工程力学材料力学弯矩计算图文..pptx
合集下载
材料力学基础—结构力学弯矩图

一 、 梁
q 2 q P
MM == P q L P L 2 =qL
L L L L L/2
( ( (1 19 0 )) ( ) 1)
P作用下的M图: qL2
2PL
qP
PL
qM=qL 2 q P=qL
LL
P=qL L
P=2qL
LL
L
( (21)1 () 2)
P作用下的M图:
( (( 31 3 )2 ))
先计算支反M= 力qL 2,再q作MP 图=q:L
(15) 1 M
(13)
2
L
q q qL
( L 1211 M)
L L (7)
P=qL
1 qL LP P= =q qL L 4
L M M L= =q qL L 142 2( qM L12 2q q )L81LqLP P= 2=q qL L
L L (8)L L
P作用下的M图:
4 qL 2
qL
1 2
M=qL 2 q
q作用q下的M图:
P=qP L
P
qL 2
L
L
L
L
(4)
qL2
q
q作q用下的M图:
1 qL 2 2
L
L
(5)
(12)
P与q作用下的M图:
3 qL 2 L
q
2
(13)
qL L L
(7)
P与q作用下的M图:
L
M
L/4
1
qL
(14)
2
L
L
2
(8)
P 2P
q LL L q q
(7)
L L L L L L
L ( ( (77 7 )) )
q 2 q P
MM == P q L P L 2 =qL
L L L L L/2
( ( (1 19 0 )) ( ) 1)
P作用下的M图: qL2
2PL
qP
PL
qM=qL 2 q P=qL
LL
P=qL L
P=2qL
LL
L
( (21)1 () 2)
P作用下的M图:
( (( 31 3 )2 ))
先计算支反M= 力qL 2,再q作MP 图=q:L
(15) 1 M
(13)
2
L
q q qL
( L 1211 M)
L L (7)
P=qL
1 qL LP P= =q qL L 4
L M M L= =q qL L 142 2( qM L12 2q q )L81LqLP P= 2=q qL L
L L (8)L L
P作用下的M图:
4 qL 2
qL
1 2
M=qL 2 q
q作用q下的M图:
P=qP L
P
qL 2
L
L
L
L
(4)
qL2
q
q作q用下的M图:
1 qL 2 2
L
L
(5)
(12)
P与q作用下的M图:
3 qL 2 L
q
2
(13)
qL L L
(7)
P与q作用下的M图:
L
M
L/4
1
qL
(14)
2
L
L
2
(8)
P 2P
q LL L q q
(7)
L L L L L L
L ( ( (77 7 )) )
材料力学4-弯矩图剪力图 PPT课件
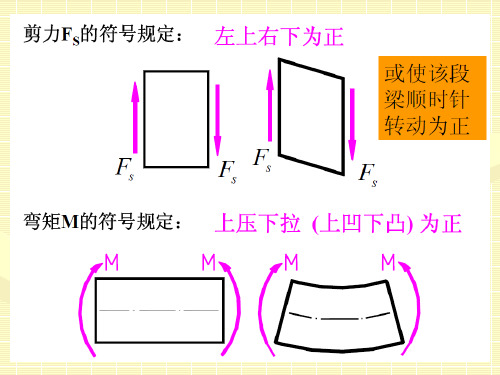
梁上最大弯矩可能发生在Fs(x) = 0 的截面上或梁段边界 的截面上。最大剪力发生在全梁或梁段的界面。
在集中力作用处剪力图有突变,其突变值等于集中力的 值。弯矩图的相应处形成尖角。
在集中力偶作用处弯矩图有突变,其突变值等于集中力 偶的值,但剪力图无变化。
矩就等于梁在各项荷载单独作用下同一 横截面上弯矩的代数和。
叠加原理:由几个外力共同作用时所引起的某一参数 (内力、应力、位移),就等于每个外力单独作用时 所引起的该参数值的代数和。
• 5.4 内力与分布荷载间的关系及其应用
剪力图上某点处的切线斜率 等于该点处荷载集度的大小
弯矩图上某点处的切线斜率 等于该点处剪力的大小。
q(x)、Fs (x)图、M(x)图三者间的关系
梁上有向下的均布荷载,即 q(x) < 0 Fs (x)图为一向右下方倾斜的 直线 M(x)图为一向下凸的二次抛 物线
• 5.3 剪力方程与弯矩方程 剪力图与弯矩图
一、剪力和弯矩方程: 剪力和弯矩沿梁长度方向的表达式,表示的是剪力和
弯矩沿轴线长度方向的分布情况
二、剪力图和弯矩图 以X轴表示横截面位置,以纵坐标表示相应截面
上的剪力Fs 、弯矩M,称为剪力图、弯矩图。 剪力图为正值画在x 轴上侧,负值画在x 轴下侧 弯矩图为正值画在x 轴下侧,负值画在x 轴上侧
作剪力图和弯矩图的几条规律
梁上集中力作用处左、右两侧横截面上,剪 力值(图)有突变,其突变值等于集中力的 数值。在此处弯矩图则形成一个尖角。
梁上集中力偶作用处左、右两侧横截面上 的弯矩值(图)也有突变,其突变值等于 集中力偶矩的数值。但在此处剪力图没有 变化。
作剪力图和弯矩图的几条规律
梁上的最大剪力发生在全梁或各梁段的边界 截面处;梁上的最大弯矩发生在全梁或各梁 段的边界截面,或Fs = 0的截面处。
经典材料力学结构力学弯矩图课件
L
L
(25)
(2(53)5)
L
L
L
L
(24) (24)
qa 2
qa
qa
1
qa
q 2q
8
1 qa2 2
a a
(26) ((2366))
aa
2L2L
qa
q
与杆件轴 线相切
qa
qa 2
q
qa 2 qa2
1 qa2 2
a
(27)
(37)
a/2
a/2பைடு நூலகம்
2a
q
1 qa2
2
1 qa2 2
q
qa 2
a
a
(28)
(38)
利用L反对称性q 作LM/图4 :
(15)1 M 2q
qq L
L
(L1211M)
LL(7)
P=qL L PP==qqLL
2PL L L PP
PL L L PL
(((22166PP)0))
L
L
从右向左作M图:
LL
LL (2) LL
PL ((66)) q
P=qL
q qq L q
(9)
PL
PP==qqLL
PL 2 3PL 2
M=PL
300 P
2qa2
2a
4a
用“局部悬臂梁法”直接作M 图,P力通过截面弯矩为0
L/2
PL
2
PL 2
PL 2
P
L/2
3PL 3PL 2
L
(19)
(27)
PL
PL
L/2
L/2
(20)
(28)
q
材料力学课件第10讲 Chapter4-2第四章 弯曲内力(剪力弯矩图)

MBMA Fs(x)dx
x2
x1
17
3 8
q
l
q
试
作
l
l
内
2
2
力 图
Fs
3 8
q
l
(1)
1 8
q
l
x
3 8
l
M
9 128
q
l2
1 16
q
l2
1 8
q
l
解:
两截面上的剪力差等于ql/2
两截面上的弯矩差等于ql2/16
18
qa
q
Pqa
2qa
q
试 作
aaa
内 力
Fs qa
qa
图
(2)
qa
1 2
q
a
解:
A FA
F
FB B
微 分
FAbl F, FBal F
C
a
b
关
l
系
Fs
b l
F
作
剪
F
力 弯
a l
F
矩
曲线在受拉侧
图
M
(2)
ab l用 微
解:
分
关
l
Fs
F
F
系
作
剪
Fl
力
曲线在受拉侧
弯
矩
M
图
(3)
13
q
利 用
解:
微
l
分 关
Fs ql
系
作 剪
1 2
q
l
2
力
曲线在受拉侧
弯
M
矩
图
(4)
14
《材料力学》课件4-2梁的剪力和弯矩.剪力图和弯矩图

实例1
实例2
实例3
03
剪力图和弯矩图的解读
剪力图和弯矩图的解读方法
截面法
通过在梁上选择若干个截面,分别计算出每个截面的剪力 和弯矩值,然后以这些值为纵坐标,以截面位置为横坐标, 绘制出剪力图和弯矩图。
微分关系法
利用剪力和弯矩的微分关系,通过积分求解出剪力图和弯 矩图。
叠加法
对于分段常数的情况,将每一段的剪力和弯矩分别叠加, 得到整体的剪力图和弯矩图。
在机械工程中,梁的剪力和弯矩分析用于设计和优化各种机 械设备,如起重机、输送机和机床等,以提高设备的性能和 可靠性。
梁的剪力和弯矩在科研中的应用
在科研领域,梁的剪力和弯矩分析也是重要的研究内容之 一。通过深入研究梁的剪力和弯矩的分布规律和影响因素 ,可以揭示材料的力学性能和结构行为的本质。
科研人员利用先进的实验技术和数值模拟方法,对梁的剪 力和弯矩进行深入探索,为材料科学、固体力学和结构工 程等领域的发展提供理论支持和实践指导。
选择截面位置
在梁上选择若干个具有代表性的截面,用于 计算剪力和弯矩。
计算剪力和弯矩
对每个截面进行受力分析,计算出剪力和弯 矩的大小。
绘制剪力图和弯矩图
根据计算结果,绘制出相应的剪力图和弯矩 图。
剪力图和弯矩图的绘制实例
悬臂梁在集中力作用下的 剪力和弯矩图
简支梁在均布载荷作用下 的剪力和弯矩图
简支梁在集中力作用下的 剪力和弯矩图
感谢您的观看
THANKS
截面法
通过在梁上选择若干个截面,计算每个截面的剪 力和弯矩,然后绘制相应的图形。
微元法
将梁分成若干个微元段,对每个微元段进行受力 分析,计算剪力和弯矩,然后绘制图形。
解析法
经典__材料力学结构力学弯矩图
P
E
C N=P/2 D
L
L LL
4m 2m
1.5L
2qL2
2qL2
铰 式 刚 架
A
B
L
(50)
4m
( (65 66 ) )
M
无 弯 矩
A
L
B
L
P (51)
P
2
2
(67)
A
4m
(56)
特点: A、B支座反力大小相向 等相 ,反 方;特点:对称结构荷 ,载 对, 称 M图对称,
四 弯、 矩三 图铰 C过 式 点刚 为架 直线D, E段弯矩为常数。C处弯矩0为 。计算A出 或B支座水平反力,
P作用下的M图:
4 qL 2
qL
1 2
M=qL 2 q
q作用q下的M图:
P=qP L
P
qL 2
L
L
L
L
(4)
qL2
q
q作q用下的M图:
1 qL 2 2
L
L
(5)
(12)
P与q作用下的M图:
3 qL 2 L
q
2
(13)
qL L L
(7)
P与q作用下的M图:
L
M
L/4
1
qL
(14)
2
L
L
2
(8)
P 2P
q作q用下的M图:
1 qL 2 L L L
2
(6)
L/2
P与q作用下的M图:
4.5qL2L 直线q 与曲L线/4相切P=qL (15) 2 qL 2
L
(9)
L
( (1 1) ) q P
P
P=qL
E
C N=P/2 D
L
L LL
4m 2m
1.5L
2qL2
2qL2
铰 式 刚 架
A
B
L
(50)
4m
( (65 66 ) )
M
无 弯 矩
A
L
B
L
P (51)
P
2
2
(67)
A
4m
(56)
特点: A、B支座反力大小相向 等相 ,反 方;特点:对称结构荷 ,载 对, 称 M图对称,
四 弯、 矩三 图铰 C过 式 点刚 为架 直线D, E段弯矩为常数。C处弯矩0为 。计算A出 或B支座水平反力,
P作用下的M图:
4 qL 2
qL
1 2
M=qL 2 q
q作用q下的M图:
P=qP L
P
qL 2
L
L
L
L
(4)
qL2
q
q作q用下的M图:
1 qL 2 2
L
L
(5)
(12)
P与q作用下的M图:
3 qL 2 L
q
2
(13)
qL L L
(7)
P与q作用下的M图:
L
M
L/4
1
qL
(14)
2
L
L
2
(8)
P 2P
q作q用下的M图:
1 qL 2 L L L
2
(6)
L/2
P与q作用下的M图:
4.5qL2L 直线q 与曲L线/4相切P=qL (15) 2 qL 2
L
(9)
L
( (1 1) ) q P
P
P=qL
经典__材料力学结构力学弯矩图

(42)
a a/2 L
Pa
Pa
2
2
Pa Pa
2 Pa
P
2
P
2Pa
a
a
((4335) )
三 、 简 支 式 刚 架
15qa2 4
21qa2 qa8 2qa2
PL
P
PL
L ( (4346) )
qa2
q
qa2
支座B无反力,AB段无变形 不用计算支反力, 直接作M图
计算A支座水平反力, 即可作M图
a
2m 2m
1 qa 2 2
q
qa 2
a
a
( 2 8 )
(38)
10010kN/m
P=40kN
60
100
80 40kN
2m 2m 2m 2m (30)
(39)
2m 2m
qL2+2cqoLs 22 α
qL2
2cos2αq
L
L
(33)
(40)
q
aa
q qa2 2
2
qa
qa
qa2
2
a
a
((4314))
15 3
3
计算A处支反力为0,直接作 M图
Pa/2 P Pa/2
A
a a/2 a/2
(55)
(65)
q=20kN/m
A
(54)
(47)
B、A处无水平支反力,直接 作M图
q=20kN/m
25kN.m
25kN.m q
65kN.m 50kN50kN
25kN.m 25kN.m
0.5m
0.5m
(48)
B、A处无水平支反力,AC、 DB无弯曲变形,EC、ED也 无弯曲变形
a a/2 L
Pa
Pa
2
2
Pa Pa
2 Pa
P
2
P
2Pa
a
a
((4335) )
三 、 简 支 式 刚 架
15qa2 4
21qa2 qa8 2qa2
PL
P
PL
L ( (4346) )
qa2
q
qa2
支座B无反力,AB段无变形 不用计算支反力, 直接作M图
计算A支座水平反力, 即可作M图
a
2m 2m
1 qa 2 2
q
qa 2
a
a
( 2 8 )
(38)
10010kN/m
P=40kN
60
100
80 40kN
2m 2m 2m 2m (30)
(39)
2m 2m
qL2+2cqoLs 22 α
qL2
2cos2αq
L
L
(33)
(40)
q
aa
q qa2 2
2
qa
qa
qa2
2
a
a
((4314))
15 3
3
计算A处支反力为0,直接作 M图
Pa/2 P Pa/2
A
a a/2 a/2
(55)
(65)
q=20kN/m
A
(54)
(47)
B、A处无水平支反力,直接 作M图
q=20kN/m
25kN.m
25kN.m q
65kN.m 50kN50kN
25kN.m 25kN.m
0.5m
0.5m
(48)
B、A处无水平支反力,AC、 DB无弯曲变形,EC、ED也 无弯曲变形
材料力学第四章弯曲内力优秀课件

工程中的弯曲构件 梁的内力及其与外力的相互关系 剪力方程与弯矩方程 载荷集度、剪力、弯矩之间的微分关系 剪力图与弯矩图 刚架的内力与内力图 结论与讨论
剪力方程与弯矩方程
•剪力、弯矩方程:剪力、弯矩沿梁轴(x轴)变化的解析表达式。
为了建立剪力方程和弯矩方程,必须首先建立Oxy坐标系,其
中O为坐标原点,x坐标轴与梁的轴线一致,坐标原点O一般取在梁
M C F A a a 2 q l0 a a 3 q 6 0 la q 6 0 a l3
思考:是否可以将梁上的分布荷载全部用静力等效后的合 力代替来求截面C的内力?
例题
建立剪力弯矩方程,并画 剪力弯矩图
q
qa2
A
B
C
a
a
x
可以不求支反力 建立坐标 建立剪力弯矩方程:
FS=-qx (0 x a) M=-qx2/2 (0 x < a)
工程中的弯曲构件
•常见静定梁
简支梁:一端固定铰支、另 一端可动铰支的梁
悬臂梁:一端固定、另一 端自由的梁
F F
外伸梁:具有一个或两个
外伸部分的简支梁
F
F
•静不定梁
约束反力数超过有效平衡方程数的梁( Ch12 研究)
常用梁截面
纵向对称面
P1
P2 纵向对称面 P1
P2 变形前
平面弯曲概念
变形后
例题
图示简支梁受到三角形分布荷载的作用,最大荷载集度为q0, 试求截面C上的内力。
y
q0l/2
q0
A
B
a
C
x
解:先求支反力 FA
l
FB
MA0 FBlq20l23l 0 MB0 FAlq20l3l 0
剪力方程与弯矩方程
•剪力、弯矩方程:剪力、弯矩沿梁轴(x轴)变化的解析表达式。
为了建立剪力方程和弯矩方程,必须首先建立Oxy坐标系,其
中O为坐标原点,x坐标轴与梁的轴线一致,坐标原点O一般取在梁
M C F A a a 2 q l0 a a 3 q 6 0 la q 6 0 a l3
思考:是否可以将梁上的分布荷载全部用静力等效后的合 力代替来求截面C的内力?
例题
建立剪力弯矩方程,并画 剪力弯矩图
q
qa2
A
B
C
a
a
x
可以不求支反力 建立坐标 建立剪力弯矩方程:
FS=-qx (0 x a) M=-qx2/2 (0 x < a)
工程中的弯曲构件
•常见静定梁
简支梁:一端固定铰支、另 一端可动铰支的梁
悬臂梁:一端固定、另一 端自由的梁
F F
外伸梁:具有一个或两个
外伸部分的简支梁
F
F
•静不定梁
约束反力数超过有效平衡方程数的梁( Ch12 研究)
常用梁截面
纵向对称面
P1
P2 纵向对称面 P1
P2 变形前
平面弯曲概念
变形后
例题
图示简支梁受到三角形分布荷载的作用,最大荷载集度为q0, 试求截面C上的内力。
y
q0l/2
q0
A
B
a
C
x
解:先求支反力 FA
l
FB
MA0 FBlq20l23l 0 MB0 FAlq20l3l 0
工程力学(静力学与材料力学)弯曲强度(剪力图与弯矩图)-PPT文档资料

第7章A 弯曲强度(1)-剪力图与弯矩图
梁的内力及其与外力的相互关系
所谓剪力和弯矩变化规律是指表示剪力和弯矩变 化的函数或变化的图线。这表明,如果在两个外力 作用点之间的梁上没有其他外力作用,则这一段梁 所有横截面上的剪力和弯矩可以用同一个数学方程 或者同一图线描述。
第7章A 弯曲强度(1)-剪力图与弯矩图
范钦珊教育与教学工作室
工程力学(静力学与材料力学)
课堂教学软件
返回总目录
工程力学(静力学与材料力学)
材料力学
弯曲强度-剪力图与弯矩图
返回总目录
第7章A 弯曲强度-剪力图与弯矩图
杆件承受垂直于其轴线的外力或位于其轴线所在平面 内的力偶作用时,其轴线将弯曲成曲线,这种受力与变形 形式称为 弯曲 ( bending )。主要承受弯曲的杆件称为 梁 (beam)。 在外力作用下,梁的横截面上将产生剪力和弯矩两种 内力。
第7章A 弯曲强度(1)-剪力图与弯矩图
工程中的弯曲构件 梁的内力及其与外力的相互关系
剪力方程与弯矩方程
载荷集度、剪力、弯矩之间的微分关系 剪力图与弯矩图
结论与讨论
返回总目录
第7章A 弯曲强度(1)-剪力图与弯矩图
工程中的弯曲构件
返回
第7章A 弯曲强度(1)-剪力图与弯矩图
在很多情形下,剪力和弯矩沿梁长度方向的分布不是 均匀的。 对梁进行强度计算,需要知道哪些横截面可能最先发 生失效,这些横截面称为危险面。弯矩和剪力最大的横截 面就是首先需要考虑的危险面。研究梁的变形和刚度虽然 没有危险面的问题,但是也必须知道弯矩沿梁长度方向是 怎样变化的。
第7章A 弯曲强度(1)-剪力图与弯矩图
返回
第7章A 弯曲强度(1)-剪力图与弯矩图
经典__材料力学结构力学弯矩图

用“局部悬臂梁法”直接作M 图
q
PL
PL
与杆件轴 线相切
qL 2 2
L
P L L
(30) (22)
(21)
(29)
用“局部悬臂梁法”直接作M图:用“局部悬臂梁法”直接作M图:
1 2 Pl 1 2 Pl
2Pl
2Pl
Pl
1 2 Pl
Pl
(31)
(32)
注:P力通过点弯矩为0
注:P力通过点弯矩为0
用“局部悬臂梁法”直接作M图:
(55)
3a
2a
(64) (54)
(65)
q=20kN/m
a/2
5qa/2
B
Pa/2
a/2
qa
2qa
q Pa/2
A
54)
(47)
(48)
B、A处无水平支反力,直接 作M图
q=20kN/m 25kN.m
2m
B、A处无水平支反力,AC、 DB无弯曲变形,EC、ED也 无弯曲变形
P
25kN.m 65kN.m 25kN.m q 0.5m
PL P PL
特点:对称结构,对称荷载,M图对称, C处弯矩为0。计算出A或B支座水平反力, 即可作M图。
2 qa/2 2 qa/2
q
2 qa/2 2 qa/2
C
C
L
A
L
B
A
a
(71) (60)
B
a
(59)
(70)
qa2
M
q
2a
A
特点:对称结构,反对称荷载,反力 L 也反对称, X A X B 0。C处弯矩为0。 (59) 即可直接作M图。
