初一数学上册有理数的认识及计算练习题精编65
初一数学上册 有理数及其运算

有理数及其运算(复习)一、正负数有理数的分类:_____________统称整数,试举例说明。
_____________统称分数,试举例说明。
____________统称有理数。
正确理解非负数和非正数。
练习:1、把下列各数填在相应额大括号内:1,-0.1,-789,25,0,-20,-3.14,-590,6/7正整数集{ …};正有理数集{ …};负有理数集{ …} 负整数集{ …};自然数集{ …};正分数集{ …} 负分数集{ …}2、某种食用油的价格随着市场经济的变化涨落,规定上涨记为正,则-5.8元的意义是 ;如果这种油的原价是76元,那么现在的卖价是 。
二、数轴规定了 、 、 的直线,叫数轴练习:1、如图所示的图形为四位同学画的数轴,其中正确的是( )2、在数轴上画出表示下列各数的点,并按从大到小的顺序排列,用“>”号连接起来。
4,-|-2|, -4.5, 1, 03、下列语句中正确的是( )A数轴上的点只能表示整数B数轴上的点只能表示分数C数轴上的点只能表示有理数D所有有理数都可以用数轴上的点表示出来4、①比-3大的负整数是_______; ②已知m是整数且-4<m<3,则m为_______________。
③有理数中,最大的负整数是 ,最小的正整数是 。
最大的非正数是 。
④与原点的距离为三个单位的点有_ _个,他们分别表示的有理数是 _和_ _。
5、在数轴上点A 表示-4,如果把原点O 向负方向移动1个单位,那么在新数轴上点A 表示的数是( ) A.-5, B.-4 C.-3 D.-26、画出数轴,把下列各组数分别在数轴上表示出来,并按从大到小的顺序排列,用“>”连接起来:⑴ 1,-2,3,-4 ⑵31,0,3,-0.2三、相反数1、像2和-2、-5和5、2.5和-2.5这样,只有 不同的两个数叫做互为相反数。
0的相反数是 。
一般地:若a 为任一有理数,则a 的相反数为-a2、相反数的相关性质:a 、相反数的几何意义:表示互为相反数的两个点(除0外)分别在原点O 的两边,并且到原点的距离相等。
北师大版七年级数学上册章节同步练习题(全册-共57页)

北师⼤版七年级数学上册章节同步练习题(全册-共57页)北师⼤版七年级数学上册章节同步练习题(全册,共57页)⽬录第⼀章丰富的图形世界1 ⽣活中的⽴体图形2 展开与折叠3 截⼀个⼏何体4 从三个⽅向看物体的形状单元测验第⼆章有理数及其运算1 有理数2 数轴3 绝对值4 有理数的加法5 有理数的减法6 有理数加减混合运算7 有理数的乘法 8 有理数的除法9 有理数的乘⽅ 10 科学记数法11 有理数的混合运算 12 ⽤计算器进⾏运算单元测验第三章整式及其加减1 字母表⽰数2 代数式3 整式4 整式的加减5 探索与表达规律单元测验第四章基本平⾯图形1 线段射线直线2 ⽐较线段的长短3 ⾓ 4⾓的⽐较5 多边形和圆的初步认识单元测验第五章⼀元⼀次⽅程1 认识⼀元⼀次⽅程2 求解⼀元⼀次⽅程3 应⽤⼀元⼀次⽅程——⽔箱变⾼了4 应⽤⼀元⼀次⽅程——打折销售5 应⽤⼀元⼀次⽅程——“希望⼯程”义演6 应⽤⼀元⼀次⽅程——追赶⼩明单元测验第六章数据的收集与整理1 数据的收集2 普查和抽样调查3 数据的表⽰4 统计图的选择第⼀章丰富的图形世界1.1⽣活中的⽴体图形(1)基础题:1.如下图中为棱柱的是()2.⼀个⼏何体的侧⾯是由若⼲个长⽅形组成的,则这个⼏何体是()A.棱柱 B.圆柱 C.棱锥 D.圆锥3.下列说法错误的是()A.长⽅体、正⽅体都是棱柱 B.三棱柱的侧⾯是三⾓形C.直六棱柱有六个侧⾯、侧⾯为矩形 D.球体和圆是不同的图形4.数学课本类似于,⾦字塔类似于,西⽠类似于,⽇光灯管类似于。
5.⼋棱柱有个⾯,个顶点,条棱。
6.⼀个漏⽃可以看做是由⼀个________和⼀个________组成的。
7.如图是⼀个正六棱柱,它的底⾯边长是3cm,⾼是5cm.(1)这个棱柱共有个⾯,它的侧⾯积是。
(2)这个棱柱共有条棱,所有棱的长度是。
提⾼题:⼀只⼩蚂蚁从如图所⽰的正⽅体的顶点A沿着棱爬向有蜜糖的点B,它只能经过三条棱,请你数⼀数,⼩蚂蚁有种爬⾏路线。
人教版初一数学上册练习题:有理数

人教版初一数学上册练习题:有理数学习是一个边学新知识边稳固的进程,对学过的知识一定要多加练习,这样才干提高。
因此,精品编辑教员为大家整理了人教版初一数学上册练习题,供大家参考。
一、选择题.1.以下说法正确的个数是 ( )①一个有理数不是整数就是分数②一个有理数不是正数就是正数③一个整数不是正的,就是负的④一个分数不是正的,就是负的A 1B 2C 3D 42.a,b是有理数,它们在数轴上的对应点的位置如以下图所示:把a,-a,b,-b依照从小到大的顺序陈列 ( )A -b-a3.以下说法正确的选项是 ( )①0是相对值最小的有理数②相反数大于自身的数是正数③数轴上原点两侧的数互为相反数④两个数比拟,相对值大的反而小A ①②B ①③C ①②③D ①②③④4.以下运算正确的选项是 ( )A .B -7-25=-95=-45C. D5.假定a+b0,那么 ( )A a0B a0C a,b两数一正一负,且正数的相对值大于正数的相对值D a,b两数一正一负,且正数的相对值大于正数的相对值6.某粮店出售的三种品牌的面粉袋上区分标有质量为(250.1)kg,(250.2)kg,(250.3)kg的字样,从中恣意拿出两袋,它们的质量最多相差 ( )A 0.8kgB 0.6kgC 0.5kgD 0.4kg7.一根1m长的小棒,第一次截去它的 ,第二次截去剩下的 ,如此截下去,第五次后剩下的小棒的长度是 ( )A.mB.C .D8.假定ab0,那么的取值不能够是 ( )A 0B 1C 2D -29.以下说法中正确的选项是 ( )A. 一定是正数B. 一定是正数C. 一定不是正数D. 一定是正数10.长城总长约为6700010米,用迷信计数法表示为(保管两位有效数字) ( )A.6.7 米B.6.7 米C.6.7 米D.6.7 米11.据报道,至2021年5月1日零时,田湾核电站1、2号两台机组往年共累计发电42.96亿千瓦时.42.96亿用迷信记数法可表示为( )A. B. C. D.12.把与6作和、差、积、商、幂的运算结果中,可以为正数的有 ( )A、4个B、3个C、2个D、1个13.数轴上的两点A、B区分表示-6和-3,那么A、B两点间的距离是 ( )A、-6+(-3)B、-6-(-3)C、|-6+(-3)|D、|-3-(-6)|14.在数-5.745,-5.75,-5.738,-5.805,-5.794,-5.845这6个数中准确到十分位得-5.8的数共有( )A、2个B、3个C、4个D、5个15.、、的大小关系为( )A. B.C. D.二、填空题.16.比大而比小的一切整数的和为 .17.假定那么2a一定是 .18.假定019.多伦多与北京的时间差为 12 小时(正数表示同一时辰比北京时间早的时数),假设北京时间是10月1日14:00,那么多伦多时间是 .20.上海浦东磁悬浮铁路全长30km,单程运转时间约为8min,那么磁悬浮列车的平均速度用迷信记数法表示约为 m/min.21.规则a﹡b=5a+2b-1,那么(-4)﹡6的值为 .22. =3,=2,且ab0,那么 = .23.a=25,b= -3,那么a99+b100的末位数字是 .24.的相反数是________,的相对值是_________25.假定 ,那么 =_________希望为大家提供的人教版初一数学上册练习题的内容,可以对大家有用,更多相关内容,请及时关注!。
初一数学《有理数及其运算》例题加练习(北师大版)

第二章:有理数及其运算知识重点:绝对值的概念和有理数的运算(包括法则、运算律、运算顺序、混合运算)是本章的重点。
知识难点:绝对值的概念及有关计算,有理数的大小比较,及有理数的运算是本章的难点。
考点:绝对值的有关概念和计算,有理数的有关概念及混合运算是考试的重点对象。
知识点:一、有理数的基础知识1、三个重要的定义:(1)正数:像1、2.5、这样大于0的数叫做正数;(2)负数:在正数前面加上“-”号,表示比0小的数叫做负数;(3)0即不是正数也不是负数。
2、有理数的分类:(1)按定义分类: (2)按性质符号分类:⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数正整数整数有理数0 ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数有理数0 3、数轴数轴有三要素:原点、正方向、单位长度。
画一条水平直线,在直线上取一点表示0(叫做原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到数轴。
在数轴上的所表示的数,右边的数总比左边的数大,所以正数都大于0,负数都小于0,正数大于负数。
4、相反数如果两个数只有符号不同,那么其中一个数就叫另一个数的相反数。
0的相反数是0,互为相反的两上数,在数轴上位于原点的两则,并且与原点的距离相等。
5、绝对值(1)绝对值的几何意义:一个数的绝对值就是数轴上表示该数的点与原点的距离。
(2)绝对值的代数意义:一个正数的绝对值是它本身;0的绝对值是0;一个负数的绝对值是它的相反数,可用字母a 表示如下:(3)两个负数比较大小,绝对值大的反而小。
二、有理数的运算 1、有理数的加法(1)有理数的加法法则:同号两数相加,取相同的符号,并把绝对值相加;绝对值不等的异号两数相加,取绝对值较大数的符号,并用较大的绝对值减去较小的绝对值;互为相反的两个数相加得0;一个数同0相加,仍得这个数。
(2)有理数加法的运算律:加法的交换律 :a+b=b+a ;加法的结合律:( a+b ) +c = a + (b +c)用加法的运算律进行简便运算的基本思路是:先把互为相反数的数相加;把同分母的分数先相加;把符号相同的数先相加;把相加得整数的数先相加。
北师大版数学七年级上册 第二章 有理数及其运算 练习题(有答案)

北师大版数学七年级上册 第二章 有理数及其运算 练习题(有答案)2.1 有理数基础题知识点1 认识正数与负数1.(连云港中考)下列各数中;为正数的是(A)A .3B .-12C .-2D .02.(临沂中考)四个数-3;0;1;2;其中负数是(A)A .-3B .0C .1D .2 3.在-1;0;1;2这四个数中;既不是正数也不是负数的是(B) A .-1 B .0 C .1 D .24.下列各数:-101.2;+18;0.002;-60;0;-45;+3.2;属于正数的有+18;0.002;+3.2;属于负数的有-101.2;-60;-45.知识点2 用正、负数表示具有相反意义的量5.(咸宁中考)冰箱冷藏室的温度零上5 ℃;记作+5 ℃;保鲜室的温度零下7 ℃;记作(B) A .7 ℃ B .-7 ℃ C .2 ℃ D .-12 ℃ 6.下列不具有相反意义的是(C) A .前进5 m 和后退5 m B .节约3 t 和浪费3 tC .身高增加2 cm 和体重减少2 kgD .超过5 g 和不足5 g7.若火箭发射点火前5秒记作-5秒;则火箭发射点火后10秒应记作(D) A .-10秒 B .-5秒 C .+5秒 D .+10秒8.如果+80 m 表示向东走80 m;那么-60 m 表示向西走60__m . 知识点3 有理数的概念及分类9.在0;1;-2;-3.5这四个数中;为负整数的是(C) A .0 B .1 C .-2 D .-3.510.有理数可按正、负性质分类;也可按整数、分数分类: ①按正、负性质分类: ②按整数、分数分类:有理数⎩⎪⎨⎪⎧正有理数⎩⎪⎨⎪⎧正整数正分数0负有理数⎩⎪⎨⎪⎧负整数负分数有理数⎩⎪⎨⎪⎧整数⎩⎪⎨⎪⎧正整数0负整数分数⎩⎪⎨⎪⎧正分数负分数 11.下列各数:3;-5;-12;0;2;0.97;-0.21;-6;9;23;85;1;其中正数有7个;负数有4个;正分数有2个;负分数有2个.12.如图是数学果园里的一棵“有理数”知识树;请仔细辨别分类;把各类数填在它所属的相应横线上.中档题13.在数-5;3;0;-32;100;0.4中;非负数有(A)A .4个B .3个C .2个D .1个 14.下列说法正确的是(D) A .+2是正数;但3不是正数 B .一个数不是正数就是负数 C .含有负号的数就是负数 D .-0.25是负分数15.请按要求填出相应的两个有理数:(1)既是正数也是分数:212;34(答案不唯一);(2)既不是负数也不是分数:2;0(答案不唯一). 16.“一只闹钟;一昼夜误差不超过±12秒.”这句话的含义是:闹钟走一天的时间比标准时间最多慢12秒或最多快12秒.17.下面是几个家庭五月份用电支出比上月支出变化情况: 赵力减少25% 肖刚增加10% 王辉减少17% 李玉增加5% 田红增加8% 陈佳减少12%分别用正、负数写出这几家五月用电支出比上月支出的增长率. 解:这六家五月用电支出比上月支出的增长率分别为:赵力-25%;肖刚+10%;王辉-17%;李玉+5%;田红+8%;陈佳-12%.18.请用两种不同的分类标准将下列各数分类:-15;+6;-2;-0.9;1;35;0;314;0.63;-4.95.解:分类一:整数:-15;+6;-2;1;0;分数:-0.9;35;314;0.63;-4.95.分类二:正数:+6;1;35;314;0.63;0;负数:-15;-2;-0.9;-4.95.19.小米家住黄河边的某市;黄河大堤高出某市区20米;另有铁塔高约58米;是该市的一大景观;小米和好朋友小华、玲玲出去玩;小米站在黄河大堤上;玲玲站在地面放风筝;顽皮的小华则爬上了铁塔顶;小米说:“以大堤为基准;记为0米;则玲玲所在的位置高为-20米;小华所在位置高为+58米.”小华说:“以铁塔顶为基准;记为0米;则玲玲所在的位置高为-58米;小米所在的位置高为-38米.”玲玲说:“小华的位置比我高58米.”他们谁说得对?解:小华和玲玲说得对.理由:用正、负数表示具有相反意义的量时;由于“基准”(0米点)的选法不同;表示的结果也不同;小米以大堤为基准;玲玲所在的位置高为-20米;小华所在位置高为38米.综合题20.将一串有理数按下列规律排列;回答下列问题:(1)在A处的数是正数还是负数?(2)负数排在A、B、C、D中的什么位置?(3)第2 017个数是正数还是负数?排在对应于A、B、C、D中的什么位置?解:(1)在A处的数是正数.(2)B和D位置是负数.(3)第2 017个数是负数;排在对应于B的位置.2.2 数轴基础题知识点1 认识数轴1.关于数轴;下列说法最准确的是(D) A .一条直线B .有原点、正方向的一条直线C .有单位长度的一条直线D .规定了原点、正方向、单位长度的直线 2.下列各图中;所画数轴正确的是(D)知识点2 在数轴上表示数 3.如图;在数轴上点A 表示(A)A .-2B .2C .±2D .04.在如图的数轴上;表示-2.75的点是(D)A .点EB .点FC .点GD .点H5.在数轴上表示数-3;0;5;2;-1的点中;在原点右边的有(C) A .0个 B .1个 C .2个 D .3个6.在数轴上;表示-2的点在原点的左侧;它到原点的距离是2个单位长度. 7.画数轴;并在数轴上表示下列各数:2;-2.5;0;13;-4.解:如图:知识点3 利用数轴比较有理数的大小 8.如图;下列说法中正确的是(B)A .a >bB .b >aC .a >0D .b >09.(成都中考)在-3;-1;1;3四个数中;比-2小的数是(A)A .-3B .-1C .1D .310.已知有理数x;y 在数轴上的位置如图所示;则下列结论正确的是(C)A .x>0>yB .y>x>0C .x<0<yD .y<x<011.把下列各数在数轴上表示出来;并用“<”把各数连接起来:-212;4;-4;0;412.解:如图;大小关系为:-4<-212<0<4<412.中档题12.下列语句中;错误的是(B)A .数轴上;原点位置的确定是任意的B .数轴上;正方向可以是从原点向右;也可以是从原点向左C .数轴上;单位长度可根据需要任意选取D .数轴上;与原点的距离等于8的点有两个13.(济宁中考)在0;-2;1;12这四个数中;最小的数是(B)A. 0 B .-2 C. 1 D.1214.数轴上的点A;B;C;D 分别表示a;b;c;d 四个数;已知A 在B 的左侧;C 在A;B 之间;D 在B 的右侧;则下列式子成立的是(A)A .a<c<b<dB .a<b<c<dC .a<d<c<bD .a<c<d<b15.将一刻度尺如图所示放在数轴上(数轴的单位长度是1 cm);刻度尺上的“0 cm ”和“15 cm ”分别对应数轴上的-3.6和x;则(C)A .9<x <10B .10<x <11C .11<x <12D .12<x <1316.若数轴上的点A 表示+3;点B 表示-4.2;点C 表示-1;则点A 和点B 中离点C 较远的是点A . 17.如图所示;数轴上的点A 向左移动2个单位长度得到点B;则点B 表示的数是-1.18.小红在做作业时;不小心将墨水洒在一个数轴上;如图所示;根据图中标出的数值;判断被墨迹盖住的整数共有多少个?解:因为-13<-12.6<-12;-8<-7.4<-7;所以此段整数有-12;-11;-10;-9;-8共5个;同理10<10.6<11;17<17.8<18;所以此段整数有11;12;13;14;15;16;17共7个;所以被墨迹盖住的整数共有5+7=12(个).19.如图;点A 表示的数是-4.(1)在数轴上表示出原点O ; (2)指出点B 所表示的数;(3)在数轴上找一点C;它与点B 的距离为2个单位长度;那么点C 表示什么数? 解:(1)如图. (2)点B 表示3. (3)点C 表示1或5.综合题20.(1)借助数轴;回答下列问题.①从-1到1有3个整数;分别是-1、0、1;②从-2到2有5个整数;分别是-2、-1、0、1、2;③从-3到3有7个整数;分别是-3、-2、-1、0、1、2、3; ④从-200到200有401个整数;⑤从-n 到n(n 为正整数)有(2n +1)个整数;(2)根据以上规律;直接写出:从-2.9到2.9有5个整数;从-10.1到10.1有21个整数;(3)在单位长度是1厘米的数轴上随意画出一条长为1 000厘米的线段AB;求线段AB 盖住的整点的个数.解:1 000个或1 001个.2.3 绝对值基础题知识点1 相反数的概念1.(河南中考)-13的相反数是(B)A .-13 B.13C .-3D .32.相反数等于本身的数为(C)A .正数B .负数C .0D .非负数 3.下列各组数中互为相反数的是(D) A .2与-3B .-3与-13C .2 016与-2 015D .-0.25与144.下列说法中正确的是(C) A .一个数的相反数是负数 B .0没有相反数C .只有一个数的相反数等于它本身D .表示相反数的两个点;可以在原点的同一侧 5.16和-16互为相反数;-2 017的相反数是2__017;1的相反数是-1. 知识点2 绝对值的意义及计算6.在数轴上表示-2的点到原点的距离等于(A) A .2 B .-2 C .±2 D .4 7.(安徽中考)-2的绝对值是(B)A .-2B .2C .±2 D.128.若|-a|=5;则a 的值是(D)A .-5B .5 C.15D .±59.-3的绝对值是3;-|-2.5|=-2.5;绝对值是6的数是±6. 10.计算:|4|+|0|-|-3|=1. 知识点3 绝对值的性质11.任何一个有理数的绝对值一定(D) A .大于0 B .小于0 C .不大于0 D .不小于0 12.在有理数中;绝对值等于它本身的数有(D) A .一个 B .两个 C .三个 D .无数个 13.(1)①正数:|+5|=5;|12|=12; ②负数:|-7|=7;|-15|=15; ③零:|0|=0;(2)根据(1)中的规律发现:不论正数、负数和零;它们的绝对值一定是非负数;即|a|≥0. 知识点4 利用绝对值比较有理数的大小 14.下列各式中正确的是(D)A .|-3|>|-4|B .-2>|-5|C .0>|-0.000 1|D .|-89|>-91015.用“>”或“<”填空: (1)-7<-6.5; (2)-3>-4;(3)-5<-4.中档题16.如果a 与1互为相反数;那么|a|等于(C) A .2 B .-2 C .1 D .-1 17.下列说法正确的是(D) A .-|a|一定是负数B .只有两个数相等时它们的绝对值才相等C .若|a|=|b|;则a 与b 相等D .若一个数小于它的绝对值;则这个数为负数18.(南京中考)数轴上点A;B 表示的数分别是5;-3;它们之间的距离可以表示为(D) A .-3+5 B .-3-5 C .|-3+5| D .|-3-5|19.如果a>0;b<0;a<|b|;那么a 、b 、-a 、-b 的大小顺序是(A) A .-b>a>-a>b B .a>b>-a>-b C .-b>a>b>-a D .b>a>-b>-a20.绝对值小于6的整数有11个;它们分别是±5;±4;±3;±2;±1;0;绝对值大于3且小于6的整数是±5;±4.21.(河北中考改编)若有理数m;n 满足|m -2|+|2 017-n|=0;则m +n =2__019. 22.比较下列各对数的大小: (1)0和|-2|; 解:0<|-2|.(2)-45和-23;解:-45<-23.(3)-(-4)和|-4|. 解:-(-4)=|-4|.23.计算:(1)|+223|×|-9|;解:原式=83×9=24.(2)|-34|÷|-178|.解:原式=34×815=25.24.光明奶粉每袋质量为500克;在质量检测中;若质量超出标准质量2克记作+2克;若质量低于标准质量3克以上;(1)这10(2)质量最大的是哪袋?它的实际质量是多少? 解:(1)第4袋和第6袋不合格.(2)质量最大的是第9袋;实际质量是505克.综合题25.已知a;b;c为有理数;且它们在数轴上的位置如图所示.(1)试判断a;b;c的正负性;(2)在数轴上分别标出a;b;c的相反数的位置;(3)根据数轴化简:①|a|=-a;②|b|=b;③|c|=c;④|-a|=-a;⑤|-b|=b;⑥|-c|=c.(4)若|a|=5.5;|b|=2.5;|c|=7;求a;b;c的值.解:(1)a为负;b为正;c为正.(2)如图.(4)a=-5.5;b=2.5;c=7.小专题(一) 绝对值的应用类型1 利用绝对值比较大小 1.比较下面各对数的大小: (1)-0.1与-0.2;解:因为|-0.1|=0.1;|-0.2|=0.2;且0.1<0.2;所以-0.1>-0.2.(2)-45与-56;解:因为|-45|=45=2430;|-56|=56=2530;且2430<2530; 所以-45>-56.2.比较下列各对数的大小:(1)-821与-|-17|;解:-|-17|=-17;因为|-821|=821;|-17|=17=321;且821>17;所以-821<-|-17|.(2)-2 0152 016与-2 0162 017.解:因为⎪⎪⎪⎪⎪⎪-2 0152 016=2 0152 016;⎪⎪⎪⎪⎪⎪-2 0162 017=2 0162 017;且2 0152 016<2 0162 017; 所以-2 0152 016>-2 0162 017.类型2 巧用绝对值的性质求字母的值3.已知|x -3|+|y -5|=0;求x +y 的值. 解:由|x -3|+|y -5|=0;得 x -3=0;y -5=0. 解得x =3;y =5. 所以x +y =3+5=8.4.若x 的相反数是-3;|y|=5;且x <y;求y -x 的值. 解:因为x 的相反数是-3;所以x =3. 因为|y|=5;所以y =±5. 因为x <y;所以x =3;y =5. 所以y -x =5-3=2.类型3 绝对值在生活中的应用5.司机小李某天下午的营运全是在南北走向的鼓楼大街进行的.假定向南为正;向北为负;他这天下午行车里程如下(单位:千米):+15;-3;+14;-11;+10;+4;-26.若汽车耗油量为0.1 L/km;这天下午汽车共耗油多少升?解:0.1×(|+15|+|-3|+|+14|+|-11|+|+10|+|+4|+|-26|)=8.3(L).6.在活动课上;有6名学生用橡皮泥做了6个乒乓球;直径可以有0.02毫米的误差;超过规定直径的毫米数记(1)(2)指出哪个同学做的乒乓球质量最好;哪个同学做的质量最差?(3)请你对6名同学做的乒乓球质量按照最好到最差排名;(4)用学过的绝对值知识来说明以上问题.解:(1)张兵、蔡伟.(2)蔡伟做的乒乓球质量最好、李明做的乒乓球质量最差.(3)蔡伟、张兵、余佳、赵平、王敏、李明.(4)这是绝对值在实际生活中的应用;对误差来说绝对值越小越好.小专题(二) 三种方法比较有理数的大小方法1 利用数轴比较大小1.如图;在数轴上有a;b;c;d 四个点;则下列说法正确的是(C)A .a>bB .c<0C .b<cD .-1>d2.有理数a 在数轴上对应的点如图所示;则a;-a;-1的大小关系是(C)A .-a<a<-1B .-a<-1<aC .a<-1<-aD .a<-a<-1 3.大于-2.5而小于3.5的整数共有(A) A .6个 B .5个 C .4个 D .3个4.在数轴上表示下列各数;并把这些数用“>”连接起来.3.5;3.5的相反数;-12;绝对值等于3的数;最大的负整数.解:各数分别为:3.5;-3.5;-12;±3;-1.在数轴上表示如图:这些数由大到小用“>”连接为:3.5>3>-12>-1>-3>-3.5.5.点A 、B 在数轴上的位置如图所示;它们分别表示数a 、b.(1)请将a;b;1;-1四个数按从小到大的顺序排列起来;(2)若将点B 向右移动3个单位长度;请将a 、b 、-1三个数按从小到大的顺序排列起来. 解:(1)b<-1<a<1. (2)-1<a<b.方法2 利用比较大小的法则比较大小 6.下列各式成立的是(B)A .-1>0B .3>-2C .-2<-5D .1<-27.(安徽中考)在-4;2;-1;3这四个数中;比-2小的数是(A) A .-4 B .2 C .-1 D .38.(西双版纳中考)若a =-78;b =-58;则a;b 的大小关系是a <b(填“>”“<”或“=”).9.已知数:0;-2;1;-3;5. (1)用“>”把各数连接起来; 解:5>1>0>-2>-3.(2)用“<”把各数的相反数连接起来; 解:-5<-1<0<2<3.(3)用“>”把各数的绝对值连接起来. 解:|5|>|-3|>|-2|>|1|>|0|. 方法3 利用特殊值比较大小10.如图;数轴上的点表示的有理数是a;b;则下列式子正确的是(B)A .-a <bB .a <bC .|a|<|b|D .-a <-b11.a;b 两数在数轴上的对应点的位置如图;下列各式正确的是(D)A.b>a B.-a<bC.|a|>|b| D.b<-a<a<-b2.4 有理数的加法第1课时 有理数的加法法则基础题知识点1 有理数的加法法则1.下列各式的结果;符号为正的是(C)A .(-3)+(-2)B .(-2)+0C .(-5)+6D .(-5)+5 2.(天津中考)计算(-3)+(-9)的结果是(B) A .12 B .-12 C .6 D .-6 3.(梅州中考)计算(-3)+4的结果是(C) A .-7 B .-1 C .1 D .7 4.已知a;b 两数互为相反数;则a +b =(C) A .2a B .2b C .0 D .1 5.下列结论不正确的是(D) A .若a>0;b>0;则a +b>0 B .若a<0;b<0;则a +b<0C .若a>0;b<0;且|a|>|b|;则a +b>0D .若a<0;b>0;且|a|>|b|;则a +b>06.在每题的横线上填写和的符号或结果. (1)(+3)+(+5)=+(3+5)=8; (2)(-3)+(-5)=-(3+5)=-8; (3)(-16)+6=-(16-6)=-10; (4)(-6)+8=+(8-6)=2; (5)(-2 015)+0=-2__015. 7.计算:(1)(-4)+(-6); 解:原式=-10.(2)(-12)+5; 解:原式=-7.(3)0+(-12);解:原式=-12.(4)(-2.5)+(-3.5). 解:原式=-6.知识点2 有理数加法的应用8.小明家冰箱冷冻室的温度为-5 ℃;调高4 ℃后的温度为(C) A .4 ℃ B .9 ℃ C .-1 ℃ D .-9 ℃9.一个物体在数轴上做左右运动;规定向右为正;按下列方式运动;列出算式表示其运动后的结果: (1)先向左运动2个单位长度;再向右运动7个单位长度.列式:-2+7; (2)先向左运动5个单位长度;再向左运动7个单位长度.列式:-5+(-7). 10.某人某天收入265元;支出200元;则该天节余65元.11.已知飞机的飞行高度为10 000 m;上升3 000 m 后;又上升了-5 000 m;此时飞机的高度是8__000m.中档题12.(玉林、防城港中考)下面的数中;与-2的和为0的是(A) A .2 B .-2 C.12 D .-1213.有理数a 、b 在数轴上对应的位置如图所示;则a +b 的值(A)A .大于0B .小于0C .小于aD .大于b 14.如果两个数的和是正数;那么(D) A .这两个数都是正数 B .一个为正;一个为零C .这两个数一正一负;且正数的绝对值较大D .必属上面三种情况之一15.一个数是25;另一个数比25的相反数大-7;则这两个数的和为(B) A .7 B .-7 C .57 D .-5716.若x 是-3的相反数;|y|=5;则x +y 的值为(D) A .2 B .8C .-8或2D .8或-217.已知A 地的海拔高度为-53米;而B 地比A 地高30米;则B 地的海拔高度为-23米. 18.如图;三个小球上的有理数之和等于-2.19.计算: (1)32+(-32); 解:原式=0.(2)116+(-4);解:原式=-256.(3)715+(-235);解:原式=+(715-235)=435.(4)-8.75+(-314).解:原式=-(8.75+314)=-12.20.已知有理数a;b;c 在数轴上的位置如图所示;请根据有理数的加法法则判断下列各式的正负性:①a ;②b ;③-c ;④a +b ;⑤a +c ;⑥b +c ;⑦a +(-b). 解:①③⑦为正;②④⑤⑥为负.综合题21.若|a -2|与|b +5|互为相反数;求a +b 的值.解:因为|a-2|与|b+5|互为相反数; 所以|a-2|+|b+5|=0.所以a=2;b=-5.所以a+b=2+(-5)=-3.第2课时 有理数的加法运算律基础题知识点1 有理数的加法运算律1.计算314+(-235)+534+(-825)时;用运算律最为恰当的是(B)A .[314+(-235)]+[534+(-825)]B .(314+534)+[(-235)+(-825)]C .[314+(-825)]+[(-235)+534]D .[(-235)+534]+[314+(-825)]2.计算512+(+4.71)+712+(-6.71)的结果为(D)A .-2B .3C .-3D .-13.在下面的计算过程后面填上运用的运算律. 计算:(-2)+(+3)+(-5)+(+4).解:原式=(-2)+(-5)+(+3)+(+4)(加法交换律) =[(-2)+(-5)]+[(+3)+(+4)](加法结合律) =(-7)+(+7) =0.4.在计算323+(-2.53)+(-235)+3.53+(-23)时;比较简便的计算方法是先计算323+(-23)和(-2.53)+3.53. 5.计算:(1)(-0.8)+1.2+(-0.7)+(-2.1) =[(-0.8)+(-0.7)+(-2.1)]+1.2 =-3.6+1.2=-2.4; (2)32.5+46+(-22.5)=[32.5+(-22.5)]+46=10+46=56. 6.运用加法的运算律计算下列各题: (1)24+(-15)+7+(-20);解:原式=(24+7)+[(-15)+(-20)] =31+(-35) =-4.(2)18+(-12)+(-18)+12;解:原式=[18+(-18)]+[(-12)+12] =0+0 =0.(3)137+(-213)+247+(-123).解:原式=(137+247)+[(-213)+(-123)]=4+(-4) =0.知识点2 有理数加法运算律的应用7.李老师的银行卡中有5 500元;取出1 800元;又存入1 500元;又取出2 200元;这时银行卡中还有3__000元钱.。
(word完整版)初一数学上册完全辅导——第一章有理数精讲
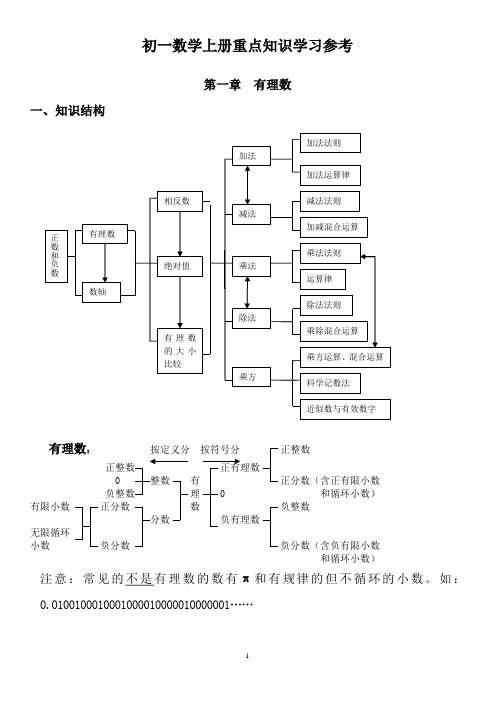
初一数学上册重点知识学习参考第一章 有理数一、知识结构有理数: 按定义分 按符号分正整数 正整数 正有理数0 整数 有 正分数(含正有限小数负整数 理 0 和循环小数)有限小数 正分数 数 负整数分数 负有理数无限循环小数 负分数 负分数(含负有限小数和循环小数)注意:常见的不是有理数的数有π和有规律的但不循环的小数。
如:0.0100100010001000010000010000001……二、掌握要点1、了解有理数的概念(什么是有理数、有理数包含的范围有哪些、有理数之间的大小比较)。
(1)大于0的数叫做正数,如3、1.8、5%等。
(2)在正数前面加上负号“—”的数叫负数,即小于0的数,如-3、-2.5、-5%等。
(3)数0既不是正数,也不是负数。
0除了表示一个也没有以外,是正数和负数的分界,是基准。
(4)在同一个问题中,分别用正数与负数表示的量具有相反的意义。
强调:用正数、负数表示实际问题中具有相反意义的量,而相反意义的量包含两个要素:一是他们的意义相反,如向东与向西、收入与支出;二是他们都是数量,而且是同类的量。
(5)正整数、0、负整数统称整数。
整数可以看作分母为1的分数。
(6)正整数、0、负整数、正分数、负分数都可以写成分数的形式,这样的数称为有理数。
(7)把一些数放在一起,就组成了一个数的集合,简称“数集”。
所有有理数组成的数集叫“有理数集”,所有整数组成的数集叫“整数集”,所有负数组成的数集叫“负数集”……数集一般用圆圈或大括号表示,因为集合中的数是无限的。
(8)有理数可以按不同的标准进行分类,标准不同,分类结果也不同。
问:有理数可分为正数和负数两大类,对吗?为什么?有理数可分为整数和分数两大类,对吗?为什么?2、有理数与数轴上的点一一对应(数轴的三要素、怎样看数轴、掌握应用数轴来进行去绝对值符号的简单运算)。
(1)通常用一条直线上的点表示数,这条直线叫数轴。
数轴三要素:原点、正方向、单位长度原点——在直线上任取一点表示数0,这个点叫原点。
初一上册数学练习题

初一上册数学练习题第一章有理数1.1 正数和负数1、在数学中,正数有无穷多个,负数也有无穷多个。
2、如果水位升高5m时水位变化记作+5m,那么水位下降3m时水位变化记作-3m,水位不升不降时水位变化记作0m。
3、在同一个问题中,分别用正数与负数表示的量具有相反的意义。
4、下列说法正确的是(B)零既不是正数也不是负数。
5、向东行进-30米表示的意义是(D)向西行进30米。
6、零上13℃记作+13℃,零下2℃可记作(B)-2℃。
7、某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高10℃。
1.2 有理数1.整数和分数统称为有理数。
2.零和负数统称为非正数,零和正数统称为非负数。
3.下列说法中正确的是(D)整数和分数统称为有理数。
4.下列说法中不正确的是(C)-2000既是负数,也是整数,但不是有理数。
5.把下列各数分别填在相应集合中:正数集合:{1.325.0.618}负数集合:{-0.20.-789.-23.13.-2004}非正数集合:{-0.20.-789.-23.13.-2004}非负数集合:{0.1.325.0.618}6.把下列各数分别填在相应的大括号里:正数集合:{5.3.7}负数集合:{-2.-3.4.-21}整数集合:{-2.5.-3.-21}有理数集合:{-2.5.-3.4.-21.3.7}1.2.2 数轴1.(2012江苏泰州市,10,3分)如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P’,则点P’表示的数是2.2.(2012山东莱芜,1,3分)如图,在数轴上点M表示的数可能是负数。
3.数轴上点A表示数a,那么A到原点的距离是什么?4.数轴上距离原点为3的数是什么?1.3 相反数、绝对值和倒数1.-2的相反数是什么?A。
B。
-。
C。
-2.D。
22.3的相反数是什么?A。
-3.B。
C。
3.D。
3.-2012的相反数是什么?A。
七年级数学上册 第二章 有理数 2.1 代数式练习题(新版)苏科版

第一节 代数式姓名________ 学校________ 等级________ 1. 代数式:用加、减、乘、除等运算符号把数或表示数的字母连结而成的式子,叫做代数式;单独的一个数或字母也是代数式备注:① 它是一个式子 ② 这个式子只有一边,任何等量或不等关系都不满足练习:1.1 判断以下各式中,哪些是代数式,哪些不是代数式?① x-1 ② -m ③ 5 ④ s=vt ⑤ x-1>0 ⑥ π ⑦ m+5 ⑧3(x+y) 正确的答案是:____________2. 单项式:数字与字母的乘积,单个的数字或者字母也是单项式〔它与分式有着本质的区别,不能弄混淆〕系数:单项式的数字局部 备注:① 这个数字不能是字母头上的 ② π是数字! 次数:字母上的指数之和读法:几次单项式练习:2.1 指出以下单项式的系数和次数① -523x y ② 3222ab π3. 多项式:假设干个单项式的和称为多项式备注:多项式是由“和〞组成的,所以每一个单项式都要加上前面的符号项:构成这个多项式的每一个单项式 注:① 注意前面符号 ② 只有字母的叫常数项 次数:由最高单项式的次数作为这个多项式的次数读法:几次几项式备注:单项式和多项式统称为整式练习:3.1 指出多项式2112m n mn -+的项、次数以及读法3.2 22321342x y x y --是_____次_____项式,其中次数最高的项是________,常数项是_________3.3 判断以下各代数式中哪些是单项式,哪些是多项式?并分别指出系数、次数以及项数2ab 、 x π、 2a b +、 222()a b -、 2a、 2413a - 3. 求代数式的值:用数值代替字母,按照运算顺序进行运算即可提高专题:一、利用概念,求字母的值提高1: 多项式3(4)b a x x x b --+-是关于x 的二次三项式,求a 、b 的值提高2: 假设单项式134m n x y +-的次数是5,且m 为质数,n 为正整数,那么m 、n 分别是多少?提高3: 假设单项式()122n n x y --是关于x y ,的三次单项式,那么n 的值是多少?提高4: 关于x 的多项式(a -1)x 5+x |b +2|-2x +b 是二次三项式,那么a 、b 分别是多少?提高5: 假设多项式()22532m x y n y +--是关于x y ,的四次二项式,求222m mn n -+的值提高6: 假设m 、n 都是自然数,请你判断多项式22m n m n +二、多种方法,求代数式的值提高1〔整体代入法〕: 代数式2346x x -+的值为9,那么2463x x -+的值是多少?思维发散1: 假设20a a +=,那么2222017a a ++的值为多少?思维发散2:代数式2346x x -+的值为9,那么2684x x -+的值为多少?思维发散3:假设2y -x =5,那么100)2(3)2(52-+---y x y x 的值是多少?提高2〔消元与整体思想〕: 假设4x y =,那么22x y x y -+的值是多少?思维发散1:3a b a b -=+,那么代数式2()4()3()a b a b a b a b +---+的值是多少?思维发散2: 3xy x y =+,那么代数式3533x xy y x xy y -+-+-的值是多少?三、代数式实际生活的应用提高1:汛期来临前,滨海区决定实施“海堤加固〞工程,某工程队承包了该工程,方案每天加固60米。
初一上册数学有理数的加减法练习题(有解析)

初一上册数学有理数的加减法练习题(有解析)想要学好数学,一定要多做同步练习,以下所介绍的七年级上册数学有理数的加减法练习题(有答案)同步练习,要紧是针对每一单元学过的知识来巩固自己所学过的内容,期望对大伙儿有所关心!一、填空题(每小题3分,共24分)1、+8与-12的和取___号,+4与-3的和取___号。
2、小华记录了一天的温度是:早晨的气温是-5℃,中午又上升了10℃,半夜又下降了8℃,则半夜的温度是____℃。
3、3与-2的和的倒数是____,-1与-7差的绝对值是____。
4、小明存折中原有450元,取出260元,又存入150元,现在存折中还有____元。
5、-0.25比-0.52大____,比- 小2的数是____。
6、若一定是____(填正数或负数)7、已知,则式子_____。
8、把下列算式写成省略括号的形式:=____。
二、选择题(每小题3分,共24分)1、已知胜利企业第一季度盈利26000元,第二季度亏本3000元,该企业上半年盈利(或亏本)可用算式表示为( )A、B、C、D、2、下面是小华做的数学作业,其中算式中正确的是( )A、①②B、①③C、①④D、②④3、小明今年在银行中办理了7笔储蓄业务:取出9.5元,存进5元,取出8元,存进12无,存进25元,取出1.25元,取出2元,这时银行现款增加了( )A、12.25元B、-12.25元C、12元D、-12元4、-2与的和的相反数加上等于( )A、-B、C、D、5、一个数加上-12得-5,那么那个数为( )A、17B、7C、-17D、-76、甲、乙、丙三地的海拔高度分别为20米,-15米和-10米,那么最高的地点比最低的地点高( )A、10米B、15米C、35米D、5米7、运算:所得结果正确的是( )A、B、C、D、8、若,则的值为( )A、B、C、D、三、解答题(共52分)1、列式并运算:(1)什么数与的和等于?(2)-1减去的和,所得的差是多少?2、运算下列各式:(1)(2)(3)3、下列是我校七年级5名学生的体重情形,(1)试完成下表:姓名小颖小明小刚小京小宁体重(千克) 34 45体重与平均体重的差-7 +3 -4 0(2)谁最重?谁最轻?(3)最重的与最轻的相差多少?4、小红和小明在游戏中规定:长方形表示加,圆形表示减,结果小者获。
北师大版七年级数学上册第二章有理数及其运算练习题及答案全套

北师大版七年级数学上第二章有理数及其运算同步练习1.数怎么不够用了一、选择题1.下面说法中正确的是().A.一个数前面加上“-”号,这个数就是负数B.0既不是正数,也不是负数C.有理数是由负数和0组成D.正数和负数统称为有理数2.如果海平面以上200米记作+200米,则海平面以上50米应记作().A.-50米B.+50米C.可能是+50米,也可能是-50米D.以上都不对3.下面的说法错误的是().A.0是最小的整数B.1是最小的正整数C.0是最小的自然数D.自然数就是非负整数二、填空题1.如果后退10米记作-10米,则前进10米应记作________;2.如果一袋水泥的标准重量是50千克,如果比标准重量少2千克记作-2千克,则比标准重量多1千克应记为________;3.车轮如果逆时针旋转一周记为+1,则顺时针旋转两周应记为______.三、判断题1.0是有理数.()2.有理数可以分为正有理数和负有理数两类.()3.一个有理数前面加上“+”就是正数.()4.0是最小的有理数.()四、解答题1.写出5个数(不许重复),同时满足下面三个条件.(1)其中三个数是非正数;(2)其中三个数是非负数;(3)5个数都是有理数.2.如果我们把海平面以上记为正,用有理数表示下面问题.一架飞机飞行高于海平面9630米;(2)潜艇在水下60米深.3.如果每年的12月海南岛的气温可以用正数去表示,则这时哈尔滨的气温应该用什么数来表示?4.某种上市股票第一天跌0.71%,第二天涨1.25%,各应怎样表示?5.如果海平面以上我们规定为正,地面的高度是否都可以用正数为表示?6.一学生参加一次智力竞赛,其中考五个题,记分标准是这样定的,如果答对一题得1分,答错或不答都扣1分,该生得了3分,问其答对了几个题?2.数轴一、选择题1.一个数的相反数是它本身,则这个数是()A.正数B.负数C.0 D.没有这样的数2.数轴上有两点E和F,且E在F的左侧,则E点表示的数的相反数应在F点表示的数的相反数的()A.左侧B.右侧C.左侧或者右侧D.以上都不对3.如果一个数大于另一个数,则这个数的相反数()A.小于另一个数的相反数B.大于另一个数的相反数C.等于另一个数的相反数D.大小不定二、填空题1.如果数轴上表示某数的点在原点的左侧,则表示该数相反数的点一定在原点的________侧;2.任何有理数都可以用数轴上的________表示;3.与原点的距离是5个单位长度的点有_________个,它们分别表示的有理数是_______和_______;4.在数轴上表示的两个数左边的数总比右边的数___________.三、判断题1.在数轴离原点4个单位长度的数是4.()2.在数轴上离原点越远的数越大.()3.数轴就是规定了原点和正方向的直线.()4.表示互为相反数的两个点到原点的距离相等.()四、解答题1.写出符合下列条件的数(1)大于而小于1的整数;(2)大于-4的负整数;(3)大于-0.5的非正整数.2.在数轴上表示下列各数,并把各数用“<”连结起来.(1)7,-3.5,0,-4.5,5,-2,3.5;(2)-500,-250,0,300,450;(3)0.1,,0.9,,1,0.3.找出下列各数的相反数(1)-0.05(2)(3)(4)-10004.如图,说出数轴上A、B、C、D四点分别表示的数的相反数,并把它们分别用标在数轴上.5.在数轴上,点A表示的数是-1,若点B也是数轴上的点,且AB的长是4个单位长度,则点B表示的数是多少?3.绝对值:一、选择题1.如果,则()A.B.C.D.2.下面说法中正确的是()A.若,则B.若,则C.若,则D.若,则3.下面说法中正确的是()A.若和都是负数,且有,则B.若和都是负数,且有,则C.若,且,则D.若都是正数,且且,则4.数轴上有一点到原点的距离是5,则()A.这一点表示的数的相反数是5 B.这一点表示的数的绝对值是5C.这一点表示的数是5 D.这一点表示的数是-5二、填空题1.已知某数的绝对值是,则是______或_______;2.绝对值最小的有理数是________;3.一个数的相反数是8,则这个数的绝对值是_________;4.已知数轴上有一点到原点的距离是3,则这点所表示的数的绝对值是________,这点所表示的数是________.三、判断题1.有理数的绝对值总是正数.()2.有理数的绝对值就等于这个有理数的相反数.()3.两个有理数,绝对值大的数反而小.()4.两个正有理数,绝对值大的数较小.()5.()四、解答题1.求下列各数的绝对值,并把它们用“<”连起来-2.37,0,,-385.7.2.把下列一组数用“>”连起来-999,,,0.01,.3.计算下列各式的值(1);(2);(3);(4)4.如图,比较和的绝对值的大小.5.计算下面各式的值(1)-(-2);(2)-(+2).4.有理数的加法:一、选择题1.两个有理数的和()A.一定大于其中的一个加数B.一定小于其中的一个加数C.和的大小由两个加数的符号而定D.和的大小由两个加数的绝对值而定2.下面计算错误的是()A.B.(-2)+(+2)=4C.D.(-71)+0=-713.如图,下列结论中错误的是()A.B.C.D.二、填空题1.两个负数相加其和为___________数.2.互为相反数的两个数的和是___________.3.绝对值不等的异号两个数相加,其和的符号与绝对值__________的加数的符号相同.三、解答题1.如图,请用表示与的和.2.计算(1);(2)(-0.19)+(-3.12);(3);(4);(5).3.计算(1)(-12.56)+(-7.25)+3.01+(-10.01)+7.25;(2)0.47+(-0.09)+0.39+(-0.3)+1.53;(3);(4)23+(-72)+(-22)+57+(-16);(5);(6)(7)4.一名外地民工10天的收支情况如下(收入为正):30元,-17元,21元,-5元,-3元,18元,-21元,45元,-10元,28元.这10天内这名外地民工净收入多少钱?5.一小商店一周的盈亏情况如下(亏为负):单位:元(1)计算出小商店一周的盈亏情况;(2)指出盈利最多一天的盈利额.6.在-49,-48,-47,…,2003这一串数中(1)前99个连续整数的和是多少?(2)前100个连续整数的和是多少?5.有理数的减法:一、选择题1.下面说法中正确的是()A.在有理数的减法中,被减数一定要大于减数B.两个负数的差一定是负数C.正数减去负数差是正数D.两个正数的差一定是正数2.下面说法中错误的是()A.减去一个数等于加上这个数的相反数B.减去一个数等于减去这个数的相反数C.零减去一个数就等于这个数的相反数D.一个数减去零仍得这个数3.甲数减乙数差大于零,则()A.甲数大于乙数B.甲数大于零,乙数也大于零C.甲数小于零,乙数也小于零D.以上都不对二、填空题1.比-3比2的数是__________,比-3少2的数是__________;2.;3..三、判断题1.若,则;()2.若成立,则;()3.若,则()四、解答题1.请举例说明两个数的差不一定小于被减数.2.如图,根据图中与的位置确定下面计算结果的正负.(1);(2);(3);(4)3.计算(1)2.7-(-3.1);(2)0.15-0.26;(3)(-5)-(-3.5);(4);(5);(6)4.1998年4月2日,长春等5个城市的最高气温与最低气温记录如下表,哪个城市的温差最大?哪个城市的温差最小?5.求数轴上表示两个数的两点间的距离.(1)表示的点与表示的点.(2)当时,表示数的点与表示的点.6.有理数的加减混合运算:一、选择题1.在1.17-32-23中把省略的“+”号填上应得到()A.1.17+32+23B.-1.17+(-32)+(-23)C.1.17+(-32)+(-23)D.1.17-(+32)-(+23)2.下面说法中正确的是()A.-2-1-3可以说是-2,-1,-3的和B.-2-1-3可以说是2,-1,-3的和C.-2-1-3是连减运算不能说成和D.-2-1-3=-2+3-13.下面说法中错误的是()A.有理数的加减混合运算都可以写成有理数的加法运算B.-5-(-6)-7不能应用加法的结合律和交换律C.如果和都是的相反数,则D.有理数的加减混合运算都可以写成有理数的减法运算二、填空题1.把下列式子变成只含有加法运算的式子.(1)-9-(-2)+(-3)-4=___________ ;(2).2.把下列各式写成省略加号的形式.(1)-7-(-15)+(-3)-(-4)=____________;(2)3.计算:(1)-5+7-15-4+2=_______________;(2)-0.5+4.3-9.6-1.8=_____________;(3)三、解答题:1.计算(1);(2);(3);(4)2.计算(1);(2);(3);(4)3.计算:(1);(2)-1999+2000-2001+2002-2003.4.小胖去年年末称体重是75千克,今年一月份小胖开始减肥,下面是小胖今年上半年体重的变化情况:负数表示比上月减少,正数表示比上月增加(1)小胖1~6月中哪个月的体重最重,是多少?(2)小胖1~6月中哪个月的体重最轻,是多少?(3)小胖6月份的体重较比去年年末是增加了还是减少了,是多少?5.存折中有2676元,取出1082元,又存入600元,在不考虑利息的情况下,你能算出存折中还有多少元钱吗?6.某校初一抽出5名同学测量体重,小明体重是55千克,其他4名同学的体重和小明体重的差数如下表:比小明重记为正,比小明轻记为负(1)哪几名同学的体重比小明重,重多少?(2)哪几名同学的体重比小明轻,轻多少?(3)写出最重和最轻的两个同学的体重,并说明这两名同学之间的体重相差多少?7.某百货商场的某种商品预计在今年平均每月售出500千克,一月份比预计平均月售出额多10千克记为+10千克,以后每月销售量和其前一个月销售量比较,其变化如下表(前11个月):(1)每月的销售量是多少?(2)前11个月的平均销售是多少?(3)要达到预计的月平均销售量,12月份还需销售多少千克?8.有理数的乘法:一、选择题1.下面说法中正确的是()A.因为同号相乘得正,所以(-2)×(-3)×(-1)=6 B.任何数和0相乘都等于0C.若,则D.以上说法都不正确2.已知,其中有三个负数,则()A.大于0B.小于0C.大于或等于0D.小于或等于03.若,其a、b、c()A.都大于0B.都小于0C.至少有一个大于0D.至少有一个小于0二、填空题1.两个数相乘,同号得___________,异号得_________,并把_________相乘;2.一个数和任何数相乘都得0,则这个数是_________;3.若干个有理数相乘,其积是负数,则积中负因数的个数是_________数.4.先填空,然后补写一个有同样特点的式子.(1)1×(-7)-1=_________,(2)9×(-9)+1=___________,12×(-7)-2=_________,98×(-9)+2=_________,123×(-7)-3=_________.987×(-9)+3=_________.__________________________.__________________________.9.有理数的除法:一、填空题1.0.25的倒数是___________-,-0.125的倒数是________,_________的倒数是;2.倒数与本身相等的数有____________.3.4.5.6.(4、5、6填“>,<,=”号)二、解答题1.计算:(1)(2)2.计算:3.在下面不正确的算式中添加负号与括号,使等式成立.(1)8×3+12÷4=-30(2)8×3+12÷4=-94.计算(1);(2)(-12)÷(-4)÷(-3)÷(-3);(3);(4)10.有理数的乘方;一、填空题1.把(-5)×(-5)×(-5)写成幂的形式是_________,底数是__________,指数是__________;2.平方等于它本身的数是_________;3.4.________的立方等于64,_________的平方等于64;5.一个数的平方等于它的绝对值,这个数是_________;6.二、判断题1.因为,所以()2.( )3.因为,所以有任何有理数的平方都是正数.()4.(n是正整数)()三、解答题: 1.计算题(1)(2)(3)2.任何整数的平方的个位数都不可能是哪些数字?3.若a是正数,请设计一个问题,使计算的结果是.4.计算1+3,1+3+5,1+3+5+7,…并找出规律,利用这个规律求1+3+5+…+19的值.5.把一个木棍第一次折成两节,第二次同时折这两节就得到四节,……,依次这样进行下去,当折十次时,将得到多少节木棍?11.有理数的混合运算: 一、选择题1.若,,则有( ) .A.B.C.D.2.已知,当时,,当时,的值是( ) .A.B.44 C.28 D.173.如果,那么的值为( ) A.0 B.4 C.-4 D.2 4.代数式取最小值时,值为( ) .A.B.C.D.无法确定5.六个整数的积,互不相等,则( ) A.0 B.4 C.6 D.86.计算所得结果为( ) .A.2 B.C.D.二、填空题1.有理数混合运算的顺序是__________________________.2.已知为有理数,则____0,____0,____0.(填“>”、“<”或“≥”=)3.平方得16的有理数是_________,_________的立方等于-8.4.__________.5.一个负数减去它的相反数后,再除以这个负数的绝对值,所得商为__________.6.1-(-2)×(-3)÷3=____________;7.1-(-2)÷(-3)×3=____________.三、解答题:1.计算(1);(2);(3);(4);(5);(6).2.计算:3.当n为奇数时,计算的值.4.试设计一个问题,使问题的计算结果是.5.某户搬入新楼,为了估计一下该月的用水量(按30天计算).对该月的头6天水表的显示数进行了记录,如下表:而在搬家之前由于搞房屋装修等已经用了15吨水.问:(1)这6在每天的用水量;(2)这6天的平均日用水量;(3)这个月大约需要用多少吨水.B组6.判断题(1)有理数和,如果,且,则.()(2)有理数和,如果,且,则()(3)表示数和的位置由下图所确定,若使,则表示数c的点的位置应在原点的右侧.()2.如图是2002年6月的日历.用一个长方形框四个数,请你认真观察框的四个数之间存在的关系..3.分别表示数和的点在数轴上的位置如图所示.(1);(2)表示数的点在数轴上运动时,将发生怎样的变化..。
人教版七年级数学上册第一章1.4有理数的乘除法-中考试题汇编含精讲解析

人教版七年级数学上册第一章1.4有理数的乘除法X年中考试题汇编含精讲解析一.选择题(共26小题)1.(X•徐州)﹣2的倒数是()A.2 B.﹣2 C.D.﹣2.(X•珠海)的倒数是()A.B.C.2 D.﹣23.(X•黄石)﹣5的倒数是()A.5 B.C.﹣5 D.4.(X•佛山)﹣3的倒数为()A.﹣B.C.3 D.﹣35.(X•自贡)的倒数是()A.﹣2 B.2 C.D.6.(X•泉州)﹣7的倒数是()A.7 B.﹣7 C.D.﹣7.(X•宿迁)的倒数是()A.﹣2 B.2 C.D.8.(X•巴中)﹣2的倒数是()A.2 B.C.﹣D.﹣29.(X•成都)﹣3的倒数是()A.﹣B.C.﹣3 D.310.(X•曲靖)﹣2的倒数是()A.﹣B.﹣2 C.D.2 11.(X•广安)的倒数是()A.5 B.﹣5 C.D.﹣12.(X•攀枝花)﹣3的倒数是()A.﹣B.3 C.D.±13.(X•毕节市)﹣的倒数的相反数等于()A.﹣2 B.C.﹣D.2 14.(X•无锡)﹣3的倒数是()A.3 B.±3 C.D.﹣15.(X•眉山)﹣2的倒数是()A.B.2 C.﹣D.﹣216.(X•龙岩)﹣1的倒数是()A.﹣1 B.0 C.1 D.±117.(X•黔东南州)的倒数是()A.B.C.D.18.(X•娄底)X的倒数为()A.﹣X B.X C.﹣D.19.(X•乌鲁木齐)﹣2的倒数是()A.﹣2 B.﹣C.D.2 20.(X•海南)﹣X的倒数是()A.﹣B.C.﹣X D.X21.(X•盐城)的倒数为()A.﹣2 B.﹣C.D.222.(X•贵港)3的倒数是()A.3 B.﹣3 C.D.﹣23.(X•义乌市)计算(﹣1)×3的结果是()A.﹣3 B.﹣2 C.2 D.324.(X•六盘水)下列运算结果正确的是()A.﹣87×(﹣83)=7221 B.﹣2.68﹣7.42=﹣10C.3.77﹣7.11=﹣4.66 D.25.(X•台湾)算式(﹣1)×(﹣3)×之值为何?()A.B.C.D.26.(X•天津)计算(﹣18)÷6的结果等于()A.﹣3 B.3 C.﹣D.二.填空题(共1小题)27.(X•湘潭)的倒数是.人教版七年级数学上册第一章1.4有理数的乘除法X年中考试题汇编含精讲解析参考答案与试题解析一.选择题(共26小题)1.(X•徐州)﹣2的倒数是()A.2 B.﹣2 C.D.﹣考点:倒数.分析:根据倒数的定义,若两个数的乘积是1,我们就称这两个数互为倒数.解答:解:∵﹣2×()=1,∴﹣2的倒数是﹣.故选D.点评:主要考查倒数的概念及性质.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数,属于基础题.2.(X•珠海)的倒数是()A.B.C.2 D.﹣2考点:倒数.分析:根据倒数的定义求解.解答:解:∵×2=1,∴的倒数是2.故选C.点评:倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.3.(X•黄石)﹣5的倒数是()A.5 B.C.﹣5 D.考点:倒数.分析:乘积是1的两数互为倒数,所以﹣5的倒数是﹣.解答:解:﹣5与﹣的乘积是1,所以﹣5的倒数是﹣.故选D.点评:本题主要考查倒数的概念:乘积是1的两数互为倒数.4.(X•佛山)﹣3的倒数为()A.﹣B.C.3 D.﹣3考点:倒数.专题:存在型.分析:根据倒数的定义进行解答即可.解答:解:∵(﹣3)×(﹣)=1,∴﹣3的倒数是﹣.故选A.点评:本题考查的是倒数的定义,即如果两个数的乘积等于1,那么这两个数互为倒数.5.(X•自贡)的倒数是()A.﹣2 B.2 C.D.考点:倒数.专题:常规题型.分析:根据倒数的定义求解.解答:解:﹣的倒数是﹣2.故选:A.点评:本题主要考查了倒数的定义,解题的关键是熟记定义.6.(X•泉州)﹣7的倒数是()A.7 B.﹣7 C.D.﹣考点:倒数.分析:根据乘积是1的两个数互为倒数,可得一个数的倒数.解答:解:﹣7的倒数是﹣,故选:D.点评:本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.7.(X•宿迁)的倒数是()A.﹣2 B.2 C.D.考点:倒数.分析:根据乘积为1的两个数互为倒数,可得答案.解答:解:的倒数是﹣2,故选:A.点评:本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.8.(X•巴中)﹣2的倒数是()A.2 B.C.﹣D.﹣2考点:倒数.分析:根据倒数定义可知,﹣2的倒数是﹣.解答:解:﹣2的倒数是﹣.故选:C.点评:主要考查倒数的定义,要求熟练掌握.需要注意的是倒数的性质:负数的倒数还是负数,正数的倒数是正数,0没有倒数.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.9.(X•成都)﹣3的倒数是()A.﹣B.C.﹣3 D.3考点:倒数.分析:根据倒数的定义,若两个数的乘积是1,我们就称这两个数互为倒数.解答:解:∵﹣3×(﹣)=1,∴﹣3的倒数是﹣.故选:A.点评:主要考查倒数的概念及性质.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数,属于基础题.10.(X•曲靖)﹣2的倒数是()A.﹣B.﹣2 C.D.2考点:倒数.分析:根据乘积是1的两个数互为倒数,可得一个数的倒数.解答:解:有理数﹣2的倒数是﹣.故选:A.点评:本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.11.(X•广安)的倒数是()A.5 B.﹣5 C.D.﹣考点:倒数.分析:根据倒数的意义,乘积是1的两个数互为倒数,求一个数的倒数就是把这个数的分子和分母调换位置.由此解答.解答:解:的倒数是5.故选A.点评:此题主要考查倒数的意义,关键是求一个数的倒数的方法.12.(X•攀枝花)﹣3的倒数是()A.﹣B.3 C.D.±考点:倒数.分析:根据倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.解答:解:﹣3的倒数是﹣.故选:A.点评:本题主要考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.13.(X•毕节市)﹣的倒数的相反数等于()A.﹣2 B.C.﹣D.2考点:倒数;相反数.分析:根据倒数和相反数的定义分别解答即可.解答:解:﹣的倒数为﹣2,所以﹣的倒数的相反数是:2.故选;D.点评:此题主要考查了倒数和相反数的定义,要求熟练掌握.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0.14.(X•无锡)﹣3的倒数是()A.3 B.±3 C.D.﹣考点:倒数.分析:根据倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.解答:解:﹣3的倒数是,故选D点评:本题主要考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.15.(X•眉山)﹣2的倒数是()A.B.2 C.﹣D.﹣2考点:倒数.分析:根据倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.解答:解:﹣2的倒数是,故选C.点评:本题主要考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.16.(X•龙岩)﹣1的倒数是()A.﹣1 B.0 C.1 D.±1考点:倒数.分析:根据乘积为1的两个数互为倒数,可得答案.解答:解:﹣1的倒数是﹣1,故选:A.点评:本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.17.(X•黔东南州)的倒数是()A.B.C.D.考点:倒数.分析:根据倒数的定义,互为倒数的两数乘积为1,﹣×(﹣)=1即可解答.解答:解:根据倒数的定义得:﹣×(﹣)=1,因此倒数是﹣.故选D.点评:本题主要考查了倒数的概念及性质.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.18.(X•娄底)X的倒数为()A.﹣X B.X C.﹣D.考点:倒数.分析:利用倒数的定义求解即可.解答:解:X的倒数为.故选:D.点评:本题主要考查了倒数的定义,解题的关键是熟记倒数的定义.19.(X•乌鲁木齐)﹣2的倒数是()A.﹣2 B.﹣C.D.2考点:倒数.分析:根据倒数的意义,乘积是1的两个数叫做互为倒数,据此解答.解答:解:∵﹣2×=1.∴﹣2的倒数是﹣,故选:B.点评:本题主要考查倒数的意义,解决本题的关键是熟记乘积是1的两个数叫做互为倒数.20.(X•海南)﹣X的倒数是()A.﹣B.C.﹣X D.X考点:倒数.分析:根据倒数的意义,乘积是1的两个数叫做互为倒数,据此解答.解答:解:∵﹣X×(﹣)=1,∴﹣X的倒数是﹣,故选:A.点评:本题主要考查倒数的意义,解决本题的关键是熟记乘积是1的两个数叫做互为倒数.21.(X•盐城)的倒数为()A.﹣2 B.﹣C.D.2考点:倒数.分析:根据倒数的意义,乘积是1的两个数叫做互为倒数,据此解答.解答:解:∵,∴的倒数为2,故选:D.点评:本题主要考查倒数的意义,解决本题的关键是熟记乘积是1的两个数叫做互为倒数.22.(X•贵港)3的倒数是()A.3 B.﹣3 C.D.﹣考点:倒数.分析:根据乘积是1的两个数互为倒数,可得一个数的倒数.解答:解:有理数3的倒数是.故选:C.点评:本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.23.(X•义乌市)计算(﹣1)×3的结果是()A.﹣3 B.﹣2 C.2 D.3考点:有理数的乘法.分析:根据有理数的乘法运算法则进行计算即可得解.解答:解:(﹣1)×3=﹣1×3=﹣3.故选A.点评:本题考查了有理数的乘法,是基础题,计算时要注意符号的处理.24.(X•六盘水)下列运算结果正确的是()A.﹣87×(﹣83)=7221 B.﹣2.68﹣7.42=﹣10C.3.77﹣7.11=﹣4.66 D.考点:有理数的乘法;有理数大小比较;有理数的减法.专题:计算题.分析:原式各项计算得到结果,即可做出判断.解答:解:A、原式=7221,正确;B、原式=﹣10.1,错误;C、原式=﹣3.34,错误;D、﹣>﹣,错误,故选A点评:此题考查了有理数的乘法,有理数的大小比较,以及有理数的减法,熟练掌握运算法则是解本题的关键.25.(X•台湾)算式(﹣1)×(﹣3)×之值为何?()A.B.C.D.考点:有理数的乘法.分析:根据有理数的乘法法则,先确定符号,然后把绝对值相乘即可.解答:解:原式=××=,故选:D.点评:本题考查的是有理数的乘法,掌握乘法法则是解题的关键,计算时,先确定符号,然后把绝对值相乘.26.(X•天津)计算(﹣18)÷6的结果等于()A.﹣3 B.3 C.﹣D.考点:有理数的除法.分析:根据有理数的除法,即可解答.解答:解:(﹣18)÷6=﹣3.故选:A.点评:本题考查了有理数的除法,解决本题的关键是熟记有理数除法的法则.二.填空题(共1小题)27.(X•湘潭)的倒数是 2 .考点:倒数.分析:根据倒数的定义,的倒数是2.解答:解:的倒数是2,故答案为:2.点评:此题主要考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.。
人教新版初一上册数学有理数的加减法试题及答案(2)

人教新版初一上册数学有理数的加减法试题及答案(2)人教新版初一上册数学有理数的加减法试题参考答案一、选择题(共13小题)1.计算﹣10﹣8所得的结果是( )A.﹣2B.2C.18D.﹣18【考点】有理数的减法.【分析】根据有理数的减法运算法则进行计算即可得解.【解答】解:﹣10﹣8=﹣18.故选D.【点评】本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.2.哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为( )A.5℃B.6℃C.7℃D.8℃【考点】有理数的减法.【专题】常规题型.【分析】根据有理数的减法,减去一个数等于加上这个数的相反数,可得答案.【解答】解:28﹣21=28+(﹣21)=7,故选:C.【点评】本题考查了有理数的减法,减去一个数等于加上这个数的相反数.3.某地某天的最高气温是8℃,最低气温是﹣2℃,则该地这一天的温差是( )A.﹣10℃B.﹣6℃C.6℃D.10℃【考点】有理数的减法.【专题】计算题.【分析】用最高温度减去最低温度,然后根据有理数的减法运算法则,减去一个数等于加上这个数的相反数进行计算即可得解.【解答】解:8﹣(﹣2)=8+2=10(℃).故选D.【点评】本题考查了有理数的减法运算法则,熟记减去一个数等于加上这个数的相反数是解题的关键.4.比1小2的数是( )A.3B.1C.﹣1D.﹣2【考点】有理数的减法.【分析】根据有理数的减法运算法则进行计算即可得解.【解答】解:1﹣2=﹣1.故选C.【点评】本题考查了有理数的减法,是基础题.5.如果崇左市市区某中午的气温是37℃,到下午下降了3℃,那么下午的气温是( )A.40℃B.38℃C.36℃D.34℃【考点】有理数的减法.【专题】应用题.【分析】用中午的温度减去下降的温度,然后根据有理数的减法运算法则进行计算即可得解.【解答】解:37℃﹣3℃=34℃.故选:D.【点评】本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.6.计算,正确的结果为( )A. B. C. D.【考点】有理数的减法.【分析】根据有理数的减法运算法则进行计算即可得解.【解答】解:﹣ =﹣ .故选D.【点评】本题考查了有理数的减法运算是基础题,熟记法则是解题的关键.7.计算:1﹣(﹣ )=( )A. B.﹣ C. D.﹣【考点】有理数的减法.【分析】根据有理数的减法法则,即可解答.【解答】解:1﹣(﹣ )=1+ = .故选:C.【点评】本题考查了有理数的减法,解决本题的关键是熟记有理数的减法法则.8.﹣2﹣1的结果是( )A.﹣1B.﹣3C.1D.3【考点】有理数的减法.【分析】根据有理数的减法法则:减去一个数等于加上这个数的相反数把原式化为加法,根据有理数的加法法则计算即可.【解答】解:﹣2﹣1=﹣2+(﹣1)=﹣3,故选:B.【点评】有本题考查的是有理数的减法法则:减去一个数等于加上这个数的相反数,掌握法则是解题的关键.9.计算2﹣3的结果是( )A.﹣5B.﹣1C.1D.5【考点】有理数的减法.【分析】减去一个数等于加上这个数的相反数,再运用加法法则求和.【解答】解:2﹣3=2+(﹣3)=﹣1.故选B.【点评】考查了有理数的减法,解决此类问题的关键是将减法转换成加法.10.桂林冬季里某一天最高气温是7℃,最低气温是﹣1℃,这一天桂林的温差是( )A.﹣8℃B.6℃C.7℃D.8℃【考点】有理数的减法.【专题】应用题.【分析】根据“温差”=最高气温﹣最低气温计算即可.【解答】解:7﹣(﹣1)=7+1=8℃.故选D.【点评】此题考查了有理数的减法,解题的关键是:明确“温差”=最高气温﹣最低气温.11.如图,这是某用户银行存折中2012年11月到2013年5月间代扣电费的相关数据,从中可以看出扣缴电费最多的一次达到( )A.147.40元B.143.17元C.144.23元D.136.83元【考点】有理数的加减混合运算;有理数大小比较.【专题】应用题.【分析】根据存折中的数据进行解答.【解答】解:根据存折中的数据得到:扣缴电费最多的一次是日期为121105,金额是147.40元.故选:A.【点评】本题考查了有理数大小比较的应用.解题的关键是学生具备一定的读图能力.12.五个城市的国际标准时间(单位:时)在数轴上表示如图所示,我市2013年初中毕业学业检测与高中阶段学校招生考试于2015年6月16日上午9时开始,此时应是(A.纽约时间2015年6月16日晚上22时B.多伦多时间2015年6月15日晚上21时C.伦敦时间2015年6月16日凌晨1时D.汉城时间2015年6月16日上午8时【考点】有理数的加减混合运算.【专题】应用题.【分析】求出两地的时差,根据北京时间求出每个地方的时间,再判断即可.【解答】解:A、∵纽约时间与北京差:8+5=13个小时,9﹣13=﹣4,∴当北京时间2015年6月16日9时,纽约时间是2015年6月15日21时,故本选项错误;B、∵多伦多时间与北京差:8+4=12个小时,9﹣12=﹣3,∴当北京时间2015年6月16日9时,纽约时间是2015年6月15日22时,故本选项错误;C、∵伦敦时间与北京差:8﹣0=8个小时,9﹣8=1,∴当北京时间2015年6月16日9时,伦敦时间是2015年6月16日1时,故本选项正确;D、∵汉城时间与北京差:9﹣8=1个小时,9+1=10,∴当北京时间2015年6月16日9时,首尔时间是2015年6月16日10时,故本选项错误;故选C.【点评】主要考查了数轴,要注意数轴上两点间的距离公式是|a ﹣b|.把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.13.与﹣3的差为0的数是( )A.3B.﹣3C.D.【考点】有理数的减法.【分析】与﹣3的差为0的数就是﹣3+0,据此即可求解.【解答】解:﹣3+0=﹣3.故选B.【点评】本题考查了有理数的减法运算,正确列出式子是关键.二、填空题(共5小题)14.计算:0﹣7= ﹣7 .【考点】有理数的减法.【分析】根据有理数的减法法则进行计算即可,减去一个数等于加上这个数的相反数.【解答】解:0﹣7=﹣7;故答案为:﹣7.【点评】此题考查了有理数的减法运算,熟练掌握减法法则是本题的关键,是一道基础题,较简单.15.计算:3﹣(﹣1)= 4 .【考点】有理数的减法.【分析】先根据有理数减法法则,把减法变成加法,再根据加法法则求出结果.【解答】解:3﹣(﹣1)=3+1=4,故答案为4.【点评】本题主要考查了有理数加减法则,能理解熟记法则是解题的关键.16.计算:3﹣4= ﹣1 .【考点】有理数的减法.【分析】本题是对有理数减法的考查,减去一个数等于加上这个数的相反数.【解答】解:3﹣4=3+(﹣4)=﹣1.故答案为:﹣1.【点评】有理数的减法法则:减去一个数等于加上这个数的相反数.17.计算:2000﹣2015= ﹣15 .【考点】有理数的减法.【专题】计算题.【分析】根据有理数的减法运算进行计算即可得解.【解答】解:2000﹣2015=﹣15.故答案为:﹣15.【点评】本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.18. |﹣7﹣3|= 10 .【考点】有理数的减法;绝对值.【专题】计算题.【分析】根据有理数的减法运算法则和绝对值的性质进行计算即可得解.【解答】解:|﹣7﹣3|=|﹣10|=10.故答案为:10.【点评】本题考查了有理数的减法运算法则和绝对值的性质,是基础题,熟记法则和性质是解题的关键初一数学复习指导一、多看主要是指认真阅读数学课本。
人教版初一数学上册知识点归纳总结及练习题

人教版七年级数学上册总复习(学生)第一章有理数1.有理数: (1)凡能写成)0p q ,p (pq≠为整数且形式的数,都是有理数, 和 统称有理数. 注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π (是不是)有理数; (2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 (3)注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;(4)自然数⇔ 0和正整数; a >0 ⇔ a 是正数; a <0 ⇔ a 是负数;a ≥0 ⇔ a 是正数或0 ⇔ a 是非负数; a ≤ 0 ⇔ a 是负数或0 ⇔ a 是非正数. 2.数轴:数轴是规定了 (数轴的三要素)的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)注意: a-b+c 的相反数是 ;a-b 的相反数是 ;a+b 的相反数是 ; (3)相反数的和为 ⇔ a+b=0 ⇔ a 、b 互为相反数.(4)相反数的商为 . (5)相反数的绝对值相等w w w .x k b 1.c o m 4.绝对值:(1)正数的绝对值等于它 ,0的绝对值是 ,负数的绝对值等于 ; 注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或 ⎩⎨⎧≤-≥=)0()0(a a a a a ;(3)0a 1aa >⇔= ;0a 1aa <⇔-=;(4) |a|是重要的非负数,即|a|≥0,非负性; 5.有理数比大小:(1)正数永远比0大,负数永远比0小; (2)正数大于一切负数;(3)两个负数比较,绝对值大的反而小; (4)数轴上的两个数,右边的数总比左边的数大; 6.倒数:乘积为1的两个数互为倒数;注意: 没有倒数; 若ab=1⇔ a 、b 互为 ; 若ab=-1⇔ a 、b 互为 .等于本身的数汇总:相反数等于本身的数:倒数等于本身的数:绝对值等于本身的数: 平方等于本身的数: 立方等于本身的数: 7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘; (2)任何数与零相乘都得零;(3)几个因式都不为零,积的符号由负因式的个数决定.奇数个负数为负,偶数个负数为正。
七年级数学上册有理数计算题专题复习50道(含答案)(K12教育文档)

(完整)七年级数学上册有理数计算题专题复习50道(含答案)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)七年级数学上册有理数计算题专题复习50道(含答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)七年级数学上册有理数计算题专题复习50道(含答案)(word版可编辑修改)的全部内容。
2017-2018学年七年级数学上册有理数计算题专题复习50道一、计算题:1.计算:—4—28—(-19)+(—24)2.计算:(+-)×(—24)3.计算:4.计算:5.计算:100÷(-2)2—(-2).6.计算:7.计算:(—2.75)×(-24); 8.9.计算:—2—|-3|+(-2)2 10.计算:-82+3×(—2)2+(—6)÷(—)211.计算:(-)2÷(—)4×(—1)6—()×48.12.计算:13.计算:14.计算:15.计算:—6+(-2)3×()÷()2÷(—3).16.计算:25。
7+(—7。
3)+(-13。
7)+7。
3。
17.计算:(—2)3+[18-(-3)×2]÷418.计算:—6—4+7 19.计算:20.计算:(-12)×(—) 21.计算:—36×(—+)22.计算:(—2)3-(—13)÷(-). 23.计算:24.计算:25.计算:26.计算:(-3。
59)×(-)—2.41×(-)+6×(—)27.计算:28.计算:29.计算:(-+)÷(-); 30.计算:31.计算:32.计算:-22÷(—1)2—×[4-(—5)2]33.计算:34.计算:35.计算:1÷(-1)+0÷(-4)×(-2010) 36.计算:(—72)+37—(—22)+(—17)37.计算:—22+(—33)×(—)3-12÷(-2)2.38.计算:—14—(1—0.5)× [10-(-2)2]—(-1)3.39.计算:—12×4—(-6)×5 40.计算:-0.52+41.计算:12-(-16)+(—4)-5 42.计算:-14-×[2-(-3)2]43.计算:3x2-3(x2-2x+1)+4 44.计算:45.计算:(—3)4÷(1.5)2-6×(-)+|-32-9|46.计算:—54×÷(—4)×47.计算:48.计算:49.计算:50.计算:参考答案1.解:原式=—32+19—24=-372。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-5 ,-2.25 ,3 ,3.5 ,1二、-22.5的绝对值是( ),-2.6的相反数是( )。
三、49的绝对值是( ),3.7的相反数是( ),-3.5的倒数是( )。
四、|-18.5|=( ),(2)2=( )。
五、计算。
4 6(-—)-(-—)+(-2) 27×[(-1)2+(-3)]7 78 1 6—+(-—)-(-—)8-(-12)-3-(-20)7 2 51(-0.2)×—×(-20) (-2)2+23(-1)197971 1 1(-—)×(-—-—)×0 11-[(-2)3-(-5)]5 5 2(—+—)-(-—) 22+(-20)+2×(-12)4 2 76 4(—-—)×(-60) (-5)2-13(-1)24715 3(-7)-(-16) 0-(-16) 7-(-11)1 1(-—)÷(-—) 5+[2-(-18-9)] (-5)4+233 929-1-(-6)+(-3) -2.4+(-9.6)-(-1.5)-9.52 1 1 4 1 4 (—-—)+(—+—) 9.7+(-—)-(-3.8)-—3 7 8 7 5 5-3 ,-3.75 ,3 ,-3 ,-8二、34的绝对值是( ),-1.8的相反数是( )。
三、41.5的绝对值是( ),0.9的相反数是( ),-9.5的倒数是( )。
四、|-43.5|=( ),(2)3=( )。
五、计算。
3 1(-—)-(-—)-(-5) 11×[(-1)3÷(-5)]7 71 1 4—-(-—)+(-—)4+(-27)-10-(-20)6 2 31(-0.6)×—÷(-2) (-3)3+32(-1)294731 1 1(-—)÷(-—-—)×0 10+[(-4)3-(-4)]4 3 2(—+—)÷(-—) 7+(-22)+10-(-19)7 2 81 3(—-—)×(-50) (-5)3-23(-1)14405 4(-16)÷(-7) 18-(-16) -15-(-10.5)1 1(-—)÷(-—) 11-[3+(-18+10)] (-4)2-347 418+16-(-10)+(-23) -7.7+(-6.3)-(-0.5)+5.52 1 1 4 9 1 (—-—)-(—-—) 8.5-(-—)+(-7.9)-—3 8 2 5 5 5-0.5 ,-3 ,1 ,-0.5 ,1二、-25.5的绝对值是( ),0.8的相反数是( )。
三、-31的绝对值是( ),-7.2的相反数是( ),6.5的倒数是( )。
四、|-13|=( ),(-2)3=( )。
五、计算。
5 5(-—)+(-—)-(-7) 18+[(-2)2×(-2)]7 74 1 10—-(-—)+(-—)27-(-30)+3×(-18)5 2 91(-0.2)÷—×(-6) (-1)4-42(-1)168781 1 1(-—)×(-—+—)×0 5×[(-2)3×(-4)]6 4 2(—+—)×(-—) 13+(-30)-1×(-11)4 7 31 9(—-—)×(-30) (-1)2-13(-1)20087 8(-14)×(-16) 2÷(-15) 1+(-19.5)1 1(-—)×(-—) 11+[-1-(-5+7)] (-2)4+339 4-39-6-(-21)+(-19) -3+(-4.4)-(-1.6)+1.32 1 1 1 9 7 (—+—)+(—+—) 5.6+(-—)+(-6.4)+—7 8 9 5 5 5-1 ,-4 ,7 ,2.5 ,-1二、28.5的绝对值是( ),-0.4的相反数是( )。
三、9的绝对值是( ),-0.1的相反数是( ),6.5的倒数是( )。
四、|-36.5|=( ),(3)2=( )。
五、计算。
1 1(-—)+(-—)+(-4) 13+[(-1)3×(-1)]7 71 1 6—-(-—)+(-—)10-(-13)+9+(-10)5 2 51(-0.2)÷—÷(-100) (-3)2-12(-1)261061 1 1(-—)÷(-—-—)×0 25-[(-3)3÷(-5)]4 7 3(—-—)-(-—) 26-(-12)-4+(-16)6 3 65 1(—-—)×(-70) (-5)4+33(-1)21806 5(-11)-(-18) 17÷(-11) 7.5+(-18)1 1(-—)÷(-—) 19-[5+(-5+2)] (-3)3-239 439-14+(-18)+(-16) 2.8-(-5.2)-(-2.8)-3.72 1 1 1 8 1 (—+—)+(—-—) 2.6+(-—)+(-3.1)+—9 3 2 5 5 5-2 ,-1.25 ,7 ,4.5 ,5二、5.5的绝对值是( ),7的相反数是( )。
三、18的绝对值是( ),5.2的相反数是( ),-6.5的倒数是( )。
四、|2|=( ),(-3)4=( )。
五、计算。
4 5(-—)+(-—)-(-5) 13+[(-1)3+(-5)]7 77 1 2—+(-—)+(-—)26+(-28)+3×(-13)8 6 31(-0.4)÷—×(-10) (-2)3-43(-1)109531 1 1(-—)÷(-—-—)×0 17×[(-3)3÷(-5)]3 2 2(—+—)×(-—) 19+(-10)-2+(-17)3 4 59 1(—-—)×(-50) (-2)2-43(-1)26138 2(-8)+(-6) 14-(-15) -3.5+(-12)1 1(-—)÷(-—) 5+[-3-(-15+10)] (-2)2-534 95-13-(-27)-(-16) -6.6-(-9.6)+(-2.2)-5.62 1 134 9 (—+—)-(—-—) 5.8+(-—)-(-3.3)+—3 5 5 7 5 5-3 ,-1.75 ,8 ,-5 ,4二、-25.5的绝对值是( ),8的相反数是( )。
三、-43的绝对值是( ),6.2的相反数是( ),-5的倒数是( )。
四、|-14|=( ),(1)4=( )。
五、计算。
3 5(-—)+(-—)+(-2) 2-[(-1)3÷(-5)]7 74 1 1—-(-—)-(-—)21-(-23)-9×(-14)5 4 31(-0.1)×—÷(-80) (-5)3-42(-1)203541 1 1(-—)÷(-—-—)×0 30+[(-2)3×(-3)]3 9 3(—-—)-(-—) 5+(-16)-10+(-17)4 2 74 1(—+—)×(-10) (-2)4-43(-1)18825 2(-11)÷(-9) 16÷(-6) -12+(-24.5)1 1(-—)-(-—) -8+[-4+(-7+9)] (-3)2-433 537-3+(-12)-(-7) -4.9-(-1.2)-(-0.6)-4.32 1 13 9 8 (—+—)-(—+—) 6.9+(-—)+(-8.8)-—5 5 9 5 5 5-5 ,-2.5 ,5 ,-0.5 ,9二、10的绝对值是( ),4.7的相反数是( )。
三、-7.5的绝对值是( ),-1的相反数是( ),9的倒数是( )。
四、|50|=( ),(3)3=( )。
五、计算。
5 3(-—)+(-—)-(-1) 17×[(-1)2÷(-4)]7 71 1 1—-(-—)-(-—)28+(-10)+8+(-15)8 4 51(-0.5)×—÷(-50) (-5)3-22(-1)218781 1 1(-—)÷(-—+—)×0 25-[(-4)2÷(-1)]3 3 7(—+—)×(-—) 3+(-18)-3×(-14)3 6 31 1(—-—)×(-40) (-5)3+33(-1)27304 2(-20)-(-16) 14-(-3) 2.5+(-25)1 1(-—)-(-—) 10-[4+(-19-1)] (-4)2+525 534+19-(-10)+(-8) 5.3+(-2.4)+(-0.7)+3.22 1 1 1 4 9 (—-—)+(—-—) 9.3-(-—)-(-7.7)+—7 4 9 7 5 5-4.5 ,-4.75 ,10 ,2 ,5二、-3的绝对值是( ),2.8的相反数是( )。
三、-16的绝对值是( ),10的相反数是( ),-1的倒数是( )。
四、|38.5|=( ),(2)2=( )。
五、计算。
6 1(-—)-(-—)+(-2) 19÷[(-2)3×(-1)]7 73 1 6—+(-—)+(-—)5+(-12)-4×(-20)4 4 71(-0.5)÷—×(-60) (-4)3-43(-1)266221 1 1(-—)×(-—+—)×0 2+[(-3)2÷(-5)]7 9 9(—-—)-(-—) 11+(-30)+6×(-17)7 2 83 8(—+—)×(-50) (-5)2-23(-1)11122 7(-11)÷(-11) 19×(-15) -1.5-(-1)1 1(-—)+(-—) -14+[3-(-15+3)] (-4)2-524 6-11+19+(-30)+(-8) -4.4-(-1.8)+(-3.7)-3.22 1 1 4 9 7(—+—)+(—-—) 6.5-(-—)-(-9.6)-—7 9 7 7 5 5-4 ,-1 ,3 ,1.5 ,-5二、24的绝对值是( ),8.3的相反数是( )。
三、9的绝对值是( ),5.8的相反数是( ),-9的倒数是( )。
四、|10.5|=( ),(1)3=( )。
五、计算。
4 5(-—)-(-—)-(-1) 26÷[(-4)3×(-5)]7 73 1 6—-(-—)-(-—)21-(-27)-10+(-20)2 8 51(-0.1)×—×(-900) (-2)3+13(-1)198891 1 1(-—)÷(-—+—)×0 26×[(-1)3×(-4)]9 5 6(—-—)-(-—) 4-(-22)+5×(-16)3 3 81 9(—+—)×(-90) (-1)2-23(-1)25418 8(-8)+(-7) 11+(-1) -12.5+(-18.5)1 1(-—)×(-—) 13-[0+(-15-10)] (-1)3-349 2-30-16-(-4)-(-20) -3.5-(-3.3)-(-1)-7.72 1 1 4 9 6 (—+—)-(—+—) 3.4-(-—)+(-1.4)+—9 6 4 7 5 5-2 ,-1.75 ,3 ,-2.5 ,-6二、23的绝对值是( ),-3.7的相反数是( )。
