四年级 相遇与追及综合
相遇追及问题综合习题

相遇追及问题综合习题相遇追及问题是数学中的一个经典问题,通常涉及到两个移动的物体在一定时间内是否会相遇,以及相遇时间和位置的计算。
这类问题涉及到物理、几何和代数等多个数学领域,需要灵活运用各种数学方法和思维方式来解决。
在解决相遇追及问题时,首先需要明确问题中所涉及到的物体的速度、起始位置和运动方向。
然后,结合方程和图形等工具,可以通过分析两个物体的运动轨迹,确定它们是否会相遇,以及相遇的时间和位置。
下面将通过一些综合习题来探讨相遇追及问题的解决方法:1. 两辆车相向而行问题:假设两辆车相向而行,车A的速度为v1,车B的速度为v2。
已知车A与车B的起始位置之差为d,问题是在多长时间内两辆车会相遇?解决这个问题可以根据两辆车相对运动的速度来计算相遇时间。
由于两辆车是相向而行,所以它们的相对速度为v1 + v2,相对速度与起始位置之差d的比值为t,即有t = d / (v1 + v2)。
2. 两辆车同向追及问题:假设两辆车同向行驶,车A的速度为v1,车B的速度为v2,车A领先车B的距离为d。
问题是在多长时间内车B会追及车A?这个问题可以通过分析车A与车B的相对速度来解决。
由于车B追及车A,所以它们的相对速度为v1 - v2,相对速度与领先距离d的比值为t,即有t = d / (v1 - v2)。
3. 船与河流相对运动问题:假设一艘船在静水中的速度为v1,河流流速为v2,船从河岸出发,沿着水流的方向航行。
问题是船在多长时间内能够到达河对岸?这个问题可以通过分析船与河流的相对速度来解决。
由于船与河流的相对速度为v1 - v2,船与河流垂直方向的移动距离为d,相对速度与移动距离的比值为t,即有t = d / (v1 - v2)。
完整版)四年级相遇追及问题专题练习

完整版)四年级相遇追及问题专题练习暑假衔接问题中,行程问题是一个常见的数学问题类型。
其中包括相遇问题、相背问题、追及问题和重复路程问题。
在相遇问题中,通常给定两个人或车从不同的地点同时出发,他们的速度也不同。
要求计算他们相遇的时间或相遇时的距离。
例如,甲乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
求两人几小时后相遇。
在相背问题中,通常给定两个人或车从相距一定距离的两个地点同时出发,他们的速度也不同。
要求计算他们相遇时的距离或相遇的时间。
例如,甲每小时行7千米,乙每小时行5千米,两人于相隔18千米的两地同时相背而行,求几小时后两人相隔54千米。
在追及问题中,通常给定一个人或车先出发,另一个人或车在一定时间后从同一地点开始追赶。
要求计算在何时何地能够追上对方。
例如,甲乙两人分别从相距24千米的两地同时向东而行,甲骑自行车每小时行13千米,乙步行每小时走5千米。
求几小时后甲可以追上乙。
在重复路程问题中,通常给定两个人或车从相距一定距离的两个地点同时出发,他们的速度也不同。
同时还有一个物体以不同的速度在两者之间往返。
要求计算当两个人或车相遇时,该物体共行了多少距离。
例如,XXX和XXX两人同时从相距2000米的两地相向而行,XXX每分钟行110米,XXX每分钟行90米。
如果一只狗与XXX同时同向而行,每分钟行500米,遇到XXX后,立即回头向XXX跑去;遇到XXX后再回头向XXX跑去。
这样不断来回,直到XXX和XXX相遇为止,狗共行了多少米。
练题:1、一辆汽车和一辆摩托车同时分别从相距900千米的甲、乙两地出发,汽车每小时行40千米,摩托车每小时行50千米。
8小时后两车相距多少千米?2、甲乙两车分别从相距480千米的A、B两城同时出发,相向而行。
已知甲车从A城到B城需6小时,乙车从B城到A城需12小时。
两车出发后多少小时相遇?3、甲车每小时行6千米,乙车每小时行5千米,两车于相隔10千米的两地同时相背而行,几小时后两人相隔65千米?4、甲每小时行9千米,乙每小时行7千米,甲从南庄向南行,同时乙从北庄向北行。
(完整版)四年级相遇与追击综合问题知识点总结

相遇和追及综合知识点总结一、基础知识点(相遇和追及):其实相遇和追及最核心的问题就是路程S、速度V和时间T的问题,基本公式就是S÷V=T以及这个公式的变形S÷T=V,V×T=S。
相遇问题:路程和S和------相遇时间T------ 速度和V和⏹S和:一定是甲乙两者共同时间内走过的路程。
如果其中一方提前走了一段路程,这个不算,需要去掉。
⏹T相遇时间:一定是在相遇过程中共同经历过的时间。
需要小心题目陷阱,如其中一方休息了一段时间,其中一方提前出发了一段时间都应该剔除。
⏹V和=V甲+ V乙⏹路程和÷速度和=相遇时间路程和÷相遇时间=速度和速度和×相遇时间=路程和追击问题:路程差S差-------追及时间T -------速度差V差⏹S差:有些题没有明确给出路程差,而是隐含在一些条件中,如甲先出发一段时间。
⏹T追及时间:一定是在追及过程中共同经历过的时间。
需要小心题目陷阱,如其中一方休息了一段时间,其中一方提前出发了一段时间都应该剔除。
⏹V和=V甲- V乙路程差÷速度差=追及时间路程差÷追及时间=速度差速速度差×追及时问=路程差二、直线的相遇与追击略三、环形跑道的相遇与追击1、同时同地每次相遇都是合走一圈S和=S甲+S乙=1圈2、同时不同地首次相遇等于初始距离,初始距离需要依据双方的运动方向确定。
每次相遇都是合走一圈S和=S甲+S乙=1圈四、火车过桥火车过杆:S火=车长火车完全过桥:S火=车长+桥长火车完全在桥上:S火= 桥长-车长超人(同向):S差=车长---等效为:人追行人错人(相向):S和=车长---等效为:车尾人与行人相遇超车(同向):S差=车长1+车长2 ---等效为:快车车尾人追慢车车头人错车(相向):S和==车长1+车长2 ---等效为:两个车尾的人相遇五、流水行船静水速度(船速),水速,顺水速度,逆水速度顺水速度=船速+ 水速逆水速度=船速- 水速船速=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2。
含答案】四年级奥数行程问题精选练习(相遇、追及)

含答案】四年级奥数行程问题精选练习(相遇、追及)小牛老师工作室精华讲义:小学奥数行程问题知识点一:相遇问题1.两辆汽车同时从相距325千米的两地相对开出。
甲车速度为35千米/时,乙车速度为30千米/时。
当甲、乙两车相遇时,它们各行驶了多少千米?解答:两车相对速度为35+30=65千米/时。
根据相遇问题,它们行驶的总时间相等,所以它们各行驶了325/2=162.5千米。
2.高小帅家距离学校3000米。
小帅妈妈从家出发接小帅放学,小帅也要从学校回家。
他们同时出发。
小帅妈妈每分钟比小帅多走24米。
30分钟后两人相遇。
那么小帅的速度是多少?解答:设小帅速度为v,则小帅妈妈速度为v+24.根据相遇问题,它们行驶的总时间相等,所以小帅行驶了30v米,小帅妈妈行驶了30(v+24)米。
因为两人相遇,所以它们行驶的总路程为3000米,即30v+30(v+24)=3000,解得v=48米/分钟,即小帅的速度为48/60=0.8米/秒。
3.甲、乙两辆汽车分别从A、B两地相对而行。
已知甲车的速度为38千米/时,乙车的速度为40千米/时。
甲车先行2小时后,乙车才开始出发,乙车行驶5小时后两车相遇。
求A、B两地的距离。
解答:设A、B两地的距离为d。
则甲车行驶了d+2×38千米,乙车行驶了5×40千米。
因为它们相遇,所以它们行驶的总路程相等,即d+2×38+5×40=2×38+5×40+d,解得d=342千米。
4.两列城际列车从两城同时相对开出,其中一列车的速度为40千米/时,另一列车的速度为45千米/时。
在行驶途中,两列车先后各停车4次,每次停车15分钟。
这样经过7小时后两车相遇。
求两城的距离。
解答:设两城的距离为d。
则两车相对速度为40+45=85千米/时。
因为两车在行驶途中各停车4次,所以它们行驶的总时间为7小时-4×4×15分钟=6.4小时。
(完整)四年级+相遇问题与追及问题

简单的相遇与追及问题一、学习目标1. 理解相遇与追及的运动模型,掌握相遇与追及这两种情况下路程、时间、速度这三个基本量之间的关系.会利用这个关系来解决一些简单的行程问题.2. 体会数形结合的数学思想方法.二、主要内容1. 行程问题的基本数量关系式:路程=时间×速度;速度=路程÷时间;时间=路程÷速度.2.相遇问题的数量关系式:相遇路程=相遇时间×速度和;速度和=相遇路程÷相遇时间;相遇时间=相遇路程÷速度和.3.追及问题的数量关系式:追及距离=追及时间×速度差;速度差=追及距离÷追及时间;追及时间=追及距离÷速度差.4. 能熟练运用路程、时间、速度这三个基本量的关系,结合图形分析,解决一些简单的行程问题.三、例题选讲例1两辆汽车同时分别从相距500千米的A,B两地出发,相向而行,速度分别为每小时40千米和每小时60千米.求几小时后两车相遇.例2甲车在乙车前200千米,同时出发,速度分别为每小时40千米与60千米.问多少小时后,乙车追上甲车.例3一辆公共汽车和一辆小轿车同时从相距598千米的两地相向而行.公共汽车每小时行40千米,小轿车每小时行52千米,问几小时后两车相距138千米?例4 甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇.求东、西两地相距多少千米?例5甲、乙两人同时从相距18千米的两地相向而行,甲每小时行4千米,乙每小时行5千米.甲带着一只狗,每小时走20千米,狗走得比人快,同甲一起出发,碰到乙后,它往甲方向奔走;碰到甲后,它又往乙方向奔走,直到甲、乙两人相遇为止,这只狗一共奔走了多少千米?例6一辆卡车和一辆摩托车同时从A、B两地相对开出,两车在途中距A地60千米处第一次相遇.然后,两车继续前进,卡车到达B地,摩托车到达A地后都立即返回,两车又在途中距B地30千米处第二次相遇.求A、B两地相距多少千米?例7甲、乙、丙三人进行100米赛跑.当甲到达终点时,乙离终点还有20米,丙离终点还有40米.如果甲、乙、丙赛跑的速度都不变,那么当乙到达终点时,丙离终点还有多远?例8小明步行上学,每分行75米,小明离家12分后,爸爸骑单车去追,每分行375米.问爸爸出发多少分后能追上小明?例9解放军某部快艇追击敌舰,追到A岛时,敌舰已逃离该岛15分钟,已测出敌舰每分钟行驶1000米,解放军快艇每分钟行驶1360米,在距离敌舰600米处可开炮射击.问解放军快艇从A岛出发经过多少分钟就可以开炮射击敌舰?例10甲、乙两人在环形跑道上以各自的不变速度跑步,如果两人同时从同地相背而行,乙跑4分钟后两人第一次相遇,已知甲跑一周需6分钟,那么乙跑一周需要多少分钟?例11两名运动员在湖周围环形道上练习长跑,甲每分跑250米,乙每分跑200米,两人同时从两地同向出发,经过45分甲追上乙,如果两人同时同地反向出发,经过多少分两人相遇?例12甲、乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米,如果她们同时分别从直路两端点出发,跑了6分,那么,这段时间内,两人共迎面相遇了多少次?四、练习题1、甲、乙两站相距980千米,两列火车由两站相对开出,快车每小时行50千米,慢车每小时行多少千米,两车经10小时能相遇?2、甲车每小时行60千米,1小时后,乙车紧紧追赶,速度为每小时80千米,几小时后乙车可追上甲车?3、早晨6时,有一列货车和一列客车同时从相距360千米的甲、乙两城相对开出,中途相遇,这期间,货车停车一次60分钟,客车停车两次各30分钟,已知货车每小时行42千米,客车每小时行78千米,问两车在几点钟相遇?4、东、西两镇相距240千米,一辆客车从上午8时从东镇开往西镇,一辆货车在上午9时从西镇开往东镇,到正午12点,两车恰好在两镇间的中点相遇,如果两车都从上午8时由两地相向开出,速度不变,到上午10时,两车还相距多少千米?5、骑单车从甲地到乙地,以每小时10千米的速度行进,下午1点到,以每小时15千米的速度行进,上午11点到.如果希望中午12点到,那么应以怎样的速度行进呢?6、A、B两地相距480千米.甲、乙两车同时从两站相对出发,甲车每小时行35千米,乙车每小时行45千米,一只燕子以每小时行50千米的速度和甲车同时出发向乙车飞去,遇到乙车又折回向甲车返飞去,遇到甲车又返飞向乙车,这样一直飞下去,燕子飞了多少米两车才相遇?7、某人由甲地去乙地,如果他从甲地先骑摩托车行了12小时,再换骑自行车行9小时,恰好到达乙地.如果他从甲地先骑自行车行了21小时,再换骑摩托车行8小时,也恰好到达乙地.问:全程骑摩托车需要多少小时才能到达乙地?8、兄妹两人同时由家上学,哥哥每分钟走90米,妹妹每分钟走60米,哥哥到校门口时,发现忘了带课本,立即沿原路返回去取,行至离校门口180米处与妹妹相遇,他们家离学校多少米?9、兄妹两人在周长300米的圆形水池边玩.从同一地点同时背向饶水池而行.哥哥每分钟走13米,妹妹每分钟走12米.他们第5次相遇时,哥哥共走了多长的路?。
四年级奥数:行程问题之相遇问题、追及问题

四年级奥数:行程问题之相遇问题、追及问题两个运动的物体,以不同的速度从不同地点出发沿同一线路相向而行,两个物体之间的距离不断缩短,直到相遇。
我们把这样的问题叫做相遇问题,相遇问题的关系式为:相遇路程=速度和×相遇时间。
解相遇问题一定要紧盯速度与相遇路程。
本篇我主要会讲到以下几种类型的题目:(1)一般相遇问题:如果两个物体是同时出发,那么相遇路程就是两个物体原来相距的路程;如果两个物体不是同时出发,那么它们的相遇路程等于两个物体原来相距的路程减去其中一个物体先走的路程;(2)中点相遇问题:相遇路程等于相遇地点与中点距离的两倍;(3)往返相遇问题:同时出发,同时停止,则中间往返的时间就是相遇时间;(4)环形相遇问题:同时、同地背向出发,相遇路程就是一周的长度。
一般相遇问题一般行程问题中,路程=速度×时间,速度=路程÷时间,时间=路程÷速度。
例题1,此类相遇问题中:相遇时间=相遇路程÷速度和。
中点相遇问题相遇问题中,路程差=速度差×时间差;速度差=路程差÷时间;时间=路程差÷速度差。
中点相遇问题中,快的多走的路程就是距离中点路程的两倍。
相遇时间=路程差÷速度差。
往返相遇问题往返相遇问题的关键是,往返行驶的时间与相遇时间相等。
环形相遇问题环形跑道上同时背向行驶,相遇几次,则相遇路程就是几个全程,再根据相遇时间=路程÷速度和求解。
在追及问题中,必定有一个物体的速度较快,而另一个物体速度较慢,解题的关键是找到追及路程。
追及问题的关系式为:追及时间×速度差=追及路程。
两种追及路线的追及路程分别是:(1)直线追及:如果两人同时同向不同地出发,那么追及路程就是两人相距的路程;如果两人同地同向不同时出发,那么追及路程就是先走的路程;(2)环形追及:如果两人同时、同地、同向出发,那么追及问题就是一周的长;如果是不同时或不同向或不同地出发,需要结合具体情景,借助示意图和列表进行分析。
四年级相遇与追及问题

四年级相遇与追及问题相遇和追及是初中数学中比较基础的运动问题。
相遇问题是指两个人从两个不同的地点出发,在途中相遇的情况。
追及问题是指一个人从后面赶上另一个人的情况。
在解决这些问题时,需要用到速度、时间和路程的关系。
具体来说,对于相遇问题,假设甲从A地到B地,乙从B地到A地。
如果两人同时出发,他们在途中相遇,实质上是甲和乙一起走了A、B之间这段路程。
如果甲的速度为v甲,乙的速度为v乙,相遇的时间为t,则相遇路程为S和=V和t,其中V和=v甲+v乙。
对于追及问题,假设甲走得快,乙走得慢。
在相同的时间(追及时间)内,甲比乙多走了一段路程,也就是追及路程。
如果甲的速度为v甲,乙的速度为v乙,速度差为V差=v甲-v乙,则追及路程为S差=V差t。
需要注意的是,在研究这些问题时,一般都隐含以下两种条件:(1)在整个被研究的运动过程中,两个物体所运行的时间相同;(2)在整个运行过程中,两个物体所走的是同一路径。
举个例子,假设XXX和明明同时从各自的家相对出发,明明每分钟走20米,XXX骑着脚踏车每分钟比明明快42米,经过20分钟后两人相遇。
那么,聪聪家和明明家的距离为S和=(20+42)×20=1640米。
在解决这些问题时,可以选择直接利用公式计算,也可以画图帮助理解。
对于刚刚研究奥数的孩子,需要引导他们认识、理解及应用公式。
已经行驶了82千米(41千米/小时×2小时),此时甲、乙两车相距770-82=688千米。
接下来,甲、乙两车相向而行,速度之和为45+41=86千米/小时。
根据“相遇时间=路程和/速度和”的公式,甲车行驶的时间为688/86=8小时。
因此,甲车行驶8小时后与乙车相遇。
答案】甲车行驶8小时后与乙车相遇。
考点】行程问题【难度】☆☆【题型】解答【解析】先求出XXX出发后,XXX所行的路程:70×5=350(米);再求出XXX返回学校和取运动服所需的时间:2×2=4(分钟);因为XXX比XXX每分钟多走40米,所以追上XXX的时间为350÷40=8.75(分钟),即约9分钟后追上XXX.答案】9分钟已知XXX和XXX同时从学校出发,XXX的速度是XXX的1.6倍,他们向同一个方向走,5分钟后XXX返回学校取运动服,这样用去了5分钟,在学校又耽误了2分钟,XXX一共耽误了12分钟。
四年级数学思维训练——追及、相遇问题

追及、相遇问题知识导航追及问题与相遇问题都属于行程问题中的一类。
其中追及问题是同向运动问题。
追及问题的基本特点是:两个物体同向运动,慢的走在前,快的走在后,它们之间的距离随着时间的推移不断地缩短,直到快者追上慢者。
追及问题中的各数量关系是:路程差二速度差X追及时间速度差=路程差F追及时间追及时间二路程差F速度差相遇问题则是反向运动问题。
相遇问题的基本特点是:两个物体反向运动,即一个物体朝着另一个物体面对面的运动,它们之间的距离随着时间的推移不断地缩短,直到两个物体碰面。
相遇问题中的各数量关系是:路程差二速度和X相遇时间速度和二路程差三相遇时间相遇时间二路程差F速度和精典例题例1:小欣在小华前面150米,小欣每秒走1米,小华有事情想找小欣于是以每秒3米的速度小跑去追小欣,问多久之后小华追上小欣?思路点拨此题为追及问题,小华每秒3米往前跑,小欣每秒1米往前走,那么小华每秒过后离小欣的距离近了3-1=2米,之前两人距离150米,所以距离缩短150米需要时间=150^2=75秒。
也可直接运用追及公式:追及时间二路程差F速度差=150F(3-1)=75秒。
模仿练习小琪早上吃完早餐后以每分钟80米的速度骑自行车去学校上学。
3分钟后,她妈妈突然发现她一本书本忘带了,于是马上以每分钟200米的速度骑自行车去追小琪给她书。
假设妈妈追到小琪的时候小琪还没到学校,问妈妈多久之后追上小琪?例2:有一个圆形跑道周长是600米,有甲乙两人同时沿顺时针方向跑,甲在乙前面240米处。
已知甲每分钟跑120米,乙每分钟跑100米,问几分钟后甲追上乙?如果追上后继续跑,问再过多少分钟,甲第三次追上乙?此题为环形跑道的追及问题,第一次甲追乙的路程差为:600-240=360米,则第一次追上的时间为:360F(240-120)=3分钟。
追上后继续跑,甲第三次追上乙,也就是说甲又沿着跑道追乙追了两圈。
则路程差为:2X600=1200米,追及时间=1200^(240-120)=10分钟。
行程问题(2)相遇与追及问题综合

行程问题(2)相遇与追及问题综合行程问题(2):相遇与追及问题题一.知识前测(1)赴援问题研究的就是两个物体同向运动的应用题。
其解题关键就是:先确认或算出赴援距离,以及两个物体的速度差。
数量关系就是:追及距离÷速度差=追及时间追及距离÷追及时间=速度差速度差×追及时间=追及距离(2)a、b两地距离150千米,两列火车从a至b地,快车每小时行75千米,慢车每小时行50千米。
当快车至b地时,慢车距b地除了多少千米?(3)甲、乙两车同时从a城开往b城,甲车每小时行120千米,乙车每小时行80千米,4小时后两车相距多少千米?(4)甲乙两人分别从西村和东村同时向东而行,甲骑著自行车每小时行14千米,乙步行每小时行5千米。
2小时后,甲甩开乙。
谋东西两村距离多少千米?(自己画图分析)(5)甲乙两人分别从相距36千米的两地同时同向而行,甲每小时行22千米,乙每小时行13千米,多少小时后,甲追上乙?此时甲走了多少千米?乙走了多少米?二.典型例题【例1】兄弟两人由家向学校出发,弟弟步行每分走50米,哥哥骑自行车每分行200米,弟弟跑了12分后,哥哥骑车离家,几分后甩开弟弟?练习:甲车以每小时55千米的速度从a在向b地开出,1小时后,乙车也从a地开向b地,速度是每小时60千米,那么乙车出发几小时后能追上甲车?【基准2】甲、乙两辆汽车同时从东、西两地并肩送出,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇。
求东、西两地间的公路长多少千米?练:练:两辆汽车同时从甲、乙两地相对送出,快车每小时行55千米,慢车每小时行45千米,碰面时,快车少于中点30千米。
甲、乙两地之间的公路短多少千米?【例3】快车和慢车同时从甲、乙两地相向开出,快车每小时行40千米,经过3小时,快车已驶进中点25千米,这时快车与慢车还距离7千米。
慢车每小时行多少千米?练习:a、b两车同时从甲、乙两城相向开出,甲车每小时行60千米,经过3小时,甲车已驶进中点20千米,这时甲车与乙车还距离8千米.乙车每小时行多少千米?(2021年世奥赛(中国区)海选赛)【例5】一辆自行车和一辆电瓶车同时从相距50千米的两地相向而行,自行车每小时行10千米,电瓶车每小时行15千米,行及了多少小时后两车距离12.5千米?择机多少小时后两车又距离12.5千米?练习:甲、乙两车早上8点分别从a、b两地同时出发相向而行,到10点时两车距离112.5千米。
简单行程问题-四年级(追及+相遇)

简单行程问题一、相遇问题二、追及问题相遇路程=相遇时间×速度和追及距离=追及时间×速度差速度和=相遇路程÷相遇时间速度差=追及距离÷追及时间相遇时间=相遇路程÷速度和追及时间=追及距离÷速度差练习题1、甲乙两地相距600千米,一辆货车以每小时48千米的速度从甲地开往乙地,一辆客车以每小时52千米的速度从乙地开往甲地,两车同时出发,经几小时两车相遇?2、快车和慢车同时从A、B两地相向而行,经过4小时相遇,已知慢车每小时行60千米,快车的速度是慢车的1.5倍,A、B两地相距多少千米?3、一列客车和一列货车,同时从相距800千米的两地相对而行,客车每小时行70千米,货车每小时行60千米,经过6小时两车相距多少千米?4、甲乙两车从相距798千米的两地相对而行,甲车先行2小时,乙车才出发,已知甲车每小时行75千米,乙车每小时行60千米,乙车开出后几小时与甲车相遇?5、两辆汽车同时从兴化沿同样的路线开往北京。
第一辆汽车每小时行65千米,第二辆汽车每小时行56千米,行了7小时后,两车相距多少千米?如果两辆汽车同时从兴化出发,相背而行,那7小时两车相距多少千米?6、甲车从南京站开往上海站,每小时行80千米,乙车同时从上海站开往南京站,每小时行60千米,两车在距离中点40千米处相遇。
相遇时甲比乙多行了多少千米?甲乙相遇时,甲行了多少千米,乙行了多少千米?甲乙两站的距离是多少千米?1、A、B、C三城在同一条直线上,甲、乙两辆汽车同时从相距90千米的AB 两城向C城驶去,甲车每小时行75千米,乙车每小时行60千米,乙车在前甲车在后,几小时后,甲车才能追上乙车?2、两船从甲码头开往乙码头,客船每小时行40千米,快艇每小时行50千米。
客船先出发1.5小时,多少小时后快艇才能追上客船?3、一辆汽车从甲地开往乙地,每小时行40千米,开出5小时后,一列火车以每小时90千米的速度也从甲地开往乙地。
小学四年级奥数-相遇追击问题

学力训练
迪斯尼乐园里,冒失的米老鼠和唐老鸭把小火车面对面地开上了同一条铁轨,米老鼠的速度是每秒10米,唐老鸭的速度是每秒11米,由于没有及时刹车,结果两列小火车相撞,加入米老鼠和唐老鸭仔相撞前( )秒同时紧急刹车,不仅可以避免两车相撞,两车车头还能保持3米的距离。(紧急刹车后米老鼠和唐老鸭的小火车分别向前滑行30米)
60米
60米
70米
210米
180米
390米
0 米
两人之间的距离为0米。
张红家距李芳家390米。两人同时从家里出发,向对方走去。李芳每分走70米,张红每分钟走60米。
同时
相向
相遇
两地
相遇问题
拓展思维能力的训练
有一段路,两人同时要走完,有几种走法? 乙走的路程 同方向走 反方向走
乙走的路程
甲走的路程
基本关系
追及时间=追及路程÷速度差
速度差=追及路程÷追及时间
追及路程=速度差×追及时间
例题求解
甲、乙两车相距90千米,两车同时相向而行,甲车每小时行65千米,乙车每小时行50千米,经过多少小时甲车能够追上乙车?
追击问题“形”变“质”不变
某港停有甲乙两船,某一天,甲船以每小时24千米,乙船以每小时16千米的速度,同时同地背向出发,2小时后,甲船因事调转船头追乙船,几小时才能追上?
面对面走
乙走的路程
甲走的路程
甲走的路程
以上情况可以看出,两个物体只要是共同行完全路程。
出发地点
行驶方向
运动 结果
开始时刻
结束时刻
属于这类题目的应用题可以根据相遇问题来解答。
同时
同时
两地
同地
相向
同向
反向
相遇与追及综合笔记

相遇与追及综合笔记一、基本公式关于s、v、t 三者的基本关系=速度×时间=路程可简记为:s vt=÷路程÷速度=时间可简记为:t s v=÷路程÷时间=速度可简记为:v s t二、相遇甲从A地到B地,乙从B地到A地,然后两人在途中相遇,实质上是甲和乙一起走了A,B之间这段路程,如果两人同时出发,那么相遇路程=甲走的路程+乙走的路程=甲的速度×相遇时间+乙的速度×相遇时间=(甲的速度+乙的速度)×相遇时间=速度和×相遇时间.一般地,相遇问题的关系式为:速度和×相遇时间=路程和,即=tS V和和三、追及有两个人同时行走,一个走得快,一个走得慢,当走得慢的在前,走得快的过了一些时间就能追上他.这就产生了“追及问题”.实质上,要算走得快的人在某一段时间内,比走得慢的人多走的路程,也就是要计算两人走的路程之差(追及路程).如果设甲走得快,乙走得慢,在相同的时间(追及时间)内:追及路程=甲走的路程-乙走的路程=甲的速度×追及时间-乙的速度×追及时间=(甲的速度-乙的速度)×追及时间=速度差×追及时间.一般地,追击问题有这样的数量关系:追及路程=速度差×追及时间,即S V=t差差四、在研究追及和相遇问题时,一般都隐含以下两种条件:(1)在整个被研究的运动过程中,2个物体所运行的时间相同(2)在整个运行过程中,2个物体所走的是同一路径。
⨯⎧⎪÷⎨⎪÷⎩÷⎧⎪⨯⎨⎪÷⎩路程=速度和相遇相遇速度和=路程相遇相遇=路程速度和追及=追及路程速度差追及追及路程=速度差追及速度差=追及路程追及。
应用题板块-行程问题之相遇追及(小学四年级奥数题)
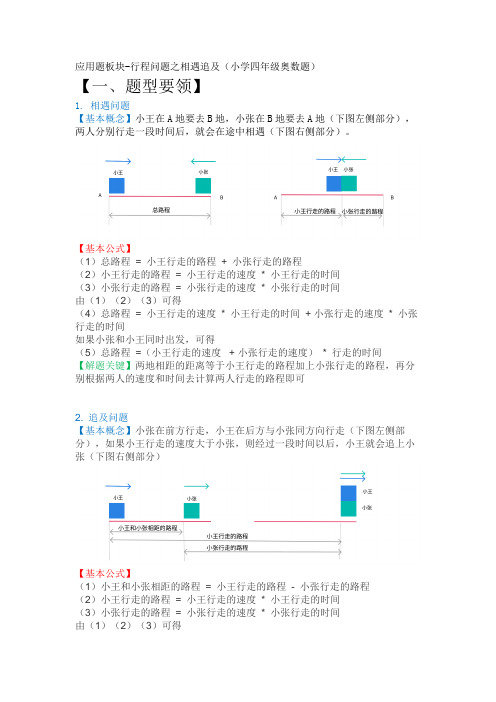
应用题板块-行程问题之相遇追及(小学四年级奥数题)【一、题型要领】1. 相遇问题【基本概念】小王在A地要去B地,小张在B地要去A地(下图左侧部分),两人分别行走一段时间后,就会在途中相遇(下图右侧部分)。
【基本公式】(1)总路程= 小王行走的路程+ 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)总路程= 小王行走的速度* 小王行走的时间+ 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)总路程=(小王行走的速度 + 小张行走的速度)* 行走的时间【解题关键】两地相距的距离等于小王行走的路程加上小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可2. 追及问题【基本概念】小张在前方行走,小王在后方与小张同方向行走(下图左侧部分),如果小王行走的速度大于小张,则经过一段时间以后,小王就会追上小张(下图右侧部分)【基本公式】(1)小王和小张相距的路程= 小王行走的路程- 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)小王和小张相距的路程 = 小王行走的速度* 小王行走的时间- 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)小王和小张相距的路程 =(小王行走的速度 - 小张行走的速度)* 行走的时间【解题关键】小王和小张相距的距离等于小王行走的路程减去小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可【举一反三】有一类题目是为赶时间,题目描述“为了节省XX时间从原本的速度x变成了之后的速度y”,解题时可以假象成另一个人以原速度提前走了XX 时间,而自身以修改后的速度从原地出发,最终两人同时到达终点,即可用“追及”问题解答【二、重点例题】例题1【题目】小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟,他们同时出发,几分钟后两人相遇?【分析】走同样长的距离,小张花费的时间是小王花费时间的36 ÷ 12 = 3(倍),因此自行车的速度是步行速度的3倍。
相遇追击问题综合题目分析_题型归纳

相遇追击问题综合题目分析_题型归纳一条街上,一个骑车人和一个步行人相向而行,骑车人的速度是步行人的3倍,每个隔10分钟有一辆公交车超过一个行人。
每个隔20分钟有一辆公交车超过一个骑车人,如果公交车从始发站每隔相同的时间发一辆车,那么间隔几分钟发一辆公交车?A 10B 8C 6D 4----------------------------------------------------------我们知道这个题目出现了2个情况,就是(1)汽车与骑自行车的人的追击问题,(2)汽车与行人的追击问题追击问题中的一个显著的公式就是路程差=速度差×时间我们知道这里的2个追击情况的路程差都是汽车的间隔发车距离。
是相等的。
因为我们要求的是关于时间所以可以将汽车的间隔距离看作单位1.那么根据追击公式(1) (V汽车-V步行)=1/10(2) (V汽车-3V步行)=1/20(1)×3-(2)=2V汽车=3/10-1/20 很快速的就能解得V汽车=1/8 答案显而易见是8再看一个例题:小明在商场的一楼要乘扶梯到二楼。
扶梯方向向上,小芳则从二楼到一楼。
已知小明的速度是小芳的2倍。
小明用了2分钟到达二楼,小芳用了8分钟到达一楼。
如果我们把一个箱子放在一楼的第一个阶梯上问多长时间可以到达二楼?跟上面一题一样。
这个题目也是2个行程问题的比较(1)小明跟扶梯之间是方向相同(1) (V小明+V扶梯)=1/2(2) 小芳跟扶梯的方向相反(2) (V小芳-V扶梯)=1/8(1)-2×(2)=3V扶梯=1/4 可见扶梯速度是1/12 答案就显而易见了。
总结:在多个行程问题模型存在的时候。
我们利用其速度差,速度和的关系将未知的变量抵消。
可以很轻松的一步求得结果!习题:1、电扶梯由下往上匀速行驶.男孩以每秒2个梯级的速度沿电扶梯往上走,40秒种可达电扶梯顶部.一女孩以每2秒3个梯级的速度往上走,50秒可以达到顶部.则静止时电扶梯的梯级数为A 80B 75C 100D 1202、2、某人沿电车线路行走,每12分钟有一辆电车从后面追上,每4分钟有一辆电车迎面而来.2个起点站的发车间隔相同,那么这个间隔是多少?。
部编版数学四年级春季第10讲.相遇与追及综合A

本讲内容1.环形跑道上的相遇与追及2.火车问题中的相遇与追及3.流水行船中的相遇与追及后续知识电梯与发车——五年级秋季第5讲(第9级下)方程法解行程——五年级秋季第14讲(第9级下)1.小明跑步的速度是5m/s,他绕400米的标准跑道跑一圈需要_________秒.2.一列长270米的火车以15m/s的速度完全经过路旁的一根电线杆需要_________秒.3.静水速度是15km/h的轮船在水速为3km/h的河里逆流而上5小时,走了________km.【分析】80;18;60.【分析】速度和:450÷6=75(米每分),艾迪用6+4=10(分)走了450米,速度为450÷10=45(米每分),薇儿的速度为:75-45=30(米每分),所以第一次相遇的地点距离A 点270米.铁路旁的人与火车问题1.人站在铁路旁不动从开始看到车头驶过到车尾离开的过程(火车与树或电线杆问题)这个过程把人看成是长度为零的桥,因此火车走过路程为一个车长.2.人在铁路旁和火车同向行走从开始看到车头驶过到车尾离开的过程这个过程实质是人和火车的追及问题,此时把人看成是可以运动长度为零的桥,追及的路程差为一个车长.3.人在铁路旁和火车相向行走从开始看到车头驶过到车尾离开的过程这个过程实质是人和火车的相遇问题,此时把人看成是可以运动长度为零的桥,相遇的路程和为一个车长.4.人坐在火车上从车窗看到外面火车车头到车尾离开的过程这个过程实质还是人和火车的相遇、追及问题.此时只是把人看成运动的速度为所坐火车的速度,长度为零的桥.一列从西向东行驶的火车车速为每秒16米,车身长300米.(1)7点整它追上了在铁路旁从西向东散步的艾迪,并于20秒后离开了他,请问艾迪步行的速度是多少?.(2)7点半,它与从东向西骑车上学的薇儿相遇,并于15秒后离开了她.请问薇儿骑车的速度是多少?【分析】(1)300÷20=15(米每秒)16-15=1(米每秒)(2)300÷15=20(米每秒)20-16=4(米每秒)艾迪和薇儿沿着铁轨旁的小路散步,迎面而来一列长98米的火车.若两人速度为1米/秒,火车从车头到车尾经过他们身边共用了7秒,求火车速度.【分析】他们与火车共同走了一个车身的长度,故速度和是98714÷=米/秒,所以火车的速度是14113-=米/秒火车问题由上可得:船速=(顺水速度+逆水速度)2÷;水速=(顺水速度-逆水速度)2÷.流水行船问题中的相遇与追及:两船在流水中的相遇与追及所需的时间与在静水中或是两车在陆地上的相遇和追及问题一样,与水速没有关系.流水行船问题有以下两个基本公式:⑴顺水速度=船速+水速,V V V =+顺船水;⑵逆水速度=船速-水速,V V V =-逆船水(其中V 船为船在静水中的速度,V 水为水流的速度).由上可得:船速=(顺水速度+逆水速度)2÷;水速=(顺水速度-逆水速度)2÷.流水行船问题中的相遇与追及:两船在流水中的相遇与追及所需的时间与在静水中或是两车在陆地上的相遇和追及问题一样,与水速没有关系.薇儿在河里逆流而上游泳的时候不小心丢了水壶,她向前又游了一会儿才发现,随后立即返回追寻,用了30分钟追回了水壶,从水壶丢掉到被发现过了多长时间?【分析】[(V +V -V 人水水)]×30=[(V -V 人水)+V 水]t30V 人=V 人tt =30(分)流水行船。
学而思四年级春季班相遇与追及综合知识总结

本讲将之前所接触过的环形跑道、火车过桥以及流水行船这几类行程问题与相遇追及结合起来。
一、环形跑道中的相遇追及在周长为600米的圆形场地的一条直径的两端,艾迪从A 点,薇儿从B 点同时骑车出发,相向而行,两人第二次恰于A 点相遇,求两人第一次相遇的地点。
【详解】两人先从AB 同时出发相向而行,第一次相遇在AB 之间某一点,第二次相遇则在A 点,我们跳出来看,相遇两次,两人所用时间是相同的,而艾迪共行了1圈,薇儿共行了0.5圈,由此可知道艾迪的速度是薇儿速度的2倍。
所以在第一次相遇时,艾迪所行路程是薇儿的2倍,即行了:600232200÷÷⨯=米,因而第一次相遇地点距离A 点200米。
二、火车过桥(其实主要是过人)中的相遇与追及小白沿着铁轨旁的小路散步,迎面而来一列长98米的火车,若小白速度为1米/秒,火车从车头到车尾经过他身边共用了7秒,求火车速度。
【详解】火车过人的相遇追及中,路程和、路程差均是车长,此处是一个相遇问题,那么路程和就是98米,又知道经过身边用7秒,那么我们马上可以求出速度和: 98714m s ÷= 从而求出火车的速度:14113m s -=练习2 练习1相遇与追及综合三、流水行船中的相遇与追迹在流水行船中,水速不会改变相遇与追及的时间,改变的是地点。
某河上下两港相距80千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行12千米,乙船逆水每小时行8千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?【详解】题目所说两船速度相等,顺逆水的速度均有,于是可以先求出船速:()128210km h +÷=,顺便可以求出水速:12102km h -=出发的同时掉下一物顺水而下,甲乙相遇用时,也就是该物漂流用时,因而可求出甲乙相遇用时:()801284h ÷+= 物体漂流距离:248km h ⨯= 甲相遇时共行:12448km h ⨯= 两者之差:48840km h -=练习3。
第五讲,相遇及追击

第五讲相遇与追及综合从去年四年级暑假班开始,我们学习了很多行程问题,从基本的相遇、追及问题,到专题性的环形跑道、火车过桥和流水行船。
今天,我们将对这些学过的行程问题做一个小的总结复习,从而起到温故而知新的效果。
一、本讲知识点概括1、直线性的基本相遇、追及问题相遇基本公式:总路程(速度甲速度乙)相遇时间追及基本公式:路程差(速度甲速读乙)追及时间2、环形跑道问题相向而行:每相遇一次,两人走得总路程是环形跑道一圈的周长同向而行:没追上一次,两人走得路程差是环形跑道一圈的周长3、火车过桥及错车问题a、完全过桥:火车所走的总路程=桥长+车长b、完全在桥上:火车所走的总路程=桥长-车长图a 图bc、人错车相遇:(车速人速)错车时间总路程(人看到车的车长)追及:(车速人速)错车时间路程差(人看到车的车长)d、车错车相遇:(快车速慢车速)错车时间总路程(两车车长和)追及:(快车速慢车速)错车时间路程差(两车车长和)4、流水行船问题a、流水中的4个速度:船速、水速、顺水速度、逆水速度(2推2.)顺水速度船速水速逆水速度船速水速船速(顺速逆速)水速(顺速逆速)注:顺速与逆速之间差2个水速。
b、流水行船中的相遇和追及问题(与水速无关)相遇问题:速度和甲顺乙逆甲水乙水甲乙追及问题:速度差甲顺乙顺甲水(乙水)甲乙二、例题讲解例1、分析:此题属于直线型的相遇问题,解题的关键在于对“客车在行驶中耽误1小时”的理解。
这句话实际的意思是:货车自己单独走了1小时。
即两车在同一时间里走的路程并不是530米,应该把货车自己单独走了1小时的路程减去。
则此题可解。
解答:530-1×50=480(米)480÷(50+70)=4(小时)客车行驶时间4×70=280(米)客车行驶路程(4+1)×50=250(米)货车行驶路程拓展练习:(1)一辆客车与一辆货车同时从甲、乙两个城市相对开出,客车每小时行46千米,火车每小时行48千米。
第十讲:相遇与追及综合

第十讲:相遇与追及综合1.公式及公式变形万年不变的基本行程公式:S(路程)=V(速度)×T(时间)相遇下的变形:路程和=速度和×相遇时间追及下的变形:路程差=速度差×追及时间2.单位的统一和判断“米/秒”可以写成“m/s”但不要写成“m/秒”利用公式可以判断单位的写法:v=s÷t;所以速度的单位就是米÷秒,即米/秒3.关键词每到行程问题,不论怎么出题,总会提到以下几个情况:同时,同地,同向,相向,背向这几个就是关键词了!是否同时同地,如果不是同时,相差几小时,谁先谁后?如果不是同地,相差多少千米,位置如何?这是每个行程问题的初始情形,基本条件,必须优先读出来。
同向,相向(背向)分别是判断追及和相遇的关键信息。
千万不要盲目的看到“几小时后两人相遇”就认定这是相遇问题!4.数形结合顾名思义:数字与图形相结合的思想,因此,行程问题,一定离不开画图。
而图的画法,将会在之后的多人行程中有更加明显的体现。
5.一题多解在最开始接触相遇和追及的时候,我们就会发现,一旦出现“问:几小时后,相距XX千米”这样的句子,答案总是会有两种可能。
这就一定要求同学们对题目考虑要足够严密;换言之,同学们一定要注意行程问题当中的多解情况。
那么,除了上面的多解情况,还会有哪些呢?例如:在环形跑道上不说明方向的相遇和追及问题。
6.方程思想方程,我们已经不再陌生,但是,仍然有些抗拒。
不过没关系,熟能生巧。
这个是我们必须攻克的难关。
为什么呢?因为到了高年级,我们逐渐发现,学会了方程,就相当于学会了应用题。
因为几乎所有的应用题,都可以通过列方程求解轻松攻克。
行程这个难题,也不例外。
所以,我们要从现在开始,尝试用方程的方法来解决一些看上去“很难”的行程问题。
1。
四年级奥数第4次课相遇追及问题综合类型

第4次课相遇追及问题综合类型相遇和追及问题的基本关系式:______________________________________________________________________________追及问题:快的追上慢的是用()来追.典型例题讲析例题1:甲乙两人在周长720米的环形跑道上沿着相同的方向同时从同一地点出发,甲每分钟走55米,乙每分钟走65米。
问:至少经过几分钟乙从甲身后追上甲?例题2.环湖一周共400米,甲、乙二人同时从同一地点同方向出发,甲过10分钟第一次从乙身后追上乙。
若二人同时从同一地点反向而行,只要2分钟二人就相遇。
求甲、乙的速度。
例题3.甲、乙、丙三人步行的速度分别是每分钟100米、90米、75米。
甲在公路上A处,乙、丙在公路上B处,三人同时出发,甲与乙、丙相向而行。
甲和乙相遇3分钟后,甲和丙又相遇了。
求A、B之间的距离。
例题4.同学们去秋游,排成一列队以每秒1米的速度行进,队伍长300米,王老师因事以每秒1.5米的速度从队伍的末尾追到排头,又立即从队伍的排头回到队尾,王老师又回到末尾时一共花了多少分钟?课堂练习:1.在300米长的环形跑道上,甲、乙二人同时同地同向跑步,甲每秒跑5米,乙每秒跑4.4米。
两人起跑后多长时间甲从乙身后追上乙?2.一个环形跑道长500米,父子二人同时从同地同方向出发,爸爸25分钟追上儿子,若两人同时同地反向而行。
两人5分钟相遇,求父子二人的速度?3.甲、乙、丙三人行走的速度分别是每分钟60米、80米、100米。
甲、乙二人在B地,丙在A地与甲、乙二人同时相向而行,丙和乙相遇后,又过2分钟和甲相遇。
求A、B两地的路程。
4.一支队伍长350米,以每秒2米的速度前进,一个人以每秒3米的速度从队尾赶到队头,然后再返回队尾,一共要用多少分钟?课后作业:1.兄弟两人在长900米的环形跑道上晨跑,两人同时从同地出发,哥哥每分钟150米,弟弟每分钟120米,两人起跑后多久哥哥从身后追上弟弟?2.在一个400米的环形跑道上兄弟两人同时从同一地点、同方向出发,哥哥10分钟后从弟弟的身后追上弟弟,如果两人同时从同一地点反向而行,只要4分钟两人就相遇,求兄弟两人的速度?3.父亲、母亲、小孩三人的步行速度分别为每分钟100米,90米,75米,父亲在公路的A处,母亲、小孩在公路的B处,三人同时出发相向而行、父亲母亲相遇了,3分钟后父亲与小孩相遇,求A、B两地的距离?4.一支队伍长450米,以每秒3米的速度前进,一个通讯员骑车以匀速从队尾赶到队头用了50秒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识总结
一、环形跑道中的相遇追及
例1、2方法:同向追及,背向相遇。
二、火车过桥中的相遇追及
例3方法:注意车长,同向追及,相向相遇
三、流水行船中的相遇追及
例4、5方法:流水行船中的速度和,速度差不受水迷影响,但具体每艘船的速度和相遇地点会受影响。
例题1
如图,周长为800米的环形跑道上,田田和阿普分别从相距200米的A、B两处同时沿相同方向出发。田田每分钟能跑200,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
练习5
某河上下游两港相距130千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为5千米/时和8千米/。平时它们相遇于距上游港60千米处。某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
课后自主练习(不强制要求)
练习1
甲、乙两人在圆形跑道上锻炼。他们分别从跑道某条直径的两端同时出发,相向而行。当乙走了100米时,他们第一次相遇。相遇后两人继续前进,在甲走完一周前60米处第二次相遇。求这条一起走圆形跑道的周长。
练习2
甲、乙、丙在湖边散步,三人同时从同一点出发,绕湖行走,甲速度是每小时5400米,乙速度是每小时400米,她们两人同方向行5分走,丙与她们反方向行走,半个小时后甲和丙相遇,再过5分钟,乙与丙相遇。那么绕湖一周的行程是多少?
练习3
一列客车长280米,一列货车长180米,两车分别以每秒17米和23米的速度相向行进,在双轨铁路上,两车从车头相遇到车尾相离共需要多少时间?
练习1
如图,周长为400米的环形跑道上田田和阿普分别从相距100米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
例题2
如图,田田和阿普分别从周长为1200米的圆形跑道上相距600米的A、B两处同时出发相向而行,6分钟后两人相遇。相遇后两人继续行进,分钟后田田恰好到达B处,问两人相遇的地点距离A点多少米?
练习4
快车长106米,慢车长74米,两车同向而行,快车追上慢车后,又经过1分钟才超过慢车;如果相向而行,车头相接后经过12秒两车完全离开。求两列火车的速度。
练习5
A,B两码头间河流长为90千米,甲、乙两船以相同速度分别从A,B码头同时起航。如果相向而行3小时相遇,而甲比乙多行了6千米,求水流动的速度。
练习2
如图,田田和阿普分别从周长600米的圆形跑道上相距300米的A、B两处同时出发相向行,6分钟后两人相遇。相遇后两人继续行进,4分钟后田田恰好到达B处,求两人相遇的地点距离A点多少米?
例题3
一列从西向东行驶的火车车速为每秒16米车身长255米,8点整它追上了在铁路旁从西向东散步的田田,并于17秒后离开了他,又过了分钟,它与从东向西散步的阿普相遇,15秒后开了他。请问田田和阿普步行的速度分别是多少?
练习4
某河上下游两港相距60千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船
顺水每小时行11千米当甲乙两船相遇时,此物距相遇地点有多远?
例题5
某河上下游两港相距150千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为6千米/时和9千米/时。平时它们相遇于距上游港70千米处,某日突下是雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
练习6
某人畅游长江,逆流而上,在A处丢失一只水壶,他向前又游了20分钟后,才发现丢失了水壶,立即返回追寻,在离A处10千米的地方追到,则他返回寻水壶用了多少分钟?
这出一加人
练习3
一列从西向东行驶的火车车速为每秒19米,车身长360米。9点整它追上了在铁路旁从西向东散步的田田,并于20秒后离开了她。又过了5分钟,它与从东向西散步的阿普相遇,18秒后离开了他。请问田田和阿普步行的速度分别是多少?
例题4
某河上下游两港相距100千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船水每小时行12千米,乙船逆水每小时行8千米,这天甲船在出发时,从船上掉下一物,此物水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
