矩阵与数值分析 误差分析
矩阵与数值分析学习指导和典型例题分析

第一章 误差分析与向量与矩阵的范数一、内容提要本章要求掌握 绝对误差、相对误差、有效数字、误差限 的定义及其相互关系;掌握 数 值稳定性 的概念、设计函数计算时的一些基本原则和误差分析 ;熟练掌握向量和矩阵范数 的 定义及其性质。
1 .误差的基本概念和有效数字 1) .绝对误差和相对误差 的基本概念设实数x 为某个精确值,a 为它的一个近似值,则 称x a 为近似值a 的绝对误差,简称x a为误差.当x 0时,=称为a 的相对误差.在实际运算中,精确值 x 往往是未知的,所x a以常把—匚作为a 的相对误差.2) .绝对误差界和相对误差界 的基本概念设实数x 为某个精确值,a 为它的一个近似值,如果有常数 e a ,使得此例计算中不难发现,绝对误差界和相对误差界并不是唯一的, 但是它们越小,说明a近似x 的程度越好,即a 的精度越好.3) .有效数字设实数x 为某个精确值,a 为它的一个近似值,写成ka 10 O.a i a 2 a n其中a i (i 1,2,)是0,1, ,9中的一个数字,q 0,k 为整数.如果x a - 10kn2则称a为x的具有n位有效数字的近似值.4) .函数计算的误差估计 如果yf(x 1,x 2, ,x n )为n 元函数,自变量*,X 2, ,X n 的近似值分别为a 1,a 2, ,a n ,称e a为a的绝对误差界或简称为误差界.称a是a的相对误差界它可以是有限或无限小数的形式, 如果a 有n 位有效数字,则a 的相对误差界满足:x a l a l1 2a 1101其中 丄_f(a 1,a 2, ,a n ),所以可以估计到函数值的误差界,近似地有Xk aXknf(X i ,X 2, ,X n ) f(a i ,a 2, ,a n ) e a取y f(x,x 2)为X i , X 2之间的四则运算,则它们的误差估计为,数相加或减时,其运算结果的精度不会比原始数据的任何一个精度高.如果x i 和X 2是两个十分接近的数,即 a i 和a 2两个数十分接近,上式表明计算的相对误差会很大,导致计算值 a i a 2的有效数字的位数将会很少。
第一章矩阵与数值分析

21!(约9.7×1020次)
使用每秒一亿次的串行计算机计算,完成运算耗时约30万年!
Cramer算法是“实际计算不了”的。为此,人们研究出著 名的Gauss消去法,它的计算过程已作根本改进,使得上述 例子的乘、除运算仅为3060次,这在任何一台电子计算机上 都能很快完成。
这是由于
x a x a x a2
a
x
ax
a
(x a)2
a x
a
x
a
a
2
1
1 xa
x
a
2
a
a
是 x 的a平方项级,故可忽略不计。
a
相对误差也可正可负,其绝对值的上界叫做相对误差界
(限)。 当绝对误差界为 e时a ,相对误差界取为
ea
相对误差界(限)
a
例1 已知 e 2.71828182 ,其近似值 a 2.718,求 a
1.2.1 误差来源与分类
用计算机解决科学计算问题时经常采用的处理方式是将连 续的问题离散化、用有限代替无限等,并且用数值分析所处理 的一些数据,不论是原始数据,还是最终结果,绝大多数都是 近似的,因此在此过程中,误差无处不在.误差主要来源于以 下四个方面:
实际问题
模型误差
计
算 机 科 学 计Βιβλιοθήκη 数学模型主要内容包括:
数值代数
Ax b
f x 0
数值逼近 微分方程数值解法
f x f x
b
a
x
f
x
dx
u f t, u, ut0 u0
具体任务: 一、构造在计算机上可行的有效算法。 二、给出可靠的理论分析:进行误差分析,讨论数值算法的 收敛性和数值稳定性。
数值分析1-误差及有效数字

(避免绝对值很大的数为乘数)
x1 1 x1 e e x ex 2 (避免 x2 为很小的数为除数) 1 2 x x x2 2 2
er x1 x2 x1 x2 er x1 er x 2 x1 x2 x1 x2
er x1 x2
这里,主要介绍计算机中浮点数的表示形式及 表示范围(4个参数):
x s p
其中, s =±0.a1a2a3………at 称为尾数∈[-1,1],
s 中的正负号用一位数字区分;
β为基数,如取2、10、8、16; p为阶数,有上限U和下限L, 由计算机存储字节长度决定。
1.4 误差危害的防止 (1)使用数值稳定的计算公式
数值稳定是指计算过程中舍入误差对计算影响不大的算法, 若第n+1步的误差en+1 与第n步的误差en满足
en 1 1 en
,则称该计算公式是绝对稳定的
例:建立积分In=
1
0
xn dx x5
(n=0,1.........,20)
递推关系式,并分析误差传播影响。
解: I +5I
n
n-1=
x 5x 0 x 5 dx
1 n n -1
1
0
x n-1dx
x n
n
1
0
1 n
I 0=
1 0 x 5dx
1
ln x 5
1 0
=ln6-ln5
1 In -5In -1 n ∴递推式: I 0 ln6 - ln5
2
x1 x 2
2
e x1 e x 2
数值分析误差限的计算公式

数值分析误差限的计算公式1、误差x∗为 x 一个近似值绝对误差:e∗=x∗−x相对误差:e∗r=e∗x=x∗−xx,由于真值 x 总是不知道的,通常取e∗r=e∗x∗=x∗−xx∗误差限:|x∗−x|≤ε∗相对误差限:ε∗r=ε∗|x∗|ε(f(x∗))≈|f′(x∗)|ε(x∗)2、插值法记ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)Lagrange 插值多项式系数:lk(xk)=(x−x0)⋯(x−xk−1)(x−xk+1)⋯(x−xn)(xk−x0)⋯(xk−xk−1)(x −xk+1)⋯(x−xn)Lagrange 插值多项式:Ln(x)=∑k=0nlk(x)yk=∑k=0nykωn+1(x)ω′n+1(xk)(x−xk) 余项:记 Mn+1=maxa≤x≤b|fn+1(x)|R(x)=fn+1(ξ)ωn+1(x)(n+1)!≤Mn+1(n+1)!|ωn+1(x)|均差与 NewTon 插值多项式一阶均差:f[x0,xk]=f(xk)−f(x0)xk−x0k 阶均差:f[x0,x1,⋯,xk]=f[x0,⋯,xk−2,xk]−f[x0,⋯,xk−2,xk−1]xk−xk−1f[x0,x1,⋯,xn]=f(n)(ξ)n!(x0,x1,⋯,xn,ξ∈[a,b])f[x0,x1,⋯,xk]=∑j=0kf(xj)ω′k+1(xj)NewTon 插值多项式:Pn(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn−1)余项:R(x)=f[x0,x1,⋯,xn]ωn+1(x)Hermite 插值Taylor 多项式:Pn(x)=f(x0)+f′(x0)(x−x0)+⋯+f(n)(x0)n!(x−x0)n余项:R(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1若已知 f(x0),f′(x1),f(x1),f(x2):P(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+A(x−x0)(x−x1)(x−x2)其中 A 由 P′(x1)=f′(x1) 可得余项:R(x)=14!f(4)(ξ)(x−x0)(x−x1)2(x−x2)两点三次 Hermite 插值多项式:H3(x)=αk(x)yk+αk+1(x)yk+1+βk(x)mk+βk+1(x)mk+1其中 mk=f′(xk),mk+1=f′(xk+1)⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧αk(x)=(1+2x−xkxk+1−xk)(x−xk+1xk−xk+1)2αk+1(x)=(1+2x−xk+1xk−xk+1)(x−xkxk+1−xk)2⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧βk(x)=(x−xk)(x−xk+1xk−xk+1)2βk+1(x)=(x−xk+1)(x−xkxk+1−xk)2余项:R(x)=f(4)(ξ)4!(x−xk)2(x−xk+1)2分段低次插值h=b−an对每个小区间使用对应插值公式求 Ih(x)余项对分段线性插值函数:maxa≤x≤b|f(x)−Ih(x)|≤M28h2对分段三次埃尔米特插值:maxa≤x≤b|f(x)−Ih(x)|≤M4384h43、数值积分代数精度定义:如果某个求积公式对于次数不超过 m 的多项式均能够准确成立,但对于 m+1 次多项式就不准确成立,则称该公式具有 m 次代数精度梯形公式公式与中矩形公式梯形公式:∫baf(x)dx≈b−a2f(a)+b−a2f(b)余项:R[f]=−(b−a)312f′′(η)(η∈(a,b))矩形公式:∫baf(x)dx≈(b−a)f(a+b2)余项:R[f]=(b−a)324f′′(η)(η∈(a,b))Newton-Cotes 公式将积分区间 [a,b] 分成 n 等分Simpson 公式(n=2):∫baf(x)dx≈b−a6f(a)+b−a6f(b)+2(b−a)3f(a+b2)余项:R[f]=−(b−a)5180∗24f(4)(η)(η∈(a,b))Cotes 公式(n=4):C=b−a90[7f(x0)+32f(x1)+12f(x2)+32f(x3)+7f(x4)]余项:R[f]=−2(b−a)7945∗46f(6)(η)(η∈(a,b))复合求积公式积分区间 [a,b] 分成 n 等分,步长 h=b−an复合梯形公式:Tn=h2[f(a)+2∑k=0n−1f(xk)+f(b)]余项:Rn(f)=−b−a12h2f′′(η)复合 Simpson 求积公式:Sn=h6[f(a)+2∑k=0n−1f(xk)+4∑k=1n−2f(x(k+1)/2)+f(b)] 其中 x(k+1)/2=xk+h2Rn(f)=−b−a180(h2)4f(4)(η)龙贝格求积算法T(0)0=h2[f(a)+f(b)]求梯形值 T0(b−a2k),利用递推公式求 T(k)0,递推公式:T2n=12Tn+h2∑k=0n−1f(xk+12)求加速值:T(k)m=4m4m−1Tk+1m−1−14m−1T(k)m−1k=1,2,⋯高斯-勒让德求积公式积分区间为 [−1,1]∫1−1f(x)dx≈∑k=0nAkf(xk)余项:n=1 时,R1[f]=1135f(4)(η)4、解线性方程组的直接方法列主元高斯消去法在每次消元时,选取列主元在最前面,列主元为该列最大值矩阵三角分解法如果 n 阶矩阵 A 的各阶顺序主子式 Dk(k=1,2,⋯,n−1) 均不为零,则必有单位下三角矩阵 L 和上三角矩阵 U,使得 A=LU,并且 L 和 U 是唯一的。
矩阵与数值分析部分习题解答

其具有6位有效数字。 故
*
而
y y* zz , 于是, y
*
1 4 1 1 k n 26 10 y y 10 10 2 2 2
y y* y z
* *
z z* z
*
0.5 104 0.5 106 59.9833 4.09407
可见,用公式 f ( x) ln x
k
k 2 k A A ( I A ) 5.证明ρ(A)<1时,
1 注意,绝对收敛的函数幂级数 f t t 1 t , t 1,则 证明(1): k 0 1 t k 1 k s t f t t f t kt kt 令 2 1 t 1 t 2 k 1 k 0
3 。 节点为: x1 h , x2 2h , x3 3h 4 8 8
相应的方程组为:
2 1 h 2 0 1 h 2 0 u1 h u2 1 2 2 u 3
2 先令 y x x 1 ,由于开方用六位函数表,则 y 的误差为已
知, 故应看成 z g ( y) ln( y) , 由 y的误差限
* ln( y ) ln( y )。 误差限
y y * 求g(y)的
解:当x=30时,求 y 30 302 1 , 用六位开方表得
xi a ih,
h 称为步长。
i 0,1,
,N, h
ba N
于是我们得区间 I=[a, b]的一个网格剖分。 xi称为网格节点,
h
a x0 x1
数值分析(01) 数值计算与误差分析

克莱姆算法步骤
1. 2.
D for 2.1. 2.2.
( j1 jn )
t ( 1 ) a1 j1 a 2 j2 a nj n
i 1 n Di
( i1 i n ) t ( 1 ) a i1 1 bi2 j a in n
Di xi D
N=[(n2-1)n!+n]flop
每周有课外练习,两周交一次作业, 一学期完成 3 个综合程序课题设计。 考试评分: 平时作业+程序占总成绩的30%,
期末考试占总成绩的70%,开卷考试。
Matlab_zm@ 密码 123456
数值分析
数值分析
第二节 数值问题与数值算法
求数学问题的数值解称为数值问题.
数值方法:适合在计算机上,按确定顺序依次进行计算 的计算公式,也就是通常所说的数值计算方法。 数值算法:从给定的已知量出发,经过有限次四则运算
有递推公式
注意
计算量 N n flop
Pn ( x) x( x( x( x(an x an1 ) an2 ) a1 ) a0
数值分析
sn an sk xsk 1 ak P n ( x) s0
k n 1,,2,1,0
数值分析
例3 矩阵乘积AB的计算量分析
第一节 数值分析的研究对象和特点
我们把在电子计算机上进行的科学工作称为科学计算。 科学研究的方法: 科学理论,科学实验,科学计算 科学计算的核心内容是以现代化的计算机及数学软件 为工具,以数学模型为基础进行模拟研究。
数值分析
数值分析
第一节 数值分析的研究对象和特点
科学计算的步骤:实际问题→数学模型→数值方法 →程序设计→上机计算→分析结果。 1、建立数学模型(实际问题数学化) 2、设计计算方案(数学问题数值化)
数值分析讲义

第1章数值分析中的误差一、重点内容误差设精确值x* 的近似值x,差e=x-x* 称为近似值x 的误差(绝对误差)。
误差限近似值x 的误差限 是误差e 的一个上界,即|e|=|x-x*|≤ε。
相对误差e r是误差e 与精确值x* 的比值,。
常用计算。
相对误差限是相对误差的最大限度,,常用计算相对误差限。
绝对误差的运算:ε(x1±x2)=ε(x1)+ε(x2)ε(x1x2)≈|x1|ε(x2)+|x2|ε(x1)有效数字如果近似值x 的误差限ε 是它某一个数位的半个单位,我们就说x 准确到该位。
从这一位起到前面第一个非0 数字为止的所有数字称为x 的有效数字。
关于有效数字:(1) 设精确值x* 的近似值x,x=±0.a1a2…a n×10ma1,a2,…,a n是0~9 之中的自然数,且a1≠0,|x-x*|≤ε=0.5×10m-l,1≤l≤n则x 有l位有效数字.(2) 设近似值x=±0.a1a2…a n×10m有n 位有效数字,则其相对误差限(3) 设近似值x=±0.a1a2…a n×10m的相对误差限不大于则它至少有n 位有效数字。
(4) 要求精确到10-3,取该数的近似值应保留4 位小数。
一个近似值的相对误差是与准确数字有关系的,准确数字是从一个数的第一位有效数字一直数到它的绝对误差的第一位有效数字的前一位,例如具有绝对误差e=0.0926 的数x=20.7426 只有三位准确数字2,0,7。
一般粗略地说,具有一位准确数字,相对于其相对误差为10% 的量级;有二位准确数字,相对于其相对误差为1% 的量级;有三位准确数字,相对于其相对误差为0.1% 的量级。
二、实例例1 设x*= =3.1415926…近似值x=3.14=0.314×101,即m=1,它的误差是0.001526…,有|x-x*|=0.001526…≤0.5×101-3即l=3,故x=3.14 有 3 位有效数字。
矩阵与数值分析

矩阵与数值分析学院电子信息与电气工程学部专业生物医学工程班级学号姓名刘江涛1:考虑计算给定向量的范数;输入向量T n x x x x ),,,(21 =,输出∞x x x ,,21,请编制一个通用程序,并用你编制的程序计算如下向量的范数:()TTn y n x ,,2,1,1,,31,21,1 =⎪⎭⎫ ⎝⎛=对1000,100,10=n 甚至更大的n 计算其范数,你会发现什么结果?你能否修改你的程序使得计算结果相对精确呢?通用求范数程序: function NORM(x) y1=sum(abs(x)); y2=(sum(x.^2))^(1/2); y3=max(abs(x));fprintf('1-范数=%g ; 2-范数= %g ; inf-范数=%g\n',y1,y2,y3); 例题的运行程序: function xianglaing(n) x=[]; y=[]; for i=1:n x(i)=1/i; y(i)=i; enddisp('x 的范数:'); NORM(x'); disp(' ')disp('y 的范数:'); NORM(y'); 运行结果如下表:根据上述的两个表的运行结果,我们可以得知无论n 的值如何变化,对于1=∞x 恒成立;n y =∞恒成立,其1-范数与2-范数随着n 的增大而增大,但是其变化越来越小,这是因为计算在进行数值计算时有误差存在,对于表达式(1)当n 很大时n1却很小,会出现“大数吃小数的现象”;修改方案:当n 很大时我们避免用n 做除数,因为当n 非常大时01→n成立;所以在求解其范数时我们从小数开始相加,无穷个非常小的数值相加也可能是个很大的数,从而可以避免两个数相加时出现“大数吃小数”的现象;2:考虑xx x f y )1ln()(+==,其中定义1)0(=f ,此时)(x f 是连续函数,用此公式计算当]10,10[1515---∈x 时的函数值,画出图像。
矩阵与数值分析公式总结

矩阵与数值分析公式总结绝对误差:a = ±1(/><0.%2 •…"“ |x-«| <^xl(/_/l ,则称a 为x 的具有n 位有效数字的近似值相对误差: 如果a 有n 位有效数字,则升詁旷;如果喘也諾护旷,则a 至 少有n 位有效数字。
近似绝对误差估计式:|/(x)- f(a)\«|/ («)||x-a\ 近似相对误差界为:喘叽關向量范数:1范数侶广刼r-12 范数:||x||2 =乞卜『=A /?7? = yl(x.x) \ f-1 °°范数:Mo =酸闻(“ \/PP 范数制卩=丈吋,l<p<+oO\ r-1/谱半径:Q (A) = max|^-|(A 的最大特征值)第二章正规矩阵:A HA = AA H,A H^A 的共轨转置。
常见的Hermite 阵(A 〃=A )、实对称矩 阵(”=A )、斜Hermite 阵(A 〃=-A )、实反对称矩阵("=「4)、酉阵 (AnA = AA H=I )和正交矩阵(/^人二必丁二/)等均为正规矩阵.正定的充分必要条件是:A 的各阶顺序主子式都为正。
A 的特征值全为正。
正交矩阵:A rA = AA r=E A~l=A r正交矩阵是实数特殊化的酉矩阵,因此总是正规 矩阵。
奇异矩阵:对应的行列式等于0的方阵。
第一章算子范数:mHili = 1^Zl rt ul (列和范数)IK = --f|^l<行和范数)■ J-1(谱范数) in nHL=E Z KI/-1 >1N 元函数误差界:1、矩阵的LU分解或Doolittle分解对于〃阶方阵A,如果存在/?阶单位下三角矩阵乙和刀阶上三角矩阵〃,使得A = LU f 则称其为矩阵A的LU分解,也称为.Gauss消去法对应的矩阵形式即为分解, 其中厶为所有行乘子组成的单位下三角矩阵,〃为Gauss消去法结束后得到的上三Ly = b<角矩阵.原方程组分解为两个三角形方程组=儿2、矩阵分解的的存在和唯一性(各阶顺丿子主子式均不为零)如果〃阶矩阵A的各阶顺序主子式卩伙= 1,2,…均不为零,则必有单位下三角矩阵£和上三角矩阵〃,使得A = LU f而且乙和卩是唯一存在的.3、矩阵的Cholesky分解或平方根法(正定矩阵)对任意"阶对称正定矩阵均存在下三角矩阵L使A = LlI f称其为对称正定矩阵A 的Cholesky分解.进一步地,如果规定工的对角元为正数,则厶是唯一确定的.原方程组= b分解为两个三角形方程组 ^' = b .L x = y利用矩阵乘法规则和厶的下三角结构可得计算次序为厶山,…人「22,4…人2,…心•由于|々|S“7, Q'、2,…、j.因此在分解 过程中I 的元素的数量级不会增长,故平方根法通常是数值稳定的,不必选主元.4、设A 为非奇异矩阵,INI 为矩阵的算子范数,称cond(A) = ||A||||A-|||为矩阵A 的条件数°条件数越大,矩阵和方程组越为病态,反之越小为良态。
讨论数值分析第五版中的误差分析方法。

讨论数值分析第五版中的误差分析方法。
原题目:讨论数值分析第五版中的误差分析方法
数值分析是解决实际问题中的数学方法,但由于测量仪器的不确定性、四舍五入误差、截断误差等因素造成了误差。
本文将讨论数值分析第五版中的误差分析方法。
误差主要分为绝对误差和相对误差。
- 绝对误差表示为 $E_a = |x - x_0|$
- 相对误差表示为 $E_r = |x - x_0|/|x_0|$
而数值分析中的误差主要分为舍入误差和截断误差:
- 舍入误差:计算时需要将无限小数缩小,所得的有限小数即为舍入误差。
- 截断误差:数值分析方法需要将所选的计算公式在某些地方进行近似,所得结果与精确解之差即为截断误差。
在实际数值分析中,误差的控制非常重要,因为误差可能会对
最终的计算结果产生很大影响。
数值分析中有很多减小误差的方法,比如增加小数位数、选择合适的计算公式和算法等等。
在实际应用中,要注意以下事项:
- 尽量避免使用不同原理的仪器测量或者使用测量范围不同的
仪器测量。
- 合理判断和控制误差对计算结果的影响。
- 遵循科学测量的要求,确保测量结果真实可靠,如果实验数
据存在异常,应根据科学理论和实验规律分析异常产生的原因,选
择合适的方法处理。
因此,在数值分析中,通过合理分析误差因素的影响,在实验
设计、计算方法选择等方面坚持精益求精,不断提高数值分析水平,是获取精确结果的重要途径。
数值分析知识点总结

数值分析知识点总结数值分析是一门研究数值计算方法的学科,它旨在研究如何使用计算机算法来解决数学问题。
数值分析广泛应用于科学与工程领域,如物理学、化学、计算机科学、经济学等,有助于我们在计算机上进行精确、高效、可靠的数值计算。
以下是数值分析的一些重要知识点。
1.数值误差:数值计算中存在着各种误差,包括舍入误差、截断误差、传播误差等。
舍入误差是由于计算机对无限小数进行近似表示而产生的误差,截断误差是由于计算方法不完全而导致的误差,传播误差是由于误差在计算过程中的传播而产生的误差。
2.插值与外推:插值是一类问题,它的目标是通过已知数据点的近似值来估计未知点的值。
插值方法包括拉格朗日插值、牛顿插值等。
外推是在已知数据点外估计函数值的方法,例如外推法、Richardson外推法等。
3.数值积分与微分:数值积分是计算函数在给定区间上的定积分的近似值的方法。
常见的数值积分方法有梯形法则、辛普森法则、龙贝格法则等。
数值微分是通过计算函数在给定点的导数的近似值来估计函数的变化率。
4.线性方程组的求解:线性方程组是数值计算中的重要问题之一,其解决方法包括直接法和迭代法。
直接法是通过代数运算求解线性方程组的精确解,如高斯消元法、LU分解法等。
迭代法是通过迭代计算逼近线性方程组的解,如雅可比迭代法、高斯-赛德尔迭代法等。
5.非线性方程的求解:非线性方程求解是指求解形式为f(x)=0的方程的根。
常用的非线性方程求解方法有二分法、牛顿法、割线法等。
6.常微分方程的数值解法:常微分方程的数值解法是指通过计算机算法来近似求解微分方程的解。
常用的数值解法包括欧拉法、改进的欧拉法、龙格-库塔法等。
7.特征值与特征向量的计算:特征值和特征向量是矩阵与线性变换中的重要概念。
求解特征值和特征向量可以帮助我们理解矩阵或线性变换的性质。
常用的特征值计算方法有幂法、反幂法等。
8.曲线拟合与回归分析:曲线拟合是通过给定的散点数据来拟合出一个函数曲线的方法。
数值分析中的微积分与矩阵分析

数值分析中的微积分与矩阵分析数值分析是数学中的一门重要学科,主要研究数值计算的方法和技术。
微积分和矩阵分析是数值分析的两个基础,它们在数值计算中扮演着重要的角色。
一、微积分微积分是数学中的一个分支,是研究变化量以及变化率的学科。
微积分的两个基本概念是导数和积分。
在数值计算中,微积分常常用于求函数的导数和积分。
在微积分中,求导数和积分是两个相对应的过程。
求导数的过程可以理解为对于一个函数f(x)求x的一个微小变化量dx,函数值的变化量df可表示为:df=f'(x)dx其中f'(x)是f(x)的导数。
求导数的过程在数值计算中的应用很广泛,比如在求解微分方程问题时,需要用到函数的导数。
另一方面,积分的过程可以理解为将一个曲线下的面积分成无数个微小的矩形,然后将各个小矩形的面积加起来,就可以得到整个曲线下的面积。
在数值计算中,积分常用于求解一些重要的物理和工程问题。
二、矩阵分析矩阵分析是数学中的一个分支,是研究矩阵性质和性质变换的学科。
在数值计算中,矩阵分析的应用也非常广泛,比如在线性代数中,矩阵乘法是基本的运算之一。
矩阵乘法是指将一个m行n列的矩阵A乘以一个n行k列的矩阵B,得到一个m行k列的矩阵C。
在实际应用中,矩阵乘法广泛应用于矩阵计算、工程计算和物理计算等领域。
除了矩阵乘法之外,矩阵分析还包括矩阵的特征值和特征向量、矩阵的逆和行列式、线性方程组和向量空间等概念。
三、微积分与矩阵分析在数值计算中的应用微积分和矩阵分析在数值计算中的应用非常广泛。
在数值计算中,微积分和矩阵分析往往被用来解决很多实际问题。
比如在求解微分方程问题时,需要用到函数的导数。
此时,可以通过微积分中的求导数方法求出函数导数,并用微分方程的数值方法来计算函数在各个点上的值。
另一方面,矩阵分析在工程计算中有着广泛应用。
比如在控制系统设计中,需要用到矩阵分析来计算系统的反馈和稳定性。
此时,可以通过矩阵分析中的特征值和特征向量来计算系统的特征和稳定性。
误差知识与算法知识

9 x 10 , x2 1. 精确解为 1
b b 2 4ac 算法1:利用求根公式 x 2a 在计算机内,109存为0.11010,1存为0.1101。做加法时, 两加数的指数先向大指数对齐,再将浮点部分相加。即1 的指数部分须变为1010,则:1 = 0.0000000001 1010,取 单精度时就成为: 109+1=0.100000001010+0.00000000 1010=0.10000000 1010
f ( n 1) ( ) n1 Rn ( x ) f ( x ) Pn ( x ) x 在 ( n 1)!
x
与0之间。
机器字长有限
—— 舍入误差 /* Roundoff Error */ 用计算机、计算器和笔算,都只能用有限位小数来 代替无穷小数或用位数较少的小数来代替位数较多的 有限小数,如:
注意此公式精确成立
( n 1, 2, , 8)
按公式就可以逐步算出
I1 1 5 I 0 0.09
I2 1 5 I1 0.05 2
What happened ?!
1 I 3 5 I 2 0.083 不稳定的算法 ! 3 1 I 4 5 I 3 0.165 4 1 I 5 5 I 4 1.025 这就是误差传播所引起的危害 ! 5 1 I 6 5 I 5 4.952 6
x1 , x2 ,, xn 的近似值为 a1 , a2 ,, an ,则 u 的近似值为
A f a1 , a2 , , an
于是函数值 u 的误差 e( A) 由Taylor展开,
得:
e( A) u A f x1 , x2 , , xn f a1 , a2 , , an
大连理工大学数值分析历年真题与答案(研究生期末卷)
;
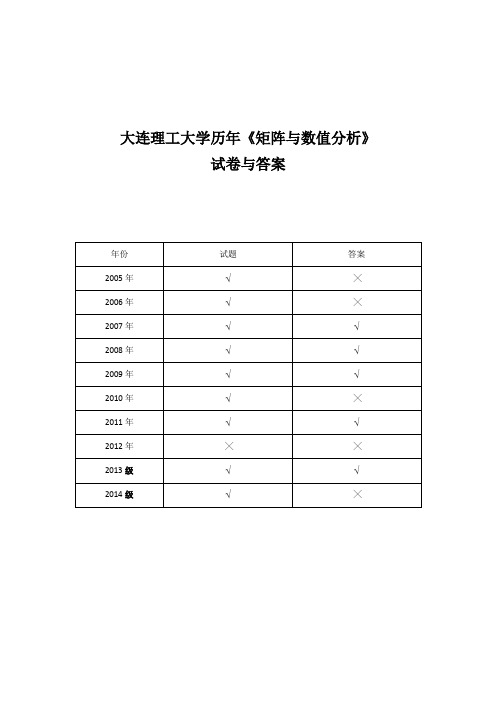
7.设 A 是 n 阶正规矩阵,则 A 2
;
8.求解一阶常微分方程初值问题 u(t ) (t 2 1)u t , u(t0 ) u0 的向后(隐式) Euler 法的显式化的格式为: 9.设 a 211.001 12 为 x 的近似值,且 x a 0.5 10 2 ,则 a 至少有 。
A-5
1 3 四、 (4 分)求 Householder 变换矩阵将向量 x 2 化为向量 y 0 . 2 0
五、 (12 分)写出解线性方程组的 Jacobi 法,G-S 法和超松弛(SOR)法的矩阵表示形式, 并根据迭代法 x ( k 1) Bx ( k ) f 对任意 x ( 0) 和 f 均收敛的充要条件为 ( B) 1 , 证明若线性方 程组 Ax b 中的 A 为严格对角占优矩阵, 则超松弛(SOR)法当松弛因子 (0,1] 时收敛.
x1 3 x2 3 x1 x2 2 x x 2 1 4 4 4 x3 7
A 1, L , U
m1
(1)列主元消元法求出上述方程组的解,并计算
和 x 2;
(2)试问用 Jacobi 迭代法和 Gauss-Seidel 迭代法求解上述方程组是否收敛? ( 3) 请给出可求出上述方程组解的收敛的 Jacobi、 Gauss-Seidel 迭代法的分量形式的迭 代公式,并说明其收敛性。
五、 (12 分)求满足下列插值条件的分段三次多项式( [3,0] 和 [0,1] ), 并验证它是不是三次样条函数.
f (3) 27 , f (2) 8 , f (1) 1 , f (0) 0 , x [3,0] ; f (0) 0 , f (0) 0 , f (1) 0 , f (1) 1 , x [0,1] .
第一章数值分析(误差分析)

* e x x * e r * * x x x x* er 则称η 为 x* 的相对误差限。 x
如果
这时 x=10,
x*=10±1;
2019/3/13
第一章 绪论与误差分析
2
本章内容安排
1. 目的意义:了解计算数学的背景知识;掌握误 差的基本知识 2.重 点:误差来源、误差表示、误差传播 及算法设计原则 3.难 点:有效数字 4.内容分配: 第 1 次:§1 计算数学研究的对象和内容 第
§2 误差的来源和分类 2 次:§3 误差的表示 §4 误差的传播 §5 算法设计的若干原则
由于计算机的字长有限,参加运算的数据以及计算结 果在计算机上存放时,计算机会按舍入原则舍去每个数据 字长之外的数字,从而产生误差,这种误差称为舍入误差 或计算误差。 例如,在十进制十位的限制下,会出现 (1.000002)2-1.000004=0
这个结果是不准确的,准确的结果应是 (1.000002)2-1.000004 =1.000004000004-1.000004=4×10-12 这里所产生的误差就是计算舍入误差。 在数值分析中,一般总假定数学模型是准确的,因而 不考虑模型误差和观测误差,主要研究截断误差和舍入误 差对计算结果的影响。
则有误差限 |x-x*|≤1= εx ,
虽然εy是εx 的3倍,但在1000内差3显然比10内差1更精确 些。这说明一个近似值的精确程度除了与绝对误差有关 外,还与精确值的大小有关,所以这时可以用相对误差 来比较这两个近似数的准确度。
2019/3/13 19
第一章 绪论与误差分析
e x x 定义1 .2 记 er x x 则称其为近似值 x *的相对误差。 由于 x 未知, 实际使用时总是将 x * 的相对误差取为
矩阵与数值分析-教学大纲
《矩阵与数值分析》教学大纲
开课院系:数学科学学院课程编号:2120020013
英文名称:Matrix and Numerical Analysis开课学期:秋
任课教师:张宏伟金光日李崇君董波孟兆良
教学对象:硕士适合专业:工科各专业
课程作用与任务:《矩阵与数值分析》课程是为工科硕士研究生开设的公共基础课程。
课程主要讲授当前科学与工程计算中所涉及的微积分、常微分方程、代数和矩阵计算等内容中数值问题的算法、理论分析等内容。
通过本课程的教学,应使学生掌握计算机现代数值方法的基本概念、基本理论与基本方法,为今后的学习、工作打下坚实基础。
教学主要内容及对学生的要求:
1、学习内容:主要涉及当前科学与工程计算中所涉及的微积分、常微分方程、代数和矩阵计算等内容中数值问题的算法及相关理论。
2、实验内容:对课程中所涉及的计算方法进行数值实验(不占教学课时)。
3、先修知识:线性代数,微积分。
考核方式:考试、闭卷
教材名称:计算机科学计算(第二版),张宏伟,金光日,施吉林高等教育出版社,2012.主要参考书目:主要参考书目:科学和工程计算基础,施妙根等编,清华大学出版社,1999
矩阵论简明教程,徐仲等,科学出版社,2001.
教学日历:
编制人签字:张宏伟(课程负责人)、金光日一级学科点长签字:主管研究生负责人签字:编制时间:2012-5-31。
数值分析知识点总结

数值分析知识点总结一、绪论数值分析是一门研究如何使用数值方法解决数学问题的学科。
它广泛应用于科学、工程、医学等领域。
在数值分析中,我们通常将实际问题转化为数学模型,然后使用计算机进行计算。
数值分析的主要内容包括:误差分析、插值与拟合、线性方程组求解、微分方程求解等。
二、误差分析误差分析是数值分析中的一个重要概念。
它包括绝对误差、相对误差和误差限等概念。
在计算过程中,误差会传递和累积,因此需要进行误差分析以评估计算结果的精度。
常用的误差分析方法有:泰勒级数展开、中点公式等。
三、插值与拟合插值与拟合是数值分析中的两个重要概念。
插值方法用于通过一组已知数据点生成一个函数,该函数能够近似地描述这些数据点之间的关系。
拟合方法则是通过一组已知数据点生成一个最佳拟合线或曲面,使得这个线或曲面与已知数据点之间的误差尽可能小。
常用的插值与拟合方法有:线性插值、多项式插值、样条插值、最小二乘法等。
四、线性方程组求解线性方程组是数值分析中经常遇到的一类方程组。
对于线性方程组,我们通常使用迭代法或直接法进行求解。
迭代法包括:雅可比迭代、高斯-赛德尔迭代、松弛法等。
直接法包括:高斯消元法、逆矩阵法等。
在实际应用中,我们通常会选择适合问题的计算方法,并根据需要进行优化。
五、微分方程求解微分方程是描述变量之间的函数关系的一类方程。
在数值分析中,我们通常使用数值方法对方程进行离散化处理,然后使用计算机进行求解。
常用的微分方程求解方法有:欧拉方法、龙格-库塔方法等。
对于复杂的微分方程,我们还可以使用谱方法、有限元方法等进行求解。
六、总结数值分析是一门应用广泛的学科,它涉及到许多数学知识和计算机技术。
在实际问题中,我们需要根据问题的特点选择合适的数值方法进行解决。
在进行计算时,需要注意误差分析、算法的稳定性和收敛性等问题。
随着计算机技术的发展,数值分析的应用领域也在不断扩大,例如、大数据分析等领域。
因此,数值分析的学习和应用具有重要意义。
机器学习中的误差分析技巧(四)

机器学习中的误差分析技巧引言在机器学习领域,误差分析是非常重要的一部分。
通过对误差的分析,我们可以了解模型在预测过程中出现的问题,从而改进模型的性能。
本文将讨论机器学习中的误差分析技巧,希望能够为读者提供一些有益的信息。
数据预处理在进行误差分析之前,首先需要对数据进行预处理。
数据预处理包括数据清洗、特征选择、特征提取等步骤。
只有当数据的质量得到保证,我们才能进行有效的误差分析。
对于数据清洗,我们需要处理缺失值、异常值和重复值。
缺失值可以通过填充或删除的方式进行处理,异常值可以通过统计学方法或者机器学习模型进行识别,重复值则可以直接删除。
在特征选择和提取方面,我们需要选择对模型有益的特征,并对特征进行转换,使其更适合模型的使用。
模型评估在进行误差分析之前,我们需要对模型进行评估。
常见的评估指标包括准确率、精确率、召回率、F1值等。
这些指标可以帮助我们了解模型的性能表现,从而确定模型的优劣。
除了这些传统的评估指标,我们还可以使用学习曲线和验证曲线来评估模型。
学习曲线可以帮助我们了解模型的训练和测试误差随着数据量的变化而变化的情况,而验证曲线则可以帮助我们了解模型的复杂度对性能的影响。
通过对模型的评估,我们可以更好地了解模型的表现,为后续的误差分析奠定基础。
误差分析一旦模型评估完成,我们就可以进行误差分析。
误差分析的目的是找出模型在预测过程中出现的问题,并加以改进。
常见的误差分析方法包括混淆矩阵分析、错误案例分析、对抗样本等。
混淆矩阵是一种展示模型分类准确性的矩阵,通过对混淆矩阵的分析,我们可以了解模型在不同类别上的性能表现。
通过混淆矩阵,我们可以找出模型在预测过程中容易出现的错误,从而有针对性地改进模型。
错误案例分析是通过对模型预测错误的样本进行分析,找出模型预测错误的原因。
通过错误案例分析,我们可以了解模型在预测过程中容易出现的问题,从而改进模型的性能。
对抗样本是一种通过对原始样本进行微小修改,从而欺骗模型的样本。
误差和数值算法设计

第一章绪论1.1 引言1.2 误差1.2.1 误差来源与分类1.2.2 绝对误差、相对误差与有效数字1.3 数值算法设计原则引言数值分析也称为数值计算方法, 它是研究用计算机求解数学问题的数值方法及其理论, 是计算数学的主体部分. 它涉及科学计算中常见问题, 如函数的插值与逼近、数值积分与数值微分、线性和非线性方程的求解、矩阵特征值问题和微分方程的数值解法等.●在学习数值分析课程时, 要掌握方法的基本原理和思想, 要注意方法处理的技巧及其与计算机的结合, 要重视误差分析、收敛性及稳定性的基本理论,达到灵活运用数值计算方法解决实际问题的目的.●用数值方法解决数学问题就是要完成如何把数学模型归结为数值问题、如何估计一个给定算法的精度、如何改进精度更高的算法、如何分析误差在计算过程中的积累和传播、如何使算法较少的占用存储量和如何分析算法的优缺点的工作. 应当指出, 数值方法的构造和分析是密可分的,二者缺一不可.数值计算方法修改 重新选择 运用计算机解决实际问题的一般流程数学模型实际问题程序设计结果分析计算机计算误差科学计算中所处理的数据和计算的结果往往都是在一定范围内的近似数值,它们与真实值之间总存在着一些偏差。
也就是说,一个物理量的真实值与计算出的值通常是不相等的,其差值称为误差。
引起误差的原因有多方面的,按误差来源分类可分为如下四类:1.模型误差2.观测误差3.截断误差4.舍入误差1.模型误差用计算机解决科学计算问题首先要建立数学模型,它是对被描述的实际问题进行抽象、简化而得到的,因而是近似的。
通常把数学模型与实际问题之间出现的这种误差称为模型误差。
2.观测误差在数学模型中往往还有一些根据观测得到的物理量,如温度、长度、电压等,这些参量显然也包含误差。
这种由观测产生的误差称为观测误差。
3.截断误差在使用无穷级数求和时,只能取前面有限项的和来近似作为该级数的和,于是就产生了有限过程代替无限过程的误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
称为近似值a 的相对误差。 相对误差也可正可负。 实际计算中,如果真值 x 未知时, 通常取
作为a的相对误差, 条件是
xa xa x a
xa 较小。 x
相对误差的绝对值上界叫做相对误差界(限), 记为:
xa a
ea a
相对误差界(限)
例
有两个量 x=3.000, a=3.100, 则其绝对误差: x a 0.1 绝对误差 其相对误差为: x a 0.1 0.333 101 , x 3.00 又有两个量 x 300.0 , a 310.0, 则其绝对误差:
1.1验并列为三大科学方法。
我们所学习的内容属于一门新学科——科学计算。
即现代意义下的计算数学。 主要研究在计算机上可计算的有效算法及相关理论。
本课程主要研究用计算机求解各种数学问题
的数值计算方法及其理论与软件实现
主要内容包括: 数值代数
Ax b
到x的前几位近似值a, 例如
x π 3.14159265
a1 0.00159265 取5位: a2 3.1416, a2 0.00000735
取3位: a1 3.14, 那么,它们的误差界的取法应为:
1 π 3.14 10 2 , 2
近似的,因此在此过程中,误差无处不在。
计 算 机 科 学 计 算 的 流 程 图
实际问题 数学模型 数值计算方法
编程实现算法 计算机数值结果
模型误差
方法误差或称为 截断误差 观测误差
舍入误差
1.模型误差 由实际问题抽象出数学模型,要简化许多 条件,这就不可避免地要产生误差.实际问题的解与数学模 型的解之间的误差
26!=4.0329×1026(次)
若使用每秒百亿次的串行计算机计算, 一年可进行的运算应为:
365(天) × 24(小时) × 3600(秒) × 1010 ≈ 3.1536 × 1017 (次) 共需要耗费时间为:
26 4.0329 10
3.1536 1017
9 1.2788 10
矩阵与数值分析
大连理工大学工科硕士研究生数学公共基础课程
大连理工大学研究生教育大楼
授课教师基本信息
• • • •
姓 名:董波 工作单位:数学科学学院 办公地点:创新园大厦(大黑楼)B1113室 EMAIL: dongbodlut@
创业园大厦
主 讲 教 材
参考书目 (Reference)
什么是有效算法?
考察线性方程组的解法
a11x1 a12 x2 a1n xn b1
a21x1 a22 x2 a2n xn b2
an1 x1 an 2 x2 ann xn bn
Cramer求解法则(18世纪)
xi
D
Di D
i 1, 2 ,
一、构造计算机可行的有效算法
二、给出可靠的理论分析,即对任意逼近达到精度要求,保证
数值算法的收敛性和数值稳定性,并可进行误差分析。 三、有好的计算复杂性,既要时间复杂性好,是指节省时 间,又要空间复杂性好,是指节省存储量,这也是建立算法要 研究的问题,它关系到算法能否在计算机上实现。 四、数值实验,即任何一个算法除了从理论上要满足上述 三点外,还要通过数值试验证明是行之有效的。
1 x a 10 k n 2
则称a为x的具有n位有效数字的近似值。
(1-15)
有 对于 e 2.71828182 ,下面的各个值的有效数字的位数。 效 1 取 a 2.718 10 0.2718 ,其绝对误差界为 数 1 3 k n 3 n 4, 10 , 字 e a 0.0003 2 位 a 是 e 的具有4位有效字的近似值。 数 1 与 取 a1 2.7182 10 0.27182 , 其绝对误差界为 小 1 3 10 , e a1 0.00009 数 2 点 故 a1是 e 的具有4位有效数字的近似值。 的 取 a 0.02718 101 0.2718 作为 x 0.0271828182 位 的近似值, 1 置 x a 0.000002 105 k n 5 n 4 。 无 2 也具有4位有效数字。 关
1.2 误差分析与数值方法的稳定性
1.2.1 误差来源与分类 1.2.2 误差的基本概念和有效数字
1.2.3 函数计算的误差估计
1.2.4 数值方法的稳定性和避免误差危害的基本原则
1.2.1 误差来源与分类
用计算机解决科学计算问题时经常采用的处理方式是将连
续的问题离散化、用有限代替无限等,并且用数值分析所处理 的一些数据,不论是原始数据,还是最终结果,绝大多数都是
(1)如果 a 有 n 位有效数字,则其相对误差界满足
1 xa 1 n 10 , 2a1 a
(2)如果其相对误差界满足
1 xa 1 n 10 , 2(a1 1) a
则 a 至少具有 n 位有效数字。
证
由(1-14)可得到
k 1 a1 10k 1 a (a1 1) 10
sx
近似代替函数 e , 则数值方法的误差是
e 2 n 1 x , Rn x e sx n 1!
x2
x2
x 2
截 断 误 差
0 1
3. 观测误差 初始数据大多数是由观测而得到的。由于观 测手段的限制,得到的数据必然有误差
4. 舍入误差 以计算机为工具进行数值运算时,由于计算 机的字长有限,原始数据在计算机上的表示往往会有误差,在 计算过程中也可能产生误差 产生的误差 例如, 用1.4142近似代替 2 ,
如果一个近似值是由精确值经四舍五入得 到的,那么,从这个近似值的末尾数向前数 起直到再无非零数字止,所数到的数字均为 有效数字
一般来说,绝对误差与小数位数有关, 相对误差与有效数字位数有关
定理
设实数 x 为某个精确值,a 为它的一个近似值,
k 其表达形式如 a 10 0. a1a2 an
13(亿年)
它远远超出目前所了解的人类文明历史!
Cramer 算法是“实际计算不了”的。
而著名的 Gauss消元法,它的计算过程已作根本改进,
成为有效算法,使得可在不到一秒钟之内即可完成上述计算 任务。 随着科学技术的发展,出现的数学问题也越来越多样化, 有些问题用消去法求解达不到精度,甚至算不出结果,从而 促使人们对消去法进行改进,又出现了主元消去法,大大提 高了消去法的计算精度。 这就是研究数值方法的必要性
n n n 1 n n 1 n 2 n n 1 3 2
n!
利用Cramer法和Laplace展开定理来求解一个n阶线性方程组,所 需的乘法运算次数就大于
(n 1)n! (n 1)!
求解25阶线性方程组
总的的乘法运算次数将达:
1.2.2 误差的基本概念和有效数字
定义 设 x 为精确值,a 为 x的一个近似值, 称
xa
通常准确值 定义
绝对误差(误差)
为近似值 a 的绝对误差, 简称误差。 误差 x a 可正可负。
x 是未知的, 因此误差 x a 也未知。
设 x 为精确值, a为 x 的一个近似值, 若有常数
ea 使得
1 π 3.1416 10 4. 2
定义
设 x 为精确值, a为x 的一个近似值,表示为:
a 10k 0. a1a2 an
(1-14)
其中 ai(i=1,2,…,n)是0到9中的 可以是有限或无限小数形式, 一个数字,a1 0, k为整数,n为正整数,如果其绝对误差界
2. 截断误差 从数学问题转化为数值问题的算法时所产 生的误差,如用有限代替无限的过程所产生的误差
例如, 给定
x求e
x2
的值的运算,我们可用无穷级数:
e
x2
4 6 2n 2 n 1 x x x x = 1 x2 2! 3! n! n 1!
我们可用它的前 n 1 项和
764.5 x 765.5,
结果说明x在区间[764.5,765.5]内。 对于一般情形 x a ea , 即可以表示为
也可以表示为
a ea x a ea ,
x a ea 。
但要注意的是,误差的大小并不能完全表示近似值的好坏。
定义
若 x 0, 则将近似值的误差与准确值的比值 xa 相对误差(误差)
的绝对误差界和相对误差界。
解: e a 0.00028182 其绝对误差界为:
相对误差界为:
ea a
e a 0.0003
0.0003 0.0001110375 0.0002。 2.718
绝对误差界和相对误差界并不是唯一的
误差界的取法
当准确值x位数比较多时,人们常常按四舍五入的原则得
占20%; 占10%;
占70%;
第1章 绪 论
作业:P27 2、3、7、8、10、12(3)、13
3、(2)x2 2c b b 4ac
2
x2
2c b b2 4ac
第1章 绪 论
1.1 计算机科学计算研究对象与特点 1.2 误差分析与数值方法的稳定性
1.3 向量与矩阵的范数
an1
b2
bn
ann
理论非常漂亮 线性方程组的求解
实际计算困难(运算量大得惊人)
计算n+1个n阶行列式 Laplace展开定理
设计算 k 阶行列式所需要的乘法运算的次数为 mk ,则
mk k k mk 1
