同济版-高等数学-课后模拟题解析
同济版-高等数学-课后习题解析

书后部分习题解答 P21页3.(3)nnn b b b a a a ++++++++∞→ΛΛ2211lim (1,1<<b a )知识点:1)等比级数求和)1(1)1(12≠--=++++-q qq a aqaq aq a n n Λ(共n 项)2)用P14例4的结论:当1<q 时,0lim =∞→nn q解:n n n b b b a a a ++++++++∞→ΛΛ2211lim ab bb a a n n n --=----=++∞→111111lim 115.(1)判断下列数列是否收敛,若收敛,则求出极限:设a 为正常数,00>x ,)(211nn n x a x x +=+ 证:由题意,0>n x ,a x a x x a x x nn n n n =⋅⋅≥+=+221)(211(数列有下界) 又02)(2121≤-=-+=-+nn n n n n n x x a x x ax x x (因a x n ≥+1)(数列单调减少) 由单调有界定理,此数列收敛;记b x n n =∞→lim ,对)(211n n n x a x x +=+两边取极限,得)(21bab b +=,解得a b =(负的舍去),故此数列的极限为a .P35页4.(8)极限=-++-+→211)1()1(lim x n x n x n x 211)1()1()]1(1[lim -++--++→x nx n x n x 21221111)1()1()1()1()1(1lim -++--+-+-+=+++→x n x n x x C x C n n n x 2)1(21+==+n n C n (若以后学了洛必达法则(00型未定型),则211)1()1(lim -++-+→x nx n x n x 2)1(2)1(lim )1(2)1())1(lim 111+=+=-+-+=-→→n n nx n x n x n n x n x ) 书后部分习题解答2 P36页8.已知当0→x 时,1cos ~1)1(312--+x ax,求常数a .知识点:1)等价无穷小的概念;2)熟记常用的等价无穷小,求极限时可用等价无穷小的替换定理。
同济大学版高等数学课后习题答案第2章

-----习题211 设物体绕定轴旋转 在时间间隔 [0 t]内转过的角度为从而转角是 t 的函数(t) 如果旋转是匀速的 那么称为该物体旋转的角速度 如果旋转t是非匀速的 应怎样确定该物体在时刻t 0 的角速度?解 在时间间隔 [t 0 t 0t] 内的平均角速度为(t 0t ) (t 0 )tt故 t 0 时刻的角速度为l i ml i m l i m(tt) (t 0) (t )t 0t 0 tt 0t2 当物体的温度高于周围介质的温度时物体就不断冷却 若物体的温度 T与时间 t 的函数关系为 T T(t) 应怎样确定该物体在时刻t 的冷却速度?解 物体在时间间隔 [t 0 t 0t]内 温度的改变量为T T(tt) T(t)平均冷却速度为T T (t t) T(t) t t故物体在时刻 t 的冷却速度为limT lim T (t t ) T (t ) T (t) t 0t t 0 t 3 设某工厂生产 x 单位产品所花费的成本是 f(x)元 此函数 f(x)称为成本函数成本函数 f(x)的导数 f (x)在经济学中称为边际成本 试说明边际成本 f (x)的实际意义解 f(x x)f(x)表示当产量由 x 改变到 x x 时成本的改变量f (x x) f (x)表示当产量由 x 改变到 x x 时单位产量的成本xf (x)lim 0f (x x) f ( x)表示当产量为 x 时单位产量的成本x x4 设 f(x)10x 2 试按定义 求 f ( 1)解 f ( 1)limf ( 1 x) f ( 1)10( 1x)2 10( 1)2xlimxxx 010 lim0 2 xx 2 10 lim ( 2x) 20xxx 05 证明 (cos x) sin x解 (cosx) limcos(x x) cosxxx2s i nx(x) s i nxlim2 2x 0 xlim [ s i nx(x ) s i n x] s i nx 2 x 0 2x26 下列各题中均假定 f (x 0)存在 按照导数定义观察下列极限指出 A 表示什么(1) lim f ( x 0x) f ( x 0 ) A xx 解 Alim0f (x 0x) f (x 0)xxl i mf ( xx) f (x 0) f ( x 0 )x 0x(2) lim f (x)A 其中 f(0) 0 且 f (0)存在x 0 x解 Alim f ( x) lim f (0 x) f (0) f (0)x 0 x x 0x (3) lim f (x 0 h) f (x 0 h)Ah 0h解A lim f ( x 0 h 0 lim[ f (xh 0limf (xh 0h)f (x 0 h) hh) f ( x 0 )] [ f (x 0 h) f (x 0)]h h) f (x 0)limf (xh) f ( x 0 ) hh 0hf (x 0) [ f (x 0)] 2f (x 0)7 求下列函数的导数(1)y x 4(2) y 3 x 2(3) y x1 6-----(4) y1 x(5) y1x23 5 x(6) y x232(7) y x x解 (1)y (x 4) 4x 4 1 4x 322 1 2 x (2) y (3 x 2 ) ( x 3 )2x 3331 3(3)y (x 1 6) 1 6x 1 6 1 1 6x 0 61 1 x(4) y ( 1) (x 2)x21 121 x 23 2(5) y(1)( x 2 )2x 3x 23 516 16 16 116 11 (6) y (x x) (x 5)x 5 x 555(7) y ( x2 3 x21 111 x ) (x 6) 1 x 6x 5665 68 已知物体的运动规律为 s t 3(m) 求这物体在 t 2 秒 (s)时的速度解 v(s) 3t 2 v|t 2 12(米 /秒)9 如果 f(x)为偶函数且 f(0)存在 证明 f(0)证明 当 f(x)为偶函数时 f( x) f(x)所以f (0) l i mf (x)f (0) l i m f (x) f (0) l i m f ( x) f (0)x 0xx 0x 0x 0x 0从而有 2f (0) 0 即 f (0) 010 求曲线 ysin x 在具有下列横坐标的各点处切线的斜率x 解 因为 y cos x 所以斜率分别为2 1k 1 c o sk 2 cos 13 2f (0)2x311 求曲线 y cos x 上点 ( , 1) 处的切线方程和法线方程式3 2解 ysin x ysin3x3 23故在点 (, 1) 处 切线方程为 y 1 3(x)3 22 23法线方程为 y 1 2(x )23 312 求曲线 y e x在点 (0 1)处的切线方程 解 y e xy |x 0 1 故在 (0 1)处的切线方程为y 1 1 (x 0)即 y x 113 在抛物线 y x 2上取横坐标为 x 1 1 及 x 2 3 的两点 作过这两点的割线问该抛物线上哪一点的切线平行于这条割线?解 yy(3) y(1)9 1 42x 割线斜率为 k132令 2x 4 得 x 2因此抛物线 y x 2 上点 (2 4)处的切线平行于这条割线 14 讨论下列函数在 x 0 处的连续性与可导性(1)y |sin x| (2) yx 2sin 1x 0xx 0解 (1)因为y(0) 0 lim y lim |sin x | lim ( sin x) 0x 0x 0x 0 lim ylim |sin x|lim sin xx 0x 0x所以函数在 x 0 处连续又因为y (0)l i m y( x)y(0) l i m |si nx | |si n0 |l i m s i nx1x 0x 0x 0x 0x 0xy (0) lim y( x) y(0) lim |sin x | |sin0|lim s i nx 1x 0 x 0 x 0x 0 x 0 x而 y (0) y (0) 所以函数在 x 0 处不可导-----解 因为 lim y(x) lim x 2sin10 又 y(0)0 所以函数在 x 0 处连续x 0 x 0x 又因为21 0y(x) y(0)xs i n1 l i mx l i ml i mxs i n 0 x 0xx 0xx 0x所以函数在点 x 0 处可导 且 y (0) 015 设函数 f (x)x 2x 1为了使函数 f(x)在 x 1 处连续且可导a b 应取什ax b x 1么值?解 因为lim f ( x) lim x 21 limf (x) lim (ax b)a b f(1) a bx 1x 1x1x 1所以要使函数在 x1 处连续 必须 a b 1 又因为当 a b1 时f (1)x 2 12l i m1x 1 xf (1) lim ax b 1 lim a( x 1) a b 1 lim a(x 1) ax 1 x 1 x 1 x 1 x 1x 1 所以要使函数在 x 1 处可导 必须 a 2 此时 b 116已知 f (x)x 2x 0求 f (0)及 f(0) 又 f (0)是否存在?x x 0解 因为f(0) lim f (x) f (0)lim x 0x 0 x x 0x f(0) lim f (x) f (0)lim x 2 0xxx 0x 而 f (0) f (0) 所以 f (0)不存在17 已知 f(x)sin x x0 求 f (x)x x解 当 x<0 时 f(x) sin x f (x) cos x 当x>0 时 f(x) x f (x) 11因为 f (0) lim f (x) f (0) lim sin x 0 1x 0 x x 0xf (0) lim f (x)f (0) lim x 0 1所以 f (0) 1 从而x 0x x 0x f (x)cosx x1 x18 证明 双曲线 xy a 2 上任一点处的切线与两坐标轴构成的三角形的面积都等于 2a 2解 由 xy a 2得 ya 2k ya 2xx 2设 (x 0 y 0)为曲线上任一点则过该点的切线方程为y a2x 0 ) y 02 ( xx 02y x 2令 y 0并注意 x 0y 0a 解得 xx 0 2x 0为切线在 x 轴上的距 a 2令 x 0并注意 x 0y 0 a 2 解得 y a 2y 2 y0 为切线在 y 轴上的距x 0 0此切线与二坐标轴构成的三角形的面积为S1|2x 0 ||2y 0 | 2|x 0 y 0 | 2a 22习题221 推导余切函数及余割函数的导数公式(cot x)csc 2x(csc x)csc xcot x解 (cot x)(cosx )sin x sin x cosx cosxsin xsin 2 x2 21 2s i nx c o s x2 2 c s cxs i nxs i nx( c sxc) ( 1 ) c o xsc s cx c o xt s i nx 2s i n x 2 求下列函数的导数(1) y4 7 2 12x 5 x 4x-----(2) y 5x 3 2x 3e x (3) y 2tan x sec x 1 (4) y sin x cos x (5) y x 2ln x (6) y 3e x cos x(7) yln xxx(8) y e 2 ln 3x(9) y x 2ln x cos x(10) s 1 sint1 cost解 (1) y ( 4 7 2 12)(4x 5 7x 4 2x 112)x 5 x 4 x20x628x52x220282x6x5x2(2) y (5x 32x 3e x ) 15x22xln2 3ex(3) y (2tan x sec x 1)2sec x tan x sec x(2sec x tan x)2sec x (4) y (sin x cos x) (sin x) cos x sin x (cos x)cos x cos x sin x ( sin x) cos 2x(5) y (x 2ln x) 2x ln x x 21 x(2ln x 1)x(6) y (3e x cos x) 3e x cos x 3e x ( sin x) 3e x(cos x sin x)ln x1 x ln x1 ln x(7) y ( ) xx x 2 x 2(8) y ( e x ln 3) e x x 2 e x 2x e x ( x 2)x 2 x 43x(9) y221cos x x 2ln x ( sin x)(x ln x cos x) 2x ln x cos x x x2x ln x cos x x cos x x 2 ln x sin x(10) s (1sin t ) cost(1 cost) (1 sin t)( sin t)1 sin t cost1 cost(1 cost)2(1 cost)23 求下列函数在给定点处的导数(1) y sin x cos x 求 y和 yxx46(2)sin1cos 求d2d4(3) f (x)3 x 2求 f (0)和 f (2)5 x 5解 (1)ycos x sin xyc o s s i n3 1 3 1x22266 6yc o s s i n22 2x2 244 4(2)dsincos1sin1sincosd22d1s i nc o s 1 2 422(1)d4 244 4 2 22 42(3) f (x)32x f (0)3 f (2) 17(5 x)2525154 以初速 v 0 竖直上抛的物体其上升高度 s 与时间 t 的关系是 s v 0t 1gt 22求(1)该物体的速度 v(t)(2)该物体达到最高点的时刻解 (1)v(t) s (t) v 0 gt(2)令 v(t) 0 即 v 0 gt 0 得 t v 0这就是物体达到最高点的时刻g5 求曲线 y 2sin x x 2 上横坐标为 x 0 的点处的切线方程和法线方程 解 因为 y 2cos x 2x y |x 0 2又当 x 0 时 y 0 所以所求的切线方程为y 2x所求的法线方程为-----y 1x即x 2y 0 26求下列函数的导数(1)y (2x 5)4(2)y cos(4 3x)(3) y e 3x 2(4)y ln(1x2)(5)y sin2x(6) y a2x2(7)y tan(x2)(8)y arctan(e x)(9)y(arcsin x)2(10) y lncos x解 (1) y4(2x 5)4 1 (2x5) 4(2x 5)3 2 8(2x 5)3 (2)y sin(4 3x) (4 3x)sin(4 3x) ( 3) 3sin(4 3x)(3) y e 3 x2 ( 3x2 )(4)y1 (1 x2)1x2(5)y 2sin x (sin x) e 3x 2(6x)6xe 3x212x2x1 x2 1 x22sin x cos x sin 2x(6) y [( a21] 1 (a211(a2 x2 ) x2) 2x2) 221 (a2x2 )1x2 ( 2x)x2 2a2 (7) y sec2(x2) (x2)2xsec2(x2)(8) y1x2 (e x)e x2x1(e ) 1 e2 arcsin x (9) y2arcsin x (arcsin x)1x2(10) y1 (cosx)1( sin x) tan xcosx cosx 7 求下列函数的导数(1) y arcsin(1 2x)(2) y11 x 2x(3) y e 2 cos3x(4) y arccos 1x(5) y1 ln x1 ln x (6) y sin 2xx(7) y arcsin x(8) y ln(x a 2 x 2 ) (9) y ln(sec x tan x)(10) y ln(csc x cot x)解 (1) y1(1 2x)21 1 (1 2x)2x x 21 (1 2x) 2(2) y [(111 1 x 2)x 2) 2]1(1 x 2) 2(1213x(1 x 2 ) 2 ( 2x)x 22(1 x 2 ) 1xxxx) cos3xx(3) y (e 2) cos3x e 2(cos3x) e 2(e 2( sin 3x)(3x)21 e xxx2 c o 3sx 3e 2 s i n3x 1e 2( c o3sx6s i n3x)22-----(4) y1 1 (1)1 1 ( 1 )|x|1 (2 x 1 ( ) 2x2x 2x21)xx1(1 l n x) (1 ln x)12(5) yxx(1ln x) 2x(1 ln x)2(6) ycos2x 2 x sin 2x 1 2x cos2x sin2xx2x2(7) y1( x)1111 ( x)21 ( x )22 x 2 x x 2(8) y1x 2 (xa 2x 2 )1x 2 [1 1(a 2 x 2) ]xa 2x a 22 a 2 x 21[112 (2x)]1x a 2 22 a 2x a 2x 2x(9) y1(secx tan x) secxtan x(10) y1(csc x cot x)csc x cot xsecx tan x sec 2x secxsecx tan x cscx cot x csc 2 x cscxcscx cot x8 求下列函数的导数(1) y (arcsin x )22(2) y ln tan x2(3) y 1 ln 2 x(4) y e arctan x(5) y sin nxcos nx(6) y arctanx 1x 1(7) y arcsinxarccosx(8) y=ln[ln(ln x)](9) y1x 1 x 1 x1 x(10) y arcsin1 x1 x解 (1) y2(arcsin x ) (arcsin x)2 22( a r c s xi)n 1( x)2 1 ( x )2 222( a r c s xi) n1 x 12 1 ( ) 222x2a r c s i n24 x 2(2) y1x (tan x) 1 x sec 2 x( x)tan 2 tan2 22 2(3) y(4) y1 2 x 1x s e c2 c s cxt a n 22 1 ln 2 x 2 1 (1 ln 2 x)1 ln2 x1 2ln x ( l nx)12ln x12 1 ln 2x2 1 ln 2xxln xx1 ln2 xearctan x(arctan x)e arctan x1 x) 2( x)1 (-----e a r c t axn11x e a r c t axn1( x)2 2 2 x(1 x)(5) y n sin n 1x (sin x) cos nx sin n x ( sin nx) (nx)n sin n 1x cos x cos nx sin n x ( sin nx) nn sin n 1x (cos x cos nx sin x sin nx) n sin n 1xcos(n 1)x(6) y1( x 1) 1(x 1) ( x 1)11 ( x 1) 2x 11 (x 1)2(x 1)2 1 x 2x 1x 11arccosx 1 arcsin x1 x2 1 x 2(7) y(arccos x)21 a r c c oxs a r c s ixn1 x22( ar c c ox)s2 1 x 2 ( a r c cxo)2s(8) y1 ln(ln x)1ln(ln x)[ln(ln x)] 11(ln x)ln(ln x) ln x 1 1 1 ln x x xln x l n ( lxn)(1 1 )( 1 x1 x) ( 1 x1 x)(1 1)(9) y2 1 x 2 1 x2 1 x 2 1 x( 1 x1 x)211 x 21 x2(10) y1 (1 x) 1 (1 x) (1 x)1 1 x 1 x 1 1 x(1 x)21 x1 x1(1 x) 2x(1 x)9. 设函数 f(x)和 g(x)可导且 f 2(x) g 2(x) 0 试求函数 y f 2 (x) g 2 (x) 的导数解 yf 1[ f 2(x) g2 (x)]22 (x)g 2(x)1[2 f (x) f ( x) 2g(x) g ( x)] 2f 2(x)g2(x)f (x) f (x)g(x)g (x)f 2 (x)g 2 (x)10设 f(x)可导求下列函数 y 的导数dy dx(1) y f(x2)(2)y f(sin2x) f(cos2x)解 (1) y f (x2) (x2)f(x2) 2x 2x f (x2)(2)y f(sin2x) (sin2x) f (cos2x) (cos2x)f(sin2x) 2sin x cos x f (cos2x) 2cosx ( sin x)sin 2x[f (sin2x)f(cos2x)]11求下列函数的导数(1)y ch(sh x )(2)y sh x e ch x(3)y th(ln x)(4)y sh3x ch2x(5)y th(1 x2)(6)y arch(x2 1)(7)y arch(e2x)(8)y arctan(th x)(9)y ln chx12 x 2ch(10)y ch2( x 1) x 1解 (1) y sh(sh x) (sh x) sh(sh x) ch x(2) y ch x e ch x sh x e ch x sh x e ch x(ch x sh2x)(3) y1(ln x)12 (ln x)2 (ln x)ch x ch-----(4) y3sh 2x ch x 2ch x sh x sh x ch x (3sh x 2) (5) ych 21 2 (1 x 2)2 2xx 2 )(1 x )ch (1 (6) y1 1(x 2 1)2x( x 2 1)x 4 2x 2 2(7) y1(e 2x)2e2x(e 2x )21 e 4 x 1 (8) y 1(th x) 1 1 1 1 1 (thx) 2 1 th 2 x ch 2 x 1 2 2sh x ch xch 2x 1 1ch 2 x sh 2x 1 2sh 2 x(9) y1 (ch x) 1 (ch 2x)ch x2ch 4 xsh x 1 2ch x shxch x2ch 4 xsh x shx sh x ch 2x shxch xch 3x ch 3xsh x (ch 2 x 1) sh 3x th 3xch 3xch 3x(10) y2ch(x1) [ch(x1)] 2ch(x1) sh(x1) ( x 1)x 1x 1x 1 x 1 x 1sh(2x 1(x 1) (x 1)2sh(2 x 1)(x 1)2( x 1)2 )x 1x 112 求下列函数的导数(1) y e x (x 2 2x 3)(2) y sin 2x sin(x 2) (3) y (arctan x )22(4) yln xx ne t e (5) ye t ett(6) y ln cos 1x(7) y e sin 2 1x(8) y x x(9) yxarcsinx4 x 22(10) y arcsin2t1 t 2解 (1) y e x (x 2 2x 3) e x (2x 2) ex( x 2 4x 5)(2) y2 222sin x cos x sin(x ) sin x cos(x ) 2xsin2x sin(x 2) 2x sin 2x cos(x 2)(3) y 2arctanx1 1 4 arctan x2 1 x 2 2 x 2 4 241 xnln x nxn 11 n ln x(4) yxx 2nx n 1(5) y(e te t )(e t e t ) (e t e t )(e te t )4e 2t(e t e t )2(e 2t 1) 211111 1 1(6) y sec x (cos x ) sec x ( sin x ) ( x 2 ) x 2tanx(7) y esin 21 ( sin 21) e sin 21xxx( 2sin 1) cos1( 1 ) xxx2122 1s i nx 2 s i nexx(8) y1x (x x )2 1 (1 1 ) 2 xxx2 x2 x 1 4 xxx(9) y arcsinxx1 12 1 ( 2x) arcsin x21 x2 2 4 x 2 24-----(10) y1 ( 2t ) 12 (1 t 2) 2t (2t) 1 (2t)2 1 t 21 ( 2t )2 (1 t 2) 21 t21 t21 t22(1 t 2)2(1 t 2)(1 t 2)2 (1 t 2 )2 |1 t 2 |(1 t 2 )习题231 求函数的二阶导数(1) y 2x 2ln x (2) y e2x 1(3) y xcos x (4) y e t sin t (5) y a 2 x 2 (6) y ln(1 x 2)(7) y tan x1(8) yx 3 12(9) y (1 x )arctan x(10) ye xx(11) y x 2xe(12) y ln( x 1 x 2 )解 (1) y 4x1 y4 1xx2(2) y e 2x 12 2e 2x 1y 2e2x 1 2 4e 2x 1(3) y xcos x y cos x xsin xy sin x sin x xcos x2sin x xcos x(4) ye tsin t e tcos t e t(cos t sin t)ye t (cos t sin t) e t ( sin t cos t) 2e t cos t(5) y21x2(a2x2)xx2a2a2a2x2x xa2ya2x2a2 x2(a2 x2 ) a2 x2(6) y11(1x2 )12x x2x2y 2(1x2 )2x (2x)2(1 x2)(1 x2 )2(1x2 )2(7) y sec2 xy2sec x (sec x)2sec x sec x tan x2sec2x tan x(8) y(x31)3x2 (x31) 2(x31)2y 6x ( x31)23x22( x31) 3x6x(2x3 1) (x3 1)4(x31)3(9) y2xarctanx(1x2)112xarctanx1 x2y2a r c t xa n2x1 x2(10)y e x x e x 1e x( x 1)x2x2y [e x( x 1) e x] x2 e x( x 1) 2x e x(x2 2x 2)x4x3(11)y e x 2x e x2(2x)e x2(12x2 )yx22x24xx22 e2x (12x )e2xe(32x )(12)y12( x1x2 )12(12x 2 )12x 1 x x 1 x 2 1 x 1 x y1(1 x2 )12x x1 x2 1 x22 1 x2)(1 x) 2 1 x-----2 设 f(x)(x6(2)?10)f解 f(x) 6(x5f(x)43 10)30(x 10) f (x) 120(x 10)f(2)120(210)32073603若 f (x)存在求下列函数 y 的二阶导数d2ydx2(1)y f(x2)(2)y ln[ f(x)]解 (1)y f(x2) (x2) 2xf(x2)y2f(x2)2x 2xf(x2)2f(x2) 4x2f(x2)(2) y1 f (x)f (x)f(x) f (x) f ( x) f(x)f( x) f (x)[ f ( x)] 2 y[ f ( x)]2[ f ( x)]24试从dx 1导出dy y(1) d 2 x ydy 2( y ) 3(2)d 3x3( y )2y y dy3( y )5解(1) d 2x d dx d1d1dx y1ydy2dy dy dy y dx y dy( y )2y( y )3(2) d3x d y d y dxdy3dy y 3dx y 3dyy ( y )3 y 3( y )2 y13( y )2 y y(y )6y(y )55已知物体的运动规律为s Asin t(A、是常数 )求物体运动的加速度并验证d 2s2 s 0dt 2解dsA cos t dt d2 s A 2 sin t dt 22d s就是物体运动的加速度dt2d2 s 2 s A 2 s i n t2 As i n t 0dt 2C1e x C2e x(6验证函数 y C1 C2是常数 )满足关系式y2y 0解y C1 e x C2 e xy C12e x C22e xy2y (C12e x C22e x)2(C1e x C2e x)(C12e x C22e x) (C12e x C22e x) 0 7验证函数 y e x sin x 满足关系式y2y2y 0解 y e x sin x e x cos x e x(sin x cos x)y e x(sin x cos x)e x(cos x sin x) 2e x cos xyx xcos x)x2y 2y 2e cos x2e (sin x2e sin x 2e x cos x2e x sin x2e x cos x2e x sin x 08求下列函数的 n 阶导数的一般表达式(1) y x n1n 12n 2n 1n 12n 都是常数)a x a x a x a (a a a(2)y sin2x(3)y xln x(4)y xe x解 (1) y nx n 1(n1)a1x n 2 (n2)a2x n 3a n 1y n(n1)x n 21 n 32n 4n 2 (n 1)(n2)a x(n 2)(n 3)a x ay(n) n(n 1)(n 2) 2 1x0 n!(2) y 2sin x cos x sin2xy 2c o 2sx 2s i n2(x)2-----y22 c o s2x()22 s i n2x( 2)22y(4)23 c o s2x(2) 23 s i n2(x 3 )22y(n)2n 1s i n2x[ (n 1)]2(3)y ln x 1y 1 x1xy ( 1)x 2y(4) ( 1)( 2)x 3y(n)(1)( 2)( 3) ( n 2)x n 1( 1)n 2(n 2)!( 1)n (n 2)!x n 1x n 1(4) y e x xe xy e x e x xe x 2e x xe xy 2e x e x xe x 3e x xe xy(n) ne x xe x e x(n x)9求下列函数所指定的阶的导数(1)y e x cos x 求 y(4)(2)y xsh x 求 y(100)(3) y x2sin 2x求y(50) .xv cos x有解 (1)令 u eu u u u(4)e xv sin x v cos x v sin x v(4) cos x所以y(4)u(4) v4u v6u v4u v u v(4)e x[cos x4(sin x)6(cos x)4sin x cos x] 4e x cos x(2)令 u x v sh x则有u 1 u0v ch x v sh x v(99)ch x v(100) sh x所以y(100)u(100)v C1 u(99) v C2u(98) v C 98 u v(98) C99 u v(99)u v(100)100100100100100ch x xsh x(3)令 u x2 v sin 2x则有u2x u 2 u0v(48)248 sin(2x48)248 s i n2x2v(49)249cos 2x v(50)250sin 2x所以y(50)u(50)v C1501u(49) v C502u(48) v C5048u v(48) C5049u v(49) u v(50)C5048u v(48)C5049u v(49) u v(50)50 492 228 sin 2x50 2x 249 c o 2sx x2 (250 s i n2x)250x2sin 2x50xc o 2sx12252 (s i n2x)2习题231求函数的二阶导数(1)y 2x2 ln x(2)y e2x 1(3)y xcos x(4)y e t sin t(5)y a2 x2(6)y ln(1 x2)(7)y tan x1(8) yx3 1(9) y (1 x2)arctan x(10) y e xx-----(11) y xe x2(12) y ln( x1x2 )解 (1) y4x1y41x x2(2) y e2x 1 2 2e2x 1y2e2x 1 2 4e2x 1(3) y xcos x y cos x xsin xy sin x sin x xcos x2sin x xcos x(4) y e t sin t e t cos t e t (cos t sin t)y e t(cos t sin t) e t (sin t cos t)2e t cos t(5) y21x2(a2x2)xx2a2a2a2x2x xx2a2ya2a2 x2(a2 x2 ) a2 x2(6) y11(1x2 )12x x2x2y 2(1x2 )2x (2x)2(1x2)(1 x2 )2(1x2 )2(7) y sec2 xy2sec x (sec x)2sec x sec x tan x2sec2x tan x(8) y(x31)3x2 (x31) 2(x31)2y 6x ( x31)23x22( x31) 3x 6x(2x3 1) (x31)4(x31)3(9) y2xarctanx(1x2)112xarctanx1 x2y2a r c t xa n 2x21 x(10)y e x x e x1 e x( x 1)x2x2y[e x ( x 1) e x ] x 2 e x ( x 1) 2x e x (x 2 2x 2)x4x3(11) ye x 2 x e x 2 (2x) e x 2 (1 2x 2 )yx 22x (1 2x 2x22e 2x ) e4x 2xe (3 2x )(12) y1( x1x 2 ) 1 (1 2x ) 1x 1 x 2x 1 x 22 1 x 21 x 2y1(1 x 2) 12xx1 x21 x 22 1 x 2)(1 x) 21 x2 设 f(x) (x 10)6f (2) ?解 f (x) 6(x 10)5 f (x) 30(x 10)4f (x) 120(x 10)3f(2) 120(2 10)3 2073603 若 f (x)存在 求下列函数(1) y f(x 2)(2) y ln[ f(x)]解 (1)yf(x 2) (x 2) 2xf (x 2) y 2f(x 2) 2x 2xf (x 2) (2) y1 f (x)f (x)f (x) f (x) f( x) f (x) y2[ f ( x)]4 试从dx 1导出dy y(1) d 2xydy 2( y ) 3(2)d 3x 3( y )2 y ydy3( y )5解 (1) d 2xd dxd 1dy2dy dydyyd 2 yy的二阶导数d x 22f (x 2) 4x 2f (x 2)f ( x) f (x) [ f ( x)] 2[ f ( x)]2d1dx y 1y dx y dy( y )2 y( y )3(2) d3x d y d y dxdy3dy y 3dx y 3dyy ( y )3 y 3( y )2 y13( y )2 y y(y )6y(y )55已知物体的运动规律为s Asin t(A、是常数 )求物体运动的加速度并验证d 2s2s 0dt 2解dsA cos t dt d2 s A 2 sin t dt 22d s就是物体运动的加速度dt2d2 s 2 s A 2 s i n t2 As i n t 0dt 2C1e x C2e x(6验证函数 y C1 C2是常数 )满足关系式y2y 0解y C1 e x C2 e xy C12e x C22e xy212e x C22x21x2e x)y (C e ) (C e C(C12e x C22e x) (C12e x C22e x) 0 7验证函数 y e x sin x 满足关系式y2y2y 0解 y e x sin x e x cos x e x(sin x cos x)y e x(sin x cos x)e x(cos x sin x) 2e x cos xyx xcos x)x2y 2y 2e cos x2e (sin x2e sin x 2e x cos x2e x sin x2e x cos x2e x sin x 08求下列函数的 n 阶导数的一般表达式(1) y x n1n 12n 2n 1n 12n 都是常数)a x a x a x a (a a a(2) y sin2x-----(3)y xln x(4)y xe x解 (1) y n 11n 2(n2 n 3n 1nx(n 1)a x2)a x ay n(n1)x n 2 (n1)(n2)a1x n 3(n 2)(n 3)a2x n 4a n 2y(n) n(n 1)(n 2) 2 1x0 n!(2) y2sin x cos x sin2xy2c o 2sx 2s i n2(x)2y22 c o s2x() 22 s i n2x( 2)22y(4) 23 cos(2x2) 23 sin(2x 3 )22(n)n 1y 2 s i n2x[ (n 1)](3)y ln x 1y 1x 1 xy ( 1)x 2y(4) ( 1)( 2)x 3(n)( 1)( 2)( 3)( n 2)x n 1( 1)n 2 (n 2)!( 1)n (n 2)!y x n 1x n 1 (4)y e x xe xy e x e x xe x 2e x xe xy 2e x e x xe x 3e x xe xy(n) ne x xe x e x(n x)9求下列函数所指定的阶的导数(1)y e x cos x 求 y(4)(2)y xsh x 求 y(100)(3)y x2sin 2x 求 y(50) .所以所以xv cos x有解 (1)令 u eu u u u(4)e xv sin x v cos x v sin x v(4)cos xy(4)u(4) v4u v6u v4u v u v(4)e x[cos x4(sin x)6(cos x)4sin x cos x] 4e x cos x(2)令 u x v sh x则有u 1 u0v ch x v sh x(99)ch x(100)sh xv vy(100) u(100) v C1 u(99)v C2u(98)v C 98 u v(98)C99 u v(99)u v(100) 100100100100(3)令 u x2u 2xv(48)100ch x xsh xv sin 2x 则有u 2 u0248 sin(2x 48 )248 s i n2x2v(49)249cos 2x v(50)250sin 2x所以y(50)u(50)v C1501u(49) v C502u(48) v C5048u v(48) C5049u v(49) u v(50) C5048u v(48) C5049u v(49) u v(50)50 492 228 sin 2x50 2x 249 c o 2sx x2 (250 s i n2x)250x 2sin 2x50xc o 2sx1 2 2 52 (2s i n2x)习题241求由下列方程所确定的隐函数 y 的导数dydx(1)y2 2x y 9 0(2)x3 y3 3axy 0(3)xy e x y(4)y 1 xe y解 (1)方程两边求导数得-----2y y 2y 2x y 0于是(y x)y yyyy x(2)方程两边求导数得3x 2 3y 2y 2ay 3axy 0于是(y 2 ax)y ayx 2yay x 2y2ax(3)方程两边求导数得yxy e x y(1 y ) 于是(x e x y )y e x y ye x yyyx e x y(4)方程两边求导数得y e y xe yy于是(1 xe y )y e yye y1 xey222在点 ( 2a, 2a) 处的切线方程和法线方程2 求曲线 x3y 3 a34 4解 方程两边求导数得 2 x31 13 2y 3 y 031于是yx31y 3在点 (2a,2a) 处 y 144所求切线方程为y2a ( x2a) 即 x y 2 a442所求法线方程为y2a (x2a) 即 x y 04423 求由下列方程所确定的隐函数 y 的二阶导数d ydx22 2(1) x y 1(2) b 2x 2 a 2y 2 a 2b 2 (3) y tan(x y)(4) y 1 xe y解 (1)方程两边求导数得2x 2yy 0yx yy ( x)y xxy xy y y 2x 21yy 2y 2y 3 y 3(2)方程两边求导数得2b 2 x 2a 2 yy 0yb 2 xa2yy x( b 2 x)b 2 y xy b 2 a 2 y ya2y2a2y 2b 2 a 2 y 2 b 2 x 2b 4a2a 2 y3a 2 y3(3)方程两边求导数得y sec 2(x y) (1 y )2y)1y s e c( x2y) 2y) 11 s e c(xc o s( x2y)21s i n(xc o s(x y)12y)y 2s i n( xy23 y23( 112 )2(1 y 2 )y 5yyy(4)方程两边求导数得yyy e xe y-----yeyeyey1 xe y1 (y 1)2 yye y y (2 y) e y ( y ) e y (3 y) y e 2 y (3 y)(2 y)2(2 y)2(2 y)34 用对数求导法求下列函数的导数(1) y ( x )x1 x (2) y5x 525 x2(3) yx 2(3 x)4( x 1)5(4) y xsin x 1e x解 (1)两边取对数得ln y xln|x| xln|1 x|,两边求导得1 y ln x x 1 l n1( x) x 1y x 1 x 于是y ( x)x[ l nx1 ]1 x 1 x 1x(2)两边取对数得ln y1ln |x 5|1l nx(22)两边求导得5251 y1 1 12x2y5 x 525 x 2于是y 1 5x 5[11 2x ]5 5 x 2 2x 5 5 x 2 2(3)两边取对数得ln y1l nx( 2) 4 l n3( x) 5l n x( 1)2两边求导得1 y 1 3 45y 2(x 2)x x 1于是yx 2(3x)4 [ 12)4 5 ](x 1)52(x x 3 x 1(4)两边取对数得ln y1ln x1ln s i nx1l n1( e x )两边求导得22 41 y1 1 c o xte xy 2x24(1 e x )于是yxs i nx 1 e x[11c o xte x]2x 2 4(1 e x )1 x 22c o tx e x ]4 xs i nx 1 e [ x e x1 dy5求下列参数方程所确定的函数的导数dxx at 2(1)y bt2x (1 sin ) (2)ycos解 (1)dyy t 3bt 2 3b tdxx t 2at 2ady ycos sin(2) dx x 1 sincos6 已知xe tsin t, 求当 t 3 时 dy的值y e tcost. dx解dy y te t cost e t sin t costsin t dxx t e tsin t e tcost sintcostdy 1 3 1 3 当 t 时 2 2 3 2dx 1 3 1 3 32 27 写出下列曲线在所给参数值相应的点处的切线方程和法线方程(1)x sin t在 t处y cos2t4x3at (2)1 t 2在 t=2 处y 3at 21 t 2解 (1) dyy t2sin 2tdxx tcost-----dy 2sin(2)当 t时42 2 2 x02y0 0 dx4cos2242所求切线方程为y 2 2(x2) 即2 2x y 2 0 2所求法线方程为y1(x 2 )即 2x 4y1222(2) y t 6at (1t2 )3at 2 2t6at(1t 2 )2(1t 2 )2x t 3a(1t 2)3at2t3a3at 2 (1t 2 )2(1t 2)2dy y t6at2tdx x t3a3at 21t 2当 t 2 时dy 2 24x 6a ydx1223050所求切线方程为012a 5y12 a 4(x6a)即 4x 3y 12a 0535所求法线方程为y12 a3(x 6a)即 3x 4y 6a 0545d 2 y 8求下列参数方程所确定的函数的二阶导数dx2x t 2(1)2y 1 t. xacost(2)y bsin t(3)x3e t y2e t(4)x f t (t )设 f(t)存在且不为零y tf t (t) f (t)dy y t1 d 2 y(y x)t1解 (1)t 21 dx x t t dx2x t t t3(2) dy y tbcostbcot tdx x t asin t ab 2 d 2 y (y x )t a csc t b dx 2 x t asin ta 2 sin 3 tdy y t 2e t22t(3) dx x t3e t3ed 2y( y x )t2 2t3 2e4 3tdx 2x t3e te9 (4) dy y t f (t) tf (t) f (t)dx x tf (t)td 2 y ( y x )t 1dx 2x tf (t)9 求下列参数方程所确定的函数的三阶导数(1) x 1 t 2y t t3(2)x ln(1 t 2) y t arctan t解 (1)dy (t t 3)1 3t2dx (1 t 2 )2t1 3t 2d 2y ( 2t )1 ( 1 3) dx 22t4 t 3 t1 1 3d 3y 4 ( t 3t )3(1 t 2)dx 32t8t 5dy (t arctan t)11(2)1 t 21 tdx [ln(1 t 2)]2t 21 t21d 2 y ( 2t) 1 t 2 dx 22t 4t1 t 23d y-----1 t 2d 3 y ( 4t ) t 4 1dx 3 2t 8t 31t 210 落在平静水面上的石头 产生同心波纹 若最外一圈波半径的增大率总是6m/s 问在 2 秒末扰动水面面积的增大率为多少?解 设波的半径为 r 对应圆面积为 S 则 S r 2 两边同时对 t 求导得S t 2 rr当 t 2 时 r 6 2 12 r t 6故 S t t 22 126 144( 米 2 秒)| 其速率为 4m 2/min11 注水入深 8m 上顶直径 8m 的正圆锥形容器中 当水深为 5m 时 其表面上升的速度为多少?解水深为 h 时 水面半径为 r1 h 水面面积为 S 1 h 21hS 1 h 1 h 224水的体积为 Vh 33 34 12dV 12 3h 2dh dh 4 dVdt dt dt h 2 dt已知 h 5(m), dV 4 (m 3/min) 因此 dh 4 dV 4 4 16(m/min)dtdt h 2 dt252512 溶液自深 18cm 直径 12cm 的正圆锥形漏斗中漏入一直径为 10cm 的圆柱形筒中 开始时漏斗中盛满了溶液 已知当溶液在漏斗中深为 12cm 时 其表面下 降的速率为 1cm/min 问此时圆柱形筒中溶液表面上升的速率为多少?解 设在 t 时刻漏斗在的水深为 y 圆柱形筒中水深为 h 于是有1 62 18 1r 2 y 52hy 3y3由 r得 r 代入上式得 6 18 31 62 18 1 ( y ) 2 y 23 3 3 5 h即162 18 1y 3 52 h 两边对 t 3 33求导得1 y2 y 52 h32t当 y 12 时 y t1 代入上式得1 122( 1) 16h t32 52 0.64 (cm/min).25。
同济大学《高等数学》[上册]的答案解析
![同济大学《高等数学》[上册]的答案解析](https://img.taocdn.com/s3/m/e852866ba5e9856a561260bf.png)
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式
练习 2-5
专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式
>>>
专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式
总习题四
专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式
练习 3-3
专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式
练习 3-4
专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
练习 4-3
专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
完美 WORD 格式
练习 4-4
专业整理 知识分享
完美 WORD 格式 专业整理 知识分享
高等数学(同济第七版下)课后习题及解答

1.设u =a -b +2c ,v =-a +3b -c .试用a ,b ,c 表示2u -3v .解2u -3v =2(a -b +2c )-3(-a +3b -c )=5a -11b +7c .2.如果平面上一个四边形的对角线互相平分,试用向量证明它是平行四边形.证如图8-1,设四边形ABCD 中AC 与BD 交于M ,已知AM =MC ,MB DM =.故DC DM MC MB AM AB =+=+=.即DC AB //且|AB |=|DC |,因此四边形ABCD是平行四边形.3.把△ABC 的BC 边五等分,设分点依次为D 1,D 2,D 3,D 4,再把各分点与点A 连接.试以AB =c ,BC =a 表向量A D 1,A D 2,A D 3,A D4.证如图8-2,根据题意知511=BD a,5121=D D a,5132=D D a,5143=D D a,故A D 1=-(1BD AB +)=-51a -cA D 2=-(2BD AB +)=-52a -c A D 3=-(3BD AB +)=-53a -c A D 4=-(4BD AB +)=-54a -c.4.已知两点M 1(0,1,2)和M 2(1,-1,0).试用坐标表示式表示向量21M M 及-221M M .解21M M =(1-0,-1-1,0-2)=(1,-2,-2).-221M M =-2(1,-2,-2)=(-2,4,4).5.求平行于向量a =(6,7,-6)的单位向量.解向量a 的单位向量为a a ,故平行向量a 的单位向量为±a a =111±(6,7,-6)=⎪⎭⎫ ⎝⎛-±116,117,116,其中11)6(76222=-++=a .6.在空间直角坐标系中,指出下列各点在哪个卦限?A (1,-2,3),B (2,3,-4),C (2,-3,-4),D (-2,-3,1).解A 点在第四卦限,B 点在第五卦限,C 点在第八卦限,D 点在第三卦限.7.在坐标面上和在坐标轴上的点的坐标各有什么特征?指出下列各点的位置:A (3,4,0),B (0,4,3),C (3,0,0),D (0,-1,0).解在坐标面上的点的坐标,其特征是表示坐标的三个有序数中至少有一个为零,比如xOy 面上的点的坐标为(x 0,y 0,0),xOz 面上的点的坐标为(x 0,0,z 0),yOz 面上的点的坐标为(0,y 0,z 0).在坐标轴上的点的坐标,其特征是表示坐标的三个有序数中至少有两个为零,比如x 轴上的点的坐标为(x 0,0,0),y 轴上的点的坐标为(0,y 0,0),z 轴上的点的坐标为(0,0,z 0).A 点在xOy 面上,B 点在yOz 面上,C 点在x 轴上,D 点在y 轴上.8.求点(a ,b ,c )关于(1)各坐标面;(2)各坐标轴;(3)坐标原点的对称点的坐标.解(1)点(a ,b ,c )关于xOy 面的对称点(a ,b ,-c ),为关于yOz 面的对称点为(-a ,b ,c ),关于zOx 面的对称点为(a ,-b ,c ).(2)点(a ,b ,c )关于x 轴的对称点为(a ,-b ,-c ),关于y 轴的对称点为(-a ,b ,-c ),关于z 轴的对称点为(-a ,-b ,c ).(3)点(a ,b ,c )关于坐标原点的对称点是(-a ,-b ,-c ).9.自点P 0),,(000z y x 分别作各坐标面和各坐标轴的垂线,写出各垂足的坐标.解设空间直角坐标系如图8-3,根据题意,P 0F 为点P 0关于xOz面的垂线,垂足F 坐标为),,000(z x ;P 0D 为点P 0关于xOy 面的垂线,垂足D 坐标为),,0(00y x ;P 0E 为点P 0关于yOz 面的垂线,垂足E 坐标为)0(0o z y ,,.P 0A 为点P 0关于x 轴的垂线,垂足A 坐标为),0,0(o x ;P 0B 为点P 0关于y 轴的垂线,垂足B 坐标为)0,,0(0y ;P 0C 为点P 0关于z 轴的垂线,垂足C 坐标为),0,0(0z .10.过点P 0),,(000z y x 分别作平行于z 轴的直线和平行于xOy 面的平面,问在它们上面的点的坐标各有什么特点?解如图8-4,过P 0且平行于z 轴的直线l 上的点的坐标,其特点是,它们的横坐标均相同,纵坐标也均相同.而过点P 0且平行于xOy 面的平面 上的点的坐标,其特点是,它们的竖坐标均相同.11.一边长为a 的正方体放置在xOy 面上,其底面的中心在坐标原点,底面的顶点在x 轴和y 轴上,求它各顶点的坐标.解如图8-5,已知AB=a ,故OA=OB=a 22,于是各顶点的坐标分别为A )0022(,,a ,B (),022,0(a ),C (-a 22,0,0),D (0,-a 22,0),E (a 22,0,a ),F (0,a 22,a ),G (-a 22,0,a ),H (0,-a 22,a ).12.求点M (4,-3,5)到各坐标轴的距离.解点M 到x 轴的距离为d 1=345)3(22=+-,点M 到y 轴的距离为d 2=415422=+,点M 到z 轴的距离为d 3=525)3(422==-+.13.在yOz 面上,求与三点A (3,1,2),B (4,-2,-2),C (0,5,1)等距离的点.解所求点在yOz 面上,不妨设为P (0,y ,z ),点P 与三点A ,B ,C,)2()1(3222-+-+=z y,)2()2(4222++++=z y.)1()5(22-+-=z y==222222)2()2(4)2()1(3++++=-+-+z y z y 22)1()5(-+-=z y ,即.)1()5()2()1(9,)2()2(16)2()1(922222222-+-=-+-+++++=-+-+z y z y z y z y 解上述方程组,得y=1,z=-2.故所求点坐标为(0,1,-2).14.试证明以三点A (4,1,9),B (10,-1,6),C (2,4,3)为顶点的三角形是等腰直角三角形.证由2798)63()14()102(,7)93()14()42(,7)96()11()410(222222222==-+++-==-+-+-==-+--+-=.+==故△ABC 为等腰直角三角形.15.设已知两点为M 1(4,2,1),M 2(3,0,2),计算向量21M M 的模、方向余弦和方向角.解向量21M M =(3-4,0-2,2-1)=(-1,-2,-1),2412-1-222==++=)()(.其方向余弦分别为cos α=-21,cos β=-22,cos γ=21.方向角分别为3,43,32πγπβπα===.16.设向量的方向余弦分别满足(1)cos α=0;(2)cos β=1;(3)cos α=cos β=0,问这些向量与坐标轴或坐标面的关系如何?解(1)由cos α=0得知2πα=,故向量与x 轴垂直,平行于yOz 面.(2)由cos β=1得知β=0,故向量与y 轴同向,垂直于xOz 面.(3)由cos α=cos β=0知2πβα==,故向量垂直于x 轴和y 轴,即与z 轴平行,垂直于xOy 面.17.设向量r 的模是4,它与u 轴的夹角为3π,求r 在u 轴上的投影.解已知|r |=4,则Prj u r=|r |cos θ=4∙cos 3π=4×21=2.18.一向量的终点在点B (2,-1,7),它在x 轴、y 轴和z 轴上的投影依次为4,-4和7,求这向量的起点A 的坐标.解设A 点坐标为(x ,y ,z ),则AB =(2-x ,-1-y ,7-z ),由题意知2-x=4,-1-y=-4,7-z=7,故x=-2,y=3,z=0,因此A 点坐标为(-2,-3,0).19.设m =3i +4j +8k ,n =2i -4j -7k 和p =5i +j -4k .求向量a =4m +3n -p 在x 轴上的投影及在y轴上的分向量.解a=4m+3n-p=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k,a在x轴上的投影为13,在y轴上的分向量为7j.1.设k j i b k j i a -+=--=2,23,求(1)b a b a ⨯⋅及;(2)b a 2b 3a 2-⨯⋅及)(;(3)b a ,的夹角的余弦.解(1)),(),,(1-2,12-1-3⋅=⋅b a ,)()()(31-2-21-13=⨯+⨯+⨯==⨯b a 121213---kj i =(5,1,7).(2)1836)(63)2(-=⨯-=⋅-=⋅-b a b a )14,2,10()7,1,5(2)(22==⨯=⨯b a b a (3222222)1(21)2()1(33),cos(-++-+-+=⋅=b a b a b a 21236143==2.设c b a ,,为单位向量,满足.,0a c c b b a cb a ⋅+⋅+⋅=++求解已知,0,1=++===c b a c b a 故0=++⋅++)()(c b a c b a .即0222222=⋅+⋅+⋅+++a c c b b a c b a .因此23-21222=++-=⋅+⋅+⋅)(c b a a c c b b a 3.已知M 1(1,-1,2),M 2(3,3,1)M 3(3,1,3).求与3221,M M M M 同时垂直的单位向量.解21M M =(3-1,3-(-1),1-2)=(2,4,-1)32M M =(3-3,1-3,3-1)=(0,-2,2)由于3221M M M M ⨯与3221,M M M M 同时垂直,故所求向量可取为M M M M a =)(由3221M M M M ⨯=220142--k j i=(6,-4,-4),17268)4()4(6222==-+-+=⨯知).172,172,173()4,4,6(1721--±=--±=a 4.设质量为100kg 的物体从点M1(3,1,8)沿直线移动到点M2(1,4,2),计算重力所作的功(坐标系长度单位为m ,重力方向为z 轴负方向).解21M M =(1-3,4-1,2-8)=(-2,3,-6)F=(0,0,-100×9.8)=(0,0,-980)W=F ∙21M M =(0,0,-980)∙(-2,3,-6)=5880(J).5.在杠杆上支点O 的一侧与点O 的距离为x 1的点P 1处,有一与1OP 成角1θ的力F 1作用着;在O 的另一侧与点O 的距离为x 2的点P 2处,有一与2OP 成角2θ的力F 2作用着(图8-6),问1θ,2θ,x 1,x 2,21,F F 符合怎样的条件才能使杠杆保持平衡?解如图8-6,已知有固定转轴的物体的平衡条件是力矩的代数和为零,又由对力矩正负符号的规定可得杠杆保持平衡的条件为0sin sin 222111=-θθx F x F ,即222111sin sin θθx F x F =.6.求向量),(4,3-4=a在向量)(1,2,2=b 上的投影.解236122)1,2,2()4,3,4(Pr 222==++⋅-=⋅=b b a a j b .7.设)4,1,2(),2,5,3(=-=b a,问μλ与有怎样的关系,能使b a μλ+与z 轴垂直?解b a μλ+=λ(3,5,-2)+μ(2,1,4)=(μλμλμλ42,5,23+-++).要b a μλ+与z 轴垂直,即要(b a μλ+)⊥(0,0,1),即(b a μλ+)∙(0,0,1)=0,亦即(μλμλμλ42,5,23+-++)∙(0,0,1)=0,故(μλ42+-)=0,因此μλ2=时能使b a μλ+与z 轴垂直.8.试用向量证明直径所对的圆周角是直角.证如图8-7,设AB 是圆O 的直径,C 点在圆周上,要证∠ACB=2π,只要证明0=⋅BCAC 即可.由BC AC ⋅=)()(OC BO OC AO +⋅+=BO OC OC AO BO AO ⋅+⋅+⋅=0=+⋅-⋅+OC AO OC AO .故BC AC⊥,∠ACB为直角.9.已知向量j i c k j i b k j i a 23,32-=+-=+-=和,计算:(1)b c a c b a )()(⋅-⋅(2))()(c b b a +⨯+(3)cb a ⋅⨯)(解(1)8)3,1,1()1,3,2(=-⋅-=⋅ba ,8)0,2,1()1,3,2(=-⋅-=⋅c a ,b c a c b a )()(⋅-⋅)24,8,0()3,1,1(8)0,2,1(8--=---=k i 248--=.(2)b a +=(2,-3,1)+(1,-1,3)=(3,-4,4),c b +=(1,-1,3)+(1,-2,0)=(2,-3,3),)()(c b b a +⨯+332443--=kj i k j --=--=)1,1,0(.(3)c b a ⋅⨯)(.2021311132=---=10.已知k j OBk i OA 3,3+=+=,求△OAB 的面积.解由向量积的几何意义知S △OAB⨯)1,3,3(310301--==⨯kj i OB OA,⨯191)3()3(22=+-+-=S △OAB219=11.已知),,(),,,(),,,(z y x z y x z y x c c c c b b b b a a a a ===,试利用行列式的性质证明:ba c a cbc b a ⋅⨯=⋅⨯=⋅⨯)()()(证因为,)(z yxz y xz y xc c c b b b a a a cb a =⋅⨯zyxz y x z y x a a a c c c b b b a c b =⋅⨯)(=⋅⨯b a c )(zyxz yxz y xb b b a a ac c c ,而由行列式的性质知z yxz y x z y x c c c b b b a a a z yx z y x z y x a a a c c c b b b ==zyxz y x z y x b b b a a a c c c ,故b ac a c b c b a ⋅⨯=⋅⨯=⋅⨯)()()(.12.试用向量证明不等式:332211232221232221b a b a b a b b b a a a ++≥++++,其中321321,,,,,b b b a a a 为任意实数.并指出等号成立的条件.证设向量=a (321,,a a a ),=b (321,,b b b ).由),cos(b a b a ba =⋅b a ≤,从而232221232221332211b b b a a a b a b a b a ++++≤++,当321,,a a a 与321,,b b b 成比例,即332211b a b a b a ==时,上述等式成立.1.求过点(3,0,-1)且与平面012573=-+-z y x 平行的平面方程.解所求平面与已知平面012573=-+-z y x 平行.因此所求平面的法向量可取为n=(3,-7,5),设所求平面为0573=++-D z y x .将点(3,0,-1)代入上式得D=-4.故所求平面方程为04573=-+-z y x .2.求过点M 0(2,9,-6)且与连接坐标原点及点M 0的线段OM 0垂直的平面方程.解.6,9,2(0)-=OM 所求平面与0OM 垂直,可取n=0OM ,设所求平面方程为0692=+-+D z y x .将点M 0(2,9,-6)代入上式得D=-121.故所求平面方程为0121692=--+z y x .3.求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程.解由0121111121212111=+---+----+--z y x ,得023=--z y x ,即为所求平面方程.注设M (x,y,z )为平面上任意一点,)3,2,1)(,,(==i z y x M i i i i 为平面上已知点.由,0)(31211=⨯⋅M M M M MM 即,0131313121212111=---------z z y y x x z z y y x x z z y y x x 它就表示过已知三点M i (i=1,2,3)的平面方程.4.指出下列各平面的特殊位置,并画出各平面:(1)x=0;(2)3y-1=0;(3)2x-3y-6=0;(4)x-3y=0;(5)y+z=1;(6)x-2z=0;(7)6x+5y-z=0.解(1)—(7)的平面分别如图8—8(a )—(g ).(1)x=0表示yOz 坐标面.(2)3y-1=0表示过点(0,31,0)且与y 轴垂直的平面.(3)2x-3y-6=0表示与z 轴平行的平面.(4)x-3y=0表示过z 轴的平面.(5)y+z=1表示平行于x 轴的平面.(6)x-2z=0表示过y 轴的平面.(7)6x+5y-z=0表示过原点的平面.5.求平面0522=++-z y x 与各坐标面的夹角的余弦.解平面的法向量为n=(2,-2,1),设平面与三个坐标面xOy ,yOz ,zOx 的夹角分别为321,,θθθ.则根据平面的方向余弦知,3111)2(2)1,0,0()1,2,2(cos cos 2221=⋅+-+⋅-=⋅==k n k n γθ,3213)0,0,1()1,2,2(cos cos 2=⋅⋅-=⋅==i n i n αθ3213)0,1,0()1,2,2(cos cos 3-=⋅⋅-=⋅==j n j n βθ.6.一平面过点(1,0,-1)且平行于向量)1,1,2(=a 和)0,1,1(-=b ,试求这个平面方程.解所求平面平行于向量a 和b ,可取平面的法向量)3,1,1(011112-=-=⨯=kj i b a n .故所求平面为0)1(3)0(1)1(1=+--⋅+-⋅z y x ,即043=--+z y x .7.求三平面322,02,13=++-=--=++z y x z y x z y x 的交点.解联立三平面方程.322,02,13=++-=--=++z y x z y x z y x 解此方程组得.3,1,1=-==z y x故所求交点为(1,-1,3).8.分别按下列条件求平面方程:(1)平行于xOz 面且经过点(2,-5,3);(2)通过z 轴和点(-3,1,-2);(3)平行于x 轴且经过两点(4,0,-2)和(5,1,7).解(1)所求平面平行于xOz 面,故设所求平面方程为0=+D By .将点(2,-5,3)代入,得05=+-D B ,即B D 5=.因此所求平面方程为05=+B By ,即05=+y .(2)所求平面过z 轴,故设所求平面为0=+By Ax .将点(-3,1,-2)代入,得03=+-B A ,即A B 3=.因此所求平面方程为03=+Ay Ax ,即03=+y x .(3)所求平面平行于x 轴,故设所求平面方程为0=++D Cz By .将点(4,0,-2)及(5,1,7)分别代入方程得2=+-D C 及07=++D C B .D B D C 29,2-==.因此,所求平面方程为0229=++-D z DDy ,即029=--z y .9.求点(1,2,1)到平面01022=-++zy x 的距离.解利用点),,(00o o z y x M 到平面0=+++D Cz By Ax 的距离公式222000C B A DCz By Ax d +++++=.1332211012221222=-=++-⋅+⋅+=1.求过点(4,-1,3)且平行于直线51123-==-z y x 的直线方程.解所求直线与已知直线平行,故所求直线的方向向量)5,1,2(=s ,直线方程即为531124-=+=-z y x .2.求过两点)1,2,3(1-M 和)2,0,1(2-M 的直线方程.解取所求直线的方向向量)1,2,4()12),2(0,31(21-=-----==M M s ,因此所求直线方程为112243-=+=--z y x .3.用对称式方程及参数方程表示直线.42,1=++=+-z y x z y x 解根据题意可知已知直线的方向向量112111-=kj i s ).3,1,2(-=取x=0,代入直线方程得.4,1=+=+-z y z y 解得.25,23==z y 这样就得到直线经过的一点(25,23,0).因此直线的对称式方程为.32512320-=-=--z y x 参数方程为.325,23,2t z t y t x +=+=-=注由于所取的直线上的点可以不同,因此所得到的直线对称式方程或参数方程得表达式也可以是不同的.4.求过点(2,0,-3)且与直线1253,0742=+-+=-+-z y x z y x 垂直的平面方程.解根据题意,所求平面的法向量可取已知直线的方向向量,即),11,14,16(253421-=--==kj i s n 故所求平面方程为.0)3(11)0(14)2(16=++-+--z y x 即.065111416=---z y x 5.求直线0123,09335=-+-=-+-z y x z y x 与直线01883,02322=-++=+-+z y x z y x 的夹角的余弦.解两已知直线的方向向量分别为),1,4,3(1233351-=--=k j i s ),10,5,10(1831222-=-=kj i s 因此,两直线的夹角的余弦212121),(cos cos s s s s s s ⋅== .010)5(10)1(4310154103222222=+-+-++⨯-⨯-⨯=6.证明直线72,72=++-=-+z y x z y x 与直线02,8363=--=-+z y x z y x 平行.证已知直线的方向向量分别是),15,3,9(112363),5,1,3(11212121---=---==--=kj i s k j i s 由123s s -=知两直线互相平行.7.求过点(0,2,4)且与两平面12=+zx 和23=-z y 平行的直线方程.解所求直线与已知的两个平面平行,因此所求直线的方向向量可取),1,3,2(31020121-=-=⨯=kj i n n s 故所求直线方程为.143220-=-=-z y x 注本题也可以这样解:由于所求直线与已知的两个平面平行,则可视所求直线是分别与已知平面平行的两平面的交线,不妨设所求直线为.3,2b z y a z x=-=+将点(0,2,4)代入上式,得.10,8-==b a 故所求直线为.103,82-=-=+z y z x 8.求过点(3,1,-2)且通过直线12354z y x =+=-的平面方程.解利用平面束方程,过直线12354z y x =+=-的平面束方程为,0)23(2354=-+=+=-z y y x λ将点(3,1,-2)代入上式得.2011=λ因此所求平面方程为,0)23(20112354=-+=+=-z y y x即.0592298=---z y x 9.求直线0,03=--=++z y x z y x 与平面01=+--z y x 的夹角.解已知直线的方向向量),2,4,2(111311-=--=k j is 平面的法向量).1,1,1(--=n 设直线与平面的夹角为,ϕ则,0)1()1(1)2(42)1()2()1(412),cos(sin 222222=-+-+-++-⋅-+-⋅+⋅=⋅==n s n s s n ϕ即.0=ϕ10.试确定下列各组中的直线和平面间的关系;(1)37423z y x =-+=-+和3224=--z y x ;(2)723z y x =-=和8723=+-z y x ;(3)431232--=+=-z y x 和.3=++z y x 解设直线的方向向量为s ,平面的法向量为n ,直线与平面的夹角为,ϕ且ns n s s n ⋅==),cos(sin ϕ.(1)),2,2,4(),3,7,2(--=--=ns,0)2()2(43)7()2()2(3)2()7(4)2(sin 222222=-+-+⋅+-+--⋅+-⋅-+⋅-=ϕ则.0=ϕ故直线平行于平面或在平面上,现将直线上的点A (-3,-4,0)代入平面方程,方程不成立.故点A 不在平面上,因此直线不在平面上,直线与平面平行.(2)),7,2,3(),7,2,3(-=-=n s 由于n s =或,17)2(37)2(377)2()2(33sin 222222=+-+⋅+-+⋅+-⋅-+⋅=ϕ知2πϕ=,故直线与平面垂直.(3)),1,1,1(),4,1,3(=-=n s 由于0=⋅n s 或,0111)4(131)4(1113sin 222222=++⋅-++⋅-+⋅+⋅=ϕ知,0=ϕ将直线上的点A (2,-2,3)代入平面方程,方程成立,即点A 在平面上.故直线在平面上.11.求过点(1,2,1)而与两直线1,012=-+-=+-+z y x z y x 和0,02=+-=+-z y x z y x 平行的平面的方程.解两直线的方向向量为),1,1,0(111112),3,2,1(11112121--=--=--=--=kj i s k j is取),1,1,1(11032121--=----=⨯=k j i s s n 则过点(1,2,1),以n 为法向量的平面方程为,0)1(1)2(1)1(1=-⋅--⋅+-⋅-z y x 即.0=+-z y x 12.求点(-1,2,0)在平面012=+-+z y x 上的投影.解作过已知点且与已知平面垂直的直线.该直线与平面的交点即为所求.根据题意,过点(-1,2,0)与平面012=+-+z y x 垂直的直线为,102211--=-=+z y x 将它化为参数方程,,22,1t z t y t x -=+=+-=代入平面方程得,01)()22(21=+--+++-t t t 整理得32-=t .从而所求点(-1,2,0)在平面012=+-+z y x 上的投影为(32,32,35-).13.求点P (3,-1,2)到直线042,01=-+-=+-+z y x z y x 的距离.解直线的方向向量).3,3,0(112111--=--=kj i s 在直线上取点(1,-2,0),这样,直线的方程可表示成参数方程形式.3,32,1t z t y x -=--==(1)又,过点P (3,-1,2),以)3,3,0(--=s 为法向量的平面方程为,0)2(3)1(3=--+-z y 即.01=-+z y (2)将式(1)代入式(2)得21-=t ,于是直线与平面的交点为(23,21,1-),故所求距离为.223)232()211()13(222=-++-+-=d 14.设M 0是直线L 外一点,M 是直线L 上任意一点,且直线的方向向量为s ,试证:点M 0到直线L的距离d =.证如图8-9,点M 0到直线L 的距离为d.由向量积的几何意义知s ⨯表示以M M 0,s 为邻边的平行四边形的面积.而表示以s 为边长的该平面四边形的高,即为点M 0到直线L 的距离.于是d =15.求直线0923,042=---=+-z y x z y x 在平面14=+-z y x 上的投影直线的方程.解作过已知直线的平面束,在该平面束中找出与已知平面垂直的平面,该平面与已知平面的交线即为所求.设过直线0923,042=---=+-z y x z y x 的平面束方程为,0)923(42=---++-z y x z y x λ经整理得.09)21()4()32(=--+--++λλλλz y x 由,01)21()1()4(4)32(=⋅-+-⋅--+⋅+λλλ得1113-=λ.代入平面束方程,得.0117373117=--+z y x 因此所求投影直线的方程为.14,0117373117=+-=--+z y x z y x 16.画出下列各平面所围成的立体的图形.(1);012243,1,2,0,0,0=-++=====z y x y x z y x(2).4,2,1,0,0yz y x z x =====解(1)如图8-10(a );(2)如图8-10(b ).1.一球面过原点及A (4,0,0),B (1,3,0)和C (0,0,-4)三点,求球面的方程及球心的坐标和半径.解设所求球面的方程为2222)()()(R c z b y a x =-+-+-,将已知点的坐标代入上式,得,2222R c b a =++(1),)4(2222R c b a =++-(2),)3()1(2222R c b a =+-+-(3)2222)4(R c b a =+++,(4)联立(1)(2)得,2=a 联立(1)(4)得,2-=c 将2=a 代入(2)(3)并联立得b=1,故R=3.因此所求球面方程为,9)2()1()2(222=++-+-z y x 其中球心坐标为),2,1,2(-半径为3.2.建立以点(1,3,-2)为球心,且通过坐标原点的球面方程.解设以点(1,3,-2)为球心,R 为半径的球面方程为,)2()3()1(2222R z y x =++-+-球面经过原点,故,14)20()30()10(2222=++-+-=R 从而所求球面方程为.14)2()3()1(222=++-+-z y x 3.方程0242222=++-++z y x z y x 表示什么曲面?解将已知方程整理成,)6()1()2()1(2222=++++-z y x所以此方程表示以(1,-2,-1)为球心,以6为半径的球面.4.求与坐标原点O 及点(2,3,4)的距离之比为1:2的点的全体所组成的曲面的方程,它表示怎样的曲面?解设动点坐标为(z y x ,,),根据题意有,21)4()3()2()0()0()0(222222=-+-+--+-+-z y x z y x 化简整理得.)2932()34()1()32(2222=+++++z y x 它表示以(34,1,32---)为球心,以2932为半径的球面.5.将xOz 坐标面上的抛物线x z 52=绕x 轴旋转一周,求所生成的旋转曲面的方程.解以22z y +±代替抛物线方程x z 52=中的z ,得222)(z y +±x 5=,即x z y 522=+.注xOz 面上的曲线0),(=z x F 绕x 轴旋转一周所生成的旋转曲面方程为0),(22=+±z y x F .6.将xOz 坐标面上的圆922=+z x 绕z 轴旋转一周,求所生成的旋转曲面的方程.解以22y x +±代替圆方程922=+z x 中的x ,得,9)(2222=++±z y x 即.9222=++z y x7.将xOy 坐标面上的双曲线369422=-y x分别绕x 轴及y 轴旋转一周,求所生成的旋转曲面的方程.解以22zy +±代替双曲线方程369422=-y x中的y ,得该双曲线绕x 轴旋转一周而生成的旋转曲面方程为,36)(942222=+±-z y x 即.36)(94222=+-z y x 以22zx +±代替双曲线方程369422=-y x中的x ,得该双曲线绕y 轴旋转一周而生成的旋转曲面方程为,369)(42222=-+±y z x 即.369)(4222=-+y z x 8.画出下列各方程所表示的曲面:(1);)2()2(222a y a x =+-(2);19422=+-y x (3);14922=+z x (4);02=-z y (5)22x z-=.解(1)如图8-11(a );(2)如图8-11(b );(3)如图8-11(c );(4)如图8-11(d );(5)如图8-11(e ).9.指出下列方程在平面解析几何中和在空间解析几何中分别表示什么图形:(1);2=x (2);1+=x y (3);422=+y x(4).122=-y x解(1)2=x 在平面解析几何中表示平行于y 轴的一条直线,在空间解析几何中表示与yOz 面平行的平面.(2)1+=x y在平面解析几何中表示斜率为1,y 轴截距也为1的一条直线,在空间解析几何中表示平行于z 轴的平面.(3)422=+y x在平面解析几何中表示圆心在原点,半径为2的圆,在空间解析几何中表示母线平行于z 轴,准线为0,422==+z y x 的圆柱面.(4)122=-y x在平面解析几何中表示以x 轴为实轴,y 轴为虚轴的双曲线,在空间解析几何中表示母线平行于z轴,准线为,122==-z y x 的双曲柱面.10.说明下列旋转曲面是怎样形成的:(1);1994222=++z y x (2);14222=+-z y x (3);1222=--z y x (4).)(222y x a z+=-解(1)1994222=++z y x 表示xOy 面上的椭圆19422=+y x 绕x轴旋转一周而生成的旋转曲面,或表示xOz 面的椭圆19422=+z x 绕x 轴旋转一周而生成的旋转曲面.(2)14222=+-z y x 表示xOy 面上的双曲线1422=-y x 绕y 轴旋转一周而生成的旋转曲面,或表示yOz 面的双曲线1422=+-z y 绕y 轴旋转一周而生成的旋转曲面.(3)1222=--z y x表示xOy 面上的双曲线122=-y x 绕x 轴旋转一周而生成的旋转曲面,或表示xOz 面的双曲线122=-z x 绕x 轴旋转一周而生成的旋转曲面.(4)222)(y x a z+=-表示xOz 面上的直线a x z +=或a x z +-=绕z 轴旋转一周而生成的旋转曲面,或表示yOz 面的直线a y z+=或a y z +-=绕z 轴旋转一周而生成的旋转曲面.11.画出下列方程所表示的曲面:(1);44222=++z y x(2);44222=--z y x(3).94322y x z +=解(1)如图8-12(a );(2)如图8-12(b );(3)如图8-12(c );12.画出下列各曲面所围立体的图形:(1)1,03,0,3,022=+=-=-==y x y x y x z z(在第一卦限内);(2)222222,,0,0,0R z y R y x z y x =+=+===(在第一卦限内).解(1)如图8-13所示;(2)如图8-14所示.1.画出下列曲线在第一卦限内的图形;(1);2,1==y x (2);0,422=---=yxyx z(3).,222222a z x a y x =+=+解(1)如图8-15(a );(2)如图8-15(b );(3)如图8-15(c ).2.指出下列方程组在平面解析几何中与在空间解析几何中分别表示什么图形:(1);32,15-=+=x y x y (2).3,19422==+y y x 解(1)32,15-=+=x y x y 在平面解析几何中表示两直线的交点.在空间解析几何中表示两平面的交线,即空间直线.(2)3,19422==+y y x 在平面解析几何中表示椭圆19422=+y x 与其切线3=y 的交点,即切点.在空间解析几何中表示椭圆柱面19422=+y x 与其切平面3=y 的交线,即空间直线.3.分别求母线平行于x 轴及y 轴而且通过曲线0,162222222=-+=++y z x z y x 的柱面方程.解在,162222222=-+=++y z x z y x 中消去x ,得,16322=-z y 即为母线平行于x 轴且通过已知曲线的柱面方程.在,162222222=-+=++y z x z y x 中消去y ,得,162322=+z x 即为母线平行于y 轴且通过已知曲线多的柱面方程.4.求球面9222=++z y x 与平面1=+z x 的交线在xOy 面上的投影的方程.解在1,9222=+=++z x z y x 中消去z ,得,9)1(222=-++x y x 即,82222=+-y x x它表示母线平行于z轴的柱面,故0,82222==+-z y x x 表示已知交线在xOy 面上的投影的方程.5.将下列曲线的一般方程化为参数方程:(1);,9222x y z y x ==++(2).0,4)1()1(222==+++-z z y x解(1)将x y=代入,9222=++z y x 得,9222=+z x 取,cos 23t x =则,sin 3t z =从而可得该曲线的参数方程tz t y t x sin 3,cos 23,cos 23===(t ≤0˂π2)(2)将z=0代入,4)1()1(222=+++-z y x 得,3)1(22=+-y x 取,cos 31t x =-则,sin 3t y =从而可得该曲线的参数方程0,sin 3,cos 31==+=z t y t x (t ≤0˂π2)6.求螺旋线θθθb z a y a x ===,sin ,cos 在三个坐标面上的投影曲线的直角坐标方程.解由θθsin ,cos a y a x==得,222a y x =+故该螺旋线在xOy 面上的投影曲线的直角坐标方程为,222==+z a y x 由θθb z a y ==,sin 得bza y sin =,故该螺旋线在yOz 面上的投影曲线的直角坐标方程为0,sin ==x bza y 由θθb z a x ==,cos 得,cos b za x =故故该螺旋线在yOz 面上的投影曲线的直角坐标方程为.0,cos ==y bza x 7.求上半球2220y x a z --≤≤与圆柱体a ax y x (22≤+>0)的公共部分在xOy 面和xOz 面上的投影.解如图8-16.所求立体在xOy 面上的投影即为ax y x ≤+22,而由axy x y x a z =+--=22222,得.2ax a z -=故所求立体在xOz 面上的投影为由x 轴,z 轴及曲线ax a z-=2所围成的区域.8.求旋转抛物面)40(22≤≤+=z y x z在三坐标面上的投影解联立422=+=z y x z ,得422=+y x.故旋转抛物面在xOy面上的投影为.0,422=≤+z y x 如图8-17.联立0,22=+=x y x z 得,2y z=故旋转抛物面在yOz 面上的投影为2y z=及4=z 所围成的区域.同理,联立0,22=+=y y x z 得,2x z =故旋转抛物面在xOz 面上的投影为2x z=及4=z 所围成的区域.。
2019年同济第六版高数答案(高等数学课后习题解答)3.doc

习题11-81. 将下列各周期函数展开成傅里叶级数(下面给出函数在一个周期内的表达式): (1))2121(1)(2<≤--=x x x f ;解 因为f (x )=1-x 2为偶函数, 所以b n =0(n =1, 2, ⋅ ⋅ ⋅), 而611)1(4)1(2/12210221020=-=-=⎰⎰dx x dx x a ,⎰-=21022/1cos )1(2/12dx x n x a n π 2212102)1(2cos )1(4ππn xdx n x n +-=-=⎰(n =1, 2, ⋅ ⋅ ⋅),由于f (x )在(-∞, +∞)内连续, 所以∑∞=+-+=12122cos )1(11211)(n n x n n x f ππ, x ∈(-∞, +∞).(2)⎪⎪⎩⎪⎪⎨⎧<≤-<≤<≤-=121 1210 101 )(x x x x x f ;解 21)(1212100111-=-+==⎰⎰⎰⎰--dx dx xdx dx x f a n ,⎰⎰⎰⎰-+==--1212100111cos cos cos cos )(xdx n xdx n xdx n x xdx n x f a n ππππ 2sin 2])1(1[122πππn n n n +--= (n =1, 2, ⋅ ⋅ ⋅),dx x n xdx n xdx n x xdx n x f b n ⎰⎰⎰⎰-+==--121210111sin sin sin sin )(πππππππn n n 12cos 2+-= (n =1, 2, ⋅ ⋅ ⋅). 而在(-∞, +∞)上f (x )的间断点为x =2k , 212+k , k =0, ±1, ±2, ⋅ ⋅ ⋅, 故 }s i n 2c o s 21c o s ]2s i n 2)1(1{[41)(122x n n n x n n n n x f n n πππππππ-++--+-=∑∞=(x ≠2k , 212+≠k x , k =0, ±1, ±2, ⋅ ⋅ ⋅).(3)⎩⎨⎧<≤<≤-+=30 1 03 12)(x x x x f .解 1])12([31)(313003330-=++==⎰⎰⎰--dx dx x dx x f a ,]3cos 3cos )12([313cos )(31300333⎰⎰⎰--++==dx x n dx x n x dx x n x f a n πππ])1(1[622n n --=π(n =1, 2, ⋅ ⋅ ⋅ ), ]3sin 3sin )12([313sin )(31300333⎰⎰⎰--++==dx x n dx x n x dx x n x f b n πππn n )1(6-=π(n =1, 2, ⋅ ⋅ ⋅ ),而在(-∞, +∞)上, f (x )的间断点为 x =3(2k +1), k =0, ±1, ±2, ⋅ ⋅ ⋅,故 }3sin 6)1(3cos])1(1[6{21)(1122∑∞=+-+--+-=n n n x n n x n n x f ππππ,(x ≠3(2k +1), k =0, ±1, ±2, ⋅ ⋅ ⋅).2. 将下列函数分别展开成正弦级数和余弦级数:(1)⎪⎩⎪⎨⎧≤≤-<≤=lx x l l x x x f 2l20 )(; 解 正弦级数:对f (x )进行奇延拓, 则函数的傅氏系数为 a 0=0(n =0, 1, 2, ⋅ ⋅ ⋅),2sin 4]sin )(sin [22221210ππππn n l dx l x n x l dx l x n x l b l n =-+=⎰⎰(n =1, 2, ⋅ ⋅ ⋅ )故 ∑∞==122sin 2sin14)(n l x n n nl x f πππ, x ∈[0, l ].余弦级数:对f (x )进行偶延拓, 则函数的傅氏系数为2])([2212100l dx x l xdx l a l =-+=⎰⎰,⎰⎰-+=l n dx l x n x l dx l x n x l a 21210]cos )(cos [2ππ])1(12cos2[222n n n l ---=ππ(n =1, 2, ⋅ ⋅ ⋅ )b n =0(n =1, 2, ⋅ ⋅ ⋅ ),故 lx n n n l l x f n n πππcos ])1(12cos2[124)(122∑∞=---+=, x ∈[0, l ].(2)f (x )=x 2(0≤x ≤2).解 正弦级数:对f (x )进行奇延拓, 则函数的傅氏系数为 a 0=0(n =0, 1, 2, ⋅ ⋅ ⋅),]1)1[()(168)1(2sin2231202--+-==+⎰n n n n n dx x n x b πππ,故 2sin }]1)1[()(168)1{()(131x n n n x f n n n πππ∑∞=+--+-=2sin}]1)1[(2)1({811x n n n n n n ππ∑∞=+--+-=, x ∈[0, 2).余弦级数:对f (x )进行偶延拓, 则函数的傅氏系数为38222020==⎰dx x a 2202)(16)1(2cos22ππn dx x n x a n n -==⎰(n =1, 2, ⋅ ⋅ ⋅),b n =0(n =1, 2, ⋅ ⋅ ⋅),故 2cos)(16)1(34)(12x n n x f n n ππ∑∞=-+=2cos)1(1634122x n n n n ππ∑∞=-+=, x ∈[0, 2].总习题十一 1. 填空: (1)对级数∑∞=1n n u , 0lim =∞→n n u 是它收敛的________条件, 不是它收敛的________条件; 解 必要; 充分.(2)部分和数列{s n }有界是正项级数∑∞=1n n u 收敛的________条件; 解 充分必要. (3)若级数∑∞=1n n u 绝对收敛, 则级数∑∞=1n n u 必定________; 若级数∑∞=1n n u 条件收敛, 则级数∑∞=1||n n u 必定________. 解 收敛; 发散.2. 判定下列级数的收敛性: (1)∑∞=11n n nn ; 解 因为11lim 11lim==∞→∞→n n n n nn n n ,而调和级数∑∞=11n n发散, 故由比较审敛法知, 级数发散. (2)∑∞=1222)!(n nn ;解 因为∞==⋅++=∞→∞→+∞→222221lim )!(2)1(2])!1[(lim lim n n n n n u u n n n n n , 故由比值审敛法知, 级数发散.(3) ∑∞=1223cos n n n n π; 解 因为n n n n n 223cos 2<π, 12121lim 2lim <==∞→∞→n n n n n n n 所以由根值审敛法, 级数∑∞=12n n 收敛; 由比较审敛法, 级数∑∞=1223cos n nn n π收敛. (4)∑∞=110ln 1n n;解 因为∞==∞→∞→nn n u n n n 10ln lim 1lim , 而调和级数∑∞=11n n 发散, 故由比较审敛法知, 原级数发散. 提示: ∞===⋅⋅⋅==⋅=∞→∞→∞→∞→∞→xx x xx x x x x x x x x x 11lim !101ln lim !101 ln lim 1011ln 101lim ln lim 9910 (5)∑∞=1n s n na (a >0, s >0). 解 因为 a n a n a sn n ns n n ==∞→∞→)(lim lim , 故由根值审敛法知, 当a <1时级数收敛, 当a >1时级数发散. 当a =1时, 原级数成为∑∞=11n s n, 这是p =s 的p -级数, 当s >1时级数收敛, 当s ≤1时级数发散. 3. 设正项级数∑∞=1n n u 和∑∞=1n n v 都收敛, 证明级数∑∞=+12)(n n n v u 与收敛. 证明 因为∑∞=1n n u 和∑∞=1n n v 都收敛, 所以0lim =∞→n n u , 0lim =∞→n n v . 又因为0)2(lim 2lim 2=+=+∞→∞→n n n nn n n n v u u v u u , 0lim lim 2==∞→∞→n n n nn v v v ,所以级数∑∞=+12)2(n n n n v u u 和级数∑∞=12n n v 都收敛, 从而级数∑∑∞=∞=+=++12122)(])2[(n n n n n n n n v u v v u u也是收敛的.4. 设级数∑∞=1n n u 收敛, 且1lim =∞→nnn u v , 问级数∑∞=1n n v 是否也收敛?试说明理由. 解 级数∑∞=1n n v 不一定收敛. 当∑∞=1n n u 和∑∞=1n n v 均为正项级数时, 级数∑∞=1n n v 收敛, 否则未必. 例如级数∑∞=-11)1(n n 收敛, 但级数∑∞=+-1]11)1[(n n n 发散, 并且有11)1(11)1(lim=-+-∞→nn n n . 5. 讨论下列级数的绝对收敛性与条件收敛性: (1)∑∞=-11)1(n p n n ; 解 ∑∑∞=∞==-111|1)1(|n p n p nnn 是p 级数. 故当p >1时级数∑∞=11n p n 是收敛的, 当p ≤1时级数∑∞=11n p n 发散. 因此当p >1时级数∑∞=-11)1(n p n n 绝对收敛. 当0<p ≤1时, 级数∑∞=-11)1(n p n n 是交错级数, 且满足莱布尼茨定理的条件, 因而收敛, 这时是条件收敛的.当p ≤0时, 由于01)1(lim ≠-∞→p nn n , 所以级数∑∞=-11)1(n p n n 发散.综上所述, 级数∑∞=-11)1(n p n n 当p >1时绝对收敛, 当0<p ≤1时条件收敛, 当p ≤0时发散.(2)∑∞=+++-1111sin )1(n n n n ππ; 解 因为1111|1s i n )1(|+++≤+-n n n n πππ, 而级数∑∞=+111n n π收敛, 故由比较审敛法知级数|1sin )1(|111∑∞=+++-n n n n ππ收敛, 从而原级数绝对收敛.(3)∑∞=+-11ln )1(n n n n ; 解 因为1ln )11ln(lim 1ln lim 1|1ln )1(|lim ==+=+=+-∞→∞→∞→e n n n n n n n n n n n n , 而级数∑∞=11n n发散, 故由比较审敛法知级数|1ln)1(|1∑∞=+-n n n n 发散, 即原级数不是绝对收敛的.另一方面, 级数∑∞=+-11ln )1(n nn n 是交错级数, 且满足莱布尼茨定理的条件, 所以该级数收敛, 从而原级数条件收敛.(4)∑∞=++-11)!1()1(n n n nn . 解 令1)!1()1(++-=n n n n n u . 因为11)11(112lim )1(12lim)!1()1()!2(lim ||||lim 121<=+⋅++=+⋅++=+⋅++∞→∞→++∞→+∞→e nn n n n n n n n n n u u n n n n n n n n n n ,故由比值审敛法知级数|)!1()1(|11∑∞=++-n n n n n 收敛, 从而原级数绝对收敛.6. 求下列级限:(1)∑=∞→+nk k k n k n 12)11(311lim ;解 显然∑=+=nk k k n k s 12)11(31是级数∑∞=+12)11(31n n n n 的前n 项部分和.因为13)11(31lim )11(31lim 2<=+=+∞→∞→e n n n n nn n n , 所以由根值审敛法, 级数∑∞=+12)11(31n n n n 收敛, 从而部分和数列{s n }收敛.因此01lim )11(311lim 12=⋅=+∞→=∞→∑n n nk k k n s n k n .(2)])2( 842[lim 312719131n n ⋅⋅⋅⋅⋅∞→.解n n nn3 27392313127191312)2( 842+⋅⋅⋅+++=⋅⋅⋅⋅⋅.显然n n n s 3 2739231+⋅⋅⋅+++=是级数∑∞=13n n n 的前n 项部分和.设∑∞=-=11)(n n nx x S , 则210)1(1]111[][])([)(x x x dx x S x S n n x-='--='='=∑⎰∞=. 因为43)311(131)31(31)31(3132111=-⋅===∑∑∞=-∞=S n n n n n n , 所以43lim =∞→n n s , 从而4331271913122lim ])2( 842[lim ==⋅⋅⋅⋅⋅∞→∞→n n s n nn .7. 求下列幂级数的收敛域:(1)∑∞=+153n n n n x n ; 解 51)53(5)53(31lim 53153lim ||lim 111=++⋅+=+⋅++=∞→++∞→+∞→n n n n n n n n n n n n n n n a a , 所以收敛半径为51=R . 因为当51=x 时, 幂级数成为]1)53[(11+∑∞=n n n , 是发散的;当51-=x 时, 幂级数成为]1)53[()1(1+-∑∞=n n n n , 是收敛的, 所以幂级数的收敛域为)51 ,51[-. (2)∑∞=+12)11(n n n x n ;解 n n n x n u 2)11(+=, 因为||||)11(lim ||lim x e x nu n n n n n =+=∞→∞→, 由根值审敛法, 当e |x |<1, 即ex e 11<<-时, 幂级数收敛; 当e |x |>1, 时幂级数发散. 当e x 1-=时, 幂级数成为∑∞=+1)1()11(2n n n e n ; 当e x 1=时, 幂级数成为∑∞=+-1)1()11()1(2n n n n e n .因为21)1ln(lim 11)11ln(lim ])11ln([lim 2022-=-+=-+=-++→+∞→+∞→t t t x x x x x x t x x , 所以 0lim )1()11(lim 21)11ln(22≠==+--+∞→∞→e ee n n n n n n n n , 因此级数∑∞=+-1)1()11()1(2n n n n e n 和∑∞=+1)1()11(2n n n e n 均发散, 从而收敛域为)1 ,1(e e -. (3)∑∞=+1)1(n n x n ; 解u n =n (x +1)n . 因为 |1||1|1lim ||lim 1+=++=∞→+∞→x x nn u u n n n n , 根据比值审敛法, 当|x +1|<1, 即-2<x <0时, 幂级数收敛; 当|x +1|>1时, 幂级数发散.又当x =0时, 幂级数成为∑∞=1n n , 是发散的; 当x =-2时, 幂级数成为∑∞=-1)1(n n n , 也是发散的, 所以幂级数的收敛域为(-2, 0). (4)∑∞=122n n n x n .解 n n n x n u 22=. 因为 221121221lim ||lim x x n n u u n n n n n n =⋅⋅+=+∞→+∞→, 根据比值审敛法, 当1212<x , 即22<<-x 时, 幂级数收敛; 当1212>x 时, 幂级数发散. 又当2±=x 时, 幂级数成为∑∞=1n n , 是发散的, 所以收敛域为)2 ,2(-.8. 求下列幂级数的和函数: (1)∑∞=--1)1(2212n n n x n ;解 设幂级数的和函数为S (x ), 则])2(2[]21[])([)(1121120'='='=∑∑⎰∞=-∞=-n n n n xx x x dx x S x S)12( )2(2]2112[22222<-+='-⋅=x x x x x , 即 )22( )2(2)(222<<--+=x x x x S . (2)∑∞=----112112)1(n n n xn ; 解 设幂级数的和函数为S (x ), 则 )1( arctan 11)1()()(20212210<=+=-='=⎰⎰∑⎰∞=--x x dx x xdx x S x S xx n n n x.因为当x =±1时, 幂级数收敛, 所以有 S (x )=arctan x (-1≤x ≤1). (3)∑∞=-1)1(n n x n ; 解 设幂级数的和函数为S (x ), 则 ])1()[1()1()1()1()(1111'--=--=-=∑∑∑∞=∞=-∞=n n n n n nx x x n x x n x S)1|1(| )2(1])1(11)[1(])1()1)[(1(211<---='----='---=∑∞=-x x x x x x x x x n n , 即 )20( )2(1)(2<<--=x x x x S .(4)∑∞=+1)1(n n n n x . 解 易知幂级数的收敛域为[-1, 1].设幂级数的和函数为S (x ), 则当x ≠0时∑∑∞=+∞=+=+=111)1(11)1(1)(n n n n x n n x x n n x Sdx dx x x dx x n x x x n n x n n ][111001101⎰⎰∑⎰∑∞=-∞===dx x x dx dx x x x x x ⎰⎰⎰--=-=000)1ln(1]11[1 )]1ln()1ln([1x x x x x-----= )1ln(11x xx --+=, x ∈[-1, 0)⋃(0, 1], 又显然S (0)=0, 因此⎪⎩⎪⎨⎧=⋃-∈--+=0 0]1 ,0()0 ,1[ )1ln(11)(x x x xx x S .9. 求下列数项级数的和: (1)∑∞=12!n n n ; 解 ∑∑∑∑∞=∞=∞=∞=+-=+-=11112!!)1(!)1(!n n n n n n n n n n n n n n n .因为n n xx n e ∑∞==1!1, 两边求导得11!-∞=∑=n n x x n n e , 再求导得22!)1(-∞=∑-=n n x x n n n e , 因此x x n n n n n n n n n n e e x x n n x n n n x x n n x n n n x n n +=+-=+-=∑∑∑∑∑∞=∞=-∞=∞=∞=221221112!!)1(!!)1(!,从而 e S n n n 2)1(!12==∑∞=. (2)∑∞=++-0)!12(1)1(n n n n . 解 ∑∑∑∞=∞=∞=+-+++-=++-000)!12(1)1(21)!12(12)1(21)!12(1)1(n n n n n nn n n n n 1sin 211cos 21)!12(1)1(21)!2(1)1(2100+=+-+-=∑∑∞=∞=n n n n n n . 提示: ∑∞=++-=012)!12(1)1(sin n n nx n x , ∑∞=++-=02)!12(12)1(cos n n n x n n x .10. 将下列函数展开成x 的幂级数: (1))1ln(2++x x ;解 ⎰⎰+='++=++xxdx x dx x x x x 0202211])1[ln()1ln(, 因为 ∑∞=---+=+=+122122!)!2(!)!12()1(1)1(11n n x n n x x , |x |≤1,故 ∑∞=++--+=++1122)12(!)!2(!)!12()1()1ln(n n n x n n n x x x (-1≤x ≤1).(2)2)2(1x -.解 ∑∞='='-='-=-02])2([21)211(21)21()2(1n n x x x x ∑∑∞=-+∞=+='=111012]21[n n n n n n x n x (-2≤x ≤2). 11. 设f (x )是周期为2π的函数, 它在[-π, π)上的表达式为 ⎩⎨⎧∈-∈=) ,0[ )0 ,[ 0)(ππx e x x f x. 将f (x )展开成傅里叶级数. 解 πππππππ11)(10-===⎰⎰-e dx e dx x f a x ,n n xn a n e nxdx e nxdx x f a 201)1(cos 1cos )(1---===⎰⎰-πππππππ, 即 ππ)1(1)1(2+--=n e a n n (n =1, 2, ⋅ ⋅ ⋅ ), ⎰⎰==-πππππ0sin 1sin )(1nxdx e nxdx x f b x nn x na nxdx e n -=-=⎰ππ0cos 1)((n =1, 2, ⋅ ⋅ ⋅ ).因此 ∑∞=-+--+-=12)sin (cos )1(1)1(21)(n n x n nx n e e x f ππππ (-∞<x <+∞且x ≠n π, n =0, ±1, ±2, ⋅ ⋅ ⋅).12. 将函数 ⎩⎨⎧≤<≤≤=πx h h x x f 00 1)( 分别展开成正弦级数和余弦级数.解 若将函数进行奇延拓, 则傅里叶系数为 a n =0(n =0, 1, 2, ⋅ ⋅ ⋅), ππππn nh nxdx nxdx x f b h n )cos 1(2sin 2sin )(200-===⎰⎰. 因此, 函数展开成正弦级数为∑∞=-=1sin cos 12)(n nx nnh x f π, x ∈(0, h )⋃(h , π),当x =h 时, 21)(=h f . 若将函数进行偶延拓, 则傅里叶系数为ππππh dx dx x f a h 22)(2000===⎰⎰, ππππn nh nxdx nxdx x f a hn sin 2cos 2cos )(200===⎰⎰(n =1, 2, ⋅ ⋅ ⋅), b n =0(n =1, 2, ⋅ ⋅ ⋅),.因此, 函数展开成余弦级数为∑∞=+=1cos sin 2)(n nx nnh h x f ππ, x ∈[0, h )⋃(h , π), 当x =h 时, 21)(=h f .总习题十二1. 填空:(1)xy '''+2x 2y '2+x 3y =x 4+1是______阶微分方程;解 是3阶微分方程.(2)若M (x , y )dx +N (x , y )dy =0是全微分方程, 则函数M 、N 应满足______;解 xN y M ∂∂=∂∂. (3)与积分方程⎰=xx dx y x f y 0),(等价的微分方程初值问题是______; 解 方程两边对x 求导得y '=f (x , y ). 显然当x =x 0时, y =0.因此与积分方程等价的微分方程初值问题是y '=f (x , y ), 0|0==x x y .(4)已知y =1、y =x 、y =x 2是某二阶非齐次线性微分方程的三个解, 则该方程的通解为______.解 容易证明非齐次线性微分方程的任意两个解的差是对应齐次线性微分方程的的解. 因此y 1=x -1和y 2=x 2-1都是对应齐次线性微分方程的的解. 显然y 1与y 2是线性无关. 所以非齐次线性微分方程的通解为y =C 1(x -1)+C 2(x 2-1)+1.2. 求以下列各式所表示的函数为通解的微分方程:(1)(x +C )2+y 2=1(其中C 为任意常数);解 将等式变形21y C x -±=+,两边对x 求导得211yy y -'±=, 从而1-y 2=y 2y '2, 即所求微分方程为y 2(1+y '2)=1.(2)y =C 1e x +C 2e 2x (其中C 1、C 2为任意常数).解 两边对x 求导得y '=C 1e x +2C 2e 2x =y +C 2e 2x ,即 y '=y +C 2e 2x ,⋅ ⋅ ⋅(1)再求导得y ''=y '+2C 2e 2x . ⋅ ⋅ ⋅(2)(2)-(1)⨯2得y ''-2y '=y '-2y ,即所求微分方程为y ''-3y '+2y =0.3. 求下列微分方程的通解:(1)xy y y x 2=+';解 将方程变形为xy x y y 1212=+', 即x y x y 121)(=+'. 其通解为)(1)1(2121C x xC dx e x e y dx x dx x +=+⎰⎰=⎰-, 即原方程的通解为xC x y 2)(+=. (2) xy 'ln x +y =ax (ln x +1);解 将方程变形为)ln 11(ln 1xa y x x y +=+', 其通解为)ln (ln 1])ln 11([ln 1ln 1C x ax x C dx e x a e y dx x x dx x x +=+⎰+⎰=⎰-, 即原方程的通解为xC ax y ln +=. (3))(ln 2x y y dx dy -=; 解 将方程变形为yy x y dy dx ln 22=+, 其通解为)21ln (1)ln 2(22222C y y y y C dy e y y e x dy y dy y +-=+⎰⎰=⎰-, 即原方程的通解为221ln yCy x +-=. (4)033=-+y x xy dxdy ; 解 将方程变形为 3231x xy dxdy y =+-, 即32222)(x xy dx y d -=---, 其通解为)())2([22222322C e e x e C dx e x e y x x x xdx xdx ++=+⎰-⎰=----⎰,即原方程的通解为1222++=-x Ce y x .(5)022=+-++yx xdy ydx ydy xdx ; 解 因为)2(22y x d y d y x d x +=+, 2222)(11y x d y y d x yx y x x d y y d x -⋅+=+- )(a r c t a n )()(112y x d y x d y x =+=,所以原方程可写成0)a r c t a n 22(22=++yx y x d , 从而原方程的通解为C yx y x =++a r c t a n 222.(6) yy ''-y '2-1=0;解 令y '=p , 则dy dp py ='', 原方程化为 012=--p dydp yp , 或 yp y dy p d 22)(22=-, 其通解为1)()2(222222-=+-=+⎰⎰=--⎰Cy C y y C dy e y e p dy y dy y . 于是 12-±='Cy y , 即dx y C dy ±=-1)(21(C =C 12), 积分得 2211)1)(l n (C x y C y C +±=-+, 化简得原方程的通解)(ch 121C x C y +±=. (7) y ''+2y '+5y =sin2x ;解 齐次方程y ''+2y '+5y =0的特征方程为r 2+2r +5=0,其根为r 1, 2=-1±2i .因为f (x )=sin2x , λ+ωi =2i 不是特征方程的根,所以非齐次方程的特解应设为y *=A cos2x +B sin2x ,代入原方程得(A +2B )cos2x +(B -4A )sin2x =sin2x , 比较系数得174-=A , 171=B , x x y 2sin 1712cos 174*+-=. 因此原方程的通解为x x x C x C e y x 2s i n 1712cos 174)2sin 2cos (21+-+=-. (8) y '''+y ''-2y '=x (e x +4);解 齐次方程y '''+y ''-2y '=0的特征方程为r 3+r 2-2r =0,其根为r 1=0, r 2=1, r 3=2.齐次方程y '''+y ''-2y '=0的通解为y =C 1+C 2e x +C 3e -2x .原方程中f (x )=f 1(x )+f 2(x ), 其中f 1(x )=xe x , f 2(x )=4x .对于方程y '''+y ''-2y '=xe x , 因为λ=1是特征方程的根, 故其特解可设为 y 1*=x (Ax +B )e x ,代入y '''+y ''-2y '=xe x 得(6Ax +8A +3b )e x =xe x , 比较系数得61=A , 94-=B , 故x e x x y )9461(*1-=. 对于方程y '''+y ''-2y '=4x , 因为λ=0是特征方程的根, 故其特解可设为 y 2*=x (Cx +D ),代入y '''+y ''-2y '=4x 得-4Cx +2C -2D =4x ,比较系数得C =-1, D =-1, 故y 2*=x (-x -1).因此原方程的通解为x x e x x e C e C C y x x x ---+++=-222321)9461(.(9) (y 4-3x 2)dy +xydx =0;解 将原方程变形为323y x y dy dx x -=-, 或32226)(y x ydy x d -=-, 其通解为)(])2([266362C y y C dy e y e x dy y dy y +=+⎰-⎰=--⎰, 即原方程的通解为x 2=y 4+Cy 6.(10)y x x y +=+'2.解 令y x u +=2, 则y =u 2-x 2, x dxdu u dx dy 22-=, 故原方程化为u x dx du u =-2, 即21)(21+=u x dx du . 这是齐次方程, 因此令z xu =, 则u =xz , dx dz x z dx du +=, 则上述齐次方程化为 2121+=+z dx dz x z , 即)112(21---=zz dx dz x , 分离变量得x dx z z zdz 21122-=--, 积分得 123ln 21)132ln(61C x z z +-=+-, 即 2z 3-3z 2+1=Cx -3)(16C e C =. 将xu z =代入上式得 2u 3-3xu 2+x 3=C , 再代入y x u +=2, 得原方程的通解C xy x y x =--+32)(2332.4. 求下列微分方程满足所给初始条件的特解:(1) y 3dx +2(x 2-xy 2)dy =0, x =1时y =1;解 原方程变形为2322x yx y dy dx -=-, 即 31222yx y dy dx x -=---, 或 31122)(yx y dy x d =+--, 其通解为)ln 2(1)2(22321C y y C dy e y e x dy +=+⎰⎰=⎰--, 即原方程的通解为y 2=x (2ln y +C ).由y |x =1=1, 得C =1. 故满足所给初始条件的特解为y 2=x (2ln y +1).(2) y ''-ay '2=0, x =0时y =0, y '=-1;解 令y '=p , 则原方程化为02=-ap dxdp .分离变量得a d x p dp =2, 两边积分得11C ax p +=-, 即11C ax y +-='. 代入初始条件y '(0)=-1得C 1=1,故 11+-='ax y . 方程两边积分得2)1l n (1C ax ay ++-=. 代入初始条件y (0)=0得C 2=0.因此满足所给初始条件的特解为)1ln(1+-=ax ay .(3) 2y ''-sin2y =0, x =0时2π=y , y '=1; 解 令y '=p , 则原方程化为02s i n 2=-y dydp p . 分离变量得2pdp =sin2ydy ,两边积分得122c o s 21C y p +-=. 代入初始条件y '(0)=1得211=C , 因而 y y y 22s i n 212c o s 21=+-=', 即 y '=sin y .分离变量得dx ydy =sin , 两边积分得2c o s 1c o s 1ln 21C x yy +=+-.代入初始条件2)0(π=y 得C 2=0. 因此满足所给初始条件的特解为yy x cos 1cos 1ln 21+-=. (4) y ''+2y '+y =cos x , x =0时y =0, 23='y . 解 齐次方程y ''+2y '+y =0的特征方程为r 2+2r +1=0,其根为r 1, 2=-1.齐次方程y ''+2y '+y =0的通解为y =(C 1+C 2x )e -x .因为f (x )=cos x , λ+ωi =i 不是特征方程的根, 所以非齐次方程的特解应设为 y *=A cos x +B sin x ,代入原方程得-2A sin x +2B cos x =cos x ,比较系数得A =0, 21=B . 故x y sin 21*=. 从而原方程的通解为 x e x C C y x s i n 21)(21++=- . 将初始条件代入通解得⎪⎩⎪⎨⎧=++-=23210211C C C , 解之得C 1=0, C 2=1.因此满足所给初始条件的特解为x xe y x sin 21+=-. 5. 已知某曲线经过点(1, 1), 它的切线在纵轴上的截距等于切点的横坐标, 求它的方程.解 设点(x , y )为曲线上任一点, 则曲线在该点的切线方程为Y -y =y '(X -x ),其在纵轴上的截距为y -xy ', 因此由已知有y -xy '=x , 即11-=-'y xy . 这是一个一阶线性方程, 其通解为)ln (])1([11C x x C dx e e y dx x dx x +-=+⎰-⎰=⎰-, 即方程的通解为y =x (C -ln x ).由于曲线过点(1, 1), 所以C =1.因此所求曲线的方程为y =x (1-ln x ).6. 已知某车间的容积为30⨯30⨯6m 3, 其中的空气含0.12%的CO 2(以容积计算). 现以含CO 20.04%的新鲜空气输入, 问每分钟应输入多少, 才能在30min 后使车间空气中CO 2的含量不超过0.06%?(假定输入的新鲜空气与原有空气很快混合均匀后, 以相同的流量排出).解 设每分钟应输入的空气为a m 3, t 时刻车间中CO 2的浓度为x (t ), 则车间中CO 2的含量(以体积计算)在t 时刻经过dt min 的改变量为30⨯30⨯6 dx =0.0004adt -axdt ,分离变量得dt a dx x 54000004.01-=-, 由于x >0.0004, 故两边积分得C t a x ln 5400)0004.0ln(+-=-, 即 t a Ce x 54000004.0-+=.由于开始时车间中的空气含0.12%的CO 2, 即当t =0时, x =0.0012, 代入上式得C =0. 0008. 因此t a e x 54000008.00004.0-+=.由上式得0008.0004.0ln 5400--=x t a . 由于要求30min 后车间中CO 2的含量不超过0.06%, 即当t =30时, x ≤0.0006, 将t =30, x =0. 0006代入上式得a =180ln 4≈250.因为054000008.05400<-='-t ae x , 所以x 是a 的减函数, 考试当a ≥250时可保证x ≤0.0006.因此每分钟输入新鲜空气的量不得小于250m 3.7. 设可导函数ϕ(x )满足1s i n )(2c o s )(0+=+⎰x t d t t x x xϕϕ, 求ϕ(x ).解 在等式两边对x 求导得ϕ'(x )cos x -ϕ(x )sin x +2ϕ(x )sin x =1,即 ϕ'(x )+tan x ϕ(x )=sec x .这是一个一阶线性方程, 其通解为)s e c ()(t a n t a n C dx xe e x xdx xdx +⎰⎰=⎰-ϕ=cos x (tan x +C )=sin x +C cos x .在已知等式中, 令x =0得ϕ(0)=1, 代入通解得C =1. 故ϕ(x )=sin x +cos x . 8. 设函数u =f (r ), 222z y x r ++=在r >0内满足拉普拉斯(Laplace)方程0222222=∂∂+∂∂+∂∂z u y u x u , 其中f (r )二阶可导, 且f (1)=f '(1)=1. 试将拉普拉斯方程化为以r 为自变量的常微分方程, 并求f (r ).解 因为rx z y x x x r =++=∂∂22222, 所以 )()(r f rx x r r f x u '=∂∂'=∂∂, )()()()(22322222r f r x r f r x r x r r f r x r f r x r x r x u '+'-=∂∂'+'∂∂-=∂∂. 同理可得)()(2232222r f ry r f r y r y u '+'-=∂∂, )()(2232222r f r z r f r z r z u '+'-=∂∂. 于是 )()(3222232222222222r f rz y x r f r z y x r z u y u x u '+++'---=∂∂+∂∂+∂∂ 22322)()(2dr u d dr du r r f r f rr+='+'=. 因此拉普拉斯方程化为0222=+dr u d dr du r , 即0222=+drdu r dr u d . 令)(r p drdu =, 则以上方程进一步变成 02=+dr dp p r , 即02=+p rdr dp , 其通解为2121rC e C p dr r =⎰=-, 即21r C dr du =. 由于f '(1)=1, 即r =1时1=drdu , 所以C 1=1, 21r dr du =. 在方程21r dr du =的两边积分得21C ru +-=. 又由于f (1)=1, 即r =1时u =1, 所以C 2=2, 从而21+-=r u , 即21)(+-=rr f .9. 设y 1(x )、y 2(x )是二阶齐次线性方程y ''+p (x )y '+q (x )y =0的两个解, 令)()()()()()()()()(21212121x y x y x y x y x y x y x y x y x W '-'=''=, 证明:(1)W (x )满足方程W '+p (x )W =0; 证明 因为y 1(x )、y 2(x )都是方程y ''+p (x )y '+q (x )y =0的解, 所以 y 1''+p (x )y 1'+q (x )y 1=0, y 2''+p (x )y 2'+q (x )y 2=0, 从而 W '+p (x )W =(y 1'y 2'+ y 1y 2''- y 1''y 2- y 1'y 2')+p (x )( y 1y 2'- y 1'y 2) =y 1[y 2''+p (x )y 2']- y 2[y 1''+p (x )y 1'] =y 1[-q (x )y 2]- y 2[-q (x )y 1] =0,即W (x )满足方程W '+p (x )W =0.(2)⎰=-x x dt t p e x W x W 0)(0)()(. 证明 已知W (x )满足方程 W '+p (x )W =0,分离变量得dx x p WdW )(-=. 将上式两边在[x 0, x ]上积分, 得 ⎰-=-x x dt t p x W x W 0)()(ln )(ln 0, 即 ⎰=-x x dt t p ex W x W 0)(0)()(.。
高等数学(同济第七版)课后答案解析

(3)相同、因为定义域、对应法则均相同.
(4)不同、因为定义域不同.
际3.设
求。(寻)“仔)・9(-骨)顽-2).并作出函数L)的囲形.
TT
S,,,T i
1(、)的,形如图丨・1所示.
S4.试让F列陥数在指定区间内的单Wi性:
第一章函故与扱限
(2)j = x+In n(0, *8).证(I) y=/(^)=rL-=-丨+宀(-8』).
F(-T)=/|(-X)+/2(F=/|(对+人(x) =F(x),
枚,(大)为偶函数.
设幻(T),&2(愛)均为奇函数.则幻(-工)=-们(*),幻(-X)=-g2(■*)•令。(])=g]())+&《]),于是
G(-X)=X|(-X)+评2(-X)=■•幻(x) -&2(1)=f),
故c(x)为奇函数.
解因为AC= 20= 15,所以,Ali= /^后IF=25.
Ih20 <2-15 <20・25可知,点P、Q在斜边AH上相讷.
令a + 2% = 15+20 + 25J!;x = 20.即当x= 2()时•点七。相遇.因此•所求函數的定义域为(0.20).
(I )当Ov — vIO时,点P在CR上•点Q在CA上(图1-5).
洎6.&卜血所考虑的函救都是定义在区间U)上的.i止明:
(1)两个偶函数的和是偶函数.两个奇函数的和是奇函数;
(2)两个偶函数的乘枳是偶函数,两个奇函数的乘枳是偶函数,偶函数与奇丽数的乗积是奇函数.
证(1)设J|(X)./2(X)均为偶函数,则乂(-X)”('),(-X)=6(x).今/⑴=/|(^)+/i(x),于是
同济大学数学系《高等数学》(第7版)(上册)-课后习题详解-第二章 导数与微分【圣才出品】

第二章 导数与微分2.2 课后习题详解习题2-1 导数概念1.设物体绕定轴旋转,在时间间隔[0,t]上转过角度θ,从而转角θ是t的函数:θ=θ(t).如果旋转是匀速的,那么称为该物体旋转的角速度.如果旋转是非匀速的,应怎样确定该物体在时刻t 0的角速度?解:物体在时间间隔上的平均角速度在时刻t 0的角速度2.当物体的温度高于周围介质的温度时,物体就不断冷却.若物体的温度T 与时间t 的函数关系为T =T(t),应怎样确定该物体在时刻t 的冷却速度?解:物体在时间间隔上平均冷却速度[,]t t t +∆在时刻t 的冷却速度3.设某工厂生产x件产品的成本为函数C(x)称为成本函数,成本函数C(x)的导数在经济学中称为边际成本.试求(1)当生产100件产品时的边际成本;(2)生产第101件产品的成本,并与(1)中求得的边际成本作比较,说明边际成本的实际意义.即生产第101件产品的成本为79.9元,与(1)中求得的边际成本比较,可以看出边际成本的实际意义是近似表达产量达到x单位时再增加一个单位产品所需的成本.4.设f(x)=10x2,试按定义求.解:5.证明证:6.下列各题中均假定存在,按照导数定义观察下列极限,指出A表示什么:以下两题中给出了四个结论,从中选出一个正确的结论:7.设则f(x)在x=1处的( ).A.左、右导数都存在B.左导数存在,右导数不存在C.左导数不存在,右导数存在D.左、右导数都不存在【答案】B【解析】 故该函数左导数存在,右导数不存在.8.设f(x)可导,,则f(0)=0是F(x)在x=0处可导的( ).A.充分必要条件B .充分条件但非必要条件C .必要条件但非充分条件D .既非充分条件又非必要条件【答案】A 【解析】 当f(0)=0时,,反之当时,f(0)=0,为充分必要条件.9.求下列函数的导数:10.已知物体的运动规律为s =t 3m ,求这物体在t =2s 时的速度.解:11.如果f(x)为偶函数,且f '(0)存在,证明f '(0)=0.证:f(x)为偶函数,得.因为所以f '(0)=0.。
(免费下载)第六版同济大学高等数学课后答案详解

同济六版高等数学课后答案全集第一章习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A \B 及A \(A \B )的表达式.解 A ⋃B =(-∞, 3)⋃(5, +∞),A ⋂B =[-10, -5),A \B =(-∞, -10)⋃(5, +∞),A \(A \B )=[-10, -5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B )C =A C ⋃B C .证明 因为x ∈(A ⋂B )C ⇔x ∉A ⋂B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ⋃B C , 所以 (A ⋂B )C =A C ⋃B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明(1)f (A ⋃B )=f (A )⋃f (B );(2)f (A ⋂B )⊂f (A )⋂f (B ).证明 因为y ∈f (A ⋃B )⇔∃x ∈A ⋃B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B )⇔ y ∈f (A )⋃f (B ),所以 f (A ⋃B )=f (A )⋃f (B ).(2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ),所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明:(1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )),所以 f -1(f (A ))⊃A .(2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f -1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A . 6. 求下列函数的自然定义域:(1)23+=x y ;解 由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解 由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞).(3)211x xy --=; 解 由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1].(4)241x y -=; 解 由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2).(5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞).(6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0, ±1, ±2, ⋅ ⋅ ⋅).(7) y =arcsin(x -3);解 由|x -3|≤1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=;解 由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3).(9) y =ln(x +1);解 由x +1>0得函数的定义域D =(-1, +∞).(10)x e y 1=.解 由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同?为什么?(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-∞, 1); (2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y , 所以函数xx y -=1在区间(-∞, 1)内是单调增加的. (2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有0l n )()l n ()l n (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以f (-x 2)<f (-x 1), -f (x 2)<-f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(-l , 0), 有f (x 1)< f (x 2), 所以f (x )在(-l , 0)内也单调增加. 11. 设下面所考虑的函数都是定义在对称区间(-l , l )上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )+g (-x )=f (x )+g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )+g (-x )=-f (x )-g (x )=-F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )⋅g (-x )=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )⋅g (-x )=[-f (x )][-g (x )]=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211xxy +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数. (3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数. 13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x -2);解 是周期函数, 周期为l =2π.(2)y =cos 4x ;解 是周期函数, 周期为2π=l . (3)y =1+sin πx ;解 是周期函数, 周期为l =2.(4)y =x cos x ;解 不是周期函数.(5)y =sin 2x .解 是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y 错误!未指定书签。
同济第六版高数答案(高等数学课后习题解答)1

习题8-31. 求下列函数的全微分: (1)yx xy z +=;解 dy y z dx x z dz ∂∂+∂∂=dy y x x dx y y )()1(2-++=.(2)xy e z =;解 xdy e x dx e x y dy y z dx x z dz y x y 12+-=∂∂+∂∂=.(3) 22y x yz +=;解 因为2/3222322)()(21y x xy y x y x z +-=+-=∂∂-, 2/3222222222)(y x x y x y x yy y x y z +=++⋅-+=∂∂, 所以 dy y x x dx y x xy dz 2/32222/322)()(+++-=)()(2/322xdy ydx y x x -+-=.(4)u =x yz . 解 因为1-⋅=∂∂yz x yz x u , x zx yu yz ln =∂∂, x yx z u yz ln =∂∂,所以 xdz yx xdy zx dx yzx du yz yz yz ln ln 1++=-.2. 求函数z =ln(1+x 2+y 2)当x =1, y =2时的全微分. 解 因为2212y x x x z ++=∂∂, 2212y x y y z ++=∂∂, 3121=∂∂==y x xz, 3221=∂∂==y x y z , 所以 dy dx dz y x 323121⋅+===.3. 求函数xyz =当x =2, y =1, ∆x =0.1, ∆y =-0.2时的全增量和全微分.解 因为xy x x y y z -∆+∆+=∆, y x x x ydz ∆+∆-=12, 所以, 当x =2, y =1, ∆x =0.1, ∆y =-0.2时,119.0211.02)2.0(1-=-+-+=∆z , 125.0)2.0(211.041-=-⨯+⨯-=dz .4. 求函数z =e xy 当x =1, y =1, ∆x =0.15, ∆y =0.1时的全微分. 解 因为y xe x ye y yz x x z dz xy xy ∆+∆=∆∂∂+∆∂∂=所以, 当x =1, y =1, ∆x =0.15, ∆y =0.1时, e e e dz 25.01.015.0=⋅+⋅=.*5. 计算33)97.1()102(+的近似值. 解 设33y x z +=, 由于y yz x x z y x y y x x ∆∂∂+∆∂∂++≈∆++∆+3333)()(332233233yx y y x x y x +∆+∆++=,所以取x =1, y =2, ∆x =0.02, ∆y =-0.03可得95.2212)03.0(2302.0321)97.1()02.1(32333=+-⋅⋅+⋅++≈+. *6. 计算(1.97)1.05的近似值(ln2=0.693). 解 设z =x y , 由于y yz x x z x x x y y y ∆∂∂+∆∂∂+≈∆+∆+)(y x x x yx x y y y ∆+∆+=-ln 1,所以取x =2, y =1, ∆x =-0.03, ∆y =0.05可得(1.97)1.05≈2-0.03+2ln2⋅0.05+1.97+0.0693 ≈2.093.*7( 已知边长为x(6m 与y(8m 的矩形( 如果x 边增加5cm 而y 边减少10cm(问这个矩形的对角线的近似变化怎样? 解 矩形的对角线为22y x z +=,)(122y y x x yx y dy dz x dx dz dz z ∆+∆+=∆+∆=≈∆,当x =6, y =8, ∆x =0.05, ∆y =-0.1时,05.0)1.0805.06(86122-=⋅-⋅+≈∆z .这个矩形的对角线大约减少5cm .*8. 设有一无盖圆柱形容器, 容器的壁与底的厚度均为0.1cm , 内高为20cm ,内半径为4厘米, 求容器外壳体积的近似值. 解 圆柱体的体积公式为V =πR 2h , ∆V ≈dV =2πRh ∆R +πR 2∆h , 当R =4, h =20, ∆R =∆h =0.1时,∆V ≈2⨯3.14⨯4⨯20⨯0.1+3.14⨯42⨯0.1≈55.3(cm 3), 这个容器外壳的体积大约是55.3cm 3.*9. 设有直角三角形, 测得其两腰的长分别为7±0.1cm 和24±0.1cm , 试求利用上述二值来计算斜边长度时的绝对误差. 解 设两直角边的长度分别为x 和y , 则斜边的长度为22y x z +=.||||||||||||y y z x x z dz z ∆⋅∂∂+∆⋅∂∂≤≈∆|)|||(122y y x x yx ∆+∆+=.令x =7, y =24, |∆x |≤0.1, |∆y |≤0.1, 则得斜边长度z 的绝对误差约为124.0)1.0241.07(247122=⋅+⋅+=z δcm .*10. 测得一块三角形土地的两边长分别为63±0.1m 和78±0.1m ,这两边的夹角为60︒±1︒, 试求三角形面积的近似值, 并求其绝对误差和相对误差.解 设三角形的两边长为x 和y , 它们的夹角z , 为则三角形面积为z xy s sin 21=.zdz xy zdy x zdx y dS cos 21sin 21sin 21++=||cos 21||sin 21||sin 21||||dz z xy dy z x dx z y dS S ++≤≈∆.令x =63, y =78, 3π=z , |dx |=0.1, |dy |=0.1, 180π=dz , 则55.2718021278631.0232631.023278=⨯⨯⨯+⨯⨯+⨯⨯≈πδs ,82.21273sin 786321=⋅⋅⋅=πS ,%29.182.212755.27==S s δ,所以三角形面积的近似值为2127.82m 2, 绝对误差为27.55m 2, 相对误差为1.29%.*11. 利用全微分证明: 两数之和的绝对误差等于它们各自的绝对误差之和.证明 设u =x +y , 则||||||||||||y x y x y yu x x u du u ∆+∆≤∆+∆=∆∂∂+∆∂∂=≈∆.所以两数之和的绝对误差|∆u |等于它们各自的绝对误差|∆x |与|∆y |的和.*12. 利用全微分证明: 乘积的相对误差等于各因子的相对误差之和; 商的相对误差等于被除数及除数的相对误差之和. 证明 设u =xy , y x v =, 则∆u ≈du =ydx +xdy ,2yxdyydx dv v -=≈∆, 由此可得相对误差;||||||||y dy x dx xy xdy ydx u du u u +=+=≈∆||||||||yyx x y dy x dx ∆+∆=+≤;||||||||2y dy x dx yx y xdy ydx v dv v v -=⋅-==∆||||||||y yx x y dy x dx ∆+∆=+≤.习题8-41. 设z =u 2-v 2, 而u =x +y , v =x -y , 求x z ∂∂, y z ∂∂.解 xv v z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂=2u ⋅1+2v ⋅1=2(u +v )=4x ,y v v z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂=2u ⋅1+2v ⋅(-1)=2(u -v )=4y .2. 设z =u 2ln v , 而y x u =, v =3x -2y , 求x z ∂∂, y z ∂∂.解 xv v z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂31ln 22⋅+⋅=v u y v u 222)23(3)23ln(2y y x x y x y x -+-=, yv v z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂)2()(ln 222-+-⋅=v u y x v u 2232)23(2)23ln(2yy x x y x y x ----=. 3. 设z =e x -2y , 而x =sin t , y =t 3, 求dtdz .解 dtdyy z dt dx x z dt dz ⋅∂∂+⋅∂∂=2223)2(cos t e t e y x y x ⋅-⋅+=--)6(cos )6(cos 22sin 223t t e t t e t t y x -=-=--.4. 设z =arcsin(x - y ), 而x +3t , y =4t 3, 求dtdz .解 dt dy y z dt dx x z dt dz ⋅∂∂+⋅∂∂=22212)(113)(11t y x y x ⋅---+⋅--= 232)43(1)41(3t t t ---=. 5. 设z =arctan(xy ), 而y =e x , 求dxdz .解 dx dy y z x z dx dz ⋅∂∂+∂∂=xxxe x x e e y x x y x y 2222221)1(11++=⋅+++=.6. 设1)(2+-=a z y e u ax , 而y =a sin x , z =cos x , 求dxdu .解 dxdz dz u dx dyy u x u dx du ⋅∂+⋅∂∂+∂∂=)sin (1cos 11)(222x a e x a a e a z y ae ax ax ax -⋅+-⋅+++-= )sin cos cos sin (122x x a x a x a a e ax ++-+=x e ax sin =. 7. 设yx z arctan =, 而x =u +v , y =u -v , 验证22v u v uv z u z +-=∂∂+∂∂. 证明 )()(v yy z v x x z u y y z u x x z v z u z ∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂=∂∂+∂∂)()(111)(11222y x yx y y x -⋅++⋅+=)1()()(111)(11222-⋅-⋅++⋅++y x yx y y x22222v u v u y x y +-=+=. 8. 求下列函数的一阶偏导数(其中f 具有一阶连续偏导数): (1) u =f (x 2-y 2, e xy );解 将两个中间变量按顺序编为1, 2号, 2122212)()(f ye f x xe f x y x f x u xy xy '+'=∂∂⋅'+∂-∂⋅'=∂∂, 212)2212)((f xe f y ye f y y x f y u xy xy '+'-=∂∂⋅'+∂-∂⋅'=∂∂. (2)) ,(zyy x f u =;解 1211)()(f y z yx f y x x f x u '=∂∂⋅'+∂∂⋅'=∂∂,)()(21z yy f y x y f y u ∂∂⋅'+∂∂'=∂∂2121f z f y x '+'-=,)()(21z y z f z x z f z u ∂∂⋅'+∂∂'=∂∂22f z y '⋅-=. (3) u =f (x , xy , xyz ).解 yz f y f f xu ⋅'+⋅'+⋅'=∂∂3211321f yz f y f '+'+'=,3232f xz f x xz f x f y u '+'=⋅'+⋅'=∂∂,33f xy xy f zu '=⋅'=∂∂.9. 设z =xy +xF (u ), 而xyu =, F (u )为可导函数, 证明xy z yz y x z x +=∂∂+∂∂⋅. 证明 y z y x z x ∂∂⋅+∂∂⋅])([])()([y u u F x x y x u u F x u F y x ∂∂'+⋅+∂∂'++=)]([)]()([u F x y u F xyu F y x '+⋅+'-+==xy +xF (u )+xy =z +xy .10. 设)(22y x f yz -=, 其中f (u )为可导函数, 验证 211y z y z y x z x =∂∂+∂∂.证明 ()()u f f xy u f x f y x z 2222'-=⋅'⋅-=∂∂, ()()u f f y u f u f y f y u f y z 2222)(1)2()('-+=-⋅'⋅-=∂∂, 所以 )(11221122u f y u f f y u f f y y z y x z x ⋅+'+'-=∂∂⋅+∂∂⋅211yz zy y =⋅.11. 设z =f (x 2+y 2), 其中f 具有二阶导数, 求22x z ∂∂, y x z ∂∂∂2, 22y z ∂∂.解 令u =x 2+y 2, 则z =f (u ), f x xu u f x z '=∂∂'=∂∂2)(,f y yu u f y z '=∂∂'=∂∂2)(,f x f x u f x f x z ''+'=∂∂⋅''+'=∂∂2224222,f xy yu f x y x z ''=∂∂⋅''=∂∂∂422,f y f yu f y f y z ''+'=∂∂⋅''+'=∂∂422222. 12. 求下列函数的22x z ∂∂,y x z ∂∂∂2,22yz ∂∂(其中f 具有二阶连续偏导数): (1) z =f (xy , y );解 令u =xy , v =y , 则z =f (u , v ).ufy v f y u f x v v f x u u f x z ∂∂=⋅∂∂+⋅∂∂=∂∂⋅∂∂+∂∂⋅∂∂=∂∂0,vfu f x v f x u f y v v f y u u f y z ∂∂+∂∂=⋅∂∂+⋅∂∂=∂∂⋅∂∂+∂∂⋅∂∂=∂∂1.因为f (u , v )是u 和v 的函数, 所以u f∂∂和vf ∂∂也是u 和v 的函数, 从而u f∂∂和vf ∂∂是以u 和v 为中间变量的x 和y 的函数. )()()(22uf x y u f y x x z x x z ∂∂∂∂=∂∂∂∂=∂∂∂∂=∂∂222222222)0()(u f y v u f y u f y x v v u f x u u f y ∂∂=⋅∂∂∂+⋅∂∂=∂∂⋅∂∂∂+∂∂⋅∂∂=,)(1)()(2uf y y u f u f y y x z y y x z ∂∂∂∂+∂∂⋅=∂∂∂∂=∂∂∂∂=∂∂∂ )(222yvv u f y u u f y u f ∂∂⋅∂∂∂+∂∂⋅∂∂+∂∂= v u fy u f xy u f v u f x u f y u f ∂∂∂+∂∂+∂∂=⋅∂∂∂+⋅∂∂+∂∂=222222)1(,)()()()(22vf y u f y x v f u f x y y z y y z∂∂∂∂+∂∂∂∂=∂∂+∂∂∂∂=∂∂∂∂=∂∂ y vv f y u u v f y v v u f y u u f x ∂∂⋅∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂=222222)( 1)1(222222⋅∂∂+⋅∂∂∂+⋅∂∂∂+⋅∂∂=vfx u v f v u f x u f x2222222vfv u f x u f x ∂∂+∂∂∂+∂∂=. (2)) ,(yx x f z =;解 令u =x ,yx v =, 则z =f (u , v ).v fy u f x v v f dx du u f x z ∂∂⋅+∂∂=∂∂⋅∂∂+⋅∂∂=∂∂1,vfy x dy dv v f y z ∂∂⋅-=⋅∂∂=∂∂2.因为f (u , v )是u 和v 的函数, 所以u f∂∂和vf ∂∂也是u 和v 的函数, 从而u f∂∂和vf ∂∂是以u 和v 为中间变量的x 和y 的函数. )(1)()1()(22v f x y u f x v f y u f x x z x x z ∂∂∂∂⋅+∂∂∂∂=∂∂⋅+∂∂∂∂=∂∂∂∂=∂∂ )(1)(222222xvv f dx du u v f y x v v u f dx du u f ∂∂⋅∂∂+⋅∂∂∂+∂∂⋅∂∂∂+⋅∂∂=22222212vfy v u f y u f ∂∂⋅+∂∂∂⋅+∂∂=,)1()(2vf y u f y x z y y x z ∂∂⋅+∂∂∂∂=∂∂∂∂=∂∂∂)(1)1()(v f y y v f y dy d u f y ∂∂∂∂⋅+∂∂⋅+∂∂∂∂= y vv f y v f y y v v u f ∂∂⋅∂∂⋅+∂∂⋅-∂∂⋅∂∂∂=22211 2232221vf y x v f y v u f y x ∂∂⋅-∂∂⋅-∂∂∂⋅-= )()()(2222vf y y x v f y x y y z y y z∂∂∂∂⋅-∂∂⋅-∂∂=∂∂∂∂=∂∂22423222322v f y x v f y x y v v f y x v f y x ∂∂⋅+∂∂⋅=∂∂⋅∂∂⋅-∂∂⋅=. (3) z =f (xy 2, x 2y );解 z x =f 1'⋅y 2+f 2'⋅2xy =y 2f 1'+2xyf 2', z y =f 1'⋅2xy +f 2'⋅x 2=2xyf 1'+x 2f 2';z xx =y 2[f 11''⋅y 2+f 12''⋅2xy ]+2yf 2''+2xy [f 21''⋅y 2+f 22''⋅2xy ] =y 4f 11''+2xy 3f 12''+2yf 2''+2xy 3f 21''+4x 2y 2 f 22'' =y 4f 11''+4xy 3f 12''+2yf 2''+4x 2y 2 f 22'',z xy =2y f 1'+y 2[f 11''⋅2xy +f 12''⋅x 2]+2xf 2'+2xy [f 21''⋅2xy +f 22''⋅x 2] =2y f 1'+2xy 3f 11''+x 2y 2 f 12''+2xf 2'+4x 2y 2f 21''+2x 3yf 22'' =2y f 1'+2xy 3f 11''+5x 2y 2 f 12''+2xf 2'+2x 3yf 22'', z yy =2xf 1'+2xy [f 11''⋅2xy +f 12''⋅x 2]+x 2[f 21''⋅2xy +f 22''⋅x 2] =2xf 1'+4x 2y 2f 11''+2x 3y f 12''+2x 3yf 21''+x 4f 22'' =2xf 1'+4x 2y 2f 11''+4x 3y f 12''+x 4f 22''. (4) z =f (sin x , cos y , e x +y ).解 z x =f 1'⋅cos x + f 3'⋅e x +y =cos x f 1'+e x +y f 3', z y =f 2'⋅(-sin y )+ f 3'⋅e x +y =-sin y f 2'+e x +y f 3', z xx =-sin x f 1'+cos x ⋅(f 11''⋅cos x + f 13''⋅e x +y ) +e x +y f 3'+e x +y (f 31''⋅cos x + f 33''⋅e x +y ) =-sin x f 1'+cos 2x f 11''+e x +y cos x f 13''+e x +y f 3' +e x +y cos x f 31''+e 2(x +y ) f 33''=-sin x f 1'+cos 2x f 11''+2e x +y cos x f 13''+e x +y f 3'+e 2(x +y ) f 33'', z xy =cos x [f 12''⋅(-sin y )+ f 13''⋅e x +y ] +e x +y f 3'+e x +y [f 32''⋅(-sin y )+ f 33''⋅e x +y ] =-sin y cos x f 12''+e x +y cos x f 13' +e x +y f 3'-e x +y sin y f 32'+e 2(x +y )f 33' =-sin y cos x f 12''+e x +y cos x f 13'' +e x +y f 3'-e x +y sin y f 32''+e 2(x +y )f 33'',z yy =-cos y f 2'-sin y [f 22''⋅(-sin y )+ f 23''⋅e x +y ] +e x +y f 3'+e x +y [f 32''⋅(-sin y )+ f 33''⋅e x +y ] =-cos y f 2'+sin 2y f 22''-e x +y sin y f 23'' +e x +y f 3'-e x +y sin y f 32''+ f 33''⋅e 2(x +y )=-cos y f 2'+sin 2y f 22''-2e x +y sin y f 23''+e x +y f 3'+f 33''⋅e 2(x +y ). 13. 设u =f (x , y )的所有二阶偏导数连续, 而23t s x -=,23t s y +=, 证明2222)()()()(t u s u y u x u ∂∂+∂∂=∂∂+∂∂及22222222t u s u y u x u ∂∂+∂∂=∂∂+∂∂.证明 因为y u x u s yy u s x x u s u ∂∂⋅+∂∂⋅=∂∂⋅∂∂+∂∂⋅∂∂=∂∂2321yu x u t yy u t x x u t u ∂∂⋅+∂∂⋅-=∂∂⋅∂∂+∂∂⋅∂∂=∂∂2123所以2222)2123()2321()()(y u x u y u x u t u s u ∂∂+∂∂-+∂∂+∂∂=∂∂+∂∂22)()(y u x u ∂∂+∂∂=. 又因为)2321()(22yu x u s s u s s u∂∂⋅+∂∂⋅∂∂=∂∂∂∂=∂∂ )(23)(21222222s y y u s x x y u s y y x u s x x u ∂∂⋅∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂= )2321(23)2321(21222222y u x y u y x u x u ∂∂⋅+∂∂∂⋅+∂∂∂⋅+∂∂⋅= 22222432341yu y x u x u ∂∂⋅+∂∂∂⋅+∂∂⋅=,)2123()(22yu x u t t u t t u∂∂⋅+∂∂⋅-∂∂=∂∂∂∂=∂∂ )(21)(23222222t y y u t x x y u t y y x u t x x u ∂∂⋅∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂-= )2123(21)2123(23222222y u x y u y x u x u ∂∂⋅+∂∂∂⋅-+∂∂∂⋅+∂∂⋅--= 22222412343y u y x u x u ∂∂⋅+∂∂∂⋅-∂∂⋅=, 所以 22222222yu x u t u s u ∂∂+∂∂=∂∂+∂∂.习题8-51. 设sin y +e x -xy 2=0, 求dxdy . 解 令F (x , y )=sin y +e x -xy 2, 则F x =e x -y 2, F y =cos y -2xy ,xyy e y xy y y e F F dx dy xy x 2cos 2cos 222--=---=-=. 2. 设x y y x arctan ln 22=+, 求dxdy .解 令xyy x y x F arctan ln ),(22-+=, 则22222222)()(11221y x y x x y xy y x x y x F x ++=-⋅+-+⋅+=,22222221)(11221y x x y x xy y x y y x F y +-=⋅+-+⋅+=, yx y x F F dx dyy x -+=-=. 3. 设022=-++xyz z y x , 求x z ∂∂及y z ∂∂.解 令xyz z y x z y x F 22),,(-++=, 则 xyz yz F x -=1, xyzxz F y -=2, xyz xyF z -=1, xy xyz xyz yz F F x z z x --=-=∂∂, xy xyz xyz xz F F y z z y --=-=∂∂2. 4. 设y z z x ln =, 求x z ∂∂及y z ∂∂,解 令yz z x z y x F ln ),,(-=, 则 z F x 1=, y y z y z F y 1)(12=-⋅-=, 2211z z x y yz z x F z +-=⋅--=, 所以 z x z F F x z z x +=-=∂∂, )(2z x y z F F yz z y +=-=∂∂.5. 设2sin(x +2y -3z )=x +2y -3z , 证明1=∂∂+∂∂y z x z证明 设F (x , y , z )=2sin(x +2y -3z )-x -2y +3z , 则 F x =2cos(x +2y -3z )-1, F y =2cos(x +2y -3z )⋅2-2=2F x , F z =2cos(x +2y -3z )⋅(-3)+3=-3F x ,313=--=-=∂∂x x z x F F F F x z ,3232=--=-=∂∂x x z y F F F F yz , 于是13231=+=--=∂∂+∂∂z z z x F F F F y z x z . 6. 设x =x (y , z ), y =y (x , z ), z =z (x , y )都是由方程F (x , y , z )=0所确定的具有连续偏导数的函数, 证明1-=∂∂⋅∂∂⋅∂∂x z z yy x .解 因为x y F F y x -=∂∂, y z F F z y -=∂∂, zx F F x z -=∂∂, 所以 1)()()(-=-⋅-⋅-=∂∂⋅∂∂⋅∂∂zx y z x y F F F F F F x z z y y x . 7. 设ϕ(u , v )具有连续偏导数, 证明由方程ϕ(cx -az , cy -bz )=0 所确定的函数z =f (x , y )满足 c y z b x z a =∂∂+∂∂.证明 因为vu uv u u b a c b a c x z ϕϕϕϕϕϕ+=⋅-⋅-⋅-=∂∂, vu v v u v b a c b a c y z ϕϕϕϕϕϕ+=⋅-⋅-⋅-=∂∂, 所以 c b a c b b a c a y z b x z a vu vv u u =+++⋅=∂∂+∂∂ϕϕϕϕϕϕ.8. 设e z-xyz =0, 求22xz∂∂.解 设F (x , y , z )=e z -xyz , 则F x =-yz , F z =e z -xy , xye yzF F x z z z x -=-=∂∂,222)()()()(xy e y x z e yz xy e x z y x z x x z z z z --∂∂--∂∂=∂∂∂∂=∂∂ 222)()(xy e xye yzyze xy ye z y zz z z ----+=32232)(22xy e e z y z xy ze y z zz ---=. 9. 设z 3-3xyz =a 3, 求yx z ∂∂∂2. 解 令F (x , y , z )=z 3-3xyz -a 3, 则 xyz yzxy z yz F F x z z x -=---=-=∂∂22333,xyz xzxy z xz F F y z z y -=---=-=∂∂22333, )()(22xyz yz y x z y y x z -∂∂=∂∂∂∂=∂∂∂ 222)()2())((xy z x yz z yz xy z y z y z --∂∂--∂∂+= 22222)()2()()(xy z x xyz xz z yz xy z xy z xz yz -----⋅-+=322224)()2(xy z y x xyz z z ---=. 10. 求由下列方程组所确定的函数的导数或偏导数: (1)设⎩⎨⎧=+++=203222222z y x y x z , 求dx dy , dx dz ;解 视y =y (x ), z =z (x ), 方程两边对x 求导得 ⎪⎩⎪⎨⎧=+++=064222dx dz z dx dy y x dx dy y x dx dz , 即⎪⎩⎪⎨⎧-=+-=-xdx dzz dxdy y x dx dz dx dy y 3222.解方程组得 )13(2)16(++-=∂∂z y z x x y , 13+=z x dx dz.(2)设⎩⎨⎧=++=++10222z y x z y x , 求dz dx ,dz dy ; 解 视x =x (z ), y =y (z ), 方程两边对z 求导得 ⎪⎩⎪⎨⎧=++=++022201z dz dy y dz dx x dz dy dz dx , 即⎪⎩⎪⎨⎧-=+-=+zdz dy y dzdxx dz dy dz dx 2221.解方程组得y x z y z x --=∂∂, yx xz z y --=∂∂. (3)设⎩⎨⎧-=+=),(),(2y v x u g v y v ux f u , 其中f , g 具有一阶连续偏导数, 求x u ∂∂,xv ∂∂; 解 视u =u (x , y ), v =v (x , y ), 方程两边对x 求偏导得 ⎪⎩⎪⎨⎧∂∂⋅'+-∂∂⋅'=∂∂∂∂⋅'+∂∂+⋅'=∂∂x v yv g xu g x v x vf x u x u f x u 21212)1()( ,即 ⎪⎩⎪⎨⎧'=∂∂⋅⋅-'+∂∂'''-=∂∂⋅'+∂∂-'121121)12()1(g x v g yv xu g f u x v f x u f x .解之得1221221)12)(1()12(g f g yv f x g f g yv f u x u ''--'-'''--''-=∂∂,1221111)12)(1()1(g f g yv f x f u f x g x v ''--'-'-'+''=∂∂.(4)设⎩⎨⎧-=+=vu e y v u e x uu cos sin , 求x u ∂∂, y u ∂∂, x v ∂∂, y v ∂∂. 解 视u =u (x , y ), v =v (x , y ), 方程两边微分得 ⎩⎨⎧+-=++=vdv u vdu du e dy vdv u vdu du e dx uu sin cos cos sin , 即 ⎩⎨⎧=+-=++dy vdv u du v e dx vdv u du v e u u sin )cos (cos )sin (, 从中解出du , dv 得 dy v v e v dx v v e v du uu 1)cos (sin cos 1)cos (sin sin +--++-=, dy v v e u e v dx v v e u e v dv u uuu ]1)cos (sin [sin ]1)cos (sin [cos +-+++--=, 从而1)cos (sin sin +-=∂∂v v e v x u u , 1)cos (sin cos +--=∂∂v v e v y u u, ]1)cos (sin [cos +--=∂∂v v e u e v x v u u , ]1)cos (sin [sin +-+=∂∂v v e u e v y v u u. 11. 设y =f (x , t ), 而t 是由方程F (x , y , t )=0所确定的x , y 的函数, 其中f , F 都具有一阶连续偏导数, 试证明:tF y F t f x F t f t F x f dx dy ∂∂+∂∂⋅∂∂∂∂⋅∂∂-∂∂⋅∂∂=.证明 由方程组⎩⎨⎧==0),,(),(t y x F t x f y 可确定两个一元隐函数⎩⎨⎧==)()(x t t x y y , 方程两边对x 求导可得⎪⎩⎪⎨⎧=⋅∂∂+⋅∂∂+∂∂⋅∂∂+∂∂=0dx dt t F dx dy y F x F dxdtt f x f dx dy ,移项得 ⎪⎩⎪⎨⎧∂∂-=∂∂+⋅∂∂∂∂=⋅∂∂-x F dx dt t F dx dy y F x f dx dt t f dx dy , 在01≠∂∂⋅∂∂+∂∂=∂∂∂∂∂∂-=y F t f t F tF y F t fD 的条件下 yFt f t F xFt f t F x f t F x F t f x f D dx dy ∂∂⋅∂∂+∂∂∂∂⋅∂∂-∂∂⋅∂∂=∂∂∂∂-∂∂-∂∂⋅=1. 习题8-61. 求曲线x =t -sin t , y =1-cos t , 2sin 4t z =在点)22 ,1 ,12 (-π处的切线及法平面方程.解 x '(t )=1-cos t , y '(t )=sin t , 2cos 2)(t t z ='. 因为点)22 ,1 ,12 (-π所对应的参数为2π=t , 故在点)22 ,1 ,12(-π处的切向量为)2 ,1 ,1(=T . 因此在点)22 ,1 ,12 (-π处, 切线方程为22211121-=-=-+z y x π, 法平面方程为0)22(2)1(1)12(1=-+-⋅++-⋅z y x π, 即422+=++πz y x .2. 求曲线t t x +=1, t t y +=1, z =t 2在对应于t =1的点处的切线及法平面方程. 解 2)1(1)(t t x +=', 21)(t t y -=', z '(t )=2t .在t =1所对应的点处, 切向量)2 ,1 ,41(-=T , t =1所对应的点为)1 ,2 ,21(, 所以在t =1所对应的点处, 切线方程为 21124121-=--=-z y x , 即8142121-=--=-z y x ; 法平面方程为0)1(2)2()21(41=-+---z y x , 即2x -8y +16z -1=0.3. 求曲线y 2=2mx , z 2=m -x 在点(x 0, y 0, z 0)处的切线及法平面方程.解 设曲线的参数方程的参数为x , 将方程y 2=2mx 和z 2=m -x的两边对x 求导, 得m dx dy y 22=, 12-=dxdz z , 所以y m dx dy =, z dxdz 21-=. 曲线在点(x 0, y 0, z 0,)的切向量为)21,,1(00z y m -=T , 所求的切线方程为0000211z z z y m y y x x --=-=-, 法平面方程为0)(21)()(00000=---+-z z z y y y m x x . 4. 求曲线⎩⎨⎧=-+-=-++0453203222z y x x z y x 在点(1, 1, 1)处的切线及法平面方程.解 设曲线的参数方程的参数为x , 对x 求导得,⎪⎩⎪⎨⎧=+-=-++053203222dx dz dx dy dx dz z dx dy y x , 即⎪⎩⎪⎨⎧=-+-=+2533222dxdz dx dy x dx dz z dx dy y . 解此方程组得z y z x dx dy 61015410----=, zy y x dx dz 610946---+=. 因为169)1,1,1(=dx dy , 161)1,1,1(-=dx dz , 所以)161 ,169 ,1(=T . 所求切线方程为1611169111--=-=-z y x , 即1191161--=-=-z y x ; 法平面方程为0)1(161)1(169)1(=---+-z y x , 即16x +9y -z -24=0. 5. 求出曲线x =t , y =t 2, z =t 3上的点, 使在该点的切线平行于平面x +2y +z =4.解 已知平面的法线向量为n =(1, 2, 1).因为x '=1, y '=2t , z '=3t 2, 所以参数t 对应的点处的切向量为T =(1, 2t , 3t 2). 又因为切线与已知平面平行, 所以T ⋅n =0, 即1+4t +3t 2=0,解得t =-1, 31-=t . 于是所求点的坐标为(-1, 1, -1)和)271 ,91 ,31(--. 6. 求曲面e z -z +xy =3在点(2,1,0)处的切平面及法线方程. 解 令F (x , y , z )=e z -z +xy -3, 则n =(F x , F y , F z )|(2, 1, 0)=(y , x , e z -1)|(2, 1, 0)=(1, 2, 0),点(2,1, 0)处的切平面方程为1⋅(x -2)+2(y -1)+0⋅(z -0)=0, 即x +2y -4=0,法线方程为02112-=-=-z y x . 7. 求曲面ax 2+by 2+cz 2=1在点(x 0, y 0, z 0)处的切平面及法线方程. 解 令F (x , y , z )=ax 2+by 2+cz 2-1, 则n =(F x , F y , F z )=(2ax , 2by , 2cz )=(ax , by , cz ).在点(x 0, y 0, z 0)处, 法向量为(ax 0, by 0, cz 0), 故切平面方程为ax 0(x -x 0)+by 0(y -y 0)+cz 0(z -z 0)=0,即 202020000cz by ax z cz y by x ax ++=++, 法线方程为00000cz z z by y y ax x x -=-=-.8. 求椭球面x 2+2y 2+z 2=1上平行于平面x -y +2z =0的切平面方程.解 设F (x , y , z )=x 2+2y 2+z 2-1, 则n =(F x , F y , F z )=(2x , 4y , 2z )=2(x , 2y , z ).已知切平面的法向量为(1, -1, 2). 因为已知平面与所求切平面平行, 所以2121z y x =-=, 即z x 21=, z y 41-=, 代入椭球面方程得1)4(2)2(222=+-+z z z ,解得1122±=z , 则1122±=x , 11221 =y . 所以切点坐标为)1122,11221,112(±± . 所求切平面方程为0)1122(2)11221()112(=±+-±z y x , 即 2112±=+-z y x . 9. 求旋转椭球面3x 2+y 2+z 2=16上点(-1, -2, 3)处的切平面与xOy 面的夹角的余弦.解 x O y 面的法向为n 1=(0, 0, 1).令F (x , y , z )=3x 2+y 2 +z 2-16, 则点(-1, -2, 3)处的法向量为 n 2=(F x , F y , F z )|(-1, -2, 3)=(6x , 2y , 2z )|(-1, -2, 3)=(-6, -4, 6). 点(-1, -2, 3)处的切平面与xOy 面的夹角的余弦为22364616||||cos 2222121=++⋅=⋅⋅=n n n n θ.10. 试证曲面a z y x =++(a >0)上任何点处的切平面在各坐标轴上的截距之和等于a .证明 设a z y x z y x F -++=),,(, 则)21,21,21(zy x =n . 在曲面上任取一点M (x 0, y 0, z 0), 则在点M 处的切平面方程为 0)(1)(1)(1000000=-+-+-z z z y y y x x x ,即 a z y x z z y y x x =++=++000000. 化为截距式, 得1000=++az z ay y ax x , 所以截距之和为a z y x a az ay ax =++=++)(000000.习题8-71. 求函数z =x 2+y 2在点(1, 2)处沿从点(1, 2)到点)32 ,2(+的方向的方向导数.解 因为从点(1, 2)到点)32 ,2(+的向量为)3 ,1(=l , 故 )cos ,(cos )23 ,21(||βα===l l e l . 又因为22)2,1()2,1(==∂∂x x z , 42)2,1()2,1(==∂∂y y z , 故所求方向导数为321234212cos cos +=⋅+⋅=∂∂+∂∂=∂∂βαy z x z l z . 2. 求函数z =ln(x +y )在抛物线y 2=4x 上点(1, 2)处, 沿这抛物线在该点处偏向x 轴正向的切线方向的方向导数.解 方程y 2=4x 两边对x 求导得2yy '=4, 解得yy 2='. 在抛物线y 2=4x 上点(1, 2)处, 切线的斜率为y '(1)=1, 切向量为l =(1, 1), 单位切向量为)cos ,(cos )21 ,21(βα==l e . 又因为31 1)2,1()2,1(=+=∂∂y x x z , 31 1)2,1()2,1(=+=∂∂y x y z , 故所求方向导数为3221312131cos cos =⋅+⋅=∂∂+∂∂=∂∂βαy z x z l z . 3. 求函数)(12222b y a x z +-=在点)2,2(b a 处沿曲线12222=+b y a x 在这点的内法线方向的方向导数.解 令1),(2222-+=by a x y x F , 则22a x F x =, 22b y F y =. 从而点(x , y )处的法向量为)2 ,2() ,(22by a x F F y x ±=±=n . 在)2,2(b a 处的内法向量为 )2 ,2()2 ,2()2,2(22ba b y a x ba-=-=n , 单位内法向量为)cos ,(cos ) ,(2222βα=+-+-=b a a b a b n e . 又因为aa x x zbab a 22)2,2(2)2,2(-=-=∂∂, b b y y zb a b a 22)2,2(2)2,2(-=-=∂∂, 所以 βαcos cos yz x z n z ∂∂+∂∂=∂∂222222b a a b b a b a +⋅++⋅=222b a ab+=.4. 求函数u =xy 2+z 3-xyz 在点(1, 1, 2)处沿方向角为3 πα=, 4 πβ=, 3πγ=的方向的方向导数. 解 因为方向向量为)21 ,22 ,21()cos ,cos ,(cos ==γβαl , 又因为1)()2,1,1(2)2,1,1(-=-=∂∂yz y x u , 0)2()2,1,1()2,1,1(=-=∂∂xz xy y u , 11)3()2,1,1(2)2,1,1(=-=∂∂xy z z u , 所以 γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂ 5211122021)1(=⋅+⋅+⋅-=. 5. 求函数u =xyz 在点(5,1,2)处沿从点(5, 1, 2)到点(9, 4, 14)的方向的方向导数.解 因为l =(9-5, 4-1, 14-2)=(4, 3, 12),)1312 ,133 ,134(||==l l e l , 并且 2)2,1,5()2,1,5(==∂∂yz xu ,10)2,1,5()2,1,5(==∂∂xz y u , 5)2,1,5()2,1,5(==∂∂xy z u , 所以 γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂ 139813125133101342=⋅+⋅+⋅=. 6. 求函数u =x 2+y 2+z 2在曲线x =t , y =t 2, z =t 3上点(1, 1, 1)处, 沿曲线在该点的切线正方向(对应于t 增大的方向)的方向导. 解 曲线x =t , y =t 2, z =t 3上点(1, 1, 1)对应的参数为t =1, 在点(1, 1,1)的切线正向为)3 ,2 ,1()3 ,2 ,1(12===t t t l ,)143,142,141(||==l l e l , 又 22)1,1,1()1,1,1(==∂∂x x u , 22)1,1,1()1,1,1(==∂∂y y u , 22)1,1,1()1,1,1(==∂∂z z u , 所以 γβαcos cos cos )1,1,1(zu y u x u l u ∂∂+∂∂+∂∂=∂∂ 1412143214221412=⋅+⋅+⋅=. 7. 求函数u =x +y +z 在球面x 2+y 2+z 2=1上点(x 0, y 0, z 0)处, 沿球面在该点的外法线方向的方向导数.解 令F (x , y , z )=x 2+y 2+z 2-1, 则球面x 2+y 2+z 2=1在点(x 0, y 0, z 0)处的外法向量为)2 ,2 ,2() , ,(000),,(000z y x F F F z y x z y x ==n , )cos ,cos ,(cos ) , ,(||000γβα===z y x n n n e , 又 1=∂∂=∂∂=∂∂zu y u x u , 所以 γβαcos cos cos zu y u x u n u ∂∂+∂∂+∂∂=∂∂ 000000111z y x z y x ++=⋅+⋅+⋅=.8. 设f (x , y , z )=x 2+2y 2+3z 2+xy +3x -2y -6z , 求grad f (0, 0, 0)及grad f (1, 1, 1).解 32++=∂∂y x x f , 24-+=∂∂x y yf , 66-=∂∂z z f . 因为 3)0,0,0(=∂∂x f, 2)0,0,0(-=∂∂yf, 6)0,0,0(-=∂∂z f , 6)1,1,0(=∂∂x f , 3)1,1,0(=∂∂y f, 0)1,1,0(=∂∂z f,所以 grad f (0, 0, 0)=3i -2j -6k ,grad f (1, 1, 1)=6i +3j .9. 设u , v 都是 x , y , z 的函数, u , v 的各偏导数都存在且连续, 证明(1) grad (u +v )=grad u + grad v ;解 k j i zv u y v u x v u v u ∂+∂+∂+∂+∂+∂=+)()()()(grad k j i )()()(zv z u y v y u x v x u ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂=)()(k j i k j i zv y v x v z u y u x u ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂= v u grad grad +=.(2) grad (uv )=v grad u +u grad v ;解 k j i zuv y uv x uv uv ∂∂+∂∂+∂∂=)()()()(grad k j i )()()(z v u z u v y v u y u v x v u x u v ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂= )()(k j i k j i zv y v x v u z u y u x u v ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂= =v grad u +u grad v .(3) grad (u 2)=2u grad u .解 k j i z u y u x u u ∂∂+∂∂+∂∂=2222)(grad k j i zu u y u u x u u ∂∂+∂∂+∂∂=222 u u zu y u x u u grad 2)(2=∂∂+∂∂+∂∂=k j i .10. 问函数u =xy 2z 在点p (1, -1, 2)处沿什么方向的方向导数最大? 并求此方向导数的最大值.解 k j i k j i 222 xy xyz z y zu y u x u u ++=∂∂+∂∂+∂∂=grad , k j i k j i +-=++=--42)2()2 ,1 ,1( )2,1,1(22xy xyz z y u grad .grad u (1, -1, 2)为方向导数最大的方向, 最大方向导数为 211)4(2|)2 ,1 ,1( 222=+-+=-u grad |.习题8-81. 求函数f (x , y )=4(x -y )-x 2-y 2的极值.解 解方程组⎩⎨⎧=--==-=024),(024),(y y x f x y x f yx , 求得驻点为(2,-2). f xx =-2, f xy =0, f yy =-2,在驻点(2,-2)处, 因为f xx f yy -f xy 2=(-2)(-2)-0=4>0, f xx =-2<0,所以在点(2, -2)处, 函数取得极大值, 极大值为f (2, -2)=8.2. 求函数f (x , y )=(6x -x 2)(4y -y 2)的极值.解 解方程组⎩⎨⎧=--==--=0)24)(6(),(0)4)(26(),(22y x x y x f y y x y x f yx , 得驻点(0, 0), (0, 4), (3, 2), (6, 0), (6,4).函数的二阶偏导数为f xx (x , y )=-2(4y -y 2), f xy (x , y )=4(3-x )(2-y ), f yy (x , y )=-2(6x -x 2). 在点(0, 0)处, 因为f xx ⋅f yy -f xy 2=0⨯0-242=-242<0,所以f (0, 0)不是极值;在点(0, 4)处, 因为f xx ⋅f yy -f xy 2=0⨯0-(-24)2=-242<0,所以f (0, 4)不是极值.在点(3, 2)处, 因为f xx ⋅f yy -f xy 2=(-8)⨯(-18)-02=8⨯18>0, f xx =-8<0,所以f (3, 2)=36是函数的极大值.在点(6, 0)处, 因为f xx ⋅f yy -f xy 2=0⨯0-(-24)2=-242>0,所以f (6, 0)不是极值.在点(6, 4)处, 因为f xx ⋅f yy -f xy 2=0⨯0-242=-242>0,所以f (6, 4)不是极值.综上所述, 函数只有一个极值, 这个极值是极大值f (3, 2)=36. 3. 求函数f (x , y )=e 2x (x +y 2+2y )的极值.解 解方程组⎩⎨⎧=+==+++=0)22(),(0)1422(),(222y e y x f y y x e y x f x yx x , 得驻点)1 ,21(-. f xx (x , y )=4e 2x (x +y 2+2y +1), f xy (x , y )=4e 2x (y +1), f yy (x , y )=2e 2x . 在驻点)1 ,21(-处, 因为 f xx ⋅f yy -f xy 2=2e ⋅2e -02=4e 2>0, f xx =2e >0, 所以2)1 ,21(e f -=-是函数的极小值. 4. 求函数z =xy 在适合附加条件x +y =1下的极大值.解 由x +y =1得y =1-x , 代入z =xy , 则问题化为求z =x (1-x )的无条件极值.x dxdz 21-=, 222-=dx z d . 令,0=dx dz 得驻点21=x . 因为022122<-==x dx zd , 所以21=x 为极大值点, 极大值为41)211(21=-=z . 5. 从斜边之长为l 的一切直角三角形中, 求有最大周界的直角三角形.解 设直角三角形的两直角边之长分别为x , y , 则周长 S =x +y +l (0<x <l , 0<y <l ).因此, 本题是在x 2+y 2=l 2下的条件极值问题, 作函数 F (x , y )=x +y +l +λ(x 2+y 2-l 2).解方程组⎪⎩⎪⎨⎧=+=+==+=222021021ly x y F x F y x λλ, 得唯一可能的极值点2l y x ==. 根据问题性质可知这种最大周界的直角三角形一定存在, 所以斜边之长为l 的一切直角三角形中, 周界最大的是等腰直角三角形.6. 要造一个容积等于定数k 的长方体无盖水池, 应如何选择水池的尺寸方可使表面积最小.解 设水池的长为x , 宽为y , 高为z , 则水池的表面积为 S =xy +2xz +2yz (x >0, y >0, z >0).本题是在条件xyz =k 下, 求S 的最大值.作函数F (x , y , z )=xy +2xz +2yz +λ(xyz -k ).解方程组⎪⎩⎪⎨⎧==++==++==++=k xyz xy y x F xz z x F yz z y F z y x 0220202λλλ, 得唯一可能的极值点)221 ,2 ,2(333k k k . 由问题本身可知S 一定有最小值, 所以表面积最小的水池的长和宽都应为.23k 高为3221k . 7. 在平面xOy 上求一点, 使它到x =0, y =0及x +2y -16=0三直线距离平方之和为最小.解 设所求点为(x , y ), 则此点到x =0的距离为|y |, 到y =0的距离为|x |, 到x +2y -16=0的距离为221|162|+-+y x , 而距离平方之和为 222)162(51-+++=y x y x z . 解方程组⎪⎩⎪⎨⎧=-++=∂∂=-++=∂∂0)162(5420)162(522y x y y z y x x x z , 即{03292083=-+=-+y x y x . 得唯一的驻点)516 ,58(, 根据问题的性质可知, 到三直线的距离平方之和最小的点一定存在, 故)516 ,58(即为所求. 8( 将周长为2p 的矩形绕它的一边旋转而构成一个圆柱体( 问矩形的边长各为多少时( 才可使圆柱体的体积为最大?解 设矩形的一边为x , 则另一边为(p -x ), 假设矩形绕p -x 旋转, 则旋转所成圆柱体的体积为V =πx 2(p -x ).由0)32()(22=-=--=x p x x x p x dx dV πππ, 求得唯一驻点p x 32=. 由于驻点唯一, 由题意又可知这种圆柱体一定有最大值, 所以当矩形的边长为32p 和3p 时, 绕短边旋转所得圆柱体体积最大. 9. 求内接于半径为a 的球且有最大体积的长方体.解 设球面方程为x 2+y 2+z 2=a 2, (x , y , z )是它的各面平行于坐标面的内接长方体在第一卦限内的一个顶点, 则此长方体的长宽高分别为2x , 2y , 2z , 体积为V =2x ⋅2y ⋅2z =8xyz .令 F (x , y , z )=8xyz +λ(x 2+y 2+z 2-a 2) .解方程组⎪⎩⎪⎨⎧=++=+==+==+=2222028028028a z y x z xy F y xz F x yz F z y x λλλ, 即⎪⎩⎪⎨⎧=++=+=+=+2222040404a z y x z xy y xz x yz λλλ, 得唯一驻点)3,3,3(a a a . 由题意可知这种长方体必有最大体积, 所以当长方体的长、宽、高都为32a 时其体积最大. 10. 抛物面z =x 2+y 2被平面x +y +z =1截成一椭圆, 求原点到这椭圆的最长与最短距离.解 设椭圆上点的坐标(x , y , z ), 则原点到椭圆上这一点的距离平方为d 2=x 2+y 2+z 2, 其中x , y , z 要同时满足z =x 2+y 2和x +y +z =1. 令 F (x , y , z )=x 2+y 2+z 2+λ1(z -x 2-y 2)+λ2(x +y +z -1).解方程组⎪⎩⎪⎨⎧=++==+-==+-=02022022212121λλλλλλz F y y F x x F z y x , 得驻点231±-==y x , 32 =z . 它们是可能的两个极值点, 由题意这种距离的最大值和最小值一定存在, 所以距离的最大值和最小值在两点处取得, 因为在驻点处359)32()231(2222222 =+±-=++=z y x d , 所以3591+=d 为最长距离;3592-=d 为最短距离.总习题八1. 在“充分”、“必要”和“充分必要”三者中选择一个正确的填入下列空格内:(1)f (x , y )在(x , y )可微分是f (x , y )在该点连续的______条件, f (x , y )在点连续是f (x , y )在该点可微分的______条件.解 充分; 必要.(2)z =f (x , y )在点(x , y )的偏导数x z ∂∂及yz ∂∂存在是f (x , y )在该点可微分的______条件, z = f (x , y )在点(x , y )可微分是函数在该点的偏导数x z ∂∂及y z ∂∂存在的______条件. 解 必要; 充分.(3)z =f (x , y )的偏导数x z ∂∂及yz ∂∂在(x , y )存在且连续是f (x , y )在该点可微分的______条件. 解 充分. (4)函数z =f (x , y )的两个二阶偏导数y x z ∂∂∂2及xy z ∂∂∂2在区域D 内连续是这两个二阶混合偏导数在D 内相等的______条件.解 充分.2. 选择下述题中给出的四个结论中一个正确的结论:设函数f (x , y )在点(0, 0)的某邻域内有定义, 且f x (0, 0)=3, f y (0, 0)=-1, 则有______.(A )dz |(0, 0)=3dx -dy .(B )曲面z =f (x , y )在点(0, 0, f (0, 0))的一个法向量为(3, -1, 1).(C )曲线⎩⎨⎧==0),(y y x f z 在点(0, 0, f (0, 0))的一个切向量为(1, 0, 3). (D )曲线⎩⎨⎧==0),(y y x f z 在点(0, 0, f (0, 0))的一个切向量为(3, 0, 1). 解 (C ).3. 求函数)1ln(4),(222y x y x y x f ---=的定义域, 并求),(lim )0,21(),(y x f y x →. 解 函数的定义域为{(x , y )| 0<x 2+y 2<1, y 2≤4x }因为D ∈)0 ,21(, 故由初等函数在定义域内的连续性有 43ln 2)1ln(4)1ln(4lim ),(lim )0,21(222222)0,21(),()0,21(),(=---=---=→→y x y x y x y x y x f y x y x .。
(完整word版)同济大学第六版高等数学课后答案详解全集

同济六版高等数学课后答案全集第一章习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A\B 及A\(A\B)的表达式.2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B)C =AC ⋃BC . .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明(1)f(A ⋃B)=f(A)⋃f(B);(2)f(A ⋂B)⊂f(A)⋂f(B).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中IX 、IY 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有IX x =x ; 对于每一个y ∈Y , 有IY y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.5. 设映射f : X →Y , A ⊂X . 证明:(1)f -1(f(A))⊃A ;(2)当f 是单射时, 有f -1(f(A))=A .6. 求下列函数的自然定义域:(1)23+=x y ;. (2)211x y -=; (3)211x x y --=;(4)241x y -=;(5)x y sin =; (6) y =tan(x +1);(7) y =arcsin(x -3); (8)x x y 1arctan 3+-=;. (9) y =ln(x +1);(10)x e y 1=.7. 下列各题中, 函数f(x)和g(x)是否相同?为什么?(1)f(x)=lg x2, g(x)=2lg x ;(2) f(x)=x , g(x)=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f(x)=1, g(x)=sec2x -tan2x .8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x)的图形.. 9. 试证下列函数在指定区间内的单调性:(1)x xy -=1, (-∞, 1);(2)y =x +ln x , (0, +∞).10. 设 f(x)为定义在(-l , l)内的奇函数, 若f(x)在(0, l)内单调增加, 证明f(x)在(-l , 0)内也单调增加.11. 设下面所考虑的函数都是定义在对称区间(-l , l)上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x2(1-x2);(2)y =3x2-x3;(3)2211x xy +-=;(4)y =x(x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x aa y -+= 13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x -2);.(2)y =cos 4x ;(3)y =1+sin πx ;(4)y =xcos x ;(5)y =sin2x .14. 求下列函数的反函数:(1)31+=x y 错误!未指定书签。
同济大学数学系《高等数学》(第7版)(上册)-课后习题(含考研真题)详解-第七章 微分方程【圣才出品

台
则
所以 y=3sinx-4cosx 是所给微分方程的解. (3)根据 y=x2ex,得
进而得
则
所以 y=x2ex 不是所给微分方程的解.
(4)根据
,得
,进而得
则
所以
是所给微分方程的解.
3.在下列各题中,验证所给二元方程所确定的函数为所给微分方程的解:
2 / 126
圣才电子书
十万种考研考证电子书、题库视频学习平
台
解:(1)在方程 x2-xy+y2=C 两端对 x 求导,得
即
所以所给二元方程所确定的函数是微分方程的解.
(2)在方程 y=ln(xy)两端对 x 求导,得
即(xy-x)y′-y=0,再在上式两端对 x 求导,得
即 给微分方程的解.
.所以所给二元方程所确定的函数是所
,即 tany·tanx=±C1,所以原方程的通解为
tany·tanx=C
(6)原方程分离变量,得 10-ydy=10xdx,两端积分得
可写成 (7)原方程为
. 分离变量得
两端积分得
或写成
,即
,
所以原方程的通解为
(ex+1)(ey-1)=C
(8)原方程分离变量,得
两端积分得
即 ln|sinysinx|=lnC1,或写成 sinysinx=±C1,所以原方程的通解为 sinysinx=C. (9)原方程分离变量,得(y+1)2dy=-x3dx.两端积分得
圣才电子书
十万种考研考证电子书、题库视频学习平 台
第七章 微分方程
7.2 课后习题详解
习题 7-1 微分方程的基本概念
1.试说出下列各微分方程的阶数:
解:(1)一阶;(2)二阶;(3)三阶;(4)一阶;(5)二阶;(6)一阶. 2.指出下列各题中的函数是否为所给微分方程的解:
高等数学(同济第七版下)课后习题及解答
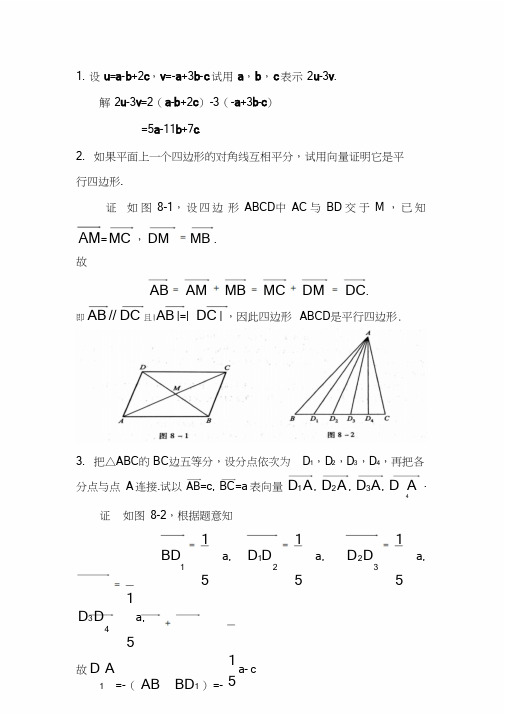
1.设u=a-b+2c,v=-a+3b-c.试用a,b,c表示2u-3v.解2u-3v=2(a-b+2c)-3(-a+3b-c)=5a-11b+7c.2.如果平面上一个四边形的对角线互相平分,试用向量证明它是平行四边形.证如图8-1,设四边形ABCD中AC与BD交于M,已知AM=MC,DM MB.故AB AM MB MC DM DC.即AB//DC且|A B|=|DC|,因此四边形ABCD是平行四边形.3.把△ABC的BC边五等分,设分点依次为D1,D2,D3,D4,再把各分点与点A连接.试以AB=c,BC=a表向量D1A,D2A,D3A,D A4.证如图8-2,根据题意知1 BD a,151D1D a,251D2D a,351 D3D a,45故D A1=-(AB BD1)=- 15a-cD2A=-(AB BD2)=- 25a-cD3A=-(AB BD3)=- 35a-cD4 A=-(AB BD)=-445a-c.4.已知两点M1(0,1,2)和M2(1,-1,0).试用坐标表示式表示向量M1M2及-2M1M2.解M1M2=(1-0,-1-1,0-2)=(1,-2,-2).-2M1M2=-2(1,-2,-2)=(-2,4,4).5.求平行于向量a=(6,7,-6)的单位向量.解向量a的单位向量为aa,故平行向量a的单位向量为a a =1(6,7,-6)=1167,,1111611 ,22 2其中a67(6)11.6.在空间直角坐标系中,指出下列各点在哪个卦限?A(1,-2,3),B(2,3,-4),C(2,-3,-4),D(-2,-3,1).解A点在第四卦限,B点在第五卦限,C点在第八卦限,D点在第三卦限.7.在坐标面上和在坐标轴上的点的坐标各有什么特征?指出下列各点的位置:A(3,4,0),B(0,4,3),C(3,0,0),D(0,-1,0).解在坐标面上的点的坐标,其特征是表示坐标的三个有序数中至少有一个为零,比如xOy面上的点的坐标为(x0,y0,0),xOz面上的点的坐标为(x0,0,z0),yOz面上的点的坐标为(0,y0,z0).在坐标轴上的点的坐标,其特征是表示坐标的三个有序数中至少有两个为零,比如x轴上的点的坐标为(x0,0,0),y轴上的点的坐标为(0,y0,0),z轴上的点的坐标为(0,0,z0).A点在xOy面上,B点在yOz面上,C点在x轴上,D点在y轴上.8.求点(a,b,c)关于(1)各坐标面;(2)各坐标轴;(3)坐标原点的对称点的坐标.解(1)点(a,b,c)关于xOy面的对称点(a,b,-c),为关于yOz面的对称点为(-a,b,c),关于zOx面的对称点为(a,-b,c).(2)点(a,b,c)关于x轴的对称点为(a,-b,-c),关于y 轴的对称点为(-a,b,-c),关于z轴的对称点为(-a,-b,c).(3)点(a,b,c)关于坐标原点的对称点是(-a,-b,-c). 9.自点P(0x0,y0,z0)分别作各坐标面和各坐标轴的垂线,写出各垂足的坐标.解设空间直角坐标系如图8-3,根据题意,P0F为点P0关于xOz 面的垂线,垂足F坐标为(x0,0,z0);P0D为点P0关于xOy面的垂线,垂足D坐标为(,,0)x0y;P0E为点P0关于yOz面的垂线,垂足E坐标为(0),y0,z o.P0A为点P0关于x轴的垂线,垂足A坐标为(x o,0,0);P0B为点P0关于y轴的垂线,垂足B坐标为(0,y0,0);P0C为点P0关于z轴的垂线,垂足C坐标为(0,0,)z.10.过点P(0x0,y0,z0)分别作平行于z轴的直线和平行于xOy面的平面,问在它们上面的点的坐标各有什么特点?解如图8-4,过P0且平行于z轴的直线l上的点的坐标,其特点是,它们的横坐标均相同,纵坐标也均相同.而过点P0且平行于xOy面的平面上的点的坐标,其特点是,它们的竖坐标均相同.11.一边长为a的正方体放置在xOy面上,其底面的中心在坐标原点,底面的顶点在x轴和y轴上,求它各顶点的坐标.2 解 如图 8-5,已知 AB=a ,故 OA=OB=a2,于是各顶点的坐 22 2 标分别为 A0 0)(a ,, ,B ((0,a ,0)),C (-a222,0,0),D 2 (0,- a 2 2 ,0),E ( a 2 2 ,0,a ),F (0, a 2 2 ,a ),G (- a2, 2 0,a ),H (0,- a 2,a ). 12.求点 M (4,-3,5)到各坐标轴的距离 .2 2解 点 M 到 x 轴的距离为 d 1=( 3) 534,点 M 到 y 22轴 的 距 离 为 d 2=4541, 点 M 到 z 轴 的 距 离 为 22.d 3=4 ( 3) 25 513.在 yOz 面上,求与三点 A (3,1,2),B (4,-2,-2),C (0,5, 1)等距离的点 .解 所求点在 yOz 面上,不妨设为 P (0,y ,z ),点 P 与三点 A ,2y 2 z 2B ,C 等距离, PA 3( 1) ( 2) , PB2 y 2 z 4 ( 2)(2) 2,PC(y 2z1) 2 .5)(由 PAPBPC 知,2( 1)2 ( 2)2 42 (2)( 2)223yz yz2( 1)2( y 5)z ,即9 ( y 1) 9 ( y 1) 2 2 2 (z 2) 16 ( y 2) 22 2 (z 2) ( y 5)( z( z21) . 2 2), 解上述方程组,得 y=1,z=-2.故所求点坐标为( 0,1,-2). 14.试证明以三点 A (4,1,9),B (10,-1,6),C (2,4,3)为顶 点的三角形是等腰直角三角形 .证 由AB (10 24)( 1 1) 2( 6 29)7, AC (2 24)( 4 1)22(3 9)7,BC(2 210)(4 1) 2(3 26)98 7 2 222知.ABAC 及 BCABAC 故△ABC 为等腰直角三角形.15. 设已知两点为 M 1(4, 2 ,1),M 2(3,0,2),计算向量 M 1M 2的模、方向余弦和方向角 .解 向量M 1M=(3-4,0-2 ,2-1)=(-1,- 2 ,-1),2其模-1 2- 2 2 12 4 2M1M()().其方向余弦分2别为cos=- 12,cos=-22,cos=12.方向角分别为23,34,3.16.设向量的方向余弦分别满足(1)cos=0;(2)cos=1;(3)cos=cos=0,问这些向量与坐标轴或坐标面的关系如何?解(1)由cos=0得知,故向量与x轴垂直,平行于2yOz面.(2)由cos=1得知=0,故向量与y轴同向,垂直于xOz面.(3)由cos=cos=0知,故向量垂直于x轴和y轴,2即与z轴平行,垂直于xOy面.,求r在u轴上的投影.17.设向量r的模是4,它与u轴的夹角为3解已知|r|=4,则Prju r=|r|cos=4?cos 3 =4×12 =2.18.一向量的终点在点B(2,-1,7),它在x轴、y轴和z轴上的投影依次为4,-4和7,求这向量的起点A的坐标.解设A点坐标为(x,y,z),则AB=(2-x,-1-y,7-z),由题意知2-x=4,-1-y=-4,7-z=7,故x=-2,y=3,z=0,因此A点坐标为(-2,-3,0).19.设m=3i+4j+8k,n=2i-4j-7k和p=5i+j-4k.求向量a=4m+3n-p在x轴上的投影及在y轴上的分向量.解a=4m+3n-p=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k,a在x轴上的投影为13,在y轴上的分向量为7j.1.设a3i j2k,b i2j k,求(1)a b及a b;(2)(-2a)3b及a2b;(3)a,b的夹角的余弦.解(1)a b(3,-1,-2)(1,2,-1)31(-12-2-1 3)()(),i j ka b31 2=(5,1,7).12 1(2)(2a)3b6(a b)6318a2b2(a b)2(5,1,7)(10,2,14)(3 cos(a,b) aabb32(1)(2)12(1)222 232 3 31462212.设a,b,c为单位向量,满足a b c0,求a b b c c a.解已知a b c1,a b c0,故(a b c)(a b c)0.22 2即2220a b c a b b c c a.因此a b b c c a 122 2(a b c)2-323.已知M1(1,-1,2),M2(3,3,1)M3(3,1,3).求与M1M2,M2M3同时垂直的单位向量.解M1M2=(3-1,3-(-1),1-2)=(2,4,-1)M 2M=(3-3,1-3,3-1)=(0,-2,2)3由于 M 1M 2 M 2M 3 与M 1M 2,M 2M 3 同时垂直,故所求向量可取为a(M M1 2M M12M M23M M2)3,ij k 由M 1M 2 M 2M 3 =2 4 1 022=(6,-4,-4),M 1M M M2 232 6 ( 24) ( 24)68 2 17 132 2知). a(6, 4, 4)(, , 2 171717174. 设质量为 100kg 的物体从点 M1(3,1,8)沿直线移动到点 M2(1,4,2), 计算重力所作的功(坐标系长度单位为 m ,重力方向为 z 轴负方向).解M 1M 2 =(1-3,4-1,2-8)=(-2,3,-6)F=(0,0,-100×9.8)=(0,0,-980)W=F?M 1M 2 =(0,0,-980)?(-2,3 ,-6 )=588(0 J ).1处,有一与O P 1 5.在杠杆上支点 O 的一侧与点 O 的距离为 x 1 的点 P 成角 1 的力 F1作用着;在 O 的另一侧与点 O 的距离为 x 2 的点 P2处,有一与OP2成角2的力F2,F1,F2作用着(图8-6),问1,2,x1,x2符合怎样的条件才能使杠杆保持平衡?解如图8-6,已知有固定转轴的物体的平衡条件是力矩的代数和为零,又由对力矩正负符号的规定可得杠杆保持平衡的条件为F1x sin1F2x2sin20,1即F1x1sin1F2x2sin2.6.求向量a(4,-3,4)在向量b(2,2,1)上的投影.a b(4,3,4)(2,2,1) 6解 2Pr j b a.22 2b 322 17.设a(3,5,2),b(2,1,4),问与有怎样的关系,能使a b与z轴垂直?解a b=(3,5,-2)+(2,1,4)=(32,5,24).要a b与z轴垂直,即要(a b)(0,0,1),即(a b)?(0,0,1)=0,亦即(32,5,24)?(0,0,1)=0,故(24)=0,因此2时能使a b与z轴垂直.8.试用向量证明直径所对的圆周角是直角.证如图8-7,设AB是圆O的直径,C点在圆周上,要证∠ACB=,2 只要证明AC BC0即可.由AC BC=(AO OC)(BO OC)2AO BO AO OC OC BO OC =2 2=0AO AO OC AO OC OC.故AC BC,∠ACB为直角.9.已知向量a2i3j k,b i j3k和c i2j,计算:(1)(a b)c(a c)b(2)(a b)(b c)(3)(a b) c 解(1)a b(2,3,1)(1,1,3)8,a c(2,3,1)(1,2,0)8,(a b)c(a c)b8(1,2,0)8(1,1,3)(0,8,24)8i24k.(2)a b=(2,-3,1)+(1,-1,3)=(3,-4,4),b c=(1,-1,3)+(1,-2,0)=(2,-3,3),i j k(a b)(b c)344(0,1,1)j k.23323 1(3)(ab) c2. 1 1 3 12 010. 已知OA i 3k,OB j 3k ,求△OAB 的面积.解 由向量积的几何意义知1△OAB= OA OB S2,ij kOA OB 1 0 3 ( 3, 3,1) , 0 1 32 2OA OB( 3) ( 3) 119S△OAB19 211. 已知( , , ), ( , , ), ( , , )a a x a a bb b b cc c c ,试利用yzxyzxyz行列式的性质证明:(a b) c (b c) a (c a) baxa yazbxbybz证因为(), a b c bbbx y z (b c) acxcyczcxc yc zaxayazcx cy cz(c a) baxayaz,bxbybz而由行列式的性质知a x a y a zb x b y b zc x c y cz b x b y b z c x c y c z = a x a y a z ,故 c x c y c z a x a y a zb x b ybz(a b) c (b c) a (c a) b .12. 试用向量证明不等式:222222a 1aabbba ba b a b ,231231 12 23 3其中a 1,a 2 ,a 3,b 1,b 2,b 3 为任意实数 . 并指出等号成立的条件.证 设向量 a ( a 1,a ,a ),b (b 1,b 2,b 3).23由ab a b cos(a, b ) a b ,从而222222 a 1ba ba baaa bbb ,1 2 23 3121 233当a 1,a 2 ,a 3与b 1,b 2 ,b 3 成比例,即a1b1a 2b2a 3b3时,上述等式成立.1.求过点(3,0,-1)且与平面3x7y5z120平行的平面方程.解所求平面与已知平面3x7y5z120平行.因此所求平面的法向量可取为n=(3,-7,5),设所求平面为3x7y5z D0.将点(3,0,-1)代入上式得D=-4.故所求平面方程为3x7y5z40.2.求过点M0(2,9,-6)且与连接坐标原点及点M0的线段OM0垂直的平面方程.解OM(2,9,6.所求平面与0)O M垂直,可取n=OM0,0设所求平面方程为2x9y6z D0.将点M0(2,9,-6)代入上式得D=-121.故所求平面方程为2x9y6z1210.3.求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程.x1y1z 1解由021212 1,得x3y2z0,11112 1即为所求平面方程.注设M(x,y,z)为平面上任意一点,M(x,y,z)(i1,2,3)i为i i i平面上已知点.由()0,M1M M M M M即1213x x1 y y1z z1x 2 x1y2y1z2z10,x 3 x1y3y1z3z1它就表示过已知三点M i(i=1,2,3)的平面方程.4.指出下列各平面的特殊位置,并画出各平面:(1)x=0;(2)3y-1=0;(3)2x-3y-6=0;(4)x-3y=0;(5)y+z=1;(6)x-2z=0;(7)6x+5y-z=0.解(1)—(7)的平面分别如图8—8(a)—(g). (1)x=0表示yOz坐标面.1(2)3y-1=0表示过点(,00,)且与y轴垂直的平面.3(3)2x-3y-6=0表示与z轴平行的平面.(4)x-3y=0表示过z轴的平面.(5)y+z=1表示平行于x轴的平面.(6)x-2z=0表示过y轴的平面.(7)6x+5y-z=0表示过原点的平面.5.求平面2x2y z50与各坐标面的夹角的余弦.解平面的法向量为n=(2,-2,1),设平面与三个坐标面xOy,yOz,zOx的夹角分别为1,2,3.则根据平面的方向余弦知cosn kcos1n k(2,222,1)(0,0,1)21( 22)113,cos2cos nnii(2, 2,1)3(1,0,0)123,cos3 cos nnjj(2, 2,1)3(10,1,0)23.6.一平面过点(1,0,-1)且平行于向量a(2,1,1)和b(1,1,0),试求这个平面方程.解所求平面平行于向量a和b,可取平面的法向量i j kn a b211(1,1,3).110故所求平面为1(x1)1(y0)3(z1)0,即x y3z40.7.求三平面x3y z1,2x y z0,x2y2z3的交点.解联立三平面方程x3y z1,2x y z0,x2y2z 3.解此方程组得x1,y1,z 3.故所求交点为(1,-1,3). 8.分别按下列条件求平面方程:(1)平行于xOz面且经过点(2,-5,3);(2)通过z轴和点(-3,1,-2);(3)平行于x轴且经过两点(4,0,-2)和(5,1,7).解(1)所求平面平行于xOz面,故设所求平面方程为By D0.将点(2,-5,3)代入,得5B D0,即D5B.因此所求平面方程为By5B0,即y50.(2)所求平面过z轴,故设所求平面为Ax By0.将点(-3,1,-2)代入,得3A B0,即B3A.因此所求平面方程为Ax3Ay0,即x3y0.(3)所求平面平行于x轴,故设所求平面方程为By Cz D0. 将点(4,0,-2)及(5,1,7)分别代入方程得2C D0及B7C D0.C D2, B92D .因此,所求平面方程为9 2DDy z D0,2即9y z20.9.求点(1,2,1)到平面x2y2z100的距离.解利用点(,,)M0x y o z o到平面Ax By Cz D0的距离公式dA xABy2B2CzC2D1 2212 22212210 331.1.求过点(4,-1,3)且平行于直线x3y z21 51的直线方程.解所求直线与已知直线平行,故所求直线的方向向量s(2,1,5),直线方程即为x 4y1z 21 5 3 .2.求过两点M1(3,2,1)和M2(1,0,2)的直线方程.解取所求直线的方向向量s M1M(13,0(2),21)(4,2,1),2因此所求直线方程为x 3y2z4 2 1 1 .3.用对称式方程及参数方程表示直线x y z1,2x y z 4.解根据题意可知已知直线的方向向量i j ks111(2,1,3).21 1取x=0,代入直线方程得yzy z1,4.3 5解得.y,z这2 2样就得到直线经过的一点(3 50,,).因此直线的对称式方程为2 2x30y z22 1 352 .参数方程为x2t,y 32t ,z 523t.注由于所取的直线上的点可以不同,因此所得到的直线对称式方程或参数方程得表达式也可以是不同的.4.求过点(2,0,-3)且与直线x2y4z70,3x5y2z10垂直的平面方程.解根据题意,所求平面的法向量可取已知直线的方向向量,即i j kn s124(16,14,11),35 2故所求平面方程为16(x2)14(y0)11(z3)0.即16x14y11z650.5.求直线5x3x3y2y3zz91 00,与直线2x3x28yyzz23180,的夹角的余弦.解两已知直线的方向向量分别为i j k i j ks533(3,4,1),s221(10,5,10), 1 232138 1因此,两直线的夹角的余弦cos(cos s1,)s2 s1s1s2s22 332410(1)4252101(1025)2100.6.证明直线x 2yz2xyz7,7与直线3x2x6yy 3zz 08,平行.证已知直线的方向向量分别是i j k i j ks 1 121(3,1,5),s2363(9,3,15), 21121 1由s23s1知两直线互相平行.7.求过点(0,2,4)且与两平面x2z1和y3z2平行的直线方程.解所求直线与已知的两个平面平行,因此所求直线的方向向量可取i j ks n1 n102(201 32,3,1),故所求直线方程为x 2 0y2z3 14.注本题也可以这样解:由于所求直线与已知的两个平面平行,则可视所求直线是分别与已知平面平行的两平面的交线,不妨设所求直线为x2z a,y3z b.将点(0,2,4)代入上式,得a8,b10.故所求直线为x2z8,y3z10.8.求过点(3,1,-2)且通过直线x54y3z2 1的平面方程.解利用平面束方程,过直线x54y3z2 1的平面束方程为x4y3y 3(z)0,52 211将点(3,1,-2)代入上式得.因此所求平面方程为20x4y311y5220 23(z) 0,即8x9y22z590.9.求直线xxyy3zz0,与平面x y z10的夹角.i j k解已知直线的方向向量(2,4,2),s113平面11 1的法向量n(1,1,1).设直线与平面的夹角为,则sin cos(n, s) ssnn 2221244((1)22)21(2)((1) 21)( 21)0,即0.10.试确定下列各组中的直线和平面间的关系;(1)x3y4z27 3和4x2y2z3;(2)x3y2z7 和3x2y7z8;(3)x32y2z134和x y z 3.解设直线的方向向量为s,平面的法向量为n,直线与平面的夹角为,且s nsin cos(n,s).s n (1)s(2,7,3),n(4,2,2),sin ( 2) ( 2 2) ( 4 2 7) ( 7) 2 3 ( 2) 2 4 3 ( ( 2 2)2) ( 2) 20, 则0.故直线平行于平面或在平面上, 现将直线上的点 A (-3,-4,0)代入平面方程,方程不成立 .故点 A 不在平面上,因此直线不在平 面上,直线与平面平行 . (2)s(3, 2,7), n (3, 2,7),由于s n 或sin 2 3 3( 3 2) 2( 2) 2 7 ( 2)2 3 7 ( 7 2) 22 71,知,故直线与平面垂直 .2(3)s( 3,1, 4), n (1,1,1),由于s n 0或sin 2 3 3 2 1 1 ( 1 1 4) 2( 4) 2 1 1 2 1 21 0, 知0,将直线上的点 A (2,-2,3)代入平面方程,方程成立,即点 A 在平面上 .故直线在平面上 . 11.求过点(1,2,1)而与两直线x x2 yy z 1 0, 2x y z z 1 0xy z 00,和 平行的平面的方程.解 两直线的方向向量为i j k i j ks 1 121(1,2,3),s2211(0,1,1), 11111 1i j k取(1,1,1),n s s12 31 201 1则过点(1,2,1),以n为法向量的平面方程为1(x1)1(y2)1(z1)0,即x y z0.12.求点(-1,2,0)在平面x2y z10上的投影.解作过已知点且与已知平面垂直的直线.该直线与平面的交点即为所求.根据题意,过点(-1,2,0)与平面x2y z10垂直的直线为x 1 1y2z21,将它化为参数方程x1t,y22t,z t,代入平面方程得1t2(22t)(t)10,整理得2t.从而所求点(-1,2,0)在平面x2y z10上的3投影为(53,23,23).13.求点P(3,-1,2)到直线x2xy z 1y z 40,的距离.i j k解直线的方向向量(0,3,3).s11 121 1在直线上取点(1,-2,0),这样,直线的方程可表示成参数方程形式x 1, y 2 3t,z 3t.(1)又,过点 P (3,-1,2),以s (0, 3, 3)为法向量的平面方程为3(y 1) 3(z 2) 0,即y z 1 0.(2)将式(1)代入式(2)得11 3t,于是直线与平面的交点为 (1, , ),2 2 2故所求距离为 d (321) ( 1 1 2 ) 2 (2 3 2 ) 2322.14.设 M 0 是直线 L 外一点,M 是直线 L 上任意一点,且直线的方向向 量为s ,试证:点 M 0 到直线 L 的距离dM M ss.证 如图 8-9,点 M 0 到直线 L 的距离为 d.由向量积的几何意义知M 0 表示以 M 0M ,s 为邻边的平行四边形的面积 .而M s M 0Mss表示以 s为边长的该平面四边形的高, 即为点 M 0 到直线L 的距离.于是dM 0 Mss.15.求直线2x3x4yy z2z0,9 0在平面4x y z1上的投影直线的方程.解作过已知直线的平面束,在该平面束中找出与已知平面垂直的平面,该平面与已知平面的交线即为所求.设过直线2x3x4yy z2z0,9 0的平面束方程为2x4y z(3x y2z9)0,经整理得(23)x(4)y(12)z90. 由(23)4(4)(1)(12)10,得1311.代入平面束方程,得17x31y37z1170.因此所求投影直线的方程为17x31y37z1170,4x y z 1.16.画出下列各平面所围成的立体的图形.(1)x0,y0,z0,x2,y1,3x4y2z120;y(2).x0,z0,x1,y2,z4解(1)如图8-10(a);(2)如图8-10(b).1.一球面过原点及A(4,0,0),B(1,3,0)和C(0,0,-4)三点,求球面的方程及球心的坐标和半径.解设所求球面的方程为2()()2 22(x a)y b z c R,将已知点的坐标代入上式,得2b c R22 2a,(1)2b2c2R2(a4),(2)( 2b2c2R2a1)(3),(3)2b2(4c)2R2a,(4)联立(1)(2)得a2,联立(1)(4)得c2,将a2代入(2)(3)并联立得b=1,故R=3.因此所求球面方程为(x2y2z2)(1)(2) 2 9,其中球心坐标为(2,1,2),半径为3.2.建立以点(1,3,-2)为球心,且通过坐标原点的球面方程.解设以点(1,3,-2)为球心,R为半径的球面方程为(x1)2y z R22 2(3)(2),球面经过原点,故2R (021) ( 0 3)2 2(02) 14,从而所求球面方程为(x1)2(y3)2(z2)214.2y z x y z2 23.方程x2420表示什么曲面?解将已知方程整理成(x2y2z1)(2)( 1) 2 2(6) ,所以此方程表示以(1,-2,-1)为球心,以6为半径的球面.4.求与坐标原点O及点(2,3,4)的距离之比为1:2的点的全体所组成的曲面的方程,它表示怎样的曲面?解设动点坐标为(x,y,z),根据题意有2(x0) (y (x22) ( y220)3)((zz220)4)12,化简整理得(x 232y2z)(1)(43)2 (它表示以(23,1,43 2)为球心,以293为25.将xOz坐标面上的抛物线z5x 绕x轴旋转一周,求所生成的旋转曲面的方程.解以2z 22y代替抛物线方程z5x中的z,得22)2(y z5x,即y2z25x.注xOz面上的曲线F(x,z)0绕x轴旋转一周所生成的旋转2z2曲面方程为(,)0F x y.2z26.将xOz坐标面上的圆x9绕z轴旋转一周,求所生成的旋转曲面的方程.解以2y22z2x代替圆方程x9中的x,得9,( 2y22z2x)2y2z2即9.x2y27.将xOy坐标面上的双曲线4x936分别绕x轴及y轴旋转一周,求所生成的旋转曲面的方程.解以2z22y2y代替双曲线方程4936x中的y,得该双曲线绕x轴旋转一周而生成的旋转曲面方程为4 2y2z2 x9(2) 36,即4x29(y2z2)36.以2z22y2x代替双曲线方程4936x中的x,得该双曲线绕y轴旋转一周而生成的旋转曲面方程为4( 2z y22 2x)936,即4(x2z2)9y236.8.画出下列各方程所表示的曲面:2y2 a2a x2 2(1));(x)y((2)1;22492z2x(3)1;9 4(4)y2z0;(5)z2x2.解(1)如图8-11(a);(2)如图8-11(b);(3)如图8-11(c);(4)如图8-11(d);(5)如图8-11(e).9.指出下列方程在平面解析几何中和在空间解析几何中分别表示什么图形:(1)x2;(2)y x1;2y22y2(3)4;x(4)x 1.解(1)x2在平面解析几何中表示平行于y轴的一条直线,在空间解析几何中表示与yOz面平行的平面.(2)y x1在平面解析几何中表示斜率为1,y轴截距也为1的一条直线,在空间解析几何中表示平行于z轴的平面.2y2(3) 4x在平面解析几何中表示圆心在原点,半径为2的圆,在空间解析几何中表示母线平行于z轴,准线为2x2y4, z0的圆柱面.(4)x2y21在平面解析几何中表示以x轴为实轴,y轴为虚轴的双曲线,在空间解析几何中表示母线平行于z轴,准线为2 x2y1,的双曲柱面.z010.说明下列旋转曲面是怎样形成的:2y2z2x(1)1;49922y z2 (2)1;x4(3)x2y2z21;(4)(z a)2x2y2.2y2z22y2 xx解(1)1表示x Oy面上的椭圆 1绕x 499492z2 x轴旋转一周而生成的旋转曲面,或表示xOz面的椭圆 1绕49x轴旋转一周而生成的旋转曲面.2 22y z2y2(2) 1x表示xOy面上的双曲线x1绕y轴4 42y2旋转一周而生成的旋转曲面,或表示yOz面的双曲线 1z4绕y轴旋转一周而生成的旋转曲面.(3)x2y2z21表示xOy面上的双曲线x2y21绕x轴2z2旋转一周而生成的旋转曲面,或表示xOz面的双曲线 1x绕x轴旋转一周而生成的旋转曲面.(4)22 2(z a)x y表示x Oz面上的直线z x a或z x a绕z轴旋转一周而生成的旋转曲面,或表示yOz面的直线z y a或z y a绕z轴旋转一周而生成的旋转曲面.11.画出下列方程所表示的曲面:(1)4x2y2z24;(2)x2y24z24;2y2z x(3).349解(1)如图8-12(a);(2)如图8-12(b);(3)如图8-12(c);12.画出下列各曲面所围立体的图形:(1)z0,z3,x y0,x3y0,x2y21(在第一卦限内);222,22 2 x0,y0,z0,x y R y z R(在第一卦(2)限内).解(1)如图8-13所示;(2)如图8-14所示.1.画出下列曲线在第一卦限内的图形;(1)xy1,2;(2)zx y4 2 x0;y 2 ,(3)2x2x2y2z2a,2a.解(1)如图8-15(a);(2)如图8-15(b);(3)如图8-15(c).2.指出下列方程组在平面解析几何中与在空间解析几何中分别表示什么图形:(1)yy5x2x1,3;(2)2x4y2y3.91,解(1)yy5x2x1,3在平面解析几何中表示两直线的交点.在空间解析几何中表示两平面的交线,即空间直线.(2)2xy 32y91,2y2x在平面解析几何中表示椭圆 1与449 其切线y3的交点,即切点.在空间解析几何中表示椭圆柱面2y2 x49与其切平面y3的交线,即空间直线. 13.分别求母线平行于x轴及y轴而且通过曲线22x2x2y2z2z2y16,的柱面方程.解在22x2x2y2zy2z216,中消去x,得3 2z2y16,即为母线平行于x轴且通过已知曲线的柱面方程.在22x2xy2z2y2z216,中消去y,得2z23x 216,即为母线平行于y轴且通过已知曲线多的柱面方程.2y z2 2x与平面x z1的交线在xOy面上的投4.求球面9影的方程.解在2x2y2z 9, 中消去z,得x z 12y2x2x y2 2 x(1)9,即2x28,它表示母线平行于z轴的柱面,故2 22x2x yz08,表示已知交线在xOy面上的投影的方程.5.将下列曲线的一般方程化为参数方程:(1)2x(x1)y x;z0.2y2z 9, (2)2 2y ( z21) 4,。
高等数学下(同济大学第五版)课后习题答案解析

word 完美格式第八章 多元函数微分法及其应用第一节 多元函数的基本概念本节主要概念,定理,公式和重要结论理解多元函数的概念,会表达函数,会求定义域; 理解二重极限概念,注意A y x f y x y x =→),(lim ),(),(00是点),(y x 以任何方式趋于),(00y x ;注意理解本节中相关概念与一元函数中相应内容的区分与联系。
习题 8-11.求下列函数表达式:(1)xy y x y x f +=),(,求),(y x xy f +解:(,)()x yxy f xy x y xyx y ++=++(2)22),(y x y x y x f -=-+,求),(y x f解:(,)()()(,)f x y x y x y x y f x y xy +-=-+⇒= 2.求下列函数的定义域,并绘出定义域的图形: (1)221)1ln(yx x y x z --+-+=解:22221011010x y x y x y x y x +->⎧+>⎧⎪-->⇒⎨⎨+<⎩⎪≥⎩(2))12ln(2+-=y x z 解:2210x y -+>(3) |)|||1ln(),(y x y x f --= 解:1||||0||||1x y x y -->⇒+< 3.求下列极限:(1)22)1,0(),(1limy x xyx y x ++-→解:22(,)(0,1)1lim1x y x xyx y →-+=+ (2)xy xy y x 42lim)0,0(),(+-→解一:(,)(0,0)(,)(0,0)(,)(0,0)18lim2lim2lim 4x y x y x y xyxy →→→=-=-=-(3)yxy x y x )sin()2(lim )0,1(),(+→(4)2222011limy x y x y x +-+→→解一:(,)(1,0)(,)(1,0)sin()sin()lim (2)lim [(2)]3x y x y xy xy x x x y xy→→+=+=解二:(,)(1,0)(,)(1,0)(,)(1,0)sin()lim (2)lim (2)lim (2)3x y x y x y xy xyx x x x y y →→→+=+=+= (4)22220011limyx y x y x +-+→→解一:2222222200000011lim lim()022x x x y y y x y y x x y x y →→→→→→==⋅=++解二:222222000000x x x y y y y x y →→→→→→===+ 4.证明下列函数当)0,0(),(→y x 时极限不存在:(1)2222),(yx y x y x f +-=解:222222222222001lim lim 1x x y kxx y x k x k x y x k x k →→=---==+++ (2)22222)(),(y x y x y x y x f -+= 解:224222400lim lim 1()x x y x x y x x y x y x →→===+- 2222200lim 0()x y x y x y x y →==+- 5.下列函数在何处是间断的? (1) yx z -=1解:x y =(2)x y xy z 2222-+=解:22y x =第二节 偏导数word 完美格式本节主要概念,定理,公式和重要结论1.偏导数:设),(y x f z =在),(00y x 的某一邻域有定义,则xy x f y x x f y x f x x ∆∆∆),(),(lim),(0000000-+=→, yy x f y y x f y x f y y ∆∆∆),(),(lim ),(0000000-+=→. ),(00y x f x 的几何意义为曲线⎩⎨⎧==0),(y y y x f z 在点)),(,,(0000y x f y x M 处的切线对x 轴的斜率.),(y x f 在任意点),(y x 处的偏导数),(y x f x 、),(y x f y 称为偏导函数,简称偏导数.求),(y x f x 时,只需把y 视为常数,对x 求导即可. 2.高阶偏导数),(y x f z =的偏导数),(),,(y x f y x f y x 的偏导数称为二阶偏导数,二阶偏导数的偏导数称为三阶偏导数,如此类推. 二阶偏导数依求导次序不同,有如下4个:xy zy x z y z x z ∂∂∂∂∂∂∂∂∂∂222222,,,,其中后两个称为混合偏导数. 若两个混合偏导数皆为连续函数,则它们相等,即可交换求偏导数的次序.高阶混合偏导数也有类似结果.习题 8-21.求下列函数的一阶偏导数:(1)xy y xz +=解:21,z z xy x x y y y∂∂=+=-+∂∂ (2)xyz arctan =解:2222222111,1()1()z y y z x y y x x x y y x x y x x∂--∂=⋅==⋅=∂+∂+++ (3))ln(22y x x z ++=解:(1z x ∂=+=∂z y ∂==∂ (4))ln(222z y x u ++=解:222222222222,,u x u y u z x x y z y x y z z x y z∂∂∂===∂++∂++∂++ (5)⎰=yzxzt dt e u 2解:22222222,,x z y z y z x z u u u ze ze ye xe x y z∂∂∂=-==-∂∂∂ (6)x y y x z cos sin = 解:2211cos cos sin sin ,cos cos sin sin z x y y x y u x x y x y x y y x x y x y y y x x y x ∂∂=+=--∂∂ (7)y x xy z ++=)1( (8))cos(ϕθϕθ-=+e u解:(1)[ln(1)],(1)[ln(1)]11x y x y z x y u x y xy xy y xy xy x x xy y xy ++∂+∂+=+++=+++∂+∂+ (8))cos(ϕθϕθ-=+e u解:[cos()sin()],[cos()sin()]u u e e θϕθϕθϕθϕθϕθϕθϕ++∂∂=---=-+-∂∂ 2.求下列函数在指定点处的一阶偏导数: (1)yxy x z arcsin)1(2-+=,求)1,0(x z 解:20(0,1)lim0x x x z x∆→∆==∆ (2)xyx e x z yarctan)1(2-+=,求)0,1(y z 解:01(1,0)lim1y y y e z y∆∆→-==-∆ 3.求下列函数的高阶偏导数:(1))ln(xy x z =, 求22x z ∂∂,22yz ∂∂,y x z∂∂∂2解:ln()1,z z x xy x y y∂∂=+=∂∂ 22222211,,z z x z x x y y x y y∂∂∂==-=∂∂∂∂ (2))2(cos 2y x z +=,求22x z ∂∂,22yz ∂∂,y x z ∂∂∂2,x y z ∂∂∂2解:2cos(2)sin(2)sin 2(2)z x y x y x y x∂=-++=-+∂word 完美格式4cos(2)sin(2)2sin 2(2)zx y x y x y y∂=-++=-+∂ 222222cos 2(2),8cos 2(2),4cos 2(2)z z zx y x y x y x y x y∂∂∂=-+=-+=-+∂∂∂∂ (3)⎰+=22 y x xtdt e z , 求22x z ∂∂, yx z∂∂∂2解:22222222222,2(12),4x y x x y x x y z z z xe e x e e xye x x x y+++∂∂∂=-=+-=∂∂∂∂ 4.设⎪⎩⎪⎨⎧=+≠++-=0 00),(22222233y x y x y x xy y x y x f ,求)0,0(xy f 和)0,0(yx f .解:00(0)(0,0)00(0,0)lim lim 0x x x f x f f x x ∆→∆→∆--===∆∆,00(0,)(0,0)00(0,0)lim lim 0y y y f y f f y y ∆→∆→∆--===∆∆4224222224(,),0()x x x y y f x y y x y x y +-=+≠+ 4224222224(,),0()y x x y y f x y x x y x y --=+≠+ 54000(0,)(0,0)(0,0)lim lim 1x x xy y y y f y f y f y y∆→∆→-∆-∆-∆===-∆∆54000(,0)(0,0)(0,0)lim lim 1x x yx x x x f x f x f x x ∆→∆→∆-∆-∆===∆∆5.设)11(y x e z +-=, 求证z y z y x z x222=∂∂+∂∂ 解: 1111()()2211,x y x y z z e ex x y y-+-+∂∂==∂∂ 111111()()()2222221122x yx y x y z z x y x e y e e z x y x y -+-+-+∂∂+=⋅+⋅==∂∂ 6.设222z y x r ++=, 证明r zr y r x r 2222222=∂∂+∂∂+∂∂证明: 22222223,r x r x r r x r r x x r x r x r r r ∂--∂∂-∂=====∂∂由轮换对称性, 2222222323,r r y r r z y r z r∂-∂-==∂∂ 222222222223321r r r r x y z r x y z r r r∂∂∂---++===∂∂∂ 第三节 全微分本节主要概念,定理,公式和重要结论1.全微分的定义若函数),(y x f z =在点),(00y x 处的全增量z ∆表示成22),(y x o y B x A z ∆+∆=+∆+∆=∆ρρ则称),(y x f z =在点),(00y x 可微,并称Bdy Adx y B x A +=+∆∆为),(y x f z =在点),(00y x 的全微分,记作dz .2.可微的必要条件:若),(y x f z =在),(00y x 可微,则 (1)),(y x f 在),(00y x 处连续;(2)),(y x f 在),(00y x 处可偏导,且),(),,(0000y x f B y x f A y x ==,从而dy y x f dx y x f dz y x ),(),(0000+=.一般地,对于区域D 内可微函数, dy y x f dx y x f dz y x ),(),(+=.3.可微的充分条件:若),(y x f z =在),(00y x 的某邻域内可偏导,且偏导数在),(00y x 处连续,则),(y x f z =在),(00y x 可微。
同济大学版高等数学课后习题答案第2章

同济大学版高等数学课后习题答案第2章习题2-11. 设物体绕定轴旋转, 在时间间隔[0, t]内转过的角度为θ, 从而转角θ是t 的函数: θ=θ(t). 如果旋转是匀速的, 那么称tθω=为该物体旋转的角速度, 如果旋转是非匀速的, 应怎样确定该物体在时刻t 0的角速度?解在时间间隔[t 0, t 0+?t]内的平均角速度ω为 tt t t t-?+=??=)()(00θθθω,故t 0时刻的角速度为)()()(lim lim lim 000000t tt t t tt t t θθθθωω'=?-?+=??==→?→?→?. 2. 当物体的温度高于周围介质的温度时, 物体就不断冷却, 若物体的温度T 与时间t 的函数关系为T =T(t), 应怎样确定该物体在时刻t 的冷却速度?解物体在时间间隔[t 0, t 0+?t]内, 温度的改变量为 ?T =T(t +?t)-T(t), 平均冷却速度为tt T t t T t T ?-?+=??)()(,故物体在时刻t 的冷却速度为)()()(lim lim 00t T tt T t t T t T t t '=?-?+=??→?→?. 3. 设某工厂生产x 单位产品所花费的成本是f(x)元, 此函数f(x)称为成本函数, 成本函数f(x)的导数f '(x)在经济学中称为边际成本. 试说明边际成本f '(x)的实际意义.解 f(x +?x)-f(x)表示当产量由x 改变到x +?x 时成本的改变量.xx f x x f ?-?+)()(表示当产量由x 改变到x +?x 时单位产量的成本. xx f x x f x f x ?-?+='→?)()(lim)(0表示当产量为x 时单位产量的成本.4. 设f(x)=10x 2, 试按定义, 求f '(-1). 解 xx x f x f f x x ?--?+-=?--?+-=-'→?→?2200)1(10)1(10lim )1()1(lim)1(20)2(lim 102lim 10020-=?+-=??+?-=→?→?x xx x x x . 5. 证明(cos x)'=-sin x .解 xxx x x x ?-?+='→?cos )cos(lim )(cos 0xxx x x +-=→?2sin )2sin(2limx x xx x x sin ]22sin )2sin([lim 0-=+-=→?. 6. 下列各题中均假定f '(x 0)存在, 按照导数定义观察下列极限, 指出A 表示什么:(1)A xx f x x f x =?-?-→?)()(lim 000;解xx f x x f A x ?-?-=→?)()(lim000)()()(lim 0000x f xx f x x f x '-=?--?--=→?-. (2)A xx f x =→)(lim 0, 其中f(0)=0, 且f '(0)存在; 解)0()0()0(lim )(lim00f x f x f x x f A x x '=-+==→→. (3)A h h x f h x f h =--+→)()(lim 000. 解hh x f h x f A h )()(lim000--+=→hx f h x f x f h x f h )]()([)]()([lim00000----+=→ hx f h x f hx f h x f h h )()(lim)()(lim 000000----+=→→ =f '(x 0)-[-f '(x 0)]=2f '(x 0). 7. 求下列函数的导数: (1)y =x 4; (2)32x y =; (3)y =x 1. 6; (4)xy 1=;(5)21xy =;(6)53x x y =;(7)5322x x x y =;解 (1)y '=(x 4)'=4x 4-1=4x 3 .(2)3113232323232)()(--=='='='x x x xy . (3)y '=(x 1. 6)'=1.6x 1. 6-1=1.6x 0. 6.(4)23121212121)()1(-----=-='='='x x x xy .(5)3222)()1(---='='='x x xy .(6)511151651653516516)()(x x x x xy =='='='-.(7)651616153226161)()(--=='='='x x x x x x y .8. 已知物体的运动规律为s =t 3(m). 求这物体在t =2秒(s)时的速度.解v =(s)'=3t 2, v|t =2=12(米/秒).9. 如果f(x)为偶函数, 且f(0)存在, 证明f(0)=0. 证明当f(x)为偶函数时, f(-x)=f(x), 所以)0(0)0()(lim 0)0()(lim 0)0()(lim)0(000f x f x f x f x f x f x f f x x x '-=-----=---=--='→-→→, 从而有2f '(0)=0, 即f '(0)=0.10. 求曲线y =sin x 在具有下列横坐标的各点处切线的斜率:π32=x , x =π.解因为y '=cos x , 所以斜率分别为 2132cos 1-==πk , 1cos 2-==πk .11. 求曲线y =cos x 上点)21 ,3(π处的切线方程和法线方程式.解y '=-sin x ,233sin3-=-='=ππx y ,故在点)21 ,3(π处, 切线方程为)3(2321π--=-x y ,法线方程为)3(3221π--=-x y .12. 求曲线y =e x 在点(0,1)处的切线方程. 解y '=e x , y '|x =0=1, 故在(0, 1)处的切线方程为 y -1=1?(x -0), 即y =x +1.13. 在抛物线y =x 2上取横坐标为x 1=1及x 2=3的两点, 作过这两点的割线, 问该抛物线上哪一点的切线平行于这条割线?解 y '=2x , 割线斜率为421913)1()3(=-=--=y y k .令2x =4, 得x =2.因此抛物线y =x 2上点(2, 4)处的切线平行于这条割线. 14. 讨论下列函数在x =0处的连续性与可导性: (1)y =|sin x|;(2)=≠=0001sin 2x x xx y . 解 (1)因为 y(0)=0,0)sin (lim |sin |lim lim 00=-==---→→→x x y x x x ,0sin lim |sin |lim lim 00===+++→→→x x y x x x ,所以函数在x =0处连续. 又因为 1sin lim 0|0sin ||sin |lim 0)0()(lim )0(000-=-=--=--='---→→→-x x x x x y x y y x x x ,1sin lim 0|0sin ||sin |lim 0)0()(lim )0(000==--=--='+++→→→+xx x x x y x y y x x x , 而y '-(0)≠y '+(0), 所以函数在x =0处不可导.解因为01sin lim )(lim 200==→→xx x y x x , 又y(0)=0, 所以函数在x =0处连续. 又因为01sin lim 01sin lim0)0()(lim 0200==-=--→→→xx x x x x y x y x x x , 所以函数在点x =0处可导, 且y '(0)=0.15. 设函数>+≤=1 1)(2x b ax x x x f 为了使函数f(x)在x =1处连续且可导, a , b 应取什么值?解因为1lim )(lim 211==--→→x x f x x , b a b ax x f x x +=+=++→→)(lim )(lim 11, f(1)=a +b ,所以要使函数在x =1处连续, 必须a +b =1 . 又因为当a +b =1时211lim )1(21=--='-→-x x f x ,a x x a xb a x a x b ax f x x x =--=--++-=--+='+++→→→+1)1(lim 11)1(lim 11lim )1(111, 所以要使函数在x =1处可导, 必须a =2, 此时b =-1. 16. 已知?<-≥=0 0)(2x x x x x f 求f +'(0)及f -'(0), 又f '(0)是否存在?解因为 f -'(0)=10lim )0()(lim00-=--=---→→xx x f x f x x , f +'(0)=00lim )0()(lim 200=-=-++→→xx x f x f x x , 而f -'(0)≠f +'(0), 所以f '(0)不存在.17. 已知f(x)=?≥<0 0sin x x x x , 求f '(x) .解当x<0时, f(x)=sin x , f '(x)=cos x ; 当x>0时, f(x)=x , f '(x)=1; 因为 f -'(0)=10sin lim )0()(lim00=-=---→→x x x f x f x x , f +'(0)=10lim )0()(lim 00=-=-++→→xx x f x f x x , 所以f '(0)=1, 从而f '(x)=?≥<0 10cos x x x .18. 证明: 双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形的面积都等于2a 2 .解由xy =a 2得xa y 2=, 22xa y k -='=.设(x 0, y 0)为曲线上任一点, 则过该点的切线方程为)(02020x x x a y y --=-. 令y =0, 并注意x 0y 0=a 2, 解得0022002x x ax y x =+=, 为切线在x轴上的距.令x =0, 并注意x 0y 0=a 2, 解得00022y y x a y =+=, 为切线在y 轴上的距.此切线与二坐标轴构成的三角形的面积为 200002||2|2||2|21a y x y x S ===.习题 2-21. 推导余切函数及余割函数的导数公式: (cot x)'=-csc 2x ; (csc x)'=-csc xcot x .解 xx x x x xx x 2sin cos cos sin sin )sin cos ()(cot ?-?-='=' x xx x x 22222csc sin 1sin cos sin-=-=+-=. x x xx x x cot csc sin cos )sin 1()(csc 2?-=-='='. 2. 求下列函数的导数: (1)1227445+-+=xxxy ;(2) y =5x 3-2x +3e x ;(3) y =2tan x +sec x -1; (4) y =sin x ?cos x ; (5) y =x 2ln x ; (6) y =3e x cos x ; (7)xx y ln =;(8)3ln 2+=xe y x;(9) y =x 2ln x cos x ; (10)tt s cos 1sin 1++=;解 (1))12274()12274(14545'+-+='+-+='---x x x xxxy2562562282022820xxxx x x +--=+--=---. (2) y '=(5x 3-2x +3e x )'=15x 2-2x ln2+3ex .(3) y '=(2tan x +sec x -1)'=2sec 2x +sec x ?tan x =sec x(2sec x +tan x).(4) y '=(sin x ?cos x)'=(sin x)'?cos x +sin x ?(cos x)' =cos x ?cos x +sin x ?(-sin x)=cos 2x . (5) y '=(x 2ln x)'=2x ?ln x +x 2?x 1=x(2ln x +1) . (6) y '=(3e x cos x)'=3e x ?cos x +3e x ?(-sin x)=3e x (cos x -sin x).(7)22ln1ln 1)ln (x x x xx x x x y -=-?='='.(8)3422)2(2)3ln (x x e x x e x e x e y x x x x -=?-?='+='. (9) y '=(x 2ln x cos x)'=2x ?ln x cos x +x 2?x1?cos x +x 2 lnx ?(-sin x)2x ln x cos x +x cos x -x 2 ln x sin x .(10)22)cos 1(cos sin 1)cos 1()sin )(sin 1()cos 1(cos )cos 1sin 1(t tt t t t t t tt s +++=+-+-+='++='.3. 求下列函数在给定点处的导数: (1) y =sin x -cos x , 求6π='x y 和4π='x y .(2)θθθρcos 21sin +=,求4πθθρ=dd .(3)553)(2x x x f +-=, 求f '(0)和f '(2) .解 (1)y '=cos x +sin x , 21321236sin 6cos 6+=+=+='=πππx y ,222224sin 4cos 4=+=+='=πππx y . (2)θθθθθθθθρcos sin 21sin 21cos sin +=-+=d d ,)21(4222422214cos 44sin 214πππππθρπθ+=?+?=+==d d . (3)x x x f 52)5(3)(2+-=', 253)0(='f , 1517)2(='f . 4. 以初速v 0竖直上抛的物体, 其上升高度s 与时间t 的关系是2021gt t v s -=. 求:(1)该物体的速度v(t); (2)该物体达到最高点的时刻. 解(1)v(t)=s '(t)=v 0-gt .(2)令v(t)=0, 即v 0-gt =0, 得gv t 0=, 这就是物体达到最高点的时刻.5. 求曲线y =2sin x +x 2上横坐标为x =0的点处的切线方程和法线方程.解因为y '=2cos x +2x , y '|x =0=2, 又当x =0时, y =0, 所以所求的切线方程为 y =2x , 所求的法线方程为x y 21-=, 即x +2y =0.6. 求下列函数的导数: (1) y =(2x +5)4 (2) y =cos(4-3x); (3)23x e y -=;(4) y =ln(1+x 2); (5) y =sin 2x ; (6)22x a y -=;(7) y =tan(x 2); (8) y =arctan(e x ); (9) y =(arcsin x)2; (10) y =lncos x .解 (1) y '=4(2x +5)4-1?(2x +5)'=4(2x +5)3?2=8(2x +5)3. (2) y '=-sin(4-3x)?(4-3x)'=-sin(4-3x)?(-3)=3sin(4-3x). (3)22233236)6()3(xx x xe x e x e y ----=-?='-?='.(4)222212211)1(11x x x x x x y +=?+='+?+='. (5) y '=2sin x ?(sin x)'=2sin x ?cos x =sin 2x . (6))()(21])[(22121222122'-?-='-='-x a x a x a y2122)2()(21x a x x x a --=-?-=-.(7) y '=sec 2(x 2)?(x 2)'=2xsec 2(x 2).(8)xx xx e e e e y 221)()(11+='?+='. (9) y '21arcsin2)(arcsin arcsin 2xx x x -='?=. (10)x x xx x y tan )sin (cos 1)(cos cos 1-=-='?='. 7. 求下列函数的导数: (1) y =arcsin(1-2x);(2)211x y -=;(3)x e y x 3cos 2-=;(4)xy 1arccos =;(5)x x y ln 1ln 1+-=;(6)xx y 2sin =; (7)x y arcsin =;(8))ln(22x a x y ++=;(9) y =ln(sec x +tan x); (10) y =ln(csc x -cot x). 解 (1)2 221)21(12)21()21(11x x x x x y --=---='-?--='.(2))1()1(21])1[(21212212'-?--='-='---x x x y 2321)1()2()1(21x x x x x --=-?--=-.(3))3)(3sin (3cos )2()3(cos 3cos )(2222'-+'-='+'='----x x e x x e x e x e y xx x x)3sin 63(cos 213sin 33cos 21222x x e x e x e xxx+-=--=---. (4)1||)1()1(11)1()1(1122222-=---='--='x x x x x x x y . (5)22)ln 1(2)ln 1(1)ln 1()ln 1(1x x x x x x xy +-=+--+-='.(6)222sin 2cos 212sin 22cos xx x x xx x x y -=?-??='.(7)2222121)(11)()(11x x x x x x y -=?-='?-='.(8)])(211[1)(12222222222'+++?++='++?++='x a x a x a x x a x x a x y 2222221)]2(211[1x a x x a x a x +=++?++=.(9)x x x x x x x x y sec tan sec sec tan sec )tan (sec tan sec 12 =++='+?+='. (10) x xx x x x x x x x y csc cot csc csc cot csc )cot (csc cot csc 12 =-+-='-?-='.8. 求下列函数的导数: (1)2)2(arcsin x y =;(2)2tan ln x y =;(3)x y 2ln 1+=;(4)x e y arctan =; (5)y =sin n xcos nx ; (6)11arctan -+=x x y ;(7)xx y arccos arcsin =;(8) y=ln[ln(ln x)] ; (9)xx x x y-++--+1111; (10)xx y +-=11arcsin.解 (1)'?=')2(arcsin )2(arcsin 2x x y )2()2(11)2(arcsin 22'?-?=x x x21)2(11(arcsin 22-?=x x . 242arcsin 2x x-=(2))2(2sec 2tan 1)2(tan 2tan 12'??='?='x x x x x yx x x csc 212sec 2tan 12=??=.(3))ln 1(ln 121ln 1222'+?+=+='x xx y )(ln ln 2ln 1212'??+=x x x x x x 1ln 2ln 1212??+=xx x2ln 1ln +=.(4))(arctan arctan '?='x e y x)()(112arctan'?+?=x x e x)1(221)(11arctan 2arctanx x e x x e x x+=?+?=.(5) y '=n sin n -1x ?(sin x)'?cos nx +sin n x ?(-sin nx)?(nx)' =n sin n -1x ?cos x ?cos nx +sin n x ?(-sin nx)?n =n sin n -1x ?(cosx ?cos nx -sin x ?sin nx)= n sin n -1xcos(n +1)x . (6)222 211)1()1()1()11(11)11()11(11x x x x x x x x x x y +-=-+--?-++='-+?-++= '.(7)222)(arccos arcsin 11arccos 11x x x x x y -+-='22)(arccos arcsin arccos 11x x x x +?-=22)(arccos 12x x -=π.(8))(ln ln 1)ln(ln 1])[ln(ln )ln(ln 1'??='?='x x x x x y)ln(ln ln 11ln 1)ln(ln 1x x x x x x ?=??=. (9)2)11()121121)(11()11)(121121(x x x x x x x x xx y -++--+--+--++-++=' 22111x x -+-=.(10)2)1()1()1(1111)11(1111x x x xx x x x x y +--+-?+--='+-?+--=')1(2)1(1x x x -+-=.9. 设函数f(x)和g(x)可导, 且f 2(x)+g 2(x)≠0, 试求函数)()(22x g x f y +=的导数.解])()([)()(212222'+?+='x g x f x g x f y )]()(2)()(2[)()(2122x g x g x f x f x g x f '+'?+=)()()()()()(22x g x f x g x g x f x f +'+'=.10. 设f(x)可导, 求下列函数y 的导数dxdy :(1) y =f(x 2);(2) y =f(sin 2x)+f(cos 2x).解 (1) y '=f '(x 2)?(x 2)'= f '(x 2)?2x =2x ?f '(x 2). (2) y '=f '(sin 2x)?(sin 2x)'+f '(cos 2x)?(cos 2x)'= f '(sin 2x)?2sin x ?cos x +f '(cos 2x)?2cosx ?(-sin x) =sin 2x[f '(sin 2x)- f '(cos 2x)]. 11. 求下列函数的导数: (1) y =ch(sh x ); (2) y =sh x ?e ch x ; (3) y =th(ln x); (4) y =sh 3x +ch 2x ; (5) y =th(1-x 2); (6) y =arch(x 2+1); (7) y =arch(e 2x ); (8) y =arctan(th x);(9)xx y 2ch 21ch ln +=; (10))11(ch 2+-=x x y解 (1) y '=sh(sh x)?(sh x)'=sh(sh x)?ch x . (2) y '=ch x ?e ch x +sh x ?e ch x ?sh x =e ch x (ch x +sh 2x) . (3))(ln ch 1)(ln )(ln ch 122x x x x y ?='?='.(4) y '=3sh 2x ?ch x +2ch x ?sh x =sh x ?ch x ?(3sh x +2) .(5))1(ch 2)1()1(ch 122222x x x x y --=-?-='. (6)222)1()1(112422++='+?++='x x x x x y .(7)12)(1)(142222-='?-='x xx x e e e e y . (8)xxx x x x x y 222222ch 1ch sh 11ch 1th 11)th ()th (11?+=?+='?+=' x x x 222sh 211sh ch 1+=+=. (9))ch (ch 21)ch (ch 124'?-'?='x x x x y x x xx x sh ch 2ch 21ch sh 4??-= xx x x x x x x 323ch sh ch sh ch sh ch sh -?=-=x xx x x x 33332th ch sh ch )1ch (sh ==-?=. (10)'+-?+-?+-='+-?+-=')11()11(sh )11(ch 2])11(ch [)11(ch 2x x x x x x x x x x y)112(sh )1(2)1()1()1()112(sh 22+-?+=+--+?+-?=x x x x x x x x .12. 求下列函数的导数: (1) y =e -x (x 2-2x +3); (2) y =sin 2x ?sin(x 2); (3)2)2(arctan x y =;(4)n xx y ln =;(5)t t t t ee e e y --+-=;(6)xy 1cos ln =;(7)x ey 1sin 2-=; (8)xx y +=;(9)242arcsin x x x y -+=;(10)212arcsint t y +=.解 (1) y '=-e -x (x 2-2x +3)+e -x (2x -2) =e -x (-x 2+4x -5).(2) y '=2sin x ?cos x ?sin(x 2)+sin 2x ?cos(x 2)?2x =sin2x ?sin(x 2)+2x ?sin 2x ?cos(x 2). (3)2arctan 44214112arctan 222x x x x y +=?+?='. (4)121ln 1ln 1+--=?-?='n n n n x x n x nx x x xy . (5)2222)1(4)())(())((+=+---++='-----t t t t t t t t t t t t e e e e e e e e e e e e y .。
同济高等数学下册课后题答案详解

第8章第1节向量及其线性运算习题8—111,12,15,17,18第8章第2节数量积、向量积、混合积习题8—23,4,6,7,9,10第8章第3节曲面及其方程习题8—32,5,7,9,10(1)(2)(3)(4)第8章第4节空间曲线及其方程习题8—43,4,7,8第8章第5节平面及其方程习题8—51,2,3,5,9第8章第6节空间直线及其方程习题8—61,2,3,4,5,8,9,10(1)(2),12,13,15第8章总复习题总复习题八1,7,8,10,11,12,13,14(1)(2),15,17,19,20第9章第1节多元函数基本概念习题9—12,5(1)(2),6(1)(2)(4)(5),7(1),8第9章第2节偏导数习题9—21(3)(4)(5) (6)(7),4,6(2),9(1)第9章第3节全微分习题9—31(1)(2)(4),2,3,5第9章第4节多元复合函数的求导法则习题9—42,4,6,7,8(1)(2),10,11,12(1)(4)第9章第5节隐函数的求导公式习题9—51,2,4,5,6,8,9,10(1)(3)第9章第6节多元函数微分学的几何应用习题9—63,4,6,7,9,10,12第9章第7节方向导数与梯度习题9—72,3,5,7,8,10第9章第8节多元函数的极值及其求法习题9—81,2,5,6,7,9,11第9章第9节二元函数泰勒公式习题9—91,3第9章总复习题总复习题九1,2,3,5,6,8,9,12,15,16,17,20第10章第1节二重积分的概念与性质习题10—12,4,5第10章第2节二重积分的计算法习题10—21(1)(3),2(3)(4),4(1)(3),6(4)(5)(6),7,89,12(1)(2)(3),14(1)(2),15(1)(2)(3),16 第10章第3节三重积分习题10—31(1)(2),2,4,5,7,8,9(1)(2),10(1)(2),11(1)第10章第4节重积分的应用习题10—41,2,5,6,8,10,14第10章总复习题总复习题十1,2(1) (3),3(1)(2)6,8(1)(2),10,11,12第11章第1节对弧长的曲线积分习题11—11,3(3)(4)(5)(7),4第11章第2节对坐标的曲线积分习题11—23(1) (2)(3) (5) (6)(7),4(1)(2)(3),7(1)(2),8第11章第3节格林公式及其应用习题11—31,2(1)(2),3,4(1)(2),5(1)(2)(4),6(1)(3)(4),8(1) (3)(5) (6)(7)第11章第4节对面积的曲面积分习题11—41,4(1)(2),5(1),6(1)(2)(3),7,8第11章第5节对坐标的曲面积分习题11—53(1)(2)(4),4(1)(2)第11章第6节高斯公式通量与散度习题11—61(1) (2)(3) (4) , 3(1)(2)第11章第7节斯托克斯公式环流量与旋度习题11—72(1) (2)(3),3(1)(2)第11章总复习题总复习题十一1,2,3,4,5,7,11第12章第1节常数项级数的概念和性质习题12—11(1)(4),2(3)(4),3,4第12章第2节常数项级数的审敛法习题12—21(1)(4) (5),2(1)(4) ,3(1)(3),4(1)(3)(5),5(1)(2)(3) (5)第12章第3节幂级数习题12—31,2第12章第4节函数展开成幂级数习题12—42,3,4,5,6第12章第7节傅里叶级数习题12—71(1)(2),2(1),3,4,5,6第12章第8节一般周期函数的傅里叶级数习题12—81(1)(2),2第12章总复习题总复习题十二1,2(1)(2)(3)(5),4,5(1)(2)(4),6(1),7(1)(2)(4),8(1)(2)(3),9(1),10(1),11。
同济第六版高数答案(高等数学课后习题解答)

习题3-31. 按(x -4)的幂展开多项式x 4-5x 3+x 2-3x +4. 解 设f (x )=x 4-5x 3+x 2-3x +4. 因为 f (4)=-56,f '(4)=(4x 3-15x 2+2x -3)|x =4=21, f ''(4)=(12x 2-30x +2)|x =4=74, f '''(4)=(24x -30)|x =4=66, f (4)(4)=24, 所以4)4(32)4(!4)4()4(!3)4()4(!2)4()4)(4()4()(-+-'''+-''+-'+=x f x f x f x f f x f =-56+21(x -4)+37(x -4)2+11(x -4)3+(x -4)4. 2. 应用麦克劳林公式, 按x 幂展开函数f (x )=(x 2-3x +1)3. 解 因为f '(x )=3(x 2-3x +1)2(2x -3),f ''(x )=6(x 2-3x +1)(2x -3)2+6(x 2-3x +1)2=30(x 2-3x +1)(x 2-3x +2), f '''(x )=30(2x -3)(x 2-3x +2)+30(x 2-3x +1)(2x -3)=30(2x -3)(2x 2-6x +3), f (4)(x )=60(2x 2-6x +3)+30(2x -3)(4x -6)=360(x 2-3x +2), f (5)(x )=360(2x -3), f (6)(x )=720;f (0)=1, f '(0)=-9, f ''(0)=60, f '''(0)=-270, f (4)(0)=720, f (5)(0)=-1080, f (6)(0)=720, 所以6)6(5)5(4)4(32!6)0(!5)0(!4)0(!3)0(!2)0()0()0()(x f x f x f x f x f x f f x f +++'''+''+'+==1-9x +30x 3-45x 3+30x 4-9x 5+x 6.3. 求函数x x f =)(按(x -4)的幂展开的带有拉格朗日型余项的3阶泰勒公式. 解 因为24)4(==f , 4121)4(421=='=-x x f , 32141)4(423-=-=''=-x x f , 328383)4(425⋅=='''=-x x f , 27)4(1615)(--=x x f , 所以4)4(32)4(!4)()4(!3)4()4(!2)4()4)(4()4(-+-'''+-''+-'+=x f x f x f x f f x ξ4732)4()]4(4[1615!41)4(5121)4(641)4(412--+⋅--+---+=x x x x x θ(0<θ<1). 4. 求函数f (x )=ln x 按(x -2)的幂展开的带有佩亚诺型余项的n 阶泰勒公式. 解 因为f '(x )=x -1, f ''(x )=(-1)x -2, f '''(x )=(-1)(-2)x -3 , ⋅ ⋅ ⋅ , nn nn x n x n x f )!1()1()1( )2)(1()(1)(--=+-⋅⋅⋅--=--; kk k k f 2)!1()1()2(1)(--=-(k =1, 2, ⋅ ⋅ ⋅, n +1), 所以])2[()2(!)2( )2(!3)2()2(!2)2()2)(2()2(ln )(32n n n x o x n f x f x f x f f x -+-+⋅⋅⋅+-'''+-''+-'+=])2[()2(2)1( )2(231)2(221)2(212ln 13322n n n n x o x n x x x -+-⋅-+⋅⋅⋅--⋅+-⋅--+=-. 5. 求函数x x f 1)(=按(x +1)的幂展开的带有拉格朗日型余项的n 阶泰勒公式. 解 因为f (x )=x -1, f '(x )=(-1)x -2, f ''(x )=(-1)(-2)x -3 , ⋅ ⋅ ⋅ , 1)1()(!)1()( )2)(1()(++--=-⋅⋅⋅--=n n n n xn xn x f ; !)1(!)1()1(1)(k k fk k k -=--=-+(k =1, 2, ⋅ ⋅ ⋅, n ),所以 )1(!3)1()1(!2)1()1)(1()1(132⋅⋅⋅++-'''++-''++-'+-=x f x f x f f x1)1()()1()!1()()1(!)1(++++++-+n n nn x n f x n f ξ 12132)1()]1(1[)1(])1( )1()1()1(1[++++++--+++⋅⋅⋅+++++++-=n n n nx x x x x x θ (0<θ<1). 6. 求函数f (x )=tan x 的带有拉格朗日型余项的3阶麦克劳林公式. 解 因为 f '(x )=sec 2x ,f ''(x )=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x ,f '''(x )=4sec x ⋅sec x ⋅tan 2x +2sec 4x =4sec 2x ⋅tan 2x +2sec 4x ,f (4)(x )=8sec 2x ⋅tan 3x +8sec 4x ⋅tan x +8sec 4x ⋅tan x xx x 52cos )2(sin sin 8+=;f (0)=0, f '(0)=1, f ''(0)=0, f '''(0)=2,所以 4523)(c o s 3]2)()[s i n s i n (31t a nx x x x x x x θθθ+++=(0<θ<1). 7. 求函数f (x )=xe x 的带有佩亚诺型余项的n 阶麦克劳林公式. 解 因为 f '(x )=e x +xe x ,f ''(x )=e x +e x +xe x =2e x +xe x , f '''(x )=2e x +e x +xe x =3e x +xe x , ⋅ ⋅ ⋅, f (n )(x )=ne x +xe x ; f (k )(0)=k (k =1, 2, ⋅ ⋅ ⋅, n ),所以 )(!)0( !3)0(!2)0()0()0()(32n nn xx o x n f x f x f x f f xe ++⋅⋅⋅⋅+'''+''+'+=)()!1(1 !2132n n x o x n x x x +-⋅⋅⋅+++=.8. 验证当210≤≤x 时, 按公式62132x x x e x +++≈计算e x 的近似值时, 所产生的误差小于0.01, 并求e 的近似值, 使误差小于0.01.解 因为公式62132x x x e x+++≈右端为e x 的三阶麦克劳林公式, 其余项为 43!4)(x e x R ξ=, 所以当210≤≤x 时,按公式62132x x x e x +++≈计算e x 的误差 01.00045.0)21(!43|!4||)(|42143<≈≤=x e x R ξ.645.1)21(61)21(212113221≈⋅+⋅++≈=e e .9. 应用三阶泰勒公式求下列各数的近似值, 并估计误差: (1)330; (2)sin18︒.解 (1)设3)(x x f =, 则f (x )在x 0=27点展开成三阶泰勒公式为2353233)27)(2792(!21)27(273127)(-⋅-⋅+-⋅+==--x x x x f4311338)27)(8180(!41)27)(272710(!31--⋅+-⋅⋅+--x x ξ(ξ介于27与x 之间).于是33823532333)272710(!313)2792(!21327312730⋅⋅⋅+⋅⋅-⋅+⋅⋅+≈---10724.3)3531311(31063≈+-+≈, 其误差为5114311431131088.13!4803278180!41|3)8180(!41||)30(|---⨯=⋅=⋅⋅⋅<⋅-⋅=ξR .(2) 已知43!4s i n !31s i n x x x x ξ+-=(ξ介于0与x 之间),所以 sin 18︒3090.0)10(!311010sin 3≈-≈=πππ,其误差为44431003.2)10(!46sin |)10(!4sin ||)10(|-⨯=<=πππξπR . 10. 利用泰勒公式求下列极限: (1))23(lim 434323x x x x x --++∞→;(2))]1ln([cos lim2202x x x e x x x -+--→;(3)2220sin )(cos 1211lim 2x e x x x x x -+-+→. 解 (1)tt t xx x x x x x t x x 430434343232131lim 12131lim)23(lim --+=--+=--++→+∞→+∞→.因为)(1313t o t t ++=+,)(211214t o t t +-=-, 所以23])(23[lim )](211[)](1[lim)23(lim 00434323=+=+--++=--++→+→+∞→t t o t t o t t o t x x x x t t x . (2)])1ln(1[)](41!21211[)](!41!211[lim)]1ln([cos lim1344244202202x x xx x xx o x x x o x x x x x e x -++⋅+--++-=-+-→-→010)1l n (1)(121lim 11340=+=-++-=-→e x x x o x x x . (3)2442442442202220))](!211())(!41!211[()](!43!211[211lim sin )(cos 1211lim 2xx o x x x o x x x o x x x x e x x x x x x +++-++-+-+-+=-+-+→→ 12123!43)(241123)(!43lim )(241123)(!43lim 2424404264440-=-=+--+=⋅+--+=→→x x o x x x o x o x x x x o x x x .习题3-41. 判定函数f (x )=arctan x -x 单调性.解 因为011111)(22≤+-=-+='x x x f , 且仅当x =0时等号成立, 所以f (x )在(-∞, +∞)内单调减少.2. 判定函数f (x )=x +cos x (0≤x ≤2π)的单调性.解 因为f '(x )=1-sin x ≥0, 所以f (x )=x +cos x 在[0, 2π]上单调增加. 3. 确定下列函数的单调区间: (1) y =2x 3-6x 2-18x -7;(2)xx y 82+=(x >0);(3)x x x y 6941023+-=;(4))1ln(2x x y ++=; (5) y =(x -1)(x +1)3;(6))0())(2(32>--=a x a a x y ; (7) y =x n e -x (n >0, x ≥0); (8)y =x +|sin 2x |.解 (1) y '=6x 2-12x -18=6(x -3)(x +1)=0, 令y '=0得驻点x 1=-1, x 2=3. 列表得可见函数在(-∞, -1]和[3, +∞)内单调增加, 在[-1, 3]内单调减少.(2) 0)2)(2(28222=+-=-='x x x x y ,令y '=0得驻点x 1=2, x 2=-2(舍去).因为当x >2时, y >0; 当0<x <2时, y '<0, 所以函数在(0, 2]内单调减少, 在[2, +∞)内单调增加. (3)223)694()1)(12(60x x x x x y +----=', 令y '=0得驻点211=x , x 2=1, 不可导点为x =0. 列表得可见函数在(-∞, 0), ]21 ,0(, [1, +∞)内单调减少, 在]1 ,21[上单调增加.(4)因为011)1221(11222>+=++++='x x x x x y , 所以函数在(-∞, +∞)内单调增加. (5) y '=(x +1)3+3(x -1)(x +1)22)1)(21(4+-=x x . 因为当21<x 时, y '<0; 当21>x 时, y '>0, 所以函数在]21 ,(-∞内单调减少, 在) ,21[∞+内单调增加.(6)32)()2(3)32(x a a x a x y ----=', 驻点为321a x =, 不可导点为22a x =, x 3=a .列表得可见函数在)2 ,(a -∞, ]32 ,2(a a , (a , +∞)内单调增加, 在) ,32[a a 内单调减少.(7)y '=e -x x n -1(n -x ), 驻点为x =n . 因为当0<x <n 时, y '>0; 当x >n 时, y '<0, 所以函数在[0, n ]上单调增加, 在[n , +∞)内单调减少.(8)⎪⎩⎪⎨⎧+<<+-+≤≤+=πππππππk x k x x k x k x x y 22sin 2 2sin (k =0, ±1, ±2, ⋅ ⋅ ⋅),⎪⎩⎪⎨⎧+<<+-+≤≤+='πππππππk x k x k x k x y 2 2c o s 212 2c o s 21(k =0, ±1, ±2, ⋅ ⋅ ⋅). y '是以π为周期的函数, 在[0, π]内令y '=0, 得驻点21π=x , 652π=x , 不可导点为23π=x .列表得根据函数在[0, π]上的单调性及y '在(-∞, +∞)的周期性可知函数在]32 ,2[πππ+k k 上单调增加, 在]22 ,32[ππππ++k k 上单调减少(k =0, ±1, ±2, ⋅ ⋅ ⋅).4. 证明下列不等式: (1)当x >0时, x x +>+1211;(2)当x >0时, 221)1ln(1x x x x +>+++; (3)当20π<<x 时, sin x +tan x >2x ;(4)当20π<<x 时, 331tan x x x +>;(5)当x >4时, 2x >x 2;证明 (1)设x x x f +-+=1211)(, 则f (x )在[0, +∞)内是连续的. 因为x x f +-='12121)(01211>+-+=xx , 所以f (x )在(0, +∞)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即 01211>+-+x x , 也就是 x x +>+1211.(2)设221)1ln(1)(x x x x x f +-+++=, 则f (x )在[0, +∞)内是连续的. 因为 0)1l n (1)11(11)1l n ()(22222>++=+-++⋅++⋅+++='x x x x x x x x x x x x f ,所以f (x )在(0, +∞)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即 01)1l n (122>+-+++x x x x , 也就是 221)1l n (1x x x x +>+++.(3)设f (x )=sin x +tan x -2x , 则f (x )在)2,0[π内连续,f '(x )=cos x +sec 2x -2xx x x 22cos ]cos )1)[(cos 1(cos ---=. 因为在)2 ,0(π内cos x -1<0, cos 2x -1<0, -cos x <0, 所以f '(x )>0, 从而f (x )在)2 ,0(π内单调增加, 因此当20π<<x 时, f (x )>f (0)=0, 即sin x +tan x -2x >0, 也就是 sin x +tan x >2x .(4)设331tan )(x x x x f --=, 则f (x )在)2 ,0[π内连续,))(t a n (t a n t a n 1s e c )(2222x x x x x x x x x f +-=-=--='. 因为当20π<<x 时, tan x >x , tan x +x >0, 所以f '(x )在)2 ,0(π内单调增加, 因此当20π<<x 时, f (x )>f (0)=0, 即031t a n 3>--x x x ,也就是 231t a n x x x +>.(5)设f (x )=x ln2-2ln x , 则f (x )在[4, +∞)内连续, 因为 0422ln 224ln 22ln )(=->-=-='e x x x f ,所以当x >4时, f '(x )>0, 即f (x )内单调增加.因此当x >4时, f (x )>f (4)=0, 即x ln2-2ln x >0, 也就是2x >x 2. 5. 讨论方程ln x =ax (其中a >0)有几个实根?解 设f (x )=ln x -ax . 则f (x )在(0, +∞)内连续, xax a x x f -=-='11)(, 驻点为a x 1=.因为当ax 10<<时, f '(x )>0, 所以f (x )在)1 ,0(a 内单调增加; 当a x 1>时, f '(x )<0, 所以f (x )在) ,1(∞+a内单调减少. 又因为当x →0及x →+∞时, f (x )→-∞, 所以如果011ln )1(>-=a a f , 即e a 1<, 则方程有且仅有两个实根; 如果011ln )1(<-=aa f , 即e a 1>, 则方程没有实根. 如果011ln )1(=-=a a f , 即e a 1=, 则方程仅有一个实根. 6. 单调函数的导函数是否必为单调函数?研究下面这个例子: f (x )=x +sin x .解 单调函数的导函数不一定为单调函数.例如f (x )=x +sin x 在(-∞,+∞)内是单调增加的, 但其导数不是单调函数. 事实上, f '(x )=1+cos x ≥0,这就明f (x )在(-∞, +∞)内是单调增加的. f ''(x )=-sin x 在(-∞, +∞)内不保持确定的符号, 故f '(x )在(-∞, +∞)内不是单调的.7. 判定下列曲线的凹凸性: (1) y =4x -x 2 ; (2) y =sh x ;(3)xy 11+=(x >0);(4) y =x arctan x ; 解 (1)y '=4-2x , y ''=-2,因为y ''<0, 所以曲线在(-∞, +∞)内是凸的. (2)y '=ch x , y ''=sh x . 令y ''=0, 得x =0.因为当x <0时, y ''=sh x <0; 当x >0时, y ''=sh x >0, 所以曲线在(-∞, 0]内是凸的, 在[0, +∞)内是凹的.(3)21x y -=', 32x y =''. 因为当x >0时, y ''>0, 所以曲线在(0, +∞)内是凹的. (4)21arctan xx x y ++=',22)1(2x y +=''.因为在(-∞, +∞)内, y ''>0, 所以曲线y =x arctg x 在(-∞, +∞)内是凹的.8. 求下列函数图形的拐点及凹或凸的区间: (1).y =x 3-5x 2+3x +5 ; (2) y =xe -x ; (3) y =(x +1)4+e x ;(4) y =ln(x 2+1); (5) y =e arctan x ; (6) y =x 4(12ln x -7),解 (1)y '=3x 2-10x +3, y ''=6x -10. 令y ''=0, 得35=x .因为当35<x 时, y ''<0; 当35>x 时, y ''>0, 所以曲线在]35 ,(-∞内是凸的, 在) ,35[∞+内是凹的, 拐点为)2720 ,35(.(2)y '=e -x -xe -x , y ''=-e -x -e -x +xe -x =e -x (x -2). 令y ''=0, 得x =2.因为当x <2时, y ''<0; 当x >2时, y ''>0, 所以曲线在(-∞, 2]内是凸的, 在[2, +∞)内是凹的, 拐点为(2, 2e -2).(3)y '=4(x +1)3+e x , y ''=12(x +1)2+e x .因为在(-∞, +∞)内, y ''>0, 所以曲线y =(x +1)4+e x 的在(-∞, +∞)内是凹的, 无拐点.(4)122+='x x y , 22222)1()1)(1(2)1(22)1(2++--=+⋅-+=''x x x x x x x y . 令y ''=0, 得x 1=-1, x 2=1. 列表得可见曲线在(-∞, -1]和[1, +∞)内是凸的, 在[-1, 1]内是凹的, 拐点为(-1, ln2)和(1, ln2).(5)2arctan 11x e y x+⋅=',)21(12arctan x x e y x-+=''. 令y ''=0得, 21=x . 因为当21<x 时, y ''>0; 当21>x 时, y ''<0, 所以曲线y =e arctg x 在]21 ,(-∞内是凹的,在) ,21[∞+内是凸的, 拐点是) ,21(21arctane. (6) y '=4x 3(12ln x -7)+12x 3, y ''=144x 2⋅ln x . 令y ''=0, 得x =1.因为当0<x <1时, y ''<0; 当x >1时, y ''>0, 所以曲线在(0, 1]内是凸的, 在[1, +∞)内是凹的, 拐点为(1, -7).9. 利用函数图形的凹凸性, 证明下列不等式:(1) nn n y x y x )2()(21+>+(x >0, y >0, x ≠y , n >1);(2))(22y x e e e yx y x ≠>++;(3)2ln)(ln ln yx y x y y x x ++>+ (x >0, y >0, x ≠y ). 证明 (1)设f (t )=t n , 则f '(t )=nt n -1, f ''(t )=n (n -1)t n -2. 因为当t >0时, f ''(t )>0, 所以曲线f (t )=t n 在区间(0, +∞)内是凹的. 由定义, 对任意的x >0, y >0, x ≠y 有)2()]()([21yx f y f x f +>+,即 nn n y x y x )2()(21+>+.(2)设f (t )=e t , 则f '(t )=e t , f ''(t )=e t . 因为f ''(t )>0, 所以曲线f (t )=e t 在(-∞, +∞)内是凹的. 由定义, 对任意的x , y ∈(-∞, +∞), x ≠y 有)2()]()([21yx f y f x f +>+,即 )(22y x ee e yx yx ≠>++.(3)设f (t )=t ln t , 则 f '(t )=ln t +1, tt f 1)(=''.因为当t >0时, f ''(t )>0, 所以函数f (t )=t ln t 的图形在(0, +∞)内是凹的. 由定义, 对任意的x >0, y >0, x ≠y 有)2()]()([21yx f y f x f +>+,即 2ln )(ln ln yx y x y y x x ++>+. 10. 试证明曲线112+-=x x y 有三个拐点位于同一直线上.证明 222)1(12+++-='x x x y ,323223)1()]32()][32()[1(2)1(2662++---+=++--=''x x x x x x x x y . 令y ''=0, 得x 1=-1, 322-=x , 323+=x . 例表得可见拐点为(-1, -1), ))32(431 ,32(---, ))32(431 ,32(+++. 因为41)1(32)1()32(431=-------, 41)1(32)1()32(431=--+--++,所以这三个拐点在一条直线上.11. 问a 、b 为何值时, 点(1, 3)为曲线y =ax 3+bx 2的拐点?解 y '=3ax 2+2bx , y ''=6ax +2b . 要使(1, 3)成为曲线y =ax 3+bx 2的拐点, 必须y (1)=3且y ''(1)=0, 即a +b =3且6a +2b =0, 解此方程组得23-=a , 29=b .12. 试决定曲线y =ax 3+bx 2+cx +d 中的a 、b 、c 、d , 使得x =-2处曲线有水平切线, (1, -10)为拐点, 且点(-2, 44)在曲线上. 解 y '=3ax 2+2bx +c , y ''=6ax +2b . 依条件有⎪⎩⎪⎨⎧=''=-'-==-0)1(0)2(10)1(44)2(y y y y , 即⎪⎩⎪⎨⎧=+=+--=+++=+-+-02604121044248b a c b a d c b a d c b a .解之得a =1, b =-3, c =-24, d =16.13. 试决定y =k (x 2-3)2中k 的值, 使曲线的拐点处的法线通过原点. 解y '=4kx 3-12kx , y ''=12k (x -1)(x +1). 令y ''=0, 得x 1=-1, x 2=1.因为在x 1=-1的两侧y ''是异号的, 又当x =-1时y =4k , 所以点(-1, 4k )是拐点. 因为y '(-1)=8k , 所以过拐点(-1, 4k )的法线方程为)1(814+-=-x k k y . 要使法线过原点, 则(0, 0)应满足法线方程, 即kk 814-=-, 82±=k .同理, 因为在x 1=1的两侧y ''是异号的, 又当x =1时y =4k , 所以点(1, 4k )也是拐点.因为y '(1)=-8k , 所以过拐点(-1, 4k )的法线方程为)1(814-=-x k k y . 要使法线过原点, 则(0, 0)应满足法线方程, 即k k 814-=-, 82±=k .因此当82±=k 时, 该曲线的拐点处的法线通过原点.14. 设y =f (x )在x =x 0的某邻域内具有三阶连续导数, 如果f ''(x 0)=0, 而f '''(x 0)≠0,试问 (x 0, f (x 0))是否为拐点?为什么?解 不妨设f '''(x 0)>0. 由f '''(x )的连续性, 存在x 0的某一邻域(x 0-δ, x 0+δ), 在此邻域内有f '''(x )>0. 由拉格朗日中值定理, 有f ''(x )-f ''(x 0)=f '''(ξ)(x -x 0) (ξ介于x 0与x 之间), 即 f ''(x )=f '''(ξ)(x -x 0).因为当x 0-δ<x <x 0时, f ''(x )<0; 当x 0<x <x 0+δ 时, f ''(x )>0, 所以(x 0, f (x 0))是拐点.习题3-51. 求函数的极值: (1) y =2x 3-6x 2-18x +7; (2) y =x -ln(1+x ) ; (3) y =-x 4+2x 2 ; (4)x x y -+=1;(5)25431x xy ++=;(6)144322++++=x x x x y ;(7) y =e xcos x ;(8)xx y 1=;(9)31)1(23+-=x y ; (10) y =x +tan x .解 (1)函数的定义为(-∞, +∞), y '=6x 2-12x -18=6(x 2-2x -3)=6(x -3)(x +1), 驻点为x 1=-1, x 2=3. 列表可见函数在 (2)函数的定义为(-1, +∞), xxx y +=+-='1111, 驻点为x =0. 因为当-1<x <0时, y '<0; 当x >0时, y '>0, 所以函数在x =0处取得极小值, 极小值为y (0)=0. (3)函数的定义为(-∞, +∞),y '=-4x 3+4x =-4x (x 2-1), y ''=-12x 2+4, 令y '=0, 得x 1=0, x 2=-1, x 3=1.因为y ''(0)=4>0, y ''(-1)=-8<0, y ''(1)=-8<0, 所以y (0)=0是函数的极小值, y (-1)=1和y (1)=1是函数的极大值.(4)函数的定义域为(-∞, 1], )112(1243121121211+---=---=--='x x x xx xy ,令y '=0, 得驻点43=x .因为当43<x 时, y '>0; 当143<<x 时, y '<0, 所以45)1(=y 为函数的极大值.(5)函数的定义为(-∞, +∞), 32)54()512(5x x y +--=', 驻点为512=x . 因为当512<x 时, y '>0; 当512>x 时, y '<0, 所以函数在512=x 处取得极大值, 极大值为10205)512(=y . (6)函数的定义为(-∞, +∞), 22)1()2(+++-='x x x x y , 驻点为x 1=0, x 2=-2.列表可见函数在x =-2处取得极小值3, 在x =0处取得极大值4.(7)函数的定义域为(-∞, +∞). y '=e x (cos x -sin x ), y ''=-e x sin x .令y '=0, 得驻点ππk x 24+=, ππ)1(24++=k x , (k =0, ±1, ±2, ⋅ ⋅ ⋅).因为0)24(<+''ππk y , 所以22)24(24⋅=++ππππk e k y 是函数的极大值. 因为y ''0])1(24[>++ππk , 所以22])1(24[)1(24⋅-=++++ππππk e k y 是函数的极小值. (8)函数xx y 1=的定义域为(0, +∞),)ln 1(121x x x y x-⋅='. 令y '=0, 得驻点x =e .因为当x <e 时, y '>0; 当x >e 时, y '<0, 所以ee e y 1)(=为函数f (x )的极大值.(9)函数的定义域为(-∞, +∞), 3/2)1(132+-='x y , 因为y '<0, 所以函数在(-∞, +∞)是单调减少的, 无极值.(10)函数y =x +tg x 的定义域为ππk x +≠2(k =0, ±1, ±2, ⋅ ⋅ ⋅). 因为y '=1+sec 2x >0, 所以函数f (x )无极值.2. 试证明: 如果函数y =ax 3+bx 2+cx +d 满足条件b 2 -3ac <0, 那么这函数没有极值 . 证明y '=3a x 2+2b x +c . 由b 2 -3ac <0, 知a ≠0. 于是配方得到y '=3a x 2+2b x +c ab ac a b x a a c x a b x a 33)3(3)332(32222-++=++=,因3ac -b 2>0, 所以当a >0时, y '>0; 当a <0时, y '<0. 因此y =ax 3+bx 2+cx +d 是单调函数, 没有极值.3. 试问a 为何值时, 函数x x a x f 3sin 31sin )(+=在3π=x 处取得极值?它是极大值还是极小值?并求此极值.解 f '(x )=a cos x +cos 3x , f ''(x )=-a sin x -3 sin x .要使函数f (x )在3π=x 处取得极值, 必有0)3(='πf , 即0121=-⋅a , a =2 .当a =2时, 0232)3(<⋅-=''πf . 因此, 当a =2时, 函数f (x )在3π=x 处取得极值, 而且取得极大值, 极大值为3)23(=f .4. 求下列函数的最大值、最小值: (1) y =2x 3-3x 2 , -1≤x ≤4; (2) y =x 4-8x 2+2, -1≤x ≤3 ; (3)x x y -+=1, -5≤x ≤1.解 (1)y '=6x 2-6x =6x (x -1), 令y '=0, 得x 1=0, x 2=1. 计算函数值得 y (-1)=-5, y (0)=0, y (1)=-1, y (4)=80,经比较得出函数的最小值为y (-1)=-5, 最大值为y (4)=80.(2)y '=4x 3-16x =4x (x 2-4), 令y '=0, 得x 1=0, x 2=-2(舍去), x 3=2. 计算函数值得 y (-1)=-5, y (0)=2, y (2)=-14, y (3)=11,经比较得出函数的最小值为y (2)=-14, 最大值为y (3)=11.(3)xy --='1211, 令y '=0, 得43=x . 计算函数值得65)5(+-=-y , 45)43(=y , y (1)=1,经比较得出函数的最小值为65)5(+-=-y , 最大值为45)43(=y .5. 问函数y =2x 3-6x 2-18x -7(1≤x ≤4)在何处取得最大值?并求出它的最大值. 解 y '=6x 2-12x -18=6(x -3)(x +1), 函数f (x )在1≤x ≤4内的驻点为x =3. 比较函数值:f (1)=-29, f (3)=-61, f (4)=-47,函数f (x )在x =1处取得最大值, 最大值为f (1)=-29.6. 问函数x x y 542-=(x <0)在何处取得最小值?解 2542x x y +=', 在(-∞, 0)的驻点为x =-3. 因为31082xy -='', 0271082)3(>+=-''y ,所以函数在x =-3处取得极小值. 又因为驻点只有一个, 所以这个极小值也就是最小值, 即函数在x =-3处取得最小值, 最小值为27)3(=-y .7. 问函数12+=x xy (x ≥0)在何处取得最大值?解 222)1(1+-='x x y . 函数在(0, +∞)内的驻点为x =1.因为当0<x <1时, y '>0; 当x >1时y '<0, 所以函数在x =1处取得极大值. 又因为函数在(0, +∞)内只有一个驻点, 所以此极大值也是函数的最大值, 即函数在x =1处取得最大值, 最大值为f (1)=21.8. 某车间靠墙壁要盖一间长方形小屋, 现有存砖只够砌20cm 长的墙壁, 问应围成怎样的长方形才能使这间小屋的面积最大?解 设宽为x 长为y , 则2x +y =20, y =20-2x , 于是面积为 S = xy =x (20-2x )=20x -2x 2. S '=20-4x =4(10-x ), S ''=-4. 令S '=0, 得唯一驻点x =10.因为S ''(10)-4<0, 所以x =10为极大值点, 从而也是最大值点. 当宽为5米, 长为10米时这间小屋面积最大.9. 要造一圆柱形油罐, 体积为V , 问底半径r 和高h 等于多少时, 才能使表面积最小?这时底直径与高的比是多少?解 由V =π r 2h , 得h =V π-1r -2. 于是油罐表面积为S =2π r 2+2π rh rVr 222+=π(0<x <+∞),224r Vr S -='π.令S '=0, 得驻点32πV r =. 因为0443>+=''r V S π, 所以S 在驻点32πVr =处取得极小值, 也就是最小值. 这时相应的高为r r Vh 2 20==π. 底直径与高的比为2r : h =1 : 1.10. 某地区防空洞的截面拟建成矩形加半圆(如图), 截面的面积为5m 2, 问底宽x 为多少时才能使截面的周长最小, 从而使建造时所用的材料最省?解 设矩形高为h , 截面的周长S , 则5)2(212=⋅+πx xh , x x h 85π-=.于是xx x x h x S 10422++=++=ππ(π400<<x ), 21041xS -+='π.令S '=0, 得唯一驻点π+=440x .因为0203>=''xS , 所以π+=440x 为极小值点, 同时也是最小值点. 因此底宽为π+=440x 时所用的材料最省.11. 设有重量为5kg 的物体, 置于水平面上, 受力F 的作用而开始移动(如图). 设摩擦系数μ=0.25, 问力F 与水平线的交角α为多少时, 才可使力F 的大小为最小?解 由F cos α =(m -F sin α)μ 得αμαμsin cos +=m F (2 0πα≤≤),2)sin (cos )cos (sin αμααμαμ+-='m F , 驻点为 α = arctan μ.因为F 的最小值一定在)2 ,0(π内取得, 而F 在)2,0(π内只有一个驻点α = arctan μ,所以α=arctan μ一定也是F 的最小值点. 从而当α=arctan0.25=14︒时, 力F 最小. 12. 有一杠杆, 支点在它的一端. 在距支点0.1m 处挂一重量为49kg 的物体. 加力于杠杆的另一端使杠杆保持水平(如图). 如果杠杆的线密度为5kg/m , 求最省力的杆长?解 设杆长为x (m), 加于杠杆一端的力为F , 则有1.049521⋅+⋅=x x xF , 即)0(9.425>+=x x x F .29.425xF -=',驻点为x =1.4. 由问题的实际意义知, F 的最小值一定在(0, +∞)内取得, 而F 在(0, +∞)内只有一个驻点x =1.4, 所以F 一定在x =1.4m 处取得最小值, 即最省力的杆长为1.4m . 13. 从一块半径为R 的圆铁片上挖去一个扇形做成一漏斗(如图),问留下的扇形的中心角ϕ取多大时, 做成的漏斗的容积最大? 解 漏斗的底周长l 、底半径r 、高h 分别为l =R ⋅ϕ, πϕ2R r =, 222242ϕππ-=-=Rr R h .漏斗的容积为22223242431ϕππϕπ-==R hr V (0<ϕ<2π). 2222234)38(24ϕπϕπϕπ--⋅='R V ,驻点为πϕ362=. 由问题的实际意义, V 一定在(0, 2π)内取得最大值, 而V 在(0, 2π)内只有一个驻点, 所以该驻点一定也是最大值点. 因此当ϕ π362=时, 漏斗的容积最大.14. 某吊车的车身高为1.5m , 吊臂长15m , 现在要把一个6m 宽、2m 高的屋架, 水平地吊到6m 高的柱子上去(如图), 问能否吊得上去?解 设吊臂对地面的倾角为ϕ时, 屋架能够吊到的最大高度为h . 在直角三角形∆EDG 中 15sin ϕ=(h -1. 5)+2+3tan ϕ,故 21tan 3sin 15--=ϕϕh ,ϕϕ2cos 3cos 15-='h . 令h '=0得唯一驻点5451arccos 3≈=ϕ︒.因为0cos sin 6sin 153<--=''ϕϕϕh , 所以ϕ=54︒为极大值点, 同时这也是最大值点. 当ϕ=54︒时, 5.721tan 3sin 15≈--=ϕϕh m .所以把此屋最高能水平地吊至7. 5m 高, 现只要求水平地吊到6m 处, 当然能吊上去. 15. 一房地产公司有50套公寓要出租. 当月租金定为1000元时, 公寓会全部租出去. 当月租金每增加50元时, 就会多一套公寓租不出去, 而租出去的公寓每月需花费100元的维修费. 试问房租定为多少可获最大收入?解 房租定为x 元, 纯收入为R 元.当x ≤1000时, R =50x -50⨯100=50x -5000, 且当x =1000时, 得最大纯收入45000元. 当x >1000时,700072501100)]1000(5150[)]1000(5150[2-+-=⋅---⋅--=x x x x x R ,72251+-='x R .令R '=0得(1000, +∞)内唯一驻点x =1800. 因为0251<-=''R , 所以1800为极大值点, 同时也是最大值点. 最大值为R =57800.因此, 房租定为1800元可获最大收入.习题3-6描绘下列函数的图形: 1. )786(5124++-=x x x y ;解 (1)定义域为(-∞, +∞);(2)23)1)(2(54)8124(51-+=+-='x x x x y ,)1)(1(512)33(542-+=-=''x x x y ,令y '=0, 得x =-2, x =1; 令y ''=0, 得x =-1, x =1.(3)列表(4)作图:2.21xx y +=;解 (1)定义域为(-∞, +∞);(2)奇函数, 图形关于原点对称, 故可选讨论x ≥0时函数的图形.(3)22)1()1)(1(x x x y ++--=', 32)1()3)(3(2x x x x y ++-='',当x ≥0时, 令y '=0, 得x =1; 令y ''=0, 得x =0, 3=x .(4)列表(5)有水平渐近线y =0; (6)作图:3.2)1(--=x e y ;解 (1)定义域为(-∞, +∞); (2))]221()][221([4)1(222)1()1(--+-=''--='----x x e y e x y x x ,令y '=0, 得x =1; 令y ''=0, 得221+=x ,221-=x .(3)列表(4)有水平渐近线y =0; (5)作图: 4.xx y 12+=;解 (1)定义域为(-∞, 0)⋃(0, +∞); (2)2321212xx xx y -=-=',333)1(222x x x y +=+='',令y '=0, 得321=x ; 令y ''=0, 得x =-1.(3)列表(4)有铅直渐近线x =0; (5)作图: 5.xxy 2cos cos =.解 (1)定义域为42ππ+≠n x (n =0, ±1, ±2, ⋅⋅⋅)(2)是偶函数, 周期为2 . 可先作[0, ]上的图形, 再根据对称性作出[-, 0)内的图形, 最后根据周期性作出[-, ]以外的图形; (3)xx x y 2cos )sin 23(sin 22-=',xx x x y 2cos )sin 4sin 123(cos 342-+⋅='',在[0,]上, 令y '=0, 得x =0, x =; 令y ''=0, 得2π=x .(4)列表(5)有铅直渐近线4π=x 及43π=x ;(6)作图:习题3-71. 求椭圆4x 2+y 2=4在点(0, 2)处的曲率. 解 两边对x 求导数得8x +2yy '=0, y x y 4-=', 244y y x y y '--=''.y '|(0, 2)=0, y ''|(0, 2)=-2.所求曲率为2)01(|2|)1(||2/322/32=+-='+''=y y K .2. 求曲线y =lnsec x 在点(x , y )处的曲率及曲率半径.解 x x x xy tan tan sec sec 1=⋅⋅=', x y 2sec =''.所求曲率为|cos |)tan 1(|sec |)1(||2/3222/32x x x y y K =+='+''=, 曲率半径为 |sec ||cos |11x x K ===ρ.3. 求抛物线y =x 2-4x +3在其顶点处的曲率及曲率半径. 解 y '=2x -4, y ''=2.令y '=0, 得顶点的横坐标为x =2. y '|x =2=0, y ''|x =2=2. 所求曲率为2)01(|2|)1(||2/322/32=+='+''=y y K , 曲率半径为211==K ρ.4. 求曲线x =a cos 3t , y =a sin 3t 在t =t 0处的曲率.解 t x a t a y tan )cos ()sin (33-=''=', tt a x a x y 43cos sin 31)cos ()tan (⋅=''-=''. 所求曲率为|2sin |32|cos sin 31|)tan 1(|cos sin 31|)1(||32/3242/32t a t t a t t t a y y K ==+⋅='+''=, |2sin |3200t a K t t ==.5. 对数曲线y =ln x 上哪一点处的曲率半径最小?求出该点处的曲率半径.解 x y 1=', 21xy -=''.2/322/3222/32)1()11(|1|)1(||x x xx y y K +=+-='+''=, xx 232)1(+=ρ,2222232212)12(1)1(2)1(23x x x x x x x x --=+-⋅⋅+='ρ.令ρ'=0, 得22=x . 因为当220<<x 时, ρ<0; 当22>x 时, ρ>0, 所以22=x 是ρ的极小值点, 同时也最小值点. 当22=x 时, 22ln =y . 因此在曲线上点)22ln ,22(处曲率半径最小, 最小曲率半径为233=ρ. 6. 证明曲线axa y ch =在点(x , y )处的曲率半径为a y 2.解 a x y sh =', axa y ch 1=''.在点(x , y )处的曲率半径为a y a x a a x a a xa x a a x y y 222/322/322/32ch |ch 1|)(ch |ch 1|)sh 1(||)1(===+='''+=ρ.7. 一飞机沿抛物线路径100002x y =(y 轴铅直向上, 单位为m )作俯冲飞行, 在坐标原点O 处飞机的速度为v =200m /s 飞行员体重G =70Kg . 求飞机俯冲至最低点即原点O 处时座椅对飞行员的反力.解 5000100002x x y ==', 50001=''y ; y '|x =0=0, 50001|0=''=x y . 500050001)01(||)1(|2/322/320=+='''+==y y x ρ.向心力56050002007022=⨯==ρmV F (牛顿). 飞行员离心力及它本身的重量对座椅的压力为 79⨯9.8+560=1246(牛顿).8. 汽车连同载重共5t , 在抛物线拱桥上行驶, 速度为21.6km/h , 桥的跨度为10m , 拱的矢高为0.25m . 求汽车越过桥顶时对桥的压力.解 如图取直角坐标系, 设抛物线拱桥方程为y =ax 2, 由于抛物线过点(5, 0.25), 代入方程得01.02525.0==a ,于是抛物线方程为y =0. 01x 2. y '=0.02x , y ''=0.02.5002.0)01(||)1(|2/322/320=+='''+==y y x ρ. 向心力为360050)3600106.21(1052332=⨯⨯==ρmV F (牛顿). 因为汽车重为5吨, 所以汽车越过桥顶时对桥的压力为 5⨯103⨯9.8-3600=45400(牛顿).*9. 求曲线y =ln x 在与x 轴交点处的曲率圆方程.*10. 求曲线y =tan x 在点)1 ,4(π处的曲率圆方程.*11. 求抛物线y 2=2px 的渐屈线方程.总习题三1. 填空:设常数k >0, 函数k exx x f +-=ln )(在(0, +∞)内零点的个数为________.解 应填写2.提示: e x x f 11)(-=', 21)(xx f -=''.在(0, +∞)内, 令f '(x )=0, 得唯一驻点x =e .因为f ''(x )<0, 所以曲线k exx x f +-=ln )(在(0, +∞)内是凸的, 且驻点x =e 一定是最大值点,最大值为f (e )=k >0.又因为-∞=+→)(lim 0x f x , -∞=+∞→)(lim x f x , 所以曲线经过x 轴两次, 即零点的个数为2.2. 选择以下题中给出的四个结论中一个正确的结论:设在[0, 1]上f ''(x )>0, 则f '(0), f '(1), f (1)-f (0)或f (0)-f (1)几个数的大小顺序为( ). (A )f '(1)>f '(0)>f (1)-f (0); (B )f '(1)>f (1)-f (0)>f '(0); (C )f (1)-f (0)>f '(1)>f '(0); (D )f '(1)>f (0)-f (1)>f '(0). 解 选择B .提示: 因为f ''(x )>0, 所以f '(x )在[0, 1]上单调增加, 从而f '(1)>f '(x )>f '(0). 又由拉格朗日中值定理, 有f (1)-f (0)=f '(ξ), ξ∈[0, 1], 所以 f '(1)> f (1)-f (0)>f '(0).3. 列举一个函数f (x )满足: f (x )在[a , b ]上连续, 在(a ,b )内除某一点外处处可导, 但在(a , b )内不存在点ξ , 使f (b )-f (a )=f '(ξ)(b -a ). 解 取f (x )=|x |, x ∈[-1, 1].易知f (x )在[-1, 1]上连续, 且当x >0时f '(x )=1; 当x >0时, f '(x )=-1; f '(0)不存在, 即f (x )在[-1, 1]上除x =0外处处可导.注意f (1)-f (-1)=0, 所以要使f (1)-f (-1)=f '(ξ)(1-(-1))成立, 即f '(ξ)=0, 是不可能的. 因此在(-1, 1)内不存在点ξ , 使f (1)-f (-1)=f '(ξ)(1-(-1)). 4. 设k x f x ='∞→)(lim , 求)]()([lim x f a x f x -+∞→.解 根据拉格朗日中值公式, f (x +a )-f (x )=f '(ξ )⋅a , ξ 介于x +a 与x 之间. 当x →∞ 时, ξ → ∞, 于是ak f a a f x f a x f x x ='=⋅'=-+∞→∞→∞→)(lim )(lim )]()([lim ξξξ.5. 证明多项式f (x )=x 3-3x +a 在[0, 1]上不可能有两个零点.证明 f '(x )=3x 2-3=3(x 2-1), 因为当x ∈(0, 1)时, f '(x )<0, 所以f (x )在[0, 1]上单调减少. 因此, f (x ) 在[0, 1]上至多有一个零点.6. 设1210++⋅⋅⋅++n a aa n =0, 证明多项式f (x )=a 0+a 1x +⋅ ⋅ ⋅+a n x n 在(0,1)内至少有一个零点.证明 设121012)(+++++=n n x n a x ax a x F , 则F (x )在[0, 1]上连续, 在(0, 1)内可导, 且F (0)=F (1)=0. 由罗尔定理, 在(0, 1)内至少有一个点ξ , 使F (ξ )=0. 而F '(x )=f (x ), 所以f (x )在(0, 1)内至少有一个零点.7. 设f (x )在[0, a ]上连续, 在(0, a )内可导, 且f (a )=0, 证明存在一点ξ∈(0, a ), 使f (ξ)+ξf '(ξ)=0.证明 设F (x )=xf (x ), 则F (x )在[0, a ]上连续, 在(0, a )内可导, 且F (0)=F (a )=0. 由罗尔定理, 在(0, a )内至少有一个点ξ , 使F (ξ )=0. 而F (x )=f (x )+x f '(x ), 所以f (ξ)+ξf '(ξ)=0.8. 设0<a <b , 函数f (x )在[a , b ]上连续, 在(a , b )内可导, 试利用柯西中值定理, 证明存在一点ξ∈(a , b )使abf b f a f ln )()()(ξξ'=-.证明 对于f (x )和ln x 在[a , b ]上用柯西中值定理, 有ξξ1)(ln ln )()(f ab a f b f '=--, ξ∈(a , b ), 即 abf b f a f ln )()()(ξξ'=-, ξ∈(a , b ).9. 设f (x )、g (x )都是可导函数, 且|f '(x )|<g '(x ), 证明: 当x >a 时, |f (x )-f (a )|<g (x )-g (a ).证明 由条件|f '(x )|<g '(x )得知,1)()(<''ξξg f , 且有g '(x )>0, g (x )是单调增加的, 当x >a 时, g (x )>g (a ).因为f (x )、g (x )都是可导函数, 所以f (x )、g (x ) 在[a , x ]上连续, 在(a , x )内可导, 根据柯西中值定理, 至少存在一点ξ∈(a , x ), 使)()()()()()(ξξg f a g x g a f x f ''=--. 因此,1)()()()(|)()(|<''=--ξξg f a g x g a f x f , |f (x )-f (a )|<g (x )-g (a ).10. 求下列极限:(1)xx x x xx ln 1lim 1+--→;(2)]1)1ln(1[lim 0xx x -+→;(3)x x x )arctan 2(lim π+∞→.(4)nxx n x x x n a a a ]/) [(lim 11211+⋅⋅⋅++∞→(其中a 1, a 2, ⋅ ⋅ ⋅, a n >0).解 (1) (x x )'=(e x l n x )'=e x l n x(ln x +1)=x x (ln x +1).xx x x xx x x x x x x x x x x x x x x x xx -+-=+-+-='+-'-=+--+→→→→1)1(ln lim11)1(ln 1lim )ln 1()(lim ln 1lim 11111 21)1)(ln 11(ln 1lim11=--+++-=+→xx x x x x x x . (2)xxx x x x x x x x x x x x x x x x ++++-='+'+-=++-=-+→→→→1)1ln(111lim ])1ln([])1ln([lim )1ln()1ln(lim ]1)1ln(1[lim 00002111)1l n (1lim )1ln()1(lim00=+++=+++=→→x x x x x x x。
同济高数课后习题答案解析

sin2 ( x − 1) 1、 lim x →1 x2 − 1 ;
解一: 原式 = lim 解二: 原式 = lim x →1
2 sin ( x − 1) cos ( x − 1) =0 x →1 2x
sin ( x − 1)
x −1
lim
x →1
sin ( x − 1)
一
− 1 ⋅( −2 ) 2t
:
原式 = lim (1 − 2t )
t →0
= e−2
解二:
原式 = lim[1 + (2 − 2 x)]
x →1
1 i ( −2) 2− 2 x
=
{lim[1 + (2 − 2 x)]
x →1
1 2 − 2 x −2
} = e−2
x − sin x lim 7、 x → 0 x3
解一: 解二:
1 = lim (1 + x ) = 1 x→ 0 1 1+ x
原 式 = lim
1 ln (1 + x )
x
1 x
x→ 0
=
1 =1 ln e
⎛ x−2⎞ lim ⎜ 5、 x →∞ ⎝ x ⎟ ⎠
⎛ 2⎞ 原式 = lim ⎜1 − ⎟ x →∞ 解一: ⎝ x⎠
解二:
x ln x−2 x
⎜ 9、 lim n→∞ ⎝ ⎛ ห้องสมุดไป่ตู้ + 2 +⋯+ n n ⎞ − ⎟ 2+ n 2⎠
⎛1 ⎞ n n + 1 ( ) ⎜2 n⎟ n 2 + n − 2n − n 2 原式 = lim ⎜ − ⎟ = lim n →∞ 2 + n 2 ⎟ n →∞ 2 ( 2 + n) ⎜ ⎝ ⎠ 解: −n 1 = lim =− n →∞ 4 + 2n 2
(完整版)高等数学第六版(同济大学)上册课后习题答案解析

高等数学第六版上册课后习题答案及解析第一章习题1—11. 设A=(-, —5)(5, +),B=[-10, 3), 写出A B,A B, A\B及A\(A\B)的表达式。
解A B=(-, 3)(5, +),A B=[-10,—5),A\B=(—, -10)(5, +),A\(A\B)=[-10, -5).2. 设A、B是任意两个集合,证明对偶律: (A B)C=A C B C。
证明因为x(A B)C x A B x A或x B x A C或x B C x A C B C,所以(A B)C=A C B C。
3. 设映射f : X Y, A X, B X。
证明(1)f(A B)=f(A)f(B);(2)f(A B)f(A)f(B).证明因为y f(A B)x A B, 使f(x)=y(因为x A或x B) y f(A)或y f(B)y f(A)f(B),所以f(A B)=f(A)f(B).(2)因为y f(A B)x A B, 使f(x)=y(因为x A且x B) y f(A)且y f(B)yf (A )f (B ),所以 f (A B )f (A )f (B )。
4。
设映射f : XY , 若存在一个映射g : Y X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个xX , 有I X x =x ; 对于每一个y Y , 有I Y y =y 。
证明:f 是双射, 且g 是f 的逆映射: g =f —1.证明 因为对于任意的yY , 有x =g (y )X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射. 又因为对于任意的x 1x 2, 必有f (x 1)f (x 2), 否则若f (x 1)=f (x 2)g [ f (x 1)]=g [f (x 2)]x 1=x 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
书后部分习题解答 P21页3.(3)nnn b b b a a a ++++++++∞→ 2211lim (1,1<<b a )知识点:1)等比级数求和)1(1)1(12≠--=++++-q qq a aqaq aq a n n (共n 项)2)用P14例4的结论:当1<q 时,0lim =∞→nn q解:nnn b b b a a a ++++++++∞→ 2211limabbb a a n n n --=----=++∞→111111lim 115.(1)判断下列数列是否收敛,若收敛,则求出极限:设a 为正常数,00>x ,)(211nn n x a x x +=+ 证:由题意,0>n x ,a x a x x a x x nn n n n =⋅⋅≥+=+221)(211(数列有下界) 又02)(2121≤-=-+=-+nn n n n n n x x a x x ax x x (因a x n ≥+1)(数列单调减少) 由单调有界定理,此数列收敛;记b x n n =∞→lim ,对)(211nn n x ax x +=+两边取极限,得)(21b a b b +=,解得a b =(负的舍去),故此数列的极限为a . P35页4.(8)极限=-++-+→211)1()1(lim x n x n x n x 211)1()1()]1(1[lim -++--++→x nx n x n x 21221111)1()1()1()1()1(1lim -++--+-+-+=+++→x n x n x x C x C n n n x 2)1(21+==+n n C n (若以后学了洛必达法则(00型未定型),则211)1()1(lim -++-+→x nx n x n x 2)1(2)1(lim )1(2)1())1(lim 111+=+=-+-+=-→→n n nx n x n x n n x n x ) 书后部分习题解答2 P36页 8.已知当0→x时,1cos ~1)1(312--+x ax ,求常数a .知识点:1)等价无穷小的概念;2)熟记常用的等价无穷小,求极限时可用等价无穷小的替换定理。
解:由题意:132231lim 1cos 1)1(lim 2203120=-=-=--+→→a x axx ax x x 得23-=a 或132]1)1()1[(211lim 1cos 1)1(lim 3123222203120=-=++++⋅--+=--+→→aax ax x ax x ax x x (根式有理化) P42页3(4) 关于间断点:xx x f 1sin 1)(=0=x 为第二类间断点说明:xx x 1sin 1lim 0→不存在(在0→x 的过程中,函数值不稳定,不趋向与∞)P43页7(1)证明方程042=-x x在)21,0(内必有一实根。
知识点:闭区间(一定要闭)上连续函数的根的存在定理证明:设x x f x 42)(-=,易知,)(x f 在]21,0[上连续; (注:设函数,闭区间)01)0(>=f ,022)21(<-=f ,故由根的存在定理,至少在)21,0(内存在一点ξ,使0)(=ξf ,即方程042=-x x在)21,0(内必有一实根.P61页 3.设)(0x f '存在,求:(1)x x x f x f x ∆∆--→∆)()(lim000(2)h h x f h x f h )()(lim 000--+→(3)tx f t x f t )()3(lim000-+→分析:因)(0x f '存在,则极限xx f x x f x ∆-∆+→∆)()(lim000的值为)(0x f '。
把(1)(2)(3)化为相应可用极限的形式 解:(1)x x x f x f x ∆∆--→∆)()(lim000)()()())((lim 0000x f x x f x x f x '=∆--∆-+=→∆ (2)h h x f h x f h )()(lim000--+→hx f h x f x f h x f h )()()()(lim 00000+---+=→)1)(()())(()()(lim00000----+--+=→h x f h x f h x f h x f h )(2)()(000x f x f x f '='+'=(3)t x f t x f t )()3(lim000-+→)(333)()3(lim 0000x f tx f t x f t '=⋅-+=→ 8.用导数的定义求⎩⎨⎧≥+<=0,)1ln(0,)(x x x x x f 在0=x 处的导数.(可参看P51例1-2) 知识点:1)导数在一点0x 处的定义:xx f x x f x f x ∆-∆+='→∆)()(lim)(0000;2)点0x 处的左右导数的定义与记号:左导数x x f x x f x f x ∆-∆+='-→∆-)()(lim )(000右导数xx f x x f x f x ∆-∆+='+→∆+)()(lim )(0003)分段函数在分界点(具体的点)处的导数必须用导数的定义或左右导数的定义做。
解:因0)0(=f (先写出0=x 处的函数值)又10lim )0()0(lim )0(00=∆-∆=∆-∆+='--→∆→∆-xx x f x f f x x(在0=x 处的左导数定义)10)1ln(lim )0()0(lim )0(00=∆-∆+=∆-∆+='-+→∆→∆+xx x f x f f x x(在0=x 处的右导数定义)而1)0()0()0(=''='+-f f f 故10.设函数⎩⎨⎧>+≤=1,1,)(2x b ax x x x f ,为了使函数在1=x 处连续且可导,b a ,应取什么值? 题型:分段函数在分界点处的连续性与导数的求法。
解:由题意,函数在1=x处连续,则1)1()01()01(==+=-f f f ,即1lim )(lim )01(211===---→→x x f f x x b a b ax x f f x x +=+==+++→→)(lim )(lim )01(11,得1=+b a 又函数在1=x处可导,则)1()1(+-'='f f而21)1(lim )1()1(lim )1(200=∆-∆+=∆-∆+='--→∆→∆-xx x f x f f x xa xb x a x f x f f x x =∆-+∆+=∆-∆+='--→∆→∆+1)1(lim )1()1(lim )1(00(用到了1=+b a ) 故1,2-==b a书后部分习题解答3(关于隐函数求导)P62页14. 设032=+-y x e xy ,求=x dxdy .分析:1)隐函数求导;2)由0=x 代入方程要求出y 的值。
解:方程两边对x 求导:032)1(2=⋅+-⋅+⋅dx dy y x dx dy x y e xy得:232yxe ye x dx dy xyxy +-= 又由0=x 代入方程,得1-=y ,所以:310==x dxdy20.已知0)sin(2=-y xy π,求)1,0(-dxdy,)1,0(22-dx y d .要点:求隐函数二阶导数的方法。
解:方程两边对x 求导:02)cos()1(2=⋅⋅-⋅+⋅dxdy y y dx dy x y ππ (1) 把1,0-==y x 代入式(1),解得π21)1,0(-=-dx dy (或由式(1)解得:x y y ydx dy -=)cos(22ππ (2) 再把点代入得π21)1,0(-=-dxdy ) (求隐函数二阶求导的方法)方法1:式(1)两边对x 求导,(记y dx dy '=,y dxyd ''=22) 02)cos(2)cos(22)sin(222=''⋅⋅-'⋅'⋅-'⋅⋅'⋅+''⋅+'+'y y y y y y y y y y y y x y y πππππππ把1,0-==y x ,π21)1,0(-=-dxdy代入,得2)1,0(2241π-=-dx y d(代入:0)1(2)1(1)21(2)1(0021212=''⋅-⋅⋅-⋅--⋅--++--y πππππ) 方法2:式(2)对x 求导:2222222])cos(2[]12)sin(2)cos(2[])cos(2[x y y y y y y y y y x y y y dx y d --'⋅-'--'=πππππππππ, 点、一阶导数直接代入(不用化简,注意式中有0处的值)即可. P62页15题.利用对数求导法求导(3)xxxy +-=112说明:1)一定要用对数求导法求导;2)取对数后,先化简. 解:取对数:)]1ln()1[ln(21ln 2ln x x x y +--+=(化简) 两边对x 求导:)1111(21121xx x y y +---+='⋅ 所以:)112(1122x x x x xy --+-=' (y 代入) 书后部分习题解答4(关于中值定理与未定式极限) P82页1.检验罗尔定理对函数)3)(2)(1()(---=x x x x f 是否成立? 分析:1)即检验是否符合罗尔定理的条件; 2)若符合,ξ是否存在?解:易知)3)(2)(1()(---=x x x x f 在[1,2],[2,3]上连续,(1,2),(2,3)内可导,且0)3()2()1(===f f f ,故符合罗尔定理的条件。
又由011123)(2=+-='x x x f ,得332±=ξ,故有)2,1(;0)(11∈='ξξf )3,2(;0)(22∈='ξξf ,符合罗尔定理的结论.故罗尔定理对函数)3)(2)(1()(---=x x x x f 成立。
4.(3)证:b a b a -≤-arctan arctan证:设x x f arctan )(=,当b a =时,等式成立;若b a <,则易知x x f arctan )(=在],[b a 上连续,在),(b a 内可导,则由拉格朗日定理 存在),(b a ∈ξ,使)(11))(()()(2a b a b f a f b f -+=-'=-ξξ 取绝对值,得a b a b a b -≤-+=-)(11arctan arctan 2ξ 同理b a >,可证b a b a -≤-arctan arctan 综合:有b a b a -≤-arctan arctan6.设函数)(x f 在闭区间[1,2]上可微,证明:ξξ2)(3)1()2(f f f '=-,其中21<<ξ. 提示:对)(x f ,2)(x x g =用柯西中值定理. 8.证明:π=--)43arccos(arccos 33x x x ,其中21≤x . 题型:证明函数为常数;用到的知识:书78页定理3.4(3)的结论,若0)(≡'x f ,则C x f ≡)(.()(0x f C =) 证明:设)43arccos(arccos 3)(3x x x x f --=,则)123()43(11)11(3)(2232x x x x x f ---+--=',整理,当21<x ,0)(='x f ,故C x f ≡)(,又πππ=-⋅=223)0(f 所以:π=--)43arccos(arccos 33x x x ,当21≤x .P89页(用洛必达法则求极限时,可以适当的化简、整理等,目的简化计算) 2(3)xxx 3tan tan lim2π→解:x x x x x x x x cos 3sin 3cos sin lim 3tan tan lim22ππ→→=xxx cos )1(3cos 1lim2⋅-⋅=→π (用到连续性与极限的运算,相当于2π=x 代入)3sin 3sin 3lim2=-=→xxx π(5))0(sin ln sin ln lim 0>+→m xmxx解:xxmmx mxx mx x x sin cos sin cos lim sin ln sin ln lim 00⋅=++→→ 1cos cos lim cos sin sin cos lim00=⋅⋅=⋅⋅=++→→xmx xmx m x mx x mx m x x (整理,等价无穷小的代换)3.(2))1(cot lim 0xx x -→ (函数差的极限,一定要整理成函数商的极限)解:)1(cot lim 0x x x -→=x x x x x x sin sin cos lim 0-→20sin cos lim x xx x x -=→ (用了等价无穷小的代换)02sin lim 2cos )sin (cos lim00=-=--+=→→xxx x x x x x x x4.(3)xx x)]1[ln(lim 0+→ (幂指函数的极限) 解:x x x)]1[ln(lim 0+→=)]1ln[ln(lim 0x x x e +→ 先求0)ln (lim 1)1(ln 1lim1)ln ln(lim )]1ln[ln(lim 02000=-=---=-=++++→→→→xx xx x x x x x x x x x (用到x x ln )1ln(-=,+→0x 时,-∞→x ln ,无穷大量的倒数为无穷小)故1)]1[ln(lim 00==+→e xx x (4)xx x )arctan 2(lim π+∞→解:)arctan 2ln(lim )arctan 2(lim x x xx x ex ππ+∞→=+∞→而22111arctan 1lim 1)ln(arctan )2ln(lim)arctan 2ln(lim xx x xx x x x x x -+⋅=+=+∞→+∞→+∞→πππ2arctan )1(lim 22-=+-=+∞→x x x x (用到1)1(lim 22-=+-+∞→x x x ,2arctan lim π=+∞→x x ) 故ππ2)arctan 2(lim -+∞→=ex x x7.试确定常数b a ,,使得2)()1ln(lim220=+-+→x bx ax x x . 解:因=+-+→220)()1ln(lim x bx ax x x xbx a x x 2)2(11lim 0+-+→, 又0→x ,上式分母02→x ,且极限存在,则必须分子0211→--+bx a x得1=a ;则xbx a x x 2)2(11lim 0+-+→=222122)1(1lim20=--=-+-→b b x x ,得25-=b 书后部分习题解答4(关于中值定理与未定式极限)P82页1.检验罗尔定理对函数)3)(2)(1()(---=x x x x f 是否成立? 分析:1)即检验是否符合罗尔定理的条件; 2)若符合,ξ是否存在?解:易知)3)(2)(1()(---=x x x x f 在[1,2],[2,3]上连续,(1,2),(2,3)内可导,且0)3()2()1(===f f f ,故符合罗尔定理的条件。
