北航研究生数值分析编程大作业1
北航数值分析大作业 第一题 幂法与反幂法

数 值 分 析(B ) 大 作 业(一)姓名: 学号: 电话:1、算法设计:①求1λ、501λ和s λ的值:s λ:s λ表示矩阵的按模最小特征值,为求得s λ直接对待求矩阵A 应用反幂法即可。
1λ、501λ:若矩阵A 的特征值满足关系 1n λλ<<且1n λλ≠,要求1λ、及501λ时,可按如下方法求解: a . 对矩阵A 用幂法,求得按模最大的特征值1m λ。
b . 按平移量1m λ对矩阵A 进行原点平移得矩阵1m BA I λ=+,对矩阵B 用反幂法求得B 的按模最小特征值2m λ。
c . 321m m m λλλ=-则:113min(,)m m λλλ=,13max(,)n m m λλλ=即为所求。
②求和A 的与数5011140k k λλμλ-=+最接近的特征值ik λ(k=0,1,…39):求矩阵A 的特征值中与P 最接近的特征值的大小,采用原点平移的方法:先求矩阵 B=A-PI 对应的按模最小特征值k β,则k β+P 即为矩阵A 与P 最接近的特征值。
在本次计算实习中则是先求平移矩阵k B A I μ=-,对该矩阵应用反幂法求得s λ,则与k μ最接近的A 的特征值为:s P λ+重复以上过程39次即可求得ik λ(k=0,1,…39)的值。
③求A 的(谱范数)条件数2cond()A 和行列式det A :在(1)中用反幂法求矩阵A 的按模最小特征值时,要用到Doolittle 分解方法,在Doolittle 分解完成后得到的两个矩阵分别为L 和U ,则A 的行列式可由U 阵求出,即:det(A)=det(U)。
求得det(A)不为0,因此A 为非奇异的实对称矩阵,则: max 2()scond A λλ=,max λ和s λ分别为模最大特征值与模最小特征值。
2、程序源代码:#include "Stdio.h"#include "Conio.h"#include "math.h"//****************************************************************************// // 在存储带状矩阵时,下面的几个量在程序中反复用到,为方便编程故把它们定义成宏.// // M :转换后的矩阵的行数,M=R+S+1。
北航研究生数值分析作业第一题

北航研究⽣数值分析作业第⼀题北航研究⽣数值分析作业第⼀题:⼀、算法设计⽅案1.要求计算矩阵的最⼤最⼩特征值,通过幂法求得模最⼤的特征值,进⾏⼀定判断即得所求结果;2.求解与给定数值接近的特征值,可以该数做漂移量,新数组特征值倒数的绝对值满⾜反幂法的要求,故通过反幂法即可求得;3.反幂法计算时需要⽅程求解中间过渡向量,需设计Doolite分解求解;4.|A|=|B||C|,故要求解矩阵的秩,只需将Doolite分解后的U矩阵的对⾓线相乘即为矩阵的Det。
算法编译环境:vlsual c++6.0需要编译函数:幂法,反幂法,Doolite分解及⽅程的求解⼆、源程序如下:#include#include#include#includeint Max(int value1,int value2);int Min(int value1,int value2);void Transform(double A[5][501]);double mifa(double A[5][501]);void daizhuangdoolite(double A[5][501],double x[501],double b[501]); double fanmifa(double A[5][501]); double Det(double A[5][501]);/***定义2个判断⼤⼩的函数,便于以后调⽤***/int Max(int value1,int value2){return((value1>value2)?value1:value2);}int Min(int value1,int value2){return ((value1}/*****************************************//***将矩阵值转存在⼀个数组⾥,节省空间***/void Transform(double A[5][501],double b,double c){int i=0,j=0;A[i][j]=0,A[i][j+1]=0;for(j=2;j<=500;j++)A[i][j]=c;i++;j=0;A[i][j]=0;for(j=1;j<=500;j++)A[i][j]=b;i++;for(j=0;j<=500;j++)A[i][j]=(1.64-0.024*(j+1))*sin(0.2*(j+1))-0.64*exp(0.1/(j+1)); i++;for(j=0;j<=499;j++)A[i][j]=b;A[i][j]=0;i++;for(j=0;j<=498;j++)A[i][j]=c;A[i][j]=0,A[i][j+1]=0;}/***转存结束***///⽤于求解模最⼤的特征值,幂法double mifa(double A[5][501]){int s=2,r=2,m=0,i,j;double b2,b1=0,sum,u[501],y[501];for (i=0;i<=500;i++){u[i] = 1.0;}do{sum=0;if(m!=0)b1=b2;m++;for(i=0;i<=500;i++)sum+=u[i]*u[i];for(i=0;i<=500;i++)y[i]=u[i]/sqrt(sum);for(i=0;i<=500;i++){u[i]=0;for(j=Max(i-r,0);j<=Min(i+s,500);j++)u[i]=u[i]+A[i-j+s][j]*y[j];}b2=0;for(i=0;i<=500;i++)b2=b2+y[i]*u[i];}while(fabs(b2-b1)/fabs(b2)>=exp(-12));return b2;}//带状DOOLITE分解,并且求解出⽅程组的解void daizhuangdoolite(double A[5][501],double x[501],double b[501]) { int i,j,k,t,s=2,r=2;double B[5][501],c[501];for(i=0;i<=4;i++){for(j=0;j<=500;j++)B[i][j]=A[i][j];}for(i=0;i<=500;i++)c[i]=b[i];for(k=0;k<=500;k++){for(j=k;j<=Min(k+s,500);j++){for(t=Max(0,Max(k-r,j-s));t<=k-1;t++)B[k-j+s][j]=B[k-j+s][j]-B[k-t+s][t]*B[t-j+s][j]; }for(i=k+1;i<=Min(k+r,500);i++){for(t=Max(0,Max(i-r,k-s));t<=k-1;t++)B[i-k+s][k]=B[i-k+s][k]-B[i-t+s][t]*B[t-k+s][k]; B[i-k+s][k]=B[i-k+s][k]/B[s][k];}}for(i=1;i<=500;i++)for(t=Max(0,i-r);t<=i-1;t++)c[i]=c[i]-B[i-t+s][t]*c[t];x[500]=c[500]/B[s][500];for(i=499;i>=0;i--){x[i]=c[i];for(t=i+1;t<=Min(i+s,500);t++)x[i]=x[i]-B[i-t+s][t]*x[t];x[i]=x[i]/B[s][i];}}//⽤于求解模最⼤的特征值,反幂法double fanmifa(double A[5][501]){int s=2,r=2,m=0,i;double b2,b1=0,sum=0,u[501],y[501];for (i=0;i<=500;i++){u[i] = 1.0;}do{if(m!=0)b1=b2;m++;sum=0;for(i=0;i<=500;i++)sum+=u[i]*u[i];for(i=0;i<=500;i++)y[i]=u[i]/sqrt(sum);daizhuangdoolite(A,u,y);b2=0;for(i=0;i<=500;i++)b2+=y[i]*u[i];}while(fabs(b2-b1)>=fabs(b1)*exp(-12));return 1/b2;}//⾏列式的LU分解,U的主线乘积即位矩阵的DET double Det(double A[5][501]) {int i,j,k,t,s=2,r=2;for(k=0;k<=500;k++){for(j=k;j<=Min(k+s,500);j++){for(t=Max(0,Max(k-r,j-s));t<=k-1;t++)A[k-j+s][j]=A[k-j+s][j]-A[k-t+s][t]*A[t-j+s][j];}for(i=k+1;i<=Min(k+r,500);i++){for(t=Max(0,Max(i-r,k-s));t<=k-1;t++)A[i-k+s][k]=A[i-k+s][k]-A[i-t+s][t]*A[t-k+s][k];A[i-k+s][k]=A[i-k+s][k]/A[s][k];}}double det=1;for(i=0;i<=500;i++)det*=A[s][i];return det;}void main(){double b=0.16,c=-0.064,p,q;int i,j;double A[5][501];Transform(A,b,c); //进⾏A的赋值cout.precision(12); //定义输出精度double lamda1,lamda501,lamdas;double k=mifa(A);if(k>0) //判断求得最⼤以及最⼩的特征值.如果K>0,则它为最⼤特征值值,//并以它为偏移量再⽤⼀次幂法求得新矩阵最⼤特征值,即为最⼤ //与最⼩的特征值的差{lamda501=k;for(i=0;i<=500;i++)A[2][i]=A[2][i]-k;lamda1=mifa(A)+lamda501;for(i=0;i<=500;i++)A[2][i]=A[2][i]+k;}else //如果K<=0,则它为最⼩特征值值,并以它为偏移量再⽤⼀次幂法//求得新矩阵最⼤特征值,即为最⼤与最⼩的特征值的差{lamda1=k;for(i=0;i<=500;i++)A[2][i]=A[2][i]-k;lamda501=mifa(A)+lamda1;for(i=0;i<=500;i++)A[2][i]=A[2][i]+k;}lamdas=fanmifa(A);FILE *fp=fopen("result.txt","w");fprintf(fp,"λ1=%.12e\n",lamda1);fprintf(fp,"λ501=%.12e\n",lamda501);fprintf(fp,"λs=%.12e\n\n",lamdas);fprintf(fp,"\t要求接近的值\t\t\t实际求得的特征值\n");for(i=1;i<=39;i++) //反幂法求得与给定值接近的特征值{p=lamda1+(i+1)*(lamda501-lamda1)/40;for(j=0;j<=500;j++)A[2][j]=A[2][j]-p;q=fanmifa(A)+p;for(j=0;j<=500;j++)A[2][j]=A[2][j]+p;fprintf(fp,"µ%d: %.12e λi%d: %.12e\n",i,p,i,q);}double cond=fabs(mifa(A)/fanmifa(A));double det=Det(A);fprintf(fp,"\ncond(A)=%.12e\n",cond);fprintf(fp,"\ndetA=%.12e\n",det);}三、程序运⾏结果λ1=-1.069936345952e+001λ501=9.722283648681e+000λs=-5.557989086521e-003要求接近的值实际求得的特征值µ1: -9.678281104107e+000 λi1: -9.585702058251e+000µ2: -9.167739926402e+000 λi2: -9.172672423948e+000µ3: -8.657198748697e+000 λi3: -8.652284007885e+000µ4: -8.146657570993e+000 λi4: -8.0934********e+000µ5: -7.636116393288e+000 λi5: -7.659405420574e+000µ6: -7.125575215583e+000 λi6: -7.119684646576e+000µ7: -6.615034037878e+000 λi7: -6.611764337314e+000µ8: -6.104492860173e+000 λi8: -6.0661********e+000µ9: -5.593951682468e+000 λi9: -5.585101045269e+000µ10: -5.0834********e+000 λi10: -5.114083539196e+000µ11: -4.572869327058e+000 λi11: -4.578872177367e+000µ12: -4.062328149353e+000 λi12: -4.096473385708e+000µ13: -3.551786971648e+000 λi13: -3.554211216942e+000µ14: -3.0412********e+000 λi14: -3.0410********e+000µ15: -2.530704616238e+000 λi15: -2.533970334136e+000µ16: -2.020*********e+000 λi16: -2.003230401311e+000µ17: -1.509622260828e+000 λi17: -1.503557606947e+000µ18: -9.990810831232e-001 λi18: -9.935585987809e-001µ19: -4.885399054182e-001 λi19: -4.870426734583e-001µ20: 2.200127228676e-002 λi20: 2.231736249587e-002µ21: 5.325424499917e-001 λi21: 5.324174742068e-001µ22: 1.043083627697e+000 λi22: 1.052898964020e+000µ23: 1.553624805402e+000 λi23: 1.589445977158e+000µ24: 2.064165983107e+000 λi24: 2.060330427561e+000µ25: 2.574707160812e+000 λi25: 2.558075576223e+000µ26: 3.0852********e+000 λi26: 3.080240508465e+000µ27: 3.595789516221e+000 λi27: 3.613620874136e+000µ28: 4.106330693926e+000 λi28: 4.0913********e+000µ29: 4.616871871631e+000 λi29: 4.603035354280e+000µ30: 5.127413049336e+000 λi30: 5.132924284378e+000µ31: 5.637954227041e+000 λi31: 5.594906275501e+000µ32: 6.148495404746e+000 λi32: 6.080933498348e+000µ33: 6.659036582451e+000 λi33: 6.680354121496e+000µ34: 7.169577760156e+000 λi34: 7.293878467852e+000µ35: 7.680118937861e+000 λi35: 7.717111851857e+000µ36: 8.190660115566e+000 λi36: 8.225220016407e+000µ37: 8.701201293271e+000 λi37: 8.648665837870e+000µ38: 9.211742470976e+000 λi38: 9.254200347303e+000µ39: 9.722283648681e+000 λi39: 9.724634099672e+000cond(A)=1.925042185755e+003detA=2.772786141752e+118四、分析如果初始向量选择不当,将导致迭代中X1的系数等于零.但是,由于舍⼊误差的影响,经若⼲步迭代后,.按照基向量展开时,x1的系数可能不等于零。
北航数值分析实验报告

北航数值分析实验报告篇一:北航数值分析报告第一大题《数值分析》计算实习报告第一大题学号:DY1305姓名:指导老师:一、题目要求已知501*501阶的带状矩阵A,其特征值满足?1?2...?501。
试求:1、?1,?501和?s的值;2、A的与数?k??1?k?501??140最接近的特征值?ik(k=1,2,...,39);3、A的(谱范数)条件数c nd(A)2和行列式de tA。
二、算法设计方案题目所给的矩阵阶数过大,必须经过去零压缩后进行存储和运算,本算法中压缩后的矩阵A1如下所示。
?0?0?A1??a1??b??c0b a2bcc bb c............c bb ccb a500b0a 3...a499c?b??a501??0?0??由矩阵A的特征值满足的条件可知?1与?501之间必有一个最大,则采用幂法求出的一个特征值必为其中的一个:当所求得的特征值为正数,则为?501;否则为?1。
在求得?1与?501其中的一个后,采用带位移的幂法则可求出它们中的另一个,且位移量即为先求出的特征值的值。
用反幂法求得的特征值必为?s。
由条件数的性质可得,c nd(A)2为模最大的特征值与模最小的特征值之比的模,因此,求出?1,?501和?s的值后,则可以求得c nd(A)2。
北航数值分析计算实习1

《数值分析》计算实习题目110091013 劳云杰一、算法设计方案根据提示的算法,首先使用幂法求出按模最大的特征值λt1,再根据已求出的λt1用带原点平移的幂法求出另一个特征值λt2,比较两个λ的大小,根据已知条件,可以得出λ1和λ501.至于λs,由于是按模最小的特征值,使用反幂法求之,由于反幂法需要解线性方程组,故对矩阵进行Doolittle分解。
再通过带原点平移的反幂法求跟矩阵的与数最接近的特征值。
对非奇异的矩阵A,根据条件数定义,取λt1/λs的绝对值,两个特征值在之前步骤中均以求得。
由于对矩阵进行了Doolittle分解,所以矩阵的行列式det A可由分解得出的上三角阵U 的对角线上元素相乘求得。
为了使A的所有零元素都不存储,使用书本25页的压缩存储法对A进行存储,在计算时通过函数在数组C中检索A中元素即可。
由于A是501*501矩阵,C应取为5*501矩阵。
由于数据不大,为了方便起见,在程序中取502*502矩阵或者502向量,C也取为6*502矩阵。
程序编写参考《数值分析》颜庆津著和[C数值算法].(美国)W ILLIAM.H.P RESS.扫描版。
二、全部源程序#include <stdio.h>#include <math.h>#define XS 1.0e-12//精度水平void fz_a();//对矩阵A赋值double js(int,int);//在压缩矩阵中检索A的元素double mf(double);//幂法double fmf(double);//反幂法int lu(double);//Doolittle分解int jfc(double[],double[]);//解方程int max(int,int);int min(int,int);double (*u)[502]=new double[502][502];//上三角阵double (*l)[502]=new double[502][502];//单位下三角阵double a[6][502];//压缩存储矩阵int max(int x,int y)//比大小函数×2{ return (x>y?x:y);}int min(int x,int y)//精度关系,比较下标用{ return (x<y?x:y);}int main(){printf("请耐心等待,先看看中间过程吧~\n");int i,k;double ldt1,ldt2,ld1,ld501,lds,mu[40],det;double ld[40];fz_a();//对A赋值ldt1=mf(0);//幂法求模最大的特征值ldt2=mf(ldt1);//以第一次求得的特征值进行平移ld1=ldt1<ldt2?ldt1:ldt2;//大的就是λ501ld501=ldt1<ldt2?ldt2:ldt1;lu(0);lds=fmf(0);//反幂法求λsdet=1;//初始化行列式for(i=1;i<=501;i++)det=det*u[i][i];//用U的对角元素求行列式for(k=1;k<=39;k++){mu[k]=ld1+k*(ld501-ld1)/40;//与数lu(mu[k]);ld[k]=fmf(mu[k]);}printf("\n 列出结果\n");printf("λ1=%1.12e λ501=%1.12e\n",ld1,ld501);printf("λs=%1.12e \n",lds);printf("cond(A)=%1.12e \n",fabs(ldt1/lds));printf("detA=%1.12e \n",det);for(k=1;k<=39;k++)//列出跟与数最接近特征值{printf("λi%d=%1.12e\t",k,ld[k]);if(k%2==0)printf("\n");}//界面友好性delete []u;delete []l;getchar();return 0;}void fz_a()//对A赋值{int i;for(i=3;i<=501;i++)a[1][i]=a[5][502-i]=-0.064;//原A矩阵的cfor(i=2;i<=501;i++)a[2][i]=a[4][502-i]=0.16;//原A矩阵的bfor(i=1;i<=501;i++)a[3][i]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i);//原对角线元素}double js(int i,int j)//对压缩矩阵检索A的元素{if(abs(i-j)<=2)return a[i-j+3][j];else return 0;}double mf(double offset)//幂法{int i,x1;double u[502],y[502];double beta=0,prebeta=-1000,yita=0;//用幂法的第一种迭代方法for(i=1;i<=501;i++) //用到了2-范数u[i]=1,y[i]=0;for(int k=1;k<=10000;k++)//对迭代次数进行限制{yita=0;for(i=1;i<=501;i++)yita=sqrt(yita*yita+u[i]*u[i]);for(i=1;i<=501;i++)y[i]=u[i]/yita;for(x1=1;x1<=501;x1++){u[x1]=0;for(int x2=1;x2<=501;x2++)u[x1]=u[x1]+((x1==x2)?(js(x1,x2)-offset):js(x1,x2))*y[x2];}prebeta=beta;beta=0;for(i=1;i<=501;i++)beta=beta+y[i]*u[i];if(fabs((prebeta-beta)/beta)<=XS){printf("offset=%f lb=%f err=%e k=%d\n",offset,(beta+offset),fabs((prebeta-beta)/beta),k);break;};}//满足误差条件后,迭代终止,并输出平移量,误差和迭代次数return(beta+offset);//加上平移量,方便比较}double fmf(double offset)//反幂法{ int i;double u[502],y[502];double beta=0,prebeta=0,yita=0;for(i=1;i<=501;i++)u[i]=1,y[i]=0; //相关量初始化for(int k=1;k<=10000;k++)//限制迭代次数{yita=0;for(i=1;i<=501;i++)yita=sqrt(yita*yita+u[i]*u[i]);for(i=1;i<=501;i++)y[i]=u[i]/yita;jfc(u,y);prebeta=beta;beta=0;for(i=1;i<=501;i++)beta=beta+y[i]*u[i];beta=1/beta;if(fabs((prebeta-beta)/beta)<=XS){printf("offset=%f lb=%f err=%ek=%d\n",offset,(beta+offset),fabs((prebeta-beta)/beta),k);break;};}//满足误差条件后,迭代终止,并输出平移量,误差和迭代次数return(beta+offset);}int lu(double offset)//Doolittle分解{int i,j,k,t;double sum;//中间量for(k=1;k<=501;k++)for(j=1;j<=501;j++){u[k][j]=l[k][j]=0;if(k==j)l[k][j]=1;}//对LU矩阵初始化for(k=1;k<=501;k++)//对式(2.12)的程序实现{for(j=k;j<=min(k+2,501);j++){sum=0;for(t=max(1,max(k-2,j-2));t<=(k-1);t++)sum=sum+l[k][t]*u[t][j];//j=k,k+1,……,nu[k][j]=((k==j)?(js(k,j)-offset):js(k,j))-sum;}if(k==501)continue;for(i=k+1;i<=min(k+2,501);i++)//i=k+1,……,n{sum=0;for(t=max(1,max(i-2,k-2));t<=(k-1);t++)sum=sum+l[i][t]*u[t][k];l[i][k]=(((i==k)?(js(i,k)-offset):js(i,k))-sum)/u[k][k];}}return 0;}int jfc(double x[],double b[])//解方程{int i,t;double y[502];double sum;y[1]=b[1];for(i=2;i<=501;i++){sum=0;for(t=max(1,i-2);t<=i-1;t++)sum=sum+l[i][t]*y[t];y[i]=b[i]-sum;}x[501]=y[501]/u[501][501];for(i=500;i>=1;i--){sum=0;for(t=i+1;t<=min(i+2,501);t++)sum=sum+u[i][t]*x[t];x[i]=(y[i]-sum)/u[i][i];}return 0;}三、结果λ1=-1.070011361502e+001λ501=9.724634098777e+000λs=-5.557910794230e-003cond(A)=1.925204273902e+003detA=2.772786141752e+118λi1=-1.018293403315e+001 λi2=-9.585707425068e+000 λi3=-9.172672423928e+000λi4=-8.652284007898e+000 λi5=-8.0934********e+000 λi6=-7.659405407692e+000λi7=-7.119684648691e+000 λi8=-6.611764339397e+000 λi9=-6.0661********e+000λi10=-5.585101052628e+000 λi11=-5.114083529812e+000 λi12=-4.578872176865e+000λi13=-4.096470926260e+000 λi14=-3.554211215751e+000 λi15=-3.0410********e+000 λi16=-2.533970311130e+000 λi17=-2.003230769563e+000 λi18=-1.503557611227e+000 λi19=-9.935586060075e -001 λi20=-4.870426738850e -001 λi21=2.231736249575e -002 λi22=5.324174742069e -001 λi23=1.052898962693e+000 λi24=1.589445881881e+000 λi25=2.060330460274e+000 λi26=2.558075597073e+000 λi27=3.080240509307e+000 λi28=3.613620867692e+000 λi29=4.0913********e+000 λi30=4.603035378279e+000 λi31=5.132924283898e+000 λi32=5.594906348083e+000 λi33=6.080933857027e+000 λi34=6.680354092112e+000 λi35=7.293877448127e+000 λi36=7.717111714236e+000 λi37=8.225220014050e+000 λi38=8.648666065193e+000 λi39=9.254200344575e+000四、讨论迭代初始向量的选取对计算结果的影响1.在反幂法中取迭代向量u[1]=1,u[i]=0,i=2,……,501,最后得出的结果中λs=2.668886923785e -002,cond(A)也随之改变成4.009204556274e+0022.在幂法中取迭代向量u[1]=1,u[i]=2,i=2,……,501,最后得出的结果不变。
北航数值分析大作业一

《数值分析B》大作业一SY1103120 朱舜杰一.算法设计方案:1.矩阵A的存储与检索将带状线性矩阵A[501][501]转存为一个矩阵MatrixC[5][501] .由于C语言中数组角标都是从0开始的,所以在数组MatrixC[5][501]中检索A的带内元素a ij的方法是:A的带内元素a ij=C中的元素c i-j+2,j2.求解λ1,λ501,λs①首先分别使用幂法和反幂法迭代求出矩阵按摸最大和最小的特征值λmax和λmin。
λmin即为λs;如果λmax>0,则λ501=λmax;如果λmax<0,则λ1=λmax。
②使用带原点平移的幂法(mifa()函数),令平移量p=λmax,求出对应的按摸最大的特征值λ,max,如果λmax>0,则λ1=λ,max+p;如果λmax<0,则λ501=λ,max+p。
3.求解A的与数μk=λ1+k(λ501-λ1)/40的最接近的特征值λik (k=1,2,…,39)。
使用带原点平移的反幂法,令平移量p=μk,即可求出与μk最接近的特征值λik。
4.求解A的(谱范数)条件数cond(A)2和行列式d etA。
①cond(A)2=|λ1/λn|,其中λ1和λn分别是矩阵A的模最大和最小特征值。
②矩阵A的行列式可先对矩阵A进行LU分解后,detA等于U所有对角线上元素的乘积。
二.源程序#include<stdio.h>#include<iostream.h>#include<stdlib.h>#include<math.h>#include<float.h>#include<iomanip.h>#include<time.h>#define E 1.0e-12 /*定义全局变量相对误差限*/int max2(int a,int b) /*求两个整型数最大值的子程序*/{if(a>b)return a;elsereturn b;}int min2(int a,int b) /*求两个整型数最小值的子程序*/{if(a>b)return b;elsereturn a;}int max3(int a,int b,int c) /*求三整型数最大值的子程序*/{ int t;if(a>b)t=a;else t=b;if(t<c) t=c;return(t);}void assignment(double array[5][501]) /*将矩阵A转存为数组C[5][501]*/{int i,j,k;//所有元素归零for(i=0;i<=4;){for(j=0;j<=500;){array[i][j]=0;j++;}i++;}//第0,4行赋值for(j=2;j<=500;){k=500-j;array[0][j]=-0.064;array[4][k]=-0.064;j++;}//第1,3行赋值for(j=1;j<=500;){k=500-j;array[1][j]=0.16;array[3][k]=0.16;j++;}//第2行赋值for(j=0;j<=500;){ k=j;j++;array[2][k]=(1.64-0.024*j)*sin((double)(0.2*j))-0.64*exp((double)(0.1/j));}}double mifa(double u[501],double array[5][501],double p) /*带原点平移的幂法*/ {int i,j; /* u[501]为初始迭代向量*/double a,b,c=0; /* array[5][501]为矩阵A的转存矩阵*/double y[501]; /*p为平移量*/for(;;){a=0;b=0;/*选用第一种迭代格式*///求ηk-1for(i=0;i<=500;i++){a=a+u[i]*u[i];}a=sqrt(a);//求y k-1for(i=0;i<=500;i++){y[i]=u[i]/a;}//求u kfor(i=0;i<=500;i++){u[i]=0;for(j=max2(i-2,0);j<=min2(i+2,500);j++){u[i]+=array[i-j+2][j]*y[j];}u[i]=u[i]-p*y[i]; /*引入平移量*/}//求βkfor(i=0;i<=500;i++){b+=y[i]*u[i];}if(fabs((b-c)/b)<=E) /*达到精度水平,迭代终止*/break;c=b;}return (b+p); /*直接返回A的特征值*/}void chuzhi(double a[]) /*用随机数为初始迭代向量赋值*/ {int i;srand((int)time(0));for(i=0;i<=500;i++){a[i]=(10.0*rand()/RAND_MAX); /*生成0~10的随机数*/}}void chuzhi2(double a[],int j) /*令初始迭代向量为e i*/{int i;for(i=0;i<=500;i++){a[i]=0;}a[j]=1;}void LU(double array[5][501]) /*对矩阵A进行Doolittle分解*/{ /*矩阵A转存在C[5][501]中*/int j,k,t; /*分解结果L,U分别存在C[5][501]的上半部与下半部*/ for(k=0;k<=500;k++){for(j=k;j<=min2((k+2),500);j++){for(t=max3(0,k-2,j-2);t<=(k-1);t++){array[k-j+2][j]-=array[k-t+2][t]*array[t-j+2][j];}}if(k<500)for(j=k+1;j<=min2((k+2),500);j++){for(t=max3(0,k-2,j-2);t<=(k-1);t++){array[j-k+2][k]-=array[j-t+2][t]*array[t-k+2][k];}array[j-k+2][k]=array[j-k+2][k]/array[2][k];}}}double fmifa(double u[501],double array[5][501],double p){ /*带原点平移的反幂法*/ int i,j;double a,b,c=0;double y[501];//引入平移量for(i=0;i<=500;i++){array[2][i]-=p;}//先将矩阵Doolittle分解LU(array);for(;;){a=0;b=0;//求ηk-1for(i=0;i<=500;i++){a=a+u[i]*u[i];}a=sqrt(a);//求y k-1for(i=0;i<=500;i++){y[i]=u[i]/a;}//回带过程,求解u kfor(i=0;i<=500;i++){u[i]=y[i];}for(i=1;i<=500;i++){for(j=max2(0,(i-2));j<=(i-1);j++){u[i]-=array[i-j+2][j]*u[j];}}u[500]=u[500]/array[2][500];for(i=499;i>=0;i--){for(j=i+1;j<=min2((i+2),500);j++){u[i]-=array[i-j+2][j]*u[j];}u[i]=u[i]/array[2][i];}//求βkfor(i=0;i<=500;i++){b+=y[i]*u[i];}if(fabs((b-c)/b)<=E) /*达到精度要求,迭代终止*/break;c=b;}return (p+(1/b)); /*直接返回距离原点P最接近的A的特征值*/ }//主函数main(){ int i;double d1,d501,ds,d,a;double u[501];double MatrixC[5][501];printf(" 《数值分析》计算实习题目第一题\n");printf(" SY1103120 朱舜杰\n");//将矩阵A转存为MatrixCassignment(MatrixC);//用带原点平移的幂法求解λ1,λ501chuzhi(u);d=mifa(u,MatrixC,0);chuzhi(u);a=mifa(u,MatrixC,d);if(d<0){d1=d;d501=a;}else{d501=d;d1=a;}printf("λ1=%.12e\n",d1);printf("λ501=%.12e\n",d501);//用反幂法求λschuzhi(u);ds=fmifa(u,MatrixC,0);printf("λs=%.12e\n",ds);//用带原点平移的反幂法求λikfor(i=1;i<=39;i++){a=d1+(i*(d501-d1))/40;assignment(MatrixC);chuzhi(u);d=fmifa(u,MatrixC,a);printf("与μ%02d=%+.12e最接近的特征值λi%02d=%+.12e\n",i,a,i,d);}//求A的条件数d=fabs((d1/ds));printf("A的(谱范数)条件数cond<A>2=%.12e\n",d);//求detAassignment(MatrixC);LU(MatrixC);a=1;for(i=0;i<=500;i++){a*=MatrixC[2][i];}printf("行列式detA=%.12e\n",a);//测试不同迭代初始向量对λ1计算结果的影响。
北航数值分析大作业一

北京航空航天大学数值分析大作业一学院名称自动化专业方向控制工程学号ZY*******学生姓名许阳教师孙玉泉日期2021 年11月26 日设有501501⨯的实对称矩阵A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=5011A a b c b c c b c b a其中,064.0,16.0),501,,2,1(64.0)2.0sin()024.064.1(1.0-==⋅⋅⋅=--=c b i e i i a ii 。
矩阵A 的特征值为)501,,2,1(⋅⋅⋅=i i λ,并且有||min ||,501150121i i s λλλλλ≤≤=≤⋅⋅⋅≤≤1λ,501λ和s λ的值。
A 的与数4015011λλλμ-+=kk 最接近的特征值)39,,2,1(⋅⋅⋅=k k i λ。
A 的(谱范数)条件数2)A (cond 和行列式detA 。
一 方案设计1 求1λ,501λ和s λ的值。
s λ为按模最小特征值,||min ||5011i i s λλ≤≤=。
可使用反幂法求得。
1λ,501λ分别为最大特征值及最小特征值。
可使用幂法求出按模最大特征值,如结果为正,即为501λ,结果为负,那么为1λ。
使用位移的方式求得另一特征值即可。
2 求A 的与数4015011λλλμ-+=kk 最接近的特征值)39,...,2,1(=k k i λ。
题目可看成求以k μ为偏移量后,按模最小的特征值。
即以k μ为偏移量做位移,使用反幂法求出按模最小特征值后,加上k μ,即为所求。
3 求A 的(谱范数)条件数2)(A cond 和行列式detA 。
矩阵A 为非奇异对称矩阵,可知,||)(min max2λλ=A cond(1-1)其中m ax λ为按模最大特征值,min λ为按模最小特征值。
detA 可由LU 分解得到。
因LU 均为三角阵,那么其主对角线乘积即为A 的行列式。
二 算法实现1 幂法使用如下迭代格式:⎪⎪⎩⎪⎪⎨⎧⋅===⋅⋅⋅=------||max |)|sgn(max ||max /),,(111111)0()0(10k k k k k k k k Tn u u Ay u u u y u u u β任取非零向量 (2-1)终止迭代的控制理论使用εβββ≤--||/||1k k k , 实际使用εβββ≤--||/||||||1k k k(2-2)由于不保存A 矩阵中的零元素,只保存主对角元素a[501]及b,c 值。
北航数值分析计算实习第一题编程

i − t + s +1,t t − k + s +1, k t = max(1,i − r ,k − s )
∑c
c
) / cs +1, k
[i = k + 1, k + 2,⋯ , min( k + r , n); k < n]
(2) 求解 Ly = b,Ux = y (数组 b 先是存放原方程右端向量,后来存放中间向量 y)
0 b a2
b c
c b a3 b c
⋯ ⋯ ⋯ ⋯ ⋯
c b a499 b c
c b a500 b 0
c ⎤ b ⎥ ⎥ a501 ⎥ ⎥ 0 ⎥ 0 ⎥ ⎦
在数组 C 中检索矩阵 A 的带内元素 aij 的方法是: A 的带内元素 aij =C 中的元素 ci − j + s +1, j
2
数值分析计算实习题目一
i −1
bi := bi −
பைடு நூலகம்
i − t + s +1,t t t = max(1,i − r )
∑c
b
(i = 2,3,⋯ , n)
xn := bn / cs +1, n
min( i + s )
xi := (bi −
t = i +1
∑c
i −t + s +1,t t
x ) / cs +1,i
(i = n − 1, n − 2,⋯ ,1)
3、Doolittle 分解求解 n 元带状线性方程组(doolittle()函数)
按照上述对带状矩阵 A 的存储方法和元素 aij 的检索方法,并且把三角分解的结果 ukj 和 lik 分 别存放在 akj 和 aik 原先的存储单元内,那么用 Doolittle 分解法求解 n 元带状线性方程组的算法 可重新表述如下(其中“:=”表示赋值) : (1) 作分解 A = LU 。 对于 k=1,2, ……,n 执行
北航数值分析-实习作业1(C语言详细注释)

《数值分析》计算实习作业《一》北航第一题 设有501501⨯的矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=501500499321a bc b a b cc b a b ccb a bc c b a b c b a A其中.064.0,16.0);501,2,1(64.0)2.0sin()024.064.1(1.0-===--=c b i e i i a i i 矩阵的特征值)501,,2,1( =i i λ满足||min ||,501150121i i s λλλλλ≤≤=<<<试求1. 5011,λλ和s λ的值2. 的与数4015011λλκλμ-+=k 最接近的特征值)39,,2,1( =K κλi3. 的(谱范数)条件数2)A (cond 和行列式A det 要求1. 算法的设计方案(A 的所有零元素都不能存储)2. 全部源程序(详细注释)。
变量为double ,精度-1210=ε,输出为e 型12位有效数字3. 特征值s 5011,,λλλ和)39,,2,1( =K κλi 以及A cond det ,)A (2的值4. 讨论迭代初始向量的选取对计算结果的影响,并说明原因解答:1. 算法设计对于s λ满足||min ||5011i i s λλ≤≤=,所以s λ是按模最小的特征值,直接运用反幂法可求得。
对于5011,λλ,一个是最大的特征值,一个是最小的特征值,不能确定两者的绝对值是否相等,因此必须首先假设||||5011λλ≠,然后运用幂法,看能否求得一个特征值,如果可以求得一个,证明A 是收敛的,求得的结果是正确的,然后对A 进行带原点平移的幂法,偏移量是前面求得的特征值,可以求得另一个特征值,最后比较这两个特征值,较大的特征值是501λ,较小的特征值就是1λ。
如果在假设的前提下,无法运用幂法求得按模最大的特征值,即此时A 不收敛,则需要将A 进行带原点平移的幂法,平移量可以选取1,再重复上述步骤即可求得两个特征值。
北航数值分析A大作业

一、算法设计方案1、解非线性方程组将各拟合节点(x i ,y j )分别带入非线性方程组,求出与(,)i i x y 相对应的数组te[i][j],ue[i][j],求解非线性方程组选择Newton 迭代法,迭代过程中需要求解线性方程组,选择选主元的Doolittle 分解法。
2、二元二次分偏插值对数表z(t,u)进行分片二次代数插值,求得对应(t ij ,u ij )处的值,即为),(j i y x f 的值。
根据给定的数表,可将整个插值区域分成 16 个小 的区域,故先判断?t ij , u ij ? 所在,的区域,再作此区域的插值,计算 z ij ,相应的Lagrange 形式的插值多项式为:°112211(,)()()(,)m n krkrk m r n p t u l t l u f t u ++=-=-=∑∑其中11()m wk w m k ww kt t l t t t +=-≠-=-∏ (k=m-1, m, m+1) °11()n wr w n r ww ry y l u y y +=-≠-=-∏ (r=n-1, n, n+1)3、曲面拟合从k=1开始逐渐增大k 的值,使用最小二乘法曲面拟合法对z=f(x,y)进行拟合,当710-<σ时结束计算。
拟合基函数φr (x)ψs (y)选择为φr (x)=x r ,ψs (y)=y s 。
拟合系数矩阵c 通过连续两次解线性方程组求得。
[]rsc *=C ,11()()T T T --=C B B B UG G G其中011101011[()]1kk r i k x x x x x x x ϕ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦B L LM M M M L ,0011101011[()]1k k s j k y y y y G y y y ψ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦L LM M M M L [(,)]i j f x y =U4、观察比较计算)5,,2,1,8,,2,1)(,(),,(****⋅⋅⋅=⋅⋅⋅=j i y x p y x f j i j i 的值并输出结果,以观察),(y x p 逼近),(y x f 的效果。
北航数值分析大作业第一题

1 算法方案 1.1 λ1,λ501,λs 的计算
(1) (2) (3) (4) (5) 将矩阵 A[501][501]以压缩存储后的形式 C[5][501]输入 使用一次幂法得到按模最大的特征值 矩阵向左平移 λm 距离(A-λmI) ,再使用一次幂法得到按模最大的特征值 s,则 λm1=s-λm1 比较 λm1 和 λm2 的大小与正负,得到 λ 和 λ501 对 A 使用一次反幂法得到按模最小的特征值 λs
while (e>=pow(10,-12)); return 1/be;//返回 1/be2 作为矩阵 m[5][501]的按模最小向量 } //333333333333333333333333333333333333333333333333333333333333333333333333 33333333333333333333333333333333333333333333333333333333333333333333333 double det(double c[1+r+s][q]) { int max3(int a,int b,int c); int fmax2(int a,int b); int fmin2(int a,int b); int i,j,k,t; double sum,det=1; for(k=1;k<=q;k++) { for(j=k;j<=fmin2(k+s,q);j++)//求 ukj { sum=0; for(t=max3(1,k-r,j-s);t<=k-1;t++) { sum=sum+c[k-t+s][t-1]*c[t-j+s][j-1]; } c[k-j+s][j-1]=c[k-j+s][j-1]-sum; }
北航数值分析第一次大作业

b2[i-1]=b[i-1]-sum3; } x[n-1]=b2[n-1]/C[s][n-1]; for(i=n-1;i>=1;i--) { double sum4=0; for(int t=i+1;t<=min(i+s,n);t++) { sum4+=C[i-t+s][t-1]*x[t-1]; } x[i-1]=(b2[i-1]-sum4)/C[s][i-1]; } } /*反幂法*/ double FMF(double C[m][n]) { LU(C); for(int k=1;k<=n;k++) u[k-1]=1; /*为迭代初始向量赋值*/ beta1=beta2=0; do { ent=0; for(int i=1;i<=n;i++) ent+=u[i-1]*u[i-1]; ent=sqrt(ent); for(i=1;i<=n;i++) y[i-1]=u[i-1]/ent; HD(C,y,u); beta1=beta2; beta2=0; for(i=1;i<=n;i++) { beta2+=y[i-1]*u[i-1]; } }while(fabs(1/beta2-1/beta1)/fabs(1/beta2)>1.0e-12); return 1/beta2; } /*求 detA*/ double det(double C[m][n]) { LU(C); double detA=1; for(int j=1;j<=n;j++)
数值分析第一次作业
姓名:吴少波 学号:SY1105513
一、算法的设计方案 1.将带状矩阵 A 压缩为矩阵 C 存储。先用幂法算出 A 按模最大的特征值,记为 maxLambda, 再 将 其 平 移 ,用 带 原点 平 移 的 幂 法求 A-maxLambdaI 按模 最 大的 特 征 值 , 记为 p1 , 记 p2=p1+maxLambda,比较 maxLambda 和 p2 的大小,大的为λ 501,小的为λ 1。 用反幂法求解λ s 时,其中需解方程 Auk=yk-1,先把矩阵 A LU 分解(不列主元) ,再在每次循环 迭代时回代求解。 2.将 A 平移μ k(k=1,2,…,39)个单位,用带原点平移的反幂法求与μ k(k=1,2,…,39) 最接近的 39 个特征值。 3.cond(A)2=│maxLambda / λ s│ A 的行列式等于把 A LU 分解后 A 所有对角线上元素的乘积。 二、源程序(VC6.0 环境下的 C 语言) #include<stdio.h> #include<stdlib.h> #include<math.h> #include<malloc.h> #define m 5 #define n 501 #define r 2 #define s 2 double C[m][n]; double u[n]; double y[n]; double ent,beta1,beta2; void YS(); /*将带状矩阵 A 压缩为 C*/ int max(int a,int b); /*两数求较大的一个*/ int min(int a,int b); /*两数求较小的一个*/ double MF(double C[m][n]); /*幂法*/ double FMF(double C[m][n]); /*反幂法*/ void LU(double C[m][n]); /*LU 分解*/ void HD(double C[m][n],double b[n],double x[n]); /*回代过程*/ double det(double C[m][n]); /*求 detA*/ double Move_MF(double C[m][n],double maxLambda); /*带原点平移的幂法*/ double Move_FMF(double C[m][n],double p); /*带原点平移的反幂法*/ /**主函数**/ void main() { /*定义变量*/ double maxLambda=0,minLambda=0,condA,detA,Lambda1,Lambda501,p1,p2,Mu_k,Lambdaik; /*算第一题*/
北航研究生数值分析编程大作业1

数值分析大作业一、算法设计方案1、矩阵初始化矩阵[]501501⨯=ij a A 的下半带宽r=2,上半带宽s=2,设置矩阵[][]5011++s r C ,在矩阵C 中检索矩阵A 中的带内元素ij a 的方法是:j s j i ij c a ,1++-=。
这样所需要的存储单元数大大减少,从而极大提高了运算效率。
2、利用幂法求出5011λλ,幂法迭代格式:0111111nk k k k kk T k k k u R y u u Ay y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止。
首先对于矩阵A 利用幂法迭代求出一个λ,然后求出矩阵B ,其中I A B λ-=(I 为单位矩阵),对矩阵B 进行幂法迭代,求出λ',之后令λλλ+'='',比较的大小与λλ'',大者为501λ,小者为1λ。
3、利用反幂法求出ik s λλ,反幂法迭代格式:0111111nk k k k kk T k k k u R y u Au y y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止,1s k λβ=。
每迭代一次都要求解一次线性方程组1-=k k y Au ,求解过程为:(1)作分解LU A =对于n k ,...,2,1=执行[][]s k n r k k k i c c c c c n s k k k j c cc c k s ks k t k s k r i t t s t i k s k i k s k i js j t k s j r k t t s t k j s j k j s j k <+++=-=++=-=+++----=++-++-++-++----=++-++-++-∑∑);,min(,...,2,1/)(:),min(,...,1,:,1,11),,1max(,1,1,1,11),,1max(,1,1,1(2)求解y Ux b Ly ==,(数组b 先是存放原方程组右端向量,后来存放中间向量y))1,...,2,1(/)(:/:),...,3,2(:,1),min(1.1.11),1max(,1--=-===-=+++-++-+--=++-∑∑n n i c x c b x c b x n i b c b b i s t n s i i t t s t i i i ns n n ti r i t t s t i i i使用反幂法,直接可以求得矩阵按模最小的特征值s λ。
北航数分大作业一

《数值分析》计算实习题第一题姓名:学号:一、 算法的设计方案 ⒈矩阵A 的存储由于A[501][501]是带状矩阵,并且阶数远大于带宽5,为节省内存空间,设置一个二维数组C[5][501]用于存放A 的带内元素。
A 中元素与C 数组中元素的对应关系,即A 的检索方式为: A 的元素ij a =C 中的元素1,i j s j C -++ 2.求解特征值λ1,λ501,λs①由于λ1‹λ2‹…‹λ501,所以在以所有特征值建立的数轴上,λ1、λ50⒊1位于数轴的两端,两者之一必为按模最大。
利用幂法,可以求出来按模最大的特征值λM ,即为λ1和λ501中一个;然后将原矩阵平移λM,再利用幂法求一次平移后矩阵的按模最大的特征值λM ′。
比较λM 和λM+λM ′大小,大者为λ501,小的为λ1。
②利用反幂法,求矩阵A 的按模最小的特征值λs 。
但是反幂法中要用到线性方程组的求解,而原矩阵A 又是带状矩阵,采用LU 分解。
所以在这之前要定义一个LU 分解子程序,将A 矩阵分解为单位下三角矩阵L 和上三角矩阵U 的乘积。
⒊求解A 的与数μk =λ1+k (λ501-λ1)/40的最接近的特征值λik(k=1,2,…,39)。
先使k 从1到39循环,求出μk 的值,然后使用带原点平移的反幂法,令平移量p=μk 。
计算过程需调用LU 分解子程序对A-u k I 矩阵进行LU 分解。
最终反幂法求出的值加上μk 即为与μk 最接近的特征值λik4.求解A的(谱范数)条件数cond(A)2和行列式detAcond(A)2=|λ1/λn|,其中λ1和λn分别是矩阵A的模最大和最小特征值,上边已经求出,可直接调用。
detA等于对A记性LU分解以后U的所有对角线上元素的乘积。
二、全部源程序#include<stdio.h>#include <math.h>/***全局变量、函数申明***/#define N 501#define EMS 1.0e-12double U[N],Y[N];double c[5][N] ;double fuzhi(); /*对A进行压缩存储*/ void DLU(double C[5][N]); /*对矩阵A进行LU分解*/ double pingyi(double C[5][N],double b); /*求矩阵的平移矩阵*/ double mifa(double c[5][N]); /*幂法计算矩阵A按模最大的特征值*/ double fmifa(double c[5][N],double b); /*反幂法求矩阵A按模最小的特征值*/void main(){double lamuda_m1,lamuda_m2,lamuda_max,lamuda_min,lamuda_sum,lamuda_s;fuzhi();lamuda_m1=mifa(c);pingyi(c, lamuda_m1);lamuda_m2 =mifa(c);lamuda_sum= lamuda_m1+ lamuda_m2;if (lamuda_m1>lamuda_sum){lamuda_max=lamuda_m1;lamuda_min=lamuda_sum;}else{lamuda_max=lamuda_sum;lamuda_min=lamuda_m1;}printf("矩阵的最大特征值为:\n lamuda_501=%.11e\n",lamuda_max); printf("矩阵的最小特征值为:\n lamuda_1=%.11e\n",lamuda_min); int i;double conda,u[39];for(i=1;i<40;i++)u[i]=lamuda_min+(lamuda_max-lamuda_min)*i/40;lamuda_s=fmifa(c,0);printf("矩阵的按模最小特征值为:\n lamuda_s=%.11e\n", lamuda_s); printf("与uk最接近的特征值如下:\n");/*求与uk接近的特征值*/for(i=1;i<40;i++)printf("u[%2d]=%.11e 与其最接近的特征值为lamuda_%2d=%.11e\n",i,u[i],i,fmifa(c,u[i]));/*求矩阵A的条件数*/conda=fabs(lamuda_m1/lamuda_s);printf("矩阵A的(谱范数)条件数为:\n cond(A)=%.11e\n", conda); /*求矩阵A的行列式*/fuzhi();double detA=1.0;DLU(c);for(i=0;i<N;i++)detA*=c[2][i];printf("矩阵A的行列式为:\n detA=%.11e\n", detA);}/*建立矩阵A的压缩存储二维数组,并对其赋值*/double fuzhi(){int i;c[0][0]=0;c[0][1]=0;c[1][0]=0;c[3][500]=0;c[4][499]=0;c[4][500]=0;for(i=2;i<N;i++)c[0][i]=-0.064;for(i=1;i<N;i++)c[1][i]=0.16;for(i=1;i<N+1;i++)c[2][i-1]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i); for(i=0;i<N-1;i++)c[3][i]=0.16;for(i=0;i<N-2;i++)c[4][i]=-0.064;return (c[5][N]);}/*求最大值*/int max(int a,int b){if(a>b) return a;else return b;}/*求最小值*/int min(int a,int b){if(a<b) return a;else return b;}/*向量乘以向量*/double xiangliangji(double G[N],double H[N]) {int i;double sum;sum=0;for(i=0;i<N;i++)sum+=G[i]*H[i];return sum;}/*向量除数*/void xlcs (double G[N],double yita){int i;for(i=0;i<N;i++)Y[i]=G[i]/yita;}/*矩阵乘向量*/void juchengxiang(double c[N][N],double G[N])int i,j;double m;for(i=0;i<N;i++)U[i]=0;for(i=0;i<N;i++){m=max(0,i-2);for(j=min(i+2,N-1);j>=m;j--)U[i]+=c[i+2-j][j]*G[j];}}/*矩阵的主对角线元素平移*/ double pingyi(double C[5][N],double b) {int i;for(i=0;i<N;i++)C[2][i]=C[2][i]-b;return C[5][N];}/*幂法求按模最大特征值*/double mifa(double c[5][N])int i,q;double sum,yita,beita,beita1,cancha; beita=0;for(i=0;i<N;i++)U[i]=1;for (q=1;;q++){beita1=beita;sum= xiangliangji(U,U);yita=sqrt(sum);xlcs (U,yita);juchengxiang (c,Y);beita=xiangliangji(Y,U);cancha=fabs((beita1-beita)/beita); if (cancha<EMS) break;}return beita;}/*矩阵的Doolittle分解*/void DLU(double C[5][N]){ int k,i,j,t;int m,l;for(k=0;k<N;k++){m=min(k+2,N-1);for(j=k;j<=m;j++){double sum=0;l=max(max(0,k-2),j-2);for(t=l;t<=k-1;t++)sum+=C[k-t+2][t]*C[t-j+2][j];C[k-j+2][j]=C[k-j+2][j]-sum;}if(k<N-1){m=min(k+2,N-1);for(i=k+1;i<=m;i++){double sum=0;l=max(max(0,i-2),k-2);for(t=l;t<=k-1;t++)sum+=C[i-t+2][t]*C[t-k+2][k];C[i-k+2][k]=(C[i-k+2][k]-sum)/C[2][k];}}}}/*反幂法求按模最小特征值*/double fmifa(double c[5][N],double b){int i,q;int m,t,p;double sum,yita,beita,beita1,cancha,lamuda;double G[N];beita=0;for(i=0;i<N;i++) /*设置初始向量U0*/{U[i]=1;}for (q=1;;q++){beita1=beita;sum=xiangliangji (U,U);yita=sqrt(sum);xlcs (U,yita);fuzhi();pingyi(c,b);DLU(c);for(i=0;i<N;i++)G[i]=Y[i];for(i=1;i<N;i++){double sum=0;m=max(0,i-2);for(t=m;t<=i-1;t++)sum+=c[i-t+2][t]*G[t];G[i]=G[i]-sum;}U[N-1]=G[N-1]/c[2][N-1]; for(i=N-2;i>=0;i--){double sum=0;p=min(i+2,N-1);for(t=i+1;t<=p;t++)sum+=c[i-t+2][t]*U[t];U[i]=(G[i]-sum)/c[2][i]; }beita=xiangliangji(Y,U);lamuda=1/beita+b;cancha=fabs((beita1-beita)/beita);if (cancha<1.0e-12) break;}printf("迭代次数%d\n",q);return lamuda;}三、计算结果矩阵的最大特征值为:lamuda_501=9.72463409878e+000矩阵的最小特征值为:lamuda_1=-1.07001136150e+001迭代次数70, 矩阵的按模最小特征值为:lamuda_s=-5.55791079423e-003与uk最接近的特征值如下:迭代次数7, u[ 1]=-1.01894949222e+001lamuda_1=-1.01829340331e+001 迭代次数226, u[ 2]=-9.67887622933e+000lamuda_ 2=-9.58570742507e+000迭代次数7, u[ 3]=-9.16825753648e+000lamuda_ 3=-9.17267242393e+000迭代次数8, u[ 4]=-8.65763884364e+000lamuda_ 4=-8.65228400790e+000迭代次数118, u[ 5]=-8.14702015079e+000lamuda_ 5=-8.0934*******e+000迭代次数16, u[ 6]=-7.63640145795e+000lamuda_ 6=-7.65940540769e+000迭代次数15, u[ 7]=-7.12578276510e+000lamuda_ 7=-7.11968464869e+000迭代次数19, u[ 8]=-6.61516407226e+000lamuda_ 8=-6.61176433940e+000迭代次数28, u[ 9]=-6.10454537941e+000lamuda_ 9=-6.0661*******e+000迭代次数21, u[10]=-5.59392668657e+000lamuda_10=-5.58510105263e+000lamuda_11=-5.11408352981e+000迭代次数13, u[12]=-4.57268930088e+000 lamuda_12=-4.57887217687e+000迭代次数290, u[13]=-4.06207060803e+000 lamuda_13=-4.09647092626e+000迭代次数13, u[14]=-3.55145191519e+000 lamuda_14=-3.55421121575e+000迭代次数6, u[15]=-3.04083322234e+000 lamuda_15=-3.0410*******e+000迭代次数1606, u[16]=-2.53021452950e+000 lamuda_16=-2.53397031113e+000迭代次数72, u[17]=-2.01959583665e+000 lamuda_17=-2.00323076956e+000迭代次数19, u[18]=-1.50897714381e+000 lamuda_18=-1.50355761123e+000迭代次数17, u[19]=-9.98358450965e-001 lamuda_19=-9.93558606008e-001迭代次数11, u[20]=-4.87739758120e-001 lamuda_20=-4.87042673885e-001迭代次数10, u[21]=2.28789347246e-002 lamuda_21=2.23173624957e-002迭代次数13, u[22]=5.33497627570e-001 lamuda_22=5.32417474207e-001迭代次数15, u[23]=1.04411632041e+000 lamuda_23=1.05289896269e+000迭代次数29, u[24]=1.55473501326e+000 lamuda_24=1.58944588188e+000迭代次数81, u[25]=2.06535370610e+000 lamuda_25=2.06033046027e+000迭代次数40, u[26]=2.57597239895e+000 lamuda_26=2.55807559707e+000迭代次数13, u[27]=3.08659109179e+000 lamuda_27=3.08024050931e+000迭代次数23, u[28]=3.59720978464e+000 lamuda_28=3.61362086769e+000迭代次数16, u[29]=4.10782847748e+000 lamuda_29=4.0913*******e+000迭代次数23, u[30]=4.61844717033e+000 lamuda_30=4.60303537828e+000迭代次数12, u[31]=5.12906586317e+000 lamuda_31=5.132********e+000迭代次数30, u[32]=5.63968455602e+000 lamuda_32=5.59490634808e+000lamuda_33=6.08093385703e+000迭代次数18, u[34]=6.66092194171e+000lamuda_34=6.68035409211e+000迭代次数74, u[35]=7.17154063455e+000lamuda_35=7.29387744813e+000迭代次数30, u[36]=7.68215932740e+000lamuda_36=7.71711171424e+000迭代次数11, u[37]=8.19277802024e+000lamuda_37=8.22522001405e+000迭代次数38, u[38]=8.70339671309e+000lamuda_38=8.64866606519e+000迭代次数10, u[39]=9.21401540593e+000lamuda_39=9.25420034458e+000矩阵A的(谱范数)条件数为:cond(A)=1.92520427390e+003矩阵A的行列式为:detA=2.77278614175e+118四、讨论迭代初始向量的选取对于计算结果的影响:1.影响迭代速度。
北航数值分析第一次大作业

一、算法的设计方案:(一)各所求值得计算方法1、最大特征值λ501,最小特征值λ1,按模最小特征值λs的计算方法首先使用一次幂法运算可以得到矩阵的按模最大的特征值λ,λ必为矩阵A的最大或最小特征值,先不做判断。
对原矩阵A进行一次移项,即(A-λI),在进行一次幂法运算,可以得到另一个按模最大特征值λ0。
比较λ和λ的大小,较大的即为λ501,较小的即为λ1。
对矩阵A进行一次反幂法运算,即可得到按模最小特征值λs。
2、A与μk 值最接近的特征值λik的计算方法首先计算出k所对应的μk 值,对原矩阵A进行一次移项,即(A-μkI),得到一个新的矩阵,对新矩阵进行一次反幂法运算,即可得到一个按模最小特征值λi 。
则原矩阵A与μk值最接近的特征值λik=λi+μk。
3、A的(谱范数)条件数cond(A)2的计算方法其中错误!未找到引用源。
矩阵A的按模最大和按模最小特征值。
(二)程序编写思路。
由于算法要求A的零元素不存储,矩阵A本身为带状矩阵,所以本题的赋值,LU分解,反幂法运算过程中,均应采用Doolittle分解法求解带状线性方程组的算法思路。
幂法、反幂法和LU分解均是多次使用,应编写子程序进行反复调用。
二、源程序:#include<stdio.h>#include<iostream>#include<stdlib.h>#include<math.h>#include<float.h>#include<iomanip> /*头文件*//*定义全局变量*/#define N 502 /*取N为502,可实现从1到501的存储,省去角标变换的麻烦*/ #define epsilon 1.0e-12 /*定义精度*/#define r 2 /*r,s为带状矩阵的半带宽,本题所给矩阵二者都是2*/ #define s 2double c[6][N]; /*定义矩阵存储压缩后的带状矩阵*/double fuzhi(); /*赋值函数*/void LUfenjie(); /*LU分解程序*/int max(int a,int b); /*求两个数字中较大值*/int min(int a,int b); /*求两个数字中较小值*/double mifa(); /*幂法计算程序*/double fanmifa(); /*反幂法计算程序*/double fuzhi() /*赋值程序,按行赋值,行从1到5,列从1到501,存储空间的第一行第一列不使用,角标可以与矩阵一一对应,方便书写程序*/{int i,j;i=1;for(j=3;j<N;j++){c[i][j]=-0.064;}i=2;for(j=2;j<N;j++){c[i][j]=0.16;}i=3;for(j=1;j<N;j++){c[i][j]=(1.64-0.024*j)*sin(0.2*j)-0.64*exp(0.1/j);}i=4;for(j=1;j<N-1;j++){c[i][j]=0.16;}i=5;for(j=1;j<N-2;j++){c[i][j]=-0.064;}return(c[i][j]);}int max(int a,int b){ return((a>b)?a:b);}int min(int a,int b){ return((a<b)?a:b);}void LUfenjie() /*LU分解程序,采用的是带状矩阵压缩存储后的LU分解法*/{double temp;int i,j,k,t;for(k=1;k<N;k++){ for(j=k;j<=min(k+s,N-1);j++){temp=0;for(t=max(1,max(k-r,j-s));t<=(k-1);t++){temp=temp+c[k-t+s+1][t]*c[t-j+s+1][j];}c[k-j+s+1][j]=c[k-j+s+1][j]-temp;}for(i=k+1;i<=min(k+r,N-1);i++){temp=0;for(t=max(1,max(i-r,k-s));t<=(k-1);t++){temp=temp+c[i-t+s+1][t]*c[t-k+s+1][k];}c[i-k+s+1][k]=(c[i-k+s+1][k]-temp)/c[s+1][k];}}}double mifa() /*幂法计算程序*/ {double u0[N],u1[N];double temp,Lu,beta=0,beta0;int i,j;for(i=1;i<N;i++) /*选取迭代初始向量*/{u0[i]=1;}do{beta0=beta;temp=0;for(i=1;i<N;i++){temp=temp+u0[i]*u0[i]; }Lu=sqrt(temp);for(i=1;i<N;i++){u1[i]=u0[i]/Lu;}for(i=1;i<N;i++){temp=0;for(j=max(i-1,1);j<=min(i+2,N-1);j++){temp=temp+c[i-j+s+1][j]*u1[j]; }u0[i]=temp;} //新的u0temp=0;for(i=1;i<N;i++){temp=temp+u1[i]*u0[i]; }beta=temp;}while(fabs(beta-beta0)/fabs(beta)>=epsilon); /*迭代运行条件判断*/return(beta);}double fanmifa() /*反幂法计算程序*/{double u0[N],u1[N],u2[N];double temp,Lu,beta=0,beta0;int i,t;for(i=1;i<N;i++) /*选取迭代初始向量*/{u0[i]=1;}do{beta0=beta;temp=0;for(i=1;i<N;i++){temp=temp+u0[i]*u0[i]; }Lu=sqrt(temp);for(i=1;i<N;i++){u1[i]=u0[i]/Lu;u2[i]=u1[i];}fuzhi();LUfenjie();/*带状矩阵压缩存储并进行LU分解后,求解线性方程组得到迭代向量u k,即程序中的u0*/for(i=2;i<N;i++){ temp=0;for(t=max(1,i-r);t<=(i-1);t++){temp=temp+c[i-t+s+1][t]*u2[t];}u2[i]=u2[i]-temp;}u0[N-1]=u2[N-1]/c[s+1][N-1];for(i=N-2;i>=1;i--){ temp=0;for(t=i+1;t<=min(i+s,N-1);t++){temp=temp+c[i-t+s+1][t]*u0[t];}u0[i]=(u2[i]-temp)/c[s+1][i];}temp=0;for(i=1;i<N;i++){temp=temp+u1[i]*u0[i]; }beta=temp;beta=1/beta; /*beta即为所求特征值,可直接返回*/}while(fabs(beta-beta0)/fabs(beta)>=epsilon); /*迭代运行条件判断*/return(beta);}void main(){double u[40]; /*定义数组,存放k值运算得到的μk值*/double lambda1,lambda501,lambdak,a,b,d,cond,det;int i,j,k;fuzhi();a=mifa(); /*幂法计算按模最大值*/fuzhi();d=fanmifa(); /*反幂法计算按模最小值*/fuzhi();for(j=1;j<N;j++){c[3][j]=c[3][j]-a;}b=mifa()+a; /*移项后幂法计算按模最大值*/if(a>b) /*比较两个按模最大值大小,并相应输出最大特征值λ501和最小特征值λ1*/ {lambda1=b;lambda501=a;printf("矩阵A最小的特征值lambda1=%13.11e\n",lambda1);printf("矩阵A最大的特征值lambda501=%13.11e\n",lambda501);}else{lambda1=a;lambda501=b;printf("矩阵A最小的特征值lambda1=%13.11e\n",lambda1);printf("矩阵A最大的特征值lambda501=%13.11e\n",lambda501);}printf("矩阵A按模最小特征值lambdas=%13.11e\n",d); /*输出按模最小特征值λs*/for(k=1;k<40;k++) /*对每一个进行移项反幂法运算,求出最接近μk的特征值并输出*/ {u[k]=(lambda501-lambda1)*k/40+lambda1;fuzhi();for(j=1;j<N;j++){c[3][j]=c[3][j]-u[k];}lambdak=fanmifa()+u[k];i=k;printf("矩阵A最接近uk特征值lambdak%d=%13.11e\n",i,lambdak);}cond=fabs(a/d);printf("A的条件数=%13.11e\n",cond); /*计算A条件数并输出*/fuzhi(); /*计算A的行列式值并输出*/LUfenjie();det=1;for(i=1;i<N;i++){det=det*c[3][i];}printf("行列式的值detA=%13.11e\n",det);}三、程序的运行结果:四、初始向量的选取对计算结果的影响:(一)选取形式不变,数值变换1、取u0为[0.5,0.5………..0.5],运行结果如下:2、取u0为[50,50………..50],运行结果如下:从运行结果来看,此类初始向量的选取对结果不会产生影响,即使选成0,结果也不变化。
北航硕士研究生数值分析大作业一

数值分析—计算实习作业一学院:17系专业:精密仪器及机械姓名:张大军学号:DY14171142014-11-11数值分析计算实现第一题报告一、算法方案算法方案如图1所示。
(此算法设计实现完全由本人独立完成)图1算法方案流程图二、全部源程序全部源程序如下所示#include <iostream.h>#include <iomanip.h>#include <math.h>int main(){double a[501];double vv[5][501];double d=0;double r[3];double uu;int i,k;double mifayunsuan(double *a,double weiyi);double fanmifayunsuan(double *a,double weiyi);void yasuo(double *A,double (*C)[501]);void LUfenjie(double (*C)[501]);//赋值语句for(i=1;i<=501;i++){a[i-1]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i);}//程序一:使用幂方法求绝对值最大的特征值r[0]=mifayunsuan(a,d);//程序二:使用幂方法求求平移λ[0]后绝对值最大的λ,得到原矩阵中与最大特征值相距最远的特征值d=r[0];r[1]=mifayunsuan(a,d);//比较λ与λ-λ[0]的大小,由已知得if(r[0]>r[1]){d=r[0];r[0]=r[1];r[1]=d;}//程序三:使用反幂法求λr[2]=fanmifayunsuan(a,0);cout<<setiosflags(ios::right);cout<<"λ["<<1<<"]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[0]<<endl;cout<<"λ["<<501<<"]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[1]<<endl;cout<<"λ[s]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[2]<<endl;//程序四:求A的与数u最接近的特征值for(k=1;k<40;k++){uu=r[0]+k*(r[1]-r[0])/40;cout<<"最接近u["<<k<<"]"<<"的特征值为"<<setiosflags(ios::scientific)<<setprecision(12)<<fanmifayunsuan(a,uu)<<endl;}//程序五:谱范数的条件数是绝对值最大的特征值除以绝对值最小的特征值的绝对值cout<<"cond(A)2="<<fabs(r[0]/r[2])<<endl;//程序六:A的行列式的值就是A分解成LU之U的对角线的乘积yasuo(a,vv);LUfenjie(vv);uu=1;for(i=0;i<501;i++){uu=uu*vv[2][i];}cout<<"Det(A)="<<uu<<endl;return 1;}double mifayunsuan(double *a,double weiyi){int i,k;double b=0.16;double c=-0.064;double ee,w,v1,v2,mm,sum;double u[501];double y[505]={0};for(i=0;i<501;i++)u[i]=1;//给u赋初值if (weiyi!=0){for (i=0;i<501;i++)a[i]-=weiyi;}ee=1;k=0;//使得初始计算时进入循环语句while(ee>1e-12){mm=0;for(i=0;i<501;i++){mm=mm+u[i]*u[i];}w=sqrt(mm);for(i=0;i<501;i++){y[i+2]=u[i]/w;//注意此处编程与书上不同,之后会解释它的巧妙之处1 }for(i=0;i<501;i++){u[i]=c*y[i]+b*y[i+1]+a[i]*y[i+2]+b*y[i+3]+c*y[i+4];//1显然巧妙之处凸显出来}sum=0;for(i=0;i<501;i++){sum+=y[i+2]*u[i];}v1=v2;v2=sum;//去除特殊情况,减少漏洞if(k==0){k++;}else{ee=fabs(v2-v1)/fabs(v2);}}if (weiyi!=0){for (i=0;i<501;i++)a[i]+=weiyi;}//还原A矩阵return (v2+weiyi);}double fanmifayunsuan(double *a,double weiyi){int i,k;double b=0.16;double c=-0.064;double ee,w,v1,v2,mm,sum;double u[501];double y[501];double C[5][501];void yasuo(double *A,double (*C)[501]);void LUfenjie(double (*C)[501]);void qiuU(double (*C)[501],double *y,double *u);//把A阵压缩到C阵中for(i=0;i<501;i++)u[i]=1;//给u赋初值if (weiyi!=0){for (i=0;i<501;i++)a[i]-=weiyi;}yasuo(a,C);LUfenjie(C);ee=1;k=0; //使得初始计算时进入循环语句while(ee>1e-12){mm=0;for(i=0;i<501;i++){mm=mm+u[i]*u[i];}w=sqrt(mm);for(i=0;i<501;i++){y[i]=u[i]/w;}qiuU(C,y,u);sum=0;for(i=0;i<501;i++){sum+=y[i]*u[i];}v1=v2;v2=sum;//去除特殊情况,减少漏洞if(k==0){k++;}else{ee=fabs(1/v2-1/v1)/fabs(1/v2);}}if (weiyi!=0){for (i=0;i<501;i++)a[i]+=weiyi;}//还原A矩阵return (1/v2+weiyi);}void yasuo(double *A,double (*C)[501]){double b=0.16;double c=-0.064;int i;for(i=0;i<501;i++){C[0][i]=c;C[1][i]=b;C[2][i]=A[i];C[3][i]=b;C[4][i]=c;}}void LUfenjie(double (*C)[501]){int k,t,j;int r=2,s=2;double sum;int minn(int ,int );int maxx(int ,int );for(k=0;k<501;k++){for(j=k;j<=minn(k+s,501-1);j++){if(k==0)sum=0;else{sum=0;for(t=maxx(k-r,j-s);t<k;t++){sum=sum+C[k-t+s][t]*C[t-j+s][j];}}C[k-j+s][j]=C[k-j+s][j]-sum;}for(j=k+1;j<=minn(k+r,501-1);j++){if(k<501-1){if(k==0)sum=0;else{sum=0;for(t=maxx(j-r,k-s);t<k;t++){sum=sum+C[j-t+s][t]*C[t-k+s][k];}}C[j-k+s][k]=(C[j-k+s][k]-sum)/C[s][k];}}}}void qiuU(double (*C)[501],double *y,double *u){int i,t;double b[501];double sum;int r=2,s=2;int minn(int ,int );int maxx(int ,int );for(i=0;i<501;i++){b[i]=y[i];}for(i=1;i<501;i++){sum=0;for(t=maxx(0,i-r);t<i;t++){sum=sum+C[i-t+s][t]*b[t];}b[i]=b[i]-sum;}u[500]=b[500]/C[s][500];for(i=501-2;i>=0;i--){sum=0;for(t=i+1;t<=minn(i+s,500);t++){sum=sum+C[i-t+s][t]*u[t];}u[i]=(b[i]-sum)/C[s][i];}}int minn(int x,int y){int min;if(x>y)min=y;elsemin=x;return min;}int maxx(int b,int c){int max;if(b>c){if(b>0)max=b;elsemax=0;}else{if(c>0)max=c;elsemax=0;}return max;}三、特征值以及的值λ[1]=-1.070011361502e+001 λ[501]=9.724634098777e+000λ[s]=-5.557910794230e-003最接近u[1]的特征值为-1.018293403315e+001最接近u[2]的特征值为-9.585707425068e+000最接近u[3]的特征值为-9.172672423928e+000最接近u[4]的特征值为-8.652284007898e+000最接近u[5]的特征值为-8.0934********e+000最接近u[6]的特征值为-7.659405407692e+000最接近u[7]的特征值为-7.119684648691e+000最接近u[8]的特征值为-6.611764339397e+000最接近u[9]的特征值为-6.0661********e+000最接近u[10]的特征值为-5.585101052628e+000最接近u[11]的特征值为-5.114083529812e+000最接近u[12]的特征值为-4.578872176865e+000最接近u[13]的特征值为-4.096470926260e+000最接近u[14]的特征值为-3.554211215751e+000最接近u[15]的特征值为-3.0410********e+000最接近u[16]的特征值为-2.533970311130e+000最接近u[17]的特征值为-2.003230769563e+000最接近u[18]的特征值为-1.503557611227e+000最接近u[19]的特征值为-9.935586060075e-001最接近u[20]的特征值为-4.870426738850e-001最接近u[21]的特征值为2.231736249575e-002最接近u[22]的特征值为5.324174742069e-001最接近u[23]的特征值为1.052898962693e+000最接近u[24]的特征值为1.589445881881e+000最接近u[25]的特征值为2.060330460274e+000最接近u[26]的特征值为2.558075597073e+000最接近u[27]的特征值为3.080240509307e+000最接近u[28]的特征值为3.613620867692e+000最接近u[29]的特征值为4.0913********e+000最接近u[30]的特征值为4.603035378279e+000最接近u[31]的特征值为5.132924283898e+000最接近u[32]的特征值为5.594906348083e+000最接近u[33]的特征值为6.080933857027e+000最接近u[34]的特征值为6.680354092112e+000最接近u[35]的特征值为7.293877448127e+000最接近u[36]的特征值为7.717111714236e+000最接近u[37]的特征值为8.225220014050e+000最接近u[38]的特征值为8.648666065193e+000最接近u[39]的特征值为9.254200344575e+000cond(A)2=1.925204273902e+003 Det(A)=2.772786141752e+118四、现象讨论在大作业的程序设计过程当中,初始向量的赋值我顺其自然的设为第一个分量为1,其它分量为0的向量,计算结果与参考答案存在很大差别,计算结果对比如下图2所示(左侧为正确结果,右侧为错误结果),导致了我花了很多的时间去检查程序算法。
北航数值分析大作业计算程序(一)

if(x>y)
return x;
return y;
}
int min(int x,int y)
{
if(x<y)
return x;
return y;
}
//向量内积函数
double innvector(double x[],double y[],int t)
{
//主函数
void main()
{ double C[m][n]={{0},{0},{0},{0},{0}};
int i,j,k;
double t1,t2,p,q,z1,z2,z3,cond,det;
double u[n];
double w[n];
double v[n]={0,0};
{
//迭代向量赋值
for(j=0;j<=n-1;j++)
{u[j]=1;}
for(i=0;i<=m-1;i++)
{for(j=0;j<=n-1;j++)
{C[i][j]=0;}
}
for(j=2;j<=n-1;j++)
{C[0][j]=-0.064;}
if(d<0)
d=-d;
if(d>r)
b=t;
else
goto P1;
}
P1:if(k<L)
return t;
else return NU NhomakorabeaL; }
//线性方程求解函数
void linequation(double C[][n],double x[],double b[])
北航数值分析B第一次上机作业算法作业

数值分析第一次上机作业 一、算法方案设计 (1)存储矩阵A (参考课本25页):矩阵A 501×501为大型带状矩阵,上半带宽S=2,下半带宽R=2,参照课本,可将其用循环语句存储在一个5行501列的二维数组A[5][501]中,使得矩阵A 的第j 列存放数组A 的第j 列带状元素,并使得矩阵的主对角元素存放在数组的第三行。
检索矩阵的元素时只要按照公式:a ij =数组a[i-j+3][j]即可。
(2)求λ1,λ501,λs :第一步,用幂法求出矩阵A 按模最大特征值,再对其判断正负,如果是正数,则该特征值为λ501,如果是负数,则该特征值为λ1。
幂法实现过程具体为:第二步,用反幂法求矩阵A 按模最小特征向量λS 。
班级:ZY16131 学号:ZY16131姓名:第三步,由于λ1≤λ2≤…..≤λ501,可采用原点平移法对矩阵A平移λ1,得到矩阵(-λ1I+A),记为矩阵B,再用用幂法求出B的模最大特征值λB,则λ501=λB+λ1。
(3)距离μk最近的特征值:还是用原点平移法,将矩阵A平移μk个单位,再用反幂法求出平移后矩阵模最小特征值ηk,矩阵A与μk最接近的特征值为:λi k = ηk + μk =ηk +(4)A的谱范数条件数与detA:a、求矩阵A的行列式值:在用反幂法时需要对矩阵A进行Doolittle三角分解,A=LU,根据det(A)=det (LU)=det(L)*det(U),其中det(L)=1,det(A)即为U矩阵的对角线元素的乘积。
b、求A的(谱范数)条件数cond(A)2:由于A是非奇异实对称阵,从而cond(A)2 =∣λ1∣/∣λs∣。
二、运行结果分析(1)取初始向量为 u_0[501]={1,1…1},计算结果截图如下:(2)讨论初始迭代向量取值对计算结果的影响在编程实现算法的过程中遇到了很多问题,多次尝试才得以解决。
例如,对各个函数的定义后需要对矩阵A进行初始化;为简化程序,方便改变变量值,应该尽可能地将某些多级变量写成函数的形式,只需要对初级变量赋值即可。
北航数值分析第一次大作业(幂法反幂法)

一、问题分析及算法描述1. 问题的提出:(1)用幂法、反幂法求矩阵A =[a ij ]20×20的按摸最大和最小特征值,并求出相应的特征向量。
其中 a ij ={sin (0.5i +0.2j ) i ≠j 1.5cos (i +1.2j ) i =j要求:迭代精度达到10−12。
(2)用带双步位移的QR 法求上述的全部特征值,并求出每一个实特征值相应的特征向量。
2. 算法的描述:(1) 幂法幂法主要用于计算矩阵的按摸为最大的特征值和相应的特征向量。
其迭代格式为:{ 任取非零向量u 0=(h 1(0),⋯,h n (0))T|h r (k−1)|=max 1≤j≤n |h r (k−1)| y ⃑ k−1=u ⃑ k−1|h r (k−1)| u ⃑ k =Ay ⃑ k−1=(h 1(k ),⋯,h n (k ))T βk =sgn (h r (k−1))h r (k ) (k =1,2,⋯) 终止迭代的控制选用≤ε。
幂法的使用条件为n ×n 实矩阵A 具有n 个线性无关的特征向量x 1,x 2,⋯,x n ,其相应的特征值λ1,λ2,⋯,λn 满足不等式|λ1|>|λ2|≥|λ3|≥⋯≥|λn |或λ1=λ2=⋯=λm|λ1|>|λm+1|≥|λm+2|≥⋯≥|λn |幂法收敛速度与比值|λ2λ1|或|λm+1λ1|有关,比值越小,收敛速度越快。
(2) 反幂法反幂法用于计算n ×n 实矩阵A 按摸最小的特征值,其迭代格式为:{任取非零向量u 0∈R nηk−1=√u ⃑ k−1T u ⃑ k−1 y ⃑ k−1=u ⃑ k−1ηk−1⁄ Au ⃑ k =y ⃑ k−1 βk =y ⃑ k−1u ⃑ k (k =1,2,⋯) 每迭代一次都要求解一次线性方程组Au ⃑ k =y ⃑ k−1。
当k 足够大时,λn ≈1βk ,y ⃑ k−1可近似的作为矩阵A 的属于λn 的特征向量。
北航研究生 算法设计与分析大作业一
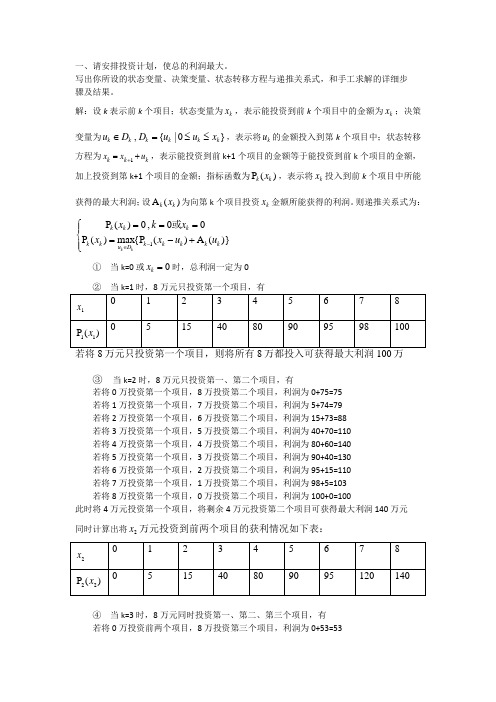
一、请安排投资计划,使总的利润最大。
写出你所设的状态变量、决策变量、状态转移方程与递推关系式,和手工求解的详细步 骤及结果。
解:设k 表示前k 个项目;状态变量为k x ,表示能投资到前k 个项目中的金额为k x ;决策变量为}0|{ , k k k k k k x u u D D u ≤≤=∈,表示将k u 的金额投入到第k 个项目中;状态转移方程为k k k u x x +=+1,表示能投资到前k+1个项目的金额等于能投资到前k 个项目的金额,加上投资到第k+1个项目的金额;指标函数为)(P k k x ,表示将k x 投入到前k 个项目中所能获得的最大利润;设)(A k k x 为向第k 个项目投资k x 金额所能获得的利润。
则递推关系式为:⎪⎩⎪⎨⎧+-====-∈)}(A )({P max )(P 00 , 0)(P 1k k k k k D u kk k k k u u x x x k x k k 或① 当k=0或0=k x 时,总利润一定为0③ 当k=2时,8万元只投资第一、第二个项目,有若将0万投资第一个项目,8万投资第二个项目,利润为0+75=75若将1万投资第一个项目,7万投资第二个项目,利润为5+74=79 若将2万投资第一个项目,6万投资第二个项目,利润为15+73=88 若将3万投资第一个项目,5万投资第二个项目,利润为40+70=110 若将4万投资第一个项目,4万投资第二个项目,利润为80+60=140 若将5万投资第一个项目,3万投资第二个项目,利润为90+40=130 若将6万投资第一个项目,2万投资第二个项目,利润为95+15=110 若将7万投资第一个项目,1万投资第二个项目,利润为98+5=103 若将8万投资第一个项目,0万投资第二个项目,利润为100+0=100此时将4万元投资第一个项目,将剩余4万元投资第二个项目可获得最大利润140万元 同时计算出将2x 万元投资到前两个项目的获利情况如下表:④ 当k=3时,8万元同时投资第一、第二、第三个项目,有 若将0万投资前两个项目,8万投资第三个项目,利润为0+53=53若将1万投资前两个项目,7万投资第三个项目,利润为5+52=57若将2万投资前两个项目,6万投资第三个项目,利润为15+51=66若将3万投资前两个项目,5万投资第三个项目,利润为40+50=90若将4万投资前两个项目,4万投资第三个项目,利润为80+45=125若将5万投资前两个项目,3万投资第三个项目,利润为90+40=130若将6万投资前两个项目,2万投资第三个项目,利润为95+26=121若将7万投资前两个项目,1万投资第三个项目,利润为120+4=124若将8万投资前两个项目,0万投资第三个项目,利润为140+0=140此时将4万元投资第一个项目,将剩余4万元投资第二个项目,第三个项目投资0元,可获得最大利润140万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值分析大作业一、算法设计方案1、矩阵初始化矩阵[]501501⨯=ij a A 的下半带宽r=2,上半带宽s=2,设置矩阵[][]5011++s r C ,在矩阵C 中检索矩阵A 中的带内元素ij a 的方法是:j s j i ij c a ,1++-=。
这样所需要的存储单元数大大减少,从而极大提高了运算效率。
2、利用幂法求出5011λλ,幂法迭代格式:0111111nk k k k kk T k k k u R y u u Ay y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止。
首先对于矩阵A 利用幂法迭代求出一个λ,然后求出矩阵B ,其中I A B λ-=(I 为单位矩阵),对矩阵B 进行幂法迭代,求出λ',之后令λλλ+'='',比较的大小与λλ'',大者为501λ,小者为1λ。
3、利用反幂法求出ik s λλ,反幂法迭代格式:0111111nk k k k kk T k k k u R y u Au y y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止,1s k λβ=。
每迭代一次都要求解一次线性方程组1-=k k y Au ,求解过程为:(1)作分解LU A =对于n k ,...,2,1=执行[][]s k n r k k k i c c c c c n s k k k j c cc c k s ks k t k s k r i t t s t i k s k i k s k i js j t k s j r k t t s t k j s j k j s j k <+++=-=++=-=+++----=++-++-++-++----=++-++-++-∑∑);,min(,...,2,1/)(:),min(,...,1,:,1,11),,1max(,1,1,1,11),,1max(,1,1,1(2)求解y Ux b Ly ==,(数组b 先是存放原方程组右端向量,后来存放中间向量y))1,...,2,1(/)(:/:),...,3,2(:,1),min(1.1.11),1max(,1--=-===-=+++-++-+--=++-∑∑n n i c x c b x c b x n i b c b b i s t n s i i t t s t i i i ns n n ti r i t t s t i i i使用反幂法,直接可以求得矩阵按模最小的特征值s λ。
求与数)39,...,2,1(4015011=-+=k k k λλλμ最接近的特征值ik λ,对矩阵IA k μ-实行反幂法,即可求出对应的k k ik k k μλλβλ+==,/1。
4、求出A 的条件数和行列式根据max 2()scond A λλ=,其中分子分母分别对应按模最大和最小的特征值。
det()A 的计算:由于A LU =,其中L 为下三角矩阵,且对角线元素为1,故det()1L =,所以有A LU U ==,又U 为上三角矩阵,故det()U 为对其对角线上各元素的乘积,最后可得det()det()A U =。
二、程序源代码(1)定义所需要的函数:#include <stdio.h>#include <conio.h>#include <math.h>#define N 501#define R 2#define S 2int min(int a,int b); // 求最小值int max(int a,int b,int c); // 求最大值double Fan_two(double x[N]);//计算二范数void FenjieLU(double (*C)[N]);//解线性方程组的LU分解过程void Solve(double (*C)[N], double *b,double *x);//解线性方程组的求解过程double PowerMethod(double C[][N],double u[N],double y[N],double bta,double D);//幂法double InversePowerMethod(double C[][N],double u[N],double y[N],double bta,double D);//反幂法};(2)程序的主函数,Main.cpp代码如下:void main(){double C[R+S+1][N];double u[N];double y[N];double miu[39];double C1[R+S+1][N];double bta = 1.0;double Namda1,Namda501,NamdaS;double Namda[39];double CondA2;double detA = 1.0;double D = 1.0e-12;int i, j, k;FILE * fp;fp = fopen("Namda.txt","w");//对数组进行初始化//int i, j;for (i = 0; i < N; i++){u[i] = 1;}for (i = 0;i< R + S + 1;i++){for (j = 0;j< N;j++){if (i==0||i==4){C[i][j]=-0.064;}else if (i==1||i==3){C[i][j]=0.16;}else if (i==2){C[i][j]=(1.64-0.024*(j+1))*sin(0.2*(j+1))-0.64*exp(0.1/(j+1));}}}//幂法求Namda1//Namda1 = PowerMethod(C, u, y, bta, D);printf("\n================================================\n"); printf("Namda1 = %12.11e", Namda1);printf("\n================================================\n"); //幂法求Namda501//bta = 1.0;for (i = 0; i < R + S + 1; i++){for (j = 0; j < N; j++){if (i == 2)C1[i][j] = C[i][j] -Namda1;elseC1[i][j] = C[i][j];}}Namda501 = algorism.PowerMethod(C1, u, y, bta, D) +Namda1;printf("\n================================================\n"); printf("Namda501 = %12.11e", Namda501);printf("\n================================================\n"); //反幂法求NamdaS//bta = 1.0;NamdaS = InversePowerMethod(C, u, y, bta, D);printf("\n================================================\n");printf("NamdaS = %12.11e", NamdaS);printf("\n================================================\n");//反幂法求Namda[k]//printf("\n================================================\n");for (k = 0; k < 39; k++){miu[k] = Namda1 + (k + 1) * (Namda501 - Namda1) / 40.0;bta = 1.0;for (i = 0; i < R + S + 1; i++){for (j = 0; j < N; j++){if (i == 2)C1[i][j] = C[i][j] - miu[k];elseC1[i][j] = C[i][j];}}Namda[k] = InversePowerMethod(C1, u, y, bta, D) + miu[k];fprintf(fp,"与%12.11e最接近的特征值为:%12.11e\n",miu[k],Namda[k]);}printf("求与miu[k]最接近的Namda[k]的计算结果已经输出到文件Namda.txt 中");printf("\n================================================\n");//求A的谱范数//printf("\n================================================\n");printf("A的谱范数为:%12.11e", sqrt(Namda501));printf("\n================================================\n");//求A的条件数//CondA2 = fabs( Namda1 / NamdaS);printf("\n================================================\n");printf("A的谱范数的条件数Cond(A)2为:%12.11e",CondA2);printf("\n================================================\n");//求det(A)2的值//for (j = 0; j < N; j++)detA *= C[2][j];printf("\n================================================\n");printf("行列式A的值为:%12.11e",detA);printf("\n================================================\n");fclose(fp);_getch();return;}(3)成员函数的实现int min(int a,int b){return a < b ? a : b;}int max(int a,int b,int c){int temp;temp = a > b ? a : b;return temp > c ? temp : c;}double Fan_two(double x[N]){double sum = 0.0;int i;for (i = 0; i < N; i++){sum += pow(x[i],2);}return sqrt(sum);}void FenjieLU(double (*C)[N]){double sum = 0;int i, j, k,t;for (k = 0; k < N; k++){j = k;i = k + 1;while (1){if (j == min(k + S + 1, N))break;for (t = max(0, k - R, j - S); t <= k - 1; t++){sum += C[k-t+S][t] * C[t-j+S][j];}C[k-j+S][j] = C[k-j+S][j] - sum;sum = 0.0;j++;if (k == N-1)break;if (i == min(k + R + 1, N))break;for (t = max(0, i - R,k - S); t <= k - 1; t++){sum += C[i-t+S][t] * C[t-k+S][k];}C[i-k+S][k] = (C[i-k+S][k] - sum) / C[S][k];sum = 0;i++;}}}void Solve(double (*C)[N], double *b,double *x){double sum = 0;int i, t;sum = 0;for (i = 1; i < N; i++){for (t = max(0, i - R); t <= i - 1; t++){sum += C[i-t+S][t] * b[t];}b[i] = b[i] - sum;sum = 0;}x[N-1] = b[N-1] / C[S][N-1];for (i = N - 2; i >= 0; i--){for (t = i+1; t <= min(i + S, N - 1); t++){sum += C[i-t+S][t] * x[t];}x[i] = (b[i] - sum) / C[S][i];sum = 0;}}double PowerMethod(double C[][N],double u[N],double y[N],double bta,double D) {double ita;double sum = 0;double temp = 0.0;int i,j,k = 0;while (fabs(bta - temp) / fabs(bta) > D){temp = bta;ita = Fan_two(u);for (i = 0; i < N; i++){y[i] = u[i] / ita;}for (i = 0; i < N; i++){for (j = max(0,i - R); j < min(i + S + 1,N); j++){sum += C[i - j + S][j] * y[j];}u[i] = sum;sum = 0;}for (i = 0; i < N; i++){sum += y[i] * u[i];}bta = sum;sum = 0;k++;}return bta;}double InversePowerMethod(double C[][N],double u[N],double y[N],double bta,double D){double TC[R+S+1][N];double ty[N];double ita;double sum = 0;double temp = 0.0;int i,j,k = 0;FenjieLU(C);while (abs(1/bta - 1/temp) / abs(1/bta) > D){temp = bta;ita = Fan_two(u);for (i = 0; i < N; i++){y[i] = u[i] / ita;}//用到临时存储数组TC[][]和ty[][]是因为函数Solve执行过程中会改变A[][]和y[][]for (i = 0; i < R + S + 1; i++){for (j = 0; j < N; j++)TC[i][j] = C[i][j];}for (i = 0; i < N; i++)ty[i] = y[i];Solve(C, y, u);for (i = 0; i < R+S+1; i++){for (j = 0; j < N; j++)C[i][j] = TC[i][j];}for (i = 0; i < N; i++)y[i] = ty[i];for (i = 0; i < N; i++){sum += y[i] * u[i];}bta = sum;sum = 0;k++;}bta = 1.0 / bta;return bta;}三、程序运行结果下图为主程序运行结果的结果输出在Namda.txt文件中,结果如下:其中ik四、分析迭代初始向量对计算结果的影响选择不同的初始向量[]u N可能会得到不同的特征值。
