基于MRT-LBM的方腔流动局部加密算法

合集下载

LBM算法原理简介

LBM算法原理
• 求解瞬态问题时，计算时间少，精度高传统方法求解的控制方程对流项是非线性的，每一个时间步都需要迭代收敛。传统软件计算瞬态问题时，给定最大迭代次数，计算并未收敛，最终影响求解精度，而且计算效率低。 LBM算法求解的Lattice-Boltzmann方程对流项是线性的，不存在这方面的问题。采用Powerflow计算瞬态问题，精度高，耗费时间大为减少。
Confidential doc of TS
1 T 2

为运动粘性, T 为温度
Confidential doc of TS
LBM算法原理
• 粒子分布函数 f 满足Lattice Boltzmann方程： 1 fi x ei t , t t fi x, t fi x, t f i eq x, t
Confidential doc of TS
LBM离散方法－2维问题
• D2Q9模型
Confidential doc of TS
LBM离散方法－2维问题
• 平衡分布函数 fi eq
f
eq 0
（根据文献[3]）
4 3 2 1 2 u 9 2c
fi fi
eq
1 3 9 3 2 2 1 2 ei 4 ei 2 u u u 9 c 2c 2c 1 3 9 3 2 2 1 2 ei 4 ei 2 u u u 36 c 2c 2c
Confidential doc of TS
LBM算法原理
• LBM方法将连续介质看作大量位于网格节点上的离散流体质点粒子. 粒子按碰撞和迁移规则在网格上运动,通过对各网格流体质点及运动特征的统计，获得流体宏观运动规律。 • 粒子分布函数f(r,e,t)drde表示在t时刻，在空间r处，粒子的速度在e到e+de的粒子数密度。

lbm 方腔自然对流程序

lbm 方腔自然对流程序自然对流是指在没有外力驱动的情况下，由于温度差异引起的流体运动。

在生活中，我们常常会遇到一些与自然对流有关的现象，比如水壶中的水会因热胀冷缩而产生热气上升的现象，热空气会从窗户朝外流出等等。

而在工程领域，我们需要对自然对流进行深入研究，以便更好地理解和应用这一现象。

为了更准确地模拟和预测自然对流的行为，科学家们开发了许多数学模型和计算方法。

其中，LB（Lattice Boltzmann）方法是一种非常常用的数值计算方法，特别适用于模拟复杂的流体运动。

LB方法将流体看作是由大量微小粒子组成的，通过在空间中构建一个网格来模拟流体的运动。

在这个网格中，每个微小粒子都有一定的速度和密度，并通过碰撞和散射的过程来描述流体的运动。

在研究自然对流的过程中，LB方法可以很好地模拟流体在容器内的温度分布、速度场以及压力场等。

通过调节初始条件和边界条件，我们可以模拟不同温度差异下的自然对流现象。

这对于很多工程问题来说具有非常重要的意义。

比如在建筑物的设计中，我们需要考虑到自然对流的影响，以便优化空调系统的设计，提高能源利用效率。

此外，在电子设备散热和核能工程等领域，自然对流也是一个重要的研究课题。

在实际应用中，LB方法的计算结果与实验结果和其他数值方法的结果进行对比，可以发现其准确性和可靠性。

同时，LB方法还具有较少的计算资源占用和较快的计算速度的优点。

这使得它在工程领域的应用非常广泛。

总之，LB方法是研究自然对流的重要工具之一。

通过模拟自然对流现象，我们可以更好地理解和预测流体的行为，并在工程实践中应用这些知识。

未来，随着计算技术的发展，LB方法还将进一步改进和应用于更多领域，从而促进工程科学的发展。

格子波兹曼方法

格子波兹曼方法
格子波兹曼方法（Lattice Boltzmann Method, LBM）是一种广泛应用于计算流
体力学领域的数值方法。

它基于分子动力学模型，通过离散化空间网格和时间步长来模拟复杂的流体流动问题。

格子波兹曼方法通过将流体宏观物理量离散化到网格上的节点，使用分布函数
描述流体粒子的运动。

流体粒子在相邻节点之间以一种特定的方式进行碰撞和传播，模拟流体的宏观行为。

格子波兹曼方法相对于传统的Navier-Stokes方程求解方法具有多个优势。

首先，它因其并行化的能力而广泛应用于高性能计算中。

其次，LBM的离散化框架使得
它在处理具有复杂边界条件和多相流问题时更加灵活。

此外，LBM对于非连续和
非均匀流体介质的模拟效果也相对较好。

格子波兹曼方法在各个领域都有广泛的应用。

在流体力学领域，LBM被用于
模拟自由表面流动、湍流现象和多孔介质中的流动行为。

在微观领域，LBM也被
用于模拟微观流体力学现象，例如微管流动和纳米颗粒悬浮体的输运行为。

除了流体力学领域，格子波兹曼方法还被应用于其他科学领域。

例如，它被用
于模拟热传导、传质过程、相变以及复杂物质的输运现象。

此外，LBM还被用于
模拟生物流体力学、地下水流动、大气动力学和地震波传播等问题。

综上所述，格子波兹曼方法是一个高效且灵活的数值方法，用于模拟复杂的流
体流动问题。

它在计算流体力学领域以及其他科学领域都有广泛的应用前景。

这种方法的进一步发展和应用将有助于我们更好地理解和预测流体行为，并解决相关领域的实际问题。

流密码详解ppt课件

2.1 流密码一般模型
自同步流密码(SSSC)
密钥流生成器是一种有记忆变换器密钥流与明文符号有关：
i 时刻的密文不仅取决于i 时刻的明文，而且与i 时刻之前的l个明文符号有关具有有限的差错传播具有自同步能力把明文每个字符扩散在密文多个字符中,强化了抗统计分析的能力
问：SSSC是如何自同步的？请email回应。
i F ( i1, k ), zi f ( i, k ), ci E (zi,m i). i:密钥流生成器的内部状态 0 :密钥流生成器的初始状态 k : 种子 (初始 )密钥 F :状态转移函数 f :密钥流生成函数
k
密钥流生成器
11
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
2.1 流密码一般模型
二元加法序列密码
明文序列: m= m1 m2 m3 …; 密钥序列: z= z1 z2 z3 …; 密文序列: c= c1 c2 c3 …; 加密变换: ci=zimi (i=1,2,3,…); 解密变换: mi=zici (i=1,2,3,…).
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
2.2 线性反馈移位寄存器序列
伪随机序列考虑二元序列: a={ai}=a0a1a2a3 ….
周期序列
定义2.1 设a= (a0, a1,…,ai,…)是一个二元序列，若存在正整数N和非负整数m，使得ai+N=ai对于任意i m成立，则称二元序列a是终归周期序列。如果 m=0，则称序列a是严格周期序列，简称周期序列。

方腔流动

边界条件
流函数边界条件：根据已知条件，在四个壁上流函数均为 0，上边界平板速度 1，根据不可滑移条件确定流函数偏导数条件。
涡量边界条件，采用（1）：
（1）可以用 Taylor 展开建立一般形式的 Thom 公式。假设某壁面切向速度 v ，沿其内法
向 n 有一节点，距离壁面距离为 h, 此点上的流函数为1 ，如果壁面上的流函数值为 0 ，那么
0
(1
0 2h2
v h)
时间导数采用向前 Euler 法，空间导数项可以用中心差分格式离散
计算步骤 1、计算 n + 1 时刻内点的涡量，需要考虑时间步长和空间步长和粘性项的关系。
2、计算 n + 1 时刻的流函数 n1 ，超松弛迭代法，松弛因子为-1.8。
3、计算 n + 1 时刻边界上的涡量
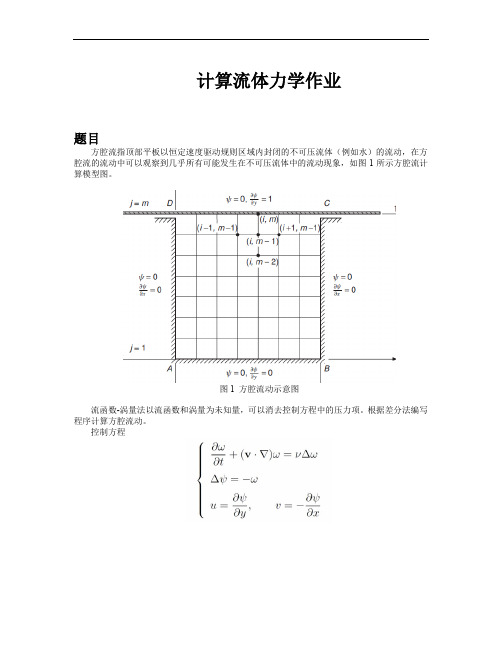
计算流体力学作业
题目
方腔流指顶部平板以恒定速度驱动规则区域内封闭的不可压流体（例如水）的流动，在方腔流的流动中可以观察到几乎所有可能发生在不可压流体中的流动现象，如图 1 所示方腔流计算模型图。
图 1 方腔流动示意图流函数-涡量法以流函数和涡量为未知量，可以消去控制方程中的压力项。根据差分法编写程序计算方腔流动。控制方程
-0.5
0
0.5
1
1.5
3.995s 方腔速度矢量图
0
0.5
1
x0=0; x1=1; dx=(x1-x0)/(N-1); %空间步长 y0=0; y1=1; dy=(y1-y0)/(M-1); %空间步长
Thom 公式
1
0.8
0.6
0.4
0.2
0
-0.2
0
0.2
0.4

lbm波尔兹曼算法

波尔兹曼方法基本原理格子Boltzmann 方法是使用简单的微观模型来模拟流体的宏观行为的一种新的方法。

格子Boltzmann 方法是建立在微观粒子运动论基础上的数值计算方法。

其求解过程一般需要通过编程来实现！一般来说研究流体的行为有两种方法：一种是从宏观的角度出发，假设流体连续分布于整个流场，注入密度、速度、压力等物理量均是时间可空间的足够光滑的函数。

另一种是从微观的角度，从非平衡统计力学的观点出发，假设流体是由大量的微观的例子组成，这些例子遵守力学定律，同时服从统计定律，运用统计的方法来讨论流体的宏观性质。

然而流体是由大量的粒子组成的，当我们从宏观的角度研究流体行为的时候，并没有涉及到单个粒子的行为。

通常我们所感兴趣的事代表某个点的宏观量，例如密度、速度、压力。

根据连续性假设我们可以推导出N-S 方程，并且利用数学上的微积分知识来求解，然而由于N-S 方程是高度非线性化的偏微分方程，仅仅一些具有简单变界或者比较严格物理闲着的现象才能够得到理论分析界，如果从微观的角度了研究单个粒子的真是行为，对于一个包含大量例子的系统来说粒子的运动方程往往是得不到解的。

统计学可以考虑整个系统所有的状态以及处理这个状态的概率来解决这些困难，对于稀薄气体所得到的就是Boltzmann 方程，但是得到的方程还不够，我们还要借助于统计方法得到流体的宏观性质，这就要求解Boltzmann 方程，然而Boltzmann 方程是一非线性微分方程，一般情况下严格求解也是非常困难的。

格子气方法是近年来发展起来的模拟流体力学以及其他系统的比较新的方法，格子气自动机模拟流场，就是将流体及其存在的时间和空间完全离散，给出离散的流体粒子之间相互作用以及迁移的规则。

流体只存在于空间网格上，用一系列布尔变量,.....,2,1)(,(b i t x n i =来描述在时刻t 位于x 处节点的每一个速度方向是否有粒子存在，其中b 表示每一个节点的速度方向的数目，粒子在每一个时间步长的演化包括两部分：()a 迁移，粒子沿它的速度方向向距离最近的节点运动；()b 碰撞，当不同的粒子同时到达某个节点时，按照一定的碰撞规则发生碰撞并改变运动的方向，格子气模型具有两重意义：()a 尽可能建立一个简单的模型是指能够用来模拟一个有大量粒子组成的系统；()b 反映粒子真实碰撞的本质，这样经过长时间我们可以获得流体的宏观特性。

lbm泊肃叶流动算例复现 -回复

lbm泊肃叶流动算例复现-回复LBM泊肃叶流动算例复现引言：LBM（Lattice Boltzmann Method，格子–玻尔兹曼方法）是一种强大的数值模拟方法，广泛应用于流体力学和热传导的模拟研究中。

其中，泊肃叶流动是流体力学中的经典问题，通过复现LBM泊肃叶流动算例，我们可以深入理解LBM的基本原理和应用。

第一步：了解原理在正式开始复现算例之前，我们需要了解一些基本的理论知识。

泊肃叶流动是指一种在圆柱外表面上产生的定常旋转流动，其中由于黏性效应，流体粘附在圆柱表面，并在表面形成一个边界层，不同于背景流体的速度也会随着距离表面的增加趋于背景速度。

第二步：建立计算模型为了复现LBM泊肃叶流动算例，我们需要建立一个合适的计算模型。

在LBM中，我们使用格子上的速度分布函数来模拟流体的运动。

对于泊肃叶流动，我们可以采用D2Q9速度模型，其中格子上有9个速度分布函数。

第三步：求解宏观量在LBM中，我们通过离散求解玻尔兹曼方程来计算速度分布函数的演化。

首先，我们需要计算格子上的宏观量，如密度和速度。

对于泊肃叶流动，由于该流动是定常流动，所以不需要迭代求解，我们可以直接计算宏观量。

第四步：边界条件处理在模拟泊肃叶流动时，我们需要处理边界条件，即圆柱的表面边界和流体的进出口边界。

对于圆柱表面，我们可以使用粘滞壁面条件，即表面的速度等于圆柱速度。

对于进出口边界，我们可以使用强出弱入条件，即进口速度恒定，出口速度根据宏观量计算。

第五步：迭代求解通过以上步骤，我们已经建立了LBM泊肃叶流动的计算模型，并处理了边界条件。

接下来，我们需要进行迭代求解，不断更新速度分布函数，直到收敛为止。

在每一次迭代中，我们需要计算新的宏观量并更新速度分布函数。

第六步：计算结果分析在完成迭代求解后，我们可以得到泊肃叶流动的计算结果。

通过分析结果，我们可以得到流体的速度、压力分布以及圆柱表面的剪切力等信息。

这些结果可以帮助我们进一步理解和研究泊肃叶流动的特性。

格子Boltzmann方法原理及其应用

格子Boltzmann方法原理及其应用摘要在上世纪八十年代后期提出的格子Boltzamnn方法克服了格子气方法的缺点，其本身也在不断的发展之中.格子Boltzamnn方法在流体运动计算方面展现了非凡的风采，成功地模拟了包括均相不可压缩湍流和多孔介质中的多相流动在内的流体动力学问题.但和成熟的流体动力学计算方法相比，特别在工程实际应用上，该方法还有许多值得研究的地方.本文主要介绍工程实际应用时，具体模型的选择问题.首先从理论上对应用最为广泛的几种基本模型进行了详尽的分析和比较.选择了Poiseuille流动，然后从计算精度、数值稳定性和收敛速度这几个方面进行了细致的比较.从理论和实验两个角度验证了D2G9模型的优越性，为工程实际应用上模型的具体选择提供了一定的参考依据.通过研究二阶精确的格子Boltzamnn模型，提出了非牛顿流体.非牛顿流动性是使用幂法则模型实现的.它可以估算出模型的精确程度，同时不会限制这个模型.二阶精度由剪切变稀和剪切增稠液体的幂法则模型参数范围给出.这些结果与Gabbanelli等人的结果相比，精确度更高，并且得到了更快的计算效率.结果表明了格子Boltzamnn方法适用于非牛顿流体模拟.对于实际流动模拟，本文应用二维9速度模型模拟了四种情况的方柱绕流问题.在第一种情况中，单个方柱位于流场中央，给出了流线图，等涡线图，模拟了卡门涡街现象，并计算了升、阻力系数，Strouhal数等参数；在第二种情况中，计算细长矩板截面柱绕流问题，得到了Strouhal数随着矩形长宽不同的比值下的变化情况；在第三种情况中，两个方柱并列位于流场中央，考察了方柱间距对于流场的影响；在第四种情况中，计算了水平来流为剪切流的方柱绕流问题，比较了速度梯度取不同值下流场的变化情况.所有有关力的求解均采用动量转换法.所得结果，包括流线、等涡线、升/阻力系数曲线等均与已有文献的实验或数值结果基本一致，显示LBM方法及其力的求解方法——动量转换法是有效的，能够精确的模拟各流场.其次，我们还引入一种两相耦合机制对D2G9模型进行了修正，从而使之可以正确处理气固两相流中输运相和颗粒相之间的相互作用.随后，我们模拟了后台阶流动，并和传统CFD方法的模拟结果以及修正其他模型的模拟结果进行了验证，得到了令人满意的结论.从一定程度上验证了两相耦合机制的可行性.通过软件模拟获得了水包油、过渡流型和油包水三种流型的典型模拟图.经分析发现：由软件模拟的流型特点和由探针获得的流型特点具有较好的一致性.在本文最后，我们介绍了以经典算例一方腔流为例，对格子Boltzamnn方法的核心代码进行了优化的方法，主要讲述对时间和空间上的优化，优化的程序使计算效率提高数倍.在并行的框架下，核心演化的代码换为优化后的程序，计算效率有大幅度的提高.关键词：格子方法；格子Boltzamnn 方法；格子气自动机；格子Boltzamnn模型.AbstractIn the latter of 80’s，the Lattice Boltzamnn Method（LBM）was introduced mainlyto cope with major drawbacks of its ancestor，the Lattice Gas Automata（LGA）．Eversince，it has undergone a number of refinements and extensions which have taken it tothe point where it can successfully compute a number of non trivial flows，raging fromhomogeneous incompressible turbulence to multiphase flows in porous geometries．Yet，when compared with conventional computational fluids dynamics methods，such as finiteelement，finite difference，it is apparent that there is still a way to go before LBM canachieve full engineering status．In this paper，we mostly focus on the choice of the basic LB models in theengineering application fields．Firstly，we expatiate the basic LB models in theory．Then，we simulate the Poiseuille flow with those basic LB models．And wecompare the simulation results from the computation precision、the numerical stabilityand the convergence rate．Finally，we draw a conclusion that the D2G9 model is the bestchoice in the engineering application fields．Simulation of Flow past square cylinder with LB Method.For the simulation of actual flow，we use D2Q9 investigate fourcases of flow past square cylinders in this paper.For case 1，one singlesquare cylinder is located at the center of the channel，we describe thestreamline contour，vortices contours，simulate the Karman vortex，then compute the lift coefficient，drag coefficient，Strouhal numbersetc.For the case 2，simulate the flow past a cylinder of rectangularcross-section;compute the change of Strouhal numbers varying withthe side ratio.For case 3:two square cylinders arranged side by side inthe center of the channel，the flow features at different spacing ratiosare studied.For case 4:we compute the linear shear flow over a squarecylinder，compare the evolution of flow with different velocitygradient.The results of thesimulation including the streamlines，vorticity contours，lift and drag coefficients etc.are agreed with thoseof available literatures，and show that LB method and itsmomentum-exchange method can achieve accurate results and obtainthe reasonable flow in detail.we employ a two-way coupling mechanisms to modify theD2G9 model．With the modified D2G9 model，we can handle with the interactionsbetween carrier phase and dispersed phase in the model．Then，we simulate abackward-facing step model，and the results are compared qualitatively with the result ofthe traditional CFD method and the other modified LB models．Though the comparison，we can see that the two-way coupling mechanisms can handle with the gas-solid twophases flows successfully．Three kinds of flow pattern，which are oil-in-water flow，transitional flow andwater-in-oil flow，have been got by simulation.According to the result of simulation，theoil-water two-phase flow pattern transition boundary model has been got by.By the analysisof simulation，the characteristic of three kinds of flow pattern of vertical oil which has beengot by analysis of the signals is consistent with results by simulation.We take the classical problem-cavity flow as an example and optimize the kerne codes of the LBM. The optimization include two aspects :time and space .The efficiency of the optimized code increased much more .In the parallel frame，the efficiency also increased if the kernel code is taken the optimized code.Key word：1atrice method；1atrice bohzmann method；lattice gas automata;LBM目录第1章概述 11.1研究格子 Boltzamnn方法的意义 11.2 格子 Boltzamnn方法的发展历程 31.2.1孕育阶段 31.2.2 萌芽到成长阶段 31.3 格子 Boltzamnn方法应用概况及优缺点 51.3.1格子Boltzamnn方法应用概况 51.3.2格子Boltzamnn的优缺点 61.4本论文的研究目的 81.5 相关研究的综述与专注情况 8第2章格子Boltzamnn方法介绍 102.1 Boltzamnn方程的产生 102.2细胞自动机（CA） 112.3格子气自动机（LGA） 122.4格子Boltzamnn方法（LBM） 132.5 格子Boltzamnn的基本结构 162.6本章小结 17第3章格子Boltzamnn方法的基本模型比较 183.1 格子 Boltzamnn 方法基本模型概述 183.2 进行常压力梯度驱动的Poiseuille流动模拟比较几种基本模型 23 3.3本章小结 27第4章格子Boltzamnn方法的算法设计 284.1格子Boltzamnn方法的算法实现 284.2格子Boltzamnn方法的高效算法设计 304.2.1优化算法 304.2.2优化实验 324.3 本章小结 34第5章格子Boltzamnn方法的实际应用 355.1二阶精确格子Boltzamnn非牛顿流体的流动模拟 35 5.1.1理论背景 355.1.2方法和计算结果分析 385.1.3 本节小结 405.2 格子Boltzamnn方法的方柱绕流模拟 405.2.1 单个方柱位于流场中央的绕流问题 405.2.2 细长矩形截面住绕流问题 425.2.3 两个并列方柱的绕流问题 445.2.4来流为剪切流的绕流问题 495.3格子Boltzamnn方法模拟气固两相流 515.3.1对气固两相流的模拟模拟对象简介 515.3.2 计算结果分析 545.3.3本节小结 565.4 格子Boltzamnn方法模拟油水两相流软件设计 565.4.1 LBM油水两相流的关键因素选取 575.4.2 软件的设计 605.4.3 本节小结 635.5 简述格子Boltzamnn方法在其他领域中的应用 645.5.1 颗粒悬浮问题的模拟 645.5.2 热导和对流—扩散问题的模拟 645.5.3 偏微分方程的模拟 655.5.4 多相流和多元流的模拟 65结论及展望 67参考文献 68第1章概述1.1研究格子Boltzamnn方法的意义自从二十世纪四十年代出现了第一台电子计算机以来，人们开始进入了电子信息时代.随着高存储、高速度计算机的出现，人们所能解决的问题也越来越广泛，同时所面临的问题也越来越复杂.在对流动现象的研究中，以往人们大部分依靠的是解析方法，但所解决的问题非常有限.而现实生活中所面临的流动问题往往十分复杂，如航空航天器的亚跨超音速飞行、舰船的航行等等，依靠解析的方法来解决这些复杂的流动现象是不可能的.到现今为止，人们对流体运动的研究主要靠实验方法和数值计算方法.实验方法具有直观、结果基本可靠的特点.但也存在较大的缺点：耗费大、周期长，并且结果受实验条件的影响也较大，尤其是如今的航空航天飞行，速度高、飞行条件复杂，用风洞来模拟困难是相当大的.而流体的运动可以由一组偏微分方程描述.在大多数情况下，这些方程（如N-S方程）都是高度非线性的，采用解析的求解方法是不实际也是不可行的.随着大型计算机的出现，使人们可以借助于计算机用数值计算方法来解决复杂的流动问题.因此，在二十世纪六十年代，用数值方法分析求解流动问题的学科——计算流体力学（CFD）逐渐发展起来.伴随着电子计算机的飞速发展以及各种新颖算法的不断出现，CFD已经形成了一门独立的学科，并且在航空航天、船舶、大型能源装置（如核电站）、新型交通工具、海洋工程、环境保护等众多工程技术部门和领域都得到了广泛的应用.随着计算技术的发展、巨型计算机的出现、计算方法的不断改进，计算流体力学在解决流动的理论和工程实际问题中愈加显示出它的巨大作用.目前，计算流体力学已经成为现代计算科学的最有力的推动力之一.在计算流体力学中，传统的数值模拟方法可以分为两大类：（1）从宏观角度出发，基于连续介质假设，采用数值计算方法，求解全位势方程或Euler方程或N-S方程；（2）从微观角度出发，采用分子动力学的方法，对流动进行数值模拟.其中，格子Boltzamnn方法就是典型的一种.格子Boltzamnn方法（Lattice Boltzamnn Method，LBM）1.1.2格子Boltzamnn法（lattice Boltzamnn method）起源于格子气自动机（Lattice Gas Automata，LGA）.LGA方法是元胞自动机（Cellular Automata，CA）在流体力学中的具体应用，是空间、时间和速度空间都离散的一个虚拟微观模型，与以连续微分方程为基础的宏观计算流体力学方法有着本质的不同.LGA的微观特性使得它的边界条件非常容易实现，并且计算也很简单.因此，LGA方法非常适于处理边界复杂的问题.更为重要的是，LGA的计算具有局部性和并行性，非常容易在并行机上实现.LGA的出现不但为并行计算提供了许多新思想，而且对并行计算机制造技术产生了重要的影响.但是，LGA方法也有许多不足之处.例如，由于含有随机因素，LGA的计算结果往往包含很大的统计噪声，LGA的宏观方程也不是标准的流体运动宏观方程.格子Boltzamnn方法是为克服LGA方法的一些内在不足而发展起来的一种新方法.LBM不但克服了LGA的缺点，继承了LGA的主要优点，而且还有许多新的优点，如计算量小、计算效率高、编程简单等.LBM的产生与发展，不仅在计算流体力学领域中产生了深远的影响，它所使用的处理方法和观点对其他许多学科也是富有启发性的.格子Boltzamnn法是一种应用非连续介质思想研究宏观物理现象，并可平行运行，求解流体力学问题的新方法.它是由格子气自动机（lattice gas automata，简称LGA）方法发展而来的.该法把流体及其存在的时间、空间完全离散，把流体看成由许多只有质量没有体积的微小粒子组成，所有这些粒子同步地随着离散的时间步长，根据给定碰撞规则在网格点上相互碰撞，并沿网格线在节点之间运动.碰撞规则遵循质量、动量和能量守恒定律.流体运动的宏观特征是由微观流体格子相互碰撞并在整体上表现出来的统计规律.该法是直接从微观模型出发，经过Boole化处理后进行计算，可认为是N-S差分法逼近的一种无限稳定的格式.被广泛应用于复杂几何边界流体流动、多孔介质流、多相流及反应流等.格子气自动机的基本思想是，把计算区域分成许多均匀的正三角形（或正方形）的网格，而那些只有质量无体积的粒子只能在网格点上存在，并沿着网格线在网格间运动.当某一个粒子从某一网格点到邻近的网格点时，有可能和从其他网格点到达该点的粒子相碰撞.根据Pauli不相容原理，在同一时刻同一点上，沿着每一网格线运动方向最多只有一个粒子，流场中的粒子速度不是0（静止）就是1（设格子边长及时间间隔都为1）.以三角形网格为例，每一个网格上在某一时刻，其周围的6个网格上粒子沿着网格线聚集到该点，加上该点可能还有一个静止粒子，这样，可能有7个粒子在该点发生碰撞，然后根据碰撞规则再散射出去，演化为新的运动粒子流向各节点的邻居，形成格子气自动机.1986年MeNamaxa和Zaneltti，提出把格子气自动机中的整数运算变成实数运算，建立了格子Boltzamnn 模型，克服了格子气自动机的数值噪声的缺点.后来陈十一和钱跃宏采用了单一时间松弛方法，满足了各项同性，GalIean不变性，并得到了独立于速度的压力项．使格子Boltzamnn模型保留了格子气自动机的优点，克服了其不足，并在理论分析和数值模拟方面都具有很大灵活性，而且程序编制简单，计算效率较高.从格子Boltzamnn方法诞生至今天已有20年，20年间，其在理论和应用研究等方面都取得了迅速发展，并逐渐成为在相关领域研究的国际热点之一，受到国内外众多学者关注.与之传统模拟方法不同，格子Boltzamnn方法基于分子动理论，具有清晰的物理背景.该方法在宏观上是离散方法，微观上是连续方法，因而被称为介观模拟方法.在许多传统模拟方法难以胜任的领域，入微尺度流动与换热、多孔介质、生物流动、磁流体、晶体生长等，格子Boltzamnn方法都可以进行有效的模拟，因此它被用于多种复杂现象的机理研究，推动了相关学科的发展.可以说，格子Boltzamnn方法不仅仅是一种数值模拟方法，而且是一项重要的科学研究手段.此外，格子Boltzamnn方法还具有天生的并行特性，以及边界条件处理简单、程序易于实施等优点.可以预计，随着计算机技术的进一步发展，以及计算方法的逐渐丰富，格子Boltzamnn方法将会取得更多成果，并为科技发展发挥更重要的作用.1.2 格子Boltzamnn方法的发展历程格子Boltzamnn方法自诞生至今年已取得了长足发展，被誉为现代流体力学的一场变革.1.2.1孕育阶段：对格子Boltzamnn方法发展使得了解，得先从格子自动机说起.格子气自动机使更广泛的元胞自动机在流体学中的应用.元胞自动机是一个时间和空间离散的数学模型.20世纪60年代，Broadwell等人首先提出了离散速度模型，用以研究流体中的激波结构.20世纪70年代，为了研究流体的运输性质，法国的Hardy、Pomeau和Pazzis提出了第一个完全离散模型，该模型命名HPP模型.这是历史上的第一个格子气自动机模型.1986年，法国的Frisch、Pomeau和美国的Hasslacher提出具有足够对称的二维正六变形格子气自动机模型，，命名为FHP模型.由于这些方法在还处在一些缺点：（1）有格子气自动机演化方程推导出来的动量方程不满足Gaililei不变形；（2）流体状态方程不仅仅依赖于密度和温度，还与宏观流速有关；（3）破装蒜子具有指数复杂性，对计算量和存储量也有较大要求.因而，我们将这一段格子气自动机的发展过程称作格子Boltzamnn方法的孕育期.1.2.2 萌芽到成长阶段：自1988年底一篇关于格子Boltzamnn方法的论文出现至今，格子Boltzamnn方法从萌芽逐渐成长壮大，并成为目前一大国际研究热点，受到越来越多学者的关注.1988年，McNamra和Zanetti提出把格子气自动机中的Bool运算变成时数运算，格子点上的粒子数不是用整数0或1来表征，而是用实数f来表示系综平均后的局部粒子分布函数，用Boltzamnn方程代替格子气自动机的演化方程，并将该模型用于流体的数值计算.这是最早的格子Boltzamnn模型，从此开启了格子Boltzamnn方法的历史大门.1989年，Higuera和Jimenez提出了一种简化模型：通过引入平衡分布函数，将碰撞算子线性化.该模型不需要碰撞模型，并忽略各自粒子间的碰撞细节，相比于多粒子碰撞模型，容易构造.同年，Higuera等进一步提出了强化碰撞算子方法，以增加模型的数值稳定性.这两模型统成为矩阵模型.经历了上述两类模型，格子Boltzamnn方法消除了统计噪声，克服了碰撞算子指数复杂性，但是由于依然使用Fermi-Dirac平衡态分布函数，格子气自动机的其他缺点仍然存在.1991年，Chen等提出了单松弛时间法，用同一个时间松弛系数来控制不同例子靠近各自平衡态的快慢，进一步简化了碰撞算子；Qian等人在1992年也提出了类似的方法，称之为格子BGK（LBGK）模型.LBGK模型与矩阵模型类似，但与前面两种模型不同的是，当粒子种类数增加时，碰撞算子本身发生生变化，不会变得复杂.至此，格子Boltzamnn方法完全克服了格子气自动机的一系列缺点，并逐渐成熟，成为国际研究的热点.早期的格子Boltzamnn模型只能用于等温不可压缩流动的模拟.但因为存在可压缩效应，会引起一定的误差.为了消除或强敌有可压缩效应引起的误差，许多学者致力于新的格子Boltzamnn模型的研究，并提出了多种等温不可压模型.而后，一些不可压缩热模型成功实现了对有效范围温度变化的热力学和传热学问题的模型.其中，最成功的要数双分布函数模型.他是在密度分布函数的基础上引入了温度分度函数、或内能分布函数、或总能分布函数，并用密度分布函数演化得到速度场，这类模型具有与等温不可压模型相同的数值稳定性，而且可以从根本上解决压缩功和耗热问题.边界处理方面，经历了20年的发展，格子Boltzamnn方法已逐渐发展出适合不同边界条件、不同模型的边界处理格式.网格划分方面，最初的格子Boltzamnn方法是基于正六边形或正四边形的均匀对称网格.由于均匀网格在计算效率、计算精度等方面的不足，从而促进了非均匀网格、多快以及多重网格、无网格等多技术出现.总的来说，这些网格技术延展了格子Boltzamnn方法的应用范围，使得格子Boltzamnn方法主机去年从理论的神殿走向更可能多的实际应用领域.1.3 格子boltzamnn方法应用概况及优缺点1.3.1格子boltzamnn方法应用概况与传统的宏观数值方法相比，具有介观特性的格子Boltzamnn方法其主要优点是物理图像清晰、便捷容易处理以及并行性能好等.因而自诞生之日起，格子Boltzamnn方法就得到了国内外学术界的广泛关注，并寄希望该方法能再注入为尺度流体、多相流、多孔介质内流动与换热、化学反应流等传统法就延受限的领域取得开拓性进展.事实上，在20年的发展过程中，格子Boltzamnn方法的确也已成一个十分活跃极具发展前景的模拟手段.并迅速在微/纳米尺度流、多孔介质流、多相多质流、非牛顿流体、粒子悬隔i浮流、湍流、化学反应流、燃烧问题、磁流体、晶体生长等许多领域得到应用.下面分别以多孔介质流、多相流和非牛顿流体三个方面为例，做较详细说明.由于格子Boltzamnn方法边界条件易于实施，在模拟具有复杂几何构型的问题具有较大的优势，因而这个方向的发展非常迅速.目前，采用格子Boltzamnn方法对多孔介质流进行模拟主要在空隙尺度和代表单元尺度上进行.在孔隙尺度上，可以直接使用格子Boltzamnn方法描述孔隙内的流体流动，多孔介质则当做固体壁面，流体与介质相互作用使用边界处理格式来描述.在多相流方面，由于真实的流动问题常常是多相的，因而对其开展研究具有重要的现实意义.由于格子Boltzamnn方法的介质特性，它可以方便地描述数流动中不同相之间的相互作用，因而在多相流领域具有较好的应用前景.按照设计方法的不用，现有模拟多相流的格子Boltzamnn模型可分为四大类：着色模型、伪势模型、自由模型和其他模型.格子Boltzamnn方法在非牛顿流体领域的应用刚刚起步，主要研究对象是非牛顿幂律流体.Aharonov等最早提出使用矩阵碰撞该算子来计算幂律流问题，即在每一个时步内，调整碰撞算自来该表局部的动力学黏性系数.Boek用该模型模拟了幂律流体在简化多孔介质中模型的流动，模拟结果与达西定律符合良好.最近，Gabbanelli又对上述模型进行了改进，引入分段幂律方程描述剪切率和表现黏度的关系.以上可看出，到目前为止，格子Boltzamnn方法的研究者主要局限在科学界.尽管如此，随着格子Boltzamnn 方法理论体系逐渐完善，以及计算机技术的进一步发展，格子Boltzamnn方法也会走向更加广泛的工业实际应用中.1.3.2格子Boltzamnn的优缺点流体力学的理论描述通常建立在纳维--斯托克斯方程的基础上，作为流体力学的基石，它已处在了一个多世纪.在通常尺度下，|人们对此方程的物理可靠性即准确性并不抱异议.理论上人们一般通过求纳维--斯托克斯方程及其各种简化形式的途径来处理复杂的流体力学问题，现行的计算流体力学研究也主要是围绕着纳维--斯托克斯方程的计算方法展开的.然而，基于其本质上的非线性以及边界条件处理的困难，除少数简单问题外，解析和数值求解纳维--斯托克斯方程都是极具挑战性的任务.除了求解的困难外，作为一种对流体物理的描述，与描述经典力学运动的牛顿运动方程，或与描述量子力学运动的薛定谔方程等原理方程不同，纳维--斯托克斯方程是从更根本的原理性方程出发，在合理地假定某些物理机制可以忽略后，经过统计平均得到的.本质上纳维--斯托克斯方程当然不可能描述那些被忽略了的物理机制带来的宏观现象，比如流体系统中的相变、非牛顿的本构关系以及在分子运动自由程尺度上的物理现象，在这些领域，纳维--斯托克斯方程明显的显示出了他的局限性.从20世纪80年代末开始，一种对于流体力学的全新的理论表相及有效的计算方法初步形成，这就是现在人们通常所谓的格子Boltzamnn方法.关于格子Boltzamnn方法的早期发展，上文已有较全面的综述，在此仅作简单介绍.从历史角度来讲，格子Boltzamnn方法最初是从所谓的格子气模型演化而来的，而后者是一种抽象简化的分子运动数学模型.格子Boltzamnn方法最初的引入有两个主要原因：一是为了降低模型导致的数值噪音；而是能够克服格子气模型里处在的非物理缺陷.可以证明，格子Boltzamnn系统的宏观表象基本满足纳维--斯托克斯方程.从而，人们可以模拟格子Boltzamnn系统地方法来间接地解纳维--斯托克斯方程.标准格子Boltzamnn方程一般用一下的数学表达式描述：式中——粒子分布函数；——碰撞项.用格子玻尔兹曼模型进行流体的数值模拟有一些明显的优越性．如，它的对流（advection）过程是通过常数值速度实现的．这相应的计算是一项极其简单的操作步骤．当适当的格子网格选定后，该过程通常可以用完全平移的方式实现．用计算数学里的常规有限插值语言来讲，它对应于上风插值．但所不同的是其对应的柯郎数（Courant Number）等于1．相比之下，纳维——斯托克思方程的对流项是一个随时空变化的非线性函数．众所周知，对于它的计算不是一项简单的事，并且，数值稳定性的要求迫使人们在实际问题的计算中只能使用比1小得多的柯朗数．在给定空间分辨度的情况下，小柯朗数意味着小时间步长，从而大大延长了计算时间：同时，小柯朗数也增大了数值扩散误差，迫使人们采用更高精度格式或隐式格式．其后果是，或者算法变得极为复杂，并行效率大大降低；或者计算只限制在处理定常流的情况下．事实上，定常流是对流动情况的极大限制．许多重要的流体力学问题，如分离流，即使我们只关心它的时间平均的结果，也是不能用定常流假设来近似的．在此我们也要提一下格子玻尔兹曼方程的另一个本质特性：所有非线性效应在格子玻尔兹曼方法里都包含在碰撞项中，并且是以纯粹局部信息的方式体现的．这进一步发挥了并行计算的长处．所有这些理由意味着格子玻尔兹曼方法是对非定常流动实行大规模并行模拟计算的一种比较优越的方法．相比之下，以流体力学方程（纳维一斯托克思方程或Burnett类型方程）宏观描述为基础的传统计算方法对许多这类问题存存基本困难．除边界条件之外，利用各种封闭性假设推导出的超越纳维一斯托克思的宏观方程直至现今仍存在对其数学规范性的疑问和争议，多相流的计算也存存同样问题．众所周知，流体系统中存在多相的物理机制是分子问的长程作用力，这种机制早已超出了流体力学方程所能描述的物理现象范围．以流体力学方程为基础的多相流计算方法必须依赖额外的模型来模拟流体力学方程本身所不包含的物理现象．除了实际数值结果显示的问题之外，这种方法本质上隐含着严重的基本物理缺陷，这种缺陷集中表现在对相交界面的准确描述上面，即在十分尖锐的相界面附近，纳维一斯托克思方程之类近平衡态的近似表象是有相当疑问的．这也反映在相界面和兀滑动（no—slip）固体边界条件的互斥性上面，为了修补这一缺憾，人们不得不引入各种滑动经验模型.反之，以细观（mesoscopic）为表象基础的格子玻尔兹曼方法可容忍更大的非平衡态程度及更广义的严格边界条件．另外，压力的状态方程在细观表象中是由粒子的相互作用自然得出的，而不用直接输入和处理．在相变情况下，物体的宏观特性将产生不连续性，而对应的微观和细观力学机制并无改变．格子玻尔兹曼方法在模拟多相流上有着广泛的使用.然而，这种为大多数人所熟悉的格子玻尔兹曼方法的理论框架存在本质上的缺陷．由于它运用逆向切普曼一安斯柯格展开的途径来适定平衡态分布函数中的关键参数，以达到复建宏观物理体系的目的，这就使其。

热格子Boltzmann法分析及应用

热格子Boltzmann法分析及应用陈杰;钱跃竑【摘要】格子Boltzmann方法(lattice Boltzmann method,LBM)是一种基于气体动理论的介观计算方法,其物理背景清晰、边界处理简单,已成功应用于等温(或无热)流动中.简要介绍现有的几种热格子Boltzmann模型,并运用几种热格子模型求解热Couette流、方腔自然对流等典型算例,对比不同热格子模型的数值稳定性、准确性、模型的计算效率等.将两种热格子模型用于多孔介质内的流动与传热问题中,对比热格子模型在处理复杂结构时的数值特性.%Lattice Boltzmann method (LBM) is a mesoscale computational method based on the gas kinetic theory. For solving Fourier-Navier-Stokes equations, the thermal lattice model has attracted much research attention. This paper compares several thermal lattice models in terms of accuracy, stability and computational efficiency. The thermal flow in pore-scale porous is also studied using different thermal lattice models.【期刊名称】《上海大学学报（自然科学版）》【年(卷),期】2012(018)005【总页数】7页(P489-495)【关键词】格子Boltzmann方法;热格子Boltzmann方法;多孔介质【作者】陈杰;钱跃竑【作者单位】上海大学上海市应用数学和力学研究所,上海200072;上海大学上海市应用数学和力学研究所,上海200072【正文语种】中文【中图分类】O351格子Boltzmann方法(lattice Boltzmann method，LBM)是近20年发展成熟起来的一种数值计算方法.LBM基于气体动理论，通过分布函数的演化获得宏观信息.作为一种简单且能处理复杂流动问题的有效数值方法［1-2］，LBM具有良好的数值稳定性、天然的并行性、简单的边界处理等优点，自出现之日起就被广泛用于多孔介质流［3］、多相流［4］、反应扩散系统［5］等诸多领域.早期的LBM只应用于等温流动(或无热流动)的模拟，但是基于这种方法具备处理复杂问题的能力以及解决传热问题的需要，研究者一直在不断地探索研究热格子Boltzmann模型，已形成了一些经过数值验证具有模拟热流动能力的热LBM［6-10］，并应用于多孔介质流动与传热、燃烧及化学反应流、湍流等问题.本研究简述了不同热格子Boltzmann模型的基本理论，并通过数值分析对比了不同热格子Boltzmann模型的计算结果及数值特性，进而用于多孔介质流动传热问题中.1 等温LBM基本原理LBM中除时间、空间被离散之外，无限维的粒子速度空间也都被离散成有限的速度序列.在标准LBM模型中，物理空间被离散成正方形(体)格子，流体粒子在格点x上碰撞并按离散速度E=［e0，e1，…，eq－1］迁移到x+eiδt格点.fi(x，t)定义为t时刻在格点x上速度为ei的粒子密度，满足如下的格子Boltzmann方程：式中为平衡态函数，ω为松弛因子.通过简单地向平衡态不断趋近的过程代替真实的复杂碰撞，即BGK(Bhatnagar-Gross-Krook)近似，所以此模型也称为LBGK 模型.平衡态分布函数的选取是LBM的关键.DnQm系列［1］中均采用式中，cs为格子声速，Wi为不同速度粒子的权重.本研究在数值模拟中均采用D2Q9模型.宏观密度和速度分别定义为2 热格子Boltzmann模型现有的热格子Boltzmann模型通常可以分为两大类：第一类是流场温度场耦合统一求解的模型，如多速格子Boltzmann模型(multi-speed LBM，MSLBM)、熵格子Boltzmann方法(entropic LBM，ELBM);另一类则是对流场与温度场分别求解，如被动标量格子Boltzmann模型(passive scalar LBM，PSLBM)、双分布函数(double-distribution-function，DDF)模型，以及其他与传统计算流体动力学(computational fluid dynamics，CFD)结合的混合方法，如混合热格子Boltzmann方法(hybrid-thermal LBM，HTLBM).2.1 多速格子Boltzmann模型(MSLBM)多速格子Boltzmann模型是等温LBM模型的直接推广，其密度、速度、内能等均由速度分布函数的各阶速度矩得到.Qian［6］基于等温LBGK模型，提出了D1Q5，D2Q13，D3Q21，D3Q25热力学LBGK模型.在这些模型中，除了要满足等温模型的守恒条件外，还应满足能量守恒和平衡态热通量为0的条件：平衡态分布函数是Maxwell分布的截断形式：式中，Ap，Bp，Dp为待定参数，由满足的守恒条件确定.平衡态包含了速度的三阶项，离散速度也在D2Q9的基础上在主坐标轴上增加了4个速度.Qian［6］采用此模型对一维激波管、二维 Rayleigh-Benard对流进行了模拟，证明了该模型的有效性.MSLBM具有良好的物理基础，宏观方程绝对耦合，已成功模拟了一些传热现象，但只能模拟狭窄的温度范围和较小的Ma数，存在稳定性问题，限制了该模型的广泛应用.2.2 熵格子Boltzmann方法(ELBM)熵格子Boltzmann方法考虑了H定理，通过在守恒约束下最小化波尔兹曼H函数求解平衡态分布函数，由此得出的正定的分布函数保证了模型的稳定性和准确性［11］.Prasianakis等［10］将ELBM拓展到热流动问题的求解中，证实了该方法的有效性，本研究参照此方法.H函数定义为平衡态分布函数则是在满足守恒约束条件：的情况下，求H函数最小值得到的，具体形式详见文献［10］.Prasianakis等［12］采用在ELBM中加入高阶量的补偿算法，较大地提高了基于D2Q9标准格子的ELBM可模拟的温差和Ma数，但是模型实施较为复杂.2.3 双分布函数模型双分布函数模型，即存在两个分布函数：密度分布函数和内能(温度或总能)分布函数，其中密度分布函数用于模拟速度场，而内能(温度或总能)分布函数则用来模拟温度场.温度、内能或总能分布函数均通过不同的方式构造，但其演化都独立于密度分布函数.2.3.1 被动标量格子Boltzmann模型(PSLBM)被动标量格子Boltzmann模型基于如下原理：在忽略压力做的功和粘性热耗散的情况下，温度可以看作是随流体运动的一个标量，遵循对流扩散方程.由于此方程与组分浓度场的控制方程一样，于是Shan［7］提出使用两组分模型模拟单组分热流动问题：组分1模拟流体的运动;组分2模拟被动的温度场.平衡态密度函数为式中，σ表示组分，两组分共享速度，2.3.2 内能双分布函数模型内能双分布函数模型最早由He等［8］提出，其速度场仍用密度分布函数演化模拟，温度场则由内能分布函数模拟.该模型的基本思想是通过对连续Boltzmann方程进行特殊的离散得到等温LBM，如果进行同样的操作，则热LBM可以由离散内能的演化方程得到.根据内能的定义ρε=∫(ξ－u)2/2f dξ，引入内能分布函数g(r，ξ，t)=(ξ－u)2f/2，并引入新的碰撞模型，得到内能分布函数满足的演化方程：式中，q=(ξ－u)·［∂tu+(ξ·)u］.然后对演化方程离散，得到可用于数值计算的离散的分布演化方程，具体的离散过程详见文献［8］.相比于PSLBM，内能DDF的构造更具有物理基础，并包含了粘性热耗散和可压缩功.相比于MSLBM，DDF模型具有更好的数值稳定性，Pr数不受限制，因此被广泛用于各种近似不可压流体流动与传热问题.2.4 混合热格子Boltzmann模型(HTLBM)HTLBM是指使用 LBM解速度场，使用传统CFD解温度场，并通过一定的方式相互影响.这种方法利用了LBM能简单处理复杂流动问题的优势以及传统CFD在传热问题上的成熟技术，可以处理一些仅仅使用传统CFD较难解决的复杂流动传热问题.最初，Lallemand等［13］将多速多松弛模型和有限差分法(finite difference method，FDM)相结合，提出了混合模型，速度场用多松弛LBM求解，温度场采用FDM求解.本研究采用有限容积法(finite volume method，FVM)与LBM相结合的混合方法，即采用如下的FVM求解能量守恒方程：式中，S为广义源项，包括压力做的功和粘性热耗散.速度场与温度场的耦合通过在LBM中添加温度相关的外力项以及在FVM中添加广义源项S来实现.此外，普朗特数、比热容等热物性以及随温度变化的输运系数可以实现相应的调节.本研究中FVM与LBM采用同一套网格系统，FVM采用绝对稳定且具有与LBM相同精度的二阶迎风格式(second-order upwind scheme，SUS).PSLBM，DDF以及HTLBM这类模型的一个关键之处在于流场与温度场之间的耦合，其模型往往不满足气体完全状态方程，温度场对速度场的影响只是通过施加一个外力来实现.如Guo等［9］针对Boussinesq方程组，通过在密度分布函数演化方程中增加一个外力项以实现温度对流场的影响.Filippova等［14］基于HTLBM研究了小Ma数下高温燃烧，用温度场修正密度场以满足状态方程.3 计算结果及分析为了进一步对比各类模型，本研究采用ELBM，PSLBM，内能DDF模型以及HTLBM，对热Couette流、封闭方腔自然对流和多孔介质内非等温流动等问题进行了模拟对比.3.1 热Couette流模拟考虑两平板间热Couette流，上平板以速度U向右运动，下板静止，且上下平板分别保持恒温Th，Tc，且Th＞Tc.横截面温度廓线的解析形式为式中，H为平板间距离，Pr=ν/χ为普朗特数，χ为热扩散系数，Ec=U2/［Cp(Th －Tc)］为埃克特数.热Couette流中不考虑流体可压缩性的影响，而粘性耗散效应明显，因而分别运用ELBM，内能DDF模型和HTLBM对该问题进行了模拟，网格数均为64×64.模拟中Re=UH/ν=20，计算结果如图1所示.固定Pr=4，Ec分别为1，10和20的无量纲温度廓线，散点为不同方法的计算值，曲线为解析解公式(10).由图可见，三种模型都成功模拟了粘性耗散效应，且与解析解吻合得很好.本工作进一步研究了三种模型的计算效率问题.图2给出了温度残差随CPU时间的变化曲线，可见ELBM和HTLBM明显优于内能DDF模型.3.2 封闭方腔自然对流模拟封闭方腔尺寸为H(正方形边长)，左右壁面分别保持恒温Th，Tc，且Th＞Tc，上下壁面绝热，四壁面速度均为无滑移边界.方腔内充满均质空气，考虑向下的重力.描述自然对流的无量纲参数Ra数定义为图1 热Couette流温度廓线Fig.1 Temperature variation of the thermal Couette flow图2 热Couette流温度残差变化曲线Fig.2 Temperature residuals variation of the thermal Couette flow式中，β为热膨胀系数.物性满足Boussinesq假设，这里通过施加外力G=－β(T－T0)g实现温度场对速度场的影响.在方腔自然对流中，可压缩效应以及粘性耗散效应可忽略不计.从模型分析可以看出，PSLBM在这种情况下与DDF模型类似，而ELBM边界实施较为复杂.因此，本研究分别采用不包含粘性耗散效应的PSLBM和HTLBM对该问题进行了模拟，模拟中Pr=0.71，Ra数分别为104，105和106.图3和图4分别为HTLBM在不同Ra数下流动稳定后得到的流线、等温线，与以往的数值及实验结果一致.由图3可见，随着Ra数的增大，方腔中心的近似圆形的涡逐渐变成椭圆形，进而分裂成两个涡.当Ra= 106时，两个涡分别向左右壁面移动，在中心出现了第三个涡.由图4可见，随着Ra数的增大，竖直的等温线逐渐变得水平，主导的传热机理由导热变为对流.为了进一步定量考核，本研究计算了努塞尔数Nu和平均努塞尔数 Numean.表1给出了热壁面的Numean、最大Nu数Numax及相应位置的yNumax、水平中心线上最大速度vmax及相应的位置x、垂直中心线上最大速度umax以及相应的位置y.HTLBM和PSLBM求解的结果与Barakos等［15］的基准解一致.同样，本研究对HTLBM和PSLBM的计算效率进行了对比，图5所示为两种方法模拟自然方腔对流Ra=105时，速度残差随CPU时间的变化曲线.可以明显看出，两种方法中残差均呈现震荡下降趋势，且HTLBM收敛快于PSLBM，HTLBM残差收敛到10－7以下时的耗时为PSLBM的57%.图3 方腔自然对流不同Ra数的流线Fig.3 Predicted streamlines of natural convection图4 方腔自然对流不同Ra数的等温线Fig.4 Predicted temperature profiles of natural convection表1 数值解与基准解对比Table 1 Comparison of numerical results between thermal models and benchmarksRa数模型 Numean Numax(y/H) umax(y/H) vmax(x/H) PSLBM 2.247 3.538(0.141) 0.194(0.824) 0.234(0.121) Ra=104 HTLBM 2.242 3.553(0.145) 0.194(0.824) 0.234(0.121) Barakos等［16］2.2453.539(0.143) 0.193(0.818) 0.234(0.119) PSLBM4.512 7.827(0.075)0.128(0.854) 0.256(0.065) Ra=105 HTLBM 4.507 7.723(0.085) 0.134(0.854) 0.260(0.065) Barakos等［16］ 4.510 7.636(0.085) 0.132(0.859) 0.258(0.066) PSLBM 8.809 17.454(0.033) 0.079(0.852) 0.261(0.037) Ra=106 HTLBM 8.792 17.435(0.040) 0.081(0.854) 0.263(0.040) Barakos等［16］ 8.80617.442(0.037) 0.077(0.859) 0.262(0.039)图5 方腔自然对流速度残差变化曲线Fig.5 Velocity residuals variation of thenatural convection3.3 多孔介质非等温流动模拟多孔介质内部结构十分复杂，其流动传热现象也相当复杂.格子Boltzmann方法在模拟孔隙内的流体运动时可以方便地使用反弹格式处理复杂流场，因此，该方法在孔隙尺度模拟多孔介质内部复杂流动上有明显的优势及较高的计算率.对于多孔介质内流动与传热的问题，以往使用比较广泛的是PSLBM和内能DDF模型.本研究将HTLBM用于多孔介质流动与传热分析中，并与PSLBM进行了对比.本研究分析了分形多孔介质中的自然对流，分形结构采用Sierpinski地毯，依次对分形等级N=2和3的Sierpinski情况进行了模拟.无量纲控制参数Pr=0.71，Ra数分别为104，105和106，固体区域温度保持线性温度分布.图6为采用HTLBM计算N= 2分形结构内自然对流得到的流线图，图7为相应的等温线.由图可见，模拟结果与PSLBM一致，随Ra数的逐步增大，传热机理由导热主导变化为对流主导.图8为N=3，Ra=106时的流线图及等温线.由图可见，固体的增多明显地抑制了对流作用.同样对HTLBM在计算效率的问题上和PSLBM进行了对比.图9为Ra=106时两种方法模拟N=2分形结构时的速度残差曲线，此时HTLBM耗时为PSLBM的76%，仍具有优势.图6 多孔介质方腔自然对流流线(N=2)Fig.6 Predicted streamlines of porous cavity(N=2)图7 多孔介质方腔自然对流等温线(N=2)Fig.7 Predicted temperature profiles of porous cavity(N=2)图8 多孔介质方腔自然对流流线及等温线(N=3)Fig.8 Predicted streamlines and temperature profiles of porous cavity(N=3)4 结论本研究简要介绍了几种热格子Boltzmann模型(MSLBM，ELBM，PSLBM，内能DDF模型及HTLBM)，并运用不同热格子模型求解了两个典型算例以及多孔介质流动传热问题，得到如下结论.图9 多孔方腔自然速度残差变化曲线Fig.9 Velocity residuals variation of porous cavity(1)速度场温度场耦合求解的模型还需要进一步发展才能被广泛应用.(2)相比于PSLBM和DDF模型，HTLBM在保证计算精度的前提下，具有较高的计算效率.(3)数值模拟验证了HTLBM在处理多孔介质复杂结构时可行、有效，且比PSLBM 的效率高.参考文献：［1］ QIANY H，D’HUMIERESD，ttice BGK models for Navier-Stokes equation ［J］.Europhysics Letters，1992，17(6)：479-484. ［2］ QIANY H，SUCCIS，ORSZAGS A.Recent advances in lattice Boltzmann computing［M］∥ DIETRICH S.Annual reviews of computational physicsⅢ.New J ersey：World Scientific Publishing Company，1995：195-224.［3］ ZHAOC Y，DAIL N，TANGG H，et al.Numerical study of natural convection in porous media(metals) using lattice Boltzmann method (LBM) ［J］.International Journal of Heat and Fluid Flow，2010，31 (5)：925-934. ［4］严永华，石自媛，杨帆.液滴撞击液膜喷溅过程的LBM模拟［J］.上海大学学报：自然科学版，2008，14(4)：399-404.［5］李青，徐旭峰，周美莲.三维斑图形成的格子Boltzmann方法模拟［J］.上海大学学报：自然科学版，2007，13(5)：516-518.［6］ QIANY H.Simulating thermohydrodynamics with lattice BGK models ［J］.Journal of Scientific Computing，1993，8(3)：231-242.［7］ SHANX.Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method［J］.Physical Review E，1997，55(3)：2780-2788. ［8］ HEX，CHENS，DOOLENG D.A novel thermal model for the latticeBoltzmann method in incompressible limit［J］.Journal of Computational Physics，1998，146 (1)：282-300.［9］ GUOZ，ZHENGC，SHIB，et al.Thermal lattice Boltzmann equationfor low Mach number flows：Decoupling model［J］.Physical Review E，2007，75 (3)：036704.［10］ PRASIANAKISN I，CHIKATAMALAS S，KARLINI V，et al.Entropic lattice Boltzmann method for simulation of thermal flows［J］.Mathematics and Computers in Simulation，2006，72(2)：179-183. ［11］ ANSUMALIS，KARLINI V，OTTINGERH C.Minimal entropic kinetic models for hydrodynamics ［J］.Europhysics Letters，2003，63(6)：798-804.［12］ PRASIANAKISN I，KARLINI ttice Boltzmann method for simulation of compressible flows on standard lattices［J］.Physical Review E，2008，78(1)：016704.［13］ LALLEMANDP，LUO L S.Theoryofthelattice Boltzmann method：Acoustic and thermal properties in two and three dimensions［J］.Physical Review E，2003，68(3)：036706.［14］ FILLIPPOVAO，HANELlD.A novellatticeBGK approach for low Mach number combustion［J］.Journal of Computational Physics，2000，158(2)：139-160.［15］ BARAKOSG，MITSOULISE，ASSIMACOPOULOSD.Natural convection flow in a square cavity revisited：Laminar and turbulent models with wall functions［J］.International Journal for Numerical Methods in Fluids，1994，18(7)：695-719.。

lbm计算公式(一)

lbm计算公式(一)LBM计算公式1. 什么是LBM？LBM（Lattice Boltzmann Method）是一种计算流体力学的数值方法，用于模拟流体的运动和流动行为。

它基于格子空间的离散形式，通过碰撞和传播规则模拟分子的运动，可以用来解决包括流动、传热、传质等问题。

2. LBM计算公式LBM方法的核心是LBGK（Lattice Bhatnagar-Gross-Krook）模型，它基于Boltzmann方程的离散形式。

下面是LBM计算公式的一些常见表达方式：流场演化LBM方法通过迭代计算流场的演化过程，使用以下公式更新流场：f_i(x + c_i, t + Δt) = f_i(x, t) - Ω(f_i(x, t) - f_i^{eq}(x, t))其中，f_i表示流场在某个节点上第i个速度方向的分布函数，c_i是对应的格点速度，t表示时间，Δt是时间步长，Ω是碰撞操作的弛豫时间，f_i^{eq}是分布函数的平衡态。

通过不断迭代，流场的分布函数将收敛到平衡态。

分布函数的计算分布函数的平衡态可以根据宏观流场的速度和密度来计算，常见的计算公式如下：f_i^{eq}(x, t) = w_i ρ(x, t) (1 + 3e_i · u(x, t) +9/2 (e_i · u)^2 - 3/2 u^2(x, t))其中，w_i是一组权重系数，ρ表示密度，u表示速度，e_i是速度方向的系数。

该公式通过在速度方向上的加权和来计算分布函数的平衡态。

3. 举例说明为了更好地理解LBM的计算公式，我们举一个具体的例子来说明。

假设我们将流体放置在一个二维正方形的容器中，初始时流场分布如下图所示：流体初始分布：我们使用LBM方法计算流场演化，通过迭代得到流体的最终分布。

根据公式，我们可以将初始分布函数f_i(x, t)代入，计算出下一个时间步的分布函数f_i(x + c_i, t + Δt)。

假设我们取Δt = 1，并使用D2Q9模型（9个速度方向），那么可以得到更新后的流体分布如下图：流体更新分布：- -经过多次迭代，流体的分布函数会逐渐趋于平衡态，最终得到稳定的流场分布。

格子botlzmann方法的原理及应用

格子botlzmann方法的原理及应用格子Boltzmann方法（Lattice Boltzmann Method，简称LBM）是一种用于模拟流体流动的计算方法。

它基于Boltzmann方程，通过离散化空间和速度空间，采用微小时间步长进行离散时间演化，来模拟流体的宏观流动行为。

LBM 的基本原理是通过碰撞和迁移两个步骤来模拟流体的运动。

LBM的基本原理可由以下几个步骤来说明：1. 离散化空间：将空间划分为一系列离散的格点（或称为格子），每个格点上的物理量（如密度、速度）用一个分布函数表示。

2. 离散化速度：对于每个格点，为其附加一个速度分布，这个分布可能是以不同速度朝不同方向运动的分布。

常用的速度模型包括D2Q9和D3Q19等。

3. 碰撞：对于每个格点的速度分布函数，根据Boltzmann方程中的碰撞项，通过碰撞模型来更新速度分布函数，使其达到平衡态。

碰撞模型通常选取BGK碰撞模型。

4. 迁移：将每个格点的速度分布函数根据其相邻格点上的速度分布函数进行迁移，即将速度信息传递给相邻的格点。

通过重复以上步骤，LBM可以模拟流体在空间和时间上的演化，从而得到流体的宏观行为。

格子Boltzmann方法具有一些明显的优势和特点，因此在流体力学领域有广泛的应用：1. 并行计算优势：LBM的计算是基于格点的，因此在并行计算方面具有很大的优势，在大规模计算的流体模拟中有很高的效率。

2. 简化边界条件：LBM可以通过对网格设置不同的物理边界条件，如固壁、自由边界和入口出口等，来模拟不同的流场。

相比传统方法，LBM不需要进行边界条件的复杂推导和处理，简化了问题的求解。

3. 适用于复杂几何形状：由于LBM的离散特性，它对于复杂几何形状的模拟相对容易。

与传统有限元方法相比，LBM更适用于较复杂的流体流动领域，如多孔介质的渗流、微尺度流体等。

4. 多相流模拟：LBM在模拟多相流动中的应用也比较广泛。

通过添加适当的边界条件和相互作用模型，可以对液体、气体和固体等不同相之间的相互作用进行有效的模拟。

lbm玻尔兹曼方法

lbm玻尔兹曼方法
LBM（Lattice Boltzmann Method，玻尔兹曼方法）是一种基于流体动力学原理的计算流体力学方法。

它通过将流体分割为一系列小的空间单元，通过每个空间单元内的碰撞和传播过程来模拟流体的运动行为。

在LBM中，每个空间单元被称为格子，它包含了一系列分布函数，用来描述流体粒子在该格子中的分布情况。

在LBM中，流体的运动是通过离散的时间步进和空间步进来模拟的。

在每个时间步中，LBM通过碰撞和传播过程来更新每个格子内的分布函数。

碰撞过程模拟了流体粒子之间的相互作用，通过将分布函数经过碰撞算子处理得到新的分布函数。

传播过程模拟了流体粒子的运动，通过将分布函数按照一定的规则传递给相邻的格子。

LBM的优点之一是其并行计算的能力。

由于LBM的计算过程可以在每个格子上独立进行，因此可以方便地将计算任务分配给不同的处理器或计算单元，实现并行计算，提高计算效率。

这使得LBM在计算流体力学领域得到了广泛的应用。

LBM在流体力学领域有着广泛的应用。

它可以用来模拟各种流体的行为，包括理想气体、不可压缩流体和多相流体等。

在研究流体的宏观行为、流体的细观结构和流体与固体的相互作用等方面，LBM都具有一定的优势。

在实际应用中，LBM可以用来模拟流体力学问题，如流体流动、传热、气体扩散等。

通过调整格子的参数和边界条件，可以模拟不同的流体行为。

此外，LBM还可以结合其他方法，如有限元法和有限差
分法等，来解决更复杂的流体力学问题。

总之，LBM是一种有效的计算流体力学方法，可以用来模拟和预测流体的运动行为，具有广泛的应用前景。

MRTN微尺度算法延伸至TN微通道顶部RANS近似

MRTN微尺度算法延伸至TN微通道顶部RANS近似微通道是一种在微尺度下具有广泛应用的狭长通道，其尺寸在纳米至毫米级别之间。

由于其特殊的几何形状和尺寸特征，微通道内部的传质和传热行为与常规尺度下的流体流动存在巨大的差异。

因此，研究微通道内部的流动特性对于提高传质和传热效率具有重要意义。

为了实现对微通道内部纳米级流动的准确描述，德国科学家发展了基于多重反射散射的微尺度算法（MRTN），其准确性已经得到广泛认可。

然而，该算法仅适用于微尺度下的MRTN流动模型，并无法直接延伸至更大尺度的TN流动模型。

因此，在本文中，我们将讨论如何将MRTN算法延伸至TN微通道顶部的RANS近似。

传统的雷诺平均粘性应力（RANS）模型在对流体流动进行建模时，采用了局部平均的方式，即假设流动中的各个物理量在时间上平均分布，这被称为时均流动。

然而，当研究对象是微通道时，RANS模型的准确性受到了挑战。

这是因为微通道内部存在的纳米级流动现象无法被时均流动所描述。

为了解决这一问题，我们将使用MRTN算法对流动进行建模，并将其与RANS模型进行融合。

MRTN算法是一种能够准确描述微尺度下流体流动的方法，它基于多重反射散射的原理。

通过考虑流动的微观粒子运动和碰撞，MRTN算法能够精确计算出流动的速度、温度和浓度等物理量。

将MRTN算法延伸至TN微通道顶部的RANS近似的关键在于融合两种模型的优点。

首先，我们用MRTN算法预测微通道内部的流动行为，得到流速、温度和浓度等物理量的准确分布。

然后，将这些分布作为边界条件输入到RANS模型中，通过局部平均的方式计算整个流道的流动特性。

这种融合的方法充分考虑了微观和宏观尺度下的流动行为，提高了模型的精度。

在实际应用中，延伸至TN微通道顶部的RANS近似可以提供更准确的流量、温度和浓度等物理量预测。

这对于微通道的设计和优化具有重要意义。

例如，在微流控领域，研究者可以利用这一模型来优化微通道的结构，从而实现更高的传质效率和传热效率。

方腔驱动流源代码(SIMPLE算法)

p
pi, j
x 0
编号为（i,j）的速度修正量 u , v 不仅与压力修正量
p 有关，还与邻近点的速度修正
量有关。SIMPLE 算法的重要假定：速度的改变只与压力的改变有关，忽略邻近点对速度修正的影响。因而得到如下速度修正量
u i, j vi, j
本算例采用求解不可压缩流动的经典算法，即 SIMPLE 算法，求解方腔内粘性不可压缩流体运动的定常解。 SIMPLE 算法的全称为 Semi-Implicit Method for Pressure-Linked Equations，即求解压力关联方程的半隐式算法。采用 SIMPLE 算法时，为了避免中心差分格式将 “棋盘” 型参量分布误认为是均匀分布，需要用交错网格对计算域进行离散。
xy M 1 M 1 1 1 M 1 M 1 ui , j ui , j Fi ,1j Fi y 0 1, j y Gi , j Gi , j 1 x pi 1, j pi , j t

Y 方向动量方程在速度 v 控制体上离散，时间采用前差

1 2 2 xy 1 M M M M aiu, j y uiM x viM 1, j u i 1, j , j vi 1, j vi , j 1 vi 1, j 1 Re x Re y t 4 4

以上是 SIMPLE 算法中离散化的动量方程
三、SIMPLE 算法基本思想
SIMPLE 算法是一种解决压力-速度耦合问题的“半隐式”算法。首先给定 M 时刻猜测的速度场 u 估计值值u

水泥3D打印喷头内浆体流动的MRT-LBM分析

水泥3D打印喷头内浆体流动的MRT-LBM分析吴伟伟;黄筱调;方成刚;李媛媛【摘要】水泥3D打印时,水泥浆体在喷头内的流动性对挤出成型有重要影响.以水泥、水、聚羧酸减水剂、改性棒土和纤维素醚作为原始打印材料,根据流变特性测试,采用Herschel-Bulkley模型作为水泥浆体的流变模型,并利用多松弛时间的格子Boltzmann方法(MRT-LBM)对浆体在喷头中的流动进行了分析,引入矩函数来描述松弛过程中的碰撞步,并利用泊肃叶流的理论解对MRT模型进行了验证.在进行实际仿真时,以雷诺数作为准则进行物理单位和格子单位之间的转换,获得相关的流线图和速度场分布图.结果表明:水泥浆体在螺槽截面的流动呈现环流形状,环流的中心在(0. 5W,0. 7h)位置处;根据速度场的分布,在螺槽横截面的左下角和右下角不存在流体流动,适当增大螺杆速度或螺槽宽度有助于水泥浆体在螺槽内的有效输送.【期刊名称】《南京工业大学学报（自然科学版）》【年(卷),期】2018(040)005【总页数】6页(P79-84)【关键词】水泥3D打印;Herschel-Bulkley流体;多松弛时间的LBM;数值模拟;流线;速度分布【作者】吴伟伟;黄筱调;方成刚;李媛媛【作者单位】南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800【正文语种】中文【中图分类】TH12对浆体在喷头内部的流动进行分析,可以很好揭示其流动规律,流线图可以描述浆体在腔体中的主要流动区域和环流的形成,速度场分布图可以描述各速度分量沿不同方向的分布情况,速度较大的区域更有利于浆体的输送,速度较小的区域往往受黏性系数和机械结构的影响,因此合理的机械结构有助于浆体在喷头内部的流动。

lbm 三维松弛矩阵 -回复

lbm 三维松弛矩阵-回复什么是LBM三维松弛矩阵(Lattice Boltzmann Method, LBM)？LBM是一种基于格子的流体模拟方法。

它通过将流体体系离散为网格，并在每个网格点上进行微观粒子状态的更新，从而模拟流体的宏观行为。

LBM是一种计算效率较高、易于并行计算、适用于多尺度流动问题的模拟方法，因此在模拟微观流动、多孔介质流动、气液两相流等领域得到了广泛的应用。

三维松弛矩阵（Three-Dimensional Relaxation Matrix）是LBM中的一个关键元素，它用来描述微观粒子在碰撞过程中的动量传递和碰撞效应。

LBM的实质是通过碰撞和碰撞后的等效演化两个步骤模拟流体的宏观行为。

在碰撞过程中，LBM使用一个松弛时间τ来描述粒子在相邻节点之间的速度，该松弛时间决定了粒子在碰撞前后的速度变化情况。

三维松弛矩阵正是用于计算碰撞过程中速度的变化。

在LBM中，流体的宏观性质通过微观粒子的分布函数来表示，而分布函数则描述了粒子在不同速度下的分布情况。

三维松弛矩阵则用于更新分布函数，从而模拟粒子在碰撞过程中的速度变化。

三维松弛矩阵可以根据流体宏观性质的不同而有所不同。

以二维方向的速度分量为u、v、w的流体为例，三维松弛矩阵可以表示为一个9×9的矩阵。

矩阵的每一个元素对应了不同速度分量下的分布函数更新方式。

在流体模拟中，三维松弛矩阵的选择对模拟结果有着重要的影响。

通常情况下，矩阵中的元素需要满足一些条件，如守恒性、粒子数守恒性、稳定性等。

通过调整矩阵中的元素，可以实现对不同流体流动行为的模拟，比如对湍流、多相流等流动过程的模拟。

除了传统的三维松弛矩阵，还有一些拓展的矩阵形式被提出，如多松弛时间模型(Multiple Relaxation Times, MRT)和连续松弛时间模型(Continuous Relaxation Times, CRT)等。

这些模型在LBM的数值计算和模拟精度方面具有一定的优势。