2014上海各区模拟考中考数学压轴题1-14浦东24
2014上海中考数学模拟测试参考答案(2014.6)

2014年上海市初中毕业生统一学业考试模拟测试数学试卷参考答案 (2014.6)说明:1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;2.第一、二大题每题评分只有满分或零分;3.第三大题中各题右端所注分数,表示考生正确做到这一步可得到的分数; 4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原.则上不超过后继部分应得分数的一半................. 一、填空题(本大题共6题,每题4分,满分24分)1. B ;2. A ;3. A ;4. B ;5. C ;6. C . 二、选择题(本大题共12题,每题4分,满分48分)7.⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+23234x x ; 8.3->x ; 9.1-; 10.75; 11.︒1440; 12.1)2(22+-=x y ; 13.554或3148; 14.b a 6161+; 15.12; 16.213±; 17.如1-=k 等,不唯一; 18.()a 12±.三、解答题(本大题共7题,满分78分) 19.解:原式aba b a b a b b a +⋅-+-+=))((………………………………………………………(3分) ba -=1………………………………………………………………………(6分) 将2=a 、1=b 代入,上式12121+=-=……………………………(10分)20.解:1232322--=+-x x x x …………………………………………………………(2分) 0322=-+x x ……………………………………………………………………(3分) ()()0132=-+x x …………………………………………………………………(5分)解得:231-=x ,12=x …………………………………………………………(7分) 经检验,当1=x 时,方程无解,舍去……………………………………………(9分)故原方程的解为23-=x …………………………………………………………(10分) 21.解:(1)22……………………………………………………………………………(2分) (2) 过O 作AB OD ⊥、过C 作OB CE ⊥,D 、E 为垂足 由题意可知:︒=∠=∠45B A22)32(2222222=+⋅==∴AO OD ……………………………(3分))32,2(A 3232tan ==∠AOC ︒=∠︒=∠∴30,60COB AOC设x EB CE ==,则x EO 3=,x OB )13(+=4)13(=+∴x 解得)13(2-=x ………………………………………(4分) )13(42-==∴x OC426sin +==∠OC OD OCA ………………………………………………(5分) (3) 过A 、B 分别作x 轴的垂线,D 、E 为垂足;过O 作AB OF ⊥,F 为垂足 ︒=90AOB ︒=∠+∠∴90COB AOC 又︒=∠+∠90OAD AOC OAD COB ∠=∠∴易证BOE OAD ∆≅∆,m BE OD ==、n OE AD ==),(m n B -∴ ……………………………………………………………………(6分)因而可求得直线AB 解析式为n m nm x n m n m y -+-⎪⎭⎫ ⎝⎛-+=22…………………(7分) 令0=y 则n m n m x ++=22 即nm n m OC ++=22……………………………… (8分)又由(2)同理可得2222n m OF +⋅=)(2)()(2sin 2222n m n m n m OC OFOCA ++⋅+==∠∴……………………………(10分)22.证明:连接GE ;过A 作BC AH ⊥,H 为垂足 47103422=+⋅=+=BC AD S AH ABCD ,3=-=AD BC BH ……………………(2分)522=+=∴BH AH AB ……………………………………………………(3分) F 为AE 中点xyOABC DExyOABC DE FEF AF =∴易证EBF AGF ∆≅∆,BE AG =……………………………………………(4分) E 为BC 中点, AB BE ==∴5ABEG ∴为菱形,GBC ABG ∠=∠,︒=∠90BFE ……………………(6分) 又CE AG //且CE AG =AECG ∴为平行四边形,GC AE //……(7分) D BFE BGC ∠=︒=∠=∠∴90……(8分) GCB DGC ∠=∠CBG GCD ∠=∠∴…………(9分) GCD ABC ∠=∠∴2………(10分) 23.解:(1) 当100≤≤x 时,设函数解析式为)0(2≠++=a c bx ax y将点)20,0(、)39,5(、)48,10(代入⎪⎩⎪⎨⎧=+=+=28101001952520b a b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=2052451c b a20524512++-=∴x x y ……………………………………………………(1分) 当2010≤≤x 时,由于函数图像为平行于x 轴的线段,故函数解析式为48=y ………………………………………………………(2分)当20≥x 时,设函数解析式为)0(≠=k xky 将点)48,20(代入解得960=k xy 960=∴……………………………………………………………………(3分) 画图正确………………………………………………………………………(4分)(2) 将6=x 代入20524512++-=x x y ,解得5208=y ……………………(5分) 将25=x 代入x y 960=,解得5192=y ……………………………………(6分)51925208> 故第6分钟学生的听课注意力更集中………………………………………(8分)(3) 把36=y 代入20524512++-=x x y 解得41=x ,202=x (不符题意,舍去)……………………………………(9分)F ABCEGDH把36=y 代入x y 960= 解得380=x ……………………………………(10分) 243684380<=-∴…………………………………………………………(11分) 故老师无法经过适当的安排,从而能使学生在听这道题时的听课注意力指数都不 低于36.…………………………………………………………………………(12分)25.解:(1)ADEF的值保持不变,证明过程如下:………………………………………(1分) 【解法一】延长FO 、DB ,相交于点G BD AB = ,D A ∠=∠∴ 易证AFO RT ∆∽DFG RT ∆DGAODF AF =∴,G AOF ∠=∠……………………………………………(2分) 又BOG AOF ∠=∠,G BOG ∠=∠∴,5==BO BG ………………(3分)315105=+=+=∴BG DB AO DF AF 又由垂径定理可知EF AF =41=+=∴DF AF AF AD EF ,是定值…………………………………………(4分) 【解法二】连接OE 、BE OB OE AO ==AEO EAB ∠=∠∴、EBO OEB ∠=∠︒=∠+∠=∠∴90OEB AEO AEB …………………………………………(2分) 又BD AB =E ∴为AD 中点,ED AE =………………………………………………(3分) 由垂径定理可知EF AF =4142===∴EF EF AE EF AD EF ,是定值………………………………………(4分). OA BCF E DG. OABCFE D(2) 连接AC 、CE ,并过E 作CD EG ⊥,G 为垂足 由(1)同理可证︒=∠90ACD 又由(1)可知E 为AD 中点【注:若上述结论在(1)中未证明,则需在(2)中给予证明】ED AD CE ==∴21…………………………………………………………(5分) y CD DG 2121==∴…………………(6分) 易证AFO RT ∆∽DGE RT ∆AODEAF DG =∴………………(7分) 5221x x y=∴ 整理得254x y =……………(9分)(3) 若圆F 与圆D 相切,这里只存在外切的可能……………………………(10分) 若两圆外切,则DE DC =易证DCE ∆为等边三角形,︒=∠60DABD ∆∴也为等边三角形,10==BD AD ………………………………(11分)521===∴AD AE BC ……………………………………………………(12分) 故当50<<BC 时,圆F 与圆D 相交;…………………………………(13分) 当5=BC 时,圆F 与圆D 相切;当105<<BC 时,圆F 与圆D 相离.…………………………………(14分). OA BCF ED G。
上海市浦东新区2014届中考数学二模试题(扫描版)

上海市浦东新区2014届九年级中考二模数学试题(扫描版)浦东新区2014年中考预测 数学试卷参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分) 1.B ;2.D ;3.B ;4.C ;5.C ;6.D .二、填空题:(本大题共12题,每题4分,满分48分) 7.2; 8.51096.6⨯; 9.6x ; 10.增大; 11.31; 12.105; 13.4-; 14.150; 15.3; 16.π34; 17.36; 18.26-.三、解答题:(本大题共7题,满分78分)19.解:原式=33-23-1++…………………………………………………… (8分)=0.………………………………………………………………………(2分)20.解:原式()()21221622+-+---+=x x x x x ………………………………………(1分) ()()()()2221622+----+=x x x x ………………………………………………(2分)()()22216442+-+--++=x x x x x ……………………………………………(2分)()()221032+--+=x x x x …………………………………………………………(1分)()()()()2225+--+=x x x x …………………………………………………………(1分)25++=x x .………………………………………………………………(1分)当23-=x 时,原式31333+=+=.………………………………(2分)21.解:(1)∵△ABE ≌△ADE ,∴∠BAE =∠CAF .∵∠B =∠FCA ,∴△ABE ∽△ACF .…………………………………(2分) ∴ACAB CF BE =.…………………………………………………………(1分) ∵AB =5,AC =9,∴95=CF BE .…………………………………………(2分)(2)∵△ABE ∽△ACF ,∴∠AEB =∠F .∵∠AEB =∠CEF ,∴∠CEF =∠F .∴CE =CF .……………………(1分) ∵△ABE ≌△ADE ,∴∠B =∠ADE ,BE =DE .∵∠ADE =∠ACE+∠DEC ,∠B =2∠ACE ,∴∠ACE =∠DEC .∴CD =DE =BE =4.………………………………………………………(2分)∵95=CF BE ,∴95=CE CD .∴536=CE .……………………………………………………………(2分)22.解:(1)根据题意,可设降价前y 关于x 的函数解析式为b kx y +=(0≠k ).…………………………………………………(1分)将()50,0,()200,30代入得⎩⎨⎧=+=.20030,50b k b …………………………(2分)解得⎩⎨⎧==.50,5b k ……………………………………………………………(1分)∴505+=x y .(300≤≤x )…………………………………(1分,1分)(2)设一共准备了a 张卡片.………………………………………………(1分) 根据题意,可得()28030%80530550=-⨯⨯+⨯+a .………………(2分) 解得50=a .答:一共准备了50张卡片.……………………………………………(1分)23.证明:(1)∵四边形ABCD 是平行四边形,∴AB ∥CD 且AB =CD .…………(2分) ∵点M 、N 分别是边CD 、AB 的中点, ∴CD CM 21=,AB AN 21=.………………………………………(1分)∴AN CM =.…………………………………………………………(1分) 又∵AB ∥CD ,∴四边形ANCM 是平行四边形.……………………(1分) ∴AM ∥CN .……………………………………………………………(1分)(2)将CN 与BH 的交点记为E .∵BH ⊥AM ,∴∠AHB =90 º.∵AM ∥CN ,∴∠NEB =∠AHB =90 º.即CE ⊥HB .………………(2分) ∵AM ∥CN ,∴EHEBAN BN =.………………………………………(2分) ∵点N 是AB 边的中点,∴AN =BN .∴EB =EH .…………………(1分) ∴CE 是BH 的中垂线.∴CH =CB .………………………………(1分) 即△BCH 是等腰三角形.(1)∵A (2,0),∴2=OA .∵OA OB 21=,∴1=OB . ∵点B 在y 轴正半轴上,∴B (0,1).……(1分) 根据题意画出图形. 过点C 作CH ⊥x 轴于点H ,可得Rt △BOA ≌Rt △AHC .可得1=AH ,2=CH .∴C (3,2).……………………………………………………………………(2分) (2)∵点B (0,1)和点C (3,2)在抛物线c bx x y ++-=265上. ∴⎪⎩⎪⎨⎧=++⨯-=.23965,1c b c 解得⎪⎩⎪⎨⎧==.1,617c b …………………………………………(3分) ∴该抛物线的表达式为1617652++-=x x y .………………………………(1分) (3)存在.……………………………………………………………………………(1分)设以AC 为直角边的等腰直角三角形的另一个顶点P 的坐标为(x ,y ). (ⅰ) 90=∠PAC ,AC =AP .过点P 作PQ ⊥x 轴于点Q , 可得Rt △QPA ≌Rt △HAC .∴1P (4,-1).(另一点与点B (0,1)重合,舍去).…………………………………………(1分) (ⅱ) 90=∠PCA ,AC =PC .过点P 作PQ 垂直于直线2=y ,垂足为点Q , 可得Rt △QPC ≌Rt △HAC .∴2P (1,3),3P (5,1).……………………………………………………(1分)∵1P 、2P 、3P 三点中,可知1P 、2P 在抛物线c bx x y ++-=265上.……………(1分)∴1P 、2P 即为符合条件的D 点.∴D 点坐标为(4,-1)或(1,3).…………………………………………………(1分)(1)联结OB .在Rt △ABC 中,90=∠C , 4=BC ,21tan =∠CAB , ∴AC =8.………………………………(1分) 设x OB =,则x OC -8=. 在Rt △OBC 中, 90=∠C ,∴()22248+-=x x .……………………………………………………………(2分) 解得5=x ,即⊙O 的半径为5.………………………………………………(1分)(2)过点O 作OH ⊥AD 于点H . ∵OH 过圆心,且OH ⊥AD .∴x AP AH 2121==.………………………(1分)在Rt △AOH 中,可得22AH AO OH -=即210042522x x OH -=-=.…………(1分) 在△AOH 和△ACD 中,OHA C ∠=∠,CAD HAO ∠=∠,∴△AOH ∽△ADC .……………………(1分) ∴ACAH CD OH =.即8242-1002xy x =+. 得410082--=xx y .………………………………………………………(1分) 定义域为540<<x .…………………………………………………………(1分)(3)∵P 是AB 的中点,∴AP =BP .∵AO =BO ,∴PO 垂直平分AB .设α=∠CAB ,可求得α=∠ABO ,α2=∠COB ,α290-=∠ OBC ,α-=∠ 90AOP ,α+=∠ 90ABD ,α+=∠=∠ 902APO APB . ∴APB ABD ∠=∠.∴△ABP ∽△ABD .…………………………(1分) ∴ABD ABP S S ∆∆2⎪⎭⎫ ⎝⎛=AB AP .………………………(1分) D ABP ∠=∠.由AP =BP 可得PAB ABP ∠=∠. ∴D PAB ∠=∠.∴54==AB BD ,即54=y .…………(1分)由410082--=xx y 可得510502-=x ,即510502-=AP .………(1分) ABD ABP S S ∆∆85580510502-=-=⎪⎭⎫ ⎝⎛=AB AP .……………………………………(1分)。
2014上海各区模拟考中考数学压轴题1-14杨浦24

例 2014年上海市杨浦区中考模拟第24题已知抛物线y =ax 2-2ax -4与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴交于点C ,△ABC 的面积为12.(1)求抛物线的对称轴及表达式;(2)若点P 在x 轴上方的抛物线上,且tan ∠PAB =21,求点P 的坐标; (3)在(2)的条件下,过C 作射线交线段AP 于点E ,使得tan ∠BCE =21,联结BE ,试问BE 与BC 是否垂直?请通过计算说明.满分解答(1)由y =ax 2-2ax -4,得C (0,-4),对称轴为直线x =1.所以OC =4. 如图1,由S △ABC =12AB OC ⋅=12,得AB =6. 由直线x =1垂直平分AB ,得A (-2, 0),B (4,0). 将B (4,0)代入y =ax 2-2ax -4,得12a =. 所以抛物线的表达式为1(2)(4)2y x x =+-2142x x =--. (2)如图2,作PH ⊥x 轴于H ,设1(,(2)(4))2P x x x +-. 由1tan 2PH PAB AH ∠==,得1(2)(4)1222x x x +-=+. 解得x =5.所以7(5,)2P .图1 图2(3)如图3,由tan ∠P AB =tan ∠ACO =tan ∠ECB =12,知∠PAB =∠ACO =∠ECB . 由∠PAB =∠ACO ,可得∠PAC =90°.由∠ACO =∠ECB ,可得∠ACE =∠BCO =45°.所以△ACE 是等腰直角三角形.因此△EMA ≌△ANC .所以EM =AN =4,MA =NC =2.所以E (2, 2).由B (4,0),C (0,-4),E (2, 2),可得CE 2=40,BC 2=32,CE 2=8.因此CE 2=BC 2+CE 2.所以∠EBC =90°.所以BE ⊥BC .【解法二】如图4,由A (-2, 0),B (4,0),C (0,-4),E (2, 2),可得CA =4CO =,CE =CB =由42CA CO ==,2CE CB ==,得CA CE CO CB=. 又因为∠ACO =∠ECB ,所以△ACO ∽△ECB .因此∠AOC =∠EBC =90°.所以BE ⊥BC .图3 图4【解法三】由△ACE 和△OCB 都是等腰直角三角形, 可得CA CE CO CB=.又因为∠ACO =∠ECB ,所以△ACO ∽△ECB . 因此∠AOC =∠EBC =90°.所以BE ⊥BC .【解法四】如图5,设CE 的中点为Q .由C (0,-4),E (2, 2),可得Q (1,-1),CE =由B (4,0),Q (1,-1),可得QB =因此QC =QE =QB .由此可得∠EBC =90°.【解法六】如图6,由∠EAB =∠ECB ,可知A 、C 、B 、E 四点共圆. 所以∠EBA =∠ECA =45°(如图7).所以∠EBC =∠EBA +∠CBA =90°.图5 图6 图7。
2014年上海市浦东新区中考数学一模试卷

2014年上海市浦东新区中考数学一模试卷一、选择题(每题3分,共18分)1.在Rt△ABC中,∠C=90°,如果∠A=α,BC=a,那么AC等于()A.a•tanαB.a•cotαC.D.【考点】锐角的三角比的概念(M361).【难度】简单题【分析】做出简图,观察已知边、角位置,最终由锐角三角函数的定义求解。
cot∠A=,∴AC=BC•cotA=a•cotA,故选B.【解答】B【点评】本题考查了考生对锐角三角函数概念的理解、应用能力,解答本题的关键是考生能够准确而迅速的进行计算。
2.如果抛物线y=mx2+(m﹣3)x﹣m+2经过原点,那么m的值等于()A.0 B.1 C.2 D.3【考点】用待定系数法求函数关系式(M414).【难度】简单题【分析】把原点坐标代入函数解析式,求出m值.∵抛物线y=mx2+(m﹣3)x﹣m+2经过原点,∴﹣m+2=0,解得m=2.故选C.【解答】C【点评】本题考查了考生利用待定系数法确定函数关系式的能力,解答本题的关键是考生能够准确而迅速的进行计算。
3.如图,已知平行四边形ABCD中,向量在,方向上的分量分别是()A. B. C.、D.、【考点】向量的加法与减法(M382).【难度】简单题【分析】∵四边形ABCD是平行四边形,∴由平行四边形法则求解即可求得答案.∵向量在,方向上的分量分别是:﹣,.故选C【解答】C【点评】此题考查了平面向量运算法则的知识.难度适中,解答本题的关键是注意对平行四边形法则的应用,并熟练掌握数形结合的思想.4.抛物线y=﹣(x﹣2)2+1经过平移后与抛物线y=﹣(x+1)2﹣2重合,那么平移的方法可以是()A.向左平移3个单位再向下平移3个单位B.向左平移3个单位再向上平移3个单位C.向右平移3个单位再向下平移3个单位D.向右平移3个单位再向上平移3个单位【考点】二次函数的图象、性质(M442).【难度】简单题【分析】总的方针是根据平移前后的抛物线的顶点坐标确定平移方法即可得解.∵抛物线y=﹣(x﹣2)2+1的顶点坐标为(2,1),抛物线y=﹣(x+1)2﹣2的顶点坐标为(﹣1,﹣2),∴顶点由(2,1)到(﹣1,﹣2)需要向左平移3个单位再向下平移3个单位.故选A.【解答】A【点评】本题侧重考查了考生对二次函数图象与几何变换的理解,解答本题的关键是利用顶点的变化确定抛物线的平移方式.当然考生也可以按照“左加右减,上加下减”的口诀来解答本题.5.在△ABC,点D、E分别在边AB、AC上,如果AD=1,BD=2,那么由下列条件能够判定DE∥BC的是()A.B.C.D.【考点】平行线分线段成比例定理(M33I)相似三角形性质、判定(M33M).【难度】简单题【分析】∵AD=1,BD=2,∴=,只有当=时,DE∥BC,理由是:∵==,∠A=∠A,∴△ADE∽△ABC,∴∠ADE=∠B,∴DE∥BC,故选D.【解答】D【点评】本题主要综合考查了考生对相似三角形的性质和判定与平行线的判定的应用能力与逻辑推理能力,解答本题的关键是考生对平面几何知识的灵活运用。
2014上海各区模拟考中考数学压轴题1-14虹口24
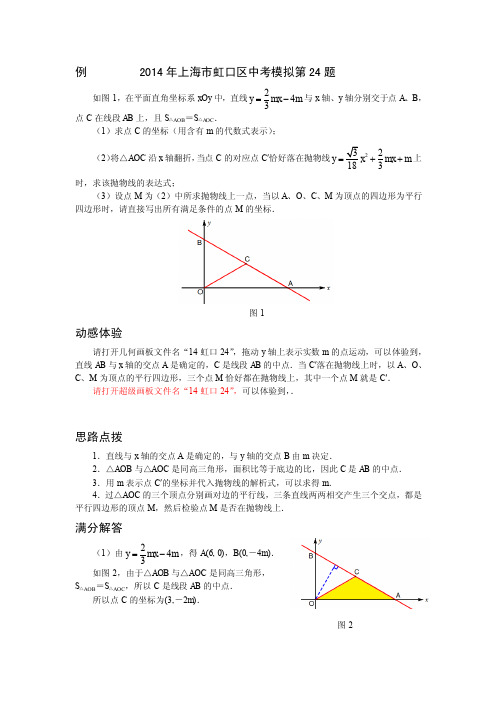
例 2014年上海市虹口区中考模拟第24题如图1,在平面直角坐标系xOy 中,直线243y mx m =-与x 轴、y 轴分别交于点A 、B ,点C 在线段AB 上,且S △AOB =S △AOC .(1)求点C 的坐标(用含有m 的代数式表示);(2)将△AOC 沿x 轴翻折,当点C 的对应点C ′恰好落在抛物线22183y x mx m =++上时,求该抛物线的表达式;(3)设点M 为(2)中所求抛物线上一点,当以A 、O 、C 、M 为顶点的四边形为平行四边形时,请直接写出所有满足条件的点M 的坐标.图1动感体验请打开几何画板文件名“14虹口24”,拖动y 轴上表示实数m 的点运动,可以体验到,直线AB 与x 轴的交点A 是确定的,C 是线段AB 的中点.当C ′落在抛物线上时,以A 、O 、C 、M 为顶点的平行四边形,三个点M 恰好都在抛物线上,其中一个点M 就是C ′. 请打开超级画板文件名“14虹口24”,可以体验到,.思路点拨1.直线与x 轴的交点A 是确定的,与y 轴的交点B 由m 决定.2.△AOB 与△AOC 是同高三角形,面积比等于底边的比,因此C 是AB 的中点.3.用m 表示点C ′的坐标并代入抛物线的解析式,可以求得m .4.过△AOC 的三个顶点分别画对边的平行线,三条直线两两相交产生三个交点,都是平行四边形的顶点M ,然后检验点M 是否在抛物线上.满分解答(1)由243y mx m =-,得A (6, 0),B (0,-4m ). 如图2,由于△AOB 与△AOC 是同高三角形,S △AOB =S △AOC ,所以C 是线段AB 的中点.所以点C 的坐标为(3,-2m ).图2(2)将C ′(3, 2m )代入223y x mx m =++,得22m m m =+.解得m =.所以抛物线的表达式为2y x x =.(3)满足条件的点M 的坐标是(3,、(-、,如图3所示. 考点伸展第(3)题的解题思路是这样的:如图3,因为A (6, 0)、O (0, 0)、C 是确定的,过△AOC 的三个顶点分别画对边的平行线,三条直线两两相交产生三个交点,都是平行四边形的顶点M .①点O (0, 0)向右平移6个单位得到点 A (6, 0),所以点C 向右平移6个单位得到点;②点A (6, 0)左平移6个单位得到点O (0, 0),所以点C 向左平移6个单位得到点(-;③点C ′(3,也是平行四边形的一个顶点.经检验,、(-、(3,三个点都在抛物线2(69)18y x x =--上.图3。
2014上海各区模拟考中考数学压轴题1-14静安24

例 2014年上海市静安区中考模拟第24题已知⊙O 的半径为3,⊙P 与⊙O 相切于点A ,经过点A 的直线与⊙O 、⊙P 分别交于点B 、C ,cos ∠BAO =13.设⊙P 的半径为x ,线段OC 的长为y .(1)求AB 的长;(2)如图1,当⊙P 与⊙O 外切时,求y 与x之间的函数关系式,并写出函数的定义域;(3)当∠OCA =∠OPC 时,求⊙P 的半径.图1 动感体验请打开几何画板文件名“14静安24”,拖动圆心P 运动,可以体验到,△OAB 与△PAC 保持相似,∠OCA 的大小保持不变.两圆外切和内切,各存在一次∠OPC =∠OCA .从图像中可以体验到,当两圆外切时,y 随x 的增大而增大.请打开超级画板文件名“14静安24”,可以体验到,.思路点拨1.第(1)题求弦AB 的长,自然想到垂径定理或三线合一.2.第(2)题构造直角三角形,使得y 成为斜边长,再用勾股定理.3.第(2)题两圆外切可以直接用第(2)的结论,两圆内切再具体分析.4.不论两圆外切还是内切,两个等腰△OAB 与△P AC 相似.满分解答(1)如图2,作OE ⊥AB ,垂足为E ,由垂径定理,得AB =2AE .在Rt △AOE 中,cos ∠BAO =13AE AO =,AO =3,所以AE =1.所以AB =2. (2)如图2,作CH ⊥AP ,垂足为H .由△OAB ∽△PAC ,得AO AP AB AC =.所以32x AC =.所以23AC x =.在Rt △ACH 中,由cos ∠CAH =13,得13AH AC CH ==.所以1239AH AC x ==,39CH AC x ==.在Rt △OCH 中,由OC 2=OH 2+CH 2,得2222)(3)9y x x =++.整理,得y =x >0.图2 图3(3)①如图3,当⊙P 与⊙O 外切时,如果∠OCA =∠OPC ,那么△OCA ∽△OPC . 因此OA OC OC OP=.所以2OC OA OP =⋅. 解方程236493(3)813x x x ++=+,得154x =.此时⊙P 的半径为154. ②如图4,图5,当⊙P 与⊙O 内切时,同样的△OAB ∽△P AC ,23AC x =. 如图5,图6,如果∠OCA =∠OPC ,那么△ACO ∽△APC . 所以AO AC AC AP=.因此2AC AO AP =⋅. 解方程22()33x x =,得274x =.此时⊙P 的半径为274.图4 图5 图6考点伸展第(3)②题也可以这样思考:如图4,图5,图6,当∠OCA =∠OPC 时,3个等腰三角形△OAB 、△PAC 、△CAO 都相似,每个三角形的三边比是3∶3∶2.这样,△CAO 的三边长为92,92,3.△PAC 的三边长为274,274,92.。
上海市初三数学一、二模考24.25压轴题收集
(3)在抛物线对称轴的右侧部分上是否存在一点P,使得
△PDC是等腰三角形?如果存在,求出符合条件的点P的坐标;如果不存在,请说明理由.
25.(本题共3小题,第(1)小题4分,第(2)、(3)小题每小题5分,满分14分)
如图,在△ABC中,AB=BC=5,AC= 6,BO⊥AC,垂足为点O.过点A作射线AE//BC,点P是边BC上任意一点,联结PO并延长与射线AE相交于点Q,设B、P两点间的距离为x.
(1)试问线段BE与OE的长度关系如何?并说明理由;
(2)当△CEF是等腰直角三角形时,求线段BE的长;
(3)设BE=x,CF=y,试求y关于x的函数解析式,并写出函数定义域.
(图8) (图9)
静安24.(本题满分12分,第(1)小题6分,第(2)小题6分)
如图,二次函数图像的顶点为坐标原点O、且经过点A(3,3),一次函数的图像经过点A和点B(6,0).
(1)求证:MN∶NP为定值;
(2)若△BNP与△MNA相似,求CM的长;
(3)若△BNP是等腰三角形,求CM的长.
宝山24.(本题满分12分,共3小题,每小题满分各4分)
如图8,已知点A(-2,4)和点B(1,0)都在抛物线 上.
(1)求 、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形
使得⊙P同时与⊙O和射线BA相切,
求所有满足条件的⊙P的半径.
虹口24.(本题满分12分,第(1)小题满分5分,第(2)小题满分4分,第(3)小题满分3分)
已知等腰 在平面直角坐标系中的位置如图9,点 坐标为 ,点 坐标为 .
(1)若将 沿 轴向左平移 个单位,此时点 恰好落在反比例函数 的图像上,求 的值;
2014上海各区模拟考中考数学压轴题1-14浦东25

2014 年上海市浦东新区中考模拟第 25 题
如图 1,已知在△ABC 中,AB=AC,BC 比 AB 大 3,sinB= 4 ,点 G 是△ABC 的重心, 5
AG 的延长线交边 BC 于点 D.过点 G 的直线分别交边 AB 于点 P、交射线 AC 于点 Q.
(1)求 AG 的长;
(2)当∠APQ=90°时,直线 PQ 与边 BC 相交于点 M,求 AQ 的值; MQ
请打开超级画板文件名“14 浦东 25”,可以体验到角三角形都是相似的,三边比为 3∶4∶5.把图形中所有 相等的锐角都标记出来,就会发现△QAG∽△QMC.
2.解第(3)题时,如果构造出了直角梯形 BB′C′C,那么思路豁然开朗.
满分解答
(1)因为 AB=AC,点 G 是△ABC 的重心,
3 11
图2
图3
(3)如图 4,过 B、C 作 BC 的垂线分别交直线 PQ 于 B′、C′.
由 BB′//AD//CC′,得 BB ' BP , CC ' CQ . AG AP AG AQ
所以 BB ' x , CC ' 15 y .因此 BB ' 8x , CC ' 120 8y 120 8 .
所以 AG 的延长线与边 BC 的交点 D 是 BC 的中点,且 AD⊥BC.
在 Rt△ABD 中,sinB= 4 ,设 AD=4m,AB=5m,那么 BD=3m.因此 BC=6m. 5
由 BC-AB=3,得 6m-5m=3.所以 m=3.
因此 AB=AC=15,BD=CD=9,AD=12.
因为点 G 是△ABC 的重心,所以 AG=8.
如图 5,此时 CC ' CQ ,即 CC ' y 15 .所以 CC ' 8y 120 8 120 .
上海市2014初三数学浦东区二模卷(含答案)

浦东新区2014年中考预测数学试卷 2014.4.15(测试时间:100分钟,满分:150分)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分) 1.下列代数式中,属于单项式的是(A )1+a ;(B )a 2;(C )a2; (D )2a . 2.数据1,3,7,1,3,3的平均数和标准差分别为(A )2,2;(B )2,4; (C )3,2;(D )3,4.3.已知抛物线2)1(+-=x y 上的两点)()(2211y x B y x A ,和,,如果121-<<x x ,那么下列结论一定成立的是 (A )021<<y y ; (B )210y y <<;(C )120y y <<;(D )012<<y y .4. 某粮食公司2013年生产大米总量为a 万吨,比2012年大米生产总量增加了10%,那么2012年大米生产总量为 (A )%)101(+a 万吨;(B )%)101(+a万吨;(C )%)101(-a 万吨; (D )%)101(-a万吨.5.在四边形ABCD 中,对角线AC 、BD 相交于点O ,CBD ADB ∠=∠,添加下列一个条件后,仍不能判定四边形ABCD 是平行四边形的是 (A )CDB ABD ∠=∠;(B )BCD DAB ∠=∠; (C )CDA ABC ∠=∠;(D )BCA DAC ∠=∠.6. 如果A 、B 分别是圆O 1、圆O 2上两个动点,当A 、B 两点之间距离最大时,那么这个最大距离被称为圆O 1、圆O 2的“远距”.已知,圆O 1的半径为1,圆O 2的半径为2,当两圆相交时,圆O 1、圆O 2的“远距”可能是 (A )3;(B )4;(C )5;(D )6.二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:π-3= ▲ .8. 化简:23410ab b a = ▲ .9.计算:xx x ---2111= ▲ . 10.正八边形的中心角等于 ▲ 度.11.如果关于x 的方程0332=+-mx x 有两个相等的实数根,那么m 的值为 ▲ . 12.请写出一个平面几何图形,使它满足“把一个图形沿某一条直线翻折过来,直线两旁的部分能够相互重合”这一条件,这个图形可以是 ▲ .13.如果关于x 的方程1+=x bx 有解,那么b 的取值范围为 ▲ . 14. 在□ABCD 中,已知AC a =,DB b =,那么用向量a 、b表示向量AB 为 ▲ .15. 把分别写有数字“1”、“2”、“3”、“4”、“5”、“6”的6张相同卡片,字面朝下随意放置在桌面上,从中任意摸出一张卡片数字是素数的概率是 ▲ .16.为了解某校九年级女生1分钟仰卧起坐的次数,从中随机抽查了50名女生参加测试,被抽查的女生中有90%的女生次数不小于30次,并绘制成频数分布直方图(如图所示),那么仰卧起坐的次数在40~45的频率是 ▲ .17.如图,已知点A 在反比例函数xky =的图像上,点B 在x 轴的正半轴上,且△OAB 是面积为3的等边三角形,那么这个反比例函数的解析式是 ▲ . 18.在Rt △ABC 中,∠ACB =90°,AC =2,23cos =A ,如果将△ABC 绕着点C 旋转至△A'B'C 的位置,使点B' 落在∠ACB 的角平分线上,A'B' 与AC 相交于点H ,那么线段CH 的长等于 ▲ .三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 计算:51555551212-⎪⎪⎭⎫ ⎝⎛++--)(.20.(本题满分10分)[来源:Z|xx|]解不等式组:⎪⎩⎪⎨⎧-≥+-<-,,x x x x 321334)1(372并把解集在数轴上表示出来.(第17题图)(每组可含最小值,不含最大值)(第16题图)(第20题图)(第22题图)已知:如图,∠P AQ =30°,在边AP 上顺次截取AB =3cm ,BC =10cm ,以BC 为直径作⊙O 交射线AQ 于E 、F 两点, 求:(1)圆心O 到AQ 的距离; (2)线段EF 的长.22.(本题满分10分,其中第(1)小题4分,第(2)小题3分,第(3)小题3分) 甲、乙两车都从A 地前往B 地,如图分别表示甲、乙两车离A 地的距离S (千米)与时间t (分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B 地,最终甲、乙两车同时到达B 地,根据图中提供的信息解答下列问题:(1)甲、乙两车行驶时的速度分别为多少? (2)乙车出发多少分钟后第一次与甲车相遇? (3)甲车中途因故障停止行驶的时间为多少分钟?[来源学科网ZXXK]23.(本题满分12分,其中每小题各6分)已知:如图,在正方形ABCD 中,点E 是边AD 的中点,联结BE ,过点A 作BE AF ⊥,分别交BE 、CD 于点H 、F ,联结BF . (1)求证:BE =BF ;(2)联结BD ,交AF 于点O ,联结OE .求证:AEB DEO ∠=∠.(第21题图) (第23题图)如图,已知在平面直角坐标系xOy 中,抛物线c bx x y ++=241与x 轴交于点A 、B (点A 在点B 右侧),与y 轴交于点C (0,-3),且OA =2OC . (1)求这条抛物线的表达式及顶点M 的坐标; (2)求M AC ∠tan 的值;(3)如果点D 在这条抛物线的对称轴上,且∠CAD =45º,求点D 的坐标.25.(本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)如图,已知在△ABC 中,AB =AC ,BC 比AB 大3,54sin =B ,点G 是△ABC 的重心,AG 的延长线交边BC 于点D .过点G 的直线分别交边AB 于点P 、交射线AC 于点Q . (1)求AG 的长;(2)当∠APQ=90º时,直线PG 与边BC 相交于点M .求MQAQ的值; (3)当点Q 在边AC 上时,设BP =x ,AQ =y ,求y 关于x 的函数解析式,并写出它的定义域.[来源:学.科.网Z.X.X.K][来源学_科_网](第24题图)(第25题图)浦东新区2014年中考预测数学试卷答案要点及评分标准一、选择题:1.D ; 2.C ; 3.A ; 4.B ; 5.D ; 6.C . 二、填空题:7.3-π; 8.ba 252;9.x1; 10.45; 11.6±; 12.圆等; 13.1≠b ;14.b a 2121+; 15.50%;16.0.62;17.xy 3-=; 18.13-. 三、解答题:19.解:原式5555555+=-+-……………………………………………………………(8分)5555155=-++-……………………………………………………………(1分)65=-…………………………………………………………………………(1分) 20.解:273(1)423133x x x x -<-⎧⎪⎨+≥-⎪⎩,.由①得2733x x -<-…………………………………………………………………(1分)化简得105<x ,………………………………………………………………………(1分) 解得:2<x .…………………………………………………………………………(1分) 由②得4932x x +≥-,………………………………………………………………(1分) 化简得66x ≥-,………………………………………………………………………(1分) 解得:1-≥x .…………………………………………………………………………(1分) ∴原不等式组的解集为.21<≤-x …………………………………………………(2分)………………………………………………(2分)21.解:(1)过点O 做OH ⊥EF ,垂足为点H . ……………………………………………(1分) ∵OH ⊥EF ,∴∠AHO =90°,在Rt △AOH 中,∵∠AHO =90°,∠P AQ =30°,∴ OH =12AO ,……………(2分) ∵BC =10cm ,∴ BO=5cm . ∵AO =AB +BO ,AB =3cm ,∴AO =3+5=8cm ,…………………………………………………………………(1分)∴OH =4cm ,即圆心O 到AQ 的距离为4cm .………………………………(1分) (2)联结OE , 在Rt △EOH 中,∵ ∠EHO =90°,∴ 222EH HO EO +=,…………(1分)∵ EO =5cm ,OH =4cm ,∴ EH =3452222=-=-OH EO cm ,……………(2分) ∵ OH 过圆心O ,OH ⊥EF ,∴ EF =2EH =6cm .………………………………………(2分) 22.解:(1)204153v ==甲(千米/分钟), ∴ 甲车的速度是43千米每分钟.……(2分) ① ②6017010v ==-乙(千米/分钟),∴ 乙车的速度是1千米每分钟.…………(2分)(2)解法①∵ 20120==乙t (分钟),∴乙车出发20分钟后第一次与甲车相遇.………(3分) 解法②设甲车离A 地的距离S 与时间t 的函数解析式为:S kt b =+(0k ≠)将点(10,0)(70,60)代入得:100,7060.k b k b +=⎧⎨+=⎩…………………………………(1分)解得:1,10.k b ==-⎧⎨⎩,即10.S t =-……………………………………………………(1分)当y =20时,解得t =30,∵ 甲车出发10分钟后乙车才出发,∴ 30-10=20分钟,乙车出发20分钟后第一次与甲车相遇.…………………(1分) (3)∵ 440303t =÷=(分钟),…………………………………………… (1分) ∵ 70-30-15=25(分钟),∴ 甲车中途因故障停止行驶的时间为25分钟.… (2分)23.证明:(1)∵四边形ABCD 是正方形,∴AB =DA=BC=CD , ∠BAD =∠ADF=∠BCF=90°,………………………(1分) ∴∠BAH +∠HAE =90°,∵ AF ⊥BE ,∴ ∠AHB =90°即∠BAH +∠ABH =90°,∴∠ABH =∠HAE ,………………………………………………………………(1分) 又∵∠BAE =∠ADF , ∴ △ABE ∽△DAF ,………………………………………………………………(1分)[来源:Z §xx §∴DFAE DA AB =,∴AE =DF .……………………………………………………………………(1分) ∵ 点E 是边AD 的中点,∴点F 是边DC 的中点,∴ CF =AE ,……………………………………………………………………(1分) 在Rt △ABE 与Rt △CBF 中, ,.AB CB AE CF =⎧⎨=⎩∴ Rt △ABE ≌Rt △CBF ,∴BE =BF .……………………………………………………………………(1分)(2)∵四边形ABCD 是正方形,∴DB 平分∠ADC ,∴∠ADB =∠CDB ,…………………………………(1分)在△DEO 与△DFO 中, ,,.ED FD ADB CDB DO DO ⎧⎪⎨⎪⎩=∠=∠= ∴△DEO ≌△DFO ,…………………………………………………………(2分)∴∠DEO =∠DFO ,…………………………………………………………(1分)∵△ABE ∽△DAF ,∴∠AEB =∠DF A ,………………………………… (1分) ∴∠AEB =∠DEO .…………………………………………………………(1分) 24.(1)解:∵C (0,-3),∴OC =3.2134y x bx =+-………………………………(1分)∵OA =2OC ,∴OA =6. ∵041>=a ,点A 在点B 右侧,抛物线与y 轴交点C (0,-3). ∴)0,6(A .…………………………………………………………………(1分)∴2134y x x =--.………………………………………………………(1分) ∴4)2(412--=x y ,∴)4,2(M . ……………………………………(1分)(2)过点M 作MH ⊥x 轴,垂足为点H ,交AC 于点N ,过点N 作NE ⊥AM 于 点E ,垂足为点E .在Rt △AHM 中,HM =AH =4,42AM =,45AMH HAM ︒∠=∠=. 求得直线AC 的表达式为132y x =-.………………(1分)∴N (2,-2).∴MN =2.…………………………………(1分) 在Rt △MNE 中,∴2ME NE ==,∴32AE =.…………………………………………(1分) 在Rt △AEN 中,221tan 33NE MAC AE =∠==.………(1分) (3)①当D 点在AC 上方时,∵1145CAD D AH HAC ︒∠=∠+∠=, 又 ∵45HAM AC AM H C ︒∠=∠+∠=,∴1D AH CAM ∠=∠. …………………………(1分) ∴1tan tan 13D AH AC M ∠=∠=. ∵点1D 在抛物线的对称轴直线x =2上, ∴1D H AH ⊥,∴4AH =.在Rt △AH 1D 中,1114tan 433D H AH D AH =⋅∠=⨯=. ∴14(2,)3D .………………………………………(1分)②当D 点在AC 下方时,∵2245D AC D AM MAC ∠=∠+∠=︒,又 ∵2245AMH D AM AD M ∠=∠+∠==︒,∴2MAC AD M ∠=∠.………………………………(1分)∴2tan tan 13AD H MAC ∠=∠= 在Rt △2D AH 中,221412tan 3AHD H AD H==÷=∠.∴2(2,12)D -.………………………………………(1分)综上所述:14(2,)3D ,2(2,12)D -.25.解:(1)在△ABC 中,∵AB =AC ,点G 是△ABC 的重心, ∴12BD DC BC ==,AD ⊥BC .………………………………………………(1分)在Rt △ADB 中,∵4sin 5AD B AB ==,∴35BD AB =. ∵3BC AB -=, ∴AB =15,BC =18.∴AD =12.………………………………………………………………………(1分) ∵G 是△ABC 的重心,∴283AG AD ==.…………………………………(1分)(2)在Rt △MDG ,∵∠GMD +∠MGD =90°, 同理:在Rt △MPB 中,∠GMD +∠B =90°,∴∠MGD =∠B .…………………………………(1分) ∴4sin sin 5MGD B ∠==, 在Rt △MDG 中,∵143DG AD ==, ∴163DM =,∴113CM CD DM =-=……(1分)在△ABC 中,∵AB =AC ,AD ⊥BC ,∴BAD CAD ∠=∠.∵90QCM CDA DAC DAC ︒∠=∠+∠∠=+, 又 ∵90QGA APQ BAD BAD ︒∠=∠+∠∠=+, ∴QCM QGA ∠=∠,………………………………(1分) 又 ∵CQM GQA ∠=∠,∴△QCM ∽△QGA .………………………………(1分) ∴2411AQ AG MQ MC ==.……………………………(1分) (3)过点B 作BE AD ,过点C 作CF AD ,分别交直线PQ 于点E 、F ,则BEAD CF .…………………………………(1分)∵BE AD ,∴AP AG BP BE =,即158x x BE-=, ∴815xBE x=-.………………………………(1分)同理可得:AQ AG QC CF =,即815y y CF=-, ∴8(15)y CF y-=.……………………………(1分) ∵BEAD CF , BD CD =,∴EG FG =.∴2CF BE GD +=,即8(15)8815y xy x-+=-.(1分) ∴75510x y x-=-,15(0)2x ≤≤.…………………(2分)。
2014上海各区模拟考中考数学压轴题1-14长宁24

例 2014年上海市长宁区中考模拟第24题如图1,在平面直角坐标系中,四边形OABC 是等腰梯形,其中OA =AB =BC =4,tan BCO ∠=(1)求经过O 、B 、C 三点的二次函数的解析式;(2)若点P 在第四象限,且△POC 与△AOB 相似,求满足条件的所有点P 的坐标;(3)在(2)的条件下,若⊙P 与以OC 为直径的⊙D 相切,请直接写出⊙P 的半径.图1满分解答(1)如图2,作AM ⊥x 轴,BN ⊥x 轴,垂足分别为M 、N ,那么OM =CN ,AM =BN ,AB =MN .在Rt △BCN 中,由tan BCO ∠=BC =4,得∠BCO =60°,CN =2,BN =所以OC =8,ON =6.所以点C 的坐标为(8, 0),点B 的坐标为(6,. 图2 因为抛物线与x 轴交于O 、C (8, 0),设抛物线的解析式为y =ax (x -8),代入点(6,B ,得12a -=6a =-.所以抛物线的解析式为2(8)663y x x x x =--=-+. (2)如图3,△AOB 是顶角为120°的等腰三角形,如果△POC 与△AOB 相似,那么△POC 也是顶角为120°的等腰三角形,存在两种情况:①如图3,当PO =PC 时,在Rt △POD 中,OD =4,∠OPD =60°,所以PD =.此时点P 的坐标为(4,. ②如图4,延长BC 到P ,使CP =CO ,作PH ⊥x 轴于H .在Rt △CPH 中,CP =8,∠PCH =60°,所以CH =4,PH =此时点P 的坐标为(12,-.图3 图4(3)①如图3,⊙D 的半径为4,圆心距PD =3.两圆内切,⊙P 在⊙D 内时,⊙P 半径为43-;两圆内切,⊙D 在⊙P 内时,⊙P 半径为43+.②如图4,在Rt △PDH 中,DH =8,PH =所以圆心距PD ==.两圆内切时,⊙P 半径为4;两圆外切时,⊙P 半径为4-.。
2014年上海市各区中考数学二模压轴题图文解析

目录
1
华东师大出版社荣誉出品 《挑战中考数学压轴题》系列产品·8
例
2014 年上海市宝山区中考模拟第 24 题
如图 1,在平面直角坐标系中,抛物线 y=mx -mx+n(m、 n 为常数)与 y 轴交于点
2
,且 tan∠ABC= 3 .如果将抛物 A(0, 2 3) ,与 x 轴交于 B、C 两点(点 C 在点 B 左侧) 线 y=mx2-mx+n 沿 x 轴向右平移 4 个单位,点 B 的对应点为 E. (1)求抛物线 y=mx -mx+n 的对称轴及其解析式; (2)联结 AE,记平移后的抛物线的对称轴与 AE 的交点为 D,求点 D 的坐标; (3)如果点 F 在 x 轴上,且△ABD 与△EFD 相似,求 EF 的长.
②当
考点伸展
如果第(3)题探究△ABC 与△EFD 相似,那么 EF 的长又是多少? 因为△ABE 是 30°底角的等腰三角形,腰长与底边的比是 1: 3 ,因此存在两种情况:
①当
EF 3 EF 1 时,EF=3 (如图 3) .②当 时,EF=1(如图 4) . ED 1 ED 3
图3
3
图4
所以点 D 的坐标为 ( ,
9 3 ). 2 2
图2 (3)因为∠BAD =∠E=30 °,所以△ABD 与△EFD 相似存在两种情况: ①当
EF AB 4 EF 4 时, .此时 EF . ED AD 3 3 3 3 EF AD 9 EF 3 3 时, .此时 EF . ED AB 4 4 3
2
华东师大出版社荣誉出品 《挑战中考数学压轴题》系列产品·8那么 EH 源自 6 9 3 . 2 2
3 ,∠E=30°, AE 4 3 . 3
2014上海各区模拟考中考数学压轴题1-14黄浦24

例 2014年上海市黄浦区中考模拟第24题在平面直角坐标系xOy 中,已知顶点为P (0, 2)的二次函数图像与x 轴交于A 、B 两点, A 点坐标为(2, 0).(1)求该二次函数的解析式,并写出点B 坐标;(2)点C 在该二次函数的图像上,且在第四象限,当△ABC 的面积为12时,求点C 坐标;(3)在(2)的条件下,点D 在y 轴上,且△APD 与△ABC 相似,求点D 坐标. 动感体验请打开几何画板文件名“14黄浦24”,拖动点D 在y 轴上运动,可以体验到,直线BC 和直线AP 与坐标轴的夹角都是45°,△APD 与△ABC 有两次机会相似. 请打开超级画板文件名“14黄浦24”,可以体验到,.思路点拨1.第(1)题设抛物线的顶点式,代入点A ,问题就解决了.2.第(2)题根据面积求得AB 边上的高,写出点C 的纵坐标,再解方程求得点C 的横坐标.3.第(3)题探求两个三角形相似的关键是寻找一组对应角,选择∠ABC =∠APD =45°,然后按照对应边成比例分两种情况计算PD 的长.满分解答(1)因为抛物线的顶点为P (0, 2),设抛物线的解析式为y =ax 2+2,代入点A (2, 0),可得12a =-. 所以抛物线的解析式为2122y x =-+. 由2112(2)(2)22y x x x =-+=--+,得B (-2, 0). (2)如图1,设AB 边上的高为h .由S △ABC =12AB h ⋅,得11242h =⨯.解得h =6. 因为点C 在第四象限,所以y C =-6. 解方程21262x -+=-,得x =±4. 所以点C 的坐标为(4,-6). 图1(3)由B (-2, 0)、C (4,-6),可知B 、C 两点间的水平距离、垂直距离都为6,因此∠ABC =45°.由A (2, 0)、P (0, 2),可知∠APO =45°.因此当D 在P 下方时,∠ABC =∠APD .所以△APD 与△ABC 相似,存在两种情况:①如图2,当PD BAPA BC ==.解得43PD =.此时点D 的坐标为2(0,)3.②如图3,当PD BCPA BA ==. 解得PD =6.此时点D 的坐标为(0,-4).图2 图3考点伸展如果我们把第(3)题中点D 的位置改在x 轴上,且△APD 与△ABC 相似,那么求点D 坐标时,我们选择∠ABC =∠PAD ,分两种情况:①如图4,当AD BAAP BC ==. 解得43AD =.此时点D 的坐标为2(,0)3.②如图5,当AD BCAP BA =4=. 解得AD =6.此时点D 的坐标为(-4,0).图4 图5。
浦东新区2014年中考预测数学试卷答案要点及评分标准(20140415)

浦东新区2014年中考预测数学试卷答案要点及评分标准一.选择题:1. D ;2. C :3. A ;4. B :5. D :6. C.二、填空题:7.8.“ :9. 1—: 10. 45: 11. ±6: 12.圆等:13. bHl :2bX1 - 1 -14. —a + —b ; 15. 50%; 16. 0.62;17V317. y=-——:1& ^3 — 1.2 2X三.解答题:19.解:原式=5_书十缪匚厚 ................................................................................... (8分)■ 6-\[s •…2x-7<3(l-x ), 20•解:打 2 -x+3>l--x (3 3 由①得2x —7 <3—3x化简得5xvl0. ............................................................................................................. (1 解得:x<2. ................................................................................................................. (1 由②得4x+9X3—2x, .................................................................................................. (1 化简得6x>-6, .............................................................................................................. (1 解得:x>-l. .................................................................................................................. (1 (2分)21•解:(1)过点O 做OH 丄EF,垂足为点H. ............................................................... (1分)VOII 丄EF. •••NAnO=90° ,在 RtAAOH 中,V ZAHO=90J , ZPAQ=30% A OH=^AO, .......................................... (22分)V BC=10cnif /• BO=5CHLTAO=AB+BO. AB=3cm» •: AO=3*5=8cnit分)••• OH=4cm , 即圆心 O 到 AQ 的距离为4cm . ............................................................................. ( 1 分) (2)联结OE, 在 RtAEOH 中,•・• ZEHO=90 ,・•・ EH 2 + HO 2 =EO 2 , ....................... (1 分) I EO=5cm, OH=4cm,・•・ EH= 7EO 2-OH 2 = yl52 -42 = 3cm, ......................... (2 分) V OH 过圆心 O, OH±EF,••• EF=2EH=6cm ・ ........................................................ (2 分)(1分)(1分分分分分分分(1=5->/?+1 +(1分)①•••原不等式组的解集为-l<x<2.Q20 422•解:(1)V 严訝=一(「米/分钟), 4•••甲车的速度是一「米每分钟.3 (2分) 60 1 v z = ----------- = 1 70-10 (2)解法① I ^= — = 20• 1 (「米/分钟),•••乙车的速度是1 T •米每分钟. (分钟),•••乙车岀发20分钟后第一次与甲车相遇. 分) 解法② 设甲车离A 地的距离S 与时间t 的怖数解析式为:S = kt+b (kH0) 10k + b = 0.70k + b = 60. 将点(10,0) (70,60)代入得:* ,即 S = t-10. ................................................... b = -10.当y=20时,解得t=30,・・・甲车出发10分钟后乙车才出发,••• 3040=20分钟,乙车出发20分钟后第一次与甲车相遇.解得:分) 4(3) I t = 40十一 =30 (分钟), ..................................3V 70-30-15=25 (分钟)■ •••甲车中途因故障停止行驶的时间为25分钟. 分) 23•证明:(1) V 四边形ABCD 是正方形, ・・・AB=D¥BC=CD, Z BAD= Z ADF= Z BCF=90 1A ZBAH+ZHAE=90° , T AF 丄BE. ••• ZAHB=90° 即ZBAH-ZABH=90" ■ AZABH=ZHAE, ...............................................................又 VZBAE=ZADF, ・•・△ABEs^DAF, ......................................................... -AB AE • • ---- = ------ ‘DA DFAAE=DF............................................................................ •・•点E 是边AD 的中点,.••点F 是边DC 的中点,・•・ CF=AE, ................................................................... 在 RtAABE 与 RtACBF 中, f AB = CB,1AE = CF .・•・ RtAABE^RtACBF,/.BE=BF. .......................................................................... (2) •・•四边形ABCD 是正方形,・・・DB 平分ZADC, ・・・ZADB=ZCDB, ............ 在ZiDEO 与 ADFO 中, ED = FD,ZADB = ZCDB, * DO = DO.AADEO^ADFO. (2分)(1分)(1分)(1 (1分)(2(1分)(1分)(1分)(1分)(1分)(1分)(1分)(2分)•••ZDEO=ZDFO, ............................................................................................. (1 •.•△ABE S GAF, A ZAEB=ZDFA, ............................................................... (1 AZAEB=ZDEO. .................................................................................................... (1)分分分24. (1)解:VC(O, -3), AOC=3. y= -x 2 +bx-3 (1分)VOA=2OC, :.OA E =6. V a = 1 > 0,点A 在点B 右侧•抛物线与y 轴交点C(0,・3). 4 ••• A(6.0)・ ............................................................................................................ (1 分)A y= —x 2 -x-3. .................................................................................................... (1 分)4 y=l(x _2)2 -4,・•・ M(2,4). ............................................................................... (1 分)4 (2)过点M 作MH 丄x 轴,垂足为点H ・交AC 于点N.过点N 作NE 丄AM f 点E,垂足为点E.在 RtAAHM 中,HN1=AH=4, AM = 4^2 , ZAMH = ZHAN1 = 45, • 求得直线AC 的表达式为y =1x —3. .............................. (1分)AN (2, -2). AN1N=2. ........................ 在 RtAMNE 中,・•・ N1E - NE- >/7 ,••• AE = 3y/2 . ..................................在 RtAAEN^P, tan ZN1AC =NE _ ^2 _ 1AE 3>/2 3 (3)①当D 点在AC 上方时,V ZCAD1 = 6 AH + ZHAC = 45°, 又 T ZHAM = ZHAC + ZCAM = 45°,(1分)(1分)(1分)AH 1在 RtA D. AH 中,D.H= ------------------- = 4*- = 12.tan ZADr H 3■A D,(2,-12) ....................................................................... (1 分)4综上所述:D 】(2,_), D.(2-12).3 ・25.解:(1)在厶ABC 中,TA^AC,点G 是△ABC 的重心,.・・ BD = DC = -BC , AD 丄BC. ........................................................................... (1 ............................................................................................................................................分)V BC-AB = 3, /.AB=15, BC=1 &AAD=12............................................................................................................... (1 ................................................................................................. 分)2JG J^AABC 的重心,A AG = -AD = 8(2)在 RtAMDG. VZGX1D+ZMGD=9O • 同理:在 RtAMPB 中,ZGMD+ZB=90> ,A ZMGD=ZB. ..................................................... (1 分) • • 4 • sill ZMGD = sillB =—5,在 RtANlDG 中,・.・ DG = £ AD = 4 ,••• DM = — , A CM = CD-DM = —……(1 分) 3 3在ZXABC 中,VAB=AC, AD 丄BC.二 ZBAD=ZCAD. J ZQCM = ZCDA+ ZDAC = 90° + ZDAC .又•: ZQGA= ZAPQ + ZBAD = 90° + ZBAD .:.ZQCM = ZQGA, .................................................... (1 分)又 V ZCQM = ZGQA,AAQCM^AQGA ................................................... (1 分) AQ AG 24• • MQ ~ MC ~ IT - ................................................... d 分〉 (3)过点B 作BEI 」AD ■过点C 作CFIJAD,分别交 直线PQ 于点E 、F,则BE LJ AD 」CFAP AG 15-x8VBEUAD--^=^^'J在RSDB 中,・二“=鴛=£BD _ 3AB 一5 •(1分)(1分) AA••• BE =8x15-x*(1分)同理町得:QC CF ' 1 15 - y CF•: BELIADLICF , BD = CD, ••• EG = FG. Z. CF+BE = 2GD ,即 8Q5_y)+ ^_ = 8(】分)y 15- x8(15—y)y(i分) 75-5x10—x(0<X<y).(2分)。
2014年上海初三年级数学所有区一模压轴18.24.25题集合

18.(2013奉贤一模)在Rt △ABC 中,∠C =90°,AB=5,BC =3,点D 、E 分别在BC 、AC 上,且BD=CE ,设点C 关于DE 的对称点为F ,若DF ∥AB ,则BD 的长为 ;24.(2013奉贤一模)(本题满分12分,每小题4分)如图,已知直线x y =与二次函数2y x bx c =++的图像交于点A 、O ,(O 是坐标原点),点P 为二次函数图像的顶点,OA=AP 的中点为B .(1)求二次函数的解析式; (2)求线段OB 的长;(3)若射线OB 上存在点Q ,使得△AOQ 与△AOP 相似,求点Q 的坐标.D第18题第24题25.(2013奉贤一模)(本题满分14分,第1小题4分,第2小题5分,第3小题5分)如图(1),已知∠MON=90°,点P 为射线ON 上一点,且OP=4,B 、C 为射线OM 和ON 上的两个动点(OP OC >),过点P 作PA ⊥BC ,垂足为点A ,且PA =2,联结BP . (1)若12PAC ABOPS S ∆=四边形时,求tan ∠BPO 的值; (2)设,,y BCABx PC ==求y 与x 之间的函数解析式,并写出定义域; (3)如图(2),过点A 作BP 的垂线,垂足为点H ,交射线ON 于点Q ,点B 、C 在射线OM 和ON 上运动时,探索线段OQ 的长是否发生变化?若不发生变化,求出它的值。
若发生变化,试用含x 的代数式表示OQ 的长.P第25题 (1)AB M OP第25题 (2)ABMOHNN18.(2013普陀一模)如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,那么四边形MABN的面积是______________.24.(2013普陀一模)(本题满分12分,其中第(1)小题2分,第(2)小题5分,第(3)小题5分)如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.(第24题)25.(2013普陀一模)(本题满分14分,其中第1小题3分,第2小题5分,第3小题6分)将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].(1)如图①,对△ABC得△AB′C′,那么AB CABCSS''∆∆= ;直线BC与直线B′C′所夹的锐角为度.(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值.(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.18.(2013闵行一模)已知在ABC Rt ∆中,︒=∠90A ,,,55sin a BC B ==点D 在边BC 上,将这个三角形沿直线AD 折叠,点C 恰好落在边AB 上,那么BD= 。
浦东新区2014年中考预测数学试卷答案要点及评分标准(20140415)

一、选择题:
1.D;2.C;3.A;4.B;5.D;6.C.
二、填空题:
7. ;8. ;9. ;10.45;11. ;12.圆等;13. ;
14. ;15. ;16. ;17. ;18. .
三、解答题:
19.解:原式 ……………………………………………………………(8分)
∴∠DEO=∠DFO,………………………………………………………………(1分)
∵△ABE∽△DAF,∴∠AEB=∠DFA,………………………………………(1分)
∴∠AEB=∠DEO.………………………………………………………………(1分)
24.(1)解:∵C(0,-3),∴OC=3. ……………………………………(1分)
又∵∠BAE=∠ADF,
∴△ABE∽△DAF,………………………………………………………………(1分)
∴ ,
∴AE=DF.…………………………………………………………………………(1分)
∵点E是边AD的中点,∴点F是边DC的中点,
∴CF=AE,…………………………………………………………………………(1分)
由②得 ,………………………………………………………………(1分)
化简得 ,………………………………………………………………………(1分)
解得: .…………………………………………………………………………(1分)
∴原不等式组的解集为 …………………………………………………(2分)
………………………………………………(2分)
在Rt△ABE与Rt△CBF中,
∴Rt△ABE≌Rt△CBF,
∴BE=BF.…………………………………………………………………………(1分)
2014上海各区模拟考中考数学压轴题1-14金山24

例 2014年上海市金山区中考模拟第24题如图1,在平面直角坐标系中,直线y =x +2与x 轴交于点A ,点B 是这条直线上第一象限内的一个点,过点B 作x 轴的垂线,垂足为D ,已知△ABD 的面积为18.(1)求点B 的坐标;(2)如果抛物线212y x bx c =-++经过点A 和点B ,求抛物线的解析式; (3)已知(2)中的抛物线与y 轴相交于点C ,该抛物线对称轴与x 轴交于点H ,P 是抛物线对称轴上的一点,过点P 作PQ //AC 交x 轴于点Q ,如果点Q 在线段AH 上,且AQ =CP ,求点P 的坐标.图1动感体验请打开几何画板文件名“14金山24”,拖动点P 运动,可以体验到,AQ =CP 有两种情况,四边形CAQP 为平行四边形或等腰梯形.请打开超级画板文件名“14金山24”,可以体验到,.思路点拨1.△ABD 是等腰直角三角形,根据面积可以求得直角边长,得到点B 的坐标.2.AQ =CP 有两种情况,四边形CAQP 为平行四边形或等腰梯形.平行四边形的情况很简单,等腰梯形求点P 比较复杂,于是我们要想起这样一个经验:平行于等腰三角形底边的直线截两腰,得到一个等腰梯形和一个等腰三角形. 满分解答(1)直线y =x +2与x 轴的夹角为45°,点A 的坐标为(-2, 0).因为△ABD 是等腰直角三角形,面积为18,所以直角边长为6.因此OD =4.所以点B 的坐标为(4, 6).(2)将A (-2, 0)、B (4, 6)代入212y x bx c =-++, 得220,84 6.b c b c --+=⎧⎨-++=⎩.解得b =2,c =6. 所以抛物线的解析式为21262y x x =-++. (3)由21262y x x =-++,得抛物线的对称轴为直线x =2,点C 的坐标为(0, 6). 如果AQ =CP ,那么有两种情况:①如图2,当四边形CAQP 是平行四边形时,AQ //CP ,此时点P 的坐标为(2, 6).②如图3,当四边形CAQP 是等腰梯形时,作AC 的垂直平分线交x 轴于点F ,那么点P 在FC 上.设点F 的坐标为(x , 0),根据FA 2=FC 2列方程,得(x +2)2=x 2+62.解得x =8.所以OF =8,HF =6. 因此39tan 642PH HF F =⋅∠=⨯=.此时点P 的坐标为9(2,)2.图2 图3考点伸展第(3)题等腰梯形CAQP 时,求点P 的坐标也可以这样思考:过点P 作PE //x 轴交AC 于E ,那么PE =PC .直线AC 的解析式为y =3x +6,设E (m , 3m +6),那么P (2, 3m +6).根据PE 2=PC 2列方程,得(2-m )2=22+(3m )2.解得12m =-.所以P 9(2,)2.图4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 2014年上海市浦东新区中考模拟第24题 如图1,已知在平面直角坐标系xOy 中,抛物线214
y x bx c =++与x 轴交于点A 、B (点A 在点B 右侧),与y 轴交于点C (0,-3),且OA =2OC .
(1)求这条抛物线的表达式及顶点M 的坐标;
(2)求tan ∠MAC 的值;
(3)如果点D 在这条抛物线的对称轴上,且∠CAD =45°,求点D 的坐标.
图1
满分解答
(1)如图2,由C (0,-3),OA =2OC ,得OC =3,OA =6.所以A (6, 0). 将A (6, 0)、C (0,-3)代入214y x bx c =
++,得960,3.b c c ++=⎧⎨=-⎩ 解得b =-1,c =-3. 所以抛物线的解析式为22113(2)444
y x x x =
--=--. 顶点M 的坐标为(2,-4).
图2 图3
(2)由A (6, 0)、M (2,-4),得A 、M 两点间的水平距离、垂直距离都为4. 所以直线AM 与坐标轴的夹角为45°.
如图3,设直线AM 与y 轴交于点N ,那么ON =OA =6.
作CH ⊥AM 于H ,作HG ⊥y 轴于G ,
那么△CHN 、△NGH 都是等腰直角三角形.
由ON =6,OC =3,得CN =3.因此NG =1.5,GO =4.5.
所以tan ∠MAC = 1.514.53
CH NH NG HA HA GO ====.
(3)如图4,设抛物线的对称轴直线x =2与x 轴的交点为E . ①当点D 在AC 上方时,因为∠CAD =∠NAO =45°,
所以∠DAE =∠CAN .
在Rt △ADE 中,AE =4,tan ∠DAE =1
3.
所以DE =4
3.此时点D 的坐标为4
(2,)3.
②当点D ′在AC 下方时,因为∠CAD =∠CAD ′=45°, 所以∠DAD ′=90°.因此∠AD ′D =∠DAE .
在Rt △AD ′E 中,AE =4,tan ∠AD ′E =1
3.
所以D ′E =12.此时点D ′的坐标为(2,-12). 图3。
