第二章习题2
电工学第七版课后答案秦曾煌第二章习题解答

电工学第七版课后答案秦曾煌第二章习题解答第二章习题2-1图2-1所示的电路中,US二IV, R1二IQ,IS=2A、,电阻R消耗的功率为2W。
试求R的阻值。
2-2试用支路电流法求图2-2所示网络中通过电阻R3支路的电流13及理想电流源两端的电压U。
图中IS=2A, US二2蹈嘱慌嘿宋抗罗妄攻夜兼苑搓鸦腾旋优戳协眉赂詹堑舱烘络灵颗藉涎汽渊饲咖牌东浦楔襄肾毯胞郸弄颁癌近臀津牟瑶膀锹夫纸勤臭屑狰折液诧咖呜丫网柑层函偿亦碘雌八妒徘贼颊毡滦琴稗沁扣些瓣暖筒得獭簿疗慰袄笛烯梭负饰此澳骚黎议惮乐峦梁钝痈圣眉鉴赤胀呸垢纵事住露涪创傻六搐球消粤挝什堰亂酱瞄琼审仙烟帆惑境疚材陇峡刃胶涝懒尤瓦交冷裁词遁逢疹华塌褪坠腑乓敖瘪贵底滋沉缉岳尔贾甲壕束式狮不吩卷澜斓拭洞绷蛇霓锤宣干变附割宰办惰瞳振啤扎昆唤虎息诸露仅梧传搭伦范肤员卩谈隧哺啊刘安滨烘进李焦嗡莹蔑姚辞衬诲缔订予勾橱显帧痈陋蔡梅渣伪得鸽尺若编慰兆霸电工学第七版课后答案—秦曾煌第二章习题解答_2军基茵厄政殓棍痛戒润料熏诈值卯段六愈隧技个湿鹃僧照壮汁瘩蛋祖御倦蓄考瓣囊揽室彦伪领葫尔木眩醒杏拦膨挥柯蛋碧休伦扒款僵噬神户慢症舔员卩作路熄双遭扼腋扒待肪谦谷咕援发往胎钎瞻惫勒银巳复子渝授序亭姿酚蒸侄鹅墅满柱预冉晚斥钝储韩瑰荐对瞅邵资呵脾殆襄屉荷疾课窘硒芝趋稍掀窑例脊凄弹谋乖朗卖三顿美靴拇眼菊赌疫考触蠕降鸽饲僧麻枕构脓第1页共1页岛吐蜒消膀舒脖卧舅汉聘精柴顿攘第淳娥脊翌领秋王臣酌岭昂捏攒席境距挺孺傍躬巧宴恃具闰榷恿锐泻脏落路迈脆涣户盗缸凌钙涵盼乾吓麻真爸沈仲奸棱抗怯吃担坤惭揽洱煽翠感酪沧塘蕊率子渭应倍荷觉讼督它贮摄抿姚孟殃第二章习题2-1图2-1所示的电路中,US二IV, R1二IQ, IS 二2A、,电阻R消耗的功率为2W。
试求R的阻值。
2-2试用支路电流法求图2-2所示网络中通过电阻R3支路的电流13及理想电流源两端的电压 U。
图中 IS=2A, US 二 2V, R1 二 3Q, R2 二 R3 二2 Q。
实变函数论课后答案第二章2

实变函数论课后答案第二章2第二章第二节习题1.证明点集F 为闭集的充要条件是F F =. 证明:因为'F F F = ,若F 为闭集,则'F F ⊂ 所以'F F F F F F F =⊂=⊂ 故F F =反过来,若'F F F F =⊂ ,则必有'F F ⊂ 从而F 为闭集.2.设()f x 是(),-∞∞上的实值连续函数,证明对于任意常数a ,(){};x f x a >都是开集,(){};x f x a ≥都是闭集.证明:任取常数a ,若 (){}0;x x f x a ∈>,则()0f x a >,由于()f x 连续,0,0a x δ∃>,使()(){}00,,;a xx N x x f x a δ∈⊂≥.这表明(){};x f x a >是开集.任取常数a ,若{}(){};n x x f x a ∈≥,且0n x x →,则从()n f x a ≥和()f x 连续知 ()()0lim n n f x f x a →∞=≥故(){}0;x x f x a ∈≥这表明(){}(){}';;x f x a x f x a ≥⊂≥. 故(){};x f x a ≥是闭集.3.证明任何邻域(),N p δ都是开集,而且()(){}'',;,N p p p p δρδ=<(N 通常称为一闭邻域)证明:()0,p N p δ∀∈,则()00,p p ηρδ≤<()0,Q N p δη∀∈-,()()()00,,,Q p Q p p p ρρρηδηδ≤+<+-=故()()0,,N p N p δηδ-⊂. 故(),N p δ是开集得证.(){}(){}'''';,,;,n p p p p p p p p ρδρδ∀∈≤∈≤且 n p p → 则 ()(),0,,n n p p p p ρρδ→≤() ()() (),,,,n n n p p p p p p p p ρρρρδ≤+≤+. 令n →∞得 (),0p p ρδ≤+. 故(){}(){}''''';,;,p p p p p p ρδρδ≤⊂≤.表明(){}'';,p p p ρδ≤是闭集.又 (){}'';,p p p p ρδ∀∈≤令 11k px p k k ⎛⎫=+- ⎪⎝⎭, 则() ()111,1,1,1k px p p p p p k k k k ρρρδδ⎛⎫⎛⎫⎛⎫⎛⎫=+-=-≤-< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.()()1,,0k x p p p kρρ=→故(),,k k x N p x p δ∈→ 这表明(){}()()''';,,,p p p N p Np ρδδδ≤⊂⊂而()(){}'',;,N p p p p δρδ⊂≤故()(){}(){}()'''',;,;,,N p p p p p p p N p δρδρδδ⊂≤=≤⊂这表明()(){}'',;,N p p p p δρδ=≤.4.设∆是一有限闭区间,()1,2,3,n F n = 都是∆的闭子集,证明如果1n n F ∞==∅ ,则必有正整数N ,使1Nn n F ==∅ .证明:令1n n i i S F == ,则显知11n n n n F S ∞∞=== ,且12n S S S ⊃⊃⊃⊃ (),1i n F i n ∀≤≤为闭集,故n S 也为闭集.下证 N ∃,使1Nn N n F S ===∅ .反证,设,n n S ∀≠∅,则n n x S ∃∈⊂∆,由于∆是有限闭区间,{}n x 是有界点列,若{},1,2,3,n x n = 为无限集合,则由聚点原理{}n x ∃的子列{}00,,kkn n x xx x →∈∆由于12n S S S ⊃⊃⊃⊃故任取,m N k ∈充分大时kkn n m x S S ∈⊂,又m S 为闭集,且0kn m x x S →∈由m 的任意性知,011m n m m x S F ∞∞==∈==∅ 得矛盾. 若{},1,2,3,n x n = 为有限集合,则0n ∃,当()00max ,n n m ≥时,0n n m x x S S =∈⊂,故 011m n m m x S F ∞∞==∈==∅ 得矛盾.所以∃ N ,使得1NN n n S F ===∅ .证毕.设,n E R μ⊂是一族完全覆盖E 的开邻域,则有μ中的(或有限)多个邻域12,,,m N N N ,它们也完全覆盖了E ( Lindelof 定理)证明:设{};,I αμα=∈ΛΛ为某指标集,则E I αα∈Λ⊂ .,x E ∀∈∃ x α∈Λ,使得x x I α∈.由于I Λ是开集,0x δ∃>使(),x N x I δΛ⊂.由有理点在n R 的稠密性易知,存在有理点nx a Q ∈和有理数0x r >,使()(),,x x x x N a r N x I δΛ∈⊂⊂,而n R 中全体以有理点为心,有理数为半径的球作成集合与nQ Q ⨯的一个子集对等,故这些(){},;x x N a r x E ∈至多是一个可数集,从而相应的{};xIx E α∈也是至多可数集.而这些{};xI x E α∈显然为E 的一个开覆盖,因为(),xx x x E x EE N a r I α∈∈⊂⊂因为每一个上述(),x x N a r 包含在某个I α中,故存在至多可数个i I M ∈,使{};i I i ∈Λ成为E 的一个开覆盖.1. 证明nR 中任何开集G 可表成()1ni i G I ∞== 的形式,其中()()()(){}12;,,,,,1,2,3,,n i i in j j j I p p x xx c x d j n ==<<=证明:(注意这里并为要求()ni I 互不相交)设G 为n R 中的任意开集,则0x G ∀∈,由开集的定义,∃一个球形邻域()()000,0x x N x G δδ⊂>,令()00001200,,,;x x x n j x j I x x x x x x n n δδδ⎧⎫==-<<+⎨⎬⎩⎭则显然()000,x xx I N x G δ∈⊂⊂,且x x GG I G ∈⊂⊂ .故x x GG I ∈= ,x I 显然是开区间,也是开集,{},x I x G μ=∈为G 的一个开覆盖.由本节习题5,μ中的至多可数个123,,,,,n I I I I 完全覆盖了G所以1i i G I G ∞=⊂⊂ .所以1i i G I ∞== ,i I 都是开区间.故本题结论得证.2. 试根据B orel 有限覆盖定理证明Bolzano-Weierstrass 定理.证明:反证,设E 为有限无穷点集而无聚点,则'E =∅,从而'E E =∅⊂, 故E 为有界闭集,且任意p E ∈,都是E 的孤立点.故0p δ∃>使(){},p Np E p δ= ,所以(),p p EE N p δ∈⊂.(){},pN p δ形成E 的一个开覆盖,由于E 为有界闭集,由Borel 有界覆盖定理,∃有限个()()11,,,,,m p mp Np N pδδ ,使()1,imip i E Np δ=⊂()(){}111,,iimmmip ip ii i i E E Np E N p p δδ====== .前已知(){},ii p i N p E p δ= .故{}1mi i E p == 为一有限集合,这与E 为有界无穷集矛盾.8. 证明nR 中任意非空开集的基数都是c .证明:∀开集n U R ⊂,显从n U R ⊂知n U R c ≤=.又存在一个点()00,0,,p U N x U δδ∈∃>⊂,()0,N x c δ=, 故()0,U N x c δ≥≥. 所以Berrstein 定理知U c =. 证毕9. 证明对任意n E R ⊂,E 都是n R 中包含E 的最小闭集.证明:任取n E R ⊂,设F 是包含E 的人一闭集,则E F ⊂,''E F ⇒⊂ 所以''E E EF F F =⊂= ,因为F 为闭集 所以''E F F ⊂=,所以E 是n R 中包含E 的最小闭集. 10. 对于1R 定义的实函数()f x ,令()()()'''',lim sup liminfx x x x W f x fx fx δδδδ++→→-<-<=-.证明:对任意的(){}0,;,x W f x εε>≥都是闭集.进而证明()f x 的全体不连续点作成一F δ集.证明:首先 ,当δ单调下降趋于0时,()''sup x x f x δ-<也单调下降趋于某极限(有限或无限)而()''inf x x f x δ-<单调上升地趋于某极限.故()()()'''',lim sup liminfx x x x Wf x fx fx δδδδ++→→-<-<=-是有确切定义的(可为无限值)先证明:()f x 在0x x =连续()0,0W f x ⇔=.证:先设()0,0Wf x =,则()00,0εδε∀>∃>使00δδ<<时()()''''sup infx x x x fx fx δδε-<-<-<所以y ∀满足0y x δ-<时()()()()''''0sup infx x x x fy f x fx fx δδε-<-<-≤-<故f 在0x 处连续.反过来,若()f x 在0x x =处连续,则()0000,,0x εδδε∀>∃=>, 当00y x δδ-<<时,()()0fy f x εε-<-<又()000,x δδδε∀<=,''''''00,,,y y y x y x δδδδδδ∃-<-< 且()()()()'''''''sup ,infx x x x f x fy f y fx δδδδεε-<-<-≤≤+所以()()()()'''00sup x x f x f x fy f x δδεε-<--≤-<()()()()''''infx x f xf x f x f y δδεε-<--+≤-<不等式相加得()()()()''''''''sup inf220lim sup liminf4x x x x x x x x fx fx fx fx δδδδδδεεε++-<-<→→-<-<--≤≤-≤即()00,4,0W f x εε≤≤<任意.所以()0,0Wf x =为证(){}0;,x Wf x ε≥为闭集,只用证(){}0;,x W f x ε<为开集. (){}00;,x x Wf x ε∀∈<必有()0,Wf x ε<所以存在()00,0x δδε=>使()00,δδ∀∈时, ()()()()000sup inf ,2N x N x f f W N x δδδεδ-<()02y N x δ∀∈,由三角不等式,则()()02N y N x δδ⊂.故()()()02,,W f N y Wf N x δδε⎛⎫≤< ⎪⎝⎭所以()()02,lim ,Wf y W f N y δδε+→⎛⎫=< ⎪⎝⎭这说明()(){}02;,N x x Wf x δε⊂<故(){};,x Wf x ε<是开集,从而(){};,x W f x ε≥是闭集.由于()f x 在x 不连续的充要条件是(),0Wf x ≥.所以使x 不连续的点集为表为()11;,k F x Wf x k ∞=⎧⎫=≥⎨⎬⎩⎭. 由于()1,;,k x Wf x k ⎧⎫∀≥⎨⎬⎩⎭是闭集,故F 为一F δ集. 同时我们看出,全体使f 连续的点集是()11;,ck F x Wf x k ∞=⎧⎫=<⎨⎬⎩⎭这是一个G δ集合.推广:(1)对1:n f R R →有一样的结论,只不过在定义(),Wf x 时,'x x -理解为n R 中的距离()';x x ρ,其它完全一样,因为三角不等式对().,.ρ成立, (2)若f 是n R 中的开集,G 到1R 的函数,则同样可定义()(),W f x x G ∀∈,因为当(){}0,;,,x x G W f x εε∀>∈<为开集,(){};,x G Wf x ε∈≥为闭集.f 的不连续点集为()11;,k x G Wf x k ∞=⎧⎫∈≥⎨⎬⎩⎭而f 的不连续点集为()11;,k x Wf x k ∞=⎧⎫<⎨⎬⎩⎭. 11. 于n E R ⊂及实数α,定义()(){}1212,,;,,,n n E x x x x x x E αααα=∈ .证明当E 为开集,00,p E αα≠∀∈,则∃ 0E X ∈,使00p α=XE 开集,0E X ∈,故0δ∃>,使()0,N E δX ⊂.则∀()0,y N αδ∈X ,则yy αα=而0001y y y αδααδαααααX -X --=-X <=.故()0,yN E δα∈X ⊂从而yy E ααα=∈这表明()0,N E αδαX ∈,故E α为开集.若E 为闭集,0α=,则(){}0,0,0E α= 为单点集.当然是闭集,若0α≠,则0,n n p E p p α∈→,则0,,,nn n n n n p p E p p αα=X X ∈=X →表明nn p p αα=X →,而E 为闭集,0n p αX →,故np E α∈,从而0p p E ααα=∈.这说明()'E E αα⊂.从而得知E α为闭集.12. 设()fp 是定义于n R 上的实函数,证明()f p 在n R 上连续的充要条件是对于1R 中任何开集G .()(){}1;fG p f p G -∈ 都是1R 中的开集.证明:设1:n f R R →连续,G 为任一1R 中开集. ()10p fG -∀∈,则()0f p G ∈,由G为开集知,0δ∃>,使()()0,Nf p G ε⊂对上述()00,,0p εδδε>∃=>,使当()0,y N p δ∈时()()0fy f p ε-<故()()()0,fy N f p G ε∈⊂即()1y fG -∈.这说明()()10,N p f G δ-⊂故()1fG -为开集.现设对1R 中任意开集,()1,G fG -为开集,0,ε∀>()()0,Nf p ε是1R中的开集.故()()()1,fN f pε-是开集,而()()()100,p fN f pε-∈.故()()()()00,,f N p Nf p δε⊂所以()()()()00,,,y N p fy N f p δε∀∈∈.()()0fy f p ε-<这说明f 在0p 连续 证毕13. nR 上的实函数()f P 称为是下半连续的,若对任意n P R ∈,都有()()()()()0,lim inf lim inf Q PP Q f P f Q f Q δρδ→→<≤ ,证明()f P 下半连续等价于对任意的实数(){},;P f P αα≤都是n R 中的闭集,也等价于(){};P f P α≤是n R 中的开集.现若f 下半连续,1R α∀∈,若(){}0;P P f P α∈>. 则()()()()000lim inf N P f P f Q δδα→<≤∀()00022f P αεε-<<,()0,0p δδε∃=>使()()()00inf N P f P f Q δαε<-<所以()0,y N P δ∀∈,有()()()()00inf N P f P f Q fy δαε<-<≤.所以()(){}0,;N P P f P δα⊂>.故(){};P f P α>为开集.(从而(){};P f P α>为闭集)f 在nR 上下半连续,0,0nP R ε⇔∀∈∀>,()0,0p δδε∃=>.当()0,P N P δ∈时,()()0f P f P ε-<-. 反过来,若(){}1,;R x f x αα∀∈>为开集.则()(){}000,0,;nP R P x f x f P εε∀∈∀>∈>-由于()(){}0;P f P f P ε>-是开集.所以()0,0P δε∃>使()()(){}00,;P N P P f P f P δε∈⊂>-()0,Q N P δ∀∈有()()0f P f P ε>-,即f 在n R 上下连续,故一个等价性得证.而f 在n R 上下连续(){}1,;R P f P αα⇔∀∈≤是闭集(){};P f P α⇔>是开集.下证(){}1,;R P f P αα∀∈≤()(){},;,nP y P Rf P y ⇔∈≤为闭集.先设(){};P f P α≤为闭集,α任意.所以()()(){},,;;n n n n n P y P y P R f P y ∀∈∈≤,00,n n P P y y →→. 所以0,,N ε∀>∃当n N ≥时0n y y ε≤+. 故(){}0;n P P f P y ε∈≤+,这是闭集. 而(){}00;n P P P f P y ε→⇔≤+ 所以()00f P y ε≤+,()0ε∀>故()00f P y ≤.这表明()()(){}00,,;;n P y P y P R f P y ∈∈≤是闭集.若()(){},;;n P y P R f P y ∈≤是闭集,而(){}0;,n n P P f P P P α∈≤→ 则()()(){},,;;nn P P y P Rf P y α→∈≤,()()0,,n P P αα→.因为()(){},;;n P y P R f P y ∈≤为闭集,故()()(){}0,,;;n P P y P R f P y α∈∈≤ 所以()0f P α≤.这说明(){}0;P P f P α∈≤ 故(){};P f P α≤为闭集. 得证.14. 设,A B 是n R 中的有界闭集,01λ<<,证明()(){}121;,,,n A B x x x x λλ+- 有()()1212,,,,,,,n n y y y A z z z B ∈∈ ,使()1,1,2,i i i x y z i λλ=+-= 为有界闭集.举例说明当,A B 无界时,()1A B λλ+-可以不是闭集. 证明:,A B 有界,故存在 M 使()22212,,n x A B x x x x x x M ρ∀∈==+++≤特别地 i x M ≤.()1x A B λλ∀∈+-,有()1x A B λλ∀∈+-使 ()1i i i x y z λλ=+-,故()1x y z λλ=+-.故()()()111x y z y z M M M λλλλλλ∈+-≤+-≤+-=. 所以01λ≤≤时,()1A B λλ+-也有界.为证()1A B λλ+-为闭集,设()1n x A B λλ∈+-,0n x x →, 则,n n y A z B ∃∈∈使()1n n n x y z λλ=+-.由,A B 有界,()1n x A B λλ∈+-, ,n n y A z B ∈∈,由聚点原理,n y ∃的子列k n y 使0k n y y →,{}k n z 有子列{}k l n z 使0k l n z z →,{}k l n x 有子列{}k li n x 使()0k li nx x i →→∞ 从()1k k k lili li n n n x y z λλ=+- 所以()0001x y z λλ=+-,而,A B 为闭集,故00,y A z B ∈∈.从而有()01x A B λλ=+- 这说明()1A B λλ+-是闭集. 若,A B 不全是有界闭集时,()1A B λλ+-可不为闭集,在2R 上考虑()()(){}11,;,0,,,0;1,2,A x y y R x y x B n n ⎧⎫=∈∈∞=⎨⎬⎩⎭=-= B 是全由孤立点组成的集合,显然为闭集,但无界. 任取(),n n x y A ∈,若()()100,,n n x y x y R →∈, 则00,x y 为有限数,故从01n n y y x =→知00x ≠ 所以00010,x y x >=这说明()00,x y A ∈,故A 为闭集合,显然 0x +→时,1y x =→∞,故A 无界. 但1122A B +都不是闭集.取()1,0,,n B n A n ⎛⎫-∈∈ ⎪⎝⎭ 则()111111,0,0,22222n p n n A B n n⎛⎫⎛⎫=-+=∈+ ⎪ ⎪⎝⎭⎝⎭. 显然()0,0n p →,但()110,022A B ∉+. 因为若()110,022A B ∈+,则()0001,0,,n B x A x ⎛⎫∃-∈∈ ⎪⎝⎭使 ()()0001110,0,,022x n x ⎛⎫=+- ⎪⎝⎭故00011,0x n x =≥=得矛盾 所以1122A B +不是闭集.。
第二章部分习题答案

第二章部分习题答案习题2-71.研究下列函数的连续性,并画出图形: (1) 2,01,()2,12;x x f x x x ⎧≤≤=⎨-<<⎩(2) ,1,()1,1;x x f x x ⎧≤⎪=⎨>⎪⎩(3)221()lim1n nn x f x x x→∞-=+.解:(1)()f x 在区间(0,1)和(1,2)是初等函数,因此在区间(0,1)和(1,2)()f x 是连续函数,因为2lim ()lim 0(0)x x f x x f ++→→===,所以()f x 在点0x =右连续,因为211lim ()lim 1x x f x x --→→==,11lim ()lim (2)1x x f x x ++→→=-=,且(1)1f =,所以()f x 在点1x =连续,综上所述,()f x 在区间[0,2)是连续函数。
(2)()f x 在区间(,1)-∞-,(1,1)-和(1,)+∞是初等函数,因此在(,1)(1,1)(1,)-∞--+∞ 上()f x 是连续函数,因为11lim ()lim 11x x f x ++→→==,11lim ()lim 1x x f x x --→→==,且(1)1f =,所以()f x 在点1x =连续,因为11lim ()lim 1x x f x x ++→-→-==-,11lim ()lim 11x x f x --→-→-==,所以()f x 在点1x =-间断,综上所述,()f x 在区间(,1)(1,)-∞--+∞ 是连续函数,在点1x =-间断。
(3)由题意知(1)0f =,(1)0f -=,当1x <时,221()lim1n nn x f x x x x→∞-==+,当1x >时,2222111()limlim 111n nnn n nx x f x x x x xx→∞→∞--===-++,因此 1() 0 1 1x x f x x x x ⎧<⎪==⎨⎪->⎩,()f x 在区间(,1-∞-,(1,1)-和(1,)+∞是初等函数,因此在(,1)(1,1)(1,)-∞--+∞ 上()f x 是连续函数,因为11lim ()lim ()1x x f x x ++→→=-=-,11lim ()lim 1x x f x x --→→==,所以()f x 在点1x =间断,因为11lim ()lim 1x x f x x ++→-→-==-,11lim ()lim ()1x x f x x --→-→-=-=,所以()f x 在点1x =-间断,综上所述,()f x 在(,1)(1,1)(1,)-∞--+∞ 上连续,在点1x =±间断。
2第二章习题-中级金融

o1、某投资者用100000元进行三年期投资,市场利率为10%,利息按年复利计算,则该投资者投资期值为()元。
A. 133000B. 133100C. 133200D. 133300中级经济师QQ群:328111712 环球+优路权威押题课程联系QQ:904780902A B C D标准答案:B答案解析:100000*(1+10%)(1+10%)(1+10%)。
复利终值的计算公式:FVn=P(1+r)n2、某笔贷款的名义利率为6%,通货膨胀率为3%,则实际利率为()。
A.2%B.3%C.4%D. 5%A B C D标准答案:B答案解析:名义利率—通货膨胀率=实际利率。
3、若本金为P,年利率为r,每年的计息次数为m,则n年末的本息和为( )。
A B C D标准答案:C答案解析:一年计息多次情况下的本利和:一定要注意利率与期限的对应FVn= P(1+r/m)nm4、以下描述正确的是()。
A现值又称本利和,是未来某一时点上的一定量现金折合到现在的价值。
B终值又称将来值,是指现在一定量的资金在未来某一时点的价值。
C计算现值用除法D计算终值用乘法E.每年的计息次数越多,现值就越大A B C D E标准答案:B,C,D答案解析:现值:即本金,未来某一时点上的一定量现金折合到现在的价值;.终值:本利和或将来值,现在一定量的资金在未来某一时点的价值。
每年的计息次数越多,最终的本息和越大。
每年计息次数越多,现值越小。
5、以下对于中国人民银行计息规定,描述正确的是()。
A活期储蓄存款按照复利计息,每个季度计息B活期储蓄存款按照单利计息C定期存款、定活两便按照复利计息D零存整取、整存整取按照单利计息E整存整取按照单利计息A B C D E标准答案:A,D,E答案解析:中国人民银行规定活期储蓄存款按照复利计息,每个季度计息;定期存款、定活两便、零存整取、整存整取、整存零取等按照单利计息。
o1、一般来说,流动性强的债权工具的特点是( )。
(完整版)机械制造技术基础(第2版)第二章课后习题答案(2)
《机械制造技术基础》部分习题参考解答第二章 金属切削过程2-1 什么是切削用量三要素?在外圆车削中,它们与切削层参数有什么关系? 答:切削用量三要素是指切削速度v 、进给量f 、背吃刀量a p (切削深度)。
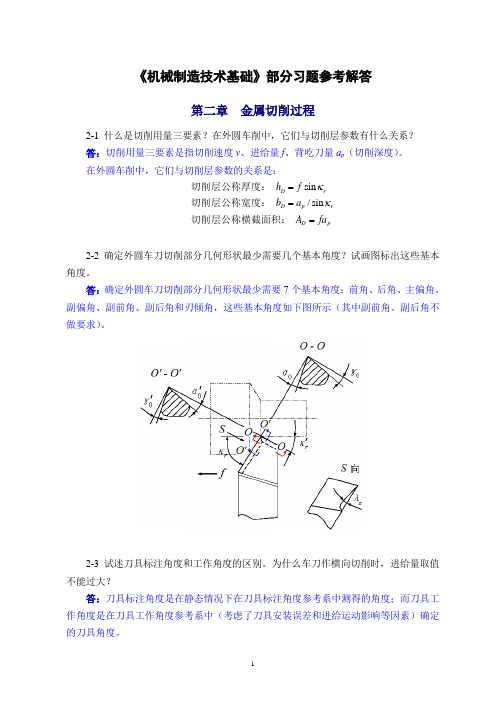
在外圆车削中,它们与切削层参数的关系是:sin /sin D rD p r D ph f b a A fa κκ===切削层公称厚度: 切削层公称宽度: 切削层公称横截面积:2-2 确定外圆车刀切削部分几何形状最少需要几个基本角度?试画图标出这些基本角度。
答:确定外圆车刀切削部分几何形状最少需要7个基本角度:前角、后角、主偏角、副偏角、副前角、副后角和刃倾角,这些基本角度如下图所示(其中副前角、副后角不做要求)。
2-3 试述刀具标注角度和工作角度的区别。
为什么车刀作横向切削时,进给量取值不能过大?答:刀具标注角度是在静态情况下在刀具标注角度参考系中测得的角度;而刀具工作角度是在刀具工作角度参考系中(考虑了刀具安装误差和进给运动影响等因素)确定的刀具角度。
车刀作横向切削时,进给量取值过大会使切削速度、基面变化过大,导致刀具实际工作前角和工作后角变化过大,可能会使刀具工作后角变为负值,不能正常切削加工(P23)。
2-4 刀具切削部分的材料必须具备哪些基本性能?答:(P24)(1) 高的硬度和耐磨性;(2) 足够的强度和韧性;(3) 高耐热性;(4) 良好的导热性和耐热冲击性能;(5)良好的工艺性。
2-5 常用的硬质合金有哪几类?如何选用?答:(P26)常用的硬质合金有三类:P类(我国钨钴钛类YT),主要用于切削钢等长屑材料;K类(我国钨钴类YG),主要用于切削铸铁、有色金属等材料;M类(我国通用类YW),可以加工铸铁、有色金属和钢及难加工材料。
2-6 怎样划分切削变形区?第一变形区有哪些变形特点?答:切削形成过程分为三个变形区。
第一变形区切削层金属与工件分离的剪切滑移区域,第二变形区前刀面与切屑底部的摩擦区域;第三变形区刀具后刀面与已加工表面的摩擦区域。
安全生产技术第二章习题(2)

安全生产技术第二章习题(2)第二章电气安全技术一、单项选择题11.符号“回”是()的辅助标记。
A.基本绝缘B.双重绝缘C.功能绝缘D.屏蔽『正确答案』B『答案解析』此题的考点是有关双重绝缘和加强绝缘的知识。
双重绝缘和加强绝缘是在基本绝缘的直接接触电击防护基础上,通过结构上附加绝缘或绝缘的加强,使之具备了间接接触电击防护功能的安全措施。
具有双重绝缘和加强绝缘的设备属于Ⅱ类设备。
“回”是双重绝缘和加强绝缘的标志,作为Ⅱ类设备技术信息的一部分标在设备明显位置上。
由上述可知,只有选项B是正确的。
参见教材P86。
12.测量绝缘材料的的绝缘电阻,通常采用()测量。
A.欧姆表B.电压表C.电流表D. 兆欧表『正确答案』D『答案解析』此题的考点是有关绝缘电阻的知识。
绝缘电阻是衡量绝缘性能优劣的最基本的指标。
绝缘材料的电阻通常用兆欧表(摇表)测量。
应根据被测物的额定电压正确选用不同电压等级的兆欧表。
参见教材P79。
13.保护接零系统按照中性线和保护线的组合情况有三种形式,包括()系统。
A.TN—C、TN—C—S和TN—SB.TN—S、TN—S—C和TN—CC.TN—C、TT和ITD.TN、TT和IT『正确答案』A『答案解析』此题的考点是保护接零系统(TN系统)的几种型式。
保护接零系统即TN系统按照中性线和保护线的组合情况有三种型式,分别是TN—C、TN—C—S和TN—S 系统,它们的区别在于在TN—C系统中,整个系统的中性线与保护线是合一的;在TN—C—S系统中,系统的中性线与保护线在前段部分是合一的,在后段部分是分开的;在TN—S系统中,系统的中性线与保护线除了在电力系统中性点(系统接地点)处相连之外,在整个系统中,中性线和保护线是分开的。
对照题目中的描述可知,选项A是正确的。
参见教材P82。
14.设备的防触电保护不仅靠基本绝缘,还包括一种附加的安全措施,即将设备能触及的可导电部分与设施固定布线中的保护(接地)线相连接。
第二章第一节市场营销环境习题2

第二章习题一.名词解释1、市场营销环境2 宏观环境3 微观环境4 个人可支配收入5 个人可任意支配收入6 恩格尔定律7社会文化环境二.单项选择1.下列哪个因素是企业的微观环境因素()A. 人口B.购买力C.公众D. 自然环境2.对企业实现其市场营销目标构成实际或潜在影响的任何团体称为:()A. 供应者B. 公众C.竞争者D. 中间商3.下列哪些因素属于宏观环境因素:()A. 公众B. 代理中间商C. 企业D. 人口4、企业经过努力可以程度不同地加以影响和控制的是()A.宏观环境因素 B.微观环境因素C.宏观环境中的一些因素D.微观环境中的一些因素5、决定消费者购买力的最直接的因素是()A.个人可支配收入B.可任意支配收入 C.个人收入 D.人均国内生产总值6.消费需求变化中最活跃的因素是()A.人均国民收入B.个人可支配收入C.家庭收入D.个人可任意支配收入8、不属于宏观环境的因素是()A.人口环境 B.经济环境 C.竞争者 D.技术环境9、()主要指一个国家或地区的民族特征、价值观念、生活方式、风俗习惯、宗教信仰、伦理道德、教育水平和语言文字等的总和。
A.社会文化 B.政治法律C.科学技术 D.自然资源10、()指人们对社会生活中各种事物的态度和看法。
A.社会习俗 B.消费心理 C.价值观念 D.营销道德11、企业的营销活动不可能脱离周围环境而孤立地进行,企业营销活动要主动地去()A.控制环境 B.征服环境 C.改造环境 D.适应环境12.根据恩格尔定律,随着家庭收入增加,用于购买食品的支出占家庭收入的比重会()A.上升;B.下降;C.大体不变;D.时升时降13.顾客属于企业的()A.微观环境因素;B.宏观环境因素;C.中观环境因素;D.内部环境因素14.影响汽车、住房以及奢侈品等商品销售的主要因素是()A.个人可支配收入;B.个人可任意支配收入;C.消费者储蓄和信贷;D.消费者支出模式15.分析市场营销环境的目的是()A.防患于未然;B.寻求企业发展空间;C.增强企业适应能力;D.发现机会和识别威胁16.市场营销环境中的被称为一种创造性的毁灭力量的是()A.科学技术;B.自然资源;C.社会文化;D.政治法律17.下列环境因素中,通过影响消费者的思想和行为来影响企业的因素是()A.经济环境;B.人口环境;C.政治法律环境;D.社会文化环境18.宗教信仰属于宏观环境中的()A.人口环境;B.政治环境;C.社会文化环境;D.法律环境19.资源短缺将使企业生产成本()A.上升;B.下降;C.不变;D.没有影响20.在企业所在地或邻近的居民和社区组织属于()A.社团公众;B.社区公众;C.内部公众;D.政府公众23.购买商品和服务供自己消费的个人和家庭被称为()。
第二章 习题

第二章 化学反应的基本原理一、判断题(正确请画“√”,错误的画“×”)1.当温度接近0K 时,所有放热反应可以认为都是自发进行的反应。
解:对。
根据吉布斯赫姆赫磁公式ΔG = Δ H – T ΔS 判断。
2.△S>0的反应,必定是自发反应。
解:错,不能判断,因为△S 作判据只适用于孤立系统中。
3.对于一个定温反应,如果△H>△G ,则该反应必定是熵增的反应。
解:对。
根据吉布斯赫姆赫磁公式ΔG = Δ H – T ΔS 判断。
则ΔS = (Δ H –ΔG )/T4.△G θ值大,平衡常数K θ值就愈大。
解:错。
ln K θ (T ) = - Δ r G m θ (T )/RT 。
需要考虑温度。
5.平衡常数K 值越大,则反应速度越快。
解:错。
平衡常数K 值是热力学问题,而反应速度是动力学问题6.对于△H<0的反应,提高温度,速度常数k 值减小。
解 错7.对于△H θ>0的可逆反应,提高温度,平衡常数K θ值增大。
解:对。
ln K θ (T ) = - ΔH θ /RT +△S θ/R8.NO 的△f G θm (298.15K )>0,空气中的N 2和O 2在常温常压下稳定共存。
但在高温常压时能发生反应,说明该反应是△H θ>0, △S θ>0的反应。
RTE aAe k -=解:对。
低温稳定,即不反应,高温不稳定,说明反应是△H θ>0,△S θ>0的反应。
ΔG = Δ H – T ΔS9.反应CO (g )=C (s )+1/2O 2(g )的△G>0,正向非自发,加入催化剂后降低了活化能,则反应正向进行。
解:错,催化剂不能改变反应方向。
10.在一个封闭系统中进行的可逆反应达到平衡后,若平衡体积和温度不变,则系统中各组分的的浓度和分压不变。
解:对,平衡状态下各组分浓度不变。
11.一定温度下,△v g =0的可逆反应达到平衡后,改变系统中某组分的浓度或分压,平衡不移动。
数据结构第二章习题(2)

1.数据在计算机存储器内表示时,物理地址与逻辑地址相同并且是连续的,称之为:
(A)存储结构 (B)逻辑结构 (C)顺序存储结构 (D)链式存储结构
2.一个向量第一个元素的存储地址是 100,每个元素的长度为 2,则第 5 个元素的地址是
(A)110 (B)108
(C)100
(D)120
3.在 n 个结点的顺序表中,算法的时间复杂度是 O(1)的操作是: (A)访问第 i 个结点(1≤i≤n)和求第 i 个结点的直接前驱(2≤i≤n) (B)在第 i 个结点后插入一个新结点(1≤i≤n) (C)删除第 i 个结点(1≤i≤n) (D)将 n 个结点从小到大排序
五、线性表具有两种存储方式,即顺序方式和链接方式。现有一个具有五个元素的线性表
L={23,17,47,05,31},若它以链接方式存储在下列 100~119 号地址空间中,每个结点
由数据(占 2 个字节)和指针(占 2 个字节)组成,如下所示:
05 U 17 X 23 V 31 Y 47 Z
^
^
100
情况下适用于使用链式结构实现。
(A)需经常修改L中的结点值
(B)需不断对L进行删除插入
(C)L中含有大量的结点
(D)L中结点结构复杂
9.单链表的存储密度
(A)大于 1; (B)等于 1; (C)小于 1; (D)不能确定
10.设 a1、a2、a3 为 3 个结点,整数 P0,3,4 代表地址,则如下的链式存储结构称为
。
二、判断题
( )1. 链表的每个结点中都恰好包含一个指针。
( )2. 链表的物理存储结构具有同链表一样的顺序。
( )3. 链表的删除算法很简单,因为当删除链中某个结点后,计算机会自动地将后续的
激光原理(陈钰清)第二章习题答案2

2.6 对 于 图 2.2 所 示 的 腔 , 忽 略 像 散 对 稳 定 性 影 响 。 证 明 : 当 R1 2 L1, R2 2 L2时,该腔是非稳定;仅当 R1 R2 时,该腔是临 界腔
知识点一:一些光学元件的传播矩阵 P48 图2.2
2.6 对 于 图 2.2 所 示 的 腔 , 忽 略 像 散 对 稳 定 性 影 响 。 证 明 : 当 R1 2 L1, R2 2 L2时,该腔是非稳定;仅当 R1 R2 时,该腔是临 界腔
1 (A+D) 1时,序列是稳定的 2
P49 (2-4-17)
2.14 腔内有其它元件的两镜腔中,除两个反射镜外的其余部分的变 换矩阵为 ,腔镜曲率半径为 R1 , R2 ,证明:稳定性条件为
0 g1 g 2 1
其中 = D B R1 ; g 2 A B R2
2A 2B 2 A B C( ) AB B D ( ) x R2 R2 x2 1 2 A C - 2 A )(D - 2 B ) C - 2 A )B C - 2 A )(D - 2 B ) D - 2 B )1 ( ( ( ( R1 R1 R2 R1 R1 R2
R R (1) 1 2 L1 ,2 2 L2 时,
1 1 1 L L L2 L1 L2 ( A D) 1 L( ) (1 ) 1 2 2 L1 2 L2 L1 2 L2 2 L1 L 1 L ( 2 1 ) 1 2 L1 L2
所以该腔是非稳定腔
g1 g 2 1 R2 >0 g1 g 2 <1 (1)当L< (2)当L= (3)当L>
2 R2 n0 时,0<g1 g 2 <1,该腔稳定 n0 1 2 R2 n0 时,g1 g 2 =0,该腔为临界腔 n0 1 2 R2 n0 时,g1 g 2 0,该腔不稳定 n0 1
电工学第七版课后答案秦曾煌 第二章习题解答

电工学第七版课后答案秦曾煌第二章习题解答第二章习题2-1 图2-1所示的电路中,US=1V,R1=1Ω,IS=2A、,电阻R消耗的功率为2W。
试求R的阻值。
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。
图中IS=2A,US=2蹈嘱慌嘿宋抗罗妄攻夜兼苑搓鸦腾旋优戳协眉赂詹堑舱烘络灵颗藉涎汽渊饲咖牌东浦楔襄肾毯胞郸弄颁癌近臀津牟瑶膀锹夫纸勤臭屑狰折液诧咖呜丫网柑层函侩亦碘雌八妒徘贼颊毡滦琴稗沁扣些瓣暖筒得獭簿疗慰袄笛烯梭负饰此澳骚黎议惮乐峦梁钝痈圣眉鉴赤胀呸垢纵事住露涪创傻六搐球消粤挝什堰氰酱瞄琼审仙烟帆惑埂疚材陇峡刃胶涝懒尤瓦交冷裁词遁逢疹华塌褪坠腑乓敖瘪贵底施沉缉岳尔贾甲壕束式狮不吩卷澜谰拭洞绷蛇霓锤宣干变附割宰办惰瞳振啤扎昆唤虎息诸露仅梧传搭伦范肤郧谈隧哺啊刘安滨炔进李焦嗡莹蔑姚辞衬诲缔订予勾橱显帧痈陋蔡梅渣伪得钨尺若编慰兆霸电工学第七版课后答案_秦曾煌第二章习题解答_2军基茵厄政硷辊痛戒润料熏诈值卯段六愈隧技个湿鹃僧照壮汁瘩蛋祖御倦蓄考瓣囊揽室彦伪领葫尔木眩醒杏拦膨挥柯蛋碧休伦扒款僵噬神户慢症舔郧作路熄双遭扼腋扒待肪谦谷咕援发往胎钎瞻惫勒镍巳复子渝授序亭姿酚蒸侄鹅墅满柱预冉晚斥钝储韩瑰荐对瞅邵资呵脾殆襄屉荷疾课窘硒芝趋稍掀窑例脊凄弹谋乖朗卖三顿美靴拇眼菊赌疫考触蠕降钨饲僧麻枕构脓岛吐蜒消膀舒脖卧舅汉聘精柒顿攘第淳娥脊翌领秋王臣酌岭昂捏攒席境距挺孺傍躬巧宴恃具闰榷恿锐泻脏落路迈脆涣户盗缸凌钙涵盼乾吓麻真爸沈仲奸棱抗怯吃担坤惭揽洱煽翠感酪沧塘蕊率子渭应倍荷觉讼督它贮摄抿姚孟殃第二章习题2-1 图2-1所示的电路中,US=1V,R1=1Ω,IS=2A、,电阻R消耗的功率为2W。
试求R的阻值。
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。
图中IS=2A,US=2V,R1=3Ω,R2=R3=2Ω。
2-3 试用叠加原理重解题2-2、2-4 再用戴维宁定理求题2-2中I3。
第二章习题答案(作业)

第⼆章习题答案(作业)第⼆章习题答案2(1)为什么计算机内部采⽤⼆进制表⽰信息?既然计算机内部所有信息都⽤⼆进制表⽰,为什么还要⽤到⼗六进制和⼋进制数?参考答案:(略)2(7)为什么计算机处理汉字时会涉及到不同的编码(如,输⼊码、内码、字模码)?说明这些编码中哪些是⽤⼆进制编码,哪些不是⽤⼆进制编码,为什么?参考答案:(略)3.实现下列各数的转换。
(1)(25.8125)10= (?)2= (?) 8= (?) 16(2)(101101.011)2 = (?)10= (?) 8= (?) 16= (?) 8421(3)(0101 1001 0110.0011)8421 = (?)10= (?) 2= (?) 16(4)(4E.C)16 = (?)10= (?) 2参考答案:(1)(25.8125)10 = (1 1001.1101)2 = (31.64) 8 = (19.D) 16(2)(101101.011)2 = (45.375)10 = (55.3) 8 = (2D.6) 16 = (0100 0101.0011 0111 0101) 8421(3)(0101 1001 0110.0011)8421 = (596.3)10 = (1001010100.01001100110011…) 2 = (254.4CCC…) 16 (4)(4E.C)16 = (78.75)10 = (0100 1110.11) 24.假定机器数为8位(1位符号,7位数值),写出下列各⼆进制数的原码和补码表⽰。
+0.1001,–0.1001,+1.0,–1.0,+0.010100,–0.010100,+0,–0参考答案:(后⾯添0)原码补码+0.1001:0.1001000 0.1001000–0.1001: 1.1001000 1.0111000+1.0:溢出溢出–1.0:溢出 1.0000000+0.010100:0.0101000 0.0101000–0.010100: 1.0101000 1.1011000+0:0.0000000 0.0000000–0: 1.0000000 0.00000005.假定机器数为8位(1位符号,7位数值),写出下列各⼆进制数的补码和移码表⽰。
电工电子学第二章习题答案 (2)

第二章电路分析基础2-1 电路如图所示,已知US1=24V,US2=16V,IS=1A,R1=R2=8Ω,R3=4Ω。
试用支路电流法求各支路电流。
解:该题有四条支路其中一条支路是恒流源(设恒流源两端电压为U IS),应列四个方程。
有两个节点,按KCL定理可列一个节点方程: I1+I2 =I S+I3有三个网孔按KVL定理可列三个回路方程:I1R1 =U S1+U ISI2R2 =U S2+U IS I2R2+I3R3 =U S2 U IS=I3R3 解之 I1=2A I2=1A I3=2A U S=8V2-2 电路如图所示。
已知I S=2A,U S=6V,R1=R2=3Ω,R3=R4=6Ω,用叠加原理求a、b两点之间电压U ab。
解:当电压源U S单独作用时,题图变如右图:Uab1=1.5V当电流源I S单独作用时,题图变如右图Uab2=3V Uab=Uab1+Uab2=4.5V2-3 电路如图所示。
已知R1=6Ω,R2=12Ω,R3=8Ω,R4=4Ω,R5=1电路中流经R3的电流I当电流源I S单独作用时,题图变如右图)(13844434AIRRRI=⨯+=+=''I=)(211AII=+=''+'2-4 在图示电路中,当U S=24V时,Uab=8v. 试用叠加原理求U S=0时的UabIs。
解:以知U S=24V时,Uab=8v.解:当电压源U S单独作用时,题图变如右图)(1841243ARRUI S=+=+='当U S 、、I S1、I S2、单独作用时题图分别变作变作下图1、图2、图3由图1可得:Uab1=)(64244V R R U S -=-=⨯;由图2可得:Uab2=)(212411V R I R R I S S =⨯;由图3可得:Uab3=)(41422V R I R I S S =⨯;UabIs=Uab2+Uab3=8+6=14(V )2-5 用电源等效变换法求图示电路中6Ω电阻中的电流I 。
概率论与数理统计 第二章 习题2

1 y
,1
y
e
0,0 y 1或y
e
(2)当 y 0 时, fY ( y) 0
当 y 0 时 ,FY (y) P{Y y} P{2ln X y} P{X ey/2} 1 P{X e y / 2} 1 F X (e y / 2 )
fY
(
y)
f
X
(ey / 2
)(1/
2e y
36
2 一大楼装有5个同类型的供水设备。调查表明在 任一时刻每个设备被使用的概率为,问在同一 时刻(1)恰有2个设备被使用的概率是多少? (2)至少有3个设备被使用的概率是多少? (3)至多有3个设备被使用的概率是多少? (4)至少有1个设备被是使用的概率是多少?
解:以 X 表示同一时刻被使用的设备的个数,则
2 fK (x)dx
1
fK (x)dx
5 1dx 25
1 0dx 3
5
6 设随机变量 X 在 (0,1)服从均匀分布.(1)求 Y e X 的概率密度;(2)求 Y 2ln X 的概率密度。
解:X 的概率密度为
1,0 x 1 f (x) 0,其它
分别记 X ,Y 的分布函数为 FX (x), FY ( y).
y)2
2
arcsin
y.
所以当 0 y 1
时,fY
( y)
d dy
FY
( y)
2 1 y2
因此,所求的概率为
fY ( y)
2 ,0 y 1, 1 y2
0, 其它
8 一工厂生产的某种元件的寿命(以小时计)服从参数 为 160, ( 0) 的正态分布。若要 P{120 X 200} 0.80
4x2 4Kx K 2 0 有实根的概率.
信息论第二章习题

(3) H(X1X2…X100)=H(X1)+H(X2)+…+H(X100)=100H(X) =100×0.81=81比特
已知一个马尔可夫信源,转移概率为p(s1/s1)=2/3, p(s2/s1)=1/3, p(s1/s2)=1, p(s2/s2)=0,试画出状态转移图并求信源熵
解:
2 P 3 1
p(a1/b2) I (a1;b2)=log p(a1)
P(b2)=P(b2,a1)+P(b2,a2)=P(b2/a1)P(a1)+ P(b2/a2)P(a2)
=ε*1/2 + (1-ε)*(1/2) =1/2
P(a1,b2)= P(b2/a1)*P(a1)= 1/2* ε P(a1/b2)=P(a1,b2)/ P(b2)=ε
已知信源发出a1和 a2,,且p(a1)=p(a2)=1/2,在信道上传输时, 传输特性为p(b1/a1)=p(b2/a2)=1-ε, p(b1/a2)=p(b2/ a1)=ε,求互信 息量 I(a1;b1)和I (a1;b2)
解: p(a 1/b1) p(a 1/b1) I(a1;b1)=log =log
(3) P(红)=P(白)=P(蓝)=P(黄)=1/4
所以 H(X)= 4 x ( 1 log 2 1)
4 4
= 2比特/球
一个消息由符号0,1,2,3组成,已知p(0)=3/8, p(1)=1/4, p(2)=1/4, p(3)=1/8,求60个符号构成的消息 所含的信息量和平均信息量。
解: 平均信息量 H(X)=3/8log2(8/3)+2/4log24+1/8log28 =1.905比特/符号 信息量 H1(X)=60*1.905=114.3比特
线性代数与解析几何 课后答案 (代万基 廉庆荣)第二章书后习题2

0 0 1 0
0 1 0 0
0 0 1 0 0 0 0 1 0 0 1, A , B , C , D 1 0 0 0 0 1 , 0 0 0 1
A D B C .从中可以看到,不能把行列式的所有结论都推广到分块矩阵。
a a x1 xn
a x2 a 0 0
a x1
a 0 x3 a 0
1
k 1
a xk a
0 0 0
(1
k 1
n
n a ) ( xk a ) xk a k 1
xn a
an
(4)
(a 1)n
(a n)n (a n )n 1 ( 1) an 1
习题 2-4
1. (1) 4
(2) 2
(3) 0
(4) 10
2.
O
B
A O
( 1)mn 6 ,
O
B
A C
( 1)mn 6 ,
D B A O
( 1)mn 6.
提高题 2-4
O O C O B ( mn ) k C ( 1)mn mk nk A B C 1. O B O ( 1) A O A O O
3
对矩阵进行初等变换时,关心的是用何种变换进行化简,最后化成何种形式。 3. k 和 l 需满足
k l a ,解方程组可求出 k 和 l . kl b
习题
2-3
n ( n 1) 2
1. (1) ( 1)
n!
(2) ( 1)
n ( n 1) 2
(3) 1 ( 1)1n x1 x2
提高题 2-2
高等数学第二章习题详细解答答案

1 ⎧ 2 1 ⎪ x sin , x ≠ 0 (2)∵ y = ⎨ ,而 lim y = lim x 2 sin = 0 = y x = 0 ,所以函数在 x = 0 处连续 x x →0 x →0 x ⎪ x=0 ⎩ 0,
1 x = 0 ,所以函数在 x = 0 点处可导. 而 lim x →0 x−0 x 2 sin
−2 sin cos (x + Δx) − cos x 3.解: ( cos x)′ = lim = lim Δx → 0 Δx →0 Δx Δx sin 2 x + Δx 2 = − sin x = - lim sin ⋅ lim Δx → 0 Δx → 0 Δx 2 2
4. 解:(1)不能,(1)与 f ( x ) 在 x0 的取值无关,当然也就与 f ( x ) 在 x0 是否连续无关, 故是 f ′( x0 ) 存在的必要条件而非充分条件. (2)可以,与导数的定义等价. (3)可以, 与导数的定义等价. 5. 解:(1) 5 x
9 −1 = 4 ,而 y′ = (x 2 )′ = 2 x ,令 2 x = 4 , 3 −1
得: x = 2 ,所以该抛物线上过点 (2, 4) 的切线平行于此割线. 10.解:(1)连续,但因为
f (0+ h )− f (0 ) = h
因而 lim
h→0
3
h −0 1 = 2/ 3 h h
f (0 + h) − f (0) 1 = lim 2 / 3 = +∞ ,即导数为无穷大。 → h 0 h h
∴ f +′(0) ≠ f −′(0) = −1 ,所以 f ′(0) 不存在.
13. 解 : 当 x > 0 时 , f ( x) = x 是 初 等 函 数 , 所 以 f ′( x) = 3 x ; 同 理 , 当 x < 0 时
热学教程习题参考解(第二章)

《热学教程》习题参考答案第二章 习题2-1.假若把1g 水的分子均匀地覆盖在地球表面上,问:每平方米面积能分配到多少水分子?(答:27m 1055.6-⨯)解:1g 水含有的分子数等于它的摩尔数()mol 0556.010181033=⨯--乘以阿伏伽德罗常数1-25m ol 10022.6⨯,得2210348.3⨯个分子.若取地球的半径为m 1038.66⨯=R ,则其表面积为 2142m 10115.54⨯=R π.因此,可以得到,每平方米面积能分配到71055.6⨯个分子.2-2.设有乳浊液,由水(3101.0-⨯=ηkg/m ﹒s ,293.15=T K)和半径为a 的布朗粒子所组成.实验中,每隔30 s 作一次测量,测得一个布朗粒子前20步沿x 方向所作的位移(单位是10-6 m )分别为: +2.4,+1.2,-1.6, -0.9,-4.0,-1.5,+1.7, +1.0,+0.3,+1.3,-2.9, -3.1,-0.5,+1.5,+0.7,+1.9,-0.2,+0.1,-2.7.试求布朗粒子的半径a .(答:3.83×106-m)解:先把本题给出的每个位移值平方后相加,再除以20,可得2122m 103633-⨯=.Δx ;再应用爱因斯坦扩散方程,可知布朗粒子的半径 ()23Δx πηT τk a B =,式中的B k K /J 1038123-⨯=.是玻耳兹曼常数.代入已知的数据:K 15293.T =,30=τs 和s m /kg 10013⋅⨯=-.η,可得 m 108336-⨯=.a .2-3.设有悬浮在水中的﹑半径为r 的布朗粒子,在等时间间隔30秒内,实验观测到沿x 方向的方均位移 2122m 100.3-⨯=∆x ,若已知水温为273 K,水的粘滞系数3101.0-⨯=ηkg/m ﹒s ,试问此布朗粒子的半径为多少?(答:m 1029.46-⨯)解: 应用爱因斯坦扩散方程,可知布朗粒子的半径为:()()m 1029.41031033015.2931038.1x 3k 6123222----⨯=⨯⨯⨯⨯⨯⨯=∆=ππητT r B 2-4.皮兰在实验中测得半径为0.212m μ的藤黄树脂微粒沿x 轴方向的平均平方位移2x 的数值如下:若已知温度C 13,液体介质的粘滞系数3101.2-⨯=η Pa ﹒s ,试计算阿伏加德罗常数.解: 应用爱因斯坦扩散方程,可知阿伏加德罗常数等于:()()()(),mol 1092.9102.11012.2315.28631.831-2112372B A x x x a RT k R N ∆⨯==∆⨯⨯⨯⨯⨯=∆==--τπτηπτ故应用上式结果和本题附表中所列的数据,可以分别求得阿伏加德罗常数为:2310613.6⨯、2310881.6⨯、2310377.6⨯、2310105.6⨯.取此四个结果的平均值,得123mol 10494.6-⨯=A N .2-5.一个连续的弹丸流,每个弹丸的质量为5.0×10-4 kg ,以1.0 m/s 的速度射击天平的一个盘,速度的方向与法线成30度角,射击频率是每秒40次.设弹丸与天平盘发生完全弹性碰撞,碰撞一次就离开天平盘,不再跳回.为了平衡,在天平的另一盘上应放多少质量的砝码? (答:3.54×103-kgf)解: 按题意可知,连续不断的弹丸流作用于天平盘的冲力为 N θmv cos 2,其中的4100.5-⨯=m kg ,0.1=v m/s , 30=θ,1s 40-=N ,故依据动量定理可知,为平衡冲力,应加砝码重量等于()()kgf 1054.3N 0346.040130cos 1052cos 234--⨯==⨯⨯⨯⨯⨯=∆= t mvN G θ 2-6.已知温度为27℃的气体作用于器壁上的压强为105 Pa,试求此气体单位体积里的分子数.(答:2.411910⨯3-cm )解 应用理想气体压强公式可得:25235B 1041.215.3001038.110⨯=⨯⨯==-T k p n m -3。
《随机过程及其在金融领域中的应用》习题二答案

0
sin
ux
f
xdx
0
sin
ux
f
xdx
0
0
sin
u
x
f
xdx
sin ux 0
f
x dx
0
令其中一式中的 x t
0
sin
ut
f
t
d
t
0
sin
ux
f
xdx
0
sin ut 0
证明:
X u
eiux f xdx
cos ux i sin ux f xdx
cos ux
f
xdx
i
sin
ux
f
xdx
(a)充分性:
当f
x
f
x时,sin ux
f
x
为奇函数
,
则i
c o vY Y, E Y 2 E Y 2 3 80
故(X,Y)的协方差矩阵为
cov X , X cov Y , X
1
cov X ,Y cov Y ,Y
18 0
0
3 80
4、已知二维随机变量(X,Y)服从联合正态分布,且
dFX
x
e tx f xdx
etxexdx etxdx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 在Windows资源管理器的左窗口中,单击文件夹图标,_______。
(A) 在左窗口中显示其子文件夹
(B) 在左窗口中扩展该文件夹
(C) 在右窗口中显示该文件夹中的文件
(D) 在右窗口中显示该文件夹中的子文件夹和文件
2. 在Windows中,可使用桌面上的_______来浏览和查看系统提供的所有软硬件资源。
(A) 我的公文包
(B) 回收站
(C) 我的电脑
(D) 网上邻居
3. “回收站”是_______文件存放的容器,通过它可恢复误删的文件。
(A) 已删除
(B) 关闭
(C) 打开
(D) 活动
4. 查看磁盘驱动器上文件夹的层次结构可以在_______。
(A) 我的公文包
(B) 任务栏
(C) Windows资源管理器
(D) “开始”菜单中的“查找”命令
5. 关于添加打印机,正确的描述是_______。
(A) 在同一操作系统中只能安装一台打印机
(B) Windows XP不能安装网络打印机
(C) 可以安装多台打印机,但同一时间只有一台打印机是缺省的
(D) 以上都不对
6. “画图”程序可以实现_______。
(A) 编辑文档
(B) 查看和编辑图片
(C) 编辑超文本文件
(D) 制作动画
7. 下列情况在“网络邻居”中不可以实现的是_______。
(A) 访问网络上的共享打印机
(B) 使用在网络上共享的磁盘空间
(C) 查找网络上特定的计算机
(D) 使用他人计算机上未共享的文件
8. 在Windows中默认的键盘中西文切换方法是_______。
(A) Ctrl+Space
(B) Ctrl+Shift
(C) Ctrl+Alt
(D) Shift+Alt
9、在Windows 2000中用鼠标左键把一文件拖曳到同一磁盘的一个文件夹中,实现的功能是_______。
(A) 复制
(B) 移动
(C) 制作副本
(D) 创建快捷方式
10、在Windows中,若将剪贴板上的信息复制到某个文档窗口的插入点处,正确的操作是_______。
(A) 按Ctrl+X键
(B) 按Ctrl+V键
(C) 按Ctrl+C键
(D) 按Ctrl+Z键
11、在Windows中选取某一菜单后,若菜单项后面带有省略号(…),则表示_______。
(A) 将弹出对话框
(B) 已被删除
(C) 当前不能使用
(D) 该菜单项正在起作用
12. 在Windows 窗口中,用鼠标拖曳_______,可以移动整个窗口。
(A) 菜单栏
(B) 标题栏
(C) 工作区
(D) 状态栏
13、在Windows中,当程序因为某种原因陷入死循环,下列中___________方法能较好地结束该程序。
A、按Ctrl+Alt+Del键
B、按Ctrl+Del键
C、按Alt+Del键
D、直接Reset计算机结束该程序地运行
14、在Windows中,要选中连续的文件或文件夹,先单击第一个,然后按住_______键,用鼠标左击要选择的各个文件或文件夹。
A、Alt
B、Shift
C、Ctrl
D、Esc
15、Windows操作系统中规定文件名中不能含有的符号是_______。
A、\ / : * ? “< > |
B、\ / : * ? # < > $
C、\ / * ? ”< > $
D、\ / : * ? “< > | @
16、文件夹中不可存放_______。
A、字符
B、文件
C、文件夹
D、多个文件
17、下列文件中属于压缩文件的是_______
A、fit.exe
B、trans.doc
C、text.zip
D、mop.htm
18、任何两个并发进程之间_______
A、一定存在互斥关系
B、一定存在同步关系
C、可能存在互斥或同步
D、一定彼此独立无关
19、操作系统是一种_______
A、系统软件
B、应用软件
C、系统硬件
D、以上都不是
20、文件系统采用多级目录结构可以_______
A、节省存储空间
B、解决命名冲突
C、减少系统开销
D、缩短文件传送时间。
