利用Matlab画频谱图
利用Matlab绘制正弦信号的频谱图并做相关分析

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求:1、信号可变(信号的赋值、相位、频率可变);2、采样频率fs可变;3、加各种不同的窗函数并分析其影响;4、频谱校正;5、频谱细化。
二、采用matlab编写如下程序:clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1:fs=100,N=1024');grid on;%两种信号叠加,x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2:fs=100,N=1024,两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3:fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4:fs=100,N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5:fs=400,N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6:fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7:fs=100,N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8:fs=100,N=1024,加汉宁窗函数');grid on;三、运行结果如下:四、分析与结论:1)从所做图像可以看出,信号的幅值均小于真实值,说明在截断信号时存在泄露。
matlab求连续信号的频谱函数和离散信号频谱函数的方法

matlab求连续信号的频谱函数和离散信号频谱函数的方法Matlab提供了多种方法来求解连续信号和离散信号的频谱函数。
在本文中,我们将分步骤介绍这些方法。
一、连续信号频谱函数的方法连续信号的频谱函数是通过对连续信号进行傅里叶变换得到的。
而在Matlab中,傅里叶变换可以通过fft函数实现。
下面是求解连续信号频谱函数的步骤:1. 定义连续信号首先,我们需要定义一个连续信号,用一个函数来表示。
例如,我们定义一个简单的三角波信号:matlabt = linspace(0, 1, 1000); 定义时间范围x = sawtooth(2*pi*5*t); 定义三角波信号2. 进行傅里叶变换接下来,我们使用fft函数对连续信号进行傅里叶变换。
傅里叶变换将信号从时域转换到频域。
matlabX = fft(x);3. 计算频谱函数通过进行傅里叶变换,我们得到了频谱函数X。
然而,频谱函数X是一个复数数组,其中包含了信号的幅度和相位信息。
为了获得真正的频谱,我们需要计算幅度谱。
matlabP2 = abs(X/length(x));P1 = P2(1:length(x)/2+1);P1(2:end-1) = 2*P1(2:end-1);在上述代码中,我们将频谱函数除以信号长度,然后计算幅度,并使用对称性将频谱函数变换为正频率部分。
最后,我们将频谱函数的第一个和最后一个值乘以2。
4. 绘制频谱图最后,我们可以使用plot函数将频谱函数可视化。
matlabfs = 1000; 采样频率f = fs*(0:(length(x)/2))/length(x);plot(f,P1)xlabel('Frequency (Hz)')ylabel('Amplitude')以上步骤可以用于求解任何连续信号的频谱函数。
二、离散信号频谱函数的方法离散信号的频谱函数可以通过对信号进行离散傅里叶变换(Discrete Fourier Transform,DFT)来获得。
用matlab画出声音的频谱

一.实验内容
任选一个声音文件,画出其波形图和频谱图。
二.算法分析和描述
(1)选择一个wav文件作为分析的对象
(2)读取音频信号的数据,并画出其时域波形和频谱图。
所使用到的几个函数如下:
1.[x,fs,bits]=wavread('filename')这是一个matlab中读取wav文件的
数据的函数。
2.[d]=fft(w,l)这是matlab中fft函数的一种输入输出形式。
3.sound(w,fs,bits)函数它将数列的数据通过声卡转化为声音。
三.实现方法(含实现思路、程序流程图和源程序列表等)clear
[y,fs,bits]=wavread(‘声音');
sound(y,fs,bits);
Y=fft(y,4096);
subplot(211);
plot(y);
title('声音信号的波形');
subplot(212)
plot(abs(Y));
title('声音信号的频谱');
四.实验结果分析(含执行结果验证、输出显示信息和图形等)通过编程实现得到下列图形:。
实验2 用MATLAB进行信号频谱分析 2

实验报告通信工程 1101学号:********* 姓名:李*实验2 用MATLAB 进行信号频谱分析一、实验目的㈠ 初步掌握MATLAB 产生常用离散时间信号的编程方法。
㈡ 学习编写简单的FFT 算法程序,对离散信号进行幅频谱分析。
㈢ 观察离散时间信号频谱的特点。
二、实验原理㈠ 常用的离散时间信号在 MATLAB 语言主要是研究离散信号的。
常用的离散信号有: 1.单位取样序列⎩⎨⎧≠==0001)(n n n δ2.单位阶跃序列⎩⎨⎧<≥=001)(n n n u3.实指数序列R a n a n x n∈∀=;)(4.复指数序列n e n x n j ∀=+)(0)(ωσ5.正(余)弦序列)cos()(0θω+=n n x n ∀ 6.周期序列n N n x n x ∀+=)()(㈡ 离散信号的产生离散信号的图形显示使用stem 指令。
在 MATLAB 中的信号处理工具箱中,主要提供的信号是离散信号。
由于MATLAB 对下标的约定为从1开始递增,例如x=[5,4,3,2,1,0],表示x(1)=5,x(2)=4,X(3)=3…因此要表示一个下标不由1开始的数组x(n),一般应采用两个矢量,如 n=[-3,-2,-1,0,l ,2,3,4,5];x=[1,-l ,3,2,0,4,5,2,1];这表示了一个含9个采样点的矢量:X(n)={x(-3),x(-2),x(-1),x(0),x(1),x(2),x(3),x(4),x(5)}。
1.单位取样序列⎩⎨⎧≠==δ0001)(n n n 这一函数实现的方法有二:方法一:可利用MATLAB 的zeros 函数。
x=zeros(1,N); %建立一个一行N 列的全零数组x(1)=1; %对X (1)赋1 方法二:可借助于关系操作符实现n=1:N;x=[n==1]; %n 等于1时逻辑关系式结果为真,x=1;n 不等于1时为假,x=0如要产生 ⎪⎩⎪⎨⎧≤<<=≤≤=-δ20210100)(10)(n n n n n n n n n n n n则可采用MATLAB 实现:n=n1:n2;x=[(n-n0)==0];%n=n0时逻辑关系式结果为真,x=1;n ≠n0时为假,x=0 2.单位阶跃序列⎩⎨⎧<≥=001)(n n n u这一函数可利用MATLAB 的ones 函数实现: x=ones(1,N);还可借助于关系操作符“>=”来实现。
用MATLAB进行FFT频谱分析

用MATLAB举止FFT频谱分解之阳早格格创做假设一旗号:画出其频谱图.分解:最先,连绝周期旗号截断对于频谱的做用.DFT变更频谱揭发的根根源基本果是旗号的截断.立即域加窗,对于应为频域卷积,果此,窗函数的主瓣宽度等便会做用到频谱.真验标明,连绝周期旗号截断时持绝时间与旗号周期呈整数倍闭系时,利用DFT变更不妨得到透彻的模拟旗号频谱.举一个简朴的例子:其周期为0.02.截断时分歧的持绝时间做用如图一.1:(对于应步调shiyan1ex1.m)图错误!文档中没有指定样式的文字。
.1其次,采样频次的决定.根据Shannon采样定理,采样戴限旗号采样频次为停止频次的二倍以上,给定旗号的采样频次应>1/7.92,与16.再次,DFT算法包罗时域采样战频域采样二步,频域采样少度M战时域采样少度N的闭系要切合M≧N时,从频谱X(k)才可真足沉修本旗号.真验中旗号R经采样后的失集旗号没有是周期旗号,然而是它又是一个无限少的旗号,果此处理常常域窗函数尽管博得宽一些已交近本质旗号.真验停止如图一.2:其中,0面位子的冲激项为曲流分量0.6制成(对于应步调为shiyan1.m)图错误!文档中没有指定样式的文字。
.2♣ARMA(Auto Recursive Moving Average)模型:将稳固随机旗号x(n)瞅做是整均值,圆好为σu2的黑噪声u(n)通过线性非移变系统H(z)后的输出,模型的传播函数为用好分圆程表示为AR(Auto Recursive)自返回模型,即ARMA模型中系数b惟有正在r=0的情况下为1,其余皆是整,赢得一个齐极面模型:好分圆程表示为:AR模型的功率谱预计为:步调:%%------------------------------------------------------------------------%%功能:利用MATLAB的FFT函数干单正弦旗号频谱分解%%------------------------------------------------------------------------fs=16;t=0:1/fs:200;x6=0.6+sin(2*pi*t/2.996)*0.1+cos(2*pi*t/7.92+2)*0.1; subplot(2,1,1);plot(t,x6);N=length(t);subplot(212);plot((-N/2:N/2-1)*fs/N,abs(fftshift(fft(x6,N)))) %画制旗号的频谱,横轴对于应本质频次axis([0 0.5 0 160]);例子:%%------------------------------------------------------------------------%%功能:连绝周期旗号截断对于频谱的做用%%------------------------------------------------------------------------fs=8000;n1=0.02;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+0.2*pi);subplot(2,2,1);plot(n,y);title('函数y=cos(100{\pi}t+0.2{\pi})');subplot(2,2,2);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期为周期整数倍,频谱图');n1=0.03;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+0.2*pi);subplot(2,2,3);plot(n,y);title('函数y=cos(100{\pi}t+0.2{\pi})');subplot(2,2,4);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期没有为周期整数倍,频谱图');。
MATLAB 频谱分析(FFT FT定义法)

X2=zeros(N/16,1);%只采样64点
for n=1:N/16
for m=1:length(X1)/2 %数据量太大显示太慢只取一半作分析
X2(n,1)=X2(n,1)+X1(m,1)*exp(-j*n*m);%将w与n同步以便于计算存储,w,n关系也可以变
subplot(244);
plot(f(1:N/2),ph(1:N/2));
xlabel('频率/Hz'),ylabel('相角'),title('录音信号相位谱');
%%%%%%%%%%%%%%%%%%录音信号FFT后频谱
subplot(245);
plot(y1)%采样后信号的FFT频谱图
title('录音信号FFT频谱图')
%%%%%%%%%%%%%%%%%%录音信号FFT后幅度
subplot(246);
plot(f(1,N/2)abs(y1(N/2)))%采样后信号的FFT幅度谱,不指定横坐标无意义请注意
title('录音信号FFT幅度谱')
%%%%%%%%%%%%%%%%%%%录音信号随频率变化的相位
ph=2*angle(y1(1:N/2));
ph=ph*180/pi;
subplot(247);
plot(f(1:N/2),ph(1:N/2));
xlabel('频率/Hz'),ylabel('相角'),title('录音信号FFT相位谱');
%%%%%%%%%%%%%%%%%%%由定义得出的FT
matlab 信号 频谱分析实验报告

MATLAB 信号频谱分析实验报告实验目的本实验旨在使用MATLAB软件进行信号频谱分析,包括对信号的时域分析和频域分析,以及频谱图的绘制和解读。
实验步骤1. 准备工作在开始实验之前,首先需要安装MATLAB软件,并启动软件。
2. 信号生成在MATLAB的命令窗口中,通过使用信号发生器生成一个信号。
可以选择使用正弦波、方波、三角波等不同类型的信号进行频谱分析。
3. 信号时域分析使用MATLAB的时域分析函数,如plot函数,绘制生成的信号的时域波形图。
plot(t, x);title('信号的时域波形图');xlabel('时间');ylabel('幅值');其中,t表示时间轴上的时间点,x表示生成的信号。
4. 信号频域分析使用MATLAB的频域分析函数,如fft函数,将时域信号转换为频域信号。
X = fft(x);可以通过计算得到信号的频率分量f和幅度谱A。
L = length(x);f = Fs*(0:(L/2))/L;A = abs(X/L);A = A(1:L/2+1);其中,Fs表示信号的采样率。
5. 绘制频谱图使用MATLAB的绘图函数,如plot函数,将频域信号的频谱绘制成图表。
plot(f, A);title('信号的频谱图');xlabel('频率');ylabel('幅值');6. 频谱图解读通过观察频谱图,可以分析信号在不同频率上的能量分布情况。
高幅度的频率分量表示信号在该频率上具有较大的能量,低幅度的频率分量表示信号在该频率上具有较小的能量。
7. 实验总结通过本次实验,我们学习了如何使用MATLAB进行信号的时域分析和频域分析。
时域分析可以帮助我们观察信号在时域上的变化情况,频域分析可以帮助我们了解信号在不同频率上的能量分布情况。
通过绘制频谱图,我们可以直观地观察信号的频谱特征,并进行进一步的信号分析和处理。
用MATLAB进行FFT频谱分析

用MATLAB进行FFT频谱分析假设一信号:()()292.7/2cos1.0996.2/2sin1.06.0+++=ttRππ画出其频谱图。
分析:首先,连续周期信号截断对频谱的影响。
DFT变换频谱泄漏的根本原因是信号的截断。
即时域加窗,对应为频域卷积,因此,窗函数的主瓣宽度等就会影响到频谱。
实验表明,连续周期信号截断时持续时间与信号周期呈整数倍关系时,利用DFT变换可以得到精确的模拟信号频谱。
举一个简单的例子:()ππ2.0100cos+=tY其周期为。
截断时不同的持续时间影响如图一.1:(对应程序)140.0160.0180.02截断时,时间间期为周期整数倍,频谱图0.0250.0320406080100截断时,时间间期不为周期整数倍,频谱图图错误!文档中没有指定样式的文字。
.1其次,采样频率的确定。
根据Shannon 采样定理,采样带限信号采样频率为截止频率的两倍以上,给定信号的采样频率应>1/,取16。
再次,DFT 算法包括时域采样和频域采样两步,频域采样长度M 和时域采样长度N 的关系要符合M ≧N 时,从频谱X(k)才可完全重建原信号。
实验中信号R 经采样后的离散信号不是周期信号,但是它又是一个无限长的信号,因此处理时时域窗函数尽量取得宽一些已接近实际信号。
实验结果如图一.2:其中,0点位置的冲激项为直流分量造成(对应程序为)0204060801001201401601802000.40.50.60.70.800.050.10.150.20.250.30.350.40.450.550100150图 错误!文档中没有指定样式的文字。
.2♣ARMA (Auto Recursive Moving Average )模型:将平稳随机信号x(n)看作是零均值,方差为σu 2的白噪声u(n)经过线性非移变系统H(z)后的输出,模型的传递函数为()()()∑∑=-=-+==Pk kk Qr r rza zb z A z B z H 111用差分方程表示为()()()∑∑==-+--=Qr r P k k r n u b k n x a n x 01AR (Auto Recursive )自回归模型,即ARMA 模型中系数b 只有在r=0的情况下为1,其余都是零,获得一个全极点模型:()()()∑=-+==Pk kk za z A z B z H 111差分方程表示为:()()()n u k n x a n x Pk k +--=∑=1AR 模型的功率谱估计为:()()()Ω-ΩΩ=j j uj x e A e A eS 12σ程序:%%------------------------------------------------------------------------%%功能:利用MATLAB 的FFT 函数做双正弦信号频谱分析 %%------------------------------------------------------------------------ fs=16; t=0:1/fs:200;x6=+sin(2*pi*t/*+cos(2*pi*t/+2)*;subplot(2,1,1);plot(t,x6);N=length(t);subplot(212);plot((-N/2:N/2-1)*fs/N,abs(fftshift(fft(x6,N)))) %绘制信号的频谱,横轴对应实际频率axis([0 0 160]);例子:%%------------------------------------------------------------------------%%功能:连续周期信号截断对频谱的影响%%------------------------------------------------------------------------fs=8000;n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,1);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,2);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期为周期整数倍,频谱图');n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,3);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,4);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期不为周期整数倍,频谱图');。
频谱图的画法
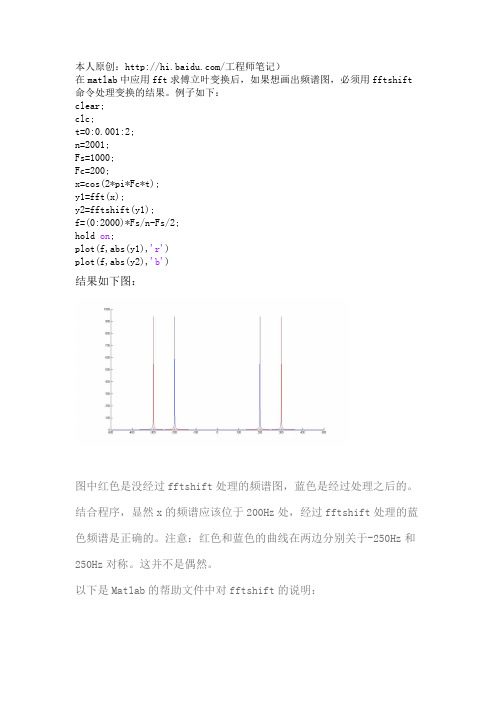
本人原创:/工程师笔记)在matlab中应用fft求傅立叶变换后,如果想画出频谱图,必须用fftshift 命令处理变换的结果。
例子如下:clear;clc;t=0:0.001:2;n=2001;Fs=1000;Fc=200;x=cos(2*pi*Fc*t);y1=fft(x);y2=fftshift(y1);f=(0:2000)*Fs/n-Fs/2;hold on;plot(f,abs(y1),'r')plot(f,abs(y2),'b')结果如下图:图中红色是没经过fftshift处理的频谱图,蓝色是经过处理之后的。
结合程序,显然x的频谱应该位于200Hz处,经过fftshift处理的蓝色频谱是正确的。
注意:红色和蓝色的曲线在两边分别关于-250Hz和250Hz对称。
这并不是偶然。
以下是Matlab的帮助文件中对fftshift的说明:Y = fftshift(X) rearranges the outputs of fft, fft2, and fftn by moving the zero-frequency component to the center of the array. It is useful for visualizing a Fourier transform with the zero-frequency component in the middle of the spectrum. For vectors, fftshift(X) swaps the left and right halves of X.由此可见,fftshift的作用正是让正半轴部分和负半轴部分的图像分别关于各自的中心对称。
将信号频率Fc改为100Hz后的频谱如下,蓝色是fftshift处理后的频谱:如何画一个信号的频谱今天终于搞明白了,这么简单的东西今天才明白如何快速的用matlab 画出,真是惭愧。
用Matlab画出信号的时域波形及频谱,观察它们的关系。

A
7
实验结果
A
8
f2(t)u(t2)u(t2)
f(t)F(j) F2(j)F2j4sa (2)
四 实验内容 1. 根据对称性得出: → MATLAB编程 R=0.05; t=-3:R:3; f2=(t>=-2)-(t>=2); subplot(1,2,1),plot(t,f2) grid on;
10
实验结果
A
11
f 3 (t) t[u (t 1) u (t 1)] f '3 (t ) f 4 (t)
MATLAB编程 R=0.05; h=0.001; t=-1.2:R:1.2; y=t.*(t>=-1)-t.*(t>=1); f4=diff(y)/h; subplot(1,2,1),plot(t,f1) Xlabel('t'),ylabel('f4') axis([-2,2,-0.5,1.5]); N=1000; k=-N:N; W1=40; W=k*W1/N; F=y*exp(-j*t'*W)*R; F=real(F); subplot(1,2,2),plot(W,F) Xlabel('W'),ylabel('F(jw)')
1 正确运用傅立叶变换
2用Matlab编程观察周期信 号的合成过程。进一步理 解周期信号的傅里叶级数 分解特性。
3.学习用Matlab绘制周期 信号频谱的方法。
A
3
三 实验原理 1. 周期矩形脉冲信号 的傅里叶展开系 数为sin 2x/2x的函数称为“采样函数”, 这个函数数据有以下特性 (1)Sa(2t)为偶函数 (2)当t→0时,Sa(t)=1是以1/t为振幅 的“正弦函数”;因而对于x的正负两半 轴都为衰减的正弦震荡; (3)在x=nπ处(n=1,2,3,…),sin x=0即Sa(t)=0;而在x=0处Sa(t)在 t→0时等于1。
MATLAB周期信号的频谱分析解读

MATLAB周期信号的频谱分析解读频谱分析是一种用于研究信号在频域上的特性的方法,对于周期信号的频谱分析尤为重要。
周期信号是在时间上有规律地重复出现的信号,例如正弦信号和方波信号。
在MATLAB中,我们可以使用傅里叶变换来进行周期信号的频谱分析。
首先,我们需要了解一些基本的概念。
频谱表示一个信号在不同频率上的能量分布,其单位通常是幅度或功率。
频谱分析可以通过计算信号的傅里叶变换来获得,傅里叶变换可以将一个信号从时间域转换到频域。
首先,我们需要生成一个周期信号。
例如,我们可以使用sin函数生成一个具有特定频率和幅度的正弦信号。
下面的代码生成了一个频率为f 的正弦信号:```matlabf=1;%信号的频率t=0:0.01:10;%时间范围x = sin(2*pi*f*t); % 生成正弦信号```接下来,我们可以使用fft函数进行信号的傅里叶变换。
傅里叶变换将信号从时域转换到频域,得到的结果是一个复数向量,其中包含了信号在不同频率上的能量信息。
我们可以使用abs函数计算傅里叶变换结果的幅度,得到频谱图。
```matlabfs = 100; % 信号的采样频率N = length(x); % 信号的长度X = fft(x); % 进行傅里叶变换X = abs(X/N); % 计算频域幅度f = (0:N-1)*(fs/N); % 计算频率轴plot(f,X) % 绘制频谱图```在上述代码中,变量fs表示信号的采样频率,N表示信号的长度。
我们需要将傅里叶变换结果除以N,以归一化频域幅度。
在频谱图中,横轴表示频率,纵轴表示信号在相应频率上的幅度。
频谱图的形状和峰值反映了信号在不同频率上的能量分布情况。
对于上述代码生成的正弦信号,频谱图应该呈现出一个峰值在f处的单个峰。
然而,由于傅里叶变换的性质,频谱图通常具有对称性。
这是由于信号的周期性导致的,正弦信号的频谱图在负频率处也有一个对称的峰。
为了更好地展示频谱图,我们可以使用fftshift函数将频谱图进行平移,将负频率部分移到频谱图的中心。
如何利用Matlab技术进行频域分析

如何利用Matlab技术进行频域分析MATLAB是一种功能强大的数学软件,被广泛应用于科学研究和工程领域。
其中的频域分析功能被广泛用于信号处理、图像处理、音频处理等领域。
本文将介绍如何利用MATLAB技术进行频域分析,以及常用的频域分析方法和技巧。
一、频域分析的基本概念在开始介绍如何利用MATLAB进行频域分析之前,我们先来了解一下频域分析的基本概念。
频域分析是指将信号从时域(时间域)转换到频域(频率域),以便更好地理解信号的频谱特性。
频域分析的基本原理是傅里叶变换。
傅里叶变换是将一个信号分解成一系列正弦函数和余弦函数的和,通过这种方式可以清晰地看到信号的频谱成分。
MATLAB中提供了多种傅里叶变换的函数,比如fft、ifft等,可以快速、方便地进行频域分析。
二、MATLAB中的频域分析函数MATLAB中提供了多种用于频域分析的函数,包括快速傅里叶变换(FFT)、离散傅里叶变换(DFT)、傅里叶逆变换(IFFT)等。
1. 快速傅里叶变换(FFT)快速傅里叶变换是一种将离散信号转换为频域表示的快速方法。
在MATLAB 中,可以使用fft函数进行快速傅里叶变换,如下所示:```MATLABX = fft(x);```其中,x为输入信号,X为傅里叶变换后的结果。
通过快速傅里叶变换,可以将信号从时域转换到频域,得到信号的频谱信息。
2. 离散傅里叶变换(DFT)离散傅里叶变换是一种将离散信号转换为频域表示的方法。
在MATLAB中,可以使用dft函数进行离散傅里叶变换,如下所示:```MATLABX = dft(x);```其中,x为输入信号,X为傅里叶变换后的结果。
3. 傅里叶逆变换(IFFT)傅里叶逆变换是一种将频域信号转换回时域信号的方法。
在MATLAB中,可以使用ifft函数进行傅里叶逆变换,如下所示:```MATLABx = ifft(X);```其中,X为输入的频域信号,x为傅里叶逆变换后的结果。
matlab绘制滤波器频谱图

题目:滤波器设计和频谱分析一.实验要求利用现有电路知识,设计低通、带通、高通、带阻滤波器,写出滤波器的频率响应函数,在matlab 中,绘制滤波器的频谱图,指出滤波器主要参数,说明对所设计的滤波器要提高这些参数该如何改进。
写出改进后滤波器的频率响应函数,绘制改进后的滤波器频谱图。
在matlab 的simulink 中,若只给出信号发生器和示波器,要求绘制所设计的一种滤波器的频谱图,并阐明试验原理。
二.设计思路和推导过程RLC 构成的无源滤波器是常见的滤波器种类,本实验即从RLC 无源滤波器出发设计低通,高通,带通,带阻滤波器,写出他们的转移函数,用matlab 画出频谱图,并且探究四种滤波器的改进方法。
1. 低通滤波器电路图:低通滤波器转移函数1C jwR 1H=,令21=H 得特征频率C R 1wc=matlab 程序w=0:10:10^7; R1=10; C1=1*10^(-3); wc1=1/(R1*C1);H1=abs(1./(1i.*w./wc1+1)); plot(log10(w./wc),20*log10(H1)); xlabel('lg(w/wc)');ylabel('|H1|/dB'); title('一阶低通'); axis([-3,5,-120,0]);频谱图:问题:通频带外下降斜率-20dB/十倍频,对带外信号的抑制效果不是很好; 改进方法:采用高阶低通滤波器,这里采用二阶低通滤波器,电路图如下转移函数H2=1/(1-w^2*R2^2*C2^2+3j*w*R2*C2),令21=H 得特征频率为wc=0.3472/(R*C). Matlab 程序如下 w=0:10:10^7; R2=10;C2=1*10^(-3);wc2=0.3472./(R2*C2);H2=abs(1./(1-w.^2.*R2.^2.*C2.^2+3i.*w.*R2.*C2)); subplot(1,2,2);plot(log10(w./wc2),20*log10(H2));axis([-3,5,-120,0]);xlabel('lg(w/wc)');ylabel('|H2|/dB');title('二阶低通');频谱图:可以看出,特征频率减小,带外斜率-40dB/十倍频,对带外信号的抑制效果增强。
matlab频率包络谱

matlab频率包络谱频率包络谱是一种用来分析信号的方法,它能够展示信号在不同频率下的能量分布。
在MATLAB中,我们可以使用一些函数和工具来计算和绘制频率包络谱,包括傅里叶变换和频率域分析工具。
首先,我们需要明确什么是频率包络谱。
频率包络谱是信号的频谱图的一个变种,它不仅显示信号的频率成分,还显示每个频率成分的能量。
在频率包络谱中,横轴表示频率,纵轴表示该频率成分的能量。
在MATLAB中,我们可以使用傅里叶变换来计算信号的频率包络谱。
傅里叶变换可以将一个信号的时域表示转换为频域表示,以便我们可以看到不同频率成分的能量。
MATLAB提供了fft函数可以对信号进行快速傅里叶变换,并得到频域表示。
假设我们有一个信号x,它是一个列向量,由n个离散时间点的采样值组成。
我们可以使用fft函数将信号x转换为频域表示X,表示为X = fft(x)。
X是一个复数矩阵,它包含了信号在频域上的各个频率成分的能量。
然而,由于傅里叶变换是基于连续时间信号的,因此在MATLAB中进行傅里叶变换之前,我们需要先将离散时间信号进行插值。
可以使用interp函数对信号进行插值,以获得更精细的频率分辨率。
插值后,我们可以对插值后的信号进行傅里叶变换,并得到信号的频率包络谱。
插值后,我们可以使用fft函数计算信号的频率包络谱,如X =fft(interp(x))。
得到频率包络谱之后,我们可以使用plot函数绘制频率包络谱图。
可以使用semilogx函数将横轴改为对数坐标轴,以便更好地展示低频和高频成分的能量分布。
可以使用xlabel和ylabel函数添加横轴和纵轴标签,以及使用title函数添加标题。
可以使用xlim和ylim函数设置横轴和纵轴的范围。
除了使用傅里叶变换计算频率包络谱外,MATLAB还提供了其他一些频率域分析工具,如功率谱密度函数(psd)和自相关函数(xcorr)。
这些函数能够更详细地分析信号的频率成分和能量分布。
matlab绘制正弦信号频谱图(虚频谱、实频谱、单、双边相位谱、单、双边幅频谱)

matlab 绘制正弦信号频谱图(虚频谱、实频谱、单、双边相位谱、单、双边幅频谱)matlab绘制正弦信号频谱图(虚、实频谱、单、双边相位谱、单、双边幅频谱) ⾸先我们今天绘制的正弦信号的函数表达式:f(x)=sin(2*π*f*t),其中f=2. 我使⽤的是matlab2020b,打开matlab后,新建脚本。
我们先画出sin(2*π*f*t)信号的图像: 函数图像如下: 然后对函数进⾏快速傅⾥叶变换、计算实部虚部,绘制幅频谱、相频谱、实频谱、虚频谱。
代码如下:f=2;T =1/f;Fs =100; %采样率Ts =1/Fs;t =0:Ts:1-Ts; %t 范围0~1,步长0.01n =length(t);y =sin(2*pi*f*t); %正弦信号函数sinplot =figure;plot(t,y) %绘制函数图像 x 轴为时间t ,y 轴为信号函数xlabel('时间(s )') %x 轴名称ylabel('信号') %y 轴名称title('原信号图像') %图像顶部名称grid on[Doain,Range]=cFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3);%离散绘制幅频谱,取消原图像⼩圆圈,线条粗细3xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1.5,1.5]) %坐标显⽰范围:x 轴-2.5~2.5,y 轴-1.5~1.5CnR =real(Doain); %实部CnI =imag(Doain); %虚部Cn =(CnR.^2+CnI.^2).^(1/2); %幅值fain =tand(CnI./CnR)/3; %相位⾓fain =fain(1,48:54); %去除影响因素figurestem(Range,CnR) %离散绘制gridaxis([-6,6,-2,2])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI,'Marker','none','LineWidth',3)axis([-2.5,2.5,-1,1])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),-fain,'Marker','none','LineWidth',3) gridaxis([-2.5,2.5,-2.5,2.5])title('双边相频谱')xlabel('Hz')ylabel('相位⾓')figurefain2=fain(1,4:7);stem(Range(1,51:54),-fain2,'Marker','none','LineWidth',3) gridaxis([-2.5,2.5,-2.5,1.5])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间(s)')ylabel('信号')title('原信号图像')grid onfunction[X,freq]=cFFT(x,Fs) %修正N=length(x);if mod(N,2)==0k=-N/2:N/2-1;elsek=-(N-1)/2:(N-1)/2;endT=N/Fs;freq=k/T;X=fft(x)/N;X=fftshift(X);end 绘制图像如下: 最后附上完整代码:f=2;T=1/f;Fs=100;Ts=1/Fs;t=0:Ts:1-Ts;n=length(t);y=sin(2*pi*f*t);sinplot=figure[Doain,Range]=cFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3); xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1.5,1.5])CnR=real(Doain);CnI=imag(Doain);Cn=(CnR.^2+CnI.^2).^(1/2);fain=tand(CnI./CnR)/3;fain=fain(1,48:54);figurestem(Range,CnR)gridaxis([-6,6,-2,2])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-1,1])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),-fain,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-2.5,2.5])title('双边相频谱')xlabel('Hz')ylabel('相位⾓')figurefain2=fain(1,4:7);stem(Range(1,51:54),-fain2,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-2.5,1.5])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间(s)')ylabel('信号')grid onfunction[X,freq]=cFFT(x,Fs)N=length(x);if mod(N,2)==0k=-N/2:N/2-1;elsek=-(N-1)/2:(N-1)/2;endT=N/Fs;freq=k/T;X=fft(x)/N;X=fftshift(X);end延迟T/4后的代码fo=2;T=1/fo;Fs=100;Ts=1/Fs;t=0:Ts:1-Ts;n=length(t);y=sin(2*pi*fo*t-pi/2);sinplot=figure[Doain,Range]=centeredFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3); xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1,1.5])CnR=real(Doain);CnI=imag(Doain);Cn=(CnR.^2+CnI.^2).^(1/2);fain=tand(CnR./CnI)*3.2;fain=fain(1,48:54);figurestem(Range,CnR,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-1,1])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI)gridaxis([-6,6,-2,2])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),abs(fain),'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-4,4])title('双边相频谱')xlabel('Hz')figurefain2=fain(1,4:7);stem(Range(1,51:54),abs(fain2),'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-4,4])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间(s)')ylabel('y')title('原信号图像')grid onfunction[X,freq]=centeredFFT(x,Fs)N=length(x);if mod(N,2)==0k=-N/2:N/2-1; % N evenelsek=-(N-1)/2:(N-1)/2; % N oddendT=N/Fs;freq=k/T; %the frequency axisaccordinglyX=fft(x)/N;X=fftshift(X);End⽂件链接: (matlabxinhao1⽂件是本⽂所提到的信号,matlabxinhao2是将本⽂提到的信号延迟T/4之后的信号绘图。
利用Matlab绘制正弦信号的频谱图并做相关分析

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求:1、信号可变(信号的赋值、相位、频率可变);2、采样频率fs可变;3、加各种不同的窗函数并分析其影响;4、频谱校正;5、频谱细化。
二、采用matlab编写如下程序:clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1:fs=100,N=1024');grid on;%两种信号叠加,x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2:fs=100,N=1024,两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3:fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4:fs=100,N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5:fs=400,N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6:fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7:fs=100,N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8:fs=100,N=1024,加汉宁窗函数');grid on;三、运行结果如下:四、分析与结论:1)从所做图像可以看出,信号的幅值均小于真实值,说明在截断信号时存在泄露。
