2015高考数学真题分类 考点36 三视图
2015年高考会这样考立体几何

【2015年高考会这样考立体几何】小题:1.以三视图为背景,考查体积;核心与难点在于三视图.2.考查线面的位置关系,核心在线面的平行与垂直.两种形式呈现:一种是符号语言表示;另一种是文字语言表示。
3.立体几何小题以考查空间想象能力为出发点,考查基本定理以及三视图,属于中等或中等偏下的题,能常出在选择题的第5—8题,容易得分。
大题:1、考查垂直,核心是线面垂直;2、考查二面角,此问可以用传统方法,也可用法向量的方法。
传统方法书写简单,但思考难度大;法向量方法思路清淅,不需要太多空间想象能力,但计算复杂,需要耐心。
3、立体向何大题一般出现在第18题,属于中等或中等偏上的题。
【复习指导】复习立体向何要先以基本的定理为基础,以解题模板训练解题的套路,关注题目的不同点,在学习中不断积累总结解题模板。
立体几何的平行与垂直知识点与题型、方法总结(一)、立体几何网络图:2、线线垂直的判断:(7)、在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
(8)、在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直。
(10)、若一直线垂直于一平面,这条直线垂直于平面内所有直线。
补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条。
4、线面垂直的判断:⑼如果一直线和平面内的两相交直线垂直,这条直线就垂直于这个平面。
⑾如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面。
⒁一直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⒃如果两个平面垂直,那么在—个平面内垂直于交线的直线必垂直于另—个平面。
判定定理:性质定理:(1)若直线垂直于平面,则它垂直于平面内任意一条直线。
即:(2)垂直于同一平面的两直线平行。
即:★判断或证明线面垂直的方法⑴利用定义,用反证法证明。
⑵利用判定定理证明。
⑶一条直线垂直于平面而平行于另一条直线,则另一条直线也垂直与平面。
2015届高考数学总复习配套课件:7-1空间几何体的结构及其三视图和直观图

阳 书
的三种视图均不相同;图④的正视图与侧视图相同.故选D.
业 有
答案:D
限 公
司
菜 单 隐藏
第二十三页,编辑于星期五:十点 十五分。
高考总复习 A 数学(文)
抓主干 考点 解密
几何体的直观图
研考向
【例3】 (2014年福州模拟)用斜二测画法画一个水平放置的平面图
要点
探 究 形的直观图为如图所示的一个正方形,则原来的图形是( )
解密
定,因为“其余各面都是三角形”并不等价于“其余各面都是有一个公
研考向
要点 探究
共顶点的三角形”,如图(1)所示;③不一定.当以斜边所在直线为旋转
悟典题 轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图(2)所示,
能力
提 升 它是由两个同底圆锥组成的几何体;④错误,棱台的上、下底面是相似
提素能 高效
抓主干 考点 解密 研考向 要点 探究 悟典题 能力 提升 提素能 高效 训练
菜 单 隐藏
高考总复习 A 数学(文)
山 东 金 太 阳 书 业 有 限 公 司
第四页,编辑于星期五:十点 十五分。
高考总复习 A 数学(文)
抓主干 考点 解密
研考向
要点
探究
____________________[通关方略]____________________
东 金
C.有两个平面互相平行,其余各面都是梯形的多面体是棱台
太 阳
D.棱台的各侧棱延长后不一定交于一点
书 业
有
限
公
司
菜 单 隐藏
第十五页,编辑于星期五:十点 十五分。
高考总复习 A 数学(文)
抓主干 考点 解密
2015高考数学第一轮复习空间几何体的结构及其三视图

4.用斜二测画法画一个水平放置的平面图形的直观图是如图所
示的一个正方形,则原来的图形是(
)
【解析】选A.由直观图的画法规则可知,平行于x轴的线段长度
不变,平行于y轴的线段长度减半.
2
则在正方形ABCD内,
OB 2 2 AB , 2 2
故侧棱长 PB PO2 OB2 3 2 5 .
4 4 2
【规律方法】三视图的画法技巧 (1)画几何体的三视图可以想象自己站在几何体的正前方、正 左方和正上方观察,它的轮廓线是什么,然后再去画图 . (2)对于简单几何体的组合体的三视图 , ①要确定正视、侧视、俯视的方向; ②要注意组合体是由哪些几何体组成 ,弄清楚它们的生成方式; ③注意它们的交线的位置.
(2)选C.在四棱锥P-ABCD中,连接AC,由正视图和侧视图可得
PC=BC=CD=1,故 AC 2, 最长的棱为 PA PC2 AC2 3.
【互动探究】若本例题(2)中的四棱锥P-ABCD为正四棱锥,且正 视图和侧视图是边长为1的正三角形,求该四棱锥的侧棱长. 【解析】如图,由条件知,正四棱锥 的底边AB=1,高 PO 3 .
第七章 立 体 几 何
第一节 空间几何体的结构及其三视图 和直观图
1.多面体的结构特征 多面体 棱柱 棱锥 棱台 结构特征 平行 且_____ 相等 ,上下底面是_____ 平行 棱柱的侧棱都_____ 全等 的多边形 且_____ 公共 棱锥的底面是任意多边形,侧面是有一个_____ 顶点 的三角形 _____ 平行于 棱台可由_______棱锥底面的平面截棱锥得到, 平行 且_____ 相似 的多边形 其上下底面是_____
2015高考数学配套课件:8-1 空间几何体的结构、三视图、直观图

自助餐
课时作业
第二十七页,编辑于星期五:十五点 九分。
高考调研
新课标版 ·高三数学(文)
(2)(2012·湖南)某几何体的正视图和侧视图均如右图所示,则
该几何体的俯视图不可能是( )
【解析】 A 图是两个圆柱的组合体的俯视图;B 图是一个 四棱柱与一个圆柱的组合体的俯视图;C 图是一个底面为等腰直 角三角形的三棱柱与一个四棱柱的组合体的俯视图,采用排除 法,故选 D.
课前自助餐
授人以渔
自助餐
课时作业
第二十九页,编辑于星期五:十五点 九分。
高考调研
新课标版 ·高三数学(文)
思考题 2 (1)如图所示,下列四个几何体中,它们各自的 三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )
A.①② C.②③ 【答案】 C
B.①③ D.①④
课前自助餐
授人以渔
自助餐
课前自助餐
授人以渔
自助餐
课时作业
第八页,编辑于星期五:十五点 九分。
高考调研
新课标版 ·高三数学(文)
3.圆柱、圆锥、圆台的特征
分别以 矩形的一边 、 直角三角形的一直角边
、
直角梯形中垂直于底边的腰所在的直线 为旋转轴,其余各边旋转
一周而形成的曲面所围成的几何体分别叫做圆柱、圆锥、圆台.
其中旋转轴叫做所围成的几何体的 轴 ;在轴上的这条边叫 做这个几何体的 高 ;垂直于轴的边旋转而成的圆面叫做这个几 何体的 底面 ;不垂直于轴的边旋转而成的曲面叫做这个几何体 的 侧面 ,无论旋转到什么位置,这条边都叫做侧面的 母线 .
第十七页,编辑于星期五:十五点 九分。
高考调研
新课标版 ·高三数学(文)
【步步高】2015届高考数学总复习 8.1空间几何体的三视图、直观图、表面积与体积配套文档 理 新人

§8.1空间几何体的三视图、直观图、表面积与体积1.空间几何体的结构特征多面体(1)棱柱的侧棱都平行且相等,上、下底面是全等的多边形.(2)棱锥的底面是任意多边形,侧面是有一个公共顶点的三角形.(3)棱台可由平行于底面的平面截棱锥得到,其上、下底面是相似多边形.旋转体(1)圆柱可以由矩形绕其任一边所在直线旋转得到.(2)圆锥可以由直角三角形绕其直角边所在直线旋转得到.(3)圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上、下底中点连线所在直线旋转得到,也可由平行于底面的平面截圆锥得到.(4)球可以由半圆或圆绕直径所在直线旋转得到.2.空间几何体的三视图是用正投影得到,这种投影下与投影面平行的平面图形留下的影子与平面图形的形状和大小是完全相同的,三视图包括正视图、侧视图、俯视图.3.空间几何体的直观图画空间几何体的直观图常用斜二测画法,基本步骤:(1)在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴、y′轴,两轴相交于点O′,且使∠x′O′y′=45°(或135°).(2)已知图形中平行于x轴、y轴的线段,在直观图中分别平行于x′轴、y′轴.(3)已知图形中平行于x轴的线段,在直观图中长度保持不变,平行于y轴的线段,长度变为原来的一半.(4)在已知图形中过O点作z轴垂直于xOy平面,在直观图中对应的z′轴也垂直于x′O′y′平面,已知图形中平行于z轴的线段,在直观图中仍平行于z′轴且长度不变.4.柱、锥、台和球的表面积和体积名称几何体表面积体积柱体(棱柱和圆柱)S表面积=S侧+2S底V=Sh锥体(棱锥和圆锥) S 表面积=S 侧+S 底 V =13Sh 台体(棱台和圆台) S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h球 S =4πR 2 V =43πR 31.判断下面结论是否正确(请在括号中打“√”或“×”) (1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.( × )(2)有一个面是多边形,其余各面都是三角形的几何体是棱锥.( × )(3)用斜二测画法画水平放置的∠A 时,若∠A 的两边分别平行于x 轴和y 轴,且∠A =90°,则在直观图中,∠A =45°.( × )(4)正方体、球、圆锥各自的三视图中,三视图均相同.( × )(5)圆柱的侧面展开图是矩形.( √ )(6)台体的体积可转化为两个锥体的体积之差来计算.( √ )2.(2013·某某)一个几何体的三视图如图所示,则该几何体的直观图可以是( )答案 D解析 由三视图可知上部是一个圆台,下部是一个圆柱,选D.3.(2013·课标全国Ⅰ)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( )A.500π3 cm 3B.866π3cm 3 C.1 372π3 cm 3D.2 048π3cm 3答案 A 解析 作出该球轴截面的图象如图所示,依题意BE =2,AE =CE =4,设DE =x ,故AD =2+x ,因为AD 2=AE 2+DE 2,解得x =3,故该球的半径AD =5,所以V =43πR 3=500π3. 4.一个三角形在其直观图中对应一个边长为1的正三角形,原三角形的面积为________. 答案 62解析 由斜二测画法,知直观图是边长为1的正三角形,其原图是一个底为1,高为6的三角形,所以原三角形的面积为62. 5.若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的体积为________.答案 33π 解析 侧面展开图扇形的半径为2,圆锥底面半径为1,∴h =22-1=3,∴V =13π×1×3=33π.题型一 空间几何体的结构特征例1 (1)下列说法正确的是( )A.有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱B.四棱锥的四个侧面都可以是直角三角形C.有两个平面互相平行,其余各面都是梯形的多面体是棱台D.棱台的各侧棱延长后不一定交于一点(2)给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②有一个面是多边形,其余各面都是三角形的几何体是棱锥;③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;④棱台的上、下底面可以不相似,但侧棱长一定相等.其中正确命题的个数是( )A.0B.1C.2D.3思维启迪从多面体、旋转体的定义入手,可以借助实例或几何模型理解几何体的结构特征.答案(1)B(2)A解析(1)A错,如图1;B正确,如图2,其中底面ABCD是矩形,可证明∠P AB,∠PCB 都是直角,这样四个侧面都是直角三角形;C错,如图3;D错,由棱台的定义知,其侧棱必相交于同一点.(2)①不一定,只有这两点的连线平行于轴时才是母线;②不一定,因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,如图1所示;③不一定,当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图2所示,它是由两个同底圆锥组成的几何体;④错误,棱台的上、下底面是相似且对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.思维升华(1)有两个面互相平行,其余各面都是平行四边形的几何体不一定是棱柱.(2)既然棱台是由棱锥定义的,所以在解决棱台问题时,要注意“还台为锥”的解题策略.(3)旋转体的形成不仅要看由何种图形旋转得到,还要看旋转轴是哪条直线.如图是一个无盖的正方体盒子展开后的平面图,A,B,C是展开图上的三点,则在正方体盒子中,∠ABC的值为()A.30°B.45°C.60°D.90°答案 C解析 还原正方体,如图所示,连接AB ,BC ,AC ,可得△ABC 是正三角形,则∠ABC =60°.题型二 空间几何体的三视图和直观图例2 (1)如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12,则该几何体的俯视图可以是( )(2)正三角形AOB 的边长为a ,建立如图所示的直角坐标系xOy ,则它的直观图的面积是________.思维启迪 (1)由正视图和侧视图可知该几何体的高是1,由体积是12可 求出底面积.由底面积的大小可判断其俯视图是哪一个.(2)按照直观图画法规则确定平面图形和其直观图面积的关系.答案 (1)C(2)616a 2 解析 (1)由该几何体的正视图和侧视图可知该几何体是柱体,且其高为1,由其体积是12可知该几何体的底面积是12,由图知A 的面积是1,B 的面积是π4,C 的面积是12,D 的面积是π4,故选C. (2)画出坐标系x ′O ′y ′,作出△OAB 的直观图O ′A ′B ′(如图).D ′为O ′A ′的中点.易知D ′B ′=12DB (D 为OA 的中点), ∴S △O ′A ′B ′=12×22S △OAB =24×34a 2=616a 2. 思维升华 (1)三视图中,正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽.即“长对正,宽相等,高平齐”.(2)解决有关“斜二测画法”问题时,一般在已知图形中建立直角坐标系,尽量运用图形中原有的垂直直线或图形的对称轴为坐标轴,图形的对称中心为原点,注意两个图形中关键线段长度的关系.(1)(2013·某某)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.2C.2-12 D.2+12(2)如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6 cm,O′C′=2 cm,则原图形是()A.正方形B.矩形C.菱形D.一般的平行四边形答案(1)C(2)C解析(1)由俯视图知正方体的底面水平放置,其正视图为矩形,以正方体的高为一边长,另一边长最小为1,最大为2,面积X围应为[1,2],不可能等于2-12.(2)如图,在原图形OABC中,应有OD=2O′D′=2×2 2=4 2 cm,CD=C′D′=2 cm.∴OC=OD2+CD2=(42)2+22=6 cm,∴OA=OC,故四边形OABC是菱形.题型三空间几何体的表面积与体积例3(1)一个空间几何体的三视图如图所示,则该几何体的表面积为()A.48B.32+817C.48+817D.80(2)已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得几何体的体积为( )A.2π3+12B.4π3+16 C.2π6+16D.2π3+12思维启迪 先由三视图确定几何体的构成及度量,然后求表面积或体积.答案 (1)C (2)C解析 (1)由三视图知该几何体的直观图如图所示,该几何体的下底面是边长为4的正方形;上底面是长为4、宽为2的矩形;两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;另两个侧面是矩形,宽为4,长为42+12=17.所以S 表=42+2×4+12×(2+4)×4×2+4×17×2=48+817. (2)由三视图确定该几何体是一个半球体与三棱锥构成的组合体,如 图,其中AP ,AB ,AC 两两垂直,且AP =AB =AC =1,故AP ⊥平面ABC ,S △ABC =12AB ×AC =12,所以三棱锥P -ABC 的体积V 1=13×S △ABC ×AP =13×12×1=16,又Rt △ABC 是半球底面的内接三角形, 所以球的直径2R =BC =2,解得R =22,所以半球的体积V 2=12×4π3×(22)3=2π6,故 所求几何体的体积V =V 1+V 2=16+2π6. 思维升华 解决此类问题需先由三视图确定几何体的结构特征,判断是否为组合体,由哪些简单几何体构成,并准确判断这些几何体之间的关系,将其切割为一些简单的几何体,再求出各个简单几何体的体积,最后求出组合体的体积.(2012·课标全国)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( )A.26B.36C.23D.22答案 A解析 由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,如图所示,S △ABC =34×AB 2=34, 高OD =12-⎝⎛⎭⎫332=63, ∴V S -ABC =2V O -ABC =2×13×34×63=26.转化思想在立体几何计算中的应用典例:(12分)如图,在直棱柱ABC —A ′B ′C ′中,底面是边长为3的等边三角形,AA ′=4,M 为AA ′的中点,P 是BC 上一点,且由P沿棱柱侧面经过棱CC ′到M 的最短路线长为29,设这条最短路线与CC ′的交点为N ,求:(1)该三棱柱的侧面展开图的对角线长;(2)PC 与NC 的长;(3)三棱锥C —MNP 的体积.思维启迪 (1)侧面展开图从哪里剪开展平;(2)MN +NP 最短在展开图上呈现怎样的形式;(3)三棱锥以谁做底好.规X 解答解 (1)该三棱柱的侧面展开图为一边长分别为4和9的矩形,故对角线长为42+92=97.[2分](2)将该三棱柱的侧面沿棱BB ′展开,如下图,设PC =x ,则MP 2=MA 2+(AC +x )2.∵MP =29,MA =2,AC =3,∴x =2,即PC =2.又NC ∥AM ,故PC P A =NC AM ,即25=NC 2. ∴NC =45.[8分] (3)S △P =12×CP ×=12×2×45=45. 在三棱锥M —P 中,M 到面P 的距离,即h =32×3=332. ∴V C —MNP =V M —P =13·h ·S △P =13×332×45=235.[12分] 温馨提醒 (1)解决空间几何体表面上的最值问题的根本思路是“展开”,即将空间几何体的“面”展开后铺在一个平面上,将问题转化为平面上的最值问题.(2)如果已知的空间几何体是多面体,则根据问题的具体情况可以将这个多面体沿多面体中某条棱或者两个面的交线展开,把不在一个平面上的问题转化到一个平面上.如果是圆柱、圆锥则可沿母线展开,把曲面上的问题转化为平面上的问题.(3)本题的易错点是,不知道从哪条侧棱剪开展平,不能正确地画出侧面展开图.缺乏空间图形向平面图形的转化意识.方法与技巧1.棱柱、棱锥要掌握各部分的结构特征,计算问题往往转化到一个三角形中进行解决.2.旋转体要抓住“旋转”特点,弄清底面、侧面及展开图形状.3.三视图画法:(1)实虚线的画法:分界线和可见轮廓线用实线,看不见的轮廓线用虚线;(2)理解“长对正、宽平齐、高相等”.4.直观图画法:平行性、长度两个要素.5.求几何体的体积,要注意分割与补形.将不规则的几何体通过分割或补形将其转化为规则的几何体求解.6.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.失误与防X1.台体可以看成是由锥体截得的,但一定强调截面与底面平行.2.注意空间几何体的不同放置对三视图的影响.3.几何体展开、折叠问题,要抓住前后两个图形间的联系,找出其中的量的关系.A组专项基础训练(时间:40分钟)一、选择题1.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( ) A.20B.15C.12D.10 答案 D解析 如图,在五棱柱ABCDE -A 1B 1C 1D 1E 1中,从顶点A 出发的对 角线有两条:AC 1,AD 1,同理从B ,C ,D ,E 点出发的对角线均有两 条,共2×5=10(条).2.(2012·某某)一个几何体的三视图形状都相同、大小均相等,那么这个 几何体不可以是( ) A.球B.三棱锥 C.正方体D.圆柱 答案 D解析 考虑选项中几何体的三视图的形状、大小,分析可得.球、正方体的三视图形状都相同、大小均相等,首先排除选项A 和C. 对于如图所示三棱锥O -ABC ,当OA 、OB 、OC 两两垂直且OA =OB =OC 时, 其三视图的形状都相同,大小均相等,故排除选项B. 不论圆柱如何设置,其三视图的形状都不会完全相同, 故答案选D.3.(2013·某某)某几何体的三视图如图所示,则该几何体的体积为( )A.5603B.5803C.200D.240 答案 C解析 由三视图知该几何体为直四棱柱,其底面为等腰梯形,上底长为2,下底长为8,高为4,故面积为S =(2+8)×42=20.又棱柱的高为10,所以体积V =Sh =20×10=200.4.如图是一个物体的三视图,则此三视图所描述物体的直观图是( )答案 D解析 由俯视图可知是B 和D 中的一个,由正视图和侧视图可知B 错.5.某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的表面积为( )A.32πB .π+ 3 C.32π+3D.52π+ 3 答案 C解析 由三视图可知该几何体为一个半圆锥,底面半径为1,高为3,∴表面积S =12×2×3+12×π×12+12×π×1×2=3+3π2.二、填空题6.如图所示,E 、F 分别为正方体ABCD —A 1B 1C 1D 1的面ADD 1A 1、面 BCC 1B 1的中心,则四边形BFD 1E 在该正方体的面DCC 1D 1上的投影 是________.(填序号)答案 ②解析 四边形在面DCC 1D 1上的投影为②:B 在面DCC 1D 1上的投影为C ,F 、E 在面DCC 1D 1上的投影应在边CC 1与DD 1上,而不在四边形的内部,故①③④错误.7.已知三棱锥A —BCD 的所有棱长都为2,则该三棱锥的外接球的表面积为________. 答案 3π解析 如图,构造正方体ANDM —FBEC .因为三棱锥A —BCD 的所有 棱长都为2,所以正方体ANDM —FBEC 的棱长为1.所以该正方体的 外接球的半径为32. 易知三棱锥A —BCD 的外接球就是正方体ANDM —FBEC 的外接球,所以三棱锥A —BCD 的外接球的半径为32.所以三棱锥A —BCD 的外接球的表面积为S 球=4π⎝⎛⎭⎫322=3π. 8.(2013·某某)如图,在三棱柱A 1B 1C 1-ABC 中,D ,E ,F 分别是AB ,AC ,AA 1的中点,设三棱锥F -ADE 的体积为V 1,三棱柱A 1B 1C 1-ABC 的体积为V 2,则V 1∶V 2=________.答案 1∶24解析 设三棱锥F -ADE 的高为h , 则V 1V 2=13h ⎝⎛⎭⎫12AD ·AE ·sin ∠DAE (2h )12(2AD )(2AE )sin ∠DAE=124. 三、解答题9.一个几何体的三视图及其相关数据如图所示,求这个几何体的表面积.解这个几何体是一个圆台被轴截面割出来的一半.根据图中数据可知圆台的上底面半径为1,下底面半径为2,高为3,母线长为2,几何体的表面积是两个半圆的面积、圆台侧面积的一半和轴截面的面积之和,故这个几何体的表面积为S=12π×12+12π×22+12π×(1+2)×2+12×(2+4)×3=11π2+3 3.10.已知一个上、下底面为正三角形且两底面中心连线垂直于底面的三棱台的两底面边长分别为30 cm和20 cm,且其侧面积等于两底面面积之和,求棱台的高.解如图所示,三棱台ABC—A1B1C1中,O、O1分别为两底面中心,D、D1分别为BC和B1C1的中点,则DD1为棱台的斜高.由题意知A1B1=20,AB=30,则OD=53,O1D1=1033,由S侧=S上+S下,得12×(20+30)×3DD1=34×(202+302),解得DD1=1333,在直角梯形O1ODD1中,O1O=DD21-(OD-O1D1)2=43,所以棱台的高为4 3 cm.B组专项能力提升(时间:30分钟)1.在四棱锥E—ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E—ABCD的体积为V,那么三棱锥M—EBC的体积为()A.25VB.13VC.23VD.310V 答案 D解析 设点B 到平面EMC 的距离为h 1,点D 到平面EMC 的距离为h 2. 连接MD .因为M 是AE 的中点, 所以V M —ABCD =12V .所以V E —MBC =12V -V E —MDC .而V E —MBC =V B —EMC ,V E —MDC =V D —EMC , 所以V E —MBC V E —MDC =V B —EMC V D —EMC =h 1h 2.因为B ,D 到平面EMC 的距离即为到平面EAC 的距离,而AB ∥CD ,且2AB =3CD ,所以h 1h 2=32. 所以V E —MBC =V M -EBC =310V . 2.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A.28+65B.30+6 5C.56+125D.60+12 5 答案 B解析 由几何体的三视图可知,该三棱锥的直观图如图所示, 其中AE ⊥平面BCD ,CD ⊥BD ,且CD =4,BD =5,BE =2,ED =3, AE =4.∵AE =4,ED =3,∴AD =5.又CD ⊥BD ,CD ⊥AE , 则CD ⊥平面ABD , 故CD ⊥AD ,所以AC =41且S △ACD =10.在Rt △ABE 中,AE =4,BE =2,故AB =2 5. 在Rt △BCD 中,BD =5,CD =4, 故S △BCD =10,且BC =41.在△ABD 中,AE =4,BD =5,故S △ABD =10. 在△ABC 中,AB =25,BC =AC =41, 则AB 边上的高h =6,故S △ABC =12×25×6=6 5.因此,该三棱锥的表面积为S =30+6 5.3.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 答案 2解析 设圆锥的母线为l ,圆锥底面半径为r .则12πl 2+πr 2=3π,πl =2πr ,∴r =1,即圆锥的底面直径为2.4.如图,在四棱锥P -ABCD 中,底面为正方形,PC 与底面ABCD 垂直, 图为该四棱锥的正视图和侧视图,它们是腰长为6 cm 的全等的等腰直角 三角形.(1)根据图所给的正视图、俯视图,画出相应的俯视图,并求出该俯视图的面积; (2)求P A .解 (1)该四棱锥的俯视图为(内含对角线),边长为6 cm 的正方形,如图, 其面积为36 cm 2. (2)由侧视图可求得PD =PC 2+CD 2=62+62=6 2.由正视图可知AD =6,且AD ⊥PD ,所以在Rt △APD 中,P A =PD 2+AD 2=(62)2+62=6 3 cm.5.已知一个圆锥的底面半径为R ,高为H ,在其内部有一个高为x 的内接圆柱. (1)求圆柱的侧面积;(2)x 为何值时,圆柱的侧面积最大? 解 (1)作圆锥的轴截面,如图所示.因为r R =H -x H ,所以r =R -R H x ,所以S 圆柱侧=2πrx=2πRx -2πR H (0<x <H ).(2)因为-2πR H <0,所以当x =2πR 4πR H=H2时,S 圆柱侧最大.故当x =H2,即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.。
2015年高考数学总复习精品课件:第13章 第1讲 空间几何体的三视图和直观图

13-4-5 所示,则相应的侧视图可以为(
)
图 13-4-5
A
B
C
D
第十九页,编辑于星期五:十一点 二十四分。
解析:(1)由俯视图和正视图可以得到几何体是一个简单的 组合体,是由一个三棱锥和被轴截面截开的半个圆锥组成, ∴侧视图是一个中间有分界线的三角形.故选 D.
答案:D
第二十页,编辑于星期五:十一点 二十四分。
直线旋转,其余各边旋转形成的曲面围成的几何体. (4)球:以半圆的直径所在的直线为旋转轴,半圆面旋转一
周形成的几何体.
第五页,编辑于星期五:十一点 二十四分。
3.空间几何体的三视图 (1)几何体的三视图包括:_______正__视__图_、_______侧__视__图_、 ___俯_视__图______,又称为主视图、左视图、俯视图. (2)三视图的长度特征:“长对正,宽相等,高平齐”,即 __正____视图和___侧___视图一样高,____正__视图和______俯视图一 样长,___侧___视图和_____俯_视图一样宽. 注意:若相邻两物体的表面相交,表面的交线是它们的分 界线,在三视图中,要注意实、虚线的画法.
(2)正棱锥:底面是正多边形,顶点在底面的射影是底面正 多边形的中心的棱锥叫做正棱锥.特别地,各棱均相等的正棱
锥叫做正多面体.反过来,正棱锥的底面是正多边形,且顶点
在底面的射影是底面正多边形的中心.
第四页,编辑于星期五:十一点 二十四分。
2.旋转体的几何特征 (1)圆柱:以矩形的一边所在的直线为旋转轴,将矩形旋转 一周而形成的曲面所围成的几何体. (2)圆锥:以直角三角形的一条直角边所在的直线为旋转 轴,将直角三角形旋转一周而形成的曲面所围成的几何体. (3)圆台:类似于棱台,圆台可看作是用一个平行于圆锥底 面的平面去截圆锥,底面与截面之间的部分.类似于圆锥的形 成过程,圆台还可以看作是一直角梯形绕垂直于底的腰所在的
2015-2019全国卷高考数学分类汇编——三视图
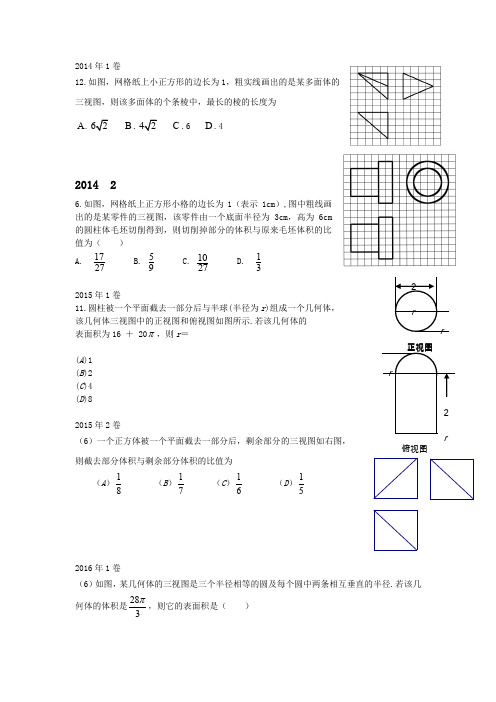
2014年1卷12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A. B.C .6 D .42014 26.如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A. 1727B. 59C. 1027D. 132015年1卷11.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体, 该几何体三视图中的正视图和俯视图如图所示.若该几何体的 表面积为16 + 20π,则r = (A )1 (B )2 (C )4 (D )82015年2卷(6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图, 则截去部分体积与剩余部分体积的比值为(A )81 (B )71 (C )61 (D )512016年1卷(6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( )2016-2(6)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A)20π(B)24π(C)28π(D)32π2016-3(9)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,学.科.网则该多面体的表面积为()(A)18+(B)54+(C)90(D)812017-17.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C .14D .162017-24.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π2018-17.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .172B .52C .3D .22018-33.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是。
2015高考数学(人教版a版)一轮配套题库:7-1空间几何体的结构特征及三视图和直观图

第一节空间几何体的结构特征及三视图和直观图时间:45分钟分值:75分一、选择题(本大题共6小题,每小题5分,共30分)1.下列结论正确的是()A.由五个面围成的多面体只能是四棱锥B.以正方形的一条对角线旋转一周围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长都相等,则此棱锥可能是正六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线解析对于选项A,五个面围成的多面体也可以是三棱柱或三棱台,所以选项A错;由正方形的一条对角线旋转一周围成的几何体为两个圆锥形成的一个组合体,选项B错;六棱锥的侧棱长大于底面多边形的边长,选项C错;选项D正确.故选D.答案 D2.(2013·四川卷)一个几何体的三视图如下图所示,则该几何体的直观图可以是()解析由俯视图知D成立.答案 D3.(2014·汕头市试题)三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则侧视图的面积为() A.8 B.4C.4 3 D. 3解析设侧棱长为x,则2·x=8,x=4,侧视图也是一个矩形,宽为等边三角形的高32·2=3,面积为43,选C.答案 C4.(2014·石家庄质检一)把边长为2的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为()A.32 B.12C.1 D.2 2解析由题意可知,三棱锥C-ABD的直观图如图所示.其中平面CBD⊥平面ABD.取BD的中点E,连接CE,AE,则CE⊥AE,Rt △AEC为三棱锥C-ABD的侧视图.∵AB=AD=BC=CD=2,∴AE=CE=1,∴S △AEC =12×1×1=12,故选B.答案 B5.(2013·湖南卷)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于( )A .1 B. 2 C.2-12 D.2+12解析 由俯视图的面积为1可得底面与水平面平行,当正方体正放时,正视图的面积最小为1,正方体旋转其正视图为其对角面时,面积最大为2,2-12<1故不可能.答案 C6.(2013·辽宁卷)已知直三棱柱ABC —A 1B 1C 1的6个顶点都在球O 的球面上.若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为( ) A.3172B .210 C.132 D .310 解析 由球心O 作平面ABC 的垂线,垂足M 落在Rt △ABC 斜边BC 的中点,AM =12BC =52,OM =12AA 1=6,所以球的半径OA =(52)2+62=132.答案 C二、填空题(本大题共3小题,每小题5分,共15分)7.在直观图(如图所示)中,四边形O′A′B′C′为菱形且边长为2 cm,则在xOy坐标系中,四边形ABCO为________,面积为________cm2.解析由斜二测画法的特点,知该平面图形的直观图的原图,即在xOy坐标系中,四边形ABCO是一个长为4 cm,宽为2 cm的矩形,所以四边形ABCO的面积为8 cm2.答案矩形88.用半径为r 的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是________.解析 由题意可知卷成的圆锥的母线长为r ,设卷成的圆锥的底面半径为r ′,则2πr ′=πr ,所以r ′=12r ,所以圆锥的高h =r 2-⎝ ⎛⎭⎪⎫12r 2=32r . 答案 32r9.用单位立方块搭一个几何体,使它的正(主)视图和俯视图如下图所示,则它的体积的最小值为________,最大值为________.解析 综合分析俯视图和正(主)视图可知单位立方块最少的情况如图①(不唯一)共10块.单位立方块最多的情况如图②,共16块.答案1016三、解答题(本大题共3小题,每小题10分,共30分)10.已知:图①是截去一个角的长方体,试按图示的方向画出其三视图;图②是某几何体的三视图,试说明该几何体的构成.解图①几何体的三视图为:图②所示的几何体是上面为正六棱柱,下面为倒立的正六棱锥的组合体.11.(2014·临沂模拟)若某几何体的三视图(单位:cm)如下图所示.求此几何体的:(1)表面积;(2)体积.解 由题意,该几何体是一个正四棱柱和一个正四棱台的一个组合体.(1)S 表=4×4×2+42+82+4×12×(4+8)×13=112+2413(cm2).(2)V=V1+V2=4×4×2+13×(42+82+42×82)×3=144(cm3).12.如下图是某几何体的三视图(单位:cm).(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.解(1)该几何体的直观图如图所示.(2)这个几何体可看成是正方体AC 1及直三棱柱B 1C 1Q —A 1D 1P 的组合体,由P A 1=PD 1=2,A 1D 1=AD =2,可得P A 1⊥PD 1.故所求几何体的表面积S =5×22+2×2×2+2×12×(2)2=(22+42)(cm 2).所以几何体的体积V =23+12×(2)2×2=10(cm 3).。
2015年全国高考-三视图专练及详细答案
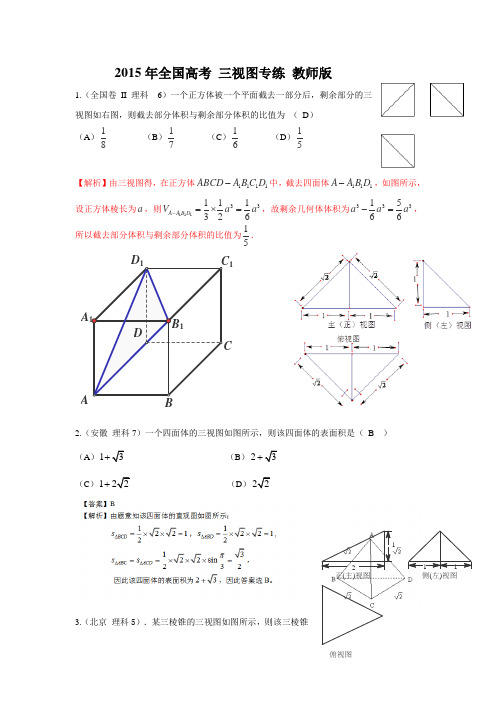
2015年全国高考 三视图专练 教师版
1.(全国卷II 理科 6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为 ( D )
(A )81 (B )71 (C )61 (D )51
【解析】由三视图得,在正方体1111ABCD A B C D -中,截去四面体111A A B D -,如图所示,设正方体棱长为a ,则11133111326A A B D V a a -=
⨯=,故剩余几何体体积为3331566a a a -=,所以截去部分体积与剩余部分体积的比值为51.
2.(安徽 理科7)一个四面体的三视图如图所示,则该四面体的表面积是( B )
(A )13+ (B )23+
(C )122+ (D )22
3.(北京 理科5).某三棱锥的三视图如图所示,则该三棱锥
C B
A D D 1C 1
B 1A 1正(主)视图11俯视图
侧(左)视图
2
1
的表面积是(C )
A .25+
B .45+
C .225+
D .5
【解析】由三视图得其几何体为右图,
4.(陕西理科5) 一个几何体的三视图如图所示,则该几何体的表面积为
A .3π
B .4π
C .24π+
D .34π+
5.(重庆理科5)某几何体的三视图如图所示,则该几何体的体积为()
A 、
13π+ B 、23
π+ C 、123π+ D 、223π+。
2015高考真题分类 考点36 三视图

考点36 三视图1.(2015.北京.理,5)某三棱锥的三视图如图所示,则该三棱锥的表面积是( )A .25+B .45+C .225+D .52.(2015.北京.文,7)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ).A.1B.2 C.3 D. 2俯视图侧(左)视图正(主)视图1113.(2015.天津.理文,10)一个几何体的三视图如图所示(单位:m ),则该几何体的体积 m 3.4.(2015.重庆.理,5)某几何体的三视图如图所示,则该几何体的体积为( )A 、13π+ B 、23π+ C 、123π+ D 、223π+ 5.(2015.重庆.文,5)某几何体的三视图如图所示,则该几何体的体积为( )A .B .C .D .正(主)视图11俯视图侧(左)视图216.(2015.湖南.理,10)某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)().A.89π B.169πC.34(21)π-D.312(21)π-7.(2015.湖南.文,10)某工作的三视图如图所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积) ( )A. 8π9B. 827πC. 324(21)π-D. 38(21)π-8.(2015.陕西.理文,5)一个几何体的三视图如图所示,则该几何体的表面积为( ) A .3πB .4πC .24π+D .34π+俯视图侧视图正视图122221。
2015年全国统一高考数学试卷(文科)(新课标ⅱ)(含答案及解析)

2015年全国统一高考数学试卷(文科)(新课标Ⅱ)一、选择题:本大题共12小题,每小题5分1.(5分)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=()A.(﹣1,3)B.(﹣1,0)C.(0,2)D.(2,3)2.(5分)若为a实数,且=3+i,则a=()A.﹣4B.﹣3C.3D.43.(5分)根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是()A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关4.(5分)=(1,﹣1),=(﹣1,2)则(2+)=()A.﹣1B.0C.1D.25.(5分)已知S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=()A.5B.7C.9D.116.(5分)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.7.(5分)已知三点A(1,0),B(0,),C(2,)则△ABC外接圆的圆心到原点的距离为()A.B.C.D.8.(5分)如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为14,18,则输出的a=()A.0B.2C.4D.149.(5分)已知等比数列{a n}满足a1=,a3a5=4(a4﹣1),则a2=()A.2B.1C.D.10.(5分)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π11.(5分)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为()A.B.C.D.12.(5分)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)二、填空题13.(3分)已知函数f(x)=ax3﹣2x的图象过点(﹣1,4)则a=.14.(3分)若x,y满足约束条件,则z=2x+y的最大值为.15.(3分)已知双曲线过点且渐近线方程为y=±x,则该双曲线的标准方程是.16.(3分)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=.三.解答题17.△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC(Ⅰ)求.(Ⅱ)若∠BAC=60°,求∠B.18.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50,60)[60,70)[70,80)[80,90)[90,100)频数2814106(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大?说明理由.19.(12分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F 分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.20.椭圆C:=1,(a>b>0)的离心率,点(2,)在C上.(1)求椭圆C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.21.设函数f(x)=lnx+a(1﹣x).(Ⅰ)讨论:f(x)的单调性;(Ⅱ)当f(x)有最大值,且最大值大于2a﹣2时,求a的取值范围.四、选修4-1:几何证明选讲22.(10分)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.五、选修4-4:坐标系与参数方程23.(10分)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α≤π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,C3:ρ=2cosθ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.六、选修4-5不等式选讲24.(10分)设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd,则+>+;(2)+>+是|a﹣b|<|c﹣d|的充要条件.2015年全国统一高考数学试卷(文科)(新课标Ⅱ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分1.(5分)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=()A.(﹣1,3)B.(﹣1,0)C.(0,2)D.(2,3)【考点】1D:并集及其运算.【专题】5J:集合.【分析】根据集合的基本运算进行求解即可.【解答】解:∵A={x|﹣1<x<2},B={x|0<x<3},∴A∪B={x|﹣1<x<3},故选:A.【点评】本题主要考查集合的基本运算,比较基础.2.(5分)若为a实数,且=3+i,则a=()A.﹣4B.﹣3C.3D.4【考点】A1:虚数单位i、复数.【专题】5N:数系的扩充和复数.【分析】根据复数相等的条件进行求解即可.【解答】解:由,得2+ai=(1+i)(3+i)=2+4i,则a=4,故选:D.【点评】本题主要考查复数相等的应用,比较基础.3.(5分)根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是()A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关【考点】B8:频率分布直方图.【专题】5I:概率与统计.【分析】A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多,故A正确;B从2007年开始二氧化硫排放量变少,故B正确;C从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C正确;D2006年以来我国二氧化硫年排放量越来越少,与年份负相关,故D错误.【解答】解:A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少,且减少的最多,故A正确;B2004﹣2006年二氧化硫排放量越来越多,从2007年开始二氧化硫排放量变少,故B正确;C从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C正确;D2006年以来我国二氧化硫年排放量越来越少,而不是与年份正相关,故D错误.故选:D.【点评】本题考查了学生识图的能力,能够从图中提取出所需要的信息,属于基础题.4.(5分)=(1,﹣1),=(﹣1,2)则(2+)=()A.﹣1B.0C.1D.2【考点】9O:平面向量数量积的性质及其运算.【专题】5A:平面向量及应用.【分析】利用向量的加法和数量积的坐标运算解答本题.【解答】解:因为=(1,﹣1),=(﹣1,2)则(2+)=(1,0)•(1,﹣1)=1;故选:C.【点评】本题考查了向量的加法和数量积的坐标运算;属于基础题目.5.(5分)已知S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=()A.5B.7C.9D.11【考点】85:等差数列的前n项和.【专题】35:转化思想;4A:数学模型法;54:等差数列与等比数列.【分析】由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3.再利用等差数列的前n项和公式即可得出.【解答】解:由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3=1.则S5==5a3=5.故选:A.【点评】本题考查了等差数列的通项公式及其性质、前n项和公式,考查了推理能力与计算能力,属于中档题.6.(5分)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.【考点】L!:由三视图求面积、体积.【专题】11:计算题;5F:空间位置关系与距离.【分析】由三视图判断,正方体被切掉的部分为三棱锥,把相关数据代入棱锥的体积公式计算即可.【解答】解:设正方体的棱长为1,由三视图判断,正方体被切掉的部分为三棱锥,∴正方体切掉部分的体积为×1×1×1=,∴剩余部分体积为1﹣=,∴截去部分体积与剩余部分体积的比值为.故选:D.【点评】本题考查了由三视图判断几何体的形状,求几何体的体积.7.(5分)已知三点A(1,0),B(0,),C(2,)则△ABC外接圆的圆心到原点的距离为()A.B.C.D.【考点】J1:圆的标准方程.【专题】5B:直线与圆.【分析】利用外接圆的性质,求出圆心坐标,再根据圆心到原点的距离公式即可求出结论.【解答】解:因为△ABC外接圆的圆心在直线BC垂直平分线上,即直线x=1上,可设圆心P(1,p),由PA=PB得|p|=,得p=圆心坐标为P(1,),所以圆心到原点的距离|OP|===,故选:B.【点评】本题主要考查圆性质及△ABC外接圆的性质,了解性质并灵运用是解决本题的关键.8.(5分)如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为14,18,则输出的a=()A.0B.2C.4D.14【考点】EF:程序框图.【专题】27:图表型;5K:算法和程序框图.【分析】模拟执行程序框图,依次写出每次循环得到的a,b的值,当a=b=2时不满足条件a≠b,输出a的值为2.【解答】解:模拟执行程序框图,可得a=14,b=18满足条件a≠b,不满足条件a>b,b=4满足条件a≠b,满足条件a>b,a=10满足条件a≠b,满足条件a>b,a=6满足条件a≠b,满足条件a>b,a=2满足条件a≠b,不满足条件a>b,b=2不满足条件a≠b,输出a的值为2.故选:B.【点评】本题主要考查了循环结构程序框图,属于基础题.9.(5分)已知等比数列{a n}满足a1=,a3a5=4(a4﹣1),则a2=()A.2B.1C.D.【考点】88:等比数列的通项公式.【专题】54:等差数列与等比数列.【分析】利用等比数列的通项公式即可得出.【解答】解:设等比数列{a n}的公比为q,∵,a3a5=4(a4﹣1),∴=4,化为q3=8,解得q=2则a2==.故选:C.【点评】本题考查了等比数列的通项公式,属于基础题.10.(5分)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π【考点】LG:球的体积和表面积.【专题】11:计算题;5F:空间位置关系与距离.【分析】当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,利用三棱锥O﹣ABC体积的最大值为36,求出半径,即可求出球O的表面积.【解答】解:如图所示,当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,设球O的半径为R,此时V O﹣ABC=V C﹣AOB===36,故R=6,则球O的表面积为4πR2=144π,故选:C.【点评】本题考查球的半径与表面积,考查体积的计算,确定点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大是关键.11.(5分)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为()A.B.C.D.【考点】HC:正切函数的图象.【分析】根据函数图象关系,利用排除法进行求解即可.【解答】解:当0≤x≤时,BP=tanx,AP==,此时f(x)=+tanx,0≤x≤,此时单调递增,当P在CD边上运动时,≤x≤且x≠时,如图所示,tan∠POB=tan(π﹣∠POQ)=tanx=﹣tan∠POQ=﹣=﹣,∴OQ=﹣,∴PD=AO﹣OQ=1+,PC=BO+OQ=1﹣,∴PA+PB=,当x=时,PA+PB=2,当P在AD边上运动时,≤x≤π,PA+PB=﹣tanx,由对称性可知函数f(x)关于x=对称,且f()>f(),且轨迹为非线型,排除A,C,D,故选:B.【点评】本题主要考查函数图象的识别和判断,根据条件先求出0≤x≤时的解析式是解决本题的关键.12.(5分)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)【考点】6B:利用导数研究函数的单调性.【专题】33:函数思想;49:综合法;51:函数的性质及应用.【分析】根据函数的奇偶性和单调性之间的关系,将不等式进行转化即可得到结论.【解答】解:∵函数f(x)=ln(1+|x|)﹣为偶函数,且在x≥0时,f(x)=ln(1+x)﹣,导数为f′(x)=+>0,即有函数f(x)在[0,+∞)单调递增,∴f(x)>f(2x﹣1)等价为f(|x|)>f(|2x﹣1|),即|x|>|2x﹣1|,平方得3x2﹣4x+1<0,解得:<x<1,所求x的取值范围是(,1).故选:B.【点评】本题主要考查函数奇偶性和单调性的应用,综合考查函数性质的综合应用,运用偶函数的性质是解题的关键.二、填空题13.(3分)已知函数f(x)=ax3﹣2x的图象过点(﹣1,4)则a=﹣2.【考点】36:函数解析式的求解及常用方法.【专题】11:计算题;51:函数的性质及应用.【分析】f(x)是图象过点(﹣1,4),从而该点坐标满足函数f(x)解析式,从而将点(﹣1,4)带入函数f(x)解析式即可求出a.【解答】解:根据条件得:4=﹣a+2;∴a=﹣2.故答案为:﹣2.【点评】考查函数图象上的点的坐标和函数解析式的关系,考查学生的计算能力,比较基础.14.(3分)若x,y满足约束条件,则z=2x+y的最大值为8.【考点】7C:简单线性规划.【专题】59:不等式的解法及应用.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点A时,直线y=﹣2x+z的截距最大,此时z最大.由,解得,即A(3,2)将A(3,2)的坐标代入目标函数z=2x+y,得z=2×3+2=8.即z=2x+y的最大值为8.故答案为:8.【点评】本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法.15.(3分)已知双曲线过点且渐近线方程为y=±x,则该双曲线的标准方程是x2﹣y2=1.【考点】KB:双曲线的标准方程.【专题】11:计算题;5D:圆锥曲线的定义、性质与方程.【分析】设双曲线方程为y2﹣x2=λ,代入点,求出λ,即可求出双曲线的标准方程.【解答】解:设双曲线方程为y2﹣x2=λ,代入点,可得3﹣=λ,∴λ=﹣1,∴双曲线的标准方程是x2﹣y2=1.故答案为:x2﹣y2=1.【点评】本题考查双曲线的标准方程,考查学生的计算能力,正确设出双曲线的方程是关键.16.(3分)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=8.【考点】6H:利用导数研究曲线上某点切线方程.【专题】26:开放型;53:导数的综合应用.【分析】求出y=x+lnx的导数,求得切线的斜率,可得切线方程,再由于切线与曲线y=ax2+(a+2)x+1相切,有且只有一切点,进而可联立切线与曲线方程,根据△=0得到a的值.【解答】解:y=x+lnx的导数为y′=1+,曲线y=x+lnx在x=1处的切线斜率为k=2,则曲线y=x+lnx在x=1处的切线方程为y﹣1=2x﹣2,即y=2x﹣1.由于切线与曲线y=ax2+(a+2)x+1相切,故y=ax2+(a+2)x+1可联立y=2x﹣1,得ax2+ax+2=0,又a≠0,两线相切有一切点,所以有△=a2﹣8a=0,解得a=8.故答案为:8.【点评】本题考查导数的运用:求切线方程,主要考查导数的几何意义:函数在某点处的导数即为曲线在该点处的导数,设出切线方程运用两线相切的性质是解题的关键.三.解答题17.△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC(Ⅰ)求.(Ⅱ)若∠BAC=60°,求∠B.【考点】HP:正弦定理.【专题】58:解三角形.【分析】(Ⅰ)由题意画出图形,再由正弦定理结合内角平分线定理得答案;(Ⅱ)由∠C=180°﹣(∠BAC+∠B),两边取正弦后展开两角和的正弦,再结合(Ⅰ)中的结论得答案.【解答】解:(Ⅰ)如图,由正弦定理得:,∵AD平分∠BAC,BD=2DC,∴;(Ⅱ)∵∠C=180°﹣(∠BAC+∠B),∠BAC=60°,∴,由(Ⅰ)知2sin∠B=sin∠C,∴tan∠B=,即∠B=30°.【点评】本题考查了内角平分线的性质,考查了正弦定理的应用,是中档题.18.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50,60)[60,70)[70,80)[80,90)[90,100)频数2814106(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大?说明理由.【考点】B8:频率分布直方图;CB:古典概型及其概率计算公式.【专题】5I:概率与统计.【分析】(I)根据分布表的数据,画出频率直方图,求解即可.(II)计算得出C A表示事件:“A地区用户的满意度等级为不满意”,C B表示事件:“B地区用户的满意度等级为不满意”,P(C A),P(C B),即可判断不满意的情况.【解答】解:(Ⅰ)通过两个地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值,B 地区的用户满意度评分的比较集中,而A地区的用户满意度评分的比较分散.(Ⅱ)A地区用户的满意度等级为不满意的概率大.记C A表示事件:“A地区用户的满意度等级为不满意”,C B表示事件:“B地区用户的满意度等级为不满意”,由直方图得P(C A)=(0.01+0.02+0.03)×10=0.6得P(C B)=(0.005+0.02)×10=0.25∴A地区用户的满意度等级为不满意的概率大.【点评】本题考查了频率直方图,频率表达运用,考查了阅读能力,属于中档题.19.(12分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F 分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.【考点】LF:棱柱、棱锥、棱台的体积;LJ:平面的基本性质及推论.【专题】15:综合题;5F:空间位置关系与距离.【分析】(Ⅰ)利用平面与平面平行的性质,可在图中画出这个正方形;(Ⅱ)求出MH==6,AH=10,HB=6,即可求平面a把该长方体分成的两部分体积的比值.【解答】解:(Ⅰ)交线围成的正方形EFGH如图所示;(Ⅱ)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为EFGH为正方形,所以EH=EF=BC=10,于是MH==6,AH=10,HB=6.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.【点评】本题考查平面与平面平行的性质,考查学生的计算能力,比较基础.20.椭圆C:=1,(a>b>0)的离心率,点(2,)在C上.(1)求椭圆C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.【考点】K3:椭圆的标准方程;KH:直线与圆锥曲线的综合.【专题】5D:圆锥曲线的定义、性质与方程.【分析】(1)利用椭圆的离心率,以及椭圆经过的点,求解椭圆的几何量,然后得到椭圆的方程.(2)设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(x M,y M),联立直线方程与椭圆方程,通过韦达定理求解K OM,然后推出直线OM的斜率与l的斜率的乘积为定值.【解答】解:(1)椭圆C:=1,(a>b>0)的离心率,点(2,)在C上,可得,,解得a2=8,b2=4,所求椭圆C方程为:.(2)设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(x M,y M),把直线y=kx+b代入可得(2k2+1)x2+4kbx+2b2﹣8=0,故x M==,y M=kx M+b=,于是在OM的斜率为:K OM==,即K OM•k=.∴直线OM的斜率与l的斜率的乘积为定值.【点评】本题考查椭圆方程的综合应用,椭圆的方程的求法,考查分析问题解决问题的能力.21.设函数f(x)=lnx+a(1﹣x).(Ⅰ)讨论:f(x)的单调性;(Ⅱ)当f(x)有最大值,且最大值大于2a﹣2时,求a的取值范围.【考点】6B:利用导数研究函数的单调性;6E:利用导数研究函数的最值.【专题】26:开放型;53:导数的综合应用.【分析】(Ⅰ)先求导,再分类讨论,根据导数即可判断函数的单调性;(2)先求出函数的最大值,再构造函数(a)=lna+a﹣1,根据函数的单调性即可求出a的范围.【解答】解:(Ⅰ)f(x)=lnx+a(1﹣x)的定义域为(0,+∞),∴f′(x)=﹣a=,若a≤0,则f′(x)>0,∴函数f(x)在(0,+∞)上单调递增,若a>0,则当x∈(0,)时,f′(x)>0,当x∈(,+∞)时,f′(x)<0,所以f(x)在(0,)上单调递增,在(,+∞)上单调递减,(Ⅱ),由(Ⅰ)知,当a≤0时,f(x)在(0,+∞)上无最大值;当a>0时,f(x)在x=取得最大值,最大值为f()=﹣lna+a﹣1,∵f()>2a﹣2,∴lna+a﹣1<0,令g(a)=lna+a﹣1,∵g(a)在(0,+∞)单调递增,g(1)=0,∴当0<a<1时,g(a)<0,当a>1时,g(a)>0,∴a的取值范围为(0,1).【点评】本题考查了导数与函数的单调性最值的关系,以及参数的取值范围,属于中档题.四、选修4-1:几何证明选讲22.(10分)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.【考点】N4:相似三角形的判定.【专题】26:开放型;5F:空间位置关系与距离.【分析】(1)通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论;(2)通过(1)知AD是EF的垂直平分线,连结OE、OM,则OE⊥AE,利用S△ABC﹣S△AEF计算即可.【解答】(1)证明:∵△ABC为等腰三角形,AD⊥BC,∴AD是∠CAB的角平分线,又∵圆O分别与AB、AC相切于点E、F,∴AE=AF,∴AD⊥EF,∴EF∥BC;(2)解:由(1)知AE=AF,AD⊥EF,∴AD是EF的垂直平分线,又∵EF为圆O的弦,∴O在AD上,连结OE、OM,则OE⊥AE,由AG等于圆O的半径可得AO=2OE,∴∠OAE=30°,∴△ABC与△AEF都是等边三角形,∵AE=2,∴AO=4,OE=2,∵OM=OE=2,DM=MN=,∴OD=1,∴AD=5,AB=,∴四边形EBCF的面积为×﹣××=.【点评】本题考查空间中线与线之间的位置关系,考查四边形面积的计算,注意解题方法的积累,属于中档题.五、选修4-4:坐标系与参数方程23.(10分)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α≤π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,C3:ρ=2cosθ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.【专题】5S:坐标系和参数方程.【分析】(I)由曲线C2:ρ=2sinθ,化为ρ2=2ρsinθ,把代入可得直角坐标方程.同理由C3:ρ=2cosθ.可得直角坐标方程,联立解出可得C2与C3交点的直角坐标.(2)由曲线C1的参数方程,消去参数t,化为普通方程:y=xtanα,其中0≤α≤π,α≠;α=时,为x=0(y≠0).其极坐标方程为:θ=α(ρ∈R,ρ≠0),利用|AB|=即可得出.【解答】解:(I)由曲线C2:ρ=2sinθ,化为ρ2=2ρsinθ,∴x2+y2=2y.同理由C3:ρ=2cosθ.可得直角坐标方程:,联立,解得,,∴C2与C3交点的直角坐标为(0,0),.(2)曲线C1:(t为参数,t≠0),化为普通方程:y=xtanα,其中0≤α≤π,α≠;α=时,为x=0(y≠0).其极坐标方程为:θ=α(ρ∈R,ρ≠0),∵A,B都在C1上,∴A(2sinα,α),B.∴|AB|==4,当时,|AB|取得最大值4.【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、曲线的交点、两点之间的距离公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.六、选修4-5不等式选讲24.(10分)设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd,则+>+;(2)+>+是|a﹣b|<|c﹣d|的充要条件.【考点】29:充分条件、必要条件、充要条件;R6:不等式的证明.【专题】59:不等式的解法及应用;5L:简易逻辑.【分析】(1)运用不等式的性质,结合条件a,b,c,d均为正数,且a+b=c+d,ab>cd,即可得证;(2)从两方面证,①若+>+,证得|a﹣b|<|c﹣d|,②若|a﹣b|<|c﹣d|,证得+>+,注意运用不等式的性质,即可得证.【解答】证明:(1)由于(+)2=a+b+2,(+)2=c+d+2,由a,b,c,d均为正数,且a+b=c+d,ab>cd,则>,即有(+)2>(+)2,则+>+;(2)①若+>+,则(+)2>(+)2,即为a+b+2>c+d+2,由a+b=c+d,则ab>cd,于是(a﹣b)2=(a+b)2﹣4ab,(c﹣d)2=(c+d)2﹣4cd,即有(a﹣b)2<(c﹣d)2,即为|a﹣b|<|c﹣d|;②若|a﹣b|<|c﹣d|,则(a﹣b)2<(c﹣d)2,即有(a+b)2﹣4ab<(c+d)2﹣4cd,由a+b=c+d,则ab>cd,则有(+)2>(+)2.综上可得,+>+是|a﹣b|<|c﹣d|的充要条件.【点评】本题考查不等式的证明,主要考查不等式的性质的运用,同时考查充要条件的判断,属于基础题.。
【高考领航】2015高考数学(理)一轮配套课件7-1 第1课时 空间几何体的结构及其三视图和直观图

转
圆台可由直角梯形绕直角腰或等腰梯形绕上下底
体 圆台 中点连线旋转得到,也可由 平行 于圆锥底面的平 面截圆锥得到. 球 球可以由半圆或圆绕 直径 所在直线旋转得到.
对点演练
(教材改编)下列说法正确的是
( A.有两个面平行,其余各面都是四边形的几何体叫棱柱 B .有两个面平行,其余各面都是平行四边形的几何体叫 棱柱 )
面上的正投影,并不是从三个方向看到的该几何体的侧 面表示的图形. (2) 在画三视图时,重叠的线只画一条,能看见的轮廓线 和棱用实线表示,挡住的线要画成虚线.
(3) 三视图的正视图、侧视图、俯视图分别是从几何体的
正前方、左方、正上方观察几何体用平行投影画出的轮 廓线.
3.对斜二测画法的认识及直观图的画法 (1)在斜二测画法中,要确定关键点及关键线段.“平行于 x 轴的线段平行性不变,长度不变,平行于 y 轴的线段平行性不 变,长度减半.” (2)按照斜二测画法得到的平面图形的直观图, 其面积与原图形 的面积有以下关系: 2 S 直观图= 4 S 原图形, S 原图形=2 2S 直观图.
题型一
空间几何体的结构特征 设有以下四个命题:
①底面是平行四边形的四棱柱是平行六面体; ②底面是矩形的平行六面体是长方体;
③直四棱柱是直平行六面体;
④棱台的相对侧棱延长后必交于一点. 共中真命题的序号是________.
题①是正确
的.底面是矩形的平行六面体的侧棱可能与底面不垂直,故 命题②是错误的.因为直四棱柱的底面不一定是平行四边形,
(二)命题趋势 1 .从考查内容看,主要侧重于对柱、锥、台、球及简单组
合体的结构特征及性质的考查,特别是常见几何体及简
单组合体的三视图,更是高考的重点和热点,几乎年年 考. 2 .从考查形式看,常以选择题、填空题的形式出现,有时 也出现在解答题中,难度不大,属中低档题.
2015高考数学热点精讲精练07之三视图(含答案)

(第三轮) 第七讲三视图与空间结构知识要点知识点1、空间几何体的三视图、直观图:(1) 正视图: 物体前后方向投影所得到的投影图; 它能反映物体的高度和长度.(2) 侧视图: 物体左右方向投影所得到的投影图; 它能反映物体的高度和宽度.(3) 俯视图: 物体上下方向投影所得到的投影图; 它能反映物体的长度和宽度.圆柱的三视图圆锥的三视图注: 三视图之间的投影规律: 正视图与俯视图---长对正; 正视图与侧视图---高平齐; 俯视图与侧视图---宽相等.(4)直观图: 一个物体, 从直观看上去的图形, 叫做直观图, 一般可用斜二测画法实现.①画出相应的x′ 轴和y′ 轴, 且使∠x′O′y′=45°或135° ;②已知图形中平行于x轴或y轴的线段,在直观图中分别画出平行于x′ 轴和y′轴的线段.③已知图形中平行于x轴的线段在直观图中长度保持不变, 平行于y轴的线段长度变成原来的一半.典例精析1、(2008广东)将正三棱柱截去三个角(如图1所示A B C,,分别是GHI△三边的中点)得到几何体如图2, 则该几何体按图2所示方向的侧视图(或称左视图)为( )2、(2009广东)用单位立方块搭一个几何体, 使它的主视图和俯视图如右图所示, 则它的体积的最小值与最大值分别为( )A. 9与13B. 7与10C. 10与16D. 10与153、(2008海南、宁夏)某几何体的一条棱长为7, 在该几何体的正视图中, 这条棱的投影是长为6的线段, 在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段, 则a+b的最大值为( )A. 22B. 23C. 4D. 25EFDIAH GB CEFDAB C侧视图1 图2BEA.BEB.BEC.BED.nmk俯视图主视图4、(2006辽宁)如图, 半径为2的半球内有一内接正六棱锥, 则此正六棱锥的侧面积是.P ABCDEF5、一个物体由几块相同的正方体叠成, 它的俯视图如图所示, 方格中的数字对应该正方体对应的层数, 请回答下列问题:(1) 该物体共有层?(2) 画出正视图与侧视图, 并涂黑以标记最高位置相应正方体.(3) 一共需要个小正方体?6、一个画家有14个边长为1m的正方体, 他在地面上把它们摆成如右图所示的形式, 分别画出该组合体的三视图, 然后他把露出的表面都涂上颜色, 那么被涂上颜色的总面积为.8、一空间几何体的三视图如图所示, 求该几何体的体积.9、一个空间几何体的正视图和侧视图都是边长为10. 右图是由一些大小相同的小正方体组成的几何体的主视图和俯视图.(1) 请你画出这个几何体的各种可能的左视图;(2) 若组成这个几何体的小正方形的块数为n, 请你写出n的所有可能值.基础过关1、(2010广东)如图1, △ ABC为三角形, AA'//BB' //CC', CC'⊥平面ABC 且3AA'=3 2BB'=CC'=AB, 则多面体△ABC -A B C'''的正视图(也称主视图)是( )2、(2013安徽)如图是一个简单的组合体的直观图与三视图.下面是一个棱长为4的正方体, 正上面放一个球, 且球的一部分嵌入正方体中, 则球的半径是( )A.12B.1 C.32D.2俯视图正视图侧视图1直观图3、如图, 动点P 在正方体1111ABCD A B C D -的对角线1BD 上. 过点P 作垂直于平面11BB D D 的直线, 与正方体表面相交于M N ,. 设BP x =, MN y =, 则函数()y f x =的图象大致是( )4、(2011浙江) 若某几何体的三视图如图所示, 则这个几何体的直观图可以是( )5、将长方体截去一个四棱锥后, 得到的几何体的直观图如右图所示, 则该几何体的俯视图为 ()6、(2010湖南)下图中的三个直角三角形是一个体积为20cm 2的几何体的三视图, 则h =cm.7、(2009泰安一模)一个几何体的三视图如图所示, 则这个几何体的体积等于 .8、(2009番禺一模)一个几何体的三视图如右图所示, 其中正视图中△ABC 是边长为2的正三角形, 俯视图为正六边形, 那么该几何体的侧视图的面积为 .9、有一堆小正方体如下图放置, 从上面拿掉一个或者几个小正方体(不能直接拿掉被压在下面的小正方体)而不改变几何体的三视图的方法有__________种.A B CD MNP A 1B 1 C1D 1y xA . Oy xB . Oy xC . OyxD . O10、己知某几何体的三视图如图所示, 则其表面积为 .11、一个几何体的三视图如图所示, 其中正视图是一个正三角形, 求这个几 何体的外接球的表面积.参考答案典例精析1、(2008广东)将正三棱柱截去三个角(如图1所示A B C ,,分别是GHI △三边的中点)得到几何体如图2, 则该几何体按图2所示方向的侧视图(或称左视图)为( A )2、(2009广东)用单位立方块搭一个几何体, 使它的主视图和俯视图 如右图所示, 则它的体积的最小值与最大值分别为( C ) A. 9与13 B. 7与10 C. 10与16 D. 10与15A B C1C1A1BD 1DEF DIA H G BC EF DABC侧视 图1图2 BEA .BEB .BEC .B ED .俯视图主视图3、(2008海南、宁夏)某几何体的一条棱长为7, 在该几何体的正视图中, 这条棱的投影是长为6的线段, 在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段, 则a+b的最大值为( C)A. 22B. 23C. 4D. 25解: 结合长方体的对角线在三个面的投影来理解计算. 如图设长方体的高宽高分别为,,m n k, 由题意得2227m n k++=, 226m k+=1n⇒=,21k a+=,21m b+=, 所以22(1)(1)6a b-+-=228a b⇒+=, 22222()282816a b a ab b ab a b+=++=+≤++=∴, 4a b⇒+≤当且仅当2a b==时取等号.4、(2006辽宁)如图, 半径为2的半球内有一内接正六棱锥P ABCDEF-, 则此正六棱锥的侧面积是.解: 显然正六棱锥P ABCDEF-的底面的外接圆是球的一个大圆, 于是可求得底面边长为2, 又正六棱锥P ABCDEF-的高依题意可得为2, 依此可求得67.5、一个物体由几块相同的正方体叠成, 它的俯视图如图所示, 方格中的数字对应该正方体对应的层数, 请回答下列问题:(1) 该物体共有层?(2) 画出正视图与侧视图, 并涂黑以标记最高位置相应正方体.(3) 一共需要个小正方体?解: (1) 三层.(2) 如右图所示.(3) 需要11块小正方体.6、一个画家有14个边长为1m的正方体, 他在地面上把它们摆成如右图所示的形式, 然后他把露出的表面都涂上颜色, 那么被涂上颜色的总面积为.解: 分别画出该组合体的三视图如下:根据三视图可知其露出的表面积为6×2+6×2+9=33(m2).nmkABCPDEF8、一空间几何体的三视图如图所示, 求该几何体的体积.解: 该空间几何体为一圆柱和一四棱锥组成的, 圆柱的底面半径为1, 高为2, 体积为2π, 四棱锥的底面边长为2, 高为3, 体积为()21232333⨯⨯=, 故该几何体的体积为2323π+. 9、一个空间几何体的正视图和侧视图都是边长为10. 右图是由一些大小相同的小正方体组成的几何体的主视图和俯视图.(1) 请你画出这个几何体的各种可能的左视图; 解: 左视图有以下五种情形:(2) 若组成这个几何体的小正方形的块数为n , 请你写出n 的所有可能值.解: n =8, 9, 10, 11.基础过关)如图1, △ ABC 为三角形, AA '//BB ' //CC ', CC '⊥平面ABC 且3AA '=32BB '=CC '=AB, 则多面体△ABC -A B C '''的正视图(也称主视图)是( D )2、(2013安徽)如图是一个简单的组合体的直观图与三视图.下面是一个棱长为4的正方体, 正上面放一个球, 且球的一部分嵌入正方体中, 则球的半径是( B )A.12B.1C.32D.23、如图, 动点P在正方体1111ABCD A B C D-的对角线1BD上. 过点P作垂直于平面11BB D D的直线, 与正方体表面相交于M N,. 设BP x=, MN y=, 则函数()y f x=的图象大致是( B )4、(2011浙江) 若某几何体的三视图如图所示, 则这个几何体的直观图可以是( B )5、将长方体截去一个四棱锥后, 得到的几何体的直观图如右图所示, 则该几何体的俯视图为( C )6、(2010湖南)下图中的三个直角三角形是一个体积为20cm2的几何体的三视图, 则h=cm. (答案: 4).俯视图正视图侧视图1直观图A BCDMNPA1 B1C1D1yxOyxOyxOyxO7、(2009泰安一模)一个几何体的三视图如图所示,则这个几何体的体积等于.(答案: 4).8、(2009番禺一模)一个几何体的三视图如右图所示, 其中正视图中△ABC是边长为2的正三角形, 俯视图为正六边形, 那么该几何体的侧视图的面积为. 答案:23.9、有一堆小正方体如下图放置, 从上面拿掉一个或者几个小正方体(不能直接拿掉被压在下面的小正方体)而不改变几何体的三视图的方法有__________种. (答案: 4).10、己知某几何体的三视图如图所示, 则其表面积为 .解: 由几何体的三视图可知该几何体为直三棱柱, 如图所示,111111111,2,2,1,2,2222,224,=2+2422464 2.CBC B ABA BCBC B ABC ABA BCD AB BB AB CD CBS SS S S SΛ⊥====∴=⨯==⨯=∴+=++=+表11、一个几何体的三视图如图所示, 其中正视图是一个正三角形, 求这个几何体的外接球的表面积.ABC1C1A1BD1D。
2015高考数学考点24三视图解析

考点24三视图【高考再现】热点一形状的判断1.(2012年高考福建卷理科4)一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是()A.球 B .三棱锥 C .正方体D.圆柱【答案】D【解析】13的正视图(主视图)、侧观图(左视图)和俯视图均为圆;三棱谁前正视图(主视图人侧视圏(左观图)和俯视图可以为全等的三形:正方障的正视图(主视图h侧视图(左视图)和俯视图均为正方形;圆枉的正视图(主视图人侧视图(左视图)为矩形,俯视图沟IB.2.(2012年高考湖南卷理科3)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是()去】A B 【答案】D【解析】本題是组合体的三视图问题,由几何体■的正视图和侧视图均如图亠所示知,原图下面图为圆柱或直四轅柱,上面是13柱或直四棱柱或下底是直甬的三棱柱.A ?吕.匕都可能是该几何即的俯观團,D不可能是该几何体的俯视團,因淘它的正视图上面应汽如图的拒孫.【方法总结】三视图的长度特征,三视图中,正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽.即“长对正,宽相等,高平齐”热点二三视图和几何体的体积相结合3. (2012年高考广东卷理科 6)某几何体的三视图如图 1所示,它的体积为(第二题图A . 12 n B.45 n C.57 n D.81 n【答案】C【解析】由三视图知』几何体为一个底面半径为3的圆柱与一个同底的圆锥组合而航所以其 体积为457T+-7rx9x4 =57JT ,故选 C,34. (2012年高考湖北卷理科4)已知某几何体的三视图如图所示,则该几何悴的体积为 ( )8TT IO TTA. —B.3 XC. --------------------D.6 n3 3【答案】B【解析】由三观图可知,该几何体为一底命半 径为1且高沟2的匮I 柱与一匾锥组合而成,所以 其体积为2兀+兀=3兀,故选B.■ 14热点三三视图和几何体的表面积相结合5.(2012年高考北京卷理科7)某三棱锥的三视图如图所示,该三梭锥的表面积是(正(主)俛图ffl {左)视是_A. 28+6-/5B. 30+6-75C. 56+ 12 V5 0.60+12 75【答案】B【解析】从所给前三视图可味得到该几何库为三棱維,如图所示,图中蓝色数:字所表示的为直援从题目所给三视图中读出的长度,黒色数字代表通过勾腌定理95计算得到的边长.本题所求表面积应为三棱锥四个面的面积之和,利用垂直关系和三角形面积公式,可得’^ = 10 ,^=10 , =10 , E盂・因此该几何体表面积6.(2012 年高考辽宁卷理科13)一个几何体的三视图如图所示,则该几何体的表面积为j 1Il 11,1 »+ 114 2 一H 1—:14[«%] 38【解析】由三视图可知该几何甲为一个长方体在中间挖去了一个等高的圆柱.其中长方冰的长、宽、高分别为4、3> 1,圆柱的底面直径淘出所以该几何体的表面积为长方体的耒面积加匾1柱的侧面积再减去僵1柱的底而积,§P^2(3x4 + 4xl+3xl) + 2^rxlxl-27T= 38【考点剖析】1.了解和正方体、球有关的简单组合体的结构特征,理解柱、锥、台、球的结构特征.2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等简易组合)的三视图,会用斜二测画法画出它们的直观图.3.会用平行投影与中心投影两种方法画出简单空间图形的三视图或直观图,了解空间图形的不同表示形式.4.能识别三视图所表示的空间几何体;理解三视图和直观图的联系,并能进行转化二.命题方向1.三视图是新增加的内容,是高考的热点和重点,几乎年年考.2.柱、锥、台、球及简单组合体的结构特征及性质是本节内容的重点,也是难点.3.以选择、填空题的形式考查,有时也会在解答题中出现三.规律总结一个规律三视图的长度特征:“长对正,宽相等,高平齐”,即正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.两个概念(1)正棱柱:侧棱垂直于底面的棱柱叫做直棱柱,底面是正多边形的直棱柱叫做正棱柱.反之,正棱柱的底面是正多边形,侧棱垂直于底面,侧面是矩形.(2)正棱锥:底面是正多边形,顶点在底面的射影是底面正多边形的中心的棱锥叫做正棱锥.特别地,各棱均相等的正三棱锥叫正四面体.反过来,正棱锥的底面是正多边形,且顶点在底面的射影是底面正多边形的中心.【基础练习】1.(课本习题改编)用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是().A .圆柱B .圆锥C.球体 D .圆柱、圆锥、球体的组合体解祈 当用过高践的平面截圆柱和圆锥时,截面分别为矩形和三角形,只有球満足任意截面都是圆面*2.(经典习题)某几何体的三视图如图所示,贝尼的体积是()•2n 8-23" C. 8-2n解析 圆锥的底面半径为1,高为二该几何体体积为正方体体积减去圆锥倣积,1即厂=2:X 2 —= X 応>< 工X 2 = § —和’正确选项为A.4 4答案A 3.(经典习题)若一个底面是正三角形的直三棱柱的正视图如图所示,则其侧面积等于( )A. ,3B . 2C . 2 . 3D . 6答案:D4. .(2011 •山东高考改编)如图是长和宽分别相等的两个矩形•给定下列三 个命题:①存在三棱柱,其正视图、俯视图如图;②存在四棱柱,其正视图、俯视图如图;③存在圆柱,其正视图、俯视图如图•其中真命题的P.曰号疋 答案;①②③解析;只要把底面为等腰直角三角形的直三棱柱的一个侧面啟在水平面 上,就可以使得这个三棱柱的正视图和附视图符合妾求,故命题①是真 命题J 把一个正四棱柱的一个侧面敢置在水平面上,目卩可使得这个四棱 柱的正视图和俯视图符合要求,命■题②是真命题:只要把圆柱侧面的一2n D.§解析:由题意可知,该直三棱柱的底面边长为2,高为1,故S 侧面=3X 2X 1 = 6.条母线战直在水平面即符合要求,命题③也是真命题.•基础扎实1.(2012届高三年级第二次综合练习文)如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长都为 1,那么这个几何体的表面积为B .C .D .【答案】D 【解析】由题意得^=(^X 1X 1)X 34-^X (V2)2 sin60°故选 D2 2 22.(北京市西城区2012届高三4月第一次模拟考试试题理 )已知正六棱柱的底面边长和侧棱长相等,体积为12 3cm ‘ .其三视图中的俯视图如图所示,则其左视图的面积是( )(A ) 4 3 cm 2 (B ) 2 3cm 2 (C ) 8cm 2 (D ) 4cm 2 【答案】A【解析】设边长为 x , V =丄 x *x *sin 60°・x =12\'3x = 2 /.2左视图是矩形,可得边长为2 3和2,•••左视图的面积是 43 cm 2故选,A3.(2012年云南省第一次统一检测理)下图是一个几何体的三视图,其中正视图是边长为 2的 等边三角形,侧视图是直角边长分别为 1与 3的直角三角形,俯视图是半径为1的半圆,则 该几何体的体积等于正视图侧视图3酹视图(A) 3二(B) _3二(C) 4 3二(D) 1二6 3 3 2答案:A 解析’ Y在几何体的三视图中,正视图是辺畏周2朗等边三第形,侧视图是直毎辺长分别为1与再的直角三角形,俯视图是半径为】的半圆.二此几何体是底面半径等于1,高等于朽的半个画锥.二该几何体的体积等于骑.64.(山西省2012年高考考前适应性训练文)已知某几何体的体积为4,它的正视图、侧视图均为边长为1的正方形,则该几何体的俯视图可以为()【答案】B2r与高h相等,此【解析】依题意得知,该几何体可是一个圆柱,其中该圆柱的底面直径2 3 H 1时相应的体积等于二r 2r=2「:r ,r ,相应的俯视图可以是B,选B.4 25.(湖北武汉2012适应性训练理)一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形•则该几何体的表面积为A. 88B. 98C. 108D. 158【答案】A【解析】依题意得叩,该几何体是一个直三棱柱,其表面积等于<1 、 2x -x6x4 十 4x4 十 2x4x6 二结E ,选扎6.(湖北省武汉市2012届高中毕业生五月供题训练(二) 理) 某几何体的正视图如左图所示,则该几何体的俯视图不可能的是答郵C解析:根据三视图的规则可知.该几何郎可能上部背一个球,底靳为一个圆枉或一个棱 柱,且球的直径与四棱枉的底面上的边长差别不犬,从上面向下看,一定看到一个圆, 再看§1或者是看不至(I —个矩舷 如正方形正观图佣视图的边长大于球的直径,刚看©I m选顼』如下面是一个圆柱,且圆柱囲底面直径与球的直径相等,看到A选项,如下面是一个袒形,且矩形的边长比球的直径大,看到H,C选项的團形不可能看钊,矩形■应是虚裁,故选:7.(湖北文科数学冲刺试卷(二))从一牛槎长为1的正方怵中切去一部分•得列一6几何律•其兰視图如右图,赠械几轉挣8a更Ut 6答案;D解析:由题意得,根据三视图的规则可知,原几何体表示一个正方体切掉一个角,正方体的体积沖巧= lxlxl=b 一个角对应的三棱锥的体和为晒二]J兀以1X1 = —32 6所以该几何体的体积为茁二*「陌故选D・68.(襄阳五中高三年级第一次适应性考试文)一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于A. 3B. 2 3 c. 3 3 D. 6 3答案:A解析:由题意得,根据三视图的规则得,棱锥以俯视图为底面,以侧视图的高为高, 由于侧视图是以2为编程的等边三角形,所以h=』3 ,1结合三视图中的数据,底面积为^-'(12) 2=3 ,2所以几何体的体积为v = 1 Sh =丄汉3汉*'3 = <3,故选A。
2015高考数学一轮课件:9-1空间几何体的结构、三视图和直观图

解析:①中其直观图是一般的平行四边形,②菱形的直观图 不一定是菱形,③正确.
答案:③
第二十一页,编辑于星期五:十三点 二十七分。
5.一个长方体去掉一个小长方体,所得几何体的正视图与 侧视图分别如图所示,则该几何体的俯视图为__________.
正(主)视图
侧(左)视图
第二十二页,编辑于星期五:十三点 二十七分。
通关训练2 三视图如图所示的几何体是( )
A.三棱锥 B.四棱锥 C.四棱台 D.三棱台
第三十六页,编辑于星期五:十三点 二十七分。
解析:由三视图知该几何体为一四棱锥,其中有一侧棱垂直 于底面,底面为一直角梯形.故选B.
答案:B
第三十七页,编辑于星期五:十三点 二十七分。
考点三 空间几何体的直观图
答案:B
第三十页,编辑于星期五:十三点 二十七分。
考点二 空间几何体的三视图 【例2】 如图,某几何体的正(主)视图与侧(左)视图都是边长
为1的正方形,且体积为12,则该几何体的俯视图可以是( )
正(主)视图
侧(左)视图
第三十一页,编辑于星期五:十三点 二十七分。
A
B
C
D
第三十二页,编辑于星期五:十三点 二十பைடு நூலகம்分。
点评:解决该类题目需准确理解几何体的定义,要真正把握 几何体的结构特征,并且学会通过反例对概念进行辨析,即要说 明一个命题是错误的,设法举出一个反例即可.
第二十八页,编辑于星期五:十三点 二十七分。
通关训练1 以下命题:
①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆
●一条规律 三视图的长度特征:“长对正,宽相等,高平齐”,即正 (主)视图和侧(左)视图一样高,正(主)视图和俯视图一样长,侧 (左)视图和俯视图一样宽. ●一点注意 若相邻两物体的表面相交,表面的交线是它们的分界线,在 三视图中,要注意实、虚线的画法.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点36 三视图
1.(2015.北京.理,5)某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
A .25+
B .45+
C .225+
D .5
2.(2015.北京.文,7)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ).
A.1
B. 2
C. 3
D. 2
俯视图
侧(左)视图
正(主)视图1
1
1
3.(2015.天津.理文,10)一个几何体的三视图如图所示(单位:m ),
则该几何体的体积 m 3
.
4.(201
5.重庆.理,5)某几何体的三视图如图所示,则该几何体的体积为( )
正(主)视图
11俯视图侧(左)视图
2
1
A、1
3
π
+B、
2
3
π
+C、
1
2
3
π
+D、
2
2
3
π
+
5.(2015.重庆.文,5)某几何体的三视图如图所示,则该几何体的体积为()
A.B.C.D.
6.(2015.湖南.理,10)某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的
一个面内,则原工件材料的利用率为(材料利用率
=新工件的体积
原工件的体积
)(). A.
8
9π
B.
16
9π
C.
3
4(21)
π
-
D.
3
12(21)
π
-
7.(2015.湖南.文,10)某工作的三视图如图所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)
( )
A. 8π
9
B.
8
27π
C.
3
24(21)
π
-
D.
3
8(21)
π
-
俯视图
侧视图
正视图
1
2
2
2
2
1
8.(2015.陕西.理文,5)一个几何体的三视图如图所示,则该几何体的表面积为( )
A .3π
B .4π
C .24π+
D .34π+
9.(2015.浙江.理文,2)某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )
A . 8cm 3
B . 12cm 3
C .
D .
10.(2015.安徽.理文,7)一个四面体的三视图如图所示,则该四面体的表面积是( )
A . 1+
B . 2+
C . 1+2
D . 2
11.(2015.福建.文,9)某几何体的三视图如图所示,则该几何体的表面积等于
A.2
2
14+ D.15
11+ C. 2
2
8+ B. 2
2
12.(2015.全国I.理,11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,
该几何体的表面积为16+20π,则r=()
(A)1 (B) 2 (C) 4 (D) 5。
