2012年福建省普通高中毕业班质量检查(理科数学)附答案
2012年5月福州市高中毕业班数学综合质检试卷(理科)(带答案)

2012年5月福州市高中毕业班数学综合质检试卷(理科)(带答案)2012年福州市高中毕业班综合练习理科数学试卷参考答案及评分参考一、选择题(本大题共10小题,每小题5分,共50分)1.B2.A3.C4.D5.B6.D7.C8.B9.D10.D二、填空题(本大题共5小题,每小题4分,共20分)11.212.1213.14.15.①④三、解答题(本大题共6小题,共80分)16.(本小题满分13分)解:(Ⅰ)记事件“小强试用的3个岗位中恰有2个在甲部门的概率”为,则.6分(Ⅱ)(元),7分(元).8分,9分.10分选择甲部门:因为,说明甲部门各岗位的工资待遇波动比乙部门小,竞争压力没有乙部门大,比较安稳.13分选择乙部门:因为,说明乙部门各岗位的工资待遇波动比甲部门大,岗位工资拉的比较开,工作比较有挑战性,能更好地体现工作价值.13分17.(本小题满分13分)解:依题意,可建立如图所示的空间直角坐标系,设,则.2分(Ⅰ)证明:由平面可知为平面的一个法向量.∴.3分∴直线与平面不平行.4分(Ⅱ)设平面的法向量为,则,5分取,则,故.6分∴,7分解得.∴.8分(Ⅲ)在平面内,分别延长,交于点,连结,则直线为平面与平面的交线.9分∵,,∴.∴,∴.11分由(Ⅱ)知,,故,∴.12分∴直线与所成的角的余弦值为.13分18.(本小题满分13分)解:(Ⅰ)设圆的半径为(),依题意,圆心坐标为.1分∵∴,解得.3分∴圆的方程为.5分(Ⅱ)把代入方程,解得,或,即点,.6分(1)当轴时,由椭圆对称性可知.7分(2)当与轴不垂直时,可设直线的方程为.联立方程,消去得,.8分设直线交椭圆于两点,则,.9分∵,∴.10分∵,11分∴,.12分综上所述,.13分19.(本小题满分13分)解:(Ⅰ)当时,,∴,1分∴,所以所求的切线的斜率为3.2分又∵,所以切点为.3分故所求的切线方程为:.4分(Ⅱ)∵,∴.5分①当时,∵,∴;6分②当时,由,得;由,得;7分综上,当时,函数在单调递增;当时,函数在单调递减,在上单调递增.8分(Ⅲ)方法一:由(Ⅱ)可知,当时,在上单调递增.9分∴当时,,即.10分令(),则.11分另一方面,∵,即,∴.12分∴().13分方法二:构造函数,9分∴,10分∴当时,;∴函数在单调递增.11分∴函数,即∴,,即12分令(),则有.13分20.(本小题满分14分)解:(Ⅰ)已知是锐角,根据三角函数的定义,得1分又,且是锐角,所以.2分所以.4分(Ⅱ)证明:依题意得,,,因为,所以,,于是有,①6分又∵,,②7分同理,,③由①,②,③可得,线段MA、NB、PC能构成一个三角形.8分(III)第(Ⅱ)小题中的三角形的外接圆面积是定值,且定值为.不妨设的边长分别为,其中角、、的对边分别为.则由余弦定理,得:9分11分因为,所以,所以,12分设的外接圆半径为R,由正弦定理,得,∴,13分所以的外接圆的面积为.14分21.(1)(本小题满分7分)选修4-2:矩阵与变换解:(Ⅰ)由条件得矩阵.2分(Ⅱ)因为矩阵的特征多项式为,令,解得特征值为,,4分设属于特征值的矩阵M的一个特征向量为,则,解得,取,得,5分同理,对于特征值,解得,取,得,6分所以是矩阵M属于特征值的一个特征向量,是矩阵M属于特征值的一个特征向量.7分(2)(本小题满分7分)选修4—4:极坐标与参数方程解:(Ⅰ)∵点、的极坐标分别为、,∴点、的直角坐标分别为、,2分∴直线的直角坐标方程为.4分(Ⅱ)由曲线的参数方程化为普通方程为,5分∵直线和曲线C只有一个交点,∴半径.7分(3)(本小题满分7分)选修4—5:不等式选讲解:(Ⅰ)∵关于的不等式对于任意的恒成立1分根据柯西不等式,有所以,当且仅当时等号成立,故.3分(Ⅱ)由(Ⅰ)得,则∴5分当且仅当,即时取等号,6分所以函数的最小值为.7分。
福建省莆田市2012届高三毕业班教学质量检试题(2012莆田质检)数学理

莆田市2012年高中毕业班教学质量检查数 学 试 题(理)参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B )如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )样本数据n x x x ,,21的标准差 锥体体积公式])()()[(122221x x x x x x n S n -++-+-=Sh V 31= 其中x 为样本平均数第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题意要求的,把答案填写在答题卷的相应位置。
1.已知a ,b 是实数,i 是虚数单位,若(1)1i ai bi +=+,则a+b 等于( )A .0B .1C .2D .-22.某社区有480户家庭,其中中等收入家庭200户,低收入家庭160户,其它为高收入家庭。
若在建设幸福社区的某次分层抽样调查中,高收入家庭被抽取了6户,则在该次调查中该社区被抽取的总户数为( )A .20B .24C .30D .363.已知,l m 为两条不同的直线,α为一个平面。
若//,l m 则“//l α”是“//m α”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.某程序框图如图所示,若程序运行后输出S 的值是25,则图中判断框①处可填入的语句是 ( )A .4?n ≤B .5?n ≤C .6?n ≤D .7?n ≤ 5.如图,由函数()x f x e e =-的图象,直线2x =及x 轴所围成的阴影部分面积等于( ) A .221e e -- B .22e e -C .22e e -D .221e e -+6.某圆柱被一平面所截得到的几何体如图(1)所示,若该几何体的正视图是等腰直角三角形,俯视图是圆(如右图),则它的侧视图是 ( )7.设()f x 是定义在R 上的奇函数,且当0x >时,()12xf x =+。
2012福建高考数学理科试题及答案

环球天下教育旗下品牌网站 美国纽交所上市公司2012年普通高等学校招生全国统一考试(福建卷)数学试题(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.理科:第Ⅱ卷第21题为选考题,其他题为必考题,满分150分.第Ⅰ卷一、选择题:(理科)本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.(文科)本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z 满足z i =1-i ,则z 等于( )A .-1-iB .1-iC .-1+iD .1+i A .3+4i B .5+4i C .3+2i D .5+2i2.等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差为( ) A .1 B .2 C .3 D .4 3.下列命题中,真命题是( ) A .x 0∈R ,0e0x ≤B .x ∈R ,2x >x 2C .a +b =0的充要条件是1ab=- D .a >1,b >1是ab >1的充分条件4.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( ) A .球 B .三棱锥 C .正方体 D .圆柱 5.下列不等式一定成立的是( )A .lg(x 2+14)>lg x (x >0) B .sin x +1sin x≥2(x ≠k π,k ∈Z )C .x 2+1≥2|x |(x ∈R )D .2111x >+(x ∈R ) 6.如图所示,在边长为1的正方形OABC 中任取一点P ,则点P 恰好取自阴影部分的概率为( )A .14 B .15 C .16 D .177.设函数1,()0,x D x x ⎧=⎨⎩为有理数,为无理数,则下列结论错误的是( )A .D (x )的值域为{0,1}B .D (x )是偶函数C .D (x )不是周期函数 D .D (x )不是单调函数8.已知双曲线22214x y b-=的右焦点与抛物线y 2=12x 的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )A .5B .42C .3D .59.若函数y =2x 图象上存在点(x ,y )满足约束条件30,230,,x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩则实数m 的最大值为( )A .12 B .1 C .32D .2 10.函数f (x )在[a ,b ]上有定义,若对任意x 1,x 2∈[a ,b ],有()()12121()22x x f f x f x +≤[+],则称f (x )在[a ,b ]上具有性质P .设f (x )在[1,3]上具有性质P ,现给出如下命题:①f (x )在[1,3]上的图象是连续不断的;②f (x 2)在[1,3]上具有性质P ;③若f (x )在x =2处取得最大值1,则f (x )=1,x ∈[1,3]; ④对任意x 1,x 2,x 3,x 4∈[1,3],有12341()44x x x x f +++≤[f (x 1)+f (x 2)+f (x 3)+f (x 4)].其中真命题的序号是( )A .①②B .①③C .②④D .③④第Ⅱ卷二、填空题:(理科)本大题共5小题,每小题4分,共20分.把答案填在答题卡的相应位置.(文科)本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.11. (a +x )4的展开式中x 3的系数等于8,则实数a =________.12.阅读右图所示的程序框图,运行相应的程序,输出的s 值等于________. 13.已知△ABC 的三边长成公比为2的等比数列,则其最大角的余弦值为________.14.数列{a n }的通项公式πcos12n n a n =+,前n 项和为S n ,则S 2 012=________. 15.对于实数a 和b ,定义运算“*”:22*.a ab a b a b b ab a b ⎧-≤=⎨->⎩,,,设f (x )=(2x -1)*(x -1),且关于x 的方程f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3的取值范围是__________.三、解答题:(理科)本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.(文科)本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:品牌 甲 乙 首次出现故障时间x (年)0<x ≤1 1<x ≤2 x >2 0<x ≤2 x >2轿车数量(辆)2 3 45 5 45 每辆利润(万元)1 2 3 1.8 2.9将频率视为概率,解答下列问题:(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率;(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X 1,生产一辆乙品牌轿车的利润为X 2,分别求X 1,X 2的分布列;(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.17.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数: ①sin 213°+cos 217°-sin13°cos17°; ②sin 215°+cos 215°-sin15°cos15°;③sin 218°+cos 212°-sin18°cos12°;④sin 2(-18°)+cos 248°-sin(-18°)cos48°;⑤sin 2(-25°)+cos 255°-sin(-25°)cos55°.(1)试从上述五个式子中选择一个,求出这个常数;(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.18.如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=AD =1,E 为CD 中点.(1)求证:B 1E ⊥AD 1.(2)在棱AA 1上是否存在一点P ,使得DP ∥平面B 1AE ?若存在,求AP 的长;若不存在,说明理由.(3)若二面角A -B 1E -A 1的大小为30°,求AB 的长.19.如图,椭圆E :22221x y a b+=(a >b >0)的左焦点为F 1,右焦点为F 2,离心率12e =.过F 1的直线交椭圆于A 、B 两点,且△ABF 2的周长为8.(1)求椭圆E 的方程;(2)设动直线l :y =kx +m 与椭圆E 有且只有一个公共点P ,且与直线x =4相交于点Q .试探究:在坐标平面内是否存在定点M ,使得以PQ 为直径的圆恒过点M ?若存在,求出点M的坐标;若不存在,说明理由.20.已知函数f (x )=e x +ax 2-e x ,a ∈R .(1)若曲线y =f (x )在点(1,f (1))处的切线平行于x 轴,求函数f (x )的单调区间;(2)试确定a 的取值范围,使得曲线y =f (x )上存在唯一的点P ,曲线在该点处的切线与曲线只有一个公共点P .21. (1)选修4-2:矩阵与变换设曲线2x 2+2xy +y 2=1在矩阵 0 1a b ⎛⎫= ⎪⎝⎭A (a >0)对应的变换作用下得到的曲线为x2+y 2=1.①求实数a ,b 的值; ②求A 2的逆矩阵.(2)选修4-4:坐标系与参数方程在平面直角坐标系中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l 上两点M ,N 的极坐标分别为(2,0),23π,32⎛⎫⎪⎪⎝⎭,圆C 的参数方程为22cos ,32sin x y θθ=+⎧⎪⎨=-+⎪⎩(θ为参数). ①设P 为线段MN 的中点,求直线OP 的平面直角坐标方程;②判断直线l 与圆C 的位置关系. (3)选修4-5:不等式选讲已知函数f (x )=m -|x -2|,m ∈R ,且f (x +2)≥0的解集为[-1,1]. ①求m 的值; ②若a ,b ,c ∈R +,且11123m a b c++=,求证:a +2b +3c ≥9.22.(文)已知函数f (x )=ax sin x -32(a ∈R ),且在[0,π2]上的最大值为π32-. (1)求函数f (x )的解析式;(2)判断函数f (x )在(0,π)内的零点个数,并加以证明.答案1. A 由z i =1-i ,得221i (1i)i i i i+11i i i 11z ---=====----. 2. B ∵a 1+a 5=10=2a 3,∴a 3=5.故d =a 4-a 3=7-5=2.3. D ∵a >1>0,b >1>0,∴由不等式的性质得ab >1, 即a >1,b >1⇒ab >1.4. D ∵圆柱的三视图中有两个矩形和一个圆, ∴这个几何体不可以是圆柱.5. C ∵x 2+1≥2|x |⇔x 2-2|x |+1≥0,∴当x ≥0时,x 2-2|x |+1=x 2-2x +1=(x -1)2≥0成立;当x <0时,x 2-2|x |+1=x 2+2x +1=(x +1)2≥0成立.故x 2+1≥2|x |(x ∈R )一定成立.6. C ∵由图象知阴影部分的面积是31220121211()d ()032326x x x x x -=⋅-=-=⎰,∴所求概率为11616=.7. C ∵D (x )是最小正周期不确定的周期函数, ∴D (x )不是周期函数是错误的.8. A 由双曲线的右焦点与抛物线y 2=12x 的焦点重合,知32pc ==,c 2=9=4+b 2,于是b 2=5,5b =.因此该双曲线的渐近线的方程为52y x =±,即520x y ±=.故该双曲线的焦点到其渐近线的距离为|35|554d ==+. 9. B 由约束条件作出其可行域如图所示:由图可知当直线x =m 经过函数y =2x的图象与直线x +y -3=0的交点P 时取得最大值,即得2x=3-x ,即x =1=m .10. D ①如图1,图 1在区间[1,3]上f (x )具有性质P ,但是是间断的,故①错.②可设f (x )=|x -2|(如图2),当x ∈[1,3]时易知其具有性质P ,但是f (x 2)=|x2-2|=222,12,2,23x x x x ⎧-≤≤⎪⎨-<≤⎪⎩不具有性质P (如图3).故②错.图2图3 ③任取x 0∈[1,3],则4-x 0∈[1,3], 1=f (2)=004()2x x f +-≤12[f (x 0)+f (4-x 0)]. 又∵f (x 0)=1,f (4-x 0)≤1, ∴12[f (x 0)+f (4-x 0)]≤1. ∴f (x 0)=f (4-x 0)=1.故③正确.④3412123422()()42x x x x x x x x f f ++++++= ≤34121()+()222x x x x f f ++⎡⎤⎢⎥⎣⎦≤14[f (x 1)+f (x 2)+f (x 3)+f (x 4)],故④正确. 11.答案:2 解析:∵T r +1=4C r a r x4-r,∴当4-r =3,即r =1时,T 2=14C ·a ·x 3=4ax 3=8x 3.故a=2.12.答案:-3解析:(1)k =1,1<4,s =2×1-1=1; (2)k =2,2<4,s =2×1-2=0; (3)k =3,3<4,s =2×0-3=-3; (4)k =4,直接输出s =-3.13.答案:24-解析:设△ABC 的最小边长为a (m >0),则其余两边长为2a ,2a ,故最大角的余弦值是22222(2)(2)2cos 42222a a a a a a aθ+--===-⋅⋅. 14.答案:3 018 解析:∵函数πcos2n y =的周期2π4π2T ==,∴可用分组求和法:a 1+a 5+…+a 2 009=50311+1=503++个…;a 2+a 6+…+a 2 010=(-2+1)+(-6+1)+…+(-2 010+1)=-1-5-…-2 009=503(12009)2--=-503×1 005;a 3+a 7+…+a 2 011=50311+1=503++个…;a 4+a 8+…+a 2 012=(4+1)+(8+1)+…+(2 012+1)=503(52013)2⨯+=503×1009;故S 2 012=503-503×1 005+503+503×1 009 =503×(1-1 005+1+1 009)=3 018.15.答案:(1316-,0) 解析:由已知,得()22200x x x f x x x x ⎧≤⎪⎨⎪⎩-,,=-+,>,作出其图象如图,结合图象可知m 的取值范围为0<m <14,当x >0时,有-x 2+x =m ,即x 2-x +m =0, 于是x 1x 2=m .当x <0时,有2x 2-x -m =0,于是31184mx -+=.故123(118)4m m x x x -+=.设h (m )=m (1-18m +),∵h ′(m )=(1-18m +)+[m (18218m-+)]=4118018mm m-+-<+,∴函数h (m )单调递减. 故x 1x 2x 3的取值范围为(1316-,0). 16.解:(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A , 则231()5010P A +==. (2)依题意得,X 1的分布列为X 1 123P125350 910X 2的分布列为X 2 1.82.9P110910(3)由(2)得,E (X 1)=1×125+2×350+3×910=14350=2.86(万元),E (X 2)=1.8×110+2.9×910=2.79(万元).因为E (X 1)>E (X 2),所以应生产甲品牌轿车.17.解:方法一:(1)选择②式,计算如下:sin 215°+cos 215°-sin15°cos15°=1-12sin30°=13144-=. (2)三角恒等式为sin 2α+cos 2(30°-α)-sin α·cos(30°-α)=34.证明如下: sin 2α+cos 2(30°-α)-sin αcos(30°-α)=sin 2α+(cos30°cos α+sin30°sin α)2-sin α·(cos30°cos α+sin30°sin α)=sin 2α+34cos 2α+32sin αcos α+14sin 2α-32sin α·cos α-12sin 2α =34sin 2α+34cos 2α=34. 方法二:(1)同方法一.(2)三角恒等式为sin 2α+cos 2(30°-α)-sin α·cos(30°-α)=34. 证明如下: sin 2α+cos 2(30°-α)-sin αcos(30°-α)=1cos21cos(602)22αα-+︒-+-sin α(cos30°cos α+sin30°sin α) =12-12cos2α+12+12(cos60°·cos2α+sin60°sin2α)-32sin αcos α-12sin 2α =12-12cos2α+12+14cos2α+34sin2α-34sin2α-14(1-cos2α) =11131cos2cos24444αα--+=.18.解:(1)以A 为原点,AB ,AD ,1AA 的方向分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图).设AB =a ,则A (0,0,0),D (0,1,0),D 1(0,1,1),E (2a,1,0),B 1(a,0,1),故1AD =(0,1,1),1B E =(2a -,1,-1),1AB =(a,0,1),AE =(2a,1,0).∵1AD ·1B E =2a-×0+1×1+(-1)×1=0,∴B 1E ⊥AD 1.(2)假设在棱AA 1上存在一点P (0,0,z 0), 使得DP ∥平面B 1AE .此时DP =(0,-1,z 0).又设平面B 1AE 的法向量n =(x ,y ,z ). ∵n ⊥平面B 1AE ,∴n ⊥1AB ,n ⊥AE ,得00.2ax z ax y +=⎧⎪⎨+=⎪⎩,取x =1,得平面B 1AE 的一个法向量n =(1,2a-,-a ). 要使DP ∥平面B 1AE ,只要n ⊥DP ,有2a -az 0=0,解得012z =. 又DP 平面B 1AE ,∴存在点P ,满足DP ∥平面B 1AE ,此时12AP =.(3)连接A 1D ,B 1C ,由长方体ABCD A 1B 1C 1D 1及AA 1=AD =1,得AD 1⊥A 1D . ∵B 1C ∥A 1D ,∴AD 1⊥B 1C .又由(Ⅰ)知B 1E ⊥AD 1,且B 1C ∩B 1E =B 1,∴AD 1⊥平面DCB 1A 1.∴1AD 是平面A 1B 1E 的一个法向量,此时1AD =(0,1,1).设1AD 与n 所成的角为θ,则1212·2cos ||||214a aAD AD aa θ--==++n n .∵二面角A -B 1E -A 1的大小为30°, ∴|cos θ|=cos30°,即233225214a a =+, 解得a =2,即AB 的长为2.19.解:方法一:(1)因为|AB |+|AF 2|+|BF 2|=8, 即|AF 1|+|F 1B |+|AF 2|+|BF 2|=8, 又|AF 1|+|AF 2|=|BF 1|+|BF 2|=2a , 所以4a =8,a =2. 又因为12e =,即12c a =,所以c =1. 所以223b a c =-=.故椭圆E 的方程是22143x y +=. (2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩,,得(4k 2+3)x 2+8kmx +4m 2-12=0.因为动直线l 与椭圆E 有且只有一个公共点P (x 0,y 0),所以m ≠0且∆=0,即64k 2m 2-4(4k 2+3)(4m 2-12)=0,化简得4k 2-m 2+3=0.(*)此时024443km k x k m =-=-+,y 0=kx 0+m =3m , 所以P (4k m -,3m).由4x y kx m =⎧⎨=+⎩,,得Q (4,4k +m ).假设平面内存在定点M 满足条件,由图形对称性知,点M 必在x 轴上. 设M (x 1,0),则0MP MQ ⋅=对满足(*)式的m ,k 恒成立.因为MP =(14k x m --,3m),MQ =(4-x 1,4k +m ), 由0MP MQ ⋅=,得211141612430kx k kx x m m m-+-+++=, 整理,得(4x 1-4)k m+x 12-4x 1+3=0.(**)由于(**)式对满足(*)式的m ,k 恒成立,所以1211440,430,x x x -=⎧⎨-+=⎩解得x 1=1.故存在定点M (1,0),使得以PQ 为直径的圆恒过点M . 方法二:(1)同方法一.(2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩,,得(4k 2+3)x 2+8kmx +4m 2-12=0.因为动直线l 与椭圆E 有且只有一个公共点P (x 0,y 0),所以m ≠0且∆=0,即64k 2m 2-4(4k 2+3)(4m 2-12)=0,化简得4k 2-m 2+3=0.(*)此时024443km k x k m =-=-+,y 0=kx 0+m =3m , 所以P (4k m -,3m ).由4x y kx m =⎧⎨=+⎩,,得Q (4,4k +m ).假设平面内存在定点M 满足条件,由图形对称性知,点M 必在x 轴上.取k =0,3m =,此时P (0,3),Q (4,3),以PQ 为直径的圆为(x -2)2+(y -3)2=4,交x 轴于点M 1(1,0),M 2(3,0);取12k =-,m =2,此时P (1,32),Q (4,0),以PQ 为直径的圆为225345()()2416x y -+-=,交x 轴于点M 3(1,0),M 4(4,0).所以若符合条件的点M 存在,则M 的坐标必为(1,0).以下证明M (1,0)就是满足条件的点:因为M 的坐标为(1,0),所以MP =(41k m --,3m),MQ =(3,4k +m ), 从而1212330k kMP MQ m m⋅=--++=, 故恒有MP MQ ⊥,即存在定点M (1,0),使得以PQ 为直径的圆恒过点M .20.解:(1)由于f ′(x )=e x+2ax -e ,曲线y =f (x )在点(1,f (1))处切线斜率k =2a =0,所以a=0,即f(x)=e x-e x.此时f′(x)=e x-e,由f′(x)=0得x=1.当x∈(-∞,1)时,有f′(x)<0;当x∈(1,+∞)时,有f′(x)>0.所以f(x)的单调递减区间为(-∞,1),单调递增区间为(1,+∞).(2)设点P(x0,f(x0)),曲线y=f(x)在点P处的切线方程为y=f′(x0)(x-x0)+f(x0),令g(x)=f(x)-f′(x0)(x-x0)-f(x0),故曲线y=f(x)在点P处的切线与曲线只有一个公共点P等价于函数g(x)有唯一零点.因为g(x0)=0,且g′(x)=f′(x)-f′(x0)=e x-e x0+2a(x-x0).(1)若a≥0,当x>x0时,g′(x)>0,则x>x0时,g(x)>g(x0)=0;当x<x0时,g′(x)<0,则x<x0时,g(x)>g(x0)=0.故g(x)只有唯一零点x=x0.由P的任意性,a≥0不合题意.(2)若a<0,令h(x)=e x-e x0+2a(x-x0),则h(x0)=0,h′(x)=e x+2a.令h′(x)=0,得x=ln(-2a),记x′=ln(-2a),则当x∈(-∞,x*)时,h′(x)<0,从而h(x)在(-∞,x*)内单调递减;当x∈(x*,+∞)时,h′(x)>0,从而h(x)在(x*,+∞)内单调递增.①若x0=x*,由x∈(-∞,x*)时,g′(x)=h(x)>h(x*)=0;x∈(x*,+∞)时,g′(x)=h(x)>h(x*)=0,知g(x)在R上单调递增.所以函数g(x)在R上有且只有一个零点x=x*.②若x0>x*,由于h(x)在(x*,+∞)内单调递增,且h(x0)=0,则当x∈(x*,x0)时有g′(x)=h(x)<h(x0)=0,g(x)>g(x0)=0;任取x1∈(x*,x0)有g(x1)>0.又当x∈(-∞,x1)时,易知g(x)=e x+ax2-[e+f′(x0)]x-f(x0)+x0f′(x0)<e x1+ax2-[e+f′(x0)]x-f(x0)+x0f′(x0)=ax2+bx+c,其中b=-[e+f′(x0)],c=e x1-f(x0)+x0f′(x0).由于a<0,则必存在x2<x1,使得ax22+bx2+c<0.所以g(x2)<0.故g(x)在(x2,x1)内存在零点,即g(x)在R上至少有两个零点.③若x0<x*,仿②并利用3e6xx>,可证函数g(x)在R上至少有两个零点.综上所述,当a<0时,曲线y=f(x)上存在唯一点P(ln(-2a),f(ln(-2a))),曲线在该点处的切线与曲线只有一个公共点P.21. (1)选修4-2:矩阵与变换解:①设曲线2x2+2xy+y2=1上任意点P(x,y)在矩阵A对应的变换作用下的像是P′(x′,y′).由1x ay b'⎛⎫⎛⎫=⎪ ⎪'⎝⎭⎝⎭x axy bx y⎛⎫⎛⎫=⎪ ⎪+⎝⎭⎝⎭,得,.x axy bx y'=⎧⎨'=+⎩又点P′(x′,y′)在x2+y2=1上,所以x′2+y′2=1,即a2x2+(bx+y)2=1,整理得(a2+b2)x2+2bxy+y2=1.依题意得222,22,a bb⎧+=⎨=⎩解得1,1,ab=⎧⎨=⎩或1,1,ab=-⎧⎨=⎩因为a>0,所以1,1. ab=⎧⎨=⎩②由①知,1 01 1⎛⎫= ⎪⎝⎭A,21 0 1 0 1 01 1 1 12 1⎛⎫⎛⎫⎛⎫==⎪⎪ ⎪⎝⎭⎝⎭⎝⎭A,所以|A 2|=1,(A 2)-1= 1 02 1⎡⎤⎢⎥-⎣⎦. (2)选修4-4:坐标系与参数方程解:①由题意知,M ,N 的平面直角坐标分别为(2,0),(0,233). 又P 为线段MN 的中点,从而点P 的平面直角坐标为(1,33),故直线OP 的平面直角坐标方程为33y x =.②因为直线l 上两点M ,N 的平面直角坐标分别为(2,0),(0,233),所以直线l 的平面直角坐标方程为33230x y +-=.又圆C 的圆心坐标为(2,3-),半径r =2, 圆心到直线l 的距离|233323|3239d r --==<+,故直线l 与圆C 相交. (3)选修4-5:不等式选讲解:①因为f (x +2)=m -|x |,f (x +2)≥0等价于|x |≤m , 由|x |≤m 有解,得m ≥0,且其解集为{x |-m ≤x ≤m }. 又f (x +2)≥0的解集为[-1,1],故m =1.②由①知111123a b c++=,又a ,b ,c ∈R +,由柯西不等式得 a +2b +3c =(a +2b +3c )(11123a b c++) ≥2111(23)923a b c a b c⋅+⋅+⋅=.。
福建省2012届普通高中毕业班4月质量检查理科综合试题.pdf

A.NH3 B.CO C.CH3CH2OH D.H2O2
②用稀土材料GeO2作催化剂,能提高YO2的转化速率。煅烧Ge(OH)CO3可制备GeO2,配平该反应的化学方程式:
Ge(OH)CO3+ O2=GeO2+ CO2+ H2O
加水的量
D.烧杯内溶液变红色
11.右下图所示原电池的总反应为Cu(s)+2Ag+(aq) Cu2+(aq)+2Ag(s),下列叙述正确的是
A.电子从银电极经导线流向铜电极
B.工作一段时间后,右烧杯中溶液的pH变小
C.电池工作时,Cu2+向铜电极移动
D.将AgNO3溶液更换为Fe(NO3)3溶液,电流计指针反向偏转
B.水对A光折射率较大
C.A光在水中传播速度较大
D A光从水中射向空气时全反射临界角较小
15. 如图为一列沿x轴正方向传播的简谐横波在t=O时刻的波形图,已知波速为20m/s,则位于x=5m处质点的振动图象
是
16. 如图所示的玩具是由弹射物、托盘、弹簧及底座组成,竖直弹焚两端分别连接在托盘和底座上,弹簧与托盘的
组别1234反应温度/℃225235225235反应前气体体积分数/%CO20022CO30302828H270707070平衡时CH3OH的体积分数
/%4.98.836.550.713.如图为一种变压器的实物图,根据其铭牌上所提供的信息,以下判断正确的是
A.这是一个升压变压器
B.原线圈的匝数比副线圈的匝数多
质世均不计。现将弹射物放在托盘上,并对其施加竖直向下的压力,使弹簧压缩。当撤去压力后,弹射物能弹离托盘
,下列说法正确的是
A. 撤去压力的瞬间,弹射物处于超重状态
2012年普通高等学校招生全国统一考试(福建卷)—数学(理)解析版

2012年普通高等学校招生全国统一考试(福建卷)数学(理科)第I 卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分·在每小题给出的四个选项中,只有一项是符合题目要求的·1、若复数z 满足i zi -=1,则z 等于( )A .i --1B .i -1C .i +-1D .i +1 考点:复数的运算· 难度:易·分析:本题考查的知识点为复数的计算,直接套用复数运算公式即可·解答:iiz -=1 111)())(1(--=--=---=i i i i i i ·2、等差数列}{n a 中,7,10451==+a a a ,则数列}{n a 的公差为( ) A .1 B .2 C .3 D .4 考点:等差数列的定义· 难度:易·分析:本题考查的知识点为复等差数列的通项公式d n a a n )1(1-+=·解答:273104211=⇒⎩⎨⎧=+=+d d a d a · 3、下列命题中,真命题是( ) A .0,00≤∈∃x eR x B .22,x R x x >∈∀C .0=+b a 的充要条件是1-=baD .1,1>>b a 是1>ab 的充分条件 考点:逻辑· 难度:易·分析:本题考查的知识点为复逻辑中的充要条件的判定· 解答:A 中,,R x ∈∀0>xe·B 中,22,4,2x x x x===∃,22,x x x<∃·C 中,⎩⎨⎧≠=+00b b a 的充要条件是1-=b a·D 中,1,1>>b a 可以得到1>ab ,当1>ab 时,不一定可以得到1,1>>b a · 4、一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )A .球B .三棱锥C .正方体D .圆柱 考点:空间几何体的三视图· 难度:易·分析:本题考查的知识点为空间几何体的三视图,直接画出即可· 解答:圆的正视图(主视图)、侧视图(左视图)和俯视图均为圆;三棱锥的正视图(主视图)、侧视图(左视图)和俯视图可以为全等的三角形; 正方体的正视图(主视图)、侧视图(左视图)和俯视图均为正方形; 圆柱的正视图(主视图)、侧视图(左视图)为矩形,俯视图为圆· 5、下列不等式一定成立的是( )A .)0(lg )41lg(2>>+x x x B .),(2sin 1sin Z k k x xx ∈≠≥+π C .)(||212R x x x ∈≥+ D .)(1112R x x ∈>+ 考点:不等式及基本不等式· 难度:中·分析:本题考查的知识点为不等式的性质及基本不等式的性质· 解答:A 中,)410(4122x x x x x =+=≥+时,当· B 中,])1,0((sin 2sin 1sin ∈≥+x x x ;))0,1[(sin 2sin 1sin -∈-≤+x xx · C 中,)(0)1|(|1||222R x x x x ∈≥-=+-·D 中,)](1,0(112R x x ∈∈+· 6、如图所示,在边长为1的正方形OABC 中任取一点P ,则点P 恰好取自阴影部分的概率为( )A .41B .51C .61D .71考点:积分的计算和几何概型·难度:中·分析:本题考查的知识点为公式法计算积分和面型的几何概型· 解答:111)(=⨯=ΩS ,⎰-=10)()(dx x x A S 61|)2132(10223=-=x x · 所以61)()()(=Ω=A S S A P ·7、设函数⎩⎨⎧=为无理数为有理数x x x D ,0,1)(,则下列结论错误的是( )A .)(x D 的值域为}1,0{B .)(x D 是偶函数C .)(xD 不是周期函数 D .)(x D 不是单调函数考点:分段函数的解析式及其图像的作法· 难度:中·分析:本题考查的知识点为分段函数的定义,单调性、奇偶性和周期性的定义和判定· 解答:A 中,)(x D 由定义直接可得,)(x D 的值域为}1,0{·B 中,)(x D 定义域为R ,)(,0,1)(x D x x x D =⎩⎨⎧=-为无理数为有理数,所以)(x D 为偶函数·C 中,)(,0,1)1(xD x x x D =⎩⎨⎧=+为无理数为有理数,所以可以找到1为)(x D 的一个周期· D 中,......1)2(,0)2(,1)1(===D D D ,所以不是单调函数·8、双曲线22214x y b-=的右焦点与抛物线x y 122=的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )A .5B .24C .3D .5考点:双曲线的定义· 难度:中·分析:本题考查的知识点为双曲线的定义,焦点,渐近线,抛物线的定义· 解答:抛物线x y 122=的焦点为)0,3(· 双曲线中,5492=-=b · 双曲线渐近线方程为x y 25±=· 所以焦点到渐近线的距离5)25(12532=+=d ·9、若直线x y 2=上存在点),(y x 满足约束条件⎪⎩⎪⎨⎧≥≤--≤-+m x y x y x 03203,则实数m 的最大值为( )A .21 B .1 C .23D .2 考点:线性规划· 难度:中·分析:本题考查的知识点为含参的线性规划,需要画出可行域的图形,含参的直线要能画出大致图像·所以,若直线x y 2=上存在点),(y x 满足约束条件⎪⎩⎪⎨⎧≥≤--≤-+m x y x y x 03203,则mm 23≥-,即1≤m ·10、函数)(x f 在],[b a 上有定义,若对任意],[,21b a x x ∈,有)]()([21)2(2121x f x f x x f +≤+,则称)(x f 在],[b a 上具有性质P ·设)(x f 在[1,3]上具有性质P ,现给出如下命题: ①)(x f 在]3,1[上的图像时连续不断的; ②)(2x f 在]3,1[上具有性质P ;③若)(x f 在2=x 处取得最大值1,则1)(=x f ,]3,1[∈x ; ④对任意]3,1[,,,4321∈x x x x ,有)]()()()([41)2(43214321x f x f x f x f x x x x f +++≤+++·其中真命题的序号是( )A .①②B .①③C .②④D .③④考点:演绎推理和函数· 难度:难·分析:本题考查的知识点为函数定义的理解,说明一个结论错误只需举出反例即可,说明一个结论正确要证明对所有的情况都成立· 解答:A 中,反例:如图所示的函数)(x f 的是满足性质P 的,但)(x f 不是连续不断的·B 中,反例:x x f -=)(在]3,1[上具有性质P ,22)(x x f -=在]3,1[上不具有性质P ·C 中,在]3,1[上,)]4()([21)2)4(()2(x f x f x x f f -+≤-+=, 1)(1)2()()4(1)2()()(2)4()(max max =⇒⎪⎩⎪⎨⎧==≤-==≤≥-+x f f x f x f f x f x f x f x f , 所以,对于任意1)(],3,1[,21=∈x f x x ·D 中,=+++)2(4321x x x x f )2)()((4321x x x x f +++)]()()()([41))]()((21))()((21[21)]2()2([21432121214321x f x f x f x f x f x f x f x f x x f x x f +++≤+++≤+++≤· 第Ⅱ卷(非选择题 共100分)二、填空题:本大题共4小题,每小题4分,共16分·把答案填在答题卡的相应位置·11、4)(x a +的展开式中3x 的系数等于8,则实数=a _________·【2】 考点:二项式定理· 难度:易·分析:本题考查的知识点为二项式定理的展开式,直接应用即可· 解答:4)(x a +中含3x 的一项为r rr r x aC T -+=441,令3=r ,则83434=-a C ,即2=a ·12、阅读右图所示的程序框图,运行相应地程序,输出的s 值等于_____________________·【3-】考点:算法初步· 难度:易·分析:本题考查的知识点为算法中流程图的读法,直接根据箭头的指向运算即可· 解答: 1,1==s k ;2,1112==-⨯=k s ; 3,0212==-⨯=k s ; 4,3302=-=-⨯=k s ;结束·13、已知ABC ∆_________·【42-】 考点:等比数列和余弦定理· 难度:易·分析:本题考查的知识点为等比数列的定义和余弦定理的应用· 解答:设ABC ∆三边为m c m b m a 2,2,===, 则可得C ∠所对的边最大,且22cos 222=-+=abc b a C · 14、数列}{n a 的通项公式12cos+=πn n a n ,前n 项和为n S ,则=2012S ___________·【3018】 考点:数列和三角函数的周期性· 难度:中·分析:本题考查的知识点为三角函数的周期性和数列求和,所以先要找出周期,然后分组计算和· 解答: 1012cos )14(12)14(cos )14(14+=+⨯+=++⨯+=+ππn n n a n , 1)24(1cos )24(12)24(cos )24(24++-=+⨯+=++⨯+=+n n n n a n ππ,10123cos )34(12)34(cos )34(34+=+⨯+=++⨯+=+ππn n n a n ,14412cos )44(12)44(cos)44(44++=+⨯+=++⨯+=+n n n n a n ππ, 所以++14n a ++24n a ++34n a 644=+n a · 即30186420122012=⨯=S · 15、对于实数b a ,,定义运算“*”:⎩⎨⎧>-≤-=*ba ab b ba ab a b a ,,22,设)1()12()(-*-=x x x f ,且关于x 的方程为)()(R m m x f ∈=恰有三个互不相等的实数根321,,x x x ,则321x x x 的取值范围是_____·【)0,1631(-】 考点:演绎推理和函数· 难度:难·分析:本题考查的知识点为新定义的理解,函数与方程中根的个数·解答:由题可得,⎩⎨⎧>--≤-=0),1(0),12()(x x x x x x x f可得0,21),41,0(132<=+∈x x x m , 且↑↑→||,,41132x x x m 所以41=m 时,=max 321||x x x 1631-, 所以∈m )0,1631(-·三、解答题:本大题共6小题,共84分·解答应写出文字说明,证明过程或演算步骤·16、(本小题满分13分)受轿车在保修期内维修费等因素的影响,企业产生每辆轿车的利润与该轿车首次出现故障的时间有关,某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年,现从该厂已售出的两种品牌轿my =车中随机抽取50辆,统计书数据如下:将频率视为概率,解答下列问题:(I )从该厂生产的甲品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率; (II )若该厂生产的轿车均能售出,记住生产一辆甲品牌轿车的利润为1X ,生产一辆乙品牌轿车的利润为2X ,分别求1X ,2X 的分布列;(III )该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌轿车,若从经济效益的角度考虑,你认为应该产生哪种品牌的轿车?说明理由· 考点:统计概率及随机变量·难度:易· 分析: 解答:(I )首次出现故障发生在保修期内的概率为2315010P +== (II )随机变量1X 的分布列为 随机变量2X 的分布列为(III )1139123 2.86255010EX =⨯+⨯+⨯=(万元) 2191.82.9 2.791010EX =⨯+⨯=(万元) 12EX EX > 所以应该生产甲品牌汽车·17、(本小题满分13分)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数· (1)02217cos 13sin 17cos 13sin -+; (2)02215cos 15sin 15cos 15sin -+;(3)02212cos 18sin 12cos 18sin -+; (4)00020248cos )18sin(48cos )13(sin --+-; (5)00020255cos )25sin(55cos )25(sin --+-·(I )试从上述五个式子中选择一个,求出这个常数;(II )根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论· 考点:三角恒等变换· 难度:中· 分析: 解答:(I )选择(2):22013sin 15cos 15sin15cos151sin 3024+-=-= (II )三角恒等式为:22003sin cos (30)sin cos(30)4αααα+---=22002222sin cos (30)sin cos(30)11sin sin )sin sin )22333sin cos 444αααααααααααα+---=++-+=+=(lby lfx )18、(本小题满分13分)如图,在长方体1111D C B A ABCD -中,11==AD AA ,E 为CD 中点· (Ⅰ)求证:11AD E B ⊥;(Ⅱ)在棱1AA 上是否存在一点P ,使得//DP 平面AE B 1?若存在,求AP 的长;若不存在,说明理由·(Ⅲ)若二面角11A E B A --的大小为030,求AB 的长·考点:立体几何· 难度:中· 分析: 解答:(Ⅰ)长方体1111D C B A ABCD -中,11==AD AA 得:1111111111,,AD A D AD A B A DA B A A D ⊥⊥=⇔⊥面11A B CD1B E ⊂面11A B CD 11B E AD ⇒⊥(Ⅱ)取1AA 的中点为P ,1AB 中点为Q ,连接PQ 在11AA B ∆中,111111//,////////22PQ A B DE A B PQ DE PD QE PD ⇒⇒⇒面AE B 1 此时11122AP AA == (Ⅲ)设11A DAD O =,连接AO ,过点O 作1OH B E ⊥于点H ,连接AH1AO ⊥面11A B CD ,1O H B E ⊥1A H B E⇒⊥ 得:AHO ∠是二面角11A E B A --的平面角30AHO ο⇒∠=在Rt AOH ∆中,30,90,2AHO AOH AH OH οο∠=∠==⇒=在矩形11A B CD 中,1,CD x AD ==11112222222228B OE x xS x ∆=--⨯-⨯=1222x =⇔=得:2AB =19、(本小题满分13分)如图,椭圆)0(1:2222>>=+b a by a x E 的左焦点为1F ,右焦点为2F ,离心率21=e ·过1F 的直线交椭圆于B A ,两点,且2ABF ∆的周长为8· (Ⅰ)求椭圆E 的方程·(Ⅱ)设动直线m kx y l +=:与椭圆E 有且只有一个公共点P ,且与直线4=x 相交于点Q ·试探究:在坐标平面内是否存在定点M ,使得以PQ 为直径的圆恒过点M ?若存在,求出点M 的坐标;若不存在,说明理由·考点:三角恒等变换·难度:难·分析:解答:(Ⅰ)设c 则2212342c e a c a b a ==⇔=⇔= 2ABF ∆的周长为22121288482,1AB AF BF AF AF BF BF a a b c ++=⇔+++=⇔=⇔===椭圆E 的方程为22143x y += (Ⅱ)由对称性可知设000(,)(0)P x y y >与(,0)M x220031434x x y y y k y '+=⇒==⇒=- 直线00000033(1):()(4,)4x x l y y x x Q y y --=--⇒ 000003(1)0()(4)0(1)(1)(3)x M P M Q x x x y x x x x y -=⇔--+⨯=⇔-=--(*) (*)对0(2,2)x ∈-恒成立1x ⇔=, 得(1,0)M20、(本小题满分14分)已知函数R a ex ax e x f x ∈-+=,)(2(Ⅰ)若曲线)(x f y =在点))1(,1(f 处的切线平行于x 轴,求函数)(x f 的单调区间;(Ⅱ)试确定a 的取值范围,使得曲线)(x f y =上存在唯一的点P ,曲线在该点处的切线与曲线只有一个公共点P ·考点:导数·难度:难·分析:解答:(Ⅰ)2()()2x x f x e ax ex f x e ax e '=+-⇒=+-由题意得:(1)200f e a e a '=+-=⇔=()01,()0x f x e e x f x x ''=->⇔><⇔<得:函数()f x 的单调递增区间为(1,)+∞,单调递减区间为(,1)-∞(Ⅱ)设00(,())P x f x ; 则过切点P 的切线方程为000()()()y f x x x f x '=-+令000()()()()()g x f x f x x x f x '=---;则0()0g x =切线与曲线只有一个公共点P ()0g x ⇔=只有一个根0x000()()()2()xx g x f x f x e e a x x '''=-=-+-,且0()0g x '=(1)当0a ≥时,00()0,()0g x x x g x x x ''>⇔><⇔<得:当且仅当0x x =时,min 0()()0g x g x ==由0x 的任意性,0a ≥不符合条件(lby lfx )(2)当0a <时,令00()2()()20ln(2)x x x h x e e a x x h x e a x x a ''=-+-⇒=+=⇔==- ①当0x x '=时,00()0,()0h x x x h x x x ''>⇔><⇔<当且仅当0x x =时,0()()0()g x g x g x ''≥=⇒在x R ∈上单调递增()0g x ⇔=只有一个根0x②当0x x '>时,()0,()0h x x x h x x x ''''>⇔><⇔<得:0()()0g x g x '''<=,又,(),,()x g x x g x ''→+∞→+∞→-∞→+∞存在两个数0x x ''<使,0()()0g x g x ''''==得:00()0()()0g x x x x g x g x '''''<⇔<<⇒<=又,()x g x '→+∞→+∞存在1x x ''>使()0g x ''=,与条件不符·③当0x x '<时,同理可证,与条件不符从上得:当0a <时,存在唯一的点(ln(2),(ln(2))P a f a --使该点处的切线与曲线只有一个公共点P21、本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分·如果多做,则按所做的前两题计分·作答时,先用2B 铅笔在答题卡上把所选题目对应题号右边的方框图黑,并将所选题号填入括号中·(1)(本小题满分7分)选修4-2:矩阵与变换设曲线12222=++y xy x 在矩阵 ⎝⎛=b a A 0(0)1a ⎫>⎪⎭对应的变换作用下得到的曲线为122=+y x ·(Ⅰ)求实数b a ,的值· (Ⅱ)求2A 的逆矩阵·解:(Ⅰ)设曲线12222=++y xy x 上任一点(,)P x y 在矩阵A 对应变换下的像是(,)P x y ''' 则220()()11x a x ax x ax ax bx y y b y bx y y bx y''=⎛⎫⎛⎫⎛⎫⎛⎫⎧==⇔⇒++=⎨ ⎪ ⎪⎪ ⎪''+=+⎝⎭⎝⎭⎝⎭⎝⎭⎩ 得:222222()212,221,1a b x bxy y a b b a b +++=⇒+==⇔==(Ⅱ)由(Ⅰ)得:21010101011111121A A ⎛⎫⎛⎫⎛⎫⎛⎫=⇒== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21101()21A A -⎛⎫=⇒= ⎪-⎝⎭【考点定位】本题主要考查矩阵与变换等基础知识,考查运算求解能力,考查转化化归思想、(2)(本小题满分7分)选修4-4:坐标系与参数方程在平面直角坐标系中,以坐标原点O 为几点,x 轴的正半轴为极轴建立极坐标系·已知直线l上两点N M ,的极坐标分别为)2,332(),0,2(π,圆C 的参数方程θθθ(sin 23cos 22⎩⎨⎧+-=+=y x 为参数)·(Ⅰ)设P 为线段MN 的中点,求直线OP 的平面直角坐标方程;(Ⅱ)判断直线l 与圆C 的位置关系·【解析】(Ⅰ)由题意知(2,0),M N ,因为P 是线段MN中点,则P因此OP 直角坐标方程为:.y x =(Ⅱ)因为直线l 上两点(2,0),(0,3M N∴l 30y -=,圆心(2,,半径2r =、32d ∴==<r ,故直线l 和圆C 相交、 【考点定位】本题主要考查极坐标与参数方程的互化、圆的参数方程等基础知识,考查运算求解能力,考查转化化归思想·(3)(本小题满分7分)选修4-5:不等式选讲已知函数R m x m x f ∈--=|,2|)(,且0)2(≥+x f 的解集为]1,1[-·(Ⅰ)求m 的值;(Ⅱ)若R c b a ∈,,,且m cb a =++31211,求证:932≥++c b a · 【解析】(1)∵(2)f x m x x +=-≥0,≤∴m ,∴0m m x m >⇒-<< (2)0111f x x m +≥⇔-≤≤⇒= (2)由(1)知1111,,,23a b c R a b c++=∈,由柯西不等式得(lby lfx ) 11123(23)()23a b c a b c a b c +++++++29≥= 【考点定位】本题主要考查绝对值不等式、柯西不等式等基本知识,考查运算求解能力,考查化归转化思想。
福建省福州市2012届高三质量检查数学(理)试题
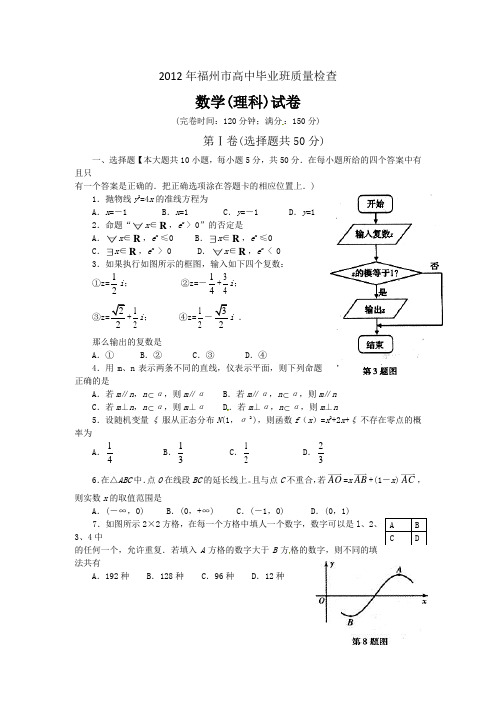
2012年福州市高中毕业班质量检查数学(理科)试卷(完卷时间:120分钟;满分:150分)第Ⅰ卷(选择题共50分)一、选择题【本大题共10小题,每小题5分,共50分.在每小题所给的四个答案中有且只有一个答案是正确的.把正确选项涂在答题卡的相应位置上.)1.抛物线y2=4x的准线方程为A.x=-1 B.x=1 C.y=-1 D.y=12.命题“x∈R,e x > 0”的否定是A .x∈R,e x ≤0B .x∈R,e x ≤0C .x∈R,e x > 0D .x∈R,e x < 03.如果执行如图所示的框图,输入如下四个复数:①z=12i;②z=-14+34i;③z=22+12i;④z=12-32i.那么输出的复数是A.① B.② C.③ D.④4.用m、n表示两条不同的直线,仪表示平面,则下列命题正确的是A.若m∥n,nα,则m∥α B.若m∥α,nα,则m∥nC.若m⊥n,nα,则m⊥αD.若m⊥α,nα,则m⊥n5.设随机变量ξ服从正态分布N(1,σ2 ),则函数f(x)=x2+2x+ξ不存在零点的概率为A.14B.13C.12D.236.在△ABC中.点O在线段BC的延长线上。
且与点C不重合,若AO=x AB+(1-x)AC,则实数x的取值范围是A.(-∞,0) B.(0,+∞) C.(-1,0) D.(0,1)7.如图所示2×2方格,在每一个方格中填人一个数字,数字可以是l、2、3、4中的任何一个,允许重复.若填入A方格的数字大于B方格的数字,则不同的填法共有A.192种 B.128种 C.96种 D.12种A B C D8.函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为42,则函数f(x)图象的一条对称轴的方程为A.x=4 B.x=2C.x=4 D.x=29.过双曲线2222x ya b=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为A.x±y=0 B.2x±y=0 C.4x±y=0 D.x±2y=010.若将有理数集Q分成两个非空的子集M与N,且满足M∪N=Q,M∩N=,M中的每一个元素都小于N中的每一个元素,则称(M,N)为有理数集的一个分割.试判断,对于有理数集的任一分割(M,N) ,下列选项中,不可能...成立的是A.M没有最大元素,N有一个最小元素 B.M没有最大元素,N也没有最小元素C.M有一个最大元素,N有一个最小元素 D.M有一个最大元素,N没有最小元素第Ⅱ卷(非选择题共100分)二、填空题(本大题共5小题,每小题4分,共20分,把答案填在答题卡的相应位置上.)11.sin47°cosl3°+sinl3°sin43°的值等于__________l2.函数f(x)=x3+ax(x∈R)在x=l处有极值,则曲线y= f(x)在原点处的切线方程是_____13.在约束条件1,2,10,xyx y,下,目标函数z=ax+by(a>0,b>0)的最大值为1,则ab的最大值等于_______14.设函数f(x)=1(1)2x(x∈Z).给出以下三个判断:①f(x)为偶函数;②f(x)为周期函数;③f(x+1)+f(x)=1.其中正确判断的序号是________(填写所有正确判断的序号).15.一个平面图由若干顶点与边组成,各顶点用一串从1开始的连续自然数进行编号,记各边的编号为它的两个端点的编号差的绝对值,若各条边的编号正好也是一串从1开始的连续自然数,则称这样的图形为“优美图”.已知图15是“优美图”,则点A、B与边a所对应的三个数分别为___________三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)16.(本小题满分13分)在数列{a n}中,a1=2,点(a n,a n+1)(n∈N*)在直线y=2x上.(Ⅰ)求数列{ a n }的通项公式;(Ⅱ)若b n=log2a n,求数列的前n项和T n.l 7.(本小题满分13分)假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5,记此时教室里敞开的窗户个数为X.(Ⅰ)求X的分布列;(Ⅱ)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为y,求y的数学期望.18.(本小题满分13分)如图,椭圆22221x ya b(a>b>0)的上、下顶点分别为A、B,已知点B在直线l:y=-1上,且椭圆的离心率e =32.(Ⅰ)求椭圆的标准方程;(Ⅱ)设P是椭圆上异于A、B的任意一点,PQ⊥y轴,Q为垂足,M为线段PQ中点,直线AM交直线l于点C,N为线段BC的中点,求证:OM⊥MN.19.(本小题满分l 4分)如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.(Ⅰ)求证:BD⊥平面POA;(Ⅱ)当PB取得最小值时,请解答以下问题:(i)求四棱锥P-BDEF的体积;(ii)若点Q满足AQ=λQP (λ>0),试探究:直线OQ与平面PBD所成角的大小是否一定大于4?并说明理由.第19题图20.(本小题满分1 3分)如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤3),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.第20题图21.本题有(1)、(2)、(3)三个选做题,每题7分,请考生任选2题作答,满分l4分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填人括号中.(1)(本小题满分7分)选修4—2:矩阵与变换利用矩阵解二元一次方程组32, 423 x yx y.(2)(本小题满分7分)选修4—4:坐标系与参数方程在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ+sinθ)=1.圆的参数方程为1cos,1sinx ry r(θ为参数,r >0),若直线l与圆C相切,求r的值.(3)(本小题满分7分)选修4—5:不等式选讲已知a2+b2+c2=1(a,b,c∈R),求a+b+c的最大值.2012年福州市高中毕业班质量检查 数学(理科)试卷参考答案及评分标准一、选择题(本大题共10小题,每小题5分,共50分.)1. A2. B3. D4. D5. C6. A7. C8. D9. B 10. C 二、填空题(本大题共5小题,每小题4分,共20分.) 11.30x y += 13. 18 14. ①②③ 15. 3、6、3三、解答题(本大题共6小题,共80分.) 16.(本小题满分13分)解:(Ⅰ)由已知得12n n a a +=,所以12n na a += 又12a =, 所以数列{}n a 是首项为2,公比为2的等比数列, ············ 3分 所以1*122()n n n a a n -=⋅=∈N . ····················· 5分 (Ⅱ)由(Ⅰ)知,2n n a =,所以2log ,n nb a n == ··········· 7分 所以11111(1)1n n b b n n n n +==-⋅⋅++, ··················· 10分 所以111111111223341n T n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭1111nn n =-=++. ······················· 13分 17.(本小题满分13分)解:(Ⅰ)∵X 的所有可能取值为0,1,2,3,4,(4,0.5)XB , ··· 1分∴4411(0)216P X C ⎛⎫=== ⎪⎝⎭,41411(1)24P X C ⎛⎫=== ⎪⎝⎭, 42413(2)28P X C ⎛⎫=== ⎪⎝⎭,43411(3)24P X C ⎛⎫=== ⎪⎝⎭, 44411(4)216P X C ⎛⎫=== ⎪⎝⎭, ···················· 6分X ∴的分布列为X 0 1 2 3 4p116 14 38 14 116········· 7分 (Ⅱ)Y 的所有可能取值为3,4,则 ·················· 8分1(3)(3)4P Y P X ====, ······················ 9分 3(4)1(3)4P Y P Y ==-==, ····················11分 Y ∴的期望值1315()34444E Y =⨯+⨯=.答:Y 的期望值()E Y 等于154. ···················· 13分18.(本小题满分13分)解:(Ⅰ)依题意,得1b =. ····················· 1分 ∵3c e a ==,2221a c b -==,∴24a =. ·············· 3分 ∴椭圆的标准方程为2214x y +=. ··················· 4分(Ⅱ)(法一)证明:设()00,P x y ,00x ≠,则0(0,)Q y ,且220014x y +=.∵M 为线段PQ 中点, ∴00,2x M y ⎛⎫⎪⎝⎭. ················ 5分又()0,1A ,∴直线AM 的方程为002(1)1y y x x -=+.000,1,x y ≠∴≠令1y =-,得00,11x C y ⎛⎫- ⎪-⎝⎭. ···················· 8分又()0,1B -,N 为线段BC 的中点,∴00,12(1)x N y ⎛⎫-⎪-⎝⎭. ········· 9分 ∴0000,122(1)x x NM y y ⎛⎫=-+ ⎪-⎝⎭. ··················· 10分∴22200000000000(1)222(1)44(1)x x x x x OM NM y y y y y y ⎛⎫⋅=-+⋅+=-++ ⎪--⎝⎭=2220000000()1(1)044(1)x x y y y y y +-+=-++=-. ········ 12分 ∴OM MN ⊥. ··························· 13分(法二)同(法一)得: 00,2x M y ⎛⎫⎪⎝⎭,00,12(1)x N y ⎛⎫- ⎪-⎝⎭. ········· 9分当00y =时,02x =,此时()()()2,0,1,0,1,1P M N -,∴0OM k =,MN k 不存在,∴OM MN ⊥.······ 10分当00y ≠时,000022OM y y k x x ==, ()()()200000000000002111221221MNy y y x k x x x y x y y y y -------====---,∵1OM MN k k ⋅=-,∴OM MN ⊥ ···················· 12分 综上得OM MN ⊥. ························· 13分 19.(本小题满分14分) (Ⅰ)证明:∵ 菱形ABCD 的对角线互相垂直,∴BD AC ⊥,∴BD AO ⊥, ····················· 1分 ∵ EF AC ⊥,∴PO EF ⊥. ∵ 平面PEF ⊥平面ABFED ,平面PEF 平面ABFED EF =,且PO ⊂平面PEF ,∴ PO ⊥平面ABFED , ······················ 2分 ∵ BD ⊂平面ABFED ,∴ PO BD ⊥. ··························· 3分 ∵ AOPO O =,∴ BD ⊥平面POA . ························ 4分 (Ⅱ)如图,以O 为原点,建立空间直角坐标系O xyz -. ·········· 5分 (ⅰ)设.AO BD H =因为60DAB ∠=︒,所以BDC ∆为等边三角形, 故4BD =,2,HB HC ==又设PO x =,则OH x =,OA x =. 所以(0,0,0)O ,(0,0,)P x,,2,0)B x ,故(2,2,)PB OB OP x x =-=-, ·················· 6分所以2222(23)22(3)10PB x x x =-++=-+,当3x =时,min 10PB =. 此时3PO =, 3.OH = ·········· 7分 由(Ⅰ)知,PO ⊥平面,BFED所以221133(42)333344P BFED BFED V S PO -=⋅⋅=⋅⨯-⨯⨯=四棱锥梯形. ····· 8分(ⅱ)设点Q 的坐标为(),0,a c ,由(i )知,3OP =,则(33,0,0)A ,(3,2,0)B ,(3,2,0)D -,(0,0,3)P . 所以()33,0,AQ a c=-,(),0,3QP a c =--,··························· 9分 ∵AQ=QP λ,∴33,3a a c cλλλ⎧-=-⎪⎨=-⎪⎩⇒33,131a c λλλ⎧=⎪⎪+⎨⎪=⎪+⎩.∴333(,0,)11Q λλλ++, ∴333(,0,)11OQ λλλ=++. ····10分 设平面PBD 的法向量为(,,)n x y z =,则0,0n PB n BD ⋅=⋅=.∵()3,2,3PB =-,()0,4,0BD =-,∴3230,40x y z y ⎧+-=⎪⎨-=⎪⎩ , 取1x =,解得:0,y =1z =, 所以(1,0,1)n =. ············· 11分 设直线OQ 与平面PBD 所成的角θ,∴222333113sin cos ,293332()()11OQ n OQ n OQ nλλλλθλλλλ+⋅+++=<>===⋅⋅+⋅+++2221961619922λλλλλ++==+++. ········ 12分又∵0λ>∴2sin θ>. ······················· 13分 ∵[0,]2πθ∈,∴4πθ>.因此直线OQ 与平面PBD 所成的角大于4π,即结论成立. ········ 14分20.(本小题满分13分)解:(Ⅰ)由已知可得ABC △为等边三角形. 因为CD AD ⊥,所以水下电缆的最短线路为CD .过D 作DE AB ⊥于E ,可知地下电缆的最短线路为DE 、AB . ······· 3分 又31,,22CD DE AB ===, 故该方案的总费用为314220.52⨯+⨯+⨯ 53=+(万元) …………6分(Ⅱ)因为0,3DCE πθθ⎛⎫∠=≤≤ ⎪⎝⎭所以1,tan ,3tan cos CE EB ED AE θθθ====-.·············· 7分 则()113sin 423tan 2223cos cos cos y θθθθθ-=⨯+⨯+-⨯=⨯+,········ 9分 令()3sin ,cos g θθθ-=则()()()222cos 3sin sin 3sin 1cos cos g θθθθθθθ-----'== , ···· 10分 因为03πθ≤≤,所以30sin 2θ≤≤, 记001sin ,(0,),33πθθ=∈当10sin 3θ≤<,即0≤0θθ<时,()0g θ'<,当13sin 3θ<≤,即0θ<θ≤3π时, ()0g θ'>, 所以()0min133()2222g g θθ-===,从而4223y ≥+, ·········· 12分 此时02tan ED θ==, 因此施工总费用的最小值为(4223+)万元,其中2ED =. ··· 13分 21.(本小题满分7分) 选修4-2,矩阵与变换解:方程组可写为312423x y ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ················· 2分系数行列式为32412⨯-⨯=,方程组有唯一解.利用矩阵求逆公式得11131242322-⎛⎫- ⎪⎛⎫= ⎪ ⎪⎪⎝⎭- ⎪⎝⎭, ··············· 5分 因此原方程组的解为111222331222x y ⎛⎫⎛⎫- ⎪ ⎪⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭- ⎪ ⎪⎝⎭⎝⎭,即1,21.2x y ⎧=⎪⎪⎨⎪=⎪⎩ ········ 7分(2)(本小题满分7分) 选修4-4:坐标系与参数方程 解:∵直线l 的极坐标方程为(cos sin )1ρθθ+=,∴直线l 的直角坐标方程为10x y +-=, ················ 2分又圆C 的普通方程为222(1)(1)x y r -+-=,所以圆心为(1,1),半径为r . ···················· 4分 因为圆心到直线l 的距离111222d +-==, ··············· 6分 又因为直线l 与圆C 相切,所以2r =. ················ 7分 (3)(本小题满分7分)选修4-5:不等式选讲(法一)解:∵ a ,b ,R c ∈,2221a b c ++=,∴ 22222222()(111)()(111)3a b c a b c a b c ++=⋅+⋅+⋅≤++++=. ······ 5分 当且仅当3a b c ===时,a b c ++3 ··········· 7分 (法二)解:∵222a b ab +≥,222b c bc +≥,222a c ac +≥ ∴ 2222()222a b c a b c ab bc ac ++=+++++222222222()()()a b c a b b c a c ≤+++++++++ ············· 3分∵ 2221a b c ++=,∴2()3a b c ++≤,当且仅当3a b c ===时等号成立, ·········· 6分 ∴a b c ++3 ······················ 7分希望对大家有所帮助,多谢您的浏览!。
2012福州质检数学答案

2012年福州市初中毕业班质量检查数学试卷参考答案及评分标准一、选择题1.A 2.B 3.C 4.C 5.D 6.A 7.D 8.A 9.B 10.C二、填空题:11.(3)(3)x x +- 12.8 13.2914.1 15.3 三、解答题:16.(1)解:1011( 3.14)2-⎛⎫-+-- ⎪⎝⎭=11122+⨯- ························································································ 4分················································································································ 7分 (2)解:()()212x x x ++-=22212x x x x +++- ·························································································· 4分=221x +, ············································································································· 5分当x ==221⨯+=5.······························································ 7分17.(1)证明:∵AB 与CD 是平行四边形ABC D 的对边,∴AB ∥CD , ······························································································· 2分∴∠F =∠F AB . ···························································································· 4分∵E 是BC 的中点, ∴BE=CE , ·································································· 5分又∵ ∠AEB =∠FEC , ·············································································· 6分∴ △ABE ≌△FCE . ·················································································· 7分(2)解:如图,a = 45°,β= 60°, AD =80.在Rt △ADB 中, ∵tan BD ADα=, ∴tan 80tan 45=80BD AD α==⨯︒ . ············· 2分 在Rt △ADC 中, ∵tan CD ADβ=,∴tan 80tan60CD AD β==⨯︒ ········ 5分∴80218.6BC BD CD =+=+.答:这栋楼高约为218.6m . ···················· 7分18.(1)a = 25 %, 90º . ················································································· 2分补全条形图. ············································································································· 4分(2)众数是5,中位数是5. ················································································ 8分(3)该市初一学生第一学期社会实践活动时间不少于5天的人数约是:20000(30%25%20%)15000⨯++=(人). ··················································· 12分 19.(1)证法一:连接AE, ····································· 1分∵AC 为⊙O 的直径,∴∠AEC =90º,即AE ⊥BC. ······························· 4分∵AB =AC,∴BE =CE ,即点E 为BC 的中点. ·················· 6分证法二:连接OE , ········································ 1分∵OE =OC,∴∠C =∠OEC.∵AB =AC,∴∠C =∠B,∴∠B =∠OEC,∴OE ∥AB. ···················································· 4分 ∴1EC OC BE AO==, ∴EC =BE ,即点E 为BC 的中点. ··················· 6分⑵∵∠COD =80º,∴∠DAC =40º . ·············································· 8分∵∠DAC +∠DEC =180º,∠BED +∠DEC =180º,∴∠BED =∠DAC =40º. ····························· 11分20.解:(1)设A 型计算器进价是x 元,B 型计算器进价是y 元, ··························· 1分 得 10888025380.x y x y +=⎧⎨+=⎩······················································································ 3分 解得40,60.x y =⎧⎨=⎩····························································································· 5分 答:每只A 型计算器进价是40元,每只B 型计算器进价是60元. ·················· 6分(2)设购进A 型计算器为z 只,则购进B 型计算器为(50-z )只,得4060(50)2520,1015(50)620.z z z z +-≤⎧⎨+-≥⎩··········································································· 9分 解得24≤z ≤26,因为z 是正整数,所以z =24,25,26. ························································ 11分答:该经销商有3种进货方案:①进24只A 型计算器,26只B 型计算器;②进25只A 型计算器,25只B 型计算器;③进26只A 型计算器,24只B 型计算器. ································ 12分21.解:(1)()4cm BE t =+, ····················································································· 1分()54cm 8EF t =+. ····················································································· 4分 (2)分三种情况讨论:①当DF EF =时,有,EDF DEF B ∠=∠=∠ ∴点B 与点D 重合,∴0.t = ········································· 5分②当DE EF =时,∴()5448t =+, 解得:12.5t =······························· 7分 ③当DE DF =时,有,DFE DEF B C ∠=∠=∠=∠ ∴△DEF ∽△ABC. ∴DE EF AB BC=, 即()54481016t +=, 解得:15625t =. ··························· 9分 综上所述,当=0t 、125或15625秒时,△DEF 为等腰三角形.(3)设P 是AC 的中点,连接BP ,∵EF ∥,AC∴△FBE ∽△ABC . ∴,EF BE AC BC = ∴.EN BE CP BC= 又,BEN C ∠=∠ ∴△NBE ∽△,PBC ∴.NBE PBC ∠=∠ ··································································································· 10分∴点N 沿直线BP 运动,MN 也随之平移.如图,设MN 从ST 位置运动到PQ 位置,则四边形PQST 是平行四边形. ········· 11分∵M 、N 分别是DF 、EF 的中点,∴MN ∥DE ,且ST =MN =1 2.2DE = 分别过点T 、P 作TK ⊥BC ,垂足为K ,PL ⊥BC ,垂足为L ,延长ST 交PL 于点R ,则四边形TKLR 是矩形,当t =0时,EF =58(0+4)=5,2TK =12EF ·1sin 2DEF ∠=·52·33;54= 当t =12时,EF =AC =10,PL =12AC ·1sin 2C =·10·3 3.5= ∴PR=PL-RL=PL-TK=3-39.44= ∴PQST S ST = ·PR=2×99.42= ∴整个运动过程中,MN 所扫过的面积为92cm 2. ··················································· 13分 解得:16,34,b c ⎧=-⎪⎨⎪=⎩ 22.解:(1)由题意得: ∴抛物线解析式为2416433y x x =-+. ·································································· 3分 (2)令0y =,得241640.33x x -+=4,4930,3c b c =⎧⎪⎨⨯++=⎪⎩………1分 ………2分解得:11x =,2x =3.∴C 点坐标为(1,0). ··········································· 4分作CQ ⊥AB ,垂足为Q ,延长CQ ,使CQ='C Q ,则点'C就是点C 关于直线AB 的对称点.由△ABC 的面积得:1122CQ AB CA OB ⋅=⋅,∵5,AB =CA =2,∴CQ =85,'CC =165. ······················································································ 6分 作'C T ⊥x 轴,垂足为T ,则△'CTC ∽△BOA. ∴''C T CC CT OA AB OB == ∴'C T =4825,CT =6425∴OT =1+6425=8925 ∴'C 点的坐标为(8925,4825) ··································· 8分 (3)设⊙D 的半径为r ,∴AE =r +3,BF =4-r ,HB =BF =4-r .∵AB =5,且AE =AH,∴r +3=5+4-r ,∴r =3. ········································· 10分HB =4-3=1.作HN ⊥y 轴,垂足为N , 则HN HB OA AB =,BN HB OB AB=, ∴HN =35,BN =45, ∴H 点坐标为(35-,245). ··············· 12分 根据抛物线的对称性,得P A =PC, ∵PH PA PH PC HC -=-≤,∴当H 、C 、P 三点共线时,PH PC -最大.∵HC∴PH PA - ······································································ 14分。
福建省福州市2012届高三毕业班综合练习数学理(2012福州5月质检).pdf

2012年福州市高中毕业班数学(理科)试卷 (完卷时间:120分钟;满分:150分) 注意事项: 1.本科考试分试题卷和答题卷,考生须在答题卷上作答,答题前,请在答题卷的密封线内填写学校、班级、准考证号、姓名; 2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟. 参考公式: 一、选择题本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中只有一项是符合题目要求的.已知,集合,则 A.B.C.D.对应的向量分别是,则复数所对应的点位于 A.第一象限B.第二象限 C.第三象限D.第四象限 3.设等比数列的前项和为,则“”是“”的 A.充分不必要B.必要不充分 C.充要D.既不充分也不必要一个几何体的三视图,正视图和侧视图均为矩形俯视图为正三角形,尺寸如图,则该几何体的积为 A B. C. D. 5.如图,执行程序框图后,输出的结果为 A.8 B.10 C.12 D.32 ,且在上单调递增的奇函数是 A.B. C.D. 7.已知,,,,则的最大值为 A. B. 2 C. D. 8.若从区间内取两个数,则这两个数之积不小于的概率 B. C. D. 9.如图,在正方体中,若平面上一动点 到和的距离相等,则点的轨迹为 A.椭圆的一部分 B.圆的一部分 C.一条线段 D.抛物线的一部分 10.将方程的正根从小到大地依次排列为,给出以下不等式:①;②; ③;④; 其中,正确的判断是A. ①③B. ①④C. ②③D. ②④ 二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡的相应位置. 11,则 . 12.已知双曲线的离心率为2,有一个焦点与抛物线的焦点重合,则 13.等差数列公差不为零,,且、、成等比数列,则的 . 14.已知三次函数的图象如图所示,则 ★★★ . 15假定平面内的一条直线将该平面内的一个区域分成,则称这条直线平分这个区域如图,是平面内的任意一个封闭区域.现给出如下结论: 过平面内的任意一点至少存在一条直线平分区域; 过平面内的任意一点至多存在一条直线平分区域; 区域内的任意一点至少存在两条直线平分区域; 平面内存在互相垂直的两条直线平分区域成四份其中正确结论的序号是 .三、解答题:本大题共6小题,共80分.解答写在答题卡相位置,应写出文字说明、证明过程或演算步骤.16.(本小题满分13分) 聘用甲乙两个部门Ⅰ)公司随机安排两个部门的3个岗位进行在甲部门 (Ⅱ)甲乙两个部门都愿意聘用甲部门不同岗位月工资(元)200240026002800获得相应岗位的概率0.40.30.20.1乙部门不同岗位月工资(元)000240028003200获得相应岗位的概率0.40.30.20.1,选择说明理由17.(本小题满分13分) 如图,三棱柱中,平面,,点上,且,. (Ⅰ)求证:直线与平面不平行; (Ⅱ)平面与平面所成的锐二面角为,若,求的; (Ⅲ)在(Ⅱ)的条件下,平面平面,求直线与所成的角的余弦值.18.(本小题满分13分) 如图,圆与轴相切于点,与轴正半轴相交于两点(点在点的左侧),且. (Ⅰ)求圆的方程;(Ⅱ)过点任作一条直线与椭圆相交于两点,连接,求证:. 19.(本小题满分13分). (Ⅰ)当时,求函数的图象在处的切线方程; (Ⅱ)判断函数的单调性; (Ⅲ)求证:(). 20.(本小题满分14分) 如图,在平面直角坐标系中,锐角、的终边分别与单位圆交于,两点. (Ⅰ)如果,点的横坐标为,求的值; (Ⅱ)的终边与单位圆交于点、、的正弦线分别为MA、NB、PC,求证:能成三角形;(III)探究第(Ⅱ)小题中的三角形的外接圆面积是否为定值? 若是,求出该定值;若不是,请说明理由. 21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中. (1)(本小题满分7分)选修4-2:矩阵与变换 设矩阵M是把坐标平面上的点的纵坐标伸长到原来的2倍,横坐标保持不变的伸缩变换. (Ⅰ)求矩阵M; (Ⅱ)求矩阵M的特征值以及属于每个特征值的一个特征向量.(2)(本小题满分7分) 选修4—4:极坐标与参数方程 在直角坐标平面内,以坐标原点为极点,轴的非负半轴为极轴建立极坐标系. 已知点、的极坐标分别为、,曲线的参数方程为为参数). (Ⅰ)求直线的直角坐标方程; (Ⅱ)若直线和曲线C只有一个交点,求的值.(3)(本小题满分7分) 选修4—5:不等式选讲 的不等式对于任意的恒成立 (Ⅰ)求的取值范围; (Ⅱ)在(Ⅰ)的条件下求函数的最小值. 2012年福州市高中毕业班综合练习 理科数学试卷参考答案及评分参考 一、选择题(本大题共10小题,每小题5分,共50分)1.B2.A3.C4.D5.B6.D7. C8. B9.D 10. D 二、填空题(本大题共5小题,每小题4分,共20分) 11. 2 12. 12 13. 14. 15. ①④ 三、解答题(本大题共6小题,共80分) 16.(本小题满分13分) 解:(Ⅰ)在甲部门,则 .6分 (Ⅱ)(元(元 ,9分 .10分 选择甲部门:因为,说明甲部门各岗位的工资待遇波动比乙部门小,竞争压力没有乙部门大,比较安稳 选择乙部门:因为,说明乙部门各岗位的工资待遇波动比甲部门大,岗位工资拉的比较开,工作比较有挑战性,能更好地体现工作价值 17.(本小题满分13分) 解:依题意,可建立如图所示的空间直角坐标系,设,则 .2分 (Ⅰ)证明:由平面可知为平面的一个法向量. ∴ .3分 ∴ 直线与平面不平行.4分 (Ⅱ)设平面的法向量,则 ,分 取,则,故.6分 ∴,7分 解得. ∴ .8分 (Ⅲ)在平面内,分别延长,交于点,连结,则直线为平面与平面的交线.9分 ∵ ,, ∴ . ∴ , ∴ .11分 由(Ⅱ)知,,故, ∴ .12分 ∴ 直线与所成的角的余弦值为.1分 18.(本小题满分13分) 解:(Ⅰ)设圆的半径为(),依题意,圆心坐标为.1分 ∵ ∴ ,解得.3分 ∴ 圆的方程为.5分 (Ⅱ)把代入方程,解得,或, 即点,.6分 当轴时,由椭圆对称性可知.7分 当与轴不垂直时,可设直线的方程为. 联立方程,消去得,.8分 设直线交椭圆于两点,则 ,.9分 ∵ , ∴ .1分,11分∴ ,.12分 综上所述,.1分19.(本小题满分13分)时,, ∴,1分 ,所以所求的切线的斜率为3. 2分,所以切点为.3分.4分, ∴.5分时,∵,∴;6分时, 由,得;由,得;7分时,函数在单调递增; 当时,函数在单调递减,在上单调递增.8分时, 在上单调递增.9分 ∴ 当时,,即.10分 令(),则.11分 另一方面,∵,即, ∴ .12分 ∴ ().13分 方法二:构造函数,9分,10分时,; ∴函数在单调递增.11分 ,即 ∴,,即12分(),则有.13分20.(本小题满分14分) 解:是锐角根据三角函数的定义,得1分,且是角,所以.分所以.分,, 因为,所以,,于是有 ,①6分, ,② 7分,③ 由①,②,③可得, 线段MA、NB、PC能成三角形分III)第(Ⅱ)小题中的三角形的外接圆面积是定值,且定值为. 不妨设的边长分别为,其中角、、的对边分别为.则由余弦定理,得: 9分 11分,所以,所以,12分的外接圆半径为R, 由正弦定理,得,∴,13分的外接圆的面积为. 14分21.(1)(本小题满分7分)选修4-2:矩阵与变换 解:(Ⅰ)由条件得矩阵.2分 (Ⅱ)因为矩阵的特征多项式为, 令,解得特征值为,,分设属于特征值的矩阵M的一个特征向量为,则,解得,取,得,分同理,对于特征值,解得,取,得,分所以是矩阵M属于特征值的一个特征向量,是矩阵M属于特征值 的一个特征向量.7分 (2)(本小题满分7分) 选修4—4:极坐标与参数方程 解:(Ⅰ)∵点、的极坐标分别为、, ∴点、的直角坐标分别为、,分∴直线的直角坐标方程为.4分 (Ⅱ)由曲线的参数方程化为普通方程为,5分 ∵直线和曲线C只有一个交点, ∴半径.7分 (3)(本小题满分7分) 选修4—5:不等式选讲 的不等式对于任意的恒成立 1分 所以,当且仅当时等号成立,故.3分 (Ⅱ)由(Ⅰ)得,则 ∴5分,即时取等号,6分的最小值为. 高考学习网( 您身边的高考专家 欢迎广大教师踊跃来稿,稿酬丰厚。
福建省泉州市普通中学2012届高中毕业班质量检查数学(理)试题

2012年泉州市普通高中毕业班质量检查理 科 数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),第Ⅱ卷第21题为选考题,其它题为必考题.本试卷共6页,满分150分.考试时间120分钟. 参考公式:样本数据1x 、2x 、…、n x 的标准差:s =x 为样本平均数; 柱体体积公式:V Sh =,其中S 为底面面积,h 为高;锥体体积公式:13V Sh =,其中S 为底面面积,h 为高; 球的表面积、体积公式:24S R π=,343V R π=,其中R 为球的半径.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题意要求的.1. 复数()1i i +等于A .1i -+B .1i +C .1i --D .1i -2. 已知集合{}13A x x =<<,{}21log 2B x x =<<,则AB 等于A.{}03x x << B.{}23x x << C.{}13x x << D.{}14x x << 3. 已知(2,1),(1,3)a b ==--,则||a b -等于 ABC .5D .254. 执行右侧框图所表达的算法,如果最后输出的S 值为12012,那么判断框中实数a 的取值范围是 A .20112012a ≤< B .20112012a <≤ C .20112012a ≤≤ D .20122013a ≤<5. 下列四个条件:①x ,y ,z 均为直线; ②x ,y 是直线,z 是平面;③x 是直线,y ,z 是平面;④x ,y ,z 均为平面. 其中,能使命题“,x y yz x z ⊥⇒⊥”成立的有A .1个B .2个C .3个D .4个6. 已知实数,x y 满足2220,0,4,x y x y x y ⎧-+≥⎪+≥⎨⎪+≤⎩则2z x y =+的最大值是 A .5 B .-1 C .2D.7. 已知二次函数2()f x ax bx =+,则“(2)0f ≥”是“函数()f x 在()1,+∞单调递增”的A .充要条件B .充分不必要条件C .必要不充分条件 D. 既不充分也不必要条件8. 已知12,A A 分别为椭圆2222:1(0)x y C a b a b+=>>的左右顶点,椭圆C 上异于12,A A 的点P 恒满足1249PA PA k k ⋅=-,则椭圆C 的离心率为A .49 B .23 C .59D.39. 为调查某校学生喜欢数学课的人数比例,采用如下调查方法:(1)在该校中随机抽取100名学生,并编号为1,2,3, (100)(2)在箱内放置两个白球和三个红球,让抽取的100名学生分别从箱中随机摸出一球,记住其颜色并放回;(3)请下列两类学生举手:(ⅰ)摸到白球且号数为偶数的学生;(ⅱ)摸到红球且不喜欢数学课的学生.如果总共有26名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是A.88%B. 90%C. 92%D.94%10. 函数的图象与方程的曲线有着密切的联系,如把抛物线2y x =的图象绕原点沿逆时针方向旋转90就得到函数2y x =的图象.若把双曲线2213x y -=绕原点按逆时针方向旋转一定角度θ后,能得到某一个函数的图象,则旋转角θ可以是A .30B .45C .60D .90第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分.将答案填在答题卡的相应位置. 11. 已知等差数列}{n a 中, 51a =,322a a =+,则11S = . 12. 一个三棱锥的正视图和侧视图及其尺寸如图所示,则该三棱锥俯视图的面积为 .13. 在ABC V 中,60,3B A C==,则ABC V 周长的最大值为 .14. 已知{}()(),min ,a b a a b a b b ≤⎧⎪=⎨>⎪⎩,设()31min ,f x x x ⎧⎫=⎨⎬⎩⎭,则由函数()f x 的图象与x 轴、直线x e =所围成的封闭图形的面积为 .15. 数学与文学之间存在着许多奇妙的联系. 诗中有回文诗,如:“云边月影沙边雁,水外天光山外树”,倒过来读,便是“树外山光天外水,雁边沙影月边云”,其意境和韵味读来真是一种享受!数学中也有回文数,如:88,454,7337,43534等都是回文数,无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“回文数”,读起来还真有趣!二位的回文数有11,22,33,44,55,66,77,88,99,共9个;三位的回文数有101,111,121,131,…,969,979,989,999,共90个; 四位的回文数有1001,1111,1221,…,9669,9779,9889,9999,共90个; 由此推测:10位的回文数总共有 个.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分13分)已知点(1,0)F ,直线:1l x =-,动点P 到点F 的距离等于它到直线l 的距离. (Ⅰ)试判断点P 的轨迹C 的形状,并写出其方程.(Ⅱ)是否存在过(4,2)N 的直线m ,使得直线m 被截得的弦AB 恰好被点N 所平分?17.(本小题满分13分)将边长为1的正三角形ABC 按如图所示的方式放置,其中顶点A 与坐标原点重合.记边AB 所在直线的倾斜角为θ,已知0,3πθ⎡⎤∈⎢⎥⎣⎦. (Ⅰ)试用θ表示BC 的坐标(要求将结果化简为形如(cos ,sin )αα的形式);(Ⅱ)定义:对于直角坐标平面内的任意两点()11,P x y 、()22,Q x y ,称123侧视图正视图1212x x y y -+-为P 、Q 两点间的“taxi 距离” ,并用符号PQ 表示.试求BC 的最大值.18.(本小题满分13分)已知12310,,,,A A A A 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为12. (Ⅰ)如果该同学10所高校的考试都参加,试求恰有2所通过的概率;(Ⅱ)假设该同学参加每所高校考试所需的费用均为a 元,该同学决定按12310,,,,A A A A 顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用ξ的分布列及数学期望.19. (本小题满分13分)如图,侧棱垂直底面的三棱柱111ABC A B C -中,AB AC ⊥,13AA AB AC ++=,(0)AB AC t t ==>,P 是侧棱1AA 上的动点.C 11C(Ⅰ)当1AA AB AC ==时,求证:11A C ABC ⊥平面; (Ⅱ)试求三棱锥1P BCC -的体积V 取得最大值时的t 值; (Ⅲ)若二面角1A BC C --t 的值. 20.(本小题满分14分)已知()0xf x x e =⋅,()()10f x f x '=,()()21f x f x '=,…,()()1n n f x f x -'=(n N *∈).(Ⅰ)请写出()n f x 的表达式(不需证明);(Ⅱ)设()n f x 的极小值点为(),n n n P x y ,求n y ;(Ⅲ)设()()22188n g x x n x n =--+-+, ()n g x 的最大值为a ,()n f x 的最小值为b ,试求a b -的最小值.21. 本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B 铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.作(1)(本小题满分7分)选修4—2:矩阵与变换若二阶矩阵M 满足127103446M ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭. (Ⅰ)求二阶矩阵M ;(Ⅱ)把矩阵M 所对应的变换作用在曲线223861x xy y ++=上,求所得曲线的方程. (2)(本小题满分7分)选修4-4:坐标系与参数方程已知在直角坐标系xOy 中,曲线C 的参数方程为2cos 2sin x t y θθ=⎧⎨=⎩(t 为非零常数,θ为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线l 的方程为sin()4πρθ-=(Ⅰ)求曲线C 的普通方程并说明曲线的形状;(Ⅱ)是否存在实数t ,使得直线l 与曲线C 有两个不同的公共点A 、B ,且10OA OB ⋅=(其中O 为坐标原点)?若存在,请求出;否则,请说明理由.(3)(本小题满分7分)选修4—5:不等式选讲已知函数()24f x x x =-+-的最小值为m ,实数,,,,,a b c n p q 满足222222a b c n p q m++=++=. (Ⅰ)求m 的值;(Ⅱ)求证:4442222n p q a b c++≥.参考解答及评分标准一、选择题:本大题考查基础知识和基本运算.每小题5分,满分50分. 1. A 2.B 3.C 4.A 5.C6. D 7.C 8.D 9.B 10.C二、填空题:本大题考查基础知识和基本运算.每小题4分,满分20分.11.33 12.1 13.14.5415.90000三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤 16. 本小题考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等.满分13分.解:(Ⅰ)因点P 到点F 的距离等于它到直线l 的距离,所以点P 的轨迹C 是以F 为焦点、直线1x =-为准线的抛物线, ………………2分 其方程为24y x =. ………………5分(Ⅱ)解法一:假设存在满足题设的直线m .设直线m 与轨迹C 交于1122(,),(,)A x y B x y ,依题意,得121284x x y y +=⎧⎨+=⎩. ………………6分①当直线m 的斜率不存在时,不合题意. ………………7分②当直线m 的斜率存在时,设直线m 的方程为2(4)y k x -=-,………8分联立方程组22(4)4y k x y x-=-⎧⎨=⎩,消去y ,得2222(844)(24)0k x k k x k --++-=,(*) ………………9分∴21228448k k x x k -++==,解得1k =. ………………10分此时,方程(*)为2840x x -+=,其判别式大于零, ………………11分 ∴存在满足题设的直线m ………………12分 且直线m 的方程为:24y x -=-即20x y --=. ………………13分解法二:假设存在满足题设的直线m .设直线m 与轨迹C 交于1122(,),(,)A x y B x y ,依题意,得121284x x y y +=⎧⎨+=⎩. ………………6分易判断直线m 不可能垂直y 轴, ………………7分 ∴设直线m 的方程为4(2)x a y -=-,………8分联立方程组24(2)4x a y y x-=-⎧⎨=⎩,消去x ,得248160y ay a -+-=, ………………9分∵216(1)480a ∆=-+>,∴直线与轨迹C 必相交. ………………10分 又1244y y a +==,∴1a =. ………………11分 ∴存在满足题设的直线m ………………12分且直线m 的方程为:24y x -=-即20x y --=. ………………13分解法三:假设存在满足题设的直线m .设直线m 与轨迹C 交于1122(,),(,)A x y B x y ,依题意,得121284x x y y +=⎧⎨+=⎩. ………………6分∵1122(,),(,)A x y B x y 在轨迹C 上,∴有2112224142y x y x ⎧=⎪⎨=⎪⎩()(),将(1)(2)-,得2212124()y y x x -=-. ………8分当12x x =时,弦AB 的中点不是N ,不合题意, ………9分 ∴12121241y y x x y y -==-+,即直线AB 的斜率1k =, ………10分注意到点N 在曲线C 的张口内(或:经检验,直线m 与轨迹C 相交)…11分 ∴存在满足题设的直线m ………………12分且直线m 的方程为:24y x -=-即20x y --=. ………………13分17. 本小题主要考查三角函数的定义、两角和与差的三角函数公式、平面向量等基础知识,考查运算求解能力,考查化归与转化思想.满分13分.解:(Ⅰ)解法一:因为()cos ,sin B θθ,cos ,sin 33C ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ……2分 所以cos cos ,sin sin 33BC ππθθθθ⎛⎫⎛⎫⎛⎫=+-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭………3分 22cos ,sin 33ππθθ⎛⎫⎛⎫⎛⎫=++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. ………7分 解法二:平移BC 到AD (B 移到A ,C 移到D ),………2分由BC 的坐标与AD 的坐标相等,都等于点D 的坐标. ………3分 由平几知识易得直线AD 的倾斜角为23πθ+, ∵||1AD =,∴根据三角函数的定义可得22cos ,sin 33D ππθθ⎛⎫⎛⎫⎛⎫++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以22cos ,sin 33BC ππθθ⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. ………7分(Ⅱ)解法一:22cos sin 33BC ππθθ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,………8分 ∵0,3πθ⎡⎤∈⎢⎥⎣⎦,∴22[,]33ππθπ+∈, ………9分 ∴22cos sin 33BC ππθθ⎛⎫⎛⎫=-+++ ⎪⎪⎝⎭⎝⎭………11分 512πθ⎛⎫=+ ⎪⎝⎭, ………12分所以当12πθ=时,BC . ………13分解法二: cos cos sin sin 33BC ππθθθθ⎛⎫⎛⎫=+-++- ⎪ ⎪⎝⎭⎝⎭,………8分 ∵03πθ≤≤,∴2333πππθπ≤+≤<,即03πθθπ≤<+<, ∴cos cos cos cos()33ππθθθθ⎛⎫+-=-+ ⎪⎝⎭. ………9分 ∵03πθ≤≤,∴()232πππθθ-≥+-,∴sin sin sin sin 33ππθθθθ⎛⎫⎛⎫+-=+- ⎪ ⎪⎝⎭⎝⎭, ………10分 ||||BC =cos cos()3πθθ-++sin sin 3πθθ⎛⎫+- ⎪⎝⎭5sin()cos())6612πππθθθ=+++=+, ………12分 所以当12πθ=时,BC. ………13分18. 本题主要考查概率与统计的基础知识,考查数据处理能力、运算求解能力以及应用用意识,考查必然与或然思想、分类与整合思想等.满分13分.解:(Ⅰ)因为该同学通过各校考试的概率均为12,所以该同学恰好通过2所高校自主招生考试的概率为2821011122P C ⎛⎫⎛⎫=- ⎪⎪⎝⎭⎝⎭451024=. ………4分 (Ⅱ)设该同学共参加了i 次考试的概率为i P (110,i i Z ≤≤∈).∵91,19,21,102ii i i Z P i ⎧≤≤∈⎪⎪=⎨⎪=⎪⎩,∴所以该同学参加考试所需费用ξ的分布列如下:ξa 2a 3a 4a 5a 6a 7a 8a 9a 10aP12 212 312 412 512 612 712 812 912 912………7分 所以2991111(12910)2222E a ξ=⨯+⨯++⨯+⨯, ………8分 令29111129222S =⨯+⨯++⨯, …(1) 则2391011111128922222S =⨯+⨯++⨯+⨯, …(2) 由(1)-(2)得291011111922222S =+++-⨯,所以2891111192222S =++++-⨯, ………11分所以289911111191022222E a ξ⎛⎫=++++-⨯+⨯ ⎪⎝⎭911122a ⎛⎫=+++⎪⎝⎭10112112a -=-101212a ⎛⎫=- ⎪⎝⎭1023512a =(元). ………13分 19. 本小题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想及应用意识. 满分13分.解:(Ⅰ)证法一:∵1AA ⊥面ABC ,∴1AA AC ⊥,1AA AB ⊥. 又∵1AA AC =,∴四边形11AAC C 是正方形, ∴11AC A C ⊥. ………1分∵11111,,,,AB AC AB AA AA AC AAC C AA AC A ⊥⊥⊂=平面,∴11AB AAC C ⊥平面. ………2分又∵111AC AAC C ⊂平面, ∴1AB AC ⊥. ………3分 ∵111,,AB AC ABC ABAC A ⊂=平面,∴11A C ABC ⊥平面. ………4分证法二:∵1AA ⊥面ABC ,∴1AA AC ⊥,1AA AB ⊥. 又∵AB AC ⊥,∴分别以1,,AB AC AA 所在直线为,,x y z 轴建立空间直角坐标系. ……1分 则11(0,0,0),(0,1,1),(1,0,0),(0,1,0),(0,0,1)A C B C A ,11(0,1,1),(0,1,1),(1,0,0)AC AC AB =-==, ∴1110,0AC AC AC AB ⋅=⋅=, …2分 ∴111,AC AC AC AB ⊥⊥. …3分 又∵111,,AB AC ABC ABAC A ⊂=平面∴11A C ABC ⊥平面. …4分证法三:∵1AA ⊥面ABC ,∴1AA AC ⊥,1AA AB ⊥.又∵AB AC ⊥,∴分别以1,,AB AC AA 所在直线为,,x y z 轴建立空间直角坐标系. ……1分 则11(0,0,0),(0,1,1),(1,0,0),(0,1,0),(0,0,1)A C B C A ,11(0,1,1),(0,1,1),(1,0,0)AC AC AB =-==. 设平面1ABC 的法向量(,,)n x y z =,则100n AC y z n AB x ⎧⋅=+=⎪⎨⋅==⎪⎩,解得0x y z =⎧⎨=-⎩.令1z =,则(0,1,1)n =-, ……3分∵1AC n =-, ∴11A C ABC ⊥平面. ……4分 (Ⅱ)∵111AA BB C C 平面,∴点P 到平面11BB C C 的距离等于点A 到平面11BB C C 的距离∴1112231113(32)(0)6232P BCC A BCC C ABC V V V V t t t t t ---====-=-<<, …5分'(1)V t t =--,令'0V =,得0t =(舍去)或1t =,列表,得(0,1)1 3(1,)2'V + 0 - V递增极大值递减∴当1t =时,max 16V =. …8分 (Ⅲ)分别以1,,AB AC AA 所在直线为,,x y z 轴建立空间直角坐标系.则11(0,0,0),(0,,32),(,0,0),(0,,0),(0,0,32)A C t t B t C t A t --,11(0,,23),(0,,32),(,0,0)AC t t AC t t AB t =-=-=, 1(0,0,32)CC t =-,(,,0)BC t t =-. ……9分设平面1ABC 的法向量1111(,,)n x y z =,则111111(32)00n AC ty t z n AB tx ⎧⋅=+-=⎪⎨⋅==⎪⎩,解得111023x t y z t =⎧⎪⎨-=⎪⎩,令1z t =,则1(0,23,)n t t =-. …10分 设平面1BCC 的法向量2222(,,)n x y z =,则2222120(32)0n BC tx ty n CC t z ⎧⋅=-+=⎪⎨⋅=-=⎪⎩. 由于302t <<,所以解得2220x y z =⎧⎨=⎩. 令21y =,则2(1,1,0)n =. …11分 设二面角1A BC C --的平面角为θ,则有1212|||cos |10||||2n n n n θ⋅===⋅. 化简得2516120t t -+=,解得2t =(舍去)或65t =. 所以当65t =时,二面角1A BC C --…13分20. 本题主要考查函数、导数、数列以及合情推理等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想及有限与无限思想.满分14分.解:(Ⅰ)()()x n f x x n e =+⋅ (n N *∈). ……4分(Ⅱ)∵()()1xn f x x n e '=++⋅,∴当()1x n >-+时,()0n f x '>;当()1x n <-+时,()0n f x '<. ∴当()1x n =-+时,()n f x 取得极小值()()()11n n f n e -+-+=-,即()1n n y e -+=-(n N *∈). ……8分 (Ⅲ) 解法一:∵()()()()2213n g x x n n =-+++-,所以()2((1))3n a gn n =-+=-.……9分 又()()()11n n b f n e -+=-+=-,∴()()213n a b n e-+-=-+,令()()()()2130x h x x ex -+=-+≥,则()()()123x h x x e -+'=--. ……10分∵()h x '在[)0,+∞单调递增,∴()()106h x h e -''≥=--, ∵()430h e-'=-<,()5420h e -'=->,∴存在()03,4x ∈使得()00h x '=. ……12分 ∵()h x '在[)0,+∞单调递增,∴当00x x ≤<时,()00h x '<;当0x x >时,()00h x '>, 即()h x 在[)0,x +∞单调递增,在[)00,x 单调递减, ∴()()()0minh x h x =,又∵()43h e -=,()541h e -=+,()()43h h >, ∴当3n =时,a b -取得最小值4e -. ……14分 解法二: ∵()()()()2213n g x x n n =-+++-,所以()2((1))3n a g n n =-+=-.……9分又()()()11n n b f n e -+=-+=-,∴()()213n a b n e -+-=-+,令()()213n n c n e-+=-+,则1211125n n n n c c n e e +++-=-+-,……10分当3n ≥时,1211125n n n n c c n ee+++-=-+-,又因为3n ≥,所以251n -≥,210n e+>,1101n e+<<,所以2111250n n n e e ++-+->,所以1n n c c +>.……12分又1232341114,1,c c c e e e=+=+=,123c c c >>,∴当3n =时,a b -取得最小值4e -. ……14分21.(1)选修4—2:矩阵与变换本题主要考查矩阵、逆矩阵、曲线的线性变换等基础知识,考查运算求解能力及函数与方程思想.满分7分.解:(Ⅰ)记矩阵1234A ⎛⎫= ⎪⎝⎭,故2A =-,故1213122A --⎛⎫⎪= ⎪-⎝⎭. ……2分 由已知得121710710123146461122M A --⎛⎫⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭. ……3分(Ⅱ)设二阶矩阵M 所对应的变换为1211x x y y '⎛⎫⎛⎫⎛⎫=⎪ ⎪⎪'⎝⎭⎝⎭⎝⎭,得2x x yy x y'=+⎧⎨'=+⎩, 解得2x x y y x y ''=-+⎧⎨''=-⎩, ……5分又223861x xy y ++=,故有223(2)8(2)()6()1x y x y x y x y ''''''''-++-+-+-=,化简得2221x y ''+=.故所得曲线的方程为2221x y +=. ……7分(2)选修4—4:坐标系与参数方程 本题主要考查曲线的参数方程、直线的极坐标方程等基础知识,考查运算求解能力以及化归与转化思想、分类与整合思想.满分7分.解:(Ⅰ)∵0t ≠,∴可将曲线C 的方程化为普通方程:2224x y t+=. ……1分①当1t =±时,曲线C 为圆心在原点,半径为2的圆; ……2分 ②当1t ≠±时,曲线C 为中心在原点的椭圆. ……3分 (Ⅱ)直线l 的普通方程为:40x y -+=. ……4分联立直线与曲线的方程,消y 得222(4)4x x t++=,化简得2222(1)8120t x t x t +++=.若直线l 与曲线C 有两个不同的公共点,则422644(1)120t t t ∆=-+⋅>,解得23t >.……5分又22121222812,,11t t x x x x t t +=-=++ ……6分 故12121212(4)(4)OA OB x x y y x x x x ⋅=+=+++121224()1610x x x x =+++=.解得23t =与23t >相矛盾. 故不存在满足题意的实数t . ……7分(3)选修4—5;不等式选讲本题主要考查绝对值的几何意义、柯西不等式等基础知识,考查运算求解能力以及推理论证能力,考查函数与方程思想以及分类与整合思想.满分7分.解:(Ⅰ)法一: 26(4)()242(24)26(2)x x f x x x x x x -≥⎧⎪=-+-=<<⎨⎪-+≤⎩,……2分 可得函数的最小值为2.故2m =. ……3分法二:()24(2)(4)2f x x x x x =-+-≥---=, ……2分 当且仅当24x ≤≤时,等号成立,故2m =. ……3分(Ⅱ) 222222222[()()()]()n p q a b c a b c++⋅++2222()n p q a b c a b c ≥⋅+⋅+⋅ ……5分即:444222()2n p q a b c ++⨯≥2222()4n p q ++=,故4442222n p q a b c++≥. ……7分。
2012年福州市5月市质检理科

一、选择题(本大题共 10小题,每小题5分,共50分.在每小题给出的四个选项中有且只有一项是符合 题目要求的,把答案填在答题卡的相应位置. 1 •已知全集U 二R ,集合M={x X 2 -X 0},则 $ M = A . {x\0 :::x ::: 1} C. { X \ X ::: 0或 X 1} 2.如图,在复平面内,若复数 点位于 A .第一象限 C .第三象限 B . {x\0<X<1} D . { X \ X _ 0或X _ 1} 乙,Z 2对应的向量分别是 OA,OB ,则复数乙Z 2所对应的 B .第二象限 D .第四象限 3 .设等比数列{a n }的前n 项和为S n ,则“ a 0 ”是 A .充分而不必要条件C.充要条件4 .若一个几何体的三视图, 如图所示,则该几何体的体积为 2 3A .一3C . .3B .必要而不充分条件 D .既不充分也不必要条件 其正视图和侧视图均为矩形 3,3 B.-2D . 2、一 35.如图,执行程序框图后,输出的结果为 A .B . 10F 列函数中,周期为二,且在A .JIC . y 二sin !2x •… \ .2丿 7 .已知 AB BC =o , A. 5 話 B.2&若从区间 第2题图 “S3 S 2 ”的 、俯视图为正三角形,尺寸 C. 12 D . 32匚2上单调递增的奇函数是B .D .第4题图y=cos 2x_;JI Iy =cosl2xI 2.丿BC| = 2, 7D DC = o ,贝y "BD C. .5 D. 2\5的最大值为(0, e)内随机取两个数,则这两个数之积不小于e 的概率为2B. 1——e开始5 = 0討— 1 站束第5题图1A . 1 一一e9. 如图,在正方体 ABCD中,若 P 到AR 和BC 的距离相等,则点 P 的轨迹为 A .椭圆的一部分B .圆的一部分C. 一条线段 D .抛物线的一部分10.C.- e 注平面2 D.-eA 1BCD 1上一动点将方程x tanx =0的正根从小到大地依次排列为 310 ::: an 1 -an22a n 1 -a n 2 ■ a n ; ② a n 1 -a^;2④ 2a n 1 < a n 2 - a n ;③其中,正确的判断是 A.①③ B.①④二、填空题:本大题共 5小题,每小题4分,共20分.C.②③ q,a 2,Hl,a n ,川,给出以下不等式:D.②④把答案填在答题卡的相应位置.fi x , xMO …11 .已知函数 f(X ) x,贝V f f -1 二 ______________ .g,x = 02 2 12.已知双曲线 —=1(m 0,n .0)的离心率为2,有一个焦点与抛物线 y 2 =16x m n 的焦点重合,贝U n= _________ . 13 .已知等差数列 Q ?的公差不为零,a a 2 a 5 13,且a > a?、成等比数列, 则a 1的取值范围为 ___________________________ . 14.已知三次函数 f(x)二ax bx ex d 的图象如图所示, 则心第14题图★ ★ ★ f (1) 15. 假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域,则称这条直线平分这个 区域.如图, ① ② ③ ④ 其中正确结论的序号是 _________________ . ....... 三、解答题:本大题共 6小题,共80分.解答写在答题卡相位置,应写出文字说明、证明过程或演 算步骤. 16. (本小题满分13分) 招聘会上,某公司决定先试用后再聘用小强,该公司的甲、乙两个部门各有 4个不同岗位. (I)公司随机安排小强在这两个部门中的 3个岗位上进行试用,求小强试用的 3个岗位中恰有2个 在甲部门的概率; (n)经试用, 表所示: 求甲、乙两部 望与方差,据此请 部门,并说明理由. 17. (本小题 如图,三棱柱 AA _平面ABC X 是平面内的任意一个圭寸闭区域.现给出如下结论: 过平面内的任意一点至少存在一条直线平分区域 :、; 过平面内的任意一点至多存在一条直线平分区域 区域内的任意一点至少存在两条直线平分区域 ; 平面内存在互相垂直的两条直线平分区域 成四份.第15题图 甲、乙两个部门都愿意聘用他•据估计,小强可能获得的岗位月工资及相应概率如下甲部门不同岗位月工资 X 1 (元) 2200 24002600 2800 获得相应岗位的概率 P 0.4 0.3 0.2 0.1 乙部门不同岗位月工资 X 2 (元) 2000 2400 2800 3200 获得相应岗位的概率 F 20.4 0.3 0.2 0.1 门月岗位工资的期 帮助小强选择一个满分13分) ABC - A BQ 1 中, ■ BAC 二 90,AB =2, AC =6, (I)求证: 点 D 在线段 BR 上,且 BD J BB i , AC A AC^ E . 3 直线 DE 与平面ABC 不平行; (n)设平面 ADO 与平面ABC 所成的锐二面角为 二,若COST - 7,求AA 的 长; (川)在(n) 角的余弦值. 的条件下,设平面 ADCJ1平面ABC =1,求直线 I 与DE 所成的 C 与y 轴相切于点T 0,2,与x 轴正半轴相交于两点 在点N 的左侧),且MN =3 . (I)求圆 18.如图,圆 (n)过点 M 任作一条直线与椭圆 C 的方程;2 2-:-y 1相交于两点4 8M, N (点 MA 、B ,连接AN 、BN ,求证: /ANM =NBNM第18题图x =0处的切线方ax19.已知函数f(x) =ln(x 1) a ,R . (I)当a =2时,求函数x +1 = f[1程;(H )判断函数 f (x )的单调性;(川)求证:In 1 -\ n(I )求直线 AB 的直角坐标方程; (H )若直线 AB 和曲线C 只有一个交点,求r 的值.(—)(本小题满分7分)选修4 —5:不等式选讲已知关于x 的不等式• ..「1 :::m 对于任意的X- [-1,2 ]恒成立(I ) 求m 的取值范围;1(n )在⑴的条件下求函数fm m 右的最小值.2012年福州市高中毕业班综合练习 理科数学试卷参考答案及评分参考一、 选择题(本大题共10小题,每小题5分,共50分) I. B 2.A—.C 4.D5.B6.D7. C 8. B 9.D10. D二、 填空题(本大题共5小题,每小题4分,共20分) II. 212. 121—. (1, ::) 14. -515.①④三、 解答题(本大题共6小题,共80分)16.(本小题满分1—分) 解:(I )记事件“小强试用的 —个岗位中恰有2个在甲部门的概率”为 A ,则...................................................................... 6 分C 8 720.(本小题满分14分) 如图, 在平面直角坐标系中,锐角 :•、 (n ) 别为MA 、 (III ) 3 如果tan 〉, B 点的横坐标为 4 若角:的终边与单位圆交于 NB 、PC,求证:线段 MA 、NB 、PC 能构成一个三角形; 探究第(H )小题中的三角形的外接圆面积是否为定值? ■-的终边分别与单位圆交于2—,求COS [二亠〕::j的值; C 点,设角:•、:、〉 若是,求出该定值;若不是,请说明理由 21.本题有(1)、(2 )、(—)三个选答题,每题 7分,请考生任选 题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用 应的题号涂黑,并将所选题号填入括号中. (1)(本小题满分7分)选修4 — 2:矩阵与变换 设矩阵M 是把坐标平面上的点的纵坐标伸长到原来的 2倍,横坐标保持不变的伸缩变换. (1) 求矩阵M ; (n )求矩阵 M 的特征值以及属于每个特征值的一个特征向量. (2) (本小题满分7分)选修4 —4:极坐标与参数方程在直角坐标平面内,以坐标原点 O 为极点,x 轴的非负半轴为极轴建立极坐标系 .已知点A 、B 的极 !x = r COS , ),曲线C 的参数方程为 (:•为参数). y = r si na 2B 铅笔在答题卡上把所选题目对 坐标分别为(1,3、(—,—=40000 ,13分选择乙部门:因为 X 甲二X 乙,D X 甲:D X 乙,说明乙部门各岗位的工资待遇波动比甲部门大,岗位 工资拉的比较开,工作比较有挑战性,能更好地体现工作价值...........17.(本小题满分13分) 解:依题意,可建立如图所示的空间直角坐标系A_xyz ,设AA 1 =h ,贝) f h ) ,A(0,0,h )G(0,6,h )E.J,3,2 \B 2,0,0 ,C 0,6,0 ,D 2,0,h.,(I)证明:由AA 1 _平面ABC 可知n 1 =]0,0,1为平面ABC 的量hhDE n 2,3,0,0,1 0 . J 6 丿' 7 6(H)设平面 ADC 1的法向量为n 2二x,y,z ,则h3 ;AD = x,y,z 2,0, H —* . .V丄h =2x 亠 z =03 ,n 2 AC t = x, y,z | i0,6, h =6y hz =0 ■取 z 二 _6,则 x =y =h ,故住二 h,h, -6 .卄J 」二 cosT = cos c n 1, n 2n 1 n 2ni n 2近1 , 2h2 367'13分个法向11分(H ) E 甲 =2200 0.4 2400 0.3 2600 0.2 2800 0.1=2400 (元),E 乙=2000 0.4 2400 0.3 2800 0.2 3200 0.1 =2400 (元).2 2 2 2D X 甲 ;=]2200 _24000.4 2400-2400 0.3 2600-2400 0.2 2800-2400 0.1........................................................................................................ 9分2 2 2 2D X 乙 i =2000-24000.4 2400-24000.3 2800-24000.2 3200-2400 0.1=160000 . ......................................................................................................................... 10 分 选择甲部门:因为 X 甲二X 乙, D X 甲:D X 乙,说明甲部门各岗位的工资待遇波动比乙部门小,竞争压力没有乙部门大,比较安稳.解得 h =6、.3 . 二 AA = 6 •. 3 ............................................................................................................. 8 分(川)在平面BCC 1B 1内,分别延长CB 、CQ ,交于点F ,连结AF ,则直线 AF 为平面AD^与平面ABC 的交线.1 1BD//CG , BD = — BB 1 = — CC 1 ,3 3 BF _ BD 1FC "CC , ~3 . 1 BF CB ,211AF =AB BF =AB CB =〕2,0,0 2, -6,0 ]:〔3,-3,0 .2 2由(H)知,h =6、.3,故 DE13分(n>0 ),依题意,圆心坐标为 (r,2).1011分 12分 13分( h=23,2,3, •.3 ,I6丿直线I 与DE 所成的角的余弦值为18. (本小题满分13分) 解:(I)设圆C 的半径为r联立方程y2 k X 2 1,消去 y 得,k 2• 2 x 2 - 2k 2x k 2 -8=0 .J 2x y =8设直线AB 交椭圆】于A X|, y 1、B X 2,y 2两点,贝V222kk -8X . X 22 , X . X 22 . ...........................k 22 k 22% 二k 为—2 , y 2 =k X 2 -2 ,kANkBN匸 %丫2 匸 k X 1-1 . k X 2 -1冷 一 4 X [ —4 卷 一 4k x 1 -1 x 2 -4 k x 2 -1 N —42 x解:(I)当 a =2时,f(x) =ln(x -1^ ------------------- ,…f (X) _x 1 (x 1)2 _(x 1)2,••• f (0) =3,所以所求的切线的斜率为3.—t —t cos ::: AF , DEgAF DE -155 -r * 2AF”DE| 12分 MN =3•r 2 I 322,解得 r 2€丿•圆C 的方程为 xI 2丿(H)把y =0代入方程 X25 42+ (y —2)25-42 + (y —2)25一,解得 X =1,或 x = 4 , 4I 2丿即点 M 1,0 , N 4,0 ..... .............. (1 )当AB _x 轴时,由椭圆对称性可知.ZANM.ZBNM . ……(2 )当AB 与x 轴不垂直时,可设直线 AB 的方程为y 二k x_1 .当x 0时,f x . f 0 =0,即卩 In x 1.10分In 1 -丄一丄(n N * ). I n 丿 n n • -x (0,1], In(1 x) - x x 2 0,即 ln(1 x) x - x 2f 1 ) 1ln 1 1 丄-\ n 12分 1 _ *令X=— ( n € N ),则有n13分(n)v fg =ln (x 1)壬(x . -1), x+1L 空」吕「a. .................................................................................................... 5分x+1(x+1) (x+1)①当 a _0 时,••• x . _1 ,••• f (x) 0 ; ............................................. 6分 ②当a :::0时,f (x ) <0 f (x ) . 0由,得 _1 ::: x ::: _1 _ a ;由 ,得 x 号 一1 _ a ; (7)分|x 乜一1x 亏一1综上,当a _0时,函数f (x )在(_1, •::)单调递增;当a :::0时,函数f (x )在(_1,_1一a )单调递减,在(_1—a,;)上单调递增. ..... 8分 (川)方法一:由(H )可知,当 a =_1时, f x =ln x ,1 -一^在0,亠「i 上单调递增.x+1方法二:构造函数 F (x )二ln ( 1 x^x x 2 , (0空x 乞1)• F '(x)11 2x 二 x(2x 1), ...................................... 10分1 +xx+1•••当 0 :: x _1 时,F'(x)0 ;•函数F(x)在(0,1]单调递增. ................................................... 11分 •函数 F(x) F(0),即 F(x) 020. (本小题满分14分)n 1 n.丿1 +1门十1 n另一方面,•- 1 1T ,即 1 — 1n n 1 n n n 11 2 , n1.. ----- n 1 1 1A —. n n............................. 12分11 * r 1、 1令 X = — ( n € N * ),贝y In .1 +— 卜一= ------- ............................. 11 分13分解:(I )已知:是锐角,根据三角函数的定义,sin 」,cos 』,55又co …壽,且]是锐角,所以sin13所以 cos (x 亠!■')二cos : cos :「sin : sin3 12 16 — —65(n )证明:依题意得, MA 二si n> ,一4 55 13 5 13NB 二sin :, PC 二sin(二• ■■-■)cosA 二 因为。
福建省惠安县2012届高三5月月考(数学理)

2012年惠安县普通高中毕业班质量检查数学(理科)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),第Ⅱ卷第21题为选考题,其他题为必考题.本试卷满分150分,考试时间120分钟.注意事项:1. 答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2. 考生作答时,请将答案答在答题卡上,请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3. 选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.4. 保持答题卡卡面清洁,不折叠,不破损.考试结束后,将本试卷和答题卡一并交回. 参考公式:样本数据12,,,n x x x L 的标准差 锥体体积公式s =13V Sh =其中x 为样本平均数 其中S 为底面面积,h 为高柱体体积公式 球的表面积、体积公式V Sh = 24S R π=,343V R π=其中S 为底面面积,h 为高. 其中R 为球的半径.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.命题“x ∀∈R ,30x x ->”的否定是( )A .x ∀∈R ,30x x -< B .x ∃∈R ,30x x -< C .x ∀∈R ,30x x -≤ D .x ∃∈R ,30x x -≤2.集合{|P x y ==,{|2}x Q y y ==,则P 与Q 关系正确的是( )A .P Q ⊆B .Q P ⊆C .P Q φ=ID .P Q =R U 3.某种菜籽在相同的条件下发芽试验,结果如下表:种子粒数 130 310 700 1500 2000 3000 5000 发芽粒数 116 286 639 1339 1810 2097 4515 发芽频率0.8920.9220.9130.8930.9050.8990.903根据上表,可以推断种子发芽的概率最有可能为( )A .0.80B .0.85C .0.90D .0.924.设7270127(1)x a a x a x a x -=++++L ,则0127,,,,a a a a L 中最大的数是( )A .3aB .4aC .5aD .3a 和4a5.“1m =”是“直线10x my m -++=与圆222x y +=相切”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 6. 已知直线,l m ,平面,αβ,且l α⊥,m β⊂,给出下列四个命题:①若//αβ,则l m ⊥;②若l m ⊥,则//αβ;③若αβ⊥,则//l m ;④若//l m ,则αβ⊥.其中正确命题的个数是( )A .0B .1C .2D .3 7.函数()sin(2))f x x x θθ=++为奇函数,且在[,0]4π-上为减函数的θ值可以是( ) A .3π-B .6π-C .56π D .23π 8.阅读右图所示的程序框图,运行相应的程序.从输出的点(,)x y 中任取一点,则该点落在不等式组30203x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩所表示的平面区域内的概率为( )A .13B .16C . 25D .159.已知定义在R 上的奇函数()f x 的图像连续不断,导函数为()f x ',当)0,(-∞∈x 时,恒有()()x f x f x '<-,设)()(x xf x F =,则满足(3)(21)F F x >-的实数x 的取值范围是( )A .1(1,)2-B .(1,2)-C .1(,2)2D .(2,1)-10.在平面直角坐标系xOy 中,抛物线24y x =的准线l 与x 轴的交点为M .过抛物线上一点P 作准线l 的垂线PN ,垂足为N ,若||PM 、||PO 、||PN 依次成等比数列,则||||PM PN -的值为( )A.2BC .2D .4第Ⅱ卷 (非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡的相应位置.11.若复数11iz i-=+,i 是虚数单位,则=||z . 12.设等差数列{}n a 的前n 项和为n S ,若376a a +=,则9S = .主视图1侧视图13.已知(,)2παπ∈,3sin()5πα-=,则 2tan cos ()42παα+-= .14.某几何体的三视图如右图所示,则该几何体体积的最大值为 .15.对于函数()f x ,如果存在锐角θ,使得将函数()f x 的图象绕坐标原点逆时针旋转θ,所得曲线仍是一个函数的图象,则称函数()f x 具有旋转性.给出如下函数: ①12()f x x =; ②()x f x e -=; ③()ln (1)f x x x =≥; ④()sin f x x =. 其中,对任意(0,)4πθ∈,均具有旋转性的函数的序号为 .(写出所有满足条件的函数的序号)三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分13分)某机床厂每月生产某种精密数控机床10件,已知生产一件合格品能盈利8万元,生产一件次品将会亏损2万元.为了估计该机床厂的盈利能力,相关部门对近24..个月..中,(Ⅰ)试估计机床厂今年第三季度中,恰有两个月生产的合格品不少于8件的概率; (Ⅱ)求机床厂每月盈利额η的数学期望.17.(本小题满分13分)如图,在平面直角坐标系xOy 内作单位圆O ,以Ox 轴为始边作任意角,αβ,它们的终边与单位圆O 的交点分别为,A B .(Ⅰ)设105α=︒,75β=︒,求OA OB ⋅uur uu u r;(Ⅱ)试证明差角的余弦公式():cos()cos cos sin sin C αβαβαβαβ--=+.18.(本小题满分13分)如图1,在等腰梯形ABCD 中,//AD BC ,1AD =,3BC =,E 为BC 上一点,且2BE EC =,1DE =.将梯形ABCD 沿DE 折成二面角B DE C --,设其大小为θ.α(Ⅰ)在上述折叠过程中,若90180θ︒≤<︒,请你动手实验并直接写出直线CD 与平面ABED 所成角的取值范围(不必证明);(Ⅱ)当90θ=︒时,连结BC ,AC ,DC ,得到如图2所示的几何体C ABED -,(i )求证:平面AEC ⊥平面ABED ;(ii )在平面BCE 上是否存在点M ,使得线段DM 的中点N 在平面ACE 上,若存在,试确定点M 的位置;若不存在,请说明理由.19.(本小题满分13分)已知椭圆E 的中心在坐标原点,焦点在x 轴上,且过双曲线2221x y -=的顶点.(Ⅰ)求椭圆E 的方程;(Ⅱ)命题:“设M 、N 是双曲线2221x y -=上关于它的中心对称的任意两点,P 为该双曲线上的动点,若直线PM 、PN 均存在斜率,则它们的斜率之积为定值,且定值是12”.试类比上述命题,写出一个关于椭圆E 的类似的正确命题,并加以证明;(Ⅲ)试推广(Ⅱ)中的命题,写出关于方程221mx ny +=(0mn ≠,,m n 不同时为负数)的曲线的统一的一般性命题(不必证明). 20.(本小题满分14分)已知函数()ln f x x ax =-,a ∈R . (Ⅰ)当1a =时,求()f x 的极值; (Ⅱ)讨论函数()y f x =的零点个数;(Ⅲ)设数列{}n a ,{}n b 均为正项数列,且满足112212n n n a b a b a b b b b +++≤+++L L ,求证:12121n bbbn a a a ⋅⋅⋅≤L .21.本题设有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2个小题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B 铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中. (1)(本小题满分7分)选修4—2:矩阵与变换已知ABC ∆经过矩阵M 的变换后变成A B C '''∆,且(1,0)A ,(1,1)B -,(0,1)C -,ABCED图2A B CD E图1(1,0)A ',(0,1)B '-.(Ⅰ)求矩阵M ,并说明它的变换类型;(Ⅱ)试求出点C '的坐标及M 的逆矩阵1-M .(2)(本小题满分7分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,直线l 的参数方程为:1,x t y t=-⎧⎨=⎩(t 为参数).在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线C 的方程为ρ= (Ⅰ)求曲线C 的直角坐标方程; (Ⅱ)设曲线C 与直线l 交于点,M N ,若点P 的坐标为(1,0),求||||P M P N ⋅的值.(3)(本小题满分7分)选修4—5:不等式选讲设不等式21|x |->的解集与关于x 的不等式20x ax b -+>的解集相同. (Ⅰ)求a ,b 的值;(Ⅱ)求函数()f x =x 的值.2012年惠安县普通高中毕业班质量检查理科数学试题参考解答及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则. 二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容与难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有严重的错误,就不再给分.三、解答右端所标注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.选择题和填空题不给中间分.一、选择题:本大题考查基础知识和基本运算.每小题5分,满分50分.1.D 2.A 3.C 4.B 5.C 6.C 7.D 8.A 9.B 10.B 二、填空题:本大题考查基础知识和基本运算.每小题4分,满分20分. 11.1 12.27 13.12014.12 15.②③④三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.本小题主要考查概率与统计、随机变量的分布列及数学期望等基础知识,考查运算求解能力以及应用意识,考查必然与或然思想.满分13分. 解:(Ⅰ)机床厂每月生产的合格品不少于8件的概率为12133-=, ……………2分 所以,今年第三季度中,恰有两个月生产的合格品不少于8件的概率223214()339P C =⋅⋅=. ……………………………6分(Ⅱ)设ξ表示机床厂每月生产合格品的数量,则1511()789108312612E ξ=⨯+⨯+⨯+⨯=, ……………………………8分 因为82(10)1020ηξξξ=--=-, ……………………………10分 所以,()(1020)10()2060E E E ηξξ=-=-=, ……………………………12分 答:该工厂每月盈利额η的数学期望为60万元. ……………………………13分17.本小题主要考查三角函数的定义、向量数量积等基础知识,考查推理论证能力,考查数形结合思想、化归与转化思想、特殊与一般思想等.满分13分.解:(Ⅰ)方法一:由已知,得,OA OB u u r u u u r 的夹角为30︒,||||1OA OB ==u u r u u u r, ……………2分||||cos302OA OB OA OB ∴⋅=︒=uu r uu u r uu r uu u r . ……………………………6分方法二:由三角函数的定义,得点(cos105,sin105)A ︒︒,(cos75,sin 75)B ︒︒, ……………………………2分cos105cos75sin105sin 75cos(10575)2OA OB ∴⋅=︒︒+︒︒=︒-︒=uu r uu u r .……6分 (Ⅱ)设,OA OB u u r u u u r的夹角为θ,因为||||1OA OB ==u u r u u u r ,所以,||||cos cos OA OB OA OB θθ⋅==u u r u u u r u u r u u u r………………8分 另一方面,由三角函数的定义,得(cos ,sin )A αα,(cos ,sin )B ββ, cos cos sin sin OA OB αβαβ∴⋅=+u u r u u u r,…………………10分 故cos cos cos sin sin θαβαβ=+,由于2,k k αβπθ-=±∈Z ,cos()cos αβθ∴-=, …………………12分 所以,cos()cos cos sin sin αβαβαβ-=+. …………………13分18.本小题主要考查空间线面关系、空间角等基础知识;考查空间想象能力、运算求解能力以及推理论证能力;考查数形结合思想、化归与转化思想等.满分13分. 解:(Ⅰ)直线CD 与平面ABED 所成角的取值范围为(0,]4π. ……………………3分(Ⅱ)(i )在图1中,过点A 作//AF DE ,交BC 于F ,由平几知识易得DE BC ⊥,在图2中,,DE BE DE CE ⊥⊥,又90BEC θ∠==︒,BE CE ∴⊥, ,,DE BE CE ∴两两互相垂直, ……………………5分 又DE BE E = ,,DE BE ⊂平面ABED ,CE ∴⊥平面ABED ,又CE ⊂平面AEC ,∴平面AEC ⊥平面ABED .……………………8分ABCDE图1F(ii )以E 为原点,,,EB EC ED 分别为,,x y z 轴,建立空间直角坐标系E xyz -,如图所示.则(0,0,0)E ,(1,0,1)A ,(2,0,0)B ,(0,1,0)C ,(0,0,1)D ,…………………………………………9分假设在平面BCE 上存在点(,,0)M x y ,使得线段DM 的中点N 在平面ACE 上,则点N 的坐标为1(,,)222x y ,且存在实数,λμ,使得EN EA EC λμ=+ ,…………………………………………10分又1(,,),(1,0,1),(0,1,0)222x y EN EA EC ===,……………………11分∴,2,21,2x yλμλ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩即1,2,x y μ=⎧⎨=⎩ ∴点(1,2,0)M μ,……………………12分 故存在满足条件的点M ,其轨迹是平行于直线EC ,且与直线EC 的距离及与点B 的距离均为1的直线. ……………………13分19.本小题主要考查椭圆、双曲线的标准方程与性质、直线与圆锥曲线的位置关系以及合情推理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想等.满分13分.解:(Ⅰ)设椭圆E 的方程为22221(0)x y a b a b+=>>,半焦距为c ,则1,2c a a ==222124c b a c ∴==-=,∴椭圆E 的方程为2241x y +=. ………………………………5分(Ⅱ)关于椭圆E 的正确命题是:设M 、N 是椭圆2241x y +=上关于它的中心对称的任意两点,P 为该椭圆上的动点,若直线PM 、PN 均存在斜率,则它们的斜率之积为定值,且定值是14-. ………………………………6分 证明如下:设点(,)P x y ,00(,)M x y ,00(,)N x y --, ………………………………7分直线PM 、PN 的斜率分别为,PM PN k k ,则2200022000PM PNy y y y y y k k x x x x x x -+-⋅=⋅=-+-, ………………………………8分点(,)P x y ,00(,)M x y 在椭圆上,∴2241x y +=,且220041x y +=,∴222200440x x y y -+-=, 即22022014y y x x -=--,…………………………9分 所以,14PM PN k k ⋅=-(定值). …………………………10分(Ⅲ)关于方程221mx ny +=(0mn ≠,,m n 不同时为负数)的曲线的统一的一般性命题是:设M 、N 是方程221mx ny +=(0mn ≠,,m n 不同时为负数)的曲线上关于它的中心对称的任意两点,P 为该曲线上的动点,若直线PM 、PN 均存在斜率,则它们的斜率之积为定值,且定值是mn-.……………………13分20.本小题主要考查函数、导数、数列、不等式等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、函数与方程思想、分类与整合思想、化归与转化思想以及有限与无限思想.满分14分. 解:(Ⅰ)当1a =时,1()1f x x'=-(0x >), 当01x <<时,()0f x '>,当1x >时,()0f x '<, ()f x ∴在(0,1)上递增,在(1,)+∞上递减,∴当1x =时,()f x 取得极大值1-,无极小值.………………………………4分(Ⅱ)方法一,由()0f x =,得ln xa x=(*), 令ln ()x g x x =,则21ln ()xg x x -'=, ……………………………5分当0x e <<时,()0g x '>,当x e >时,()0g x '<, ()g x ∴在(0,)e 上递增,在(,)e +∞上递减,m a x 1()()g x g e e∴==, ……………………………6分又当0x →时,()g x →-∞;当x e >时,ln ()0xg x x=>,……………8分 ∴当0a ≤或1a e =时,方程(*)有唯一解,当10a e <<时,方程(*)有两个不同解,当1a e>时,方程(*)无解,所以,当0a ≤或1a e=时,()y f x =有1个零点;当10a e <<时,()y f x =有2个零点;当1a e>时,()y f x =无零点. …………………………10分方法二,由()0f x =,得ln x ax =,()y f x ∴=的零点个数为ln y x =和y ax =的图象交点的个数. ……………5分由ln y x =和y ax =的图象可知:当0a ≤时,()y f x =有且仅有一个零点;……………………………6分当0a >时,若直线y a x =与ln y x =相切,设切点为00(,)P x y ,因为1(ln )y x x''==, 000ln 1x k x x ∴=切=,得0x e =,1k e ∴切=, 故当1a e =时,()y f x =有且仅有一个零点; …………………………8分当10a e <<时,()y f x =有两个零点;当1a e>时,()y f x =无零点,综上所述,当0a ≤或1a e=时,()y f x =有1个零点;当10a e <<时,()y f x =有2个零点;当1a e>时,()y f x =无零点. …………………………10分(Ⅲ)由(Ⅰ)知,当(0,)x ∈+∞时,ln 1x x ≤-.0,0n n a b >>Q ,ln 1n n a a ∴≤-,从而有ln n n n n n b a b a b ≤-,即ln n b n n n n a b a b ≤-(*n ∈N ), …………………………12分111ln inn nb ii i i i i i ab a b ===∴≤-∑∑∑,112212n nn a b a b a b b b b +++≤+++Q L L ,即110n ni i i i i b a b ==-≤∑∑, 1l n 0inb i i a=∴≤∑,即1212ln()0n b b b n a a a ⋅⋅⋅≤L ,12121n b b b n a a a ∴⋅⋅⋅≤L . …………………………14分21.(1)(本小题满分7分)选修4—2:矩阵与变换本小题主要考查矩阵与变换等基础知识,考查运算求解能力,考查数形结合思想等.满分7分.解:(Ⅰ)设M =⎣⎢⎡⎦⎥⎤a b c d ,依题意得⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤10=⎣⎢⎡⎦⎥⎤10,且⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤ 1-1=⎣⎢⎡⎦⎥⎤0-1, ∴⎩⎪⎨⎪⎧a =1,c =0,a -b =0,c -d =-1.解得,⎩⎪⎨⎪⎧a =1,b =1,c =0,d =1.∴M =⎣⎢⎡⎦⎥⎤110 1,它是沿x 轴方向的切变变换. ………………………………4分(Ⅱ)∵⎣⎢⎡⎦⎥⎤110 1 ⎣⎢⎡⎦⎥⎤0-1=⎣⎢⎡⎦⎥⎤-1-1,故点C ′的坐标是(-1,-1), 又||10=≠M ,11101--⎛⎫∴=⎪⎝⎭M . ………………………………7分(2)(本小题满分7分)选修4—4:坐标系与参数方程本小题主要考查参数方程、极坐标方程等基础知识,考查运算求解能力,考查化归与转化思想等.满分7分.解:(Ⅰ)由ρ=,得25ρ=,∴225x y +=,曲线C 的直角坐标方程为225x y +=. ………………………………3分 (Ⅱ)把直线的参数方程代入到曲线C 的直角坐标方程,得22(1)5t t -+=,即220t t --=,由于30∆=>,故可设12,t t 是上述方程的两实根,所以122t t =-,又直线l 过点(1,0)P ,故由上式及t 的几何意义,得2|||||4PM PN ⋅==.………………………………7分(3)(本小题满分7分)选修4—5:不等式选讲本小题主要考查绝对不等式、一元二次不等式、柯西不等式等基础知识,考查推理论证能力, 考查化归与转化思想等.满分7分.解:(Ⅰ)不等式21|x |->的解集为{|13}x x x <>或,所以,不等式20x ax b -+>的解集为{|13}x x x <>或,4,3a b ∴==. ………………………………3分(Ⅱ)函数的定义域为]5,3[,显然有0>y ,由柯西不等式可得: 25)5()3(3453342222=-+-⨯+≤-+-=x x x x y ,当且仅当3354-=-x x 时等号成立,即25107=x 时,函数取得最大值25. ………………………………7分。
2012年高考理科数学福建卷(含答案解析)

数学试卷 第1页(共21页)数学试卷 第2页(共21页) 数学试卷 第3页(共21页)绝密★启用前2012年普通高等学校招生全国统一考试(福建卷)数学试题(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数z 满足i 1i z =-,则z 等于( )A .1i --B .1i -C .1i -+D .1i +2. 等差数列{}n a 中,1510a a +=,47a =,则数列{}n a 的公差为( )A .1B .2C .3D .4 3. 下列命题中,真命题是( )A .0x ∃∈R ,0e 0x ≤B .x ∀∈R ,22x x >C .0a b +=的充要条件是1ab=-D .1a >,1b >是1ab >的充分条件4. 一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是 ( )A .球B .三棱锥C .正方体D . 圆柱 5. 下列不等式一定成立的是( )A .21lg()lg (0)4x x x +>>B .1sin 2(π,k )sin x x k x +≠∈≥ZC .22||(x x x ∈+1≥R)D .211()1x x ∈+>R6. 如图所示,在边长为1的正方形OABC 中任取一点P ,则点P 恰好取自阴影部分的概率为( )A .14 B .15 C .16D .177. 设函数1,()0,x D x x ⎧=⎨⎩为有理数,为无理数,则下列结论错误的是 ( )A .()D x 的值域为{0,1}B .()D x 是偶函数C .()D x 不是周期函数D .()D x 不是单调函数8. 已知双曲线22214x y b-=的右焦点与抛物线212y x =的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )AB.C .3D .59. 若函数2x y =图象上存在点(,)x y 满足约束条件30,230,,x y x y x m +-⎧⎪--⎨⎪⎩≤≤≥则实数m 的最大值为( )A .12 B .1 C .32D .210. 函数()f x 在[,]a b 上有定义,若对任意12,[,]x x a b ∈,有12121()[()()]22x x f f x f x ++≤,则称()f x 在[,]a b 上具有性质P .设()f x 在[1,3]上具有性质P ,现给出如下命题: ①()f x 在[1,3]上的图象是连续不断的; ②2()f x在上具有性质P ;③若()f x 在2x =处取得最大值1,则()1f x =,[1,3]x ∈; ④对任意1x ,2x ,3x ,4[1,3]x ∈,有123412341()[()()()()]44x x x x f f x f x f x f x ++++++≤.其中真命题的序号是( )A .①②B .①③C .②④D .③④第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡的相应位置. 11.4()a x +的展开式中3x 的系数等于8,则实数a =_______. 12.阅读右图所示的程序框图,运行相应的程序,输出的s 值等于________.13.已知ABC △的等比数列,则其最大角的余弦值为________.14.数列{}n a 的通项公式ππcos12n n a =+,前n 项和为n S ,则2012S =________.15.对于实数a 和b ,定义运算“*”;22,,*,.a ab a b a b b ab a b ⎧-=⎨-⎩≤>设()(21)*(1)f x x x =--,且关于x 的方程()(f x m m =∈R)恰有三个互不相等的实数根1x ,2x ,3x ,则123x x x 的取值范围是_______.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16.(本小题满分13分)受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已将频率视为概率,解答下列问题:(Ⅰ)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率;(Ⅱ)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为1X ,生产一辆乙品牌轿车的利润为2X ,分别求1X ,2X 的分布列;(Ⅲ)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应产生哪种品牌的轿车?说明理由.--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共21页)数学试卷 第5页(共21页)数学试卷 第6页(共21页)17.(本小题满分13分)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数: (1)22sin 13cos 17sin13cos17+-; (2)22sin 15cos 15sin15cos15+-; (3)22sin 18cos 12sin18cos12+-; (4)22sin (18)cos 48sin(18)cos48-+--; (5)22sin (25)cos 55sin(25)cos55-+--.(Ⅰ)试从上述五个式子中选择一个,求出这个常数;(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.18.(本小题满分13分)如图,在长方体1111ABCD A B C D -中,11AA AD ==,E 为CD 中点. (Ⅰ)求证:11B E AD ⊥;(Ⅱ)在棱1AA 上是否存在一点P ,使得DP ∥平面1B AE ?若存在,求AP 的长;若不存在,说明理由;(Ⅲ)若二面角11A B E A --的大小为30,求AB 的长.19.(本小题满分13分)如图,椭圆E :22221(0)x y a b a b +=>>的左焦点为1F ,右焦点为2F ,离心率12e =.过1F 的直线交椭圆于A 、B 两点,且2ABF △的周长为8. (Ⅰ)求椭圆E 的方程;(Ⅱ)设动直线l :y kx m =+与椭圆E 有且只有一个公共点P ,且与直线4x =相交于点Q .试探究:在坐标平面内是否存在定点M ,使得以PQ 为直径的圆恒过点M ?若存在,求出点M 的坐标;若不存在,说明理由.20.(本小题满分14分)已知函数2()e e x f x ax x =+-,a ∈R .(Ⅰ)若曲线()y f x =在点(1(1))f ,处的切线平行于x 轴,求函数()f x 的单调区间; (Ⅱ)试确定a 的取值范围,使得曲线()y f x =上存在唯一的点P ,曲线在该点处的切线与曲线只有一个公共点P .21.本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B 铅笔在答题卡上把所选题目对应题号右边的方框涂黑,并将所选题号填入括号中.(1)(本小题满分7分)选修4—2:矩阵与变换设曲线22221x xy y ++=在矩阵01a A b ⎛⎫= ⎪⎝⎭(0)a >对应的变换作用下得到的曲线为221x y +=.(Ⅰ)求实数a ,b 的值;(Ⅱ)求2A 的逆矩阵.(2)(本小题满分7分)选修4—4:坐标系与参数方程在平面直角坐标系中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l 上两点M ,N 的极坐标分别为(2,0),π)2,圆C的参数方程为22cos ,2sin x y θθ=+⎧⎪⎨=⎪⎩(θ为参数). (Ⅰ)设P 为线段MN 的中点,求直线OP 的平面直角坐标方程; (Ⅱ)判断直线l 与圆C 的位置关系. (3)(本小题满分7分)选修4—5:不等式选讲已知函数|2|f x m x =--(),m ∈R ,且2()0f x +≥的解集为[1,1]-. (Ⅰ)求m 的值; (Ⅱ)若,,a b c ∈R ,且11123m a b c++=,求证:239a b c ++≥.2012年普通高等学校招生全国统一考试(福建卷)数学试题(理工农医类)答案解析又双曲线的渐近线方程故选B.30x y+-≤⎧数学试卷第7页(共21页)数学试卷第8页(共21页)数学试卷第9页(共21页)数学试卷 第10页(共21页)数学试卷 第11页(共21页)数学试卷 第12页(共21页)(2)1f =,又42x f +⎛ ⎝又()1f x ≤1≤,所以对于④,f ⎛⎛ ⎝4)()]f x +216,1()E X >可知甲品牌轿车首次出现故障发生在保修期内的轿车数数学试卷 第13页(共21页)数学试卷 第14页(共21页)数学试卷 第15页(共21页)21315cos 15sin15cos151sin3024+-=-=;3(30)sin cos(30)4ααα---=,(30)sin cos(30)ααα---2131⎫⎛【提示】(Ⅰ)选择②,由22sin 15cos 15sin15cos151sin3024+-=-=,可得这个常数的值.(Ⅱ)推广,得到三角恒等式223sin cos (30)sin cos(30)4αααα+---=,直接利用两角(0,1,1)AD ∴=,a B E ⎛=- ,(,0,1)AB a =,,1,0a AE ⎛= 1101102aAD B E =-⨯+⨯+,11B E AD ∴⊥;(Ⅱ)假设在棱,使得DP ∥平面此时(0,DP =-的法向量(,,)n x y z =n ⊥平面1B AE ,n AB ⊥,n AE ⊥,得,02ax y +=⎩取1x =,得平面AE 的一个法向量1,,2a n ⎛=- ⎝⎭,只要n DP ⊥,有2a n DP =-1AP =; 11B C A D ∥1AD B ∴⊥11EB C B =1AD ∴⊥平面平面11A B CD ,AD ∴是平面的一个法向量,此时(0,1,1)AD =,设AD 与n 所成的角为11cos ||||n AD n AD θ==,二面角A -的大小为30, cos30,即y 轴,可求出向量AD 与B E 的坐标,验证其数量积为30建立关于||F =0MP MQ =①,①对0(0,2)x ∈数学试卷 第16页(共21页)数学试卷 第17页(共21页)数学试卷 第18页(共21页)③当0<x x '时,同理可证,与条件不符;∴当<0a 时,存在唯一的点[]ln(2),ln(2)P a f a ⎡⎤--⎣⎦使该点处的切线与曲线只有一个公共点P .【提示】(Ⅰ)求导函数,利用曲线()f x 在点[]1,(1)f 处的切线平行于x 轴,可求a 的值,令()e e 0xf x '=-<,可得函数()f x 的单调减区间;令()0f x '>,可得单调增区间;(Ⅱ)设点[]00,()P x f x ,曲线()y f x =在点P 处的切线方程为000()()()y f x x x f x '=-+, 令000()()()()()g x f x f x x x f x '=---,曲线在该点处的切线与曲线只有一个公共点P 等价于()g x 有唯一零点,求出导函数,再进行分类讨论:(Ⅰ)若0a ≥,()g x 只有唯一零点0x x =,由P 的任意性0a ≥不合题意;(Ⅱ)若<0a ,令00()e e 2()x xh x a x x =-+-,则()0h x =,()e 2xh x a '=+,可得函数的单调性,进而可研究()g x 的零点,由此可得结论.【考点】利用导数研究曲线上某点切线方程,利用导数研究函数的单调性 21.【答案】(Ⅰ)1a =1b =(Ⅱ)2110()21-⎛⎫= ⎪-⎝⎭A【解析】(Ⅰ)设曲线22221x xy y ++=上任一点(,)P x y ,在矩阵A 对应变换下的项是(),P x y ''',则220()()11x a x ax x axax bx y y b y bx y y bx y''=⎛⎫⎛⎫⎧⎛⎫⎛⎫==⇒⇒++=⎨ ⎪ ⎪ ⎪ ⎪''+=+⎝⎭⎝⎭⎝⎭⎝⎭⎩, 2222()21a b x bxy y ∴+++=, 222a b ∴+=,22b =,1a ∴=,1b =;(Ⅱ)由(Ⅰ)得:21010101011111121⎛⎫⎛⎫⎛⎫⎛⎫=⇒== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭A A , 2110||1()21-⎛⎫=⇒= ⎪-⎝⎭A A .【提示】(Ⅰ)确定点在矩阵0(0)1a a b ⎛⎫=> ⎪⎝⎭A 对应的变换作用下得到点坐标之间的关系,利用变换前后的方程,即可求得矩阵A ;23.【答案】(Ⅰ)(2)||0f x m x +=-≥,||x m ∴≤,>0<<m m x m ⇒-,(2)011f x x +≥⇒-≤≤,1m ∴=;(Ⅱ)由(Ⅰ)知111123a b c++=,a ,b ,c ∈R , 由柯西不等式得:211123(23)2392323a b c a b c a bc a b c a bc ⎛⎫+++++++≥++= ⎪⎪⎝⎭⎭. 【提示】(Ⅰ)由条件可得(2)||f x m x +=-,故有||0m x -≥的解集为[]1,1-,即||x m ≤的解集为[]1,1-,故1m =;(Ⅱ)根据111233223(23111232233)a b c a c a b a b c a b c a b a b b c c c ⎛⎫++=++++++++ ⎪⎝⎭++=++,利用基本不等式证明它大于或等于9.【考点】带绝对值的函数,不等式的证明数学试卷第19页(共21页)数学试卷第20页(共21页)数学试卷第21页(共21页)。
