02第二篇回归分析与相关分析业题

合集下载

回归分析练习试题和参考答案解析

1 下面是7个地区2000年的人均国内生产总值（GDP）和人均消费水平的统计数据：求：(1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。

(2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。

(3)求出估计的回归方程，并解释回归系数的实际意义。

(4)计算判定系数，并解释其意义。

α=)。

(5)检验回归方程线性关系的显著性(0.05(6)如果某地区的人均GDP为5000元，预测其人均消费水平。

(7)求人均GDP为5000元时，人均消费水平95％的置信区间和预测区间。

解：（1）可能存在线性关系。

（2）相关系数：系数a模型非标准化系数标准系数t Sig.相关性B标准误差试用版零阶偏部分1(常量).003人均GDP.309.008.998.000.998.998.998 a. 因变量: 人均消费水平有很强的线性关系。

（3）回归方程：734.6930.309y x=+系数a模型非标准化系数标准系数t Sig.相关性回归系数的含义：人均GDP没增加1元，人均消费增加元。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1（常量）人均GDP（元）%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（4）模型汇总模型R R 方调整 R 方标准估计的误差1.998a.996.996a. 预测变量: (常量), 人均GDP。

人均GDP对人均消费的影响达到%。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

模型摘要模型R R 方调整的 R 方估计的标准差1.998(a)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（5）F检验：Anova b模型平方和df均方F Sig.1回归.6801.680.000a 残差5总计.7146a. 预测变量: (常量), 人均GDP。

回归与相关分析

回归分析和相关分析早在十九世纪后半期就已经开始应用，随着工业生产和科学技术的发展，在生物学界人类学界以及社会科学领域里需要回答如何度量现象之间的关系，在1877年以及1892年美国有两位学者都对此做出过尝试，但较有成效的要归功于英国学者，英国遗传学家高尔登（Francis Galton）对遗传问题进行了大量的研究1877-1889年十年间高尔登得出了一个数学公式，这个公式用来度量孩子身高与父母平均身高之间的关系，根据统计测定，假如父母身高在人类平均身高上下y英寸，则他们的子女身高在人类平均身高上下2|3y英寸，他发现了一个规律，及子女的平均高度有恢复到人类总高度的倾向，这就是回归法则，虽然2|3这个数值并未作出最后的定论，回归一词已经成为统计上研究事物相互关系的通用语。

1890年高尔登的学生皮尔逊初次床用积距相关系数，其后这个方法被广泛的运用于各个领域，如1901年Hooker用这种相关系数研究结婚率和贸易之间的关系，Yule用此方法研究出生率死亡率与贸易间的关系。

近年来相关与回归分析方法被广泛的应用于生物学心理学社会学医学扥领域。

首先理清相关关系与函数关系事物的联系是普遍的。

因此，客观世界中的许多事物之间都存在着相互影响、相互制约、相互关联的关系。

客观现象尤其是经济现象之间的这种相互联系都可以通过一定的数量关系形式反应出来。

而现象之间的数量关系，又可以区分成两种不同的类型；函数关系和统计相关关系。

函数关系是指现象之间存在的确定性的数量依存关系。

相关关系，是指现象之间存在的非确定性的数量依存关系。

即一个现象发生数量上的变化，另一个现象数量水平也会相应的发生变化，但这种数量并不是一一对应的关系，一个变量的取值变化时另一个变量并不会有一个数值与之对应，而是可能存在许多不同的值，不过这些值会围绕某个数值上下波动。

统计学相关与回归分析试题

相关与回归分析试题一、单项选择题1、自然界和人类社会中的诸多关系基本上可归纳为两种类型，这就是（）A.函数关系和相关关系B.因果关系和非因果关系C.随机关系和非随机关系D.简单关系和复杂关系 2、相关关系是指变量间的（）A.严格的函数关系B.简单关系和复杂关系C.严格的依存关系D.不严格的依存关系3.具有相关关系的两个变量的关系是（）A.一个变量的取值不能由另一个变量唯一确定B.一个变量的取值由另一个变量唯一决定C.变量之间的一种确定性的数量关系D.变量之间存在的一种函数关系 4.当变量x 的值增加时，变量y 的值也随之增加，那么变量x 和变量y 之间存在着（）。

A.正相关系 B.负相关系C.不确定关系D.非线性相关关系 5.下列相关系数的取值不正确的是（）A. 0B. -0.96C.0.87D.1.066.两个变量之间的线性相关关系越不密切，相关系数r 值就越接近（） A.-1 B.+1D.0 D.大于-1或小于+1 7.相关系数的值越接近-1，表明两个变量间（）A.正线性相关关系越弱B.负线性相关关系越强C.负线性相关关系越弱D.正线性相关关系越强 8.回归分析中，被解释的变量称为（）A.自变量B.因变量C.随机变量D.非随机变量 9.根据最小二乘法配合线性回归方程是使（）A.最小）（=∑2y ˆ-y B.最小）（=∑y ˆ-yC.最小）（=∑2y -y D.最小）（=∑y -y10.回归方程 1.5x 123yˆ+=中回归系数的意思是，当自变量每增加一个单位时，因变量（）A.增加1.5个单位B.平均增加1.5个单位C.增加123个单位D.平均增加123个单位11.若回归系数b 大于0，表明回归直线是上升的，此时相关系数r 的值（） A.一定大于0 B.一定小于0 C.等于0 D.无法判断 12.在回归分析中，F 检验主要用来检验（）A.相关系数的显著性B.回归系数的显著性C.线性关系的显著性D.估计标准误差的显著性13.在多元线性回归方程k k 22110x b x b x b b yˆ++++= 中，回归系数i b 表示（） A.自变量i x 每变动一个单位因变量y 的平均变动量 B.自变量i x 每变动一个单位因变量y 的变动总量C.在其他条件不变的情况下，自变量i x 每变动一个单位因变量y 的平均变动量D.在其他条件不变的情况下，自变量i x 每变动一个单位因变量y 的变动总量 14.在多元线性回归分析中，t 检验用来检验（）A.总体线性关系的显著性B.各回归系数的显著性C.样本线性关系的显著性D.各相关系数的显著性15.在多元线性回归分析中，如果F 检验表明线性关系显著，则意味着（） A.至少有一个自变量与因变量之间的线性关系是显著的 B.所有自变量与因变量之间的线性关系都是显著的C.至少有一个自变量与因变量之间的线性关系是不显著的D.所有自变量与因变量之间的线性关系都是不显著的16.在多元线性回归分析中，若自变量i x 对因变量y 的影响很小，则回归系数i b （） A.可能接近0 B.可能接近1 C.可能小于0 D.可能大于1 二、多项选择题1.下列关系中属于相关关系的是（）A.家庭收入与消费支出的关系B.商品价格与商品需求量的关系C.速度不变，路程与时间的关系D.肥胖程度和死亡率的关系E.利率变动与居民储蓄存款额的关系2.判断变量之间相关关系形态及密切程度的方法有（） A.回归方程 B.散点图 C.相关系数 D.回归系数3.回归方程可用于（）A.根据自变量预测因变量B.根据给定因变量推算自变量C.确定两个变量之间的相关程度D.解释自变量与因变量的数量依存关系 4.在回归分析中要建立有意义的线性回归方程，应该满足的条件是（） A.现象间存在着显著性的线性相关关系 B.相关系数必须等于1C.在两个变量中须确定自变量和因变量D.相关数列的项数应足够多 5.对于简单线性回归方程的回归系数b ，下列说法中正确的是（）A.b 是回归直线的斜率B.b 的绝对值介于0~1之间C.b 接近0表明自变量对因变量的影响不大D.b 与r 有相同的符号三、计算题1、为探讨某产品的耗电量x （单位：度）与日产量y （单位：件）的相关关系，随机抽选了10个企业，经计算得到：，，，，要求：①计算相关系数；②建立直线回归方程，解释回归系数的经济意义。

应用回归分析_第2章课后习题参考答案

2.1 一元线性回归模型有哪些基本假定？答：1. 解释变量 1x , ,2x ,p x 是非随机变量，观测值,1i x ,,2 i x ip x 是常数。

2. 等方差及不相关的假定条件为⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧≠=====j i n j i j i n i E j i i ,0),,2,1,(,),cov(,,2,1,0)(2 σεεε 这个条件称为高斯-马尔柯夫(Gauss-Markov)条件，简称G-M 条件。

在此条件下，便可以得到关于回归系数的最小二乘估计及误差项方差2σ估计的一些重要性质，如回归系数的最小二乘估计是回归系数的最小方差线性无偏估计等。

3. 正态分布的假定条件为⎩⎨⎧=相互独立n i n i N εεεσε,,,,,2,1),,0(~212 在此条件下便可得到关于回归系数的最小二乘估计及2σ估计的进一步结果，如它们分别是回归系数的最及2σ的最小方差无偏估计等，并且可以作回归的显著性检验及区间估计。

4. 通常为了便于数学上的处理，还要求,p n >及样本容量的个数要多于解释变量的个数。

在整个回归分析中，线性回归的统计模型最为重要。

一方面是因为线性回归的应用最广泛；另一方面是只有在回归模型为线性的假设下，才能的到比较深入和一般的结果；再就是有许多非线性的回归模型可以通过适当的转化变为线性回归问题进行处理。

因此，线性回归模型的理论和应用是本书研究的重点。

1. 如何根据样本),,2,1)(;,,,(21n i y x x x i ip i i =求出p ββββ,,,,210 及方差2σ的估计;2. 对回归方程及回归系数的种种假设进行检验；3. 如何根据回归方程进行预测和控制，以及如何进行实际问题的结构分析。

2.2 考虑过原点的线性回归模型 n i x y i i i ,,2,1,1 =+=εβ误差n εεε,,,21 仍满足基本假定。

求1β的最小二乘估计。

答：∑∑==-=-=ni ni i i i x y y E y Q 1121121)())(()(ββ∑∑∑===+-=--=∂∂n i n i ni i i i i i i x y x x x y Q111211122)(2βββ 令,01=∂∂βQ即∑∑===-n i ni i i i x y x 11210β 解得,ˆ1211∑∑===ni ini i i xyx β即1ˆβ的最小二乘估计为.ˆ1211∑∑===ni ini ii xyx β2.3 证明： Q (β，β1)= ∑(y i-β0-β1x i)2因为Q (∧β0,∧β1)=min Q (β0,β1 )而Q (β0,β1) 非负且在R 2上可导,当Q 取得最小值时，有即-2∑(y i -∧β0-∧β1x i )=0 -2∑(y i-∧β0-∧β1x i ) x i=0又∵e i =yi -( ∧β0+∧β1x i )= yi -∧β0-∧β1x i ∴∑e i =0，∑e i x i =0（即残差的期望为0，残差以变量x 的加权平均值为零）2.4 解：参数β0，β1的最小二乘估计与最大似然估计在εi~N(0, 2 ) i=1,2，……n 的条件下等价。

第2章习题

3. 美国各航空公司业绩的统计数据公布在《华尔街日报 1999 年年鉴》（The Wall Street Journal Almanac 1999）上。航班正点到达的比率和每 10 万名乘客投诉的次数的数据如下。
航空公司名称
航班正点率（%）
投诉率（次/10 万名乘客）
西南(Southwest)航空公司
D （X，Y）
16. 以 Y 表示实际观测值， Yˆ 表示 OLS 估计回归值，则用 OLS 得到的样本回归直线
Yˆ i＝βˆ0 + βˆ1Xi 满足（）
∑ A （Yi－Yˆ i）＝0 ∑ B （Yi－Yi）2＝0 ∑ C （Yi－Yˆ i）2＝0 ∑ D （Yˆ i－Yi）2＝0
17. 若一正常商品的市场需求曲线向下倾斜，则可断定（） A 它具有不变的价格弹性 B 随需求量增加，价格下降 C 随需求量增加，价格上升 D 需求无弹性
6. 在总体回归直线 E（Yˆ ）＝β0 + β1X 中， β1表示（） A 当 X 增加一个单位时，Y 增加 β1 个单位 B 当 X 增加一个单位时，Y 平均增加 β1 个单位 C 当 Y 增加一个单位时，X 增加 β1 个单位 D 当 Y 增加一个单位时，X 平均增加 β1 个单位
7. 最小二乘准则是指使（
C Yi＝βˆ0 + βˆ1Xi + ei
D Yˆ i＝βˆ0 + βˆ1Xi + ei
E E(Yi )＝βˆ0 + βˆ1Xi
4. Yˆ 表示 OLS 估计回归值，u 表示随机误差项。如果 Y 与 X 为线性相关关系，则下列哪些
是正确的（
）
A Yi＝β0 + β1Xi
B Yi＝β0 + β1Xi＋ui

回归分析课后习题

第一章习题1.1变量间统计关系和函数关系的区别是什么？1.2回归分析与相关分析的区别和联系是什么？1.3回归模型中随机误差项的意义是什么？1.4线性回归模型中的基本假设是什么？1.5回归变量设置的理论依据是什么？在设置回归变量时应注意哪些问题？1.6收集、整理数据包括哪些基本内容？1.7构造回归理论模型的基本依据是什么？1.8为什么要对回归模型进行检验？1.9回归模型有哪几个方面的应用？1.10为什么强调运用回归分析研究经济问题要定性分析和定量分析相结合？第二章习题2.1一元线性回归模型有哪些基本假定？ 2.2 考虑过原点的线性回归模型1,1,,i i i y x i n βε=+=误差1,,n εε仍满足基本假定。

求1β的最小二乘估计。

2.3证明（2.27）式，10nii e==∑，10ni i i x e ==∑。

2.4回归方程01Ey x ββ=+的参数01,ββ的最小二乘估计与极大似然估计在什么条件下等价？给出证明。

2.5 证明0ˆβ是0β的无偏估计。

2.6 证明(2.42)式 ()()222021,i x Var n x x βσ⎡⎤=+⎢⎥-⎢⎥⎣⎦∑成立 2.7 证明平方和分解式SST SSR SSE =+2.8 验证三种检验的关系，即验证：（1）t ==（2）2212ˆ1ˆ2xx L SSR F t SSE n βσ===-2.9 验证（2..63）式：()()221var 1i i xx x x e n L σ⎡⎤-=--⎢⎥⎢⎥⎣⎦2.10 用第9题证明()2211ˆˆ2n i ii y y n σ==--∑是2σ的无偏估计。

2.11* 验证决定系数2r 与F 值之间的关系式 22Fr F n =+-以上表达式说明2r 与F 值是等价的，那么我们为什么要分别引入这两个统计量，而不是只使用其中的一个。

2.12* 如果把自变量观测值都乘以2，回归参数的最小二乘估计0ˆβ和1ˆβ会发生什么变化？如果把自变量观测值都加上2，回归参数的最小二乘估计0ˆβ和1ˆβ会发生什么变化？ 2.13 如果回归方程01ˆˆˆy x ββ=+相应的相关系数r 很大，则用它预测时，预测误差一定较小。

《应用回归分析》课后题答案[整理版]

《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系，而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。

1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。

区别有a.在回归分析中，变量y称为因变量，处在被解释的特殊地位。

在相关分析中，变量x和变量y处于平等的地位，即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。

b.相关分析中所涉及的变量y与变量x全是随机变量。

而在回归分析中，因变量y是随机变量，自变量x可以是随机变量也可以是非随机的确定变量。

C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。

而回归分析不仅可以揭示变量x 对变量y的影响大小，还可以由回归方程进行预测和控制。

1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项，正是由于随机误差项的引入，才将变量间的关系描述为一个随机方程，使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系，由于客观经济现象是错综复杂的，一种经济现象很难用有限个因素来准确说明，随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。

1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的，观测值xi1.xi2…..xip是常数。

2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。

4.样本容量的个数要多于解释变量的个数，即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量，即便是不显著的，如果理论上无法判断那么可以采用统计方法来判断，解释变量和被解释变量存在统计关系。

题目：基于R对国内各省市区主要经济指标的相关性分析与回归分析 (2)

基于R对国内各省、市、区GDP与主要经济指标的回归分析学号：107551300678 姓名：杨治峰班级：地矿学院（“三矿”专业）摘要：基于对2012年国内生产总值的数据分析，找出我国GDP 与多个指标，尤其是对投资、消费、出口等基本指标的依赖关系，运用相关分析和回归分析方法，建立回归模型，找出我国GDP的增长受社会固定资产依赖性较强，尤其是东部的山东省，也受制于出口收入，而我国消费水平依然不高的问题并为之提出改进措施和经济发展的预测，对国家各地区经济的科学发展建言献策关键词：R语言、相关分析、回归分析、中国GDP1 引言在当前复杂多变的国际经济形势下，我国国民生产总值（GDP）依然保持较快发展，国民生产总值是一个综合指标，依赖于多个指标的良性组合。

世界各国都十分重视GDP结构问题的研究。

本文基于对2012年国内生产总值的数据分析，找出我国GDP 与多个指标，尤其是对投资、消费、出口等基本指标的依赖关系，建立回归模型，尝试着探索出我国GDP 存在的结构性问题和不足之处，并为之提出改进措施和经济发展的预测，对国家各地区经济的科学发展建言献策！2.数据与分析方法2.1.数据描述性统计2.1.1.数据源的格式化处理R软件在读入excel数据源的时候，必须先对数据源进行格式化处理和调整才可以达到R软件的读取标准。

如表头的单行单列、文字间空格符号的消除等，调整完后，依据个人习惯将数据存入txt文本格式，命名为“ryuan.txt”。

2.1.2.数据的读取> A=read.table("ryuan.txt",header=T)> A#解析变量成y,x1,x2,x3,x4,x5,x6,x7,;X=A[,c(1,4,2,9,6,8,3)]Xy=A[,c(1)]#地区生产总值（亿元）yy2=A[,c(4)]#人均地区生产总值(元)y2x1=A[,c(2)]#社会固定资产投资（亿元)x1x2=A[,c(9)]#出口总额（亿美元）x2x3=A[,c(6)]#城镇人均消费支出（元）x3x4=A[,c(8)]#农民人均消费支出（元）x4x5=x3+x4#各地区人均消费总额(元)x5x6=A[,c(3)]#各地区居民消费价格指数x6B=data.frame("地区生产总值（亿元）"=y,"社会固定资产投资（亿元)"=x1,"出口总额（亿美元）"=x2,"各地区人均总额（元）"=x5)2.1.3.对读入的数据进行描述性统计。

河南财经政法大学统计学练习题相关与回归分析习题

第八章相关与回归分析一、单项选择题1、自然界和人类社会中的诸多关系基本上可归纳为两种类型，这就是（）①函数关系和相关关系②因果关系和非因果关系③随机关系和非随机关系④简单关系和复杂关系2、相关关系是指变量间的（）①严格的函数关系②简单关系和复杂关系③严格的依存关系④不严格的依存关系3、单相关也叫简单相关，所涉及变量的个数为（）①一个②两个③三个④多个4、直线相关即（）①线性相关②非线性相关③曲线相关④正相关5、多元相关关系即（）①复杂相关关系②三个或三个以上变量的相关关系③三个变量的相关④两个变量之间的相关关系6、相关系数的取值范围是（）①（0，1）②[0，1]③（-1，1）④[-1，1]7、相关系数为零时，表明两个变量间（）①无相关关系②无直线相关关系③无曲线相关关系④中度相关关系8、相关系数的绝对值为1时，表明两个变量间存在着（）①正相关关系②负相关关系③完全线性相关关系④不完全线性相关关系9、两个变量间的线性相关关系愈不密切，样本相关系数r值就愈接近（）①-1 ②+1③0 ④-1或+110、相关系数的值越接近-1，表明两个变量间（） ①正线性相关关系越弱 ②负线性相关关系越强 ③线性相关关系越弱 ④线性相关关系越强11、如果协方差02<xy σ，说明两变量之间（）①相关程度弱 ②负相关 ③不相关 ④正相关 12、样本的简单相关系数r=0.90时，说明（） ①总体相关系数ρ=0.90 ②总体相关系数90.0<ρ③总体相关系数90.0>ρ④总体的相关程度需进行统计估计和检验13、进行简单直线回归分析时，总是假定（） ①自变量是非随机变量、因变量是随机变量 ②自变量是随机变量、因变量是确定性变量③两变量都是随机变量 ④两变量都不是随机变量14、在直线回归模型i i x y10ˆˆˆββ+=中，回归系数1ˆβ的大小（） ①表明两变量线性关系密切程度的高低②表明两变量关系的独立程度 ③不能用于判断两变量的密切程度15、回归方程i i x y 5.1123ˆ+=中的回归系数数值表明：当自变量每增加一个单位时，因变量（）①增加1.5个单位 ②平均增加1.5个单位 ③增加123个单位 ④平均增加123个单位16、若回归系数1ˆβ大于0，表明回归直线是上升的，此时相关系数r 的值（） ①一定大于0 ②一定小于0 ③等于0 ④无法判断 17、下列回归方程中，肯定错误的是（）①88.0,32ˆ=+=r x y i i ②88.0,32ˆ=+-=r x yi i ③88.0,32ˆ-=+-=r x yi i ④88.0,32ˆ-=-=r x yi i 18、若根据资料计算得到的回归方程为5ˆ=y，则相关系数r 为（）①-1 ②0 ③1 ④0.519、根据回归方程ii x y10ˆˆˆββ+=（） ①只能由变量i x 去预测变量i y ②只能由变量i y 去预测变量i x ③可以由变量i x 去预测变量i y ，也可以由变量i y 去预测变量i x ④能否相互预测，取决于变量i x 和变量i y 之间的因果关系 20、下列现象的相关密切程度高的是（）。

应用回归分析-第2章课后习题参考答案

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n）仍满足基本假定。

求β1的最小二乘估计解：得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =02.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

21112)ˆ()ˆ(ini i n i i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi i i i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，上式恰好就是最小二乘估计的目标函数相同。

值得注意的是：最大似然估计是在εi ~N (0, σ2 )的假设下求得，最小二乘估计则不要求分布假设。

第二章(简单线性回归模型)2-1答案

2.1回归分析与回归函数一、判断题1. 总体回归直线是解释变量取各给定值时被解释变量条件期望的轨迹。

（T ）2. 线性回归是指解释变量和被解释变量之间呈现线性关系。

（ F ）3. 随机变量的条件期望与非条件期望是一回事。

（F ）4、总体回归函数给出了对应于每一个自变量的因变量的值。

（F ）二、单项选择题1．变量之间的关系可以分为两大类，它们是（ A ）。

A ．函数关系与相关关系B ．线性相关关系和非线性相关关系C ．正相关关系和负相关关系D ．简单相关关系和复杂相关关系2．相关关系是指（ D ）。

A ．变量间的非独立关系B ．变量间的因果关系C ．变量间的函数关系D ．变量间不确定性的依存关系3．进行相关分析时的两个变量（ A ）。

A ．都是随机变量B ．都不是随机变量C ．一个是随机变量，一个不是随机变量D ．随机的或非随机都可以4．回归分析中定义的（ B ）。

A.解释变量和被解释变量都是随机变量B.解释变量为非随机变量，被解释变量为随机变量C.解释变量和被解释变量都为非随机变量D.解释变量为随机变量，被解释变量为非随机变量5．表示x 和y 之间真实线性关系的总体回归模型是（ C ）。

A ．01ˆˆˆt t Y X ββ=+B ．01()t t E Y X ββ=+C ．01t t t Y X u ββ=++D ．01t t Y X ββ=+6.一元线性样本回归直线可以表示为（ C ）A ．i i X Y u i 10++=ββ B. i 10X )(Y E i ββ+=C. i i e X Y ++=∧∧i 10ββ D. i 10X i Y ββ+=∧7．对于i 01i i ˆˆY =X +e ββ+，以ˆσ表示估计标准误差，r 表示相关系数，则有（ D）。

A ．ˆ0r=1σ＝时，B ．ˆ0r=-1σ＝时，C ．ˆ0r=0σ＝时，D ．ˆ0r=1r=-1σ＝时，或8．相关系数r 的取值范围是（ D ）。

回归分析参考答案

回归分析参考答案回归分析参考答案回归分析是一种常用的统计方法，用于研究变量之间的关系。

它可以帮助我们理解和预测变量之间的依赖关系，并且在实际应用中具有广泛的应用场景。

本文将介绍回归分析的基本概念、方法和应用，并提供一些参考答案，以帮助读者更好地理解和运用回归分析。

一、回归分析的基本概念回归分析是一种用于研究因变量和自变量之间关系的统计方法。

它基于一组观测数据，通过建立数学模型来描述因变量与自变量之间的关系，并用统计方法对模型进行估计和推断。

回归分析的目标是通过自变量的变化来预测因变量的值。

在回归分析中，因变量是我们想要预测或解释的变量，而自变量是我们用来解释因变量变化的变量。

回归分析可以分为简单线性回归和多元回归两种类型。

简单线性回归是指只有一个自变量和一个因变量的情况，而多元回归则是指有多个自变量和一个因变量的情况。

二、回归分析的方法回归分析的方法主要包括建模、参数估计和模型评估三个步骤。

1. 建模：在回归分析中，我们需要选择适当的模型来描述因变量和自变量之间的关系。

常见的模型包括线性模型、非线性模型和广义线性模型等。

选择合适的模型需要根据具体问题和数据特点来决定。

2. 参数估计：在建立模型之后，我们需要对模型的参数进行估计。

参数估计的方法有最小二乘法、最大似然估计和贝叶斯估计等。

最小二乘法是一种常用的参数估计方法，它通过最小化观测值与模型预测值之间的差异来估计参数。

3. 模型评估：在参数估计之后，我们需要对模型进行评估，以确定模型的拟合程度和预测能力。

模型评估的指标包括残差分析、方差分析和回归系数的显著性检验等。

通过这些指标，我们可以判断模型是否合理，并对模型进行改进。

三、回归分析的应用回归分析在实际应用中具有广泛的应用场景。

下面将介绍一些常见的应用领域和相应的参考答案。

1. 经济学：回归分析在经济学中常用于研究经济变量之间的关系。

例如，我们可以使用回归分析来研究收入和消费之间的关系，以及利率和投资之间的关系。

应用回归分析+第2章详细答案

2.3由⎪⎪⎩⎪⎪⎨⎧=β-β-=β∂∂=β-β-=β∂∂∑∑=β=β=β=βn1i i i 10i ˆ1n 1i i 10i ˆ00x )x ˆˆy (Q 0)x ˆˆy (Q 1100得⎪⎪⎩⎪⎪⎨⎧==-==-∑∑∑∑====n 1i n 1i i i i i i n 1i n1i i i i 0x e x )y ˆy (0e )y ˆy (2.4在),0(N ~2i σε的正态分布假定下，10,ββ的最小二乘估计与最大似然估计等价，求对数似然函数的极大值等价于对∑=β+β-n1i 2i 10i )]x (y [求极小值，至此与最小二乘估计原理完全相同2.52.62n1i 2i212210])x x()x (n 1[)ˆvar()x (n 1)x ˆy var()ˆvar(σ-+=β+σ=β-=β∑=2.7SSR SSE )y y ˆ)(y ˆy (2)y y ˆ()y ˆy ()y y ˆyˆy ()y y (SST n1i i i i n 1i 2i n 1i 2i i n 1i 2i i i n 1i 2i +=--+-+-=-+-=-=∑∑∑∑∑=====2.8（1）22i2i 2i2i 2i2i2i i2i i xx1xx 1r 12n r )y y ()y y ˆ(12n r )y y ()y yˆ()y y (2n r )y y ()yˆy (2n r )y ˆy (2n L ˆˆL ˆt --=----=-----=---=--β=σβ=∑∑∑∑∑∑∑∑（2）F )2n /(SSE 1/SSR SSE SSR )2n (SSTSSR 1SST SSR)2n (r 1r )2n (t 222=-=-=--=--= 2.92xxi 2i10L )x x (n 1)x ˆˆvar(σ-+σ=β+β xx2i 2xx i 2i i 2xx i i i i 2i 1i L )x x (n 1)L y )x x (,y cov(n 1)L y )x x ()x x (,y cov(n 1))x x (ˆy ,y cov(-+σ=-+σ=--+σ=-β+∑2xx 2i 22i1i i 10i i i i n11[L )x x (n 1))x x (ˆy ,y cov(2)x ˆˆvar()y var()y y var()e var(--=σ--σ-σ=-β+-β+β+=-=2.1022xx2i i 2i 2i 2i i 2)L )x x (1n (2n 1))e (E )e (var(2n 1)e (E 2n 1))y ˆy (2n 1(E )ˆ(E σ=σ----=--=-=--=σ∑∑2.112n F F )2n /(SSE SSE SSR )2n /(SSE SSR )2n /(SSE SST )2n /(SSE SSR SSTSSR r 2-+=-+-=--==如果一个线性回归方程通过F 检验，只能说明x 与y 之间的线性关系是显著的，不能说明数据拟合得很好，决定系数r 2是一个回归直线与样本观测值拟合优度的相对指标。

回归分析练习题及参考答案

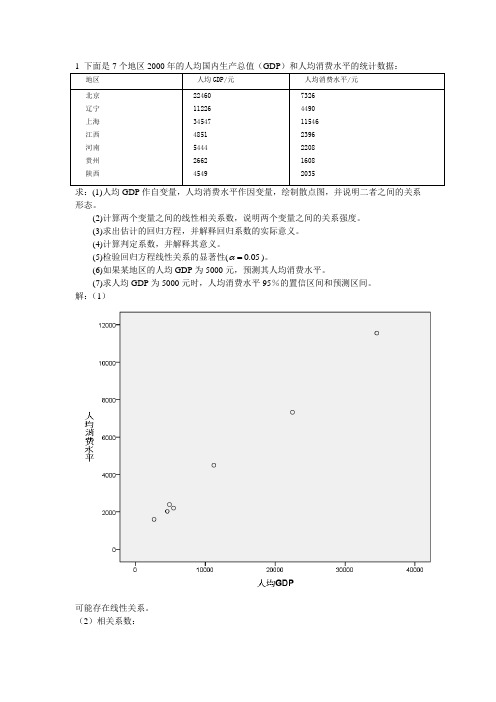
求：(1)人均GDP 作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。

(2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。

(3)求出估计的回归方程，并解释回归系数的实际意义。

(4)计算判定系数，并解释其意义。

(5)检验回归方程线性关系的显著性(0.05α=)。

(6)如果某地区的人均GDP 为5000元，预测其人均消费水平。

(7)求人均GDP 为5000元时，人均消费水平95％的置信区间和预测区间。

解：（1）可能存在线性关系。

（2）相关系数：（3）回归方程：734.6930.309y x=+回归系数的含义：人均GDP没增加1元，人均消费增加0.309元。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 （常量）734.693 139.540 5.265 0.003人均GDP（元）0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平（元）%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%人均GDP对人均消费的影响达到99.6%。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

模型摘要模型R R 方调整的R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP（元）。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（5）F 检验：回归系数的检验：t 检验注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

系数(a)模型非标准化系数标准化系数t 显著性B 标准误 Beta1（常量） 734.693 139.540 5.2650.003 人均GDP （元）0.3090.0080.99836.4920.000a. 因变量: 人均消费水平（元）%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（6）某地区的人均GDP 为5000元，预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。

简单线性回归模型试题及答案

第二章简单线性回归模型、单项选择题:1、回归分析中定义的（B ）C 、解释变量和被解释变量都为非随机变量D 解释变量为随机变量，被解释变量为非随机变量 &下面哪一个必定是错误的（ C ）。

A Y?=30+0.2X i ,以丫 =0.8B 、= —75 + 1.5X i ,気=0.91 C 2.1X i , r XY =0.78 D 、 Y? = —12 —3.5X i , r XY = —0.969、产量（X ,台）与单位产品成本（Y ,元/台）之间的回归方程为Y? = 356 -1.5X ，这说明（D 。

A 产量每增加一台，单位产品成本增加356元B 、产量每增加一台，单位产品成本减少1.5元C 、产量每增加一台，单位产品成本平均增加 356元D 、产量每增加一台，单位产品成本平均减少1.5元10、回归模型Yi 八。

「X i , i = 1 ，…，25中，总体方差未知，检验H 。

： r =0时，所用的检验统计量 —L 服从（D 。

S目A 2（n -2）B 、t （n-1）C 、2（n"）D 、t （n-2）11、对下列模型进行经济意义检验，哪一个模型通常被认为没有实际价值的（ B ）。

A 、Ci （消费）=500弋.8^ （收入）B 、Qdi （商品需求）=10・0.81［（收入）0.9Pi （价格）CQ si （商品供给）二20（价格）D Y （产出量）765K 役（资本）L ："（劳动）12、进行相关分析时，假定相关的两个变量（A ）。

A 、解释变量和被解释变量都是随机变量2、 A 3最小二乘准则是指使（ D n Z （Y t -Y ） B 下图中“{”所指的距离是（）达到最小值的原则确定样本回归方程。

nE Y -Y? C 、max Y r -Y Dt -1n、' (Y t -Y?)2t 丄 5、 6、线性 B 、无偏性 C、有效性 D参数-的估计量？具备有效性是指（B ）Var （ ?） =0 B 、Var （ ?）为最小 C 亠0反映由模型中解释变量所解释的那部分离差大小的是总体平方和 B 、回归平方和 C 、残差平方和7、 (B )。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二篇回归分析和相关分析1 证明题⑴ 试证 ① ])(1][)(1[/)()())((222222∑∑∑∑∑∑∑∑∑∑---=----=i i i i iiii iii iy ny x n x nyx y x y y x x y y x x R ;② ∑∑∑∑∑∑∑--=---=222)()())((iiiiiiii ix x n y x y x n x x y y x x b .⑵ 假定bx a y +=的反函数为y b a x '+'=。

对于观测数据，考虑模型残差，我们有i i i x b a y ε++=ˆˆ, ii i y b a x ε'+'+'=ˆˆ. 试证2ˆˆR b b='。

这里R 为相关系数。

⑶ 对于一元线性回归分析，试证明=----=∑∑22)ˆ(11)ˆ(iiiyy m n y y F )1(1122R m n R ---.⑷ 对于一元线性回归分析，试证明F R m n R sb t b =---==)1(11ˆ2.⑸ 我们知道，一元线性方程的回归系数b 和相关系数R 可以表作xx xy b S S =, yyxx xyR S S S =, 式中∑=-=n i i x x xx 12)(S , ∑=-=ni i y y yy 12)(S分别为x 和y 的校正平方和。

要求：① 建立回归系数和相关系数的关系。

② 证明对于标准化的x 和y 值，必有b R =。

提示：数据标准化的公式为,*jjij ij x x x σ-=（m j n i ,,2,1;,,2,1 ==）式中∑==ni ijj xnx 11为第j 个变量的平均值，而2/112])(11[∑=--=ni j ijj x xn σ为基于抽样方差的标准差。

⑹ 以二元线性回归方程2211x b x b a y ++=,为例，证明如下问题两个问题，并借助计算结果进行检验。

① 对于标准化的自变量，建立矩阵X *，则[]22**)(1⨯==ij T R X X nC为自变量x 1和x 2的简单相关系数矩阵。

② C 的逆矩阵[][]ijijv R C ==--11的对角线的元素等于方程膨胀因子（VIF ）值。

③ 借助第3题第（1）小题的问题和数据检验这种推导结果。

⑺ VIF 计算公式的证明。

考虑线性回归方程2211x b x b a y ++=,以二元线性回归为例，证明如下问题。

① 对于标准化的自变量，建立矩阵X*，则[]22**)(1⨯==ij T R X X nC为自变量x 1和x 2的简单相关系数矩阵。

② C 的逆矩阵[][]ij ijv R C ==--11的对角线的元素等于方程膨胀因子（VIF ）值。

2 计算题（一元回归分析）为了估计山上积雪溶化后对河流下游灌溉的影响，在山上建立观测站，测得连续10年的观测数据如下表（见下表1-1）。

表1-1 年份最大积雪深度x (米)灌溉面积y (千亩)x i 2 y i 2 x i y i 预测值残差1971 15.2 28.6 1972 10.4 19.3 197321.240.51974 18.6 35.6 1975 26.4 48.9 1976 23.4 45.0 1977 13.5 29.2 1978 16.7 34.1 1979 24.0 46.7 1980 19.137.4∑利用本节公式，借助Excel 计算： ① 表中各项指标；② 回归参数a 、b ，并给出回归模型；③ 计算总平方和SS t 即Syy 、剩余平方和SS e 及回归平方和SS r ； ④ 验证如下关系0)(1=-∑=ni iy y,0)ˆ(1=-∑=ni i iyy,0)ˆ(1=-∑=ni iy y,0)ˆ)(ˆ(1=--∑=ni i i iy y yy. ⑤ 验证如下关系：SS t =SS r +SS e ，即222)ˆ( )ˆ()(∑∑∑-+-=-y yyy y y i i i i . ⑥ 相关系数R 和标准误差s ；⑦ 计算F 值、t 值和DW 值；⑧ 计算残差和自变量的相关系数，分析结果。

⑨ 假定1981的积雪深度为27.5米，估计当年的灌溉面积大约为多少？3 计算题（多元回归分析）⑴ 为了考察工业、农业和固定资产投资对交通运输业的影响，利用SPSS 统计分析软件对某省1970－1987年18年的产值数据进行多元回归分析和逐步回归分析，指出多重共线性的问题实质所在（见下表1-2）。

表1-2 序号年份工业产值x 1 农业产值x 2 固定资产投资x 3运输业产值y1 1970 57.82 27.05 14.54 3.09 2 1971 58.05 28.89 16.83 3.40 3 1972 59.15 33.02 12.26 3.884 1973 63.83 35.23 12.87 3.905 1974 65.36 24.94 11.65 3.22 6 1975 67.26 32.95 12.87 3.76 7 1976 66.92 30.35 10.80 3.598 1977 67.79 38.70 10.93 4.03 9 1978 75.65 47.99 14.71 4.34 10 1979 80.57 54.18 17.56 4.65 11 1980 79.02 58.73 20.32 4.78 12198180.5259.8518.675.0413 1982 86.88 64.57 25.34 5.5914 1983 95.48 70.97 25.06 6.0115 1984 109.71 81.54 29.69 7.0316 1985 126.50 94.01 43.86 10.0317 1986 138.89 103.23 48.90 10.8318 1987 160.56 119.33 60.98 12.90资料来源：李一智等，1991。

⑵以国内生产总值（GDP）为因变量，分别借助Excel和SPSS对我国1995年社会经济发展的8项指标进行多元回归分析和逐步回归分析（见下表1-3）。

表1-3地区国内生产总值工业总产值固定资产投资全社会货物周转量职工平均工资居民消费水平消费价格指数商品零售价格指数北京1394.89 1908.62 519.01 373.9 8144 2505 117.3 112.6 天津920.11 2094.01 345.46 342.8 6501 2720 115.3 110.6 河北2849.52 3995.72 704.87 2033.3 4839 1258 115.2 115.8 山西1092.48 1753.58 290.90 717.3 4721 1250 116.9 115.6 内蒙832.88 781.73 250.23 781.7 4134 1387 117.5 116.8 辽宁2793.37 4974.90 887.99 1371.1 4911 2397 116.1 114.0 吉林1129.20 1428.96 320.45 497.4 4430 1872 115.2 114.2 黑龙江2014.53 2203.78 435.73 824.8 4145 2334 116.1 114.3 上海2462.57 5128.97 996.48 207.4 9279 5343 118.7 113.0 江苏5155.25 11812.86 1434.95 1025.5 5943 1926 115.8 114.3 浙江3524.79 8087.75 1006.39 754.4 6619 2249 116.6 113.5 安徽2003.58 3155.88 474.00 908.3 4609 1254 114.8 112.7 福建2160.52 2800.68 553.97 609.3 5857 2320 115.2 114.4 江西1205.11 1291.37 282.84 411.7 4211 1182 116.9 115.9 山东5002.34 8456.32 1229.55 1196.6 5145 1527 117.6 114.2 河南3002.74 4715.11 670.35 1574.4 4344 1034 116.5 114.9 湖北2391.42 4102.58 571.68 849.0 4685 1527 120.0 116.6 湖南2195.70 2451.47 422.61 1011.8 4797 1408 119.0 115.5 广东5381.72 9535.42 1639.83 656.5 8250 2699 114.0 111.6 广西1606.15 1666.10 382.59 556.0 5105 1314 118.4 116.4 海南364.17 193.26 198.35 232.1 5340 1814 113.5 111.3 四川3534.00 4426.37 822.54 902.3 4645 1261 118.5 117.0 贵州630.07 557.14 150.84 301.1 4475 942 121.4 117.2 云南1206.68 1206.55 334.00 310.4 5149 1261 121.3 118.1 西藏55.98 8.99 17.87 4.2 7382 1110陕西1000.03 1182.72 300.27 500.9 4396 1208 119.0 117.0 甘肃553.35 824.73 114.81 507.0 5493 1007 119.8 116.5 青海165.31 148.64 47.76 61.6 5753 1445 118.0 116.3 宁夏169.75 197.50 61.98 121.8 5079 1355 117.1 115.3⑶现有某地区15个房地产的售价、居住面积、评估价格和建筑等价（高、中、低）等数据，试以售价为因变量，根据下表中资料拟合售价的预测模型（表1-4）。

表1-4价格居住面积评估价格建筑等级26.0 521 7.8 低31.0 661 23.8 低37.4 694 28.0 中34.8 743 26.2 中39.2 787 22.4 中38.0 825 28.2 中39.6 883 25.8 中31.2 920 20.8 低37.2 965 14.6 中38.4 1011 26.0 中43.6 1047 30.0 中44.8 1060 29.2 高40.6 1079 24.2 中41.8 1164 29.4 高45.2 1298 23.6 高资料来源：于洪彦，2001。

02第二篇回归分析与相关分析业题

回归分析练习试题和参考答案解析

回归与相关分析

统计学相关与回归分析试题

应用回归分析_第2章课后习题参考答案

第2章习题

回归分析课后习题

相关和回归分析练习题

《应用回归分析》课后题答案[整理版]

题目：基于R对国内各省市区主要经济指标的相关性分析与回归分析 (2)

河南财经政法大学统计学练习题相关与回归分析习题

应用回归分析-第2章课后习题参考答案

相关分析与回归分析同步练习试卷2(题后含答案及解析)

第二章(简单线性回归模型)2-1答案

回归分析参考答案

应用回归分析+第2章详细答案

相关和回归分析例题

回归分析练习题及参考答案

简单线性回归模型试题及答案

02第二篇 回归分析与相关分析业题

回归分析练习试题和参考答案解析

回归与相关分析

统计学相关与回归分析试题

应用回归分析_第2章课后习题参考答案

第2章习题

回归分析课后习题

相关和回归分析练习题

《应用回归分析》课后题答案[整理版]

题目：基于R对国内各省市区主要经济指标的相关性分析与回归分析 (2)

河南财经政法大学统计学练习题相关与回归分析习题

应用回归分析-第2章课后习题参考答案

相关分析与回归分析同步练习试卷2(题后含答案及解析)

第二章(简单线性回归模型)2-1答案

回归分析参考答案

应用回归分析+第2章详细答案

相关和回归分析例题

回归分析练习题及参考答案

简单线性回归模型试题及答案

02第二篇回归分析与相关分析业题