回归分析练习题与参考答案
应用回归分析课后习题参考答案

第4章违背根本假设的情况思考及练习参考答案4.1 试举例说明产生异方差的原因。
答:例:截面资料下研究居民家庭的储蓄行为Y i=β0+β1X i+εi其中:Y i表示第i个家庭的储蓄额,X i表示第i个家庭的可支配收入。
由于高收入家庭储蓄额的差异较大,低收入家庭的储蓄额那么更有规律性,差异较小,所以εi的方差呈现单调递增型变化。
例4.2:以某一行业的企业为样本建立企业生产函数模型Y i=A iβ1K iβ2L iβ3eεi被解释变量:产出量Y,解释变量:资本K、劳动L、技术A,那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
由于每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。
这时,随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。
4.2 异方差带来的后果有哪些?答:回归模型一旦出现异方差性,如果仍采用OLS估计模型参数,会产生以下不良后果:1、参数估计量非有效2、变量的显著性检验失去意义3、回归方程的应用效果极不理想总的来说,当模型出现异方差性时,参数OLS估计值的变异程度增大,从而造成对Y的预测误差变大,降低预测精度,预测功能失效。
4.3 简述用加权最小二乘法消除一元线性回归中异方差性的思想及方法。
答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数一样,是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下,平方和中的每一项的地位是不一样的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。
所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。
第七章回归与相关分析练习及答案

第七章回归与相关分析一、填空题1.现象之间的相关关系按相关的程度分为、和;按相关的形式分为和;按影响因素的多少分为和。
2.两个相关现象之间,当一个现象的数量由小变大,另一个现象的数量,这种相关称为正相关;当一个现象的数量由小变大,另一个现象的数量,这种相关称为负相关。
3.相关系数的取值X围是。
4.完全相关即是关系,其相关系数为。
5.相关系数,用于反映条件下,两变量相关关系的密切程度和方向的统计指标。
6.直线相关系数等于零,说明两变量之间;直线相关系数等1,说明两变量之间;直线相关系数等于—1,说明两变量之间。
7.对现象之间变量的研究,统计是从两个方面进行的,一方面是研究变量之间关系的,这种研究称为相关关系;另一方面是研究关于自变量和因变量之间的变动关系,用数学方程式表达,称为。
8.回归方程y=a+bx中的参数a是,b是。
在统计中估计待定参数的常用方法是。
9. 分析要确定哪个是自变量哪个是因变量,在这点上它与不同。
10.求两个变量之间非线性关系的回归线比较复杂,在许多情况下,非线性回归问题可以通过化成来解决。
11.用来说明回归方程代表性大小的统计分析指标是。
12.判断一条回归直线与样本观测值拟合程度好坏的指标是。
二、单项选择题1.下面的函数关系是( )A销售人员测验成绩与销售额大小的关系 B圆周的长度决定于它的半径C家庭的收入和消费的关系 D数学成绩与统计学成绩的关系2.相关系数r的取值X围( )A -∞<r<+∞B -1≤r≤+1C -1<r<+1D 0≤r≤+13.年劳动生产率z(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均( )A增加70元 B减少70元 C增加80元 D减少80元4.若要证明两变量之间线性相关程度是高的,则计算出的相关系数应接近于( )A+1 B 0 C 0.5 D [1]5.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( ) A线性相关还是非线性相关 B正相关还是负相关C完全相关还是不完全相关 D单相关还是复相关6.某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建=a+b x。
回归分析练习试题和参考答案解析

1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
α=)。
(5)检验回归方程线性关系的显著性(0.05(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:系数a模型非标准化系数标准系数t Sig.相关性B标准误差试用版零阶偏部分1(常量).003人均GDP.309.008.998.000.998.998.998 a. 因变量: 人均消费水平有很强的线性关系。
(3)回归方程:734.6930.309y x=+系数a模型非标准化系数标准系数t Sig.相关性回归系数的含义:人均GDP没增加1元,人均消费增加元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1(常量)人均GDP(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1.998a.996.996a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的 R 方估计的标准差1.998(a)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F检验:Anova b模型平方和df均方F Sig.1回归.6801.680.000a 残差5总计.7146a. 预测变量: (常量), 人均GDP。
回归分析练习题及参考答案
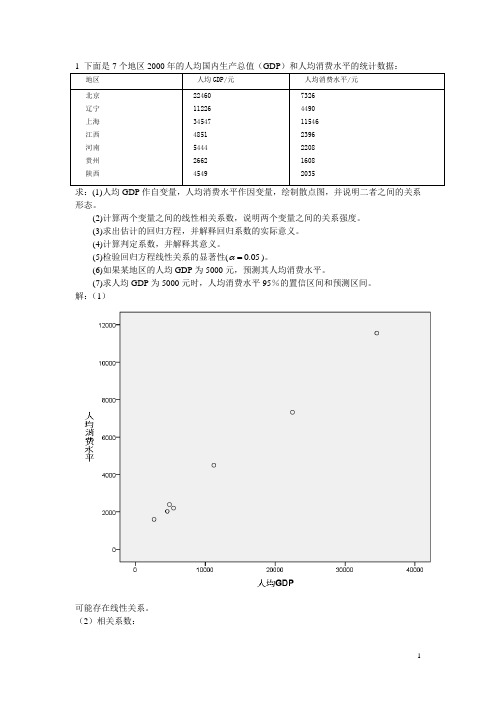
1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
回归分析时间序列分析答案

回归分析时间序列分析答案一、单项选择题1、下面的关系中不是相关关系的是(D )A、身高与体重之间的关系B、工资水平与工龄之间的关系C、农作物的单位面积产量与降雨量之间的关系D、圆的面积与半径之间的关系2、具有相关关系的两个变量的特点是(A )A、一个变量的取值不能由另一个变量唯一确定B、一个变量的取值由另一个变量唯一确定C、一个变量的取值增大时另一个变量的取值也一定增大D、一个变量的取值增大时另一个变量的取值肯定变小3、下面的假定中,哪个属于相关分析中的假定(B)A、两个变量之间是非线性关系B、两个变量都是随机变量C、自变量是随机变量,因变量不是随机变量D、一个变量的数值增大,另一个变量的数值也应增大4、如果一个变量的取值完全依赖于另一个变量,各观测点落在一条直线上,则称这两个变量之间为(A )A、完全相关关系B、正线性相关关系C、非线性相关关系D、负线性相关关系 5、根据你的判断,下面的相关系数取值哪一个是错误的( C )A、–0.86B、0.78C、1.25D、0x6、某校经济管理类的学生学习统计学的时间()与考试成绩(y)之间建立线性回归方程yx=a+b。
经计算,方程为y =200—0.8x,该方程参数的计算(C) ccA a值是明显不对的B b值是明显不对的C a值和b值都是不对的D a值和b值都是正确的 7、在回归分析中,描述因变量y如何依赖于自变量x和误差项ε的方程称为(B)A、回归方程B、回归模型C、估计回归方程D、经验回归方程,,,x,,8、在回归模型y=中,ε反映的是(C ) 01A、由于x的变化引起的y的线性变化部分B、由于y的变化引起的x的线性变化部分C、除x和y的线性关系之外的随机因素对y的影响D、由于x和y的线性关系对y的影响9、如果两个变量之间存在负相关关系,下列回归方程中哪个肯定有误(B),,A、=25–0.75xB、= –120+ 0.86x yy,,C、=200–2.5xD、= –34–0.74x yy10、说明回归方程拟合优度的统计量是(C )A、相关系数B、回归系数C、判定系数D、估计标准误差211、判定系数R是说明回归方程拟合度的一个统计量,它的计算公式为(A ) SSRSSRSSESSTA、 B、 C、 D、 SSTSSESSTSSR12、为了研究居民消费(C)与可支配收入(Y)之间的关系,有人运用回归分析的方法,得到以下方程:在该方程中0.76的含义是(B ) LnC,2.36,0.76LnY,A、可支配收入每增加1元,消费支出增加0.76元B、可支配收入每增加1%,消费支出增加0.76%C、可支配收入每增加1元,消费支出增加76%D、可支配收入每增加1%,消费支出增加76%13、年劳动生产率z(千元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均(A)A增加70元 B减少70元 C增加80元 D减少80元14、下列回归方程中哪个肯定有误(A),,A、y=15–0.48x,r=0.65B、y= –15 - 1.35x,r=-0.81,,C、yy=-25+0.85x,r=0.42D、=120–3.56x,r=-0.96215、若变量x与y之间的相关系数r=0.8,则回归方程的判定系数R为(C )A、0.8B、0.89C、0.64D、0.40 16、对具有因果关系的现象进行回归分析时(A)A、只能将原因作为自变量B、只能将结果作为自变量C、二者均可作为自变量D、没有必要区分自变量二、多项选择题1(下列哪些现象之间的关系为相关关系(ACD)A家庭收入与消费支出关系 B圆的面积与它的半径关系C广告支出与商品销售额关系 D单位产品成本与利润关系E在价格固定情况下,销售量与商品销售额关系2(相关系数表明两个变量之间的(DE)A线性关系 B因果关系 C变异程度 D相关方向 E相关的密切程度3、如下的现象属于负相关的有(BCD)。
专题05 回归分析(解析版)

专题5 回归分析例1.已知回归方程y=5x+1,则该方程在样本(1,4)处的残差为()A.﹣2B.1C.2D.5【解析】解:当x=1时,y=5x+1=6,∴方程在样本(1,4)处的残差是4﹣6=﹣2.故选:A.例2.研究变量x,y得到一组样本数据,进行回归分析,有以下结论①残差平方和越小的模型,拟合的效果越好;②用相关指数R2来刻画回归效果,R2越小说明拟合效果越好;③在回归直线方程y=−0.2x+0.8中,当解释变量x每增加1个单位时,预报变量y平均减少0.2个单位;④若变量y和x之间的相关系数为r=﹣0.9462,则变量y和x之间的负相关很强.以上正确说法的是①③④.【解析】解:①可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故①正确;②用相关指数R2来刻画回归效果,R2越大说明拟合效果越好,故②错误;③在回归直线方程y=−0.2x+0.8中中,当解释变量x每增加1个单位时,预报变量y平均减少0.2个单位,故③正确;④若变量y和x之间的相关系数为r=﹣0.9462,r的绝对值趋向于1,则变量y和x之间的负相关很强,故④正确.故答案为:①③④.例3.下列命题中,正确的命题有②③.①回归直线y=b x+a恒过样本点中心(x,y),且至少过一个样本点;②用相关指数R2来刻画回归效果,表示预报变量对解释变量变化的贡献率,R2越接近于1说明模型的拟合效果越好;③残差图中残差点比较均匀的落在水平的带状区域中,说明选用的模型比较合适;④两个模型中残差平方和越大的模型的拟合效果越好.【解析】解:①回归直线y=b x+a恒过样本点中心(x,y),不一定过样本点,故①正确;②用相关指数R2来刻画回归效果,表示预报变量对解释变量变化的贡献率,R2越接近于1说明模型的拟合效果越好,正确;③残差图中残差点比较均匀的落在水平的带状区域中,说明选用的模型比较合适,正确;④两个模型中残差平方和越大的模型的拟合效果越差.故④错误,故正确的是②③,故答案为:②③例4.下列命题:①相关指数R2越小,则残差平方和越大,模型的拟合效果越好.②对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”可信程度越大.③残差点比较均匀地落在水平带状区域内,带状区域越宽,说明模型拟合精度越高.④两个随机变量相关性越强,则相关系数的绝对值越接近0.其中错误命题的个数为4.【解析】解:对于①,相关指数R2越小,则残差平方和越大,此时模型的拟合效果越差,所以①错误;对于②,对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”可信程度越小,所以②错误;对于③,残差点比较均匀地落在水平带状区域内,带状区域越宽,说明模型拟合精度越低,所以③错误;对于④,两个随机变量相关性越强,则相关系数的绝对值越接近1,所以④错误.综上知,错误命题的序号是①②③④,共4个.故答案为:4.例5.垃圾是人类日常生活和生产中产生的废弃物,由于排出量大,成分复杂多样,且具有污染性,所以需要无害化、减量化处理.某市为调査产生的垃圾数量,采用简单随机抽样的方法抽取20个县城进行了分析,得到样本数据(x i,y i)(i=1,2,……,20),其中x i和y i分别表示第i个县城的人口(单位:万人)和该县年垃圾产生总量(单位:吨),并计算得∑20i=1x i=80,∑20i=1y i=4000,∑20i=1(x i−x)2=80,∑20i=1(y i−y)2=8000,∑20i=1(x i−x)(y i−y)=7000.(1)请用相关系数说明该组数据中y与x之间的关系可用线性回归模型进行拟合;(2)求y关于x的线性回归方程;(3)某科研机构研发了两款垃圾处理机器,如表是以往两款垃圾处理机器的使用年限(整年)统计表:1年2年3年4年5年使用年限台数款式甲款520151050乙款152010550某环保机构若考虑购买其中一款垃圾处理器,以使用年限的频率估计概率.根据以往经验估计,该机构选择购买哪一款垃圾处理机器,才能使用更长久?参考公式:相关系数r=∑n i=1i−x)(y i−y)√∑i=1(x i−x)∑i=1(y i−y)2.对于一组具有线性相关关系的数据(x i,y i)(i=1,2,……,n),其回归直线y=b x+a的斜率和截距的最小二乘估计分别为:b=∑ni=1(x i−x)(y i−y)∑n i=1(x i−x)2,a=y−b x.【解析】解:(1)由题意知相关系数r=∑20i=1i−x)(y i−y)√∑i=1(x i−x)2∑i=1(y i−y)2=√80×8000=78=0.875,因为y与x的相关系数接近1,所以y与x之间具有较强的线性相关关系,可用线性回归模型进行拟合.(2)由题意可得,b=∑20i=1(x i−x)(y i−y)∑20i=1(x i−x)2=70080=8.75,a=y−b x=400020−8.75×8020=200−8.75×4=165,所以y=8.75x+165.(3)以频率估计概率,购买一台甲款垃圾处理机器节约政府支持的垃圾处理费用X(单位:万元)的分布列为X﹣50050100P0.10.40.30.2E(X)=﹣50×0.1+0×0.4+50×0.3+100×0.2=30(万元)购买一台乙款垃圾处理机器节约政府支持的垃圾处理费用Y(单位:万元)的分布列为:Y﹣302070120P0.30.40.20.1E(Y)=﹣30×0.3+20×0.4+70×0.2+120×0.1=25(万元)因为E(X)>E(Y),所以该县城选择购买一台甲款垃圾处理机器更划算.例6.某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.据统计该基地的西红柿增加量y(百斤)与使用某种液体肥料x(千克)之间对应数据为如图所示的折线图.(1)依据数据的折线图,请计算相关系数r(精确到0.01),并以此判定是否可用线性回归模型拟合y 与x的关系?若是请求出回归直线方程,若不是请说明理由;(2)过去50周的资料显示,该地周光照量X(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量X限制,并有如表关系:周光照量X(单位:小时)30<X<5050≤X≤70n≥2光照控制仪最多可运行台数542若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了5台光照控制仪,求商家在过去50周每周利润的平均值.附:对于一组数据(x1,y1),(x2,y2),……,(x n,y n),其相关系数公式r=∑n i=1i−x)(y i−y)√∑i=1i−x)2∑i=1i−y)2,回归直线y=b x+a的斜率和截距的最小二乘估计分别为:b=∑ni=1(x i−x)(y i−y)∑n i=1(x i−x)2=∑ni=1x i y i−nxy∑n i=1(x i−x)2,a=y−b x,参考数据√0.3≈0.55,√0.9≈0.95.【解析】解:(1)由已知数据可得x=2+4+5+6+85=5,y=3+4+4+4+55=4,因为∑5i=1(x i−x)(y i−y)=(−3)×(−1)+0+0+0+3×1=6,√∑5i=1(x i−x)2=√(−3)2+(−1)2+02+12+32=2√5,√∑5i=1(y i−y)2=√(−1)2+02+02+02+12=√2.所以相关系数r=∑n i=1i−x)(y i−y)√∑i=1i −x)2√∑i=1i−y)2=2√5⋅√2=√910≈0.95,因为r>0.75,所以可用线性回归模型拟合y与x的关系,因为b=∑ni=1(x i−x)(y i−y)∑n i=1(x i−x)2=620=0.3,a=y−b x=2.5,所以回归直线方程y=0.3x+2.5.(2)记商家周总利润为Y元,由条件可得在过去50周里:X>70时,共有10周,只有2台光照控制仪运行,周总利润Y=2×3000﹣3×1000=3000元,当50≤X≤70时,共有35周,有4台光照控制仪运行,周总利润Y=4×3000﹣1×1000=11000元,当X<50时,共有5周,5台光照控制仪都运行,周总利润Y=5×3000=15000元,所以过去50周每周利润的平均值Y=3000×10+11000×35+15000×550=9800元,所以商家在过去50周每周利润的平均值为9800元.例7.湖南省从2021年开始将全面推行“3+1+2”的新高考模式,新高考对化学、生物、地理和政治等四门选考科目,制定了计算转换T分(即记入高考总分的分数)的“等级转换赋分规则”(详见附1和附2),具体的转换步骤为:①原始分Y等级转换;②原始分等级内等比例转换赋分.某校的一次年级统考中,政治、生物两选考科目的原始分分布如表:等级A B C D E比例约15%约35%约35%约13%约2%政治学科各等级对应的原始分区间[81,98][72,80][66,71][63,65][60,62]生物学科各等级对应的原始分区间[90,100][77,89][69,76][66,68][63,65]现从政治、生物两学科中分别随机抽取了20个原始分成绩数据,作出茎叶图:(1)根据茎叶图,分别求出政治成绩的中位数和生物成绩的众数;(2)该校的甲同学选考政治学科,其原始分为82分,乙同学选考生物学科,其原始分为91分,根据赋分转换公式,分别求出这两位同学的转化分;(3)根据生物成绩在等级B的6个原始分和对应的6个转化分,得到样本数据(Y i,T i),请计算生物原始分Y i与生物转换分T i之间的相关系数,并根据这两个变量的相关系数谈谈你对新高考这种“等级转换赋分法”的看法.附1:等级转换的等级人数占比与各等级的转换分赋分区间等级A B C D E原始分从高到低排序的等级人数占比约15% 约35% 约35% 约13% 约2%转换分T 的赋分区间[86,100] [71,85][56,70] [41,55] [30,40]附2:计算转换分T 的等比例转换赋分公式:Y 2−Y Y−Y 1=T 2−T T−T 1.(其中:Y 1,Y 2别表示原始分Y 对应等级的原始分区间下限和上限;T 1,T 2分别表示原始分对应等级的转换分赋分区间下限和上限.T 的计算结果按四舍五入取整).附3:∑ 6i=1(Y i −Y )(T i −T )=74,√∑ 6i=1(Yi −Y)2∑ 6i=1(T i −T)2=√5494≈74.12,r =∑n i=1i −Y)(T i −T)√∑i=1i −Y)2∑i=1i −T)2.【解析】解:(1)根据茎叶图知,政治成绩的中位数为72,生物成绩的众数为73; (2)甲同学选考政治学科的等级为A ,由转换赋分公式:98−8282−81=100−T T−86,解得T =87;乙同学选考生物学科的等级为A ,由赋分转换公式:100−9191−90=100−T T−86,解得T =87;所以甲、乙两位同学的转换分都是87分. (3)由题意知,r =∑n i=1i −Y)(T i −T)√∑ i=1(Y i −Y)2∑ i=1(T i −T)2=7474.12≈0.998, 说法1:等级转换赋分公平,因为相关系数十分接近1,接近函数关系,因此高考这种“等级转换赋分”具有公平性与合理性.说法2:等级转换赋分法不公平,在同一等级内,原始分与转化分是确定的函数关系,理论上原始分与转化分的相关系数为1,在实际赋分过程中由于数据的四舍五入,使得实际的转化分与应得的转化分有一定的误差,极小部分同学赋分后会出现偏高或偏低的现象. (只要说法有道理,都可以得分).例8.某市房管局为了了解该市市民2018年1月至2019年1月期间买二手房情况,首先随机抽样其中200名购房者,并对其购房面积m (单位:平方米,60≤m ≤130)进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价y (单位:万元/平方米),制成了如图2所示的散点图(图中月份代码1﹣13分别对应2018年1月至2019年1月).(Ⅰ)试估计该市市民的购房面积的中位数m0;(Ⅱ)现采用分层抽样的方法从购房面积位于[110,130]的40位市民中随机抽取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在[120,130]的概率;(Ⅲ)根据散点图选择y=a+b√x和y=c+d lnx两个模型进行拟合,经过数据处理得到两个回归方程,分别为y=0.9369+0.0285√x和y=0.9554+0.0306lnx,并得到一些统计量的值如表所示:y=0.9369+0.0285√x y=0.9554+0.0306lnx ∑13i=1(y i−y i)20.0005910.000164∑13i=1(y i−y)20.006050请利用相关指数R2判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出2019年12月份的二手房购房均价(精确到0.001).【参考数据】ln2≈0.69,ln3≈1.10,ln23≈3.14,ln25≈3.22,√2≈141,√3≈1.73,√23≈4.80.【参考公式】R2=1−∑ni=1(y i−y i)2∑n i=1(y i−y)2.【解析】解:(I)由频率分布直方图,可得,前三组频率和为0.05+0.1+0.2=0.35,前四组频率和为0.05+0.1+0.2+025=0.6,故中位数出现在第四组,且m0=90+10×0.150.25=96.(Ⅱ)设从位于[110,120)的市民中抽取x人,从位于[120,130]的市民中抽取y人,由分层抽样可知:440=x30=y10,则x=3,y=1,在抽取的4人中,记3名位于[11,120)的市民为A1,A2,A3,位于[120,130]的市民为B则所有抽样情况为:(A1,A2),(A1,A3),(A1,B),(A2,A3),(A2,B),(A3,B)共6种.而其中恰有一人在位于购房面积[120,130]的情况共有3种,故所求概率P=36=12,(III)设模型y=0.9369+0.0285√x和y=0.955+0.0306lnx的相关指数分别为R12,R22,则R12=1−0.0005910.006050,R22=1−0.0001640.006050,显然R12<R22,故模型y=0.9554+0.0306lnx的拟合效果更好.由2019年12月份对应的代码为24,则y=0.9554+0.0306ln24=0.9554+0.0306(3ln2+ln3)≈1.052万元/平方米.例9.某汽车公司拟对“东方红”款高端汽车发动机进行科技改造,根据市场调研与模拟,得到科技改造投入x(亿元)与科技改造直接收益y(亿元)的数据统计如表:x2346810132122232425y1322314250565868.56867.56666当0<x≤16时,建立了y与x的两个回归模型:模型①:y=4.1x+11.8;模型②:y=21.3√x−14.4;当x>16时,确定y与x满足的线性回归方程为:y=−0.7x+a.(Ⅰ)根据下列表格中的数据,比较当0<x≤16时模型①、②的相关指数R2,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为16亿元时的直接收益.回归模型模型①模型②回归方程y=4.1x+11.8y=21.3√x−14.4∑7i=1(y i−y i)2182.479.2(附:刻画回归效果的相关指数R2=1−∑n i=1(y i−y i)2∑n i=1(y i−y)2.)(Ⅱ)为鼓励科技创新,当科技改造的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较科技改造投入16元与20亿元时公司实际收益的大小;(附:用最小二乘法求线性回归方程y=b x+a的系数公式b=∑ni=1x i y i−nx⋅y∑n i=1x i2−nx2=∑ni=1(x i−x)(y i−y)∑n i=1(x i−x)2;a=y−b x)(Ⅲ)科技改造后,“东方红”款汽车发动机的热效率X大幅提高,X服从正态分布N(0.52,0.012),公司对科技改造团队的奖励方案如下:若发动机的热效率不超过50%但不超过53%,不予奖励;若发动机的热效率超过50%但不超过53%,每台发动机奖励2万元;若发动机的热效率超过53%,每台发动机奖励4万元.求每台发动机获得奖励的数学期望.(附:随机变量ξ服从正态分布N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=0.6827,P(μ﹣2σ<ξ<μ+2σ)=0.9545.)【解析】解:(Ⅰ)由表格中的数据,有182.4>79.2,即182.4∑7i=1(y i−y)2>79.2∑7i=1(y i−y)2,∴模型①的R2小于模型②的R2,说明模型②的刻画效果更好.∴当x=16亿元时,科技改造直接收益的预测值为y=21.3×√16−14.4=70.8(亿元);(Ⅱ)由已知可得,x−20=0.5+2+3.5+4+55=3,则x=23,y−60=8.5+8+7.5+6+65=7.2,则y=67.2,∴a=y−0.7x=67.2+0.7×23=83.3,∴当x>16亿元时,y与x满足线性回归方程y=−0.7x+83.3,当x=20亿元时,科技改造直接收益的预测值为y=−0.7×20+83.3=69.3.∴当x=20亿元时,实际收益的预测值为69.3+10=79.3亿元>70.8亿元.∴科技改造投入20亿元时,公司的实际收益更大;(Ⅲ)∵P(0.52﹣0.02<X<0.52+0.02)=0.9545,∴P(X>0.50)=1+0.95452=0.97725,P(X≤0.50)=1−0.95452=0.02275,∵P(0.52﹣0.01<X<0.52+0.01)=0.6827,∴P(X>0.53)=1−0.68272=0.15865,∴P(0.50<X≤0.53)=0.97725﹣0.15865=0.8186.设每台发动机获得的奖励为Y(万元),则Y的分布列为:Y024P0.022750.81860.15865∴每台发动机获得的奖励的数学期望为:E(Y)=0×0.02275+2×0.8186+4×0.15865=2.2718(万元).例10.某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系,从若干个高中男学生中抽取了1000个样本,得到如下数据.数据一:身高在[170,180)(单位:cm)的体重频数统计体重(kg)[50,55)[55,60)[60,65)[65,70)[70,75)[75,80)[80,85)[85,90)人数206010010080201010数据二:身高所在的区间含样本的个数及部分数据身高x(cm)[140,150)[150,160)[160﹣170)[170﹣180)[180﹣190)平均体重y(kg)4553.66075(Ⅰ)依据数据一将下面男高中生身高在[170﹣180)(单位:cm)体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在[170﹣180)(单位:cm)的中学生的平均体重;(保留小数点后一位)(Ⅱ)依据数据一、二,计算身高(取值为区间中点)和体重的相关系数约为0.99,能否用线性回归直线来刻画中学生身高与体重的相关关系,请说明理由;若能,求出该回归直线方程;(Ⅲ)说明残差平方和或相关指数R2与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)参考公式:b=∑ni=1(x i−x)(y i−y)∑n i=1(x i−x)2=∑ni=1x i y i−nx⋅y∑n i=1x i2−nx2,a=y−b x.参考数据:(1)145×45+155×53.6+165×60+185×75=38608;(2)1452+1552+1652+1752+1852﹣5×1652=1000.(3)663×175=116025,664×175=116200,665×175=116375.(4)728×165=120120.【解析】解:(1)身高在[170,180)的总人数为:20+60+100+100+80+20+10+10=400,体重在[55﹣60)的频率为:60400=0.15,体重在[70﹣75)的 频率为:80400=0.2,平均体重为:52.5×0.05+57.5×0.15+62.5×0.25+67.5×0.25+72.5×0.2 +77.5×0.05+82.5×0.025+87.5×0.025≈66.4,(2)因为 r =0.99→1,线性相关很强,故可以用线性回归直线来 刻画中学生身高与体重的相关, x =145+155+165+175+1855=165,y =45+75+60+53.6+66.45=60,b =∑ 8i=1x i y i −8x⋅y ∑ 8i=1x i 2−8x2=38608+175×66.4−5×165×601000=0.728, a =y −b x =60−0.728×165=−60.12, 所以回归直线方程为:y =0.728x −60.12,(3)残差平方和越小或相关指数 R 2 越接近于1,线性回归模型拟合效果越好.例11.2019年的“金九银十”变成“铜九铁十”,国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.如图是该地某小区2018年11月至2019年1月间,当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码1~13分别对应2018年11月~2019年11月)根据散点图选择y =a +b √x 和y =c +dlnx 两个模型进行拟合,经过数据处理得到两个回归方程分别为y ^=0.9369+0.0285√x和y^=0.9554+0.0306lnx,并得到以下一些统计量的值:y^=0.9369+0.0285√x y^=0.9554+0.0306lnx ∑13i=1(y i−y^i)20.0005910.000164∑13i=1(y i−y)20.006050(1)请利用相关指数R2判断哪个模型的拟合效果更好;(2)某位购房者拟于2020年4月购买这个小区m(70≤m≤160)平方米的二手房(欲购房为其家庭首套房).若购房时该小区所有住房的房产证均已满2但未满5年,请你利用(1)中拟合效果更好的模型解决以下问题:(i)估算该购房者应支付的购房金额;(购房金额=房款+税费,房屋均价精确到0.001万元/平方米)(ii)若该购房者拟用不超过100万元的资金购买该小区一套二手房,试估算其可购买的最大面积.(精确到1平方米)附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格(计税价格=房款)进行征收的.房产证满2年但未满5年的征收方式如下:首套面积90平方米以内(含90平方米)为1%;首套面积90平方米以上且140平方米以内(含140平方米)1.5%;首套面积140平方米以上或非首套为3%.参考数据:ln2≈0.69,ln3≈1.10,ln17≈2.83,ln19≈2.94,√2≈1.41,√3≈1.73,√17≈4.12,√19≈4.36.参考公式:相关指数R2=1−∑ni=1(y i−y^i)2∑n i=1(y i−y)2.【解析】解:(1)模型一中,y=0.9369+0.0285√x的残差平方和为0.000591,相关指数为R21−0.0005910.006050≈0.923,模型二中,y=0.9554+0.0306lnx的残差平方和为0.000164,相关指数为 R 21−0.0001640.006050≈0.973,∴ 相关指数较大的模型二拟合效果好些. (2)通过散点图确定2020年4月对应的 x =18, 代入(1)中拟合效果更好的模型二,代入计算 y =0.9554+0.0306ln18 =0.9554+0.0306×(ln 2+2ln 3) =0.9554+0.0306×(0.69+2×1.10) ≈1.044 (万元/平方米),则2020年4月份二手房均价的预测值为1.044(万元/平方米).(i )设该购房者应支付的购房金额 h 万元,因为税费中淵方只需缴纳契税, ①当70⩽m ⩽90 时,契税为计税价格的 1%, 故h =m ×1.044×(1%+1)=1.05444m ; ②当90<m ⩽144 时,契税为计税价格的 1.5%, 故h =m ×1.044×(1.5%+1)=1.05966m ; ③当144<m ⩽160 时,契税为计税价格的 3%, 故h =m ×1.044×(3%+1)=1.07532m ;∴ℎ={1.05444m ,70⩽m ⩽901.05966m ,90<m ⩽1441.07532m ,144<m ⩽160;∴ 当 70⩽m ⩽90 时购房金额为 1.05444m 万元, 当 90<m ⩽144 时购房金额为 1.05966m 万元, 当 144<m ⩽160 时购房金额为 1.07532m 万元.(ii )设该购房者可购买该小区二手房的最大面积为 t 平方米,由(i ) 知,当70⩽m ⩽90时,应支付的购房金额为 1.05444t ,又1.05444t ⩽1.05444×90<100, 又因为房屋均价约为1.044万元/平方米,所以 t <100,所以90⩽t <100, 由1.05966t ⩽100,解得 t ⩽1001.05966,且1001.05966≈94.4,所以该购房者可购买该小区二手房的最大面积为94平方米.例12.某新兴科技公司为了确定新研发的产品下一季度的营销计划,需了解月宣传费x (单位:万元)对月销售量y(单位:千件)的影响,收集了2020年3月至2020年8月共6个月的月宣传费x和月销售量y的数据如表:月份345678宣传费x5678910月销售量y0.4 3.5 5.27.08.610.7现分别用模型①y=b x+a和模型②y=e m x+n对以上数据进行拟合,得到回归模型,并计算出模型的残差如表:(模型①和模型②的残差分别为e1和e2,残差=实际值﹣预报值)x5678910y0.4 3.5 5.37.08.610.7e1﹣0.60.540.280.12﹣0.24﹣0.1e2﹣0.63 1.71 2.10 1.63﹣0.7﹣5.42(1)根据上表的残差数据,应选择哪个模型来拟合月宣传费x与月销售量y的关系较为合适,简要说明理由;(2)为了优化模型,将(1)中选择的模型残差绝对值最大所对应的一组数据(x,y)剔除,根据剩余的5组数据,求该模型的回归方程,并预测月宣传费为12万元时,该公司的月销售量.(剔除数据前的参考数据:x=7.5,y=5.9,∑6i=1x i y i=299.8,∑6i=1x i2=355,z=lny.z≈−1.41,∑6i=1x i y i=−73.10,ln10.7≈2.37,e4.034≈56.49.)参考公式:b=∑ni=1x i y i−nxy∑n i=1x i2−nx2,a=y−b x.【解析】解:(1)应选择模型①,因为模型①每组数据对应的残差绝对值都比模型②的小,残差波动小,残差点比较均匀地落在水平的带状区域内,说明拟合精度高.(2)由(1)知,需剔除第一组数据,则剔除后的x=7.5×6−55=8,y=5.9×6−0.45=7,5xy=280,5x2=320,∑5i=1x i y i=299.8−5×0.4=297.8,∑5i=1x i2=355−25=330.∴b=∑5i=1x i y i−5xy∑5i=1x i2−5x2=297.8−280330−320=1.78,a=y−b x=7−1.78×8=−7.24.得①的回归方程为y=1.78x−7.24,则当x=12时,y=1.78×12−7.24=14.12.故月宣传费为12万元时,该公司的月销售量为14.12千件.例13.新型冠状病毒肺炎COVID﹣19疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.如表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.日期代码x12345678累计确诊人数y481632517197122为了分析该国累计感染人数的变化趋势,小王同学分别用两种模型:①y=bx2+a,②y=dx+c对变量x和y的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差e î=y i−y î):经过计算得它∑8i=1(x i−x)(y i−y)=728,∑8i=1(x i−x)2=42,∑8i=1(z i−z)(y i−y)=6868,∑8i=1(z i−z)2=3570,其中z i=x i2,z=18∑8i=1z i.(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由;(2)根据(1)问选定的模型求出相应的回归方程(系数均保留两位小数);(3)由于时差,该国截止第9天新型冠状病毒感染确诊的累计人数尚未公布.小王同学认为,如果防疫形势没有得到明显改善,在数据公布之前可以根据他在(2)问求出的回归方程来对感染人数做出预测,那么估计该地区第9天新型冠状病毒感染确诊的累计人数是多少?附:回归直线的斜率和截距的最小二乘估计公式分别为:b=∑8i=1(x i−x)(y i−y)∑8i=1(x i−x)2,a=y−b x.【解析】解:(1)选择模型①,理由如下:根据残差图可以看出,模型①的估计值和真实值相对比较接近,模型②的残差相对比较大,所以模型①的拟合效果相对较好;(2)由(1)可知y关于x的回归方程为y=bx2+a,令z=x2,则y=bz+a,由所给的数据可得:z=18(1+4+9+16+25+36+49+64)=25.5,y=18(4+8+16+31+51+71+97+122)=50,b=∑8i=1(z i−z)(y i−y)∑8i=1(z i−z)2=68683570≈1.92,则a=y−b z≈50﹣1.92×25.5=1.04,所以y关于x的回归方程为y=1.92x2+1.04;(3)将x=9代入回归方程,可得y=1.92×92+1.04=156.56≈157(人),所以预测该地区第9天新型冠状病毒感染确诊的累计人数约为157人.例14.H市某企业坚持以市场需求为导向,合理配置生产资源,不断改革、探索销售模式.下表是该企业每月生产的一种核心产品的产量x(吨)与相应的生产总成本y(万元)的五组对照数据.产量x(件)12345生产总成本y(万元)3781012(Ⅰ)根据上达数据,若用最小二乘法进行线性模拟,试求y关于x的线性回归方程y=b x+a;参考公式:b=∑ni=1x i y i−nxy∑n i=1x i2−nx2,a=y−b x.(Ⅱ)记第(Ⅰ)问中所求y与x的线性回归方程y=b x+a为模型①,同时该企业科研人员利用计算机根据数据又建立了y与x的回归模型②:y=12x2+1.其中模型②的残差图(残差=实际值﹣预报值)如图所示:请完成模型①的残差表与残差图,并根据残差图,判断哪一个模型更适宜作为y关于x的回归方程?并说明理由;(Ⅲ)根据模型①中y与x的线性回归方程,预测产量为6吨时生产总成本为多少万元?【解析】解:(Ⅰ)计算x=15(1+2+3+4+5)=3,y=15(3+7+8+10+12)=8,∑5i=1x i2=12+22+32+42+52=55,∑5i=1x i y i=1⋅3+2⋅7+3⋅8+4⋅10+5⋅12=141,b=∑5i=1x i y i−nxy∑5i=1x i2−nx2=141−5×3×855−5×9=2.1,a=y−b x=8−2.1×3=1.7,因此,回归直线方程为y=2.1x+1.7.(Ⅱ)模型①的残差表为:x12345y3781012 y 3.8 5.9810.112.2 e﹣0.8 1.10﹣0.1﹣0.2画出残差图,如图所示;结论:模型①更适宜作为y关于x的回归方程,因为:理由1:模型①的4个样本点的残差点落在的带状区域比模型②的带状区域更窄;理由2:模型①的4个样本点的残差点比模型②的残差点更贴近进x轴..(不列残差表不扣分,写出一个理由即可得分.)(Ⅲ)根据模型①中y与x的回归直线方程,计算x=6时,y=2.1×6+1.7=14.3,所以预测产量为6吨时生产总成本为14.3万元.例15.为了解某企业生产的某产品的年利润与年广告投入的关系,该企业对最近一些相关数据进行了调查统计,得出相关数据见表:23456年广告投入x(万元)346811年利润y(十万元)根据以上数据,研究人员分别借助甲.乙两种不同的回归模型,得到两个回归方程,方程甲:方程甲:y(1)=b(x﹣1)2+2.75,方程乙:y(2)=c x﹣1.6.(1)求b(结果精确到0.01)与c的值.(2)为了评价两种模型的拟合效果,完成以下任务.①完成下表(备注:e î=y i−y î,e î称为相应于点(x i,y i)的残差;年广告投入x(万元)23456年利润y(十万元)346811模型甲估计值y î(1)残差e î(1)模型乙估计值y î(2)残差e î(2)②分别计算模型甲与模型乙的残差平方和Q1及Q2,并通过比较Q1,Q2的大小,判断哪个模型拟合效果更好.【解析】解:(1)设t=(x﹣1)2,则t=15(1+4+9+16+25)=11.∵y=6.4,∴6.4=b×11+2.75,解得b≈0.33.又x=4,∴6.4=c×4−1.6,即c=2.(2)①经计算,可得下表:年广告投入x(万元)23456年利润y(十万元)346811模型甲估计值y î(1) 3.08 4.07 5.728.0311残差e î(1)﹣0.08﹣0.070.28﹣0.030模型乙估计值y î(2) 2.4 4.4 6.48.410.4残差e î(2)0.6﹣0.4﹣0.4﹣0.40.6②Q1=(−0.08)2+(−0.07)2+0.282+(−0.03)2=0.0906.Q2=0.62×2+(−0.4)2×3=1.2.∵Q1<Q2,∴模型甲的拟合效果更好.。
简单线性回归模型试题及答案

第二章 简单线性回归模型、单项选择题:1、回归分析中定义的(B )C 、解释变量和被解释变量都为非随机变量D 解释变量为随机变量,被解释变量为非随机变量 &下面哪一个必定是错误的( C )。
A Y?=30+0.2X i ,以丫 =0.8B 、= —75 + 1.5X i ,気=0.91 C 2.1X i , r XY =0.78 D 、 Y? = —12 —3.5X i , r XY = —0.969、 产量(X ,台)与单位产品成本(Y ,元/台)之间的回归方程为Y? = 356 -1.5X ,这说明(D 。
A 产量每增加一台,单位产品成本增加356元B 、产量每增加一台,单位产品成本减少1.5元C 、产量每增加一台,单位产品成本平均增加 356元D 、产量每增加一台,单位产品成本平均减少1.5元10、 回归模型Yi 八。
「X i , i = 1 ,…,25中,总体方差未知,检验H 。
: r =0时,所用的检验 统计量 —L 服从(D 。
S目A 2(n -2)B 、t (n-1)C 、2(n")D 、t (n-2)11、 对下列模型进行经济意义检验,哪一个模型通常被认为没有实际价值的( B )。
A 、Ci (消费)=500弋.8^ (收入)B 、Qdi (商品需求)=10・0.81[(收入)0.9Pi (价格)CQ si (商品供给)二20(价格)D Y (产出量)765K 役(资本)L :"(劳动)12、进行相关分析时,假定相关的两个变量(A )。
A 、解释变量和被解释变量都是随机变量2、 A 3最小二乘准则是指使( D n Z (Y t -Y ) B 下图中“{”所指的距离是( )达到最小值的原则确定样本回归方程。
nE Y -Y? C 、max Y r -Y Dt -1n、' (Y t -Y?)2t 丄 5、 6、 线性 B 、无偏性 C、有效性 D参数-的估计量?具备有效性是指(B )Var ( ?) =0 B 、Var ( ?)为最小 C 亠0反映由模型中解释变量所解释的那部分离差大小的是 总体平方和 B 、回归平方和 C 、残差平方和7、 (B )。
第11章多重线性回归分析思考与练习参考答案

0.674
5
0.795
0.809
1.734
1.715
0.549
0.654
6
0.787
0.779
1.509
1.474
0.782
0.571
7
0.933
0.880
1.695
1.656
0.737
0.803
8
0.799
0.851
1.740
1.777
0.618
0.682
9
0.945
0.876
1.811
三、计算题
为确定老年妇女进行体育锻炼还是增加营养会减缓骨骼损伤,一名研究者用光子吸收法测量了骨骼中无机物含量,对三根骨头主侧和非主侧记录了测量值,结果见教材表11-20。分别用两种桡骨测量结果作为反应变量对其他骨骼测量结果作多重线性回归分析,提出并拟合适当的回归模型,分析残差。
解:答案提示,需要对自变量进行筛选,而且要考虑是否存在多重共线性,如果存在,应进行适当的处理。
5.如何判断、分析自变量间的交互作用?
答:基于专业背景知识,构造可能的交互作用项,并检验交互作用项是否有统计学意义。
6.多重线性回归模型的基本假定有哪些?如何判断资料是否满足这些假定?如果资料不满足假定条件,常用的处理方法有哪些?
答:多重线性回归的前提条件是线性、独立性、正态性和等方差性,可以借助残差分析等方法判断资料是否满足条件。如果资料不满足前提条件,可以采用变量变换和非线性回归等方法处理。
19
0.856
0.786
1.390
1.324
0.578
0.610
20
0.890
0.950
2.187
应用回归分析课后习题参考答案 全部版 何晓群,刘文卿

第一章回归分析概述1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
第11章 多重线性回归分析思考与练习参考答案

第11章多重线性回归分析思考与练习参考答案一、最佳选择题1.逐步回归分析中,若增加自变量的个数,则(D)。
A.回归平方和与残差平方和均增大B.回归平方和与残差平方和均减小C.总平方和与回归平方和均增大D.回归平方和增大,残差平方和减小E.总平方和与回归平方和均减小2.下面关于自变量筛选的统计学标准中错误的是(E)。
A.残差平方和(SS残差)缩小B.确定系数(R)增大2C.残差的均方(MS残差)缩小D.调整确定系数(Rad)增大2E.Cp统计量增大3.多重线性回归分析中,能直接反映自变量解释因变量变异百分比的指标为(C)。
A.复相关系数B.简单相关系数C.确定系数D.偏回归系数E.偏相关系数4.多重线性回归分析中的共线性是指(E)。
A.Y关于各个自变量的回归系数相同B.Y关于各个自变量的回归系数与截距都相同C.Y变量与各个自变量的相关系数相同D.Y与自变量间有较高的复相关E.自变量间有较高的相关性5.多重线性回归分析中,若对某一自变量的值加上一个不为零的常数K,则有(D)。
A.截距和该偏回归系数值均不变B.该偏回归系数值为原有偏回归系数值的K 倍C.该偏回归系数值会改变,但无规律D.截距改变,但所有偏回归系数值均不改变E.所有偏回归系数值均不会改变二、思考题1.多重线性回归分析的用途有哪些?答:多重线性回归在生物医学研究中有广泛的应用,归纳起来,可以包括以下几个方面:定量地建立一个反应变量与多个解释变量之间的线性关系,筛选危险因素,通过较易测量的变量估计不易测量的变量,通过解释变量预测反应变量,通过反应变量控制解释变量。
2.多重线性回归模型中偏回归系数的含义是什么?答:偏回归系数的含义是:在控制其他自变量的水平不变的情况下,该自变量每改变一个单位,反应变量平均改变的单位数。
3.请解释用于多重线性回归参数估计的最小二乘法的含义。
答:最小二乘法的含义是:残差的平方和达到最小。
4.如何判断和处理多重共线性?答:如果自变量之间存在较强的相关,则存在多重共线性。
相关分析与回归分析练习试卷1(题后含答案及解析)

相关分析与回归分析练习试卷1(题后含答案及解析) 题型有:1. 单选题 2. 多选题单项选择题以下每小题各有四项备选答案,其中只有一项是正确的。
1.根据散点图8-1,可以判断两个变量之间存在( )。
A.正线性相关关系B.负线性相关关系C.非线性关系D.函数关系正确答案:A 涉及知识点:相关分析与回归分析2.假设某品牌的笔记本市场需求只与消费者的收入水平和该笔记本的市场价格水平有关。
则在假定消费者的收入水平不变的条件下,该笔记本的市场需求与其市场价格水平的相关关系就是一种( )。
A.单相关B.复相关C.偏相关D.函数关系正确答案:C解析:在某一现象与多种现象相关的场合,假定其他变量不变,专门考察其中两个变量的相关关系称为偏相关。
在假定消费者的收入水平不变的条件下,该笔记本的市场需求与其市场价格水平的关系就是一种偏相关。
知识模块:相关分析与回归分析3.相关图又称( )。
A.散布表B.折线图C.散点图D.曲线图正确答案:C解析:相关图又称散点图,是指把相关表中的原始对应数值在乎面直角坐标系中用坐标点描绘出来的图形。
知识模块:相关分析与回归分析4.下列相关系数取值中错误的是( )。
A.-0.86B.0.78C.1.25D.0正确答案:C解析:相关系数r的取值介于-1与1之间。
知识模块:相关分析与回归分析5.如果相关系数r=0,则表明两个变量之间( )。
A.相关程度很低B.不存在任何关系C.不存在线性相关关系D.存在非线性相关关系正确答案:C解析:相关系数r是根据样本数据计算的度量两个变量之间线性关系强度的统计量。
如果相关系数r=0,说明两个变量之间不存在线性相关关系。
知识模块:相关分析与回归分析6.当所有观测值都落在回归直线上,则两个变量之间的相关系数为( )。
A.1B.-1C.+1或-1D.大于-1,小于+1正确答案:C解析:当所有观测值都落在回归直线上时,说明两个变量完全线性相关,所以相关系数为+1或-1。
回归分析练习题及参考答案
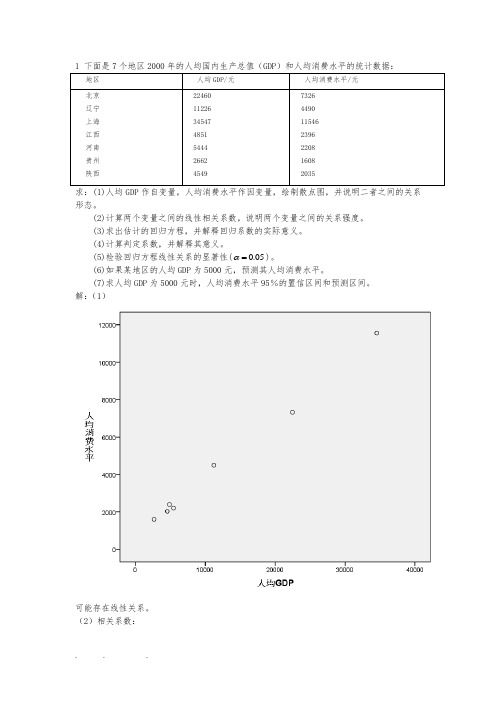
1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
回归分析习题答案

回归分析习题答案回归分析习题答案回归分析作为一种常用的统计方法,被广泛应用于各个领域。
它能够帮助研究者理解变量之间的关系,并预测未来的趋势。
在回归分析的学习过程中,习题是不可或缺的一部分,通过解答习题,我们可以更好地掌握回归分析的原理和应用。
本文将回答一些常见的回归分析习题,帮助读者更好地理解回归分析的概念和方法。
1. 问题:某公司想要预测销售额与广告投入之间的关系,他们收集了过去12个月的数据,包括每个月的广告投入和销售额。
请用简单线性回归模型拟合数据,并预测下个月的销售额。
答案:简单线性回归模型可以表示为:销售额= β0 + β1 * 广告投入。
通过最小二乘法估计参数,可以得到回归方程。
使用软件或计算器进行计算,得到β0和β1的估计值。
然后,将下个月的广告投入代入回归方程,即可得到预测的销售额。
2. 问题:某研究人员想要研究学生的考试成绩与学习时间之间的关系。
他们随机选择了100名学生,记录了他们的学习时间和考试成绩。
请用多元线性回归模型拟合数据,并解释模型中的系数。
答案:多元线性回归模型可以表示为:考试成绩= β0 + β1 * 学习时间+ β2 *年级+ ε。
其中,学习时间和年级是自变量,考试成绩是因变量。
通过最小二乘法估计参数,可以得到回归方程。
系数β1表示学习时间对考试成绩的影响,系数β2表示年级对考试成绩的影响。
如果β1和β2的估计值显著不为零,说明学习时间和年级对考试成绩有显著影响。
3. 问题:某研究人员想要研究气温对冰淇淋销量的影响。
他们收集了每天的气温和冰淇淋销量数据,发现两者呈现正相关关系。
请用非线性回归模型拟合数据,并解释模型中的参数。
答案:非线性回归模型可以表示为:冰淇淋销量= β0 + β1 * 气温+ β2 * 气温^2 + ε。
其中,气温是自变量,冰淇淋销量是因变量。
通过最小二乘法估计参数,可以得到回归方程。
系数β1表示气温对冰淇淋销量的线性影响,系数β2表示气温对冰淇淋销量的非线性影响。
回归分析试题答案
诚信应考 考出水平 考出风格浙江大学城市学院2011 — 2012 学年第一学期期末考试卷《 回归分析 》开课单位: 计算分院 ;考试形式:开卷(A4纸一张);考试时间:2011年01月6日; 所需时间: 120 分钟一.计算题(10分。
)1,考虑过原点的线性回归模型1,1,2,...,i i i y x i n βε=+=误差1,...,n εε仍满足基本假定。
求1β的最小二乘估计。
并求出1β 的期望和方差,写出1β的分布。
1221111111121,1,2,...,ˆ()()2()0ˆi i i nni i i i i i ni i i i ni ii nii y x i n Q y yy x Qy x x x yxβεββββ======+==-=-∂=--=∂=∑∑∑∑∑解:第1页共 6 页二. 证明题(本大题共2小题,每小题7分,共14分。
)1,证明:(1)22()1var()[1]i i xxx x e n L σ-=--(2)2211ˆˆ()2n i ii y y n σ==--∑是2σ的无偏估计。
011111122ˆˆˆ()()1()()1var()var[()()]()1var()var((()))()12cov[,(())](1(i i i i i nn i i j j jj j xx ni i i j j j xx ni i j j j xx ni i j j j xxe y y y x x x x y y x x y n L x x e y x x y n L x x y x x y n L x x y x x y n L x n ββσσ======-=----=----=-+--=++---+-=++∑∑∑∑∑解(1):222122222221212211)()1())2()()()11(12()]()1[1]1ˆˆ(2)()(())21ˆ[()]2()111var()[1]2212n i i j j xx xxi i xx xxi xx ni i i ni i i n n i i i i xx x x x x x L n L x x x x n L n L x x n L E E y y n E y y n x x e n n n L n σσσσσ=====----+--=++-+-=--=--=---==----=-∑∑∑∑∑22(11)n σσ--=三.填空题.(每空2分,共46分)1.为了研究家庭收入和家庭消费的关系,通过调查得到数据如下:6.22893,29.12349,43008,97.29,5422=====∑∑∑xy yxy x1)用最小二乘估计求出线性回归方程的参数估计值0ˆβ= 。
相关分析与回归分析同步练习试卷2(题后含答案及解析)

相关分析与回归分析同步练习试卷2(题后含答案及解析)题型有:1. 单项选择题 3. 名词解释题 4. 简答题 5. 计算分析题单项选择题每小题1分,在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
多选无分。
1.总体总量指标的点估计值是()A.平均数乘以样本成数B.样本容量乘以样本成数C.样本指标值乘以总体单位数D.样本指标的区间估计值乘以总体单位数正确答案:C 涉及知识点:相关分析与回归分析2.理论上最符合抽样调查随机原则的形式是()A.整群抽样B.类型抽样C.阶段抽样D.简单随机抽样正确答案:D 涉及知识点:相关分析与回归分析3.()是其他抽样方式的基础,也是衡量其他抽样方式抽样效果的标准。
()A.简单随机抽样B.等距抽样C.类型抽样D.整群抽样正确答案:A 涉及知识点:相关分析与回归分析4.为了解职工家庭生活水平状况,决定采用等距抽样进行调查,首先把职工按工资水平的高低进行排队,此种排队方法属于A.按无关标志排队B.按有关标志排队C.按简单标志排队D.按复杂标志排队正确答案:B 涉及知识点:相关分析与回归分析5.产品的单位成本随着劳动生产率的不断提高而下降,此种现象属于()A.完全相关B.不完全相关C.正相关D.负相关正确答案:D 涉及知识点:相关分析与回归分析6.只反映一个自变量和一个因变量韵相关关系是()A.正相关B.负相关C.单相关D.复相关正确答案:C 涉及知识点:相关分析与回归分析7.当相关关系的—个变量变动时,另—变量也相应地发生大致均等的变动,这种相关关系称为()A.线性相关B.非线性相关C.单相关D.完全相关正确答案:A 涉及知识点:相关分析与回归分析8.完全相关关系就是()A.函数关系B.因果关系C.狭义的相关关系D.广义的相关关系正确答案:A 涉及知识点:相关分析与回归分析9.大多数相关关系属于()A.不相关B.完全相关C.不完全相关D.无法判断正确答案:C 涉及知识点:相关分析与回归分析10.制作双变量分组相关表,应将自变量放在()A.横栏B.纵栏C.中间栏D.任意一栏正确答案:A 涉及知识点:相关分析与回归分析11.相关系数的取值范围是()A.-1≤r≤lB.-1≤r≤lC.-1<r<lD.-1≤r<1正确答案:B 涉及知识点:相关分析与回归分析12.两个变量问的相互依存程度越高,则二者之间的相关系数值越接近于()A.1B.-1C.0D.1或-1正确答案:D 涉及知识点:相关分析与回归分析13.两个现象之间相互依存关系程度越弱,则相关系数r()A.越接近于0B.越接近于-1C.越接近于1D.越接近于0.5正确答案:A 涉及知识点:相关分析与回归分析14.在相关分析中,要求相关的两个变量()A.至少有一个是随机变量B.因变量是随机变量C.都不是随机变量D.自变量是随机变量正确答案:A 涉及知识点:相关分析与回归分析名词解释题每小题3分15.一元线性回归模型正确答案:一元线性回归模型又称简单直线回归模型,它是根据两个变量的成对数据,配合直线方程式,再根据自变量的变动值,来推算因变量的估计值的一种统计分析方法。
应用回归分析试题

应用回归分析试题(一)一、选择题1. 两个变量与x的回归模型中,通常用2R来刻画回归的效果,则正确的叙述是( D )A. 2R越小,残差平方和越小B. 2R越大,残差平方和越大C. 2R与残差平方和无关D. 2R越小,残差平方和越大2.下面给出了4个残差图,哪个图形表示误差序列是自相关的(B)(A) (B)(C)(D)3.在对两个变量x,y进行线性回归分析时,有下列步骤:i ,…,①对所求出的回归直线方程作出解释; ②收集数据(i x,i y),1,2n;③求线性回归方程; ④求未知参数; ⑤根据所搜集的数据绘制散点图如果根据可行性要求能够作出变量,x y具有线性相关结论,则在下列操作中正确的是( D )A.①②⑤③④ B.③②④⑤①C.②④③①⑤ D.②⑤④③①4.下列说法中正确的是(B )A.任何两个变量都具有相关关系B.人的知识与其年龄具有相关关系C.散点图中的各点是分散的没有规律 D.根据散点图求得的回归直线方程都是有意义的5. 下面的各图中,散点图与相关系数r不符合的是(B )二、填空题1. OLSE估计量的性质线性、无偏、最小方差。
2. 学习回归分析的目的是对实际问题进行预测和控制。
3. 检验统计量t 值与P 值的关系是P(|t |>|t 值|)=P 值,P 值越小,|t 值| 越大 ,回归方程越显著。
4. 在一元线性回归中,SST 自由度为n-1, SSE 自由度为n-2, SSR 自由度为1。
5. 在多元线性回归中,样本决定系数2R = 1SSR SSESSTSST =-。
三、叙述题1. 叙述一元线性回归模型中回归方程系数的求解过程及结果(OLSE 法)答案:定义离差平方和2^1)()(i ni i y y Q ∑=-=β最小二乘思想找出参数10,ββ的估计值^1^0,ββ。
使得离差平方和最小,使^1^0,ββ满足下述条件:∑∑==--=-=ni i i ni i i x y x y Q 1210,121^^010)(min ),(),(1ββββββββ根据微分中值定理可得:0)(2|0)(2|^11^01^11^11^00^00=---=∂∂=---=∂∂∑∑====i i n i i i n i i x x y Qx y Qββββββββββ求解正规方程组得到:⎪⎪⎪⎩⎪⎪⎪⎨⎧---=-=∑∑=-=----n i i n i i i x x y y x x xy 121^11^^0)())((βββ 令 --=-=--==--=--=-=-=∑∑∑∑y x n y x y y x x L xn x x x L ni i i i ni i xy ni ini i xx 1121212)()()(则一元线性回归模型中回归方程系数可表示为⎪⎪⎩⎪⎪⎨⎧=-=--xx xy L L x y ^1^1^0βββ2. 叙述多元线性回归模型的基本假设 答案:假设1.解释变量12,,,K X X X L 是非随机的 假设(i ε)=0;假设(i ε)=2σ,i =1,2,……ncov(,i j εε)=0,i j ≠, ,i j =1,2,……n; 假设4.解释变量12,,,K X X X L 线性无关;假设5.2(0,)i N εσ:3. 回归模型中随机误差项ε的意义是什么?答案:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y 与12,,px x x L 的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
回归分析练习题及参考答案

1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
整理回归分析练习题与参考答案

20 年 月 日
A4打印 / 可编辑
2019
年招收攻读硕士学位研究生入学
考试试题
2019年招收攻读硕士学位研究生入学考试试题
********************************************************************************************招生专业与代码:流行病与卫生统计学100401、劳动卫生与环境卫生学100402、营养与食品卫生学100403、儿少卫生与妇幼保健学100404、卫生毒理学100405、公共卫生(专业学位)105300考试科目名称及代码:卫生综合353
整理丨尼克
本文档信息来自于网络,如您发现内容不准确或不完善,欢迎您联系我修正;如您发现内容涉嫌侵权,请与我们联系,我们将按照相关法律规定及时处理。
Logistic_回归分析作业答案[3页]
![Logistic_回归分析作业答案[3页]](https://img.taocdn.com/s3/m/bfd1a26871fe910ef02df8a6.png)
第六章 Logistic回归练习题 (操作部分:部分参考答案)1. 下面问题的数据来自“ch6-logistic_exercise”,数据包含受访者的人口学特征、劳动经济特征、流动身份。
数据的变量及其定义如下:变量名变量的定义age 年龄,连续测量degree 受教育程度:1=未上过学;2=小学;3=初中;4=高中;5=大专;6=大学;7=研究生girl 性别:1=女性;0=男性hanzu 民族:1=汉族;0=少数民族hetong 劳动合同:1=固定合同;2=非固定合同;3=无合同income 月收入ldhour 每周劳动时间married 婚姻状态:1=在婚;0=其他(未婚、离异、再婚、丧偶,等)migtype4 流动身份:1=本地市民;2=城-城流动人口;3=乡-城流动人口pid IDss_jobloss 失业保险:1=有;0=无ss_yanglao 养老保险:1=有;1=无这里的研究问题是,流动人口与流入地居民在社会保障、劳动保护和居住环境等方面是否存在显著差别。
流动人口被区分为城-城流动人口(即具有城镇户籍、但离开户籍地半年以上之人)和乡-城流动人口(即具有农村户籍、且离开户籍地半年以上之人)。
因此,样本包含三类人群:本地市民、城-城流动人口、乡-城流动人口及相应特征。
说明:(1)你需要对数据进行一些必要的处理,才能正确回答研究问题;(2)将变量hetong的缺失数据作为一个类别;(3)将degree合并为四类:<=小学,初中、高中、>高中. use "D:\course\integration of theory andmethod\8_ordered\chapter8-logistic_exercise.dta", clear*重新三个社会保障变量. gen ss_jobl=ss_jobloss==1. gen ss_ylao=ss_yanglao==1. gen ss_yili=ss_yiliao ==1*重新code受教育程度. recode degree (1/2=1) (3=2) (4=3)(5/7=4)*将劳动合同的缺失作为一个分类. recode hetong (.=4)请基于该数据,完成以下练习,输出odds ratio的分析结果:其一,运用二分类Logistic模型,探讨流动人口的社会保障机会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1下面是7个地区2000年的人均国生产总值(GDP)与人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京上海 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间与预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 .540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规排版。
模型摘要模型R R 方调整的 R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:Anova b模型 平方与 df均方 F Sig. 1回归 81444968.680 1 81444968.680 1331.692.000a残差 305795.034 5 61159.007总计81750763.7146a. 预测变量: (常量), 人均GDP 。
b. 因变量: 人均消费水平回归系数的检验:t 检验%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规排版。
系数(a)模型 非标准化系数标准化系数 t 显著性B 标准误Beta1(常量) 734.693 .540 5.2650.003 人均GDP (元)0.3090.0080.99836.4920.000a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的人均GDP 为5000元,预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。
(7)人均GDP 为5000元时,人均消费水平95%的置信区间为[1990.74915,2565.46399],预测区间为[1580.46315,2975.74999]。
2 从n =20的样本中得到的有关回归结果是:SSR (回归平方与)=60,SSE (误差平方与)=40。
要检验x 与y 之间的线性关系是否显著,即检验假设:01:0H β=。
(1)线性关系检验的统计量F 值是多少? (2)给定显著性水平0.05α=,F α是多少? (3)是拒绝原假设还是不拒绝原假设?(4)假定x 与y 之间是负相关,计算相关系数r 。
(5)检验x 与y 之间的线性关系是否显著?解:(1)SSR 的自由度为k=1;SSE 的自由度为n-k-1=18;因此:F=1SSR k SSE n k --=6014018=27 (2)()1,18F α=()0.051,18F =4.41 (3)拒绝原假设,线性关系显著。
(4)=0.7746,由于是负相关,因此r=-0.7746(5)从F 检验看线性关系显著。
(1)用广告费支出作自变量x ,销售额作因变量y ,求出估计的回归方程。
(2)检验广告费支出与销售额之间的线性关系是否显著(0.05α=)。
(3)绘制关于x 的残差图,你觉得关于误差项ε的假定被满足了吗? (4)你是选用这个模型,还是另寻找一个更好的模型? 解:(1)系数(a)模型 非标准化系数标准化系数 t 显著性B 标准误Beta1(常量)29.399 4.807 6.1160.002 广告费支出(万元)1.5470.4630.8313.3390.a. 因变量: 销售额(万元)(2)回归直线的F 检验:ANOVA(b)模型 平方与 df均方 F 显著性1回归 691.723 1 691.72311.147.(a)残差310.277562.合计1,002.000 6a. 预测变量:(常量), 广告费支出(万元)。
b. 因变量: 销售额(万元)显著。
回归系数的t检验:系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)29.399 4.807 6.116 0.002广告费支出(万元) 1.547 0.463 0.831 3.339 0.a. 因变量: 销售额(万元)显著。
(3)未标准化残差图:标准化残差图:(4)应考虑其他模型。
可考虑对数曲线模型:y=b0+b1ln(x)=22.471+11.576ln(x)。
4 根据下面SPSS输出的回归结果,说明模型中涉及多少个自变量?多少个观察值?写出回归方程,并根据F,s e,R2及调整的2aR的值对模型进行讨论。
模型汇总b模型R R 方调整 R 方标准估计的误差1 0.8424070.7096500.630463109.429596Anova b模型平方与df 均方 F Sig.1 回归321946.8018 3 107315.6006 8.9617590.002724残差131723.1982 11 11974.84总计453670 14解:自变量3个,观察值15个。
回归方程:ˆy=657.0534+5.710311X1-0.416917X2-3.471481X3拟合优度:判定系数R2=0.70965,调整的2aR=0.630463,说明三个自变量对因变量的影响的比例占到63%。
估计的标准误差yxS=109.429596,说明随即变动程度为109.429596回归方程的检验:F检验的P=0.002724,在显著性为5%的情况下,整个回归方程线性关系显著。
回归系数的检验:1β的t检验的P=0.008655,在显著性为5%的情况下,y与X1线性关系显著。
2β的t检验的P=0.222174,在显著性为5%的情况下,y与X2线性关系不显著。
β的t检验的P=0.034870,在显著性为5%的情况下,y与X3线性关系显3著。
因此,可以考虑采用逐步回归去除X2,从新构建线性回归模型。
5 下面是随机抽取的15家大型商场销售的同类产品的有关数据(单位:元)。
求:(1)计算y与x1、y与x2之间的相关系数,是否有证据表明销售价格与购进价格、销售价格与销售费用之间存在线性关系?(2)根据上述结果,你认为用购进价格与销售费用来预测销售价格是否有用?α=)。
(3)求回归方程,并检验模型的线性关系是否显著(0.05(4)解释判定系数R2,所得结论与问题(2)中是否一致?(5)计算x1与x2之间的相关系数,所得结果意味着什么?(6)模型中是否存在多重共线性?你对模型有何建议?解:(1)y与x1的相关系数=0.309,y与x2之间的相关系数=0.0012。
对相关性进行检验:相关性销售价格购进价格销售费用销售价格Pearson 相关性 1 0.309 0.001显著性(双侧)0.263 0.997N 15 15 15 购进价格Pearson 相关性0.309 1 -.853(**)显著性(双侧)0.263 0.000N 15 15 15销售费用 Pearson 相关性 0.001 -.853(**)1显著性(双侧) 0.997 0.000 N151515**. 在 .01 水平(双侧)上显著相关。
可以看到,两个相关系数的P 值都比较的,总体上线性关系也不现状,因此没有明显的线性相关关系。
(2)意义不大。
(3)回归统计Multiple R 0.593684 R Square 0.35246 Adjusted R Square 0.244537 标准误差 69.75121 观测值 15方差分析dfSSMSFSignificance F回归分析 2 31778.1539 15889.08 3.265842 0.073722 残差 12 58382.7794 4865.232 总计14 90160.9333Coefficie nts 标准误差 t Stat P-value L ower 95% U pper 95% 下限 95.0% 上限95.0% (常量) 375.6018 339.410562 1.10663 0.290145 -363.91 1115.114 -363.91 1115.114 购进价格x1 0.537841 0.21044674 2.555711 0.0252 0.079317 0.996365 0.079317 0.996365 销售费用x2 1.457194 0.66770659 2.182386 0.049681 0.002386 2.912001 0.002386 2.912001 从检验结果看,整个方程在5%下,不显著;而回归系数在5%下,均显著,说明回归方程没有多大意义,并且自变量间存在线性相关关系。
(4)从R 2看,调整后的R 2=24.4%,说明自变量对因变量影响不大,反映情况基本一致。
(5)方程不显著,而回归系数显著,说明可能存在多重共线性。
(6)存在多重共线性,模型不适宜采用线性模型。
6 一家电器销售公司的管理人员认为,每月的销售额是广告费用的函数,并想通过广告费用对月销售额作出估计。
下面是近8个月的销售额与广告费用数据:求:(1)用电视广告费用作自变量,月销售额作因变量,建立估计的回归方程。
(2)用电视广告费用与报纸广告费用作自变量,月销售额作因变量,建立估计的回归方程。
