强伪Ockham代数与剩余格
colombeau 代数

colombeau 代数
Colombeau代数是一种用于处理广义函数的数学工具。
广义函数是一类在数学物理中经常出现的对象,它们不满足普通函数的性质,例如可微性和有界性。
Colombeau代数的目的是为了给这些广义函数提供一个合适的代数结构,使得可以在其上定义代数运算,并且能够进行一些传统函数上的操作,比如乘法、除法和微分等。
Colombeau代数最早由法国数学家J.F. Colombeau在20世纪80年代提出,并且得到了广泛的应用。
它的基本思想是通过将广义函数表示为等价类的形式,然后定义代数运算在这些等价类上。
这种方法使得可以在广义函数上进行类似于普通函数的运算,同时也能够保持一些传统函数的性质,比如可微性和有界性。
Colombeau代数在偏微分方程、泛函分析、弹性力学和量子场论等领域都有着重要的应用。
它为处理一些传统数学工具无法处理的问题提供了一种新的途径,使得可以更加灵活地处理广义函数,并且在一定程度上克服了传统分布理论的局限性。
总的来说,Colombeau代数是一种重要的数学工具,它为处理广义函数提供了一种新的代数结构,并且在数学物理和工程领域有
着广泛的应用前景。
通过对广义函数的代数化处理,Colombeau代数为研究人员提供了更加灵活和强大的数学工具,有助于解决一些传统方法难以处理的问题。
gamma代数

gamma代数Gamma代数是一种代数结构,它包括了布尔代数和Heyting代数,常用于形式化逻辑和计算机科学中。
Gamma代数的定义包括了以下几个基本要素:一个非空集合G,一个二元运算符∧,一个二元运算符∨和一个一元运算符¬。
并且这些运算符都符合一定的公理。
其中∧和∨运算符都是交换的、结合的,并且满足分配律。
¬运算符是单调的。
此外,Gamma代数还满足一些特殊的公理。
总的来说,Gamma代数在形式化逻辑和计算机科学中都有广泛的应用。
在形式化逻辑中,Gamma代数可以用来研究逻辑公式的连通性、可满足性和等价性等问题。
在计算机科学中,Gamma代数可以用于语言处理、自动机理论和计算复杂性。
尽管Gamma代数在学术界中有广泛的应用,但是对于普通人来说,Gamma代数可能相对陌生。
不过,我们可以通过一些例子来加深理解。
首先,让我们考虑一个例子——开关。
如果我们有两盏灯,可以打开或关闭,那么这两盏灯就可以被看作是一个Gamma代数。
我们可以用1表示灯开,用0表示灯关。
∧可以表示“与”,∨可以表示“或”,¬可以表示“取反”。
假设我们有两盏灯,灯A和灯B。
如果我们想要两盏灯都亮着,那么可以表示为A∧B=1。
如果我们想要其中任何一盏灯亮着,那么可以表示为A∨B=1。
如果我们想要灯A不亮着,那么可以表示为¬A=0。
我们还可以通过Gamma代数来描述逻辑运算。
比如,如果我们有两个命题P和Q,并且我们想知道它们同时为真的情况,那么可以表示为P∧Q=1。
如果我们想知道它们中任意一个为真的情况,那么可以表示为P∨Q=1。
如果我们想知道P不为真的情况,那么可以表示为¬P=0。
总的来说,Gamma代数是一个非常重要的数学工具,可以用于解决许多实际问题。
如果我们可以熟练掌握它们,那么就可以在学术界和实际应用中走得更远。
逻辑代数知识点总结

逻辑代数知识点总结逻辑代数的研究领域非常广泛,其知识点也十分丰富,下面我将就逻辑代数的相关知识点进行总结,以便更好地理解和应用逻辑代数的理论和方法。
一、集合论集合论是逻辑代数中的基础概念之一,它研究集合的属性、运算和关系。
集合是由若干个元素组成的整体,集合的运算包括并集、交集、补集和差集等。
集合的关系包括包含关系、相等关系和重叠关系等。
1.1 集合的基本概念集合的基本概念包括集合的元素、空集、全集、子集和集合的基数等。
其中,集合的元素是构成集合的个体,空集是不包含任何元素的集合,全集是包含所有元素的集合,子集是包含于另一个集合中的集合,集合的基数是集合中元素的个数。
1.2 集合的运算集合的运算包括并集、交集、补集和差集等。
并集是将两个集合中的所有元素组成的集合,交集是两个集合中共有的元素组成的集合,补集是在全集中不属于某个集合的元素组成的集合,差集是在一个集合中但不在另一个集合中的元素组成的集合。
1.3 集合的关系集合的关系包括包含关系、相等关系和重叠关系等。
包含关系是一个集合中的所有元素都属于另一个集合,相等关系是两个集合中的元素完全相同,重叠关系是两个集合中存在共同的元素。
二、布尔代数布尔代数是逻辑代数中的一个重要概念,它研究布尔变量、布尔运算和布尔函数等。
布尔代数在计算机科学、电路设计和逻辑推理等领域有广泛的应用。
2.1 布尔变量和布尔运算布尔变量只有两种取值,分别为真和假,用1和0来表示。
布尔运算包括与运算、或运算、非运算和异或运算等。
与运算是当且仅当两个布尔变量同时为真时结果为真,或运算是当且仅当两个布尔变量至少一个为真时结果为真,非运算是将一个布尔变量取反,异或运算是当且仅当两个布尔变量不同时为真时结果为真。
2.2 布尔函数布尔函数是布尔变量和布尔运算组成的算式。
布尔函数有多种表达形式,包括逻辑表达式、真值表和卡诺图等。
逻辑表达式是用布尔变量和布尔运算表示的算式,真值表是列出布尔函数的所有输入值和输出值的表格,卡诺图是用矩形和圆圈表示布尔函数的图形方法。
逻辑代数的基本公式和常用公式

逻辑代数的基本公式和常用公式一.基本定义与运算代数是以字母代替数,称因变量为自变量的函数,函数有定义域和值域。
——这些都是大家耳熟能详的概念。
如或;当自变量的取值(定义域)只有0和1(非0即1)函数的取值也只有0和1(非0即1)两个数——这种代数就是逻辑代数,这种变量就是逻辑变量,这种函数就是逻辑函数。
逻辑代数,亦称布尔代数,是英国数学家乔治布尔(George Boole)于1849年创立的。
在当时,这种代数纯粹是一种数学游戏,自然没有物理意义,也没有现实意义。
在其诞生100多年后才发现其应用和价值。
其规定:1.所有可能出现的数只有0和1两个。
2.基本运算只有“与”、“或”、“非”三种。
与运算(逻辑与、逻辑乘)定义为(为与运算符,后用代替)00=0 01=0 10=0 11=1 或00=0 01=0 10=0 11=1或运算(逻辑或、逻辑加)定义为(为或运算符,后用+代替)00=0 01=1 10=1 11=1 或0+0=0 0+1=1 1+0=1 1+1=1非运算(取反)定义为:至此布尔代数宣告诞生。
二、基本公式如果用字母来代替数(字母的取值非0即1),根据布尔定义的三种基本运算,我们马上可推出下列基本公式:A A=A A+A=AA0=0 A+0=AA1=A A+1=1=+=上述公式的证明可用穷举法。
如果对字母变量所有可能的取值,等式两边始终相等,该公式即告成立。
现以=+为例进行证明。
对A、B两个逻辑变量,其所有可能的取值为00、01、10、11四种(不可能有第五种情况)列表如下:由此可知:=+成立。
用上述方法读者很容易证明:三、常用公式1.左边==右边2.左边==右边例题:将下列函数化为最简与或表达式。
(公式1:)= (公式2:)()练习题:3.异或运算和同或运算(放到最小项卡诺图中讲)四、逻辑函数1.定义:如果有若干个逻辑变量(如A、B、C、D)按与、或、非三种基本运算组合在一起,得到一个表达式L。
【国家自然科学基金】_广义模糊算子_基金支持热词逐年推荐_【万方软件创新助手】_20140803
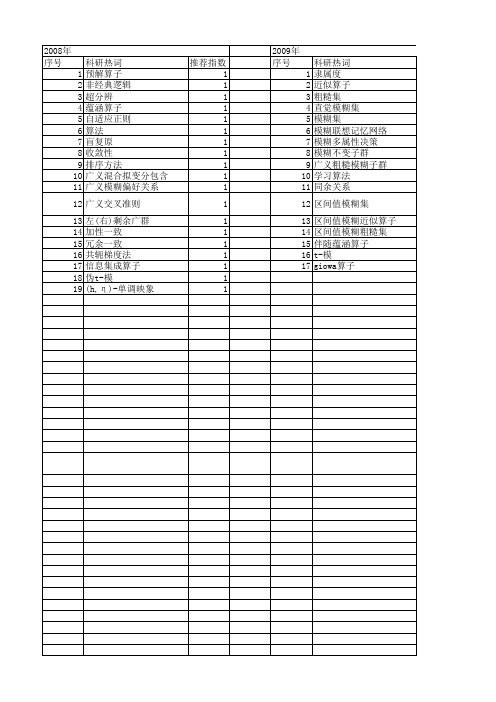
科研热词 推荐指数 剩余格 2 非可换模糊逻辑 1 隶属度 1 近似推理 1 边缘检测 1 辨识矩阵 1 诱导算子 1 覆盖上、下近似算子 1 蕴涵 1 聚合算子 1 约简 1 算子选择 1 直觉模糊集 1 目标匹配 1 模糊集 1 模糊逻辑 1 模糊蕴涵算子 1 模糊联想记忆 1 模糊神经网络 1 模糊特征平面 1 模糊推理系统 1 模糊关系方程 1 模糊 1 检测算子 1 柔性形态学 1 有序加权平均(owa)算子 1 指纹 1 拟加法 1 拟乘法 1 强伪ockham代数 1 强ockham代数 1 强de morgan代数 1 广义模糊算子 1 广义有序加权平均(gowa)算子 1 广义sugeno模糊积分 1 对比度增强 1 学习算法 1 多属性评价 1 多属性决策 1 合成推理规则 1 决策 1 信息量 1 伪ockham代数 1 t-范数 1 sobel算子 1 ockham代数 1 k-拟可加模糊测度 1 hough变换 1 canny算子 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
科研热词 推荐指数 集成算子 1 轨道电路 1 粗糙集 1 粗糙近似 1 直觉模糊不确定语言变量 1 模糊近似空间 1 模糊联想记忆网络 1 模糊神经网络 1 故障预测 1 广义概率积 1 广义概率和 1 广义vague集 1 广义vague粗糙集 1 学习算法 1 区间值模糊集 1 区间值模糊粗糙近似算子 1 区间值模糊关系 1 公理化规划 1 公理化方法 1 伴随蕴涵算子 1 三角模 1 vague集 1 t-模 1 archimedean三角模 1
Strongart数学笔记:代数K理论的代数基础小结

Strongart数学笔记:代数K理论的代数基础小结.doc 代数K理论的代数基础小结最近我在读一点代数K理论,尽管这是个比较年轻的分支,但是却在代数数论、代数几何、代数拓扑、算子代数等理论中都有着广泛的应用,可以说是代数学中的“泛函分析”。
代数K理论自然是建立抽象代数的基础之上,特别需要交换与非交换环的内容,下面我就结合环上K0、K1群,对所需的代数基础作一点简单的小结。
所谓环R的K0群,就是R上的f.g.(有限生成)投射模在同构下的等价类的半群完备化,也就是相应等价类的Grothendieck群。
这里考虑f.g.条件,是因为在无限生成的条件下,会出现类似Hilbert Hotel的情况,使得K=2K?K=0.这样一来,环上的f.g.投射模就比一般的投射模更受关注,最常见的问题就是问它们什么时候是自由的。
一个答案是需要环是PID,因为PID上f.g.模有类似Abel群的结构定理;另一个答案则是局部环(未必交换),这可以通过推广Nakayama lemma来证明。
顺便说一下,即使不要求f.g.条件,在局部环上的投射模也都是自由的,只是证明起来要麻烦一些啊~对于K0.K1群而言,比较重要的一类环就是Dedekind domain(DD),它是交换的遗传环,有着各种等价的描述:1)从环的结构上看,DD就是一维的Noether的整闭整环。
这里的整闭条件常常用来说明某个环不是DD,比如Z[?-5]就是PID但不是DD的典型例子。
2)从局部化构造来看,DD是Noether的局部DVR.这就使得对任意素理想p,都可以做p-adic赋值。
3)从理想的角度来看:DD的分式理想构成群。
此等价于其任意(分式)理想均可逆。
4)从模的角度来看:DD的f.g.投射模是理想的直和。
注意比较一下遗传条件,其理想实际上就是投射模。
此外,DD还有一些重要的性质:a)1+1/2的Noether性:理想由两个元素生成,并且其中一个元素可以事先给定。
(5)-第三章-同余、剩余类、完全剩余系

第17页,共39页。
显 然 , a 对 模 m的 逆 c不 是 惟 一 的 .当c 是 a 对 模 m 的 逆 时 , 任 一 c ' c (mod m)也 一 定 是 a 对 模 m 的 逆;由 性 质 知 , a 对 模 m 的 任 意 两 个 逆 c1,c2必 有 c1 c2 ( mo d m) .
证 由 定 理 知 , 存 在 x0, y0,使 得 a x0 m y0 1 . 取 c x0 既 满 足 要 求 .
由 此 提 供 一 种 求 a1(mo d m)有 效 的 方 法 , 这是Euclid算法的又一重要应用.
116
第16页,共39页。
例 求模 p 11所有元的逆元. 解 由 1( - 1 0 ) + 1 1 = 1 得 11 (10) 1 (mod 11) 由 2 ( - 5 ) + 1 1 = 1 得 21 ( 5) 6 (mod 11); 同样计算得: a 1 2 3 4 5 6 7 8 9 10 a1 1 6 4 3 9 2 8 7 5 10
证 同余式( 7) 即m c(a b), 这等价于
m c (a b). (c,m) (c,m)
由 定 理 及 ( m / (c,m),c / (c,m)) = 1 知 ,
这等价于 m (a b).
115
(c, m)
第15页,共39页。
性 质 若 m 1,(a,m) 1,则 存 在 c 使 得 ca 1 (mod m),我 们 把 c 称 为 是 a 对 模 m 的 逆 , 记 作 a1 b ( mo d m)或 a1.
明年的今天(2016年4月8日)是星期五
4 第4页,共39页。
定 义 给 定 一 个 正 整 数 m,把 它 叫 做 模. 如 果 用 m去除任意两个整数a与b所得的余数相同, 我们 就 说 a ,b 对 模 m同 余,记 作 a b (mod m). 如 果 余 数 不 同,我 们 就 说 a ,b 对 模 m 不 同 余,记 作 a b (mod m).
剩余类、剩余系、完全剩余系和简化剩余系学习笔记

剩余类、剩余系、完全剩余系和简化剩余系学习笔记经常在⼀些数论题题解中看到剩余类、剩余系、完全剩余系、简化剩余系这⼏个名词,但总感觉⾃⼰对它们的概念理解得不是很深,⽽且还经常混淆,故写篇博客记录下⾃⼰所理解的剩余系相关知识,如有错误,欢迎路过的⼤佬指正。
剩余类(同余类)定义n n r∈[0,n−1]n C r=n∗x+r,x∈Znn=1145,r=14C14=1145x+141145−1131,14,1159性质剩余系定义n n n x x xnn=1145r={11,4,5,14}114514性质完全剩余系(完系)定义n n n n nnn=5{0,1,2,3,4}5{5,1,8,−3,14}5性质n r a∈Z,b∈Z gcd(n,a)=1a∗r i+b (i∈[0,n−1])n证明:命题 1 :如果r是⼀个模n的剩余系,那r i+b⼀定也构成⼀个模n的完全剩余系。
反证法,若r i+b不构成⼀个模n的完全剩余系,则存在两个元素同余n,即有r x+b≡r y+b(mod n),同余式两边同时减去b,有r x≡r y(mod n),与r是⼀个模n的剩余系这⼀前提⽭盾,命题 1 得证。
命题 2:若r是⼀个模n的完全剩余系,对于任意的整数a,若有gcd(a,n)=1,则a∗r i也构成⼀个模n的完全剩余系。
同样是反证法,若结论不成⽴,则有a∗r x≡a∗r y(mod n),因为gcd(a,n)=1,所以⼀定存在a mod p的逆元inv(a),同余式两边同时乘以inv(a),则有r x≡r y(mod n),与前提⽭盾,命题 2 得证。
这俩个命题都得证,所以a∗r i构成⼀个模n的完全剩余系,a∗r i+b也构成⼀个模n的完全剩余系,故性质得证。
简化剩余系(既约剩余系、缩系)定义nφ(n)n r nφ(n)φ(n)nn=10{1,3,7,9}10n=5{1,8,7,14}5n n性质n r a∈Z gcd(n,a)=1a∗r i n 参考资料国际惯例。
逻辑代数的公式与基本定理

逻辑代数的公式与基本定理逻辑代数是一门研究命题和命题逻辑关系的数学分支。
它通过符号表示和操作来研究命题的逻辑结构。
在逻辑代数中,有一些重要的公式和基本定理,它们对于理解和应用逻辑代数具有重要的意义。
一、公式1. 吸收律(Absorption Law):a∨(a∧b)=aa∧(a∨b)=a这个定律表明,当两个命题中一个包含另一个时,可以通过去除其中一个命题来简化表达式。
2. 结合律(Associative Law):(a∨b)∨c=a∨(b∨c)(a∧b)∧c=a∧(b∧c)这个定律表明,当有多个命题连接在一起时,可以改变它们的组合方式而不改变逻辑等价关系。
3. 分配律(Distributive Law):a∨(b∧c)=(a∨b)∧(a∨c)a∧(b∨c)=(a∧b)∨(a∧c)这个定律表明,当一个命题与两个命题的逻辑运算混合时,可以通过改变运算的顺序来简化表达式。
4. 归纳法则(Inductive Law):a∨¬a=1a∧¬a=0这个定律表明,任何命题与其否定的逻辑运算结果为真或假。
二、基本定理1. 双重否定定理(Double Negation Theorem):¬(¬a)=a这个定理表明,一个命题的否定再次否定后与原命题等价。
2. 德·摩根定理(De Morgan's Theorem):¬(a∨b)=¬a∧¬b¬(a∧b)=¬a∨¬b这个定理表明,一个命题的合取或析取的否定可以分别表示为各个命题的否定的合取或析取。
3.等幂律(Law of Identity):a∧1=aa∨0=a这个定理表明,一个命题与恒等元素进行合取或析取运算后仍等于原命题。
4. 否定消除律(Law of Noncontradiction):a∨¬a=1a∧¬a=0这个定理表明,一个命题与其否定进行合取或析取运算后结果为真或假。
西格玛代数

西格玛代数西格玛代数,也称西格玛群代数,是一种数学系统,可以用来表示数字、函数、操作、向量和多维空间等概念。
西格玛代数是一种构造代数,其研究内容主要是这种代数系统的性质。
西格玛代数在几何学、微分几何学、数学物理学、概率论以及各种应用科学和工程学中都扮演着重要的角色。
西格玛代数的发明是由欧拉发现的所谓“恒等式”推导而来的。
恒等式是一些恒定的数学函数,这些函数能够用于描述数字的变化和表示某种物理的变化。
1811年,欧拉发现了这些恒等式,他给它们起了一个名字叫做“西格玛群”。
受欧拉的激励,接着有一些数学家开始研究西格玛群,以求得一种可表达西格玛群的数学结构。
两位着名的德国数学家尤金西格玛和卡尔施密特在1841年共同发表了西格玛代数的完整形式,可以说其发现实现了欧拉的抱负,以此奠定了西格玛代数的基础。
西格玛代数具有许多独特的性质。
它的结构涉及集合论、群论和抽象代数学,使得它不仅仅是一种简单的数学概念,而是一种表达事物概念的工具。
西格玛代数具有“稳定”、“可求逆”、“有界”、“正定”等等性质,从而解决了众多领域中的复杂问题。
西格玛代数的应用非常广泛。
它在线性代数、微分几何学和力学领域的应用尤其丰富,而它的数学原理也被用在电子计算机和自动控制系统中。
西格玛代数也是研究量子力学的重要工具,通过它可以表示和计算纳米尺度的一些复杂的模型。
此外,西格玛代数也被广泛应用在航空航天、建筑结构和机械等领域。
在总结西格玛代数特性方面,西格玛代数具有四大特点:结构化、稳定性、可逆性和有界性。
第一个特点是“结构化”,即西格玛代数定义了一些数学函数,这些函数在一个特定的范围内具有相同的性质,比如可以表示向量和函数,数字的变化,以及表示物理概念的空间。
第二个特点是“稳定性”,即西格玛代数可以表示的是普遍的性质,而不是特殊的性质。
第三个特点是“可逆性”,即西格玛代数可以通过某种操作实现反向操作,使得数据在某一点之间可以完全恢复。
最后一个特点是“有界性”,即西格玛代数是一种有界结构,这就意味着数据不会随时间而无限增长或变化。
伪补对称扩张Ockham代数

伪补对称扩张Ockham代数张雄盛;方捷【摘要】研究peO代数类中的子类pe2,0K1,1,即满足恒等式f 3=f和k2=idL的peO-代数.利用同余和代数的次直不可约,有如下的主要结果:如果L∈pe2,0K1,1,则L是真次直不可约当且仅当Con L?{ω}⊕[G,Φ]⊕{ι}.这里ω 和ι 分别表示相等关系和泛关系,Φ表示由f(x)=f(y)确定的一个同余,G表示Glivenko同余.【期刊名称】《纯粹数学与应用数学》【年(卷),期】2017(033)003【总页数】12页(P314-325)【关键词】p-代数;Ockham代数;扩张Ockham代数【作者】张雄盛;方捷【作者单位】广东技术师范学院数学与系统科学学院,广东广州 510665;广东技术师范学院数学与系统科学学院,广东广州 510665【正文语种】中文【中图分类】O153.1;O153.2一个p-代数(或称伪补代数)是指一个具有最小元0的格L且赋予映射∗:L→L使得对任意x∈L存在 x∗=max{y∈L|x∧y=0};等价地,x∧y=0⇔ y 6 x∗.一个Ockham代数是一个有界分配格L并赋予对偶自同态f:L→L.在Ockham代数(L;f)中,K1,1-代数是它的一个重要的子类,其中f满足条件:f3=f.有关p-代数和Ockham 代数的基本性质,见文献[1-2].在文献 [3]中,作者介绍了 pO-代数.确切地来说,一个 pO-代数是代数 (L;f,∗),其中(L;f)是 Ockham代数,(L;∗)是p-代数.同时,一元运算f和∗可相互交换.随后在2008年,文献[4]研究了扩张Ockham代数簇eO;即代数(L;f,k),其中L是有界分配格,f和k是 L的两个一元运算,使得 (L;f)是一个 Ockham代数,k是 (L;f)上的自同态.特别地,当k2=idL时,这样的代数(L;f,k)称之为对称扩张Ockham代数.他们在该文中特别刻画了对称扩张Ockham代数类中的一个子类e2,0M,即称为对称扩张de Morgan代数(L;f,k)的次直不可约性.这里的一元运算f和k满足条件:f2=idL和k2=idL.有关这些代数类的基本性质,见文献[2-4]或文献[6-8].本文将考虑包含对称扩张Ockham代数和p-代数的一个代数类.定义如下:一个伪补对称扩张K1,1代数,是指代数(L;f,k,∗).其中L是有界分配格,f,k和∗是L上的三个一元运算并且满足如下条件:(1)(L;f,k)是一个扩张Ockham代数;(2)(L;∗)是一个p-代数;(3)f3=f且k2=idL;(4)f,k和∗可相互交换.我们将用pe2,0K1,1表示伪补对称扩张K1,1-代数类.例 1.1[4] 每个有限布尔格(B;∧,∨,′,0,1)都可以被看作一个 pe2,0K1,1-代数.实际上,令A={a0,a1,···,an}为B的所有原子组成的集合,而且定义映射f:B→B使得和映射k:B→B使得对于x∈B有k(x)=[f(x)]′.于是,如文献[4]例1.4所示,f2=idB和k2=idB.从而知,(L;f,k)是对称扩张de Morgan代数.显然,例 1.2 考虑下面所给出的代数L如图1,表1所示:通过简单的观察,可以发现都是pe2,0K1,1-代数.设(E;6)是一个有序集,a,b∈E.如果a?b同时b?a,则称a和b不可比较;否则称为可比较.我们将用a∥b表示a和b不可比较,用a∦b表示a和b可比较.下面是文中所需要的引理:引理 2.1(见文献[4,6]) 如果(L;f,k)是一个对称扩张Ockham代数,则(1)(∀x∈L)x=k(x)或x∥k(x);(2)对于x,y∈L并且x6y,如果x∧k(x)=y∧k(y)同时x∨k(x)=y∨k(y),则x=y.引理 2.2(见文献 [2]) 如果 (L;∗)是一个p-代数,则定理 2.1 如果L∈pe2,0K1,1,则下面论断成立:证明 (1)如果x ∈ L 则 x 6 x∗∗,所以 f(x)>f(x∗∗)=[f(x)]∗∗>f(x),由此可得f(x∗∗)=f(x).(2)令x∈L,由(1)可得由此推知,(f(L);∗)是布尔代数.类似地,(fk(L);∗)也是布尔代数.为了术语上的便利,将 f(x)记为x◦,k(x)记为 x+并且将 pe2,0K1,1-代数 (L;f,k,∗)记为(L;◦,+,∗).同样,将 f(L)记为L◦={x◦|x∈L}和 fk(L)记为L◦+={x◦+|x∈ L}.pe2,0K1,1-代数(L;◦,+,∗)上的一个同余,是指一个格同余ϑ使得设(L;◦,+,∗)是一个 pe2,0K1,1-代数.用 ConL表示 L的同余格;用 ConlatL表示格 L 的格同余格.用符号ω和ι分别表示 L的相等关系和泛关系.正如文献 [1,6]所见,Glivenko同余 G,给出由(x,y)∈ G ⇔ x∗=y∗,是 p-代数 (L;∗)的一个同余.同时,由(x,y)∈Φ⇔f(x)=f(y)给出的关系Φ是K1,1-代数的一个同余.我们有如下的定理: 定理 2.2 设(L;◦,+,∗)∈pe2,0K1,1.则 G 和Φ 都是 L的同余并且G 6 Φ.证明如文献 [6],G是一个∗-同余.为证 G也是一个(◦,+)-同余,令(x,y)∈G则有x∗=y∗.故有从而推知因此,G是(◦,+)-同余,从而它是L的一个同余.类似可证,Φ也是L的同余.最后,设(x,y)∈G.则 x∗=y∗.由定理 2.1,有因此,(x,y)∈Φ.从而得到G 6 Φ.定理 2.3 设(L;◦,+,∗)∈pe2,0K1,1.则下列论断成立:(1)G=ω⇔ (L;∗)是布尔代数;(2)Φ = ω ⇔ (∀x ∈ L)x∗∗=x◦◦=x;(3)Φ =G ⇔ (∀x ∈ L)x∗∗=x◦◦.证明 (1)如果G=ω,则对任意x∈L,有(x∨x∗,1)∈G=ω.于是得x∨x∗=1.因此(L;∗)是布尔代数.反过来显然成立.(2)如果Φ= ω,则由定理 2.2知,G=ω.因此由 (1),对任意x∈L,有 x∗∗=x.由于(x,x◦◦)∈Φ=ω,于是有x◦◦=x.故结论成立.反过来显然成立.(3)如果Φ=G,则对x∈L,由于(x,x◦◦)∈ Φ=G,因此有故由定理2.1(1)知,反之,对于任意x∈L,如果则现若(x,y)∈ Φ 则x◦=y◦,由此推知故(x,y)∈G.从而有Φ 6 G.因此由定理2.2推知,Φ=G.给定a,b∈L并且a 6 b,用θ(a,b)表示关于a和b的主同余;即由a和b生成的(L;◦,+,∗)上的最小同余;用θlat(a,b)表示相应地格L上的主格同余;用θ∗(a,b)表示(L;∗)的主∗-同余;用θ◦(a,b)表示(L;◦)的主◦-同余.正如文献 [1,6]中所述,有下面给出pe2,0K1,1-代数的主同余表示:定理 2.4 若(L;◦,+,∗)∈pe2,0K1,1及a,b∈L 并且 a 6 b,则证明令φ(a,b)为(†)中右边的第一个等式.显然有φ(a,b)6 θ(a,b).如文献 [6]的 41页 (3)和定理 5.9 中所见,θ◦(a,b)∨ θ◦(a+,b+)是(◦,+)-同余,θ∗(a,b)和θ∗(a+,b+)是∗-同余.因此为证φ(a,b)是一个同余,只需证明θ◦(a,b)∨θ◦(a+,b+)是∗-同余同时θ∗(a,b)∨θ∗(a+,b+)是(◦,+)-同余.为此,只需观察如下事实:则后者给出 x∗∧q◦∗=y∗∧q◦∗,从而由定理 2.1 推知 x∗∨q◦=y∗∨q◦.前者给出因此得到 (x∗,y∗) ∈ θlat(p◦,q◦).则从而推知因此得到 (x∗,y∗)∈ θlat((a∗∧ b)∗+,1).类似地,如果于是有因此由定理2.1可得再由定理2.1,有从而得到综上所述,可推知φ(a,b)是一个同余.故θ(a,b)6 φ(a,b).显然,有和故φ(a,b)6 θ(a,b).因此等式成立.推论 2.1 设L∈pe2,0K1,1.如果a,b∈L◦使得a 6 b,则证明因为(L◦;∗)是布尔代数,所以有注意到 a∗∗=a 和 b∗∗=b,于是有类似地,可证θ∗(a+,b+)=θlat(a+,b+).因此由定理 2.4,等式(‡)成立.推论 2.2 设L∈pe2,0K1,1.如果a,b∈L并且a 6 b使得(a,b)∈G,则证明设(a,b)∈G 并且 a 6 b,则 a∗=b∗.因G 6 Φ,故a◦=b◦.从而由定理 2.4,等式成立.本节中,我们将考虑次直不可约pe2,0K1,1-代数.我们说一个代数L是次直不可约,如果存在L的一个同余α使得对于所有θ∈ConL且θ≠ω,都有α>θ.这样的一个同余α被称为L的唯独元.余唯独元可对偶地定义.一个次直不可约代数是单纯的,如果其同余格ConL是一个2-元素链ω<ι,即Co nL={ω,ι}.称一个次直不可约代数是真次直不可约,如果它不是单纯的.设Fix+(L)={x∈L|x+=x}.定理 3.1 设L∈pe2,0K1,1.若L是次直不可约,则有(1)ω≼G;(2)(∀x∈L)|[x]G∩Fix+(L)|6 2;(3)(∀x∈L)|[x]G|6 4.确切地说,[x]G是一个单元素集,或是以下两种形状中的一种,如图 2,图3所示:证明 (1)假设G̸=ω.因L是次直不可约的,故存在L的一个唯独元α使得因而有a,b∈L且a<b使得α=θ(a,b)6G.又因a̸=b,故由引理 2.1有不妨假定a∧a+̸=b∧b+,则因此由推论2.2推知令则在ConlatL中,有不难看出,β∧G是L的同余.从而得后面一种情况是不可能的,因为它给出α=α∧β∧G=α∧β=ω,一个矛盾.因此必有β∧G=ω.于是得故G是L的唯独元.(2)用反证法.假设存在一个 [x]G,它至少包含 Fix+(L)中的三个元素,即a,b,c∈L且a<b<c使得则由定理2.4,有这与L的次直不可约性相矛盾.因此必有|[x]G∩Fix+(L)|6 2.(3)假若存在xi∈L(i=1,2,3,4)使得则有以及由 (2),存在某个i∈{1,2,3}使得从而由引理 2.1推知,xi=xi+1,这与假设矛盾.因此必有|[x]G|6 4.再由(2),得到所要求的Hasse图.记定理 3.2 设L∈pe2,0K1,1是次直不可约.则有证明设则故由定理2.1知x∗和x是互补元.如果x/∈Fix◦(L)则由推论 2.1,有由L的次直不可约性推知,故x∧x◦=0,因而又由L的分配性,得x◦=x∗.再由推论2.1,有由此知因而有x∈{0,1},从而得相反的包含关系是显然的.题设的等式成立.定理 3.3 若L∈pe2,0K1,1是次直不可约,则S(L)是单纯代数.证明只需证明,对任意x,y∈S(L)及x<y,有假设则由引理 2.1,有不妨假定x∧x+<y∧y+.则由定理3.2,有或者或者这三种情况都蕴含着θ(x∧x+,y∧y+)=ι,由此推知θ(x,y)=ι.结论对x∨x+≠y∨y+的情况同样成立.因此,S(L)是单纯的.推论 3.1 若L∈pe2,0K1,1是次直不可约,则Φ是L的余唯独元.证明因为L/Φ≃S(L),所以有由定理 3.3可知,区间[Φ,ι]是一个 2-元素链.故结论成立.设A和B是两个不相交的有序集.将用A⊕B表示由A∪B生成的线性和,其序关系由下面所给出:定理 3.4 设L∈pe2,0K1,1.则L是真次直不可约当且仅当ConL≃{ω}⊕[G,Φ]⊕{ι}.证明 (⇒:)设L是真次直不可约,则由推论 3.1有Φ≺ι,同时由定理2.3和定理3.1,Φ≠ω.由后者,存在L的一个唯独元α使得ω≺α 6 Φ.有x,y∈L且x<y使得如果G=ω,则由定理2.3知(L;∗)是布尔代数,因而有故类似于定理3.1(1)中的证明,可得从而有另一方面,若G≠ω,则由定理3.1和定理3.3,结论成立.(⇐:)这是显然的.例 3.1 例1.2中所描述的两个pe2,0K1,1-代数(L;f1,+,∗)和(L;f2,+,∗),它们都是次直不可约.其中(L;f1,+,∗)的同余格是一个3-元素链:ω≺G=Φ≺ι,这里G=Φ=θ(a,d);(L;f2,+,∗)的同余格是一个4-元素链:ω≺G≺Φ≺ι,这里G=θ(a,d)和Φ=θ(0,d).例 3.2 考虑由下面的Hasse图所确定的pe2,0K1,1-代数(L;◦,+,∗),如图4,表2所示: 显然,L是次直不可约的且ConL诱导出一个3-元素链:ω=G≺Φ≺ι,其中Φ=θ(0,c).例 3.3 考虑由下面 Hasse图所确定的 pe2,0K1,1-代数(L;◦,+,∗),如图 5,表 3所示:可以看出,L的同余格ConL具有如下形式,如图6所示:【相关文献】[1]Blyth T S,Varlet J C.Ockham Algebras[M].Oxford:Oxford University Press,1994.[2]Fang Jie.Distributive Lattices with Unary Operations[M].Beijing:Science Press,2011.[3]Blyth T S,Fang Jie,Varlet J C.Ockham algebras withpseudocomplementation[J].Communications in Algebra,1997,25(11):3605-3615.[4]Blyth T S,Fang Jie.Extended Ockham algebras[J].Communications inAlgebra,2008,25:1271-1284.[5]Fang Jie.Pseudocomplemented MS-algebras[J].Algebra Colloquium,1996,3(1):59-65.[6]Blyth T S,Fang Jie.Symmetric extended Ockham algebras[J].AlgebraColloquium,2003,10(4):479-489.[7]Berman J.Distributive lattices with an additional unary operation[J].Aequationes Math.,1977,16:165-171.[8]Gratzer G,Lakser H.The structure of pseudo-complemented distributivelatticeⅡ,Congruence extension and amalgamation[J].Trans.Amer.Math.Soc.,1971,156:343-358.。
19_代数格

x x = x ( x (xx) ) = x (两次应用吸收律)
同理可证:x x = x
6
关于格的对偶命题
对偶命题的例子
ab≼a和ab≽a互为对偶命题
对偶命题构成规律
格元素名不变
≼与≽,与全部互换。
7
格的对偶原理
如果命题P对一切格为真,则P的对偶命题P*也对 一切格为真。
证明思路:证明P*对任意格(S, ≼)为真 定义S上的二元关系≼*, a,bS, a≼*b b≼a, 显然≼* 是偏序。 a,bS, a*b=ab, a*b=ab 所以(S, ≼*)也是格
这里a*b, a*b分别是a,b关于偏序≼*的最大下界和最小上界。
P*在(S, ≼)中为真当且仅当 P在(S, ≼*)中为真。 P在一切格中为真,P*在一切格中为真。a (bc)
设(S, ≼)是格,则(S, , )有下列性质:
交换律:ab = ba, ab = ba
吸收律: a (ab) = a, a (ab)=a
3
代数格(定义)
设L是一个集合, 和是L上的二元运算,且满足结合律、 交换律、吸收律,则称(L, , )是代数格。
x, yB, 定义 x ≼ y iff xy =x (即 xy =y)
证明这个关系满足自反性、反对称性、传递性。
这个偏序构成一个格。
lub{x,y} 即为 xy。 glb{x,y} 即为 xy。
5
代数格等同于(偏序)格
格的代数性质
结合律 交换律
吸收律 幂等律
逻辑代数公式

逻辑代数公式
1. 否定(Negation):
用符号“~”表示,即~P表示“非P”。
2. 合取(Conjunction):
用符号“∧”表示,即P∧Q表示“P且Q”。
3. 析取(Disjunction):
用符号“∨”表示,即P∨Q表示“P或Q”。
4. 异或(Exclusive or):
用符号“⊕”表示,即P⊕Q表示“P与Q互斥”。
5. 蕴含(Implication):
用符号“→”表示,即P→Q表示“如果P,则Q”。
6. 等价(Equivalence):
用符号“↔”表示,即P↔Q表示“P当且仅当Q”。
7. 空集(Empty set):
用符号“∅”表示,即表示一个没有任何元素的集合。
8. 全集(Universal set):
用符号“U”表示,即表示包含所有元素的集合。
用符号“C”表示,即表示补充一个集合的元素,例如A表示集合A 的补集。
10. 交集(Intersection):
用符号“∩”表示,即A∩B表示A和B的交集。
11. 并集(Union):
用符号“∪”表示,即A∪B表示A和B的并集。
12. 集合包含(Subset):
用符号“⊆”表示,即A⊆B表示A是B的子集。
13. 集合包含真(Proper subset):
用符号“⊂”表示,即A⊂B表示A是B的真子集。
平衡伪补Ockham代数的O-理想

平衡伪补Ockham代数的O-理想
赵秀兰;蒋红敬
【期刊名称】《汕头大学学报(自然科学版)》
【年(卷),期】2016(031)004
【摘要】在平衡伪补Ockham代数上,引入O-理想的概念,利用平衡伪补Ockham 代数核理想和余核滤子同余关系表达式,获得了平衡伪补Ockham代数上的理想成为O-理想的充要条件.
【总页数】5页(P19-23)
【作者】赵秀兰;蒋红敬
【作者单位】黄河科技学院数理部,河南郑州,450063;黄河科技学院数理部,河南郑州,450063
【正文语种】中文
【中图分类】O151
【相关文献】
1.双重伪补Ockham代数的理想与滤子同余关系的注记 [J], 赵秀兰;初元红;史西专
2.拟伪补Ockham代数的同余与核理想 [J], 王钊
3.平衡拟补Ockham代数的理想格 [J], 赵秀兰;方捷
4.拟伪补Ockham代数的同余与核理想 [J], 王钊;
5.平衡双重伪补Ockham代数的核理想与O-理想 [J], 赵秀兰
因版权原因,仅展示原文概要,查看原文内容请购买。
sigma代数

sigma代数个人实分析拙劣的笔记,仅供鄙薄.参考书籍:Folland,《Real Analysis, Modern Techniques andTheir Applications》(Second Edition)设是一个集合,由子集构成的对象我们称上的集类,其是幂集\mathcal{P}()的一个子集.我们来研究一些特殊的集类.定义2.1:设是非空集合,\mathcal{A}是上的集类,若其对有限集合的并及集合的补运算封闭,则称其上的代数(algebra);对可列集合的并封闭的代数称为\sigma-代数.注记:部分书籍将代数称为域(field),相应地,\sigma-代数称为\sigma-域.很明显,(\sigma-)代数具有这样的性质(证明从略,利用Demorgan律):命题2.1:代数对有限交也是封闭的;\sigma-代数对可列交也是封闭的.\emptyset及均属于A.命题2.2:设\mathcal{A}是代数,若其对可数个不交集合的并封闭,则其是\sigma-代数.Proof:\ 设\left\lbrace E_k\right\rbrace_{k=1}^{\infty}是\mathcal{A}中集列,令F_k=E_k\backslash \left[ \bigcup_{j=1}^{k-1}{E_j} \right] \\则F_k两两不交,且\bigcup_{k=1}^{\infty}F_k=\bigcup_{j=1}^{\infty}E_j.\blacksquare 下面给一些\sigma-代数的例子.例2.1:设是任意非空集合,\mathcal{P}()和\left\lbrace\emptyset,\right\rbrace 则是\sigma-代数.这也是最简单的两个\sigma-代数,称为平凡\sigma-代数.例2.2:设是一不可数集,则\mathcal{A}=\left\{ E\subset :E\text{可数或}E^c\text{可数} \right\} \\是一\sigma-代数,称为可数或余可数集合的\sigma-代数.命题2.3:设是一非空集合,\mathcal{M}_\alpha(\alpha\in A)是上的一族\sigma-代数,则\bigcap_{\alpha \in A}{\mathcal{M}_{\alpha}} \\仍然是上的\sigma-代数.Proof:证明从略.\blacksquare推论2.1:设\mathcal{E}是上一个集类,则存在包含\mathcal{E}的最小集类,记为\mathcal{M}(\mathcal{E}),称之为由\mathcal{E}生成的最小\sigma-代数.Proof:首先包含\mathcal{E}的\sigma-代数必然是存在的,幂集就是这样一个家伙.因而对包含\mathcal{E}的所有\sigma-代数取交即是包含\mathcal{E}的最小\sigma-代数.(根据上一命题)\blacksquare 以下引理虽然简单,但是耐用.证明从略.引理2.1:设\mathcal{E}\subset\mathcal{M}(\mathcal{F}),则\mathcal{M}(\mathcal{E})\subset\mathcal{M}(\mathcal{F}).定义2.2:设是任意度量空间,中所有开集生成的\sigma-代数称为Borel\sigma-代数,记之为\mathcal{B}_.显然\mathcal{B}_包含了所有的开集,以及一列开集的交,一列闭集的并.事实上,我们也给它们起了棒棒的名字:定义2.3:可数个开集的交集称为G_\delta集;可数个闭集的并集称为F_\sigma集.可数个G_\delta集的并集称为G_{\delta\sigma}集;可数个F_\sigma集的交集称为F_{\sigma\delta}集;以此类推下去.\mathbb{R}上的Borel\sigma-代数在实分析理论中扮演着非常重要的角色,我们对它做一点简单讨论.命题2.4:\mathcal{B}_\mathbb{R}可以由以下集类生成.(a).开区间类:\mathcal{E}_1=\left\lbrace(a,b):a<b\right\rbrace ;\ (b).闭区间类:\mathcal{E}_2=\left\lbrace [a,b]:a<b\right\rbrace ;\ (c).半开区间类:\mathcal{E}_3=\left\lbrace\left( a,b\right] :a<b\right\rbrace 或\mathcal{E}_4=\left\lbrace \left[ a,b\right) \right\rbrace ;\ (d).半开半无穷区间类:\mathcal{E}_5=\left\lbrace(a,\infty):a\in\mathbb{R}\right\rbrace 或\mathcal{E}_6=\left\lbrace (-\infty,a):a\in\mathbb{R}\right\rbrace .\ (e).半闭半无穷区间类:\mathcal{E}_7=\left\lbrace[ a,\infty) :a\in\mathbb{R}\right\rbrace 或\mathcal{E}_8=\left\lbrace (-\infty,a] :a\in\mathbb{R}\right\rbrace .Proof:我们企图利用引理2.1,首先要回忆起实直线上开集的构造定理.该定理说明所有的开集构成的集合属于\mathcal{M}(\mathcal{E}_1),继而\mathcal{B}_\mathbb{R}\subset \mathcal{M}(\mathcal{E}_1),反向"属于"号是显然的.因此,对于(b)情形只需要说明闭区间是一列开区间经过开或者并得到,从而闭区间类生成的\sigma-代数包含开区间类,因而包含Borel\sigma-代数.反向亦是如此.类似可证(c),(d),(e).\blacksquare下面来谈谈乘积\sigma-代数.我们给出一个在指标集A可数情形下乘积\sigma-代数直觉化的刻画: Proof:记\left\{ \prod_{\alpha \in A}{E_{\alpha}:}E_{\alpha}\in\mathcal{M}_{\alpha} \right\} \\生成的\sigma-代数为\mathcal{M}'.一方面,\forallE_\alpha\in\mathcal{M}_\alpha,有反之,注意到\prod_{\alpha \in A}{E_{\alpha}}=\bigcap_{\alpha \in A}{\pi _{\alpha}^{-1}\left( E_{\alpha} \right)} \\注记:你可能会问哪里用到了A的可数性,事实上,由于A可数故\bigcap_{\alpha\in A}是一个可数交,从而利用\sigma-代数对可数交运算的封闭性.实际上我们还可以进一步弱化乘积\sigma-代数.\mathcal{H}=\left\{ E_{\alpha}\subset _{\alpha}:\pi_{\alpha}^{-1}\left( E_{\alpha} \right) \in\mathcal{M}\left( \mathcal{F}_1 \right) \right\} . \\(2).我们特别发现(2)增加了一个条件_\alpha \in\mathcal{E}_\alpha,当然这是必须的.由命题2.5,我们知道\mathcal{H}=\left\{ E_{\alpha}\subset _{\alpha}:\prod_{\beta \in A}{E_{\beta}}\in \mathcal{M}\left( \mathcal{F}_2\right) ,E_{\beta}=_{\beta}\left( \beta \ne \alpha \right)\right\} \\\mathcal{F}=\left\{ \pi _{j}^{-1}\left( U_j\right) :U_j\text{在}_j\text{中开},1\le j\le n \right\} \\(2).看到问题自然会想到可分性是如何发挥作用的,我们先给出证明再阐释这一点.设C_j是_j中可数稠密子集,\mathcal{E}_j是_j中球心落于C_j且具有有理半径的开球全体构成的集合.则_j中每一开集都是\mathcal{E}_j中集合的(可数)并.这就说明\mathcal{B}_{_j}=\mathcal{M}\left( \mathcal{E}_j \right) \\进一步,中第j个坐标落于C_j(\forall j)的所有点构成的集合是可数稠密子集.而中半径为r的球体恰恰是_j中半径为r的球体的乘积.因此\mathcal{B}_=\mathcal{M}\left( \left\{ \prod_1^n{E_j}:E_j\in \mathcal{E}_j \right\} \right) \\我们希望应用命题2.6(2)的结论,则问题直接OK了,但是缺一个条件:_j\in\mathcal{E}_j.事实上,令\mathcal{E}'_j=\mathcal{E}_j\cup _j \\代替\mathcal{E}_j即可.二者生成的\sigma-代数是一样的,因_j可以由\mathcal{E}_j中集合并运算得到.\blacksquare注记:我们对(2)的证明做一些阐释.在去掉_j可分的条件下,如果\mathcal{E}_j直接取_j中开集族是否可行,此时非常大的问题在于\mathcal{B}_=\mathcal{M}\left( \left\{ \prod_1^n{E_j}:E_j\in \mathcal{E}_j \right\} \right) \\这个等式不成立了.实际上,可分性的条件使得中开集的结构更加特别了.最后我们来介绍一个非常有用的集族:基础族(elementary family)定义2.5:设是非空集合,\mathcal{E}是上的集族,其满足:(1).\emptyset\in\mathcal{E};(2).若E,F\in\mathcal{E},则E\cap F\in\mathcal{E};(3).E\in\mathcal{E}则E^c是\mathcal{E}中有限个集合的不交并;则称\mathcal{E}上的基础族.命题2.8:设\mathcal{E}是一个基础族,则\mathcal{E}中有限个不交并构成的集族是代数.Proof:证明从略.\blacksquare。
代数变形工具总结打印收藏版

a = cos A , b = cos B , c = cosC ,
( ) ( ) 解 (a + b + c)5 − a5 + b5 + c5 = 5(a + b)(b + c)(c + a) a2 + b2 + c2 + ab + bc + ca
其中 A + B + C = π
abc = 1
a = x , b = y , c = z 或 a = x2 , b = y2 , c = z2
⎜⎝
n i =1
ai 2
⎞⎛ ⎟⎠ ⎜⎝
n i =1
bi 2
⎞ ⎟⎠
−
⎛ ⎜⎝
n i =1
aibi
⎞2 ⎟⎠
=
n 1≤i< j≤n
aibj − a jbi
2
增量换元 三角消元
三角换元
齐次换元 均值换元 三边换元
常见的换元与轮换式
常见的换元
常见的轮换式
a>b a>b>c a2 + b2 =1 a+b =1 a2 + b2 + c2 =1
B
+ sin C )
=
a2 + b2
4(cot A + cot
+ c2
B + cot C )
外接圆半径 R
=
abc ,内切圆半径 r 4S
=
s p
,高
ha
=
2S a
,中线 ma
=
1 2
2b2
+
2c2
−
a2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3 期
张隆传, : 等 强伪 O ka 代数与剩余格 chm
7 5
余格等概念,均参阅文献 [ 中的定义. 面在文 8 ] 下 献 [ 的基础上给出伪 O ka 4 ] chm代数 的概念.
格, 则 , , , , ,) A V g 0 1 构成一个伪 O ka chm代数当
且仅当 , , , , ,÷ 0 1 V A o L,, ) 是分配剩余格且满足
强伪 O k a chm代数与剩余格
张 隆传 。张 小红
( 宁波大学 理学院,浙江 宁波 3 5 1 数 的概念 ,讨论 了伪 O ka 代 数 与剩余格 的关 系. 一 步 引入 强伪 chm chm 进
O ka chm代数概念, 并给 出了它的基本性质. 然后, 将著名的 0 蕴涵和 0 算子推广到伪 O k a chm
1 预 备知 识
因篇幅所限, 文中涉及到的 O ka chm代数与剩
格的重要性, 它成为多个数学分支的研究课题, 从 而也造成了其定义的多样性 . 通常模 糊逻辑 中剩
收稿 日期 :20—21 0 90-4 宁 波大学 学报 ( 工版 )网址 :t :3bnueuc 理 ht / x b . p/ d n 基金项目:国家 自然科学基金 ( 07 08); 67 5 3 宁波市 自然科学基金 ( 09 6 07 );宁波大学王宽诚幸福基金. 20 A 108 第一作者:张隆传 ( 9 4 18 一), 江西玉山人,在读硕士研究生, 男, 主要研究方向: 代数学. — i z—ogh a8 6 . m Ema :h l cun @13c l n o 通 讯作 者:张小 红 (16 一 ), ,陕西南 郑人 , 士墩 授 , 95 男 博 主要 研究 方 向:代数学 等 . - i z agioog b uc Ema :hnxah n@nue . l d n
第 2 卷 第 3期 3 2 1 年 7月 00
宁 波 大 学 学 报 (理 工 版 )
J U NA I O R LOFN NGB NI E S T NS E) O U V R I Y( E
Vb 3 NO 3 l 2 . J l 01 u y2 0
文章编 号 : 0 . 12( 0 0) 30 7 —5 1 15 3 2 1 0 .0 40 0
代数上, 证明 了添加广义 o 蕴涵和广义 0 算子后 的伪 O k a chm代数 成为剩余格的充要条件是
为强伪 Ochm 代 数.最后 给 出注记 ,以此说 明强伪 Ochm 代数 的条件是 独 立的. ka ka
关键 词 :非 可换模 糊逻 辑;伪 Oc hm 代 数 ;剩余格 ;强伪 O k a 代数 ka chm 中 图分类 号: 5 . O1 31 文献标 识码 : A
∈ £有 : 1ro= , 1= ; ()1 g 1 0 () 八 () )1 )0 g0= , () .2 / i = ) )/ ,(v )AxA )gx y= ()gy, (v V ) xy= )Av; (A )gxv ()gx J
入了双重 O k a 代数和交换双重 O k a 代数, chm ch m
深入研究强伪 O k a chm代数在何种 l 青 况下构成剩余
格. 由于 O k a 代数本身并没有蕴涵运算 , ch m
研究了一类双重 O k a chm代数 ; , , , v ^. 即赋予
和 g 偶格 同态 [5 是 41 -;另一 方面 , 现代 模糊 逻辑 理 在
O ka ch m代数与剩余格都是与非经典数理逻辑
余格的定义【 实质上是指可换剩余格 . 6 】 , 在非可换 模糊逻辑的研究 中涉及非可换 的剩余格, 与文 它
献[] 7中的 也不尽相同. 为了不引起混乱, 我们
( 尤其是模糊逻辑) 密切相关 的代 数结构 . 一方面, O k a 代数是格论的一个重要分支, chm 其研究始于 17 7年 B r a[ 9 e n] m  ̄ 关于
O k a 代数;引入强伪 O k a 代数概念, chm chm 进而
格的一个特殊子类( chm 代数是对偶 自同态 的 O ka
有 界分配格 ) 2 . 0世 纪 9 年代 , l h等 [ 1 0 By t 2 在 - 3 O ka chm代数 、D ra 代数和 MS eMogn 代数上做 了 大量工作. 9 4 By 和 V r t 18 年, l h t al 引入了双重 MS e 代数, 后来, eui 将其扩充到双重 , S qe a r 代数. 我 国学者 Wu F n 介绍了双重 . 和 ag 1 代数, 并相继 引
,
子簇的工作. 作为分配
使用 “ 可换剩余格”和 “ 一般剩余格”的名称, 且 要求是有界格 、1既是最大元又是最小元( 中的 文 “ 剩余格”是非可换剩余格, 即一般剩余格) . 笔者在文献 [ 8 ] 4 . 基础上,引入了伪 O k a ,9 chm 代数 的概 念 , 论剩 余格 在何 种情 况下 构成 伪 讨
条件: A ) v 一 ( y ( y一 y , A ) x 一 x 证明 ~V ,∈ . , xJ ,
定义 1 一个伪 O ka chm代数是一个型为(, , 22
1 10 0的代数 , , , g 0 1 即 , , , 0 ,,,) A V , , ) . AV , 1 ) 和 , , , , , ) O k a A Vg 0 1 是 chm代数, 且对任意 X ,
和相应的⑧ 运算, 故需要基于伪 O ka 代数的序 chm
结构成为剩余格.
1 对可交换一元运算 .和 g的有界分配格, 厂 其中。 厂 结构构造 出恰当的 ,L和o 以使产生的新代数 + ,
论 中, 剩余格是公认的最重要的代数结构, 已成为 模糊逻辑系统 中相当理想的代数框架 . 因为剩余
