流体力学计算题练习

合集下载

流体力学计算题及答案.docx

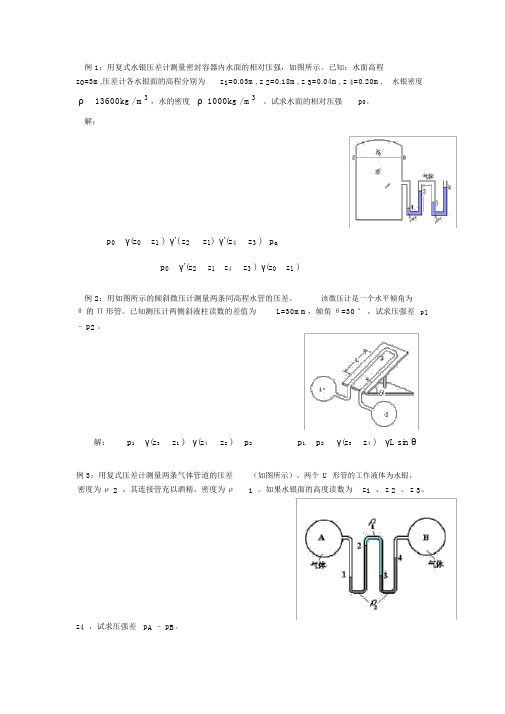
例 1：用复式水银压差计测量密封容器内水面的相对压强，如图所示。

已知：水面高程z0=3m,压差计各水银面的高程分别为z1=0.03m, z 2=0.18m, z 3=0.04m, z 4=0.20m,水银密度ρ13600kg / m3，水的密度ρ 1000kg / m3。

试求水面的相对压强p0。

解：p0γ(z0 z1 ) γ'( z2z1) γ'(z4z3 ) p ap0γ'(z2z1 z4z3 ) γ(z0 z1 )例 2：用如图所示的倾斜微压计测量两条同高程水管的压差。

该微压计是一个水平倾角为θ的Π形管。

已知测压计两侧斜液柱读数的差值为L=30mm，倾角θ=30 °，试求压强差p1– p2。

解：p1γ(z3z1 )γ(z4z2 ) p2p1p2γ(z3z4 )γL sinθ例 3：用复式压差计测量两条气体管道的压差（如图所示）。

两个U形管的工作液体为水银，密度为ρ2，其连接管充以酒精，密度为ρ 1 。

如果水银面的高度读数为z1、 z 2、 z 3、z4，试求压强差p A– p B。

解：点 1 的压强： p A点2的压强： p2p Aγ2( z2z1 )点 3的压强： p3 p Aγ2( z2z1 )γ1( z2 z3 )p4p Aγ2( z2z1 ) γ1(z2z3 ) γ2( z4z3 ) p Bp A p Bγ2(z2 z1 z4z3 ) γ1( z2z3 )例 4：用离心铸造机铸造车轮。

求A-A 面上的液体总压力。

解：p 1 2r2gz C p 1 2r2gz p a22在界面 A-A 上： Z = - hp 1 2r2gh p a F( p p a ) 2 rdr 21 2 R41ghR2R2082例 5：在一直径 d = 300mm，而高度 H= 500mm的园柱形容器中注水至高度h1 = 300mm，使容器绕垂直轴作等角速度旋转。

如图所示。

(1) 试确定使水之自由液面正好达到容器边缘时的转数n1；(2)求抛物面顶端碰到容器底时的转数 n2，此时容器停止旋转后水面高度 h2将为多少？解： (1)由于容器旋转前后，水的体积不变( 亦即容器中空气的体积不变 ) ，有：图1d 2L1 d 2 (H h1 )424L 2( H h1 ) 400 mm0.4 m在 xoz 坐标系中，自由表面2 r 2 1 的方程：z02g对于容器边缘上的点，有：d0.15m z0 r22gz0 2 9.80.4 r 20.152∵ 2 n / 60L0.4m18.67( rad / s)n1606018.672178.3 (r / min)2(2) 当抛物面顶端碰到容器底部时，这时原容器中的水将被甩出一部分，液面为图中2所指。

流体力学期末复习,计算部分

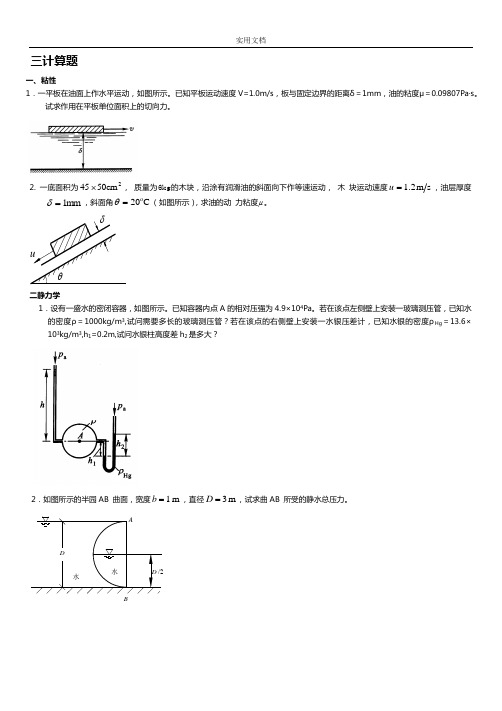
三计算题一、粘性1．一平板在油面上作水平运动，如图所示。

已知平板运动速度V=1.0m/s，板与固定边界的距离δ＝1mm，油的粘度μ＝0.09807Pa·s。

试求作用在平板单位面积上的切向力。

2. 一底面积为2cm5045⨯，质量为6kg的木块，沿涂有润滑油的斜面向下作等速运动，木块运动速度sm2.1=u，油层厚度mm1=δ，斜面角C02ο=θ（如图所示），求油的动力粘度μ。

δuθ二静力学1．设有一盛水的密闭容器，如图所示。

已知容器内点A的相对压强为4.9×104Pa。

若在该点左侧壁上安装一玻璃测压管，已知水的密度ρ＝1000kg/m3,试问需要多长的玻璃测压管？若在该点的右侧壁上安装一水银压差计，已知水银的密度ρHg＝13.6×103kg/m3,h1=0.2m,试问水银柱高度差h2是多大？2．如图所示的半园AB 曲面，宽度m1=b，直径m3=D，试求曲AB 所受的静水总压力。

D/2AB水水DαO B O A Hp a3. 如下图，水从水箱经管路流出，管路上设阀门K ，已知L=6m,α=30°,H=5m, B 点位于出口断面形心点。

假设不考虑能量损失，以O-O 面为基准面，试问：阀门K 关闭时，A 点的位置水头、压强水头、测压管水头各是多少？4. 位于不同高度的两球形容器，分别贮有2m kN 9.8=g A ρ的油和2m kN 00.10=g B ρ的盐水，差压计内工作液体为水银。

m 21=h ，m 32=h ，m 8.03=h ，若B 点压强2cm N 20=B p ，求A 点压强A p 的大小。

••M MA B汞h h h γγAB1235. 球形容器由两个半球面铆接而成，有8个铆钉，球的半径m 1=R，内盛有水，玻璃管中液面至球顶的垂直距离2m . 1=H ，求每个铆钉所受的拉力。

RH6．设有一盛静水的密闭容器，如图所示。

由标尺量出水银压差计左肢内水银液面距A 点的高度h 1=0.46m ，左右两侧液面高度差h 2=0.4m ，试求容器内液体中A 点的压强，并说明是否出现了真空。

流体力学计算题（有答案）

《流体力学》计算题及答案。

2、当压强增加4×104Pa 时，某种液体的密度增长0.015%，求该液体的压缩系数。

解：0=+=⇒=dV Vd dM V M ρρρρρd dV V -=N m dp d dp V dV p /1075.3104%015.011294-⨯=⨯==-=ρρβ3、将一根长度L 为800mm ，直径d 为45mm 的圆轴水平放置于内径D 为50mm 的圆管中央，圆柱体与圆管的间隙充满密度为925kg/m 3、运动粘度s m /105.624-⨯=ν的油液。

求将圆柱体以0.8m/s 的速度作水平移动时所需的拉力F 为多少牛顿？（间隙中的速度分布可认为是线性分布）。

答案： N F 8.21=4、(将一根长度L 为1m ，直径d 为200mm 的圆柱体水平放置于内径D 为206mm 的圆管中央，圆柱体与圆管的间隙充满密度为920kg/m 3的油液。

测得将圆柱体以1m/s 的速度作水平移动时的拉力F 为108牛顿，求该油液的运动粘度（间隙中的速度分布可认为是线性分布）。

答案：运动粘度s m /106.524-⨯=ν6、液体通过装置DV 的阻力损失由倒置U 形差压计测量。

液体的密度为1500kg/m 3。

差压计中的指示液体使用密度为750 kg/m 3的油。

求如图所示标定值时，A 和B 的压强水头变化。

解：设差压计中的工作液体密度为Pam8、已知速度场⎪⎩⎪⎨⎧-=-=)/()/(2222x y ax x y ay u υ，其中a 为常数。

（１）试求流线方程（２）判断流动是否无旋，若无旋则求速度势ϕ。

答案：（１）流线方程C y x =-22（２）因为22y x x y u +=∂∂-∂∂υ除了０点外，022≠+=∂∂-∂∂y x xy u υ，所以是有旋的，不存在速度势。

9、在平面不可压缩流动中，已知速度势函数233xy x -=ϕ，求相应的流函数。

答案：10、已知某不可压缩流体平面流动的速度分布规律为：⎩⎨⎧--=-+=yxy yx x u 22422υ判断说明该流动是否连续？是否无旋？并求出流函数。

流体力学练习题及参考答案

水力学练习题及参考答案一、是非题(正确的划“√”，错误的划“×)1、理想液体就是不考虑粘滞性的实际不存在的理想化的液体。

（√）2、图中矩形面板所受静水总压力的作用点与受压面的形心点O重合。

(×)3、园管中层流的雷诺数必然大于3000。

×4、明槽水流的急流和缓流是用Fr判别的，当Fr＞1为急流。

(√)5、水流总是从压强大的地方向压强小的地方流动。

（×）6、水流总是从流速大的地方向流速小的地方流动。

（×）6、达西定律适用于所有的渗流。

（×）7、闸孔出流的流量与闸前水头的1/2次方成正比。

（√）8、渐变流过水断面上各点的测压管水头都相同。

(√)9、粘滞性是引起液流运动能量损失的根本原因。

(√)10、直立平板静水总压力的作用点就是平板的形心。

（×）11、层流的沿程水头损失系数仅与雷诺数有关。

√12、陡坡上出现均匀流必为急流，缓坡上出现均匀流必为缓流。

(√)13、在作用水头相同的条件下，孔口的流量系数比等直径的管嘴流量系数大。

(×)14、两条明渠的断面形状、尺寸、糙率和通过的流量完全相等，但底坡不同，因此它们的正常水深不等。

(√)15、直立平板静水总压力的作用点与平板的形心不重合。

（√）16、水力粗糙管道是表示管道的边壁比较粗糙。

×17、水头损失可以区分为沿程水头损失和局部水头损失。

(√)18、牛顿内摩擦定律适用于所有的液体。

(×)19、静止液体中同一点各方向的静水压强数值相等。

（√）20、明渠过流断面上各点的流速都是相等的。

×21、缓坡上可以出现均匀的急流。

(√)22、静止水体中,某点的真空压强为50kPa，则该点相对压强为-50 kPa。

(√)24、满宁公式只能适用于紊流阻力平方区。

(√)25、水深相同的静止水面一定是等压面。

(√)26、恒定流一定是均匀流，层流也一定是均匀流。

（×）27、紊流光滑区的沿程水头损失系数仅与雷诺数有关。

工程流体力学经典计算题

工程流体力学经典计算题1、相对密度0.89的石油，温度20ºC 时的运动粘度为40cSt ，求动力粘度为多少？解：89.0==水ρρd ν＝40cSt ＝0.4St ＝0.4×10-4m 2/s μ＝νρ＝0.4×10-4×890＝3.56×10-2 Pa ·s2、图示一平板在油面上作水平运动，已知运动速度u=1m/s ，板与固定边界的距离δ=1，油的动力粘度μ＝1.147Pa ·s ，由平板所带动的油层的运动速度呈直线分布，求作用在平板单位面积上的粘性阻力为多少？解：233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 3、如图所示活塞油缸，其直径D ＝12cm ，活塞直径d ＝11.96cm ，活塞长度L ＝14cm ，油的μ＝0.65P ，当活塞移动速度为0.5m/s 时，试求拉回活塞所需的力F=？解：A ＝πdl , μ＝0.65P ＝0.065 Pa ·s ,Δu ＝0.5m/s , Δy=(D-d)/2，()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ4、在一直径D ＝300mm 、高H ＝500mm 的圆柱形容器中注入水至高度h 1＝300mm ，然后使容器绕其垂直轴旋转。

①试求能使水的自由液面到达容器上部边缘时的转数n 1。

②当转数超过n 1时，水开始溢出容器边缘，而抛物面的顶端将向底部接近。

试求能使抛物面顶端碰到容器底时的转数n 2，在容器静止后水面高度h 2将为多少？解：自由液面方程：gr z s 222ω=注：抛物体的体积是同底同高圆柱体体积的一半gR R g R V 422142222πωπω=⋅=抛① ()12122h H R V h R V H R -=⇒=-πππ抛抛()()11112421244n Rh H g h H R gR πωππω=-=⇒-=()()min /34.178/97.21015014.3103005008.93311r s r Rh H g n =⨯⨯⨯-⨯=-=--π ② 2/2H R V π=抛()min/4.199/323.31015014.32105008.922423322422r s r RgH n H R gR n ==⨯⨯⨯⨯==⇒=--ππππ③mm H h 250250022===附证明：抛物体的体积是同底同高圆柱体体积的一半gR R g R V 422142222πωπω=⋅=抛⎪⎪⎭⎫ ⎝⎛=======⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==⎰⎰⎰⎰g r g r r z r V V gr r gdr r gdr g r r gr d r dz r V r r r z z 2221442224022********020423022202220200πωωπππωπωπωωπωππ柱柱抛5、某处装置一安全闸门，门宽B 为0.6米，门高H 为1.0米。

《流体力学与流体机械》计算题及答案

Q v1A1 v2 A2
Q
v2 A2
4
0.12
3
0.0234 m3
/
s
v1
4Q
d12
4 0.0234
0.152
1.3
3
6 m
/
s
编辑ppt
• 习题3-15 判断流动 ux = xy；uy = -xy 是否满足不可压缩流动的连续性条件。 • 解：因为 ux = xy；uy = -xy 与时间无关，所以流动定常，根据定常不可压微分形式连续方程，
•
图示为一轴流风机，已测得进口相对压力p1= -103 Pa，出口相对压力p2 = 150 Pa。设截面
1-2间压力损失 100Pa，求风机的全压P ( P为风机输送给单位体积气体的能量 ) 。
• 解：
p1
1
2
v12
z2
z1 ga
p
p2
2
2
v22
ghw
1000 0 p 150100
P 1250 Pa
第一章流体及其物理性质
•
• 例1－2 相距为h=10 mm的两固定平板间充满动力粘度μ=1.49 Pa·s的甘油，若两板间甘油的速度分布为u=4000y(h-y)
•
(1) 若上板的面积A=0.2 m2，求使上板固定不动所需的水平作用力F；
•
(2) 求y=h/3和2h/3处的内摩擦应力，
并说明正负号的意义。
有一圆桶，半径R=1m，高H=3.5m，桶内盛有高度h=2.5m的水。圆桶绕中心
轴匀速旋转。问水恰好开始溢出时，转速ω为多少？而此时距中心线r=0.4m处桶底面上A点的压力是多少?
• 解：(1) 求旋转速度ω

流体力学计算题练习及答案

练习题1. 如右图所示，在一密闭容器中，上部装有密度ρ1=0.8×103kg/m 3的油，下部为密度ρ2=103 kg/m 3的水，已知h 1=0.4m ，h 2=0.2m 。

测压管中水银柱的读数h =0.5m ，水银的密度为ρ1=13.6×103 kg/m 3。

求密闭容器中油液面上的压强p 0。

2. 图示为一水暖系统，为了防止水温升高时体积膨胀将水管胀裂，在系统顶部设一膨胀水箱，使水有膨胀的余地。

若系统内水的总体积为8m3，加温前后温差为50℃，在其温度范围内水的膨胀系数为βT ＝9×10－4 1/℃，求膨胀水箱的最小容积。

3. 当温度不变，压强从0.20 MPa 增加到10 MPa 时，某种液体的体积减小0.49%，求该液体的体积模量。

4. 两个充满空气的封闭容器互相隔开，左边压力表M 的读数为100kPa ，右边真空计V 的读数为 3.5mH2O ，试求连接两容器的水银压差计中h 的读值。

5. 已知流体运动的速度场为：3231yv xy v y x ==，，试求t=2时过点()()x y z ，，，，=312处的流线方程。

hp ap 0h 1h 2ρ1ρ2ρ36. 如图所示，水在压强作用下从密封的下水箱沿竖直管道流入上水箱中，已知h ＝50cm ，H ＝3m ，管道直径D ＝25mm ，λ＝0.02，各局部阻力系数分别为ζ1＝0.5，ζ2＝5.0，ζ3＝1.0，求：为维持稳定的管中流速V ＝1m/s ，下水箱的液面压强应保持在多少Pa?7. 右图为毕托管示意图。

液体自左向右流动，直管和直角弯管直接插入管道内的液体中，弯管开口迎着流动方向。

测得A 点的液柱高度为hA =170 mm ，B 点的液柱高度为hB = 230 mm ，已知液体的密度为 =990 kg/m3，忽略阻力损失，试计算管内液体的流速uA 。

8. 如右图所示为一壁厚可以忽略的大容器，在其下部开一直径为d =12mm 的小孔口，水自孔口流出后进入另一液面比大容器液面低H =1.2m 的容器中，两容器内的水位始终保持不变。

流体力学计算题

[1]
6．高压管末端的喷嘴如图，出口直径d=10cm，管端直径D=40cm，流量Q=0.4m3/s，喷嘴和管以法兰盘连接，共用12个螺栓，不计水头损失，不计水和管嘴的重量，求每个螺栓受力为多少。
[1]
7．矩形断面的平底渠道。已知渠道宽度B=2.7m，渠道河床在某断面有一上升坎，坎高度h1=0.5m，坎上游渐变流断面上的水深H=2m，坎后水面下降h2=0.15m，忽略边壁和底部摩擦阻力，试求水流对底坎的推力R。
[1]
10．一水平放置的突然扩大管路，直径由d1=50mm扩大到d2=100mm，在扩大前后断面接出的双液比压计中上部为水，下部为=15.7kN/m3的四氯化碳，当流量Q=16 m3/h时的比压计读数h=173mm，求突然扩大的局部阻力系数，并与理论计算值进行比较。
【题型：计算】【100分】【限300个汉字以内】
[1]
11．直径为0.5m的通风管道，流动属紊流粗糙区，当空气流量为3m3/s，在400m长的管段上的压差值为20cm水柱高，温度为10ºC时的空气密度为1.25kg/m3，沿程摩阻系数。求管壁的当量粗糙高度ks。
【题型：计算】【100分】【限300个汉字以内】
[1]
12．薄壁孔口出流，直径d=2cm，。水箱水位恒定H=2m，试求：（1）孔口流量Q；（2）此孔口外接圆形管嘴的流量Qn；（3）管嘴收缩断面的真空高度。
[1]
4．有一圆滚门，长度l=20m，直径D=4m，上游水深H1=4m，下游水深H2=2m。求作用于圆滚门上的水平和铅直分压力。
1]
5.钢储罐内装满10°C的水，密封加热到75°C，在加热增压的温度和压强范围内，水的热膨胀系数α= 4.1×10-4/°C，体积弹性模量E= 2×109 N/m2，罐体坚固，假设容积不变，试估算因加热罐壁承受的压强。

工程流体力学习题及答案

工程流体力学习题及答案（1）1 某种液体的比重为3，试求其比容。

（答：3.3×10-4米3/公斤）2 体积为5.26米3的某种油，质量为4480公斤，试求这种油的比重、密度与重度。

（答：0.85；851公斤/米3；8348牛/米3）3 若煤油的密度为0.8克/厘米3，试求按工程单位计算的煤油的重度、密度与比容。

（答：800公斤力/米3；81.56公斤力·秒2/米4；1.25×10-3米3/公斤力） 4 试计算空气在温度t=4℃，绝对压力P=3.4大气压下的重度、密度与比容。

(答：42.4牛/米3；4.33公斤/米3；0.231米3/公斤）5 试计算二氧化碳在温度为t=85℃，绝对压力P=7.1大气压下的重度、密度与比容。

（答：104牛/米3；10.6公斤/米3；0.09厘米3/公斤）6 空气在蓄热室内于定压下，温度自20℃增高为400℃，问空气的体积增加了多少倍？（答：1.3倍）7 加热炉烟道入口烟气的温度900=t 入℃，烟气经烟道及其中设置的换热器后，至烟道出口温度下降为500=t 出℃，若烟气在0℃时的密度为28.10=ρ公斤/米3，求烟道入口与出口处烟气的密度。

（答：298.0=ρ人公斤/米3；452.0=ρ出公斤/米3） 8 试计算一氧化碳在表压力为0.3大气压、温度为8℃下的重度。

（答：15.49牛/米3）9 已知速度为抛物线分布，如图示 y=0，4，8，12，17厘米处的速度梯度。

又若气体的绝对粘性系数为1013.25-⨯=μ牛·秒/米3，求以上各处气体的摩擦切应力。

9 题图10 夹缝宽度为h ，其中所放的很薄的大平板以定速v 移动。

若板上方流体的粘性系数为μ，下方流体的粘性系数为K μ，问应将大平板放在夹缝中何处，方能使其移动时阻力为最小？（答:h kk kh =++11或）11 如图所示，一正方形b ×b=67×67厘米2、质量为12公斤的平板，在厚3.1=δ毫米的油膜支承下，以匀速v=0.18米/秒沿一斜面滑下，问油的粘性系数是多少？10 题图 11 题图（答：0.728牛·秒/米2）12 如图所示，气缸直径D 1=16厘米，活塞直径D 2=16厘米，质量0.97公斤，若活塞以匀速0.05米/秒在气缺内下降，试求油的粘性系数是多少？12 题图 15 题图（答：0.63牛·秒/米2）13 直径为150毫米的圆柱，固定不动。

流体力学静水压强练习题

流体力学静水压强练习题一、基本概念题1. 列出静水压强的定义。

2. 静水压强与哪些因素有关？3. 什么是绝对压强和相对压强？4. 简述液体压强随深度的变化规律。

5. 如何计算液体在某一点的静水压强？二、公式应用题1. 已知水的密度为1000 kg/m³，求深度为10m处的静水压强。

2. 某容器内液体深度为5m，液体密度为800 kg/m³，求容器底部的静水压强。

3. 一根直径为0.1m的管道内，水流速度为2m/s，求管道中心处的静水压强。

4. 某封闭容器内气体压强为1.5×10^5 Pa，容器内液体深度为3m，液体密度为1200 kg/m³，求气体对容器底部的压强。

5. 在一水坝底部，水深为20m，求水坝底部的静水压强。

三、综合分析题1. 分析液体内部压强分布规律，并说明原因。

2. 举例说明静水压强在实际工程中的应用。

3. 讨论液体静压强与液体密度的关系。

4. 如何利用静水压强原理计算液体在容器内的压力？5. 分析在深海潜水过程中，潜水员所承受的静水压强变化。

四、计算题1. 已知一圆形水池直径为10m，水深为4m，求水池底部的静水压强。

2. 一矩形水槽长20m，宽5m，水深6m，求水槽底部的静水压强。

3. 某圆柱形容器高1m，直径0.5m，容器内液体密度为1500kg/m³，求容器底部的静水压强。

4. 一潜水员在海底作业，水深为50m，求潜水员所承受的静水压强。

5. 一艘船在海上航行，船底距海平面深度为15m，求船底的静水压强。

五、判断题1. 液体内部的压强处处相等。

（）2. 静水压强与液体深度成正比。

（）3. 液体压强与液体密度无关。

（）4. 绝对压强总是大于相对压强。

（）5. 液体静压强在水平方向上是不变的。

（）六、选择题A. 液体的密度B. 液体的温度C. 液体的深度D. 重力加速度2. 在同一液体中，下列哪个深度处的静水压强最大？A. 5m深处B. 10m深处C. 15m深处D. 20m深处A. 静水压强随深度增加而减小B. 静水压强在液体表面处最大C. 静水压强在液体内部处处相等D. 静水压强与液体密度成正比4. 在一个密闭容器内，液体上方气体的压强为50kPa，液体深度为2m，液体密度为1000 kg/m³，容器底部的总压强为多少？A. 100 kPaB. 150 kPaC. 200 kPaD. 250 kPaA. P = ρghB. P = ρgh^2C. P = ρg/hD. P = ρg^2h七、填空题1. 液体的静水压强是由__________、__________和__________共同作用产生的。

流体力学考试题及答案

流体力学考试题及答案一、选择题（每题2分，共20分）1. 流体力学中，流体的基本假设是什么？A. 流体是不可压缩的B. 流体是完全弹性体C. 流体是完全塑性体D. 流体是连续介质答案：D2. 流体静力学中，压力的分布规律是什么？A. 与深度成正比B. 与深度成反比C. 与深度无关D. 与深度的平方成正比答案：A3. 流体的粘性是由什么决定的？A. 温度B. 压力C. 密度D. 以上都是答案：A4. 伯努利方程描述了什么？A. 流体的静压和动压关系B. 流体的压缩性C. 流体的粘性D. 流体的热力学性质答案：A5. 流体的雷诺数是用来描述什么的？A. 流体的密度B. 流体的粘性C. 流体的惯性力与粘性力的比值D. 流体的压缩性答案：C6. 什么是流体的不可压缩性条件？A. 密度不变B. 温度不变C. 压力不变D. 速度不变答案：A7. 流体的连续性方程描述了什么？A. 流体的动量守恒B. 流体的动能守恒C. 流体的质量守恒D. 流体的热能守恒答案：C8. 流体的湍流与层流的区别是什么？A. 湍流有粘性，层流没有B. 湍流是有序的流动，层流是无序的C. 湍流是无序的流动，层流是有序的D. 湍流和层流都是有序的流动答案：C9. 流体的边界层厚度与什么有关？A. 流体的密度B. 流体的速度C. 流体的粘性D. 流体的压缩性答案：C10. 什么是流体的临界雷诺数？A. 流体开始流动的雷诺数B. 流体从层流转变为湍流的雷诺数C. 流体达到最大速度的雷诺数D. 流体达到最大压力的雷诺数答案：B二、简答题（每题10分，共30分）1. 简述流体力学中的纳维-斯托克斯方程及其物理意义。

答案：纳维-斯托克斯方程是描述流体运动的基本方程，它将流体的动量守恒定律与流体的粘性联系起来。

方程表明，流体的加速度不仅与压力梯度有关，还与粘性力有关。

物理意义上，它描述了流体内部的动量传递过程。

2. 描述流体的粘性对流动的影响。

答案：流体的粘性对流动有显著影响。

(完整版)流体力学练习题及答案

(完整版)流体力学练习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN流体力学练习题及答案一、单项选择题1、下列各力中，不属于表面力的是（）。

A ．惯性力B ．粘滞力C ．压力D ．表面张力2、下列关于流体粘性的说法中，不准确的说法是（）。

A ．粘性是实际流体的物性之一B ．构成流体粘性的因素是流体分子间的吸引力C ．流体粘性具有阻碍流体流动的能力D ．流体运动粘度的国际单位制单位是m 2/s3、在流体研究的欧拉法中，流体质点的加速度包括当地加速度和迁移加速度，迁移加速度反映（）。

A ．由于流体质点运动改变了空间位置而引起的速度变化率B ．流体速度场的不稳定性C ．流体质点在流场某一固定空间位置上的速度变化率D ．流体的膨胀性4、重力场中平衡流体的势函数为（）。

A ．gz -=πB ．gz =πC ．z ρπ-=D ．z ρπ=5、无旋流动是指（）流动。

A ．平行B ．不可压缩流体平面C ．旋涡强度为零的D ．流线是直线的6、流体内摩擦力的量纲[]F 是（）。

A . []1-MLtB . []21--t MLC . []11--t ML D . []2-MLt 7、已知不可压缩流体的流速场为xyj zi x 2V 2+= ，则流动属于（）。

A ．三向稳定流动B ．二维非稳定流动C ．三维稳定流动D ．二维稳定流动8、动量方程的不适用于(??? ??) 的流场。

A ．理想流体作定常流动B ．粘性流体作定常流动C ．不可压缩流体作定常流动D ．流体作非定常流动9、不可压缩实际流体在重力场中的水平等径管道内作稳定流动时，以下陈述错误的是：沿流动方向 ( ) 。

A ．流量逐渐减少B ．阻力损失量与流经的长度成正比C ．压强逐渐下降D ．雷诺数维持不变10、串联管道系统中,其各支管内单位质量流体的能量损失（）。

A ．一定不相等B ．之和为单位质量流体的总能量损失C ．一定相等D ．相等与否取决于支管长度是否相等11、边界层的基本特征之一是（）。

流体力学试题及答案4

流体力学试题及答案4一、选择题（每题2分，共10分）1. 流体力学中，描述流体运动的基本概念是（）。

A. 质量B. 密度C. 速度D. 压力答案：C2. 流体静力学基本方程中，描述流体静压力与深度关系的公式是（）。

A. P = ρghB. P = ρgh²C. P = ρgh³D. P = ρg答案：A3. 在不可压缩流体中，连续性方程表明（）。

A. 质量守恒B. 能量守恒C. 动量守恒D. 角动量守恒答案：A4. 流体力学中的雷诺数是用来描述（）。

A. 流体的密度B. 流体的粘度C. 流体流动的层流与湍流状态D. 流体的压缩性答案：C5. 根据伯努利方程，流体在管道中流动时，流速增加会导致（）。

A. 压力增加B. 压力减小C. 温度增加D. 密度增加答案：B二、填空题（每题2分，共10分）1. 流体力学中，流体的粘性系数通常用符号________表示。

答案：μ2. 当流体流动时，如果流体的流线不相交，则该流动称为________流动。

答案：层流3. 流体力学中，流体的惯性力与流体的________和________有关。

答案：密度，速度4. 流体力学中，流体的表面张力是由分子间的________力引起的。

答案：吸引力5. 流体力学中，流体的压缩性是指流体在压力作用下体积的________。

答案：变化三、简答题（每题10分，共20分）1. 简述流体力学中的边界层概念及其重要性。

答案：边界层是指流体在固体表面附近流动时，由于粘性作用，流体速度从零逐渐增加到与主流速度相近的区域。

边界层的存在对流体的流动特性、摩擦阻力和流体的传热、传质等过程有重要影响。

2. 描述流体力学中的能量守恒定律，并给出其数学表达式。

答案：能量守恒定律表明，流体系统中能量的总量在没有外力作用的情况下是守恒的。

数学表达式为：ρu(E + p/ρ + gz) = constant，其中ρ是流体密度，u是流体速度，E是单位质量流体的内能，p是压力，g是重力加速度，z是垂直高度。

流体力学--第3章习题

1
1 2 2
解：（1）列两自由液面的伯努利方程，只计沿程损失，得到
H hf
2
64 l v 32lQ 128 lQ hf 4 Re d 2 g gd 4 gd 4
校核流态
2.73 0.006 Re 1918 2320 6 8.54 10 vd
层流
沿程阻力系数
一、选择题
C 1. 圆管紊流过渡区的沿程阻力系数________ 。 A. 与雷诺数Re有关； B. 与管壁相对粗糙度△/d有关； C. 与Re和△/d有关； D. 与Re和管长l有关。 B 2. 圆管紊流粗糙区的沿程阻力系数________ 。 A. 与雷诺数Re有关； B. 与管壁相对粗糙度△/d有关； C. 与Re和△/d有关； D. 与Re和管长l有关。
解: 列橡皮管进, 出口两端伯努利方程：
pm
L v2 ( ) d 2g
2 pm
v
L d
2 5.49 105 5.024m s

18 1000 (7.5 0.024 ) 0.012
6. 长管输送液体只计沿程损失，已知 H=127.4m, L=500m, 管路末端可用水头 h=2H/3，管路末端可用功率为 1000Kw, λ=0.024,求管路的输送流量与管路直径。
3. 圆管层流，实测管轴线上流速为4m／s，则断面平均流速为： C A. 4m／s B. 3.2m／s C. 2m／s D. 1m／s
二、计算题
1. ρ=0.85g/cm3、v=0.18cm2/s的油在管径为100mm的管中以 v =6.35cm/s的速度作层流运动，求（1）管中心处的最大流速；（2）在离管中心r=20mm处的流速；（3）沿程阻力系数λ ；（4）管壁切应力τ0及每1000km管长的水头损失。

流体力学题及答案

流体力学题及答案(总15页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--C (c) 盛有不同种类溶液的连通器DC D水油BB (b) 连通器被隔断AA(a) 连通容器1. 等压面是水平面的条件是什么2. 图中三种不同情况，试问：A-A 、B-B 、C-C 、D-D 中哪个是等压面哪个不是等压面为什么3 已知某点绝对压强为80kN/m 2，当地大气压强p a =98kN/m 2。

试将该点绝对压强、相对压强和真空压强用水柱及水银柱表示。

4. 一封闭水箱自由表面上气体压强p 0=25kN/m 2，h 1=5m ，h 2＝2m 。

求A 、B 两点的静水压强。

答：与流线正交的断面叫过流断面。

过流断面上点流速的平均值为断面平均流速。

引入断面平均流速的概念是为了在工程应用中简化计算。

8．如图所示，水流通过由两段等截面及一段变截面组成的管道，试问：(1)当阀门开度一定，上游水位保持不变，各段管中，是恒定流还是非恒定流是均匀流还是非均匀流(2)当阀门开度一定，上游水位随时间下降，这时管中是恒定流还是非恒定流(3)恒定流情况下，当判别第II 段管中是渐变流还是急变流时，与该段管长有无关系9 水流从水箱经管径分别为cmd cm d cm d 5.2,5,10321===的管道流出，出口流速sm V /13=，如图所示。

求流量及其它管道的断面平均流速。

解：应用连续性方程（1）流量：==33A v Q s l /103-⨯(2) 断面平均流速s m v /0625.01=, s m v /25.02= 。

10如图铅直放置的有压管道，已知d 1=200mm ，d 2=100mm ，断面1-1处的流速v 1=1m/s 。

求（1）输水流量Q ；（2）断面2-2处的平均流速v 2；（3）若此管水平放置，输水流量Q 及断面2-2处的速度v 2是否发生变化（4）图a 中若水自下而上流动，Q 及v 2是否会发生变化解：应用连续性方程（1）4.31=Q s l / （2）s m v /42= （3）不变。

流体力学计算题(精选.)

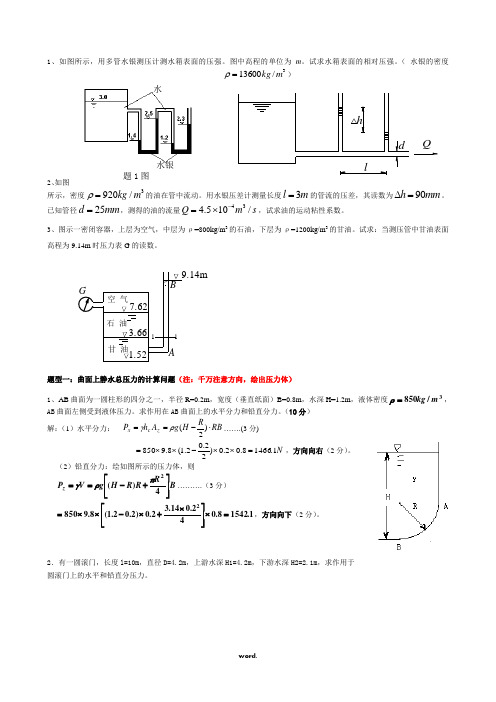
水水银题1图1、如图所示，用多管水银测压计测水箱表面的压强。

图中高程的单位为m 。

试求水箱表面的相对压强。

（水银的密度3/13600m kg =ρ）2、如图所示，密度3920/kg m ρ=的油在管中流动。

用水银压差计测量长度3l m =的管流的压差，其读数为90h mm ∆=。

已知管径25dmm =，测得的油的流量434.510/Q m s -=⨯，试求油的运动粘性系数。

3、图示一密闭容器，上层为空气，中层为ρ=800kg/m 3的石油，下层为ρ=1200kg/m 3的甘油。

试求：当测压管中甘油表面高程为9.14m 时压力表G 的读数。

题型一：曲面上静水总压力的计算问题（注：千万注意方向，绘出压力体）1、AB 曲面为一圆柱形的四分之一，半径R=0.2m ，宽度（垂直纸面）B=0.8m ，水深H=1.2m ，液体密度3/850m kg =ρ，AB 曲面左侧受到液体压力。

求作用在AB 曲面上的水平分力和铅直分力。

（10分）解：（1）水平分力：RB RH g A h P z c x ⋅-==)2(ργ…….(3分) N 1.14668.02.0)22.02.1(8.9850=⨯⨯-⨯⨯=，方向向右（2分）。

（2）铅直分力：绘如图所示的压力体，则B R R R H g V P z ⎥⎥⎦⎤⎢⎢⎣⎡+-==4)(2πργ……….（3分）1.15428.042.014.32.0)2.02.1(8.98502=⨯⎥⎥⎦⎤⎢⎢⎣⎡⨯+⨯-⨯⨯=，方向向下（2分）。

2．有一圆滚门，长度l=10m ，直径D=4.2m ，上游水深H1=4.2m ，下游水深H2=2.1m ，求作用于圆滚门上的水平和铅直分压力。

ldQhG BA空气石油甘油7.623.661.529.14m11解题思路：（1）水平分力：l H H p p p x )(21222121-=-=γ 方向水平向右。

（2）作压力体，如图，则l D Al V p z 4432πγγγ⨯=== 方向垂直向上。

流体力学例题

h4=300mm，h5=500mm，ρ1=1000㎏/m3，ρ2=800㎏ /m3，ρ3=13598㎏/m3，试拟定Ａ和Ｂ两点旳压强差。
【解】根据等压面条件，图中1—1，2—2，3—3均为等压面。可应用流体静力学基本方程式逐渐推算。
P1=p2+ρ1gh1
p2=p1-ρ3gh2
p3=p2+ρ2gh3
则 Rx qV (v2 v1 cos ) P2 P1 cos 0.1 (3.18 1.42 cos 60 ) 5.40 12.43cos 60 0.56（8 kN）
沿y轴方向 P1 sin R y qV (0 v1 sin )
R y P1 sin qV v1 sin
2g H
0.6 pa
g
2 9.806 2.8 0.6 98060 20.78
9806 （m/s）
所以管内流量
qV
4
d
2V2
0.785 0.122 20.78 0.235
m3/s）
【例3-8】水流经过如下图所示管路流入大气，已知：
Ｕ形测压管中水银柱高差Δh=0.2m，h1=0.72m H2O，管径d1=0.1m，管嘴出口直径d2=0.05m，不计管中水头损失，试求管中流量qv。
12.43sin 60 0.11.42 sin 60 10.88（kN）
管壁对水旳反作用力
图 3-22
【解】当阀门全开时列1-l、2-2截面旳伯努利方程
H pa 0 0 pa 0.6 pa V22
g
g
2g
当阀门关闭，据压强计旳读数，用流体静力学基本方程求出Ｈ值
pa gH pa 2.8 pa
H
2.8 pa
g
2.8 98060 9806

流体力学习题及答案

题2－8图题2－9图
2－9有一半封闭容器，左边三格为水，右边一格为油(比重为0.9)。试求A、B、C、D四点的相对压力。
2－10一小封闭容器放在大封闭容器中，后者充满压缩空气。测压表A、B的读数分别为8.28kPa和13.80kPa，已知当地大气压为100kPa，试求小容器内的绝对压力。
题2－10图题2－11图
题2－30图题2－31图
2－31有一三角形闸门，可绕AB轴旋转，油液的重度为γ，求液体对闸门的总压力及总压力对AB轴的力矩。
2－32倾斜的矩形平板闸门，长为AB，宽b＝2m，设水深h＝8m，试求作用在闸门上的静水总压力及其对端点A的力矩。
题2－32图题2－33图
2－33矩形平板闸门，宽b＝0.8m，高h＝1m，若要求箱中水深h1超过2m时闸门即可自动开启，铰链的位置y应设在何处？
1－16空气中水滴直径为0.3mm时，其内部压力比外部大多少？
1－17在实验室中如果用内径0.上升高度各为多少？
1－18两块竖直的平行玻璃平板相距1mm，求其间水的毛细升高值。
《流体力学》习题（二）
2－1质量为1000kg的油液(S＝0.9)在有势质量力 (N)的作用下处于平衡状态，试求油液内的压力分布规律。
1－4图示为一水暖系统，为了防止水温升高时体积膨胀将水管胀裂，在系统顶部设一膨胀水箱，使水有膨胀的余地。若系统内水的总体积为8m3，加温前后温差为50℃，在其温度范围内水的膨胀系数为βT＝9×10－41/℃，求膨胀水箱的最小容积。
题1－4图题1－5图
1－5图示为压力表校正器。器内充满压缩系数为βp＝4.75×10－101/Pa的油液，器内压力为105Pa时油液的体积为200mL。现用手轮丝杆和活塞加压，活塞直径为1cm，丝杆螺距为2mm，当压力升高至20MPa时，问需将手轮摇多少转？

工程流体力学计算题集(含答案)

30.(6分)飞机在10000m 高空(T=223.15K,p=0.264bar)以速度800km/h 飞行，燃烧室的进口扩压通道朝向前方，设空气在扩压通道中可逆压缩，试确定相对于扩压通道的来流马赫数和出口压力。

(空气的比热容为C p =1006J/(kg ·K)，等熵指数为k=1.4，空气的气体常数R 为287J/(kg ·K))T 0=T ∞+v C p ∞=+⨯⨯232222315*********21006/.()/()=247.69KM ∞=v a ∞∞=⨯⨯⨯=(/)...80010360014287223150743 P 0=p ∞11221+-⎡⎣⎢⎤⎦⎥∞-k M k k =0.26411412074038214141+-⨯⎡⎣⎢⎤⎦⎥=-.....bar31.(6分)一截面为圆形风道，风量为10000m 3/h ，最大允许平均流速为20m/s ，求：(1)此时风道内径为多少?(2)若设计内径应取50mm 的整倍数，这时设计内径为多少? (3)核算在设计内径时平均风速为多少? 依连续方程（ρ=C ）v 1A 1=v 2A 2=q v(1)v 1π412d q v = d 1=100004360020⨯⨯π=0.42m=420mm (2)设计内径应取450mm 为50mm 的9倍，且风速低于允许的20m/s (3) 在设计内径450mm 时，风速为 v q d m s v 2222441000036000451746==⨯⨯=ππ../ 32.(7分)离心式风机可采用如图所示的集流器来测量流量，已知风机入口侧管道直径d=400mm,U 形管读数h=100mmH 2O ，水与空气的密度分别为ρ水=1000kg/m 3，ρ空=1.2kg/m 3，忽略流动的能量损失，求空气的体积流量q v 。

由伯努利方程0+0+0=p gρ+0+v g 22得v=-2p ρ由静力学方程p+ρ水gh=0⇒p=-ρ水gh 代入得 v=22980701100012ghρρ水=⨯⨯⨯...=40.43m/s q v =v •=⨯⨯=ππ44043404508223d m s .(.)./33.(7分)要为某容器底部设计一个带水封的疏水管，结构如图示：容器内部的压强值，最高时是表压强p e =1500Pa,最低时是真空值p v =1200Pa,要求疏水管最高水位应低于容器底部联接法兰下a=0.1m ，最低水位应在疏水管口上b=0.2m(水密度ρ=1000kg/m 3，重力加速度g=9.8m/s 2)求：(1)疏水管长度L 。

流体力学计算题

四．计算题（05）1-1 若某油箱中有体积为5.0m 3的油所受的重力为41313N ，试确定这种油的密度。

解：因为Vg mg G ρ== 液体密度()31.90081.9541313mkg VgG =⨯==ρ1-2 某容器内有体积为500cm 3的某种液体，在天平上称得液体的质量为0.453kg ，试求该液体的密度和相对密度。

解：V m=ρ= 906 kg/m 3 9.01000906===水ρρd 061-3 已知密度为900kg/m 3的石油所受的重力为3.175×106N ，试确定其体积。

解：Vg mg G ρ==()36081.99003175000=⨯==gGv ρ1-4 温度为20℃的水每小时流入加热器的体积为60m 3，经过加热后，水温升高到80℃。

若水的体积膨胀系数βt 为550×10-6l/℃，那么水从加热器中流出时，每小时流出的体积为多少？解：dt dVV t 1=β 所以 dV=t β.V .dt=1.98m 3 dV=V 2－V 1 所以V 2＝dV ＋V 1＝61.9m 3五．计算题(05)2-1 在海面以下h=30m 处测得相对压力为3.09×105Pa ，试确定海水的密度。

解: 所以Kg/m 32-2 气压计读数为755mmHg ，求位于水面以下7.6m 深处的绝对压强。

解:＝74556(Pa) Pa ＝755×=760101325100658.39 (Pa)P 绝＝P 表+ Pa ＝17521.439 (pa)2-3 某容器中液面上的压强p 0=1×104Pa ，液体密度ρ=1000kg/m 3，试求在液面下h=2m 处M 点的绝对压强和表压强。

解:＝1000×9.81×2＝19620(pa )P 绝＝P 表+P 0＝19620+105＝119620(Pa)2-4 某圆柱形容器内装三种液体，如图题2-4所示，上层油的相对密度d 1=0.8，中层水的相对密度d 2=1，下层汞的相对密度d 3=13.6。