流体力学计算题及答案.docx
流体力学题库(附答案)

流体力学题库(附答案)一、单选题(共48题,每题1分,共48分)1.()管路各段阻力损失相同。
A、短管管系B、串联管系C、并联管系D、分支管系正确答案:C2.理想液体的特征是( )A、不可压缩B、符合牛顿内摩擦定律的C、无粘性D、粘度为常数正确答案:C3.当容器内工质压力大于大气压力时,工质处于()状态。
A、标准B、正压C、负压D、临界正确答案:B4.某点的真空压力是65000pa,当地大气压为0.1MPa,该点的绝对压强为()。
A、165000PaB、65000PaC、55000PaD、35000Pa正确答案:D5.在圆管流中,层流的断面流速分布为()。
A、均匀规律B、直线变化规律C、抛物线规律D、对数曲线规律正确答案:C6.抽气器的工作原理是()A、动量方程B、静力学基本方程C、连续性方程D、伯努利方程正确答案:D7.伯努利方程说明,流体在水平管内定常流动中,流速降低()A、压力下降B、都可能C、压力上升D、压力不变正确答案:C8.那个设备压力是真空压力()。
A、再热器B、凝汽器C、过热器D、给水泵正确答案:B9.伯努利方程中Z+P/ρg表示()A、单位体积流体具有的机械能B、通过过流断面的流体所具有的总机械能C、单位质量流体具有的机械能D、单位重量流体具有的测压管能头正确答案:D10.超临界机组主蒸汽压力最接近的是()。
A、5个大气压B、26兆帕C、50巴D、5公斤正确答案:B11.静止的流体中存在()。
A、压应力、拉应力和剪切力B、压应力和拉应力C、压应力D、压应力和剪切力正确答案:C12.将极细测压管插入水中,毛细现象会使得液位()A、下降B、不变C、都有可能D、上升正确答案:D13.一个标准大气压(1atm)等于()。
A、Hg780mmB、101.325kPaC、720mmHgD、110.325kPa正确答案:B14.流体在管道内的流动阻力分为()两种。
A、阀门阻力、三通阻力B、沿程阻力、局部阻力C、流量孔板阻力、水力阻力D、摩擦阻力、弯头阻力正确答案:B15.主机润滑油压力为130千帕,其是多少米水柱()。
《流体力学与流体机械》计算题及答案

Q v1A1 v2 A2
Q
v2 A2
4
0.12
3
0.0234 m3
/
s
v1
4Q
d12
4 0.0234
0.152
1.3
3
6 m
/
s
编辑ppt
• 习题3-15 判断流动 ux = xy;uy = -xy 是否满足不可压缩流动的连续性条件 。 • 解: 因为 ux = xy;uy = -xy 与时间无关,所以流动定常,根据定常不可压微分形式连续方程,
•
图示为一轴流风机,已测得进口相对压力p1= -103 Pa,出口相对压力p2 = 150 Pa。设截面
1-2间压力损失 100Pa,求风机的全压P ( P为风机输送给单位体积气体的能量 ) 。
• 解:
p1
1
2
v12
z2
z1 ga
p
p2
2
2
v22
ghw
1000 0 p 150100
P 1250 Pa
第一章 流体及其物理性质
•
• 例1-2 相距为h=10 mm的两固定平板间充满动力粘度μ=1.49 Pa·s的甘油, 若两板间甘油的速度分布为u=4000y(h-y)
•
(1) 若上板的面积A=0.2 m2,求使上板固定不动所需的水平作用力F;
•
(2) 求y=h/3和2h/3处的内摩擦应力,
并说明正负号的意义。
有一圆桶,半径R=1m,高H=3.5m,桶内盛有高度h=2.5m的水。圆桶绕中心
轴匀速旋转。问水恰好开始溢出时,转速ω为多少?而此时距中心线r=0.4m处桶底 面上A点的压力是多少?
• 解:(1) 求旋转速度ω
流体力学试题(含答案)

流体力学试题(含答案)一、选择题(每题10分,共40分)1. 流体力学研究的对象是:A. 固体B. 液体C. 气体D. 所有流体答案:D2. 下列哪个物理量表示流体的压强?A. 力B. 压力C. 压力系数D. 压强答案:D3. 在伯努利方程中,流速增加时,下列哪个物理量会减小?A. 压强B. 动能C. 位能D. 总能量答案:A4. 下列哪个现象说明流体具有粘性?A. 流体在管道中流动B. 流体在容器中静止C. 流体表面形成波纹D. 流体在流动过程中产生涡旋答案:D二、填空题(每题20分,共60分)5. 流体力学的基本方程之一是______方程,它描述了流体在流动过程中质量守恒的规律。
答案:连续性方程6. 在不可压缩流体中,流线是指______。
答案:流速矢量线7. 伯努利方程适用于______流体。
答案:理想流体8. 流体的粘性使得在流动过程中产生______,从而导致能量损失。
答案:摩擦力三、计算题(每题25分,共50分)9. 一水平管道内,水以0.5 m/s的速度流动。
管道直径由0.2 m渐变至0.4 m。
求管道渐变处的流速。
解:根据连续性方程,流体在流动过程中质量守恒,即流速与截面积的乘积保持不变。
设管道渐变前后的流速分别为v1和v2,截面积分别为A1和A2。
由连续性方程可得:v1 * A1 = v2 * A2代入已知数据:0.5 m/s * π * (0.2 m)^2 = v2 * π * (0.4m)^2解得:v2 = 0.25 m/s答案:0.25 m/s10. 一水平管道内,水以2 m/s的速度流动,管道直径为0.1 m。
管道入口处的压强为100 kPa。
求管道出口处的压强。
解:根据伯努利方程,流速增加时,压强会减小。
设管道入口处的流速为v1,压强为p1;管道出口处的流速为v2,压强为p2。
伯努利方程为:p1/ρg + v1^2/2g + z1 = p2/ρg + v2^2/2g + z2由于管道水平,所以z1 = z2,且水的密度ρ = 1000 kg/m^3,重力加速度g = 9.8 m/s^2。
流体力学习题及参考答案

09流体力学习题1及参考答案一、单项选择题(共15分,每小题1分)1、下列各力中,属于质量力的是( )。
A .离心力B .摩擦力C .压力D .表面张力2、下列关于流体粘性的说法中,不准确的说法是( )。
A .粘性是实际流体的固有属性B .构成流体粘性的因素是流体分子间的吸引力C .流体粘性具有传递运动和阻碍运动的双重性D .动力粘度与密度之比称为运动粘度3、在流体研究的欧拉法中,流体质点的加速度由当地加速度和迁移加速度组成,当地加速度反映()。
A .流体的压缩性B .由于流体质点运动改变了空间位置而引起的速度变化率C .流体速度场的不稳定性D .流体速度场的不均匀性4、重力场中流体的平衡微分方程为( )。
A .gdz dp -=B .gdz dp ρ=C .dz dp ρ-=D .gdz dp ρ-=5、无旋流动是指( )的流动。
A .速度环量为零B .迹线是直线C .流线是直线D .速度环量不为零6、压强的量纲[]p 是( )。
A.[]2-MLt B.[]21--t ML C.[]11--t ML D.[]1-MLt7、已知不可压缩流体的流速场为 则流动不属于( )。
A .非均匀流B .非稳定流动C .稳定流动D .三维流动8、动量方程的适用条件是( ) 。
0 ),,(),(⎪⎩⎪⎨⎧===w t z x f z y f u υin out QV QV F )()(ρρ∑-∑=∑A.仅适用于理想流体作定常流动B.仅适用于粘性流体作定常流动C.适用于理想流体与粘性流体作定常或非定常流动D.适用于理想流体与粘性流体作定常流动9、在重力场中作稳定流动的系统,沿流动方向总水头线维持水平的条件是 ( ) 。
A.管道是水平放置的B.流体为不可压缩流体C.管道是等径管D.流体为不可压缩理想流体10、并联管道系统中,其各支管内单位质量流体的能量损失()。
A.不相等 B.之和为总能量损失 C.相等D.不确定11、边界层的基本特征之一是()。
流体力学习题库(含答案)

流体力学习题库(含答案)一、单选题(共70题,每题1分,共70分)1、低温泵的气相平衡线的作用是防止泵的( )。
A、憋压B、超温C、汽蚀D、汽缚正确答案:D2、若被输送液体的黏度增大时,离心泵的效率( )。
A、减小B、增大C、不变D、不定正确答案:A3、当地大气压为745mmHg测得一容器内的绝对压强为350mmHg,则真空度为( )A、395mmHgB、350mmHgC、410mmHg正确答案:A4、单位质量的流体所具有的( )称为流体的比容。
A、位能B、动能C、体积D、黏度正确答案:C5、喷射泵是利用流体流动时的( )的原理来工作的。
A、动能转化为静压能B、热能转化为静压能C、静压能转化为动能正确答案:C6、机械密封与填料密封相比( )的功率消耗较大。
A、填料密封B、机械密封C、差不多正确答案:A7、下列不属于离心泵的主要构件是 ( )A、泵轴B、泵壳C、叶轮D、轴封装置正确答案:A8、一台离心泵开动不久,泵入口处的真空度正常,泵出口处的压力表也逐渐降低为零,此时离心泵完全打不出水。
发生故障的原因是( )A、吸入管路堵塞B、忘了灌水C、吸入管路漏气D、压出管路堵塞正确答案:A9、某液体在内径为D0的水平管路中稳定流动,其平均流速为u0,当它以相同的体积流量通过等长的内径为D2(D2=D0/2)的管子时,若流体为层流,则压降ΔP为原来的( )倍。
A、32B、8C、4D、16正确答案:A10、造成离心泵气缚原因是( )A、泵不能抽水B、安装高度太高C、入口管路阻力太大D、泵内流体平均密度太小正确答案:D11、离心泵的轴功率N和流量Q的关系为( )A、Q增大,N增大B、Q增大,N先增大后减小C、Q增大,N减小D、Q增大,N先减小后增大正确答案:A12、在静止的连通的同一种连续流体内,任意一点的压强增大时,其他各点的压强则( )A、减小B、不变C、相应增大D、不一定正确答案:C13、往复泵的流量调节采用( )A、出口支路B、出口阀开度C、入口阀开度D、入口支路正确答案:A14、为了防止( )现象发生,启动离心泵时必须先关闭泵的出口阀A、汽蚀B、电机烧坏C、气缚D、叶轮受损正确答案:B15、某泵在运行的时候发现有汽蚀现象应( )A、停泵向泵内灌液B、降低泵的安装高度C、检查进口管路是否漏液D、检查出口管阻力是否过大正确答案:C16、选离心泵是根据泵的( )A、扬程和轴功率选择B、转速和轴功率选择C、轴功率和流量选择D、扬程和流量选择正确答案:D17、流体运动时,能量损失的根本原因是由于流体存在着 ( )。
流体力学计算题及答案

流体力学计算题及答案第二章例1:用复式水银压差计测量密封容器内水面的相对压强,如图所示。
已知:水面高程z 0=3m,压差计各水银面的高程分别为z 1=0.03m , z 2=0.18m , z 3=0.04m, z 4=0.20m, 水银密度3/13600m kg ρ=',水的密度3/1000m kg ρ= 。
试求水面的相对压强p 0。
解:ap z z γz z γz z γp =-----+)(')(')(3412100)()('1034120z z γz z z z γp ---+-=∴例2:用如图所示的倾斜微压计测量两条同高程水管的压差。
该微压计是一个水平倾角为θ的在xoz 坐标系中,自由表面1的方程:gr z 2220ω=对于容器边缘上的点,有:m L z m d r 4.015.02==== )/(67.1815.04.08.922220s rad r gz =⨯⨯==∴ω∵ωπ=260n /∴==⨯=n r 160260186721783ωππ..(/min)(2)当抛物面顶端碰到容器底部时,这时原容器中的水将被甩出一部分,液面为图中2所指。
在'''x o z 坐标系中:自由表面2的方程: gr z 2220ω'='当m H z m dr 5.0,15.02=='==时)/(87.2015.05.08.92222s rad r z g =⨯⨯='='ωmin)/(3.199287.20602602r ππωn =⨯='=∴这时,有:14214222ππd H d H h ⋅=-()mm Hh Hh H 2502222==∴=-∴例6:已知:一块平板宽为 B ,长为L,倾角θ,顶端与水面平齐。
求:总压力及作用点。
解:总压力:LB θL γA h γF c 2sin ⋅==压力中心D :方法一:dA θy γy ydF dM sin ==3sin sin sin 322L BθγBdy y θγdA y θγM L A===⎰⎰DFy M = L F M yD32/==∴方法二:62212123LL BL L BL L A y J y y c cx c D +=+=+=例7:如图,已知一平板,长L,宽B,安装于斜壁面上,可绕A 转动。
流体力学题及答案
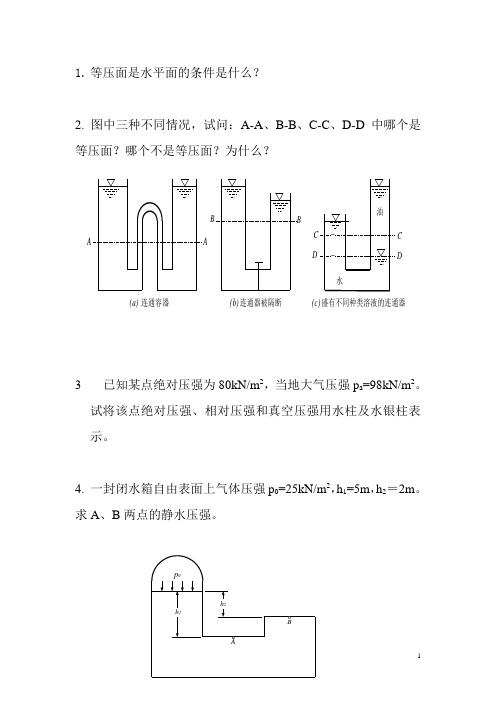
C (c) 盛有不同种类溶液的连通器DC D水油BB (b) 连通器被隔断AA(a) 连通容器1. 等压面是水平面的条件是什么?2. 图中三种不同情况,试问:A-A 、B-B 、C-C 、D-D 中哪个是等压面?哪个不是等压面?为什么?3 已知某点绝对压强为80kN/m 2,当地大气压强p a =98kN/m 2。
试将该点绝对压强、相对压强和真空压强用水柱及水银柱表示。
4. 一封闭水箱自由表面上气体压强p 0=25kN/m 2,h 1=5m ,h 2=2m 。
求A 、B 两点的静水压强。
速?答:与流线正交的断面叫过流断面。
过流断面上点流速的平均值为断面平均流速。
引入断面平均流速的概念是为了在工程应用中简化计算。
8.如图所示,水流通过由两段等截面及一段变截面组成的管道,试问:(1)当阀门开度一定,上游水位保持不变,各段管中,是恒定流还是非恒定流?是均匀流还是非均匀流?(2)当阀门开度一定,上游水位随时间下降,这时管中是恒定流还是非恒定流?(3)恒定流情况下,当判别第II 段管中是渐变流还是急变流时,与该段管长有无关系?9 水流从水箱经管径分别为cm d cm d cm d 5.2,5,10321===的管道流出,出口流速s m V /13=,如图所示。
求流量及其它管道的断面平均流速。
解:应用连续性方程(1)流量:==33A v Q 4.91s l /103-⨯ (2) 断面平均流速s m v /0625.01= , s m v /25.02= 。
10如图铅直放置的有压管道,已知d 1=200mm ,d 2=100mm ,断面1-1处的流速v 1=1m/s 。
求(1)输水流量Q ;(2)断面2-2处的平均流速v 2;(3)若此管水平放置,输水流量Q 及断面2-2处的速度v 2是否发生变化?(4)图a 中若水自下而上流动,Q 及v 2是否会发生变化?解:应用连续性方程 (1)4.31=Q s l / (2)s m v /42= (3)不变。
流体力学计算题及答案

第二章例1:用复式水银压差计测量密封容器内水面的相对压强,如图所示。
已知:水面高程z 0=3m,压差计各水银面的高程分别为z 1=0.03m, z 2=0.18m, z 3=0.04m, z 4=0.20m, 水银密度3/13600m kg ρ=',水的密度3/1000m kg ρ= 。
试求水面的相对压强p 0。
解:ap z z γz z γz z γp =-----+)(')(')(3412100)()('1034120z z γz z z z γp ---+-=∴例2:用如图所示的倾斜微压计测量两条同高程水管的压差。
该微压计是一个水平倾角为θ的Π形管。
已知测压计两侧斜液柱读数的差值为L=30mm ,倾角θ=30∘,试求压强差p 1 – p 2 。
解: 224131)()(p z z γz z γp =-+-- θL γz z γp p sin )(4321=-=-∴例3:用复式压差计测量两条气体管道的压差(如图所示)。
两个U 形管的工作液体为水银,密度为ρ2 ,其连接管充以酒精,密度为ρ1 。
如果水银面的高度读数为z 1 、 z 2 、 z 3、z 4 ,试求压强差p A – p B 。
解: 点1 的压强 :p A )(21222z z γp p A --=的压强:点)()(33211223z z γz z γp p A -+--=的压强:点B A p z z γz z γz z γp p =---+--=)()()(3423211224 )()(32134122z z γz z z z γp p B A ---+-=-∴例4:用离心铸造机铸造车轮。
求A-A 面上的液体总压力。
解: C gz r p +⎪⎭⎫ ⎝⎛-=2221ωρ a p gz r p +⎪⎭⎫ ⎝⎛-=∴2221ωρ在界面A-A 上:Z = - ha p gh r p +⎪⎭⎫⎝⎛+=∴2221ωρ⎪⎭⎫⎝⎛+=-=∴⎰2420218122)(ghR R rdr p p F a Rωπρπ例5:在一直径d=300mm ,而高度H=500mm 的园柱形容器中注水至高度h 1 = 300mm ,使容器绕垂直轴作等角速度旋转。
《流体力学与流体机械》计算题及答案

1 2
总结词
掌握流体流动阻力和能量损失的计算方法,了解 流体流动过程中阻力和能量的变化规律。
流体流动阻力计算
根据流体流动的雷诺数和流体性质,计算流体在 管道中的流动阻力,包括直管阻力和局部阻力。
3
能量损失计算
根据伯努利方程和流体流动的能量守恒原理,计 算流体在管道中的能量损失,包括沿程损失和局 部损失。
分析流体在流动过程中 的温度变化,以及由此
产生的热能转换。
03
探讨流体流动与热能转 换之间的关系,以及其 对流体机械性能的影响。
05
详细描述
02
计算流体在流动过程中 由于热传导、对流和辐 射等热传递方式而产生
的热量交换。
04
流体流动与化学能转换计算
总结词:计算流体在流动 过程中由于化学反应而产 生的化学能转换。
详细描述
分析流体在流动过程中可 能发生的化学反应,以及 由此产生的化学能转换。
探讨流体流动与化学能转 换之间的关系,以及其在 化工、制药等领域中的应 用。
计算化学反应过程中流体 的能量变化,以及其对流 体机械性能的影响。
THANKS
感谢观看
计算流体在流动过程中由于机械能转换 而产生的能量损失或增益。
分析流体在流动过程中所受的阻力,如 摩擦力和局部阻力,对机械能转换的影 响。
详细描述
计算流体在管道中流动时的压力能变化 ,以及由此产生的速度和流量的变化。
流体流动与热能转换计算
总结词:计算流体在流 动过程中由于温度变化
而产生的热能转换。
01
必需汽蚀余量(NPSHr)
泵开始发生汽蚀时,所必须的最低有效汽蚀余量。
有效汽蚀余量(NPSHa)
泵在实际运行中,所实际具有的有效汽蚀余量。
(完整版)流体力学练习题及答案

流体力学练习题及答案一、单项选择题1、下列各力中,不属于表面力的是( )。
A .惯性力B .粘滞力C .压力D .表面张力2、下列关于流体粘性的说法中,不准确的说法是( )。
A .粘性是实际流体的物性之一B .构成流体粘性的因素是流体分子间的吸引力C .流体粘性具有阻碍流体流动的能力D .流体运动粘度的国际单位制单位是m 2/s3、在流体研究的欧拉法中,流体质点的加速度包括当地加速度和迁移加速度,迁移加速度反映( )。
A .由于流体质点运动改变了空间位置而引起的速度变化率B .流体速度场的不稳定性C .流体质点在流场某一固定空间位置上的速度变化率D .流体的膨胀性4、重力场中平衡流体的势函数为( )。
A .gz -=πB .gz =πC .z ρπ-=D .z ρπ=5、无旋流动是指( )流动。
A .平行B .不可压缩流体平面C .旋涡强度为零的D .流线是直线的6、流体内摩擦力的量纲[]F 是( )。
A . []1-MLt B . []21--t ML C . []11--t MLD . []2-MLt 7、已知不可压缩流体的流速场为xyj zi x 2V 2+= ,则流动属于( )。
A .三向稳定流动B .二维非稳定流动C .三维稳定流动D .二维稳定流动8、动量方程 的不适用于( ) 的流场。
A .理想流体作定常流动in out QV QV F )()(ρρ∑-∑=∑B.粘性流体作定常流动C.不可压缩流体作定常流动D.流体作非定常流动9、不可压缩实际流体在重力场中的水平等径管道内作稳定流动时,以下陈述错误的是:沿流动方向( ) 。
A.流量逐渐减少B.阻力损失量与流经的长度成正比C.压强逐渐下降D.雷诺数维持不变10、串联管道系统中,其各支管内单位质量流体的能量损失()。
A.一定不相等B.之和为单位质量流体的总能量损失C.一定相等D.相等与否取决于支管长度是否相等11、边界层的基本特征之一是()。
流体力学期末复习试题含答案(大学期末复习资料)

流体力学期末复习试题含答案(大学期末复习资料)流体力学是应用数学和物理学原理来研究流体运动规律的一门科学。
以下是一篇针对大学本科生流体力学课程的期末复习试题及答案,内容涵盖了流体力学的基本概念、原理和计算方法。
流体力学期末复习试题一、选择题(每题5分,共25分)1. 流体的连续性方程描述的是()A. 流体的运动状态B. 流体的连续性C. 流体的能量转换D. 流体的动量变化2. 在不可压缩流体中,流速和截面积的乘积是一个()A. 常数B. 变量C. 随时间变化的量D. 随空间变化的量3. 下列哪个方程描述了流体的动量守恒()A. 连续性方程B. 动量方程C. 能量方程D. 伯努利方程4. 在理想流体中,下列哪个力是忽略不计的()A. 粘滞力B. 压力C. 重力D. 外力5. 在流体力学中,下列哪个概念描述了单位时间内通过某一截面的流体体积()A. 流速B. 流量C. 动压力D. 马赫数二、填空题(每题5分,共25分)6. 在流体的连续性方程中,流速和截面积的乘积等于__________。
7. 在不可压缩流体中,流体的密度__________(填“变化”或“不变”)。
8. 流体力学中的伯努利方程描述了__________(填“静压”、“动压”或“全压”)与流速之间的关系。
9. 在理想流体中,__________(填“存在”或“不存在”)粘滞力。
10. 流体的粘度是描述流体__________(填“流动”或“粘性”)的物理量。
三、计算题(每题25分,共75分)11. 一根直径为10cm的管道中,水的流速为2m/s。
求通过该管道的水的流量。
答案:流量Q = v × A = 2 m/s × π × (0.05 m)^2= 0.157 m^3/s12. 一不可压缩流体在水平管道中流动,管道截面积在某一截面处为0.01m^2,流速为2m/s。
求该截面处的压力。
答案:根据伯努利方程,P1 + 0.5ρv1^2 = P2 +0.5ρv2^2由于是不可压缩流体,ρ为常数,且v2未知,所以无法直接求解。
(完整word版)流体力学与流体机械习题(含答案)参考答案

高等学校教学用书主讲:张明辉中国矿业大学出版社张景松编.流体力学与流体机械, 徐州:中国矿业大学出版社,2001.6(2005.1重印)删掉的题目:1-14、2-6、2-9、2-11、2-17、3-10、3-19、4-5、4-13《流体力学与流体机械之流体力学》第一章 流体及其物理性质1-8 1.53m 的容器中装满了油。
已知油的重量为12591N 。
求油的重度γ和密度ρ。
解:312591856.5kg/m 9.8 1.5m V ρ===⨯;38394N/m g γρ== 1-11 面积20.5m A =的平板水平放在厚度10mm h =的油膜上。
用平力拉它以0.8m/s U =速度移动(图1-6)。
若油的密度3856kg/m ρ=。
求油的动力粘度和运动粘度。
解:29.6N/m F A τ==,Uh τμ=, 所以,0.12Pa s hU τμ==g ,42/0.12/856 1.410m /s νμρ-===⨯ 1-12 重量20N G =、面积20.12m A =的平板置于斜面上。
其间充满粘度0.65Pa s μ=g 的油液(图1-7)。
当油液厚度8mm h =时。
问匀速下滑时平板的速度是多少。
解:sin 20 6.84F G N ==o ,57Pa s FAτ==g , 因为Uhτμ=,所以570.0080.7m/s 0.65h U τμ⨯=== 1-13 直径50mm d =的轴颈同心地在50.1mm D =的轴承中转动(图1-8)。
间隙中润滑油的粘度0.45Pa s μ=g 。
当转速950r/min n =时,求因油膜摩擦而附加的阻力矩M 。
解:将接触面沿圆柱展开,可得接触面的面积为:20.050.10.016m A dL ππ==⨯⨯=接触面上的相对速度为:2 2.49m/s 2260d d nu πω=== 接触面间的距离为:0.05mm 2D dδ-==接触面之间的作用力:358.44N du F AA dy uδμμ=== 则油膜的附加阻力矩为:8.9N m 2dM F==g 1-14 直径为D 的圆盘水平地放在厚度为h 的油膜上。
计算流体力学试题(含答案08)

一.简要回答以下问题(20分)1.差分格式的基本特征相容性,稳定性,收敛性,守恒性,有界性,真实性,精确性2.差分格式的稳定性和收敛性的关系对于适定的线性微分方程的初值问题,与之相容的差分方程稳定的充分必要条件是差分格式收敛。
3.显格式和隐格式显格式:离散方程的解可以直接求解隐格式:离散方程的解需要通过求解线性代数方程组的形式来获得隐格式具有较高的稳定性4.列举四种常用的流体力学数值计算模型(方法)边界元法,有限差分法,有限体积法,有限元法,有限分析法,谱方法等5.二阶偏微分方程有那些基本类型,试举例说明 椭圆型方程:02222=∂∂+∂∂yu x u 抛物型方程:022=∂∂+∂∂y u xu 双曲型方程:02222=∂∂-∂∂yu x u 二.写出函数),,(t y x u 在时间t 附近的泰勒展开式(仅对时间项)(保留到3阶)(15分)))(()(),,(61)(),,(21),,(),,(),,(4333222t O t tt y x u t t t y x u t t t y x u t y x u t t y x u ∆+∆∂∂+∆∂∂+∆∂∂+=∆+三.分别写出微分xy x u a ∂∂),(的UDS ,CDS ,FDS ,BDS 差分格式(15分) UDS :xu u a a x u u a a x u a i i i i ∆--+∆-+=∂∂+-1122 CDS :xu u a x u a i i ∆-=∂∂-+211 BDS :xu u a x u a i i ∆-=∂∂-1 FDS :xu u a x u ai i ∆-=∂∂+1四.采用有限体积法离散下列积分方程(假设数值网格为等距网格)(15分)⎰⎰∇⋅Γ=∂∂ds dV t t y x φφn ),,()2()2(1n P n S n N n P n W n E n P n P yx x y y x t φφφφφφφφ-+∆∆Γ+-+∆∆Γ=∆∆∆-+五.给出圆球无粘性绕流的定解条件(15分)⎪⎩⎪⎨⎧-=∂∂=∇xUn n φφ02六.采用有限差分法离散对流扩散方程,并分析其稳定性。
工程流体力学计算题集(含答案)

30.(6分)飞机在10000m 高空(T=223.15K,p=0.264bar)以速度800km/h 飞行,燃烧室的进口扩压通道朝向前方,设空气在扩压通道中可逆压缩,试确定相对于扩压通道的来流马赫数和出口压力。
(空气的比热容为C p =1006J/(kg ·K),等熵指数为k=1.4,空气的气体常数R 为287J/(kg ·K))T 0=T ∞+v C p ∞=+⨯⨯232222315*********21006/.()/()=247.69KM ∞=v a ∞∞=⨯⨯⨯=(/)...80010360014287223150743 P 0=p ∞11221+-⎡⎣⎢⎤⎦⎥∞-k M k k =0.26411412074038214141+-⨯⎡⎣⎢⎤⎦⎥=-.....bar31.(6分)一截面为圆形风道,风量为10000m 3/h ,最大允许平均流速为20m/s ,求:(1)此时风道内径为多少?(2)若设计内径应取50mm 的整倍数,这时设计内径为多少? (3)核算在设计内径时平均风速为多少? 依连续方程(ρ=C )v 1A 1=v 2A 2=q v(1)v 1π412d q v = d 1=100004360020⨯⨯π=0.42m=420mm (2)设计内径应取450mm 为50mm 的9倍,且风速低于允许的20m/s (3) 在设计内径450mm 时,风速为 v q d m s v 2222441000036000451746==⨯⨯=ππ../ 32.(7分)离心式风机可采用如图所示的集流器来测量流量,已知风机入口侧管道直径d=400mm,U 形管读数h=100mmH 2O ,水与空气的密度分别为ρ水=1000kg/m 3,ρ空=1.2kg/m 3,忽略流动的能量损失,求空气的体积流量q v 。
由伯努利方程0+0+0=p gρ+0+v g 22得v=-2p ρ由静力学方程p+ρ水gh=0⇒p=-ρ水gh 代入 得 v=22980701100012ghρρ水=⨯⨯⨯...=40.43m/s q v =v •=⨯⨯=ππ44043404508223d m s .(.)./33.(7分)要为某容器底部设计一个带水封的疏水管,结构如图示:容器内部的压强值,最高时是表压强p e =1500Pa,最低时是真空值p v =1200Pa,要求疏水管最高水位应低于容器底部联接法兰下a=0.1m ,最低水位应在疏水管口上b=0.2m(水密度ρ=1000kg/m 3,重力加速度g=9.8m/s 2)求:(1)疏水管长度L 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 1:用复式水银压差计测量密封容器内水面的相对压强,如图所示。
已知:水面高程z0=3m,压差计各水银面的高程分别为z1=0.03m, z 2=0.18m, z 3=0.04m, z 4=0.20m,水银密度ρ13600kg / m3,水的密度ρ 1000kg / m3。
试求水面的相对压强p0。
解:p0γ(z0 z1 ) γ'( z2z1) γ'(z4z3 ) p ap0γ'(z2z1 z4z3 ) γ(z0 z1 )例 2:用如图所示的倾斜微压计测量两条同高程水管的压差。
该微压计是一个水平倾角为θ的Π形管。
已知测压计两侧斜液柱读数的差值为L=30mm,倾角θ=30 °,试求压强差p1– p2。
解:p1γ(z3z1 )γ(z4z2 ) p2p1p2γ(z3z4 )γL sinθ例 3:用复式压差计测量两条气体管道的压差(如图所示)。
两个U形管的工作液体为水银,密度为ρ2,其连接管充以酒精,密度为ρ 1 。
如果水银面的高度读数为z1、 z 2、 z 3、z4,试求压强差p A– p B。
解:点 1 的压强: p A点2的压强: p2p Aγ2( z2z1 )点 3的压强: p3 p Aγ2( z2z1 )γ1( z2 z3 )p4p Aγ2( z2z1 ) γ1(z2z3 ) γ2( z4z3 ) p Bp A p Bγ2(z2 z1 z4z3 ) γ1( z2z3 )例 4:用离心铸造机铸造车轮。
求A-A 面上的液体总压力。
解:p 1 2r2gz C p 1 2r2gz p a22在界面 A-A 上: Z = - hp 1 2r2gh p a F( p p a ) 2 rdr 21 2 R41ghR2R2082例 5:在一直径 d = 300mm,而高度 H= 500mm的园柱形容器中注水至高度h1 = 300mm,使容器绕垂直轴作等角速度旋转。
如图所示。
(1) 试确定使水之自由液面正好达到容器边缘时的转数n1;(2)求抛物面顶端碰到容器底时的转数 n2,此时容器停止旋转后水面高度 h2将为多少?解: (1)由于容器旋转前后,水的体积不变( 亦即容器中空气的体积不变 ) ,有:图1d 2L1 d 2 (H h1 )424L 2( H h1 ) 400 mm0.4 m在 xoz 坐标系中,自由表面2 r 2 1 的方程:z02g对于容器边缘上的点,有:d0.15m z0 r22gz0 2 9.80.4 r 20.152∵ 2 n / 60L0.4m18.67( rad / s)n1606018.672178.3 (r / min)2(2) 当抛物面顶端碰到容器底部时,这时原容器中的水将被甩出一部分,液面为图中2所指。
在 x o z 坐标系中:2r 2自由表面 2 的方程:z02 gd当r 0.15m时, z0 H 0.5m 22gz0 2 9.80.520.87(rad / s)r 20.152n260ω60 20.87π2199.3(r / min)π2这时,有:1d 2H1d 2 ( H h2 )424Hh2HH h2250mm22例 6:已知:一块平板宽为 B ,长为 L, 倾角,顶端与水面平齐。
求:总压力及作用点。
解:总压力:Fγh c A γL sinθLB 2压力中心 D:方法一: dM ydF yγy sin θdAL3M γsin θ y2 dA2 Bdyγsin θB Lγsin θ yA03M Fy D y D M / F 2 L3Jcx L 1 BL3L L方法二:y D y c12y c A2L BL262例 7:如图,已知一平板,长L, 宽 B, 安装于斜壁面上,可绕 A 转动。
已知L,B,L 1, θ。
求:启动平板闸门所需的提升力F。
解:f 11γL sin θBL22Lf 2 γL 1 sin θBLFL cosf 1 3 Lf22F1 2 f 1 1 f 2cos32例 8:平板 A B, 可绕 A 转动。
长 L=2m,宽 b=1m,θ=60°, H 1=1.2m,H 2=3m 为保证平板不能自转,求自重 G 。
解:F 1H 1bH 18153 NF 2L sin θ 16986 NγγbL2 sin θ2F 3 γ(H 2 L sin θ)bL 24870 NG Lcos θ F 1 L 1 H 1F 2 2 LF 3L23 sin θ3 2G 69954 N例 9:与水平面成45°倾角的矩形闸门 AB( 图 1) ,宽 1m ,左侧水深h 1 = 3m ,右侧水深 h 2 = 2m ,试用图解法求作用在闸门上的静水总压 图 1力的大小和作用点。
解:如图 2 所示,作出闸门两侧的静水压强分布图,并将其合成。
AEh 1 h 2 11414. (m)sin 45° sin 45°EBh 2 2 2.828(m)sin 45° sin 45°P 11 b1(h 1h 2 ) AE b1 9.8 (3 2) 1.414 1 6.93( KN )22AD 12AE21.4140.943 (m)33P2 2 b(h1 h2 )BE b9.8 (3 2) 2.828 1 27.71( KN )ED2111414. (m) EB 2.82822AD2AE ED2 1414.1414. 2.828( m)静水总压力:P P1P2 6.93 27.7134.64( KN )设合力的作用点 D 距 A 点的距离为l ,则由合力矩定理:P l P1AD1P2AD2P1AD1P2AD2 6.930.943 27.71 2.828 lP 2.45 m34.64即,静水总压力的作用点 D 距 A 点的距离为 2.45m。
例 10:如图,一挡水弧形闸门,宽度为b(垂直于黑板) , 圆心角为θ,半径为 R,水面与绞轴平齐。
试求静水压力的水平分量F x与铅垂分量 F z。
F x 1解:γ Rsinθ bR sinθ2压力体如图所示:F zγb θπR21R sin θ R cosθ2π2例 11:一球形容器由两个半球铆接而成( 如图 1所示 ) ,铆钉有 n 个,内盛重度为的液体,求每一铆钉所受的拉力。
解:如图 2 所示,建立坐标系xoyz取球形容器的上半球面ABC作为研究对象,显然由于ABC在 yoz 平面上的两个投影面大小相等、方向相反,故x 方向上的静水总压力P x0 ;同理 P y0 。
即: ABC仅受铅垂方向的静水总压力P z V P而: V P V园柱V半球R 2 ( R H )1 4 R 3 R2 (R H )2 R 32 33图 2R 2( R H2R)R 2 (HR )33故: P Z V PR 2R ( H) 方向铅垂向上, 即3铆钉受拉力。
每一铆钉 所 受 的拉力为:F ZP Z 1 R 2( HR )nn3第三章例 1:已知 u = - (y+t2) , v =x+t , w =0 。
求 t=2 ,经过点( 0, 0)的流线方程。
解: t=2 时, u = - (y+4) , v =x+2 , w =0流线微分方程:dx dy ( y 4)x 21(x 2)21( y 4)2c22流线过点( 0, 0) ∴ c=10流线方程为:(x+2)2+(y+4) 2=20例 2:已知某流场中流速分布为: u = -x , v = 2y ,w = 5-z 。
求通过点 (x,y,z)=(2,4,1)的流线方程。
解: 流线微分方程为:dxdy dzdx dy dz uvwx2 y5 zdx 1 d (2y) d (5 z) x2 2 y5 zdx 1 d ( 2y)x22 y dx d (5 z)x5 z由上述两式分别积分,并整理得: x y c 1①xc 2 z 5c 2即流线为曲面x y c 1 和平面 x c 2 z 5c 20 的交线。
将 ( x, y, z)(2,4,1) 代入①可确定 c 1和 c 2 :c1 4,c21 2故通过点 (2,4,1)的流线方程为:x y42x z 5 0例 3. 求小孔出流的流量:解:如图,对断面0-0 和断面 1-1 列伯努利方程,不计能量损失,有:z0p0α0V02z1p aα1V12γ2gγ2gV1 2 g z0z12gh QμV1 AμA 2gh 上式中:A为小孔的面积, A 为1-1断面的面积。
例 4. 用文丘里流量计测定管道中的流量:解:如图,在1-1 及 2-2断面列伯努利方程,不计能量损失有:z1p1α1V12z2p2α2V22由于:V1 A1 V2 A2γ2gγ2g故:V221 A22z1p1z2p22g A12γγ又p1γz1z3p2γz2z4γz4z3z1p1z2p2γ1 z4z3z2p2ρ1 z4 z3γγγγρV221A22ρ 1h2g A12ρρ ρ 1 2g hμV 2 A 2V 22Q1 A2 A 1:考虑能量损失及其它因素所加的系数。
<1。
例 5:输气管入口,已知:ρ’ =1000kg/m 3,ρ =1.25kg/m 3, d = 0.4m ,h = 30mm 。
求:Q = ?解:对 0— 0 和 1— 1 断面列伯努利方程, 不计损失, 有:z 0 p a z 1p 1 α1V 1 2γγ 2g又因为:α1 1.0,z 0 z 1,p 1 γhp aV 1γ2ghρ2gh 21.784m / sγ ρQ V 1 πd 22.737m 3 / s4例 6:如图,已知: V 1 、 A 1 、 A 2 ; θ;相对压强 p 1 ;且管轴线在水平面内,试确定水流对弯管的作用力。
解:对 1-1 及 2-2 断面列伯努利方程,不计水头损失,有:p 1 V 12 p 2 V 22 γ 2gγ 且: Q V 1 A 1 V 2 A 22g可求出: V 2和 p 2。
在 x 方向列动量方程,有:F x p 1 A 1 p 2 A 2 cos θ ρQ (V 2 cos θ V 1 )F x p 1 A 1 p 2 A 2 cos θ ρQ(V 2 cos θ V 1 )在 y 方向列动量方程,有:F y p 2 A 2 sin θ ρQV 2 sin θF y p 2 A 2 sin θ ρQV 2 sin θ例 7:水渠中闸门的宽度 B = 3.4m 。
闸门上、下游水深分别为h 1 = 2.5m, h 2 = 0.8m,求:固定闸门应该施加的水平力F 。
解:对 1-1 及 2-2 断面列伯努利方程,不计水头损失,有:h 1p a V 12 p a V 22 h 2γ又: Q V 1h 1B V 2h 2 Bγ 2g2g以上两式联解,可得:V 1 1.95m / s,V 2 6.095m / s所以: Q V 1h 1B16.575m 3 / s在水平方向列动量方程,有:Fh 1h 1Bh 2(V 1 )2 2 h 2 BQ V 2FB 22 ρQ (V 2 V 1 )故:F24812 N 。
