《力学》质点运动学
01 力学:第一章 质点运动学-课堂练习及部分习题解答

xM h2 = x h1 − h2 dxM h1 dx vM = = dt h1 − h2 dt
h2
x
· x
M
M
x
《学习指导》第1章·典型例题3
Zhang Shihui
题. 距河岸(看成直线)500m处有一艘静止的船,船上的探 照灯以转速为n=1r/min转动。当光束与岸边成60°角时, 光束沿岸边移动的速度的大小是多少? 解:首先建立 p 的运动方程 x(t)
Zhang Shihui
题. 一艘正在沿直线行驶的电艇,在发动机关闭后,其 加速度方向与速度方向相反,大小与速度平方成正比, 即 dv dt = − kv 2。式中k为常数,试求电艇在关闭发动 机后行驶x距离时的速度。 dv dv dx 2 解:已知 = − kv ⇒ = − kv 2 dt dx dt
《学习指导》第1章·典型例题7
Zhang Shihui
题. 物体悬挂在弹簧上作竖直振动,加速度为a=-ky,k为 常数,y是以平衡位置为原点测得的坐标,假定振动的物 体在坐标y0处的速度为v0,求速度v和坐标y的函数关系。
dv dv dy dv 解: 由 a = = −ky ⇒ = − ky ⇒ v = − ky dt dy dt dy
《学习指导》第1章·典型例题2
Zhang Shihui
题. 灯距地面高度为h1,一只鸵鸟身高为h2,在灯下以匀 速率v沿水平直线行走,如图所示,则它的头顶在地上的 影子M点沿地面移动的速度为多少? 解:建立如图所示的坐 标系,鸵鸟坐标为x, M点的坐标为xM
dx dxM = v, vM = =? dt dt
α h
O
vp
x
θ P
《学习指导》第1章·习作题1
大学物理质点力学第一章 质点运动学 PPT

方向:
cosa
=
x r
cosβ=
y r
cosγ=
z r
路程:质点所经路径得总长度。
三、速度
描述位置矢量随时间变化快慢得物理量
1、平均速度
在移质为点r由)A,到单B的位过时程间中内(的所平用均时位间移为称为t该,质所点发在生该的过位
程中的平均速度。
v
=
Δ Δ
r t
=
Δx Δt
i
+ΔΔ
y t
j
+
Δ Δ
0
Δx
Δ t —割线斜率(平均速度)
dx —切线斜率(瞬时速度) dt
x~t图
t tt
1
2
2、 v ~ t 图
v ~ t图
割线斜率:
Δv Δt = a
v v2
切线斜率:
dv dt
=a
v1
v ~ t 图线下得面积(位移):
0 t1
t2
x2
dt dx x2 x1 x
t1
x1
t2 t
3、 a ~ t 图
=
dθ
dt
B
Δθ A
θ
0
x
(3)、角加速度
β =ΔΔωt
β
=
lim
Δt
Δω
0Δ t
=ddωt
=ddθt2 2
(4)、匀变速率圆周运动
0
t
1 2
t2
0 t
2
2 0
2
(5)、线量与角量得关系
Δ s = rΔθ
lim Δ s
Δt 0Δ t
=
lim
Δt 0
r
Δθ
第1章-质点运动学
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
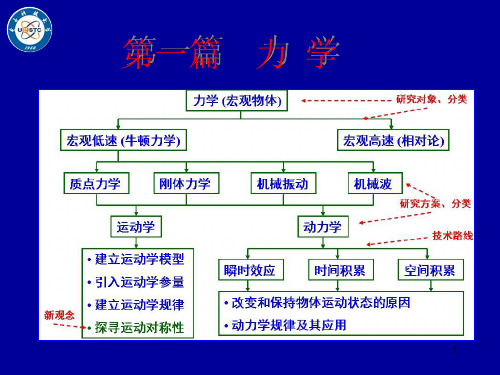
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
大学物理《力学1·质点运动学》复习题及答案

[]
6.在相对地面静止的坐标系内, A、B 二船 都以 3ms1 的速率匀速行驶, A 船沿 x 轴正 向, B 船沿 y 轴正向,今在船 A 上设置与静 止坐标系方向相同的坐标系 ( x、y方向单 位矢量i、j用表示 ), 那么在 A 船上的坐标 系中, B 船的速度(以 m·s1 为单位)为
(A) 3i 3 j, (C) 3i 3 j,
(B) 3i 3 j, (D) 3i 3 j,
[]
7.一运动质点在某瞬时位于矢径r (x,y) 的端 点处,其速度大小为
( A ) dr dt
(B) dr dt
dr (C )
dt
(D)
dx dt
2
dy dt
H
H'
的高度
S
A 15 cm
30cm M
o
C
解:先求质点的位置
t 2s,
s 20 2 5 22 60 (m)( 在大圆)
v ds / dt 20 10t ,
v(2) 40 m/s
a
t 2s时
at dv / dt 10m/s
an
an v2 / R
an
160 / 3m/ s2。
解:根据机械能守 恒定律,小球与斜
h
v2
面碰撞时的速度
H
H'
为
v1 2 gh
S
h 为小球碰撞前自由下落的距离。
因为是完全弹性碰撞,小球弹射的速度大 小为
v2 v1 2 gh
v2的方向是沿水平方向,故小球与斜面碰 撞后作平抛运动,弹出的水平距离为
s v2t 式中t 2(H h ) g
力学(漆安慎)课件 2-1,2描述质点运动的物理量

v v r = r (t) —— 运动函数(运动方程 )。 运动函数(
v v v v r (t) = x(t)i + y(t) j + z(t)k
x = x(t)
y = y(t) z = z(t)
或
由各个时刻的矢径端点连接而描 由各个时刻的矢径端点连接而描 矢径端点 画出的曲线就是质点运动的轨迹 质点运动的轨迹。 画出的曲线就是质点运动的轨迹。
x
位矢长度的变化
x22 + y22 + z22 − x12 + y12 + z12
第二章 质点运动学
讨论 位移与路程 位移与路程:
(A)P1P2 两点间的路程 ) 不唯一的, 是不唯一的 可以是∆s 或 ∆s ' v 是唯一的 而位移 ∆r 是唯一的. (B) 一般情况 位移 ) 一般情况, 大小不等于路程. 大小不等于路程
只要在研究问题中,物体的体积和形状是无关紧要的, 只要在研究问题中,物体的体积和形状是无关紧要的, 我们就可以看作质点。 我们就可以看作质点。 对于同一物体,由于研究的不同,有时可看作质点, 对于同一物体,由于研究的不同,有时可看作质点,有 时不行。 时不行。
第二章 质点运动学
·
物体可以作为质点处理的条件: 物体可以作为质点处理的条件:大小和形状对运 动没有影响或影响可以忽略。 动没有影响或影响可以忽略。 例:研究地球公转
v r (t + ∆t)
∆s v ∆r
A
质点的平均速度
第二章 质点运动学 一、 位置矢量(position vector)
由参考系上的坐标原点引 向质点所在位置的矢量称为质 点的位置矢量 简称位矢 位置矢量, 位矢。 点的位置矢量,简称位矢。
力学第二章质点运动学(PDF)

2.1一、质点把所研究的物体视为无形状大小但有一定质量的点。
•能否看成质点依研究问题而定。
例:地球绕太阳公转:地球→质点地球半径<<日地距离6.4×103 km 1.5×108 km地球自转:地球≠质点•复杂物体可看成质点的组合。
二、位置矢量与运动方程1、位置矢量k z j y i x r v v v v ++=定义:从坐标原点O 指向质点位置P 的有向线段位置矢量的直角坐标分量:===++=r z r y r x z y x r γβαcos ,cos ,cos 222方向:大小:γβαP (x,y,z )r v z y xo2、运动方程k t z j t y i t x r vv v v )()()(++=矢量形式参数形式===)()()(t z z t y y t x x 3、轨道方程(轨迹)== → ===0),,(0),,()()()(z y x G z y x F t z z t y y t x x t 消去•要尽可能选择适当的参照物和坐标系,以使运动方程形式最简,从而减少计算量。
三、位移和路程O P P ’r ∆v )(t r v )(t t r ∆+v s ∆•••1、位移'()()r PP r t t r t ∆==+∆−v v v 2、路程'()()s PP s t t s t ∆==+∆−注意(1) 位移是矢量(有大小,有方向)位移不同于路程(2) 位移与参照系位置的变化无关r s ∆≠∆v 与Δr 的区别r v ∆分清O r v ∆r v∆O r∆••O PP ’r ∆v )(t r v )(t t r ∆+v s∆•••思考:什么情况下位移的大小等于路程?[例题]一质点在xOy平面内依照x= t 2 的规律沿曲线y = x3/ 320运动,求质点从第2 秒末到第4秒末的位移(式中t的单位为s;x,y的单位为cm)。
[解] ()()r r t t r t ∆=+∆−v v v 1212.6i j=+v v(cm)2121()()x x i y yj=−+−v v [()()][()()]x t t i y t t j x t i y t j =+∆++∆−+v v v v[()()][()()]x t t x t i y t t y t j=+∆−++∆−v v 66222121()()320320t t t t i j=−+−v v 662242(42)()320320i j =−+−vv 17.4 cm r ∆==v 与水平轴夹角Δarctan 46.4Δyx ϕ=o=2.2一、速度O P P ’r∆v )(t r v )(t t r ∆+vs∆•••反映质点运动的快慢和方向的物理量1、速度的概念平均速度:平均速率:v v v v v r t r t t r t t==+−∆∆∆∆()()tt s t t s t s v ∆∆∆∆)()(−+==瞬时速度:瞬时速率:O P P ’r∆v)(t r v)(t t r ∆+vs∆•••vv v v =≠vv ,瞬时速度沿轨道切线方向2、速度的直角坐标分量()()()()::cos ,cos ,cos x y z y x z r r t x t i y t j z t kdr dx dy dz v i j k v i v j v k dt dt dt dt v v v v v v v αβγ==++==++=++ = ===v v v v vv v v v v v v v 大小方向101552r i tj t k=−++v v v v [例题]某质点的运动学方程为求:t = 0和1s 时质点的速度矢量。
第一章 质点运动学

z
r rA rB
B
y
平均速度的方向与t时间内位移的方向一致。
§1-2 质点运动的描述
第1章 质点运动学
A
2. 瞬时速度(速度) 能精细地描述 z 质点在某时刻的运动情况。 r dr v lim O t d t t 0 x 速度的方向为轨道上质点所在
处的切线方向。
r rA rB
B
dr dx dy dz v i j k dt dt dt dt
v
r
2 z
y
A
B
v vx i v y j vz k
速度的大小: v v
dx dy dz vx , v y , vz dt dt dt
§1-2 质点运动的描述
第1章 质点运动学
速度(speed)----描述质点运动的快慢和方向。
定义:单位时间内质点所发生的位移。 1. 平均速度(mean speed) 设质点:
A
t 时刻: A, rA t t 时刻: B, rB O 位移: r x r 平均速度: v 单位:ms-1 t
大小: r
单位矢量:i , j , k
2 2
r
x y z
2
x y z 方向: cos cos cos r r r
cos cos cos 1
2 2 2
特性:矢量性、 瞬时性、相对性
§1-2 质点运动的描述
第1章 质点运动学
2. 运动方程(equation of motion): 质点运动时位置随时 间变化的规律。 z
ax 0 (2) x : vx 5 y : v y 15 10t a y 10 g
力学习题-第1章质点运动学(含答案)

第一章质点运动学单元测验题一、选择题1.一质点沿x 轴运动,加速度与位置的关系为a (x )=2x +4x 2(SI 单位).已知质点在x =0处的速度为2m/s ,则质点在x =3m 处的速度为A.42m/s; B.26m/s ; C.94m/s ; D.34m/s .答案:C 解:根据题意:224dv a x x dt ==+,两边同乘dx 有:2(24)dv dx x x dx dt ⋅=+⋅由dx v dt=,上式化为:2(24)v dv x x dx ⋅=+对上式两边积分得到:223423v x x c =++由x =0,v =2m/s ,确定c =2.则当x =3m 时,解得:v =94m/s.2.一质点沿x 轴做直线运动,其速度v 随时间t 的变化关系如图所示.则下列哪个图可表示质点加速度a 随时间t 变化关系?2-•/s m a 2-•/s m a AB C答案:B 解:依据质点在一维运动时,速度-时间曲线的斜率对应加速度可知B 为加速度曲线.3.质点的运动学方程为33(21)t t =++r i j (SI 单位).则t =1s 时质点的速度为(SI单位)A.ji 6+3; B.j i 3+3; C.j i 6+6; D.j i 3+6.答案:A解:根据题意:33(21)t t =++r i j ,微分得:236d t dt ==+r v i j ,()136=+v i j 4.质点运动学方程为:kbt j t a i t a r +sin +cos =ωω,其中a 、b 、ω均为正的常数.问质点作什么运动?A.平面圆周运动;B.平面椭圆运动;C.螺旋运动;D.三维空间的直线运动.答案:C解:把质点的运动分解到三个方向上:cos sin x a t y a t z bt ωω===,,整理可知:222x y a z bt+==,则质点是以z 5.如图所示,在桌面的一边,—小球作斜抛运动,初速度v 0=4.7m/s.已知桌面宽a =2.0m.欲使小球能从桌面的另—边切过,小球的抛射角θ为A.30°;B.38°;C.50°;D.58°.答案:D 解:根据题意,小球沿x 和y 方向的运动方程为:t v x ⋅=θcos 0,201sin 2y v t gt θ=⋅-由x =2.0m 时,y =0,解得:o 58θ=.6.如图,有一半径为R 的定滑轮,沿轮周绕着一根绳子,悬在绳子一端的物体按s =(1/2)bt 2的规律向下运动.若绳子与轮周间没有相对滑动,轮周上一点A 在任一时刻t 的总加速度大为A.2t b a ;B.222/=R t b a ;C.b a =;D.R t b b a /+=22.答案:A 解:已知221bt s =,微分可得速度大小:t b dtds v ⋅==切向加速度大小:b dt dv a ==τ;法向加速度大小:Rt b R v a n 222==总加速度大小:a ==.7.当蒸汽船以15km/h 的速度向正北方向航行时,船上的人观察到船上的烟囱里冒出的烟飘向正东方向.过一会儿,船以24km/h 的速度向正东方向航行,船上的人则观察到烟飘向正西北方向.若在这两次航行期间风速不变,则风速的大小为A.9km/h; B.17.5km/h ; C.26.9km/h ; D.41km/h.答案:B解:地面为静系,船为动系,风为研究对象,则风对地的速度为绝对速度:风v v =船对地的速度为牵连速度:船牵连v v =风对船的速度为相对速度:风对船牵连v v =由绝对速度、牵连速度和相对速度的关系可得v v v =+船风对船,其矢量几何关系如图所示由此几何关系可得:1cos v v θ=船风,o 2145sin v v ctg v θ-=风船船联立解得:o 31θ=,5.17=v km /h .8.一个自由落体在它运动的最后一秒内所通过的路程等于全程的1/3.则物体通过全程所需的时间为A.3s ;B.6-3s ;C.6+3s ;D.6s答案:C解:设自由落体的全程下落时间和下落的高度分别为t 、S t 。
力学中的质点运动学

力学中的质点运动学力学是研究物体运动的科学,其中质点运动学是力学中的重要分支之一。
质点运动学主要研究质点在空间中发生的运动,探索了质点运动的规律和特性。
通过深入理解质点运动学,我们可以更好地理解和描述物体在空间中的运动情况。
一、质点的定义和描述1.1 质点的概念在力学中,将没有大小和形状的物体称为质点。
由于没有具体尺寸,故忽略了它们所占据的体积。
1.2 质点的位置表示质点在坐标系中位置的表示通常采用直角坐标系或极坐标系来进行描述。
直角坐标系使用x、y、z轴分别表示空间中三个方向上的位移;而极坐标系则通过径向距离r和极角θ来描述位置。
二、位移与速度2.1 位移与平均速度质点从初始位置到最终位置所经过的路径称为路径s,而两个位置之间的位移Δs等于最终位置减去初始位置。
平均速度V_avg等于位移Δs除以经过时间Δt,即V_avg=Δs/Δt。
2.2 瞬时速度瞬时速度V是指在某一瞬间的瞬时位移对应的速度。
当时间趋于无穷小(即Δt→0)时,质点的平均速度趋近于瞬时速度,即V_avg→V。
三、加速度和运动图像3.1 加速度加速度a定义为单位时间内质点速度的变化率。
当质点在匀加速运动下,由初始速度v₀和加速度a所决定的位移s与时间t之间满足s=v₀·t+1/2·a·t²。
3.2 运动图像运动图像是描述物体运动过程中位置随时间变化情况的一种方法。
根据不同类型的质点运动学模式,可以绘制出直线运动、曲线运动等不同形式的运动图像。
四、匀变速直线运动4.1 定义与表达式匀变速直线运动是指物体在直线上以恒定加速度a进行运动的情况。
其位移与时间之间存在着关系s=v₀·t+1/2·a·t²。
4.2 特殊情况:匀速直线运动与匀减速直线运动当加速度a为0时,质点在直线上做匀速直线运动;当加速度a小于0时,质点在直线上做匀减速直线运动。
五、曲线运动5.1 圆周运动圆周运动是指质点沿着一条固定半径的圆形路径进行的运动。
第1章质点运动学

2.几种典型的坐标系 几种典型的坐标系 (1).直角坐标系 直角坐标系
z P
r 直角坐标系中, 直角坐标系中,任意矢量 A 可表示为 r r r r A= A i + Ay j + A k x z
矢量的大小或模 矢量的大小或模表示为
x
γ
O
A
α
β
y
A = A2 + A2 + A2 x y z
方向余弦满足关系
cos2 α +cos2 β +cos2 γ =1
r dk =0 dt
直角坐标系中,坐标轴的单位矢量是常矢量, 直角坐标系中,坐标轴的单位矢量是常矢量,满足
r di =0 dt
r dj =0 dt
3
(2).自然坐标系 自然坐标系 为坐标原点, 在已知运动轨迹上任取一点O为坐标原点,用质点距离原点的轨 来确定质点任意时刻的位置, 道长度s来确定质点任意时刻的位置,以轨迹切向和法向的单位 矢量( 作为其独立的坐标方向,这样的坐标系,称为自然坐 矢量(τ、n)作为其独立的坐标方向,这样的坐标系,称为自然坐 称为自然坐标 自然坐标。 标系 s 称为自然坐标。
在第6章 狭义相对论中讲授 在第6
10
§1.3.2 描述一般曲线运动的线参量
线参量: 线参量: 位置矢量、位移矢量、 位置矢量、位移矢量、 速度矢量和加速度矢量
z P(x,y,z)
γ α
r
z
β
1.位置矢量与运动方程 1.位置矢量与运动方程
x x
o
y y
(1).位置矢量: 由坐标原点指向质点的有向线段。 (1).位置矢量:时刻t,由坐标原点指向质点的有向线段。 位置矢量
β
大学物理力学习题
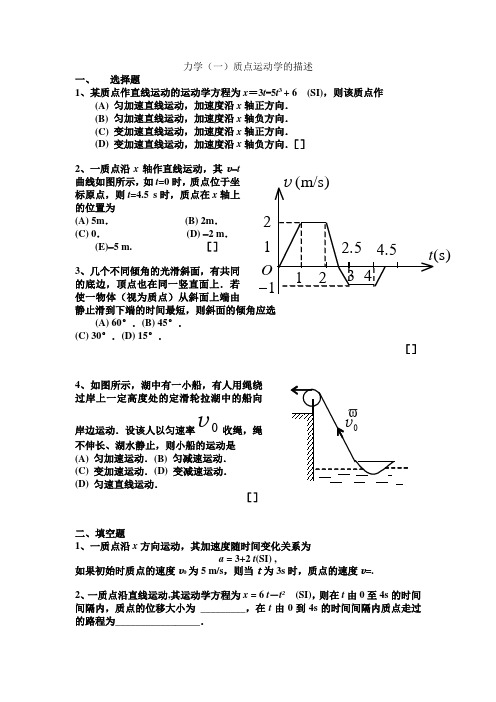
力学(一)质点运动学的描述一、 选择题1、某质点作直线运动的运动学方程为x =3t -5t 3 + 6 (SI),则该质点作(A) 匀加速直线运动,加速度沿x 轴正方向. (B) 匀加速直线运动,加速度沿x 轴负方向. (C) 变加速直线运动,加速度沿x 轴正方向. (D) 变加速直线运动,加速度沿x 轴负方向.[]2、一质点沿x 轴作直线运动,其v -t 曲线如图所示,如t =0时,质点位于坐标原点,则t =4.5 s 时,质点在x 轴上的位置为(A) 5m . (B) 2m . (C) 0. (D) -2 m .(E)-5 m. []3、几个不同倾角的光滑斜面,有共同的底边,顶点也在同一竖直面上.若使一物体(视为质点)从斜面上端由静止滑到下端的时间最短,则斜面的倾角应选(A) 60°.(B) 45°. (C) 30°.(D) 15°.[]4、如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率0v 收绳,绳不伸长、湖水静止,则小船的运动是 (A) 匀加速运动.(B) 匀减速运动. (C) 变加速运动.(D) 变减速运动. (D) 匀速直线运动.[]二、填空题1、一质点沿x 方向运动,其加速度随时间变化关系为a = 3+2 t (SI) ,如果初始时质点的速度v 0为5 m/s ,则当t为3s 时,质点的速度v =. 2、一质点沿直线运动,其运动学方程为x = 6 t -t 2 (SI),则在t 由0至4s 的时间间隔内,质点的位移大小为 _________,在t 由0到4s 的时间间隔内质点走过的路程为_________________.-12O3、灯距地面高度为h 1,一个人身高为h 2,在灯下以匀速率v 沿水平直线行走,如图所示.他的头顶在地上的影子M 点沿地面移动的速度为v M =.三、计算题 1、一质点沿x 轴运动,其加速度a 与位置坐标x 的关系为a =2+6 x 2 (SI)如果质点在原点处的速度为零,试求其在任意位置处的速度.2、有一质点沿x 轴作直线运动,t 时刻的坐标为x = 4.5 t 2– 2 t 3 (SI) .试求:(1) 第2秒内的平均速度; (2) 第2秒末的瞬时速度; (3) 第2秒内的路程. 一、 DBBC 二、23m/s 3分8 m2分10 m 2分h 1v /(h 1-h 2) 3分 三、解:设质点在x 处的速度为v ,62d d d d d d 2x tx x t a +=⋅==v v 2分()x x xd 62d 02⎰⎰+=v v v2分()2 213x x +=v 1分解:(1) 5.0/-==∆∆t x v m/s 1分(2) v = d x /d t = 9t - 6t 21分 v (2) =-6 m/s 1分(3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m 2分力学(二)圆周运动与相对运动一、 选择题1、质点沿半径为R 的圆周作匀速率运动,每T 秒转一圈.在2T 时间间隔中,其平均速度大小与平均速率大小分别为(A) 2p R /T , 2p R/T .(B) 0 , 2πR /T(C) 0 , 0. (D) 2πR /T , 0. []2、对于沿曲线运动的物体,以下几种说法中哪一种是正确的: (A) 切向加速度必不为零.(B) 法向加速度必不为零(拐点处除外).(C) 由于速度沿切线方向,法向分速度必为零,因此法向加速度必为零. (D) 若物体作匀速率运动,其总加速度必为零.(E) 若物体的加速度a ϖ为恒矢量,它一定作匀变速率运动.[] 3、质点作半径为R 的变速圆周运动时的加速度大小为(v 表示任一时刻质点的速率)(A)t d d v . (B) R 2υ.(C)R t 2d d v v +. (D) 2/1242d d ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛R t v v . []4、在相对地面静止的坐标系内,A 、B 二船都以2 m/s 速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向.今在A 船上设置与静止坐标系方向相同的坐标系(x 、y 方向单位矢用i ϖ、j ϖ表示),那么在A 船上的坐标系中,B 船的速度(以m/s为单位)为 (A) 2i ϖ+2jϖ. (B) -2i ϖ+2j ϖ.(C) -2i ϖ-2j ϖ. (D) 2i ϖ-2jϖ.[]二、填空题1、质点沿半径为R 的圆周运动,运动学方程为223t+=θ (SI) ,则t时刻质点的法向加速度大小为a n =;角加速度β=.2、设质点的运动学方程为j t R i t R r ϖϖϖsin cos ωω+= (式中R 、ω 皆为常量) 则质点的vϖ=___________,d v /d t =_________________.3、如图所示,小船以相对于水的速度vϖ与水流方向成α角开行,若水流速度为uϖ,则小船相对于岸的速度的大小为_______________,与水流方向的夹角为_________________.三、计算题1、质点M 在水平面内的运动轨迹如图所示,OA 段为直线,AB 、BC 段分别为不同半径的两个1/4圆周.设t =0时,M 在O 点,已知运动学方程为S =30t +5t 2 (SI)αu ϖv ϖ求t =2 s 时刻,质点M 的切向加速度和法向加速度.2、一质点沿半径为R 的圆周运动.质点所经过的弧长与时间的关系为221ct bt S +=其中b 、c 是大于零的常量,求从0=t开始到切向加速度与法向加速度大小相等时所经历的时间.一、 选择题1、两个质量相等的小球由一轻弹簧相连接,子剪断的瞬间,球1和球2的加速度分别为 (A) a 1=g,a 2=g. (B) a 1=0,a 2=g. (C)a 1=g,a 2=0. (D) a 1=2g,a 2=0.2、水平地面上放一物体A ,它与地面间的滑动摩擦系数为μ.现加一恒力F ϖ如图所示.欲使物体A 有最大加速度,则恒力F ϖ与水平方向夹角θ 应满足(A) sin θ =μ.(B) cos θ =μ.(C) tg θ =μ. (D) ctg θ =μ.[]B3、一只质量为m 的猴,原来抓住一根用绳吊在天花板上的质量为M 的直杆,悬线突然断开,小猴则沿杆子竖直向上爬以保持它离地面的高度不变,此时直杆下落的加速度为(A) g .(B)g M m .(C) g MmM +. (D)g m M m M -+ . (E) g MmM -.[ ]4、一公路的水平弯道半径为R ,路面的外侧高出内侧,并与水平面夹角为θ.要使汽车通过该段路面时不引起侧向摩擦力,则汽车的速率为(A)Rg . (B)θtg Rg .(C) θθ2sin cos Rg . (D)θctg Rg[]二、填空题1、沿水平方向的外力F 将物体A 压在竖直墙上,由于物体与墙之间有摩擦力,此时物体保持静止,并设其所受静摩擦力为f 0,若外力增 至2F ,则此时物体所受静摩擦力为_____________.2、如图,在光滑水平桌面上,有两个物体A 和B 紧靠在一起.它们的质量分别为m A =2 kg ,m B =1 kg .今用一水平力F =3 N 推物体B ,则B 推A 的力等于______________.如用同样大小的水平力从右边推A ,则A 推B 的力等于___________________.3、一圆锥摆摆长为l 、摆锤质量为m ,在水平面上作匀速圆周运动,摆线与铅直线夹角θ,则(1) 摆线的张力T=_____________(2) 摆锤的速率v=_____________.三、计算题1、如图所示,质量为m的摆球A悬挂在车架上.求在下述各种情况下,摆线与竖直方向的夹角α和线中的张力T.(1)小车沿水平方向作匀速运动;(2)小车沿水平方向作加速度为a的运动.2、一质量为60 kg的人,站在质量为30 kg的底板上,用绳和滑轮连接如图.设滑轮、绳的质量及轴处的摩擦可以忽略不计,绳子不可伸长.欲使人和底板能以1 m/s2的加速度上升,人对绳子的拉力T2多大?人对底板的压力多大? (取g=10 m/s2)一、 DCCB 二、f 0 3分)/(m M F + 2分)/(m M MF + 2分θcos /mg 1分θθcos sin gl2分 三、解:(1)0=α 1分mg T = 1分(2) ma T =αsin ,mg T =αcosg a /tg =α [或)/(tg 1g a -=α] 1分22g a m T += 2分解:人受力如图(1) 图2分 a m g m N T 112=-+ 1分底板受力如图(2) 图2分 a m g m N T T 2221=-'-+ 2分 212T T = 1分 N N ='由以上四式可解得 a m m g m g m T )(421212+=-- ∴5.2474/))((212=++=a g m m T N1分5.412)(21=-+=='T a g m N N N 1分力学(四)功、势能一、 选择题1、一辆汽车从静止出发在平直公路上加速前进.如果发动机的功率一定,下面哪一种说法是正确的?(A) 汽车的加速度是不变的.图(1)ϖa ϖ图(2) T ϖ g m 1(B) 汽车的加速度随时间减小.(C) 汽车的加速度与它的速度成正比. (D) 汽车的速度与它通过的路程成正比. (E) 汽车的动能与它通过的路程成正比.[]2、一个质点同时在几个力作用下的位移为:k j i r ρρρρ654+-=∆(SI)其中一个力为恒力k j i F ρρρρ953+--=(SI),则此力在该位移过程中所作的功为(A)-67 J . (B) 17 J .(C) 67 J . (D) 91 J .[]3、对功的概念有以下几种说法:(1) 保守力作正功时,系统内相应的势能增加. (2) 质点运动经一闭合路径,保守力对质点作的功为零. (3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零.在上述说法中:(A) (1)、(2)是正确的. (B) (2)、(3)是正确的. (C) 只有(2)是正确的. (D) 只有(3)是正确的.[]4、有一劲度系数为k 的轻弹簧,原长为l 0,将它吊在天花板上.当它下端挂一托盘平衡时,其长度变为l 1.然后在托盘中放一重物,弹簧长度变为l 2,则由l 1伸长至l 2的过程中,弹性力所作的功为(A) ⎰-21d l l x kx . (B) ⎰21d l l x kx .(C)⎰---0201d l l l l x kx . (D)⎰--0201d l l l l x kx .[]二、填空题1、已知地球质量为M ,半径为R .一质量为m 的火箭从地面上升到距地面高度为2R 处.在此过程中,地球引力对火箭作的功为_____________________.2、如图所示,一斜面倾角为θ,用与斜面成α角的恒力F ρ将一质量为m 的物体沿斜面拉升了高度h ,物体与斜面间的摩擦系数为μ.摩擦力在此过程中所作的功W f =________________________. 三、 计算题1、一物体按规律x =ct 3 在流体媒质中作直线运动,式中c 为常量,t 为时间.设媒质对物体的阻力正比于速度的平方,阻力系数为k ,试求物体由x =0运动到x =l 时,阻力所作的功.2、一质量为m 的质点在Oxy 平面上运动,其位置矢量为j t b i t a r ρρρωωsin cos +=(SI)式中a 、b 、ω是正值常量,且a >b .(1)求质点在A 点(a ,0)时和B 点(0,b )时的动能;(2)求质点所受的合外力F ρ以及当质点从A 点运动到B 点的过程中F ρ的分力x F ρ和y F ρ分别作的功.一、 BCCC 二、)131(R R GMm -或 RGMm 32- 3分θαμθμsin sin ctg Fh mgh +-3分Fα θ三、解:由x =ct 3可求物体的速度:23d d ct tx==v 1分 物体受到的阻力大小为:343242299x kc t kc k f ===v 2分力对物体所作的功为:⎰=W W d =⎰-lx x kc 03432d 9=7273732l kc - 2分解:(1)位矢j t b i t a r ρρρωωsin cos += (SI) 可写为t a x ωcos =,t b y ωsin =t a t x x ωωsin d d -==v ,t b ty ωωcos d dy -==v在A 点(a ,0) ,1cos =t ω,0sin =t ωE KA =2222212121ωmb m m y x =+v v 2分在B 点(0,b ) ,0cos =t ω,1sin =t ωE KB =2222212121ωma m m y x =+v v 2分(2) j ma i ma F y x ρρρ+==j t mb i t ma ρρωωωωsin cos 22-- 2分由A →B ⎰⎰-==020d cos d a a x x x t a m x F W ωω=⎰=-022221d a ma x x m ωω 2分⎰⎰-==b b y y t b m y F W 020dy sin d ωω=⎰-=-b mb y y m 022221d ωω 2分习题(五)动能定理、功能原理、机械能宁恒一、 选择题1、质量为m 的一艘宇宙飞船关闭发动机返回地球时,可认为该飞船只在地球的引力场中运动.已知地球质量为M ,万有引力恒量为G ,则当它从距地球中心R 1处下降到R 2处时,飞船增加的动能应等于(A)2R GMm (B)22R GMm(C) 2121R R R R GMm -(D) 2121R R R GMm -(E) 222121R R R R GMm[ ]2、今有一劲度系数为k 的轻弹簧,竖直放置,下端悬一质量为m 的小球,开始时使弹簧为原长而小球恰好与地接触,今将弹簧上端缓慢地提起,直到小球刚能脱离地面为止,在此过程中外力作功为(A)kg m 422 (B)kg m 322(C)kg m 222(D)kg m 222(E)kg m 224[]3、如图所示,子弹射入放在水平光滑地面上静止的木块而不穿出.以地面为参考系,下列说法中正确的说法是(A) 子弹的动能转变为木块的动能. (B) 子弹─木块系统的机械能守恒. (C) 子弹动能的减少等于子弹克服木块阻力所作的功. (D) 子弹克服木块阻力所作的功等于这一过程中产生的热.[]二、填空题1、如图所示,质量m=2 kg的物体从静止开始,沿1/4圆弧从A滑到B,在B处速度的大小为v=6 m/s,已知圆的半径R=4 m,则物体从A到B的过程中摩擦力对它所作的Array功W=_________.2、质量m=1kg的物体,在坐标原点处从静止出发在水平面内沿x轴运动,其所受合力方向与运动方向相同,合力大小为F=3+2x(SI),那么,物体在开始运动的3 m内,合力所作的功W=________________;且x=3 m时,其速率v=_________________.三、计算题1、某弹簧不遵守胡克定律. 设施力F,相应伸长为x,力与伸长的关系为F=52.8x+38.4x2(SI)求:(1)将弹簧从伸长x1=0.50 m拉伸到伸长x2=1.00 m时,外力所需做的功.(2)将弹簧横放在水平光滑桌面上,一端固定,另一端系一个质量为2.17 kg 的物体,然后将弹簧拉伸到一定伸长x2=1.00 m,再将物体由静止释放,求当弹簧回到x1=0.50 m时,物体的速率.(3)此弹簧的弹力是保守力吗?2、如图所示,质量m为0.1 kg的木块,在一个水平面上和一个劲度系数k为20 N/m的轻弹簧碰撞,木块将弹簧由原长压缩了x=0.4 m.假设木块与水平面间的滑动摩擦系数 k为0.25,问在将要发生碰撞时木块的速率v为多少?CCC-42.4 J18 J6 m/s解:(1) 外力做的功=31 J(2) 设弹力为F ′= 5.34 m/s(3) 此力为保守力,因为其功的值仅与弹簧的始末态有关.解:根据功能原理,木块在水平面上运动时,摩擦力所作的功等于系统(木块和弹簧)机械能的增量.由题意有222121v m kx x f r -=-而mg f k r μ=由此得木块开始碰撞弹簧时的速率为mkx gx k 22+=μv= 5.83 m/s[另解]根据动能定理,摩擦力和弹性力对木块所作的功,等于木块动能的增量,应有20210v m kxdx mgx x k -=--⎰μ其中2021kx kxdx x =⎰力学(六)动量守恒定律一、 选择题⎰⎰⋅+==21d )4.388.52(d 2x x xx x xF W ρρ⎰⎰⋅=-==1212d d 21'2x x x x Wx F x F m ρρv mW2=v︒30v ϖ2 1、质量为m 的质点,以不变速率v 沿图中正三角形ABC 的水平光滑轨道运动.质点越过A 角时,轨道作用于质点的冲量的大小为(A) m v . (B)m v .(C) m v . (D) 2m v .[]2、质量为20 g 的子弹沿X 轴正向以500 m/s 的速率射入一木块后,与木块一起仍沿X 轴正向以50 m/s 的速率前进,在此过程中木块所受冲量的大小为 (A) 9 N·s . (B) -9 N·s .(C)10 N·s . (D) -10 N·s .[]3、在水平冰面上以一定速度向东行驶的炮车,向东南(斜向上)方向发射一炮弹,对于炮车和炮弹这一系统,在此过程中(忽略冰面摩擦力及空气阻力) (A) 总动量守恒.(B) 总动量在炮身前进的方向上的分量守恒,其它方向动量不守恒. (C) 总动量在水平面上任意方向的分量守恒,竖直方向分量不守恒. (D) 总动量在任何方向的分量均不守恒.[]4、质量为20 g 的子弹,以400 m/s 射入一原来静止的质量为980 g 的摆球中,(A) 2 m/s . (B) 4 m/s .(C) 7 m/s . (D) 8 m/s .[]二、填空题1、两块并排的木块A和B,质量分别为m 1和m 2 ,静止地放置在光滑的水平面上,一子弹水平地穿过两木块,设子弹穿过两木块所用的时间分别为∆t 1 和∆t 2 ,木块对子弹的阻力为恒力F ,则子弹穿出后,木块A 的速度大小为____ ,木块B 的速度大小为______.2、一物体质量M =2 kg ,在合外力i t F ϖ)23(+=(SI )的作用下,从静止开始运动,式中i ϖ为方向一定的单位矢量,则当t=1 s 时物体的速度1v ϖ=_________.A CA B233、一质量为30 kg的物体以10 m·s-1的速率水平向东运动,另一质量为20 kg 的物体以20 m·s-1的速率水平向北运动。
物理力学知识点归纳总结

物理力学知识点归纳总结一、基本概念物理力学的基本概念包括:质点、力、运动、运动学、动力学等。
1. 质点质点是物理力学研究的基本对象,它被看作一个具有质量但没有体积的点。
在质点模型中,物体的形状和大小被忽略,只考虑其质量、速度和位置等运动状态。
2. 力力是导致物体产生运动或形变的原因。
在物理力学中,力被描述为对物体的作用,其大小和方向决定了物体的运动状态。
力的单位是牛顿(N)。
3. 运动运动是物体相对于参考点的位置随时间的变化。
物体在空间中的位置随着时间的推移而改变,这种变化被称为运动。
运动学研究物体的位置、速度和加速度等与运动有关的量。
4. 运动学运动学是物理力学的一个分支,研究物体的运动状态和运动规律。
通过描述物体的位置、速度和加速度等参数,可以描绘物体的运动轨迹和运动规律。
5. 动力学动力学是物理力学的另一个分支,研究力和物体的运动之间的相互作用。
通过分析物体所受的外力和内力之间的关系,可以揭示物体的运动规律和动力学规律。
二、牛顿运动定律牛顿运动定律是物理力学的重要基础,它包括三条定律:惯性定律、动量定律和作用反作用定律。
1. 惯性定律惯性定律又称牛顿第一定律,它指出:物体如果没有外力作用,将保持静止或匀速直线运动的状态。
这一定律表明,物体的运动状态在没有外力作用时将保持不变,这种性质被称为惯性。
2. 动量定律动量定律又称牛顿第二定律,它表明:物体的加速度与作用在其上的力成正比,与物体的质量成反比。
具体表达为:F=ma,其中F为作用在物体上的力,m为物体的质量,a为物体的加速度。
这一定律描述了力和运动之间的关系,为分析物体的运动提供了基本原理。
3. 作用反作用定律作用反作用定律又称牛顿第三定律,它指出:两个物体之间的相互作用力,大小相等、方向相反,且作用在不同的物体上。
这一定律阐明了物体之间的相互作用规律,为研究物体的相互作用提供了基本原理。
三、运动的描述物体的运动状态可以通过位置、速度和加速度等参数来描述。
力学 第二章 质点运动学

v
arccos vz 5618'
v
二、平均加速度与瞬时加速度
1、平均加速度:速度矢量对时间的平均变化率。
a v v(t t) v(t)
t
t
v(t )
v
速度矢端曲线
v( t t )
§2.3 质点的直线运动(x vx ax )
一、运动学方程
x xt
二、速度和加速度
1、速度(瞬时速度)
vx
dx dt
大小表示质点在t时刻运动的快慢;
正负分别对应于质点沿Ox正向和负向运动。
2、加速度
ax
dvx dt
d2x dt 2
ax与vx同号,则加速;ax与vx反号,则减速。
4、质点的运动学轨迹方程
质点运动时描出的轨迹称为质点的轨迹。 也就是位置矢量的矢端曲线。
质点在平面Oxy上运动,
轨迹方程: y y(x) 或者:f (x, y, z) 0
例题:r R cos tiˆ R sin tˆj, 求:轨迹方程。
y R
解: x2 y2 R2.
x
二、位移
v
v
v
4、注意:
(1)平均速度的大小不等于平均速率。 (2)瞬时速度的大小等于瞬时速率。 (3)即使位置矢量的大小不变,也可以有速度。
ΔS
r(t )
r
S
r(
t
t
)
o
dr / dt
r(t )
ΔS
S
r
r( t t )
第1章:质点运动学

dr C) dt
dr B) dt
dx dy D) ( ) ( ) dt dt
2 2
1.3
1.3.1
加速度
加速度
v 平均加速度:a t a 与 v 同方向。
瞬时加速度:
y
A
O
vA
B
vB
v dv a lim t 0 t dt 2 d r 2 dt
x
vA
v
解:(1)由运动方程消去 时间 t 得质点轨迹方程:
R
x y R
2 2
2
质点的运动轨迹是一 个半径为 R 的园。
O r2
a r t r1
v
p1 x
r
p2
r xi yj R costi R sin tj dr v R sin ti R cos tj dt
ds 2 v 10t 0.3t dt dv 10 0.6t 切向加速度大小为 a dt
v (10t 0.3t ) 法向加速度大小 an R 300
2
2 2
总加速度矢量为
(10t 0.3t 2 ) 2 a (10 0.6t ) n 300 当t =1.0s 时 a 9.4 0.314 n
s vav t
无限短时间段中的平均速率可以定义为 质点在该时刻 t 的瞬时速率:
s ds v(t ) lim t 0 t dt
r d r 瞬时速度: v (t ) lim t 0 t dt d ( xi yj zk ) v (t ) dt dx dy dz i j k dt dt dt
dv v a a a dt
大学物理 第一章 质点运动学

是否等于瞬时速率? t 时刻位矢
瞬时速度的大小是否
r
等于瞬时速率?
A
r
r1
B t 时间内位移
x
t +t 时刻位矢
平面直角坐标系中的瞬时速度(简称速度)
v lim r dr
t0 t
dt
r(t) x(t)i y(t) j
v d r
dx
i
d
y
j
y
vy
v
dt dt dt
vx
vxi vy j
力 学
§1-1 参照系 &坐标系 质点 §1-2 位移、速度和加速度 §1-3 圆周运动 §1-5 牛顿运动定律 §1-6 牛顿运动定律的应用举例
1. 运动的绝对性 绝对静止的物体是没有的
地球自转 太阳表面的运动
太阳随银河系运动
为了确定一个物体的位置和描述一个物体的机
械运动,必须另选一个物体或内部无相对运动的物
3. 坐标系 为了定量地描述物体相对于参考系的 运动情况,要在参考系上选择一个固定的坐标系
坐标系选定后,运动物体A 中任一点 P 的位置
就可以用它在此坐标系中的坐标来描述
运动物体
运动参考系
y
A P(x,y,z)
运动物体
O
z 参考系
x
地面参考系
常用坐标系: 平面直角坐标系和自然坐标系
一、质点 一般情况下,运动物体的形状和大小都可能变化
y
y z koj
r
i
x
*P
x
方向的单位矢量.
z
位矢r 的值为
r
xi
yj
zk
r r x2 y2 z2
位矢 r 的方向余弦
力学舒幼生第一章质点运动学

P
yj
r(t tx)i
O
x
加速度 a d d v td d2r 2 td dxv i td dyv tjr
15
例 空心入篮
抛射角 12
xvct o2s1 2g2tsin1
yvst in21 2g2tco1s
y0
t 2vsin2 g cos1
第一章 质点运动学
0
1.1 空间和时间
时间和空间的测量
绝对时空观 绝对空间,就其本性来说,与任何外在的情况无关,
始终保持着相似和不变。 绝对的、纯粹的数学的时间,就其本性来说,均匀地
流逝而与任何外在的情况无关。 牛顿——《自然哲学的数学原理》
时间和空间的测量与物体的存在和运动没有任何关系
参考系
参考物:选取的一个有固定大小和形状的物体。 相对参考物,可以确定其它物体的位置。
9
vv0a0(tt0)1 2b(tt0)2
再求 t 时刻的位置
微分关系式 dxvdt
两边积分 tt0 d x tt0 v dtt0[v t0 a 0 (t t0 ) 1 2 b (t t0 )2 ]d
x x 0 v 0 (t t0 ) 1 2 a 0 (t t0 )2 1 6 b (t t0 )3
a心 d d vtvddtR ddtR 2 a切dd/vt/Rd dt R
与速度垂直,改变速度方向
与速度平行,改变速度大小
18
无限小角位移矢量
ddk
r(tt)
d r(t)
⊙k
初、末态矢量与转动正方向满足右手螺旋法则
无限小角位移与有限角位移的区别?
19
有限角位移不是矢量
不满足矢量加法的交换律
新概念物理教程力学赵凯华

θ
y
r
y
θ
0
x
x
Φ
极轴
直角坐标系
球坐标系
极坐标系
坐标系实际上是由实物构成的参考系的数学抽象。
精选课件
6
§2. 时间和空间的计量
一.时间的计量
时间是表征物质运动的持续性。通常采用能够重复出现的周 期现象来计量时间。
时间计量的实物基准——地球自转
1956年,国际计量会议规定:
1 平均太阳秒=平均太阳日×(1/86400)
在科学记数法中指数相差1,即代表数目大10倍或小10倍,叫 做一个“数量级”
为了方便,通常采用词头来代表一个单位得十进倍数或十进分 数。如千(kilo),厘(centi)等,现在已有20个词头。见表1-2 (p13 )
精选课件
15
3.2 空间尺度
人们已研究的领域中,空间尺度跨越了42了数量级。
在物理上把原子尺度的客体叫做微观系统,大小在人体尺度 上下几个数量级范围之内的客体,叫做宏观系统;微观系统 和宏观系统最重要的区别是服从的物理规律不同。呈现出微 观特征的宏观系统,叫做有质量,没有大小、形状的理想物体。
抽象条件:物体运动过程中,物体的大小和形状对研究的问 题影响很小,可忽略不计。
理论方法:对复杂的运动进行抽象提出物理模型研究物体 运动的基本规律。
质点模型意义: ①机械运动中,质点是最简单、最基本的单元 ②易于描述和研究基本的运动规律 ③复杂的物体可以看成是由许多质点组成的系统(即质点系)
最大的动物(鲸)体长十米,即101m的数量级 最大的植物(红杉树)高达百米以上,即102m的数量级 最高的山(珠穆朗玛峰)高8.84km,即104m的数量级 最深的海(马里亚纳海沟)深11.022km, 也是104m的数量级
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参考系:用来描述物体运动而选作参考的物体
或物体系。
运动学中参考系可任选,不同参考系中物体
的运动形式(如轨迹、速度等)可以不同。
常用的参考系:
▲太阳参考系(太阳一恒星参考系)▲地心参考系(地球一片旦星参考系)▲地面参考系或实验室参考系▲质心参考系(第三章§3.6)
■
质点
1.质点的定义
只具有质量而没有大小和形状的理想物体。
2•质点模型抽象条件
形状、大小不起作用的运动,如平动; 物体线度远小于研究的尺寸,如地球公转。
3.建立模型的意义
对事物的认识总是从简单入手的;
复杂问题只有忽略次要因素,才能突出主 要因素,找到其运动规律。3
本章目录
§1.1参考系、坐标系(书§1.1)™
§ 1・2质点的位置矢量、运.3)ch
§1.4匀加速运动(书§1・4、§ 1.5、§1.6)™
§1・7相对运动(书§1.8)®
§1.1参考系、坐标系
一•参考系(frame of reference, reference system )
