数据结构中有向图和无向图的C语言实现
数据结构中有向图和无向图的c语言实现

#include<iostream.h>
#include<malloc.h>
#define M 50
typedef char vextype;//顶点数据类型char
typedef struct node //定义表结点类型
{
int adjvex;//邻接点域
struct node *link;//指针域
}
cout<<"以(0,0)为输入结束符"<<endl;
cout<<"输入一条边依附的两个顶点序号:";
cin>>i>>j;
while((i>0)&&(j>0))//输入的(i,j)为(0,0)作为结束符号
{
p=(edgenode*)malloc(sizeof(edgenode));//生成邻接序号为j的表结点
break;
default:cout<<"输入错误,程序结束!"<<endl;
return;
}
cout<<endl;
cout<<"是否继续?(输入n结束,输入y有效!)"<<endl;
cin>>flag;
}
cout<<"程序结束,再见!"<<endl;
}
}edgenode,*Edgenode;
typedef struct headnode//定义表头结点类型
{
vextype vexdata;//顶点数据域
算法与数据结构课设(有向图,无向图,有向网,无向网)

算法与数据结构课程设计报告系(院):计算机科学学院专业班级:教技1001姓名:李##学号: ******### 指导教师:***设计时间:2012.6.16 - 2012.6.24设计地点:4号楼2号机房目录一、设计方案 (1)二、实现过程以及代码 (2)三、测试 (20)四、结论和分析 (23)五、难点和收获 (23)一、 设计方案1.程序设计基本过程:拿到课程设计任务书,按照要求,需要设计有向图、有向网、无向图 、无向网四种图,以及邻接矩阵、邻接表两种数据存储结构,三层以上的显示菜单。
图的操作中又包含了有关线性表、栈和队列的基本操作。
由于显示菜单已给出,剩下的任务就是把函数写入其中。
2.程序流程图:预定义 定义结构体 定义变量 各种函数3.程序设计的原理:图的操作都是以两种存储结构为基础的:邻接矩阵存储结构和邻接表存储结构,如有向图,有向网,无向图,无向网的创建,其他的操作都是在四种图创建后才开始进行的。
所以,首先必须理解两种存储结构的定义。
图的邻接矩阵存储结构即图的数组表示法。
用两个数组分别存储数据元素(如顶点)的信息和数据元素之间的关系(如边或弧)的信息。
用邻接矩阵存储结构的图具有以下几点特征:(一):顶点数:vexnum ,边(弧)数:arcnum ,图的种类:kind ;(二):邻接矩阵:arcs(1顶点关系类型:adj 2相关信息:*info);(三):顶点向量(顶点名):vexs[];其优点是以二维数组表示有n 个顶点的图时,需存放n 个顶点的信息和n*n 条弧的信息存储量。
借助邻接矩阵容易判定任意两个顶点之间是否有边或弧相连,并容易求出各个顶点的度。
缺点是时间复杂度是O (n*n ),例如,构造一个具有n 个顶点和e 条边的无向网的时间复杂度为O (n*n+e*n )。
图的邻接表存储结构是图的一种链式存储结构。
对图中的每个顶点建立一个单链表,每个结点由三个域组成,邻接点域adjvex (弧尾在邻接表链表中的位序),链域nextarc (下一条弧),数据域info(权值)。
无向图C程序代码

}
void DFSTraverseM(MGraph *G)
{
int i;
for(i=0;i<G->n;i++)
visited[i]=FALSE; //访问标志数组初始化
for(i=0;i<G->n;i++) //可用于非连通图的遍历
if(!visited[i])
DFSM(G,i); //对未访问的顶点调用DFSM
}
int main() //主函数的调用
{
MGraph G;
CreateUDG (&G);
DFSTraverseM(&G);
rerintf("深度优先遍历:顶点%d/n",G->vexs[i]); //访问顶点vi
printf("\n");
visited[i]=TRUE; //访问第i个顶点
for(j=0;j<G->n;j++) //依次搜索vi邻接点
if(G->arcs[i][j]==1 && !visited[j]) //对尚未访问的邻接顶点j递归调用DFSM
#include <stdio.h>
#define NAX_VERTEX_NUM 20
typedef enum{FALSE,TRUE}Boolean;
Boolean visited[NAX_VERTEX_NUM];
typedef struct
{
int vexs[NAX_VERTEX_NUM]; //顶点向量
scanf("%d %d",&(G->n),&(G->e));
数据结构(C语言版) 第七章 图

路径与连通性
路径、简单路径、回路(环)、简单回路
顶点之间的连通性、无向连通图、有向强连通
图
4/46
7.1 图的定义和术语(3)
路径与连通性
对于有向图G1
V1V3V4V1V2 是从V1 到V2 的路径, 不是简单路径;
V1V2是简单路径; V1V3V4V1V3V4V1是环,不是简单环; V1V3V4V1是简单环。
3/46
7.1 图的定义和术语(2)
有向图
弧<v,w> ∊ E (v,w ∊V),w为弧头, v为弧尾; 顶点v
邻接到顶点w,顶点w 邻接自顶点v,弧< v, w >和 顶点v、w相关联。
顶点v 的入度是以v 为弧头的弧的数目,记为ID(v); v 的出度是以v为弧尾的弧的数目,记为OD(v); v 的度是TD(v) = ID(v) + OD(v)。
}VNode, AdjList[MAX_VERTEX_NUM];
这种存储结构适合于进行first_adj(G,v) 找v的第一个邻接点的操作
邻接矩阵的方法适合存储稠密图
26/46
7.2.2 邻接表--- 链式存储结构
邻接表是一种顺序存储与链式结构相结 合的存储方式,类似于树的孩子链表。
对每个顶点建立一个单链表,第i个单链 表中的结点表示依附于顶点vi的边。
邻接矩阵
从邻接矩阵M中可以看出该图 共有( )个顶点;如果是有 向图该图共有( )条弧,如 果是无向图,则共有( )边。
AB CD
G
25/46
邻接矩阵存储的特点
无向图的邻接矩阵是对称的,对n个顶 点的无向图只需要存入下三角矩阵,即 需要n(n-1)/2个存储单元。
有向图的邻接矩阵所需要的存储单元不 一定,需要N*N个存储单元
数据结构C语言版-无向图的邻接多重表存储表示和实现

数据结构C语言版无向图的邻接多重表存储表示和实现.txt只要你要,只要我有,你还外边转什么阿老实在我身边待着就行了。
听我的就是,问那么多干嘛,我在你身边,你还走错路!跟着我!不能给你幸福是我的错,但谁让你不幸福,我TMD去砍了他/* 数据结构C语言版无向图的邻接多重表存储表示和实现P166编译环境:Dev-C++ 4.9.9.2日期:2011年2月15日*/#include <stdio.h>#include <malloc.h>#define MAX_NAME 3 // 顶点字符串的最大长度+1#define MAX_INFO 80 // 相关信息字符串的最大长度+1typedef char InfoType;typedef char VertexType[MAX_NAME]; // 字符串类型// AMLGraph.h 无向图的邻接多重表存储表示#define MAX_VERTEX_NUM 20typedef enum{unvisited,visited}VisitIf;typedef struct EBox{VisitIf mark; // 访问标记int ivex,jvex; // 该边依附的两个顶点的位置struct EBox *ilink,*jlink; // 分别指向依附这两个顶点的下一条边InfoType *info; // 该边信息指针}EBox;typedef struct{VertexType data;EBox *firstedge; // 指向第一条依附该顶点的边}VexBox;typedef struct{VexBox adjmulist[MAX_VERTEX_NUM];int vexnum,edgenum; // 无向图的当前顶点数和边数}AMLGraph;typedef int QElemType;// 单链队列--队列的链式存储结构typedef struct QNode{QElemType data; //数据域struct QNode *next; //指针域}QNode,*QueuePtr;typedef struct{QueuePtr front,//队头指针,指针域指向队头元素rear; //队尾指针,指向队尾元素}LinkQueue;// 若G中存在顶点u,则返回该顶点在无向图中位置;否则返回-1int LocateVex(AMLGraph G,VertexType u){int i;for(i=0;i<G.vexnum;++i)if(strcmp(u,G.adjmulist[i].data)==0)return i;return -1;}// 采用邻接多重表存储结构,构造无向图Gint CreateGraph(AMLGraph *G){int i,j,k,l,IncInfo;char s[MAX_INFO];VertexType va,vb;EBox *p;printf("请输入无向图G的顶点数,边数,边是否含其它信息(是:1,否:0): ");scanf("%d,%d,%d",&(*G).vexnum,&(*G).edgenum,&IncInfo);printf("请输入%d个顶点的值(<%d个字符):\n",(*G).vexnum,MAX_NAME);for(i=0;i<(*G).vexnum;++i) // 构造顶点向量{scanf("%s",(*G).adjmulist[i].data);(*G).adjmulist[i].firstedge=NULL;}printf("请顺序输入每条边的两个端点(以空格作为间隔):\n");for(k=0;k<(*G).edgenum;++k) // 构造表结点链表{scanf("%s%s%*c",va,vb); // %*c吃掉回车符i=LocateVex(*G,va); // 一端j=LocateVex(*G,vb); // 另一端p=(EBox*)malloc(sizeof(EBox));p->mark=unvisited; // 设初值p->ivex=i;p->jvex=j;p->info=NULL;p->ilink=(*G).adjmulist[i].firstedge; // 插在表头(*G).adjmulist[i].firstedge=p;p->jlink=(*G).adjmulist[j].firstedge; // 插在表头(*G).adjmulist[j].firstedge=p;if(IncInfo) // 边有相关信息{printf("请输入该弧的相关信息(<%d个字符):",MAX_INFO);gets(s);l=strlen(s);if(l){p->info=(char*)malloc((l+1)*sizeof(char));strcpy(p->info,s);}}}return 1;}// 返回v的值VertexType* GetVex(AMLGraph G,int v){if(v>=G.vexnum||v<0)exit(0);return &G.adjmulist[v].data;}// 对v赋新值valueint PutVex(AMLGraph *G,VertexType v,VertexType value){int i;i=LocateVex(*G,v);if(i<0) // v不是G的顶点return 0;strcpy((*G).adjmulist[i].data,value);return 1;}// 返回v的第一个邻接顶点的序号。
数据结构C语言版第七章 图

第七章图重点难点要求掌握图的基本概念和术语;熟悉图的各种存储结构及其构造算法,了解各种存储结构的特点及其选用原则;熟练掌握图的两种遍历算法,熟练掌握图在实际应用中的主要算法:最小生成树算法、最短路径算法、拓扑排序和关键路径算法。
典型例题1在下图所示的有向图中:(1) 该图是强连通的吗? 若不是,则给出其强连通分量。
(2) 请给出所有的简单路径及有向环。
(3) 请给出每个顶点的度,入度和出度。
(4) 请给出其邻接表、邻接矩阵及逆邻接表。
答:(1)该图是强连通的,所谓强连通是指有向图中任意顶点都存在到其他各顶点的路径。
(2)简单路径是指在一条路径上只有起点和终点可以相同的路径:有v1v2、v2v3、v3v1、v1v4、v4v3、v1v2v3、v2v3v1、v3v1v2、v1v4v3、v4v3v1、v3v1v4、另包括所有有向环,有向环如下:v1v2v3v1、v1v4v3v1(这两个有向环可以任一顶点作为起点和终点)(3)每个顶点的度、入度和出度:D(v1)=3 ID(v1)=1 OD(v1)=2D(v2)=2 ID(v2)=1 OD(v2)=1D(v3)=3 ID(v3)=2 OD(v3)=1D(v4)=2 ID(v4)=1 OD(v4)=1(4)邻接表:(注意边表中邻接点域的值是顶点的序号,这里顶点的序号是顶点的下标值-1) vertex firstedge next┌─┬─┐┌─┬─┐┌─┬─┐0│v1│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘1│v2│─→│ 2│∧│├─┼─┤├─┼─┤2│v3│─→│ 0│∧│├─┼─┤├─┼─┤3│v4│─→│ 2│∧│└─┴─┘└─┴─┘逆邻接表:┌─┬─┐┌─┬─┐0│v1│─→│ 2│∧│├─┼─┤├─┼─┤1│v2│─→│ 0│∧│├─┼─┤├─┼─┤┌─┬─┐2│v3│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘3│v4│─→│0│∧│└─┴─┘└─┴─┘邻接矩阵:0 1 0 10 0 1 01 0 0 00 0 1 02.对n个顶点的无向图和有向图,采用邻接矩阵和邻接表表示时,如何判别下列有关问题?(1) 图中有多少条边?(2)任意两个顶点i和j是否有边相连?(3) 任意一个顶点的度是多少?【解】对于n个顶点的无向图和有向图,用邻接矩阵表示时:(1)设m为矩阵中非零元素的个数无向图的边数=m/2有向图的边数=m(2)无论是有向图还是无向图,在矩阵中第i行,第j列的元素若为非零值,则该两顶点有边相连。
算法与数据结构课程设计(有向图,无向图,有向网,无向网)

算法与数据结构课程设计报告系(院):计算机科学学院专业班级:教技1001班*名:***学号:*********指导教师:***设计时间:2012.6.16 - 2012.6.24设计地点:4号楼2号机房目录一、设计方案及实现过程******************第3页二、实现代码***********************************第4页三、测试******************************************第19页四、难点与收获********************************第21页一、设计方案及实现过程这次课程设计要求实现无向图、有向图、无向网以及有向网的一些基本操作以及应用,大体的方案是先进入界面后,选择无向图、有向图、无向网、无向网中的一个,然后创建相应的图或者网,创建好后,在此基础上选择进行相关的操作,具体的函数放在main函数前面,通过多次函数调用已达到具体操作的实现。
流程图如下:进入选择界面1 无向图创建无向图1 创建无向图的邻接矩阵函数调用2 创建无向图的邻接表函数调用3无向图的深度优先遍历函数调用4 无向图的广度优先遍历函数调用5 返回选择主界面2 有向图3 无向网4 有向网5 退出有向图、无向网、有向网的操作和无向图类似,在这里不一一列举。
二、实现代码#include<stdio.h># include <stdlib.h># define maxlen 10# define large 999# define true 1# define false 0# define ok 1# define error 0# define overflow -2# define null 0typedef int status;#include <ctype.h>#include <string.h>#include <queue>#include <stack>#include <process.h>using namespace std;#define MAX_VERTEX_NUM 20#define MAX 1000typedef struct{int a[maxlen],b[maxlen],h[maxlen];char vexs[maxlen];int vexnum,arcnum;int kind;int arcs[maxlen][maxlen];}graph;typedef struct node{int adjvex;int info;struct node *next;}edgenode;typedef struct{int id;char data;edgenode *link;}vexnode;typedef struct{vexnode adjs[maxlen];int vexnum,arcnum;int kind;}adjlist;typedef struct qnode{int data;struct qnode *next;}linkqlist;typedef struct{linkqlist *front;linkqlist *rear;} linkqueue;typedef struct{int stack[maxlen];int top;}stackstru;int cnull=-1;graph g;adjlist adjl;stackstru *t;stackstru *s;linkqueue *q;graph printf_adjmatrix(graph g){int i,j;printf("邻接矩阵:\n");printf("vertex\t");for (i=0;i<g.vexnum;i++) printf("%4c",g.vexs[i]);printf("\n");for(i=0;i<g.vexnum;i++){printf("% 4c \t",g.vexs[i]);for(j=0;j<g.vexnum;j++) printf("%4d",g.arcs[i][j]);printf("\n");}return g;}void create_2(graph g){ //构造有向图int i,j,k,c=0;for (i=0;i<g.vexnum;i++)for(j=0;j<g.vexnum;j++)g.arcs[i][j]=c;for(k=0;k<g.arcnum;k++)g.arcs[g.a[k]-1][g.b[k]-1]=1;printf_adjmatrix(g);}void create_1(graph g){ //构造无向图int i,j,k,c=0;for (i=0;i<g.vexnum;i++)for(j=0;j<g.vexnum;j++)g.arcs[i][j]=c;for(k=0;k<g.arcnum;k++){g.arcs[g.a[k]-1][g.b[k]-1]=1;g.arcs[g.b[k]-1][g.a[k]-1]=1;}printf_adjmatrix(g);}graph create_4(graph g){ //构造有向网int i,j,k,c=999;for (i=0;i<g.vexnum;i++)for(j=0;j<g.vexnum;j++)g.arcs[i][j]=c;for(k=0;k<g.arcnum;k++)g.arcs[g.a[k]-1][g.b[k]-1]=g.h[k];printf_adjmatrix(g);return g;}graph create_3(graph g){ //构造无向网int i,j,k,c=999;for (i=0;i<g.vexnum;i++)for(j=0;j<g.vexnum;j++)g.arcs[i][j]=c;for (k=0;k<g.arcnum;k++){g.arcs[g.a[k]-1][g.b[k]-1]=g.h[k];g.arcs[g.b[k]-1][g.a[k]-1]=g.h[k];}printf_adjmatrix(g);return g;}void creategraph(graph g){switch(g.kind){case 1:create_1(g);break;case 2:create_2(g);break;case 3:create_3(g);break;case 4:create_4(g);break;default:printf("Error\n");}}adjlist createlist (graph g ,adjlist adjl){ //创建邻接表int i;edgenode *p;if(g.kind==1||g.kind==3){//创建有向邻接表for(i=0;i<adjl.arcnum;i++){p=(edgenode*)malloc(sizeof(edgenode));p->adjvex=g.b[i];p->info=g.h[i];p->next=adjl.adjs[g.a[i]-1].link;adjl.adjs[g.a[i]-1].link=p;}}if(g.kind==2||g.kind==4){//创建无向邻接表for(i=0;i<adjl.arcnum;i++){p=(edgenode*)malloc(sizeof(edgenode));p->info=g.h[i];p->adjvex=g.b[i];p->next=adjl.adjs[g.a[i]-1].link;adjl.adjs[g.a[i]-1].link=p;p=(edgenode*)malloc(sizeof(edgenode));p->info=g.h[i];p->adjvex=g.a[i];p->next=adjl.adjs[g.b[i]-1].link;adjl.adjs[g.b[i]-1].link=p;}}printf("邻接表为:\n");for(i=0;i<g.vexnum;i++){printf("[%d,%c]=>",i+1,adjl.adjs[i].data);p=adjl.adjs[i].link;while(p!=null){printf("[%c,%d]-->",adjl.adjs[(p->adjvex)-1].data,p->info);p=p->next;}printf("^\n");}return adjl;}void initqueue(linkqueue *p){ //构造空队列p->front=(linkqlist *)malloc(sizeof(linkqlist));p->rear=p->front;(p->front)->next=null;}status empty(linkqueue *q){ //判断是否为空int v;if(q->front==q->rear) v=true;else v=false;return v;}int addqueue(linkqueue *q,int e){q->rear->next=(linkqlist *)malloc(sizeof(linkqlist));q->rear=q->rear->next;if(!q->rear) return -1;q->rear->data=e;q->rear->next=null;return ok;}status delqueue(linkqueue *q){ //linkqlist *p;int e;if (q->front==q->rear)printf("the linklist is overflow");else p=(q->front)->next;(q->front)->next=p->next;e=p->data;if(q->rear==p)q->rear=q->front;free(p);return(e);}bool visit[maxlen]; //深度优先搜索void DFS(adjlist adjl,int i){edgenode *p;visit[i]=1;printf("%c ",adjl.adjs[i].data);for(p=adjl.adjs[i].link;p;p=p->next){if(!visit[p->adjvex]) DFS(adjl,p->adjvex);}}void DFSTraverse(adjlist adjl){int i;printf("\t\t深度优先搜索:");for( i=0;i<maxlen;i++)visit[i]=false;for( i=0;i<=adjl.vexnum;i++)if(!visit[i]) DFS(adjl,i);}queue <int> Q;void BFSTraverse(adjlist adjl) { //广度优先搜索edgenode *w;int i,j;printf("\n\t\t广度优先搜索:");for( i=0;i<maxlen;i++)visit[i]=0;for(i=0;i<=adjl.vexnum;i++){if(!visit[i]){visit[i]=1;printf("%c ",adjl.adjs[i].data);Q.push(i);while(!Q.empty()){j=Q.front();Q.pop();for( w=adjl.adjs[i].link;w;w=w->next)if(!visit[w->adjvex]){visit[w->adjvex]=1;printf("%c ",adjl.adjs[w->adjvex-1].data);Q.push(w->adjvex);}}}}}status initstack(stackstru *s){ //构造空栈s->top=0;return ok;}status push(stackstru *s,int x) { //进栈if (s->top==maxlen)printf("the stack is overflow!\n");else{s->top=s->top+1;s->stack[s->top]=x;}return 1;}status pop(stackstru *s) //出栈{int y;if(s->top==0)printf("the stack is empty!\n");else{y=s->stack[s->top];s->top=s->top-1;}return y;}status stackempty(stackstru *s) //判断栈是否为空{ if (s->top==maxlen) return (true);else return (false);}int TopologicalSort(adjlist adjl) //拓扑排序{stack <int> S;edgenode *p;int i,j,count=0;printf("\n拓扑排序:");for(i=0;i<=adjl.vexnum;i++)if(adjl.adjs[i].id==0)S.push(i);count=0;while(!S.empty()){j=S.top(); S.pop();count++;printf("(%d %c) ",j,adjl.adjs[j].data);for(p=adjl.adjs[i].link;p;p=p->next){int k=p->adjvex;int d=--(adjl.adjs[k].id);if(!d)S.push(k);}}if(count<adjl.vexnum){ printf("\n网中有环!\n");return error;}else return ok;}void prim(graph g){int i,j,k,min;int lowcost[maxlen];int closet[maxlen];printf("最小生成树的边为:\n");for(i=1;i<g.vexnum;i++){lowcost[i]=g.arcs[0][i];closet[i]=1;}closet[1]=0;j=1;for(i=1;i<g.vexnum;i++){min=lowcost[j];k=i;for(j=1;j<g.vexnum;j++)if(lowcost[j]<min&&closet[j]!=0){min=lowcost[j];k=j;}printf("(%c,%c),",g.vexs[k-1],g.vexs[closet[k-1]]);closet[k]=0;for(j=1;j<g.vexnum;j++)if(g.arcs[k][j]<lowcost[j]&&closet[j]!=0){lowcost[j]=g.arcs[k][j];closet[j]=k;}}}int ve[maxlen];int vl[maxlen];status toporder(adjlist adjl,stackstru *t){ //关键路径int i,j,count,k;edgenode *p;initstack(s);initstack(t);for(i=0;i<adjl.vexnum;i++)if(adjl.adjs[i].id==0) push(s,i);count=0;for(i=0;i<adjl.vexnum;i++) ve[i]=0;while(!stackempty(s)){j=pop(s);push(t,j);++count;for(p=adjl.adjs[j].link;p;p=p->next){k=p->adjvex;if(--adjl.adjs[k-1].id==0) push(s,k-1);if(ve[j]+(p->info)>ve[k-1]) ve[k-1]=ve[j]+(p->info);}}if(count<adjl.vexnum) return error;else return ok;}int criticalpath(adjlist adjl){int i,j,k,dut,ee,el;edgenode *p;if(!toporder(adjl,t)) return error;for(i=0;i<adjl.vexnum;i++) vl[i]=ve[i-1];printf("关键路径为:\n");while(!stackempty(t))for(j=pop(t), p=adjl.adjs[j].link;p;p=p->next){k=p->adjvex; dut=(p->info);if(vl[k]-dut<vl[j]) vl[j]=vl[k]-dut;}for(j=0;j<adjl.vexnum;++j)for(p=adjl.adjs[j].link;p;p=p->next){k=p->adjvex;dut=p->info;ee=ve[j];el=vl[k-1]-dut;if(ee==el) printf("(%c,%c)->",adjl.adjs[j].data,adjl.adjs[k-1].data);}return ok;}void shortpath_dijkstra(graph g) //有向网的最短路径{int cost[maxlen][maxlen];int dist[maxlen];int path[maxlen];int s[maxlen];int i,j,v0,min,u;printf("\n请输入起点的编号:");scanf("%d",&v0);v0--;for(i=0;i<g.vexnum;i++){for(j=0;j<g.vexnum;j++)cost[i][j]=g.arcs[i][j];}for(i=0;i<g.vexnum;i++){dist[i]=cost[v0][i];if(dist[i]<large&&dist[i]>0) path[i]=v0;s[i]=0;}s[v0]=1;for(i=0;i<g.vexnum;i++){min=large;u=v0;for(j=0;j<g.vexnum;j++)if(s[j]==0&&dist[j]<min){min=dist[j];u=j;}s[u]=1;for(j=0;j<g.vexnum;j++)if(s[j]==0&&dist[u]+cost[u][j]<dist[j]){dist[j]=dist[u]+cost[u][j];path[j]=u;}}printf("\n顶点%d到各顶点的最短路径长度为:\n",v0);for(i=0;i<g.vexnum;i++)if(s[i]==1){u=i;while(u!=v0){ printf("%4c<-",g.vexs[u]);u=path[u];}printf("%4c",g.vexs[u]);printf(":%d\n",path[i]);}else printf("%4c<-%4c:无路径\n",g.vexs[i],g.vexs[v0]);}void ShowMainMenu(){printf("\n");printf("**************图的基本操作及应用***************\n");printf("* 1 无向图的基本操作及应用*\n");printf("* 2 有向图的基本操作及应用*\n");printf("* 3 无向网的基本操作及应用*\n");printf("* 4 有向网的基本操作及应用*\n");printf("* 5 退出\n");printf("***********************************************\n");}void UDG(){int n;do{printf("\n");printf("**************无向图的基本操作及应用***************\n");printf("* 1 创建无向图的邻接矩阵*\n");printf("* 2 创建无向图的邻接表*\n");printf("* 3 无向图的深度优先遍历*\n");printf("* 4 无向图的广度优先遍历*\n");printf("* 5 退出\n");printf("***************************************************\n");printf("请选择:");scanf("%d",&n);switch(n){case 1:printf("----------wait-------");creategraph(g);break; //邻接矩阵case 2:printf("----------wait-------");createlist (g,adjl);break; //邻接表case 3:printf("----------wait-------");DFSTraverse(adjl);break; //深度优先搜索case 4:printf("----------wait-------");BFSTraverse(adjl);break; //广度优先搜索case 5:break;default:printf("ERROR!");}}while(n!=5);}void DG(){int n;do{printf("\n");printf("**************有向图的基本操作及应用***************\n");printf("* 1 创建有向图的邻接矩阵*\n");printf("* 2 创建有向图的邻接表*\n");printf("* 3 拓扑排序*\n");printf("* 4 退出*\n");printf("***************************************************\n");printf("请选择:");scanf("%d",&n);switch(n){case 1:printf("--------wait-------");creategraph(g);break; //邻接矩阵case 2:printf("--------wait-------");createlist (g,adjl);break; //邻接表case 3:printf("--------wait-------");createlist(g,adjl);TopologicalSort(adjl);break; //拓扑排序case 4:break; //退出default:printf("ERROR!");}}while(n!=4);}void UDN(){int n;do{printf("\n");printf("**************无向网的基本操作及应用***************\n");printf("* 1 创建无向网的邻接矩阵*\n");printf("* 2 创建无向网的邻接表*\n");printf("* 3 Prim算法求最小生成树*\n");printf("* 4 kraskal算法求最小生成树*\n");printf("* 5 退出\n");printf("***************************************************\n");printf("请选择:");scanf("%d",&n);switch(n){case 1:printf("---------wait-------");creategraph(g);break; // 创建无向网的邻接矩阵case 2:printf("--- ----wait-------");createlist (g,adjl);break; // 创建无向网的邻接表case 3:printf("---------wait-------");prim(g);break; //Prim算法求最小生成树case 4:printf("---------wait-------");break;case 5:break;default:printf("ERROR!");}}while(n!=5);}void DN(){int n;do{printf("\n");printf("**************有向网的基本操作及应用***************\n");printf("* 1 创建有向网的邻接矩阵*\n");printf("* 2 创建有向网的邻接表*\n");printf("* 3 关键路径*\n");printf("* 4 单源顶点最短路径问题*\n");printf("* 5 退出\n");printf("***************************************************\n");printf("请选择:");scanf("%d",&n);switch(n){case 1:printf("---------wait-------");creategraph(g);break; //创建有向网的邻接矩阵case 2:printf("---------wait-------");createlist (g,adjl);break; //创建有向网的邻接表case 3:printf("---------wait-------");criticalpath(adjl);break; //关键路径case 4:printf("---------wait-------");criticalpath(adjl);break; //单源顶点最短路径问题case 5:break; //退出default:printf("ERROR!");}while(n!=5);}void main(){int i,j,k,h,n;do{ShowMainMenu();printf("请选择:");scanf("%d",&n);if(n>5) error;else{g.kind=n;h=n;printf("请输入顶点数,边数:");scanf("%d,%d",&i,&j);g.vexnum=i;adjl.vexnum=i;g.arcnum=j;adjl.arcnum=j;for (i=0;i<g.vexnum;i++){printf("第%d个顶点的信息:",i+1);scanf("%s",&g.vexs[i]);adjl.adjs[i].data=g.vexs[i];adjl.adjs[i].link=null;adjl.adjs[i].id=0;}for (k=1;k<=g.arcnum;k++){//label:if (g.kind==2||g.kind==4)printf("第%d条边的起点编号,终点编号:",k);else printf("第%d条边的两个顶点的编号:",k);scanf("%d,%d",&i,&j);g.a[k-1]=i;g.b[k-1]=j;while (i<1||i>g.vexnum||j<1||j>g.vexnum){printf(" 编号超出范围,重新输入");//goto label;}if (g.kind==3||g.kind==4){printf("\t该边的权值:");scanf("%d",&h);g.h[k-1]=h;}else g.h[k-1]=null;adjl.adjs[i].id++;}switch(n){case 1:UDG();break;case 2:DG();break;case 3:UDN();break;case 4:DN();break;case 5:break;default:printf("ERROR!");break;}}while(n!=5);}三、测试a)程序开始运行,进入选择界面b)选择无向图,并创建无向图C)基于已创建的的无向图选择各项具体的操作四、难点与收获这次的实习报告相对我而言算是比较难的,因为在学这门课程的时候就没怎么专心听讲,所以在拿到计划书的时候,对很多地方感觉很陌生,甚至有一种没办法动手的感觉,加之开始学JAVA以后就很少用C语言编写程序,导致对很多很简单的东西都很陌生,所以熟悉整个C语言的编程环境都花了一段时间。
数据结构 C语言版(严蔚敏版)第7章 图

1
2
4
1
e6 2 4
2016/11/7
29
7.3 图的遍历
从已给的连通图中某一顶点出发,沿着一 些边访遍图中所有的顶点,且使每个顶点 仅被访问一次,就叫做图的遍历 ( Graph Traversal )。 图中可能存在回路,且图的任一顶点都可 能与其它顶点相通,在访问完某个顶点之 后可能会沿着某些边又回到了曾经访问过 的顶点。 为了避免重复访问,可设置一个标志顶点 是否被访问过的辅助数组 visited [ ]。
2
1 2
V2
V4
17
结论:
无向图的邻接矩阵是对称的; 有向图的邻接矩阵可能是不对称的。 在有向图中, 统计第 i 行 1 的个数可得顶点 i 的出度,统计第 j 行 1 的个数可得顶点 j 的入度。 在无向图中, 统计第 i 行 (列) 1 的个数可得 顶点i 的度。
2016/11/7
18
2
邻接表 (出度表)
adjvex nextarc
data firstarc
0 A 1 B 2 C
2016/11/7
1 0 1
逆邻接表 (入度表)
21
网络 (带权图) 的邻接表
6 9 0 2 1 C 2 8 3 D
data firstarc Adjvex info nextarc
2016/11/7
9
路径长度 非带权图的路径长度是指此路径 上边的条数。带权图的路径长度是指路径 上各边的权之和。 简单路径 若路径上各顶点 v1,v2,...,vm 均不 互相重复, 则称这样的路径为简单路径。 回路 若路径上第一个顶点 v1 与最后一个 顶点vm 重合, 则称这样的路径为回路或环。
数据结构之图C源代码

玩转算法与数据结构之图—HIT2000鲁天伟图在数据结构中比前面的链表和二叉树要复杂一些,复杂在无固定的造型。
比如让大家画一个链表,画一个二叉树,大家应该画的差不多一个样子。
但是图就不行,让大家画个图可能就千差万别了,我们数据结构里面常用的图是由顶点和边构成的图。
有长度的边叫加权边。
由加权边构成的图叫带权图。
研究的无向图基本上都是连通图(图中任意两个顶点之间都连通,即任两点间都有一条通路连接)。
所研究的有向图,也是在无向图的基础上,在每条边上加上指示方向的箭头,并能够从图(有向图按无向图使用算法)中从任一个顶点开始进行先深搜索(DFS)算法或是先广搜索(BFS)算法遍历找到所有顶点。
关于图中度的概念,简单来说,无向图顶点的度是指该顶点连接几条边,连几条边,就是几度,无向图中所有顶点的总度数是边数的两倍。
有向图顶点的度分入度和出度,入度是指向该顶点的边总和,出度是以该点为起点指向其他顶点的边总和。
无向图的应用主要是在连通图中寻找任意顶点到其它顶点间的最短路径,用最小代价连通各个顶点的最小生成树。
有向图的应用主要在工程方面,使用AOV(顶点表示活动)网和AOE(边表示活动)网。
AOV网用来表示活动的先后顺序,可用拓扑排序来找出活动的先后顺序。
AOE网用来找出关键路径(从起始点到终止点最长的一条路径)。
AOV和AOE网都是无环有向图。
图表 1 无向图图表 2 有向图如上图1表示无向图,这个无向图的边没有标明长度,只有邻接关系。
可以用邻接矩阵来表示,即用一个二维的数组存放顶点间的关系(表示两顶点是否有线连接)。
邻接矩阵既可以存无向图的顶点关系也可以存有向图的顶点关系。
边没有长度时,在二维数组邻接两点对应的坐标位置填1表示有邻接,不邻接的两点确定的坐标位置填0表示不邻接。
如果边有长度设定,可以在坐标位写入加权边的长度值。
图表 3 邻接矩阵如上左图是图1的邻接矩阵。
右图是图2的邻接矩阵。
那么对于有向图,我们还可以用邻接表来存储。
C语言实现常用数据结构——图
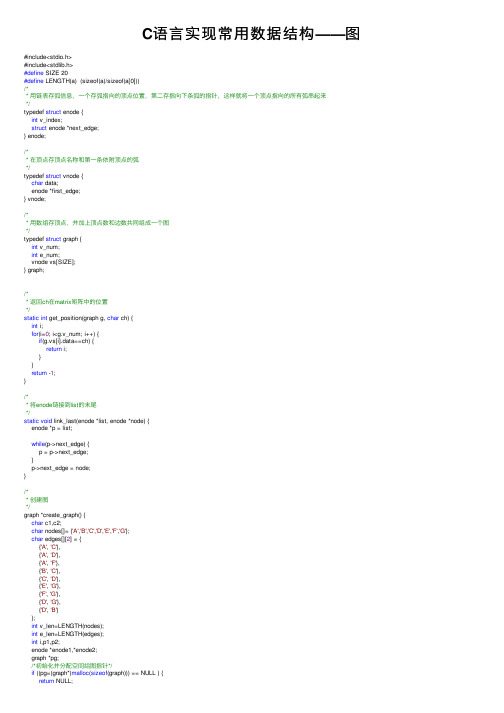
C语⾔实现常⽤数据结构——图#include<stdio.h>#include<stdlib.h>#define SIZE 20#define LENGTH(a) (sizeof(a)/sizeof(a[0]))/** ⽤链表存弧信息,⼀个存弧指向的顶点位置,第⼆存指向下条弧的指针,这样就将⼀个顶点指向的所有弧串起来*/typedef struct enode {int v_index;struct enode *next_edge;} enode;/** 在顶点存顶点名称和第⼀条依附顶点的弧*/typedef struct vnode {char data;enode *first_edge;} vnode;/** ⽤数组存顶点,并加上顶点数和边数共同组成⼀个图*/typedef struct graph {int v_num;int e_num;vnode vs[SIZE];} graph;/** 返回ch在matrix矩阵中的位置*/static int get_position(graph g, char ch) {int i;for(i=0; i<g.v_num; i++) {if(g.vs[i].data==ch) {return i;}}return -1;}/** 将enode链接到list的末尾*/static void link_last(enode *list, enode *node) {enode *p = list;while(p->next_edge) {p = p->next_edge;}p->next_edge = node;}/** 创建图*/graph *create_graph() {char c1,c2;char nodes[]= {'A','B','C','D','E','F','G'};char edges[][2] = {{'A', 'C'},{'A', 'D'},{'A', 'F'},{'B', 'C'},{'C', 'D'},{'E', 'G'},{'F', 'G'},{'D', 'G'},{'D', 'B'}};int v_len=LENGTH(nodes);int e_len=LENGTH(edges);int i,p1,p2;enode *enode1,*enode2;graph *pg;/*初始化并分配空间给图指针*/if ((pg=(graph*)malloc(sizeof(graph))) == NULL ) {return NULL;}memset(pg, 0, sizeof(graph));pg->v_num = v_len;pg->e_num = e_len;/*初始化所有顶点*/for(i=0; i<pg->v_num; i++) {pg->vs[i].data = nodes[i];pg->vs[i].first_edge = NULL;}/*初始化所有边,⽆向图的边为两个顶点共有,按指向顶点来定义可以算两条边,因此要挂在两个顶点的邻接表后⾯*/ for(i=0; i<pg->e_num; i++) {/*获取顶点名*/c1 = edges[i][0];c2 = edges[i][1];/*获取顶点在数组中的位置*/p1 = get_position(*pg, c1);p2 = get_position(*pg, c2);enode1 = (enode*)malloc(sizeof(enode));enode1->v_index = p2;/*若边所依附的顶点尚⽆第⼀条边,则将这条边赋给顶点的first_edge,否则加在顶点的边链表的最末尾*/if(pg->vs[p1].first_edge == NULL) {pg->vs[p1].first_edge = enode1;} else {link_last(pg->vs[p1].first_edge, enode1);}enode2 = (enode*)malloc(sizeof(enode));enode2->v_index = p1;if(pg->vs[p2].first_edge == NULL) {pg->vs[p2].first_edge = enode2;} else {link_last(pg->vs[p2].first_edge, enode2);}}return pg;}/** 打印邻接表图*/void print_graph(graph g){int i,j,k;enode *node;printf("List Graph:\n");for (i = 0; i < g.v_num; i++){printf("%d(%c): ", i, g.vs[i].data);node = g.vs[i].first_edge;while (node != NULL){printf("%d(%c) ", node->v_index, g.vs[node->v_index].data);node = node->next_edge;}printf("\n");}}main() {/*创建图,并打印图*/graph *pg = create_graph();print_graph(*pg);}List Graph:0(A): 2(C) 3(D) 5(F)1(B): 2(C) 3(D)2(C): 0(A) 1(B) 3(D)3(D): 0(A) 2(C) 6(G) 1(B)4(E): 6(G)5(F): 0(A) 6(G)6(G): 4(E) 5(F) 3(D)。
有向图的C#实现

有向图的C#实现using System;using System.Collections;using System.Text;namespace myWorkFlow.kernel{//边表结点类public class EdgeNode{public int adjvex;public EdgeNode next;public EdgeNode(){next=null;}}////顶点表结点类public class VertexNode{public object vertex;public EdgeNode firstedge;public VertexNode(){firstedge=null;}}//图的类型public enum GraphType{UnDiGraph = 0,//⽆向图DiGraph = 1//有向图}//图类public class ALGraph{public VertexNode[] AdjList;//顶点表public int VertexNodeCount;//顶点数public int BordeCount;//边数public GraphType theType;//图的类型public ALGraph( int n,int e ,GraphType cuType){VertexNodeCount = n;BordeCount= e;AdjList = new VertexNode[n];theType = cuType;}}//图对象操作类public class GraphOperation{private bool[] visited;private StringBuilder sb ;public GraphOperation(){}///<summary>///建全⼀个有向图对象/// (不是建⽴ ^_^)///</summary>///<param name="G"></param>public void CreateALGraph(ALGraph G){int i,j,k;EdgeNode s;for(int vnc = 0 ;vnc < G.VertexNodeCount; vnc++){VertexNode cuVN = new VertexNode();Console.Write("请输⼊顶点的编号 : ");cuVN.vertex = Console.ReadLine();cuVN.firstedge = null;G.AdjList[vnc]=cuVN;}for(k = 0; k < G.BordeCount; k++){Console.Write("请输⼊边开始顶点的序号 : ");i = int.Parse(Console.ReadLine());Console.Write("请输⼊边结束顶点的序号 : ");j =int.Parse(Console.ReadLine());s = new EdgeNode();s.adjvex = j;s.next = G.AdjList[i].firstedge;//邻接表头插法G.AdjList[i].firstedge = s;//建⽴⽆向图if(G.theType == GraphType.UnDiGraph){s = new EdgeNode();s.adjvex = i;s.next = G.AdjList[j].firstedge;G.AdjList[j].firstedge = s;}}}///<summary>///深度优先遍历以邻接表表⽰的图G.///</summary>///<param name="G"></param>public void DFSTraverse(ALGraph G){visited = new bool[G.VertexNodeCount];sb = new StringBuilder();for(int i = 0;i < G.VertexNodeCount;i++){visited[i] = false;}for(int i = 0;i < G.VertexNodeCount;i++){if(!visited[i]){DFS(G,i);}}Console.Write("深度优先遍历以邻接表表⽰的图G 的结果:\n "); Console.Write(sb);}private void DFS(ALGraph G,int i){EdgeNode p;sb.Append(G.AdjList[i].vertex.ToString()+"--->");visited[i] = true;p = G.AdjList[i].firstedge;while(p != null){if(!visited[p.adjvex]){DFS(G,p.adjvex);//递归}p = p.next;}}///<summary>///⼴度优先遍历以邻接表表⽰的图G///</summary>///<param name="G"></param>public void BFSTraverse(ALGraph G){visited = new bool[G.VertexNodeCount];sb = new StringBuilder();for(int i = 0;i < G.VertexNodeCount;i++){visited[i] = false;}for(int i = 0;i < G.VertexNodeCount;i++){if(!visited[i]){BFS(G,i);}}Console.Write("⼴度优先遍历以邻接表表⽰的图G 的结果:\n "); Console.Write(sb);}private void BFS(ALGraph G,int k){int i;Queue Q;EdgeNode p;Q = new Queue();sb.Append(G.AdjList[k].vertex.ToString()+"--->");visited[k] = true;Q.Enqueue(k);while(Q.Count != 0){i = (int)Q.Dequeue();p = G.AdjList[i].firstedge;while(p != null){if(!visited[p.adjvex]){sb.Append(G.AdjList[p.adjvex].vertex.ToString()+"--->");visited[p.adjvex] = true;Q.Enqueue(p.adjvex);}p = p.next;}}}///<summary>///有向图⽆前驱的顶点优先之拓扑排序///</summary>///<param name="G"></param>public void NonPreFirstTopSort(ALGraph G){if(G.theType == GraphType.UnDiGraph){Console.Write("对⽆向图进⾏拓扑排序是不对的!"); return;}StringBuilder SB = new StringBuilder() ;int [] indegree = new int[G.VertexNodeCount];Stack S;int i,j,count = 0;EdgeNode p;for(i = 0;i < G.VertexNodeCount;i++){indegree[i] = 0;}for(i = 0;i < G.VertexNodeCount;i++){for(p = G.AdjList[i].firstedge; p != null;p = p.next) {indegree[p.adjvex]++;}}S = new Stack();for(i = 0;i < G.VertexNodeCount; i++){if(indegree[i] == 0){S.Push(i);}}while(S.Count != 0){i = (int)S.Pop();SB.Append(G.AdjList[i].vertex.ToString()+"--->"); count++;for(p = G.AdjList[i].firstedge; p != null; p = p.next) {j = p.adjvex;indegree[j]--;if(indegree[j] == 0){S.Push(j);}}}if(count < G.VertexNodeCount){Console.Write("图中有环,排序失败");}else{Console.Write("拓扑排序结果如下 : \n"+SB);}}}}//测试⽂件 GraphTest.csusing System;using System.Collections;using System.Text;namespace myWorkFlow.kernel{///<summary>/// Class1 的摘要说明。
【数据结构】有向图(1.基于邻接表的C++实现)

【数据结构】有向图(1.基于邻接表的C++实现) 先说优缺点吧:优点是基本功能都有了,⽽且还有Dijkstra算法求最短路径,使⽤的模板,适合各种数据;缺点是并不像他所说的那样适合⼤数据的图,另外就是要求⼀个顶点的逆邻接表(即所有以该顶点为弧头的边)时⽐较⿇烦。
我做过测试,加⼊10W条边需要20+ minutes,这是个让⼈⽆法忍受的时间。
⼤家可以⾃⼰试⼀下,找找到底是哪⾥花费了⼤量时间。
下⼀个博⽂分析算法效率低劣的原因,然后过⼏天会另外发⼀个基于⼗字链表的实现⽅式,⽽且效率⾄少提少2个数量级。
声明类头⽂件:#ifndef __GRAPH_H__#define __GRAPH_H__#include <vector>#define IN#define OUT#define INOUTusing namespace std;namespace graphspace{template <typename weight>struct Edge //边{int nDestVertex; //邻接顶点编号weight edgeWeight; //边权重Edge<weight> *pNextEdge; //下⼀条边Edge(int d, weight c, Edge<weight> *p = NULL):nDestVertex(d), edgeWeight(c), pNextEdge(p){}};template <typename vertexNametype, typename weight>struct Vertex //顶点{vertexNametype vertexName; //顶点名Edge<weight> *pAdjEdges; //邻接边链表Vertex(vertexNametype x, Edge<weight> *p = NULL):vertexName(x), pAdjEdges(p){}};//adjacency list based graphtemplate <typename vertexNametype, typename weight>class ALGraph{public:explicit ALGraph();~ALGraph();public://插⼊结点bool insertAVertex(IN const vertexNametype vertexName);//插⼊边bool insertAEdge(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2, IN const weight edgeWeight);//边是否存在bool edgeExist(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2);//输出顶点的邻接表void vertexAdjEdges(IN const vertexNametype vertexName);//删除边bool removeAEdge(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2, IN const weight edgeWeight);//获取最⼩权weight getMinWeight(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2);//获取顶点索引int getVertexIndex(IN const vertexNametype vertexName);int getVertexNumber();//获取顶点名vertexNametype getData(IN int index);//迪科斯彻算法,最短路径int Dijkstra(IN const vertexNametype vertexName1);//输出迪科斯彻void DijkstraPrint(IN int index, IN int sourceIndex, IN vector<int> vecPreVertex);friend ostream& operator<<(OUT ostream &out, IN const ALGraph<vertexNametype,weight> &graphInstance); public://获取边权weight getEdgeWeight(IN const Edge<weight> *pEdge);//将顶点的所有邻接边的权值放⼊数组或者vector中void getVertexEdgeWeight(IN const int v1, OUT vector<weight> &DistanceArray);vector< Vertex<vertexNametype, weight> > m_vertexArray;};#include "ALGraph_realize.h"}#endif实现类头⽂件:#ifndef __GRAPH_REALIZE__H_#define __GRAPH_REALIZE__H_template<typename vertexNametype, typename weight>ALGraph<vertexNametype, weight>::ALGraph(){//没做重复顶点处理,因为我需要的数据是从另⼀个系统所得,已经确保没有重复节点if (!m_vertexArray.empty()){m_vertexArray.clear();}}template<typename vertexNametype, typename weight>ALGraph<vertexNametype, weight>::~ALGraph(){vector< Vertex<vertexNametype, weight> >::iterator iter;for(iter = m_vertexArray.begin(); iter != m_vertexArray.end(); iter++) //删除每个结点的邻接链表{Edge<weight> *p = iter->pAdjEdges;while(NULL != p) //删除邻接链表{iter->pAdjEdges = p->pNextEdge;delete p;p = iter->pAdjEdges;}}if (!m_vertexArray.empty()){m_vertexArray.clear();}}template<typename vertexNametype, typename weight>bool ALGraph<vertexNametype, weight>::insertAVertex(IN const vertexNametype vertexName){int v = getVertexIndex(vertexName);if (-1 != v){cerr << "There vertex "<<vertexName<<" is existed!" << endl;return false;}Vertex<vertexNametype, weight> VertexInstance(vertexName, NULL);m_vertexArray.push_back(VertexInstance);template<typename vertexNametype, typename weight>bool ALGraph<vertexNametype, weight>::insertAEdge(IN const vertexNametype vertexName1,IN const vertexNametype vertexName2, IN const weight edgeWeight){int v1 = getVertexIndex(vertexName1);if (-1 == v1){cerr << "There is no vertex 1" << endl;return false;}int v2 = getVertexIndex(vertexName2);if (-1 == v2){cerr << "There is no vertex 2" << endl;return false;}Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;while(p != NULL && p->nDestVertex != v2) //邻接链表是否存在,并且搜索V2是否已经在邻接表中了{p = p->pNextEdge;}if (NULL == p) //邻接表为空,或没找到顶点V2,则添加⼀条边{p = new Edge<weight>(v2, edgeWeight, m_vertexArray.at(v1).pAdjEdges);m_vertexArray.at(v1).pAdjEdges = p;return true;}if (v2 == p->nDestVertex) //若V1,V2之间已有⼀条边,则加⼀条新的边到已存在的第⼀条V1->V2边之后 {Edge<weight> *q = p;p = new Edge<weight>( v2, edgeWeight, q->pNextEdge );q->pNextEdge = p;return true;}return false;}template<typename vertexNametype, typename weight>bool ALGraph<vertexNametype, weight>::edgeExist(IN const vertexNametype vertexName1,IN const vertexNametype vertexName2){int v1 = getVertexIndex(vertexName1);if (-1 == v1){cerr << "There is no vertex 1" << endl;return false;}int v2 = getVertexIndex(vertexName2);if (-1 == v2){cerr << "There is no vertex 2" << endl;return false;}Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;while(p != NULL && p->nDestVertex != v2){p = p->pNextEdge;}if(NULL == p){cout<<"dont exist"<<endl;return false;}if(v2 == p->nDestVertex){cout<<"exist"<<endl;cout << vertexName1 << ": ";while(p != NULL && p->nDestVertex == v2) //如果v1->v2之间有⼏条不同的边,都输出{cout << "(" << vertexName1 << "," << vertexName2 << "," << p->edgeWeight << ") ";p = p->pNextEdge;}cout << endl;}template<typename vertexNametype, typename weight>void ALGraph<vertexNametype, weight>::vertexAdjEdges(IN const vertexNametype vertexName){int v1 = getVertexIndex(vertexName);if( -1 == v1){cerr<<"There is no vertex: "<<vertexName<<endl;return ;}Edge<weigh> *p = m_vertexArray.at(v1).pAdjEdges;cout << vertexName << ": ";while( p != NULL){cout<<"(" << vertexName << "," << getData(p->nDestVertex) <<"," << p->edgeWeight <<") ";}cout<<endl;}template<typename vertexNametype, typename weight>bool ALGraph<vertexNametype, weight>::removeAEdge(IN const vertexNametype vertexName1,IN const vertexNametype vertexName2, IN const weight edgeWeight){int v1 = getVertexIndex(vertexName1);if (-1 == v1){cerr << "There is no vertex 1" << endl;return false;}int v2 = getVertexIndex(vertexName2);if (-1 == v2){cerr << "There is no vertex 2" << endl;return false;}Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;Edge<weight> *q = NULL;while(p != NULL && p->nDestVertex != v2 ){q = p;p = p->pNextEdge;}if (NULL == p){cerr << "Edge is not found" << endl;return false;}while( edgeWeight != p->edgeWeight && p->nDestVertex == v2) //搜索相同边{q = p;p = p->pNextEdge;}if (v2 != p->nDestVertex){cerr << "Edge is not found" << endl;return false;}if( q == NULL ) //m_vertexArray.at(v1).pAdjEdges所指的值即为所求时m_vertexArray.at(v1).pAdjEdges = p->pNextEdge;elseq->pNextEdge = p->pNextEdge; //这⾥如果同⼀条边有好⼏个相同值,只会删除⼀次delete p;return true;}template<typename vertexNametype, typename weight>weight ALGraph<vertexNametype, weight>::getEdgeWeight(IN const Edge<weight> *pEdge){return pEdge->edgeWeight;}template<typename vertexNametype, typename weight>void ALGraph<vertexNametype, weight>::getVertexEdgeWeight(IN const int v1, OUT vector<weight> &DistanceArray) {Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;int prevIndex = -1;while(NULL != p){//需考虑相同边的存在,取最⼩的⼀个值if (prevIndex == p->nDestVertex){if (tmp > p->edgeWeight){DistanceArray[prevIndex] = p->edgeWeight;}}else{DistanceArray[p->nDestVertex] = p->edgeWeight;prevIndex = p->nDestVertex;tmp = p->edgeWeight;}p = p->pNextEdge;}}template<typename vertexNametype, typename weight>weight ALGraph<vertexNametype, weight>::getMinWeight(IN const vertexNametype vertexName1, IN const vertexNametype vertexName2){Edge<weight> *pEdge = NULL;int v1 = getVertexIndex(vertexName1);if (-1 == v1){cerr << "There is no vertex 1" << endl;return false;}int v2 = getVertexIndex(vertexName2);if (-1 == v2){cerr << "There is no vertex 2" << endl;return false;}Edge<weight> *p = m_vertexArray.at(v1).pAdjEdges;while (p != NULL && p->nDestVertex != v2){p = p->pNextEdge;}if (NULL == p){pEdge = NULL;return weight(0);}weight tmp = getEdgeWeight(p);pEdge = p;while (NULL != p && v2 == p->nDestVertex) //相同边,取权值最⼩的⼀条{if (tmp > getEdgeWeight(p)){tmp = getEdgeWeight(p);pEdge = p;}p = p->pNextEdge;}return tmp;}template<typename vertexNametype, typename weight>int ALGraph<vertexNametype, weight>::getVertexIndex(IN const vertexNametype vertexName){for (int i = 0; i < m_vertexArray.size(); i++){if (vertexName == getData(i)){return i;}}return -1;}template<typename vertexNametype, typename weight>int ALGraph<vertexNametype, weight>::getVertexNumber(){return m_vertexArray.size();}template<typename vertexNametype, typename weight>vertexNametype ALGraph<vertexNametype, weight>::getData(IN int index){return m_vertexArray.at(index).vertexName;}template<typename vertexNametype, typename weight>int ALGraph<vertexNametype, weight>::Dijkstra(IN const vertexNametype vertexName1){int sourceIndex = getVertexIndex(vertexName1);if (-1 == sourceIndex){cerr << "There is no vertex " << endl;return false;}int nVertexNo = getVertexNumber();//the array to record the points have been included, if included the value is true//else is falsevector<bool> vecIncludeArray;vecIncludeArray.assign(nVertexNo, false);vecIncludeArray[sourceIndex] = true;//the array to record the distance from vertex1vector<weight> vecDistanceArray;vecDistanceArray.assign(nVertexNo, weight(INT_MAX));vecDistanceArray[sourceIndex] = weight(0);//prev array to record the previous vertexvector<int> vecPrevVertex;vecPrevVertex.assign(nVertexNo, sourceIndex);getVertexEdgeWeight(sourceIndex, vecDistanceArray);int vFrom, vTo;while(1){weight minWeight = weight(INT_MAX);vFrom = sourceIndex;vTo = -1;for (int i = 0; i < nVertexNo; i++){if (!vecIncludeArray[i] && minWeight > vecDistanceArray[i]){minWeight = vecDistanceArray[i];vFrom = i;}}if (weight(INT_MAX) == minWeight){break;}vecIncludeArray[vFrom] = true;Edge<weight> *p = m_vertexArray[vFrom].pAdjEdges;while (NULL != p){weight wFT = p->edgeWeight;vTo = p->nDestVertex;if (!vecIncludeArray[vTo] && vecDistanceArray[vTo] > wFT + vecDistanceArray[vFrom]) {vecDistanceArray[vTo] = wFT + vecDistanceArray[vFrom];vecPrevVertex[vTo] = vFrom;}p = p->pNextEdge;}}//print the shortest route of all vertexesfor (int i = 0; i < nVertexNo; i++){if (weight(INT_MAX) != vecDistanceArray[i]){cout << getData(sourceIndex) << "->" << getData(i) << ": ";DijkstraPrint(i, sourceIndex, vecPrevVertex);cout << "" << vecDistanceArray[i];cout << endl;}}return0;}template<typename vertexNametype, typename weight>void ALGraph<vertexNametype, weight>::DijkstraPrint(IN int index, IN int sourceIndex, IN vector<int> vecPreVertex) {if (sourceIndex != index){DijkstraPrint(vecPreVertex[index], sourceIndex, vecPreVertex);}cout << getData(index) << "";}template<typename vertexNametype, typename weight>ostream& operator<<(OUT ostream &out, IN ALGraph<vertexNametype,weight> &graphInstance){int vertexNo = graphInstance.getVertexNumber();out << "This graph has " << vertexNo << "vertexes" << endl;for(int i = 0; i < vertexNo; i++){vertexNametype x1 = graphInstance.getData(i);out << x1 << ": ";Edge<weight> *p = graphInstance.m_vertexArray.at(i).pAdjEdges;while (NULL != p){out << "(" << x1 << "," << graphInstance.getData(p->nDestVertex) << "," << p->edgeWeight << ") ";p = p->pNextEdge;}out << endl;}return out;}#endif主程序:#include <iostream>#include <ctime>#include <string>#include "ALGraph.h"using namespace std;using namespace graphspace;int main(){ALGraph<string, int> g;clock_t start1,finish1;double duration;g.insertAVertex("A");g.insertAVertex("B");g.insertAEdge("A", "B", 16);g.insertAEdge("A", "B", 26);g.insertAEdge("A", "B", 36);g.insertAEdge("A", "B", 46);g.insertAEdge("A", "B", 6);g.insertAVertex("C");g.insertAVertex("D");g.insertAVertex("E");g.insertAVertex("F");cout<<g<<endl<<endl;g.insertAEdge("A", "B", 6);g.insertAEdge("A", "C", 3);g.insertAEdge("B", "C", 2);g.insertAEdge("B", "D", 5);g.insertAEdge("C", "D", 3);g.insertAEdge("C", "E", 4);g.insertAEdge("D", "E", 2);g.insertAEdge("D", "F", 3);g.insertAEdge("E", "F", 5);g.insertAEdge("B", "A", 6);g.insertAEdge("C", "A", 3);g.insertAEdge("C", "B", 2);g.insertAEdge("D", "B", 5);g.insertAEdge("D", "C", 3);g.insertAEdge("E", "C", 4);g.insertAEdge("E", "D", 2);g.insertAEdge("F", "D", 3);g.insertAEdge("F", "E", 5);cout<<g<<endl<<endl;g.Dijkstra("A");/*char vertex[9];srand((unsigned)time(0));string str[10000];for(int i=0; i<10000; i++) //随机⽣成1 W个顶点{for(int j=0; j<8; j++){vertex[j] = rand()%26 + 97;str[i] += vertex[j];}g.insertAVertex(str[i]);}cout<<g<<endl<<endl;for(int i=0; i<100000; i++) //随机⽣成10W条边{int num1 = rand()%10000;int num2 = rand()%10000;int num3 = rand()%10;g.insertAEdge(str[num1], str[num2], num3);}string lastname = "test";g.insertAVertex(lastname);for(int i=0; i<5000; i++) //单个顶点关联的边并不多,这⾥单独加⼀个顶点,关联5K条边 {int num5 = rand()%10000;int num6 = rand()%10000;g.insertAEdge(lastname, str[num5], num6);}cout<<g<<endl<<endl;string vertex1;string vertex2;cout<<"entry 2 vertem name"<<endl;cin>>vertex1;cin>>vertex2;while(vertex1 != "q"){start1 = clock();g.edgeExist(vertex1, vertex2);finish1 = clock();duration = (double)(finish1 - start1) / CLOCKS_PER_SEC;cout<<duration<<" seconds"<<endl;cout<<"entry 2 vertem name"<<endl;cin>>vertex1;cin>>vertex2;}*/system("pause");return0;}运⾏结果:。
【算法导论】--C++实现随机生成100个顶点的无向图和有向图

【算法导论】--C++实现随机⽣成100个顶点的⽆向图和有向图⼀、题⽬算法实验⼀(主要是为之后的图算法做前期准备⼯作)->⽣成100个顶点的图,随机⽣成顶点->⽆向图⼤约1000条边->有向图⼤约2000条边->计算每个顶点的度->⾸先默认每条边的权重为1,随之后的实验内容再进⾏修改⼆、实现使⽤邻接矩阵的⽅式存储该图。
三、代码(具体解释都在注释中)1/*****************************************************************************2*算法实验⼀;3*->⽣成100个顶点的图,随机⽣成顶点4*->⽆向图⼤约1000条边5*->有向图⼤约2000条边6*->计算每个顶点的度7*****************************************************************************/8 #include<iostream>9 #include<cmath>10 #include<ctime>11using namespace std;1213#define maxvertexnum 100 /*最⼤顶点数设为100*/14#define infinity 2147483647 /*当两点不连通时,则它们之间距离为最⼤值*/15 typedef int vertextype;/*顶点的类型为整型*/16 typedef int edgetype;/*边的权重为整形*/1718enum GraphType{DG,UG};/*有向图,⽆向图*/19struct MGraph//邻接矩阵表⽰法的结构和类型声明20 {21 vertextype V[maxvertexnum];//顶点集22 edgetype E[maxvertexnum][maxvertexnum];//边集23int n,e;//顶点数,边数24enum GraphType GType;//设定图的类型25 };2627int randomnum()//返回⼀个0-99之间的随机数28 {29int a;30//srand(time(NULL));//设置随机数种⼦,使每次运⾏获取的随机数不同31 a=rand()%100;3233return a;34 }35int* countedge(MGraph *G)//函数返回⼀个数组36 {37int i,j,countnum=0;38int *sum=new int[100];39for(i=0;i<G->n;i++)40 {41 countnum=0;//到达下⼀个顶点时置042for(j=0;j<G->n;j++)43 {44if(G->E[i][j]==1)45 {46 countnum+=1;47 sum[i]=countnum;//计算每⼀个顶点的度48 }49 }50 }51return sum;53 }5455void CreateMGraphUG(MGraph *G)//⽣成⽆向图56 {57int i,j,k,w;58 G->GType=UG;//⽆向图59 G->n=100;60 G->e=1000;61for(i=0;i<G->n;i++)62 {63 G->V[i]=i;//为每个顶点都编号从0-9964 }6566for(i=0;i<G->n;i++)67 {68for(j=0;j<G->n;j++)69 {70 G->E[i][j]=0;//初始化邻接矩阵71 }72 }7374for(k=0;k<G->e;k++)75 {76 i=randomnum();//随机⽣成任意两顶点77 j=randomnum();78//cout<<i<<" "<<j<<"\t";79 G->E[i][j]=1;//建⽴邻接矩阵,边的权重都为180 G->E[j][i]=1;//因为是⽆向图,所以要对称81 }8283 }8485void CreateMGraphDG(MGraph *G)//⽣成有向图86 {87int i,j,k,w;88 G->GType=DG;//有向图89 G->n=100;90 G->e=2000;91for(i=0;i<G->n;i++)92 {93 G->V[i]=i;//为每个顶点都编号从0-9994 }9596for(i=0;i<G->n;i++)97 {98for(j=0;j<G->n;j++)99 {100 G->E[i][j]=infinity;//初始化邻接矩阵101 }102 }103104for(k=0;k<G->e;k++)105 {106 i=randomnum();//随机⽣成任意两顶点107 j=randomnum();108 G->E[i][j]=1;//建⽴邻接矩阵,边的权重都为1109 }110111 }112113int main()114 {115 MGraph *UGG=new MGraph;//⽆向图116 MGraph *DGG=new MGraph;//有向图117int *ug=new int[100];118int *dg=new int[100];119120 cout<<"在⽆向图中"<<endl;121 CreateMGraphUG(UGG);122 ug=countedge(UGG);123for(int i=0;i<100;i++)124 {125 cout<<"顶点【"<<UGG->V[i]<<"】的度为"<<ug[i]<<endl; 126 }127128 cout<<"在有向图中"<<endl;129 CreateMGraphUG(DGG);130 dg=countedge(DGG);131for(int i=0;i<100;i++)132 {133 cout<<"顶点【"<<DGG->V[i]<<"】的度为"<<dg[i]<<endl; 134 }135136return0;137 }上述代码还有很多需要改进之处,期待指正和探讨。
c++随机生成带权联通无向图

c++随机⽣成带权联通⽆向图提⽰1、请使⽤c++11 编译运⾏2、默认⽣成 100 个输出⽂件,⽂件名为data1.in到data100.in,如有需要⾃⾏修改3、50000 以下的点 1s内可以运⾏结束,50000−300000 的点在 30s内运⾏结束, 300000 以上看⼈品4、⽣成的图为⽆向连通图,因此如果边数⼩于点数 −1,程序⾃动终⽌5、如果边数点数⼤于 10000000 或者为负数,程序⾃动终⽌6、如果运算量过⼤,程序⾃⾏终⽌7、默认带有边权以及参数k8、4 到 7 条可以⾃⾏修改9、输出到屏幕中的⽂字不会输出到⽂件中代码#include<bits/stdc++.h>using namespace std;#define rg registerconst int maxn=1e7+5,maxm=1e3+5;int n,m,cnt,fa[maxn];char s[maxm][maxm];int zhao(rg int xx){if(fa[xx]==xx) return xx;else return fa[xx]=zhao(fa[xx]);}int main(){fprintf(stderr,"This program is used to generate undirected connected graphs with n nodes, m edges and K weights.\n"); fprintf(stderr,"The program generates 100 input files by default.\n");fprintf(stderr,"For each input file, you must enter three parameters, N, m, and K.\n");fprintf(stderr,"Please make sure that 0<=n<=10000000 0<=m<=10000000 m>=n-1.\n");fprintf(stderr,"N is the number of nodes in the graph, M is the number of edges in the graph\n");fprintf(stderr,"and K is some parameters in the graph. If you do not want to output K.\n");fprintf(stderr,"Please delete the code yourself.\n");default_random_engine engine(time(NULL));srand(time(NULL));for(rg int i=1;i<=100;i++){rg int cntt[9];memset(cntt,0,sizeof(cntt));rg int Num=-1,now=i;while(now){cntt[++Num]=now%10;now/=10;}s[i][0]='d',s[i][1]='a',s[i][2]='t',s[i][3]='a';for(rg int j=4;j<=Num+4;j++){s[i][j]=cntt[Num+4-j]+'0';}s[i][Num+5]='.',s[i][Num+6]='i',s[i][Num+7]='n';}for(rg int kk=1;kk<=100;kk++){long long now=0;if(kk>=2) fprintf(stderr,"Last num:%d is OK\n.",kk-1);fprintf(stderr,"Now the %dth set of data is generated.\n",kk);fprintf(stderr,"please enter n m k\n");fprintf(stderr,"And then waiting....\n");freopen(s[kk],"w",stdout);cnt=0;rg int jl=0,n,m,k;scanf("%d%d%d",&n,&m,&k);uniform_int_distribution<> dis(1,0x3f3f3f3f);printf("%d %d %d\n",n,m,k);if(m<n-1){fprintf(stderr,"Wrong!m must be bigger than n-1.\n");fprintf(stderr,"The %dth data is not generated.\n",kk);continue;}if(m<0 || m>10000000){fprintf(stderr,"Wrong!m is too big or too small.\n");fprintf(stderr,"The %dth data is not generated.\n",kk);continue;}if(n<0 || n>10000000){fprintf(stderr,"Wrong!n is too big or too small.\n");fprintf(stderr,"The %dth data is not generated.\n",kk);continue;}for(rg int i=1;i<=n;i++) fa[i]=i;while(cnt<n-1){now++;if(now>=10000000000){fprintf(stderr,"Too large to build\n");jl=1;Processing math: 100%break;}rg int x=dis(engine)%n+1,y=dis(engine)%n+1,x1=zhao(x),y1=zhao(y),z=1LL*rand()*rand()%10000000+1; if(x1!=y1){fa[x1]=y1,cnt++;printf("%d %d %d\n",x,y,z);}}if(jl){fprintf(stderr,"The %dth data is not generated.\n",kk);continue;}m=m-(n-1);for(rg int i=1;i<=m;i++){rg int x=dis(engine)%n+1,y=dis(engine)%n+1,z=1LL*rand()*rand()%10000000+1;printf("%d %d %d\n",x,y,z);}}return 0;}。
【数据结构】有向图、无向图以及最短路(Dijkstra)算法的C#实现(Template模式)

【数据结构】有向图、⽆向图以及最短路(Dijkstra)算法的C#实现(Template模式)为了写个“运筹学”的⼩⼯具,发现必须⽤到数据结构中的图。
找了⼀圈没有找到⾃⼰满意的,只能⾃⼰写⼀个。
所有代码基于C#,完全模板实现。
⾸先是顶点的定义,顶点可以是任意类型,但其ID为Int32,该ID只是Graph内部使⽤。
public sealed class GraphVertex<M>{#region Constructorpublic GraphVertex(){}#endregion#region Fieldsprivate Int32 nID = default(Int32);private M objData = default(M);#endregion#region Propertiespublic Int32 ID{get { return nID; }set { nID = value; }}public M Data{get { return objData; }set { objData = value; }}#endregion}然后是Edge的定义,这⾥有⼀个辅助的Struct:GraphEdgeCore,其负责真正的边的识别::public struct GraphEdgeCore : IEquatable<GraphEdgeCore>{public GraphEdgeCore(Int32 i1, Int32 i2){ID1 = i1;ID2 = i2;}public Int32 ID1;public Int32 ID2;public Boolean IsValidated(){if (ID1 == -1 || ID2 == -1)return false;if (ID1 == ID2)return false;return true;}#region IEquatable<GraphEdgeCore> Memberspublic bool Equals(GraphEdgeCore other){if (ID1 != other.ID1) return false;if (ID2 != other.ID2) return false;return true;}#endregion#region Operatorspublic static Boolean operator == (GraphEdgeCore ec1, GraphEdgeCore ec2){return ec1.Equals(ec2);}public static Boolean operator != (GraphEdgeCore ec1, GraphEdgeCore ec2){return !(ec1 == ec2);}#endregionpublic override int GetHashCode(){return base.GetHashCode();}public override bool Equals(object obj){return (this == (GraphEdgeCore)obj);}}public sealed class GraphEdge<N>{#region Constructorpublic GraphEdge(Int32 n1, Int32 n2, N obj){edge.ID1 = n1;edge.ID2 = n2;objData = obj;}#endregion#region Fieldsprivate GraphEdgeCore edge;private N objData = default(N);#endregion#region Propertiespublic GraphEdgeCore EdgeCore{get { return edge; }}public N Data{get { return objData; }set { objData = value; }}#endregion}最⼤的难点来了:既然全部是模板,就不可避免会遇到权重的⽐较,因为是模板,所以必须定义⼀个额外的辅助类来实现:public abstract class ACGraphEdgeWeightAssistant<N> //: IComparable, IComparable<ACGraphEdgeWeightAssistant<N>>{#region Propertiespublic abstract N MinimumValue { get; }public abstract N MaximumValue { get; }#endregion#region Abstract methodspublic abstract N Add(N n1, N n2);public abstract N Subtract(N n1, N n2);public abstract Boolean Equals(N n1, N n2);public abstract Int32 Compare(N n1, N n2);public abstract Boolean IsMaximumValue(N nVal);#endregion//#region IComparable<ACGraphEdgeWeightAssistant<N>> Members//public int CompareTo(ACGraphEdgeWeightAssistant<N> other)//{// throw new NotImplementedException();//}//#endregion//#region IComparable Members//public int CompareTo(object obj)//{// return CompareTo(obj as ACGraphEdgeWeightAssistant<N>);//}//#endregion}最后是图的定义:public sealed class Graph<M, N> // where N : ValueType{#region Constructorpublic Graph(ACGraphEdgeWeightAssistant<N> objAss){System.Diagnostics.Debug.Assert(objAss != null);pAssist = objAss;}#endregion#region Fieldsprivate Dictionary<Int32, GraphVertex<M>> dictNodes = new Dictionary<int, GraphVertex<M>>();private List<GraphEdge<N>> listEdges = new List<GraphEdge<N>>();private Int32 nVertexID = 0;// Assistant for working for Nprivate ACGraphEdgeWeightAssistant<N> pAssist = null;#endregion#region Propertiespublic Int32 NodesAmount{get { return dictNodes.Count; }}public Int32 EdgesAmount{get { return listEdges.Count; }}#endregion#region Public methodspublic void InsertVertex(GraphVertex<M> objVertex){System.Diagnostics.Debug.Assert(objVertex != null);objVertex.ID = nVertexID++;dictNodes.Add(objVertex.ID, objVertex);}public void InsertEdge(GraphEdge<N> objEdge){System.Diagnostics.Debug.Assert(objEdge != null);if (!objEdge.EdgeCore.IsValidated())return;if (!dictNodes.ContainsKey(objEdge.EdgeCore.ID1))return;if (!dictNodes.ContainsKey(objEdge.EdgeCore.ID2))return;listEdges.Add(objEdge);}public GraphEdge<N>[] GetEdges(GraphEdgeCore objEdgeCore){List<GraphEdge<N>> lists = new List<GraphEdge<N>>();foreach (GraphEdge<N> ge in listEdges){if (ge.EdgeCore == objEdgeCore)lists.Add(ge);}return lists.ToArray();}public GraphEdge<N>[] GetEdges(Int32 nID, Boolean bSource){List<GraphEdge<N>> lists = new List<GraphEdge<N>>();foreach (GraphEdge<N> ge in listEdges){if (bSource){if (ge.EdgeCore.ID1 == nID)lists.Add(ge);}else{if (ge.EdgeCore.ID2 == nID)lists.Add(ge);}return lists.ToArray();}public GraphEdge<N>[] GetAllEdges(){return listEdges.ToArray();}public GraphVertex<M>[] GetAllVerteics(){List<GraphVertex<M>> listVer = new List<GraphVertex<M>>();foreach (GraphVertex<M> gv in dictNodes.Values)listVer.Add(gv);return listVer.ToArray();}// Get shortest path// Note: call this method before you make sure that the weight should not negative.public void DijkstraShortestPath(Int32 nSource, Int32 nTarget, List<GraphPath<N>> listPaths) {System.Diagnostics.Debug.Assert(listPaths != null);listPaths.Clear();GraphPath<N> gp = null;if (!dictNodes.ContainsKey(nSource))return;if (!dictNodes.ContainsKey(nTarget))return;if (nSource == nTarget){gp = new GraphPath<N>();gp.CurrentCost = pAssist.MinimumValue;gp.PathNodes.Add(nSource);listPaths.Add(gp);return;}Dictionary<Int32, N> dictPSet = new Dictionary<Int32, N>();Dictionary<Int32, N> dictTSet = new Dictionary<Int32, N>();// InitializedictPSet.Add(nSource, pAssist.MinimumValue);foreach (Int32 nVer in dictNodes.Keys){if (nVer != nSource)dictTSet.Add(nVer, pAssist.MaximumValue);}while (!dictPSet.ContainsKey(nTarget)){// Go through each item in P Setforeach (Int32 nID in dictPSet.Keys){foreach (GraphEdge<N> ge in GetEdges(nID, true)){if (dictTSet.ContainsKey(ge.EdgeCore.ID2)){// Update the T value: min { P(X) + W, T(X) }N nTValue = dictTSet[ge.EdgeCore.ID2];N nPValue = dictPSet[nID];N nVal = pAssist.Add(nPValue, ge.Data);if (pAssist.IsMaximumValue(nTValue)){dictTSet[ge.EdgeCore.ID2] = nVal;}else{if (pare(nTValue, nVal) > 0){dictTSet[ge.EdgeCore.ID2] = nVal;}}}}}// Get the minimum of TSetInt32 nTID = default(Int32);N ntmp = pAssist.MaximumValue;foreach (KeyValuePair<Int32, N> kvp in dictTSet)if (pare(kvp.Value, ntmp) < 0){ntmp = kvp.Value;nTID = kvp.Key;}}if (nTID == default(Int32))break;dictTSet.Remove(nTID);dictPSet.Add(nTID, ntmp);}// OKay, we get the final result, parse the result outgp = new GraphPath<N>();gp.CurrentID = nTarget;gp.CurrentCost = dictPSet[nTarget];gp.PathNodes.Add(nTarget);listPaths.Add(gp);Boolean bEnd = false;Boolean bExisted = false;List<GraphPath<N>> listTempPaths = new List<GraphPath<N>>();while (!bEnd){bExisted = false;listTempPaths.Clear();foreach (GraphPath<N> gpath in listPaths){if (gpath.DeadPath)continue;foreach (GraphEdge<N> ge in GetEdges(gpath.CurrentID, false)){//dictPSet[ge.Data]if (dictPSet.ContainsKey(ge.EdgeCore.ID1)&&pare(gpath.CurrentCost, pAssist.Add(ge.Data, dictPSet[ge.EdgeCore.ID1])) == 0) {if (!bExisted){gpath.CurrentID = ge.EdgeCore.ID1;gpath.PathNodes.Add(ge.EdgeCore.ID1);gpath.CurrentCost = dictPSet[ge.EdgeCore.ID1];bExisted = true;}else{// Existed already in currentGraphPath<N> gp2 = new GraphPath<N>(gpath);gp2.CurrentID = ge.EdgeCore.ID1;gp2.PathNodes.Add(ge.EdgeCore.ID1);gp2.CurrentCost = dictPSet[ge.EdgeCore.ID1];listTempPaths.Add(gp2);}}}if (!bExisted){gpath.DeadPath = true;}}foreach (GraphPath<N> gpath in listTempPaths)listPaths.Add(gpath);foreach (GraphPath<N> gpath in listPaths){if ((!gpath.DeadPath) && gpath.PathNodes.Contains(nSource)){bEnd = true;break;}}}// Finalize the result outputforeach (GraphPath<N> gpth in listPaths){if (gpth.DeadPath)listPaths.Remove(gpth);elsegpth.CurrentCost = dictPSet[nTarget];}}#endregion}其中,代表路径使⽤了另外⼀个类:public sealed class GraphPath<N> : ICloneable{#region Constructorpublic GraphPath() { }public GraphPath(GraphPath<N> other): this(){if (other != null){nCurID = other.nCurID;curCost = other.curCost;foreach (Int32 n in other.listPath)listPath.Add(n);}}#endregion#region Fieldsprivate List<Int32> listPath = new List<Int32>();private Int32 nCurID = default(Int32);private N curCost = default(N);private Boolean bDeadPath = false;#endregion#region Propertiespublic List<Int32> PathNodes{get { return listPath; }}public Int32 CurrentID{get { return nCurID; }set { nCurID = value; }}public N CurrentCost{get { return curCost; }set { curCost = value; }}public Boolean DeadPath{get { return bDeadPath; }set { bDeadPath = value; }}#endregion#region ICloneable Memberspublic object Clone(){return new GraphPath<N>(this);}#endregion}使⽤实例:public sealed class ACGraphEdgeWeightSingleAssistant : ACGraphEdgeWeightAssistant<Single> {public override float MinimumValue{get { return0; }}public override float MaximumValue{get { return Single.MaxValue; }}public override float Add(float n1, float n2){return n1 + n2;}public override float Subtract(float n1, float n2){return n1 - n2;}public override bool Equals(float n1, float n2){return n1 == n2;}public override int Compare(float n1, float n2){if (n1 > n2) return1;if (n1 < n2) return -1;return0;}public override bool IsMaximumValue(float nVal){return nVal == Single.MaxValue;}}ACGraphEdgeWeightSingleAssistant objWSA = new ACGraphEdgeWeightSingleAssistant();Dictionary<Char, Int32> dictVer = new Dictionary<Char, Int32>();Graph<Char, Single> gph = new Graph<Char, Single>(objWSA);GraphVertex<Char> gv = new GraphVertex<char>();gv.Data = '1'; gph.InsertVertex(gv);dictVer.Add('1', gv.ID);gv = new GraphVertex<char>(); gv.Data = '2'; gph.InsertVertex(gv); dictVer.Add('2', gv.ID);gv = new GraphVertex<char>(); gv.Data = '3'; gph.InsertVertex(gv); dictVer.Add('3', gv.ID);gv = new GraphVertex<char>(); gv.Data = '4'; gph.InsertVertex(gv); dictVer.Add('4', gv.ID);gv = new GraphVertex<char>(); gv.Data = '5'; gph.InsertVertex(gv); dictVer.Add('5', gv.ID);gv = new GraphVertex<char>(); gv.Data = '6'; gph.InsertVertex(gv); dictVer.Add('6', gv.ID);GraphEdge<Single> ge = new GraphEdge<float>(dictVer['1'], dictVer['2'], 4);gph.InsertEdge(ge);ge = new GraphEdge<float>(dictVer['1'], dictVer['3'], 3);gph.InsertEdge(ge);ge = new GraphEdge<float>(dictVer['2'], dictVer['4'], 3);gph.InsertEdge(ge);ge = new GraphEdge<float>(dictVer['2'], dictVer['5'], 2);gph.InsertEdge(ge);ge = new GraphEdge<float>(dictVer['3'], dictVer['5'], 3);gph.InsertEdge(ge);ge = new GraphEdge<float>(dictVer['4'], dictVer['6'], 2);gph.InsertEdge(ge);ge = new GraphEdge<float>(dictVer['5'], dictVer['6'], 2);gph.InsertEdge(ge);List<GraphPath<Single>> listPaths = new List<GraphPath<Single>>();gph.DijkstraShortestPath(dictVer['1'], dictVer['6'], listPaths);注意:对Dijkstra算法来说,其基本要求权重必须⾮负!根据上述代码可以轻易的实现对权重⽆要求的Floyd算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p=p->link;//查找下一个邻接点
}
}/*DFS*/
void blt(vexnode ag[],int n)//对图按深度优先遍历搜索
{
int i;
int flag[M];
for(i=1;i<=n;i++)
flag[i]=0;//初始化标志组flag
//无向图的邻接表生成算法
void creatlist1(vexnode ag[],int n)
{
edgenode *p;
int i,j;
char ch;
cout<<"请输入顶点个数:";
cin>>n;
for(i=1;i<=n;i++)
{
cout<<"第"<<i<<"个顶点为:";
cin>>ch;//读入顶点信息
cout<<"深度遍历为:";
DFS(v2,k,f);//深度遍历
cout<<endl;
for(i=0;i<M;i++)
f[i]=0;
cout<<"广度遍历为:";
BFS(v2,k,f);//广度遍历
break;
default:cout<<"输入错误,程序结束!"<<endl;
return;
}
cout<<endl;
}edgenode,*Edgenode;
typedef struct headnode//定义表头结点类型
{
vextype vexdata;//顶点数据域
struct node *firstarc;//指针域指向链表中的第一个结点
}vexnode,*Vexnode;
typedef vexnode adjlist[M];//adjlist为邻接表类型
{
edgenode *p;
int i,j;
char ch;
cout<<"请输入顶点个数:";
cin=n;i++)
{
cout<<"第"<<i<<"个顶点为:";
cin>>ch;//读入顶点信息
ag[i].vexdata=ch;//设顶点为字符型
ag[i].firstarc=NULL;//将每个链表初始化为空
p->adjvex=j;
p->link=ag[i].firstarc;
ag[i].firstarc=p;//结点j插入到第i个链表
cout<<"输入下一条边的两个顶点序号:";
cin>>i>>j;//再次输入下一条边的两个顶点序号
}
}/*creatlist2*/
void DFS(vexnode ag[],int v,int flag[])//从序号为v的顶点对图进行深度优先遍历
q[0]=v;
while(f<=r)
{
v=q[f++];
p=g[v].firstarc;
while(p!=NULL)
{
v=p->adjvex;
if(c[v]==0)
{
c[v]=1;
cout<<g[v].vexdata<<" ";
q[++r]=v;
}
p=p->link;
}
}
}/*BFS*/
void main()
cout<<"是否继续?(输入n结束,输入y有效!)"<<endl;
cin>>flag;
}
cout<<"程序结束,再见!"<<endl;
}
p->adjvex=i;
p->link=ag[j].firstarc;
ag[j].firstarc=p;//结点i插入到第j个链表的头部
cout<<"输入下一条边的两个顶点序号:";
cin>>i>>j;//再次输入下一条边的两个顶点序号
}
}/*creatlist1*/
//有向图邻接表生成算法
void creatlist2(vexnode ag[],int n)
#include<stdio.h>
#include<iostream.h>
#include<malloc.h>
#define M 50
typedef char vextype;//顶点数据类型char
typedef struct node //定义表结点类型
{
int adjvex;//邻接点域
struct node *link;//指针域
{
p=(edgenode*)malloc(sizeof(edgenode));//生成邻接序号为j的表结点
p->adjvex=j;
p->link=ag[i].firstarc;
ag[i].firstarc=p;//结点j插入到第i个链表
p=(edgenode*)malloc(sizeof(edgenode));//生成临界点序号为i的表结点
{
int n=0,j,k,kind,i;
char flag='y';
int f[M];
vexnode v1[M],v2[M];
while(flag=='y')
{
cout<<"请选择图的种类(1代表有向图,2代表无向图)"<<endl;
cin>>kind;//输入图的种类
switch(kind)
{
case 1:cout<<"---------------创建有向图---------------"<<endl;
for(i=1;i<=n;i++)
if(flag[i]==0)
DFS(ag,i,flag);//调用深度优先算法DFS
}
void BFS(Vexnode g,int v,int c[])//对图进行广度遍历
{
int q[M],r=0,f=0;
Edgenode p;
c[v]=1;
cout<<g[v].vexdata<<" ";
BFS(v1,j,f);//广度遍历
break;
case 2:cout<<"---------------创建无向图----------------"<<endl;
creatlist2(v2,n);//创建无向图
cout<<"开始遍历的结点序号为:";
cin>>k;
for(i=0;i<M;i++)
f[i]=0;
creatlist1(v1,n);//创建有向图
cout<<"开始遍历的结点序号为:";
cin>>j;
for(i=0;i<M;i++)
f[i]=0;
cout<<"深度遍历为:";
DFS(v1,j,f);//深度遍历
cout<<endl;
for(i=0;i<M;i++)
f[i]=0;
cout<<"广度遍历为:";
{
edgenode *p;
int i;
flag[v]=1;
cout<<ag[v].vexdata<<" ";
p=ag[v].firstarc;//p最初指向v的第一个邻接点
while(p!=NULL)
{
i=p->adjvex;//取出p指针所指向的邻接点的序号
if(flag[i]==0)
DFS(ag,i,flag);
}
cout<<"以(0,0)为输入结束符"<<endl;
cout<<"输入一条边依附的两个顶点序号:";
cin>>i>>j;
while((i>0)&&(j>0))//输入的(i,j)为(0,0)作为结束符号
{
p=(edgenode*)malloc(sizeof(edgenode));//生成邻接序号为j的表结点
ag[i].vexdata=ch;//设顶点为字符型
ag[i].firstarc=NULL;//将每个链表初始化为空
}
cout<<"以(0,0)为输入结束符"<<endl;
cout<<"输入一条边依附的两个顶点序号:";
cin>>i>>j;
while((i>0)&&(j>0))//输入的(i,j)为(0,0)作为结束符号
