MATLAB通信建模实验仿真实验报告
通信原理MATlAB简单仿真报告

MATLAB简单仿真实验一、实验目的:学会利用MATLAB软件进行简单的仿真。
通过实验提高学生实际动手能力和编程能力,为日后从事通信工作奠定良好的基础。
二、实验内容:(1)绘制函数y=xe-x在0≤x≤1时的曲线。
(2)将输入的一段二进制代码编成单极性不归零码和双极性不归零码。
(3)学习使用simulink进行仿真建模三、仿真和实验结果:(1)x=0:0.1:1 %定义自变量的采样点取值数组y=x.*exp(-x) %利用数组运算计算各自变量采样点上的函数值plot(x,y),xlabel('x'),ylabel('y'),title('y=x*exp(-x)') %绘图(2)(a)单极性不归零码程序function y=snrz(x)t0=300;t=0:1/t0:length(x);for i=1:length(x)if(x(i)==1) %如果信息位为1for j=1:t0y((i-1)*t0+j)=1;%该码元对应的点值取1endelsefor j=1:t0y((i-1)*t0+j)=0; %否则,取0endendendy=[y,x(i)];%为了画图,要将y序列加上最后一位M=max(y);m=min(y);subplot(2,1,1)plot(t,y);grid on;axis([0,i,m-0.1,M+0.1]);title('1 0 0 1 1 0 0 0 0 1 0 1');(b)双极性码程序(3)a)在MATLAB的命令窗运行指令simulink,或点击命令窗中的图标,便打开如图所示的SIMULINK模型库浏览器(simulink Library Browser)。
b)在库浏览器中直接点击左侧分类目录中的Source子库,便可以看到各种信源模块,如图所示。
c)点击工具条上的图标,打开一个名为untitled的空白模型窗口。
Matlab与通信仿真课程设计报告

Matlab与通信仿真课程设计报告Matlab与通信仿真课程设计报告班级:12通信(1)班姓名:诸葛媛学号:Xb12680129实验⼀S-函数&锁相环建模仿真⼀、实验⽬的1.了解S函数和锁相环的⼯作原理2.掌握⽤S函数建模过程,锁相环载波提取仿真⼆、实验内容1、⽤S函数编写Similink基本模块(1)信源模块实现⼀个正弦波信号源,要求其幅度、频率和初始相位参数可以由外部设置,并将这个信号源进⾏封装。
(2)信宿和信号显⽰模块实现⼀个⽰波器⽊块,要求能够设定⽰波器显⽰的扫描周期,并⽤这个⽰波器观察(1)的信源模块(3)信号传输模块实现调幅功能,输⼊⽤(1)信源模块,输出⽤(2)信宿模块;基带信号频率1KHz,幅度1V;载波频率10KHz,幅度5V实现⼀个压控正弦振荡器,输⼊电压u(t)的范围为[v1,v2]V,输出正弦波的中⼼频率为f0Hz,正弦波的瞬时频率f随控制电压线性变化,控制灵敏度为kHz/V。
输⼊⽤(1)信源模块,输出⽤(2)信宿模块2、锁相环载波提取的仿真(1)利⽤压控振荡器模块产⽣⼀个受10Hz正弦波控制的,中⼼频率为100Hz,频偏范围为50Hz到150Hz的振荡信号,并⽤⽰波器模块和频谱仪模块观察输出信号的波形和频谱。
(2)构建⼀个抑制载波的双边带调制解调系统。
载波频率为10KHz,被调信号为1KHz正弦波,试⽤平⽅环恢复载波并进⾏解调。
(3)构建⼀个抑制载波的双边带调制解调系统。
载波频率为10KHz,被调信号为1KHz正弦波,试⽤科斯塔斯环恢复载波并进⾏解调。
(4)设参考频率源的频率为100Hz,要求设计并仿真⼀个频率合成器,其输出频率为300Hz。
并说明模型设计上与实例3.26的主要区别三、实验结果分析1、⽤S函数编写Similink基本模块(3)为了使S函数中输⼊信号包含多个,需要将其输⼊变量u初始为制定维数或⾃适应维数,⽽在S函数模块外部采⽤Simulink基本库中的复⽤器(Mux)将3⾏的信号矩阵。
通信系统仿真实验报告

通信系统仿真实验报告摘要:本篇文章主要介绍了针对通信系统的仿真实验,通过建立系统模型和仿真场景,对系统性能进行分析和评估,得出了一些有意义的结果并进行了详细讨论。
一、引言通信系统是指用于信息传输的各种系统,例如电话、电报、电视、互联网等。
通信系统的性能和可靠性是非常重要的,为了测试和评估系统的性能,需进行一系列的试验和仿真。
本实验主要针对某通信系统的部分功能进行了仿真和性能评估。
二、实验设计本实验中,我们以MATLAB软件为基础,使用Simulink工具箱建立了一个通信系统模型。
该模型包含了一个信源(source)、调制器(modulator)、信道、解调器(demodulator)和接收器(receiver)。
在模型中,信号流经无线信道,受到了衰落等影响。
在实验过程中,我们不断调整系统模型的参数,例如信道的衰落因子以及接收机的灵敏度等。
同时,我们还模拟了不同的噪声干扰场景和信道状况,以测试系统的鲁棒性和容错性。
三、实验结果通过实验以及仿真,我们得出了一些有意义的成果。
首先,我们发现在噪声干扰场景中,系统性能并没有明显下降,这说明了系统具有很好的鲁棒性。
其次,我们还测试了系统在不同的信道条件下的性能,例如信道的衰落和干扰情况。
测试结果表明,系统的性能明显下降,而信道干扰和衰落程度越大,系统则表现得越不稳定。
最后,我们还评估了系统的传输速率和误码率等性能指标。
通过对多组测试数据的分析和对比,我们得出了一些有价值的结论,并进行了讨论。
四、总结通过本次实验,我们充分理解了通信系统的相关知识,并掌握了MATLAB软件和Simulink工具箱的使用方法,可以进行多种仿真。
同时,我们还得出了一些有意义的结论和数据,并对其进行了分析和讨论。
这对于提高通信系统性能以及设计更加鲁棒的系统具有一定的参考价值。
matlab高级编程与应用-通讯工程仿真实验报告
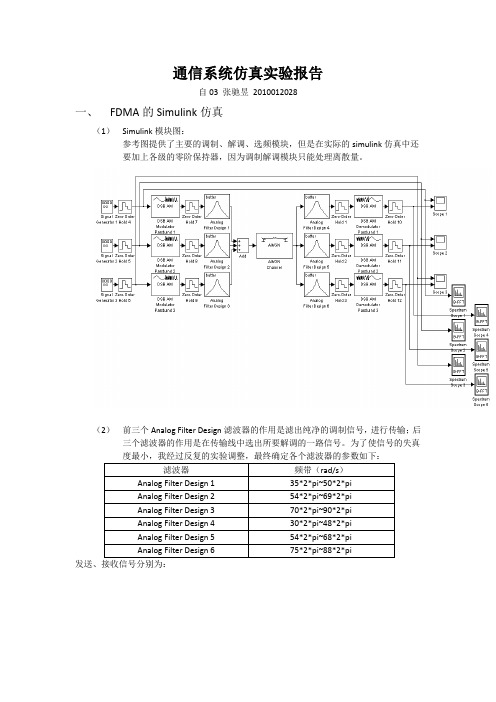
通信系统仿真实验报告自03 张驰昱2010012028一、FDMA的Simulink仿真(1)Simulink模块图:参考图提供了主要的调制、解调、选频模块,但是在实际的simulink仿真中还要加上各级的零阶保持器,因为调制解调模块只能处理离散量。
(2)前三个Analog Filter Design滤波器的作用是滤出纯净的调制信号,进行传输;后三个滤波器的作用是在传输线中选出所要解调的一路信号。
为了使信号的失真度最小,我经过反复的实验调整,最终确定各个滤波器的参数如下:发送、接收信号分别为:Scope2(3)用Spectrum Scope进行频谱分析注意要设置各个频谱分析仪的采样周期要与之前的临界采样器一样,不然频谱上的频率就不是实际频率了。
频域采样的精细程度可以用FFT length来调。
这里采用的频域宽度为-10Hz到10Hz,spectrum units用Watts/Hertz.正弦信号的发送、接收频谱:方波信号的发送、接收频谱:方波信号的发送、接收频谱:由于滤波不是非常精确,所以正弦波频谱的包络不是很精确,但是三角波和方波的频谱还是比较准确的,传输前后基本无差别。
二、TDMA的Simulink仿真TDMA仿真图:(1)Multiplex单元:其中Pulse Generator的参数设置如下:0.003秒的周期即延时环节周期的三倍,所以33.33%的占空比配合两个延时环节正好可以把一个周期的脉冲时间满打满算分为三个通道实现时分多址。
(2)接收单元应该与发送单元完全一样。
门控脉冲时间也完全一样,即各个通道每次都是发送端与接收端同时选中。
(3)接收端波形:三、CDMA的Simulink仿真各模块参数设置如下:伯努利随机序列发生器Bernoulli Binary Generator1 Initial seed:20Sample time:1/8000(2和3的initial seed为40和60)中继器Relay 1、2、3、7、8、9Switch on point: 0.8Switch off point: -0.2Output when on: 1Output when off:-1中继器Relay 4、5、6Switch on point: 0.5Switch off point: -0.5Output when on: 1Output when off:-1高斯白噪声信道AGWN Channel:Initial seed:67Mode:Signal to noise ratioEb/No:100M序列生成器PN Sequence Generator:Sample time:1/8000/50数字滤波器Digital Filter Design:要设计成低通滤波器Response Type: LowpassFs:200Fpass: 10Fstop: 15其余用默认设置即可。
Matlab与通信仿真课程设计报告

《MATLAB与通信仿真》课程设计指导老师: 张水英、汪泓班级:07通信(1)班学号:E07680104姓名:林哲妮目录目的和要求 (1)实验环境 (1)具体内容及要求 (1)实验内容题目一 (4)题目内容流程图程序代码仿真框图各个参数设置结果运行结果分析题目二 (8)题目内容流程图程序代码仿真框图各个参数设置结果运行结果分析题目三 (17)题目内容流程图程序代码仿真框图各个参数设置结果运行结果分析题目四 (33)题目内容流程图程序代码仿真框图各个参数设置结果运行结果分析心得与体会 (52)目的和要求通过课程设计,巩固本学期相关课程MATLAB与通信仿真所学知识的理解,增强动手能力和通信系统仿真的技能。
在强调基本原理的同时,更突出设计过程的锻炼。
强化学生的实践创新能力和独立进行科研工作的能力。
要求学生在熟练掌握MATLAB和simulink仿真使用的基础上,学会通信仿真系统的基本设计与调试。
并结合通信原理的知识,对通信仿真系统进行性能分析。
实验环境PC机、Matlab/Simulink具体内容及要求基于MATLAB编程语言和SIMULINK通信模块库,研究如下问题:(1)研究BFSK在加性高斯白噪声信道下(无突发干扰)的误码率性能与信噪比之间的关系;(2)研究BFSK在加性高斯白噪声信道下(有突发干扰)的误码率性能与信噪比之间的关系;分析突发干扰的持续时间对误码率性能的影响。
(3)研究BFSK+信道编码(取BCH码和汉明码)在加性高斯白噪声信道下(无突发干扰)的误码率性能与信噪比之间的关系;分析不同码率对误码率性能的影响。
比较不同信道编码方式的编码增益性能。
(4)研究BFSK+信道编码(取BCH码和汉明码)在加性高斯白噪声信道下(有突发干扰)的误码率性能与信噪比之间的关系;分析突发干扰的持续时间对误码率性能的影响。
分析不同码率对误码率性能的影响。
比较不同信道编码方式的编码增益性能。
题目一题目内容:研究BFSK 在加性高斯白噪声信道下(无突发干扰)的误码率性能与信噪比之间的关系 流程图是不是程序代码:clc clearecho on %x 表示信噪比x=0:15; % y 表示信号的误码比特率,它的长度与x 相同 y=x; % BFSK 调治的频率间隔等于24kHz FrequencySeparation=24000; %信源产生信号的bit 率等于10kbit/s BitRate=10000; % 仿真时间设置为10秒SimulatonTime=10; % BFSK 调质信号每一个符号的抽样数等于2 SamplesPerSymbol=2;开始 读懂题目,确定仿真框图 确定参数编写程序代码 运行程序,得出结果图 得出的结果是理想的结果? 修改参数 得出最终结果for i=1:length(x)%信道的信噪比依次取X中的元素SNR=x(i); %运行仿真程序,得到的误码率保存在工作区变量BitErrorRate中sim('shiyanyi1');%计算BitErrorRate的均值作为本次仿真的误码率 y(i)=mean(BitErrorRate);end% 准备一个空白的空间% hold off;figure% 绘制x和y的关系曲线图,纵坐标采用对数表示semilogy(x,y,'-*'); %对y取对数画图xlabel('信噪比'); %写X坐标ylabel('误码率'); %写y坐标title('BFSK在无突发干扰下误码率与信噪比的关系'); %写标题grid on; %画网格图仿真框图各个参数设置Random Integer GeneratorM-FSK Modulator BasebandAWGN ChannelTo Workspace运行结果结果分析:BFSK在无突发干扰下误码率随着信噪比的增大而减小题目二题目内容:研究BFSK在加性高斯白噪声信道下(有突发干扰)的误码率性能与信噪比之间的关系;分析突发干扰的持续时间对误码率性能的影响。
移动通信仿真实验-MATLAB仿真

2012级移动通信仿真实验——1234567 通信S班一、实验目的:(1)通过利用matlab语言编程学会解决移动通信中基本理论知识的实验分析和验证方法;(2)巩固和加深对移动通信基本理论知识的理解,增强分析问题、查阅资料、创新等各方面能力。
二、实验要求:(1)熟练掌握本实验涉及到的相关知识和相关概念,做到原理清晰,明了;(2)仿真程序设计合理、能够正确运行;(3)按照要求撰写实验报告(基本原理、仿真设计、仿真代码(m文件)、仿真图形、结果分析和实验心得)三、实验内容:1、分集技术在Rayleigh衰落信道下的误码率分析内容要求:1)给出不同调制方式(BPSK/MPSK/QPSK/MQAM任选3种,M=4/8/16)在AWGN和Rayleigh衰落环境下的误码率性能比较,分析这些调制方式的优缺点;2)给出Rayleigh衰落信道下BPSK在不同合并方式(MRC/SC/EGC)和不同路径(1/2/3)时的性能比较,分析合并方式的优缺点;3)给出BPSK在AWGN和Rayleigh衰落信道下1条径和2条径MRC合并时理论值和蒙特卡洛仿真的比较。
3、直接扩频技术在Rayleigh衰落信道下的误码率分析内容要求:1)m-序列、Gold序列和正交Gold序列在AWGN信道下的QPSK误码率分析;2)m-序列、Gold序列和正交Gold序列在Rayleigh信道下的QPSK误码率分析;3)m-序列在AWGN和Rayleigh信道下的QPSK误码率分析;4)m-序列Rayleigh信道下不同调制方式MQAM(M=4/8/16)时的误码率分析。
四、实验数据1、基于MATLAB中的BPSK误码性能研究BPSK(Binary Phase Shift Keying )即双相频移键控,是把模拟信号转换成数据值的转换方式之一。
利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
本实验将简要介绍BPSK调制方式的特点,调制解调方法,以及在Matlab中在AWGN信道中的误码性能。
基于MATLAB的通信系统的仿真报告参考例文

摘要Simulink是Mathworks公司推出的基于Matlab平台的著名仿真环境Simulin作为一种专业和功能强大且操作简单的仿真工具,目前已被越来越多的工程技术人员所青睐,它搭建积木式的建模仿真方式既简单又直观,而且已经在各个领域得到了广泛的应用。
本文主要是以simulink为基础平台,对2ASK、2FSK、2PSK信号的仿真。
文章第一章内容是对simulink的简单介绍和通信技术的目前发展和未来展望;第二章是对2ASK、2FSK和2PSK信号调制及解调原理的详细说明;第三章是本文的主体也是这个课题所要表现的主要内容,第三章是2ASK、2FSK和2PSK信号的仿真部分,调制和解调都是simulink建模的的方法,在解调部分各信号都是采用相干解调的方法,而且在解调的过程中都对整个系统的误码率在display模块中有所显示本文的主要目的是对simulink的熟悉和对数字通信理论的更加深化和理解。
关键词:2ASK、2FSK、2PSK,simulink,调制,相干解调目录第一章绪论 (31)1.1 MATLAB/Smulink的简介 (31)1.2 通信发展简史........................................ 错误!未定义书签。
1 1.3 通信技术的现状和发展趋势............................ 错误!未定义书签。
4 第二章 2ASK、2FSK、2PSK和2DPSK的基本原理和实现....... 错误!未定义书签。
7 2.1 2ASK的基本原理和调制解调实现...................... 错误!未定义书签。
8 2.2 2FSK的基本原理和调制解调实现..................... 错误!未定义书签。
11 2.3 2PSK的基本原理和调制解调实现.................... 错误!未定义书签。
14 2. 2DPSK的基本原理和调制解调实现.................... 错误!未定义书签。
实验一 模拟通信的MATLAB仿真..

实验一 模拟通信的MATLAB 仿真姓名:左立刚 学号:031040522简要说明:实验报告注意包括AM ,DSB ,SSB ,VSB ,FM 五种调制与解调方式的实验原理,程序流程图,程序运行波形图,simulink 仿真模型及波形,心得体会,最后在附录中给出了m 语言的源程序代码。
一.实验原理1.幅度调制(AM )幅度调制(AM )是指用调制信号去控制高频载波的幅度,使其随调制信号呈线性变化的过程。
AM 信号的数学模型如图3-1所示。
图2-1 AM 信号的数学模型为了分析问题的方便,令δ=0,1.1 AM 信号的时域和频域表达式()t S AM=[A 0+m ()t ]cos t cω (2-1)()t S AM =A 0π[()()ωωωωδC C ++-]+()()[]ωωωωc c M M ++-21(2-2)AM 信号的带宽2=BAMfH(2-3)式中,fH为调制信号的最高频率。
2.1.3 AM 信号的功率P AM 与调制效率ηAMP AM=()2222t m A +=PP mc + (2-4)式中,P C=2A为不携带信息的载波功率;()22t m P m=为携带信息的边带功率。
()()t t m A m PP AMCAM222+==η(2-5) AM 调制的优点是可用包络检波法解调,不需要本地同步载波信号,设备简单。
AM 调制的最大缺点是调制效率低。
2.2、双边带调制(DSB )如果将在AM 信号中载波抑制,只需在图3-1中将直流 A 0去掉,即可输出抑制载波双边带信号。
2.2.1 DSB 信号的时域和频域表达式()()t t m t cDSB S ωcos= (2-6)()()()[]ωωωωωC C DSBM M S ++-=21 (2-7) DSB 信号的带宽fB BHAM DSB2== (2-8)DSB 信号的功率及调制效率由于不再包含载波成分,因此,DSB 信号的功率就等于边带功率,是调制信号功率的一半,即()()t t m PS P CDSB DSB 2221=== (2-9) 显然,DSB 信号的调制效率为100%。
Matlab实验报告

实验结果及分析实验1:程序如下x=1:10y=2*x;plot(x,y)仿真结果:实验结果分析:仿真结果是条很规则的直线,X轴和Y轴一一对应,清楚明了,而序又特别简单。
所以用Maltab 软件很方便地画出规则的直线,方便研究。
实验结果及分析1、A=2、A=1A=实验结果及分析实验三 Matlab在信号与系统中的应用实验名称实验1、掌握信号与系统课程中基本知识的Matlab编程、仿真方法目的实验原理实验1程序:b=[1];a=[1 1];p=;t=0:p:5;x=exp(-3*t);subplot(1,2,1);impulse(b,a,0:p:5);title('冲激响应');subplot(1,2,2);step(b,a,0:p:5);title('阶跃响应');实验内容<设计性实验>1、用MATLAB在时域中编程求解y′(t)+y(t)=f(t), f(t)= exp(-3t)ε(t)的冲激响应、阶跃响应。
在simulink仿真环境下,设计系统框图,分析系统的冲激响应、阶跃响应。
<设计性实验>(选做)2、用MATLAB在时域中编程求解y′(t)+y(t)=f(t), f(t)=(1+exp(-3t))ε(t)的冲激响应、阶跃响应,要求用conv编程实现系统响应。
在simulink仿真环境下,设计系统框图,分析系统的冲激响应、阶跃响应。
实验结果及分析实验1仿真结果:simulink仿真环境下冲激响应阶跃响应实验名称实验四 Matlab在数字信号处理中的应用实验结果及分析实验1仿真结果:6khz12kHZ。
MATLAB通信系统仿真实验报告

MATLAB通信系统仿真实验报告(2014-2015 学年第2 学期)实验一、MATLAB的基本使用与数学运算目的:学习MATLAB的基本操作,实现简单的数学运算程序。
内容:1、要求在闭区间[0,2π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
2、用M文件建立大矩阵x:[0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.91.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.93.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9]3、已知A=[5,6;7,8],B=[9,10;11,12],用MATLAB分别计算A+B、A*B、A.B、A^3、A.^3、A/B、A\B。
4、任意建立矩阵A,然后找出在[10,20]区间的元素位置。
程序代码及运行结果:1.(1)程序代码:方法1: a = 0:2*pi/10:2*pi方法2: a1 = inspace(0,2*pi,10)(2)运行结果如图1-1所示:图 1- 12.(1)程序代码:x=[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9;1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9;2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9;3.1,3.2,3.3,3.4,3.5,3.6,3.7,3.8,3.9]运行结果如图1-2所示:图 1-23.(1)程序代码:A=[5,6;7,8];B=[9,10;11,12];C=A+BD=A*BE=A.*BF=A^3G=A.^3H=A/BI=A\B(2)运行结果:C =14 1618 20D =111 122151 166E =45 6077 96F =881 10261197 1394G =125 216343 512H =3.0000 -2.00002.0000 -1.0000I =-3.0000 -4.00004.00005.00004.(1)程序代码:>>A=[4,15,-45,10,6;56,0,17,-45,0] B=find(A>=10&A<=20)(2)运行结果:A=4 15 -45 10 656 0 17 -45 0B=367总结:通过本次实验学习MATLAB的基本操作,实现简单的数学运算程序。
MATLAB通信系统仿真实验报告

MATLAB通信系统仿真实验报告实验一、MATLAB的基本使用与数学运算目的:学习MATLAB的基本操作,实现简单的数学运算程序。
内容:1-1 要求在闭区间[0,2π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
运行代码:x=[0:2*pi/9:2*pi]运行结果:1-2 用M文件建立大矩阵xx=[ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.91.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.93.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9]代码:x=[ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.91.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.93.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9]m_mat运行结果:1-3已知A=[5,6;7,8],B=[9,10;11,12],试用MATLAB分别计算A+B,A*B,A.*B,A^3,A.^3,A/B,A\B.代码:A=[5 6;7 8] B=[9 10;11 12] x1=A+B X2=A-B X3=A*B X4=A.*B X5=A^3 X6=A.^3 X7=A/B X8=A\B运行结果:1-4任意建立矩阵A,然后找出在[10,20]区间的元素位置。
程序代码及运行结果:代码:A=[12 52 22 14 17;11 10 24 03 0;55 23 15 86 5 ] c=A>=10&A<=20运行结果:1-5 总结:实验过程中,因为对软件太过生疏遇到了些许困难,不过最后通过查书与同学交流都解决了。
例如第二题中,将文件保存在了D盘,而导致频频出错,最后发现必须保存在MATLAB文件之下才可以。
matlab 仿真实验报告

matlab 仿真实验报告Matlab 仿真实验报告引言:在科学研究和工程应用中,仿真实验是一种非常重要的手段。
通过在计算机上建立数学模型和进行仿真实验,我们可以更好地理解和预测现实世界中的各种现象和问题。
Matlab作为一种强大的科学计算软件,被广泛应用于各个领域的仿真实验中。
本文将介绍我进行的一次基于Matlab的仿真实验,并对实验结果进行分析和讨论。
实验背景:在电子通信领域中,信号的传输和接收是一个重要的研究方向。
而在进行信号传输时,会受到各种信道的影响,如噪声、衰落等。
为了更好地理解信道的特性和优化信号传输方案,我进行了一次关于信道传输的仿真实验。
实验目的:本次实验的目的是通过Matlab仿真,研究不同信道条件下信号传输的性能,并对比分析不同传输方案的优劣。
实验步骤:1. 信道建模:首先,我需要建立信道的数学模型。
根据实际情况,我选择了常见的高斯信道模型作为仿真对象。
通过Matlab提供的函数,我可以很方便地生成高斯噪声,并将其加入到信号中。
2. 信号传输方案设计:接下来,我需要设计不同的信号传输方案。
在实验中,我选择了两种常见的调制方式:频移键控(FSK)和相移键控(PSK)。
通过调整不同的调制参数,我可以模拟不同的传输效果。
3. 信号传输仿真:在信道模型和传输方案设计完成后,我开始进行信号传输的仿真实验。
通过Matlab提供的信号处理函数,我可以很方便地生成调制后的信号,并将其传输到信道中。
4. 信号接收和解调:在信号传输完成后,我需要进行信号接收和解调。
通过Matlab提供的信号处理函数,我可以很方便地对接收到的信号进行解调,并还原出原始的信息信号。
5. 仿真结果分析:最后,我对仿真结果进行分析和讨论。
通过对比不同信道条件下的传输性能,我可以评估不同传输方案的优劣,并得出一些有价值的结论。
实验结果与讨论:通过对不同信道条件下的信号传输仿真实验,我得到了一些有价值的结果。
首先,我观察到在高斯噪声较大的信道条件下,PSK调制比FSK调制具有更好的抗干扰性能。
matlab与通信仿真实验报告

matlab与通信仿真实验报告《Matlab与通信仿真实验报告》摘要:本实验报告通过使用Matlab软件进行通信仿真实验,对通信系统的性能进行了评估和分析。
首先介绍了通信系统的基本原理和模型,然后利用Matlab软件搭建了通信系统的仿真模型,并进行了实验验证。
通过实验结果的分析,得出了通信系统的性能指标,为通信系统的设计和优化提供了重要参考。
一、引言通信系统是现代信息社会中不可或缺的基础设施,它承载着各种类型的信息传输和交换。
通信系统的性能直接影响着信息传输的质量和效率,因此对通信系统的性能评估和分析具有重要意义。
Matlab软件是一种功能强大的科学计算软件,它提供了丰富的工具和函数库,可以用于通信系统的建模、仿真和分析。
本实验报告将利用Matlab软件进行通信系统的仿真实验,对通信系统的性能进行评估和分析。
二、通信系统的基本原理和模型通信系统由发送端、信道和接收端组成,发送端将信息转换成电信号发送出去,经过信道传输后,接收端将电信号转换成信息。
通信系统的性能评估主要包括信号传输质量、误码率、信噪比等指标。
在本实验中,我们将以常见的调制解调技术为例,建立通信系统的仿真模型。
三、Matlab软件在通信系统仿真中的应用Matlab软件提供了丰富的工具和函数库,可以用于通信系统的建模、仿真和分析。
在本实验中,我们将利用Matlab软件搭建通信系统的仿真模型,包括信号调制、信道传输、信号解调等过程。
通过Matlab软件的仿真实验,我们可以得到通信系统的性能指标,如误码率、信噪比等。
四、实验结果分析通过Matlab软件进行通信系统的仿真实验,我们得到了一系列实验结果。
通过对实验结果的分析,我们可以评估通信系统的性能,比如误码率随信噪比的变化规律、不同调制方式的性能比较等。
这些实验结果对于通信系统的设计和优化具有重要的参考价值。
五、结论本实验报告利用Matlab软件进行通信系统的仿真实验,对通信系统的性能进行了评估和分析。
MATLAB通信建模实验仿真实验报告

实验1:上采样与内插一、实验目的1、了解上采样与内插的基本原理和方法。
2、掌握上采样与内插的matlab程序的设计方法。
二、实验原理上采样提高采样频率。
上采样使得周期降低M倍,即新采样周期Tu和原有采样周期Ts的关系是T u=T s/M,根据对应的连续信号x(t),上采样过程从原有采样值x(kT s)生成新采样值x(kT u)=x(kT s/M)。
操作的结果是在每两个采样值之间放入M-1个零值样点。
更实用的内插器是线性内插器,线性内插器的脉冲响应定义如下:上采样值x(kT u)=x(kT s/M)通过与线性内插器的脉冲响应的卷积来完成内插。
三、实验内容仿真正弦波采样和内插,通过基本采样x(k),用M=6产生上采样x u(k),由M=6线性内插得到样点序列x i(k)。
四、实验程序% File: c3_upsampex.mM = 6; % upsample factorh = c3_lininterp(M); % imp response of linear interpolatort = 0:10; % time vectortu = 0:60; % upsampled time vectorx = sin(2*pi*t/10); % original samplesxu = c3_upsamp(x,M); % upsampled sequencesubplot(3,1,1)stem(t,x,'k.')ylabel('x')subplot(3,1,2)stem(tu,xu,'k.')ylabel('xu')xi = conv(h,xu);subplot(3,1,3)stem(xi,'k.')ylabel('xi')% End of script file.% File: c3_upsample.mfunction out=c3_upsamp(in,M)L = length(in);out = zeros(1,(L-1)*M+1); for j=1:Lout(M*(j-1)+1)=in(j); end% End of function file.% File: c3_lininterp.m function h=c3_lininterp(M) h1 = zeros(1,(M-1)); for j=1:(M-1) h1(j) = j/M; endh = [0,h1,1,fliplr(h1),0]; % End of script file.四、 实验结果012345678910x0102030405060x u01020304050607080-11x i实验二:QPSK、16QAM信号的散点图、正交、同相分量波形图一、实验目的1、了解QPSK、16QAM调制的基本原理。
Matlab通信系统仿真实验报告

Matlab通信原理仿真学号: 2142402 姓名:圣斌实验一 Matlab 基本语法与信号系统分析一、 实验目的:1、掌握MATLAB 的基本绘图方法;2、实现绘制复指数信号的时域波形。
二、 实验设备与软件环境:1、实验设备:计算机2、软件环境:MATLAB R2009a三、 实验内容:1、MATLAB 为用户提供了结果可视化功能,只要在命令行窗口输入相应的命令,结果就会用图形直接表示出来。
MATLAB 程序如下:x = -pi::pi;y1 = sin(x); y2 = cos(x); %准备绘图数据 figure(1); %打开图形窗口subplot(2,1,1); %确定第一幅图绘图窗口 plot(x,y1); %以x ,y1绘图title('plot(x,y1)'); %为第一幅图取名为’plot(x,y1)’ grid on; %为第一幅图绘制网格线 subplot(2,1,2) %确定第二幅图绘图窗口 plot(x,y2); %以x ,y2绘图xlabel('time'),ylabel('y')%第二幅图横坐标为’time ’,纵坐标为’y ’运行结果如下图:-1-0.500.51plot(x,y1)-1-0.500.51timey2、上例中的图形使用的是默认的颜色和线型,MATLAB中提供了多种颜色和线型,并且可以绘制出脉冲图、误差条形图等多种形式图:MATLAB程序如下:x=-pi:.1:pi;y1=sin (x);y2=cos (x);figure (1);%subplot (2,1,1);plot (x,y1);title ('plot (x,y1)');grid on%subplot (2,1,2);plot (x,y2);xlabel ('time');ylabel ('y')subplot(1,2,1),stem(x,y1,'r') %绘制红色的脉冲图subplot(1,2,2),stem(x,y1,'g') %绘制绿色的误差条形图运行结果如下图:3、一个复指数信号可以分解为实部和虚部两部分。
通信原理Matlab仿真实验报告

实验二1、用Matlab模拟图形A律解码⑴Matlab程序代码:①建立函数ADecode()function y=ADecode(code,n) codesize=size(code);cr_len=codesize(1);cl_len=codesize(2);ca=zeros(1,cl_len-1);for i=1:cr_lenca=code(i,2:n);s=0;for j=1:n-1s=s+ca(j)*2^(n-1-j);enda=code(i,1);y(i)=s*((-1)^(a+1)); endy=y/(2^(n-1));A=87.6;A1=1+log(A);for j=1:length(y)if(y(j)>=0)if(y(i)<=1/A1)y(j)=y(j)*A1/A;elsey(j)=exp(y(j)*A1-1/A);endelsetemp=-y(j);if(temp<=1/A1)y(j)=-temp*A1/A;elsey(j)=-exp(temp*A1-1)/A;endendend②建立函数APCM()function code=APCM(x,n)xmax=max(abs(x));x=x/xmax;xlen=length(x);y=zeros(1,xlen);A=87.6;A1=1+log(A);for i=1:xlenif x(i)>=0if x(i)<=1/Ay(i)=(A*x(i))/A1;elsey(i)=(1+log(A*x(i)))/A1;endelsex1=-x(i);if x1<=1/Ay(i)=-(A*x1)/A1;elsey(i)=-(1+log(A*x1))/A1;endendendy1=y*(2^(n-1)-1);y1=round(y1);code=zeros(length(y1),n); c2=zeros(1,n-1);for i=1:length(y1)if(y1(i)>0)c1=1;elsec1=0;y1(i)=-y1(i);endfor j=1:n-1r=rem(y1(i),2);y1(i)=(y1(i)-r)/2;c2(j)=r;endc2=fliplr(c2);code(i,:)=[c1 c2];实验三1、用Matlab模拟双极性归零码⑴ Matlab程序代码:function y=drz(x)t0=300;x=[1 0 0 1 1 0 0 0 0 1 0 1];t=0:1/t0:length(x);for i=1:length(x);if(x(i)==1)for j=1:t0/2y(t0/2*(2*i-2)+j)=1;y(t0/2*(2*i-1)+j)=0;endelsefor j=1:t0/2y(t0/2*(2*i-2)+j)=-1;y(t0/2*(2*i-1)+j)=0;endendendy=[y,x(i)];M=max(y);m=min(y); subplot(211)plot(t,y);grid on;axis([0,i,m-0.1,M+0.1]);title('1 0 0 1 1 0 0 0 0 1 0 1 ');⑵Matlab仿真结果:2、用Matlab产生2FSK信号⑴ Matlab程序代码:①建立函数fskdigital()function fskdigital(s,f1,f2) t=0:2*pi/99:2*pi;m1=[];c1=[];b1=[];for n=1:length(s)if s(n)==0;m=ones(1,100);c=sin(f2*t);b=zeros(1,100) else s(n)==1;m=ones(1,100);c=sin(f1*t);b=ones(1,100)endm1=[m1 m]; c1=[c1 c]; b1=[b1 b]; endfsk=c1.*m1;subplot(211);plot(b1,'r')title('原始信号');axis([0 100*length(s) -0.1 1.1]);grid on;subplot(212);plot(fsk)title('2FSK信号');⑵仿真结果:①三角波原图②用矩形波近似的冲击函数③分解后的三角波④经低通还原的三角波。
(完整word版)matlab实验报告

《通信系统仿真》实验报告姓名:杨仕浩专业:通信工程学号: 2014111347实验一 MATLAB环境的熟悉与基本运算一、实验目的:1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识:1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器文件和搜索路径浏览器。
变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英文字母开头(3)长度不大于31个(4)区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
三、实验内容1、学习安装MATLAB软件。
2、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)3、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
4、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、 exerc3……),学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
注意:每一次M-file的修改后,都要存盘。
练习A:(1) help rand,然后随机生成一个2×6的数组,观察command window、command history和workspace等窗口的变化结果。
(2)学习使用clc、clear,了解其功能和作用。
(3)输入C=1:2:20,则C(i)表示什么?其中i=1,2,3, (10)(4)输入A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2; 3 3 3],在命令窗口中执行下列表达式,掌握其含义:A(2, 3) A(:,2) A(3,:) A(:,1:2:3) A(:,3).*B(:,2)A(:,3)*B(2,:) A*B A.*B A^2 A.^2 B/A B./A (5)二维数组的创建和寻访,创建一个二维数组(4×8)A,查询数组A 第2行、第3列的元素,查询数组A第2行的所有元素,查询数组A第6列的所有元素。
中国地质大学基于MATLAB通信仿真实验报告

中国地质大学(武汉)通信原理matlab仿真报告姓名: 张彪_班号: 075112 _学号:20111002253院系:_机电学院专业:_通信工程指导教师:_赵娟老师联系方式:预留指导时间:1、选题为3.周期信号m(t),周期为2,在区间[0,2]内定义为:m(t)=t , 1=<t=<2;m(t)=2-t , 1=<t<=2。
(1)以时间间隔为0.1 的步长对此信号进行8 电平的均匀量化,画出量化输出波形;(2)求各量化点的量化误差,画出量化误差波形;(3)通过计算误差信号的功率,求该系统的SNRq(以dB 计)。
2、解题原理与思路模拟信号的取值范围:a~b,量化电平数=M则均匀量化时的量化间隔为:(b-a)/M且量化区间的端点mi=a+i v i=0,1,…,M 若量化输出电平qi取量化间隔的中点,则qi=[mi+m (i-1)]/2 i=1,2…,M .我的解题思路很简单,大致分为三部分,第一部分构造出题中所给的分段函数;第二部分自定义均匀量化函数,并一并写入计算信噪比等功能;第三部分将第一部分带入自定义函数并求出量化误差波形,最后输出波形,完成题目要求。
思路框图3、实验代码及注释:(1)分段函数的构造并代入自定义函数及求量化误差。
clear all;x1=0:0.1:1;y1=x1;x2=1:0.1:2y2=-x2+2;y3(1:11)=y1;y3(11:21)=y2; %构造出分段函数x=0:0.1:2;plot(x,y3); %输出分段函数w=juny(y3,1,8); %代入自定义函数求值plot(x,y3,x,w); %输出原波形与量化波形title('原波形与量化波形')figure(2)z=abs(y3-w); %求量化误差plot(x,z) %输出量化误差波形title('量化误差波形')(2)自定义函数:量化函数的实现function h=juny(f,v,L)%f是量化的信号序列%v是量化电平最大值%L是量化电平数n=length(f);t=2*v/L; %纵坐标取间隔p=zeros(1,L+1); %确定范围及初始化for i=1:L+1,p(i)=-v+(i-1)*t; %确定原信号抽样值endfor i=1:n %求量化值if f(i)>=v %在此范围内的量化取值(大于量化电平最大值时)h(i)=v;endif f(i)<=-v %在此范围内的量化取值(小于量化电平最小值时)h(i)=-v;endflag=0; %设立标志for j=2:L/2+1 %对量化电平数即纵坐标取半if flag==0if f(i)<p(j) %原信号与抽样信号循环比较h(i)=(p(j-1)+p(j))/2; %确定量化电平flag=1;endendendfor j=L/2+2:L+1 %另一部分的量化(同上)if flag==0if f(i)<p(j)h(i)=(p(j-1)+p(j))/2;flag=1;endendendendnq=v^2/(3*L^2); %计算量化噪声功率nq %显示量化噪声功率Am=2;snr=(3/2)*(Am/v)^2*L^2; %计算信噪比snr %显示信噪比snr=10*log(snr)/log(10); %将信噪比改为dB表示snr4、运行结果:运算结果:nq =0.0052 snr =384 snr =25.8433dB5、分析:在实验过程中出现许多问题,比如分段函数的构造写了一下午,本来是很简单,可以直接是一个三角函数,调用即可,不过如果是其他形式的分段函数就不能了,所以过程中用if 语句等等去做,不过都没做好,最后想起来用的这种方法构造的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验1:上采样与内插一、实验目的1、了解上采样与内插的基本原理和方法。
2、掌握上采样与内插的matlab程序的设计方法。
二、实验原理上采样提高采样频率。
上采样使得周期降低M倍,即新采样周期Tu和原有采样周期Ts的关系是T u=T s/M,根据对应的连续信号x(t),上采样过程从原有采样值x(kT s)生成新采样值x(kT u)=x(kT s/M)。
操作的结果是在每两个采样值之间放入M-1个零值样点。
更实用的内插器是线性内插器,线性内插器的脉冲响应定义如下:上采样值x(kT u)=x(kT s/M)通过与线性内插器的脉冲响应的卷积来完成内插。
三、实验内容仿真正弦波采样和内插,通过基本采样x(k),用M=6产生上采样x u(k),由M=6线性内插得到样点序列x i(k)。
四、实验程序% File: c3_upsampex.mM = 6; % upsample factorh = c3_lininterp(M); % imp response of linear interpolatort = 0:10; % time vectortu = 0:60; % upsampled time vectorx = sin(2*pi*t/10); % original samplesxu = c3_upsamp(x,M); % upsampled sequencesubplot(3,1,1)stem(t,x,'k.')ylabel('x')subplot(3,1,2)stem(tu,xu,'k.')ylabel('xu')xi = conv(h,xu);subplot(3,1,3)stem(xi,'k.')ylabel('xi')% End of script file.% File: c3_upsample.mfunction out=c3_upsamp(in,M)L = length(in);out = zeros(1,(L-1)*M+1); for j=1:Lout(M*(j-1)+1)=in(j); end% End of function file.% File: c3_lininterp.m function h=c3_lininterp(M) h1 = zeros(1,(M-1)); for j=1:(M-1) h1(j) = j/M; endh = [0,h1,1,fliplr(h1),0]; % End of script file.四、 实验结果012345678910x0102030405060x u01020304050607080-11x i实验二:QPSK、16QAM信号的散点图、正交、同相分量波形图一、实验目的1、了解QPSK、16QAM调制的基本原理。
2、理解QPSK、16QAM散点图和其正交、同相分量波形图。
3、掌握QPSK、16QAM散点图和其正交、同相分量波形图的matlab程序设计。
4、二、实验原理如下是数字调制器的模型:散点图是以正交分量x qk(t)和x dk(t)的函数画出来的图,为了构成一个QPSK信号,数据符号a k是通过每次取两个二进制符号构成的,本次实验中每个符号的d k和q k我们定义了+1和-1两个值,16-QAM中每个符号的d k和q k我们选择+1、-1、+3、-3四个值,脉冲成型滤波器选择六阶的巴特沃斯滤波器,通过六阶巴特沃斯滤波器后可以画出散点图。
同时可以分别画出同相和正交分量的时域波形图。
三、实验内容设计matlab程序,画出16-QAM的符号的散点图和通过六阶巴特沃斯滤波器后的散点图,以及16-QAM的符号的同相和正交分量的时域波形图。
四、实验程序% File: c4_qamdemo.mlevelx = input('Number of D levels > ');levely = input('Number of Q levels > ');m = input('Number of symbols > ');n = input('Number of samples per symbol > ');bw = input('Filter bandwidth, 0<bw<1 > ');[xd,xq] = qam(levelx,levely,m,n);[b,a] = butter(6,bw); % determine filter coefficientsyd = filter(b,a,xd); % filter direct coefficientyq = filter(b,a,xq); % filter quadrature coefficient subplot(2,2,1) % first paneplot(xd,xq,'o') % unfiltered scatterplota = 1.4;maxd = max(xd); maxq = max(xq);mind = min(xd); minq = min(xq);axis([a*mind a*maxd a*minq a*maxq])axis equalxlabel('xd'); ylabel('xq')subplot(2,2,2) % second paneplot(yd,yq) % filtered scatterplotaxis equal;xlabel('xd'); ylabel('xq');sym = 30; % number of symbols in time plot nsym = (0:sym*n)/n; % x axis vector for time plots subplot(2,2,3) % third paneplot(nsym(1:sym*n),yd(1:sym*n)) % filtered direct component xlabel('symbol index');ylabel('xd');subplot(2,2,4) % fourth paneplot(nsym(1:sym*n),yq(1:sym*n)) % filtered quadrature component xlabel('symbol index');ylabel('xq');% End of script file.子程序:% File: qam.mfunction [xd,xq] = qam(levelx,levely,m,n)xd = mary(levelx,m,n);xq = mary(levely,m,n);% End of function file.子程序:% File: mary.mfunction y= mary(levels,m,n)% m = number of symbols% n = samples per symboll = m*n; % Total sequence lengthy = zeros(1,l-n+1); % Initalize output vectorlm1 = levels-1;x=2*fix(levels*rand(1,m))-lm1;for i = 1:m % Loop to generate info symbolsk = (i-1)*n+1;y(k) = x(i);endy = conv(y,ones(1,n)); % Make each symbol n samples % End of function file.五、 实验结果-505-4-2024xdx q-505-202xdx q102030-4-2024symbol indexx d102030-4-2024symbol indexx q实验三:冲激不变、阶跃不变、双线性法实现IIR滤波器一、实验目的1、掌握冲激不变、阶跃不变、双线性三种滤波器的设计原理及其三者之间的差别。
2、掌握三种滤波器的matlab的程序的设计。
二、实验原理1、冲激不变滤波器假设数字滤波器的单位冲激响应,除了幅度比例有差别外,等于模拟滤波器冲激响应的采样,这样的数字滤波器就称为模拟滤波器的冲激不变实现,该滤波器的传递函数定义为:其中表示拉普拉斯反变换,Z表示z变换,H a(s)表示模拟原型的传递函,T表示采样周期。
2、阶跃不变滤波器对于阶跃不变滤波器而言,数字滤波器的单位阶跃响应等价于模拟滤波器阶跃响应的采样,其阶跃不变滤波器的传递函数:3、双线性z变换滤波器双线性z变换综合方法采用简单的代数变换,将模拟原型Ha(s)映射为一个数字滤波器,具体来讲,该数字滤波器的传递函数可以定义为:三、实验内容1、假设采样频率为100HZ,模拟滤波器的3dB频率为10HZ,设计matlab 程序,比较三种滤波器的响应。
2、基于前面的例子,考虑一个具有1dB通带波纹和一个最小20dB的阻带衰减,进行五阶椭圆滤波器的综合设计。
四、实验程序例5-5程序:% File: c5_threefilters.mT = 0.01;f = 0:0.1:50;z = exp(-i*2*pi*f*T); % see (5.4)a0 = 0.239057; a1 = 0.239057; b1 = 0.521886; % bilinear invariant num = a0+a1*z;den = 1-b1*z;ampx = abs(num./den);a0 = 0.628319; b1 = 0.533488; % impulse invariantnum = a0;den = 1-b1*z;ampy = abs(num./den);a0 = 1.0; a1 = 0.533488; b1 = 0.533488; % step invriantnum = (a0-a1)*z;den = 1-b1*z;ampz = abs(num./den);plot(f,ampx,f,ampy,f,ampz)xlabel('Frequency - Hz')ylabel('Amplitude Response')例5-6程序:% File: c5_ellipexam.mfs = 100; % set sampling frequencyfc = 20; % set cuttoff frequencyf = 0:0.1:50; % define frequency vector[b,a] = ellip(5,1,20,2*pi*fc,'s');h = freqs(b,a,2*pi*f); % amp. resp. of analog filte[bz1,az1] = impinvar(b,a,fs); % impulse invariant digital filter h1 = freqz(bz1,az1,f,fs); % amplitude response of above [bz2,az2] = bilinear(b,a,fs); % bilinear z filter (not prewarped) h2 = freqz(bz2,az2,f,fs); % amplitude response of above [bz3,az3] = bilinear(b,a,fs,fc); % bilinear z filter (prewarped) h3 = freqz(bz3,az3,f,fs); % amplitude response of above subplot(211) % subplot 1plot(f,abs(h),f,abs(h1)) % plotxlabel('Frequency - Hz') % label x axisylabel('Amplitude Response') % label y axissubplot(212) % subplot 2plot(f,abs(h2),f,abs(h3))xlabel('Frequency - Hz') % label x axisylabel('Amplitude Response') % label y axis五、实验结果例5-5实验结果:051015202530354045500.20.40.60.811.21.4Frequency - HzA m p l i t u d e R e s p o n s e例5-6实验结果:051015202530354045500.511.5Frequency - HzA m p l i t u d e R e s p o n s e051015202530354045500.511.5Frequency - HzA m p l i t u d e R e s p o n s e实验四、FTR滤波器设计与实现一、实验目的1、掌握根据幅度响应进行设计FIR滤波器的原理和方法及其matlab程序设计。
