高中数学必修2立体几何常考题型:直线与平面、平面与平面平行的性质正式版
高中数学-直线与平面平行、平面与平面平行的性质

【证明】证法一:如图所示,分别取AA1,A1B1 的中点M,N,连接MN,NQ,MP.
∵P,Q分别是面AA1 D1D,面A1B1C1D1的中点,
∴MP∥AD, MP=
NQ=
1 2
A1D1.
1 2
AD,NQ∥A1D1,
∴MP∥NQ且MP=NQ.
∴四边形PQNM为平行四边形.
∴PQ∥MN.
∵MN AA1B1B,
∵CQ∥
∴CQ∥MN.
∵EF是△ABC的中位线,∴M是PC的中点,
则N是PQ的中点,即PQ被平面EFGH平分.
【点评】P,C,Q三点所确定的辅助平面是解决本题的 核心.有了面PCQ,就有了连接CD与面EFGH的桥梁, 线面平行的性质才能得以应用.
返回
如图2-3-4所示,已知ABCD是平行四边形,点P是平面 ABCD外一点,M是PC的中点,在DM上取一点G,过G 和AP作平面交平面BDM于GH.求证:AP∥GH.
.
∴AC∥MN∥AC,且AC= 13AC.
∴AC∥平面ABC.
同理,A′B′∥平面ABC.
又∵AC∩A′B′=A′,
∴平面A′B′C′∥平面ABC.
1
1
(2)同理A′B′= AB3 , B=C BC3 ,
∴△A′B′C′∽△ABC.
∴S△A′B′C′
S△ABC =1:9.
返回
1.如何理解线面平行的性质定理?
表示平面的平行四边形的外面,并且使它与平行四边形的一 边或平行四边形内的一条线段平行.
返回
2.如何理解两个平面平行的性质定理?
平面平行的性质是根据面面平行、线面平行、线线平行的 定义直接给出的;判定直线与直线平行,进而判定直线与 平面平行和平面与平面平行,或者反过来由后者判定前者, 是立体几何最基本又最常见的一类问题.证明线面平行往往 转化为证明面面平行.
高考数学复习—立体几何:(二)空间直线平面关系判断与证明—平行与垂直关系证明(试题版)
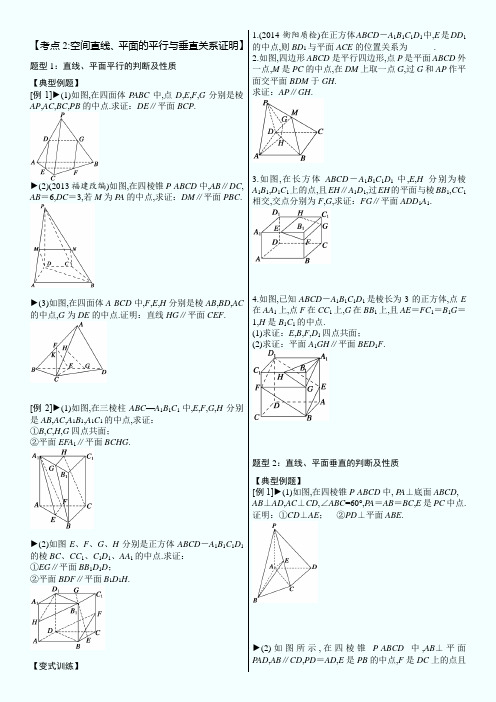
【考点2:空间直线、平面的平行与垂直关系证明】题型1:直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证:DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB=6,DC=3,若M为P A的中点,求证:DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明:直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:①B,C,H,G四点共面;②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:①EG∥平面BB1D1D;②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH .3.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.4.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F .题型2:直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC中点. 证明:①CD⊥AE;②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△P AD中AD边上的高.①证明:PH⊥平面ABCD;②证明:EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(I)求证:EF⊥平面BCG;(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA1,D是棱AA1的中点.(I)证明:平面BDC1⊥平面BDC;(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.①求证:PC⊥BC;②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A=PB=AB =BC,∠PBC=90°,D为AC的中点,AB⊥PD.(1)求证:平面P AB⊥平面ABC;(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.☆题型3:直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α∥β,l∥α,则l∥β;④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.(I)求证:平面ABE⊥平面B1BCC1;(II)求证:C1F∥平面ABE;(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5. 求证:(I)直线P A∥平面DEF;(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积;(II)证明:四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证:DE∥平面A1CB;(II)求证:A1F⊥BE;(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β=c.给出下列命题:①若a与b是异面直线,则c至少与a,b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证: (1)P A ⊥底面ABCD ; (2)BE ∥平面P AD ;(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB =BC=12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证:BC ⊥平面P AC ; (2)设Q 为P A 的中点,G 为△AOC 的重心,求证:QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P - ABD 的体积V =34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E . 求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3. (1)证明:BC ∥平面PDA ; (2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE . (Ⅰ)证明:CD ⊥平面A 1OC ;(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值.17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置. (1)证明:AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点. (1)证明MN ∥平面P AB ;(2)求四面体N -BCM 的体积.19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ; (2)若PA =PD =AB =DC ,∠ADP =90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。
必修二立体几何线线平行、面面平行、线面垂直判定及性质练习

必修二立体几何线线平行、面面平行、线面垂直判定及性质练习本文档将介绍必修二立体几何中关于线线平行、面面平行、线面垂直的判定方法和性质,并提供相关练题。
一、线线平行的判定和性质1. 判定方法- 定理1:若两线的任意一对对应角相等,则这两条线平行。
定理1:若两线的任意一对对应角相等,则这两条线平行。
- 定理2:若一条直线与两平行线相交,则所成的对应角相等。
定理2:若一条直线与两平行线相交,则所成的对应角相等。
2. 性质- 平行线之间的距离相等。
- 平行线截取的两个平行线段成比例。
- 平行线相交的任意两对内错角相等,外错角相等。
- 平行线与一个横截线相交,所成的相应角、对应角均相等。
二、面面平行的判定1. 判定方法- 定理3:若两平面有一对平行线,则这两个平面平行。
定理3:若两平面有一对平行线,则这两个平面平行。
- 定理4:若两平面分别与一直线平行,则这两个平面平行。
定理4:若两平面分别与一直线平行,则这两个平面平行。
2. 性质- 平行面之间的距离相等。
三、线面垂直的判定1. 判定方法- 定理5:一条直线与平面垂直的充分必要条件是直线与平面内的任意一条短线都垂直。
定理5:一条直线与平面垂直的充分必要条件是直线与平面内的任意一条短线都垂直。
2. 性质- 垂直于同一平面的两条直线平行。
四、练题1. 若两线段的长度相等,能判断这两条线段平行吗?若能,请说明理由。
2. 若两平行线上的两点与另外一直线上的两点分别相连,那么这四条线段相交于一点还是两点?请说明理由。
3. 若两平面平行,能判断这两个平面之间的距离吗?请说明理由。
以上是必修二立体几何中关于线线平行、面面平行、线面垂直的判定方法和性质的介绍及练题。
通过理解和练这些内容,你将更好地掌握立体几何的基本概念和性质。
希望对你有帮助!。
高中数学必修二2.2-直线、平面平行的判定及其性质课堂练习及答案

2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号表示:a αb β => a∥αa∥b●知能训练一.选择题1.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是()A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥βC.若m∥α,m∥β,则α∥βD.若m⊥α,n⊥α,则m∥n2.若直线l不平行于平面α,且l⊄α,则()A.α内存在直线与l异面B.α内存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交3.如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交;②过M点有且只有一条直线与直线AB、B1C1都垂直;③过M点有且只有一个平面与直线AB、B1C1都相交;④过M点有且只有一个平面与直线AB、B1C1都平行.其中真命题是()A.②③④B.①③④C.①②④D.①②③4.正方体ABCD-A1B1C1D1中M,N,Q分别是棱D1C1,A1D1,BC的中点.P在对角线BD1上,且BP=BD1,给出下面四个命题:(1)MN∥面APC;(2)C1Q∥面APC;(3)A,P,M三点共线;(4)面MNQ∥面APC.正确的序号为()A.(1)(2)B.(1)(4)C.(2)(3)D.(3)(4)5.在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中,任取两点连成直线,所连的直线中与A1BC1平行的直线共有()A.12条B.18条C.21条D.24条6.直线a∥平面α,P∈α,那么过P且平行于a的直线()A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内7.如果直线a∥平面α,那么直线a与平面α内的()A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交8.如图在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是()A.DD1B.A1D1C.C1D1D.A1D9.如图,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1上的一点,若BC1∥平面AB1D1,则等于()A.1/2B.1 C.2 D.310.下面四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是()A.①②B.①④C.②③D.③④11.如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=,则下列结论中错误的是()A.AC⊥BEB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值二.填空题12.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H,M分别是棱AD,DD1,D1A1,A1A,AB的中点,点N在四边形EFGH的四边及其内部运动,则当N只需满足条件时,就有MN⊥A1C1;当N只需满足条件时,就有MN∥平面B1D1C.13.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于.三.解答题14.如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.(1)求证:AB 1∥平面BC1D;(2)若BC=3,求三棱锥D-BC1C的体积.2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
立体几何直线平面平行的判定和性质课件文

2023-11-06•直线与平面平行的判定•直线与平面平行的性质•直线与平面平行的重要结论•立体几何直线平面平行问题建模•立体几何直线平面平行问题的求解策略目录01直线与平面平行的判定直线与平面平行是指直线与平面内任意一条直线都无公共点,即直线与平面平行。
直线与平面平行的基本性质是:如果直线与平面平行,则直线与平面内的任意一条直线都平行。
直线与平面平行的定义直线与平面平行的判定定理如果一条直线与一个平面平行,那么这条直线与此平面内的任何一条直线都平行。
如果一条直线与一个平面平行,那么这条直线的方向向量与此平面的法向量垂直。
如果一条直线与一个平面平行,那么这条直线的斜率与此平面的法向量的斜率互为相反数的倒数。
在工程学中,直线与平面平行的判定定理也被广泛应用,例如在机械加工、建筑设计等领域中,都需要用到这个定理来计算和设计物体的位置和形状。
直线与平面平行判定的应用在立体几何中,我们常常需要判断一条直线是否与一个平面平行,或者判断一个平面是否与另一个平面平行。
通过直线与平面平行的判定定理,我们可以很容易地判断出直线与平面的位置关系,从而解决一些立体几何的问题。
02直线与平面平行的性质直线与平面平行的性质定理直线与平面平行,则该直线与平面内的任意一条直线均无交点,因此它们平行或异面。
若直线与平面平行,则该直线与平面的垂线互相垂直。
若两条直线都与同一平面平行,则它们的夹角为0度。
直线与平面平行性质的应用在建筑学中,可以利用直线与平面平行的性质来设计建筑物的结构,确保其稳定性和安全性。
在机械加工中,可以利用直线与平面平行的性质来加工和测量工件的尺寸和形状。
在实际生活中,可以利用直线与平面平行的性质来检测平直的物体或线段是否平行。
直线与平面平行性质的证明方法方法一01利用直线与平面平行的判定定理证明直线与平面平行,然后根据性质定理得出结论。
方法二02利用反证法证明直线与平面平行。
假设直线与平面不平行,根据性质定理可得出矛盾,从而证明直线与平面平行。
高中数学必修二 8 5 2 直线与平面平行(第2课时)直线与平面平行的性质 练习(含答案)

8.5.2 直线与平面平行第2课时 直线与平面平行的性质一、选择题1.已知直线l 和平面α,若//l α,P α∈,则过点P 且平行于l 的直线( )A .只有一条,不在平面α内B .只有一条,且在平面α内C .有无数条,一定在平面α内D .有无数条,一定不在平面α内【答案】B【解析】假设过点P 且平行于l 的直线有两条m 与n ,∴//m l 且//n l ,由平行公理得//m n ,这与两条直线m 与n 相交与点P 相矛盾.故选:B .2.如图,在长方体1111ABCD A B C D -中,E 、F 分别是棱1AA 和1BB 的中点,过EF 的平面EFGH 分别交BC 和AD 于点G 、H ,则GH 与AB 的位置关系是( )A .平行B .相交C .异面D .平行或异面【答案】A 【解析】在长方体1111ABCD A B C D -中,11//AA BB ,E 、F 分别为1AA 、1BB 的中点,//AE BF ∴, ∴四边形ABFE 为平行四边形,//EF AB ∴,EF ⊄平面ABCD ,AB 平面ABCD ,//EF ∴平面ABCD ,EF ⊂平面EFGH ,平面EFGH平面ABCD GH =,//EF GH ∴,又//EF AB ,//GH AB ∴,故选A.3.如图,在三棱柱ABC -A 1B 1C 1中,AM =2MA 1,BN =2NB 1,过MN 作一平面交底面三角形ABC 的边BC 、AC 于点E 、F ,则 ( )A.MF∥NEB.四边形MNEF为梯形C.四边形MNEF为平行四边形D.A1B1∥NE【答案】B【解析】∵在AA 1B1B中,AM=2MA1,BN=2NB1,∴AM//BN,∴MN//AB.又MN⊄平面ABC,AB⊂平面ABC,∴MN∥平面ABC.又MN⊂平面MNEF,平面MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB,显然在△ABC中EF≠AB,∴EF≠MN,∴四边形MNEF为梯形.故选B.4.如图,四棱锥S-ABCD的所有棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为()A.B.C.D.【答案】C【解析】因为AB=BC=CD=DA=2,所以四边形ABCD是菱形,所以CD∥AB,又CD⊄平面SAB,AB⊂平面SAB,所以CD∥平面SAB.又CD⊂平面CDEF,平面CDEF∩平面SAB=EF,所以CD∥EF,所以EF∥AB.又因为E为SA中点,所以EF=12AB=1.又因为△SAD和△SBC都是等边三角形,所以所以四边形DEFC 的周长为:故选C.5.(多选题)在梯形ABCD 中,AB CD ∥,AB平面α,CD ⊄平面α,则直线CD 与平面α内的直线的位置关系只能是( )A .平行B .异面C .相交D .共面 【答案】AB【解析】∵AB CD ∥,AB 平面α,CD ⊄平面α,∴CD ∥平面α,∴直线CD 与平面α内的直线没有公共点,直线CD 与平面α内的直线的位置关系可能平行,也可能异面,故选A B .6.(多选题)在空间四边形ABCD 中,,,,E F G H 分别是,,,AB BC CD DA 上的点,当//BD 平面EFGH 时,下面结论正确的是( )A .,,,E F G H 一定是各边的中点B .,G H 一定是,CD DA 的中点C .::AE EB AH HD =,且::BF FC DG GC =D .四边形EFGH 是平行四边形或梯形【答案】CD【解析】由//BD 平面EFGH ,所以由线面平行的性质定理,得//BD EH ,//BD FG ,则::AE EB AH HD =,且::BF FC DG GC =,且//EH FG ,四边形EFGH 是平行四边形或梯形.故选:CD .二、填空题7.如图,在三棱柱111ABC A B C -中,D 是BC 的中点,E 是11A C 上一点,但1//A B 平面1B DE ,则11A E EC 的值为_______. 【答案】12【解析】如下图所示,连接1BC 交1B D 于点F ,连接EF .在三棱柱111ABC A B C -中,11//BC B C ,11BDF C B F ∴∆∆, D 为BC 的中点,111122BD BC B C ∴==,11112BF BD FC B C ∴==. 1//A B 平面1B DE ,1A B ⊂平面11A BC ,平面11A BC ⋂平面1B DE EF =,1//A B EF ∴,11112A E BF EC FC ∴==,故答案为12. 8.正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在1CC 上,若//EF 平面1AB C ,则EF =_____.【解析】取1AA 中点M ,连接,EM MFE 为AD 的中点,M 为1AA 中点⇒11EMA D EMBC ⇒⇒//EM 平面1AB C又因为://EF 平面1AB C ⇒ 平面//EMF 平面1AB C ⇒ //MF 平面1AB C ,因为MF ⊂平面11,AA C C 平面11AAC C 平面1AB C AC =MF AC ⇒⇒F 为1CC 中点.在Rt ECF ∆中,计算知:EF =9.如图,长方体1111ABCD A B C D -中,DD 18= ,E ,F 分别是侧棱1AA ,1CC 上的动点,8AE CF +=,点P 在棱1AA 上,且2AP =,若//EF 平面PBD ,则__________CF =.【答案】2【解析】连接AC ,交BD 于点O ,连接PO .因为//EF 平面PBD ,EF ⊂平面EACF ,平面EACF 平面PBD PO =,所以//EF PO ;在1PA 上截取2PQ AP ==,连接QC ,则//QC PO ,所以//EF QC ,所以易知四边形EFCQ 为平行四边形,则CF EQ =.又8AE CF +=,18AE A E +=,所以11122A E CF EQ AQ ====,故2CF =. 故答案为:2.10.如图在四面体ABCD 中,若截面PQMN 是正方形,则在下列命题中正确的有______.(填上所有正确命题的序号)AC BD ⊥①,AC BD =②,//AC ③截面PQMN ,④异面直线PM 与BD 所成的角为45.【答案】①③④【解析】解:在四面体ABCD 中,截面PQMN 是正方形,//PQ MN ∴,PQ ⊄平面ACD ,MN ⊂平面ACD ,//PQ ∴平面ACD .平面ACB ⋂平面ACD AC =,//PQ AC ∴,可得//AC 平面PQMN .同理可得//BD 平面PQMN ,//BD PN .PN PQ ⊥,AC BD ∴⊥.由//BD PN ,MPN ∴∠是异面直线PM 与BD 所成的角,且为45.由上面可知://BD PN ,//PQ AC .PN AN BD AD ∴=,MN DN AC AD=, 而AN DN ≠,PN MN =,BD AC ∴≠.综上可知:①③④都正确.故答案为①③④.利用线面平行与垂直的判定定理和性质定理、正方形的性质、异面直线所成的角即可得出.三、解答题11.如图所示,P 为平行四边形ABCD 所在平面外一点,M,N 分别为AB,PC 的中点,平面PAD 平面PBC =l .(1)求证:BC ∥l ;(2)MN 与平面PAD 是否平行?试证明你的结论.【答案】(1)见解析;(2)见解析【解析】(1)证明 因为BC ∥AD ,AD ⊂平面PAD ,BC ⊄平面PAD ,所以BC ∥平面PAD.又平面PAD∩平面PBC =l ,BC ⊂平面PBC ,所以BC ∥l.(2)解 MN ∥平面PAD.证明如下:如图所示,取PD 中点E ,连结AE ,EN.又∵N 为PC 的中点,∴//12EN CD =又∵//12AM CD = ∴//AM EN =即四边形AMNE 为平行四边形.∴AE ∥MN ,又MN ⊄平面PAD ,AE ⊂平面PAD.∴MN ∥平面PAD.12.如图,在四棱锥P ABCD -中,底面ABCD 为菱形,60BAD ∠=︒,Q 为AD 的中点,点M 在侧棱PC 上,且PM tPC =,若//PA 平面MQB ,试确定实数t 的值.【答案】13【解析】如图,连接BD AC AC ,,交BQ 于点N ,交BD 于点O ,连接MN ,易知O 为BD 的中点.∵,BQ AO 分别为正三角形ABD 的边,AD BD 上的中线,∴N 为正三角形ABD 的中心.设菱形ABCD 的边长为a,则AN =,AC =. ∵//PA 平面MQB ,PA ⊂平面PAC ,平面PAC平面MQB MN =, ∴//PA MN ,∴13a PM AN PC AC === 即13PM PC =,∴实数t 的值为13.。
高中数学必修2立体几何常考题型:直线与平面、平面与平面垂直的性质(复习课)全面版

直线与平面、平面与平面垂直的性质( 复习课 )【常考题型】题型一、线面、面面垂直的综合问题【例 1】如图,已知直线a⊥ α,直线 b⊥ β,且 AB⊥ a,AB⊥ b,平面α∩β= c.求证: AB∥ c.[ 证明 ]如图,过点 B 作直线 a′ ∥a, a′与 b 确立的平面设为γ.由于 a′ ∥a,AB⊥a,所以 AB ⊥a′,又 AB⊥b, a′∩ b= B,所以 AB ⊥γ.由于 b⊥β, c? β,所以 b⊥c.①由于 a⊥α, c? α,所以 a⊥c,又 a′ ∥a,所以 a′ ⊥c.②由①②可得c⊥γ,又 AB⊥γ,所以 AB∥c.【类题通法】判断线线、线面的平行或垂直关系,一般要利用判断定理和性质定理,有时也能够放到特殊的几何体中(如正方体、长方体等)而后再判断它们的地点关系.【对点训练】1.如下图:平面α,β,直线a,且α⊥ β,α∩ β=AB,a∥ α,a⊥ AB.求证: a⊥ β.证明:∵a∥α,过 a 作平面γ交α于 a′,则 a∥a′∵a⊥AB ,∴a′ ⊥AB.∵α⊥β,α∩β= AB,∴a′ ⊥β,∴a⊥β.题型二、求点到面的距离 【例2】 已知△ABC , AC =BC =1, AB =2,又已知S 是△ ABC所在平面外一点,SA= SB = 2, SC =5,点P 是 SC 的中点,求点P 到平面ABC的距离.[ 解] 法一: 如下图,连结 PA , PB.易知△SAC ,△ACB 是直角三角形,所以 SA ⊥AC ,BC ⊥AC.取 AB 、 AC 的中点 E 、F ,连结 PF , EF ,PE ,则 EF ∥BC ,PF ∥SA.所以 EF ⊥AC , PF ⊥AC.由于 PF ∩ EF =F ,所以 AC ⊥平面 PEF.又 PE? 平面 PEF ,所以 PE ⊥AC.易证△SAC ≌△SBC.由于 P 是 SC 的中点,所以 PA =PB .而 E 是 AB 的中点,所以 PE ⊥AB .由于 AB ∩ AC =A ,所以 PE ⊥平面 ABC.进而 PE 的长就是点 P 到平面 ABC 的距离.151 2在 Rt △AEP 中, AP =2SC = 2 ,AE =2AB = 2 ,225 1 3所以 PE = AP -AE =4- 2= 2 , 即点 P 到平面 ABC 的距离为3 2.法二: 如下图,过 A 作 AE ∥BC ,过 B 作 BF ∥AC ,交 AE 于点 D ,则四边形 ACBD 为正方形.连结 SD.由于 AC ⊥SA , AC ⊥AD , SA ∩ AD = A ,所以 AC ⊥平面 SDA.所以 AC ⊥SD.又由题意,可知BC ⊥SB.由于 BC ⊥BD ,SB ∩ BD = B ,所以 BC ⊥平面SDB ,所以 BC ⊥SD.又 BC ∩ AC =C ,于是 SD ⊥平面 ACBD .所以 SD 的长为点 S到平面 ABC 的距离.在 Rt△SDA 中易得 SD=SA2-AD 2= 22- 12= 3.由于 P 为 SC 的中点,故点P 到平面 ABC 的距离为13 2SD=2 .【类题通法】求点到面的距离的重点是确立过点与平面垂直的线段.可经过外形进行转变,转变为易于求解的点,等体积法也是求点到平面的距离的常用方法.【对点训练】2.如下图,正四棱柱 ABCD - A1B1C1D1中,底面边长为 2 2,侧棱长为 4, E, F 分别为棱 AB ,BC 的中点, EF∩ BD =G.(1)求证:平面 B1EF⊥平面 BDD 1B1;(2)求点 D1到平面 B1EF 的距离.解:证明: (1)连结 AC.∵正四棱柱 ABCD - A1B1C1D1的底面是正方形,∴AC⊥BD .又 AC ⊥DD 1,且 BD ∩DD 1= D,故 AC⊥平面 BDD 1B1,∵E, F 分别为棱 AB, BC 的中点,故EF ∥AC,∴EF⊥平面 BDD 1B1,∴平面 B1EF ⊥平面 BDD 1B1.(2)解题流程:题型三、折叠问题【例 3】如图,在矩形ABCD中,AB=2AD,E是AB的中点,沿 DE 将△ ADE 折起.(1)假如二面角 A- DE -C 是直二面角,求证: AB=AC ;(2) 假如 AB= AC,求证:平面ADE ⊥平面 BCDE .[证明 ] (1)过点 A 作 AM ⊥DE 于点 M,则 AM ⊥平面 BCDE ,∴AM ⊥BC.又 AD= AE,∴M 是 DE 的中点.取BC 中点 N,连结 MN , AN,则 MN ⊥BC.又 AM ⊥BC,AM∩ MN=M,∴BC⊥平面 AMN ,∴AN⊥BC.又∵N 是 BC 中点,∴AB= AC.(2)取 BC 的中点 N,连结 AN.∵AB= AC,∴AN⊥BC.取 DE 的中点 M,连结 MN , AM,∴MN ⊥BC.又 AN∩MN=N,∴BC⊥平面 AMN ,∴AM ⊥BC.又 M 是 DE 的中点, AD= AE,∴AM⊥DE .又∵DE 与 BC 是平面 BCDE 内的订交直线,∴AM ⊥平面 BCDE .∵AM ? 平面 ADE ,∴平面 ADE ⊥平面 BCDE .【类题通法】解决折叠问题的策略(1) 抓住折叠前后的变量与不变量.一般状况下,在折线同侧的量,折叠前后不变,“ 越过”折线的量,折叠前后可能会发生变化,这是解决这种问题的重点.(2) 在解题时认真审察从平面图形到立体图形的几何特点的变化状况.注意相应的点、直线、平面间的地点关系,线段的长度,角度的变化状况.【对点训练】3.如下图,在平行四边形 ABCD 中,已知 AD =2AB= 2a,BD = 3a, AC∩ BD= E,将其沿对角线 BD 折成直二面角.求证: (1) AB⊥平面 BCD ;(2) 平面 ACD ⊥平面 ABD .证明: (1) 在△ABD 中, AB= a,AD = 2a, BD =3a,222∴AB +BD =AD ,∴∠ABD = 90°,∴AB⊥BD.又∵平面 ABD ⊥平面 BCD ,平面 ABD ∩平面 BCD =BD ,AB? 平面 ABD,∴AB⊥平面 BCD .(2)∵折叠前四边形 ABCD 是平行四边形,且 AB⊥BD ,∴CD ⊥BD .∵AB⊥平面 BCD ,∴AB⊥CD .又∵AB∩ BD=B,∴CD ⊥平面 ABD.又∵CD ? 平面 ACD,∴平面 ACD ⊥平面 ABD .【练习反应】1.如下图,三棱锥P,A,B 是定点,则动点P-ABC 的底面在平面C 运动形成的图形是(α上,且)AC ⊥PC,平面PAC⊥平面PBC,点A.一条线段B.一条直线分析:选 D∵平面PAC⊥平面PBC,AC⊥PC,AC?平面PAC,且平面PAC∩平面 PBC =∴AC⊥平面 PBC.又∵BC? 平面 PBC ,∴AC ⊥BC,∴∠ACB= 90°,∴动点 C 运动形成的图形是以AB 为直径的圆,除掉 A 和 B 两点,应选 D.2.在三棱锥P— ABC 中,平面 PAC⊥平面角形, PC= 4,M 是 AB 边上的一动点,则PM ABC,∠ PCA = 90°,△ ABC 是边长为 4 的正三的最小值为 ()A.23B.27C.43D.47分析:选B连结CM ,则由题意PC⊥平面 ABC,可得PC⊥CM ,所以 PM=PC 2+CM 2,要求PM的最小值只需求出CM的最小值即可,在△ABC 中,当CM ⊥AB 时CM有最小值,此时有CM=4×32 =23,所以 PM 的最小值为 2 7.3.若组成教室墙角的三个墙面记为α,β,γ,交线记为BA,BC,BD ,教室内一点墙面α,β,γ的距离分别为 3 m, 4 m,1 m ,则 P 与墙角 B 的距离为 ________ m.P 到三分析:过点P 向各个面作垂线,组成以BP为体对角线的长方体.|BP|=32+ 42+ 1=26.答案:264.如下图,平面α⊥平面β, A∈ α, B∈ β, AA′⊥ A′ B′, BB′⊥ A′ B′,且 AA′= 3, BB′= 4,A′ B′= 2,则三棱锥 A— A′ BB′的体积 V= ________.分析:由题意 AA1⊥面A′ BB′,BB′ ⊥面A′ B′A,则三棱锥 A—A′ BB′中,AA′为高,底面△A′ BB′为 Rt△.∴V A-′BB′ =1△′BB′=1×3×1× 2×4= 4.AA′ ·S323答案: 45.如图,已知平面α⊥平面γ,平面β⊥平面γ.α∩ γ= a,β∩γ=b,且 a∥b,求证:α∥ β.证明:在平面γ内作直线c⊥a.∵α⊥γ,α∩ γ= a,∴c⊥α.∵a∥b,∴c⊥b.又∵β⊥γ,β∩ γ= b,∴c⊥β,∴α∥β.你曾落的泪,最都会成阳光,照亮脚下的路。
高中数学必修2立体几何常考题型:直线与平面、平面与平面平行的判定正式版

直线与平面、平面与平面平行的判定知识梳理】1.直线与平面平行的判定表示定理图形 文字 符号直线与平面平行 的判定定理平面外一条直线与此 平面内一直线平行,则该 直线与此平面平行a?α b? α a ∥b? a ∥ α表示位置图形 文字 符号平面与平面平行 的判定定理一个平面内的两条 相交直线与另一个平面 平行,则这两个平面平 行a? βb? β a ∩b = P ? α∥β a ∥α b ∥α常考题型】题型一、直线与平面平行的判定【例 1】 已知公共边为 AB 的两个全等的矩形 ABCD 和 ABEF 不在同一平面内, P ,Q 分 别是对角线 AE ,BD 上的点,且 AP = DQ (如图 ).求证: PQ ∥平面 CBE.[证明] 作PM ∥AB 交 BE 于点 M ,作 QN ∥AB 交BC 于点 N ,连接 MN ,如图,∴EP = BQ.又 AB =CD ,∴PM 綊 QN , ∴四边形 PMNQ 是平行四边形, ∴PQ ∥MN .则 PM ∥QN , PM=EP ,QN =BQ. AB =EA ,CD =BD .EA =BD , AP =DQ ,又PQ?平面CBE,MN? 平面CBE,∴PQ∥平面CBE.【类题通法】利用直线和平面平行的判定定理证明线面平行的关键是在平面内找一条直线与已知直线平行,常利用平行四边形、三角形中位线、平行公理等.【对点训练】1.如图,在四棱锥P-ABCD 中,底面ABCD 是矩形,E,F分别是PB,PC 的中点.证明:EF∥平面PAD.证明:在△PBC 中,E,F 分别是PB,PC的中点,∴EF∥BC.又BC∥AD ,∴EF ∥AD .∵AD? 平面PAD,EF?平面PAD,∴EF∥平面PAD .题型二、面面平行的判定【例2】如图,在正方体ABCD—A1B1C1D1 中,M、E、 F 、N 分别是A1B1、B1C1、C1D1、D1A1的中点.求证:(1)E、 F 、B、 D 四点共面;(2)平面MAN ∥平面EFDB .[证明] (1)连接B1D1,∵E、F 分别是边B1C1、C1D1 的中点,∴EF∥B1D 1.而BD∥B1D1,∴BD∥EF.∴E、F、B、D 四点共面.(2)易知MN ∥B1D1,B1D1∥BD,∴MN ∥BD. 又MN?平面EFDB ,BD? 平面EFDB.∴MN ∥平面EFDB .连接MF.∵M、F 分别是A1B1、C1D1的中点,∴MF ∥A1D 1,MF =A1D1.∴MF ∥AD ,MF =AD.∴四边形ADFM 是平行四边形,∴ AM ∥DF . 又AM?平面BDFE ,DF? 平面BDFE,∴AM ∥平面BDFE .又∵AM∩MN=M,∴平面MAN ∥平面EFDB .类题通法】两个平面平行的判定定理是确定面面平行的重要方法.解答问题时一定要寻求好判定定理所需要的条件,特别是相交的条件,即与已知平面平行的两条直线必须相交,才能确定面面平行.对点训练】2.如图,已知四棱锥P-ABCD 中,底面ABCD 为平行四边形,点M,N,Q 分别在PA,BD,PD 上,且PM∶MA=BN∶ND =PQ∶QD.求证:平面MNQ ∥平面PBC.证明:∵PM∶MA=BN∶ND=PQ∶QD ,∴MQ∥AD,NQ∥BP.∵BP? 平面PBC,NQ?平面PBC,∴NQ∥平面PBC.又底面ABCD 为平行四边形,∴BC ∥AD ,∴MQ ∥BC.∵BC? 平面PBC,MQ?平面PBC,∴MQ∥平面PBC.又MQ∩ NQ=Q,根据平面与平面平行的判定定理,得平面MNQ ∥平面PBC.题型三、线线平行与面面平行的综合问题【例 3】 如图,在四棱锥 O - ABCD 中,底面 ABCD 是边长为 1 的菱形, M 为 点,N 为BC 的中点.证明:直线 MN ∥平面 OCD.[证明] 如图,取 OB 中点 E ,连接 ME ,NE ,则 ME ∥AB .又∵AB ∥CD , ∴ME ∥CD .又∵ME?平面 OCD , CD? 平面 OCD , ∴ME ∥平面OCD .又∵NE ∥OC ,且 NE?平面 OCD , OC? 平面 OCD , ∴NE ∥平面OCD.又∵ME ∩NE = E ,且 ME ,NE? 平面 MNE , ∴平面MNE ∥平面OCD .∵MN? 平面 MNE ,∴MN ∥平面OCD . 类题通法】解决线线平行与面面平行的综合问题的策略(1)立体几何中常见的平行关系是线线平行、线面平行和面面平行,这三种平行关系不是孤立的,而是相互联系、相互转化的.(2)判定判定―→ 线面平行 ――面面平行线线平行 OA 的中G( )所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理.对点训练】∴直线EG ∥平面BDDB .(2)连接 SD ,∵F ,G 分别是 DC ,SC 的中点,∴FG ∥SD.又∵SD? 平面 BDD 1B 1,FG ?平面 BDD 1B 1, ∴FG ∥平面BDDB .又 EG ∥平面BDD B ,且 EG? 平面 EFG ,FG? 平面 EFG ,EG ∩FG =G ,∴平面 EFG ∥平面BDD B .练习反馈】解析: 选 C 可借助于长方体判断两平面对应平行或相交.2.能保证直线 a 与平面 α平行的条件是 ( )A . b? α,a ∥ b则这两个平面的位置关A .一定平行B .一定相交C .平行或相交D .以上判断都不对3.如图,在正方体 ABCD -A 1B 1C 1D 1中,S 是B 1D 1的中点, E ,F ,∴EG ∥SB.又∵SB? 平面 BDD 1B 1,EG?平面 BDD 1B 1. 1.若一个平面内的两条直线分别平行于另一个平面内的两条直线, 分别是 BC ,DC ,SC 的中点.求证: (1)直线 EG ∥平面 BDD B ;(2)平面 EFG ∥平面 BDD 1B 1. 证明: (1) 如图,连接 SB ,∵E ,G 分别是 BC ,SC 的中点, 系是B .b? α,c ∥α,a ∥b , a ∥cC .b? α,A 、B ∈ a ,C 、D ∈b ,且 AC ∥BD D . a?α,b? α, a ∥b解析: 选 D 由线面平行的判定定理可知, D 正确.置关系是解析: 如右图所示,连接 BD 交 AC 于点 O. 在正方体中容易得到点 O 为BD 的中点.又因为 E 为 DD 1 的中点,所以 OE ∥BD 1.又∵OE? 平面 ACE , BD 1?平面 ACE ,∴BD 1∥平面ACE.答案: 平行4.下列命题真命题序号为 _______① 若一个平面内有两条直线都与另一个平面平行,则这两个平面平行; ② 若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;③ 若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行; ④若一个平面内的两条相交直线分别平行于另一个平面,则这两个平面平行.解析: ①错,应为一平面内两相交直线与另一平面平行;②当两平面相交时,一面内也有 无数条直线均与另一平面平行,②也不对;③中任意直线都与另一平面平行,也有两相交直线 与另一平面平行,故③为真;④为两平面平行的判定定理,故④也为真.答案: ③④5.如图,正方形 ABCD 和四边形 ACEF 所在平面相交. EF ∥ AC , AB = 2,EF =1.求证: AF ∥平面 BDE.证明: 设 AC , BD 交于点 G ,因为 EF ∥AC ,且 EF = 1,易得AG = 12AC =1,所以四边形 AGEF 为平行四边形,所以 AF ∥EG.因为 AF?平面 BDE ,EG? 平面 BDE , 所以 AF ∥平面BDE.学习不是一朝一夕的事情,需要平时积累,需要平时的勤学苦练。
高中数学必修2 直线、平面平行的判定与性质

两个防范(1)在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.答案 A5.(2012·衡阳质检)在正方体________.解析如图.连接AC、BD交于ACE.答案平行在四棱锥PABCD中,底面求证:PB∥平面ACM.[审题视点] 连接MO,证明证明连接BD,MO.中点,所以PB∥MO.利用判定定理时关键是找平面内与已知直线平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线.在正方体ABCDA1B1C1D1求证:平面MNP∥平面[审题视点] 证明MNMP∥C1B.(1)面面平行的定义;下面给出证明:如图,取BB1的中点则DF∥B1C1.∵AB的中点为E,连接结论成立的充分条件,规范解答13——怎样证明线线、线面、面面平行与垂直的综合性问题【问题研究】高考对平行、垂直关系的考查主要以线面平行、线面垂直为核心,以多面体为载体结合平面几在四棱台ABCDA1B1C1D1BAD=60°.(1)证明:AA1⊥BD;(2)如图,连结AC,A1C1设AC∩BD=E,连结EA1因为四边形ABCD为平行四边形,明的依据是空间线面关系的判定定理和性质定理.如图,在多面体ABCDEF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB;β=b)平行的直线②④β=则,bm不平行于平面又∵AE∥CD且∴FM綉AE,即四边形证明如下:如图,取。
(完整版)高中数学立体几何经典常考题型

高中数学立体几何经典常考题型题型一:空间点、线、面的位置关系及空间角的计算空间点、线、面的位置关系通常考查平行、垂直关系的证明,一般出现在解答题的第(1)问,解答题的第(2)问常考查求空间角,求空间角一般都可以建立空间直角坐标系,用空间向量的坐标运算求解.【例1】如图,在△ABC中,∠ABC=π4,O为AB边上一点,且3OB=3OC=2AB,已知PO⊥平面ABC,2DA=2AO=PO,且DA∥PO.(1)求证:平面PBD⊥平面COD;(2)求直线PD与平面BDC所成角的正弦值.(1)证明∵OB=OC,又∵∠ABC=π4,∴∠OCB=π4,∴∠BOC=π2.∴CO⊥AB.又PO⊥平面ABC,OC?平面ABC,∴PO⊥OC.又∵PO,AB?平面PAB,PO∩AB=O,∴CO⊥平面PAB,即CO⊥平面PDB.又CO?平面COD,∴平面PDB⊥平面COD.(2)解以OC,OB,OP所在射线分别为x,y,z轴,建立空间直角坐标系,如图所示.设OA=1,则PO=OB=OC=2,DA=1.则C(2,0,0),B(0,2,0),P(0,0,2),D(0,-1,1), ∴PD →=(0,-1,-1),BC →=(2,-2,0),BD →=(0,-3,1). 设平面BDC 的一个法向量为n =(x ,y ,z ), ∴⎩⎪⎨⎪⎧n ·BC →=0,n ·BD →=0,∴⎩⎨⎧2x -2y =0,-3y +z =0,令y =1,则x =1,z =3,∴n =(1,1,3). 设PD 与平面BDC 所成的角为θ, 则sin θ=⎪⎪⎪⎪⎪⎪⎪⎪PD →·n |PD →||n | =⎪⎪⎪⎪⎪⎪1×0+1×(-1)+3×(-1)02+(-1)2+(-1)2×12+12+32=22211. 即直线PD 与平面BDC 所成角的正弦值为22211. 【类题通法】利用向量求空间角的步骤 第一步:建立空间直角坐标系. 第二步:确定点的坐标.第三步:求向量(直线的方向向量、平面的法向量)坐标. 第四步:计算向量的夹角(或函数值). 第五步:将向量夹角转化为所求的空间角.第六步:反思回顾.查看关键点、易错点和答题规范.【变式训练】 如图所示,在多面体A 1B 1D 1-DCBA 中,四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,E 为B 1D 1的中点,过A 1,D ,E 的平面交CD 1于F . (1)证明:EF ∥B 1C .(2)求二面角E -A 1D -B 1的余弦值.(1)证明 由正方形的性质可知A 1B 1∥AB ∥DC ,且A 1B 1=AB =DC ,所以四边形A 1B 1CD 为平行四边形,从而B 1C ∥A 1D ,又A 1D?面A 1DE ,B 1C?面A 1DE ,于是B 1C ∥面A 1DE.又B 1C?面B 1CD 1,面A 1DE ∩面B 1CD 1=EF ,所以EF ∥B 1C.(2)解 因为四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,所以AA 1⊥AB ,AA 1⊥AD ,AB ⊥AD 且AA 1=AB =AD .以A 为原点,分别以AB →,AD →,AA 1→为x 轴,y 轴和z 轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A (0,0,0),B (1,0,0),D (0,1,0),A 1(0,0,1),B 1(1,0,1),D 1(0,1,1),而E 点为B 1D 1的中点,所以E 点的坐标为⎝ ⎛⎭⎪⎫12,12,1.设平面A 1DE 的一个法向量n 1=(r 1,s 1,t 1),而该面上向量A 1E →=⎝ ⎛⎭⎪⎫12,12,0,A 1D →=(0,1,-1),由n 1⊥A 1E →,n 1⊥A 1D →得r 1,s 1,t 1应满足的方程组⎩⎨⎧12r 1+12s 1=0,s 1-t 1=0,(-1,1,1)为其一组解,所以可取n 1=(-1,1,1).设平面A 1B 1CD 的一个法向量n 2=(r 2,s 2,t 2),而该面上向量A 1B 1→=(1,0,0),A 1D →=(0,1,-1),由此同理可得n 2=(0,1,1).所以结合图形知二面角E -A 1D -B 1的余弦值为 |n 1·n 2||n 1|·|n 2|=23×2=63.题型二:立体几何中的探索性问题此类试题一般以解答题形式呈现,常涉及线、面平行、垂直位置关系的探究或空间角的计算问题,是高考命题的热点,一般有两种解决方式: (1)根据条件作出判断,再进一步论证;(2)利用空间向量,先假设存在点的坐标,再根据条件判断该点的坐标是否存在.【例2】如图,在四棱锥P -ABCD 中,平面PAD⊥平面ABCD ,PA ⊥PD ,PA =PD ,AB ⊥AD ,AB =1,AD =2,AC =CD = 5. (1)求证:PD⊥平面PAB ;(2)求直线PB 与平面PCD 所成角的正弦值;(3)在棱PA 上是否存在点M ,使得BM∥平面PCD 若存在,求AMAP的值;若不存在,说明理由.(1)证明 因为平面PAD⊥平面ABCD ,平面PAD∩平面ABCD =AD ,AB ⊥AD , 所以AB⊥平面PAD ,所以AB⊥PD.又PA⊥PD,AB ∩PA =A ,所以PD⊥平面PAB. (2)解 取AD 的中点O ,连接PO ,CO. 因为PA =PD ,所以PO ⊥AD.因为PO?平面PAD ,平面PAD ⊥平面ABCD , 所以PO ⊥平面ABCD.因为CO?平面ABCD ,所以PO ⊥CO. 因为AC =CD ,所以CO ⊥AD.如图,建立空间直角坐标系O -xyz.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1).设平面PCD 的一个法向量为n =(x ,y ,z ),则 ⎩⎪⎨⎪⎧n ·PD →=0,n ·PC →=0,即⎩⎨⎧-y -z =0,2x -z =0,令z =2,则x =1,y =-2. 所以n =(1,-2,2).又PB →=(1,1,-1),所以cos 〈n ,PB →〉=n ·PB →|n ||PB →|=-33.所以直线PB 与平面PCD 所成角的正弦值为33.(3)解设M是棱PA上一点,则存在λ∈0,1],使得AM→=λAP→.因此点M(0,1-λ,λ),BM→=(-1,-λ,λ).因为BM?平面PCD,所以要使BM∥平面PCD,则BM→·n=0,即(-1,-λ,λ)·(1,-2,2)=0,解得λ=1 4 .所以在棱PA上存在点M,使得BM∥平面PCD,此时AMAP=14.【类题通法】(1)对于存在判断型问题的求解,应先假设存在,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.(2)对于位置探究型问题,通常借助向量,引进参数,综合已知和结论列出等式,解出参数.【变式训练】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,∠PAD=45°,E为PA的中点.(1)求证:DE∥平面BPC;(2)线段AB上是否存在一点F,满足CF⊥DB若存在,试求出二面角F-PC-D的余弦值;若不存在,请说明理由.(1)证明取PB的中点M,连接EM和CM,过点C作CN⊥AB,垂足为点N.∵CN⊥AB,DA⊥AB,∴CN∥DA,又AB∥CD,∴四边形CDAN为平行四边形,∴CN=AD=8,DC=AN=6,在Rt△BNC中,BN BC2-CN2=102-82=6,∴AB=12,而E,M分别为PA,PB的中点,∴EM∥AB且EM=6,又DC∥AB,∴EM ∥CD 且EM =CD ,四边形CDEM 为平行四边形, ∴DE ∥CM.∵CM?平面PBC ,DE?平面PBC , ∴DE ∥平面BPC.(2)解 由题意可得DA ,DC ,DP 两两互相垂直,如图,以D 为原点,DA ,DC ,DP 分别为x ,y ,z 轴建立空间直角坐标系D -xyz , 则A (8,0,0),B (8,12,0),C (0,6,0),P (0,0,8). 假设AB 上存在一点F 使CF ⊥BD , 设点F 坐标为(8,t ,0),则CF →=(8,t -6,0),DB →=(8,12,0), 由CF →·DB →=0得t =23.又平面DPC 的一个法向量为m =(1,0,0), 设平面FPC 的法向量为n =(x ,y ,z ). 又PC →=(0,6,-8),FC →=⎝ ⎛⎭⎪⎫-8,163,0.由⎩⎪⎨⎪⎧n ·PC →=0,n ·FC →=0,得⎩⎨⎧6y -8z =0,-8x +163y =0,即⎩⎪⎨⎪⎧z =34y ,x =23y , 不妨令y =12,有n =(8,12,9).则cos 〈n ,m 〉=n ·m |n ||m |=81×82+122+92=817.又由图可知,该二面角为锐二面角, 故二面角F -PC -D 的余弦值为817. 题型三:立体几何中的折叠问题将平面图形沿其中一条或几条线段折起,使其成为空间图形,这类问题称为立体几何中的折叠问题,折叠问题常与空间中的平行、垂直以及空间角相结合命题,考查学生的空间想象力和分析问题的能力. 【例3】如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =54,EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置,OD ′=10.(1)证明:D ′H ⊥平面ABCD ; (2)求二面角B -D ′A -C 的正弦值.(1)证明 由已知得AC ⊥BD ,AD =CD . 又由AE =CF 得AE AD =CFCD,故AC ∥EF . 因此EF ⊥HD ,从而EF ⊥D ′H .由AB =5,AC =6得DO =BO =AB 2-AO 2=4. 由EF ∥AC 得OH DO =AE AD =14.所以OH =1,D ′H =DH =3.于是D ′H 2+OH 2=32+12=10=D ′O 2,故D ′H ⊥OH . 又D ′H ⊥EF ,而OH ∩EF =H , 所以D ′H ⊥平面ABCD .(2)解 如图,以H 为坐标原点,HF →的方向为x 轴正方向,建立空间直角坐标系H -xyz . 则H (0,0,0),A (-3,-1,0),B (0,-5,0),C (3,-1,0),D ′(0,0,3),AB →=(3,-4,0),AC →=(6,0,0),AD ′→=(3,1,3). 设m =(x 1,y 1,z 1)是平面ABD ′的一个法向量, 则⎩⎪⎨⎪⎧m ·AB →=0,m ·AD ′→=0,即⎩⎨⎧3x 1-4y 1=0,3x 1+y 1+3z 1=0,所以可取m =(4,3,-5).设n =(x 2,y 2,z 2)是平面ACD ′的一个法向量, 则⎩⎪⎨⎪⎧n ·AC →=0,n ·AD ′→=0,即⎩⎨⎧6x 2=0,3x 2+y 2+3z 2=0,所以可取n =(0,-3,1).于是cos 〈m ,n 〉=m ·n |m ||n |=-1450×10=-7525.sin 〈m ,n 〉=29525.因此二面角B -D ′A -C 的正弦值是29525. 【类题通法】立体几何中的折叠问题,关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况,一般地翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化. 【变式训练】如图1,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =1,AD =2,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置,如图2.(1)证明:CD ⊥平面A 1OC ;(2)若平面A 1BE ⊥平面BCDE ,求平面A 1BC 与平面A 1CD 夹角的余弦值. (1)证明 在题图1中,因为AB =BC =1,AD =2,E 是AD 的中点,∠BAD =π2,所以BE ⊥AC .即在题图2中,BE ⊥OA 1,BE ⊥OC , 从而BE ⊥平面A 1OC .又CD ∥BE ,所以CD ⊥平面A 1OC . (2)解 由已知,平面A 1BE ⊥平面BCDE , 又由(1)知,BE ⊥OA 1,BE ⊥OC ,所以∠A 1OC 为二面角A 1-BE -C 的平面角,所以∠A 1OC =π2.如图,以O 为原点,OB →,OC →,OA 1→分别为x 轴、y 轴、z 轴正方向建立空间直角坐标系,因为A 1B =A 1E =BC =ED =1,BC ∥ED ,所以B ⎝ ⎛⎭⎪⎫22,0,0,E ⎝ ⎛⎭⎪⎫-22,0,0,A 1⎝ ⎛⎭⎪⎫0,0,22,C ⎝ ⎛⎭⎪⎫0,22,0,得BC →=⎝ ⎛⎭⎪⎫-22,22,0,A 1C →=⎝⎛⎭⎪⎫0,22,-22,CD →=BE →=(-2,0,0).设平面A 1BC 的一个法向量n 1=(x 1,y 1,z 1),平面A 1CD 的一个法向量n 2=(x 2,y 2,z 2),平面A 1BC 与平面A 1CD 的夹角为θ,则⎩⎪⎨⎪⎧n 1·BC →=0,n 1·A 1C →=0,得⎩⎨⎧-x 1+y 1=0,y 1-z 1=0,取n 1=(1,1,1);⎩⎪⎨⎪⎧n 2·CD →=0,n 2·A 1C →=0, 得⎩⎨⎧x 2=0,y 2-z 2=0,取n 2=(0,1,1),从而cos θ=|cos 〈n 1,n 2〉|=23×2=63, 即平面A 1BC 与平面A 1CD 夹角的余弦值为63.。
高中数学(人教版必修2)直线、平面平行的判定及其性质配套练习(有答案)

§2.2直线、平面平行的判定及其性质2.2.1直线与平面平行的判定一、基础过关1.直线m∥平面α,直线n∥m,则() A.n∥αB.n与α相交C.n⊂αD.n∥α或n⊂α2.棱台的一条侧棱所在的直线与不含这条侧棱的侧面所在的平面的位置关系是() A.平行B.相交C.平行或相交D.不相交3.已知a,b是两条相交直线,a∥α,则b与α的位置关系是() A.b∥αB.b与α相交C.b⊂αD.b∥α或b与α相交4.一条直线l上有相异三个点A、B、C到平面α的距离相等,那么直线l与平面α的位置关系是() A.l∥αB.l⊥αC.l与α相交但不垂直D.l∥α或l⊂α5. 如图,在长方体ABCD-A1B1C1D1的面中:(1)与直线AB平行的平面是______;(2)与直线AA1平行的平面是______;(3)与直线AD平行的平面是______.6.已知不重合的直线a,b和平面α.①若a∥α,b⊂α,则a∥b;②若a∥α,b∥α,则a∥b;③若a∥b,b⊂α,则a∥α;④若a∥b,a∥α,则b∥α或b⊂α,其中正确命题的个数是________.7.在正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1∥平面AEC.8. 如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点.求证:AB∥平面DCF.二、能力提升9.在空间四边形ABCD中,E、F分别是AB和BC上的点,若AE∶EB=EF∶FB=1∶3,则对角线AC和平面DEF的位置关系是()A.平行B.相交C.在内D.不能确定10.过直线l外两点,作与l平行的平面,则这样的平面() A.不存在B.只能作出一个C.能作出无数个D.以上都有可能11.过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有________条.12.如图,在平行四边形ABCD中,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,F为线段A′C的中点.求证:BF∥平面A′DE.三、探究与拓展13. 正方形ABCD与正方形ABEF所在平面相交于AB,在AE,BD上各有一点P,Q,且AP=DQ.求证:PQ∥平面BCE.(用两种方法证明)答案1.D 2.B 3.D 4.D5.(1)平面A1C1和平面DC1(2)平面BC1和平面DC1(3)平面B1C和平面A1C1 6.17.证明如图,连接BD交AC于F,连接EF.因为F为正方形ABCD对角线的交点,所以F为AC、BD的中点.在三角形DD1B中,E、F分别为DD1、DB的中点,所以EF∥D1B.又EF⊂平面AEC,BD1⊄平面AEC,所以BD1∥平面AEC.8.证明连接OF,∵O为正方形DBCE对角线的交点,∴BO=OE,又AF=FE,∴AB∥OF,⎭⎬⎫AB⊄平面DCFOF⊂平面DCFAB∥OF⇒AB∥平面DCF.9.A10.D11.1212.证明取A′D的中点G,连接GF,GE,由条件易知FG∥CD,FG=12CD,BE∥CD,BE=12CD,所以FG∥BE,FG=BE,故四边形BEGF为平行四边形,所以BF∥EG.因为EG⊂平面A′DE,BF⊄平面A′DE,所以BF∥平面A′DE.13.证明如图所示,连接AQ并延长交BC于K,连接EK.∵KB∥AD,∴DQBQ=AQQK.∵AP=DQ,AE=BD,∴BQ=PE.∴DQBQ=APPE.∴AQQK=APPE.∴PQ∥EK.又PQ⊄平面BCE,EK⊂平面BCE,∴PQ∥平面BCE.2.1.2 空间中直线与直线之间的位置关系一、基础过关1.分别在两个平面内的两条直线间的位置关系是( )A .异面B .平行C .相交D .以上都有可能2.若AB ∥A ′B ′,AC ∥A ′C ′,则有( )A .∠BAC =∠B ′A ′C ′ B .∠BAC +∠B ′A ′C ′=180°C .∠BAC =∠B ′A ′C ′或∠BAC +∠B ′A ′C ′=180°D .∠BAC >∠B ′A ′C ′3.空间四边形的两条对角线相互垂直,顺次连接四边中点的四边形一定是 ( )A .空间四边形B .矩形C .菱形D .正方形4.“a 、b 为异面直线”是指:①a ∩b =∅,且aD \∥b ;②a ⊂面α,b ⊂面β,且a ∩b =∅;③a ⊂面α,b ⊂面β,且α∩β=∅;④a ⊂面α,b ⊄面α;⑤不存在面α,使a ⊂面α,b ⊂面α成立. 上述结论中,正确的是( )A .①④⑤B .①③④C .②④D .①⑤5.如果两条直线a 和b 没有公共点,那么a 与b 的位置关系是________. 6.已知正方体ABCD —A ′B ′C ′D ′中: (1)BC ′与CD ′所成的角为________; (2)AD 与BC ′所成的角为________.7.如图所示,四边形ABEF 和ABCD 都是直角梯形,∠BAD =∠F AB=90°,BC 綊12AD ,BE 綊12F A ,G 、H 分别为F A 、FD 的中点.(1)证明:四边形BCHG 是平行四边形; (2)C 、D 、F 、E 四点是否共面?为什么?8.如图,正方体ABCD -EFGH 中,O 为侧面ADHE 的中心,求:(1)BE 与CG 所成的角; (2)FO 与BD 所成的角. 二、能力提升9.如图所示,已知三棱锥A -BCD 中,M 、N 分别为AB 、CD 的中点,则下列结论正确的是( )A .MN ≥12(AC +BD )B .MN ≤12(AC +BD )C .MN =12(AC +BD )D .MN <12(AC +BD )10.如果两条异面直线称为“一对”,那么在正方体的十二条棱中共有异面直线( )A .12对B .24对C .36对D .48对11.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论:①AB ⊥EF ;②AB 与CM 所成的角为60°; ③EF 与MN 是异面直线; ④MN ∥CD .以上结论中正确的序号为________.12.已知A 是△BCD 平面外的一点,E ,F 分别是BC ,AD 的中点,(1)求证:直线EF 与BD 是异面直线;(2)若AC ⊥BD ,AC =BD ,求EF 与BD 所成的角. 三、探究与拓展13.已知三棱锥A —BCD 中,AB =CD ,且直线AB 与CD 成60°角,点M 、N 分别是BC 、AD 的中点,求直线AB 和MN 所成的角.答案1.D 2.C 3.B 4.D 5.平行或异面 6.(1)60° (2)45°7.(1)证明 由已知FG =GA ,FH =HD ,可得GH 綊12AD .又BC 綊12AD ,∴GH 綊BC ,∴四边形BCHG 为平行四边形.(2)解 由BE 綊12AF ,G 为F A 中点知,BE 綊FG ,∴四边形BEFG 为平行四边形,∴EF ∥BG . 由(1)知BG 綊CH ,∴EF ∥CH , ∴EF 与CH 共面.又D ∈FH ,∴C 、D 、F 、E 四点共面.8.解 (1)如图,∵CG ∥BF ,∴∠EBF (或其补角)为异面直线BE 与CG 所成的角,又△BEF 中,∠EBF =45°,所以BE 与CG 所成的角为45°.(2)连接FH ,BD ,FO ,∵HD 綊EA ,EA 綊FB , ∴HD 綊FB ,∴四边形HFBD 为平行四边形, ∴HF ∥BD ,∴∠HFO (或其补角)为异面直线FO 与BD 所成的角. 连接HA 、AF ,易得FH =HA =AF , ∴△AFH 为等边三角形,又依题意知O 为AH 中点,∴∠HFO =30°,即FO 与BD 所成的角是30°.9.D 10.B 11.①③12.(1)证明 假设EF 与BD 不是异面直线,则EF 与BD 共面,从而DF 与BE 共面,即AD 与BC 共面,所以A 、B 、C 、D 在同一平面内,这与A 是△BCD 平面外的一点相矛盾.故直线EF 与BD 是异面直线.(2)解 取CD 的中点G ,连接EG 、FG ,则EG ∥BD ,所以相交直线EF 与EG 所成的角,即为异面直线EF 与BD 所成的角.在Rt △EGF 中,由EG =FG =12AC ,求得∠FEG =45°,即异面直线EF 与BD 所成的角为45°.13.解 如图,取AC 的中点P .连接PM 、PN ,则PM ∥AB ,且PM =12AB ,PN ∥CD ,且PN =12CD ,所以∠MPN 为直线AB 与CD 所成的角(或所成角的补角). 则∠MPN =60°或∠MPN =120°, 若∠MPN =60°,因为PM ∥AB ,所以∠PMN 是AB 与MN 所成的角(或所成角的补角). 又因AB =CD ,所以PM =PN ,则△PMN 是等边三角形, 所以∠PMN =60°,即AB 与MN 所成的角为60°.若∠MPN =120°,则易知△PMN 是等腰三角形.所以∠PMN =30°, 即AB 与MN 所成的角为30°.故直线AB 和MN 所成的角为60°或30°.2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系一、基础过关1.已知直线a∥平面α,直线b⊂α,则a与b的位置关系是() A.相交B.平行C.异面D.平行或异面2.直线l与平面α不平行,则() A.l与α相交B.l⊂αC.l与α相交或l⊂αD.以上结论都不对3.如果直线a∥平面α,那么直线a与平面α内的() A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交4.如果平面α外有两点A、B,它们到平面α的距离都是a,则直线AB和平面α的位置关系一定是() A.平行B.相交C.平行或相交D.AB⊂α5.直线a⊂平面α,直线b⊄平面α,则a,b的位置关系是________.6.若a、b是两条异面直线,且a∥平面α,则b与α的位置关系是________.7.平面α内有无数条直线与平面β平行,那么α∥β是否正确?说明理由.8. 如图,直线a∥平面α,a⊂β,α∩β=b,求证:a∥b.二、能力提升9.下列命题正确的是() A.若直线a在平面α外,则直线a∥αB.若直线a与平面α有公共点,则a与α相交C.若平面α内存在直线与平面β无交点,则α∥βD.若平面α内的任意直线与平面β均无交点,则α∥β10.教室内有一根直尺,无论怎样放置,在地面上总有这样的直线与直尺所在的直线() A.异面B.相交C.平行D.垂直11.若不在同一条直线上的三点A、B、C到平面α的距离相等,且A、B、CD/∈α,则面ABC 与面α的位置关系为________.12. 如图,平面α、β、γ满足α∥β,α∩γ=a,β∩γ=b,判断a与b、a与β的关系并证明你的结论.三、探究与拓展13.正方体ABCD—A1B1C1D1中,点Q是棱DD1上的动点,判断过A、Q、B1三点的截面图形的形状.答案1.D2.C3.D4.C5.平行、相交或异面6.b⊂α,b∥α或b与α相交7.解不正确.如图,设α∩β=l,则在α内与l平行的直线可以有无数条,如a1,a2,…,a n,它们是一组平行线,这时a1,a2,…,a n与平面β平行,但此时α与β不平行,α∩β=l.8.证明∵直线a∥平面α,∴直线a与平面α无公共点.∵α∩β=b,∴b⊂α,b⊂β.∴直线a与b无公共点.∵a⊂β,∴a∥b.9.D10.D11.平行或相交12.解由α∩γ=a知a⊂α且a⊂γ,由β∩γ=b知b⊂β且b⊂γ,∵α∥β,a⊂α,b⊂β,∴a、b无公共点.又∵a⊂γ且b⊂γ,∴a∥b.∵α∥β,∴α与β无公共点,又a⊂α,∴a与β无公共点,∴a∥β.13.解由点Q在线段DD1上移动,当点Q与点D1重合时,截面图形为等边三角形AB1D1,如图(1)所示;当点Q与点D重合时,截面图形为矩形AB1C1D,如图(2)所示;图(1)图(2)当点Q不与点D,D1重合时,截面图形为等腰梯形AQRB1,如图(3)所示.图(3)2.2.2平面与平面平行的判定一、基础过关1.直线l∥平面α,直线m∥平面α,直线l与m相交于点P,且l与m确定的平面为β,则α与β的位置关系是() A.相交B.平行C.异面D.不确定2.平面α与平面β平行的条件可以是() A.α内的一条直线与β平行B.α内的两条直线与β平行C.α内的无数条直线与β平行D.α内的两条相交直线分别与β平行3.给出下列结论,正确的有()①平行于同一条直线的两个平面平行;②平行于同一平面的两个平面平行;③过平面外两点,不能作一个平面与已知平面平行;④若a,b为异面直线,则过a与b平行的平面只有一个.A.1个B.2个C.3个D.4个4.若正n边形的两条对角线分别与面α平行,则这个正n边形所在的平面一定平行于平面α,那么n的取值可能是() A.12 B.8 C.6 D.55.已知平面α、β和直线a、b、c,且a∥b∥c,a⊂α,b、c⊂β,则α与β的关系是________.6.有下列几个命题:①平面α内有无数个点到平面β的距离相等,则α∥β;②α∩γ=a,α∩β=b,且a∥b(α,β,γ分别表示平面,a,b表示直线),则γ∥β;③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边,则α∥β;④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行,则α∥β.其中正确的有________.(填序号)7.如图所示,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,求证:AE∥平面DCF.8. 在长方体ABCD—A1B1C1D1中,E、F、E1、F1分别是AB、CD、A1B1、C1D1的中点.求证:平面A1EFD1∥平面BCF1E1.二、能力提升9.α、β是两个不重合的平面,a、b是两条不同的直线,在下列条件下,可判定α∥β的是() A.α,β都平行于直线a、bB.α内有三个不共线的点到β的距离相等C.a,b是α内两条直线,且a∥β,b∥βD.a、b是两条异面直线,且a∥α,b∥α,a∥β,b∥β10. 正方体EFGH—E1F1G1H1中,下列四对截面中,彼此平行的一对截面是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G11. 如图所示,在正方体ABCD—A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________时,有MN∥平面B1BDD1.12.已知在正方体ABCD—A1B1C1D1中,M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点.求证:(1)E、F、D、B四点共面;(2)平面AMN∥平面EFDB.三、探究与拓展13.如图所示,B为△ACD所在平面外一点,M、N、G分别为△ABC、△ABD、△BCD的重心.(1)求证:平面MNG∥平面ACD;(2)求S△MNG∶S△ADC.答案1.B 2.D 3.B 4.D 5.相交或平行 6.③7.证明 由于AB ∥CD ,BE ∥CF ,故平面ABE ∥平面DCF .而直线AE 在平面ABE 内,根据线面平行的定义,知AE ∥平面DCF . 8.证明 ∵E 、E 1分别是AB 、A 1B 1的中点,∴A 1E 1∥BE 且A 1E 1=BE .∴四边形A 1EBE 1为平行四边形. ∴A 1E ∥BE 1.∵A 1E ⊄平面BCF 1E 1, BE 1⊂平面BCF 1E 1. ∴A 1E ∥平面BCF 1E 1. 同理A 1D 1∥平面BCF 1E 1, A 1E ∩A 1D 1=A 1,∴平面A 1EFD 1∥平面BCF 1E 1. 9.D 10.A 11.M ∈线段FH12.证明 (1)∵E 、F 分别是B 1C 1、C 1D 1的中点,∴EF 綊12B 1D 1,∵DD 1綊BB 1,∴四边形D 1B 1BD 是平行四边形, ∴D 1B 1∥BD . ∴EF ∥BD ,即EF 、BD 确定一个平面,故E 、F 、D 、B 四点共面. (2)∵M 、N 分别是A 1B 1、A 1D 1的中点, ∴MN ∥D 1B 1∥EF . 又MN ⊄平面EFDB , EF ⊂平面EFDB . ∴MN ∥平面EFDB .连接NE ,则NE 綊A 1B 1綊AB . ∴四边形NEBA 是平行四边形.∴AN ∥BE .又AN ⊄平面EFDB ,BE ⊂平面EFDB .∴AN ∥平面EFDB . ∵AN 、MN 都在平面AMN 内,且AN ∩MN =N , ∴平面AMN ∥平面EFDB .13.(1)证明 连接BM 、BN 、BG 并延长交AC 、AD 、CD 分别于P 、F 、H .∵M 、N 、G 分别为△ABC 、△ABD 、△BCD 的重心,则有BM MP =BN NF =BGGH =2.连接PF 、FH 、PH ,有MN ∥PF . 又PF ⊂平面ACD ,MN ⊄平面ACD , ∴MN ∥平面ACD .同理MG ∥平面ACD ,MG ∩MN =M , ∴平面MNG ∥平面ACD .(2)解 由(1)可知MG PH =BG BH =23,∴MG =23PH .又PH =12AD ,∴MG =13AD .同理NG =13AC ,MN =13CD .∴△MNG ∽△DCA ,其相似比为1∶3, ∴S △MNG ∶S △ADC =1∶9.2.2.3 直线与平面平行的性质一、基础过关1.a ,b 是两条异面直线,P 是空间一点,过P 作平面与a ,b 都平行,这样的平面( ) A .只有一个 B .至多有两个 C .不一定有D .有无数个2. 如图,在四面体ABCD 中,若截面PQMN 是正方形,则在下列命题中,错误的为( )A .AC ⊥BDB .AC ∥截面PQMNC .AC =BDD .异面直线PM 与BD 所成的角为45°3. 如图所示,长方体ABCD -A 1B 1C 1D 1中,E 、F 分别是棱AA 1和BB 1的中点,过EF 的平面EFGH 分别交BC 和AD 于G 、H ,则HG 与AB 的位置关系是( )A .平行B .相交C .异面D .平行和异面4.直线a ∥平面α,α内有n 条直线交于一点,则这n 条直线中与直线a 平行的直线( ) A .至少有一条 B .至多有一条 C .有且只有一条D .没有5.设m 、n 是平面α外的两条直线,给出三个论断:①m ∥n ;②m ∥α;③n ∥α.以其中的两个为条件,余下的一个为结论,构造三个命题,写出你认为正确的一个命题:______________.(用序号表示)6. 如图所示,ABCD —A 1B 1C 1D 1是棱长为a 的正方体,M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =a3,过P ,M ,N 的平面交上底面于PQ ,Q 在CD 上,则PQ =________.7. ABCD 是平行四边形,点P 是平面ABCD 外一点,M 是PC 的中点,在DM 上取一点G ,过G 和AP 作平面交平面BDM 于GH ,求证:AP ∥GH .8. 如图所示,三棱锥A —BCD 被一平面所截,截面为平行四边形EFGH .求证:CD∥平面EFGH.二、能力提升9.如图所示,平面α∩β=l1,α∩γ=l2,β∩γ=l3,l1∥l2,下列说法正确的是()A.l1平行于l3,且l2平行于l3B.l1平行于l3,且l2不平行于l3C.l1不平行于l3,且l2不平行于l3D.l1不平行于l3,但l2平行于l310.如图所示,已知A、B、C、D四点不共面,且AB∥平面α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG的形状是________.10题图11题图11.如图所示,在空间四边形ABCD中,E、F、G、H分别是四边上的点,它们共面,并且AC∥平面EFGH,BD∥平面EFGH,AC=m,BD=n,当四边形EFGH是菱形时,AE∶EB =________.12. 如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面P AD∩平面PBC=l.(1)求证:BC∥l;(2)MN与平面P AD是否平行?试证明你的结论.三、探究与拓展13.如图所示,三棱柱ABC—A1B1C1,D是BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,求证:平面A1BD1∥平面AC1D.答案1.C 2.C 3.A 4.B5.①②⇒③(或①③⇒②) 6.223a7.证明 如图所示,连接AC 交BD 于O ,连接MO ,∵ABCD 是平行四边形,ABCD 是平行四边形,点P 是平面ABCD 外一点,M 是PC 的中点,在DM 上取一点G ,过G 和AP 作平面交平面BDM 于GH ,求证:AP ∥GH .∴O 是AC 中点,又M 是PC 的中点, ∴AP ∥OM .根据直线和平面平行的判定定理, 则有P A ∥平面BMD .∵平面P AHG ∩平面BMD =GH , 根据直线和平面平行的性质定理, 则有AP ∥GH .8.证明 ∵四边形EFGH 为平行四边形, ∴EF ∥GH .又GH ⊂平面BCD ,EF ⊄平面BCD . ∴EF ∥平面BCD .而平面ACD ∩平面BCD =CD ,EF ⊂平面ACD ,∴EF ∥CD . 而EF ⊂平面EFGH ,CD ⊄平面EFGH , ∴CD ∥平面EFGH . 9.A 10.平行四边形 11.m ∶n12.(1)证明 因为BC ∥AD ,AD ⊂平面P AD ,BC ⊄平面P AD ,所以BC ∥平面P AD .又平面P AD ∩平面PBC =l ,BC ⊂平面PBC ,所以BC ∥l . (2)解 MN ∥平面P AD . 证明如下:如图所示,取PD 中点E . 连接EN 、AE .又∵N 为PC 中点,∴EN 綊12AB∴EN綊AM,∴四边形ENMA为平行四边形,∴AE∥MN.又∵AE⊂平面P AD,MN⊄平面P AD,∴MN∥平面P AD.13.证明连接A 1C交AC1于点E,∵四边形A1ACC1是平行四边形,∴E是A1C的中点,连接ED,∵A1B∥平面AC1D,平面A1BC∩平面AC1D=ED,∴A1B∥ED,∵E是A1C的中点,∴D是BC的中点.又∵D1是B1C1的中点,∴BD1∥C1D,又∵C1D⊂平面AC1D,BD1⊄平面AC1D,∴BD1∥平面AC1D,又A1B∩BD1=B,∴平面A1BD1∥平面AC1D.2.2.4 平面与平面平行的性质一、基础过关1.已知平面α∥平面β,过平面α内的一条直线a 的平面γ,与平面β相交,交线为直线b ,则a 、b 的位置关系是( ) A .平行B .相交C .异面D .不确定2.已知a 、b 表示直线,α、β表示平面,下列推理正确的是( )A .α∩β=a ,b ⊂α⇒a ∥bB .α∩β=a ,a ∥b ⇒b ∥α且b ∥βC .a ∥β,b ∥β,a ⊂α,b ⊂α⇒α∥βD .α∥β,α∩γ=a ,β∩γ=b ⇒a ∥b3. 如图所示,P 是三角形ABC 所在平面外一点,平面α∥平面ABC ,α分别交线段P A 、PB 、PC 于A ′、B ′、C ′,若P A ′∶AA ′=2∶3,则S △A ′B ′C ′∶S △ABC 等于( )A .2∶25B .4∶25C .2∶5D .4∶54.α,β,γ为三个不重合的平面,a ,b ,c 为三条不同的直线,则有下列命题,不正确的是( )①⎭⎪⎬⎪⎫a ∥c b ∥c ⇒a ∥b; ② ⎭⎪⎬⎪⎫a ∥γb ∥γ⇒a ∥b ; ③⎭⎪⎬⎪⎫α∥c β∥c ⇒α∥β; ④ ⎭⎪⎬⎪⎫α∥γβ∥γ⇒α∥β;⑤⎭⎪⎬⎪⎫α∥c a ∥c ⇒α∥a; ⑥⎭⎪⎬⎪⎫α∥γa ∥γ⇒a ∥α. A .④⑥ B .②③⑥ C .②③⑤⑥ D .②③5.分别在两个平行平面的两个三角形.(填“相似”“全等”) (1)若对应顶点的连线共点,那么这两个三角形具有______关系; (2)若对应顶点的连线互相平行,那么这两个三角形具有________关系.6.已知平面α∥β∥γ,两条直线l 、m 分别与平面α、β、γ相交于点A 、B 、C 与D 、E 、F .已知AB =6,DE DF =25,则AC =______.7.如图,在三棱柱ABC -A 1B 1C 1中,M 是A 1C 1的中点,平面AB 1M ∥平面BC 1N ,AC ∩平面BC 1N =N .求证:N 为AC 的中点.8. 如图所示,在底面是平行四边形的四棱锥P -ABCD 中,点E 在PD 上,且PE ∶ED =2∶1,在棱PC 上是否存在一点F ,使BF ∥平面AEC ?并证明你的结论.二、能力提升9.设α∥β,A ∈α,B ∈β,C 是AB 的中点,当A 、B 分别在平面α、β内运动时,得到无数个AB 的中点C ,那么所有的动点C( )A .不共面B .当且仅当A 、B 分别在两条直线上移动时才共面C .当且仅当A 、B 分别在两条给定的异面直线上移动时才共面D .不论A 、B 如何移动,都共面10.已知平面α∥平面β,P 是α,β外一点,过点P 的直线m 与α,β分别交于点A ,C ,过点P 的直线n 与α,β分别交于点B ,D ,且P A =6,AC =9,PD =8,则BD 的长为( )A .16B .24或245 C .14 D .2011.对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α、β都垂直于γ;②存在平面γ,使α、β都平行于γ;③α内有不共线的三点到β的距离相等;④存在异面直线l ,m ,使得l ∥α,l ∥β,m ∥α,m ∥β.其中可以判断两个平面α与β平行的条件有________个.12. 如图所示,平面α∥平面β,△ABC 、△A ′B ′C ′分别在α、β内,线段AA ′、BB ′、CC ′共点于O ,O 在α、β之间,若AB =2,AC =1,∠BAC =90°,OA ∶OA ′=3∶2. 求△A ′B ′C ′的面积.三、探究与拓展13.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.§2.3直线、平面垂直的判定及其性质2.3.1直线与平面垂直的判定一、基础过关1.已知直线a∥b,平面α∥β,a⊥α,则b与β的位置关系是() A.b⊥βB.b∥βC.b⊂βD.b⊂β或b∥β2.直线a⊥直线b,b⊥平面β,则a与β的关系是() A.a⊥βB.a∥βC.a⊂βD.a⊂β或a∥β3.空间四边形ABCD的四边相等,则它的两对角线AC、BD的关系是() A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交4.如图所示,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定5. 在正方体ABCD-A 1B1C1D1中,(1)直线A1B与平面ABCD所成的角是________;(2)直线A1B与平面ABC1D1所成的角是________;(3)直线A1B与平面AB1C1D所成的角是______.6. 如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是棱AA1和AB上的点,若∠B1MN是直角,则∠C1MN=______.7.如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱B1C1、B1B的中点.求证:CF⊥平面EAB.8. 如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱P A垂直于底面,E、F分别是AB、PC的中点,P A=AD.求证:(1)CD⊥PD;(2)EF⊥平面PCD.二、能力提升9. 如图所示,P A⊥平面ABC,△ABC中BC⊥AC,则图中直角三角形的个数为()A.4 B.3 C.2 D.110.已知矩形ABCD,AB=1,BC=2,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中() A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直11.在直三棱柱ABC—A1B1C1中,BC=CC1,当底面A1B1C1满足条件________时,有AB1⊥BC1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况).12. 如图所示,在正方体ABCD-A1B1C1D1中,P为DD1的中点,O为ABCD的中心,求证:B1O⊥平面P AC.三、探究与拓展13.已知平面α外两点A、B到平面α的距离分别为1和2,A、B两点在α内的射影之间距离为3,求直线AB和平面α所成的角.答案1.A 2.D 3.C 4.B 5.(1)45° (2)30° (3)90° 6.90°7.证明 在平面B 1BCC 1中, ∵E 、F 分别是B 1C 1、B 1B 的中点, ∴△BB 1E ≌△CBF , ∴∠B 1BE =∠BCF ,∴∠BCF +∠EBC =90°,∴CF ⊥BE , 又AB ⊥平面B 1BCC 1,CF ⊂平面B 1BCC 1, ∴AB ⊥CF ,又AB ∩BE =B , ∴CF ⊥平面EAB .8.证明 (1)∵P A ⊥底面ABCD , ∴CD ⊥P A .又矩形ABCD 中,CD ⊥AD ,且AD ∩P A =A ,∴CD ⊥平面P AD ,∴CD ⊥PD .(2)取PD 的中点G ,连接AG ,FG .又∵G 、F 分别是PD 、PC 的中点,∴GF 綊12CD ,∴GF 綊AE ,∴四边形AEFG 是平行四边形,∴AG ∥EF . ∵P A =AD ,G 是PD 的中点, ∴AG ⊥PD ,∴EF ⊥PD , ∵CD ⊥平面P AD ,AG ⊂平面P AD . ∴CD ⊥AG .∴EF ⊥CD .∵PD ∩CD =D ,∴EF ⊥平面PCD . 9.A 10.B 11.∠A 1C 1B 1=90°12.证明 连接AB 1,CB 1,设AB =1.∴AB 1=CB 1=2,∵AO =CO ,∴B 1O ⊥AC .连接PB1.∵OB21=OB2+BB21=32,PB21=PD21+B1D21=94,OP2=PD2+DO2=34,∴OB21+OP2=PB21.∴B1O⊥PO,又∵PO∩AC=O,∴B1O⊥平面P AC.13.解(1)如图①,当A、B位于平面α同侧时,由点A、B分别向平面α作垂线,垂足分别为A1、B1,则AA1=1,BB1=2,B1A1= 3.过点A作AH⊥BB1于H,则AB和α所成角即为∠HAB.而tan∠BAH=2-13=33.∴∠BAH=30°.(2)如图②,当A、B位于平面α异侧时,经A、B分别作AA1⊥α于A1,BB1⊥α于B1,AB∩α=C,则A1B1为AB在平面α上的射影,∠BCB1或∠ACA1为AB与平面α所成的角.∵△BCB1∽△ACA1,∴BB1AA1=B1CCA1=2,∴B1C=2CA1,而B1C+CA1=3,∴B1C=233.∴tan∠BCB1=BB1B1C=2233=3,∴∠BCB1=60°.综合(1)、(2)可知:AB与平面α所成的角为30°或60°.2.3.2平面与平面垂直的判定一、基础过关1.过两点与一个已知平面垂直的平面() A.有且只有一个B.有无数个C.一个或无数个D.可能不存在2.不能肯定两个平面一定垂直的情况是() A.两个平面相交,所成二面角是直二面角B.一个平面经过另一个平面的一条垂线C.一个平面垂直于另一个平面内的一条直线D.平面α内的直线a与平面β内的直线b是垂直的3.设有直线m、n和平面α、β,则下列结论中正确的是()①若m∥n,n⊥β,m⊂α,则α⊥β;②若m⊥n,α∩β=m,n⊂α,则α⊥β;③若m⊥α,n⊥β,m⊥n,则α⊥β.A.①②B.①③C.②③D.①②③4.设l是直线,α,β是两个不同的平面,下列结论中正确的是() A.若l∥α,l∥β,则α∥βB.若l∥α,l⊥β,则α⊥βC.若α⊥β,l⊥α,则l⊥βD.若α⊥β,l∥α,则l⊥β5.过正方形ABCD的顶点A作线段AP⊥平面ABCD,且AP=AB,则平面ABP与平面CDP 所成的二面角的度数是________.6.如图所示,已知P A⊥矩形ABCD所在的平面,图中互相垂直的平面有________对.7.在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.求证:平面EFG⊥平面PDC.8. 如图所示,四棱锥P—ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,P A⊥底面ABCD,P A= 3.(1)证明:平面PBE⊥平面P AB;(2)求二面角A—BE—P的大小.二、能力提升9.在边长为1的菱形ABCD 中,∠ABC =60°,把菱形沿对角线AC 折起,使折起后BD =32,则二面角B -AC -D 的余弦值为( )A.13B.12C.223D.32 10.在正四面体P -ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,下面四个结论中不成立的是( )A .BC ∥面PDFB .DF ⊥面P AEC .面PDF ⊥面ABCD .面P AE ⊥面ABC11.如图,在直三棱柱ABC —A 1B 1C 1中,E 、F 分别是A 1B 、A 1C 的中点,点D 在B 1C 1上,A 1D ⊥B 1C . 求证:(1)EF ∥平面ABC ; (2)平面A 1FD ⊥平面BB 1C 1C .12.如图,在三棱锥P —ABC 中,P A ⊥底面ABC ,P A =AB ,∠ABC =60°,∠BCA =90°,点D 、E 分别在棱PB 、PC 上,且DE ∥BC .(1)求证:BC ⊥平面P AC .(2)是否存在点E 使得二面角A —DE —P 为直二面角?并说明理由. 三、探究与拓展13.如图所示,三棱锥P —ABC 中,D 是AC 的中点,P A =PB =PC =5,AC =22,AB =2,BC = 6.(1)求证:PD ⊥平面ABC ; (2)求二面角P —AB —C 的正切值.答案1.C 2.D 3.B 4.B5.45°6.57.证明因为MA⊥平面ABCD,PD∥MA,所以PD⊥平面ABCD.又BC⊂平面ABCD,所以PD⊥BC.因为四边形ABCD为正方形,所以BC⊥DC.又PD∩DC=D,所以BC⊥平面PDC.在△PBC中,因为G、F分别为PB、PC的中点,所以GF∥BC,所以GF⊥平面PDC.又GF⊂平面EFG,所以平面EFG⊥平面PDC.8.(1)证明如图所示,连接BD,由ABCD是菱形且∠BCD=60°知,△BCD是等边三角形.因为E是CD的中点,所以BE⊥CD.又AB∥CD,所以BE⊥AB.又因为P A⊥平面ABCD,BE⊂平面ABCD,所以P A⊥BE.而P A∩AB=A,因此BE⊥平面P AB.又BE⊂平面PBE,所以平面PBE⊥平面P AB.(2)解由(1)知,BE⊥平面P AB,PB⊂平面P AB,所以PB⊥BE.又AB⊥BE,所以∠PBA是二面角A—BE—P的平面角.=3,则∠PBA=60°.在Rt△P AB中,tan∠PBA=P AAB故二面角A—BE—P的大小是60°.9.B 10.C11.证明(1)由E、F分别是A1B、A1C的中点知EF∥BC.因为EF⊄平面ABC,BC⊂平面ABC.所以EF∥平面ABC.(2)由三棱柱ABC—A1B1C1为直三棱柱知CC1⊥平面A1B1C1.又A1D⊂平面A1B1C1,故CC1⊥A1D.又因为A1D⊥B1C,CC1∩B1C=C,故A1D⊥平面BB1C1C,又A1D⊂平面A1FD,所以平面A1FD⊥平面BB1C1C.12.(1)证明∵P A⊥底面ABC,∴P A⊥BC.又∠BCA=90°,∴AC⊥BC.又∵AC∩P A=A,∴BC⊥平面P AC.(2)解∵DE∥BC,又由(1)知,BC⊥平面P AC,∴DE⊥平面P AC.又∵AE⊂平面P AC,PE⊂平面P AC,∴DE⊥AE,DE⊥PE.∴∠AEP 为二面角A —DE —P 的平面角. ∵P A ⊥底面ABC ,∴P A ⊥AC , ∴∠P AC =90°.∴在棱PC 上存在一点E , 使得AE ⊥PC .这时∠AEP =90°,故存在点E ,使得二面角A —DE —P 为直二面角. 13.(1)证明 连接BD ,∵D 是AC 的中点,P A =PC =5, ∴PD ⊥AC .∵AC =22,AB =2,BC =6, ∴AB 2+BC 2=AC 2.∴∠ABC =90°,即AB ⊥BC .∴BD =12AC =2=AD .∵PD 2=P A 2-AD 2=3,PB =5, ∴PD 2+BD 2=PB 2.∴PD ⊥BD . ∵AC ∩BD =D ,∴PD ⊥平面ABC .(2)解 取AB 的中点E ,连接DE 、PE ,由E 为AB 的中点知DE ∥BC , ∵AB ⊥BC ,∴AB ⊥DE . ∵PD ⊥平面ABC ,∴PD ⊥AB .又AB ⊥DE ,DE ∩PD =D ,∴AB ⊥平面PDE ,∴PE ⊥AB . ∴∠PED 是二面角P —AB —C 的平面角.在△PED 中,DE =12BC =62,PD =3,∠PDE =90°,∴tan ∠PED =PDDE = 2.∴二面角P —AB —C 的正切值为 2.2.3.3 直线与平面垂直的性质 2.3.4 平面与平面垂直的性质一、基础过关1.已知两个平面互相垂直,那么下列说法中正确的个数是( )①一个平面内的直线必垂直于另一个平面内的无数条直线;②一个平面内垂直于这两个平面交线的直线必垂直于另一个平面内的任意一条直线; ③过一个平面内一点垂直于另一个平面的直线,垂足必落在交线上; ④过一个平面内的任意一点作交线的垂线,则此直线必垂直于另一个平面. A .4B .3C .2D .1 2.在圆柱的一个底面上任取一点(该点不在底面圆周上),过该点作另一底面的垂线,则这条垂线与圆柱的母线所在直线的位置关系是( ) A .相交B .平行C .异面D .相交或平行3.若m 、n 表示直线,α表示平面,则下列命题中,正确命题的个数为( )①⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α; ② ⎭⎪⎬⎪⎫m ⊥αn ⊥α⇒m ∥n ; ③⎭⎪⎬⎪⎫m ⊥αn ∥α⇒m ⊥n; ④⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥α. A .1 B .2C .3D .4 4.在△ABC 所在的平面α外有一点P ,且P A =PB =PC ,则P 在α内的射影是△ABC 的( )A .垂心B .内心C .外心D .重心5. 如图所示,AF ⊥平面ABCD ,DE ⊥平面ABCD ,且AF =DE ,AD =6,则EF =________.6.若α⊥β,α∩β=AB ,a ∥α,a ⊥AB ,则a 与β的关系为________. 7. 如图,在三棱锥P -ABC 中,P A ⊥平面ABC ,平面P AB ⊥平面PBC .求证:BC ⊥AB .8. 如图所示,在正方体ABCD —A 1B 1C 1D 1中,M 是AB 上一点,N 是A 1C 的中点,MN ⊥平面A 1DC . 求证:(1)MN ∥AD 1; (2)M 是AB 的中点.二、能力提升9. 如图所示,平面α⊥平面β,A ∈α,B ∈β,AB 与两平面α、β所成的角分别为π4和π6.过A 、B 分别作两平面交线的垂线,垂足分别为A ′、B ′,则AB ∶A ′B ′等于( )A .2∶1B .3∶1C .3∶2D .4∶310.设α-l -β是直二面角,直线a ⊂α,直线b ⊂β,a ,b 与l 都不垂直,那么( )A .a 与b 可能垂直,但不可能平行B .a 与b 可能垂直,也可能平行C .a 与b 不可能垂直,但可能平行D .a 与b 不可能垂直,也不可能平行11.直线a 和b 在正方体ABCD -A 1B 1C 1D 1的两个不同平面内,使a ∥b 成立的条件是________.(只填序号)①a 和b 垂直于正方体的同一个面; ②a 和b 在正方体两个相对的面内,且共面; ③a 和b 平行于同一条棱;④a 和b 在正方体的两个面内,且与正方体的同一条棱垂直. 12.如图所示,在多面体P —ABCD 中,平面P AD ⊥平面ABCD ,AB ∥DC ,△P AD 是等边三角形,已知BD =2AD =8,AB =2DC =4 5. (1)设M 是PC 上的一点, 求证:平面MBD ⊥平面P AD ; (2)求四棱锥P —ABCD 的体积. 三、探究与拓展13.如图,直三棱柱ABC -A 1B 1C 1中,AC =BC =12AA 1,D 是棱AA 1的中点,DC 1⊥BD . (1)证明:DC 1⊥BC ;(2)求二面角A 1-BD -C 1的大小.答案1.B 2.B 3.C 4.C 5.6 6.a ⊥β7.证明 在平面P AB 内,作AD ⊥PB 于D . ∵平面P AB ⊥平面PBC , 且平面P AB ∩平面PBC =PB . ∴AD ⊥平面PBC . 又BC ⊂平面PBC , ∴AD ⊥BC .又∵P A ⊥平面ABC , BC ⊂平面ABC ,∴P A ⊥BC ,∴BC ⊥平面P AB . 又AB ⊂平面P AB , ∴BC ⊥AB .8.证明 (1)∵ADD 1A 1为正方形, ∴AD 1⊥A 1D .又∵CD ⊥平面ADD 1A 1, ∴CD ⊥AD 1. ∵A 1D ∩CD =D , ∴AD 1⊥平面A 1DC . 又∵MN ⊥平面A 1DC , ∴MN ∥AD 1.(2)连接ON ,在△A 1DC 中, A 1O =OD ,A 1N =NC .∴ON 綊12CD 綊12AB ,∴ON ∥AM . 又∵MN ∥OA ,∴四边形AMNO 为平行四边形, ∴ON =AM . ∵ON =12AB ,∴AM =12AB ,∴M 是AB 的中点. 9.A 10.C 11.①②③12.(1)证明 在△ABD 中,∵AD =4,BD =8,AB =45, ∴AD 2+BD 2=AB 2.∴AD ⊥BD .又∵面P AD ⊥面ABCD ,面P AD ∩面ABCD =AD ,BD ⊂面ABCD ,∴BD ⊥面P AD ,又BD ⊂面BDM , ∴面MBD ⊥面P AD . (2)解 过P 作PO ⊥AD , ∵面P AD ⊥面ABCD , ∴PO ⊥面ABCD ,即PO 为四棱锥P —ABCD 的高. 又△P AD 是边长为4的等边三角形, ∴PO =2 3.在底面四边形ABCD 中,AB ∥DC ,AB =2DC ,∴四边形ABCD 为梯形.在Rt △ADB 中,斜边AB 边上的高为4×845=855,此即为梯形的高. ∴S 四边形ABCD =25+452×855=24. ∴V P —ABCD =13×24×23=16 3.13.(1)证明 由题设知,三棱柱的侧面为矩形.由于D 为AA 1的中点,故DC =DC 1.又AC =12AA 1,可得DC 21+DC 2=CC 21,所以DC 1⊥DC .而DC 1⊥BD ,CD ∩BD =D ,所以DC 1⊥平面BCD .因为BC ⊂平面BCD ,所以DC 1⊥BC .(2)解 DC 1⊥BC ,CC 1⊥BC ⇒BC ⊥平面ACC 1A 1⇒BC ⊥AC ,取A 1B 1的中点O ,过点O 作OH ⊥BD 于点H ,连接C 1O ,C 1H ,A 1C 1=B 1C 1⇒C 1O ⊥A 1B 1,面A 1B 1C 1⊥面A 1BD ⇒C 1O ⊥面A 1BD ,又∵DB ⊂面A 1DB ,∴C 1O ⊥BD ,又∵OH ⊥BD ,∴BD ⊥面C 1OH ,C 1H ⊂面C 1OH ,∴BD ⊥C 1H ,得点H 与点D 重合,且∠C 1DO 是二面角A 1-BD -C 的平面角,设AC =a ,则C 1O =22a ,C 1D =2a =2C 1O ⇒∠C 1DO =30°,故二面角A 1-BD -C 1的大小为30°.章末检测一、选择题1.下列推理错误的是() A.A∈l,A∈α,B∈l,B∈α⇒l⊂αB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A∈l,l⊂α⇒A∈α2.长方体ABCD-A1B1C1D1中,异面直线AB,A1D1所成的角等于() A.30°B.45°C.60°D.90°3.下列命题正确的是() A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行4.在空间四边形ABCD的边AB,BC,CD,DA上分别取E、F、G、H四点,如果EF,GH交于一点P,则() A.P一定在直线BD上B.P一定在直线AC上C.P一定在直线AC或BD上D.P既不在直线AC上,也不在直线BD上5.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是() A.①和②B.②和③C.③和④D.②和④6.已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是() A.AB∥m B.AC⊥m C.AB∥βD.AC⊥β7.如图(1)所示,在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,如图(2)所示,那么,在四面体S-EFG中必有()。
高一数学必修二2.2.3直线与平面平行的性质2.2.4平面与平面平行的性质导学案(解析版)

2.2.3直线与平面平行的性质2.2.4平面与平面平行的性质一、课标解读1、掌握直线与平面平行的性质定理及其应用;2、学生通过观察与类比,借助实物模型理解性质及应用。
3、进一步提高学生空间想象能力、思维能力;二、自学导引问题1:在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之.问题2:上述定理通常称为直线与平面平行的性质定理,该定理用符号语言可怎样表述?问题3:直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?问题4:平面与平面平行的性质定理:问题5:符号语言表述:问题6:面与面平行的性质定理有何作用?三、合作探究探究1:如果直线a 与平面α平行,那么直线a 与平面α内的直线有哪些位置关系?探究2:若直线a 与平面α平行,那么在平面α内与直线a 平行的直线有多少条?这些直线的位置关系如何?探究3:如果直线a 与平面α平行,那么经过平面α内一点P 且与直线a 平行的直线怎样定位?探究4:如果α∥β,,,βα⊂⊂b a 则直线a 与直线b 的位置关系如何?四、典例精析例1 如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.已知:βαβα//,//,a a l =求证:l a //变式训练1 已知,,321l l l ===γβγαβα ,1l ∥2l .求证:3l ∥1l ,3l ∥2l例2.如图所示,三棱椎BCD A -被一平面所截,截面为平行四边形EFGH .求证:CD ∥平面EFGH变式训练2 在长方体1111ABCD A BC D -中,点重合)不与11,(B B BBP ∈M BA PA =1 N BC PC =1 ,求证:MN ∥平面AC例 3 已知N M CD AB ,,之间的线段,,是夹在两个平行平面βα分别为CD AB ,的中点.求证:MN ∥α变式训练3 如图所示,在正方体1111ABCD A BC D -中,P N M ,,分别为11111,,B A D B B A上的点,若311111==BA BM D B N B ,又PN ∥11D A ,求证:MN ∥平面11BCC B例4 如图所示,已知的分别是所在平面外一点,是平行四边形PC AB N M ABCD P ,,中点,平面l PBC PAD =平面 .(1) 求证:l ∥BC(2) MN 与平面PAD 是否平行?证明你的结论.五、自主反馈 1.平面α∩平面β=a ,平面β∩平面γ=b ,平面γ∩平面a =c ,若a ∥b ,则c 与a ,b的位置关系是( )A .c 与a ,b 都异面B .c 与a ,b 都相交C .c 至少与a ,b 中的一条相交D .c 与a ,b 都平行2.如果两个相交平面分别经过两条平行线中的一条,那么它们的交线和这两条平行线的位置关系是( )A .都平行B .都相交C .一个相交,一个平行D .都异面 3.对于直线m 、n 和平面α,下面命题中的真命题是A .如果m n m ,,αα⊄⊂、n 是异面直线,那么α//nB .如果m n m ,,αα⊄⊂、n 是异面直线,那么α与n 相交C .如果m n m ,//,αα⊂、n 共面,那么n m //D .如果m n m ,//,//αα、n 共面,那么n m //4.已知m 、n 是不重合的直线,α、β是不重合的平面,有下列命题①若m ⊂α,n ∥α,则m ∥n ;②若m ∥α,m ∥β,则α∥β;③若α∩β=n ,m ∥n ,则m ∥α且m ∥β;其中真命题的个数是A .0B .1C .2D .35.A 、B 是不在直线l 上的两点,则过点A 、B 且与直线l 平行的平面的个数是 ( )A .0个B .1个C .无数个D .以上三种情况均有可能 6 用一个平面去截正方体,所得的截面可能是______________________________;7.三个平面两两相交,有三条交线,则这三条交线的位置关系为__________;8. 在△ABC 中,AB =5,AC =7,∠A =60°,G 是重心,过G 的平面α与BC 平行,AB ∩α=M ,AC ∩α=N ,则MN ___________;9. P 是边长为8的正方形ABCD 所在平面外的一点,且PA =PB =PC =PD =8,M 、N 分别在PA 、BD 上,且53==ND BN MA PM ,则MN =_________; 答案2.2.3 直线与平面平行的性质2.2.4 平面与平面平行的性质例1 证明:过b a 于交作平面αγb a a //,//∴α,于交平面作平面过c βδα βββ⊂⊄∴c b c b c a a ,,//,//,//又l a l b l b b //,//,,,//∴∴=⊂∴βααβ 又例2 略例3 证明:情形一:若ABCD CD AB 在同一平面内,则平面, BD AC BD AC //,//,,∴βαβα 的交线为,与BD MN CD AB N M //,,∴的中点,为又αα平面平面又//,MN BD ∴⊂P AE E CD AE A CD AB 中点,取于交作异面,过情形二:若α//, 连接AEDC CD AE CD AE ED BE PN MP 确定平面,,//,,,,∴ 且平面AC ED AEDC ,的交线为,与βα的中点分别为又CD AE N P ED AC ,,,//,//∴βααα//,//,//,//MP BE MP PN ED PN ∴∴∴同理可证 αα//,,//MN MPN MN MPN ∴⊂∴平面又平面例4 证明:(1)PAD AD PAD BC AD BC 平面平面⊂⊄,,// l PAD PBC PAD BC =∴平面平面,又平面 //l BC //∴(2)平行证明:取NE AE E PD ,,连接的中点AM NE AM NE =且可得,//是平行四边形可知四边形AMNEPAD MN AE MN 平面//,//∴∴变式训练1.略2.证明:M BA PA AA BB BA B A =11111,// 且中,在平面 1111,,CC PB MA PM CC AA AA PB MA PM =∴==∴又 ① N BC PC CC BB BCC B =11111,// 且中,在平面1CC PB NC PN =∴ ② 由①②得AC MN NC PN MA PM //,∴=AC MN AC AC AC MN 平面,平面平面//,∴⊂⊄3.证明:31,31,//11111111==A B P B D B N B D A PN 得由 ,//,3111BB PM BA BM ∴=又 11111,BCC B BB BCC B PM 平面平面又⊂⊄ 11111111//,////C B D A D A PN BCC B PM ,又平面∴ 111111//,C B PN BCC B C B ∴⊂平面1111//BCC B PN BCC B PN 平面,平面又∴⊄ 11//,BCC B PMN P PN PM 平面平面又∴= 11//,BCC B MN PMN MN 平面平面∴⊂ 自主反馈答案1.D2.A3.C4.A5.D6. 3,4,5,6边形7. 平行或交于一点 8.3392 9. 19。
人教版必修2《直线与平面、平面与平面平行的判定及其性质》知识点 练习 答案

直线与平面、平面与平面平行的判定及其性质一、知识点:1、直线与平面的位置关系有且只有三种:⎪⎩⎪⎨⎧⎩⎨⎧;:;:;:没有公共点直线与平面平行有且只有一个公共点直线与平面相交直线在平面外有无数个公共点直线在平面内 2、平面与平面的位置关系有两种: ⎩⎨⎧;:;:有且只有一条公共直线两个平面相交没有公共点两个平面平行3、定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补;4、①直线与平面平行的判定定理:平面外一条直线与平面内一条直线平行, 则该直线与此平面平行;简称“线线平行⇒线面平行”;用数学符号表示为:,,b a αα⊂⊄ a ∥b (3个条件,缺一不可)⇒a ∥α;②直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线 的任一平面与此平面的交线与该直线平行;简称“线面平行⇒线线平行”;用数学符号表示为:a ∥α,b ,a =⊂βαβ (3个条件,缺一不可)⇒a ∥b ;5、①平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行;简称“线面平行⇒面面平行”; 用数学符号表示为:P ,b ,a ,b a =⊂⊂ ββa ∥α,b ∥α5个条件,缺一不可)⇒β∥α;②平面与平面平行的判定定理:如果两个平行平面同时和第三个平面 相交,它们的交线平行;简称“面面平行⇒线线平行”; 用数学符号表示为:α∥β,b a ,==γβγα (3个条件,缺一不可)⇒a ∥b ;6、证明直线与平面平行的另一种方法:先证明这条直线所在的平面与另一个平面平行,则这条直线与另一个平面平行。
二、范例精讲例1 已知a ,b ,c 是三条不重合的直线,,αβ,γ是三个不重合的平面, ①a ∥c ,b ∥c ⇒a ∥b ; ②a ∥γ,b ∥⇒γa ∥b ; ③a ∥c ,c ∥a ⇒α∥α; ④a ∥γ,α∥γ⇒a ∥α; ⑤,a α⊄,b α⊂a ∥b ⇒a ∥α。
其中正确的命题个数是( ) A.1 B.2 C.3 D.4 例2 下列说法正确的是( )A.直线l 平行于平面α内的无数条直线,则l ∥α;B.若a 直线在平面α外,a ∥α;C.若直线,b a φ= 直线α⊂b ,则a ∥α;D.若直线a ∥b ,,b α⊂则a ∥α或α⊂a 。
高中数学必修2考点知识专题训练10---直线与平面平行的性质(含答案解析)

B.相交 D.不确定
解析:∵BB1∥CC1,BB1⊄平面 CDD1C1,CC1⊂平面 CDD1C1,∴BB1∥平面 CDD1C1.
2 / 10
又 BB1⊂平面 BEE1B1,平面 BEE1B1∩平面 CDD1C1=EE1,
∴BB1∥EE1.
答案:A
5.如图,在三棱锥 A-BCD 中,E,F,G,H 分别是 AB,BC,CD,DA 上的点,当 BD∥平面 EFGH
答案:B 2.若直线 a∥平面 α,α 内有 n 条直线交于一点,则这 n 条直线中与直线 a 平行的直线 () A.至少有一条 B.至多有一条 C.有且只有一条 D.没有
解析:设这 n 条直线的交点为 P,则点 P 不在直线 a 上,那么直线 a 和点 P 确定一个平面 β, 则点 P 既在平面 α 内又在平面 β 内,则平面 α 与平面 β 相交.设交线为直线 b,则直线 b 过 点 P.又直线 a∥平面 α,a⊂平面 β,则 a∥b.很明显这样作出的直线 b 有且只有一条,那么 直线 b 可能在这 n 条直线中,也可能不在,即这 n 条直线中与直线 a 平行的直线至多有一 条.
10 / 10
9 / 10
又 EF⊂平面 EFQ,平面 EFQ∩平面 PCD=GH, ∴EF∥GH. ∵EF∥AB, ∴AB∥GH. ★8.如图,在空间四边形 ABCD 中,AC,BD 为其对角线,E,F,G,H 分别为 AC,BC,BD,AD 上 的点.若四边形 EFGH 为平行四边形,求证:AB∥平面 EFGH.
∴CD∥ME.
ெ ெ
ൌ
ாா.
同理可得
ா ா
ൌ
ேே,
ெ ெ
ൌ
ே ே
(完整版)高中数学立体几何经典常考题型

高中数学立体几何经典常考题型题型一:空间点、线、面的位置关系及空间角的计算空间点、线、面的位置关系通常考查平行、垂直关系的证明,一般出现在解答题的第(1)问,解答题的第(2)问常考查求空间角,求空间角一般都可以建立空间直角坐标系,用空间向量的坐标运算求解. 【例1】如图,在△ABC 中,∠ABC =π4,O 为AB 边上一点,且3OB =3OC =2AB ,已知PO ⊥平面ABC ,2DA =2AO =PO ,且DA ∥PO. (1)求证:平面PBD ⊥平面COD ;(2)求直线PD 与平面BDC 所成角的正弦值.(1)证明 ∵OB =OC ,又∵∠ABC =π4, ∴∠OCB =π4,∴∠BOC =π2. ∴CO ⊥AB. 又PO ⊥平面ABC , OC ⊂平面ABC ,∴PO ⊥OC.又∵PO ,AB ⊂平面PAB ,PO ∩AB =O , ∴CO ⊥平面PAB ,即CO ⊥平面PDB. 又CO ⊂平面COD , ∴平面PDB ⊥平面COD.(2)解 以OC ,OB ,OP 所在射线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示.设OA =1,则PO =OB =OC =2,DA =1.则C(2,0,0),B(0,2,0),P(0,0,2),D(0,-1,1), ∴PD→=(0,-1,-1),BC →=(2,-2,0),BD →=(0,-3,1).设平面BDC 的一个法向量为n =(x ,y ,z ), ∴⎩⎪⎨⎪⎧n ·BC →=0,n ·BD →=0,∴⎩⎨⎧2x -2y =0,-3y +z =0,令y =1,则x =1,z =3,∴n =(1,1,3). 设PD 与平面BDC 所成的角为θ, 则sin θ=⎪⎪⎪⎪⎪⎪⎪⎪PD→·n |PD →||n | =⎪⎪⎪⎪⎪⎪1×0+1×(-1)+3×(-1)02+(-1)2+(-1)2×12+12+32=22211. 即直线PD 与平面BDC 所成角的正弦值为22211. 【类题通法】利用向量求空间角的步骤 第一步:建立空间直角坐标系. 第二步:确定点的坐标.第三步:求向量(直线的方向向量、平面的法向量)坐标. 第四步:计算向量的夹角(或函数值). 第五步:将向量夹角转化为所求的空间角.第六步:反思回顾.查看关键点、易错点和答题规范.【变式训练】 如图所示,在多面体A 1B 1D 1DCBA 中,四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,E 为B 1D 1的中点,过A 1,D ,E 的平面交CD 1于F . (1)证明:EF ∥B 1C .(2)求二面角E -A 1D B 1的余弦值.(1)证明 由正方形的性质可知A 1B 1∥AB ∥DC ,且A 1B 1=AB =DC ,所以四边形A 1B 1CD 为平行四边形,从而B 1C ∥A 1D ,又A 1D ⊂面A 1DE ,B 1C ⊄面A 1DE ,于是B 1C ∥面A 1DE.又B 1C ⊂面B 1CD 1,面A 1DE ∩面B 1CD 1=EF ,所以EF ∥B 1C.(2)解 因为四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,所以AA 1⊥AB ,AA 1⊥AD ,AB ⊥AD 且AA 1=AB =AD .以A 为原点,分别以AB →,AD →,AA 1→为x 轴,y 轴和z 轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A (0,0,0),B (1,0,0),D (0,1,0),A 1(0,0,1),B 1(1,0,1),D 1(0,1,1),而E 点为B 1D 1的中点,所以E 点的坐标为⎝ ⎛⎭⎪⎫12,12,1.设平面A 1DE 的一个法向量n 1=(r 1,s 1,t 1),而该面上向量A 1E →=⎝ ⎛⎭⎪⎫12,12,0,A 1D →=(0,1,-1),由n 1⊥A 1E →,n 1⊥A 1D →得r 1,s 1,t 1应满足的方程组⎩⎪⎨⎪⎧12r 1+12s 1=0,s 1-t 1=0,(-1,1,1)为其一组解,所以可取n 1=(-1,1,1).设平面A 1B 1CD 的一个法向量n 2=(r 2,s 2,t 2),而该面上向量A 1B 1→=(1,0,0),A 1D →=(0,1,-1),由此同理可得n 2=(0,1,1).所以结合图形知二面角E -A 1D B 1的余弦值为 |n 1·n 2||n 1|·|n 2|=23×2=63.题型二:立体几何中的探索性问题此类试题一般以解答题形式呈现,常涉及线、面平行、垂直位置关系的探究或空间角的计算问题,是高考命题的热点,一般有两种解决方式: (1)根据条件作出判断,再进一步论证;(2)利用空间向量,先假设存在点的坐标,再根据条件判断该点的坐标是否存在.【例2】如图,在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,PA ⊥PD ,PA =PD ,AB ⊥AD ,AB =1,AD =2,AC =CD = 5. (1)求证:PD ⊥平面PAB ;(2)求直线PB 与平面PCD 所成角的正弦值;(3)在棱PA 上是否存在点M ,使得BM ∥平面PCD ?若存在,求AMAP 的值;若不存在,说明理由.(1)证明 因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,AB ⊥AD , 所以AB ⊥平面PAD ,所以AB ⊥PD.又PA ⊥PD ,AB ∩PA =A ,所以PD ⊥平面PAB. (2)解 取AD 的中点O ,连接PO ,CO. 因为PA =PD ,所以PO ⊥AD.因为PO ⊂平面PAD ,平面PAD ⊥平面ABCD , 所以PO ⊥平面ABCD.因为CO ⊂平面ABCD ,所以PO ⊥CO. 因为AC =CD ,所以CO ⊥AD.如图,建立空间直角坐标系O -xyz.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1).设平面PCD 的一个法向量为n =(x ,y ,z ),则 ⎩⎪⎨⎪⎧n ·PD →=0,n ·PC →=0,即⎩⎨⎧-y -z =0,2x -z =0,令z =2,则x =1,y =-2. 所以n =(1,-2,2).又PB →=(1,1,-1),所以cos 〈n ,PB →〉=n ·PB →|n ||PB →|=-33.所以直线PB 与平面PCD 所成角的正弦值为33.(3)解 设M 是棱P A 上一点,则存在λ∈0,1],使得AM →=λAP →.因此点M (0,1-λ,λ),BM→=(-1,-λ,λ).因为BM ⊄平面PCD ,所以要使BM ∥平面PCD ,则BM →·n =0,即(-1,-λ,λ)·(1,-2,2)=0,解得λ=14. 所以在棱P A 上存在点M ,使得BM ∥平面PCD ,此时AM AP =14.【类题通法】(1)对于存在判断型问题的求解,应先假设存在,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等. (2)对于位置探究型问题,通常借助向量,引进参数,综合已知和结论列出等式,解出参数.【变式训练】如图,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,DC =6,AD =8,BC =10,∠P AD =45°,E 为P A 的中点. (1)求证:DE ∥平面BPC ;(2)线段AB 上是否存在一点F ,满足CF ⊥DB ?若存在,试求出二面角F -PC -D 的余弦值;若不存在,请说明理由.(1)证明 取PB 的中点M ,连接EM 和CM ,过点C 作CN ⊥AB ,垂足为点N .∵CN ⊥AB ,DA ⊥AB ,∴CN ∥DA ,又AB ∥CD ,∴四边形CDAN 为平行四边形, ∴CN =AD =8,DC =AN =6, 在Rt △BNC 中,BN =BC 2-CN 2=102-82=6,∴AB =12,而E ,M 分别为P A ,PB 的中点, ∴EM ∥AB 且EM =6,又DC ∥AB ,∴EM ∥CD 且EM =CD ,四边形CDEM 为平行四边形, ∴DE ∥CM.∵CM ⊂平面PBC ,DE ⊄平面PBC , ∴DE ∥平面BPC.(2)解 由题意可得DA ,DC ,DP 两两互相垂直,如图,以D 为原点,DA ,DC ,DP 分别为x ,y ,z 轴建立空间直角坐标系D -xyz , 则A (8,0,0),B (8,12,0),C (0,6,0),P (0,0,8). 假设AB 上存在一点F 使CF ⊥BD , 设点F 坐标为(8,t ,0),则CF→=(8,t -6,0),DB →=(8,12,0), 由CF→·DB →=0得t =23. 又平面DPC 的一个法向量为m =(1,0,0), 设平面FPC 的法向量为n =(x ,y ,z ). 又PC→=(0,6,-8),FC →=⎝ ⎛⎭⎪⎫-8,163,0. 由⎩⎪⎨⎪⎧n ·PC →=0,n ·FC →=0,得⎩⎪⎨⎪⎧6y -8z =0,-8x +163y =0,即⎩⎪⎨⎪⎧z =34y ,x =23y , 不妨令y =12,有n =(8,12,9). 则cos 〈n ,m 〉=n ·m|n ||m |=81×82+122+92=817. 又由图可知,该二面角为锐二面角, 故二面角F -PC -D 的余弦值为817. 题型三:立体几何中的折叠问题将平面图形沿其中一条或几条线段折起,使其成为空间图形,这类问题称为立体几何中的折叠问题,折叠问题常与空间中的平行、垂直以及空间角相结合命题,考查学生的空间想象力和分析问题的能力. 【例3】如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =54,EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置,OD ′=10. (1)证明:D ′H ⊥平面ABCD ; (2)求二面角B -D ′A -C 的正弦值.(1)证明 由已知得AC ⊥BD ,AD =CD . 又由AE =CF 得AE AD =CFCD ,故AC ∥EF . 因此EF ⊥HD ,从而EF ⊥D ′H .由AB =5,AC =6得DO =BO =AB 2-AO 2=4. 由EF ∥AC 得OH DO =AE AD =14.所以OH =1,D ′H =DH =3. 于是D ′H 2+OH 2=32+12=10=D ′O 2,故D ′H ⊥OH . 又D ′H ⊥EF ,而OH ∩EF =H , 所以D ′H ⊥平面ABCD .(2)解 如图,以H 为坐标原点,HF →的方向为x 轴正方向,建立空间直角坐标系H -xyz .则H (0,0,0),A (-3,-1,0), B (0,-5,0),C (3,-1,0),D ′(0,0,3),AB →=(3,-4,0),AC →=(6,0,0),AD ′→=(3,1,3). 设m =(x 1,y 1,z 1)是平面ABD ′的一个法向量, 则⎩⎪⎨⎪⎧m ·AB →=0,m ·AD ′→=0,即⎩⎨⎧3x 1-4y 1=0,3x 1+y 1+3z 1=0,所以可取m =(4,3,-5).设n =(x 2,y 2,z 2)是平面ACD ′的一个法向量, 则⎩⎪⎨⎪⎧n ·AC →=0,n ·AD ′→=0,即⎩⎨⎧6x 2=0,3x 2+y 2+3z 2=0,所以可取n =(0,-3,1). 于是cos 〈m ,n 〉=m ·n |m ||n |=-1450×10=-7525.sin 〈m ,n 〉=29525.因此二面角B -D ′A -C 的正弦值是29525.【类题通法】立体几何中的折叠问题,关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况,一般地翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化. 【变式训练】如图1,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =1,AD =2,E 是AD的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置,如图2.(1)证明:CD ⊥平面A 1OC ;(2)若平面A 1BE ⊥平面BCDE ,求平面A 1BC 与平面A 1CD 夹角的余弦值.(1)证明 在题图1中,因为AB =BC =1,AD =2,E 是AD 的中点,∠BAD =π2,所以BE ⊥AC .即在题图2中,BE ⊥OA 1,BE ⊥OC , 从而BE ⊥平面A 1OC .又CD ∥BE ,所以CD ⊥平面A 1OC . (2)解 由已知,平面A 1BE ⊥平面BCDE , 又由(1)知,BE ⊥OA 1,BE ⊥OC ,所以∠A 1OC 为二面角A 1-BE -C 的平面角,所以∠A 1OC =π2.如图,以O 为原点,OB →,OC →,OA 1→分别为x 轴、y 轴、z 轴正方向建立空间直角坐标系,因为A 1B =A 1E =BC =ED =1,BC ∥ED ,所以B ⎝ ⎛⎭⎪⎫22,0,0,E ⎝ ⎛⎭⎪⎫-22,0,0,A 1⎝ ⎛⎭⎪⎫0,0,22,C ⎝ ⎛⎭⎪⎫0,22,0,得BC →=⎝ ⎛⎭⎪⎫-22,22,0,A 1C →=⎝⎛⎭⎪⎫0,22,-22,CD →=BE →=(-2,0,0). 设平面A 1BC 的一个法向量n 1=(x 1,y 1,z 1),平面A 1CD 的一个法向量n 2=(x 2,y 2,z 2),平面A 1BC 与平面A 1CD 的夹角为θ,则⎩⎪⎨⎪⎧n 1·BC →=0,n 1·A 1C →=0,得⎩⎨⎧-x 1+y 1=0,y 1-z 1=0,取n 1=(1,1,1);⎩⎪⎨⎪⎧n 2·CD →=0,n 2·A 1C →=0,得⎩⎨⎧x 2=0,y 2-z 2=0,取n 2=(0,1,1),从而cos θ=|cos 〈n 1,n 2〉|=23×2=63, 即平面A 1BC 与平面A 1CD 夹角的余弦值为63.。
高中数学必修二考点知识专题讲解27---直线与平面平行的性质

高中数学必修二考点知识专题讲解(二十七)直线与平面平行的性质1.已知直线a∥平面α,直线b⊂平面α,则()A.a∥b B.a与b异面C.a与b相交D.a与b无公共点解析:选D由题意可知直线a与平面α无公共点,所以a与b平行或异面,所以两者无公共点.故选D.2.若直线l∥平面α,则过l作一组平面与α相交,记所得的交线分别为a,b,c,…,那么这些交线的位置关系为()A.都平行B.都相交且一定交于同一点C.都相交但不一定交于同一点D.都平行或交于同一点解析:选A因为直线l∥平面α,所以根据直线与平面平行的性质知l∥a,l∥b,l∥c,…,所以a∥b∥c∥….故选A.3.已知m,n为两条不同的直线,α,β为两个不同的平面,则下列结论中正确的是()A.m∥α,m∥n⇒n∥αB.m∥α,n∥α⇒m∥nC.m∥α,m⊂β,α∩β=n⇒m∥nD.m∥α,n⊂α⇒m∥n解析:选C A中,n还有可能在平面α内;B中m,n可能相交、平行、异面;由线面平行的性质定理可得C正确;D中m,n可能异面.故选C.4.在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,当BD∥平面EFGH时,下面结论正确的是()A.E,F,G,H一定是各边的中点B.G,H一定是CD,DA的中点C.BE∶EA=BF∶FC,且DH∶HA=DG∶GCD.AE∶EB=AH∶HD,且BF∶FC=DG∶GC解析:选D由于BD∥平面EFGH,所以有BD∥EH,BD∥FG,则AE∶EB=AH∶HD,且BF∶FC=DG∶GC.故选D.5.如图,已知S为四边形ABCD外一点,G,H分别为SB,BD上的点,若GH∥平面SCD,则()A.GH∥SAB.GH∥SDC.GH∥SCD.以上均有可能解析:选B因为GH∥平面SCD,GH⊂平面SBD,平面SBD∩平面SCD=SD,所以GH∥SD,显然GH与SA,SC均不平行.故选B.6.α,β,γ是三个平面,a,b是两条直线,有下面三个条件:①a∥γ,b⊂β;②a∥γ,b∥β;③a⊂γ,b∥β.命题“α∩β=a,b⊂γ,且________,则a∥b”是真命题(在横线处填写条件).解析:①中a∥γ,b⊂β,γ∩β=b,得出a∥b;③中a⊂γ,b∥β,b⊂γ,α∩β=a,β∩γ=a ,得出a ∥b .答案:①或③7.如图所示,四边形ABCD 是梯形,AB ∥CD ,且AB ∥平面α,AD ,BC 与平面α分别交于点M ,N ,且点M 是AD 的中点,AB =4,CD =6,则MN =________.解析:因为AB ∥平面α,AB ⊂平面ABCD ,平面ABCD ∩平面α=MN ,所以AB ∥MN ,又点M 是AD 的中点,所以MN 是梯形ABCD 的中位线,故MN =5.答案:58.如图,在正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上. 若EF ∥平面AB 1C ,则线段EF 的长度等于________.解析:因为EF ∥平面AB 1C ,平面AC ∩平面AB 1C =AC ,EF ⊂平面AC ,所以EF ∥AC . 又E 为AD 的中点,所以F 为DC 的中点,EF =12AC = 2.答案: 29.如图所示,已知AB ∥平面α,AC ∥BD ,且AC ,BD 与α分别相交于点C ,D .求证:AC =BD .证明:如图所示,连接CD ,因为AC ∥BD ,所以AC 与BD 确定一个平面β,又因为AB ∥α,AB ⊂β,α∩β=CD , 所以AB ∥CD .所以四边形ABDC 是平行四边形. 所以AC =BD .10.如图所示,E,F,G,H为空间四边形ABCD的边AB,BC,CD,DA上的点,且EH∥FG.求证:EH∥BD.证明:因为EH∥FG,EH⊄平面BCD,FG⊂平面BCD,所以EH∥平面BCD.又因为EH⊂平面ABD,平面ABD∩平面BCD=BD,所以EH∥BD.B级——面向全国卷高考高分练1.在梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α内的直线的位置关系只能是()A.平行B.平行或异面C.平行或相交D.异面或相交解析:选B由AB∥CD,AB⊂平面α,CD⊄平面α,得CD∥α,所以直线CD与平面α内的直线的位置关系是平行或异面.故选B.2.如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是()A.异面B.平行C.相交D.以上均有可能解析:选B因为A1B1∥AB,AB⊂平面ABC,A1B1⊄平面ABC,所以A1B1∥平面ABC.又A1B1⊂平面A1B1ED,平面A1B1ED∩平面ABC=DE,所以DE∥A1B1.又AB∥A 1B 1,所以DE ∥AB .故选B.3.如图,已知四棱锥P -ABCD 的底面是平行四边形,AC 交BD 于点O ,E 为AD 中点,F 在P A 上,AP =λAF ,PC ∥平面BEF ,则λ的值为( )A .1 B.32 C .2D .3解析:选D 设AO 交BE 于点G ,连接FG (图略). 因为O ,E 分别是BD ,AD 的中点,所以AG AO =23,AG AC =13. 因为PC ∥平面BEF ,平面BEF ∩平面P AC =GF ,所以GF ∥PC ,所以AFAP =AG AC =13,即λ=3.故选D.4.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,点P 是面AA 1D 1D 的中心,点Q 是面A 1B 1C 1D 1的对角线B 1D 1上一点,且PQ ∥平面AA 1B 1B ,则线段PQ 的长为( )A.22B.32 C .1D. 2解析:选A 如图,连接AD 1,AB 1, ∵PQ ∥平面AA 1B 1B ,平面AB 1D 1∩平面AA 1B 1B =AB 1,PQ ⊂平面AB 1D 1, ∴PQ ∥AB 1,∴PQ =12AB 1=1212+12=22.故选A.5.如图所示,已知A ,B ,C ,D 四点不共面,且AB ∥α,CD ∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG的形状是______.解析:平面ADC∩α=EF,且CD∥α,得EF∥CD;同理可证GH∥CD,EG∥AB,FH∥A B.所以GH∥EF,EG∥FH.所以四边形EFGH是平行四边形.答案:平行四边形6.直线a∥平面α,α内有n条直线交于一点,则这n条直线中与直线a平行的直线有________条.解析:过直线a与交点作平面β,设平面β与α交于直线b,则a∥b,若所给n 条直线中有1条是与b重合的,则此直线与直线a平行,若没有与b重合的,则与直线a平行的直线有0条.答案:0或17.如图所示的直三棱柱ABC-A1B1C1中,如何作出过点A1,B,C1的平面与平面ABC的交线?并说明理由.解:在平面ABC中,过点B作直线l,使l∥AC,则l即为平面BA1C1与平面ABC 的交线.证明如下:在三棱柱ABC-A1B1C1中,A1C1∥AC,AC⊂平面ABC,A1C1⊄平面ABC,所以A1C1∥平面ABC.又A1C1⊂平面A1BC1,平面A1BC1∩平面ABC=l,所以A1C1∥l.又因为直线l过点B,且l⊂平面ABC.根据线面平行的性质定理,l 即为所求.C 级——拓展探索性题目应用练如图,在三棱柱ABC -A 1B 1C 1中,点E ,F 分别是棱CC 1,BB 1上的点,点M 是线段AC 上的动点,EC =2FB =2,若MB ∥平面AEF ,试判断点M 在何位置.解:若MB ∥平面AEF ,如图过F ,B ,M 作平面FBMN 交AE于N ,连接MN ,NF .因为BF ∥平面AA 1C 1C ,BF ⊂平面FBMN ,平面FBMN ∩平面AA 1C 1C =MN ,所以BF ∥MN .又MB ∥平面AEF ,MB ⊂平面FBMN ,平面FBMN ∩平面AEF =FN ,所以MB ∥FN ,所以BFNM 是平行四边形, 所以MN ∥BF ,MN =BF =1. 而EC ∥FB ,EC =2FB =2, 所以MN ∥EC ,MN =12EC =1, 故MN 是△ACE 的中位线.所以当M 是AC 的中点时,MB ∥平面AEF .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线与平面、平面与平面平行的性质
【知识梳理】
1.线面平行的性质定理
(1)文字语言:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. (2)图形语言:
(3)符号语言:
⎭
⎪⎬⎪⎫a ∥αa ⊂βα∩β=b ⇒a ∥b
(4)作用:线面平行⇒线线平行.
2.面面平行的性质定理
(1)文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
(2)图形语言:
(3)符号语言:
⎭
⎪⎬⎪⎫α∥βα∩γ=a β∩γ=b ⇒a ∥b
(4)作用:面面平行⇒线线平行.
【常考题型】
题型一、线面平行的性质及应用
【例1】 如图所示,已知三棱锥A —BCD 被一平面所截,截面为▱EFGH ,求证:CD ∥平面EFGH .
[证明]∵EFGH为平行四边形,∴EF∥GH.
又GH⊂平面BCD,EF⊄平面BCD,
∴EF∥平面BCD.
而平面ACD∩平面BCD=CD,EF⊂平面ACD,
∴EF∥CD.
又EF⊂平面EFGH,CD⊄平面EFGH,
∴CD∥平面EFGH.
【类题通法】
运用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与平面相交的交线,然后确定线线平行.证题过程应认真领悟线线平行与线面平行的相互转化关系.【对点训练】
1.求证:如果一条线和两个相交平面都平行,那么这条直线和它们的交线平行.
已知:α∩β=l,a∥α,a∥β,求证:a∥l.
证明:如图,过a作平面γ交α于b.
∵a∥α,∴a∥b.过a作平面ε交平面β于c.∵a∥β,
∴a∥c,∴b∥c.
又b⊄β且c⊂β,∴b∥β.
又平面α过b交β于l,∴b∥l.
∵a∥b,∴a∥l.
题型二、面面平行的性质及应用
【例2】如图所示,两条异面直线BA,DC与两平行平面α,β分别
交于B,A和D,C,M,N分别是AB,CD的中点.求证:MN∥平面α.
[证明]过A作AE∥CD交平面α于点E,取AE的中点P,
连接MP,PN,BE,ED,AC.
∵AE∥CD,∴AE,CD确定平面AEDC.
则平面AEDC∩α=DE,平面AEDC∩β=AC.
∵α∥β,∴AC∥DE.
又∵P,N分别为AE,CD的中点,
∴PN∥DE.∵PN⊄α,DE⊂α,∴PN∥α.
又∵M,P分别为AB,AE的中点,
∴MP∥BE.又∵MP⊄α,BE⊂α,
∴MP∥α.∵MP,PN⊂平面MPN,且MP∩PN=P,
∴平面MPN∥α.
又∵MN⊂平面MPN,∴MN∥α.
【类题通法】
1.把握面面平行性质定理的关键
(1)成立的条件:两平面平行,第三个平面与这两个平面均相交.
(2)定理的实质:面面平行⇒线线平行,体现了转化思想与判定定理交替使用,可实现线面、线线、面面平行间的相互转化.
2.面面平行的性质定理的几个推论
(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.
(2)夹在两平行平面间的平行线段相等.
(3)经过平面外的一点有且只有一个平面与已知平面平行.
(4)两条直线被三个平行平面所截,截得的对应线段成比例.
【对点训练】
2.如图所示,在矩形ABCD 中,AB =2BC =2a ,E 为AB 上一点,将
B 点沿线段E
C 折起至点P ,连接P A 、PC 、P
D ,取PD 中点F ,若有AF
∥平面PEC ,试确定E 点的位置.
解:取PC 的中点G ,连接GE ,GF .如右图.
由条件知GF ∥CD ,
EA ∥CD ,∴GF ∥EA ,则G ,E ,A ,F 四点共面.
∵AF ∥平面PEC ,
平面GEAF ∩平面PEC =GE ,
∴AF ∥GE .∴四边形GEAF 为平行四边形.
∵GF =12CD ,∴EA =12CD =12
BA , ∴E 为AB 的中点.
题型三、线面平行和面面平行的综合问题
【例3】 在正方体ABCD -A 1B 1C 1D 1中,如图.
(1)求证:平面AB 1D 1∥平面C 1BD ;
(2)试找出体对角线A 1C 与平面AB 1D 1和平面C 1BD 的交点E ,F ,
并证明:A 1E =EF =FC .
[解] 证明:(1)因为在正方体ABCD -A 1B 1C 1D 1中,AD 綊B 1C 1,
所以四边形AB 1C 1D 是平行四边形,所以AB 1∥C 1D .
又因为C 1D ⊂平面C 1BD ,AB 1⊄平面C 1BD .
所以AB 1∥平面C 1BD .
同理B1D1∥平面C1BD.
又因为AB1∩B1D1=B1,AB1⊂平面AB1D1,B1D1⊂平面AB1D1,
所以平面AB1D1∥平面C1BD.
(2)如图,连接A1C1交B1D1于点O1,连接AO1与A1C交于点E.
又因为AO1⊂平面AB1D1,所以点E也在平面AB1D1内,
所以点E就是A1C与平面AB1D1的交点;
连接AC交BD于O,连接C1O与A1C交于点F,则点F就是A1C与平面C1BD的交点.下面证明A1E=EF=FC.
因为平面A1C1C∩平面AB1D1=EO1,
平面A1C1C∩平面C1BD=C1F,
平面AB1D1∥平面C1BD,所以EO1∥C1F.
在△A1C1F中,O1是A1C1的中点,所以E是A1F的中点,
即A1E=EF;
同理可证OF∥AE,所以F是CE的中点,
即CF=FE,
所以A1E=EF=FC.
【类题通法】
1.在遇到线面平行时,常需作出过已知直线与已知平面相交的辅助平面,以便运用线面平行的性质.
2.要灵活应用线线平行、线面平行和面面平行的相互联系、相互转化.在解决立体几何中的平行问题时,一般都要用到平行关系的转化.转化思想是解决这类问题的最有效的方法.【对点训练】
3.如图,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,E ,F ,P ,Q 分别
是BC ,C 1D 1,AD 1,BD 的中点.
(1)求证:PQ ∥平面DCC 1D 1;
(2)求PQ 的长;
(3)求证:EF ∥平面BB 1D 1D .
解:(1)证明:如图所示.
连接AC ,CD 1,
∵P ,Q 分别是AD 1,AC 的中点,
∴PQ ∥CD 1.又PQ ⊄平面DCC 1D 1,
CD 1⊂平面DCC 1D 1,
∴PQ ∥平面DCC 1D 1.
(2)由(1)易知PQ =12D 1C =22
a . (3)证明:取B 1C 1的中点E 1,连接EE 1,FE 1,则有FE 1∥B 1D 1,EE 1∥BB 1,∴平面EE 1F ∥平面BB 1D 1D .
又EF ⊂平面EE 1F ,所以EF ∥平面BB 1D 1D .
【练习反馈】
1.梯形ABCD 中,AB ∥CD ,AB ⊂平面α,CD ⊄平面α,则直线CD 与平面α内的直线的位置关系只能是( )
A .平行
B .平行或异面
C .平行或相交
D .异面或相交
解析:选B 由题意,CD ∥α,则平面α内的直线与CD 可能平行,也可能异面.
2.如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN
∥平面P AD,则()
A.MN∥PD
B.MN∥P A
C.MN∥AD
D.以上均有可能
解析:选B∵MN∥平面P AD,平面P AC∩平面P AD=P A,MN⊂平面P AC,∴MN∥P A.
3.过正方体ABCD-A1B1C1D1的顶点A1,C1,B的平面与底面ABCD所在的平面的交线为l,则l与A1C1的位置关系是________.
解析:由于平面ABCD∥平面A1B1C1D1,平面A1B1C1D1∩平面A1C1B=A1C1,平面ABCD∩平面A1C1B=l,所以l∥A1C1.
答案:平行
4.如图所示,平面四边形ABCD所在的平面与平面α平行,且四边
形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形,则四边
形ABCD的形状一定是________.
解析:由平行投影的定义,AA1∥BB1,而ABCD所在面与面α平行,
则AB∥A1B1,且四边形ABB1A1为平行四边形;同理四边形CC1D1D为平行四边形.∴AB綊CD,从而四边形ABCD为平行四边形.
答案:平行四边形
5.如图所示,P为▱ABCD所在平面外一点,点M,N分别为AB,PC
的中点,平面P AD∩平面PBC=l.
(1)求证:BC∥l;
(2)MN与平面P AD是否平行?证明你的结论.
解:(1)证明:因为四边形ABCD是平行四边形,所以BC∥AD.又因AD⊂平面P AD,BC⊄平面P AD,所以BC∥平面P AD.又因为平面PBC∩平面P AD=l,BC⊂平面PBC,所以BC∥l.
(2)MN∥平面P AD.证明如下:如图所示,取PD的中点E,连接NE,
AE ,所以NE ∥CD ,NE =12
CD . 而CD 綊AB ,M 为AB 中点,所以NE ∥AM ,NE =AM ,所以四边形MNEA 是平行四边形,所以MN ∥AE .又AE ⊂平面P AD ,MN ⊄平面P AD ,所以MN ∥平面P AD .。
