次态卡诺图在时序逻辑电路分析和设计中的运用
时序电路的基本分析与设计方法

时序电路的基本分析与设计方法时序逻辑电路时序逻辑电路——电路任何一个时刻的输出状态不仅取决于当时的输入信号,还与电路的原状态有关。
时序电路中务必含有具有经历能力的存储器件。
时序电路的逻辑功能可用逻辑表达式、状态表、卡诺图、状态图、时序图与逻辑图6种方式表示,这些表示方法在本质上是相同的,能够互相转换。
一、时序电路的基本分析与设计方法 (一)分析步骤1.根据给定的时序电路图写出下列各逻辑方程式: (1)各触发器的时钟方程。
(2)时序电路的输出方程。
(3)各触发器的驱动方程。
2.将驱动方程代入相应触发器的特性方程,求得各触发器的次态方程,也就是时序逻辑电路的状态方程。
3.根据状态方程与输出方程,列出该时序电路的状态表,画出状态图或者时序图。
4.根据电路的状态表或者状态图说明给定时序逻辑电路的逻辑功能。
【例1】分析时序电路(1)时钟方程:CP CP CP CP ===012输出方程:nnQ Q Y 21=驱动方程:⎪⎩⎪⎨⎧======n n n nnn Q K Q J Q K Q J Q K Q J 202001011212(2)求状态方程JK 触发器的特性方程:n n n Q K Q J Q+=+1将各触发器的驱动方程代入,即得电路的状态方程:⎪⎩⎪⎨⎧=+=+==+=+==+=+=+++n n n n n n n n n n n n n n n n n nn n n n n n Q Q Q Q Q Q K Q J Q Q Q Q Q Q Q K Q J Q Q Q Q Q Q Q K Q J Q 202020000100101011111112121222212(3)计算、列状态表nn nn nn n n Q Q Y Q Q Q Q Q Q 21210011112=⎪⎩⎪⎨⎧===+++(4)画状态图及时序图(5)逻辑功能有效循环的6个状态分别是0~5这6个十进制数字的格雷码,同时在时钟脉冲CP 的作用下,这6个状态是按递增规律变化的,即:000→001→011→111→110→100→000→…因此这是一个用格雷码表示的六进制同步加法计数器。
时序逻辑电路的自启动设计
图化简得到最简单的形式:
Q1n+1 = Q3 Q2n+1 = Q1
Q3n+1 = Q2
Q3Q2Q1的无效状 态000、011、101 、110、111分别 带入,得到如下图 中的实线链连接的
状态转换图。
显然设计的电路不能自启动
为保持移位寄存器内部结构不变,只允许修改第一位触发器的 输入。所以修改Q1,
Q1n+1 = Q2 Q3 Q2n+1 = Q1 + Q2 Q3 Q3n+1 = Q2,
修改后的电路状态转换图如下:
例2 设计一个能自启动的3位环形计数器。要求它的有效循环状态为 100010 001 100
解:根据题目要求的状态循环,电路的状态转换图和次态卡诺图如图:
如只考虑使状态方程图化简方案的 方法使电路具有自启动功能。
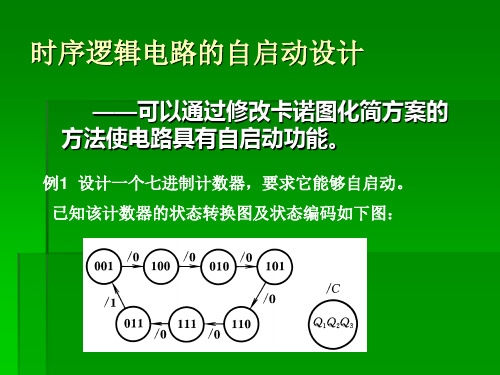
例1 设计一个七进制计数器,要求它能够自启动。 已知该计数器的状态转换图及状态编码如下图:
根据状态转换图,可以得到:
按照卡诺图化简的最简 要求可得到方程:
Q1n+1 = Q2 Q3 Q2n+1 = Q1 Q3n+1 = Q2
得到修改后的次态卡诺图如下:
修改后的状态方程如:
Q1n+1 = Q1 Q2 Q2n+1 = Q1 Q3n+1 = Q2
若选用D触发器构造此计数器,驱动方程为: D1 = Q1n+1 = Q1 Q2 = Q1 + Q2 D2 = Q2n+1 = Q1 D3 = Q3n+1 = Q2
逻辑图如下:
实际上,包括在圈里的任意项取为1,而在圈外的任意项取 为0。即无效状态的次态已被指定。
若这个指定的次态属于有效循环中的状态,电路可以自启 动;反之则不可以自启动。
次态卡诺图在时序逻辑电路自启动设计中的应用

( Ph y s i c s De p a r t me n t o f B a o j i Co l l e g e o f Ar t s a n d S c i e n c e s ,Ba o j i 7 2 1 0 1 6,Ch i n a )
问题 , 修 改 次态卡 诺 图 , 为 次 态卡 诺 图 中的无 效状 态指 定 次 态, 指 定 的次 态属 于有 效循 环状 态。利 用该 方
法 实 现 了逻 辑 电路 的 自启 动 。
关键 词 : 卡诺 图; 自启 动 ; 无 效循 环 ; 时 序 逻 辑 电 路
中 图分类 号 : TN 7 9 文 献标 志码 : B
a nd Sys t e ms , 2 0 05, 15 6( 2): 20 8 — 2 25 .
在 时序逻 辑 分 析设 计 和 电 子 技术 教 学 活 动 中 , 时序 逻辑 电路 的 自启 动 是 经 常 遇 到 的 一 个 实 际 问 题, 而且 是数 字 电子 技术 基 础 教 学 中的 重 点 和难 点
态, 从 而 实 现 自启 动 。
1 电路 不 能 自启 动 的原 因
p r o b l e ms .Mo d i f y t h e n e x t s t a t e Ka r n a u g h ma p f o r n e x t s t a t e Ka r n a u g h ma p i n t h e i n v a l i d s t a t e d e s i g n a t e d o f s e c o n d a r y
Ab s t r a c t : I n t h e d e s i g n p r o c e s s o f s e q u e n t i a l l o g i c c i r c u i t ,t h e c i r c u i t i s t h e k e y p a r t o f t h e d i g i t a l e l e c t r o n i c t e c h n o l o g y
联合卡诺图在时序逻辑电路设计中的应用

驱动函数的确定
n Q0 +1 = Q3Q2.Q0
Qn+1 = Q0Q1 + Q0Q 1 1
n Q3 +1 = Q2QQ0 Q3 + Q2Q3 1
n Q2 +1 = QQ0 Q2 + Q3QQ0.Q3 1 1
设计步骤
(1)逻辑抽象,得出描述对象过程的原始状态转换; 逻辑抽象,得出描述对象过程的原始状态转换; (2)状态化简; 状态化简; (3)状态赋值,也叫状态编码; 状态赋值,也叫状态编码; (4)作出次态联合卡诺图; 作出次态联合卡诺图; (5)确定触发器,直接用次态联合卡诺图得出最简次 确定触发器, 态函数,在化简的过程中同时考虑自启动的问题; 态函数,在化简的过程中同时考虑自启动的问题; (6)将次态函数与触发器的特性方程相比较,确定各 将次态函数与触发器的特性方程相比较, 触发器的驱动函数; 触发器的驱动函数; (7)根据输出要求确定输出函数; 根据输出要求确定输出函数; (8)画出逻辑电路。 画出逻辑电路。
卡诺图的属性
●卡诺图是二维真值表。 卡诺图是二维真值表。 ●卡诺图可以用来描述任何逻辑电 既可以描述组合逻辑电路, 路,既可以描述组合逻辑电路, 又可以描述时序电路。 又可以描述时序电路。
次态联合卡诺图的结构
●次态联合卡诺图是二维状态转换表。 次态联合卡诺图是二维状态转换表。 ●次态联合卡诺图是表格式的状态转换图。 次态联合卡诺图是表格式的状态转换图。
1 同步时序逻辑电路的联合卡诺图设计法 1.1 设计方法
时序逻辑电路经典的设计方法, 时序逻辑电路经典的设计方法,或者是根据 驱动表确定的驱动函数卡诺图得出最简驱动 函数, 函数,或者是根据分列的次态函数卡诺图确 定最简次态函数, 定最简次态函数,再与触发器的特性方程相 比较,得出最简驱动函数。 比较,得出最简驱动函数。 联合卡诺图设计法与经典的设计步骤完全相 同,其不同点是直接根据联合次态卡诺图确 定最简次态函数。 定最简次态函数。
卡诺图在数字电路分析和设计中的应用

卡诺图在数字电路分析和设计中的应用数字电路是高科技产业中的关键技术,卡诺图是一种模型可以用来分析和设计数字电路的工具。
一般来说,理解数字电路的复杂结构要求精心的设计和分析,这一专业的技术可以帮助工程师在有限的时间内降低工程的问题复杂程度。
卡诺图是一种用于描述逻辑回路的图形化方法,主要用于便捷地描述数字逻辑系统中的组件模型和关系。
它由许多模型元素组成,可以很容易地表达电路的抽象模型,并使整个系统的结构清晰可见。
卡诺图的主要组成部分有:结点、线条和标记。
结点可以用来表示输出信号或输入信号,线条用来连接结点,绘制出连接信号和表达式,而标记则用来描述逻辑运算方式。
卡诺图的优势在于,它可以清晰地表达复杂的逻辑结构,而且不需要写出许多复杂的表达式就可以准确地描述电路,从而简化了分析和设计的工作量。
卡诺图最初由EDVAC(电子数据处理计算机)的构建者John von Neumann提出,并由Edward F. Codd在1952年的一篇论文中发表了详细的说明。
在此后的几十年中,卡诺图在电路分析和设计中广泛使用。
据不完全统计,截止到2019年,有超过三千万的数字电路技术利用卡诺图来分析和设计。
在卡诺图应用于数字电路分析和设计中,它可以用来完成很多步骤,比如从软件层面分析电路,指出设计中可能出现的漏洞,以及构建和模拟不同的电路架构,等等。
使用卡诺图可以准确地表达数字电路,以确保设计正确性。
此外,它还可以检查电路中可能出现的更多问题,比如检查电路是否能够满足特定的性能要求,检查电路的可靠性,判断电路的功耗,甚至可以用来识别和防止设计错误。
同时,卡诺图还可以用来降低设计成本和简化流程,例如卡诺图可以帮助工程师快速分析和搭建电路,从而节省大量的时间和工作量。
而且,由于它可以完整表达电路结构,可以让工程师有更多的机会和空间进行实验和修正,从而提高整个电路设计的质量。
卡诺图在数字电路分析和设计中的应用无处不在。
它的优势在于可以极大地提高数字电路设计的效率,并使分析和设计变得更加简单。
卡诺图在数字电路分析和设计中的应用

卡诺图在数字电路分析和设计中的应用
摘要:卡诺图是计算机科学中的一种计算技术,可用于数字电路分析和设计。
本文旨在阐述卡诺图在电路分析和设计中的应用。
首先,文章介绍了卡诺图的基本概念和基本原理,然后对其主要应用进行详细介绍,包括模拟电路分析、组合电路分析、时间延迟测量等。
总结来说,卡诺图在数字电路分析和设计中有着重要的应用。
关键词:卡诺图;电路分析;数字电路;时间延迟
1.言
着计算机科学的发展,卡诺图作为一种快速分析复杂电路的有效技术,被广泛应用到计算机技术领域中,其在数字电路分析和设计中有重要意义。
本文将深入介绍卡诺图在数字电路分析和设计中的应用。
2.诺图的基本概念和基本原理
诺图是一种使用节点和支路来绘制电路图的灵活方法,它由卡诺Niklas1945年提出,是一种连续系统和电路分析的表达方式。
卡诺
图的主要优点是可以将复杂的电路表示为简单的图形,从而可以更容易地理解和分析电路结构,以及更加便捷地操纵其中的参数。
3.诺图的应用
诺图的主要应用有模拟电路分析、组合电路分析等,其中模拟电路分析用于求解两个或多个节点之间的电压,组合电路分析用于求解节点之间的电流。
此外,还可以利用卡诺图进行时间延迟测量,并可以在电路中发现和诊断故障。
4.论
上所述,卡诺图是一种能够快速分析复杂电路的有效技术,可以用于数字电路分析和设计中,这些分析方法可以用来求解节点之间的电压、电流、甚至时间延迟等参数,这对于识别并定位故障也很有帮助。
总之,卡诺图在数字电路分析和设计中有着重要的应用意义。
卡诺图在数字电路分析和设计中的应用

卡诺图在数字电路分析和设计中的应用
最近,随着计算机科学和技术的发展,数字电路分析和设计成为一项十分重要的任务。
在这项任务中,卡诺图技术作为一种强大的工具在应用中现已受到越来越多的关注。
卡诺图可以被用来快速分析和设计数字电路。
此外,它还可以用来解决复杂的数字电路问题。
首先,卡诺图是一种强大的数字电路分析和设计工具。
它可以帮助计算机科学家们快速分析数字电路并对其进行设计,从而提高计算机知识的效率。
此外,卡诺图还可以被用来检查数字电路设计时的错误,在检查完成之后,可以便捷地修正错误。
此外,卡诺图在多层电路中也有着重要的应用,尤其是在大规模集成电路(IC)设计方面十分有用。
此外,卡诺图技术还可以被用来快速解决复杂的数字电路问题。
它可以被用来模拟计算机的行为,对控制程序的可靠性提供可靠的指导,它可以被用来识别任务的主要功能,从而提供适当的设计方案。
此外,卡诺图还可以帮助计算机科学家们快速识别数字电路中的故障,从而可以有效地进行修复。
总之,卡诺图技术是一种强大的工具,可以帮助科学家们快速分析和设计数字电路,解决复杂的数字电路问题,以及帮助计算机科学家们发现数字电路中的故障,从而确保数字电路的正确性和安全性。
因此,卡诺图在数字电路分析和设计中已被广泛应用,并可能会给计算机科学带来更多新的突破。
- 1 -。
使用卡诺图的技巧

使用卡诺图的技巧摘要:卡诺图是一种常用于简化逻辑表达式和优化电路的工具。
它通过比较不同的组合输入和输出值,帮助我们找到最小化逻辑电路所需要的最简化表达式。
本文将介绍一些使用卡诺图的技巧,包括如何使用它来快速找到最简逻辑表达式、使用简化的布尔代数来简化电路等内容。
关键词:卡诺图、逻辑表达式、电路、布尔代数、优化正文:卡诺图是一种非常有用的工具,尤其是在电路设计和逻辑优化的过程中。
它的本质原理是比较不同输入和输出组合,以此来确定最小化逻辑电路所需要的最简化表达式。
下面介绍一些利用卡诺图的技巧:1. 确定卡诺图大小当我们需要使用卡诺图来简化逻辑表达式时,首先需要确定卡诺图的大小。
卡诺图的大小通常取决于所涉及的变量的数量。
计算出变量的数量后,我们可以使用下表来确定卡诺图的大小:变量(数目) | 卡诺图大小--------------|-------------1 | 2x12 | 2x23 | 4x44 | 4x45 | 8x86 | 8x87 | 8x88 | 8x82. 组织卡诺图一旦我们知道了卡诺图的大小,接下来的步骤就是将逻辑表达式中的每个变量映射到卡诺图中的一个格子上。
这样做的时候,可以采用灵活的方法,比如按字典顺序排列或按变量重要性对格子进行排序。
3. 找到主项和独立项在卡诺图中找到主项或者独立项,是确定最简逻辑表达式所必需的步骤。
主项代表着其输入变量的组合可以覆盖整个逻辑表达式中的输出。
独立项表示在逻辑表达式中单独出现的变量,可以使用这些项来表示逻辑表达式中的重复项。
4. 简化布尔代数卡诺图可以帮助我们简化布尔代数。
布尔代数也是一种常用于逻辑电路的表达式,通常包括AND、OR和NOT这些运算符。
卡诺图可以将不同的逻辑表达式映射到一个单一的布尔表达式,并消除其中的冗余项。
总之,卡诺图是一种非常有用的工具。
通过使用它,我们可以快速找到最简逻辑表达式和优化电路,以及简化布尔代数表达式。
在电路设计和逻辑优化中,熟练掌握卡诺图的技巧将是一个非常有用的技能。
卡诺图在数字电路分析和设计中的应用

卡诺图在数字电路分析和设计中的应用数字电路是现代计算机,称为最重要的组成部分,也是计算机领域最为广泛的技术和研究领域之一。
数字电路的分析和设计涉及到一系列的技术,例如电路分析、模拟数字电路、硬件电路设计、控制结构设计、系统调试等。
而卡诺图正是在这一系列研究手段中扮演着十分重要的作用。
卡诺图是一种形式化的图形化语言,在数字电路分析和设计中被用作代码编写和测试程序,可以将电路建模为一个可视化的形式,以更好地研究电路模型。
此外,卡诺图还可以用来分析正常电路和故障电路,以及进行电路模拟和仿真,由此可以有效地将数字电路简化成一个易于理解的模型。
首先,可以使用卡诺图来编写和调试代码。
数字电路分析和设计需要编写复杂的代码,而卡诺图可以让用户将复杂的代码表示为一幅图形。
操作者可以更容易地检查和调试代码,便于发现程序中的错误。
此外,卡诺图还可以用来分析正常电路和故障电路。
卡诺图可以描述一系列的逻辑表达式,而这些表达式可以通过模拟和仿真环境来测试和分析。
因此,卡诺图可以帮助分析师在正常电路和故障电路中分析电路,以了解其运作原理。
另外,卡诺图还可以用于硬件电路设计。
电路设计师可以使用卡诺图来描述电路,并在仿真环境中测试和调试设计。
此外,卡诺图还可以用于硬件系统的控制结构设计,帮助硬件设计师更好地实现其系统模型。
最后,卡诺图可以用于系统调试。
系统调试主要是检查系统中的软件模块,并在故障发生时定位问题,以便及早发现并修复问题。
数字电路分析和设计中的系统调试也可以使用卡诺图,可以有效地检查和修复系统中的故障。
因此,卡诺图在数字电路分析和设计中扮演着重要的角色,可以帮助用户编写代码、分析正常电路和故障电路、仿真电路模型、以及进行系统调试。
因此,卡诺图在数字电路分析和设计中越来越受到重视,越来越多的电路分析师和设计师都在使用卡诺图来解决问题,以更好地研究数字电路。
次态卡诺图在时序逻辑电路中的应用

V 1 6, . o . No 2
Jn 2 0 u .。0 6
文 章 编 号 :6 1 44 (0 6 0 0 7 — 3 17 — 6 4 20 )2— 0 1 0
次 态 卡 诺 图在 时序 逻 辑 电路 中 的应 用
吴 恒 玉 , 民 丽 唐
( 南软件 职 业技 术 学 院 信 息管理 系, 南 琼海 海 海
态 卡诺 图 , 中 Q = 其 ! 0部分 , 即编 号为 0 14、 、、 5的小 格 部分 表示 ; ! 部 分 , Q =1 即编 号 为 2、、 、 3 67的小
格部分表示 , 若把这一部分各 小格 的值取 反, 即表
示 。
1 触发器 的状态 控 制 方程 、 状态 方程 在 卡 诺 图上 的 表 示
=
T触发 器的特 性 方程 为 “ =
+
=
Q “I 0 9 = Q “I = 0 p
() 2 () 3
①Q , 将此式两边 同时异或 Q , ?可得状态控制方 程为: Q ①Q “
= =
=
¨l 0+ ¨I 1 Q 一 Q 一
( 又称驱动 方 程 、 励 方 程 ) 次态 卡 诺 图上 的表 示 激 在
方法。 1 1 J 触发 器 . K
式 ( ) 明 , , Q “ 的卡 诺 图相 同。 4表 D和
1 3 T触发 器 .
由 J 触 发 器 的 特性 方 程 Q “ = Q , K + Q ¨ 可得状 态 控制 方 程为 : 刮
有 m个输 入变 量 、 X , n个触 发 器 ( XA 由 其 现态 为 Q 、 !AQ ) 成 的 时 序 逻 辑 电路 , 个 触 Q 、 :构 各 发 器的状 态方 程 , 即次 态 方 程 均 可表 示 成 如 下 的 函 数形 式 :
浅谈卡诺图在数字电路学习中的应用

0 0
O 1
l 1 1 O
O ’ —
l 7
8 — l 5
1÷ _
+6 一
9— ÷I 4 _1
2 —
+ 一5
1 O— +_ 3 -l
3 上
十4 一
1 1 +. 2 _1
值 进 行取 反运 算 ,即 “ ”变 为 “ ” “ ”变 为 “ ” 0 1、 1 0 ,便得 到该 函
字 逻 辑 电路 中的应 用 ,体现 了卡诺 图的实用 性 。系 统地 掌握 卡 诺 图 的应用 可 以使 学 习者在 学 习过程 中达 到事 半 功倍 的效 果 。 二 、卡 诺图 在数 字 电路 中的应 用 ( )卡诺 图用 于记忆 格 雷码 一 格 雷码( ry oe,是一 种无 权码 ,广泛 应用 于数 字 系统 中 。 G a d) c
0
1 2 3 4
O
0 0 0 0
0
O O O 1
摘要 :在 数 字 电路 中 ,卡诺 图是 表 示逻辑 关 系的 一种 几何 图形 ,主要 用在 对逻 辑 函数 的化 简上 。本 文是 在传 统使 用 方 法 的基础 上介 绍 了卡 诺 图的几 点灵 活运 用 。 关键 词 :卡 诺 图 ;数 字 电路 ;应 用
中图分类号 :T 9 文献标识码 :A 文章编号:10 — 59(02 0— 0 1 0 N7 1 07 99 2 1) 9 06 - 2
数 反 函数 的卡 诺 图 。
图 1 格雷 码 的卡 诺 图表示 方法 表 1 格 雷码 的编 码表 格雷码
十进 制 数
A B C D
卡诺图在数字电路分析和设计中的应用

卡诺图在数字电路分析和设计中的应用卡诺图是一种用于分析和设计数字电路的图形工具。
在过去的几十年中,它已广泛应用于电路设计和分析,并被认为是一种简单而有效的信号流分析工具。
与标准的逻辑图相比,卡诺图可以表现出一种更清晰的信号流结构,有助于快速确定系统行为,从而简化设计过程。
这一点尤其重要,因为数字电路有着复杂的建模和设计过程,经常需要多次迭代才能得到最终的设计结果。
卡诺图可以帮助设计人员快速捕捉特定电路的特性,并确定其行为。
这通常是通过构建复杂的电路网络来实现的,然后使用卡诺图作为分析工具对电路的非线性行为进行分析,以确定每个信号的行为,以及各个信号之间的关系。
此外,还可以使用卡诺图进行建模,以确定某些信号结构的状态,例如时序问题,以及表示这些信号的信号的极限值。
此外,卡诺图还可以用于调试数字电路,以确定系统中可能存在的潜在问题。
这包括检测系统中可能存在的逻辑问题,以及追踪某些信号的行为和变化。
使用卡诺图进行调试也可以帮助设计师快速发现可能发生故障的状态,以及定位和修复故障的部分。
卡诺图也可以用来绘制数字电路,以及创建输入/输出表以及数据流图。
这些图形可以清晰地表示出系统的行为,并可以帮助设计师快速找出问题,调整设计,并最终完成系统的设计。
可以说,卡诺图是一种重要的工具,可以帮助设计师在进行数字电路分析和设计时降低分析和设计的复杂度。
它可以帮助设计师可视化地捕捉电路的特性,并有助于快速定位和解决设计问题。
此外,卡诺图还可以帮助设计师追踪信号的行为,帮助他们调试系统,构建数字电路,以及创建图形化输入/输出表和数据流图。
因此,可以断言,卡诺图在数字电路分析和设计中大有裨益,将继续发挥其重要作用。
卡诺图在逻辑电路分析与设计中的巧用

r
O
I
图 6次态卡诺图 ( 3 ) 作状态转换 图
图 4实现 y ; A 曰 + A C + B C的组合电路 4 利用卡诺图分析时序逻辑 电路 对于时序逻辑 电路 的分析,其传统作法是: 写
根 据次 态卡 诺图中Q : Q ? Q : 对于的 状 态转 换 作
-
只限于用来化简逻辑函数, 在逻辑 电路的分析和设 计中占有重要的地位, 因此 , 在教学过程中, 要打破
个 实现 逻 辑 函 数 Y = A B + AC + B C的组 合 电路 .用卡
卡诺 图法是最简便和最直观 的方法.
判断方法: 凡是卡诺 图中存在相切而不相交的 卡诺圈, 则该逻辑 电路存在着竞争 冒险 , 所谓卡诺 圈相切是指两个 卡诺圈之间存在 不被 同一卡诺圈
包含 的相邻最 小项 . 消 除 方法 : 消 除 卡 诺 图 中相 切 的卡 诺 圈 , 破 坏 卡 诺 圈 的单独 相 切 性. 具 体做 法 是加 上 一个 与 两 相 切 卡诺 圈相 交的 一个 卡诺 圈.
图 7状 态转换 图
一
( 4 ) 分析逻辑功能 ‘ 由图 7所示 的状 态转 换 图可 以看 出 , 该 电路是 个可 自启 动 的同步 五进 制计 数器 . 通过以上案例分析可 以看 出, 卡诺图的用途不
图 5时 序 逻 辑 电路
5结 束语
( 1 ) 写方程式
输出 方程为 y = Q : 驱动方程为 J o : 一 Q  ̄
时, 传统的代数法需要对逻辑 函数进行变换或对逻 辑表达式进行类 比, 因此 , 需要娴熟 的表达式变换
技巧 , 过程繁琐 , 且不直观 , 容 易 出错 . 如 果采 用 卡
卡诺图在《数字电子技术》中的应用

卡诺图在《数字电子技术》中的应用摘要:卡诺图通常是在化简逻辑函数时引入的,并且大多只介绍如何使用卡诺图化简逻辑函数,其实卡诺图在数字电子技术中还有很多不同的用途,灵活运用卡诺图,可以达到事半功倍的效果。
关键词:数字电子技术;卡诺图;逻辑函数卡诺图是1953年美国贝尔实验室的电信工程师Maurice Karnaugh在维奇图的基础上提出的一种用于化简逻辑函数的方法[1]。
在学习了卡诺图的化简之后,后续章节或多或少都应用到了卡诺图,但这些应用相对较为分散,缺少概括总结。
本文将介绍卡诺图在数字电子技术中的一些应用,使学生对卡诺图的使用融会贯通,达到事半功倍的效果。
一、卡诺图在逻辑函数运算中的应用用卡诺图可以直观快速求出逻辑函数的与、或、非、异或、同或等逻辑运算的结果[2]。
当两个函数进行与运算时,只要画出两个函数的卡诺图,再将两个函数卡诺图中对应的方格相与(同为1填1,其他填0),便得到这两个函数相与的卡诺图当两个函数进行或运算时,只要画出两个函数的卡诺图,再将两个函数卡诺图中对应的方格相或(有1填1,全0填0),便得到这两个函数相与的卡诺图。
当对一个函数进行非运算时,只要画出该函数的卡诺图,再将卡诺图中的1变为0,0变为1(0填1,1填0),便得到该函数的反函数的卡诺图。
当两个函数进行异或运算时, 只要画出两个函数的卡诺图, 再将两个函数卡诺图中对应的方格相异或(相异填1,相同填0),便得到这两个函数异或的卡诺图。
当两个函数进行同或运算时, 只要画出两个函数的卡诺图, 再将两个函数卡诺图中对应的方格相同或(相同填1,相异填0),便得到这两个函数同或的卡诺图。
综上,利用卡诺图不仅可以对函数进行逻辑运算,而且过程简单、明了。
以上得到的仅仅是逻辑运算后的卡诺图,若要得到逻辑运算后的结果,需要进行必要的化简。
二、卡诺图在记忆格雷码中的应用格雷码是一种常用的无权可靠性代码,由于首、尾两个码组也具有单位距离码的特性,又称为循环码[1]。
卡诺图在时序逻辑电路设计中的应用

图 2中 , “ 一 ” 为约束项 , 在 这 一 方 面往 往 存 在 很 多 问题 , 也 比较
诺 图应 用 中存 在 的重 点 问 题 进 行 分 析 。 与代 数 化 简 法 相 比 , 卡诺 图 难 理 解 。所 谓 约 束 项 , 简单的理解为该项 的函数值为 “ 0 ” , 也 就是 化 简 更 加 的直 观 和 形 象 , 在 变 量 个 数 低 于 5个 的 逻 辑 代 数 化 简 中 , 说, 四项 约 束 条 件 的 和 为 0 , 即 每 一 项 函 数值 都是 O , 否 则 约束 条件
在 同步 时 序 电路 设 计 中 , 卡诺 图 的应 用 流 程 如 图 3所 是一种最小项方块图 , 按照循环码排列变量 , 其 本 质 上 是 对 一 个 实 的核 心 内容 。 物进行描述 。 这 与逻辑 图、 真值表及逻 辑表达式是相 同的 , 只 是 表 示 . 设 计 有 状 态 图 或 文 字 描 述 进行 , 首先 抽象逻辑问题 , 然 后 得 到 现的形式存在差异 . 卡 诺 图建 模 过 程 如 图 1 所示 : 状态转化 图. 利 用 卡 诺 图对 状 态 转 化 图 进 行 化 简 , 以状 态 方 程 和输 出方 程 的形 式 表 达 出来 ,然后 对 触 发 器 特 性 方 程 与 状 态 方 程 进 行
对比. 可得 到驱动方程 , 在 驱 动 方 程 基 础 上得 到 逻 辑 电 路 图 , 最 后 对 所 得 电路 进 行 检 查 , 看是否能启动。整个过程中 , 因为 设 计 的是
瓷油柱
( 1 】 回 圆
.
同步 时序 电路 , 可 随时 对 时 钟 方 向 进 行 确 定 , 也 就 是 说 在 异 步 时序
一
卡诺图在数字电路分析和设计中的应用

卡诺图在数字电路分析和设计中的应用
第一次20世纪50年代,卡诺图在数字电路分析和设计中的应用被提出,它极大简化了电路的分析和设计。
卡诺图是一种可视化工具,它可以让我们更好地理解复杂的数字电路系统。
卡诺图可以将复杂系统拆分成不同的组件,从而使系统中元件之间的关系更明了。
卡诺图在数字电路分析和设计中的应用主要有三个方面:第一是电路分析。
通过将复杂的数字电路系统分解成相对简单的子电路,卡诺图有助于我们更清楚地了解系统内部的信号流动特性。
第二是电路设计。
卡诺图可以帮助我们更有效地组织和实现复杂的数字电路系统,从而更快地完成系统的设计。
第三是故障诊断。
卡诺图可以帮助我们更准确地分析故障,从而发现故障原因,有助于提高故障排除及系统维护的效率。
卡诺图给数字电路分析和设计带来了巨大的便利,但也有几个需要注意的问题。
首先,卡诺图的应用需要良好的图形技术,能够清晰地表达各个元件间的信号传播情况和时序关系。
其次,卡诺图的应用还需要考虑复杂的控制机制,如控制信号的传播路径和时序关系。
最后,卡诺图也可能不能有效地处理复杂的数字电路系统,比如需要大量深度分析量才能分析出问题的系统。
总之,卡诺图是一种非常有用的可视化工具,它可以极大地简化数字电路分析和设计,使我们从复杂的系统中萃取有价值的信息。
尽管它有一些局限性,但它仍然是实现电路分析和设计的有效工具,可以有效节约我们的时间和精力。
联合卡诺图在时序逻辑电路设计中的应用PPT学习教案

其一,无CP(CP=0)时,触发器的次态保持原来 的状态不变。
其二,有CP(CP=1)时,触发器的次态由电路的 输入信号和现态的组合以及触发器的特性方程决定
。
次态方程
Qn1 i
F
(
X1,
X
2
,..... X m
,
Q1,
Q2
,......Qn
).CP
Qi
.CP
是异步时序逻辑电路联合卡诺图设计法的理论基础。
第28页/共30页
谢谢大家!
第29页/共30页
EN D
第19页/共30页
CP的选择(续)
(5)当内部时钟脉冲恰好覆盖高位触发器的翻转区 时,则该触发器接成计数模式即可;
(6)当内部时钟脉冲覆盖的范围大于高位触发器的 翻转区时,则该触发器的驱动设计有驱动函数法和计 数模式法;
(7)内部时钟脉冲的选择,可以直接在联合卡诺图 中用观察法确定,也可以用波形图(时序图)辅助分 析。
第4页/共30页
设计步骤
(1)逻辑抽象,得出描述对象过程的原始状态转换; (2)状态化简; (3)状态赋值,也叫状态编码;
(4)作出次态联合卡诺图; (5)确定触发器,直接用次态联合卡诺图得出最简次
态函数,在化简的过程中同时考虑自启动的问题;
(6)将次态函数与触发器的特性方程相比较,确定各 触发器的驱动函数;
第3页/共30页
1 同步时序逻辑电路的联合卡诺图设计法
1.1 设计方法
时序逻辑电路经典的设计方法,或者是根据 驱动表确定的驱动函数卡诺图得出最简驱动 函数,或者是根据分列的次态函数卡诺图确 定最简次态函数,再与触发器的特性方程相 比较,得出最简驱动函数。 联合卡诺图设计法与经典的设计步骤完全相 同,其不同点是直接根据联合次态卡诺图确 定最简次态函数。
卡诺图在时序逻辑电路设计中的应用

卡诺图在时序逻辑电路设计中的应用何金保;骆再飞;诸葛霞【摘要】卡诺图是分析和设计数字电路的重要工具,本文首先阐述卡诺图模型建立方法,然后通过时序逻辑电路设计实例讨论卡诺图的应用方法,最后对卡诺图应用进行剖析.本文总结归纳了初学者理解上容易犯错的关键点,可使学生学习卡诺图时避开一些误区,从而熟练掌握和运用卡诺图工具.【期刊名称】《宁波工程学院学报》【年(卷),期】2016(028)002【总页数】4页(P1-4)【关键词】卡诺图;数电;时序逻辑电路【作者】何金保;骆再飞;诸葛霞【作者单位】宁波工程学院,浙江宁波315016;宁波工程学院,浙江宁波315016;宁波工程学院,浙江宁波315016【正文语种】中文【中图分类】TN791卡诺图是1953年由贝尔实验室工程师卡诺(Karnaugh)提出,目前已应用于许多领域,在数电课程中,卡诺图作为一种重要的化简工具,应用十分广泛[1-3],对于卡诺图的理解和应用是学习过程的关键环节。
本文着重对卡诺图在应用过程中关键问题进行讨论。
卡诺图化简相对于代数化简方法,具有直观形象的优点,十分适合变量个数少于5个的逻辑代数化简。
在教学过程中,笔者发现学生能够按部就班完成常规的化简工作,但是遇到稍微的变化就束手无策,究其原因,学生对于卡诺图理解不够透彻,因而尚不能灵活运用卡诺图。
鉴于上述原因,本文通过卡诺图的在时序逻辑电路中应用实例,详细阐述卡诺图运用方法,着重对于卡诺图几个关键问题的理解进行讨论,帮助初学者掌握卡诺图。
时序逻辑电路设计是数电课程中综合性最强的部分,本文试图通过时序逻辑电路的设计的阐述,让学习者对此融会贯通。
1.1 不带约束的卡诺图卡诺图是按循环码排列变量的一种最小项方块图。
卡诺图本质上与真值表、逻辑图、逻辑表达式等一样都是在描述同一个实物,只是表示形式不同而已。
图1是卡诺图建模过程,图1(a)是两个变量4个最小项表示方法,图1(b)是m表示最小项,下标是最小项的编码,图1(c)是在实际运用时,卡诺图的表示方法。
基于次态卡诺图的J、K激励函数最小化方法及时序逻辑电路自启动

第37卷第4期 2010年7月浙江大学学报(理学版JJournal of Zhejiang University(Science Edition基于次态卡诺图的tJr、K激励函数最小化方法及时序逻辑电路自启动设计任骏原(渤海大学物理系,辽宁锦州121000搐要:分析了JK触发嚣的激励函数和次态函数的关系并在卡诺图上建立二者的联系,提出了在触发器的次态卡诺图上直接求解最小化.,、K激励函数的方法,讨论了无效状态的赋值问题及自启动设计方法,对简化时序逻辑电路的设计过程具有实用意义.关键词:JK触发器;激励函数;自启动;时序逻辑电路设计中图分类号:TP 332.1文献标志码:A 文章编号:1008—9497(201004—425—03REN Jun-yuan(Department of Physics,Bohai University,Jinzhou 121000,Liaoning Province,China Minimization method of J and K excitation function based Oil next-state karnau【gh maps and self-starting design of sequential logic circuits.Journal of Zhejiang University(Science Edition,2010,37(4:425--427Abstract:The relation between excitation function and next—state function of JK flip-flop was analyzed based on Kar-naugh maps.Themethod of solving 1and K excitation function based on next—state Karnaugh maps was proposed and the assignment for inactive state and the design of self-starting were discussed。
