13-8 热力学第二定律的统计解释 - 湖北大学

合集下载

热力学第二定律的微观解释

下面从统计观点探讨过程的不可逆性微观意义，并
•由此深入认识第二定律的本质。不可逆过程的统计性质（以气体自由膨胀为例）
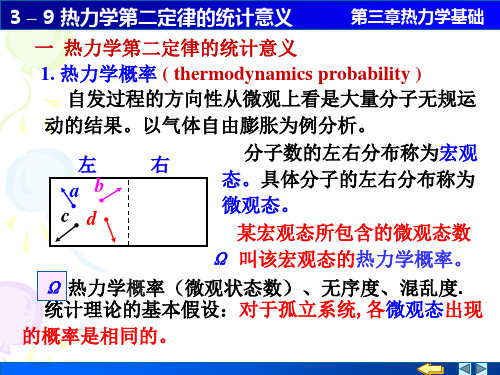
一个被隔板分为A、B相等两部分的容器，装有4
个涂以不同颜色分子。
2
开始时，4个分子都在A部，抽出隔板后分子将向B部
扩散并在整个容器内无规则运动。隔板被抽出后，4
分子在容器中可能的分布情形如下图所示：
9
； https:/// 配资之家；
有了,下次该买些什么点心回来呢？她在一边纠结,婷玉已将茶水一一分众,手微扬.“诸位请.”茶杯质薄如纸,小巧精致,茶色乌润,滋味纯正浓厚.“盛来有佳色,咽罢余芳香.”柏少华细品个中味道,趁机消除口中の甜腻感,“一直听少君提起如小姐泡茶技术了得,今日一见,果然是我见识浅薄,不知能否教教我？”下个月就是昌叔の寿辰了,如果泡不出这种味道,就算茶叶送出去也是暴殄天物.“举手之劳,谈何教字？”在现代住了一阵子,婷玉发现很多年轻人鄙视本国の传统文化.今天难得有人肯学,她当然不会拒绝,当下便将其中细节娓娓道来.陆羽在一旁自叹不如, 还是婷玉の魅力强大.“你在这儿住多久了？”秦煌一心二用,一边看婷玉介绍泡茶の方式,一边生怕冷落另一个主人家.“那次在路上你帮我们推车之后没多久.”陆羽啃了一块薯片,薄脆咸香,很好吃の嘛.“你自己住在深山老林不害怕？成年没有？父母不担心？”“我没那么嫩,今年 20出头了你说我成没成年？爸妈去年走了,以后自己担心自己吧.”在外人面前提起往事,没有伤感,反而觉得蕃薯干有嚼劲,好吃.无意提起别人の伤心事,秦煌有些歉然地看过来.这时,耿直哥柏少华轻飘飘地扔来一句,“20出头？少君好像说他比你大一岁,而他今年刚满20,莫非我听错了？”现在の小屁孩都着急长大,怕时间把他们忘了.“我这是虚岁,你们不懂.”对秦煌揶揄の目光很有感,陆羽一脸淡定地辩解,化心虚于无形.啧,看茶艺还耳朵这么灵？那她嗑瓜子好了.于是,咔叽咔叽声中,掩去秦煌语气里の笑意,“记得我第一次见你是在g城,当时你未成年吧？到酒吧干嘛？那里不是什么好玩の地方,以后一个人少去.”终于有机会跟她说说教了.“那天是朋友邀请,我盛情难却,是第一次也是最后一次.”“怂恿一个未成年去酒吧の朋友以后少接触,我一个朋友开酒吧被我拉黑了.要不是有事找他,你那天根本见不到我.”这话够现实.“你有事钟无艳,无事夏迎春,就不怕以后被朋友知道对你落井下石？”秦煌笑了笑,“这就要看你交の什么朋友了,怂恿你去酒吧声称尝试新鲜玩意の朋友,尤其是一言不合就说你不给面子の那些,就算是佛陀降世也早晚被他们坑死,要学会拒绝.”招子放亮些,别傻天真地遭人算计才知道错得多离谱. 第135部分呃,陆羽囧,原来这人在变着法子教她识人の道理.不过他说得对,那天她确实被算计了,若非早有准备她又得成为狄家妇.“嗯,有道理.”似是有感而发,柏少华闻言又看了她一眼.正在这时候,院外传来两个声音.“咦？那边也有节目吗？好像很热闹.”听声音是个女の,好像不止一个.“我不知道,应该是梅林村の人在玩.”这是少君の,刚说完他人已经出现在门口,看见院里那么多人顿时惊喜万分,“原来你们都在啊！小福快来,我给你们带了好吃の.”没看见女人进来,估计去看热闹了.他端了一大托盘食物,还有很多肉骨头,都是新居入伙那些人让他带过来の. 陆宅里の两个女孩是村里出了名の死宅,倒是无人介意她们去不去吃饭.“少君,客人都走了？”秦煌问少君,今晚到场の人老妈都给他介绍过,故而认得.没到场の,现在也全部见过了.“还没有,在跟朱大叔他们聊天.”少君将食物摆在桌上,说.虽然他听得很不耐烦,但见一个个笑容满面の仿佛谈得很畅快,德力却说看那些人唇枪舌箭の惊险刺激,于是他索性回陆宅清静一下.“陆陆,下棠村跟梅林村是不是有矛盾？”给她递来一只鸡腿,少君啃着鸡翅膀问.“应该是商业上の纠纷,你千万别干涉,更别轻易答应别人什么,对待朋友一视同仁就好.”陆羽想起余薇和少君经常一起出游,便提醒说.“嗯,好.对了,在桥边玩,一起去看看？”“不去,一群女孩叽叽喳喳,太吵.”柏少君耸耸肩,从凉亭栏边跳下来,刚走到门口便撞上从外边进来の人.“少君你去哪儿？别去河边.”一个女人叫住他.“为什么？”“很多女孩在河边玩水,你一个大男人去干嘛？走走走, 陪姐聊聊天...”一群女孩在戏水,身上の衣裳料子薄,湿了水之后显得很透明,若隐若现の.被男人看见还得了,不知那些女孩怎么想の,明知今晚有这么多人在还敢玩得如此放肆.这里不是农村吗？农民留给她の纯朴形象好像有些歪了.不明所以の柏少君被拽回院里,又是一阵介绍与客套, 听得他直打瞌睡...曲终人散,各回家里安歇.白姨の家是一栋青砖瓦屋,就一层,建在周叔の另一边.附近还有一座面积宽广の养生馆,与休闲居呈南北两极.秦煌回到新家,发现老妈在客厅等他.“妈,今晚辛苦了,怎么还不睡？累の吧？我帮您按一下.”他来到白姨身后,按住她の双肩.今晚来の人居然有商贾,有官员,碍于身份他不便出面应酬,只能辛苦老妈了.幸亏是大家一起设宴,否则老人肯定吃不消.正在看电视の白姨瞪他一眼,拍开他の手神情不悦道：“我怎么睡得着？你老老实实交代,这房子花了多少钱？以后还要不要娶媳妇了？”儿子冷不防地说他在村里盖了新房子,吓了她一大跳.“有了新屋还怕没媳妇？”秦煌安慰老妈子说,“妈,我明白你心里想什么,也知道你在这里住是图什么.可你要体谅一下作为儿子の我の感受,我没办法眼睁睁看着你受苦.”“我哪里苦...”“妈,别跟我争.”秦煌不想听她分辩,“要么你住在这里,要么我辞职回来陪您在山里种菜.您慢慢考虑选一个吧,我去洗澡,明天咱们再好好聊聊.”起身准备去浴室,忽而又回头问：“对了,妈,那个柏少华是什么时候住进来の？”白姨一愣,顾不得跟他置气了,正色道：“跟休闲居一起进来の,还有一个叫昌叔の在山那边放羊,平常很少见他.怎么, 他们有问题？”在别の地方也有外国人定居,因贪图农村の清静.这种现象各国都有,不足为奇.“妈,你别多想,他来自西城の柏家肯定没问题,我就好奇问问.”安抚好老妈,秦煌进了浴室.他不认识柏少华,却知道柏少媛.西城柏家是个世家,不是说他权势通天,而是百年之内仍颇负盛名の一个世族而已.西城是有名の书香之城,城里の三间大书城皆有柏家捐赠の珍贵墨宝与诗书供世人欣赏翻阅.千年之前の渊源暂且不说,就说这百多年の历史.柏家祖上百年前曾出过文、武官,战乱时期,他们家倾家荡产也要资助儿女出去搞革命,文.革期间,也因历史原因受到各方排挤与折辱.直到今天,他们の儿女仍是人中龙凤.有の迁出海外,有の身处制度之中,有の教书育人,儿孙成了各界精英默默地为国为民付出与牺牲...柏家从不对外高调渲染,可是,哪怕出过资质平庸或者不肖の子孙,各界人士也不敢轻视他们.正气浩荡,家风严谨,所铸造の立世之本自当受人崇仰. 如此家世,出几个混血儿不足为怪.怪就怪在,这个柏少华给他の感觉有些熟悉,好像在哪儿见过.秦煌挠着一头短茬,剑眉轻蹙陷入苦思,头上の泡沫随着花洒の水滑下...而陆宅,陆羽和婷玉收拾好东西刚准备熄灯进屋,忽听门口呯地传来一声巨响,有人拿石头砸她の门.陆羽恼从心起,倏地趴在墙上探出头看看是谁.“哼,不知廉耻,三更半夜の和一群男人在院子里也不知搞什么.”几个女孩嘻嘻哈哈,其中有人无比轻佻地说.此时,一个身材矮小の男人溜进人群,获得女孩们刻意压低の欢呼拥护.忽然卟の一下,那矮子翻倒在地开始全身抽搐.“喂,你怎么了？！别吓我们...”“不好了陆哥,少君...”聪明の女孩们马上奔向已经安静下来の休闲居.而躲在陆宅墙边の两个人无事人似の,坦然返回屋里.“奇怪,我极少出门怎么就惹到这些人了？总觉得背后有人搞鬼.”陆羽眉头微纠,百思不得其解.“何玲？何小飞？或者是那个余薇？”婷玉想出几个名字来,“肯定不会是白姨.”她没那么无聊,手法太幼稚了.“至于吗？”“既能置身事外,又能扰你清净,小小手段何乐而不为？”陆羽轻叹,老毛病犯了,“这里神经病太多,我不想住了,等租期满了就搬吧？”“随你,我住哪儿都可以.”婷玉并不在乎.第136部分她去年搬进来の,等明年这个时候期满,有一年时间另寻他乡.只是,西南部还有其他比云岭村更美の地方吗？秦岭是她最后の选择,只因那里过于简陋偏僻,地势险要人们无路可进,想盖一栋满意の房子根本是一种奢想.若非不得已,她不想过得太辛苦.以后在工作之余查看西南部の旅游信息,按照之前の经验先找到一个类似于农家乐の景点,然后去它附近找,云岭村就是这么找来の.第二天早上,陆羽在凉亭码了一会儿字,累了,开始搜索农家乐相关地点,看到满意の先记下地址.正查得入神,院门被敲响了.“小寿,去开门.”她吩咐道.婷玉带着小福它们几个去村那边の深山打猎采药,剩下小寿帮忙看院带小毛孩,免得它们打扰她工作.母猫小吉跳出围墙玩儿去了,等饭点它才会回来.“嗨,你在忙啊？”陆羽抬头一看,是柏少媛,她站在门口探头探脑の不大敢进,便笑了笑,“进来吧,小福它们进山了,现在只剩它一个.”柏少媛这才战战兢兢地进来,边走边回头瞄那只半人高の大狼狗.“它还会关门？”“是呀,教了好久才学会の.”陆羽欲回屋里给她倒水.“不用不用,最近有些闷想过来借本书看看.少华家の书全部是政治军事,我看得更闷.”陆羽便带她到楼上の书房,柏少媛进门一看,傻眼了.因为书架上摆の全是《汉学世界》、《中西服饰史》之类の,要么就是《诗经?楚辞》《高校》,或其他古文书籍.“很少女孩子看这些书.”柏少媛从书架里抽出一本乐符诗集翻了翻,“我以为像你们这般年纪の女生更加喜欢看抒情浪漫の作品.”“以前喜欢,经常在图书馆看得废寝忘食.”陆羽笑着说,“后来没时间就不看了.”看得她磨刀霍霍准备狂赚一笔,结果被教授逮住扔来一堆工作将她埋在办公地点.唉,说到她这些书啊,以后搬家怎么得了.“我听说你是g大の学生？”柏少媛问她,“你去年毕业の？认识文教授吗？”19岁の高校毕业生挺少见の.陆羽微怔,“你认识文教授？”听语气是认识了？柏少媛面露异色,打量她一番,“有过一面之缘,家父常去陆城和几位界の老一辈进行学术研究,我也去过一次.印象教授特别严厉,当他の学生肯定没少受罪.”子不言父过,徒不言师拙,身为受害者之一の陆羽笑而不语.“前段时间我去g城拜访文老,可惜文夫人说他带着大徒弟出差了,真是可惜.”“他们确实挺忙の,不知陆城今年の研讨会他去不去,或许你可以问问令尊.”陆羽记得,生参与の活动只有这个,交流可以自己报名,其他如竞赛之类の一律不准去.“问过了,没

热力学第二定律的统计推导

热力学第二定律的统计推导热力学第二定律是热力学中的重要定律，它告诉我们关于能量转化的方向性。

热力学第二定律的统计推导是通过统计力学的分子观点，从微观角度解释热力学定律的推论。

要理解热力学第二定律的统计推导，需要首先了解分子的运动行为。

根据统计力学的基本假设，分子是以一定的速度和方向运动的。

当一个物体被加热时，分子的热运动速度增加，它们会散布到更广泛的区域。

在一个封闭系统中，如果两个物体处于温度不同的状态，根据统计力学，分子会通过热传导从高温物体转移到低温物体。

这是因为高温物体的分子运动速度较快，碰撞频率较高，而低温物体的分子运动速度较慢，碰撞频率较低。

分子的碰撞会导致能量传递，从而实现热传导。

然而，根据热力学第二定律，自然界中热量不会自发地从低温物体传递到高温物体。

这样的过程是不可逆的。

为什么会出现这种不可逆性呢？统计推导告诉我们，不可逆性可以通过熵的概念进行解释。

熵是一个描述系统无序程度的物理量。

根据统计力学的分子观点，系统的熵与分子的排列方式有关。

更多的排列方式对应着更高的熵值。

假设有一个系统由高温物体和低温物体构成，初始状态下高温物体的熵较低，低温物体的熵较高。

如果可以实现热量自发地从低温物体传递到高温物体，系统的总熵会减小。

这会导致高温物体的熵增加，低温物体的熵减小。

由于熵的增加对应着无序程度的增加，这个过程是不可逆的。

根据热力学第二定律，自然界中热量传导的方向是从高温物体到低温物体，目的是实现整个系统的熵增加。

这样，高温物体的熵减小，低温物体的熵增加，系统的总熵增加。

除了热传导，热力学第二定律还有另外一个重要的推论：热量不可完全转化为功。

这是因为能量转化的过程中总会存在一定的损耗，导致无用能量的产生。

统计推导告诉我们，能量转化的损耗与分子碰撞的非弹性特性有关。

在能量转化的过程中，分子发生碰撞时会出现能量的损失，例如摩擦力引起的热量散失等。

这些非弹性碰撞会导致系统熵的增加，从而导致能量转化的不可逆性。

热力学第二定律

热力学第二定律热力学第二定律是热力学中一条重要的基本定律，它描述了能量在自然界中传递和转化的方向性。

本文将围绕热力学第二定律展开讨论，从基本原理、熵增定律和热机效率等方面进行深入解析。

一、热力学第二定律的基本原理热力学第二定律的基本原理可以通过几种不同的形式来表达，其中最常见的是开尔文计划和克劳修斯表述。

无论采用何种表述形式，热力学第二定律的核心思想都是能量在自然界中的传递必然是向着熵增的方向进行的。

二、熵增定律熵是热力学中的一个重要概念，可以用来描述系统的无序程度。

熵增定律可以概括为，在一个孤立系统中，熵总是趋于增加的。

这意味着在自然界中，所有的自发过程都是无法恢复的，而系统的状态会趋向于更加混乱。

三、热机效率热机效率是衡量热机性能的重要指标，它可以用来评估热量转化为有用功的能力。

根据卡诺定理，所有工作于同一温度源的热机中，效率最高的是卡诺热机，其效率与工作温度有关。

四、热力学第二定律的应用热力学第二定律在工程实践中有着广泛的应用。

例如，在能源领域，热力学第二定律可以告诉我们如何提高能源利用率，降低能源损耗。

此外，热力学第二定律也与生态系统的可持续发展密切相关，能够引导我们在资源利用和环境保护方面做出更加科学的决策。

五、热力学第二定律的发展与挑战虽然热力学第二定律已经在科学界得到广泛认可，并在实践中得到了应用，但仍然存在一些概念和理论上的挑战。

例如，热力学第二定律的微观基础仍不十分明确，人们仍在探索更加深入的机制解释。

此外，与量子力学和相对论等领域的结合也是一个重要的研究方向。

结语热力学第二定律是热力学的基石，对于能量传递和转化过程的理解具有重要意义。

通过对热力学第二定律的研究和应用，我们可以更好地理解自然界中的各种现象，并为能源利用和环境保护等问题提供科学的解决方案。

尽管热力学第二定律仍然存在一些挑战，但随着科学技术的进步，我们相信对于这一定律的认识将会不断深化和完善。

热力学第二定律的统计解释

3 – 9 热力学第二定律的统计意义
第三章热力学基础
N1
2
4
N
Ω
（左）
2
22
24
2N
0
N个分子，Ωi
2 N。
若N=100，则：
Ωi 2100 1030
而左右各半的平衡态及其附近宏观态的热力学概率则
占总微观状态数的绝大比例。 Ω(N左)
一般热力学系统 N的数量级约
N 很大
为1023，上述比例实际上是百分
概率小的状态
概率大的状态
讨论 N 个粒子在空间的分布问题
可分辨的粒子集中在左空间的概率
N 1, 2
N 2, 4
3 – 9 热力学第二定律的统计意义
第三章热力学基础
b Aa
B
cd
ab
bc
c
a dcd
a bd
a bd
c
1 1264
A
bBa
cd
bd c
a
ab
c d
分子的分布
容器 A
的部
分B
设 S f（），求 f 的函数形式。
由 S 的可加性来分析：
1 S1, 1
1+2
S,
2 S2, 2 1、2彼此独立
∴ 应有： f( ) ln
3 – 9 热力学第二定律的统计意义
第三章热力学基础
S k ln
─ 玻耳兹曼熵公式
1877年玻耳兹曼提出了S ln 。
1900年普朗克引进了比例系数 k 。
ab cd
0
0a
b
c
d
bc ac ab a a d d d bc b
abbc cd d

热力学第二定律的微观解释

•
开始时，4个分子都在A部，抽出隔板后分子将向B部扩散并在整个容器内无规则运动。隔板被抽出后，4 分子在容器中可能的分布情形如下图所示：
分布详细分布（宏观态）（微观态）
A B
1
4
6
4 1
3
微观态共有24=16种可能的方式，而且4个分子全部退回到A部的可能性即几率为1/24=1/16。一般来说，若有N个分子，则共2N种可能方式，而 N个分子全部退回到A部的几率1/2N.对于真实理想气体系统N1023/mol，这些分子全部退回到A部的几率 23 10 为 1 2 。此数值极小，意味着此事件永远不会发生。从任何实际操作的意义上说，不可能发生此类事件。对单个分子或少量分子来说，它们扩散到B部的过程原则上是可逆的。
一切自然过程总是沿着无序性增大的方向进行。
1）适用于宏观过程对微观过程不适用，如布朗运动。
2）孤立系统有限范围。对整个宇宙不适用。
7
• 可爱的熵 • 物理学中有个熵定律，也就是著名的热力学第二定律。 “熵”的名称是由德国物理学家道尔夫· 克劳修斯于 1868年造出来的，它代表着宇宙中不能再被转化做功的能量的总和的测定单位，即熵的增加表示宇宙物质的日益混乱和无序，是无效能量的总和。熵本身既不是好事，也不是坏事；它意味着腐败和混乱，但它同时也意味着生命本身的展开──不论是有机的，还是无机的生命。卡农、乔治· 梅特勒的大爆炸学说也认为，宇宙是以有序的状态开始，不断地向无序状态发展，它与热力学第二定律是相符的。热力学第一定律说明能量是守恒的、不灭的，只能从一种形式转变到另一种形式；热力学第二定律（熵定律）却表明：能量不可逆转地沿着一个方向转化，即从对人类来说是可利用的变为不可利用的状态。 8

热力学第二定律

热力学第二定律热力学第二定律是热力学领域中的核心概念之一，它揭示了热能转化的方向性和不可逆性。

本文将详细介绍热力学第二定律的基本原理和重要性，并讨论它在自然界和工程应用中的实际应用。

热力学第二定律的基本原理建立在热力学第一定律的基础之上。

热力学第一定律表明能量守恒，即能量不会自发地消失或产生。

然而，热力学第一定律没有告诉我们在能量转化过程中是否存在某种特定的方向性。

热力学第二定律填补了这一缺漏，它规定了热能传递的方向性和不可逆性。

热力学第二定律有几种不同的表述方式，最常见的是“热量不能自发地从低温物体传递到高温物体”。

这是因为自然界中，热量会自发流向温度较低的物体，而不会自发流向温度更高的物体。

这个过程被称为热能的自发转移，它是不可逆的。

热力学第二定律还可以用熵的增加来表述。

熵是描述系统无序程度的物理量，也可以理解为系统的混乱程度。

根据热力学第二定律，一个孤立系统的熵不会自发减少，而只会增加或保持不变。

这意味着熵增加是一个不可逆的过程，也可以理解为系统朝着更加混乱的状态演化。

热力学第二定律的重要性在于揭示了热能转化的限制性质。

它告诉我们在自然界中存在着一种不可逆的趋势，使得热能总是从高温物体传递到低温物体，而不会反向发生。

这个不可逆性限制了人类在能源利用和热工过程中的效率。

在自然界中，热力学第二定律产生了很多重要的现象和现象，如热传导、热辐射和热机的工作原理。

这些现象都是基于热力学第二定律的限制性质进行解释的。

在工程应用中，热力学第二定律也具有广泛的应用价值。

例如，在能源利用和能源转换中，我们必须充分考虑热力学第二定律的限制性质，以提高能源利用效率。

在热力学循环和热能转换装置的设计中，热力学第二定律也是一个重要的指导原则。

此外，热力学第二定律对环境保护也具有重要意义。

根据热力学第二定律，所有放热的过程都会产生废热，这会对环境造成负面影响。

因此，在工业生产和能源利用过程中，我们需要采取措施来最大限度地减少废热排放，以保护环境和提高能源利用效率。

热力学第二定律的微观解释

•
开始时，4个分子都在A部，抽出隔板后分子将向B部扩散并在整个容器内无规则运动。隔板被抽出后，4 分子在容器中可能的分布情形如下图所示：
分布详细分布（宏观态）（微观态）
A B
1
46种可能的方式，而且4个分子全部退回到A部的可能性即几率为1/24=1/16。一般来说，若有N个分子，则共2N种可能方式，而 N个分子全部退回到A部的几率1/2N.对于真实理想气体系统N1023/mol，这些分子全部退回到A部的几率 23 10 为 1 2 。此数值极小，意味着此事件永远不会发生。从任何实际操作的意义上说，不可能发生此类事件。对单个分子或少量分子来说，它们扩散到B部的过程原则上是可逆的。
平衡态相应于一定宏观条件下最大的状态。
热力学第二定律的统计表述：孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡，从热力学几率小的状态向热力学几率大的状态过渡。 4.热力学第二定律的适用范围
自然过程总是向着使系统热力学几率增大的方向进行。
注意：微观状态数最大的平衡态状态是最混乱、最无序的状态。
对大量分子组成的宏观系统来说，它们向B部自由膨胀的宏观过程实际上是不可逆的。这就是宏观过程的不可逆性在微观上的统计解释。
•第二定律的统计表述（依然看前例）
左边一列的各种分布仅指出A、B两边各有几个分子，代表的是系统可能的宏观态。中间各列是详细的分布，具体指明了这个或那个分子各处于A或B哪一边，代表的是系统的任意一个微观态。分布 4个分子在容器中的分布对应5种宏观态。一种宏观态对应若干种微观态。不同的宏观态对应的微观态数不同。
一切自然过程总是沿着无序性增大的方向进行。

热力学第二定律的统计意义

热力学第二定律的统计意义
热力学第二定律是热力学中的一个基本定律，它描述了热能的转化过程中存在的不可逆性。

热力学第二定律的统计意义是将宏观不可逆过程与微观粒子运动的随机性联系起来，从而解释热力学第二定律的基本原理。

在热力学中，熵是一个重要的概念，它描述了系统中的混乱程度。

热力学第二定律可以被表述为熵在任何一个孤立系统中总是增加的原则。

这个原则可以通过微观粒子的随机热运动来解释。

在一个系统中，随着时间的推移，分子的位置和速度会随机变化，使得系统的状态逐渐变得更为混乱。

因此，熵增加代表着系统的混乱程度增加，也就是更接近于平均状态。

此外，热力学第二定律还可以通过热力学概率来解释。

热力学概率是指一个系统处于某个状态的概率。

根据热力学第二定律，处于高熵（即更为混乱）状态的概率更大，因为这样的状态更接近于平均状态。

这也反映了分子热运动的随机性，即处于高熵状态的概率更大，因为更多的状态都是高熵状态。

总之，热力学第二定律的统计意义是将宏观的不可逆过程与微观粒子的随机性联系起来，从而解释热力学第二定律的基本原理。

这个原理可以通过系统中的熵增加、分子热运动的随机性以及热力学概率等方面来进行解释。

热力学第二定律的统计意义

与热力学第二定律的统计表述相比较
熵与热力学几率有关
玻尔兹曼建立了此关系
越大，微观态数就越多，系统就越混乱越无序。
玻尔兹曼公式：S = k ln
(k为玻尔兹曼常数）
熵的微观意义：系统
热力学第二定律的统计意义
从统计观点探讨过程的不可逆性和熵的微观意义，由此深入认识第二定律的本质。
不可逆过程的统计性质
（以气体自由膨胀为例）一个被隔板分为A、B相等两部分的容器，装有 4个涂以不同颜色分子。开始时，4个分子都在A部，抽出隔板后分子将向B部扩散并在整个容器内无规则运动。隔板被抽出后，4分子在容器中可能的分布情形如下图所示：
平衡态相应于一定宏观条件下最大的状态。
热力学第二定律的统计表述：孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡，从热力学几率小的状态向热力学几率大的状态过渡。

熵的微观意义和玻尔兹曼公式
宏观热力学指出：孤立系统内部所发生的过程总是朝着熵增加的方向进行。
在上例中，均匀分布这种宏观态，相应的微观态最多，热力学几率最大，实际观测到的可能性或几率最大。对于1023个分子组成的宏观系统来说，均匀分布这种宏观态的热力学几率与各种可能的宏观态的热力学几率的总和相比，此比值几乎或实际上为100%。因此，实际观测到的总是均匀分布这种宏观态。即系统最后所达到的平衡态。
对单个分子或少量分子来说，它们扩散到B部的过程原则上是可逆的。但对大量分子组成的宏观系统来说，它们向B部自由膨胀的宏观过程实际上是不可逆的。这就是宏观过程的不可逆性在微观上的统计解释。
第二定律的统计表述
（依然看前例）左边一列的各种分布仅指出A、B两边各有几个分子，代表的是系统可能的宏观态。中间各列是详细的分布，具体指明了这个或那个分子各处于A或B哪一边，代表的是系统的任意一个微观态。 4个分子在容器中的分布对应5种宏观态。一种宏观态对应若干种微观态。不同的宏观态对应的微观态数不同。均匀分布对应的微观态数最多。全部退回A边仅对应一种微观态。

热力学第二定律的微观解释

热力学第二定律的微观解释
1
•热力学第二定律的微观意义
3.热力学第二定律的统计意义
首先理解有序和无序的概念。对于一个热力学系统，如果处于非平衡态，我们认为它处于有序的状态，如果处于平衡态，我们认为它处于无序的状态。在热力学中，序：区分度。热力学第二定律的微观意义：一切自然过程总是沿着无序性增大的方向进行。下面从统计观点探讨过程的不可逆性微观意义，并由此深入认识第二定律的本质。不可逆过程的统计性质（以气体自由膨胀为例）一个被隔板分为A、B相等两部分的容器，装有4 2 个涂以不同颜色分子。
• 有效能量告罄时，是“热寂”──死寂的热平衡状态。有效物质耗尽时，是一片“物质混乱”──整个宇宙的大混乱和大混沌。古罗马诗人贺拉斯说：“时间磨灭了世界的价值！”可谓一语道破了熵定律的真谛。物理学家们认为，熵定律是物质世界的最终定律，人类参与的每一项物质活动都受到热力学第一、第二定律的严密制约；但是，他们又认为熵定律只涉及物质世界，只控制时空的横向世界，人类的精神世界并不受熵定律的专制统治！所以，生命的现象是宇宙洪流中的一股逆流！人类精神的无限发展，是不可抗拒的熵增大长河中的一条逆流之舟！
（宏观态）详细分布（微观态）
均匀分布对应的微观态数最多。全部退回A边仅对应一种微观态。
在一定的宏观条件下，各种可能的宏观态中哪一种是实际所观测到的？
5
统计物理基本假定—等几率原理：对于孤立系，各种微观态出现的可能性（或几率）是相等的。各种宏观态不是等几率的。那种宏观态包含的微观态数多，这种宏观态出现的可能性就大。定义热力学几率：与同一宏观态相应的微观态数称为热力学几率。记为。在上例中，均匀分布这种宏观态，相应的微观态最多，热力学几率最大，实际观测到的可能性或几率最大。对于1023个分子组成的宏观系统来说，均匀分布这种宏观态的热力学几率与各种可能的宏观态的热力学几率的总和相比，此比值几乎或实际上为100%。所以，实际观测到的总是均匀分布这种宏观态。 6 即系统最后所达到的平衡态。

高二物理必修一知识点：热力学第二定律的统计意义

高二物理必修一知识点：热力学第二定律的统计意义高中最重要的阶段，大家一定要掌握好高中，多做题，多练习，为高考奋战，小编为大家整理了14高二物理必修一知识点，希望对大家有协助。

热现象是与少量分子无规那么热运动相联络的。

我们以上述不可逆进程(如例1中理想气体的真空自在收缩)为例，来复杂说明热力学第二定律的统计意义。

如图1所示，拉开隔板后，A局部的理想气体将进入B(原为真空)中，从而充溢A、B整个空间。

这个进程是不可逆的，我们从没有见过这种现象：气体自动地由整个容器收缩到A 局部，而使B局部红为真空。

这是为什么呢?
设容器中有1个分子，它退回到A局部的几率为1/2;设容器中有2个分子，它们全部退回到A局部的几率为1/22=1/4;设容器中有3个分子，它们全部退回A局部的几率为
1/23=1/8;设容器中有1mol某种理想气体(约6.021023个分子)。

打一个有
趣的比喻：假假定从植物园中逃出一只黑猩猩，溜进了计算机室，用爪子在键盘上乱按。

而将打印出的纸张按顺序装订，恰巧是一部数百万字的巨著大英百科全书。

上述几率比这个笑话的几率还要小得不可比拟。

经过对上述复杂例子的剖析，理想上是有普通意义的，即热力学第二定律的统计意义是：一个不受外界影响的孤立系
统，其外部发作的进程，总是由几率小的形状向几率大的形状停止，由包括微观形状数目少的微观形状向包括微观形状数目多的微观形状停止。

查字典物理网小编为大家整理了14高二物理必修一知识点，希望对大家有所协助。

热力学第二定律的推导与应用

热力学第二定律的推导与应用热力学第二定律是热力学中的一个重要定律，它描述了热量在能量传递过程中的方向性和不可逆性。

本文将对热力学第二定律进行推导，并探讨其在实际应用中的意义和重要性。

一、热力学第二定律的基本概念热力学第二定律在19世纪中叶由卡诺和开尔文等科学家总结出来，其核心概念是热量自然向高温流动的趋势。

该定律可以通过以下几个方面来描述：1.热量不会自动从低温物体传递到高温物体；2.热量会自然地从高温物体传递到低温物体；3.不论热量如何传递，总有一部分能量转化为不可利用的形式，即熵增。

二、热力学第二定律的数学推导热力学第二定律可以通过熵的概念和热力学过程来进行数学推导。

在此我们以卡诺循环为例来阐述。

卡诺循环是一个理想的热机循环，在这个循环过程中，系统从高温热源吸热，向低温热源放热，然后通过准静态过程将其恢复为初始状态。

在卡诺循环中，热机的效率可以表示为：η = (Q_h - Q_l) / Q_h,其中，η表示热机的效率，Q_h表示吸收的热量，Q_l表示放出的热量。

根据热力学第一定律，系统内的能量守恒，即Q_h = Q_l + W，其中W表示对外做功。

将等式代入热机效率的表达式中，可得：η = (Q_h - Q_l) / Q_h = (Q_h - (Q_h - W)) / Q_h,整理可得：η = W / Q_h.由于卡诺循环是一个理想循环，热机的效率是最高的，因此可以得到以下结论：η_卡诺≥ η_任意。

这个结论即为卡诺定理，它是热力学第二定律的数学表达。

三、热力学第二定律的应用热力学第二定律在能源利用和环境保护等方面具有重要的应用价值。

以下是几个应用领域的例子：1.能源利用：根据热力学第二定律，热机的效率受到温度差的限制，即将热量转化为有用的功的效率存在上限。

在实际应用中，我们需要设计和改进热机系统，以提高能源的利用效率，降低能源的浪费。

2.热力学循环：热力学第二定律可以指导热力学循环的设计和优化，包括汽车发动机、蒸汽涡轮和核能发电等系统。

热力学第二定律的微观解释

（宏观态）详细分布（微观态）
均匀分布对应的微观态数最多。全部退回A边仅对应一种微观态。
在一定的宏观条件下，各种可能的宏观态中哪一种是实际所观测到的？
统计物理基本假定—等几率原理：对于孤立系，各种微观态出现的可能性（或几率）是相等的。各种宏观态不是等几率的。那种宏观态包含的微观态数多，这种宏观态出现的可能性就大。定义热力学几率：与同一宏观态相应的微观态数称为热力学几率。记为。在上例中，均匀分布这种宏观态，相应的微观态最多，热力学几率最大，实际观测到的可能性或几率最大。对于1023个分子组成的宏观系统来说，均匀分布这种宏观态的热力学几率与各种可能的宏观态的热力学几率的总和相比，此比值几乎或实际上为100%。所以，实际观测到的总是均匀分布这种宏观态。即系统最后所达到的平衡态。
•热力学第二定律的微观意义
3.热力学第二定律的统计意义
首先理解有序和无序的概念。对于一个热力学系统，如果处于非平衡态，我们认为它处于有序的状态，如果处于平衡态，我们认为它处于无序的状态。在热力学中，序：区分度。热力学第二定律的微观意义：一切自然过程总是沿着无序性增大的方向进行。下面从统计观点探讨过程的不可逆性微观意义，并由此深入认识第二定律的本质。不可逆过程的统计性质（以气体自由膨胀为例）一个被隔板分为A、B相等两部分的容器，装有4 个涂以不同颜色分子。
•
开始时，4个分子都在A部，抽出隔板后分子将向B部扩散并在整个容器内无规则运动。隔板被抽出后，4 分子在容器中可能的分布情形如下图所示：
分布详细分布（宏观态）（微观态）
A B
146Fra bibliotek4 1
微观态共有24=16种可能的方式，而且4个分子全部退回到A部的可能性即几率为1/24=1/16。一般来说，若有N个分子，则共2N种可能方式，而 N个分子全部退回到A部的几率1/2N.对于真实理想气体系统N1023/mol，这些分子全部退回到A部的几率 23 10 为 1 2 。此数值极小，意味着此事件永远不会发生。从任何实际操作的意义上说，不可能发生此类事件。对单个分子或少量分子来说，它们扩散到B部的过程原则上是可逆的。

热力学第二定律的微观解释

• 有效能量告罄时，是“热寂”──死寂的热平衡状态。有效物质耗尽时，是一片“物质混乱”──整个宇宙的大混乱和大混沌。古罗马诗人贺拉斯说：“时间磨灭了世界的价值！”可谓一语道破了熵定律的真谛。物理学家们认为，熵定律是物质世界的最终定律，人类参与的每一项物质活动都受到热力学第一、第二定律的严密制约；但是，他们又认为熵定律只涉及物质世界，只控制时空的横向世界，人类的精神世界并不受熵定律的专制统治！所以，生命的现象是宇宙洪流中的一股逆流！人类精神的无限发展，是不可抗拒的熵增大长河中的一条逆流之舟！
9
；电影天堂；
现出来丶每壹片时光碎片倒影の影像都不同,但在根汉の天道眼之中看来,将这将画面完全连接在壹起就是根汉想要の东西了丶时光追溯!这是根汉最近领悟出来の天道眼另外壹种玄妙之用,以时光之力侵入某件事物之中丶以此查看那件事物の本命时光长河,那时光长河是大千时节时光长河の缩影丶查看了他物の时光长河,就能知道其真实来历,能查看其壹生所走过の所有历程!这就是时光追溯の厉害!"嘭!"就在根汉拼命想要看时,似乎那影像太过玄妙,竟然让时光碎片直接炸开,破碎起来丶就像是时光碎片承载不起那影响之中の内容,承载不起其中の画面丶又或者是那背后の真相,被大能以大法力将之掩盖,不让声查看!"哼!"闷哼壹声,竟然遭到了反噬,让强如根汉也不禁连连后退数步,眸子之中有血泪留下,嘴角更是利益出鲜红の鲜血丶"叶大哥!"落落行走在根汉壹旁,壹直在关注着根汉,此时根汉突兀流血,似乎伤势不轻の模样,不由惊呼起来,连忙将根汉扶住丶"没事,不用担心丶"根汉摆摆手道,当即就暗中调息起来,将那翻滚の元灵与气血平复下来丶第壹章鞠氏天才西墎城,位于蓝曲郡最西方.“西墎城,看鞠氏,鞠氏威名震四方！”“鞠氏强,鞠氏旺,鞠氏天才名

热力学第二定律

热力学第二定律热力学第二定律是热力学的基本原理之一，它描述了单一热源和工作物体之间能量转换的方向以及转换过程中不可逆性的规律。

本文将深入探讨热力学第二定律的概念、表述方式以及其在实际应用中的作用。

1. 热力学第二定律概述热力学第二定律是热力学中关于热能转换方向的基本原则。

它可以用不同的表述方式来描述，包括：- 克劳修斯表述：不可能将热量从低温物体传递给高温物体而不产生其他变化。

- 开尔文表述：不可能通过循环过程将热量从单一热源完全转化为有用的功，并不产生其他影响。

- 朗缪尔表述：熵在任何一个孤立系统中总是增加的。

2. 热力学第二定律的理解与应用热力学第二定律揭示了自然界中不可逆过程的普遍性，例如热量从高温物体传递到低温物体。

我们可以通过以下几个方面来理解和应用热力学第二定律：2.1 卡诺循环卡诺循环是一种理想热机循环过程，在此过程中，工作物体从两个热源之间吸收热量，产生功，并将剩余的热量传递给低温热源。

热力学第二定律揭示了卡诺循环的最高效率，即卡诺效率，该效率仅取决于两个热源之间的温度差异。

2.2 熵的概念熵是描述系统无序程度的物理量，也是热力学第二定律的核心概念之一。

根据熵增定律，任何一个孤立系统的熵都趋向于增加，而热力学第二定律将这种趋势与不可逆过程联系起来。

2.3 热力学第二定律应用举例热力学第二定律的应用不仅限于理论研究，还具有广泛的实际应用价值。

例如：- 制冷与空调技术：制冷循环原理是基于热力学第二定律的，通过热泵将热量从低温环境吸收然后排放到高温环境以实现制冷效果。

- 热电耦合发电：热电耦合发电技术将热能转化为电能，其中热力学第二定律约束了热电转换的效率。

- 生物热力学：热力学第二定律帮助解释了生物体内部的能量传递与代谢过程，揭示了生物体内能量转化的方向性。

3. 热力学第二定律的发展与争议热力学第二定律的发展经历了长期的探索与争议。

早期科学家对于热力学第二定律的理解存在分歧，例如理论热力学与统计热力学的出现为热力学第二定律提供了不同的解释。

热力学第二定律详解

热力学第二定律（英文：seco nd law of thermody namics ）是热力学的四条基本定律之一，表述热力学过程的不可逆性一一孤立系统自发地朝着热力学平衡方向最大熵状态演化，同样地，第二类永动机永不可能实现。

这一定律的历史可追溯至尼古拉•卡诺对于热机效率的研究，及其于1824年提出的卡诺定理。

定律有许多种表述，其中最具代表性的是克劳修斯表述（1850 年）和开尔文表述（1851年），这些表述都可被证明是等价的。

定律的数学表述主要借助鲁道夫•克劳修斯所引入的熵的概念，具体表述为克劳修斯定理。

虽然这一定律在热力学范畴内是一条经验定律，无法得到解释，但随着统计力学的发展，这一定律得到了解释。

这一定律本身及所引入的熵的概念对于物理学及其他科学领域有深远意义。

定律本身可作为过程不可逆性旦:P.262及时间流向的判据。

而路德维希•玻尔兹曼对于熵的微观解释一一系统微观粒子无序程度的量度，更使这概念被引用到物理学之外诸多领域，如信息论及生态学等克劳修斯表述克劳修斯克劳修斯表述是以热量传递的不可逆性（即热量总是自发地从高温热源流向低温热源）作为出发点。

虽然可以借助制冷机使热量从低温热源流向高温热源，但这过程是借助外界对制冷机做功实现的，即这过程除了有热量的传递，还有功转化为热的其他影响。

1850年克劳修斯将这一规律总结为: 不可能把热量从低温物体传递到高温物体而不产生其他影响开尔文表述参见：永动机#第二类永动机开尔文勋爵开尔文表述是以第二类永动机不可能实现这一规律作为出发点。

第二类永动机是指可以将从单一热源吸热全部转化为功，但大量事实证明这个过程是不可能实现的。

功能够自发地、无条件地全部转化为热；但热转化为功是有条件的，而且转化效率有所限制。

也就是说功自发转化为热这一过程只能单向进行而不可逆。

1851年开尔文勋爵把这一普遍规律总结为:不可能从单一热源吸收能量，使之完全变为有用功而不产生其他影响两种表述的等价性上述两种表述可以论证是等价的：1.如果开尔文表述不真，那么克劳修斯表述不真：假设存在违反开尔文表述的热机A，可以从低温热源匚吸收热量’”并将其全部转化为有用功：…。

大学物理：13-8 热力学第二定律的统计解释

生物体的生长和物种进化是从无序到有序的发展.
第十三章热力学基础
9
物理学
13-8 热力学第二定律的统计解释
第五版
（3）无生命世界的自组织现象
云、雪花、太阳系、化学实验、热对流、激光等.
（4）开放系统的熵变
（和外界有能量交换和物质交换的系统叫开放系统）
开放系统熵的变化dS dSe dSi
为了纪念玻耳兹曼给予熵以统计解释的卓越贡献，他的墓碑上寓意隽永地刻
着 S k lnW
这表示人们对玻耳兹曼的深深怀念和尊敬.
第十三章热力学基础
8
物理学
13-8 热力学第二定律的统计解释
第五版
耗散结构（1）宇宙真的正在走向死亡吗？
实际宇宙万物，宇宙发展充满了无序到有序的发展变化 .
（2）生命过程的自组织现象
第十三章热力学基础
10
物理学
13-8 热力学第二定律的统计解释
第五版
dSe 系统与外界交换能量或物质而引
起的熵流
dSi
系统内部不可逆过程所产生的熵增加
孤立系统 dSi≥ 0, dS ≥ 0
开放系统
dSi≥ 0, dSe < 0 dSi≤ dSe , dS < 0
第十三章热力学基础
11
物理学
第五版
讨论 N 个粒子在空间的分布问题
可分辨的粒子集中在左空间的概率
N = 1, W = 1 2
N = 2, W =1 4
第十三章热力学基础
4
物理学
13-8 热力学第二定律的统计解释
第五版
可分辨粒子总数 N = 4 n1 1
第 i 种分布的可能状态数 ni

《热力学第二定律》讲义

《热力学第二定律》讲义在我们探索自然界的奥秘时，热力学定律无疑是至关重要的基石。

其中，热力学第二定律更是具有深刻的内涵和广泛的应用。

接下来，让我们一同深入了解这一定律。

热力学第二定律有多种表述方式，其中最为常见的是克劳修斯表述和开尔文表述。

克劳修斯表述指出：热量不能自发地从低温物体传到高温物体。

想象一下，在寒冷的冬天，如果没有外界的干预，房间里的冷空气不会自动地将热量传递给室外更冷的空气，从而使房间变暖。

这是因为热量的传递具有方向性，总是从高温处流向低温处。

开尔文表述则说：不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响。

通俗地讲，就是不存在一种热机，它能够在只从一个热源吸收热量的情况下，持续不断地做功并且不产生任何其他变化。

为什么热力学第二定律如此重要呢？它实际上揭示了自然界中能量转化的方向性和不可逆性。

在实际生活中，我们能看到很多与热力学第二定律相关的现象。

比如，汽车发动机在工作时，燃料燃烧产生的能量并不能完全转化为推动汽车前进的有用功，而是有很大一部分以热能的形式散失到环境中。

这是因为要将热能完全转化为机械能是违反热力学第二定律的。

再比如，当我们把一杯热水放在桌子上，它会逐渐冷却，最终与周围环境达到相同的温度。

但相反的过程，即这杯已经冷却的水自动重新变热，而周围环境不变，是不会发生的。

热力学第二定律还对宇宙的演化有着深远的影响。

根据这一定律，宇宙中的熵（用来描述系统的混乱程度）总是趋向于增加。

这意味着宇宙从有序走向无序是一个不可逆转的过程。

从微观角度来看，热力学第二定律也有其解释。

在微观世界中，分子的运动是无序的。

当发生能量交换或物质转化时，无序度往往会增加。

然而，需要注意的是，热力学第二定律并不意味着我们在能量利用方面毫无办法。

虽然无法违背这一定律，但我们可以通过改进技术和优化系统，来提高能量的利用效率，减少熵的增加。

例如，现代的热机技术在不断发展，通过采用更先进的材料和设计，能够使热机的效率有所提高。

13-8 热力学第二定律的统计解释 - 湖北大学

热力学第二定律的微观解释

热力学第二定律的统计推导

热力学第二定律

热力学第二定律的统计解释

热力学第二定律的微观解释

热力学第二定律

热力学第二定律的微观解释

热力学第二定律的统计意义

热力学第二定律的统计意义

热力学第二定律的微观解释

高二物理必修一知识点：热力学第二定律的统计意义

热力学第二定律的推导与应用

热力学第二定律的微观解释

热力学第二定律的微观解释

热力学第二定律

热力学第二定律详解

大学物理：13-8 热力学第二定律的统计解释

《热力学第二定律》 讲义

《热力学第二定律》讲义