BAMCG模型周期解的全局指数稳定性
合集下载
【国家自然科学基金】_bam神经网络_基金支持热词逐年推荐_【万方软件创新助手】_20140801
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 bam神经网络 神经网络 时滞 故障诊断 故障树分析 指数稳定性 拓扑度 微分不等式 平衡点 全局指数稳定性 lyapunov泛函
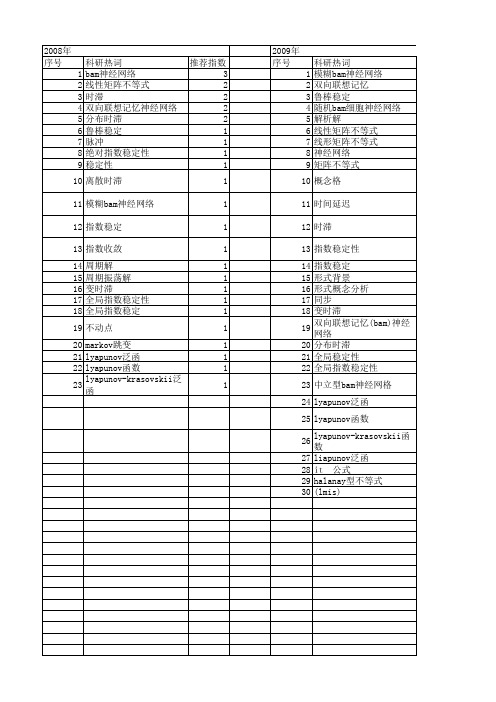
2009年 序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 halanay型不等式 30 (lmis)
科研热词 模糊bam神经网络 双向联想记忆 鲁棒稳定 随机bam细胞神经网络 解析解 线性矩阵不等式 线形矩阵不等式 神经网络 矩阵不等式 概念 时间延迟 时滞 指数稳定性 指数稳定 形式背景 形式概念分析 同步 变时滞 双向联想记忆(bam)神经网络 分布时滞 全局稳定性 全局指数稳定性 中立型bam神经网格 lyapunov泛函 lyapunov函数 lyapunov-krasovskii函数 liapunov泛函
推荐指数 2 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2011年 科研热词 推荐指数 时滞 3 双向联想记忆神经网络 3 脉冲 1 稳定性 1 概周期解 1 振动性 1 平衡点 1 存在性 1 周期解 1 双向联想记忆神经网络:m-矩阵 1 分布时滞 1 全局渐近稳定性 1 全局指数稳定性 1 不稳定性 1 n个神经元bam神经网络 1 mawhin连续定理 1
2014年 序号 1 2 3 4
2014年 科研热词 随机 指数同步 s-分布时滞 bam神经网络 推荐指数 1 1 1 1
具有比例时滞和D算子的BAM神经网络概周期解的存在性与稳定性
具有比例时滞和D算子的BAM神经网络概周期解的存在性
与稳定性
赵莉莉
【期刊名称】《青海师范大学学报（自然科学版）》
【年(卷),期】2024(40)1
【摘要】为了探讨一类含比例时滞和D算子的中立型BAM神经网络的概周期解的存在性与广义指数稳定性,首先,通过构造概周期函数空间,并利用压缩不动点原理,得到确保系统概周期解存在的充分条件,其次,使用微分不等式技巧得到确保系统概周期解广义指数稳定的充分条件.发现若系统的参数满足一定的条件,那么系统的概周期解是存在的,且是广义指数稳定的,而且所得结果与比例时滞无关.所得结论推进了现有文献中的相关工作.
【总页数】8页(P32-39)
【作者】赵莉莉
【作者单位】云南大学数学与统计学院
【正文语种】中文
【中图分类】O221.6
【相关文献】
1.时间尺度上时滞Cohen-Grossberg BAM神经网络系统概周期解的全局指数稳定性
2.变系数变时滞BAM神经网络概周期解的存在性与全局吸引性(英文)
3.时间尺度上具有泄漏时滞的一般BAM神经网络概周期解的存在性和指数稳定性
4.时间
尺度上漏项中具有变时滞的中立型模糊BAM神经网络的概周期解5.具有时变时滞的复值BAM神经网络的概周期解
因版权原因，仅展示原文概要，查看原文内容请购买。
神经甾体——一类新的神经调节剂
神经甾体——一类新的神经调节剂
李文姬;李绍顺
【期刊名称】《药学进展》
【年(卷),期】1997(021)003
【摘要】神经甾体是由中枢，周围神经组织及腺体产生的对中枢神经系统具有重要调节作用的一类甾体化合物，它不同于经典的皮质激素和性激素，在体内有特定的生物合成，代谢及调节机制，具有多种生理作用，如中枢抑制，记忆增强，神经保护等，本文概述了近年关于神经甾体类化合物的生物合成，代谢，生理药理学作用及其作用机制等方面研究的一些新进展。
【总页数】7页(P129-135)
【作者】李文姬;李绍顺
【作者单位】第二军医大学基础部;第二军医大学基础部
【正文语种】中文
【中图分类】R971
【相关文献】
1.一类时滞BAM神经网络的全局指数稳定性的新准则 [J], 贾秀玲;段誉
2.一类时滞模糊BAM神经网络周期解的全局指数稳定性的新准则 [J], 王继禹;贾秀玲;段誉
3.一类时滞BAM神经网络的全局指数稳定性的新准则 [J], 贾秀玲;段誉;
4.一类时滞模糊BAM神经网络周期解的全局指数稳定性的新准则 [J], 王继禹;贾秀玲;段誉;
5.一类非自治的高阶BAM神经网络周期解的全局指数稳定性的新准则 [J], 王继禹;常彦妮
因版权原因，仅展示原文概要，查看原文内容请购买。
具时滞和脉冲的随机BAM型Cohen-Grossberg神经网络的稳定性分析
∑ （ （ ｔ ） ） ｄ （ ｔ ） ， ∑ａ ｊ ｉ （ ｘ ｄ ｔ ） ） ｄ ｗ ｉ （ ｔ ） 记为随机扰动；
Ｊ＝ １ ｚ＝ ｌ
＝（ ％）
和 ＝（ ｉ ）
表示
扩散 系数 矩 阵； ｗ（ ｔ ） ＝（ Ｗ１ （ ） ， 叫 ２ （ ￡ ） ， …， Ｗ （ ￡ ） ） Ｔ、 面（ ｔ ） ＝（ 面１ （ ） ， 面 ２ （ ） ， …， 面 （ ） ） Ｔ为定 义 在概 率 空 间 （ ， ｛ ｝ ｔ ０ ， Ｐ） 上具有 自然滤 波 ｛ ｝ ｔ ＞ ｏ Ｂ ｒ ｏ ｗ ｎ运 动 ．
Ｍ Ｒ（ ２ ０ ０ ０ ）主题分 类： ９ ３ Ｄ２ ０ ； ３ ４ Ｋ ２ ０ 中图分类号 ： Ｏ１ ７ ５ 文献标识码： Ａ 文章编号：１ ０ ０ ３ — ３ ９ ９ ８ （ ２ ０ １ ３ ） ０ ５ — ９ ３ ７ — １ ４
ｌ 引言
１ ９ ８ ３年 由 Ｃ ｏ ｈ ｅ ｎ和 Ｇｒ ｏ ｓ ｓ ｂ ｅ ｒ ｇ提 出的 Ｃ — Ｇ［ ］ 神 经 网络 被人 们逐 步关 注：在这类 神经 网 络里 考虑 时滞 ［ ２ － ２ １ ］ 和脉 冲 ［ ５ － １ ０ ， ２ ２ － ２ ７ ］ 已经很 常见 ；单 纯地 在 Ｃ — Ｇ 神经 网络里 引入随 机 因
＋ ∑ （ ｙ ｊ （ ｔ ） ） ｄ ｆ Ｊ ｊ （ ｔ ） ，ｉ ∈ ， ｔ ≠ｔ ｋ ， ｔ （ ＋ ） ＝ ｔ （ ｔ 一 ） ＋厶 ％ （ ｔ （ 一 ） ） ，ｔ ＝ｔ ｋ ， ∈Ｎ，
Ｉ ／ 扎 、 Ｊ
ｄ ｙ ｊ （ ｔ ） ：ｌ Ｌ — ｃ ｊ （ （ ｔ ） ） （ ＼ ｄ ｊ （ ｙ ｊ （ ｔ ） ） 一∑的 ｔ （ ｔ ） （ （ ） ） 一 ∑叫 Ｊ （ ｔ ） （ ｔ （ 一 ） ） 一 Ｊ ｊ （ ｔ ） ） Ｉ ｄ ｔ １ ｔ ＝１ ／Ｊ
Ｊ＝ １ ｚ＝ ｌ
＝（ ％）
和 ＝（ ｉ ）
表示
扩散 系数 矩 阵； ｗ（ ｔ ） ＝（ Ｗ１ （ ） ， 叫 ２ （ ￡ ） ， …， Ｗ （ ￡ ） ） Ｔ、 面（ ｔ ） ＝（ 面１ （ ） ， 面 ２ （ ） ， …， 面 （ ） ） Ｔ为定 义 在概 率 空 间 （ ， ｛ ｝ ｔ ０ ， Ｐ） 上具有 自然滤 波 ｛ ｝ ｔ ＞ ｏ Ｂ ｒ ｏ ｗ ｎ运 动 ．
Ｍ Ｒ（ ２ ０ ０ ０ ）主题分 类： ９ ３ Ｄ２ ０ ； ３ ４ Ｋ ２ ０ 中图分类号 ： Ｏ１ ７ ５ 文献标识码： Ａ 文章编号：１ ０ ０ ３ — ３ ９ ９ ８ （ ２ ０ １ ３ ） ０ ５ — ９ ３ ７ — １ ４
ｌ 引言
１ ９ ８ ３年 由 Ｃ ｏ ｈ ｅ ｎ和 Ｇｒ ｏ ｓ ｓ ｂ ｅ ｒ ｇ提 出的 Ｃ — Ｇ［ ］ 神 经 网络 被人 们逐 步关 注：在这类 神经 网 络里 考虑 时滞 ［ ２ － ２ １ ］ 和脉 冲 ［ ５ － １ ０ ， ２ ２ － ２ ７ ］ 已经很 常见 ；单 纯地 在 Ｃ — Ｇ 神经 网络里 引入随 机 因
＋ ∑ （ ｙ ｊ （ ｔ ） ） ｄ ｆ Ｊ ｊ （ ｔ ） ，ｉ ∈ ， ｔ ≠ｔ ｋ ， ｔ （ ＋ ） ＝ ｔ （ ｔ 一 ） ＋厶 ％ （ ｔ （ 一 ） ） ，ｔ ＝ｔ ｋ ， ∈Ｎ，
Ｉ ／ 扎 、 Ｊ
ｄ ｙ ｊ （ ｔ ） ：ｌ Ｌ — ｃ ｊ （ （ ｔ ） ） （ ＼ ｄ ｊ （ ｙ ｊ （ ｔ ） ） 一∑的 ｔ （ ｔ ） （ （ ） ） 一 ∑叫 Ｊ （ ｔ ） （ ｔ （ 一 ） ） 一 Ｊ ｊ （ ｔ ） ） Ｉ ｄ ｔ １ ｔ ＝１ ／Ｊ
时滞BAM神经网络周期振荡解的存在性和指数收敛性
时 滞 的 ＢＡ 神经 网络 周 期 振荡 解 的存在 性 与 指数 收敛 性 ，导 出 了周 期 振荡 解 存 在 和指 数 收敛 的充 Ｍ 分 判 据 ，对 激 励 函数 的 限制 较 少 ，得 到 的充 分 判 据 具 有 较 小 的保 守 性 ， 因而 有 助 于 周 期 振荡 时 滞
维普资讯
第２ ２卷
２ ０ 年 ０８
第 １ 期
２ 月
五邑大学学报 （自然科学版 ）
Ｊ Ｕ Ａ Ｏ ＷＵＹ Ｕ Ｖ ＳＴ （ ａ ｒｌ ｃ ｎｅ ｄｔ ｎ Ｏ ＲＮ Ｌ Ｆ Ｉ ＮＩＥＲ ＩＹ Ｎ ｔ ａ ｕ Ｓｉ ｃ Ｅ ｉｏ ） ｅ ｉ
Ｖ＿ ．２ ＮＯ． ０ ２ Ｉ １
ｎ ｔ ｒｓ ｅ ｗｏ ｋ ｗｉｈ ｅ ａ ｓ ｓ ｔ ｄ ｌ ｙ ｉ ｄｉ ｃ ｓ ｅ ｂ ｕ ｉ ｇ ｆｘ ｄ ｐ ｉ ｔ ｈ ｏ ｅ ｓ ｕ ｓ ｄ ｙ ｓ ｎ ｉ ｅ － ｏ ｎ ｔ ｅ ｒ ｍ， ｃ ｎ ｔ ｕ ｔ ｎ ｕ ｔ ｂ ｅ ｙ ｐ ｎ ｖ ｏ ｓ ｒ ｃ ｉ ｇ ｓ ｉ ｌ Ｌ ａ ｕ ｏ ａ ｆ ｎ ｔｏ ｓ ｎｄ ｓ ｍｅ ａ ａ ｙ ｉ ｅ ｈｎ ｑ ｅ ．Ｓ ｍｅ ｓ ｆｉ ｉ ｎ ｏ ｉｉ ｎ ｒ ｅ ｉ ｅ ｉ ｈ ａ ｅ ｏ ｒ ａ ｕ ｃ ｉ ｎ ，ａ ｏ ｎ ｌ ｓ ｓ ｔ ｃ ｉ ｕ ｓ ｏ ｕ ｆｃ ｅ ｔ ｃ ｎｄ ｔｏ ｓ ａ ｅ ｄ ｒｖ ｄ ｗｈ ｃ ｒ ｆ ｇ ｅ ｔ ｓ ｇ ｉｉ ａ ｅ ｉ ｈｅ ｄ ｓ ｇ ｎ ｐｐ ｉ ａ ｉ ｎ ｆ ＢＡＭ ｔ ｅ ａ ｓ ｈ ｏ ｄ ｔｏ ｓ ａ ｅ ｅ ｓ ｏ ｃ ｅ ｋ ｉ ｉ ｎ ｆｃ ｎｃ ｎ ｔ ｅ ｉ ｎ ａ ｄ ａ ｌｃ ｔｏ ｓ ｏ ｗｉ ｄ ｌ ｙ ．Ｔ ｅ ｃ ｎ ｉｉ ｎ ｒ ａ ｙ ｔ ｈ ｃ ｎ ｈ ｐ ａ ｔｃ ｙ ｓ ｍｐ ｅ ａ ｇ ｂ ａ ｃ ｍｅ ｈ ｄ ．Ｆｉ ａ ｌ ，ａ ｘ ｍｐ ｅ ｉ ｉ ｅ ｏ ｉｌ ｓ ｒ ｔ ｈ ｆｅ ｔ ｖ ｎ ｓ ｆ ｒ ｃ ｉｅ ｂ ｉ ｌ ｌｅ ｒ ｉ ｔ ｏ ｓ ｎ ｌｙ ｎ ｅ ａ ｌ ｓ ｇ ｖ ｎ ｔ ｌｕ ｔａ ｅ ｔ ｅ ｅ ｆ ｃ ｉ ｅ ｅ ｓ ｏ ｏ ｒｒ ｓ ｌ． ｕ ｅ ｕ ｔ
时滞BAM神经网络的p-类全局指数稳定性分析
（ 军 航 空工 程 学 院 海 ａ 基础 部 系统 科 学 与 数 学研 究 所 ， ． 础 部 ； ． ｂ基 山东 烟 台 ２ 一０ ） ６－ １ ￣ ０
摘 要 ： 先 给 出 了 Ｐ 类 全 局 指 数 稳 定 的概 念 ， 激 励 函数 满 足 全 局 Ｌｐｃｉ 连 续 的 条 仁 下 ， 用 不 等 式 和 分 首 一 在 ｉ ｈｚ ｓ ｔ ＝ 利
兴 趣
． 文 ［－４ ８ ，４ １ ］ 如 ３＿ ，＿９ １— ６ 等就 通过 构造 Ｌａｕｏ 泛 函或利 用 Ｍ 矩阵 、 ｙｐｎｖ 拓扑 度理 论 等方 法研
究 网络 的指数 稳定 性． 而文 ［ ，２ １ ］ 则 研究 了 网络 的渐 近稳 定 性 ． 经元 的响 应 时滞 会 影 响 网络 ２ １— ３ 等 神 的稳定 性 ， 引起 网络 的振 荡或不 稳定 ． 在设 计神 经元 电路 时 ， 仅要 考虑 系统稳定 的问题 ， 为重 要 的是 不 更 还 要考 虑 网络 的收敛行 为 ， 尤其 需要 设计 出以指数 速率 收敛 的网络 以保证 网络 的快速 响应 ， 这就 需要确
２８ ０
鲁 东大学学报 （ 自然科学 版）
第２ ８卷
文 中记 Ａ ＝ ｍ ｘ ａ
～
￣ｃ ，， ＝ 一 ｌｖｉ ， ｍ ｌ ， （ ＰＡ （ １ ｍｃ（） １ ｐ 笔 ＩＡ Ａ 。 Ｉａ ＝ ＝ ． － Ｉ ｐ
， ＝ ｛ ，｝＞。 。 ， ｃ＝ｍｘＡ， ｝ ＝２ａ（ １ｌ ａ／＇ ＇ ／ ｘ ｍｘ 慧 ｍ ｃＡ
理论 和实践 中都具 有重 要意 义． 于此并 受文 ［ ］ 基 ９ 的启 发 ， 文 首先 进 一 步提 出 了 Ｂ Ｍ 神 经 网络 Ｐ 类 本 Ａ 一
全局指 数稳定 的概 念 ， 然后结 合不 等式技 巧 ， 纯粹 数 学 分析 的方法 给 出了 网络 Ｐ 类全 局 指数 稳 定 的 用 ．
摘 要 ： 先 给 出 了 Ｐ 类 全 局 指 数 稳 定 的概 念 ， 激 励 函数 满 足 全 局 Ｌｐｃｉ 连 续 的 条 仁 下 ， 用 不 等 式 和 分 首 一 在 ｉ ｈｚ ｓ ｔ ＝ 利
兴 趣
． 文 ［－４ ８ ，４ １ ］ 如 ３＿ ，＿９ １— ６ 等就 通过 构造 Ｌａｕｏ 泛 函或利 用 Ｍ 矩阵 、 ｙｐｎｖ 拓扑 度理 论 等方 法研
究 网络 的指数 稳定 性． 而文 ［ ，２ １ ］ 则 研究 了 网络 的渐 近稳 定 性 ． 经元 的响 应 时滞 会 影 响 网络 ２ １— ３ 等 神 的稳定 性 ， 引起 网络 的振 荡或不 稳定 ． 在设 计神 经元 电路 时 ， 仅要 考虑 系统稳定 的问题 ， 为重 要 的是 不 更 还 要考 虑 网络 的收敛行 为 ， 尤其 需要 设计 出以指数 速率 收敛 的网络 以保证 网络 的快速 响应 ， 这就 需要确
２８ ０
鲁 东大学学报 （ 自然科学 版）
第２ ８卷
文 中记 Ａ ＝ ｍ ｘ ａ
～
￣ｃ ，， ＝ 一 ｌｖｉ ， ｍ ｌ ， （ ＰＡ （ １ ｍｃ（） １ ｐ 笔 ＩＡ Ａ 。 Ｉａ ＝ ＝ ． － Ｉ ｐ
， ＝ ｛ ，｝＞。 。 ， ｃ＝ｍｘＡ， ｝ ＝２ａ（ １ｌ ａ／＇ ＇ ／ ｘ ｍｘ 慧 ｍ ｃＡ
理论 和实践 中都具 有重 要意 义． 于此并 受文 ［ ］ 基 ９ 的启 发 ， 文 首先 进 一 步提 出 了 Ｂ Ｍ 神 经 网络 Ｐ 类 本 Ａ 一
全局指 数稳定 的概 念 ， 然后结 合不 等式技 巧 ， 纯粹 数 学 分析 的方法 给 出了 网络 Ｐ 类全 局 指数 稳 定 的 用 ．
时间尺度上时滞Cohen-Grossberg BAM神经网络系统概周期解的全局指数稳定性
在实 践和应用 中，连 续和离散 系统都很重 要的，然而，这是 非常麻烦 的分开去 研 究连 续和离 散 系统 的稳定性 ．因此，研究 时间尺 度理论 去统一离散和 连续 系统是 有意义 的．
关键词 指 数稳定；Ｃｏｈｅｎ－Ｇｒｏｓｓｂｅｒｇ ＢＡＭ 神经 网络；概周期解；时间尺度；时滞
中图分 类号 Ｏ１７５．１４
Ｇ ｌｏｂａｌ Ｅｘｐｏｎｅｎｔｉａｌ Ｓｔａｂｉｌｉｔｙ ｏｆ Ａ ｌｍ ｏｓｔ Ｐｅｒｉｏｄｉｃ Ｓｏｌｕｔｉｏｎ ｔｏ Ｃｏｈｅｎ．Ｇ ｒｏｓｓｂｅｒｇ ＢＡ Ｍ Ｎ ｅｕｒａｌ Ｎ ｅｔｗ ｏｒｋｓ ｗ ｉｔｈ Ｄ ｅｌａｙｓ
吕小俊
（云南大学旅游文化学院，信息学院，丽江 ６７４１９９）
摘 要 本文通过使用李雅谱诺夫函数和不等式技巧等，在时间尺度上研究时滞 Ｃｏｈｅｎ－ Ｇｒｏｓｓｂｅｒｇ ＢＡＭ 神经 网络系 统概周期解 的全局指数稳定性，在此，不需要假设反应 函数 的有界性．最后，获得一些使 其存在全局指数稳 定 的概周期解 的分条件，并给 出例 子 去验 证结果 的有效 性．
ｏｎ Ｔｉｍ ｅ Ｓｃａｌｅｓ
ＬＵ Ｘｉａ￣ｊｕｎ （Ｄｅｐａｒｔｍｅｎｔ ｏｆ Ｉｎｆｏｒｍａｔｉｏｎ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ，Ｔｏｕｒｉｓｍ ａｎｄ Ｃｕｌｔｕｒｅ Ｃｏｌｌｅｇｅ，Ｙｕｎｎａｎ Ｕｎｉｖｅｒｓｉｔｙ，Ｌｉｊｉａｎｇ
６７４１９９，Ｃｈｉｎａ）
Ａ ｂｓｔｒａｃｔ Ｉｎ ｔｈｉｓ ｐａｐｅｒ．ｔｈｅ ｇｌｏｂａｌ ｅｘｐｏｎｅｎｔｉａｌ ｓｔａｂｉｌｉｔｙ ｏｆ ａｌｍｏｓｔ ｐｅｒｉｏｄｉｃ ｓｏｌｕｔｉｏｎ ｔｏ Ｃｏｈｅｎ－Ｇｒｏｓｓｂｅｒｇ ＢＡＭ ｎｅｕｒａｌ ｎｅｔｗｏｒｋｓ ｗｉｔｈ ｄｅｌａｙｓ ｏｎ ｔｉｍｅ ｓｃａｌｅｓ ｉｓ ｓｔｕｄｉｅｄ．Ｗ ｉｔｈｏｕｔ ａｓｓｕｍ ｉｎｇ ｂｏｕｎｄｅｄ ｃｏｎｄｉｔｉｏｎｓ ｏｎ ｔｈｅｓｅ ａｃｔｉｖａｔｉｏｎ ｆｕｎｃｔｉｏｎｓ．Ｕｓｉｎｇ Ｌｙａｐｕｎｏｖ ｆｕｎｃｔｉｏｎａｌ ａｎｄ ｉｎｅｑｕａｌｉｔｙ ｓｋｉｌｌｓ，ｗｅ ｆｉｎｄ ｓｏｍ ｅ ｓｕｆｉ ｃｉｅｎｔ ｃｏｎｄｉｔｉｏｎｓ ｅｎｓｕｒｉｎｇ ｔｈｅ ｅｘｉｓｔｅｎｃｅ ａｎｄ ｇｌｏｂａｌ ｅｘｐｏｎｅｎｔｉａｌ ｓｔａｂｉｌｉｔｙ ｏｆ ａｌｍ ｏｓｔ ｐｅｒｉｏｄｉｃ ｓｏｌｕｔｉｏｎ ｔｏ Ｃｏｈｅｎ－Ｇｒｏｓｓｂｅｒｇ ＢＡＭ ｎｅｕｒａｌ ｎｅｔｗｏｒｋｓ ｗｉｔｈ ｄｅｌａｙｓ ｏｎ ｔｉｍｅ ｓｃａｌｅｓ．Ａｎ ｅｘａｍｐｌｅ ｉｓ ｇｉｖｅｎ ｔｏ ｓｈｏｗ ｔｈｅ ｅｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ｔｈｅ ｏｂｔａｉｎｅｄ ｒｅｓｕｌｔｓ．
多元产品价格互惠时滞模型的周期解和概周期解及其全局稳定性
：
十 面’ｌ） （ （ ， 一
面
＋ 型’ ｝ ） （ ，ｏ 堕） ）
， ∈【 】利用归纳法不难推 ｔ ０ ＿ ，
＋
ｔ
（ 笪 ＾ ，。 一 ｄ （ 塑 ０ 面 一 ） （ ｌ） ｆ＿ ，。 ， 。 ＋ （ ’ ｕ ｌ） 叭
从而
（ ０ 即 ｔ ） ，
Ｍ Ｒ（ ０ ０ ２ ０ ）主题分类 ：３ Ｋ５ ； ２ ５ ６ Ｈ１ 中图分类号 ：０２ １ 文献标识码 ：Ａ ５ ７ ９ Ｄ２ ； ０ ０ １． ４
文章编号：１０—９８２ １）６１１—２ ０３ ９（０１０—７８１ ３
１ 引 言
众所周 知 ， Ｌ ｔａＶ ｌ ｒａ 型是 生态 系统最早 和最典 型的模 型 ，但近年来 ，人 们开 始 ｏｋ－ｏ ｅｒ 模 ｔ 将其 应 用于市 场结 构演 化 ，投 资竞 争 ［ ４ 商 品价 格波 动 ［ ７ 等经 济 问题 研 究．本文 从 以 １ ］ －， ５ ］ －
式得 到
－ ￣－） ｔ 面一 ｒｅ Ｋ（ ｓ ｉ Ｉ
０
ｔ
一 １ｓ ａ－ ￣＋ ｔ ｄ ＜ ｅ Ｋｔ ｅ Ｋ（ ｓ － ｉ－） ｔ 尬 一 Ｉ ｄ ｓ
为 ｂ２＞０ 和 ｂ１＞０， １（ ） ２（ ）于是 Ｕ ２的变 化对 Ｕ ｌ产生促进 作用 ，反过 来 Ｕ １的变 化对 札 也 有促 ２ 进作 用 ，由此推 出二元产 品价 格互惠关 系为
＝， （ ｌＵ ＋ “ ） “ 。 一ｂｌ ｌ 。，
ｄｕ２
＝“ （２ ２ 一ｂ２２． ２。 ＋ｂ１ １ １ｕ ）
，
（） ９
存在，而且 也 型
的解 ．
． 我们进一步证 明 ＝型 ＝乱ｔ ０ ） （ ） （ ） （ （∈［ ］是初值问题 （）（ ） ， １，２ ）
十 面’ｌ） （ （ ， 一
面
＋ 型’ ｝ ） （ ，ｏ 堕） ）
， ∈【 】利用归纳法不难推 ｔ ０ ＿ ，
＋
ｔ
（ 笪 ＾ ，。 一 ｄ （ 塑 ０ 面 一 ） （ ｌ） ｆ＿ ，。 ， 。 ＋ （ ’ ｕ ｌ） 叭
从而
（ ０ 即 ｔ ） ，
Ｍ Ｒ（ ０ ０ ２ ０ ）主题分类 ：３ Ｋ５ ； ２ ５ ６ Ｈ１ 中图分类号 ：０２ １ 文献标识码 ：Ａ ５ ７ ９ Ｄ２ ； ０ ０ １． ４
文章编号：１０—９８２ １）６１１—２ ０３ ９（０１０—７８１ ３
１ 引 言
众所周 知 ， Ｌ ｔａＶ ｌ ｒａ 型是 生态 系统最早 和最典 型的模 型 ，但近年来 ，人 们开 始 ｏｋ－ｏ ｅｒ 模 ｔ 将其 应 用于市 场结 构演 化 ，投 资竞 争 ［ ４ 商 品价 格波 动 ［ ７ 等经 济 问题 研 究．本文 从 以 １ ］ －， ５ ］ －
式得 到
－ ￣－） ｔ 面一 ｒｅ Ｋ（ ｓ ｉ Ｉ
０
ｔ
一 １ｓ ａ－ ￣＋ ｔ ｄ ＜ ｅ Ｋｔ ｅ Ｋ（ ｓ － ｉ－） ｔ 尬 一 Ｉ ｄ ｓ
为 ｂ２＞０ 和 ｂ１＞０， １（ ） ２（ ）于是 Ｕ ２的变 化对 Ｕ ｌ产生促进 作用 ，反过 来 Ｕ １的变 化对 札 也 有促 ２ 进作 用 ，由此推 出二元产 品价 格互惠关 系为
＝， （ ｌＵ ＋ “ ） “ 。 一ｂｌ ｌ 。，
ｄｕ２
＝“ （２ ２ 一ｂ２２． ２。 ＋ｂ１ １ １ｕ ）
，
（） ９
存在，而且 也 型
的解 ．
． 我们进一步证 明 ＝型 ＝乱ｔ ０ ） （ ） （ ） （ （∈［ ］是初值问题 （）（ ） ， １，２ ）