福建省2012年高考数学最新联考试题分类大汇编(15)算法框图、选修系列试题

合集下载

2012高考福建理科数学精彩试题及问题详解(高清版)

2012年普通高等学校夏季招生全国统一考试数学理工农医类(福建卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．理科：第Ⅱ卷第21题为选考题，其他题为必考题，满分150分．第Ⅰ卷一、选择题：(理科)本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．(文科)本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z 满足z i ＝1－i ，则z 等于( )A ．－1－iB ．1－iC ．－1＋iD ．1＋i A ．3＋4i B ．5＋4i C ．3＋2i D ．5＋2i2．等差数列{a n }中，a 1＋a 5＝10，a 4＝7，则数列{a n }的公差为( ) A ．1 B ．2 C ．3 D ．4 3．下列命题中，真命题是( )A ．x 0∈R ，0e 0x≤ B ．x ∈R ，2x＞x 2C ．a ＋b ＝0的充要条件是1ab=- D ．a ＞1，b ＞1是ab ＞1的充分条件4．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是( ) A ．球 B ．三棱锥 C ．正方体 D ．圆柱 5．下列不等式一定成立的是( )A ．lg(x 2＋14)＞lg x (x ＞0) B ．sin x ＋1sin x≥2(x ≠k π，k ∈Z )C ．x 2＋1≥2|x |(x ∈R ) D ．2111x >+(x ∈R ) 6．如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为()A ．14 B ．15 C ．16 D ．177．设函数1,()0,x D x x ⎧=⎨⎩为有理数，为无理数，则下列结论错误的是( )A ．D (x )的值域为{0,1}B ．D (x )是偶函数C ．D (x )不是周期函数 D ．D (x )不是单调函数8．已知双曲线22214x y b-=的右焦点与抛物线y 2＝12x 的焦点重合，则该双曲线的焦点到其渐近线的距离等于( )AB．．3 D ．59．若函数y ＝2x图象上存在点(x ，y )满足约束条件30,230,,x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩则实数m 的最大值为( )A ．12 B ．1 C ．32D ．2 10．函数f (x )在［a ，b ］上有定义，若对任意x 1，x 2∈［a ，b ］，有()()12121()22x x f f x f x +≤［＋］，则称f (x )在［a ，b ］上具有性质P ．设f (x )在［1,3］上具有性质P ，现给出如下命题：①f (x )在［1,3］上的图象是连续不断的；②f (x 2)在［1］上具有性质P ；③若f (x )在x ＝2处取得最大值1，则f (x )＝1，x ∈［1,3］；④对任意x 1，x 2，x 3，x 4∈［1,3］，有12341()44x x x x f +++≤［f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)］．其中真命题的序号是( )A ．①②B ．①③C ．②④D ．③④第Ⅱ卷二、填空题：(理科)本大题共5小题，每小题4分，共20分．把答案填在答题卡的相应位置．(文科)本大题共4小题，每小题4分，共16分．把答案填在答题卡的相应位置．11． (a ＋x )4的展开式中x 3的系数等于8，则实数a ＝________．12．阅读右图所示的程序框图，运行相应的程序，输出的s 值等于________． 13．已知△ABC的等比数列，则其最大角的余弦值为________．14．数列{a n }的通项公式πcos12n n a n =+，前n 项和为S n ，则S 2 012＝________． 15．对于实数a 和b ，定义运算“*”：22*.a ab a b a b b ab a b ⎧-≤=⎨->⎩，，，设f (x )＝(2x －1)*(x －1)，且关于x 的方程f (x )＝m (m ∈R )恰有三个互不相等的实数根x 1，x 2，x 3，则x 1x 2x 3的取值范围是__________．三、解答题：(理科)本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．(文科)本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．16．受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率；(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X 1，生产一辆乙品牌轿车的利润为X 2，分别求X 1，X 2的分布列；(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．17．某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：①sin 213°＋cos 217°－sin13°cos17°；②sin 215°＋cos 215°－sin15°cos15°；③sin 218°＋cos 212°－sin18°cos12°；④sin 2(－18°)＋cos 248°－sin(－18°)cos48°；⑤sin 2(－25°)＋cos 255°－sin(－25°)cos55°． (1)试从上述五个式子中选择一个，求出这个常数；(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论． 18．如图，在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝1，E 为CD 中点．(1)求证：B 1E ⊥AD 1．(2)在棱AA 1上是否存在一点P ，使得DP ∥平面B 1AE ？若存在，求AP 的长；若不存在，说明理由．(3)若二面角A －B 1E －A 1的大小为30°，求AB 的长．19．如图，椭圆E ：22221x y a b +=(a ＞b ＞0)的左焦点为F 1，右焦点为F 2，离心率12e =．过F 1的直线交椭圆于A 、B 两点，且△ABF 2的周长为8．(1)求椭圆E 的方程；(2)设动直线l ：y ＝kx ＋m 与椭圆E 有且只有一个公共点P ，且与直线x ＝4相交于点Q ．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M 的坐标；若不存在，说明理由．20．已知函数f(x)＝e x＋ax2－e x，a∈R．(1)若曲线y＝f(x)在点(1，f(1))处的切线平行于x轴，求函数f(x)的单调区间；(2)试确定a的取值范围，使得曲线y＝f(x)上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P．21． (1)选修4－2：矩阵与变换设曲线2x2＋2xy＋y2＝1在矩阵1ab⎛⎫= ⎪⎝⎭A(a＞0)对应的变换作用下得到的曲线为x2＋y2＝1．①求实数a，b的值；②求A2的逆矩阵．(2)选修4－4：坐标系与参数方程在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为(2,0)，π32⎛⎫⎪⎪⎝⎭，圆C的参数方程为22c o s,2s i nxyθθ=+⎧⎪⎨=⎪⎩(θ为参数)．①设P为线段MN的中点，求直线OP的平面直角坐标方程；②判断直线l与圆C的位置关系．(3)选修4－5：不等式选讲已知函数f(x)＝m－|x－2|，m∈R，且f(x＋2)≥0的解集为［－1,1］．①求m的值；②若a，b，c∈R＋，且11123ma b c++=，求证：a＋2b＋3c≥9．22．(文)已知函数f(x)＝ax sin x－32(a∈R)，且在［0，π2］上的最大值为π32-．(1)求函数f(x)的解析式；(2)判断函数f(x)在(0，π)内的零点个数，并加以证明．1． A 由z i＝1－i，得221i(1i)i i i i+11ii i11z---=====----．2． B ∵a1＋a5＝10＝2a3，∴a3＝5．故d＝a4－a3＝7－5＝2．3． D ∵a＞1＞0，b＞1＞0，∴由不等式的性质得ab＞1，即a＞1，b＞1⇒ab＞1．4． D ∵圆柱的三视图中有两个矩形和一个圆，∴这个几何体不可以是圆柱．5． C ∵x2＋1≥2|x|⇔x2－2|x|＋1≥0，∴当x≥0时，x2－2|x|＋1＝x2－2x＋1＝(x－1)2≥0成立；当x＜0时，x2－2|x|＋1＝x2＋2x＋1＝(x＋1)2≥0成立．故x2＋1≥2|x|(x∈R)一定成立．6． C∵由图象知阴影部分的面积是3122121211)d()32326x x x x=⋅-=-=⎰，∴所求概率为11616=．7． C ∵D (x )是最小正周期不确定的周期函数， ∴D (x )不是周期函数是错误的．8． A 由双曲线的右焦点与抛物线y 2＝12x 的焦点重合，知32pc ==，c 2＝9＝4＋b 2，于是b 2＝5，b =2y x =±20y ±=．故该双曲线的焦点到其渐近线的距离为d == 9． B 由约束条件作出其可行域如图所示：由图可知当直线x ＝m 经过函数y ＝2x的图象与直线x ＋y －3＝0的交点P 时取得最大值，即得2x＝3－x ，即x ＝1＝m ．10． D ①如图1，图1在区间［1,3］上f (x )具有性质P ，但是是间断的，故①错．②可设f (x )＝|x －2|(如图2)，当x ∈［1,3］时易知其具有性质P ，但是f (x 2)＝|x2－2|＝222,1x x x x ⎧-≤≤⎪⎨-<≤⎪⎩P (如图3)．故②错．图2图3③任取x 0∈［1,3］，则4－x 0∈［1,3］， 1＝f (2)＝004()2x x f +-≤12［f (x 0)＋f (4－x 0)］．又∵f (x 0)＝1，f (4－x 0)≤1， ∴12［f (x 0)＋f (4－x 0)］≤1． ∴f (x 0)＝f (4－x 0)＝1．故③正确．④3412123422()()42x x x x x x x x f f ++++++= ≤34121()+()222x x x x f f ++⎡⎤⎢⎥⎣⎦≤14［f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)］，故④正确．11．答案：2 解析：∵T r ＋1＝4C ra r x4－r，∴当4－r ＝3，即r ＝1时，T 2＝14C ·a ·x 3＝4ax 3＝8x 3．故a＝2．12．答案：－3解析：(1)k ＝1,1＜4，s ＝2×1－1＝1； (2)k ＝2,2＜4，s ＝2×1－2＝0； (3)k ＝3,3＜4，s ＝2×0－3＝－3； (4)k ＝4，直接输出s ＝－3．13．答案：4-解析：设△ABC 的最小边长为a (m ＞0)，2a ，故最大角的余弦值是2222cos 4θ===-． 14．答案：3 018 解析：∵函数πcos2n y =的周期2π4π2T ==，∴可用分组求和法：a 1＋a 5＋…＋a 2 009＝50311+1=503++个…；a 2＋a 6＋…＋a 2 010＝(－2＋1)＋(－6＋1)＋…＋(－2 010＋1)＝－1－5－…－2 009＝503(12009)2--＝－503×1 005；a 3＋a 7＋…＋a 2 011＝50311+1=503++个…；a 4＋a 8＋…＋a 2 012＝(4＋1)＋(8＋1)＋…＋(2 012＋1)＝503(52013)2⨯+＝503×1009；故S 2 012＝503－503×1 005＋503＋503×1 009 ＝503×(1－1 005＋1＋1 009)＝3 018．15．答案：，0)解析：由已知，得()22200x x x f x x x x ⎧≤⎪⎨⎪⎩－，，＝－＋，＞，作出其图象如图，结合图象可知m 的取值范围为0＜m ＜14，当x ＞0时，有－x 2＋x ＝m ，即x 2－x ＋m ＝0，于是x 1x 2＝m ．当x ＜0时，有2x 2－x －m ＝0，于是314x =．故123(14m x x x =．设h (m )＝m (1，∵h ′(m )＝(1＋［m()］＝10<，∴函数h (m )单调递减．故x 1x 2x 3的取值范围为，0)． 16．解：(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A ，则231()5010P A +==． (2)依题意得，X 1X 2的分布列为(3)由(2)得，E (X 1)＝1×125＋2×50＋3×10＝50＝2.86(万元)，E (X 2)＝1.8×110＋2.9×910＝2.79(万元)．因为E (X 1)＞E (X 2)，所以应生产甲品牌轿车．17．解：方法一：(1)选择②式，计算如下： sin 215°＋cos 215°－sin15°cos15°＝1－12sin30°＝13144-=．(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下： sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝sin 2α＋(cos30°cos α＋sin30°sin α)2－sin α·(cos30°cos α＋sin30°sin α)＝sin 2α＋34cos 2α＋2sin αcos α＋14sin 2α－2sin α·cos α－12sin 2α＝34sin 2α＋34cos 2α＝34．方法二：(1)同方法一．(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下： sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝1cos21cos(602)22αα-+︒-+－sin α(cos30°cos α＋sin30°sin α)＝12－12cos2α＋12＋12(cos60°·cos2α＋sin60°sin2α)－sin αcos α－12sin 2α＝12－12cos2α＋12＋14cos2ααα－14(1－cos2α)＝11131cos2cos24444αα--+=．18．解：(1)以A 为原点，AB ，AD ，1AA 的方向分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图)．设AB ＝a ，则A (0,0,0)，D (0,1，0)，D 1(0,1,1)，E (2a，1,0)，B 1(a,0,1)，故1AD ＝(0,1,1)，1B E ＝(2a -，1，－1)，1AB ＝(a,0,1)，AE ＝(2a，1,0)．∵1AD ·1B E ＝2a-×0＋1×1＋(－1)×1＝0，∴B 1E ⊥AD 1．(2)假设在棱AA 1上存在一点P (0,0，z 0)，使得DP ∥平面B 1AE ．此时DP ＝(0，－1，z 0)．又设平面B 1AE 的法向量n ＝(x ，y ，z )． ∵n ⊥平面B 1AE ，∴n ⊥1AB ，n ⊥AE ，得00.2ax z ax y +=⎧⎪⎨+=⎪⎩，取x ＝1，得平面B 1AE 的一个法向量n ＝(1，2a-，－a )．要使DP ∥平面B 1AE ，只要n ⊥DP ，有2a－az 0＝0，解得012z =．又DP 平面B 1AE ，∴存在点P ，满足DP ∥平面B 1AE ，此时12AP =．(3)连接A 1D ，B 1C ，由长方体ABCD A 1B 1C 1D 1及AA 1＝AD ＝1，得AD 1⊥A 1D ． ∵B 1C ∥A 1D ，∴AD 1⊥B 1C ．又由(Ⅰ)知B 1E ⊥AD 1，且B 1C ∩B 1E ＝B 1，∴AD 1⊥平面DCB 1A 1．∴1AD 是平面A 1B 1E 的一个法向量，此时1AD ＝(0,1,1)．设1AD 与n 所成的角为θ，则11·cos ||||a aAD AD θ--==n n ．∵二面角A －B1E －A 1的大小为30°， ∴|cos θ|＝cos303a =，解得a ＝2，即AB 的长为2．19．解：方法一：(1)因为|AB |＋|AF 2|＋|BF 2|＝8，即|AF 1|＋|F 1B |＋|AF 2|＋|BF 2|＝8，又|AF 1|＋|AF 2|＝|BF 1|＋|BF 2|＝2a ，所以4a ＝8，a ＝2．又因为12e =，即12c a =，所以c ＝1．所以b故椭圆E 的方程是22143x y +=． (2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩，，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0．因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且∆＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0．(*)此时024443km k x k m =-=-+，y 0＝kx 0＋m ＝3m ，所以P (4k m -，3m )．由4x y kx m =⎧⎨=+⎩，，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．设M (x 1,0)，则0MP MQ ⋅=对满足(*)式的m ，k 恒成立．因为MP ＝(14k x m --，3m)，MQ ＝(4－x 1,4k ＋m )，由0MP MQ ⋅=，得211141612430kx k k x x m m m-+-+++=，整理，得(4x 1－4)k m＋x 12－4x 1＋3＝0．(**)由于(**)式对满足(*)式的m ，k 恒成立，所以1211440,430,x x x -=⎧⎨-+=⎩解得x 1＝1．故存在定点M (1,0)，使得以PQ 为直径的圆恒过点M ．方法二：(1)同方法一．(2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩，，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0．因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且∆＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0．(*)此时024443km k x k m =-=-+，y 0＝kx 0＋m ＝3m ，所以P (4k m -，3m )．由4x y kx m =⎧⎨=+⎩，，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．取k ＝0，m =此时P (0)，Q (4)，以PQ 为直径的圆为(x －2)2＋(y)2＝4，交x 轴于点M 1(1,0)，M 2(3,0)；取12k =-，m ＝2，此时P (1，32)，Q (4,0)，以PQ 为直径的圆为225345()()2416x y -+-=，交x 轴于点M 3(1,0)，M 4(4,0)．所以若符合条件的点M 存在，则M 的坐标必为(1,0)．以下证明M (1,0)就是满足条件的点：因为M 的坐标为(1,0)，所以MP ＝(41k m --，3m)，MQ ＝(3,4k ＋m )，从而1212330k kMP MQ m m⋅=--++=，故恒有MP MQ ⊥，即存在定点M (1,0)，使得以PQ 为直径的圆恒过点M ．20．解：(1)由于f ′(x )＝e x＋2ax －e ，曲线y ＝f (x )在点(1，f (1))处切线斜率k ＝2a ＝0，所以a ＝0，即f (x )＝e x－e x ．此时f ′(x )＝e x－e ，由f ′(x )＝0得x ＝1．当x ∈(－∞，1)时，有f ′(x )＜0；当x ∈(1，＋∞)时，有f ′(x )＞0．所以f (x )的单调递减区间为(－∞，1)，单调递增区间为(1，＋∞)．(2)设点P(x0，f(x0))，曲线y＝f(x)在点P处的切线方程为y＝f′(x0)(x－x0)＋f(x0)，令g(x)＝f(x)－f′(x0)(x－x0)－f(x0)，故曲线y＝f(x)在点P处的切线与曲线只有一个公共点P等价于函数g(x)有唯一零点．因为g(x0)＝0，且g′(x)＝f′(x)－f′(x0)＝e x－e x0＋2a(x－x0)．(1)若a≥0，当x＞x0时，g′(x)＞0，则x＞x0时，g(x)＞g(x0)＝0；当x＜x0时，g′(x)＜0，则x＜x0时，g(x)＞g(x0)＝0．故g(x)只有唯一零点x＝x0．由P的任意性，a≥0不合题意．(2)若a＜0，令h(x)＝e x－e x0＋2a(x－x0)，则h(x0)＝0，h′(x)＝e x＋2a．令h′(x)＝0，得x＝ln(－2a)，记x′＝ln(－2a)，则当x∈(－∞，x*)时，h′(x)＜0，从而h(x)在(－∞，x*)内单调递减；当x∈(x*，＋∞)时，h′(x)＞0，从而h(x)在(x*，＋∞)内单调递增．①若x0＝x*，由x∈(－∞，x*)时，g′(x)＝h(x)＞h(x*)＝0；x∈(x*，＋∞)时，g′(x)＝h(x)＞h(x*)＝0，知g(x)在R上单调递增．所以函数g(x)在R上有且只有一个零点x＝x*．②若x0＞x*，由于h(x)在(x*，＋∞)内单调递增，且h(x0)＝0，则当x∈(x*，x0)时有g′(x)＝h(x)＜h(x0)＝0，g(x)＞g(x0)＝0；任取x1∈(x*，x0)有g(x1)＞0．又当x∈(－∞，x1)时，易知g(x)＝e x＋ax2－［e＋f′(x0)］x－f(x0)＋x0f′(x0)＜e x1＋ax2－［e＋f′(x0)］x－f(x0)＋x0f′(x0)＝ax2＋bx＋c，其中b＝－［e＋f′(x0)］，c＝e x1－f(x0)＋x0f′(x0)．由于a＜0，则必存在x2＜x1，使得ax22＋bx2＋c＜0．所以g(x2)＜0．故g(x)在(x2，x1)内存在零点，即g(x)在R上至少有两个零点．③若x0＜x*，仿②并利用3e6xx>，可证函数g(x)在R上至少有两个零点．综上所述，当a＜0时，曲线y＝f(x)上存在唯一点P(ln(－2a)，f(ln(－2a)))，曲线在该点处的切线与曲线只有一个公共点P．21． (1)选修4－2：矩阵与变换解：①设曲线2x2＋2xy＋y2＝1上任意点P(x，y)在矩阵A对应的变换作用下的像是P′(x′，y′)．由1x ay b'⎛⎫⎛⎫=⎪ ⎪'⎝⎭⎝⎭x axy bx y⎛⎫⎛⎫=⎪ ⎪+⎝⎭⎝⎭，得,.x axy bx y'=⎧⎨'=+⎩又点P′(x′，y′)在x2＋y2＝1上，所以x′2＋y′2＝1，即a2x2＋(bx＋y)2＝1，整理得(a2＋b2)x2＋2bxy＋y2＝1．依题意得222,22,a bb⎧+=⎨=⎩解得1,1,ab=⎧⎨=⎩或1,1,ab=-⎧⎨=⎩因为a＞0，所以1,1. ab=⎧⎨=⎩②由①知，1 01 1⎛⎫= ⎪⎝⎭A，21 0 1 0 1 01 1 1 12 1⎛⎫⎛⎫⎛⎫==⎪⎪ ⎪⎝⎭⎝⎭⎝⎭A，所以|A2|＝1，(A2)－1＝1 02 1⎡⎤⎢⎥-⎣⎦．(2)选修4－4：坐标系与参数方程解：①由题意知，M，N的平面直角坐标分别为(2,0)，(0，3)．又P 为线段MN 的中点，从而点P 的平面直角坐标为(1，3)，故直线OP 的平面直角坐标方程为3y x =．②因为直线l 上两点M ，N 的平面直角坐标分别为(2,0)，(0，3)，所以直线l 30y +-=．又圆C 的圆心坐标为(2，)，半径r ＝2，圆心到直线l 的距离32d r ==<，故直线l 与圆C 相交． (3)选修4－5：不等式选讲解：①因为f (x ＋2)＝m －|x |，f (x ＋2)≥0等价于|x |≤m ，由|x |≤m 有解，得m ≥0，且其解集为{x |－m ≤x ≤m }．又f (x ＋2)≥0的解集为［－1,1］，故m ＝1． ②由①知111123a b c++=，又a ，b ，c ∈R ＋，由柯西不等式得 a ＋2b ＋3c ＝(a ＋2b ＋3c )(11123a b c++)≥29＝．。

2012年福建省高考数学试卷(理科)答案与解析

2012年福建省高考数学试卷（理科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出分四个选项中，只有一项是符合题目要求的．===≤的充要条件是，但是4．（5分）（2012•福建）一个几何体的三视图形状都相同，大小均相等，那么这个几何体不sinx+≥（x∈R）时，不等式两边相等；sinx+6．（5分）（2012•福建）如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（）By=（（﹣=取自阴影部分的概率为=7．（5分）（2012•福建）设函数，则下列结论错误的是（）=（8．（5分）（2012•福建）已知双曲线﹣=1的右焦点与抛物线y2=12x的焦点重合，则B∵双曲线的右焦点与抛物线∴双曲线的一条渐近线方程为∴双曲线的焦点到其渐近线的距离等于9．（5分）（2012•福建）若函数y=2x图象上存在点（x，y）满足约束条件，B10．（5分）（2012•福建）函数f（x）在[a，b]上有定义，若对任意x1，x2∈[a，b]，有在[1，3]上具有性质P，现给出如下命题：①f（x）在[1，3]上的图象是连续不断的；②f（x2）在[1，]上具有性质P；③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；④对任意x1，x2，x3，x4∈[1，3]，有[f（x1）+f（x2）+f（x3）+f（x4）]其中真命题的序号是（）在]（≤=[f二、填空题：本大题共5小题，每小题4分，共20分，把答案填在答题卡的相应位置．11．（4分）（2012•福建）（a+x）4的展开式中x3的系数等于8，则实数a=2．×12．（4分）（2012•福建）阅读图所示的程序框图，运行相应地程序，输出的s值等于﹣3．13．（4分）（2012•福建）已知△ABC得三边长成公比为的等比数列，则其最大角的余弦值为．据三角形三边长成公比为，aaa﹣14．（4分）（2012•福建）数列{a n}的通项公式a n=ncos+1，前n项和为S n，则S2012= 3018．cos ncos的规律，即可求出数列的规律即可求出结ncos=0ncos的每四项和为15．（4分）（2012•福建）对于实数a和b，定义运算“*”：a*b=设f（x）=（2x﹣1）*（x﹣1），且关于x的方程为f（x）=m（m∈R）恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是．=）轴的左边，得到，），又在，）上成立，y=（，即故答案为：三、解答题：本大题共5小题，共80分，解答题写出文字说明，证明过程或演算步骤．16．（13分）（2012•福建）受轿车在保修期内维修费等因素的影响，企业产生每辆轿车的利润与该轿车首次出现故障的时间有关，某轿车制造厂生产甲、乙两种品牌轿车，保修期均为（Ⅰ）从该厂生产的甲品牌轿车中随机抽取一辆，求首次出现故障发生在保修期内的概率；（Ⅱ）若该厂生产的轿车均能售出，记住生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列；（Ⅲ）该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌轿车，若从经济效益的角度考虑，你认为应该产生哪种品牌的轿车？说明理由．××+3×=2.86×+2.9×××+3×=2.86××=2.7917．（13分）（2012•福建）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数．（1）sin213°+cos217°﹣sin13°cos17°（2）sin215°+cos215°﹣sin15°cos15°（3）sin218°+cos212°﹣sin18°cos12°（4）sin2（﹣18°）+cos248°﹣sin2（﹣18°）cos48°（5）sin2（﹣25°）+cos255°﹣sin2（﹣25°）cos55°（Ⅰ）试从上述五个式子中选择一个，求出这个常数；（Ⅱ）根据（Ⅰ）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．﹣，可得这个常数的=++sin2，化简可得结果．sin30．．++sin sin﹣sin=++（）﹣﹣+cos2﹣=1﹣+．18．（13分）（2012•福建）如图，在长方体ABCD﹣A1B1C1D1中AA1=AD=1，E为CD中点．（Ⅰ）求证：B1E⊥AD1；（Ⅱ）在棱AA1上是否存在一点P，使得DP∥平面B1AE？若存在，求AP的长；若不存在，说明理由．（Ⅲ）若二面角A﹣B1E﹣A1的大小为30°，求AB的长．为原点，，，为原点，，，的方向为，，，==（•．此时的法向量=⊥平面⊥，⊥=，﹣，﹣，只要⊥，即有•，有此得t=，AP=的一个法向量，此时与==|，解得19．（13分）（2012•福建）如图，椭圆E：的左焦点为F1，右焦点为F2，离心率e=．过F1的直线交椭圆于A、B两点，且△ABF2的周长为8．（Ⅰ）求椭圆E的方程．（Ⅱ）设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．，；，，∴的方程为．（Ⅱ）由===，），此时，，，，﹣），交20．（14分）（2012•福建）已知函数f（x）=e x+ax2﹣ex，a∈R．（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求函数f（x）的单调区间；（Ⅱ）试确定a的取值范围，使得曲线y=f（x）上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P．==，则c=，使得四、选考题（题设有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分。

2012福建高考数学理科试题及答案

环球天下教育旗下品牌网站美国纽交所上市公司2012年普通高等学校招生全国统一考试（福建卷）数学试题（理工农医类）本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．理科：第Ⅱ卷第21题为选考题，其他题为必考题，满分150分．第Ⅰ卷一、选择题：(理科)本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．(文科)本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z 满足z i ＝1－i ，则z 等于( )A ．－1－iB ．1－iC ．－1＋iD ．1＋i A ．3＋4i B ．5＋4i C ．3＋2i D ．5＋2i2．等差数列{a n }中，a 1＋a 5＝10，a 4＝7，则数列{a n }的公差为( ) A ．1 B ．2 C ．3 D ．4 3．下列命题中，真命题是( ) A ．x 0∈R ，0e0x ≤B ．x ∈R ，2x ＞x 2C ．a ＋b ＝0的充要条件是1ab=- D ．a ＞1，b ＞1是ab ＞1的充分条件4．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是( ) A ．球 B ．三棱锥 C ．正方体 D ．圆柱 5．下列不等式一定成立的是( )A ．lg(x 2＋14)＞lg x (x ＞0) B ．sin x ＋1sin x≥2(x ≠k π，k ∈Z )C ．x 2＋1≥2|x |(x ∈R )D ．2111x >+(x ∈R ) 6．如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为( )A ．14 B ．15 C ．16 D ．177．设函数1,()0,x D x x ⎧=⎨⎩为有理数，为无理数，则下列结论错误的是( )A ．D (x )的值域为{0,1}B ．D (x )是偶函数C ．D (x )不是周期函数 D ．D (x )不是单调函数8．已知双曲线22214x y b-=的右焦点与抛物线y 2＝12x 的焦点重合，则该双曲线的焦点到其渐近线的距离等于( )A ．5B ．42C ．3D ．59．若函数y ＝2x 图象上存在点(x ，y )满足约束条件30,230,,x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩则实数m 的最大值为( )A ．12 B ．1 C ．32D ．2 10．函数f (x )在［a ，b ］上有定义，若对任意x 1，x 2∈［a ，b ］，有()()12121()22x x f f x f x +≤［＋］，则称f (x )在［a ，b ］上具有性质P ．设f (x )在［1,3］上具有性质P ，现给出如下命题：①f (x )在［1,3］上的图象是连续不断的；②f (x 2)在［1，3］上具有性质P ；③若f (x )在x ＝2处取得最大值1，则f (x )＝1，x ∈［1,3］； ④对任意x 1，x 2，x 3，x 4∈［1,3］，有12341()44x x x x f +++≤［f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)］．其中真命题的序号是( )A ．①②B ．①③C ．②④D ．③④第Ⅱ卷二、填空题：(理科)本大题共5小题，每小题4分，共20分．把答案填在答题卡的相应位置．(文科)本大题共4小题，每小题4分，共16分．把答案填在答题卡的相应位置．11． (a ＋x )4的展开式中x 3的系数等于8，则实数a ＝________．12．阅读右图所示的程序框图，运行相应的程序，输出的s 值等于________． 13．已知△ABC 的三边长成公比为2的等比数列，则其最大角的余弦值为________．14．数列{a n }的通项公式πcos12n n a n =+，前n 项和为S n ，则S 2 012＝________． 15．对于实数a 和b ，定义运算“*”：22*.a ab a b a b b ab a b ⎧-≤=⎨->⎩，，，设f (x )＝(2x －1)*(x －1)，且关于x 的方程f (x )＝m (m ∈R )恰有三个互不相等的实数根x 1，x 2，x 3，则x 1x 2x 3的取值范围是__________．三、解答题：(理科)本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．(文科)本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．16．受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：品牌甲乙首次出现故障时间x (年)0＜x ≤1 1＜x ≤2 x ＞2 0＜x ≤2 x ＞2轿车数量(辆)2 3 45 5 45 每辆利润(万元)1 2 3 1.8 2.9将频率视为概率，解答下列问题：(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率；(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X 1，生产一辆乙品牌轿车的利润为X 2，分别求X 1，X 2的分布列；(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．17．某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数： ①sin 213°＋cos 217°－sin13°cos17°； ②sin 215°＋cos 215°－sin15°cos15°；③sin 218°＋cos 212°－sin18°cos12°；④sin 2(－18°)＋cos 248°－sin(－18°)cos48°；⑤sin 2(－25°)＋cos 255°－sin(－25°)cos55°．(1)试从上述五个式子中选择一个，求出这个常数；(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．18．如图，在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝1，E 为CD 中点．(1)求证：B 1E ⊥AD 1．(2)在棱AA 1上是否存在一点P ，使得DP ∥平面B 1AE ？若存在，求AP 的长；若不存在，说明理由．(3)若二面角A －B 1E －A 1的大小为30°，求AB 的长．19．如图，椭圆E ：22221x y a b+=(a ＞b ＞0)的左焦点为F 1，右焦点为F 2，离心率12e =．过F 1的直线交椭圆于A 、B 两点，且△ABF 2的周长为8．(1)求椭圆E 的方程；(2)设动直线l ：y ＝kx ＋m 与椭圆E 有且只有一个公共点P ，且与直线x ＝4相交于点Q ．试探究：在坐标平面内是否存在定点M ，使得以PQ 为直径的圆恒过点M ？若存在，求出点M的坐标；若不存在，说明理由．20．已知函数f (x )＝e x ＋ax 2－e x ，a ∈R ．(1)若曲线y ＝f (x )在点(1，f (1))处的切线平行于x 轴，求函数f (x )的单调区间；(2)试确定a 的取值范围，使得曲线y ＝f (x )上存在唯一的点P ，曲线在该点处的切线与曲线只有一个公共点P ．21． (1)选修4－2：矩阵与变换设曲线2x 2＋2xy ＋y 2＝1在矩阵 0 1a b ⎛⎫= ⎪⎝⎭A (a ＞0)对应的变换作用下得到的曲线为x2＋y 2＝1．①求实数a ，b 的值； ②求A 2的逆矩阵．(2)选修4－4：坐标系与参数方程在平面直角坐标系中，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．已知直线l 上两点M ，N 的极坐标分别为(2,0)，23π,32⎛⎫⎪⎪⎝⎭，圆C 的参数方程为22cos ,32sin x y θθ=+⎧⎪⎨=-+⎪⎩(θ为参数)． ①设P 为线段MN 的中点，求直线OP 的平面直角坐标方程；②判断直线l 与圆C 的位置关系． (3)选修4－5：不等式选讲已知函数f (x )＝m －|x －2|，m ∈R ，且f (x ＋2)≥0的解集为［－1,1］． ①求m 的值； ②若a ，b ，c ∈R ＋，且11123m a b c++=，求证：a ＋2b ＋3c ≥9．22．(文)已知函数f (x )＝ax sin x －32(a ∈R )，且在［0，π2］上的最大值为π32-． (1)求函数f (x )的解析式；(2)判断函数f (x )在(0，π)内的零点个数，并加以证明．答案1． A 由z i ＝1－i ，得221i (1i)i i i i+11i i i 11z ---=====----． 2． B ∵a 1＋a 5＝10＝2a 3，∴a 3＝5．故d ＝a 4－a 3＝7－5＝2．3． D ∵a ＞1＞0，b ＞1＞0，∴由不等式的性质得ab ＞1，即a ＞1，b ＞1⇒ab ＞1．4． D ∵圆柱的三视图中有两个矩形和一个圆， ∴这个几何体不可以是圆柱．5． C ∵x 2＋1≥2|x |⇔x 2－2|x |＋1≥0，∴当x ≥0时，x 2－2|x |＋1＝x 2－2x ＋1＝(x －1)2≥0成立；当x ＜0时，x 2－2|x |＋1＝x 2＋2x ＋1＝(x ＋1)2≥0成立．故x 2＋1≥2|x |(x ∈R )一定成立．6． C ∵由图象知阴影部分的面积是31220121211()d ()032326x x x x x -=⋅-=-=⎰，∴所求概率为11616=．7． C ∵D (x )是最小正周期不确定的周期函数， ∴D (x )不是周期函数是错误的．8． A 由双曲线的右焦点与抛物线y 2＝12x 的焦点重合，知32pc ==，c 2＝9＝4＋b 2，于是b 2＝5，5b =．因此该双曲线的渐近线的方程为52y x =±，即520x y ±=．故该双曲线的焦点到其渐近线的距离为|35|554d ==+． 9． B 由约束条件作出其可行域如图所示：由图可知当直线x ＝m 经过函数y ＝2x的图象与直线x ＋y －3＝0的交点P 时取得最大值，即得2x＝3－x ，即x ＝1＝m ．10． D ①如图1，图 1在区间［1,3］上f (x )具有性质P ，但是是间断的，故①错．②可设f (x )＝|x －2|(如图2)，当x ∈［1,3］时易知其具有性质P ，但是f (x 2)＝|x2－2|＝222,12,2,23x x x x ⎧-≤≤⎪⎨-<≤⎪⎩不具有性质P (如图3)．故②错．图2图3 ③任取x 0∈［1,3］，则4－x 0∈［1,3］， 1＝f (2)＝004()2x x f +-≤12［f (x 0)＋f (4－x 0)］．又∵f (x 0)＝1，f (4－x 0)≤1， ∴12［f (x 0)＋f (4－x 0)］≤1． ∴f (x 0)＝f (4－x 0)＝1．故③正确．④3412123422()()42x x x x x x x x f f ++++++= ≤34121()+()222x x x x f f ++⎡⎤⎢⎥⎣⎦≤14［f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)］，故④正确． 11．答案：2 解析：∵T r ＋1＝4C r a r x4－r，∴当4－r ＝3，即r ＝1时，T 2＝14C ·a ·x 3＝4ax 3＝8x 3．故a＝2．12．答案：－3解析：(1)k ＝1,1＜4，s ＝2×1－1＝1； (2)k ＝2,2＜4，s ＝2×1－2＝0； (3)k ＝3,3＜4，s ＝2×0－3＝－3； (4)k ＝4，直接输出s ＝－3．13．答案：24-解析：设△ABC 的最小边长为a (m ＞0)，则其余两边长为2a ，2a ，故最大角的余弦值是22222(2)(2)2cos 42222a a a a a a aθ+--===-⋅⋅． 14．答案：3 018 解析：∵函数πcos2n y =的周期2π4π2T ==，∴可用分组求和法：a 1＋a 5＋…＋a 2 009＝50311+1=503++个…；a 2＋a 6＋…＋a 2 010＝(－2＋1)＋(－6＋1)＋…＋(－2 010＋1)＝－1－5－…－2 009＝503(12009)2--＝－503×1 005；a 3＋a 7＋…＋a 2 011＝50311+1=503++个…；a 4＋a 8＋…＋a 2 012＝(4＋1)＋(8＋1)＋…＋(2 012＋1)＝503(52013)2⨯+＝503×1009；故S 2 012＝503－503×1 005＋503＋503×1 009 ＝503×(1－1 005＋1＋1 009)＝3 018．15．答案：(1316-，0) 解析：由已知，得()22200x x x f x x x x ⎧≤⎪⎨⎪⎩－，，＝－＋，＞，作出其图象如图，结合图象可知m 的取值范围为0＜m ＜14，当x ＞0时，有－x 2＋x ＝m ，即x 2－x ＋m ＝0，于是x 1x 2＝m ．当x ＜0时，有2x 2－x －m ＝0，于是31184mx -+=．故123(118)4m m x x x -+=．设h (m )＝m (1－18m +)，∵h ′(m )＝(1－18m +)＋［m (18218m-+)］＝4118018mm m-+-<+，∴函数h (m )单调递减．故x 1x 2x 3的取值范围为(1316-，0)． 16．解：(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A ，则231()5010P A +==． (2)依题意得，X 1的分布列为X 1 123P125350 910X 2的分布列为X 2 1.82.9P110910(3)由(2)得，E (X 1)＝1×125＋2×350＋3×910＝14350＝2.86(万元)，E (X 2)＝1.8×110＋2.9×910＝2.79(万元)．因为E (X 1)＞E (X 2)，所以应生产甲品牌轿车．17．解：方法一：(1)选择②式，计算如下：sin 215°＋cos 215°－sin15°cos15°＝1－12sin30°＝13144-=． (2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下： sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝sin 2α＋(cos30°cos α＋sin30°sin α)2－sin α·(cos30°cos α＋sin30°sin α)＝sin 2α＋34cos 2α＋32sin αcos α＋14sin 2α－32sin α·cos α－12sin 2α ＝34sin 2α＋34cos 2α＝34．方法二：(1)同方法一．(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下： sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝1cos21cos(602)22αα-+︒-+－sin α(cos30°cos α＋sin30°sin α) ＝12－12cos2α＋12＋12(cos60°·cos2α＋sin60°sin2α)－32sin αcos α－12sin 2α ＝12－12cos2α＋12＋14cos2α＋34sin2α－34sin2α－14(1－cos2α) ＝11131cos2cos24444αα--+=．18．解：(1)以A 为原点，AB ，AD ，1AA 的方向分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图)．设AB ＝a ，则A (0,0,0)，D (0,1，0)，D 1(0,1,1)，E (2a，1,0)，B 1(a,0,1)，故1AD ＝(0,1,1)，1B E ＝(2a -，1，－1)，1AB ＝(a,0,1)，AE ＝(2a，1,0)．∵1AD ·1B E ＝2a-×0＋1×1＋(－1)×1＝0，∴B 1E ⊥AD 1．(2)假设在棱AA 1上存在一点P (0,0，z 0)，使得DP ∥平面B 1AE ．此时DP ＝(0，－1，z 0)．又设平面B 1AE 的法向量n ＝(x ，y ，z )． ∵n ⊥平面B 1AE ，∴n ⊥1AB ，n ⊥AE ，得00.2ax z ax y +=⎧⎪⎨+=⎪⎩，取x ＝1，得平面B 1AE 的一个法向量n ＝(1，2a-，－a )．要使DP ∥平面B 1AE ，只要n ⊥DP ，有2a －az 0＝0，解得012z =．又DP 平面B 1AE ，∴存在点P ，满足DP ∥平面B 1AE ，此时12AP =．(3)连接A 1D ，B 1C ，由长方体ABCD A 1B 1C 1D 1及AA 1＝AD ＝1，得AD 1⊥A 1D ． ∵B 1C ∥A 1D ，∴AD 1⊥B 1C ．又由(Ⅰ)知B 1E ⊥AD 1，且B 1C ∩B 1E ＝B 1，∴AD 1⊥平面DCB 1A 1．∴1AD 是平面A 1B 1E 的一个法向量，此时1AD ＝(0,1,1)．设1AD 与n 所成的角为θ，则1212·2cos ||||214a aAD AD aa θ--==++n n ．∵二面角A －B 1E －A 1的大小为30°， ∴|cos θ|＝cos30°，即233225214a a =+，解得a ＝2，即AB 的长为2．19．解：方法一：(1)因为|AB |＋|AF 2|＋|BF 2|＝8，即|AF 1|＋|F 1B |＋|AF 2|＋|BF 2|＝8，又|AF 1|＋|AF 2|＝|BF 1|＋|BF 2|＝2a ，所以4a ＝8，a ＝2．又因为12e =，即12c a =，所以c ＝1．所以223b a c =-=．故椭圆E 的方程是22143x y +=． (2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩，，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0．因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且∆＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0．(*)此时024443km k x k m =-=-+，y 0＝kx 0＋m ＝3m ，所以P (4k m -，3m)．由4x y kx m =⎧⎨=+⎩，，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．设M (x 1,0)，则0MP MQ ⋅=对满足(*)式的m ，k 恒成立．因为MP ＝(14k x m --，3m)，MQ ＝(4－x 1,4k ＋m )，由0MP MQ ⋅=，得211141612430kx k kx x m m m-+-+++=，整理，得(4x 1－4)k m＋x 12－4x 1＋3＝0．(**)由于(**)式对满足(*)式的m ，k 恒成立，所以1211440,430,x x x -=⎧⎨-+=⎩解得x 1＝1．故存在定点M (1,0)，使得以PQ 为直径的圆恒过点M ．方法二：(1)同方法一．(2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩，，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0．因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且∆＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0．(*)此时024443km k x k m =-=-+，y 0＝kx 0＋m ＝3m ，所以P (4k m -，3m )．由4x y kx m =⎧⎨=+⎩，，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．取k ＝0，3m =，此时P (0，3)，Q (4，3)，以PQ 为直径的圆为(x －2)2＋(y －3)2＝4，交x 轴于点M 1(1,0)，M 2(3,0)；取12k =-，m ＝2，此时P (1，32)，Q (4,0)，以PQ 为直径的圆为225345()()2416x y -+-=，交x 轴于点M 3(1,0)，M 4(4,0)．所以若符合条件的点M 存在，则M 的坐标必为(1,0)．以下证明M (1,0)就是满足条件的点：因为M 的坐标为(1,0)，所以MP ＝(41k m --，3m)，MQ ＝(3,4k ＋m )，从而1212330k kMP MQ m m⋅=--++=，故恒有MP MQ ⊥，即存在定点M (1,0)，使得以PQ 为直径的圆恒过点M ．20．解：(1)由于f ′(x )＝e x＋2ax －e ，曲线y ＝f (x )在点(1，f (1))处切线斜率k ＝2a ＝0，所以a＝0，即f(x)＝e x－e x．此时f′(x)＝e x－e，由f′(x)＝0得x＝1．当x∈(－∞，1)时，有f′(x)＜0；当x∈(1，＋∞)时，有f′(x)＞0．所以f(x)的单调递减区间为(－∞，1)，单调递增区间为(1，＋∞)．(2)设点P(x0，f(x0))，曲线y＝f(x)在点P处的切线方程为y＝f′(x0)(x－x0)＋f(x0)，令g(x)＝f(x)－f′(x0)(x－x0)－f(x0)，故曲线y＝f(x)在点P处的切线与曲线只有一个公共点P等价于函数g(x)有唯一零点．因为g(x0)＝0，且g′(x)＝f′(x)－f′(x0)＝e x－e x0＋2a(x－x0)．(1)若a≥0，当x＞x0时，g′(x)＞0，则x＞x0时，g(x)＞g(x0)＝0；当x＜x0时，g′(x)＜0，则x＜x0时，g(x)＞g(x0)＝0．故g(x)只有唯一零点x＝x0．由P的任意性，a≥0不合题意．(2)若a＜0，令h(x)＝e x－e x0＋2a(x－x0)，则h(x0)＝0，h′(x)＝e x＋2a．令h′(x)＝0，得x＝ln(－2a)，记x′＝ln(－2a)，则当x∈(－∞，x*)时，h′(x)＜0，从而h(x)在(－∞，x*)内单调递减；当x∈(x*，＋∞)时，h′(x)＞0，从而h(x)在(x*，＋∞)内单调递增．①若x0＝x*，由x∈(－∞，x*)时，g′(x)＝h(x)＞h(x*)＝0；x∈(x*，＋∞)时，g′(x)＝h(x)＞h(x*)＝0，知g(x)在R上单调递增．所以函数g(x)在R上有且只有一个零点x＝x*．②若x0＞x*，由于h(x)在(x*，＋∞)内单调递增，且h(x0)＝0，则当x∈(x*，x0)时有g′(x)＝h(x)＜h(x0)＝0，g(x)＞g(x0)＝0；任取x1∈(x*，x0)有g(x1)＞0．又当x∈(－∞，x1)时，易知g(x)＝e x＋ax2－［e＋f′(x0)］x－f(x0)＋x0f′(x0)＜e x1＋ax2－［e＋f′(x0)］x－f(x0)＋x0f′(x0)＝ax2＋bx＋c，其中b＝－［e＋f′(x0)］，c＝e x1－f(x0)＋x0f′(x0)．由于a＜0，则必存在x2＜x1，使得ax22＋bx2＋c＜0．所以g(x2)＜0．故g(x)在(x2，x1)内存在零点，即g(x)在R上至少有两个零点．③若x0＜x*，仿②并利用3e6xx>，可证函数g(x)在R上至少有两个零点．综上所述，当a＜0时，曲线y＝f(x)上存在唯一点P(ln(－2a)，f(ln(－2a)))，曲线在该点处的切线与曲线只有一个公共点P．21． (1)选修4－2：矩阵与变换解：①设曲线2x2＋2xy＋y2＝1上任意点P(x，y)在矩阵A对应的变换作用下的像是P′(x′，y′)．由1x ay b'⎛⎫⎛⎫=⎪ ⎪'⎝⎭⎝⎭x axy bx y⎛⎫⎛⎫=⎪ ⎪+⎝⎭⎝⎭，得,.x axy bx y'=⎧⎨'=+⎩又点P′(x′，y′)在x2＋y2＝1上，所以x′2＋y′2＝1，即a2x2＋(bx＋y)2＝1，整理得(a2＋b2)x2＋2bxy＋y2＝1．依题意得222,22,a bb⎧+=⎨=⎩解得1,1,ab=⎧⎨=⎩或1,1,ab=-⎧⎨=⎩因为a＞0，所以1,1. ab=⎧⎨=⎩②由①知，1 01 1⎛⎫= ⎪⎝⎭A，21 0 1 0 1 01 1 1 12 1⎛⎫⎛⎫⎛⎫==⎪⎪ ⎪⎝⎭⎝⎭⎝⎭A，所以|A 2|＝1，(A 2)－1＝ 1 02 1⎡⎤⎢⎥-⎣⎦． (2)选修4－4：坐标系与参数方程解：①由题意知，M ，N 的平面直角坐标分别为(2,0)，(0，233)．又P 为线段MN 的中点，从而点P 的平面直角坐标为(1，33)，故直线OP 的平面直角坐标方程为33y x =．②因为直线l 上两点M ，N 的平面直角坐标分别为(2,0)，(0，233)，所以直线l 的平面直角坐标方程为33230x y +-=．又圆C 的圆心坐标为(2，3-)，半径r ＝2，圆心到直线l 的距离|233323|3239d r --==<+，故直线l 与圆C 相交． (3)选修4－5：不等式选讲解：①因为f (x ＋2)＝m －|x |，f (x ＋2)≥0等价于|x |≤m ，由|x |≤m 有解，得m ≥0，且其解集为{x |－m ≤x ≤m }．又f (x ＋2)≥0的解集为［－1,1］，故m ＝1．②由①知111123a b c++=，又a ，b ，c ∈R ＋，由柯西不等式得 a ＋2b ＋3c ＝(a ＋2b ＋3c )(11123a b c++) ≥2111(23)923a b c a b c⋅+⋅+⋅＝．。

2012高考福建文科数学试题及答案(高清版)

2012年普通高等学校夏季招生全国统一考试数学文史类(福建卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．理科：第Ⅱ卷第21题为选考题，其他题为必考题，满分150分．第Ⅰ卷一、选择题：(理科)本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．(文科)本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．复数(2＋i)2等于()A．3＋4i B．5＋4i C．3＋2i D．5＋2i2．已知集合M＝{1,2,3,4}，N＝{－2,2}，下列结论成立的是()A．N M B．M∪N＝MC．M∩N＝N D．M∩N＝{2}3．已知向量a＝(x－1,2)，b＝(2,1)，则a⊥b的充要条件是()A．12x=-B．x＝－1C．x＝5 D．x＝04．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是()．A．球B．三棱锥C．正方体D．圆柱5．已知双曲线22215x ya-=的右焦点为(3,0)，则该双曲线的离心率等于()A．14B4C．32D．436．阅读下图所示的程序框图，运行相应的程序，输出的s值等于()A．－3 B．－10 C．0 D．－27．直线x＋－2＝0与圆x2＋y2＝4相交于A，B两点，则弦AB的长度等于()A．B．C D．18．函数f(x)＝sin(x－π4)的图象的一条对称轴是… ()A．π4x=B．π2x=C．π4x=-D．π2x=-9．设1,0,()0,0,1,0,xf x xx>⎧⎪==⎨⎪-<⎩1,()xg xx⎧=⎨⎩为有理数，，为有理数，则f(g(π))的值为()A．1 B．0 C．－1 D．π10．若函数y＝2x图象上存在点(x，y)满足约束条件30,230,,x yx yx m+-≤⎧⎪--≤⎨⎪≥⎩则实数m的最大值为()A．12B．1 C．32D．211．数列{a n}的通项公式πcos2nna n=，其前n项和为S n，则S2 012等于()A．1 006 B．2 012 C．503 D．012．(文)已知f(x)＝x3－6x2＋9x－abc，a＜b＜c，且f(a)＝f(b)＝f(c)＝0．现给出如下结论：①f(0)f(1)＞0；②f(0)f(1)＜0；③f(0)f(3)＞0；④f(0)f(3)＜0．其中正确结论的序号是()A．①③B．①④C．②③D．②④第Ⅱ卷二、填空题：(理科)本大题共5小题，每小题4分，共20分．把答案填在答题卡的相应位置．(文科)本大题共4小题，每小题4分，共16分．把答案填在答题卡的相应位置．13．在△ABC中，已知∠BAC＝60°，∠ABC＝45°，BC=，则AC＝__________．14．一支田径队有男女运动员98人，其中男运动员有56人．按男女比例用分层抽样的方法，从全体运动员中抽出一个容量为28的样本，那么应抽取女运动员人数是__________．15．已知关于x的不等式x2－ax＋2a＞0在R上恒成立，则实数a的取值范围是__________．16．某地区规划道路建设，考虑道路铺设方案．方案设计图中，点表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10．现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为__________．三、解答题：(理科)本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．(文科)本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．17．在等差数列{a n}和等比数列{b n}中，a1＝b1＝1，b4＝8，{a n}的前10项和S10＝55．(1)求a n和b n；(2)现分别从{a n}和{b n}的前3项中各随机抽取一项，写出相应的基本事件，并求这两项的值相等的概率．18．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试(1)求回归直线方程 y bx a=+，其中b＝－20，a y b x=-；(2)预计在今后的销售中，销量与单价仍然服从(Ⅰ)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本) 19．如图，在长方体ABCD－A1B1C1D1中，AB＝AD＝1，AA1＝2，M为棱DD1上的一点．(1)求三棱锥A－MCC1的体积；(2)当A1M＋MC取得最小值时，求证：B1M⊥平面MAC．20．某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：①sin213°＋cos217°－sin13°cos17°；②sin215°＋cos215°－sin15°cos15°；③sin218°＋cos212°－sin18°cos12°；④sin2(－18°)＋cos248°－sin(－18°)cos48°；⑤sin2(－25°)＋cos255°－sin(－25°)cos55°．(1)试从上述五个式子中选择一个，求出这个常数；(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．21．如图，等边三角形OAB的边长为E：x2＝2py(p＞0)上．(1)求抛物线E的方程；(2)设动直线l与抛物线E相切于点P，与直线y＝－1相交于点Q．证明以PQ为直径的圆恒过y轴上某定点．22．已知函数f(x)＝ax sin x－32(a∈R)，且在［0，π2］上的最大值为π32-．(1)求函数f(x)的解析式；(2)判断函数f(x)在(0，π)内的零点个数，并加以证明．1．A(2＋i)2＝4＋4i＋i2＝4＋4i－1＝3＋4i．2． D ∵M ＝{1,2,3,4}，N ＝{－2,2}，∴M ∩N ＝{2}． 3． D ∵a ＝(x －1,2)，b ＝(2,1)，a ⊥b ，∴a ·b ＝(x －1，2)·(2,1)＝2(x －1)＋2×1＝2x ＝0，即x ＝0．4． D ∵圆柱的三视图中有两个矩形和一个圆， ∴这个几何体不可以是圆柱．5． C 由双曲线的右焦点为(3,0)知c ＝3，即c 2＝9，又∵c 2＝a 2＋b 2，∴9＝a 2＋5，即a 2＝4，a ＝2．故所求离心率32c e a ==．6． A (1)k ＝1,1＜4，s ＝2×1－1＝1； (2)k ＝2,2＜4，s ＝2×1－2＝0； (3)k ＝3,3＜4，s ＝2×0－3＝－3； (4)k ＝4，输出s ＝－3．7． B 圆心O 到直线AB的距离1d ==，所以||AB ===． 8． C 函数f (x )＝sin(x －π4)的图象的对称轴是x －π4＝k π＋π2，k ∈Z ，即x ＝k π＋3π4，k ∈Z ．当k ＝－1时x ＝－π＋3π4＝π4-．故选C ．9．B ∵g (π)＝0，∴f (g (π))＝f (0)＝0．10． B 由约束条件作出其可行域如图所示：由图可知当直线x ＝m 经过函数y ＝2x的图象与直线x ＋y －3＝0的交点P 时取得最大值，即得2x ＝3－x ，即x ＝1＝m ．11． A ∵函数πcos 2n y =的周期2π4π2T ==，∴可分四组求和：a 1＋a 5＋…＋a 2 009＝0，a 2＋a 6＋…＋a 2 010＝－2－6－…－2 010＝503(22010)2⨯--＝－503×1 006，a 3＋a 7＋…＋a 2 011＝0，a 4＋a 8＋…＋a 2 012＝4＋8＋…＋2 012＝503(42012)2⨯+＝503×1 008．故S 2 012＝0－503×1 006＋0＋503×1 008＝503×(－1 006＋1 008)＝1 006．12． C 设g (x )＝x 3－6x 2＋9x ＝0，则x 1＝0，x 2＝x 3＝3，其图象如下图：要使f (x )=x 3－6x 2+9x －abc 有3个零点，需将g (x )的图象向下平移，如图所示：又f ′(x )=3x 2－12x +9=0时，x 1=1，x 2=3，即得f (1)是极大值，f (3)是极小值．故由图象可知f (0)·f (1)＜0，f (0)·f (3)＞0．13．解析：如图：由正弦定理得sin sin AC BC BA=，即sin 45sin 60AC =︒︒22=，故AC =14．答案：12 解析：∵282987=，即每7人抽取2人，又知女运动员人数为98－56＝42(人)，∴应抽取女运动员人数为42×27＝12(人)．15．答案：(0,8) 解析：∵x 2－ax ＋2a ＞0在R 上恒成立，∴∆＝(－a )2－4·2a ＜0，即a 2－8a ＜0,0＜a ＜8．故a 的取值范围是(0,8)．16．答案：16解析：由题意知，各城市相互到达，且费用最少为1＋2＋2＋3＋3＋5＝16＝FG ＋GD ＋AE ＋EF ＋GC ＋BC ．17．解：(1)设{a n }的公差为d ，{b n }的公比为q ．依题意得S 10＝10＋1092⨯d ＝55，b 4＝q 3＝8，解得d ＝1，q ＝2，所以a n ＝n ，b n ＝2n －1．(2)分别从{a n }和{b n }的前3项中各随机抽取一项，得到的基本事件有9个：(1,1)，(1,2)，(1,4)，(2,1)，(2,2)，(2,4)，(3,1)，(3,2)，(3,4)．符合题意的基本事件有2个：(1,1)，(2,2)．故所求的概率29P =．18．解：(1)由于x ＝16(x 1＋x 2＋x 3＋x 4＋x 5＋x 6)＝8.5，y ＝16(y 1＋y 2＋y 3＋y 4＋y 5＋y 6)＝80，所以a ＝y －b x ＝80＋20×8.5＝250，从而回归直线方程为 y ＝－20x ＋250． (2)设工厂获得的利润为L 元，依题意得 L ＝x (－20x ＋250)－4(－20x ＋250) ＝－20x 2＋330x －1 000 ＝－20(x －334)2＋361.25，当且仅当x ＝8.25时，L 取得最大值．故当单价定为8.25元时，工厂可获得最大利润． 19．解：(1)由长方体ABCD -A 1B 1C 1D 1知，AD ⊥平面CDD 1C 1，故点A 到平面CDD 1C 1的距离等于AD ＝1．又∵111121122M C C S C C C D ∆=⋅=⨯⨯=，∴111133A M C C M C C V A D S -∆⋅＝＝．(2)将侧面CDD 1C 1绕DD 1逆时针转90°展开，与侧面ADD 1A 1共面(如图)，当A 1，M ，C ′共线时，A 1M +MC 取得最小值．由AD =CD =1，AA 1=2，得M 为DD 中点．连结C 1M ，在△C 1MC 中，1M C =，MC =，CC 1=2，∴CC 12=MC 12+MC 2，得∠CMC 1=90°，即CM ⊥MC 1．又由长方体ABCD －A 1B 1C 1D 1知，B 1C 1⊥平面CDD 1C 1， ∴B 1C 1⊥CM ．又B 1C 1∩C 1M =C 1，∴CM ⊥平面B 1C 1M ，得CM ⊥B 1M ．同理可证，B 1M ⊥AM ，又AM ∩MC =M ，∴B 1M ⊥平面MAC ．20．(理17，文20)解：方法一：(1)选择②式，计算如下： sin 215°＋cos 215°－sin15°cos15°＝1－12sin30°＝13144-=．(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下： sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝sin 2α＋(cos30°cos α＋sin30°sin α)2－sin α·(cos30°cos α＋sin30°sin α)＝sin 2α＋34cos 2α＋2sin αcos α＋14sin 2α－2sin α·cos α－12sin 2α＝34sin 2α＋34cos 2α＝34．方法二：(1)同方法一．(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下： sin 2α＋cos 2(30°－α)－sin αcos(30°－α) ＝1cos21cos(602)22αα-+︒-+－sin α(cos30°cos α＋sin30°sin α) ＝12－12cos2α＋12＋12(cos60°·cos2α＋sin60°sin2α)－2sin αcos α－12sin 2α＝12－12cos2α＋12＋14cos2α4sin2α－4sin2α－14(1－cos2α)＝11131cos2cos24444αα--+=．21．解：方法一：(1)依题意，||O B =BOy ＝30°．设B (x ，y )，则x ＝|OB |sin30°＝ y ＝|OB |·cos 30°＝12．因为点B(12)在x 2＝2py 上，所以(2＝2p ×12，解得p ＝2．故抛物线E 的方程为x 2＝4y ．(2)由(1)知214y x =，12y'x =．设P (x 0，y 0)，则x 0≠0，且直线l 的方程为y －y 0＝12x 0(x －x 0)，即y ＝12x 0x －14x 02．由20011,241,y x x x y ⎧=-⎪⎨⎪=-⎩得2004,21.x x x y ⎧-=⎪⎨⎪=-⎩ 所以Q (20042x x -，－1)．设M (0，y 1)，令0M P M Q ⋅= 对满足20014y x =(x 0≠0)的x 0，y 0恒成立．由于M P ＝(x 0，y 0－y 1)，M Q ＝(20042x x -，－1－y 1)，由0M P M Q ⋅= ，得20042x x -－y 0－y 0y 1＋y 1＋y 12＝0，即(y 12＋y 1－2)＋(1－y 1)y 0＝0．(*) 由于(*)式对满足20014y x =(x 0≠0)的y 0恒成立，所以121110,20,y y y -=⎧⎨+-=⎩解得y 1＝1．故以PQ 为直径的圆恒过y 轴上的定点M (0,1)．方法二：(1)同方法一． (2)由(1)知214y x =，12y'x =．设P (x 0，y 0)，则x 0≠0，且直线l 的方程为 y －y 0＝12x 0(x －x 0)，即y ＝12x 0x －14x 02．由20011,241,y x x x y ⎧=-⎪⎨⎪=-⎩得2004,21.x x x y ⎧-=⎪⎨⎪=-⎩ 所以Q (20042x x -，－1)．取x 0＝2，此时P (2,1)，Q (0，－1)，以PQ 为直径的圆为(x －1)2＋y 2＝2，交y 轴于点M 1(0,1)或M 2(0，－1)；取x 0＝1，此时P (1，14)，Q (32-，－1)，以PQ 为直径的圆为(x ＋14)2＋(y ＋38)2＝12564，交y 轴于M 3(0,1)或M 4(0，74-)．故若满足条件的点M 存在，只能是M (0,1)．以下证明点M (0,1)就是所要求的点．因为M P ＝(x 0，y 0－1)，M Q ＝(20042x x -，－2)，M P M Q ⋅ ＝2042x -－2y 0＋2＝2y 0－2－2y 0＋2＝0．故以PQ 为直径的圆恒过y 轴上的定点M ． 22．解：(1)由已知得f ′(x )＝a (sin x ＋x cos x )，对于任意x ∈(0，π2)，有sin x ＋x cos x ＞0．当a ＝0时，3()2f x =-，不合题意；当a ＜0，x ∈(0，π2)时，f ′(x )＜0，从而f (x )在(0，π2)内单调递减，又f (x )在［0，π2］上的图象是连续不断的，故f (x )在［0，π2］上的最大值为3(0)2f =-，不合题意；当a ＞0，x ∈(0，π2)时，f ′(x )＞0，从而f (x )在(0，π2)内单调递增，又f (x )在［0，π2］上的图象是连续不断的，故f (x )在［0，π2］上的最大值为π()2f ，即π3π3222a --=，解得a ＝1．综上所述，得f (x )＝x sin x －32．(2)f (x )在(0，π)内有且只有两个零点．证明如下：由(1)知，f (x )＝x sin x 32-，从而有f (0)＝32-＜0，ππ3()022f -=>，又f(x)在［0，π2］上的图象是连续不断的，所以f(x)在(0，π2)内至少存在一个零点．又由(1)知f(x)在［0，π2］上单调递增，故f(x)在(0，π2)内有且仅有一个零点．当x∈［π2，π］时，令g(x)＝f′(x)＝sin x＋x cos x．由g(π2)＝1＞0，g(π)＝－π＜0，且g(x)在［π2，π］上的图象是连续不断的，故存在m∈(π2，π)，使得g(m)＝0．由g′(x)＝2cos x－x sin x，知x∈(π2，π)时，有g′(x)＜0，从而g(x)在(π2，π)内单调递减．当x∈(π2，m)时，g(x)＞g(m)＝0，即f′(x)＞0，从而f(x)在(π2，m)内单调递增，故当x∈［π2，m］时，ππ3()()022f x f-≥=>，故f(x)在［π2，m］上无零点；当x∈(m，π)时，有g(x)＜g(m)＝0，即f′(x)＜0，从而f(x)在(m，π)内单调递减．又f(m)＞0，f(π)＜0，且f(x)在［m，π］上的图象是连续不断的，从而f(x)在(m，π)内有且仅有一个零点．综上所述，f(x)在(0，π)内有且只有两个零点．。

福建省高考数学最新联考试题分类大汇编(5)三角函数试题

福建省2012年高考数学最新联考试题分类大汇编（5）三角函数试题一、选择题：8．(福建省福州市2012年3月高中毕业班质量检查理科)函数)0,0)(cos(2)(πφωφω<<>+=x x f 为奇函数，该函数的部分图象如图所示，点B A ,分)0,0)(cos(2)(πφωφω<<>+=x x f 是奇函数，图象过原点，所以2πϕ=，因此()2s i n ,4f x x π=函数)(x f 图象的一条对称轴的方程为2=x .3sin ,25απα=+则sin()=（ B ）A ．1225-B ．2425-C ．1225D ．242510．(福建省厦门市2012年3月高三质量检查文科)在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，3B π=，且sin :sin 3:1A C =，则:b c 的值为（ C ）A B ．2C D ．7甲同学在ABC ∆中用余弦定理解得AC =Rt ACH ∆中解得1cos 72AC =︒，据此可得cos72︒的值所在区间为（ C ）A ．（0.1,0.2）B ．（0.2,0.3）C ．（0.3,0.4）D ．（0.4,0.5）4．(福建省宁德市2012年高三毕业班质量检查文科)将函数sin()4y x π=+的图象上各点的纵坐标不变，横坐标伸长到原来的2倍，所得图象的函数解析式是（ D ）A ．cos 2y x =B ．sin(2)4y x π=+ C ．1sin()28y x π=+D ．1sin()24y x π=+3．(福建省宁德市2012年高三毕业班质量检查理科)为了得到函数sin 2y x =的图象，可将函数sin(2)6y x π=+的图象（ C ）A ．向右平移6π个单位 B ．向左平移6π个单位C ．向右平移12π个单位 D ．向左平移12π个单位10．(福建省莆田市2012年3月高三毕业班教学质量检查文科)已知角α的顶点在原点，始边与x 轴的正半轴重合，终边与单位圆交点的横坐标为35-，若(0,)a π∈，则t an α=（ D ）A ．34B ．34-C ．43D ．43-二、填空题：11. (福建省福州市2012年3月高中毕业班质量检查理科)oo43sin 13sin 13cos 47sin 0+的值等于 ____ ．0000sin 47cos13sin13sin 43sin 47cos13cos 47sin13sin 60o o o +=+= .的值是．4511．(福建省莆田市2012年3月高三毕业班教学质量检查理科)已知角α的顶点在坐标原点，始边与x 轴的正半轴重合，终边与单位交点的横坐标是35-，若(0,)απ∈，则tan α= 。

2012年普通高等学校招生全国统一考试(福建卷)—数学(理)解析版

2012年普通高等学校招生全国统一考试（福建卷）数学（理科）第I 卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分·在每小题给出的四个选项中，只有一项是符合题目要求的·1、若复数z 满足i zi -=1，则z 等于（）A ．i --1B ．i -1C ．i +-1D ．i +1 考点：复数的运算· 难度：易·分析：本题考查的知识点为复数的计算，直接套用复数运算公式即可·解答：iiz -=1 111)())(1(--=--=---=i i i i i i ·2、等差数列}{n a 中，7,10451==+a a a ，则数列}{n a 的公差为（） A ．1 B ．2 C ．3 D ．4 考点：等差数列的定义· 难度：易·分析：本题考查的知识点为复等差数列的通项公式d n a a n )1(1-+=·解答：273104211=⇒⎩⎨⎧=+=+d d a d a · 3、下列命题中，真命题是（） A ．0,00≤∈∃x eR x B ．22,x R x x >∈∀C ．0=+b a 的充要条件是1-=baD ．1,1>>b a 是1>ab 的充分条件考点：逻辑· 难度：易·分析：本题考查的知识点为复逻辑中的充要条件的判定· 解答：A 中，,R x ∈∀0>xe·B 中，22,4,2x x x x===∃，22,x x x<∃·C 中，⎩⎨⎧≠=+00b b a 的充要条件是1-=b a·D 中，1,1>>b a 可以得到1>ab ，当1>ab 时，不一定可以得到1,1>>b a · 4、一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（）A ．球B ．三棱锥C ．正方体D ．圆柱考点：空间几何体的三视图· 难度：易·分析：本题考查的知识点为空间几何体的三视图，直接画出即可· 解答：圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆；三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形；正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形；圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆· 5、下列不等式一定成立的是（）A ．)0(lg )41lg(2>>+x x x B ．),(2sin 1sin Z k k x xx ∈≠≥+π C ．)(||212R x x x ∈≥+ D ．)(1112R x x ∈>+ 考点：不等式及基本不等式· 难度：中·分析：本题考查的知识点为不等式的性质及基本不等式的性质· 解答：A 中，)410(4122x x x x x =+=≥+时，当· B 中，])1,0((sin 2sin 1sin ∈≥+x x x ；))0,1[(sin 2sin 1sin -∈-≤+x xx · C 中，)(0)1|(|1||222R x x x x ∈≥-=+-·D 中，)](1,0(112R x x ∈∈+· 6、如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为（）A ．41B ．51C ．61D ．71考点：积分的计算和几何概型·难度：中·分析：本题考查的知识点为公式法计算积分和面型的几何概型· 解答：111)(=⨯=ΩS ，⎰-=10)()(dx x x A S 61|)2132(10223=-=x x · 所以61)()()(=Ω=A S S A P ·7、设函数⎩⎨⎧=为无理数为有理数x x x D ,0,1)(，则下列结论错误的是（）A ．)(x D 的值域为}1,0{B ．)(x D 是偶函数C ．)(xD 不是周期函数 D ．)(x D 不是单调函数考点：分段函数的解析式及其图像的作法· 难度：中·分析：本题考查的知识点为分段函数的定义，单调性、奇偶性和周期性的定义和判定· 解答：A 中，)(x D 由定义直接可得，)(x D 的值域为}1,0{·B 中，)(x D 定义域为R ，)(,0,1)(x D x x x D =⎩⎨⎧=-为无理数为有理数，所以)(x D 为偶函数·C 中，)(,0,1)1(xD x x x D =⎩⎨⎧=+为无理数为有理数，所以可以找到1为)(x D 的一个周期· D 中，......1)2(,0)2(,1)1(===D D D ，所以不是单调函数·8、双曲线22214x y b-=的右焦点与抛物线x y 122=的焦点重合，则该双曲线的焦点到其渐近线的距离等于（）A ．5B ．24C ．3D ．5考点：双曲线的定义· 难度：中·分析：本题考查的知识点为双曲线的定义，焦点，渐近线，抛物线的定义· 解答：抛物线x y 122=的焦点为)0,3(· 双曲线中，5492=-=b · 双曲线渐近线方程为x y 25±=· 所以焦点到渐近线的距离5)25(12532=+=d ·9、若直线x y 2=上存在点),(y x 满足约束条件⎪⎩⎪⎨⎧≥≤--≤-+m x y x y x 03203，则实数m 的最大值为（）A ．21 B ．1 C ．23D ．2 考点：线性规划· 难度：中·分析：本题考查的知识点为含参的线性规划，需要画出可行域的图形，含参的直线要能画出大致图像·所以，若直线x y 2=上存在点),(y x 满足约束条件⎪⎩⎪⎨⎧≥≤--≤-+m x y x y x 03203，则mm 23≥-，即1≤m ·10、函数)(x f 在],[b a 上有定义，若对任意],[,21b a x x ∈，有)]()([21)2(2121x f x f x x f +≤+，则称)(x f 在],[b a 上具有性质P ·设)(x f 在[1,3]上具有性质P ，现给出如下命题： ①)(x f 在]3,1[上的图像时连续不断的； ②)(2x f 在]3,1[上具有性质P ；③若)(x f 在2=x 处取得最大值1，则1)(=x f ，]3,1[∈x ； ④对任意]3,1[,,,4321∈x x x x ，有)]()()()([41)2(43214321x f x f x f x f x x x x f +++≤+++·其中真命题的序号是（）A ．①②B ．①③C ．②④D ．③④考点：演绎推理和函数· 难度：难·分析：本题考查的知识点为函数定义的理解，说明一个结论错误只需举出反例即可，说明一个结论正确要证明对所有的情况都成立· 解答：A 中，反例：如图所示的函数)(x f 的是满足性质P 的，但)(x f 不是连续不断的·B 中，反例：x x f -=)(在]3,1[上具有性质P ，22)(x x f -=在]3,1[上不具有性质P ·C 中，在]3,1[上，)]4()([21)2)4(()2(x f x f x x f f -+≤-+=， 1)(1)2()()4(1)2()()(2)4()(max max =⇒⎪⎩⎪⎨⎧==≤-==≤≥-+x f f x f x f f x f x f x f x f ，所以，对于任意1)(],3,1[,21=∈x f x x ·D 中，=+++)2(4321x x x x f )2)()((4321x x x x f +++)]()()()([41))]()((21))()((21[21)]2()2([21432121214321x f x f x f x f x f x f x f x f x x f x x f +++≤+++≤+++≤· 第Ⅱ卷（非选择题共100分）二、填空题：本大题共4小题，每小题4分，共16分·把答案填在答题卡的相应位置·11、4)(x a +的展开式中3x 的系数等于8，则实数=a _________·【2】考点：二项式定理· 难度：易·分析：本题考查的知识点为二项式定理的展开式，直接应用即可· 解答：4)(x a +中含3x 的一项为r rr r x aC T -+=441，令3=r ，则83434=-a C ，即2=a ·12、阅读右图所示的程序框图，运行相应地程序，输出的s 值等于_____________________·【3-】考点：算法初步· 难度：易·分析：本题考查的知识点为算法中流程图的读法，直接根据箭头的指向运算即可· 解答： 1,1==s k ；2,1112==-⨯=k s ； 3,0212==-⨯=k s ； 4,3302=-=-⨯=k s ；结束·13、已知ABC ∆_________·【42-】考点：等比数列和余弦定理· 难度：易·分析：本题考查的知识点为等比数列的定义和余弦定理的应用· 解答：设ABC ∆三边为m c m b m a 2,2,===，则可得C ∠所对的边最大，且22cos 222=-+=abc b a C · 14、数列}{n a 的通项公式12cos+=πn n a n ，前n 项和为n S ，则=2012S ___________·【3018】考点：数列和三角函数的周期性· 难度：中·分析：本题考查的知识点为三角函数的周期性和数列求和，所以先要找出周期，然后分组计算和· 解答： 1012cos )14(12)14(cos )14(14+=+⨯+=++⨯+=+ππn n n a n ， 1)24(1cos )24(12)24(cos )24(24++-=+⨯+=++⨯+=+n n n n a n ππ，10123cos )34(12)34(cos )34(34+=+⨯+=++⨯+=+ππn n n a n ，14412cos )44(12)44(cos)44(44++=+⨯+=++⨯+=+n n n n a n ππ，所以++14n a ++24n a ++34n a 644=+n a · 即30186420122012=⨯=S · 15、对于实数b a ,，定义运算“*”：⎩⎨⎧>-≤-=*ba ab b ba ab a b a ,,22，设)1()12()(-*-=x x x f ，且关于x 的方程为)()(R m m x f ∈=恰有三个互不相等的实数根321,,x x x ，则321x x x 的取值范围是_____·【)0,1631(-】考点：演绎推理和函数· 难度：难·分析：本题考查的知识点为新定义的理解，函数与方程中根的个数·解答：由题可得，⎩⎨⎧>--≤-=0),1(0),12()(x x x x x x x f可得0,21),41,0(132<=+∈x x x m ，且↑↑→||,,41132x x x m 所以41=m 时，=max 321||x x x 1631-，所以∈m )0,1631(-·三、解答题：本大题共6小题，共84分·解答应写出文字说明，证明过程或演算步骤·16、（本小题满分13分）受轿车在保修期内维修费等因素的影响，企业产生每辆轿车的利润与该轿车首次出现故障的时间有关，某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年，现从该厂已售出的两种品牌轿my =车中随机抽取50辆，统计书数据如下：将频率视为概率，解答下列问题：（I ）从该厂生产的甲品牌轿车中随机抽取一辆，求首次出现故障发生在保修期内的概率；（II ）若该厂生产的轿车均能售出，记住生产一辆甲品牌轿车的利润为1X ，生产一辆乙品牌轿车的利润为2X ，分别求1X ，2X 的分布列；（III ）该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌轿车，若从经济效益的角度考虑，你认为应该产生哪种品牌的轿车？说明理由· 考点：统计概率及随机变量·难度：易· 分析：解答：（I ）首次出现故障发生在保修期内的概率为2315010P +== （II ）随机变量1X 的分布列为随机变量2X 的分布列为（III ）1139123 2.86255010EX =⨯+⨯+⨯=(万元) 2191.82.9 2.791010EX =⨯+⨯=(万元) 12EX EX > 所以应该生产甲品牌汽车·17、（本小题满分13分）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数· （1）02217cos 13sin 17cos 13sin -+；（2）02215cos 15sin 15cos 15sin -+；（3）02212cos 18sin 12cos 18sin -+；（4）00020248cos )18sin(48cos )13(sin --+-；（5）00020255cos )25sin(55cos )25(sin --+-·（I ）试从上述五个式子中选择一个，求出这个常数；（II ）根据（Ⅰ）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论· 考点：三角恒等变换· 难度：中· 分析：解答：（I ）选择（2）：22013sin 15cos 15sin15cos151sin 3024+-=-= （II ）三角恒等式为：22003sin cos (30)sin cos(30)4αααα+---=22002222sin cos (30)sin cos(30)11sin sin )sin sin )22333sin cos 444αααααααααααα+---=++-+=+=（lby lfx ）18、（本小题满分13分）如图，在长方体1111D C B A ABCD -中，11==AD AA ，E 为CD 中点· （Ⅰ）求证：11AD E B ⊥；（Ⅱ）在棱1AA 上是否存在一点P ，使得//DP 平面AE B 1？若存在，求AP 的长；若不存在，说明理由·（Ⅲ）若二面角11A E B A --的大小为030，求AB 的长·考点：立体几何· 难度：中· 分析：解答：（Ⅰ）长方体1111D C B A ABCD -中，11==AD AA 得：1111111111,,AD A D AD A B A DA B A A D ⊥⊥=⇔⊥面11A B CD1B E ⊂面11A B CD 11B E AD ⇒⊥（Ⅱ）取1AA 的中点为P ，1AB 中点为Q ，连接PQ 在11AA B ∆中，111111//,////////22PQ A B DE A B PQ DE PD QE PD ⇒⇒⇒面AE B 1 此时11122AP AA == （Ⅲ）设11A DAD O =，连接AO ，过点O 作1OH B E ⊥于点H ，连接AH1AO ⊥面11A B CD ，1O H B E ⊥1A H B E⇒⊥ 得：AHO ∠是二面角11A E B A --的平面角30AHO ο⇒∠=在Rt AOH ∆中，30,90,2AHO AOH AH OH οο∠=∠==⇒=在矩形11A B CD 中，1,CD x AD ==11112222222228B OE x xS x ∆=--⨯-⨯=1222x =⇔=得：2AB =19、（本小题满分13分）如图，椭圆)0(1:2222>>=+b a by a x E 的左焦点为1F ，右焦点为2F ，离心率21=e ·过1F 的直线交椭圆于B A ,两点，且2ABF ∆的周长为8· （Ⅰ）求椭圆E 的方程·（Ⅱ）设动直线m kx y l +=:与椭圆E 有且只有一个公共点P ，且与直线4=x 相交于点Q ·试探究：在坐标平面内是否存在定点M ，使得以PQ 为直径的圆恒过点M ？若存在，求出点M 的坐标；若不存在，说明理由·考点：三角恒等变换·难度：难·分析：解答：（Ⅰ）设c 则2212342c e a c a b a ==⇔=⇔= 2ABF ∆的周长为22121288482,1AB AF BF AF AF BF BF a a b c ++=⇔+++=⇔=⇔===椭圆E 的方程为22143x y += （Ⅱ）由对称性可知设000(,)(0)P x y y >与(,0)M x220031434x x y y y k y '+=⇒==⇒=- 直线00000033(1):()(4,)4x x l y y x x Q y y --=--⇒ 000003(1)0()(4)0(1)(1)(3)x M P M Q x x x y x x x x y -=⇔--+⨯=⇔-=--（*）（*）对0(2,2)x ∈-恒成立1x ⇔=，得(1,0)M20、（本小题满分14分）已知函数R a ex ax e x f x ∈-+=,)(2（Ⅰ）若曲线)(x f y =在点))1(,1(f 处的切线平行于x 轴，求函数)(x f 的单调区间；（Ⅱ）试确定a 的取值范围，使得曲线)(x f y =上存在唯一的点P ，曲线在该点处的切线与曲线只有一个公共点P ·考点：导数·难度：难·分析：解答：（Ⅰ）2()()2x x f x e ax ex f x e ax e '=+-⇒=+-由题意得：(1)200f e a e a '=+-=⇔=()01,()0x f x e e x f x x ''=->⇔><⇔<得：函数()f x 的单调递增区间为(1,)+∞，单调递减区间为(,1)-∞（Ⅱ）设00(,())P x f x ；则过切点P 的切线方程为000()()()y f x x x f x '=-+令000()()()()()g x f x f x x x f x '=---；则0()0g x =切线与曲线只有一个公共点P ()0g x ⇔=只有一个根0x000()()()2()xx g x f x f x e e a x x '''=-=-+-，且0()0g x '=（1）当0a ≥时，00()0,()0g x x x g x x x ''>⇔><⇔<得：当且仅当0x x =时，min 0()()0g x g x ==由0x 的任意性，0a ≥不符合条件（lby lfx ）（2）当0a <时，令00()2()()20ln(2)x x x h x e e a x x h x e a x x a ''=-+-⇒=+=⇔==- ①当0x x '=时，00()0,()0h x x x h x x x ''>⇔><⇔<当且仅当0x x =时，0()()0()g x g x g x ''≥=⇒在x R ∈上单调递增()0g x ⇔=只有一个根0x②当0x x '>时，()0,()0h x x x h x x x ''''>⇔><⇔<得：0()()0g x g x '''<=，又,(),,()x g x x g x ''→+∞→+∞→-∞→+∞存在两个数0x x ''<使，0()()0g x g x ''''==得：00()0()()0g x x x x g x g x '''''<⇔<<⇒<=又,()x g x '→+∞→+∞存在1x x ''>使()0g x ''=，与条件不符·③当0x x '<时，同理可证，与条件不符从上得：当0a <时，存在唯一的点(ln(2),(ln(2))P a f a --使该点处的切线与曲线只有一个公共点P21、本题设有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分·如果多做，则按所做的前两题计分·作答时，先用2B 铅笔在答题卡上把所选题目对应题号右边的方框图黑，并将所选题号填入括号中·（1）（本小题满分7分）选修4-2：矩阵与变换设曲线12222=++y xy x 在矩阵 ⎝⎛=b a A 0(0)1a ⎫>⎪⎭对应的变换作用下得到的曲线为122=+y x ·（Ⅰ）求实数b a ,的值· （Ⅱ）求2A 的逆矩阵·解：（Ⅰ）设曲线12222=++y xy x 上任一点(,)P x y 在矩阵A 对应变换下的像是(,)P x y ''' 则220()()11x a x ax x ax ax bx y y b y bx y y bx y''=⎛⎫⎛⎫⎛⎫⎛⎫⎧==⇔⇒++=⎨ ⎪ ⎪⎪ ⎪''+=+⎝⎭⎝⎭⎝⎭⎝⎭⎩ 得：222222()212,221,1a b x bxy y a b b a b +++=⇒+==⇔==（Ⅱ）由（Ⅰ）得：21010101011111121A A ⎛⎫⎛⎫⎛⎫⎛⎫=⇒== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21101()21A A -⎛⎫=⇒= ⎪-⎝⎭【考点定位】本题主要考查矩阵与变换等基础知识，考查运算求解能力，考查转化化归思想、（2）（本小题满分7分）选修4-4：坐标系与参数方程在平面直角坐标系中，以坐标原点O 为几点，x 轴的正半轴为极轴建立极坐标系·已知直线l上两点N M ,的极坐标分别为)2,332(),0,2(π，圆C 的参数方程θθθ(sin 23cos 22⎩⎨⎧+-=+=y x 为参数）·（Ⅰ）设P 为线段MN 的中点，求直线OP 的平面直角坐标方程；（Ⅱ）判断直线l 与圆C 的位置关系·【解析】（Ⅰ）由题意知(2,0),M N ，因为P 是线段MN中点，则P因此OP 直角坐标方程为：.y x =（Ⅱ）因为直线l 上两点(2,0),(0,3M N∴l 30y -=，圆心(2,，半径2r =、32d ∴==<r ,故直线l 和圆C 相交、【考点定位】本题主要考查极坐标与参数方程的互化、圆的参数方程等基础知识，考查运算求解能力，考查转化化归思想·（3）（本小题满分7分）选修4-5：不等式选讲已知函数R m x m x f ∈--=|,2|)(，且0)2(≥+x f 的解集为]1,1[-·（Ⅰ）求m 的值；（Ⅱ）若R c b a ∈,,，且m cb a =++31211，求证：932≥++c b a · 【解析】（1）∵(2)f x m x x +=-≥0,≤∴m ，∴0m m x m >⇒-<< (2)0111f x x m +≥⇔-≤≤⇒= （2）由（1）知1111,,,23a b c R a b c++=∈,由柯西不等式得（lby lfx ） 11123(23)()23a b c a b c a b c +++++++29≥= 【考点定位】本题主要考查绝对值不等式、柯西不等式等基本知识，考查运算求解能力，考查化归转化思想。

12年高考真题——理科数学(福建卷)-推荐下载

x m
）
-1-/8
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电通，力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置，机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2，荷试而下卷且高总可中体保资配障料置各试时类卷，管调需路控要习试在题验最到；大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资，常料要工试加况卷强下安看与全22过，22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资；中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整，高核或中对者资定对料值某试，些卷审异弯核常扁与高度校中固对资定图料盒纸试位，卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置，地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中，案资要，料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气，设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术，技槽以来术、及避管系免架统不等启必多动要项方高方案中式；资，对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资，件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调，并试合且技理进术利行，用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活：。。在对对分于于线调差盒试动处过保，程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试，题技应，术采作是用为指金调发属试电隔人机板员一进，变行需压隔要器开在组处事在理前发；掌生同握内一图部线纸故槽资障内料时，、，强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试，卷卷线试切缆验除敷报从设告而完与采毕相用，关高要技中进术资行资料检料试查，卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

2012年普通高等学校招生全国统一考试福建卷(数学理)Word版

2012年普通高等学校招生全国统一考试福建卷（数学理）Word版第I卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出分四个选项中，只有一项是符合题目要求的。

1.若复数z满足zi=1-i，则z等于A.-1-IB.1-iC.-1+ID.1=i2.等差数列{a n}中，a1+a5=10,a4=7,则数列{a n}的公差为A.1B.2C.3D.43.下列命题中，真命题是A.B.C.a+b=0的充要条件是ab=-1D.a>1,b>1是ab>1的充分条件4.一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是A.球B.三棱柱C.正方形D.圆柱5.下列不等式一定成立的是A.B.C.D.6.如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为A.14B.15C.16D.177.设函数则下列结论错误的是A.D（x）的值域为{0,1}B. D（x）是偶函数C. D（x）不是周期函数D. D（x）不是单调函数8.已知双曲线22214x yb-=的右焦点与抛物线y2=12x的焦点重合，则该双曲线的焦点到其渐近线的距离等于A. B. C.3 D.59.若函数y=2x图像上存在点（x，y）满足约束条件，则实数m的最大值为A．12B.1C.32D.210.函数f（x）在[a,b]上有定义，若对任意x1，x2∈[a,b]，有则称f（x）在[a,b]上具有性质P。

设f（x）在[1,3]上具有性质P，现给出如下命题：①f（x）在[1,3]上的图像时连续不断的；②f（x2）在上具有性质P；③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1,3]；④对任意x1，x2，x3，x4∈[1,3]，有其中真命题的序号是A.①②B.①③C.②④D.③④第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，每小题4分，共20分，把答案填在答题卡的相应位置。

2012年高考理数真题试卷(福建卷)

（
Ⅰ
）
求
证
：
B1E⊥AD1
；
（Ⅱ）在棱 AA1 上是否存在一点 P，使得 DP∥平面 B1AE？若存在，求 AP 的长；若不存在，说明理由．
第 3页，总 20页
…………○…………内…………○…………装…………○…………订…………○…………线…………○………… ※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
A . lg（x2+ ）＞lgx（x＞0）
B . sinx+
≥2（x≠kx，k∈Z）
C . x2+1≥2|x|（x∈R） D .
（x∈R）
第 1页，总 20页
…………○…………内…………○…………装…………○…………订…………○…………线…………○………… ※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
………○…………外…………○…………装…………○…………订…………○…………线…………○…………
5. （2012•福建）若函数 y=2x 图象上存在点（x，y）满足约束条件为（）
A.
B.1 C.
D.2
6. （2012•福建）下列命题中，真命题是（） A . ∃x0∈R， ≤0 B . ∀x∈R，2x＞x2
………○…………外…………○…………装…………○…………订…………○…………线…………○…………
（ Ⅲ ）若二面角 A ﹣ B1E ﹣ A1 的大小为 30° ，求 AB 的长．
7. （ 2012• 福建）选修 4 ﹣ 4 ：坐标系与参数方程在平面直角坐标系中，以坐标原点 O 为极点，x 轴的正半轴为极轴建立极坐标系．已知直线 l 上两点 M，

北京2012年高考数学最新联考试题分类大汇编(15)算法框图试题解析.pdf

一、学——目标自学、自主学习（一）学习目标： 1、有感情地朗读诗歌，体会作者的思想感情。

2、揣摩、品味诗歌的语言，体会诗中哲理性的语句。

? 3、联系实际，树立远大理想，并为之奋斗。

（二）作家作品： 1、走近作者：流沙河，原名余勋坦，四川金堂县人，生于1931年。

早在解放前，他在成都二中读书时，就是一个追求光明、酷爱文学的少年。

他加入了进步学生团体“十月读书会”，并在进步报刊上发表文章。

新中国成立时他17岁，正在四川大学农化系读书。

他痛恨自己的地主家庭，决计脱离它而独立生活，毅然辍学前往山区当了小学教员。

1952年转入四川省文联搞专业创作。

1957年1月，流沙河、白航等四位年青诗人在成都创办《星星》诗刊。

“反右”开始，《星星》被指控为“反党刊物”， 1979年底，身穿破棉袄的流沙河又回到《星星》编辑部。

他一边在复刊后的《星星》作编辑工作，一边勤奋地写作。

22年的灾难，不仅没有使他消沉，反而使他的诗更充满激情，更深沉感人，…… 代表作：短篇小说集《窗》、诗歌集《农村夜曲》、《告别火星》、组诗《草木篇》、《故园六咏》流沙河诗歌特色：1.构思奇妙，富于浪漫色彩。

2.民族化、群众化结合。

3.形式上：标准的新格律诗，标准的自由体诗。

3、学诗方法：诗是语言的艺术。

诗人的语言就好比画家笔下的线条或色彩，带有一定的灵动性。

理解鉴赏诗歌，就要用普通话正确、流利、有感情地朗读全诗，反复咀嚼这些诗句，细心揣摩诗人的心理历程。

从准确把握诗歌的朗读节奏入手,联系自己的生活体验和阅读积累，感悟诗的意境、情感及表现技巧。

（三）基础自测 1、给加点字注音或根据拼音写汉字。

倔强 ( ) ( ) 鬓发( ) 洗濯 ( ) 黎明( ) 庸人( ) 船舶 ( ) 寂寥（）脊梁( ) 连zhuì( ) tuì( )变哭qì( ) 扒窃( ) diàn( )污 zǔ zhòu( )( )榆阳( ) 荣yù( ) 2、根据课文内容把下列词语填充完整。

2012年高考数学试题解析分项版之专题15 算法框图学生版文.pdf

题型专项(四)　圆的有关计算及证明本专项主要以圆为背景考查线段、角、弧长等有关的计算常与三角形、四边形等简单几何图形综合考查属于中档题．且近两年的安徽中考对圆的考查有加强的态势分值较大复习时应予以重视．类型1　1．(2015·眉山)如图是△ABC的外接圆＝45则∠B的度数为( ) 2．(2015·酒泉)△ABC为⊙O的内接三角形若∠AOC＝160则∠ABC的度数是( )或100(2015·南通)如图为⊙O的直径为⊙O上一点弦AD平分∠BAC交BC于点E＝6＝5则AE的长为( ) 如图是⊙O的直径是弦于E交于D.(1)请写出四个不同类型的正确结论； (2)若BC＝8＝2求⊙O的半径．(2015·安徽)在⊙O中直AB＝6是弦＝30点P在BC上点Q在⊙O上且OP⊥PQ.(1)如图1当PQ∥AB时求PQ的长度； (2)如图2当点P在BC上移动时求PQ长的最大值．(2015·永州)如图已知△ABC内接于⊙O且AB＝AC直径AD交BC于点E是OE上的一点使CF∥BD.(1)求证：BE＝CE； (2)试判断四边形BFCD的形状并说明理由；(3)若BC＝8＝10求CD的长．(2015·德州)如图的半径为1是⊙O上的四个点＝∠CPB＝60(1)判断△ABC的形状：__________；(2)试探究线段PA之间的数量关系并证明你的结论； (3)当点P位于的什么位置时四边形APBC的面积最大？求出最大面积．类型2　圆中弧长与扇形面积的计算(2015·福建)在半径为6的⊙O中°圆心角所对的弧长是( )(2015·西宁)如图在半径为2圆心角为90的扇形内以BC为直径作半圆交AB于点D连接CD则阴影部分的面积是( )π－1 π－2－2 ．－1 (2015·咸宁)如图在△ABC中＝CB＝90以AB的中点D为圆心作圆心角为90的扇形DEF点C恰在EF上设∠BDF＝α(090°)，当α由小到大变化时图中阴影部分的面积( ) 由小到大由大到小不变先由小到大后由大到小(2015·南通)如图分别与⊙O相切于A两点＝60(1)求∠P的度数； (2)若⊙O的半径长为4 求图中阴影部分的面积．(2015·随州)如图射线PA切⊙O于点A连接PO.(1)在PO的上方作射线PC使∠OPC＝∠OPA(用尺规在原图中作保留痕迹不写作法)并证明：PC是⊙O的切线； (2)在(1)的条件下若PC切⊙O于点B＝AP＝4求的长．(2015·吉林)如图1半径为R圆心角为n的扇形面积是S扇形＝由弧长l＝得S扇形＝＝·R＝通过观察我们发现S扇形＝类似于S三角形＝底×高．类比扇形我们探索扇环(如图2两个同心圆围成的圆环被扇形截得的一部分叫作扇环)的面积公式及其应用．(1)设扇环的面积为S扇环的长为l的长为l线段AD的长为h(即两个同心圆半径R与r的差)．类比S梯形＝(上底＋下底)×高用含l的代数式表示S扇环并证明； (2)用一段长为40 的篱笆围成一个如图2所示的扇环形花园线段AD的长h为多少时花园的面积最大最大面积是多少？类型1　2.　3. 4.(1)不同类型的正确结论有：①BE＝CE；②＝；③∠BED＝90；④∠BOD＝∠A；⑤AC∥OD；⑥AC⊥BC；⑦OE＋BE＝OB；⑧S＝BC·OE；⑨△BOD是等腰三角形；⑩△BOE∽△BAC等等．OD⊥BC，∴BE＝CE＝＝4.设⊙O的半径为R则OE＝OD－DE＝R－2.在中由勾股定理得OE＋BE＝OB即(R－2)＋42＝R解得R＝5.⊙O的半径为5. 5.(1)连接OQ. PQ⊥OP，∴∠QPO＝90＝90直径AB＝6＝30＝＝＝点P在BC上移动要使PQ最大则必须OP最小．根据垂线段最短得当BC⊥OP时OP最小．由＝得＝即OP＝＝＝ 6.AD是直径＝∠ACD＝90在和中∴Rt△ABD≌Rt△ACD(HL)．∠BAD＝∠CAD.AB＝AC＝CE.四边形BFCD是菱形．理由：AD是直径＝AC＝CE.CF∥BD，∴∠FCE＝∠DBE.在△BED和△CEF中∴△BED≌△CEF(ASA)．CF＝BD.四边形BFCD是平行四边形．∠BAD＝∠CAD＝CD.四边形BFCD是菱形． (3)AD是直径＝CE由△CED∽△AEC得CE2＝DE·AE.设DE＝xBC＝8＝10＝x(10－x)．解得x＝2或x＝8(舍去)．在中＝＝＝. 7.(1)等边三角形　在PC上截取PD＝AP连接AD. ∠APC＝60是等边三角形．AD＝AP＝PD＝60＝120∠APB＝∠APC＋∠BPC＝120＝∠APB.在△APB和△ADC中∴△APB≌△ADC(AAS)．BP＝CD.PD＝AP＝BP＋AP.(3)当点P为的中点时四边形APBC的面积最大．理由：过点P作PE⊥AB垂足为E.过点C作CF⊥AB垂足为F.S△APE＝ABC＝S四边形APBC＝(PE＋CF)．当点P为的中点时＋CF＝PC为⊙O的直径此时四边形APBC的面积最大．⊙O的半径为1其内接正三角形的边长AB＝四边形APBC＝＝类型2　2.　3. 4.(1)连接OA、OB. PA、PB是⊙O的切线＝∠OBP＝90∠AOB＝2∠C＝120＝360－(90＋90＋120)＝60＝60连接OP.PA、PB是⊙O的切线＝＝30在中＝＝＝＝4()．S阴影＝2(S－S扇形)＝2×(－)＝(16－)()． 5.(1)作图如图．连接OA过O作OB⊥PC. PA切⊙O于点AOPC＝∠OPA＝OB即d＝r.PC是⊙O的切线．PA、PC是⊙O的切线＝PB.AB＝AP＝4是等边三角形．∠APB＝60＝120＝60在中＝＝＝＝ 6.(1)S扇环＝(l＋l)h，证明：设大扇形半径为R小扇形半径为r圆心角度数为n则由l＝得R＝＝图中扇环的面积S＝－＝－l＝(l－l)＝(l＋l)(l1－l)＝·(R－)(l1＋l)＝(l＋l2)(R－r)＝(l＋l2)h故猜想正确．根据题意得：l＋l＝40－2h则S扇环＝(l＋l)h＝(40－2h)h＝－h＋20h＝－(h－10)＋100.－1＜0开口向下有最大值当h＝10时最大值是100.所以线段AD的长h为10 时花园的面积最大最大面积是100 初中学习网，资料共分享！我们负责传递知识！。

2012年福建高考理科数学试卷及答案解析(Word)

2012年普通高等学校夏季招生全国统一考试数学理工农医类(福建卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．理科：第Ⅱ卷第21题为选考题，其他题为必考题，满分150分．第Ⅰ卷一、选择题：(理科)本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．(文科)本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z 满足z i ＝1－i ，则z 等于( )A ．－1－iB ．1－iC ．－1＋iD ．1＋i A ．3＋4i B ．5＋4i C ．3＋2i D ．5＋2i2．等差数列{a n }中，a 1＋a 5＝10，a 4＝7，则数列{a n }的公差为( ) A ．1 B ．2 C ．3 D ．4 3．下列命题中，真命题是( ) A ．x 0∈R ，0e0x ≤B ．x ∈R ，2x ＞x 2C ．a ＋b ＝0的充要条件是1ab=- D ．a ＞1，b ＞1是ab ＞1的充分条件4．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是( ) A ．球 B ．三棱锥 C ．正方体 D ．圆柱 5．下列不等式一定成立的是( ) A ．lg(x 2＋14)＞lg x (x ＞0) B ．sin x ＋1sin x≥2(x ≠k π，k ∈Z ) C ．x 2＋1≥2|x |(x ∈R ) D ．2111x >+(x ∈R ) 6．如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为( )A ．14 B ．15 C ．16 D ．177．设函数1,()0,x D x x ⎧=⎨⎩为有理数，为无理数，则下列结论错误的是( )A ．D (x )的值域为{0,1}B ．D (x )是偶函数C ．D (x )不是周期函数 D ．D (x )不是单调函数8．已知双曲线22214x y b-=的右焦点与抛物线y 2＝12x 的焦点重合，则该双曲线的焦点到其渐近线的距离等于( )AB． C ．3 D ．59．若函数y ＝2x 图象上存在点(x ，y )满足约束条件30,230,,x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩则实数m 的最大值为( )A ．12 B ．1 C ．32D ．2 10．函数f (x )在［a ，b ］上有定义，若对任意x 1，x 2∈［a ，b ］，有()()12121()22x x f f x f x +≤［＋］，则称f (x )在［a ，b ］上具有性质P ．设f (x )在［1,3］上具有性质P ，现给出如下命题：①f (x )在［1,3］上的图象是连续不断的； ②f (x 2)在［1P ；③若f (x )在x ＝2处取得最大值1，则f (x )＝1，x ∈［1,3］； ④对任意x 1，x 2，x 3，x 4∈［1,3］，有12341()44x x x x f +++≤［f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)］．其中真命题的序号是( )A ．①②B ．①③C ．②④D ．③④第Ⅱ卷二、填空题：(理科)本大题共5小题，每小题4分，共20分．把答案填在答题卡的相应位置．(文科)本大题共4小题，每小题4分，共16分．把答案填在答题卡的相应位置．11． (a ＋x )4的展开式中x 3的系数等于8，则实数a ＝________．12．阅读右图所示的程序框图，运行相应的程序，输出的s 值等于________． 13．已知△ABC________． 14．数列{a n }的通项公式πcos12n n a n =+，前n 项和为S n ，则S 2 012＝________． 15．对于实数a 和b ，定义运算“*”：22*.a ab a b a b b ab a b ⎧-≤=⎨->⎩，，，设f (x )＝(2x －1)*(x －1)，且关于x 的方程f (x )＝m (m ∈R )恰有三个互不相等的实数根x 1，x 2，x 3，则x 1x 2x 3的取值范围是__________．三、解答题：(理科)本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．(文科)本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．16．受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率；(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X 1，生产一辆乙品牌轿车的利润为X 2，分别求X 1，X 2的分布列；(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．17．某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数： ①sin 213°＋cos 217°－sin13°cos17°； ②sin 215°＋cos 215°－sin15°cos15°； ③sin 218°＋cos 212°－sin18°cos12°； ④sin 2(－18°)＋cos 248°－sin(－18°)cos48°； ⑤sin 2(－25°)＋cos 255°－sin(－25°)cos55°． (1)试从上述五个式子中选择一个，求出这个常数；(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论． 18．如图，在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝1，E 为CD 中点．(1)求证：B 1E ⊥AD 1．(2)在棱AA 1上是否存在一点P ，使得DP ∥平面B 1AE ？若存在，求AP 的长；若不存在，说明理由．(3)若二面角A －B 1E －A 1的大小为30°，求AB 的长．19．如图，椭圆E ：22221x y a b+=(a ＞b ＞0)的左焦点为F 1，右焦点为F 2，离心率12e =．过F 1的直线交椭圆于A 、B 两点，且△ABF 2的周长为8．(1)求椭圆E 的方程；(2)设动直线l ：y ＝kx ＋m 与椭圆E 有且只有一个公共点P ，且与直线x ＝4相交于点Q ．试探究：在坐标平面内是否存在定点M ，使得以PQ 为直径的圆恒过点M ？若存在，求出点M 的坐标；若不存在，说明理由．20．已知函数f (x )＝e x ＋ax 2－e x ，a ∈R ．(1)若曲线y＝f(x)在点(1，f(1))处的切线平行于x轴，求函数f(x)的单调区间；(2)试确定a的取值范围，使得曲线y＝f(x)上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P．21．(1)选修4－2：矩阵与变换设曲线2x2＋2xy＋y2＝1在矩阵1ab⎛⎫= ⎪⎝⎭A(a＞0)对应的变换作用下得到的曲线为x2＋y2＝1．①求实数a，b的值；②求A2的逆矩阵．(2)选修4－4：坐标系与参数方程在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为(2,0)，π2⎫⎪⎪⎝⎭，圆C的参数方程为22cos,2sinxyθθ=+⎧⎪⎨=⎪⎩(θ为参数)．①设P为线段MN的中点，求直线OP的平面直角坐标方程；②判断直线l与圆C的位置关系．(3)选修4－5：不等式选讲已知函数f(x)＝m－|x－2|，m∈R，且f(x＋2)≥0的解集为［－1,1］．①求m的值；②若a，b，c∈R＋，且11123ma b c++=，求证：a＋2b＋3c≥9．22．(文)已知函数f(x)＝ax sin x－32(a∈R)，且在［0，π2］上的最大值为π32-．(1)求函数f(x)的解析式；(2)判断函数f(x)在(0，π)内的零点个数，并加以证明．2012年普通高等学校夏季招生全国统一考试数学理工农医类(福建卷)答案详解1． A 由z i ＝1－i ，得221i (1i)i i i i+11i i i 11z ---=====----． 2． B ∵a 1＋a 5＝10＝2a 3， ∴a 3＝5．故d ＝a 4－a 3＝7－5＝2．3． D ∵a ＞1＞0，b ＞1＞0，∴由不等式的性质得ab ＞1，即a ＞1，b ＞1⇒ab ＞1．4． D ∵圆柱的三视图中有两个矩形和一个圆， ∴这个几何体不可以是圆柱．5． C ∵x 2＋1≥2|x |⇔x 2－2|x |＋1≥0，∴当x ≥0时，x 2－2|x |＋1＝x 2－2x ＋1＝(x －1)2≥0成立；当x ＜0时，x 2－2|x |＋1＝x 2＋2x ＋1＝(x ＋1)2≥0成立．故x 2＋1≥2|x |(x ∈R )一定成立．6． C ∵由图象知阴影部分的面积是31220121211)d ()032326x x x x =⋅-=-=⎰，∴所求概率为11616=．7． C ∵D (x )是最小正周期不确定的周期函数， ∴D (x )不是周期函数是错误的．8． A 由双曲线的右焦点与抛物线y 2＝12x 的焦点重合，知32pc ==，c 2＝9＝4＋b 2，于是b 2＝5，b =2y x =±20y ±=．故该双曲线的焦点到其渐近线的距离为d ==． 9． B 由约束条件作出其可行域如图所示：由图可知当直线x ＝m 经过函数y ＝2x 的图象与直线x ＋y －3＝0的交点P 时取得最大值，即得2x ＝3－x ，即x ＝1＝m ．10． D ①如图1，图1在区间［1,3］上f (x )具有性质P ，但是是间断的，故①错．②可设f (x )＝|x －2|(如图2)，当x ∈［1,3］时易知其具有性质P ，但是f (x 2)＝|x 2－2|＝222,1x x x x ⎧-≤≤⎪⎨-≤⎪⎩P (如图3)．故②错．图2图3③任取x 0∈［1,3］，则4－x 0∈［1,3］， 1＝f (2)＝004()2x x f +-≤12［f (x 0)＋f (4－x 0)］．又∵f (x 0)＝1，f (4－x 0)≤1， ∴12［f (x 0)＋f (4－x 0)］≤1． ∴f (x 0)＝f (4－x 0)＝1．故③正确．④3412123422()()42x x x x x x x x f f ++++++= ≤34121()+()222x x x x f f ++⎡⎤⎢⎥⎣⎦≤14［f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)］，故④正确． 11．答案：2解析：∵T r ＋1＝4C r a r x 4－r ，∴当4－r ＝3，即r ＝1时，T 2＝14C ·a ·x 3＝4ax 3＝8x 3．故a ＝2．12．答案：－3解析：(1)k ＝1,1＜4，s ＝2×1－1＝1； (2)k ＝2,2＜4，s ＝2×1－2＝0； (3)k ＝3,3＜4，s ＝2×0－3＝－3； (4)k ＝4，直接输出s ＝－3． 13．答案：解析：设△ABC 的最小边长为a (m ＞0)，2a ，故最大角的余弦值是2222cos 4θ===-． 14．答案：3 018 解析：∵函数πcos2n y =的周期2π4π2T ==，∴可用分组求和法：a 1＋a 5＋…＋a 2 009＝50311+1=503++个…；a 2＋a 6＋…＋a 2 010＝(－2＋1)＋(－6＋1)＋…＋(－2 010＋1)＝－1－5－…－2 009＝503(12009)2--＝－503×1 005；a 3＋a 7＋…＋a 2 011＝50311+1=503++个…；a 4＋a 8＋…＋a 2 012＝(4＋1)＋(8＋1)＋…＋(2 012＋1)＝503(52013)2⨯+＝503×1 009；故S 2 012＝503－503×1 005＋503＋503×1 009 ＝503×(1－1 005＋1＋1 009)＝3 018． 15．答案：(116，0) 解析：由已知，得()22200x x x f x x x x ⎧≤⎪⎨⎪⎩－，，＝－＋，＞，作出其图象如图，结合图象可知m 的取值范围为0＜m ＜14，当x＞0时，有－x2＋x＝m，即x2－x＋m＝0，于是x1x2＝m．当x＜0时，有2x2－x－m＝0，于是3x=．故123x x x=．设h(m)＝m(1，∵h′(m)＝(1＋［m()］＝10<，∴函数h(m)单调递减．故x1x2x3的取值范围为，0)．16．解：(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A，则231 ()5010 P A+==．(2)依题意得，X1的分布列为X2的分布列为(3)由(2)得，E(X1)＝1×125＋2×50＋3×10＝50＝2.86(万元)，E(X2)＝1.8×110＋2.9×910＝2.79(万元)．因为E (X 1)＞E (X 2)，所以应生产甲品牌轿车． 17．解：方法一：(1)选择②式，计算如下： sin 215°＋cos 215°－sin15°cos15°＝1－12sin30°＝13144-=． (2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下：sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝sin 2α＋(cos30°cos α＋sin30°sin α)2－sin α·(cos30°cos α＋sin30°sin α)＝sin 2α＋34cos 2αsin αcos α＋14sin 2αα·cos α－12sin 2α ＝34sin 2α＋34cos 2α＝34．方法二：(1)同方法一．(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin α·cos(30°－α)＝34．证明如下：sin 2α＋cos 2(30°－α)－sin αcos(30°－α) ＝1cos21cos(602)22αα-+︒-+－sin α(cos30°cos α＋sin30°sin α)＝12－12cos2α＋12＋12(cos60°·cos2α＋sin60°sin2α)－2sin αcos α－12sin 2α＝12－12cos2α＋12＋14cos2α＋4sin2α－4sin2α－14(1－cos2α) ＝11131cos2cos24444αα--+=． 18．解：(1)以A 为原点，AB ，AD ，1AA 的方向分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图)．设AB ＝a ，则A (0,0,0)，D (0,1，0)，D 1(0,1,1)，E (2a，1,0)，B 1(a,0,1)，故1AD ＝(0,1,1)，1B E ＝(2a -，1，－1)，1AB ＝(a,0,1)，AE ＝(2a，1,0)．∵1AD ·1B E ＝2a-×0＋1×1＋(－1)×1＝0， ∴B 1E ⊥AD 1．(2)假设在棱AA 1上存在一点P (0,0，z 0)，使得DP ∥平面B 1AE ．此时DP ＝(0，－1，z 0)．又设平面B 1AE 的法向量n ＝(x ，y ，z )． ∵n ⊥平面B 1AE ，∴n ⊥1AB ，n ⊥AE ，得00.2ax z ax y +=⎧⎪⎨+=⎪⎩，取x ＝1，得平面B 1AE 的一个法向量n ＝(1，2a-，－a )．要使DP ∥平面B 1AE ，只要n ⊥DP ，有2a －az 0＝0，解得012z =．又DP平面B 1AE ，∴存在点P ，满足DP ∥平面B 1AE ，此时12AP =． (3)连接A 1D ，B 1C ，由长方体ABCD -A 1B 1C 1D 1及AA 1＝AD ＝1，得AD 1⊥A 1D ． ∵B 1C ∥A 1D ，∴AD 1⊥B 1C ．又由(Ⅰ)知B 1E ⊥AD 1，且B 1C ∩B 1E ＝B 1，∴AD 1⊥平面DCB 1A 1．∴1AD 是平面A 1B 1E 的一个法向量，此时1AD ＝(0,1,1)．设1AD 与n 所成的角为θ，则11·cos ||||a aAD AD θ--==n n∵二面角A －B 1E －A 1的大小为30°，∴|cos θ|＝cos30°3a=，解得a ＝2，即AB 的长为2．19．解：方法一：(1)因为|AB |＋|AF 2|＋|BF 2|＝8，即|AF 1|＋|F 1B |＋|AF 2|＋|BF 2|＝8，又|AF 1|＋|AF 2|＝|BF 1|＋|BF 2|＝2a ，所以4a ＝8，a ＝2．又因为12e =，即12c a =，所以c ＝1．所以b故椭圆E 的方程是22143x y +=． (2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩，，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0．因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且∆＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0．(*) 此时024443km k x k m =-=-+，y 0＝kx 0＋m ＝3m，所以P (4k m -，3m)．由4x y kx m =⎧⎨=+⎩，，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．设M (x 1,0)，则0MP MQ ⋅=对满足(*)式的m ，k 恒成立．因为MP ＝(14k x m --，3m)，MQ ＝(4－x 1,4k ＋m )，由0MP MQ ⋅=，得211141612430kx k k x x m m m-+-+++=，整理，得(4x 1－4)km＋x 12－4x 1＋3＝0．(**) 由于(**)式对满足(*)式的m ，k 恒成立，所以1211440,430,x x x -=⎧⎨-+=⎩解得x 1＝1．故存在定点M (1,0)，使得以PQ 为直径的圆恒过点M ．方法二：(1)同方法一．(2)由22143y kx m x y =+⎧⎪⎨+=⎪⎩，，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0．因为动直线l 与椭圆E 有且只有一个公共点P (x 0，y 0)，所以m ≠0且∆＝0，即64k 2m 2－4(4k 2＋3)(4m 2－12)＝0，化简得4k 2－m 2＋3＝0．(*) 此时024443km k x k m =-=-+，y 0＝kx 0＋m ＝3m，所以P (4k m -，3m)．由4x y kx m =⎧⎨=+⎩，，得Q (4,4k ＋m )．假设平面内存在定点M 满足条件，由图形对称性知，点M 必在x 轴上．取k ＝0，m ，此时P (0，Q (4，以PQ 为直径的圆为(x －2)2＋(y2＝4，交x 轴于点M 1(1,0)，M 2(3,0)；取12k =-，m ＝2，此时P (1，32)，Q (4,0)，以PQ 为直径的圆为225345()()2416x y -+-=，交x 轴于点M 3(1,0)，M 4(4,0)．所以若符合条件的点M 存在，则M 的坐标必为(1,0)．以下证明M (1,0)就是满足条件的点：因为M 的坐标为(1,0)，所以MP ＝(41k m --，3m)，MQ ＝(3,4k ＋m )，从而1212330k kMP MQ m m⋅=--++=，故恒有MP MQ ⊥，即存在定点M (1,0)，使得以PQ 为直径的圆恒过点M ． 20．解：(1)由于f ′(x )＝e x ＋2ax －e ，曲线y ＝f (x )在点(1，f (1))处切线斜率k ＝2a ＝0，所以a ＝0，即f (x )＝e x －e x ．此时f ′(x )＝e x －e ，由f ′(x )＝0得x ＝1．当x ∈(－∞，1)时，有f ′(x )＜0；当x ∈(1，＋∞)时，有f ′(x )＞0．所以f (x )的单调递减区间为(－∞，1)，单调递增区间为(1，＋∞)．(2)设点P (x 0，f (x 0))，曲线y ＝f (x )在点P 处的切线方程为y ＝f ′(x 0)(x －x 0)＋f (x 0)，令g (x )＝f (x )－f ′(x 0)(x －x 0)－f (x 0)，故曲线y ＝f (x )在点P 处的切线与曲线只有一个公共点P 等价于函数g (x )有唯一零点．因为g (x 0)＝0，且g ′(x )＝f ′(x )－f ′(x 0)＝e x －e x 0＋2a (x －x 0)．(1)若a≥0，当x＞x0时，g′(x)＞0，则x＞x0时，g(x)＞g(x0)＝0；当x＜x0时，g′(x)＜0，则x＜x0时，g(x)＞g(x0)＝0．故g(x)只有唯一零点x＝x0．由P的任意性，a≥0不合题意．(2)若a＜0，令h(x)＝e x－e x0＋2a(x－x0)，则h(x0)＝0，h′(x)＝e x＋2a．令h′(x)＝0，得x＝ln(－2a)，记x′＝ln(－2a)，则当x∈(－∞，x*)时，h′(x)＜0，从而h(x)在(－∞，x*)内单调递减；当x∈(x*，＋∞)时，h′(x)＞0，从而h(x)在(x*，＋∞)内单调递增．①若x0＝x*，由x∈(－∞，x*)时，g′(x)＝h(x)＞h(x*)＝0；x∈(x*，＋∞)时，g′(x)＝h(x)＞h(x*)＝0，知g(x)在R上单调递增．所以函数g(x)在R上有且只有一个零点x＝x*．②若x0＞x*，由于h(x)在(x*，＋∞)内单调递增，且h(x0)＝0，则当x∈(x*，x0)时有g′(x)＝h(x)＜h(x0)＝0，g(x)＞g(x0)＝0；任取x1∈(x*，x0)有g(x1)＞0．又当x∈(－∞，x1)时，易知g(x)＝e x＋ax2－［e＋f′(x0)］x－f(x0)＋x0f′(x0)＜e x1＋ax2－［e ＋f′(x0)］x－f(x0)＋x0f′(x0)＝ax2＋bx＋c，其中b＝－［e＋f′(x0)］，c＝e x1－f(x0)＋x0f′(x0)．由于a＜0，则必存在x2＜x1，使得ax22＋bx2＋c＜0．所以g(x2)＜0．故g(x)在(x2，x1)内存在零点，即g(x)在R上至少有两个零点．③若x0＜x*，仿②并利用3e6xx>，可证函数g(x)在R上至少有两个零点．综上所述，当a＜0时，曲线y＝f(x)上存在唯一点P(ln(－2a)，f(ln(－2a)))，曲线在该点处的切线与曲线只有一个公共点P．21．(1)选修4－2：矩阵与变换解：①设曲线2x2＋2xy＋y2＝1上任意点P(x，y)在矩阵A对应的变换作用下的像是P′(x′，y′)．由1x ay b'⎛⎫⎛⎫=⎪ ⎪'⎝⎭⎝⎭x axy bx y⎛⎫⎛⎫=⎪ ⎪+⎝⎭⎝⎭，得,.x axy bx y'=⎧⎨'=+⎩又点P′(x′，y′)在x2＋y2＝1上，所以x′2＋y′2＝1，即a2x2＋(bx＋y)2＝1，整理得(a2＋b2)x2＋2bxy＋y2＝1．依题意得222,22,a bb⎧+=⎨=⎩解得1,1,ab=⎧⎨=⎩或1,1,ab=-⎧⎨=⎩因为a＞0，所以1,1. ab=⎧⎨=⎩②由①知， 1 01 1⎛⎫=⎪⎝⎭A ，21 0 1 0 1 01 1 1 12 1⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭A ，所以|A 2|＝1，(A 2)－1＝ 1 02 1⎡⎤⎢⎥-⎣⎦． (2)选修4－4：坐标系与参数方程解：①由题意知，M ，N 的平面直角坐标分别为(2,0)，(0)．又P 为线段MN 的中点，从而点P 的平面直角坐标为(1，故直线OP 的平面直角坐标方程为y x =．②因为直线l 上两点M ，N 的平面直角坐标分别为(2,0)，(0，所以直线l 30y +-=．又圆C 的圆心坐标为(2，，半径r ＝2，圆心到直线l 的距离32d r ==<，故直线l 与圆C 相交． (3)选修4－5：不等式选讲解：①因为f (x ＋2)＝m －|x |，f (x ＋2)≥0等价于|x |≤m ，由|x |≤m 有解，得m ≥0，且其解集为{x |－m ≤x ≤m }．又f (x ＋2)≥0的解集为［－1,1］，故m ＝1． ②由①知111123a b c++=，又a ，b ，c ∈R ＋，由柯西不等式得 a ＋2b ＋3c ＝(a ＋2b ＋3c )(11123a b c++)≥29＝．。

福建省高考数学联考试题分类大汇编算法框图选修系列试题

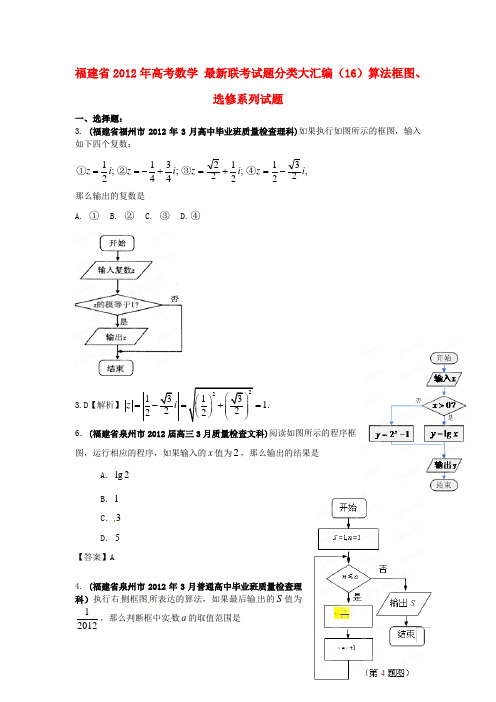
福建省2012年高考数学最新联考试题分类大汇编（16）算法框图、选修系列试题一、选择题：3. (福建省福州市2012年3月高中毕业班质量检查理科)如果执行如图所示的框图，输入如下四个复数： ;21i z =①;4341i z +-=②;2122i z +=③,2321i z -=④ 那么输出的复数是A. ①B. ②C. ③D.④3.D 【解析】221313 1.2222z i ⎛⎫⎛⎫=-=+= ⎪ ⎪ ⎪⎝⎭⎝⎭6．(福建省泉州市2012届高三3月质量检查文科)阅读如图所示的程序框图，运行相应的程序，如果输入的x 值为2，那么输出的结果是A ．lg 2B ．1C ．3D ．5【答案】A4. (福建省泉州市2012年3月普通高中毕业班质量检查理科）执行右侧框图所表达的算法，如果最后输出的S 值为12012，那么判断框中实数a 的取值范围是A ．20112012a ≤<B ．20112012a <≤C ．20112012a ≤≤D ．20122013a ≤< 4.A 【解析】4．(福建省厦门市2012年3月高三质量检查理科)执行右边的程序框图，输出S的值等于（ B ）A ．10B ．6C ．3D ．27．(福建省宁德市2012年高三毕业班质量检查理科)运行如右所示的程序框图，输入下列四个函数，则可以输出的函数是（ D ）A ．2()f x x =B ．()cos 2f x x =C ．()x f x e =D ．()sin f x x =4．(福建省莆田市2012年3月高三毕业班教学质量检查理科)某程序框图如图所示，若程序运行后输出S 的值是25，则图中判断框①处可填入的语句是（ B ）A ．4?n ≤B ．5?n ≤C ．6?n ≤D ．7?n ≤二、填空题：15．(福建省宁德市2012年高三毕业班质量检查文科)运行如图所示的程序框图，若输出的结果是7，则判断框中的横线上可以填入的最大整数为 9 。

2012年高考理科数学福建卷(含答案解析)

数学试卷第1页（共21页）数学试卷第2页（共21页）数学试卷第3页（共21页）绝密★启用前2012年普通高等学校招生全国统一考试(福建卷)数学试题(理工农医类)本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题共50分)一、选择题：本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数z 满足i 1i z =-,则z 等于（）A .1i --B .1i -C .1i -+D .1i +2. 等差数列{}n a 中,1510a a +=,47a =,则数列{}n a 的公差为（）A .1B .2C .3D .4 3. 下列命题中,真命题是（）A .0x ∃∈R ,0e 0x ≤B .x ∀∈R ,22x x ＞C .0a b +=的充要条件是1ab=-D .1a ＞,1b ＞是1ab ＞的充分条件4. 一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是（）A .球B .三棱锥C .正方体D . 圆柱 5. 下列不等式一定成立的是（）A .21lg()lg (0)4x x x +＞＞B .1sin 2(π,k )sin x x k x +≠∈≥ZC .22||(x x x ∈+1≥R)D .211()1x x ∈+＞R6. 如图所示,在边长为1的正方形OABC 中任取一点P ,则点P 恰好取自阴影部分的概率为（）A .14 B .15 C .16D .177. 设函数1,()0,x D x x ⎧=⎨⎩为有理数，为无理数，则下列结论错误的是（）A .()D x 的值域为{0,1}B .()D x 是偶函数C .()D x 不是周期函数D .()D x 不是单调函数8. 已知双曲线22214x y b-=的右焦点与抛物线212y x =的焦点重合,则该双曲线的焦点到其渐近线的距离等于（）AB.C .3D .59. 若函数2x y =图象上存在点(,)x y 满足约束条件30,230,,x y x y x m +-⎧⎪--⎨⎪⎩≤≤≥则实数m 的最大值为（）A .12 B .1 C .32D .210. 函数()f x 在[,]a b 上有定义,若对任意12,[,]x x a b ∈,有12121()[()()]22x x f f x f x ++≤,则称()f x 在[,]a b 上具有性质P .设()f x 在[1,3]上具有性质P ,现给出如下命题： ①()f x 在[1,3]上的图象是连续不断的； ②2()f x在上具有性质P ；③若()f x 在2x =处取得最大值1,则()1f x =,[1,3]x ∈； ④对任意1x ,2x ,3x ,4[1,3]x ∈,有123412341()[()()()()]44x x x x f f x f x f x f x ++++++≤.其中真命题的序号是（）A .①②B .①③C .②④D .③④第Ⅱ卷(非选择题共100分)二、填空题：本大题共5小题,每小题4分,共20分.把答案填在答题卡的相应位置. 11.4()a x +的展开式中3x 的系数等于8,则实数a =_______. 12.阅读右图所示的程序框图,运行相应的程序,输出的s 值等于________.13.已知ABC △的等比数列,则其最大角的余弦值为________.14.数列{}n a 的通项公式ππcos12n n a =+,前n 项和为n S ,则2012S =________.15.对于实数a 和b ,定义运算“*”；22,,*,.a ab a b a b b ab a b ⎧-=⎨-⎩≤＞设()(21)*(1)f x x x =--,且关于x 的方程()(f x m m =∈R)恰有三个互不相等的实数根1x ,2x ,3x ,则123x x x 的取值范围是_______.三、解答题：本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16.（本小题满分13分）受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已将频率视为概率,解答下列问题：（Ⅰ）从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率；（Ⅱ）若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为1X ,生产一辆乙品牌轿车的利润为2X ,分别求1X ,2X 的分布列；（Ⅲ）该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应产生哪种品牌的轿车？说明理由.--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷第4页（共21页）数学试卷第5页（共21页）数学试卷第6页（共21页）17.（本小题满分13分）某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数： (1)22sin 13cos 17sin13cos17+-； (2)22sin 15cos 15sin15cos15+-； (3)22sin 18cos 12sin18cos12+-； (4)22sin (18)cos 48sin(18)cos48-+--； (5)22sin (25)cos 55sin(25)cos55-+--.（Ⅰ）试从上述五个式子中选择一个,求出这个常数；（Ⅱ）根据（Ⅰ）的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.18.（本小题满分13分）如图,在长方体1111ABCD A B C D -中,11AA AD ==,E 为CD 中点. （Ⅰ）求证：11B E AD ⊥；（Ⅱ）在棱1AA 上是否存在一点P ,使得DP ∥平面1B AE ？若存在,求AP 的长；若不存在,说明理由；（Ⅲ）若二面角11A B E A --的大小为30，求AB 的长.19.（本小题满分13分）如图,椭圆E ：22221(0)x y a b a b +=＞＞的左焦点为1F ,右焦点为2F ,离心率12e =.过1F 的直线交椭圆于A 、B 两点,且2ABF △的周长为8. （Ⅰ）求椭圆E 的方程；（Ⅱ）设动直线l ：y kx m =+与椭圆E 有且只有一个公共点P ,且与直线4x =相交于点Q .试探究：在坐标平面内是否存在定点M ,使得以PQ 为直径的圆恒过点M ？若存在,求出点M 的坐标；若不存在,说明理由.20.（本小题满分14分）已知函数2()e e x f x ax x =+-,a ∈R .（Ⅰ）若曲线()y f x =在点(1(1))f ，处的切线平行于x 轴,求函数()f x 的单调区间；（Ⅱ）试确定a 的取值范围,使得曲线()y f x =上存在唯一的点P ,曲线在该点处的切线与曲线只有一个公共点P .21.本题设有（1）、（2）、（3）三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B 铅笔在答题卡上把所选题目对应题号右边的方框涂黑,并将所选题号填入括号中.（1）（本小题满分7分）选修4—2：矩阵与变换设曲线22221x xy y ++=在矩阵01a A b ⎛⎫= ⎪⎝⎭(0)a ＞对应的变换作用下得到的曲线为221x y +=.（Ⅰ）求实数a ,b 的值；（Ⅱ）求2A 的逆矩阵.（2）（本小题满分7分）选修4—4：坐标系与参数方程在平面直角坐标系中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l 上两点M ,N 的极坐标分别为(2,0),π)2,圆C的参数方程为22cos ,2sin x y θθ=+⎧⎪⎨=⎪⎩（θ为参数）. （Ⅰ）设P 为线段MN 的中点,求直线OP 的平面直角坐标方程；（Ⅱ）判断直线l 与圆C 的位置关系. （3）（本小题满分7分）选修4—5：不等式选讲已知函数|2|f x m x =--（）,m ∈R ,且2()0f x +≥的解集为[1,1]-. （Ⅰ）求m 的值；（Ⅱ）若,,a b c ∈R ,且11123m a b c++=,求证：239a b c ++≥.2012年普通高等学校招生全国统一考试（福建卷）数学试题(理工农医类)答案解析又双曲线的渐近线方程故选B．30x y+-≤⎧数学试卷第7页（共21页）数学试卷第8页（共21页）数学试卷第9页（共21页）数学试卷第10页（共21页）数学试卷第11页（共21页）数学试卷第12页（共21页）(2)1f =，又42x f +⎛ ⎝又()1f x ≤1≤，所以对于④，f ⎛⎛ ⎝4)()]f x +216，1()E X >可知甲品牌轿车首次出现故障发生在保修期内的轿车数数学试卷第13页（共21页）数学试卷第14页（共21页）数学试卷第15页（共21页）21315cos 15sin15cos151sin3024+-=-=；3(30)sin cos(30)4ααα---=，(30)sin cos(30)ααα---2131⎫⎛【提示】（Ⅰ）选择②，由22sin 15cos 15sin15cos151sin3024+-=-=，可得这个常数的值．（Ⅱ）推广，得到三角恒等式223sin cos (30)sin cos(30)4αααα+---=，直接利用两角(0,1,1)AD ∴=，a B E ⎛=- ，(,0,1)AB a =，,1,0a AE ⎛= 1101102aAD B E =-⨯+⨯+，11B E AD ∴⊥；（Ⅱ）假设在棱，使得DP ∥平面此时(0,DP =-的法向量(,,)n x y z =n ⊥平面1B AE ，n AB ⊥，n AE ⊥，得，02ax y +=⎩取1x =，得平面AE 的一个法向量1,,2a n ⎛=- ⎝⎭，只要n DP ⊥，有2a n DP =-1AP =； 11B C A D ∥1AD B ∴⊥11EB C B =1AD ∴⊥平面平面11A B CD ，AD ∴是平面的一个法向量，此时(0,1,1)AD =，设AD 与n 所成的角为11cos ||||n AD n AD θ==，二面角A -的大小为30， cos30，即y 轴，可求出向量AD 与B E 的坐标，验证其数量积为30建立关于||F =0MP MQ =①，①对0(0,2)x ∈数学试卷第16页（共21页）数学试卷第17页（共21页）数学试卷第18页（共21页）③当0<x x '时，同理可证，与条件不符；∴当<0a 时，存在唯一的点[]ln(2),ln(2)P a f a ⎡⎤--⎣⎦使该点处的切线与曲线只有一个公共点P ．【提示】（Ⅰ）求导函数，利用曲线()f x 在点[]1,(1)f 处的切线平行于x 轴，可求a 的值，令()e e 0xf x '=-<，可得函数()f x 的单调减区间；令()0f x '>，可得单调增区间；（Ⅱ）设点[]00,()P x f x ，曲线()y f x =在点P 处的切线方程为000()()()y f x x x f x '=-+，令000()()()()()g x f x f x x x f x '=---，曲线在该点处的切线与曲线只有一个公共点P 等价于()g x 有唯一零点，求出导函数，再进行分类讨论：（Ⅰ）若0a ≥，()g x 只有唯一零点0x x =，由P 的任意性0a ≥不合题意；（Ⅱ）若<0a ，令00()e e 2()x xh x a x x =-+-，则()0h x =，()e 2xh x a '=+，可得函数的单调性，进而可研究()g x 的零点，由此可得结论．【考点】利用导数研究曲线上某点切线方程，利用导数研究函数的单调性 21.【答案】（Ⅰ）1a =1b =（Ⅱ）2110()21-⎛⎫= ⎪-⎝⎭A【解析】（Ⅰ）设曲线22221x xy y ++=上任一点(,)P x y ，在矩阵A 对应变换下的项是(),P x y '''，则220()()11x a x ax x axax bx y y b y bx y y bx y''=⎛⎫⎛⎫⎧⎛⎫⎛⎫==⇒⇒++=⎨ ⎪ ⎪ ⎪ ⎪''+=+⎝⎭⎝⎭⎝⎭⎝⎭⎩， 2222()21a b x bxy y ∴+++=， 222a b ∴+=，22b =，1a ∴=，1b =；（Ⅱ）由（Ⅰ）得：21010101011111121⎛⎫⎛⎫⎛⎫⎛⎫=⇒== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭A A ， 2110||1()21-⎛⎫=⇒= ⎪-⎝⎭A A ．【提示】（Ⅰ）确定点在矩阵0(0)1a a b ⎛⎫=> ⎪⎝⎭A 对应的变换作用下得到点坐标之间的关系，利用变换前后的方程，即可求得矩阵A ；23.【答案】（Ⅰ）(2)||0f x m x +=-≥，||x m ∴≤，>0<<m m x m ⇒-，(2)011f x x +≥⇒-≤≤，1m ∴=；（Ⅱ）由（Ⅰ）知111123a b c++=，a ，b ，c ∈R ，由柯西不等式得：211123(23)2392323a b c a b c a bc a b c a bc ⎛⎫+++++++≥++= ⎪⎪⎝⎭⎭．【提示】（Ⅰ）由条件可得(2)||f x m x +=-，故有||0m x -≥的解集为[]1,1-，即||x m ≤的解集为[]1,1-，故1m =；（Ⅱ）根据111233223(23111232233)a b c a c a b a b c a b c a b a b b c c c ⎛⎫++=++++++++ ⎪⎝⎭++=++，利用基本不等式证明它大于或等于9．【考点】带绝对值的函数，不等式的证明数学试卷第19页（共21页）数学试卷第20页（共21页）数学试卷第21页（共21页）。

2012年普通高等学校招生全国统一考试高考数学教师精校版含详解福建理

2012年福建理一、选择题（共10小题；共50分）1. 若复数z满足z i=1−i，则z等于 A. −1−iB. 1−iC. −1+iD. 1+i2. 等差数列a n中，a1+a5=10，a4=7，则数列a n的公差为 A. 1B. 2C. 3D. 43. 下列命题中，真命题是 A. ∃x0∈R，e x0≤0B. ∀x∈R，2x>x2C. a+b=0的充要条件是ab=−1 D. a>1，b>1是ab>1的充分条件4. 一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是 A. 球B. 三棱锥C. 正方体D. 圆柱5. 下列不等式一定成立的是 A. lg x2+14>lg x x>0B. sin x+1sin x≥2x≠kπ,k∈ZC. x2+1≥2∣x∣x∈RD. 1x2+1>1x∈R6. 如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为 A. 14B. 15C. 16D. 177. 设函数D x=1,x为有理数,0,x为无理数,则下列结论错误的是 A. D x的值域为0,1B. D x是偶函数C. D x不是周期函数D. D x不是单调函数8. 已知双曲线x24−y2b2=1的右焦点与抛物线y2=12x的焦点重合，则该双曲线的焦点到其渐近线的距离等于 A. 5B. 42C. 3D. 59. 若函数y=2x图象上存在点x,y满足约束条件x+y−3≤0,x−2y−3≤0,x≥m,则实数m的最大值为 A. 12B. 1 C. 32D. 210. 函数f x在a,b上有定义，若对任意x1,x2∈a,b，有f x1+x22≤12f x1+f x2，则称f x在a,b上具有性质P．设f x在1,3上具有性质P，现给出如下命题：①f x在1,3上的图象是连续不断的；②f x2在1,3上具有性质P；③若f x在x=2处取得最大值1，则f x=1，x∈1,3；④对任意x1,x2,x3,x4∈1,3，有f x1+x2+x3+x44≤14f x1+f x2+f x3+f x4．其中真命题的序号是 A. ①②B. ①③C. ②④D. ③④二、填空题（共5小题；共25分）11. a+x4的展开式中x3的系数等于8，则实数a=．12. 阅读如图所示的程序框图，运行相应的程序，输出的s值等于．13. 已知△ABC的三边长成公比为2的等比数列，则其最大角的余弦值为．14. 数列a n的通项公式a n=n cos nπ2+1，前n项和为S n，则S2012=．15. 对于实数a和b，定义运算" ∗ "：a∗b=a2−ab,a≤b,b2−ab,a>b.设f x=2x−1∗x−1，且关于x的方程f x=m m∈R恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是．三、解答题（共8小题；共104分）16. 受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：将频率视为概率，解答下列问题：（1）从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率；（2）若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列；（3）该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车?请说明理由．17. 某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：①sin213∘+cos217∘−sin13∘cos17∘；②sin215∘+cos215∘−sin15∘cos15∘；③sin218∘+cos212∘−sin18∘cos12∘；④sin2−18∘+cos248∘−sin−18∘cos48∘；⑤sin2−25∘+cos255∘−sin−25∘cos55∘．（1）试从上述五个式子中选择一个，求出这个常数；（2）根据（1）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．18. 如图，在长方体ABCD−A1B1C1D1中，AA1=AD=1，E为CD的中点．（1）求证：B1E⊥AD1；（2）在棱AA1上是否存在一点P，使得DP∥平面B1AE ?若存在，求AP的长；若不存在，请说明理由；（3）若二面角A−B1E−A1的大小为30∘，求AB的长．19. 如图，椭圆E:x2a +y2b=1a>b>0的左焦点为F1，右焦点为F2，离心率e=12，过F1的直线交椭圆于A，B两点，且△ABF2的周长为8．（1）求椭圆E的方程；（2）设动直线l:y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M ?若存在，求出点M的坐标；若不存在，请说明理由．20. 已知函数f x=e x+ax2−e x，a∈R．（1）若曲线y=f x在点1,f1处的切线平行于x轴，求函数f x的单调区间；（2）试确定a的取值范围，使得曲线y=f x上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P．21. 设曲线2x2+2xy+y2=1在矩阵A=a0b1a>0对应的变换作用下得到的曲线为x2+y2=1．（1）求实数a，b的值；（2）求A2的逆矩阵．22. 在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为2,0，233,π2，圆C的参数方程为x=2+2cosθ,y=−3+2sinθ（θ为参数）．（1）设P为线段MN的中点，求直线OP的平面直角坐标方程；（2）判断直线l与圆C的位置关系．23. 已知函数f x=m−∣x−2∣,m∈R，且f x+2≥0的解集为−1,1，（1）求m的值；（2）若a,b,c∈R+，且1a +12b+13c=m，求证：a+2b+3c≥9．答案第一部分 1. A 2. B 【解析】由 2a 1+4d =10a 1+3d =7⇒ a 1=1d =2.3. D4. D5. C【解析】此类题目可用筛选法．对于A ，当x =12时，两边相等，故A 错误；对于B ，具有基本不等式的形式，但是sin x 不一定大于零，故B 错误；对于C ，x 2+1≥2∣x∣⇔x 2±2x +1≥0⇔ x ±1 2≥0，显然成立；对于D ，对任意x 都不成立． 6. C【解析】由题图可得，图中阴影部分的面积S =x−x 10d x = 23x 3−12x 2 ∣∣∣01=23−12=16,由此可得点P 恰好取自阴影部分的概率P =16÷ 1×1 =16． 7. C8. A9. B【解析】如图，当直线x =m 经过函数y =2x 的图象与直线x +y −3=0的交点时，函数y =2x 的图象上仅有一个点在可行域内，由方程组 y =2x ,x +y −3=0得x =1，所以m ≤1． 10. D【解析】提示：①②我们可举反例说明错误．①中我们令f x = 2−x ,x ∈ 1,3 2,x =3，②中我们令f x =−x ．③可用图象说明其正确性．我们来看④，作变形x 1+x 2+x 3+x 44=x 1+x 22+x 3+x 422即可．第二部分 11. 2 12. −3 13. −24【解析】不妨设△ABC 的三边分别为a 、 2a 、2a ,则最大边长为2a ，该边所对的角最大，且最大角θ的余弦值为cos θ=2222a ×2a=−24． 14. 3018【解析】∵a n=n cos nπ2+1，∴当n为奇数时，a n=1；当n=4k+2，k∈N时，a n=−n+1；当n=4k，k∈N∗时，a n=n+1．∴数列a n的前4项和为1+−1+1+5=6；第5至第8项和为1+−5+1+9=6；⋯，由此可得a n+a n+1+a n+2+a n+3=1+−n−1+1+1+n+3+1=6（n+3是4的倍数，n∈N∗）．故S2012=S4×503=503×6=3018．15. 1−316,0【解析】由已知条件可得f x=2x−1∗x−1=2x2−x,x≤0,−x2+x,x>0,该函数的图象如图所示，当0<m<14时，方程f x=m有三个不同的实数根，不妨设x1<x2<x3,由图可知1−34<x1<0<x2<12<x3<1,且x2+x3=1,根据均值不等式，得x2x3<x2+x322=14,即x2x3<14,所以0>x1x2x3>14x1>14×1−34=1−316,即x1x2x3∈1−316,0.第三部分16. （1）设"甲品牌轿车首次出现故障发生在保修期内"为事件A，则P A=2+3=1.（2）依题意得X1的分布列为X1123P139 X2的分布列为X2 1.8 2.9P 110910（3）由（2）得E X1=1×125+2×350+3×910=2.86万元,E X2=1.8×110+2.9×910=2.79万元.因为E X1>E X2，所以应生产甲品牌轿车．17. （1）选择②式，计算如下：sin215∘+cos215∘−sin15∘cos15∘=1−1sin30∘=3.（2）三角恒等式为sin2α+cos230∘−α−sinαcos30∘−α=3 .证明如下：sin2α+cos230∘−α−sinαcos30∘−α=1−cos2α+1+cos60∘−2α−sinαcos30∘cosα+sin30∘sinα=12−12cos2α+12+12cos60∘cos2α+sin60∘sin2α−32sinαcosα−12sin2α=1−1cos2α+1+1cos2α+3sin2α−3sin2α−11−cos2α=1−1cos2α−1+1cos2α=3 .18. （1）以A为原点，AB，AD，AA1的方向分别为x轴，y轴，z轴的正方向建立空间直角坐标系（如图）．设AB=a，则A0,0,0,D0,1,0,D10,1,1,E a,1,0,B1a,0,1,故AD1=0,1,1,B1E= −a2,1,−1,AB1=a,0,1,AE=a2,1,0,因为AD1⋅B1E=0,所以B 1E ⊥AD 1.（2）假设在棱AA 1上存在一点P 0,0,z 0 ，使得DP ∥ 平面 B 1AE ．此时DP = 0,−1,z 0 ．又设平面B 1AE 的法向量n = x ,y ,z ．因为n ⊥ 平面 B 1AE ，所以n ⊥AB 1 ，n⊥AE ，得 ax +z =0,ax 2+y =0.取x =1，得平面B 1AE 的一个法向量n = 1,−a2,−a ．要使DP ∥ 平面 B 1AE ，只要n ⊥DP ，有a2−az 0=0，解得z 0=12. 又DP ⊄ 平面 B 1AE ，所以存在点P ，满足DP ∥ 平面 B 1AE ，此时AP =12．（3）连接A 1D ，B 1C ，由长方体ABCD −A 1B 1C 1D 1及AA 1=AD =1，得AD 1⊥A 1D ．因为B 1C ∥A 1D ，所以AD 1⊥B 1C ．又由（1）知B 1E ⊥AD 1，且B 1C ∩B 1E =B 1，所以AD 1⊥平面 DCB 1A 1，AD 1 是平面A 1B 1E 的一个法向量，此时AD 1 = 0,1,1 ．设AD 1 与n所成的角为θ，则 cos θ=n ⋅AD 1∣n ∣∣∣AD 1 ∣∣=−a 2−a2⋅ 1+4+a 2因为二面角A −B 1E −A 1的大小为30∘，所以∣cos θ∣=cos30∘，即3a 22⋅ 1+4= 3, 解得a =2,即AB 的长为2． 19. （1）因为∣AB ∣+∣AF 2∣+∣BF 2∣=8,即∣AF 1∣+∣F 1B ∣+∣AF 2∣+∣BF 2∣=8,又∣AF1∣+∣AF2∣=∣BF1∣+∣BF2∣=2a,所以4a=8,a=2.又因为e=12，即ca=12，所以c=1，所以b=a2−c2= 3.故椭圆E的方程是x2 4+y23=1.（2）由y=kx+m,x2+y2=1,得4k2+3x2+8kmx+4m2−12=0.因为动直线l与椭圆E有且只有一个公共点P x0,y0，所以m≠0且Δ=0，即64k2m2−44k2+34m2−12=0,化简得4k2−m2+3=0.此时x0=−4km4k2+3=−4km,y0=kx0+m=3 ,所以P −4km ,3m．由x=4,y=kx+m,得Q4,4k+m．假设平面内存在定点M满足条件，由图形对称性知，点M必在x轴上．取k=0，m=3，此时P 0,3，Q 4,3，以PQ为直径的圆为x−22+ y−32=4,交x轴于点M11,0，M23,0；取k=−12，m=2，此时P1,32，Q4,0，以PQ为直径的圆为x−52+ y−32=45,交x轴于点M31,0，M44,0．所以若符合条件的点M存在，则M的坐标必为1,0．以下证明M1,0就是满足条件的点：因为M的坐标为1,0，所以MP= −4km−1,3m,MQ=3,4k+m,从而MP⋅MQ=−12km−3+12km+3=0,故恒有MP⊥MQ，即存在定点M1,0，使得以PQ为直径的圆恒过点M．20. （1）对f x求导可得f′x=e x+2ax−e,曲线y=f x在点1,f1处切线斜率k=2a=0，所以a=0，即f x=e x−e x.此时f′x=e x−e，由f′x=0，得x=1，当x∈−∞,1时，有f′x<0；当x∈1,+∞时，有f′x>0．所以f x的单调递减区间为−∞,1，单调递增区间为1,+∞．（2）设点P x0,f x0，曲线y=f x在点P处的切线方程为y=f′x0x−x0+f x0,令g x=f x−f′x0x−x0−f x0,故曲线y=f x在点P处的切线与曲线只有一个公共点P等价于函数g x有唯一零点．因为g x0=0，且g′x=f′x−f′x0=e x−e x0+2a x−x0.（i）若a≥0，当x>x0时，g′x>0，则x>x0时，g x>g x0=0；当x<x0时，g′x<0，则x<x0时，g x>g x0=0．故g x只有唯一零点x=x0．由P的任意性知，a≥0不合题意．（ii）若a<0，令 x=e x−e x0+2a x−x0，则 x0=0, ′x=e x+2a．令 ′x=0，得x=ln−2a，记x∗=ln−2a，则当x∈−∞,x∗时， ′x<0，从而 x在−∞,x∗内单调递减；当x∈x∗,+∞时， ′x>0，从而 x在x∗,+∞内单调递增．①若x0=x∗，由x∈−∞,x∗时，g′x= x> x∗=0；x∈x∗,+∞时，g′x= x> x∗=0．知g x在R上单调递增．所以函数g x在R上有且只有一个零点x=x∗．②若x0>x∗，由于 x在x∗,+∞内单调递增，且 x0=0，则当x∈x∗,x0时有g′x= x< x0=0，g x>g x0=0；任取x1∈x∗,x0有g x1>0．又当x∈−∞,x1时，易知g x=e x+ax2−e+f′x0 x−f x0+x0f′x0<e x1+ax2−e+f′x0 x−f x0+x0f′x0=ax2+bx+c,其中b=− e+f′x0,c=e x1−f x0+x0f′x0.由于a<0，则必存在x2<x1，使得ax22+bx2+c<0．所以g x2<0，故g x在x2,x1内存在零点．即g x在R上至少有两个零点．③若x0<x∗，仿②并利用e x>x36，可证函数g x在R上至少有两个零点．综上所述，当a<0时，曲线y=f x上存在唯一点P ln−2a,f ln−2a，曲线在该点处的切线与曲线只有一个公共点P．21. （1）设曲线2x2+2xy+y2=1上任意点P x,y在矩阵A对应的变换作用下的像是P′x′,y′．由x′y′=a0b1xy=axbx+y,得x′=ax,y′=bx+y,又点P′x′,y′在x2+y2=1上，所以xʹ2+yʹ2=1,即a2x2+bx+y2=1,整理得a2+b2x2+2bxy+y2=1.依题意得a2+b2=2,2b=2,解得a=1, b=1,或a=−1, b=1.因为a>0，所以a=1,b=1.（2）由（1）知，A=1011,A2=101110 11=1021.所以∣A2∣=1,A2−1=10−21.22. （1）由题意知，M，N的平面直角坐标分别为2,0，0,233．又P为线段MN的中点，从而点P的平面直角坐标为1,33，故直线OP的平面直角坐标方程为y=33x．（2）因为直线l上两点M，N的平面直角坐标分别为2,0，0,233，所以直线l的平面直角坐标方程为3x+3y−23=0.又圆C的圆心坐标为2,−3，半径r=2，圆心到直线l的距离d=∣23−33−23∣3+9=32<r,故直线l与圆C相交．23. （1）因为f x+2=m−∣x∣，f x+2≥0等价于∣x∣≤m，由∣x∣≤m有解，得m≥0，且其解集为x∣−m≤x≤m．又f x+2≥0的解集为−1,1，故m=1.（2）由（1）知1 a +12b+13c=1.又a,b,c∈R+，由柯西不等式得a+2b+3c=a+2b+3c 1+1+1≥aa 2b⋅2b3c⋅3c2=9.当且仅当a=2b=3c时上式取等号．。

2012年高考数学试题解析分项版之专题15 算法框图--学生版文

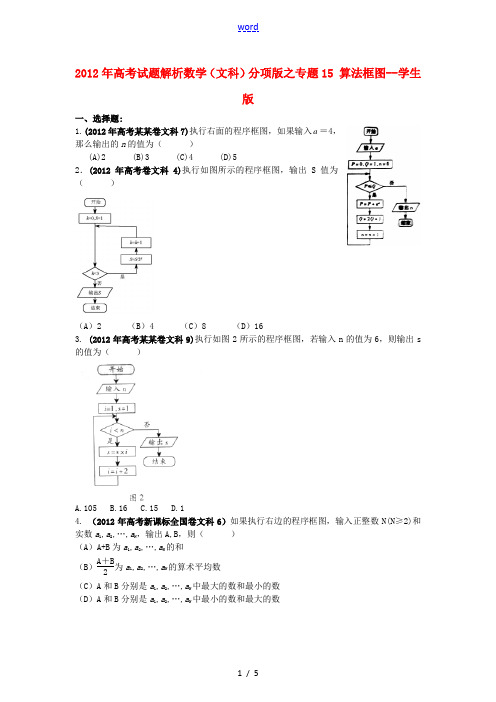
2012年高考试题解析数学（文科）分项版之专题15 算法框图--学生版一、选择题:1.(2012年高考某某卷文科7)执行右面的程序框图，如果输入a ＝4，那么输出的n 的值为（）(A)2 (B)3 (C)4 (D)52．(2012年高考卷文科4)执行如图所示的程序框图，输出S 值为（）（A ）2 （B ）4 （C ）8 （D ）163. (2012年高考某某卷文科9)执行如图2所示的程序框图，若输入n 的值为6，则输出s 的值为（）A.105B.16C.15D.14. （2012年高考新课标全国卷文科6）如果执行右边的程序框图，输入正整数N(N ≥2)和实数a 1,a 2,…,a N ，输出A,B ，则（）（A ）A+B 为a 1,a 2,…,a N 的和（B ）A ＋B 2为a 1,a 2,…,a N 的算术平均数（C ）A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数（D ）A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数5.（2012年高考某某卷文科6）如图所示，程序框图（算法流程图）的输出结果是（）（A ） 3 （B ）4 （C ） 5 （D ）8 开始A=xB=x x ＞A 否输出A ，B是输入N ，a 1,a 2,…,a N结束x <Bk ≥N k =1,A =a 1,B=a 1k =k+1x =a k是否否是6.（2012年高考某某卷文科10）执行如图所示的程序框图，则输出的S的值是（）(A) 4 (B) 3 2(C)23(D) 17. (2012年高考某某卷文科3)阅读右边的程序框图，运行相应的程序，则输出S的值为（）（A）8 （B）18 （C）26 （D）808. (2012年高考某某卷文科6)阅读右图所示的程序框图，运行相应的程序，输出s值等于（）A -3B -10C 0D -29. (2012年高考某某卷文科5)下图是计算某年级500名学生期末考试（满分为100分）及格率q的程序框图，则图中空白框内应填入（）A. q=NMB 。