典型相关分析论文
毕业论文中如何正确运用相关性分析和因子分析

毕业论文中如何正确运用相关性分析和因子分析在毕业论文中,正确运用相关性分析和因子分析是非常重要的。
相关性分析是一种用于确定变量之间关系的统计方法,而因子分析则是用于确定潜在因素的方法。
本文将探讨如何正确运用这两种分析方法,并提供几个例子来说明它们在毕业论文中的应用。
第一部分:相关性分析相关性分析是通过计算变量之间的相关系数来确定它们之间关系的一种方法。
相关系数的范围从-1到+1,-1表示完全负相关,+1表示完全正相关,0表示没有相关性。
在毕业论文中,相关性分析可以用于研究两个或多个变量之间的关系。
例如,在教育领域的研究中,一个研究者可能对学生的成绩和参与课外活动之间的关系感兴趣。
通过进行相关性分析,可以确定这两个变量之间的关系强度和方向。
在运用相关性分析时,研究者需要注意以下几点:1. 确定要分析的变量:在进行分析之前,需要明确要研究的变量。
在上述例子中,研究者需要确定他们要分析的是学生的成绩和参与课外活动。
2. 收集数据:研究者需要收集相关的数据,例如学生的成绩和他们的课外活动参与情况。
数据可以通过问卷调查、观察或其他方法获得。
3. 计算相关系数:通过计算相关系数,研究者可以确定变量之间的相关性。
常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数适用于连续变量,而斯皮尔曼相关系数适用于有序变量。
举个例子,研究者收集了100名学生的成绩和他们的课外活动参与情况。
通过计算皮尔逊相关系数,研究者发现成绩和课外活动参与之间存在正相关关系,相关系数为0.7,说明两者之间的关系较为密切。
第二部分:因子分析因子分析是一种用于确定潜在因素的方法。
在毕业论文中,因子分析可以用于确定一组变量背后的共同因素。
它可以帮助研究者简化数据集,并找到隐藏的模式和关联。
在运用因子分析时,研究者需要注意以下几点:1. 确定要进行因子分析的变量:在进行因子分析之前,需要明确要进行分析的变量。
例如,在心理学研究中,研究者可能想要确定一组变量(如压力水平、焦虑水平和抑郁水平)背后的共同因素。
管理学案例分析论文六篇

管理学案例分析论文六篇管理学案例分析论文范文1【关键词】网络环境财务管理案例教学教学模式案例教学法是一种启发式、争论式、互动式的教学方法,以典型案例为载体,引导同学阅读、思索、争论案例,在互动争论中关心同学把握和运用理论学问,并培育同学分析、推断、表达以及运用所学学问处理问题的力量。
传统的案例教学采纳在课堂中集中争论的教学形式,由于受课堂教学时间和条件的限制,同学难以在短时间内对案例绽开全面分析。
尤其是财务管理教学中的一些案例,案例内容包括公司背景状况、经营状况说明以及许多报表数据,同学很难在短时间内把其中的财务问题分析清晰,更难以提出有效的对策建议,大大降低了案例教学的效果。
网络科技的进展,多媒体教学平台的广泛应用,为财务管理教学模式的创新和改革供应了有力的技术支持。
网络环境下建设网络案例教学平台,给同学供应自主探究、协作学习的环境,使得教学活动突破时间和空间的限制,同学能够实现更具弹性的自主学习。
利用网络教学平台,可以供应参考资料、案例答疑以及争论区,增加同学与老师间、同学与同学间的教学沟通,可以提高同学的参加度,增加教学效果。
本文结合教学实践,构建了网络环境下财务管理案例教学模式。
一、网络环境下财务管理案例教学的理论依据建构主义理论、情境学习理论是构建网络环境下财务管理案例教学模式的重要理论依据。
建构主义关于教学的基本观点:同学是认知的主体,是意义的主动建构者,老师是意义建构的指导者、促进者,而不是学问的灌输者;情境对意义建构具有重要作用,要尽量创设能够促进同学乐观主动地建构学问的情景;注意协作学习,通过同学与老师之间、同学与同学之间沟通争论建构自己的学问结构;学习环境的设计具有重要意义,要细心设计教学环境,让同学能够利用各种工具和资源来达到学习目标。
建构主义理论的启示是:利用网络平台创建“学习社区”,在老师指导下,同学对案例情景绽开自主探究、协作学习,最终提高同学分析问题、解决问题的力量。
典型相关分析论文

海南省备市县农村住户结构特性经济活动特性与经济活动后果三者相关分析吴学品李均立傅国华冯子华摘要:本文在建立海南省农村住户结构特性、经济活动特性、经济活动后果三者评价指标体系的基础上,依据海南省第一次农业普查资料,利用多元统计中的主成分分析和典型相关分析方法,对上述三者的各指标体系进行分析。
主成分分析方法概述:主成分分析方法是处理多变量(多指标)问题的一种方法,即将研究对象的多个相关变量(指标)化为少数几个不相关的变量,而这较少的不相关变量尽可能地反映原变量提供的大部分信息。
典型相关分析概述:研究多个变量之间的相关性的一种方法。
本文把上述两种方法有机结合起来,先利用主成分的降维思想,分别对各市县农村住户结构特性,经济活动特性,经济活动后果进行主成分分析,然后对上述三者的主成分进行典型相关分析。
1.各市县农住户结构特性的主成分分析1.l评价指标体系及各指标水平见《海南省农村住户结构特性的研究》。
1.2程序:DATA HNO1;INPUT X1-X11;LABEL X1=“民族乡占乡镇百分比”......Xl1=“非农村住户农业生产经营单位从事种植业率”;(依各指标水平顺序) CARDS:(按INPUT格式输入数据);PROC PRINCOMP OUT=PRINHNO1;PREFIX=APRIN;RUN;PROC PRINT;VAR APRIN1-APRIN4;RUN;1.3结果分析1.3.1运行结果显示,X1,X2,X3,X4的标准差较大,它们相对应的指标为民族乡占乡镇百分比,老边区占乡镇百分比,山区占乡镇百分比,乡镇平均土地面积,这说明各省县区的生活居住条件极其不平衡,还有X7、X8、X9、X10、Xl1也较大,它们相对应的指标为文盲半文盲占农村住户从业人员百分比(住户成员个体的素质),及住户成员个体户的经济活动(X8-X11)相对指标的总称也极不平衡,从附表1的(1)~(2)相关表中可看出X9与大多数变量都为负相关(即X9与X1、X2、X3、X4、X6、X10),结合他们本身意义,相当于农村住户从业人员在农村从事非农业率与生活居住条件(Xl-X4),住户类型(X6),从业人员从事种植业率(Xl0)有很大的负相关关系,从附表1的(3)给出的特征值和各成分所占的贡献率可以看出:前4个特征及相应的累计贡献率为85%,因此可从说,前4个主成分几乎已经概括了大部分信息,后7个主成分的贡献率小于5.5%,因此,我们可以取4个主成分作为该问题的主成分。
【毕业论文】相关分析和回归分析
相关分析和回归分析客观事物之间的关系分为函数关系和统计关系,函数关系也就是我们通常所说的一一对应的关系,而统计关系是指两事物之间的一种非一一对应的关系,即当一个变量x取一定值时,另一变量y无法依确定的函数取唯一确定的值。
事物之间的统计关系是普遍存在,且有的关系强,有的关系弱。
相关分析和回归分析都是以不同方式测度事物之间统计关系的有效工具。
实际应用中。
这两种分析方法经常互相结合渗透。
一、相关分析相关分析通过图形和数值两种方式,能够有效的揭示事物之间统计关系的强弱程度。
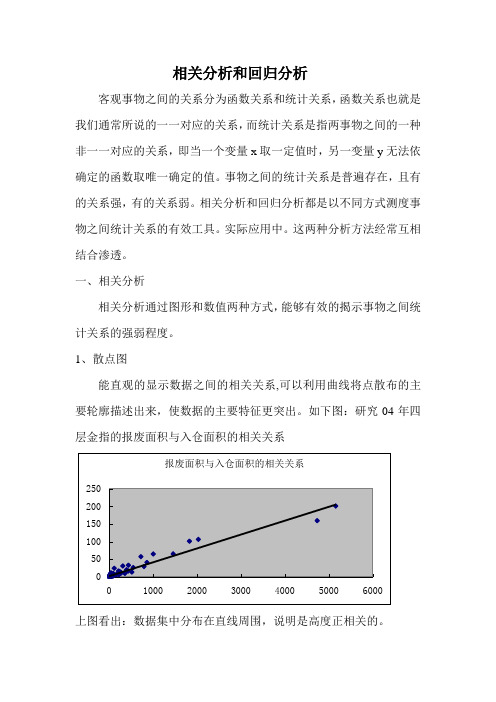
1、散点图能直观的显示数据之间的相关关系,可以利用曲线将点散布的主要轮廓描述出来,使数据的主要特征更突出。
如下图:研究04年四层金指的报废面积与入仓面积的相关关系上图看出:数据集中分布在直线周围,说明是高度正相关的。
2、相关系数散点图能直观的展现变量之间的统计关系,但并不精确。
相关系数以数值的方式精确的反映了两个变量间线形相关的强弱程度。
➢ R=yyxx xy L L L ,其中xx L =∑=--ni ix x12)(,∑=----=ni i i xy y y x x L 1))((,∑=--=ni i yy y y L 12)(.➢ 相关系数R 的取值在-1~+1之间。
➢ R>0表示两变量之间存在正的线性相关关系;R<0表示两变量之间存在负的线性相关关系。
➢ R=1表示两变量存在完全正相关;R=-1表示两变量存在完全负相关;R=0表示两变量不存在线性相关关系。
➢ |R|>0.8表示两变量之间具有较强的线性关系;|R|<0.3表示两变量之间的线性相关关系较弱。
上例中,R=0.974,说明报废面积与入仓面积之间是强正相关的。
二、一元线性回归在实际应用中,我们常常需要考虑某一现象与影响它的最主要因素的关系,回归分析不仅可以揭示变量x 对变量y 的影响大小,还可以由回归方程进行预测和控制。
一元线性回归是最简单的回归模型。
会计案例研究论文六篇

会计案例研究论文六篇会计案例讨论论文范文1一、案例教学应是一种综合性的教学形式笔者认为,目前所进行的案例教学一般来说还是一种综合性的课堂教学形式,它是将课堂讲授(老师预备案例和对同学分析与报告内容的点评等)、争论、试验(同学实际操作)和习题(撰写分析报告)等教学形式相结合的课堂教学形式。
在案例教学中,老师需要在大量收集资料的基础上形成需要进行分析的案例内容,在同学对案例进行分析、报告以及争论后要对分析报告的内容和争论的状况进行点评,这些工作都是与课堂讲授有关的内容。
成本会计学案例分析中有的内容是需要同学进行实际计算与复核(如成本核算案例中的计算与复核),撰写分析报告,所做工作类似于同学做习题和试验。
同学就案例作分析报告和问答是争论教学形式的运用。
而成本会计学案例教学的深化进展应是将课堂教学形式与现场教学形式相结合,在老师的引导下,将同学分为若干组到企业单位实地调查和实习,收集第一手资料,编写企业单位的成本会计案例和分析报告,在肯定程度上还可以依据所学学问解决实际问题。
课堂教学与现场教学相结合的形式在成本会计学课程的特地实习或学年实习条件下采纳比较合适。
二、案例教学应注意所学学问的融会贯穿和综合力量的培育成本会计学案例教学一般是在已经学习了肯定的成本会计学学问的基础上进行的。
因此,进行案例教学首先是检测和巩固所学学问,然后才是在这一基础上进行问题分析和提出解决问题的对策。
在案例教学的学问检测和巩固部分,要求同学能结合所学学问进行推断,通过同学的推断来检查同学对有关学问的把握程度。
通过这种教学方法,可以有效地发觉同学对有关概念和方法理解上的偏差或错误,从而在老师讲解点评时予以准时订正,加速同学对有关学问点、方法和相互关系的熟悉。
在案例教学其次部分的分析与解决问题中,同学通过案例分析和解决问题对策的讨论,提高发觉问题、分析问题和解决问题的力量,团队合作的力量,分析报告的文字表述和口头表述的力量以及课件的制作力量。
(概率论与数理统计专业论文)Copula理论与相关性分析

华中科技大学博士学位论文Copula理论与相关性分析姓名:***申请学位级别:博士专业:概率论与数理统计指导教师:任佳刚;刘次华20091024华中科技大学博士学位论文摘要本文主要研究利用Copula理论分析多维随机变量的相关性及其应用。
Copula是一个“连接”多维联合分布及其边缘分布的函数,其优点主要有两点:第一,它能完整地刻划变量之间的相关性结构;其次,它可以将单个随机变量的边缘分布与变量间的相关结构拆开来处理,然后再加以整合,这样能生成灵活多样的高维概率分布。
论文首先分析了多元Copula函数的特点,然后基于Copula理论研究了随机变量的相关性,探讨了多元Copula参数模型的选择问题,以及利用Copula函数在多元极值理论中获得了一些成果,最后研究了Copula模型在金融和保险等领域的应用。
本文的创新点和主要工作如下:1. 深入分析了Copula理论在研究多变量的相关性中的重要作用,与传统的相关性分析方法相比,Copula函数所具有的优势和特点。
讨论了当边缘分布是连续和非连续的两种情形时Sklar定理的不同结果,并用一种新的方法更简单地证明了此定理。
利用Copula理论研究了Kendall’s τ系数与 Spearman’s ρ系数之间的关系,得到了两者比值ρτ变化的不等式。
针对一类Copula参数族,证明了比值ρτ的极限值是3/2.2. 如何选取合适的Copula函数来描述多维随机变量的相关性结构是目前Copula 理论研究中的一个难题。
论文讨论了一类多元Copula参数模型的选择问题,其Copula 函数能与一个一元函数构成一一对应的关系,从而达到降维的目的。
研究了4种此类常见的Copula模型的性质和图形,并分别在参数已知或未知两种情况下进行了拟合优度检验。
对中国股市的上证指数与深证综指作了实证分析,结果表明两者存在着较强的正相关性,相关性模型选取Gumbel Copula模型最合适。
相关分析构建原理分析论文

相关分析的构建原理分析摘要:联系是自然现象、社会现象普遍具备的特点。
通过各种形态的联系,事物间构成了一个相互影响、相互制约的整体系统。
人们在各类实践活动中,总结和积累了大量的有着明显类别之分的专业知识。
其中大量的知识是关于事物、现象间联系问题的探讨、研究、总结。
从某个角度讲,关于事物、现象之间联系的方式、特点、规律的信息构成人类的全部知识。
关键词:联系相关分析统计中根据联系在数学上的特点的不同,将联系区分为两大类:函数关系、相关关系。
函数关系指如果事物间的联系可以用明确的函数表达式进行描述,那么这种关系称为函数关系。
相关关系与函数关系相对应,指如果事物间存在关联,但关联并不能描述为明确的函数表达式,那么这种关联称为相关关系。
函数关系简洁、直观,如确定了自变量数值大小,就能唯一确定因变量数值大小,为我们掌握事物变化规律提供了一条捷径。
然而,这种理想色彩浓厚的联系形式在揭示客观事物变化,尤其是揭示社会、经济现象变化时,显得过于呆板,常常漏洞百出。
与函数关系相比相关关系对关联特征的描述更具灵活性。
由于事物间的联系以相关关系的形态为表现具有普遍性,并且也是确定事物间函数关系的前提,所以相关关系的研究具有重要意义,引入相关关系来完善联系的类别结构也显得十分必要。
相关关系根据相关的程度可以分为完全相关、不完全相关、不相关;根据相关的方向可以划分为正相关和负相关;根据涉及变量的多少可以分为单相关、复相关、偏相关;根据计量结果是否与实际吻合可分为真实相关和虚假相关;根据的曲线特征的不同,相关关系又可以区分为线性相关和非线性相关两种类型。
线性相关如果现象之间的关系大致呈现为线性的特征,称之为线性相关。
其线性相关的程度可由指标相关系数(r)进行测度。
相关系数的测度公式:x:表示某一指标 y:表示相关联的另一指标这一公式包括分子和分母两个部分,我们对两部分分别进行探讨。
1 分子部分cov(x,y)是两个变量之间的协方差。
典型火灾事故案例分析论文范文

典型火灾事故案例分析论文范文随着城市现代化建设的不断推进,大型商业建筑、高层住宅、办公楼等高耸入云的建筑层出不穷,加之近年来天气异常,气温不断飙升,空气湿度不足等情况,火灾事故也愈加频繁。
为了更好地预防和处理火灾事故,进行典型火灾事故案例分析就显得尤为必要。
本文将从火灾事故的成因以及防范措施、相关的法律法规和典型火灾安全事故案例等方面进行分析。
一、火灾事故的成因以及防范措施1.火源环境火源环境是指火灾发生的物理环境,包括温度、湿度、氧气含量等。
夏季气温高、空气干燥、氧气含量低,这都是火源环境的助长因素。
针对该环境,采取的防范措施包括提高建筑的抗火等级和隔热等级,加强消防设施建设,增加灭火器和消防栓等装备的数量。
2.人为因素人为因素是造成火灾事故最主要的原因。
通常是由于人们的不注意,例如抽烟、使用明火、乱扔火柴等,结果导致火灾。
针对这种情况,应对普及消防知识,增强公众消防意识,并提高消防设施和人员的防范及应急处理能力。
3.电气因素电气因素是造成火灾的常见原因。
这包括电线电缆的老化、接头松动、负载过重、电器故障等因素。
针对这种原因,应对建筑物内部的电线电缆进行定期检查和维护,稳定电网负荷,也可设置电器安全开关等装置,确保电路的安全性。
二、相关的法律法规火灾事故的相应法律法规颇为完善。
如《消防法》和《建筑法》、《安全生产法》等都对防范火灾、保护建筑和人员安全等方面的内容进行了详细规定。
其中重要的一项法规是《消防法》第六十二条规定,规定建筑物、构筑物内应当设置火灾自动报警系统,装配必要的灭火设备;同时也明确规定各级政府、国有企事业单位和其他有管理权限的组织,应当成立消防组织,配备专职消防队伍,指定专人负责组织实施消防安全预防措施。
三、典型火灾安全事故案例1. 沈阳防控三期工地火灾2015年10月4日下午4点许,沈阳某工地发生火灾,当时现场有8名工人正在作业,事故造成2死6伤。
指向该事件的原因是由于建筑工程进展速度较快,钢汁液体未及时清理过滤,致使热量积聚导致发生火源,后来短时间内火源迅速扩散。
相关性分析论文怎么写

相关性分析论文怎么写
相关分析的主要方法有比较分析法、比率分析法、因素分析法。
比较分析法
比较分析法,是通过对比两期或连续数期财务报告中的相同指标,确定其增减变动的方向、数额和幅度,来说明企业财务状况或经营成果变动趋势的一种方法。
采用这种方法,可以分析引起变化的主要原因、变动的性质,并预测企业未来的发展趋势。
比较分析法的具体运用主要有重要财务指标的比较、会计报表的比较和会计报表项目构成的比较三种方法。
比率分析法
比率分析法是通过计算各种比率指标来确定财务活动变动程度
的方法。
比率指标的类型主要有构成比率、效率比率、相关比率三类。
因素分析法
因素分析法是依据分析指标与其影响因素的关系,从数量上确定各因素对分析指标影响方向和影响程度的一种方法。
因素分析法具体有两种:连环替代法和差额分析法。
相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法。
论文部分 相关性分析过程

问题一中求两组品酒员的评价结果有无显著性差异,由此我们考虑到利用相关性分析检验,将每一组中十名品酒员对每种葡萄酒的每种样品进行品尝评分的结果做相关性分析。
每组的十名品酒员评分之间的相关性系数越大,则表明该组品酒员之间的评价误差越小,即评价结果越准确。
(其中相关性系数的绝对值大于等于0.8则为高度相关,在0.5和0.8之间则为中度相关。
)相关性系数可由SPSS软件及EXCEL求得,这里只介绍前者。
将两组品酒员对白葡萄酒中的28份葡萄酒样品进行品尝后所评的分导入到SPSS中,得到56组十名品酒员评价之间的相关性系数;同理,将两组品酒员对红葡萄酒中的27份葡萄酒样品进行品尝后所评的分导入到SPSS中,得到54组十名品酒员评价之间的相关性系数。
再将所有的110组相关性系数单独分析,选出所有组中所有相关性系数大于0.9的葡萄酒样品,再选出所有组中部分相关性系数介于0.5和0.8之间的葡萄酒样品。
分析结果可知:(1)第一组十名品酒员对白葡萄酒的28份样品所评的分之间相关性系数全都大于0.9的有:样品4。
相关性系数中有部分介于0.8和0.9之间的有:样品1、样品2、样品6、样品7、样品9、样品11、样品12、样品13、样品16、样品17、样品19、样品23、样品25、样品26、样品27。
相关性系数中有部分介于0.5和0.8之间的有:样品5、样品8、样品10、样品14、样品15、样品18、样品20、样品21、样品22、样品24。
(2)第一组十名品酒员对红葡萄酒的27份样品所评的分之间相关性系数全部大于0.9的有:样品2、样品12、样品20、样品23。
相关性系数中有部分介于0.8和0.9之间的有:样品3、样品5、样品6、样品10、样品13、样品16、样品17、样品21、样品22、样品24、样品25、样品26。
部分相关性系数介于0.5和0.8之间的有:样品1、样品4、样品8、样品9、样品11、样品14、样品15、样品18、样品19、样品27。
皮尔逊相关关系论文分析

皮尔逊相关关系论文分析卡尔.皮尔逊(karl pearson,1857~1936)是英国著名科学家和自由思想家。
他的科学哲学代表作是《科学规范》,这部初版于1892年的名著又相继出了第二版和第三版,并被译成多种文字在世界范围内广为流传(上海辛垦书店于1934年出版了中文节译本)。
其实,早在该书初版的前一年(1891年3、4月间),皮尔逊在为格雷沙姆学院讲座准备讲演提纲时,就勾勒出《科学规范》的蓝图。
本文拟以《科学规范》为据,简要论述一下皮尔逊的科学哲学。
1)以感觉论为基石的观念论哲学作为批判学派的主要成员之一,皮尔逊与另一位代表人物马赫一样,也把其哲学建立在感觉论的基石上。
不过,马赫标榜他的“要素(感觉)一元论”是超越物质论和观念论的,或者说填补了“物体和感觉之间、内部和外部之间,物质世界和精神世界之间以前所指的那种鸿沟”。
而皮尔逊则在《科学规范》第2版的序言中公开申明他的观念论立场:“健全的观念论(sound idealism)作为自然哲学的基础正在取代旧物理学家的粗糙的物质论(the crude materialism)。
”([2],p.vi)皮尔逊从“外部物体”出发建立他的感觉论。
他以黑板为例:我们通过感官获得了关于黑板的感觉印象(sense-impression),我们同时把我们过去的关于黑板的经验也加诸于黑板。
因此,黑板存在的绝对必要条件首先是某种感觉印象,是某些感觉印象的恒久的结合群。
在皮尔逊看来,决定外部物体实在性的感觉印象可能是十分稀少的,对象也许主要是由推理和联想构造出来的,但是我们要称它是真实的对象而不是我们想象的产物的话,那么就必须要有某些感觉印象。
一定数目的感觉印象群的存在导致我们推断我们接受到的其他感觉印象群的存在的可能性,如果乐意的话,我们能把这种可能性提交检验。
因此,“外部物体一般说来是建构(construct),是直接的感觉印象与过去的或储存的感觉印象的组合。
事物的实在性取决于它作为直接的感觉印象群整体地或部分地发生的可能性。
典型相关分析及其应用实例

摘要典型相关分析是多元统计分析的一个重要研究课题.它是研究两组变量之间相关的一种统计分析方法,能够有效地揭示两组变量之间的相互线性依赖关系.它借助主成分分析降维的思想,用少数几对综合变量来反映两组变量间的线性相关性质.目前它已经在众多领域的相关分析和预测分析中得到广泛应用. 本文首先描述了典型相关分析的统计思想,定义了总体典型相关变量及典型相关系数,并简要概述了它们的求解思路,然后深入对样本典型相关分析的几种算法做了比较全面的论述.根据典型相关分析的推理,归纳总结了它的一些重要性质并给出了证明,接着推导了典型相关系数的显著性检验.最后通过理论与实例分析两个层面论证了典型相关分析的应用于实际生活中的可行性与优越性.【关键词】典型相关分析,样本典型相关,性质,实际应用ABSTRACT The Canonical Correlation Analysis is an important studying topic of theMultivariate Statistical Analysis. It is the statistical analysis method which studies thecorrelation between two sets of variables. It can work to reveal the mutual linedependence relation availably between two sets of variables. With the help of thethought about the Principal Components we can use a few comprehensive variablesto reflect the linear relationship between two sets of variables. Nowadays It hasalready been used widely in the correlation analysis andforecasted analysis. This text describes the statistical thought of the Canonical Correlation Analysisfirstly and then defines the total canonical correlation variables and canonicalcorrelation coefficient and sum up their solution method briefly. After it I go deepinto discuss some algorithm of the sample canonical correlation analysis thoroughly.According to the reasoning of the Canonical Correlation Analysis sum up some of itsimportant properties and give the identification following it I infer the significancetesting about the canonical correlation coefficient. According to the analysis from thetheories and the application we can achieve the possibility and the superiority fromcanonical correlation analysis in the real life.【Key words】Canonical Correlation Analysis,Sample canonical correlation,Character,Practical applications 目录前言...............................................................1第1章典型相关分析的数学描述......................................2第2章典型变量与典型相关系数......................................3 2.1 总体典型相关................................................3 2.2 样本典型相关................................................4 2.2.1 第一对典型相关变量的解法...............................4 2.2.2 典型相关变量的一般解法.................................8 2.2.3 从相关矩阵出发计算典型相关.............................9第3章典型相关变量的性质.........................................11第4章典型相关系数的显著性检验...................................15第5章典型相关分析的计算步骤及应用实例...........................18 5.1 典型相关分析的计算步骤.....................................18 5.2 实例分析...................................................19结语..............................................................26致谢..............................................................27参考文献...........................................................28附录..............................................................29 西北第二民族学院学士学位论文前言典型相关分析Canonical Correlation Analysis CCA作为多元统计学的一个重要部分,是相关分析研究的一个主要内容.典型相关分析不仅其方法本身具有重要的理论意义,而且它还可以作为其他分析方法,如多重回归、判别分析和相应分析的工具,因此在多元分析方法中占有特殊的地位. 典型相关的概念是在两个变量相关的基础上发展起来的.我们知道,两个随机变量的相关关系可以用它们的简单相关系数来衡量;一个随机变量与一组随机变量之间的相关关系可以用复相关系数来衡量.但考虑一组随机变量与另一组随机变量的关系时,如果运用两个变量的相关关系,分别考虑第一组每个变量和第二组中每个变量的相关,或者运用复相关关系,考虑一组变量中的每个变量和另一组变量的相关,这样做比较繁琐,抓不住要领.因此,为了用比较少的变量来反映两组变量之间的相关关系,一种考虑的思路就是类似主成分分析,考虑两组变量的线性组合,从这两个线性组合中找出最相关的综合变量,通过少数几个综合变量来反映两组变量的相关性质,这样便引出了典型相关分析. 典型相关分析的基本思想是首先在每组变量中找出变量的线性组合,使其具有最大相关性,然后再在每组变量中找出第二对线性组合,使其分别与第一对线性组合不相关,而第二对本身具有最大的相关性,如此继续下去,直到两组变量之间的相关性被提取完毕为止.有了这样线性组合的最大相关,则讨论两组变量之间的相关,就转化为只研究这些线性组合的最大相关,从而减少研究变量的个数. 典型相关分析是由Hotelling 于1936 年提出的.就目前而言,它的理论己经比较完善,计算机的发展解决了典型相关分析在应用中计算方面的困难,成为普遍应用的进行两组变量之间相关性分析技术.如在生态环境方面,用典型相关理论对预报场与因子场进行分析,实现了短期气象预测;借助典型相关,分析了植被与环境的关系;在社会生活领域,应用典型相关分析了物价指标和影响物价因素的相关关系等等. 第1 页共33 页西北第二民族学院学士学位论文第1章典型相关分析的数学描述一般地,假设有一组变量X 1 X 2 X p 与另一组变量Y1 Y2 Yq ,我们要研究这两组变量之间的相关关系,如何给两组变量之间的相关性以数量的描述. 当p q 1 时,就是我们常见的研究两个变量X 与Y 之间的简单相关关系,其相关系数是最常见的度量,定义为:Cov X Y xy Var X Var Y 当p 1 q 1 (或q 1 p 1 )时,p 维随机向量X X 1 X 2 X p ,设X 11 12Y N p 1 ,,其中,11 是第一组变量的协方差阵,12 是21 22第一组与第二组变量的协方差阵,22 是第二组变量的协方差阵. 则称 1 2111 12R 为Y 与X 1 X 2 X p 的全相关系数,全相关系数用于度量一个随22机变量Y 与另一组随机变量X 1 X 2 X p 的相关系数. 当p q 1 时,利用主成分分析的思想,可以把多个变量与多个变量之间的相关化为两个新的综合变量之间的相关.也就是做两组变量的线性组合即U 1 X 1 2 X 2 p X p X V 1Y1 2Y2 q Yq Y其中,1 2 p 和1 2 q 为任意非零向量,于是我们把研究两组变量之间的问题化为研究两个变量U与V 之间的相关问题,希望寻求,使U ,V 之间最大可能的相关,我们称这种相关为典型相关,基于这种原则的分析方法就是典型相关分析. 第 2 页共33 页西北第二民族学院学士学位论文第2章典型变量与典型相关系数2.1 总体典型相关设有两组随机变量X X 1 X 2 X p Y Y1 Y2 Yq 分别为p维和q维随机向量,根据典型相关分析的思想,我们用X 和Y 的线性组合X 和Y 之间的相关性来研究两组随机变量X 和Y 之间的相关性.我们希望找到和,使得(‘ X Y)最大.由相关系数的定义Cov X Y X Y Var X Var Y 易得出对任意常数e f c d ,均有e X f c Y d X Y 这说明使得相关系数最大的X Y 并不唯一.因此,为避免不必要的结果重复,我们在求综合变量时常常限定Var X 1 ,Var Y 1 于是,我们就有了下面的定义:设有两组随机变量X X 1 X 2 X p ,XY Y1 Y2 Yq ,p q 维随机向量的均值向量为零,协方差阵0 (不Y妨设p q ).如果存在 1 11 p1 和 1 11 q1 ,使得在约束条件Var X 1 ,Var Y 1 下,1 X 1Y max X Y 则称1 X 1Y 是X Y 的典型相关变量,它们之间的相关系数称为典型相关系数;其他典型相关变量定义如下:定义了前k 1 对典型相关变量之后,第k 对典型相关变量定义为:如果存在k 1k pk 和k 1k qk ,使得⑴k X k Y 和前面的k 1 对典型相关变量都不相关;第 3 页共33 页西北第二民族学院学士学位论文⑵Var k X 1 ,Var k Y 1 ;⑶k X和k Y 的相关系数最大,则称k X和k Y 是X Y 的第k 对(组)典型相关变量,它们之间的相关系数称为第k 个典型相关系数(k 2p ).2.2 样本典型相关以上是根据总体情况已知的情形进行,而实际研究中,总体均值向量和协方差阵通常是未知的,因而无法求得总体的典型相关变量和典型相关系数,首先需要根据观测到的样本数据阵对进行估计.2.2.1 第一对典型相关变量的解法设总体Z X 1 X p Y1 Yq ,已知总体的n 次观测数据为:X t Z t (t 12 n ),Y t p q 1于是样本数据阵为x11 x12 x1 p y11 y12 y1q x x 22 x2 p y 21 y 22 y 2q 21 x n1 x n 2 x np y n1 yn2 y nq n p q 若假定Z N p q 则由参考文献【2】中定理 2.5.1 知协方差阵的最大似然估计为1 n n t 1 Z t Z Z t Z 1 n其中Z Z t ,样本协方差矩阵S 为:n t 1 S S12 S 11 S 21 S 22式中第 4 页共33 页西北第二民族学院学士学位论文1 n S11 n j 1 X j X X j X 1 n S12 X j X Y j Y n j 1 1 n S 21 Y j Y X j X n j 1 1 n S 22 n j 1 Y j Y Y j Y 1 n 1 n X Xj ,n j 1 Y Y j n j 1令U j X j ,V j Y j ,则样本的相关系数为n U j 1 j U V j V r U j V j n n U j 1 j U 2 V j 1 j V 2 1 n 1 n 1 n又因为:U U j n X j n X j X n j 1 j 1 j 1 1 n 1 n 1 n V n j 1 V j Y j Y j Y n j 1 n j 1 1 n 1 n SU jV j n j 1 U j U V j V X j X Y j Y S12 n j 1 1 n 1 n S U jU j n j 1 U j U U j U X j X X j X S11 n j 1 1 n 1 n S V jV j V j V V j V n Y j Y Y j Y S 22 n j 1 j 1所以S12 r U j V j S11 S 22 由于U j ,V j 乘以任意常数并不改变他们之间的相关系数,即不妨限定取标准化的U j 与V j ,即限定U j 及V j 的样本方差为1,故有:第 5 页共33 页西北第二民族学院学士学位论文SU jU j SV jV j 1 (2.2.1)则r U j V j S12 (2.2.2)于是我们要求的问题就是在(2.2.1)的约束条件下,求R p ,R q ,使得式(2.2.2)达到最大.这是条件极值的问题,由拉格朗日乘子法,此问题等价于求,,使S12 S11 1 S 22 1 (2.2.3)2 2达到最大.式中,,为拉格朗日乘数因子.对上式分别关于,求偏导并令其为0,得方程组:S12 S11 0 (2.2.4)S 21 S 22 0分别用,左乘方程(2.2.4)得S12 S11 S 21 S 22又S12 S 21所以S 21 S12 也就是说,正好等于线性组合U 与V 之间的相关系数,于是(2.2.4)式可写为:S12 S11 0 S11 S12 或0 (2.2.5)S 21 S 22 0 S 21 S 22而式(2.2.5)有非零解的充要条件是:S11 S12 0 (2.2.6).。
受贿犯罪的原因分析论文

受贿犯罪的原因分析论文受贿罪,是指国家工作人员利用职务上的便利,索取他人财物的,或者非法收受他人财物,为他人谋取利益的行为。
“利用职务上的便利”,是指利用本人职务范围内的权力,即自己职务上主管、负责或者承办某项公共事务的职权及其所形成的便利条件。
索取他人财物的,不论是否“为他人谋取利益”,均可构成受贿罪。
非法收受他人财物的,必须同时具备“为他人谋取利益”的条件,才能构成受贿罪。
但是为他人谋取的利益是否正当,为他人谋取的利益是否实现,不影响受贿罪的认定。
受贿犯罪的原因分析全文如下:尽管我国对受贿犯罪一直保持着严打高压的态势,但犯罪势头依然不减,形势相当严峻。
根据监视世界各国腐败行为的非政府组织“透明国际”2021年10月26日发布的本年度全球腐败指数评估,我国的“清廉度”在178个国家和地区中排名第78位。
这样的评估是否准确当然可以探讨,但至少说明,我国的腐败问题仍较为严重。
受贿作为腐败犯罪中非常典型的职务犯罪行为,是伴随着国家权力的出现而出现,其明显特征就是国家公职人员利用手中的公权力为自己谋取私利,是公共权力的非公共利用。
它是社会肌体中的一个毒瘤,危害极大,不仅损害了国家利益,败坏了社会风气,更为严重的是损害了政府的公信力,动摇了党的执政根基,危及社会稳定。
一、我国当前受贿犯罪的主要特点当前,我国的受贿犯罪呈现出以下五方面的特点:一受贿犯罪量急剧上升随着我国经济的快速发展,无论是受贿犯罪的立案数量还是收受金额,都呈现不断向上“飙升”的态势。
就受贿犯罪的立案数量而言,根据相关年度的《中国检察年鉴》统计,全国检察机关立案侦查的国家公职人员贪污受贿等职务犯罪案件,1994年为36 471件,2000年为45 000件,2021年为115 420件;就受贿犯罪的收受金额而言,20世纪80年代初期,受贿上万元即是足以轰动社会的大案要案了,到了80年代后期,受贿犯罪金额呈逐渐上升之势,从几万元到十几万元再到几十万元。
商业企业人力资本与公司业绩的相关性分析本科毕业论文

商业企业人力资本与公司业绩的相关性分析本科毕业论文标题:商业企业人力资本与公司业绩的相关性分析摘要:本篇毕业论文旨在探讨商业企业的人力资本与公司业绩之间的相关性,并通过相关性分析来验证两者之间的关系。
通过对相关研究文献的梳理和统计数据的分析,研究发现人力资本与公司业绩之间存在着正向的相关关系。
因此,合理管理和培养企业的人力资本,对于提升企业业绩具有重要的积极影响。
关键词:商业企业、人力资本、公司业绩、相关性分析1.引言人力资本是指企业拥有的一切包括员工技能、知识、健康与动力的资源。
在现代商业中,企业的人力资本已经成为竞争力和成功的重要因素之一、企业的人力资本不仅仅是员工数量的总和,还包括员工的能力、技能、经验、教育背景等。
而公司业绩则是衡量企业发展和运营状况的重要指标,对于企业的生存和发展至关重要。
因此,人力资本与公司业绩之间的关系备受关注。
2.文献综述许多研究都指出,人力资本与公司业绩之间存在着正向的关联关系。
例如,费加罗(1995年)的研究发现,人力资本的投资对于公司的业绩具有显著的正向影响。
而哈尔沃感(1999年)则发现,人力资本的组织内部转移对于公司业绩具有正向影响。
此外,博斯(2001年)的研究表明,拥有高质量的人力资本的公司,在市场竞争中更具优势,并获得更好的业绩。
因此,这些研究结果都对人力资本与公司业绩之间的正向关系提供了支持。
3.数据和方法本论文采用相关性分析来验证人力资本与公司业绩之间的关系。
首先,收集了一批商业企业的人力资本和公司业绩的数据,并进行数据的清洗和整理。
然后,通过计算人力资本和公司业绩之间的相关系数来分析两者之间的关系。
4.结果分析通过相关性分析,我们发现人力资本与公司业绩之间存在着显著的正向相关关系。
相关系数为0.7,具有高度的相关性。
这表明,人力资本的增加将会对公司的业绩产生积极的影响。
这与之前的研究结果相一致。
5.讨论和结论本研究的结果表明,商业企业的人力资本与公司业绩之间存在着正向的相关关系。
毕业论文写作中的统计分析案例

毕业论文写作中的统计分析案例在毕业论文写作中,统计分析案例是一种非常重要的方法,可以帮助研究者得出准确的结论,并支持研究的目的和假设。
本文将以一个虚拟的案例来说明如何运用统计分析方法进行毕业论文写作。
引言在本次研究中,我们将通过统计分析方法探讨某公司员工的工作满意度与其绩效之间的关系。
通过统计分析,我们可以找出是否有相关性存在,以及这种相关性的程度。
这将对公司管理层提供决策方向和参考依据。
数据收集首先,我们需要收集相关数据以进行统计分析。
我们从目标公司的员工数据库中获取了500名员工的工作满意度和其绩效评分。
工作满意度采用1到10的评分进行衡量,绩效评分则使用0到100的评分体系。
这些数据将作为我们进行统计分析的样本。
描述统计分析我们将首先进行描述统计分析,以便更好地理解我们的样本数据。
描述统计分析可以提供样本的中心趋势、离散程度、分布形态等信息。
中心趋势我们计算了工作满意度和绩效评分的均值、中位数和众数,以了解其中的中心趋势。
根据计算结果,工作满意度的均值为7.2,中位数为7,众数为8;而绩效评分的均值为75,中位数为76,众数为80。
这些数值可以帮助我们了解样本中的典型情况。
离散程度通过计算标准差和范围,我们可以了解样本数据的离散程度。
工作满意度的标准差为1.5,范围为1到10;而绩效评分的标准差为15,范围为30到100。
这些数值可以帮助我们判断数据的变化幅度,并了解样本的一致性。
分布形态为了了解数据的分布形态,我们可以画出工作满意度和绩效评分的频率分布直方图。
从直方图中可以判断数据是否呈正态分布或偏态分布。
此外,我们还可以通过绘制箱线图来观察数据是否存在离群值。
推断统计分析在描述统计分析的基础上,我们还需要进行推断统计分析,以便推断出总体的特征并进行显著性检验。
相关性分析我们将使用相关分析方法来探讨工作满意度和绩效评分之间的相关性。
通过计算相关系数(如皮尔逊相关系数),我们可以了解两个变量之间的线性关系强度。
相关性分析论文

相关性分析论文
以下是一些关于相关性分析的论文:
1. "A Review of Correlation Analysis Techniques for Big Data" - 这篇论文综述了用于大数据相关性分析的各种技术。
它提供了对常用方法的概述,并讨论了这些方法的优点和缺点。
2. "Correlation-Based Feature Selection for Machine Learning" - 这篇论文介绍了基于相关性的特征选择方法,以提高机器学习算法的性能。
它详细说明了如何计算特征之间的相关性,并提出了一种基于相关性的特征选择算法。
3. "Detecting and Modeling Correlations in Time Series Data" - 这篇论文研究了如何检测和建模时间序列数据中的相关性。
它介绍了一种基于小波变换的方法,能够在时间序列数据中发现隐含的相关性。
4. "Correlation Analysis of Social Media Data for Sentiment Analysis" - 这篇论文探讨了如何利用社交媒体数据进行情感分析,并通过相关性分析来研究不同社交媒体平台上用户之间的情感关联。
这些论文提供了关于相关性分析在不同领域的应用和方法的信息,可以用于深入研究相关性分析的原理和实践。
李彦军案件法律分析论文(3篇)

第1篇摘要:本文以李彦军案件为切入点,通过对案件事实、法律适用、判决结果等方面的分析,探讨我国刑法中关于职务侵占罪、挪用资金罪等相关法律规定,旨在为类似案件提供法律参考,并对相关法律适用提出建议。
关键词:李彦军案件;职务侵占罪;挪用资金罪;法律分析一、引言近年来,随着我国经济的快速发展,职务犯罪案件日益增多,其中,职务侵占罪和挪用资金罪案件尤为突出。
李彦军案件作为一起典型的职务犯罪案件,引起了社会广泛关注。
本文将对李彦军案件进行法律分析,以期为类似案件提供借鉴。
二、案件事实李彦军,原系某公司总经理,在职期间,利用职务便利,非法占有公司资金共计人民币1000万元。
具体事实如下:1. 李彦军通过虚构项目、伪造合同等手段,将公司资金划拨至个人账户,用于个人消费。
2. 李彦军擅自将公司资金借给他人使用,未按规定办理审批手续。
3. 李彦军侵占公司资金后,隐瞒事实,未按规定进行财务处理。
三、法律适用1. 职务侵占罪根据《中华人民共和国刑法》第二百七十一条第一款规定:“公司、企业或者其他单位的人员,利用职务上的便利,将本单位财物非法占为己有,数额较大的,处五年以下有期徒刑或者拘役;数额巨大的,处五年以上有期徒刑,可以并处没收财产。
”本案中,李彦军作为公司总经理,利用职务上的便利,非法占有公司资金1000万元,其行为已构成职务侵占罪。
2. 挪用资金罪根据《中华人民共和国刑法》第二百七十二条第一款规定:“公司、企业或者其他单位的工作人员,挪用本单位资金归个人使用或者借贷给他人,数额较大、超过三个月未还的,或者虽未超过三个月,但数额较大、进行营利活动的,或者进行非法活动的,处三年以下有期徒刑或者拘役;数额巨大或者有其他严重情节的,处三年以上七年以下有期徒刑。
”本案中,李彦军擅自将公司资金借给他人使用,未按规定办理审批手续,其行为已构成挪用资金罪。
四、判决结果法院经审理认为,李彦军的行为构成职务侵占罪和挪用资金罪,依法判处其有期徒刑八年,并处罚金人民币100万元。
论文中相关性分析结果表达

论文中相关性分析结果表达相关性分析——比如最常见的Pearson相关性分析——是极具价值的统计学方法,用以确定变量之间是否存在相关关系以及相关程度的大小。
然而,人们对这一类分析结果的意义以及如何对结果进行表述经常有误解。
我们今天就要把这个问题搞清楚。
首先,最佳步骤是参考期刊的指南。
那些经常用到相关性分析的期刊通常对报告指标有明确要求,或者会提出参考其它机构的要求。
这种情况下,请遵循这些特定的指南。
其次,在期刊没有特殊要求的情况下,你可以采取以下这些方法。
必须要报告的内容有:相关系数(r)或决定系数(r2)两个系数一起报告很有意义,但至少要报告其中一个。
既然r2可以从r推导出来,通常报告一个就可以了。
这通常跟目标变量有关。
例如,求模型契合度时,主要关注的是相关性的强度(r),而一个自变量可以解释因变量的变化的比例(r2)则用来表达一个变量对另一个变量所产生的影响的重要性。
p值p值在假设检验中被用来判断所检验的关系是否存在统计显著性。
需要注意的是,不要认为p值跟所检验的关系的强度或重要性有任何关联。
自由度现在许多期刊要求此项,因为自由度提供了计算统计学参数所使用的数据量的必要信息。
样本大小报告上述统计信息时并不一定要同时报告样本大小,但实验设计一定要清楚地表明用于相关性分析的样本大小。
最后,明智的做法是为所有相关性分析附上散点图。
因为相关性的强度是一个主观上的评价,所以应该给读者们一个直观评估数据的机会。
作者不应该隐藏那些造成统计显著相关性的异常数据,比如聚集在相关关系两端的数据群。
另外,把相关性分析中生成的回归方程放在图中也很重要。
法学案例分析论文范文3篇

法学案例分析论⽂范⽂3篇保险学案例教学法特征分析论⽂摘要:保险学是⼀门理论性与实践性并重的课程。
案例教学可以增强学⽣对保险学理论的理解,提⾼学⽣兴趣,是⼀种⾏之有效的教学⽅式。
在保险学案例教学中,应遵循相关性、典型性和正⾯引导的原则合理筛选案例。
同时,案例教学不能取代其他教学⼿段,在进⾏案例教学时,应注重多种教学的互相配合。
关键词:保险学;案例;教学⼀、案例教学在保险学教学中的重要性对传统保险学教学⽅式进⾏改⾰,案例教学是⼀项必然选择。
从保险学案例教学实践来看,教学效果明显。
(⼀)案例教学有助于提⾼学习兴趣在枯燥乏味的课堂教学中增加有趣的案例,能起到很好的调剂作⽤,学⽣的学习兴趣变浓厚了。
在课堂上,案例教学经常能起到化腐朽为神奇的效果。
如果⽼师只是平平淡淡地把知识点介绍给学⽣,这种满堂灌式的教学⽅法很难激发学⽣的学习兴趣和学习主动性,课堂⽓氛⽐较沉闷。
⽐如说,保险业的经营与管理是⼀个⽐较枯燥的实务问题,学⽣学习兴趣不⾼,笔者尝试在教学中增加了相关的案例,如保险⼈引发的保险纠纷、理赔过程中的代位追偿问题等等,明显感觉到学⽣听课的注意⼒集中了,课堂⽓氛也活跃了。
(⼆)案例教学有助于增进师⽣互动在课堂教学中,传统的教学⽅式是以教师为主体,表现为⽼师⼀味地讲课,学⽣⼀味做笔记,下课后师⽣就形同陌路,这不仅不利于师⽣的交流与合作,也不会取得好的教学效果。
⽽案例教学中学⽣分析、⽼师点评的⽅式使学⽣之间的交流增加,学⽣也更乐于在课后和⽼师探讨⼀些学业上的问题,师⽣的关系变融洽了。
师⽣互动的结果⼀⽅⾯促使学⽣不断进步,不断向上突破;另⼀⽅⾯事实上也给⽼师提出了更⾼的要求,促使⽼师不断更新知识结构,不断加强⾃⾝的理论素养,形成“教学相长”的良好氛围。
(三)案例教学有助于引导学⽣思考保险学的专业术语和基本原理是⽐较繁杂的,很多学⽣⼀学期下来还没有完全明⽩保险学的⼀些基本概念。
⽽案例能引导学⽣去思考相关的原理,真正把理论与实务紧密结合起来,使学⽣更好地掌握保险学的专业知识并能学以致⽤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海南省备市县农村住户结构特性经济活动特性与经济活动后果三者相关分析吴学品李均立傅国华冯子华摘要:本文在建立海南省农村住户结构特性、经济活动特性、经济活动后果三者评价指标体系的基础上,依据海南省第一次农业普查资料,利用多元统计中的主成分分析和典型相关分析方法,对上述三者的各指标体系进行分析。
主成分分析方法概述:主成分分析方法是处理多变量(多指标)问题的一种方法,即将研究对象的多个相关变量(指标)化为少数几个不相关的变量,而这较少的不相关变量尽可能地反映原变量提供的大部分信息。
典型相关分析概述:研究多个变量之间的相关性的一种方法。
本文把上述两种方法有机结合起来,先利用主成分的降维思想,分别对各市县农村住户结构特性,经济活动特性,经济活动后果进行主成分分析,然后对上述三者的主成分进行典型相关分析。
1.各市县农住户结构特性的主成分分析1.l评价指标体系及各指标水平见《海南省农村住户结构特性的研究》。
1.2程序:DATA HNO1;INPUT X1-X11;LABEL X1=“民族乡占乡镇百分比”......Xl1=“非农村住户农业生产经营单位从事种植业率”;(依各指标水平顺序) CARDS:(按INPUT格式输入数据);PROC PRINCOMP OUT=PRINHNO1;PREFIX=APRIN;RUN;PROC PRINT;VAR APRIN1-APRIN4;RUN;1.3结果分析1.3.1运行结果显示,X1,X2,X3,X4的标准差较大,它们相对应的指标为民族乡占乡镇百分比,老边区占乡镇百分比,山区占乡镇百分比,乡镇平均土地面积,这说明各省县区的生活居住条件极其不平衡,还有X7、X8、X9、X10、Xl1也较大,它们相对应的指标为文盲半文盲占农村住户从业人员百分比(住户成员个体的素质),及住户成员个体户的经济活动(X8-X11)相对指标的总称也极不平衡,从附表1的(1)~(2)相关表中可看出X9与大多数变量都为负相关(即X9与X1、X2、X3、X4、X6、X10),结合他们本身意义,相当于农村住户从业人员在农村从事非农业率与生活居住条件(Xl-X4),住户类型(X6),从业人员从事种植业率(Xl0)有很大的负相关关系,从附表1的(3)给出的特征值和各成分所占的贡献率可以看出:前4个特征及相应的累计贡献率为85%,因此可从说,前4个主成分几乎已经概括了大部分信息,后7个主成分的贡献率小于5.5%,因此,我们可以取4个主成分作为该问题的主成分。
1.3.2对于第一主成分,除X9,X2,Xll的分量绝对值较小外,其余几乎都在0.1~0.4之间,说明影响农村住户结构特性因素有共同的原因,所以可把第一主成分称为指标因子。
从原指标水平及附表一的(8)也可看出,各市县的各项指标值大的,它们的第一主成分值也较高。
从第二主成分可看出X7,X8,X9,X11的系数较高,相应于评价指标体系就是个体的素质(X7),从业人员在本乡从业率(X8),从业人员在农村从事非农业率(X11),所以第二主成分主要反映了从业人员的素质和经济活动因素。
第三主成分的分量中X2的值特别大,这主要反映老边区占乡镇百分比的因素。
从第四主成分的向量分量中注意到X2、X3、X4、Xll的系数都为正且都较大,而其余分量的系数都为负,所以第四主成分主要反应生活居住条件(X2-X4)和非农村住户农业生产经营单位从事种植业率因素与其它农村住户结构特性(X5-Xl0)的对比。
2.各市县农村经济活动特性的主成分分析2.1评价指标体系及各指标水平见《海南省农村住户经济活动特性研究》2.2程序:DATA HN02;TNPUT Y1-Y2;LABEL Y1=“家庭外雇人员三个月以下占全部外雇人员百分比”......Y22=“平均每户鸡鸭鹅存栏数”(依各指标水平顺序)CSRDS;(按INPUT格式输入数据)PROC PRINCOMP OUT=PRINHNO2;PREFIX=BPRIN;PROC PRINT;VAR BPRIN1-BPRIN6;RUN;2.3结果分析2.3.1运行结果显示,Y1、Y2、Y7、Yl0、Y12、Y17、Y16、Y22等指标的方差很大(除Y8、Yl4、Yl8-Y21较小以外),结合它们原指标水平的意义,即各市县的外雇人员情况(Y1-Y2)住户经营类别,农户用地情况,农作物种植情况,农业技术应用部分情况及牲畜与家禽饲养情况极不平衡。
前6个主成分相应的累计贡献率已达到87%,所以可以认为前6个主成分几乎概括了所有的信息,而剩下的16个主成分的贡献率均小4,所以取前6个主成分为该问题的主成分。
2.3.2从第一主成分的分量可看出,所有分量的绝对值相差不大,且有正有负,除分量Y20、Y22的绝对值较小外,其他负的分量都对应于各项指标的百分比,所以第一主成分主要反映各项指标中的非百分比因素。
第二主成分的Y1、Y3、Y5的值较大,Y20、Y21的值也较大,结合它们的意义,所以第二主成分表示外雇人员三个月以下占全部外雇人员百分比(Yl),收入来源于农业占收入主要来源户数的百分比(Y3),农业收入中主要来源于种植业的户数所占百分比(Y5),平均每月存栏数(Y20),平均每月猪存栏数(Y22)等因素。
第三主成分中相应于Y2、Y3、Y10的值较大,相应地主要反映了家庭外雇人员三个月以上占全部外雇人员百分比(Y2),收入来源于农业占收入主要来源户数的百分比(Y3),粮食训种植占农作物种值面积的百分比(Yl0)等因素。
第四主成分到第六主成分的贡献率都小于10%,这里不述。
3.各市县农村经济活动后果的数据分析3.1评价指标体系及各指标水平3.2程序:DATA HN03;INPUT Z1-Z24;LABEL Z1=“户均农业增加值”......Z24=“户均纯收入”(按指标水平顺序);CARDS;(按INPUT的格式输入数据);PROC PRINCOMP OUT= PRINHN03;PREFIX=CPRIN;RUN;PROC PRINT;VAR CPRINl-CPRIN7;RUN;3.3结果分析3.3.1运行结果显示,各市县的经济活动后果的标准差非常大,其中较小的为Z13与Z16,其它的都很大,可见对于海南各市县来说,各种经济活动后果极不均匀。
导致各市县的收入极不平衡,贫富差距非常大。
3.3.2前7个特征值所对应的主成分为该问题的主成分,可看出,前7个主成分的累计贡献率已达83%,基本上已概括了所有的信息。
3.3.3第一主成分中Z22-Z24的值较大,相对应于Z22-Z24的指标是收入,也就是说第一主成分主要反映收入情况,而收入主要是由各项经济活动结果所影响,第二主成分分量值较大的是Z22(林业增加值)、Z11(户均橡胶产量),与其它分量绝对值相差较大,即第二主成分主要反映林业增加值及橡胶的因素。
从第三主成分的分量上看,Z3、Z4、Z7的值较大,所以第三主成分主要反映牧渔业增加值和户均甘蔗产量的因素,而第四主成分Z1、Z5的值较大,主要反映了农业增加值与户均粮食产量的因素,其它主成分的贡献率小于5%,不述。
4.农村住户结构、经济活动特性和经济活动后果三者之间相关分析利用主成分的降维思想,农村住户结构、经济活动特性、经济活动后果三者之间的典型相关,可通过三者主成分之间的典型相关得到。
4.1农村住户结构与经济活动特性的相关4.1.1程序:DATA HN12;INPUT APRIN1-APRIN4 BPRIN1-BPRIN6;CARDS;(按INPUT格式把附表1的(5)APRIN1-APRIN4,把附表2的(5)BPRIN1-BPRIN6依数据输入)PROC CANCORR ALL;VAR APRIN1-APRIN4;WITH BPRIN1-BPRIN6;RUN;4.1.2结果分析(1)第一典型相关系数为0.982381,第二典型相关系数为0.872052,两个相关系数比两组主成分之间任一相关系数都大,检验总体所有典型相关系数假设,概率水平为0.0001及0.0811,故在X=0.10的显著水平下,否定所有典型相关系数均为0的假设。
(2)农村住户结构特性的主成分的第一典型变量为:V1=0.8948APRIN1-0.2568APRIN2-0.2689APRIN3-0.2471APRIN4来自农村住户活动特性的主成分的第一典型变量为:W1=0.7821BPRIN1+0.1560BPRIN2+0.4452BPRIN3+0.1305BPRIN4+0.3849BPRIN5-0.0269BPRIN6相关系数为0.982381从第一对典型变量可看出APRIN1与BPRIN1有较强的相依关系,结合两个主成分的意义,即农村结构特性与农村活动特性有很强的相关关系。
来自农村住户结构特性的主成分和活动,特性的主成分的第二典型变量为:V2=0.2226APRIN1+0.8043APRIN2+0.3577APRIN3-0.4191APRIN4W2=-0.0886BPRIN1+0.9258BPRIN2+0.1086BPRIN3-0.1203BPRIN4+0.0061BPRIN5+0.3299BPRIN6第二对典型相关的相关系数为0.872052,主要反映了APRIN2与BPRIN2有较强的相关关系,结合两个主成分的意义,主要反映了从业人员的素质和经济活动与外雇人员情况及牲畜与家禽饲养有很强的相关关系。
4.2对农村住户结构特性与农村经济活动后果的相关关系4.2.1程序类似于4.1.1程序4.2.2结果分析运行结果得到全部变量的均值、方差和它们之间的相关系数,以及两对显著的典型相关变量:第一对典型相关变量为:V1=-0.8005APRIN1+0.5015APRIN2+0.2916APRIN3+0.1507APRIN4W1=0.5659CRIN1-0.7248CPRIN2+0.2695CPRIN3-0.1800CPRIN4-0.106CPRIN5+0.1351CPRIN6+0.1408CPRIN7它们的典型相关系数为0.938376,由上可以看出,APRIN2与BPRIN1有较强的相依关系,结合它们的意义即为农村住户结构中从业人员的素质和经济活动(APRIN2)与经济活动后果的收入(CPRINl)有很大的相关关系。
第二对典型相关变量为:V2=0.4735APRIN1+0.7105APRIN2+0.2984APRIN3-0.4266APRIN4W2=-0.5847CPRIN1-0.6434CPRIN2-0.3021CPRIN3-0.3368CPRIN4+0.1559CPRIN5+0.1064CPRIN6+0.0621CPRIN7它们的相关系数为0.842080由上可知APRIN2与CPRIN4有很大的相关关系。
