湖南四大名校内部资料初二八年级下册数学反比例函数测试题及试卷答案

合集下载

八年级下反比例函数单元测评卷含答案

反比例函数单元测评卷;（满分：100分时间：60分钟;）一、选择题（每题4分，共32分）;;1．下列问题中，两个变量成反比例的是 ( ）A ．长方形的周长确定，它的长与宽B ．长方形的长确定，它的周长与宽C ．长方形的面积确定，它的长与宽D ．长方形的长确定，它的面积与宽2．若反比例函数1k y x-=的图象位于第二、四象限，则k 的取值可以是 ( )A ．0B ．1C ．2D ．以上都不是3．若反比例函数的图象经过点(3，2)，则该反比例函数的关系式是( )A ．y ＝23xB ．y ＝6xC ．y ＝3xD ．y ＝2x －44．对于反比例函数y ＝1x ，下列说法正确的是 ( )A ．图象经过点（1，－1）B ．图象位于第二、四象限C ．图象是中心对称图形D ．当x <0时，y 随x 的增大而增大;5．函数y ＝2x 与函数y ＝1x-在同一平面直角坐标系中的大致图象是( )6．已知力F所做的功是15焦（功＝力×物体在力的方向上通过的距离），则力F与物体在力的方向上通过的距离s之间的函数图象大致是( )7．如图，一次函数与反比例函数的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是( )A．x<－1 B．－1<x<0或x>2C．x>2 D．x<－1或0<x<2的图象上关于原点对称的任意两点，8．如图，A、B是函数y＝2xBC∥x轴，AC∥y轴，若△ABC的面积记为S，则( ) A．S＝2 B．S＝4 C．2<S<4 D．S>4二、填空题（每题4分，共24分）的图象经过（1，－2），则k＝_______．9．已知反比例函数y＝kx10．已知y与x成反比例，当x＝3时，y＝1，则y与x之间的函数关系式为_______．和y＝3x＋n的图象交于点A（－2，m），则m n＝11．函数y＝2x_______．在第一象限内的图象，且过点A(2，12．如图，l1是反比例函数y＝kx1)，l2与l1关于x轴对称，那么图象l2的函数关系式为_______(x>0)．，过y1上的任13．双曲线y、y在第一象限的图象如图所示，y1＝4x意一点A，作x轴的平行线交y2于B，交y轴于C．若S△AOB ＝1，则y2的函数关系式是_______．(x>0)的图象如图所示，则结论：①两14．函数y1＝x(x≥0)，y2＝9x函数图象的交点A的坐标为(3，3)；②当x>3时，y2>y1；③当x＝1时，BC＝8；④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．其中正确结论的序号是_______．三、解答题（共44分）15．（6分）已知y＝y1－y2，y1与x成反比例，y2与x－2成正比例，并且当x＝3时，y＝5；当x＝1时，y＝－1．求y与x之间的函数关系式．的16．（6分）已知关于x的一次函数y＝k x－3和反比例函数y＝6x 图象都经过点（2，m）．求一次函数的关系式．17．（7分）如图，在平面直角坐标系x O y中，一次函数y＝－2x的图象的一个交点为A(－1，n)．的图象与反比例函数y＝kx(1)求反比例函数y＝k的关系式；x(2)若P是坐标轴上一点，且满足PA＝OA，直接写出点P的坐标．18．（7分）一名司机驾驶汽车从甲地去乙地，以80千米／时的平均速度用了6小时到达目的地．(1)当他按原路匀速返回时，求汽车速度v（千米／时）与时间t（小时）之间的函数关系式；(2)如果该司机匀速返回时用了4.8小时，求返回时的速度．19．（8分）如图，一次函数y＝k x＋b的图象与反比例函数y＝－8x 的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是－2．(1)求一次函数的关系式；(2)求△AOB的面积．20．（10分）“保护生态环境，建设绿色社会”已经从理念变为人们的行动，某化工厂2009年1月的利润为200万元，设2009年1月为第1个月，第x个月的利润为y万元．由于排污超标，该厂决定从2009年1月底起适当限产，并投入资金进行治污改造，导致月利润明显下降，从1月到5月，y与x成反比例．到5月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加20万元（如图）．(1)分别求该化工厂治污期间及治污改造工程完工后，y与x之间对应的函数关系式；(2)治污改造工程完工后经过几个月，该厂月利润才能达到2009年1月的水平？(3)当月利润少于100万元时为该厂资金紧张期，则该厂资金紧张期共有几个月？参考答案一、1．C 2．A 3．B 4．C 5．B 6．B 7．D 8．B二、9．－2 10．y＝3x 11．－1 12．y＝－2x13．y2＝6x14．①③④三、15．y＝3x＋4x－8 16．一次函数的关系式为y＝3x－3 17．(1)y＝－2x (2)点P的坐标为（－2，0）或(0，4) 18．(1)480vt(2)100(千米／时) 19．(1) y＝－x＋2 (2)6 20．(1)y＝200x(x≤5) y＝20x －60 (2)8个月(3)5个月。

八年级数学下册《反比例函数》测试卷含答案

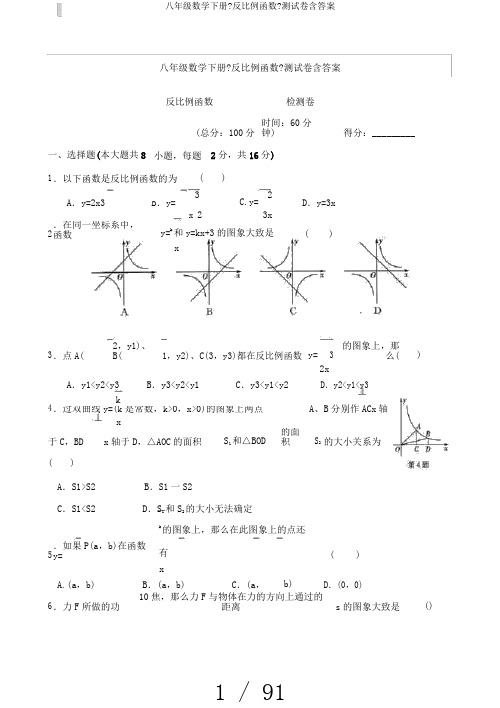
八年级数学下册?反比例函数?测试卷含答案反比例函数检测卷(总分：100分时间：60分钟)得分：_________一、选择题(本大题共8小题，每题2分，共16分) 1．以下函数是反比例函数的为()A．y=2x33C.y=2D．y=3x B．y=23xx2．在同一坐标系中，函数y=k和y=kx+3的图象大致是()x3．点A(2，y1)、B(1，y2)、C(3，y3)都在反比例函数y=3的图象上，那么()2xA．y1<y2<y3B．y3<y2<y1C．y3<y1<y2D．y2<y1<y34kA、B分别作ACx轴．过双曲线y=(k是常数，k>0，x>0)的图象上两点x于C，BD x轴于D，△AOC的面积S1和△BOD 的面积S2的大小关系为()A．S1>S2B．S1一S2C．S1<S2D．S1和S2的大小无法确定5．如果P(a，b)在函数y=k的图象上，那么在此图象上的点还有()xA.(a，b)B．(a，b)C．(a，b)D．(0，0)6．力F所做的功10焦，那么力F与物体在力的方向上通过的距离s的图象大致是()17．假设点M(2，2)和N(b， 1 n2)是反比例函数y=k的图象上的两个点，那么一次函数y=kx+b的x图象经过()A．第一、二、三象限B．第一、二、四象限C．第一、三、四象限D．第二、三、四象限8．在反比例函数y=4的图象中，阴影局部的面积等于4的有()xA．1个B．2个C．3个D．4个二、填空题(本大题共10小题，每题2分，共20分)9．y与x成反比例，当x=3时，y=1，那么y与x间的函数关系式为_________．10．点P在反比例函数y=6P的纵坐标是2，那么的图象上，且点x P的横坐标是_________．11．假设反比例函数y=k的图象过点A(1，2)，那么k=_________．k x12．反比例函数(x>0)图象如下列图，那么y随x的增大_________．y=x 13．假设反比例函数y=1的图象上有两点A(1，y1)，B(2，y2)，那么y1_________y2(填“>〞、“<〞x或“=〞)．14．在△ABC的三个顶点A(2，3)，B(4，k 5)，C(3，2)中，可能在反比例函数y=(k>0)x的图象上的点是_________．215．有反比例函数y=kx 1，(x 1，y 1)、(x 2，y 2)其象上的两点，假设x 1<0<x 2，y 1>y 2，k 的取范是_________．l6．如，反比例函数y= 5 的象与直y=kx(k>o)相交于A 、B 两点，AC ∥y ，BC ∥x ，x△ABC 的面等于_________个面位．17．假设一次函数y=2xk 的象与反比例函数y=k5的象相交，其中一个交点坐4，x此交点坐_________．18．如所示，P 1(x 1，y 1)、P 2(x 2，y 2)、⋯、P n (x n ，y n )在函数y=9 (x>o)的象上，△OP l A 1、△xP 2A 1A 2、△P 3A 2A 3、⋯、△P n A n1A n 都是等腰直角三角形，斜 O 1A l 、A 1A 2、⋯、A n 1A n 都在x 上，y 1+y 2+⋯+y n =_________．三、解答(本大共10小，共64分)519．(本小5分)正比例函数y=kx 与反比例函数 y=的象都 A(m ，1)点，求此正比x例函数解析式．20．(本小5分)点 A(2， k+2)在双曲 y=k上．求常数 k 的．x21．(本小5分)y=y 1 y 2，y 1与x 成正比例，y 2与x+3成反比例，当x=0，y= 2；当3x=3时，y=2；求y与x的函数关系式，并指出自变量的取值范围.22．(本小题5分)一定质量的氧气，它的密度(kg／m3)是它的体积V(m3)的反比例函数，当V=10 m3时，kg／m3．求与V的函数关系式；(2)求当V=2m3时，求氧气的密度．23．(本小题5分)一次函数y=kx+b(k≠o)和反比例函数y=k的图象交于点A(1，1)．2x求两个函数的解析式’(2)假设点B是x轴上一点，且△AOB是直角三角形，求B点的坐标．24．(本小题7分)反比例函数y=k的图象与一次函数y=kx+m的图象相交于点(2，1)．x分别求出这两个函数的解析式’试判断点P(1，5)关于x轴的对称点P’是否在一次函数y=kx+m的图象上．25．(本小题7分)假设反比例函数y1=6与一次函数y2=mx 4的图象都经过点A(a，2)、B(1，b)．x求一次函数y2=mx4的解析式；(2)在同一直角坐标系中，画出两个函数的图象，并求当x取何值时有y2<y1；(3)求△AOB的面积．426．(本小题7分)反比例函数y=2的图象与一次函数y=kx+b的图象交于点A(m，2)、点B(2，x，一次函数的图象与y轴的交点为C．求一次函数解析式；求C点的坐标；求△AOC的面积．k27．(本小题9分)如图，直线y=kx+b与反比例函数y= (x<0)的图象相交于点A、点B，与x轴x交于点C，其中点A的坐标为( 2，4)，点B的横坐标为4．(1)试确定反比例函数的关系式；(2)求△AOC的面积．28．(本小题9分)假设一次函数y=2x 1和反比例函数y=k的图象都经过点(1，1)．2x求反比例函数的解析式；(2)点A在第三象限，且同时在两个函数的图象上，求点A的坐标。

初二反比例函数复习题及答案

反比例函数综合复习题一、选择题1．反比例函数y ＝xn 5图象经过点（2，3），则n 的值是（）． A 、－2 B 、－1 C 、0 D 、1 2．若反比例函数y ＝xk（k≠0）的图象经过点（－1，2），则这个函数的图象一定经过点（）． A 、（2，－1） B 、（－21，2） C 、（－2，－1） D 、（21，2）3．已知甲、乙两地相距s （km ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h ）与行驶速度v （km/h ）的函数关系图象大致是（）4．若y 与x 成正比例，x 与z 成反比例，则y 与z 之间的关系是（）．A 、成正比例B 、成反比例C 、不成正比例也不成反比例D 、无法确定 5．一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝xk满足（）． A 、当x ＞0时，y ＞0 B 、在每个象限，y 随x 的增大而减小C 、图象分布在第一、三象限D 、图象分布在第二、四象限第6题图 6．如图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线PQ 交双曲线y ＝x1于点Q ，连结OQ ，点P 沿x 轴正方向运动时， Rt △QOP 的面积（）．A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定 7．在一个可以改变容积的密闭容器，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变．ρ与V 在一定围满足ρ＝Vm，它的图象如图所示，则该气体的质量m 为（）．A 、1.4kgB 、5kgC 、6.4kgD 、7kg 第7题图 8．若A （－3，y 1），B （－2，y 2），C （－1，y 3）三点都在函数y ＝－x1的图象上，则y 1，y 2，y 3的大小关系是（）．Q pxyot /hO t /hOt /hOt /hv /(km/h)OA ．B ．C ．D ．A 、y 1＞y 2＞y 3B 、y 1＜y 2＜y 3C 、y 1＝y 2＝y 3D 、y 1＜y 3＜y 2 9．已知反比例函数y ＝xm21-的图象上有A （x 1，y 1）、B （x 2，y 2）两点，当x 1＜x 2＜0时，y 1＜y 2，则m 的取值围是（）．A 、m ＜0B 、m ＞0C 、m ＜21 D 、m ＞21 10．如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值围是（）．A 、x ＜－1B 、x ＞2C 、－1＜x ＜0或x ＞2D 、x ＜－1或0＜x ＜2 第10题图二、填空题11．某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12．已知反比例函数xky =的图象分布在第二、四象限，则在一次函数b kx y +=中，y 随x 的增大而（填“增大”或“减小”或“不变”）．13．若反比例函数y ＝xb 3-和一次函数y ＝3x ＋b 的图象有两个交点，且有一个交点的纵坐标为6，则b ＝．14．反比例函数y ＝（m ＋2）xm2－10的图象分布在第二、四象限，则m 的值为．15．有一面积为S 的梯形，其上底是下底长的31，若下底长为x ，高为y ，则y 与x 的函数关系是． 16．如图，点M 是反比例函数y ＝xa（a ≠0）的图象上一点，过M 点作x 轴、y 轴的平行线，若S 阴影＝5，则此反比例函数解析式为．第16题图第19题图第20题图17．使函数y ＝（2m 2－7m －9）xm2－9m ＋19是反比例函数，且图象在每个象限y 随x 的增大而减小，则可列方程（不等式组）为． 18．过双曲线y ＝xk（k≠0）上任意一点引x 轴和y 轴的垂线，所得长方形的面积为____ __．19. 如图，直线y ＝kx(k ＞0)与双曲线xy 4交于A （x 1，y 1），B （x 2，y 2）两点，则2x 1y 2－7x 2y 1＝___________． 20．如图，长方形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上，点B 的坐标为B （－320，5），D 是AB 边上的一点，将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是．三、解答题21．如图，已知A （x 1，y 1），B （x 2，y 2）是双曲线y ＝xk在第一象限的分支上的两点，连结OA 、OB ．（1）试说明y 1＜OA ＜y 1＋1y k ；（2）过B 作BC⊥x 轴于C ，当m ＝4时，求△BOC 的面积．22．如图，已知反比例函数y ＝－x8与一次函数y ＝kx ＋b 的图象交于A 、B 两点，且点A 的横坐标和点B 的纵坐标都是－2．求：（1）一次函数的解析式；（2）△AOB 的面积．23．如图，一次函数y ＝ax ＋b 的图象与反比例函数y ＝xk的图象交于M 、N 两点．（1）求反比例函数与一次函数的解析式；（2）根据图象写出使反比例函数的值大于一次函数的值的x 的取值围．24．如图，已知反比例函数y ＝xk的图象与一次函数y ＝a x ＋b 的图象交于M （2，m ）和N （－1，－4）两点．（1）求这两个函数的解析式；（2）求△MON 的面积；（3）请判断点P （4，1）是否在这个反比例函数的图象上，并说明理由．25．如图，点P 的坐标为（2，23），过点P 作x 轴的平行线交y 轴于点A ，交双曲线x k y =(x>0)于点N ；作PM⊥AN 交双曲线xky =(x>0)于点M ，连结AM.已知PN=4. （1）求k 的值.（2）求△APM 的面积.26．如图，已知直线12y x =与双曲线(0)ky k x=>交于A B ，两点，且点A 的横坐标为4．（1）求k 的值；（2）若双曲线(0)ky k x=>上一点C 的纵坐标为8，求AOC △的面积；（3）过原点O 的另一条直线l 交双曲线(0)ky k x=>于P Q ，两点（P 点在第一象限），若由点A B P Q ，，，为顶点组成的四边形面积为24，求点P 的坐标．O x Ay B27．如图8，直线b kx y +=与反比例函数xk y '=（x ＜0）的图象相交于点A 、点B ，与x 轴交于点C ，其中点A 的坐标为（－2，4），点B 的横坐标为－4.（1）试确定反比例函数的关系式；（2）求△AOC 的面积.28．已知：如图，正比例函数y ax =的图象与反比例函数ky x=的图象交于点()32A ，．（1）试确定上述正比例函数和反比例函数的表达式；（2）根据图象回答，在第一象限，当x 取何值时，反比例函数的值大于正比例函数的值？（3）()M m n ，是反比例函数图象上的一动点，其中03m <<，过点M 作直线MN x ∥轴，交y 轴于点B ；过点A 作直线AC y ∥轴交x 轴于点C ，交直线MB 于点D ．当四边形OADM 的面积为6时，请判断线段BM 与DM 的大小关系，并说明理由．yxOAD MCB参考答案DACBD ； CDBDD ． 11、y ＝x 1000； 12、减小； 13、5 ； 14、－3 ；15、y ＝x s 23 ； 16、y ＝－x5；17、⎩⎨⎧---=+-0972119922＞m m m m ； 18、|k|； 19、 20； 20、y ＝－x 12． 21、解：（1）过点A 作AD⊥x 轴于D ，则OD ＝x 1，AD ＝y 1，因为点A （x 1，y 1）在双曲线y ＝xk上，故x 1＝1y k ，又在Rt △OAD 中，AD ＜OA ＜AD ＋OD ，所以y 1＜OA ＜y 1＋1y k；（2）△BOC 的面积为2． 22、解：（1）由已知易得A （－2，4），B （4，－2），代入y ＝kx ＋b 中，求得y ＝－x ＋2；（2）当y ＝0时，x ＝2，则y ＝－x ＋2与x 轴的交点M （2，0），即|OM|＝2，于是S △AOB ＝S △AOM ＋S △BOM ＝21|OM|·|y A |＋21|OM|·|y B |＝21×2×4＋21×2×2＝6．23、解：（1）将N （－1，－4）代入y ＝xk ，得k ＝4．∴反比例函数的解析式为y ＝x 4．将M （2，m ）代入y ＝x 4，得m ＝2．将M （2，2），N （－1，－4）代入y ＝ax ＋b ，得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y ＝2x －2．（2）由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值． 24．解（1）由已知，得－4＝1-k ，k ＝4，∴y＝x 4．又∵图象过M （2，m ）点，∴m＝24＝2， ∵y＝a x ＋b 图象经过M 、N 两点，∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y＝2x －2．（2）如图，对于y ＝2x －2，y ＝0时，x ＝1，∴A （1，0），OA ＝1，∴S △MON ＝S △MOA ＋S △NOA ＝21OA·MC＋21OA·ND ＝21×1×2＋21×1×4＝3．（3）将点P （4，1）的坐标代入y ＝x4，知两边相等，∴P 点在反比例函数图象上． 26．解：(1)∵当 x = 4时，y = 2 .∴ 点A 的坐标为（ 4，2 ）. ∵ 点A 是直线与双曲线（k>0）的交点 ,∴ k = 4 ×2 = 8 . (2) 解法一：如图12-1，∵ 点C 在双曲线上，当y = 8时，x = 1 ∴ 点C 的坐标为 ( 1, 8 ) . 过点A 、C 分别做x 轴、y 轴的垂线，垂足为M 、N ，得矩形DMON . S 矩形ONDM = 32 ， S △ONC = 4 ， S △CDA = 9， S △OAM = 4 . S △AOC = S 矩形ONDM - S △ONC - S △CDA - S △OAM = 32 - 4 - 9 - 4 = 15 .（3）∵ 反比例函数图象是关于原点O 的中心对称图形 ,∴ OP=OQ ，OA=OB .∴ 四边形APBQ 是平行四边形 .x y 21xy 8=∴ S△POA = S平行四边形APBQ = ×24 = 6 .设点P的横坐标为m（m> 0且4m≠）, 得P ( m, ) .过点P、A分别做x轴的垂线，垂足为E、F，∵ 点P、A在双曲线上，∴S△POE = S△AOF = 4 .若0＜m＜4，如图12-3，∵ S△POE+ S梯形PEFA= S△POA + S△AOF,∴ S梯形PEFA = S△POA = 6∴18(2)(4)62mm+⋅-=.解得m= 2，m= - 8(舍去) . ∴ P（2，4）.若m＞ 4，如图12-4，∵ S△AOF+ S梯形AFEP = S△AOP+ S△POE,∴ S梯形PEFA = S△POA= 6 .∴18(2)(4)62mm+⋅-=，解得m = 8，m = - 2 (舍去) .∴ P（8，1）. ∴ 点P的坐标是P（2，4）或P（8，1）.28.（1）y=；y=x；（2）0<x<3；（3）BM=DM，41m8。

八年级数学下册《反比例函数》单元检测练习试卷及答案有详细解析

八年级数学下册《反比例函数》单元检测练习试卷一、选择题1、如图，已知函数，点A 在正y 轴上，过点A 作轴，交两个函数的图象于点B 和C ，若，则k 的值是( )A ．6B ．3C ．－3D ．－62、直线l 与双曲线C 在第一象限相交于点A 、B 两点，其图像信息如图4所示，则阴影阴部分（包括边界）横纵坐标都是整数的点（俗称格点）有( ) A. 4个 B. 5个 C. 6个 D. 8个（第1题图）（第2题图）（第3题图）3、如图，已知双曲线y ＝（k>0）经过Rt △OAB 斜边OB 的中点D ，与直角边AB 相交于点C ．若△OBC 的面积为6，则k 的值为( ) A. 1 B. 2 C. 3 D. 44、若A(x 1，y 1)、B(x 2，y 2)、C(x 3，y 3)是反比例函数y ＝图象上的点，且x 1<x 2<0<x 3，则y 1、y 2、y 3的大小关系正确的是( )A ．y 3>y 1>y 2B ．y 1>y 2>y 3C ．y 2>y 1>y 3D ．y 3>y 2>y 1 5、若反比例函数y ＝（m －2）x的图象经过第二、四象限，则m 的值为( )A ．3B ．－3C ．±3D ．±1 6、如图，过y 轴正半轴上的任意一点P ，作x 轴的平行线，分别与反比例函数y ＝－和y ＝的图象交于点A 和点B ，若点c 是x 轴上任意一点，连接AC 、BC ，则△ABC 的面积为( )A. 3B. 4C. 5D. 67、若某反比例函数的图象经过点（－1，6），则下列各点中，此函数图象也经过的点是( )A ．(－3，2)B ．(3，2)C ．(2，3)D ．(6，1)8、如图，直线l 和双曲线y ＝（k>0）交于A 、B 两点，P 是线段AB 上的点（不与A 、B 重合），过点A 、B 、P 分别向x 轴作垂线，垂足分别是C 、D 、E ，连接OA 、OB 、OP ．设△AOC 面积是S 1、△BOD 面积是S 2、△POE 面积是S 3，则( ) A. S 1<S 2<S 3 B. S 1>S 2>S 3 C. S 1＝S 2>S 3 D. S 1＝S 2<S 39、关于反比例函数的图象，下列说法正确的是（）A ．必经过点（2，-2）B ．两个分支分布在第二、四象限C ．两个分支关于x 轴成轴对称D ．两个分支关于原点成中心对称10、已知正比例函数y ＝k 1x （k 1≠0）与反比例函数y ＝（k 2≠0）的图象有一个交点的坐标为（－2，－1），则它们的另一个交点的坐标为( )A ．(2，1)B ．（－1，－2)C ．（－2，1)D ．（2，－1)二、填空题11、如图，在反比例函数y ＝ (x>0)的图象上，有点P 1、P 2、P 3、P 4，它们的横坐标依次为1、2、3、4．分别过这些点作x 轴与y 轴的垂线，图中所构成的阴影部分的面积从左到右依次为S 1、S 2、S 3，则S 1＋S 2＋S 3＝_______。

八年级下《反比例函数》单元测试题含答案

八年级下《反比例函数》单元测试题含答案反比例函数单元测试题（时间：90分钟满分：120分）（班级：姓名：得分：）一、选择题（第小题3分，共30分） 1. 观察下列函数：2015y x =，2016x y =-，20181y x =-，2014y x-=.其中反比例函数有（）A. 1个B. 2个C. 3个D. 4个 2. 反比例函数2018y x =，2016y x =-，12019y x=的共同特点是（） A. 图像位于相同的象限内 B. 自变量的取值范围是全体实数 C. 在第一象限内y 随x 的增大而减小 D. 图像都不与坐标轴相交 3. 在反比例函数2015ky x -=图像的每一支曲线上，y 都随x 的增大而增大，则k 的值可以是（） A .2016 B.0 C.2015 D.2016-4. 已知函数210(2)m y m x-=+是反比例函数，且图像在第二、四象限内，则m 的值是（）A.3B.3-C.3±D.13- 5.如图，正比例函数y 1=k 1x 和反比例函数y 2=2k x的图像交于A （-1,2）, B （1,-2）两点,若y 1 ＜y 2，则x 的取值范围是（）A.x ＜-1或x ＞1B. x ＜-1或0＜x ＜1C. -1＜x ＜0或 0＜x ＜1D. -1＜x ＜0或x ＞1 6.如果反比例函数=ky x的图像经过点A(－1，－2)，则当x ＞1时，函数值y 的取值范围是（） A.y ＞1 B. 0＜ y ＜2 C. y ＞2 D.0＜y ＜1 7. 反比例函数2016y x=图像上的两点为（x 1,y 1）,(x 2,y 2)，且x 1<x 2,则下列关系成立的是（） A.y 1>y 2 B.y 1<y 2 C.y 1=y 2 D.不能确定 8.当a ≠0时，函数y=ax+1与函数y=xa在同一坐标系中的图像可能是（）9.如图，若点M 是x 轴正半轴上的任意一点，过点M 作PQ ∥y 轴，分别交函数xk 1y =（x ＞0）和xk 2y =（x ＞0）的图像于点P 和Q ，连接OP ,OQ,则下列结论正确的是（） A.∠POQ 不可能等于900 B.21K K QM PM= C.这两个函数的图像一定关于x 轴对称 D. △POQ 的面积是）（|k ||k |2121+第9题图10.如图，过点C （1,2）分别作x 轴、y 轴的平行线，交直线y=-x+6于A,B 两点，若反比例函数ky x=（x ＞0）的图像与△ABC 有公共点，则k 的取值范围是（） A ．2≤k ≤8 B. 2≤k ≤9 C. 2≤k ≤5 D. 5≤k ≤8 二、填空题（第小题4分，共32分） 11.已知函数y=－12016x，当x ＜0时，y__________0，此时，其图像的相应部分在第__________象限.12. 若正比例函数y=kx 在每一个象限内y 随x 的增大而减小，那么反比例函数ky x=-在每一个象限内y 随x 的增大而_________.13. 在同一坐标系内，正比例函数20182015y x =-与反比例函数2016y x=-图像的交点在第_____象限 . 14. 若A （x 1,y 1）,B(x 2，y 2)，C （x 3,y 3）都是反比例函数y=－x1的图像上的点，且x 1＜0＜x 2＜x 3，则y 1,y 2,y 3由小到大的顺序是__________. 15. 点A(2，1)在反比例函数y kx=的图像上，当1﹤x ﹤4时，y 的取值范围是 . 16. 设函数2y x=与1y x =-的图像的交点坐标为() , a b ，则11a b -的值为________17. 如图，点A 在双曲线 1y x=上，点B 在双曲线 3y x =上，且AB ∥x 轴，点C 和点D 在x 轴上，若四边形ABCD为矩形，则矩形ABCD 的面积为 .18.如图，直线y=k 1x+b 与双曲线y=2k x交于Ａ,B 两点，其横坐标分别为1和5，则不等式k 1x ＜2k x-b 的解集是 .xyCBAO三、解答题（共58分）19.(10分)已知y=y 1-y 2，y 1与x 成反比例，y 2与x-2成正比例，并且当x=3时，y=5；当x=1时，y=-1. （1）y 与x 的函数表达式；（2）当1x =-时，求y 的值.20.(10分)已知一次函数y ＝3x+m 与反比例函数y ＝xm 3-的图像有两个交点. (1)当m 为何值时，有一个交点的纵坐标为6? (2)在(1)的条件下，求两个交点的坐标. 21.(12分)如图，直线y ＝k 1x ＋b 与双曲线y ＝2k x相交于A （1，2），B （m ，－1）两点．（1）求直线和双曲线的表达式；（2）若A 1（x 1，y 1），A 2（x 2，y 2），A 3（x 3，y 3）为双曲线上的三点，且x 1＜x 2＜0＜x 3，请直接写出y 1，y 2，y 3的大小关系；（3）观察图像，请直接写出使不等式k 1x ＋b ＞2k x成立的x 的取值范围．22.(12分)某气球内充满了一定质量的气球,当温度不变时,气球内气球的压强p(千帕)是气球的体积V(米3)的反比例函数,其图像如图所示.（1）写出这个函数的表达式；（2）当气球的体积为0.8米3时,气球内的气压是多少千帕？（3）当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少？23.(14分)已知一次函数m x y +=1的图像与反比例函数xy 62=的图像交于A ，B 两点，当1>x 时，21y y >；当10<<x 时，21y y <.⑴求一次函数的表达式；⑵已知一次函数在第一象限上有一点C 到y 轴的距离为3，求△ABC 的面积.参考答案一、1.B 2. D 3. A 4. B 5. D 6. B 7. D 8. C 9. D 10. B 14. .y 2＜y 3＜y 1 15.12y ＜＜2 二、11.＞二 12. .减小 13. 二、四 16. 12-17. 2 18.0＜x ＜1或x ＞5三、19.解：（1）设()()112212,2 0k y y k x k k x==-≠，则y=x k 1-k 2(x-2).由题意，得⎪⎩⎪⎨⎧-=+=-.1,532121k k k k 解得⎩⎨⎧-==.4,321k k 所以y 与x 的函数表达式为y=x 3+4（x-2).（2）当1x =-时，()()3342412151y x x =+-=+--=--. 20.解：(1)把y ＝6分别代入y ＝3x+m 和y ＝xm 3-, 得 3x+m ＝6,xm 3-＝6. 解得m ＝5. (2)由(1)得一次函数为y ＝3x+5，反比例函数为y ＝x 2. 解352y x y x =+⎧⎪⎨=⎪⎩得∴两个函数图像的交点为(-2，-1)和(31,6). 21.解：（1）∵双曲线y ＝2k x 经过点A （1，2），∴k 2＝2．∴双曲线的表达式为y ＝2x． ∵点B(m ，－1)在双曲线y ＝2x上，∴m ＝－2，则B （－2，－1）．由点A （1，2），B （－2，－1）在直线y ＝k 1x ＋b 上，得112,2 1.k b k b +=⎧⎨-+=-⎩解得11,1.k b =⎧⎨=⎩∴直线的表达式为y ＝x ＋1．（2）y 2＜y 1＜y 3．（3）x ＞1或－2＜x ＜0． 22. （1）96P v=（2）当 4.8v =米3时，961204.8P ==20千帕（3）∵96144P v=≤，∴23v ≥.为了安全起见,气球的体积应不小于23米3.23.解：(1)根据题意知，点A 的坐标为（1，6），代人y 1=x+m ，得m=5.∴ 一次函数的表达式为y 1=x+5.（2）如图，过点B 作直线BD 平行于x 轴，交AC 的延长线于D. ∵点C 到y 轴的距离为3，∴C 点的横坐标为3.又C 在双曲线上，∴y=623=,即C （3，2）. 解56y x y x =+⎧⎪⎨=⎪⎩得12126116x x y y =-=⎧⎧⎨⎨=-=⎩⎩，∴B （-6，-1）. 设AC 的表达式为y=k 1x+b 1，把点A （1，6），点C （3，2）代入，得⎩⎨⎧=+=+.23,61111b k b k 解得k 1=-2,b 1=8.∴直线AC 的表达式为y=－2x+8. 当y=－1时－1=－2x+8, x=4.5,即点D （4.5，－1） ∴ABC ABD BCD S S S =-△△△=1211217-32222⨯⨯⨯⨯=21.。

八年级下《反比例函数》检测题含答案

八年级下《反比例函数》检测题含答案反比例函数检测题（满分：100分，时间：90分钟）一、选择题(每小题3分，共30分) 1.下列函数是反比例函数的是（）A.y x =B.1y kx -=C.8y x =-D.28y x= 2.若反比例函数8y x=的图象经过点(2,)m -，则m 的值是（） A.14 B.14- C.－4 D.4 3.在同一坐标系中，函数ky x=和3y kx =+的图象大致是（）4.当k ＞0,x ＜0时，反比例函数ky x=错误！未找到引用源。

的图象在（） A.第一象限 B.第二象限 C.第三象限 D.第四象限5.若函数错误！未找到引用源。

的图象经过点（3，－7），则它一定还经过点( ) A.(3，7) B.(－3，－7) C.(－3，7) D.(2，－7)6.如图，菱形OABC 的顶点C 的坐标为（3，4）．顶点A 在x 轴的正半轴上，反比例函数(0)ky x x=>的图象经过顶点B ，则k 的值为（）A.12B.20C.24D.32第6题图第7题图7.如图，A 为反比例函数ky x=图象上一点，AB 垂直于x 轴于点B ，若3AOB S =△，则k 的值为( ）A.6B.3C.23D.不能确定 8.已知点1(2,)A y -、2(1,)B y -、3(3,)C y 都在反比例函数4y x=的图象上，则1y 、2y 、3y 错误！未找到引用源。

的大小关系是( ）A.123y y y <<错误！未找到引用源。

B.321y y y <<错误！未找到引用源。

C.312y y y <<错误！未找到引用源。

D.213y y y <<错误！未找到引用源。

9.在反比例函数1ky x-=的图象的每一条曲线上，y 都随x 的增大而增大，则k 的值可以第19题图是（）A.－1B.0C.1D.2 10.已知1(1,)A y -，2(2,)B y 两点在双曲线32my x+=上，且12y y >，则m 的取值范围是（） A.0m < B.0m > C.32m >- D.32m <-二、填空题（每小题3分，共24分）11.已知y 错误！未找到引用源。

八年级下《反比例函数》单元测试含答案

1 2
1
2
3
知为参数数，曲线 C 的极坐标方程为
cos ．
知Ⅰ数写出曲线 C 的直角坐标方程，并指明 C 是什么曲线；知Ⅱ数设直线 l 与曲线 C 相交于，两点，求䁯䁯的值．
16.已知函数知函数知Ⅰ数若知函数
3函
3䁯函䁯
1
．
知Ⅱ数判断函 t h 时，函数知函数的单调性；
2，求 x 的值；
2，
h，求得函
6，
．
6．
第 5页，共 5页
函
19. 解：知1数把知1，数代入
解得；
得
1
，
知2数由 B 是 AC 的中点可得 B 点的纵坐标是 A 点纵坐标的一半，即把知3数由 A、B 点的坐标求得直线 AB 的解析式为令角点的坐标为知3，h数 t 角的面积为2
1
2 代入
函
求得函 3， 3
2，故 B 点的坐标为知2，2数； 2函
13. 已知函数
______ ．
函
的图象经过知
1，3数点，如果点知2，数也在这个函数图象上，则
第 2页，共 5页
1 . 已知点 A 是函数三、解答题
则 t 的面积为______ ．
函
的图象上的一点，过 A 点作
函轴，垂足为 M，连接 OA，
15.已知极坐标系的极点在平面直角坐标系的原点处，极轴与 x 轴的正半轴重合.直线 l 的参数方程为函
和 B 重合数，过 P 点分别作 x、y 轴的垂线 PC、PD 交
反比例函数图象于点 M、N，则四边形 PMON 面积的
12. 如图，在平面直角坐标系中，M 为 y 轴正半轴上一点，过点 M 的直线 tt函轴，l 分别与反比例函数

反比例函数》测试题(含答案)

反比例函数》测试题(含答案)1、选择题（每小题5分，共50分）1、若点（x1.-1）、(x2.-2)、(x3.1)都在反比例函数y= k/x 上，则它们之间的大小关系是（）A．x1<x3<x2B．x2<x1<x3C．x1<x2<x3D．x2<x3<x12、若反比例函数y=k/x的图象经过点(m，3m)，其中m≠0，则此反比例函数的图象在（）A．第一、二象限；B．第一、三象限；C．第二、四象限；D．第三、四象限3、在直角坐标系中，点A是x轴正半轴上的一个定点，点B是双曲线y=3/x上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小4、函数y=-kx与函数y=k/x的图象的交点个数是（）A。

0B。

1C。

2D.不确定5、函数y=6-x与函数y=k/x的图象交于A、B两点，设点A的坐标为（x1,y1），则边长分别为x1、y1的矩形面积和周长分别为（）A。

4，12B。

4，6C。

8，12D。

8，66、已知y1+y2=y，其中y1与x成反比例,且比例系数为k1，而y2与x2成正比例,且比例系数为k2，若x=-1时,y=0，则k1,k2的关系是( )A.k1+k2=0B.k1k2=1C.k1-k2=0D.k1k2=-17、正比例函数y=2kx与反比例函数y=k/(x-1)在同一坐标系中的图象不可能是（）18、如图，直线y=mx与双曲线y=k/(x-1)交与A、B两点，过点A作AM⊥x轴，垂足为M，连接BM，若S△ABM=2，则k的值是（）A、2B、m-2C、mD、49、如图，点A在双曲线y=6/x上，且OA＝4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为( )A.47B.5C.27D.2210、如图，反比例函数y= k/x的图象经过点(1,2)，则k=（）。

二、填空题（每小题5分，共20分）11、若y=k/x是反比例函数，且x1y1=x2y2，则k=______。

八年级下反比例函数单元测评卷含答案

八年级下反比例函数单元测评卷含答案反比例函数单元测评卷（满分：100分时间：60分钟）一、选择题（每题4分，共32分）1．下列问题中，两个变量成反比例的是(）A ．长方形的周长确定，它的长与宽B ．长方形的长确定，它的周长与宽C ．长方形的面积确定，它的长与宽D ．长方形的长确定，它的面积与宽2．若反比例函数1k y x-=的图象位于第二、四象限，则k 的取值可以是()A ．0B ．1C ．2D ．以上都不是3．若反比例函数的图象经过点(3，2)，则该反比例函数的关系式是()A ．y ＝23xB ．y ＝6xC ．y ＝3xD ．y ＝2x －44．对于反比例函数y ＝1x，下列说法正确的是()A ．图象经过点（1，－1）B ．图象位于第二、四象限C ．图象是中心对称图形D ．当x <0时，y 随x 的增大而增大5．函数y ＝2x 与函数y ＝1-在同一平面直角坐标系中的大致图象是()6．已知力F 所做的功是15焦（功＝力×物体在力的方向上通过的距离），则力F 与物体在力的方向上通过的距离s 之间的函数图象大致是()7．如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是()A ．x <－1B ．－1<x <0或x >2C ．x >2D ．x <－1或0<x <28．如图，A 、B 是函数y ＝2x的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴，若△ABC 的面积记为S ，则()A ．S ＝2B ．S ＝4C ．2<S<4D ．S>4二、填空题（每题4分，共24分）9．已知反比例函数y ＝k x的图象经过（1，－2），则k ＝_______．10．已知y 与x 成反比例，当x ＝3时，y ＝1，则y 与x 之间的函数关系式为_______．11．函数y ＝2x和y ＝3x ＋n 的图象交于点A （－2，m ），则m n ＝_______．12．如图，l 1是反比例函数y ＝k x在第一象限内的图象，且过点A(2，1)，l 2与l 1关于x 轴对称，那么图象l 2的函数关系式为_______(x >0)．13．双曲线y 、y 在第一象限的图象如图所示，y 1＝4x，过y 1上的任意一点A ，作x 轴的平行线交y 2于B ，交y 轴于C ．若S △AOB ＝1，则y 2的函数关系式是_______．14．函数y 1＝x (x ≥0)，y 2＝9x(x >0)的图象如图所示，则结论：①两函数图象的交点A 的坐标为(3，3)；②当x >3时，y 2>y 1；③当x ＝1时，BC ＝8；④当x 逐渐增大时，y 1随着x 的增大而增大，y 2随着x 的增大而减小．其中正确结论的序号是_______．三、解答题（共44分）15．（6分）已知y ＝y 1－y 2，y 1与x 成反比例，y 2与x －2成正比例，并且当x ＝3时，y ＝5；当x ＝1时，y ＝－1．求y 与x 之间的函数关系式．16．（6分）已知关于x的一次函数y＝k x－3和反比例函数y＝6x的图象都经过点（2，m）．求一次函数的关系式．17．（7分）如图，在平面直角坐标系x O y中，一次函数y＝－2x的图象与反比例函数y＝kx的图象的一个交点为A(－1，n)．(1)求反比例函数y＝kx的关系式；(2)若P是坐标轴上一点，且满足PA＝OA，直接写出点P的坐标．18．（7分）一名司机驾驶汽车从甲地去乙地，以80千米／时的平均速度用了6小时到达目的地．(1)当他按原路匀速返回时，求汽车速度v（千米／时）与时间t（小时）之间的函数关系式；(2)如果该司机匀速返回时用了4.8小时，求返回时的速度．19．（8分）如图，一次函数y＝k x＋b的图象与反比例函数y＝－8x的图象交于A、B 两点，且点A的横坐标和点B的纵坐标都是－2．(1)求一次函数的关系式；(2)求△AOB的面积．20．（10分）“保护生态环境，建设绿色社会”已经从理念变为人们的行动，某化工厂2009年1月的利润为200万元，设2009年1月为第1个月，第x个月的利润为y万元．由于排污超标，该厂决定从2009年1月底起适当限产，并投入资金进行治污改造，导致月利润明显下降，从1月到5月，y与x成反比例．到5月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加20万元（如图）．(1)分别求该化工厂治污期间及治污改造工程完工后，y与x之间对应的函数关系式；(2)治污改造工程完工后经过几个月，该厂月利润才能达到2009年1月的水平？(3)当月利润少于100万元时为该厂资金紧张期，则该厂资金紧张期共有几个月？参考答案一、1．C2．A3．B4．C5．B6．B7．D8．B二、9．－210．y＝3x11．－112．y＝－2x13．y2＝6x14．①③④三、15．y＝3x＋4x－816．一次函数的关系式为y＝3x－317．(1)y＝－2x(2)点P的坐标为（－2，0）或(0，4)18．(1)480vt(2)100(千米／时)19．(1)y＝－x＋2(2)620．(1)y＝200x(x≤5)y＝20x－60(2)8个月(3)5个月。

湖南四大名校内部资料反比例函数测试卷带答案

1第五章反比例函数测试卷一、选择题1. 下列函数中，y 是x 的反比例函数是（）A y= 11-x B x y 21= C 22x y = D 2=x y2.关于反比例函数4y x=的图象，下列说法正确的是（） A ．必经过点（1，1）B ．两个分支分布在第二、四象限C ．两个分支关于x 轴成轴对称D ．两个分支关于原点成中心对称 3.函数2y x =与函数1y x-=在同一坐标系中的大致图像是( )4.某反比例函数的图象经过点（-1,6），则下列各点中，此函数图象也经过的点是（） A. （-3,2） B. （3,2） C. （2，3） D. （6,1）5.若双曲线y=x k 12-的图象经过第二、四象限，则k 的取值范围是( )A.k ＞21 B. k ＜21 C. k =21D. 不存在 6.反比例函数ky x=的图象经过点A (-1,-2).则当x ＞1时，函数值y 的取值范围是（）A.y＞1 B.0＜y ＜1 C. y ＞2 D.0＜ y ＜27. 矩形的长为x ，宽为y ，面积为9，则y 与x 之间的函数关系用图象表示大致为（）8. 已知点（-1，1y ），（2，2y ），（3，3y ）在反比例函数xk y 12--=的图像上. 下列结论中正确的（） A ．321y y y >> B ．231y y y >> C ．213y y y >> D ．132y y y >> 9. 如图，正比例函数y 1=kx 和反比例函数y 2=2k x的图像交于A （-1,2）、（1,-2）两点，若y 1 ＜y 2，则x 的取值范围是（）A.x ＜-1或x ＞1B. x ＜-1或0＜x ＜1C. -1＜x ＜0或 0＜x ＜1D. -1＜x ＜0或x ＞1 10. 如图，过点C （1,2）分别作x 轴、y 轴的平行线，交直线y=-x+6于A 、B 两点，若反比例函数ky x=（x ＞0）的图像与△ABC 有公共点，则k 的取值范围是（） A ．2≤k ≤9 B. 2≤k ≤8 C. 2≤k ≤5 D. 5≤k ≤8二、填空题11. 若反比例函数的图像过点P （-1,4），则它的函数关系是 .12.若函数xm y 2+=图象在其象限内y 的值随x 值的增大而增大，则m 的取值范围是 . 13.如图：点A 在双曲线ky x=上，AB ⊥x 轴于B ，且△AOB 的面积S △AOB =2，则k=______．14. 如图，点A 在双曲线1y x =上，点B 在双曲线3y x=上，且AB ∥x轴，C 、D 在x 轴上，若四边形ABCD 的面积为矩形，则它的面积为 .15. 如图，已知第一象限内的图象是反比例函数y=图象的一个分支，第二象限内的图象是反比例函数y=﹣图象的一个分支，在x 轴的上方有一条平行于x 轴的直线l 与它们分别交于点A 、B ，过点A 、B 作x 轴的垂线，垂足分别为C 、D ．若四边形ABCD 的周长为8且AB ＜AC ，则点A 的坐标为．214题 15题三、解答题16. （10分）如图9，已知双曲线ky x=和直线y=mx+n 交于点A 和B ，B 点的坐标是（2，-3），AC 垂直y 轴于点C ，AC=32；（1）求双曲线和直线的解析式；（2）求△AOB 的面积。

八年级下册反比例函数练习题(含答案)

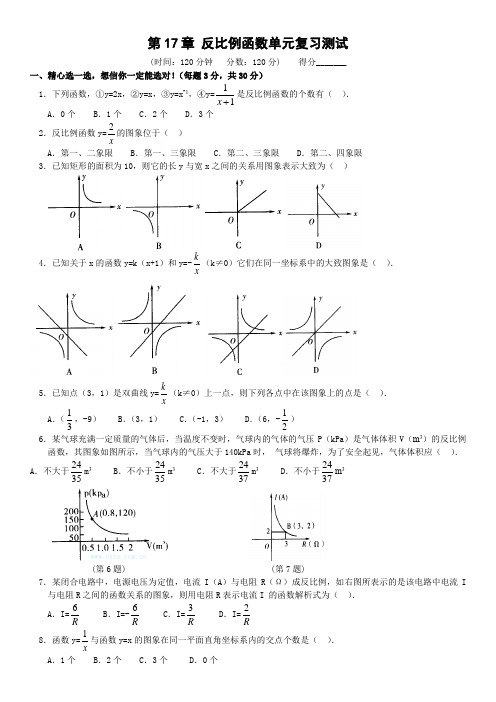
第17章反比例函数单元复习测试(时间：120分钟分数：120分) 得分_______ 一、精心选一选，想信你一定能选对！（每题3分，共30分）1．下列函数，①y=2x，②y=x，③y=x-1，④y=11x是反比例函数的个数有（）．A．0个 B．1个 C．2个 D．3个2．反比例函数y=2x的图象位于（）A．第一、二象限 B．第一、三象限 C．第二、三象限 D．第二、四象限3．已知矩形的面积为10，则它的长y与宽x之间的关系用图象表示大致为（）4．已知关于x的函数y=k（x+1）和y=-kx（k≠0）它们在同一坐标系中的大致图象是（• ）．5．已知点（3，1）是双曲线y=kx（k≠0）上一点，则下列各点中在该图象上的点是（）．A．（13，-9） B．（3，1） C．（-1，3） D．（6，-12）6．某气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P（kPa）是气体体积V（m3）的反比例函数，其图象如图所示，当气球内的气压大于140kPa时，•气球将爆炸，为了安全起见，气体体积应（）．A．不大于2435m3 B．不小于2435m3 C．不大于2437m3 D．不小于2437m3(第6题) (第7题)7．某闭合电路中，电源电压为定值，电流I（A）与电阻R（Ω）成反比例，如右图所表示的是该电路中电流I 与电阻R之间的函数关系的图象，则用电阻R表示电流I•的函数解析式为（）．A．I=6RB．I=-6RC．I=3RD．I=2R8．函数y=1x与函数y=x的图象在同一平面直角坐标系内的交点个数是（）．A．1个 B．2个 C．3个 D．0个9．若函数y=（m+2）|m|-3是反比例函数，则m 的值是（）．A ．2B ．-2C ．±2D ．×210．已知点A （-3，y 1），B （-2，y 2），C （3，y 3）都在反比例函数y=4x的图象上，则（）． A ．y 1<y 2<y 3 B ．y 3<y 2<y 1 C ．y 3<y 1<y 2 D ．y 2<y 1<y 3二、细心填一填，相信你填得又快又准！（每题3分，共27分） 11．一个反比例函数y=k x（k ≠0）的图象经过点P （-2，-1），则该反比例函数的解析式是________． 12．已知关于x 的一次函数y=kx+1和反比例函数y=6x 的图象都经过点（2，m ），则一次函数的解析式是________． 13．一批零件300个，一个工人每小时做15个，用关系式表示人数x•与完成任务所需的时间y 之间的函数关系式为________．14．正比例函数y=x 与反比例函数y=1x的图象相交于A 、C 两点，AB ⊥x 轴于B ，CD•⊥x 轴于D ，如图所示，则四边形ABCD 的为_______．(第14题) (第15题) (第19题)15．如图，P 是反比例函数图象在第二象限上的一点，且矩形PEOF 的面积为8，则反比例函数的表达式是_________．16．反比例函数y=21039n n x --的图象每一象限内，y 随x 的增大而增大，则n=_______．17．已知一次函数y=3x+m 与反比例函数y=3m x -的图象有两个交点，当m=_____时，有一个交点的纵坐标为6． 18．若一次函数y=x+b 与反比例函数y=k x 图象，在第二象限内有两个交点，•则k______0，b_______0，（用“>”、“<”、“＝”填空）19．两个反比例函数y=3x ，y=6x 在第一象限内的图象如图所示，点P 1，P 2，P 3……P 2005，在反比例函数y=6x的图象上，它们的横坐标分别是x 1，x 2，x 3，…x 2005，纵坐标分别是1，3，•5•……，•共2005年连续奇数，过点P 1，P 2，P 3，…，P 2005分别作y 轴的平行线与y=3x 的图象交点依次是Q 1（x 1，y 1），Q 2（x 2，y 2），Q 3（x 3，y 3），…，Q 2005（x 2005，y 2005），则y 2005=________．三、耐心选一选，千万别漏选！（每题4分，共8分，错选一项得0分，•对而不全酌情给分）20．当>0时，两个函数值y ，一个随x 增大而增大，另一个随x 的增大而减小的是（ •）．A ．y=3x 与y=1x B ．y=-3x 与y=1xC ．y=-2x+6与y=1xD ．y=3x-15与y=-1x21．在y=1x的图象中，阴影部分面积为1的有（）．四、用心做一做，培养你的综合运用能力．22．（8分）如图，已知一次函数y=kx+b（k≠0）的图象与x轴、y轴分别交于A、B•两点，且与反比例函数y=mx （m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D，•若OA=OB=OD=1．（1）求点A、B、D的坐标;（2）求一次函数和反比例函数的解析式．23．（10分）如图，已知点A（4，m），B（-1，n）在反比例函数y=8x的图象上，直线AB•分别与x轴，y轴相交于C、D两点，（1）求直线AB的解析式．（2）C、D两点坐标．（3）S△AOC：S△BOD是多少？24．（11分）已知y=y1-y2，y1y与x成反比例，且当x=1时，y=-14，x=4时，y=3．求（1）y与x之间的函数关系式．（2）自变量x的取值范围．（3）当x=14时，y的值．25．（12分）如图，一次函数y=kx+b的图象与反比例函数y=mx的图象交于A、B两点．（1）利用图中的条件，求反比例函数和一次函数的解析式．（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．26．（14分）如图，双曲线y=5x在第一象限的一支上有一点C（1，5），•过点C•的直线y=kx+b（k>0）与x轴交于点A（a，0）．（1）求点A的横坐标a与k的函数关系式（不写自变量取值范围）．（2）当该直线与双曲线在第一象限的另一个交点D的横坐标是9时，求△COA•的面积．答案:1．B 2．D 3．A 4．A 5．B 6．B 7．A 8．B 9．A 10．D11．y=2x 12．y=x+1 13．y= 14．2 15．y=-8x16．n=-3 17．m=5 18．<，> 19．2004．5 20．A 、B 21．A 、C 、D22．解：（1）∵OA=OB=OD=1，∴点A 、B 、D 的坐标分别为A （-1，0），B （0，1），D （1，0）．（2）∵点AB 在一次函数y=kx+b （k ≠0）的图象上， ∴ 解得 ∴一次函数的解析式为y=x+1，∵点C 在一次函数y=x+1的图象上，•且CD ⊥x 轴，∴C 点的坐标为（1，2），又∵点C 在反比例函数y=m x（m ≠0）的图象上， ∴m=2，•∴反比例函数的解析式为y=2x ． 23．（1）y=2x-6；（2）C （3，0），D （0，-6）；（3）S △AOC ：S △BOD =1：1．（2）自变量x 取值范围是x>0．25．解：（1）由图中条件可知，双曲线经过点A （2，1）∴1=，∴m=2，∴反比例函数的解析式为y=2x．又点B 也在双曲线上，∴n==-2，∴点B 的坐标为（-1，-2）． ∵直线y=kx+b 经过点A 、B ．∴ 解得 ∴一次函数的解析式为y=x-1．（2）根据图象可知，一次函数的图象在反比例函数的图象的上方时，•一次函数的值大于反比例函数的值，即x>2或-1<x<0．26．解：（1）∵点C （1，5）在直线y=-kx+b 上，∴5=-k+b ，又∵点A （a ，0）也在直线y=-kx+b 上，∴-ak+b=0，∴b=ak将b=ak 代入5=-k+a 中得5=-k+ak ，∴a=+1．（2）由于D 点是反比例函数的图象与直线的交点20x 01k b b -+=⎧⎨=⎩11k b =⎧⎨=⎩2m 21-122k b k b =+⎧⎨-=-+⎩11k b =⎧⎨=-⎩5k∴ ∵ak=5+k ，∴y=-8k+5 ③ 将①代入③得：=-8k+5，∴k=，a=10． ∴A （10，0），又知（1，5），∴S △COA =12×10×5=25． 599y y k ak⎧=⎪⎨⎪=-+⎩5959。

初二数学反比例函数试题答案及解析

初二数学反比例函数试题答案及解析1.如图，在平面直角坐标系中，双曲线经过点B，连结OB．将OB绕点O按顺时针方向旋转90°并延长至A，使OA＝2OB，且点A的坐标为（4，2）．（1）求过点B的双曲线的函数关系式；（2）根据反比例函数的图像，指出当x＜－1时，y的取值范围；（3）连接AB，在该双曲线上是否存在一点P，使得S△ABP ＝S△ABO，若存在，求出点P坐标；若不存在，请说明理由．【答案】（1）双曲线的函数关系式为y=﹣；（2）当x＜﹣1时，0＜y＜2；（3）存在；点P坐标为（﹣，4）．【解析】（1）作AM⊥x轴于点M，BN⊥x轴于点N，由相似三角形的判定定理得出△AOM∽△OBN，OA=2OB，再根据OA=2OB，点A的坐标为（4，2）可得出B点坐标，进而得出反比例函数的关系式；（2）由函数图象可直接得出结论；（3）根据AB两点的坐标可知AB∥x轴，S△ABP =S△ABO=5，再分当点P在AB的下方与当点P在x轴上方两种情况即可得出结论．试题解析：（1）作AM⊥x轴于点M，BN⊥x轴于点N，∵OB⊥OA，∠AMO=∠BNO=90°，∴∠AOM=∠NBO，∴△AOM∽△OBN．∵OA=2OB，∴，∵点A的坐标为（4，2），∴BN=2，ON=1，∴B（﹣1，2）．∴双曲线的函数关系式为y=﹣；（2）由函数图象可知，当x＜﹣1时，0＜y＜2；（3）存在．∵yA =yB，∴AB∥x轴，∴S△ABP =S△ABO=5，∴当点P在AB的下方时，点P恰好在x轴上，不合题意舍去；当点P在x轴上方时，点P在第二象限，得AB•（yP ﹣2）=5，即×5×（yP﹣2）=5，解得yP=4，∴点P坐标为（﹣，4）．【考点】1、相似三角形的判定与性质；2、待定系数法；3、函数大小的比较；4、反比例函数2.已知点A（1，y1）、B（2，y2）、C（﹣3，y3）都在反比例函数的图象上，则y1、y2、y3的大小关系是____________________．【答案】y3＜y2＜y1．【解析】∵k=6＞0，∴图象在一、三象限，且在每一象限内y随x的增大而减小．∵x1＜x2，∴y1＞y2＞0，∵x3＜0，∴y3＜0，∴y3＜y2＜y1．故答案是y3＜y2＜y1．【考点】反比例函数图象上点的坐标特征．3.已知反比例函数y=的图象上有三个点（2，）,(3,),(,),则，，的大小关系是（）A．＞＞B．＞＞C．＞＞D．＞＞【答案】A.【解析】试题解析：∵-k2-1＜0∴反比例函数y=的图象在第二、四象限∴＞＞故选A.【考点】反比例函数图象上点的坐标特征．4.已知长方形的面积为10，则它的长y与宽x之间的关系用图象大致可表示为图中的（）A．B．C．D．【答案】A【解析】由长方形的面积公式得y=，且x＞0，y＞0，而B中有x＜0，y＜0的情况，C，D中有x=0或y=0的情况，据此即可得出结果．解：∵xy=10∴y=，（x＞0，y＞0）故选A．点评：现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．5.已知反比列函数y=的图象在每一条曲线上，y都随x的增大而增大，（1）求k的取值范围；（2）在曲线上取一点A，分别向x轴、y轴作垂线段，垂足分别为B、C，坐标原点为O，若四边形ABOC面积为12，求此函数的解析式．【答案】（1）k＜0 （2）y=﹣【解析】（1）直接根据反比例函数的性质求解即可，k＜0；（2）直接根据k的几何意义可知：过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，所以|k|=12，而k＜0，则k=﹣12．解：（1）∵反比列函数y=的图象在每一条曲线上，y都随x的增大而增大，∴k＜0；（2）设A（x，y），由已知得，|xy|=|k|=12，∵k＜0，∴k=﹣12，所以，反比例函数的解析式为y=﹣．点评：主要考查了反比例函数中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．6.在同一平面直角坐标系中，正比例函数y=（m﹣1）x与反比例函数y=的图象的大体位置不可能是（）A．B．C．D．【答案】D【解析】根据题意，依次分析选项中的图象，根据图象，求出其参数的范围，并解看有无公共解，若有，则可能是它们的图象，若无解，则不可能是它们的图象；即可得答案．解：依次分析选项可得：A、4m＞0，m﹣1＞0；解可得m＞1；故可能是它们的图象．B、4m＞0，m﹣1＜0；解可得0＜m＜1；故可能是它们的图象．C、4m＜0，m﹣1＜0；解可得m＜1；故可能是它们的图象．D、4m＜0，m﹣1＞0；无解；故不可能是它们的图象．故选D．点评：本题考查正比例函数与反比例函数的图象性质，注意①正比例函数与反比例函数的图象与k的关系，②两个函数中参数的关系．7.若A（，b）、B（－1，c）是函数的图象上的两点，且＜0，则b与c的大小关系为（）A．b＜c B．b＞c C．b=c D．无法判断【答案】B【解析】反比例函数的性质：当时，图象在第一、三象限，在每一象限内，y随x的增大而减小；当时，图象在第二、四象限，在每一象限内，y随x的增大而增大.解：∵，∴故选B.【考点】反比例函数的性质点评：反比例函数的性质是初中数学的重点，是中考中比较常见的知识点，一般难度不大，需熟练掌握.8.如图，在直角坐标平面内，函数的图象经过A（1，4），B(a，b)，其中a>1，过点B作轴垂线，垂足为C，连接AC、AB.（1）m= ；（2）若△ABC的面积为4，则点B的坐标为【答案】（1）4；（2）【解析】（1）把A的坐标代入反比例函数的解析式，即可求出m和得出反比例函数的解析式；（2）设B的坐标是（a，b），根据B在反比例函数上得出ab的值，再根据△ABC的面积为4求解即可．（1）把A（1，4）代入得；（2）设B的坐标是（a，b），∵B在反比例函数上，∴ab=4∵△ABC的面积为4，∴×a×（4-b）=4，∴2a ab=4，∴2a-2=4，a=3，∵ab=4，∴b=．则点B的坐标为（3，）．【考点】反比例函数图象上点的坐标特征，用待定系数法求反比例函数的解析式，三角形的面积点评：待定系数法求函数的解析式是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.9.如图，双曲线在第一象限内如图所示作一条平行y轴的直线分别交双曲线于A、B两点，连OA、OB，则S＝。

初中数学八年级下册反比例函数同步测试题及参考答案

初中数学八年级下册反比例函数同步测试题及参考答案选择题1. 对于反比例函数y =x5，下列结论中正确的是（） A.y 取正值 B.y 随x 的增大而增大 C.y 随x 的增大而减小 D.y 取负值 2.下列各点中，在双曲线xy 2=上的是（） A.（1，2） B.（2，2） C.（4，2） D.（0，2） 3. 下列函数中，图象经过点(11)-，的反比例函数解析式是（）A ．1y x =B ．1y x -=C ．2y x =D ．2y x -= 4.函数x k y =的图象经过点（-4，6），则下列个点中在xky =图象上的是（）A.（3，8 ）B.（-3，8）C.（-8，-3）D.（-4，-6）5. 在下图中，反比例函数xk y 12+=的图象大致是（）6. 已知反比例函数xky =的图象在第二、第四象限内，函数图象上有两点A (72，y 1)、B (5，y 2)，则y 1与y 2的大小关系为（）。

A 、y 1＞y 2B 、y 1＝y 2C 、y 1＜y 2D 、无法确定7.函数y =mx 922--m m 的图象是双曲线，且在每个象限内函数值y 随x 的增大而减小，则m 的值是（）A.－2B.4C.4或－2D.－18. 若反比例函数y =xk的图象经过点(－2, 4)，那么这个函数是（） A.y =x 8 B.y =8x C.y =－x 8 D.y =－8x9.反比例函数xm y 5-=的图象的两个分支分别在二、四象限内，那么m 的取值范围是（）A.0<mB.0>mC.5>mD.5<m10. 如图，反比例函数ky x=的图象经过点A ，则k 的值是（）A.2B. 1.5C.3-D. 32-11. 如图，P P P 123、、是双曲线上的三点，过这三点分别作yP A OP A OP A O 112233、、，设它们的面积分别是S S S 123、、，则（）A ． S S S 123<<B ． SS S 213<< C ． S S S 132<<D ． S S S 123==12. 反比例函数ky x=与正比例函数2y x =图像的一个交点的横坐标为1，则反比例函数的图像大致为（）13. 函数y x m =+与(0)my m x=≠在同一坐标系内的图象可以是（）14. 如图，反比例函数xy 5=的图象与直线)0(>=k kx y 相交于B 两点，AC ∥y 轴，BC ∥x 轴，则△ABC 的面积等于个面积单位.A.4B.5C.10D.20 二、填空题15. 如果点(a ,－3a )在双曲线y =xk上，那么k _________0.xA ．xB ．xC ． xD ．16. y 与x +1成反比例，当x =2时，y =1，则当y =－1时，x =_________. 17. 函数y =xk(k ＞0)的图象上两点A (x 1, y 1)和B (x 2, y 2),且x 1＞x 2＞0，分别过A 、B 向x 轴作AA 1⊥x 轴于A 1，BB 1⊥x 轴于B 1，则O AA S 1∆_________O BB S 1∆ (填“＞”“=”或“＜”)，若O AA S 1∆=2，则函数解析式为_________.18. （08四川省资阳市）若A (1x ，1y )、B (2x ，2y )在函数12y x=的图象上，则当1x 、2x 满足_______________时，1y ＞2y . 19. 已知12y y y =+，其中1y 与1x成反比例且比例系数为1k ，2y 与2x 成正比例且比例系数为2k ，若1-=x 时，0=y ，则1k 与2k 的关系为 20. 已知（11,y x ）、（22,y x ）为反比例函数xky =图象上的点，当2121,0y y x x <<<时，则k 的一个值为（只符合条件的一个即可）.21. 近视眼镜的度数y （度）与镜片焦距x （米）成反比例，已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y 与镜片焦距x 之间的函数关系式为．三、解答题（本大题24分）22.甲、乙两地相距100km ，一辆汽车从甲地开往乙地，把汽车到达乙地所用的时间)(h t 表示为汽车速度)/(h km v 的函数，并画出函数图象.23已知函数y = y 1－y 2，y 1与x 成反比例，y 2与x －2成正比例，且当x = 1时，y =－1；当x = 3时，y = 5.求当x ＝5时y 的值。

八年级数学反比例函数综合检测题(含答案)

反比例函数综合检测题一、选择题（每小题3分，共30分） 1、反比例函数y ＝xn 5+图象经过点（2，3），则n 的值是（）． A 、－2 B 、－1 C 、0 D 、12、若反比例函数y ＝xk（k ≠0）的图象经过点（－1，2），则这个函数的图象一定经过点（）． A 、（2，－1） B 、（－21，2） C 、（－2，－1） D 、（21，2）3、(08双柏县)已知甲、乙两地相距s （km ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h ）与行驶速度v （km/h ）的函数关系图象大致是（）4、若y 与x 成正比例，x 与z 成反比例，则y 与z 之间的关系是（）．A 、成正比例B 、成反比例C 、不成正比例也不成反比例D 、无法确定 5、一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝xk满足（）． A 、当x ＞0时，y ＞0 B 、在每个象限内，y 随x 的增大而减小 C 、图象分布在第一、三象限 D 、图象分布在第二、四象限6、如图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线PQ 交双曲线y ＝x1于点Q ，连结OQ ，点P 沿x 轴正方向运动时，Rt △QOP 的面积（）． A 、逐渐增大 B 、逐渐减小 C 、保持不变 D 、无法确定7、在一个可以改变容积的密闭容器内，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变．ρ与V 在一定范围内满足ρ＝Vm，它的图象如图所示，则该气体的质量m 为（）．A 、1.4kgB 、5kgC 、6.4kgD 、7kg8、若A （－3，y 1），B （－2，y 2），C （－1，y 3）三点都在函数y ＝－x1的图象上，则y 1，y 2，y 3的大小关系是（）．A 、y 1＞y 2＞y 3B 、y 1＜y 2＜y 3C 、y 1＝y 2＝y 3D 、y 1＜y 3＜y 2 9、已知反比例函数y ＝xm21-的图象上有A （x 1，y 1）、B （x 2，y 2）两点，当x 1＜x 2＜0时，y 1＜y 2，则m 的取值范围是（）．A 、m ＜0B 、m ＞0C 、m ＜21 D 、m ＞21 10、如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（）．A 、x ＜－1B 、x ＞2C 、－1＜x ＜0或x ＞2D 、x ＜－1或0＜x ＜2A ．B ．C ．．二、填空题（每小题3分，共30分）11.某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12、已知反比例函数xky =的图象分布在第二、四象限，则在一次函数b kx y +=中，y 随x 的增大而（填“增大”或“减小”或“不变”）． 13、若反比例函数y ＝xb 3-和一次函数y ＝3x ＋b 的图象有两个交点，且有一个交点的纵坐标为6，则b ＝．14、反比例函数y ＝（m ＋2）xm 2－10的图象分布在第二、四象限内，则m 的值为．15、有一面积为S 的梯形，其上底是下底长的31，若下底长为x ，高为y ，则y 与x 的函数关系是．16、如图，点M 是反比例函数y ＝xa（a ≠0）的图象上一点，过M 点作x 轴、y 轴的平行线，若S 阴影＝5，则此反比例函数解析式为． 17、使函数y ＝（2m 2－7m －9）xm2－9m ＋19是反比例函数，且图象在每个象限内y 随x 的增大而减小，则可列方程（不等式组）为．18、过双曲线y ＝xk（k ≠0）上任意一点引x 轴和y 轴的垂线，所得长方形的面积为______． 19. 如图，直线y ＝kx(k ＞0)与双曲线xy 4=交于A （x 1，y 1），B （x 2，y 2）两点，则2x 1y 2－7x 2y 1＝___________．20、如图，长方形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上，点B 的坐标为B （－320，5），D 是AB 边上的一点，将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是．三、解答题（共60分）21、（8分）如图，P 是反比例函数图象上的一点，且点P 到x 轴的距离为3，到y 轴的距离为2，求这个反比例函数的解析式．22、（9分）请你举出一个生活中能用反比例函数关系描述的实例，写出其函数表达式，并画出函数图象．举例：函数表达式：23、（10分）如图，已知A （x 1，y 1），B （x 2，y 2）是双曲线y ＝xk在第一象限内的分支上的两点，连结OA 、OB ．（1）试说明y 1＜OA ＜y 1＋1y k ；（2）过B 作BC ⊥x 轴于C ，当m ＝4时，求△BOC 的面积．24、（10分）如图，已知反比例函数y ＝－x8与一次函数y ＝kx ＋b 的图象交于A 、B 两点，且点A 的横坐标和点B 的纵坐标都是－2．求：（1）一次函数的解析式；（2）△AOB 的面积．25、（11分）如图，一次函数y ＝ax ＋b 的图象与反比例函数y ＝xk的图象交于M 、N 两点．（1）求反比例函数与一次函数的解析式；（2）根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．26、（12分）如图，已知反比例函数y ＝xk的图象与一次函数y ＝a x ＋b 的图象交于 M （2，m ）和N （－1，－4）两点．（1）求这两个函数的解析式；（2）求△MON 的面积；（3）请判断点P （4，1）是否在这个反比例函数的图象上，并说明理由．参考答案:一、选择题1、D ；2、A ；3、C ；4、B ；5、D ；6、C7、D ；8、B ；9、D ； 10、D ．二、填空题 11、y ＝x 1000； 12、减小； 13、5 ； 14、－3 ；15、y ＝x s 23 ； 16、y ＝－x5； 17、⎩⎨⎧---=+-0972119922＞m m m m ； 18、|k|； 19、 20； 20、y ＝－x 12．三、解答题 21、y ＝－x6． 22、举例：要编织一块面积为2米2的矩形地毯，地毯的长x （米）与宽y （米）间函数关系式为y ＝x2（x ＞0）．（只要是生活中符合反比例函数关系的实例均可）画函数图象如右图所示．23、（1）过点A 作AD ⊥x 轴于D ，则OD ＝x 1，AD ＝y 1，因为点A （x 1，y 1）在双曲线y ＝x k 上，故x 1＝1y k，又在Rt △OAD 中，AD ＜OA ＜AD ＋OD ，所以y 1＜OA ＜y 1＋1y k；（2）△BOC 的面积为2． 24、（1）由已知易得A （－2，4），B （4，－2），代入y ＝kx ＋b 中，求得y ＝－x ＋2；（2）当y ＝0时，x ＝2，则y ＝－x ＋2与x 轴的交点M （2，0），即|OM|＝2，于是S △AOB ＝S △AOM ＋S △BOM ＝21|OM|·|y A |＋21|OM|·|y B |＝21×2×4＋21×2×2＝6．25、（1）将N （－1，－4）代入y ＝x k ，得k ＝4．∴反比例函数的解析式为y ＝x 4．将M （2，m ）代入y ＝x4，得m ＝2．将M （2，2），N （－1，－4）代入y ＝ax ＋b ，得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y ＝2x －2．（2）由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值． 26、解（1）由已知，得－4＝1-k ，k ＝4，∴y ＝x 4．又∵图象过M （2，m ）点，∴m ＝24＝2，∵y ＝a x ＋b 图象经过M 、N 两点，∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y ＝2x －2．（2）如图，对于y ＝2x －2，y ＝0时，x ＝1，∴A （1，0），OA ＝1，∴S △MON ＝S △MOA ＋S △NOA ＝21OA ·MC ＋21OA ·ND ＝21×1×2＋21×1×4＝3．（3）将点P （4，1）的坐标代入y ＝x4，知两边相等，∴P 点在反比例函数图象上．。

八年级数学下册(反比例函数)练习题试题

轧东卡州北占业市传业学校保靖县水田河镇民族八年级数学下册<反比例函数>练习题湘教(检测时间50分钟总分值100分)一、选择题:(每题3分,共18分)1.以下函数中,是反比例函数的是( )A.y=-3xB.y=-31x- 1 C.y=-32x D.y=-32x - 2.如果双曲线y=k x过点A(3,-2),那么以下各点在双曲线上的是( ) A.(2,3) B.(6,1) C.(-1,-6) D.(-3,2)3.一定质量的二氧化碳,当它的体积V=53m ,密度p=1.98kg/3m 时,p 与V 之间的函数关系式是( ) A.p=V B.9.9V ρ= C.9.9V ρ= D.29.9V ρ= 4.假设点A(-2,1y ),B(-1,2y ),C(1,3y )在反比例函数y=1x 的图象上, 那么以下结论正确的选项是( )A.1y >2y >3yB.3y >1y >2yC.2y >1y >3yD.3y >2y >1y5.1y +2y =y,其中1y 与1x 成反比例,且比例系数为1k ,而2y 与2x 成正比例,且比例系数为2k ,假设x=-1时,y=0,那么1k ,2k 的关系是( )A.12k k + =0B.12k k =1C.12k k - =0D.12k k =-16.一次函数y=1k x+b,y 随x 的增大而减小,且b>0,反比例函数y=2k x 中的2k 与1k 的值相等,那么它们在同一坐标系内的图象只可能是( )二、填空题:(每题4分,共28分)1.y 与2x+1成反比例,且当x=1时,y=2,那么当x=0时,y=________.2.函数y=221(1)k k kx ---,当k=____时,它的图象是双曲线. 3.函数y=36k x-在每个象限内,y 随x 的减小而减小,那么k 的取值范围是_______. 4.反比例函数y=12k kx -,当x>0时,y 随x 的________而增大.5.正比例函数y=kx(k≠0),y 随x 的增大而减小,那么反比例函数y=k x ,当x< 0时,y 随x 的增大而_______.6.假设函数y=k x的图象在第二、四象限,那么函数y=kx-1的图象经过第____象限. 7.假设反比例函数y=(2m-1)22m x - 的图象在第一、三象限,那么函数的解析式为______.三、根底训练:(每题12分,共24分)1.矩形的面积为48c 2m ,求矩形的长y(cm)与宽x(cm)之间的函数关系式, 并写出自变量的取值范围,画出图象.2.如下列图,一个反比例函数的图象在第二象限内,点A 是图象上的任意一点,AM⊥x 轴于M,O 是原点,假设S △AOM =3,求该反比例函数的解析式,并写出自变量的取值范围.四、提高训练:(共15分)如下列图,Rt△AOB 中,∠ABO=90°,点B 在x 轴上,点A 是直线y=x+m 与双曲线y=m x 在第一象限的交点,且S △AOB =3.(1)求m 的值.(2)求△ACB 的面积. 五、中考题竞赛题:(共15分) (2003,)如图4所示,一次函数y =kx+b(k≠0)的图象与x 轴、y 轴分别交于A,B 两点,且与反比例函OC B Ax y CBy数y=mx(m≠0)的图象在第一象限交于C点,CD⊥x轴, 垂足为D,假设OA=OB=OD=1.(1)求点A,B,D坐标.(2)求一次函数和反比例函数的关系式.答案:。

八年级数学反比例函数综合检测题(含答案)

反比例函数练习一、选择题（每小题3分，共30分） 1、反比例函数y ＝xn 5图象经过点（2，3），则n 的值是（）． A 、－2 B 、－1 C 、0 D 、12、若反比例函数y ＝xk（k ≠0）的图象经过点（－1，2），则这个函数的图象一定经过点（）． A 、（2，－1） B 、（－21，2） C 、（－2，－1） D 、（21，2）3、(08双柏县)已知甲、乙两地相距s （km ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h ）与行驶速度v （km/h ）的函数关系图象大致是（）4、若y 与x 成正比例，x 与z成反比例，则y 与z 之间的关系是（）． A 、成正比例 B 、成反比例C 、不成正比例也不成反比例D 、无法确定 5、一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝xk满足（）． A 、当x ＞0时，y ＞0 B 、在每个象限内，y 随x 的增大而减小 C 、图象分布在第一、三象限 D 、图象分布在第二、四象限6、如图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线PQ 交双曲线y ＝x1于点Q ，连结OQ ，点P 沿x 轴正方向运动时，Rt △QOP 的面积（）． A 、逐渐增大 B 、逐渐减小 C 、保持不变 D 、无法确定7、在一个可以改变容积的密闭容器内，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变．ρ与V 在一定范围内满足ρ＝Vm，它的图象如图所示，则该气体的质量m 为（）．A 、1.4kgB 、5kgC 、6.4kgD 、7kg8、若A （－3，y 1），B （－2，y 2），C （－1，y 3）三点都在函数y ＝－x1的图象上，则y 1，y 2，y 3的大小关系A ． B ． C ．．是（）．A 、y 1＞y 2＞y 3B 、y 1＜y 2＜y 3C 、y 1＝y 2＝y 3D 、y 1＜y 3＜y 2 9、已知反比例函数y ＝xm21-的图象上有A （x 1，y 1）、B （x 2，y 2）两点，当x 1＜x 2＜0时，y 1＜y 2，则m 的取值范围是（）．A 、m ＜0B 、m ＞0C 、m ＜21 D 、m ＞21 10、如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（）．A 、x ＜－1B 、x ＞2C 、－1＜x ＜0或x ＞2D 、x ＜－1或0＜x ＜2 二、填空题（每小题3分，共30分）11.某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12、已知反比例函数xky =的图象分布在第二、四象限，则在一次函数b kx y +=中，y 随x 的增大而（填“增大”或“减小”或“不变”）． 13、若反比例函数y ＝xb 3-和一次函数y ＝3x ＋b 的图象有两个交点，且有一个交点的纵坐标为6，则b ＝．14、反比例函数y ＝（m ＋2）xm2－10的图象分布在第二、四象限内，则m 的值为．15、有一面积为S 的梯形，其上底是下底长的31，若下底长为x ，高为y ，则y 与x 的函数关系是．16、如图，点M 是反比例函数y ＝xa（a ≠0）的图象上一点，过M 点作x 轴、y 轴的平行线，若S 阴影＝5，则此反比例函数解析式为． 17、使函数y ＝（2m 2－7m －9）xm2－9m ＋19是反比例函数，且图象在每个象限内y 随x 的增大而减小，则可列方程（不等式组）为．18、过双曲线y ＝xk（k ≠0）上任意一点引x 轴和y 轴的垂线，所得长方形的面积为______．19. 如图，直线y ＝kx(k ＞0)与双曲线xy 4=交于A （x 1，y 1），B （x 2，y 2）两点，则2x 1y 2－7x 2y 1＝___________．20、如图，长方形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上，点B 的坐标为 B （－320，5），D 是AB 边上的一点，将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是．三、解答题（共60分）21、（8分）如图，P 是反比例函数图象上的一点，且点P 到x 轴的距离为3，到y 轴的距离为2，求这个反比例函数的解析式．22、（9分）请你举出一个生活中能用反比例函数关系描述的实例，写出其函数表达式，并画出函数图象．举例：函数表达式：23、（10分）如图，已知A （x 1，y 1），B （x 2，y 2）是双曲线y ＝xk在第一象限内的分支上的两点，连结OA 、OB ．（1）试说明y 1＜OA ＜y 1＋1y k ；（2）过B 作BC ⊥x 轴于C ，当m ＝4时，求△BOC 的面积．24、（10分）如图，已知反比例函数y ＝－x8与一次函数y ＝kx ＋b 的图象交于A 、B 两点，且点A 的横坐标和点B 的纵坐标都是－2．求：（1）一次函数的解析式；（2）△AOB 的面积．25、（11分）如图，一次函数y ＝ax ＋b 的图象与反比例函数y ＝xk的图象交于M 、N 两点．（1）求反比例函数与一次函数的解析式；（2）根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．26、（12分）如图，已知反比例函数y ＝xk的图象与一次函数y ＝a x ＋b 的图象交于 M （2，m ）和N （－1，－4）两点．（1）求这两个函数的解析式；（2）求△MON 的面积；（3）请判断点P （4，1）是否在这个反比例函数的图象上，并说明理由．一、选择题1、D ；2、A ；3、C ；4、B ；5、D ；6、C7、D ；8、B ；9、D ； 10、D ．二、填空题 11、y ＝x 1000； 12、减小； 13、5 ； 14、－3 ；15、y ＝x s 23 ； 16、y ＝－x5； 17、⎩⎨⎧---=+-0972119922＞m m m m ； 18、|k|； 19、 20； 20、y ＝－x 12．三、解答题 21、y ＝－x6． 22、举例：要编织一块面积为2米2的矩形地毯，地毯的长x （米）与宽y （米）间函数关系式为y ＝x2（x ＞0）．23、（1）过点A 作AD ⊥x 轴于D ，则OD ＝x 1，AD ＝y 1，因为点A （x 1，y 1）在双曲线y ＝xk上，故x 1＝1y k ，又在Rt △OAD 中，AD ＜OA ＜AD ＋OD ，所以y 1＜OA ＜y 1＋1y k；（2）△BOC 的面积为2． 24、（1）由已知易得A （－2，4），B （4，－2），代入y ＝kx ＋b 中，求得y ＝－x ＋2；（2）当y ＝0时，x ＝2，则y ＝－x ＋2与x 轴的交点M （2，0），即|OM|＝2，于是S △AOB ＝S △AOM ＋S △BOM ＝21|OM|·|y A |＋21|OM|·|y B |＝21×2×4＋21×2×2＝6．25、（1）将N （－1，－4）代入y ＝x k ，得k ＝4．∴反比例函数的解析式为y ＝x 4．将M （2，m ）代入y ＝x4，得m ＝2．将M （2，2），N （－1，－4）代入y ＝ax ＋b ，得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y ＝2x －2．（2）由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值． 26、解（1）由已知，得－4＝1-k ，k ＝4，∴y ＝x 4．又∵图象过M （2，m ）点，∴m ＝24＝2，∵y ＝a x ＋b 图象经过M 、N 两点，∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y ＝2x －2．（2）如图，对于y ＝2x －2，y ＝0时，x ＝1，∴A （1，0），OA ＝1，∴S △MON ＝S △MOA ＋S △NOA ＝21OA ·MC ＋21OA ·ND ＝21×1×2＋21×1×4＝3．（3）将点P （4，1）的坐标代入y ＝x4，知两边相等，∴P 点在反比例函数图象上．。

湖南四大名校内部资料初二八年级下册数学反比例函数测试题及试卷答案

八年级下反比例函数单元测评卷含答案

八年级数学下册《反比例函数》测试卷含答案

初二反比例函数复习题及答案

八年级数学下册《反比例函数》单元检测练习试卷及答案有详细解析

八年级下《反比例函数》单元测试题含答案

八年级下《反比例函数》检测题含答案

八年级下《反比例函数》单元测试含答案

反比例函数》测试题(含答案)

八年级下反比例函数单元测评卷含答案

湖南四大名校内部资料反比例函数测试卷带答案

八年级下册反比例函数练习题(含答案)

初二数学反比例函数试题答案及解析

初中数学八年级下册反比例函数同步测试题及参考答案

八年级数学反比例函数综合检测题(含答案)

八年级数学下册(反比例函数)练习题 试题

八年级数学反比例函数综合检测题(含答案)

八年级数学下册(反比例函数)练习题试题