二次根式讲义
初三数学上册二次根式讲义

二次根式讲义知识点一:二次根式的概念和性质1定义:形如()的式子叫做二次根式。
注:在二次根式中,被开放数可以是数,也可以是单项式、多项式、分式等代数式,把握的重点:(1)二次根式是形式上定义的,必须含有二次根号。
(2)被开方数a必须是非负数,即a≧0(3)的根指数是2,一般省略根指数2,写作,这一点一定要切实注意,不可误认为根指数为“1”,“0”。
2.性质1、两个非负性:(1)根号下的a必须是非负数,表示为a≥0;(2)a(a≥0≥02、a(a≥0)的平方根是±a,a(a≥0)的算术平方根是a3a│=要特别注意:不能直接将根号、平方一起去掉,应该有绝对值号,然后再计算绝对值。
计算绝对值的时候,要注意绝对值内代数式的正负性,绝对值内是一个整体4、2=a(a≥0)注意:与的异同点1、不同点:与表示的意义是不同的,表示一个正数a的算术平方根的平方,而表示一个实数a的平方的算术平方根;在中,而中a可以是正实数,0,负实数。
但与都是非负数,即,。
因而它的运算的结果是有差别的,,而a(a≥0)-a(a<0)2、相同点:当被开方数都是非负数,即时,=;时,无意义,而.知识点二:二次根式的乘除运算1乘法公式1a≥0,b≥0)即二次根式相乘,把被开方数相乘,根指数不变。
注意(1)在进行二次根式乘法运算中,一定不要忽略被开方数a,b均为非负数。
(2)此法则可以推广到多个二次根式相乘的运算。
(3)若含有系数的二次根式相乘,可类比单项式的乘法法则,将它分为系数和根式两部分的运算,然后相乘。
公式2(a≥0,b≥0)要注意式子成立的条件限制。
2除法公式1=(a≥0,b>0)即两个二次根式相除,把被开方数相除,根指数不变。
注意(1)除法运算的结果也要进行化简(2)在运算过程中要注意条件(a≥0,b>0)(3)若含有系数的二次根式相除,可类比单项式的除法法则,将它分为系数和根式两部分分别运算,然后想乘。
公式2=(a≥0,b>0)3最简二次根式(1)应满足的条件:(1)被开方数不含分母或分母中不含二次根式;(2)被开方数中不含开得尽方的因数或因式最简二次根式定义中第(1)条说明被开方数不含有分母;分母是1的例外。
《二次根式》 讲义

《二次根式》讲义一、二次根式的定义形如\(\sqrt{a}(a\geq 0)\)的式子叫做二次根式。
其中,\(\sqrt{}\)称为二次根号,\(a\)叫做被开方数。
需要特别注意的是,二次根式有两个非常重要的限制条件:一是根指数为 2;二是被开方数必须是非负数。
例如,\(\sqrt{5}\),\(\sqrt{16}\),\(\sqrt{x^2 +1}\)(其中\(x\)为任意实数)等都是二次根式;而\(\sqrt{-5}\)就不是二次根式,因为被开方数\(-5\)是负数。
二、二次根式的性质1、\(\sqrt{a^2} =|a|\)当\(a \geq 0\)时,\(\sqrt{a^2} = a\);当\(a < 0\)时,\(\sqrt{a^2} = a\)。
例如,\(\sqrt{3^2} = 3\),\(\sqrt{(-5)^2} = 5\)。
2、\((\sqrt{a})^2 = a\)(\(a\geq 0\))例如,\((\sqrt{7})^2 = 7\)。
3、\(\sqrt{ab} =\sqrt{a} \cdot \sqrt{b}\)(\(a\geq 0\),\(b\geq 0\))例如,\(\sqrt{12} =\sqrt{4\times 3} =\sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\)。
4、\(\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}\)(\(a\geq 0\),\(b > 0\))例如,\(\sqrt{\dfrac{18}{2}}=\dfrac{\sqrt{18}}{\sqrt{2}}=\dfrac{3\sqrt{2}}{\sqrt{2}}= 3\)。
三、二次根式的化简化简二次根式是二次根式运算中的重要环节,其目的是将二次根式化为最简二次根式。
最简二次根式需要满足以下两个条件:1、被开方数不含分母;2、被开方数中不含能开得尽方的因数或因式。
二次根式辅导讲义

二次根式一、知识梳理1、二次根式的概念和性质二次根式的定义:形如a (0a ≥)的式子叫做二次根式.注意点:(1)被开方数是正数或0;(2)二次根式a (0a ≥)表示非负数a 的算术平方根.二次根式的性质:(1)二次根式的非负性:0a ≥;(2)2()(0)a a a =≥;(3)2(0)(0)(0)a a a a a a a a >⎧⎪===⎨⎪-<⎩;(4)当0a ≥时,22()a a =.2、最简二次根式最简二次根式最简二次根式的定义:①被开方数的因数是整数,因式是整式(分母中不含根号);②被开方数中不含能开 得尽方的因数或因式.这样的二次根式叫做最简二次根式.最简二次根式的满足条件:(1)被开放数的因数是整数,因式是整式(被开方数不能存在小数、分数形式);(2)被开方数中不含能开得尽方的因数或因式;(3)分母中不含二次根式.说明:二次根式的计算结果要写成最简根式的形式.3、二次根式的加减同类二次根式几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫同类二次根式.二次根式的加减同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次 根式.合并同类二次根式:()a x b x a b x +=+,同类二次根式才可加减合并.分母有理化分母有理化:把分母中的根号化去叫做分母有理化.互为有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,说这两个代数式互为有理化因式.a b+与a b-互为有理化因式;分式有理化时,一定要保证有理化因式不为0.4、二次根式综合运算二次根式的综合运算法则:先算乘除法,再算加减法,有括号的先算括号里面的,最终结果二次根式部分要化为最简二次根式.注意:在二次根式的计算题中,如果题目中没有明确说明字母的取值范围,按照字母使二次根式有意义计算.5、二次根式化简求值二次根式的化简求值:先把二次根式化为最简二次根式,然后进行二次根式的加减乘除运算,化为较为简单的一个式子(或直接得出结果),最后代入未知数的值求解,有时候也会存在整体代入的情况.注意:对于二次根式的化简求值如果字母没有明确说明取值范围,必须要进行分类讨论.6、根式的大小比较比较大小的方法1.作差法:比较a、b的大小,0,0,0,a b a b a ba b>>⎧⎪-==⎨⎪<<⎩2.作商法:比较a、b的大小,当0,0a b>>时,可以采用作商法,1,1,1,a b aa b ba b>>⎧⎪==⎨⎪<<⎩二次根式比较大小的方法(1)0a b a b>>⇔>(2)二次根式比较大小:能直接比较大小的直接比较;不能直接比较大小的,先平方再比较.(3)估算法(4)分子有理化(5)倒数法7、二次根式的乘除二次根式的乘除法二次根式的乘法法则:a b ab⋅=(0a≥,0b≥).二次根式的除法法则:a abb=(0a≥,0b>).说明:利用乘除法则时注意a、b的取值范围,对于ab a b=⋅,a、b都非负,否则不成立.二、典型例题题型一、二次根式的概念和性质例1: 函数1x y x =-中自变量x 的取值范围是( ) A .1x ≥B .1x <且0x ≠C .1x >D .1x ≥且0x ≠【答案】C【解析】该题考查的是函数的定义域.根式下的式子在非负条件下有意义,分数在分母不为0的条件下有意义,综上所述,10x -≥,且10x -≠,∴1x >,故本题答案为C .例2: 若320-+-=x y ,则xy 的值为____.A .8B .6C .5D .9【答案】A【解析】该题考查的是的非负性.根据题意得:3020x y -=⎧⎨-=⎩解得:32x y =⎧⎨=⎩∴32x y =,故选A .变式: 已知:()322512012x x y x -+-=+--,求x y 的值. 【答案】25【解析】该题考查的是二次根式的性质.∵()322512012x xy x -+-=+--有意义∴()32020120120x x x ⎧-≥⎪⎪-≥⎨⎪--≠⎪⎩所以2x =,055y =+=∴2525x y ==题型二、最简二次根式例1、下列二次根式中,最简二次根式是( )A .22xB .0.5C .22x y +D .1x 【答案】C【解析】该题考查最简二次根式.A 、x x 222=被开方数含能开得尽方的因数,不是最简二次根式;故本选项错误; B 、120.522==,被开方数含分母,不是最简二次根式;故本选项错误; C 、22x y +满足最简二次根式的定义,是最简二次根式;D 、1x x x=,被开方数含能开得尽方的因数,不是最简二次根式. 故选C .例2、若最简二次根式2342a +与22613a -是同类二次根式,则a =_________【答案】1±【解析】该题考查的是二次根式.满足下列两个条件的二次根式,叫做最简二次根式:(1)被开方数的因数是整数,因式是整式;(2)被开方数中不含能开得尽方的因数或因式.几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式. 根据题意可列:22461a a +=-解得:1a =±变式、若2,m ,4为三角形三边,化简:()()2226m m -+-=____________.【答案】4【解析】该题考查的是根式的化简求值.∵2,m ,4为三角形三边,可知包括如下关系:①24m +>,即6m <②24m +>,即2m >∴原式264m m =-+-=题型三、二次根式的加减例1、计算124183-⨯=__________.【答案】6【解析】该题考查的是二次根式的计算.原式346923=⨯-⨯⨯326323=-⨯ 2666=-=例2、111115533131317+++=++++____.【答案】1714-【解析】该题考查根式的分母有理化.11115135133171317144444155********-----+++=+++=++++ 故答案为1714-. 变式、已知32x =+,32y =-,则33_________x y xy +=.【答案】10【解析】因为32x =+,32y =-,所以()()32321xy =+-=,()()323223x y +=++-=,所以()()()22332221232110x y xy xy x y xy x y xy ⎡⎤⎡⎤+=+=+-=⨯-⨯=⎢⎥⎣⎦⎣⎦题型四、二次根式综合运算例1、化简:2244112a a a a -+--+(112a ≤≤)【答案】32a -【解析】()()222244112211211a a a a a a a a -+--+---=---,因为112a ≤≤,所以原式21121132a a a a a =---=-+-=-例2、若352x y +=-,325x y -=-,求xy .【答案】52-【解析】2()352x y +=-;2()325x y -=-∴22()()352(325)5244x y x y xy +-----===-变式、化简22691025a a a a +++-+【答案】当3a <-时,原式=22a -+;当35a -≤<时,原式=8;当5a ≥时,原式=22a -;【解析】()()22226910253535a a a a a a a a +++-+=++-=++-,当3a <-时,原式353522a a a a a =++-=---+=-+;当35a -≤<时,原式35358a a a a =++-=+-+=;当5a ≥时,原式353522a a a a a =++-=++-=-题型五、二次根式化简求值例1、化简:()221269x x x -+-+=____【答案】43x -【解析】该题考查根式的化简.()()2221269123x x x x x -+-+=-+-∵由题得120x -≥,12x ≤∴()2333x x x -=-=-.∴原式12343x x x =-+-=-.故答案为43x -.例2、化简:108322++.【答案】42+【解析】22108322108(12)108(12)1882(42)42++=++=++=+=+=+变式、化简:(1)412-(2)415+【答案】(1)31-(2)1062+【解析】(1)()24124233131-=-=-=- (2)221064158215(53)222++=+=+=题型六、根式的大小比较例1、比较大小:512-_______12.(填“>”、“<”或“=”). 【答案】>【解析】该题考查的是二次根式比大小.5115115254022222------===>,即511022-->, 即51122->. 例2、设120082006,2007A B =-=,比较大小:A ____B .【答案】A B >【解析】222008200620082006A ==+-,22220072007B ==;2008200622007+< ∴22A B< ∴A B >变式、已知21a =-,226b =-,62c =-,那么a ,b ,c 的大小关系是( )A .a b c >>B .b a c >>C .c b a >>D .c b a <<【答案】B【解析】()()221,223,2322a b c ⎛⎫=-=-=- ⎪ ⎪⎝⎭2222(231)2(13)(2223)0222b a -=--+=-+=+->,b a > 2222(132)2(13)(2223)0222a c -=--+=-+=+->,a c >b ac >>题型七、二次根式的乘除例1、下列计算正确的是( )A .235⋅=B .236⋅=C .84=D .2(3)3-=-【答案】B【解析】根据二次根式的乘法运算法则,可得236⋅=,故答案为B 选项.例2、下列计算结果正确的是( )A .257+=B .2510⨯=C .3223-=D .25105=【答案】B【解析】该题考查的是二次根式计算.A 选项2与5不是同类项,不能合并,故本选项错误;B 选项252510⨯=⨯=,故本选项正确;C 选项32222-=,故本选项错误;D 选项21055=,故本选项错误. 故答案是B .变式、已知:4322232b a a =-+-+,求11a b +的平方根.【答案】2±【解析】该题考查的是二次根式.4322232b a a =-+-+,根据被开方数的非负性我们知道320230a a -≥⎧⎨-≥⎩,所以23a =, 代入得43222322b a a =-+-+=,所以1131222a b +=+=,平方根为2±三、课堂巩固1、函数11y x =-中自变量的取值范围是( B )A .1x ≠B .1x >C .1x ≥D .1x ≥-2、对于所有实数,a b ,下列等式总能成立的是( C )A .()2a b a b +=+B .22a b a b +=+C .()22222a b a b +=+ D .()2a b a b +=+ 3、函数12y x =+中,自变量x 的取值范围是2->x 4、实数P 在数轴上的位置如图所示,化简()()2223p p -+-=15、计算:=⨯121726,=--)84)(213(24, =⨯-03.027.02-0.18,=÷-327348-5.6、化简:()221269x x x -+-+=x 34-.7、设120082006,2007A B =-=,比较大小:A >B . 8、已知: 21x =-,求223x x +-的值.()()()()2222231322-=-+=+-=-+x x x x 9、已知:,x y 为实数,且113y x x <-+-+,化简:23816y y y ---+. 1=x 3<y 原式=()1-4343=---=---y y y y1 2 3 4 p课后作业1、函数2x y x-=中,自变量x 的取值范围是( A ) A .2x ≤且0x ≠B .2x ≤C .2x <且0x ≠D .0x ≠2、若()424A a =+,则A =( A ) A .24a +B .22a +C .()222a + D .()224a + 3、若2(2)10m n ++-= 则m n -= -3 .4、在下列二次根式22211025312232322a a a a b m x a b x a b +-++,,,,,,,,,,中,最简二次根式有6个.5、若最简二次根式35a -与3a +是同类二次根式,则a =___4___.6、若231604b a a +-+=-,则3223a b a b +=-___-18___.7、比较大小:512-___>___12.(填“>”、“<”或“=”). 8、计算:01186(121)221+---- 原式=01232212=--++9、化简:(1)412-原式=()13132-=- (2)415+221064158215(53)222++=+=+=。
二次根式讲义(初次、基础版)

二次根式【知识要点】 必杀技:要注意二次根式中字母的取值范围: 被开方数必须是非负数.1. 二次根式的主要性质: ①⎩⎨⎧<-≥==002a a a a a a ; ②()a a =2(),0≥a ; ③()0,0≥≥⋅=b a b a ab ④()0,0>≥==b a b ab ba b a ; ⑤()()b a b a b a b a ba b a --=-+-=+1; ⑥b a b a ba -+=-1. A 、最简二次根式:被开方数中不含分母,并且被开方数中不含开的尽方的因数或因式,像这样的二次根式成为最简二次根式最简二次根式的条件:①根号内不含有开的尽方的因数或因式②根号内不含有分母③分母不含有根号B 、同类二次根式:被开方数相同的最简二次根式叫做同类二次根式C 、乘法公式:)0,0______(≥≥=⋅b a b a ;反之:)0,0_______(≥≥=b a abD 、除法公式:)0,0______(>≥=b a ba ;反之:)0,0______(>≥=b a b a E 、合并同类二次根式:__________________;=-=+a n a m a n a m【典型例题】例1.x 是怎样的实数时,下列二次根式有意义?(1)1+x ; (2)23-x ; (3)123+x ; (4)x231-. 例2.若a a ---33有意义,则a 的值为______________.例3.若22)2()2(-=-x x ,则x 的取值范围是________________.例4.已知2<x <3,化简:3)2(2-+-x x . 例5.数a 、b 在数轴上的位置如图所示,化简222)()1()1(b a b a ---++.例1、乘法运算(1))169()25(-⨯- (2)1527⨯ (3)228n m (4)a a 122532⋅- 例2:除法运算(1)354- (2)531513÷ (3)921.15004.0⨯⨯ (4)2294a b 例3:加减混合运算二次根式加减时,可以先将二次根式化简成最简二次根式,再合并同类二次根式,一般步骤为: 化简→分类→合并例1、计算:(1)ab ab ab b a ÷+-)3(33,其中0,0>>b a(4)20)21()23(3632918-+-++-- 【变式练习】 计算:6、27348612421-+-; (2))312218(21812-+-- (3)a ab a b ab a 4322763232+-,其中0>ab (4)33)2321418(÷--- 【课堂练习】 1.如果03332=⎪⎪⎭⎫ ⎝⎛-++y x ,那么()=2005xy .2.已知y x ,的实数,214422-+-+-=x x x y ,则y x 43+的值为 . 3.化简下列各式:(1)()()()44322>---a a a (2)()()233522-+---4.已知23-=a ,求121232---++a aa a a 的值. 【贴近中考】1. (2011江苏省南京市)计算)(12=___________. 2. (2011江苏省扬州市)=_______________.3. (2011内蒙古包头市)_________ 4. (2011青海省)___________.5. (2011 山东省菏泽市) 实数a 在数轴上的位置如图所示,则化简后为( )A. 7B. -7C. 2a -15D. 无法确定 6. (2011 山东省济宁市) 下列各式计算正确的是( )A=B.2=C.=D.2=7. (2011山东省聊城市)=_____________.8. (2011 山东省临沂市)计算的结果是( )A.B.5C .5D .0 5 a 10。
二次根式讲义

二次根式辅导讲义同步知识梳理一:二次根式得概念二次根式得定义形如得式子叫二次根式,其中叫被开方数,只有当就是一个非负数时,才有意义.二:二次根式得性质1、非负性:a a()≥0就是一个非负数.注意:此性质可作公式记住,后面根式运算中经常用到.2、()() a aa20=≥.注意:此性质既可正用,也可反用,反用得意义在于,可以把任意一个非负数或非负代数式写成完全平方得形式:a a a=≥()()203、a aa aa a20 ==≥-<⎧⎨⎩||()()注意:(1)字母不一定就是正数.(2)能开得尽方得因式移到根号外时,必须用它得算术平方根代替.(3)可移到根号内得因式,必须就是非负因式,如果因式得值就是负得,应把负号留在根号外.4、公式a aa aa a2==≥-<⎧⎨⎩||()()与()()a aa20=≥得区别与联系(1)a2表示求一个数得平方得算术根,a得范围就是一切实数.(2)()a2表示一个数得算术平方根得平方,a得范围就是非负数.(3)a2与()a 2得运算结果都就是非负得.三:最简二次根式与同类二次根式2a B、1--3<0,则化简(1)148 (2)4337- (3)11212 (4)13550-【例14】把下列各式分母有理化(1)328x x y(2)38xx【例15】把下列各式分母有理化:(1)221- (2)5353+- (3)333223- 举一反三:1、已知2323x -=+,2323y +=-,求下列各式得值:(1)x y x y +-(2)223x xy y -+专题五:二次根式计算——二次根式得乘除【例16】化简(1)916⨯ (2)1525⋅ (3)229x y (0,0≥≥y x ) (4)12×632⨯ 【例17】计算(1)(2) (3) (4)(5) (6) (7) (8)【例18】化简:(1)364 (2)22649b a )0,0(≥>b a (2)2964xy )0,0(>≥y x (4)25169x y )0,0(>≥y x【例19】计算:(1)123 (2)3128÷ (3)11416÷(4)648【例20】能使等式22xxx x =--成立得得x 得取值范围就是( )A 、2x >B 、0x ≥C 、02x ≤≤D 、无解专题六:二次根式计算——二次根式得加减【例20】计算(1)11327520.53227--+-; (2)12543102024553457⎛⎫⎛⎫+-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭; 【例21】(1)224344x y x y x y x y --+--+ (2)a b a ba b a b--+-+ 专题七:二次根式计算——二次根式得混合计算与求值1、ab b a ab b 3)23(235÷-⋅ 2、 22 (212 +418-348 ) 3、132x y ·(-42y x)÷162x y 4、673)32272(-⋅++5、62332)(62332(+--+)6、1110)562()562(+-【例21】 1.已知:,求得值.2.已知,求得值。
第二十一章二次根式 辅导讲义

求:(1) ;(2) ;(3)你会算 吗?
6.当x= 时,求 + 的值.(结果用最简二次根式表示)
教师评定:
1、学生上次作业评价:○好○较好○一般○差○没做作业
2、学生本次上课情况评价:○好○较好○一般○差
教师签字:
家长签字:___________
4.同学们,我们以前学过完全平方公式a2±2ab+b2=(a±b)2,你一定熟练掌握了吧!现在,我们又学习了二次根式,那么所有的正数(包括0)都可以看作是一个数的平方,如3=( )2,5=( )2,你知道是谁的二次根式呢?下面我们观察:
( -1)2=( )2-2·1· +12=2-2 +1=3-2
反之,3-2 =2-2 +1=( -1)2
例2.判断下列各式是否正确,不正确的请予以改正:
(1)
(2) × =4× × =4 × =4 =8
例3.已知 ,且x为偶数,求(1+x) 的值.
例4.观察下列各式,通过分母有理化,把不是最简二次根式的化成最简二次根式:
= = -1,
= = - ,
同理可得: = - ,……
从计算结果中找出规律,并利用这一规律计算
A.13 B. C.10 D.5
4.( -3 +2 )× 的值是().
A. -3 B.3 - C.2 - D. -
5.计算( + )( - )的值是().
A.2 B.3 C.4 D.1
二、填空题
1.在 、 、 、 、 、3 、-2 中,与 是同类二次根式的有________.
2.计算二次根式5 -3 -7 +9 的最后结果是________.
二次根式讲义

二次根式讲义 一、知识点梳理 1.二次根式式子)0(≥a a 叫做二次根式,二次根式必须满足:含有二次根号“”;被开方数a必须是非负数。
2.定义重点①式子有意义:)0(≥a a 中必须,否则,式子没有意义②隐含条件:)0(≥a a ,则,即也为非负数4. 二次根式的乘除运算b a ab ⋅=(00≥≥b a ,))0,0(≥≥=b a b ab a根式中分母不能含有根号,且要变为最简。
6.最简二次根式若二次根式满足:被开方数的因数是整数,因式是整式;被开方数中不含能开得尽方的因数或因式,这样的二次根式叫做最简二次根式。
化二次根式为最简二次根式的方法和步骤:(1)如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简。
(2)如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来。
三、典型例题讲解 例11、用代数式表示:(1)面积为S 的正方形的边长为______.(2)•面积为10•的直角三角形的两直角边的比为1:•2,•则这两条直角边分别为______.2、在二次根式1a -中,字母a 的取值范围是( )A .1<aB .1≤aC .1≥aD .1>a 3、下列式子中,是二次根式的有( )①22x +,②3x ,③32,④2()x -A .1个B .2个C .3个D .4个 4、(1)若0≥a ,则a _____0.(2)若021=++-x y ,则=x _____,=y ______. 5、求使式子有意义的实数x 的取值范围.(1)2x - (2)11x - 例21、计算:(1)=2)3(______;(2)=-2)52(_____. 2、下列式子正确的个数是( )①2)4(4±=;②3)3(2-=--;③1)2()3(22=-;④2)7(7=.A .1个B .2个C .3个D .4个3、在实数范围内分解因式792-a .解:=-=-222)7()3(79a a ( )·( )4、计算:(1)22=______.(2)2(5)-=_____; (3)2211010-==______.5、计算: (1)2(2)x -(2≤x ) (2)2(32)- (3)-2(3.14)π-例31、计算:(1)2×7=______.(2)12×8=______; (3)0.1×100=_______.2、下列运算不正确的是( )A .0.40.6⨯=0.2×0.6=1.2B .4×36=2×6=12C .0.4 3.60.4 3.6 1.44⨯=⨯===1.2D .a ·3=3a (0≥a ) 3、计算:(1)3×(-212) (2)2×6×13(3)2ab ·1b (4)-12xy ·(-4y )4、计算:(1)812=______;(2)126=_____.5、计算:(1)318÷2=_____;(2)293x y xy ÷=______. 例41、化简:(1)8=______;(2)1327=____.2、化简:(1)3a =_____;(2)2316x y =_____.3、化简:(1)56=______; (2)-125015⨯=______; (3)2332ab c=______;4、下列计算正确的是( )A .-1210×2=-1220B .y x xy x xy x 31313313=⋅=⋅C .112882887272⨯=⨯=4=2 D .534=5435、把38化为最简二次根式为_______.6、下列二次根式中,不是最简二次根式的是( )A .aB .31C .1x D .21a +四、举一反三 1.(2012义乌)一个正方形的面积是15,估计它的边长大小在( ) A .2与3之间 B .3与4之间 C .4与5之间 D .5与6之间2.(2012杭州)已知)212()33(-⨯-=m ,则有( )A .5<m <6B .4<m <5C .-5<m <-4D .-6<m <-5 3.(2012泰安)下列运算正确的是( )A .2(5)5-=- B .21()164--= C .632x x x ÷= D .325()x x =4.(2012德阳)使代数式12-x x有意义的x 的取值范围是( )A . 0≥xB .21≠x C .0≥x 且21≠x D .一切实数5.(2011山东菏泽)实数a 在数轴上的位置如图所示,则22(4)(11)a a -+- 化简后为( )A . 7B . -7C .152-aD . 无法确定6.(2011山东济宁)若0)3(12=++-+y y x ,则y x -的值为 ( )A .1B .-1C .7D .-77.(2011山东烟台)如果aa 21)12(2-=-,则( )A .21<a B. 21≤a C. 21>a D. 21≥a8.(2011山东日照)已知x ,y 为实数,且满足x +1y y ---1)1(=0,那么20112011y x -= .9. (2011山东枣庄)对于任意不相等的两个实数a 、b ,定义运算※如下:a※b =b a b a -+,如3※2=32532+=-.那么8※12= .10.已知a ,b ,c 为△ABC 的三边长,化简22()()a b c b a c +-+---a b c --.a 105第2题图第4题图 五、过关测试二次根式的定义 1、二次根式11x --有意义,则实数x 的取值范围为_____. 2、矩形面积为12cm 2,矩形的长与宽之比为3:2,则矩形长为_____cm ,宽为____cm . 3、无论实数x 取何值下列式子总有意义为( )A .2(1)x -- B .21x -+ C .21x + D .1x -4、如图所示,方格图中小正方形的边长为1,将方格图中阴影部分剪下来,再把剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( ) A .3 B .2 C .5 D .65、如图所示,在平面直角坐标系中,A (-2,3),B (-4,0),C (-2,0)是三角形的三个顶点,求三角形各边的长.6、已知1433b a --与114+-b a 互为相反数,试求a ,b 的值.7、已知x ,y 为实数,且y =1122x x -+-+12,求x ,y 的值.二次根式的性质1、计算:(1)=2)75(____________; (2)=-2)2(x ______.2、(1)当0≥x 时,=-2x ______________;(2)当0≤x 时,2x =______. 3、下列式子计算不正确的是( )A .3)3(2=B .a a =-2)((0≥a )C .2(32)-=3-2D .15)53(2-=- 4、计算:(1)22)3553()54(- (2)22(6)(8)-+-(3)2)52(494-⋅+ (4)2230.6--5、已知实数x 在数轴上的位置如图所示,化简2222(1)(2)x x x --+-.6、(改错题)计算:(2x -)2+2(3)x - 解:(2x -)2+2(3)x -=2-x +x -3 ① =-1 ②你认为上述解答过程是错在第_____步,为什么?并求出正确的结果.二次根式的乘法 1、计算:(1)-122×3=_____; (2)18×(-32)=_____. 2、计算:(1)110×110=______; (2)131x·3xy =______. 3、化简:(1)3a -=_____;(2)34m n (0<m )=______. 4、若)2)(1(21--=-⋅-x x x x .则x 的取值范围是( )A .1>xB .2≥xC .2>xD .1≥x 5、定义运算“@”运算法则,x@y@z =xyz ,则2@3@6值为( )A .3B .2C .6D .126、下列各等式成立的是( )A .45×25=85B .53×42=205C .43×32=75D ,53×42=20 7、已知2=a ,则200的值为( )A .a 2B .a 3C .a 10D .a 8 8、下列计算正确的是( )A .(121)(9)1219-⨯-=-⨯-=33B .23x =x 3C .(16)(25)1625-⨯-=⨯=20D .249x -=32-x 9、阅读解答题:因为23=223⨯=12 ①-23=2(2)3-⨯=12 ②所以23=-23 ③ 即2=-2导致以上出现错误的结果错因在第几步( ) A .① B .② C .③ D .④ 10、化简:(1)2000 (2)250a b (0<a ,0>b )(3)18×3220×(-1315) (4)627×(-23)(5)2xy ×12x (6)115×23×(-1210)11、计算(1)5xy ×(-323x y )×361y (2)32ab b ·(-323a b )·3ab(0<a ,0>b )(3))))((abx ax x a b x ab --- (0>a ,0>b ,0>x )12、将aa 1-括号外的因式a 移到括号内部.二次根式的除法及最简二次根式 1、计算:(1)49=_____________;(2)2764=______.2、计算:(1)0.680.17=__________;(2)328=______. 3、计算:(1)0.48=______;(2)512=_____. 4、若2211x xx x--=++,则x 取值范围为_______. 5、下列各式是最简二次根式为( ) A .15B .24C .28D .7326、如图所示,小芳想在墙壁上钉一个三角形架,•其中两直角边的长度之比为3:2,斜边长为520,则较短直角边的长度为( ) A .40 B .210 C .410 D .426 7、化去下列各式中根号内的分母正确的是( ) A .2225555== B .22151535=⨯ C .3333n n mn m m m ==(0>m ,0>n ) D .11aa a a===a 8、下列各式计算正确的是( )A .442939---==---=23B .238499==2132C .3163727÷= D .825=58 9、把下列二次根式化为最简二次根式: (1)338=_______; (2)712=_______;(3)2.11.0⋅=_______;(4)3273x =_______; 10、计算:(1)48÷(32·3)(2)43623x x ÷(3)3520÷(-136)(4)8243311、计算:(1)3223×(-1815)÷1225(2)-4318÷(28×1354)。
二次根式讲义 Word

二次根式及其运算概述:二次根式的概念、性质以及运算法则是根式运算的基础,在进行根式运算时,往往用到绝对值、整式、分式、因式分解,以及配方法、换元法、待定系数法等有关知识与解题方法。
知识盘点:1、二次根式的性质:2、二次根式的运算法则:(5)3、设a,b,c,d,m是有理数,且m不是完全平方数,则当且仅4、当两个含有二次根式的代数式相乘时,如果它们的积不含有二次根式,则这两个代数式互为有理化因式.典典例精析:例1 化简:点评:若根式中的字母给出了取值范围,则应在这个范围内进行化简;若没有给出取值范围,则应在字母允许取值的范围内进行化简.例2 化简:点评:两个题分母均含有根式,若按照通常的做法是先分母有理化,这样计算化简较繁.我们可以先将分母因式分解后,再化简.解法1 配方法.配方法是要设法找到两个正数x,y(x>y),使x+y=a,xy=b,则解法2 待定系数法.例4 化简:点评:(1)将被开方数的化成分母是2的分数就可以按例3的方法解决了,还要注意开方时考虑符号;(2)这是多重复合二次根式,可从里往外逐步化简。
例5:(2010湖北省荆门市)已知a =2b =2a b -的值. 点评:由于a+b 和ab 都是有理数,所以整体代人较为简便。
点评:考虑到被开方数的平方差特点待定系数法设原式为x ,两边平方可以使原式简化。
例7:化简441296222+--+-+++x x x x x x点评:本题的解法叫零点法,也叫分段讨论法,是解决绝对值题型的基本方法。
例8:设154-=a ,试求a a a 4223--的值。
点评:原式=a(a 2-2a-4)=a(a 2-2a+1)-5a ….通过配方巧妙解答,流畅自然。
例9:计算10121011101144++-++点评:设10,10,10424===a a a 则达到化繁为简之妙。
例10:已知a 、b 都是有理数,且347-是方程02=++b ax x 的解,求a+b 。
二次根式知识点讲义

第一章 二次根式知识点一: 二次根式的概念 知识点二:取值范围:二次根式()的双重非负性PS;单项式和多项式统称整式。
单项式:由数字与字母或字母与字母的相乘组成的代数式叫做单项式(单独的一个数字或字母也是单项式)形如()的式子叫做二次根式。
注:在二次根式中,被开放数可以是数,也可以是单项式、多项式、分式等代数式,但必须注意:因为负数没有平方根,所以是为二次根式的前提条件,如,,等是二次根式,而,等都不是二次根式。
例1下列各式13)-其中是二次根式的是_________(填序号). 例2、求下列二次根式中字母的取值范围(1)x x --+315;(2)22)-(x知识点三:与的异同点1、不同点:与表示的意义是不同的,表示一个正数a 的算术平方根的平方,而表示一个实数a 的平方的算术平方根;在中,而中a 可以是正实数,0,负实数。
但与都是非负数,即,。
因而它的运算的结果是有差别的,,而2、相同:当被开方数是非负数,即时,=;时,无意义,而.例3、(1)-2)3(; (2)2)32(; (3) 2)(b a + (a+b ≥0)知识点四 .最简二次根式:必须同时满足下列条件:⑴被开方数中不含开方开的尽的因数或因式;⑵被开方数中不含分母;⑶分母中不含根式。
例4、(1__ __;(2=___ __;(3=____;(40,0)x y≥≥=___ _;(5)_______420=-。
例5、在根式1) ,最简二次根式是()A.1) 2) B.3) 4) C.1) 3) D.1) 4)知识点五.二次根式的运算:PS把多项式中同类项合成一项,叫做合并同类项1同类二次根式:二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式底数幂相乘,底数不变,指数相加。
即:a m﹒a n=a m+n。
幂的乘方,底数不变,指数相乘。
(a m)n =a m n积的乘方,等于把积中的每个因式分别乘方,然后把所得的幂相乘。
二次根式讲义

7. 若 ,求 的值。
8、化简:
【例二】若y= + +2009,则x+y=
【例三】若a、b为实数,且满足|a-2|+ =0, 则b-a的 值为( )
A.2 B.0 C.-2 D.以上都不对
【例四】若 是二次根式,则字母a应满足的条件是( )
A. B. C. D.
3、化简
【例五】 的平方根是( )
A.5B. -5C.± D.±5
【例六】计算 +|-11|- ,正确的结果是( )
6、分母有理化
在二次根式的运算中,把分母中的根号化去的过程称为分母有理化。
方法一: (a≥0,b≥0)
方法二: (a≥0,b≥02、二次根式的化简和混合运算
三、经典例题
1、求二次根式的值
【例一】当x=-2时,二次根式 的值为_______.
2、利用二次根式非负性解题
满足:(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式。
4同类二次根式:
把几个二次根式化为最简二次根式,如果被开方数相同,那么这几个二次根式叫做同类二次根式。
5、二次根式的运算
(1)乘法 (a≥0,b≥0)
(2)除法运算: (a≥0,b>0)
(3)加减运算:先把各个二次根式化成最简二次根式,在合并同类二次根式。
2、(2013,永州)已知 ,则 的值为
A. 0 B. C. 1 D.2
3、(2013,上海)下列式子中,属于最简二次根式的是( )
4、(2012,陕西)计算: .
A. ;B. ;C. ;D. .
5、(2013,佛山)化简 的结果是( )
A. B. C. D.
二次根式基础讲义

二次根式复习讲义(MS )一、基础知识(一)二次根式的概念:(1)二次根式:式子a (a ≥0)叫做二次根式.(2)最简二次根式:①被开方数不含分母;②被开方数中不含能开得尽方的因数或因式.把满足这两个条件的二次根式,叫做最简二次根式。
(3)同类二次根式:化成最简二次根式后,如果被开方数相同。
,这几个二次根式就叫做同类二次根式.(4)分母有理化:把分母中的根号化去,叫做分母有理化。
(5)有理化因式:两个含有二次根式的代数式相乘,如果它们的积为有理式,我们说这两个代数式互为有理化因式.(6)代数式:用基本运算符号(加、减、乘、除、乘方和开方)把数和表示数的字母连接起来的式子叫代数式。
(二).同类二次根式:二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式。
(三)二次根式的性质.20)(0);,(0)0,(0),(0)0,0)____(0,0);a a a a a a a a a a b a b ≥=≥>⎧⎪===⎨⎪-<⎩=≥≥=≥>是一个非负数;(*)(三)二次根式的运算:(1)二次根式的加减:先将二次根式化成最简二次根式,然后合并同类二次根式。
(20,0,0)a b a b =≥≥=≥>注意:做乘法时要灵活运用乘法分式;做除法时,有时要写为分数形式,然后分母有理化; 化简时要注意a 的正负性,尤其是隐含的正负性.二、分类考点 二次根式的定义例: ) A 、6个 B 、5个 C 、4个 D 、3个练习:下列各式中,哪些是二次根式,哪些不是二次根式?1.求a 为何值时,下列各式有意义. (1)a a 212-+ (2)32-+a a (4)215.0-a练习1、 53+-x 的取值范围是 _________________练习2有意义的x 的取值范围是 _________________ 练习3、x x --+315的取值范围是 _________________练习4、若31-+a 在实数范围内有意义, 则a 满足的条件是( )A.2=aB. 2≥a C .4-≤a D. 2≥a 或4-≤a例1: 在根式1) ) A .1) 2) B .3) 4) C .1) 3) D .1) 4)例2.在二次根式45, 2x 3, 11, 54, x 4中,最简二次根式个数是( ) A .1个 B.2个 C.3个 D.4个例1.把下列各式中根号外的因式适当改变后移到根号里面(1)53- (2)3.010 (3)1832 (4)616 (5)2142-例2、将根号外的数移到根号内(1)33 (2)717(3)x 2 (4)x x 2练习1.计算化简(1)226061- (2)84252.0b a (3)b b 42-(4)b a 325(0<b ) (5)2211b a -(b a <)练习3.求值(1)当211=x 时,求2244x x x +--的值;(2)当3-=a 时,求4152+-⋅-a a a 的值.练习4.求值22)2()1(+--b a ,其中3,14==b a .练习5、10)21()2006(312-+---+;练习5、已知AB,试比较A 与B 的大小。
二次根式的讲解

二次根式的概念与性质一、知识结构:知识要点梳理知识点一:二次根式的概念一般地,我们把形如(a≥0)•的式子叫做二次根式,“”称为二次根号.要点诠释:二次根式的两个要素:①根指数为2;②被开方数为非负数.(1)被开方数的因数是整数,因式是整式;(2)被开方数中不含能开得尽方的因数或因式。
如不是最简二次根式,因被开方数中含有4是可开得尽方的因数,又如,,..........都不是最简二次根式,而,,5,都是最简二次根式。
(2) 3.同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式。
如, , 就是同类二次根式,因为=2,=3,它们与的被开方数均为2。
4.有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,则说这两个代数式互为有理化因式。
如与,a+与a-,-与+,互为有理化因式。
关于二次根式的概念,要注意以下几点:(1)从形式上看,二次根式是以根号“”表示的代数式,这里的开方运算是最后一步运算。
如,等不是二次根式,而是含有二次根式的代数式或二次根式的运算;(2)当一个二次根式前面乘有一个有理数或有理式(整式或分式)时,虽然最后运算不是开方而是乘法,但为了方便起见,我们把它看作一个整体仍叫做二次根式,而前面与其相乘的有理数或有理式就叫做二次根式的系数;(3)二次根式的被开方数,可以是某个确定的非负实数,也可以是某个代数式表示的数,但其中所含字母的取值必须使得该代数式的值为非负实数;(4)象“,”等虽然可以进行开方运算,但它们仍属于二次根式。
知识点二:二次根式的性质1.;2.;3.;4. 积的算术平方根的性质:;5. 商的算术平方根的性质:.(6)若,则。
注意与的逆用。
要点诠释:二次根式(a≥0)的值是非负数,其性质可以正用亦可逆用,正用时去掉根号起到化简的作用;逆用时可以把一个非负数写成完全平方的形式,有利于在实数范围内进行因式分解.要注意以下问题:(1)因为被开方数a2≥0(非负数),所以a可以取任意实数。
第三讲 二次根式讲义

第三讲 二次根式一、课标下复习指南 (一)二次根式的有关概念 1.二次根式形如)0(≥a a 的式子叫做二次根式.2.最简二次根式(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.满足上述两个条件的二次根式叫做最简二次根式. (二)二次根式的主要性质1.)0(≥a a 是一个非负数; 2.);0()(2≥=a a a 3.⎩⎨⎧<-≥==);0(),0(||2a a a a a a4.);0,0(≥≥⋅=b a b a ab5.);0,0(>≥=b a ba ba6.若a >b ≥0,则.b a >(三)二次根式的运算 1.二次根式的加减二次根式加减时,先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.2.二次根式的乘除二次根式相乘除,把被开方数相乘除,根指数不变. *3.分母有理化把分母中的根号化去,分式值不变,叫做分母有理化. 常用的二次根式的有理化因式:(1)a 与a 互为有理化因式;(2)b a +与b a -,一般的,b c a +与b c a -互为有理化因式;(3)b a +与b a -,一般的,b d a c +与b d a c -互为有理化因式. 二、例题分析例1 当x 为何值时,下列代数式有意义?.1)2(;322)1(232x x x x x -+----解 (1)欲使3222---x x x 有意义,只要使⎩⎨⎧=/--≥-.032,022x x x 即⎩⎨⎧≠-=/≥.31,2x x x 且 解得x ≥2且x ≠3. ∴当x ≥2且x ≠3时,3222---x x x 有意义.(2)欲使231x x -+-有意义,只要使-x 2≥0,解得x =0. ∴当x =0时,231x x -+-有意义.说明 代数式有意义的条件:分式有意义的条件是分式的分母不为零;二次根式有意义的条件是被开方数为非负数;由实际意义得到的代数式还要符合实际意义.例2 化简:(1);14962123xx x x x -+ *(2)已知1<x <2,化简122+-x x .442x x +-+ 解 (1)原式x x x x x x 4221-+=x x 23-=(2)∵1<x <2,∴x -1>0,2-x >0.224412x x x x +-++-∴22)2()1(x x -+-==|x -1|+|2-x |=(x -1)+(2-x )=1.说明 (1)二次根式的化简要考虑最简二次根式的两个条件,根号内是多项式时,要考虑是否是完全平方式;(2)化简2a 时,要考虑字母a 的取值范围;(3)在二次根式运算中,根号外的因式可以平方后作为被开方数的因式移进根号内,从而使运算简化.例3 计算:(1);22)8321464(÷+- (2)+⋅-+-5()625()2332(202.)6219 解 (1)原式22)262264(÷+-= .232+=(2)原式=5)(625[()1861212(-++-62561230)625()]6219-+-=-⋅+.61435-=说明 整式和分式的运算性质在二次根式的运算中同样适用,乘法公式、分配律、约分等都有可能简化运算过程,要根据式子的结构特征灵活使用.例4 已知xy =3,求yxyx y x+的值. 分析 因为xy =3,所以x ,y 同正或同负,要分情况讨论.解 当x >0,y >0时, 原式.322==+=xy xy xy 当x <0,y <0时,原式.322-=-=--=xy xy xy 综上可知,原式.32±= 三、课标下新题展示例5 若n 20是整数,则满足条件的最小正数n 为( ). A .2 B .3C .4D .5解 D .说明 对于二次根式的性质:||);0()(22a a a a a =≥=,会有多种形式进行考查,要熟练掌握.例6 对正实数a ,b ,定义,*b a ab b a +-=若4*x =44,则x 的值是______. 解 依题意,得.4444=+-x x 整理,得.484=+x x 变形,得.4912)(2=++x x.49)1(2=+∴x71=+∴x 或,71-=+x 6=x 或8-=x (舍).∴x =36.经检验,x =36是原方程的解. ∴x 的值是36.说明 此题考查了阅读理解能力、完全平方公式、二次根式的性质、配方法解方程,是一道代数综合题,要求每个基本知识点都熟练掌握. 四、课标考试达标题(一)选择题1.在根式⑤④③②①;2;15;;5223a b a a -2;12aa ⑥中,最简二次根式是( ). A .②③⑤ B .②③⑥C .②③④⑥D .①③⑤⑥2.如果最简根式a b b -3和22+-a b 是同类二次根式,那么a 、b 的值分别是( ).A .a =0,b =2B .a =2,b =0C .a =-1,b =1D .a =1,b =-23.下列各式中,运算正确的是( ). A .553322=+ B .236=÷ C .632=D .12233=-(二)填空题4.当x 满足______条件时,32++-x x在实数范围内有意义. 5.若式子|2|)1(2-+-x x 化简的结果为2x -3,则x 的取值范围是______. 6.已知x 为整数,且满足32≤≤-x ,则x =______.7.观察下列各式:=+=+412,312311514513,413=+…请你将发现的规律用含自然数n 的等式表示出来______.(n ≥1)(三)解答题 8.计算:.)2(xy yxxyxy ⋅+-9.化简:.)23(36329180-++--10.先化简,再求值:423)225(--÷---a a a a ,其中.33-=a*11.观察下列分母有理化的运算:-=+2121=+-=+321,23231,1,32-251+.,25 -= 从计算结果中找出规律,并利用这一规律计算:+++++++ 321231121().12010()200920101+⋅+参考答案第三讲 二次根式1.B . 2.A . 3.B . 4.-3≤x <0. 5.x ≥2. 6.-1,0,1. 7.21)1(21++=++n n n n . 8.xy -2y +x . 9.⋅2210.-2(a +3),.32- 11.2009.。
八年级二次根式 教师讲义带答案

第五章二次根式知识网络知识点一:二次根式的概念形如的式子叫做二次根式;注:在二次根式中,被开方数可以是数,也可以是单项式、多项式、分式等代数式,但必须注意:因为负数没有平方根,所以是为二次根式的前提条件,如,,等是二次根式,而,等都不是二次根式;知识点二:取值范围1. 二次根式有意义的条件:由二次根式的意义可知,当a≧0时,有意义,是二次根式,所以要使二次根式有意义,只要使被开方数大于或等于零即可;2. 二次根式无意义的条件:因负数没有算术平方根,所以当a﹤0时,没有意义;知识点三:二次根式的非负性表示a的算术平方根,也就是说,是一个非负数,即0;注:因为二次根式表示a的算术平方根,而正数的算术平方根是正数,0的算术平方根是0,所以非负数的算术平方根是非负数,即0,这个性质也就是非负数的算术平方根的性质,和绝对值、偶次方类似;这个性质在解答题目时应用较多,如若,则a=0,b=0;若,则a=0,b=0;若,则a=0,b=0;知识点四:二次根式的性质文字语言叙述为:一个非负数的算术平方根的平方等于这个非负数;注:二次根式的性质公式是逆用平方根的定义得出的结论;上面的公式也可以反过来应用:若,则,如:,.知识点五:二次根式的性质文字语言叙述为:一个数的平方的算术平方根等于这个数的绝对值;注:1、化简时,一定要弄明白被开方数的底数a是正数还是负数,若是正数或0,则等于a本身,即;若a是负数,则等于a的相反数-a,即;2、中的a的取值范围可以是任意实数,即不论a取何值,一定有意义;3、化简时,先将它化成,再根据绝对值的意义来进行化简;知识点六:与的异同点1、不同点:与表示的意义是不同的,表示一个正数a的算术平方根的平方,而表示一个实数a的平方的算术平方根;在中,而中a可以是正实数,0,负实数;但与都是非负数,即,;因而它的运算的结果是有差别的,,而2、相同点:当被开方数都是非负数,即时,=;时,无意义,而.知识点七:二次根式的运算1.二次根式的乘除运算1运算结果应满足以下两个要求:①应为最简二次根式或有理式;②分母中不含根号.2注意知道每一步运算的算理;3乘法公式的推广:2.二次根式的加减运算先化为最简二次根式,再类比整式加减运算,明确二次根式加减运算的实质;3.二次根式的混合运算1对二次根式的混合运算首先要明确运算的顺序,即先乘方、开方,再乘除,最后算加减,如有括号,应先算括号里面的;2二次根式的混合运算与整式、分式的混合运算有很多相似之处,整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用.要点诠释:怎样快速准确地进行二次根式的混合运算.1.明确运算顺序,先算乘方,再算乘除,最后算加减,有括号先算括号里面的;2.在二次根式的混合运算中,原来学过的运算律、运算法则及乘法公式仍然适用;3.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能收到事半功倍的效果.1加法与乘法的混合运算,可分解为两个步骤完成,一是进行乘法运算,二是进行加法运算,使难点分散,易于理解和掌握.在运算过程中,对于各个根式不一定要先化简,可以先乘除,进行约分,达到化简的目的,但最后结果一定要化简.例如进行化简,使计算繁琐,可以先根据乘法分配律进行乘法运算,43+=+=+通过约分达到化简目的;2多项式的乘法法则及乘法公式在二次根式的混合运算中同样适用.如:221+-=-=,利用了平方差公式.所以,在进行二次根式的混合运算时,借助乘法公式,会使运算简化. 4.分母有理化把分母中的根号化去,分式的值不变,叫做分母有理化.两个含有二次根式的代数式相乘,若它们的积不含二次根式,则这两个代数式互为有理化因式.常用的二次根式的有理化因式:2a a +-互为有理化因式;一般地a a +--互为有理化因式;一般地+-式.专题总结及应用一、知识性专题专题1 二次根式的最值问题专题解读涉及二次根式的最值问题,应根据题目的具体情况来决定应采用的方法,不能一概而论,但一般情况下利用二次根式的非负性来求解.例1 当x 取何值时,3的值最小最小值是多少分析 00,因为3是常数,3的最小值为3.0,33≥,∴当9x +1=0,即19x =-时,3有最小值,最小值为3.解题策略解决此类问题一定要熟练掌握二次根式的非负性,0a ≥0. 专题2 二次根式的化简及混合运算专题解读对于二次根式的化简问题,可根据定义,也可以利用||a =这一性质,但应用性质时,要根据具体情况对有关字母的取值范围进行讨论.例2 下列计算正确的是 分析 根据具体选项,应先进行化简,再计算. A 选项中,==B 选若可化为=,C 选项逆用平方差公式可求得2(=4-5=-1,而D 得22=.故选A.例3 计算2006200721)21)的结果是 分析 本题可逆用公式ab m=a m b m及平方差公式,将原式化为2006[(21)(21)]21)2 1.=故选D.例4 书知2228442142x x y x x x y y x x++=--+,求的值. 分析 本题主要利用二次根式的定义及非负性确定x 的值,但要注意所得x 的值应使分式有意义.解:由二次根式的定义及分式性质,得2240,4,2,20,x x x x ⎧-⎪-∴=⎨⎪+⎩≥≥0≠解题策略 本题中所求字母x 的取值必须使原代数式有意义. 例5 223541294-202522a a a a a -++-(≤≤).解题策略 本题应根据条件直接进行化简,2(0)||-(0).a a a a a a ⎧==⎨⎩≥,<例6 已知实数,a ,b ,c 在数轴上的位置如图21-8所示,化简222||()().a a c c a b -+-解:由a ,b ,c 在数轴上的位置可知:解题策略 利用间接给出的或隐含的条件进行化简时,要充分挖掘题目中的隐含条件,再进行化简.规律·方法 对于无约束条件的化简问题需要分类讨论,用这种方法解题分为以下步骤:首先,求出绝对值为零时未知数的值,这些未知数的值在数轴上的对应点称为零点;其次,以这些零点为分点,把数轴划分为若干部分,即把实数集划分为若干个集合,在每个集合中分别进行化简,简称“零点分区间法”.例8 已知3,12,.a ba b ab ba b a+=-=求的值 图21-8分析 这是一道二次根式化简题,在化为最简二次根式的过程中,要注意a ,b 的符号,本题中没明确告诉,a ,b 的符号,但可从a +b =-3,ab =12中分析得到.解:∵a +b =-3,ab =12,∴a <0,b <0.解题策略 本题最容易出现的错误就是不考虑a ,b 的符号,把所求的式子化简,直接代入.专题3 利用二次根式比较大小、进行计算或化简例9 的运算结果应在 A. 6到7之间 B. 7到8之间 C. 8到9之间D. 9到10之间分析 本题应计算出所给算式的结果,原式4==+,由于即2 2.5849+,所以<. 故选C.例10 已知m 是,n ,求m nm n-+的值. 解:∵9<13<16,即3 43,即m =3,3,即,∴m n m n -===+ 二、规律方法专题专题4 配方法专题解读 把被开方数配方,a |化简.例11 化简规律·方法一般地,对于a±型的根式,可采用观察法进行配方,即找出x,yx>y>0,使得xy=b,x+y=a,则2a±=,于是==,.例12 若a,b为实数,且b15,值.分析本题中根据b15可以求出a,b,对.解:由二次根式的性质得3503350..5305aa aa-⎧∴-=∴=⎨-⎩≥,≥,当3215.55a b====,时,原式解题策略对于形如22b a b aa b a b++-+或形式的代数式都要变为2()a bab+或2()a bab-的形式,当它们作为被开方式进行化简时,要注意.a b a b ab+-和以及的符号专题5 换元法专题解读通过换元将根式的化简和计算问题转化为方程问题.例13计算解:令x两边同时平方得:∴x2=33专题6 代入法专题解读通过代入求代数式的值.例14 已知22==a b ab2400,5760,.专题7 约分法专题解读通过约去分子和分母的公因式将第二次根式化简.例15 化简例16 化简).≠x y三、思想方法专题专题8 类比思想专题解读类比是根据两对象都具有一些相同或类似的属性,并且其中一个对象还具有另外某一些属性,从而推出另一对象也具有与该对象相同或相似的性质.本章类比同类项的概念,得到同类二次根式的概念,即把二次根式化简成最简二次根式后,若被开方数相同,则这样的二次根式叫做同类二次根式.我们还可以类比合并同类项去合并同类二次根式.例17 计算.解:1原式2原式=3+2.解题策略对于二次根式的加减法,应先将各式化为最简二次根式,再类比合并同类项的方法去合同类二次根式.专题9 转化思想专题解读当问题比较复杂难于解决时,一般应采取转化思想,化繁为简,化难为易,本章在研究二次根式有意义的条件及一些化简求值问题时,常转化为不等式或分式等知识加以解决.例18 函数y 24x -中,自变量x 的取值范围是 .分析 本题比较容易,主要考查函数自变量的取值范围的求法,24x -是二次根式,所以被开方数2x -4≥0,所以x ≥2.故填x ≥2.例19 如图21-9所示的是一个简单的数值运算程序,若输入x 3,则输出的数值为 .图21-9分析 本题比较容易,根据程序给定的运算顺序将问题化为二次根式求值问题,易知图中所表示的代数式为21x -,3-1=2.故填2.专题10 分类讨论思想专题解读 当遇到某些数学问题存在多种情况时,应进行分类讨论.本意在运用公式2||a a =进行化简时,若字母的取值范围不确定,应进行分类讨论.例20 若化简2|1|816x x x ---+25x -,则x 的取值范围是 A. x 为任意实数 B. 1≤x ≤4 C. x ≥1 D. x ≤4分析 由题意可知|1||4|25x x x ---=-,由此可知|1|1x x -=-,且|4|4x x -=-,由绝对值的意义可知10x -≥,且40x -≥,所以14x x ≤≤,即的取值范围是14x ≤≤.故选B.解题策略 2a |a |形式的式子的化简都应分类讨论.例21 如图21-10所示的是一块长、宽、高分别为7cm,5cm 和3cm 的长方体木块,一只蚂蚁要从长方体木块的一个顶点A 处,沿着长方体的表面爬到和顶点A 相对的顶点B 处吃食物,那么它要爬行的最短路径的长是多少分析 这是一个求最短路径的问题,一个长方体有六个面,蚂蚁有三种不同的爬行方法,计算时要分类讨论各种方法,进而确定最佳方案.解:沿前、右两个面爬,=cm. 沿前、上两个面爬,=cm. 沿左、上两个面爬,=cm.所以它要爬行的最短路径长为规律·方法 沿表面从长方体的一个顶点爬到相对的顶点去,共有三个爬行路线,每个路线长分别是它爬行两个展开图的对角线的长.二次根式单元测试题一判断题:每小题1分,共5分1.ab 2)2(-=-2ab .………………… 2.3-2的倒数是3+2. 3.2)1(-x =2)1(-x .… 4.ab 、31b a 3、bax 2-是同类二次根式.… 5.x 8,31,29x +都不是最简二次根式. 二填空题:每小题2分,共20分 6.当x __________时,式子31-x 有意义. 7.化简-81527102÷31225a= . 8.a -12-a 的有理化因式是____________.9.当1<x <4时,|x -4|+122+-x x =________________.10.方程2x -1=x +1的解是____________. 11.已知a 、b 、c 为正数,d 为负数,化简2222dc abd c ab +-=______.12.比较大小:-721_________-341.13.化简:7-522000·-7-522001=______________. 14.若1+x +3-y =0,则x -12+y +32=____________.15.x ,y 分别为8-11的整数部分和小数部分,则2xy -y 2=____________. 三选择题:每小题3分,共15分16.已知233x x +=-x 3+x ,则………………A x ≤0B x ≤-3C x ≥-3D -3≤x ≤017.若x <y <0,则222y xy x +-+222y xy x ++=……………………… A2x B2y C -2x D -2y18.若0<x <1,则4)1(2+-x x -4)1(2-+xx 等于……………………… A x2 B -x2 C -2x D2x19.化简aa 3-(a <0)得……………………………………………………………… A a - B -a C -a - D a20.当a <0,b <0时,-a +2ab -b 可变形为……………………………………… A 2)(b a + B -2)(b a - C 2)(b a -+- D 2)(b a ---四计算题:每小题6分,共24分 21.235+-235--;22.1145--7114--732+;23.a 2m n -m ab mn +m n n m ÷a 2b 2mn ; 24.a +ba abb +-÷b ab a ++a ab b --ab b a +a ≠b .五求值:每小题7分,共14分25.已知x =2323-+,y =2323+-,求32234232y x y x y x xy x ++-的值. 26.当x =1-2时,求2222ax x a x x+-++222222ax x x a x x +-+-+221ax +的值.六、 解答题:每小题8分,共16分 27.计算25+1211++321++431++…+100991+. 28. 若x ,y 为实数,且y =x 41-+14-x +21.求x y y x ++2-xyy x +-2的值. 一判断题:每小题1分,共5分 1、提示2)2(-=|-2|=2.答案×. 2、提示231-=4323-+=-3+2.答案×.3、提示2)1(-x =|x -1|,2)1(-x =x -1x ≥1.两式相等,必须x ≥1.但等式左边x 可取任何数.答案×. 4、提示31b a 3、bax 2-化成最简二次根式后再判断.答案√.5、29x +是最简二次根式.答案×. 二填空题:每小题2分,共20分6、提示x 何时有意义x ≥0.分式何时有意义分母不等于零.答案x ≥0且x ≠9.7、答案-2a a .点评注意除法法则和积的算术平方根性质的运用.8、提示a -12-a ________=a 2-22)1(-a .a +12-a .答案a +12-a . 9、提示x 2-2x +1= 2,x -1.当1<x <4时,x -4,x -1是正数还是负数 x -4是负数,x -1是正数.答案3.10、提示把方程整理成ax =b 的形式后,a 、b 分别是多少12-,12+.答案x =3+22.11、提示22d c =|cd |=-cd .答案ab +cd .点评∵ ab =2)(ab ab >0,∴ ab -c 2d 2=cd ab +cd ab -.12、提示27=28,43=48.答案<.点评先比较28,48的大小,再比较281,481的大小,最后比较-281与-481的大小. 13、提示-7-522001=-7-522000·_________-7-52.7-52·-7-52=1.答案-7-52.点评注意在化简过程中运用幂的运算法则和平方差公式. 14、答案40.点评1+x ≥0,3-y ≥0.当1+x +3-y =0时,x +1=0,y -3=0. 15、提示∵ 3<11<4,∴ _______<8-11<__________.4,5.由于8-11介于4与5之间,则其整数部分x =小数部分y =x =4,y =4-11答案5.点评求二次根式的整数部分和小数部分时,先要对无理数进行估算.在明确了二次根式的取值范围后,其整数部分和小数部分就不难确定了. 三选择题:每小题3分,共15分 16、答案D .点评本题考查积的算术平方根性质成立的条件,A 、C 不正确是因为只考虑了其中一个算术平方根的意义.17、提示∵ x <y <0,∴ x -y <0,x +y <0. ∴222y xy x +-=2)(y x -=|x -y |=y -x . 222y xy x ++=2)(y x +=|x +y |=-x -y .答案C .点评本题考查二次根式的性质2a =|a |.18、提示x -x 12+4=x +x 12,x +x 12-4=x -x 12.又∵ 0<x <1, ∴ x +x 1>0,x -x1<0.答案D .点评本题考查完全平方公式和二次根式的性质.A 不正确是因为用性质时没有注意当0<x <1时,x -x1<0.19、提示3a -=2a a ⋅-=a -·2a =|a |a -=-a a -.答案C . 20、提示∵ a <0,b <0,∴ -a >0,-b >0.并且-a =2)(a -,-b =2)(b -,ab =))((b a --. 答案C .点评本题考查逆向运用公式2)(a =aa ≥0和完全平方公式.注意A 、B 不正确是因为a <0,b <0时,a 、b 都没有意义. 四计算题:每小题6分,共24分21、提示将35-看成一个整体,先用平方差公式,再用完全平方公式. 解原式=35-2-2)2(=5-215+3-2=6-215. 22、提示先分别分母有理化,再合并同类二次根式. 解原式=1116)114(5-+-711)711(4-+-79)73(2--=4+11-11-7-3+7=1.23、提示先将除法转化为乘法,再用乘法分配律展开,最后合并同类二次根式. 解原式=a 2m n -m ab mn +m n n m ·221b a n m=21b n m m n ⋅-mab 1n m mn ⋅+22b ma n nmn m ⋅ =21b-ab 1+221ba =2221b a ab a +-.24、提示本题应先将两个括号内的分式分别通分,然后分解因式并约分. 解原式=ba ab b ab a +-++÷))(())(()()(b a b a ab b a b a b a b b b a a a -+-+-+--=b a b a ++÷))((2222b a b a ab b a b ab b ab a a -++----=b a b a ++·)())((b a ab b a b a ab +-+-=-b a +. 点评本题如果先分母有理化,那么计算较烦琐. 五求值:每小题7分,共14分25、提示先将已知条件化简,再将分式化简最后将已知条件代入求值. 解∵ x =2323-+=2)23(+=5+26, y =2323+-=2)23(-=5-26. ∴ x +y =10,x -y =46,xy =52-262=1.32234232yx y x y x xy x ++-=22)())((y x y x y x y x x +-+=)(y x xy y x +-=10164⨯=652. 点评本题将x 、y 化简后,根据解题的需要,先分别求出“x +y ”、“x -y ”、“xy ”.从而使求值的过程更简捷.26、提示注意:x 2+a 2=222)(a x +, ∴ x 2+a 2-x 22a x +=22a x +22a x +-x ,x 2-x 22a x +=-x 22a x +-x .解原式=)(2222x a x a x x-++-)(22222x a x x a x x -++-+221ax +=)()()2(22222222222x a x a x x x a x x a x x a x x -++-+++-+-=)()(22222222222222x a x a x x x a x x a x a x x x-++-+++++-=)()(222222222x a x a x x a x x a x -+++-+=)()(22222222x a x a x x x a x a x -++-++=x1.当x =1-2时,原式=211-=-1-2.点评本题如果将前两个“分式”分拆成两个“分式”之差,那么化简会更简便.即原式=)(2222x a x a x x-++-)(22222x a x x a x x -++-+221ax +=)11(2222a x xa x +--+-)11(22x x a x --++221a x +=x 1. 六、解答题:每小题8分,共16分27、提示先将每个部分分母有理化后,再计算.解原式=25+11212--+2323--+3434--+…+9910099100--=25+112-+23-+34-+…+99100- =25+11100- =925+1.点评本题第二个括号内有99个不同分母,不可能通分.这里采用的是先分母有理化,将分母化为整数,从而使每一项转化成两数之差,然后逐项相消.这种方法也叫做裂项相消法.28、提示要使y 有意义,必须满足什么条件].014041[⎩⎨⎧≥-≥-x x 你能求出x ,y 的值吗].2141[⎪⎪⎩⎪⎪⎨⎧==y x 解要使y 有意义,必须⎩⎨⎧≥-≥-014041[x x ,即⎪⎪⎩⎪⎪⎨⎧≥≤.4141x x ∴ x =41.当x =41时,y =21.又∵ xy y x ++2-xy y x +-2=2)(xy y x+-2)(xy y x -=|xy yx+|-|xy y x-|∵ x =41,y =21,∴y x <x y . ∴ 原式=x y y x +-y x x y +=2yx 当x =41,y =21时,原式=22141=2.点评解本题的关键是利用二次根式的意义求出x 的值,进而求出y的值.。
二次根式讲义

【知识回顾】1.二次根式:式子a (a ≥0)叫做二次根式。
2.最简二次根式:必须同时满足下列条件:⑴被开方数中不含开方开的尽的因数或因式; ⑵被开方数中不含分母; ⑶分母中不含根式。
3.同类二次根式:二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式。
4.二次根式的性质:(1)(a )2=a (a ≥0); (2)==a a 2 5.二次根式的运算:(1)因式的外移和内移:如果被开方数中有的因式能够开得尽方,那么,就可以用它的算术根代替而移到根号外面;如果被开方数是代数和的形式,那么先解因式, 变形为积的形式,再移因式到根号外面,反之也可以将根号外面的正因式平方后移到根号里面.(2)二次根式的加减法:先把二次根式化成最简二次根式再合并同类二次根式. (3)二次根式的乘除法:二次根式相乘(除),将被开方数相乘(除),所得的积(商)仍作积(商)的被开方数并将运算结果化为最简二次根式.=·(a≥0,b≥0);(b≥0,a>0). (4)有理数的加法交换律、结合律,乘法交换律及结合律, 乘法对加法的分配律以及多项式的乘法公式,都适用于二次根式的运算.【典型例题】 1.概念与性质例1下列各式1), 其中是二次根式的是_________(填序号).例2求下列二次根式中字母的取值范围(1)x x --+315;(2)22)-(x例3在根式1),最简二次根式是( ) A .1) 2) B .3) 4) C .1) 3) D .1) 4)例4已知:的值。
求代数式22,211881-+-+++-+-=x yy x x yy x x x y例5已知数a ,b ,若=b -a ,则 ( )A. a>bB. a<bC. a≥bD. a≤bab a b b ba a=22211,2)5,3)2,4)4,5)(),6)1,7)2153x a a a --+---+222;2);3);4)275xa b x xy abc +-2()a b -( >0)( <0)0 ( =0);2.二次根式的化简与计算例6将根号外的a移到根号内,得() A. ; B. -; C. -; D.例7把(a-b )-1a-b化成最简二次根式例8计算:例9先化简,再求值:,其中a=,b=.例10如图,实数a、b在数轴上的位置,化简:222()a b a b---3.比较数值(1)、根式变形法当0,0a b>>时,①如果a b>,则a b>;②如果a b<,则a b<。
二次根式及其运算知识讲义(解析版)
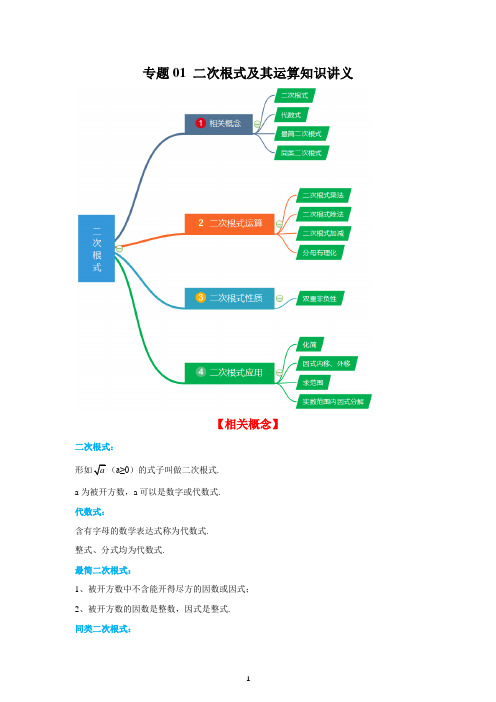
专题01 二次根式及其运算知识讲义【相关概念】二次根式:a≥0)的式子叫做二次根式.a为被开方数,a可以是数字或代数式.代数式:含有字母的数学表达式称为代数式.整式、分式均为代数式.最简二次根式:1、被开方数中不含能开得尽方的因数或因式;2、被开方数的因数是整数,因式是整式.同类二次根式:几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式.【二次根式运算】乘法=a≥0,b≥0)除法=(a≥0,b >0)加(减)法先把各根式化成最简根式,再合并同类根式分母有理化====【二次根式性质】,a≥0非负数:|a|,a 2n()()00a a a a ≥⎧=⎨-≤⎩2a =【二次根式应用】因式的内移和外移:(1)负号不能移到根号下;(2)根号下的负号不能移到根号外.【题型一】二次根式有意义条件例1. (2020·m 能取的最小整数值是()A .m = 0B .m = 1C .m = 2D .m = 3【答案】B.3m -1≥0,解得:m≥13, 所以,m 能取的最小整数值是1.故答案为:B .例2. (2020·=-,那么x 的取值范围是_______. 【答案】-3≤x≤0.【解析】解:∵233x x +-∴x≤0,且x+3≥0,解得:-3≤x≤0,故答案为:-3≤x≤0.例3.(2019·=x 的取值范围是______. 【答案】x≥2.=∴x≥0,x−2≥0,∴x≥2.故答案为:x≥2.【题型二】同类二次根式例4. (2020·是同类二次根式,那么满足条件的m 中最小正整数是________.【答案】4.【解析】解:当5m+8=7时,m=-15,不合题意,,即5m+8=28时,m=4,是同类二次根式,那么m 的最小正整数是4,故答案为:4.例5. mn =_________.【答案】10.∴n=2,2m-5=5,∴m=5,n=2∴mn=10故答案为:10.例6. mn=________.【答案】21.∴1221343nm m-=⎧⎨-=-⎩,解得,73mn=⎧⎨=⎩,∴mn=21故答案为:21.【题型三】变式考查例7. (2020·浙江宁波市期中)我们把形如b(a,b为最简二次根式)32是()A型无理数B C型无理数D型无理数【答案】B.【解析】解:2故答案为:B.例8. (1n所有可能的值;(2是整数,求正整数n的最小值.【答案】(1)自然数n 的值为2、9、14、17、18;(2)正整数n 的最小值为6.【解析】解:(1是整数,∴18-n=0或1或4或9或16,解得:n=18或17或14或9或2,则自然数n 的值为2,9,14,17,18;(2=是整数,n 为正整数,∴正整数n 的最小值为6.例9.(2020·21x =-,则x=__________. 【答案】12或1.21x =-,∴2x-1=0或2x-1=1,解得:x=12或x=1. 故答案为12或1. 【题型四】二次根式运算例10.(2020·周长为( )A .B .C .D .无法确定【答案】A.若,,则周长为若,∴,此三角形不存在,∴个三角形的周长为故答案为:A .例11)2211-.)2211--1313=--+-=例12.(2020·福建省泉州月考)已知1x =,x 的整数部分为a ,小数部分为b ,求a b的值..【解析】解:∵3,∴+1<4,故a=3,-2,∴)3232274a b ====-. 例13.(2020·广东佛山市月考)先阅读,再解答:由222=-= 可以看出,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式,在进行二次根式计算时,利用有理化因式,有时可以化去分母中的根号,例如:==,请完成下列问题:1的有理化因式是;(2)= .(直接写结果)>或<)(4)利用你发现的规律计算下列式子的值:)1+【答案】(1+1;(2);(3)<;(4)2017.【解析】解:(1+1;(2333==+;(3=>(4)原式=)120181+=)11=2018-1=2017.例14. 若a,b都是正整数,且a<b是可以合并的二次根式,是否存在a,b,=a,b的值;若不存在,请说明理由.【答案】当a=3,b=48;当a=12,b=27.,m、n为正整数,m<n,∴m=1,n=4或m=2,n=3故a=3,b=48或a=12,b=27.例15.(2019·辽宁大连市期中)[观察]请你观察下列式子的特点,并直接写出结果:11112=+-=;11123=+-=;11134=+-=;……[发现]根据你的阅读回答下列问题:(1)请根据上面式子的规律填空:=(n为正整数);(2)请证明(1) 中你所发现的规律.[应用]请直接写出下面式子的结果:11n++=.【答案】[观察]32,76,1312;[发现](1)1111n n+-+或221n nn n+++;(2)证明见解析;[应用]221n nn++.【解析】[观察]32,76,1312,[发现](1)1111n n+-+或221n nn n+++(2)左边=====∵n 为正整数,∴()11111011n n n n +-=+>++ ∴左边=右边[应用11n +++111111111111223341n n =+-++-++-+++-+…… 1111n n =⨯+-+ 1n n n =++ 22=1n n n ++. 【题型五】化简求值例16. (2021·江苏南通市期末)化简2+的结果是( ) A .152x -B .1-C .27x -D .1 【答案】A.【解析】解:∵二次根式被开方数为非负数,∴7-x≥0,则x≤7∴x-8<0,原式=7-x+8-x=15-2x故答案为:A .例17.(2020·浙江杭州期中)实数a ,b 在数轴上的位置如图,||a b -的结果为( )A .2aB .2a -C .2bD .2b -【答案】B.【解析】解:由题意得:a >b ,|a |<|b |,a >0,b <0,∴a -b >0,a +b <0,∴原式=-a -b -a +b =-2a ,故答案为:B .例18.若数轴上表示数x 的点在原点的左边,则化简3x + ) A .4x - B .4x C .2x - D .2x【答案】C.【解析】解:∵数x 的点在原点的左边,∴x <0,∴原式=|3x +|x ||=|3x -x |=|2x |=-2x .故答案为:C .例19.(2020·温州月考)下列四个式子中,与(a -的值相等的是() AB .CD .【答案】D.【解析】解:由题意得:2021-a>0,得:a<2021,∴a-2021<0,∴原式=(2021a --== 故答案为:D . 例20.下列给出的四个命题:①若a b = ,则a a b b =;②若a 2﹣5a+5=01a =- ;③(1a -=其中是真命题是【答案】②.【解析】解:①当a=-1,b=1时,命题不成立,是假命题,②a 2=5a-5,∴5a-5≥0,即a≥1,,是真命题;③(a -==,是假命题, 故答案为:②.【题型六】阅读材料例21.(2021·北京延庆区期末)我们规定用(a ,b )表示一对数对.给出如下定义:记m=,n = a > 0,b > 0),将(m ,n )与(n ,m )称为数对(a ,b )的一对“对称数对”.例如:(4,1)的一对“对称数对”为(12,1)和(1,12); (1)数对(9,3)的一对“对称数对”是 ;(2)若数对(3,y )的一对“对称数对”相同,则y 的值为 ;(3)若数对(x ,2)的一个“对称数对”,1),则x 的值为 ;(4)若数对(a ,b )的一个“对称数对”,,求ab 的值.【答案】(1)1(3与1)3, ;(2)13;(3)1 ;(4)16或6.【解析】解:(1)由题意得13=,∴数对(9,3)的一对“对称数对”是1(3与1)3,;(2)由题意得,∴数对(3,y )的一对“对称数对”为⎝与⎭, ∵数对(3,y )的一对“对称数对”相同,= ∴y=13;(3)∵数对(x ,2)的一对“对称数对”是与而数对(x ,2)的一个“对称数对”,1), 1=, ∴x=1;(4)∵数对(a ,b)的一对“对称数对”是与,而数对(a ,b)的一个“对称数对”是,==1,183a b == ∴11863ab =⨯=;==1,318a b ==, ∴113186ab =⨯=,综上所述,16ab =或6ab =. 例22. 阅读理解:二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式..11==. 类比应用:(1= ; (29++=+ . 拓展延伸:的矩形叫黄金矩形.如图①,已知黄金矩形ABCD 的宽AB =1. (1)黄金矩形ABCD 的长BC = ;(2)如图②,将图①中的黄金矩形裁剪掉一个以AB 为边的正方形ABEF ,得到新的矩形DCEF ,猜想矩形DCEF 是否为黄金矩形,并证明你的结论;(3)在图②中,连结AE ,则点D 到线段AE 的距离为 .【答案】类比应用:(1);(2)2;拓展延伸:(1)12;(2)矩形DCEF为黄金矩形,理由见解析;(3【解析】解:类比应用:(1)根据题意可得:== (2)根据题意可得:9++(9+++19-+-1=2;拓展延伸:(1的矩形叫黄金矩形, 若黄金矩形ABCD 的宽AB =1,则黄金矩形ABCD 的长BC; (2)矩形DCEF 为黄金矩形,理由是:由裁剪可知:AB=AF=BE=EF=CD=1,根据黄金矩形的性质可得:AD=BC=1=∴FD=EC=AD-AF=112-=12,∴DF EF =11122÷=,故矩形DCEF 为黄金矩形;(3)连接AE ,DE ,过D 作DG ⊥AE 于点G ,∵AB=EF=1,,∴=在△AED 中,S △AED =1122AD EF AE DG ⨯⨯=⨯⨯,即AD EF AE DG ⨯=⨯1DG =,解得∴点D 到线段AE 的距离为4+. 例23. (2019·四川月考)阅读下列材料,然后回答问题.一样的式子,其实我们还可以将其进一步化简:====1以上这种化简的步骤叫做分母有理化.②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 a +b =2,ab = -3 ,求 a 2 + b 2 .我们可以把a +b 和ab 看成是一个整体,令 x =a +b , y = ab ,则 a 2 + b 2 = (a + b)2 - 2ab = x 2- 2y = 4+ 6=10.这样,我们不用求出a ,b ,就可以得到最后的结果.(1...+(2)已知 m 是正整数, ab且 2a 2+ 1823ab + 2b 2 = 2019 .求 m . (31=【答案】(1)12;(2)2;(3)9. 【解析】解:(1)原式12019+2222=+++2019++== (2)∵ab∴=2(2m+1),=1∵2a 2+ 1823ab + 2b 2 = 2019∴2(a 2+b 2)+1823=2019∴a 2+b 2=98∴4(2m+1)2=100∴m=2或m=-3∵m是正整数∴m=2.(31=,得:21=20=2281=-+=0≥≥.例24.(2020·湖南怀化市期末)同学们,我们以前学过完全平方公式222)2(a ab b a b ±+=±,你一定熟练掌握了吧!现在,我们又学习了二次根式,那么所有的非负数(以及0)都可以看作是一个数的平方,如23=,25=,下面我们观察:)2221211213=-⨯=-=-23211)-=-=,∴231)-=1= 求:(1;(2(3=,则m 、n 与a 、b 的关系是什么?并说明理由.【答案】(11;(21;(3)m+n=a ,mn=b ,理由见解析.【解析】解:(11;(21==;(3)m+n =a ,mn =b.=∴2a =+,∴,∴m+n =a ,mn =b.例25.(2020·安徽安庆市)阅读理解题,下面我们观察:2221)211213=-⨯=-=-反之23211)-=-=,所以231)-=1= 完成下列各题:(1)在实数范围内因式分解:(2(3.【答案】(1)2(1+;(21;(3【解析】解:(1)22231(1+=+=+(21==(3==。
专题02 二次根式【课件精讲】

A.2 3 B.3
C.2 2 D.2
【答案】A 【分析】将被开方数 12 写成平方数 4 与 3 的乘积,再将 4 开出来为 2,易知化简 结果为 2 3 .
【详解】解: 12 43 22 3 =2 3 ,
故选:A.
3.下列各式中与 3 是同类二次根式的是(
)
A. 6 B. 9 C. 12 D. 18
(3)
2
3 1
3 2
3
2 ;(4)
8
2
18
24
1 6
3
【答案】(1) 5
2 ;(2)
2 ;(3) 3 2
3 ;(4)5 11 2
6
【分析】(1)先化为最简二次根式,再计算加减法;
(2)先算乘方和开方,去绝对值,再算加减法;
(3)利用完全平方公式和平方差公式展开,再合并计算;
1 x2
1 y2
1 z2
11 xy
1 z
(结论不需要证明)
例如: 1 22
1 32
1 52
1 22
1 32
(
1 5)2
11 1 2 3 (5)
19 30
根据以上阅读,请解决下列问题:
【基础训练】(1)求
1 12
1 22
1 32
的值;
S
【能力提升】(2)设
1
1 12
1 22
1
1 22
1 32
1
1 20192
03
考点ห้องสมุดไป่ตู้解
【考点1】二次根式的概念
【例 1】(2022·江苏连云港)函数 y x 1中自变量 x 的取值范围是( ) A. x 1 B. x 0 C. x 0 D. x 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次根式讲义-CAL-FENGHAI.-(YICAI)-Company One1二次根式复习讲义知识点一:二次根式的概念【知识要点】二次根式的定义: 形如的式子叫二次根式,其中a 叫被开方数,只有当a 是一个非负数时,才有意义.【典型例题】【例1】下列各式1)22211,2)5,3)2,4)4,5)(),6)1,7)2153x a a a --+---+, 其中是二次根式的是_________(填序号).举一反三:1、下列各式中,一定是二次根式的是( )A 、aB 、10-C 、1a +D 、21a +2、在a 、2a b 、1x +、21x +、3中是二次根式的个数有______个.【例2】若式子3x -有意义,则x 的取值范围是 . 举一反三: 1、使代数式43--x x 有意义的x 的取值范围是( ) A 、x>3 B 、x ≥3C 、 x>4D 、x ≥3且x ≠4 2、如果代数式mn m 1+-有意义,那么,直角坐标系中点P (m ,n )的位置在( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限【例3】若y=5-x +x -5+2009,则x+y=解题思路:式子a (a ≥0),50,50x x -≥⎧⎨-≥⎩ 5x =,y=2009,则x+y=2014 举一反三:111x x --2()x y =+,则x -y 的值为( )A .-1B .1C .2D .32、若x 、y 都是实数,且y=4x 233x 2+-+-,求xy 的值【例4】已知a b 是12a b ++的值。
举一反三:1、若3的整数部分是a ,小数部分是b ,则=-b a 3 。
知识点二:二次根式的性质 【知识要点】1. 非负性:a a ()≥0是一个非负数.注意:此性质可作公式记住,后面根式运算中经常用到.2. ()()a a a 20=≥.注意:此性质既可正用,也可反用,反用的意义在于,可以把任意一个非负数或非负代数式写成完全平方的形式:a a a =≥()()203. a a a a a a 200==≥-<⎧⎨⎩||()() 注意:(1)字母不一定是正数.(2)能开得尽方的因式移到根号外时,必须用它的算术平方根代替.(3)可移到根号内的因式,必须是非负因式,如果因式的值是负的,应把负号留在根号外.4. 公式a a a a a a 200==≥-<⎧⎨⎩||()()与()()a a a 20=≥的区别与联系 (1)a 2表示求一个数的平方的算术根,a 的范围是一切实数.(2)()a 2表示一个数的算术平方根的平方,a 的范围是非负数.(3)a 2和()a 2的运算结果都是非负的.【典型例题】题型一:二次根式的双重非负性【例5】若()2240a c --=,则=+-c b a .举一反三:1、若0)1(32=++-n m ,则m n +的值为 。
二次根式的性质2 (公式)0()(2≥=a a a 的运用)【例6】化简:21a -+的结果为( )A 、4—2aB 、0C 、2a —4D 、4举一反三:1、在实数范围内分解因式:429__________,2__________x x -=-+= 二次根式的性质3 (公式⎩⎨⎧<-≥==)0a (a )0a (a a a 2的应用) 【例7】已知2x <,)A 、2x -B 、2x +C 、2x --D 、2x -举一反三: 1( )A .-3B .3或-3C .3D .92、若a -3<0,则化简a a a -++-4962的结果是( )(A) -1 (B) 1 (C) 2a -7 (D) 7-2a【例8】如果表示a ,b 两个实数的点在数轴上的位置如图所示,那么化简│a -b │+ 的结果等于( )A .-2bB .2bC .-2aD .2a举一反三:实数a 在数轴上的位置如图所示:化简:1______a -=.【例9】化简1x -2x -5,则x 的取值范围是()(A )x 为任意实数 (B )1≤x ≤4 (C ) x ≥1 (D )x ≤10 o ba举一反三:若代数式2,则a 的取值范围是( )(A )4a ≥(B )2a ≤ (C )24a ≤≤ (D )2a =或4a = 【例10】化简二次根式22a a a +-的结果是( ) (A )2--a (B)2---a (C)2-a (D)2--a举一反三:1、把二次根式a a -1化简,正确的结果是( ) A. -aB. --aC. -aD.a 知识点三:最简二次根式和同类二次根式【知识要点】1、最简二次根式:最简二次根式的定义:①被开方数是整数,因式是整式;②被开方数中不含能开得尽方的数或因式. 2、同类二次根式(可合并根式):几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式,即可以合并的两个根式。
【典型例题】 下列根式中,不是..最简二次根式的是( )AB C . 21 D【例11】举一反三:1、下列根式不是最简二次根式的是( )2、在根式,最简二次根式是( ) A .1) 2) B .3) 4) C .1) 3) D .1) 4)3、把下列各式化为最简二次根式: (1)12 (2)b a 245【例12】下列根式中能与3是合并的是( ) A.8 B. 27 5 D.21 举一反三:1、下列各组根式中,是可以合并的根式是( )A 2、在二次根式:①12;② 32;③32;④27中,能与3合并的二次根式是 。
知识点四:二次根式计算——分母有理化【知识要点】1.分母有理化 定义:把分母中的根号化去,叫做分母有理化。
2.有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,就说这两个代数式互为有理化因式。
有理化因式确定方法如下:a =b a -与b a -等分别互为有理化因式。
②两项二次根式:利用平方差公式来确定。
如a 与a3.分母有理化的方法与步骤:①先将分子、分母化成最简二次根式;②将分子、分母都乘以分母的有理化因式,使分母中不含根式;③最后结果必须化成最简二次根式或有理式。
【典型例题】【例13】 把下列各式分母有理化(1(2 (3(4)【例14】把下列各式分母有理化:(1(2(3举一反三:1、已知x =,y =,求下列各式的值:(1)x y x y +-(2)223x xy y -+知识点五:二次根式计算——二次根式的乘除【知识要点】1.积的算术平方根的性质:积的算术平方根,等于积中各因式的算术平方根的积。
2.二次根式的乘法法则:两个因式的算术平方根的积,等于这两个因式积的算术平方根。
3.商的算术平方根的性质:商的算术平方根等于被除式的算术平方根除以除式的算术平方根4.二次根式的除法法则:两个数的算术平方根的商,等于这两个数的商的算术平方根。
注意:乘、除法的运算法则要灵活运用,在实际运算中经常从等式的右边变形至等式的左边,同时还要考虑字母的取值范围,最后把运算结果化成最简二次根式.【典型例题】【例15】化简(1)1525⋅32⨯【例16】化简: )0,0(≥>b a )0,0(>≥y x知识点六:二次根式计算——二次根式的加减【知识要点】需要先把二次根式化简,然后把被开方数相同的二次根式(即同类二次根式)的系数相加减,被开方数不变。
注意:对于二次根式的加减,关键是合并同类二次根式,通常是先化成最简二次根式,再把同类二次根式合并.但在化简二次根式时,二次根式的被开方数应不含分母,不含能开得尽的因数. 【典型例题】【例17】计算(1) (2)⎛- ⎝;【例18】(3)3213273108334a a a a a a a -+- (4)114a a b b a b ⎛⎫+-- ⎪ ⎪⎝⎭【例19】1、a b b a ab b 3)23(235÷-⋅ 2、 132x y ·(-42y x )÷162x y3、673)32272(-⋅++4、1110)562()562(+-)【例20】求的值.知识点七:根式比较大小【知识要点】1、根式变形法 当0,0a b >>时,①如果a b >a b >a b <,则a b <2、平方法 当0,0a b >>时,①如果22a b >,则a b >;②如果22a b <,则a b <。
3、分母有理化法 通过分母有理化,利用分子的大小来比较。
4、分子有理化法 通过分子有理化,利用分母的大小来比较。
5、倒数法6、媒介传递法 适当选择介于两个数之间的媒介值,利用传递性进行比较。
【典型例题】【例21】 比较的大小。
【例22】【例23】【例24】33的大小。
