参考范围-运筹学2018-2019-1
2019年青岛大学全日制博士研究生招生考试参考范围

2019年全日制博士生入学考试参考范围物理科学学院:070200物理学:考试范围:《固体物理学》路栋,第一版,2006年,上海科技出版社;《材料科学基础》张联盟,第一版,2004年,武汉理工大学出版社;《无机材料物理性能》关振铎,第一版,1992年,清华大学出版社;《量子力学教程》周世勋,第二版,2009年,高等教育出版社加试科目:热力学:《热力学统计物理(1—4章)》汪志诚,第三版,2001年,高教出版社。
材料分析测试方法:《材料近代分析测试方法》,常铁军,哈尔滨工业大学出版社,1999年。
统计物理:《热力学统计物理(6—9章)》汪志诚,第三版,2001年,高教出版社。
物理化学:《物理化学》傅献彩,第四版,2000年,高教出版社。
经济学院:0202应用经济学经济学主要参考书目:1、平狄克等著,李彬等译,《微观经济学》(第八版),中国人民大学出版社,2013.6;2、多恩布什等著,王志伟译,《宏观经济学》(第十版),中国人民大学出版社,2010.1。
计量经济学主要参考书目:1、李子奈、潘文卿著,《计量经济学》(第四版),高等教育出版社,2015.9;2、达摩达尔·N·古扎拉蒂、唐·C·波特著,费剑平改编,《计量经济学基础》(第五版),中国人民大学出版社,2011.6。
加试科目:1、国际经济学李坤望主编,《国际经济学》(第三版),高等教育出版社,2010.6。
2、统计学李洁明、祁新娥著,《统计学原理》(第六版),复旦大学出版社,2014.1。
商学院:120100管理科学与工程参考用书:1、高级微观经济学:参考书目——(美)范里安著,费方域等译,《微观经济学》:现代观点(第八版),格致出版社,2011年1月。
考试范围:供求均衡机制、生产与成本理论、厂商理论、非完全竞争理论、博弈论及其应用、经济机制设计理论、微观主体行为最优化理论、要素市场理论、福利经济学等。
2、运筹学:参考书目——《运筹学》,运筹学教材编写组编,清华大学出版社(第三版),2006。
硕士研究生入学考试《运筹学》考试大纲

硕士研究生入学考试《运筹学》考试大纲
一、考试性质
运筹学是交通运输工程专业硕士生选考的一门专业基础课程。
它的评价标准是优秀本科毕业生能达到的水平,以保证被录取者具有较好的运筹学理论基础。
二、考试形式与试卷结构
1、答卷方式:闭卷,笔试。
2、题型:填空、判断、计算、应用。
3、内容:线性规划基本概念,单纯形法,对偶原理,灵敏度分析,运输模型,整数规划,动态规划,图论与网络分析,目标规划,排队论。
4、参考书目:《管理运筹学》,韩大卫编,大连理工大学出版社,2011年版。
三、考查要点
1、线性规划的基本性质
会建立线性规划问题的数学模型;理解可行解、可行域、最优解、最优值、基本解等概念,了解线性规划解的性质。
2、单纯形法、对偶原理、灵敏度分析
会用单纯形法求解线性规划问题,掌握线性规划的对偶关系及对偶性质,掌握灵敏度分析的思想、方法。
3、运输模型
运输问题及其数学模型,会对有关应用问题建立模型;表上作业法的应用。
4、整数规划
整数规划问题及其数学模型;整数规划的一般解法;OT规划的分支定界法;指派问题及其解法。
5、动态规划
动态规划的基本概念;离散确定性典例。
6、网络分析
最小树问题的解法;最短路问题的标号算法;最大流问题的标号算法;最小费用最大流的求法。
7、排队论
排队论基本概念;指数服务排队模型的解法;其他模型。
8、目标规划
目标规划的模型、解法及应用。
南开大学运筹学(人工智能学院)考研大纲2018年与2019年对比一览表

南开大学运筹学(人工智能学院)考研大纲2018年与2019年对比一览表
南开大学运筹学(计控学院)2019年考研大纲已经公布,但是考研的同学都清楚何如利用吗?考研大纲是目标院校唯一官方指定的硕士研究生入学考试命题的唯一依据,是规定研究生入学考试相应科目的考试范围、考试要求、考试形式、试卷结构等权威指导性文件。
考研大纲作为唯一官方的政策指导性文件在专业课备考中的作用是不言而喻的。
然而,各大高校的考试大纲均在9月中旬左右才公布,对参照前一年的考研大纲已经复习大半年的莘莘学子来说可谓姗姗来迟。
借此,我们天津考研网特别推出考研大纲的对比、变化情况的系列专题,及时反映相关的考研动态,以此来消除学子们的复习误区;使学子们尽早捕捉到官方的细微变化。
为考研之路保驾护航!
以上是南开大学808运筹学(计控学院)2018年与2019年考研大纲的对比情况,从对比文件可以看出,南开大学808运筹学(计控学院)的考研大纲基本没有发生变化。
所以,报考目标院校目标专业的研友们可以安心的按照已定计划去复习备考,在报考的时候请注意。
南开大学808运筹学(计控学院)考研资料请到天津考研网官网咨询查看。
运筹学基础及应用课后习题答案(第一二章习题解答)

运筹学基础及应用课后习题答案(第一二章习题解答)第一章:线性规划一、选择题1. 线性规划问题中,目标函数可以是()A. 最大化B. 最小化C. A和B都对D. A和B都不对答案:C解析:线性规划问题中,目标函数可以是最大化也可以是最小化,关键在于问题的实际背景。
2. 在线性规划问题中,约束条件通常表示为()A. 等式B. 不等式C. A和B都对D. A和B都不对答案:C解析:线性规划问题中的约束条件通常包括等式和不等式两种形式。
二、填空题1. 线性规划问题的基本假设是______。
答案:线性性2. 线性规划问题中,若决策变量个数和约束条件个数相等,则该问题称为______。
答案:标准型线性规划问题三、计算题1. 求解以下线性规划问题:Maximize Z = 2x + 3ySubject to:x + 2y ≤ 83x + 4y ≤ 12x, y ≥ 0答案:最优解为 x = 4, y = 2,最大值为 Z = 14。
解析:画出约束条件的图形,找到可行域,再求目标函数的最大值。
具体步骤如下:1) 将约束条件化为等式,画出直线;2) 找到可行域的顶点;3) 将顶点代入目标函数,求解最大值。
第二章:非线性规划一、选择题1. 以下哪个方法适用于求解非线性规划问题()A. 单纯形法B. 拉格朗日乘数法C. 柯西-拉格朗日乘数法D. A和B都对答案:B解析:非线性规划问题通常采用拉格朗日乘数法求解,单纯形法适用于线性规划问题。
2. 非线性规划问题中,以下哪个条件不是K-T条件的必要条件()A. 梯度条件B. 正则性条件C. 互补松弛条件D. 目标函数为凸函数答案:D解析:K-T条件包括梯度条件、正则性条件和互补松弛条件,与目标函数是否为凸函数无关。
二、填空题1. 非线性规划问题中,若目标函数和约束条件都是凸函数,则该问题称为______。
答案:凸非线性规划问题2. 非线性规划问题中,K-T条件是求解______的必要条件。
运筹学实验报告五最优化问题

2018-2019学年第一学期《运筹学》实验报告(五)班级:交通运输171学号: **********姓名: *****日期: 2018.12.6654321m in x x x x x x z +++++=..ts 6,...,2,1,0302050607060655443322116=≥≥+≥+≥+≥+≥+≥+i x x x x x x x x x x x x x x i i 均为整数,且实验一:一、问题重述某昼夜服务的公共交通系统每天各时间段(每4个小时为一个时段)所需的值班人数如下表所示。
这些值班人员在某一时段开始上班后要连续工作8个小时(包括轮流用膳时间)。
问该公交系统至少需要多少名工作人员才能满足值班的需要?设该第i 班次开始上班的工作人员的人数为x i 人,则第i 班次上班的工作人员将在第(i+1)班次下班。
(i=1,2,3,4,5,6)三、数学模型四、模型求解及结果分析Global optimal solution found.Objective value: 150.0000Objective bound: 150.0000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 4Variable Value Reduced CostX1 60.00000 1.000000X2 10.00000 1.000000X3 50.000001.000000X4 0.000000 1.000000X5 30.00000 1.000000X6 0.000000 1.000000Row Slack or Surplus DualPrice1 150.0000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 10.00000 0.0000007 0.000000 0.000000根据Lingo程序运行结果分析可知:当第i班次开始上班的工作人员排布如下时,所需人力最少,为150人。
贵州大学2022年硕士研究生招生考试自命题科目参考书目
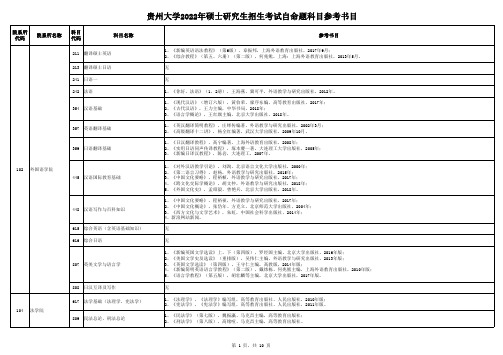
1、《普通生物化学》,陈钧辉、张冬梅编著,高等教育出版社,2015年。
1、《药物分析》(第8版),杭太俊,人民卫生出版社; 2、《药物化学》,尤启东,人民卫生出版社,2016年2月; 3、《药理学》,朱依谆,人民卫生出版社,2011年; 4、《药剂学》(第7版),崔福德,人民卫生出版社。
3、《有机化学》(第三版),王积涛等编,南开大学出版社,2009年。
115 化学与化工学院
828 物理化学一(不含结构化学) 830 化工原理
1、《物理化学》(第五版),傅献彩等编,高等教育出版社,2006年。 1、《化工原理》(第四版),谭天恩编,化学工业出版社,2013年。
925 物理化学三
1、《物理化学》(第二版),安燕主编,贵州大学出版社,2019年; 2、《物理化学》(第五版),天津大学物理化学教研室编,高等教育出版社,2017年。
1、《模拟电子技术基础》(第五版),童诗白、华成英主编,高等教育出版社; 2、《数字电子技术基础》(第六版),阎石、王红主编,高等教育出版社。
834 电子技术基础
1、《模拟电子技术基础》(第五版),童诗白、华成英主编,高等教育出版社; 2、《数字电子技术基础》(第六版),阎石、王红主编,高等教育出版社。
1、《管理学:原理与方法》(第七版),周三多,复旦大学出版社,2018年。
1、《运筹学教程》(第四版),胡运泉、郭耀煌,清华大学出版社,2018年。
1、《管理学:原理与方法》(第七版),周三多,复旦大学出版社,2018年。
1、《社会工作概论》(第3版),王思斌,高等教育出版社,2014年; 2、《社会工作理论》(第2版),何雪松,格致出版社,2017年; 3、《社会及行为科学研究法(二)质性研究法》(第1版),瞿海源、毕恒达等主编,社会科学出版社,2013年。 1、《社会工作实务》(中级),2021年全国社会工作职业水平考试指导教材,中国社会出版社,2021年; 2、《社会工作实务基础——专业服务技巧的综合与运用》,童敏,2019年。
运筹学完整版

绪论
国际上运筹学的思想可追溯到1914年,当时的 兰彻斯特提出了军事运筹学的作战模型。1917年, 丹麦工程师埃尔朗在研究自动电话系统中通话线路 与用户呼叫的数量关系问题时,提出了埃尔朗公式, 研究了随机服务系统中的系统排队与系统拥挤问题。 存储论的最优批量公式是( Operations Research )
第一章
运
决
筹
胜
帷 幄之
绪论
千
里
中
之
外
Introduction
绪论
本章主要内容: (1)运筹学简述 (2)运筹学的主要内容 (3)本课程的教材及参考书 (4)本课程的特点和要求 (5)本课程授课方式与考核 (6)运筹学在经济管理中的应用
绪论
绪论
绪论
20世纪50年代中期,钱学森、许国志等教授在国内全面介 绍和推广运筹学知识,1956年,中国科学院成立第一个运筹学研 究室,1957年运筹学运用到建筑和纺织业中,1958年提出了图上 作业法,山东大学的管梅谷教授提出了“中国邮递员问题”, 1970年,在华罗庚教授的直接指导下,在全国范围内推广统筹方 法和优选法。
1978年11月,在成都召开了全国数学年会,对运筹学的理论 与应用研究进行了一次检阅,1980年4月在山东济南正式成立了 “中国数学会运筹学会”,1984年在上海召开了“中国数学会运 筹学会第二届代表大会暨学术交流会”,并将学会改名为“中国 运筹学会”。
绪论
运筹学的发展趋势
成熟的学科分支向纵深发展 新的研究领域产生 与新的技术结合 与其他学科的结合加强 传统优化观念不断变化
x1 0xn 0
n
简写为: max(min)Z cj xj j1
n
aij xj ( ) bi (i 1 2m)
《运筹学》课程考试试卷试题(含答案)

《运筹学》课程考试试卷试题(含答案)一、选择题(每题5分,共25分)1. 运筹学的核心思想是()A. 最优化B. 系统分析C. 预测D. 决策答案:A2. 在线性规划中,约束条件可以用()表示。
A. 等式B. 不等式C. 方程组D. 矩阵答案:B3. 以下哪个不是运筹学的基本模型?()A. 线性规划B. 整数规划C. 非线性规划D. 随机规划答案:D4. 在目标规划中,以下哪个术语描述的是决策变量的偏离程度?()A. 目标函数B. 约束条件C. 偏差变量D. 权重系数答案:C5. 在动态规划中,以下哪个概念描述的是在决策过程中,某一阶段的最优决策对后续阶段的影响?()A. 最优子结构B. 无后效性C. 最优性原理D. 阶段性答案:B二、填空题(每题5分,共25分)1. 运筹学是一门研究在复杂系统中的______、______和______的科学。
答案:决策、优化、实施2. 在线性规划中,若目标函数为最大化,则其标准形式为______。
答案:max z = c^T x3. 在非线性规划中,若目标函数和约束条件均为凸函数,则该规划问题为______。
答案:凸规划4. 在目标规划中,若决策变量x_i的权重系数为w_i,则目标函数可以表示为______。
答案:min Σ(w_i d_i^+ + w_i d_i^-)5. 在动态规划中,若状态变量为s_n,决策变量为u_n,则状态转移方程可以表示为______。
答案:s_{n+1} = f(s_n, u_n)三、判断题(每题5分,共25分)1. 线性规划问题的最优解一定在可行域的顶点处取得。
()答案:正确2. 在整数规划中,若决策变量为整数,则目标函数和约束条件也必须为整数。
()答案:错误3. 目标规划中的偏差变量可以是负数。
()答案:正确4. 在动态规划中,最优策略具有最优子结构。
()答案:正确5. 在非线性规划中,若目标函数为凸函数,则约束条件也必须为凸函数。
《运筹学》习题与答案

《运筹学》习题与答案(解答仅供参考)一、名词解释1. 线性规划:线性规划是运筹学的一个重要分支,它主要研究在一系列线性约束条件下,如何使某个线性目标函数达到最大值或最小值的问题。
2. 动态规划:动态规划是一种解决多阶段决策问题的优化方法,通过把原问题分解为相互联系的子问题来求解,对每一个子问题只解一次,并将其结果保存起来以备后续使用,避免了重复计算。
3. 整数规划:整数规划是在线性规划的基础上,要求决策变量取值为整数的一种优化模型,用于解决实际问题中决策变量只能取整数值的情形。
4. 马尔可夫决策过程:马尔可夫决策过程是一种随机环境下的决策模型,其中系统的状态转移具有无后效性(即下一状态的概率分布仅与当前状态有关),通过对每个状态采取不同的策略(行动)以最大化期望收益。
5. 最小费用流问题:最小费用流问题是指在网络流模型中,每条边都有一个容量限制和单位流量的成本,寻找满足所有节点流量平衡的同时使得总成本最小的流方案。
二、填空题1. 运筹学的主要研究对象是系统最优化问题,其核心在于寻求在各种(约束条件)下实现(目标函数)最优的方法。
2. 在运输问题中,供需平衡指的是每个(供应地)的供应量之和等于每个(需求地)的需求量之和。
3. 博弈论中的纳什均衡是指在一个博弈过程中,对于各个参与者来说,当其他所有人都不改变策略时,没有人有动机改变自己的策略,此时的策略组合构成了一个(纳什均衡)。
4. 在网络计划技术中,关键路径是指从开始节点到结束节点的所有路径中,具有最长(总工期)的路径。
5. 对于一个非负矩阵A,如果存在一个非负矩阵B,使得AB=BA=A,则称A为(幂等矩阵)。
三、单项选择题1. 下列哪项不是线性规划的标准形式所具备的特点?(D)A. 目标函数是线性的B. 约束条件是线性的C. 决策变量非负D. 变量系数可以为复数2. 当线性规划问题的一个基解满足所有非基变量的检验数都非正时,那么该基解(C)。
A. 不是可行解B. 是唯一最优解C. 是局部最优解D. 不一定是可行解3. 下列哪种情况适合用动态规划法求解?(B)A. 问题无重叠子问题B. 问题具有最优子结构C. 问题不能分解为多个独立子问题D. 子问题之间不存在关联性4. 在运输问题中,如果某条路线的运输量已经达到了其最大运输能力,我们称这条路线处于(A)状态。
《运筹学》(A)参考答案.docx

《运筹学》(A)参考答案一、不定项选择题(每小题3分,共9分)1.线性规划的标准型有特点(B D )0A、右端项非零;B、目标求最大;C、有等式或不等式约束;D、变量均非负。
2.一个线性规划问题(P)与它的对偶问题(D)有关系(BCD)。
A、(P)无可行解则(D) 一定无可行解;B、(P)、(D)均有可行解则都有最优解;C、(P)的约束均为等式,则(D)的所有变量均无非负限制;D、若(D)是(P)的对偶问题,则(P)是(D)的对偶问题。
3.关于动态规划问题的下列命题中(B )是错误的。
A、动态规划阶段的顺序与求解过程无关;B、状态是由决策确定的;C、用逆序法求解动态规划问题的重要基础之一是最优性原理;D、列表法是求解某些离散变量动态规划问题的有效方法。
二、判断题(每小题2分,共10分)1.若某种资源的影子价格等于Q在其他条件不变的情况下,当该种资源增加5个单位时,相应的目标函数值将增大5k个单位。
(X)2.如果运输问题单位运价表的某一行(或某一列)元素分别加上一个常数久最优调运方案将不会发生变化。
(V)3.运输问题是一种特殊的线性规划模型,因而求解结果也可能出现下列四种情况之一:有唯一最优解,有无穷多最优解,无界解,无可行解。
(X )4.用割平面法求解纯整数规划问题时,要求包括松弛变量在内的全部变量必须取整数值。
(V )5.如图中某点匕有若干个相邻点,与其距离最远的相邻点为耳,则边卩,刀必不包含在最小支撑树内。
(X)三(20分)、考虑下列线性规划:max z = 3xj + 5x2 + x34xj + 2X2+x3 < 14< X] + x2 + x3 < 4Xj > 0, j = 1,2,31(10分)、写出此线性规划的最优解、最优值、最优基B和它的逆沪;2(2分)、求线性规划的对偶问题的最优解;3(4分)、试求C2在什么范围内,此线性规划的最优解不变;4 (4分)、若^=14变为9,最优解及最优值是什么?解:1(10分)、写出此线性规划的最优解、最优值、最优基B和它的逆沪;标准形式:max z = 3xj + 5x2 + x34xj + 2*2 + X3 + 卩=14< X] + *2 + X3 + x5 = 4X j > 0, j = 1,2,3,4,5最优解 X' =(0,4,0,6,0)『 最优值r =20 ---------------- (1分) 最优基5 = P 2]---------------- (2分)0 1 "1 -2B~l= o ]---------------- (2 分)2(2分)、求线性规划的对偶问题的最优解; 对偶问题的最优解厂=(0,5)3(4分)、试求c?在什么范围内,此线性规划的最优解不变;(1分)(2分)要使得原最优解不变,则所有检验数非正,即 3 — c 2 W 0 <1-C 2 <0 ,解得c 2 >3--------------- (2 分)~C 2 - 04(4分)、若$=14变为9,最优解及最优值是什么?-2j9 1 4最优值r =20-四(10分)、下述线性规划问题:max z = 10“ + 24x 2 + 20x 3 + 2O.r 4 + 25x 5X] + x 2 + 2x, + 3X 4 + 5X 5 < 19 < 2x 1 + 4X 2 + 3x, + 2X 4 + x 5 < 57 ">(2分)(2分)0, j =l,2,---,5以几,力为对偶变量写出其对偶问题。
《运筹学》期末考试试卷A-答案

《运筹学》期末考试试卷A-答案一、选择题(每题5分,共25分)1. 运筹学是一门研究在复杂系统中进行决策的科学,以下哪个选项不属于运筹学的研究内容?A. 优化问题B. 随机过程C. 系统建模D. 心理咨询答案:D2. 在线性规划中,若一个线性规划问题的可行域是空集,则该问题称为:A. 无界问题B. 无解问题C. 无可行解问题D. 有解问题答案:C3. 线性规划问题中,目标函数和约束条件均为线性函数的是:A. 线性规划B. 非线性规划C. 动态规划D. 随机规划答案:A4. 在整数规划中,若决策变量只能取整数值,则该问题称为:A. 线性规划B. 整数规划C. 非线性规划D. 动态规划答案:B5. 在排队论中,以下哪个因素对服务效率影响最大?A. 服务速率B. 到达率C. 排队长度D. 服务时间答案:A二、填空题(每题5分,共25分)1. 运筹学的基本方法是________、________和________。
答案:模型化、最优化、计算机模拟2. 线性规划的标准形式包括________、________和________。
答案:目标函数、约束条件、非负约束3. 在非线性规划中,目标函数和约束条件至少有一个是________函数。
答案:非线性4. 动态规划适用于解决________决策问题。
答案:多阶段5. 排队论中的基本参数包括________、________和________。
答案:到达率、服务率、服务台数量三、简答题(每题10分,共30分)1. 请简要介绍线性规划的基本概念。
答案:线性规划是运筹学的一个基本分支,主要研究在一定的线性约束条件下,如何求解目标函数的最大值或最小值问题。
线性规划问题通常包括目标函数、约束条件和非负约束。
目标函数是决策者要优化的目标,约束条件是决策者需要满足的条件,非负约束要求决策变量取非负值。
2. 请简要阐述整数规划的特点。
答案:整数规划是线性规划的一种特殊情况,要求决策变量取整数值。
902运筹学与统计学考试内容

902运筹学与统计学考试内容如下:
运筹学部分:
1.线性规划:包括线性规划的基本概念、标准形式、几何意义,
以及求解线性规划的方法(单纯形法)。
2.整数规划:介绍整数规划的基本概念、性质和求解方法,包括
分支定界法等。
3.动态规划:主要介绍动态规划的基本概念、原理和求解方法,
包括状态转移方程、最优解的性质和求解步骤等。
4.图论:介绍图论的基本概念、最短路径问题、最小生成树问题
等。
5.决策分析:介绍决策分析的基本概念、不确定型决策和风险型
决策的方法,以及贝叶斯定理等。
统计学部分:
1.描述性统计:介绍描述性统计的基本概念和方法,如均值、方
差、协方差、相关系数等。
2.概率论:介绍概率论的基本概念、概率分布和随机变量的性质
等。
3.参数估计:介绍参数估计的基本概念和方法,包括最大似然估
计和最小二乘估计等。
4.假设检验:介绍假设检验的基本原理和方法,包括显著性检验
和置信区间的计算等。
5.方差分析:介绍方差分析的基本原理和方法,包括单因素方差
分析和双因素方差分析等。
6.回归分析:介绍回归分析的基本原理和方法,包括一元线性回
归和多元线性回归等。
7.时间序列分析:介绍时间序列分析的基本概念和方法,包括平
稳性检验、季节性分解和预测方法等。
2019年研究生入学考试运筹学考试大纲

2019年研究生入学考试《运筹学》考试大纲第一部分考试说明一、考试性质全国硕士研究生入学考试是为高等学校招收硕士研究生而设置的。
其中运筹学是为管理科学与工程专业考生设置的专业基础课程考试科目,属招生学校自行命题性质。
其评分标准是高等学校优秀本科生能达到的及格或及格以上水平,以保证被录取者具有坚实的运筹学与管理科学基本理论和较强的分析实际问题的能力,有利于招生学校在专业上择优录取。
二、考试的学科范围应考范围包括:线性规划、对偶理论及灵敏度分析、运输问题、整数规划、目标规划、动态规划、图与网络分析、网络计划、存贮论、对策论。
具体考查要点详见本纲第二部分。
三、评价目标运筹学考试的目标在于考查学生运筹学的基本概念、基本理论和方法的掌握以及对实际问题的分析、建立必要的数学模型和求解问题的能力。
考生应能:1. 正确理解运筹学中的基本概念和基本理论。
2. 正确分析实际问题并建立相应的数学模型。
3. 掌握求解运筹学中常见问题的方法。
4. 能正确的解释所求问题的计算结果。
四、考试形式与考卷结构答卷形式:闭卷、笔试;试卷中的所有题目全部为必答题。
答题时间:180分钟。
试卷分数:满分为150分。
试卷结构及考查比例:试卷主要分为三部分,即:问题建模20%,基本理论和方法40%,分析题40%。
试卷题型:简答题 20%、计算及应用题 80%第二部分考查要点1.线性规划(1)了解:经济管理中常见的线性规划问题:生产计划与组织问题、工农业布局问题、合理下料问题、配料问题、运输问题、指派问题等。
(2)理解:线性规划问题数学模型的三个要素(决策变量、约束条件、目标函数),线性规划问题数学模型的一般形式及标准形式,线性规划问题解的概念,线性规划问题的几何意义,线性规划解的基本定理,利用单纯形法求解线性规划问题的思路,线性规划问题解的几种情况。
(3)掌握:简单线性规划问题的建模,线性规划问题的图解法,线性规划问题的单纯形法计算,单纯形法求解中解的判别。
武汉科技大学817运筹学2018--2019+答案考研初试真题

A 20 B
15 10
E5 5
10
F G
20 10
20
10
10
20
30 D
H
C
5、( 15 分)用单纯形表求解线性规划问题
MaxZ=2X1+5X2 X1≤4
2X1≤12 3X1+2X2≤18
X1,X2≥0
五、建模题( 共 1 小题,共 20 分) 1、( 20 分)某种钢材每根长度为 3795mm,要将其截成 423mm,1053mm, 503mm 三种长度的材料各 90 根,应如何安排,才能使消耗的钢材的根数最 少?试建立模型。
么 B 在集合 A 的 ________。
3、( 3 分)线性规划问题 MaxZ=CX;AX=b,X≥0(A 为 kxl 的矩阵,且 l>k)的基
的最多个数为_______,基的可行解的最多个数为__________。
4、( 3 分)线性规划问题的所有可行解构成的集合是________,它们有有限个
二、 填空题(共 5 小题,每小题 3 分,共 15 分) 1、( 3 分)人为将线性规划变成标准型,而人为添加的变量。 2、( 3 分)顶点地方取得。 3、( 3 分)__Clk_, _ Clk_。
4、( 3 分)____凸集____, ____顶点_____, ___顶点_____。 5、( 3 分)_____m*n ___个, ____ m+n-1____个。
运筹学实验报告六综合类问题

2018-2019学年第一学期《运筹学》实验报告(六)班级:交通运输171学号:1700000000女姓名: *****日期:2018.12.26实验一:一、问题重述一汽车厂生产小、中、大三种类型的汽车,已知各类型每辆车对钢材、劳动时间的需求、利润以及每月工厂钢材、劳动时间的现有量如下表所示。
试问如何制定月生产计划,使工厂的利润最大。
优的生产计划应作何改变?二、模型假设及符号说明模型一:设该汽车厂生产小、中、大型的汽车数量分别为X1, X2, X3;记总利润为z;模型二:在模型一的符号假设基础上增设y i, y2, y3,分别表示是否生产小、中、大型的汽车,若生产,则为1,若不生产,则为0;三、数学模型模型一:max z 2x1 3x2 4x31.5x i 3x2 5x3 600乩* 280x1250x2400x360000.x2,x30,且均为整数模型二:max z 2x1 3x2 4x3f1 .5 x1 3 x 2 5 x 3600280 x! 250 x 2400 x 360000S.t. x i 1000 y ix i 80 y ii x i均为整数,y j 0或1,i 1,2 ,3四、模型求解及结果分析根据模型一运行结果分析可得:当生产小型车64辆、中型车168辆时,该汽车厂所得利润最大,此时为632万元;根据模型二运行结果分析可分:当生产小型车80辆、中型车150辆时,该汽车厂在该前提下所得利润最大,此时为610万元。
五、附录(程序)模型一运行程序:max=2*x1+3*x2+4*x3; 1.5*x1+3*x2+5*x3<=600;280*x1+250*x2+400*x3<=60000; @gin (x1); @gin (x2); @gin (x3); end模型一运行结果:Global optimal soluti on found. Objective value: Objective bound: In feasibilities:Exte nded solver steps: Total solver iteratio ns:VariableValue Reduced Cost X1 64.00000 -2.000000 X2168.0000 -3.000000 X30.000000-4.000000Row Slack or Surplus Dual Price1632.0000 1.000000 2 0.000000 0.000000 380.00000 0.000000模型二运行程序:max=2*x1+3*x2+4*x3; 1.5*x1+3*x2+5*x3<=600; 280*x1+250*x2+400*x3<=60000; x1>=80*y1; x1<=1000*y1; x2>=80*y2; x2<=1000*y2; x3>=80*y3; x3<=1000*y3;@gi n (x1); @gi n (x2); @gi n (x3); @bin (y1); @bin (y2);@bin (y3);End模型二运行结果:Global optimal soluti on found. Objective value: 610.0000 Objective bou nd: 610.0000 In feasibilities:0.000000632.0000 632.0000 0.000000《运筹学》实验报告Variable Value Reduced Cost X1 80.00000 -2.000000 X2 150.0000 -3.000000 X3 0.000000 -4.000000 Y1 1.000000 0.000000 Y2 1.000000 0.000000 Y30.0000000.000000Row Slack or Surplus DualPrice 1 610.0000 1.000000 2 30.00000 0.000000 3 100.0000 0.000000 4 0.000000 0.000000 5 920.0000 0.000000 6 70.00000 0.000000 7 850.0000 0.000000 8 0.000000 0.000000 90.0000000.000000Exte nded solver steps:Total solver iteratio ns:0 15实验二:一、问题重述某架货机有三个货舱:前舱、中舱、后场。
运筹学实验报告四整数规划

2018-2019学年第一学期《运筹学》实验报告(四)班级:交通运输171学号: 1000000000姓名: *****日期: 2018.11.22实验一:用Lingo 软件求解下列整数规划问题(要求附程序和结果)12121212max 25062210,1,2i z x x x x x x x x x i =++≤⎧⎪-+≤⎪⎨+≤⎪⎪≥=⎩且取整数12312323123123123max 232452244,,01z x x x x x x x x x x x x x x x x x =+-++≤⎧⎪+≤⎪⎪+-≤⎨⎪+-≤⎪=⎪⎩或解:例题(左)解题程序及运行结果如下:sets :bliang/1,2/:x,a; yshu/1,2,3/:b;xshu(yshu,bliang):c; endsets data : a=2,1; b=5,0,21; c=1,1 -1,1 6,2; enddatamax =@sum (bliang(i):a(i)*x(i));@for (yshu(j):@sum (bliang(i):x(i)*c(j,i))<=b(j)); @for(bliang(i):@gin(x(i)));Global optimal solution found.Objective value: 7.000000 Objective bound: 7.000000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 0Variable Value Reduced CostX( 1) 3.000000 -2.000000X( 2) 1.000000 -1.000000A( 1) 2.000000 0.000000A( 2) 1.000000 0.000000B( 1) 5.000000 0.000000B( 2) 0.000000 0.000000B( 3) 21.00000 0.000000C( 1, 1) 1.000000 0.000000C( 1, 2) 1.000000 0.000000C( 2, 1) -1.000000 0.000000C( 2, 2) 1.000000 0.000000C( 3, 1) 6.000000 0.000000C( 3, 2) 2.000000 0.000000Row Slack or Surplus Dual Price1 7.0000001.0000002 1.000000 0.0000003 2.000000 0.0000004 1.000000 0.000000例题(右)解题程序及运行结果如下:sets:bliang/1,2,3/:x,a;yshu/1,2,3,4/:b;xshu(yshu,bliang):c;endsetsdata:a=2,1,-1;b=2,5,2,4;c=1,3,10,4,11,2,-11,4,-1;enddatamax=@sum(bliang(i):a(i)*x(i));@for(yshu(j):@sum(bliang(i):x(i)*c(j,i))<=b(j));@for(bliang(i):@bin(x(i)));Global optimal solution found.Objective value: 2.000000Objective bound: 2.000000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value ReducedCostX( 1) 1.000000 -2.000000X( 2) 0.000000 -1.000000X( 3) 0.000000 1.000000A( 1) 2.000000 0.000000A( 2) 1.000000 0.000000A( 3) -1.000000 0.000000B( 1) 2.000000 0.000000B( 2) 5.000000 0.000000B( 3) 2.0000000.000000B( 4) 4.000000 0.000000C( 1, 1) 1.000000 0.000000C( 1, 2) 3.000000 0.000000C( 1, 3) 1.000000 0.000000C( 2, 1) 0.000000 0.000000C( 2, 2) 4.000000 0.000000C( 2, 3) 1.000000 0.000000C( 3, 1) 1.000000 0.000000C( 3, 2) 2.000000 0.000000C( 3, 3) -1.000000 0.000000C( 4, 1) 1.000000 0.000000C( 4, 2) 4.000000 0.000000C( 4, 3) -1.000000 0.000000Row Slack or Surplus Dual Price1 2.0000001.0000002 1.000000 0.0000003 5.000000 0.0000004 1.000000 0.0000005 3.000000 0.000000实验二:一、问题重述某学校规定,运筹学专业的学生毕业时必须至少学习过两门数学课、三门运筹学课和两门计算机课。
《运筹学》考试大纲

硕士研究生入学考试《运筹学》考试大纲
一、考试形式和试卷结构
1、试卷满分及考试时间
本试卷满分为IOO分,考试时间为120分钟。
2、答题方式
答题方式为闭卷、笔试。
3、试卷题型结构
(1)计算题70分
(2)证明题30分
二、考试范围
1.运筹学模型和建模的方法与思路。
2.熟练线性规划的单纯形法原理与计算方法,线性规划的对偶理论与灵敏度分析。
3.线性规划的典型应用,如人力资源分配的问题、生产计划的问题、配料问题、投资问题。
4.运输问题的表上作业求解法及应用。
5.掌握整数规划的应用、会利用0-1变量为某些整数线性规划问题的建模。
6.掌握整数规划的分支定界法。
7.有优先权的目标规划、复杂情况下有优先权的目标规划及加
权目标规划。
8.掌握动态规划基本概念、最优化原理和基本方程。
9.动态规划模型结构、逆序法算法原理。
10.动态规划在资源分配、生产与存储等问题方面的应用。
11.最小树、最短路、最大流、最小费用最大流问题的内涵及其解法。
12.确定型存贮模型、随机型的建模和求解方法。
13.掌握单服务台负指数分布排队模型。
14.掌握多服务台负指数分布排队模型,排队系统设计的最优化。
15.矩阵对策的求解方法。
16.风险决策、效用理论及灵敏度分析方法。
(完整版)《运筹学》复习参考资料知识点及习题

第一部分线性规划问题的求解一、两个变量的线性规划问题的图解法:㈠概念准备:定义:满足所有约束条件的解为可行解;可行解的全体称为可行(解)域。
定义:达到目标的可行解为最优解。
㈡图解法:图解法采用直角坐标求解:x1——横轴;x2——竖轴。
1、将约束条件(取等号)用直线绘出;2、确定可行解域;3、绘出目标函数的图形(等值线),确定它向最优解的移动方向;注:求极大值沿价值系数向量的正向移动;求极小值沿价值系数向量的反向移动。
4、确定最优解及目标函数值。
㈢参考例题:(只要求下面这些有唯一最优解的类型)例1:某厂生产甲、乙两种产品,这两种产品均需在A、B、C三种不同的设备上加工,每种产品在不同设备上加工所需的工时不同,这些产品销售后所能获得利润以及这三种加工设备因各种条件限制所能使用的有效加工总时数如下表所示:问:该厂应如何组织生产,即生产多少甲、乙产品使得该厂的总利润为最大?(此题也可用“单纯形法”或化“对偶问题”用大M法求解)解:设x 1、x 2为生产甲、乙产品的数量。
max z = 70x 1+30x 2 s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+072039450555409321212121x x x x x x x x ,可行解域为oabcd0,最优解为b 点。
由方程组⎩⎨⎧=+=+72039450552121x x x x 解出x 1=75,x 2=15 ∴X *=⎪⎪⎭⎫⎝⎛21x x =(75,15)T∴max z =Z *= 70×75+30×15=5700⑴⑵ ⑶ ⑷ ⑸、⑹max z = 6x 1+4x 2 s.t.⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x , 解:可行解域为oabcd0,最优解为b 点。
由方程组⎩⎨⎧=+=+81022121x x x x 解出x 1=2,x 2=6 ∴X *=⎪⎪⎭⎫⎝⎛21x x =(2,6)T∴max z = 6×2+4×6=36⑴⑵ ⑶ ⑷ ⑸、⑹min z =-3x 1+x 2 s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤+≥+≤≤08212523421212121x x x x x x x x , 解:可行解域为bcdefb ,最优解为b 点。
《管理科学与工程学科基础知识》考试大纲 .doc

《管理科学与工程学科基础知识》考试大纲一、参考教材⑴《运筹学》(第4版)(面向21世纪课程教材(信息管理与信息系统专业教材系列)),《运筹学》教材编写组,清华大学出版社,2012-09-01。
⑵《管理学》(第五版),周三多,高等教育出版社,2018年03月。
二、考核要求明确管理科学与工程的研究对象、基本假设;明确管理科学与工程的研究对象-管理活动、管理情景、管理优化特征;掌握特定情境下管理活动内容、活动重点以及组织形式变化对应的管理理论的变化,掌握管理的内涵、职能,管理者的角色与技能,管理理论的形成与发展趋势。
明确运筹学的内涵、原则、工作步骤、建模方法及其应用环境,熟练掌握线性规划的建模与算法。
三、考试内容、比例(一)管理学 40%⑴管理理论的形成与发展管理的内涵、职能,管理者的角色与技能,管理理论的形成与发展。
⑵管理道德与企业社会责任伦理道德的内涵与类型,道德管理的特征与影响因素,社会责任。
⑶互联网时代的管理互联网的基本特征、发展趋势,互联网时代管理面临的挑战与转型之路(二)规划论 60%⑴运筹学概论运筹学的内涵、原则、工作步骤、建模方法,运筹学的应用。
⑵线性规划与单纯形线性规划问题建模与单纯形法。
⑶对偶单纯形对偶问题与对偶单纯形。
⑷运输问题运输问题建模与表上作业法。
⑸线性目标规划线性目标规划问题建模与算法。
⑹整数线性规划整数线性规划问题建模与算法。
四、考试题型理论分析与模型构建、定量优化计算。
五、考试时间本科目考试时间为180分钟。
《管理学》入学考试大纲一、考试说明本课程考试范围为管理学基础知识,主要测试考生对管理学的基本概念、基本理论、各项管理职能、管理方法等掌握的程度;测试考生融会贯通灵活运用现代管理学理念和知识的能力;考察测试学生发现问题、分析问题和解决问题的能力,并考核学生对管理实践热点及管理研究动态的了解情况。
1、参考教材《管理学—原理与方法》(第五版),周三多等编著,复旦大学出版社,2011年《管理学》(第11版),[美]斯蒂芬·P·罗宾斯等著,中国人民大学出版社,2012年2、题型及分数比例名词解释30分、选择或判断题30分、简答题50分、论述题(或案例分析)40分二、考试内容1、管理活动与管理理论1.1管理的定义及其内涵;管理的职能;管理的两重性原理;管理者的角色和技能;了解管理中的人性假设。
武汉科技大学817运筹学2018--2019+答案考研真题

2、( 2 分)线性规划最优解不唯一是指( )。
A.可行解集合无界 ;
B.存在某个检验数 k 0 且 aik 0(i 1, 2...m) ;
C.可行解集合是空集; D.最优表中存在非基变量的检验数非零;
3、( 2
分)使用人工变量法求解极大化线性规划问题时,当所有的检验数
j 0 在基变量中仍含有非零的人工变量,表明该线性规划问题 ( )
故此时最优基保持不变,最优解如下
X=(0,1,1,0,0)T minz=11
1 (3)、B-1b11= 2
02 2 11 3 0
此时最优基改变,采用对偶单纯形法,得最后结果如下
X=(3/2,0,1/2,0,0)T minz=10
(4)、将x1-
5、( 15 分)
解:化为标准型,然后利用单纯形法求解,如下
Cj
2
5
00 0
CB XB X1 X2 X3 X4 X5
b
0 X3 1
0
10
0
4
0 X4 2
0
01
0
12
0 X5
3 [2] 0 0
1
18
检验数
2
5
00
0
0 X3 1
0
10
0
4
0 X4 2
0
01
0
12
5 X2 1.5 1 检验数 -5.5 0
四、计算题( 共 5 小题,共 80分)
1、( 20 分)用单纯形法求解线性规划问题,并进行灵敏度分析:
min z 4x1 3x2 8x3
s.t
x1 x2
x3 2 x3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.计算下图所示网络中从A点到F点的最短路线及其长度
2.已知建设一个汽车库及引道的作业明细表如表所示。
工序代号工序名称工序时间(天)紧前工序
a 清理场地,准备施工10 ——
b 备料8 ——
c 车库地面施工 6 a、b
d 预制墙及房顶的桁架16 b
e 车库混凝土地面保养24 c
f 立墙架 4 d、e
g 立房顶桁架 4 f
h 装窗及边墙10 f
i 装门 4 f
j 装天花板12 g
k 油漆16 h、i、j
l 引道混凝土施工8 c
m 引道混凝土保养24 l
n 清理场地,交工验收 4 k、m
要求:a) 绘制网络图并计算网络时间;
b) 根据网络图,找出关键工序和关键路线;
c) 若要求该项工程在70天内完工,又知各道工序按正常进度的工序
时间与每天的费用以及赶工作业的工序时间与每天的费用如表—11所示,试确定在保证70天内完成,又使全部费用最低的施工方案。
3.某企业生产一种新产品,为了满足可能出现的高需求,可以增添某些附加设备。
但一旦出现高需求后,不能确切知道高需求是否长期持续。
根据对今后八年市场需求的预测,对该种新产品的需求估计见表
据此有两种投资方案:方案A为一次投资10万元,碰到高需求时每年盈利40000元,低需求时每年盈利5000元;方案B为分阶段投资,开始投一笔,三年后再根据情况确定是否投。
执行方案B,在碰到高需求时头三年每年盈利30000元,如不增加投资,后五年每年盈利20000元,如增加投资,后五年每年盈利40000元;在碰到低需求时,头三年每年盈利30000元,不增加投资时后五年每年仍为30000元,增加投资时后五年每年盈利10000元。
又分阶段投资时,期初投资额为70000元,后期增加额应为45000元。
试用决策树法确定最优的投资策略。
4.某投资人现有下列四种投资机会, 三年内每年年初都有3万元(不计利息)可供投资:
方案一:在三年内投资人应在每年年初投资,一年结算一次,年收益率是20%,下一年可继续将本息投入获利;
方案二:在三年内投资人应在第一年年初投资,两年结算一次,收益率是50%,下一年可继续将本息投入获利,这种投资最多不超过2万元;
方案三:在三年内投资人应在第二年年初投资,两年结算一次,收益率是60%,这种投资最多不超过1.5万元;
方案四:在三年内投资人应在第三年年初投资,一年结算一次,年收益率是30%,这种投资最多不超过1万元.
投资人应采用怎样的投资决策使三年的总收益最大,建立数学模型.
5.考虑线性规划
⎪⎪⎩⎪⎪⎨
⎧≥≥+≥+≥++=0
,73225442012min 2121212121x x x x x x x x x x Z
(1)说明原问题与对偶问题都有最优解;
(2)通过解对偶问题由最优表中观察出原问题的最优解; (3)利用公式C B B -1求原问题的最优解; (4)利用互补松弛条件求原问题的最优解.
6. 现有一面粉加工厂,每星期上五天班。
生产成本和需求量见下表。
表
面粉加工没有生产准备成本,每袋面粉的存储费为h k=0.5元/袋,按天交货,分别比较下列两种方案的最优性,求成本最小的方案。
(1)星期一早上和星期五晚的存储量为零,不允许缺货,仓库容量为S=40袋;
(2)其它条件不变,星期一初存量为8。
7. 友谊农场有3万亩农田,今欲种植玉米、大豆和小麦等三种农作物。
各种农作物每亩需施化肥分别为0.12吨、0.20吨和0.15吨。
预计秋后玉米每亩可收获500千克,售价为0.24元/千克,大豆每亩可收获200千克,售价为1.20元/千克,小麦每亩可收获300千克,售价为0.70元/千克。
农场年初规划时依目标重要性顺序考虑如下几个方面:
(1)年终总收益不低于350万元,赋予优先权P1 ;
(2)年总产量不低于1.25万吨,赋予优先权P2 ;
(3)小麦产量以0.5万吨为宜,赋予优先权P3 ;
(4)大豆产量不少于0.2万吨,赋予优先权P4 ;
(5)玉米产量不超过0.6万吨,赋予优先权P5 ;
(6)农场现能提供5000吨化肥,若不够,可在市场上高价购买,但希望高价采购量愈少愈好;赋予优先权P6 。
试就该农场年生产计划建立目标规划的数学模型。
8.有一个车队总共有车辆100辆,分别送两批货物去A、B两地,运到A地去的利润与车辆数目满足关系100x,x为车辆数,车辆抛锚率为30%,运到B地的利润与车辆数y关系为80y,车辆抛锚率为20%,总共往返3轮。
请设计使总利润最高的车辆分配方案。
9.有甲、乙、丙、丁四个人,要分别指派他们完成A、B、C、D四项不同的工作,每人所做各项工作所消耗的时间如下表:
问:应如何指派,才能让总消耗时间最少?
10.已知某工厂计划生产I、II、III三种产品,各产品需要在A、B 、C三种设备
上加工,各有关数据见如下表,试回答:
(1)如何充分发挥设备能力,使生产盈利最大?
(2)若为了增加产量,可借用别的工厂的设备B,每月可借用60台时,租金为1.8万元,问借用设备B是否合算?
(3)若另有两种新产品IV、V,其中IV需用设备A—12台时,B—5台时,C —10台时,单位产品盈利2.1千元;V需用设备A—4台时,B—4台时,C —12台时,单位产品盈利1.87千元。
如果A、B 、C三种设备台时不增加,分别回答这两种新产品投产在经济上是否合算?
(4)若对产品工艺重新进行设计和结构改造,而改进后生产每件产品I需用设备A—9台时,设备B—12台时,设备C—4台时,单位产品盈利4.5千元,问这对原计划有何影响?。
