八年级第一学期期末考试试卷

合集下载

北京市西城区2023-2024学年八年级上学期期末语文试题(含答案)

北京市西城区2023—2024学年度第一学期期末试卷八年级语文 2024.1注意事项：1．本试卷共11页，共五道大题，25道小题，满分100分。

考试时间120分钟。

2．在试卷和答题卡上准确填写学校、班级、姓名和学号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题用2B铅笔作答，其他试题用黑色字迹签字笔作答。

5．考试结束，请将考试材料一并交回。

一、基础·运用（共16分）班级组织同学们开展主题为“中轴话鸟，和谐共生”的跨学科实践活动。

各学习小组准备在本班的微信公众号上推送学习成果，你参与了文稿的编审工作，请完成以下任务。

栏目一：文物探“鸟”历史小组走进中轴线上的博物馆。

找到不少中国古代带有鸟类造型的文物，搜集了一些资料。

其中有两段配图的文字，还需审核完善。

春秋莲鹤方壶（收藏于故宫博物院）西汉彩绘雁鱼青铜釭灯（收藏于中国国家博物馆）莲鹤方壶形体巨大，有1米多高。

双层镂雕莲瓣盏上立有一只展翅欲飞的仙鹤，铸造得①。

据记载，复杂青铜器的铸造、通常会使用失蜡法、分铸法等工艺。

本器的仙鹤、双龙耳与器身主体采用分铸法，显示了高超的铸造技术。

雁鱼青铜釭灯整体造型为鸿雁双足站立并回首叼着一条鱼。

位于雁背部的灯盘带有手柄，其上的灯罩可转动开合，以便调节灯光照射方向和防yù（）来风。

雁腹内可盛清水，灯烟经雁颈“suì（）道”溶入水中，可减少污染。

这样的设计达到了器物形式与功能的完美统一，堪称②。

1．对文段中加点字的读音和填入括号中的汉字进行判断，下列说法正确的一项是（）（2分）A．“镂雕”的“镂”应读作“lóu”“防yù”应写为“防御”B．“镂雕”的“镂”应读作“lòu”“防yù”应写为“防卸”C．“记载”的“载”应读作“zǎi”“suì道”应写为“隧道”D．“记载”的“载”应读作“zài”“suì道”应写为“邃道”2．在文段横线处填入成语，最恰当的一项是（）（2分）A．①入木三分②妙手偶得 B．①入木三分②巧妙绝伦C．①惟妙惟肖②妙手偶得 D．①惟妙惟肖②巧妙绝伦栏目二：胡同寻“鸟”地理小组走进中轴线附近的胡同，寻找各种各样“鸟”的踪迹。

黑龙江省牡丹江市2023-2024学年八年级上学期期末考试数学试卷(含解析)

2023-2024学年黑龙江省牡丹江市八年级（上）期末数学试卷一、单项选择题（本题12个小题，每小题3分，共36分）1．（3分）习近平总书记强调，“垃圾分类工作就是新时尚”．下列垃圾分类标识的图形中，轴对称图形个数是（）A．1个B．2个C．3个D．4个2．（3分）下列运算正确的是（）A．a3•a4＝a12B．2b+5a＝7abC．（a+b）2＝a2+b2D．（a2b3）2＝a4b63．（3分）2023年9月9日，上海微电子研发的28nm浸没式光刻机的成功问世，标志着我国在光刻机领域迈出了坚实的一步．已知28nm为0.000000028米，数据0.000000028用科学记数法表示为（）A．2.8×10﹣10B．2.8×10﹣8C．2.8×10﹣6D．2.8×10﹣94．（3分）下列各式，，，，，中，最简分式的个数是（）A．4B．3C．2D．15．（3分）将一把直角三角尺和一把直尺按如图所示的位置放置．若∠1＝65°，则∠2等于（）A．145°B．150°C．155°D．160°6．（3分）若分式的值是整数，则满足条件的所有正整数m的和等于（）A．9B．8C．7D．57．（3分）如图，在等腰直角三角形ABC中，AB＝AC，∠BAC＝90°，∠ABC外角平分线交CA延长线于点D，DE⊥BC，垂足是E，若△ABC周长是8，则线段CD的长为（）A．B．9C．8D．78．（3分）如果x2﹣2（m﹣1）x+5﹣2m是一个完全平方式，则满足条件的整数m的个数是（）A．1B．2C．3D．49．（3分）有两个正方形A，B，现将B放在A的内部，得到图①，将A，B并列放置后构成新的正方形，得到图②．若图①和图②中的阴影面积分别是3和8，则正方形A，B的面积之和是（）A．9B．11C．12D．1510．（3分）某地开展建设绿色家园活动，活动期间，计划每天种植相同数量的树木．该活动开始后，实际每天比原计划多植树20棵，实际植树800棵所需时间与原计划植树600棵所需时间相同．设实际每天植树x 棵，则下列方程正确的是（）A．B．C．D．11．（3分）一组按规律排列的式子：，，，，…，第n个式子是（n为正整数）（）A．B．C．D．12．（3分）在以“长方形的折叠”为主题的数学活动课上，某位同学进行了如下操作：第一步：在长方形纸片ABCD的BC边上取一点E，将△ABE沿AE翻折，使点B落在点B'处，边EB'交AD于点F，第二步：将△ECD沿DE翻折，点C的对应点C′恰好落在线段EB'上．根据以上的操作，若BC＝6，C'是EB'的中点，则线段AF的长为（）A．B．3C．D．4二、填空题（本题8个小题，每小题3分，共24分）13．（3分）如图，∠CAB＝∠DBA，只需补充一个条件，就可以根据“ASA”得到△ABC≌△BAD．14．（3分）若分式的值为0，则m的值为．15．（3分）如图，在△ABC中，AB＝AC＝8，∠BAC＝150°，点P，Q分别在边AB，BC上，则AQ+PQ的最小值为．16．（3分）若x m＝4，x n＝6，则x3m﹣n的值为．17．（3分）如图，网格内每个小正方形的边长都是1个单位长度，A，B，C，D都是格点，AB与CD相交于点P，则∠A+∠D＝．18．（3分）关于x的分式方程的解是非负数，则m的取值范围是．19．（3分）等腰三角形ABC中，高BD与一腰所夹的锐角是40°，则等腰三角形ABC底角的度数为．20．（3分）如图，在△ABC中，AB＝AC，点D在AC边上，点F在AB边上，过点D作DE⊥BC，垂足是E，∠FED＝∠B，4∠FDE﹣∠A＝180°．下列结论：①2∠CDE＝∠A；②BC＝BF+CD；③△DEF是等边三角形；④过点D作DM⊥DE，交AB边于点M，若M是AF的中点，DM＝3，则BC＝9．其中正确的是．三、解答题（60分）21．（18分）（1）计算：（﹣1）2024+（）﹣2﹣（π﹣3）0；（2）计算：（m﹣n）2﹣2m（m﹣n）；（3）因式分解：a2（x﹣y）+4（y﹣x）；（4）解分式方程：﹣3＝．22．（6分）先化简：，再从﹣2，﹣1，﹣6，中选择一个适合的数x代入求值．23．（7分）如图，在平面直角坐标系中，△ABC的顶点A，B，C在格点上．（1）请在图中作出△ABC关于y轴对称的△A′B′C'；（2）写出点B'，点C'的坐标，以A'，B，C′为顶点的三角是三角形；（3）点P在图中格点上，若△PBC是等腰三角形，则点P的个数是．24．（9分）在△ABC中，∠BAC＝∠BCA，D是平面内一点，∠DAB＝∠ABC＝90°，点E在AB边所在直线上，CE⊥BD，垂足是F．（1）当点E在线段AB上时，如图①，求证：AE+AD＝BC；（2）当点E在线段BA延长线上时，如图②；当点E在线段AB延长线上时，如图③，请猜想并直接写出线段AE，AD，BC的数量关系；（3）如图③，若BF+CF＝6，则S四边形ADFC﹣S△BEF＝．25．（10分）2024年是中国农历甲辰龙年．元旦前，某商场进货员预测一种“吉祥龙”挂件能畅销市场，就用6000元购进一批这种“吉祥龙”挂件，面市后果然供不应求，商场又用12800元购进了第二批这种“吉祥龙”挂件，所购数量是第一批购进数量的2倍，但每件的进价贵了4元．（1）该商场购进第一批、第二批“吉祥龙”挂件每件的进价分别是多少元？（2）若两批“吉祥龙”挂件按相同的标价销售，要使两批“吉祥龙”挂件全部售完后获利不低于7300（不考虑其他因素），且最后的50件“吉祥龙”挂件按八折优惠售出，那么每件“吉祥龙”挂件的标价至少是多少元？26．（10分）如图，△ABC在平面直角坐标系中，顶点B（m，0），C（n，0）在x轴上，顶点A在y轴的正半轴上，BD⊥AC，垂足是D，BD交AO于点E，∠AED﹣∠BAO＝45°，（m+4）2+（n﹣6）2＝0．请解答下列问题：（1）求点B、点C的坐标；（2）求线段AE的长；（3）连接CE．若OE＝2，在坐标轴上是否存在点F，使S△ACF＝S△ACE？若存在，请直接写出点F的个数和其中一个点F的坐标；若不存在，请说明理由．参考答案与解析一、单项选择题（本题12个小题，每小题3分，共36分）1．（3分）习近平总书记强调，“垃圾分类工作就是新时尚”．下列垃圾分类标识的图形中，轴对称图形个数是（）A．1个B．2个C．3个D．4个【解答】解：左起第一、第四个图形不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形．第二、第三这两个图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形．故选：B．2．（3分）下列运算正确的是（）A．a3•a4＝a12B．2b+5a＝7abC．（a+b）2＝a2+b2D．（a2b3）2＝a4b6【解答】解：A、原式＝a7，不符合题意；B、原式不能合并，不符合题意；C、原式＝a2+2ab+b2，不符合题意；D、原式＝（a2）2•（b3）2＝a4b6，符合题意．故选：D．3．（3分）2023年9月9日，上海微电子研发的28nm浸没式光刻机的成功问世，标志着我国在光刻机领域迈出了坚实的一步．已知28nm为0.000000028米，数据0.000000028用科学记数法表示为（）A．2.8×10﹣10B．2.8×10﹣8C．2.8×10﹣6D．2.8×10﹣9【解答】解：0.000000028＝2.8×10﹣8．故选：B．4．（3分）下列各式，，，，，中，最简分式的个数是（）A．4B．3C．2D．1【解答】解：＝＝﹣，＝5a，＝，都不是最简分式，，，是最简分式，故选：B．5．（3分）将一把直角三角尺和一把直尺按如图所示的位置放置．若∠1＝65°，则∠2等于（）A．145°B．150°C．155°D．160°【解答】解：∵直尺的两边互相平行，∠1＝65°，∴∠3＝∠1＝65°，∴∠4＝∠3＝65°，∴∠2＝∠4+90°＝65°+90°＝155°．故选：C．6．（3分）若分式的值是整数，则满足条件的所有正整数m的和等于（）A．9B．8C．7D．5【解答】解：∵分式的值是整数，∴m+1是6的约数，即m+1＝1或2或3或6，解得：m＝0（舍去）或1或2或5，则满足条件的所有正整数m的和为1+2+5＝8．故选：B．7．（3分）如图，在等腰直角三角形ABC中，AB＝AC，∠BAC＝90°，∠ABC外角平分线交CA延长线于点D，DE⊥BC，垂足是E，若△ABC周长是8，则线段CD的长为（）A．B．9C．8D．7【解答】解：在等腰直角三角形ABC中，AB＝AC，∠BAC＝90°，设AB＝AC＝x，则BC＝x，∵△ABC周长是8，∴x+x+x＝8，∴x＝8﹣4，∴AB＝AC＝8﹣4，BC＝（8﹣4）×＝8﹣8，∵BD是∠ADE的角平分线，DE⊥BE，AB⊥AD，∴BE＝AB＝8﹣4，又∵BD＝BD，∴Rt△BDE≌Rt△BDA（HL），∴DE＝DA，设CD＝m，则AD＝DE＝m﹣8+4，∵S，∴（m﹣8+4）×＝（8﹣4）（2m﹣8+4），解得m＝8，即CD＝8，故选：C．8．（3分）如果x2﹣2（m﹣1）x+5﹣2m是一个完全平方式，则满足条件的整数m的个数是（）A．1B．2C．3D．4【解答】解：∵x2﹣2（m﹣1）x+5﹣2m是一个完全平方式，∴（m﹣1）2＝5﹣2m，解得m＝±2．故选：B．9．（3分）有两个正方形A，B，现将B放在A的内部，得到图①，将A，B并列放置后构成新的正方形，得到图②．若图①和图②中的阴影面积分别是3和8，则正方形A，B的面积之和是（）A．9B．11C．12D．15【解答】解：设正方形A、B的边长分别是a、b，则正方形A，B的面积之和是a2+b2．根据题意，图①中阴影部分的图形是正方形，边长为（a﹣b），图②中新正方形的边长为（a+b），根据图①和图②中的阴影面积分别是3和8，得，经整理，得，∴a2+b2＝11，∴正方形A，B的面积之和是11．故选：B．10．（3分）某地开展建设绿色家园活动，活动期间，计划每天种植相同数量的树木．该活动开始后，实际每天比原计划多植树20棵，实际植树800棵所需时间与原计划植树600棵所需时间相同．设实际每天植树x 棵，则下列方程正确的是（）A．B．C．D．【解答】解：由题意可得：＝，故选：B．11．（3分）一组按规律排列的式子：，，，，…，第n个式子是（n为正整数）（）A．B．C．D．【解答】解：∵第奇数个式子的符号为“负”，∴第n个式子的符号可用（﹣1）n表示．∵分母中单项式的系数分别为1，2，3...n，字母a的指数分别是1，2，3...n，∴第n个式子的分母可表示为：na n．∵分子分别是2，5，8，11...（3n﹣1），∴第n个式子的分母是3n﹣1．∴第n个式子为：（﹣1）n．故选：D．12．（3分）在以“长方形的折叠”为主题的数学活动课上，某位同学进行了如下操作：第一步：在长方形纸片ABCD的BC边上取一点E，将△ABE沿AE翻折，使点B落在点B'处，边EB'交AD于点F，第二步：将△ECD沿DE翻折，点C的对应点C′恰好落在线段EB'上．根据以上的操作，若BC＝6，C'是EB'的中点，则线段AF的长为（）A．B．3C．D．4【解答】解：∵四边形ABCD是矩形，∴AB＝CD，AD＝BC＝6，∠B＝∠C＝90°由折叠的性质可得：AB＝AB'＝CD＝C'D，∠B＝∠B'＝90°＝∠C＝∠DC'E，BE＝B'E，CE＝C'E，∵点C'恰好为EB'的中点，∴B'E＝2C'E，∴BE＝2CE，∴BC＝AD＝3EC，∴CE＝2，BE＝4，∵AE2＝AB2+BE2，DE2＝DC2+CE2，AD2＝AE2+DE2，∴AB2+16+8+DC2+4＝36，∴AB＝CD＝2，∵∠B'＝∠DC'F＝90°，∠AFB'＝∠DFC'，AB'＝C'D＝CD＝2，∴△AB'F≌△DC'F（AAS），∴AF＝DF＝AD＝3，故选：B．二、填空题（本题8个小题，每小题3分，共24分）13．（3分）如图，∠CAB＝∠DBA，只需补充一个条件　AC＝BD　，就可以根据“ASA”得到△ABC≌△BAD．【解答】解：补充条件AC＝BD．理由：在△ABC和△BAD中，，△ABC≌△BAD（SAS）．故答案为：AC＝BD．14．（3分）若分式的值为0，则m的值为　1　．【解答】解：由题意得，，解得m＝1，故答案为：1．15．（3分）如图，在△ABC中，AB＝AC＝8，∠BAC＝150°，点P，Q分别在边AB，BC上，则AQ+PQ的最小值为　4　．【解答】解：作点A关于直线BC的对称点E，连接EB、AE、PE，作EF⊥AB于点F，∵AB＝AC＝8，∠BAC＝150°，∴∠ABC＝∠C＝×（180°﹣150°）＝15°，∵BC垂直平分AE，∴EB＝AB＝8，∴∠EBC＝∠ABC＝15°，∴∠ABE＝2∠ABC＝30°，∵∠BFE＝90°，∴EF＝EB＝4，∵EQ+PQ≥PE，PE≥EF，且EQ＝AQ，∴AQ+PQ≥EF，∴AQ+PQ≥4，∴AQ+PQ的最小值为4，故答案为：4．16．（3分）若x m＝4，x n＝6，则x3m﹣n的值为．【解答】解：x3m﹣n＝x3m÷x n＝43÷6＝＝．故答案为：．17．（3分）如图，网格内每个小正方形的边长都是1个单位长度，A，B，C，D都是格点，AB与CD相交于点P，则∠A+∠D＝　135°　．【解答】解：如图，过点B作BF∥CD，连接EF，由勾股定理得：BE＝＝，EF＝，BF＝，∴BE＝EF，∵BE2+EF2＝BF2，∴∠BEF＝90°，∴∠EBF＝45°，∴∠APD＝∠EBF＝45°，∴∠A+∠D＝180°﹣45°＝135°，故答案为：135°．18．（3分）关于x的分式方程的解是非负数，则m的取值范围是　m≥1且m≠4　．【解答】解：原方程去分母得：m﹣4＝x﹣3，解得：x＝m﹣1，∵x﹣3≠0，∴x≠3，∴m﹣1≠3，∴m≠4，∵关于x的分式方程的解是非负数，∴x≥0，即m﹣1≥0，解得：m≥1，又∵m≠4，∴m的取值范围是m≥1且m≠4．故答案为：m≥1且m≠4．19．（3分）等腰三角形ABC中，高BD与一腰所夹的锐角是40°，则等腰三角形ABC底角的度数为　50°或65°或25°　．【解答】解：依题意有以下两种情况：（1）△ABC为锐角三角形时，此时又有两种情况：①当BD是等腰△ABC底边上的高时，如图1所示：∵BD为等腰三角形底边AC上的高，∴∠ADB＝90°，∴∠ABD+∠A＝90°，∵高BD与一腰所夹的锐角是40°，∴∠BAD＝40°，∴∠A＝90°﹣∠BAD＝50°；②当BD是等腰△ABC腰上的高时，如图2所示：∵BD为等腰三角形腰AC上的高，∴∠ADB＝90°，∴∠A+∠ABD＝90°，∵高BD与一腰所夹的锐角是40°，∴∠ABD＝40°，∴∠A＝90°﹣∠ABD＝50°，∵AB＝AC，∴∠ABC＝∠C＝（180°﹣∠A）＝（180°﹣50°）＝65°．（2）当等腰△ABC为钝角三角形时，则顶角为钝角，此时高BD只能是腰上的高，如图3所示：∵BD为等腰三角形腰AC上的高，∴∠ADB＝90°，∴∠DAB+∠ABD＝90°，∵高BD与一腰所夹的锐角是40°，∴∠ABD＝40°，∴∠DAB＝90°﹣∠ABD＝50°，∴∠BAC＝180°﹣∠DAB＝130°，∵AB＝AC，∴∠ABC＝∠C＝（180°﹣∠BAC）＝（180°﹣130°）＝25°．综上所述：等腰三角形ABC底角的度数为50°或65°或25°．故答案为：50°或65°或25°．20．（3分）如图，在△ABC中，AB＝AC，点D在AC边上，点F在AB边上，过点D作DE⊥BC，垂足是E，∠FED＝∠B，4∠FDE﹣∠A＝180°．下列结论：①2∠CDE＝∠A；②BC＝BF+CD；③△DEF是等边三角形；④过点D作DM⊥DE，交AB边于点M，若M是AF的中点，DM＝3，则BC＝9．其中正确的是　①②④　．【解答】解：①在△ABC中，AB＝AC，∴∠B＝∠C，∴∠A＝180°﹣2∠C，∵DE⊥BC，∠CDE＝90°﹣∠C，∴∠CDE＝2∠A，故结论①正确；②设∠B＝∠C＝α，则∠FED＝∠B＝∠C＝α，∴∠A＝180°﹣2α，∵4∠FDE﹣∠A＝180°，∴4∠FDE﹣（180°﹣2α）＝180°，∴∠FDE＝90°﹣α，∴∠DFE＝180°﹣（FED+∠FDE）＝180°﹣（α+90°﹣α）＝90°﹣α，∴∠FDE＝∠DFE，∴DE＝EF，∵DE⊥BC，∴∠CDE+∠C＝90°，∠BEF+∠FED＝90°，∵∠C＝∠FED＝α，∴∠CDE＝∠BEF，在△CDE和△BEF中，，∴△CDE≌△BEF（AAS），∴CD＝BE，CE＝BF，∴BC＝CE+BE＝BF+CD，故结论②正确；③不妨假设△DEF是等边三角形，∴∠FED＝60°，∴∠B＝∠FED＝60°，∴△ABC是等边三角形，根据已知条件，无法判定△ABC是等边三角形，∴假设是错误的．故结论③不正确．④∵DM⊥DE，DE⊥BC，∴DM∥BC，∠MDE＝90°，∴∠AMD＝∠B，∠ADM＝∠C，∠MDF+∠FDE＝90°，∵∠B＝∠C，∴∠AMD＝∠ADM，∴△AMD为等腰三角形，∵△CDE≌△BEF，∴∠DEC＝∠EFB＝90°，∴∠EFM＝90°，即∠MFD+∠EFD＝90°，∵∠FDE＝∠DFE，∴∠MDF＝∠MFD，∴DM＝FM＝3，∵点M是AF的中点，∴AM＝FM＝DM＝3，∴△AMD为等边三角形，∴∠ADM＝∠AMD＝∠A＝60°，AM＝DM＝AD＝3，∴∠FMD＝120°，∴∠MDF＝∠MFD＝（180°﹣∠FMD）＝（180°﹣120°）＝30°，∴∠ADF＝∠ADM+∠MDF＝60°+30°＝90°，在Rt△ADF中，AF＝AM+FM＝6，AD＝3，由勾股定理得：FD＝＝，∵∠AMD＝∠B＝60°，∠ADM＝∠C＝60°，∴△ABC为等边三角形，∴BC＝AB，∵∠FED＝∠B＝60°，DE＝EF，∴△DEF为等边三角形，∴EF＝FD＝，∵∠EFB＝90°，∠B＝90°，∴∠BEF＝30°，在Rt△BEF中，∠BEF＝30°，∴BE＝2BF，由勾股定理得：BE2﹣BF2＝EF2，即（2BF）2﹣BF2＝，∴BF＝3，∴AB＝AF+BF＝6+3＝9，∴BC＝AB＝9．故结论④正确．综上所述：正确的结论是①②④．故答案为：①②④．三、解答题（60分）21．（18分）（1）计算：（﹣1）2024+（）﹣2﹣（π﹣3）0；（2）计算：（m﹣n）2﹣2m（m﹣n）；（3）因式分解：a2（x﹣y）+4（y﹣x）；（4）解分式方程：﹣3＝．【解答】解：（1）（﹣1）2024+（）﹣2﹣（π﹣3）0＝1+9﹣1＝9；（2）（m﹣n）2﹣2m（m﹣n）＝m2﹣2mn+n2﹣2m2+2mn＝n2﹣m2；（3）a2（x﹣y）+4（y﹣x）＝a2（x﹣y）﹣4（x﹣y）＝（x﹣y）（a2﹣4）＝（x﹣y）（a+2）（a﹣2）；（4）﹣3＝，方程两边都乘x﹣2，得3﹣3（x﹣2）＝1﹣x，3﹣3x+6＝1﹣x，﹣3x+x＝1﹣6﹣3，﹣2x＝﹣8，x＝4，检验：当x＝4时，x﹣2≠0，所以分式方程的解是x＝4．22．（6分）先化简：，再从﹣2，﹣1，﹣6，中选择一个适合的数x代入求值．【解答】解：＝•＝＝＝，∵x＝﹣1，﹣2时，原分式无意义，∴x可以为﹣6或，当x＝﹣6时，原式＝＝2．23．（7分）如图，在平面直角坐标系中，△ABC的顶点A，B，C在格点上．（1）请在图中作出△ABC关于y轴对称的△A′B′C'；（2）写出点B'，点C'的坐标，以A'，B，C′为顶点的三角是　等腰直角　三角形；（3）点P在图中格点上，若△PBC是等腰三角形，则点P的个数是　10个　．【解答】解：（1）如图，△A′B′C'即为所求．（2）由图可得，B'（﹣3，2），C'（﹣2，﹣1）．由勾股定理得，A'B＝＝，A'C'＝＝，BC'＝＝，∴A'B＝A'C'，A'B2+A'C'2＝BC'2，∴∠BA'C'＝90°，∴△A'BC'为等腰直角三角形．故答案为：等腰直角．（3）如图，点P1，P2，P3，P4，P5，P6，P7，P8，P9，P10均满足题意，∴点P的个数是10个．故答案为：10个．24．（9分）在△ABC中，∠BAC＝∠BCA，D是平面内一点，∠DAB＝∠ABC＝90°，点E在AB边所在直线上，CE⊥BD，垂足是F．（1）当点E在线段AB上时，如图①，求证：AE+AD＝BC；（2）当点E在线段BA延长线上时，如图②；当点E在线段AB延长线上时，如图③，请猜想并直接写出线段AE，AD，BC的数量关系；（3）如图③，若BF+CF＝6，则S四边形ADFC﹣S△BEF＝　18　．【解答】（1）证明：由题意得，△ABC为等腰直角三角形，则AB＝BC，∵∠ABD+∠CBF＝90°，∠CBF+∠FCB＝90°，∴∠ABD＝∠BCF，∵∠EBC＝∠DBA＝90°，AB＝BC，∴△EBC≌△DAB（ASA），∴BE＝AD，则BC＝AB＝AE+BE＝AE+DA；（2）解：当点E在线段BA延长线上时，BC＝AD﹣AE，理由：由（1）同理可得：△EBC≌△DAB（ASA），∴BE＝AD，则BC＝AB＝BE﹣AE＝AD﹣AE；当点E在线段AB延长线上时，BC＝AE﹣AD，理由：由（1）同理可得：△EBC≌△DAB（ASA），∴BE＝AD，则BC＝AB＝AE﹣BE＝AE﹣AD；（3）解：如图③，设EF＝a，BF＝x，则FC＝6﹣x，则BC2＝x2+（6﹣x）2，由（1）同理可得：△EBC≌△DAB（ASA），则S△EBC＝S△DAB，则S四边形ADFC﹣S△BEF＝S△EBC+S△DAB+S△ABC﹣2S△BEF＝2S△EBC+S△ABC﹣2S△BEF＝（a+6﹣x）x﹣[（6﹣x）2+x2]﹣ax＝ax+6x﹣x2+18﹣6x+x2﹣ax＝18，故答案为：18．25．（10分）2024年是中国农历甲辰龙年．元旦前，某商场进货员预测一种“吉祥龙”挂件能畅销市场，就用6000元购进一批这种“吉祥龙”挂件，面市后果然供不应求，商场又用12800元购进了第二批这种“吉祥龙”挂件，所购数量是第一批购进数量的2倍，但每件的进价贵了4元．（1）该商场购进第一批、第二批“吉祥龙”挂件每件的进价分别是多少元？（2）若两批“吉祥龙”挂件按相同的标价销售，要使两批“吉祥龙”挂件全部售完后获利不低于7300（不考虑其他因素），且最后的50件“吉祥龙”挂件按八折优惠售出，那么每件“吉祥龙”挂件的标价至少是多少元？【解答】解：（1）设该商场购进第一批“吉祥龙”挂件的进价是x元/件，则第二批“吉祥龙”挂件的进价是（x+4）元，根据题意得：＝×2，解得：x＝60，经检验，x＝60是所列方程的解，且符合题意，∴x+4＝60+4＝64（元/件）．答：该商场购进第一批“吉祥龙”挂件的进价是60元/件，第二批“吉祥龙”挂件的进价是64元；（2）该商场购进第一批“吉祥龙”挂件的数量是6000÷60＝100（件），该商场购进第二批“吉祥龙”挂件的数量是12800÷64＝200（件）．设每件“吉祥龙”挂件的标价是y元，根据题意得：（100+200﹣50）y+50×0.8y﹣6000﹣12800≥7300，解得：y≥90，∴y的最小值为90．答：每件“吉祥龙”挂件的标价至少是90元．26．（10分）如图，△ABC在平面直角坐标系中，顶点B（m，0），C（n，0）在x轴上，顶点A在y轴的正半轴上，BD⊥AC，垂足是D，BD交AO于点E，∠AED﹣∠BAO＝45°，（m+4）2+（n﹣6）2＝0．请解答下列问题：（1）求点B、点C的坐标；（2）求线段AE的长；（3）连接CE．若OE＝2，在坐标轴上是否存在点F，使S△ACF＝S△ACE？若存在，请直接写出点F的个数和其中一个点F的坐标；若不存在，请说明理由．【解答】解：（1）∵（m+4）2+（n﹣6）2＝0，则m+4＝0且n﹣6＝0，解得：m＝﹣4且n＝6，故点B、C的坐标分别为：（﹣4，0）、（6，0）；（2）∵BD是△ABC的高，∴BD⊥AC，∴∠BDC＝∠BDA＝90°，∴∠DAE+∠DEA＝90°．∵x轴⊥y轴，∴∠AOB＝∠AOC＝90°，∴∠DAE+∠ACB＝90°，∴∠ACB＝∠DEA．∵∠ACB﹣∠BAO＝45°，∴∠DEA﹣∠BAO＝45°．∵∠DEA﹣∠BAO＝∠ABD，∴∠ABD＝45°．∵∠BDA＝90°，∴∠BAD＝90°﹣∠ABD＝45°，∴BD＝AD．在△DBC和△DAE中，，∴△DBC≌△DAE（AAS），∴AE＝BC＝6+4＝10；（3）由（2）知，AE＝10，则点A、E的坐标分别为：（0，12）、（0，2），由点A、C的坐标得，直线AC的表达式为：y＝﹣2x+12，∵S△ACF＝S△ACE，故取AE的中点N（0，7），过点N作直线n∥AC，取AM＝AN，过点M（0，17）作直线m∥AC，则直线m、n和x坐标轴的交点即为点F，故共有4个，为点M、N以及m、n和x轴的交点，∵n∥AC，则直线n的表达式为：y＝﹣2x+7，则直线n和坐标轴的交点坐标为：（0，7）、（3.5，0）；同理可得直线m和坐标轴的交点坐标为：（0，17）、（8.5，0）；综上，符合条件的点F有4个，坐标为：（0，7）或（3.5，0）或（0，17）或（8.5，0）．。

浙江省杭州市钱塘区2023-2024学年八年级上学期期末考试语文试卷(含答案)

2023-2024学年浙江省杭州市钱塘区八年级（上）期末语文试卷一、寻访山水美景（39分）大自然的山山水水，蕴含着丰富的文化内涵，是人类的宝贵财富。

班级开展“寻访山水”为主题的综合实践活动，让我们一起参与其中吧！活动一：访山水之妙西湖的一汪碧水，悄悄注入杭州的灵魂，三秋桂子、十里荷花的胜景，烟柳画桥、风帘翠幕的诗情，自出（xīn）裁在杭州；远离喧（xiāo）、清闲自得的山水，保留着中国文化精致的记忆，寄托着人们诗意栖居的美好愿望。

如此____的山水与文化紧密相连，山水是文化的载体，文化是山水的灵魂。

作为历史文化名胜，杭州的山水因为人的居住和参与，逐渐演变成了生动的人文意象与城市肌理，并与现代城市生活（róng）为一体，在历史与现实的交汇中展露出了自身的个性。

1.根据拼音写汉字或给加点字选择正确的读音。

（4分）①自出（xīn）裁②喧（xiāo）③载体（A.zǎi B.zài）④（róng）为一体2.填入横线处的成语，最恰当的一项是（3分）A.惟妙惟肖B.无动于衷C.巧妙绝伦D.妙手偶得活动二：赏文化精神3．（8分）请在横线处填写相应的诗文。

中国文人流连钟情于山水，山水给予中国文人太多的灵感与情思。

“（1），隐天蔽日”，是郦道元对山峡壮阔的描绘；“夕日欲颓，（2）”，是陶弘景笔下灵动的美景；“（3）？烟波江上使人愁。

”，是崔颢抒写的浓烈乡愁；“树树皆秋色，（4）”，是王绩勾勒的山野秋景；“（5），绿水逶迤”，是欧阳修短浆轻舟的惬意；“争渡，争渡，（6）”，是李清照遇见的惊喜；“（7），（8）”，是白居易钱塘湖春行耳闻目睹的莺歌燕语。

4．（4分）山水是风景，也是险阻；是历练，也是见证。

在《红星照耀中国》《长征》的“跋山涉水”中，你读到了中国共产党人怎样的精神？请选择下列事件中的一项进行分析。

A.四渡赤水河B.巧渡金沙江C.飞夺泸定桥活动三：探发展理念厚植绿水青山，描绘美丽中国新画卷。

辽宁省大连市中山区2023-2024学年八年级上学期期末考试语文试卷(含答案)

2023-2024学年辽宁省大连市中山区八年级（上）期末语文试卷一、积累与运用。

（17分）1．（2分）下列词语中加点字的字音、字形完全正确的一项是（）A．要塞（sāi）粗糙（cāo）洗涤（dí）秉息敛声（bǐng）B．仲裁（cái）窒息（zhì）序幕（mù）抑扬顿挫（cuò）C．咆哮（páo）琐屑（xiè）曼延（màn）张目结舌（jiē）D．周济（jì）倔强（juè）瞻仰（zhān）烙绎不绝（luò）2．（2分）依次填入下面句子横线处的词语最恰当的一项是（）ㅤㅤ人生路上，目的地_______重要，所谓实现目标是通向幸福的道路。

_______赶路途中的风景亦不可错过，有时不妨放缓脚步，冷静就难，淡定受喜，说不准能在欣赏到平日________的风景、捕捉到生活的美好细节之余，还能更利于________目标呢。

A．显然但漫不经心完成B．显然因熟视无睹达到C．固然但熟视无睹达到D．固然因漫不经心完成3．（2分）下列各项中分析有误的一项是（）ㅤㅤ在与自然长期打交道的过程中，勤劳而智慧的劳动人民就地取材，创造出多样的民间艺术表现形式和内容。

中国民间艺术深深地根植于具有几千年农耕文明的土壤之上，它带有泥土的芬芳和百姓最为质朴的情感。

早在三千多年前，先民就注重通过收集民间的诗歌而了解民风，《诗经》中的“国风”汇集了周初至春秋间各诸侯国的民间诗歌，其内容表达了劳动人民最真实的生活以及他们对美好生活向往的愿景。

A．“中国民间艺术深深地根植于具有几千年农耕文明的土壤之上。

”这句话主干是“艺术根植土壤之上。

”B．“它带有泥土的芬芳和百姓最为质朴的情感。

”用符号分析句子成分为：它//带有（泥土的）芬芳和（百姓最为质朴的）情感。

C．“早在三千多年前，先民就注重通过收集民间的诗歌而了解民风。

”“早在三千多年前”和“就”都是状语。

部编版八年级上学期语文《期末考试试卷》及答案解析

(选自郦道元《三峡》)
[乙]山川之美,古来共谈.高峰入云,清流见底.两岸石壁,五色交辉.青林翠竹,四时俱备.晓雾将歇,猿鸟乱鸣；夕日欲颓,沉鳞竞跃.实是欲界之仙都.自康乐以来,未复有能与其奇者.
(选自陶弘景《答谢中书书》)
15. 解释下列句子中加点词的意思.
(1)则素湍绿潭湍(2)晓雾将歇歇
16. 将下面句子翻译成现代汉语
(1)东风不与周郎便,_______________.(杜牧《赤壁》
(2)________________,塞上燕脂凝夜紫.(李贺《雁门太守行》
(3)_________________,悠然见南山.(陶渊明《饮酒(其五)》)
(4)入则无法家拂士,_________________,国恒亡 (《生于忧患,死于安乐》)
7. 选段说明的主要内容是什么？请用一句话概括.
8. “初月出云,长虹饮涧”是什么意思？
9. 作者引用张嘉贞的话的目的是什么？
10. 说明文的语言必须准确,讲究用语的分寸.写出下面句中加点词语的表达作用.
①全桥只有一个大拱,长达37.4米,在当时可算是世界上最长的石拱.
② 大拱的两肩上,各有两个小拱.
“24小时城市书房”的特点：____________________________________________.
二．现代文阅读(共25分)
(一)(共11分)
阅读下面的文章,完成下列小题.
赵州桥非常雄伟,全长50.82米,两端宽9.6米,中部略窄,宽9米.桥的设计完全合乎科学原理,施工技术更是巧妙绝伦.唐朝的张嘉贞说它“制造奇特,人不知其所以为”.这座桥的特点是：(一)全桥只有一个大拱,长达37.4米,在当时可算是世界上最长的石拱.桥洞不是普通半圆形,而是像一张弓,因而大拱上面的道路没有陡坡,便于车马上下.(二)大拱的两肩上,各有两个小拱.这个创造性的设计,不但节约了石料,减轻洪水对桥身的冲击.同时,拱上加拱,桥身也更美观.(三)大拱由28道拱圈拼成,就像这么多同样的弓合拢在一起,做成一个弧形的桥洞.每道拱圈都能独立支撑上面的重量,一道坏了,其他各道不致受到影响.(四)全桥结构匀称,和四周景色配合得十分和谐；桥上的石栏石板也雕刻得古朴美观.唐朝的张说,远望这座桥就像“初月出云,长虹饮涧”.赵州桥高度的技术水平和不朽的艺术价值,充分显示了我国劳动人民的智慧和力量.桥的主要设计者李春就是一位杰出的工匠,在桥头的碑文里刻着他的名字.

2023-2024学年度第一学期期末考试试题八年级数学+答案解析

2023-2024学年度第一学期期末考试八年级数学试卷试卷满分：150分考试时间：120分钟一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将该选项的字母代号填涂在答题卡相应位置上）1．下列几种著名的数学曲线中，不是轴对称图形的是（▲）A ．B ．C ．D ．2．有下列实数：，1.8－，9，3，33，其中无理数有（▲）A ．1个B ．2个C ．3个D ．4个3．下列数据中不能确定物体位置的是（▲）A ．电影票上的“5排8号”B ．小明住在某小区3号楼7号C ．南偏西37°D ．东经130°，北纬54°的城市4．如图，AD 为∠BAC 的角平分线，添加下列条件后，不能证明△ABD ≌△ACD 的是（▲）A ．∠B ＝∠C B ．∠BDA ＝∠CDA C ．AB ＝AC D ．BD ＝CD 5．在等腰三角形ABC 中，∠A =100°，则底角的度数是（▲）A ．100°B ．80°C ．50°D ．40°6．如图，△AOB 是边长为2的等边三角形，点B 在x 轴上，则点A 关于x 轴的对称点的坐标为（▲）A ．（1，－3）B ．（1，3）C ．（－1，－3）D ．（－1，3）7．一次函数b ax y ＋＝1与正比例函数bx y ＝－2在同一坐标系中的图像大致是（▲）A ．B ．C ．D ．8．如图，△ABC 中，∠ACB ＝90°，BC =6，AC ＝8，点D 是AB 的中点，将△ACD 沿CD 翻折得到△ECD ，连接AE ，BE ，则线段AE 的长等于（▲）A ．75B ．548C ．53D ．514第4题图第6题图第8题图二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）9．36的平方根是▲．10．扬州市面积约为6591平方公里，数据6591用四舍五入法精确到百位，并用科学记数法表示为▲．11．比较大小：3▲1－π（用“>”、“<”或“＝”填空）．12．如果将直线y ＝2x －1向上平移3个单位，那么所得直线的函数表达式是▲．13．已知点A （1，m ），B （32，n ）在一次函数y ＝3x ＋1的图像上，则m ▲n （用“>”、“<”或“＝”填空）．14．如图，在△ABC 中，AB ＝AC ，AD 是BC 边上的高，点E 、F 是AD 的三等分点，若BC ＝3cm ，AD ＝4cm ，则图中阴影部分的面积是▲cm 2．15．如图，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y 轴于点N ，再分别以点M 、N 为圆心，大于MN 的长为半径画弧，两弧在第二象限交于点P ．若点P 的坐标为()a a －，＋112，则a 的值为▲．16．如图，在Rt △ABC 中，AC ＝4，AB ＝5，∠C ＝90°，BD 平分∠ABC 交AC 于点D ，则DC 的长是▲．17．已知A 、B 两地是一条直路，甲骑自行车从A 地到B 地，乙骑摩托车从B 地到A 地，两人同时出发，乙先到达目的地，两人之间的距离s （km ）与运动时间t （h ）的函数关系大致如图所示，则下列结论正确的有▲．①两人出发2h 后相遇；②甲骑自行车的速度为60km/h ；③乙比甲提前2h 到达目的地；④乙到达目的地时两人相距200km ．第14题图第15题图第16题图第17题图18．定义：在平面直角坐标系xOy 中，O 为坐标原点，任意两点P （x 1，y 1）、Q （x 2，y 2），称2121y y x x ＋＋＋的值为P 、Q 两点的“坐标和距离”．若P （1，－3），Q 为直线y ＝x ＋2上任意一点，则P ，Q 的“坐标和距离”的最小值为▲．三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）19．（本题满分8分）（1）计算：9)1(6423--+；（2）求27)4(3-=-x 中x 的值．20．（本题满分8分）已知2a ＋1与a －4是b 的两个不相等的平方根，求b －1的立方根．21．（本题满分8分）已知y 与2x －3成正比例，且当x ＝2时，y ＝2．（1）求y 与x 的函数关系式；（2）求当x ＝21时的函数值．22．（本题满分8分）已知：如图，在△ABC 中，∠BAC ＝90°，AB ＝3，AC ＝4，AD ⊥BC ，垂足为点D ，求BC ，AD 的长．23．（本题满分10分）如图，在平面直角坐标系中，△ABC 各顶点的坐标分别为：A （﹣2，4），B （﹣4，2），C （﹣3，1），按下列要求作图．（1）画出△ABC 关于y 轴对称的图形△A 1B 1C 1（点A 、B 、C 分别对应A 1、B 1、C 1）；（2）△A 1B 1C 1的面积＝▲；（3）若M （x ，y ）是△ABC 内部任意一点，请直接写出这点在△A 1B 1C 1内部的对应点M 1的坐标▲；（4）P 是x 轴上一点，满足线段B 1P ＋BP 的值最小，画出P 点，并写出P 点坐标▲．24．（本题满分10分）已知：如图，∠ABC ＝∠ADC ＝90°，M 、N 分别是AC 、BD 的中点，连接BM 、DM ．（1）求证：BM ＝DM ；（2）求证：MN ⊥BD ．25．（本题满分10分）在四边形ABCD 中，O 是边BC 上的一点．若△OAB ≌△OCD ，则点O 叫做该四边形的“全等点”．（1）如图，已知在四边形ABCD 中，∠BAO ＝85°,∠B ＝40°，求∠AOD 的度数；（2）如图，在四边形ABCD 中，边BC 上的点O 是四边形ABCD 的“全等点”，已知CD ＝32，OA ＝5，BC ＝12，连接AC ，求AC 的长．26．（本题满分10分）如图，一次函数343+-=x y 的图像分别于x 轴、y 轴交于点A 、B ，以线段AB 为边在第一象限内作等腰直角△ABC ,∠BAC ＝90°．（1）求过B 、C 两点的直线的函数解析式；（2）在x 轴上取一点M ，使△AMC 是等腰三角形，直接写出符合条件的所有M 的坐标．27．（本题满分12分）如图，深50cm 的圆柱形容器，底部放入一个长方体的铁块，现在以一定的速度向容器内注水，右图为容器顶部离水面的距离y （cm ）随时间t （分钟）的变化图像．（1）求放入的长方体的高度；（2）求该容器注满水所用的时间；（3）若长方体铁块的底面积为6cm 2，求圆柱体的底面积．28．（本题满分12分）已知，△ABC 是等边三角形，点D 为射线BC 上一动点，连接AD ，以AD 为边在直线AD 右侧作等边△ADE ．图1图2图3（1）如图1，点D 在线段BC 上，连接CE ，若AB ＝4，且CE ＝1，求线段CD 的长；（2）如图2，点D 是BC 延长线上一点，过点E 作EF ⊥AC 于点F ，求证：CF ＝AF ＋CD ；（3）如图3，若AB ＝8，点D 在射线BC 上运动，取AC 中点G ，连接EG ，请直接写出EG 的最小值．2023-2024学年度第一学期期末考试八年级数学参考答案一、选择题(每题3分，共24分)题号12345678答案DBCDDACB二、填空题(每题3分，共30分)9.±6;10.3106.6⨯;11.<;12.22+=x y ;13.<；14.3；15.－2；16.23；17.①②④;18.2．三、解答题19．（1）计算：9)1(6423--+解：原式＝2……………………4分（2）求27)4(3-=-x 中x 的值．解：x ＝1……………………8分20．解：2a ＋1＋a －4＝0a ＝1……………………4分b ＝9b －1的立方根为2……………………8分21．（1）解：设y ＝k （2x －3）（k ≠0）x ＝2，y ＝2k ＝2y ＝4x －6……………………4分（2）解：当21＝x 时y ＝－4……………………8分22．（1）BC =5……………………4分（2）AD =512……………………8分23．（1）图略……………………2分（2）2……………………4分（3）（－x ，y ）……………………6分（4）作出点P 图略…………………8分（0，0）……………………10分24．（1）在△ABC 中，∵∠ABC ＝90°，M 是AC 的中点∴BM =21AC 同理DM =21AC∴BM =DM ……………………5分（2）在△MBD 中，BM =DM∵N 是BD 的中点∴MN ⊥BD……………………10分25．（1）70；……………………5分（2）80或54……………………10分26．（1）371+=x y ；……………………5分（2）（-1，0）、（9，0）、（10，0）（649，0）……………………10分（其中前3个1分1个，最后一个2分）27．（1）20cm ；……………………4分（2）21分钟；……………………8分（3）8cm 2……………………10分28．（1）3；……………………4分（2）在AC 上取一点G ，使CG =CD ，连EG先证△ABD ≌△ACE 得到∠ACE =∠DCE =60°再证△EGC ≌△EDC 得EG =EA 又∵EF ⊥AC ∴AF =FG ∴CF =AF +CD……………………8分（3）12或32……………………12分。

四川省成都市新都区2023-2024学年八年级上学期期末考试语文试卷(含解析)

四川省成都市新都区2023-2024学年八年级上学期期末语文试卷一、基础知识（共12分）1．下面加点字注音有误的一项是（）（3分）A．凌．空（líng）浩瀚．（hàn）屏息敛．声（lǎn）B．绯．红（fēi）佃．农（diàn）藏污纳垢．（gòu）C．燥．热（zào）婆娑．（suō）触．目伤怀（chù）D．卑．微（bēi）格调．（diào）惟妙惟肖．（xiào）2．下列语句中书写正确的一项是（）（3分）A．阶砌旁边栽着几丛书带草，墙上曼延着爬山虎或者蔷薇木香。

B．远远望去，在一座雄伟峻俏的山里，游击队员们正穿过树林。

C．据后代文人考定，《清明上河图》可能作于政和至宣和年间。

D．它们那些略带蓝色荧光的美丽轮廓，也许正闪耀在黑暗之中。

3．下列语句中加点的成语使用有误的一项是（）（3分）他是一个和颜悦色．．．．继承了父母的家业，在他的．．．．的人，总能非常友好地对待身边人。

他在三十岁时白手起家领导下，他的公司变成了国际型的大公司。

做事一丝不苟．．．．的他总能轻松应对工作中的挑战，当然，在成功的路上，他也遇见了许多困难，但他那不折不挠．．．．的精神品质始终支撑着他向前走，寻找着更多的可能性。

A．和颜悦色B．白手起家C．一丝不苟D．不折不挠4．下列句子没有语病的一项是（）（3分）A．学校开展和筹划了一场趣味运动会，让同学们在这个冬天感受到了运动的快乐。

B．经过了激烈的比赛，中国代表队在成都国际乒联混合团体世界杯中获得了冠军。

C．考生在考试前如果吃得太饱，可能会延长消化时间，降低做题效率和考试状态。

D．学校此次的表彰对象，主要是面向参与过班级自主管理并且表现突出的学生们。

二、文言文阅读（共12分）5．阅读下面两篇文章，完成问题。

（12分）甲自三峡七百里中，两岸连山，略无阙处。

重岩叠嶂，隐天蔽日，自非亭午夜分，不见曦月。

至于夏水襄陵，沿溯阻绝。

河南省洛阳市嵩县2022-2023学年八年级上学期期末语文试题(含答案)

2022--2023学年第一学期期末考试八年级语文试卷注意事项1.本试卷共6页，四道大题，满分120分，考试时间120分钟。

2.本试卷上不要答题，请按答题卡上注意事项的要求，直接把答案填写在答题卡上。

答在试卷上的答案无效。

一、积累与运用（共28分）1.阅读下面语段，回答问题。

（共4分）书是知识的山峰，是人类思维之花，生命之源，具有用之不竭．的力量。

高尔基曾经说过“书①是人类进步的阶梯”。

阅读一本好书，如同与一位知识渊博的学者谈话，他们的言语中闪烁着智慧的火花，传达着高尚的修养。

读书，不仅能丰富我们的知识，还能教会我们明②是非、惩恶扬善的人生哲理。

好．读书，读好书，才能不断汲取丰厚的营养，从而充实自己的人生。

(1)依次给语段中加点的字注音，全都正确．．．．的一项是A.jié hǎoB.jié hàoC.è hàoD.è hǎo(2)在语段横线处填入汉字，全都正确．．．．的一项是A.①籍②辩B.①藉②辨C.①籍②辨D.①藉②辩2.古诗文默写。

（8分）诗中有景，“树树皆秋色，①”（王绩《野望》），这是傍晚时分，诗人遥望山野所见的浓浓秋意；“② ,谁家新燕啄春泥”（白居易《钱塘湖春行》），这是初春时节，诗人游湖所见的莺歌燕舞的勃勃生气。

诗中有情，“③,④”（李贺《雁门太守行》），这是边关战场上，将士们誓死报国的凌云壮志；“⑤,⑥”（杜甫《春望》），这是国破家亡背景下，诗人思念亲人，渴望与亲人互通音讯的心声。

“⑦,⑧”（晏殊《浣溪沙》）这是诗人对光阴流转，物是人非的无限感慨和惆怅。

3.名著阅读。

（4分）在学校组织的名著阅读交流会上，针对八年级上册所涉及的《红星照耀中国》和《昆虫记》两本书，八（1)班张浩同学谈了自己的阅读体会：“初读《红星照耀中国》，如偶遇一位风尘仆仆的长者，虽交流有些困难，待深谙其身世后会愈加敬重；随意翻开《昆虫记》，就像一下子闯进了鲁迅先生笔下的百草园，邂逅了不少自然界的朋友，找回了几多童年的奇趣。

2022-2023学年度第一学期期末考试八年级语文试卷

3.（本题2分）C（海春轩塔属于物质文化遗产）
4.（本题7分）（1）示例：高大的战马腾空跃起，新四军战士手握盒子枪，策马飞驰，冲锋陷阵，锐不可当。（3分，未使用成语扣1分，表达方式不正确另外酌情扣分）（2）示例：你用嘀嘀嗒嗒的马蹄声谱曲，豪迈东进是最激越的一章。（2分，句式、修辞须跟例句一致，字数不要求完全相同。内容不契合雕塑图片及介绍文字不得分）（3）示例：吴先生，您创作的《新四军东进》雕塑有什么深刻内涵？这尊雕塑对新时期的东台有何特别意义？（2分）
（三）（9分）
12.（本题2分）（1）北京冬奥场馆建设融合科技与艺术，场馆内的科技元素引人关注；（1分）（2）绿色冬奥成色十足，实施节能减排，实现碳中和目标。（1分）
13.（本题3分）举例子。（1分）列举国家跳台滑雪中心的例子，（1分）具体说明了在设计与建筑过程中，北京冬奥会的场馆实现了科学、艺术和文化的完美融合。（1分）
14.（本题4分）（1）“仅”是只的意思，（1分）说明国家速滑馆“冰丝带”屋面相比于传统屋面用钢量之少，突出其采用技术之先进。（1分）（2）“所有”指一切，全部，（1分）说明北京冬奥会场馆实现了绿电供应的全覆盖，无一例外，突出其在奥运史上的首创地位。（1分）
（四）（16分）
15.（本题4分）（1）淡泊名利，清正自律。（2）礼贤下士，尊重人才。（3）非凡的卓识、视野和胸襟。（4）高尚而谦逊的人格。（每点1分）
16.（本题5分）“不像”：梅贻琦帮助夫人在清华大学附近摆摊，贴补家用；（1分）每次教授开会，梅贻琦像茶役一样为教授续茶，不发表看法，服从教授意见。（1分） “像”：被清华师生拥护、爱戴；（1分）以自己的“做”“实干”奠定了清华大学的格局；（1分）使清华大学发展成大师林立、闪耀而强大的大学，跻身国内名牌大学之列。（1分）

湖南省长沙市明德中学2024届八年级数学第一学期期末综合测试试题含解析

湖南省长沙市明德中学2024届八年级数学第一学期期末综合测试试题考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题（每题4分，共48分）1．如图，在△PAB 中，∠A =∠B ，D 、E 、F 分别是边PA 、PB 、AB 上的点，且AD =BF ，BE =AF ．若∠DFE =34°，则∠P 的度数为（）A ．112°B ．120°C ．146°D ．150°2．一个三角形的三条边长分别为4,7,x ，则x 的值有可能是下列哪个数（） A ．3B ．7C ．11D ．123．等腰三角形的两边长分别为4cm 和8cm ，则它的周长为（） A ．16cmB ．17cmC ．20cmD ．16cm 或20cm4．如图，在ABC 中，90,4,3C AC BC ∠=︒==，将ABC 绕点A 逆时针旋转，使点C 恰好落在线段AB 上的点E 处，点B 落在点D 处，则B D ，两点间的距离为（）A 10B 8C ．3D ．55．如图，在△ABC 中，AB ＝6，BC ＝5，AC ＝4，AD 平分∠BAC 交BC 于点D ，在AB 上截取AE ＝AC ，则△BDE 的周长为( )A ．8B ．7C ．6D ．56．如图，在△ABC 和△DEF 中，∠B＝∠DEF，AB ＝DE ，若添加下列一个条件后，仍然不能证明△ABC≌△DEF，则这个条件是( )A ．∠A＝∠DB ．BC ＝EF C ．∠ACB＝∠FD ．AC ＝DF7．若1x =-使某个分式无意义，则这个分式可以是（） A ．121x x -- B ．211x x ++ C ．211x x -- D ．121x x ++ 8．如图，直线a ，b ，c 表示三条公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）A ．一处B ．两处C ．三处D ．四处9．下列因式分解正确的是( ) A ．256(5)6m m m m -+=-+ B ．2241(21)m m -=- C ．2244(2)m m m +-=+ D ．241(21)(21)m m m -=+-10．如果把分式2aba b+中的a 、b 同时扩大为原来的2倍，那么得到的分式的值（） A ．不变B ．扩大为原来的2倍C ．缩小到原来的12D ．扩大为原来的4倍．11．已知△ABC 中，AB=8,BC=5,那么边AC 的长可能是下列哪个数（） A ．15B ．12C ．3D ．212．如图，在△ABC 中，∠C=90°，∠BAC=30°，AB=12，AD 平分∠BAC ，点PQ 分别是AB 、AD 边上的动点，则BQ+QP 的最小值是（）A．4 B．5 C．6 D．7二、填空题（每题4分，共24分）13．已知甲、乙两地间的铁路长1480千米，列车大提速后，平均速度增加了70千米/时，列车的单程运行时间缩短了3小时．设原来的平均速度为x千米/时，根据题意，可列方程为______________．14．计算：6x2÷2x= ．15．邮政部门规定：信函重100克以内（包括100克）每20克贴邮票0.8元，不足20克重以20克计算；超过100克，先贴邮票4元，超过100克部分每100克加贴邮票2元，不足100克重以100克计算．八（9）班有11位同学参加项目化学习知识竞赛，若每份答卷重12克，每个信封重4克，将这11份答卷分装在两个信封中寄出，所贴邮票的总金额最少是_________元．16．若32x 有意义，则x的取值范围是__________．17．若实数，满足，则______.18．如图，某风景区的沿湖公路AB=3千米，BC=4千米，CD=12千米，AD=13千米，其中AB^BC，图中阴影是草地，其余是水面．那么乘游艇游点C出发，行进速度为每小时11713千米，到达对岸AD最少要用小时．三、解答题（共78分）19．（8分）（1）如图1，在△ABC 中，∠ABC 的平分线BF 交AC 于F，过点F 作DF∥BC，求证：BD=DF．（2）如图2，在△ABC 中，∠ABC 的平分线BF 与∠ACB 的平分线CF 相交于F，过点F 作DE∥BC，交直线AB 于点D，交直线AC 于点E．那么BD，CE，DE 之间存在什么关系？并证明这种关系．（3）如图3，在△ABC 中，∠ABC 的平分线BF 与∠ACB 的外角平分线CF 相交于F，过点F 作DE∥BC，交直线AB 于点D，交直线AC 于点E．那么BD，CE，DE 之间存在什么关系？请写出你的猜想．（不需证明）20．（8分）如图，在等边ABC ∆中，点D ，E 分别是AC ，AB 上的动点，且AE CD =，BD 交CE 于点P ．（1）如图1，求证120BPC ︒∠=；（2）点M 是边BC 的中点，连接PA ，PM ．①如图2，若点A ，P ，M 三点共线，则AP 与PM 的数量关系是；②若点A ，P ，M 三点不共线，如图3，问①中的结论还成立吗？若成立，请给出证明，若不成立，请说明理由．21．（8分）甲、乙、丙三明射击队员在某次训练中的成绩如下表：队员成绩（单位：环）甲 6 6 7 7 8 9 9 9 9 10 乙 6 7 7 8 8 8 8 9 9 10 丙66677810101010针对上述成绩，三位教练是这样评价的：教练A ：三名队员的水平相当；教练B ：三名队员每人都有自己的优势；教练C ：如果从不同的角度分析，教练A 和B 说的都有道理. 你同意教练C 的观点吗？通过数据分析，说明你的理由.22．（10分）如图1，直线AB ∥CD ，直线l 与直线AB ，CD 相交于点E ，F ，点P 是射线EA 上的一个动点（不包括端点）（1）若∠CFE ＝119°，PG 交∠FEB 的平分线EG 于点G ，∠APG ＝150°，则∠G 的大小为．（2）如图2，连接PF ．将△EPF 折叠，顶点E 落在点Q 处．①若∠PEF ＝48°，点Q 刚好落在其中的一条平行线上，请直接写出∠EFP 的大小为． ②若∠PEF ＝75°，∠CFQ ＝12∠PFC ，求∠EFP 的度数．23．（10分）如图所示，在△ABC 中，已知AB ＝AC ，∠BAC ＝120°，AD ⊥AC ，DC ＝6 求BD 的长.24．（10分）已知等腰三角形底边长为a ，底边上的高的长为h ，求作这个等腰三角形．（要求：写作法，用尺规作图，保留作图痕迹）．25．（12分）某服装商预测一种应季衬衫能畅销市场，就用8000元购进一批衬衫，面市后果然供不应求，该服装商又用17600元购进了第二批这种衬衫，所购数量是第一批购进数量的2倍，但单价贵了8元．请问该服装商第一批进货的单价是多少元？26．如图，在ABC ∆中，,=⊥AB AC AD BC 于D（1）若52C BAC ∠=∠，求BAD ∠的度数（2）若点E 在AB 上，EF//AC 交AD 的延长线于点F 求证：AE=FE参考答案一、选择题（每题4分，共48分） 1、A【分析】根据等边对等角得到∠A=∠B ，证得△ADF ≌△BFE ，得∠ADF=∠BFE ，由三角形的外角的性质求出∠A=∠DFE=42°，根据三角形内角和定理计算即可．【题目详解】解：∵PA=PB ， ∴∠A=∠B ，在△ADF 和△BFE 中，AD BF A B AF BE =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△BFE （SAS ）， ∴∠ADF=∠BFE ，∵∠DFB=∠DFE+∠EFB=∠A+∠ADF ， ∴∠A=∠DFE=34°， ∴∠B =34°，∴∠P=180°-∠A-∠B=112°，故选：A ．【题目点拨】本题考查的是等腰三角形的性质、全等三角形的判定和性质、三角形的外角的性质，掌握等边对等角、全等三角形的判定定理和性质定理、三角形的外角的性质是解题的关键． 2、B【分析】已知两边，则第三边的长度应是大于两边的差而小于两边的和，这样就可求出第三边长的范围，从而得出结果．【题目详解】解：根据题意得：7-4＜x ＜7+4，即3＜x ＜11，故选：B ．【题目点拨】本题考查三角形的三边关系，关键是理解如何根据已知的两条边求第三边的范围．3、C【解题分析】试题分析：分当腰长为4cm 或是腰长为8cm 两种情况：①当腰长是4cm 时，则三角形的三边是4cm ，4cm ，8cm ，4cm+4cm=8cm 不满足三角形的三边关系；当腰长是8cm 时，三角形的三边是8cm ，8cm ，4cm ，三角形的周长是20cm ．故答案选C ．考点：等腰三角形的性质；三角形三边关系． 4、A【分析】连接BD ，利用勾股定理求出AB ，然后根据旋转的性质可得AC=AE=4，∠AED=∠C=90°，BC=DE=3，从而求出∠DEB 和BE ，最后利用勾股定理即可求出结论．【题目详解】解：连接BD∵90,4,3C AC BC ∠=︒== ∴225AC BC +由旋转的性质可得AC=AE=4，∠AED=∠C=90°，BC=DE=3 ∴∠DEB=180°－∠AED=90°，BE=AB －AE=1 在Rt △DEB 中，2210+=BE DE 故选A ．【题目点拨】此题考查的是勾股定理和旋转的性质，掌握勾股定理和旋转的性质是解决此题的关键． 5、B【题目详解】解：∵AD 是∠BAC 的平分线， ∴∠EAD =∠CAD 在△ADE 和△ADC 中， AE =AC ， ∠EAD =∠CAD ， AD =AD ，∴△ADE ≌△ADC (SAS)，∴ED =CD ，∴BC =BD +CD =DE +BD =5，∴△BDE 的周长=BE +BD +ED =(6−4)+5=7 故选B ．【题目点拨】本题考查全等三角形的应用.三角形全等的判定定理有：边边边（SSS ）、边角边（SAS ）、角边角（ASA ）、角角边（AAS ）、HL.通过证明三角形全等可以得到相等的边或角，可将待求量进行转化，使问题迎刃而解． 6、D【解题分析】解：∵∠B =∠DEF ，AB =DE ，∴添加∠A =∠D ，利用ASA 可得△ABC ≌△DEF ； ∴添加BC =EF ，利用SAS 可得△ABC ≌△DEF ； ∴添加∠ACB =∠F ，利用AAS 可得△ABC ≌△DEF ；故选D ．点睛：本题考查了全等三角形的判定，掌握全等三角形的判定方法：SSS 、ASA 、SAS 、AAS 和HL 是解题的关键． 7、B【分析】根据分式无意义的条件，对每个式子进行判断，即可得到答案. 【题目详解】解：A 、由210x -=，得12x =，故A 不符合题意； B 、由10x +=，得1x =-，故B 符合题意； C 、由10x -=，得1x =，故C 不符合题意； D 、由210x +=，得12x =-，故D 不符合题意；故选：B. 【题目点拨】本题考查了分式无意义的条件，解题的关键是掌握分式无意义的条件，即分母等于0. 8、D【分析】根据角平分线上的点到角两边的距离相等作图即可得到结果．【题目详解】解：如图所示，可供选择的地址有4个，故选：D 【题目点拨】本题主要考查的是角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键． 9、D【分析】因式分解：把一个整式化为几个因式的积的形式．从而可以得到答案．【题目详解】A 没有把256m m -+化为因式积的形式，所以A 错误， B 从左往右的变形不是恒等变形，因式分解是恒等变形，所以B 错误， C 变形也不是恒等变形所以错误，D 化为几个因式的积的形式，是因式分解，所以D 正确．故选D ．【题目点拨】本题考查的是多项式的因式分解，掌握因式分解的定义是解题关键． 10、B【分析】依题意分别用2a 和2b 去代换原分式中的a 和b ，利用分式的基本性质化简即可【题目详解】分别用2a 和2b 去代换原分式中的a 和b ，得22242222a b ab aba b a b a b⨯⨯==⨯+++，可见新分式是原分式的2倍．故选：B ．【题目点拨】本题考查了分式的基本性质．解题的关键是抓住分子、分母变化的倍数，解此类题首先把字母变化后的值代入式子中，然后约分，再与原式比较，最终得出结论． 11、B【解题分析】根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边列出不等式即可．【题目详解】解：根据三角形的三边关系，8−5＜AC ＜8＋5，即3＜AC ＜13，符合条件的只有12，故选：B ．【题目点拨】本题考查的是三角形的三边关系，掌握三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边是解题的关键． 12、C【分析】如图，作点P 关于直线AD 的对称点P′，连接QP′，由△AQP ≌△AQP′，得PQ=QP′，欲求PQ+BQ 的最小值，只要求出BQ+QP′的最小值，即当BP′⊥AC 时，BQ+QP′的值最小，此时Q 与D 重合，P′与C 重合，最小值为BC 的长．【题目详解】解：如图，作点P 关于直线AD 的对称点P′，连接QP′，△AQP 和△AQP′中，''⎧=⎪∠=∠⎨⎪=⎩AP AP QAP QAP AQ AQ ，∴△AQP ≌△AQP′， ∴PQ=QP′∴欲求PQ+BQ 的最小值，只要求出BQ+QP′的最小值，∴当BP′⊥AC 时，BQ+QP′的值最小，此时Q 与D 重合，P′与C 重合，最小值为BC 的长．在Rt △ABC 中，∵∠C=90°，AB=12，∠BAC=30°， ∴BC=12AB=6， ∴PQ+BQ 的最小值是6，故选：C ．【题目点拨】本题考查了勾股定理、轴对称中的最短路线问题、垂线段最短等知识，找出点P 、Q 的位置是解题的关键．二、填空题（每题4分，共24分）13、14801480370x x =++ 【解题分析】试题解析：设原来的平均速度为x 千米/时，列车大提速后平均速度为x+70千米/时，根据走过相同的距离时间缩短了3小时，列方程：1480x ＝148070x +＋3，故答案为1480x ＝148070x +＋3. 14、3x ．【解题分析】试题解析：6x 2÷2x=3x ．考点：单项式除以单项式．15、5.1【分析】由题意知，把它分成两个小于或等于100克的信封比较省钱，设其中一个信封装x 份答卷，根据重量小于等于100列出方程组求出x 的取值范围，然后分情况计算所贴邮票的总金额即可.【题目详解】解：11份答卷以及两个信封总计：12×11＋2×4＝140（克），由题意知，把它分成两个小于或等于100克的信封比较省钱，设其中一个信封装x 份答卷，则另一个信封装（11−x ）份答卷，由题意得：()12410012114100x x +≤⎧⎨-+≤⎩，解得：3≤x≤8，∴共有三种情况：①一个信封装3份答卷，另一个信封装8份答卷，装3份答卷的信封重量为12×3＋4＝40（克），装8份答卷的信封重量为140－40＝100（克），此时所贴邮票的总金额为：0.8×2＋0.8×5＝5.1（元）；②一个信封装4份答卷，另一个信封装7份答卷，装4份答卷的信封重量为12×4＋4＝52（克），装7份答卷的信封重量为140－52＝88（克），此时所贴邮票的总金额为：0.8×3＋0.8×5＝1.4（元）；③一个信封装5份答卷，另一个信封装1份答卷，装5份答卷的信封重量为12×5＋4＝14（克），装1份答卷的信封重量为140－14＝71（克），此时所贴邮票的总金额为：0.8×4＋0.8×4＝1.4（元）；∴所贴邮票的总金额最少是5.1元，故答案为：5.1．【题目点拨】本题考查了一元一次不等式组的实际应用，正确理解题意，分析得出把它分成两个小于或等于100克的信封比较省钱，进而列出方程组是解题的关键.16、一切实数【分析】根据使立方根有意义的条件解答即可.【题目详解】解:立方根的被开方数可以取一切实数,所以x可以取一切实数.故答案为:一切实数.【题目点拨】本题考查使立方根有意义的条件,理解掌握该知识点是解答关键.17、1.5【解题分析】根据非负数的性质列式求出m，n的值，然后代入代数式进行计算即可得解．【题目详解】解：根据题意得：，∴∴；故答案为：.【题目点拨】本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0，解题的关键是利用非负性正确求值.18、0.1【分析】连接AC，在直角△ABC中，已知AB，BC可以求AC，根据AC，CD，AD的长度符合勾股定理确定AC⊥CD，则可计算△ACD的面积，又因为△ACD的面积可以根据AD边和AD边上的高求得，故根据△ACD的面积可以求得C到AD的最短距离，即△ACD中AD边上的高．【题目详解】解：连接AC，在直角△ABC中，AB=3km，BC=1km，则22，34∵CD=12km，AD=13km，故存在AD2=AC2+CD2∴△ACD为直角三角形，且∠ACD=90°，∴△ACD的面积为12×AC×CD=30km2，∵AD=13km，∴AD边上的高，即C到AD的最短距离为7150 1313=km，游艇的速度为11601313150⨯km/小时，需要时间为601313150⨯小时=0.1小时．故答案为0.1．点睛：本题考查了勾股定理在实际生活中的应用，考查了直角三角形面积计算公式，本题中证明△ACD是直角三角形是解题的关键．三、解答题（共78分）19、（1）见详解；（2）BD+CE＝DE，证明过程见详解；（3）BD﹣CE＝DE，证明过程见详解【分析】（1）根据平行线的性质和角平分线定义得出∠DFB＝∠CBF，∠ABF＝∠CBF，推出∠DFB＝∠DBF，根据等角对等边推出即可；（2）与（1）证明过程类似，求出BD＝DF，EF＝CE，即可得出结论；（3）与（1）证明过程类似，求出BD＝DF，EF＝CE，即可得出结论．【题目详解】解：（1）∵BF平分∠ABC，∴∠ABF＝∠CBF，∵DF∥BC，∴∠DFB＝∠CBF，∴∠DFB＝∠DBF，∴BD＝DF；（2）BD+CE＝DE，理由是：∵BF平分∠ABC，∴∠ABF＝∠CBF，∵DF∥BC，∴∠DFB＝∠CBF，∴∠DFB＝∠DBF，∴BD＝DF；同理可证：CE ＝EF ，∵DE ＝DF +EF ，∴BD +CE ＝DE ；（3）BD ﹣CE ＝DE ．理由是：∵BF 平分∠ABC ，∴∠ABF ＝∠CBF ，∵DF ∥BC ，∴∠DFB ＝∠CBF ，∴∠DFB ＝∠DBF ，∴BD ＝DF ；同理可证：CE ＝EF ，∵DE ＝DF ﹣EF ，∴BD ﹣CE ＝DE ．【题目点拨】本题考查了角平分线定义，平行线的性质，等腰三角形的判定等知识点，本题具有一定的代表性，三个问题证明过程类似．20、（1）证明过程见详解；（2）①2AP PM =；②结论成立，证明见详解【分析】（1）先证明()AEC CDB SAS ≌，得出对应角相等，然后利用四边形的内角和和对顶角相等即可得出结论；（2）①2AP PM =；由等边三角形的性质和已知条件得出AM ⊥BC ，∠CAP ＝30°，可得PB ＝PC ，由∠BPC ＝120°和等腰三角形的性质可得∠PCB ＝30°，进而可得AP ＝PC ，由30°角的直角三角形的性质可得PC ＝2PM ，于是可得结论；②延长BP 至D ，使PD ＝PC ，连接AD 、CD ，根据SAS 可证△ACD ≌△BCP ，得出AD ＝BP ，∠ADC ＝∠BPC ＝120°，然后延长PM 至N ，使MN ＝MP ，连接CN ，易证△CMN ≌△BMP （SAS ），可得CN ＝BP ＝AD ，∠NCM ＝∠PBM ，最后再根据SAS 证明△ADP ≌△NCP ，即可证得结论．【题目详解】（1）证明：因为△ABC 为等边三角形，所以60A ACB ∠=∠=︒∵AC BC A ACB AE CD =⎧⎪∠=∠⎨⎪=⎩，∴()AEC CDB SAS ≌ ，∴AEC CDB ∠=∠，在四边形AEPD 中，∵360AEC EPD PDA A ∠+∠+∠+∠=︒，∴18060360AEC EPD CDB ∠+∠+︒-∠+︒=︒，∴120EPD ∠=︒，∴120BPC ∠=︒；（2）①如图2，∵△ABC 是等边三角形，点M 是边BC 的中点，∴∠BAC ＝∠ABC ＝∠ACB ＝60°，AM ⊥BC ，∠CAP ＝12∠BAC ＝30°，∴PB ＝PC ， ∵∠BPC ＝120°，∴∠PBC ＝∠PCB ＝30°，∴PC ＝2PM ，∠ACP ＝60°﹣30°＝30°＝∠CAP ，∴AP ＝PC ，∴AP ＝2PM ；故答案为：2AP PM ；②AP ＝2PM 成立，理由如下：延长BP 至D ，使PD ＝PC ，连接AD 、CD ，如图4所示：则∠CPD ＝180°﹣∠BPC ＝60°，∴△PCD 是等边三角形，∴CD ＝PD ＝PC ，∠PDC ＝∠PCD ＝60°，∵△ABC 是等边三角形，∴BC ＝AC ，∠ACB ＝60°＝∠PCD ，∴∠BCP ＝∠ACD ，∴△ACD ≌△BCP （SAS ），∴AD ＝BP ，∠ADC ＝∠BPC ＝120°，∴∠ADP ＝120°﹣60°＝60°，延长PM 至N ，使MN ＝MP ，连接CN ，∵点M 是边BC 的中点，∴CM ＝BM ，∴△CMN ≌△BMP （SAS ），∴CN ＝BP ＝AD ，∠NCM ＝∠PBM ，∴CN ∥BP ，∴∠NCP +∠BPC ＝180°，∴∠NCP ＝60°＝∠ADP ，在△ADP 和△NCP 中，∵AD=NC ，∠ADP =∠NCP ，PD=PC ，∴△ADP ≌△NCP （SAS ），∴AP ＝PN ＝2CM ；【题目点拨】本题是三角形的综合题，主要考查了等边三角形的判定与性质、全等三角形的判定与性质、含30°角的直角三角形的性质等知识；熟练掌握等边三角形的判定与性质，证明三角形全等是解题的关键．21、同意教练C 的观点，见解析【分析】依次求出甲、乙、丙三名队员成绩的平均数、中位数、方差及众数，根据数据的稳定性即可判断.【题目详解】解：依题意渴求得：甲队员成绩的平均数为6677899991010+++++++++=8；乙队员成绩的平均数为6778888991010+++++++++=8；丙队员成绩的平均数为6667781010101010+++++++++=8；甲队员成绩的中位数为898.52+=，乙队员成绩的中位数为8882+=，丙队员成绩的中位数为787.52+=，甲队员成绩的方差为2s 甲=110 [（6−8）2＋（6−8）2＋（7−8）2＋（7−8）2＋（8−8）2＋（9−8）2＋（9−8）2＋（9−8）2＋（9−8）2＋（10−8）2]＝1.8;乙队员成绩的方差为2s 乙=110[（6−8）2＋（7−8）2＋（7−8）2＋（8−8）2＋（8−8）2＋（8−8）2＋（8−8）2＋（9−8）2＋（9−8）2＋（10−8）2]＝1.2; 丙队员成绩的方差为2s 丙=110 [（6−8）2＋（6−8）2＋（6−8）2＋（7−8）2＋（7−8）2＋（8−8）2＋（10−8）2＋（10−8）2＋（10−8）2＋（10−8）2]＝3; 由于甲、乙、丙三名队员成绩的平均数分别为：8x =甲，8x =乙，8x =丙，所以，三名队员的水平相当.故，教练A 说的有道理.由于甲、乙、丙三名队员的成绩的中位数分别为：8.5；8；7.5.所以，从中位数方面分析，甲队员有优势.由于甲、乙、丙三名队员的成绩的方差分别为：2 1.8s =甲，2 1.2s =乙，23s =丙.所以，从方差方面分析，乙队员有优势.由于甲、乙、丙三名队员的成绩的众数分别为：9；8；10.所以，从众数方面分析，丙队员有优势.故，教练B说的有道理.所以，同意教练C的观点.【题目点拨】此题主要考查数据分析的应用，解题的关键是熟知平均数、中位数、方差及众数的求解方法.22、（1）29.5°；（2）①42°或66°；②35°或63°．【分析】（1）根据平行线的性质和三角形的内角和即可得到结论；（2）①Ⅰ、当点Q落在AB上时，利用三角形内角和定理计算即可．Ⅱ、当点Q落在CD上时，∠PQF＝∠PEF＝48°，利用平行线的性质，三角形的内角和定理计算即可．②分两种情形：Ⅰ、当点Q在平行线AB，CD之间时．Ⅱ、当点Q在CD下方时，分别构建方程即可解决问题．【题目详解】（1）∵直线AB∥CD，∴∠BEF＝∠CFE＝119°，∠PEF＝180°﹣∠CFE＝61°，∵EG平分∠BEF，∴∠FEG＝12∠BEF＝59.5°，∵∠APG＝150°，∴∠EPF＝30°，∴∠G＝180°﹣30°﹣61°﹣59.5°＝29.5°；故答案为：29.5°；（2）①Ⅰ、当点Q落在AB上时，易证PF⊥AB，可得∠EPF＝90°，∴∠EFP＝90°﹣∠PEF＝90°﹣48°＝42°．Ⅱ、当点Q落在CD上时，∠PQF＝∠PEF＝48°，∵AB∥CD，∴∠EPQ+∠PQF＝180°，∴∠EPQ＝132°，∵∠EPF＝∠QPF，∴∠EPF＝12×132°＝66°，∴∠EFP＝180°﹣48°﹣66°＝66°．综上所述，满足条件的∠EFP的值为42°或66°，故答案为：42°或66°．②Ⅰ、当点Q在平行线AB，CD之间时．设∠PFQ＝x，由折叠可知∠EFP＝x，∵2∠CFQ＝∠CFP，∴∠PFQ＝∠CFQ＝x，∴75°+3x＝180°，∴x＝35°，∴∠EFP＝35°．Ⅱ、当点Q在CD下方时，设∠PFQ＝x，由折叠可知∠EFP＝x，∵2∠CFQ＝∠CFP，∴∠PFC＝23x，∴75°+23x+x＝180°，解得x＝63°，∴∠EFP＝63°．【题目点拨】本题考查了三角形的角度问题，掌握平行线的性质和三角形的内角和定理是解题的关键．23、1．【题目详解】试题分析：由题意先求得∠B=∠C=10°，再由AD⊥AC，求得∠ADC=60°，则∠BAD=10°，然后得出AD=BD．∵AB=AC，∠BAC=120°，∴∠B=∠C=10°，∵AD⊥AC，DC=6，∴AD=12CD=1，∠ADC=60°.∴∠B=∠BAD=10°.∴AD=BD=1．考点：1.含10度角的直角三角形；2.等腰三角形的判定与性质．24、详见解析.【解题分析】根据题目要求画出线段a、h，再画△ABC，使AB=a，△ABC的高为h；首先画一条直线，再画垂线，然后截取高，再画腰即可．【题目详解】解：作图：①画射线AE ，在射线上截取AB=a ，②作AB 的垂直平分线，垂足为O ，再截取CO=h ，③再连接AC 、CB ，△ABC 即为所求．【题目点拨】此题主要考查了复杂作图，关键是掌握垂线的画法，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．25、该服装商第一批进货的单价是80元.【分析】设第一批进货的单价为x 元，则第二批进货单价为()8x +元，据此分别表示出两批进货的数量，然后根据“第二批所购数量是第一批购进数量的2倍”列出方程求解，然后检验得出答案即可.【题目详解】设第一批进货的单价为x 元，则第二批进货单价为()8x +元，则：80001760028x x ⨯=+，解得：80x =，经检验，80x =是原方程的解，答：该服装商第一批进货的单价是80元.【题目点拨】本题主要考查了分式方程的实际应用，准确找出等量关系是解题关键.26、（1）50°；（2）见解析【分析】（1）根据等腰三角形的性质得到∠BAD=∠CAD ，根据52C BAC ∠=∠设∠C=2x ，∠BAC=5x ，根据三角形的内角和求出x ，即可得到结果；（2）根据等腰三角形的性质得到∠BAD=∠CAD 根据平行线的性质得到∠F=∠CAD ，等量代换得到∠BAD=∠F ，于是得到结论．【题目详解】解：（1）∵AB=AC ，AD ⊥BC 于点D ，∴∠BAD=∠CAD ，∠ADC=∠ADB=90°，∵52C BAC ∠=∠，设∠C=2x ，∠BAC=5x ，则∠B=2x，则2x+2x+5x=180，解得：x=20，∴∠BAC=100°，∴∠BAD=50°；（2）∵AB=AC，AD⊥BC于点D，∴∠BAD=∠CAD，∵EF∥AC，∴∠F=∠CAD，∴∠BAD=∠F，∴AE=FE．【题目点拨】本题考查了等腰三角形的性质，平行线的性质，正确的识别图形是解题的关键．。

八年级上册期末考试试卷含详细答案

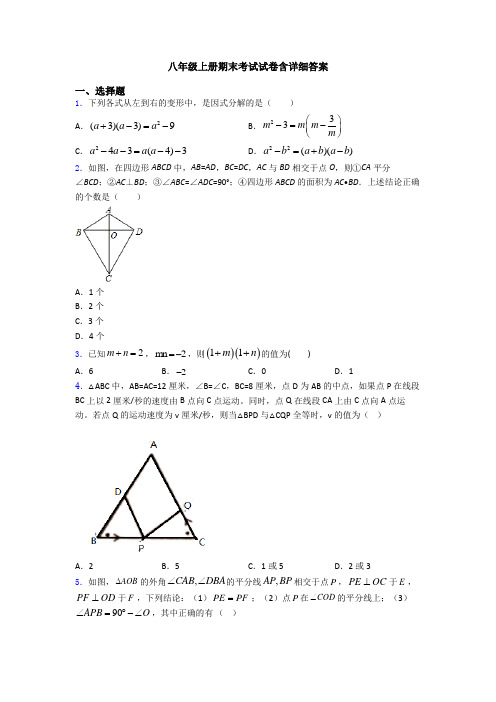
八年级上册期末考试试卷含详细答案一、选择题1．下列各式从左到右的变形中，是因式分解的是（）A ．2(3)(3)9a a a +-=-B ．233m m m m ⎛⎫-=- ⎪⎝⎭C ．243(4)3a a a a --=--D ．22()()a b a b a b -=+-2．如图，在四边形ABCD 中，AB =AD ，BC =DC ，AC 与BD 相交于点O ，则①CA 平分∠BCD ；②AC ⊥BD ；③∠ABC =∠ADC =90°；④四边形ABCD 的面积为AC •BD ．上述结论正确的个数是（）A ．1个B ．2个C ．3个D ．4个3．已知2m n +=，m n 2=-，则()()11m n ++的值为( )A ．6B ．2-C ．0D ．14．△ABC 中，AB=AC=12厘米，∠B=∠C ，BC=8厘米，点D 为AB 的中点，如果点P 在线段BC 上以2厘米/秒的速度由B 点向C 点运动。

同时，点Q 在线段CA 上由C 点向A 点运动。

若点Q 的运动速度为v 厘米/秒，则当△BPD 与△CQP 全等时，v 的值为（）A ．2B ．5C ．1或5D ．2或35．如图，AOB ∆的外角,CAB DBA ∠∠的平分线,AP BP 相交于点P ，PE OC ⊥于E ，PF OD ⊥于F ，下列结论：（1）PE PF =；（2）点P 在COD ∠的平分线上；（3）90APB O ∠=︒-∠，其中正确的有（）A ．0个B ．1个C ．2个D ．3个6．如图，△ABC 中，AB =AC ，AD ⊥BC 于点D ，点E 是AB 的中点，点F 在AD 上，当△BEF 周长最小时，点F 的位置在（）A ．AD 的中点B ．△ABC 的重心 C ．△ABC 三条高线的交点D ．△ABC 三边中垂线的交点 7．已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比是3：1，这个多边形的边数是( )A ．8B ．9C ．10D ．12 8．有下列说法：①轴对称的两个三角形形状相同；②面积相等的两个三角形是轴对称图形；③轴对称的两个三角形的周长相等；④经过平移、翻折或旋转得到的三角形与原三角形是形状相同的．其中正确的有（）A ．4个B ．3个C ．2个D ．1个 9．如图，在ABC ∆中，AD 平分BAC ∠，2B ADB ∠=∠，4,7AB CD ==，则AC 的长为（）A ．3B ．11C ．15D ．910．设,,a b c 是三角形的三边长，且满足222a b c ab bc ca ++=++，关于此三角形的形状有以下判断：①是直角三角形； ②是等边三角形； ③是锐角三角形；④是钝角三角形，其中正确的说法的个数有（）A ．1个B ．2个C ．3个D ．4个二、填空题11．如图，在△ABC 中，AB ＝10，AC ＝8，∠ABC 、∠ACB 的平分线相交于点O ，MN 过点O ，且MN ∥BC ，分别交AB 、AC 于点M 、N ．则△AMN 的周长为_______．12．如图，已知：AB ∥CD ，DB ⊥BC ，∠1＝40°，求∠2的度数．完成下面的证明过程：证明：∵AB ∥CD （）， ∴∠1＝∠BCD ＝40°（）．∵BD ⊥BC ，∴∠CBD ＝．∵∠2+∠CBD+∠BCD ＝（），∴∠2＝．13．化简分式22214ac a bc- 的结果为_____． 14．如图，直线a 平移后得到直线b ，若170∠=，则23∠-∠=______.15．()()()243232121211++⋯++计算结果的个位数字是______________． 16．已知直角三角板和直尺如图放置，若∠1=20°，则∠2的度数为___________．17．求220191222++++的值，可令22019S 1222=++++，则23202022222S =++++，因此2020221S S -=-．仿照以上推理，计算出23201911112222++++的值为______． 18．从A 沿北偏东60︒的方向行驶到B ，再从B 沿南偏西20︒方向行驶到C ，则ABC ∠=______.19．在多项式241x +中添加一个单项式，使其成为一个完全平方式，则添加的单项式是______（只写出一个即可）．20．当 x_____ 时，分2x x+式有意义．三、解答题21．如图，等边ABC 中，D 为BC 边中点，CP 是BC 的延长线．按下列要求作图并回答问题：（要求：尺规作图，不写作法，保留作图痕迹）（1）作ACP ∠的平分线CF ；（2）作60ADE ∠=︒，且DE 交CF 于点E ；（3）在（1），（2）的条件下，可判断AD 与DE 的数量关系是__________；请说明理由．22．已知：如图，AD 垂直平分BC ，D 为垂足，DM ⊥AB ，DN ⊥AC ，M 、N 分别为垂足．求证：DM=DN ．23．先化简，再求值：2()()(2)()x y x y y x y x y +-++--，其中3x =，13y =-．24．如图，点B ，E ，C ，F 在一条直线上，AB=DE ，AC=DF ，BE=CF ．试说明：（1）ABC DEF ≅；（2）A EGC ∠=∠．25．先化简，再求值：（a ＋2）2－（a ＋1）（a －1），其中a ＝32-． 26．如图，四边形ABCD 是长方形，E 是边CD 的中点，连接AE 并延长交边BC 的延长线于F ，过点E 作AF 的垂线交边BC 于M ，连接AM ．（1）请说明 ΔADE ≌ ΔFCE ；（2）试说明AM = BC + MC ；（3）设S △AEM = S 1，S △ECM = S 2，S △ABM = S 3，试探究S 1，S 2，S 3三者之间的等量关系，并说明理由．27．已知，//AB CD ，点M 在AB 上，点N 在CD 上．（1）如图1中，BME E END ∠∠∠、、的数量关系为：________；（不需要证明）如图2中，BMF F FND ∠∠∠、、的数量关系为：__________；（不需要证明）（2）如图3中，NE 平分FND ∠，MB 平分FME ∠，且2180E F ∠+∠=︒，求FME ∠的度数；（3）如图4中，60BME ∠=︒，EF 平分MEN ∠，NP 平分END ∠，且//EQ NP ，则FEQ ∠的大小是否发生变化，若变化，请说明理由，若不变化，求出FEQ ∠的度数．28．如图①所示是一个长为2m ，宽为2n(m n)>的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图2的方式拼成一个正方形()1如图②中的阴影部分的正方形的边长等于______(用含m 、n 的代数式表示)； ()2请用两种不同的方法列代数式表示图②中阴影部分的面积：方法①：______；方法②：______；()3观察图②，试写出2(m n)+、2(m n)-、mn 这三个代数式之间的等量关系：______；()4根据()3题中的等量关系，若m n 12+=，mn 25=，求图②中阴影部分的面积．29．在学习分式计算时有这样一道题：先化简1(1+)2x -÷22214x x x -+-，再选取一个你喜欢且合适的数代入求值．张明同学化简过程如下：解：1(1+)2x -÷22214x x x -+- =212x x -+-÷2(1)(2)(2)x x x -+-（） =21(2)(2)2(1)x x x x x -+-⋅-- （） =21x x +- （）（1）在括号中直接填入每一步的主要依据或知识点；（2）如果你是张明同学，那么在选取你喜欢且合适的数进行求值时，你不能选取的数有__________．30．如图，△ACF ≌△DBE ，其中点A 、B 、C 、D 在一条直线上.（1）若BE ⊥AD ，∠F=62°，求∠A 的大小.（2）若AD=9cm ，BC=5cm ，求AB 的长.【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【解析】【分析】直接利用因式分解的定义得出答案．【详解】A 、2(3)(3)9a a a +-=-，是整式乘法，故此选项不合题意；B 、233m m m m ⎛⎫-=- ⎪⎝⎭，不符合因式分解的定义，故此选项不合题意； C 、243(4)3a a a a --=--，不符合因式分解的定义，故此选项不合题意；D 、22()()a b a b a b -=+-是分解因式，符合题意；故选：D ．【点睛】此题主要考查了因式分解的意义，正确分解因式是解题关键．2．B解析：B【解析】【分析】证明△ABC 与△ADC 全等，即可解决问题.【详解】解：在△ABC 与△ADC 中，AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩， ∴△ABC ≌△ADC （SSS ），∴∠ACB =∠ACD ，故①正确，∵AB =AD ，BC =DC∴AC 是BD 的垂直平分线，即AC ⊥DB ，故②正确；无法判断∠ABC =∠ADC =90°，故③错误，四边形ABCD 的面积=S △ADB +S △BCD =12DB ×OA +12DB ×OC =12AC •BD ，故④错误；故选B ．【点睛】此题考查全等三角形的判定和性质，关键是根据SSS 证明△ABC 与△ADC 全等． 3．D解析：D【解析】【分析】根据整式乘法法则去括号，再把已知式子的值代入即可．【详解】∵2m n +=，m n 2=-，∴原式()11221m n mn =+++=+-=．故选：D ．解析：D【解析】【分析】此题要分两种情况：①当BD=PC时，△BPD与△CQP全等，计算出BP的长，进而可得运动时间，然后再求v；②当BD=CQ时，△BDP≌△QCP，计算出BP的长，进而可得运动时间，然后再求v．【详解】解：当BD=PC时，△BPD与△CQP全等，∵点D为AB的中点，∴BD=12AB=6cm，∵BD=PC，∴BP=8-6=2（cm），∵点P在线段BC上以2厘米/秒的速度由B点向C点运动，∴运动时间时1s，∵△DBP≌△PCQ，∴BP=CQ=2cm，∴v=2÷1=2；当BD=CQ时，△BDP≌△QCP，∵BD=6cm，PB=PC，∴QC=6cm，∵BC=8cm，∴BP=4cm，∴运动时间为4÷2=2（s），∴v=6÷2=3（m/s）．故v的值为2或3．故选择：D．【点睛】此题主要考查了全等三角形的判定，关键是要分情况讨论，不要漏解，掌握全等三角形的判定方法：SSS、SAS、ASA、AAS、HL．5．C解析：C【解析】【分析】过点P作PG⊥AB，由角平分线的性质定理，得到PE PG PF==，可判断（1）（2）正确；由12APB EPF∠=∠，180EPF O∠+∠=︒，得到1902APB O∠=︒-∠，可判断（3）错误；即可得到答案．解：过点P 作PG ⊥AB ，如图：∵AP 平分∠CAB ，BP 平分∠DBA ，PE OC ⊥，PF OD ⊥，PG ⊥AB ，∴PE PG PF ==；故（1）正确；∴点P 在COD ∠的平分线上；故（2）正确； ∵12APB APG BPG EPF ∠=∠+∠=∠，又180EPF O ∠+∠=︒，∴11(180)9022APB O O ∠=⨯︒-∠=︒-∠；故（3）错误； ∴正确的选项有2个；故选：C ．【点睛】本题考查了角平分线的判定定理和性质定理，解题的关键是熟练掌握角平分线的判定和性质进行解题．6．B解析：B【解析】【分析】连接EC ，与AD 交于点P ，由题意易得BD=DC ，根据等腰三角形的“三线合一”可得当△BEF 周长最小时，即为BE+CE 的长，最后根据中线的交点可求解．【详解】解：连接EC ，与AD 交于点P ，如图所示：△ABC 中，AB =AC ，AD ⊥BC 于点D ，∴BD=DC ，点F 在AD 上，当△BEF 周长最小时，即BE+BF+EF 为最小，由轴对称的性质及两点之间线段最短可得：BE+BF+EF 为最小时即为BE+CE 的长；点F的位置即为点P的位置，根据三角形的重心是三角形三条中线的交点；故选B．【点睛】本题主要考查等腰三角形及轴对称的性质和三角形的重心，熟练掌握等腰三角形及轴对称的性质和三角形的重心是解题的关键．7．A解析：A【解析】试题分析：设这个多边形的外角为x°，则内角为3x°，根据多边形的相邻的内角与外角互补可的方程x+3x=180，解可得外角的度数，再用外角和除以外角度数即可得到边数．解：设这个多边形的外角为x°，则内角为3x°，由题意得：x+3x=180，解得x=45，这个多边形的边数：360°÷45°=8，故选A．考点：多边形内角与外角．8．B解析：B【解析】【分析】根据平移、翻折或旋转的性质逐项判断可求解．【详解】解：①轴对称的两个三角形形状相同，故正确；②面积相等的两个三角形形状不一定相同，故不是轴对称图形，故错误；③轴对称的两个三角形的周长相等，故正确；④经过平移、翻折或旋转得到的三角形与原三角形是形状相同的，故正确．故选：B．【点睛】本题考查了图形的变换，掌握平移、翻折或旋转的性质是解题的关键．9．B解析：B【解析】【分析】在AC上截取AE＝AB，连接DE，如图，先根据SAS证明△ABD≌△AED，然后根据全等三角形的性质和已知条件可得∠BDE＝∠AED，进而可得CD＝EC，再代入数值计算即可．【详解】解：在AC上截取AE＝AB，连接DE，如图，∵AD平分∠BAC，∴∠BAD＝∠DAC，又∵AD=AD，∴△ABD ≌△AED （SAS ），∴∠B ＝∠AED ，∠ADB ＝∠ADE ，∵∠B ＝2∠ADB ，∴∠AED ＝2∠ADB ，而∠BDE ＝∠ADB +∠ADE ＝2∠ADB ，∴∠BDE ＝∠AED ，∴∠CED ＝∠EDC ，∴CD ＝CE ，∴AC ＝AE +CE ＝AB +CD ＝4+7＝11．故选：B ．【点睛】本题考查了全等三角形的判定和性质、等腰三角形的判定、角平分线的性质，正确作出辅助线、构造全等三角形是解题的关键．10．B解析：B【解析】【分析】先将原式转化为完全平方公式，再根据非负数的性质得出a b c ==．进而判断即可．【详解】∵222a b c ab bc ca ++=++，∴222222222a b c ab bc ca ++=++，即()()()2220a b b c a c -+-+-=，∴a b c ==，∴此三角形为等边三角形，同时也是锐角三角形．故选：B ．【点睛】本题考查了因式分解的应用，根据式子特点，将原式转化为完全平方公式是解题的关键．二、填空题11．18【解析】【分析】由在△ABC 中，∠ABC 与∠ACB 的平分线相交于点O ，过点O 作MN∥BC，易证得△BOM 与△CON 是等腰三角形，继而可得△AMN 的周长等于AB+AC ．【详解】解析：18【解析】【分析】由在△ABC中，∠ABC与∠ACB的平分线相交于点O，过点O作MN∥BC，易证得△BOM 与△CON是等腰三角形，继而可得△AMN的周长等于AB+AC．【详解】∵在△ABC中，∠ABC、∠ACB的平分线相交于点O，∴∠ABO＝∠OBC，∵MN∥BC，∴∠MOB＝∠OBC，∴∠ABO＝∠MOB，∴BM＝OM，同理CN＝ON，∴△AMN的周长是：AM+NM+AN＝AM+OM+ON+AN＝AM+BM+CN+AN＝AB+AC＝10+8＝18．故答案为：18．【点睛】本题考查等腰三角形的判定与性质，角平分线的性质，平行线的判定，三角形周长的求法，等量代换等知识点．12．已知；两直线平行，同位角相等；90°；180°；三角形内角和定理；50°【解析】【分析】由平行线的性质和垂线的定义可得∠1＝∠BCD＝40°，∠CBD＝90°，由三角形内角和定理可求∠2的度数解析：已知；两直线平行，同位角相等；90°；180°；三角形内角和定理；50°【解析】【分析】由平行线的性质和垂线的定义可得∠1＝∠BCD＝40°，∠CBD＝90°，由三角形内角和定理可求∠2的度数．【详解】∵AB∥CD（已知），∴∠1＝∠BCD＝40°（两直线平行，同位角相等）．∵BD⊥BC，∴∠CBD＝90°．∵∠2+∠CBD+∠BCD＝180°（三角形内角和定理），∴∠2＝50°．故答案为：已知，两直线平行，同位角相等，90°，180°，三角形内角和定理，50°．本题考查了平行线的性质，垂线的定义，三角形内角和定理，熟练运用三角形内角和定理是本题的关键．13．【解析】【分析】把分子分母中的公因式2ac约去即可．【详解】解：原式＝＝．故答案为:．【点睛】本题考查约分：约去分式的分子与分母的公因式，不改变分式的值，这样的分式变形叫做分式的约解析：7c ab-【解析】【分析】把分子分母中的公因式2ac约去即可．【详解】解：原式＝227ac c ac ab -＝7c ab-．故答案为:7c ab-．【点睛】本题考查约分：约去分式的分子与分母的公因式，不改变分式的值，这样的分式变形叫做分式的约分．14．110°.【解析】【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可．【详解】延长直线,如图：∵直线a平移后得到直线b，∴a∥b，∴∠5=180°−∠1=180°−70°解析：110°.【解析】【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可．【详解】延长直线,如图：∵直线a平移后得到直线b，∴a∥b，∴∠5=180°−∠1=180°−70°=110°，∵∠2=∠4+∠5，∠3=∠4，∴∠2−∠3=∠5=110°，故答案为110°.【点睛】此题考查平移的性质，解题关键在于作辅助线.15．6【解析】【分析】根据平方差公式化简所求，再根据2的n次幂的变化规律即可求解．【详解】=====∵21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128解析：6【解析】【分析】根据平方差公式化简所求，再根据2的n 次幂的变化规律即可求解．【详解】()()24323212121(1++⋯++）=()()()()22432212121211-++⋯++ =()()()44322121211-+⋯++=323221)2((1)1-++=64211-+=642∵21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128，28＝256，…∴64÷4=16∴个位数为6故答案为：6．【点睛】本题考查了平方差公式的应用，解此题的关键是熟知平方差公式的特点，题型较好，难度适中，是一道不错的题目，通过此题能培养学生的观察能力．16．40°【解析】【分析】如图，过E 作EF∥AB，则AB∥EF∥CD，根据平行线的性质和三角形的内角和定理即可求得答案．【详解】解：如图，过E 作EF∥AB，则AB∥EF∥CD，∴∠1＝∠3，解析：40°【解析】【分析】如图，过E 作EF ∥AB ，则AB ∥EF ∥CD ，根据平行线的性质和三角形的内角和定理即可求得答案．【详解】解：如图，过E 作EF ∥AB ，则AB ∥EF ∥CD ，∴∠1＝∠3，∠2＝∠4，∵∠3+∠4＝180°－90°－30°=60°，∴∠1+∠2＝60°，∵∠1＝20°，∴∠2＝40°．故答案为：40°．【点睛】本题以三角板为载体，主要考查了平行线的性质和三角形的内角和定理，正确添加辅助线、熟练掌握平行线的性质是解题的关键．17．【解析】【分析】根据题目所给计算方法，令，再两边同时乘以，求出，用，求出的值，进而求出的值．【详解】解：令，则，∴，∴，则．故答案为：【点睛】本题考查了同底数幂的乘法，利用错解析：2019112【解析】【分析】根据题目所给计算方法，令23201911112222S，再两边同时乘以12，求出12S ，用12S S ，求出12S 的值，进而求出S 的值．【详解】解：令23201911112222S ，则22023401111122222S ， ∴2020111222S S ， ∴2020111222S ，则2019112S ．故答案为：2019112【点睛】本题考查了同底数幂的乘法，利用错位相减法，消掉相关值，是解题的关键．18．40【解析】【分析】根据方位角的概念，画图正确表示出行驶的过程，再根据已知转向的角度结合三角形的内角和与外角的关系求解．【详解】如图，A 沿北偏东60°的方向行驶到B ，则∠BAC=90°-解析：40【解析】【分析】根据方位角的概念，画图正确表示出行驶的过程，再根据已知转向的角度结合三角形的内角和与外角的关系求解．【详解】如图，A 沿北偏东60°的方向行驶到B ，则∠BAC=90°-60°=30°，B 沿南偏西20°的方向行驶到C ，则∠BCO=90°-20°=70°，又∵∠ABC=∠BCO-∠BAC ，∴∠ABC=70°-30°=40°．故答案为40°【点睛】解答此类题需要从运动的角度，正确画出方位角，再结合三角形的内角和与外角的关系求解．19．或【解析】【分析】【详解】设这个单项式为Q ，如果这里首末两项是2x 和1这两个数的平方，那么中间一项为加上或减去2x 和1积的2倍，故Q=±4x；如果这里首末两项是Q 和1，则乘积项是4x2=2解析：4x ±或416x【解析】【分析】【详解】设这个单项式为Q ，如果这里首末两项是2x 和1这两个数的平方，那么中间一项为加上或减去2x 和1积的2倍，故Q=±4x ；如果这里首末两项是Q 和1，则乘积项是4x 2=2⋅2x 2，所以Q=4x 4；如果该式只有4x 2项或1，它也是完全平方式，所以Q=-1或-4x 2．解：∵4x 2+1±4x=（2x±1）2；4x 2+1+4x 4=（2x 2+1）2；4x 2+1-1=（±2x ）2；4x 2+1-4x 2=（±1）2．∴加上的单项式可以是±4x 、4x 4、-4x 2、-1中任意一个．20．【解析】【分析】直接利用分式有意义的条件分析得出即可．【详解】解：根据分式有意义得：2+x≠0，解得：x≠-2．故答案为：≠-2．【点睛】本题考查了分式有意义的条件，关键是熟练掌握解析：2≠-【解析】【分析】直接利用分式有意义的条件分析得出即可．【详解】解：根据分式有意义得：2+x≠0，解得：x≠-2．故答案为：≠-2．【点睛】本题考查了分式有意义的条件，关键是熟练掌握知识点：分式有意义，分母不为0．三、解答题21．（1）见解析；（2）见解析；（3）AD DE =，见解析【解析】【分析】（1）根据角平分线的作法作图即可；（2）根据作一个角等于已知角的方法作图即可；（3）连接AE ，首先根据等边三角形的性质计算出30BAD EDC ∠=∠=︒，30DEC EDC ∠=∠=︒，进而得到CE CD BD ==，然后证明ABD ACE ∆≅∆可得AD AE =，再由60ADE ∠=︒，可得ADE ∆是等边三角形，进而得到AD DE =．【详解】（1）尺规作图，如下图；（2）尺规作图，如下图；（3）AD DE =理由如下：如图，连接AE∵等边ABC 中，D 为BC 边中点，∴BD DC =，90ADB ADC ∠=∠=︒，∵60B ADE ∠=∠=︒，∴30BAD EDC ∠=∠=︒，∵120ACP ∠=︒，CE 为ACP ∠的平分线，∴60ACE ECP ∠=∠=︒，∴30DEC ECP EDC ∠=∠-∠=︒，∴30DEC EDC ∠=∠=︒，∴CE CD BD ==，在ABD △和ACE △中，∵AB AC =，60B ACE ∠=∠=︒，BD CE =，∴ABD ACE SAS △≌△()，∴AD AE =，又∵60ADE ∠=︒，∴ADE 是等边三角形，∴AD DE =.【点睛】此题主要考查了基本作图，以及全等三角形的判定与性质，解题的关键是正确掌握全等三角形的判定方法．22．见解析．【解析】【分析】根据垂直平分线的性质得到AC=AB ，再利用等腰三角形的性质得到AD 是角平分线，最后利用角平分线的性质即可得到结论．【详解】证明：∵AD 垂直平分BC ，∴AC=AB ，即ABC 是等腰三角形，∴AD 平分∠BAC ，∵DM ⊥AB ，DN ⊥AC ，∴DM=DN ．【点睛】本题考查了垂直平分线的性质，等腰三角形的判定与性质，角平分线的性质，熟练掌握各性质判定定理是解题的关键．23．3xy ，3-．【解析】【分析】先计算平方差公式、完全平方公式、整式的乘法，再计算整式的加减法，然后将x 、y 的值代入即可得．【详解】原式222222(2)x y xy y x xy y =-++--+，2222222x y xy y x xy y =-++-+-，3xy =，将3x =，13y =-代入得：原式133333xy ⎛⎫==⨯⨯-=- ⎪⎝⎭．【点睛】本题考查了平方差公式、完全平方公式、整式的加减法与乘法，熟记公式和整式的运算法则是解题关键．24．（1）见解析；（2）见解析【解析】【分析】（1）根据等式性质，由BE=CF 得BC=EF ，再根据SSS 定理得△ABC ≌△DEF 即可；（2）由全等三角形得∠B=∠DEF ，由平行线的判定定理得AB ∥DE ，再根据平行线的性质得∠A=∠EGC ．【详解】（1）∵BE CF =，∴BE EC CF EC +=+，即BC EF =，在△ABC 与△DEF 中，AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩， ∴(SSS)ABC DEF ≅△△；（2）∵△ABC ≌△DEF ，∴∠B=∠DEF ，∴AB ∥DE ，∴∠A=∠EGC ．【点睛】本题考查了全等三角形的判定和性质，平行线的性质与判定，解题的关键是正确寻找全等三角形全等的条件，属于中考常考题型．25．－1.【解析】分析：原式利用完全平方公式，以及平方差公式化简，去括号合并得到最简结果，把a 的值代入计算即可求出值．详解：原式=a 2+4a +4﹣a 2+1=4a +5当a =32-时，原式=﹣6+5=﹣1．点睛：本题考查了整式的混合运算﹣化简求值，熟练掌握运算法则是解答本题的关键．26．（1）见解析；（2）见解析；（3）S 3=2S 1-4S 2，理由见解析．【解析】【分析】（1）根据ASA 可证得 ΔADE ≌ ΔFCE ；（2）由（1）可得AE=EF ，AD=CF ，根据垂直平分线的性质可得再由线段等量关系即可说明AM = BC + MC ；（3）由AE=EF 得出S △ECF =S 1-S 2，再由底和高的倍数关系得到S △ABF =4S △ECF =4S 1-4S 2，从而根据S 3=S △ABF -S △MAF 得到结果．【详解】解：（1）∵E 是边CD 的中点，∴DE=CE ，∵∠D=∠DCF=90°，∠DEA=∠ECF ，∴△ADE ≌△FCE （ASA ）；（2）由（1）得AE=EF ，AD=CF ，∴点E 为AF 中点，∵ME ⊥AF ，∴AM=MF ，∵MF=CF+MC ，∵AD=BC=CF ，∴MF=BC+MC ，即AM=BC+MC ；（3）S 3=2S 1-4S 2，理由是：由（2）可知：AE=EF ，AD=BC=CF ，∴S 1=S △MEF =S 2+S △ECF ，∴S △ECF =S 1-S 2，∵AB=2EC ，BF=2CF ，∠B=∠ECF=90°，∴S △ABF =4S △ECF =4S 1-4S 2，∴S 3=S △ABF -S △MAF =S △ABF -2S 1=2S 1-4S 2．【点睛】本题考查了长方形的性质，全等三角形的判定与性质，线段垂直平分线的性质，勾股定理。

天津市河东区2023-2024学年八年级上学期期末考试英语试题(含答案)

2023~2024学年度第一学期期末质量检测八年级英语注意：本试卷共100分，考试时长90分钟。

第Ⅰ卷（选择题共65分）一、听力理解（共15小题，每小题1分，满分15分）A）在下列每小题内，你将听到一个或两个句子并看到供选择的A、B、C三幅图画。

找出与你所听句子内容相匹配的图画。

1.A B C2.A B C3.A B C4.A B CB）下面你将听到五组对话，每组对话有一个问题。

根据对话内容，从所给的A、B、C三个选项中找出能回答问题的最佳选项。

5. How long does it take the woman to go to work?A. About 5 minutes.B. About 10 minutes.C. About 15 minutes.6. What’s Harry’s favourite sport?A. Football.B. Table tennis.C. Basketball.7. How many people are there in Shanghai?A. 30 million.B. 13 million.C. 15 million.8. Why is Betty going to the post office?A. To send a letter.B. To buy a stamp.C. To get a letter.9. When was John born?A. On May 14, 1986.B. On May 24, 1986.C. On May 14, 1988.C）听下面的长对话或独白，每段长对话或独白后都有几个问题，从题中所给的A、B、C三个选项中选出最佳选项。

听下面一段材料，回答第10-12题。

10. Where does the new student come from?A. England.B. America.C. Australia.11. How many languages can the new student speak?A. 2.B. 3.C. 4.12. What languages can he speak?A. English, Chinese and French.B. English and German.C. English, Chinese, French and German.听下面一段材料，回答第13-15题。

八年级第一学期期末考试数学试卷(带答案)

八年级第一学期期末考试数学试卷（带答案）（时间:120分钟满分:120分）一、选择题（共10小题，每题3分，共30分）1．下列图形中，既是轴对称图形又是中心对称图形的是（）A． B．C．D．2．下列等式从左边到右边的变形，属于因式分解的是（）A．x（x﹣1）＝x2﹣x B．x2﹣2x+1＝（x﹣1）2C．x2+3x﹣4＝x（x+3）﹣4 D．y3﹣4y2+y＝y（y2﹣4y）3.如图，在平行四边形ABCD中，∠A的平分线AE交CD于E，AB＝8，BC＝6，则EC等于（）A．1 B．1.5 C．2 D．34.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如表所示：选手甲乙丙丁平均数（环）7 8 8 7方差（环2）0.9 1.1 0.9 1则这四人中成绩好且发挥最稳定的是（） A．甲 B．乙 C．丙 D．丁5.下列说法正确的是（）A．一组对边平行，另一组对边相等的四边形是平行四边形 B．平行四边形的对角互补C．有两组对角相等的四边形是平行四边形 D．平行四边形的对角线平分每一组对角6.如图，将△ABC绕顶点A逆时针旋转得到△AB′C′，点B的对应点B′在BC上，若∠B＝70°，则∠C′AC的度数是（）A．40° B．50°C．60° D．70°7.若在x+y2xy中的x和y都扩大到原来的2倍．那么分式的值（）A．缩小为原来的一半 B．不变C．扩大为原来的4倍 D．扩大为原来的2倍8.如果一个多边形的内角和是它的外角和的5倍，则这个多边形是（）A．十一边形 B．十二边形 C．十三边形 D．十边形9.如图，将直角三角形ABC沿AB方向平移2cm得到△DEF，DF交BC 于点H，CH＝2cm，EF＝5cm，则阴影部分的面积为（）第6题图第3题图A ．6cm 2B ．8cm 2C ．12cm 2D ．16cm 210.如图，四边形ABCD 是平行四边形，点E 是边CD 上一点，且BC ＝EC ，CF ⊥BE 交AB 于点F ，P 是EB 延长线上一点，下列结论：①BE 平分∠CBF ；②CF 平分∠DCB ；③BF ＝BE ；④PF ＝PC ．其中正确的个数为（） A ．1个 B ．2个 C ．3个 D ．4个二、填空题（共8小题，11-14题每题3分，15-18题每题4分，共28分）11．使分式12+-x x 有意义的x 的取值范围为___________.12．在平行四边形ABCD 中，若∠A +∠C ＝80°，则∠B 的度数是________°.13．某校举行广播体操比赛，评分项目包括服装统一度、进退场秩序、动作规范整齐度这三项，每项满分10分，总成绩按以上三项得分2：3：5的比例计算，总成绩满分10分．已知八（1）班在比赛中三项得分依次为10分、8分、9分，则八（1）班这次比赛的总成绩为分． 14.已知ab ＝7，a+b ＝6，则多项式a 2b+ab 2的值为___________．15.如图，小明从A 点出发，沿直线前进5米后向左转72°，再沿直线前进5米，又向左转72°，…，照这样走下去，他第一次回到出发点A 时，共走路程为________米．16．已知关于x 的分式方程3x x−2=m 2−x+1,若此方程的解为正数，则m 的取值范围为．17．如图，在四边形ABCD 中，AD ∥BC ，∠A ＝90°，AD ＝6，BC ＝9，点P 从点A 出发，沿射线AD 以每秒2个单位长度的速度向右运动，同时点Q 从点C 出发，沿CB 方向以每秒1个单位长度的速度向点B 运动．当点Q 到达点B 时，点P ，Q 停止运动，设点Q 运动时间为t 秒．在运动的过程中，当t =__________时，使以P ，D ，C ，Q 为顶点的四边形为平行四边形？18．已知a 是不为1的有理数，我们把11−a称为a 的差倒数，如：2的差倒数是11−2=−1，﹣1的差倒数是11−(−1)=12，已知a 1=−13，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数，…，依此类推，则a 2024＝．三、解答题（共7小题，共62分，解答写出必要的文字说明或计算步骤） 19．（本题满分9分）因式分解：（1）3x ﹣12x 2 （2） ﹣a 3b +10a 2b ﹣25ab ；（3）9a 2（x ﹣y ）+4b 2（y ﹣x ）．第10题图第17题图第15题图20．（本题满分7分）(1)计算：（mn）2⋅nm÷（−mn2）；(2)先化简，再求值：x+1x2−2x+1÷(2x−1+1)，请在﹣1＜x≤1范围内选择一个你喜欢的整数x代入求值．21.（本题满分8分）为引导激励青少年学生爱读书、读好书、善读书，切实增强历史自觉和文化自信，着力培养德智体美劳全面发展的社会主义建设者和接班人．某校开展主题为“乐学悦读，打造未来工匠“读书月活动，要求每人读2至5本名著，活动结束后随机抽查了若干名学生每人的读书量，并分为四种类型，A：2本；B：3本；C：4本；D：5本，将各类的人数绘制成如下的扇形统计图和条形统计图（不完整）．根据以上信息，解答下列问题：（1）本次抽查学生______人，a=__________,将条形统计图补全；（2）本次抽取学生的读书量的众数是本，中位数是本；（3）学校拟将读书量超过4本（不含4本）的学生评为“最佳悦读之星”予以表扬，已知该校有1000名学生，请估计该校此次受表扬的学生人数．22．（本题满分8分）在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：（1）作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标；（2）作出△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标；(3)△A2B2C2可看作△A1B1C1以点（，）为旋转中心，旋转180°得到的．23.（本题满分8分）如图1，在△ABC中，D、E分别为AB、AC的中点，延长BC至点F，使CF＝BC，连接CD和EF．（1）求证：四边形DEFC是平行四边形．（2）如图2，当△AB C是等边三角形且边长是8，求四边形DEFC的面积．24．（本题满分10分）某商店计划购进甲乙两种商品，已知一件甲商品的进价比一件乙商品的进价少2元，且用80元购进甲商品的数量与用100元购进乙商品的数量相同．（1）求甲、乙两种商品每件进价分别是多少元？（2）第一批销售完后，进价不变，该商店再次购进甲商品的数量比购进乙商品的数量的3倍少5件，且两种商品总数量不超过95件，计划将甲、乙两种商品分别按12元/件、15元/件销售完后两种商品的总利润超过371元，则该商店会有哪几种购进方案？25. （本题满分12分）如图① ABCD 的对角线AC 和BD 相交于点O ，EF 过点O 且与边AB ，CD 分别相交于点E 和点F ．（1）求证：OE ＝OF（2）如图②，已知AD ＝1，BD ＝2，AC ＝2√2，∠DOF ＝∠α ①当∠α为多少度时，EF ⊥AC ？②在①的条件下，连接AF ，求△ADF 的周长．参考答案及评分标准一、选择题（每题 3 分，共 30 分）题号 1 2 3 4 5 6 7 8 9 10 答案DBCCCAABBC二．填空题（共8小题,11-14题每题3分，15-18题每题4分，共28分） 11． x ≠-1 12． 140 13． 8.9 14. 42 ． 15．25 16． m ＜-2且m≠-6 17. 2或6 18. 43．三．解答题（共7小题，共62分） 19．（共9分）解：（1）（1）3x ﹣12x 2＝3x （1﹣4x ）； ------------------------3分（2）﹣a 3b +10a 2b ﹣25ab＝﹣ab（a2﹣10a+25）＝﹣ab（a﹣5）2；---------------------------------------------6分（3）9a2（x﹣y）+4b2（y﹣x）＝9a2（x﹣y）﹣4b2（x﹣y）＝（x﹣y）（9a2﹣4b2）＝（x﹣y）（3a+2b）（3a﹣2b）．------------------------------9分20.（1）原式=-n ------------------------------3分（2）先化简，再求值：x+1x2−2x+1÷(2x−1+1)，请在﹣1＜x≤1范围内选择一个你喜欢的整数x代入求值．原式=x+1(x−1)2÷2+x−1x−1=x+1(x−1)2•x−1 x+1=1x−1--------------------------------------------------------------6分∵x＝1或﹣1时，原分式无意义，﹣1＜x≤1∵x可以取得整数为0当x＝0时，原式=10−1=−1．------------------------------------------------7分21.（8分）解：（1）35÷35%＝100（人）D组：5本的学生人数为：100﹣5﹣40﹣35＝20（人），a=20补全条形统计图如下：-----------------------------3分（2）众数是3本，中位数是4本，-----------------------------5分（3）1000×＝200（人）答：该校有1000名学生中此次受表扬的学生人数大约有200人．--------8分22.（8分）解：（1）如图，△A1B1C1为所作，点C1的坐标为（﹣1，2）；--------3分（2）如图，△A2B2C2为所作，C2（﹣3，﹣2）；--------6分△A2B2C2可看作△A1B1C1以点（﹣2，0）为旋转中心，旋转180°得到的．--------------------------8分23.（8分）（1）证明：∵D、E分别为AB、AC的中点∴DE是△ABC的中位线BC，DE∥BC∴DE=12BC∵CF=12∴DE＝CF∴四边形DEFC是平行四边形．---------------------------4分（2）解：过点D作DH⊥BC于H，如图2所示：∵△ABC是等边三角形，D为AB的中点AB＝4∴∠B＝60°，BD=12∵∠DHB＝90°∴∠BDH＝30°DB＝2∴BH=12∴DH=√BD2−BH2=√42−22=2√3CB＝4∵CF=12∴S＝CF•DH＝4×2√3=8√3．----------------------------8分四边形DEFC24.（10分）解：（1）设乙种商品每件进价为x元，则甲种商品每件进价为（x﹣2）元由题意得：＝解得：x＝10，----------------------------3分经检验，x＝10是原方程的解，且符合题意，---------------------------4分∴x﹣2＝10﹣2＝8答：甲种商品每件进价为8元，乙种商品每件进价为10元；----------------5分（2）设购进乙种商品y件，则购进甲种商品（3y﹣5）件．由题意得：解得：23＜y≤25．----------------7分∵y为整数∴y＝24或25．∴共有2种购进方案：方案一：购进甲种商品67件，乙商品件24件；方案二：购进甲种商品70件，乙种商品25件．---------------10分25.（12分）解：证明：（1）∵四边形ABCD是平行四边形∴OB＝OD，AB∥CD．∴∠EBO＝∠FDO．又∵∠BOE＝∠DOF∴△BOE ≌△DOF （ASA ）．∴OE ＝OF ； ---------------------------4分（2）①∵四边形ABCD 是平行四边形 ∴OD =12BD ＝1，OA =12AC =√2 又AD ＝1∴AD 2+OD 2＝OA 2．∴∠ADO ＝90°，∠AOD ＝45°．∴∠α＝90°﹣45°＝45． ---------------------------8分 ②由（1）可得：EF 垂直平分AC ∴AF ＝FC又AB =√12+22=√5=CD∴△ADF 的周长＝AD +DF +F A ＝AD +CD ＝1+√5．----------------------------12分。

广东省深圳市南山区2022-2023学年八年级上学期期末考试数学试卷(解析版)

2022—2023学年度第一学期期末教学质量监测八年级数学试题一、选择题1. 4的平方根是（）A. ±2B. 2C. ﹣2D. 16 【答案】A【解析】【分析】根据平方根的定义，求数a 的平方根，也就是求一个数x ，使得x 2=a ，则x 就是a 的一个平方根．【详解】∵（±2 ）2=4，∴4的平方根是±2，故选A ．【点睛】本题主要考查平方根的定义，熟练掌握平方根的定义是解题的关键.2. 下列运算错误的是（）A.2=B.1=C. 2=D. =【答案】D【解析】【分析】直接利用二次根式的性质，二次根式的乘法运算法则和平方差公式计算，进而得出答案．详解】解：A2=，故此选项正确，不符合题意； B、321−=−=，故此选项正确，不符合题意； C 2=，故此选项正确，不符合题意；D=故选：D ．【点睛】本题主要考查了二次根式的性质以及二次根式的乘法运算，平方差公式，正确掌握相关运算法则是解题关键．3. 在一次校园歌曲演唱比赛中，小红对七位评委老师给自己打出的分数进行了分析，并制作如下表格：平均数众数中位数方差【9.15 9.2 9.1 0.2如果去掉一个最高分和一个最低分，那么表格中数据一定不会发生变化的是（）A. 中位数B. 众数C. 平均数D. 方差【答案】A【解析】【分析】根据中位数的定义：位于中间位置或中间两数的平均数可以得到去掉一个最高分和一个最低分不影响中位数．【详解】解：去掉一个最高分和一个最低分对中位数没有影响，故选：A ．【点睛】本题考查了统计量的选择，解题的关键是了解中位数、众数、平均数及方差的定义．4. 将一副直角三角尺如图放置，已知AE ∥BC ，则∠AFD 的度数是（）A. 45°B. 50°C. 60°D. 75°【答案】D【解析】【分析】本题主要根据直角尺各角的度数及三角形内角和定理解答．【详解】解：∵∠C=30°，∠DAE=45°，AE ∥BC ，∴∠EAC=∠C=30°，∠FAD=45﹣30=15°，在△ADF 中根据三角形内角和定理得到：∠AFD=180﹣90﹣15=75°．故选D ．5. 下列命题：①当n 取正整数时，231n n ++的值是质数；②22a b =，则a b =；③如果1∠和2∠是对顶角，那么12∠=∠；④以8，15，19为边长的三角形是直角三角形．是真命题的有（）A. 1个B. 2个C. 3个D. 4个【答案】A【解析】【分析】通过举反例即可判断①，由两个数的平方相等，那么这两个数相等或互为相反数可判断②，由对顶角相等可判断③，由勾股定理的逆定理可判断④，即可解答．【详解】当6n =时，2231636155n n +++×+而55511=×不是一个质数，则①不是真命题；若22a b =，则a b =±，则②不是真命题；如果1∠和2∠是对顶角，那么12∠=∠，则③是真命题；∵22281519+≠，∴以8，15，19为边长的三角形不是直角三角形，则④不是真命题；综上所述，是真命题的有1个，故选：A ．【点睛】本题考查了命题的真假，涉及质数、开平方、对顶角相等和勾股定理的逆定理，熟练掌握知识点是解题的关键．6. 在直角坐标系中，已知点3,2A m ，点B n是直线()0y kx b k =+<上的两点，则m ，n 的大小关系是（）A. m n <B. m n >C. m n ≥D. m n ≤【答案】A【解析】【分析】因为直线()0y kx b k =+<，所以随着自变量的增大，函数值会减小，根据这点即可得到问题解答．【详解】解：∵因为直线()0y kx b k =+<， ∴y 随着x 的增大而减小，∵32>2，∴32> ∴m <n ，故选：A ．【点睛】此题考查了一次函数的图象和性质，解题的关键是正确判断一次函数的增减性并灵活运用． 7. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．”诗中后面两句的意思是：如果一间客房住7人，那么有7人无房可住；如果一间客房住9人，那么就空出一间客房，若设该店有客房x 间，房客y 人，则列出关于x 、y 的二元一次方程组正确的是（）A. ()7791x y x y −= −=B. ()7791x y x y += −=C. 7791x y x y += −=D. 7791x y x y −= −=【答案】B【解析】【分析】设该店有客房x 间，房客y 人；根据题意一房七客多七客，一房九客一房空得出方程组即可．【详解】解：设该店有客房x 间，房客y 人；根据题意得：()7791x y x y +=−= ，故选：B ．【点睛】本题考查了二元一次方程组的应用；根据题意得出方程组是解决问题的关键．8. 如图，13AB AC ==，BP CP ⊥，8BP =，6CP =，则四边形ABPC 的面积为（）A. 48B. 60C. 36D. 72【答案】C【解析】【分析】连接BC ，过点A 作AD BC ⊥于点D ，勾股定理求得BC ，根据等腰三角形的性质得出152CD DB BC ===，在Rt △ABD 中，勾股定理求得AD ，进而根据1122ABC PBC S S BC AD PC PB −=×−× ，即可求解．详解】解：如图，连接BC ，过点A 作AD BC ⊥于点D ，∵BP CP ⊥，8BP =，6CP =，∴10BC ，【∵13AB AC ==，AD BC ⊥， ∴152CD DB BC ===，在Rt △ABD 中，12AD∴四边形ABPC 的面积为1122ABC PBC S S BC AD PC PB −=×−× 1110126860243622=××−××=−=，故选：C ．【点睛】本题考查了等腰三角形的性质，勾股定理，掌握勾股定理是解题的关键．9. 甲、乙两位同学放学后走路回家，他们走过的路程s （千米）与所用的时间t （分钟）之间的函数关系如图所示．根据图中信息，下列说法错误的是（）A. 前10分钟，甲比乙的速度慢B. 经过20分钟，甲、乙都走了1.6千米C. 甲的平均速度为0.08千米/分钟D. 经过30分钟，甲比乙走过的路程少【答案】D【解析】【分析】结合函数关系图逐项判断即可．【详解】A 项，前10分钟，甲走了0.8千米，乙走了1.2千米，则甲比乙的速度慢，故A 项正确，故不符合题意；B 项，前20分钟，根据函数关系图可知，甲、乙都走了1.6千米，故B 正确，故不符合题意；C 项，甲40分钟走了3.2千米，则其平均速度为：3.2÷40=0.08千米/分钟，故C 项正确，故不符合题意；D 项，经过30分钟，甲走了2.4千米，乙走了2.0千米，则甲比乙多走了0.4千米，故D 项错误，故符合题意；故选：D ．【点睛】本题考查了一次函数的图像及其在行程问题中的应用，理解函数关系图是解答本题的关键． 10. 如图，A ABC CB =∠∠，BD 、CD 、AD 分别平分ABC 的内角ABC ∠、外角ACF ∠、外角EAC ∠，以下结论：①AD BC ∥；②ACBADB ??；③12BDC BAC ∠=∠；④90ADC ABD ∠+∠=°．其中正确的结论有（）A. 1个B. 2个C. 3个D. 4个【答案】C【解析】【分析】根据角平分线的定义得出，22ABC ABD DBC ∠=∠=∠，2EAC EAD ∠=∠，2ACF DCF ∠=∠，根据三角形的内角和定理得出，180BAC ABC ACB ∠+∠+∠=°，根据三角形外角性质得出EAC ABC ACB ACF ABC BAC ∠=∠+∠∠=∠+∠，，根据已知结论逐步推理，即可判断各项．【详解】解：①∵AD 平分EAC ∠，∴2EAC EAD ∠=∠，∵EAC ABC ACB ∠=∠+∠，A ABC CB =∠∠，∴2EAC ABC ∠=∠，∴EAD ABC ∠=∠，∴AD BC ∥，故①正确；②∵AD BC ∥，∴ADB DBC ∠=∠，∵BD 平分ABC ∠，A ABC CB =∠∠，∴22ABC ACB DBC ADB ∠=∠=∠=∠，故②错误；③∵180DCF ACD ACB ∠°+∠+∠=，ACD DCF ∠=∠，∴2180DCF ACB ∠+∠=°，∵BDC DBC DCF ∠+∠=∠，∴22180BDC DBC ACB °∠+∠+∠=，∴2180ABC BDC ACB ∠°+∠+∠=，∵180BAC ABC ACB ∠+∠+∠=°，∴2BAC BDC ∠=∠， ∴12BDC BAC ∠=∠，故③正确； ④∵BD 平分ABC ∠，∴ABD DBC ∠=∠，∵AD BC ∥，∴ADB DBC ∠=∠，∴ABD ADB ∠=∠，∵CD 平分ACF ∠，∴2ACF DCF ∠=∠，∵2180ADB CDB DCF DCF ACB ∠+∠=∠∠+∠=°，，∴222180DCF ABC DCF ABD °∠+∠=∠+∠=，∴90DCF ABD ∠+∠=°，∵AD BC ∥，∴ADC DCF ∠=∠，∴90ADC ABD ∠+∠=°，故④正确；综上，正确的有①③④，共3个，故选：C ．【点睛】本题考查了三角形外角的性质、角平分线的定义、平行线的性质、三角形内角和定理的应用，主要考查学生的推理能力，有一定难度．二、填空题11.在实数范围内有意义，则x 的取值范围为______．【答案】x ≥-3【解析】【分析】直接利用二次根式的定义分析得出答案．【详解】解：依题意有x +3≥0，解得：x ≥-3．故答案为：x ≥-3．【点睛】此题主要考查了二次根式有意义条件，正确掌握定义是解题关键．12. 如图是国庆阅兵时，战机在空中展示的轴对称队形．以飞机B ，C 所在直线为x 轴、队形的对称轴为的y 轴，建立平面直角坐标系，若飞机E 的坐标为()40,35−，则飞机D 的坐标为________．【答案】()40,35−−【解析】【分析】根据轴对称的性质即可得到结论．【详解】解：∵飞机()40,35E −与飞机D 关于y 轴对称，∴飞机D 坐标为()40,35−−，故答案为：()40,35−−．【点睛】本题考查了轴对称的性质，准确理解题意，熟练掌握知识点是解题的关键．13. 一次函数y kx b =+的图像经过点()2,3A ，每当x 增加1个单位时，y 增加3个单位，则此函数图像向上平移2个单位长度的表达式是________．【答案】31y x =−．【解析】【分析】根据平面直角坐标系中平移的性质求出函数经过的另一点，再根据待定系数法即可求出函数解析式．【详解】解：∵函数图像经过点()23A ，，每当x 增加1个单位时，y 增加3个单位， ∴函数图像经过点()36，， ∴根据题意可得方程：3263k b k b =+ =+∴解方程得：33k b = =− ∴一次函数的解析式为：33y x =−，的∴函数图像向上平移2个单位长度的表达式为：33231y x x −+−,故答案为：31y x =−．【点睛】本题考查了确定一次函数解析式的方法待定系数法，函数图像平移的相关知识点，掌握一次函数平移规律是解题的关键．14. 若关于x ，y 的方程组111222a x b y c a x b y c += += 的解为56x y = = ，则方程组()()()()1112221111a x b y c a x b y c −++= −++= 的解为____________．【答案】65x y = =【解析】【分析】设x ﹣1＝m ，y +1＝n ，方程组变形后求出解得到m 与n 的值，进而求出x 与y 的值即可；【详解】解：设x ﹣1＝m ，y +1＝n ，则方程组可化为111222a m b n c a m b n c += += ， ∵关于x ，y 的方程组111222a x b y c a x b y c += += 的解为56x y = = ∴解得：56m n = =，即1516x y −= +=，所以65x y = =，故答案为：65x y = =. 【点睛】此题考查了解解二元一次方程组，以及二元一次方程组的解，熟练掌握方程组的解法是解本题的关键．15. 教材上曾让同学们探索过线段的中点坐标：在平面直角坐标系中，若两点A （x 1，y 1）、B （x 2，y 2），所连线段AB 的中点是M ，则M 的坐标为（122x x +，122y y +），例如：点A （1，2）、点B （3，6），则线段AB 的中点M 的坐标为（132+，262+），即M （2，4）请利用以上结论解决问题：在平面直角坐标系中，若点E （a ﹣1，a ），F （b ，a ﹣b ），线段EF 的中点G 恰好位于x 轴上，且到y 轴的距离是2，则2a ＋b 的值等于_____．【答案】203或﹣4 【解析】【分析】根据线段的中点坐标公式即可得到结论．【详解】解：∵点E （a ﹣1，a ），F （b ，a ﹣b ），∴中点G （a-1+b 2，2a-b 2）， ∵中点G 恰好位于x 轴上，且到y 轴的距离是2， ∴a-1+b =222a-b =02，解得：115a =310b =3，22a =-1b =-2 ， ∴2a ＋b ＝203或﹣4；故答案为：203或﹣4．【点睛】此题考查坐标与图形性质，中点坐标公式，关键是根据线段的中点坐标公式解答．三、解答题16. 计算：（1（2；（3(101212− +−−+− ．【答案】（1；（2）1；（3）8．【解析】【分析】（1）根据二次根式的性质计算即可求解；（2）根据立方根，二次根式的乘除法法则计算即可；（3）根据负整数指数幂，零指数幂的法则计算即可求解．【小问1详解】；【小问2详解】3=3=−32=−1=；【小问3详解】(101212− −−+− ()4121=+−−+4121=+++8=．【点睛】本题考查了二次根式的混合运算、负整数指数幂和零指数幂，掌握相关的运算法则是解题的关键．17. 解方程组：111,522x y x y +− −=− +=．【答案】13x y =−= 【解析】【分析】原方程组化简后用代入消元法求解．详解】解：原方程组化简，得25172x y x y −=− +=①②，【②×5+①，得7x=-7，∴x=-1，把x=-1代入②，得-1+y=2，∴y=3，∴13xy=−=．【点睛】本题考查了二元一次方程组的解法，其基本思路是消元，消元的方法有：加减消元法和代入消元法两种，灵活选择合适的方法是解答本题的关键．18. 某单位计划从内部招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如表所示：根据录用程序，组织200名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐1人）如图所示，每得一票记1分．测试项目测试成绩/分甲乙丙笔试75 80 90面试93 70 68（1）请算出三人的民主评议得分，甲得_____分，乙得______分，丙得______分；（2）根据实际需要，单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩，那么谁将被录用？【答案】（1）50,80,70（2）丙将被录用【解析】【分析】（1）用200分别乘以扇形统计图中甲、乙、丙的百分比即可；（2）根据加权平均数的计算方法分别计算三人的个人成绩，进行比较即可．【小问1详解】甲：20025%50×=分，乙：20040%80×=分，丙：20035%70×=分．故答案为：50,80,70；【小问2详解】如果将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩，那么，甲的个人成绩为：47539335072.9433×+×+×=++（分）乙的个人成绩为：48037038077433×+×+×=++（分）．丙的个人成绩为：49036837077.4433×+×+×=++（分）由于丙的个人成绩最高，所以候选人丙将被录用．【点睛】本题考查加权平均数的计算和扇形统计图，要注意各部分的权重与相应的数据的关系，牢记加权平均数的计算公式是解题的关键．19. 如图，一个无盖长方体的小杯子放置在桌面上，6cm AB BC ==，10cm CD =；（1）一只蚂蚁从A 点出发，沿小杯子外表面爬到D 点，求蚂蚁怎样走最短，最短路程是多少？（2）为了怕杯子落入灰尘又方便使用，现在需要给杯子盖上盖子，并把一双筷子放进杯子里，请问，筷子的最大长度是多少？【答案】（1）如方法一的路线最短，最短路线为（2）筷子的最大长度是【解析】【分析】（1）分别讨论将面ABEF 和面BCDE 展开，将面ABEF 和上底面展开两种情况，再利用勾股定理计算，进而比较即可求解；（2）当筷子沿AD 倾斜放的时候，能够放的最长，利用勾股定理计算即可．【小问1详解】方法一：将面ABEF 和面BCDE 展开，如图，∵6cm AB BC ==，10cm CD =，∴12cm,90AC C =∠=°，由勾股定理得AD ；方法二：将面ABEF 和上底面展开，如图，∵6cm AB DE ==，10cm BE =，∴16cm,90DB B =∠=°，由勾股定理得AD ===；所以，如方法一的路线最短，最短路线为；【小问2详解】如图，当筷子沿AD 倾斜放的时候，能够放的最长，∵6cm AB BC ==，10cm CD =，∴由勾股定理得AC，∴AD =，所以，筷子的最大长度是．【点睛】本题考查了勾股定理的应用，准确理解题意，熟练掌握勾股定理是解题的关键．20. 某商场第1次用39万元购进A ，B 两种商品，销售完后获得利润6万元，它们的进价和售价如表（总利润=单价利润×销售量）：价格商品进价（元/件）售价（元/件） A1200 1350 B 1000 1200（1）该商场第1次购进A ，B 两种商品各多少件？（2）商场第2次以原进价购进A ，B 两种商品，购进A 商品的件数不变，而购进B 商品的件数是第1次的2倍，A 商品按原售价销售，而B 商品打折销售，若两种商品销售完毕，要使得第2次经营活动获得利润等于5.4万元，则B 种商品是按几折销售的？【答案】（1）商场第1次购进A 商品200件，B 商品150件（2）B 种商品打九折销售的【解析】【分析】（1）设第1次购进A 商品x 件，B 商品y 件，根据该商场第1次用39万元购进A 、B 两种商品且销售完后获得利润6万元，即可得出关于x 、y 的二元一次方程组，解之即可得出结论；（2）设B 商品打m 折出售，根据总利润＝单件利润×销售数量，即可得出关于m 的一元一次方程，解之即可得出结论．【小问1详解】解：设第1次购进A 商品x 件，B 商品y 件．根据题意得：()()12001000390000135012001200100060000x y x y += −+−= ，解得：200150x y = =．答：商场第1次购进A 商品200件，B 商品150件．【小问2详解】设B 商品打m 折出售．根据题意得：()200135012001502120010005400010m ×−+×××−=，解得：9m =．答：B 种商品打九折销售的．【点睛】本题考查了二元一次方程组的应用以及一元一次方程的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）找准等量关系，正确列出一元一次方程．21. 如图，在平面直角坐标系中，一次函数1210y x =−+的图象与x 轴交于点A ，与一次函数2223y x =+的图象交于点B ．（1）求点B 的坐标；（2）C 为x 轴上点A 右侧一个动点，过点C 作y 轴的平行线，与一次函数1210y x =+的图象交于点D ，与一次函数2223y x =+的图象交于点E ．当3CE CD =时，求DE 的长；（3）直线y kx k =−经过定点()1,0，当直线与线段AB （含端点）有交点时k 的正整数值是________．【答案】（1）()3,4（2）8 （3）1或2【解析】【分析】（1）联立可直接得点B 的坐标；（2）设点C 的横坐标为m ，则(),210D m m −+，2,23E m m +，由3CE CD =求出m ，即可得DE 的长；（3）分别求解当直线y kx k =−也经过点()3,4B 时，当直线y kx k =−也经过点A 时k 的值即可求解．【小问1详解】解：令221023x x −++，解得3x =，4y ∴=，B ∴点坐标为()3,4．【小问2详解】解：设点C 的横坐标为m ，则(),210D m m −+，2,23E m m +， 223CE m ∴=+，210CD m =−， 3CE CD = ， ∴()2232103m m +=−，解得6m =． ()6,2D ∴−，()6,6E ，8DE ∴=．【小问3详解】直线y kx k =−经过定点()1,0，当直线y kx k =−经过点()3,4B 时，43k k =−，解得2k =；当直线y kx k =−经过点A 时，解得0k =；∴直线y kx k =−经过定点()1,0，当直线与线段AB （含端点）有交点时k 的正整数值是1或2，故答案为：1或2．【点睛】本题是一次函数综合题，考查了待定系数法求一次函数解析式，函数图象上点的坐标特征，两点的距离等知识，灵活运用这些知识解决问题是本题的关键．22. 如图，长方形ABCD （对边平行且相等，四个角都是直角）中，6,8AB AD ==，点P 在边BC 上，且不与点B 、C 重合，直线AP 与DC 的延长线交于点E ．（1）当点P 是BC 的中点时，求证：ABP ECP △≌△；（2）将APB △沿直线AP 折叠得到APB ′ ，点B ′落在长方形ABCD 的内部，延长PB ′交直线AD 于点F ．①证明FA FP =，并求出在（1）条件下AF 的值；②连接B C ′，求PCB ′△周长的最小值．【答案】（1）见解析（2）①证明见解析，132AF =；②PCB ′△周长的最小值为12．【解析】【分析】（1）根据长方形的性质得AB CD ∥，可得BAP E B BCE ∠=∠∠=∠，，利用AAS 即可得出结论；（2）①根据平行线的性质和折叠的性质得出FAP APF ∠=∠，等角对等边即可得FA FP =，设FA x =，在Rt AB F ′△中，由勾股定理求即可解；②可得PCB ′△的周长8CP P C CB C B B B B C ′′′=+++=+′=，当点B ′恰好位于对角线AC 上时，CB AB ′+′最小，在Rt ABC △中，由勾股定理得10AC =，据此求解即可得PCB ′△周长的最小值．【小问1详解】证明：∵长方形ABCD 中，∴AB CD ∥，∴BAP E B BCE ∠=∠∠=∠，，∵点P 是BC 的中点，∴BP CP =，∴(AAS)ABP ECP △≌△；【小问2详解】解：①∵长方形ABCD 中，∴AD BC ∥，∴APB FAP ∠=∠，由折叠得APB APF ∠=∠，∴FAP APF ∠=∠，∴FA FP =，长方形ABCD 中，68AB AD ==，，∴8BC AD ==，∵点P 是BC 的中点，∴4BP CP ==，由折叠得6A B B A ′==，4PB PB ′==，90B AB P AB F ∠=∠=∠=′′°，设FA x =，则FP x =，∴4FB x ′=−，在Rt AB F ′△中，222AF F B A B ′+′=，∴222(4)6x x =−+，解得132x =，即132AF =； ②由折叠得6A B B A ′==，4PB PB ′==， ∴PCB ′△的周长8CP P C CB C B B B B C ′′′=+++=+′=，连接B C AC ′，，∵AB B C AC ′′+>，∴当点B ′B ′恰好位于对角线AC 上时，CB AB ′+′最小，在Rt ABC △中，68AB BC ==，，∴10AC =，∴CB ′的最小值4AC AB ′=−=，∴PCB ′△周长的最小值88412CB ′=+=+=．【点睛】本题属于四边形综合题，考查了折叠的性质，全等三角形的判定和性质，等腰三角形的判定和性质以及勾股定理等知识，掌握折叠是一种轴对称，折叠前后的图形对应角相等、对应边相等，灵活运用相关的性质是解题的关键．。

山东省济南市历下区2023-2024学年八年级上学期期末考试物理试题(含答案)

山东省济南市历下区2023~2024学年第一学期八年级期末教学质量检测物理试题（LX2024.1）本试题共6页．分选择题部分和非选择题部分，选择题部分40分，非选择题部分60分．全卷满分100分，考试用时60分钟．答题前，请考生务必将自己的学校、班级、姓名、座号、准考证号写在答题卡的规定位置，并同时将学校、班级、姓名、座号写在试卷的规定位置．答题时，选择题部分每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．非选择题部分，用0.5毫米黑色签字笔在答题卡上题号所提示的答题区域作答．直接在试题上作答无效．本考试不允许使用计算器．考试结束后，将本试题和答题卡一并交回．选择题部分共40分一、单项选择题（本大题共10小题，每小题2分，共20分．每小题给出的四个选项中，只有一个选项最符合题目的要求）1．2022年10月12日，“天宫课堂”第三课在每天要绕地球转15圈半的“问天实验舱”内正式开讲．在水球变“懒”实验中，水球在微重力作用下呈现椭圆形静止在支架上，如图所示．我们说水球静止，所选择的参照物是（）A．问天实验舱B．地面演播室C．地球D．太阳2．如图所示的“圭表”是我国古代天文学家发明的一种通过度量日影长度来测定节气的观测仪器，它由相互垂直的“圭”和“表”两部分组成．为了让“表”处于竖直位置，古代天文学家用重垂线进行校正，这种做法主要利用了（）A．重力的大小与质量有关B．重力的方向总是竖直向下C．力可以改变物体的形状D．重力作用点在其几何中心3．科技感爆棚的山东省科技馆新馆成为新晋网红打卡处．如图所示是“声聚焦”装置，可以使远处传来的声音在其表面发生反射而会聚，从而使微弱的声音被放大．由此可知“声聚焦”装置主要增大了声音的（）A．音调B．音色C．频率D．响度4．如图甲所示，在“探究凸透镜成像规律”的实验中，选取焦距为10cm的凸透镜，将一个F型LED灯依次放在光具座A、B、C三点处，所成像如图乙所示，则人眼在透镜右侧观察到的像先后顺序是（）甲乙A．③②①B．③①②C．②③①D．②①③5．如图所示，一同学将手臂水平前伸，另一位同学用大小相同的力向相同方向，分别对手臂的A、B、C不同部位施加水平推力，来比较哪种情况下更容易推动手臂，这是体验影响力的效果因素中的（）A．力的大小B．力的方向C．力的作用点D．三者都有6．如图为高速摄像机拍摄的子弹穿过柿子的照片．若子弹的平均速度是900m/s，则子弹穿过柿子的时间大约为（）A．0.1μs B．0.1ms C．0.1s D．0.1min7．“锲而不舍，金石可镂”．如图所示，雕刻之后，印章石的（）A．体积减少，密度减小B．质量减少，密度减小C．质量减少，密度不变D．体积、质量和密度都减小8．牛顿第一定律是在大量经验事实的基础上，通过推理抽象概括出来的．当年，牛顿还曾用这一方法研究过另一个问题：人们沿水平方向抛出去的石块，运动一段距离后会落回地面：沿水平方向抛石块的力越大，石块的落地点就会越远，如果使用一门大炮用非常非常大的力沿水平方向将石块抛出，会怎样呢？考虑到地球是圆的，因此可以推理，石块将会（）A．在半空中静止不动B．会落回大炮发射的位置C．绕地球做圆周运动D．会一直做匀速直线运动9．生活中人们常常利用物体的惯性．下列描述正确的是（）甲乙丙丁A．图甲，运动员扔标枪时要助跑，利用了运动员的惯性B．图乙，紧固锤头时撞击锤柄下端，利用了锤柄的惯性C．图丙，拍打棉被清除上面的浮灰，利用了棉被的惯性D．图丁，渔民将手中的渔网抛出时，利用了渔网的惯性10．2023年10月6日，杭州第19届亚运会举重女子87公斤级比赛，中国选手梁小梅夺得金牌．如图所示是梁小梅举重的场景，下列说法中正确的是（）A．人所受到的重力和地面对人的支持力是一对平衡力B．杠铃受到的重力和人对杠铃的支持力是一对平衡力C．人对地面的压力和地面对人的支持力是一对平衡力D．杠铃对人的压力与人对杠铃的支持力是一对平衡力二、多项选择题（本大题共5小题，每小题4分，共20分．每小题给出的四个选项中，至少有两个选项符合题目的要求．）11．“估测”是物理学中常用的一种方法．下面数据中，比较接近实际的是（）A．教室内中学生使用的课桌高度约为82BB．小梅步行上学时正常走路速度约18km/hC．小明站在水平体重计上对其压力约500ND．一本初中八年级物理课本的质量约4kg12．如图所示是北京2022冬奥会速度滑冰场馆安装的超高速4K轨道摄像机．这款“猎豹”4K高清摄像机能紧跟400米速滑道上飞奔的运动员们，进行全过程精准拍摄．下列说法正确的是（）A．轨道摄像机的镜头相当于凸透镜B．摄像机成像的原理与放大镜相同C．运动员通过摄像机成缩小的实像D．运动员远离摄像机成的像会变小13．汽车的发明促进了人类文明的发展，它是我们现代生活中不可或缺的交通工具．下列有关汽车中各部件的说法中正确的是（）A．汽车后视镜是利用光的反射来扩大司机视野B．倒车雷达是利用超声波来探测车后方情况的C．汽车的车身显白色是因为吸收所有颜色的光D．汽车装有消声器的目的是在接收处减弱噪声14．第24届冬季奥林匹克运动会由北京市和张家口市联合举办．如图为冰球选手备战训练的瞬间，下列说法中正确的是（）A．运动员用球杆推着冰球在冰面上加速滑行，说明力是维持物体运动的原因B．运动员手持球杆击球时，球杆对球的力与球对球杆的力是一对相互作用力C．运动员推出的冰球在水平冰面上滑行时，冰球受到重力、支持力和摩擦力D．运动员在弯道减速滑行过程中，若外力全部消失，运动员将匀速直线运动15．如图所示，对以下实验的说法正确的是（）甲乙丙丁A．图甲，使用刻度尺测量物理课本的长度和宽度时，采用多次测量可减小误差B．图乙，探究斜面上小车速度的变化时，尽量选定路程测时间并使坡度缓一些C．图丙，将有反射光的光屏向后折转，反射光的位置和方向不会跟随发生改变D．图丁，探究物重与物体质量关系，可得物体所受的重力大小与其质量成正比非选择题部分共60分三、非选择题（本大题共12小题，共60分）16．我国新一代“人造太阳”装置建成并实现放电．如图所示，装置采用很强的磁场将高温粒子束缚在真空室有限的环形轨道内运动，说明力可以改变物体的_____________．设备几乎监测不到放电过程的爆裂声是因为_____________．17．小鹏去电影院观看电影《志愿军》，影院里的观众在各个角度都能看到银幕上的影像，这是因为光在银幕上发生了_____________（选填“漫”或者“镜面”）反射；银幕上显示的彩色画面是由红、_____________、蓝三种色光混合而成的．18．晋代张华的《博物志》记载了我国劳动人民用冰取火的过程，利用凸透镜对光的_____________作用将物体点燃，如图所示．用这类透镜制作的眼镜片，可以用来矫正_____________眼．19．如图所示，物块在两侧钩码共同的作用下处于静止状态．每个钩码的质量是50g ，取，则图中物块受到的合力大小为_____________．钩码对物块施加拉力的同时，物块也对钩码有拉力的作用，这说明力的作用是_____________的．20．请在答题卡相应位置画出入射光线AO 经界面折射后的折射光线并标出折射角．21．如图所示，重600N 的滑雪运动员从高山上加速下滑，请在答题卡相应位置画出该运动员所受重力的示意图．22．如图所示，具有立体触控技术的手机屏幕，可以称量物体的质量．取，请根据屏幕上所显示的数据，求该水果受到的重力．23．（7分）人工智能逐渐融入我们的生活，一些餐厅、饭店等餐饮场所开始使用机器人送餐．如图所示是某餐厅的送餐机器人，在1min 内匀速直线运动72m ．当该送餐机器人托着质量为5kg的物体送餐时，机器人和10N /kg g =10N /kg g =所托物体受到的总重力是490N ，机器人受到的阻力约为其总重力的0.08倍．取，通过计算回答：（1）此次送餐过程的1min 内，机器人的速度是多少？（2）该送餐机器人自身质量是多少？（3）机器人在匀速直线运动时受到的牵引力是多少？24．在提倡“低碳生活”的今天，自行车成为人们“绿色出行”的首选工具，越来越多的年轻人喜欢上了自行车运动．如图所示为一款碳纤维自行车，其相关数据见下表．通过计算回答：品牌名称*******变速档位24速产品功能竞赛/运动/娱乐车架质量 4.5kg 车架材质航太级碳纤维车架材质密度（1）碳纤维车架的体积是多少？（2）若仅将车架换成铁材质（铁的密度取），车架质量是多少？25．（7分）如图甲、乙两张图片记录了小林在一次骑行中，分别两次从自行车后视镜（平面镜）看到弟弟的像．根据这个现象，她来到实验室里利用图丙中的器材“探究平面镜成像特点”．甲乙丙（1）实验中用玻璃板代替平面镜的目的是便于_____________．该实验需要的测量工具是_____________．（2）如图丙所示，把点燃的蜡烛A 放在玻璃板前，将另一支完全相同、未点燃的蜡烛B 放在玻璃板的后面，实验时小林应在蜡烛_____________（选填“A ”或“B ”）一侧观察玻璃板中的像．（3）调整后，小林通过多次实验发现：蜡烛A 无论靠近还是远离玻璃板，通过移动蜡烛B 都能与蜡烛A 的像10N /kg g =331.810kg /m ⨯337.910kg /m ⨯完全重合．由此小林判断出：从图甲到图乙，弟弟在后视镜里的像的大小是_____________（选填“变大”“不变”或“变小”）的．（4）实验中，为得到像与物体关于平面镜的位置关系，小林将蜡烛B在水平桌面的纸上移动，让它与蜡烛A 的像完全重合，在纸上描出此时蜡烛、玻璃板和像的位置，接下来的操作是_____________．26．（8分）生活生产中存在着大量与摩擦力有关的现象．在学习摩擦力的课上，老师让同学们感受一下手掌在桌面上滑动时的摩擦力，同学们积极进行体验，有的同学用不同的压力去滑动，有的同学还将手压在书上滑动……同学们纷纷根据体验提出如下猜想：A．滑动摩擦力大小与压力大小有关B．滑动摩擦力大小与接触面积大小有关C．滑动摩擦力大小与接触面的粗糙程度有关（1）小明同学列举了一个生活中的事例：下雪天给自行车轮胎撒点气，就不打滑．因此他猜想，滑动摩擦力的大小与接触面积大小有关，老师认为这个事例不能支持他的猜想，你认为其原因是_____________．设计好实验方案后，同学们用一个长方体物块、长木板、弹簧测力计、砝码和细线等器材进行“探究影响滑动摩擦力大小因素”的实验．甲乙丙（2）用弹簧测力计沿水平方向拉着长方体物块做_____________运动，其目的是使弹簧测力计示数等于滑动摩擦力的大小．如图甲，此时滑动摩擦力的大小为_____________N．（3）根据甲、乙两图，可以得出的结论是：_____________．（4）现已完成对猜想A的探究，如要用如图丙物块的上、前、底三个面完成对另外两个猜想的探究，下列各图能够完成探究任务的是（图中有花纹的代表接触面更粗糙）：_____________．A．B．C．D．27．（10分）在“探究固体的质量与体积的关系”实验中，所用的实验器材有托盘天平，量筒，甲、乙两种不同材料的固体．图甲（1）将天平放在水平工作台上，把游码移到称量标尺左端的零刻度线处，分度盘上的指针如图甲所示，此时应将平衡螺母向_____________（选填“左”或“右”）调节，使天平横梁平衡；（2）在其中一次测量质量时，将最小为5g 的砝码放入托盘天平的右盘后，分度盘上的指针也如图甲所示，为了使天平的横梁平衡，应该_____________（填正确的字母序号）；A ．把横梁两端的平衡螺母向右调节B ．不取下这个砝码，把标尺上的游码向右移C ．取下这个砝码，把标尺上的游码向右移（3）他们分别测出甲、乙两种物质的质量及体积，记录数据如下表所示．实验序号物质种类质量/g 体积/12710 2.725420 2.738130 2.74甲10840 2.75201026402027603028乙80402根据表中的数据，请在图乙相应位置的坐标纸上描点，并用平滑曲线画出物质乙质量与体积关系的图像．（4）比较表中甲和乙的实验数据，可得出结论：不同物质的_____________一般是不同的，物理学中把它定义为物质的密度．甲乙丙（5）小明通过所学的知识测量鹅卵石的密度，所测数据如图丙和图丁所示，该鹅卵石的密度为_____________；（6）实验结束后小明发现天平右边托盘下一直沾着一点泥土，通过与组里的同学们分析讨论，可知所测鹅卵3cm 3/g cm -⋅质量体积3kg /m石的质量会_____________（选填“变大”“变小”或“不变”），理由是________________．山东省济南市历下区2023~2024学年第一学期八年级期末教学质量检测物理试题参考答案及评分意见选择题部分共40分一、单项选择题本大题包括10小题，每小题2分，共20分．题号12345678910答案A B D A C B C C D B二、多项选择题本大题包括5小题，每小题4分，共20分．题号1112131415答案AC ACD AB BCD ABCD非选择题部分共60分三、非选择题本大题包括12小题，共60分．16．运动状态：真空不能传声17．漫；绿18．会聚；远视（老花）19．0N（或0）；相互20．如题图答．21．如题图答．评分意见：20题3分，画出法线且折射光线在左下区域的按以下标准得分：折射角明显小于入射角、折射光线画成实线且有箭头、标对折射角位置各得1分．法线画成实线的扣1分.21题3分，画对力的方向的按以下标准得分：力的大小（标出）、方向、作用点各得1分．22．解：答：该水果受到的重力是23．解：（1）（2）由公式，得：（3）600NG=251.7g 5.1710kgm-==⨯25.1710kg10N/kg0.517NG mg-==⨯⨯=0.517N72m1min60s, 1.2m/s60sst vt=====G mg=490N49kg10N/kgGmg===总总()49kg5kg44kgm m m=--=总人物0.080.08490N39.2Nf G==⨯=总因为机器人做匀速直线运动，所以答：（1）此次送餐过程的1min 内，机器人的速度是1.2m/s ；（2）该送餐机器人自身质量是是44kg ；（3）机器人在匀速直线运动时受到的牵引力是39.2N ．24．解：（1）由公式，得：（2）答：（1）碳纤维车架的体积是；（2）车架质量是19.75kg ．25．（1）确定像的位置刻度尺（2）A （3）不变（4）（用直线连接蜡烛和像，）用刻度尺分别量出蜡烛和像到玻璃板的距离（或将纸沿玻璃板的位置对折，观察蜡烛和像的位置是否重合）．（4）2分．其他答案合理的同样给分．26．（8分）（1）此时自行车轮胎受到的摩擦力不是滑动摩擦力（2）匀速直线 1.2（3）当接触面积和接触面的粗糙程度相同时，压力越大，滑动摩擦力越大（4）AC评分意见：本小题7分．（1）2分．答出自行车轮胎受到的“静摩擦力”或“滚动摩擦”，或答成“接触面的粗糙程度发生改变”同样得分．（2）2分．每空1分．（3）2分．（4）2分．部分选对得1分．27．（1）右（2）B （3）如题图答（4）质量与体积的比（值）（5）（6）不变在测量前调节天平平衡时，已经避免了左、右两盘质量不同带来的影响．39.2NF f ==牵m V ρ=33334.5kg 2.510m 1.810kg /m m V ρ-===⨯⨯碳碳33337.910kg /m 2.510m 19.75kgm V ρ-==⨯⨯⨯=铁铁332.510m -⨯32.710⨯。

江苏省南通市海门区2023-2024学年八年级上学期期末语文试题(含答案)

2023~2024学年度第一学期期末试卷八年级语文注意事项考生在答题前请认真阅读本注意事项及各题答题要求：1．本卷共8页，满分150分，考试时间150分钟。

2．答题前，请务必核对答题纸上的条形码姓名、考试号。

3．须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置，在其它位置作答无效。

如需改动，请用橡皮擦干净后，再书写其它答案。

4．请直接将答案书写在答题纸上。

一（30分）江南霜雪晚，初冬正佳时。

小文随家人赴一场研学之旅——寻根人文印记，溯源传统文化。

第一站：【江苏省江海博物馆】江海博物馆是中国唯一以江海文化为主题的博物馆，是海门打造江海特色花园城市最为厚重和最有看点的文化地标， A 。

走进博物馆，我们可以听到海门先民战江斗海的动人故事，可以看到今日海门人追江赶海的jué jiàng身影。

这里真实jì zǎi了江海文明的前世今生，体现了浓郁的江海文化韵味，是传承和hóng yáng江海文化最主要的公益性文化阵地。

1．根据拼音在横线上用行楷写出相应的汉字。

（3分）__________ __________ __________2．选择条理最为清晰、语言最为连贯的句子填写在A处：__________（只填序号）（2分）A．是体现江海魅力文化、保护江海城市记忆、延续江海历史文脉的主要载体。

B．是保护江海城市记忆、延续江海历史文脉、体现江海魅力文化的主要载体。

C．是延续江海历史文脉、体现江海魅力文化、保护江海城市记忆的主要载体。

3．博物馆展出了清朝胡义赞的《归棹洛阳图轴》，图上附录了唐代韦应物的一首诗。

因年代久远，有一字模糊不清。

小文根据律诗的相关知识，推断该字是：（）（2分）凄凄去亲爱，泛泛入烟雾。

归棹洛阳人，残钟广陵（）。

今夕为此别，何处还相遇。

世事波上舟，沿洄安得住。

A．楼 B．月 C．树 D．舟第二站：【青龙港1806】拥有200多年历史的青龙港，是长江下游江海地区联结上海的航运枢纽，史称“长江第一渡”。

八年级上学期期末考试2022-2023第一学期8年级语文试题

2022—2023学年第一学期期末调研考试八年级语文试题温馨提示: 1.本试卷共6页，22道小题，满分为120分，考试时间为120分钟。

2.本次考试实行网阅，请根据提示要求在答题卡上作答，在试卷上作答无效。

第一部分（1-4题，23分）1．阅读下列文字，按要求回答问题。

（6分）时间往往是最好的检验器。

时间的流逝可以让盛极一时的东西永远xiāo声匿迹，也可以让默默无闻的坚守者显现出巨大的价值。

那些事物能够经受住岁月淘洗的原因，是因为它们总会留下不同凡响的价值。

在时代变革的大背景下，如何能够让事物[甲] （延伸/ 延续）不断？恐怕只因“认真”两个字。

当我们面对复杂多变的挑战和[乙] （层出不穷/变化无穷）的机遇而茫茫不得其要的时候，当我们忧心时代大浪滔滔不绝、淘洗不尽的时候，不妨告诉自己，匠心传承，唯“真”传承．。

①根据拼音写汉字，给加点字注音。

（2分）xiāo（）声匿迹传承．（）②从文段中括号内选择符合语境的词语填入[甲][乙]两处横线上。

（2分）[甲] [乙]③文中画线句有一处语病，请改正。

（2分）2. 依次填入下面一段文字横线处的词语,最恰当的一项是( )（2分）在信息化技术发展迅速的今天，个人信息泄露的风险，因此，为公民信息撑起一把安全“保护伞”，不仅，更是刻不容缓。

同时，当个人安全信息遭遇侵害时，应当，勇于维护自己的合法权益。

A.无孔不入势不可挡挺身而出B.无处不在势不可挡奋不顾身C.无孔不入势在必行奋不顾身D.无处不在势在必行挺身而出3. 古诗文背诵与默写。

（7分）①“山”天然灵秀，意蕴丰厚。

“树树皆秋色，”是秋意浓浓的山野之美，“采菊东篱下，”是人菊合一的山中闲情，“风休住，”是浪漫神话中的美好归处。

②“水”变幻多姿，含情寄思。

“，”是《渡荆门送别》中情谊深厚的长江水，触发了李白的思乡之情；“，”是《三峡》中春冬季节富有色彩又动感十足的长江水，寄寓了郦道元的无限情思。

4.阅读下面两则材料，回答问题。

八年级第一学期期末考试试卷【含答案】

八年级第一学期期末考试试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪种现象属于光的反射？A. 彩虹B. 镜子中的倒影C. 日食D. 月食2. 在电路中，电阻的单位是？A. 安培B. 伏特C. 欧姆D. 瓦特3. 下列哪个是单质？A. 氧气B. 水C. 二氧化碳D. 盐酸4. 哪个是生物的基本单位？A. 细胞B. 原子C. 分子D. 阳离子5. 地球上最大的生物圈是？A. 海洋生物圈B. 陆地生物圈C. 大气生物圈D. 淡水生物圈二、判断题（每题1分，共5分）1. 地球围绕太阳转是正确的。

（）2. 长度单位厘米是国际单位制中的基本单位。

（）3. 0℃的水比0℃的冰重。

（）4. 人类是由单细胞生物进化而来的。

（）5. 光的传播速度在真空中是最慢的。

（）三、填空题（每题1分，共5分）1. 地球上最大的生物圈是______。

2. 光的反射定律包括入射角等于______。

3. 电路中，电阻的单位是______。

4. 细胞是生物的______。

5. 地球围绕太阳转是______。

四、简答题（每题2分，共10分）1. 简述光的反射定律。

2. 解释电阻的概念。

3. 什么是单质？4. 生物的基本单位是什么？5. 地球上最大的生物圈是哪个？五、应用题（每题2分，共10分）1. 如果一个物体的质量是5kg，加速度是10m/s²，求物体所受的力。

2. 如果一个电池的电压是9V，电路中的电阻是3Ω，求电路中的电流。

3. 如果一个单质元素的原子量是20，它的分子量是多少？4. 如果一个细胞分裂成两个细胞，每个新细胞的大小是原来细胞的一半，新细胞的数量是多少？5. 如果地球上最大的生物圈是海洋生物圈，那么海洋生物圈中有哪些生物？六、分析题（每题5分，共10分）1. 分析光的反射定律在生活中的应用。

2. 分析电阻在电路中的作用。

七、实践操作题（每题5分，共10分）1. 设计一个实验，验证光的反射定律。