北京市海淀区2017年九年级上期中数学试题(含答案)

合集下载

2017-2018学年北京市海淀区九年级上期中数学试题含答案

第 1 页共 14 页初三第一学期期中学业水平调研数学2017.11学校班级___________姓名成绩一、选择题（本题共24分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的．请将正确选项前的字母填在表格中相应的位置．1．一元二次方程3610x x --=的二次项系数、一次项系数、常数项分别是 A ．3，6，1B ．3，6，1-C ．3，6-，1D ．3，6-，1-2．把抛物线2y x =向上平移1个单位长度得到的抛物线的表达式为 A ．21y x =+ B ．21y x =- C ．21y x =-+D ．21y x =--3．如图，A ，B ，C 是⊙O 上的三个点. 若∠C =35°，则∠AOB 的大小为 A ．35° B ．55° C ．65° D ．70° 4．下列手机手势解锁图案中，是中心对称图形的是A B C D 5．用配方法解方程2420x x -+=，配方正确的是 A ．()222x -= B．()222x +=C ．()222x -=-D ．()226x -=6．风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转n °后能与原来的图案重合，那么n 的值可能是A ．45B ．60C ．90D ．120第 1 页共 14 页7．二次函数21y ax bx c =++与一次函数2y mx n =+2ax bx c mx n ++>+的x 的取值范围是A ．30x -<<B ．3x <-或0x >C ．3x <-或1x >D ．03x <<8．如图1，动点P 从格点A 出发，在网格平面内运动，设点P 走过的路程为s ，点P 到直线l 的距离为d . 已知d 与s 的关系如图2所示．下列选项中，可能是点P 的运动路线的是A B C D二、填空题（本题共24分，每小题3分）9．点P （1-，2）关于原点的对称点的坐标为________． 10．写出一个图象开口向上，过点（0，0）的二次函数的表达式：________．11．如图，四边形ABCD 内接于⊙O ，E 为CD 的延长线上一点．若∠B =110°，则∠ADE 的大小为________． 12．抛物线21y x x =--与x 轴的公共点的个数是________． 13．如图，在平面直角坐标系xOy 中，点A ，点B 的坐标分别为（0，2），（1-，0），将线段AB 绕点O 顺时针旋转，若点A 的对应点A '的坐标为（2，0），则点B 的对应点B '的坐标为________．14．已知抛物线22y x x =+经过点1(4)y -，，2(1)y ，，则1y ________2y （填“＞”，“=”，或“＜”）．15．如图，⊙O 的半径OA 与弦BC 交于点D ，若OD =3，AD =2， BD =CD ，则BC 的长为________．lllll。

北京市海淀区-九年级上期中数学复习试卷含解析.doc

2016-2017学年北京市海淀区普通中学九年级（上）期中数学复习试卷（因式分解）一、选择题1．分解因式：16﹣x2=（）A．（4﹣x）（4+x）B．（x﹣4）（x+4）C．（8+x）（8﹣x）D．（4﹣x）22．下列因式分解错误的是（）A．2a﹣2b=2（a﹣b）B．x2﹣9=（x+3）（x﹣3）C．a2+4a﹣4=（a+2）2 D．﹣x2﹣x+2=﹣（x﹣1）（x+2）3．把8a3﹣8a2+2a进行因式分解，结果正确的是（）A．2a（4a2﹣4a+1）B．8a2（a﹣1）C．2a（2a﹣1）2D．2a（2a+1）2 4．若实数x、y、z满足（x﹣z）2﹣4（x﹣y）（y﹣z）=0，则下列式子一定成立的是（）A．x+y+z=0 B．x+y﹣2z=0 C．y+z﹣2x=0 D．z+x﹣2y=05．小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：a﹣b，x﹣y，x+y，a+b，x2﹣y2，a2﹣b2分别对应下列六个字：昌、爱、我、宜、游、美，现将（x2﹣y2）a2﹣（x2﹣y2）b2因式分解，结果呈现的密码信息可能是（）A．我爱美B．宜昌游C．爱我宜昌D．美我宜昌二、填空题6．如图中的四边形均为矩形，根据图形，写出一个正确的等式．7．分解因式：（x﹣8）（x+2）+6x=．8．若整式x2+ky2（k为不等于零的常数）能在有理数范围内因式分解，则k的值可以是（写出一个即可）．9．分解因式：（2a+b）2﹣（a+2b）2=．10．已知实数a，b满足：a2+1=，b2+1=，则2015|a﹣b|=．三、解答题11．分解因式：（1）3x2﹣27；（2）4+12（x﹣y）+9（x﹣y）2；（3）8（x2﹣2y2）﹣x（7x+y）+xy．12．若△ABC的三边长分别为a，b，c，且a+2ab=c+2bc，判断△ABC的形状．13．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．14．设a=m+1，b=m+2，c=m+3，求代数式a2+2ab+b2﹣2ac﹣2bc+c2的值．15．设y=kx，是否存在实数k，使得代数式（x2﹣y2）（4x2﹣y2）+3x2（4x2﹣y2）能化简为x4？若能，请求出所有满足条件的k的值；若不能，请说明理由．2016-2017学年北京市海淀区普通中学九年级（上）期中数学复习试卷（因式分解）参考答案与试题解析一、选择题1．分解因式：16﹣x2=（）A．（4﹣x）（4+x）B．（x﹣4）（x+4）C．（8+x）（8﹣x）D．（4﹣x）2【考点】因式分解-运用公式法．【分析】直接利用平方差公式分解因式得出答案．【解答】解：16﹣x2=（4﹣x）（4+x）．故选：A．【点评】此题主要考查了公式法分解因式，熟练应用平方差公式是解题关键．2．下列因式分解错误的是（）A．2a﹣2b=2（a﹣b）B．x2﹣9=（x+3）（x﹣3）C．a2+4a﹣4=（a+2）2 D．﹣x2﹣x+2=﹣（x﹣1）（x+2）【考点】因式分解-运用公式法；因式分解-提公因式法；因式分解-十字相乘法等．【分析】根据公式法分解因式的特点判断，然后利用排除法求解．【解答】解：A、2a﹣2b=2（a﹣b），正确；B、x2﹣9=（x+3）（x﹣3），正确；C、a2+4a﹣4不能因式分解，错误；D、﹣x2﹣x+2=﹣（x﹣1）（x+2），正确；故选C．【点评】本题主要考查了因式分解，关键是对于完全平方公式和平方差公式的理解．3．把8a3﹣8a2+2a进行因式分解，结果正确的是（）A．2a（4a2﹣4a+1）B．8a2（a﹣1）C．2a（2a﹣1）2D．2a（2a+1）2【考点】提公因式法与公式法的综合运用．【分析】首先提取公因式2a，进而利用完全平方公式分解因式即可．【解答】解：8a3﹣8a2+2a=2a（4a2﹣4a+1）=2a（2a﹣1）2．故选：C．【点评】此题主要考查了提取公因式法以及公式法分解因式，熟练应用完全平方公式是解题关键．4．若实数x、y、z满足（x﹣z）2﹣4（x﹣y）（y﹣z）=0，则下列式子一定成立的是（）A．x+y+z=0 B．x+y﹣2z=0 C．y+z﹣2x=0 D．z+x﹣2y=0【考点】完全平方公式．【分析】首先将原式变形，可得x2+z2+2xz﹣4xy+4xz+4y2﹣4yz=0，则可得（x+z﹣2y）2=0，则问题得解．【解答】解：∵（x﹣z）2﹣4（x﹣y）（y﹣z）=0，∴x2+z2﹣2xz﹣4xy+4xz+4y2﹣4yz=0，∴x2+z2+2xz﹣4xy+4y2﹣4yz=0，∴（x+z）2﹣4y（x+z）+4y2=0，∴（x+z﹣2y）2=0，∴z+x﹣2y=0．故选：D．【点评】此题考查了完全平方公式的应用．解题的关键是掌握：x2+z2+2xz﹣4xy+4y2﹣4yz=（x+z﹣2y）2．5．小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：a﹣b，x﹣y，x+y，a+b，x2﹣y2，a2﹣b2分别对应下列六个字：昌、爱、我、宜、游、美，现将（x2﹣y2）a2﹣（x2﹣y2）b2因式分解，结果呈现的密码信息可能是（）A．我爱美B．宜昌游C．爱我宜昌D．美我宜昌【考点】因式分解的应用．【分析】对（x2﹣y2）a2﹣（x2﹣y2）b2因式分解，即可得到结论．【解答】解：∵（x2﹣y2）a2﹣（x2﹣y2）b2=（x2﹣y2）（a2﹣b2）=（x﹣y）（x+y）（a﹣b）（a+b），∵x﹣y，x+y，a+b，a﹣b四个代数式分别对应爱、我，宜，昌，∴结果呈现的密码信息可能是“爱我宜昌”，故选C．【点评】本题考查了公式法的因式分解运用，熟练掌握因式分解的方法是解本题的关键．二、填空题6．如图中的四边形均为矩形，根据图形，写出一个正确的等式am+bm+cm=m（a+b+c）．【考点】因式分解-提公因式法．【分析】直接利用矩形面积求法结合提取公因式法分解因式即可．【解答】解：由题意可得：am+bm+cm=m（a+b+c）．故答案为：am+bm+cm=m（a+b+c）．【点评】此题主要考查了提取公因式法分解因式，正确利用矩形面积求出是解题关键．7．分解因式：（x﹣8）（x+2）+6x=（x+4）（x﹣4）．【考点】因式分解-运用公式法．【分析】原式去括号、合并同类项后，运用平方差公式分解即可得到结果．【解答】解：原式=x2+2x﹣8x﹣16+6x=x2﹣16=（x+4）（x﹣4），故答案为：（x+4）（x﹣4）．【点评】此题考查了因式分解﹣运用公式法，熟练掌握整式的化简、平方差公式是解题的关键．8．若整式x2+ky2（k为不等于零的常数）能在有理数范围内因式分解，则k的值可以是﹣1（写出一个即可）．【考点】因式分解-运用公式法．【分析】令k=﹣1，使其能利用平方差公式分解即可．【解答】解：令k=﹣1，整式为x2﹣y2=（x+y）（x﹣y），故答案为：﹣1．【点评】此题考查了因式分解﹣运用公式法，熟练掌握平方差公式是解本题的关键．9．分解因式：（2a+b）2﹣（a+2b）2=3（a+b）（a﹣b）．【考点】因式分解-运用公式法．【分析】原式利用平方差公式分解即可．【解答】解：原式=（2a+b+a+2b）（2a+b﹣a﹣2b）=3（a+b）（a﹣b）．故答案为：3（a+b）（a﹣b）．【点评】此题考查了因式分解﹣运用公式法，熟练掌握平方差公式是解本题的关键．10．已知实数a，b满足：a2+1=，b2+1=，则2015|a﹣b|=1．【考点】因式分解的应用；零指数幂．【分析】由于a2+1=，b2+1=，两式相减可得a2﹣b2=﹣，则有（a+b）（a﹣b）=，分解因式可得a=b，依此可得2015|a﹣b|=20150，再根据零指数幂的计算法则计算即可求解．【解答】解：∵a2+1=，b2+1=，两式相减可得a2﹣b2=﹣，（a+b）（a﹣b）=，[ab（a+b）+1]（a﹣b）=0，∴a﹣b=0，即a=b，∴2015|a﹣b|=20150=1．故答案为：1．【点评】考查了因式分解的应用，零指数幂，本题关键是得到a=b．三、解答题11．分解因式：（1）3x2﹣27；（2）4+12（x﹣y）+9（x﹣y）2；（3）8（x2﹣2y2）﹣x（7x+y）+xy．【考点】提公因式法与公式法的综合运用．【分析】利用提公因式法、公式法进行因式分解即可．【解答】解：（1）3x2﹣27=3（x2﹣9）=3（x﹣3）（x+3）；（2）4+12（x﹣y）+9（x﹣y）2=[2+3（x﹣y）]2=（2+3x﹣3y）2；（3）8（x2﹣2y2）﹣x（7x+y）+xy=8x2﹣16y2﹣7x2﹣xy+xy=x2﹣16y2=（x+4y）（x﹣4y）．【点评】本题考查的是多项式的因式分解，掌握提公因式法、公式法因式分解是解题的关键．12．若△ABC的三边长分别为a，b，c，且a+2ab=c+2bc，判断△ABC的形状．【考点】因式分解的应用．【分析】通过对a+2ab=c+2bc的变形得到2b（a﹣c）=0，由此求得a=c，易判断△ABC的形状．【解答】解：∵a+2ab=c+2bc，∴2b（a﹣c）=0，∵b≠0，∴a﹣c=0，∴a=c，∴△ABC是等腰三角形．【点评】该题主要考查了因式分解及其应用问题；解题的关键是牢固掌握掌握分组分解法或提公因式法，灵活选用有关方法来变形、化简、求值或证明．13．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．【考点】多项式乘多项式．【分析】先根据题意画出图形，然后求出长方形的长和宽，长为a+2b，宽为a+b，从而求出长方形的面积．【解答】解：如图：或a2+3ab+2b2=（a+b）（a+2b）．【点评】考查多项式与多项式相乘问题；根据面积的不同表示方法得到相应的等式是解决本题的关键．14．设a=m+1，b=m+2，c=m+3，求代数式a2+2ab+b2﹣2ac﹣2bc+c2的值．【考点】因式分解的应用．【分析】首先把代数式a2+2ab+b2﹣2ac﹣2bc+c2利用完全平方公式因式分解，再代入求得数值即可．【解答】解：a2+2ab+b2﹣2ac﹣2bc+c2=（a+b）2﹣2c（a+b）+c2=（a+b﹣c）2当a=m+1，b=m+2，c=m+3时，原式=[m+1+m+2﹣（m+3）]2=m2．【点评】此题考查代数式求值，注意利用完全平方公式因式分解，简化计算的方法与步骤．15．设y=kx，是否存在实数k，使得代数式（x2﹣y2）（4x2﹣y2）+3x2（4x2﹣y2）能化简为x4？若能，请求出所有满足条件的k的值；若不能，请说明理由．【考点】因式分解的应用．【分析】先利用因式分解得到原式=（4x2﹣y2）（x2﹣y2+3x2）=（4x2﹣y2）2，再把当y=kx 代入得到原式=（4x2﹣k2x2）2=（4﹣k2）x4，所以当4﹣k2=1满足条件，然后解关于k的方程即可．【解答】解：能；（x2﹣y2）（4x2﹣y2）+3x2（4x2﹣y2）=（4x2﹣y2）（x2﹣y2+3x2）=（4x2﹣y2）2，当y=kx，原式=（4x2﹣k2x2）2=（4﹣k2）2x4，令（4﹣k2）2=1，解得k=±或±，即当k=±或±时，原代数式可化简为x4．【点评】本题考查了因式分解的运用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．。

2017-2018学年北京市海淀区九年级上期中数学试题含答案

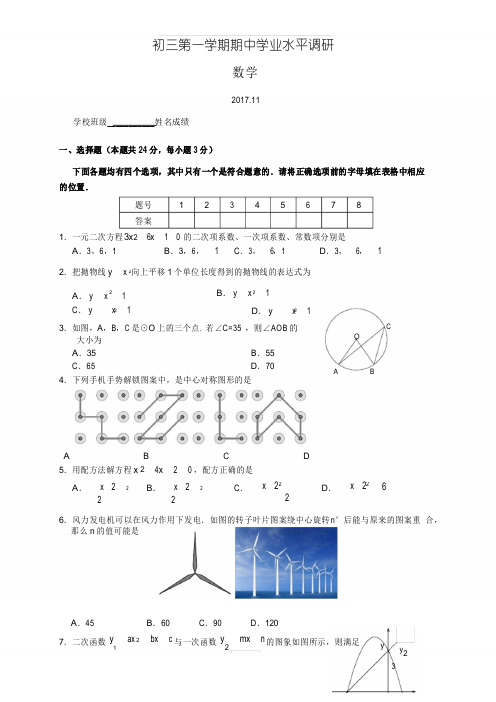
初三第一学期期中学业水平调研数学2017.11学校班级___________姓名成绩一、选择题（本题共 24 分，每小题 3 分）下面各题均有四个选项，其中只有一个是符合题意的．请将正确选项前的字母填在表格中相应的位置．题号答案12 3 4 5 6 7 81．一元二次方程 3x 2 6 x 1 0的二次项系数、一次项系数、常数项分别是A ．3，6，1B ．3，6，1C ．3， 6，1D ．3， 6，12．把抛物线 y x 向上平移 1 个单位长度得到的抛物线的表达式为A ． y x 1C ． yx 1B ． y x 1D ． yx 13．如图，A ，B ，C 是⊙O 上的三个点. 若∠C =35°，则∠AOB 的C大小为 A ．35° B ．55° C ．65° D ．70° 4．下列手机手势解锁图案中，是中心对称图形的是OA BAB C D5．用配方法解方程 x 2 4 x 2 0 ，配方正确的是A ．x 222B ．x 222C ．x 22D ．x 266．风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转n °后能与原来的图案重合，那么 n 的值可能是A ．45B ．60C ．90D ．1207．二次函数yax 2 bx c与一次函数y mx n的图象如图所示，则满足．． 2 222 2 22ax2bx c mx n的x的取值范围是A．3x 0C．x 3或x 1 8．如图1，动点P从格点AB．x 3或x 0D．0x 3出发，在网格平面内运动，设点P走过的路程为s，点P到直线l的距离为d.已知d与s的关系如图2所示．下列选项中，可能是点P的运动路线的是l d43A21 l l l lO图1A A A AA B C D二、填空题（本题共24分，每小题3分）9．点P（1，2）关于原点的对称点的坐标为________．12345图2s10．写出一个图象开口向上，过点（0，0）的二次函数的表达式：________．A B11．如图，四边形ABCD内接于⊙O，E为CD的延长线上一点．若∠B=110°，则∠ADE的大小为________．OE D C12．抛物线y x2x 1与x轴的公共点的个数是________．13．如图，在平面直角坐标系xOy中，点A，点B的坐标分别为（0，2），（1，0），将线段AB绕点O顺时针旋转，若y A点A的对应点A的坐标为（2，0），则点B的对应点B 的坐标为________．BO A'x14．已知抛物线y x22x经过点(4，y )，(1，y )12，则y 1________y（填“＞”，“=”，或“＜”）．215．如图，⊙O的半径OA与弦BC交于点D，若OD=3，AD=2，BD=CD，则BC的长为________．OB DAC16．下面是“作已知三角形的高”的尺规作图过程．已知△：ABC．AB C 求作：BC边上的高AD．作法：如图，1（1）分别以点A和点C为圆心，大于AC的2长为半径作弧，两弧相交于P，Q两点；A POD Q B C（2）作直线PQ，交AC于点O；（3）以O为圆心，OA为半径作⊙O，与CB的延长线交于点D，连接AD．线段AD即为所作的高．请回答：该尺规作图的依据是_______________________________________________．三、解答题（本题共72分，第17题4分，第18~23题，每小题5分，第24~25题，每小题7分，第26~ 28题，每小题8分）17．解方程：x24x 30．18．如图，等边三角形ABC的边长为3，点D是线段BC上的点，CD=2，以AD 为边作等边三角形ADE，连接CE．求CE的长．AEB D C19．已知m 是方程x23x 10的一个根，求m 32m 2m 2的值．20．如图，在⊙O中，AB CD．求证：∠B=∠C．BO C A D21．如图，ABCD是一块边长为4米的正方形苗圃，园林部门拟将其改造为矩形A EFG的形状，其中点E在AB边上，点G在AD的延长线上，DG=2BE．设BE的长为x米，改造后苗圃A EFG的面积为y平方米．（1）y与x之间的函数关系式为_____________________（不需写自变量的取值范围）；（2）根据改造方案，改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等，请问此时BE的长为多少米？A D GEH FB C22．关于x的一元二次方程x22m 1x m210有两个不相等的实数根x,x12．（1）求实数m的取值范围；（2）是否存在实数m，使得x x 012由．成立？如果存在，求出m的值；如果不存在，请说明理23．古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家——“代数学之父”阿尔·花拉子米．在研究一元二次方程解法的过程中，他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”．»»以x210x 39为例，花拉子米的几何解法如下：如图，在边长为x的正方形的两个相邻边上作边长分别为x和x55的矩形，再补上一个边长为5的小正方形，最终把图形补成一个大正方形．通过不同的方式来表示大正方形的面积，可以将原方程化为x xx55x ____239____，从而得到此方程的正根是________．524．如图，在平面直角坐标系xOy中，点A的坐标为（1，0），点P 的横坐标为2，将点A绕点P旋转，使它的对应点B恰好落在x轴上（不与A点重合）；再B绕点O逆时针旋转90°得到点C．（1）直接写出点B和点C的坐标；（2）求经过A，B，C三点的抛物线的表达式．yPO A x将点25．如图，AB为⊙O的直径，点C在⊙O上，过点O作OD⊥BC交BC于点E，交⊙O于点D，CD∥AB．（1）求证：E为OD的中点；（2）若CB=6，求四边形CAOD的面积．C DEA O B26．在平面直角坐标系xOy中，已知抛物线C：y x24x 4和直线l：y kx 2k(k 0)．（1）抛物线C的顶点D的坐标为________；（2）请判断点D是否在直线l上，并说明理由；x 2 4x 4，x 2,（3）记函数ykx 2k，x 2的图象为G，点M(0,t)，过点M垂直于y轴的直线与图象G交于点P(x，y )11，Q(x，y)22．当1t 3时，若存在t使得x x124成立，结合图象，求k的取值范围．y6543x27．对于平面直角坐标系xOy中的点P，给出如下定义：记点P到x轴的距离为d，到y轴的距1离为d2，若d d12，则称d1为点P的“引力值”；若d d12，则称d2为点P的“引力值”．特别地，若点P在坐标轴上，则点P的“引力值”为0．例如，点P（2力值”为2．，3）到x 轴的距离为3，到y轴的距离为2，因为23，所以点P的“引（1）①点A（1，4）的“引力值”为________；②若点B（a，3）的“引力值”为2，则a的值为________；（2）若点C在直线y 2x 4y8765432上，且点C的“引力值”为2，求点C的坐标；1–4 –3–2–1O–1–2–3–412345678xy8765（3）已知点M是以D（3，4）为圆心，半径为2上的一个动点，那么点M的“引力值”d 4321的圆的取值范围是．–4 –3–2–1O–112345678x–2–3–428．在△R t ABC中，斜边AC的中点M关于BC的对称点为点O，△将ABC绕点O 顺时针旋转至△DCE，连接BD，BE，如图所示．（1）在①∠BOE，②∠ACD，③∠COE中，等于旋转角的是________（填出满足条件的的角的序号）；（2）若∠A=α，求∠BEC 的大小（用含 α 的式子表示）；（3）点 N 是 BD 的中点，连接 MN ，用等式表示线段 MN 与 BE 之间的数量关系，并证明．ADMNBCEO初三第一学期期中学业水平调研数学参考答案一、选择题（本题共 24 分，每小题 3 分）2017．11题号答案1D 2A 3D 4B 5A 6D 7A 8D二、填空题（本题共 24 分，每小题 3 分）9．（1，2 ）10．答案不唯一，例如yx211．110°12．213．（0，1）14．＞15．816．①到线段两端点距离相等的点在线段的垂直平分线上；②直径所对的圆周角是直角；③两点确定一条直线．（注：写出前两个即可给 3 分，写出前两个中的一个得 2 分，其余正确的理由得 1 分）三、解答题（本题共 72 分）17．解法一：解： x2 4 x 4 1，x 221，………………2 分x 21，x11，x3 2．………………4 分解法二：解：x 1x 3，………………2 分x 10或 x 3 0，18．解：∵△ABC是等边三角形，∴AB =BC =AC ，∠BAC =60°. ∴∠1+∠3=60°.………………1 分 ∵△ADE 是等边三角形，A1 3 2∴AD =AE ，∠DAE =60°.∴∠2+∠3=60°.………………2 分E∴∠1=∠2.在△ABD 与△ACE 中AB AC12 ，BDCAD AE ∴△ABD ≌△ACE （SAS ）. ∴CE =BD .………………4 分 ∵BC =3，CD =2， ∴BD =BC -CD =1.∴CE =1．………………5 分 19．解：∵m 是方程 x 3 x 1 0的一个根，∴ m 23m 1 0.………………2 分∴ m 2 3m1 .∴原式m 2 6m 9 m 2m 23m 53 ．………………5 分24………………4 分20．方法 1：AB CD ，证明：∵在⊙O 中，∴∠AOB =∠COD .………………2 分 ∵OA =OB ，OC =OD ， 1∴在△AOB 中， B 90 AOB ， 21在△COD 中， C 90COD .………………4 分 2BOCAD∴∠B =∠C ．………………5 分方法 2：证明：∵在⊙O 中， AB CD，∴AB =CD .………………2 分 ∵OA =OB ，OC =OD ，∴△AOB ≌△COD （SSS ）.………………4 分 ∴∠B =∠C ．………………5 分2» »» »）………………3分21．解：（1）y 2x24x 16（或y4x 42x（2）由题意，原正方形苗圃的面积为16平方米，得2x24x 1616.解得：x 2，x 0（不合题意，舍去）.………………5分12答：此时BE的长为2米.有两个不相等的实数根，22．解：（1）∵方程x22m 1x m 210∴4，m 124m 218m 80∴m 1．………………2分0.（2）存在实数m使得x x12x x 0，即是说0是原方程的一个根，则m210.………………3分12解得：m 1或m 1.………………4分当m 1时，方程为x20，有两个相等的实数根，与题意不符，舍去．∴m．………………5分123．通过不同的方式来表示大正方形的面积，可以将原方程化为x 5………………1分23925………………3分从而得到此方程的正根是3．………………5分24．（1）点B的坐标为（3，0），点C 的坐标为（0，3）；………………2分（2）方法1：设抛物线的解析式为y ax2bx c. 因为它经过A（1，0），B（3，0），C（0，3），a b c 0,则9a 3b c 0,………………4分c 3.a 1,解得b 4,………………6分c 3.方法2：抛物线经过点A（1，0），B（3，0），故可设其表达式为………………4分因为点C（0，3）在抛物线上，a 01033，得a1.………………6分所以y a(x 1)(x 3)(a 0).∴经过A,B,C三点的抛物线的表达式为y x24x 3．………………7分方法3：抛物线经过点A（1，0），B（3，0），则其对称轴为x 2.设抛物线的表达式为y a x 22k.………………4分将A（1，0），C（0，3）代入，得a k 0, 4a k 3.解得a 1,k 1.………………6分∴经过A,B,C三点的抛物线的表达式为y x24x 3．………………7分25．（1）证明：∵在⊙O中，OD⊥BC于E，∴CE=BE.………………1分∵CD∥AB，∴∠DCE=∠B.………………2分AC DEO B在△DCE与△OBE 中DCE B,CE BE,CED BEO.∴△DCE≌△OBE（ASA）.∴DE=OE.∴E为OD 的中点．………………4分（2）解：连接OC.∵AB 是⊙O 的直径，∴∠ACB=90°.∵OD⊥BC，∴∠CED=90°=∠ACB.∴AC∥OD.………………5分AC DEO B∵CD∥AB，∴四边形CAOD 是平行四边形.∵E是OD 的中点，CE⊥OD，∴OC=CD.∵OC=OD，∴OC=OD=CD.∴△OCD是等边三角形.∴∠D=60°.………………6分∴∠DCE=90°-∠D=30°. ∴在△R t CDE中，CD=2DE.∵BC=6，∴CE=BE=3.∵C E2DE2CD24D E2，∴DE 3，C D 23.∴O D CD 23.∴S四边形C AODOD CE 63.………………7分26．（1）（2，0）；………………2分（2）点D 在直线l上，理由如下：直线l 的表达式为y kx 2k(k 0)，∵当x 2时，y 2k 2k 0，………………3分∴点D（2，0）在直线l 上．………………4分注：如果只有结论正确，给1分.（3）如图，不妨设点P在点Q左侧.由题意知：要使得x x 4成立，即是要求点P 与12y 6 5点Q 关于直线x 2对称.又因为函数y x24x 4的图象关于直线x 2对称，所以当1t 3时，若存在t使得x x 4 成立，即要求点Q12在y x24x 4(x 2,1y 3)的图象–2–14321OBP QA123456x上.………………6分根据图象，临界位置为射线y kx 2k(k 0,x 2)过–1–2y x24x 4(x 2)与y 1的交点A(3,1)处，以及射线y kx 2k(k 0,x 2)过y x24x 4(x 2)与y 3的交点B(23,3)处.此时k 1以及k 3，故k的取值范围是1k 3.………………8分27．（1）①1，②2；………………2分注：错一个得1分.（2）解：设点C的坐标为（x，y）.由于点C 的“引力值”为2，则x 2或y 2，即x 2，或y 2.当x 2时，y 2x 40，此时点C的“引力值”为0，舍去；当x2时，y 2x 48，此时C 点坐标为（-2，8）；当y 2时，2x 42，解得x 1，此时点C 的“引力值”为1，舍去；当y 2时，2x 42，x 3，此时C 点坐标为（3，-2）；综上所述，点C的坐标为（2，8）或（3，2）.………………5分注：得出一个正确答案得2 分.（3）1d 772.………………8分注：答对一边给2分；两端数值正确，少等号给2分；一端数值正确且少等号给1分.28．（1）③；………………1分（2）连接BM，OB，OC，OE.∵△R t ABC中，∠ABC=90°，M为AC的中点，1∴MA=MB=MC=AC.………………2分2∴∠A=∠ABM.∵∠A=α，∴∠BMC=∠A+∠ABM=2α.∵点M 和点O关于直线BC对称，AMNB CD∴∠BOC=∠BMC=2α.………………3分E ∵OC=OB=OE，∴点C，B，E 在以O 为圆心，OB为半径的圆上.O1∴BEC BOC2.………………4分（3）MN 12BE，证明如下：连接BM并延长到点F，使BM=MF，连接FD.∵∠A=α，∠ABC=90°，∴∠ACB=90°-∠A=90°-α.∴∠DEC=∠ACB=90°-α.A F∵∠BEC=α，D∴∠BED=∠BEC+∠DEC=90°.∵BC=CE，∴∠CBE=∠CEB=α.MN∵MB=MC，B C∴∠MBC=∠ACB=90°-α.∴∠MBE=∠MBC+∠CBE=90°.E ∴∠MBE+∠BED=180°.∴BF∥DE.………………6分∵BF=2BM，AC=2BM，∴BF=AC.∵AC=DE，∴BF=DE.∴四边形BFDE是平行四边形.………………7分∴DF=BE.∵BM=MF，BN=ND，1∴MN=DF.21∴MN=BE.………………8分2O注：如果只有结论正确，给1分.解答题解法不唯一，如有其它解法相应给分.。

北京市海淀区九年级数学上学期期中试题(含解析) 新人教版

AOA '北京市海淀区2017届九年级数学上学期期中试题学校姓名学号一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的．请将正确选项前的字母填在表格中相应的位置．1．一元二次方程320x x --=的二次项系数、一次项系数、常数项分别是 A ．3，1-，2- B ．3，1，2- C ．3，1-，2 D ．3，1，22．里约奥运会后，受到奥运健儿的感召，群众参与体育运动的热度不减，全民健身再次成为了一种时尚，球场上也出现了更多年轻人的身影．请问下面四幅球类的平面图案中，是中心对称图形的是A B C D 3．用配方法解方程2620x x ++=，配方正确的是A ．()239x += B ．()239x -= C ．()236x += D ．()237x += 4．如图，小林坐在秋千上，秋千旋转了80°，小林的位置也从A 点运动到了A '点，则'OAA ∠的度数为A ．40° B．50° C ．70° D．80°5．将抛物线22y x =平移后得到抛物线221y x =+，则平移方式为 A ．向左平移1个单位B ．向右平移1个单位C ．向上平移1个单位D ．向下平移1个单位6．在△ABC 中，90C ︒∠=，以点B 为圆心，以BC 长为半径作圆，点A 与该圆的位置关系为 A ．点A 在圆外 B ．点A 在圆内 C ．点A 在圆上 D．无法确定 7．若扇形的圆心角为60°，半径为6，则该扇形的弧长为A ．πB ．2πC ．3πD ．4π 8．已知2是关于x 的方程230x ax a +-=的根，则a 的值为A ．4-B ．4C ．2D ．459．给出一种运算：对于函数nx y =，规定1-='n nx y ．例如：若函数41y x =，则有314y x '=．函数32y x =，则方程212y '=的解是A ．14x =，24x =-B ．1x =，2x =-C ．021==x xD ．12x =，22x =-10．太阳影子定位技术是通过分析视频中物体的太阳影子变化，确定视频拍摄地点的一种方法．为了确定视频拍摄地的经度，我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻．在一定条件下，直杆的太阳影子长度l （单位：米）与时刻t （单位：时）的关系满足函数关系2l at bt c =++（a ，b ，c 是常数），如图记录了三个时刻的数据，根据上述函数模型和记录的数据，则该地影子最短时，最接近的时刻t 是 A ．12.75B ．13C ．13.33D ．13.5二、填空题（本题共18分，每小题3分） 11．方程02=-x x 的解为．12．请写出一个对称轴为3x =的抛物线的解析式．13．如图，用直角曲尺检查半圆形的工件，其中合格的是图（填“甲”、“乙”或“丙”），你的根据是_______________________________________________________ _______________________________________________________．14．若关于x 的方程220x x k --=有两个相等的实数根，则k 的值是． 15．如图，△ABC 内接于⊙O ，∠C =45°，半径OB 的长为3，则AB的长为．16．CPI 指居民消费价格指数，反映居民家庭购买消费商品及服务的价格水平的变动情况．CPI 的涨跌率在一定程度受到季节性因素和天气因素的影响．根据北京市2015年与2016年CPI 涨跌率的统计图中的信息，请判断2015年1~8月份与2016年1~8月份，同月份比较CPI 涨跌率下降最多的月份是月；请根据图中提供的信息，预估北京市2016年第四季度CPI 涨跌率变化趋势是，你的预估理由是．2015与2016年CPI 涨跌率（%）l (米A三、解答题（本题共72分，第17~26题，每小题5分，第27题7分，第28题7分，第29题8分） 17．解方程：246x x +=．18．求抛物线22y x x =-19．如图，A ，D 是半圆上的两点，O 为圆心，BC 是直径，∠D =35°，求∠OAC 的度数．20．已知：2230m m +-=．求证：关于x 的方程2220x mx m --=有两个不相等的实数根．21．如图，在等边△ABC 中，点D 是 AB 边上一点，连接CD ，将线段CD 绕点C 按顺时针方向旋转60°后得到CE ，连接AE ．求证：AE ∥BC ．B CDA E图222．如图1，在线段AB 上找一点C ，C 把AB 分为AC 和CB 两段，其中BC 是较小的一段，如果2BC AB AC ⋅=，那么称线段AB 被点C 黄金分割．为了增加美感，黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域．如图2，在我国古代紫禁城的中轴线上，太和门位于太和殿与内金水桥之间靠近内金水桥的一侧，三个建筑的位置关系满足黄金分割，已知太和殿到内金水桥的距离约为100丈，求太和门2.2）．23．如图1是某公园一块草坪上的自动旋转喷水装置，这种旋转喷水装置的旋转角度为240°，它的喷灌区是一个扇形．小涛同学想了解这种装置能够喷灌的草坪面积，他A C B图1测量出了相关数据，并画出了示意图．如图2，A ，B 两点的距离为18米，求这种装置能够喷灌的草坪面积．24．下表是二次函数2y ax bx c =++的部分x ，y 的对应值：）二次函数图象的开口向，顶点坐标是，的值为；（2）当0x ＞时，y 的取值范围是；（3）当抛物线2y ax bx c =++的顶点在直线y x n=+的下方时，n 的取值范围是．25．如图，在△ABC 中，AB =BC ，以AB 为直径的⊙O 分别交AC ，BC 于点D ，E ，过点A 作⊙O 的切线交BC 的延长线于点F ，连接AE ．（1）求证：∠ABC =2∠CAF ；（2）过点C 作CM ⊥AF 于M 点，若CM = 4，BE = 6，求AE 的长．26．小华在研究函数1y x =与22y x =图象关系时发现：如图所示，当1x =时，11y =，22y =；当2x =时，A图212y =，24y =；…；当x a =时，1y a =，22y a =．他得出如果将函数1y x =图象上各点的横坐标不变，纵坐标变为原来的2倍，就可以得到函数22y x =的图象．类比小华的研究方法，解决下列问题：（1）如果函数3y x =图象上各点横坐标不变，纵坐标变为原来的3倍，得到的函数图象的表达式为；（2）①将函数2y x =图象上各点的横坐标不变，纵坐标变为原来的倍，得到函数24y x =的图象；②将函数2y x =图象上各点的纵坐标不变，横坐标变为原来的2倍，得到图象的函数表达式为．27．在平面直角坐标系xOy 中，抛物线21y x mx n =++-的对称轴为2x =．（1）m 的值为；（2）若抛物线与y 轴正半轴交于点A ，其对称轴与x 轴交于点B ，当△OAB 是等腰直角三角形时，求n 的值；（3）点C 的坐标为（3，0），若该抛物线与线段OC 有且只有一个交点，求n 的取值范围．28．在菱形ABCD 中，∠BAD =α，E 为对角线AC 上的一点（不与A ，C 重合），将射线EB 绕点E 顺时针旋转β角之后，所得射线与直线AD 交于F 点．试探究线段EB 与EF 的数量关系．小宇发现点E 的位置，α和β的大小都不确定，于是他从特殊情况开始进行探究．（1）如图1，当α=β=90°时，菱形ABCD 是正方形．小宇发现，在正方形中，AC 平分∠BAD ，作EM ⊥AD 于M ，EN ⊥AB 于N ．由角平分线的性质可知EM =EN ，进而可得EMF ENB △≌△，并由全等三角形的性质得到EB 与EF 的数量关系为．（2）如图2，当α=60°，β=120°时，①依题意补全图形；②请帮小宇继续探究（1）的结论是否成立．若成立，请给出证明；若不成立，请举出反例说明；（3）小宇在利用特殊图形得到了一些结论之后，在此基础上对一般的图形进行了探究，设∠ABE =γ，若旋转后所得的线段EF 与EB 的数量关系满足（1）中的结论，请直接写出角α，β，γ满足的关系：．29．点P 到AOB ∠的距离定义如下：点Q 为AOB ∠的两边上的动点，当PQ 最小时，我们称此时PQ的长度为点P 到AOB ∠的距离，记为()d P AOB ∠，．特别的，当点P 在AOB ∠的边上时，()0d P AOB ∠=，．在平面直角坐标系xOy 中，A ()40，．（1）如图1，若M （0，2），N （1-，0），则()d M AOB ∠=，，()d N AOB ∠=，；FEM CD A N B 图1 图2图1（2）在正方形OABC 中，点B （4，4）．①如图2，若点P 在直线34y x =+上，且()d P AOB ∠=，，求点P 的坐标；②如图3，若点P 在抛物线24y x =-上，满足()d P AOB ∠=，P 有个，请你画出示意图，并标出点图2图3北京市海淀区2017届九年级第一学期期中考试数学试题答案及解析一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的．请将正确选项前的字母填在表格中相应的位置．1．一元二次方程的二次项系数、一次项系数、常数项分别是（）A．，，B．，，C．，，D．，，【考点】一元二次方程的有关概念【答案】A【解析】∵x²前面的数字是二次项系数，x前面的是一次项系数，数字是常数项ax²（二次项，a是系数）+bx（一次项，b是系数）+c（常数项）=0∴二次项系数、一次项系数、常数项分别是．，，。

人教版九年级数学上《圆》期中复习试卷含答案解析初三数学

北京市海淀区-九年级（上）期中数学复习试卷（圆）（解析版）一、填空题1．如图，AB为⊙O的直径，弦CD⊥AB，E为上一点，若∠CEA=28°，则∠ABD=度．2．如图，AB为圆O的直径，弦CD⊥AB，垂足为点E，连接OC，若OC=5，CD=8，则AE=．3．如图，AB是⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，连接OC，AC．若∠D=50°，则∠A的度数是．4．（秋•海淀区期中）已知AB是直径，∠C等于15度，∠BAD的度数=．5．（秋•海淀区期中）如图，PA，PB分别与相⊙O切于点A，B，连接AB．∠APB=60°，AB=5，则PA的长是．6．在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2．下列说法中不正确的是（）A．当a＜5时，点B在⊙A内B．当1＜a＜5时，点B在⊙A内C．当a＜1时，点B在⊙A外D．当a＞5时，点B在⊙A外7．已知⊙O的半径是5，OP的长为7，则点P与⊙O的位置关系是（）A．点P在圆内B．点P在圆上C．点P在圆外D．不能确定8．已知扇形的半径为3，扇形的圆心角是120°，则该扇形面积为．9．如图，四边形ABCD内接于⊙O，若∠BOD=138°，则它的一个外角∠DCE等于．10．平面上有⊙O及一点P，P到⊙O上一点的距离最长为6cm，最短为2cm，则⊙O的半径为cm．11．（秋•海淀区期中）如图，四边形ABCD内接于⊙O，∠ABC=130°，求∠OAC的度数．12．（秋•陇西县期末）如图，AB是⊙O的直径，CD是弦，CD⊥AB于点E，点G在直径DF的延长线上，∠D=∠G=30．（1）求证：CG是⊙O的切线；（2）若CD=6，求GF的长．13．（秋•海淀区期中）已知：如图，PA，PB分别与⊙O相切于A，B两点．求证：OP 垂直平分线段AB．14．（秋•海淀区期中）已知：如图，Rt△ABC中，∠ACB=90°，以AC为直径的半圆O 交AB于F，E是BC的中点．求证：直线EF是半圆O的切线．15．（秋•海淀区期中）已知：⊙O的半径OA=1，弦AB、AC的长分别为，，求∠BAC的度数．16．（秋•海淀区期中）已知：⊙O的半径为25cm，弦AB=40cm，弦CD=48cm，AB∥CD．求这两条平行弦AB，CD之间的距离．-学年北京市海淀区九年级（上）期中数学复习试卷（圆）参考答案与试题解析一、填空题1．如图，AB为⊙O的直径，弦CD⊥AB，E为上一点，若∠CEA=28°，则∠ABD=度．【考点】垂径定理；圆周角定理．【分析】本题关键是理清弧的关系，找出等弧，则可根据“同圆中等弧对等角”求解．【解答】解：由垂径定理可知，又根据在同圆或等圆中相等的弧所对的圆周角也相等的性质可知∠ABD=∠CEA=28度．故答案为：28．【点评】本题综合考查了垂径定理和圆周角的求法及性质．解答这类题一些学生不会综合运用所学知识解答问题，不知从何处入手造成错解．2．如图，AB为圆O的直径，弦CD⊥AB，垂足为点E，连接OC，若OC=5，CD=8，则AE=．【考点】垂径定理；勾股定理．【分析】根据垂径定理可以得到CE的长，在直角△OCE中，根据勾股定理即可求得．【解答】解：∵AB为圆O的直径，弦CD⊥AB，垂足为点E．∴CE=CD=4．在直角△OCE中，OE===3．则AE=OA﹣OE=5﹣3=2．故答案为：2．【点评】此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．3．如图，AB是⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，连接OC，AC．若∠D=50°，则∠A的度数是．【考点】切线的性质．【分析】根据切线的性质求出∠OCD，求出∠COD，求出∠A=∠OCA，根据三角形的外角性质求出即可．【解答】解：∵CD切⊙O于C，∴OC⊥CD，∴∠OCD=90°，∵∠D=50°，∴∠COD=180°﹣90°﹣50°=40°，∵OA=OC，∴∠A=∠OCA，∵∠A+∠OCA=∠COD=40°，∴∠A=20°．故答案为：20°．【点评】本题考查了三角形的外角性质，三角形的内角和定理，切线的性质，等腰三角形的性质的应用，主要考查学生运用这些性质进行推理的能力，题型较好，难度也适中，是一道比较好的题目．4．（秋•海淀区期中）已知AB是直径，∠C等于15度，∠BAD的度数=．【考点】圆周角定理．【分析】连接BD，根据圆周角定理得到∠B=∠C=15°，根据直角三角形的性质计算即可．【解答】解：连接BD，∠B=∠C=15°，∵AB是直径，∴∠ADB=90°，∴∠BAD=90°﹣15°=75°，故答案为：75°．【点评】本题考查的是圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等是解题的关键．5．（秋•海淀区期中）如图，PA，PB分别与相⊙O切于点A，B，连接AB．∠APB=60°，AB=5，则PA的长是．【考点】切线的性质．【分析】利用切线长定理得出PA=PB，再利用等边三角形的判定得出△PAB是等边三角形，即可得出答案．【解答】解：∵PA，PB分别与⊙O相切于点A，B，∴PA=PB，∵∠APB=60°，∴△PAB是等边三角形，∴AB=PA=5，故答案为：5．【点评】此题主要考查了切线长定理以及等边三角形的判定与性质，得出△PAB是等边三角形是解题关键．6．在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2．下列说法中不正确的是（）A．当a＜5时，点B在⊙A内B．当1＜a＜5时，点B在⊙A内C．当a＜1时，点B在⊙A外D．当a＞5时，点B在⊙A外【考点】点与圆的位置关系．【分析】先找出与点A的距离为2的点1和5，再根据“点与圆的位置关系的判定方法”即可解．【解答】解：由于圆心A在数轴上的坐标为3，圆的半径为2，∴当d=r时，⊙A与数轴交于两点：1、5，故当a=1、5时点B在⊙A上；当d＜r即当1＜a＜5时，点B在⊙A内；当d＞r即当a＜1或a＞5时，点B在⊙A外．由以上结论可知选项B、C、D正确，选项A错误．故选：A．【点评】本题考查点与圆的位置关系的判定方法．若用d、r分别表示点到圆心的距离和圆的半径，则当d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．7．已知⊙O的半径是5，OP的长为7，则点P与⊙O的位置关系是（）A．点P在圆内B．点P在圆上C．点P在圆外D．不能确定【考点】点与圆的位置关系．【分析】直接根据点与圆的位置关系即可得出结论．【解答】解：∵⊙O的半径是5，OP的长为7，5＜7，∴点P在圆外．故选C．【点评】本题考查的是点与圆的位置关系，熟知点与圆的三种位置关系是解答此题的关键．8．已知扇形的半径为3，扇形的圆心角是120°，则该扇形面积为．【考点】扇形面积的计算．【分析】直接根据扇形的面积公式进行计算即可．【解答】解：∵扇形的圆心角为120°，其半径为3，==3π．∴S扇形故答案为：3π．【点评】本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．9．如图，四边形ABCD内接于⊙O，若∠BOD=138°，则它的一个外角∠DCE等于．【考点】圆内接四边形的性质．【分析】由∠BOD=138°，根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠A的度数，又由圆的内接四边四边形的性质，求得∠BCD的度数，继而求得∠DCE的度数【解答】解：∵∠BOD=138°，∴∠A=∠BOD=69°，∴∠BCD=180°﹣∠A=111°，∴∠DCE=180°﹣∠BCD=69°．故答案为：69°．【点评】此题考查了圆周角定理与圆的内接四边形的性质．此题比较简单，解题的关键是注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半与圆内接四边形的对角互补定理的应用．10．平面上有⊙O及一点P，P到⊙O上一点的距离最长为6cm，最短为2cm，则⊙O的半径为cm．【考点】点与圆的位置关系．【分析】解答此题应进行分类讨论，点P可能位于圆的内部，也可能位于圆的外部．【解答】解：当点P在圆内时，则直径=6+2=8cm，因而半径是4cm；当点P在圆外时，直径=6﹣2=4cm，因而半径是2cm．所以⊙O的半径为4或2cm．故答案为：4或2．【点评】考查了点与圆的位置关系，解决本题的关键是首先要进行分类讨论，其次是理解最长距离和最短距离和或差的意义．11．（秋•海淀区期中）如图，四边形ABCD内接于⊙O，∠ABC=130°，求∠OAC的度数．【考点】圆内接四边形的性质；圆周角定理．【分析】先根据圆内接四边形的性质推出∠ADC=50°，再根据圆周角定理推出∠AOC=100°，然后根据等腰三角形的性质及三角形内角和定理即可得出∠OAC的度数．【解答】解：∵四边形ABCD内接于⊙O，∴∠ADC+∠ABC=180°，∵∠ABC=130°，∴∠ADC=180°﹣∠ABC=50°，∴∠AOC=2∠ADC=100°．∵OA=OC，∴∠OAC=∠OCA，∴∠OAC=（180°﹣∠AOC）=40°．【点评】本题主要考查圆内接四边形的性质、圆周角定理、等腰三角形的性质及三角形内角和定理，关键在于求出∠AOC的度数．12．（秋•陇西县期末）如图，AB是⊙O的直径，CD是弦，CD⊥AB于点E，点G在直径DF的延长线上，∠D=∠G=30．（1）求证：CG是⊙O的切线；（2）若CD=6，求GF的长．【考点】切线的判定．【分析】（1）连接OC，根据三角形内角和定理可得∠DCG=180°﹣∠D﹣∠G=120°，再计算出∠GCO的度数可得OC⊥CG，进而得到CG是⊙O的切线；（2）设EO=x，则CO=2x，再利用勾股定理计算出EO的长，进而得到CO的长，然后再计算出FG的长即可．【解答】（1）证明：连接OC．∵OC=OD，∠D=30°，∴∠OCD=∠D=30°．∵∠G=30°，∴∠DCG=180°﹣∠D﹣∠G=120°．∴∠GCO=∠DCG﹣∠OCD=90°．∴OC⊥CG．又∵OC是⊙O的半径．∴CG是⊙O的切线．（2）解：∵AB是⊙O的直径，CD⊥AB，∴CE=CD=3．∵在Rt△OCE中，∠CEO=90°，∠OCE=30°，∴EO=CO，CO2=EO2+CE2．设EO=x，则CO=2x．∴（2x）2=x2+32．解得x=（舍负值）．∴CO=2．∴FO=2．在△OCG中，∵∠OCG=90°，∠G=30°，∴GO=2CO=4．∴GF=GO﹣FO=2．【点评】此题主要考查了切线的判定，关键是掌握切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．13．（2015秋•海淀区期中）已知：如图，PA，PB分别与⊙O相切于A，B两点．求证：OP垂直平分线段AB．【考点】切线的性质．【分析】由PA与PB为圆的两条切线，根据切线长定理得到PA=PB，且PO平分两切线的夹角，进而得到三角形PAB为等腰三角形，根据三线合一得到PC为高，PC为中线，可得出OP垂直平分线段AB，得证．【解答】证明：∵PA，PB分别为⊙O的切线，∴PA=PB，PO为∠APB的平分线，∴PO⊥AB，C为AB的中点，则OP垂直平分线段AB．【点评】此题考查了切线的性质，涉及的知识有：切线长定理，以及等腰三角形的性质，熟练掌握切线长定理是解本题的关键．14．（2015秋•海淀区期中）已知：如图，Rt△ABC中，∠ACB=90°，以AC为直径的半圆O交AB于F，E是BC的中点．求证：直线EF是半圆O的切线．【考点】切线的判定．【分析】连接OF，CF，利用等边对等角即可证得OF⊥EF，从而证得EF是圆的切线．【解答】证明：连接OF，CF．∵AC是直径，∴∠AFC=90°，∴∠BFC=90°，又∵E是BC的中点，∴EF=EC，∴∠EFC=∠ECF，∵OC=OF，∴∠OFC=∠FCO，∵∠ACB=∠FCO+∠ECF=90°，∴∠EFC+∠OFC=90°，即∠EFO=90°，∴OF⊥EF，∴EF是⊙O的切线．【点评】本题考查了切线的判定，直角三角形的性质等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．解决本题的关键是正确作出辅助线．15．（2015秋•海淀区期中）已知：⊙O的半径OA=1，弦AB、AC的长分别为，，求∠BAC的度数．【考点】垂径定理；解直角三角形．【分析】根据题意画出图形，作出辅助线，由于AC与AB在圆心的同侧还是异侧不能确定，故应分两种情况进行讨论．【解答】解：分别作OD⊥AB，OE⊥AC，垂足分别是D、E．∵OE⊥AC，OD⊥AB，∴AE=AC=，AD=AB=，∴sin∠AOE===，sin∠AOD==，∴∠AOE=60°，∠AOD=45°，∴∠BAO=45°，∠CAO=90°﹣60°=30°，∴∠BAC=45°+30°=75°，或∠BAC′=45°﹣30°=15°．∴∠BAC=15°或75°．【点评】本题考查的是垂径定理及直角三角形的性质，解答此题时进行分类讨论，不要漏解．16．（2015秋•海淀区期中）已知：⊙O的半径为25cm，弦AB=40cm，弦CD=48cm，AB ∥CD．求这两条平行弦AB，CD之间的距离．【考点】垂径定理；勾股定理．【分析】分情况进行讨论，（1）如图，AB和CD再圆心的同侧，连接OB，OD，作OM ⊥AB交CD于点N，由AB∥CD，即可推出ON⊥CD，则MN为AB，CD之间的距离，通过垂径定理和勾股定理即可推出OM和ON的长度，根据图形即可求出MN=OM﹣ON，通过计算即可求出MN的长度，（2）AB和CD在圆心两侧，连接OB，OD，做直线OM⊥AB交CD于点N，由AB∥CD，即可推出MN⊥CD，则MN为AB，CD之间的距离，通过垂径定理和勾股定理即可推出OM和ON的长度，根据图形即可求出MN=OM+ON，通过计算即可求出MN的长度．【解答】解：（1）如图1，连接OB，OD，做OM⊥AB交CD于点N，∵AB∥CD，∴ON⊥CD，∵AB=40cm，CD=48cm，∴BM=20cm，DN=24cm，∵⊙O的半径为25cm，∴OB=OD=25cm，∴OM=15cm，ON=7cm，∵MN=OM﹣ON，∴MN=8cm，（2）如图2，连接OB，OD，做直线OM⊥AB交CD于点N，∵AB∥CD，∴ON⊥CD，∵AB=40cm，CD=48cm，∴BM=20cm，DN=24cm，∵⊙O的半径为25cm，∴OB=OD=25cm，∴OM=15cm，ON=7cm，∵MN=OM+ON，∴MN=22cm．∴平行弦AB，CD之间的距离为8cm或22cm．【点评】本题主要考查垂径定理和勾股定理的运用，平行线间的距离的定义，平行线的性质等知识点，关键在于根据题意分情况进行讨论，正确的做出图形，认真的做出辅助线构建直角三角形，熟练运用垂径定理和勾股定理推出OM和ON的长度，利用数形结合的思想即可求出结果．。

北京XX为学校2017届九年级上期中数学试卷含答案解析

23．如图，以□ABCD 的顶点 A 为圆心，AB 为半径作⊙A，分别交 BC，AD 于 E，F 两点，交 BA 的延长线于 G，判断和是否相等，并说明理由．
24．对于抛物线 y=x2﹣4x+3．
2016-2017 学年北京 X为X学校九年级（上）期中数学试卷
一、选择题（本题共 30 分，每小题 3 分，）下列各题均有四个选项，其中只有一个是符合题意的． 1．下列图形中，是中心对称图形的为（）
A．
B．
C．
D．
2．如图，⊙O 的半径为 5，AB 为弦，OC⊥AB，垂足为 C，如果 OC=3，那么弦 AB 的长为（）
A．30° B．45° C．50° D．70° 7．如图，将△ABC 绕着点 C 按顺时针方向旋转 20°，B 点落在 B′位置，A 点落在 A′位置，若 AC⊥A′B′，则∠BAC 的度数是（）
A．50° B．60° C．70° D．80° 8．函数 y=ax2﹣2x+1 和 y=ax+a（a 是常数，且 a≠0）在同一直角坐标系中的图象可能是（） NhomakorabeaA．
B．
C．
D．
9．小宏用直角三角板检查某些工件的弧形凹面是否是半圆，下列工件的弧形凹面一定是半圆的是（）
20．已知抛物线 y=﹣x2+2x+3 与 x 轴交于 A，B 两点，点 A 在点 B 的左侧．（1）求 A，B 两点的坐标和此抛物线的对称轴；（2）设此抛物线的顶点为 C，点 D 与点 C 关于 x 轴对称，求四边形 ACBD 的面积． 21．列方程或方程组解应用题：某公司在 2013 年的盈利额为 200 万元，预计 2015 年的盈利额达到 242 万元，若每年比上一年盈利额增长的百分率相同，求该公司这两年盈利额的年平均增长率是多少？ 22．如图，在方格网中已知格点△ABC 和点 O．（1）画△A′B′C′和△ABC 关于点 O 成中心对称；（2）请在方格网中标出所有使以点 A、O、C′、D 为顶点的四边形是平行四边形的 D 点．

2017年北京市海淀区九年级数学上期中试题(附答案)

2017年北京市海淀区九年级数学上期中试题（附答案）初三第一学期期中学业水平调研数学 2017.11 学校班级___________姓名成绩一、选择题（本题共24分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的．请将正确选项前的字母填在表格中相应的位置．题号 1 2 3 4 5 6 7 8 答案 1．一元二次方程的二次项系数、一次项系数、常数项分别是 A．3，6，1 B．3，6， C．3，，1 D．3，， 2．把抛物线向上平移1个单位长度得到的抛物线的表达式为 A． B． C． D． 3．如图，A，B，C是⊙O上的三个点. 若∠C=35°，则∠AOB的大小为 A．35° B．55° C．65° D．70° 4．下列手机手势解锁图案中，是中心对称图形的是 A B C D 5．用配方法解方程，配方正确的是 A． B． C． D． 6．风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转n°后能与原来的图案重合，那么n的值可能是 A．45 B．60 C．90 D．120 7．二次函数与一次函数的图象如图所示，则满足的x的取值范围是 A． B．或 C．或 8．如图1，动点P从格点出发，在网格平面内运动，设点P走过的路程为s，点P到直线l的距离为d. 已知d与s的关系如图2所示．下列选项中，可能是点P的运动路线的是A B C D二、填空题（本题共24分，每小题3分） 9．点P（，2）关于原点的对称点的坐标为________． 10．写出一个图象开口向上，过点（0，0）的二次函数的表达式：________． 11．如图，四边形ABCD 内接于⊙ ，E为CD的延长线上一点．若∠B=110°，则∠ADE的大小为________． 12．抛物线与x轴的公共点的个数是________． 13．如图，在平面直角坐标系xOy中，点A，点B的坐标分别为（0，2），（，0），将线段AB绕点O顺时针旋转，若点A 的对应点的坐标为（2，0），则点B的对应点的坐标为________． 14．已知抛物线经过点，，则 ________ （填“＞”，“=”，或“＜”）． 15．如图，⊙ 的半径OA与弦BC交于点D，若OD=3，AD=2， BD=CD，则BC的长为________．16．下面是“作已知三角形的高”的尺规作图过程．已知：△ABC．求作：BC边上的高AD．作法：如图，（1）分别以点A和点C为圆心，大于 AC的长为半径作弧，两弧相交于P，Q两点；（2）作直线PQ，交AC于点O；（3）以O为圆心，OA为半径作⊙O，与CB的延长线交于点D，连接AD．线段AD即为所作的高．请回答：该尺规作图的依据是_______________________________________________ ．三、解答题（本题共72分，第17题4分，第18~23题，每小题5分，第24~25题，每小题7分，第26~ 28题，每小题8分） 17．解方程：．18．如图，等边三角形ABC的边长为3，点D是线段BC上的点，CD=2，以AD为边作等边三角形ADE，连接CE．求CE的长．19．已知m是方程的一个根，求的值．20．如图，在⊙O中，．求证：∠B=∠C．21．如图，ABCD是一块边长为4米的正方形苗圃，园林部门拟将其改造为矩形AEFG的形状，其中点E在AB边上，点G在AD的延长线上，DG=2BE．设BE的长为x米，改造后苗圃AEFG的面积为y平方米．（1）y与x之间的函数关系式为_____________________（不需写自变量的取值范围）；（2）根据改造方案，改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等，请问此时BE的长为多少米？22．关于的一元二次方程有两个不相等的实数根．（1）求实数的取值范围；（2）是否存在实数，使得成立？如果存在，求出的值；如果不存在，请说明理由．23．古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家――“代数学之父”阿尔•花拉子米．在研究一元二次方程解法的过程中，他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”．以为例，花拉子米的几何解法如下：如图，在边长为的正方形的两个相邻边上作边长分别为和 5的矩形，再补上一个边长为5的小正方形，最终把图形补成一个大正方形．通过不同的方式来表示大正方形的面积，可以将原方程化为，从而得到此方程的正根是________． 24．如图，在平面直角坐标系xOy中，点A的坐标为（1，0），点P的横坐标为2，将点A绕点P旋转，使它的对应点B恰好落在x轴上（不与A点重合）；再将点B绕点O逆时针旋转90°得到点C．（1）直接写出点B和点C的坐标；（2）求经过A，B，C三点的抛物线的表达式．25．如图，AB为⊙O的直径，点C在⊙O上，过点O作OD⊥BC交BC于点E，交⊙O于点D，CD∥AB．（1）求证：E为OD的中点；（2）若CB=6，求四边形CAOD的面积．26．在平面直角坐标系中，已知抛物线C：和直线l：．（1）抛物线C的顶点D的坐标为________；（2）请判断点D是否在直线l 上，并说明理由；（3）记函数的图象为G，点，过点垂直于轴的直线与图象G交于点，．当时，若存在使得成立，结合图象，求的取值范围． 27．对于平面直角坐标系xOy中的点P，给出如下定义：记点P到x轴的距离为，到y轴的距离为，若，则称为点P的“引力值”；若，则称为点P的“引力值”．特别地，若点P在坐标轴上，则点P的“引力值”为0．例如，点P（，3）到x轴的距离为3，到y轴的距离为2，因为，所以点P的“引力值”为2．（1）①点A（1，）的“引力值”为________；②若点B（a，3）的“引力值”为2，则a的值为________；（2）若点C在直线上，且点C 的“引力值”为2，求点C的坐标；（3）已知点M是以D（3，4）为圆心，半径为2的圆上的一个动点，那么点M的“引力值”d的取值范围是．28．在Rt△ABC中，斜边AC的中点M关于BC的对称点为点O，将△ABC 绕点O顺时针旋转至△DCE，连接BD，BE，如图所示．（1）在①∠BOE，②∠ACD，③∠COE中，等于旋转角的是________（填出满足条件的的角的序号）；（2）若∠A=α，求∠BEC的大小（用含α的式子表示）；（3）点N是BD的中点，连接MN，用等式表示线段MN与BE之间的数量关系，并证明．初三第一学期期中学业水平调研数学参考答案2017．11 一、选择题（本题共24分，每小题3分）题号 1 2 3 4 5 6 7 8 答案 D A D B A D A D 二、填空题（本题共24分，每小题3分）9．（1，）10．答案不唯一，例如 11．110° 12．2 13．（0，1）14．＞15．8 16．①到线段两端点距离相等的点在线段的垂直平分线上；②直径所对的圆周角是直角；③两点确定一条直线．（注：写出前两个即可给3分，写出前两个中的一个得2分，其余正确的理由得1分）三、解答题（本题共72分） 17．解法一：解：，， (2)分，，．………………4分解法二：解：，………………2分或，，．………………4分 18．解：∵△ABC是等边三角形，∴AB=BC=AC，∠BAC=60°. ∴∠1+∠3=60°.………………1分∵△ADE是等边三角形，∴AD=AE，∠DAE=60°.∴∠2+∠3=60°.………………2分∴∠1=∠2. 在△ABD与△ACE中，∴△ABD≌△ACE（SAS）. ∴CE=BD.………………4分∵BC=3，CD=2，∴BD=BC-CD=1. ∴CE=1．………………5分 19．解：∵m是方程的一个根，∴ ...................2分∴ . ∴原式 (4)分．………………5分 20．方法1：证明：∵在⊙O中，，∴∠AOB=∠COD.………………2分∵OA=OB，OC=OD，∴在△AOB中，，在△COD中，.………………4分∴∠B=∠C．………………5分方法2：证明：∵在⊙O中，，∴AB=CD.………………2分∵OA=OB，OC=OD，∴△AOB≌△COD（SSS）.………………4分∴∠B=∠C．..................5分 21．解：（1）（或） (3)分（2）由题意，原正方形苗圃的面积为16平方米，得 . 解得：，（不合题意，舍去）...................5分答：此时BE的长为2米. 22．解：（1）∵方程有两个不相等的实数根，∴ ，∴ ． (2)分（2）存在实数使得 . ，即是说是原方程的一个根，则.………………3分解得：或.………………4分当时，方程为，有两个相等的实数根，与题意不符，舍去．∴ ．………………5分23．通过不同的方式来表示大正方形的面积，可以将原方程化为………………1分………………3分从而得到此方程的正根是．………………5分24．（1）点B的坐标为（3，0），点C的坐标为（0，3）； (2)分（2）方法1：设抛物线的解析式为 . 因为它经过A（1，0），B （3，0），C（0，3），则………………4分解得………………6分∴ 经过三点的抛物线的表达式为．………………7分方法2：抛物线经过点A（1，0），B（3，0），故可设其表达式为. ………………4分因为点C（0，3）在抛物线上，所以，得.………………6分∴经过三点的抛物线的表达式为．………………7分方法3：抛物线经过点A（1，0），B（3，0），则其对称轴为 . 设抛物线的表达式为.………………4分将A（1，0），C（0，3）代入，得解得………………6分∴经过三点的抛物线的表达式为．………………7分 25．（1）证明：∵在⊙O 中，OD⊥BC于E，∴CE=BE.………………1分∵CD∥AB，∴∠DCE=∠B.………………2分在△DCE与△OBE中∴△DCE≌△OBE（ASA）. ∴DE=OE. ∴E为OD的中点． (4)分（2）解：连接OC. ∵AB是⊙O的直径，∴∠ACB=90°.∵OD⊥BC，∴∠CED=90°=∠ACB. ∴AC∥OD.………………5分∵CD∥AB，∴四边形CAOD是平行四边形. ∵E是OD的中点，CE⊥OD，∴OC=CD. ∵OC=OD，∴OC=OD=CD. ∴△OCD是等边三角形.∴∠D=60°.………………6分∴∠DCE=90°-∠D=30°. ∴在Rt△CDE中，CD=2DE. ∵BC=6，∴CE=BE=3. ∵ ，∴ ，. ∴ . ∴ ...................7分26．（1）（2，0）；..................2分（2）点D在直线l上，理由如下：直线l的表达式为，∵当时，，..................3分∴点D（2，0）在直线l上． (4)分注：如果只有结论正确，给1分. （3）如图，不妨设点P在点Q 左侧. 由题意知：要使得成立，即是要求点P与点Q关于直线对称. 又因为函数的图象关于直线对称，所以当时，若存在使得成立，即要求点Q在的图象上.………………6分根据图象，临界位置为射线过与的交点处，以及射线过与的交点处. 此时以及，故k的取值范围是.………………8分27．（1）①1，② ；………………2分注：错一个得1分. （2）解：设点C的坐标为（x，y）. 由于点C的“引力值”为2，则或，即，或 . 当时，，此时点C的“引力值”为0，舍去；当时，，此时C点坐标为（-2，8）；当时，，解得，此时点C的“引力值”为1，舍去；当时，，，此时C点坐标为（3，-2）；综上所述，点C的坐标为（，8）或（3，）.………………5分注：得出一个正确答案得2分. （3）.………………8分注：答对一边给2分；两端数值正确，少等号给2分；一端数值正确且少等号给1分.28．（1）③；..................1分（2）连接BM，OB，OC，OE. ∵Rt△ABC 中，∠ABC=90°，M为AC的中点，∴MA=MB=MC= AC. (2)分∴∠A=∠ABM. ∵∠A=α，∴∠BMC=∠A+∠ABM=2α. ∵点M和点O关于直线BC对称，∴∠BOC=∠BMC=2α.………………3分∵OC=OB=OE，∴点C，B，E在以O为圆心，OB为半径的圆上.∴ .………………4分（3），证明如下：连接BM并延长到点F，使BM=MF，连接FD. ∵∠A=α，∠ABC=90°，∴∠ACB=90°-∠A=90°-α. ∴∠DEC=∠ACB=90°-α. ∵∠BEC=α，∴∠BED=∠BEC+∠DEC=90°. ∵BC=CE，∴∠CBE=∠CEB=α. ∵MB=MC，∴∠MBC=∠ACB=90°-α. ∴∠MBE=∠MBC+∠CBE=90°.∴∠MBE+∠BED=180°. ∴BF∥DE.………………6分∵BF=2BM，AC=2BM，∴BF=AC. ∵AC=DE，∴BF=DE. ∴四边形BFDE是平行四边形.………………7分∴DF=BE. ∵BM=MF，BN=ND，∴MN= DF. ∴MN = BE.………………8分注：如果只有结论正确，给1分. 解答题解法不唯一，如有其它解法相应给分.。

北京市海淀区九年级数学上学期期中试题(扫描版) 新人

北京市海淀区2017届九年级数学上学期期中试题九年级第一学期期中练习数学答案 2016．11一、选择题（本题共30分，每小题3分）二、填空题（本题共18分，每小题3分）11．1201x x ==，； 12．()23y x =-（答案不唯一）；13．乙，90°的圆周角所对的弦是直径； 14．1-； 15．16．8，第二空填“上涨”、“下降”、“先减后增”等，第三空要能支持第二空的合理性即可．三、解答题（本题共72分，第17~26题，每小题5分，第27题7分，第28题7分，第29题8分） 17．解法一：解：244x x ++=，----------------------------------------------------------------------------------1分 ()2210x +=，-------------------------------------------------------------------------------------3分2x =-±，12x =-，22x =- -------------------------------------------------------------5分解法二：解：246x x +-=，----------------------------------------------------------------------------1分x ==，----------------------------------------------------3分2x =-±，12x =-，22x =- -------------------------------------------------------------5分18．解：()211y x =--，-----------------------------------------------------------------------------------1分∴对称轴为1x =． --------------------------------------------------------------------------------2分顶点为()11-，． ----------------------------------------------------------------------------------3分----------------------------------------------------------------------------5分 19．解法一：解：∵35D ∠=°，∴35B D ∠=∠=°． ---------------------------------------------1分 ∵BC 是直径， ∴90BAC ∠=°．∴90ACB ∠=°55ABC -∠=°．∵OA OC =，∴55OAC OCA ∠=∠=°． --------------------------------------5分解法二：解：∵35D ∠=°， ∴270AOC D ∠=∠=°． ---------------------------------------------------------------------1分∵OA OC =， ∴OAC OCA∠=∠，----------------------------------------------------------------------------3分∵180OAC OCA AOC ∠+∠+∠=°， ∴55OAC ∠=°． --------------------------------------------------------------------20．解：∵2230m m +-=， ∴223m m +=． ---------------------------------------------------------------------------------1分 ∴248m m ∆=+-----------------------------------------------------------------------------------2分()242120m m =+=＞，------------------------------------------------------------------4分 ∴原方程有两个不相等的实数根． -------------------------------------------------------------5分 21．解：∵等边ABC △，∴AC BC =，60B ACB ∠=∠=°． ∵线段CD 绕点C 顺时针旋转60°得到CE ， ∴CD CE =，60DCE ∠=°． ∴DCE ACB ∠=∠．------------------------------------------------1分即1223∠+∠=∠+∠．∴13∠=∠． -----------------------------------------------------------------------------------------2分在BCD △与ACE △中，13BC AC CD CE =⎧⎪∠=∠⎨⎪=⎩，，， ∴BCD△≌ACE △． ------------------------------------------------------------------------3分∴60EAC B ∠=∠=°． ∴EAC ACB ∠=∠．--------------------------------------------------------------------------------4分∴AE BC ∥． -------------------------------------------------------------------------321DB CA E22．解：设太和门到太和殿的距离为x丈，-----------------------------------------------------------1分由题意可得，()2100100x x =-.----------------------------------------------------------------------------3分150x =-+，250x =--（舍）.--------------------------------------------4分 5050 2.260x ≈-+⨯=．答：太和门到太和殿的距离为60丈． ------------------------------------------------------------5分 23．解：过点O 作OC AB ⊥于C 点． ∵OC AB ⊥，18AB =，∴192AC AB ==． ---------------------------------------1分 ∵OA OB =，360AOB ∠=°240-°120=°，∴1602AOC AOB ∠=∠=°．在Rt OAC △中，222OA OC AC =+，又∵12OC OA =，∴r OA == -----------------------------------------4分 ∴240360S =πr 2=72π（m 2）．----------------------------------5分 24．（1）上；()12-，；2；（说明：每空1分）------------------------------------------------------3分（2）2y ≥-；------------------------------------------------------------------------------------------4分（3）3n >-． -------------------------------------------------------------------------------------------5分 25．（1）连接BD ， ∵AB 是直径，∴90ADB ∠=°． --------------------------1分 ∵AF 是⊙O 的切线， ∴90BAF ∠=°.∴1290BAC BAC ∠+∠=∠+∠=°． ∴12∠=∠. ∵AB=BC ， ∴2122ABC ∠=∠=∠． ---------------------------------------------------------------------2分（2）∵12334∠=∠=∠∠=∠，，∴24∠=∠． ∵AB 是直径， ∴CE ⊥AE ．--------------------------------------------------------------------------------------------3分 ∵CM ⊥AF ，CM =4, ∴CE =CM =4． --------------------------------------------------------------------------------------4分 ∵BE =6,∴AB =BC =BE +EC =10．在Rt △ABE 中，8AE =． ----------------------------------------------------5分 26．（1）9y x =;-------------------------------------------------------------------------------------------1分（2）①4；----------------------------------------------------------------------------------------------3分 ②214y x =． --------------------------------------------------------------------------------------5分 27．（1）4-． ----------------------------------------------------------------------------------------------1分（2）241y x x n =-+-， ()01A n -，，()20B ，　，------------------------------------------------------------------2分 12n -=，3n =． ----------------------------------------------------------------------------------------3分（3）如图1，当抛物线顶点在x轴上时，5n =，------------------------------------------------4分如图2，当抛物线过点C (3，0)时，4n =，---------------------------------------------5分如图3，当抛物线过原点时，1n =，---------------------------------------------------------6分结合图象可得，14n ≤<或5n =．------------------------------------------------------------7分28．（1）EB=EF ；------------------------------------------------------------------------------------------1分（2）①；---------------------------------------------------------------------2分 ②结论依然成立EB =EF ． -----------------------------------3分证法1：过点E 作EM ⊥AF 于M ，EN ⊥AB 于N ．∵四边形ABCD 为菱形，∴12∠=∠．∵EM ⊥AF ，EN ⊥AB ．∴=90FME N ∠=∠°，EM=EN ． -------------------4分 ∵60BAD ∠=°，120BEF ∠=°，∴3360F ∠+∠=°180BAD BEF -∠-∠=°． ∵3180EBN ∠+∠=°， ∴F EBN ∠=∠．------------------------------------------------------------------------------5分在△EFM 与△EBN 中，F EBN FME N EM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩，，，∴△EFM ≌△EBN ． ∴EF=EB ． ------------------------------------------------------------------------------------6分证法2：连接ED\∵四边形ABCD 是菱形， ∴AD =AB ，∠DAC =∠BAE ．又∵AE =AE ,∴△ADE ≌△ABE ．∴ED =EB ，∠ADE =∠ABE ． ------------------------4分又∵∠DAB =60°，∠BEF =120°． ∴∠F +∠ABE =180°．又∵∠ADE +∠FDE =180°， --------------------------5分 ∴∠F =∠FDE ． ∴EF =ED ． ∴EF =EB ． -------------------------------------------------------------------------------------6分（3）+=180αβ°或++=18022αβγ°． ------------------------------------------------------7分29．（1）1；1．（说明：每空1分）--------------------------------------------------------------------2分（2）①如图，点P 在EF 上时，OP = 设P （x ，3x +4），()22348x x ++=， 12225x x =-=-，（舍）， P ()22--，， --------------------------------4分点P 在射线FG 上时，P 到射线OB 的距离为点P 与点C 重合，P ()04，， -------------------------------------5分 ∴P ()22--，，()04，． ②4． -------------------------------------------------------------------------------------------------6分-------------------------------------------------------------8分（说明：每标对两个点得1分）。

北京市海淀区初三数学第一学期期中试题及答案初中数学

北京市海淀区初三数学第一学期期中试题及答案初中数学海淀区九年级第一学期期中练习数学试卷答宴及谗分捻考16医号9 10 11 12•'•斗=4內=-2・ .................. ................................ 5分x-l»±3.A x} «4.r;■・2・................. ….................................. 5分14.计％彳34（护*声・1卜（一2）°.tt： ®St-2v3-3+^3-l^l ............................................ ........................2 •=373-4-1,15.计算2 (272-3)(72 + 1). 解：原式=4 42的一 3运一31-72.16.解法r 违按OC.OZXA ZJCO = 90°. Z/DO = 90°「・•\ m } +2m-5 = 0.•*• rn‘+・5/w ・9-刃（亦十2加-5）-9V AO&^B 的I ［径，C. £）两点在上.4 RtA ACO 和 RtA /DO 中.促OB 的宣径• C\ D 两点在O B 匕Z^CC? = 90% "DO 二AC. AD 3分4分AD^S.解法二连接OC.OD2分••• AC^ADr4分I 4C-5. A 4D = 5.AC^ AD.\OC^OD. imo ・ 0••• RtA ACO 4 RU ADO.7.風 I 刖她方程，+ 2上一5M 0的一个根.$分2 •18・解! （I ） •即为所球.（不写结论的不扣分） 3C.......................................................... 3分（2） 2鬲・ .............................. 3分四.解备题（本題共20分.毎小題5分） 19・解：设这种药品平均每次降价的百分率足工依题意.得200(1-x)2 =不合注意■舍去〉. 解鸭勺亦2卫卒这种药品号均毎伙降价的百分20%・ .............20・解，如田•当弦CQ 与半径。

北京海淀区初三上学期数学期中考试试卷(附答案)

(1) y 与 x 之间的函数关系式为
（不需写自变量的取值范围）；
(2) 根据改造方案，改造后的矩形苗圃 AEF G 的面积与原正方形苗圃 ABCD 的面积相
等，请问此时 BE 的长为多少米?
21. 关于 x 的一元二次方程 x2 + 2 (m − 1) x + m2 − 1 = 0 有两个不相等的实数根 x = x1，x = x2． (1) 求实数 m 的取值范围；
=
2
(m2
−
) 3m
+
5
= 3.
19. ∵ 在 ⊙O 中，AB = CD， ∴ ∠AOB = ∠COD． ∵ OA = OB，OC = OD， ∴ 在 △AOB 中，∠B = 90◦ − 1 ∠AOB， 2 在 △COD 中，∠C = 90◦ − 1 ∠COD． 2 ∴ ∠B = ∠C．
20. (1) y = −2x2 + 4x + 16（或 y = (4 − x) (4 + 2x)） (2) 由题意，原正方形苗圃的面积为 16 平方米，得 −2x2 + 4x + 16 = 16.
x2 + 10x = 39 为例，花拉子米的几何解法如下：
如图，在边长为 x 的正方形的两个相邻边上作边长分别为 x 和 5 的矩形，再补上一个边长为 5 的小正方形，
最终把图形补成一个大正方形．
通过不同的方式来表示大正方形的面积，可以将原方程化为 (x + )2 = 39 + ，从而得到此方程的正
∠ADE 的大小为
．
12. 抛物线 y = x2 − x − 1 与 x 轴的公共点的个数是
．
13. 如图，在平面直角坐标系 xOy 中，点 A，点 B 的坐标分别为 (0, 2)，(−1, 0)，将线段 AB 绕点 O 顺时针旋转，若点 A 的对应点 A′ 的坐标为 (2, 0)，则点 B 的对应点 B′ 的坐标为．

2017年海淀区九年级第一学期期中数学试题答案正式

初三第一学期期中学业水平调研数学参考答案2017．11一、选择题（本题共24分，每小题3分）二、填空题（本题共24分，每小题3分）9．（1，2-） 10．答案不唯一，例如2y x = 11．110° 12．2 13．（0，1）14．＞15．816．①到线段两端点距离相等的点在线段的垂直平分线上；②直径所对的圆周角是直角；③两点确定一条直线．（注：写出前两个即可给3分，写出前两个中的一个得2分，其余正确的理由得1分）三、解答题（本题共72分） 17．解法一：解：2441x x -+=，()221x -=，………………2分21x -=±，11x =，23x =．………………4分解法二：解：()()130x x --=，………………2分 10x -=或30x -=，11x =，23x =．………………4分 18．解：∵△ABC 是等边三角形， ∴AB =BC =AC ，∠BAC =60°. ∴∠1+∠3=60°.………………1分 ∵△ADE 是等边三角形， ∴AD =AE ，∠DAE =60°.∴∠2+∠3=60°.………………2分 ∴∠1=∠2.在△ABD 与△ACE 中12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩， ∴△ABD ≌△ACE （SAS ）. ∴CE =BD .………………4分 ∵BC =3，CD =2， ∴BD =BC -CD =1.321EDCBA∴CE =1．………………5分19．解：∵m 是方程2310x x -+=的一个根，∴2310m m -+=.………………2分 ∴231m m -=-.∴原式22694m m m =-++-………………4分()2235m m =-+3=．………………5分20．方法1：证明：∵在⊙O 中，»»AB CD=， ∴∠AOB =∠COD .………………2分 ∵OA =OB ，OC =OD ，∴在△AOB 中，1902B AOB ∠=︒-∠，在△COD 中，1902C COD ∠=︒-∠.………………4分∴∠B =∠C ．………………5分方法2：证明：∵在⊙O 中，»»AB CD=， ∴AB =CD .………………2分 ∵OA =OB ，OC =OD ，∴△AOB ≌△COD （SSS ）.………………4分 ∴∠B =∠C ．………………5分21．解：（1）22416y x x =-++（或()()442y x x =-+）………………3分（2）由题意，原正方形苗圃的面积为16平方米，得2241616x x -++=. 解得：12x =，20x =（不合题意，舍去）.………………5分答：此时BE 的长为2米. 22．解：（1）∵方程()222110xm x m +-+-=有两个不相等的实数根，∴()()224141880m m m ∆=---=-+>，∴1m <．………………2分（2）存在实数m 使得120x x =.120x x =，即是说0是原方程的一个根，则210m -=.………………3分解得：1m =-或1m =.………………4分当1m =时，方程为20x =，有两个相等的实数根，与题意不符，舍去．∴1m =-．………………5分23．通过不同的方式来表示大正方形的面积，可以将原方程化为()25 x +………………1分39 25 =+………………3分从而得到此方程的正根是 3 ．………………5分24．（1）点B 的坐标为（3，0），点C 的坐标为（0，3）；………………2分（2）方法1：设抛物线的解析式为2y ax bx c =++. 因为它经过A （1，0），B （3，0），C （0，3），则0,930,3.a b c a b c c ++=⎧⎪++=⎨⎪=⎩………………4分解得1,4,3.a b c =⎧⎪=-⎨⎪=⎩………………6分∴ 经过,,A B C 三点的抛物线的表达式为243y x x =-+．………………7分方法2：抛物线经过点A （1，0），B （3，0），故可设其表达式为(1)(3)(0)y a x x a =--≠. ………………4分因为点C （0，3）在抛物线上，所以()()01033a --=，得1a =.………………6分∴经过,,A B C 三点的抛物线的表达式为243y x x =-+．………………7分方法3：抛物线经过点A （1，0），B （3，0），则其对称轴为2x =. 设抛物线的表达式为()22y a x k =-+.………………4分将A （1，0），C （0，3）代入，得0,4 3.a k a k +=⎧⎨+=⎩解得1,1.a k =⎧⎨=-⎩………………6分∴经过,,A B C 三点的抛物线的表达式为243y x x =-+．………………7分25．（1）证明：∵在⊙O 中，OD ⊥BC 于E ， ∴CE =BE .………………1分 ∵CD ∥AB ，∴∠DCE =∠B .………………2分在△DCE 与△OBE 中,,.DCE B CE BE CED BEO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△DCE ≌△OBE （ASA ）. ∴DE =OE .∴E 为OD 的中点．………………4分（2）解：连接OC .∵AB 是⊙O 的直径， ∴∠ACB =90°. ∵OD ⊥BC ， ∴∠CED =90°=∠ACB . ∴AC ∥OD .………………5分 ∵CD ∥AB ，∴四边形CAOD 是平行四边形. ∵E 是OD 的中点，CE ⊥OD ， ∴OC =CD . ∵OC =OD ， ∴OC =OD =CD . ∴△OCD 是等边三角形. ∴∠D =60°.………………6分 ∴∠DCE =90°-∠D =30°. ∴在Rt △CDE 中，CD =2DE . ∵BC =6， ∴CE =BE =3.∵22224CE DE CD DE +==，∴DE =CD =∴OD CD ==∴CAOD S OD CE =⋅=四边形………………7分AAB26．（1）（2，0）；………………2分（2）点D 在直线l 上，理由如下：直线l 的表达式为2(0)y kx k k =->，∵当2x =时，220y k k =-=，………………3分 ∴点D （2，0）在直线l 上．………………4分注：如果只有结论正确，给1分.（3）如图，不妨设点P 在点Q 左侧.由题意知：要使得124x x =+成立，即是要求点P 与点Q 关于直线2x =对称.又因为函数244y x x =-+的图象关于直线2x =对称，所以当13t <<时，若存在t 使得124x x =+成立，即要求点Q在244(2,13)y x x x y =-+><<的图象上.………………6分根据图象，临界位置为射线2(0,2)y kx k k x =->>过244(2)y x x x =-+>与1y =的交点(3,1)A 处，以及射线2(0,2)y kx k k x =->>过244(2)y x x x =-+>与3y =的交点(2B 处.此时1k =以及k=k的取值范围是1k <<………………8分27．（1）①1，②2±；………………2分注：错一个得1分.（2）解：设点C 的坐标为（x ，y ）.由于点C 的“引力值”为2，则2x =或2y =，即2x =±，或2y =±. 当2x =时，240y x =-+=，此时点C 的“引力值”为0，舍去；当2x =-时，248y x =-+=，此时C 点坐标为（-2，8）；当2y =时，242x -+=，解得1x =，此时点C 的“引力值”为1，舍去；当2y =-时，242x -+=-，3x =，此时C 点坐标为（3，-2）；综上所述，点C 的坐标为（2-，8）或（3，2-）.………………5分注：得出一个正确答案得2分. （3）1d ≤≤………………8分注：答对一边给2分；两端数值正确，少等号给2分；一端数值正确且少等号给1分.28．（1）③；………………1分（2）连接BM，OB，OC，OE.∵Rt△ABC中，∠ABC=90°，M为AC的中点，∴MA=MB=MC=12 AC.………………2分∴∠A=∠ABM.∵∠A=α，∴∠BMC=∠A+∠ABM=2α.∵点M和点O关于直线BC对称，∴∠BOC=∠BMC=2α.………………3分∵OC=OB=OE，∴点C，B，E在以O为圆心，OB为半径的圆上.∴12BEC BOCα∠=∠=.………………4分（3）12MN BE=，证明如下：连接BM并延长到点F，使BM=MF，连接FD. ∵∠A=α，∠ABC=90°，∴∠ACB=90°-∠A=90°-α.∴∠DEC=∠ACB=90°-α.∵∠BEC=α，∴∠BED=∠BEC+∠DEC=90°.∵BC=CE，∴∠CBE=∠CEB=α.∵MB=MC，∴∠MBC=∠ACB=90°-α.∴∠MBE=∠MBC+∠CBE=90°.∴∠MBE+∠BED=180°.∴BF∥DE.………………6分∵BF=2BM，AC=2BM，∴BF=AC.∵AC=DE，∴BF=DE.∴四边形BFDE是平行四边形.………………7分∴DF=BE.∵BM=MF，BN=ND，∴MN=12 DF.∴MN =12 BE.………………8分注：如果只有结论正确，给1分.OMNABDCEBD解答题解法不唯一，如有其它解法相应给分.。

北京XX为学校2017届九年级上期中数学试卷含答案解析

果调整商品售价，每降价 1 元，每星期可多卖出 20 件．设每件商品降价 x 元
后，每星期售出商品的总销售额为 y 元，则 y 与 x 的关系式为（）
A．y=60（300+20x） B．y=（60﹣x）（300+20x）
9．小宏用直角三角板检查某些工件的弧形凹面是否是半圆，下列工件的弧形凹
面一定是半圆的是（）
A． B． C． D．
（2）分别作 AC，BC 的垂直平分线，两条垂直平分线交于 O 点；所以点 O 就是
所求弧 AB 的圆心．
老师说：“小亮的作法正确．
请你回答：小亮的作图依．
2．如图，⊙O 的半径为 5，AB 为弦，OC⊥AB，垂足为 C，如果 OC=3，那么弦
AB 的长为（）
A．4 B．6 C．8 D．10
3．⊙O 的半径为 3cm，如果圆心 O 到直线 l 的距离为 d，且 d=5cm，那么⊙O
10．如图 1，在△ABC 中，AB=AC，∠BAC=120°，点 O 是 BC 的中点，点 D 沿
B→A→C 方向从 B 运动到 C．设点 D 经过的路径长为 x，图 1 中某条线段的长为
y，若表示 y 与 x 的函数关系的图象大致如图 2 所示，则这条线段可能是图 1 中
A．50° B．60° C．70° D．80°
8．函数 y=ax2﹣2x+1 和 y=ax+a（a 是常数，且 a≠0）在同一直角坐标系中的图
象可能是（）
A． B． C． D．
（1）画△A′B′C′和△ABC 关于点 O 成中心对称；
（2）请在方格网中标出所有使以点 A、O、C′、D 为顶点的四边形是平行四边

北京海淀区九年级第一学期期中数学答案

海淀区九年级第一学期期中练习2013.11数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3.评分参考中所注分数,表示考生正确做到此步应得的累加分数. 一、选择题（本题共32分，每小题4分）二、填空题（本题共16分，每小题4分）9．45°；10．20x x -=(二次项系数不为0,且常数项为0均正确)；11．50°；12．21，622+-n n (每空2分)．三、解答题（本题共30分,每小题5分） 13．（本小题满分5分）解：36324⨯+÷………………………………………………………………………2分2322+=…………………………………………………………………4分 25=.……………………………………………………………………………5分14．（本小题满分5分）解：原方程可化为2+410x x -=，……………………………………………………1分141a ,b ,c ===-,2441(1)=20>0,∆=-⨯⨯-…………………………………………………………2分方程有两个不相等的实数根,2x ===-4分即1222x =-=-5分15．（本小题满分5分）结论:CD BE =．……………………………………………………………………1分证明：Θ△ABC 与△AED 是等边三角形，∴AE AD =，AB AC =，60CAB DAE ∠=∠=o．…2分 ∴CAB DAB DAE DAB ∠-∠=∠-∠，即CAD BAE ∠=∠．………………………………3分在△CAD 和△BAE 中，EDCBAAC AB,CAD BAE,AD AE,=⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△BAE ．…………………………………………………………4分 ∴CD =BE ．…………………………………………………………………5分16．（本小题满分5分）解：Θ15-=x ，∴1x +=∴5)1(2=+x ．………………………………………………………………1分∴2215x x ++=．………………………………………………………………2分∴224x x +=．…………………………………………………………………3分 ∴225451x x +-=-=-．……………………………………………………5分17．（本小题满分5分）证明：过点O 作AB OM ⊥于M ，…………………………1分由垂径定理可得DM CM BM AM ==,．……………3分∴DM BM CM AM -=-．…………………………4分即BD AC =．…………………………………………5分18．（本小题满分5分）解：设小路的宽度是x 米．………………………………………………………1分由题意可列方程，3(20)(12)20124x x --=⨯⨯．……………………………2分化简得, 232600x x -+=．解得, 12302x ,x ==．………………………………………………………3分由题意可知3020x =>不合题意舍去，2x =符合题意.…………………4分答：小路的宽度是2米.……………………………………………………5分四、解答题（本题共20分，每小题5分） 19．（本小题满分5分）解：（1）∵关于x 的一元二次方程210x mx m -++=的一个根为2，∴22210m m -++=.……………………………………………………1分 ∴5m =.……………………………………………………………………2分 ∴一元二次方程为2560x x -+=.解得1223x ,x ==.…………………………………………………………3分∴5m =，方程另一根为3.（2）当长度为2的线段为等腰三角形底边时，则腰长为3，此时三角形的周长为2+3+3=8；………………………………………………………………4分当长度为3的线段为等腰三角形底边时，则腰长为2，此时三角形的周长为2+2+3=7. ………………………………………………………………5分20．（本小题满分5分）解：（1）过点O 作OM ⊥BC 于M .由垂径定理可得：BM=CM .…1分∵30DAC ∠=o , ∴12OM OA =.∵直径DE =10， EA =1，∴=5OD OC OE ==.∴516OA OE EA =+=+=. ∴3OM =.…………………2分在R t △COM 中，222225316CM OC OM =-=-=. ∴4CM =. ∴4BM =.∴+8BC BM CM ==.……………………………………………………3分 (2)在R t △AOM 中，222226327AM OA OM =-=-=.∴AM =.……………………………………………………………………4分∴+4AC AM CM ==. ∵OM ⊥AC ,∴114)3622AOC S AC OM =⋅=⨯⨯=V .……………………………5分21．（本小题满分5分）解：(1)∵关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根,∴224(1)4=8+4>0k k k ∆=+-.………………………………………………2分 ∴1>2k -.…………………………………………………………………3分 (2)∵当1-=x 时，左边=222(1)x k x k -++22(1)2(1)(1)k k =--+⨯-+223k k =++…………………………………………4分 2(+1)20k =+>．而右边=0,∴左边≠右边．∴1-=x 不可能是此方程的实数根．……………………………………5分22.（本小题满分5分）（1）正确画出34P P 、点（图略）．………………………………………………1分224=P P P P ．……………………………………………………………………2分（2）（-4，-2）．…………………………………………………………………3分（0,2）．……………………………………………………………………5分五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23.（本小题满分7分）解：（1）由题意可知0m ≠．2(21)42m m ∆=+-⨯⨯22=441(21)0m m m -+=-≥．……………………………………………2分∴此方程总有两个实数根．（2）方程的两个实数根为x =，∴1212x ,x m==．…………………………………………………………4分 ∵方程的两个实数根都是整数，且m 为整数，∴1m =±．…………………………………………………………………5分（3）∵原方程的两个实数根分别为1x 、2x ，∴211(21)20mx m x -++=222(21)20mx m x -++=．……………………………………………………6分∴5)(2))(12()(2122213231+++++-+x x x x m x x m=1323211222[(21)2]+[(21)2]+5mx m x x mx m x x -++-++ =12211222[(21)2]+[(21)2]+5x mx m x x mx m x -++-++ =12005x x ⨯+⨯+=5．…………………………………………………………………………7分24.（本小题满分8分）（1）AE ⊥CM ，AE =CM ．……………………………………………………2分（2）如图，过点A 作AG ⊥AB ,且AG =BM,，连接CG 、FG ,延长AE 交CM 于H .∵ο90=∠ACB ,26==CB CA ,∴∠CAB =∠CBA =45°，12=. ∴∠GAC =∠MBC =45°. ∵AB CD ⊥,∴CD=AD=BD =162AB =. ∵M 是DB 的中点, ∴3BM DM ==. ∴3AG =.∵2AF FD =,∴4 2.AF DF ==，∴+2+3=5.FM FD DM == ∵AG ⊥AF ,∴FG∴.FG FM =……………………………………………………………………3分在△CAG 和△CBM 中， CA CB CAG CBM AG BM =⎧⎪∠=∠⎨⎪=⎩，，， ∴△CAG ≌△CBM ．∴CG =CM ,ACG BCM ∠=∠．∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠=o ．………………………4分在△FCG 和△FCM 中， CG CM FG FM CF CF =⎧⎪=⎨⎪=⎩，，， ∴△FCG ≌△FCM ．∴FCG FCM ∠=∠．………………………………………………………5分 ∴45FCH ∠=o .由（1）知AE ⊥CM ， ∴90CHN ∠=o∴ο45=∠CNE .………………………………………………………………6分（3）存在.AF =8.…………………………………………………………………………8分25.（本小题满分7分）（1）5;…………………………………………………………………………………1分（2）如图1, 过点C 分别作CP ⊥x 轴于P ，CQ ⊥y 轴于Q ．∴∠CQB =∠CP A =90°，∵∠QOP =90°，∴∠QCP =90°．∵∠BCA =90°， ∴∠BCQ =∠ACP ． ∵BC=AC ，∴△BCQ ≌△ACP ．∴CQ=CP ．………………………………3分 ∵点C 在第一象限,∴不妨设C 点的坐标为(a ，a )(其中0a ≠)．设直线OC 所对应的函数解析式为kx y =，∴a ka =，解得k =1，∴直线OC 所对应的函数解析式为x y =．…………………………………4分（3）取DE 的中点N ，连结ON 、NG 、OM .∵∠AOB=90°，∴OM =152AB =．同理ON =5．∵正方形DGFE ，N 为DE 中点，DE=10， ∴NG===在点M 与G 之间总有MG ≤MO +ON +NG (如图2)，由于∠DNG 的大小为定值，只要12DON DNG ∠=∠,且M 、N 关于点O 中心对称时，M 、O 、N 、G 四点共线,此时等号成立（如图3）.………………………5分∴线段MG 取最大值10+55．………………6分此时直线MG 的解析式x y 251+-=．……………………………………7分。

北京市海淀区九年级数学上学期期中试题新人教版

数学试卷（分数：120分时间：120分钟）班级姓名学号成绩试题答案一律填涂或书写在答题卡上,在试卷上做答无效. 一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．一元二次方程2230x x --=的二次项系数、一次项系数、常数项分别是A. 1,2,3--B. 1,-2,3C. 1,2,3D. 1,2,3- 2．在角、等边三角形、平行四边形、圆中，既是中心对称图形又是轴对称图形的是 A ．角B ．等边三角形 C ．平行四边形 D ．圆 3．函数2y x =-中，自变量x 的取值范围是A ．2≠xB ．2≤xC ．2>xD ．2≥x4．如图，点A 、B 、C 在O ⊙上，若110AOB ∠=，则ACB ∠的大小是 A ．35B ．45 C ．55D ．1105．用配方法解方程09102=++x x ,配方正确的是 A ．16)5(2=+x B ．34)5(2=+x C ．16)5(2=-x D ．25)5(2=+x6．如图所示的图案绕旋转中心旋转一定角度后能够与自身重合，那么这个旋转角可能是 A ．60B ．72 C ．90D ．120 7．若230a b ++-=，则a b +的值为A ．-1B ．1C ．5D ．68．如图，⊙O 的半径为5，点P 到圆心O 的距离为10，如果过点P 作弦，那么长度为整数值的弦的条数为OCBAPOA ．3B ．4C ．5D ．6二、填空题（本题共16分，每小题4分）9．如图，将ABC △绕点C 顺时针旋转至''A B C △的位置，若 15ACB ∠=，120B ∠=，则'A ∠的大小为________．10．已知一元二次方程有一个根是0，那么这个方程可以是（填上你认为正确的一个方程即可）．11．如图，AB 是⊙O 的直径，点C 、D 为⊙O 上的两点，若40=∠ABD ，则BCD ∠的大小为．12．下面是一个按某种规律排列的数阵：1 第1行23 2 第2行 5 6 7 22 3第3行 10 11 23 13 14 15 4第4行根据数阵排列的规律，则第5行从左向右数第5个数为，第n （3≥n ，且n 是整数）行从左向右数第5个数是（用含n 的代数式表示）．三、解答题（本题共30分，每小题5分） 13．计算：36324⨯+÷．14．用公式法解一元二次方程：241x x +=．15．如图，ABC △与AED △均是等边三角形，连接BE 、CD ．请在图中找出一条与CD 长度相等的线段，并证明你的结论．结论：CD =．证明：16．当15-=x 时，求代数式522-+x x 的值．O D CA ED C B A17．如图，两个圆都以点O 为圆心，大圆的弦AB 交小圆于C 、D 两点．求证：AC =BD ．证明：18．列方程（组）解应用题：如图，有一块长20米，宽12米的矩形草坪，计划沿水平和竖直方向各修一条宽度相同的小路，剩余的草坪面积是原来的34，求小路的宽度．解：四、解答题（每小题5分，共20分）19．已知关于x 的一元二次方程210x mx m -++=的一个根为2. (1) 求m 的值及另一根；（2）若该方程的两个根分别是等腰三角形的两条边的长，求此等腰三角形的周长．20．如图，DE 为半圆的直径，O 为圆心，DE =10，延长DE 到A ，使得EA =1，直线AC 与半圆交于B 、C 两点，且 30=∠DAC ．（1）求弦BC 的长；（2）求AOC △的面积．21．已知关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根．（1）求k 的取值范围；（2）求证：1-=x 不可能是此方程的实数根．22．阅读下面的材料：小明在研究中心对称问题时发现：如图1，当点1A 为旋转中心时，点P 绕着点1A 旋转180°得到1P 点，点1P 再绕着点1A 旋转180°DCBA O ECADBO得到2P 点，这时点P 与点2P 重合.如图2，当点1A 、2A 为旋转中心时，点P 绕着点1A 旋转180°得到1P 点，点1P 绕着点2A 旋转180°得到2P 点，点2P 绕着点1A 旋转180°得到3P 点，点3P 绕着点2A 旋转180°得到4P 点,小明发现P 、4P 两点关于点2P 中心对称.（1）请在图2中画出点3P 、4P ，小明在证明P 、4P 两点关于点2P 中心对称时，除了说明P 、2P 、4P 三点共线之外，还需证明；（2）如图3，在平面直角坐标系xOy 中，当)3,0(1A 、)0,2(2-A 、)0,2(3A 为旋转中心时，点)4,0(P 绕着点1A 旋转180°得到1P 点；点1P 绕着点2A 旋转180°得到2P 点；点2P 绕着点3A 旋转180°得到3P 点；点3P 绕着点1A 旋转180°得到点4P 点. 继续如此操作若干次得到点56P P 、、，则点2P 的坐标为，点2017P 的坐为．五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23．已知关于x 的一元二次方程02)12(2=++-x m mx ．图3图2图1（1）求证：此方程总有两个实数根；（2）若此方程的两个实数根都是整数，求m 的整数值；（3）若此方程的两个实数根分别为1x 、2x ，求代数式5)(2))(12()(2122213231+++++-+x x x x m x x m 的值．24．已知在ABC △中，90=∠ACB ，26==CB CA ，AB CD ⊥于D ，点E 在直线CD 上，CD DE 21=，点F 在线段AB 上，M 是DB 的中点，直线AE 与直线CF 交于N 点. （1）如图1，若点E 在线段CD 上，请分别写出线段AE 和CM 之间的位置关系和数量关系：___________，___________；（2）在（1）的条件下，当点F 在线段AD 上，且2AF FD =时，求证：45=∠CNE ；（3）当点E 在线段CD 的延长线上时，在线段AB 上是否存在点F ，使得 45=∠CNE ．若存在，请直接写出AF 的长度；若不存在，请说明理由．DCBA25．在平面直角坐标系xOy 中，点A 、B 分别在x 轴、y 轴的正半轴上，且10=AB ，点M 为线段AB 的中点．（1）如图1，线段OM 的长度为________________；（2）如图2，以AB 为斜边作等腰直角三角形ACB ，当点C 在第一象限时，求直线OC 所对应NFECBA的函数的解析式；（3）如图3，设点D 、E 分别在x 轴、y 轴的负半轴上，且10=DE ，以DE 为边在第三象限内作正方形DGFE ，请求出线段MG 长度的最大值，并直接写出此时直线MG 所对应的函数的解析式．海淀区九年级第一学期期中练习2013.11数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3.评分参考中所注分数,表示考生正确做到此步应得的累加分数. 二、填空题（本题共16分，每小题4分）9．45°；10．20x x -=(二次项系数不为0,且常数项为0均正确)；11．50°；12．21，622+-n n (每空2分)．三、解答题（本题共30分,每小题5分） 13．（本小题满分5分）解：36324⨯+÷2分2322+=…………………………………………………………………4分 25=.……………………………………………………………………………5分图1图2CxyOABM BAOyx14．（本小题满分5分）解：原方程可化为2+410x x -=，……………………………………………………1分141a ,b ,c ===-,2441(1)=20>0,∆=-⨯⨯-…………………………………………………………2分方程有两个不相等的实数根,2x ===-，……………………………………4分即1222x =-=-．……………………………………………………5分15．（本小题满分5分）结论:CD BE =．……………………………………………………………………1分证明： △ABC 与△AED 是等边三角形，∴AE AD =，AB AC =，60CAB DAE ∠=∠=．…2分 ∴CAB DAB DAE DAB ∠-∠=∠-∠，即CAD BAE ∠=∠．………………………………3分在△CAD 和△BAE 中， AC AB,CAD BAE,AD AE,=⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△BAE ．…………………………………………………………4分 ∴CD =BE ．…………………………………………………………………5分16．（本小题满分5分）解： 15-=x ，∴1x +∴5)1(2=+x ．………………………………………………………………1分∴2215x x ++=．………………………………………………………………2分∴224x x +=．…………………………………………………………………3分 ∴225451x x +-=-=-．……………………………………………………5分17．（本小题满分5分）证明：过点O 作AB OM ⊥于M ，…………………………1分由垂径定理可得DM CM BM AM ==,．……………3分∴DM BM CM AM -=-．…………………………4分即BD AC =．…………………………………………5分18．（本小题满分5分）解：设小路的宽度是x 米．………………………………………………………1分由题意可列方程，3(20)(12)20124x x --=⨯⨯．……………………………2分化简得, 232600x x -+=．E DCBA解得, 12302x ,x ==．………………………………………………………3分由题意可知3020x =>不合题意舍去，2x =符合题意.…………………4分答：小路的宽度是2米.……………………………………………………5分四、解答题（本题共20分，每小题5分） 19．（本小题满分5分）解：（1）∵关于x 的一元二次方程210x mx m -++=的一个根为2，∴22210m m -++=.……………………………………………………1分 ∴5m =.……………………………………………………………………2分∴一元二次方程为2560x x -+=.解得1223x ,x ==.…………………………………………………………3分∴5m =，方程另一根为3.（2）当长度为2的线段为等腰三角形底边时，则腰长为3，此时三角形的周长为2+3+3=8；………………………………………………………………4分当长度为3的线段为等腰三角形底边时，则腰长为2，此时三角形的周长为2+2+3=7. ………………………………………………………………5分20．（本小题满分5分）解：（1）过点O 作OM ⊥BC 于M .由垂径定理可得：BM=CM .…1分∵30DAC ∠=, ∴12OM OA =.∵直径DE =10， EA =1，∴=5OD OC OE ==.∴516OA OE EA =+=+=. ∴3OM =.…………………2分在R t △COM 中，222225316CM OC OM =-=-=. ∴4CM =. ∴4BM =.∴+8BC BM CM ==.……………………………………………………3分 (2)在R t △AOM 中，222226327AM OA OM =-=-=.∴AM =.……………………………………………………………………4分∴+4AC AM CM ==. ∵OM ⊥AC ,∴114)3622AOCSAC OM =⋅=⨯⨯=.……………………………5分21．（本小题满分5分）解：(1)∵关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根,∴224(1)4=8+4>0k k k ∆=+-.………………………………………………2分 ∴1>2k -.…………………………………………………………………3分 (2)∵当1-=x 时，左边=222(1)x k x k -++22(1)2(1)(1)k k =--+⨯-+223k k =++…………………………………………4分 2(+1)20k =+>．而右边=0,∴左边≠右边．∴1-=x 不可能是此方程的实数根．……………………………………5分22.（本小题满分5分）（1）正确画出34P P 、点（图略）．………………………………………………1分224=P P P P ．……………………………………………………………………2分（2）（-4，-2）．…………………………………………………………………3分（0,2）．……………………………………………………………………5分五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23.（本小题满分7分）解：（1）由题意可知0m ≠．2(21)42m m ∆=+-⨯⨯22=441(21)0m m m -+=-≥．……………………………………………2分∴此方程总有两个实数根．（2）方程的两个实数根为x =∴1212x ,x m==．…………………………………………………………4分 ∵方程的两个实数根都是整数，且m 为整数，∴1m =±．…………………………………………………………………5分（3）∵原方程的两个实数根分别为1x 、2x ，∴211(21)20mx m x -++= 222(21)20mx m x -++=．……………………………………………………6分∴5)(2))(12()(2122213231+++++-+x x x x m x x m=1323211222[(21)2]+[(21)2]+5mx m x x mx m x x -++-++=12211222[(21)2]+[(21)2]+5x mx m x x mx m x -++-++=12005x x ⨯+⨯+=5．…………………………………………………………………………7分24.（本小题满分8分）（1）AE ⊥CM ，AE =CM ．……………………………………………………2分（2）如图，过点A 作AG ⊥AB ,且AG =BM,，连接CG 、FG ,延长AE 交CM 于H .∵ 90=∠ACB ,26==CB CA ,∴∠CAB =∠CBA =45°，12.∴∠GAC =∠MBC =45°. ∵AB CD ⊥,∴CD=AD=BD =162AB =. ∵M 是DB 的中点, ∴3BM DM ==. ∴3AG =. ∵2AF FD =,∴4 2.AF DF ==，∴+2+3=5.FM FD DM == ∵AG ⊥AF ,∴FG =∴.FG FM =……………………………………………………………………3分在△CAG 和△CBM 中， CA CB CAG CBM AG BM =⎧⎪∠=∠⎨⎪=⎩，，， ∴△CAG ≌△CBM ．∴CG =CM ,ACG BCM ∠=∠．∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠=．………………………4分在△FCG 和△FCM 中， CG CM FG FM CF CF =⎧⎪=⎨⎪=⎩，，， ∴△FCG ≌△FCM ．∴FCG FCM ∠=∠．………………………………………………………5分 ∴45FCH ∠=.由（1）知AE ⊥CM ， ∴90CHN ∠=∴ 45=∠CNE .………………………………………………………………6分（3）存在.AF =8.…………………………………………………………………………8分25.（本小题满分7分）（1）5;…………………………………………………………………………………1分（2）如图1, 过点C 分别作CP ⊥x 轴于P ，CQ ⊥y 轴于Q ．∴∠CQB =∠CPA =90°，∵∠QOP =90°，∴∠QCP =90°． ∵∠BCA =90°，∴∠BCQ =∠ACP ．11 ∵BC=AC ，∴△BCQ ≌△ACP ．∴CQ=CP ．………………………………3分∵点C 在第一象限,∴不妨设C 点的坐标为(a ，a )(其中0a ≠)．设直线OC 所对应的函数解析式为kx y =，∴a ka =，解得k =1， ∴直线OC 所对应的函数解析式为x y =．…………………………………4分（3）取DE 的中点N ，连结ON 、NG 、OM . ∵∠AOB=90°， ∴OM =152AB =．同理ON =5． ∵正方形DGFE ，N 为DE 中点，DE=10， ∴NG===．在点M 与G 之间总有MG ≤MO +ON +NG (如图2)，由于∠DNG 的大小为定值，只要12DON DNG ∠=∠,且M 、N 关于点O 中心对称时，M 、O 、N 、G 四点共线,此时等号成立（如图3）.………………………5分∴线段MG 取最大值10+55．………………6分此时直线MG 的解析式x y 251+-=．……………………………………7分。

北京海淀初三(九年级)上学期数学期中试题及答案

北京海淀初三(九年级)上学期数学期中试题及答案
6、如图所示的图案绕旋转中心旋转一定角度后能够与自身重合，那么这个旋转角可能是
A、60°
B、72°
C、90°
D、120°
7、若，则a+b的值为
A、-1
B、 1
C、5
D、6
8、如图，⊙O的半径为5，点P到圆心O的距离为，如果过点P作弦，那么长度为整数值的弦的条数为
A、 3
B、 4
C、 5
D、6
二、填空题(本题共16分，每小题4分)
9、如图，将△ABC绕点C顺时针旋转至△A’B’C’的位置，若∠ACB=15°∠B=120°，∠A’的大小为____
北京海淀2019-2019初三(九年级)上学期数学期中试题及答案
以上“北京海淀2019-2019初三(九年级)上学期数学期中试题及答案”的全部内容是由数学网整理的，更多数学期中试题请查看数学网。

2019寒春尖子班来袭，快来巨人搜课网疯狂抢购!。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

九年级数学试卷第1页（共14页）
初三第一学期期中学业水平调研
数学
2017.11
学校班级___________姓名成绩一、选择题（本题共24分，每小题3分）
下面各题均有四个选项，其中只有一个．．是符合题意的．请将正确选项前的字母填在表格中相应的位置．
1．一元二次方程3610x x --=的二次项系数、一次项系数、常数项分别是 A ．3，6，1
B ．3，6，1-
C ．3，6-，1
D ．3，6-，1-
2．把抛物线2
y x =向上平移1个单位长度得到的抛物线的表达式为 A ．2
1y x =+ B ．2
1y x =- C ．21y x =-+
D ．2
1y x =--
3．如图，A ，B ，C 是⊙O 上的三个点. 若∠C =35°，则∠AOB 的大小为 A ．35° B ．55° C ．65° D ．70° 4．下列手机手势解锁图案中，是中心对称图形的是
A B C D
5．用配方法解方程2
420x x -+=，配方正确的是
A ．()222x -= B
．()2
22x +=
C ．()2
22x -=-
D ．()2
26x -=
6．风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转n °后能与原来的图案重合，那么n 的值可能是
A ．45
B ．60
C ．90
D ．
120。

北京市海淀区2017年九年级上期中数学试题(含答案)

2017-2018学年北京市海淀区九年级上期中数学试题含答案

最新海淀区九年级第一学期数学期中测评答案.doc

北京市海淀区-九年级上期中数学复习试卷含解析.doc

2017-2018学年北京市海淀区九年级上期中数学试题含答案

北京市海淀区九年级数学上学期期中试题(含解析) 新人教版

人教版九年级数学上《圆》期中复习试卷含答案解析初三数学

北京XX为学校2017届九年级上期中数学试卷含答案解析

2017年北京市海淀区九年级数学上期中试题(附答案)

北京市海淀区九年级数学上学期期中试题(扫描版) 新人

北京市海淀区初三数学第一学期期中试题及答案初中数学

北京海淀区初三上学期数学期中考试试卷(附答案)

2017年海淀区九年级第一学期期中数学试题答案正式

北京XX为学校2017届九年级上期中数学试卷含答案解析

北京海淀区九年级第一学期期中数学答案

北京市海淀区九年级数学上学期期中试题 新人教版

北京海淀初三(九年级)上学期数学期中试题及答案

北京市海淀区九年级数学上学期期中试题新人教版