四章习题答案
第四章习题

第四章第二节习题:一、判断题:1、资本成本通常用相对数表示,即用资本占用成本与资本取得成本之和除以筹资总额。
()2、通常将资本成本视为投资项目的“最低收益率”,只要预期报酬率大于资本成本,投资项目就具有经济上的可行性。
()3、一般而言,债券成本要高于长期借款成本。
()4、综合资本成本是指企业全部长期资本成本中的各个个别资本成本的平均数。
()二、单选:1、下列筹资方式中,一般情况下资本成本最高的是()A普通股 B长期借款 C长期债券 D留存收益2、用于追加筹资决策的资本成本是()A个别资本成本 B综合资本成本 C边际资本成本 D加权资本成本3、某公司债券票面利率为9%,每年付息一次,发行费率为1%,所得税率为33%,则该债券的资金成本()A.6%B.6.09%C.9%D.9.09%4、某笔银行借款,年利息率为6%,筹资费用率为1%,所得税率为33%,则该笔银行借款的资金成本()A.4.06%B.4.10%C.9.05%D.12.53%5、某公司普通股发行价为20元,筹资费率为5%,第一年发放现金股利1元,以后每年增长2%。
假定所得税率为33%,则该股票成本为()A.5.53%B.7.26%C.7.36%D.12.53%三、多项选择题:1、能够在所得税前列支的费用有()A长期借款利息 B优先股股利 C普通股股利D债券利息 E资本取得成本2、决定综合资本成本高低的因素有()A个别资本的数量 B个别资本的权重 C个别资本成本D总资本的数量 E个别资本的种类3、下列项目中,计入债券资金成本的筹资费用是()A.债券利息B.发行印刷费C.发行手续费D.债券注册费4、决定加权平均资金成本的因素是()A.个别资金成本B.边际资金成本C.资金筹资渠道D.各种资金所占的权重四、计算题:1、F公司的贝他系数β为1.45,无风险利率为10%,股票市场平均报酬率为16%,求该公司普通股的资本成本率。
2、公司现有优先股:面值100元,股息率10%,每季付息的永久性优先股。
第4章课后习题及答案

返 回
第 4 章 供 电 与 用 电
练习题解答
4.1.1 某三相同步发电机,三相绕组联结成星形时的线电压为 10.5kV,若将它联结成三角形,则线电压是多少?若联结成星形 时,L2相绕组的首末端接反了,则三个线电压的有效值U12 , U23 和U31各是多少? · · · · U31= U3 -U1 · -U2 解: 星形联结时UlY = 10.5kV U3 · U 3 UlY 10.5 = kV = 6.06kV ∴UpY = · · U 1=U23 √ 3 √3 · ·-U =U 三角形联结时相电压不变, 2 3 · UlY = UpY =6.06kV L2首末端接反的相量图如图所示:
· · · 0 0 0 IL2 = I2 - I1 ( 8 . 8 30 8 . 8 0 ) A 4 . 56 105 A · · · 0 0 0 IL3 = I3 - I2 ( 8 . 8 30 8 . 8 30 ) A 8 . 8 90 A
XL= Z sin = 77.1×0.6 Ω = 46.3 Ω
返 回 上一题 下一题
第 4 章 供 电 与 用 电
4.3.2 某三相负载,额定相电压为220V,每相负载的电阻为4Ω,感 抗为3Ω,接于线电压为380V的对称三相电源上,试问该负载应
采用什么联结方式?负载的有功功率、无功功率和视在功率?
· I
l2
· I
l3
· I
2
· I
3
-jXC
解: 负载为不对称三相负载
· · 0 U U 220 120 2 23 · 0 I2 = Z = -jX = 8 . 8 30 A -j25 2 C
返 回 上一题 下一题
第四章习题及参考答案

第四章习题及参考答案第四章抽样与抽样估计⼀、单项选择题1、实际⼯作中,⼩样本是指()A、样本容量⼤于30的样本B、样本容量⼩于30的样本C、样本容量等于30的样本D、样本容量⼩于等于30的样本2、从5个字母中随机抽取2个字母作为样本,采⽤重复抽样,考虑顺序,则可能的样本个数为()A、10个B、20个C、25个D、30个3、当总体⽅差未知,且样本容量⼩于30时,进⾏正态总体均值的区间估计应采⽤的临界值为()A、F值B、Z值C、t值D、2x值4、当总体⽅差已知,⽆论样本容量n的⼤⼩如何,进⾏正态总体均值的区间估计应采⽤的临界值为()A、F值B、Z值C、t值D、2x值5、在总体内部情况复杂、且各单位之间差异程度⼤、单位数⼜多的情况下,宜采⽤()A、等距抽样B、整群抽样C、简单随机抽样D、类型抽样6、根据重复抽样的资料,甲单位⼯⼈⼯资⽅差为25,⼄单位为100,⼄单位抽的⼈数⽐甲单位多3倍,则抽样平均误差()A、甲单位较⼤B、甲单位较⼤C、⽆法判断D、甲、⼄单位相同7、某学校在全校学⽣中随机重复抽取100⼈调查⾝⾼,计算出抽样平均误差为5cm。
如果改⽤不重复抽样⽅法,在其他条件不变时,其抽样平均误差将会()A、⼤于5cmB、⼩于5cmC、等于5cmD、不确定8、纯随机重复抽样条件下,样本容量扩⼤为原来的9倍,其它条件不变,则()A、抽样允许误差不变B、抽样允许误差缩⼩为原来的九分之⼀C、抽样允许误差缩⼩为原来的三分之⼀D、抽样允许误差增⼤为原来的九倍⼆、多项选择题1、影响抽样平均误差的因素主要有()A、总体⽅差或标准差B、样本容量C、抽样⽅法D、抽样组织⽅式E、抽样的对象2、下列说法中错误的有()A、抽样误差是不可避免的B、抽样误差是可以避免的C、抽样误差可以计算但不能加以控制机D、抽样误差是由于抽样的随机性⽽产⽣的样本估计量与总体参数之间的代表性误差 E、抽样误差是指登记性误差3、评价估计量的优劣常⽤下列三个标准()A、⼀致性B、有效性C、合理性D、代表性E、⽆偏性4、抽样推断过程包括相互联系的三项内容()A、随机抽样B、统计估计C、假设检验D、抽样精度E、置信度5、下列说法正确的有()A、总体参数是唯⼀的、确定的,但⼜是未知的B、总体参数是随机变量C、样本统计量是随机变量D、样本统计量是唯⼀的、确定的E、样本所包含的总体单位个数称为样本容量6、概率抽样最基本的组织⽅式有()A、简单随机抽样B、分层抽样C、等距抽样D、整群抽样E、配额抽样7、抽样估计中的抽样误差()A、⽆法避免B、可以控制C、只能在估计结束才能知道D、可以计算E、不可控制8、抽样平均误差是指()A、所有可能样本的样本指标与总体指标的平均离差B、所有可能样本的样本指标对总体指标的标准差C、已抽出样本的标准差D、等价于极限误差E、已抽出样本的平均差三、填空题1、概率抽样也叫随机抽样,是指按照原则抽取样本。
(完整版)第四章生产者行为理论习题及答案

第四章 生产者行为理论一、单项选择题1.根据可变要素的总产量曲线、平均产量曲线和边际产量曲线之间的关系,可将生产划分为三个阶段,任何理性的生产者都会将生产选择在( )。
A.第Ⅰ阶段;B.第Ⅱ阶段;C.第Ⅲ阶段。
2.在维持产量水平不变的条件下,如果企业增加二个单位的劳动投入量就可以减少四个单位的资本投入量,则有( )。
A.RTS LK =2,且2=LK MP MP ; B.RTS LK =21,且2=L K MP MP ; C.RTS LK =2,且21=L K MP MP ; D .RTS LK =21,且21=L K MP MP 。
3.在以横坐标表示劳动数量,纵坐标表示资本数量的平面坐标中所绘出的等成本线的斜率为( )。
A.γω;B.- γω;C.ωγ;D.- ωγ。
4.当边际产量大于平均产量时( )。
A.平均产量递减;B.平均产量递增;C.平均产量不变;D.总产量递减。
5.如图所示,厂商的理性决策应在( ) A .0<L <7;B.4.5<L <7;C .3<L <4.5;D.0<L <4.5。
6.已知某企业的生产函数Q=10K L (Q 为产量,L 和K 分别为劳动和资本),则( )。
A .生产函数是规模报酬不变;B .生产函数是规模报酬递增;C .生产函数是规模报酬递减;D .无法判断7.等成本曲线绕着它与纵轴Y的交点向外移动表明( )。
A.生产要素Y的价格下降了;B.生产要素x的价格上升了;C. 生产要素x的价格下降了;D. 生产要素Y的价格上升了。
8.总成本曲线与可变成本曲线之间的垂直距离()。
A.随产量减少而减少;B.等于平均固定成本;C.等于固定成本;D.等于边际成本。
9.随着产量的增加,短期固定成本()。
A.增加;B.减少;C.不变;D.先增后减。
10.已知产量为8个单位时,总成本为80元,当产量增加到9个单位时,平均成本为11元,那么,此时的边际成本为()。
A.1元;B.19元;C.88元;D.20元。
西方经济学课后答案--第四-十章

第四章课后习题答案一、名词解释1.边际报酬递减:是指在生产技术不变的条件下,若其他投入不变,只是不断增加某一种要素投入,则该种投入要素的边际产量最终会逐渐减少.2.等产量线:也叫等生产线,是表示生产技术不变时生产同一产量某种产品的不同的投入组合的轨迹。
3.边际技术替代率:是指在维持产量水平不变的条件下,增加一单位某种生产要素投入量时所减少的另一种要素的投入数量.4.等成本线:是指在既定的成本预算和生产要素价格条件下,生产者可以购买到的两种生产要素不同数量组合的轨迹.5.生产者均衡:是指在既定的成本条件下的最大产量或既定产量条件下的最小成本。
6.扩展线:是表示生产技术和要素价格不变的条件下,生产者在不同的生产规模上将采用的最佳投入组合的轨迹。
7.规模经济:由于产出水平的提高,或者说因为生产规模的扩大而引起的单位成本下降。
规模不经济:由于产出水平的提高,或者说因为生产规模的扩大而引起的单位成本下上升。
8.外在经济:是指由于厂商的生产活动所依赖的外部环境得到改善从而引起的平均成本下降。
外在不经济:由于厂商生产活动所依赖的外部环境恶化而引起的单位成本上升.9.机会成本:是指由于使用特定资源而放弃的该资源其他用途所能获得的最高收益。
会计成本:是指需要现实的货币支付,会在厂商的会计账目上记录和反映出来的成本。
沉没成本:是指已经发生和支付且无法收回的成本.显性成本:是指厂商支付给各要素所有者的报酬而形成的成本.隐性成本:是指应该计算为成本但却未在形式上进行货币支付的厂商本身所拥有的生产要素的报酬.10.短期:是指生产者来不及调整全部生产要素投入数量,至少有一种生产要素投入数量是固定不变的时间周期。
长期:是指生产者可以调整全部生产要素投入数量的时间周期。
正常利润:是指厂商自有生产资源应该获得的正常报酬。
经济利润:是厂商销售收益扣减经济成本的余额.11.短期总成本:是厂商在一定时期内生产一定数量产品的全部成本.短期内它由固定成本和可变成本之和构成。
第四、五、六章练习题答案

图3-18
14.利用影响线,求得结构在图3-20所示荷载作用下,C截面的剪力等于-20kN。(×)
15.结构的附属部分某截面某量值的影响线在基本部分的影响线竖标为零。(√)
第六章力法
1.超静定结构中有几个多余约束就有几个建立力法方程的变形条件。(√)
7.图3-14a所示梁的剪力图,竖标 是截面C左的剪力值,图3-14b是截面C的剪力影响线,竖标- 也是表示在移动荷载作用下截面C左的剪力值。(×)
图3-14
8.图3-15b可以代表图3-15a所示梁EF段任意截面的剪力影响线。(√)
图3-15
9.任何静定结构的支座反力、内力影响线,军事有一段或是数段直线组成。(√)
2.力法方程中的主系数的符号在任何情况下都取正值。(√)
3.把超静定结构的基本未知力求出来后,画最后内力图时,实际上是在画静定结构的内力图。(√)
4.图5-14所示超静定结构当支座A发生位移时,构建CD不会产生内力。(√)
图5-14
5.对图5-15(a)所示超静定刚架,若进行内力分析时采用5-15b所示的基本结构,并画出了最后的内力图,当计算C点的竖向位移时可选用图5-15 C所示的基本结构。(√)
2.剪力的结构包络图表示梁在已知荷载作用下各截面剪力可能变化的极限范围。(√)
3.静定桁架的影响线在结点之间必是一条直线。(√)
4.下图3-10所示两根梁的MC影响线不相同。(×)
图3-10图3-11
5.同4题图所示两根梁的QC影响线不相同。(√)
6.图3-11所示单位荷载在AB区间移动,绘制界面C的某内力影响线时,也应限制在AB区间内。(√)
10.静定梁某截面弯矩的临界荷载位置一般就是最不利荷载位置。(×)
第4章习题答案(科学出版社)

第四章相平衡思考题1.什么叫自由度?相律的内容是什么?它能够解决什么问题?答:在不引起旧相消失和新相形成的前提下,可以在一定范围内独立变动的强度性质称为系统的自由度。
相律就是在平衡系统中,系统内相数、组分数、自由度数及影响物质性质的外界因素(如温度、压力、重力场、磁场、表面能等)之间关系的规律。
相律是一个定性规律,可以指示相平衡体系中有几个相,可以指导如何去识别由实验绘制的相图。
2.水的三相点与冰点是否相同?答:不相同。
纯水的三相点是气-液-固三相共存,其温度和压力由水本身性质决定,这时的压力为610.62Pa,温度为273.16K。
热力学温标1K就是取水的三相点温度的1/273.16K。
5 水的冰点是在大气压力下,水的三相共存点的温度。
由于冰点受外界压力影响,在10Pa压力下,温度下降0.00747K,由于水中溶解了空气,温度又下降0.0024K,所以在大气压力为105Pa时,水的冰点为273.15K。
3.相点与物系点有什么区别?答:相点是相图中表示某平衡相组成的点。
从相点位置可看出该相的状态、组成、温度、压力等。
相点位置可随压力、温度的改变而改变。
在单组分系统的相图上,所有点全部是相点。
物系点是在多组分系统的相图上表示系统总组成的点,在单相区,物系点可与相点重合,而在两相区内只有物系点。
该物系所对应的两个相组成由两个相点表示。
在T-x图上,物系点可沿着与温度坐标平行的直线上下移动;在水盐系统图上,随着水的含量不同,物系点可沿着与组成坐标平行的直线左右移动。
4.单组分系统的三相点与低共熔点有何异同点?答:共同点:都是三相共存。
不同点:单组分系统的三相点是气-液-固三相共存,这时的自由度为零,它的压力、温度由系统自身性质决定,不受外界因素影响。
而二组分系统的低共熔点在等压的条件下自由度为零。
外压改变,低共熔点的温度和组成也会随之而改变。
5.米粉和面粉混合得十分均匀。
再也无法彼此分开,这时混合体系有几相?答:两相6.金粉和银粉混合后加热,使之熔融后冷却,得到的固体是一相还是两相?答:一相7.低共熔物能不能看作是化合物?答:不能。
操作系统第4章习题带答案

操作系统第4章习题带答案第四章⼀、问答题1、同步机制应遵循的准则是什么?2、死锁产⽣的4个必要条件是什么?它们是彼此独⽴的吗?3、简述死锁的定义和死锁产⽣的原因。
4、简述死锁定理和解除死锁的⽅法。
5、什么是安全状态?怎么判断系统是否处于安全状态?6、同步机制应遵循的准则是什么?7、死锁产⽣的4个必要条件是什么?它们是彼此独⽴的吗?⼆、计算题(共20分)1、当前系统中出现下述资源分配情况:利⽤银⾏家算法,试问如果进程P2提出资源请求Request(1,2,2,2)后,系统能否将资源分配给它?答:Request(1,2,2,2)<=(2,3,5,6)申请合法Request(1,2,2,2)<=Available,开始试探性分配,Available=(0,4,0,0) 测试系统是否安全:work= Available,finish=1没有进程的need满⾜<=work系统处于不安全状态,系统拒绝此次资源分配。
2、当前某系统有同类资源7个,进程P,Q所需资源总数分别为5,4。
它们向系统申请资源的次序和数量如表所⽰。
回答:问:采⽤死锁避免的⽅法进⾏资源分配,请你写出系统完成第3次分配后各进程占有资源量,在以后各次的申请中,哪次的申请要求可先得到满⾜?答:第1次申请,Q申请资源2,系统安全,分配第2次申请,P申请资源1,系统安全,分配第3次申请,Q申请资源1,系统安全,分配资源剩余3个,P占有1个资源,Q占有3个资源,第4次分配不安全,拒绝,第5分配系统安全,满⾜。
3、⼀个计算机系统有6个磁带驱动器和4个进程。
每个进程最多需要n个磁带驱动器。
问当n为什么值时,系统不会发⽣死锁?并说明理由答:n=2理由同第4题(进程资源最⼤需求-1)×进程数量+1≤系统资源数量4、若系统有某类资源m×n+1个,允许进程执⾏过程中动态申请该类资源,但在该系统上运⾏的每⼀个进程对该资源的占有量任何时刻都不会超过m+1个。
第四章 习题答案
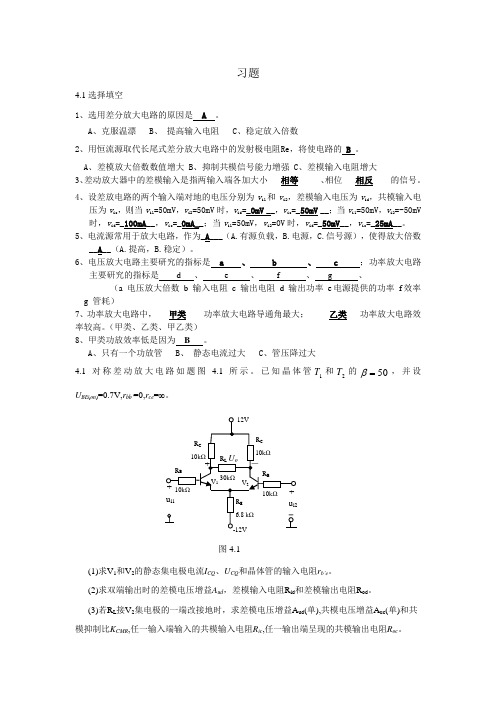
习题4.1选择填空1、选用差分放大电路的原因是 A 。
A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ,将使电路的 B 。
A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。
4、设差放电路的两个输入端对地的电压分别为v i1和v i2,差模输入电压为v id ,共模输入电压为v ic ,则当v i1=50mV ,v i2=50mV 时,v id =_0mV __,v ic =_50mV __;当v i1=50mV ,v i2=-50mV 时,v id =_100mA __,v ic =_0mA__;当v i1=50mV ,v i2=0V 时,v id =_50mV __,v ic =_25mA __。
5、电流源常用于放大电路,作为_A ___(A.有源负载,B.电源,C.信号源),使得放大倍数__A __(A.提高,B.稳定)。
6、电压放大电路主要研究的指标是 a 、 b 、 c ;功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、(a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗)7、功率放大电路中,___甲类____功率放大电路导通角最大;_____乙类___功率放大电路效率较高。
(甲类、乙类、甲乙类) 8、甲类功放效率低是因为 B 。
A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。
已知晶体管1T 和2T 的50=β,并设U BE (on )=0.7V,r bb ’=0,r ce =∞。
(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。
(2)求双端输出时的差模电压增益A ud ,差模输入电阻R id 和差模输出电阻R od 。
电子技术基础第四章 习题答案

4.3 在分析反相加法、差分式减法、反相积分和微分电路中,所根 据的基本概念是什么?KCL是否得到应用?如何导出它们输入-输出的 关系?
答:所根据的基本概念是虚短、虚断。KCL在分析反馈电流与比较 电流的关系时得到应用。根据反馈电流与比较电流的关系导出输出-输 入的关系。
第4章 习 题
4.1 在反相求和电路中,集成运放的反相输入端是如何形成虚地 的?该电路属于何种反馈类型?
答:在反相求和电路中,集成运放的反相输入端是等于同相输入端 的电压,而同相端接地,所以在反相形成虚地。该电路属于电压并联负 反馈
4.2 说明在差分式减法电路中,运放的两输入端存在共模电压,为 提高运算精度,应选用何种运放?
输出波形如图(b)。传输特性如图(c).
答: 4.10求图所示电路的输出电压uo,设运放是理想的
; ; ; ; 将电路中的电阻参数代入上式得
; ;;
整理后: 代入 中 =2.31u3+1.16u4-2u2-1.25u1 4.11 画出实现下述运算的电路:
uo=2ui1-6ui2+3ui3-0.8ui4
4.12 图为积分求和运算电路,设运放是理想的,试推导输出电压与 各输入电压的关系式。
解:根据虚断:i1+i2+i3=if 4.13 实用积分电路如图所示,设运放和电容均为理想的。 (1)试求证:;
(2)说明运放A1、A2各起什么作用?
解:
;; ∵ Rf=R2 R1=R3 ∴ ∵ ①;将 代入①后u01得:
对等式两边积分得: - 4.14 求图所示比较器的阀值,画出传输特性。又若输入电压uI波形 如图所示时,画出uo波形(在时间上必须与uI对应)。 解:uo=6V时 uo=-6V时
统计学4章练习题+答案

第4章练习题1、一组数据中出现频数最多的变量值称为(A)A.众数B.中位数C.四分位数D.平均数2、下列关于众数的叙述,不正确的是(C)A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响3、一组数据排序后处于中间位置上的变量值称为(B)A.众数B.中位数C.四分位数D.平均数4、一组数据排序后处于25%和75%位置上的值称为(C)A.众数B.中位数C.四分位数D.平均数5、非众数组的频数占总频数的比例称为(A)A.异众比率B.离散系数C.平均差D.标准差6、四分位差是(A)A.上四分位数减下四分位数的结果B.下四分位数减上四分位数的结果C.下四分位数加上四分位数D.下四分位数与上四分位数的中间值7、一组数据的最大值与最小值之差称为(C)A.平均差B.标准差C.极差D.四分位差8、各变量值与其平均数离差平方的平均数称为(C)A.极差B.平均差C.方差D.标准差9、变量值与其平均数的离差除以标准差后的值称为(A)A.标准分数B.离散系数C.方差D.标准差10、如果一个数据的标准分数-2,表明该数据(B)A.比平均数高出2个标准差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差11、经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范围之内大约有(B)A.68%的数据B.95%的数据C.99%的数据D.100%的数据12、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=4,其意义是(C)A.至少有75%的数据落在平均数加减4个标准差的范围之内B. 至少有89%的数据落在平均数加减4个标准差的范围之内C. 至少有94%的数据落在平均数加减4个标准差的范围之内D. 至少有99%的数据落在平均数加减4个标准差的范围之内13、离散系数的主要用途是(C)A.反映一组数据的离散程度B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平14、比较两组数据离散程度最适合的统计量是(D)A.极差B.平均差C.标准差D.离散系数15、偏态系数测度了数据分布的非对称性程度。
(完整word版)第四章 习题答案

第四章的习题及答案4-1 设有一台锅炉,水流入锅炉是之焓为62.7kJ ·kg -1,蒸汽流出时的焓为2717 kJ ·kg -1,锅炉的效率为70%,每千克煤可发生29260kJ 的热量,锅炉蒸发量为4.5t ·h -1,试计算每小时的煤消耗量。
解:锅炉中的水处于稳态流动过程,可由稳态流动体系能量衡算方程:Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换:0=s W ,并忽 动能和位能的变化, 所以: Q H =∆设需要煤mkg ,则有:%7029260)7.622717(105.43⨯=-⨯m解得:kg m 2.583=4-2 一发明者称他设计了一台热机,热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ,规定这热机的高温与低温分别为670K 与330K ,试判断此设计是否合理?解:可逆热机效率最大,可逆热机效率:507.06703301112max =-=-=T T η 热机吸收的热量:1m in210005.042000-⋅=⨯=kJ Q热机所做功为:1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为:486.02100010200==-=Q W η 该热机效率小于可逆热机效率,所以有一定合理性。
4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点,并在沸点下完全蒸发。
试问加给水的热量有多少可能转变为功?环境温度为293 K 。
解:查水蒸气表可得始态1对应的焓和熵为:H 1=83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为:H 2=2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子,此加热过程的总熵变为多少?由于过程的不可逆性损失了多少功? 解:此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体,400K 下在气缸内进行恒温不可逆压缩,由0.1013MPa 压缩到1.013MPa 。
第四章 习题答案

一、名词解释1.群体: 群体是两人或两人以上的集合体,他们遵守共同的行为规范,在心理上相互作用,在情感上互相依赖,在思想上互相影响,在利益上相互联系、相互依存,而且有着共同的奋斗目标。
2.群体结构: 指群体成员的相互关系以及保证群体有序运行的特征。
3. 社会惰化: 指一种倾向,一个人在群体中工作不如单独一个人工作时更努力。
4. 角色:人们对在某个社会性单位中占有一定职位的人所期望的一系列行为模式。
5. 地位:是他人对于群体或群体成员的位置或层次进行的一种社会界定,也可以说是个体在群体中的相对社会职位或等级。
6. 群体动力:群体是处于均衡状态的各种力的一种“力场”。
这些力涉及群体成员在其中活动的环境,还涉及群体成员的个性、感情及其相互间的看法。
人和群体的行为方向取决于内部力场和情境力场(环境因素)的相互作用。
7. 群体规范:是群体成员所共同接受并遵守的行为标准与行为准则,它是一个群体能保持一致的基本因素,它是由价值观、心理、行为方面的相互接近达成一致而形成的。
8. 群体压力:指由于群体规范的形成而对成员在心理上产生的压力。
群体对个体行为的影响主要通过群体规范所形成的群体压力而起作用。
9. 从众行为:是个体在群体的压力下改变个人意见而与多数人取得一致认识的行为倾向。
10. 冒险转移现象:又称极端性转移,是指群体决策比个人决策更容易出现冒险倾向。
11. 小集团思想:小集团思想指的是群体中成员的一种思想作风,认为追求思想一致比现实地评价各种可能行动方案更为重要,因此也称作小群体意识。
12. 正式群体: 正式群体是由组织正式文件明文规定的,群体的成员有固定的编制,有规定的权利和义务,有明确的职责分工。
13. 非正式群体: 非正式群体是组织中没有正式规定的群体,成员间可能因为住得近、有共同的兴趣爱好,或互相满足需要而形成群体,成员之间的相互关系带有明显的情感色彩。
13. 群体决策: 是群体成员共同参与作出决定。
数字电子技术基础第四章习题及参考答案

数字电子技术基础第四章习题及参考答案第四章习题1.分析图4-1中所示的同步时序逻辑电路,要求:(1)写出驱动方程、输出方程、状态方程;(2)画出状态转换图,并说出电路功能。
CPY图4-12.由D触发器组成的时序逻辑电路如图4-2所示,在图中所示的CP脉冲及D作用下,画出Q0、Q1的波形。
设触发器的初始状态为Q0=0,Q1=0。
D图4-23.试分析图4-3所示同步时序逻辑电路,要求:写出驱动方程、状态方程,列出状态真值表,画出状态图。
CP图4-34.一同步时序逻辑电路如图4-4所示,设各触发器的起始状态均为0态。
(1)作出电路的状态转换表;(2)画出电路的状态图;(3)画出CP作用下Q0、Q1、Q2的波形图;(4)说明电路的逻辑功能。
图4-45.试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0,并说明它的功能(假设初态Q0Q1=00)。
CPQ1Q0CP图4-56.分析如图4-6所示同步时序逻辑电路的功能,写出分析过程。
Y图4-67.分析图4-7所示电路的逻辑功能。
(1)写出驱动方程、状态方程;(2)作出状态转移表、状态转移图;(3)指出电路的逻辑功能,并说明能否自启动;(4)画出在时钟作用下的各触发器输出波形。
CP图4-78.时序逻辑电路分析。
电路如图4-8所示:(1)列出方程式、状态表;(2)画出状态图、时序图。
并说明电路的功能。
1C图4-89.试分析图4-9下面时序逻辑电路:(1)写出该电路的驱动方程,状态方程和输出方程;(2)画出Q1Q0的状态转换图;(3)根据状态图分析其功能;1B图4-910.分析如图4-10所示同步时序逻辑电路,具体要求:写出它的激励方程组、状态方程组和输出方程,画出状态图并描述功能。
1Z图4-1011.已知某同步时序逻辑电路如图4-11所示,试:(1)分析电路的状态转移图,并要求给出详细分析过程。
(2)电路逻辑功能是什么,能否自启动?(3)若计数脉冲f CP频率等于700Hz,从Q2端输出时的脉冲频率是多少?CP图4-1112.分析图4-12所示同步时序逻辑电路,写出它的激励方程组、状态方程组,并画出状态转换图。
第4章习题及答案_无机材料科学基础

第四章非晶态结构与性质4-1名词解释熔体与玻璃体分化(解聚)与缩聚网络形成体网络中间体网络改变体桥与非桥氧硼反常现象单键强度晶子学说与无规则网络学说4-2试简述硅酸盐熔体聚合物结构形成的过程和结构特点。
4-3试用实验方法鉴别晶体SiO2、SiO2玻璃、硅胶和SiO2熔体。
它们的结构有什么不同?4-4 试述石英晶体、石英熔体、Na2O·2SiO2熔体结构和性质上的区别。
4-5影响熔体粘度的因素有哪些?试分析一价碱金属氧化物降低硅酸盐熔体粘度的原因。
4-6熔体粘度在727℃时是107Pa·s,在1156℃时是103 Pa·s,在什么温度下它是106 Pa·s?(用lnη=A+B/T解之)4-7 SiO2熔体的粘度在1000℃时为1014 Pa·s,在1400℃时为107 Pa·s。
SiO2玻璃粘滞流动的活化能是多少?上述数据为恒压下取得,若在恒容下获得,你认为活化能会改变吗?为什么?4-8一种熔体在1300℃的粘度是310 Pa·s,在800℃是107 Pa·s,在1050℃时其粘度为多少?在此温度下急冷能否形成玻璃?4-9试用logη=A+B/(T-T0)方程式,绘出下列两种熔体在1350~500℃间的粘度曲线(logη~1/T)。
两种熔体常数如下:4-10派来克斯(Pyrex)玻璃的粘度在1400℃时是109 Pa·s,在840℃是1013Pa·s。
请回答:(1)粘性流动活化能是多少?(2)为了易于成形,玻璃达到105Pa·s的粘度时约要多高的温度?4-11一种玻璃的工作范围是870℃(η=106Pa·s)至1300℃(η=102.5Pa·s),估计它的退火点(η=1012Pa·s)?4-12一种用于密封照明灯的硼硅酸盐玻璃,它的退火点是544℃,软化点是780℃。
第四章习题答案

一、填空题1.几何公差的形状公差有6项,它们的名称和代号分别是(直线度)、(平面度)、(圆度)、(圆柱度)、(线轮廓度)和(面轮廓度)。
2.几何量公差的跳动公差有2项,它们的名称和代号分别为(圆跳动)和(全跳动)。
3.端面对轴线的垂直度(小)于端面圆跳动。
4.某轴尺寸为Φ10-0.018-0.028 mm ,轴线对基准A 的垂直度公差为Φ0.01 mm ,被测要素给定的尺寸公差和几何公差采用最大实体要求,则垂直度公差是被测要素在(最大实体状态)时给定的。
当轴实际尺寸为(Φ9.972)mm 时,允许的垂直度误差达最大,可达(0.02)mm 。
5.独立原则是指图样上给定的(尺寸)公差与(几何)公差各自独立,分别满足要求的公差原则。
6.包容要求采用(最大实体)边界,最大实体要求采用(最大实体实效)边界。
7.某孔尺寸为Φ40+0.119 +0.030○E mm ,实测得其尺寸为Φ40.09mm ,则其允许的几何误差数值是(Φ0.06)mm ,当孔的尺寸是(Φ40.119)mm 时,允许达到的几何误差数值为最大。
8.某孔尺寸为Φ40+0.119+0.030mm ,轴线直线度公差为 Φ0.005 mm ,实测得其局部实际尺寸为Φ40.09mm ,轴线直线度误差为Φ0.003mm ,则孔的最大实体尺寸是(Φ40.030)mm ,最小实体尺寸是(Φ40.119)mm ,体外作用尺寸是(Φ40.087)mm 。
9.若某轴标注为则该零件的MMS 为(φ30mm ),又称为该零件的(最大)极限尺寸;其LMS 为(φ29.979mm ),又称为该零件的(最小)极限尺寸;零件采用的公差要求为(最大实体要求),若加工后测得某孔的实际尺寸为φ29.98mm ,直线度误差为0.015mm ,则该零件(是)(是、否)合格。
10.若某孔的尺寸标注为,则该零件采用的公差原则为(最大实体要求),其MMS 为(Φ20mm ),此时的几何公差值为(Φ0.02)mm ;其LMS 为(Φ20.05mm )mm ,此时的形位公差值为(Φ0.07)mm ;其MMVS 为(Φ19.98)mm 。
高等数学 线性代数 习题答案第四章

习题 4-11.验证函数f (x )=lnsin x 在[π5π,66]上满足罗尔定理的条件,并求出相应的ξ,使f ′(ξ)=0.解: 显然()ln sin f x x =在5π,66x ⎡⎤⎢⎥⎣⎦上连续,在π5π,66⎛⎫⎪⎝⎭内可导,且π5π()()ln 266f f ==-,满足罗尓定理的条件. 令cos ()cot 0sin x f x x x '===,则π2x = 即存在ππ5π(,)66ξα=∈,使()0f ξ'=成立.2. 下列函数在指定区间上是否满足罗尔定理的三个条件?有没有满足定理结论中的ξ ?[][][]2(1)()1,;(2)(),;1,10,21sin ,0π(3)()0,π1,0e x f x f x x x x f x x =-=--<≤⎧=⎨=⎩解: (1) 2()1e x f x =-在[]1,1-上连续,在()1,1-内可导,且(1)1,(1)1,e e f f -=-=- 即 (1)(1)f f -= () f x ∴在[]1,1-上满足罗尓定理的三个条件. 令 2()20ex f x x '==得 0x =,即存在0(1,1)ξ=∈-,使()0f ξ'=.(2) 101()1112x x f x x x x -≤<⎧==-⎨-≤≤⎩显然()f x 在(0,1),(1,2)内连续,又1111(10)lim ()lim(1)0,(10)lim ()lim(1)0,(10)(10)(1)0,即x x x x f f x x f f x x f f f --++→→→→-==-=+==-=-=+==所以()f x 在1x =处连续,而且22(00)lim ()lim(1)1(0),(20)lim ()lim(1)1(2),x x x x f f x x f f f x x f ++--→→→→+==-==-==-==即()f x 在0x =处右连续,在2x =处左连续,所以()f x 在[]0,2 上连续.又1111()(1)1(1)lim lim 1,11()(1)1(1)lim lim 111x x x x f x f xf x x f x f xf x x --++-→→+→→--'===-----'===--(1)(1)()f f f x -+''∴≠∴在1x =处不可导,从而()f x 在(0,2)内不可导.又 (0)(2)1f f == 又由 101()112x f x x -<<⎧'=⎨<<⎩知 ()0f x '≠综上所述,函数()f x 满足罗尓定理的条件(1),(3)不满足条件(2),没有满足定理结论的ξ.(3) 由0(00)lim sin 0(0)1x f x f +→+==≠=知()f x 在0x =不右连续, () f x ∴在[]0,π上不连续, 显然()f x 在()0,π上可导,又(0)1,(π)0f f ==,即(0)(π)f f ≠,且()cos (0,π) f x x x '=∈,取π(0,π)2ξ=∈,有π()cos cos 02f ξξ'===. 综上所述,函数()f x 满足罗尓定理的条件(2),不满足条件(1),(3),有满足定理结论的ξ,ξ=π2.3. 不用求出函数()(1)(2)(3)f x x x x =---的导数,说明方程()0f x '=有几个实根,并指出它们所在的区间.解: 显然()f x 在[]1,2上连续,在()1,2内可导,且(1)(2)0f f ==,由罗尓定理知,在()1,2内至少存在一点1ξ,使1()0f ξ'=,即()0f x '=在()1,2内至少有一个实根.同理 ()0f x '=在()2,3内也至少有一个实根2ξ.又()0f x '=是二次方程,最多有两个实根,故()0f x '=有两个实根,分别在区间()1,2和()2,3内.4. 验证拉格朗日中值定理对函数3()2f x x x =+在区间[0,1]上的正确性.解: 显然3()2f x x x =+在[0,1]上连续,在()0,1内可导,满足拉格朗日中值定理的条件.若令2(1)(0)()32310f ff x x -'=+==-则x =,取ξ=,即存在(0,1)3ξ=∈,使得(1)(0)()10f f f ξ-=-成立. 从而拉格朗日中值定理对函数3()2f x x x =+在[0,1]上成立.5. 已知函数f (x )在[a ,b ]上连续,在(a ,b )内可导,且f (a )=f (b )=0,试证:在(a ,b )内至少存在一点ξ,使得f (ξ)+f ′(ξ) = 0,ξ∈(a ,b ). 证: 令()()e xF x f x =,则()()()e e xxF x f x f x ''=+由e x 在(),-∞+∞上连续,可导,()f x 在[],a b 上连续,在(),a b 内可导,知()F x 在[],a b 上连续,在(),a b 内可导,而且()()0,()()0,()()e e 即abF a f a F b f b F a F b =====,由罗尓定理至少存在一点(,)a b ξ∈使()0F ξ'=. 即 ()()0e e f f ξξξξ'+= 而0e ξ≠ 故 ()()0f f ξξ'+=即在(),a b 内至少存在一点ξ,使得()()0f f ξξ'+=. 6.若方程10110n n n a x a x a x --+++= 有一个正根x 0,证明方程12011(1)0n n n a nx a n x a ---+-++=必有一个小于0x 的正根. 证: 令1011()…nn n f x a x a xa x --=+++,显然()f x 在[]00,x 连续,在()00,x 内可导,且(0)0f =,依题意知0()0f x =.即有0(0)()f f x =.由罗尓定理,至少存在一点0(0,)x ξ∈,使得()0f ξ'=成立,即12011(1)0…n n n a n a n a ξξ---+-++=成立,这就说明ξ是方程12011(1)0n n n a nx a n x a ---+-++= 的一个小于0x 的正根.7. 设f (a ) = f (c ) = f (b ),且a <c <b , f ″(x )在[a ,b ]上存在,证明在(a ,b )内至少存在一点ξ,使f ″(ξ)= 0.证: 显然()f x 分别在[],a c 和[],c b 上满足罗尓定理的条件,从而至少存在1(,)a c ξ∈,2(,)c b ξ∈,使得12()()0f f ξξ''==.又由题意知()f x '在[]12,ξξ上满足罗尓定理的条件,从而至少存在一点12(,)(,)a b ξξξ∈⊂,使得()0f ξ''=.即在(,)a b 内至少存在一点ξ,使()0f ξ''=.习题4-21.利用洛必达法则求下列极限:(1) sin3lim tan5x xxπ→; (2) 0e 1lim (e 1)x x x x x →---;(3)lim m m n n x a x a x a →--; (4) 20()lim x xx a x a x →+-,(a >0); (5) 0ln lim cot x xx+→; (6) 0lim sin ln x x x +→; (7) 1ln(1)lim arccot x x x →+∞+; (8) 0e 1lim()e 1x x x x →--; (9) 10lim(1sin )xx x →+; (10) 2lim (arctan )πx x x →+∞(11) c s c 03e lim()2x x x x →-+ ; (12) 2120lim e x x x →;(13) lim )x x →+∞; (14) 1101lim (1)e xxx x →⎡⎤+⎢⎥⎣⎦.解:222000011sin 33cos33(1)limlim lim cos3cos 5tan 55sec 5533(1)(1)5511(2)lim lim lim (1)111lim 22(3)lim lim lim πππe e e e e e e e e x x x x x xx x x x x xx x x x m m m n n n x a x a x a x x x x x x x x x x x x a mx x a nx →→→→→→→--→→→==⋅=⋅-⋅-=----==--+++==+-==-.m n m nm m x a n n --=2002220()ln ln()()(4)lim lim 21()()()ln ln()()lim2x xxxx x x x x x x a x a a a x a x a a x x xa x a x a x a a a x a x a x a x →→→⎡⎤+-++⎢⎥+-+⎣⎦=⎡⎤++++-++⎢⎥+++⎣⎦=[]200021()ln ln 012 aa a a aa a a a ++-⋅+==2200000000001ln sin 2sin cos (5)lim lim lim lim cot csc 12sin 0cos 001ln sin (6)lim sin ln lim lim lim tan csc csc cot sin lim lim tan 100x x x x x x x x x x x x x x x x x x x x x x x xx x x xxx x ++++++++++→→→→→→→→→→==-=--=-⋅====-⋅-=-⋅=-⨯=222221111ln(1)111(7)lim lim lim lim 111cot 11arc x x x x xx x x x x x x x x →+∞→+∞→+∞→+∞-++++====+-++ 20002200001(1)(8)lim()lim lim 1(1)21443limlim 12022e e e e e e e e e e e e e e e e e e e x x x x x x x x x x x xxxxx x x x x x x xx x x x x x →→→→→-----==-------====+-++0002cos 11ln(1sin )cos 1sin ln(1sin )lim limlim 11sin 12112ln(arctan )arctan 1limlim 112ln(arctan )(9)lim(1sin )lim 2(10)lim (arctan )lim πππee =e ee ee eeπx x x x x xx xx x xxxxx x x x x x x x xxx x x x →→→→+∞→+∞++++→→⋅⋅+-→+∞→+∞+========221lim12lim(1)arctan (1)arctan πeeex x x xx xx→+∞→+∞--+-+===020033lnln322csc ln lim csc 2sin sin 0002(2)(3)33(2)limlim 1(3)(2)cos cos 3(11)lim()lim lim 21e e e e e e e e eee ee exxxx x x x x x x x e e e x x x x xxxxx x x x x x x x xxx →→→---+++→→→+-+--⋅----+--+-===+====2221111220000221()(12)lim lim lim lim 11()e e ee x xx x x x x x x x x x→→→→'⋅====∞'202211ln(1)1ln(1)1limlim lim 0(13)lim )lim1111lim31(14)lim (1) eeee x x x x x x x x xx xxx x x x x →→→+∞→+∞+-+-→=++===⎡⎤===+⎢⎥⎣⎦00111211lim2(1)2eex x xx →→-+--+==2.设 21lim 1x x mx nx →++-=5,求常数m ,n 的值.解: 1lim(1)0, x x →-= 而21lim 51x x mx n x →++=-21lim()0 x x mx n →∴++= 且21()lim 5(1)x x mx n x →'++='-即 10m n ++= 且 1l i m (2)5x x m →+= 即 1m n +=- 且 25m += 于是得 3,4m n ==-. 3.验证极限sin lim x x xx→∞+存在,但不能由洛必达法则得出.解: sin 1limlim(1sin )1x x x x x x x→∞→∞+=+=,极限存在,但若用洛必达法则,有sin lim lim(1cos )x x x xx x→∞→∞+=+因lim cos x x →∞不存在,所以不能用洛必达法则得出.4.设f (x )二阶可导,求2()2()()limh f x h f x f x h h →+-+-.解: 这是型未定式,利用洛必达法则有 [][]200000()2()()()()limlim2()()()()1lim 21()()1()()11lim lim ()()2222().h h h h h f x h f x f x h f x h f x h h hf x h f x f x h f x hf x h f x f x h f x f x f x h h f x →→→→→''+-+-+--=''''-+---=''''+---''''=+=+-''=5.设f (x )具有二阶连续导数,且f (0) = 0,试证g (x ) = (),0'(0),0f x x x f x ⎧≠⎪⎨⎪=⎩可导,且导函数连续. 证: 当0x ≠时,2()()()()()f x xf x f x g x x x '-''==当0x =时,由200000()(0)()(0)()(0)lim lim lim 00()(0)1()(0)1lim lim (0)2202x x x x x f x f g x g f x xf x x x x f x f f x f f x x →→→→→'-'--==--''''--''===- 即 1(0)(0)2g f '''=所以 2()(),0()1(0),02xf x f x x xg x f x '-⎧≠⎪⎪'=⎨⎪''=⎪⎩由(),()f x f x '的连续性知()g x '在0x ≠处连续,又20000()()()()()lim ()limlim211lim ()(0)(0)22x x x x xf x f x f x xf x f x g x x xf x fg →→→→'''''-+-'=='''''===故()g x '在0x =处连续,所以()g x '在(),-∞+∞内处处连续.综上所述,(),0()(0),0f x xg x x f x ⎧≠⎪=⎨⎪'=⎩可导,且导函数连续.习题4-31.求函数f (x ) =e x x 的n 阶马克劳林公式.解:()()(1),()(1)(2),()()…x x x x x x k x f x e xe e x f x e x e e x f x e k x '=+=+''=++=+=+()()(0)1(0),(1,2,3,)!!(1)!k k f k fk k k k k ∴====-又 (0)0f =321(1)()(01)2!(1)!(1)!n x n x x e n x f x x x x n n θθθ+++∴=+++++<<-+2.当01x =-时,求函数f (x ) = 1x的n 阶泰勒公式. 解:()()[]23()2341()1()112212!3!!()(1),()(1),()(1),,()(1)!(1)(1)!(1)(1)!1,(0,1,2,)!!(1)()(1)1(1)111(1) … n n n n n n n n n nn n f x f x f x f x x x x x n f n f n n n n x f x x x x x θ-++++''''''=-=-=-=-∴-=-⋅=----==-=+∴=-+-⎡⎤+++++++⎣⎦-++ (01)θ<<3.按(4)x -的乘幂展开多项式432()53 4.f x x x x x =-+-+解: 函数432()534f x x x x x =-+-+,根据泰勒公式按(4)x -的幂的展开式是2(4)34(4)()(4)(4)(4)(4)2!(4)(4)(4)(4)3!4! f f x f f x x f f x x '''=+-+-'''+-+- 而[][][]432324244(4)(4)454434456,(4)21,41523(4)137,123022!2(4)111,24303!3!(4)12414!4!x x x f f x x x f x x f x f ====-⨯+-⨯+=-'==-+-''==-+'''==-=⨯=所以,234()5621(4)37(4)11((4)(4)f x x x x x =-+-+-+-+-.4.利用泰勒公式求下列极限:(1) 30sin limx x x x →-; (2) 21lim ln(1)x x x x →+∞⎡⎤-+⎢⎥⎣⎦. 解: (1) 利用泰勒公式,有34sin ()3!x x x o x =-+所以 343300430()sin 3!lim lim 1()1lim()66x x x x o x x x x x o x x →→→--==-= (2) 利用泰勒公式,有221111ln(1)()2o x x x x+=-+,所以222222221111lim lim ln(1)(())21()1111lim lim .()1222x x x x x x x x o x x x x o x x o x x →+∞→+∞→+∞→+∞⎡⎤⎡⎤=-+--+⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎡⎤==-=-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦ 习题4-41. 求下面函数的单调区间与极值:(1)32()26187f x x x x =---; (2)()ln f x x x =-; (3)23()1(2)f x x =--; (4)()(4)f x x x =-. 解: (1) 2()612186(1)(3),f x x x x x '=--=+-令()0f x '=得驻点121,3,x x =-=-在()(),,13,-∞-+∞上,()0f x '>,在()1,3-上()0f x '< ∴ ()f x 在(,1],[3,)-∞-+∞上单调增加,在[]1,3-上单调减少.当 1x =-时, ()f x 有极大值,极大值为(1)3f -=, 当 3x =时, ()f x 有极小值,极小值为(3)61f =-.(2) 11()1x f x x x-'=-=,令()0f x '=得驻点1x = 在()0,1上,()0f x '<;在()1,+∞上,()0f x '> ∴ ()f x 在(0,1]上单调递减;在[1,)+∞上单调递增. 当1x =时,()f x 有极小值,极小值为(1)1f =. (3)()()0f x f x ''=≠ 但当2x =时,()f x '不存在, 在(,2)-∞上,()0f x '>;在(2,)+∞上,()0f x '<, ∴ ()f x 在(,2]-∞上单调递增;在[2,)+∞上单调递减. 当2x =时, ()f x 有极大值,极大值为(2)1f =.(4) 2240()40x xx f x x xx ⎧-≥=⎨-+<⎩ ,则 240()240x x f x x x ->⎧'=⎨-+<⎩且当 0x =时,()f x '不存在,又令()0f x '=得2x = 在(,0),(2,)-∞+∞上,()0f x '>,在(0,2)上()0f x '< ∴ ()f x 在(,0],[2,)-∞+∞上单调递增;在[0,2]上单调递减; 当0x =时,()f x 有极大值,极大值为(0)0f =; 当2x =时, ()f x 有极小值,极小值为(2)4f =-. 2. 试证方程sin x = x 只有一个根.证: 显然0x =是方程sin x x =得一个根(亦可将()sin f x x x =-运用零点定理).令()sin f x x x =-,则()cos 10f x x '=-≤,而()0f x '=的点不是单调区间的分界点,故()f x 在(,)-∞+∞内单调下降,所以()f x 在(,)-∞+∞内只有一个零点,即方程sin x x =只有0x =一个根.3. 已知()([0,))f x C ∈+∞,若f (0) = 0, f ′(x )在[0,)+∞内存在且单调增加,证明()f x x在[0,+∞)内也单调增加.解: 0 x ∀>,由题意知()f x 在[]0,x 上满足拉格朗日中值定理的条件,利用拉格朗日中值定理得,(0,) x ξ∃∈,使()(0)()f x f xf ξ'-=, 因 ()f x '在[0,)+∞单调增加,且(0)0f =,所以()()()f x xf xf x ξ''=≤ 即 ()()0xf x f x '-≥令 ()()(0) f x F x x x=>,则 2()()()0xf x f x F x x '-'=≥ 所以()F x 单调递增,即 ()f x x在(0,)+∞内单调增加.4. 证明下列不等式:(1) 1+12x x >0; (2)2ln(1)(0)2 x x x x x -<+<>.证: (1) 令 1()12f x x =+则1()(12f x '=, 当 0x >时1,()0f x '<>即()f x 单调递增,从而()(0)0f x f >=,故112x +>. (2) 令 2()ln(1)2x f x x x =+-+,则 21()111x f x x x x'=-+=++当 0x >时,有()0f x '>,即()f x 单调递增,从而()(0)0f x f >= ,即2ln(1)2x x x +>-又令 ()ln(1)g x x x =-+,则1()111xg x x x'=-=++ 当 0x >时,()0g x '>,即 ()g x 单调递增,从而()(0)0g x g >=,即ln(1)x x >+.综上所述,当0x >时有2ln(1)2x x x x -<+<. 5. 试问a 为何值时,f (x ) = a sin x +13sin 3x 在x =3π处取得极值?是极大值还是极小值?并求出此极值.解: ()cos cos3f x a x x '=+若3πx =为极值点,则cos cos 03ππa +=,所以2a =.又()2sin 3sin 3,()03πf x x x f ''''=--=<故函数在3πx =处取得极大值,极大值为()3πf =习题4 - 51. 某个体户以每条10元的价格购进一批牛仔裤,设此批牛仔裤的需求函数为402Q P =-,问该个体户应将销售价定为多少时,才能获得最大利润? 解: 利润2()10260400L P PQ Q P P =-=-+-, ()460L P P '=-+,令 ()0L P '=得 P =15所以应将销售价定为每条15元,才能获得最大利润.2.设 f (x ) = cx α (c >0,0<α<1)为一生产函数,其中c 为效率因子,x 为投入量,产品的价格P 与原料价格Q 均为常量,问:投入量为多少时可使利润最大? 解: 依题意,总利润()()()L x Pf x Q x P cx Qx α=-=⋅- 则 1()L x Pc xQ αα-'=- 令 ()0L x '=得 11Q x Pc αα-⎛⎫=⎪⎝⎭所以,投入量为11Q Pc αα-⎛⎫⎪⎝⎭时利润最大.3. 某产品的成本函数为23()156C Q Q Q Q =-+,(1) 生产数量为多少时,可使平均成本最小?(2) 求出边际成本,并验证边际成本等于平均成本时平均成本最小. 解: (1) 2()()156C Q C Q Q Q Q==-+ 令 260()Q C Q '=-=⎡⎤⎣⎦得Q =3 故 生产数量3Q =时,可使平均成本最小. (2) 2()15123MC C Q Q Q '==-+当 3Q =时,15123396MC =-⨯+⨯= 2()156336C Q =-⨯+=即边际成本等于平均成本时平均成本最小. 4. 已知某厂生产Q 件产品的成本为C =25000+2000Q +1402Q (元). 问:(1) 要使平均成本最小,应生产多少件产品?(2) 若产品以每件5000元售出,要使利润最大,应生产多少件产品? 解: (1) 平均成本 250001()200040C Q Q Q =++ 边际成本1()200020C Q Q '=+. 当()()C Q C Q '=时,平均成本最小,由()()C Q C Q '=即2500011200020004020Q Q Q ++=+ 得1000Q =(负值不合题意已舍去). 所以要使平均成本最小,应生产1000件产品.(2)221()5000()500025000200040130002500040L Q Q C Q Q Q Q Q Q =-=---=-+-令 1()3000020L Q Q '=-+=, 得60000Q =(件) 所以应生产60000件产品.5. 某厂全年消耗(需求)某种钢材5170吨,每次订购费用为5700元,每吨钢材单价为2400元,每吨钢材一年的库存维护费用为钢材单价的13.2%,求: (1) 最优订购批量; (2) 最优批次; (3) 最优进货周期; (4) 最小总费用.解: 由题意 215170,5700,1,240013.2%316.8 R C T C ====⨯= 则(1)最优订购批量70*431.325q === (2)最优批次 5170*12*431.325R n q ==≈(次)(3)最优进货周期 36530.452*12T t n ===(天) (4)最小总费用*136643.9E ==≈(元)6. 用一块半径为R 的圆形铁皮,剪去一圆心角为α的扇形后,做成一个漏斗形容器,问α为何值时,容器的容积最大?解: 设漏斗的底面半径为r ,高为h ,为了计算方便令2ϕπα=-,则2,,2ππR r R r h ϕϕ====漏斗的容积2322123(83)πππV hr V ϕϕ==<<'=-令 0V '=得10ϕ=(舍之),2ϕ=,34222237),40,9πππV V ϕϕϕ''=-+-⎫''=-<⎪⎭故当ϕ=时漏斗得容积最大.由2πϕα=-得2π2πα==, 所以,当2πα=-时,容积最大. 7. 工厂生产出的酒可即刻卖出,售价为k ;也可窖藏一个时期后再以较高的价格卖出.设售价V 为时间t 的函数V = k (k >0)为常数.若贮存成本为零,年利率为r ,则应何时将酒售出方获得最大利润(按连续复利计算). 解: ()e rtrtA t k k -=⋅=令()0rt r A t k ⎫'-==⎪⎭得214t r = 所以,应窖藏214r 时以后售出可获得最大利润. 8. 若火车每小时所耗燃料费用与火车速度的三次方成正比,已知速度为20km/h ,每小时的燃料费用40元,其他费用每小时200元,求最经济的行驶速度. 解: 设火车每小时所耗燃料费为Q ,则 3Q k v = (k 为比例常数) 依题意得 34020k =⋅, 解得 1200k =, 又设火车行驶()km s 后,所耗费用为, 32200(200)()s E kv kv s v v=+⋅=+ 令 2200()0100v E s v'=-=, 得27.14v =≈ (km/h), 所以,最经济得行驶速度为27.14 km/h.习题 4-61. 讨论下列函数的凸性,并求曲线的拐点:(1) y =2x -3x ; (2) y = ln(1+2x ); (3) y = x e x; (4) y = 4(1)x ++e x; (5) y =2(3)x x +; (6) y=arctan e x. 解: (1)223,126,0.3令 得 y x x y x y x '=-''''=-==当13x <时,0y ''>; 当13x >时,0y ''<,且12()327f = 所以,曲线23y x x =-在1(,)3-∞内是下凸的,在1(,)3+∞内是上凸的,点12(,)327是曲线的拐点.(2) 222222222(1)222(1),1(1)(1)x x x x x y y x x x +-⋅--'''===+++, 令0y ''=得,121,1x x =-=,这两点将定义域(,)-∞+∞分成三个部分区间,列表考察各部分区间上二阶导数得符号.所以,曲线2l n (1)y x =+在(,1)-∞-及(1,)+∞内是上凸的,在(1,1)-内是下凸的,点(1,ln 2)±是曲线的拐点.(3) 324(1),12(1)0xxy x e y x e '''=++=++> 所以,曲线在定义域(,)-∞+∞内处处下凸,没有拐点.(4) 343212,(3)(3)x x y y x x --'''==++,令 0y ''=得6x = 当 6x <时,0y ''<,当6x >时,0y ''>;又2(6)27f =,函数的定义域为(,3)(3,)-∞--+∞ ;所以曲线在(,3),(3,6)-∞--内上凸,在(6,)+∞内下凸,点2(6,)27是拐点. (6)arctan 2arctan arctan arctan 2222221112(12)(1)(1)(1)x x x x y e x x x ey e e x x x '=⋅+-''=⋅-⋅=+++令 0y ''= 得 12x =当 12x <时,0y ''>,当12x >时,0y ''<,且 1arctan 21()2e f =,所以曲线在1(,)2-∞内向下凸,在1(,)2+∞内向上凸,点1arctan 21(,)2e是拐点. 2. 利用函数的凸性证明下列不等式:(1) e e 2x y +>2e x y+, x ≠y ;(2) x ln x +y ln y >(x +y )ln2x y +,x >0,y >0,x ≠y .证: (1) 令()e x f x =,则()e x f x '=,()0e xf x ''=>,所以函数()f x 的曲线在定义域(,)-∞+∞内是严格下凸的,由曲线下凸的定义有: ()(),()()22x y f x f y x y f x y ++∀≠<≠ 即 22e e ex y x y ++< 即2()2e e e x yx y x y ++>≠.(2) 令()ln f x x x =,则1()1ln ,()f x x f x x'''=+=当 0x >时,恒有()0f x >,所以()f x 的曲线在(0,)+∞内是严格下凸的,由曲线下凸的定义有, 0,0,,x y x y ∀>>≠有()()()22f x f y x y f ++>即ln ln ()ln222x x y x y x y+++> 即 ln ln ()ln 2x yx x y y x y ++>+.3. 当a ,b 为何值时,点(1,3)为曲线y =a 3x +b 2x 的拐点. 解: 因为32y ax bx =+是二阶可导的,所以在拐点处0y ''=,而232,62y a x b x y a x b'''=+=+ 所以 620a b += 又拐点(1,3)应是曲线上的点,所以3a b +=解方程6203a b a b +=⎧⎨+=⎩ 得 39,22a b =-=所以当39,22a b =-=时,点(1,3)为曲线32y ax bx =+的拐点. 4. 求下列曲线的渐近线:(1) y = ln x ; (2)y =22x -; (3) y = 23xx -; (4) y = 221x x -.解: (1) 0lim lim ln x x y x ++→→==-∞,所以ln y x =有垂直渐近线 0x =. 又 lim x y →+∞=+∞,但1ln lim lim lim 01x x x y xx y x x→+∞→+∞→+∞====,lim (0)x y x →+∞-⋅=∞,所以不存在水平或斜渐近线.(2) 220x x -=,所以有水平渐近线0y =,又2lim 0x x x y x -→∞→∞== ,所以没有斜渐近线,又函数22x y -=没有间断点,因而也没有垂直渐近线. (3) 221limlim 0331x x xxx x →∞→∞==--,所以有水平渐近线0y =,又函数23x y x ==-有两个间断点x x ==,且22,,3x x x xx x=∞=∞--所以有两条垂直渐近线x =x =又 21lim lim 3x x y x x →∞→∞==∞-,所以没有斜渐近线.(4) 2lim lim 21x x x y x →∞→∞==∞- ,所以没有水平渐近线,又 函数221x y x =-有间断点12x =,且212lim 21x x x →=∞-,所以有垂直渐近线12x =. 又 1limlim 212x x y x x x →∞→∞==- 2111l i m ()l i m ()l i m 22122(21)4x x x x x y x x x x →∞→∞→∞-=-==-- 所以有斜渐近线1124y x =+. 5.作出下列函数的图形: (1) f (x ) =21xx+; (2) ()2arctan f x x x =- (3) ()2,(0,)e xf x x x -=∈+∞. 解: (1) (i) 定义域为(,)-∞+∞.()()f x f x -=- ,故曲线关于原点对称.(ii) 21lim limlim 012x x x x y x x→∞→∞→∞===+ ,故曲线有渐近线0y =.(iii) 222222121,(1)(1)x x x x y x x +-⋅-'==++ 22223322423232(1)(1)2(1)222442(3)(1)(1)(1)x x x x x x x x x x x y x x x -+--⋅+⋅---+-''===+++,令0y '=即210x -=得驻点1x =±,又使0y ''=的点为0,x =.图4-1(2) (i) 定义域为(,)-∞+∞.又 ()arctan y x x x y -=-+=-,故为奇函数.(ii) 2arctan lim ,limlim (1)1,x x x y x y x x→±∞→±∞→±∞=∞=-=πlim ()lim (2arctan )(2)()π2x x y x x →±∞→±∞-=-=-±= 所以有渐近线πy x = .(iii) 222211,11x y x x -'=-=++ 2222222(1)(1)24,(1)(1)x x x x x y x x +--⋅''==++令 0y '=得驻点1x =±,又使0y ''=的点为0x =. 列表如下:图4-2(3) (i) 定义域为(,)-∞+∞,且()((,))f x C ∈-∞+∞. (ii) ()2(1),()2(2),e e xxf x x f x x --'''=-=-由()0f x '=得1x =,由()0f x ''=得2x =,把定义域分为三个区间 (,1),(1,2),(2,);-∞+∞(iv) lim ()0x f x →+∞=,故曲线()y f x =有渐近线0y =,lim ()x f x →+∞=-∞.(v) 补充点(0,0)并连点绘图,如图所示:图4-3。
第四章 消化系统习题及答案

3.消化管、消化腺
4.口腔、咽、食管、胃、小肠、大肠
5.脐与右髂前上棘连线的中、外1/3
6.贲门部、胃底、胃体、幽门部、贲门、幽门
7.盲肠、结肠、直肠、肛管
8. 十二指肠、空肠、回肠
二、选择题(单项或多项选择)
1.C 2.D 3.D 4.B 5.C 6.AB 7.BC 8.BD 9.ABCD 10.BCD 11.ACD 12.BCD
6.消化系统由口、咽、食管、胃、小肠、大肠构成。( )
7.咽是消化和呼吸系统共同的通道。( )
四.名词解析
1.内脏
2.肝门
3.肝外胆道系统
五.问答题
1、试论与小肠强大的消化吸收功能相适应的解剖结构有哪些?
第四章 消化系统习题答案一.填空题
1.胸腔,腹腔,盆腔,管道,消化系统,泌尿系统,生殖系统,呼吸系统
一、填空题
1.内脏是指主要位于( )、( )、和( )内,并有( )管道直接或间接与外界相同的器官。它包括( )、( )、( )和 ( )四大系统。
2.( )系统、( )系统、( )系统和( )系统合称为内脏。
3.消化系统包括( )和( )。
4.消化管包括( )、( )、( )、( )、( )和( )等器官。
三.判断题
1. × 2. √ 3. × 4. × 5. √ 6. × 7. √
四、名词解释
1.主要指位于胸腔、腹腔和盆腔内并有管道直接或间接与外界相通的器官,包括消化系统、呼吸系统、泌尿系统和生殖系统。
2.位于肝膈面中间的横沟处,是门静脉、肝动脉、肝管、淋巴管和神经出入肝的门户。
3.包括肝左管、肝右管、肝总管、胆囊、胆囊管和胆总管。胆汁出肝后,经肝外胆道系统运输至十二指肠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四章习题答案一、命名(1)2-丙醇 (2)环己醇 (3)2-甲基-3-戊醇(4)2-甲基-2-丙醇 (5)邻甲苯酚 (6)5-甲基-3-烯-2-己醇 (7)1,3,5-三苯酚 (8)1,3,5-三溴苯酚 (9)2-萘酚 (10)对硝基苯酚 (11)1,2,4-三苯酚 (12)对苯醚(13)二苯酮 (14)肉桂醛 (15)对苯二甲酸 (16)2-丁酮 (17)丙烯醛 (18)丁二醛 (19)环己酮 (20)2,2-二甲基丙醛 (21)肉桂醛(22)2-甲基丁酸 (23)丙烯酸 (24)顺丁烯二酸 (25)水杨酸 (26)乙酸乙烯酯 (27)乙二酸二乙酯 (28)乙丙酐 (29)乙酰胺 (30)N-甲基-N-乙基-乙酰胺 二、1、CH 3CH CH 2C H 2O HCH 32、C H 3C H C H C H 2O HC H 3C H 33、C H 2=C H -O-C H 2C H 2C H 2C H 34、C H 3O C H 2C H C H 3C H 35、C H 2=C HO C H=C H 26、H O C H 2-C-C H 2O HC H 2O HC H 2O H7、C H 2O H8、HOCH 2O HCH 3CH 39、N OH10、C H OO H11、C H =C H C H O12、C HCl 313、H 3CC O O C 2H 514、C H 2=C-C O O C H 3C H 315、C H 3-C-NOH 3C H 316、C H 3H 2-C H-C H 3C H 3O17、C H 2O H C HO HC H 2O H18、C O O HC O O H19、C H2-O-C-C H3C H2-O-C-C H3OO 20、C H2-O-C H221、B rB rB rO H22、C H2-C H-C H2O C l 23、C H3C H2C H2C HC NO H24、OH3C H325、C H3-C-C H-C H2C H3OC H326、C H3C H=C H-C H=N-N H27、C H3C HC-ClC H3O28、(C H3C H2C H2CO)2O29、C H3C-O-OC-ClO30、C H3-C-C H2C H3N-O H31、O HNO2 32、C HONO2 33、C-C H3ONO234、CCOOO35、O HNO2O2NNO2 36、C H2=C-C O O HC l三、鉴别1、在室温下加入卢卡试剂,出现浑浊的是2-甲基2-戊醇2、加入金属钠,发生反应的是苯甲醇3、加入金属钠,发生反应的是2-丁醇4、加入银氨溶液,发生银镜反应的是丙醛5、加入次碘酸钠,有沉淀生成的是2-戊醇6、加入银氨溶液,无现象的是丙酮,另二种样品加入希夫试剂,褪色的是甲醛7、加入卢卡试剂,立即浑浊的是叔丁醇,放置片刻浑浊的是异丙醇,室温无现象,加热才浑浊的是乙醇8、用PH试纸检验,显酸性的是乙酸,另二种样品加入银氨溶液,有银镜反应的是乙醛9、加入银氨溶液,发生反应的是苯甲醛10、加入三氯化铁溶液,显色的是水杨酸,另二种加入碳酸钠加加热,发生反应有气泡的是苯甲酸11、加入硝酸银的乙醇溶液,有沉淀生成的是乙酰氯,另三种加碳酸钠,有气泡的是乙酸,余下二种加入氢氧化钠,有气泡生成的是乙酰胺,无现象的是乙酸乙酯12、加入次碘酸钠,有沉淀生成的是乙醇13、加入三氯化铁溶液,显色的是苯酚,余下的样品加入金属钠,有气泡生成的是1-苯基乙醇14、加入2,4-二硝基苯肼,无现象的是2-丁醇,余下样品加入银氨溶液,发生反应的是丁醛15、加水,有气泡生成的是乙酰氯,无现象的是氯乙酸16、加入次碘酸钠,有沉淀生成的是2-戊酮17、加入银氨溶液,发生银镜反应的是甲酸,余下样品加入高锰酸钾,褪色的是丙烯酸18、加入银氨溶液,发生反应的是苯甲醛,余下样品中加入碳酸钠,有气泡生成的是苯甲酸19、加入银氨溶液,发生反应的是甲酸,余下样品加热产生气体通入澄清石灰水,变浑浊的是丙二酸20、加入高锰酸钾,无现象的是乙酸,余下的为乙二酸四、分离混合物1、加少量水,用分液漏斗分液2、加浓硫酸,乙醚溶于浓硫酸中3、加入氢氧化钠溶液,苯酚和苯甲酸溶解,再通入二氧化碳,苯酚钠生成苯酚而分离4、加入次碘酸钠,2-戊酮发生反应有沉淀生成5、加入氢氧化钠溶液,溶解后通入二氧化碳,苯酚分离出6、加入氢氧化钠,分离出环己酮,再通入二氧化碳,分离出苯酚,再加入碳酸氢钠,苯甲酸生成苯甲酸钠溶解7、先加氢氧化钠溶解,通入二氧化碳,邻甲苯酚不溶于水8、加入金属钠,1-戊醇溶解,加饱和亚硫酸氢钠,戊醛生成沉淀分离9、加入饱和亚硫酸氢钠,分离出丁醛,再加入浓硫酸,丁醚溶解10、加入饱和亚硫酸氢钠,环戊酮生成沉淀11、加入氢氧化钠,苯酚溶解12、加入氢氧化钠,苯甲酸、苯酚溶解,通入二氧化碳分离出苯酚,另二种样品中加浓硫酸,丁醚溶解于浓硫酸中13、加入碳酸氢钠,正丁酸溶解,加入氢氧化钠,正戊醇溶解五、1、丙二酸﹥甲酸﹥丁酸﹥丁二酸﹥乙酸乙醇2、三氟乙酸﹥三氯乙酸﹥氯乙酸﹥乙酸3、对硝基苯甲酸﹥苯甲酸﹥邻硝基苯酚﹥苯酚﹥对甲基苯酚4、苦味酸﹥2,4-二硝基苯酚﹥邻硝基苯酚﹥苯酚﹥对甲基苯酚六、1、甲醇﹥乙醇﹥异丙醇﹥叔丁醇2、甲醛﹥乙醛﹥丙酮﹥2-戊酮﹥苯甲醛﹥二苯酮3、乙酰氯﹥乙酸酐﹥乙酸乙酯﹥乙酰胺4、A:2,2-二甲基丁醇﹤2,3-二甲基丁醇﹤2-甲基戊醇﹤3-甲基戊醇﹤正己醇﹤正庚醇B:乙醇﹤甘醇﹤2-甲氧基-1,3-丙二醇﹤3-甲氧基-1,2-丙二醇﹤甘油C:丁烷﹤乙醚﹤氯丁烷﹤丁醇﹤丁酰胺﹤丁酸七、1、C H3C HC H2C H3O H224140C H3C HC H2C H3C H3C HC H2C H3O2、C H2C H3Cl2C H C H3l3、C H3C H C H2C H3OHC H3C C H2C H3O4、OH+HC l l5、C H2-C H2OC H2C H2O H C lH2O H C H2N H2H2O H C H2O C H2C H3C H2O H C H2O H6、O HO HN O2+O HN O2OHB rB rB rO-C-C H3OOHO HO-C H3O7、C H3C H=C H2Cl2500C H2C H=C H2C lH ClOC H2C H-C H2C l O H C lC a(O H)260C H2-C H-C H2O H O H C lN a O HC H2-C H-C H2O H O H O H8、C H2=C H C H3C H OH2C H3C H2Cl2C H Cl39、(C H3)3C C Na O H(C H3)3C C O O H+(C H3)3C C H2O H10、(C H3)3CC HO+HC HO NaO H(C H3)3CC H2O H+HCO O Na11、C H3C H2C HO+C H3C H2Mg Br C H3C H2C HC H2C H3O Mg Br12、(C H3)2C HO H227H+(C H3)2C HOZn-HgHC H3C H2C H313、CH3CH2CH2O HK M n O4H+CH3CH2CO ONH33CH2CO N H2O H2CH3CH2NH214、(C H3)2C HC O O2(C H3)2C HC ClOK O H2(C H3)2C HC O O HKO H25(C H3)2C HC-O C2H5O15、C H3CO O C2H5+C H3C H2MgBrC2H5O C2H5C H3-C-O-C2H5O MgBrC H2C H316、C H3C H2C HC H3O C H3HIC H3I+C H3C H2C HC H3O H17、C H3C H2C HC H3O HNaIO C H3C H2C HC H3HNaIOC H3C H2CO O Na+C HI3八、1、C H3C HC H2C H3BrNaB H42C H3C HC H2C H3O H2、C H2=C HC H2C H3H+C H3C HC H2C H3O H3、C H3C C H2C H3ONa B H4C H3C HC H2C H3O H4、C H3C HO+C H3C H2Mg X C H3C HC H2C H3O H九、1、C H2C H22H3C HO Na O H C H3C H=C HC HO H3C H2C H2C H2O H2、C H2C H222H3CC H3C H2Mg XC H3C H2-C-O Mg XHC H3 H+C H3C H2C HC H3O H24C H3C H2C H=C HH B r22C H3C H2C H2C H2B rC H3C H2C H2C H2O H十、1、C HO+HC N C HO HC N2、C C H3O+C6H5N H N H2C6H5C C H3N N HC6H53、C HO+Na HS O3C HO HO3Na4、C C H3OC I3O O Na+C HI35、C HO+HC HO Na O HHO2C H2O H+HC O O Na十一、二醇内分子间氢键最强,故沸点最高,一醇次之,醚类分子间无氢键存在,故沸点最低十二、1、O H25%H NO3O HNO2+HO NO22、O H Br2O HBrBrBr3、O H24O HSO3H+O HSO3H十三、1 C6H5C HO +C H3C C H2C H2C HOZn-HClC6H5C H3+C H3C H2C H2C H2C H3C6H5C HOC6H5Mg BrC6H5C HO Mg BrC6H52、C H3C C H2C H2C H3O65C6H5-C-O Mg BrC H3C H2C H2C H33、C6H5C HOAg(N H3)2O HC6H5C O O N H4+Ag+22N H33+HO2C H3C C H2C H2C H3OAg(N H3)2O H4、C6H5C HOC H3C C H2C H2C H3O4C6H5C O O HK Mn O4C H3C O O H+C H3C H2C H2C O O H+C H3C H2C O O H+HC O O H5、C6H5C HOC H3C C H2C H2C H3OC6H5C H652N-N HC6H5C6H5N H N H2C H3C H2C H2C=N-N HC6H5C H36、C6H5C HOC H3C C H2C H2C H3OC H3C H2O H2C6H5C H(O C H2C H3)2C H3C H2O H7、C6H5C HOC H3C C H2C H2C H3O3C6H5C HO HS O3NaC H3C H2C H2C-C H3O HS O3Na8、C6H5C HOC H3C C H2C H2C H3OBr2Br2Na O H C HBr39、C6H5C HOC H3C C H2C H2C H3ONa O HNa O HC6H5C O O Na+C6H5C H2O HC H3C H2C H2C-C H2-C C H2C H2C H3C H3HO10、C6H5C HOC H3C C H2C H2C H3OC6H5C H2O HH2H2C H3C HC H2C H2C H3O H十四、1、C H3C H2C H2C HO4C H3C H2C H2C O O H2、C H3C H2C H2C HO4C H3C H2C H2C O O HC H3C C H2C H2C H3O3C H3C H2C H2C O O H+HC O O H3、C H3C H2C H2C H=C HC H2C H2CD H34HC H3C H2C H2CO O H4、C H3C H2C H2BrHC NC H3C H2C H2C N+H3C H2C H2C NOH+C H3C H2C H2C O O H十五、1、醛2、酮3、乙醇、具有C H3C H(R)-O H结构的醇十六、1、C H3C H2O HNa C NC H3C H2C NH+H3C H2C O OH2C H3C H2C H2O H24C H3C H=C H2(O)C H3C C H3OC H3C H2C H2O H HBr H3C H2C H2BrM g2525C H3C H2CH2H3C H2C H2C C H3O HC H32、C H2C H222C H3C HO Na O H C H3C H=C HC HOH2H3C H2C H2C H2O H3、C H2=C H C H326C H3C H2C H2)3HO2H3C H2C H2O H24H3C H2C H2O C H2C H2C H34、C H2C H22C H2-C H2OH+C H2-C H2O H O H324C H2O C H3C H2O C H35、C HC H HC N C H2=C HC NH+C H2=C HCO OC H3O HC H2=C HCO O C H36、C H 2=C HC H 3HO 24C H 3C HC H 3O HC H 3C C H 3OHC NC H 3-C-C H 3O H C N24C H 2=C-C H C O O HH 2C H 3C HC H 3C O O H7、C HH 2H 2Mg ClH 2C O O H8、C H 3CH 2O H(O)C H 3C O O C H 2C O O HC lNa C NC H 2C O O HC N2524C H 2C O O C 2H 5C O O C 2H 59、C H 2=C HC H HO 2C H 3C HC H 3O H H 3C C H 3O C H 2=C HC H 3H BrC H 3C HC H 3BrM g2525C H 3C HC Mg BrH 3-C H-C-C H 3C H 3C H 3O H10、C H 3-C H=C HHO 24C H 3C HC H O HH 3C C H 3OrM g2525Mg BrC O Mg Br C H 3C H 3C O H C H 3C H 311、C H2=C H2HO2H3C H2O HC uC H2=C H2H B rC H3C H2Br2525C H3C HOC H3C H2MgBrC H3C HC H2C H3O Mg Br H+C H3C HC H2C H3O HH3C HC H2C H3O12、C HOO HO Cl 3H3C CO13、C H2=C HC H4H3C O O HLiAl H4C H3C H2O H24170C H2=C H HB r H3C H2BrM g2525C H3C H2Mg BrC H2=C HC H3HB r22H3C H2C H2Na O HCH3C H2C H2O H3C H2C HO+C H3C H2C HC H2C H3O HC H3C H2C C H2C H3O14、C H3C H=C H26C H3C H2C H2O H C H3C H2C HOC H3C H=C H2H C l C H3C HC H3C lM g2525(C H3)2C H Mg ClH+C H3C H-C H-C H2C H3C H3O H15、C H4Cl2C H3HO2O HH3O H24C H3O C H316、C H3C H2C H3Cl2H3C HC HC l24C H2=C HC H3Cl2H2=C HC H2ClHClO C H2-C H-C H2C l O H C l O H C H2-C H-C H2O H O H O H3C H2-O-NO2C H-O-NO2C H2-O-NO217、C H3C H2O HBrHC H3C H2Br25C H3C H2C O O HC H3C H2O H24C H3C H2C O O C H2C H3Na C NC H3C H2C NH+218、C H3C H2C H2C H2O H HBr C H3C H2C H2C H2BrNa C N25C H3C H2C H2C H2C NH+2C H3C H2C H2C H2C O O H2H3C H2C H2C HC O O HC lH2S O4C H3C H2C H=C HC O O H十七、1、A:C H3C HC HC H3O H C H3 B:C H3C C HC H3O C H3 C:C H3C H=CC H3C H3C H3C H=C(C H3)24C H3C O O H+C H3C C H3OC H3-C H-C H-C H3H C H324C H3C H=C(C H3)2C H3-C H-C H(C H3)2O HC H3-C-C H(C H3)2O2、A:C H3C H2C H2C H2BrB:C H3C H2C H=C H2C:C H3C H2CO O HD:C H3C H2C HC H3B r3、A:O C H3B:O HC:C H3IO C H O HC H3IH I+C H3I+Ag NO3AgI+C H3NO34、A:C H3C H2C H2C H2O HB:C H3C H2C H2C H2ClC:C H3C H2C H=C H2 D:C H3C H2C HC H3C lE:C H3C H2CO O HC H 3C H 2C H 2C H 2O H SO Cl 2H 3C H 2C H 2C H 2Cl C H 3C H 2C H 2C H 2O H 24C H 3C H 2C H=C H 2C H 3C H 2C H 2C H 2Cl C H 3C H 2C H=C H 2Na O H C H 3C H 2C H=C H 2H C l C H 3C H 2C HClC H 3C H 3C H 2C H=C H 2K Mn O 4C H 3C H 2C O O H255、H 3C-C-C H 2-C H=C H 2O6、HOC H=C HC O O H7、HOC C H 3OHOC C H 3O+NO 2NO 2N H N H 2HOC C H 3N N HO 2N NO 2HOC-O Na OHOC C H 3O+Na O I3+C HI 38、A :H 3C OC H 2CC H 3OB :H 3C OC H 2C HC H 3O HC:HO C H2C C H3OD:HO C H2C H2C H3HO C H2C H2C H3H3C O C H2C C H3O4C H2C HC H3O HH3C OH3C O C H2C C H3OIHO C H2C C H3OZn-HgH9、甲:C H3HC H3O HC H3乙:C H3C C H(C H3)2O丙:C H3C H=C(C H3)2C H3C HC HC H3O H C H3C H3C C H(C H3)2OC H3C C H(C H3)2O+H2N N HC6H5C H3-C=N-N HC6H5C H(C H3)2C H3C C H(C H3)2O+Na O I3(C H3)2C HC-O-NaO+C HI3C H3C HC HC H3O H C H3H2SO4C H3C H=C(C H3)2C H3C H=C(C H3)24C H3C O O H+C H3C C H3O10、A:C H3C H2CO O HB:C H3C H2O HC:C H3C H2BrD:C H3C H2C NC H3C H2C O O HC H3C H2O H C H3C H2BrC H3C H2C NC H3C H2C-O C2H5OC H3C H2C O O H+C H3C H2O H3C H3C H2Br+K C N+HB rC H3C H2C N H+11、甲:C H 3-C-O-C H=C H 2O 乙:C H 2=C H-C-O C H 3O12、A :C H 3C H 2CO O HB :HC-O-C H 2C H 3O C :C H 3-C-O -C H 3O13、H 3C-C-C H 2C H 2C O O HO14、A :C H 3C H 2C H 2C N H 2OB ;C H 3C H 2C N HC H 3OC ;C H 3C NHC H 2C H 3O15、A :C H 3-C-C H-C H 3C H 3O H C H 3B :C H 3-C=C H-C H 3C H 3C H 3C :C H 3-C-C H 3O16、A :C H 3-C=C H-C H 2-C H 2-C-C H 3C H 3OB :HO O C-C H 2-C H 2-C-C H 3O。
