第二章 插值b
计算方法-插值b

…………
2
f [ x , x 0 , x1 ]
x x1
f [ x , x 0 , ... , x n 1 ] f [ x 0 , ... , x n ] ( x x n ) f [ x , x 0 , ... , x n ]
n1
1
←
←
3
←……
←
n1
f ( x ) f ( x 0 ) f [ x 0 , x 1 ]( x x 0 ) f [ x 0 , x 1 , x 2 ]( x x 0 )( x x 1 ) ...
(k+1)阶差商:
f [ x0 , x1 , ... , xk ] f [ x1 , ... , xk , xk 1 ] f [ x0 , ... , xk 1 ] x 0 x k 1 f [ x0 , ... , xk 1 , xk ] f [ x0 , ... , xk 1 , xk 1 ] x k x k 1
( )
实际计算过程为
x0 x1 x2 …
xn1 xn
k !
, ( x min , x max )
f (x0) f (x1) f (x2) … f (xn1) f (xn)
xn+1 f (xn+1)
f [x0, x1] f [x1, x2] …… …… f [xn1, xn] f [xn, xn+1]
f [x0, x1 , x2] …… …… f [xn2, xn1, xn] f [xn1, xn, xn+1]
f [x0, …, xn] f [x1, …, xn+1]
f [x0, …, xn+1]
第2章插值法

2.1 引 言
2.1.1 插值问题的提出
许多实际问题都用函数 y= f(x)来表示某种内在 规律的关系,其中相当一部分函数是通过实验或观 测得到的. 虽然f(x)在某个区间[a , b] 上是存在的, 有的还是连续的,但却只能给出[a , b] 上一系列点 的xi函数值yi=f(xi) (i=0,1,...,n),这只是一张函数表. 有的函数虽有解析表达式,但由于计算复杂,使用 不方便,通常也造一个函数表,如大家熟悉的三角 函数表、对数表、平方根和立方根表等.
上页 下页
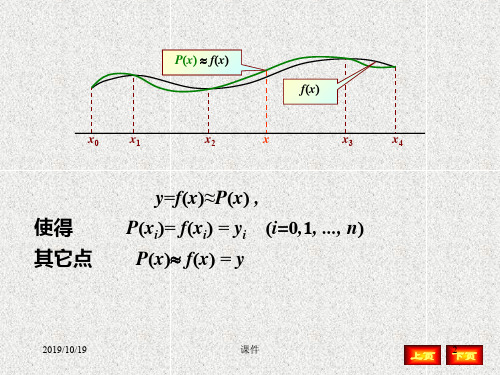
从几何上看,插值法就是求曲线 y=P(x), 使其 通过给定的n+1个点(xi, yi), i=0,1, … ,n,并用它近似 已知曲线y=f(x),见下图.
上页 下页
2.1.2 多项式插值
设在区间[a , b]上给定n+1个点
a≤x0<x1<…<xn≤b
上的函数值yi=f(xi), (i=0,1,…,n),求次数不超过n的 多项式(1.2),使
对n=1及n=2时的情况前面已经讨论. 用类似 的推导方法,可得到n次插值基函数为
lk
(
x)
(x ( xk
x0 x0
) )
( x xk1 )( x xk1 ) ( x xn ) ( xk xk1 )( xk xk1 ) ( xk xn )
(k 0,1, ,n)
(2.8)
上页 下页
显然它满足条件(2.7). 于是,满足条件(2.6)的插值多
(x
xk )
(点斜式)
(2.1)
L1 ( x)
yk
xk1 x xk1 xk
yk1
x xk xk1 xk
数值分析第二章 插值法

(j,k=0,1,…,n)
( x x0 )( x xk 1 )( x xk 1 )( x xn ) lk ( x ) ( xk x0 )( xk xk 1 )( xk xk 1 )( xk xn )
n1 ( x ) ( x xk ) n1 ' ( xk )
n
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
• 性质 (2)k阶均差可重新写为:
f [ x1 , x2 ,, xk ] f [ x0 , x1 , xk 1 ] f [ x0 , x1 , xk ] xk x0
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
类似地称 2 f k f k 1 f k 为 xk 处的二阶差分. 一般地称 n f k n1 f k 1 n1 f k 为 xk 处的n阶差分.
• 均差与差分关系
• 牛顿前插公式
n f k (1) f nk j , j 0 j
求5、6月份的日照时间的变化规律。 • 多项式插值的存在唯一性
一、引言
2.多项式插值
• 一个例子 日照时间的变化设为 y(x)=a0+ a1x + a2x2, 根据三组数据: (1, 13.53), (31, 14.21),(61, 14.40), 导出关于a0,a1,a2的线性方程组
a0 a1 a2 13.53 2 a0 31a1 (31) a2 14.21 2 a0 61a1 (61) a2 14.40
三、均差与牛顿插值
3.差分形式的牛顿插值公式
若x0,x1,…,xn 为等距节点,即xk=x0+kh (k=0,1,...,n) 时,可将牛顿插值公式简化
第二章 插值方法

x0
x1
x2
x3
x4
x
插值多项式的存在唯一性
利用范德蒙行列式及克莱姆法则证明
插值基函数
由线性空间Pn(x)的不同基底出发构造满足插
值条件的多项式的方法称为基函数法; 基函数法求插值多项式的步骤有两个:1、首 先定义n+1个线性无关的特殊代数多项式, 称为插值基函数,其次利用插值条件确定n次 插值多项式的系数。
Pn ( x) a0l0 ( x) a1l1 ( x) anln ( x)
其中a0、a1、 、an为待定参数
令
即
Pn ( xi ) f ( xi ) yi
i 0,1,2 ,, n i 0,1,2 ,, n
a l (x )
j 0 j j i
n
yi
ai yi
当p(x)为多项式时,该插值方法称为代数多项式插值, p(x)为插值多项式。
插值问题的提法
已知y=f(x)的函数表,且xi(i=0,1,…,n)两两互异,
x y x0 x1 …xn y0 y1 …yn
xi a, b ,求次数不超过n的多项式
Pn ( x) a0 a1 x a2 x 2 ... an x n
则f ( x)的二次Lagrange 插值基函数为
( x x1 )( x x2 ) ( x 169 )( x 225 ) l0 ( x ) ( x0 x1 )( x0 x2 ) 2025 ( x x0 )( x x2 ) ( x 144 )( x 225 ) l1 ( x ) ( x1 x0 )( x1 x2 ) 1400 ( x x0 )( x x1 ) ( x 144 )( x 169 ) l2 ( x ) ( x2 x0 )( x2 x1 ) 4536
第2章1-4节 插 值 法

12
图2-3
13
2.
n次插值多项式
根据插值的定义
Ln ( x j ) y j
Ln (x) 应满足
( j 0,1, , n).
为构造 L
n
( x),
先定义 n 次插值基函数.
14
定义1 若
n 次多项式 L j ( x) ( j 0,1, , n) 在 n 1 个节点
x0 x1 xn
b, Ln ( x)
( n1)
定理2 设 f
(n)
( x)
( x ) 在 ( a, b) 内
存在,节点 a x0 x1 xn
是满足条件
的插值多项式,则对任何 x [a, b] ,插值余项
Rn ( x) f ( x) Ln ( x) f
( n 1
( )
(n 1)!
11
显然,lk (x) 及 lk 1 ( x) 也是线性插值多项式,在节点 xk 及 上满足条件
lk ( xk ) 1, lk 1 ( xk ) 0, lk ( xk 1 ) 0, lk 1 ( xk 1 ) 1,
xk 1
称
lk (x) 及 lk 1 ( x) 为线性插值基函数, 图形见图2-3.
( xk 1 , yk 1 )
的直线. 如图2-2.
图2-2
10
由
L1 ( x)
的几何意义可得到表达式
yk 1 y k xk 1 xk ( x xk )
L1 ( x ) yk
(点斜式), (两点式),
L1 ( x )
xk 1 x xk 1 xk
yk
x xk xk 1 xk
第2章_插值法

13.214 285 71
175 13.228756555322952...
考虑通过 + 1个节点0 < 1 < ⋯ < 的次插值
多项式 (),满足条件
= ,
= 0,1, … ,
希望找到 li(x),i = 0, …, n, 使得
= ; = ,
n次插值多项式, 插值节点为{ xi }in 0 [ a , b],则x [ a , b],有
f ( n 1) ( )
Rn (x )
n 1 ( x)
Lagrange型余项
(n 1)!
n
其中 n 1 ( x ) ( x xi ) , ( a , b) , 且依赖于 x.
满足条件P(xi) = f(xi) (i = 0, … n)。 P(x) 称
为f(x) 的插值函数。
P(x) f(x)
x0
x1
x2
x
x3
x4
定理1:设插值节点 ≠ ( ≠ ),则满足条件
= , = 0,1, … , 的插值多项式
= 0 + 1 + ⋯ +
− , , + 线性无关。
二次插值多项式
= − − + + + + ()
满足 = ( = − , , + )
例1:
已知 f ( x )满足 f (144) 12 , f (169) 13, f ( 225) 15
i 0
一次及二次差值余项
1 ′′
1 = − 0 − 1 ,
第2章 插值法

2.3.2 均差及其性质
差商的基本性质:
由(3.4)得差商表:
k xk f(xk) 一阶差商 二阶差商 三阶差商 …
0 x0 f(x0) 1 x1 f(x1) 2 x2 f(x2) 3 x3 f(x3) 4 x4 f(x4) ┆ ┆┆
f[x0, x1] f[x1, x2] f[x2, x3] f[x3, x4]
。
1.0
这说明用高次插值多项
式Ln(x)近似f(x)效果并不
0.5
好,因而通常不用高次
插值,而用分段低次插值。
-5
0
5x
二、分段线性插值 所谓分段线性插值就是用通过插值点的折线段逼近f(x).
二、分段三次埃尔米特插值 分段线性插值函数导数间断,若已知节点上函数值和
导数,可构造一个导数连续的插值函数Ih(x),满足
yk
0
xk
y=L1(x) y=f(x)
yk+1
xk+1
x
y
1 1 图 2-3
1
0
xk
xk+1
x
几何上就是通过三点(xk-1,yk-1),(xk,yk),(xk+1,yk+1)的抛物线。
y 1
0
Xk-1
x xk Xk+1
图 2-4
2.2.2 拉格朗日插值多项式
需要指出(2.3)式与(2.5)式是当n=1和n=2时的特殊 情形。
例1 已知sin0.32=0.314567, sin0.34=0.333487, sin0.36=
0.352274,用抛物插值计算sin0.3367的值, 并估计误差.
§2.3 差商与牛顿插值
2.3.1 插值多项式的逐次生成
第二章插值法

线性插值的几何意义:用 通过点 A(x0 , f (x0 )) 和 B(x1, f (x1 )) 的直线近似地代替曲线 y=f(x)由解析几何知道, 这条直线用点斜式表示为
y=f(x)
p(x)=ax+b
A(x.0,f(x.0)) B(x.1,f(x.1))
p(x)
y0
y1 x1
y0 x0
(x
x0 )
解: 用待定系数法, 将各节点值依次代入所求多项式, 得
解上述方程, 将求出的a0, a1, a2 代入 p(x) = a0 + a1x + a2x2 即得所求二次多项式
例2.5 求过点(0,1)、(1,2)、(2,3)的三点插值多项式
P(x) an x n an1 x n1 a1x a0
满足
P(x) an x n an1 x n1 a1 x a0 P(xi ) f (xi ) (i 0,1,2, , n)
则称P(x)为f(x)的n次插值多项式。这种插值法通常称
为代数插值法。其几何意义如下图所示
y y=P(x) y=f(x)
lk ( xi ) ki
1 0
(i k ) (i k )
l0 (x) 与 l1(x) 称为线性插值基函数。且有
lk (x)
1 j0
x xj , xk x j
jk
k 0,1
于是线性插值函数可以表示为与基函数的线性组合
p(x) l0 (x) y0 l1 (x) y1
例2.1 已知 100 10 , 121 11 , 求 y 115
为已知 f (x0 ), f (x1), , f (xn ) ,即 yi f (xi ) 若存在一个
f(x)的近似函数 (x),满足
第二章插值(2012)

( 2 . 1 . 3 ) ( 反复使用 )
( t ) f ( t ) L n ( t ) k ( x ) ( t x 0 ) ( t x 1 ) ( t x n ),
Rolle 定理
( n 1)
有 ( x 0 , x n ), 使 故 k (x) 误差限 f
解上述方程组得
y1x0 y0x1 a0 x0 x1
y0 y1 a1 x0 x1
y x y x y x x x x 1 0 0 1 y 0 1 0 1 L ( x ) x y y 1 0 1 x x x x x x x x 0 1 0 1 0 1 1 0
五、Lagrange算法: step1:输入插值节点数n,插值点序列(xi,yi),i=0,1, …n,
待计算的函数点x;
step2: for i=0 to n {{ 2.1 for j=0 to n /*对于给定的x计算基函数li(x)*/ if(j!= i) temp=temp*(x-xj)/(xi-xj);
2 . 插值多项式的存在唯一 性 定理 2 .1 :在 n 1 个 互异 x k 处满足插值条件 p x x k 0 , 1 ,2 ,....., n ) n( k)f ( k) (
的次数不超过 n 的多项式 p x ) 存在且唯一 n(
证:
设 p n ( x ) a 0 a 1 x ...... a n x n . 代入插值条件得 :
§2.2 Newton插值公式
一.差商 1.定义
f x 0 , x1 f ( x1 ) f ( x 0 ) 为 f 在 x 0 , x1的一阶差商(均差) x1 x 0
第2章 插值法(演示)

第二章 插值法在科学研究与工程技术中,常常遇到这样的问题:由实验或测量得到一批离散样点,要求作出一条通过这些点的光滑曲线,以便满足设计要求或进行加工。
反映在数学上,即已知函数在一些点上的值,寻求它的分析表达式。
此外,一些函数虽有表达式,但因式子复杂,不易计算其值和进行理论分析,也需要构造一个简单函数来近似它。
解决这种问题的方法有两类:一类是给出函数()f x 的一些样点,选定一个便于计算的函数()x ϕ形式,如多项式、分式线性函数及三角多项式等,要求它通过已知样点,由此确定函数()x ϕ作为()f x 的近似,这就是插值法;另一类方法在选定近似函数的形式后,不要求近似函数过已知样点,只要求在某种意义下在这些样点上的总偏差最小。
这类方法称为曲线(数据)拟合法。
设已知区间[,]a b 上的实值函数f 在1n +个相异点[,]i x a b ∈处的函数值(),0,1,,i i f f x i n == ,要求构造一个简单函数()x ϕ作为函数()f x 的近似表达式()()f x x ϕ≈使得()(),0,1,,i i i x f x f i n ϕ=== (2-1)这类问题称为插值问题。
称f 为被插值函数;()x ϕ为插值函数;0,,nx x 为插值节点;(2-1)为插值条件。
若插值函数类{()}x ϕ是代数多项式,则相应的插值问题为代数插值。
若{()}x ϕ是三角多项式,则相应的插值问题称为三角插值。
若{()}x ϕ是有理分式,则相应的插值问题称为有理插值。
§1 Lagrange 插值1.1 Lagrange 插值多项式设函数f在1n +个相异点01,,,n x x x 上的值(),0,1,i i f f x i n == 是已知的,在次数不超过n 的多项式集合n P 中,求()n L x 使得(),0,1,,n i i L x f n n == (2-2)定理1 存在惟一的多项式n nL P ∈满足插值条件(2-2)。
第二章 插值法-数值分析

1 1
x0 x1
2 n x0 x0 2 n x1 x1
2 n 1 xn xn xn Nhomakorabea
0 i j n
( x j - xi ) 0
由克莱默法则知,方程组有唯一解 a0 , a1 , , an .
§2 Lagrange Polynomial
唯一性的另一证明 满足 P( xi ) yi , i 0, ... , n 的 n 阶插 值多项式是唯一存在的。
分别利用x0, x1 以及 x1, x2 计算
x0
利用 x1 , x2
4
3
~ 5 0 . 00538 R 0.00660 sin 50 0.76008, 1 18
内插 /* interpolation */ 的实际误差 0.00596
§1 Lagrange Polynomial
i 0 n
多项式,其中 p( x )可以是任意多项式。
Interpolation polynomial
2-2 线性插值与抛物插值 1. 线性插值
f (x)
(x0 ,y0) (x1 ,y1)
P1(x)
x0
x1
y1 - y 0 ( x - x0 ) 直线方程为: y - y 0 x1 - x0 x - x0 x - x1 等价变形为: y x - x y 0 x - x y1 0 1 1 0
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
记为: L1 ( x)
引入记号:
x - x1 l 0 ( x) , l1 ( x) x - x0 x0 - x1 x1 - x0
第2章 插值法(1)

现要构造一个二次函数
φ(x)=P2(x)=ax2+bx+c 近似地代替f(x),并满足插值原则(4―2)
《 数 值 分 析 》
(2―6) (2―7)
P2(xi)=yi, i=0,1,2,… 由(2―7)式得
2 ax0 bx0 c y0 2 ax1 bx1 c y1 ax 2 bx c y 2 2 2
(2―5)
第2章 插值法
2.2 二次插值
二次插值又称为抛物线插值,也是常用的代数多项 式 插 值 之 一 。 设 已 知 函 数 f(x) 的 三 个 互 异 插 值 基 点
《 数 值 分 析 》
x0,x1,x2的函数值分别为y0,y1,y2,见下表所示:
x y
xo y0
x1 y1
x2 y2
第2章 插值法
(2―15)
第2章 插值法
显然
0, j i li ( x j ) , i, j 0,1,2, 1, j i
,n
《 数 值 分 析 》
(2―14)式的Pn(x)是n+1个n次多项式li(x)(i=0,1,2,…,n)的 线性组合,因而Pn(x)的次数不高于n。我们称形如多项式 (2―14)的Pn(x)为拉格朗日插值多项式。Pn(x)还可以写成下 列较简单的形式:
f ( n ) ( x0 ) ( x x0 ) n n!
第2章 插值法
取前n+1项的部分和Pn(x)作为f(x)的近似式,也即
Pn ( x ) f ( x0 ) f ( x0 )( x x0 )
《 数 值 分 析 》
f ( n ) ( x0 ) ( x x0 ) n n!
第二章:插值法

满足(2.1)式的 l i(x) 是否存在?若存在,具有什么形式呢?
先考虑 l0(x)。因 l0(x)是以 x1, x2 为零点的二次多项式,
所以它可写成 l0(x)= 0(x -x1)(x -x2), 其中0 是待定系 数。 又因为 l0( x0)=1,所以0(x0-x1)(x0-x2)=1,则可有
n
| x - xi |
i=0
作为误差估计上限。
当 f(x) 为任一个次数 n 的多项式时, f (n1)( x) 0,
可知 Rn ( x) 0 ,即插值多项式对于次数 n 的多项式 是精确的。
例1 求经过A(0,1),B(1,2),C(2,3)三个插值点的插值多项式. 解:三个插值节点及对应的函数值为
-
3
);
1 2
cos x
3 2
0.00044
R2
5
18
0.00077
sin 50 = 0.7660444…
2次插值的实际误差 0.00061
高次插值通常优于 低次插值
但绝对不是次数越 高就越好,嘿 嘿……
例3 考虑下述的插值法问题:求二次多项式P(x),满足 P(x0) = y0, P(x1) = y1,P(x2 ) = y2, 其中 x0 x2,y0、y1、y2 是已给的数据并给出使这一问题的解存在且唯一的条件.
x0 )(x -
x1 ),
[ x0 , x1 ]
当n = 2时 , 抛 物 插 值 的 余 项 为
R2 ( x) =
1 6
f ( )( x -
x0 )(x -
x1 )(x -
x2 ),
[x0 , x2 ]
注: 通常不能确定 x , 而是估计 f (n1)( x) Mn1 , x(a,b)
数值分析课件-第02章插值法

目录
• 插值法基本概念与原理 • 拉格朗日插值法 • 牛顿插值法 • 分段插值法 • 样条插值法 • 多元函数插值法简介
01 插值法基本概念与原理
插值法定义及作用
插值法定义
插值法是一种数学方法,用于通过已知的一系列数据点,构造一个新的函数, 使得该函数在已知点上取值与给定数据点相符,并可以用来估计未知点的函数 值。
06 多元函数插值法简介
二元函数插值基本概念和方法
插值定义
通过已知离散数据点构造一个连 续函数,使得该函数在已知点处
取值与给定数据相符。
插值方法分类
根据构造插值函数的方式不同, 可分为多项式插值、分段插值、
样条插值等。
二元函数插值
针对二元函数,在平面上给定一 组离散点,构造一个二元函数通 过这些点,并满足一定的光滑性
差商性质分析
分析差商的性质,如差商 的对称性、差商的差分表 示等,以便更好地理解和 应用差商。
差商与导数关系
探讨差商与原函数导数之 间的关系,以及如何利用 差商近似计算导数。
牛顿插值法优缺点比较
构造简单
牛顿插值多项式构造过程相对简 单,易于理解和实现。
差商可重用
对于新增的插值节点,只需计算 新增节点处的差商,原有差商可 重用,节省了计算量。
要求。
多元函数插值方法举例
多项式插值
分段插值
样条插值
利用多项式作为插值函数,通 过已知点构造多项式,使得多 项式在已知点处取值与给定数 据相符。该方法简单直观,但 高阶多项式可能导致Runge现 象。
将整个定义域划分为若干个子 区间,在每个子区间上分别构 造插值函数。该方法可以避免 高阶多项式插值的Runge现象 ,但可能导致分段点处的不连 续性。
数值分析--第2章插值法
2019/10/19
课件
上页 下2 页
2.1 引言
2.1.1 插值问题
设 y= f(x) 是区间[a , b] 上的一个实函数, xi ( i=0,
1, ... ,n)是[a,b]上n+1个互异实数,已知 y=f(x) 在 xi 的
值 yi=f(xi) (i=0,1,...,n), 求一个次数不超过n的多项式
由克莱姆法则知方程组 (5-3) 的解存在唯一. 证毕。
2019/10/19
课件
上页 下7 页
2.2 拉格朗日插值
2.2.1 基函数
考虑最简单、最基本的插值问题. 求n次插值多项式 l i(x) (i=0,1, …,n), 使其满足插值条件
Lagrange 法1736-1813
0, ji li(xj) 1, ji (j0,1, ,n )
称为拉格朗日插值多项式,再由插值多项式的唯一性,
得
P n(x)L n(x)
特别地, 当 n =1时又叫线性插值,其几何意义为 过两点的直线. 当 n =2时又叫抛物(线)插值, 其几 何意义为过三点的抛物线.
2019/10/19
课件
上页 1下4 页
注意 :
(1) 对于插值节点,只要求它们互异,与大小次序无关;
2019/10/19
课件
上页 1下3 页
2.2.2 拉格朗日插值多项式
利用拉格朗日基函数l i(x), 构造次数不超过n的多项式 n
L n (x ) y 0 l0 (x ) y 1 l1 (x ) y n ln (x )y ili(x )
i 0
可知其满足 L n (x j) y j j 0 ,1 , ,n
第二章 插值

注: 通常不能确定 , 而是估计 f ( n1) ( x ) M n1 ,
M n 1 n x(a,b),将 | x xi | 作为误差估计上限。 ( n 1)! i 0
通常取
M n 1 max | f ( n 1) ( x ) |
a x b
( x) 0 , 当 f(x) 为任一个次数 n 的多项式 时,f 可知 Rn ( x ) 0 ,即插值多项式对于次数 n 的多项 式是精确的。
Rn ( x) 也称为Lagrange插值多项式的插值余项。
当n = 1时,线性插值的余项
f ( ) R1 ( x) ( x x0 )( x x1 ), ( x0 , x1 ) 2
当n = 2时,抛物插值的余项
f ( ) R2 ( x) ( x x0 )( x x1 )( x x2 ), ( x0 , x2 ) 6
插值函数的类型有很多种,最常用的插值函数 是 代数多项式。
用代数多项式作插值函数的插值称为代数插值,即选取次 数不超过n的多项式 Pn(x) ,使得 Pn (xj) = yj (j = 0, 1,…, n)
(2.1.2)
代 数 插 值
一、插值多项式的存在唯一性? 二、插值多项式的常用构造方法?
L* ( x ) n
x n1
图2.1 前后两组插值节点的划分
x x0 ( Ln ( x) L* ( x)) 插值余项可表示成 Rn ( x) f ( x) Ln ( x) n x0 xn 1
例:已知 sin 1 , sin 1 , sin 3
第2章插值法

Rn (x)
f (n1) ( )
(n 1)!
n1
(
x)
(2.9)
x
其中 n1(x) n (x xi ) , (a,且b)依赖于 。
证明 点都是
由插i值0 条件
知
的零点,故可设Pn(xi)f(xi)
Rn (xi ) 0(i 0,,1,即插, n值) 节
当复杂,使用起来很不方便。面对这些情况,总希望 根据所得函数表(或结构复杂的解析表达式),构造
某个简单函数P(x)作为 的近似。
插值法是解决此类问题的一种比较古老的、
然而却是目前常用f 的x方法,它不仅直接广泛地
应用于生产实际和科学研究中,而且也是进一 步学习数值计算方法的基础。
4
现在你正浏览到当前第四页,共一百零三页。
(图2-3
例1 已知
分别用线性插值和抛物插值
求
的1值0 。1 0,012 11,1 14 1 42
115
15
现在你正浏览到当前第十五页,共一百零三页。
解 因为115在100和121之间,故取节点x0=100,x1=121相应地有 y0=10,y1=11,于是,由线性插值公式(2.5)可得
L1
(
x)
17
现在你正浏览到当前第十七页,共一百零三页。
输入xi,yi,n,x
j=0,1,```,n
P=1
y=0
k=0,1,```,n
k=j?
否 P=P*(x-xj)(xk-xj)
是
输出x,y
图2-4
y=y+P*yk
18
现在你正浏览到当前第十八页,共一百零三页。
lk (x)
数值分析第2章插值法

0.32 0.34
0.34 0.32
0.330365.
截 断 误 差 为 :R1x
f
1
2!
2
x
M2 2
x
x0 x
x1 , 其 中 :
M2
max
x0 x x1
f x,f x sin x,f x
sin x,M2
sin x1
0.3335
R1 0.3367
sin0.3367
L1 0.3367
x a, b,插 值余 项Rn x
f x Ln x
f n1 n 1!
n1
x
,
其
中
a,
b,
与x有 关,n1x
n
x
k0
xk
.
n
性质: lk x 1. k0
5
例1、证明: ( xi x)2 li ( x) 0, 其中li ( x)是关于点x0 , x1 ,, x5的插值 i0
基 函 数.
2.2 拉格朗日插值
2.2.1、线性插值与抛物插值
1、 线 性 插 值 :
设 yk f xk , yk1 f xk1 , xk xk1 求 一 次 多 项 式 L1 x, 满 足 :L1 xk yk,L1 xk1 yk1
L1 x
yk
yk1 xk1
yk xk
x xk
求n次 插 值 多 项 式Ln x, 满 足 :Ln xi yi i 0,1,2,,n
Ln
x
n
lk
x
yk
k0
lk
xj
1,k j
kj 0,k j
j 0,1,2,,n
lk x
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L1*(x)在每个小区间是上 在每个小区间是上f(x)的插值一次式,因此称为分段线 的插值一次式, 在每个小区间是上 的插值一次式 因此称为分段线 性插值。 性插值。
失去了原函数的光滑性。 失去了原函数的光滑性。 光滑性
同理,可以进行分段抛物线插值 (分段二次插值 同理,可以进行分段抛物线插值 分段二次插值) 分段二次插值
f [ xi , x j ] − f [ x j , xk ] f [ xi , x j , xk ] = (i ≠ k ) xi − xk
2阶差商 阶差商
§2 Newton’s Interpolation
(k+1)阶差商: 阶差商: 阶差商 f [ x0 , x1 , ... , xk ] − f [ x1 , ... , xk , xk +1 ] f [ x0 , ... , xk +1 ] = x 0 − x k +1 f [ x0 , ... , xk −1 , xk ] − f [ x0 , ... , xk −1 , xk +1 ] = x k − x k +1
§2 Newton’s Interpolation
牛顿公式
Nn ( x) = f ( x0 ) + f [ x0 , x1](x − x0 ) + ...+ f [ x0 , ... , xn ](x − x0 )...(x − xn−1 )
牛顿前差公式 /* Newton’s forward-difference formula */ 设 x = x 0 + t h ,则 N n ( x ) = N n ( x 0 + t h ) = Σ t ∆k f ( x 0 )
f [x0, x1 , x2] …… …… f [xn−2, xn−1, xn] − − f [xn−1, xn, xn+1] −
f [x0, …, xn] f [x1, …, xn+1] f [x0, …, xn+1]
§2 Newton’s Interpolation
等距节点公式 /* Formulae with Equal Spacing */ 等距分布时 当节点等距分布时: 当节点等距分布时 x i = x 0 + i h ( i = 0 , ... , n ) 向前差分
§2 Newton’s Interpolation
牛顿插值 /* Newton’s Interpolation */
Nn ( x) = a0 + a1 ( x − x0 ) + a2 ( x − x0 )(x − x1 ) + ... + an ( x − x0 )...(x − xn−1 )
f ( x) = f ( x0 ) + ( x − x0 ) f [ x, x0 ]
向后差分
/* backward difference */
中心差分
/* centered difference */
δ k f i = δ k −1 f i + − δ k − 1 f i −
1 2
1 2
h 其中 f i ± = f ( x i ± 2 )
1 2
§2 Newton’s Interpolation
∇ k f ( xn )
时用前插, 时用后插, 注:一般当 x 靠近 x0 时用前插,靠近 xn 时用后插,故两 种公式亦称为表初公式 表末公式。 表初公式和 种公式亦称为表初公式和表末公式。
§4 分段低次插值
/* piecewise polynomial approximation */
1 1 + x2
1 + (x − x0) × 2 + … … + (x − x0)…(x − xn−1) × −
n−1 −
f ( x ) = f ( x0 ) + f [ x0 , x1 ]( x − x0 ) + f [ x0 , x1 , x2 ]( x − x0 )( x − x1 ) + ...
+ f [ x 0 , ... , x n ]( x − x 0 )...( x − x n −1 )
Nn( x) = f ( xn ) + f [xn , xn−1](x − xn ) + ...+ f [xn , ..., x0 ](x − xn )...(x − x1 )
设 x = x n + t h ,则 N n ( x ) = N n ( xn + t h) = Σ (−1)k
k =0
n
−t k
函数值可由差分值算出: 函数值可由差分值算出:
f [ x0 , ... , x k ] = ∆k f 0 k! hk
f n+k = Σ n ∆ j f k j j =0
n
由 Rn 表达式
f
(k )
∇k f n f [ xn , xn −1 , ... , xn − k ] = k ! hk
∆k f 0 (ξ ) = k h
差分的重要性质: 差分的重要性质: 线性: 线性:例如 ∆ ( a f ( x ) + b g ( x )) = a ∆ f + b ∆ g 若 f (x)是 m 次多项式,则 ∆k f ( x) (0 ≤ k ≤ m) 是 m − k 次多项 是 次多项式, k 式,而 ∆ f ( x ) = 0 ( k > m ) 差分值可由函数值算出: 差分值可由函数值算出:
只附加一项上去即可。 只附加一项上去即可。 上去即可 差商( 差商(亦称均差) /* divided difference */
f ( xi ) − f ( x j ) f [ xi , x j ] = xi − x j (i ≠ j, xi ≠ x j )
1阶差商 /* the 1st 阶差商
divided difference of f w.r.t. xi and xj */
f ( xi ) 事实上 f [ x0 , ... , xk ] = ∑ ′ i = 0 ω k +1 ( x i )
′ 其中 ω k +1 ( x ) = ∏ ( x − xi ) , ω k + 1 ( x i ) = ∏ ( x i − x j )
i =0
j=0 j≠i
k
k
k
Warning: my head is exploding… 差商的值与 of的顺序无关! What is the pointxi 的顺序无关! this formula?
f ( k ) (ξ ) f [ x 0 , ... , x k ] = , ξ ∈ ( x min , x max ) k!
实际计算过程为
f (x0) f (x1) f (x2) … f (xn−1) − f (xn) f (xn+1) f [x0, x1] f [x1, x2] …… …… f [xn−1, xn] − f [xn, xn+1]
+ f [ x , x0 , ... , xn ]( x − x0 )...( x − xn−1 )( x − xn )
Nn(x)
ai = f [ x0, …, xi ]
Rn(x)
§2 Newton’s Interpolation
注:
由唯一性可知 Nn(x) ≡ Ln(x), 只是算法不同,故其 , 只是算法不同, 余项也相同, 余项也相同,即 f ( n +1 ) (ξ x ) f [ x , x 0 , ... , x n ]ω k +1 ( x ) = ω k +1 ( x ) ( n + 1) !
/* forward difference */
∆ f i = f i +1 − f i ∆k f i = ∆k − 1 ( ∆ f i ) = ∆k − 1 f i + 1 − ∆k − 1 f i ∇f i = f i − f i−1 − ∇ k fi = ∇ k −1 f i − ∇ k −1 f i −1
n ∆ f k = Σ ( − 1) f n+ k − j j j=0
n j n
∇ f k = Σ (−1)n− j
n j =0
n
n f k + j −n j
其中
n n ( n − 1 )...( n − j + 1 ) = j j!
/* binomial coefficients */
f ( n+1) (ξ ) Rn ( x ) = t ( t − 1)...( t − n)hn+1 , ξ ∈ ( x0 , x n ) ( n + 1)!
k =0 n
k
牛顿后差公式 /* Newton’s backward-difference formula */ 将节点顺序倒置: 将节点顺序倒置:
f [ x, x0 ] = f [ x0 , x1 ] + ( x − x1 ) f [ x, x0 , x1 ]
1 2
n−1 −
…………
f [ x, x0 , ... , xn−1 ] = f [ x0 , ... , xn ] + ( x − xn ) f [ x, x0 , ... , xn ] n−
§3 牛顿插值
/* Newton’s Interpolation */
Lagrange 插值虽然易算,但若要增加一个节点时, 插值虽然易算,但若要增加一个节点时, 都需重新算过。 全部基函数 li(x) 都需重新算过。
? ? 将 Ln(x) 改写成 a0?+ a1( x − x0 ) + a2 ( x − x0 )(x − x1 ) + ... + a? ( x − x0 )...(x − xn−1 ) 的形式,希望每加一个节点时, 的形式,希望每加一个节点时, n
