03_第二章222,223牛顿插值法
牛顿插值法ppt课件

为 在点
处的二阶差商
称
f[x 0 ,x 1 , x n ] f[x 0 ,x 1 , ,x x n 0 1 ] x n f[x 1 ,x 2 , x n ]
为f (x)在点
处的n阶差商。
--
9
差商表
x
f(x)
一阶差 商
二阶差商
三阶差商
x0
f(x0)
x1
f(x1) f [x0,x1]
x2
f(x2) f [x1,x2] f [x0,x1,x2]
--
14
例题分析(续1)
f
(x0, x1)
y1 x1
y0 x0
12 1(1)
1 2
f
(x1,
x2)
y2 x2
y1 x1
11 21
0
f
(x0, x1, x2)
f
(x1,x2) f (x0,x1) x2 x0
02((1/12))
1 6
--
15
例题分析(续2)
f (x)N2(x) f (x0)f[x0,x1](xx0)
令 xx0得: Nn(x0)c0y0f(x0); 令 xx1得: Nn(x1)c0c1(x1x0)y1f(x1); 由此可c0解 ,c1;c出 i 依: 次类推。
--
6
具有承袭性的插值公式
线性插值公式可以写成如下形式:
其中
p 1 x p 0 x c 1 x x 0
p0xfx0,其修正项的系数 c1
f
x1f x0
x1 x0
再修正 p1 x 可以进一步得到拋物插值公式
p 2 x p 1 x c 2 x x 0 x x 1
其中
第2章02牛顿插值

m
由m阶差商定义和上面两式知 1 f [ x0 ,, xm ] f [ x0 ,, xm2 , xm ] f [ x0 ,, xm1 ] xm xm1
上页
下页 返回
1 1 f ( x j ) x x m2 x x 1 j m j m 1 j 0 ( x j x0 )( x j x j 1 )( x j x j 1 )( x j xm 2 ) xm xm 1 f ( xm ) 1 ( xm x0 )( xm xm2 ) xm xm1 f ( xm1 ) 1 ( xm1 x0 )( xm1 xm2 ) xm xm1
x4=1,作出(x)关于x0,x1,x2,x3,x4的差商表.
解
xk x0=-1 x1=-0.8 x2=0 x3=0.5 x4=1
差商表为
ƒ(xk) -1 0.16032 1 1.15625 3 一阶差商 二阶差商 三阶差商 四阶差商
5.8016 1.0496 0.3125 3.6875
-4.752 -0.567 3.375
f ( k ) ( ) f [ x0 , x1 ,, xk ] k!
用余项的 相等证明
上页
下页 返回
(4)(多项式的差商)设f(x)为n次多项式,则其一 阶差商
f [ x] f [ xi ] f [ x, xi ] x xi
是x的n-1次多项式 推论 n次多项式pn(x)的k阶差商pn[x0,…xk],当k≤n时 是n-k次多项式,当k>n时恒为0
2.79 2.19
上页
-0.3
下页 返回
二、牛顿插值公式
设插值多项式
N n ( x ) a0 a1 ( x x0 ) a2 ( x x0 )( x x1 ) ... an ( x x0 )...( x xn1 )
第二章插值法

lk ( xk 1 ) 0
n=2的情况,假定插值节点为
xk 1 , xk , xk 1 , 要求一个二次插值多项式L2 ( x),使它满足 L2 ( x j ) y j ( j k 1, k , k 1)
y L2 ( x)在几何上就是通过三点(xk-1 , yk 1 ),(xk , yk ),(xk+1, yk 1 )的抛物线
插值法
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 §2.7 引言 拉格朗日插值 均差与牛顿插值公式 差分与等距节点插值 埃尔米特插值 分段低次插值 三次样条插值
一、插值问题
或者函数本身只是 一组实验数据,很 难对函数的性质进 行分析
对函数f (x),其函数形式可能很复杂且不利于在计算机上 ,
设函数
y f ( x ) 在区间 [a, b] 上有定义,且已知在
a x0 x1 x2 xn b
f ( xi ) yi , i 0,1,, n
如果存在一个简单函数 P ( x ),使得
P( xi ) f ( xi ) yi , i 0,1,, n
xx x x
如函数y sin x, 若给定 0, ]上5个等分点 [
其插值函数的图象如图
对于被插函数 ( x)和插值函数 ( x) f P
在节点xi处的函数值必然相等
但在节点外 ( x)的值可能就会偏离 ( x) P f 因此P( x)近似代替 ( x)必然存在着误差 f
整体误差的大小反映了插值函数的好坏
成立,则称 P ( x ) 为 f ( x ) 的插值函数
称点 xi , i 0,1,2,, n为插值节点
称区间 a , b]为插值区间 [
牛顿插值法原理及应用
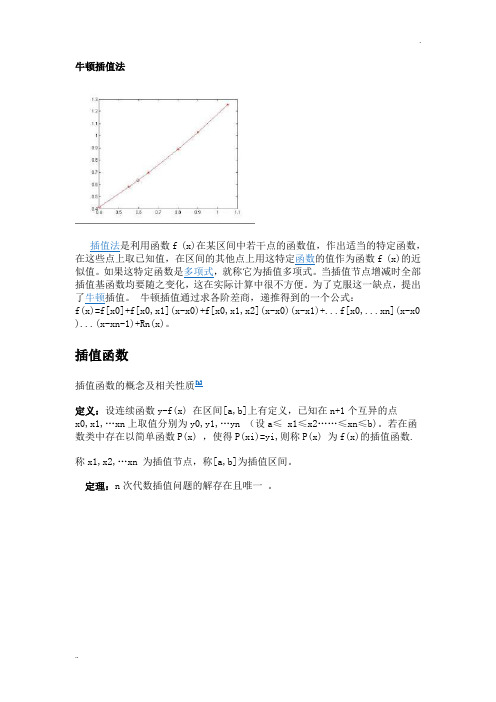
牛顿插值法插值法是利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
如果这特定函数是多项式,就称它为插值多项式。
当插值节点增减时全部插值基函数均要随之变化,这在实际计算中很不方便。
为了克服这一缺点,提出了牛顿插值。
牛顿插值通过求各阶差商,递推得到的一个公式:f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0 )...(x-xn-1)+Rn(x)。
插值函数插值函数的概念及相关性质[1]定义:设连续函数y-f(x) 在区间[a,b]上有定义,已知在n+1个互异的点x0,x1,…xn上取值分别为y0,y1,…yn (设a≤ x1≤x2……≤xn≤b)。
若在函数类中存在以简单函数P(x) ,使得P(xi)=yi,则称P(x) 为f(x)的插值函数.称x1,x2,…xn 为插值节点,称[a,b]为插值区间。
定理:n次代数插值问题的解存在且唯一。
牛顿插值法C程序程序框图#include<stdio.h>void main(){float x[11],y[11][11],xx,temp,newton;int i,j,n;printf("Newton插值:\n请输入要运算的值:x=");scanf("%f",&xx);printf("请输入插值的次数(n<11):n=");scanf("%d",&n);printf("请输入%d组值:\n",n+1);for(i=0;i<n+1;i++){ printf("x%d=",i);scanf("%f",&x[i]);printf("y%d=",i);scanf("%f",&y[0][i]);}for(i=1;i<n+1;i++)for(j=i;j<n+1;j++){ if(i>1)y[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-i]);elsey[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-1]);printf("%f\n",y[i][i]);}temp=1;newton=y[0][0];for(i=1;i<n+1;i++){ temp=temp*(xx-x[i-1]);newton=newton+y[i][i]*temp;}printf("求得的结果为:N(%.4f)=%9f\n",xx,newton);牛顿插值法Matlab程序function f = Newton(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等!');return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f); %将插值多项式展开f = vpa(f, 6);endend牛顿插值法摘要:值法利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
第2章 3.牛顿插值公式

r yi r 1 yi r 1 yi 1
中心差分
/ centered difference /
r y i r 1 y i r 1 y i
1 2
1 2
其中 yi 1 y( xi h ) 2
2
差分的重要性质: 线性:例如 (a f ( x ) b g( x )) a f b g 若 f (x)是 m 次多项式,则 k f ( x) (0 k m) 是 m k 次多项 k 式,而 f ( x) 0 (k m) 差分值可由函数值算出:
同理有:N 2 ( x ) f ( x0 ) f [ x0 , x1 ]( x x0 ) f [ x0 , x1 , x2 ]( x x0 )( x x1 )
1 ( 3) f [ x0 , x1 , x2 , x ] f ( ) 3!
一般地f ( x)在x0 , x1 , xn为插值结点的n次插值多项式为
牛顿插值公式
邹昌文
问题的提出
以x0 , x1为插值结点的一阶插值公式为 x x0 x x1 L1 ( x ) y0 y1 x0 x1 x1 x0 y1 y0 y0 ( x x0 ) x1 x0
现考虑增加一个插值结x2,且使原有项不变 点
可令
L2 ( x) L1 a( x x0 )( x x1 )
设x x0 th 则N n ( x ) N n ( x0 th)
f ( x0 ) f [ x0 , x1 ]( x x0 ) f [ x0 , x1 , x2 ]( x x0 )( x x1 ) f [ x0 , x1 , xn ]( x x0 )( x x1 )( x xn1 )
第2章_插值法

13.214 285 71
175 13.228756555322952...
考虑通过 + 1个节点0 < 1 < ⋯ < 的次插值
多项式 (),满足条件
= ,
= 0,1, … ,
希望找到 li(x),i = 0, …, n, 使得
= ; = ,
n次插值多项式, 插值节点为{ xi }in 0 [ a , b],则x [ a , b],有
f ( n 1) ( )
Rn (x )
n 1 ( x)
Lagrange型余项
(n 1)!
n
其中 n 1 ( x ) ( x xi ) , ( a , b) , 且依赖于 x.
满足条件P(xi) = f(xi) (i = 0, … n)。 P(x) 称
为f(x) 的插值函数。
P(x) f(x)
x0
x1
x2
x
x3
x4
定理1:设插值节点 ≠ ( ≠ ),则满足条件
= , = 0,1, … , 的插值多项式
= 0 + 1 + ⋯ +
− , , + 线性无关。
二次插值多项式
= − − + + + + ()
满足 = ( = − , , + )
例1:
已知 f ( x )满足 f (144) 12 , f (169) 13, f ( 225) 15
i 0
一次及二次差值余项
1 ′′
1 = − 0 − 1 ,
计算方法—插值法

2018/10/20
lk ( x) lk 1 ( x) 1
13
2.2 拉格朗日插值
Chapter2 插值法
L1(X)
L1(X)
∴ lg2.718 ≈L1 (2.718)=0.43428
2018/10/20 14
2.2 拉格朗日插值
2-2 线性插值与抛物插值
利用线性插值法对函数y=f(x) 进行逼近时,即用直线y=L1(x)代替 曲线y=f(x)。
Chapter2 插值法
显然当插值区间较大或曲线[x0,x1]凸凹变化大时,线 性插值的误差很大。 为了减小这种误差,我们用简单的曲线(抛物线)去近似
代替复杂曲线y=f(x) 。二次多项式函数的曲线为抛物线, 所以我们构造插值函数L2(x) ,即n=2。
2018/10/20 15
2.2 拉格朗日插值
5
2018/10/20
2.1 引言
多项式插值
Chapter2 插值法
对于n+1个基点的插值问题,如果要求插值函数是次 数不超过n的多项式,记为Pn(x),则相应的问题就是多项 式插值,并且把Pn(x)称为插值多项式。 实际上,我们所考虑的插值函数通常都是多项式函数
或分段多项式函数。由于次数不超过n的多项式的一般形 式为: Pn(x)=a0+a1x+a2x2+…+anxn
当n=20,在109次/秒的计算机上计算需几万年!
2018/10/20 12
2.2 拉格朗日插值
2-2 线性插值与抛物插值 已知函数y=f(x)的函数 插值法
y yk
yk+1
求次数不超过1的多项式L1(x)=a0+a1x 满足插值条件L1(xk)=yk, L1(xk+1)=yk+1。
计算方法插值法(均差与牛顿插值公式)

为f ( x)关于节点 x0 , xk 一阶均差 (差商)
2018/11/7
5
2018/11/7
6
二、均差具有如下性质:
f [ x0 , x1 ,, xk 1 , xk ]
j 0
k
f (x j ) ( x j x0 )( x j x j 1 )(x j x j 1 )( x j xk )
2018/11/7
27
fk fk 1 fk 为f ( x)在 xk 处的二阶向前差分
2
依此类推
m f k m1 f k 1 m1 f k
为f ( x)在 xk 处的m阶向前差分
2018/11/7
28
差分表
xk f k 一阶差分 x0 f 0 x1 f 1 二阶差分 三阶差分 四阶差分
2018/11/7
31
等距节点插值公式
一、牛顿前插公式
2018/11/7
32
2018/11/7
33
二、牛顿插值公式与拉格朗日插值相比
牛顿插值法的优点是计算较简单,尤其是增加 节点时,计算只要增加一项,这是拉格朗日插值 无法比的. 但是牛顿插值仍然没有改变拉格朗日插值的 插值曲线在节点处有尖点,不光滑,插值多 项式在节点处不可导等缺点.
2018/11/7
25
2018/11/7
26
§
2.3.4 差分及其性质
一、差分
fk , 定义3. 设f ( x)在等距节点xk x0 kh 处的函数值为 k 0 ,1, , n , 称
f k f k 1 f k
k 0,1,, n 1
为f ( x)在 xk 处的一阶向前差分
牛顿插值法原理及应用
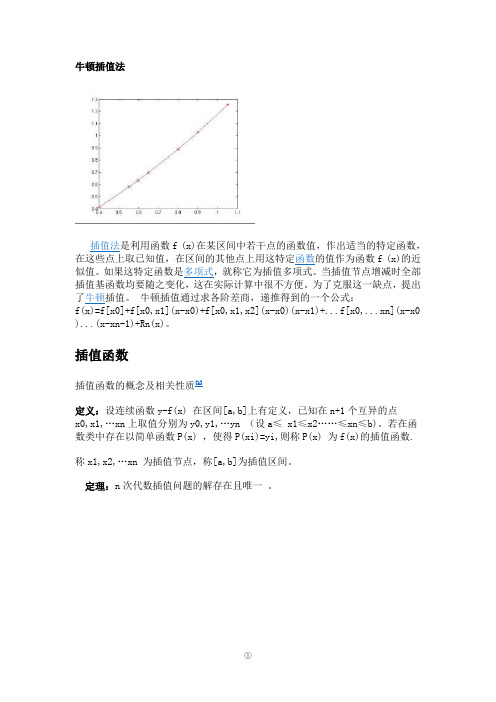
牛顿插值法插值法是利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
如果这特定函数是多项式,就称它为插值多项式。
当插值节点增减时全部插值基函数均要随之变化,这在实际计算中很不方便。
为了克服这一缺点,提出了牛顿插值。
牛顿插值通过求各阶差商,递推得到的一个公式:f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0 )...(x-xn-1)+Rn(x)。
插值函数插值函数的概念及相关性质[1]定义:设连续函数y-f(x) 在区间[a,b]上有定义,已知在n+1个互异的点x0,x1,…xn上取值分别为y0,y1,…yn (设a≤ x1≤x2……≤xn≤b)。
若在函数类中存在以简单函数P(x) ,使得P(xi)=yi,则称P(x) 为f(x)的插值函数.称x1,x2,…xn 为插值节点,称[a,b]为插值区间。
定理:n次代数插值问题的解存在且唯一。
牛顿插值法C程序程序框图#include<stdio.h>void main(){float x[11],y[11][11],xx,temp,newton;int i,j,n;printf("Newton插值:\n请输入要运算的值:x=");scanf("%f",&xx);printf("请输入插值的次数(n<11):n=");scanf("%d",&n);printf("请输入%d组值:\n",n+1);for(i=0;i<n+1;i++){ printf("x%d=",i);scanf("%f",&x[i]);printf("y%d=",i);scanf("%f",&y[0][i]);}for(i=1;i<n+1;i++)for(j=i;j<n+1;j++){ if(i>1)y[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-i]);elsey[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-1]);printf("%f\n",y[i][i]);}temp=1;newton=y[0][0];for(i=1;i<n+1;i++){ temp=temp*(xx-x[i-1]);newton=newton+y[i][i]*temp;}printf("求得的结果为:N(%.4f)=%9f\n",xx,newton);牛顿插值法Matlab程序function f = Newton(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等!');return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f); %将插值多项式展开f = vpa(f, 6);endend牛顿插值法摘要:值法利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
牛顿插值

§4 Newton’s Interpolation
注:
由唯一性可知 Nn(x) ≡ Ln(x), 只是算法不同,表达 , 只是算法不同, 形式不同,故其余项也相同, 形式不同,故其余项也相同,即
f ( n +1) (ξ x ) ωn +1 ( x ) f [ x, x0 , ... , xn ]ωn +1 ( x ) = ( n + 1) !
+ f [ x , x0 , ... , xn ]( x − x0 )...( x − xn−1 )( x − xn )
Nn(x)—n次多 次 项式,满足: 项式,满足: Nn(xi)= f(xi)
ai = f [ x0, …, xi ]
Nn(x) ≡ Ln(x),??? ,
Rn(x)—插值余项, 插值余项, 插值余项 满足R , 满足 n(xi)=0, i=0,…,n
差分计算可通过构造差分表得到
xk f ( xk ) =fk ∆fk x0 f0 x1 f1 x2 f2 x3 f3 x4 f4
增加
1
t
t(t-1)/2! t(t-1)(t-2)/3!
∆2 fk
2
∆3 fk ∆4 fk
3 4
∆f0 ∆f1 ∆f2 ∆f3 ∆f4
∆2 f0 ∆3 f0 ∆4 f0 ∆5 f0 ∆ f1 ∆ f1 ∆ f1 ∆ f2 ∆ f2
f ( k ) (ξ ) f [ x 0 , ... , x k ] = , ξ ∈ ( x min , x max ) k!
实际计算过程为
f (x0) f (x1) f (x2) … f (xn−1) − f (xn) f [x0, x1] f [x1, x2] …… …… f [xn−1, xn] − f [xn, xn+1]
牛顿插值法原理及应用

牛顿插值法插值法是利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
如果这特定函数是多项式,就称它为插值多项式。
当插值节点增减时全部插值基函数均要随之变化,这在实际计算中很不方便。
为了克服这一缺点,提出了牛顿插值。
牛顿插值通过求各阶差商,递推得到的一个公式:f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0)...(x-xn-1)+Rn(x)。
插值函数插值函数的概念及相关性质[1]定义:设连续函数y-f(x) 在区间[a,b]上有定义,已知在n+1个互异的点x0,x1,…xn 上取值分别为y0,y1,…yn (设a≤ x1≤x2……≤xn≤b)。
若在函数类中存在以简单函数P(x) ,使得P(xi)=yi,则称P(x) 为f(x)的插值函数.称x1,x2,…xn 为插值节点,称[a,b]为插值区间。
定理:n次代数插值问题的解存在且唯一。
牛顿插值法C程序程序框图#include<>void main(){float x[11],y[11][11],xx,temp,newton;int i,j,n;printf("Newton插值:\n请输入要运算的值:x=");scanf("%f",&xx);printf("请输入插值的次数(n<11):n=");scanf("%d",&n);printf("请输入%d组值:\n",n+1);for(i=0;i<n+1;i++){ printf("x%d=",i);scanf("%f",&x[i]);printf("y%d=",i);scanf("%f",&y[0][i]);}for(i=1;i<n+1;i++)for(j=i;j<n+1;j++){ if(i>1)y[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-i]);elsey[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-1]);printf("%f\n",y[i][i]);}temp=1;newton=y[0][0];for(i=1;i<n+1;i++){ temp=temp*(xx-x[i-1]);newton=newton+y[i][i]*temp;}printf("求得的结果为:N(%.4f)=%9f\n",xx,newton);牛顿插值法Matlab程序function f = Newton(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = ;elsedisp('x和y的维数不相等!');return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f); %将插值多项式展开f = vpa(f, 6);endend牛顿插值法摘要:值法利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
正文牛顿插值法

牛顿插值法摘要:值法利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
如果这特定函数是多项式,就称它为插值多项式。
利用插值基函数很容易得到拉格朗日插值多项式,公式结构紧凑,在理论分析中甚为方便,但当插值节点增减时全部插值基函数均要随之变化,整个公式也将发生变化,这在实际计算中是很不方便的,为了克服这一缺点,提出了牛顿插值。
牛顿插值通过求各阶差商,递推得到的一个公式:f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x 0)...(x-xn-1)+Rn(x)关键词:牛顿插值法流程图程序实现一、插值法的由来在许多实际问题及科学研究中,因素之间往往存在着函数关系,然而,这种关系经常很难有明显的解析表达,通常只是由观察与测试得到一些离散数值。
有时,即使给出了解析表达式,却由于表达式过于复杂,不仅使用不便,而且不易于进行计算与理论分析。
解决这类问题的方法有两种:一种是插值法,另一种是拟合法。
插值法是一种古老的数学方法,它来自生产实践,早在一千多年前,我国科学家在研究历法上就应用了线性插值与二次插值,但它的基本理论却是在微积分产生之后才逐渐完善的,其应用也日益增多,特别是在计算机软件中,许多库函数,如等的计算实际上归结于它的逼近函数的计算。
逼近函数一般为只含有算术运算的简单函数,如多项式、有理分式(即多项式的商)。
在工程实际问题当中,我们也经常会碰到诸如此类的函数值计算问题。
被计算的函数有时不容易直接计算,如表达式过于复杂或者只能通过某种手段获取该函数在某些点处的函数值信息或者导数值信息等。
因此,我们希望能用一个“简单函数”逼近被计算函数,然后用该简单函数的函数值近似替代被计算函数的函数值。
这种方法就叫插值逼近或者插值法。
逐次线性插值法优点是能够最有效地计算任何给定点的函数值,而不需要写出各步用到的插值多项式的表达式。
数值分析牛顿插值法

因此可得
f(x ) f0 f[x ,x 0 ]x ( x 0 )
f 0 ( f [ x 0 , x 1 ] f [ x , x 0 , x 1 ] x ( x 1 )x ) x 0 ) (
f 0 f [ x 0 , x 1 ] x x ( 0 ) f [ x , x 0 , x 1 ] x x ( 0 ) x x ( 1 )
华长生制作
11
下面推导余项的另外一种形式 若x将 xi,(i0,1, ,n)视为一 ,则个节点
f[x 0,x 1, ,xk,x]f[x0,x1, ,xk]x kf [x x0,x1, ,xk 1,x] f[x 0,x 1 , ,x k 1 ,x ] f [ x 0 , x 1 , , x k ] f [ x 0 , x 1 , , x k , x ] x x k ( )
有 P(x0)f0a0
a0 f0
P (x 1 ) f1 a 0 a 1 (x 1 x 0 )
a1
f1 x1
f0 x0
P ( x 2 ) f 2 a 0 a 1 ( x 2 x 0 ) a 2 ( x 2 x 0 ) x 2 ( x 1 )
f2 f0 f1 f0
a2
x2
可以证明
mfk mfkm
如
fk fk1
2fk 2fk2 3fk 3fk3
华长生制作
16
差分表
xk fk 一阶差分 二阶差分
x0 f0
x1 f1 x2 f2 x3 f3 x4 f4
f0
f1
f1
f2
f2
f3
f 3 f4
2 f0
2 f2
f2
1 2 f3
f2 2 2 f4
三阶差分
最新文档-Newton插值-PPT精品文档

f[20,21, ,27]f(7 7)! ()7 7!!1
f[20,21, ,28]f(8 8)! ()8 0!0
数计学院-黄陈思
上面我们讨论了节点任意分布的插值公式,但实际应 用时经常会遇到等距节点的情形,这时插值公式可以 进一步简化,计算也简单多了,为了给出等距节点的 插值公式,我们先来看一个新概念;
数计学院-黄陈思
k 1
k1
k 1
k (x) (x x j ) (x0 thx0 jh) (t j)h
j0
j0
j0
则插值公式
n
Nn(x) f0 f[x0,x1, ,xk]k(x) k1
化为
Nn(x0th)
f0
n
[
k 1
若 用 插 值 基 函 数 表 示 , 则 在 整 个 区 间 [a,b]上 Ih(x)为
n
Ih(x)=fjlj(x) j=0
x xj
xj1 xj1
,xj1
x
xj
(
j
0略去)
其中,lj
(x)=xxj
xj1 xj1
,xj
x
xj1( j
n略去)
a n(xx0)x (x1) (xxn 1)
其 中 a 0 ,a 1 ,… … a n 为 待 定 系 数
数计学院-黄陈思
P(x)应满足插 P(xi)值 fi ,条 i0,件 1, ,n
有 P(x0)f0a0
a0 f0
P ( x 1 ) f1 a 0 a 1 ( x 1 x 0 )
2fkfk1fk 为f (x)在xk 处的二阶向前差分 2fk fk fk1 为f (x)在xk 处的二阶向后差分
牛顿插值法.doc

牛顿插值法数值计算实习课程的设计名称:张广玉讲师;谭高山学生人数: 目录1190841691.实验目的2.问题的提出3.牛顿插值法原理4.差商概念的推导5.牛顿插值公式和其他公式6、牛顿插值法计算步骤7、牛顿插值多项式程序实现8.图像对比度牛顿插值多项式9、牛顿插值多项式总结10.附件111.附件21.实验:的目的是了解牛顿插值多项式的原理及其通过Matlab程序解决实际问题的能力。
2.问题的提出我们知道拉格朗日插值多项式的插值基函数在理论分析中非常方便,但是当插值节点增加或减少时,所有的插值基函数都会改变,整个公式也会改变,这在实际计算中非常不方便。
虽然拉格朗日插值很容易计算,但是如果增加一个节点,所有的基函数都需要重新计算。
3.牛顿插值多项式的原理我们知道两点直线的公式是:让我们考虑点偏斜,其中两点是((x0,y0)(x1,y1)),那么线性方程是:然后,在此基础上添加一个节点(x2,y2),通过这三个点的插值多项式为:C(x)应该是二次多项式。
根据插值条件显示插值条件:您可以找到:重写p2(x):是.4.下面介绍差商和差的定义:一阶差商二阶差商n一阶差商可以证明差商具有以下性质:(2) k 阶差商关于节点对称,或者平均差与节点顺序无关,即平均差表具有零阶平均差一阶平均差二阶平均差三阶平均差x0f (x0) x1f (x1) f [x0,x1] x2f (x2) f [x0,x1,x2]x3f[x1,x2……5.牛顿插值公式和其他公式如下:……(1)……(2)和(n 1)具有:其间6、牛顿插值法计算步骤:牛顿插值法是利用一定区间内几个点的函数值来构造牛顿插值多项式。
已知值取自这些点,牛顿插值多项式的值用作区间中其他点的函数值的近似值。
1.输入值和(;要计算的功能点。
2.对于由计算的给定值。
3.输出。
7.Matlab程序实现示例:f(x)=lnx的值如表所示。
构造牛顿插值多项式,计算ln0.53的值。
牛顿插值法

牛顿插值法(1)牛顿真是牛,拉格朗日插值法只能算是数学意义上的插值,从插值基函数的巧妙选取,已经构造性的证明了插值法的存在性和惟一性,但是从实现的角度看并不很好,而牛顿很好的解决了这个问题。
牛顿插值是基于下面这些的公式:f[x0,x1,...xk]=(f[x1,...xk]-f[x0,...xk-1])/(xk-x0)f[x]=f(x)f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0)...(x-xn-1)+Rn(x)前两个是均差的递推关系式,而后一个就是牛顿插值公式,其中N(x)=f(x)-Rn(x),即目标多项式,Rn(x)是n阶插值余项,我们就是用N(x)去近似f(x)。
可以构造这样一个均方差表:xk f(xk) 一阶均差二阶均差 ...x0 f(x0)x1 f(x1) f[x0,x1]x2 f(x2) f[x1,x2] f[x0,x1,x2]...如果有n个点插值,表会有(n*n)/2+n个表项,如果直接编程会有O(n*n)的空间复杂度,编程时做个简单的改进,不难发现在这个表中只有部分数据有用,对角线(斜行)它们是目标值,用来表示多项式的,左边的两纵行(实际上只需要x一行)以及最底下的一行,表示当前插值的状态。
经过改进后只需要O(n)的空间复杂度。
两个过程:1,新增加一个点时的更新。
只须更新最底下一行数据,其递推关系由均差公式给出,最后算出高一队的均差值,需时O(n)2,插入点完成后如何计算多项式在另外给定点的值N(x)。
由牛顿插值公式,最终的表达式为:N(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0)...(x-xn-1)如果直接将它展开,再算实在麻烦,实际上大可不必这样做,还记得多项式求值的秦九韶算法吗?将多项式‘叠’起来,从内层括号往外一层层拨开,n次多项多的计算,只需要做n次乘法,同样的思想,将上式改写成:N(x)=f[x0]+(x-x0){f[x0,x1]+(x-x1){f[x0,x1,x2]+(x-x2){...{f[x0,...xn-1]+(x-xn-1)f[x0, (x)n]}...}就可以同样简单的计算了,时间复杂度O(n)综合起来的性能:对于n个点的插值,产生多项式的时间复杂度是O(n*n),最终进行一个点的计算的时间复杂度是O(n)。
牛顿插值法

x2-x1
依次递推可得到a3, …, an. 为写出系数 ak的一般表达式,
➢差商(均差)定义
2.3.2 均差及其性质
1、差商(均差)的定义
称
f [x0 , xk ] =
f ( xk ) - f ( x0 ) xk - x0
为 f ( x关) 于点 x的0 ,一xk阶差商。
称
f [ x0 , x1, xk ] =
-
f ( x1)
-பைடு நூலகம்
f ( x0 )
( x1 - x0 )( xk - x1) ( x0 - x1)( xk - x1)
=
f (x0 )
+
f (x1)
+
f (xk )
(x0 - x1)( x0 - xk ) (x1 - x0 )( x1 - xk ) (xk - x0 )( xk - x1)
一般有
f [ x0 , x1,, xk ] =
注:差商与节点的排列次序无关——差商 的对称性
f[x0,x1,…,xn]= f[x1,x0,x2,…,xn]=… = f[x1, …, xn ,x0]
因此 f [ x0 , x1,, xk ] = f [ x1, xk-1, x0 , xk ] = f [ x1, x2 ,, xk-1, xk ] - f [ x1, x2 ,, xk-1, x0 ] xk - x0 = f [ x1, x2 ,, xk-1, xk ] - f [ x0 , x1, x2 ,, xk-1] xk - x0
=
f[x0,x2] - f[x0,x1]
x2 - x1
= f[x0,x1,x2] ;
P2(x)=f(x0) + f[x0,x1](x-x0) + f[x0,x1,x2](x-x0)(x-x1)
牛顿插值法ppt课件

f (m0 (m0
1)( )
1)!
(
x
x0
)(
m0
1)
19
Hermite插值多项式(续2)
已知函数 y f (x)在区间[a,b]上n个互异点 x0 , x1,L , xn 处的函数值 y0 , y1,L , yn , 以及导数值m0 , m1,L , mn ,求 H2n1(x) P2n1 使得满足插值条件
0 (x),1(x), 0 (x), 1(x)
使之满足
0 (x0 ) 1
00
( x1 (x0
) )
0 0
0 (x1) 0
0 (x0 ) 0 0 (x1) 1 0 (x0 ) 0 0 (x1) 0
0 (x0 ) 0
0 0
( x1 ) (x0 )
0 1
0 (x1) 0
0 (x0 ) 0
增加一个点后
Nn1(x) c0 c1(x x0 ) c2(x x0)(x x1) L cn (x x0)(x x1)L (x xn1) cn1(x x0 )(x x1)L (x xn1)(x xn )
5
Newton插值
关键是ci的求法! 可仿照泰勒公式里系数 的求法!
Nn (x) c0 c1(x x0 ) c2 (x x0 )(x x1) cn (x x0 )(x x1) (x xn1)
1.53427 2.18224 x 0.761677 x2 0.113706 x3
ln 1.5 = 0.409074
28
一般的Hermit插值
设在n+1个节点 a x0 x1 L xn b
给出函数值和导数值 y0 , y1,L , yn 及y0 , y1,L , yn
第二章牛顿插值法

3 fi3 3!h3
f [xi , xi1 ,, xim ]
m fi m!hm
m fim m!hm
f [x0 , x1 ,, xk ]
k f0 k!hk
k fk k!hk
1.Newton向前(差分)插值公式
如果节点 x0 , x1 ,, xn是等距节点 ,即
y2 ,
(a b)3 a3 3a2b 3ab2 b3
归纳4 y可0 知 ,3k2y阶y10差商3y可10表示yy4为04yy2326yy12y40y1 y0
4kyy1 iC32ky0y2y1ik3yCy21k1yiyyk5114yy342C6ykyk231yiy411y2 C kkyy1 i
fi xi
fi fi1 hh
f [xi , xi1 , xi2 ]
f [ xi , xi1 ] f [ xi1 , xi2 ] xi xi2
fi fi1 2h2
2 fi 2h2
fi1 fxi2 2h2
2 fi2 2h2
xk
x0
kh,k
0,1,, n, h
f [xi , xi1 , xi2 , xi3 ]
f [ xi , xi1 , xi2 ] f [ xi1 , xi2 , xi3 ] xi xi3
2 fi 2 fi1 3 2h3
3 fi 3!h3
依此类推
2
fi2 2 fxi3 3 2h3
xk f (xk ) 一阶差商 x0 f ( x0 )
x1 f ( x1 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
k 1
n
f0 f [x0 , x1 , , xk ] (x xj ) f [x, x0 , x1 , , xn ] (x xj )
k 1
j0
j0
华长生制作
12
n
Nn(x) f [x, x0 , x1 , , xn ] (x xj ) j0
Nn(x) Rn(x)
因此
Rn ( x)
k!
华长生制作
Newton插值 估计误差的 重要公式
13
练习 设当xi 1,2,3,4,5时, f (xi ) 1,4,7,8,6. 求四次牛顿 插值多项式.
k xk f(xk) 一阶差商 二阶差商 三阶差商 四阶差商 0 11
1 24 3
2 37 3
0
3 48 1
-1
-1/3
4 5 6 -2
-3/2 -1/6
1/24
N4(x) 1 (x 1) 3 (x 1)(x 2) 0
(x 1)(x 2)(x 3) ( 13) (x 1)(x 2)(x 3)(x 4) (214)
1
华长生制2作4
x4
9 12
x3
83 24
x2
33 12
x
1
14
2.2.3 等距节点插值公式
定义. 设f (x)在等距节点xk x0 kh处的函数值为fk , k 0,1, , n , 称
若将x xi ,(i 0,1, , n)视为一个节点 ,则
f [x0 , x1 ,
, xk , x]
f [ x0 , x1 ,
, xk ] f [x0 , x1 , xk x
, xk 1 , x]
f [x0 , x1 , , xk 1 , x] f [x0 , x1 , , xk ] f [x0 , x1 , , xk , x]( x xk )
j0
21
称
Nn(x0 th)
n
f0
k 1
[ k f0 k!
k 1
(t j)]
j0
为Newton向前插值公式(又称为表初公式)
如果假设
x x0 th
由差商与向前差分的关系
华长生制作
f [x0 , x1 ,
, xk ]
k f0 k!hk
20
k 1
k 1
k 1
k (x) (x xj ) (x0 th x0 jh) (t j)h
j 0
j0
j0
则插值公式
n
Nn(x) f0 f [x0 , x1 , , xk ]k (x) k 1
差分表
xk fk 一阶差分
x0 f0 x1 f1
f0
f1
x2 f2
f1
f2
x3 f3
f2
f3
x4 f4
f3 f4
二阶差分
2 f0
2 f2
2 f1 2 f3 2 f2 2 f4
三阶差分
3 f0
3 f3
3 f1
3 f4
四阶差分
4 f0
4 f4
华长生制作
17
在等距节点的前提下,差商与差分有如下关系
f [ xi , xi1 ]
华长生制作
2
显然,多项式组
1, x x0 , (x x0 )( x x1 ), , (x x0 )( x x1 ) (x xn1 )
线性无关,因此,可以作为插值基函数
设插值节点为 xi , 函数值为 fi f (xi ) , i 0,1,L , n
hi xi1 xi , i 0,1,2, , n 1
f (n1) ( )
(n 1)!
n 1
(
x
)
f [x, x0 , x1 , , xn ]n1(x)
一般 Rk ( x) f [x0 , x1 , , xk 1 ]k 1(x)
kn
另外
f [x, x0 , x1 ,
, xn ]
f (n1)( )
(n 1)!
f [x0 , x1 ,
, xk ]
f (k )( )
华长生制作
15
依此类推
m fk m1 fk 1 m1 fk 为f ( x)在 xk 处的m阶向前差分 m fk m1 fk m1 fk 1 为f ( x)在 xk 处的m阶向后差分
可以证明
m fk m fk m
如
fk fk 1
2 fk 2 fk 2
3 fk 3 fk 3
华长生制作
16
设插值多项式
P(x) a0 a1(x x0 ) a2(x x0 )(x x1 ) an(x x0 )(x x1 ) (x xn1 )
满足插值条件
P(xi ) fi , i 0,1, , n
则待定系数为
a0 f0
a1 f [x0 , x1 ]
a2 f [x0 , x1 , x2 ]
h
max i
hi
插值条件为 P(xi ) fi , i 0,1, , n
设插值多项式 P(x)具有如下形式
P(x) a0 a1(x x0 ) a2(x x0 )(x x1 ) an(x x0 )(x x1 ) (x xn1 )
华长生制作
3
P(x)应满足插值条件 P(xi ) fi , i 0,1, , n
化为
Nn(x0
th)
f0
n k 1
[
k f0 k!hk
k 1
(t j)h]
j0
n
f0
k 1
[ k f0 k!
k 1
(t j)]
j0
其余项
Rn ( x)
f (n1) ( )
(n 1)!
n 1
(
x)
化为
华长生制作
Rn(x0 th)
f (n1)( )
(n 1)!
n
hn1 (t j)
an f [x0 , x1 , , xn ]
华长生制作
10
定义3. 称 Nn(x) a0 a1(x x0 ) a2(x x0 )(x x1 )
an(x x0 )(x x1 ) (x xn1 )
k 1
k (x) (x xj ) j 0 为k次多项式
n
k 1
f0 f [x0 , x1 , , xk ] (x xj )
Ax b
§ 2.2.2 Newton插值法
§
a11
A
a21
2.2.3
a12 a22
等距节点插值公式
a1n a2n
xi
bi
i1
lij x j
j1
lii
an1
an2
ann
i 2,3, , n
我们知道,Lagrange插值多项式的插值基函数为
l j(x)
n i0
(x xi ) (x j xi )
(3) 当f(k )(x)在包含节点 x0 , x1 , , xk的区间存在时 ,
在x0 , x1 , , xk之间必存在一点 ,使得
f [x0 , x1 ,
, xk ]
f (k )( )
k!
华长生制作
用余项的 相同证明
7
差商的计算方法(表格法):
差商表 Chashang.m
xk f (xk ) 一阶差商 x0 f ( x0 )
x1 f ( x1 )
f [ x0 , x1 ] f [x1 , x2 ]
x2 f ( x2 )
f [ x2 , x3 ]
x3 f ( x3 )
f [ x3 , x4 ]
x4 f (x4 )
二阶差商
f [x0 , x1 , x2 ] f [x1 , x2 , x3 ] f [x2 , x3 , x4 ]
fk fk 1 fk k 0,1, ,n 1 为f (x)在 xk 处的一阶向前差分
fk fk fk1 k 1,2, ,n 为f (x)在 xk 处的一阶向后差分
2 fk fk 1 fk 为f (x)在 xk 处的二阶向前差分
2 fk fk fk 1 为f (x)在 xk 处的二阶向后差分
三阶差商 四阶差商
f [x0 , x1 , x2 , x3 ]
f [x0 , x1 , , x4 ]
f [x1 , x2 , x3 , x4 ]
华长生制作
规定函数值为零阶差商
8
例1 值
求
f(xi)=
x3在节点
x=0,
2,
3,
5,
6上的各阶差商
解: 计算得如下表
xi f[xi] f[xi,xi+1] f[xi,xi+1,xi+2] f[xi,xi+1,xi+2 ,xi+2]
fi1 xi 1
fi xi
fi fi1 hh
f [xi , xi1 , xi2 ]
f [ xi , xi1 ] f [ xi1 , xi2 ] xi xi2
fi fi1 2h2
2 fi 2h2
fi1 fi2 2h2
2 , xi3 ]
i j
j 0,1,2, ,n
形式上太复杂,计算量很大,并且重复计算也很多
由线性代数的知识可知,任何一个n次多项式都可以表示成
1, x x0 , (x x0 )( x x1 ), , (x x0 )( x x1 ) (x xn1 )
共n+1个多项式的线性组合
那么,是否可以将这n+1个多项式作为插值基函数呢?
m fim m!hm
f [x0 , x1 ,
, xk ]
k f0 k!hk
k fk k!hk
