山东省德州市2013届高三上学期期末校际联考数学(理)
2013高考数学试题分类汇编:专题08 平面向量(解析版)

专题08 平面向量一、选择题:1. (山东省济南市2013年1月高三上学期期末理10)非零向量,a b 使得||||||a b a b +=-成立的一个充分非必要条件是A. //a bB. 20a b +=C. ||||a ba b =D. a b =2.(山东省德州市2013年1月高三上学期期末校际联考理11)若12,e e是平面内夹角为60的两个单位向量,则向量12122,32a e e b e e =+=-+的夹角为( )A .30B .60C .90D .1203. (山东省烟台市2013年1月高三上学期期末理6)在△ABC 中,AB=3,AC=2,1,2BD BC =uu u r uu u r则AD BD ⋅uuu r uu u r的值为A.52-B.52C.54-D.54【答案】C【解析】因为1,2BD BC =uu u r uu u r 所以点D 是BC 的中点,则1()2AD AB AC =+,11()22BD BC AC AB ==- ,所以11()()22AD BD AB AC AC AB ⋅=+⋅-2222115()(23)444AC AB =-=-=- ,选C.4. (山东省济宁市2013届高三1月份期末测试理8)已知点P 是ABC ∆所在平面内一点,则PA PB PC AB ++=是点P 在线段AC 上的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.(山东省诸城市2013届高三12月月考理)已知a 、b 、c 是共起点的向量,a 、b不共线,且存在m ,n∈R 使c ma nb =+ 成立,若a 、b 、c的终点共线,则必有A .m+n=0B .m -n= 1C .m+n =1D .m+ n=-16. (山东省诸城市2013届高三12月月考理)若向量(1,2),(4,)a x b y =-= 相互垂直,则93x y +的最小值为 A .6B .23C .32D .127.(山东省青岛一中2013届高三1月调研理)已知两点(1,0),3),A B O 为坐标原点,点C 在第二象限,且120=∠AOC ,设2,(),OC OA OB λλλ=-+∈R则等于A .1-B .2C .1D .2-8.(山东省诸城市2013届高三12月月考理)已知各项均不为零的数列{a n },定义向量*1(,),(,1),n n n n c a a b n n n N +==+∈。
山东省德州市2013届高三上学期期末校际联考

山东省德州市2013届高三上学期期末校际联考化学试题第I卷(选择题共45分)一、选择题(本题包括15,小题,每小题3分,共45分。
每小题只有一项最符合题目要求)1.化学在生产和日常生活中有着重要的应用。
下列说法错误的是A.外加电源的负极连接在海水中的钢铁闸门上,可保护闸门不生锈B.发酵粉中主要含有碳酸氢钠,能使焙制出的糕点疏松多孔C.14C可用于文物年代的鉴定,14C与12C互为同素异形体D.金属钠、钙等活泼金属着火时,不能使用泡沫灭火器来灭火2.下列关于有机化合物的认识不正确...的是A.油脂在空气中完全燃烧转化为水和二氧化碳B.蔗糖、麦芽糖的分子式都是C12H22O11,二者互为同分异构体C.乙烯通人高锰酸钾溶液褪色是因为发生了加成反应D.在浓硫酸存在下,苯与浓硝酸共热生成硝基苯的反应属于取代反应3.NA代表阿伏加德罗常数的值,下列叙述正确的是A.标准状况下,5.6 L一氧化氮和5.6L氧气混合后的分子总数为0.5N AB.在H2O2+Cl2==2HCl+O2反应中,每生成32g氧气,则转移2N A个电子C.1 mol乙烷分子中含有8N A个共价键D.58.5 g的氯化钠固体中含有N A个氯化钠分子4.对滴有酚酞试液的下列溶液,操作后颜色变深的是A.明矾溶液加热B.CH3COONa溶液加热C.氨水中加入少量NH4Cl固体D.小苏打溶液中加入少量NaCl固体5.下列叙述不正确...的是A.在家用电热水器不锈钢内胆镶嵌镁棒,以防止内胆腐蚀B.草木灰(主要成分K2CO3)和铵态氮肥混合使用会降低肥效C.施用适量石灰乳可降低盐碱地(含较多NaCl、Na2CO3)的碱性D.除去废水中的Cu2+、Ag+等重金属离子可选用硫化钠溶液6.A.B、C、X均为中学化学常见物质,一定条件下它们有如下转化关系(其它产物已略去),下列说法错误的是:,则A可为硫A.若X为OB.若X为KOH溶液,则A可能为AlCl3C.若X为HNO3,则C可能为Fe(NO3)3'D.若A、B、C均为焰色反应呈黄色的化合物,则X可能为CO27.制备乙酸乙酯的绿色合成路线之一为下列说法正确的是A.淀粉与纤维素互为同分异构体B.M的分子式为C12H22O11C.N的结构简式为C2H4O2D.④的反应类型属于取代反应8.用下列实验装置进行相应实验,能达到实验目的的是A.用图l所示装置蒸干AIC13饱和溶液制备AlCl3晶体B.用图2所示装置证明非金属性Cl>C>SiC.用图3所示装置分离CCl4萃取溴水后已分层的有机层和水层D.用图4所示装置制取少量Cl2气体9.下列说法中,正确的是A.酸性:盐酸>氢硫酸(H2S),故非金属性:Cl>SB.第二周期元素的最高正化合价从左到右依次升高C.元素原子的最外层电子数越多,得电子能力越强,失电子能力越弱D.共价化合物中只存在共价键,离子化合物中一定含有离子键10.下列有关工业生产的叙述正确的是A.电解精炼铜时,阳极溶解的金属的质量与阴极析出的金属的质量不相等B.电解饱和食盐水制烧碱采用离子交换膜法,可防止阴极室产生的Cl2进入阳极室C.合成氨生产过程中增大N2的浓度可同时提高N2、H2的转化率D.硫酸工业中,使用催化剂是为了提高SO2转化为SO3的转化率11.元素的原子结构决定其性质和在周期表中的位置。
山东省2014届理科数学一轮复习试题选编29:二项式定理

山东省2014届理科数学一轮复习试题选编29:二项式定理一、选择题 1.(山东省淄博市2013届高三上学期期末考试数学(理))若()()()()()()923112012311132222xx a a x a x a x a x +-=+-+-+-+⋅⋅⋅+-,则1211a a a ++⋅⋅⋅+的值为( )A .0B .5-C .5D .255【答案】C【 解析】令2x =,则290(21)(23)5a =+-=-.令3x =,则01110a a a ++⋅⋅⋅+=,所以1110(5)5a a a +⋅⋅⋅+=-=--=,选C .2 .(山东省德州市2013届高三上学期期末校际联考数学(理))51()(21)ax x x+-的展开式中各项系数的和为2,则该展开式中常数项为 ( )A .-20B .—10C .10D .20【答案】C【解析】令1x =,可得各项系数和为5(1)(21)12a a +-=+=,所以1a =.所以555111()(21)()(21)()(12)ax x x x x x x x x+-=+-=-+-,5(12)x -的展开式的通项公式为155(2)(2)k k k k k k T C x x C +=-=-,当1k =时,125(2)10T C x x =-=-;所以展开式的常数项为1(10)10x x-⨯-=,选 C .3 .(山东省2013届高三高考模拟卷(一)理科数学)若2013(2)x -220130122013a a x a x a x =++++ ,则02420121352013a a a a a a a a ++++=++++( )A .201320133131+-B .201320133131+--C .201220123131+-D .201220123131+--【答案】B 【解析】令1=x 得01234520131a a a a a a a +++++++= ①,令1-=x 得201301234520133a a a a a a a -+-+-+-= ②,由①②联立,可得2012420a a a a ++++ 2013312+=,++31a a 52013a a ++ 2013132-=,从而02420121352013a a a a a a a a ++++++++ 20132013312132+=-201320133131+=--. 4 .(山东省枣庄市2013届高三3月模拟考试数学(理)试题)若4(1,)a a b +=+为有理数,则a+b=( )A .36B .46C .34D .44【答案】D二项式的展开式为11223344441118928C C C ++++=+++=+,所以28,16a b ==,281644a b +=+=,选 D .5 .(山东省济南市2013届高三3月高考模拟理科数学)二项式8(2x-的展开式中常数项是 ( )A .28B .-7C .7D .-28【答案】C展开式的通项公式为488831881()(()(1)22k k k k k k k k x T C C x ---+==-,由4803k -=得6k =,所以常数项为6866781()(1)72T C -=-=,选C .6 .(山东省临沂市2013届高三第三次模拟考试 理科数学)51()(2)x a x x+-的展开式中各项系数的和为2,则该展开式中常数项为 ( )A .-40B .-20C .20D .40【答案】 .A .7 .(山东省潍坊市2013届高三第二次模拟考试理科数学)设0(cos sin )a x x dx π=⎰-,则二项式26()a x x+展开式中的3x 项的系数为 ( )A .-20B .20C .-160D .160【答案】C 因为00(cos sin )(sin cos )2a x x dx x x ππ=⎰-=+=-,所以二项式为26262()()a x x x x+=-,所以展开式的通项公式为261231662()()(2)kk k k k k k T C x C x x--+=-=-,由1233k -=得3k =,所以333346(2)160T C x x =-=-,所以3x 项的系数为160-.选C .8 .(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))设a=π0⎰sin x d x ,则二项式6⎛⎝的展开式的常数项是( )A .160B .-160C .240D .-240【答案】B【解析】由2)cos (sin 00=-=⎰ππx xdx ,所以2=a ,所以二项式为6)12(xx -,展开式的通项为22666661)1(2)1()2(k k kk k k k k k xxC xx C T ----+-=-=k k k k x C ---=366)1(2,所以当3=k ,为常数,此时160)1(23336-=-C ,选B .9 .(山东省青岛市2013届高三第一次模拟考试理科数学)已知()|2||4|f x x x =++-的最小值为n ,则二项式1()n x x-展开式中2x 项的系数为 ( )A .15B .15-C .30D .30-【答案】A 因为函数()|2||4|f x x x =++-的最小值为4(2)6--=,即6n =.展开式的通项公式为6621661()(1)k k k k k k k T C x C x x--+=-=-,由622k -=,得2k =,所以222236(1)15T C x x =-=,即2x 项的系数为15,选A .10.(山东省济宁市2013届高三4月联考理科数学)设221(32)=⎰-a x x dx ,则二项式261()-ax x展开式中的第4项为( )A .31280-xB .1280-C .240D .240-【答案】A11.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )(82展开式中不含..4x项的系数的和为( )A .-1B .1C .0D .2【答案】C12.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)设22(13)40a x dx =-+⎰,则二项式26()a x x+展开式中不含..3x 项的系数和是( )A .160-B .160C .161D .161-【答案】C13.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)()5a x x R x ⎛⎫+∈ ⎪⎝⎭展开式中3x 的系数为10,则实数a 等于 ( )A .-1B .12C .1D .2【答案】D14.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)若2012(3)nnn x a a x a x a x -=++++ ,其二项式系数的和为16,则012n a a a a ++++=( )A .8B .16C .32D .64【答案】B15.(山东省潍坊市2013届高三上学期期末考试数学理( )A .)若()()()()()()923112012311132222x x a a x a x a x a x +-=+-+-+-+⋅⋅⋅+-,则1211a a a ++⋅⋅⋅+的值为 ( )A .0B .5-C .5D .255【答案】C【解析】令3x =,则有012110a a a a +++⋅⋅⋅+=,令2x =,则290(21)(23)5a =+-=-,所以121105a a a a ++⋅⋅⋅+=-=,选C .二、填空题16.(山东省夏津一中2013届高三4月月考数学(理)试题)若52345012345(12),x a a x a x a x a x a x +=+++++则a 3=______________.【答案】8017.(山东省凤城高中2013届高三4月模拟检测数学理试题 )若261()xax -的二项展开式中3x 项的系数为52,则实数a =_______.【答案】-218.(山东省莱芜五中2013届高三4月模拟数学(理)试题)若31()nx x-展开式中的所有二项式系数和为512,则该展开式中3x 的系数为______.【答案】84;19.(2013届山东省高考压轴卷理科数学)(2013滨州市一模)设6sin (a xdx,π=⎰则二项式的展开式中的常数项等于________.【答案】-160词 【解析】,3,2)1(,)12()1(,2|)cos (sin 36616600=∴-=-=-∴=-==--+⎰r x C T x x x x a x dx x a r r r r r ππ所以常数项为-160.20.(山东省威海市2013届高三上学期期末考试理科数学)8(2x -的展开式中,常数项为___________. 【答案】7展开式的通项公式为488831881()((1)()22k k k k k k kk x T C C x ---+==-,由4803k -=,解得6k =,所以常数项为226781(1)()72T C =-=.21.(山东省烟台市2013届高三3月诊断性测试数学理试题)若(x 2-nx)1的展开式中含x 的项为第6项,设(1-3x)n=a o +a 1x+a 2x 2++a n x n,则a l +a 2++a n 的值为_____________ 【答案】255展开式(x 2-n x )1的通项公式为22311()()(1)k n k k kk n k k n n T C x C x x--+=-=-,因为含x 的项为第6项,所以5,231k n k =-=,解得8n =,令1x =,得88018(13)2a a a +++=-= ,又01a =,所以81821255a a ++=-= .22.(山东省德州市2013届高三第二次模拟考试数学(理)试题)二项式)10的展开式中含x 的正整数指数幂的项数是____________. 【答案】523.(2013年山东临沂市高三教学质量检测考试理科数学)在62(x )x-的二项展开式中,常数项等于_______. 【答案】 【答案】160- 展开式的通项公式为6621662()(2)k k k k k kk T C x C x x--+=-=-,由620k -=,得3k =,所以3346(2)160T C =-=-,即常数项为160-.24.(山东省济南市2013届高三4月巩固性训练数学(理)试题)设dx x )12(20-⎰,则二项式4⎪⎭⎫ ⎝⎛+x a x 的展开式中的常数项为__________.___【答案】2425.(2011年高考(山东理))若62(x x -展开式的常数项为60,则常数a 的值为_________.【答案】解析:6(x 的展开式616(k k k k T C x -+=636(kk C x -=,令630,2,k k -==226(1560,4C a a ===,答案应填:4.26.(山东省济宁市2013届高三第一次模拟考试理科数学 )25(ax的展开式中各项系数的和为243,则该展开式中常数项为 【答案】10【解析】因为展开式中各项系数的和为243,所以当1x =时,5(1)243a +=,解得2a =,展开式的通项公式为5102552155(2)2k kkk k kk T C x C x ---+==,由51002k -=,解得4k =,所以常数项为455210T C =⨯=.27.(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)二项式6213x x ⎛⎫+ ⎪⎝⎭的展开式中,常数项等于______(用数字作答). 【答案】1215展开式的通项公式为666316621(3)()3kk k k k kk T C x C x x---+==,由630k -=得2k =,所以常数项为423631215T C ==.28.(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)设6sin (a xdx,π=⎰则二项式的展开式中的常数项等于________.【答案】160-00sin =cos 2a xdx x ππ=-=⎰,所以二项式的展开式为663166(((1)2k k kk k k k k T C C x ---+==-⋅⋅,由30k -=时,3k =,所以常数项为33346(1)2160T C =-⋅=-.29.(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)若22nx ⎫⎪⎭展开式中只有第六项的二项式系数最大,则展开式中的常数项是_________.【答案】180。
山东省2014届理科一轮复习试题选编38:算法初步(含解析)
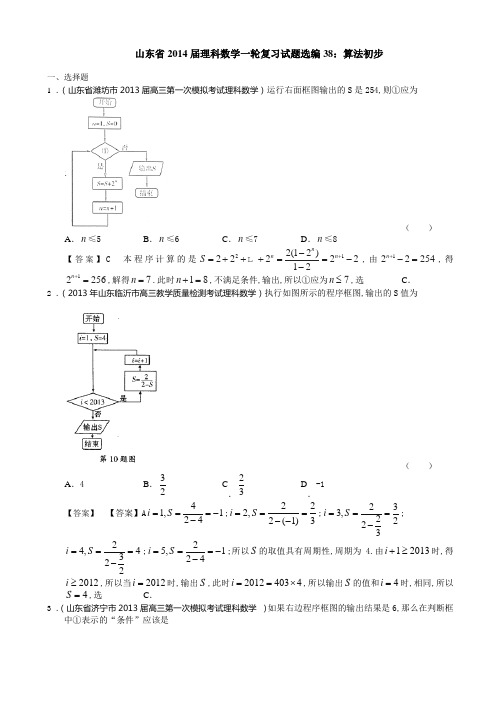
山东省2014届理科数学一轮复习试题选编38:算法初步一、选择题 1 .(山东省潍坊市2013届高三第一次模拟考试理科数学)运行右面框图输出的S 是254,则①应为( )A .n ≤5B .n ≤6C .n ≤7D .n ≤8【答案】C 本程序计算的是212(12)2222212n nn S +-=+++==-- ,由122254n +-=,得12256n +=,解得7n =.此时18n +=,不满足条件,输出,所以①应为7n ≤,选C . 2 .(2013年山东临沂市高三教学质量检测考试理科数学)执行如图所示的程序框图,输出的S 值为( )A .4B .32 C.23D .-1 【答案】 【答案】A 41,124i S ===--;222,2(1)3i S ===--;233,2223i S ===-;24,4322i S ===-;25,124i S ===--;所以S 的取值具有周期性,周期为 4.由12013i +≥时,得2012i ≥,所以当2012i =时,输出S ,此时20124034i ==⨯,所以输出S 的值和4i =时,相同,所以4S =,选 C .3 .(山东省济宁市2013届高三第一次模拟考试理科数学 )如果右边程序框图的输出结果是6,那么在判断框中①表示的“条件”应该是( )A .i≥3B .i≥4C .i≥5D .i≥6 【答案】D【解析】第一次循环,264,6410,2m s i =-+==+==;第二次循环,2262,10212,3m s i =-⨯+==+==;第三次循环,2360,12,4m s i =-⨯+===;第四次循环,2462,12210,5m s i =-⨯+=-=-==;第五次循环,2564,1046,6m s i =-⨯+=-=-==;此时满足条件输出6s =,所以条件应为,6i ≥选D .4 .(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知数列{}11,1,n n n a a a a n +==+中,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是( )A .11?n ≤B .10?n ≤C .9?n ≤D .8?n ≤【答案】C 5 .(山东省临沂市2013届高三5月高考模拟理科数学)执行如图所示的程序框图,输出的结果是( )A .11B .12C .13D .14【答案】C 第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选 C . 6 .(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)若程序框图如图所示,则该程序运行后输出k 的值是( )A .4B .5C .6D .7【答案】B第一次35116,1n k =⨯+==;第二次168,22n k ===;第三次84,32n k ===;第四次42,42n k ===;第五次21,52n k ===此时满足条件输出5k =,选 B . 7 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)定义某种运算⊗,a b ⊗的运算原理如图 所示.设x x f ⊗=1)(.()f x 在区间[2,2]-上的最大值为. ( )A .-2B .-1C .0D .2【答案】D 8 .(山东省济宁市2013届高三4月联考理科数学)左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7.98.6 3 89.3 9 8 8 4 1 5 10.3 1 11.4 ( )A .7B .8C .9D .10【答案】D9 .(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)执行如图所示的程序框图,若输出结果为3,则可输入的实数x 值的个数为( )A .1B .2C .3D .4【答案】C 由题意知221,2log ,2x x y x x ⎧-≤=⎨>⎩.当2x ≤时,由213x -=,得24x =,解得2x =±.当2x >时,由2log 3x =,得8x =,所以输入的实数x 值的个数为3个,选 C .10.(山东省德州市2013届高三第二次模拟考试数学(理)试题)执行如图所示的程序框图,若输入n 的值为≤≥16,则输出s 的值为( )A .17B .16C .10D .9【答案】C 11.(山东省2013届高三高考模拟卷(一)理科数学)执行如图所示的程序框图,若输入5=p ,6=q ,则输出a ,i 的值分别为( )A .5,1B .30,3C .15.3D .30.6【答案】D 【解析】执行程序框图可知,当1=i 时,15⨯=a ;当2=i 时,25⨯=a ;;当6=i 时,65⨯=a ,即a 能被q 整除,退出循环,输出i a ,的值分别为30,6. 12.(山东省德州市2013届高三3月模拟检测理科数学)如图所示,程序框图运行后输出k 的值是( )A .4B .5C .6D .7【答案】B 第一次循环,35116,1n k =⨯+==;第二次循环,168,22n k ===; 第三次循环,84,32n k ===;第四次循环,42,42n k ===;第五次循环,21,52n k ===,此时输出5k =,选B . 13.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)阅读程序框图,若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是( )A .i>5?B .i>6?C .i>7?D .i>8?【答案】A14.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)右图给出的是计算111124620++++ 的值的一个框图,其中菱形判断框内应填入的条件是 ( )A .10>iB .10<iC .11>iD .11<i【答案】A15.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )若右边的程序框图输出的S 是254,则条件①可为( )A .5n ≤B .6n ≤C .7n ≤D .8n ≤【答案】C16.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)如图是一个算法的流程图,若输出的结果是31,则判断框中整数M 的值是( )A .3B .4C .5D .6【答案】B本程序计算的是21222AS =++++ ,即11122112A A S ++-==--,由121=31A +-得12=32A +,解得4A =,则15A +=时,条件不成立,所以4M =,选B . 17.(山东省莱芜五中2013届高三4月模拟数学(理)试题)执行如图所示的程序框图,则输出的结果为( )A .2B .1C .21 D .1-【答案】C 18.(山东省凤城高中2013届高三4月模拟检测数学理试题 )阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )ABC.D.【答案】A19.(山东省文登市2013届高三3月二轮模拟考试数学(理))右面的程序框图中,若输出S 的值为126,则图中应填上的条件为( ) A .5n ≤ B .6n ≤C .7n ≤D .8n ≤【答案】B 20.(2012年山东理)(6)执行下面的程序图,如果输入a=4,那么输出的n 的值为( )C .4D .5【答案】:312,140,00=+==+==q p n ;716,541,11=+==+==q p n ;15114,2145,22=+==+==q p n ,q p n >=,3.答案应选 B .21.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)右图是某算法的程序框图,则程序运行后输出的结果是( )A .6B .27C .124D .168【答案】B 22.(山东省潍坊市2013届高三第二次模拟考试理科数学)运行如图所示的程序,若结束时输出的结果不小于3,则t 的取值范围为( )A .14t ≥B .18t ≥C .14t ≤D .18t ≤ 【答案】B 第一次循环,2,2,211n x t a ===-=;第二次循环,4,4,413n x t a ===-=;第三次循环,6,8,633n x t a ===-=,此时满足条件输出83x t a =,由题意知833x t a =≥,解得81t ≥,即18t ≥,选B .23.(山东省济南市2013届高三3月高考模拟理科数学)阅读右边的程序框图,运行相应的程序,输出的结果为( )A .1311B .2113C .813D .138【答案】D第7题图第一次循环,112,1,2z x y =+===;第二次循环,123,2,3z x y =+===;第三次循环,235,3,5z x y =+===;第四次循环,358,5,8z x y =+===;第五次循环,5813,8,13z x y =+===;第六次循环,81321z =+=,不满足条件输出138y x =,选 D . 24.(山东省夏津一中2013届高三4月月考数学(理)试题)如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是( )A .2012i ≤B .i >2012C .1006≤iD .i >1006【答案】A 25.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)如果执行下面的程序框图,输出的S=110,则判断框处为( )A .10<k ?B .11≥k ?C .10≤k ?D .11>k ?【答案】C【 解析】由程序可知该程序是计算(22)242(1)2k k S k k k +=+++==+ ,由(1)110S k k =+=得10k =,则当10k =时,110111k k =+=+=不满足条件,所以条件为10k ≤,选 C .26.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)右图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有( )A .1个B .2个C .3个D .4个【答案】C27.(山东威海市2013年5月高三模拟考试数学(理科))一算法的程序框图如右图所示,若输出的12y =,则输入的x 可能为 ( )A .1-B .1C .1或5D .1-或1【答案】 B . 二、填空题 28.(2013届山东省高考压轴卷理科数学)执行如右图的程序框图,那么输出S 的值是________.第5题图【答案】1-【解析】由框图知:12,1;1,2;,3;2S k S k S k ===-===2,4;1,5,S k S k ===-=不满足条件,输出S 的值是1-.29.(2013山东高考数学(理))执行右图的程序框图,若输入的ε的值为0.25,则输出的n 的值为_____.,10123,312,2F F n =+==-==,此时1110.253F =≤不成立.第二次循环,10235,523,3F F n =+==-==,此时1110.255F =≤成立,输出3n =. 30.(山东省济南市2013届高三上学期期末考试理科数学)已知程序框图如右图所示,则输出的i =________;【答案】9【 解析】第一次循环,133,5S i =⨯==;第二次循环,3515,7S i =⨯==;第三次循环,157105,9S i =⨯==;第四次循环,满足条件输出9i =. 31.(山东省德州市2013届高三上学期期末校际联考数学(理))执行如图所示程序框图,输出结果S=.【答案】1【解析】第一次循环1(1)2,3,2S T n =--===;第二次循环23(1)21,5,3S T n =--⨯===;第三次循环35(1)6,7,4S T n =--===;第四次循环47(1)61,9,5S T n =--⨯===,第五次循环,满足条件,输出1S =. 32.(2011年高考(山东理))执行右图所示的程序框图,输入2,3,5l m n ===,则输出的y 的值是______.【答案】解析:1406375278,y =++=278105173,17310568y y =-==-=.答案应填:68. 33.(山东省烟台市2013届高三3月诊断性测试数学理试题)执行如右图所示的程序框图,输出的S 值为___________【答案】10第一次循环,1,1,2i S i ==-=;第二次循环,22,123,3i S i ==-+==; 第三次循环,23,336,4i S i ==-=-=;第四次循环,24,6410,5i S i ==-+==,此时不满足条件,输出10S =. 34.(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)执行如图所示的程序框图,输出S 的值为__________.【答案】-2 35.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)执行如图所示的程序框图,若输出的结果是8,则输入的数是______.【答案】2或22- 由a b ≥得23x x ≥,解得1x ≤.所以当1x ≤时,输出2a x =,当1x >时,输出3b x =.所以当1x ≤时,由28a x ==,解得822x =-=-.若1x >,由38b x ==,得2x =,所以输入的数为2或22-. 36.(2010年高考(山东理))执行右图所示的程序框图,若输入10x =,则输出y 的值为_____________.【答案】54-【解析】当x=10时,y=110-1=42⨯,此时|y-x|=6; 当x=4时,y=14-1=12⨯,此时|y-x|=3;当x=1时,y=111-1=-22⨯,此时|y-x|=32;当x=12-时,y=115-1=-224⨯-(),此时|y-x|=3<14,故输出y 的值为54-.【命题意图】本题考查程序框图的基础知识,考查了同学们的试图能力.37.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))如果执行右面的程序框图,那么输出的S =______.【答案】 20【解析】第一次循环:2,220==+=k S ;第二次循环:3,642==+=k S ;第三次循环:4,1266==+=k S ;第四次循环:5,20812==+=k S ;第五次循环:输出20=S .38.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)执行如图的程序框图,如果输入的n 是4,则输出的p 是______【答案】3 39.(山东省青岛市2013届高三第一次模拟考试理科数学)某程序框图如右图所示,若3a=,则该程序运行后,输出的x 值为【答案】31 第一次循环,2317,2x n =⨯+==;第二次循环,27115,3x n =⨯+==;第三次循环,215131,4x n =⨯+==.此时不满足条件,输出31x =. 40.(2009高考(山东理))执行右边的程序框图,输入的T= .【答案】【解析】:按照程序框图依次执行为S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30 答案:30。
无锡新领航教育特供:山东省德州市2013届高三上学期校际联考试题

小升初 中高考 高二会考 艺考生文化课 一对一辅导 /wxxlhjy QQ:157171090 无锡新领航教育特供:高中三年级校际联考地理试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷1至6页,第II 卷7至8 页,共100分,考试时间90分钟。
注意事项:1. 答第I 卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮 擦干净,再选涂其它答案。
不能答在试卷上。
3. 考试结束,将答题纸和答题卡一并交回。
第I 卷(选择题共60分)一、单项选择题(本题共30小题,每小题2分,共计60分。
在每小题列出的四个选项中,只 有一项是最符合题目要求的。
)读“世界某区域的经纬网图”,图中箭头为地球自转方向,阴影为黑夜,此时在丙地正好可以看到日落的景观,完成1 ~2题。
1. 若此刻丙地是17: 30,此时有一架飞机从乙地取最短路径飞往甲地,行程用了3小时30 分钟,则下列说法正确的是A. 飞机先向东北后向东南飞B. 抵达甲地时,当地时间为当日17:40C. 飞机先向东南后向东北飞D. 抵达甲地时,当地时间为当日17:20【答案】B 【解析】根据自转方向为逆时针,可知为北半球,从乙地飞往甲地的最短路径偏向北极点,即先向西北再向西南;乙地经度为东经25度,时间为17: 30,甲地经度为西经25度,飞机从乙地起飞时,甲地时间为14:10,再加上路上时间3小时30 分钟,所以到达甲地时,时间为17:40。
2. 当乙地正午太阳高度达最大值时,下列叙述可信的是A.北印度洋洋流向西流B.黄河正处于主汛期。
山东省2014届理科数学一轮复习试题选编22:一元二次不等式

山东省2014届理科数学一轮复习试题选编22:一元二次不等式及其它简单不等式的问题一、选择题1 .(2013重庆高考数学(文))关于x 的不等式22280x ax a --<(0a >)的解集为12(,)x x ,且:2115x x -=,则a = ( )A .52B .72C .154D .152【答案】A .2 .(2013大纲卷高考数学(文))不等式222x -<的解集是( )A .()-1,1B .()-2,2C .()()-1,00,1D .()()-2,00,2【答案】D .3 .已知2()4(0)f x ax ax b a =-+>,则不等式(25)(4)f x f x +<+的解集为( )A .5(,1)3--B .5(,)(1,)3-∞-⋃-+∞C .5(1,)3D .5(,1)(,)3-∞⋃+∞【答案】 答案A 提示:2()4(0)f x ax ax b a =-+>的对称轴为2x =,由0a >可知,距离对称轴越远函数值越大.故(25)(4)|252||42|f x f x x x +<+⇔+-<+-22(23)(2)x x ⇔+<+23850x x ⇔++<513x ⇔-<<-,故选答案A4 .(山东省德州市2013届高三上学期期末校际联考数学(理))如果不等式57|1|x x ->+和不等式220ax bx +->有相同的解集,则( )A .8,10a b =-=-B .1,9a b =-=C .4,9a b =-=-D .1,2a b =-=【答案】C【解析】由不等式57|1|x x ->+可知50x ->,两边平方得22(5)49(1)x x ->+,整理得24920x x ++<,即24920x x --->.又两不等式的解集相同,所以可得4,9a b =-=-,选C .5 .(2013安徽高考数学(理))已知一元二次不等式()<0f x 的解集为{}1|<-1>2x x x 或,则(10)>0x f 的解集为( )A .{}|<-1>lg2x x x 或B .{}|-1<<lg2x xC .{}|>-lg2x x D .{}|<-lg2x x【答案】 D 【解析】 由题知,一元二次不等式2ln 211-),21(-1,的解集为0)(-<⇒<<>x e x x 即所以选 D .6 .(山东省实验中学2013届高三第一次诊断性测试数学(理)试题)不等式3≤l5 - 2xl<9的解集是( )A .(一∞,-2)U(7,+co)B .[1,4]C .[-2,1】U 【4,7】D .(2,1][4,7)-【答案】D【解析】由3|52|9x ≤-<得3259x ≤-<,或9253x -<-≤-,即47x ≤<或21x -<≤,所以不等式的解集为(2,1][4,7)- ,选D .7 .(2012年大纲版高考压轴卷)设min{, }p q 表示p ,q 两者中的较小的一个,若函数221()min{3log , log }2f x x x =-,则满足()1f x <的x 的集合为 ( )A .(0,B .(0, +)¥C .(0, 2)(16,)+ UD .1(, )16+ 【答案】C .8 .(山东省烟台市莱州一中2013届高三第三次质量检测数学(理)试题)不等式02ax +bx+c >的解集为{|24}x x <<,则不等式20cx bx a ++<的解集为( )A .11{|}24x x x ><或 B .1{|}4x x <C .1{|}2x x >D .11{|}24x x << 【答案】A 【解析】因为不等式02ax +bx+c >的解集为{|24}x x <<,所以0a <,且2,4是方程02ax +bx+c =的两个根,所以246b a +=-=,248ca⨯==,所以68b a c a =-=,,所以不等式20cx bx a ++<等价为2860ax ax a -+<,即28610x x -+>,所以(21)(41)0x x -->,解得1124x x 或><,所以不等式20cx bx a ++<的解集为11{|}24x x x ><或,选A 二、填空题9 .(山东省济宁市2013届高三4月联考理科数学)已知不等式2x x ++≤a 的解集不是空集,则实数a 的取值范围是______________ 【答案】a ≥210.(山东省济宁邹城市2013届高三上学期期中考试数学(理)试题)已知定义域为(-1,1)函数32(),(3)(9)0,f x x x f a f a a =---+-<且则的取值范围是____.【答案】11.(辽宁大连高三二模理科)若函数141log (1)(0)1(),()22(0)x x x f x f x x -+≥⎧⎪=≤-⎨⎪<⎩则的解集为_________.【答案】(,1][1,)-∞-+∞12.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)若存在实数x 使|||1|3x a x -+-≤成立,则实数a 的取值范围是___________.【答案】42≤≤-a13.(2013上海高考数学(文))不等式021xx <-的解为_________. 【答案】 1(0,)2【解析】)21,0(0)12(∈⇒<-x x x14.(2009高考(山东理))不等式0212<---x x 的解集为 .【答案】{|11}x x -<<,原不等式等价于不等式组①221(2)0x x x ≥⎧⎨---<⎩或②12221(2)0x x x ⎧<<⎪⎨⎪-+-<⎩ 或③12(21)(2)0x x x ⎧≤⎪⎨⎪--+-<⎩不等式组①无解,由②得112x <<,由③得112x -<≤,综上得11x -<<,所以原不等式的解集为{|11}x x -<<.15.(2012年湖南省十二校第二次联考(文数,word 版))已知函数2,(0)()2,(0)xx f x x x ≥⎧⎪=⎨⎪<⎩,则不等式()1f x ≥的解集为______________.【答案】(,1][2,)-∞-+∞16.(2013广东高考数学(理))不等式220x x +-<的解集为___________.【答案】()2,1-;易得不等式220x x +-<的解集为()2,1-.17.(北京市师大附中2012届下学期高三年级开学检测数学文试卷)已知)(x f y =是偶函数,)(x g y =是奇函数,它们的定义域均为]3,3[-,且它们在]3,0[∈x 上的图像如图所示,则不等式0)()(<x g x f 的解集是___________.【答案】 )3,2()1,0()1,2( --18.(2013四川高考数学(理))已知()f x 是定义域为R 的偶函数,当x ≥0时,2()4f x x x =-,那么,不等式(2)5f x +<的解集是____________.【答案】 答案 {x |-7<x <3}解析 令x <0,则-x >0,∵x ≥0时,f (x )=x 2-4x ,∴f (-x )=(-x )2-4(-x )=x 2+4x ,又f (x )为偶函数,∴f (-x )=f (x ),∴x <0时,f (x )=x 2+4x ,故有f (x )=⎩⎪⎨⎪⎧x 2-4x ,x ≥0,x 2+4x ,x <0.再求f (x )<5的解,由⎩⎪⎨⎪⎧x ≥0,x 2-4x <5,得0≤x <5;由⎩⎪⎨⎪⎧x <0,x 2+4x <5,得-5<x <0,即f (x )<5的解为(-5,5).由于f (x )向左平移两个单位即得f (x +2),故f (x +2)<5的解集为{x |-7<x <3}.19.(山东省实验中学2013届高三第三次诊断性测试理科数学)记c bx ax x f +-=2)(,若不等式0)(>x f 的解集为(1,3),试解关于t 的不等式)2()8|(|2t f t f +<+.【答案】由题意知)3)(1())(()(21--=--=x x a x x x a x f .且0<a 故二次函数在区间),2[+∞上是增函数 又因为22,8||82≥+>+t t ,故由二次函数的单调性知不等式)2()8|(|2t f t f +<+ 等价于22||8t t +>+即06||||2<--t t 故3||<t 即不等的解为:33<<-t20.(山东省凤城高中2013届高三4月模拟检测数学理试题 )若不等式2210x ax -+≥对任意1x ≥恒成立,则实数a 的取值范围为________.【答案】(,1]-∞21.已知函数⎪⎩⎪⎨⎧<-≥+=)0(,4)0(,4)(22x x x x x x x f ,若)()2(2a f a f >-,则a 的范围是________【答案】)(ln 2*N n n ∈+由图像或导数可判断)(x f 在R 上是增函数122)()2(22<<-⇔>-⇔>-∴a a a a f a f22.(山东省2013届高三高考模拟卷(一)理科数学)对任意的实数R x ∈,不等式01||2≥++x a x恒成立,则实数a 的取值范围是________.【答案】 ),2[+∞-【解析】当0=x 时,R a ∈;当0=/x 时,原不等式变形可得)||1|(|x x a +-≥,因为2||1||≥+x x (当且仅当1||=x 时,等号成立),所以2)||1|(|-≤+-x x ,即)||1|(|x x +-的最大值是2-,所以2-≥a .23.(2012年高考(湖南文))不等式2560x x -+≤的解集为______.【答案】{}23x x ≤≤【解析】由x 2-5x+6≤0,得(3)(2)0x x --≤,从而的不等式x 2-5x+6≤0的解集为{}23x x ≤≤.三、解答题24.(山东省日照市2013届高三12月份阶段训练数学(理)试题)已知函数()1.f x x x=-(I)若()2f x =,求x 的值;(II)若()()20tf t mf t +≥对于[]2,4t ∈恒成立,求实数m 的取值范围.【答案】解:(Ⅰ)当0<x 时,()0f x <;当0≥x 时,1()f x x x=-由条件可知 12x x-=,即 2210x x --=,解得 1x =0x > ,1x ∴=+ (Ⅱ)因为[]2,4t ∈,所以()1f t t t=-, ()2221f t t t =-, ()()20tf t mf t +≥恒成立即22110t t m t t t ⎛⎫⎛⎫-+-≥ ⎪ ⎪⎝⎭⎝⎭恒成立,即()2110t t m t ⎛⎫-++≥ ⎪⎝⎭,又[]2,4t ∈,所以10t t->. 所以210t m ++≥恒成立. 即2(1)m t ≥-+恒成立又[]2,4t ∈,∴2max (1)m t ⎡⎤≥-+⎣⎦.即5m ≥-。
山东省2014届理科数学一轮复习试题选编38:算法初步(教师版)
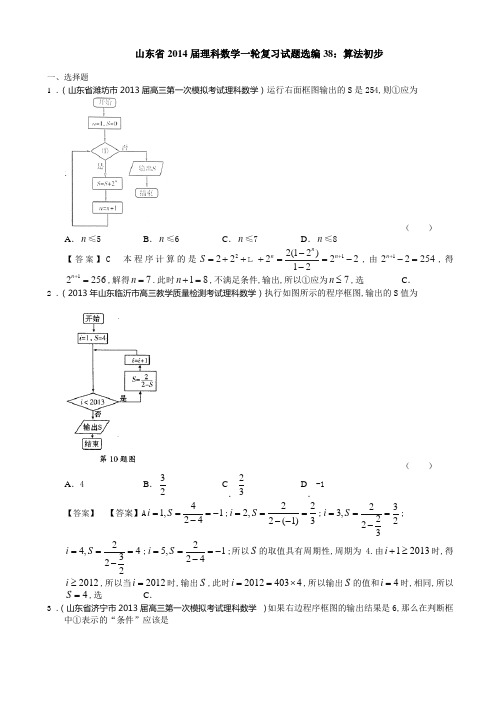
山东省2014届理科数学一轮复习试题选编38:算法初步一、选择题 1 .(山东省潍坊市2013届高三第一次模拟考试理科数学)运行右面框图输出的S 是254,则①应为( )A .n ≤5B .n ≤6C .n ≤7D .n ≤8【答案】C 本程序计算的是212(12)2222212n nn S +-=+++==-- ,由122254n +-=,得12256n +=,解得7n =.此时18n +=,不满足条件,输出,所以①应为7n ≤,选C . 2 .(2013年山东临沂市高三教学质量检测考试理科数学)执行如图所示的程序框图,输出的S 值为( )A .4B .32 C.23D .-1 【答案】 【答案】A 41,124i S ===--;222,2(1)3i S ===--;233,2223i S ===-;24,4322i S ===-;25,124i S ===--;所以S 的取值具有周期性,周期为 4.由12013i +≥时,得2012i ≥,所以当2012i =时,输出S ,此时20124034i ==⨯,所以输出S 的值和4i =时,相同,所以4S =,选 C .3 .(山东省济宁市2013届高三第一次模拟考试理科数学 )如果右边程序框图的输出结果是6,那么在判断框中①表示的“条件”应该是( )A .i≥3B .i≥4C .i≥5D .i≥6 【答案】D【解析】第一次循环,264,6410,2m s i =-+==+==;第二次循环,2262,10212,3m s i =-⨯+==+==;第三次循环,2360,12,4m s i =-⨯+===;第四次循环,2462,12210,5m s i =-⨯+=-=-==;第五次循环,2564,1046,6m s i =-⨯+=-=-==;此时满足条件输出6s =,所以条件应为,6i ≥选D .4 .(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知数列{}11,1,n n n a a a a n +==+中,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是( )A .11?n ≤B .10?n ≤C .9?n ≤D .8?n ≤【答案】C 5 .(山东省临沂市2013届高三5月高考模拟理科数学)执行如图所示的程序框图,输出的结果是( )A .11B .12C .13D .14【答案】C 第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选 C . 6 .(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)若程序框图如图所示,则该程序运行后输出k 的值是( )A .4B .5C .6D .7【答案】B第一次35116,1n k =⨯+==;第二次168,22n k ===;第三次84,32n k ===;第四次42,42n k ===;第五次21,52n k ===此时满足条件输出5k =,选 B . 7 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)定义某种运算⊗,a b ⊗的运算原理如图 所示.设x x f ⊗=1)(.()f x 在区间[2,2]-上的最大值为. ( )A .-2B .-1C .0D .2【答案】D 8 .(山东省济宁市2013届高三4月联考理科数学)左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7.98.6 3 89.3 9 8 8 4 1 5 10.3 1 11.4 ( )A .7B .8C .9D .10【答案】D9 .(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)执行如图所示的程序框图,若输出结果为3,则可输入的实数x 值的个数为( )A .1B .2C .3D .4【答案】C 由题意知221,2log ,2x x y x x ⎧-≤=⎨>⎩.当2x ≤时,由213x -=,得24x =,解得2x =±.当2x >时,由2log 3x =,得8x =,所以输入的实数x 值的个数为3个,选 C .10.(山东省德州市2013届高三第二次模拟考试数学(理)试题)执行如图所示的程序框图,若输入n 的值为≤≥16,则输出s 的值为( )A .17B .16C .10D .9【答案】C 11.(山东省2013届高三高考模拟卷(一)理科数学)执行如图所示的程序框图,若输入5=p ,6=q ,则输出a ,i 的值分别为( )A .5,1B .30,3C .15.3D .30.6【答案】D 【解析】执行程序框图可知,当1=i 时,15⨯=a ;当2=i 时,25⨯=a ;;当6=i 时,65⨯=a ,即a 能被q 整除,退出循环,输出i a ,的值分别为30,6. 12.(山东省德州市2013届高三3月模拟检测理科数学)如图所示,程序框图运行后输出k 的值是( )A .4B .5C .6D .7【答案】B 第一次循环,35116,1n k =⨯+==;第二次循环,168,22n k ===; 第三次循环,84,32n k ===;第四次循环,42,42n k ===;第五次循环,21,52n k ===,此时输出5k =,选B . 13.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)阅读程序框图,若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是( )A .i>5?B .i>6?C .i>7?D .i>8?【答案】A14.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)右图给出的是计算111124620++++ 的值的一个框图,其中菱形判断框内应填入的条件是 ( )A .10>iB .10<iC .11>iD .11<i【答案】A15.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )若右边的程序框图输出的S 是254,则条件①可为( )A .5n ≤B .6n ≤C .7n ≤D .8n ≤【答案】C16.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)如图是一个算法的流程图,若输出的结果是31,则判断框中整数M 的值是( )A .3B .4C .5D .6【答案】B本程序计算的是21222AS =++++ ,即11122112A A S ++-==--,由121=31A +-得12=32A +,解得4A =,则15A +=时,条件不成立,所以4M =,选B . 17.(山东省莱芜五中2013届高三4月模拟数学(理)试题)执行如图所示的程序框图,则输出的结果为( )A .2B .1C .21 D .1-【答案】C 18.(山东省凤城高中2013届高三4月模拟检测数学理试题 )阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )ABC.D.【答案】A19.(山东省文登市2013届高三3月二轮模拟考试数学(理))右面的程序框图中,若输出S 的值为126,则图中应填上的条件为( ) A .5n ≤ B .6n ≤C .7n ≤D .8n ≤【答案】B 20.(2012年山东理)(6)执行下面的程序图,如果输入a=4,那么输出的n 的值为( )C .4D .5【答案】:312,140,00=+==+==q p n ;716,541,11=+==+==q p n ;15114,2145,22=+==+==q p n ,q p n >=,3.答案应选 B .21.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)右图是某算法的程序框图,则程序运行后输出的结果是( )A .6B .27C .124D .168【答案】B 22.(山东省潍坊市2013届高三第二次模拟考试理科数学)运行如图所示的程序,若结束时输出的结果不小于3,则t 的取值范围为( )A .14t ≥B .18t ≥C .14t ≤D .18t ≤ 【答案】B 第一次循环,2,2,211n x t a ===-=;第二次循环,4,4,413n x t a ===-=;第三次循环,6,8,633n x t a ===-=,此时满足条件输出83x t a =,由题意知833x t a =≥,解得81t ≥,即18t ≥,选B .23.(山东省济南市2013届高三3月高考模拟理科数学)阅读右边的程序框图,运行相应的程序,输出的结果为( )A .1311B .2113C .813D .138【答案】D第7题图第一次循环,112,1,2z x y =+===;第二次循环,123,2,3z x y =+===;第三次循环,235,3,5z x y =+===;第四次循环,358,5,8z x y =+===;第五次循环,5813,8,13z x y =+===;第六次循环,81321z =+=,不满足条件输出138y x =,选 D . 24.(山东省夏津一中2013届高三4月月考数学(理)试题)如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是( )A .2012i ≤B .i >2012C .1006≤iD .i >1006【答案】A 25.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)如果执行下面的程序框图,输出的S=110,则判断框处为( )A .10<k ?B .11≥k ?C .10≤k ?D .11>k ?【答案】C【 解析】由程序可知该程序是计算(22)242(1)2k k S k k k +=+++==+ ,由(1)110S k k =+=得10k =,则当10k =时,110111k k =+=+=不满足条件,所以条件为10k ≤,选 C .26.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)右图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有( )A .1个B .2个C .3个D .4个【答案】C27.(山东威海市2013年5月高三模拟考试数学(理科))一算法的程序框图如右图所示,若输出的12y =,则输入的x 可能为 ( )A .1-B .1C .1或5D .1-或1【答案】 B . 二、填空题 28.(2013届山东省高考压轴卷理科数学)执行如右图的程序框图,那么输出S 的值是________.第5题图【答案】1-【解析】由框图知:12,1;1,2;,3;2S k S k S k ===-===2,4;1,5,S k S k ===-=不满足条件,输出S 的值是1-.29.(2013山东高考数学(理))执行右图的程序框图,若输入的ε的值为0.25,则输出的n 的值为_____.,10123,312,2F F n =+==-==,此时1110.253F =≤不成立.第二次循环,10235,523,3F F n =+==-==,此时1110.255F =≤成立,输出3n =. 30.(山东省济南市2013届高三上学期期末考试理科数学)已知程序框图如右图所示,则输出的i =________;【答案】9【 解析】第一次循环,133,5S i =⨯==;第二次循环,3515,7S i =⨯==;第三次循环,157105,9S i =⨯==;第四次循环,满足条件输出9i =. 31.(山东省德州市2013届高三上学期期末校际联考数学(理))执行如图所示程序框图,输出结果S=.【答案】1【解析】第一次循环1(1)2,3,2S T n =--===;第二次循环23(1)21,5,3S T n =--⨯===;第三次循环35(1)6,7,4S T n =--===;第四次循环47(1)61,9,5S T n =--⨯===,第五次循环,满足条件,输出1S =. 32.(2011年高考(山东理))执行右图所示的程序框图,输入2,3,5l m n ===,则输出的y 的值是______.【答案】解析:1406375278,y =++=278105173,17310568y y =-==-=.答案应填:68. 33.(山东省烟台市2013届高三3月诊断性测试数学理试题)执行如右图所示的程序框图,输出的S 值为___________【答案】10第一次循环,1,1,2i S i ==-=;第二次循环,22,123,3i S i ==-+==; 第三次循环,23,336,4i S i ==-=-=;第四次循环,24,6410,5i S i ==-+==,此时不满足条件,输出10S =. 34.(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)执行如图所示的程序框图,输出S 的值为__________.【答案】-2 35.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)执行如图所示的程序框图,若输出的结果是8,则输入的数是______.【答案】2或22- 由a b ≥得23x x ≥,解得1x ≤.所以当1x ≤时,输出2a x =,当1x >时,输出3b x =.所以当1x ≤时,由28a x ==,解得822x =-=-.若1x >,由38b x ==,得2x =,所以输入的数为2或22-. 36.(2010年高考(山东理))执行右图所示的程序框图,若输入10x =,则输出y 的值为_____________.【答案】54-【解析】当x=10时,y=110-1=42⨯,此时|y-x|=6; 当x=4时,y=14-1=12⨯,此时|y-x|=3;当x=1时,y=111-1=-22⨯,此时|y-x|=32;当x=12-时,y=115-1=-224⨯-(),此时|y-x|=3<14,故输出y 的值为54-.【命题意图】本题考查程序框图的基础知识,考查了同学们的试图能力.37.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))如果执行右面的程序框图,那么输出的S =______.【答案】 20【解析】第一次循环:2,220==+=k S ;第二次循环:3,642==+=k S ;第三次循环:4,1266==+=k S ;第四次循环:5,20812==+=k S ;第五次循环:输出20=S .38.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)执行如图的程序框图,如果输入的n 是4,则输出的p 是______【答案】3 39.(山东省青岛市2013届高三第一次模拟考试理科数学)某程序框图如右图所示,若3a=,则该程序运行后,输出的x 值为【答案】31 第一次循环,2317,2x n =⨯+==;第二次循环,27115,3x n =⨯+==;第三次循环,215131,4x n =⨯+==.此时不满足条件,输出31x =. 40.(2009高考(山东理))执行右边的程序框图,输入的T= .【答案】【解析】:按照程序框图依次执行为S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30 答案:30。
高三数学:专题07 不等式 理(教师版)

山东省2013届高三数学 各地市最新模拟理数试题精品分类汇编 专题07 不等式 理(教师版)一、选择题:1. (山东省济南市2013年1月高三上学期期末理3)设0.30.33,log 3,log a b c e π===则,,a b c 的大小关系是A .a b c <<B .c b a <<C .b a c <<D .c a b <<2. (山东省济南市2013年1月高三上学期期末理8)设实数,x y 满足不等式组 1103300x y x y x +-≤⎧⎪-+≤⎨⎪≥⎩,则 2z x y =+的最大值为 A. 13 B. 19 C. 24D. 293.(山东省德州市2013年1月高三上学期期末校际联考理3)设,,,,a b R ∈则“1a ≥且1b ≥”是“2a b +≥”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】若1a ≥,1b ≥,则2a b +≥。
若2a b +≥时,当15,2a b ==时有2a b +≥成立,但1b ≤,所以“1a ≥且1b ≥”是“2a b +≥”的充分而不必要条件,选A. 4.(山东省德州市2013年1月高三上学期期末校际联考理6)如果不等式57|1|x x ->+和不等式220ax bx +->有相同的解集,则A .8,10a b =-=-B . 1,9a b =-=C .4,9a b =-=-D .1,2a b =-=5.(山东省德州市2013年1月高三上学期期末校际联考理7)已知变量x 、y ,满足202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩,则41(24)z og x y =++的最大值为 A .23B .1C .32D .26. (山东省烟台市2013年1月高三上学期期末理5)若实数x y 、满足240 00x y x y +-≤⎧⎪≥⎨⎪≥⎩,则21y z x +=-的取值范围为A.2(,4][,)3-∞-⋃+∞ B.2(,2][,)3-∞-⋃+∞ C.2[2,]3-D.2[4,]3-7. (山东省烟台市2013年1月高三上学期期末理10)已知第一象限的点(a,b )在直线2x+3y -1=0上,则代数式23ab+的最小值为 A.24B.25C.26D.278. (山东省泰安市2013年1月高三上学期期末理3)设0.533,log 2,cos 2a b c ===,则 A.c <b a < B.c a b << C.a <b c <D.b <c a <9. (山东省泰安市2013年1月高三上学期期末理9)已知不等式组210y x y kx y ≤-+⎧⎪≤-⎨⎪≥⎩所表示的平面区域的面积等于14的三角形,则实数k 的值为A.1-B.12-C.12D.110.(山东省枣庄三中2013届高三上学期1月阶段测试理)设x , y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ,若目标函数z ax by =+(a .>0,b >0),最大值为12,则b a 32+ 的最小值为A.724 B.625 C. 5 D. 411.(山东省师大附中2013届高三第四次模拟测试1月理)已知x y 、满足5030x y x x y -+≥⎧⎪≤⎨⎪+≥⎩,则24z x y =+的最小值为( )A. 5B. -5 C . 6 D. -6【答案】D【解析】做出可行域如图:由24z x y =+,得124z y x =-+,平移直线,由图象可知当直线124z y x =-+经过点C 时,直线124z y x =-+的截距最小,此时z 最小。
山东省2014届理科数学一轮复习试题选编5:指数函数、对数函数、幂函数(学生版)

山东省2014届理科数学一轮复习试题选编5:指数函数、对数函数、幂函数一、选择题1 .(山东省烟台市2013届高三3月诊断性测试数学理试题)已知幂函数y=f(x)的图象过点(1,22),则log 2f(2)的值为 ( )A .12 B .-12C .2D .-22 .(山东省德州市2013届高三上学期期末校际联考数学(理))已知a>0,b>0,且1ab =,则函数()x f x a =与函数()1b g x og x =的图象可能是3 .(山东省实验中学2013届高三第一次诊断性测试数学(理)试题)下列函数图象中,正确的是4 .(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)已知1()x f x a =,2()a f x x =,3()log a f x x =,(0a >且1a ≠),在同一坐标系中画出其中两个函数在( )A .BC .D5 .(2012年高考(四川文))函数(0,1)xy a a a a =->≠的图象可能是6 .(山东省曲阜市2013届高三11月月考数学(理)试题)函数log (||1)(1)a y x a =+>的大致图象是 ( )A .B .C .D .7 .(山东省潍坊市2013届高三第二次模拟考试理科数学)已知函数9()4(1)1f x x x x =-+>-+,当x=a 时,()f x 取得最小值,则在直角坐标系 中,函数11()()x g x a+=的大致图象为8 .(2013陕西高考数学(文))设a , b , c 均为不等于1的正实数, 则下列等式中恒成立的是 ( )A .·log log log a c c b a b =B .·log lo log g a a a b a b =C .()log g o lo g a a a b c bc =D .()log g og o l l a a a b b c c +=+9 .(2013辽宁高考数学(文))已知函数()()2ln1931,f x x x =+-+则()1lg 2lg 2f f ⎛⎫+= ⎪⎝⎭( )A .1-B .0C .1D .210.(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))若点(a,9)在函数3xy =的图象上,则tan 3πa 的值为 ( )A .0B .33- C .1 D .3-11.(2012年高考(四川理))函数1(0,1)xy a a a a=->≠的图象可能是12.(2009高考(山东理))函数x xx xe ey e e--+=-的图像大致为13.(2011年高考(山东理))若点(,9)a 在函数3xy =的图象上,则tan 6a π的值为 ( )A .0B 3C .1D 314.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)设11333124log ,log ,log ,233a b c ===则a,b,c 的大小关系是( )A .a b cB .c b aC .b a cD .b c a1 xy 1OxyO 1 1 B xy O 1 1 C x y 1 1 O15.(山东省潍坊市四县一校2013届高三11月期中联考(数学理))若函数⎪⎩⎪⎨⎧<->=0),(log 0,log )(212xx x x x f ,若0)(>-a af ,则实数a 的取值范围是( ) A .)()(1,00,1⋃- B .),(),(∞+⋃-∞-11 C .),()(∞+⋃-10,1 D .)(),(1,01⋃-∞- 16.已知曲线221:9436C x y +=,曲线12:3x C y +=,则1C 与2C 的交点个数为( )A .0B .1C .2D .317.(山东省日照市2013届高三12月份阶段训练数学(理)试题)已知函数()2log ,0,2,0.x x x f x x >⎧=⎨≤⎩若()12f a =,则a 等于 ( ) A .1-或2 B .2 C .1- D .1或2-18.(2013福建高考数学(文))函数)1ln()(2+=x x f 的图象大致是( )A .B .C .D .19.(2013上海春季数学(理))函数12()f x x-=的大致图像是20.(山东省潍坊市2013届高三第二次模拟考试理科数学)已知1122log (4)log (32)x y x y ++<+-,若x y λ-<恒成立, 则λ的取值范围是( )A .(],10-∞B .(),10-∞C .[)10,+∞D .()10,+∞21.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)幂函数()y f x =的图象经过点(4,12),则f(14)的值为( )A .1B .2C .3D .422.(山东省烟台市2013届高三上学期期中考试数学试题(理科))已知()()()2,log 0,1x a f x a g x x a a -==>≠,若()()440f g ⋅-<,则y=()f x ,y=()g x 在同一坐标系内的大致图象是x y 0xy BA0 x y C0 x yD23.(山东省烟台市2013届高三上学期期中考试数学试题(理科))设5.205.2)21(,5.2,2===c b a,则c b a ,,的大小关系是 ( )A .b c a >>B .b a c >>C .c a b >>D .c b a >>二、填空题24.(2013安徽高考数学(文))函数1ln(1)y x=++_____________. 25.(2013北京高考数学(文))函数f(x)=12log ,12,1x x x x ≥⎧⎪⎨⎪<⎩的值域为_________. 26.若12()1f x x--=+,且(1)(102)f a f a +<-,则a 的取值范围为______.27.(2012年高考(上海文))方程03241=--+x x 的解是_________.28.(2012年高考(山东文))若函数()(0,1)x f x a a a =>≠在[-1,2]上的最大值为4,最小值为m ,且函数()(14g x m =-在[0,)+∞上是增函数,则a =____.29.(山东省实验中学2013届高三第三次诊断性测试理科数学)若直线a y 2=与函数|1|-=x a y ()10≠>a a 且的图像有两个公共点,则a 的取值范围是____________.30.函数122(2)y xx --=-的定义域为_______________31.(山东省济宁邹城市2013届高三上学期期中考试数学(理)试题)当1{1,,1,3},2∈-时幂函数a y x =的图象不奇能经过第_____象限.山东省2014届理科数学一轮复习试题选编5:指数函数、对数函数、幂函数参考答案一、选择题1. 【答案】A 设幂函数为()f x x α=,则11()()222f α==,解得12α=,所以()f x =所以(2)f =即221log (2)log 2f ==,选A.2. 【答案】D【解析】因为对数函数()1b g x og x =的定义域为(0,)+∞,所以排除A,C.因为1ab =,所以1b a=,即函数()xf x a =与()1bg x og x =的单调性相反.所以选D.3. 【答案】C【解析】A 中幂函数中0a <而直线中截距1a >,不对应.B 中幂函数中12a =而直线中截距1a >,不对应.D 中对数函数中1a >,而直线中截距01a <<,不对应,选C. 4. 【答案】B【解析】A 中1()x f x a =单调递增,所以1a >,而幂函数2()a f x x =递减,0a <,所以不正确.B 中3()log a f x x =单调递增,所以1a >,而幂函数2()a f x x =递增,,所以正确.C 中1()x f x a =单调递增,所以1a >,而3()log a f x x =递减,01a <<,所以不正确.D 中1()x f x a =单调递减,所以01a <<,而幂函数2()a f x x =递增,0a >,所以不正确.所以正确的是B.5. [答案]C[解析]采用特殊值验证法. 函数(0,1)xy a a a a =->≠恒过(1,0),只有C 选项符合. 6. B7. 【答案】B 9941+511y x x x x =-+=+-++,因为1x >-,所以910,01x x +>>+,所以由均值不等式得91+5511y x x =+-≥-=+,当且仅当911x x +=+,即2(1)9x +=,所以13,2x x +==时取等号,所以2a =,所以1111()()()2x x g x a ++==,又1111(),11()()222,1x x x x g x x +++⎧≥-⎪==⎨⎪<-⎩,所以选B.8. B 解:a, b,c≠1. 考察对数2个公式: abb y x xyc c a a a a log log log ,log log log =+=对选项A: b ab a b bc c a c c a log log log log log log =⇒=⋅,显然与第二个公式不符,所以为假.对选项B: abb b a bc c a c c a log log log log log log =⇒=⋅,显然与第二个公式一致,所以为真.对选项C: c b bc a a alog loglog ⋅=)(,显然与第一个公式不符,所以为假. 对选项D: c b c b a a alog log )log +=+(,同样与第一个公式不符,所以为假. 所以选B9. [答案]D()3)1f x x -=+所以()()2f x f x +-=,因为lg 2,1lg 2为相反数,所以所求值为2.10. D 【解析】因为点(,9)a 在函数3xy =的图象上,所以39a =,解得2a =,所以2tan tan 33a ππ==选D11. [答案]C[解析]采用排除法. 函数(0,1)xy a a a a =->≠恒过(1,0),选项只有C 符合,故选C.12. 【解析】:函数有意义,需使0xxe e--≠,其定义域为{}0|≠x x ,排除C,D,又因为22212111x x x x x x xe e e y e e e e --++===+---,所以当0x >时函数为减函数,故选A.答案:A.13.解析:2393a==,2a =,tantan 63a ππ==答案应选D. 14. B15. A 【解析】若0a >,则由0)(>-a af 得, 12log 0a a >,解得01a <<,若0a <,则由0)(>-a af 得,2log ()0a a ->,即2log ()0a -<解得01a <-<,所以10a -<<,综上01a <<或10a -<<,选A.16. C17. A 【解析】若0a >,则由()12f a =得,21log 2a =,解得a =若0a ≤,则由()12f a =得122a =,解得1a =-,所以a =1a =-,选A.18. A 【解析】本题考查的是对数函数的图象.由函数解析式可知)()(x f x f -=,即函数为偶函数,排除C;由函数过)0,0(点,排除B,D.19. A20. 【答案】C 要使不等式成立,则有40320432x y x y x y x y ++>⎧⎪+->⎨⎪++>+-⎩,即403203x y x y x ++>⎧⎪+->⎨⎪<⎩,设z x y =-,则y x z =-.作出不等式组对应的平面区域如图,平移直线y x z =-,由图象可知当直线y x z =-经过点B 时,直线的截距最小,此时z 最大,由403x y x ++=⎧⎨=⎩,解得73y x =-⎧⎨=⎩,代入z x y =-得3710z x y =-=+=,所以要使x y λ-<恒成立,则λ的取值范围是10λ≥,即[)10,+∞,选C.21. B22. B 【解析】由()()440f g ⋅-<知04log ,04log 2<∴<⋅a a a )(.10x f a ∴<<∴为减函数,因此可排除A 、C,而)(x g 在0>x 时也为减函数,故选B.23. D 【解析】,10,1,1<<=>c b a 所以c b a >>.故选D二、填空题24. (]0,1 解:2110011011x x xx x ⎧+>⇒><-⎪⎨⎪-≥⇒-≤≤⎩或,求交集之后得x 的取值范围(]0,1 25. (-∞,2) [解析] 函数y =log 12x 在(0,+∞)上为减函数,当x ≥1时,函数y =log 12x 的值域为(-∞,0];函数y =2x 在上是增函数,当x <1时,函数y =2x的值域为(0,2),所以原函数的值域为(-∞,2).26.由12()1f x x-=+为定义在(0,)+∞上的减函数,可知101(1)(102)102053511023a a f a f a a a a a a a +>>-⎧⎧⎪⎪⎪⎪+<-⇔->⇔<⇔<<⎨⎨⎪⎪+>->⎪⎪⎩⎩27. [解析] 0322)2(2=-⋅-x x ,0)32)(12(=-+x x ,32=x,3log 2=x .28. 答案:14 解析:当1a >时,有214,a a m -==,此时12,2a m ==,此时()g x x =-为减函数,不合题意.若01a <<,则124,a a m -==,故11,416a m ==,检验知符合题意.另解:由函数()(14)g x m x =-在[0,)+∞上是增函数可知41,041<>-m m ; 当1>a 时()x f x a =在[-1,2]上的最大值为=2a 4,解得2=a ,最小值为211==-a m 不符合题意,舍去;当10<<a 时,()x f x a =在[-1,2]上的最大值为41=-a,解得41=a ,此时最小值为411612<==a m ,符合题意, 故a =41.29. 1(0,)2【解析】因为1x y a =-的图象是由x y a =向下平移一个单位得到,当1a >时,作出函数1x y a =-的图象如图,此时22y a =>,如图象只有一个交点,不成立.当01a <<时,022a <<,要使两个函数的图象有两个公共点,则有021a <<,即102a <<,所以a的取值范围是1(0,)2.30. (2,)(,0)+∞⋃-∞.由1222(2)2y x x x x-=-=-,故由2202x x x ->⇒>或0x <.31.二、四。
山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题(学生版)

山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题一、选择题 1 .(山东省实验中学2013届高三第三次诊断性测试理科数学)已知等差数列{}n a 的公差d 不为0,等比数列{}n b 的公比q 是小于1的正有理数.若d a =1,,21d b =且321232221b b b a a a ++++是正整数,则q 的值可以是( )A .71 B .-71 C .21 D .-21 2 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)已知数列{},{}n n a b 满足113a b ==,113n n n nb a a b ++-==,n N +∈,若数列{}n c 满足n n a c b =,则2013c = ( )A .20129B .201227C .20139D .2013273 .(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知各项均不为零的数列{}n a ,定义向量()()1,,,1,n n n n c a a b n n n N *+==+∈ .下列命题中真命题是( )A .若n N *∀∈总有n n c b ⊥成立,则数列{}n a 是等比数列B .若n N *∀∈总有//n n c b 成立,则数列{}n a 是等比数列C .若n N *∀∈总有n n c b ⊥成立,则数列{}n a 是等差数列D .若n N *∀∈总有//n n c b 成立,则数列{}n a 是等差数列二、填空题 4 .(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知等差数列{}n a 中,有11122012301030a a a a a a ++++++=成立.类似地,在正项等比数列{}n b 中,有_____________________成立.三、解答题 5 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)已知数列{}n a 满足13a =,*133()n n n a a n N +-=∈,数列{}n b 满足3nn na b =. (1)证明数列{}n b 是等差数列并求数列{}n b 的通项公式; (2)求数列}{n a 的前n 项和n S .6 .(山东省济宁市2013届高三第一次模拟考试理科数学 )已知数列{n a }的前n 项和1122n *n n S a ()(n N )-=--+∈,数列{n b }满足n b =2n n a .(I)求证数列{n b }是等差数列,并求数列{n a }的通项公式;(Ⅱ)设2n n n c log a =,数列{22n n c c +}的前n 项和为T n ,求满足2521*n T (n N )<∈的n 的最大值.7 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)在等差数列{}n a 中,345842,30a a a a ++==.(1)求数列{}n a 的通项公式; (2)若数列{}n b满足2n a n b λ+=+(R λ∈),则是否存在这样的实数λ使得{}n b 为等比数列;(3)数列{}n c 满足112,1,2n n n n n c T a n --⎧⎪=⎨⎪⎩为奇数,为偶数为数列{}n c 的前n 项和,求2n T .8 .(山东省凤城高中2013届高三4月模拟检测数学理试题 )设等比数列{}n a 的前项和为n S ,已知122n n a S +=+,(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)在n a 与1n a +之间插入n 个数,使这2+n 数组成公差为n d 的等差数列,求1{}nd 的前n 项和n T .9 .(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知数列{}n a 的前n 项和n S 满足21n n S a =-,等差数列{}n b 满足11b a =,43b S =.(1)求数列{}n a 、{}n b 的通项公式; (2)设11n n n c b b +=,数列{}n c 的前n 项和为n T ,问n T >10012012的最小正整数n 是多少?10.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)等差数列}{n a 中,9,155432==++a a a a .(Ⅰ)求数列}{n a 的通项公式; (Ⅱ)设213+=n a n b ,求数列n n a 1{,b }2+的前n 项和n S .11.(山东省德州市2013届高三上学期期末校际联考数学(理))数列{a n }的前n 项和为1,2(1)n n n S S n +=-+,等差数列{}n b 的各项为正实数,其前n 项和为31122339,,,n T T a b a b a b =+++,且又成等比数列. (I)求数列{a n }、{}n b 的通项公式;(2)若.n n n c a b =,当n≥2时,求数列{}n c 的前n 项和A n .12.(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知等差数列{}n a 的首项13,0a d =≠公差,其前n 项和为n S ,且1413,,a a a 分别是等比数列{}n b 的第2项,第3项,第4项. (I)求数列{}n a 与{}n b 的通项公式;(II)证明1211113.34n S S S ≤++⋅⋅⋅+< 13.(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)设等比数列{}n a 的前n 项和为,415349,,,n S a a a a a =-成等差数列.(I)求数列{}n a 的通项公式;(II)证明:对任意21,,,k k k R N S S S +++∈成等差数列.14.(山东师大附中2013届高三第四次模拟测试1月理科数学)已知数列{}n a 是等差数列,{}n b 是等比数列,且112a b ==,454b =,12323a a a b b ++=+.(1)求数列{}n a 和{}n b 的通项公式(2)数列{}n c 满足n n n c a b =,求数列{}n c 的前n 项和n S .15.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知{}n a 是公差为2的等差数列,且317111a a a +++是与的等比中项.(1)求数列{}n a 的通项公式;(2)令()12n n na b n N *-=∈,求数列{}n b 的前n 项和Tn. 16.(2012年山东理)(20)在等差数列{}n a 中,345984,73a a a a ++==.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)对任意*m ∈N ,将数列{}n a 中落入区间2(9,9)m m 内的项的个数记为{}n b ,求数列{}n b 的前m 项和m S .17.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)已知数列{}n a 的前n 项和为1,3n n n S a S n +=-+且,1,2n a ∈=+N .(Ⅰ)求数列{}n a 的通项; (Ⅱ)设()2n n nb n S n =∈-++N 的前n 项和为n T ,证明:n T <34. 18.(山东省日照市2013届高三12月份阶段训练数学(理)试题)已知{}n a 是公差不为零的等差数列,11391,,,a a a a =成等比数列.求: (I)数列{}n a 的通项公式; (II)数列{}2an n a ⋅的前n 项和n S19.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )设数列{}n a 为等差数列,且145=a ,720a =,且132(2,)n n S S n n N -=+≥∈;, (Ⅰ(Ⅱ为数列{}n c 的前n 项和. T n <m 恒成立对N n *∈,求m 的最小值.20.(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知数列n a 满足222121na a a n n =+⋅⋅⋅++- (Ⅰ)求数列{}n a 的通项; (Ⅱ)若nn a nb =,求数列{}n b 的前n 项的和n S .21.(山东师大附中2013届级高三12月第三次模拟检测理科数学)数列{}n a 的前n 项的和为n S ,对于任意的自然数0n a >,()241n n S a =+(Ⅰ)求证:数列{}n a 是等差数列,并求通项公式 (Ⅱ)设3nn na b =,求和12n n T b b b =+++ 22.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)设等比数列{}n a 的前n 项和为n S ,已知122(n n a S n +=+∈N *).(1)求数列{}n a 的通项公式;(2)在n a 与1n a +之间插入n 个数,使这n+2个数组成公差为n d 的等差数列,求数列1n d ⎧⎫⎪⎨⎬⎪⎭⎩的前n 项和n T . 23.(山东省潍坊市四县一校2013届高三11月期中联考(数学理))已知各项均为正数的数列{}n a 前n 项和为n S ,首项为1a ,且n n S a ,,21等差数列. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若n b n a )21(2=,设n n n a b c =,求数列{}n c 的前n 项和n T .24.(山东省夏津一中2013届高三4月月考数学(理)试题)在等比数列}{n a 中,412=a ,512163=⋅a a .设22122log 2log 2nn n a a b +=⋅,n T 为数列{}n b 的前n 项和.(Ⅰ)求n a 和n T ;(Ⅱ)若对任意的*∈N n ,不等式n n n T )1(2--<λ恒成立,求实数λ的取值范围.25.(山东省济南市2013届高三3月高考模拟理科数学)数列{}n a 的前n 项和为n S ,11a =,121n n a S +=+*()n N ∈,等差数列{}n b 满足 353,9b b ==.(1)分别求数列{}n a ,{}n b 的通项公式; (2)设*22()n n n b c n N a ++=∈,求证113n n c c +<≤.26.(山东省济南市2013届高三上学期期末考试理科数学)已知等差数列{}n a 的前n 项和为n S ,365,36a S ==,(1)求数列{}n a 的通项公式;(2) 设2n an b =,求数列{}n b 的前n 项和n T .27.(山东省潍坊市2013届高三上学期期末考试数学理(A ))设数列{}n a 为等差数列,且9,553==a a ;数列{}n b 的前n 项和为n S ,且2=+n n b S .(I)求数列{}n a ,{}n b 的通项公式; (II)若()+∈=N n b a c nnn ,n T 为数列{}n c 的前n 项和,求n T .28.(山东威海市2013年5月高三模拟考试数学(理科))已知{}n a 为等差数列,n S 为其前n 项和,且222n n S a n =+.(Ⅰ)求,n n a S ;(Ⅱ)若2221,,k k k a a a -+成等比数列,求k 的值及公比.山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题参考答案一、选择题1. C 【解析】由题意知21312,23a a d d a a d d =+==+=,22222131,b b q d q b b q d q ====,所以2222221232222212349141a a a d d d b b b d d q d q qq++++==++++++,因为321232221b b b a a a ++++是正整数,所以令2141t q q=++,t 为正整数.所以2114t q q ++=,即21014t q q ++-=,解得5613t q +-+===,因为t 为正整数,所以当8t =时,12122q -+===.符合题意,选C2. D3. D 【解析】由//nn c b 得,1(1)n n na n a +=+,即11n n a a n n +=+,所以11n n a n a n ++=,所以1n a na =,故数列{}n a 是等差数列,选D.二、填空题4. 由算术平均数类比几何平均数,容易得出30302110201211b b b b b b =. 三、解答题5. 解(1)证明:由3n n n a b =,得1113n n n a b +++=, ∴1111333n n n n n n a a b b +++-=-=所以数列{}n b 是等差数列,首项11b =,公差为13∴121(1)33n n b n +=+-=(2)13(2)3n n n n a b n -==+⨯n n a a a S +++=∴ 2113)2(3413-⨯+++⨯+⨯=n n ----① n n n S 3)2(343332⨯+++⨯+⨯=∴ -------------------②①-②得n n n n S 3)2(33313212⨯+-++++⨯=--n n n 3)2(3331212⨯+-+++++=-n n n 3)2(233⨯+-+=23)2(433nn n n S +++-=∴6. 解:(Ⅰ)在2)21(1+--=-n n n a S 中,令n=1,可得1121a a S n =+--=,即211=a . 当2≥n 时,2)21(211+--=---n n n a S ∴111)21(---++-=-=n n n n n n a a S S a ,∴11)21(2--+=n n n a a ,即12211+=--n n n n a a .∵n n n a b 2=,∴11+=-n n b b ,即当2≥n 时,11=--n n b b . 又1211==a b ,∴数列{b n }是首项和公差均为1的等差数列.于是n n n a n n b 21)1(1==⋅-+=,∴nn n a 2= (Ⅱ)∵nn a nc 2log ==n n =2log 2, ∴22211(2)2n n+==-c c n n+n n+, ∴)211()1111()5131()4121()311(+-++--++-+-+-=n n n n T n =2111211+-+-+n n 由n T 2125<,得2111211+-+-+n n 2125<,即42132111>+++n n , =)(n f 2111+++n n 单调递减,∵4213)5(,209)4(==f f , ∴n 的最大值为47. 解:(1)因为{}n a 是一个等差数列,所以34544342,14a a a a a ++==∴=.设数列{}n a 的公差为d ,则84416d a a =-=,故4d =;故4(4)42n a a n d n =+-=-(2)29n a n n b λλ+=+=+.假设存在这样的λ使得{}n b 为等比数列,则212n n n b b b ++=⋅,即122(9)(9)(9)n n n λλλ+++=+⋅+,整理可得0λ=. 即存在0λ=使得{}n b 为等比数列(3)∵12,23,n n n c n n -⎧=⎨-⎩为奇数为偶数,∴242221(223)2(243)22(223)n n T n -=+⨯-++⨯-++++⨯- 242212224(12)3n n n -=++++++++-214(1)414321423n n n n n n n -+-=+⨯-=+-- 8. 解:(Ⅰ)由122(n n a S n +=+∈ N +)得122(n n a S n -=+∈N +,2n ≥), 两式相减得:12n n n a a a +-=, 即13(n n a a n +=∈N +,2n ≥),∵{}n a 是等比数列,所以213a a = ; 又2122,a a =+则11223a a +=,∴12a =, ∴132-⨯=n n a(Ⅱ)由(1)知132-⨯=n n a ,则nn a 321⨯=+∵1(1)n n n a a n d +=++ , ∴1341+⨯=-n d n n∵123111n T d d d =+++1nd + ∴1210341344343342-⨯+++⨯+⨯+⨯=n n n T ① nn n n n T 34134344343342311321⨯++⨯++⨯+⨯+⨯=- ② ①-②得nn n n T 3413413413413413423213210⨯+-⨯++⨯+⨯+⨯+⨯=-n n n 3413113113141211⨯+--⎪⎭⎫ ⎝⎛-⨯+=-n n 385285⨯+-= ∴1316521615-⨯+-=n n n T 9. 解:(1)当1n =时,11121a S a ==-,∴11a =当2n ≥时,111(21)(21)22n n n n n n n a S S a a a a ---=-=---=-, 即12nn a a -= ∴数列{}n a 是以11a =为首项,2为公比的等比数列,∴12,21n n n n a S -==- 设{}n b 的公差为,d 111b a ==,4137b d =+=,∴2d = ∴1(1)221n b n n =+-⨯=-(2)111111()(21)(21)22121n n n c b b n n n n +===--+-+ ∴11111111(1...)(1)2335212122121n n T n n n n =-+-++-=-=-+++ 由n T >10012012,得21n n +>10012012,解得n >100.1∴n T >10012012的最小正整数n 是10110.解:(Ⅰ)设数列{}由题意得首项的公差为,1a d a n且⎩⎨⎧=+=+⎩⎨⎧==++941563915115432d a d a a a a a 即 解得⎩⎨⎧==211d a所以数列{}12-=n a a n n 的通项公式为 (Ⅱ)由(Ⅰ)可得n n n ab 3231==+所以n n n n b a3..21=+所以+++=323.33.23.11n S 13.+n n两式相减得++++-=433333(22n S 13.)3+++n n n 10 分43).12(323..1233.31313111+++-+=-+=+---=n n n n n n S n n n 即)()(11.12.13.14. 【解析】:(Ⅰ)设{}n a 的公差为d ,{}n b 的公比为q由341b b q =,得354272q ==,从而3q = 因此11132--⋅=⋅=n n n q b b又123223361824a a a a b b ++==+=+=,28a ∴= 从而216d a a =-=,故466)1(1-=⋅-+=n n a a n (Ⅱ)13)23(4-⋅-⋅==n n n n n b a c令122103)23(3)53(373431--⋅-+⋅-++⨯+⨯+⨯=n n n n n Tn n n n n T 3)23(3)53(37343131321⋅-+⋅-++⨯+⨯+⨯=-两式相减得13)13(3313)23(333333331211321--⨯+=⋅--⨯++⨯+⨯+⨯+=---n nn n n Tnn 3)23(⋅--n 1n 9(31)13n 2)32--=+--⋅(73(67)44n n n T -∴=+,又n n n S 4T 7(6n 7)3==+-⋅15.16. (20)解:(Ⅰ)因为{}n a 是一个等差数列,所以3454384a a a a ++==,即428a =. 所以,数列{}n a 的公差9473289945a a d --===-, 所以,*4(4)289(4)98()n a a n d n n n =+-=+-=-∈N (Ⅱ)对*m ∈N ,若 299m m n a <<,则 298998m m n +<<+,因此 121919m m n --+≤≤, 故得 2199m m m b -=-(lb ylfx) 于是 123...m m S b b b b =++++35212121(999...9)(199...9)9(181)19181199109180m m m m m m --+=++++-++++⨯--=----⨯+=17.解:(Ⅰ)()113,213n n n n a S n n a S n +-=-+≥=--+ 时, ,,12,111-=-=-∴++n n n n n a a a a a 即 112(1),(2,),n n a a n n +∴-=-≥∈N* 2221(1)232n n n a a --∴-=-=∙=n a ⎩⎨⎧≥+∙=-2,1231,22n n n (Ⅱ)113322n n n S a n n -+=+-=∙+- ,123-∙=∴n n nb⎪⎭⎫⎝⎛++++=∴-1222322131n n n T⎪⎭⎫ ⎝⎛++++=n n n T 2232221312132 相减得,⎪⎭⎫⎝⎛-++++=-n n n n T 22121211312112 ,n n n nT 23221134∙-⎪⎭⎫ ⎝⎛-=∴﹤34∴结论成立.18.解:(Ⅰ)设等差数列{}n a 的公差为d ,由题设知0d ≠,由11391,,,a a a a =成等比数列,得1218112d dd++=+ 解得1,0d d ==(舍去).故{}n a 的通项公式为11)1=+(n a n n -⨯=(Ⅱ)由(I)知22n a n n a n ⋅=⋅,1231122232(1)22n n n S n n -=⨯+⨯+⨯++-⨯+⨯ , (1)23412122232(1)22n n n S n n +⨯=⨯+⨯+⨯++-⨯+⨯ ,(2) (1)(2)-,得123122222n n n S n +-=++++-⨯所以11222.12n n n S n ++--=-⨯-从而1(1)2 2.=nS n +-⨯+19.∵T n <m 恒成立对N n *∈∴2≥m ∴m 的最小值是220.解:(Ⅰ)2111==a n 时222213221na a a a n n =+++- (1)21222123221-=+++--n a a a a n n (2) (1)-(2)得2121=-n n a 即n n a 21=(n 2≥),又211=a 也适合上式∴n n a 21=21.解 :(1)令(2)-(1)是等差数列(2)---①---②①-②所以22. (1)由122(n n a S n +=+∈ Z *)得122(n n a S n -=+∈ Z *,2n ≥),两式相减得:12n n n a a a +-=, 即13(n n a a n +=∈ Z *,2n ≥),∵{}n a 是等比数列,所以213a a = ; 又2122,a a =+则11223a a +=,∴12a =, ∴132-⨯=n n a(2)由(1)知132-⨯=n n a ,则n n a 321⨯=+ ∵1(1)n n n a a n d +=++ ,∴1341+⨯=-n d n n∵123111n T d d d =+++1nd +∴1210341344343342-⨯+++⨯+⨯+⨯=n n n T ① nn n n n T 34134344343342311321⨯++⨯++⨯+⨯+⨯=- ② ①-②得nn n n T 3413413413413413423213210⨯+-⨯++⨯+⨯+⨯+⨯=- n n n 3413113113141211⨯+--⎪⎭⎫ ⎝⎛-⨯+=-nn 385285⨯+-= ∴1316521615-⨯+-=n n n T 23.解(1)由题意知0,212>+=n n n a S a当1=n 时,21212111=∴+=a a a当2≥n 时,212,21211-=-=--n n n n a S a S两式相减得1122---=-=n n n n n a a S S a整理得:21=-n n a a∴数列{}n a 是以21为首项,2为公比的等比数列.211122212---=⨯=⋅=n n n n a a(2)42222--==n b n n a∴n b n 24-=,nn n n n nn a b C 28162242-=-==-nn n nn T 28162824282028132-+-⋯+-++=- ① 13228162824202821+-+-+⋯++=n n n n n T ② ①-②得1322816)212121(8421+--+⋯++-=n n n nT 1112816)211442816211)2112184+-+----=----⋅-=n n n nn (( n n 24= .28n n n T =∴24.解:(Ⅰ)设}{n a 的公比为q ,由5121161552263==⋅=q q a a a 得21=q , ∴n n n q a a )21(22=⋅=-22211211()2122()2log 2log 2=log 2log 21111()(21)(21)22121n n nn n a a b n n n n -++=⋅⋅==--+-+∴)1211215131311(21+--++-+-=n n T n 111)22n 121nn =-=++( (Ⅱ)①当n 为偶数时,由2-<n T n λ恒成立得,322)12)(2(--=+-<nn n n n λ恒成立,即m in )322(--<nn λ, 而322--n n 随n 的增大而增大,∴2=n 时0)322(m in =--nn ,∴0<λ; ②当n 为奇数时,由2+<n T n λ恒成立得,522)12)(2(++=++<nn n n n λ恒成立,即m in )522(++<n n λ,而95222522=+⋅≥++n n n n ,当且仅当122=⇒=n nn 等号成立,∴9<λ综上,实数λ的取值范围0∞(-,)25.解:(1)由121n n a S +=+----① 得121n n a S -=+----②,①-②得112()n n n n a a S S +--=-,13n n a a +∴=13n n a -∴=;5326,3b b d d ∴-==∴= 36n b n ∴=-(2)因为 1223,3n n n a b n +++==所以 1333n n nn nc+==所以032111<-=-++n n n nc c1113n n c c c +<<⋅⋅⋅<=所以113n n c c +<≤26.解: (1)设{}n a 的公差为d , 36535a S =⎧∴⎨=⎩;则1125656362a d a d +=⎧⎪⎨⨯+=⎪⎩即112556a d a d +=⎧⎨+=⎩,解得112a d =⎧⎨=⎩,*12(1)21,()n a n n n N ∴=+-=-∈(2) 2122na n nb -==135212222n n T -∴=++++2(14)2(41)143n n --==-27.28.解:(Ⅰ)∵{}n a 为其等差数列,设公差为d1n =,则有11112a a =+,∴12a = 2n =,有122142a a a +=+,∴24a =,∴21422d a a =-=-=∴2+2(1)2n a n n =-=,(22)(1)2n n n S n n +==+ (Ⅱ)若2221,,k k k a a a -+成等比数列,则有22221k k k a a a -+= 即24(22)22(21)k k k -=⋅+,整理得22940k k -+=, 解得4k =或12k =(舍) ∴469,,a a a 成等比数列,6432a q a ==。
(中学联盟)德州市2013届高三1月份期末校际联考(基本能力)

山东省德州市2013届高三上学期期末校际联考基本能力试题本试卷分为两部分,满分100分,考试时间90分钟。
考试结束后,将答题卡交回。
考生注意1.答题前,考生务必在试卷和答题卡上用黑色签字笔清楚填写姓名、准考证号,并用2B 铅笔在答题卡上正确填涂准考证号。
2.每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不涂在答题卡上,只答在试题卷上不得分。
第一部分单项选择题,共70题,每题1分,共70分,在每题给出的四个选项中,只有一个选项符合题目要求。
春节俗称“年节”,是中华民族最隆重的传统佳节。
2013年是农历癸已年,蛇年。
完成l~6题。
1.贴年画,祭天祈年是年俗的重要内容。
下列年画为祭祀灶神的是2.春联是中国特有的文学艺术形式,春联的内容往往是社会历史变迁的写照。
据此判断以下农家百姓春联出现的先后顺序是①新四军拼命抗日,老百姓安心过年②改革开放同添异彩,经济建设共展宏图③口诛笔伐批斗四人帮,千歌万曲赞颂党中央④粮补机补肥补补农民幸福,医保社保低保保百姓平安A.①②③④B.①④③②C.①③④②D.①③②④3.下列古诗句中,不是描写春节的是A.千门万户瞳瞳日,总把新桃换旧符B.听烧爆竹童心在,看换桃符老兴偏C.历添新岁月,客满旧山河D.今宵注眼看不见,更许萤火争清寒4.小海同学自制了电子贺卡给老师祝贺春节。
下图为电子贺卡效果图,序号①②③④显示的效果在工具栏上对应的操作按钮依次是A.d a b c B.c d a b C.d b a c D.d c a b5.2013年是小海父亲的“知命之年”,小海和他爸爸是同一个属相,由此我们可以推断小海出生于A.1977年B.1997年C.1983年D.1987年6.二十四节气歌,体现着我国古代劳动人民的劳动智慧。
2013年2月10日,是我国蛇年春节,由此可推断离蛇年春节最近的节气是A.小寒B.大寒C.立春D.雨水7.右图是我国发行的首套京剧题材邮票《梅兰芳舞台艺术》之《贵妃醉酒》,下列有关说法不正确的是A.京剧与武术、中医、书法并称“四大国粹”,在世界上有着重要的影响B.《贵妃醉酒》主人公是杨玉环,她生活的时期发生了安史之乱C.“一骑红尘妃子笑,无人知是荔枝来”说的是唐太宗为了讨杨贵妃的喜欢而劳民伤财从南方快马运荔枝到长安的故事D.《贵妃醉酒》又名《百花亭》,经京剧大师梅兰芳倾尽毕生心血精雕细刻、加工点缀,是梅派经典代表剧目之一2012年11月14日,中国共产党第十八次全国代表大会在雄壮的《国际歌》中胜利闭幕。
2013高考数学试题分类汇编:专题13 复数与推理证明(解析版)

专题13 复数与推理证明一、选择题:1.(山东省济南市2013年1月高三上学期期末文1)复数31ii+=+ A .i 21+ B .i 21- C .i +2 D .i -22.(山东省德州市2013届高三上学期期末校际联考文2)已知复数z 1,z 2在复平面上对应的点分别为A (l ,2),B (-1,3),则21z z =: A .1+i B .iC .1-iD .一i3.(山东省青岛即墨市2013届高三上学期期末考试文1)已知),(2R b a i b iia ∈+=+,其中i 为虚数单位,则=-a bA.-1B.1C.2D.34.(山东省青岛一中2013届高三1月调研考试文)2013i 的值为( )A . 1B .iC .-1D .i -5.(山东省师大附中2013届高三第四次模拟测试1月文)设()2112i iz +++=,则z =A . 2B .1C .2D .36.(山东省潍坊市四县一区2013届高三11月联考文)已知{}n a 中n n a )31(=,把数列{}n a 的各项排列成如下的三角形状,记),n m A (表示第m 行的第n 个数,则)(12,10A = A.9331)( B.9231)( C.9431)( D.11231)(7.(山东省济南外国语学校2013届高三上学期期中考试文) 复数512ii-=( ) A.2i - B.12i - C.2i -+ D.12i -+8.(山东省聊城市东阿一中2013届高三上学期期初考试)是虚数单位i ,复数ii+1= ( )A.i -1B.i +1C.i +-1D.i9.(山东省师大附中2013届高三12月第三次模拟检测文)复数12()1iz i i-=-为虚数单位在复平面上对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限10.(山东省兖州市2013届高三9月入学诊断检测文)复数122ii+=-( ) A.i -B.iC.5iD.45i +二、填空题:11. (山东省泰安市2013届高三上学期期末文14)下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第n 个图形中小正方形的个数是___________.【答案】(1)2n n + 【解析】12341,3,6,10a a a a ====,所以2132432,3,4a a a a a a -=-=-=,1n n a a n --=,等式两边同时累加得123n a a n -=+++ ,即(1)122n n n a n +=+++=,所以第n 个图形中小正方形的个数是(1)2n n + 12. (山东省青岛即墨市2013届高三上学期期末考试文16)研究问题:“已知关于x 的不等式02>+-c bx ax 的解集为(1,2),解关于x 的不等式02>+-a bx cx ”,有如下解法:由0)1()1(022>+-⇒>+-x c x b a c bx ax ,令x y 1=,则)1,21(∈y ,所以不等式02>+-a bx cx 的解集为),(121。
2013高考数学试题分类汇编:专题01 集合(解析版)

专题01 集合一、选择题1. (山东省济南市2013年1月高三上学期期末理1)设全集U R =,集合2{|230}M x x x =+-≤,{|14}N x x =-≤≤,则M N 等于A .{|14}x x ≤≤B .}31|{≤≤-x xC .{|34}x x -≤≤D .{|11}x x -≤≤2.(山东省德州市2013年1月高三上学期期末校际联考理1)已知全集U={l ,2,3,4,5,6},集合A={l ,2.4:6},集合B={l ,3,5},则U A B ð( ) A .{l,2,3,4,5,6}B .{1,2,4,6}C .{2,4,6}D .{2,3,4,5,6}3.(山东省淄博市2013届高三上学期期末理1)全集U=R ,集合{}02|2≥+=x x x A ,则[U A= A .[]0,2-B .()0,2-C .(][)+∞⋃-∞-,02,D .[]2,04. (山东省烟台市2013年1月高三上学期期末理1)设集合}{}{{}20,1,2,3,4,5,1,2,540,U A B x Z x x ===∈-+<则()U C A B ⋃A.{0,1,2,3,}B.{5}C.{1,2,4}D. {0,4,5}5.(山东省青岛一中2013届高三1月调研理)设集合}1,0,1{-=M ,},{2a a N =则使M N N = 成立的a 的值是A .1B .0C .-1D .1或-16.(山东省师大附中2013届高三第四次模拟测试1月理)设全集()()2,{|21},{|ln 1}x x U R A x B x y x -==<==-,则右图中阴影部分表示的集合为( )A .{|1}x x ≥B .{|12}x x ≤<C .{|01}x x <≤D .{|1}x x ≤7.(山东省枣庄三中2013届高三上学期1月阶段测试理)设集合P ={1,2,3,4},集合Q ={3,4,5} ,全集U =R ,则集合R P Q ðA. {1,2}B. {3,4}C. {1}D. {-2,-1,0,1,2}8.(山东省诸城市2013届高三12月月考理)设非空集合A ,B 满足A ⊆B ,则A .o x ∃∈A ,使得x o ∈B B .x ∀∈A,有 x ∈BC .o x ∃∈B ,使得x o ∉AD .x ∀∈B,有x ∈A【答案】 BU【解析】根据集合关系的定义可知选B.9.(山东省烟台市莱州一中2013届高三10月月考理)集合{x x y R y A ,lg =∈=>}{}2,1,1,2,1--=B 则下列结论正确的是A.{}1,2--=⋂B AB.()()0,∞-=⋃B A C RC.()+∞=⋃,0B AD.(){}1,2--=⋂B A C R10.(山东省烟台市2013届高三上学期期中考试理)已知函数()()lg 1f x x =-的定义域为M ,函数1y x=的定义域为N ,则M N = A. {}10x x x <≠且 B . {}10x x x ≤≠且 C. {}1x x > D. {}1x x ≤11.(山东省烟台市莱州一中20l3届高三第二次质量检测 理)已知全集U R =,集合{0A x =<2x <}1,{3log B x x =>}0,则()U A C B ⋂=A.{x x >}1B.{x x >}0C.{0x <x <}1D.{x x <}012.(山东省潍坊市四县一区2013届高三11月联考理)设集合}31|{},23|{≤<-∈=<<-∈=n N n B m Z m A ,则=⋂B AA.{0,1}B.{-1,0,1}C.{0,1,2}D.{-1,0,1,2}13.(山东省泰安市2013届高三上学期期中考试数学理)全集{}{}{}1,2,3,4,5,6,2,3,4,4,5U M N ===,则()U C M N ⋃等于A.{}1,3,5B.{}2,4,6C.{}1,5D.{}1,614.(山东省实验中学2013届高三第三次诊断性测试理)设}{}2,1{2a N M ==,,则”“1=a 是”“M N ⊆的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件15.(山东省师大附中2013届高三上学期期中考试数学理)已知全集U R =,集合{}{}()3021,log 0,x U A x B x x A C B =<<=>⋂=则A.{}1x x >B.{}0x x >C.{}01x x <<D.{}0x x <16.(山东省实验中学2013届高三第二次诊断性测试理)设全集{}N x x x x Q ∈≤-=,052|2,且Q P ⊆,则满足条件的集合P 的个数是A.3B.4C.7D.817.(山东省师大附中2013届高三12月第三次模拟检测理)若全集为实数集R ,集合A =12{|log (21)0},R x x C A ->则=( )A .1(,)2+∞B .(1,)+∞C .1[0,][1,)2+∞D .1(,][1,)2-∞+∞【答案】D【解析】121{|log (21)0}{0211}{1}2x x x x xx ->=<-<=<<,所以1{1}2R A x x x =≥≤或ð,即1(,][1,)2R A =-∞+∞ ð,选D.18.(山东省聊城市东阿一中2013届高三上学期期初考试理)已知集合m A B A mx x B A 则且,},1|{},1,1{===-= 的值为 ( )A .1或-1或0B .-1C .1或-1D .19.(山东省临沂市2013届高三上学期期中考试理)设2{|1,},{|2,}x P y y x x Q y y x ==-+∈==∈R R ,则A .P Q ⊆B .Q P ⊆C .R C P Q ⊆D .R Q C P ⊆20.(山东省青岛市2013届高三上学期期中考试理)已知全集R U =,集合{}{}237,7100A x x B x x x =≤<=-+<,则()U A B ⋂=ðA.()()+∞⋃∞-,53,B.(]()+∞⋃∞-,53,C.(][)+∞⋃∞-,53,D.()[)+∞⋃∞-,53,21.(山东省济南外国语学校2013届高三上学期期中考试理科)设集合U={1,2,3,4,5},A={1,3,5},B={2,5},则A ∩(C U B)等于( )A.{2}B.{2,3}C.{3}D.{1,3}22.(山东省德州市乐陵一中2013届高三10月月考理)已知全集R U =,集合11{20},{2}4x A x x B x -=-≤<=<,则)()(=⋂B A C RA.),1[)2,(+∞-⋃--∞B.),1(]2,(+∞-⋃--∞C.),(+∞-∞D. ),2(+∞-二、解答题:23.(山东省枣庄三中2013届高三上学期1月阶段测试理)(本小题满分12分) 已知二次函数2()f x ax x =+,若对任意12,x x R ∈,恒有12122()()()2x x f f x f x +≤+成立,不等式()0f x <的解集为A(Ⅰ)求集合A ;(Ⅱ)设集合{}4,B x x a =+<,若集合B 是集合A 的子集,求a 的取值范围24.(山东省潍坊市四县一区2013届高三11月联考理)(本小题满分12分)已知集合}032|{)},(0)1(|{2≤--=∈<--=x x x N R a a x x x M ,若N N M =⋃,求实数a 的取值范围.25.(山东省泰安市2013届高三上学期期中考试数学理)(本小题满分12分)已知集合A 为函数()()()lg 1lg 1f x x x =+--的定义域,集合{}22120B x a ax x =---≥.(I )若112A B xx ⎧⎫⋂=≤<⎨⎬⎩⎭,求a 的值; (II )求证2a ≥是A B φ⋂=的充分不必要条件. 【解析】26.(山东省烟台市莱州一中20l3届高三第二次质量检测理17)已知全集U=R ,非空集合{23x A xx -=-<}0,{()()22B x x a x a =---<}0. (1)当12a =时,求()U C B A ⋂;(2)命题:p x A ∈,命题:q x B ∈,若q 是p 的必要条件,求实数a 的取值范围. 【解析】27.(山东省烟台市莱州一中2013届高三10月月考理17)(12分)已知{}{}m x x S x x x P ≤-=≤--=1,02082(1)若P S P ⊆⋃,求实数m 的取值范围;(2)是否存在实数m ,使得“P x ∈”是“S x ∈”的充要条件,若存在,求出m 的取值范围;若不存在,请说明理由. 【解析】。
山东省德州市高三数学上学期期末校际联考 理 新人教B

山东省德州市2013届高三上学期期末校际联考数学(理)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟. 注意事项:1.答第Ⅰ卷前考生务必将自己的姓名、准考证号、考试科目用2B 铅笔涂写在答题卡上. 2.选择题为四选一题目,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上, 第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分,把正确答案涂在答题卡上. 1.已知全集U={l ,2,3,4,5,6},集合A={l ,2.4:6},集合B={l ,3,5},则U A B U ð( )A .{l,2,3,4,5,6}B .{1,2,4,6}C .{2,4,6}D .{2,3,4,5,6}2.已知复数z 1,z 2在复平面上对应的点分别为A (l ,2),B (-1,3),则21z z =:( ) A .1+iB .iC .1-iD .一i 3.设,,,,a b R ∈则“a≥1且b≥l”是“a+b≥2”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.已知函数1,0(),()(1)03,0gx x f x f a f x x >⎧+=⎨+≤⎩若,则实数a 的值等于( ) A .-3 B .-l 或3 C . 1D .-3或l5.已知a>0,b>0,且ab=1,则函数()xf x a = 与函数()1bg x og x =的图象可能是( )6.如果不等式57|1|x x ->+和不等式220ax bx +->有相同的解集,则 ( )A .a=-8,b=-10B .a=-1,b=9C .a=-4,b= -9D .a=-1,b=27.已知变量x 、y ,满足4202301(24)0x y x y z og x y x -≤⎧⎪-+≥=++⎨⎪≥⎩,则的最大值为A .23B .1C .32D .28.在等比数列{a n }中,1234,n a a a +=·164,n a -=且前n 项和62n S =,则项数n 等于( ) A .4B .5C .6D .79.51()(21)ax x x+-的展开式中各项系数的和为2,则该展开式中常数项为( ) A .-20 B .—10C .10D .20' '10.双曲线22221(0,0)x y a b a b-=>> 的左、右焦点分别为F 1,F 2,渐近线分别为12,l l ,点P在第一象限内且在1l 上,若2l ⊥PF 1,1l //PF 2,则双曲线的离心率是( ) AB .2CD11.若e 1,e 2是平面内夹角为60o的两个单位向量,则向量a =2 e l +e 2,b=-3 e 1+2 e 2的夹角为( ) A .30oB .60oC .90oD .120o12.已知P 是直线:34110l f x y -+=上的动点,PA 、PB 是圆222210x y x y +--+=的两条切线,C 是圆心,那么四边形PACB 面积的最小值是( ) AB .CD .第II 卷(共90分)二、填空题:本大题共4小题,每小题4分.共16分.把答案填在答题纸的相应位置13.某市居民用户12月份燃气用量(单位:m 3)的 频率分布直方图如图所示,现抽取了500户 进行调查,则用气量在[26,36)的户数为。
山东省德州市2013届高三第二次模拟考试数学理题目

山东省德州市2013届高三第二次模拟考试数学(理)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟。
注意事项:选择题为四选一题目.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上。
第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.把正确答案涂在答题卡上. 1.设集合U={0,l ,2,3,4,5,6},M ={l ,3,5},N={2,4,6},则(U M ð)(U N ð)=A .{0}B .{1,3,5}C . {2,4,6}D .{0,1,2,3,4,5,6}2.设i 为虚数单位,则复数3412ii-++=A .-1 +2iB .1+2iC .-1-2iD .1-2i3.已知不同的直线m ,n ,l ,不重合的平面,αβ,则下列命题正确的是 A .m//α,n ∥α,则m ∥n B .m//α,m//β,则α//β C .m ⊥l ,n ⊥l ,则m ∥nD .m ⊥α,m ⊥β,则α//β4.不等式|2x +3 |≥7成立的充要条件是A .{x|x≥2}B .{x|x≤-5}C .{xlx≤-5或x≥2}D .{x|x≠0}5.执行如图所示的程序框图,若输入n 的值为6,则输出s 的值为A .17B .16C .10D .96.已知向量a=(sin α,1),b=(2,2cos α-,(2παπ<<),若a ⊥b ,则sin (4πα-)=A .B .-12C .12D7.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程0.6854.6y x =+表中有一个数据模糊不清,请你推断出该数据的值为 A .68 B . 68.2 C .69D .758.已知变量x ,y 满足约束条件221x y x y x +≤⎧⎪-≤⎨⎪≥⎩,若2x y a +≥恒成立,则实数a 的取值范围为A .(-∞,-1]B .(-∞,2]C .(-∞,3]D .[-1,3]9.已知双曲线22221x y a b-=(a>0,b>0)的离心率为2,该双曲线与抛物线y 2= 16x 的准线交于A ,B 两点,若A .2213y x -=B .22126x y -= C .23x -y 2 =1D .221412x y -= 10.在长为12cm 的线段AB 上任取一点C ,以AC 、BC 的长为邻边作一个矩形,则该矩形的面积小于32cm 2的概率为 A .45B .23C .13D .1611.若对于定义在R 上的函数f (x ),存在常数()t t R ∈,使得f (x+t )+tf (x )=0对任意实数x 均成立,则称f (x )是阶回旋函数,则下面命题正确的是 A .f (x )=2x 是12-阶回旋函数 B .f (x )=sin (πx )是1阶回旋函数 C .f (x )=x 2是1阶回旋函数D .f (x )=log a x 是0阶回旋函数12.已知定义在R 上的函数f (x ),g (x )满足()()x f x a g x =,且f '(x )g (x )(1)(1)5()(),(1)(1)2f f f x g x g g -'>+=-,若有穷数列*()()()f n n N g n ⎧⎫∈⎨⎬⎩⎭的前n 项和等于126,则n 等于 A .4 B .5C .6D .7第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题纸的相应位置.13.曲线y=e x 与x =0,x=l ,y=0所围成的图形的面积为 。
山东省德州市2013届高三上学期期末校际联考

山东省德州市2013届高三上学期期末校际联考语文试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共150分,考试时间150分钟。
第Ⅰ卷(选择题,共36分)一、(15分,每小题3分)1.下列词语中加点的字,每对读音都相同的二组是()A.络绎/落枕富饶/妖娆漱口/追本溯源称颂/瞠目结舌B.难点/难民锐意/蜕变谛听/有的放矢着装/不着边际C.赝品/吞咽脉络/山脉储备/处变不惊冠名/羽扇纶巾D.付梓/渣滓缜密/枕藉怡然/颐指气使市侩/脍炙人口2.下列词语中,没有错别字的一组是()A.暮霭闭门羹水泄不通鹬蚌相争,鱼人得利B.原凶一幅画身体厉行金玉其外,败絮其中C.悲怆亲和力怨天尤人城门失火,殃及池鱼D.汗颜竞技场宣宾夺主为渊趋鱼,为丛趋雀3.依次填人下列横线处的词语,最恰当的一组是()①这项惠及全市人民的工程在今午春节前完成,现在工人们正加班加点,以保证按时交付使用。
②第49届台湾电影金马奖名单今晚公布。
娄烨执导的内地影片《浮城谜事》成为最大热门。
③大学生有创新意识,却在实践中屡屡碰壁,主要是因为对市场风险考虑不够,____ 创业失败。
A.预定提名以致B.预定题名以至C.预订提名以至D.预订题名以致4.下列各句中,加点的熟语使用最恰当的一句是()A.对于航空公司来说,如何未雨绸缪,提前制定策略应对极端天气,消除运行隐患,降低安全风险,是保证运行顺畅打赢春运攻坚战的关键。
B.近来有关于“车牌抠掉小圆点能防电子眼”的说法,引得部分市民纷纷效仿,果真有效吗?市交警大队工作人员表示,这纯属不刊之论。
C.对于多数家庭来说,利用小长假外出旅行会花费一定的积蓄,但这种寅吃卯粮的消费不会给他们以后的生活带来太大的压力。
D.几天来,他用尽了各种办法也没有解出这道题。
老师的一句点拨让他豁然开期,他感到了从未有过的轻松,心想:早知今日,何必当初啊!5.下列各句中,没有语病、句意明确的一句是()A.据最新统计,上映18天的电影《泰囧》以9.4亿元的票房超越《画皮2》,成为最卖座的国产电影,观影人次近3000万左右,超过了《阿凡达》和《变形金刚3》。
山东省德州市2013届高三第一次模拟考试理科数学试卷-推荐下载

C. c a b
。
x 2y
。
D. a c b
。
82 为次品,现随机抽取这两种元件各 100 件进行检测,检测结果统计如下:
测试指标 70, 76 70,82 82,88 88,94 94,100
元件 A
元件 B
8
7
(1)试分别估计元件 A,元件 B 为正品的概率;
(4)已知 a, b R , 2a b 1, 则 2 1 8 。其中正确命题的序号为
ab
三、解答题:本大题共 6 小题,共 74 分,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分 12 分)
在△ABC 中,角 A,B,C 的对边分别为 a,b,c,已知角 A , sin B 3sin C. 3
山东省德州市 2013 届高三第一次模拟考试
数学(理)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150 分,测试时间 120 分钟。 注意事项: 选择题为四选一题目,每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号 涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上。
x (, 0) f (x) xf '(x) 0 成立若
a=(20.2)·
f
(20.2 ), b
(1n2) ·
f
(1n2), c
第 2 页 共 11 页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省德州市2013届高三上学期期末校际联考
数学(理)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟. 注意事项: 1.答第Ⅰ卷前考生务必将自己的姓名、准考证号、考试科目用2B 铅笔涂写在答题卡上. 2.选择题为四选一题目,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如
需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上,
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分,把正确答案涂在答题卡上.
1.已知全集U={l ,2,3,4,5,6},集合A={l ,2.4:6},集合B={l ,3,5},则U A B ð( ) A .{l,2,3,4,5,6}
B .{1,2,4,6}
C .{2,4,6}
D .{2,3,4,5,6}
2.已知复数z 1,z 2在复平面上对应的点分别为A (l ,2),B (-1,3),则21
z z =:
( )
A .1+i
B .i
C .1-i
D .一i 3.设,,,,a b R ∈则“a ≥1且b ≥l”是“a +b≥2”的
( )
A .充分而不必要条件
B .必要而不充分条件
C .充分必要条件
D .既不充分也不必要条件
4.已知函数1,0(),()(1)03,0
gx x f x f a f x x >⎧+=⎨
+≤⎩若,则实数a 的值等于 ( )
A .-3
B .-l 或3
C .1
D .-3或l
5.已知a>0,b>0,且ab=1,则函数()x f x a = 与函数()1b g x og x =的图象可能是 ( )
6.如果不等式57|1|x x ->+和不等式2
20ax bx +->有相同的解集,则 ( )
A .a=-8,b=-10
B .a=-1,b=9
C .a=-4,b= -9
D .a=-1,b=2
7.已知变量x 、y ,满足4202301(24)0x y x y z og x y x -≤⎧⎪
-+≥=++⎨⎪≥⎩
,则的最大值为
A .
23
B .1
C .
32
D .2
8.在等比数列{a n }中,1234,n a a a +=·164,n a -=且前n 项和62n S =,则项数n 等于( ) A .4 B .5 C .6 D .7
9.5
1()(21)ax x x
+
-的展开式中各项系数的和为2,则该展开式中常数项为
( )
A .-20
B .—10
C .10
D .20
' ' 10.双曲线
222
2
1(0,0)x y a b a
b
-
=>> 的左、右焦点分别为F 1,F 2,渐近线分别为12,l l ,点P 在第
一象限内且在1l 上,若2l ⊥PF 1,1l //PF 2,则双曲线的离心率是 ( )
A .
B .2
C D
11.若e 1,e 2是平面内夹角为60 的两个单位向量,则向量a =2 e l +e 2,b=-3 e 1+2 e 2的夹角为( ) A .30
B .60
C .90
D .120
12.已知P 是直线:34110l f x y -+=上的动点,PA 、PB 是圆222210x y x y +--+=的两条切 线,C 是圆心,那么四边形PACB 面积的最小值是 ( )
A .
B .2 C
D .
第II 卷(共90分)
二、填空题:本大题共4小题,每小题4分.共16分.把答案填在答题纸的相应位置 13.某市居民用户12月份燃气用量(单位:m 3)的 频率分布直方图如图所示,现抽取了500户 进行调查,则用气量在[26,36)的户数为 。
14.执行如图所示程序框图,输出结果 S= 。
15.抛物线y=x 2在A (l ,1)处的切线与y 轴及该抛物线所围成的图形面积为 .
16.已知2
1221(),()(1),,()()x f x xe g x x a x x R f x g x ==-++∃∈≤若使得)成立,则实数a 的取
值范围是 。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)
若函数2
()22cos f x x x m =++在区间[0,
]2
π
上的最大值为2,将函数()f x 图象上所
有点的横坐标伸长为原来的2倍(纵坐标不变),再将图象上所有的点向右平移
6
π
个单位,得到
函数()g x 的图象. (1)求函数()f x 解析式;
(2)在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,又8(),225
g A b π
-=
=,△ABC 的面
积等于3,求边长a 的值, 18.(本小题满分12分)
甲、乙两人进行乒乓球比赛,已知一局中甲胜乙的概率为0.6,现实行三局两胜制,假设各局比赛结果相互独立- (1)求甲获胜的概率;
(2)用x 表示甲获胜的局数,求x 的分布列和数学期望E (X ). 19.(本小题满分12分)
数列{a n }的前n 项和为1,2(1)n n n S S n +=-+,等差数列{}n b 的各项为正实数,其前n 项和为
31122339,,,n T T a b a b a b =+++,且又成等比数列.
(I )求数列{a n }、{}n b 的通项公式;
(2)若.n n n c a b =,当n≥2时,求数列{}n c 的前n 项和A n 。
20.(本小题满分12分)
某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为
8元,今年,工厂第一次投入100万元,并计划以后每年比上一年多投入100万元,预计销售
量从今年开始每年比上一年增加10万只,第n 次投入后,每只产品的固定成本为()0,,)
g n k k n N =
>∈为常数,若产品销售价保持不变,第n 次投入后的年利润为
()f n 万元.
(1)求k 的值,并求出()f n 的表达式;
(2)若今年是第1年,则第几年年利润最高?最高利润为多少万元?
21.(本小题满努13分)
已知椭圆C 的中心为原点,点F (l ,0)是它的一个焦点,直线l 过点F 与椭圆C 交于A ,B
两点,且当直线l 垂直于x 轴时O A ·
OB =-1
3
(1)求椭圆C 的标准方程;
(2)若点P 在直线x=3上,是否存在斜率为k 的直线l ,使得△ABP 为正三角形,若存在,求
出直线l 的方程;若不存在,说明理由.
22.(本小题满分13分)
已知函数2(),()1(1)f x ax x g x n x =+=+.
(1)若a=l ,求()()()F x g x f x =-在(1,)-+∞上的最大值; (2)利用(1)的结论证明:对任意的正整数n ,不等式2
34121(1)49n n n n
++++>+
都成立:
(3)是否存在实数a (a>0),使得方程
2(1)
'()(41)g x f x a x
-=--在区间1
(,)e e
内有且只有两
个不相等的实数根?若存在,请求出a 的取值范围;若不存在,请说明理由.。
