2004年全国初中数学竞赛
2002~2013年全国初中数学竞赛试题及答案(完整版)

2002年全国初中数学竞赛试题一、选择题1.设a <b <0,a 2+b 2=4ab ,则ba ba -+的值为【 】 A 、3 B 、6 C 、2 D 、32.已知a =1999x +2000,b =1999x +2001,c =1999x +2002,则多项式a 2+b 2+c 2-ab -bc -ca 的值为【 】A 、0B 、1C 、2D 、33.如图,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则ABCDAGCD S S 矩形四边形等于【 】A 、65 B 、54 C 、43 D 、32ABC DEF G4.设a 、b 、c 为实数,x =a 2-2b +3π,y =b 2-2c +3π,z =c 2-2a +3π,则x 、y 、z 中至少有一个值【 】A 、大于0B 、等于0C 、不大于0D 、小于0 5.设关于x 的方程ax 2+(a +2)x +9a =0,有两个不等的实数根x 1、x 2,且x 1<1<x 2,那么a 的取值范围是【 】A 、72-<a <52 B 、a >52 C 、a <72- D 、112-<a <06.A 1A 2A 3…A 9是一个正九边形,A 1A 2=a ,A 1A 3=b ,则A 1A 5等于【 】 A 、22b a + B 、22b ab a ++ C 、()b a +21D 、a +b 二、填空题7.设x 1、x 2是关于x 的一元二次方程x 2+ax +a =2的两个实数根,则(x 1-2x 2)(x 2-2x 1)的最大值为 。
8.已知a 、b 为抛物线y =(x -c)(x -c -d)-2与x 轴交点的横坐标,a <b ,则b c c a -+-的值为 。
9.如图,在△ABC 中,∠ABC =600,点P 是△ABC 内的一点,使得∠APB =∠BPC =∠CPA ,且PA =8,PC =6,则PB = 。
历届(第1-23届)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题......................003-0052.希望杯第一届(1990年)初中一年级第二试试题......................010-0123.希望杯第二届(1991年)初中一年级第一试试题...... 0错误!未定义书签。
-0204.希望杯第二届(1991年)初中一年级第二试试题...... 0错误!未定义书签。
-0265.希望杯第三届(1992年)初中一年级第一试试题...... 0错误!未定义书签。
-0326.希望杯第三届(1992年)初中一年级第二试试题...... 0错误!未定义书签。
-0407.希望杯第四届(1993年)初中一年级第一试试题...... 0错误!未定义书签。
-0508.希望杯第四届(1993年)初中一年级第二试试题...... 0错误!未定义书签。
-0589.希望杯第五届(1994年)初中一年级第一试试题...... 0错误!未定义书签。
-06610.希望杯第五届(1994年)初中一年级第二试试题..... 0错误!未定义书签。
-07311.希望杯第六届(1995年)初中一年级第一试试题..... 0错误!未定义书签。
-080 12希望杯第六届(1995年)初中一年级第二试试题..... 0错误!未定义书签。
-08713.希望杯第七届(1996年)初中一年级第一试试题..... 0错误!未定义书签。
-09814.希望杯第七届(1996年)初中一年级第二试试题....... 错误!未定义书签。
-10515.希望杯第八届(1997年)初中一年级第一试试题....... 错误!未定义书签。
-11316.希望杯第八届(1997年)初中一年级第二试试题....... 错误!未定义书签。
-12017.希望杯第九届(1998年)初中一年级第一试试题....... 错误!未定义书签。
2004年度全国中学生数学奥林匹克竞赛全国决赛获奖名单
成都七中
苏勇
华东师范大学附属第二中学
章尧
人大附中
王国桢
兰州一中
杜松沛
河南师大附中
张娜
太原五中
李舟
武钢三中
张凌人
上海中学
刘扬阳
长沙市一中
甄一村
成都七中
王晟
杭州外国语学校
陈世腾
海南中学
赵琳博
北大附中
郑志诚
莆田一中
左力
陕西省西安中学
支持
镇海中学
胡 劲
华师一附中
祖鹏鹤
河南师大附中
李杨佳
长沙市一中
傅列
华东师大二附中
王枫
安师大附中
毛智超
西北工大附中
杨健慧
河师大附中
荣 膺
福州一中
曹楠
东北师大附中
万时凯
景德镇市一中
陈子娟
长沙市一中
魏崟泷
蚌埠二中
李思其
金陵中学
赵 沨
石家庄二中
林 嵩
深圳中学
张辉
利津一中
吴昊
北京二十二中
戴莽原
新疆实验中学
雷慧天
武钢三中
赵煦
北京二中
龙忠慧
湖南师大附中
周桐
山西大学附属中学
王一壘
绍兴一中
孙毅然
北京四中
陈宗文
上海中学
邢硕博
清华附中
茅越
江苏省启东中学
俞能昆
马鞍山二中
田 伟
石家庄二中
三等奖(31名)
杨磊
长沙市雅礼中学
藏经涛
哈师大附中
李邱华
江苏省启东中学
曹志敏
江苏省华罗庚中学
新学校新同学

为了进一步扩大教育教学 交流,展示南海学校的名 师风采,并为《新课标》 的全面推广在理论和实践 上做好铺垫效应。12月10 日,南海实验学校初中部 的12名优秀教师在本校多 媒体教室公开教学示范课 共12节。内容涉及语文、 数学、英语、自然、社会 等学科。据悉,来自市内 外42所中学的332名教师到 场观摩,市区教研员也来 到现场指导,此外,本校 的100多名教师也参加了此 次活动。
我校被中共 舟山市委 舟山市人民 政府命名为 2002—— 2003年度市 级文明单位
打开出国留学的便捷之门-南海与加拿大教育合作项目 在温哥华签约
2004-04-28 加拿大东部时间4月19日14时30分、北京时间4月20 日5时30分,祝幸安同志与加拿大菲莎河谷大学(UCFV)校长 巴士.福特博士就我校高中毕业生赴加拿大菲莎河谷大学留学合 作项目正式签约。这是我校继在全市中小学第一家获得外国文 教专家资格、第一家获得接收外国学生资格后,又首家与国外 大学建立了稳定的教育合作关系,为南海实验学校高中毕业生 打开了便捷的出国留学之门。学校的国际交流工作迈上了新的 台阶。 菲莎河谷大学是加拿大不列颠哥伦比亚省公立本科大学,位 于大温哥华地区,现有在校生7500人,外国学生400人,其学分 可在该省内一些大学通用。 双方协议约定:从今年起加拿大方 面同意每年接收50-100名南海实验学校高中毕业生赴菲莎河谷 大学留学。菲莎河谷大学愿为有赴加留学意愿的高中新生从进 入南海起每年提供注册并保留学额,直至高中毕业生留学成行。 其中高一时学生将接到加方欢迎信函及有关资料;高二时将收 到加方预备录取书,并赴该大学访问;高三时接收到正式录取 书。
新学校,新同学
青春调色板
请同学们用一种颜色来描绘 你心目中的初中新生活
我爱新学校
2004年全国初中数学竞赛.
桐乡十中
刘绵福
247
许佳萍
永秀中心
骆克双
248
屠小飞
洲中
徐登峰
249
何晓红
建设中学
朱年荣
250
朱旭明
王店镇中学
吴勇
251
王思加
秀洲现代实验学校
陆长林
252
戴跃
曹桥中学
顾其根
253
陆晓燕
全塘中学
夏海英
254
商忠伟
高桥初中
255
沈冲
河山镇中心学校
彭延盛
256
陈林
民合中心学校
周新鸣
257
金秋杰
南日初中
顾春江
桐乡八中
沈建松
155
王志杰
桐乡九中
柏雪
156
杨诚纯
桐乡六中
杜建民
157
黄秋婧
桐乡六中
徐惠荣
158
沈思遥
桐乡六中
杜建民
159
陆静
桐乡求是中学
陈小春
160
朱国强
洲中
沈海松
161
孙漪
新塍镇中学
吴小英
162
俞佳佳
油车港镇中学
朱圣东
163
顾陇兵
曹桥中学
毛夏平
164
李星童
城关中学
刘金付/徐明芳
165
蒋佳骏
城关中学
蒋根荣
166
陈天笑
当湖初中
沈秀中/杨爱萍
167
陈洲
东湖中学
山引珠
168
倪勤宣
东湖中学
郭照明
169
费建
东湖中学
2004年全国初中数学联赛试题及答案(修正版)

NABCDP2004年全国初中数学联合数学竞赛试题第一试一.选择题1.已知abc ≠0,且a +b +c =0, 则代数式 a 2bc +b 2ca +c 2ab的值是( )(A) 3 (B) 2 (C) 1 (D) 02.已知p ,q 均为质数,且满足5p 2+3q =59,则以p +3,1-p +q ,2p +q -4为边长的三角形是( )(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 等腰三角形3. 一个三角形的边长分别为a ,a ,b ,另一个三角形的边长分别为b ,b ,a ,其中a >b ,若两个三角形的最小内角相等,则 a b的值等于( )(A)3+1 2 (B) 5+1 2 (C) 3+2 2 (D) 5+224.过点P (-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作( ) (A) 4条 (B) 3条 (C) 2条 (D) 1条5.已知b 2-4ac 是一元二次方程ax 2+bx +c =0(a ≠0)的一个实数根,则ab 的取值范围为( ) (A) ab ≥1 8(B) ab ≤1 8(C) ab ≥1 4(D) ab ≤1 46.如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( )(A) 24 (B) 38 (C) 46 (D) 50二.填空题1.计算1 1+2+1 2+3+1 3+4+……+12003+2004= .2.如图ABCD 是边长为a 的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ,延长AP 交BC 于点N ,则BNNC = .3.实数a ,b 满足a 3+b 3+3ab =1,则a +b = .4.设m 是不能表示为三个合数之和的最大整数,则m = .l G B C H F A E P QMD 第二试一、 已知方程x 2-6x -4n 2-32n =0的根都是整数,求整数n 的值。
初三数学完美正方巧妙构造
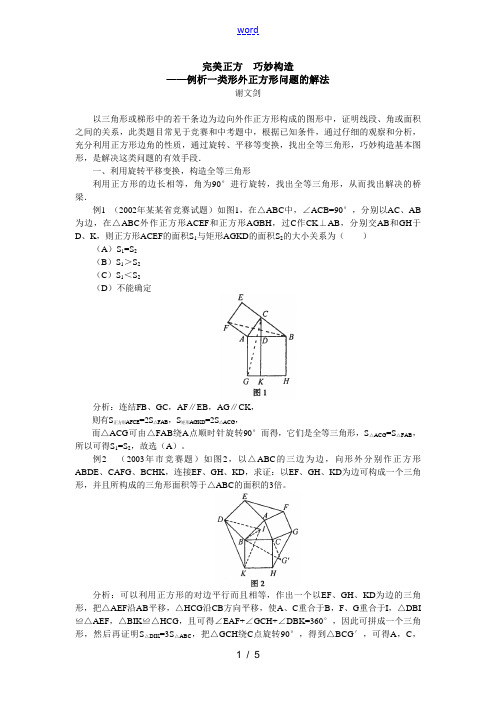
完美正方巧妙构造——例析一类形外正方形问题的解法谢文剑以三角形或梯形中的若干条边为边向外作正方形构成的图形中,证明线段、角或面积之间的关系,此类题目常见于竞赛和中考题中,根据已知条件,通过仔细的观察和分析,充分利用正方形边角的性质,通过旋转、平移等变换,找出全等三角形,巧妙构造基本图形,是解决这类问题的有效手段.一、利用旋转平移变换,构造全等三角形利用正方形的边长相等,角为90°进行旋转,找出全等三角形,从而找出解决的桥梁.例1 (2002年某某省竞赛试题)如图1,在△ABC中,∠ACB=90°,分别以AC、AB 为边,在△ABC外作正方形ACEF和正方形AGBH,过C作CK⊥AB,分别交AB和GH于D、K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系为()(A)S1=S2(B)S1>S2(C)S1<S2(D)不能确定分析:连结FB、GC,AF∥EB,AG∥CK,则有S正方形AFCE=2S△FAB,S矩形AGKD=2S△ACG,而△ACG可由△FAB绕A点顺时针旋转90°而得,它们是全等三角形,S△ACG=S△FAB,所以可得S1=S2,故选(A)。
例2 (2003年市竞赛题)如图2,以△ABC的三边为边,向形外分别作正方形ABDE、CAFG、BCHK,连接EF、GH、KD,求证:以EF、GH、KD为边可构成一个三角形,并且所构成的三角形面积等于△ABC的面积的3倍。
分析:可以利用正方形的对边平行而且相等,作出一个以EF、GH、KD为边的三角形,把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,△DBI ≌△AEF,△BIK≌△HCG,且可得∠EAF+∠GCH+∠DBK=360°,因此可拼成一个三角形,然后再证明S△DIK=3S△ABC,把△GCH绕C点旋转90°,得到△BCG′,可得A,C,G ′在一条直线上,且C 为AG ′的中点。
初中数学竞赛专题6:因式分解

专题6:因式分解第1讲 因式分解赛题练习一、选择题1.(第17届希望杯竞赛题)若22222006200620072007m =+⨯+,则m ( ) A .是完全平方数,还是奇数 B .是完全平方数,还是偶数 C .不是完全平方数,但是奇数D .不是完全平方数,但是偶数2.(第17届希望杯竞赛题)There is a two-placed number 10ab a b =+satisfying that ab ba + is a complete square number ,then total number of those like ab is ( ) A .4B .6C .8D .10(英汉词典:two-placed number 两位数;number 数;to satisfy 满足;complete square 完全平方(数);total 总的,总数)3.(2005年全国初中数学竞赛题)若223894613M x xy y x y =-+-++(x ,y 是实数),则M 的值一定是( ) A .正数B .负数C .零D .整数4.(北京市竞赛题)44a +分解因式的结果是( ) A.()()222222a a a a +--+ B.()()222222a a a a +--- C.()()222222a a a a ++--D.()()222222a a a a ++-+5.(2006年希望杯竞赛题)实数320052005m =-,下列各数中不能整除m 的是( ) A.2006B.2005C.2004D.20036.(2005年武汉市竞赛题)若3234x kx -+被31x -除后余3,则k 的值为( ) A.2B.4C.9D.107.(第13届希望杯竞赛题)已知a b c >>,222M a b b c c a =++,222N ab bc ca =++,则M 与N 的大小关系是( ) A.M N <B.M N >C.M N =D.不能确定8.(美国犹他州竞赛题)322136x x x +-+的因式是( ) A.21x - B.2x + C.3x -D.21x +E.21x +9.(2005年全国初中数学竞赛题)若22389M x xy y =-+-4613x y ++(x 、y 是实数),则M 的值一定是( ) A.正数B.负数C.零D.整数10.(武汉市竞赛题)如果328x ax bx +++有两个因式1x +和2x +,则a b +=( ) A.7 B.8C.15D.21二、填空题11.(第7届五羊杯竞赛题)把()()()()16a b c d b c a d c a b d a b c d abcd ++++--+--+--+因式分解为________.12.(第18届五羊杯竞赛题)在实数范围内分解因式:432344x x x x +---=________. 13.(第18届五羊杯竞赛题)分解因式:2226773x xy y x y --+++=________.14.(2004年全国初中数学竞赛题)已知实数a ,b ,x ,y 满足2a b x y +=+=,5ax by +=,则()()2222ab xy ab x y +++=________.15.(2007年全国初中数学联赛题)若10064a +和20164a +均为四位数,且均为完全平方数,则整数a 的值是________.16.(北京市竞赛题)已知222246140x y z x y z ++-+-+=,则2002()x y z --=__________. 17.(2004年广西竞赛题)已知()22210x y x y +--+=,则()999x y +=__________.18.(北京市竞赛题)1~100若存在整数n ,使2x x n +-能分解为两个整系数一次式的乘积,这样的n 有____________个.19.(郑州市竞赛题)分解因式:22423a b a b -+++=_______________________________________. 20.(2004年河南省竞赛题)分解因式:229643x x y y --+-=_______________________________. 21.(第16届希望杯竞赛题)分解因式:()()221ab a b a b +-++=_____________________________. 22.(2004年全国初中数学竞赛题)已知实数a 、b 、x 、y 满足2a b x y +=+=,5ax by +=,则()()2222ab xy ab x y +++=___________________.23.(第15届江苏省竞赛题)已知26x x +-是多项式43221x x ax bx a b +-+++-的因式,则a =___________,b =___________.24.(第18届五羊杯竞赛题)在实数范围内分解因式:432344x x x x +---=___________. 25.(大连市第8届育英杯竞赛题)分解因式:()()112x x y y xy -++-=____________. 三、解答题26.(1991年黄冈初中数学竞赛题)已知a 是自然数,且3221215a a a +-+表示质数,求这个质数.27.(1999年天津市数学竞赛题)当k 为何值时,多项式222352x xy ky x y -++-+能分解成两个一次因式的积?28.(第9届华杯赛总决赛题)计算;()()()()()()()()()()444444444476415642364316439643641164196427643564++++++++++.29.(第10届希望杯竞赛题)272-1能被500与600之间的若干整数整除,请找出三个这样的整数,它们是________.30.(第10届希望杯竞赛题)若233x x x k +-+有一个因式是x +1,求k 的值.31.(第6届希望杯竞赛题)计算:2211100.010.01101001000⎛⎫⎛⎫++++- ⎪ ⎪⎝⎭⎝⎭.32.(第9届五羊杯竞赛题)当n =1,x =2时,求多项式51n n x x ++的两个因式的和.33.(2000年美国犹他州中学数学竞赛题)如果328x ax bx +++有两个因式x +1和x +2,求a +b 的值.34.(第5届美国数学邀请赛试题)计算:()()()()()()()()()()44444444441032422324343244632458324432416324283244032452324++++++++++.35.(第37届美国中学生数学竞赛题)设543269569106910695691N =+⨯+⨯+⨯+⨯+.问:有多少个正整数是N 的因数?36.(第9届莫斯科奥林匹克试题)证明:对任何整数x 和y ,343223453515412x x y x y x y xy y +--++的值都不会等于33.37.(第37届美国中学生数学竞赛题)已知b ,c 是整数,二次三项式2x bx c ++既是42625x x ++的一个因式,也是4234285x x x +++的一个因式,求当x =1时,2x bx c ++的值.38.(祖冲之杯竞赛题)分解因式:32539x x x ++-.39.(北京市竞赛题)证明恒等式:()244422()2a b a b a ab b +++=++.40.(江苏省竞赛题)已知x 、y 为正偶数,且2296x y xy +=,求22x y +的值.41.(希望杯竞赛题)分解因式:()()()2221x y xy x y xy +-+-+-.42.(第12届五羊杯竞赛题)分解因式:()()42424310x x x x +-+++.43(2006年希望杯培训题)计算:32322007220072005200720072008-⨯-+-.44.(太原市竞赛题)已知关于x 、y 的二次式22754324x xy ay x y ++-+-可分解为两个一次因式的乘积,求a 的值.45.(2005年莫斯科市竞赛题)对方程22222004a b a b ++=,求出至少一组整数解.46.(2006年创新杯培训题)已知n 是正整数,且4216100n n -+是质数,求n .47.(2006年全国初中数学竞赛题)计算 (252)(472)(692)(8112)(200420072)(142)(362)(582)(7102)(200320062)⨯+⨯+⨯+⨯+⨯⨯⨯+⨯+⨯+⨯+⨯+⨯⨯⨯+48.计算:(1)(第15届希望杯竞赛题)2220034004200320024008200320042003300520032003200520053005-⨯+⨯-⨯-⨯-⨯+⨯;(2)(第九届华杯赛竞赛题)()()()()()()()()()()444444444476415642364316439643641164196427643564++++++++++49.分解因式: (1)4464a b +; (2)4224x x y y ++; (3)()2222(1)x x x x ++++;(4)(昆明市竞赛题)()()()24c a b c a b ----;(5)(第15届希望杯竞赛题)432234232a a b a b ab b ++++; (6)(重庆市竞赛题)32256x x x +--.50.(重庆市竞赛题)分解因式: (1)224443x x y y --+-; (2)343115x x -+.问题解决例1.分解因式:()()()3332332125x y x y x y -+---=______. 例2.把下列各式分解因式: (1)()()22525312x x x x ++++-; (2)()()()()21236x x x x x +++++; (3)()()()()211x y x y xy xy xy +++++-.例3.阅读理解:观察下列因式分解的过程: (1)244x xy x y -+-原式()()()()()()24444x xy x y x x y x y x y x =-+-=-+-=-+. (2)2222a b c bc --+原式()()()()222222a b c bc a b c a b c a b c =-+-=--=+--+.第(1)题分组后能直接提公因式,第(2)题分组后能直接运用公式.仿照上述分解因式的方法,把下列各式分解因式: (1)2a ab ac bc -+-; (2)22244x y z yz --+.例4.分解因式:326116x x x +++.例5.把下列各式分解因式: (1)261110y y --; (2)22823x xy y --.数学冲浪 知识技能广场1.分解因式:(1)()()22162x x x ---=______; (2)()()4a b a b ab --+=______; (3)276ax ax a -+=______. 2.分解因式:(1)3222a ab a b +-=______;(2)()()21211x x ---+=______; (3)2221a ab b -+-=______; (4)2244x y x --+=______. 3.分解因式:(1)323412x x x +--=______; (2)()()2223238x xx x +-+-=______.4.若()()23x x m x x n ++=-+对x 恒成立,则n =______.5.把多项式22344x y xy x --分解因式的结果是( ). A.()34xy x y x --B.()22x x y --C.()2244x xy y x --D.()2244x xy y x --++6.()()()()()()656565323322134x x x x x x x xx +-+++-+++-与下列哪一个式子相同( ).A.()()653421x x x -+ B.()()653423x x x -+ C.()()653421x x x --+D.()()653423x x x --+7.把多项式22243x y x y ----因式分解之后,正确的结果是( ) A.()()31x y x y ++-- B.()()13x y x y +--+ C.()()31x y x y +--+D.()()13x y x y ++--8.已知212x ax +-能分解成两个整系数的一次因式的乘积,则符合条件的整数a 的个数是( ) A.3个B.4个C.6个D.8个9.先阅读以下材料,然后解答问题.分解因式:()()()()mx nx my ny mx nx my ny x m n y m n +++=+++=+++=()()m n x y ++;也可以()()()()()()mx nx my ny mx my nx ny m x y n x y m n x y +++=+++=+++=++. 以上分解因式的方法称为分组分解法. 请用分组分解法分解因式:3322a b a b ab -+-.10.分解因式:(1)22463a b a b -+-;(2)222944a b bc c -+-; (3)()()()2a c a c b b a +-+-; (4)()()221212x x x x ++++-; (5)()22223122331x x x x -+-+-; (6)()()()213512x x x -+++.思维方法天地11.分解因式:()()()()()12345x x x x x x ++++++=______. 12.分解因式:()()()33322x y x y -----=______.13.已知()()()()1931131713171123x x x x -----可因式分解为()()8ax b x c ++,其中a ,b ,c 均为整数,则a b c ++=______.14.已知1x -得多项式33x x k -+的一个因式,那么k =______;将这个多项式分解因式,得______. 15.44a +分解因式的结果是( ).A.()()222222a a a a +--+B.()()222222a a a a +---C.()()222222aa a a ++-- D.()()222222aa a a ++-+16.实数320052005m =-,下列各数中不能整除m 的是( ) A.2006B.2005C.2004D.200317.已知3a b -=,5b c +=-,则代数式2ac bc a ab -+-的值为( ) A.15-B.2-C.6-D.618.已知a ,b ,c 是ABC ∆的三边长,且满足()222220a b c b a c ++-+=,则此三角形是( ). A.等腰三角形 B.等边三角形 C.直角三角形 D.不能确定19.分解因式:(1)224443x x y y --+-;(2)()()()2221x y xy x y xy +-+-+-; (3)343115x x -+; (4)32539x x x ++-.应用探究乐园20.已知在ABC ∆中,三边长a ,b ,c 满足等式222166100a b c ab bc --++=.求证:2a c b +=.21.下金蛋的鸡法国数学家费马(1601-1665)一生中提出了不少猜想,最著名的是“费马大定理”:关于x ,y ,z 的方程n n n x y z +=(n 为大于2的整数)没有正整数解.直到350年之后,这个猜想才由英国数学家怀尔斯(1953— )于1994年证明.德国数学家希尔伯特(1862-1943)将费马大定理称为“一只会下金蛋的鸡”,因为在攻克它的漫漫征程中,不但引出了许多数学概念和方法,而且促进了一些新的分支的创立和发展.这些远比证明定理本身更重要!不过费马的猜想并不总是正确的.他考察了12215+=,222117+=,3221257+=,422165537+=,发现结果都是素数(也称质数),于是猜想:对任意正整数n ,221n+(即()221n+)都是素数.瑞士数学家欧拉(1707-1783)指出,5221+并不是素数.我国数学家华罗庚(1910—1985)在他的著作《数论导引》中给出一种简明的证法:设72a =,5b =,可算得()524442111ab a a b +=++-,可见5221+必有除1和本身以外的约数______(填较简单的一个,用含a ,b 的式子表示),即5221+能被______整除(填入具体数值),所以不是素数.第2讲 因式分解的应用赛题练习1.(2004年重庆市竞赛题)已知2310x x x +++=,则220041x x x ++++的值为( )A.0B.1C.1-D.20042.(第19届江苏省竞赛题)若432237x x ax x b -+++能被22x x +-整除,则:a b 的值是 ( ) A.2-B.12-C.6D.43.(第14届希望杯竞赛题)若1x y +=-,则43222234585x x y x y x y xy xy y ++++++的值为( ) A.0B.1-C.1D.34.(第17届江苏省竞赛题)a 、b 、c 是正整数,a b >,且27a ab ac bc --+=,则a c -的值为( ) A.1-B.1-或7-C.1D.1或75.(中学生智能通讯赛试题)设()()322320042003200420052003200220012002a -⨯+=⨯--,()()322320052004200520062004200320022003b -⨯+=⨯--,则a 、b 的大小关系是( ) A.a b >B.a b =C.a b <D.不能确定6.(湖北省竞赛题)设a 是正数,且21a a -=,那么224a a-的值为( ) A.3-B.1C.3D.57.(2005年全国初中数学竞赛题)已知2221114834441004A ⎛⎫=⨯+++⎪---⎝⎭,则与A 最接近的正整数是( ) A.18B.20C.24D.258.(2007年全国初中数学竞赛题)方程323652x x x y y ++=-+的整数解(),x y 的个数是( ) A.0B.1C.3D.无穷多9.(第17届希望杯竞赛题)若22222006200620072007m =+⨯+,则m ( ) A.是完全平方数,还是奇数 B.是完全平方数,还是偶数 C.不是完全平方数,但是奇数D.不是完全平方数,但是偶数10.(2002年全国初中数学联赛题)若22m n =+,22()n m m n =+≠,则332m mn n -+的值为( ) A.1B.0C.1-D.2-11.(2003年全国初中数学联赛题)满足等式2003=的正整数对(),x y 的个数是( )A.1B.2C.3D.412.(第14届希望杯竞赛题)已知54410a a b a a b --+--=,且231a b -=,则33a b +的值为___________.13.(全国初中数学竞赛题)已知a 、b 、x 、y 满足2a b x y +=+=,5ax by +=,则()()2222ab xy ab x y +++=___________.14.(第17届希望杯竞赛题)A 、n 都是自然数,且21526A n n =++是一个完全平方数,则n =_____________.15.(四川省竞赛题)对一切大于2的正整数n ,数5354n n n -+的最大公约数是____________. 16.(2001年全国初中数学联赛题)一个正整数,若分别加上100和168,则可得到两个完全平方数,这个正整数为___________.17.(第9届华杯赛试题)a 、b 、c 是正整数,并且满足等式12004abc ab ac bc a b c +++++++=,那么a b c ++的最小值是__________.18.(祖冲之杯竞赛题)整数a 、b 满足6910303ab a b =-+,则a b +=___________.19.(第18届五羊杯竞赛题)若P 是两位的正整数,则以下等式中有可能成立的式子的个数是______________.①22006(34)(59)x Px x x ++=--; ②22006(17)(118)x Px x x ++=--; ③22006(34)(59)x Px x x --=+-; ④22006(17)(118)x Px x x --=+-; ⑤22006(1)(2006)x Px x x +-=-+.20.(2001年全国初中数学联赛题)若214x xy y ++=,228y xy x ++=,则x y +的值为___________. 21.(2005年四川省竞赛题)对于一个正整数n ,如果能找到正整数a 、b ,使得n a b ab =++,则称n 为一个“好数”,例如31111=++⨯,3就是一个“好数”,那么,在1~20这20个正整数中,好数有___________个.22.(2004年北京市竞赛题)已知x 、y 为正整数,且满足22222341x y x y +=+,则22x y +__________. 23.(第10届希望杯竞赛题)7221-能被500与600之间的若干整数整除,请找出3个这样的整数,它们是__________.24.(2008年天津市竞赛题)已知4个实数a 、b 、c 、d ,且a b ≠,c d ≠.若4个关系式:22a ac +=,22b bc +=,24c ac +=,24d ad +=同时成立,则6232a b c d +++的值为___________. 25.(五城市联赛题)若a 是自然数,则4239a a -+是质数还是合数?给出你的证明.26.(全国初中数学联赛题)某校在向“希望工程”捐款活动中,甲班的m 个男生和11个女生的捐款总数与乙班的9个男生和n 个女生的捐款总数相等,都是()911145mn m n +++元,已知每人的捐款数相同,且都是整数,求每人的捐款数.27.(2006年俄罗斯萨温市竞赛题)(1)证明:19992000200120032004200536⨯⨯⨯⨯⨯+是一个完全平方数.(2)证明:数848497n n ++-对于任何自然数n 都能被20整除.28.(江苏省竞赛题)(1)证明:791381279--能被45整除;(2)证明:当n 为自然数时,()221n +形式的数不能表示为两个整数的平方差;(3)计算:44444444441111124681044444111111357944444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭29.(2005年太原市竞赛题)二次三项式22x x n --能分解为两个整系数一次因式的乘积. (1)若130n ≤≤,且n 是整数,则这样的n 有多少个? (2)当2005n ≤时,求最大的整数n .30.(重庆市竞赛题)按下面规则扩充新数:已有两数a 、b ,可按规则c ab a b =++扩充一个新数,在a 、b 、c 三个数中任取两数,按规则又可扩充一个新数,…,每扩充一个新数叫做一次操作.现有数1和4. (1)求按上述规则操作三次得到扩充的最大新数; (2)能否通过上述规则扩充得到新数1999,并说明理由.问题解决例1.方程2270xy x y --+=的整数解(x y ≤)为______. 例2.1621-能分解成n 个质因数的乘积,n 的值是( ). A.6 B.5 C.4 D.3例3.计算:(1)2220034004200320024008200320042003300520032003200520053005-⨯+⨯-⨯-⨯-⨯+⨯;(2)()()()()()()()()()()444444444476415642364316439643641164196427643564++++++++++. 例4.设9310382a =+-,证明:a 是37的倍数.例5.已知n 是正整数,且4216100n n -+是质数,求n 的值.例6.(1)实数x ,y 满足221252810x xy y y ++-+=,则22x y -=______.(2)在平面直角坐标系中,满足不等式2222x y x y +≤+的整数点坐标(),x y 的个数为( ). A.10B.9C.7D.5数学冲浪 知识技能广场1.设y ax =,若代数式()()()23x y x y y x y +-++化简的结果为2x ,则a =______.2.如图,有三种卡片,其中边长为a 的正方形卡片1张,边长分别为a ,b 的长方形卡片6张,边长为b 的正方形卡片9张,用这16张卡片拼成一个正方形,则这个正方形的边长为______. 3.如果实数x ,y 满足方程组1,2225,x y x y ⎧-=-⎪⎨⎪+=⎩那么22x y -的值为______.4.已知2m ≥,2n ≥,且m ,n 均为正整数,如果将n m 进行如下方式的“分解”,那么下列三个叙述:(1)在52的“分解”中最大的数是11; (2)在34的“分解”中最小的数是13;(3)若3m 的“分解”中最小的数是23,则m 等于5. 其中正确的是______.5.若实数x ,y ,z 满足()()()240x z x y y z ----=,则下列式子一定成立的是( ) A.0x y z ++= B.20x y z +-= C.20y z x +-=D.20z x y +-=6.边长为a ,b 的矩形的周长为14,面积为10,则22a b ab +的值为( ) A.140B.70C.55D.247.设n 为某一自然数,代入代数式3n n -计算其值时,四个学生算出了下列四个结果,其中正确的结果是( ). A.5814B.5841C.8415D.84518.a ,b ,c 是正整数,a b >,27a ab ac bc --+=,则a c -等于( ) A.1- B.1-或7- C.1 D.1或79.计算:(1)32322004220042002200420042005-⨯-+-; (2)44444444441111124681044444111111357944444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.10.选取二次三项式()20ax bx c a ++≠中的两项,配成完全平方式的过程叫配方. ①选取二次项和一次项配方:()224222x x x -+=--;②选取二次项和常数项配方:(()22424x x x x -+=+,或((32424x x x x -+=-+;③选取一次项和常数项配方:22242x x x -+=-.根据上述材料,解决下面的问题.(1)写出284x x -+的两种不同形式的配方;(2)已知22330x y xy y ++-+=,求y x 的值.思维方法天地11.若两个不等实数m ,n 满足22m m a -=,22n n a -=,225m n +=,则实数a 的值为______. 12.已知a ,b ,x ,y 满足2a b x y +=+=,5ax by +=,则()()2222a b xy ab x y +++=______. 13.整数x ,y 满足方程283xy x y ++=,则x y +=______.14.A ,n 都是自然数,且21526A n n =++是一个完全平方数,则n =______. 15.若22222006200620072007m =+⨯+,则m ( ). A.是完全平方数,还是奇数 B.是完全平方数,还是偶数 C.不是完全平方数,但是奇数D.不是完全平方数,但是偶数16.设n 为某一正整数,代入代数式2n n -计算其值时,四个学生算出了下列四个结果,其中仅有一个是正确的,则这个正确的结果是( ) A.7770B.7775C.7776D.777917.方程222334x xy y ++=的整数解(),x y 的组数为( ). A.3B.4C.5D.618.黑板上写有1,12,…,1100共100个数字,每次操作先从黑板上的数中选取两个数a ,b ,然后删去a ,b ,并在黑板上写上数a b ab ++,则经过99次操作后黑板上剩下的数是( ). A.2012B.101C.100D.9919.已知()()222012a b c b a c +=+=,且a b ≠,求()2c a b +的值.20.计算:()()()()()()()()()()424242424242424242422214416618881010133155177199111111++++++++++++++++++++.应用探究乐园21.当我们看到下面这个数学算式333337133713503724613724++==++时,大概会觉得算题的人错用了运算法则吧,因为我们知道3333a b a bc d c d++≠++,但是,如果你动手计算一下,就会发现上式并没有错,不仅如此,我们还可以写出任意多个这种等式:333331313232++=++,333352525353++=++,333373737474++=++,3333107107103103++=++,…,你能发现以上等式的规律吗?22.按下面规则扩充新数:已有两数a ,b ,可按规则c ab a b =++扩充一个新数,在a ,b ,c 三个数中任取两数,按规则又可扩充一个新数……每扩充一个新数叫做一次操作.现有数1和4. (1)求按上述规则操作三次得到扩充的最大新数; (2)能否通过上述规则扩充得到新数1999,并说明理由.。
二次函数竞赛题

二次函数竞赛题1.二次函数c bx x y ++=2的图象的顶点为D ,与x 轴正方向从左至右依次交于A ,B 两点,与y 轴正方向交于C 点,若△ABD 和△OBC 均为等腰直角三角形(O 为坐标原点),则=+c b 2 .2.在直角坐标系中有三点A (0,1),B (1,3),C (2,6);已知直线b ax y +=上横坐标为0、1、2的点分别为D 、E 、F .试求b a ,的值使得AD 2+BE 2+CF 2达到最小值.3.(2004年“TRULY @信利杯”全国初中数学竞赛试题)实数x 、y 、z 满足x +y +z =5,xy +yz +zx =3,则z 的最大值是_______.4.已知直线32+-=x y 与抛物线2x y =相交于A 、B 两点,O 为坐标原点,那么△OAB 的面积等于___________。
5.(2003年“TRULY @信利杯”全国初中数学竞赛试题)已知二次函数y =ax 2+bx +c (其中a 是正整数)的图象经过点A (-1,4)与点B (2,1),并且与x •轴有两个不同的交点,则b +c 的最大值为________.6.设抛物线()452122++++=a x a x y 的图象与x 轴只有一个交点,(1)求a 的值;(2)求618323-+a a 的值.7. 通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散. 学生注意力指标数y 随时间x (分钟)变化的函数图象如图所示(y 越大表示学生注意力越集中). 当100≤≤x 时,图象是抛物线的一部分,当2010≤≤x 和4020≤≤x 时,图象是线段.(1)当100≤≤x 时,求注意力指标数y 与时间x 的函数关系式; (2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排, 使学生在听这道题时,注意力的指标数都不低于36.8.课题研究:现有边长为120厘米的正方形铁皮,准备将它设计并制成一个开口..的水槽,使水槽能通过的水的流量最大.初三(1)班数学兴趣小组经讨论得出结论:在水流速度一定的情况下,•水槽的横截面面积越大,则通过水槽的水的流量越大.为此,•他们对水槽的横截面进行了如下探索: (1)方案①:把它折成横截面为直角三角形的水槽(如图a ).若∠ACB =90°,设AC =x 厘米,该水槽的横截面面积为y 厘米2,请你写出y 关于x 的函数关系式(不必写出x 的取值范围),并求出当x 取何值时,y 的值最大,最大值又是多少?方案②:把它折成横截面为等腰梯形的水槽(如图b ).若∠ABC =120°,•请你求出该水槽的横截面面积的最大值,并与方案①中的y 的最大值比较大小.(2)假如你是该兴趣小组中的成员,请你再提供两种方案,•使你所设计的水槽的横截面面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).9.如图,抛物线2(0)y ax bx a =+>与双曲线ky x=相交于点A ,B . 已知点A 的坐标为(1,4),点B 在第三象限内,且△AOB 的面积为3(O 为坐标原点).(1)求实数a ,b ,k 的值;(2)过抛物线上点A 作直线AC ∥x 轴,交抛物线于另一点C ,求所有满 足△EOC ∽△AOB 的点E 的坐标.10.如图,抛物线()2230y mx mx m m =-->与x 轴交于A B 、两点,与y 轴交于C 点.(1)请求出抛物线顶点M 的坐标(用含m 的代数式表示),A B 、两点的坐标; (2)经探究可知,BCM △与ABC △的面积比不变,试求出这个比值;(3)是否存在使BCM △为直角三角形的抛物线?若存在,请求出;如果不存在,请说明 理由.11.已知抛物线2y x =与动直线c x t y --=)12(有公共点),(11y x ,),(22y x ,且3222221-+=+t t x x . (1)求实数t 的取值范围;(2)当t 为何值时,c 取到最小值,并求出c 的最小值.12.已知0<a ,0≤b ,0>c ,且ac b ac b 242-=-,求ac b 42-的最小值.13. 在自变量x 的取值范围59≤x ≤60内,二次函数212y x x =++的函数值中整数的个数是( ) A .59 B .120 C .118 D .6014. 在直角坐标系中,抛物线223(0)4y x mx m m =+->与x 轴交于A ,B 的两点.若A ,B 两点到原点的距离分别为OA ,OB ,且满足1123OB OA -=,则m =__ ___.15. Rt △ABC 的三个顶点A ,B ,C 均在抛物线2x y =上,并且斜边AB 平行于x 轴.若斜边上的高为h ,则( )(A )h <1 (B )h =1 (C )1<h <2 (D )h >216. 设0<k <1,关于x 的一次函数)1(1x kkx y -+=,当1≤x ≤2时的最大值是( ) (A )k (B )k k 12- (C )k1(D )k k 1+17. 平面直角坐标系中,如果把横坐标、纵坐标都是整数的点叫做整点,那么函数1212-+=x x y 的图象上整点的个数是 ( )(A )2个 (B )4个 (C )6个 (D )8个18. 函数1422-+=x x y 的最小值是 .19.对220b a ab ≠≠,,二次函数))((b x a x y --=的最小值为 ( )A . 2)2(b a + B . 2)2(b a +- C . 2)2(b a - D . 2)2(b a --20.两抛物线222b ax x y ++=和222b cx x y -+=与x 轴交于同一点(非原点),且a 、b 、c 为正数,a ≠c ,则以a 、b 、c 为边的三角形一定是 ( ) A . 等腰直角三角形 B . 直角三角形 C . 等腰三角形 D . 等腰或直角三角形21.当n =1,2,3,……,2003,2004时,二次函数1)12()(22++-+=x n x n n y 的图象与x 轴所截得的线段长度之和为( ) A . 20032002B .20042003C .20052004D .2006200522.已知二次函数c bx ax y ++=2图象如图6-2所示,则下列式子: ab ,ac ,a +b +c ,a -b +c ,2a +b ,2a -b 中,其值为正的式子共有 个.23.如果当m 取不等于0和1的任意实数时,抛物线mm x m x m m y 3212--+-=在平面直角坐标系上都过两个定点,那么这两个定点间的距离为_______24.已知抛物线1)1(2+++=x k x y 与x 轴两个交点A 、B 不全在原点的左侧,抛物线顶点为C ,要使△ABC 恰为等边三角形,那么k 的值为_______25.设x 为实数,则函数12156322++++=x x x x y 的最小值是______26.设二次函数q px x y ++=2的图象经过点(2,-1), 且与x 轴交于不同的两点A (x 1,0) B (x 2,0),M为二次函数图象的顶点,求使△AMB 面积最小时的二次函数的解析式.27.已知:3x 2+2y 2=6x , x 和y 都是实数,求:x 2+y 2的最大、最小值.28.ABC ∆中,∠B =60,AC =1,求BA +BC 的最大值及这时三角形的形状.29.如图,点G 、D 、C 在直线a 上,点E 、F 、A 、B 在直线b 上,若a b ∥,Rt GEF ∆从如图所示 的 位置出发,沿直线b 向右匀速运动,直到EG 与BC 重合.运动过程中GEF ∆与矩形ABCD 重合部分....的面积()S 随时间()t 变化的图象大致是( )FEGABCD N MH GFEDC BAkg )30.(南京)如图,E 、F 分别是边长为4的正方形ABCD 的边BC CD ,上的点,413CE CF ==,,直线EF 交AB 的延长线于G ,过线段FG 上的一个动点H 作HM AG ⊥,HN AD ⊥,垂足分别为M N ,,设HM x =,矩形AMHN 的面积为y⑴ 求y 与x 之间的函数关系式;⑵ 当x 为何值时,矩形AMHN 的面积最大,最大面积为多少?31.已知某种水果的批发单价与批发量的函数关系如图(1)所示. (1)请说明图中①、②两段函数图象的实际意义.(2)写出批发该种水果的资金金额w (元)与批发量m (kg )之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg 以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.32.函数623)12(222+-+--=k k x k x y 的最小值为m ,则当m 达到最大时,x =______ (2004年全国初中数学联赛)33.设a ,b 为实常数,k 取任意实数时,函数)3()(2)1(2222b ak k x k a x k k y ++++-++=的图像与x 轴-2-1O1x2交于点A (1,0)(1)求a ,b 的值(2)若函数与x 轴的另一个交点为B ,当k 变化时,求AB 的最大值34.(2007年福州)如图所示,二次函数2y ax bx c =++(a ≠0)的图象经过点(-1,2),且与x 轴交点的横坐标分别为1x 、2x ,其中-2<1x <-1,0<2x <1,下列结论:①420a b c -+<;②20a b -<;③a <-1;④284b a ac +>.其中正确的有:( )A 、1个B 、2个C 、3个D 、4个35.(2007年天门)施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM 为12米,现在O点为原点,OM 所在直线为x 轴建立直角坐标系(如图所示). (1)直接写出点M 及抛物线顶点P 的坐标; (2)求出这条抛物线的函数解析式;(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD ,使A 、D 点在抛物线上,B 、C 点在地面OM 上.为了筹备材料,需求出“脚手架”三根木杆AB 、AD 、DC 的长度之和的最大值是多少?请你帮施工队计算一下.36.(2009年天津市)已知函数212y x y x bx c αβ==++,,,为方程120y y -=的两个根,点()1M T ,在函数2y 的图象上. (Ⅰ)若1132αβ==,,求函数2y 的解析式; (Ⅱ)在(Ⅰ)的条件下,若函数1y 与2y 的图象的两个交点为A B ,,当ABM △的面积为112时,求t 的值; (Ⅲ)若01αβ<<<,当01t <<时,试确定T αβ,,三者之间的大小关系,并说明理由.37. 已知点A (0,3),B (-2,-1),C (2,-1) P (t ,t 2)为抛物线y =x 2上位于三角形ABC 内(包括边界)的一动点,BP 所在的直线交AC 于E , CP 所在的直线交AB 于F 。
2004年全国初中数学竞赛试题及参考答案

2004年全国初中数学竞赛试题及参考答案2004年全国初中数学竞赛试题(由网友Alpha提供一部分,余下系本人整理)(考试时间120分钟,满分140分)一、选择题(共5小题,每小题8分,满分40分)1,已知实数a不等于b且满足(a+1)^2=3-3(a+1),3(b+1)=3-(b+1)^2。
则b√(b/a)+a√(a/b)的值为()A 23B -23C -2D -132,若直角三角形的两条直角边长为a,b,斜边长为c,斜边上的高为h,则有()A, ab=h^2 B, 1/a+1/b=1/hC,1/a^2+1/b^2=1/h^2 D, a^2+b^2=2h^23,一条抛物线y=ax^2+bx+c顶点为(4,-11),且与x轴的两个交点的横坐标为一正一负,则a,b,c中为正数的()A,只有a B ,只有b C,只有c D,只有a和b4,△ABC中,DE平行于AB平行于FG,且FG到DE,AB的距离比为1/2。
若△ABC 面积为32,△CDE面积为2,则△CFG面积S为()。
A, 6 B, 8 C, 10 D, 125,如果x和y是非零实数,使得│x│+y=3,│x│y+x^3=0,那么x+y等于()A, 3 B,√13 C,(1-√13)/2 D,4-√13二、填空题(共5小题,每小题8分,满分40分)6,如图所示,在△ABC中,AB=AC,AD=AE,∠BAD=60°,则∠EDF=(度)。
7,据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数m、n(单位:万人)以及两个城市间的距离d(单位:km)E有T=kmn/d^2的关系(k为常数)。
现测得A、B、C三个城市的人口及它们之间距离如图所示,且已知A、 B两个城市间每天的电话通话次数为t,那么B、C两个城市间的每天的电话通话次数为次(用t表示)。
8,已知实数a,b,x,y满足a+b=x+y=2,ax+by=5,则(a^2+b^2)xy+ab(x^2+y^2)= 。
初中数学竞赛专题4:整式

3、选择题则第二周工资总额与第一周工资总额相比([9](江苏省“数学文化节”试题)有甲、乙两种糖果,原价分别为每千克调查,将两种糖果按甲种糖果m kg 与乙种糖果n kg 的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价上涨 c%,乙种糖果单价下跌 d%,但按原比例混合的糖果单价恰好不变,那么m等于().nAac A .bd[10]如图①,将一个边长为 a 的正方形纸片剪去两个小矩形,得到一个“专题4:整式33 7 9 11,4313 15 17 19, ”,右m 分裂后,其中有 个奇数是 2013,A.43B.44C.45D.46[3]若一个两位数恰等于它的各位数字之和的4倍,则这个两位数称为“巧数” 两位数的个数是()。
A.82B.84C.86D.88[4]已知a b 0,ab ,则化简baa 2 ab 2 得( b)。
A. 2aB. 2bC. 4D. 4⑸已知2ab3, 2 c6 , 2 12 , 则a , b , c 的关系是()A. 2b a cB. 2b a cC. 2b a cD. a大于[2] 则m 的值是(,则不是“巧数”的第二周每小时工资增加小王第一周每小时工资为 a 元,工作b 小时, [1]1时,代数式2ax 3bx 8的值为18,那么,代数式9b6a 2A.28B.-28C.32D.-3231的正整数m 的三次幕可“分裂”成若干个连续奇数的和,如2 3 5 =,10%,工作总时间减少 10%,A.增加1%B.减少1%C.减少1.5% [7]已知有理数 a,b, c 在数轴上的位置如图D.不变丄b所示,且|a | |b|,则代数式|a | | c a| |c b| | b| 的值为()。
A. 2cB. 0C. 2cD. 2a 2b 2c [8]当x 1时, ax b 1的值为-2,贝U a b 1 1 a b 的值为(A.-16B.-8C.8D.16a 元和b 元.根据柜台组D .虫ac ”的图案,如图②所示,再将剪下的两个小矩形拼成一个新的矩形,如图③所示,则新矩形的周长可表示为(3A. 2a 3b D. 4a 10bB. 4a 8bC.2a 4b[11]已知a, b ,c满足a 2 2b 7 , 2b 2c21 , c 6a 17 , 则a bA.2B.3C.4D.5[12]把255,443 ,533, 622这4个数从小到大排列, 正确的是()55 44 33 22 55 33 22 44A. 2 3 5 6B. 2 5 6 3亠55 22 33 44 55 22 44 33C. 2 6 5 3D. 2 6 3 5[13]若a m. n b 2 2n 2ma b 5 3ab , 则mn的值为(( )A.3B. 2C.1D.[14]已知a 31 4181 , b 27 , c 961, 则a , b,c的大小关系;是(是().A. a b cB. a c bC. a b cD.b[15](第15届希望杯竞赛题)式子a b c d 去括号后是().A. a b c dB. a b c dC. a b c dD.[16] (2007 年浙江省竞赛题)若 3 x 2 x x 1 0,则x2725x 川 1x是()c的值等于(3c aa b c1 x III 26xx27的值-1[17]已知25x 2000,80y 20001丄等于yA.2B.1C ED.-2[18]乘积539422的结果的位数是(A.41B.61C.51D.47[19](五羊杯竞赛题)老师报出一个五位数,同学们将它的顺序倒排后得到的五位数减去原数,生甲、乙、丙、丁的结果分别是34567, 34056, 23456,34956,老师判定4个结果中只有1 个正确, 答对的是().A •甲B .乙C .丙26 [20]若x x 212 11 10a12x aux aexIII ax a o, 则a i2 a10 a s a6 a4 a2 ( )A. 32B.0C.32D.64[21](第16届希望杯竞赛题)有三组数为X1,X2, X3 ;y1 , y2, y3 ;乙, Z2 , Z3 .它们的平均数分别是 a , b , c,那么为y z , x? y2 Z2 , x3 y3 Z3的平均数是()•[22](第17届江苏省初中数学竞赛题)下列四个数中可以写成100个连续自然数之和的是(A . 1627384950 B. 2345678910 C. 3579111300 D. 4692581470[23](第17届江苏省初中数学竞赛题)若代数式 23x 2x 6的值为8, 则代数式-x2 x 1的值为2[24](第18届五羊杯竞赛题)计算:2.5 3 2 (2 9 8 1 4.5 4).409[25]( 安徽省竞赛题果对于某一特定范任意允许值,2X |1 3x 1 9x| |1 10x的值恒为一常数,则此值为().[26](第17届希望杯竞赛题)已知a, b, c都是整数,m a b\ |bA . m 一定是奇数B . m 一定是偶数C.仅当a, b, c同奇或同偶时, m是偶数 D . m的奇偶性不能确定[27](重庆市竞赛题)给出两列数: 3, 5, 乙9,…,2001 和1, 6, 11, 16, 21,…,2001 , 同时出现在这两列数中的数的个数为().A . 199B .200 C .201D . 202[28](第17届江苏省初中数学竞赛题)用min a,b表示a , b两数中的较小者,用max a,b表示a , b两数中的较大者. 例如:min 3,5 3 , max 3,5 5 ;min 3,3 3 , max 5,5 5 .设a , b ,c ,d 是互不相等的自然数,min a,b p , min c,d q , max p,q x , max a,b m , max c,d n ,D . x y 和x y 都有可能[36]把2009表示成两个整数的平方差的形式,则不同的表示法有(2002 2002x y , b , c , d 从小到大排列的顺序是( ).A . abedmin m,n y ,则()•A . 0B . 1C .1D . 2004[30](第17 届五 羊杯 竞 赛题)已知 有 理 数a ,b , e , d 满足3a 2005 3b 20273e 2822 d 32820 , 那么().A . a e b dB . b d a eC . e a b dD . d b a e( ).[31](第15届希望杯竞赛题)当x31时,代数式2ax 3bx 8的值为18,这时,代数式9b 6a2A . 2B .2C . 4D . 4[33] ( 2004年河北省竞赛题)已知2a3 b,2 e6 , 2 12 2002,则x2002y , b ,e 的关系是( )A . 2ba eB.2b a eC . 2b a eD . a b e[34]如果a 2b 3e 12,且 2.2a b2e ab be ea ,贝U.23a b e的值是 ()A.12B.14C.16D.18[35]如果x 2 2y 1, x y 3,那么3x 3y 的值为()[32] ( 2005年广西竞赛题)如果).A.2B.3C.4D.5[29] ( 2004年重庆初中数学决赛题)已知1 XX2 x 30,则 1 XX 2 x 32004x的值为A . 28B . 28C . 32D . 32 ―—,那么2 a 2 bb 2的值等于(1 a 1 bA.16 种B.14 种C.12 种D.10 种[37](北京市迎春杯竞赛题)已知 2 219x 143xy 19y 2005 , b 344, c 533, d622,那么[38] ( 2004年河北省竞赛题)若x 123456789 小关系是().123456786, y 123456788 123456787,则 x , y 大D .不能确定[44]当克拉拉计算自己各科测试成绩的总分时,无意识地将某一科分数的十位与个位交换了位置, 则最有可能是错误的总分与正确的总分相差的分数是( )A.45B.46C.47D.48E.49[45] 一根铁丝对折,再对折,对折n 次之后n 2,从中间剪断,这根铁丝被剪成()段。
奥赛 三角形面积(含答案)

A、4B、5C、6D、
(江苏省第十五届初中数学竞赛初二第1试试题)10、已知凸四边形ABCD的面积是 ,E、F、G、H分别是AB、BC、CD、DA的中点,那么图中阴影部分的总面积是。
A.4∶9B.2∶3C.1∶2D2∶5
(2003年嵊州市初二数学竞赛试卷)10.观察下列图形
则图②中的三角形的个数为_________,图③中的三角形的个数为___________.
(2003年嵊州市初二数学竞赛试卷)12.已知△ABC为等腰三角形,由A点所引BC边的高线恰好等于BC边长的一半,则∠BAC的度数为______________.
(嵊州市2004年初三数学竞赛试题)5.如图,平行四边形ABCD中,E是AD上的一点,且AE= AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果 ABCD的面积为S,那么,△GEF的面积为( )
A.
B.
C.
D.
(嵊州市2004年初一数学竞赛试题)10.在等腰△ABC(AB=AC≠BC)所在的平面上有一点P,使得△PAB,△PAC都是等腰三角形,则满足此条件的点有( )
(A)3种(B)4种(C)5种(D)6种
(江苏省第十七届初中数学竞赛初一年级第1试)8.如图所示,一个大长方形被两条线段AB、CD分成四个小长方形.如果其中图形Ⅰ、Ⅱ、Ⅲ的面积分别为8、6、5,那么阴影部分的面积为().
(A) (B) (C) (D)
(江苏省第十八届初中数学竞赛初一年级第1试)13.如图,一个大正方形被两条线段分割成两个小正方形和两个长方形,如果S1=75cm2,S2=15cm2,那么大正方形的面积是S=_____________cm2
《中等数学》2004年总目次

2004 年第 6 期
关于 2003 年全国高中数学联赛第二题 (王景周 崔建英 6·13)
我为数学竞赛命题
从函数方程到初中联赛试题
(罗增儒 1·13)
同旁内角的计数 ———从具体到抽象 (罗增儒 3·14)
负数进入应用题
(罗增儒 5·15)
巧思妙解
好题与巧解
(解兴武 2·14)
巧思探求的过程 妙解本质的揭示
(方廷刚 2·9)
用三角代换解竞赛题
(齐文友 2·12)
含绝对值竞赛题的求解策略
(王启东 3·8)
数学竞赛中的计数问题
(费振鹏 3·11)
关于两道高中联赛题的背景研究 (刘培杰 4·8)
解数学竞赛题的局部调整策略 (郑日锋 4·10)
让向量进入竞赛数学
(邹 明 5·9)
一道全国初中竞赛题的解法研究 (江明芬 5·14)
48
中等数学
《中等数学》2004 年总目次
数学活动课程讲座
·初中·
几何计数问题 (下)
(罗增儒 1·3)
存在性问题
(李建泉 2·2)
好玩的平移
(周春荔 3·2)
构造法在初中数学竞赛中的应用
(王盛裕 4·2 ,5·2)
一元二次方程根的分布问题
(杨贵武 6·2)
·高中·
根轴的性质及应用
(沈文选 1·6)
学生习作
一道数学奥林匹克问题的思考 一道 IMO 试题的推广及简证 一个几何不等式的简证
短论集锦
(石文博 5·18) (程 俊 5·19) (崔振嵛 5·20)
简证一道国家集训队选拔考试题 (胡昱希 1·17) 边长为 1 ,2 ,3 , …的正方形铺砌问题 (吴振奎 1·17) 一个集组计数问题的简证 (王景周 崔建英 1·18)
全国初中数学竞赛(联赛)分类题型详解-几何

历年(95-10)年全国数学竞赛(联赛)分类题型详解 - 几何(1)选择题(30道题)1. 如果边长顺次为25、39、52与60的四边形内接于一圆,那么此圆的周长为[ ]A.62πB.63π C.64πD.65π1995年全国初中数学联赛试题答案: D详解:四个选择支表明,圆的周长存在且唯一,从而直径也存在且唯一.又由AB2+AD2 =252+602 =52×(52+122)=52×132=(32+42)×132 =392+522 =BC2+CD2故可取BD=65为直径,得周长为65π,选D.2. 设AB是⊙O的一条弦,CD是⊙O的直径,且与弦AB相交,记M=|S△CAB-S△DAB|,N=2S△OAB,则[ ]A.M>N B.M=N C.M<N D.M、N的大小关系不确定1995年全国初中数学联赛试题答案: B详解1: 不失一般性,设CE≥ED,在CE上取CF=ED,则有OF=OE,且S△ACE-S△ADE=S△AEF=2S△AOE.同理,S△BCE-S△BDE=2S△BOE.相加,得S△ABC-S△DAB=2S△OAB,即M=N.选B.详解2: 若过C、D、O分别作AB的垂线(图3),CE⊥AB、DF⊥AB、OL⊥AB,垂足分别为E、F、L.连CF、DE,可得梯形CEDF.又由垂径分弦定理,知L是EF的中点.根据课本上做过的一道作业:梯形对角线中点的连线平行底边,并且等于两底差的一半,有|CE-DF|=2OL.即M=N.选B.3.如图,A是半径为1的圆O外的一点,OA=2,AB是圆O的切线,B是切点,弦BC∥OA,连结AC,则阴影部分的面积等于[ ]1996年全国初中数学联赛试题答案: B4.如果一个三角形的面积和周长都被一直线所平分,那么该直线必通过这个三角形的[ ]A.内心B.外心C.重心D.垂心1996年全国初中数学联赛试题答案: A5.如果20个点将某圆周20等分,那么顶点只能在这20个点中选取的正多边形的个数有[ ]A.4个B.8个 C.12个 D.24个1996年全国初中数学联赛试题答案: C6. 在△ABC中,已知BD和CE分别是两边上的中线,并且BD⊥CE,BD=4,CE=6,那么△ABC的面积等于()(A)12(B)14(C)16(D)181998年全国数学联赛试卷答案: C详解: 连ED,则又因为DE是△ABC两边中点连线,所以故选C.7.一个凸n边形的内角和小于1999°,那么n的最大值是().A.11 B.12 C.13 D.141999年全国初中数学竞赛答案: C8.在三角形ABC 中,D 是边BC 上的一点,已知AC=5,AD=6,BD=10,CD=5,那么三角形ABC 的面积是( ).A .30B .36C .72D .1251999年全国初中数学竞赛答案: B9.在正五边形ABCDE 所在的平面内能找到点P ,使得△PCD 与△BCD 的面积相等,并且△ABP 为等腰三角形,这样的不同的点P 的个数为( ).A .2B .3C .4D .51999年全国初中数学竞赛答案: D10. 设a ,b ,c 分别是△ABC 的三边的长,且cb a ba b a +++=,则它的内角∠A 、∠B 的关系是( )。
初中数学重点梳理:根式及其运算

根式及其运算知识定位根式是初中数学的重要内容之一,也是近年各类初中数学竞赛中常常涉及到的知识点.解此类有关根式计算题的关键在于将无理式进行有理化.但是在很多竞赛题中我们遇到的计算式子却非常复杂和灵活,其中对根式的计算要求技巧性较强,因而计算的难度较大.在进行根式运算时,往往用到绝对值、整式、分式、因式分解,以及配方法、换元法、待定系数法等有关知识与解题方法,也就是说,根式的运算,可以培养同学们综合运用各种知识和方法的能力.知识梳理二次根式的概念:式子a (a ≥0)叫二次根式。
二次根式的性质: (1)()()02≥=a a a ;(2)⎪⎩⎪⎨⎧<-=>==00002a ,a a ,a ,a a a二次根式的运算法则:(1)c )b a (c b c a ±=± (0≥c ); (2)ab b a =⋅ (00≥≥b ,a );(3)baba =(00>≥b ,a ); (4)()()0≥=a a a m m若0>>b a ,则b a >。
设m ,d ,c ,b ,a 是有理数,且m 不是完全平方数,则当且仅当d b ,c a ==时,m d c m b a +=+ 。
形如b a x +=,b a y -=的这两个根式互称为共轭根式。
当两个含有二次根式的代数式相乘时,如果它们的积不含有二次根式,则这两个代数式互为有理化因式.例题精讲◆专题一:共轭因式法【试题来源】2006年第十七届“希望杯”数学竞赛第二试 【题目】设0>m ,m x x =--+13,则代数式13-++x x 的值是 (用m 表示).【答案】m4 【解析】观察此题中13--+x x 与13-++x x 恰是共轭因式,因此想到将两式相乘得:()()()()413131322=--+=-++•--+x x x x x x即()433=-++•x x m ,所以mx x 413=-++. 点评:我们把形如b a +、b a -的两个根式互称为共轭因式,共轭因式相乘就恰好将无理式化为有理式,从而此题轻松解决. 【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】2◆专题二:有理化法【试题来源】2008年全国初中数学联赛第一试 【题目】已知实数x 、y 满足()()20082008200822=----y y x x ,则2007332322--+-y x y x 的值为( )【选项】(A)-2008 (B) 2008 (C)-1 (D)1 【答案】D 【解析】由已知()()20082008200822=----y y x x 可得:200820081200822--=--y y x x然后将等式左边分子有理化得:()()200820082008200820082222--=-+-+--y y x x x x x x()20082008200820082222--=-+--y y x x x x200820082008200822--=-+y y x x∴ 2008200822--=-+y y x x ①同理可得:2008200822-+=--y y x x ②由①、②得:x = y ∴ ()2008200822=--x x变形得: 20082008200822--=--x x x x将等式的左边分子有理化得:200820082008200822--=-+x x x x∴ 2008200822-+=--x x x x∴020082=-x ,即20082=x∴原式=120072008200720073323222=-=-=--+-x x x x x .故选D.点评:有理化法是解二次根式计算题的常用方法,就其形式来说可分为分母有理化和分子有理化两类.具体方法是在分式的分母(或分子)同时乘以原二次根式的有理化因式,从而达到化无理式为有理式的目的. 【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】2◆专题三:因式分解法常用方法:利用配方法将被开方数配成完全平方式或者立方式 【试题来源】2006年第十七届“希望杯”数学竞赛第二试【题目】计算-++++12862231286223+---,得 .【答案】2-【解析】此题分子、分母均含根式,如果按照通常的做法是先分母有理化,这样计算较繁.若观察到分母可进行因式分解,先将分母因式分解后,再化简.原式()()32432223++++=()()32432223-----()()423223+++=()()423223----421421-++=222222-++-=2-=点评:从此题我们可得到这样的启发:当分子分母均含有根式时,可用因式分解法先将式子化简,再进行计算,这样能起到化繁为简的作用. 【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】2【试题来源】【题目】化简:2008200820082008100435715337++⎪⎭⎫⎝⎛,得到 . 【答案】1 【解析】解:原式.【知识点】根式及其运算【适用场合】当堂练习题 【难度系数】3【试题来源】 【题目】化简:)23)(36(23346++++,最后得_________【答案】23+【解析】原式633332(32)(63)(63)(32)(63)(32)(32)(63)++===+++++++62【知识点】根式及其运算 【适用场合】当堂练习题 【难度系数】3◆专题四:换元法【试题来源】2004年全国初中数学联赛 【题目】已知8a ≥1, 则333183131831-+-+-++a a a a a a 的值是( )【选项】 (A)1 (B) 23a (C)a 8 (D)不能确定【答案】A【解析】解析:设318-=a x ,则8132+=x a ,83312+=+x a原式()3228313x x x +++=()3228313xx x +-++3238133+++=x x x 3238133+-+-+x x x ()3381+=x ()3381x -+2121x x -++==1 选A.点评:此题若用常规方法根本无法入手进行解答,此处换元法的运用妙在能达到化无理式为有理式的目的,从而使问题迎刃而解. 【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】2◆专题五:裂项法【试题来源】2003年第十四届“希望杯”全国数学竞赛第二试 【题目】对于正整数n,有111111+-=+++n nn n n )n (,若某个正整数k 满足32111433413223121121=+++++++++k k k )k (,则k=______. 【答案】8【解析】解析:由公式111111+-=+++n nn n n )n (,因此有()111433413223121121++++++++++k k k k11131212111+-++-+-=k k111+-=k32111=+-k 3111=+∴k 8=∴k点评:裂项法在很多有关分式和分数的计算题中经常用到,我们仔细观察会发现能应用此方法进行计算的式子都有着某种特殊的规律.常用的裂项形式主要有以下几种: (1)()11111+-=+n n n n .如:200820071431321211⨯++⨯+⨯+⨯ 200812007131212111-++-+-= 200811-= 20082007=(2)()⎪⎭⎫⎝⎛+-=+k n n k k n n 1111.如:2008200511071741411⨯++⨯+⨯+⨯ ⎪⎭⎫ ⎝⎛-++-+-⨯=2008120051714141131 ⎪⎭⎫ ⎝⎛-⨯=20081131 2008200731⨯= 2008669=(3)111111+-=+++n n n n n )n (.如本题中()111433413223121121++++++++++k k k k11131212111+-++-+-=k k111+-=k .【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】3【试题来源】 【题目】4947474917557153351331++++++++【答案】73 【解析】考虑一般情形(21)(21)(21)(21)2121(2121)n n n n n n n n ==+-+-++-++-(2121)(2121)1(22121(2121)221212121n n n n n n n n n n n n +--+--===+-+-++--+原式11113{()(()2217713354749=+++-=-=【知识点】根式及其运算 【适用场合】当堂练习题 【难度系数】3◆专题六:条件转化法【试题来源】2006年第十七届“希望杯”数学竞赛第一试【题目】已知x =22+1,则分式15119232----x x x x 的值等于__________.【答案】2【解析】由x =22+1得:221=-x两边平方得:()()22221=-x ,即722+=x x所以原式()()1511729272--+--+=x x x x x 154222---=x x()1547222--+-=x x12--==2点评:此题先通过乘方的方法将已知条件中的无理式x =22+1,转化为有理式722+=x x .再代入所求代数式中,通过逐步降次,从而求得代数式的值,因此这种方法称为条件转化法. 【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】3【试题来源】 【题目】设215-=a ,则=-+---+aa a a a a a 3234522 . 【答案】-2 【解析】解:,,因此,本题正确答案是-2.【知识点】根式及其运算 【适用场合】当堂练习题 【难度系数】3◆专题七:配方及平方法【试题来源】2008年第十九届“希望杯”数学竞赛第二试 【题目】当2>x 时,化简代数式1212--+-+x x x x ,得 .【答案】12-x【解析】法一:解析:应用配方法可得:()112112+-+-=-+x x x x()2211121+•-+-=x x()211+-=x 同理可得:=--12x x ()211--x∴1212--+-+x x x x()()221111--++-=x x1111--++-=x x∵2>x∴原式12-=x .点评:配方法是化简多重根式的常用方法.其根本做法是把被开方式b a 2±配方成完全平方式()2y x ±的形式()0,0≥≥y x ,即是要设法找到两个正数x ,y(x >y),使x+y=a ,xy=b ,则()y x yx xy y x b a ±=±=±+=±222,其中(x >y).法二: 对于上面的例子还可以进行另一种思考:由于12-+x x 与12--x x 互为有理化因式(共轭因式),则有()()2222121212-=--=--•-+x x x x x x x ,因此原式平方后是一个有理式,所以上题还可以用平方法. 解析:设1212--+-+=x x x x y ,则y >0.将上式两边分别平方得:()()1212122122--+--•-++-+=x x x x x x x x y()221222--+=x x x44222+-+=x x x ()2222-+=x x222-+=x x∵2>x ,∴442-=x y ∴1244-=-=x x y点评:解答含根式的计算题,关键在于如何将无理式转化成有理式.如果原无理式直接平方后就能从无理式转化为有理式,那么我们不妨用平方法,这种方法的解题思路更加自然流畅,计算过程也更加简便易行.【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】3【试题来源】武汉市选拔赛试题 【题目】化简22)1(111+++n n ,所得的结果为( )A .1111+++n nB .1111++-n nC .1111+-+n nD .1111+--n n【答案】C【解析】待选项不再含根号,从而可预见被开方数通过配方运算后必为完全平方式形式.原式222221*********(1)()()(1)(1)11n n n n n n n n n n n n n ++++-+-+=-=-++++选(C )【知识点】根式及其运算 【适用场合】当堂练习题 【难度系数】3◆专题八:巧用乘法公式解题【试题来源】2004年第十五届“希望杯”数学竞赛第二试 【题目】对于任意的自然数n ,有f(n)=323232121121+-+-+++n n n n n , 则f(1)+f(3)+f(5)+…+f(999)= . 【答案】5【解析】注意到f(n)表达式的分母可整理成:()()2333231111-+-•+++n n n n ,形如22b ab a ++的形式,类似于立方差公式的一部份,因此考虑用立方差公式. 由立方差公式:()()2233bab a b a b a ++-=-有()()333311--+n n()()()⎥⎦⎤⎢⎣⎡-+-•+++--+=23332333111111n n n n n n即()()()⎥⎦⎤⎢⎣⎡-+-•+++•--+=233323331111112n n n n n n∴1=()()()⎥⎦⎤⎢⎣⎡-+-•+++•--+2333233311111121n n n n n n将其代入f(n)表达式得:f(n )=()()()()()23332323332333111111111121-+-•+++⎥⎦⎤⎢⎣⎡-+-•+++•--+•n n n n n n n n n n=()331121--+•n n∴f(1)+f(3)+f(5)+…+f(999)()()()()33333333998100021462124210221-•++-•+-•+-•=()3333333310009989984422021+-++-+-+-= 1021⨯= 5=点评:此题用常规方法无法入手进行解答,已知条件中的表达式也比较复杂,这时我们从表达式的形式上进行分析,得到22b ab a ++的形式,自然联想到立方差公式,然后运用乘法公式将条件进行转化,从而找到解决问题的捷径. 【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】3◆专题九:活用整数、根式的性质解题【试题来源】2006年第十七届“希望杯”数学竞赛第一试【题目】计算2200612008200720062005-+⨯⨯⨯的结果是__________. 【答案】2005【解析】:注意到此题中2005、2006、2007、2008是四个连续的正整数,而四个连续的正整数的积与1的和是一个完全平方数.因此本题有了如下的简便解法:原式()()()2200612200612006200612006-++⨯+⨯⨯-==()[]()()[]2200612200612006120062006-++⨯-⨯+⨯=()()2222006122006200620062006-+-+⨯+()()22222006120062006220062006-++-+= ()2222006120062006--+=222006120062006--+==2005点评:正整数具有这样的性质“四个连续的正整数的积与1的和是一个完全平方数”,而本题恰是灵活运用了正整数的这一性质进行解答的.我们可以看到正整数的某些性质恰是解决有关正整数问题的金钥匙.【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】3【试题来源】重庆市竞赛题【题目】已知254245222+-----=xx x x y ,则22y x += .【答案】6【解析】因一个等式中含两个未知量,初看似乎条件不足,不妨从二次根式的定义入手.二次根式有如下重要性质:(1)0≥a ,说明了a 与a 、n a 2一样都是非负数;(2) a a =2)( (≥a 0),解二次根式问题的途径——通过平方,去掉根号有理化;(3) a a =2)(,揭示了与绝对值的内在一致性.著名数学教育家玻利亚曾说,“回到定义中去”,当我们面对条件较少的问题时,记住玻利亚的忠告,充分运用概念解题.提示:22222205420,262045x x x y x y x x⎧-≥⎪⎪-→-==→+=⎨-⎪≥⎪-⎩ 【知识点】根式及其运算 【适用场合】当堂例题 【难度系数】3习题演练【试题来源】 【题目】计算:(11014152110141521+--+++;(23151026332185231--+-+++【答案】(1)562- (2)233-【解析】(1)原式101415212(57)3(57)(23)(57)101415212(57)3(57)(23)(57)+--+-+-+==++++++++(23)(32)(526)265==--=(2315102633218(31510)(1826)(332)52315231--+-+-+-+-=++++5(332)23(332)(332)(332)(5231)33252315231-+-+--++===++++【知识点】根式及其运算 【适用场合】随堂课后练习 【难度系数】3【试题来源】“希望杯”邀请赛试题 【题目】计算223810++ 【答案】24+【解析】原式222108122(2)108(12)108(12)=+++++++2224242(2)(42)42=++=+=【知识点】根式及其运算 【适用场合】随堂课后练习 【难度系数】4【试题来源】湖北省孝感市“英才杯”竞赛题 【题目】计算1212--+-+a a a a 【答案】见解析【解析】通过配方可以简化一重根号,本题的关键是就a 的取值情况讨论,解决含根号、绝对值符号的综合问题.原式222222121(1)121(1)(11)(11)a a a a a a =+-+---+-=+---2111112112a a a a a a a ⎧-≤≤≤⎪=--=⎨-->⎪⎩ 当1,即12时 当>1,即时 【知识点】根式及其运算 【适用场合】随堂课后练习 【难度系数】3【试题来源】山东省竞赛题【题目】已知521332412---=----+c c b a b a ,求c b a ++的值. 【答案】20【解析】思路点拨 已知条件是一个含三个未知量的等式,三个未知量,一个等式怎样才能确定未知量的值呢?考虑从配方的角度试一试.原式可化为:222221[(1)211][(2)2212][(3)2339]2a ab ac c ---+---+=----+即2221(11)(22)]33)02a b c -+-+-=,因此有110a -=,得2a =;220b -=,得6b =330c -=,得12c =。
2004年全国初中数学竞赛

223
俞彬杰
新埭中学
王根方
224
唐伟杰
新埭中学
张军
225
顾特卫
乍浦镇初中
毛利忠
226
邓忠杰
大麻学校
邱国昌
227
陆艳丽
河山镇中心学校
周洪兵
228
朱世杰
河山镇中心学校
褚中乔
229
陈佳慧
留良初中
俞永泽
230
沈婷
留良初中
于亚军
231
朱卉
桐乡六中
陈国祥
232
陈球
桐乡六中
钟维廉
233
钱蕊莎
桐乡六中
顾金梅
234
111
张冬
新埭中学
王根方
112
祝燕琼
海盐县武原镇中学
汤菊英
113
王惠峰
东栅中学
张瑞英
114
陶新恩
二十一世纪外国语学校
李培林
115
刘剑清
洪波中学
吴红平
116
郑嘉
吉水中学
包珏晔
117
沈哲伦
嘉兴三中
徐韬
118
叶莹
穆湖实验学校
钟林芳
119
徐跃飞
新丰镇中学
黄德正
120
王利民
余新镇中学
周晓红
121
金晓萍
王店镇中学
殳卓琳
桐乡六中
陈国祥
189
盛锦辉
桐乡六中
凌柏明
190
朱晓明
屠甸中学
张雪英
191
顾琴芳
乌镇初中
192
沈晓燕
洲中
田世均
奥数-2004年重庆市初中数学竞赛决赛试题(七年级

2004年重庆市初中数学竞赛决赛试题(七年级)(全卷共三个大题,考试时间120分钟,满分100分)一、 选择题:(每小题5分,共35分)1. 春节晚会上,电工师傅在礼堂四周挂了一圈只有绿、黄、蓝、红四种颜色的彩灯,起排列规则是:绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红……,那么,第2004个彩灯的颜色是( ) A 绿色 B 黄色 C 红色 D 蓝色2. 根据图中小立方体的三种不同的状态显示的数字,推出?处的数字是( )A1 B2 C3 D63. 已知有理数x 、y 、z 两两不等,则yx xz x z z y z y y x ------,,中负数的个数是( ) A1个 B2个 C3个 D4个 4.把10个相同的小正方体按如图的位置堆放,他的外表会有若干个小正方形,如果将图中表有字母P 的一个小正方体搬去,这时外表含有的小正方形的个数与搬动前相比( ) A 不增不减 B 减少1个 C 减少2个 D 减少3个5.有A 、B 、C 、D 、E 共五位同学一起比赛象棋,每两人之间只比赛1盘,比赛过程中间统计比赛的盘数知A 赛了4盘,B 赛了3盘,C 赛了2盘,D 赛了1盘,那么同学E 所赛的盘数为( ) A1 B2 C3 D46.一椭圆形地块,打算分A 、B 、C 、D 四个局域栽种观赏植物,要求同一种区域种同一种植物,相邻的两块种不同的植物,现在有4种不同的植物可供选择,那么所有的种栽方案的个数为( ) A66 B72 C60 D847.甲乙两人轮流在黑板上写下不超过10的自然数,规定禁止在黑板上写下已经写过的数的约数,最后不能写得为失败者,如果甲写第一个,甲要必胜,甲应写数字( ) A10 B9 C8 D6 二、填空题:(每小题5分,共35分)1. 当整数m = 时,代数式136-m 的值是整数2. 已知:a 、b 、c 都不为0,且abcabc c c b b a a +++的最大值为m ,最小值为n ,则5 4112 34 5?A B C D P2004)(n m +=3. 若n是正整数,定义123)2()1(!⨯⨯⨯⨯-⨯-⨯= n n n n ,设!2004!2003!4!3!2!1++++++= m ,则m 的末两位数字之和为4. 如图,一个面积为50平方厘米的正方形与另一个小正方形并排放在一起,则△ABC 的面积是 平方厘米5. 小华、小亮、小红3位同学分别发出新年贺卡x 、y 、z 张,如果已知x 、y 、z 的最小公倍数是60;x 、y 的最大公约数是4;y 、z 的最大公约数是3,已知小华至少发出5张贺卡,那么,小华发出的新年贺卡是 张 6. 小敏购买4种数学用品:计算器、圆规、三角板、量角器的件数和用钱总数列下表:品名件数 计算器 圆规 三角板 量角器 总数 第一次购件数 1 3 4 5 78 第二次购件数157998则4种数学用品各买一件共需 元7. 某中学举行运动会,以年级为单位参加,设跳高、跳远和100米赛跑三项,各项均取前三名,第一名可得5分,第二名可得3分,第三名可得1分,已知七年级和八年级总分相等,并列第一名,且八年级进入前三名的人数是七年级的两倍,那么九年级的总分是 分三、 解答题:(每小题15分,共30分)1. 甲乙两人到特价商店购买商品,商品里每件商品的单价只有8元和9元两种,以后至来了个人购买商品的件数相同,且两人购买商品以共花费了172元,求两人共购买两种商品各几件?2. 长方形四边的长度都是小于10的整数(单位:厘米),这四个长度数可以构成一个四位数,这个四位数的千位数字与百位数字相同,并且这个四位数是一个完全平方数,求这个长方形的面积C BA。
全国初中数学竞赛试题及答案(2004年)

2004年全国初中数学联合数学竞赛试题第一试一.选择题1.已知abc ≠0,且a+b+c =0, 则代数式222a b c bc ca ab++的值是( ) (A) 3 (B) 2 (C) 1 (D) 02.已知p,q 均为质数,且满足5p 2+3q=59,则以p+3,1-p+q,2p+q-4为边长的三角形是( )(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 等腰三角形 3. 一个三角形的边长分别为a,a,b ,另一个三角形的边长分别为b,b,a ,其中a>b ,若两个三角形的最小内角相等,则ab的值等于( )(A)12 (B) 12 (C) 22 (D) 224.过点P(-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作( )(A) 4条 (B) 3条 (C) 2条 (D) 1条5.已知b 2-4ac 是一元二次方程ax 2+bx+c=0(a ≠0)的一个实数根,则ab 的取值范围为( ) (A) 18ab ≥(B) 18ab ≤ (C) 14ab ≥ (D) 14ab ≤ 6.如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( )(A) 24 (B) 38 (C) 46 (D) 50二.填空题 1.计算2003+++= .2.如图ABCD 是边长为a 的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ,延长AP 交BC 于点N ,则BNNC= .D AB3.实数a,b满足a3+b3+3ab=1,,则a+b= .4.设m是不能表示为三个合数之和的最大整数,则m= .第二试(A)一.已知方程x2-6x-4n2-32n=0的根都是整数,求整数n的值。
二.已知如图,梯形ABCD中,AD∥BC, 以两腰AB,CD为一边分别向两边作正方形ABGE和DCHF,设线段AD的垂直平分线l交线段EF于点M,EP⊥l于P,FQ⊥l于Q。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2004年全国初中数学竞赛嘉兴市三等奖说明:由嘉兴市数学会颁发证书。
序号姓名学校指导老师1王林军海盐县澉浦中学张进良2黄斌璐海盐县官堂中学孙建华3郑琳海盐县武原中学朱汉华4顾丹虹海盐县武原中学朱汉华5金峰嘉善四中俞亚芳6胡逸飞嘉善四中周建方7徐剑峰海盐县秦山中学尧满远8顾峰磊海盐县实验中学陆菊芳9高培军海盐县武原中学王建芬10费忠嘉善里泽中学朱惠良11薛嘉晓嘉善四中周建方12张荣嘉善新世纪学校吕浩13赵璋嘉善一中潘慧丰14潘旻嘉善一中顾群15陆伟峰海盐县武原中学戎海滨16周艳婷海盐县武原中学朱汉华17张祎晨海盐县武原中学朱汉华18张斌海海盐县武原中学王建芬19孙雪燕海盐县元通中学张佩良20俞振佳新仓初中周树华21陈晓燕嘉善干窑中学何栋梁22王华杰嘉善干窑中学孙凤根23严彬蔚嘉善四中周建方24朱叶波海盐县澉浦中学朱国芳25马海惠海盐县官堂中学孙建华26陈龙飞海盐县横港中学陆海琴27马敏辉海盐县秦山中学尧满远28步平飞海盐县秦山中学尧满远29王勋海盐县沈荡中学张丽萍30王宇翔海盐县实验中学富旭东31何俊杰海盐县实验中学陆菊芳32沈海涛海盐县武原中学周利君33韦力海盐县武原中学朱汉华34王龙海盐县武原中学王建芬35田叶琴海盐县元通中学肖燕36张龙马桥初中孙芬华37朱琰上外附属浙江宏达学校马金康等38张呤啸实验初中方王兴39钟弢洪波中学张政杰40殷琰洪波中学张政杰41吴悦嘉兴三中张燕宁42宋翰卿嘉兴三中张燕宁43葛康嘉兴秀州中学分校汝彩英44张真三水湾中学王培荣/陈二军45江如俊余新镇中学吴允仁46沈芳嘉善魏塘中学罗旭47富强嘉善新世纪学校章加华48沈佳龙嘉善新世纪学校田应强49许永明嘉善一中顾群50陈阳嘉善一中潘慧丰51汪颖枭嘉善一中周晓峰52方正嘉善一中潘慧丰53周波海盐县官堂中学孙建华54黄灵毓海盐县秦山中学尧满远55赵军海盐县通元中学袁社英56夏春蕾海盐县武原镇中学余晓明57胡瑞海盐县武原中学朱汉华58梁一舒海盐县武原中学朱汉华59姚峰海海盐县元通中学郑马荣60沈斌海宁一中计惠英61曹宇音洪波中学张政杰62顾振雄嘉兴清河中学于国华63李琛超嘉兴三中徐唤民64刘砾嘉兴秀州中学分校赵有红65吴佳青三水湾中学王培荣/陈二军66凌夏珏秀洲现代实验学校袁天红67王嘉黛嘉善四中吴泉林68沈嘉桢嘉善泗洲中学柴国忠69周静中嘉善陶庄中学黄永新70韩佳燕嘉善新世纪学校田应强71史佳伟嘉善杨庙中学樊根平72冯一欣嘉善一中顾群73张逸超城关中学刘金付74徐佳伟城关中学蒋根荣75施文杰城关中学蒋根荣76蒋巍亮东湖中学顾菊根77金必卿东湖中学蒋建强78施布恩东湖中学沈兴旺79缪芸东湖中学郭照明80顾立佳海盐县沈荡中学苏娟芳81张吉斯海宁一中王娟益82王芳实验初中孙永良83王旭炳大桥镇中学刘洋84戎朕远二十一世纪外国语学校沈其豪85马维娜二十一世纪外国语学校张庆忠86张伟超吉水中学包珏晔87于沁嘉兴三中孙松林88范中远嘉兴三中孙松林89沈琪嘉兴三中张燕宁90殷晟聪嘉兴三中姚宏91于成龙嘉兴三中徐唤民92王鉴嘉兴三中徐韬93许昂嘉兴秀州中学分校汝彩英94张思杰嘉兴秀州中学分校汝彩英95王宇喆嘉兴秀州中学分校徐琪96钟嘉龙穆湖实验学校钟林芳97秦峰余新镇中学周晓红98钱学伟余新镇中学陆晨阳99金佳圆南汇中学胡坤华100陈志敏新塍镇中学李科梅101朱立成秀洲现代实验学校袁天红102马瑶嘉善四中吴泉林103邱涛嘉善四中吴泉林104张严平嘉善五中陈华105孙晨良嘉善杨庙中学樊根平106王金花嘉善姚庄中学唐建红107成盖天城关中学蒋根荣108钱琰君东湖中学山引珠109俞山杰林埭中学孙跃平110沈燕新仓中学李洪根/朱川丽111张冬新埭中学王根方112祝燕琼海盐县武原镇中学汤菊英113王惠峰东栅中学张瑞英114陶新恩二十一世纪外国语学校李培林115刘剑清洪波中学吴红平116郑嘉吉水中学包珏晔117沈哲伦嘉兴三中徐韬118叶莹穆湖实验学校钟林芳119徐跃飞新丰镇中学黄德正120王利民余新镇中学周晓红121金晓萍王店镇中学吴勇122何晨王江泾镇中学许荣林123盖静佳曹桥中学毛夏平124殳辰杰城关中学刘金付/徐明芳125缪慎杰东湖中学蒋建强126沈筱旖东湖中学咸桂杰127张虬海盐县横港中学韩庆伟128钱颖乐海盐县于城中学吴会琴129蒋娟凤河山镇中心学校周洪兵130谢晓峰桐乡六中顾金梅131谢闻达桐乡六中顾金梅132吴叶超桐乡六中顾金梅133戴一帆洪波中学张政杰134万芸穆湖实验学校钟林芳135寿魏维清河中学屠强华136陆天乐三水湾中学王培荣/陈二军137俞晓莉三水湾中学王培荣/陈二军138顾志清新丰镇中学陆雪祥139周淳迪秀州中学分校倪建荣140杜佳燕余新镇中学干启勇141姚龙锋洛东中学邬洪彪142徐琳悦洛东中学陈跃勇143周晓娟栖真中学吴良伯144仲耀华秀洲现代实验学校张何农145金振宇城关中学刘金付146许敏磊东湖中学咸桂杰147陆奕雯东湖中学顾菊根148盛佳妮东湖中学山引珠149汤腾蛟东湖中学郭照明150姚春平新仓中学李洪根/朱川丽151王小英城西初中胡林152夏丹邵逸夫中学姚建学153洪超石门中学陆岳明154顾春江桐乡八中沈建松155王志杰桐乡九中柏雪156杨诚纯桐乡六中杜建民157黄秋婧桐乡六中徐惠荣158沈思遥桐乡六中杜建民159陆静桐乡求是中学陈小春160朱国强洲中沈海松161孙漪新塍镇中学吴小英162俞佳佳油车港镇中学朱圣东163顾陇兵曹桥中学毛夏平164李星童城关中学刘金付/徐明芳165蒋佳骏城关中学蒋根荣166陈天笑当湖初中沈秀中/杨爱萍167陈洲东湖中学山引珠168倪勤宣东湖中学郭照明169费建东湖中学咸桂杰170陶丽娇广陈中学华明中171李静林埭中学吴水良172张浩海盐县澉浦中学朱国芳173许敏丽海盐县石泉中学郁卫军174陈燕歌海盐县于城中学谢寒175魏锋城西初中胡林176徐跃飞高桥初中177张亚芳民合中心学校周新鸣178谢一飞南日初中冯荣方179陈凯骑塘初中姚菊芬180张笑丽邵逸夫中学夏琦学181曹敏邵逸夫中学李伟昌182朱鑫炎邵逸夫中学周国平183朱晓强邵逸夫中学周国平184吕辰健邵逸夫中学周国平185闻君侠同福初中祝红娟186倪红燕桐乡八中沈建松187杨铮园桐乡六中陈国祥188殳卓琳桐乡六中陈国祥189盛锦辉桐乡六中凌柏明190朱晓明屠甸中学张雪英191顾琴芳乌镇初中192沈晓燕洲中田世均193陈林洛东中学邬洪彪194怀万里南汇中学宋海斌195裘智远王店镇中学陈晓群196郭松秀洲现代实验学校陆长林197叶灵宇秀洲现代实验学校张何农198戚海平黄姑中学陶国梁199朱斌健林埭中学吴水良200陆慧新埭中学洪雪峰201王君良新埭中学金亚英202陆凤麟海盐县西塘中学王锋203徐新伟高桥初中204姚汉铭河山镇中心学校周洪兵205吴祁欢南日初中郁银海206施耀飞青石初中沈国华207郑伟潮邵逸夫中学李伟昌208徐凌蔚邵逸夫中学李伟昌209孙爱飞同福初中潘咏竹210沈明丽同福初中祝红娟211陈良同福初中周夜飞212沈晓峰桐乡三中陆菊英213徐洁桐乡三中陆菊英214柴云洁桐乡四中高月良215李心瑶桐乡四中高月良216张龙屠甸中学张雪英217夏幸炬芝村初中钟敏218俞开明洲中田世均219胡勤芳洪合镇中学李培根220张亮南汇中学胡坤华221吴春涛塘汇实验学校朱锦祥222袁立谅新塍镇中学(八字)夏音223俞彬杰新埭中学王根方224唐伟杰新埭中学张军225顾特卫乍浦镇初中毛利忠226邓忠杰大麻学校邱国昌227陆艳丽河山镇中心学校周洪兵228朱世杰河山镇中心学校褚中乔229陈佳慧留良初中俞永泽230沈婷留良初中于亚军231朱卉桐乡六中陈国祥232陈球桐乡六中钟维廉233钱蕊莎桐乡六中顾金梅234程深桐乡六中顾金梅235莫自楷桐乡六中张翠娜236陆丽萍桐乡七中马娟文237邱俊桐乡七中程锡坤238沈国宾桐乡七中叶伟学239许晓燕桐乡求是中学吴玥霞240黄海桐乡三中施宋学241朱建海桐乡三中徐东红242庄林泉桐乡三中张忠梅243周建强桐乡十中朱林祥244任春燕桐乡十中徐伟245李斌桐乡十中徐伟246徐明桐乡十中刘绵福247许佳萍永秀中心骆克双248屠小飞洲中徐登峰249何晓红建设中学朱年荣250朱旭明王店镇中学吴勇251王思加秀洲现代实验学校陆长林252戴跃曹桥中学顾其根253陆晓燕全塘中学夏海英254商忠伟高桥初中255沈冲河山镇中心学校彭延盛256陈林民合中心学校周新鸣257金秋杰南日初中冯荣方258范冰骑塘初中黄呈瑞259沈晓栋邵逸夫中学李伟昌260张迅博桐乡六中杜建民261李晶桐乡六中顾金梅262吴晓林桐乡七中叶伟学263黄雁青桐乡求是中学吴玥霞264陈颖桐乡求是中学陈小春265蒋少良乌镇中学王峰湖266俞晓明新生初中许少琴267沈权锋洲中徐登峰268杨峰洪合镇中学杨松269张佳锋秀洲现代实验学校陆长林270葛佳伟秀洲现代实验学校高爱民271曹贇轩秀洲现代实验学校高爱民272郑晓辰秀洲现代实验学校高爱民273程丽斌黄姑中学陶国梁274董玉凤羔羊中学徐月江275庄煜顺高桥初中276徐倩莲南日初中冯荣方277陈怡邵逸夫中学李伟昌278曹丽娟桐乡十中朱林祥279章瑰玮桐乡四中高月良280马海峰芝村初中徐积萱281朱笑丽洲中钱吉锋282徐美霞新仓中学李洪根/朱川丽283张佩乍浦镇初中毛利忠284姚政国乍浦镇初中毛利忠285肖伟钟埭中学李连根286李佳钟埭中学俞浩287张凌乍浦中学王飞嘉兴市教育研究院嘉兴市教育学会中学数学分会嘉兴市数学会2004年5月10日。
