广西南宁市东盟中学2020届高三一轮复习天天练48-53解析几何(无答案)
广西南宁市东盟中学2020届高考冲刺理科数学限时训练5(无答案)

选择填空限时训练五(限时40分钟)1. 已知集合(){}(),11,,2,2⎭⎬⎫⎩⎨⎧+-====x x y y x B x y y x A 为则B A IA. φB.{-1,-2}C. {(1,2)}D. {(-1,-2)} 2.复数z 满足的最大值是则z i z ,12=+- A.5 B.6 C.15+ D.15-3.设实数x,y 满足约束条件⎪⎩⎪⎨⎧≤≥-+≤--,2,04,022y y x y x 则12-+=x y z 的最小值是A.32 B.54 C.78D.4 4.运行如图1所示的程序框图,若输入 的)4,3,2,1(=i a i 分别为1,2,4,16,则输出值为A.25B.5.5C.5D.45. 已知m,n 是两条不同的直线,α,β是两个不同的平面,给出下列命题: ①;则若βααβ⊥⊂⊥,,,//m n n m ①;或则,若βαβαβα⊥⊥⊥=⊥n n m n m ,,I①;或则若βαβαβα⊥⊂⊥⊥//,,,n n m m①.////,,,//βαβαβαn n n n m n m 且则,若⊄⊄=I其中正确命题的序号是A. ①①B. ①①C.①①D.①①6. 已知在ΔABC 中,M,N 分别是边AB,AC 上的点,且 CM BN NC AN MB AM 与,3,2==相交于点P ,记AC b AB a ==,,用b a ,表示AP 的结果是A.b a AP 3231+= B.b a AP 3121+= C. b a AP 3152+= D. b a AP 2131+=7.已知()512-⎪⎭⎫ ⎝⎛+x x a x 的展开式中各项系数和为3,则()=+-⎰dx x x a 024 A.22π+B.π+2C. π24+D. π44+8.“双11”促销活动中,某商场为了吸引顾客,搞好促销活动,采用“双色球”定折扣的方式促销,即:在红、黄的两个纸箱中分别装有大小完全相同的红、黄球各5个,每种颜色的5个球上标有1,2,3,4,5等5个数字,顾客结账时,先分别从红、黄的两个纸箱中各取一球,按两个球的数字之和为折扣打折。
广西南宁市东盟中学2020届高三一轮复习天天练54-55算法和统计(无答案)

天天练习(54)算法1.右图是求样本1210,,,x x x L 平均数x 的程序框图,图中空白框中应填入的内容为( ) (A)S=S +x n(B)S =S +n x n (C)S =S +n (D)S =S +1n 2.如果执行右面的程序框图,输入正整数n ,m ,满足n ≥m ,那么输出的P 等于( )(A )1m n C - (B) 1m n A - (C) m n C (D) m nA3.某程序框图如图所示,若输出的S=57,则判断框内应填入( )(A ) k >4? (B )k >5? (C ) k >6? (D )k >7?4.阅读右边的程序框图,若输出s 的值为-7,则判断框内可填写 ( )(A)i <3? (B )i <4? (C )i <5? (D )i <6?5.如图所示,程序框图(算法流程图)的输出值x =________.6.执行如图所示的程序框图,若输入10x =,则输出y 的值为 .7.若某程序框图如图所示,则该程序运行后输出的k 的值为 .8.若执行如图所示的框图,输入,2,3,2,1321====x x x x 则输出的数等于______.第1题 第2题 第3题 第4题第5题 第6题 第7题 第8题天天练习(55)随机抽样1.某产品的广告费用x 与销售额y 的统计数据如下表:根据上表可得回归方程ˆˆˆybx a =+中的ˆb为9.4,据此模型预报广告费用为6万元时销售额为( )(A )63.6万元 (B )65.5万元 (C )67.7万元 (D )72.0万元2.样本()12,,n x x x L ,的平均数为x ,样本()12,,m y y y L ,的平均数为()y x y ≠.若样本()1212,,,,,n m x x x y y y L L ,,的平均数()1z x y αα=+-,其中102α<<,则,n m 的大小关系为( )(A) n m < (B )n m > (C )n m = (D )不能确定3.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[]1,450的人做问卷A ,编号落入区间[]451,750的人做问卷B ,其余的人做问卷C.则抽到的人中,做问卷B 的人数为( )(A )7 (B )9 (C )10 (D )154.总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字,则选出来的第5个个体的编号为( )7816 6572 0802 6314 0702 4369 9728 01983204 9234 4935 8200 3623 4869 6938 7481A.08B.07 5.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50), [50,60), [60,70),[70,80), [80,90), [90,100]加以统计,得到如图所示的频率分布直方图。
广西南宁市东盟中学2020届高三一轮复习天天练58-59概率、分布列、期望(无答案)

天天练习(58)概率1.两个实习生每人加工一个零件.加工为一等品的概率分别为23和34,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )(A )12 (B)512 (C)14(D)162.甲、乙两队进行排球决赛.现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军.若两队胜每局的概率相同,则甲队获得冠军的概率为( ) (A )12 (B )35 (C )23 (D )343.如图,矩形ABCD 中,点E 为边CD 的中点,若在矩形ABCD 内部随机取一个点Q ,则点Q 取自△ABE 内部的概率等于( ) (A)14 (B)13 (C)12 (D)234.有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( ) (A )13 (B )12 (C )23 (D )345.有5本不同的书,其中语文书2本,数学书2本,物理书1本.若将其随机地抽取并排摆放在图书架的同一层上,则同一科目的书都不相邻的概率是( ) (A )15 (B )25 (C )35 (D )456.从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B ∩A)=( ) (A)18 (B)14 (C)25 (D)127.甲乙两人一起去游“2011西安世园会”,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是( ) (A )136 (B )19 (C )536(D )168.小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若此点到圆心的距离大于12,则周末去看电影;若此点到圆心的距离小于14,则去打篮球;否则,在家看书,则小波周末不在家看书的概率为 . 9.在区间[]1,2-上随机取一个数x ,则x 1≤的概率为10.盒中装有形状、大小完全相同的5个球,其中红色球3个,黄色球2个.若从中随机取出2个球,则所取出的2个球颜色不同的概率等于_______.11.某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于 0.128 .12. 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为 和 . 24 23天天练习(59)分布列、期望和方差1.某种种子每粒发芽的概率都为0.9,现播种了1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X ,则X 的数学期望为( )(A )100 (B )200 (C )300 (D )400 2.已知随机变量ξ服从正态分布2N(0,)σ,若P(>2)=0.023ξ,则P(-22)=ξ≤≤( )(A)0.477 (B)0.628 (C)0.954 (D)0.977 3.已知离散型随机变量X 的分布列为则X 的数学期望E (x )=( ) A.32B. 2C.52D 34.如图,将一个各面都凃了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的油漆面数为X ,则X 的均E(X)=( ) A.125126 B. 56C.125168 D 575.某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为23,得到乙、丙两公司面试的概率均为p ,且三个公司是否让其面试是相互独立的.记X 为该毕业生得到面试的公司个数.若1(0)12P X ==,则随机变量X 的数学期望()E X = . 536.设非零常数d 是等差数列12319,,,,x x x x L 的公差,随机变量ξ等可能地取值12319,,,,x x x x L ,则方差_______D ξ=230d7.某学校高一年级男生人数占该年级学生人数的40%.在一次考试中,男、女生平均分数分别是75、80,则这次考试该年级学生平均分数为 .78.8.已知箱中装有4个白球和5个黑球,且规定:取出一个白球得2分,取出一个黑球得1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X 为取出此3球所得分数之和. 则X 的数学期望E (X )=______.9.红队队员甲、乙、丙与蓝队队员A ,B ,C 进行围棋比赛,甲对A ,乙对B ,丙对C 各一盘.已知甲胜A 、乙胜B 、丙胜C 的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.用ξ表示红队队员获胜的总盘数,则ξ的分布列和数学期望E ξ=________.10.某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成4小块地,在总共8小块地中,随机选4小块地种植品种甲,另外4小块地种植品种乙.在第一大块地中,种植品种甲的小块地的数目记为X ,则EX=_________.X 1 2 3 p0.60.30.1。
广西南宁市东盟中学2020届高三一轮复习天天练40-47立体几何(无答案)
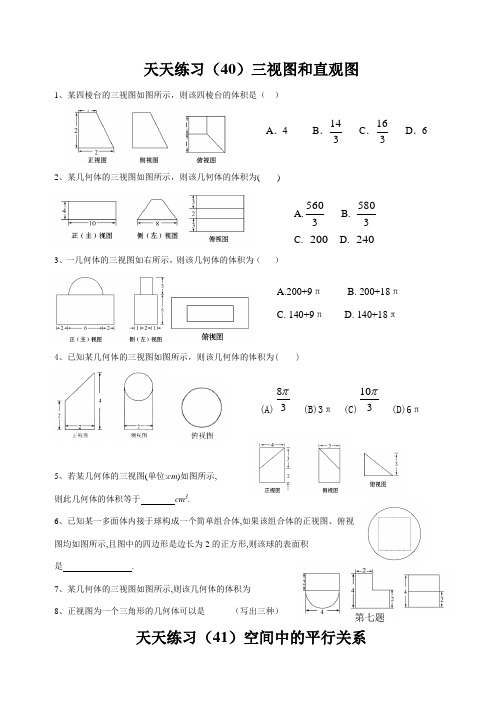
天天练习(40)三视图和直观图1、某四棱台的三视图如图所示,则该四棱台的体积是( )2、某几何体的三视图如图所示,则该几何体的体积为( )3、一几何体的三视图如右所示,则该几何体的体积为( )4、已知某几何体的三视图如图所示,则该几何体的体积为( )5、若某几何体的三视图(单位:cm )如图所示, 则此几何体的体积等于 cm 3.6、已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是 .7、某几何体的三视图如图所示,则该几何体的体积为_____ 8、正视图为一个三角形的几何体可以是______(写出三种)天天练习(41)空间中的平行关系A.3560 B. 3580 C. 200 D. 240A .4B .143 C .163D .6 A.200+9π B. 200+18π C. 140+9π D. 140+18π(A)83π (B)3π (C)103π(D)6π第七题BAD C P NQM1、在空间,下列命题正确的是( )(A )平行直线的平行投影重合 (B )平行于同一直线的两个平面平行 (C )垂直于同一平面的两个平面平行 (D )垂直于同一平面的两条直线平行 2、设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是( )(A )若lm ⊥,m α⊂,则l α⊥ (B )若l α⊥,l m //,则m α⊥(C )若l α//,m α⊂,则l m // (D )若l α//,m α//,则l m //3、已知a ,b ,c 为三条不重合的直线,α,β是两个不重合的平面,给出下列四个命题①//,////a b b c a c ⇒; ②//,////a b a b αα⇒③//,////a αβααβ⇒ ④,,////.a b a b a ααα⊄⊂⇒其中正确的命题是( ) A .①④ B .①② C .②③ D .③④4、如图,已知,,,M N P Q 分别是空间四边形ABCD 的边,,,AB BC CD DA 的中点.求证:(I)线段MP 和NQ 相交且互相平分。
广西南宁市东盟中学2020届高三高考数学《高考中的多选题》(详解)

18.(2014新课标Ⅰ改编)不等式组 的解集记为D.下面四个命题中,是真命题是()
A. B. ,
C. D. .
答案AB
【解析】画出可行域如图中阴影部分所示,由图可知,
当目标函数 经过可行域内的点A(2,-1)时,取得最小值0,故 ,因此 是真命题.
19.(2010安徽改编)若 ,则下列不等式对一切满足条件的 恒成立的是().
A.给定向量 ,总存在向量 ,使 ;
B.给定向量 和 ,总存在实数 和 ,使 ;
C.给定单位向量 和正数 ,总存在单位向量 和实数 ,使 ;
D.给定正数 和 ,总存在单位向量 和单位向量 ,使 ;
答案AB
【解析】利用向量加法的三角形法则,易的A是对的;利用平面向量的基本定理,易的B是对的;以 的终点作长度为 的圆,这个圆必须和向量 有交点,这个不一定能满足,C是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须 ,所以D是假命题.12安徽改编)设 的内角 所对的边为 ;则下列命题正确的是.
A.若 ;则 B.若 ;则
C.若 ;则 D.若 ;则
答案ABC
【解析】A.
B.
C.当 时, 与 矛盾
D.取 满足 得:
六、平面向量
17.(2013广东改编)设 是已知的平面向量且 ,关于向量 的分解,若向量 , 和 在同一平面内且两两不共线,下列命题中的则真命题的是()
当 时, ,若 在 单调递增,则 ,即 ,因为 ,故C正确.
15.(2011安徽改编)设 = ,其中 , ,若 对一切则 恒成立,则以下结论正确的是().
A.
B. <
C. 既不是奇函数也不是偶函数
D. 的单调递增区间是
广西南宁市东盟中学2020届高三选择填空限时训练四(无答案)

选择填空限时训练四(限时40分钟)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目.1. 已知集合()(){}11,22=+-=y x y x A ,()(){}21,-==x y y x B ,则A∩B 中元素的个数为 A.1 B.2 C.3 D.02.已知bi a z +=,R b a ∈,,满足()52bi i a =+,则z = A.5 B.5 C.3 D.33. 已知空间中的两条直线a ,b 和两个平面α,β,若,,βα⊂⊂b a 则,b a ⊥是βα⊥的A. 充分不必要B.必要不充分C.充要条件D.既不充分也不必要4. 无字证明(proof without words )是指仅用图形或图象而无需文字解释就能不证自明的数学 命题。
虽然无字证明只是用图形来说明一个证明中的特例,不够严密,但其不证自明的特性,使得这种证明方式被认为比严格的数学证明更为优雅。
根据如图1甲中菱形的面积与乙中各矩形面积之和的关系,你认为该图所验证的一个三角恒等式为A.βsin αcos βcos αsin )βαsin(+=+B.βsin αcos -βcos αsin )β-αsin(=C.βsin αsin -βcos αcos )βα(cos =+D.βsin αsin βcos αcos )β-α(cos +=5.李华同学利用“随机模拟的方法”估计图2中由曲线x y 2log =与两直线2=x 及0=y 所围成的阴影部分的面积S ,他用计算机分别产生了15个在区间[1,2]上的均匀随机数i x 和15个在区间[0,1]上的均匀随机数,151,,*≤≤∈i N i y i 其数据如下表的前两行.根据以上数据可估算S 的一个近似值为A.157B.158C.53D.32 6.执教如图3所示的程序框图,输出的x 的值为A.-2B.31- C.21 D.3 7. 已知3log ,2log ,5432ln ===c b a ,则a,b,c 的大小关系为A. c b a >>B.b c a >>C.a b c >>D.b a c >>8. 已知函数,2,01)sin(2)(⎪⎭⎫ ⎝⎛<>-+=πϕωϕωx x f ,3)(-=αf .1)(-=βf 若βα-的最小值是43π,且)(x f 的图像关于点),(14-π对称,则函数)(x f 的单调递增区间为A.2,2,2k k k Z p p p p 轾++?犏犏臌B.3,3,2k k k Z p p p p 轾++?犏犏臌C.52,2,2k k k Z p p p p 轾++?犏犏臌D.53,3,2k k k Z p p p p 轾++?犏犏臌 9.在ABC D 中,M,N 分别为边BC,AC 的中点,且向量BN AM 与的夹角为1500,,,32==BN AM 则AC AB ⋅的值为A.9133-B.9236-C.9339-D.94312- 10.在平面四边形ABCD 中,2==AD AB ,2===DB CD BC ,现将ΔABD 沿BD 折起,使二面角A -BD -C 的大小为600.若A,B,C,D 四点在同一个球的球面上,则该球的表面积为 A.π313 B.π314 C.π952 D.π956 11.已知离心率为1e 的椭圆C 1:)0(111212212>>=+b a b y a x 和离心率为2e 的双曲线)0,0(1-:222222222>>=b a b y a x C 有公共的焦点F 1,F 2,P 是它们在第一象限的交点,且02160=∠PF F ,则2221e e +的最小值为A.23B.231+C.232+D.233+ 12.已知函数(),)2(2x ex x a x f --=(),)1(x e a x g +=其中R a ∈.若函数()x f 和()x g 的图像有两个公共点,则c 的取值范围为A.)0,1[)1()1(2-⎭⎬⎫⎩⎨⎧-+Y e e eB.)0,1[-C.]1,)1()1([1132--+⎭⎬⎫⎩⎨⎧-+e e e e e YD.]1,)1()1([2--+e e e 题号1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题:本大题共4小题,每小题5分,共20分。
广西南宁市东盟中学2020届高三一轮复习天天练1-2常用逻辑用语(无答案)

天天练习(1)命题及其关系、充分条件与必要条件“”“”p q p q ∧∨1.如果命题与命题都是假命题,那么( ).A p q ⌝⌝命题与命题的真值不同 .B p q ⌝命题与命题的真值相同.C q p ⌝命题与命题的真值相同 .D p q ⌝∧⌝命题“()()”是真命题(2.)p q 已知命题:所有有理数都是实数;命题:正数的对数都是负数,则下列命题中为真命题的是 ()()()()( ) A p q B p q C p q D p q ∨∧∧∨.┐ . .┐┐ .┐┐23.p :x R,x 210;,sinx 1.x q x R ∀∈-+>∃∈=已知命题命题:则下列判断正确的是( ).q .q .p .p A B C D ⌝⌝是假命题 是假命题 是假命题 是真命题|4.|12p x q x a p q a >>⌝⌝已知条件:+,条件:,且是的充分不必要条件,则的取值范围是( ).1133Aa a a a ≥≤≥-≤- B. C. D.3()5. 0,20x A x R lgx B x R tanx C x R x D x R ∃∈∃∈∀∈∀∈>>下列命题中的假命题是 .,=0.,=1 ., . 6.下面四个条件中,使a b >成立的充分而不必要的条件是A .1>+a bB .1>-a bC .22>a bD .33>a b 7.cos ABC ∆在中,条件甲:A<B;条件乙:2A>cos2B,则甲是乙的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件8.在∆ABC 中,“π3=A ”是“sin =A ) A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件9.“11≥-x ”是“1log 2≥x ”成立的______________________条件.10.“a =18”是“对任意的正数x,2x +a x≥1”的___________________条件. 11.112x m x a -<<<如果不等式成立的充分不必要条件是,则实数的取值范围是_____.12.p q s q t s t p _____________.命题是命题是充分不必要条件,命题是命题的必要但不充分条件, 命题是命题的充要条件,则是的条件天天练习(2)简单的逻辑联结词、全称量词与存在词1.命题“若一个数是负数,则它的平方是正数”的逆命题是( )A .“若一个数是负数,则它的平方不是正数”B .“若一个数的平方是正数,则它是负数”C .“若一个数不是负数,则它的平方不是正数”D .“若一个数的平方不是正数,则它不是负数”2.若命题p的否命题是q,命题q 的逆命题是r ,则r 是p 的逆命题的A .原命题B .逆命题C .否命题D .逆否命题+a b a c b c >>+3.命题“若,则”的逆否命题是A .“+<<+a b a c b c 若,则 ”B .“+≤≤+a b a c b c 若,则 ”C .“+<+<a c b c a b 若,则”D .“+≤+≤a c b c a b 若,则”,2x x R ∃∈4."使>3"的否定是A .“,2x x R ∃∈使<3 ”B .“,2x x R ∃∈≤使3 ”C .“,2x x R ∀∈使<3”D .“,2x x R ∀∈≤使3”5.已知p :函数()||f x x a =+在(,1)-∞-上是单调函数;q :函数()log (1)a g x x =+ (0a >且1)a ≠在(1,)-+∞上是增函数;则p ⌝成立是q 成立的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件326."10"x R x x ∈≤命题:对任意的,-+的否定是________()27."110"______.x x a x a ∃∈-R 若命题,使得++<是真命题,则实数的取值范围是28."10"______.x x ax a a ∀∈-≥R 若命题,使得++是真命题,则实数的取值范围是()212519.:30,:0,________.66p log x q x x p q ->-+>已知则是的条件 ()()()1011273_____|(_|_)_x x x m f x m m R .有两个命题:不等式+->的解集是;函数=--是减函数.如果这两个命题中有且只有一个是真命题,则实数的取值范围是.211.6032___________.x x x x +-><->命题“不等式的解或”的逆否命题是。
广西南宁市东盟中学2020届高三一轮复习天天练8-11基本初等函数(无答案)

1.函数2(33)x y a a a =-+是指数函数,则a 的取值范围是( ) A.12a a ==或 B.2a = C.1a = D.()0,12a a a ∈+∞≠≠且2.,(2),(3),(4)x x x x y a y b y c y d ====的图象,则,,,a b c d 与1大小关系是( )3.设 1.71.70.30.3,b 0.2,c 1.7a ===,则( )(A ) a b c >> (B )b c a >> (C )a c b >> (D )a b c >> 4.若函数f (x )=⎩⎪⎨⎪⎧a x,x >1(4-a2)x +2,x ≤1是R 上的增函数,则实数a 的取值范围为( ) A .(1,+∞) B .(1,8) C .(4,8) D .[4,8) 5.函数y =(12)1-x 的单调增区间为( )A .(-∞,+∞)B .(0,+∞)C .(1,+∞)D .(0,1)231()4xxx +-<6.不等式2的解集是_________ 7.若函数()()2x u f x e --=的最大值为m ,且f (x )是偶函数,则m +u =________.8.函数221(01)x x y a a a a =+->≠且在区间[11]-,上有最大值14,则a 的值是_______.9.已知m x f x +-=132)(是奇函数,则m =________.1.设f (x )=lg(21-x +a )是奇函数,则使f (x )<0的x 的取值范围是( )A .(-1,0)B .(0,1)C .(-∞,0)D .(-∞,0)∪(1,+∞)2.已知函数()()()5lnx,g lg ,log ,f x x x h x x ===直线y=a(a<0)与这三个函数图象的交点的横坐标分别是123,,,x x x 则123,,x x x 的大小关系是( ) A. 231x x x << B. 132x x x <<C. 123x x x <<D. 213x x x <<3. 0.50.6a log b c ===,,则( ) A.a <b <cB.b <a <cC.a <c <bD.c <a <b4.设0.3113211log 2,log ,32a b c ⎛⎫=== ⎪⎝⎭,则 ( )A .a <b <cB .a <c <bC .b <c <aD .b <a <c5.函数()()213log 54f x x x=-- 的单调减区间为( )A.(-∞,-2)B.[-2,+∞]C.(-5,-2)D.[-2,1]6.已知函数()()y f x x R =∈满足()()2f x f x +=,且当[]1,1x ∈-时,()2f x x = ,则()y f x =与7log y x = 的图象的交点的个数为( )A.3B.4C.5D.67. ()1225254log _______⎡⎤-+=⎣⎦8. ()2lg 2lg 2lg5lg5______++=g9.函数y =log 3(x 2-2x )的单调减区间是________. 10.函数y=)x log 1(log 2221+的定义域为 .天天练习(10)幂函数与二次函数1.如图给出4个幂函数大致的图象,则图象与函数对应正确的是()A.①13y x = ②2y x =③12y x = ④1y x -= B.①3y x =②2y x =③12y x =④1y x -= C.①2y x =②3y x =③12y x =④1y x -= D.①13y x =②12y x =③2y x =④1y x -= 2.设0abc >,二次函数()2f x ax bx c =++的图象可能是( )(A) (B)(C) (D)3.设函数1-x 22x 1()1-log x x 1f x ⎧≤=⎨⎩,,,>,则满足()2f x ≤的x 的取值范围是( )(A )[-1,2] (B )[0,2] (C )[1,+∞) (D )[0,+∞)()()4.y 3- x 6x =+的最大值为A.9B.92C.3D.3225.若当x ∈(1,2)时,不等式2+40x mx +<恒成立,则m 的取值范围为 .()()()2-3+2=0,,f x f x f x π⎧-≤≤⎪⎨⎩=⎪-2xcos 1x 12x 1x 1,则关于x 的方程>,6.已知函数的实根的个数是__ 7.方程x 2-mx +1=0的两根为α,β,且α>0,1<β<2,则实数m 的取值范围是 . 8.已知函数()ax bf x x b+=-,其图象关于点(-3,2)对称,则()2f 的值是________. 天天练习(11)函数的图像1.函数y =2x -4sin x ,x ∈[-π2,π2]的图象大致是( D )2.函数f (x )=2e -x2-x的图象大致是( B ) 3.函数231x x y =-的图象大致是( B )4.已知函数1()ln(1)f xx x=+-;则()y f x=的图像大致为B5.已知10≠>a a且,若函数)(log )(2k x x x f a ++=在),(+∞-∞上既是奇函数,又是增函数,则函数k x x g a -=log )(的图像是A6.函数y=f(x)与y=g(x)的图象如图,则函数y=f(x)·g(x)的图象可能是( )7.已知函数()xf x e x=+,若关于x 的方程()f x k =有两个不同的实根,则实数k 的取值范围是 .。
广西南宁市东盟中学2020届高三一轮复习天天练36-39不等式(无答案)

11.f(x)x 2(0)A.0 B.0 C.-4 D.-x x=+-<已知函数,则f(x)有最大值为 最小值为 最大值为 最小值为4 2.下列不等式一定成立的是 A. ()21lg lg 04x x x ⎛⎫+>> ⎪⎝⎭ B. ()1sin 2,sin x x k k Z xπ+≥≠∈ C. ()R x x x ∈≥+212 D. ()R x x ∈>+11123.已知一元二次不等式()<0f x 的解集为1x|<-1>2⎧⎫⎨⎬⎩⎭或x x ,则(10)>0xf 的解集为 ( )A . {}|<-1>lg2x x x 或 B.{}|-1<<lg2x x C. {}|>-lg2x x D.{}|<-lg2x x4.若直线),(+∈=-+R b a by ax 012平分圆064222=---+y x y x ,则21a b+的最小值是________5.2,0_____1||2|__|a a a b bb a ++=>=设则取得当时,最小值。
()26.sin 0sin x x x函数的最小值是_______p +<<7.2x 函数f(x)=_______(8.2x 函数f(x)=的最大值是_______-()289.?1x f x x +=-函数() 1x >的最小值为_______ 10.设x,y )41)(1(,02222y xy x xy R ,++≠∈则且的最小值为_______ 11.设,x y 为实数,若2241,x y xy ++=则2x y +的最大值是 . 12.设a ∈R ,若x >0时均有[(a-1)x-1](x 2-ax-1)≥0,则a=_________.1. 设a b c 、、均为正数,且1a b c ++=,证明:(Ⅰ)13ab bc ac ++≤; (Ⅱ)2221a b c b c a ++≥2.若0,0a b >>,且11a b+=.(Ⅰ)求33a b +的最小值; (Ⅱ)是否存在,a b ,使得236a b +=?并说明理由.3.若0,0a b >>,且1a b +=。
广西壮族自治区南宁市东盟中学高三数学文测试题含解析

广西壮族自治区南宁市东盟中学高三数学文测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知抛物线:的焦点为,准线为,是上一点,是直线与的一个交点,若,则=A. B. C. D.参考答案:B2. 已知f(x)在R上是奇函数,且满足f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f (2015)=()A. 2 B.﹣2 C.8 D.﹣8参考答案:考点:函数解析式的求解及常用方法.专题:计算题;函数的性质及应用.分析:由题意知函数的周期为4,故f(2015)=f(﹣1),又由奇函数可求f(﹣1)=﹣f(1)=﹣2.解答:解:∵f(x+4)=f(x),∴f(2015)=f(504×4﹣1)=f(﹣1),又∵f(x)在R上是奇函数,∴f(﹣1)=﹣f(1)=﹣2.故选B.点评:本题考查了函数的奇偶性与周期性的应用,属于基础题.3. 设、、是三个不同的平面,a、b是两条不同的直线,给出下列4个命题:①若a∥,b∥,则a∥b;②若a∥,b∥,a∥b,则∥;③若a⊥,b⊥,a⊥b,则⊥;④若a、b在平面内的射影互相垂直,则a⊥b. 其中正确命题是A. ④B. ③C. ①③D. ②④参考答案:B略4. 已知全集U={1,2,3,4,5,6},集合M={1,3,5},则=(A){2,4,6} (B){l,3,5}(C) {1,2,3,4,5,6} (D)参考答案:A略5. 给定函数①,②,③,④,其中在区间上单调递减的函数序号是A.①②B.②③C.③④D.①④参考答案:B略6. △ABC中,若,,则=( )A.B.C.D.参考答案:B略7. 给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是()A.①和② B.②和③ C.③和④ D.②和④参考答案:D8. 已知向量是与单位向量夹角为的任意向量,则对任意的正实数,的最小值是()A.0 B. C. D.1参考答案:C略9. 极坐标方程分别是ρ=cosθ和ρ=sinθ的两个圆的圆心距是()A.2B.C.1 D.参考答案:D10. 如果角的终边经过点,则( )A. B. C. D.参考答案:D略二、填空题:本大题共7小题,每小题4分,共28分11. 已知平面向量=(1,﹣3),=(4,﹣2),λ+与垂直,则λ= .参考答案:﹣1考点:数量积判断两个平面向量的垂直关系.专题:计算题.分析:先求出互相垂直的2个向量的坐标,再利用这2个向量的数量积等于0,求出待定系数λ的值.解答:解:,()?(λ+4)×1+(﹣3λ﹣2)×(﹣3)=0?λ=﹣1,故答案为﹣1.点评:本题考查2个向量坐标形式的运算法则,及2个向量垂直的条件是他们的数量积等于0.12. 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD的中点.若=2,=1,且BAD=60o,则。
广西南宁市东盟中学2020届高三一轮复习天天练3-7集合和函数概念(无答案)

天天练习(3)集合{}{}{}()1.U 1,2,3,4,1,2,3,2,3,4,=U M N M N ===I 设集合则C ( )A .{}12,B .{}23,C .{}2,4D .{}1,4M {01234}N {135}P M P ,N ===I 2.已知集合,,,,,,,,则的子集共有( )A .2个B .4个C .6个D .8个3.已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;则B 中所含元素的个数为( )A .3B .6C .8D .104.已知集合{1,3,}A m =,{1,}B m =,A B A =U ,则m =( )A .03或B .03或C .13或D .13或 5.已知集合{}022>-=x x x A ,{}55B <<-=x x ,则( )A .AB =ΦI B .A B =R UC .A B ⊆D .B A ⊆()()()U U I I U U U A B m A B n A B A B 6.已知全集=中有个元素,中有个元素.若非空,则的 元素个数为 痧 A .mn B .+m n C .-n m D .-m n{}{}27.230,22=A x x x B x x A B =--≥=-≤<I 已知集合,则( )A .[]2,1--B .[1,2-)C .[]1,1-D .[1,2){}{}U Z A 1,3,5,7,9B 1,2,3,4,5_______===8.设,,,则图中阴影部分表示的集合是{}{}25,113m ___.A x xB x m x m A B A =-<<=+<<-=I 9.设,若,则实数的取值范围是()()A {0,11,1(-12)}B {(x y)|x+y-10x y Z}A B ____.∈I 10.已知集合=,,,,=,=,,,则=天天练习(4)函数及其表示第8题1.函数y = )A .[1,)+∞B .23(,)+∞ C .23[,1] D .23(,1]2.若函数y =f (x )的定义域是[0,2],则函数g (x )=f (2x )ln x的定义域是( )A .[0,1]B .[0,1)C .[0,1)∪(1,4]D .(0,1)3.下列函数中,与函数()f x = ).A .1sin y x =B .ln x y x =C .x y xe =D .sin xy x=4.已知函数224,0()4,0x x x f x x x x ⎧+≥=⎨-<⎩若2(2)(),f a f a ->则实数a 的取值范围是 A(,1)(2,)-∞-⋃+∞ B (1,2)- C (2,1)- D (,2)(1,)-∞-⋃+∞5.已知函数f (x )=⎩⎨⎧≤>.0,2,0,12x x x og x若f (a )=21,则a 等于______ A .-1或2 B .2 C .-1 D .1或-26.设2,0.()log ,0.x e x g x x x ⎧≤=⎨>⎩则1(())2g g =__________7.若函数1,0()1(),03x x x f x x ⎧<⎪⎪=⎨⎪≥⎪⎩ 则不等式1|()|3f x ≥的解集为____________.8.()1()2()0,()=____________f x f x x f x x+=≠已知则天天练习(5)函数的单调性1.函数()=-2f x x x 的单调减区间是( ) A .[1,2] B .[-1,0] C .[0,2]D .[)2+∞,2.函数()212()=log 23f x x x -+1的递减区间是( )A .()1+∞,B .3-4⎛⎤∞ ⎥⎝⎦,C .1+2⎛⎫∞ ⎪⎝⎭,D .3+4⎡⎫∞⎪⎢⎣⎭, 3.已知(31)4,1()log ,1a a x a x f x x x -+≤⎧=⎨>⎩是(,)-∞+∞上的减函数,那么a 的取值范围是A.(0,1)B.1(0,)3C.11[,)73D.1[,1)74.已知函数y=f(x)满足:f(x)=f(4-x)(x ∈R),且在[2,+∞)上为增函数,则( ) A.f(4)>f(1)>f(0.5) B.f(1)>f(0.5)>f(4) C.f(4)>f(0.5)>f(1) D.f(0.5)>f(4)>f(1)5.设()f x 是定义在R 上的增函数,且对任意x ,都有()()-+0f x f x =恒成立,如果实数,m n 满足不等式()()22616+80f m m f n n -+-<,那么nm取值范围是 A.(724 ,+∞) B.(-∞,724) C. (0,724) D. B. (-∞,0)∪(724,+∞)6.0____()____y x x ≥函数的最大值为7.()23(211)g x log ax x =+-若函数有最大值, a 则实数_______的值为8.()20()(1,)f x A f a a +∞=-+已知在,上为减函数,则 3 4B f ⎛⎫⎪⎝⎭=的大小关系为_____ 9、定义在R 上的函数()f x 满足:(1)()()()=1f x y f x f y +++(2)当()()01,(3)1 1.x f x f >>-=时,不等式()()22+14f x x f x +->的解集是________天天练习(6)函数的奇偶性1.下列函数中,既是偶函数,又在()0+∞, 单调递增的函数是A .3y x =B .1y x =+C .21y x =-+ D .2xy -=2. 设函数()f x ,()g x 的定义域都为R ,且()f x 是奇函数,()g x 是偶函数,则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数3.若定义在R 上的偶函数f (x )和奇函数()g x 满足()()(),=_____x f x g x e g x +=则A .xxe e -- B .()12x x e e -+ C .()12x xe e -- D .()12x xe e -- 4.()f x R 是上的奇函数,)()2(x f x f -=+,当10≤≤x 时,x x f =)(,则(7.5)f =___A .0.5B .0.5-C .1.5D . 1.5-5.若1()21xf x a =+-是奇函数,则a = .12 6.已知2)(x x f y +=是奇函数,且1)1(=f ,若2)()(+=x f x g ,则=-)1(g 。
广西南宁市东盟中学2020届高考冲刺理科数学限时训练1(无答案)

选择填空限时训练一(限时40分钟)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数i i a z ++=12是实数(i 为虚数单位),则实数的值是 A. 1 B. 2 C. 3 D. 42.已知集合A={y|R x y x ∈-=,32},B={x |()2lg -=x y },则下列结论正确的是A. -3∈AB. 3∉BC. A∈B=BD. A∩B=B3.定义在⎪⎭⎫ ⎝⎛-2323ππ,上的函数的图象大致形状如A. B. C. D.4.已知正三角形ABC 的边长为32,重心为G ,P 是线段AC 上一点,则AP GP ⋅的最小值为A.41-B. -2C.43- D. -1 5.设F 2是双曲线()0,012222>>=-b a by a x 的右焦点,过F 2作其中一条渐近线的垂线,垂足为H ,若O 为原点且|OF 2|=2|OH|,则双曲线C 的离心率为A. 2B. 3C. 4D. 56.我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”,设∈ABC 的三个内角A 、B 、C 所对的变分别为a 、b 、c ,面积为S ,则“三斜公式”为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+-=222222241b c a c a S ,若3,sin 4sin 2π==B C A c ,则用“三斜公式”求得∈ABC 的面积为A.3B.5C.6D.77.某算法的程序框图如图1所示,若a=90 ,b=120,输入 58,92,61,74,89,93,101,120,99,135,则输出的结果为A. 3B. 4C. 5D. 68.学校足球赛决赛计划在周三、周四、周五三天中的某一天进行,如果这一天下雨则推迟至后一天,如果这三天都下雨则推迟至下一周,已知这三天下雨的概率均为,则这周能进行决赛的概率为A. B. C. D.9.如图,在直三棱柱ABC -A 1B 1C 1 中,∈BAC=,AB=AC=2AA 1,则异面直线AC 1与A 1B 所成角的余弦值为A. B. - C.D. - 10.已知函数在上有两个零点,则的取值范围为 A.⎪⎭⎫ ⎝⎛617611, B.⎪⎭⎫⎢⎣⎡617611, C.⎪⎭⎫ ⎝⎛3835, D. ⎪⎭⎫⎢⎣⎡3835, 11.函数()x f y =的定义域为R,()00≠f ,当0>x 时,()1>x f ;对任意的()()()b f a f b a f R b a =+∈,,.下列结论:∈()10=f ;∈对任意R x ∈,有()0>x f ;∈()x f 是R 上的减函数.正确的有A. 0个B. 1个C. 2个D. 3个12.设直线l 过椭圆C :13422=+y x 的左焦点F 1与椭圆交于A 、B 两点,F 2是椭圆的右焦点,则∈ABF 2的内切圆的面积的最大值为A.πB.169πC. 43πD. 49π二、填空题:本题共4小题,每小题5分.13.曲线21xy e =-在点(0,0)处的切线方程为______________; 14.已知实数x,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥+≤-02200y x y x y x ,则y x z -=2 的取值范围是______;15.已知sin cos sin cos 0αααα+-=,则sin 2α=________;16.正三棱锥的四个顶点都在同一球面上,若该棱锥的底面边长为32,侧棱与侧棱所成角的余弦值为41,则该球的表面积为___________;。
广西壮族自治区南宁市东盟中学2020-2021学年高三数学理模拟试卷含解析

广西壮族自治区南宁市东盟中学2020-2021学年高三数学理模拟试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 若,则|z|=()A.B.1 C.5 D.25参考答案:B【考点】A5:复数代数形式的乘除运算.【分析】利用复数的运算法则、共轭复数的定义、模的计算公式即可得出.【解答】解: ==,则|z|==1.故选:B.【点评】本题考查了复数的运算法则、共轭复数的定义、模的计算公式,考查了推理能力与计算能力,属于基础题.2. 储油30 m3的油桶,每分钟流出m3的油,则桶内剩余油量Q(m3)以流出时间t(分)为自变量的函数的定义域为()A.[0,+∞)B.[0,]C.(-∞,40] D.[0,40]参考答案:D3. 若用相关指数来刻画回归效果,回归模型3的相关指数,回归模型4的相关指数,则模型3的拟合效果更好。
参考答案:B 略4. 各项均为正数的等比数列的前n项和为S n,若S n=2,S30=14,则S40等于(A)80(B)30 (C)26 (D)16参考答案:答案:B解析:由等比数列的性质可知选B5. 集合,则()A. B. C. D.参考答案:无略6. 当前,某城市正分批修建经济适用房以解决低收入家庭住房紧张问题.已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户,若第一批经济适用房中有90套住房用于解决这三个社区中90户低收入家庭的住房问题,先采用分层抽样的方法决定各社区户数,则应从乙社区中抽取低收入家庭的户数为(A)40 (B)36 (C)30 (D)20参考答案:C略7. 已知集合A={x|x2>1},B={x|log2x>0},则A∩B=( )A.{x|x<﹣1} B.{x|>0} C.{x|x>1} D.{x|x<﹣1或x>1}参考答案:C考点:交集及其运算.专题:不等式的解法及应用.分析:化简A、B两个集合,利用两个集合的交集的定义求出A∩B.解答:解:集合A={x|x2>1}={x|x>1或x<﹣1},B={x|log2x>0=log21}={x|x>1},A∩B={x|x>1},故选:C.点评:本题考查集合的表示方法,两个集合的交集的定义和求法,化简A、B两个集合是解题的关键.8. 已知函数恰有两个零点,则实数的取值范围是()A.(-1,0) B.(-1,+∞) C.(-2,0) D.(-2,-1)参考答案:A9. 已知抛物线上一点M(1,m)到其焦点的距离为5,则该抛物线的准线方程为()A.x=8 B.x=-8 C.x=4 D.x=-4参考答案:A略10. 已知{a n}是正项等比数列,且a1a8=4a5,a4与2a6的等差中项为18,则a5=()A. 2B. 4C. 8D. 16参考答案:C【分析】根据条件列关于首项与公比的方程组,解得首项与公比,再根据等比数列通项公式得结果.【详解】设正项等比数列{a n}的公比为q>0,∵a1a8=4a5,a4与2a6的等差中项为18,∴a12q7=4a1q4,a4+2a6=36即a1(q3+2q5)=36,解得a1=,q=2,则a5= a1q4=8.故选:C.【点睛】本题考查等比数列基本量,考查基本分析求解能力,属基础题.二、填空题:本大题共7小题,每小题4分,共28分11. 复数的实部是。
广西南宁市东盟中学2020届高三一轮复习天天练32-35数列(无答案)

天天练习(32)数列的通项公式1、数列{}n a 满足()()2132321++=++++n n n na a a a n Λ,则=n a2、数列{}n a 的前n 项和为22n S n n =-,=n a 。
3、数列{}n a 的前n 项和为322+-=n n S n ,=n a 。
4、设数列{}n a 的前n 项和为n S ,已知22n n n S a =-, 则n a =________..5、若数列{}n a 的前n 项和为3132n +=n a S ,则n a =____________. 6、已知数列{}n a 满足1a =1,131n n a a +=+.则n a =________. 7、数列{}n a 满足()*1132,1N n a a a n n ∈+==+.则na =________. 8、数列{}n a 中,()12,011-+==+n a a a n n ,则n a =________.9、设数列{}n a 满足21112,32n n n a a a -+=-=⋅ ,则n a =________.10、数列{}n a 中,112,22n n n a a a +==+,则n a =________.11、已知数列{}n a 满足115a =且当112,,14n n n a n n N a a *--≥∈=+,则n a =________. 12已知数列{}n a 满足121,2a a ==,212133n n n a a a ++=+,求n a 。
天天练习(33)等差数列1 .下面是关于公差0d >的等差数列()n a 的四个命题:{}1:n p a 数列是递增数列;{}2:n p na 数列是递增数列; 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列; {}4:3n p a nd +数列是递增数列; 其中的真命题为 (A)12,p p (B)34,p p (C)23,p p (D)14,p p2、已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =A .138B .135C .95D .233、如果等差数列{}n a 中,34512a a a ++=,那么127...a a a +++=(A )14 B )21 (C )28 (D )354、设n S 为等差数列{}n a 的前n 项和,若11a =,公差2d =,224k k S S +-=,则k =A .8B .7C .6D .55、设等差数列{}n a 的前n 项和为n S ,若21-=-m S ,0=m S ,31=+m S ,则=m(A )3 (B )4 (C )5 (D )66、设n S 是等差数列{}n a 的前项和,且141,7a a ==,则5S =________7、n S 为等差数列{a n }的前n 项和,S 2=S 6,a 4=1,则a 5=____________.—18、设等差数列{}n a 的前n 项和为n S ,若972S =,则249a a a ++= 。
广西南宁市东盟中学2020届高考冲刺理科数学限时训练7(无答案)

选择填空限时训练七(限时40分钟)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.2020-2021学年衡水中学学业考复习已知集合{1,0,1}A =-,{0,1,2}B =,则A B =U A .{0,1} B .{0,1,2} C .{1,0,1,2}- D .{1,0,0,1,1,2}-2.复数z 满足1iz i=+,则在复平面内复数z 对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限 3.下列四个结论:①在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;②某学校有男教师60名、女教师40名,为了解教师的体育爱好情况,在全体教师中抽取20名调查,则宜采用的抽样方法是分层抽样; ③线性相关系数r 越大,两个变量的线性相关性越弱;反之,线性相关性越强;④在回归方程$0.52y x =+中,当解释变量x 每增加一个单位时,预报变量$y 增加0.5个单位. 其中正确的结论是A .①②B .①④C .②③D .②④4.已知{}n a 是正项等比数列,若1a 是2a ,3a 的等差中项,则公比q =A .-2B .1C .0D .1,-25.已知a r ,b r 均为单位向量,若2a b -=r ra r 与b r 的夹角为A .6π B .3πC .23πD .56π6.下列说法正确的是A .若两个平面和第三个平面都垂直,则这两个平面平行B .若两条直线和一个平面所成的角相等,则这两条直线平行C .若一个平面内的所有直线都和另一个平面平行,则这两个平面平行D .若两条平行直线中的一条和一个平面平行,则另一条也和这个平面平行7.小明早上步行从家到学校要经过有红绿灯的两个路口,根据经验,在第一个路口遇到红灯的概率为0.4,在第二个路口遇到红灯的概率为0.5,在两个路口连续遇到红灯的概率是0.2.某天早上小明在第一个路口遇到了红灯,则他在第二个路口也遇到红灯的概率是 A .0.2 B .0.3 C .0.4 D .0.5 8.已知抛物线C :22(0)y px p =>,O 是坐标原点,点P 是抛物线C 在第一象限内的一点,若点P 到y 轴的距离等于点P 到抛物线C 的焦点的距离的一半,则直线OP 的斜率为A .12 B .13C .2D .3 9.设()f x 是(,0)(0,)-∞+∞U 上的偶函数,当0x >时,()ln f x x x =,则()f x 在(1,(1))f --处的切线方程为( )A .10x y --=B .10x y +-=C .10x y -+=D .10x y ++=10.已知函数,0()ln ,0x e a x f x x x ⎧+≤⎪=⎨>⎪⎩,()()g x f x x =+,若()g x 有且仅有一个零点,则a 的取值范围是( )A .(,1)-∞-B .[1,)-+∞C .(,0)-∞D .[0,)+∞11.2020-2021学年衡水中学学业考复习直线l 与双曲线2212y x -=交于A ,B 两点,以AB 为直径的圆C 的方程为22240x y x y m ++++=,则m =( ) A .-3 B .3 C.5- D.12.在三棱锥A BCD -中,60BAC BDC ∠=∠=︒,二面角A BC D --的余弦值为13-,当三棱锥A BCD -) A .5二、填空题(本大题共4小题,每小题5分,共20分)13.若x ,y 满足约束条件2002x y x y x +-≥⎧⎪-≥⎨⎪≤⎩,则2z x y =+的最小值为_____.14.记n S 为数列{}n a 的前n 项和,2(1)n n S a =+,则4a =_____. 15.用数字0,1,2,3,4,5组成无重复数字且为5的倍数的四位数,把所组成的全部四位数从小到大排列起来,则3125是第_____个数.16.下列关于函数()2sin cos f x x x =+的描述中,正确的是______.(填写正确命题的序号) ①π是()f x 的一个周期; ②()f x 是偶函数; ③1()f x ≤≤;④()y f x =,[0,]x π∈与2y =有且只有2个公共点.。
广西南宁市东盟中学2020届高考冲刺之解三角形能力检测(无答案)

南宁市东盟中学 校本教材 能力检测解三角形能力检测(一)姓名:___________ 班级:___________ 成绩:___________一、选择题(单选题,每小题5分,共60分)1.在ABC ∆中,060,2A AB ∠==,且ABC ∆的面积为2,则BC 的长为( ) AB .3 CD .72.在锐角ABC ∆中,3,4AB AC ==,其面积ABC S ∆=BC =( ) A .5 B.CD3.ABC ∆的内角,,A B C 的对边分别为,,a b c,,,64ABC B C S ππ∆===,则c =( ) AC .2 D4.已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,且sin sin sin c b Ac a C B-=-+,则B =( ) A .6π B .4π C .3πD .34π5.在ABC ∆中,内角,,A B C 的对边分别是,,a b c ,若2c a =,1sin sin sin 2b B a A a C -=,则sin B 为( ) A.34 CD .136.ABC ∆中,若2lg sin lg lg lg -==-B c a 且)2,0(π∈B ,则ABC ∆的形状是( )A. 等边三角形B. 等腰三角形C. 等腰直角三角形D. 直角三角形 7.在ABC ∆中,若3sin 4cos 6A B +=,4sin 3cos 1B A +=,则角C 为( )A .30oB .30o或150oC .150oD .60o8.已知,,a b c 分别为ABC ∆内角,,A B C 的对边,2sin 2sin sin B A C =,且1,cos 4a c B >=,则ac=( ) A .2 B .12 C .3 D .139.在中,内角的对边分别为.若,)10.在ABC △中,2a =,1c =,则角C 的取值范围是( )A .0 2π⎛⎫ ⎪⎝⎭,B . 63ππ⎛⎫ ⎪⎝⎭,C . 62ππ⎛⎫ ⎪⎝⎭, D .(0 ]6π,ABC ∆,,A B C ,,a b c 2220b c bc a ++-=11.在ABC ∆中,角A B C 、、所对边的长为a b c 、、,设AD 为BC 边上的高,且AD a =,则b c c b+的最大值是( )A .2 BCD .412.△ABC 中,三边长a ,b ,c 满足a 3+b 3=c 3,那么△ABC 的形状为( )A .锐角三角形B .钝角三角形C .直角三角形D .以上均有可能二、填空题(每小题5分,共40分)13.在ABC ∆中,内角C B A ,,的对边分别是c b a ,,,若C a A a B b sin 23sin sin =-,且ABC ∆的面积为B a sin 2,则=B cos ______.14.在ABC ∆中,角A ,B ,C 所对边长分别为a ,b ,c ,若2222a b c +=,则cos C 的最小值为_________. 15.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知cos cos 2b C c B b +=,则ab= . 16.在ABC ∆中,4,5,6a b c ===,则sin 2sin AC= . 17.已知△ABC 的面积为S ,三内角A ,B ,C 的对边分别为a ,b ,c .若2224S a b c +=+,则sin cos()4C B π-+取最大值时C = .18.已知ABC △的三个内角A ,B ,C 的对边分别为a ,b ,c ,若2a =,3A π=,()sin sin 2B C B --=,则ABC △面积为 .19.在ABC △中,角A B C ,,所对的边分别为a b c ,,,且()362cos cos 0A C c a c B b C ==--=,,,则ABC △的面积是_____________. 20.已知ABC ∆,若存在111A B C ∆,满足111cos cos cos 1sin sin sin A B CA B C ===,则称111A B C ∆是ABC ∆的一个“友好”三角形. 在满足下述条件的三角形中,存在“友好”三角形的是____:(请写出符合要求的条件的序号)①90,60,30A B C =︒=︒=︒ ;②75,60,45A B C =︒=︒=︒; ③75,75,30A B C =︒=︒=︒ ;④70,65,45A B C =︒=︒=︒。
广西南宁市东盟中学2020届高三一轮复习天天练60-61参数方程与极坐标(无答案)

1.在极坐标系中,圆=2cos ρθ的垂直于极轴的两条切线方程分别为 ( )A.=0()cos=2∈R θρρ和B.ρρπθ=(∈R)和cos =22C. πθ=(ρ∈R)和ρcos =12D.θ=0(ρ∈R)和ρcos =1 2.如图, 以过原点的直线的倾斜角θ为参数, 则圆220y x x +-=的参数方程为 . 为参数)(θθθθ,sin cos cos 2⎩⎨⎧⋅==y x 3.设曲线C 的参数方程为2x=ty=t ⎧⎨⎩(t 为参数),若以直角坐标系的原点为极点,x 轴的正半轴为极轴建立极坐标系,则曲线C 的极坐标方程为_______.2cos sin 0ρθ-θ= 4.在极坐标系中,曲线cos 1ρθ=+与cos 1ρθ=的公共点到极点的距离为________152+ 5.已知圆的极坐标方程为ρ=4cos θ,圆心为C,点P 的极坐标为4,3π⎛⎫ ⎪⎝⎭,则CP= . 23 6.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.若极坐标方程为cos 4ρθ=的直线与曲线23x t y t ⎧=⎨=⎩(t 为参数)相交于A 、B 两点,则AB = 16 7.在直角坐标系xOy 中,椭圆C 的参数方程为(φ为参数,a>b>0),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线l 与圆O 的极坐标方程分别为2sin 42m πρθ⎛⎫+= ⎪⎝⎭ (m 为非零数)与ρ=b.若直线l 经过椭圆C 的焦点,且与圆O 相切,则椭圆C 的离心率为 .10.已知抛物线的参数方程为22,2.x pt y pt ⎧=⎨=⎩(t 为参数),其中p>0,焦点为F,准线为l ,过抛物线上一点M 作l 的垂线,垂足为E ,若|EF|=|MF|,点M 的横坐标为3,则p =________.1、已知曲线1C 的参数方程是)(3sin y 2cos x 为参数ϕϕϕ⎩⎨⎧==,以坐标原点为极点,x 轴的正半轴为极轴建立坐标系,曲线2C 的极坐标系方程是2=ρ,正方形ABCD 的顶点都在2C 上, 且,,,A B C D 依逆时针次序排列,点A 的极坐标为(2,)3π。
广西南宁市东盟中学2020届高三一轮复习天天练56-57计数原理、排列组合、二项式(无答案)

天天练习(56)两个计数原理1.(2011新)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为A .13 B .12 C .23 D .342.(2012新)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )()A 12种 ()B 10种 ()C 9种 ()D 8种 3.(2013一)为了解某地区中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是(A )简单的随机抽样 (B )按性别分层抽样(C )按学段分层抽样 (D )系统抽样4.(2013二)从n 个正整数1,2,3,4,5,…,n 中任意取出两个不同的数,若其和为5的概率是141,则n = 。
5. (2014一)4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .786. (2014二)某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )A. 0.8B. 0.75C. 0.6D. 0.457.(2015长春二模)已知随机变量ξ服从正态分布()21N σ,,若()()20.15,01=p p ξξ>=≤≤则A. 0.85B. 0.70C. 0.35D. 0.158.(2015梧州二模)把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”,则()P B A =A .37B .38C .58D .789.从1,3,5,7,9这5个奇数中选取3个数字,从2,4,6,8这4个偶数中选取2个,再将5个数值组成没有重复数字的五位数,且奇数数字与偶数数字相间排列,这样的五位数的个数是A. 180B. 360C.480D. 720天天练习(57)二项式定理1. (1+2x )5的展开式中,x 2的系数等于( )(A )80 (B )40 (C )20 (D )102. 6(42)x x --(x ∈R )展开式中的常数项是( )(A )20- (B )15- (C )15 (D )20 3.在6的二项展开式中,2x 的系数为 ( ) (A )154- (B )154 (C )38- (D )38 4. 5221(2)1x x ⎛⎫+- ⎪⎝⎭的展开式的常数项是( ) ()A 3- ()B 2- ()C 2 ()D 35.5()a x x +(x R ∈)展开式中3x 的系数为10,则实数a 等于( )(A )-1 (B )12 (C)1 (D)2 6. 512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2,则该展开式中常数项为( ) (A )-40 (B )-20 (C )20 (D )407.设a ∈Z ,且0≤a ﹤13,若512012+a 能被13整除,则a=( )(A)0 (B)1 (C)11 (D)128.261(1)()x x x x ++-的展开式中的常数项为______-5_. 9.6⎛⎫展开式中,3x 的系数等于_______15_. 10.设2121221021)1x a x a x a a x ++++=-Λ(,则1110a a += .011. 72()x x x -的展开式中,4x 的系数是____84__ (用数字作答). 12.若62x x ⎛⎫- ⎪ ⎪⎝⎭的展开式的常数项为60,则常数a 的值为 .4 13.设二项式6(x -(0)a >的展开式中3x 的系数为A ,常数项为B ,若4B A =,则a 的值是 .2。
2020版广西高考人教版数学(文)一轮复习考点规范练:48 直线与圆锥曲线 Word版含解析

(2)除 H 以外,直线 MH 与 C 是否有其他公共点?说明理由.
( )������2
解(1)由已知得 M(0,t),P 2������,������ .
又 N 为 M 关于点 P 的对称点,
( ) ( ) ������2
������
2������2
2������2
故 N ������ ,������ ,ON 的方程为 y=������x,代入 y2=2px 整理得 px2-2t2x=0,解得 x1=0,x2= ������ .因此 H ������ ,2������ .
1
联立,消去 y 得 3x2-10x+3=0,解得 x1=3,x2=3.
因为 M 在 x 轴的上方,所以 M(3,2 3).
因为 MN⊥l,且 N 在 l 上,所以 N(-1,2 3).
因为 F(1,0),所以直线 NF:y=- 3(x-1).
|
所以 M 到直线 NF 的距离为
3 × (3 - 1) + 2 3|
所以除 H 以外直线 MH 与 C 没有其他公共点.
������2 ������2
25
10.(2018 福建厦门第一次质检)设 O 为坐标原点,椭圆 C:������2 + ������2=1(a>b>0)的左焦点为 F,离心率为 5 .
直线 l:y=kx+m(m>0)与 C 交于 A,B 两点,AF 的中点为 M,|OM|+|MF|=5.
∵P(0,1),������������·������������=-4, ∴(x1,y1-1)·(x2,y2-1)=x1x2+y1y2-(y1+y2)+1=-4,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天天练习(48)直线的方程、两直线位置关系1.已知直线l 的倾斜角α满足条件1sin cos 5αα+=则l 的斜率为( ) 4343A. B. C D 3434.-.- 2.已知点A(1,-2),B(m,2),且线段AB 的垂直平分线的方程是x+2y-2=0,则实数m 的值是( )A.-2B.-7C.3D.13.经过点P(1,4)的直线在两坐标轴上的截距都是正值,且截距之和最小,则直线的方程为( ) A .x +2y -6=0 B .2x +y -6=0 C .x -2y +7=0 D .x -2y -7=04.直线Ax +By -1=0在y 轴上的截距是-1,而且它的倾斜角是直线3x y 33-= 的倾斜角的2倍,则( ) A . A=3 B =1 B . A=3 B =-1 C . A=3- B =-1 D .A=3- B =15.在等腰直角三角形ABC 中,=4AB AC =,点P 是边AB 上异于,A B 的一点,光线从点P 出发,经,BC CA 发射后又回到原点P (如图1).若光线QR 经过ABC ∆的重心,则AP 等于( ) A .2 B .1 C .83 D .436.已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( ) A.(0,1) B.211,22⎛⎫-⎪ ⎪⎝⎭ C. 211,23⎛⎤- ⎥ ⎦⎝D. 11,32⎡⎫⎪⎢⎣⎭ 7.已知两点A(3,2)和B(-1,4)到直线mx +y +3=0的距离相等,则m 的值为( ) A. 0或12-B. 12或-6C. 12-或12D. 0或128.若动点A,B 分别在直线l 1:x+y-7=0和l 2:x+y-5=0上移动,则AB 的中点M 到原点的距离的最小值为( ) A. 33B. 332C. 32D. 429.直线x-2y+1=0关于x=3对称的直线方程为 .10.若直线3x+4y-3=0与直线6x+my+14=0平行,则它们之间的距离为 .11.在平面直角坐标系内,到点A(1,2),B(1,5),C(3,6),D(7,-1)的距离之和最小的点的坐标是 .天天练习(49)圆的方程1.已知圆22:40C xy x +-=,l 是过点()3,0P 的直线,则( )(A) l 与C 相交 (B) l 与C 相切 (C) l 与C 相离 (D) 以上三个选项均有可能 2.过圆x 2+y 2=1上一点作圆的切线与x 轴、y 轴的正半轴交于A ,B 两点,则|AB|的最小值为( )C.2D.33.设m,n R ∈,若直线()()m 1120x n y +++-=与圆()()22111x y -+-=相切,则m n +的取值范围是( )(A)1⎡⎣ (B) (),11⎡-∞+∞⎣U(C) 2⎡-+⎣(D) (),22⎡-∞-++∞⎣U4.已知圆1C :22(2)(3)1x y -+-=,圆2C :22(3)(4)9x y -+-=,M 、N分别是圆1C 、2C 上的动点,P 为x 轴上的动点,则PM PN+的最小值为 ( )A.425- B.117- C.226- D.175.圆心在直线y=-4x 上,并且与直线l :x+y-1=0相切于点P(3,-2)的圆的方程为___________.6.过点A(4,1)的圆C 与直线10x y --=相切于点B(2,1).则圆C 的方程为 .7.已知圆心在x O 位于y 轴左侧,且与直线x+y=0相切,则圆O 的方程是8.在平面直角坐标系xOy 中,已知圆422=+y x 上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c 的取值范围是___________9.已知圆C 过点(1,0),且圆心在x 轴的正半轴上,直线l :1y x =-被圆C 所截得的弦长为则过圆心且与直线l 垂直的直线的方程为 . 10.在平面直角坐标系xoy 中,圆C 的方程为228150xy x +-+=,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是 .天天练习(50)曲线与方程1.已知定点F 1(-2,0),F 2(2,0),N 是圆O:x 2+y 2=1上任意一点,点F 1关于点N 的对称点为M,线段F1M 的中垂线与直线F 2M 相交于点P,则点P 的轨迹是 ( ) A.椭圆 B.双曲线 C.抛物线 D.圆2.动点P(x ,y)|3x +4y-11|,则点P 的轨迹是( ) A.椭圆 B.双曲线 C.抛物线 D.直线3.在△ABC 中,A 为动点,B,C 为定点,,0,,022a a B C ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭(a>0),且满足条件sin C-sin B =sin A ,则动点A 的轨迹方程是____.4.如果三个数 且a ≠1)成等差数列,那么点P(x ,y)在平面直角坐标系内的轨迹是( )A.一段圆弧B.椭圆的一部分C.双曲线的一部分D.抛物线的一部分5.设圆锥曲线Γ的两个焦点分别为F 1,F 2,若曲线Γ上存在点P 满足1122::PF F F PF =4:3:2,则曲线Γ的离心率等于( )(A )1322或 (B )23或2 (C )12或2 (D )2332或 6. x y1a 2a-+=与x,y 轴交点的连线的中点的轨迹方程是____. 7.平面直角坐标系中,已知两点A(3,1),B(-1,3),若点C 满足12OC OA OB λλu u u r u u u r u u u r=+ (O 为原点),其中λ1,λ2∈R ,且λ1+λ2=1,则点C 的轨迹方程为______.8.曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >的点的轨迹.给出下列三个结论:①曲线C 过坐标原点; ②曲线C 关于坐标原点对称; ③若点P 在曲线C 上,则12F PF ∆的面积不大于212a . 其中所有正确的结论的序号是 .天天练习(51)椭圆1.椭圆2214x y +=的左、右焦点分别为F 1,F 2,过F 1作垂直于x 轴的直线与椭圆相交,一个交点为P ,则|PF 2|=( ) 73A. B. C. 3 D.422 2.已知椭圆22122:1x y C a b +=(a >b >0)与双曲线222:14y C x -=有公共的焦点,2C 的一条渐近线与以1C 的长轴为直径的圆相交于,A B 两点,若1C 恰好将线段AB 三等分,则( )(A )2132a = (B )2a =13 (C )212b = (D )2b =23.椭圆22221x y a b+=(a >b >0)的两顶点为A(a,0),B(0,b),且左焦点为F ,△FAB 是以B 为直角顶点的直角三角形,则椭圆的离心率e 为( )31511531A. B. C. D.--++ 4.椭圆22221x y a b+=(a >b >0)的左、右顶点分别是A ,B ,左、右焦点分别是F 1,F 2.若|AF 1|,|F 1F 2|,|F 1B|成等比数列,则此椭圆的离心率为( ) (A)14 (B) 5 (C )12(D) 5-25.(2014·梅州模拟)以F 1(-1,0),F 2(1,0)为焦点且与直线x-y+3=0有公共点的椭圆中,离心率最大的椭圆方程是( )22222222x y x y x y y x A. 1 B.1 C. 1 D.12019985498+=+=+=+= 6.如图,中心均为原点O 的双曲线与椭圆有公共焦点,M ,N 是双曲线的两顶点.若M ,O ,N 将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是( ) (A)3 (B)2 (C)3 (D) 27.设12,F F 分别为椭圆2213x y +=的左、右焦点,点,A B 在椭圆上,若125F A F B =u u u r u u u u r ,则点A 的坐标是 .8.以椭圆的两个焦点为直径的端点的圆与椭圆有四个不同的交点,顺次连接这四个点和两个焦点,恰好得到一个正六边形,那么这个椭圆的离心率等于_______.9.已知椭圆C :22+12x y =的两焦点为F 1,F 2,点P(x0,y0)满足22000+12x y <<, 则|PF 1|+|PF 2|的取值范围为_____________,直线00+12x xy y =与椭圆C 的公共点个数为_________.10.若椭圆22221x y a b +=的焦点在x 轴上,过点112⎛⎫⎪⎝⎭,作圆22+1x y =的切线,切点分别为A ,B ,直线AB 恰好经过椭圆的右焦点和上顶点,则椭圆方程是_______.天天练习(52)双曲线1.双曲线2228xy -=的实轴长是( )(A)2 (B)22(C)4 (D)422.设双曲线19222=-y ax (a>0)的渐近线方程为320x y ±=,则a 的值为( ) (A )4 (B )3 (C )2 (D )13.已知双曲线22221x y a b-=(a>0,b>0)的两条渐近线均和圆C :x 2+y 2-6x+5=0相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为( )(A )22154x y -= (B )22145x y -= (C )221x y 36-= (D )221x y 63-= 4.设直线l 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,l 与C 交于A ,B 两点,AB 为C 的实轴长的2倍,则C 的离心率为( ) (A )2 (B )3 (C )2 (D )35.如图,F 1,F 2分别是双曲线C :22221x y a b-=(a,b >0)的左、右焦点,B 是虚轴的端点,直线F 1B 与C 的两条渐近线分别交于P,Q 两点,线段PQ 的垂直平分线与x 轴交于点M ,若|MF 2|=|F 1F 2|,则C 的离心率 是( )(A)233 (B) 62(C) 2 (D) 3 6.已知双曲线C :22x a -22y b=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C 的方程为( )(A)220x -25y =1 (B)25x -220y =1 (C)280x -220y =1 (D)220x -280y =17.已知双曲线22214x y b-=的右焦点与抛物线212y x =的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )(A)5 (B) 42 (C)3 (D)58.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A ,B 两点,43AB =,则C 的实轴长为( ) (A)2 (B) 22 (C)4 (D)89.已知双曲线22221(0b 0)x y a a b -=>,>和椭圆22x y =1169+有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .10.已知点(2,3)在双曲线C :22221(0b 0)x y a a b-=>,>上,C 的焦距为4,则它的离心率为_________.天天练习(53)抛物线1.设抛物线的顶点在原点,准线方程为2x =-,则抛物线的方程是( ) (A )28y x =- (B )28y x = (C )24y x =- (D )24y x =2.已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A,B 两点,AB =12,P 为C 的准线上一点,则∆ABP 的面积为( )(A )18 (B )24 (C )36 (D )48 3.已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,=3AF BF +,则线段AB 的中点到y 轴的距离为( ) (A)34 (B)1 (C)54 (D)744.过抛物线24y x =的焦点F 的直线交该抛物线于A 、B 两点, O 为坐标原点,若3AF =,则△AOB的面积为( )(A )2(B (C )2(D )5.设M (0x ,0y )为抛物线C :28x y =上一点,F 为抛物线C 的焦点,以F 为圆心、FM为半径的圆和抛物线C 的准线相交,则0y 的取值范围是( )(A)(0,2) (B)[0,2] (C)(2,+∞) (D)[2,+∞)6.已知双曲线22221(0,0)x y a b a b-=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )(A )(B (C )(D )7.已知双曲线C 1:22221x y a b-=(a,b >0)的离心率为2.若抛物线C 2:()220x py p =>的焦点到双曲线C 1的渐近线的距离为2,则抛物线C 2的方程为( )(A) 2xy =(B) 2xy =(C) 28xy = (D) 216xy =8.过抛物线24y x =的焦点F 的直线交该抛物线于A,B 两点,若3AF=,则BF =______.9.已知抛物线的顶点在原点,对称轴为y 轴,抛物线上一点Q(-3,m)到焦点的距离是5,则抛物线的方程为________.10.设抛物线y 2=mx 的准线与直线x =1的距离为3,则抛物线的方程为________。
