MATLAB实验报告7
MATLAB实验报告

实验一MATLAB操作基础实验目的和要求:1、熟悉MATLAB的操作环境及基本操作方法。
2、掌握MATLAB的搜索路径及设置方法。
3、熟悉MATLAB帮助信息的查阅方法实验内容:1、建立自己的工作目录,再设置自己的工作目录设置到MA TLAB搜索路径下,再试验用help命令能否查询到自己的工作目录。
2、在MA TLAB的操作环境下验证课本;例1-1至例1-4,总结MATLAB的特点。
例1-1例1-2例1-3例1-43、利用帮助功能查询inv、plot、max、round等函数的功能。
4、完成下列操作:(1)在matlab命令窗口输入以下命令:x=0:pi/10:2*pi;y=sin(x);(2)在工作空间窗口选择变量y,再在工作空间窗口选择回绘图菜单命令或在工具栏中单击绘图命令按钮,绘制变量y的图形,并分析图形的含义。
5、访问mathworks公司的主页,查询有关MATLAB的产品信息。
主要教学环节的组织:教师讲授实验目的、开发环境界面、演示实验过程,然后同学上机练习。
思考题:1、如何启动与退出MA TLAB集成环境?启动:(1)在windows桌面,单击任务栏上的开始按钮,选择‘所有程序’菜单项,然后选择MA TLAB程序组中的MA TLABR2008b程序选项,即可启动MATLAB系统。
(2)在MA TLAB的安装路径中找到MA TLAB系统启动程序matlab.exe,然后运行它。
(3)在桌面上建立快捷方式后。
双击快捷方式图标,启动MA TLAB。
退出:(1)在MA TLAB主窗口file菜单中选择exitMATLAB命令。
(2)在MA TLAB命令窗口中输入exit或quit命令。
(3)单击MATLAB主窗口的关闭按钮。
2、简述MATLAB的主要功能。
MATLAB是一种应用于科学计算领域的数学软件,它主要包括数值计算和符号计算功能、绘图功能、编程语言功能以及应用工具箱的扩展功能。
3、如果一个MATLAB命令包含的字符很多,需要分成多行输入,该如何处理?使用‘;’隔开4、Help命令和lookfor命令有何区别?help是显示matlab内置的帮助信息一般是help 命令;而lookfor 关键词是通过关键词查找,“关键词”就是你要找的词语5、在MA TLAB环境下,建立了一个变量fac,同时又在当前目录下建立了一个m文件fac.m,如果需要运行fac.m文件,该如何处理?实验二MATLAB矩阵及运算实验目的和要求:1、掌握MATLAB数据对象的特点及运算规则2、掌握MATLAB建立矩阵的方法及矩阵处理的方法3、掌握MATLAB分析的方法实验内容:1.求下列表达式的值(1)(2)(3)(4)2.已知A=[-1,5,-4;0,7,8;3,61,7],B=[8,3,-1;2,5,3;-3,2,0] 求下列表达式的值:(1)A+6B和A^2-B+I(其中I为单位矩阵)。
matlab实验报告总结精选

matlab实验报告总结电气工程学院自动化102班 2012年12月21日实验一 MATLAB环境的熟悉与基本运算一、实验目的1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令变量与运算符变量命名规则如下:变量名可以由英语字母、数字和下划线组成变量名应以英文字母开头长度不大于31个区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式的基本运算表7 两种运算指令形式和实质内涵的异同表的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、新建一个文件夹2、启动,将该文件夹添加到MATLAB路径管理器中。
3、保存,关闭对话框4、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye5、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
6、初步程序的编写练习,新建M-file,保存,学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
注意:每一次M-file的修改后,都要存盘。
练习A:help rand,然后随机生成一个2×6的数组,观察command window、command history和workspace等窗口的变化结果。
学习使用clc、clear,了解其功能和作用。
答:clc是清除命令窗体内容 clear是清除工作区间输入C=1:2:20,则C表示什么?其中i=1,2,3,?,10。
基于matlab的实验报告

基于matlab的实验报告实验报告:基于MATLAB 的实验一、实验目的通过使用MATLAB 软件,掌握如何进行数据分析、图像处理、算法实现等一系列实验操作,提高实验者的实践能力和动手能力。
二、实验原理MATLAB 是一种在科学计算和技术开发领域广泛应用的计算机软件。
它能进行矩阵计算、绘制函数和数据图像、实现算法以及进行数据分析等。
通过掌握MATLAB 的使用,能够快速、高效地解决各种科学和工程问题。
三、实验内容1. 数据分析:使用MATLAB 的数据分析工具进行数据的导入、处理和分析。
2. 图像处理:利用MATLAB 的图像处理工具包对图像进行滤波、增强、分割等操作。
3. 算法实现:使用MATLAB 实现常用的算法,如排序、搜索、图像压缩等。
四、实验步骤1. 数据分析:(1)使用MATLAB 的读取数据函数将数据导入MATLAB 环境中。
(2)利用MATLAB 的数据处理函数进行数据清洗和预处理。
(3)使用MATLAB 的统计工具进行数据分析,如求平均值、标准差等。
(4)利用MATLAB 的绘图函数将分析结果可视化。
2. 图像处理:(1)使用MATLAB 的读取图像函数将图像导入MATLAB 环境中。
(2)利用MATLAB 的图像处理工具包进行滤波操作,如均值滤波、中值滤波等。
(3)使用MATLAB 的图像增强函数对图像进行锐化、变换等操作。
(4)利用MATLAB 的图像分割算法对图像进行分割。
3. 算法实现:(1)使用MATLAB 编写排序算法,如冒泡排序、快速排序等。
(2)使用MATLAB 编写搜索算法,如二分查找、线性搜索等。
(3)使用MATLAB 实现图像压缩算法,如离散余弦变换(DCT)。
五、实验结果实验中,我们使用MATLAB 完成了数据分析、图像处理和算法实现的一系列实验操作。
通过数据分析,我们成功导入了数据并对其进行了清洗和预处理,最后得到了数据的统计结果。
在图像处理方面,我们对图像进行了滤波、增强和分割等操作,最终得到了处理后的图像。
matlab仿真实验报告

matlab仿真实验报告Matlab仿真实验报告引言:Matlab是一种广泛应用于科学和工程领域的数值计算软件,它提供了强大的数学和图形处理功能,可用于解决各种实际问题。
本文将通过一个具体的Matlab 仿真实验来展示其在工程领域中的应用。
实验背景:本次实验的目标是通过Matlab仿真分析一个电路的性能。
该电路是一个简单的放大器电路,由一个输入电阻、一个输出电阻和一个放大倍数组成。
我们将通过Matlab对该电路进行仿真,以了解其放大性能。
实验步骤:1. 定义电路参数:首先,我们需要定义电路的各个参数,包括输入电阻、输出电阻和放大倍数。
这些参数将作为Matlab仿真的输入。
2. 构建电路模型:接下来,我们需要在Matlab中构建电路模型。
可以使用电路元件的模型来表示电路的行为,并使用Matlab的电路分析工具进行仿真。
3. 仿真分析:在电路模型构建完成后,我们可以通过Matlab进行仿真分析。
可以通过输入不同的信号波形,观察电路的输出响应,并计算放大倍数。
4. 结果可视化:为了更直观地观察仿真结果,我们可以使用Matlab的图形处理功能将仿真结果可视化。
可以绘制输入信号波形、输出信号波形和放大倍数的变化曲线图。
实验结果:通过仿真分析,我们得到了以下实验结果:1. 输入信号波形与输出信号波形的对比图:通过绘制输入信号波形和输出信号波形的变化曲线,我们可以观察到电路的放大效果。
可以看到输出信号的幅度大于输入信号,说明电路具有放大功能。
2. 放大倍数的计算结果:通过对输出信号和输入信号的幅度进行计算,我们可以得到电路的放大倍数。
通过比较不同输入信号幅度下的输出信号幅度,可以得到放大倍数的变化情况。
讨论与分析:通过对实验结果的讨论和分析,我们可以得出以下结论:1. 电路的放大性能:根据实验结果,我们可以评估电路的放大性能。
通过观察输出信号的幅度和输入信号的幅度之间的比值,可以判断电路的放大效果是否符合设计要求。
MATLAB实验报告

仿真程序:
I. 傅里叶正变换的m函数
II. 傅里叶反变换的m函数
图像:
正变换图像:
反变换图像:
二、能量信号的能量谱密度仿真
【例二】(矩形脉冲的能量谱密度) 宽度为 的矩形脉冲的表达式为
g(t)=
其能量谱密度为
Eg(f)= =
参考仿真程序:
图像:
图像:
三、信号通过线性系统
若线性系统的输入是x(t),输出是y(t),则输出与输入的关系可以用卷积来描述y(t)= (式4),其中h(t)是系统的单位冲激相应。
在离散时间和截短的情况下,式4对应到离散卷积
仿真中更为简便的做法是借助频域关系来实现滤波
Y(y)=H(f)X(f)
【例三】(矩形脉冲通过巴特沃斯低通滤波器) 将一个宽为 =1ms的矩形脉冲通过一个3dB带宽为500Hz的6阶巴特沃思滤波器。矩形脉冲的主瓣带宽为1khz。仿真中设置的时间分辨率为1/32ms,频谱分辨率为1/64khz,抽样率为fs=32khz,总观察时间为T=64ms。参考仿真程序:图像:心得体会:
通过此次仿真实验实验中,我学会了如何使用MATLAB建立脚本文件实现函数之间的调用
也学到了通信原理中周期函数的频谱使用MATLAB仿真实现,收获了傅里叶正变换与傅里叶反变换图像十分清晰可见,有助于我对傅里叶变换更加深入地学习。有信号能量密度的仿真图像可知傅里叶反变换与傅里叶正变换是不同的。信号通过线性系统是傅里叶正变换为不规则的频谱,傅里叶反变换时为规则的矩形谱。不管怎么样自己动手做出来的收获就是不一样。
一、周期信号的频谱仿真
虽然Matlab中有许多现成的频域分析工具,如fft、ifft等,但对通信原理的学习者来说,直接进行傅里叶变换更为直观。为此,我们用Matlab提供的函数为基础,编制了两个m函数t2f.m及f2t.m。t2f是傅里叶正变换,对应
matlab实验报告

matlab实验报告实验1 熟悉matlab 的开发环境及矩阵操作⼀、实验的教学⽬标通过本次实验使学⽣熟悉MATLAB7.0的开发环境,熟悉MA TLAB ⼯作界⾯的多个常⽤窗⼝包括命令窗⼝、历史命令窗⼝、当前⼯作⽬录窗⼝、⼯作空间浏览器窗⼝等。
掌握建⽴表达式书写规则及常⽤函数的使⽤,建⽴矩阵的⼏种⽅法。
⼆、实验环境计算机、MATLAB7.0集成环境三、实验内容1、熟悉命令窗⼝的使⽤,⼯作空间窗⼝的使⽤,⼯作⽬录、搜索路径的设置。
命令历史记录窗⼝的使⽤,帮助系统的使⽤。
2、在当前命令窗⼝中输⼊以下命令:x=0:2:10 y=sqrt(x),并理解其含义。
3、求下列表达式的值(1)w=)1034245.01(26-?+?(2)x=ac b e abc cb a ++-+++)tan(22ππ,其中a=3.5,b=5,c=-9.8 四、实验总结1、熟悉了命令窗⼝的使⽤,⼯作空间窗⼝的使⽤。
2、了解了⼯作⽬录、搜索路径的设置⽅法。
---5317383399351542实验2 MATLAB 基本运算⼀、实验的教学⽬标通过本次实验使学⽣掌握向量和矩阵的创建⽅法;掌握矩阵和数组的算术运算、逻辑运算和关系运算;掌握字符数组的创建和运算;了解创建元胞数组和结构体的⽅法。
⼆、实验环境计算机、MATLAB7.0集成环境三、实验内容1、要求在闭区间]2,0[π上产⽣具有10个等距采样点的⼀维数组。
试⽤两种不同的指令实现。
(提⽰:冒号⽣成法,定点⽣成法)2、由指令rng('default'),A=rand(3,5)⽣成⼆维数组A ,试求该数组中所有⼤于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
(提⽰:find 和sub2ind )3、创建3阶魔⽅矩阵a 和3阶对⾓阵b ,c=a(1:3,1:3)(1)计算矩阵a,b 和c 的⾏列式、逆矩阵并进⾏最⼤值的统计。
(2)⽐较矩阵和数组的算术运算:b 和c 的*、/、^和.*、./、.^。
数值分析matlab实验报告

数值分析matlab实验报告《数值分析MATLAB实验报告》摘要:本实验报告基于MATLAB软件进行了数值分析实验,通过对不同数学问题的数值计算和分析,验证了数值分析方法的有效性和准确性。
实验结果表明,MATLAB在数值分析领域具有较高的应用价值和实用性。
一、引言数值分析是一门研究利用计算机进行数值计算和分析的学科,其应用范围涵盖了数学、物理、工程等多个领域。
MATLAB是一种常用的数值计算软件,具有强大的数值分析功能,能够进行高效、准确的数值计算和分析,因此在科学研究和工程实践中得到了广泛的应用。
二、实验目的本实验旨在通过MATLAB软件对数值分析方法进行实验验证,探究其在不同数学问题上的应用效果和准确性,为数值分析方法的实际应用提供参考和指导。
三、实验内容1. 利用MATLAB进行方程求解实验在该实验中,利用MATLAB对给定的方程进行求解,比较数值解和解析解的差异,验证数值解的准确性和可靠性。
2. 利用MATLAB进行数值积分实验通过MATLAB对给定函数进行数值积分,比较数值积分结果和解析积分结果,验证数值积分的精度和稳定性。
3. 利用MATLAB进行常微分方程数值解实验通过MATLAB对给定的常微分方程进行数值解,比较数值解和解析解的差异,验证数值解的准确性和可靠性。
四、实验结果与分析通过对以上实验内容的实际操作和分析,得出以下结论:1. 在方程求解实验中,MATLAB给出的数值解与解析解基本吻合,验证了MATLAB在方程求解方面的高准确性和可靠性。
2. 在数值积分实验中,MATLAB给出的数值积分结果与解析积分结果基本吻合,验证了MATLAB在数值积分方面的高精度和稳定性。
3. 在常微分方程数值解实验中,MATLAB给出的数值解与解析解基本吻合,验证了MATLAB在常微分方程数值解方面的高准确性和可靠性。
五、结论与展望本实验通过MATLAB软件对数值分析方法进行了实验验证,得出了数值分析方法在不同数学问题上的高准确性和可靠性。
MATLAB实验报告

页脚内容1实验一 名称:连续时间信号分析姓名:王嘉琦 学号:201300800636 班级:通信二班一、实验目的(一)掌握使用Matlab 表示连续时间信号1、学会运用Matlab 表示常用连续时间信号的方法2、观察并熟悉常用信号的波形和特性(二)掌握使用Matlab 进行连续时间信号的相关运算1、学会运用Matlab 进行连续时间信号的时移、反褶和尺度变换2、学会运用Matlab 进行连续时间信号微分、积分运算3、学会运用Matlab 进行连续时间信号相加、相乘运算4、学会运用Matlab 进行连续时间信号卷积运算二、实验条件Matlab三、实验内容1、利用Matlab 命令画出下列连续信号的波形图。
(1))4/3t (2cos π+代码:页脚内容2k=2;w=3;phi=pi/4;t=0:0.01:3;ft=k*cos(w*t+phi);plot(t,ft),grid on;axis([0,3,-2.2,2.2])title('余弦信号')(2))t (u )e 2(t -- 代码:页脚内容3k=-1;a=-1;t=0:0.01:3;ft=2-k*exp(a*t);plot(t,ft),grid onaxis([0,3,2,3])title('指数信号')(3))]2()(u )][t (cos 1[--+t u t π代码:页脚内容4k=1;w=pi;phi=0;t=0:0.01:2;ft=1+k*cos(w*t+phi);plot(t,ft),grid on;axis([0,3,0,2])title('余弦信号')2、利用Matlab 命令画出复信号)4/t (j 2e )t (f π+=的实部、虚部、模和辐角。
代码:页脚内容5t=0:0.01:10;k=2;a=0;b=1;phi=pi/4;ft=k*exp(a+i*(b*t+phi));subplot(2,2,1);plot(t,real(ft));title('实部');axis([0,10,-2.2,2.2]);grid on; subplot(2,2,2);plot(t,imag(ft));title('虚部');axis([0,10,-2.2,2.2]);grid on; subplot(2,2,3);plot(t,abs(ft));title('模');axis([0,10,0,6]);grid on;subplot(2,2,4);plot(t,angle(ft));title('相角');axis([0,10,-4,4]);grid on;3、已知信号的波形(课本P13例题1-1),画出()()()()2332----t f t f t f t f ,,,的波形图。
matlab 实验报告

matlab 实验报告Matlab 实验报告引言:Matlab(Matrix Laboratory)是一种强大的科学计算软件,它为科学家、工程师和研究人员提供了一个强大的计算环境。
本实验报告旨在介绍我对Matlab的实验结果和使用体验,以及对其优点和局限性的思考。
一、Matlab的基本功能和特点Matlab是一种高级编程语言和开发环境,它具有广泛的数学和工程计算功能。
通过Matlab,我可以进行矩阵运算、数值计算、数据可视化、算法开发等一系列操作。
Matlab的语法简洁易懂,可以快速实现复杂的计算任务。
此外,Matlab还提供了大量的工具箱,如信号处理、控制系统、图像处理等,使得各种领域的科学研究和工程应用变得更加便捷。
二、实验结果与应用案例在本次实验中,我选择了一个经典的数值计算问题——求解非线性方程。
通过Matlab的数值计算能力,我可以使用不同的迭代方法来求解方程的根。
在实验中,我使用了牛顿迭代法、二分法和割线法来求解方程。
通过对比这些方法的收敛速度和精度,我得出了不同方法的优缺点。
在实际应用中,Matlab可以广泛应用于信号处理、图像处理、数据分析等领域。
例如,在信号处理中,我可以使用Matlab的信号处理工具箱来进行滤波、频谱分析等操作。
在图像处理中,我可以利用Matlab的图像处理工具箱进行图像增强、边缘检测等操作。
这些应用案例充分展示了Matlab在科学计算和工程应用中的重要性和灵活性。
三、Matlab的优点1. 强大的计算功能:Matlab提供了丰富的数学和工程计算函数,可以高效地进行复杂的计算任务。
2. 简洁的语法:Matlab的语法简洁易懂,使得编程变得更加高效和便捷。
3. 丰富的工具箱:Matlab提供了大量的工具箱,覆盖了各种领域的科学计算和工程应用需求。
4. 可视化能力强:Matlab提供了丰富的绘图函数,可以直观地展示数据和计算结果。
四、Matlab的局限性1. 高昂的价格:Matlab是一款商业软件,其价格较高,对于个人用户而言可能不太容易承受。
matlab实验报告

matlab实验报告Matlab实验报告实验题目:利用Matlab进行数据处理与分析实验目的:通过使用Matlab进行数据处理与分析的实践,掌握Matlab的基本操作和数据处理的方法。
实验内容:1. 数据读取:从文件中读取原始数据,并进行初步的观察和分析。
2. 数据清洗:对原始数据进行清洗,包括去除空值、异常值等。
3. 数据可视化:利用Matlab的绘图函数,将数据可视化呈现,以方便对数据进行进一步的分析和理解。
4. 数据分析:对清洗后的数据进行统计分析,包括求平均值、方差、相关系数等。
5. 模型建立:根据数据分析的结果,建立合适的数学模型,并使用Matlab进行参数估计和模型验证。
6. 结果验证:利用实验数据和模型进行实验结果的对比,验证模型的准确性和可靠性。
实验步骤:1. 准备实验数据:从实验样本中获得原始数据,并将其存储为文本文件。
2. 使用Matlab导入数据:使用Matlab的数据导入函数,将文本文件中的数据导入到Matlab的工作空间中。
3. 数据分析与处理:使用Matlab的数据处理函数,对导入的数据进行清洗和处理,去除异常值和空值,并进行初步的数据观察和分析。
4. 数据可视化:利用Matlab的绘图函数,绘制数据的直方图、散点图、折线图等,以展示数据的分布和趋势。
5. 数据统计分析:使用Matlab的统计分析函数,对处理后的数据进行统计分析,包括计算平均值、方差、相关系数等。
6. 模型建立与验证:根据数据分析的结果,建立合适的数学模型,并使用Matlab进行参数估计和模型验证。
7. 结果对比和讨论:将实验结果与模型预测结果进行对比,并进行结果的讨论和分析。
8. 实验结论:总结实验结果并给出结论。
实验结果:根据实验数据的分析和处理,得出如下结论:1. 数据呈现正态分布,符合正态性假设。
2. 数据之间存在显著的正相关关系,相关系数为0.8,结果具有统计学意义。
3. 建立的数学模型与实验数据拟合良好,模型预测结果与实验结果吻合度高。
(完整word)Matlab实验报告
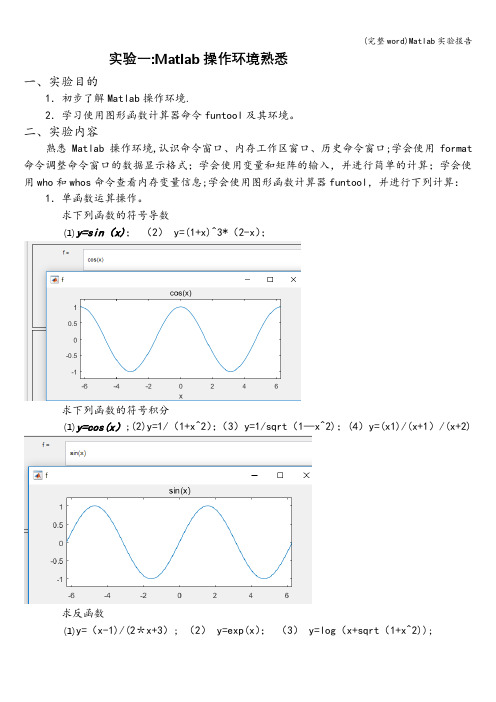
实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境.2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format 命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
求下列函数的符号导数(1)y=sin(x);(2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1—x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x);(3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x—4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x—3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2)y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6) y6=x^2/2 3.两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(—x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x—1)/(x—2); 求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二:MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
matlab入门 实验报告

matlab入门实验报告Matlab入门实验报告一、引言Matlab是一种功能强大的数学软件,广泛应用于科学计算、数据分析和工程设计等领域。
本实验报告将介绍Matlab的基本使用方法和一些常见的数学计算实例。
二、Matlab的基本操作1. Matlab的安装和启动Matlab可以从官方网站下载并安装在计算机上。
安装完成后,双击桌面上的Matlab图标即可启动软件。
2. Matlab的界面和基本操作Matlab的界面由主窗口、命令窗口和编辑器等组成。
在命令窗口中可以输入和执行Matlab命令,编辑器可以编写和保存Matlab脚本。
3. Matlab的数据类型和变量Matlab支持多种数据类型,包括数值型、字符型、逻辑型等。
可以使用赋值语句将值存储在变量中,例如:x = 5。
4. Matlab的基本数学运算Matlab可以进行基本的数学运算,如加减乘除、幂运算等。
例如,输入命令:y = 2*x + 3,即可计算出变量y的值。
三、Matlab的数学函数1. Matlab的数学函数库Matlab内置了大量的数学函数,可以进行各种复杂的数学运算和数据处理。
例如,sin函数用于计算正弦值,sqrt函数用于计算平方根。
2. Matlab的矩阵运算Matlab是一个强大的矩阵计算工具,可以进行矩阵的加减乘除、转置、求逆等运算。
例如,输入命令:A = [1 2; 3 4],即可创建一个2x2的矩阵。
3. Matlab的符号计算Matlab还支持符号计算,可以进行代数运算和求解方程等。
例如,输入命令:syms x; solve(x^2 - 2*x - 3 = 0, x),即可求解方程的根。
四、Matlab的数据可视化1. Matlab的绘图功能Matlab提供了丰富的绘图函数,可以绘制各种类型的图形,如曲线图、散点图、柱状图等。
例如,输入命令:plot(x, y),即可绘制x和y的曲线图。
2. Matlab的图像处理Matlab还可以进行图像处理,如读取、显示和编辑图像。
MATLAB实验报告(word文档良心出品)

《MATLAB/Simulink与控制系统仿真》实验报告专业:班级:学号:姓名:指导教师:实验1、MATLAB/Simulink 仿真基础及控制系统模型的建立一、实验目的1、掌握MATLAB/Simulink 仿真的基本知识;2、熟练应用MATLAB 软件建立控制系统模型。
二、实验设备电脑一台;MATLAB 仿真软件一个 三、实验内容1、熟悉MATLAB/Smulink 仿真软件。
2、一个单位负反馈二阶系统,其开环传递函数为210()3G s s s=+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
图 1系统结构图图 2示波器输出结果图3、某控制系统的传递函数为()()()1()Y s G s X s G s =+,其中250()23s G s s s+=+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MA TLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
图 3系统结构图 图 4 示波器输出结果图图 5 工作空间中仿真结果图形化输出4、一闭环系统结构如图所示,其中系统前向通道的传递函数为320.520()0.11220s G s s s s s+=+++g ,而且前向通道有一个[-0.2,0.5]的限幅环节,图中用N 表示,反馈通道的增益为1.5,系统为负反馈,阶跃输入经1.5倍的增益作用到系统。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
图 6 系统结构图图 7 示波器输出结果实验2 MATLAB/Simulink 在控制系统建模中的应用一、实验目的1、掌握MATLAB/Simulink 在控制系统建模中的应用; 二、实验设备电脑一台;MA TLAB 仿真软件一个 三、实验内容1、给定RLC 网络如图所示。
matlab 实验报告

matlab 实验报告Matlab实验报告引言:Matlab是一种强大的数值计算和可视化软件,广泛应用于科学、工程和经济等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和结果。
实验一:矩阵运算在这个实验中,我使用Matlab进行了矩阵运算。
首先,我创建了一个3x3的矩阵A和一个3x1的矩阵B,并进行了矩阵相乘运算。
通过Matlab的矩阵乘法运算符*,我得到了一个3x1的结果矩阵C。
接着,我对矩阵C进行了转置操作,得到了一个1x3的矩阵D。
最后,我计算了矩阵C和矩阵D的点积,并将结果输出。
实验二:数据可视化在这个实验中,我使用Matlab进行了数据可视化。
我选择了一组实验数据,包括时间和温度两个变量。
首先,我将数据存储在一个矩阵中,并使用Matlab的plot函数将时间和温度之间的关系绘制成曲线图。
接着,我使用Matlab的xlabel、ylabel和title函数添加了横轴、纵轴和标题。
最后,我使用Matlab的legend函数添加了图例,以便更好地理解图表。
实验三:数值积分在这个实验中,我使用Matlab进行了数值积分。
我选择了一个函数f(x)进行积分计算。
首先,我使用Matlab的syms函数定义了符号变量x,并定义了函数f(x)。
接着,我使用Matlab的int函数对函数f(x)进行积分计算,并将结果输出。
为了验证结果的准确性,我还使用了Matlab的diff函数对积分结果进行了求导操作,并与原函数f(x)进行了比较。
实验四:信号处理在这个实验中,我使用Matlab进行了信号处理。
我选择了一个音频文件,并使用Matlab的audioread函数读取了该文件。
接着,我使用Matlab的fft函数对音频信号进行了傅里叶变换,并将结果绘制成频谱图。
为了进一步分析信号的特征,我还使用了Matlab的spectrogram函数绘制了信号的时频图。
通过对信号的频谱和时频图的观察,我可以更好地理解信号的频率和时域特性。
matlab上机实验报告

matlab上机实验报告《Matlab上机实验报告:探索数据分析与图像处理的奇妙世界》摘要:本实验报告基于Matlab平台,探索了数据分析与图像处理的应用。
通过实验,我们发现Matlab具有强大的数据处理和图像处理能力,能够帮助我们快速高效地分析数据和处理图像。
本文将详细介绍实验过程和结果,以及对Matlab在数据分析与图像处理中的应用前景进行探讨。
1. 实验目的本次实验旨在通过Matlab平台进行数据分析与图像处理实验,探索Matlab在这两个领域的应用能力,为学习者提供实践机会,加深对数据分析与图像处理的理解,并为未来的科研工作和工程实践提供技术支持。
2. 实验内容2.1 数据分析我们首先使用Matlab对一组实验数据进行分析,包括数据的可视化、统计特征提取、数据拟合等操作。
通过Matlab强大的数据处理工具,我们可以快速准确地分析数据,提取出其中的规律和特征,为后续的决策和应用提供支持。
2.2 图像处理其次,我们利用Matlab对一组图像进行处理,包括图像的增强、滤波、边缘检测等操作。
通过Matlab丰富的图像处理工具,我们可以对图像进行各种操作,改善图像质量,提取图像特征,甚至实现图像识别和分析。
3. 实验结果在数据分析方面,我们利用Matlab对实验数据进行了可视化展示,并提取了数据的统计特征,得到了数据的分布规律和趋势。
在图像处理方面,我们利用Matlab对图像进行了增强和边缘检测,得到了处理后的图像,观察到了图像质量的改善和边缘特征的提取。
4. 实验结论通过本次实验,我们深刻认识到Matlab在数据分析与图像处理领域的强大能力,能够帮助我们快速高效地分析数据和处理图像,为科研工作和工程实践提供技术支持。
我们相信,在未来的发展中,Matlab将在数据分析与图像处理领域发挥越来越重要的作用。
5. 展望基于本次实验的结果,我们对Matlab在数据分析与图像处理领域的应用前景进行了展望。
我们相信,随着科技的不断发展,Matlab将在数据分析与图像处理领域发挥越来越重要的作用,为人类社会的进步和发展做出更大的贡献。
matlab实验报告

matlab实验报告Matlab实验报告引言:Matlab(Matrix Laboratory)是一种高级的计算机编程语言和环境,主要用于数值计算、数据分析和可视化。
它的功能强大,被广泛应用于科学研究、工程设计和教学实验等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和收获。
一、Matlab的基本语法和数据类型Matlab的语法与其他编程语言相比较简单,但仍然需要掌握一些基本的语法规则。
例如,Matlab中的变量命名不区分大小写,但建议使用小写字母来命名变量。
Matlab支持多种数据类型,包括数值型、字符型、逻辑型等。
在实验中,我常常使用数值型数据进行计算和分析。
二、Matlab中的矩阵运算矩阵运算是Matlab的重要特性之一,它使得处理大量数据变得更加高效和简便。
我在实验中经常使用矩阵运算来进行数据的处理和分析。
例如,我可以使用矩阵乘法来计算两个矩阵的乘积,或者使用矩阵的转置来进行数据的重排和变换。
Matlab还提供了丰富的矩阵运算函数,如求逆矩阵、特征值分解等,这些函数大大简化了复杂计算的过程。
三、Matlab的数据可视化Matlab提供了强大的数据可视化功能,可以帮助我们更直观地理解和展示数据。
在实验中,我常常使用Matlab绘制曲线图、散点图和柱状图等,以便更清晰地观察数据的分布和趋势。
Matlab的绘图函数丰富多样,可以根据不同的需求选择合适的图形类型和样式。
此外,Matlab还支持图像处理和三维可视化等高级功能,这些功能在科学研究和工程设计中有着广泛的应用。
四、Matlab的编程和调试Matlab不仅是一种计算工具,还是一种编程语言。
通过编写脚本和函数,我们可以实现更复杂的计算和操作。
在实验中,我常常使用Matlab编写自定义函数来实现特定的功能。
编程过程中,我注意到Matlab的调试功能非常强大,可以帮助我们找出代码中的错误和问题。
Matlab提供了断点调试、变量监视和错误提示等功能,这些功能对于提高代码的可靠性和效率非常有帮助。
matlab实验报告

matlab实验报告实验名称:MATLAB数值分析实验报告摘要:本实验通过使用MATLAB软件,实现了一些数值分析中重要的算法,包括线性方程组求解、非线性方程求根、数值积分与微分以及常微分方程求解。
在算法实现的过程中,通过观察输出结果验证了算法的正确性和可靠性,并探讨了一些算法实现中需要注意的问题。
1.线性方程组求解线性方程组求解是数值分析中的重要算法之一,是很多数学问题的基础。
本实验中使用了三种求解线性方程组的算法:高斯消元法、LU分解法和共轭梯度法。
在实验中,我们需要注意选取矩阵的条件数,使用一些特殊矩阵,如对角矩阵、三对角矩阵和希尔伯特矩阵等来验证算法的正确性。
2.非线性方程求根非线性方程求根是MATLAB中一个非常实用的函数,能够快速解决大量的非线性方程。
本实验中,我们更深入地探讨了二分法、牛顿法和割线法等算法,通过实现代码,实现了对非线性方程的求解。
同时,对不同的算法进行比较,从而选择合适的算法。
3.数值积分与微分数值积分与微分是宏观物理中需要用到的重要数学问题之一。
本实验中,我们使用了梯形法、辛普森法和龙贝格法等多种数值积分算法实现了函数的数值积分。
同时,也对数值微分的误差和稳定性进行了研究和探讨。
4.常微分方程求解常微分方程求解是MATLAB中最常用的功能之一。
本实验中,我们实现了欧拉法、龙格-库塔法等常微分方程求解算法。
并不断尝试对算法进行改进,提高其效率和精度。
实验结果表明,使用MATLAB实现数值分析算法是非常可靠和高效的。
同时,也需要注意在算法实现中注意问题和选择合适的算法。
matlab 模拟 实验报告

matlab 模拟实验报告《利用Matlab模拟的实验报告》摘要:本实验利用Matlab软件对某一特定系统进行了模拟实验。
通过对系统的建模和仿真,我们得出了一些有价值的结论,并对系统的性能进行了评估。
本文将详细介绍实验的目的、方法、结果和分析,以及对实验结果的讨论和总结。
1. 引言Matlab是一种强大的数学建模和仿真工具,广泛应用于工程、科学和技术领域。
利用Matlab进行系统仿真可以帮助我们更好地理解系统的行为和性能,优化系统设计,并预测系统在不同条件下的表现。
本实验旨在利用Matlab对某一特定系统进行仿真,以验证系统的性能和稳定性。
2. 实验目的本实验的主要目的是利用Matlab对某一特定系统进行建模和仿真,分析系统的动态响应和稳定性,并评估系统的性能。
具体来说,我们将通过仿真实验探讨系统的频率响应、阶跃响应和脉冲响应,以及系统的稳定性和鲁棒性。
3. 实验方法首先,我们对系统进行了建模,包括系统的传递函数、状态空间模型等。
然后,利用Matlab软件进行仿真实验,分别对系统的频率响应、阶跃响应和脉冲响应进行了分析。
最后,我们对仿真结果进行了统计和评估,得出了一些有价值的结论。
4. 实验结果与分析通过Matlab的仿真实验,我们得到了系统的频率响应曲线、阶跃响应曲线和脉冲响应曲线。
通过对这些曲线的分析,我们可以得出系统的动态特性和稳定性。
同时,我们还对系统的性能进行了评估,包括系统的超调量、调节时间等指标。
5. 结果讨论与总结通过对实验结果的讨论和总结,我们得出了一些结论和建议。
我们对系统的性能和稳定性进行了评估,发现系统在某些条件下存在一些问题,提出了一些建议和改进措施。
同时,我们也对Matlab软件在系统仿真中的应用进行了总结和展望。
结论本实验利用Matlab对某一特定系统进行了建模和仿真,得出了一些有价值的结论。
通过对系统的动态响应和稳定性进行分析,我们发现了系统存在的一些问题,并提出了一些建议和改进措施。
matlab实验报告

matlab实验报告实验名称熟悉matlab环境课程名称数值分析学生姓名乔幸帅学号 331201000018专业信号与信息处理一、实验目的本次实验的目的是在理论基础的学习前提下熟悉matlab的基本操作,学会matlab的基本绘图以及函数的编写,为学习数值分析这门课奠定基础,并为以后在其他学习和工程使用中打下基础。
二、实验内容1.熟悉matlab的三种指令输入方式2.学会简单的绘图命令3.用matlab编程学会创建函数三、实验步骤3.1 matlab的三种指令输入方式3.1.1 在指令框中直接输入指令并查看结果,如图所示:3.1.2 创建M文件写入指令并运行○1点击matlab的FILE按键选中NEW-Script创建一个如图所示:○2在M文件中输入想要运行的程序并保存○3点击debug中的Run按键运行程序显示结果如图:012345678910matlab Notebook的启动点击matlab左下角的start按钮,点击里面的notebook选项即可新建一个类似word的文档,在里面输入程序,并在Notebook下拉菜单选择Define Input Cell,继续选择Ealuate Input Cell,即得结果如图所示3.2 matlab的简单绘图绘制图像的最基本函数是plot(),其基本调用格式是plot(x,y)如果要绘制多个图像可以使用subplot函数,即在同一个窗口绘制多个子图。
用subplot函数花多个子图。
t=0:pi/100:2*pi;y1=sin(t);y2=cos(t);y3=sin(t)+cos(t);y4=sin(t).*cos(t);subplot(2,2,1)plot(t,y1)xlabel('\itt\rm/s');ylabel('y_1=sin(t)');subplot(2,2,2)plot(t,y2)xlabel('\itt\rm/s'); ylabel('y_2=cos(t)'); subplot(2,2,3) plot(t,y3) gridxlabel('\itt\rm/s'); ylabel('y_3=sin(t)+cos(t)'); subplot(2,2,4) plot(t,y4) gridxlabel('\itt\rm/s'); ylabel('y_4=sin(t)*cos(t)'); 程序运行结果如图所示2468-1-0.500.51t /sy 1=s i n (t )02468-1-0.500.51t /sy 2=c o s (t )2468-2-1012t /sy 3=s i n (t )+c o s (t )02468-0.50.5t /sy 4=s i n (t )*c o s (t )3.3 用 matlab 编写函数MATLAB 的 M 函数是由 function 语句引导的,其基本格式如下: function [返回变量列表] = 函数名 (输入变量列表)[例子]:假设我们想生成一个 n*m 阶的 Hilbert 矩阵, 它的第 i 行第 j 列的元素值为 1/(i+j-1)。
matlab实验报告

《MATLAB及其工程应用》实验报告专业:班级:学号:姓名:指导老师:实验一实验名称:Practice how to initialize/save/load the MATLAB实验时间:第六周周三7-8节 实验目的:1、熟练的掌握MATLAB 变量的使用规则,学会创建变量。
2、熟练的掌握数组的相关知识并能加以运用。
实验要求:1、熟练命名合法的变量名。
2、能够应对关于数组的相关问题,如:数组的大小,子数组等。
实验步骤:1.4 假设u=1和v=3,用MATLAB 语句编写下列语句 a. v u 34 b.22)(2v u v +- c.333u v v - d.234v π 解:打开matlab7.0程序,新建一个M-file ,M-file 中输入:u=1;v=3;a=4*u/(3*v);b=2*v^(-2)/(u+v)^2;c=v^3/(v^3-u^3);d=4*pi*v^2/3;abcd然后点击运行,将得到以下结果:a =0.4444b =0.0139c =1.0385d =37.6991实验二实验名称:Practice how to use the MATLAB operators.实验时间:第七周周三7-8节实验目的:1、熟练的掌握数组和矩阵的使用规则。
2、熟练的掌握数组和矩阵的相关知识并能加以运用。
实验要求:1、熟练命名合法的变量名。
2、能够应对关于数组和矩阵的相关问题。
实验步骤:2.1看下面的数组回答有关问题⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=0.01.10.01.54.13.14.03.01.01.24.38.26.61.10.00.65.31.20.01.11array a. array1的大小是多少?b. array1(4,1)的值是多少?c. array1(:,1:2)的大小和值为多少?d. array1([1 3],end)的大小和值为多少?解:打开matlab7.0程序,新建一个M-file ,M-file 中输入:array1=[1.1,0.0,2.1,-3.5,6.0;0.0,1.1,-6.6,2.8,3.4;2.1,0.1,0.3,-0.4,1.3;-1.4,5.1,0.0,1.1,0.0];size(array1) %2.11aarray1(4,1) %2.1barray1(:,1:2) %2.1csize(array1(:,1:2)) %2.1carray1([1 3],end) %2.1dsize(array1([1 3],end)) %2.1d然后点击运行,将得到以下结果:ans =4 5ans =-1.4000ans =1.1000 00 1.10002.1000 0.1000-1.4000 5.1000ans =4 2ans =6.00001.3000ans =2 12.3 写出下面的数组的大小和内容.注意后面的数组可能根据前面数组的定义.a. a=1:2:5;b. b=[a' a' a'];c. c=b(1:2:3,1:2:3);d. d=a+b(2,:);e. w=[zeros(1,3) ones(3,1)' 3:5'];f. b([1 3],2)=b([3 1],2);解:>> a=1:2:5a =1 3 5>> size(a)ans =1 3>> b=[a' a' a']b =1 1 13 3 35 5 5>> size(b)ans =3 3>> c=b(1:2:3,1:2:3)c =1 15 5>> size(c)ans =2 2>> d=a+b(2,:)d =4 6 8>> size(d)ans =1 3>> w=[zeros(1,3) ones(3,1)' 3:5'w =0 0 0 1 1 1 3 4 5>> size(w)ans =1 9>> b([1 3],2)=b([3,1],2)b =1 5 13 3 35 1 5>> size(b)ans =3 32.4数组定义如下,写下面的子数组的内容⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=0.01.10.01.54.13.14.03.01.01.24.38.26.61.10.00.65.31.20.01.11array a. array1(3,:)b. array1(:,3)c. array1(1:2:3,[3 3 4])d. array1([1 1],:)解:>> array1=[1.1 0.0 2.1 -3.5 6.0;0.0 1.1 -6.6 2.8 3.4;2.1 0.1 0.3 -0.4 1.3 ;-1.45.1 0.0 1.1 0.0]array1 =1.1 02.1 -3.5 60 1.1 -6.6 2.8 3.42.1 0.1 0.3 -0.4 1.3-1.4 5.1 0 1.1 0>> array1(3,:)ans =2.1 0.1 0.3 -0.4 1.3>> array1(:,3)ans =2.1-6.60.3>> array1(1:2:3,[3 3 4])ans =2.1 2.1 -3.50.3 0.3 -0.4>> array1([1 1],:)ans =1.1 02.1 -3.5 61.1 02.1 -3.5 6实验三实验名称:Practice MATLAB display and plotting functions.实验时间:第九周周三7-8节实验目的:1、掌握三种常见函数:disp ,fprintf ,plot2、掌握画图函数的使用方法实验要求:1、熟练掌握plot 函数的使用方法2、能运用画图函数画一些较简单的图形实验步骤:2.10 球的位置和速度.如果一静止小球在离地h 0的地方以初速度v 0做垂直运动,其等等式为o o h t v gt t h ++=221)( (2.10) o v gt t v +=)( (2.11)其中g 为重力加速度(9.81m/(s*s)),h (t )代表在t 时刻小球的高度.v (t )代表在时刻t 小球的速度.编写一个MATLAB 程序,计算出每一秒钟的速度和高度,并打印出h ,v 关于时间t 的函数.确保在你的图中有合适的标签.解:v0=input('v0=');h0=input('h0=');t=-10:0.01:10;h=0.5.*(-9.81).*t.^2+v0.*t+h0;v=(-9.81).*t+v0;plot(t,h,'r--',t,v,'g');axis([-10,10,-50,50]);xlabel('t');ylabel('h and v');legend('h','v')结果:v0=10h0=102.13双曲余弦.双曲余弦的定义如下2cosh xx e e x -+=编写一个程序,计算出用户指定的x 的值对应的双曲余弦值.用这个程序计算3.0的双曲余弦值.和MATLAB 中的内建函数cosh(x)得到的值是否完全相同.用MATLAB 打印出这个函数的图象.当x 为何值时,这个函数有最小值?最小值为多少?解:注:以下结果均为x=3.0时的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验(7):最优化实验(Optimization)1.Carpenter Problem.
A carpenter makes tables and bookcases. He is trying to determine how many
each type of furniture he should make each week
多达) 600 board feet of lumber to devote weekly to the project
He estimates that it requires 20 board feet of lumber and 5 hours of labor to
complete a table and 30 board feet of lumber and 4 hour of labor for a bookcase.
Moreover, he signed a contract to deliver four tables and two bookcases each
week. The carpenter wishes to determine a weekly production schedule for tables and bookcases that maximize his profits.
设桌子的个数为x1,书架的个数为x2
f=[-25,-30];
A=[20 30;5 4];
b=[600;120];
Aeq=[];beq=[];
lb=[4;2];
ub=[inf,inf];
[x,feval]=linprog(f,A,b,Aeq,beq,lb,ub)
Optimization terminated.
x =
17.1429
8.5714
feval =
-685.7143
则最优解为桌子17.1429 书架8.5714
最大利润为685.7143
2. Solve the Ladder Problem by using three methods. (Animation is optional)
Suppose there is a big house with two levels. A flower house made of glass is
next to it.
On the side where the two houses are next to each other, there is a window.
Assume we put a ladder onto the wall over the glass house, so that we can
clean the window by standing on top of the ladder.
实验(7):最优化实验(Optimization)
What is the shortest length of the ladder?
设房屋的高度为H=10米,花房高度为h=5米,宽度s=3米。
(1)第一种解法:
设梯子总长为z,上半段长为x,下半段长为y,则有
条件:
x/(x+y)=s/(s+(y^2-h^2)^(1/2))即为x*(y^2-25)(1/2)-3*y=0
x^2-s^2<=(H-h)^2,y>0即为x^2<=34
求解:
Min z=x+y
代码:
function f=fun(x)
f=x(1)+x(2)
function [c,ceq]=confun(x)
c=[]
ceq=[x(1)*(x(2)^2-25)^(1/2)-3*x(2)]
[x,fval]=fmincon(@fun,[4,6],[],[],[],[],[0,0],[34^(1/2),inf],@confun) 结果
No active inequalities.
x =
4.6531 6.5410
实验(7):最优化实验(Optimization)
fval =
11.1941
(2)第二种解法:
设梯上小三角形高度为x,下小三角形的底为y,则
条件:
x/(x+h)=s/(s+y)即为xy=sh
0<x<H-h,y>0
求解:
Min z=(x^2+s^2)^(1/2)+(y^2+h^2)^(1/2)
代码:
function f=fun(x)
f=(x(1)+9)^(1/2)+(x(2)+25)^(1/2)
function [c,ceq]=confun(x)
c=[]
ceq=[x(1)*x(2)-15]
[x,fval]=fmincon(@fun,[3,5],[],[],[],[],[0,0],[5,inf],@confun)
结果:
No active inequalities.
x =
4.6531 6.5410
fval =
11.1941
(3)第三种解法
设三角形的底角为x,上小三角形的高为s*tanx,斜边长为s/cosx,同理下三角形的斜边长为h/sinx,
条件:s*tanx<H-h
Pi/2>x>0
求解:
Min z=s/cosx+h/sinx
代码:
function f=fun(x)
f=3/cos(x)+5/sin(x)
function [c,ceq]=confun(x)
c=[3*tanx<5]
实验(7):最优化实验(Optimization )
ceq=[]
[x,fval]=fmincon(@fun,[pi/4],[],[],[],[],[0],[pi/2],@confun) 结果:
No active inequalities. x =
0.8701 fval =
11.1941
3.求解非线性规划问题:
123max ..
x x x s t
123123
1222202272101020
x x x x x x x x x -++≥⎧⎪++≤⎪⎨
-=⎪⎪≤≤⎩ fun='-x(1)*x(2)*x(3)'; x0=[0 0 0]; A=[1 -2 -2;1 2 3]; b=[0;72]; Aeq=[1 -1 0]; beq=10;
lb=[-inf 10 -inf]; ub=[inf 20 inf];
[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Active inequalities (to within options.TolCon = 1e-006): lower upper ineqlin ineqnonlin 2 x =
22.5851 12.5851 8.0816
实验(7):最优化实验(Optimization)
fval =
-2.2971e+003
4. 制定配棉方案
棉纺厂的主要原料是棉花,一般要占总成本的70%左右。
所谓配棉问题,就是要根据棉纱的质量指标,采用各种价格不同的棉花,按一定的比例
制成纱,使其既达到质量指标,又使总成本最低。
棉纱的质量指标一般由棉结和品质指标来决定。
这两项指标都可用数量
形式来表示。
一般来说,棉结粒数越少越好,品质指标越大越好。
一个年纺纱能力为15000锭的小厂在采用最优化方法配棉前,某一种产
品32D纯棉纱的棉花配比,
数据文件:OptimizationExpData.xls中,
有关部门对32D纯棉纱规定的质量指标为棉结不多于70粒,品质指标不
A=[60 65 80;-3800 -3500 -2500];
b=[70;-2900];
Aeq=[1 1 1];
beq=[1];
lb=[0 0 0];
ub=[];
[x,feval]=linprog(f,A,b,Aeq,beq,lb,ub)
Optimization terminated.
x =
0.0000
0.6667
0.3333
实验(7):最优化实验(Optimization)feval =
7.2333e+003。
