混凝土梁柱极限挠度和裂缝宽度计算
混凝土裂缝宽度计算公式

混凝土裂缝宽度计算公式简介混凝土裂缝宽度是评估混凝土结构强度和稳定性的重要指标。
准确计算混凝土裂缝宽度可以帮助工程师提前发现潜在问题并采取相应的预防和修补措施。
本文档将介绍一种常用的混凝土裂缝宽度计算公式,供工程师参考使用。
计算公式根据国内外研究和实践,混凝土裂缝宽度可通过以下公式进行计算:w = (K × f_ck × c_s) / (sqrt(f_t × E_s) × (d - c_w))其中,w代表混凝土裂缝宽度(mm),K为修正系数,f_ck 为混凝土抗压强度(MPa),c_s为混凝土应力矩引起的裂缝宽度影响系数,f_t为钢筋抗拉强度(MPa),E_s为钢筋弹性模量(MPa),d为截面受拉方向上的混凝土到钢筋中心距离(mm),c_w为保护层厚度(mm)。
参数说明以下是各参数的详细说明:- 修正系数K:随环境、材料和结构特性的不同而变化,具体数值需根据实际情况进行确定。
- 混凝土抗压强度f_ck:根据混凝土的质量和配比进行实测或参考相关标准。
- 混凝土应力矩引起的裂缝宽度影响系数c_s:根据结构的几何形状和荷载条件进行计算或根据相关经验值选择合适的数值。
- 钢筋抗拉强度f_t:根据所使用的钢筋型号和相关标准进行查询或实测。
- 钢筋弹性模量E_s:根据所使用的钢筋型号和相关标准进行查询或实测。
- 混凝土到钢筋中心距离d:根据结构设计图纸或实测取得。
- 保护层厚度c_w:根据结构设计图纸或实测取得。
注意事项在使用该计算公式进行混凝土裂缝宽度计算时,需注意以下事项:1. 参数的准确性:确保各参数数值的准确性,尽量从相关实测数据或权威标准中获取。
2. 环境和材料特性:修正系数K的值受环境和材料特性的影响,需根据具体情况进行修正。
3. 结构设计相关:提供参数值的结构设计图纸或实测数据应符合相关规范和标准。
4. 其他因素考虑:该计算公式只考虑了一些基本因素,对于特殊情况或特定结构需进行适当的修正或采用其他计算方法。
钢筋混凝土受弯构件的裂缝宽度和挠度验算
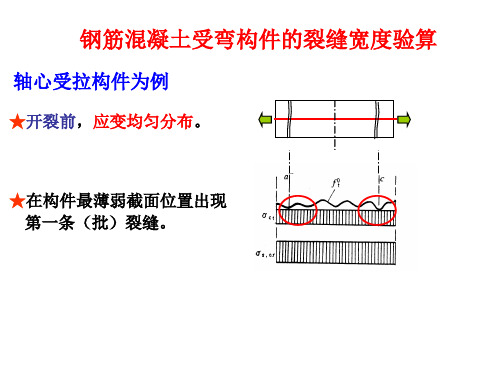
受压翼缘加强系数
3、钢筋应变不均匀系数
sm sk s sm s sk
钢筋应力不均匀系数 是反映裂缝间混凝土参加受拉工作 程度的影响系数。 越小,裂缝之间的混凝土协助钢筋抗拉的
作用越强。
1.1 0.65 ftk s sk te
sk分布图
1.1 0.65 ftk s sk te
sm sk
Sm cm cck
sm
cm
c
(
' f
Mk
0 )bh02Ec
cm
Mk
bh02 Ec
sm
Mk
Ash0 Es
ቤተ መጻሕፍቲ ባይዱ
Bs
Mk
M k h0
sm cm
cm
Mk
bh02 Ec
Bs
1
Ash02 Es
1
bh03 Ec
Bs
Es Ash02
E
E 0.2 6 E
1 3.5 f
Bs
1.15
Es Ash02 0.2
6E
1 3.5 f
1.1 0.65 ftk s sk te
在短期弯矩Mk=(0.5~0.7)Mu范围,三个参数、 和 中, 和 为常数,而 随弯矩增长而增大。
wm smlm cmlm
εsm、εcm——分别为裂缝间钢筋及砼的平均应变; lm——裂缝间距。
平均裂缝宽度wm
wm smlm cmlm
sm
(1
cm sm
建筑结构-钢筋混凝土构件裂缝宽度和挠度验算

Bl
Bl
M l (
Ms 1)
Ms
Bs
…8-6
Ms ––– 荷载短期效应组合算得的弯矩。 (恒载+活载) ––– 标准值。
Ml ––– 荷载长期效应组合算得的弯矩。
(恒载+活载q) ––– 标准值。
––– 挠度增大系数。 = 2.0 0.4' /
Bs ––– 短期刚度按式(8-5)计算。
3). 最小刚度原则:
e0
e0
Ns Ns
(a)
Ns
Ts
Ns
(b)
Ns
Ns
(c)
图8-1
(d T
(e)
非
为防止温度应力过大引起的开裂,规定了最
荷 载
大伸缩缝之间的间距。表8-1
引
起
为防止由于钢筋周围砼过快的碳化失去对钢
的
筋的保护作用,出现锈胀引起的沿钢筋纵向
裂 缝
的裂缝,规定了钢筋的混凝土保护层的最小
厚度。
通常,裂缝宽度和挠度一般可分别用控制最大 钢筋直径和最大跨高比来控制,只有在构件截面尺 寸小,钢筋应力高时进行验算。
2 裂缝宽度验算
随机性 《规范》在若干假定的基础上,根据裂缝出
现机理,建立理论公式,然后按试验资料确定系 数,得到相应的裂缝宽度计算经验式。
Ns
NNcr
1
ct=ftk
1
NNcr
Ns
(a)
ftk (b)
s ss
max
(c)
图8-2
(d)
1). 裂缝的出现和开展
出现:
当c ftk,在某一薄弱环节第一条裂缝出现,
1). 短期刚度 Bs的计算
M 1 EI r
混凝土梁挠度计算公式

混凝土梁挠度计算公式
概述:
混凝土梁的挠度是指梁的弯曲变形程度,是衡量梁的刚度和受力性能的重要参数。
计算混凝土梁的挠度可以帮助工程师确定梁的设计是否满足要求,并进行必要的调整。
常用公式:
1. 单跨梁的挠度计算公式:
梁的挠度 = (5 * q * L^4) / (384 * E * I)
公式中的变量含义如下:
挠度:梁的弯曲变形程度,单位为米。
q:集中载荷,单位为牛顿。
L:梁的跨度,单位为米。
E:混凝土的弹性模量,单位为帕斯卡。
I:梁的截面惯性矩,单位为米的四次方。
2. 多跨梁的挠度计算公式:
梁的挠度 = (q * L^4) / (E * I) * ( (L^2) / 2 - L * x + x^2 / 3 )
公式中的变量含义如下:
挠度:梁的弯曲变形程度,单位为米。
q:集中载荷,单位为牛顿。
L:梁的跨度,单位为米。
E:混凝土的弹性模量,单位为帕斯卡。
I:梁的截面惯性矩,单位为米的四次方。
x:距离梁的起点的长度,单位为米。
注意事项:
1. 当梁的截面形状不规则或荷载不均匀分布时,需要根据具体
情况进行修正。
2. 在实际工程中,通常需要考虑梁的自重、弯矩和剪力等因素,并使用更复杂的公式进行计算。
参考资料:
[1] 林将进, 林曦然. 标准化建筑工程交底书[M]. 科学技术文献
出版社, 2014.
[2] 中国土木工程学会. 建筑结构设计规范[M]. 中国建筑工业出
版社, 2018.。
裂缝宽度计算方法

裂缝宽度计算方法裂缝宽度是指裂缝之间的距离,是评估建筑物安全性和耐久性的重要指标。
在计算裂缝宽度时,需要考虑多个因素,如混凝土强度、环境条件、荷载大小等。
本文将介绍几种常见的裂缝宽度计算方法,并分析其适用范围和优缺点。
一、通过裂缝宽度计算公式计算公式法是计算裂缝宽度的一种常用方法,其基本原理是根据材料的力学性能和裂缝周围的应力分布,利用数学公式来计算裂缝宽度。
常用的裂缝宽度计算公式有:1. 莫尔-库伦理论公式该公式适用于混凝土材料,根据混凝土的强度等级和荷载大小,可以计算出裂缝宽度。
该方法的优点是简单易行,缺点是忽略了其他因素的影响,如环境条件、荷载组合等。
2. 临界裂缝截面厚度公式该公式适用于建筑物中的受拉区,可以根据混凝土的强度等级和配筋情况,计算出临界裂缝截面厚度和裂缝宽度。
该方法的优点是考虑了混凝土的力学性能和配筋情况,缺点是忽略了其他因素的影响。
二、通过测量计算测量法是通过测量裂缝之间的距离,来计算裂缝宽度的方法。
常用的测量方法有:1. 塞尺测量法该方法是通过塞尺将裂缝之间的距离测量的方法。
适用于较小的裂缝宽度,且测量精度要求不高的情况。
2. 千分尺测量法该方法是通过千分尺等精密测量工具,对裂缝之间的距离进行精确测量的方法。
适用于较大裂缝宽度的测量,但测量成本较高。
三、通过经验公式计算经验公式是根据实践经验总结出来的计算裂缝宽度的公式,适用于特定的建筑物或结构。
常见的经验公式有:1. 温度裂缝经验公式该公式适用于温度变化引起的裂缝宽度变化较大的情况,可以根据温度变化系数和建筑物使用年限,计算出裂缝宽度。
2. 地基沉降裂缝经验公式该公式适用于地基沉降不均匀引起的裂缝宽度计算,可以根据地基沉降量和其他相关因素,计算出裂缝宽度。
注意事项:在进行裂缝宽度计算时,需要考虑建筑物的使用年限、环境条件、荷载大小等因素,并结合实际情况选择合适的计算方法。
此外,对于较大的裂缝宽度,建议采用精密测量工具进行测量,以确保测量结果的准确性和可靠性。
钢筋混凝土受弯构件的裂缝宽度和挠度计算

钢筋混凝土受弯构件的裂缝宽度和挠度计算钢筋混凝土受弯构件在使用过程中常常会出现裂缝,这对其承载能力和使用寿命产生了直接影响。
因此,正确计算裂缝宽度和挠度是保证构件安全和性能的重要环节。
本文将就钢筋混凝土受弯构件的裂缝宽度和挠度计算进行详细介绍,希望对相关工程人员有所指导。
首先,我们来介绍裂缝宽度的计算方法。
裂缝宽度主要受到荷载、构件尺寸、材料性能以及钢筋布置等因素的影响。
一般而言,裂缝宽度的计算可以采用两种方法:一是基于应变的方法,二是基于变形的方法。
基于应变的方法是通过计算构件内部混凝土的应变来确定裂缝宽度。
根据国内外的研究成果,一些常用的裂缝宽度计算公式可以参考,比如“行位裂缝宽度计算公式”和“游离裂缝宽度计算公式”。
这些公式可以根据结构的具体情况进行选择和应用。
另一种方法则是基于构件变形的方法,即根据构件变形的大小和变形能力来确定裂缝宽度。
这种方法一般采用挠度与裂缝宽度之间的经验关系,通过实测数据或者试验结果来获得。
此外,挠度也是钢筋混凝土受弯构件在设计和施工过程中需要考虑的一个重要参数。
挠度主要受到荷载、构件尺寸、材料性能等因素的影响。
正确计算挠度可以保证构件的稳定性和使用性能。
挠度的计算需要通过结构的静力分析和动力分析来确定。
静力分析方法一般适用于简单的构件,通过使用梁的弯曲理论可以求解得到挠度。
而动力分析方法适用于复杂结构和地震荷载作用下的构件,需要借助于数值计算和计算机模拟来完成。
通过合理地计算裂缝宽度和挠度,可以帮助我们了解钢筋混凝土受弯构件的行为,进一步指导施工过程中的操作,并保证结构的安全和使用寿命。
因此,工程人员在进行相关计算时应注意选取合适的计算方法,并结合实际情况进行验证和调整,以达到设计要求和规范的要求。
综上所述,钢筋混凝土受弯构件的裂缝宽度和挠度计算是保证结构安全和性能的重要环节。
正确计算裂缝宽度和挠度需要综合考虑荷载、构件尺寸、材料性能等因素,并采用合适的计算方法。
梁裂缝宽度、挠度计算计算书完整版

θ=2
回目录
f lim 1/300l0
20.0000
满足?OK!!!
OK!!!
OK!!!
计算说明:
1.本计算为梁跨中挠度及裂缝宽度连续计算表。
2.可自动计算梁内力,荷载计算考虑梁受均布荷载作用。( 梁内力按1/10ql2计算)
3.梁挠度计算公式为一端固定一端铰接梁 受 4.均按布表荷中载红作色用标下记的顺挠序度填。出个体工程计算 参 5.数梁值受。拉黑纵色向数钢据筋切实不配可面改积动及。直径可调 整,对计算结果较敏感。
梁截面特征 梁宽(mm) 梁高(mm) 梁压区翼缘板计算宽度(mm) 梁压区翼缘板计算高度(mm)
受拉钢筋合力点距离(mm) 梁钢筋保护层厚度(mm)
梁裂缝宽度、挠度计算书
b
h b'f h'f a(单排35;双排60~80)
C(25<C<32)
250 450 1500 100
70 30
材料特性 梁砼强度等级 砼轴心抗压强度(N/mm2) 砼轴心抗拉强度(N/mm2) 砼的弹性模量(N/mm2) 钢筋的抗拉强度(N/mm2) 钢筋的弹性模量(N/mm2)
10 6 2 0.5 4 6 2.8125
内力计算 标准组合弯矩(Kn*m) 准永久值组合弯矩(Kn*m)
Mk=1/10ql2 Mq=1/10ql2
161.33 146.93
梁跨中挠度计算 梁受拉纵向钢筋配筋率 钢筋与砼弹性模量比值 受拉翼缘面积与腹板有效面积比值 短期刚度(n.mm2) 受弯构件截面刚度(N.mm2) 梁跨中挠度计算(mm) 挠度控制值(mm) 裂缝验算结果
梁上荷载计算 梁上墙体荷载 楼板恒载(Kn/m2) 楼板活载(Kn/m2) 活载准永久值系数 梁荷载分布计算宽度(m) 梁计算跨度(m) 梁自重(Kn/m)
钢筋混凝土受弯构件的裂缝宽度和挠度计算

钢筋混凝土受弯构件的裂缝宽度和挠度计算摘要:一、钢筋混凝土受弯构件的裂缝宽度计算1.裂缝宽度的定义2.影响裂缝宽度的因素3.裂缝宽度计算的方法二、钢筋混凝土受弯构件的挠度计算1.挠度的定义2.影响挠度的因素3.挠度计算的方法三、计算示例及结果分析1.裂缝宽度计算示例2.挠度计算示例3.结果分析正文:钢筋混凝土受弯构件在工程中应用广泛,其裂缝宽度和挠度的计算是设计中必须要考虑的问题。
一、钢筋混凝土受弯构件的裂缝宽度计算1.裂缝宽度的定义裂缝宽度是指在受弯构件的表面上,两个相邻的裂缝之间的距离。
裂缝宽度的大小直接影响到构件的承载能力和使用寿命。
2.影响裂缝宽度的因素影响裂缝宽度的因素主要有混凝土的强度、钢筋的直径和间距、受力状态等。
3.裂缝宽度计算的方法根据规范,裂缝宽度可以通过计算得到。
一般采用经验公式计算,例如我国常用的裂缝宽度计算公式为:V = Aεf其中,V 为裂缝宽度,A 为受力钢筋面积,εf 为混凝土的抗拉强度与钢筋的弹性模量的比值。
二、钢筋混凝土受弯构件的挠度计算1.挠度的定义挠度是指受弯构件在受力过程中产生的弯曲变形。
挠度的大小影响到构件的使用性能和安全性。
2.影响挠度的因素影响挠度的因素主要有混凝土的强度、钢筋的直径和间距、受力状态等。
3.挠度计算的方法钢筋混凝土受弯构件的挠度计算一般采用弹性理论方法,即根据受力钢筋和混凝土的弹性模量、截面几何参数等计算出截面的弯曲刚度,然后根据荷载条件计算出挠度。
三、计算示例及结果分析1.裂缝宽度计算示例假设某受弯构件的混凝土强度为C30,钢筋直径为25mm,钢筋间距为300mm。
根据规范,εf=0.8,代入裂缝宽度计算公式,可得:V = π(d/2)^2εf = π(25/2)^2×0.8 = 318.5mm2.挠度计算示例假设某受弯构件的混凝土强度为C30,钢筋直径为25mm,钢筋间距为300mm。
根据规范,查表可得该构件的截面弯曲刚度为:Bl = 8000mm^3根据荷载条件,可计算出挠度:δ= Ql^4/Bl^3 = 1000000×(1000/8000)^3 = 157mm3.结果分析根据计算结果,该受弯构件的裂缝宽度为318.5mm,挠度为157mm。
钢筋混凝土受弯构件的裂缝宽度和挠度计算

【钢筋混凝土受弯构件的裂缝宽度和挠度计算】一、引言钢筋混凝土结构是现代建筑中常见的结构形式之一,而受弯构件作为其重要组成部分,其裂缝宽度和挠度的计算是设计过程中的关键内容。
在本文中,我将分析钢筋混凝土受弯构件的裂缝宽度和挠度计算,并对其进行深度探讨,希望能为您提供有价值的信息。
二、裂缝宽度计算1.裂缝宽度计算公式钢筋混凝土受弯构件的裂缝宽度计算可以使用以下公式进行:\[w_k = k \times \frac{f_s}{f_y} \times \frac{M_s}{b \times d}\]其中,\(w_k\)为裂缝宽度,\(k\)为调整系数,\(f_s\)为梁内应力,\(f_y\)为钢筋的屈服强度,\(M_s\)为抗弯强度矩,\(b\)为截面宽度,\(d\)为截面有效高度。
2.裂缝宽度计算包含的因素在裂缝宽度计算中,需要考虑梁内应力、钢筋的屈服强度以及抗弯强度矩等因素。
通过对这些因素的综合考虑,可以准确计算出钢筋混凝土受弯构件的裂缝宽度,从而确保结构的安全性。
三、挠度计算1.挠度计算公式钢筋混凝土受弯构件的挠度计算可以使用以下公式进行:\[f = \frac{5 \times q \times l^4}{384 \times E \times I}\]其中,\(f\)为挠度,\(q\)为荷载,\(l\)为构件长度,\(E\)为弹性模量,\(I\)为惯性矩。
2.挠度计算的影响因素在挠度计算中,荷载、构件长度、弹性模量和惯性矩等因素都会对挠度产生影响。
通过对这些因素进行综合考虑,并结合实际工程情况,可以准确计算出钢筋混凝土受弯构件的挠度,从而满足设计要求。
四、个人观点和理解钢筋混凝土受弯构件的裂缝宽度和挠度计算是结构设计中的重要内容,它直接关系到结构的安全性和稳定性。
在实际工程中,我们需要充分理解裂缝宽度和挠度计算的原理和方法,结合设计规范和实际情况,确保结构设计的合理性和可行性。
五、总结与展望通过本文的分析,我们深入探讨了钢筋混凝土受弯构件的裂缝宽度和挠度计算,并对其进行了详细介绍。
梁裂缝宽度、挠度计算(excel)

材料特性 梁砼强度等级 砼轴心抗压强度 砼轴心抗拉强度 钢筋等级 钢筋的弹性模量
内力计算 固端弯矩 跨中弯矩
梁支座裂缝计算 梁拉区翼缘板计算宽度 梁拉区翼缘板计算高度 梁受拉纵向钢筋实配面筋 梁受拉纵向钢筋等效直径 梁纵向钢筋的应力 有效钢筋配筋率 钢筋应变不均匀系数 梁裂缝宽度 裂缝控制值 裂缝验算结果
梁跨中裂缝计算 梁受拉纵向钢筋实配面筋 梁受拉纵向钢筋等效直径 梁纵向钢筋的应力 有效钢筋配筋率 钢筋应变不均匀系数 梁裂缝宽度 裂缝控制值 裂缝验算结果
梁裂缝宽度计算书
b(mm) h(mm) a(单排35mm;双排60mm~80mm) C(mm) (25<C<32)
9/5/20
(红色为输入数值) 800 750 70 30
C?(20,25,30,35,40) fc ftk fy
30 14.3
2.01 300 200000
1392.00 734.50
bf(mm)
hf(mm)
As
deq σsk=Mk/0.87/h0/As ρte =(As+Ap)/Ate; Ate=0.5bh+(bf-b)hf ψ=1.1-0.65*ftk/ρte/σsk(0.2<ψ<1) ωmax=αcr*ψ*σsk/Es*(1.9c+0.08deq/ρte)
ωlim (mm) 满足?OK!!!
2000
100 11000 28 213.90 0.0262 0.867 0.2775
0.4000 OK!!!
As
deq σsk=Mk/0.87/h0/As ρte =(As+Ap)/Ate; Ate=0.5bh ψ=1.1-0.65*ftk/ρte/σsk(0.2<ψ<1) ωmax=αcr*ψ*σsk/Es*(1.9c+0.08deq/ρte) ωlim (mm)
钢筋混凝土构件的裂缝宽度和挠度计算

钢筋混凝土构件的裂缝宽度和挠度计算钢筋混凝土结构是一种广泛应用的建筑结构形式。
在使用的过程中,由于各种因素的影响,钢筋混凝土构件会出现裂缝和挠度。
裂缝宽度和挠度的计算是设计和施工中非常重要的一步,下面将详细介绍钢筋混凝土构件的裂缝宽度和挠度计算的方法。
首先,我们先来了解什么是裂缝宽度。
裂缝宽度是裂缝两侧的最大间隔距离,通常用毫米来表示。
裂缝宽度的计算与构件所承受的荷载大小有关。
弹性模量法是一种基于线弹性理论的裂缝宽度计算方法。
该方法假设构件的截面保持线弹性行为,并且裂缝开口处的应力等于截面中的应力。
根据这个假设,可以通过使用构件的几何特征、材料性质以及荷载情况来进行计算。
弹性模量法的计算步骤如下:1.确定构件的几何特征,包括构件的截面形状、尺寸和钢筋的分布情况。
2.根据构件的截面形状和计算荷载,计算构件的抗弯承载力和抗剪承载力。
3.根据构件的弹性模量、截面的惯性矩和荷载情况,计算出构件所受到的弯矩和剪力。
4.计算裂缝宽度,可以使用一些经验公式或者根据经验计算裂缝宽度的公式,如ACI224R-01中给出的公式。
极限平衡法是一种基于非线性分析的计算方法,广泛用于钢筋混凝土构件的裂缝宽度计算。
该方法考虑了材料的非线性行为和构件在承受荷载过程中的变形情况。
极限平衡法的计算步骤如下:1.确定构件的几何特征和材料性质。
2.将构件的截面划分为若干离散截面,然后使用有限元或其他非线性分析方法计算每个离散截面的受力情况。
3.根据计算出的应力分布,计算裂缝宽度。
可以使用一些经验公式或者根据经验计算裂缝宽度的公式。
除了计算裂缝宽度,钢筋混凝土构件的挠度也是需要考虑的。
挠度是构件在受到荷载作用后产生的弯曲变形,通常用单位长度的偏移量表示。
挠度的计算方法与裂缝宽度计算类似,可以使用弹性模量法和极限平衡法等进行计算。
总而言之,钢筋混凝土构件的裂缝宽度和挠度的计算是设计和施工中的关键步骤。
正确的计算方法能够保证构件的安全性和使用寿命,并且提供准确的数据指导设计和施工。
混凝土梁的挠度计算

混凝土梁的挠度计算一、概述混凝土梁是建筑结构中常见的构件之一,承受着房屋和建筑物的重量和荷载。
在设计混凝土梁时,其挠度是一个必须要考虑的因素。
挠度是梁在荷载作用下发生的变形,是衡量梁的刚度和稳定性的一个重要指标。
因此,对混凝土梁的挠度进行计算和评估是十分必要的。
二、计算方法混凝土梁的挠度计算可以通过以下方法进行。
1. 简化法简化法是一种快速计算混凝土梁挠度的方法,适用于简单的梁结构。
其基本思路是将梁看作一个简单支承梁,并假设荷载均匀分布在梁的整个跨度上。
其计算公式为:δ=5wl^4/(384EI)其中,δ为梁的挠度,w为单位长度的荷载,l为梁的跨度,E为混凝土的弹性模量,I为梁的截面惯性矩。
2. 复杂法复杂法是一种更加精确的计算混凝土梁挠度的方法,适用于复杂的梁结构。
其基本思路是将梁的跨度分为若干小段,并在每段上分别计算挠度。
其计算公式为:δ=∑(wi^2l^4)/(8EI)其中,i为梁的小段编号,wi为该小段的荷载,l为该小段的长度,E 为混凝土的弹性模量,I为梁的截面惯性矩。
3. 有限元法有限元法是一种计算混凝土梁挠度的高精度方法,适用于复杂的梁结构和非线性分析。
其基本思路是将梁的跨度离散化为若干个小单元,再通过计算每个小单元的应力和变形来确定整个梁的挠度。
该方法需要使用专业的有限元软件进行计算。
三、影响因素混凝土梁的挠度受到多种因素的影响,包括以下几个方面。
1. 荷载荷载是影响混凝土梁挠度的主要因素之一。
荷载越大,梁的挠度就越大。
此外,荷载的位置和分布也会对梁的挠度产生影响。
2. 梁的截面形状和尺寸梁的截面形状和尺寸是影响混凝土梁挠度的重要因素。
一般来说,梁的截面越大,挠度就越小。
此外,梁的形状也会影响挠度,比如梁的高宽比、截面形状等。
3. 混凝土的强度和材料特性混凝土的强度和材料特性也会对梁的挠度产生影响。
强度越高的混凝土梁,挠度就越小。
此外,混凝土的弹性模量和泊松比等材料特性也会影响梁的挠度。
钢筋混凝土受弯构件的裂缝宽度和挠度计算

钢筋混凝土受弯构件的裂缝宽度和挠度计算【最新版】目录1.钢筋混凝土受弯构件裂缝宽度和挠度计算的背景和意义2.裂缝宽度和挠度计算的理论基础3.裂缝宽度和挠度计算的方法和步骤4.计算结果的分析和应用5.结论和展望正文钢筋混凝土受弯构件的裂缝宽度和挠度计算是建筑结构设计中的重要环节,关系到结构的安全性、稳定性和耐久性。
在实际工程中,裂缝宽度和挠度通常是混凝土结构受弯构件的主要设计控制参数,因此,对它们的精确计算和分析具有重要的现实意义。
一、钢筋混凝土受弯构件裂缝宽度和挠度计算的理论基础裂缝宽度和挠度是受弯构件的两个主要变形参数。
其中,裂缝宽度是指混凝土受弯构件在弯曲过程中,由于内部应力达到极限而产生的裂缝的宽度;而挠度则是指受弯构件在弯曲过程中,构件的中性轴线偏离原位置的距离。
二、裂缝宽度和挠度计算的方法和步骤在实际工程中,裂缝宽度和挠度的计算通常采用以下的方法和步骤:1.确定受弯构件的材料性能参数,包括混凝土的抗压强度、抗拉强度、弹性模量等;2.根据受弯构件的几何参数和荷载条件,确定构件的截面几何形状和尺寸;3.采用适当的数学方法(如有限元法、矩方法等)计算受弯构件在荷载作用下的应力和应变分布;4.根据计算结果,确定裂缝宽度和挠度的数值。
三、计算结果的分析和应用裂缝宽度和挠度的计算结果可以反映受弯构件在弯曲过程中的变形情况,为结构设计提供重要的依据。
通常,我们需要对计算结果进行以下的分析和应用:1.检验裂缝宽度和挠度是否符合设计规范的要求;2.如果不符合要求,则需要调整设计参数(如增加截面尺寸、改变材料性能等)重新计算,直到满足设计要求;3.根据裂缝宽度和挠度的计算结果,确定受弯构件的耐久性和安全性。
四、结论和展望钢筋混凝土受弯构件的裂缝宽度和挠度计算是建筑结构设计的重要内容。
随着计算机技术和数学方法的发展,计算方法和工具也越来越精确和便捷。
混凝土结构变形裂缝宽度及混凝土结构耐久性计算

混凝土结构变形裂缝宽度及混凝土结构耐久性计算
一、混凝土结构变形裂缝宽度计算
变形裂缝宽度是混凝土结构设计中需要考虑的一个重要参数。
混凝土
结构在受到荷载作用时,会产生变形,如果此时混凝土受力过大,就会发
生裂缝。
变形裂缝宽度是用来评估混凝土结构的变形程度和结构的安全性。
1.收缩和膨胀引起的裂缝宽度计算
混凝土的收缩和膨胀是由于水化反应引起的,当混凝土的含水量发生
变化时,就会引起收缩和膨胀。
收缩引起的裂缝宽度一般不会超过0.3mm,膨胀引起的裂缝宽度一般不会超过0.1mm。
2.温度引起的裂缝宽度计算
W=αLΔT
1.混凝土的质量
混凝土的质量对混凝土结构的耐久性有着重要的影响。
混凝土应具有
足够的抗压强度和耐久性,可以通过混凝土的抗压强度和氯离子渗透性试
验等进行评估。
2.混凝土结构的设计
3.混凝土结构的施工和维护
总结起来,混凝土结构变形裂缝宽度及耐久性的计算是混凝土结构设
计中不可或缺的一部分。
通过合理的设计、施工和维护,可以确保混凝土
结构的变形裂缝宽度和耐久性满足设计要求,保证结构的安全性和可靠性。
混凝土结构09挠度、裂缝宽度验算及延性和经久性

延性和经久性的定义和要求
延性
结构在发生破坏前具有较大的变形能力,能够吸收和分散荷载。
经久性
结构在使用寿命内能够满足设计要求,不出现过度变形、破坏和损坏。
延性和经久性的评价和检验方法
结构破坏
评价结构是否具有足够的延性和 经久性的关键因素。
定期维护
通过定期检查和维护,延长结构 的使用寿命。
混凝土测试
2ห้องสมุดไป่ตู้
挤压挠度
由于混凝土的收缩和膨胀引起的变形,需要控制在允许范围内。
3
剪切挠度
主要考虑梁柱节点的剪切变形,应满足相关规范要求。
裂缝宽度的验算方法
应力平衡法
通过考虑混凝土的应力平衡条 件,计算裂缝的宽度。
应变调整法
通过考虑混凝土的温度变形和 收缩变形,计算裂缝的宽度。
静惯性法
通过考虑结构惯性和刚度,计 算裂缝的宽度。
通过对混凝土进行强度、硬度等 参数的测试,评估结构的延性和 经久性。
混凝土结构设计中的注意事项
1 合理的梁、柱布局
通过合理的布局,减小结构的变形和应力集中。
2 正确选择混凝土强度等级
根据结构的要求和使用条件,选择合适的混凝土强度等级。
3 考虑温度和湿度变化
混凝土在干燥或潮湿环境下会发生收缩或膨胀,需要考虑这些因素。
混凝土结构09挠度、裂缝 宽度验算及延性和经久性
本演示将介绍混凝土结构中的挠度、裂缝宽度的验算方法,以及延性和经久 性的定义、评价和检验方法。
设计要求
混凝土结构设计应符合建筑设计规范和强度要求,并考虑结构的安全性、可靠性和经济性。
混凝土的挠度验算
1
弯曲挠度
通过梁的截面形状和受力状态计算得出,应满足设计要求。
钢筋混凝土构件的裂缝宽度和挠度计算课件

可以采用水准仪、全站仪、挠度计等测量设备监测结构的挠 度。也可以通过观察结构表面是否出现明显的弯曲变形来判 断挠度大小。
05
钢筋混凝土构件的工程实例分析
工程实例一:某大桥的裂缝宽度和挠度计算
总结词
大型桥梁结构,受力复杂,需要精确计算裂缝宽度和挠度。
详细描述
某大型桥梁采用钢筋混凝土结构,由于承受较大的车辆载荷和风载,需要对裂缝宽度和挠度进行精确 计算。通过建立有限元模型,分析不同工况下的应力分布,并采用相应的规范公式计算裂缝宽度和挠 度。
裂缝宽度的控制标准
根据不同的使用环境和结构类型,规范规定了裂缝宽度的限值。超过限值则需要 进行加固或修复。
挠度的控制标准
为了保证结构的正常使用,规范要求在正常荷载作用下,结构的最大挠度应不超 过允许值。
裂缝宽度和挠度的监测方法
裂缝宽度的监测方法
可以采用肉眼观察、刻度放大镜、裂缝测宽仪等方法监测裂 缝宽度。对于细微的裂缝,可以采用涂色或贴石膏条等方法 观察。
钢筋混凝土构件的裂缝宽度和挠度 计算课件
目 录
• 钢筋混凝土构件的基本知识 • 钢筋混凝土构件的裂缝宽度计算 • 钢筋混凝土构件的挠度计算 • 钢筋混凝土构件的裂缝宽度和挠度的关系 • 钢筋混凝土构件的工程实例分析
contents
01
钢筋混凝土构件的基本知识
钢筋混凝土构件的组成
钢筋
钢筋与混凝土的粘结力
钢筋混凝土构件的应用
桥梁
作为主要的承载结构,广 泛应用于各类桥梁工程中。
建筑
高层建筑、大跨度结构等 都采用钢筋混凝土作为主 要结构材料。
水利工程
大坝、水闸等水利设施中 广泛应用钢筋混凝土结构。
02
混凝土梁柱极限挠度和裂缝宽度计算

件能承受的最大弯矩和最大剪力。代入求得最大弯矩
为 179.507kN ·m, 最 大 剪 力 为 71.8kN。
1!0=
"$,'")2
/02 *
'
(2)
式中: 为计算截面的剪跨比,=3/'0,3 为集中荷
载作用点距支座截面或节点边缘的距离;当 <1.5时
取 1.5;当 >3时取 3。由公式(2)可计算箍筋。截面配
心受拉构件,取 *+=2.7;45 为最外层纵向受拉钢筋外
边 缘 至 受 拉 区 底 边 的 距 离 , 当 45<20mm 时 ,取
45=20mm;当 45>65mm时,取 45=65mm。由公式(4)计
算得跨中最大挠度变形为 11.872mm;由公式(5)计算
得最大裂缝宽度为 0.414mm。
"!#=20.1N/mm2,"$=1.43N/mm2,"$#=2.01N/mm2,%&=3.00× 104N/mm2,'(=460mm。 钢 筋 材 料 参 数 :")=360N/mm2, %*=2.00×105N/mm2。
+ "!,-.")/0
(1)
=.")/(0 '0-2- )
式中:1混凝土强度等级小于获等于 C50时,取 1=1.0。纵筋面积 /0=1256mm2。由公式(1)可计算出构
典型的受弯构件正截面试验梁一般为单筋矩形 截面简支梁,该梁应具有足够的抗剪能力,以保证在 受弯实验中不发生剪切破坏。其加载方式为集中荷载 跨中加载,荷载逐级加载,由零开始直至梁正截面受
. A弯l破l 坏R,i此gh时t跨s中R变es形e最rv大e,d即.为最大挠度,同时也是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6789:;<=>?@AB>CD
(安徽天成建设有限公司 ,安徽 六安 237000)
EFGHIJKLM 安徽建筑
% &在竖向荷载作用下,截面 250mm×500mm,净跨 5m的 钢筋混凝土梁发生弯曲变形。混凝土开裂前钢筋混凝土协同工 作,混凝土开裂后,混凝土退出工作,构件进入带裂缝工作阶段 直到钢筋屈服,记录此状态下最大挠度变形和裂缝宽度;在竖 向和水平荷载作用下,截面 400mm×400mm,高度 3m的钢筋 混凝土柱发生大偏心受压,计算其最大挠度和裂缝宽度。 ' ( ) 简支梁;偏心受压柱;极限挠度;极限裂缝宽度 *+,-.!"#$% /0123& / 4 5 . $''()(#*+ %'$+ '$)''(%)'# ,-.$'/$0##'12345673$''(8(#*+3%'$+3'$3'#'
图4
(a)
图5
(b)
给定的轴压比为 =0.4,由此计算出轴力 N、e,基
本公式如下。
=7 !*6
(6)
70!8 6, =1!* 9)+!8 '6, '
72=1!*
9)(:0-2) )+!8
';,(':0-(,
')
(7)
求得 7=915200N,2=399mm
3.5.1短期刚度 E, 计算
同时承受轴力和弯矩的构件为偏心受压构件,轴 力 N和弯矩 M的共同作用等效于一个偏心距 20=M/N 的偏心压力的作用,因此偏心受压构件不仅是最基 本、应用最广泛的构件之一。如图 2所示的钢筋混凝 土柱受到水平力 P和竖向轴压力 N的作用,相当于 偏心受压。柱在给定轴压比、纵筋、箍筋的条件下验算 其承载力,计算其最大变形、最大裂缝宽度。柱截面配 筋见图 4,纵筋单侧配筋率为 0.6%,即 6,=942mm2;全 部纵筋配筋率为 1.2%,在要求范围内(0.5%~5.0%)。
不考虑荷载的长期作用,即不考虑受压区混凝土
2<2=
0
: +
>(,
2
=
=2*
+2(
,2(
"'()
+*,$,****
?
2 =
*
7
?=@$
由上式求得:?=200.429kN·m,@=67kN。
(9)
在给定箍筋配筋的情况下须验证柱子能承受的
最大剪力,柱子两端在压力的作用下对其抗剪能力有
一定的提高,量化后具体为 0.07N(7'() 为 0.3!*6)
净跨为 5m,保护层厚度 !=20mm,纵筋和箍筋都为 钢筋应变不均匀系数,当 <0.2时取 0.2,当 >1.0时
HRB400 混 凝 土 材 料 参 数 :"!=14.3N/mm2, 取 1.0,对直接承受重复荷载的构件取 =1.0;"'为受
压翼缘加强系数,对矩形截面,"'=0。
! " # $ 涂好祖(1975-),男,安徽六安人,毕业于皖西学院土木工程 专业,本科,工学学士,硕士,工程师。专业方向:建筑工程。
"!#=20.1N/mm2,"$=1.43N/mm2,"$#=2.01N/mm2,%&=3.00× 104N/mm2,'(=460mm。 钢 筋 材 料 参 数 :")=360N/mm2, %*=2.00×105N/mm2。
+ "!,-.")/0
(1)
=.")/(0 '0-2- )
式中:1混凝土强度等级小于获等于 C50时,取 1=1.0。纵筋面积 /0=125筋混凝土梁开裂后的短 期刚度 4*=3.15×1013N·mm2
安徽建筑
!" #$# $%%&
(4)
'()=*+
,.,
(&'(/,0)'*%
1232
)
(5)
式中:*+ 为构件受力特征系数,对受弯、偏心受
压构件,取 *+=1.9;对偏心受拉构件,取 *+=2.4;对轴
件能承受的最大弯矩和最大剪力。代入求得最大弯矩
为 179.507kN ·m, 最 大 剪 力 为 71.8kN。
1!0=
"$,'")2
/02 *
'
(2)
式中: 为计算截面的剪跨比,=3/'0,3 为集中荷
载作用点距支座截面或节点边缘的距离;当 <1.5时
取 1.5;当 >3时取 3。由公式(2)可计算箍筋。截面配
A=1.+715!3 9:0+!8B
6,B 5
:0+0.077
: <
CD
-+
0
7=0.3!* 6
(10)
由上式求得柱子能承受的最大剪力为 204kN,大
于水平力 @,故柱子抗剪能力满足要求。
由图 5(a)所示,柱最大变形发生在柱顶,根据结 构力学图乘法可求得变形量大小,如图 5(b)所示。
心受拉构件,取 *+=2.7;45 为最外层纵向受拉钢筋外
边 缘 至 受 拉 区 底 边 的 距 离 , 当 45<20mm 时 ,取
45=20mm;当 45>65mm时,取 45=65mm。由公式(4)计
算得跨中最大挠度变形为 11.872mm;由公式(5)计算
得最大裂缝宽度为 0.414mm。
筋见图 3。
图3
图 1 集中荷载加载图 图 2 柱加载图
2
40=
%* /* '0
1.15+0.2+ 6%
1+3.5"'
(3)
式中:40 为钢筋混凝土梁开裂后的短期刚度,由
于不考虑荷载的长期作用,即不考虑受压区混凝土发
混凝土使用 C30,梁截面尺寸为 250mm×250mm, 生的徐变,所以采用短期刚度; 为裂缝间纵向受拉
