第11章 习题
大学物理习题答案第十一章

[习题解答]11-7 在磁感应强度大小为B = 0.50 T 的匀强磁场中,有一长度为l = 1.5 m 的导体棒垂直于磁场方向放置,如图11-11所示。
如果让此导体棒以既垂直于自身的长度又垂直于磁场的速度v 向右运动,则在导体棒中将产生动生电动势。
若棒的运动速率v = 4.0 m ⋅s -1 ,试求:(1)导体棒内的非静电性电场K ;(2)导体棒内的静电场E ;(3)导体棒内的动生电动势ε的大小和方向;(4)导体棒两端的电势差。
解(1)根据动生电动势的表达式,由于()的方向沿棒向上,所以上式的积分可取沿棒向上的方向,也就是d l 的方向取沿棒向上的方向。
于是可得.另外,动生电动势可以用非静电性电场表示为.以上两式联立可解得导体棒内的非静电性电场,为,方向沿棒由下向上。
图11-11(2)在不形成电流的情况下,导体棒内的静电场与非静电性电场相平衡,即,所以,E 的方向沿棒由上向下,大小为.(3)上面已经得到,方向沿棒由下向上。
(4)上述导体棒就相当一个外电路不通的电源,所以导体棒两端的电势差就等于棒的动生电动势,即,棒的上端为正,下端为负。
11-8 如图11-12所表示,处于匀强磁场中的导体回路ABCD ,其边AB 可以滑动。
若磁感应强度的大小为B = 0.5 T ,电阻为R = 0.2 Ω,AB 边长为 l = 0.5 m ,AB 边向右平移的速率为v = 4 m ⋅s -1 ,求:(1)作用于AB 边上的外力;(2)外力所消耗的功率;(3)感应电流消耗在电阻R 上的功率。
解(1)当将AB 向右拉动时,AB 中会有电流通过,流向为从B 到A 。
AB 中一旦出现电流,就将受到安培力F 的作用,安培力的方向为由右向左。
所以,要使AB 向右移动,必须对AB施加由左向右图11-12的力的作用,这就是外力F外。
在被拉动时,AB中产生的动生电动势为,电流为.AB所受安培力的大小为,安培力的方向为由右向左。
外力的大小为,外力的方向为由左向右。
细胞生物学第十一章细胞增殖习题及答案 done

第11章细胞增殖及其调控1.高等生物内所有细胞依繁殖状态可分为哪几类?各有何特征?答:大体可以分为四类:(1)G1期细胞(DNA合成前期):细胞代谢活跃,细胞生长、体积增大,主要进行大部分蛋白质和RNA的合成工作。
(2)S期细胞(DNA合成期):此阶段细胞内完成DNA的复制,以及组蛋白、非组蛋白合成与核小体结构的复制。
(3)G2期细胞(DNA合成后期):此阶段的细胞做分列前的最后准备,合成周期蛋白、微管蛋白等。
(4)M期:细胞进入分裂过程,分裂中,细胞内生化合成活动减弱,例如:RNA合成停止,蛋白质合成减少,此期仍有少量非组蛋白合成。
又分前、中、后、末四个状态。
(a)前期主要事件:染色体凝缩,分裂极确定,核仁解体和核膜消失。
(b)中期此期染色体全部移到赤道板位置排列“染色体列队”,是由于以两极对染色体牵引为动态平衡所致。
(c)后期此期主要事件:染色体着丝粒粒区纵向断裂,一分为二。
两姐妹染色单体分别趋向两极。
(d)末期此期的主要事件:子核形成的胞质分裂。
胞质分裂是指核分裂以外的细胞质部分分裂。
动物细胞是以中部缢缩方式,而植物细胞是以形成细胞壁方式进行胞质分裂的。
2.运用3H—TdR的脉冲标况技术如何测定推测细胞周期?答:此内容不考,飘过。
P.S.要看看细胞周期同步化的内容。
3.简述细胞周期中DNA、RNA,组蛋白和非组蛋白的合成概况。
答:见习题1。
4.细胞周期中有哪几个重要的检验点,各有何作用?答:所熟知的有3个检验点:(1)G1->S的检验点:检查G1期的蛋白质、RNA合成工作是否完成。
细胞增殖行为会在G1期之后发生分歧,分为周期细胞和G0期细胞或终端分化细胞。
(2)G2->M期的检验点:检查M期之前的物质、能量准备工作,并进行G2向M期的转变。
该过程由CDK激酶进行调控,CDK1使组蛋白H1磷酸化,促进染色质凝集;使核纤层蛋白磷酸化,使核纤层解聚;核仁蛋白磷酸化,促使核仁解体等等。
第11章 收入习题

第11章收入习题一、判断题1.收入能够导致企业所有者权益增加,因此,能导致所有者权益增加的就应确认为企业的收入。
()解释:收入能够导致企业所有者权益增加,但导致所有者权益增加的并不一定都是收入。
收入能够导致所有者权益增加,因为收入会导致企业利润增加,从而导致盈余公积和未分配利润这两个所有者权益项目增加,但是除了这两个项目外,所有者权益还包括实收资本和资本公积项目,企业增资扩股等业务会导致实收资本和资本公积项目增加,从而导致所有者权益增加,但并不是企业的收入。
2.企业无法支付的应付账款,经批准计入“营业外收入”,该收入不属于狭义的收入。
()3.企业的“主营业务收入”科目,核算日常活动形成的收入,而“其他业务收入”核算非日常活动形成的收入。
()4.企业只要将商品所有权上的主要风险和报酬转移给了购货方,就可以确认收入。
()解释:企业商品销售收入的确认应同时符合五个条件:5.企业在确定商品销售收入时,不考虑各种可能发生的现金折扣和销售折让。
()解释:现金折扣在实际发生时计入当期财务费用;销售折让应在实际发生时冲减发生当期的收入(非日后事项)。
6.企业对于已经发出但尚未确认销售收入的商品成本,应借记“在途物资”科目。
()7.企业销售商品时,收到购货方用以结算货款的银行汇票结算凭证,应借记“其他货币资金—银行汇票存款”。
()8.在采用只收取手续费委托代销销售方式下,委托方应在收到代销产品的货款时确认收入。
()9.采用视同买断方式代销商品的,受托方应在商品销售后按双方协议价格确认收入。
()解释:采用视同买断方式代销商品的,受托方应在商品销售后按不含税的销售价款确认收入。
10.对于在合同中规定了买方有权退货条款的销售,如无法合理确定退货的可能性,销货方应在退货期满时确认收入。
()11.售后回购是指商品销售的同时,销售方同意日后重新买回这批商品,在这种情况下,就视为融资行为,不确认为收入。
()解释:售后回购行为的实质是以商品作抵押,融得一笔资金的使用权。
11结构的稳定计算习题解答

第11章 结构的稳定计算习题解答习题11.1 是非判断题(1)要提高用能量法计算临界荷载的精确度,不在于提高假设的失稳曲线的近似程度,而在于改进计算工具。
( )(2)对称结构承受对称荷载时总是按对称形式失稳。
( )(3)刚架的稳定问题总是可以简化为具有弹性支座的单根压杆进行计算。
( ) (4)结构稳定计算时,叠加原理已不再适用。
( )(5)有限自由度体系用能量法求出的临界荷载是精确解。
( )(6)当结构处于不稳定平衡状态时,可以在原结构位置维持平衡,也可以在新的形式下维持平衡。
( )【解】(1)错误。
能量法计算临界荷载的精确度,直接取决于所假设的失稳曲线的近似程度。
(2)错误。
既可按对称形式失稳也可按反对称形式失稳。
(3)错误。
在能求出刚度系数的情况下,才可简化为具有弹性支座的单根压杆进行计算。
(4)正确。
一般情况下,结构的稳定计算中,既要考虑几何非线性也要考虑材料非线性,因此,不能采用适用于线性弹性理论的叠加原理。
(5)正确。
(6)错误。
习题 12.2 填空题(1)结构由稳定平衡到不稳定平衡,其临界状态的静力特征是平衡形式的 。
(2)临界荷载与压杆的支承情况有关,支承的刚度越大,则临界荷载越 。
(3)用能量法求无限自由度体系的临界荷载时,所假设的失稳曲线y (x )必须满足 条件,并尽量满足 条件。
(4)利用对称性,求习题11.2(4)图所示结构的临界荷载F Pcr = 。
习题11.2(4)图(5)习题11.2(5)图(a )所示结构可简化为习题11.2(5)图(b )所示单根压杆计算,则弹簧抗转动刚度系数k = 。
1=l3EI(a) (b)习题11.2(5)图(6)习题11.2(6)图(a )所示结构可简化为习题11.2(6)图(b )计算,则抗移动弹簧刚度系数k 1= ,抗转动弹簧刚度系数k 2= 。
(a)(b)习题11.2(6)图【解】(1)二重性。
(2)大。
(3)位移边界;力的边界。
《高数》下册第十一章练习题

第十一章 曲线积分与曲面积分习题 11-11.设在xOy 面内有一分布着质量的曲线弧L ,在点(x,y )处它的线密度为μ(x,y )。
用对弧长的曲线积分分别表达:(1)这曲线弧对x 轴,对y 轴的转动惯量x I ,y I(2)这曲线弧的质心坐标x ,y2.利用对弧长的曲线积分的定义证明性质33.计算下列对弧长的曲线积分: (1)22(x y )nLds +⎰,其中L 为圆周x cos t,y sin (0t 2)a a t π==≤≤(2)(x y)ds L+⎰,其中L 为连接(1,0)及(0,1)两点的直线段(3)x Lds ⎰,其中L 为由直线y=x 及抛物线2y x =所围成的区域的整个边界 (4)22x y Leds +⎰,其中L 为圆周222x y a +=,直线y=x 及x 轴在第一象限内所围成的扇形的整个边界(5)2221ds x y z Γ++⎰,其中Γ为曲线cos ,sin ,t t tx e t y e t z e ===上相应于t 从0变到2的这段弧 (6)2x yzds Γ⎰,其中Γ为折线ABCD ,这里A,B,C,D 依次为点(0,0,0),(0,0,2),(1,0,2),(1,3,2) (7)2Ly ds ⎰,,其中L 为摆线的一拱(t sin ),y (1cos )(0t 2)x a t a t π=-=-≤≤(8)22(x )ds Ly +⎰,其中L 为曲线(cos sin ),y (sin cos )(0t 2)x a t t t a t t t π=+=-≤≤4.求半径为a,中心角为2ϕ的均匀圆弧(线密度1μ=)的质心5.设螺旋形弹簧一圈的方程为cos ,sin ,x a t y a t z kt ===,其中02t π≤≤,它的线密度222(x,y,z)x y z ρ=++.求: (1)它关于z轴的转动惯量z I(2)它的质心。
习题 11-21.设L 为xOy 面内直线x a =上的一段,证明:(x,y)dx 0LP =⎰2.设L 为xOy 面内x 轴上从点(a,0)到点(b,0)的一段直线,证明:(x,y)dx (x,0)dxbLaP P =⎰⎰3.计算下列对坐标的积分: (1)22(xy )Ldx-⎰,其中L 是抛物线2y x =上从点(0,0)到点(2,4)的一段弧(2)Lxydx⎰,其中L 为圆周222(x )a a y a -+=(>0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行) (3)Lydx xdy+⎰,其中L 为圆周cos ,sin x R t y R t ==上对应t 从0到2π的一段弧(4)22(x y)dx (x y)dy L x y +--+⎰,其中L 为圆周222+y x a =(按逆时针方向绕行) (5)2x dx zdy ydzΓ+-⎰,其中Γ为曲线cos ,sin x k y a z a θ,θθ===上对应θ从0到π的一段弧 (6)(x y 1)dz xdx ydy Γ+++-⎰,其中Γ是从点(1,1,1)到点(2,3,4)的一段直线(7)+y dx dy dzΓ-⎰,其中Γ为有向闭折线ABCD ,这里的A,B,C 依次为点(1,0,0),(0,1,0),(0,0,1) (8)22(x2xy)dx (y 2xy)dyL-+-⎰,其中L 是抛物线2y x =上从点(-1,1)到点(1,1)的一段弧 4.计算(x y)dx (y x)dy L++-⎰,其中L 是:(1)抛物线2y x =上从点(1,1)到点(4,2)的一段弧(2)从点(1,1)到点(4,2)的直线段(3)先沿直线从点(1,1)到点(1,2),然后再沿直线到点(4,2)的折线(4)曲线2221,1x t t y t =++=+上从点(1,1)到点(4,2)的一段弧 5.一力场由沿横轴正方向的恒力F 所构成,试求当一质量为m 的质点沿圆周222x y R +=按逆时针方向移过位于第一象限的那一段弧时场力所做的功6.设z 轴与动力的方向一致,求质量为m 的质点从位置(x,y,z )沿直线移到(x,y,z )时重力所做的功7.把对坐标的曲线积分(x,y)dx Q(x,y)dyLP +⎰化成对弧长的积分曲线,其中L 为:(1)在xOy 面内沿直线从点(0,0)到点(1,1)(2)沿抛物线2y x =从点(0,0)到点(1,1)(3)沿上半圆周222x y x +=从点(0,0)到点(1,1) 8.设Γ为曲线23,,x t y t z t ===上相应于t 从0变到1的曲线弧,把对坐标的曲线积分Pdx Qdy RdzΓ++⎰化成对弧长的曲线积分习题 11-31.计算下列曲线积分,并验证格林公式的正确性: (1)22(2xy x )dx (x y )dyL-++⎰,其中L 是由抛物线2y x =和2y x =所围成的区域的正向边界曲线 (2)222(x xy )dx (y 2xy)dyL-+-⎰,其中L 是四个顶点分别为(0,0),(2,0),(2,2),(0,2)的正方形区域的正想边界2.利用曲线积分,求下列曲线所围成的图形的面积 (1)星形线33cos ,sin x a t y a t ==(2)椭圆229+16y 144x = (3)圆222x y ax +=3.计算曲线积分22ydx 2(x y )L xdy -+⎰,其中L 为圆周22(x 1)2y -+=,L 的方向为逆时针方向4.证明下列曲线积分在整个xOy 面内与路径无关,并计算积分值(1)(2,3)(1,1)(x y)dx (x y)dy++-⎰(2)(3,4)2322(1,2)(6xy y )dx (63)dy x y xy -+-⎰(3)(2,1)423(1,0)(2xy y 3)dx (x 4xy )dy-++-⎰5.利用格林公式,计算下列曲线积分: (1)(2x y 4)dx (5y 3x 6)dyL-+++-⎰,其中L 为三顶点分别为(0,0),(3,0)和(3,2)的三角形正向边界;(2)222(cos 2sin )(x sinx 2ye )dyx x Lx y x xy x y e dx +-+-⎰,其中L 为正向星形线222333(a 0)x y a +=>(3)3222(2xy y cosx)(12ysinx 3x y )dyLdx -+-+⎰,其中L 为在抛物线22x y π=上由点(0,0)到(2π,1)的一段弧(4)22(xy)dx (x sin y)dyL--+⎰,其中L 是在圆周22y x x =-上由点(0,0)到点(1,1)的一段弧6.验证下列(x,y)dx (x,y)dy P Q +在整个xOy 平面内是某一函数u(x,y)的全微分,并求这样的一个u(x,y):(1)(2)(2)x y dx x y dy +++(2)22xydx x dy + (3)4sin sin3cos 3cos3cos 2x y xdx y xdy -(4)2232(38)(812)y x y xy dx x x y ye dy ++++ (5)22(2cos cos )(2sin sin )x y y x dx y x x y dy ++- 7.设有一变力在坐标轴上的投影为2,28X x y Y xy =+=-,这变力确定了一个力场。
国际贸易实务习题第章

国际贸易实务习题第章第11章第十一章商品检验、索赔、不可抗力和仲裁一、单项选择题1、以仲裁方式解决贸易争议的必要条件是()A、双方当事人订有仲裁协议B、双方当事人订有合同C、双方当事人无法以协商解决D、一方因诉讼无果而提出2、“离岸重量、到案品质”是指()A、装运港检验B、目的港检验C、出口国检验、进口国复验D、装运港检验重量、目的港检验品质3、在众多检验商品品质的方法中,最常用的是()A、装运港检验B、目的港检验C、出口国检验、进口国复验D、装运港检验重量、目的港检验品质4、在国际货物买卖合同中,作为卖方的A公司和作为买方的B公司,B在合同签订后将10万美元定金先付给A公司,后A公司没有履行合同,问A公司应该返还B公司多少万美元()A、10B、20C、5D、255、短交在多数情况下,应该向谁索赔()A、保险公司B、买方C、卖方D、承运人6、我国某公司与新加坡一家公司以CIF新加坡的条件出口一批土产品,订约时,我国公司已知道该批货物要转销美国。
该货物到新加坡后,立即转运美国。
其后新加坡的买主凭美国商检机构签发的在美国检验的证明书,向我提出索赔。
问,美国的检验证书是否有效()A、有效B、无效,应要求新加坡商检机构出具证明C、无效,应由合理第三国商检机构出具证明D、其它7、我某粮油食品进出口公司与美国田纳西州某公司签订进口美国小麦合同,数量为100万公吨。
麦收前田纳西州暴雨成灾,到10月份卖方应交货时小麦价格上涨。
美方未交货。
合同订有不可抗力条款,天灾属于该条款的范围,美方据此要求免责。
此时,我方应()A、不可抗力,予以免责,并解除合同。
B、未构成不可抗力,坚持美方应按合同规定交货。
C、构成不可抗力,可以解除合同,但要求损害赔偿。
D、成不可抗力,但不要求损害赔偿,亦不解除合同,而要求推迟到下年度交货。
8、下列关于仲裁裁决的效力描述不正确的是()A、凡由中国国际经济贸易仲裁委员会做出的裁决一般是终局性的,对双方都有约束力。
第11章-作业及习题参考答案

第11章(8分)将下面程序划分为基本块,并画出其基本块程序流图。
(1) if a<b goto (3)(2) halt(3) if c<d goto (5)(4) goto (8)(5) t1:=y+z(6) x :=t1(7) goto (1)(8) t2:=y-z(9) x :=t2(10) goto (1)11.1答:所谓代码优化即对代码进行等价变换,使得变换后的代码与变换前代码运行结果相同,而运行速度加快或占用存储空间少,或两者兼有。
进行优化的基础是中间或目标代码生成,以及基本块的识别、控制流分析和数据流分析。
2答:根据不同的阶段,分为中间代码优化和目标代码的优化。
根据优化所涉及的程序范围,又可分为局部优化、循环优化和全局优化。
3答:最常用的代码优化技术有:(1)删除多余运算(2)代码外提(3)强度削弱(4)变换循环控制条件(5)合并已知量和复写传播(6)删除无用赋值4 图11.23是图11.22的C代码的部分四元式代码序列(1) 请将图11.23的四元式代码序列划分为基本块并做出其流图?(2) 将每个基本块的公共子表达式删除?(3) 找出流图中的循环,将循环不变量计算移出循环外?(4) 找出每个循环中的归纳变量,并且在可能的地方删除它们图11.22void quicksort(m,n)int m,n;1 / 10{ int i,j;int v,x; if (n<=m) return;/* fragment begins here */ i = m-1;j = n;v = a[n];while(1) {do i = i+1;while (a[i]<v);do j = j-1; while (a[j]>v);if (i>=j) break;x = a[i];a[i] = a[j];a[j] = x;}x = a[i];a[i] = a[n];a[n] = x;/* fragment ends here */ quicksort (m,j);quicksort(i+1,n);}图11.23(1) i:=m-1(2)j:=n(3) t1:=4*n(4) v:=a[t1](5) i:=i+1(6) t2:=4*i(7) t3:=a[t2](8) if t3< v goto (5)(9) j:=j-1(10)t4:=4*j(11)t5:=a[t4](12)if t5> v goto (9)(13)if i >= j goto (23)(14)t6:=4*i(15)x:=a[t6] (16) t7:=4*i(17) t8:=4*j(18) t9:=a[t8](19) a[t7]:=t9(20) t10:=4*j(21) a[t10]:=x(22) goto (5)(23) t11:=4*i(24) x:=a[t11](25) t12:=4*i(26) t13:=4*n(27) t14:=a[t13](28) a[t12]:=t14(29) t15:=4*n(30) a[t15]:=x答:(1)1-4为第1块,5-8为第2块,9-12为第3块,13句为第4块,14-22为第5块,23-30句为第6块。
人教版物理八年级下册第十一章 功和机械能 复习题(包含答案)
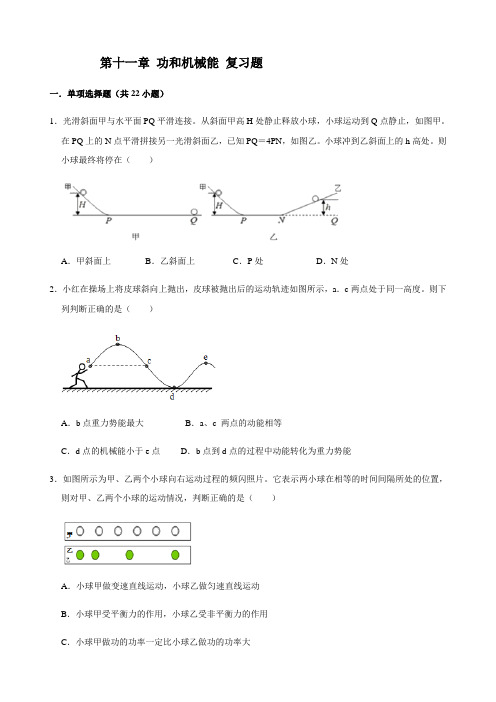
第十一章功和机械能复习题一.单项选择题(共22小题)1.光滑斜面甲与水平面PQ平滑连接。
从斜面甲高H处静止释放小球,小球运动到Q点静止,如图甲。
在PQ上的N点平滑拼接另一光滑斜面乙,已知PQ=4PN,如图乙。
小球冲到乙斜面上的h高处。
则小球最终将停在()A.甲斜面上B.乙斜面上C.P处D.N处2.小红在操场上将皮球斜向上抛出,皮球被抛出后的运动轨迹如图所示,a.c两点处于同一高度。
则下列判断正确的是()A.b点重力势能最大B.a、c 两点的动能相等C.d点的机械能小于e点D.b点到d点的过程中动能转化为重力势能3.如图所示为甲、乙两个小球向右运动过程的频闪照片。
它表示两小球在相等的时间间隔所处的位置,则对甲、乙两个小球的运动情况,判断正确的是()A.小球甲做变速直线运动,小球乙做匀速直线运动B.小球甲受平衡力的作用,小球乙受非平衡力的作用C.小球甲做功的功率一定比小球乙做功的功率大D.小球甲的机械能比小球乙的机械能小4.某同学站立在匀速上升的电梯里,则此过程中()A.人的动能转化为其重力势能B.人的机械能总量保持不变C.电梯对人的支持力做功为零D.电能转化为机械能5.请判断下列哪种情况下人对物体做了功()A.举着一个重物B.推墙C.推车上坡D.看书6.如图所示,重为12N的物体A放在足够长的水平桌面上,通过轻质细绳与滑轮相连,不计绳重与滑轮间的摩擦,动滑轮重为2N,重为6N的物体B通过滑轮拉动物体A向右做匀速直线运动的速度为0.2m/s,2min后,物体B着地,以下说法正确的是()A.物体A受到的摩擦力为3N B.1min内拉力对物体A做功为36JC.2min内B物体的重力做功为144J D.若用一个向左的拉力F使A向左匀速运动,则F=8N 7.关于火箭加速上升的过程中,下列说法正确的是()A.动能变小,势能变大,机械能保持不变B.动能变大,势能变小,机械能保持不变C.动能变小,势能变大,机械能变大,内能转化为机械能D.动能变大,势能变大,机械能变大,内能转化为机能能8.如图所示是体能测试中掷出的实心球运动的情景,下列说法正确的是()A.实心球从a点运动到b点的运动过程中,惯性越来越小B.实心球在b点时,受推力和重力的作用C.实心球从b点运动到c点的过程中,重力势能转化为动能D.实心球在c点时,内能为零9.如图所示,钩码A的重力大于钩码B,用手托钩码A使两者处于静止状态。
11 章 思考题 习题答案

NaBH4
OH O CH3CH2CHCH COCH2CH3
CH3
HCN (5) HC CH
CH2 CHCN
H2O,H+
CH3OH H+
CH2
CHCOOCH3
O
(6)
CH3OH/H+ NaBH4 HO CO2H
CO2CH3
OH
(7)格式试剂与二氧化碳反应 CH3CHCH3 HBr
Mg/醚
1)CO2 CH3CHCOOH
COOC2H5 CH2=CHCH2-C-CH3
COOC2H5
(1) OH-,H2O (2) H3O+
CH2=CHCH2CHCOOH CH3
思考题 11-19 写出反应产物 O + NCCH2COOH CH3COONH4
答案:为活泼亚甲基与酮的 Knoevenagel 反应: O + NCCH2COOH CH3COONH4
CH3CCH3
CH3CHCH3
答案:β-二羰基的互变性。与 2,4-二硝基苯肼反应的为(a)、(b),(a)使 Br2/CCl4
褪色。
思考题 11-17 由乙酰乙酸乙酯合成
O -C-CH3
答案:为乙酰乙酸乙酯合成环状取代丙酮的方法:
OO
OO
CH3CCH2COC2H5
(1)C2H5ONa (2)Br(CH2)4Br
HOCH2CH2CH2CH2OH
思考题 11-15 由对羟基苯胺合成药物泰诺林的有效成分对乙酰氨基酚
答案:为酰胺的制备 HO-
OO -NH2 + CH3COCCH3 吡啶 HO-
O -NH-CCH3
3
思考题 11-16 用化学方法鉴别下列化合物
第十、11章习题

第十、11章习题第十章检验、索赔与定金罚款一、单项选择题1.交易一方认为对方未能全部或部分履行合同规定责任与义务而引起的纠纷是()。
A.争议B.违约C.索赔D.理赔2.方当事人在合同中明确规定“货物运抵目的港后30天内索赔”。
这种索赔期限是()A.法定索赔期限B.约定索赔期限C.固定索赔期限D.变动索赔期限3.合同中对卖方较为有利的索赔期可规定为()A.货物运抵目的港(地)后××天内B.货物运抵目的港(地)后卸离海轮后××天C.货物运抵最终目的地后××天内D.货物装上船后××天内4.合同和法律规定,是索赔时的()A.事实依据B.法律依据C.违约证据D.违约事实5.我国法律规定,合同中违约金过高或过低时()A.可酌情调高B.可酌情调低C.可酌情调整D。
为无效6.英美法认为是无效的,不可强制执行的违约金是()A.预约赔偿金B.罚金C.赔偿性违约金D.惩罚性违约金7.《联合国国际货物销售合同公约》规定的索赔期限为买方实际收到货物后()A.半年内B.1年内C.1年半内D.2年内8.国际上应用较广泛的商品检验时间、地点的规定方法是()A.装船前装运港检验B.出口国装运港(地)检验,进口国目的港(地)复验C.装运港(地)检验重量,目的港(地)检验品质D.进口国目的港(地)检验9.在下列各项中,不属于商检证书作用的是()A.作为索赔和理赔的依据之一B.作为仲裁机构受理案件的依据之一C.作为银行付款的单据之一D.作为海关验关放行的依据之一10.国际标准化组织的英文缩写是()A.ISO B.UL C.IWS .SGS二、多项选择题1.国际贸易中的索赔案件,多数愿因是()A.卖方所交货物品质与合同规定不符B.卖方所交货物数量与合同规定不符C. 卖方不按期交货D. 买方未及时开证2.涉及国际货物买卖的索赔,通常包括()A.买卖双方之间的贸易索赔B.卖方向承运人提出的运输索赔C.买方向承运人提出的运输索赔 D. 卖方向保险人提出的保险索赔3.索赔期限的规定方法有()A.约定索赔期限B.货到目的港后××天索赔 C.货到目的港卸至码头D.货到追中目的地后××天4.进出口合同中索赔条款有两种规定方式()A.异议条款B.索赔条款C.罚金条款D.异议和索赔条款5.异议和索赔条款包括()A.索赔依据B.索赔期限C.索赔处理办法D.索赔金额6.合同中的违约金条款应订明()A.违约金的金额B.违约金的计算方法C.违约金的功能 D.违约金的起算日期7.大陆法系国家认为,违约金的功能是( )A.制裁违约B.保证合同履行C.赔偿损失D.预防违约8.商品检验证书在国际贸易中的作用是()A.证明卖方所交货物是否符合合同规定的依据B.对外索赔的依据C.通关放行的有效证件D.银行付款的主要依据9.我国商检局的主要任务是()A.实施法定检验B.实施监督管理C.办理公证鉴定业务D.进行对外索赔三、判断题1.索赔和理赔是两种不同的事情()2.遭受损害的一方向违约方要求赔偿,这是理赔()3.逾期提赔是无效的()4.受害人在向违约方索赔时,必须符合合同和有关国家法律规定()5.各国的法律对违约的解释不同()6. 合同一经成立,违约金条款就发生实效()7. 如果买方在规定的索赔期内做不出最终结论,可以在原定索赔期限内通知卖方,要求延展该期限()8.买方对货物的检验权是强制性的,是接受货物的前提条件()9.由于国际贸易中大多采用装运港交货的贸易术语成交,因此,在合同中规定检验地点时,应采用“离岸品质、离岸重量”的方法()10.商检机构的鉴定业务是强制性的()11.复验期限实际上就是索赔期限()四、填空题1.索赔的事实依据是指违约的_______﹑_______及其______。
第11-14章练习题

第11章练习题(一)填空题1、清廷改革中央官制,御前会议确定按照“五不议”的原则进行。
2、中国法制史上首部具有近代宪法意义的法律文件是《钦定宪法大纲》。
3、外国侵略者强迫中国缔结的不平等条约中所规定的一种非法特权是领事裁判权。
4、清末修订法律,确定了“参考古今,博稽中外”的修律方针。
5、清廷在大理院内设立总检察厅,作为最高检察机关。
6、1908年清政府颁发的《钦定宪法大纲》共二十三条,内容包括君上大权和臣民权利义务两部分。
7、清末新修订的刑法有两部,一部是《大清现行刑律》,另一部为《大清新刑律》。
8、清廷为“新政”需要,在立宪的同时对旧律进行修订,为此设立修订法律专门机关修订法律馆。
9、清末成立的修订法律馆由当时刑部左侍郎沈家本主持。
10、中国历史上第一部近代化的专门刑法典是《大清新刑律》,中国历史上第一部独立的商法是《钦定大清商律》,中国历史上第一部民法典为《大清民律草案》。
(二)单项选择题1、模仿资产阶级国家制定的我国第一个单行法院组织法规是(B、《大理院审判编制法》)。
2、在我国,程序法和实体法分开,始于(B、鸦片战争后清朝)。
3、鸦片战争后清朝专门负责来司法行政的机关是(D、法部)。
4、清末成立(B、修订法律馆),进行大规模的修律。
5、旧中国起草的第一部半殖民地半封建的民法典是(D、《大清民律草案》)。
6、中国封建王朝最后而且是最进步的一部刑法典是(D、《大清现行刑律》)。
7、中国历史上第一次分总则和分则的刑法典是(C、《大清新刑律》)。
8、《钦定宪法大纲》的附录是(D、臣民权利义务) 。
9、鸦片战争后清朝最高审判机关是(D、大理院)。
10、辛亥革命后,清廷仅用三天时间便制定和通过了(B、《十九信条》)。
11、清末“预备立宪”过程中清政府设立的地方咨询机构是(A、谘议局)。
12、清末“预备立宪”过程中清政府设立的中央咨询机构是(B、资政院)。
13、《谘议局章程》和《谘议局议员选举章程》是由下列哪有机关草拟的(B、宪政编查馆)。
【习题】第十一章 长期负债及借款费用

第十一章长期负债及借款费用[题目答案分离版] 字体:大中小一、单项选择题1、符合资本化条件的资产所发生的借款费用在予以资本化时,要与资产支出相挂钩的是()。
A、专门借款利息B、专门借款的溢价摊销C、一般借款利息D、外币专门借款的汇兑差额【正确答案】C【答案解析】本题考核借款费用资本化的核算。
专门借款发生的借款费用不需要考虑资产支出。
【该题针对“借款费用的范围”知识点进行考核】【答疑编号10532857,点击提问】2、A公司于2012年2月1日经临时股东大会批准,决定建造一栋办公楼,为此于2012年2月15日向某银行申请贷款8 000万元;2012年3月1日工程动工兴建,并于当日领用自产建材一批,共计80万元;2012年4月1日,上述贷款获准发放到位,并于当日开始计息;2012年4月15日支付在建工程人员职工薪酬95万元。
除上述专门借款外,该项工程未占用其他借款;预计工期为2年。
不考虑其他因素,则该项工程借款费用开始资本化的时点为()。
A、2012年2月15日B、2012年3月1日C、2012年4月1日D、2012年4月15日【正确答案】C【答案解析】本题考核开始资本化时点的确定。
开始资本化时点需要同时满足为使资产达到预定可使用或可销售状态所必要的购建或生产活动已经开始、资产支出已经发生、借款费用已经发生三个条件。
【该题针对“借款费用的确认”知识点进行考核】【答疑编号10532856,点击提问】3、2012年1月1日,甲企业融资租入一台设备。
租赁资产原账面价值为35万元,合同规定每年年末支付10万元租金,租赁期为4年,承租人无优惠购买选择权,租赁开始日估计资产余值为4万元,承租人的母公司提供资产余值的担保金额为2万元,另外担保公司提供资产余值的担保金额为1万元。
在租赁开始日为安装设备支付工程承包商设备安装费15万元;按照合同约定从租赁期的第二年起,再按本项目营业收入的3%收取租金(假定2012年度本项目营业收入为1 000万元),则最低租赁付款额为()万元。
第十一章 习题参考答案

x=0处的光程差为
x=0处为第k=7级明纹时
11-19在双缝干涉实验装置中,屏幕到双缝的距离D远大于双缝之间的距离d,对于钠黄光( nm),产生的干涉条纹,相邻两明条纹的角距离(即两相邻的明条纹对双缝处的张角)为 。
(1)对于什么波长的光,这个双缝装置所得相邻两条纹的角距离比用钠黄光测得的角距离大10%?
11-29 1000条/mm; ;不变
11-30 0.139 mm
11-31 281 m
11-32 0.416 nm;0.395 nm
11-33 I1
11-34
11-35
11-15凸面镜的曲率半径为0.400m,物体置于凸面镜左边0.500m处,求物体的像位置。
解:根据成像公式 ,其中
则
解得
11-16一双凸透镜由火石玻璃制成,其折射率nL=1.61,曲率半径分别为0.332 m和0.417 m,求透镜在空气中的焦距。
解:
11-25用波长 =400 nm和 =700 nm的混合光垂直照射单缝,在衍射图样中 的第k1级明纹中心位置恰与 的第k2级暗纹中心位置重合。求k1和k2。
解:
即:
11-26在复色光照射下的单缝衍射图样中,其中某一未知波长光的第三级明纹极大位置恰与波长为 =600 nm光的第二级明纹极大位置重合,求这种光波的波长。
解:
,
11-21柱面平凹透镜A,曲率半径为R,放在平玻璃片B上,如题11-21图所示。现用波长为 的平行单色光自上方垂直往下照射,观察A和B间空气薄膜的反射光的干涉条纹。设空气膜的最大厚度 。
(1)求明条纹极大位置与凹透镜中心线的距离r;
(2)共能看到多少条明条纹;
第十一章流水施工习题

第11章流水施工基本原理一、思考题:1.什么是依次施工、平行施工和流水施工?2. 说明依次施工的特点(优点缺点)。
3.说明流水施工的特点。
3.说明平行施工的特点。
4.说明流水参数的概念和种类。
5.试述划分施工段的原则。
6.简述工艺参数的概念和种类。
7.简述空间参数的概念和种类。
8.简述时间参数的概念和种类。
9.流水施工按节奏特征不同可分为哪几种方式,各有什么特点?二、名词解释:1流水施工:2流水强度:3工作面4施工段:5流水节拍:6流水步距:7工作面:8施工段:9分别流水:三、选择题:(每题的备选答案中,只有一个最符合题意)1相邻两个施工过程先后进入流水施工的时间间歇称为()。
A.流水节拍B.流水步距C.工艺间歇D.流水间歇2在加快成倍节拍流水中,任何两个相邻专业工作队之间的流水步距等于所有流水节拍中的()。
A.最大值B.最小值C.最大公约数D.最小公约数3在组织流水施工时,通常施工段数目m与施工过程数n之间的关系应该是()。
470A.m≥n B.m≤n C.m=n D.无关系4在组织加快成倍节拍流水施工时,施工段数m与施工队总数∑b i之间的关系应该是()。
479 A.m≥∑b i B.m≤∑b i C.m=∑b i D.无关系5()是建筑施工流水作业组织的最大特点。
464A.划分施工过程B.划分施工段C.组织专业工作队施工D.均衡、连续施工6选择每日工作班次,每班工作人数,是在确定()参数时需要考虑的。
471A.施工过程数B.施工段数C.流水步距D.流水节拍7下列()参数为工艺参数。
A.施工过程数B.施工段数C.流水步距D.流水节拍8在使工人人数达到饱和的条件下,下列()说法是错误的。
469A.施工段数越多,工期越长B .施工段数越多,所需工人越多C .施工段数越多,越有可能保证施工队连续施工D .施工段数越多,越有可能保证施工段不空闲9某施工段的工程量为200m 3 ,施工队的人数为25人,日产量 0.8 m 3 /人,则该队在该施工段的流水节拍为( )。
第11章-卤素习题

第11章卤素习题一.选择题1.卤素的原子特性是( )1). 最外电子层结构是ns np2). 半径随原子序数增加而增大3). 都有获得一个电子成为卤离子的强烈倾向4). 随着原子序数增加,核外价电子的引力逐渐增大A. 1和3B. 2和4C. 1,3,4D. 1,2,32.下列关于氟和氯性质的说法正确的是( )A. 氟的电子亲和势(绝对值)比氯小B. 氟的离解能比氯高C. 氟的电负性比氯大D. F-的水合能(绝对值)比Cl-小E. 氟的电子亲和势(绝对值)比氯大3.按F--Cl--Br--I顺序,下列性质递变规律不正确的是( )A. X-离子半径:F-<Cl-<Br-<I-B. 电负性:F>Cl>Br>IC. 电子亲和能:F>Cl>Br>ID. X-离子水和热(绝对值):F->Cl->Br->I-4.卤素单质的颜色随分子量的增大而加深的原因是( )A. 卤素单质的极化作用不同B. 卤素原子价电子能量高低不同C. 卤原子的电离能不同D. 卤原子的电子亲和能不同5.下列物质中具有漂白作用的是( )A. 液氯B. 氯水C. 干燥的氯气D. 氯酸钙6.氟与水猛烈反应,并伴随燃烧现象,其主要反应产物有( )A. HF和O2B. HF和FOHC. HF、O2和FOHD. HF和O37.溴和碘都能与磷作用,反应生成物分别为( )A. PBr5和PI3B. PBr3和PI3C. PBr5和PI5D. PBr3和PI58.氯气中毒时,可以吸入何种物质做解毒剂( )A. 乙醚蒸气B. 氧气和乙醚的混合气体C. 水蒸气和酒精蒸气的混合气体D. 酒精和乙醚的混合蒸气E. 氨水蒸气9.氟表现出最强的非金属性,具有很大的化学反应活性,是由于( )A. 氟元素电负性最大,原子半径小B. 单质熔、沸点高C. 氟分子中F--F键离解能高D. 分子间的作用力小E. 单质氟的氧化性强10.实验室中常用浓HCl与下列哪一些氧化剂反应,均可制取Cl2? ( )A. MnO2、KMnO4和CuOB. K2Cr2O4和CuOC. MnO2和CuOD. MnO2、K2Cr2O4和KMnO411.实验室制备Cl2,需通过下列物质洗涤,正确的一组为( )A. NaOH溶液,浓H2SO4B. 浓H2SO4,NaOH溶液C. NaCl饱和水溶液,浓H2SO4D. 浓H2SO4,H2O12.从海水中提取溴时,海水的酸碱性必须控制在以下哪个范围( )A. 酸性B. 碱性C. 中性D. 微碱性13.下列各物质分别盛装在洗气瓶中,若实验室制备的Cl2,按书写顺序通过,洗气的方式正确的是( )1. NaOH2. 浓H2SO43. CaCl24. P2O55. 饱和NaCl溶液6. 变色硅胶A. 3,1,6B. 1,3C. 3,2,5D. 5,214.电解熔融KHF2和无水HF的混合物制取F2时,常加入少量LiF或AlF3,其作用是( )A. 作催化剂,加快反应速度B. 作配合剂C. 降低电解质熔点,减少HF挥发D. 作氧化剂15.溴常以碱金属和碱土金属卤化物形式存在于海水中,若某一海水中含Br-为60ppm,如使一吨海水中的Br-完全被氧化为Br2,理论上需通入Cl2( )升. (标准状况下) (原子量: Br:79.9 Cl:35.5)A. 0.84升B. 8.4升C. 42升D. 4.2升16.液态氟化氢不能用来电解制备氟是因为( )A. 液态HF是电的不良导体B. 液态HF具有腐蚀性C. 液态HF酸是弱酸D. HF分子间存在氢键17.下列物质中,还原能力最强的是( )A.NaClB. NaBrC. NaID. NaF18.下列关于HX性质的叙述正确的是( )A. HX极易液化,液态HX不导电B. HX都是极性分子,按HF→HI分子极性递增C. HX都具有强烈刺激性气味的有色气体D. HX水溶液的酸性:HI>HClE. HX还原性:HF→HI依次减弱19.对碘化氢,下列说法中正确的是( )A. 碘化氢的有机溶液是一种良好导体B. 在水溶液中,碘化氢是一种强酸C. 碘化氢在水溶液中具有强氧化性D. 碘化氢分子间只有取向力E. 在加热时,碘化氢气体迅速分解20.铅,铜等金属可用于制造盛氢氟酸的容器,其原因是( )A. 氢氟酸是弱酸,无腐蚀性B. 氢氟酸根本不与以上金属作用C. 在金属表面生成了氧化物薄膜,具有保护作用D. 在上述金属表面生成了不溶性氟化物薄膜,使金属免于进一步腐蚀21.氯化氢易溶于水,在标准状态下,把充满干燥HCl的集气瓶倒置水面,水徐徐上升,当水充满整个集气瓶时,此HCl溶液的百分含量是( )A. 0.261%B. 0.163%C. 0.131%D. 0.098%22.NaBr与下列哪一种酸作用可制取相当纯的HBr?( )A. 浓HClB. 纯HAcC. 浓H2SO4D. 浓H3PO423.由单质直接合成HX的方法,对于下列哪一种HX的制备有实用价值( )A. HBrB. HFC. HClD. HI24.实验室不宜用浓H2SO4与金属卤化物制备的HX气体有( )A. HF和HIB. HBr和HIC. HF、HBr和HID. HF和HBr25.实验室中,用NaBr和H3PO4作用制取HBr气体,当有1mol H3PO4完全反应时,生成的HBr气体折合成标准状况下的体积是( )A. 67.2升B. 44.8升C. 11.2升D. 22.4升26.工业盐酸常显黄色是因含( )A. FeCl3B. Cl2C. FeCl2D. HClO27.对于下列反应: 3HClO====2HCl+HClO3反应条件是( )A. 加热B. 光照C. CoO氧化D. NiO催化28.106AA02 下列反应是HClO水溶液在各种条件下的分解反应,光照条件下发生的反应是( )A. 2HClO==Cl2O+H2OB. 3HClO==HClO3+2HClC. 2HClO==2HCl+O2D. 以上三种都是29.对于NaClO下列说法正确的是( )A. 在碱液中不分解B. 在稀溶液中不能氧化非金属单质C. 可作为配合剂D. 能使淀粉--KI溶液变蓝E. 加热易歧化30.对于HClO4,下列说法正确的是( )A. 在水中部分电离B. 与活泼金属反应都可得到Cl2C. 能氧化一些非金属单质D. 反应后都可被还原为Cl-E. 是无机酸中最强酸31.对于HClO在水溶液中的表现,下列说法正确的是( )A. 不分解为HClO3和HClB. 不能全部电离C. 不能作为氧化剂D. 不能作为还原剂32.下列氯的含氧酸溶液中,氧化性最强的是( )A. HClO4B. HClO3C. HClO2D. HClO33.氯的含氧酸的酸性大小顺序是( )A. HClO>HClO2>HClO3>HClO4B. HClO3>HClO4>HClO2>HClOC. HClO>HClO4>HClO3>HClO2D. HClO4>HClO3>HClO2>HClO34.下列酸根在酸性条件下氧化能力强弱顺序正确的是( )A. ClO4->ClO3->ClO2->ClO-B. ClO3->ClO4->ClO2->ClO-C. ClO->ClO4->ClO3->ClO2-D. ClO->ClO2->ClO3->ClO4-35.在酸性条件下,下列各组混合溶液中,可能发生氧化还原反应的是( )A. NaCl+Br2B. NaBr+I2C. KBrO3+Cl2D. KClO3+Br236.下列说法正确的是( )A. 氯的电负性比氧的要小,因而氯不易获得电子,其氧化能力比氧要小;B. 卤素单质与水作用,水解程度由F I依次增大;C. HBrO4是无机酸中氧化能力和酸性最强的酸;D. 卤酸盐还原为X-的氧化能力大小由Br--Cl--I依次减小;37.氢氰酸的水溶液是( )A. 强酸B. 中强酸C. 弱酸D. 极弱酸38.下列四种反应中,哪一种反应是真正可以进行的( )A. (CN)2+3H2O=2NH3+N2O3B. (CN)2+H2O=HCN+HCNOC. (CN)2+2H2O=2HCN+2OH-D. 2(CN)2+2H2O=4HCN+O239.拟卤素与卤素性质相似的主要原因是( )A. 在游离态都是二聚体B. 有相似的外层电子结构C. 都易形成配合物D. 与金属反应都生成一价阴离子盐40.下列关于(CN)2的反应中,不象卤素的反应为( )A. 在碱性溶液中生成CN-和OCN-B. 与卤素反应生成CNCl,CNBr等C. 与Ag,Hg,Pb反应得难溶盐D. 可在空气中燃烧41.区别HCl(g)和Cl2(g)的方法应选用( )A. AgNO3溶液B. 观察颜色C. NaOH溶液D. 湿淀粉KI试纸E. 干的有色布条42.能够鉴别HF,HCl,HBr,HI四种溶液的是( )A. CaCl2和苯B. AgNO3C. AgNO3和NH3H2OD. SiO2和氯水43.Cl2在水溶液中发生歧化反应的条件是( )A. pH>3B. pH<4C. pH>4D. pOH>1244.下列说法中,性质变化规律正确的是( )A. 酸性:HI>HBr>HCl>HFB. 还原性:HF>HCl>HBr>HIC. 沸点:HI>HBr>HCl>HFD. 熔点:HF>HCl>HBr>HIE. 还原性:HF<HCl<HBr<HI45.下列各组物质相互作用时,有蓝色现象出现的是( )A. 淀粉溶液与KI溶液混合B. 淀粉溶液与KI和Cl2混合C. 淀粉溶液与Cl2水混合D. 淀粉溶液与H2SO4混合46.根据卤素性质递变规律,试推断原子序数为53的卤素X最不可能具备的性质是( )A. X是一种挥发性元素B. X2能将水中的Fe氧化为FeC. AgX不溶于水D. 氯水可将X氧化成XO3-47.关于从HF到HI酸性递增的主要原因,下列叙述正确的是( )A. HF--→HI 键能减弱B. 从F--→I 原子电负性减小C. 从F--→I 原子电子密度减小D. 从F--→I 原子电子亲和能减小48.知:I2(s)+2e=2I-E=0.535VI2(aq)+2e=2I-E=0.621V计算碘的饱和溶液的浓度(mol·L)是( )A. 3.48×10B. 1.22×10C. 2.915D. 1.45849.卤素的成键特征叙述不正确的是( )A. 常温下以非极性共价键组成双原子分子B. 卤素与活泼金属化合生成离子型盐,键是离子键C. 在某些化合物中,氟,氯,溴,碘可显正氧化态(+1,+3,+5,+7),键是极性共价键D. 卤素与电负性较小的非金属元素化合时,能形成极性共价键化合物二.填空题1.氟在自然界的分布主要以萤石和冰晶石矿物存在,它们的化学式分别是______________,___________________.2.随原子序数的增大,ⅦA单质的熔沸点依次__________,这是因为_________________3.卤素单质中,从氯到碘键能逐渐_____,分子间力逐渐_________.4.氯气与氢氧化钙反应生成漂白粉,其化学反应方程式为:_________________________________.漂白粉的有效成分是________.5.目前世界上的碘主要来源于__________,其分子式为__________.6.制备F2只能采用______________法来实现,主要原料是_________________________的混合物.7.使用氢氟酸时必须戴_____________和________________8.氢卤酸在一定压力下能组成__________溶液,将氢卤酸蒸馏最后会达到_____________的状态.9.制备HF的主要方法是_____________________作用,其反应方程式为:_______________________________________.10.市售盐酸的百分比浓度为______,其物质的量浓度为________.11.KClO3和S混合,受到撞击产生爆炸,其反应方程式为:___________________________________________________________.12.工业上制备KClO3,通常用无隔膜电解槽,电解_________溶液得到___________,再与KCl进行复分解反应而制得.13.电解NaCl水溶液时,以汞作阴极,其阴极反应为______________,而电解NaCl水溶液时,以Fe做阴极,则其阴极反应为:___________________. 14.亚氯酸可用_____________________反应而制得水溶液,它极不稳定迅速分解,反应式为____________________________________15.在含有I-的酸性溶液中,加入含有Fe的溶液时,生成_________和______.(已知:E I2/I-=0.535V E Fe/Fe=0.77V)三.问答题1.卤素原子都有ns np的电子构型,为什么氟和氯、溴、碘不同,它并不呈现变价?2.比较F、Cl、Br、I的电子亲和势递变的顺序,并简述理由.3.在常态下,为何氟和氯是气体,溴是液体,碘是固体?4.写出从海水提取Br2的过程及反应方程式,注明反应条件.5.为什么配制碘酒时要加入适量的KI?6.写出大量制备F2和Cl2的方法及反应方程式:7.写出用NaIO3与NaHSO3反应制备I2的步骤及反应方程式:8.卤化氢在空气中为什么冒烟?9.卤化氢中HF分子的极性特强,熔、沸点特高,但其水溶液的酸性却最小,试分析其原因.10.与其它氢卤酸相比较,氢氟酸具有哪些特性?11.为何要在HI水溶液中加入少量的铜?12.一溶液中含有相同浓度的Br-离子和I-离子,逐滴加入AgNO3溶液时,你能否从结构观点判断哪种物质先沉淀析出.简要说明理由.13.实验室中有溴和红磷,如何制取HBr?并写出反应方程式.14.为什么可用浓H2SO4与NaCl制备HCl气体,而不能用浓H2SO4和KI来制备HI气体?(用反应方程式表示)15.ClO-,BrO2-,IO3-,ClO4-,IO65-离子的空间构型和中心原子的杂化方式分别是什么?16.在碘酸盐和碘化物的溶液中加入Al2(SO4)3溶液会得到什么产物?并加以解释.17.写出以盐酸为原料制备次氯酸的化学方程式(可添加必要原料)18.试讨论氢卤酸的酸性,还原性,热稳定性的变化规律.19.为什么AgF,AgCl,AgBr,AgI的溶解度依次降低?20.已知下列元素的电势图:1.69 1.23 1.19 0.53MnO——MnO2——Mn,IO——I2——I-|__________________| |_____________|1.51 1.08写出当pH=0时,在下列条件下,KMnO4与KI反应的离子方程式:(a) 碘化钾过量(b)高锰酸钾过量21.向KI溶液中通入足量的Cl2,溶液开始变黄,接着颜色褪去,试写出反应方程式.四.计算题1.HCl与MnO2反应制取Cl2时,所需HCl的最低浓度是多少?MnO2+4H++2e=Mn2++2H2O E=1.23VCl2+2e=2Cl-E=1.36V P Cl2=1atm2.从下列元素电势图中的已知标准电极电势,求E BrO3-/Br-,并判断哪种物质可发生歧化反应,为什么?并计算K.1.50 1.59 1.07BrO3-————HBrO————Br2————Br-3.已知下列元素电势图:1.45 0.53IO3-——HIO———I2———I-└───1.20 ──┘1.计算: E IO3-/I-=? E IO3-/HIO=?2.电势图中哪种物质能发生歧化反应,并写出反应方程式,计算反应的K.五.判断推理题1.今有白色的钠盐晶体A和B,A和B都溶于水,A的水溶液呈中性,B的水溶液呈碱性,A溶液与FeCl3溶液作用溶液呈棕色,A溶液与AgNO3溶液作用有黄色沉淀析出,晶体B与浓HCl反应有黄绿色气体生成,此气体同冷NaOH作用,可得含B的溶液,向A溶液中滴加B溶液时,溶液呈红棕色,若继续加过量B溶液,则溶液的红棕色消失,试问A,B为何物?写出有关方程式2.有一种可溶性的白色晶体A(钠盐),加入无色油状液体B的浓溶液,可得一种紫黑色固体C,C在水中溶解度较小,但可溶于A的溶液成棕黄色溶液D,将D分成两份,一份中加入一种无色(钠盐)溶液E,另一份中通入过量气体F,都变成无色透明溶液,E溶液中加入盐酸时,出现乳白色混浊,并有刺激性气体逸出,E溶液中通入过量气体F后再加入BaCl2溶液有白色沉淀产生,该沉淀不溶于HNO3. 问:1). A,B,C,D,E,F,各是何物?2). 写出下列反应方程式:A+B-→C E+HCl-→D+F-→E+F-→3.今有白色的钠盐晶体A和B. A和B都溶于水,A 的水溶液呈中性,B 的水溶液呈碱性. A溶液与FeCl3溶液作用溶液呈棕色. A溶液与AgNO3溶液作用,有黄色沉淀析出. 晶体B与浓HCl反应有黄绿气体生成,此气体同冷NaOH作用,可得到含B的溶液. 向A溶液中滴加B溶液时,溶液呈红棕色; 若继续滴加过量B溶液,则溶液的红棕色消失. 试问A,B为何物?写出上述反应式.第11章卤素习题解答一.选择题二.填空题1.CaF2,Na3AlF62.升高,X2为双原子分子,随之增大,色散力增大3.减小增大4.2Cl2+2Ca(OH)2=CaCl2+Ca(ClO)2+2H2OCa(ClO)25.智利硝石NaIO36.电解氧化无水HF和KHF27.防毒面具,橡皮手套8.恒沸,溶液的组成和沸点恒定9.萤石(CaF2)和浓H2SO4△CaF 2+H 2SO 4(浓)==CaSO 4+2HF↑10. 37% 12mol·L 2KClO 3撞击 2KCl+3O 2↑ S+O 2△ SO 2或: 2KClO 3+3S=2KCl+3SO 2↑11. 热NaCl NaClO 312. Na ++e==Na 2H 2O+2e=H 2↑+2OH -13. Na ++e==Na 2H 2O+2e=H 2↑+2OH -14. Ba(ClO 2)2和稀H 2SO 44HClO 2==3ClO 2+12 Cl 2+2H 2O15. Fe 和I 2 三.问答题1. Cl 、Br 、I 原子中有与ns 、np 能级相近的nd 轨道,只要供给一定的能量,其np 甚至ns 电子就会激发到nd 轨道上去,从而呈现变价,而F 原子电负性最大,且无d 价电子轨道,故不呈现变价.2. 电子亲和势:F<Cl>Br>I ,随原子半径增大,核对外层电子引力减小,电子亲和势趋于减小,但氟反常.因其原子半径特别小,电子云密度特大,对外来电子斥力较大,这种斥力部分抵消了获得一个电子所放出的能量,故其电子亲和势比氯小.3. 由F 2→I 2分子的半径越来越大,变形性也越来越大,色散力随之增强,故其分子间的作用力依次增大.所以在常态下,从F 2到I 2的物态由气体变为液体再到固体.4. 1). 将盐卤加热到363K 后控制pH 值为3.5,通Cl 2置换出溴: 2Br -+Cl 2=Br 2+2Cl -2). 用空气将Br 2吹出且以Na 2CO 3吸收3Br 2+3Na 2CO 3=5NaBr+NaBrO 3+3CO 2↑3). 酸化,即得溴: 5NaBr+NaBrO 3+3H 2SO 4=3Br 2+3Na 2SO 4+ 3H 2O5. 为了增加I 2的溶解度.因加入KI 发生如下反应:I 2+I -=I 3- 因此加入KI 使I 2的溶解度增大,且使I 2变得更加稳定,保持其消毒杀菌的性能.6. 制备F 2采用:电解氧化法,温度373K ,电解熔融的KHF 2和无水氢氟酸.2KHF 2电解 F 2↑+H 2↑+2KF(阳极) (阴极)制备Cl 2采用电解饱和食盐水溶液:2NaCl+2H 2O 电解 Cl 2↑+H 2↑+2NaOH(阳极) (阴极)7. 1). 先用适量的NaHSO 3将NaIO 3还原为I -:IO 3-+3HSO 3-==3SO 4+I -+3H +2). 再用所得的酸性 I -离子溶液与适量IO 3-溶液作用:IO 3-+5I -+6H +=3I 2+3H 2O8. 卤化氢与空气中水蒸汽相遇时,便形成氢卤酸HX ,这一现象表明HX 对H 2O有很大的亲和能,所形成的酸皆以小雾滴状分散在空气中,如同酸雾.9. 卤原子中,由于F 原子半径特小,电负性特大,所以HF 分子中的共用电子对强烈的偏向于F 原子一方,因而HF 具有强烈极性,也决定了HF 分子间会产生氢键而缔合,故HF 与其它HX 相比有高的熔、沸点,至于HF 水溶液的酸性比其它氢卤酸都弱,主要是和它具有最大的键能和多分子缔合结构有关。
第11章固有免疫应答.

《医学免疫学》练习题第十一章固有免疫应答一、选择题【 A 型题】1.参与固有免疫的效应分子不包括A. 防御素B.补体系统C.细胞因子D.溶菌酶E. 外毒素2. 下列关于固有免疫哪种说法不正确A. 在是机体抵御病原微生物感染的第一道防线B.是个体与生俱来的一种生理功能C.识别特点是泛特异性的,仅能识别不同类型的微生物D. 通过模式识别受体识别病原相关的分子模式E. 模式识别受体的基因在个体发育过程中重排,且受体呈克 3. 上皮细胞及其附属成分的作用不包括A . 皮肤黏膜上皮细胞及其附属成分构成的物理屏障B . 皮肤黏膜分泌物中的杀菌物质构成的化学屏障C . 皮肤和腔道黏膜表面的正常菌群构成D . 皮肤黏膜中的γδT 细胞识别抗原发挥E. 机械阻挡作用4. 下列哪些不属于固有免疫的效应分子A. 补体B.抗体C.反应蛋白 E. 细胞因子5. 下列关于适的A. 与非特异性免疫关 . 高度的特异性C . 具有耐受性具有记忆性E. 具有多样6. 感染急性期蛋白是A . . 热休克蛋白 C. C4结合蛋白 D .免疫球蛋白【A 96小时之内 B. 48小时 C. 96小时之后 D . E. 数周1. B-1细胞接受抗原刺激到抗体产生的时间约为2. 早期非特异性免疫应答发生于感染后3.特异性免疫应答诱导阶段发生于感染A . NK 细胞B. γδT 细胞 C.中性粒细胞 D . 巨噬细胞 E. B-1B 细胞4.在抗化脓菌免疫中发挥强大吞噬杀菌作用的细胞是5.在非特异性和特异性免疫应答各阶段均起重要作用的细胞是《医学免疫学》练习题6. 具有自我更新能力 , 表面标志为 CD5+、 SmIgM 的淋巴细胞是7.胞浆含大量嗜天青颗粒 , 表面标志为 CD3+CD56+CD16+的淋巴细胞是8.分布于粘膜和上皮组织中, 表面标志为 CD3+CD4-CD8-的淋巴细胞是【 C 型题】A. 参与特异性细胞免疫应答B.参与非特异性免疫C. 两者均可D.两者均否1. 干扰素2.溶菌酶3.防御素4. IL-1A. 参与特异性免疫应答B.参与非特异性免疫C. 两者均可D.两者均否5. 单核 -巨噬细胞6. B1细胞7. B2细胞8. NK细胞【 X 型题】1. 皮肤、黏膜分泌的杀菌物质是 :A. 溶菌酶B.不饱和脂肪酸抗体E.乳酸2. 固有免疫的生物学意义A.参与调控特异性免疫应B. 影响答C.影响特异性免疫应D. 维持免疫维持自身耐受1. 固有免疫化过程中逐渐形成 , 其特点是 :________、 ________、__________、或 ________。
初三物理十一章练习题

初三物理十一章练习题1. 问题描述根据初三物理教材第十一章《声学》中的内容,完成以下练习题。
2. 练习题1) 什么是声波?声波由什么产生?答:声波是一种机械波,是由物体的振动产生的。
当物体振动时,会使周围介质(如空气)中的分子振动,分子间的相互作用将传递振动,从而形成了声波。
2) 声波和光波有什么不同?答:声波是机械波,需要介质传播,而光波是电磁波,可以在真空中传播;声波振动的方向与传播方向垂直,而光波振动方向与传播方向平行;声波的频率范围通常在20Hz到20kHz,而光波的频率范围在数百THz到数百PHz。
3) 声音的速度和频率有什么关系?声音在不同介质中传播速度是否相同?答:声音的速度和频率无直接关系,它们是独立的物理量。
声音在空气中的速度约为340m/s,但在其他介质中速度不同,例如在水中约为1498m/s。
然而,声音的频率越高,其在某介质中的传播速度一般会略有提高。
4) 什么是声音的音强和音量?它们有什么关系?答:声音的音强是指单位面积上通过的声能,单位是瓦特/平方米。
音量是人耳对声音强度的主观感受,它与声音的音强不是线性关系。
通常情况下,音强和音量存在正相关关系,即音强较大的声音也会被感觉为较大的音量。
5) 噪声和声音有什么区别?答:噪声是一种杂乱无序的声音,非常不规则和不和谐,通常具有较高的音强。
而声音更多地指的是具有一定频率和调性的可辨识的声波。
噪声会对人的生理和心理产生负面影响,而声音有时可以给人带来愉悦的感受。
3. 总结以上是初三物理教材第十一章《声学》练习题的解答,包括声波的产生、声波和光波的区别、声音速度与频率的关系、音强与音量的关系,以及噪声与声音的区别等内容。
通过解答这些问题,可以加深对声学知识的理解,提升学习效果。
通过对初三物理十一章练习题的解答,我们对声学的相关概念有了更加深入的了解。
希望这些解答能为你的学习提供一些帮助。
第十一章习题解答

第十一章习题解答Last revision on 21 December 2020第十一章 微分方程习题11-11.说出下列各微分方程的阶数:(1)20dy dy x y dx dx ⎛⎫+-= ⎪⎝⎭; (2)220d Q dQ Q L Rdt dt C -+=; (3)220xy y x y '''''++= ; (4)()d (76)0x y y x y dx ++-=; (5)2sin y y y x '''++= ; (6)2d sin .d ρρθθ+= 解:(1)一阶;(2)二阶;(3)三阶;(4)一阶;(5)二阶;(6)一阶. 2.指出下列各函数是否为所给微分方程的解: (1)22 , 5;xy y y x '==(2)0 , 3sin 4cos ;y y y x x ''+==-(3)221, ;y x y y x''=+=(4)21221 , sin cos .2x x d y y e y C x C x e dx +==++解:(1)∵ 10 y x '=,代入方程得 21025x x x ⋅=⋅∴25y x =是方程的解.(2)∵ 3cos 4sin ,3sin 4cos y x x y x x '''=+=-+,代入方程,得∴ 3sin 4cos y x x =-是方程的解. (3)∵ 2312,y y x x '''=-=,代入方程,得 23221x x x≠+ ∴1y x=是方程的解. (4)∵ 21212211cos sin ,sin cos 22x x dy d y C x C x e C x C x e dx dx =-+=--+,代入方程, 得 121sin cos 2x C x C x e ⎛⎫--++ ⎪⎝⎭121sin cos 2x x C x C x e e ⎛⎫++= ⎪⎝⎭∴121sin cos 2x y C x C x e =++是方程的解.3.在下列各题中,验证所给二元方程所确定的函数为所给微分方程的解: (1)()2222 , ;x y y x y x xy y C '-=--+= (2)()220 , ln().xy x y xy yy y y xy '''''-++-==解:(1)在二元方程22 x xy y C -+=的两边同时对x 求导,得 移项后即得 ()22 x y y x y '-=-故二元方程22x xy y C -+=所确定的函数是所给微分方程的解.(2)在 ln()y xy =两边对x 求导,得11 ()y y y xy xy x y '''=+=+, 即 yy xy x'=-()()()()()232223122 y xy x y y xy xy y yxy xy xyy xy x xy x xy x ''--+-'--+-+-''===---,代入微分方程,得故 ln()y xy =所确定的函数是所给微分方程的解.4.在下列各题中,确定函数关系式中所含的参数,使函数满足所给的初始条件: (1)2220 , |1;x x xy y C y =-+==(2)()1200 , |0 , |1;x x x y C C x e y y =='=+== (3)1200cos sin , | 1 , |.t t x C t C t x x ωωω=='=+== 解:(1)∵ 0 |1x y ==∴222 =0011C -+=即 221x xy y -+=(2)()122 x y C C x C e '=++,由00 |0 , |1x x y y =='==,得 11201C C C =⎧⎨+=⎩∴12 =0 , =1C C , x y xe =(3)12sin cos x C t C t ωωωω'=-+,由00| 1 , |t t x x ω=='==,得 121C C ωω=⎧⎨=⎩∴12 =1 , =1C C , cos sin x t t ωω=+5.写出由下列条件确定的曲线所满足的微分方程:(1)曲线在点(,)x y 处切线的斜率等于该点横坐标的平方;(2)曲线上点(,)P x y 处的法线与x 轴的交点为Q ,且线段PQ 被y 轴平分. 解:(1)设曲线的方程为()y y x =,则曲线上点(,)x y 处切线的斜率为y ',由条件知2y x '=,此即为所求曲线的微分方程.(2)设曲线的方程为()y y x =,则曲线上点(,)P x y 处法线的斜率为1y -',由条件知线段PQ 中点的横坐标为0,所以Q 的坐标为(,0)x -,则有 即所求曲线的微分方程为 20yy x '+=.习题11-21.求下列微分方程的通解:(1)ln 0;xy y y '-= (2)23550;x x y '+-= (3'= (4)2();y xy a y y '''-=+ (5)cos sin d sin cos d 0;x y x x y y += (6)2d (4)d 0.y x x x y +-= 解:(1)原方程可写为ln 0dyxy y dx-=,分离变量,得d 1,ln y dx y y x = 两端积分,得 11ln dy dx y y x=⎰⎰ 即 ln ln ln ln ln y x C Cx =+=,亦即ln y Cx = ,故通解为Cx y e = (2)原方程可写为235dy x x dx =+,两端分离变量并积分,得 23()5dy x x dx =+⎰⎰, 故通解为231125y x x C =++ .(3)原方程可写为dy dx =,两端分离变量并积分,得=,故通解为arcsin arcsin y x C =+.(4)原方程可写为21dy ay dx x a=--,两端分离变量并积分,得211ady dx y x a =--⎰⎰,故通解为1ln 1a x a C y=+-+. (5)分离变量,得cos cos d d sin sin y x y x y x =- ,两端积分,得 cos cos d d sin sin y xy x y x=-⎰⎰ , 1ln sin ln sin y x C =-+,1ln sin sin x y C ⋅=,故通解为sin sin x y C = ,其中1C C e =±为任意常数. (6)分离变量,得,24dx dyx x y=-积分,得 1144dy dx x x y ⎛⎫+= ⎪-⎝⎭⎰⎰, 即 4ln ln(4)ln ln x x C y --+=,故通解为4(4)x y Cx -=. 2.求下列微分方程满足所给初始条件的特解:(1)20,|0;x y x y e y -='== (2)0cos sin d cos sin d ,|;4x x y y y x x y π===(3)2sin ln ,|;x y x y y y e π='== (4)0cos d (1)sin d 0,|;4xx y x e y y y π-=++==(5)2d 2d 0,|1;x x y y x y =+== (6)220(+)d ()d 0,| 1.x xy x x x y y y y =+-==解:(1)分离变量并积分得, 2y x e dy e dx =⎰,即通解为 212y x e e C =+,由条件0|0x y ==,得112C =+, 12C =,故满足初始条件的特解 21(1)2y x e e =+ .(2)分离变量并积分得,sin sin d d cos cos y xy x y x=⎰⎰, 即 ln(cos )ln(cos )ln y x C -=--, 亦即通解为cos cos y C x =,由条件0|4x y π==,得 coscos 04C π=,C =,故满足初始条件的特解 cos 0x y -=. (3)分离变量并积分得,1csc ln dy xdx y y=⎰⎰, 即ln(ln )ln(tan )ln 2x y C =+,亦即通解为ln tan 2xy C =,由条件2|x y e π==,得ln tan 4e C π=,1C =,故满足初始条件的特解ln tan2xy =. (4)分离变量并积分得,tan 1x xe ydy dx e-=+⎰⎰,通解为(1)sec xe y C +=,由条件0|4x y π==,得C =(1)sec x e y +=.(5)分离变量并积分得,12dy dx y x=-⎰⎰,通解为2x y C =由条件2|1x y ==,得4C =,故满足初始条件的特解24x y =. (6)分离变量并积分得,2211y x dy dx y x=+-⎰⎰,通解为22(1)(1)x y C -+= 由条件0|1x y ==,得2C =,故满足初始条件的特解22(1)(1)2x y -+=. 3.求下列齐次方程的通解:(1)0;xy y '-= (2)d ln ;d y yxy x x= (3)22()d d 0;x y x xy y +-= (4)332()d 3d 0;x y x xy y +-=(5) ;y xyy e x '=+ (6)(12)d 21d 0.x xy y x e x e y y ⎛⎫++-= ⎪⎝⎭解:(1)原方程可写为dy y dx x =y u x =,则 ,y ux =d d ,d d y u u x x x =+代入原方程,得dd uu xu x +=+1dx x =,积分得 ln(ln ln u x C =+,即u Cx =,亦即y Cx x +=,原方程的通解2y Cx =.(2)原方程可写为d ln d y y y x x x =,令y u x =,则 ,y ux =d d ,d d y uu x x x=+ 代入原方程,得d ln d uu xu u x+=,分离变量积分得 ()11ln 1du dx u u x =-⎰⎰, 即 ln(ln 1)ln ln u x C -=+,亦即 ln 1y Cx x =+,原方程的通解ln 1yCx x=+. (3)原方程可写为d d y y x x x y =+,令y u x =,则 ,y ux =d d ,d d y uu x x x=+ 代入原方程,得d 1d u u xu x u +=+,分离变量积分得 1udu dx x=⎰⎰, 即 22ln u x C =+,,将yu x =代入上式得原方程的通解22(2ln )y x x C =+.(4)原方程可写为22d d 33y y x x x y =+,令y u x =,则 ,y ux =d d ,d d y uu x x x=+代入原方程,得2d 1d 33u u u x x u+=+,分离变量积分得 233112u du dx u x =-⎰⎰, 即 311ln(12)ln 2u x C --=+,亦即 3221C u x =-,其中1C C e =,将yu x =代入上式,得原方程的通解332x y Cx -=. (5)令y u x =,则 ,y ux =d d ,d d y u y u x x x '==+代入原方程,得d d u uu x e u x+=+,即 ln ueCx --=,将yu x=代入上式,得原方程的通解ln 0yx e Cx -+=.(6)原方程可写为12d d 12xy xyx ey x ye ⎛⎫- ⎪⎝⎭=+,令x u y =,则 ,x u y =d d ,d d x u u y y y =+ 代入原方程,得d 2(1)dy 12u uu e u u y e -+=+,分离变量积分得 1212u u e du dy u e y +=-+⎰⎰, 即 ln(2)ln ln u u e y C +=-+,亦即 (2)u y u e C +=,将yu x=代入上式,得原方程的通解2x yx ye C +=4.求下列线性微分方程的通解:(1)d ;d x yy e x-+= (2)232;xy y x x '+=++ (3)tan sin 2;y y x x '+= (4)d 32;d ρρθ+=(5)ln d (ln )d 0;y y x x y y +-= (6)2d (6)20.d yy x y x -+=解:(1)原方程是()1P x =,()x Q x e -=的一阶非齐次线性方程.由通解公式得原方程的通解为()()dx dxx x xx x y e e e dx C eee dx C e x C -----⎛⎫⎰⎰=⋅+=⋅+=+ ⎪⎝⎭⎰⎰.(2)原方程可化为123y y x x x '+=++,它是1()P x x =,2()3Q x x x=++的一阶非齐次线性方程.由通解公式得原方程的通解为()11221332dx dx x x y e x e dx C x x dx C x x -⎡⎤⎛⎫⎰⎰⎡⎤=++⋅+=+++⎢⎥ ⎪⎣⎦⎝⎭⎣⎦⎰⎰213232C x x x =+++; (3)原方程是()tan P x x =,()sin 2Q x x =的一阶非齐次线性方程.由通解公式得原方程的通解为tan tan 2sin 2sin 2cos cos 2cos cos xdx xdx x y e x e dx C x dx C C x x x -⎛⎫⎛⎫⎰⎰=⋅+=+=- ⎪ ⎪⎝⎭⎝⎭⎰⎰. (4)原方程是()3P θ=,()2Q θ=的一阶非齐次线性方程.由通解公式得333332223333d d C C Ce e d e e dx e θθθθθρθ---⎛⎫⎛⎫⎰⎰=⋅+=+=+ ⎪ ⎪⎝⎭⎝⎭⎰⎰ ,即原方程的通解为 332Ce θρ-=+. (5)原方程可化为1=ln dx x dy y y y +,它是1()ln P y y y =,1()Q y y=的一阶非齐次线性方程.由通解公式得112ln ln 11111ln ln 2ln 2ln 22dy dyy y y y C C C x e e dy ydy y y y y y -⎛⎫⎛⎫⎰⎰⎛⎫=⋅+=⋅+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰⎰, 即原方程的通解为22ln ln x y y C =+.(6)原方程可化为3=2dx x y dy y --,它是3()P y y =-,()2yQ y =-的一阶非齐次线性方程.由通解公式得33323311222dy dy y y y y x e e dy C y dy C y Cy y -⎡⎤⎛⎫⎰⎰⎛⎫=-⋅+=-⋅+=+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦⎰⎰. 5.求下列微分方程满足所给初始条件的特解: (1)0d tan sec ,|0;d x y y x x y x =-== (2)21d 4,| 2 ;d x y yx y x x=+== (3)cos 2d cot 5,|4;d x x y y xe y x π=+==- (4)0d 38,| 2 d x yy y x =+==.解:(1)由公式可得一阶线性微分方程通解为()tan tan 11sec sec cos cos cos xdxxdx y e x e dx C x xdx C x C x x -⎡⎤⎰⎰⎡⎤=⋅+=⋅+=+⎢⎥⎣⎦⎣⎦⎰⎰由0|0x y ==得0C =,故特解为cos xy x=. (2)由公式可得一阶线性微分方程通解为由12x y==得1C =,故特解为31y x x=+. (3) 由公式可得一阶线性微分方程通解为 由24x yπ==得1C =,故特解为cos 151sin x y e x⎡⎤=-+⎣⎦,即 cos sin 51x y x e +=. (4)由公式可得一阶线性微分方程通解为由0| 2 x y ==得23C =-,故特解为32(4)3x y e -=-.6.求下列伯努利方程的通解:(1)2d (cos sin );d y y y x x x +=- (2)33d 22 .d yxy x y x+= 解:方程两边同除以2y ,得21d cos sin d yy y x x x --+=- 令1z y =,2d d y dz y x dx -=-,则原方程变为sin cos dzz x x dx-=-,故将1z y =代入上式,得原方程通解为1sin x Ce x y =-.1sin x x Ce y=-+; (2)方程两边同除以3y ,得323d 22d yy xy x x--+= 令21z y =,3d 1d 2y dz y x dx -=-,则原方程变为344dz xz x dx-=-,故 将21z y =代入上式,得原方程通解为222212x y Ce x -=++. 7.用适合的变量代换将下列方程化为可分离变量的方程,然后求出通解: (1)2d ();d yx y x=+ (2)d 11;d y x x y =+- (3)(ln ln );xy y y x y '+=+ (4)212x y y e +-'=-.解:(1)令u x y =+,则1dy du dx dx =-,从而原方程可化为21du u dx=+,分离变量积分得21dudx u=+⎰⎰,即arctan x u C =+. 将u x y =+代入,得原方程的通解为arctan()x x y C =++,即tan()y x x C =-++.(2)令u x y =-,则1dy du dx dx =-,从而原方程可化为1du dx u -=,分离变量积分得udu dx =-⎰⎰,即2112x u C +=. 将u x y =-代入,得原方程的通解为2()2x y x C -=-+ (其中12C C =).(3)令u xy =,则2,duxuu dydx y x dx x-==,从而原方程可化为21()ln du u u u x u x dx x x x -+=,分离变量积分得ln dx dux u u =⎰⎰,即 ln ln ln(ln )x C u +=,亦即C x u e =,将u xy =代入,得原方程的通解为1C x y e x=.(4)令21u x y =+-,则2dy du y dx dx '==-,从而原方程可化为u du e dx=,分离变量积分得udx e du -=⎰⎰,即u e C x -=-. 将21u x y =+-代入,得原方程的通解为12ln y x C x =---.8.判别下列方程中哪些是全微分方程,并求全微分方程的通解:(1)(cos cos )d (sin sin )d 0x y x y y y x x ++-=; (2)2()0x y dx xdy --=; (3)22()0x y dx xydy ++= ; (4)22(1)20e d e d θθρρθ++=. 解:(1)这里(,)sin sin , (,)cos cos P x y y y x Q x y x y x =-=+,cos sin P Q y x y x∂∂=-=∂∂,所以(1)是全微分方程.取000 , 0x y ==, 根据公式00(,)(,)(,)x yx y u x y P x y dx Q x y dy =+⎰⎰,有于是全微分方程的通解为sin cos x y y x C +=.. (2)这里2(,),(,)P x y x y Q x y x =-=-,于是有1P Qy x∂∂=-=∂∂,所以(2)是全微分方程.取000 , 0x y ==,根据公式00(,)(,)(,)xy x y u x y P x y dx Q x y dy =+⎰⎰,有于是全微分方程的通解为33x xy C =+.(3)这里22(,),(,),P x y x y Q x y xy =+=2P y y ∂=∂,Q y x∂=∂,显然P Q y x ∂∂≠∂∂,所以(3)不是全微分方程.(4)22(1)20e d e d θθρρθ++=.这里22(,)1,(,)2P e Q e θθρθρθρ=+=,显然22P Qe θθρ∂∂==∂∂,所以(4)是全微分方程,取000 , 0ρθ==,根据公式00(,)(,)(,)u P d Q d ρθρθρθρθρρθθ=+⎰⎰ ,有于是全微分方程的通解为2(1)e C θρ+=.9.求一曲线的方程,这曲线通过原点,并且它在点(,)x y 处的切线斜率等于2x y +.9. 2(1)x y e x =--.解:设曲线的方程为()y y x =,由题意知2y x y '=+,0|0x y ==,于是()()222122dx dx x x x x xy e x e dx C e xe dx C e x e C Ce x ---⎛⎫⎰⎰⎡⎤=⋅+=+=-++=-- ⎪⎣⎦⎝⎭⎰⎰由0|0x y ==,得2C =,于是所求曲线的方程为2(1)x y e x =--10.质量为lg (克)的质点受外力作用作直线运动,这外力和时间成正比,和质点运动的速度成反比.在10s t =时,速度等于50cm/s ,外力为24g cm/s ⋅,问从运动开始经过了一分钟后的速度是多少解 :已知t F k v =⋅,并且10t s =时50/v cm s =,4/F g cm s =⋅,故10450k =⋅,从而20k =,因此20t F v =⋅.又由牛顿定律F ma =,即201t dvv dt⋅=⋅,故20vdv tdt =,积分得221102v t C =+,即v ,再代入初始条件得2250C =,因此所求特解为v 60t s =时269.3(/)v cm s ==≈.11.镭的衰变有如下的规律:镭的衰变速度与它的现存量R 成正比.由经验材料得知,镭经过1600年后,只余原始量0R 的一半.试求镭的量R 与时间t 的函数关系. 解: 设比例系数0λ>,则由题意可得dR R dt λ=-⋅.分离变量积分可得dR dt Rλ=-⎰⎰,即1ln R t C λ=-+,从而1()C t R C e C e λ-=⋅=,因为0t =时0R R =,所以0R C =,即0t R R e λ-=⋅.又因为1600t =时02R R =,所以1600002R R e λ-=⋅,从而ln 21600λ=,因此镭的量R 与时间t 的函数关系为ln 20.000433160000t t R R eR e --==,.时间以年为单位.12.设有连结点(0,0)O 和(1,1)A 的一段向上凸的曲线弧OA ,对于OA 上任一点(,)P x y ,曲线弧OP 与直线段OP 所围图形的面积为2x ,求曲线弧OA 的方程.解: 曲线弧OA 的方程为()y y x =,由题意得 两边求导得11()()()222y x y x xy x x '--=,即4yy x'=-, 令y u x =,则 ,y ux =d d ,d d y u u x x x =+上式可化为4dux dx=-,分离变量积分得4ln u x C =-+.将yu x=代入,得 4ln y x x Cx =-+.由于(1,1)A 在曲线上,因此(1)1y =,代入得1C =,从而曲线弧OA 的方程为(14ln )y x x =-,01x <≤;当0x =时0y =.13.设有一质量为m 的质点作直线运动.从速度等于零的时刻起,有一个与运动方向一致、大小与时间成正比(比例系数为1k )的力作用于它,此外还受一与速度成正比(比例系数为2k )的阻力作用.求质点运动的速度与时间的函数关系. 解 由牛顿定律知12dv mk t k v dt =-,即21kk dv v t dt m m+=,因此 由0t =时0v =得122k m C k =,故22211122222kkkt t t m mm k k m k m v e te e k k k -⎛⎫=-+ ⎪⎝⎭,即质点运动的速度与时间的函数关系为211222(1)kt m k k mv t e k k -=--.习题11-31.求下列各微分方程的通解:(1)2290;4d y x dx -= (2);x y xe '''=(3)2(1)2;x y xy '''+= (4)220.1y y y'''-=- 解:(1)原方程变形,得2294d y x dx =,对所给方程接连积分两次,得2198y x C '=+, 31238y x C x C =++ ,这就是所求的通解.(2)对所给方程接连积分三次,得 2123(3)x y x e C x C x C =-+++. 这就是所求的通解.(3)令(),y p x y p ''''==,原方程可化为2(1)2x p xp '+=,即221dp xdx p x =+,积分得21ln ln(1)ln p x C =++,亦即21(1)p C x =+,21(1)y C x '=+,所以就是原方程的通解.(4)令()y p y '=,则dpy p dy ''=,原方程化为2201dp p p dy y -=-,即201dp p p dy y ⎡⎤-=⎢⎥-⎣⎦, 当0p =时,得原方程的一个解为y C =,它不是通解; 当0p ≠时,约去p ,分离变量积分,得2(1)p y C -=,即2(1)dy Cp dx y ==-,从而2(1)y dy Cdx -=,积分得312(1)y C x C -=+,其中13C C =,因此原方程的通解为312(1)y C x C -=+.2.求下列各微分方程满足所给初始条件的特解: (1)111, |||0 ;x x x x y e y y y ===''''''====(2)00| 1 , | 2 ;x x y y y =='''=== (3)2000 , ||0 ;y x x y e y y =='''-=== (4)31110 , | 1 , |0 x x y y y y =='''+===.解:(1)1+C x x y e dx e ''==⎰,由1|0 x y =''=得,1C e =-,即x y e e ''=-,2()+C x x y e e dx e ex '=-=-⎰,由1|0 x y ='=得,20C =,即x y e ex '=-,23()+C 2x x e y e ex dx e x =-=-⎰,由1|0 x y ==得,32eC =-,故222x e ey e x =-- 为 原方程的所求特解 .(2)令()y p y '=,那末 dp y pdy ''=,得dppdy=,即pdp =, 积分得3221122p y C =+,由00 | 1 , |2x x y y =='==得10C =,从而342y p y '==±,又y ''=,可知342y y '=,即342y dy dx -=,积分得14242y x C =+,由0 | 1 x y ==,得24C =,所以4112y x ⎛⎫=+ ⎪⎝⎭为所求特解.(3)令()y p y '=,那末dp y pdy ''=,得20y dpp e dy-=,即2y pdp e dy =,积分得2211122yp e C =+,由000x x y y=='==得112C =-,从而22()1,y y e y ''=-=dx =±y dx -=±,积分得2arcsin y e x C --=±+,由00x y==,得22C π=-,所以sin()cos 2y e x x π-=±+=,原方程特解为lnsec y x =. (4) 令y p '=,则dp y pdy ''=,原方程变为31dpy pdy=-,从而3pdp y dy -=-,积分得2121p C y =+,即2121()y C y'=+,由111,0x x y y =='==得11C =-,从而221()1y y'=-,即y '=dx =±,积分得2x C =±+,再由11x y ==得21C =,因此所求特解为(1)x =±-,即221(1)y x -=-亦即222x y x +=,或y =(舍去y =,因为11x y ==).3.试求y x ''=的经过点(0,1)M 且在此点与直线12xy =+相切的积分曲线. 解:由积分曲线经过点(0,1)M 知,01x y ==,又由积分曲线在点(0,1)M 与直线12x y =+相切知,012x y ='=. 对方程y x ''=积分得,2112y xdx x C '==+⎰,利用条件012x y ='=,从而112C =,即21122y x '=+,再积分得,3262x x y C =++,利用条件01x y==,从而21C =,于是3162x xy =++.4.下列函数组在其定义区间内哪些是线性无关的(1)2cos , ;x x (2)22,5 ;x x (3)22,3;x x e e (4)2sin ,1 ;x (5)cos 2,cos sin ;x x x (6)22,;x x e xe (7)ln ,2ln ;x x (8)1212,().x x e e λλλλ≠ 解:(1)、(4)、(5)、(6)、(8)线性无关.因为:对于定义在区间I 上的两个函数1()y x 与2()y x ,如果1()y x 与2()y x 在区间I 上线性相关,则存在两个不全为0的常数12 , k k ,使得对于∀x I ∈恒有1122()()0k y x k y x +=成立,即12()()y x y x 或21()()y x y x 恒为常数.因而如果12()()y x y x 或21()()y x y x 均不为常数,则称1()y x 与2()y x 在区间I 上一定线性无关.(1)、(4)、(5)、(6)、(8)中的两个函数之比均不为常数,所以这五组函数均线性无关.相反地(2)(3)(7)线性相关.5.验证21x y e -=及62x y e -=都是方程8120y y y '''++=的解,并写出该方程的通解. 解: 因为21x y e -=,22112,4x x y e y e --'''=-=,62x y e -=,66226,36x x y e y e --'''=-=,所以21x y e -=和 62x y e -=都是已知方程的解.由于24162xx x y e e y e--==不为常数,因此1y 与2y 线性无关,所给方程的通解为2612x x y C e C e --=+.6.验证1sin y x =及2cos y x =都是方程0y y ''+=的解,并写出该方程的通解. 解: 因为1sin y x =,11cos ,sin y x y x '''==-,2cos y x =,22sin ,cos y x y x '''=-=-,所以1sin y x =何2cos y x =都是已知方程的解.由于12tan y x y =不为常数,因此1y 与2y 线性无关,所给方程的通解为12sin cos y C x C x =+.7.求下列微分方程的通解:(1)3100;y y y '''--= (2)40;y y '''-= (3)20; y y ''+= (4)8160;y y y '''++=(5)22d d 690;d d x xx t t-+= (6)220y y y '''++=.解:(1)特征方程为23100r r --=,解得122,5r r =-=,故方程的通解2512x x y C e C e -=+.(2)特征方程为240r r -=,特征根为120,4r r ==,故方程的通解为412x y C C e =+.(3)特征方程为220r +=,解得1,2r =,故方程的通解12y C C =+.(4)特征方程为28160r r ++=,特征根为124r r ==-,故方程的通解为412()x y C C x e -=+.(5)特征方程为2690r r -+=,特征根为123r r ==,故方程的通解为312()t x C C t e =+.(6)特征方程为2220r r ++=,特征根为1,221i 21r -±==-±⨯,故方程的通解为12(cos sin )x y e C x C x -=+.8.求下列微分方程满足所给初始条件的特解: (1)00680,|1,|6;x x y y y y y ==''''-+=== (2)00440,|2,|0;x x y y y y y ==''''++=== (3)00340,|0,|5;x x y y y y y ==''''--===- (4)006130,|3,|1x x y y y y y ==''''++===-.解:(1)特征方程为2680r r -+=,特征根为122,4r r ==,故方程的通解为2412x x y C e C e =+代入初始条件00|1,|6x x y y =='==,得12121246C C C C +=⎧⎨+=⎩,解之得1212C C =-⎧⎨=⎩,从而所求特解为242x x y e e =-+.(2)特征方程为24410r r ++=,特征根为121,3r r ==,故方程的通解为312x x y C e C e =+代入初始条件002,0x x y y =='==,得12126310C C C C +=⎧⎨+=⎩,解之得1242C C =⎧⎨=⎩,从而所求特解为342x x y e e =+.(3) 特征方程为2340r r --=,特征根为121,4r r =-=,故方程的通解为412x x y C e C e -=+代入初始条件000,5x x y y =='==-,得1212045C C C C +=⎧⎨-+=-⎩,解之得1211C C =⎧⎨=-⎩, 从而所求特解为4x x y e e -=-(4)特征方程为26130r r ++=,特征根为1,232i r ==-±,故方程的通解为312(cos 2sin 2)x y e C x C x -=+代入初始条件00|3,|1x x y y =='==-,得1123321C C C =⎧⎨-+=-⎩,解之得1234C C =⎧⎨=⎩,从而所求特解为3(3cos 24sin 2)x y e x x -=+.9.写出下列各微分方程的待定特解的形式(不用解出): (1)355;x y y y e '''-+= (2)3;y y '''-=(3)2276(521);x y y y x x e '''-+=-- (4)369(1)x y y y x e '''-+=+.解(1)特征方程为2350r r -+=,解得1,2331i 2122r ±==±⨯. 又因为()5x f x e =,1λ=是特征根,故待定特解的形式为*x y ae =. (2)特征方程为20r r -=,特征根为120,1r r ==.又因为()3f x =,0λ=是特征根,故待定特解的形式为*y ax =. (3)特征方程为2760r r -+=,特征根为1216r r ==.又因为22()(521)x f x x x e =--, 2λ=不是特征根,故待定特解的形式为*22()x y ax bx c e =++.(4) 特征方程为2690r r -+=,特征根为123r r ==.又因为3()(1)x f x x e =+,3λ=是特征根,故待定特解的形式为*23()x y x ax b e =+. 10.求下列各微分方程满足已给初始条件的特解: (1)sin 20, |1, |1;x x y y x y y ππ=='''++=== (2)00325, |1, |2;x x y y y y y ==''''-+=== (3)004, |0, |1;x x x y y xe y y =='''-=== (4)0045, |1, |0x x y y y y ==''''-===.解:(1)特征方程为210r +=,解得1,2i r =±,对应齐次方程的通解为12cos sin y C x C x =+因()sin 2f x x =-,i 2i αβ±=±不是特征根,所以设原方程的特解为*cos 2sin 2y A x B x =+,*()2sin 22cos 2y A x B x '=-+,*()4cos 24sin 2y A x B x ''=--,代入原方程得3cos23sin 2sin 20A x B x x --+=,30 , 310A B -=-+=,即10,3A B ==, *1sin 23y x =.故原方程的通解为又122sin cos cos 23y C x C x x '=-++,代入初始条件1,1x x yy ππ=='==,得112211 1,2313C C C C =-⎧⎪⇒=-=-⎨=+⎪⎩,从而所求特解为11cos sin sin 233y x x x =--+.(2)特征方程为210r +=,解得121,2r r ==,对应齐次方程的通解为 因()5f x =,0λ=不是特征根,所以设原方程的特解为*y A =, 代入原方程 ,得 25A = 即 52A =,*52y =.故原方程的通解为 又2122x x y C e C e '=+,代入初始条件00 |1, |2x x y y =='==,得121212517 5,2222C C C C C C ⎧++=⎪⇒=-=⎨⎪+=⎩, 从而所求特解为275522x x y e e =-++.(3)特征方程为2320r r -+=,解得121,1r r ==-,对应齐次的通解为 而()4x f x xe =-,1λ=是特征方程的单根,故可设原方程的特解为 代入原方程整理得比较系数,得1,1A B ==-,所以*(1)x y x x e =-.故原方程的通解为 将条件00,1x x yy =='==代入,得12121211 , 111C C C C C C +=⎧⇒==-⎨--=-⎩, 从而所求特解为2()x x x y e e x x e -=-+-.(4)特征方程为240r r -=,解得120,4r r ==,对应齐次方程的通解为412x y C C e =+ 因()5f x =,0λ=是特征方程的单根,所以设原方程的特解为*y Ax =,代入原方程 ,得 45A -= 即 54A =-,*54y x =-.故原方程的通解为又42544x y C e '=-,代入初始条件00|1, |0x x y y =='==,得121221115 ,51616404C C C C C +=⎧⎪⇒==⎨-=⎪⎩, 从而所求特解为4115516164x y e x =+-. 11.设函数()x ϕ连续,且满足求()x ϕ.解: 方程两边同时对x 求导,得0()()xx x e t dt ϕϕ'=-⎰,()()x x e x ϕϕ''=-,(0) 1 , (0)1ϕϕ'== 从而 ()()x x x e ϕϕ''+=又该方程对应齐次方程的特征方程为210r +=,特征根为1,2i r =±,故齐次方程的通解为 通过观察易知*12x e ϕ=为方程()()x x x e ϕϕ''+=的一个特解,从而该方程的通解为 将初始条件(0)1,(0)1ϕϕ'==代入,得11221112 1212C C C C ⎧=+⎪⎪⇒==⎨⎪=+⎪⎩, 故总习题十一1.单项选择题:(1)下列微分方程中是线性方程的是( ).(A ) cos()y y e x '+= (B ) 22x xy y x y e '''+-=(C )()250y y '+= (D )sin 8y y x ''+=(2)下列方程中是一阶微分方程的是( ).(A ) 2()20x y yy x ''++= (B ) ()()245750y y y x '''+-+=(C )0xy y y '''++= (D )(4)5cos 0y y x '+-=(3)微分方程20ydy dx -=的通解是( ).(A ) 2y x C -= (B ) 2y x C +=(C )y x C =+ (D )y x C =-+(4)微分方程0y y ''+=满足初始条件001 , 1x x y y =='==的特解是( ).(A ) cos y x = (B ) sin y x =(C )cos sin y x x =+ (D )12cos sin y C x C x =+(5)下列函数是微分方程20y y y '''-+=的解是( ).(A ) 2x x e (B ) 2x x e -(C ) x xe - (D ) x xe解:(1)(B ) ; (2)(A ); (3)(A ); (4)(C ); (5)(D ).2.填空题:(1)以22()1x C y ++=(其中C 为任意常数)为通解的微分方程为22(1)1y y '+=. (2)以212x x y C e C e =+(其中1C 、2C 为任意常数)为通解的二阶常系数齐次线性微分方程为320y y y '''-+=.(3)微分方程x y y e -'=的通解为y x e e C =+.(4)方程cot 2sin y y x x x '-=的通解为2()sin y x C x =+.(5) 设方程()()()y p x y q x y f x '''++=的三个特解是2123 ,,x x y x y e y e ===,则此方程的通解为2212()()x x x y C x e C x e e =-+-+.3.求下列微分方程的通解:(1)2(12)(1)0y xdx x dy +++=; (2)x y y x +'=-; (3)d d 2(ln )y y x y x =- ; (4)5d d y y xy x-=; (5)20y y y '''+-=; (6)22x y y y e '''+-= ;(7)sin y y x ''+=; (8)25sin 2y y y x '''++=.解:(1)分离变量积分,得 21121x dy dx y x=-++⎰⎰, 即 ()2ln 12ln(1)ln y x C +=-++,亦即 2(1)(12)x y C ++=故原方程所求通解为 2(1)(12)x y C ++=.(2) 原方程变形为11y y x'+=-,这是一阶线性方程,其通解为 即原方程通解为22xy x C +=.(3)原方程变形为d 22ln d x y x y y y+=,这是一阶线性方程,其通解为 即原方程通解为21ln 2x Cy y -=+-. (4)这是5n =的伯努利方程. 方程两端同除以5y ,得54dy y y x dx ---=,令4z y -=,便有44dz z x dx+=-,此方程为一阶非齐次线性方程,其通解为 将4z y -=代入,得原方程的通解为4414x y Ce x --=-+. (5)特征方程为220r r +-=,解得122,1r r =-=,故方程的通解、212x x y C e C e -=+.(6)特征方程为2210r r +-=,解得1211,2r r =-=,对应齐次的通解为 而()2x f x e =,1λ=不是特征方程的根,故可设原方程的特解为代入原方程整理得 1A =,所以*x y e = 故原方程的通解为212x x x y C e C e e -=++.(7)特征方程为210r +=,解得1,2i r =±,对应齐次方程的通解为因()sin f x x =,i i αβ±=±是特征根,所以设原方程的特解为()*cos sin y x A x B x =+,又 ()*()sin cos cos sin y x A x B x A x B x '=-+++,()*()2(cos sin )cos sin y B x A x x A x B x ''=--+,代入原方程,得()()2(cos sin )cos sin cos sin sin B x A x x A x B x x A x B x x --+++=,21, 20A B -==, 即1,02A B =-=, *1cos 2y x x =-.故原方程的通解为 (8)25sin 2y y y x '''++=其特征方程为2250r r ++=,特征根为1,212r i =-±,从而其对应齐次方程的通解为12(cos 2sin 2)x y e C x C x -=+.又()sin 2f x x =,i 2i αβ±=±不是特征根,所以设原方程的特解为*cos 2sin 2y A x B x =+,*()2sin 22cos 2y A x B x '=-+,*()4cos 24sin 2y A x B x ''=--,代入原方程得()()4cos24sin 2sin 2A B x B A x x ++-=,4041 , 411717A B A B B A +=⎧⇒=-=⎨-=⎩,所以*41cos 2sin 21717y x x =-+. 故原方程的通解为1241(cos 2sin 2)cos 2sin 21717x y e C x C x x x -=+-+. 4.求下列微分方程满足所给初始条件的特解:(1)222(3+2)d (2)d 0 , 1x xy y x x xy y x -+-==时1y =;(2)2cos , 0y y y x x '''++==时30 , 2y y '==.解:(1)222(,)3+2 ,(,)2P x y x xy y Q x y x xy =-=-,于是有22P Q x y y x∂∂=-=∂∂,所以方程(1)是全微分方程.因为 所以方程(1)的通解为322x x y xy C +-=,又1x =时,1y =,从而1C =于是原方程的特解为3221x x y xy +-=.(2)特征方程为2210r r ++=,解得121r r ==-,对应齐次方程的通解为因()cos f x x =,i i αβ±=±不是特征根,所以设原方程的特解为*cos sin y A x B x =+,又 *()sin cos y A x B x '=-+,()*()cos sin y A x B x ''=-+,代入原方程,得()cos sin A x B x -+2sin 2cos A x B x -++cos sin cos A x B x x +=,20, 21A B -==, 即10,2A B ==, *1sin 2y x =.故原方程的通解为1sin 2x y xe x -=+ 由条件0x =时30 , 2y y '==,得210 1322C C =⎧⎪⇒⎨+=⎪⎩121,0C C == 所以原方程的特解为1sin 2x y xe x -=+. 5.已知某曲线经过点(1,1),它的切线在纵轴上的截距等于切点的横坐标,求它的方程.解:设曲线的方程为()y y x =,其上任一点(,)x y 处的切线方程为()Y y y X x '-=-,切线在纵轴上的截距为y xy '-,由题意有y xy x '-=,即1y y x'-=-,其通解为 又因为曲线过点(1,1) ,所以1C =,从而所求曲线方程为(1ln )y x x =-.6.设可导函数()x ϕ满足求()x ϕ.解:方程两边同时对x 求导得即()cos ()sin 1x x x x ϕϕ'+=,亦即()tan ()sec x x x x ϕϕ'+=,其通解为在0()cos 2()sin 1xx x t tdt x ϕϕ+=+⎰中,令0x =得(0)1ϕ=,故 因此()cos sin x x x ϕ=+.7.一链条挂在一钉子上,起动时一端离开钉子8m,另一端离开钉子12m ,分别在以下两种情况下求链条滑下来所需要的时间:(1)若不计钉子对链条产生的摩擦力;(2)若摩擦力为1m 长的链条的重量.解: (1) 设在时刻t 时,较长的一段链条垂下 m x ,且设链条的密度为ρ,则向下拉链条的作用力由牛顿第二定律可知202(10)x g x ρρ''=-,即 10g x x g ''-=- 该方程对应的齐次方程的特征方程为2010g r -=,特征根为1,2r =程的通解为通过观察知*10x =为非齐次方程10g x x g ''-=-的一个特解,因而原方程的通解为又12x e '=且(0)12,(0)0x x '==,可得1212122 10C C C C C C +=⎧⇒==⎨-+=⎩,因此10x e=++;当20x =,即链条全部滑下来,有10e =+,解得所需时间t =+(秒). (2) 此时向下拉链条的作用力变为(20)1(221)F x g x g g g x ρρρρ=---⋅=-.由牛顿第二定律可知20(221)x g x ρρ''=-,即 1.0510g x x g ''-=-.类似于(1)中解法可得此方程通解为 1210.5t t x C e C =++由初始条件得1234C C ==,因而所求特解为 3310.544x e =++当20x =时有39.54e ⎛⎫=+ ⎪ ⎪⎝⎭,解之得所需时间为193t +=(秒).。
初二上册十一章数学练习题

初二上册十一章数学练习题初二上册第十一章数学练习题1. 小明有10元钱,他买了两本书,每本书的价格是3.5元,请问小明还剩下多少钱?解法:两本书的总价格 = 3.5元/本 × 2本 = 7元小明还剩下的钱 = 10元 - 7元 = 3元2. 请计算:7 × (4 - 3) + 2 × 5 的结果。
解法:首先计算括号里的结果,4 - 3 = 1然后计算乘法,7 × 1 = 7,2 × 5 = 10最后计算加法,7 + 10 = 17所以,7 × (4 - 3) + 2 × 5 = 173. 有一条长方形的长为8米,宽为6米,请问长方形的周长是多少米?解法:周长 = 2 × (长 + 宽)周长 = 2 × (8米 + 6米)周长 = 2 × 14米周长 = 28米4. 小华每天早上骑自行车去学校,全程4公里。
她上学的时间是30分钟,请问她每小时骑自行车的速度是多少公里?解法:每天骑行的路程 = 4公里每天骑行的时间 = 30分钟 = 0.5小时每小时骑行的路程 = 每天骑行的路程 / 每天骑行的时间每小时骑行的路程 = 4公里 / 0.5小时每小时骑行的路程 = 8公里/小时5. 两个数的和是32,大的数是18,请问小的数是多少?解法:两个数的和 = 32大的数 = 18小的数 = 两个数的和 - 大的数小的数 = 32 - 18小的数 = 146. 小明参加马拉松比赛,他用1小时35分钟跑完42.195公里,请问他的平均速度是多少?解法:总路程 = 42.195公里总时间 = 1小时35分钟 = 1.58小时平均速度 = 总路程 / 总时间平均速度 = 42.195公里 / 1.58小时平均速度≈ 26.75公里/小时7. 请计算下面等式的值:12 + 4 × (8 - 6) ÷ 2 = ?解法:首先计算括号里的结果,8 - 6 = 2然后计算乘法和除法,4 × 2 ÷ 2 = 4最后计算加法,12 + 4 = 16所以,12 + 4 × (8 - 6) ÷ 2 = 16通过以上数学练习题的解答,我们能够加深对初二上册第十一章数学知识的理解和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章 光学
11
物理学
第五版
第十一章 习题
11 把折射率n=1.40的薄膜放入迈克耳孙干 涉仪的一臂,如果由此产生了7.0条条纹的 移动,求膜厚.设入射光的波长为589 nm.
第十一章 光学
12
物理学
第五版
第十一章 习题
12 如图如示,折射率n2=1.2 的油滴落在n3=1.5的平板玻璃 上,形成一个上表面近似于 球面的油膜,测得油膜中心
第十一章 光学
8
物理学
第五版
第十一章 习题
8 如图所示,利用空气劈尖测细丝直径, -2 已知=859.3 nm ,L=2.88810 m,测得30 -3 条条纹的总宽度为4.29510 m ,求细丝直 径d.
d L 第8题图 第9题图 A B
第十一章 光学
9
物理学
第五版
第十一章 习题
9 集成光学中的楔形薄膜耦合器原理如图 所示.沉积在玻璃衬底上的是氧化钽(Ta2O5) 薄膜,其楔形端从A到B厚度逐渐减小为零. 为测定薄膜的厚度,用波长=632.8 nm的 He-Ne激光垂直照射,观察到薄膜楔形端共 出现11条暗纹,且A处对应一条暗纹,试求 氧化钽薄膜的厚度(Ta2O5对632.8 nm 激光 的折射率为2.21).
第十一章 光学
1
物理学
第五版
第十一章 习题
S1
S
S‘ S2
O
第1题图
第十一章 光学
2
物理学
第五版
第十一章 习题
2 如图所示,两个直径有微小差别的彼此 平行的滚柱之间的距离为L,夹在两块平面 晶体的中间,形成空气劈形膜,当单色光垂 直入射时,产生等厚干涉条纹,如果滚柱之 间的距离L变小,则在L范围内干涉条纹的 ( )
第十一章 光学
4
物理学
第五版
第十一章 习题
4 在双缝干涉实验中,用波长=546.1 nm 的单色光照射,双逢与屏的距离d´=300 mm, 测得中央明纹两侧的两个第五级明条纹的 间距为12.2 mm ,求双缝间的距离.
第十一章 光学
5
物理学
第五版
第十一章 习题
5 一双缝装置的一个缝被折射率为1.40的 薄玻璃片所遮盖,另一个缝被折射率为1.70 的薄玻璃片所遮盖.在玻璃片插入以后,屏 上原来的中央极大所在点,现变为第五级 明纹.假定=480 nm ,且两玻璃片厚度均为 d,求d.
第十一章 光学
10
物理学
第五版
第十一章 习题
10 利用牛顿环测未知单色光波长实验,用 波长为589.3 nm的钠黄光垂直照射时,测得 -3 第一和第四暗环的距离为r=4.010 ;当用 波长未知的单色光垂直照射时,测得第一 -3 和第四暗环的距离为r´=3.8510 ,求该 单色光的波长.
第十一章 光学
20
物理学
第五版
第十一章 习题
19 用一毫米内有500条刻痕的平面透射光 栅观察钠光谱( =589 nm),设透镜焦距 问:(1)光线垂直入射时,最多能看到第 几级光谱;(2)光线以入射角30 入射时, 最多能看到第几级光谱;(3)若用白光垂 直照射光栅,求第一级光谱的线宽度.
第十一章 光学
22
物理学
第五版
第十一章 习题
21 测得从一池静水的表面反射出来的太阳 光是线偏振光,求此时太阳处在地平线的 多大仰角处(水的折射率为1.33)?
第十一章 光学
23
物理学
第五版
第十一章 习题
22 使自然光通过两个偏振化方向相交的偏振 片,透射光强为,今这这两个偏振片之间插 入另一偏振片,它的方向下前两个偏振片均 成角,则透射光强为多少?
第十一章 光学
18
-4
物理学
第五版
第十一章 习题
17 迎面而来的一辆汽车的两车头灯相距为 1.0 m, 问在汽车离人多远时,它们刚能为 人眼所分辩?设瞳孔直径为3.0 mm,光在 空气中的波长=500 nm.
第十一章 光学
19
物理学
第五版
第十一章 习题
18 一束平行光垂直入射到某个光栅上,该 光束有两种波长的光, 1=440 nm和2=660 nm ,实验发现,两种波长的谱线(不计中 央明纹)第二次重合于衍射角 = 60 的方向 上,求此光栅的光栅常数.
Байду номын сангаас
第十一章 光学
6
物理学
第五版
第十一章 习题
6 白光垂直照射到空气中一厚度为380 nm 的肥皂膜上.设肥皂的折射率为1.32.试问 该膜 的正面呈现什么颜色?背面呈现什 么颜色?
第十一章 光学
7
物理学
第五版
第十一章 习题
7 在折射率为n3=1.52的照相机镜头表面涂 有一层折射率n2=1.38的MgF2增透膜,若 此膜仅适用于波长=550 nm的光,则此膜 的最小厚度为多少?
第十一章 光学
24
物理学
第五版
第十一章 习题
23 一束光是自然光和平面线偏振光的混合, 当它通过一偏振片时发现透射光的强度取决 于偏振片的取向,其强度可以变化5倍,求入 射光中两种光的强度各占总入射光强度的几 分之几.
第十一章 光学
25
(A)数目减小,间距变大 (B)数目减小,间距不变 (C)数目不变,间距变小 (D)数目增加,间距变小
第十一章 光学
L 第2题图
3
物理学
第五版
第十一章 习题
3 在单缝夫琅禾费衍射实验中,波长为的 单色光垂直入射在宽度为3 的单缝上,对 应于衍射角为30º 的方向,单缝处波阵面可 分成的半波带数目为( ) (A)2个 (B) 3个 (C) 4个 (D) 6个
物理学
第五版
第十一章 习题
1 在双缝干涉实验中,若单色光源S到两缝 S1、S2距离相等,则观察屏上中央明条纹位 于图中O处,现将光源S向下移动到示意图 中的S´位置,则() (A)中央明纹向上移动,且条纹间距增大 (B)中央明纹向上移动,且条纹间距不变 (C)中央明纹向下移动,且条纹间距增大 (D)中央明纹向下移动,且条纹间距不变
第十一章 光学
16
物理学
第五版
第十一章 习题
15 一单色平行光垂直照射于一单缝,若其 第三条明纹位置正好和波长为600 nm的单 色光入射时的第二级明纹位置一样,求前 一种单色光的波长.
第十一章 光学
17
物理学
第五版
第十一章 习题
16 已知单缝宽度b=1.010 ,透镜焦距 f=0.50m,用1=400 nm和2=760 nm的单色 平行光分别垂直照射,求这两种光的第一 级明纹离屏中心的距离,以及这两条明纹 之间的距离.若用每厘米刻有1 000条刻线的 光栅代替这个单缝,则这两种单色光的第 一级明纹分别距屏中心多远?这两条明纹 之间的距离又是多少?
第十一章 光学
14
物理学
第五版
第十一章 习题
L P
b
f
x
o
第13题图
第十一章 光学
15
物理学
第五版
第十一章 习题
14 单缝的宽度b=0.40,以波长=589 nm的 单色光垂直照射,设透镜的焦距f=1.0 m.求: (1)第一级暗纹距中心的距离;(2)第 二级明纹距中心的距离;(3)如单色光以 入射角i=30º 斜射到单缝上,则上述结果有 何变动.
dm
n2 n3
最高处的高度dm=1.1 m ,用=600 nm的单 色光垂直照射油膜.求(1)油膜周边是暗环 还是明环?(2)整个油膜可看到几个完整 暗环?
第十一章 光学
13
第12题图
物理学
第五版
第十一章 习题
13 如图如示,狭缝的宽度b=0.60 mm,透 镜焦距f=0.40 m ,有一与狭缝平行的屏放置 在透镜的焦平面处.若以单色光垂直照射狭 缝,则在屏上离点O为x=1.4 mm的点P看到 衍射明条纹.试求:(1)该入射光的波长; (2)点P条纹的级数;(3)从点P看,对 该光波而言,狭缝处的波阵面可作半波带 的数目.
第十一章 光学
21
物理学
第五版
第十一章 习题
20 波长为600 nm的单色光垂直入射在一光 栅上,第二级主极大出现在sin =0.2处 , 第四级缺级.试问(1)光栅上相邻两缝的 间距是多少?(2)光栅上狭缝的宽度有多 大?(3)在-90 < < 90 范围内,实际呈 现的全部级数.
