《计算方法》复习资料
华南农业大学精品复习资料计算思维补充内容

1.4 计算思维概述思维是指人脑对客观事物本质属性和内部规律的间接或概括的反映过程。
科学思维通常是指理性认识及其过程,即经过感性阶段获得的大量材料,通过整理和改造,形成概念、判断和推理,以便反映事物的本质和规律。
人们在科学研究过程中采取的各种手段和途径叫科学方法。
科学界一般认为,科学方法分为理论、实验和计算三大类。
理论科学、实验科学和计算科学作为科学发现三大支柱,正推动着人类文明进步和科技发展,该说法已被科学文献广泛引用。
与三大科学方法相对应的是人类认识世界和改造世界的三大科学思维,即理论思维、实验思维和计算思维,这三种思维基本涵盖了目前为止科学思维的全部内容,见表1.6。
2006年3月,美国卡内基·梅隆大学计算机科学系周以真教授提出:计算思维是运用计算机科学的基础概念进行问题求解、系统设计、以及人类行为理解等涵盖计算机科学之广度的一系列思维活动。
计算思维强调的抽象和构造、可解,强调用自动方式逐步求解。
对于上述定义需要强调以下三点。
①求解问题中的计算思维利用计算手段求解问题的过程是:首先要把实际的应用问题转换为数学问题,然后建立模型、设计算法和编程实现,最后在实际的计算机中运行并求解。
前两步是计算思维中的抽象,后两步是计算思维中的自动化。
②设计系统中的计算思维任何自然系统和社会系统都可视为一个动态演化系统,演化伴随着物质、能量和信息的交换,这种交换可以映射为符号变换,使之能用计算机实现离散的符号处理。
当动态演化系统抽象为离散符号系统后,就可以采用形式化的规范来描述,通过建立模型、设计算法和开发软件来揭示演化的规律,实时控制系统的演化并自动执行。
③理解人类行为中的计算思维计算思维是基于可计算的手段,以定量化的方式进行的思维过程。
利用计算手段来研究人类的行为,即通过各种信息技术手段,设计、实施和评估人与环境之间的交互。
社会计算涉及人们的交互方式、社会群体的形态及其演化规律等问题。
研究生命的起源与繁衍、理解人类的认识能力、了解人类与环境的交互以及国家的福利与安全等,都属于社会计算的范畴,这些都与计算思维密切相关。
数学史复习资料

一、单项选择题1.关于古埃及数学的知识,主要来源于( )。
A.埃及纸草书和苏格兰纸草书B.兰德纸草书和莫斯科纸草书C.莫斯科纸草书和希腊纸草书D. 兰德纸草书和尼罗河纸草书2.以“万物皆数”为信条的古希腊数学学派是( )。
A.爱奥尼亚学派B.伊利亚学派C.诡辩学派D.毕达哥拉斯学派3.最早记载勾股定理的我国古代名著是( )。
A.《九章算术》B.《孙子算经》C.《周髀算经》D.《缀术》4.首先使用符号“0”来表示零的国家或民族是( )。
A.中国B.印度C.阿拉伯D.古希腊5.欧洲中世纪漫长的黑暗时期过后,第一位有影响的数学家是( )。
A.斐波那契B.卡尔丹C.塔塔利亚D.费罗6.对微积分的诞生具有重要意义的“行星运行三大定律”,其发现者是( )。
A.伽利略B.哥白尼C.开普勒D.牛顿7.对古代埃及数学成就的了解主要来源于( )A.纸草书B.羊皮书C.泥版D.金字塔内的石刻8.公元前4世纪,数学家梅内赫莫斯在研究下面的哪个问题时发现了圆锥曲线?( )A.不可公度数B.化圆为方C.倍立方体D.三等分角9.《九章算术》中的“阳马”是指一种特殊的( )A.棱柱B.棱锥C.棱台D.楔形体10.印度古代数学著作《计算方法纲要》的作者是( )A.阿耶波多B.婆罗摩笈多C.马哈维拉D.婆什迦罗11.射影几何产生于文艺复兴时期的( )A.音乐演奏B.服装设计C.雕刻艺术D.绘画艺术12.微分符号“d”、积分符号“”的首先使用者是( )A.牛顿B.莱布尼茨C.开普勒D.卡瓦列里13.作为“非欧几何”理论建立者之一的年轻数学家波尔约是( )A.俄国人B.德国人C.葡萄牙人D.匈牙利人14.最早证明了有理数集是可数集的数学家是( )A.康托尔B.欧拉C.魏尔斯特拉斯D.柯西15.在1900年巴黎国际数学家大会上提出了23个著名的数学问题的数学家( )A.希尔伯特B.庞加莱C.罗素D.克莱因16.《周髀算经》和()是我国古代两部重要的数学著作。
中考物理复习《浮力液面高度变化量计算方法与技巧》
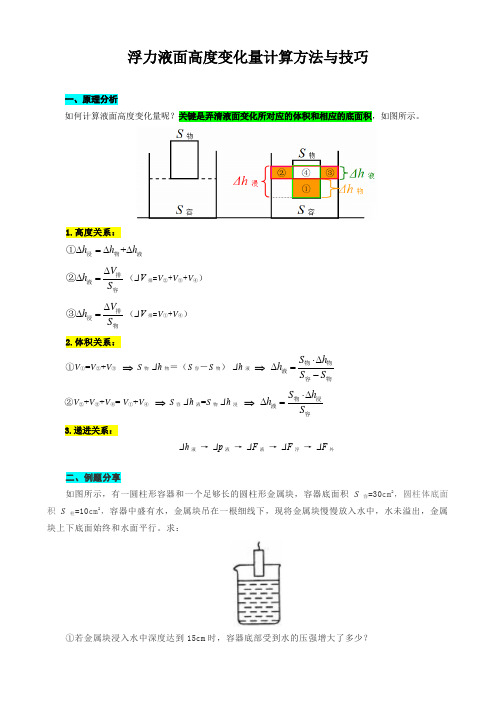
浮力液面高度变化量计算方法与技巧一、原理分析如何计算液面高度变化量呢?关键是弄清液面变化所对应的体积和相应的底面积,如图所示。
1.高度关系:+h h h ∆=∆∆浸物液①V h S ∆∆=排液容②(ΔV 排=V ②+V ③+V ④)V h S ∆∆=排浸物③(ΔV 排=V ①+V ④)2.体积关系:①V ①=V ②+V ③ ⇒ S 物·Δh 物=(S 容-S 物)·Δh 液 ⇒ S h h S S ⋅∆∆=-物物液物容②V ②+V ③+V ④= V ①+V ④ ⇒ S 容·Δh 液=S 物·Δh 浸 ⇒ S h h S ⋅∆∆=浸物液容3.递进关系:Δh 液 → Δp 液 → ΔF 液 → ΔF 浮 → ΔF 外二、例题分享如图所示,有一圆柱形容器和一个足够长的圆柱形金属块,容器底面积S 容=30cm 2,圆柱体底面积S柱=10cm 2,容器中盛有水,金属块吊在一根细线下,现将金属块慢慢放入水中,水未溢出,金属块上下底面始终和水面平行。
求:①若金属块浸入水中深度达到15cm 时,容器底部受到水的压强增大了多少?②若绳子从金属块底部刚好接触到水面时开始向下放下15cm时,容器底部受到水的压强增了多少?1.第1小问分析过程:要求水对容器底部增加的压强,也就是求水位增加的高度。
如何求水位增加的高度呢?思维过程如下:当圆柱体浸入水中15cm时,实际上是一个动态过程,圆柱体一边下降,水位一边上升,圆柱体下降的深度加上水位上升的高度刚好为15cm。
由此可见,如何将动态变化过程转化为静态过程才是解题关键。
多数同学可能有这样的思维过程:假设原来水位不变,我们把圆柱体浸入水中后排开的水用容器接到,然后将排开的水再倒回容器中。
这个时候有两种思考:(1)倒入圆柱体两边的空白处,这样水位上升的高度,Δh=V排/(S容-S柱)。
显然,圆柱体浸入水中的深度就是15cm+Δh,跟题意矛盾。
人教版数学四年级上册-六《除数是两位数的除法》整理和复习说课稿

人教版数学四年级上册-六《除数是两位数的除法》整理和复习说课稿一. 教材分析《除数是两位数的除法》是人教版数学四年级上册第六单元的内容。
本节课的主要内容是让学生掌握除数是两位数的除法的计算方法和步骤,以及能够灵活运用这种方法解决实际问题。
教材通过详细的例题和练习,帮助学生理解和掌握这一知识点。
二. 学情分析在四年级的学生中,他们已经掌握了除数是一位数的除法的计算方法,对于除法的概念和步骤也有一定的理解。
但是,他们在面对除数是两位数的情况时,可能会遇到一些困难,例如计算过程比较复杂,容易出错。
因此,在教学过程中,我们需要注重引导学生理解和掌握计算方法,提高他们的计算能力。
三. 说教学目标1.知识与技能目标:学生能够理解除数是两位数的除法的计算方法和步骤,能够正确地进行计算。
2.过程与方法目标:通过学生的自主探究和合作交流,培养学生的动手操作能力和解决问题的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养他们的自信心和克服困难的勇气。
四. 说教学重难点1.教学重点:除数是两位数的除法的计算方法和步骤。
2.教学难点:如何引导学生理解和掌握计算方法,提高他们的计算能力。
五. 说教学方法与手段在本节课的教学过程中,我将采用启发式教学法和小组合作学习法。
通过引导学生自主探究和合作交流,激发他们的学习兴趣和动力。
同时,我还会运用多媒体教学手段,如PPT和教学软件,以直观的方式展示除法的计算过程,帮助学生理解和掌握。
六. 说教学过程1.导入:通过复习除数是一位数的除法,引导学生自然过渡到除数是两位数的情况。
2.新课导入:介绍除数是两位数的除法的概念和计算方法。
3.例题讲解:通过具体的例题,引导学生理解和掌握计算方法。
4.练习环节:布置一些相关的练习题,让学生独立完成,巩固所学知识。
5.应用拓展:通过一些实际问题,让学生运用所学的除法知识解决问题。
6.总结环节:对本节课的内容进行总结,强调重点和难点。
五年级数学上册各单元重难点及复习资料

五年级数学上册各单元重难点及复习资料第一单元《小数乘法》知识点小数加减法的计算方法:计算小数加减法;要先把小数点对齐;然后按照整数加减法的法则进行计算。
1.小数乘整数意义:求几个相同加数的和的简便运算。
如:3.6×5表示5个3.6的和是多少或者3.6的5倍是多少。
小数乘小数的意义:就是求这个数的几分之几是多少。
如:2.6×0.4就是求2.4的十分之四是多少。
8.5×3.4就是求8.5的3.4倍是多少。
2.小数乘法的计算方法:计算小数乘法;先按整数乘法算出积(也就是末位要对齐);再看因数中一共有几位小数;就从积的右边起数出几位;点上小数点;乘得积的小数位数不够时;要在前面用0补足;再点小数点;小数末尾有0的要去掉。
3.一个数(0除外)乘大于1的数;积比原来的数大;一个数(0除外)乘小于1的数;积比原来的数小。
4.小数四则运算顺序跟整数是一样的:即有括号的要先算括号里的;没有括号的要先算乘除法;后算加减法;同级运算按照从左往右的顺序计算。
5.整数乘法的交换律、结合律、分配律;对于小数乘法也适用。
6.小数点向右移:小数点向右移动一位;小数就扩大到原数的10倍;小数点向右移动两位;小数就扩大到原数的100倍;小数点向右移动三位;小数就扩大到原数的1000倍;……小数点向左移:小数点向左移动一位;小数就缩小到原数的;小数点向左移动两位;小数就缩小到原数的;小数点向左移动三位;小数就缩小到原数的;……第二单元《小数除法》知识点1.小数除法的意义:已知两个因数的积与其中的一个因数;求另一个因数的运算。
如:2.6÷1.3表示已知两个因数的积2.6与其中的一个因数1.3;求另一个因数的运算。
2、小数除法的计算方法:(1)计算除数是整数的小数除法:按整数除法的计算方法去除;商的小数点要和被除数的小数点对齐;除到哪一位;商就写在哪一位的上面。
整数部分不够除;商0;点上小数点;继续除;如果有余数;要添0再除。
第2章 《整式的加减》章节复习资料【7】

第2章《整式的加减》章节复习资料【7】1.下列计算正确的有()(1)5a3﹣3a3=2;(2)﹣10a3+a3=﹣9a3;(3)4x+(﹣4x)=0;(4)(﹣xy)﹣(+xy)=﹣xy;(5)﹣3mn﹣2nm=﹣5mn.A.1个B.2个C.3个D.4个2.下列各式中去括号正确的是()A.a2﹣(2a﹣b2+b)=a2﹣2a﹣b2+b B.﹣(2x+y)﹣(﹣x2+y2)=﹣2x+y+x2﹣y2C.2x2﹣3(x﹣5)=2x2﹣3x+5 D.﹣a3﹣[﹣4a2+(1﹣3a)]=﹣a3+4a2﹣1+3a3.若5x2y|m|﹣(m+1)y2﹣3是三次三项式,则m等于()A.±1 B.1 C.﹣1 D.以上都不对4.若多项式3x2﹣2xy﹣y2减去多项式M所得的差是﹣5x2+xy﹣2y2,则多项式M是()A.﹣2x2﹣xy﹣3y2B.2x2+xy+3y2C.8x2﹣3xy+y2D.﹣8x2+3xy﹣y25.已知x+y+2(﹣x﹣y+1)=3(1﹣y﹣x)﹣4(y+x﹣1),则x+y等于()A.﹣ B.C.﹣D.6.如图1,将一个边长为a的正方形纸片剪去两个矩形,得到一个“S”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为()A.2a﹣3b B.2a﹣4b C.4a﹣8b D.4a﹣10b7.如果m是三次多项式,n是三次多项式,那么m+n一定是()A.六次多项式B.次数不高于三的整式C.三次多项式D.次数不低于三的整式8.若关于x,y的多项式化简后不含二次项,则m=()A.B.C.D.09.一家商店以每包a元的价格进了30包甲种茶叶,又以每包b的价格买进60包乙种茶叶.如果以每包元的价格卖出这两种茶叶,则卖完后,这家商店()A.赚了B.赔了C.不赔不赚D.不能确定赔或赚10.若A与B都是二次多项式,则A﹣B:(1)一定是二次式;(2)可能是四次式;(3)可能是一次式;(4)可能是非零常数;(5)不可能是零.上述结论中,不正确的有()个.A.5 B.4 C.3 D.211.已知多项式x|m|+(m﹣2)x﹣10是二次三项式,m为常数,则m的值为.12.若代数式mx2+5y2﹣2x2+3的值与字母x的取值无关,则m的值是.13.甲、乙、丙三人拿出同样多的钱,合伙订购同种规格的若干件商品.商品买来后,甲、乙分别比丙多拿了12、9件商品,最后结算时,乙付给丙20元,那么,甲应付给丙元.14.若a<0,则|1﹣a|+|2a﹣1|+|a﹣3|=.15.如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a﹣b)米.问小明家楼梯的竖直高度(即:BC的长度)为米.16.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.(﹣x2+3xy﹣y2)﹣(﹣x2+4xy﹣y2)=﹣x2+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是.17.某校为适应电化教学的需要新建阶梯教室,教室的第一排有a个座位,后面每一排都比前一排多一个座位,若第n排有m个座位,则a、n和m之间的关系为m=.18.定义一种新运算:a※b=,则当x=3时,2※x﹣4※x的结果为.19.已知a2+ab=3,ab+b2=1,试求a2+2ab+b2=,a2﹣b2=.20.已知,则代数式(m+2n)﹣(m﹣2n)的值为.21.将多项式按字母X的降幂排列.22.已知a,b为常数,且三个单项式4xy2,axy b,﹣5xy相加得到的和仍然是单项式.那么a和b的值可能是多少?说明你的理由.23.先化简,再求值:已知2(﹣3xy+x2)﹣[2x2﹣3(5xy﹣2x2)﹣xy],其中x,y满足|x+2|+(y﹣3)2=0.24.试至少写两个只含有字母x、y的多项式,且满足下列条件:(1)六次三项式;(2)每一项的系数均为1或﹣1;(3)不含常数项;(4)每一项必须同时含字母x、y,但不能含有其他字母.25.已知关于x的多项式(a﹣1)x2+x|a+2|﹣2x+b,问是否存在实数a,b,使得这个多项式为二次三项式?若存在,请求出a,b的值,若不存在,请说明理由.26.观察下面有规律的三行单项式:x,2x2,4x3,8x4,16x5,32x6,…①﹣2x,4x2,﹣8x3,16x4,﹣32x5,64x6,…②2x2,﹣3x3,5x4,﹣9x5,17x6,﹣33x7,…③(1)根据你发现的规律,第一行第8个单项式为;(2)第二行第n个单项式为;(3)第三行第8个单项式为;第n个单项式为.27.已知关于x、y的多项式5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1(1)若该多项式不含三次项,求m的值;(2)在(1)的条件下,当x2+y2=13,xy=﹣6时,求这个多项式的值.28.已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的还多1岁,求这三名同学的年龄的和.29.学规律在数学中有着极其重要的意义,我们要善于抓住主要矛盾,提炼出我们需要的信息,从而解决问题.(1)观察下列算式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…,通过观察,用你所发现的规律确定32014的个位数字是;(2)观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是;根据此规律,如果a n(n为正整数)表示这个数列的第n项,那么a18=,a n=;(3)观察下面的一列单项式:x,﹣2x2,4x3,﹣8x4,…根据你发现的规律,第5个单项式为;第7个单项式为;第n个单项式为.30.马虎的李明在计算多项式M加上x2﹣3x+7时,因错看成加上x2+3x+7,尽管计算过程没有错误,也只能得到一个错误的答案为5x2+2x﹣4.(1)求多项式M;(2)求出本题的正确答案.第2章《整式的加减》章节复习资料参考答案与试题解析一.选择题(共10小题)1.(2014秋•赛罕区校级期末)下列计算正确的有()(1)5a3﹣3a3=2;(2)﹣10a3+a3=﹣9a3;(3)4x+(﹣4x)=0;(4)(﹣xy)﹣(+xy)=﹣xy;(5)﹣3mn﹣2nm=﹣5mn.A.1个B.2个C.3个D.4个【解答】解:5a3﹣3a3=2a3;﹣10a3+a3=﹣9a3;4x+(﹣4x)=0;(﹣xy)﹣(+xy)=﹣xy;﹣3mn﹣2nm=﹣5mn.故选C.2.(2014•新泰市校级模拟)下列各式中去括号正确的是()A.a2﹣(2a﹣b2+b)=a2﹣2a﹣b2+bB.﹣(2x+y)﹣(﹣x2+y2)=﹣2x+y+x2﹣y2C.2x2﹣3(x﹣5)=2x2﹣3x+5D.﹣a3﹣[﹣4a2+(1﹣3a)]=﹣a3+4a2﹣1+3a【解答】解:A、a2﹣(2a﹣b2+b)=a2﹣2a+b2﹣b,故A错误;B、﹣(2x+y)﹣(﹣x2+y2)=﹣2x﹣y+x2﹣y2,故B错误;C、2x2﹣3(x﹣5)=2x2﹣3x+15,故C错误;D、﹣a3﹣[﹣4a2+(1﹣3a)]=﹣a3﹣(﹣4a2+1﹣3a)=﹣a3+4a2﹣1+3a,故D正确.故选D.3.(2014秋•温州期末)若5x2y|m|﹣(m+1)y2﹣3是三次三项式,则m等于()A.±1 B.1 C.﹣1 D.以上都不对【解答】解:由题意可得,解得m=1.故选B.4.(2016春•启东市月考)若多项式3x2﹣2xy﹣y2减去多项式M所得的差是﹣5x2+xy﹣2y2,则多项式M是()A.﹣2x2﹣xy﹣3y2B.2x2+xy+3y2C.8x2﹣3xy+y2D.﹣8x2+3xy﹣y2【解答】解:根据题意得:M=3x2﹣2xy﹣y2﹣(﹣5x2+xy﹣2y2)=3x2﹣2xy﹣y2+5x2﹣xy+2y2=8x2﹣3xy+y2.故选C.5.(2014秋•淄川区期末)已知x+y+2(﹣x﹣y+1)=3(1﹣y﹣x)﹣4(y+x﹣1),则x+y等于()A.﹣ B.C.﹣D.【解答】解:方法1:∵x+y+2(﹣x﹣y+1)=3(1﹣y﹣x)﹣4(y+x﹣1)∴x+y﹣2x﹣2y+2=3﹣3y﹣3x﹣4y﹣4x+4∴﹣x﹣y+2=7﹣7y﹣7x∴6x+6y=5∴x+y=方法2:∵x+y+2(﹣x﹣y+1)=3(1﹣y﹣x)﹣4(y+x﹣1)∴(x+y)﹣2(x+y)+2=3﹣3(x+y)﹣4(x+y)+4∴(x+y)﹣2(x+y)+3(x+y)+4(x+y)=3+4﹣2∴6(x+y)=5∴x+y=故选D.6.(2015•廊坊二模)如图1,将一个边长为a的正方形纸片剪去两个矩形,得到一个“S”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为()A.2a﹣3b B.2a﹣4b C.4a﹣8b D.4a﹣10b【解答】解:根据题意得:新矩形的长为a﹣b,宽为a﹣3b,则新矩形周长为2(a﹣b+a﹣3b)=2(2a﹣4b)=4a﹣8b,故选C.7.(2015秋•南通期中)如果m是三次多项式,n是三次多项式,那么m+n一定是()A.六次多项式B.次数不高于三的整式C.三次多项式D.次数不低于三的整式【解答】解:若两个三次多项式中,三次项的系数不相等,这两个三次多项式相减后就仍为三次多项式;若两个三次多项式中,三次项的系数相等,这两个三次多项式相减后三次多项式就会变为低于三次的整式.故选B.8.(2016春•台州校级月考)若关于x,y的多项式化简后不含二次项,则m=()A.B.C.D.0【解答】解:∵原式=x2y+(6﹣7m)xy+y3,若不含二次项,即6﹣7m=0,解得m=.故选B.9.(2004•梅州)一家商店以每包a元的价格进了30包甲种茶叶,又以每包b的价格买进60包乙种茶叶.如果以每包元的价格卖出这两种茶叶,则卖完后,这家商店()A.赚了 B.赔了C.不赔不赚 D.不能确定赔或赚【解答】解:根据题意,列式(30+60)﹣(30a+60b)=15(a﹣b),当b<a时,盈利,当b=a时,不赚不赔,当b>a时,亏损,由于不知a,b具体值,所以无法确定.故选D.10.(2014秋•临海市校级期中)若A与B都是二次多项式,则A﹣B:(1)一定是二次式;(2)可能是四次式;(3)可能是一次式;(4)可能是非零常数;(5)不可能是零.上述结论中,不正确的有()个.A.5 B.4 C.3 D.2【解答】解:∵多项式相减,也就是合并同类项,而合并同类项时只是把系数相加减,字母和字母的指数不变,∴结果的次数一定不高于2次,当二次项的系数相同时,合并后结果为0,所以(1)和(2)(5)是错误的.故选C.二.填空题(共10小题)11.(2016•河北模拟)已知多项式x|m|+(m﹣2)x﹣10是二次三项式,m为常数,则m的值为﹣2.【解答】解:因为多项式x|m|+(m﹣2)x﹣10是二次三项式,可得:m﹣2≠0,|m|=2,解得:m=﹣2,故答案为:﹣212.(2012秋•武侯区期末)若代数式mx2+5y2﹣2x2+3的值与字母x的取值无关,则m的值是2.【解答】解:mx2+5y2﹣2x2+3=(m﹣2)x2+5y2+3,∵代数式mx2+5y2﹣2x2+3的值与字母x的取值无关,则m﹣2=0,解得m=2.13.(2012•万州区校级二模)甲、乙、丙三人拿出同样多的钱,合伙订购同种规格的若干件商品.商品买来后,甲、乙分别比丙多拿了12、9件商品,最后结算时,乙付给丙20元,那么,甲应付给丙50元.【解答】解:(12+9)÷3=7,乙比丙多拿了2件,所以一件是20÷2=10元.10×(12﹣7)=50.甲付给丙50元.故答案为:5014.若a<0,则|1﹣a|+|2a﹣1|+|a﹣3|=5﹣4a.【解答】解:依题意得:原式=(1﹣a)+(﹣2a+1)+(﹣a+3)=5﹣4a.15.(2015秋•双城市期末)如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a﹣b)米.问小明家楼梯的竖直高度(即:BC的长度)为(a﹣2b)米.【解答】解:(3a﹣b)﹣(2a+b)=3a﹣b﹣2a﹣b=a﹣2b(米).故小明家楼梯的竖直高度(即:BC的长度)为(a﹣2b)米.故答案为:(a﹣2b).16.(2014秋•上杭县校级月考)下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.(﹣x2+3xy﹣y2)﹣(﹣x2+4xy﹣y2)=﹣x2+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是﹣xy.【解答】解:根据题意得:﹣x2+3xy﹣y2+x2﹣4xy+y2+x2﹣y2=﹣xy,故答案为:﹣xy.17.(2013秋•滨湖区校级期末)某校为适应电化教学的需要新建阶梯教室,教室的第一排有a个座位,后面每一排都比前一排多一个座位,若第n排有m个座位,则a、n和m之间的关系为m=a+n﹣1.【解答】解:由题意得:后面每一排都比前一排多一个座位及第一排有a个座位可得出第n排的座位数第n排的座位数:a+(n﹣1)又第n排有m个座位故a、n和m之间的关系为m=a+n﹣1.18.(2015秋•沛县期末)定义一种新运算:a※b=,则当x=3时,2※x﹣4※x的结果为8.【解答】解:当x=3时,原式=2※3﹣4※3=9﹣(4﹣3)=9﹣1=8,故答案为:819.(2015春•万源市校级月考)已知a2+ab=3,ab+b2=1,试求a2+2ab+b2=4,a2﹣b2=2.【解答】解:∵a2+ab=3,ab+b2=1,∴a2+2ab+b2=(a2+ab)+(ab+b2)=3+1=4,a2﹣b2=(a2+ab)﹣(ab+b2)=3﹣1=2.故答案为:4,2.20.(2014•贵池区校级模拟)已知,则代数式(m+2n)﹣(m﹣2n)的值为﹣5.【解答】解:原式=(m+2n)﹣(m﹣2n)=4n,当时,原式=.故答案为:﹣5.三.解答题(共10小题)21.(2015秋•太康县期中)将多项式按字母X的降幂排列.【解答】解:将多项式按字母x的降幂排列为:﹣7x4y2+3x2y﹣xy3+.22.(2009•余杭区模拟)已知a,b为常数,且三个单项式4xy2,axy b,﹣5xy相加得到的和仍然是单项式.那么a和b的值可能是多少?说明你的理由.【解答】解:(1)若axy b与﹣5xy为同类项,∴b=1,∵和为单项式,∴;(2)若4xy2与axy b为同类项,∴b=2,∵axy b+4xy2=0,∴a=﹣4,∴.23.(2015秋•渝北区期末)先化简,再求值:已知2(﹣3xy+x2)﹣[2x2﹣3(5xy﹣2x2)﹣xy],其中x,y满足|x+2|+(y﹣3)2=0.【解答】解:原式=﹣6xy+2x2﹣[2x2﹣15xy+6x2﹣xy]=﹣6xy+2x2﹣2x2+15xy﹣6x2+xy=﹣6x2+10xy∵|x+2|+(y﹣3)2=0∴x=﹣2,y=3,∴原式=﹣6x2+10xy=﹣6×(﹣2)2+10×(﹣2)×3=﹣24﹣60=﹣84.24.(2015秋•太和县校级期中)试至少写两个只含有字母x、y的多项式,且满足下列条件:(1)六次三项式;(2)每一项的系数均为1或﹣1;(3)不含常数项;(4)每一项必须同时含字母x、y,但不能含有其他字母.【解答】解:此题答案不唯一,如:x3y3﹣x2y4+xy5;﹣x2y4﹣xy﹣xy2.25.已知关于x的多项式(a﹣1)x2+x|a+2|﹣2x+b,问是否存在实数a,b,使得这个多项式为二次三项式?若存在,请求出a,b的值,若不存在,请说明理由.【解答】解:若(a﹣1)x2+x|a+2|﹣2x+b,是二次三项式,可得a=﹣1,b≠0或a=﹣3,b≠0或a=0,a=﹣4,b≠0所以当a=﹣1,b≠0或a=﹣3,b≠0或a=﹣4,b≠0.得(a﹣1)x2+x|a+2|﹣2x+b为二次三项式.26.(2013秋•硚口区期中)观察下面有规律的三行单项式:x,2x2,4x3,8x4,16x5,32x6,…①﹣2x,4x2,﹣8x3,16x4,﹣32x5,64x6,…②2x2,﹣3x3,5x4,﹣9x5,17x6,﹣33x7,…③(1)根据你发现的规律,第一行第8个单项式为128x8;(2)第二行第n个单项式为(﹣2)n x n;(3)第三行第8个单项式为﹣129x9;第n个单项式为(﹣1)n+1(1+2n﹣1)x n+1.【解答】解:因为第一行的每个单项式,数字因数后面都是前面的2倍,字母次数与这个单项式是第几个有关,根据这个规律可得第一行第8个单项式为128x8;因为第二行的每个单项式,数字因数后面都是前面的(﹣2)倍,字母次数与这个单项式是第几个有关,根据这个规律可得第n个单项式为(﹣2)n x n;通过观察第三行的这组单项式,这组单项式符合(﹣1)n+1(1+2n﹣1)x n+1,第8个单项式是﹣129x9;第n个单项式为(﹣1)n+1(1+2n﹣1)x n+1.故答案为:(1)128x8,(2)(﹣2)n x n,(3)﹣129x9 ,(﹣1)n+1(1+2n﹣1)x n+127.(2015秋•和平区期中)已知关于x、y的多项式5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1 (1)若该多项式不含三次项,求m的值;(2)在(1)的条件下,当x2+y2=13,xy=﹣6时,求这个多项式的值.【解答】解:(1)5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1=5x2﹣2xy2﹣(3xy+4y2+9xy﹣2y2﹣2mxy2+7x2)﹣1=5x2﹣2xy2﹣(12xy+2y2﹣2mxy2+7x2)﹣1=5x2﹣2xy2﹣12xy﹣2y2+2mxy2﹣7x2﹣1=﹣2x2﹣2y2﹣12xy+(﹣2+2m)xy2﹣1,∵该多项式不含三次项,∴﹣2+2m=0,故m的值为:1;(2)∵原式=﹣2x2﹣2y2﹣12xy+(﹣2+2m)xy2﹣1=﹣2(x2+y2)﹣12xy﹣1=﹣2×13﹣12×(﹣6)﹣1=45.28.(2015秋•永川区校级期中)已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的还多1岁,求这三名同学的年龄的和.【解答】解:由题意可知:小红的年龄为(2m﹣4)岁,小华的年龄为岁,则这三名同学的年龄的和为:=m+2m﹣4+(m﹣2+1)=4m﹣5.答:这三名同学的年龄的和是4m﹣5岁.29.(2015秋•富顺县校级期中)学规律在数学中有着极其重要的意义,我们要善于抓住主要矛盾,提炼出我们需要的信息,从而解决问题.(1)观察下列算式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…,通过观察,用你所发现的规律确定32014的个位数字是9;(2)观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是2;根据此规律,如果a n(n为正整数)表示这个数列的第n项,那么a18=218,a n=2n;(3)观察下面的一列单项式:x,﹣2x2,4x3,﹣8x4,…根据你发现的规律,第5个单项式为16x5;第7个单项式为64x7;第n个单项式为(﹣2)n﹣1x n.【解答】解:(1)式子末尾数字以3、9、7、1这4个一循环,2014÷4=503…2,所以32014的末位数字是9.(2)每一项与前一项之比是一个常数,这个常数是2,所以a18=218,a n=2n;(3)由题意可知,第5个单项式为16x5,第7个单项式为64x7.第n个单项式是(﹣2)n﹣1x n.故答案为:9;2,218,2n;16x5,64x7,(﹣2)n﹣1x n.30.(2014秋•盐都区期末)马虎的李明在计算多项式M加上x2﹣3x+7时,因错看成加上x2+3x+7,尽管计算过程没有错误,也只能得到一个错误的答案为5x2+2x﹣4.(1)求多项式M;(2)求出本题的正确答案.【解答】解:(1)根据题意列得:M=5x2+2x﹣4﹣(x2+3x+7)=4x2﹣x﹣11;(2)正确答案为:4x2﹣x﹣11+(x2﹣3x+7)=4x2﹣x﹣11+x2﹣3x+7=5x2﹣4x﹣4.。
苏教版二年级数学上册《表内除法一》复习教案

苏教版二年级数学上册《表内除法一》复习教案一、教学目标1. 知识与技能:学生能够熟练掌握表内除法的计算方法,能够运用除法解决简单的实际问题。
2. 过程与方法:通过观察、操作、思考等活动,培养学生的动手能力和解决问题的能力。
3. 情感态度与价值观:激发学生对数学的兴趣,培养他们善于观察、思考和合作的良好品质。
二、教学重点和难点重点:表内除法的计算方法和实际应用。
难点:理解除法的意义,掌握除法运算的规则,解决复杂的实际问题。
三、教学过程1. 导入:回顾旧知,通过提问学生关于除法的相关知识,引出表内除法一的复习。
2. 新授:(1)除法运算的复习:通过例题和练习,让学生掌握除法的基本计算方法,理解除法的意义。
(2)除法的实际应用:结合生活实际,引导学生运用除法解决简单的实际问题,如平均分配、计算时间等。
(3)复杂问题的解决:通过一些复杂的实际问题,让学生了解如何运用除法进行推理和分析,培养学生的思维能力。
3. 巩固:通过多种形式的练习,如计算题、应用题等,让学生熟练掌握除法的计算方法和实际应用。
4. 拓展:引导学生自主探究除法的变形和应用,如乘法和除法的关系、商不变的规律等。
5. 总结:对本节课所学内容进行总结,让学生明确自己的学习成果和不足之处。
四、教学方法和手段1. 讲授法:讲授除法的基本概念和计算方法,帮助学生建立正确的概念和理解。
2. 讨论法:组织学生进行小组讨论,互相交流学习心得和解题方法,培养学生的合作精神和沟通能力。
3. 练习法:通过大量的练习,让学生熟练掌握除法的计算方法和实际应用。
4. 任务驱动法:通过布置任务的方式,引导学生自主探究和学习,提高他们的学习能力和解决问题的能力。
5. 互动教学法:通过师生互动、生生互动的方式,激发学生的学习兴趣和参与度,提高教学效果。
五、课堂练习、作业与评价方式1. 课堂练习:课堂上组织学生进行即时练习,通过练习巩固所学知识,提高学生的应用能力。
2. 作业:布置一定量的课后作业,让学生在家中继续练习,加深对所学知识的理解和记忆。
数学史复习资料.doc

数学史复习资料1.世界上第一个把n计算到3.1415926< n <3.1415927的数学家是(祖冲之)。
2.亚力山大晚期一位重要的数学家是(帕波斯),他唯一的传世之作《数学汇编》是一部荟萃总结前人成果的典型著作。
3.古希腊亚历山大时期的数学家阿波罗尼兹在前人工作的基础上创立了相当完美的圆锥曲线理论,其著作《圆锥曲线》代表了希腊演绎几何的最高成就。
4.我国的数学教育有悠久的历史,(隋唐)代开始在国子寺里设立“算学”,唐至五代代则在科举考试中开设了数学科目,叫“明算科”。
5.《几何基础》的作者是(希尔伯特),该书所提出的公理系统包括(五)组公理。
6.用“分割法”建立实数理论的数学家是(戴德金),该理论建立于(19)世纪。
7.费马大定理证明的最后一步是英国数学家(怀尔斯)于1994年完成的,他因此于1996年获得了(沃尔夫)奖。
8.“蓦势既同,则积不容异”是我国古代数学家(刘徽)首先明确提出的,这一原理在西方文献中被称作(〈瓦列利)原理。
9.创造并首先使用“阿拉伯数码”的国家或民族是(印度),而首先使用十进位值制记数的国家或民族则是(中国)。
10.古希腊的三大著名几何问题是化圆为方、倍立方和三等分角。
11.我国元代数学著作《四元玉鉴》的作者是(朱世杰),《海岛算经》的作者是—刘徽12.就微分学与积分学的起源而言(积分学早于微分学)13.在现存的中国古代数学著作中,《周髀算经》是最早的一部。
卷上叙述的关于荣方与陈子的对话,包含了勾股定理的一般形式。
14.希尔伯特在历史上第一次明确地提出了选择和组织公理系统的原则,即:相容性、完备性、独立性。
15.二项式展开式的系数图表,在中学课本中称其为_杨辉一三角,而数学史学者常常称它为贾宪三角。
16.阿拉伯数学家花拉子米的《代数学》第一次给出了一次和二次方程的一般解法,并用—几何—方法对这一解法给出了证明。
17.被称为“现代分析之父”的数学家是(柯西),被称为“数学之王”的数学家是(高斯)。
《数值计算方法》试题集及答案(1-6)-2..

《计算方法》期中复习试题一、填空题:1、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用辛普生(辛卜生)公式计算求得⎰≈31_________)(dx x f ,用三点式求得≈')1(f 。
答案:2.367,0.252、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L3、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;4、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );答案)(1)(1n n n n n x f x f x x x '---=+5、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );6、计算方法主要研究( 截断 )误差和( 舍入 )误差;7、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n a b );8、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 ); 11、 两点式高斯型求积公式⎰1d )(xx f ≈(⎰++-≈1)]3213()3213([21d )(f f x x f ),代数精度为( 5 );12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5,1 ,进行两步后根的所在区间为 0.5,0.75 。
计算思维复习
网络层
功能:主要完成信息传递和处理。 组成:两个部分:接入单元、接入网络。
接入单元是连接感知层的网桥,它汇聚从感知层获得的数据,并将 数据发送到接入网络。 接入网络即现有的通信网络,包括移动通信网、有线电话网、有线 宽带网等。通过接入网络,人们将数据最终传入互联网。 关键技术:包含了现有的通信技术,如移动通信技术、有线宽带技 术、公共交换电话网(PSTN)技术、Wi-Fi通信技术等,也包含了 终端技术,如实现传感网与通信网结合的网桥设备、为各种行业 终端提供通信能力的通信模块等。
在2006 年,个人用户才刚刚迈进TB时代,全球 一共新产生了约180EB的数据;
在2011 年,这个数字达到了1.8ZB。
而有市场研究机构预测: 到2020 年,整个世界的数据总量将会增长44 倍, 达到35.2ZB(1ZB=10 亿TB)!
想驾驭这庞大的数据,我们必 须了解大数据的特征。
什么是大数据: Big Data名词由来
普适计算
普适计算(Pervasive Computing/Ubiquitous Computing),指无所不在的、随时随地可 以进行计算的一种方式——无论何时何地,只要需要,就可以通过某种设备访问到所 需的信息。
普适计算(又叫普及计算)的思想源于1991年Mark Weiser在《Scientific American》的 “The Computer for the 21st Century”中提出的,强调把计算机嵌入到环境或日常工具中 去,让计算机本身从人们的视线中消失,使人们注意的中心回归到要完成的任务本身上。
数据库
软件
MapReduce
• MapReduce是Google公司于2004年提出来的一种并行的程序处 理技术
《数值计算方法》复习资料

实用文档《数值计算方法》复习资料第一章数值计算方法与误差分析第二章非线性方程的数值解法第三章线性方程组的数值解法第四章插值与曲线拟合第五章数值积分与数值微分第六章常微分方程的数值解法自测题课程的性质与任务数值计算方法是一门应用性很强的基础课,在学习高等数学,线性代数和算法语言的基础上,通过本课程的学习及上机实习、使学生正确理解有关的基本概念和理论,掌握常用的基本数值方法,培养应用计算机从事科学与工程计算的能力,为以后的学习及应用打下良好基础。
第一章数值计算方法与误差分析一考核知识点误差的来源类型;绝对误差和绝对误差限,相对误差和相对误差限,有效数字;绝对误差的传播。
二复习要求1.知道产生误差的主要来源。
2.了解绝对误差和绝对误差限、相对误差和相对误差限和有效数字等概念以及它们之间的关系。
3.知道四则运算中的误差传播公式。
实用文档三例题例 1 设x*= =3.1415926⋯近似值 x=3.14 = 0.314× 101,即 m=1,它的绝对误差是- 0.001 592 6 ,⋯有即 n=3,故 x=3.14 有 3 位有效数字 .x=3.14准确到小数点后第 2 位 .又近似值 x=3.1416,它的绝对误差是0.0000074 ⋯,有即 m=1,n= 5, x=3.1416 有 5 位有效数字 .而近似值x=3.1415,它的绝对误差是0.0000926 ⋯,有即 m=1,n= 4, x=3.1415 有 4 位有效数字 .这就是说某数有s 位数,若末位数字是四舍五入得到的,那么该数有s 位有效数字;例 2指出下列各数具有几位有效数字,及其绝对误差限和相对误差限:2.000 4-0.002 009 0009 000.00解因为 x1=2.000 4= 0.200 04× 101, 它的绝对误差限 0.000 05=0.5 × 10 1―5,即m=1,n=5, 故 x=2.000 4 有 5 位有效数字 . a1=2,相对误差限x2=- 0.002 00,绝对误差限0.000 005,因为 m=-2,n=3 ,x2=- 0.002 00 有 3 位有效数字 . a1=2 ,相对误差限r ==0.002 5实用文档x3=9 000 ,绝对误差限为0.5× 100,因为 m=4, n=4, x3=9 000 有 4 位有效数字, a=9 ,相对误差限r== 0.000 056x4=9 000.00 ,绝对误差限0.005,因为 m=4, n=6, x4=9 000.00 有 6 位有效数字,相对误差限为r== 0.000 000 56由 x3与 x4可以看到小数点之后的0,不是可有可无的,它是有实际意义的.例 3 ln2=0.69314718⋯,精确到10-3的近似值是多少?解精确到 10-3= 0.001,意旨两个近似值x1,x2满足,由于近似值都是四舍五入得到的,要求满足,近似值的绝对误差限应是=0.0005,故至少要保留小数点后三位才可以。
2022版步步高《大一轮复习讲义》人教版第1章 第5讲 微专题4 化学计算的常用方法

4 化学计算的常用方法一、应用化学方程式计算方法 1.应用化学方程式列比例最重要的基础方法,关键抓对应项列比例,且“上下单位统一,左右单位相当”。
2.关系式法——一种快速高效的化学方程式计算方法(1)关系式法是一种巧妙利用已知量与未知量之间的关系进行解题的一种方法,一般适用于多步进行的连续反应,因前一个反应的产物是后一个反应的反应物,可以根据中间物质的传递关系,找出原料和最终产物的相应关系式。
(2)列关系式通常有如下几种方法:①有关化学方程式的计量数关系;②原子守恒关系;③得失电子守恒关系。
3.差量法(1)所谓“差量”就是指反应过程中反应物的某种物理量之和(始态量)与同一状态下生成物的相同物理量之和(终态量)的差,这种物理量可以是质量、物质的量、气体体积、气体压强、反应过程中的热效应等。
根据化学方程式求出理论上的差值(理论差量),结合题中的条件求出或表示出实际的差值(实际差量),根据比例关系建立方程式并求出结果。
(2)差量法的解题关键是找准研究对象。
通常有:①固体的质量差,研究对象就是固体。
②气体的质量差,研究对象就是气体。
③液体的质量,研究对象就是液体。
4.列方程组进行的混合物计算计算中的数学思想:在两种物质组成的混合物中。
一般可设两个未知数x 、y ,题目中通常给出两个已知量(设为A 、B ),寻找x 、y 与A 、B 的数学关系,由此建立二元一次方程组进行联解⎩⎪⎨⎪⎧A =f 1(x ,y )B =f 2(x ,y )。
1.取3.38 g K 2CO 3和KHCO 3的混合物溶于水配成25 mL 溶液,往溶液中加入25 mL Ba(OH)2溶液恰好使生成白色沉淀的量最多,反应后溶液中c (OH -)=0.8 mol·L -1(忽略混合后溶液体积变化),则原混合物中K 2CO 3和KHCO 3 物质的量之比为( ) A .1∶2 B .1∶1 C .2∶1 D .2∶3 答案 A解析 设原混合物中n (K 2CO 3)=x mol ,n (KHCO 3)=y mol , 根据总质量可得:138x +100y =3.38①往溶液中加入Ba(OH 2)溶液,恰好使生成白色沉淀的量最多,反应后剩余的氢氧根的物质的量n (OH -)=0.8 mol·L -1×0.05 L =0.04 mol 。
《计算方法》复习资料

二单项选择题1. 已知近似值1x ,2x ,则()12,x x ()=A. ()()2112x x x x + B 。
()()12x x +C. ()()1122x x x x + D 。
()()12x x2. 已知求积公式()()211211()(2)636f x dx f Af f ≈++⎰,则A =( ) A . 16 B 。
13 C 。
12 D. 233. 已知2112A ⎡⎤=⎢⎥⎣⎦,则化为A 为对角阵的平面旋转变换角θ=( ) A .6π B 。
4π C 。
3π D. 2π 4. 设求方程()0f x =的根的切线法收敛,则它具有( )敛速。
A . 线性 B. 超越性 C 。
平方 D 。
三次5。
改进欧拉法的局部截断误差为( )A . ()5O h B. ()4O h C. ()3O h D 。
()2O h填空题1。
π的近似值3.1428是准确到 近似值。
2. 满足()a a f x x =,()b b f x x =,()c c f x x =的拉格朗日插值余项为 。
3。
用列主元法解方程组时,已知第2列主元为()142a 则()142a = 。
4.乘幂法师求实方阵 的一种迭代方法。
5. 欧拉法的绝对稳定实区间为 。
计算题1. 用已知函数表求抛物插值多项式,并求1()2f 的近似值。
2. 用紧凑格式解方程组123410114130141x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦3. 已知方程组123210113110121x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(1) 证明高斯-塞德尔法收敛;(2) 写出高斯-塞德尔法迭代公式; (3) 取初始值()()00,0,0TX=,求出()1X 。
4. 用4n =复化辛卜公式计算积分1011dx x +⎰,并估计误差。
5. 用一般迭代法求方程[]0,0.5内的根。
《概率论与数理统计》总复习资料

《概率论与数理统计》总复习资料概率论部分1.古典概型中计算概率用到的基本的计数方法。
例1:袋中有4个白球,5个黑球,6个红球,从中任意取出9个球,求取出的9个球中有1个白球、3个黑球、5个红球的概率.解:设B ={取出的9个球中有1个白球、3个黑球、5个红球}样本空间的样本点总数:915C n ==5005事件B 包含的样本点:563514C C C r ==240,则P (B )=240/5005=0.048例2:在0~9十个整数中任取四个,能排成一个四位偶数的概率是多少?解:考虑次序.基本事件总数为:410A =5040,设B ={能排成一个四位偶数}。
若允许千位数为0,此时个位数可在0、2、4、6、8这五个数字中任选其一,共有5种选法;其余三位数则在余下的九个数字中任选,有39A 种选法;从而共有539A =2520个。
其中,千位数为0的“四位偶数”有多少个?此时个位数只能在2、4、6、8这四个数字中任选其一,有4种选法;十位数与百位数在余下的八个数字中任选两个,有28A 种选法;从而共有428A =224个。
因此410283945)(A A A B P -==2296/5040=0.4562.概率的基本性质、条件概率、加法、乘法公式的应用;掌握事件独立性的概念及性质。
例1:事件A 与B 相互独立,且P (A )=0.5,P (B )=0.6,求:P (AB ),P (A -B ),P (A B )解:P (AB )=P (A )P (B )=0.3,P (A -B )=P (A )-P (AB )=0.2,P (A B )=P (A )+P (B )-P (AB )=0.8例2:若P (A )=0.4,P (B )=0.7,P (AB )=0.3,求:P (A -B ),P (A B ),)|(B A P ,)|(B A P ,)|(B A P 解:P (A -B )=0.1,P (A B )=0.8,)|(B A P =)()(B P AB P =3/7,)|(B A P =)()()()()(B P AB P B P B P B A P -==4/7,|(B A P =)(1)()()(B P B A P B P B A P -==2/33.准确地选择和运用全概率公式与贝叶斯公式。
《简便计算总复习》教案

1.教学重点
(1)乘法口诀的熟练运用:强调学生对乘法口诀的记忆和应用,如“一一得一”、“二二得四”等,以便在简便计算中迅速得出结果。
(2)四则运算定律的理解与应用:包括加法结合律、交换律,减法的性质,乘法分配律,除法的性质等,使学生能够灵活运用这些定律简化计算过程。
(3)简便计算方法的掌握:如利用加、减法的性质进行简算,以及利用乘法分配律进行简算等。
五、教学反思
在今天的教学过程中,我发现同学们在简便计算总复习这一章节中,对乘法口诀和四则运算定律的掌握程度参差不齐。让我印象深刻的是,有些同学能够迅速准确地运用这些知识点简化计算过程,而部分同学在这一方面还存在一定的困难。
在导入新课环节,通过提问同学们在日常生活中遇到的计算问题,成功引起了他们的兴趣和好奇心。这个环节让我意识到,将生活实际与教学内容相结合,能够激发学生的学习兴趣,提高他们的学习积极性。
举例:在计算“123 + 456”时,可以运用加法交换律,将其变为“456 + 123”,简化计算过程。
2.教学难点
(1)乘法口诀的灵活运用:学生在实际计算中,往往难以迅速准确地应用乘法口诀,导致计算速度慢、准确性低。
解决方法:通过设计相关练习题,让学生反复练习,提高乘法口诀的熟练度。
(2)四则运算定定律简化计算。
学生小组讨论环节,同学们围绕简便计算在实际生活中的应用展开讨论。这个环节让我看到了学生的创新意识和解决问题的能力。同时,我也发现部分同学在思考问题时,容易陷入思维定势,需要我在教学中多设计一些开放性问题,引导他们拓展思维,提高解决问题的能力。
通过这次教学,我认识到以下几点需要在今后的教学中注意:
1.针对学生掌握程度的差异,因材施教,关注每一个学生的成长。
成人教育《计算方法 提纲》期末考试复习题及参考答案

一、单项选择题1、Jacobi迭代法解方程组Ax = b的必要条件是( C ).A.A的各阶顺序主子式不为零 B.ρ(A)<1C. D.|A|≤12、设,均差( B )A.3B. -3C. 5D.03、设,则ρ(A)为( C ).A. 2B. 5C. 7D. 34、三点的高斯求积公式的代数精度为( B ).A. 2B.5C. 3D. 45、幂法的收敛速度与特征值的分布( A )。
A. 有关B. 不一定C. 无关6、求解线性方程组Ax=b的分解法中,A须满足的条件是( B )。
A. 对称阵B. 正定矩阵C. 任意阵D. 各阶顺序主子式均不为零7、舍入误差是( A )产生的误差。
A.只取有限位数B.模型准确值与用数值方法求得的准确值C. 观察与测量D.数学模型准确值与实际值8、3.141580是π的有( B )位有效数字的近似值。
A.6B.5C. 4D. 79、幂法是用来求矩阵( A )特征值及特征向量的迭代法。
A. 按模最大B. 按模最小C. 所有的D. 任意一个10、用1+x近似表示所产生的误差是( C )误差。
A. 模型B. 观测C.截断D. 舍入11、解线性方程组的主元素消去法中选择主元的目的是( A )。
A.控制舍入误差B. 减小方法误差C.防止计算时溢出D. 简化计算12、解线性方程组Ax=b的迭代格式收敛的充要条件是( D )。
A. |M|<1B. ρ(A)<1C. |ρ(M)|<1D. ρ(M)<113、用近似表示所产生的误差是( D )误差。
A. 舍入B. 观测C.模型D. 截断14、-324.7500是舍入得到的近似值,它有( C )位有效数字。
A. 5B. 6C.7D. 815、反幂法是用来求矩阵( B )特征值及相应特征向量的一种向量迭代法。
A. 按模最大B. 按模最小C.全部D. 任意一个16、用表示自由落体运动距离与时间的关系式( g为重力加速度),是在时间t内的实际距离,则是( C )误差。
(完整版)水文水利计算复习资料

水文计算1.水文现象的基本特点及水文学的研究方法是什么.基本规律( 1)成因规律(确立性规律)(2)统计规律(随机性规律)(3)地域性规律研究方法成因解析法、数理统计法、地理综合法2.流域均匀雨量计算有哪几种方法.算数均匀法、泰森多边形法、等雨量线图法3.径流有哪些表示方法.流量( Q):单位时间经过河流某断面的水量径流量( W):时段 ?t 内经过河流某一断面的总水量径流深( R) :径流量平铺在整个流域面积上的水层深度R=QT/1000F径流模数 (M): 流域出口断面流量与流域面积的比值M=1000Q/F径流系数(α):某一时段的径流深与相应的降雨深度的比值α=R/P4.生么是概率、频次?两者的关系。
概率:表示随机事件出现的可能性或几率,是用来胸怀可能性大小的数值,常用百分数表示。
频次:必然程度上反应了事件出现的可能性大小。
两者关系 :概率是理论值,是固定不变的,能够依据公式开初计算出来。
拥有先验性;而频次是计算值,是可变的(拥有显然的随机性)、试验的(不吻合古典概率公式的事件,他们的概率只能经过多次察看试验来推求)。
概率是指随机变量某值在整体中的出现机遇;频次是指随机变量某值在样本中的出现机遇。
当样本足够大时,频次拥有必然的坚固性;当样本无量增大时,频次趋于概率。
所以,频次能够作为概率的近似值。
5.重现期( T)与频次( P)有什么关系, P=80%的枯水年,其重现期 (T)为多少年?含有是什么。
频次与重现期的关系有两种:(1)当研究暴雨洪水问题时,研究的目的是防洪,一般设计频次 P< 50%,则T=1/P (X ≥Xp)T---重现期P---频次 (%)(2)当考虑水库兴利调理研究枯水问题时,研究的目的是浇灌、发电、供水等兴利目的,更关怀小于等于某一数值出现的可能性大小,设计频次P>50%,则11T1 P(x x p)P( x< x p)1T(5年)180%P=80%的枯水年,它表示小于等于P=80%的枯水流量在长久间内均匀 5 年出现一次。
《计算方法》期末复习

《计算方法》期末复习计算方法是计算机科学与技术专业的一门基础课程,它主要涉及计算机中的常用数值计算方法及其应用。
期末复习是为了帮助学生巩固课程知识、理解和掌握具体的计算方法,以提高数学计算和算法实现的能力。
在期末复习中,需要复习的内容主要包括数值计算方法的原理、基本原则、具体的计算方法及其常见应用等。
下面是计算方法期末复习的一个大纲,可供参考:一、计算方法基础知识回顾1.数值计算及其应用的概念和基本原理2.计算机中数的表示形式及其精度3.计算机中常用的数学运算法则4.误差的类型和度量方法二、线性方程组的数值解法1.线性方程组的矩阵表示、高斯消元法和矩阵消去法2.矩阵LU分解法和逆矩阵法3.迭代法解线性方程组(雅可比方法、高斯-赛德尔方法、逐次超松弛方法)4.带主元的高斯消元法5.矩阵的特征值和特征向量的计算(幂法、反幂法、QR分解法)三、非线性方程的求根方法1.非线性方程求根的基本概念和定理2.二分法、简单迭代法和牛顿法的原理和应用3.割线法和弦截法四、插值与逼近1.插值与逼近的基本概念和分类2.拉格朗日插值多项式及其误差估计3.牛顿插值多项式及其差商表示4.埃尔米特插值多项式与三次样条插值5.最小二乘法曲线拟合及其应用五、数值积分与数值微分1.数值积分的基本概念和定义2.梯形公式、辛普森公式和复化求积公式3.数值积分的误差估计和自适应积分方法4.复化求积公式的收敛性和数值稳定性5.数值微分的基本概念和定义6.差商和差商表及其应用六、常微分方程的数值解法1.常微分方程(ODE)的基本概念和分类2.欧拉法和改进欧拉法3.龙格-库塔法(RK4法)4.多步法(Adams-Bashforth法、Milne法)5.预测-校正法(Adams-Moulton法)6.刚体现象方程的数值解法七、矩阵特征值与特征向量的计算1.矩阵特征值与特征向量的原理和定义2.幂法和反幂法的原理和应用3.QR分解法与带位移的QR分解法4.雅可比迭代法和带位移的雅可比迭代法八、常见数值计算问题的MATLAB实现1.线性方程组的解法2.非线性方程求根的方法3.插值与逼近的应用4.数值积分与数值微分的计算5.常微分方程的数值解法6.矩阵特征值与特征向量的计算以上是《计算方法》期末复习的一个大纲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二单项选择题1. 已知近似值1x ,2x ,则()12,x x ()=A. ()()2112x x x x +B. ()()12x x +C. ()()1122x x x x +D. ()()12x x 2. 已知求积公式()()211211()(2)636f x dx f A f f ≈++⎰,则A =( ) A .16B.13C. 12D.233. 已知2112A ⎡⎤=⎢⎥⎣⎦,则化为A 为对角阵的平面旋转变换角θ=( ) A .6πB.4πC.3πD.2π4. 设求方程()0f x =的根的切线法收敛,则它具有( )敛速。
A . 线性 B. 超越性 C. 平方 D. 三次5. 改进欧拉法的局部截断误差为( )A . ()5O h B. ()4O h C. ()3O h D. ()2O h填空题1. π的近似值3.1428是准确到 近似值。
2. 满足()a a f x x =,()b b f x x =,()c c f x x =的拉格朗日插值余项为 。
3. 用列主元法解方程组时,已知第2列主元为()142a 则()142a = 。
4.乘幂法师求实方阵 的一种迭代方法。
5. 欧拉法的绝对稳定实区间为 。
计算题1. 用已知函数表求抛物插值多项式,并求1()2f 的近似值。
2. 用紧凑格式解方程组 123410114130141x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦3. 已知方程组 123210113110121x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(1) 证明高斯-塞德尔法收敛;(2) 写出高斯-塞德尔法迭代公式; (3) 取初始值()()00,0,0TX=,求出()1X。
4. 用4n =复化辛卜公式计算积分1011dx x+⎰,并估计误差。
5. 用一般迭代法求方程[]0,0.5内的根。
(1) 对方程同解变形,并检验压缩条件; (2) 写出一般迭代法迭代公式; (3) 选初始值00.5x =,求出1x 。
证明题1. 设x Bx b **=+,1B <证明由公式()()1m m xBxb +=+,0,1,m = ,得到的序列(){}m x收敛于x*。
2.证明计算)0α>的切线法迭代公式为 11()2n n nx x x α+=+, ()0,1,n =二一、单项选择题1. A2. D3. B4. C5. C 二、填空题1. 210- 2. ()()()()()3!a b c f R x x x x x x x ξ'''=---3. ()()114222m ax i i αα≥= 4.按规模最大的特征值与特征向量 5. []2,0-三、计算题 1. 作差商表:()()()()2210011N x x x x x =+-+--=+21151.25224f N ⎛⎫⎛⎫≈==⎪ ⎪⎝⎭⎝⎭2. 解:(1)完成分解A LR =114r =,121r =-,130r =, 2114l =,310l =,22115444r =-=,231r =-,32415l =,335615r =所以矩阵的三角分解A LR = 14101151144456011515A ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦ (2)解方程组L Y b =,11y =,2134y =,32815y =(3)解方程组RX Y =,312x =,21x =,112x =所以11(,1,)22TX =3. (1)因为A 严格对角占优矩阵,所以高斯-塞德尔迭代法收敛。
(2)高斯-塞德尔法迭代公式为: ()()()()()()()()()()112112131132112113112m m m m m m m x x x x x x x +++++⎧=-⎪⎪⎪=---⎨⎪⎪=-⎪⎩(3)取初值()()00,0,0TX=,计算得()1112x =,()1212x =-,()1334x =4. 用4n =复化辛卜公式计算得:101144411240.693251126572dx x⎡⎤⎛⎫≈+⨯+⨯++≈ ⎪⎢⎥+⎝⎭⎣⎦⎰因为()11f x x=+, ()()()45241fx x =+,()()44m ax 24M fx ==所以,()44241288021920R f ≤=⨯5. (1)在[]0,0.5上将方程同解变形为 ()()3114x x x ϕ=+=而()233m ax m ax1416x xρϕ'===<(2)一般迭代法公式为:()3111,0,1,4n nx xn +=+=··· (3)由00.5x =,计算得10.28125x ≈ 四、证明题 1.证明 由公式()()1m m xBxb +=+和x Bx b **=+两式相减得()()1m m x xBxx-**-≤-≤···()0mBxx *≤-所以有:()()0,,()m m xx x x m **-→→→∞2.证明)0α>等同于求方程20x α-=的正根,令()()2,2f x x f x x α'=-=,代入切线法迭代公式得:211()22n n n n nnx x x x x x αα+-=-=+,0,1,n =···三单项选择题1. 以下误差公式不正确的是( )A .()1212x x x x ∆-≈∆-∆B .()1212x x x x ∆+≈∆+∆C .()122112x x x x x x ∆≈∆+∆D .1122()x x x x ∆≈∆-∆2. 已知等距节点的插值型求积公式()()352kkk f x dx A f x =≈∑⎰,那么3kk A==∑( )A .1 B. 2 C. 3 D. 4 3. 辛卜生公式的余项为( ) A .()()32880b a f η-''-B .()()312b a f η-''-C .()()()542880b a fη--D .()()()452880b a fη--4. 用紧凑格式对矩阵4222222312A -⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦进行的三角分解,则22r =( ) A .1 B .12C .–1D .–25. 用一般迭代法求方程()0f x =的根,将方程表示为同解方程()x x ϕ=的,则()0f x = 的根是( )A . y x =与()y x ϕ=的交点B . y x =与与x 轴的交点的横坐标的交点的横坐标C . y x =与()y x ϕ=的交点的横坐标D . ()y x ϕ=与x 轴的交点的横坐标填空题1. 取 3.142x =作为 3.141592654x =┅的近似值,则x 有 位有效数字.2. 消元法的步骤包括 .3. 龙贝格积分法是将区间[],a b 并进行适当组合而得出的积分近似值的求法。
4.乘幂法可求出实方阵A 的 特征值及其相应的特征向量. 5. 欧拉法的绝对稳定实区间为 。
计算题6.已知函数211y x=+的一组数据:求分段线性插值函数,并计算()1.5f 的近似值. 7. 求矩阵10101022A -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦的谱半径. 8. 已知方程组123210113110121x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(1) 证明高斯-塞德尔法收敛; (2) 写出高斯-塞德尔法迭代公式; (3) 取初始值()()00,0,0TX=,求出()1X。
4. 4n =时,用复化梯形与复化辛卜生公式分别计算积分124x dx x +⎰.5. 用改进平方根法求解方程组233351035916591730x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦证明题证明向量X 的范数满足不等式 (1)2X X∞∞≤≤ (2)111XXXn∞≤≤三参考答案一.单选题1. D2.C3.C4.A5. C 二.填空题1. 42. 消元和回代3. 逐次分半4. 按模最大5. []2,0- 三.计算题1. 解 []0,1x ∈, ()1010.510.50110x x Lx x --=⨯+⨯=--- []1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为()[][]10.50,10.80.31,2x x L x x x ⎧-∈⎪=⎨-∈⎪⎩ 10分 ()1.50.80.3 1.50.35L=-⨯= 12分2. 解 ()()1010101322I A λλλλλλλ--=-=--- 4分 矩阵A 的特征值为1230,1,3λλλ=== 8分 所以谱半径(){}max 0,1,33A ρ== 12分3. 1)因为A 严格对角占优矩阵,所以高斯-塞德尔迭代法收敛。
(2)高斯-塞德尔法迭代公式为: ()()()()()()()()()()112112131132112113112m m m m m m m x x x x x x x +++++⎧=-⎪⎪⎪=---⎨⎪⎪=-⎪⎩(3)取初值()()00,0,0TX=,计算得()1112x =,()1212x =-,()1334x =4. 解 10.2544b a h -=== 2分用复化梯形公式计算:124x dx x +⎰()()()()()()0.25020.250.50.7512f f f f f ⎡⎤≈++++⎣⎦=0.110 892 27 7分用复化辛卜生公式计算得:124x dx x +⎰()()()()()()0.25040.250.7520.513f f f f f ⎡⎤≈++++⎣⎦=0.111 581 85 12分5. 解 由公式计算得1111121213133,3,5;r a r a r a ====== 312121311111351,33a a l l r r =====22222121232321135132,9154r a lr ralr =-=-⨯==-=-⨯= ()233233333113322322422,23r l r a l r l r r ====-+=4分再得 123410,6,3y y y ===8分得()1,1,2TX =- 12分证明(1)设j x 是向量X 的分量,则22221m ax ni ii i Xx x n X∞∞=⎡⎤=≤≤⎣⎦∑,所以由向量范数的概念可知,结论成立。
5分 (2)由1111max ni i i i Xx x Xn n∞=⎡⎤=≥=⎣⎦∑11m a x ni i i i Xx x X∞=⎡⎤=≤=⎣⎦∑所以结论成立。
