筒仓中粮食卸料动压力的数值模型
粮食立筒仓弹性变形对卸料动压力的影响与计算

粮食立筒仓弹性变形对卸料动压力的影响与计算粮食立筒仓是一种常用于粮食储存的设备。
在粮食储存在立筒仓中的过程中,粮食堆积在上部时会产生一定的压力,称为卸料动压力。
而粮食的立体弹性特性则会对这个卸料动压力产生影响。
下面将对粮食的弹性变形对卸料动压力的影响进行分析,并介绍相应的计算方法。
粮食的立体弹性变形对卸料动压力的影响是通过实际情况和材料性质两个方面来考虑的。
第一方面,实际情况。
卸料过程中,粮食由上部向下部流动,受到上层粮食的压力作用。
同时,下层的粮食也会受到上层粮食的压力,从而对容器内壁施加一个向外的动压力。
粮食的弹性变形使得上层粮食的重力分布不均匀,导致下层粮食的压力也不均匀。
在实际情况中,粮食的形状、密度等因素会影响到卸料动压力的分布。
第二方面,材料性质。
粮食的弹性变形取决于粮食的物理性质,如弹性模量、泊松比等。
粮食的弹性模量指的是单位应力下产生的单位应变,是描述粮食弹性特性的指标。
粮食的泊松比则表示了粮食在拉伸和压缩变形中横向收缩的程度。
这些材料性质的不同都会对粮食的弹性变形和卸料动压力产生影响。
计算粮食立筒仓卸料动压力时,需要考虑宏观力学和微观力学两个层面。
宏观力学上,可以通过传统的结构力学方法来计算。
首先需要建立立筒仓的弹性力学模型,将粮食视为弹性固体,并考虑粮食的重力和粮食对容器壁施加的力。
可以利用等效应力原理和平衡条件,建立方程组,并求解得到粮食的应力和变形分布。
通过将关键参数带入这些方程,可以计算出粮食在不同位置的动压力。
微观力学上,可以通过颗粒力学来计算粮食的弹性变形和卸料动压力。
颗粒力学是一种用来研究颗粒体系的力学方法,可以考虑颗粒间的接触力和颗粒的相对位移。
通过建立颗粒间的力学模型,可以计算出粮食颗粒的变形和应力分布。
然后将微观尺度上的结果转化为宏观力学上的结果,得到卸料动压力。
总之,粮食立筒仓的粮食弹性变形对卸料动压力的影响是一个很复杂的问题,需要综合考虑不同因素的影响。
粮食钢板筒仓设计规范 荷载与荷载效应组合 粮食荷载

4.2.1 考虑粮食对筒仓的作用时,应包括以下四种力:1 作用于筒仓仓壁的水平压力;2 作用于筒仓仓壁的竖向摩擦力;3 作用于筒仓仓底的竖向压力;4 作用于筒仓仓顶的吊挂电缆拉力。
4.2.2 深仓储粮静态压力的标准值,应按下列公式计算(图4.2.2):1 计算深度S处,储粮作用于仓壁单位面积上的水平压力标准值按下式计算:2 计算深度S处,储粮作用于单位水平面上的竖向压力标准值按下式计算:3 计算深度S处,储粮作用于仓壁单位面积上的竖向摩擦力标准值按下式计算:4 计算深度S处,储粮作用于仓壁单位周长上的总摩擦力标准值按下式计算:4.2.3 在深仓卸粮过程中,储粮作用于筒仓仓壁的动态压力标准值,应以其静态压力标准值乘以动态压力修正系数。
深仓储粮动态压力修正系数,应按表4.2.3 取值。
4.2.4 浅仓储粮压力的标准值,应按下列公式计算(图4.2.4):1 计算深度S处,作用于仓壁单位面积上的水平压力标准值按下式计算:2 若储粮计算高度hn大于或等于15m,且筒仓内径dn大于或等于10m时,储粮水平压力除按上式计算外,尚应按本规范(4.2.2-1)式计算,二者计算结果取大值;此外,还应按下式计算筒仓内壁单位面积上的竖向摩擦力标准值:3 计算深度S处,作用于单位水平面上的竖向压力标准值按下式计算:4.2.5 作用于圆形漏斗壁上的储粮压力标准值可按下式计算:1 漏斗壁单位面积上的法向压力标准值为:2 漏斗壁单位面积上的切向压力标准值为:4.2.6 吊挂于仓顶的测温电缆,计算其作用于仓顶结构的吊挂荷载时,应考虑电缆自重、粮食摩擦力及电缆突出物对储粮阻滞而产生的拉力。
当电缆为圆截面,且直径无变化,表面无突出物时,储粮摩擦引起的电缆总拉力标准值,应按下式计算:。
筒仓贮料流态的颗粒流数值模拟

文章编号:100926825(2008)3520090203筒仓贮料流态的颗粒流数值模拟收稿日期:2008208204作者简介:翟振威(19802),男,硕士,焦作一建建设工程有限公司,河南焦作 454100原国平(19772),男,助理工程师,焦作一建建设工程有限公司,河南焦作 454100张峰涛(19822),男,助理工程师,焦作匠人工程技术咨询有限公司,河南焦作 454100翟振威 原国平 张峰涛摘 要:采用基于离散单元法的颗粒流程序建立了一种筒仓缩尺模型,对筒仓缩尺模型进行了静态侧压力的数值模拟,并把模拟结果与原型筒仓的Janssen 计算值进行了比较,发现模拟结果与试验和理论值吻合较好,对该模型筒仓进行了卸料过程的模拟,得到了贮料的流动形态。
关键词:筒仓模型,物料流态,颗粒流中图分类号:TU311文献标识码:A0 引言立筒仓属于特种结构,由于其仓储物料的散体介质特性使其设计计算不同于其他一般的结构形式。
立筒仓结构设计的关键在于其工况荷载———贮料侧压力的正确计算和确定。
卸料是筒仓物料的流态,是影响侧压力的一个重要因素。
很多学者证实:当贮料流动时会产生不同的流动形态,而流动形态的不同对仓壁侧压力的大小的影响也不同。
贮料的流动形态,归纳起来可分为两种类型,一种属于整体流动,即卸料时整个贮料随之而动;另一种属于管状流动或称为漏斗状流动,即卸料时贮料从其内部形成的流动腔中流动,如图1所示。
贮料处于管状流动时所产生的动态侧压力,要大大小于整体流动时所产生的动态侧压力。
数值模拟法研究筒仓贮料流态是学者们常用的一种手段,这0.32/2)=5.07kN ・m 。
3)恒荷载作用下梁的内力计算:M =1/12ql 2=1/12×4.8×7.52=22.5kN ・m 。
4)活荷载作用下梁的内力计算:考虑两种内力组合:1.2恒载+1.4活载和1.2恒载+0.5活载+1.3地震梁。
M 1=1.2×22.5+1.4×9.38=40.14kN ・m 。
筒仓的受力分析及静力学计算
6736
D 34 d=300
2120 × 2120
h2
h1
h
2 已知参数
仓体材料:Q 2 3 5 B 许用应力 [σ]=17000N/cm2 筒仓自重:W 自 筒仓容重:W 容
3 筒仓结构强度计算
由于筒仓柱体和锥体连接处用 槽钢作环箍,可视作固支连接。因 此,连接处既存在薄膜应力,又存在 局部弯矩和剪力,其应力最大,强度
N2
柱壳由于下端支承(边界效应
另 作 计 算 )。 则:X = 0 Y = 0 Z = γ·α =13000 α
图3
由图 3 有:
由(3 )式得环向拉力:
N2 = RZ = R γα 当α = h1 时 N 2 为柱壳最大环向拉力 即:N2 = R γα 则环向拉应力为:
又:N2 = RZ 式中:
5 压实功能
同普通振动压路机的操控完全 一样,用高速冲击加宽频宽幅力的非 对称激振模式的混沌激振压路机通过 调整液压马达的ω,可得以下功能:
10g(非对称激振力 / 对称激力最 大力幅) 之傅立叶变换的绝对值
当∣ω∣小,振动轮可得低速
非对称多频冲击及连续宽频混沌激
振力激振。
当ω>0 对双挡振动压路机,振
故:N1 = 0 3.2 锥壳边缘处薄膜应力(图 3)
(1)
N1
W
R
N1
R1
(2)
h1
N2 = RZ 式中:X、Y 及 Z 为柱壳所受荷载
分别在纵向、环向及法向的分量;N 1、 N 2 及 S 为纵向拉压力、环向拉压力及 平错力;R 为单元薄壳曲率半径。
动轮可得强非对称多频冲击及连续
宽频混沌激振力激振。
粮仓特种结构课程设计计算书

特种结构课程设计计算书一、计算参数1.平面组合形式:2×3排列2.筒仓储料品种:稻谷3.筒仓内径:12米4.筒仓装粮高度:26米5.混凝土强度等级采用C30,钢筋采用HRB335。
6.粮食设计参数稻谷的重力密度为6kN/m3,内摩擦角为35°。
7.地震设防烈度6度;风载按当地情况查取。
二、筒仓的结构选型1.筒仓的仓壁、筒壁及角锥形漏斗宜采用等厚度截面,其厚度为:直径小于或等于15m的圆形筒仓仓壁厚度:t=d n/100+100=12000/100+100=220mm厚度可以取250mm2.圆形筒仓仓顶可采用钢筋混凝土梁板结构。
3.仓顶板厚度为150mm三、筒仓结构上的荷载仓壁上作用的荷载主要有仓顶板自重、女儿墙自重(G1k+G2k),女儿墙高度为1.3m。
G1k+G2k=25×3.14×6.22×0.15+1.3×25×0.2×3.14×12.2=701.633kN四、筒仓仓壁配筋计算1.仓壁配筋计算仓壁厚度为250mm,混凝土保护层厚度为30mm。
具体计算见附件一。
2.仓壁裂缝宽度验算具体计算见附件二。
五、锥形漏斗配筋计算1.锥形漏斗配筋计算锥形漏斗壁与水平方向的夹角为60º锥形漏斗出粮口直径d1=500mm锥斗的高度h n=(d n-d1)·tan50°/2=9.96m具体计算见附件三2.锥形漏斗径向裂缝宽度验算具体计算见附件四。
3.锥形漏斗环向裂缝宽度验算具体计算见附件五。
附表三锥形漏斗配筋计算表附表四锥形漏斗径向裂缝宽度验算附表五锥形漏斗环向裂缝宽度验算。
筒仓中粮食卸料动压力的数值模型

中国粮油 学报
J un lo eC ie eC rasa d Oi s cain o ra ft hn s e el n l Aso it h s o
V0 . 6. . 12 No 4
Ap . 01 r2 1
筒 仓 中粮 食 卸 料 动 压 力 的数值 模 型
基 金 项 目 : 家 科技 支 撑 计 划 (o 9 AD 0 o 5 国 20 B A B 4— ) 收 稿 日期 :0 0—0 0 2 1 4— 8 作 者 简 介 : 绪 铎 , ,97年 出 生 , 授 , 食储 藏 程 男 15 教 粮
因子 随粮食 深度 的增加 而增加 , 于 直径 1 的 筒仓 ( 对 0m P=8 0 k/n , =2 . 。 = . Q=1 0 k h = 0 gI 5 0 , 0 4, . t , /
0 4 E =3 . a , . , 0 0MP ) 粮食 深 度从 2 0m 增加 到 2 . I , 压 因子从 约 13 . 4 0I 时 超 T .3增加 到 1 8 ; 食 卸料 时超压 .7 粮 因子 随粮食 流量 的增 大 而增 大 , 随粮 食体 积 弹性模 量 的增 大而增 大 , 随粮食 和 仓壁 摩擦 系数 的增 大 而增 大 , 随 粮食 内摩擦 角的增 大而减 小 ; 藏静 压 力和 卸 料 动压 力都 随粮 食 和 仓壁 摩擦 系数 的增 大 而减 小 , 随粮食 内 储 都 摩擦 角 的增 大而减 小。
难 确定 。苏乐 逍 等 提 出筒仓 卸 料 时 , 食 不 断地 粮
结 拱 , 不 断地 塌 拱 , 于结 拱 就 阻 碍 了拱 以 上 部 又 由
基 于结 拱 ( 态拱 ) 论 , 结 拱 时 拱 上 方 的粮 瞬 理 将
基于EDEM的筒仓静置与卸料侧压力模拟

D O I : 1 0 . 1 3 7 3 3  ̄ . j e a m. i s s n . 2 0 9 5 - 5 5 5 3 . 2 0 1 5 . 0 2 . 0 2 8
中国 农 机 化 学报
J o u na r l o f C h i n e s e Ag ic r u l t u r a l Me c h a n i z a t i o n
数值 及 单 位
0. 2 5、0 . 2 8
者 们 的注 意 .在 国内外有 关 筒仓 卸料 侧压 力 的研 究有
很多 V i d a 1 . P 等使 用A N S Y S 分析 了偏 心 卸料 对筒 仓侧
料 过 程 中 关 键 词 :E D E M :筒 仓 ; 离 散元 ;侧 压 力 中 图 分 类 号 :T U 2 4 9 . 3 文献 标 识 码 :A 文 章 编 号 :2 0 9 5 — 5 5 5 3 f 2 0 1 5 1 0 2 — 0 1 0 4 — 0 4
刘 震, 王学 文 , 杨 兆 建. 基于 E D E M 的筒 仓 静 置 与卸 料 侧 压力 模 拟m. 中 国农 机 化学 报 , 2 0 1 5 , 3 6 ( 2 ) : 1 0 4 ~ 1 0 6 , 7 2 L i u Z h e n , Wa n g X u e w e n , Y a n g Z h a o j i a n . S i m u l a t i o n o f l a t e r a l p r e s s u r e d u r i n g s t e w i n g a n d d i s c h a r g i n g i n s i l o s b a s e d o n E D E M 【 J 1 . J o u na r l o f C h i ・ n e s e A c u l t u r a l Me c h a n i z a t i o n , 2 0 1 5 , 3 6 ( 2 ) : 1 4- 0 1 0 6 , 7 2
筒仓中人粮自动分级的动力学分析及缓解措施研究

国内外对粮食 自动分级 的现象有大量 的报导 , 但都是对 自动分级现象的定性叙述 ,理论上 的定量 分析很少。本文依据动力学原理,研究粮粒人仓动 力学 的特性 ,分 析 了粮食 自动 分级 的形成原 因 ,并 提 出了一些 缓解 自动 分级 的人 粮方案 。
1 颗粒在筒仓 内下落过程的动力学分析
要 简述 了 自动 分级在 筒仓储粮 中的危 害 。依 据动 力 学原 理 ,建 立 了颗粒 下落 的动
力学 方程 ,并推 导 出颗 粒 下 落深度 与飘移 距 离之 间 的关 系方 程 。通过 计算 得 出颗粒 的水平 飘 移距 离随 着 下 落深度 的增加 而增 加 ;在 筒仓 内的 同一 下 落深 度 ,颗粒 水平 飘移 距 离随着 密度 的增加 而减小;在 筒仓 内的同一下落深度 ,颗粒水平飘移距 离随着半径的增加而增加 。针对 颗 粒 飞行 的动 力 学特性 ,提 出 了几种缓 解 自动 分 级 的措 施 。
第 4 卷 1
筒仓 C 粮 自 A. 动分级 的动力学分析及缓解措施研究
z= 一 r D O c s
・1 7・
() 6
由 ( ) 5 、( )式得 : 4 、( ) 6
F =
p ( 。2 +  ̄s O。 d ) fs s oi cs O n O
() 7
即: 一号 △ F
关键词 筒仓 自 动分级
动力学 缓解措施
特别 多 ,粮 食 的品质 较差 , 自动分级 严重 ,在 筒仓 的仓 壁边上 ,形成 了很 厚 的轻 颗粒 区域 ,这 些地 方 空 隙特别小 ,同时有 大量 的霉 菌孳生 ,水分 含量 也
粮堆是 非 均质 的粮 粒 聚集 体 ,粮粒 有饱满 、瘪 瘦 、完 整 、破碎 之分 ,水 分 含 量也 不 尽相 同;粮 粒 有轻重 、形状与 大 小 的不 同 ,粮堆 还 含 有土块 、秸 秆等杂质。因此 ,粮食在人仓过程 中,各个粮粒所 受 的碰撞力、重力和空气 的阻力不同,自然会引起
混凝土筒仓仓壁计算

待完善,請多提建議,聯係請加QQ:38090514 謝謝!
水平压力 筒仓水平净 ph=Ch*γ *ρ 侧压力系数 仓壁分n段后 截面的水力 贮料压力修 k=tg2(45o-φ 摩擦折减系数- *(1-e-μ ks/ρ )/μ 半径ρ 每段至仓顶深 正系数Ch =d0/4(m) 度S(m) /2) μ ks/ρ (kPa) 5.3 3 1.53399504 0.33333333 -0.341555556 32.14013871 10.3 3 1.94342432 0.33333333 -0.663777778 68.268128 15.3 3 2.2 0.33333333 -0.986 99.87707581 20.3 3 2.2 0.33333333 -1.308222222 116.2487326 25.3 3 2.2 0.33333333 -1.630444444 128.1106064 30.3 3 2.2 0.33333333 -1.952666667 136.7049749 35.3 3 2.2 0.33333333 -2.274888889 142.9319142 40.3 3 2.2 0.33333333 -2.597111111 147.4435631 裂缝宽度验算结果
仓壁环向拉力 标准值 Nhs=ph*d0/2 (kN/m) 192.8408323 409.608768 599.2624548 697.4923958 768.6636387 820.2298491 857.591485 884.6613788
强度配筋值 (HRB335级 钢)mm2/m 835.6436066 1774.971328 2596.803971 3022.467048 3330.875768 3554.329346 3716.229768 3833.532641
筒仓粮堆内部竖向压力计算方法

粮食 等散 体 物料 具 有 复 杂 的力 学 特性 。不 同 于 固体 ,散粒 体不 能 承受 或 只 能 承受 较 小 的拉 力 ,但 可 以承 受较 大 的压力 和 剪 力 ;也 不 同于 液 体 ,散 粒体 虽 可 以向各 方 向传 递 压 强 ,但 并 不 相 等 。 由此 造 成 粮 堆 内部存 在如 边坡 稳 定性 、筒仓 结 拱 、筒 仓 超 压等 诸 多 问题 ¨ 。在处 理这 些 问题 时 ,国 内外 学者 大多 把 研 究集 中在在 如何 确定 粮堆 边界 上 的压力 u4 J,较 少 粮 堆 内部 的空 间压 力 分 布 情 况 。然 而 ,要 解 决 这 些 问题 ,仅考 虑粮 堆边 界 上 的 压 力是 远 远 不够 的 ,因 为 这 些 问题 或者 其 本 质 就 是 粮 堆 的 空 间压 力 问 题 ,或 者 是 以粮 堆 的空 间 压 力 为 基 础 的 问题 。 目前 ,鲜 有 学 者对 粮堆 内部任 意 一 点 的压 力 进行 研 究 。如果 把 对 粮堆 压力 的研 究从 粮 堆 的 边 界 转 向 “空 间 ”,给 出 粮 堆 的空 间压 力 场 模 型 ,大有 可 能 解 决 很 多 仓 储 方 向 尚未解决 的问题 。
方筒仓侧压力的PFC-(3D)模拟
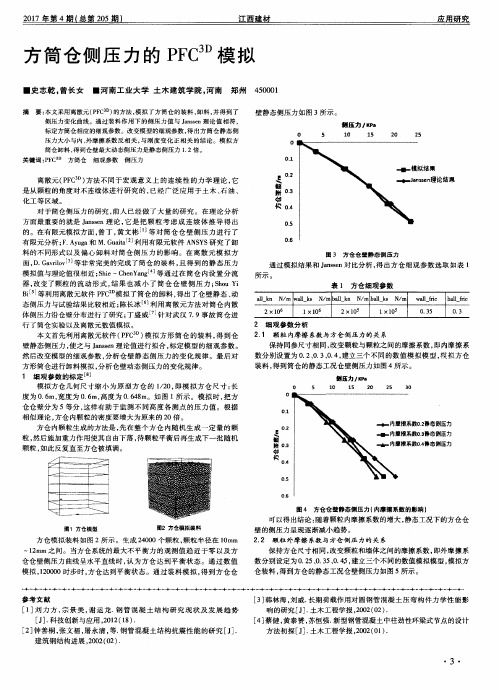
表 1 方 仓 细 观参 数
a l l k n N/ m wa n k s N / m b a l l k n N / m b a l l k s N/ m
_
w a l lf t i c
2 0 1 7年 第 4期 ( 总第 研 究
方 筒仓 侧 压 力 的 P F C 3 D 模 拟
■史志乾 , 曾长 女
摘
一 河南 工 业大 学 土 木 建 筑 学 院 , 河南
郑州
4 5 0 0 0 1
壁静态侧压力如图 3所示 。
侧压力, * P a
o O 5 l O l 5 2O 2 5
~
关键词 : P F C 。 方筒仓
细观参数
侧压力
0l
累
离散元 ( P F C ) 方法不 同于宏观意 义上 的连续性 的力 学理论 , 它 是从颗粒 的角度对不连续体进行研究 的 , 已经 广泛应用 于土木 、 石油、 化 工 等 区域 。
对于筒仓侧压力的研究 , 前 人 已 经 做 了大 量 的 研 究 。 在 理 论 分 析 方面最重要 的就是 J a n s s e n理 论 , 它 是把 颗粒考 虑成 连续 体推 导得 出
_
b a l lf le i
_
2 X1 0 6
1 X1 0 6
2 X1 0 5
1 X1 0 5
0 . 3 5
0 . 3
2 细 观 参 数 分 析
2 . 1 颗 粒 内摩 擦 系数 与 方 仓 侧 压 力 的 关 系
保持 同参尺寸相同 , 改变颗粒与颗粒之 间的摩擦系数 , 即内摩擦 系 数分别设置为 0 . 2、 0 . 3 、 0 . 4, 建立三个 不同的数值模 拟模型 , 模拟方仓 装料 , 得 到筒仓 的静态工况仓壁侧压力 如图 4所示。
筒仓中粮食卸料动压力的数值模型

筒仓中粮食卸料动压力的数值模型摘要:本文主要研究了粮食筒仓卸料动压力的数值模型,通过对物料压力的数值模拟,分析探究了物料在多种压入参数情况下的压力分布变化特征以及影响因素,为研制筒仓产品提供了有效参考依据和理论支持。
一、前言粮食筒仓是为了长期贮存大粮小粮而设计的圆筒形贮存设备,它占有效利用空间,减少贮存成本,增加空间的利用率,保护贮存的粮食安全等众多优势,受到了行业的广泛认可与应用。
但是,由于其特殊工作原理,粮食筒仓在卸料过程中会面临着很大的压力。
为了更进一步弄清其背后的数学原理,本文就其压力特征及影响因素等展开研究,为此提出了一个简单的数值模型,以便更直观地反映压力特性及影响因素,为筒仓生产企业提供建设性的参考依据和有效的理论支撑。
二、模型原理1. 基于物料的压缩限制,建立卸料过程的数学模型,因将平面切割为圆柱面,所以假定卸料行为为层层压缩,允许物料内部的细小应变,即可以看作单一室内的动压力的问题;2. 以真实粮仓容积容积作为假定空间,由入口宽度、出口宽度以及长度确定;3. 用三维向量表示卸料粮仓行为,即筒仓直径、筒仓高度以及容积,可以从而确定各种参数;4. 首先,通过对压力分布的数值模拟,分析探究物料在多种压入参数情况下的压力分布变化特征,确定物料压力的变化规律;5. 其次,在这一数值模拟的基础上,探究不同参数的影响及其力学特性;6. 最后,按照已知参数以及变化规律,以空间参数为基础,建立粮仓仓内物料压力的动压力数值模型,用以研究物料行为。
三、结论与展望1. 通过本次数值模拟,发现入口处物料压力大于出口处,两者之间呈锯齿状变化, These results are in line with the actual operating condition of the material in the pressure vessel.2. 在参数调节的影响上,筒仓长度越长,物料压力越高,出口宽度越大,物料压力越小,这与实际现象相一致。
筒仓装卸料时力场及流场的离散单元法模拟

筒仓装卸料时力场及流场的离散单元法模拟离散单元法(DEM)是一种基于颗粒动力学的数值模拟方法,适用于
研究颗粒体系的运动、变形和相互作用等问题。
在筒仓装卸料时,颗粒的
运动和相互作用是主要的物理过程,因此DEM方法可以用来模拟力场和流场。
DEM方法将颗粒视为离散的质点,并考虑它们之间的相互作用。
在筒
仓装卸料时,颗粒之间的相互作用包括摩擦力、弹性碰撞力和重力等,这
些作用力可以用DEM方法进行模拟。
对于流场的模拟,DEM方法通常结合其他数值模拟方法(如CFD方法)来处理。
由于颗粒的形状和大小不同,流场的变化也很复杂,因此需要在DEM模拟中引入其他的物理过程和数值方法。
总的来说,DEM方法在筒仓装卸料时的应用还需要进一步的研究和发展,以提高其精度和应用范围。
散体物料压力理论

本章,作者大致按照时间顺序总结介绍了以下几项实验。
1
2
12-2 Tachtamishev的实验 S.G.Tachtamishev因第一个运用全尺寸工业筒仓进行精确实验而成名。他揭示了在卸料过程中物料的流动类型和他们对侧压力的影响。在1938到1939年之间,S.G.Tachtamishev在Baku(USSR)进行了一系列关于散体物料的实验,他指出,在卸料过程中,筒壁的侧压力是运用Janssen方法得到结果的2到3倍。
1941年,他运用混凝土筒仓又进行了砂子和小麦的卸料实验。结果表明,在卸料过程中,物料为砂子的筒壁侧压力值为静态侧压力的1.65倍,小麦的也达到了1.35倍。
通过观察,他把流动分为两种基本类型。一种叫做nondynami流动(图12-1a),这种流动中,卸料口的上方形成了一个中心柱,它一直延伸到物料的顶部,物料主要沿着这个“柱子”向下流动,而周围的物料保持不动。现在这种流动被称为漏斗或者岩心流动。
12-1 历史背景
M.S.Ketchum总结了了几个早期在欧美国家进行的实验,同时也包括他自己的几项实验。这些实验包括实验和真实的粮仓模型,但所使用的压力测试设备的灵敏度都不十分精确。在大多数情况下,这些实验都没能检测出物料在流动过程中的压力变化(高于静态值)。因此,不论是通过Janssen还是Airy方法得到的实验结果与实际中筒仓散体物料的压力值相近的结论都是不正确的。然而,尽管其中的一些实验考虑了漏斗位置的变化对于筒仓侧壁压力值的影响,但在设计中却没有针对这一影响提出解决方案。
同时,要指出的是,depression column仅仅适用于非粘性材料。即便是对于有轻微粘性的材料也不合适。
02
1948到1953年之间,V.S.Kim在Soviet Union进行了很多实验模型和全尺寸模型实验,其目的是研究阻止在粮食输送过程中的筒壁裂缝。这些裂缝被认为是在卸料过程中的动态压力产生的。
筒仓装卸料力学过程的数值模拟

筒仓装卸料力学过程的数值模拟
李巍;俞良群
【期刊名称】《煤矿设计》
【年(卷),期】1992(000)001
【摘要】目前,筒仓仓壁所受的压力,一般采用测试方法(包括现场实测和室内模型试验)和理论计算方法确定.但是,这两种方法都有其缺陷,前者往往由于放置的传感元件精度不高,使测出的压力值失真,而且很难捕捉到瞬间的临界荷载;后者所用的理论公式没有考虑许多重要的影响因素,如颗粒密度、级配和装料方式等,用其计算筒仓所受的动压未免有大的出入.另外,学术界对于筒仓在装卸料时的压力变化的认识尚未统一.
【总页数】3页(P41-43)
【作者】李巍;俞良群
【作者单位】不详;不详
【正文语种】中文
【中图分类】TU311
【相关文献】
1.多点卸料浅筒仓力学性能检测 [J], 汪少宁
2.双侧壁卸料筒仓动态压力及流态的数值模拟研究 [J], 姜学佳;原方;张健;庞照昆
3.筒仓动态卸料过程侧压力模拟与验证 [J], 张大英;许启铿;王树明;梁醒培
4.基于离散元模拟筒仓贮料卸料成拱过程及筒仓壁压力分布 [J], 刘克瑾;肖昭然;王
世豪
5.钢筋混凝土立筒仓卸料过程侧压力模拟 [J], 丁永刚;周秀;许启铿;郭呈周
因版权原因,仅展示原文概要,查看原文内容请购买。
200t筒仓计算说明书

1.3.3有地震作用参与组合时,粮食荷载取0.9;地震作用取1.0;雪荷载取0.5;
风荷载不计,楼面可变荷载:按实际考虑时取1.0;按等效均部荷载时取0.6。
1.4钢板筒仓的风载体型系数可按如下取值
1.4.1仓壁稳定计算:取1.0;
鹤壁二矿筒仓计算说明书
1.设计资料
1.1贮料物理特性
松散物料的性能参数
储量荷载计算系数
1.2分项系数的取值
1.2.1永久荷载分项系数:对结构不利时,取1.2;筒仓抗倾覆计算,取0.9
1.2.2可变荷载分项系数:储粮荷载去1.3;其它可变荷载取1.4
1.2.3地震作用取1.3
1.3可变荷载组合系数
1.3.1无风荷载参与组合时,取1.0
验 算 人:肖极木
完成日期:2009.9.30
5.参考文献
1.国家粮食局.粮食钢板筒仓.北京:中华人民共和国建设部,2001
2.JB/T4735—1997《钢制焊接常压容器》99页—123页
3.中国煤炭建设协会. 钢筋混凝土筒仓设计规范. 北京:新华书店北京发行,200454页—55页
4.陈宜通、盛春芳、陈润余. 混凝土机械. 北京:中国建材工业出版社,200250页—54页
图2.3 圆锥漏斗内力计算示意图
3.粉煤灰
3.1仓的容积和外形尺寸
图3.1 粉煤灰二维图图3.2 仓壁厚为10mm的三维图
3.2 仓厚度的计算和检验
图3.3圆锥漏斗内力计算示意图
4.计算总结
经过这次200t的筒仓设计,让我掌握了基本的筒仓外形尺寸计算、仓壁强度和稳定性的验算。但是由于仓上没有建筑,忽略了一些可变荷载作用于仓壁单位周长上的竖向压力,没有准确的计算出 。在验算强度时,由于不知道加劲肋的尺寸,无法计算出加劲肋组合构建的截面强度计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 16 )
· i ¨
( 27 ) x 为第 i 层的速度, x i 为第 i 层的加速度。 其中, 令:
式中: m 为各层的质量。 系统的弹性势能为: Ve = 1 2
n n -1 2
∑ k i ( z i +1 - z i - d i - λ i )
i =1
( 17 )
x n +i = · xi
· ¨ · mx 1 + k ( x1 - x2 ) = ( - x1 / x1 ) C dμ p hs ( nd)
图4
筒仓内粮食系统的振动模型
z2 , …, z n 为系统的广义坐 选各粮食层的高度 z1 , 标, 振动时, 系统的动能为: T = 1 2
n ·2 mz ∑ i i =1
mx i + k( 2 x i - x i -1 - x i +1 ) = · · ( - x i / x i ) Cdμp hs ( nd + d - id) , ( i = 2, ..., n - 1) · ¨ · mx n + k ( x n - x n - 1 ) = ( x n / x n ) C dμ p hs ( d)
对仓壁产生的动压力的研究是从理论和试验两个方 向进行的。Moriyama 等
[6 ]
提出的粮食动压力是粮食
卸载时仓内粮食由主动应力状态转换成被动应力状 态的结果。这个理论很难确定主动应力状态转换成
[7 ] 被动应力状态的条件和区域。Xu S 等 提出粮食动
是0. 7 到 2. 4 。 研究发现许多因数对最大动压力有 影响 , 这些因数是粮食颗粒大小 、 卸料速率 、 仓高与 直径的比 、 仓墙沟纹 、 漏 斗 设 计、 卸 料 偏 心 率、 仓墙 刚度 。 研究结果一致 表 明 卸 料 时 作 用 于 仓 墙 上 动 对 压力超过 由 Janssen 方 程 预 计 的 静 压 力 。 然 而 , 于动态压力的大小和位置 , 试 验 结 果 是 不 一 致 的, 动压力与静压力之比从较低的 1. 25 ~ 1. 5 到 较 高 [12] 的 3. 5 ~ 4. 0 。 基于结拱 ( 瞬态拱 ) 理论, 将结拱时拱上方的粮 食分成等厚的许多层, 将其简化成多层弹簧振子系 统, 从而求出结拱时粮食流动时的惯性力, 进而有动 量定理求出粮食对仓壁的动压力 。
pv =
( 10 ) ( 11 )
δ =
ph ቤተ መጻሕፍቲ ባይዱ dv = (1 + ) p hs g dt
( 12 )
粮食卸料结拱时的惯性加速度的确定 由式( 11 ) 、 式( 12 ) 知, 要求得粮食卸料结拱时的
侧向压应力和超压因子的值需先确定粮食薄层的惯 dv 的值。 性加速度 dt 2. 2. 1 筒仓中粮食系统的弹簧振子模型 将筒仓中拱上方的粮食分为 n 层, 每层的厚度 ( 13 ) ( 14 )
[9 - 13]
1
粮食储藏时对仓壁的侧压力
。 Takhtamishev 在圆筒仓试验中测
粮食静止储藏时, 粮食处在主动应力状态。 假 设粮食密度 ρ、 仓墙和粮食间摩擦系数 μ、 内摩擦角 φ 是常数, 压 力 大 小 不 随 半 径 的 大 小 和 方 向 而 变 化。 图 1 是一个圆筒仓和粮食表面下深度 y 处粮食微元 层示意图。
( 4)
2
2. 1
粮食卸料结拱时的动压力
粮食卸料结拱时的动压力公式 设 t 时刻在深度 y 处结拱, 由于结拱, 使正在以
相等为 d, 质量相等为 m, 且有, d = Hg / n m = πD H g ρ 4n
2
速度 v 流动的粮食突然减缓下来, 流速迅速达到零, 故产生一惯性力, 其方向与粮食的流速方向相同。 粮食结拱层受力图见图 2 。
H g 为筒仓圆筒 式中: D 为筒仓圆筒部分的直径, 中拱上部的高。 假设每相邻两层被一个弹簧连接。 第 i 层的压 缩值 λ i 为: ( i = 1, …, n) λ i = mg( n - i) / k 式中: k 为筒仓中粮食每层的刚度。 ( 15 )
筒仓中拱的上方粮食系统被简化成多层弹簧振 子系统( 图 3 、 图 4) 。
· i
( i = 2, …, n) ( 21 ) 式中: M 为拱的上方谷物的总质量, 且 M = nm 。 系统的 Lagrang 方程为: d T T V ( ) - + = Fi dt · zi z i z i ( i = 1, 2, …, n) ( 22 ) 将式( 16 ) ~ 式( 21 ) 代入 式( 22 ) , 得系统的动力 学方程为:
( i = 1, 2, …, n)
( 28 )
系统的重力势能为: Vg = mgz i ∑ i =1 ( 18 )
系统的总势能为: V = Ve + Vg 系统的广义力为: F1 = Mg + ( - · z1 / · z1 ) Cd μp hs ( nd) F i = ( - z / z ) Cd μp hs ( nd + d - id)
压力是粮食卸料时仓内粮食横向膨胀的结果, 当粮 食卸料时 , 由于粮食的相对运 动 , 竖直方向的剪切 产生 , 剪切可视为两个带锯齿表面的刚块的竖直剪 切, 这样 , 粮食水平方向膨胀发生 , 这个膨胀决定于 锯齿表面的膨胀角 , 但这个理论的问题是膨胀角很 难确定 。 苏乐逍等
[8]
提出筒仓卸料时 , 粮食不断地
因子随粮食流量的增大而增大, 随粮食体积弹性模量的增大而增大 , 随粮食和仓壁摩擦系数的增大而增大, 随 粮食内摩擦角的增大而减小; 储藏静压力和卸料动压力都随粮食和仓壁摩擦系数的增大而减小, 都随粮食内 摩擦角的增大而减小。 关键词 筒仓 粮食卸料 结拱 超压因子 中图分类号: TS210. 4 文献标识码: A 文章编号: 1003 - 0174 ( 2011 ) 04 - 0089 - 06 筒仓中粮食卸料动压力的研究从 20 世纪中叶 开始, 一直持续到现在
· i · i
( 19 ) ( 20 )
结合式( 27) , 式( 28) , 得系统的动力学方程组为: · x i = x n +i , ( i = 1, 2, ..., n) k · x n + 1 = ( x2 - x1 ) + ( - · x1 / · x1 m) Cd μp hs ( nd) m k · x n +i = ( x i +1 + x i -1 - 2 x i ) + m ( -· xi / · ( i = 2, …, n - 1) x i m) Cd μp hs ( nd + d - id) , k · x2 n = ( x n - 1 - x n ) + ( - · xn / · m ) C d p ( d ) μ xn hs m ( 29 ) 系统的初始条件为: xi ( 0) = 0, ( i = 1, …, n) x n +1 ( 0 ) = 0 x n +i ( 0 ) = - v, ( i = 2, …, n)
2011 年 4 月 第 26 卷第 4 期
中国粮油学报
Journal of the Chinese Cereals and Oils Association
No. 4 Vol. 26 , Apr. 2011
筒仓中粮食卸料动压力的数值模型
程绪铎 唐福元 石翠霞 陆琳琳
( 南京财经大学食品科学与工程学院 ,南京 210003 ) 筒仓中粮食卸料时拱不断形成并不断坍塌 。以这些不稳定拱( 瞬态拱) 为依据, 建立一个预测筒 结拱层上方的粮食视为多层弹簧振子系统, 建立该 仓中粮食卸料动压力的数值模型。将粮食分成许多薄层, 摘 要 系统的振动方程, 从而解出结拱层的加速度, 再对结拱层运用动量定理, 推导出粮食卸料时对仓壁的动压力。 计算结果表明: 粮食卸料时粮食对筒仓壁产生的动压力大于 Janssen 方程计算的储藏静压力, 粮食卸料时超压
3 Q = 1. 0 kt / h, 因子随粮食深度的增加而增加, 对于直径 10 m 的筒仓 ( ρ = 800 kg / m , φ = 25. 0 ° , μ = 0. 4 , ν= E v = 30. 0 MPa) , 0. 4 , 粮食深度从 2. 0 m 增加到 24. 0 m 时, 超压因子从约 1. 33 增加到 1. 87 ; 粮食卸料时超压
[1 - 5 ]
。筒仓中粮食卸料时粮食
出卸仓超 压 因 子 在 2 到 3 之 间 ; Platonov 和 Kovtun 在高与直径的比为 6. 67 的圆筒仓试验中测出超压
[12] [13] 因子 在 1. 67 到 2. 32 之 间 。 Manbeeck 等 对 平底深仓 ( H / D = 5 ) 进行卸仓试验 , 得出超压因子
μk s 1 dv ρgR (1 + ) ( 1 - e- R y) g dt μk s μk s 1 dv ρgR ph = (1 + ) ( 1 - e- R y) g dt μ 比较式( 4 ) 、 式( 11 ) 得超压因子为:
C 为 仓 的 周 长, dy 式中: A 为仓的 横 截 面 面 积, g 为重力加速度, p hs 为粮食内侧压 为是粮食层厚度, p vs 为粮食内竖直压应力。 应力, 粮食处在主动应力状态时侧压应力和竖直压应 力之比 k s 为: k s = p hs / p vs = ( 1 - sinφ) / ( 1 + sinφ) ( 2) 2. 2 将式( 2 ) 代入式 ( 1 ) , 得粮食内竖直压应力表达 : 式为 p vs ( y) = ( ρgR / k s μ) ( 1 - e - k s μy / R ) 式中: R = A / C 为仓内水力半径。 作用在仓墙上的侧压力为: p hs = kp vs = ( ρgR / μ) ( 1 - e - k s μy / R ) ( 3)
