小升初第八讲 测试
小升初数学专项题-第八讲 和差倍分问题通用版

第八讲 和差倍分问题【基础概念】:1、和差问题:知道大小两个数的和与差,求这两个数是多少,数量关系式:(和+差)÷2=大数,(和-差)÷2=小数;2、和倍问题:已知两个数的和及两个数间的倍数关系,求这两个数各是多少,数量关系式:两数和÷(倍数+1)=小数,小数×倍数=大数;3、差倍问题:已知两个数的差及两个数间的倍数关系,求这两个数各是多少,数量关系式:两个数的差÷(倍数-1)=小数,小数×倍数=大数。
【典型例题1】:有两筐苹果,第一筐重30kg ,如果从第一筐中取出12kg 放入第二筐,则两筐苹果同样重.两筐苹果一共重多少千克?【思路分析】:第一筐重30kg ,如果从第一筐中取出12 kg 放入第二筐,第一筐剩30-12 kg ,因为两筐苹果同样重,所以用30- 12 kg 乘以2即可得两筐苹果一共重多少千克。
解答:(30-12 )×2=592 ×2=59(千克)答:两筐苹果一共重59千克 。
【小结】:解决这类问题的关键是要弄清楚前后的质量关系。
【巩固练习】1、甲、乙两筐苹果共重100千克,如果从甲筐取出12千克放到乙筐,则甲、乙两筐苹果一样重.甲乙两筐苹果原来各多少千克?2、有甲、乙两筐苹果,甲筐的重量是乙筐的90%.如果从乙筐拿5千克到甲筐,则两筐苹果一样重.两筐苹果共多少千克?【典型例题2】:果园里有桃树32棵,梨树是桃树的2倍,苹果树比桃树和梨树的总数多54棵.果园里有苹果树多少棵?【思路分析】:由题意知,梨树为桃树的2倍,求出梨树的棵数后加桃树的棵数,然后再加上54棵,就是苹果树的棵数。
解答:32×2+32+54=64+32+54=96+54=150(棵)答:果园里有苹果树150棵。
【小结】:解决此类问题的关键是先求出梨树的棵数,然后再根据苹果树与桃树、梨树棵树的关系求苹果树的棵数即可。
【巩固练习】3、果园有苹果树48棵,桃树的棵数是苹果树的4倍,梨树的棵数比苹果树和桃树的总数少12棵,果园有梨树多少棵?4、果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵数是苹果树的3倍,桃树的棵数是苹果树的6倍.求梨树、桃树和苹果树各有多少棵?5、果园里有桃树、梨树、苹果树共552棵.桃树比梨树的2倍多12棵,苹果树比梨树少20棵.梨树有多少棵?答案及解析:1.【解析】由“从甲筐取出12千克放到乙筐,则甲、乙两筐苹果一样重”,可知甲筐比乙筐重(12×2)千克,因此,乙筐原有苹果(100-12×2)÷2,甲筐原有苹果的重量就好求了。
小升初语文阅读技巧第八讲:分析标题的作用(含例题精析+答案)
小升初语文阅读技巧第八讲:分析标题的作用(含例题精析+答案)标题是文章的重要组成部分,或限定题材范围、指明描写对象或议论中心,或直接概括文章的主要内容、表明作者主张等。
它的作用、好处、妙处是记叙文中常考的题型,一般与文章是内容、情感、主旨、结构、写法等有着密切的关系。
巧记公式:前言(一)《十毫升母爱》①这半年,我一边上班一边照顾孩子,疲惫不堪,吃不好睡不好,身体慢慢变差。
虽已立春,但春寒料峭,凛冽的风仍不时从门缝往里吹。
瘦弱的我受了风寒,终于熬不住,病倒了。
②丈夫建议:“要不把孩子的姥姥接过来吧?帮忙带带孩子!”我却犹豫了。
③我从小就怕母亲。
记忆中,母亲脾气暴躁,一直以凶神恶煞的面目出现。
我有丝毫让她不满意的地方,她便会严厉地指责我,给我幼小的心灵留下了浓浓的阴影。
④母亲几乎没有夸奖过我,也许是没有文化的缘故,她甚至不懂得在我难过之际给予一点安慰。
高考结束,我的成绩不太理想,母亲却没有安慰我,只是忙着做自己的事。
拿到录取通知书时,我递给母亲看,她没有接,低着头冷冷地说:“叫你不要报这么差的大学。
”我默默收回了通知书,流着泪转身离去。
⑤这些年,我们母女的关系一直淡淡的,交流很少,彼此都习惯了对方的淡漠。
⑥丈夫瞒着我给母亲打了电话。
没想到,她竟然很快从千里之外坐车赶来了。
打开门,看见母亲扶着墙壁站在我面前时,我竟有些不知所措。
母亲晕车厉害,一上车便开始吐。
等到下车,虚弱得像丢了半条命。
⑦我赶紧把母亲迎进门,母亲顾不上自己身体不适,一个劲盯着我看,说:“就你逞能,都累成这样了!”语气一如既往的不中听。
我已经习惯了,无声地笑了笑。
⑧母亲来了,我的担子被她分去一部分,顿感轻松多了。
我的病却很奇怪,药吃了一周,不见好。
尽管穿着厚厚的棉服,还是咬着牙关瑟瑟发抖。
晚上我早早地躲进被窝,母亲则在客厅打电话。
连续几个晚上,她都在电话里和她的老姐妹拉家常。
⑨一天早上,母亲从外面回来,放下包便进了厨房。
许久,从厨房猫着腰出来了,手里端着一碗冒着热气的汤水,递给我,催促我快点喝完。
2023学年小学语文六年级小升初阅读理解专项训练08 分析人物形象

小升初语文阅读理解专项训练第八讲分析人物形象考点解读分析人物形象,要由浅入深地分析人物的性格特点、思想品质。
答题思路是:先通读全文,筛选与人物相关的重要信息,探究人物思想品格、性格特点。
然后按总分方式先用一句话整体对人物作出评价,再从几方面分条分析;也可从几个方面具体分析,再用一句话作定性式总结。
具体方法有:①事件提炼法:分析文章所写的典型的事例,在事件中提炼出人物形象。
②言行提炼法:品析最能体现人物特征的外貌、语言、行为和心理等各方面的描写,深入细致分析,提炼人物特点。
③提关键词句法:文中的总领句、过渡句、段落中心句、首尾段中的某些关键词,会直接点明该人物的性格特点,这些关键词句可直接借用。
④侧面解读法:某些环境描写、其他人物的表现或评价,也是对该人物的一种烘托,可以探究品读关语句,准确把握人物特点。
考点训练智取生辰纲(节选)施耐庵杨志想赶快催促着运送生辰纲的军卒走过这个黄泥冈,谁知众军卒都在树荫下,横竖四地躺着不动。
过了一会儿,只见远处一个汉子,挑着副担桶,一边往冈上走,一边唱山歌:“赤日炎炎似火烧,野田禾稻半枯焦。
农夫心内如汤煮,公子王孙把扇摇!”军卒们又热又渴,便商量着凑钱买酒解渴去暑。
杨志喝道:“好大胆!没有我的话,怎敢随便买酒吃?”又要动手打人。
众军卒说:“我们买碗酒吃,又有何碍,也来打人!”杨志说:“你晓得什么,有多少好汉被蒙汗药麻翻了!”这时,松林里贩枣子的客人跑出来要买酒吃。
挑酒的说:“不卖!这位客官说我酒里有蒙汗药!”他们央求了好一会儿,买了一桶,每人拿了椰瓢分着吃了。
有一个贩枣的客人乘卖酒的收钱的时候,揭开另一桶的桶盖,舀了一瓢便吃。
挑酒的汉子去夺时,他便跑到松林里。
挑酒的去赶上,夺回来往桶里一倒,盖上盖,把瓢往地上一丢,还抢白了那舀酒的客人一顿。
军卒们见了,都馋得厉害,说道:“这里没处讨水喝,那贩枣子的已买了一桶吃了,我们也买些润一润喉咙才好。
”杨志见那一桶酒吃了,这一桶也有人吃了一瓢,都没有事,想来酒是好的,就说:“既然大家都要买些吃,就买吧,吃了好赶路。
六年级下册数学试题小升初专题训练:第08讲浓度问题人教版

第八讲浓度问题例1.将20克盐加入300克水中,得到的盐水浓度为百分之几?例2.有含糖6%的糖水650克,加入浓度10%的糖水350克,浓度为多少?例3.在浓度为20%的糖水中加入50克糖,浓度变为40%,再加入多少克水,糖水浓度变为25%?例4.现有浓度为10%盐水8千克,要得到浓度为20%盐水,用什么方法可以得到?具体怎么操作?(至少两种做法)例5.蜜蜂采的花蜜,含有70%的水分,蜜蜂用这种花蜜酿成只含水分17%的蜂蜜l千克,需这样的花蜜多少千克?(精确到0.01)例6、一种35%的农药,如稀释到1.75%时,治虫最有效。
用多少千克浓度为35%的农药加多少千克水,才能配成1.75%的农药800千克?例7、现有浓度为10%的盐水20千克。
再加入多少千克浓度为30%的盐水,可以得到浓度为22%的盐水?例8、将20%的盐水与5%的盐水混合,配成15%的盐水600克,需要20%的盐水和5%的盐水各多少克?例9、浓度为70%的酒精溶液500克与浓度为50%的酒精溶液300克混合后所得到的酒精溶液的浓度是多少?例10. 20%的食盐水与5%的食盐水混合,要配制成15%的食盐水900克,问:20%与5%的食盐水各需要多少克?例11.甲容器中有纯酒精11升,乙容器中有水15升,第一次把甲中的一部分倒入乙中,使酒精与水混合,第二次把乙中的一部分混合物倒入甲中,这样甲中纯酒精的含量为62.5%,乙中的纯酒精含量为25%,那么第二次从乙中倒入甲中的混合物是多少升?例12.甲种酒精4升,乙种酒精6升,混合成的酒精含纯酒精62%,如果甲种酒精和乙种酒精一样多,混合成后酒精含纯酒精61%。
甲、乙两种酒精各含纯酒精百分之几?练习:1、现在有浓度为20%的糖水300克,要把它变成浓度为40%的糖水,需要加糖多少克?2、有含盐15%的盐水20千克,要使盐水的浓度为20%,需加盐多少千克?3、两种钢分别含镍5%和40%,要得到140吨含镍30%的钢,需要含镍5%的钢和含镍40%的钢各多少吨?4、有甲、乙两个瓶子,甲瓶里装了200毫升清水,乙瓶里装了200毫升的纯酒精。
最新2020小升初数学总复习同步拓展-第八讲.用“组合法”解工程问题(不含答案) 全国通用

用“组合法”解工程问题【知识、方法梳理】在解答工程问题时,如果对题目提供的条件孤立、分散、静止地看,则难以找到明确的解题途径,若用“组合法”把具有相依关系的数学信息进行恰当组合,使之成为一个新的基本单位,便会使隐蔽的数量关系立刻明朗化,从而顺利找到解题途径。
【典例精讲】【例题1】一项工程,甲、乙两队合作15天完成,若甲队做5天,乙队做3天,只能完成工程的7/30,乙队单独完成全部工程需要几天?【思路导航】此题已知甲、乙两队的工作效率和是1/15,只要求出甲队货乙队的工作效率,则问题可解,然而这正是本题的难点,用“组合法”将甲队独做5天,乙队独做3天,组合成甲、乙两队合作了3天后,甲队独做2天来考虑,就可以求出甲队2天的工作量7/30-1/15×3=1/30,从而求出甲队的工作效率。
所以1÷【1/15-(7/30-1/15×3)÷(5-3)】=20(天)答:乙队单独完成全部工程需要20天。
练习1:1.师、徒二人合做一批零件,12天可以完成。
师傅先做了3天,因事外出,由徒弟接着做1天,共完成任务的3/20。
如果这批零件由师傅单独做,多少天可以完成?2.某项工程,甲、乙合做1天完成全部工程的5/24。
如果这项工程由甲队独做2天,再由乙队独做3天,能完成全部工程的13/124。
甲、乙两队单独完成这项工程各需多少天?3.甲、乙两队合做,20天可完成一项工程。
先由甲队独做8天,再由乙队独做12天,还剩这项工程的8/15。
甲、乙两队独做各需几天完成?【例题2】一项工程,甲队独做12天可以完成。
甲队先做了3天,再由乙队做2天,则能完成这项工程的1/2。
现在甲、乙两队合做若干天后,再由乙队单独做。
做完后发现两段所用时间相等。
求两段一共用了几天?【思路导航】此题很容易先求乙队的工作效率是:(1/2-1/12×3)÷2=1/8;再由条件“做完后发现两段所用时间相等”的题意,可组合成由两个乙队和一个甲队合做需若干天完成,即可求出相等的时间。
【精品】小升初语文满分夺冠秘籍第8讲:图文转换专题-对联专题(word版-含答案)

【导入新课】教学建议:教师可根据实际学生水平,选择相应的导学内容,建议用时不超过5分钟。
从上述漫画中,我们得到了哪些信息?漫画的主题是什么?地球受到污染。
爱护地球,保护环境。
【专题精讲】图文表文转换知识梳理1、专题特点:近年小升初语文科的命题,内容更贴近现实,体现语文学科的基础性、工具性特点,更加突出对考生语文综合能力的考查,注重考生创造能力的发挥。
2、表格材料信息提炼方法指导:①认真阅读题目和表头,明确被调查对象和调查内容。
②横读、纵读表格数据,察看最大值和最小值,寻找数据变化规律。
③判定调查结果,确定材料信息。
[被调查对象 + 调查内容 + 数值变化规则]3、解答图表分析题要把握好五个方面:(1)注重整体阅读。
对这类考题,应当先对材料或图表资料等有一个整体的了解,把握一个大主题或方向。
要通过整体阅读,搜索有效信息。
(2)重视数据变化。
我们要重视图表中的数据变化,数据的变化的往往说明了某个问题,而这可能正是这个材料的重要之处,这也是得到观点的源头。
(3)注意图表细节。
图表中一些细节不能忽视,它往往起提示作用。
如图表下的“注”等。
(4)把握考题要求。
根据考题要求进行回答,才能有的放矢;同时考题要求往往对内容有一定的提示性。
这样,比较分析内容,就可准确回答问题。
(5)简要归纳概括。
解答这类问题的共同点是归纳概括。
解答前,要正确分析图表中所列内容的相互联系,从中找出规律性的东西。
分析出有关材料的内在联系,再归纳概括为一个结论,也就符合简答要求了。
图文转换题解题的基本流程:图表(源信息)一观察认读一分析理解一归纳概括一文字表达。
要综合分析三个难度:横向角度、纵向角度、斜向角度(主要是数据变化)。
对联知识梳理1.专题特点对联,和律诗、京剧一样,都属于中国文化的“国粹”。
从宋代开始,人们就有贴春联的习俗了。
对联不仅是优秀传统文化的重要组成部分,它对培养小朋友思维的深刻性、敏捷性,以及灵活用词、简洁造句等方面的能力,也有十分独特的作用。
六年级下册小升初全复习-第8讲 统计表的应用-北师大(2014年秋)(含答案)

第八讲统计表的应用例1、某校有若干学生,全校男、女生人数之比是5:3,低、中、高三个年级段总人数之比是7:10:15。
中年级男、女生和高年级男、女生的人数比都是3:2;已知低年级的女生比男生少135人。
那么这个学校共有学生多少人?巩固练习11、家禽场里鸡、鸭、鹅三种家禽中,公禽与母禽数量之比是2:3,已知鸡、鸭、鹅数量之比是8:7:5,公鸡、母鸡数量的比是1:3,公鸭、母鸭数量的比是3:4,公鹅、母鹅的数量之比是多少?2、一个工厂有三个车间,全厂男、女职工人数之比是4:3,三个分厂的人数之比是9:8:11。
第一分厂男、女职工人数的比是2:1;第二分厂男女职工人数的比是5:3;第三分厂男职工比女职工少40人,那么这个工厂共有多少人?3、育才体操队的男、女运动员人数之比是3:2,分为甲、乙、丙三个小组,已知甲、乙、丙三组的人数之比是10:8:7。
甲组中男、女运动员人数的比是3:1;乙组中男、女运动员人数的比是5:3;丙组的男运动员比女运动员少48人,那么体操队一共有多少名运动员?例2、甲、乙两个长方形的长、宽都为整数厘米,且它们的周长相等。
已知甲长方形的长与乙长方形的长之比为7:3,甲长方形的宽与乙长方形的宽之比为5:8,那么这两个长方形的面积之和至少为多少平方厘米?1、 边长都为整数的甲、乙两个长方形,它们的周长相等。
甲长方形的长是乙长方形长的94,乙长方形的宽是甲长方形宽的52,那么两个长方形的面积之和至少是多少?2、甲、乙两班同学人数相等,已知甲班男生人数是乙女生人数的51,乙班男生人数是甲女生人数的61,甲班女生人数是乙女生人数的几分之几?3、甲、乙两班同学人数相等,各有一些同学参加天文小组,甲班参加天文小组的人数恰好是乙班没有参加的31,乙班参加天文小组的人数是甲班没有参加的41。
问甲班没有参加的人数是乙班没有参加的几分之几?例3、一批工人到甲、乙两个工地进行清理工作,甲工地的工作量是乙工地的工作量的121 倍。
部编语文小升初【阅读理解】训练、理解短文的主要内容 +20篇阅读理解题和答案

部编语文小升初【阅读理解】训练、理解短文的主要内容 +20篇阅读理解题和答案第八讲、理解短文的主要内容我们阅读文章一般是从整体到部分再到整体,读了一遍文章,我们就要大致了解它的主要内容,然后再理解重点词句的意思。
我们只有弄懂了文章的主要内容,才能给文章分段,才能理解文章的中心思想,才能有自己的感受。
我们如何概括文章的主要内容呢?段意合并法。
一篇文章可以分为几段,每一个段落大意都概括了一个段落的主要意思,把各段的段意综合起来,就能归纳岀文章的主要内容了。
综合组织各段的大意为主要内容,并不等于各段大意的总和,概括时一定要注意区别重点段落与次要段落,做到有详有略,重点突出。
如《新型玻璃》一文,我们通过通读知道文章分别介绍夹丝网防盗玻璃、夹丝玻璃、变色玻璃、吸热玻璃、吃音玻璃等五种新型玻璃的特点和它们在现代生活中的广泛应用,我们把这几种玻璃名称提岀来,把“特点和它们在现代生活中的广泛应用”保留,就是文章的主要内容。
要素串联法。
对于文中有时间、地点、主要人物、重点事件(包括起因、经过、结果等基本要素)的,我们把这些基本要素弄出来,再用合适的词语把它们串起来,大致就是这篇文章的主要内容,这种方法一般用于写人记事类的文章。
例如《金色的鱼钩》一文,时间是“1935年秋天”,地点是“草地“,人物是“老班长、'我'和另外两个伤员”,事件起因是指导员让老班长照顾三个伤员,经过是老班长钓到鱼做成了鱼汤,自己不喝,全给了三个伤员,而自己却只吃鱼骨头,结果是老班长最后牺牲在草地上。
我们把这些要素串起来就是这篇课文的主要内容。
内容借助法。
这种方法主要是借助文章中的句段来总结主要内容,这种句段主要是课文中的中心句或中心段。
如《彩色的非洲》一文中的开头“非洲真是一个色彩斑斓的世界啊”和结尾“啊,非洲,好一个多姿多彩的世界”就可以概括本篇课文的主要内容。
问题自答法。
我们在阅读完一篇文章后,可以自我提问,主要是这样的几个问题:写人和事的文章是“谁在干什么?经过如何?结果怎样呢?”状物类的文章是“什么(事物)东西怎么样?”当我们提出问题后,就要认真阅读课文,然后抓住关键词句来回答,这样就概括岀了文章的主要内容。
第8讲-小数四则运算(知识梳理+易错专练)-2023-2024学年六年级小升初数学备战专项讲义

第8讲-小数四则运算(知识梳理+易错专练)2023-2024学年六年级小升初数学备战专项讲义1、小数加法。
小数加法的意义与整数加法的意义相同。
是把两个数合并成一个数的运算。
2、小数减法。
小数减法的意义与整数减法的意义相同。
已知两个加数的和与其中的一个加数,求另一个加数的运算.3、小数乘法。
小数乘整数的意义和整数乘法的意义相同,就是求几个相同加数和的简便运算;一个数乘纯小数的意义是求这个数的十分之几、百分之几、千分之几……是多少。
4、小数除法。
小数除法的意义与整数除法的意义相同,就是已知两个因数的积与其中一个因数,求另一个因数的运算。
5、小数四则运算的运算顺序和整数四则运算顺序相同。
一.选择题(共8小题,满分16分,每小题2分)1.(2分)如图竖式中,“45”乘“6”得到的“270”表示()A.270个一B.270个十分之一C.270个百分之一D.270个千分之2.(2分)小马虎在计算一道小数减法时,把减数百分位上的“5”看成了“2”,得到的结果是12.73,正确的结果是()A.12.76 B.12.43 C.15.73 D.12.73.(2分)如图竖式中的余数“3“表示()A.3 B.0.3 C.0.03 D.0.0034.(2分)□.3表示一个一位小数,那么6.8⨯□.3的积可能是()A.1.74 B.20.6 C.36.04 D.70.245.(2分)已知“□.5 2.⨯□9”是一个一位小数乘两位小数的算式,下面四个数中有可能是它的得数的是()A.0.435 B.9.405 C.7.25 D.33.975 6.(2分)59.999.99⨯的结果()A.比600小B.比600大C.等于600 D.不能估算7.(2分)小虎在计算减法时把被减数十分位上的“8”错看成了“3”,把减数百分位上的“1”错看成了“7”,得到的错误答案是6.38。
这道减法算式的正确答案应该是()A.6.94 B.6.82 C.5.82⋅D.5.948.(2分)小雪在解决“一根彩带长41.3米,如果将它剪成每根长0.6米的包装绳,可以剪成多少根?还剩多长?”的数学问题时,写出了如图的竖式,圆圈中的“5”表示还剩()A.5米B.5分米C.5厘米D.5毫米二.填空题(共8小题,满分16分,每小题2分)9.(2分)甲数除以乙数的商是1.5,如果甲数增加20,则甲数是乙数的2倍.原来甲数是 .10.(2分)小马虎计算30.6除以一个数时,由于将除数的小数点向右点错了一位,结果得204,正确的除数是 。
小升初数学第八讲:分数应用题(学生版)

分数应用题学生姓名年级学科授课教师日期时段核心内容解决复杂分数应用题课型一对一教学目标1、使学生学会掌握“已知一个数,求它的几分之几和比它多(或少)几分之几的数是多少”及"已知一个数的几分之几和比它多(或少)几分之几数是多少,求这个数””的应用题的解答方法,并能熟练地列方程解答这类应用题。
2、进一步培养学生自主探索解决问题的能力和加强分析、推理和判断等思维能力,提高解答应用题的能力。
重、难点重点:弄清单位“1”的量,会分析题中的数量关系。
掌握常用的解决稍复杂分数应用题的技巧难点:灵活运用技巧解决分数应用题课首沟通1、上次的作业完成了没有?有不会的题吗?2、你会解答哪些类型的分数乘除应用题,举例说明?3、如何理解“量率”对应关系?画线段图分析题意,什么情况画单线段图?什么情况画双线段图?课首小测1. 先找出对应分率,再列式,不用计算。
2. 看图列式3. 把下面的应用题补充完整后再列出算式。
一本书,已看了25页,还有20页没有看,_____________①已看的页数是未看的几分之几? _________ ②未看的页数是已看的几分之几? _________③已看的页数比未看的多几分之几? _________④未看的页数比已看的少几分之几? _________⑤已看的页数是全书的几分之几? _________ ⑥未看的页数是全书的几分之几? _________4. (2012年大联盟试题)) 工程队用3天修完一段路,第一天修的是第二天的,第三天修的是第二天的倍,已知第三天比第一天多修270米,这段路长多少米?5. (2013年大联盟试题)) 某工程队修一条路,第一天修了比全长的多2米,第二天修了比剩下的少4米,还剩下200米没有修,这段路全长多少米?6. (2013年小联盟试题)) 有一些数字卡片,上面写的数全部都是3或4的倍数,其中是3的倍数的卡片占,是4的倍数的卡片占,12的倍数的卡片有20张,求一共有多少张卡片.知识梳理解答分数应用题,首先要确定单位“1”,在单位“1”确定以后,一个具体数量总与一个具体分数(分率)相对应,这种关系叫“量率对应”,这是解答分数应用题的关键。
小升初暑假衔接 第八讲 阅读 段落作用 专题卷-2023-2024学年语文(统编版)

小升初语文暑假衔接第八讲·阅读段落作用专题卷(一)千金一诺①真爱的方式有许多种,实现诺言也是爱的一种方式。
②8岁时,我上小学三年级,我的姐姐当时正读初中,她是个很美的姑娘,亲朋们因此很宠爱她。
春节前,从广州出差回来的姑姑给她一件样式别致、颜色粉红的上衣作为新年的礼物。
在我饱含羡慕甚至是嫉妒的目光中,姐姐小心翼翼地把衣服藏在柜子里,急切地盼着新年的到来。
③可是就在腊月二十九那天,邻居大哥的女朋友第一次上门做客,仓促之下伯父伯母没有准备好给她的礼物。
正在他们手足无措之际,父亲毫不犹豫地把姐姐的新衣服送了过去,于是促成了一桩美满的婚事。
④晚上,伯父来到我家,连连称谢并送来了买衣服的钱,父亲执意不收。
送走了伯父,他喝住了正幸灾乐祸挖苦姐姐的我,然后安慰姐姐并答应新年那天一定让她穿上新衣服。
姐姐不理睬父亲,躲在母亲怀里委屈地哭个不停。
⑤那时候爸爸妈妈两个人的工资不足100元钱,家中的经济一点儿也不富裕,而且在我们居住的偏僻小城里根本买不到那样漂亮的衣服。
所以姐姐认为重新拥有那片粉红只不过是个奢望罢了。
⑥第二天就是大年三十,父亲一大早就拿着家里仅有的30元钱去赶北京的长途汽车,西单、东单、王府井、大栅栏……他跑遍城内大大小小的商业市场,最后终于买到了和姑姑送的样式、颜色都一样的上衣。
⑦在黄昏的暮色中,父亲风尘仆仆地赶回家,把衣服放到满脸惊诧的姐姐手上,没有说一句话。
⑧看看母亲给父亲清洗包扎挤车碰破的手臂,我问:“爸爸,你为什么一定要去买衣服?”父亲轻轻抚摩着我的头,淡淡地说了一句:“让姐姐过个愉快的新年呀。
”⑨泪水渐渐遮住了我的视线,一种深厚无比的爱意沿着父亲的手指抵达我幼小心灵的最深处。
1.文题“千金一诺”的意思是什么?它带有怎样的感情色彩?___________________________________________________________________ ___________________________________________________2.文章开头一句话在文中有什么样的作用?___________________________________________________________________ ___________________________________________________3.说明下面句子的表达作用。
小升初 8 测试卷
小升初 8 测试卷(时间:60分钟满分:100分)一、英汉互译。
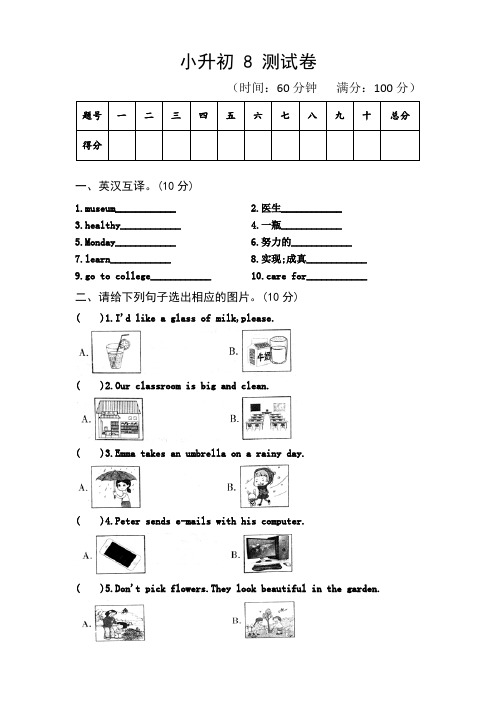
(10分)1.museum____________2.医生____________3.healthy____________4.一瓶____________5.Monday____________6.努力的____________7.learn____________ 8.实现;成真____________9.go to college____________ 10.care for____________二、请给下列句子选出相应的图片。
(10分)( )1.I'd like a glass of milk,please.( )2.Our classroom is big and clean.( )3.Emma takes an umbrella on a rainy day.( )4.Peter sends e-mails with his computer.( )5.Don't pick flowers.They look beautiful in the garden.三、请从下列选项中选出最怡当的一项完成各小题。
(20分)( )1.I use the _______ to cut the paper.A.glueB.townC.scissorsD.e-mail( )2.Look,Lisa!There _______ lots of beautiful flowers over there.A.isB.areC.wasD.were( )3.I'd like a __________ of bread.A.cupB.pairC.glassD.piece( )4.Little Liu Wei lost his arms __________ he was 9 years old.A.orB.whenC.andD.so( )5.Jackson does well __________ the boys' throwing.A.inB.toC.byD.on( )6.Nina is so ________.She can speak English and Chinese well.A.cleverzyC.hungryD.dirty( )7.Our school __________ a sale in the library next Monday.A.hasB.haveC.hadD.will have( )8.Tomorrow is Kate's birthd ay.I want to __________ for her.A.study the starsB.make a cakeC.play footballD.cut down the trees( )9.—__________ do you wear on a sunny day?—I often wear my sunglasses.A.WhoB.WhereC.WhatD.How( )10.—__________.Where is the Children's Park?一It's on Happy Road.A.Excuse meB.Here you areC.Thank youD.S ounds great四、连词成句。
小升初数学课程:第八讲 组合图形和阴影部分计算

第八讲组合图形和阴影部分计算一、知识梳理(一)常用的面积公式及其联系图(二)几种常见的解题方法对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:1.直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
2.相加、相减求面积:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出所求图形的面积。
3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
二、例题精讲1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例1:求下图阴影部分的面积(单位:厘米)。
解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:×2×4=4(平方厘米)变式1:如图,求下列图形总面积【解析】如图所示,该图形由三角形和平行四边形组成。
面积=三角形面积+平行四边形面积故总面积=10*32*1/2+20*32=800变式2:如图求下列图形总面积【解析】该图形由一个梯形和直角三角形组成。
总面积=(6+20)*15*1/2+3*4*1/2=201例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?解答:两个正方形的面积:+=41(平方厘米)三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米)阴影部分的面积:41-33=8(平方厘米)变式1:如图,两个正方形边长分别为9厘米、6厘米,求图中阴影部分面积。
小升初第8讲:不定方程和方程组(教师版)

□ □ □ □ 7 □ □ 30那么被纸片盖住的第一个数是 .分析:设第一个数是x ,第二个数是y ,则八个数依次为.138,85,53,32,2,,,y x y x y x y x y x y x y x ++++++由⎩⎨⎧=+=+30138732y x y x 解得.2,21==y x例3.几何应用题如图,平行四边形ABCD 周长为75厘米.以BC 为底时高是14厘米,以CD 为底时高是16厘米.那么平行四边形ABCD 的面积为 .分析:由平行四边形面积公式知AE ⨯BC =AF ⨯CD ,即14BC =16CD ① 又 2⨯(BC +CD )=75 ②联立①、②解得BC =20,CD =17.5.因此,平行四边形ABCD 的面积为14BC =280(平方厘米). 例4.年龄应用题甲、乙、丙、丁四人,每三个人的平均年龄加上余下一人的年龄分别为29、23、21和17.这四人中最大年龄与最小年龄的差是 .分析:设四人的年龄分别是x 、y 、z 、w .依题意,得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++=+++=+++=+++173213233293z y x w y x w z x w z y w z y x 所以 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++++=++++=++++=++++17323213232332329323z w z y x y w z y x x w z y x w w z y x 比较①,②,③,④易知 z <y <x <w . ①-④整理得 ()1232=-z w ,故w -z =18,即最大年龄与最小年龄之差为18. 例5.销售问题甲、乙、丙三个业主,在同一公司购得相同货物,甲购得12包鞋、7包夹克、17包裤子,用一个集装箱发回,货款及运费共付1012万元.乙和丙发货时每包运费为2000元,乙购得5包鞋、6包夹克、4包裤子,共付货款及运费453万元.乙和丙付的运费是甲所付运费的53.丙每样货购一包,丙付货款及运费共多少元? ABCD 14cm6cm936=÷=a c .故19964=++=++c b a .2. 一个六位数它能被9和11整除,去掉这个六位数的首、尾两个数字,中间的四个数字是1997.那么这个六位数是 .设这个数为b a 1997.由能被9整除,推知a +b =1或10;由能被11整除,推知a -b =5或b -a =5.综上求得a =2,b =8. 3.如图,在矩形ABCD 中,放入六个形状、大小相同的长方形,所标尺寸如图所示.试求图中阴影部分的总面积.设小长方形的长为x ,宽为y ,依题意得⎩⎨⎧=-+=+62)(143y y x y x 解得 x =8,y =2.则AD =6+2y =6+2⨯2=10.矩形ABCD 面积=14⨯10=140(平方厘米).阴影部分总面积=140-6⨯2⨯8=44(平方厘米).4.某校初一有甲、乙、丙三个班,甲班比乙班多4个女同学,乙班比丙班多1个女同学,如果把甲班的第一组调到乙班,乙班的第一组调到丙班,丙班的第一组调到甲班,则三个班女生人数相等.已知丙班第一组有2个女同学.问甲、乙两班第一组各有女同学多少人?设丙班有n 个女同学,甲班第一组有x 个女同学,乙班第一组有y 个女同学,则乙班原有n +1个女同学,甲班原有n +5个女同学,依题意,列出方程(n +5)-x +2=(n +1)-y +x =n -2+y 7-x =1-y +x =y -2 即 ⎩⎨⎧-=+-=-,221127y x yx 解得 x =5,y =4.答:甲班第一组有5个女同学,乙班第一组有4个女同学.5.某车间有三个小组,甲组比乙组多3人,乙组比丙组多4人;甲组每人每天比乙组每人每天少生产2个工件,乙组每人每天比丙组每人每天少生产5个工件;又知甲组每天比乙组多生产9个工件,乙组比丙组多生产5个工件,问各组有多少人,每人每天生产多少个工件?分析:设丙组x 人,甲组每人每天生产y 个工件,则乙组x +4人,甲组(x +4)+3=x +7人;乙组每人每天生产y +2个工件,丙组每人每天生产(y +2)+5=y +7个工件,依题意,得⎩⎨⎧++=+++++=+5)7()2)(4(9)2)(4()7(y x y x y x y x 解得 x =11,y =13.所以x +4=15,x +7=18;y +2=15,20. 答:各组分别有18,15,11人,每人每天生产13,15,20个工件.6.一水池有A 、B 两个进水龙头和一个出水龙头C ,如果在水池空时同时将A 、C 打开,2小时可注满水池;同时ABCD14cm6cm打开B 、C 两龙头3小时可注满水池.当水满时,先打开C ,7小时后把A 、B 同时打开(C 仍开着),1小时后水池可注满.那么单独打开A ,几小时可注满水池?分析:设单独打开A 、B 龙头(或C 龙头),分别可在x 、y (或z )小时内注满水池(或放尽池水),依题意,得122=-zx ① 133=-z y ②1)111(71=+++-z y x z ,(7≥z ) ③或 1111=-+zy x (z <7) ④ 联立①、②、③解得⎪⎪⎪⎩⎪⎪⎪⎨⎧===.536,1736,2336z y x 联立①、②、④解得⎪⎪⎩⎪⎪⎨⎧===6,2,23z y x 答:当独打开C 龙头放完一池水所需时间不少于7小时(事实上为536小时)时,单独打开A 龙头,2326小时可注满水池,当单独打开C 龙头放完一池水所需时间少于7小时(事实上为6小时)时,单独打开A 龙头,23小时可注满用如图1中的长方形和正方形纸板做侧面和底面,做成如图2的竖式和横式两种无盖纸盒. 现在仓库里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?分析:我们已经知道已知量有正方形纸板的总数1000,长方形纸板的总数2000,未知量是竖式纸盒的个数和横式纸盒的个数. 而且每个竖式纸盒和横式纸盒都要用一定数量的正方形纸板和长方形纸板做成,如果我们知道这两种纸盒分别要用多少张正方形纸板和长方形纸板,就能建立起如下的等量关系:每个竖式纸盒要用的正方形纸板数 × 竖式纸盒个数 + 每个横式纸盒要用的正方形纸板数 × 横式纸盒个数 = 正方形纸板的总数每个竖式纸盒要用的长方形纸板数 × 竖式纸盒个数 + 每个横式纸盒要用的长方形纸板数 × 横式纸盒个数 = 长方形纸板的总数通过观察图形,可知每个竖式纸盒分别要用1张正方形纸板和4张长方形纸板,每个横式纸盒分别要用2张正方形纸板和3张长方形纸板.解:由题中的等量关系我们可以得到下面图表所示的关系.设竖式纸盒做x 个,横式纸盒做y 个. 根据题意,得①×4-②,得 5y=2000,解得 y=400.把y=400代入①,得 x+800=1000,解得 x=200.所以方程组的解为因为200和400均为自然数,所以这个解符合题意.答: 竖式纸盒做200个,横式纸盒做400个,恰好将库存的纸板用完.1.不定方程172112=+y x 的整数解是多少?分析:没有整数解.若方程有整数解,则x 123,y 213,因此y x 21123+,且3|17,产生矛盾,因此原方程没有整数解2.有两种不同规格的油桶若干个,大的能装8千克油,小的能装5千克油,44千克油恰好装满这些油桶。
小升初奥数专题-第八讲比和比例关系

第八讲比和比例关系比和比例,是小学数学中的最后一个内容,也是学习更多数学知识的重要基础.有了“比”这个概念和表达方式,处理倍数、分数等问题,要方便灵活得多.我们希望,小学同学学完这一讲,对“除法、分数、比例实质上是一回事,但各有用处”有所理解.这一讲分三个内容:一、比和比的分配;二、倍数的变化;三、有比例关系的其他问题.8.1 比和比的分配最基本的比例问题是求比或比值.从已知一些比或者其他数量关系,求出新的比.例1甲、乙两个长方形,它们的周长相等.甲的长与宽之比是3∶2,乙的长与宽之比是7∶5.求甲与乙的面积之比.解:设甲的周长是2.甲与乙的面积之比是答:甲与乙的面积之比是864∶875.作为答数,求出的比最好都写成整数.例2 如右图,ABCD是一个梯形,E是AD的中点,直线CE把梯形分成甲、乙两部分,它们的面积之比是10∶7.求上底AB与下底CD的长度之比.解:因为E是中点,三角形CDE与三角形CEA面积相等.三角形ADC与三角形ABC高相等,它们的底边的比AB∶CD=三角形ABC的面积∶三角形ADC的面积=(10-7)∶(7×2)= 3∶14.答:AB∶CD=3∶14.两数之比,可以看作一个分数,处理时与分数计算几乎一样.三数之比,却与分数不一样,因此是这一节讲述的重点.例3 大、中、小三种杯子,2大杯相当于5中杯,3中杯相当于4小杯.如果记号表示2大杯、3中杯、4小杯容量之和,求与之比.解:大杯与中杯容量之比是5∶2=10∶4,中杯与小杯容量之比是4∶3,大杯、中杯与小杯容量之比是10∶4∶3.∶=(10×2+4×3+3×4)∶(10×5+4×4+3×3)=44∶75.答:两者容量之比是44∶75.把5∶2与4∶3这两个比合在一起,成为三样东西之比10∶4∶3,称为连比.例3中已告诉你连比的方法,再举一个更一般的例子.甲∶乙=3∶5,乙∶丙=7∶4,3∶5=3×7∶5×7=21∶35,7∶4=7×5∶4×5=35∶20,甲∶乙∶丙=21∶35∶20.花了多少钱?解:根据比例与乘法的关系,连比后是甲∶乙∶丙=2×16∶3×16∶3×2=32∶48∶63.答:甲、乙、丙三人共花了429元.例5有甲、乙、丙三枚长短不相同的钉子,甲与乙,而它们留在墙外的部分一样长.问:甲、乙、丙的长度之比是多少?解:设甲的长度是6份.∶x=5∶4.乙与丙的长度之比是而甲与乙的长度之比是 6∶5=30∶25.甲∶乙∶丙=30∶25∶26.答:甲、乙、丙的长度之比是30∶25∶26.于利用已知条件6∶5,使大部分计算都整数化.这是解比例和分数问题的常用手段.例6 甲、乙、丙三种糖果每千克价分别是22元、30元、33元.某人买这三种糖果,在每种糖果上所花钱数一样多,问他买的这些糖果每千克的平均价是多少元?解一:设每种糖果所花钱数为1,因此平均价是答:这些糖果每千克平均价是27.5元.上面解法中,算式很容易列出,但计算却使人感到不易.最好的计算方法是,用22,30,33的最小公倍数330,乘这个繁分数的分子与分母,就有:事实上,有稍简捷的解题思路.解二:先求出这三种糖果所买数量之比.不妨设,所花钱数是330,立即可求出,所买数量之比是甲∶乙∶丙=15∶11∶10.平均数是(15+11+10)÷3=12.单价33元的可买10份,要买12份,单价是下面我们转向求比的另一问题,即“比的分配”问题,当一个数量被分成若干个数量,如果知道这些数量之比,我们就能求出这些数量.例7 一个分数,分子与分母之和是100.如果分子加23,分母加32,解:新的分数,分子与分母之和是(10+23+32),而分子与分母之比2∶3.因此例8加工一个零件,甲需3分钟,乙需3.5分钟,丙需4分钟,现有1825个零件要加工,为尽早完成任务,甲、乙、丙应各加工多少个?所需时间是多少?解:三人同时加工,并且同一时间完成任务,所用时间最少,要同时完成,应根据工作效率之比,按比例分配工作量.三人工作效率之比是他们分别需要完成的工作量是所需时间是700×3=2100分钟)=35小时 .答:甲、乙、丙分别完成700个,600个,525个零件,需要35小时.这是三个数量按比例分配的典型例题.例9某团体有100名会员,男会员与女会员的人数之比是14∶11,会员分成三个组,甲组人数与乙、丙两组人数之和一样多.各组男会员与女会员人数之比是:甲:12∶13,乙:5∶3,丙:2∶1,那么丙有多少名男会员?解:甲组的人数是100÷2=50(人).乙、丙两组男会员人数是 56-24=32 (人).答:丙组有12名男会员.上面解题的最后一段,实质上与“鸡兔同笼”解法一致,可以设想,“兔例10 一段路程分成上坡、平路、下坡三段,各段路程长之比依次是1∶2∶3.小龙走各段路程所用时间之比依次是4∶5∶6.已知他上坡时速度为每小时3千米,路程全长50千米.问小龙走完全程用了多少时间?解一:通常我们要求出小龙走平路与下坡的速度,先求出走各段路程的速度比.上坡、平路、下坡的速度之比是走完全程所用时间答:小龙走完全程用了10小时25分.上面是通常思路下解题.1∶2∶3计算中用了两次,似乎重复计算,最后算式也颇费事.事实上,灵活运用比例有简捷解法.解二:全程长是上坡这一段长的(1+2+3)=6(倍).如果上坡用的时设小龙走完全程用x小时.可列出比例式8.2 比的变化已知两个数量的比,当这两个数量发生增减变化后,当然比也发生变化.通过变化的描述,如何求出原来的两个数量呢?这就是这一节的内容.例11 甲、乙两同学的分数比是5∶4.如果甲少得22.5分,乙多得22.5分,则他们的分数比是5∶7.甲、乙原来各得多少分?解一:甲、乙两人的分数之和没有变化.原来要分成5+4=9份,变化后要分成5+7=12份.如何把这两种分法统一起来?这是解题的关键.9与12的最小公倍数是36,我们让变化前后都按36份来算.5∶4=(5×4)∶(4×4)=20∶16.5∶7=(5×3)∶(7×3)=15∶21.甲少得22.5分,乙多得22.5分,相当于20-15=5份.因此原来甲得22.5÷5×20=90(分),乙得 22.5÷5×16=72(分).答:原来甲得90分,乙得72分.我们再介绍一种能解本节所有问题的解法,也就是通过比例式来列方程.解二:设原先甲的得分是5x,那么乙的得分是4x.根据得分变化,可列出比例式.(5x-22.5)∶(4x+22.5)=5∶7即 5(4x+22.5)=7(5x-22.5)15x=12×22.5x=18.甲原先得分18×5=90(分),乙得18×4=72(分).解:其他球的数量没有改变.增加8个红球后,红球与其他球数量之比是5∶(14-5)=5∶9.在没有球增加时,红球与其他球数量之比是1∶(3-1)=1∶2=4.5∶9.因此8个红球是5-4.5=0.5(份).现在总球数是答:现在共有球224个.本题的特点是两个数量中,有一个数量没有变.把1∶2写成4.5∶9,就是充分利用这一特点.本题也可以列出如下方程求解:(x+8)∶2x=5∶9.例13 张家与李家的收入钱数之比是8∶5,开支的钱数之比是8∶3,结果张家结余240元,李家结余270元.问每家各收入多少元?解一:我们采用“假设”方法求解.如果他们开支的钱数之比也是8∶5,那么结余的钱数之比也应是8∶5.张家结余240元,李家应结余x元.有240∶x=8∶5,x=150(元).实际上李家结余270元,比150元多120元.这就是8∶5中5份与8∶3中3份的差,每份是120÷(5-3)=60.(元).因此可求出答:张家收入720元,李家收入450元.解二:设张家收入是8份,李家收入是5份.张家开支的3倍与李家开支的8倍的钱一样多.我们画出一个示意图:张家开支的3倍是(8份-240)×3.李家开支的8倍是(5份-270)×8.从图上可以看出5×8-8×3=16份,相当于270×8-240×3=1440(元).因此每份是1440÷16=90(元).张家收入是90×8=720(元),李家收入是90×5=450(元).本题也可以列出比例式:(8x-240)∶(5x-270)=8∶3.然后求出x.事实上,解方程求x的计算,与解二中图解所示是同一回事,图解有算术味道,而且一些数量关系也直观些.例14 A和B两个数的比是8∶5,每一数都减少34后,A是B的2倍,求这两个数.解:减少相同的数34,因此未减时,与减了以后,A与B两数之差并没有变,解题时要充分利用这一点.8∶5,就是8份与5份,两者相差3份.减去34后,A是B的2倍,就是2∶1,两者相差1.将前项与后项都乘以3,即2∶1=6∶3,使两者也相差3份.现在就知道34是8-6=2(份)或5-3=2(份).因此,每份是34∶2=17.A数是17×8=136,B数是17×5=85.答:A,B两数分别是136与85.本题也可以用例13解一“假设”方法求解,不过要把减少后的2∶1,改写成8∶4.例15小明和小强原有的图画纸之比是4∶3,小明又买来15张.小强用掉了8张,现有的图画纸之比是5∶2.问原来两人各有多少张图画纸?解一:充分利用已知数据的特殊性.4+3=7,5+2=7,15-8=7.原来总数分成7份,变化后总数仍分成7份,总数多了7张,因此,新的1份=原来1份+1原来4份,新的5份,5-4=1,因此新的1份有15-1×4=11(张).小明原有图画纸11×5-15=40(张),小强原有图画纸11×2+8=30(张).答:原来小明有40张,小强有30张图画纸.解二:我们也可采用例13解一的“假设”方法.先要将两个比中的前项化成同一个数(实际上就是通分)4∶3=20∶155∶2=20∶8.但现在是20∶8,因此这个比的每一份是当然,也可以采用实质上与解方程完全相同的图解法.解三:设原来小明有4“份”,小强有3“份”图画纸.把小明现有的图画纸张数乘2,小强现有的图画纸张数乘5,所得到的两个结果相等.我们可以画出如下示意图:从图上可以看出,3×5-4×2=7(份)相当于图画纸15×2+8×5=70(张).因此每份是10张,原来小明有40张,小强有30张.例11至15这五个例题是同一类型的问题.用比例式的方程求解没有多大差别.用算术方法,却可以充分利用已知数据的特殊性,找到较简捷的解法,也启示一些随机应变的解题思路.另外,解方程的代数运算,对小学生说来是超前的,不容易熟练掌握.例13的解一,也是一种通用的方法.“假设”这一思路是很有用的,希望读者能很好掌握,灵活运用.从课外的角度,我们更应启发小同学善于思考,去找灵巧的解法,这就要充分利用数据的特殊性.因此我们总是先讲述灵巧的解法,利于心算,促进思维.例16粗蜡烛和细蜡烛长短一样.粗蜡烛可以点5小时,细蜡烛可以点4小时.同时点燃这两支蜡烛,点了一段时间后,粗蜡烛长是细蜡烛长的2倍.问这两支蜡烛点了多少时间?我们把问题改变一下:设细蜡烛长度是2,每小时点等需要时间是答:这两支蜡烛点了3小时20分.把细蜡烛的长度和每小时烧掉的长度都乘以2,使原来要考虑的“2倍”变成“相等”,思考就简捷了.解这类问题这是常用的技巧.再请看一个稍复杂的例子.例17箱子里有红、白两种玻璃球,红球数是白球数的3倍多2只.每次从箱子里取出7只白球,15只红球,经过若干次后,箱子里剩下3只白球,53只红球,那么,箱子里原来红球数比白球数多多少只?解:因为红球是白球的3倍多2只,每次取15只,最后剩下53只,所以对3倍的白球,每次取15只,最后应剩51只.因为白球每次取7只,最后剩下3只,所以对3倍的白球,每次取 7×3=21只,最后应剩 3×3= 9只.因此.共取了(51- 3×3)÷(7×3-15)= 7(次).红球有 15×7+ 53= 158(只).白球有 7×7+3=52(只).原来红球比白球多 158-52=106(只).答:箱子里原有红球数比白球数多106只.8.3 比例的其他问题,这里必须用分数来说,而不能用比.实际上它还是隐含着比例关系:(甲-7)∶乙= 2∶3.因此,有些分数问题,就是比例问题.加33张,他们两人取的画片一样多.问这些画片有多少张?答:这些画片有261张.解:设最初的水量是1,因此最后剩下的水是样重,就有因此原有水的重量是答:容器中原来有8.4千克水.例18和例19,通常在小学数学中,叫做分数应用题.“比”有前项和后项,当两项合在一起写成一个分数后,才便于与其他数进行加、减运算.这就是把比(或除法)写成分数的好处.下面一个例题却是要把分数写成比,计算就方便些.例20 有两堆棋子, A堆有黑子 350个和白子500个, B堆有黑子堆中拿到 A堆黑子、白子各多少个?子100个,使余下黑子与白子之比是(40-100)∶100=3∶1.再要从 B堆拿出黑子与白子到A堆,拿出的黑子与白子数目也要保持3∶1的比.现在 A堆已有黑子 350+ 100= 450个),与已有白子500个,相差从B堆再拿出黑子与白子,要相差50个,又要符合3∶1这个比,要拿出白子数是50÷(3-1)=25(个).再要拿出黑子数是 25×3= 75(个).答:从B堆拿出黑子 175个,白子25个.人,问高、初中毕业生共有多少人?解一:先画出如下示意图:6-5=1,相当于图中相差 17-12=5(份),初中总人数是 5×6=30份,因此,每份人数是520÷(30-17)= 40(人).因此,高、初中毕业生共有40×(17+12)= 1160(人).答:高、初中毕业生共1160人.计算出每份是例21与例14是完全一样的问题,解一与例14的解法也是一样的.(你是否发现?)解二是通常分数应用题的解法,显然计算不如解一简便.例18,19,20,21四个例题说明分数与比例各有好处,你是否从中有所心得?当然关键还是在于灵活运用.下的钱共有多少元?解:设钢笔的价格是1.这样就可以求出,钢笔价格是张剩下的钱数是李剩下的钱数答:张、李两人剩下的钱共28元.题中有三个分数,但它们比的基准是不一样的.为了统一计算单位,设定钢笔的价格为1.每个人原有的钱和剩下的钱都可以通过“1”统一地折算.解分数应用题中,设定统一的计算单位是常用的解题技巧.作为这一讲最后的内容,我们通过两个例题,介绍一下“混合比”.用100个银币买了100头牲畜,问猪、山羊、绵羊各几头?这是十八世纪瑞士大数学家欧拉(1707~1783)提出的问题.们设1头猪和5头绵羊为A组,3头山羊和2头羊绵为B组.A表示A组的数,B表示B 组的数,要使(1+ 5)× A+(3+ 2)× B=100,或简写成 6A+5B=100.就恰好符合均价是1.类似于第三讲鸡兔同笼中例17,很明显,A必定是5的整数倍.A=5, B= 4, 6×5+ 5×4=50,50是 100的约数,符合要求.A=5,猪 5头,绵羊 25头,B=4,山羊12头,绵羊8头.猪∶山羊∶绵羊=5∶12∶(25+8).现在已把1∶5和3∶2两种比,组合在一起通常称为混合比.要注意,这样的问题常常有多种解答.A= 5, B=14或 A=15,B=2才能产生解答,相应的猪、山羊、绵羊混合比是5∶42∶53或15∶6∶79.答:有三组解答.买猪、山羊、绵羊的头数是10,24,66;或者5,42,53;或者15,6,79.求混合比是一种很实用的方法,对数学有兴趣的小学同学,学会这种方法是有好处的,会增加灵活运用比例的技巧.通常求混合比可列下表:下面例题与例23是同一类型,但由于题目的条件,解法上稍有变化.例24某商品76件,出售给33位顾客,每位顾客最多买三件,买 1件按定价,买2件降价 10%,买 3件降价 20%.最后结算,平均每件恰好按原定价的 85%出售,那么买3件的顾客有多少人?解:题目已给出平均数 85%,可作比较的基准.1人买3件少 5%×3;1人买2件多 5%×2;1人买1件多 15%×1.1人买3件与1人买1件成A组,即按1∶1比例,2人买3件与3人买2件成B组,即按2∶3的比例.A组是2人买4件,每人平均买2件.B组是5人买12件,每人平均买2.4件.现在已建立了一个鸡兔同笼型问题:总脚数76,总头数33,兔脚数2.4,鸡脚数2.B组人数是(76-2×33)÷(24-2)= 25(人),A组人数是 33-25=8(人),其中买 3件4人,买 1件4人.10+ 4= 14(人).答:买3件的顾客有14位.建立两种比的A组和B组,与例23的解题思路完全一致,只是后面解法稍有不同.因为对A组和B组,不仅要从人数考虑满足2A+5B=33,还要从买的件数考虑满足 4A+12B=76.这已完全确定了A组和B组的数,不必再求混合比.。
六年级上册数学小升初常考奥数第8讲 转化单位“1”(三)

第8讲 转化单位“1”(三)一、知识要点解答较复杂的分数应用题时,我们往往从题目中找出不变的量,把不变的量看作单位“1”,将已知条件进行转化,找出所求数量相当于单位“1”的几分之几,再列式解答。
二、精讲精练【例题1】有两筐梨。
乙筐是甲筐的53,从甲筐取出5千克梨放入乙筐后,乙筐的梨是甲筐的7/9。
甲、乙两筐梨共重多少千克?解:5÷(5/(5+3)-9/(7+9))=80(千克) 答:甲、乙两筐梨共重80千克。
练习1:1、某小学低年级原有少先队员是非少先队员的31,后来又有39名同学加入少先队组织。
这样,少先队员的人数是非少先队员的87。
低年级有学生多少人?解:39÷(7/ 7+8-1/ 1+3) =39÷(7/15-1/4) =39÷13/60 =39×60/13 =180(名)答:低年级有学生180名.2、王师傅生产一批零件,不合格产品是合格产品的191,后来从合格产品中又发现了2个不合格产品,这时算出产品的合格率是94%。
合格产品共有多少个?19x -2/19x +x ×100%=94% x=10那么合格产品共有19x -2=19×10-2=188(个) 答:合格产品共有188个.3、某校六年级上学期男生占总人数的54%,本学期转进3名女生,转走3名男生,这时女生占总人数的48%。
现在有男生多少人?设原来总人数为x 人,则男生为0.54x 人,女生为0.46x 人由于转走的人数和转进的人数一样多,那么现在班级的总人数也为x 人.根据题意列出方程,解得人.则现在的女生人数为人.【例题2】某学校原有长跳绳的根数占长、短跳绳总数的83。
后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的127。
这个学校现有长、短跳绳的总数是多少根?练习2:1、阅览室看书的同学中,女同学占53,从阅览室走出5位女同学后,看数的同学中,女同学占,原来阅览室一共有多少名同学在看书? 3/(5-3)- 4/(7-4)= 1/6 5÷ 1/6=30(名)30÷( 5-3)/5=75(名)答:原来阅览室一共有75名同学在看书.742、一堆什锦糖,其中奶糖占45%,再放入16千克其他糖后,奶糖只占25%,这堆糖中有奶糖多少千克?解:16÷(1÷25%-1÷45%) =9(千克)3、数学课外兴趣小组,上学期男生占5/9,这学期增加21名女生后,男生就只占2/5了,这个小组现有女生多少人?设兴趣小组共有x 人, 5/9x=(x+21)×2/5 x=5454×(1-5/9)+21=45(人)【例题3】有两段布,一段布长40米,另一段长30米,把两段布都用去同样长的一部分后,发现短的一段布剩下的长度是长的一段布所剩长度的53,每段布用去多少米?解:40-(40-30)÷(1-3/5)=15(米) 答:每段布用去15米。
小升初专题-年龄问题

分析:每过1年爸妈的年龄和比李爷爷追回1岁。 4÷1=4(岁) 答:4年后一样大。
例5、 今年,费叔叔的年龄比小悦、冬冬、阿奇三人年龄的总和还多6岁。多少年后,费叔叔的年龄将比他们三人年龄的总和少6岁?
分析:每过1年费叔叔的年龄 被小悦、冬冬、阿奇三人年龄的总和追回2岁。 经过:6÷2=3(年)后年龄一样 再经过:6÷2=3(年)后费叔叔的年龄将比他们三人年龄的总和少6岁。 3+3=6(年) 答:6年后费叔叔的年龄将比他们三人年龄的总和少6岁。
第八讲年龄问题
求年龄间的和差倍关系。
年龄差不变。
例1、今年冬冬10岁,爸爸40岁,那么爸爸比冬冬大多少岁?2年前爸爸比冬冬大多少岁?3年后爸爸比冬冬大多少岁?
今年爸爸比冬冬大:40-10=30(岁) 两年后爸爸比冬冬大:42-12=30(岁) 三年后爸爸比冬冬大::43-13=30(岁) 答:今年、两年后、-1=12(份) 孙子的年龄:(72-12)÷12=5(岁) 2008-(12-5)=2001(年) 答:2001年爷爷的年龄是孙子的13倍。 练习2、2008年,爷爷72岁,孙子12岁,哪一年爷爷的年龄是孙子的5倍,哪一年爷爷的年龄是孙子的13倍?
(2)孙子的年龄:1份
练习5、今年费叔叔的年龄是28岁,小悦、冬冬、阿奇的年龄之和为30岁。多少年后小悦、冬冬、阿奇年龄和比费叔叔的年龄多10岁?
经过:(10-2)÷2=4(年)后小悦、冬冬、阿奇年龄和比费叔叔的年龄多10岁。 答:4年后小悦、冬冬、阿奇年龄和比费叔叔的年龄多10岁。 .
年龄差不变。 求年龄间的和差倍关系。 画1倍量 画多倍量 标数 求1倍量
添加标题
练习1、今年爸爸32岁,爷爷61岁,那么7年前爷爷比爸爸大多少岁?
六年级上册数学讲义-小升初培优:第08讲 等积变形(解析版)全国通用

第八讲等积变形1、理解并掌握等积变形的思想方法;2、能正确运用等积变形的思想方法解决一些实际问题;3、让学员在操作、观察、讨论、归纳等数学活动过程中,体会等积变形、转化等数学思想方法。
我们已经知道三角形面积的计算公式:三角形面积=底×高÷2从这个公式可以发现:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化。
同时也告诉我们:面积相同三角形有无数多个不同的形状。
在实际问题的研究中,我们还会常常用到以下结论:(1)等底等高的两个三角形面积相等。
(2)夹在一组平行线之间的等积变形,如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,那么ACD BCDS S∆∆=;反之,如果ACD BCDS S∆∆=,则可知直线AB平行于CD。
(备注:长方形和正方形的对边就是一组平行线。
)讲演者:得分:如图,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米。
求长方形的宽。
【解析】连接AG,则可以依据题目条件求出三角形AGB的面积,因为DG已知,进而可以求三角形AGD的高,也就是长方形的宽,问题得解。
解答:长方形的宽的长是6.4厘米。
讲演者:得分:如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米。
请问图中阴影部分的面积是多少平方分米?【解析】连结FD。
根据等底等高的三角形面积相等可得S△AFD=S△FDC,而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,从而得到△AFC=S△AHC+S△HCD=S△ADC=0。
正方形ABCD面积依此即可求。
解答:图中阴影部分的面积是32平方分米。
如图,已知梯形ABCD的面积为5,DA与EB平行,ED与CA平行,求四边形EDAC的面积。
【解析】连接EA、DB,根据平行线间的距离处处相等,和等底等高的三角形的面积相等,可得△EDC的面积=△EDA的面积、△EDA的面积=△DAB的面积、△DAB的面积=△CAB的面积;据此可得△EDC的面积=△CAB的面积;据此可得四边形EDAC的面积=△EDC的面积+△CDA的面积=△CAB的面积+△CDA的面积=梯形ABCD的面积=5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北 京 四 中 网 校 小 升 初语 文 试 题姓名注意事项:1.考试时间150分钟,全卷总分120分,其中卷面与书写共4分。
2.答题前请将姓名填写清楚。
3.用黑、蓝水性或油性笔直接答在试卷上。
4.答题精彩奖励1分,全卷奖励分共5分。
一、积累(共38分)1.默写。
(14分)①_ _____ _____ _ _,行舟绿水前。
(王湾《次北固山下》) ②东风不与周郎便,___ _ ______ _ ____。
(杜牧《赤壁》)③山下兰芽短浸溪,松间沙路净无泥, 。
(苏轼《浣溪沙·游蕲水清泉寺》)④__ __ __ ____,冷露无声湿桂花。
(王建《十五夜望月》) ⑤不应有恨,_____ __?(苏轼《水调歌头》)⑥____ ___ _ __ ____,绝胜烟柳满皇都。
(韩愈《早春呈水部张十八员外》) ⑦旧时茅店社林边,__ ___ _____ ____。
(辛弃疾《西江月(夜行黄沙道中)》) ⑧ ,便引诗情到碧霄。
(刘禹锡《秋词》) ⑨ ,自将磨洗认前朝。
(杜牧《赤壁》) ⑩起舞弄清影,__ ____ ___ ____。
(苏轼《水调歌头》)⑾__ _________ ____,草色遥看近却无。
(韩愈《早春呈水部张十八员外》) ⑿ __ ,清风半夜鸣蝉。
(辛弃疾《西江月(夜行黄沙道中)》) ⒀潮平两岸阔, 。
(王湾《次北固山下》) ⒁但愿人长久,_ ___ ____ ______。
(苏轼《水调歌头》)2.在括号里填上正确的字。
(6分)谈笑风()不骄不()莫()其妙()流不息阴谋()计迫不()待3.下列加点的字注音完全正确的一项是()。
(2分)A、暂时(zàn)魁梧(wú)潜移默化(qiǎn)B、伶俐(lì)萦绕(yíng)掺和(cān)窈窕(tiǎo)C、惩罚(chãng)勉强(qiǎng)惟妙惟肖(xiào)D、胆怯(qiâ)处理(chù)扣人心弦(xián)4.选出和“树林一直在唱着那首愉快的歌”修辞方法相同的一项是( ) (2分)A.这里的人们非常好客,火一般热情。
B.一路上,稻田绿、菜花黄、江水银,绘成了一幅幅田园巨画。
C.生命是一条河流,有奔腾也有平缓。
D.天气炎热,那张乒乓球桌子也在睡觉。
5.选择正确的句子,将序号填入括号中,使文段完整通顺。
(4分)不是所有的笑容都有表示喜悦,();不是所有的喝彩都表示赞颂,();不是所有的顺从都表示虔敬,();不是所有的顺利都表示成功,( )。
①就像不是所有的反对都表示憎恶②就像不是所有的眼泪都表示悲痛③就像不是所有的沉默都表示否定④就像不是所有的挫折都表示不幸6.下面这段文字中每一句都有语病或不得体,请改正.(4分)感谢各位参加我13岁生日晚会。
①看见桌上放着许多大家送来的生日礼物,②我不禁回忆起了从前的往事。
我尤其想起了我的同桌张晓波,③他是一个多么好的小胖墩啊!他为了帮助我学习数学,竟然放弃了参加奥数的赛前训练。
在他的帮助下,④我在数学上取得了巨大的成就。
①句改为②句去掉③句不得体,应改为:④句改为7.口语交际中听出对方言语中的言外之意是一种很重要的能力。
请你根据下面的情景,按要求填空。
(4分)小明正在阳台上浇花,楼下的刘阿姨说:“小李,你真爱美啊,我晒的被子上也锦上添花了。
”刘阿姨的言外之意是 。
(不超过20字)如果你是小明,你会说 。
(不超过35字)8.每年的4月23日定为“世界图书和版权日”(也译为“世界读书日”、“世界书香日”),鼓励人们尤其是年轻人发现读书的乐趣,并以此对那些推动人类社会和文化进步的人们所做出的伟大贡献表示感谢和尊重。
你所在的学校准备举办“读书节”活动,作为一名中学生,你应该积极行动起来,主动参与到这一活动中去。
请你为这次活动拟写一条宣传标语。
(2分)二、阅读(40分)(一)(共13分)智子疑邻宋有富人,天雨墙坏。
其子曰:“不筑,必将有盗。
”其邻人之父亦云。
暮而果大亡其财,其家甚智其子,而疑邻人之父。
1.解释下列划横线的字词。
(4分) ①暮而果大亡其财 ( ) ②其家甚智其子,而疑邻人之父。
( ) ③宋有富人,天雨墙坏。
( ) ④不筑 ( ) 2.翻译句子。
(6分) ①宋有富人,天雨墙坏。
译: ②其子曰:“不筑,必将有盗。
”译: ③暮而果大亡其财,其家甚智其子,而疑邻人之父。
译:3.《智子疑邻》有何寓意?这对我们有何启示?(3分)答:(二)(共10分)蝉①今年,蝉鸣得早。
杜鹃花还没零落,就听见断续的蝉声了。
近月来,窗外蝉更知知不休,使事忙的人听了很烦。
②一天,在树下拾得一只病蝉,透明的翅收敛了,身躯微微颤动,没有声响。
它就是曾知知不休的在树上过日子的小东西。
那么小,却那么响,竟响彻一个夏天!曾这样问:何必聒聒?那只不过是夏天罢了!③朋友说:知道么?它等了17年,才等到一个夏天。
就只有这个夏天,它从泥土中出来,从幼虫成长过来。
等秋风一吹,它的生命就完结了。
④17年埋在泥中,出来就活一个夏天,为什么呢?⑤朋友说:那本来的生活历程就是这样。
它为了生命延续,必须好好活着。
哪管是90年,90天,都不过要好好的过。
⑥哦!那是蝉的生命意义!⑦斜阳里,想起秋风颜色,就宽恕了那烦人的聒聒!1.文章开头写蝉“知知不休”地叫,让人听了很烦,你认为这样写的目的是什么?(3分)2.第②段画线句中的一个“竟”字,表达了作者怎样的思想感情?(2分)3.第⑥段“哦,那是蝉的生命意义!”中的“那”具体指代的内容是什么?(2分)4.你认为这篇文章表达了怎样的人生哲理?(3分)(三)(共15分)五十元钱公司组织旅行,去西部的一处风景地。
在车上,导游就告诫我们:到了那儿,一不要和当地的小孩拍照;二不要购买当地小孩兜售的所谓纪念品;三不要和当地的小孩搭讪。
否则,很可能会惹上麻烦。
这“三个不要”,我们都默记在心。
那天刚下车,还没来得及望一眼好山好水好风景,正如导游所说,一大群当地的小孩就围了上来。
干燥黝黑的脸,凌乱纠结的头发,脏乱破旧的衣服,七嘴八舌地问着,“要合影吗?”“拍一张只要5元钱,3元也行……”“这是我自己做的纪念品,很便宜,买一个吧!”对于他们的要求,我们统统都说“不要”。
但是,他们很执著,没有放弃的意思。
一个小男孩一直贴着我走,手里拿着若干染了色的石头。
他也就10岁的样子,跟着我,喋喋不休。
但我却始终不为所动。
末了,他仰着头对我讲:“那么,你就给我1元钱吧,我去买写字的本子。
”这句话让我停了下来。
我想,他真的缺这1元买本子的钱吗?而上学,倒确是一个要钱的好理由。
我想给他,但是,这小男孩的眼睛出卖了他。
我从这双混沌无神的眼睛里,读出的是“理所当然”、“无所谓”之类的意思,是一种久经世故的熟练。
但我觉得自己的举动真有一点不可思议,鬼使神差地,我从包里拿出了50元钱,递给了那个男孩:“我知道你问我要那1元钱一定不会去买本子,现在,我给你50元,我希望你至少去买一本本子,一支笔。
”小男孩接过了钱,有那么一瞬间,他的眼里闪过一丝不知所措。
然后,他没有再看我一眼,也没有说声“谢谢”,就一溜烟地跑了。
其实,我给他50元钱,一来是想求个安静,二来也是为了一种莫名的心安,虽然我知道,他不会用其中的1分钱去买书或笔。
即使有了这一段插曲,该地区的绝美风光仍然弥补了开初的些微不愉快,也让我很快忘了那个男孩。
在大自然的怀抱里我们流连忘返,当夕阳西下的时候,才依依不舍地回到停车场。
没想到,在我们的大巴旁,我又见到了那个男孩,说起来,是那个男孩认出了我。
他径直跑来,不知塞了一样什么在我手里,然后说了声“谢谢你”,又一溜烟跑了。
借着车子的前灯,我看见男孩给我的是一块有着漂亮花纹的天然石头,还有一张纸,上面用铅笔端端正正地写着:“我会用你给我的钱去买书和笔的,一定,谢谢你。
”字极不好看,但是,我的眼泪还是落下来了。
后来,听司机说,男孩在车旁等了很久很久。
我知道50元钱其实改变不了什么,但是,我知道,它起了作用。
他有了变化,这就够了。
1.在文章第一段中,作者极力着墨“三不要”有何作用?(2分)2.“我”给“他”50元钱的原因是什么?(2分)3.文中画线句子运用了怎样的人物描写方式?有什么作用?(4分)4.“字极不好看,但是,我的眼泪还是落下来了”,“我”为什么流泪了?(3分)5. 阅读下列链接材料,结合上文,谈谈你的一点感悟。
(4分)【材料一】记者从江北区教委了解到,从明年春季开学起,江北区辖区内的义务教育阶段的娃娃将免除学杂费,小学每生每期205元,初中每生每期295元。
如果该政策顺利实施,江北区辖区内中小学适龄儿童将只缴纳课本费。
(摘自《重庆晨报》)【材料二】随着西部大开发号角的吹响,西部地区成为人们关注的热点。
“西部大开发,教育要先行”已成为全社会的共识。
然而,由于西部大多是经济不发达地区,绝大多数贫困儿童都生活在西部。
一些适龄儿童和少年由于家庭条件困难,交不起学费而辍学在家。
(蒋夫尔《多关注西部贫困儿童就学》)三、作文(40分)提示:1.从下面两个题目中任选一题,写一篇不少于400字的文章,除诗歌外,文体不限。
2.要真实、有个性地表达,凡抄袭、套写的文章均酌情扣分。
3.文中的人名、校名、地名一律用化名,以免透露有关信息,影响得分。
题目一:那年六·一题目二:在同学们成长的过程中,都会遇到一些使自己心灵受到震动的事。
这些事一定会深深地留在你的记忆深处,请你写下来,题目自拟。
