《24.7弧长和扇形面积》经典题
弧长及扇形面积的计算(习题精选)

弧长及扇形面积的计算(历年中考题)1如图,半径为1cm ,圆心角为90°的扇形OAB 中,分别以OA 、OB 为直径作半圆,则图中阴影部分的面积为2 如图,一枚直径为4cm 的圆形古钱币沿着直线滚动一周,圆心移动的距离是3 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A 、B 、C 为格点.作△ABC 的外接圆⊙O ,则弧AC 的长等于4 (2011•桂林)如图,将边长为a 的正六边形A 1A 2A 3A 4A 5A 6在直线l 上由图1的位置按顺时针方向向右作无滑动滚动,当A 1第一次滚动到图2位置时,顶点A 1所经过的路径的长为( )A .3324+∏a B. 3348+∏a C. 334+∏a D. 6324+∏a5 如图(甲),水平地面上有一面积为30πcm 2的灰色扇形OAB ,其中OA 的长度为6cm ,且与地面垂直.若在没有滑动的情况下,将图(甲)的扇形向右滚动至OB 垂直地面为止,如图(乙)所示,则O 点移动的距离为( )A.20cmB. 24cmC. 10∏cmD. 30∏cm6.如图为某物体的三视图,友情提醒:在三视图中,AB=BC=CD=DA=EI=IG=NZ=MZ=KY=YL ,θ=60°,FE=GH=KN=LM=YZ .现搬运工人小明要搬运此物块边长为acm 物块ABCD 在地面上由起始位置沿直线l 不滑行地翻滚,翻滚一周后,原来与地面接触的面ABCD 又落回到地面,则此时点B 起始位置翻滚一周后所经过的长度是( )A . 3132+∏a B. 2aC. 3a ∏ D. a ∏7、如图,将边长为2cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动6次后,正方形的中心O经过的路线长是cm.(结果保留π)8、如图,一根木棒(AB)长为2a,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)3 )a,B端沿直线OM向右滑动到B′,则木棒为60°,当木棒A端沿N0向下滑动到A′,AA′=( 2中点从P随之运动到P′所经过的路径长为9、已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50米,半圆的直径为4米,则圆心O所经过的路线长是米.10.如图1,图2…、图m是边长均大于2的三角形、四边形、…、凸n边形.分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、n条弧.(1)图1中3条弧的弧长的和为,图2中4条弧的弧长的和为;(2)求图m中n条弧的弧长的和(用n表示).11、(2010•台州)如图,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π)..12、(2011•东营)如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABCD的周长为15.(1)求此圆的半径;(2)求图中阴影部分的面积13、某校研究性学习小组在研究相似图形时,发现相似三角形的定义、判定及其性质,可以拓展到扇形的相似中去.例如,可以定义:“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”;相似扇形有性质:弧长比等于半径比、面积比等于半径比的平方….请你协助他们探索这个问题.(1)写出判定扇形相似的一种方法:若,则两个扇形相似;(2)有两个圆心角相等的扇形,其中一个半径为a、弧长为m,另一个半径为2a,则它的弧为;(3)如图1是一完全打开的纸扇,外侧两竹条AB和AC的夹角为120°,AB为30cm,现要做一个和它形状相同、面积是它一半的纸扇(如图2),求新做纸扇(扇形)的圆心角和半径14.(2010•温州)如图,在正方形ABCD中,AB=4,O为对角线BD的中点,分别以OB,OD为直径作⊙O1,⊙O2.(1)求⊙O1的半径;(2)求图中阴影部分的面积.15、(2010•邵阳)阅读下列材料,然后解答问题.经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形.如图,已知正四边形ABCD的外接圆⊙O,⊙O的面积为S1,正四边形ABCD的面积为S2,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H.设由OE、OF、弧EF及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①(1)当OM经过点A时(如图①),则S、S1、S2之间的关系为:S= (用含S1、S2的代数式表示);(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由;(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.16、如图,已知⊙O的半径为R,直径AB⊥CD以B为圆心,以BC为半径作弧CED.求弧CED与弧CAD围成的新月形ACED的面积S.17、如图,已知半圆的直径AB=12cm,点C、D是这个半圆的三等分点,求弦AC、AD有弧CD围成的阴影部分的面积.(结果用π表示)18、如图,⊙C经过原点且与两坐标轴分别交于A、B两点,点A的坐标是(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标.19、如图,在⊙M中,弦AB所对的圆心角为120度,已知圆的半径为2cm,并建立如图所示的直角坐标系.(1)求圆心M的坐标;(2)求经过A,B,C三点的抛物线的解析式;(3)设点P是⊙M上的一个动点,当△PAB为Rt△PAB时,求点P的坐标.20.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.(1)求∠ACB的大小;(2)写出A,B两点的坐标;(3)试确定此抛物线的解析式;(4)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.。
人教版九年级数学上册《24.4弧长及扇形的面积》同步练习题(附答案)

人教版九年级数学上册《24.4弧长及扇形的面积》同步练习题(附答案)姓名班级学号成绩一、选择题:(本题共8小题,每小题5分,共40分.)1.若扇形的弧长是16cm,面积是56cm2,则它的半径是()A.2.8cm B.3.5cm C.7cm D.14cm2.已知一个扇形的半径为R,圆心角为n°,当这个扇形的面积与一个直径为R的圆面积相等时,则n等于()A.180 B.120 C.90 D.603.如图,放置在直线l上的扇形OAB.由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的最短路径的长是()A.2π+2 B.3πC.D. +24.如图,一块直角三角板的60°角的顶点A落在⊙O上,两边分别交⊙O于B,C两点,若⊙O的半径是1,则的长是()A.B.C.D.5.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为()A.B.πC.2πD.4π6.如图,在△ABC中,∠A=40°,BC=3,分别以点B,C为圆心,BC长为半径在BC右侧画弧,两弧交于点D,与AB,AC的延长线分别交于点E,F,则弧DE和弧DF的长度和为()A.B.C.D.2π7.如图,是的直径,且,是上一点,将沿直线翻折,若翻折后的圆弧恰好经过点,则图中阴影部分的面积为().A.B.C.D.8.如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则与的弧长之和为()A.B.C.D.二、填空题:(本题共5小题,每小题3分,共15分.)9.扇形弧长为5πcm,面积为60πcm2,则扇形半径为.10.如图,的外接圆O的半径为3,则劣弧的长是.11.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC= ,则图中阴影部分的面积是12.如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心,半径r为,点A,B是圆上的两点,圆心角,则的长为.(结果保留)13.如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E,F,则图中阴影部分的面积为.三、解答题:(本题共5题,共45分)14.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,求弧AD的长15.如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.16.如图,在△ABC中,AB=AC,以AB为直径作⊙O,⊙O交BC于点D,交CA的延长线于点E.过点D作DF ⊥AC,垂足为F.(1)求证:DF为⊙O的切线;(2)若AB=4,∠C=30°,求劣弧的长.17.如图,已知过菱形的三个顶点A,B,D,连接,过点A作交的延长线于点E.(1)求证:为的切线;(2)若的半径为2,求图中阴影部分的面积.18.如图,在中,以边为直径作分别交,于点D,E,点D是中点,连接OE,OD.(1)求证:是等腰三角形.(2)若,求的长和扇形的面积.参考答案:1.C 2.C 3.C 4.C 5.C 6.B 7.D 8.A 9.24cm10.11.12.13.14.解:∵在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1 ∴AB=2BC=2,∠ABC=90°-∠BAC=60°∴∠ABD=180°-∠ABC=120°∴弧AD=故答案为.15.解:过点O作OC⊥AB于C点.∵OC⊥AB,AB=18∴∵OA=OB,∠AOB=360°﹣240°=120°∴°.在Rt△OAC中,OA2=OC2+AC2又∵∴.∴πr2=72π(m2)16.(1)证明:如图,连接OD∵AB=AC∴∠B=∠C∵OB=OD∴∠B=∠ODB∴∠C=∠ODB∴OD// AC∵DF⊥AC∴DF⊥ODDF为⊙O的切线(2)解:如图,连接OE∵∠B=∠C=30°∴∠EAB=∠B+∠C=60°∴∠EOB=2∠EAB=120°∴的长=. 17.(1)证明:连接交于点P∵四边形是菱形∴∴∵∴∴∵为的半径∴为的切线;(2)解:∵四边形是菱形∴∵∴∴是等边三角形∴∵∴∴∴∴. 18.(1)证明:连接∵为直径∴,即又∵D是中点∴是线段的中垂线∴∴是等腰三角形(2)解:∵∴∴∵∴∴∵∴∴∴∴。
弧长以及扇形面积的计算-练习题含答案

连接 OD、OE,先证明
、
是等边三角形,得出
,
求出
,再由弧长公式即可得出答案.
本题考查了等边三角形的性质与判定、弧长公式;熟练掌握弧长公式,证明三角形是等 边三角形是解决问题的关键.
三、解答题(本大题共 1 小题,共分) 9. 如图,AB 为半圆 O 的直径,AC 是
的一条弦,D
为 的中点,作
,交 AB 的延长线于点 F,
弧长以及扇形面积的计算
副标题
题号 得分
一
二
三
总分
一、选择题(本大题共 3 小题,共分)
1. 如图,在
中,
,
,以 BC 的中
点 O 为圆心 为 A.
分别与 AB,AC 相切于 D,E 两点,则 的长
B.
C. D.
【答案】B
【解析】解:连接 OE、OD,
设半径为 r,
分别与 AB,AC 相切于 D,E 两点,
2. 一个扇形的弧长是
,面积是
,则此扇形的圆心角的度数是
A. 【答案】B
【解析】解:
B.
一个扇形的弧长是
C.
,面积是
D.
,
,即
,
解得:
,
,
解得:
,
故选 B 利用扇形面积公式 1 求出 R 的值,再利用扇形面积公式 2 计算即可得到圆心角度数. 此题考查了扇形面积的计算,以及弧长的计算,熟练掌握扇形面积公式是解本题的关键.
,
,
,
故
,
.
【解析】 直接利用切线的判定方法结合圆心角定理分析得出
,即可得出答
案;
直接利用得出
,再利用
,求出答案.
专题3弧长和扇形面积(专项练习含答案

专题3.24 弧长和扇形面积(专项练习1)一、单选题知识点一、求弧长1.如图,PA 、PB 是⊙O 的切线,切点分别为A 、B ,若OA =2,⊙P =60°,则AB 的长为( )A .23πB .πC .43πD .53π 2.如图,在扇形AOB 中,AC 为弦,140AOB ∠︒=,60CAO ∠︒=,6OA =,则BC 的长为( )A .43πB .83πC .D .2π 3.如图,半径为1的⊙O 与正五边形ABCDE 相切于点A ,C ,则劣弧AC 的长度为( )A .25π B .23π C .34π D .45π 知识点二、求半径4.一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为( )A .6厘米B .12厘米C .厘米D 厘米 5.若扇形的圆心角为90︒,弧长为3π,则该扇形的半径为( )A B .6 C .12 D .,圆心角是150,则它的半径长为()6.已知一个扇形的弧长为5cmA.6cm B.5cm C.4cm D.3cm 知识点三、求圆心角7.已知扇形半径为3,弧长为π,则它所对的圆心角的度数为()A.120°B.60°C.40°D.20°8.圆锥的地面半径为10cm.它的展开图扇形半径为30cm,则这个扇形圆心角的度数是()A.60°B.90°C.120°D.150°9.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是()A.90°B.120°C.180°D.135°知识点四、求点的运动路径长10.如图,在边长为1的正方形组成的网格中,⊙ABC的顶点都在格点上,将⊙ABC绕点C 顺时针旋转60°,则顶点A所经过的路径长为()A.10πBC D.π11.如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°时,点B运动路径的长度为()A.πB.2πC.3πD.4π12.如图,已知□ABCD的对角线BD=4cm,将□ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )A .4π cmB .3π cmC .2π cmD .π cm知识点五、求扇形面积13.如图,AB 为半圆的直径,其中4AB =,半圆绕点B 顺时针旋转45︒,点A 旋转到点A '的位置,则图中阴影部分的面积为( )A .πB .2πC .2πD .4π14.如图,AB 是⊙O 的直径,CD 是弦,⊙BCD=30°,OA=2,则阴影部分的面积是( )A .3πB .23πC .πD .2π15.如图,等边三角形ABC 内接于O ,若O 的半径为2,则图中阴影部分的面积等于( )A .3πB .23πC .43πD .2π知识点六、求旋转扫过的面积16.如图,C 是半圆⊙O 内一点,直径AB 的长为4cm ,⊙BOC =60°,⊙BCO =90°,将⊙BOC 绕圆心O 逆时针旋转至⊙B′OC′,点C′在OA 上,则边BC 扫过的区域(图中阴影部分)的面积为( )A .43πB .πC .4πD 17.在⊙ABC 中,⊙C=90°,BC=4cm ,AC=3cm ,把⊙ABC 绕点A 顺时针旋转90°后,得到⊙A 1B 1C 1(如图所示),则线段AB 所扫过的面积为( )A .2B .254πcm 2C .252πcm 2D .5πcm 218.如图,直径AB 为6的半圆,绕A 点逆时针旋转60°,此时点B 到了点B′,则图中阴影部分的面积是( )A .6πB .5πC .4πD .3π知识点七、求弓形的面积19.如图,在O 中,2OA =,45C ∠=︒,则图中阴影部分的面积为( )A.2πB .πC .22π- D .2π-20.如图,阴影表示以直角三角形各边为直径的三个半圆所组成的两个新月形,若127S S +=,且8AC BC +=,则AB 的长为( )A .6B .7C .8D .1021.如图,某商标是由三个半径都为R 的圆弧两两外切得到的图形,则三个切点间的弧所围成的阴影部分的面积是( )A .(√3﹣12π)R 2B .(√3+12π)R 2C .(√32﹣π)R 2D .(√32+π)R 2知识点八、求不规则图形面积22.如图,在菱形ABCD 中,点E 是BC 的中点,以C 为圆心、CE 为半径作弧,交CD 于点F ,连接,AE AF .若6AB =,60B ∠=,则阴影部分的面积为( )A .3πB .2πC .9π-D .6π 23.如图,直径6AB =的半圆,绕B 点顺时针旋转30︒,此时点A 到了点A ',则图中阴影部分的面积是( ).A .2πB .34πC .πD .3π24.如图,菱形ABCD 的边长为4cm ,⊙A =60°,弧BD 是以点A 为圆心,AB 长为半径的弧,弧CD 是以点B 为圆心,BC 长为半径的弧,则阴影部分的面积为( )A .2cm 2B .2C .4cm 2D .πcm 2二、填空题 知识点一、求弧长25.如图,边长为的正六边形螺帽,中心为点O ,OA 垂直平分边CD ,垂足为B ,AB =17cm ,用扳手拧动螺帽旋转90°,则点A 在该过程中所经过的路径长为_____cm .26.一个扇形的圆心角是120°.它的半径是3cm .则扇形的弧长为__________cm . 27.如图,在66⨯的方格纸中,每个小方格都是边长为1的正方形,其中A 、B 、C 为格点,作ABC 的外接圆,则BC 的长等于_____.知识点二、求半径28.已知扇形的圆心角为120°,弧长为6π,则它的半径为________.29.若扇形的圆心角为120°,弧长为18πcm ,则该扇形的半径为_____cm .30.如图,⊙O 的半径为6cm ,B 为⊙O 外一点,OB 交⊙O 于点A ,AB=OA ,动点P 从点A 出发,以π cm/s 的速度在⊙O 上按逆时针方向运动一周回到点A 立即停止.当点P 运动的时间为______时,BP 与⊙O 相切.知识点三、求圆心角31.一个扇形的弧长是20cm π,面积是2240cm π,则这个扇形的圆心角是___度. 32.如图,点A 、B 、C 在半径为9的⊙O 上,AB 的长为,则⊙ACB 的大小是___.33.若一个扇形的弧长是2πcm ,面积是26πcm ,则扇形的圆心角是__________度.知识点四、求点的运动路径长34.如图,扇形AOB 中,10,36OA AOB =∠=︒.若将此扇形绕点B 顺时针旋转,得一新扇形A O B '',其中A 点在O B '上,则点O 的运动路径长为_______cm .(结果保留π)35.将边长为2的正六边形ABCDEF 绕中心O 顺时针旋转α度与原图形重合,当α最小时,点A 运动的路径长为_____.36.如图,在扇形铁皮AOB中,OA=10,⊙AOB=36°,OB在直线l上.将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA第5次落在l上时,停止旋转.则点O所经过的路线长为_____.知识点五、求扇形面积37.如图,在正六边形ABCDEF中,分别以C,F为圆心,以边长为半径作弧,图中阴影部分的面积为24π,则正六边形的边长为_____.38.一个扇形的半径为3cm,面积为 2cm,则此扇形的圆心角为______.39.如图,矩形ABCD的对角线交于点O,以点A为圆心,AB的长为半径画弧,刚好过点O,以点D为圆心,DO的长为半径画弧,交AD于点E,若AC=2,则图中阴影部分的面积为_____.(结果保留π)知识点六、求旋转扫过的面积40.如图,在⊙ABC 中,⊙ABC =45°,⊙ACB =30°,AB =2,将⊙ABC 绕点C 顺时针旋转60°得⊙CDE ,则图中线段AB 扫过的阴影部分的面积为_____.41.如图,在⊙ABC 中,AB =5,AC =3,BC =4,将⊙ABC 绕点A 逆时针旋转30°后得到⊙ADE ,点B 经过的路径为弧BD ,则图中阴影部分的面积为________.42.如图,将ABC 绕点A 逆时针旋转120︒得ADE ,已知4AB =,1AC =,那么图中阴影部分的面积是________.(结果保留π)知识点七、求弓形的面积43.如图,⊙O 的半径为2,点A ,B 在⊙O 上,⊙AOB =90°,则阴影部分的面积为________.44.如图,点A 、B 、C 在⊙O 上,若⊙BAC =45°,OB =2,则图中阴影部分的面积为_____.45.如图,点C 是以AB 为直径的半圆O 的三等分点,2AC = ,则图中阴影部分的面积是 _______.知识点八、求不规则图形面积46.如图,边长为2的正方形ABCD 中心与半径为2的⊙O 的圆心重合,E 、F 分别是AD 、BA 的延长与⊙O 的交点,则图中阴影部分的面积是______.(结果保留π)47.如图,AB 是O 的直径,点E 是BF 的中点,过点E 的切 线分别交AF AB ,的延长线于点D C ,,若C 30∠=,O 的半径是2,则图形中阴影部分的面积是_______.48.如图所示的扇形AOB 中,920,OA B OB AO ∠===︒,C 为AB 上一点,30AOC ∠=︒,连接BC ,过C 作OA 的垂线交AO 于点D ,则图中阴影部分的面积为_______.三、解答题知识点一、求弧长49.如图,PC是⊙O的直径,PA切⊙O于点P,OA交⊙O于点B,连结BC.已知⊙O的半径为2,⊙C=35°(1)求⊙A的度数;(2)求BC的长.知识点二、求半径50.在⊙O中,弦AB所对的圆周角为30°,且5cmAB=,求AB的长.嘉琪的解法如下:⊙弦AB所对的圆周角是30°,AB∴的长为3055(cm) 1806ππ⨯=.请问嘉琪的解法正确吗?如果不正确,请给出理由.知识点三、求圆心角51.若一条圆弧所在圆半径为9,弧长为52π,求这条弧所对的圆心角.知识点四、求点的运动路径长52.如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕点O顺时针旋转180°,试解决下列问题:(1)画出四边形ABCD旋转后的图形;(2)求点C在旋转过程中经过的路径长.知识点五、求扇形面积53.如图,AB是O的直径,点D是AB延长线上的一点,点C在O上,且AC=CD,=.∠︒120ACD()求证:CD是O的切线;1()若O的半径为3,求图中阴影部分的面积.2知识点六、求旋转扫过的面积54.如图所示,在平面直角坐标系中,Rt⊙ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).(1)将⊙ABC以点C为旋转中心逆时针旋转90°,画出旋转后对应的⊙A1B1C;(2)图中⊙ABC外接圆的圆心的坐标是,⊙ABC外接圆的面积是平方单位长度.知识点七、求弓形的面积55.如图,以AB为直径的⊙O经过AC的中点D,DE⊙BC于点E.(1)求证:DE是⊙O的切线;(2)当AB=⊙C=30°时,求图中阴影部分的面积(结果保留根号和π).知识点八、求不规则图形面积56.如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.(1)求证:AC平分⊙DAB;(2)若BE=3,参考答案1.C【解析】试题解析:⊙P A、PB是⊙O的切线,⊙⊙OBP=⊙OAP=90°,在四边形APBO中,⊙P=60°,⊙⊙AOB =120°,⊙OA =2,⊙AB 的长l =12024=1803ππ⨯. 故选C.2.B【分析】连接OC ,根据等边三角形的性质得到80BOC ∠︒=,根据弧长公式计算即可.【详解】连接OC ,60OA OC CAO ∠︒=,=,AOC ∴为等边三角形,60AOC ∴∠︒=,1406080BOC AOB AOC ∴∠∠-∠︒-︒︒===,则BC 的长80681803ππ⨯==, 故选B . 【点拨】本题考查弧长的计算,等边三角形的判定和性质,掌握弧长公式:180n r l π=是解题的关键.3.D【分析】连接OA 、OC ,如图,根据正多边形内角和公式可求出⊙E 、⊙D ,根据切线的性质可求出⊙OAE 、⊙OCD ,从而可求出⊙AOC ,然后根据圆弧长公式即可解决问题.【详解】连接OA 、OC ,如图.⊙五边形ABCDE 是正五边形, ⊙⊙E =⊙D =(52)1805︒-⨯=108°.⊙AE 、CD 与⊙O 相切,⊙⊙OAE =⊙OCD =90°,⊙⊙AOC =(5﹣2)×180°﹣90°﹣108°﹣108°﹣90°=144°,⊙劣弧AC 的长为144141805ππ⨯=. 故选D .【点拨】本题主要考查了切线的性质、正五边形的性质、多边形的内角和公式、圆弧长公式等知识,求出圆弧所对应的圆心角是解决本题的关键.4.A【解析】 l=180n R π⨯, 由题意得,2π=60180R π⨯, 解得:R=6cm .故选A .故选A .【点睛】运用了弧长的计算公式,属于基础题,熟练掌握弧长的计算公式是关键. 5.B 【分析】根据弧长公式180n r l π=可以求得该扇形的半径的长度. 【详解】 解:根据弧长的公式180n r l π=,知 180180390l r n πππ⨯===6, 即该扇形的半径为6.故选:B .【点拨】本题考查了弧长的计算.解题时,主要是根据弧长公式列出关于半径r 的方程,通过解方程即可求得r 的值.6.A【分析】设扇形半径为rcm ,根据扇形弧长公式列方程计算即可.【详解】设扇形半径为rcm , 则150180r π=5π,解得r =6cm . 故选A.【点拨】本题主要考查扇形弧长公式.7.B【解析】【详解】解:根据l=3180180n r n ππ⨯==π, 解得:n=60°,故选B .【点拨】本题考查弧长公式,在半径为r 的圆中,n°的圆心角所对的弧长为l=180n r π. 8.C【解析】【分析】根据圆锥的侧面展开图为扇形,圆锥的底面圆的周长等于扇形的弧长得到圆锥的展开图扇形的弧长=2π•10,然后根据扇形的弧长公式l =180n R π 计算即可求出n . 【详解】解:设圆锥的展开图扇形的圆心角的度数为n .⊙圆锥的底面圆的周长=2π•10=20π,⊙圆锥的展开图扇形的弧长=20π,⊙20π=30180n π⋅⋅, ⊙n =120°.故答案选:C .【点拨】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,圆锥的底面圆的周长等于扇形的弧长,母线长等于扇形的半径.也考查了扇形的弧长公式.9.C【分析】根据弧长公式:l =180n R π(弧长为l ,圆心角度数为n ,圆的半径为R ),代入即可求出圆心角的度数.【详解】解:由题意得,2π=2180n π⨯, 解得:n =180.即这条弧所对的圆心角的度数是180°.故选C .【点拨】本题考查了弧长的计算,解答本题关键是熟练掌握弧长的计算公式,及公式字母表示的含义.10.C【详解】如图所示:在Rt⊙ACD 中,AD=3,DC=1,根据勾股定理得:又将⊙ABC 绕点C 顺时针旋转60°,则顶点A 所经过的路径长为=. 故选C.11.A【分析】B 点的运动路径是以A 点为圆心,AB 长为半径的圆的14的周长,然后根据圆的周长公式即可得到B 点的运动路径长度为π.【详解】解:⊙B 点的运动路径是以A 点为圆心,AB 长为半径的圆的14的周长, ⊙9022360,故选:A .【点拨】本题考查了弧长的计算,熟悉相关性质是解题的关键.12.C【分析】点D 所转过的路径长是一段弧,是一段圆心角为180°,半径为OD 的弧,故根据弧长公式计算即可.【详解】解:BD=4, ⊙OD=2⊙点D 所转过的路径长=1802180π⨯=2π. 故选:C .【点拨】本题主要考查了弧长公式:180n r l π=. 13.B【分析】由旋转的性质可得:AB A B BAA S S S S ''+=+阴影半圆半圆扇形,从而可得BAA S S '=阴影扇形,利用扇形面积公式计算即可.【详解】解:半圆AB 绕点B 顺时针旋转45︒,点A 旋转到A '的位置, AB A B S S '∴=半圆半圆,45ABA '∠=︒.AB A B BAA S S S S ''+=+阴影半圆半圆扇形,BAA S S '∴=阴影扇形24542360ππ⨯==. 故选B . 【点拨】本题考查的是旋转的性质,扇形面积的计算,掌握以上知识是解题的关键. 14.B【分析】根据圆周角定理可以求得⊙BOD 的度数,然后根据扇形面积公式即可解答本题.【详解】⊙⊙BCD=30°,⊙⊙BOD=60°,⊙AB 是⊙O 的直径,CD 是弦,OA=2,⊙阴影部分的面积是:236236020ππ⨯⨯=, 故选B .【点拨】本题考查扇形面积的计算、圆周角定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.15.C【分析】连接OC ,如图,利用等边三角形的性质得120AOC ∠=,AOB AOC SS =,然后根据扇形的面积公式,利用图中阴影部分的面积AOC S =扇形进行计算.【详解】解:连接OC ,如图, ABC 为等边三角形,120AOC ∠∴=,AOB AOC S S =,∴图中阴影部分的面积212024.3603AOC S 扇形ππ⋅⨯===故选C .【点拨】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了等边三角形的性质.16.B【解析】【分析】根据直角三角形的性质求出OC 、BC ,根据扇形面积公式:2360n r S π=计算即可. 【详解】解:⊙⊙BOC=60°,⊙BCO=90°,⊙⊙OBC=30°,⊙OC=12OB=1,则边BC 扫过的区域的面积为:2212021120111136023602ππ⨯⨯+-- =πcm 2.故答案为B .【点拨】本题主要考查扇形面积公式,三角形的性质.正确计算扇形面积是解题的关键. 17.B【解析】【分析】首先求出AB ,然后根据扇形面积公式计算即可.【详解】解:,⊙线段AB 所扫过的面积为:290525=3604ππ⋅⋅, 故选:B.【点拨】本题主要考查扇形面积计算,熟练掌握扇形面积计算公式是解题关键. 18.A【详解】试题分析:根据题意可得:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB 为直径的半圆的面积=扇形ABB′的面积=26066360ππ⨯=,故选A . 考点:图形旋转的性质、扇形的面积.19.D【分析】根据圆周角定理得出⊙AOB=90°,再利用S 阴影=S 扇形OAB -S ⊙OAB 算出结果.【详解】解:⊙⊙C=45°,⊙⊙AOB=90°,⊙OA=OB=2,⊙S阴影=S扇形OAB-S⊙OAB=29021223602π⋅⋅-⨯⨯=2π-,故选D.【点拨】本题考查了圆周角定理,扇形面积计算,解题的关键是得到⊙AOB=90°.20.A【分析】根据勾股定理得到AC2+BC2=AB2,根据扇形面积公式、完全平方公式计算即可.【详解】解:由勾股定理得,AC2+BC2=AB2,⊙S1+S2=7,⊙12×π×(2AC)2+12×π×(2BC)2+12×AC×BC−12×π×(2AB)2=7,⊙AC×BC=14,AB6,故选:A.【点拨】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.21.A【解析】【分析】由题意知,得到的如图三角形是等边三角形,边长也为R,阴影的部分的面积等于等边三角形的面积减去三个弓形的面积.而一个弓形的面积等于圆心角为60度的半径为R 的扇形的面积减去边长为R的等边三角形的面积.【详解】解:边长为R的等边三角形的面积SΔ=12×sin60°R2=√34R2;半径为R的扇形的面积S扇形=60πR2360=πR26;⊙一个弓形的面积S扇形=πR26−√34R2,⊙阴影的部分的面积=√34R 2−3×(πR 26−√34R 2)=(√3−12π)R 2. 故选:A .【点拨】本题考查了等边三角形的性质和面积的求法,及扇形,弓形的面积的求法. 22.A【分析】连接AC ,根据菱形的性质求出BCD ∠和6BC AB ==,求出AE 长,再根据三角形的面积和扇形的面积求出即可.【详解】连接AC ,⊙四边形ABCD 是菱形,⊙6AB BC ==,⊙60B ∠=,E 为BC 的中点,⊙3CE BE CF ===,ABC ∆是等边三角形,//AB CD ,⊙60B ∠=,⊙180120BCD B ∠=-∠=,由勾股定理得:AE ==⊙11622AEB AEC AFC S S S ∆∆∆==⨯⨯==,⊙阴影部分的面积212033360AEC AFC CEFS S S S ππ∆∆⨯=+-==扇形, 故选A .【点拨】本题考查了等边三角形的性质和判定,菱形的性质,扇形的面积计算等知识点,能求出AEC ∆、AFC ∆和扇形ECF 的面积是解此题的关键.23.D【分析】由半圆A′B 面积+扇形ABA′的面积-空白处半圆AB 的面积即可得出阴影部分的面积.【详解】解:⊙半圆AB,绕B点顺时针旋转30°,⊙S阴影=S半圆A′B+S扇形ABA′-S半圆AB= S扇形ABA′=2630 360π⋅=3π故选D.【点拨】本题考查了扇形面积的计算以及旋转的性质,熟记扇形面积公式和旋转前后不变的边是解题的关键.24.B【解析】【分析】连接BD,判断出⊙ABD是等边三角形,根据等边三角形的性质可得⊙ABD=60°,再求出⊙CBD=60°,DB=BC=AD,从而确定S扇形BDC=S扇形ABD,然后求出阴影部分的面积=S扇形BDC -(S扇形ABD-S⊙ABD)=S⊙ABD,计算即可得解.【详解】解:如图,连接BD,⊙四边形ABCD是菱形,⊙AB=AD=BC,⊙⊙A=60°,⊙⊙ABD是等边三角形,⊙⊙ADB=60°,AD=DB=BC=4又⊙菱形的对边AD⊙BC,⊙⊙CBD=⊙ADB=60°,⊙S扇形BDC=S扇形ABD⊙S阴影=S扇形BDC-(S扇形ABD-S⊙ABD)=S⊙ABD24cm2.故选B.【点拨】本题考查了菱形的性质,等边三角形的性质和面积,熟记性质并作辅助线构造出等边三角形是解题的关键.25.10π【分析】利用正六边形的性质求出OB的长度,进而得到OA的长度,根据弧长公式进行计算即可.【详解】解:连接OD,OC.⊙⊙DOC=60°,OD=OC,⊙⊙ODC是等边三角形,⊙OD=OC=DC=cm),⊙OB⊙CD,⊙BC=BD cm),⊙OB=3(cm),⊙AB=17cm,⊙OA=OB+AB=20(cm),⊙点A在该过程中所经过的路径长=9020180π⋅⋅=10π(cm),故答案为:10π.【点拨】本题考查了正六边形的性质及计算,扇形弧长的计算,熟知以上计算是解题的关键.26.2π【解析】分析:根据弧长公式可得结论. 详解:根据题意,扇形的弧长为1203180π⨯=2π, 故答案为:2π点睛:本题主要考查弧长的计算,熟练掌握弧长公式是解题的关键.27 【分析】由AB 、BC 、AC 长可推导出⊙ACB 为等腰直角三角形,连接OC ,得出⊙BOC =90°,计算出OB 的长就能利用弧长公式求出BC 的长了.【详解】⊙每个小方格都是边长为1的正方形,⊙AB =AC ,BC ,⊙AC 2+BC 2=AB 2,⊙⊙ACB 为等腰直角三角形,⊙⊙A =⊙B =45°,⊙连接OC ,则⊙COB =90°,⊙OB⊙BC 的长为:90180π⋅=2.【点拨】本题考查了弧长的计算以及圆周角定理,解题关键是利用三角形三边长通过勾股定理逆定理得出⊙ACB 为等腰直角三角形.28.9【分析】根据弧长公式L =180n R π求解即可. 【详解】 ⊙L =180n R π, ⊙R =1806120ππ⨯=9. 故答案为9.【点拨】本题考查了弧长的计算,解答本题的关键是掌握弧长公式:L =180n R π. 29.27【解析】【分析】根据弧长公式即可得解.【详解】解:设扇形的半径为r (cm ),则18π=120180r π⨯⨯, 解得:r=27.故答案为27.【点拨】本题考查扇形的弧长公式,l=180n r π,l 是弧长,n 是圆心角的度数,r 是半径. 30.2或10【分析】根据切线的判定与性质进行分析即可.若BP 与⊙O 相切,则⊙OPB=90°,又因为OB=2OP ,可得⊙B=30°,则⊙BOP=60°;根据弧长公式求得弧AP 长,除以速度,即可求得时间.【详解】连接OP⊙当OP⊙PB 时,BP 与⊙O 相切,⊙AB=OA ,OA=OP ,⊙OB=2OP ,⊙OPB=90°;⊙⊙B=30°;⊙⊙O=60°;⊙OA=6cm ,弧AP=606180π⨯=2π, ⊙圆的周长为:12π,⊙点P 运动的距离为2π或12π-2π=10π;⊙当t=2秒或10秒时,有BP 与⊙O 相切.故答案为:2或10【点拨】本题考查的是切线的性质及弧长公式,解答此题时要注意过圆外一点有两条直线与圆相切,不要漏解.31.150【分析】根据弧长公式计算.【详解】 根据扇形的面积公式12S lr =可得: 1240202r ππ=⨯, 解得r =24cm , 再根据弧长公式20180n r l cm ππ==, 解得150n =︒.故答案为:150.【点拨】本题考查了弧长的计算及扇形面积的计算,要记熟公式:扇形的面积公式12S lr =,弧长公式180n r l π=. 32.20°. 【分析】连接OA 、OB ,由弧长公式的92180n ππ⨯⨯=可求得⊙AOB ,然后再根据同弧所对的圆周角等于圆心角的一半可得⊙ACB.【详解】解:连接OA、OB,由弧长公式的92180nππ⨯⨯=可求得⊙AOB=40°,再根据同弧所对的圆周角等于圆心角的一半可得⊙ACB=20°.故答案为:20°【点拨】本题考查弧长公式;圆周角定理,题目难度不大,掌握公式正确计算是解题关键.33.60【分析】根据扇形的面积公式求出半径,然后根据弧长公式求出圆心角即可.【详解】解:扇形的面积=12lr=6π,解得:r=6,又⊙6180nlπ⨯==2π,⊙n=60.故答案为:60.【点拨】此题考查了扇形的面积和弧长公式,解题的关键是掌握运算方法.34.4π.【分析】根据弧长公式,此题主要是得到⊙OBO′的度数.根据等腰三角形的性质即可求解.【详解】解:根据题意,知OA=OB.又⊙AOB=36°,⊙⊙OBA=72°.⊙点O 旋转至O′点所经过的轨迹长度=7210180π︒⨯⨯︒=4πcm . 故答案是:4π. 【点拨】本题考查了弧长的计算、旋转的性质.解答该题的关键是弄清楚点O 的运动轨迹是弧形,然后根据弧长的计算公式求解.35.23π . 【详解】试题分析:根据题意α最小值是60°,然后根据弧长公式即可求得.⊙正六边形ABCDEF 绕中心O 顺时针旋转α度与原图形重合,α最小值是60°, ⊙点A 运动的路径长=60221803. 故答案为23π. 考点:轨迹;旋转对称图形.36.60π.【解析】【分析】点O 所经过的路线是2段弧和一条线段,一段是以点B 为圆心,10为半径,圆心 角为90°的弧,另一段是一条线段,和弧AB 一样长的线段,最后一段是以点A 为圆心,10为半径,圆心角为90°的弧,从而得出答案.【详解】当OA 第1次落在l 上时:点O 所经过的路线长为:90π1036π1090π10216π1012π.180180180180⨯⨯⨯⨯++== 则当OA 第5次落在l 上时:点O 所经过的路线长=12π×5=60π.故答案是:60π.【点拨】本题考查了轨迹:利用特殊几何图形描述点运动的轨迹,然后利用几何性质计算相应的几何量.37.6【分析】根据多边形的内角和公式求出扇形的圆心角,然后按扇形面积公式列方程求解计算即可.【详解】解:⊙正六边形的内角是120度,阴影部分的面积为24π,设正六边形的边长为r,⊙2120224360rππ⨯⨯=,2224,3rππ∴=236,r∴=解得r=6.(负根舍去)则正六边形的边长为6.故答案为:6.【点拨】本题考查的是正多边形与圆,扇形面积,掌握以上知识是解题的关键.38.40°.【详解】解:根据扇形的面积计算公式可得:23360n=π,解得:n=40°,即圆心角的度数为40°.考点:扇形的面积计算.39.4π【分析】由图可知,阴影部分的面积是扇形ABO和扇形DEO的面积之和,然后根据题目中的数据,可以求得AB、OA、DE的长,⊙BAO和⊙EDO的度数,从而可以解答本题.【详解】解:⊙四边形ABCD是矩形,⊙OA=OC=OB=OD,⊙AB=AO,⊙⊙ABO是等边三角形,⊙⊙BAO=60°,⊙⊙EDO =30°,⊙AC =2,⊙OA =OD =1,⊙图中阴影部分的面积为:22601301+=3603604ππ⨯⨯⨯⨯π, 故答案为:4π. 【点拨】本题主要考查扇形面积、矩形的性质及等边三角形的性质与判定,熟练掌握扇形面积、矩形的性质及等边三角形的性质与判定是解题的关键.40.3【分析】作AF ⊙BC 于F ,解直角三角形分别求出AC 、BC ,根据扇形面积公式、三角形面积公式计算即可.【详解】作AF ⊙BC 于F ,⊙⊙ABC =45°,⊙AF =BF =2AB 在Rt⊙AFC 中,⊙ACB =30°,⊙AC =2AF =FC =tan ∠AF ACF , 由旋转的性质可知,S ⊙ABC =S ⊙EDC ,⊙图中线段AB 扫过的阴影部分的面积=扇形DCB 的面积+⊙EDC 的面积﹣⊙ABC 的面积﹣扇形ACE 的面积=扇形DCB 的面积﹣扇形ACE 的面积﹣260360π⨯,.【点拨】本题考查的是扇形面积计算,掌握扇形面积公式S=2360n Rπ是解题的关键.41.25 12π【解析】【详解】由题意得,S⊙AED=S⊙ABC,由题图可得,阴影部分的面积= S⊙AED+S扇形ABD-S⊙ABC,⊙阴影部分的面积= S扇形ABD=2 30525π36012π⨯=.故答案为25 12π.42.5π【分析】根据旋转的性质可以得到阴影部分的面积=扇形DAB的面积-扇形EAC的面积,利用扇形的面积公式即可求解.【详解】解:⊙将ABC绕点A逆时针旋转120︒得ADE,⊙S⊙ABC= S⊙ADE,⊙阴影部分的面积=扇形DAB的面积+S⊙ADE-扇形EAC的面积-S⊙ABC=扇形DAB的面积-扇形EAC的面积⊙阴影部分的面积221205 12041360360πππ⨯⨯⨯=-=⨯,故答案为:5π.【点拨】本题考查了旋转的性质以及扇形的面积公式,根据旋转的性质推出:阴影部分的面积=扇形DAB的面积-扇形EAC的面积是解题关键.43.π-2【解析】【分析】先求出扇形面积,再求三角形面积,阴影面积=扇形面积-三角形面积.【详解】由已知可得,S 阴影=S 扇形OAB -S ⊙OAB =290212223602ππ-⨯⨯=-. 故答案为π-2【点睛】本题考核知识点:扇形面积. 解题关键点:熟记扇形面积公式,用求差法得到阴影面积.44.π﹣2【分析】先根据圆周角定理证得⊙BOC=90°,从而得出⊙OBC 是等腰直角三角形,然后根据S 阴影=S 扇形OBC -S ⊙OBC 即可求得.【详解】解:⊙⊙BAC=45°,⊙⊙BOC=90°,⊙⊙OBC 是等腰直角三角形,⊙OB=2,⊙S 阴影=S 扇形OBC -S ⊙OBC =14π×22-12×2×2=π-2. 故答案为π﹣2【点拨】本题考查的是圆周角定理及扇形的面积公式,熟记扇形的面积公式是解答此题的关键.45.43π【解析】【分析】连接OC,用扇形OBC 的面积减去OBC 的面积即可.【详解】如图:连接OC,点C 是以AB 为直径的半圆O 的三等分点,60,120,AOC BOC ∴∠=∠=,OA OC =OAC ∴是等边三角形,60,2,A OA OC AC ∴∠====S 扇形OBC 2120π24π.3603⨯== 1111122tan 603,22222OBC ABC S S AC BC ==⨯⋅=⨯⨯⨯=则阴影部分的面积为:43π故答案为43π 【点拨】考查不规则图形面积的计算,掌握扇形的面积公式是解题的关键.46.π-1【分析】延长DC ,CB 交⊙O 于M ,N ,根据圆和正方形的面积公式即可得到结论.【详解】解:延长DC ,CB 交⊙O 于M ,N ,则图中阴影部分的面积=14×(S 圆O −S 正方形ABCD )=14×(4π−4)=π−1, 故答案为π−1.【点拨】本题考查了圆中阴影部分面积的计算,正方形的性质,正确的识别图形是解题的关键.472π3- 【分析】先根据已知条件证明四边形AOEF 为菱形,再得到ΔEOB 为等边三角形,求出AE 的长,得到弓形的面积,再利用ΔFDE S S S =-阴弓即可求解.【详解】解:连接OE EF ,连接OF 交AE 与点G .连接BE⊙点E 是BF 的中点即=EF BE ,C 30∠=︒.⊙EF BE DAB 60∠==︒,又OF AO =⊙AEC 90ΔAFO ∠=︒,为等边三角形⊙AF AO OE EF ===,即四边形AOEF 为菱形,⊙EF AO ,从而DFE FAO 60∠∠==︒⊙AB 为直径⊙AEB 90∠=︒又⊙CD 为切线⊙OE CD ⊥⊙EOC 60∠=︒又OE OB =,⊙ΔEOB 为等边三角形.⊙BE 2=,EBA 60∠=︒,⊙AEsin EBA sin60AB ∠=︒=,即AE AB sin604=⋅︒==.2AOE AOEF 114π2S S S π22323=-=⨯-⨯⨯=-弓EF 扇菱形即2πS 3=弓在RT⊙FDE 中,DEsin DFE sin60EF ∠=︒=即ED EFsin6022=︒=⨯=⊙DF 1==⊙ΔFDE 12π2πS S S 12323⎛=-=⨯=- ⎝阴弓.2π3-.【点拨】此题主要考查了扇形的面积计算以及三角形面积求法等知识,根据图形的特点求出弓形的面积是解题的关键.48.232π- 【分析】先根据题目条件计算出OD ,CD 的长度,判断BOC 为等边三角形,之后表示出阴影面积的计算公式进行计算即可.【详解】在Rt COD 中,30,2AOC OC OA ︒∠===⊙1,CD OD ==⊙90AOB ︒∠=⊙60BOC ︒∠=⊙OB OC =⊙BOC 为等边三角形⊙BOC =COD BOC S S S S +-△△阴影扇形221602122360π⨯=+-232π=-故答案为:232π-【点拨】本题考查了阴影面积的计算,熟知不规则阴影面积的计算方法是解题的关键. 49.(1)⊙A =20°;(2)119π.【分析】(1)根据圆周角定理求出⊙AOP ,根据切线的性质计算,得到答案;(2)根据弧长公式计算即可.【详解】解:(1)由圆周角定理得,⊙AOP =2⊙C =70°⊙P A 切⊙O 于点P ,⊙⊙APO =90°,⊙⊙A =20°;(2)⊙BOC =180°﹣⊙AOP =110°, ⊙1102180BA π==119π. 【点拨】本题考查的是切线的性质、弧长的计算,掌握圆的切线垂直于经过切点的半径是解题的关键.50.嘉琪的解法不正确,见解析【分析】连接AO ,OB ,根据圆周角定理可得60AOB ∠=︒,进而得到OAB ∆是等边三角形,然后根据弧长计算公式可得答案.【详解】解:嘉琪的解法不正确,理由如下:如图,连接AO ,OB ,AB 所对的圆周角为30,60AOB ∴∠=︒,AO BO =,OAB ∴∆是等边三角形,5AB cm =,∴AB 的长为:6055()1803cm ππ⨯=. 【点拨】此题主要考查了圆周角定理和弧长计算公式,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.注意:弧长公式。
圆的弧长与扇形面积综合练习题

圆的弧长与扇形面积综合练习题题1:已知一个半径为3cm的圆的弧长为12πcm,求扇形的面积。
题解:求扇形的面积时,需要知道扇形的圆心角和半径。
已知圆的弧长是12πcm,可以计算出圆心角的大小。
因为弧长等于半径乘以圆心角的弧度,所以可以得到12π = 3cm × 圆心角。
解方程可以得到圆心角为4π/3弧度。
扇形的面积等于圆心角占据的比例乘以整个圆的面积,所以扇形的面积为(4π/3)(π(3)^2) = 12π平方cm。
题2:若一个圆的半径是5cm,那么它的弧长和扇形面积各是多少?题解:已知圆的半径是5cm,它的弧长可以计算得出。
弧长等于半径乘以圆心角的弧度,所以弧长等于5cm ×圆心角。
圆心角的弧度可以通过圆弧长除以半径得到。
假设圆心角为θ弧度,则弧长为5θ。
要求扇形的面积,也需要知道圆心角的大小。
同样,我们可以利用扇形的面积公式,并确认圆心角的弧度为θ。
扇形的面积等于圆心角占据的比例乘以整个圆的面积。
所以扇形的面积为θ(π(5)^2) = 25θπ平方cm。
题3:已知一个扇形的半径是8m,扇形的面积是12π平方m,求圆心角和弧长各是多少?题解:已知扇形的半径是8m,扇形的面积是12π平方m。
要求圆心角的大小,可以利用扇形面积的公式,并确认圆心角的弧度为θ。
扇形的面积等于圆心角占据的比例乘以整个圆的面积,所以12π平方m = θ(π(8)^2)。
解方程可以得到θ = 3π/4。
要求弧长的大小,同样可以利用扇形的面积公式,但是需要先计算出圆心角的弧度。
扇形的面积等于圆心角占据的比例乘以整个圆的面积,所以12π平方m = (3π/4)(π(8)^2)。
解方程可以得到弧长为6πm。
题4:一个扇形的圆心角是π/2,弧长是4,求扇形的面积。
题解:已知扇形的圆心角是π/2,弧长是4。
要求扇形的面积,需要用到圆心角和半径的关系。
圆心角所占的比例乘以整个圆的面积就是扇形的面积。
所以扇形的面积等于(π/2)(πr^2),其中r表示圆的半径。
弧长与扇形面积练习题与答案

知识点:1、 弧长公式: l n R(牢记)180在半径是 R 的圆中, 360 度的圆心角多对的弧长就是圆的周长 Cn R2 12、扇形面积公式: S扇形=或 S 扇形= 1lR (牢记) 360 23、圆锥的侧面积和全面积(难点) 圆锥的侧面展开图形是一个扇形,这个扇形的半径是圆锥的母线长R ,扇形的弧长是圆锥底面圆的周长。
典型例题1.已知圆锥的高是 30cm ,母线长是 50cm ,则圆锥的侧面积是 【关键词】圆锥侧面积、扇形面积答案:22000 cm 2;2. (2010 年福建省晋江市) 已知:如图,有一块含 30 的直角三角板 OAB 的直角边长 BO的长恰与另一块等腰直角三角板 ODC 的斜边 OC 的长相等,把该套三角板放置在平面 直角坐标系中,且 AB 3.(1) 若双曲线的一个分支恰好经过点A ,求双曲线的解析式;(2) 若把含 30 的直角三角板绕点 O 按顺时针方向旋转后,斜边 OA 恰好与 x 轴重叠,点 A 落在点 A ,试求图中阴影部分的面积 (结果保留 ).弧长和扇形面积答案:解: (1) 在 Rt OBA 中, AOB 30 , AB 3,OBcot AOB ,AB∴ OB AB cot30 3 3 ,∴点 A 3,3 3设双曲线的解析式为 ykk 0x∴3 3 k, k 9 393 ,则双曲线的解析式为 y3x(2) 在 Rt OBA 中,AOB 30 , AB 3 ,AB3sin AOB , sin30 ,OAOA∴ OA 6.关键词】反比例函数、扇形面积 yBO C AyA由题意得: AOC 60 ,260 62360在 Rt OCD 中, DOC 45 , OC OB 3 3 ,OD OC cos45332 3622212 1 3627.S ODC OD2224S阴=S扇形 AOA'SODC6 2743. (2010 年浙江省东阳市)在如图的方格纸中,每个小方格 都是边长为 1 个单位的正方形, △ABC 的三个顶点 都在 格点上(每个小方格的顶点叫格点) .( 1)如果建立直角坐标系,使点 B 的坐标为(- 5,2 ),点C 的坐标为(- 2, 2),则点 A 的坐标为 ▲ ; (2) 画出 △ABC 绕点P顺时针旋转 90 后的△A 1B1C,并求线段 BC 扫过的面积 .关键词:扇形面积公式 答案:(1)A(-4,4)(2)图略线段 BC 扫过的面积= (4 -1 )= 15444、( 2010 福建德化) 已知圆锥的底面半径是 3cm ,母线长为 6cm ,则侧面积为__________________________________________________________ cm 2.(结果保留 π) 关键词:圆锥侧面积答案: 185、已知圆锥的底面半径为 关键词:圆锥的高 3,侧面积为 15 ,则这个圆锥的高为 ▲ 答案: 4S扇形 AOA'6(2010年门头沟区).如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为 AB 的等腰梯形,上底CD的端点在圆周上,且 CD=10cm.求图中阴影部分的面积.【关键词】圆、梯形、阴影部分面积答案】 解:连结 OC , OD ,过点 O 作 OE ⊥CD 于点 E. ∵OE ⊥CD ,∴CE=DE=5, ∴OE= CO 2CE 2102 52 =5 3,∵∠ OED=9°0 ,DE= 1 OD , ∴∠DOE=3°0 ,∠DOC=6°0 . 2S△ OCD =2·OE ·CD= 25 3 (cm 2)50 2∴S 阴影 = S 扇形 - S △OCD = ( π- 25 3) cm3 50∴阴影部分的面积为 ( 530π- 25 3) cm 2.60102∴ S扇形36050(cm 2)33分7. (2010 年山东省济南市)如图,四边形 OABC 为菱形,点 ⌒B 、C 在以点 O 为圆心的 EF 上,若 OA =1,∠ 1=∠2,则扇形 OEF 的面积为 π π πA. B. C. 6 4 3 【关键词】扇形的面积 【答案】 C D.2πO8. ( 2010年台湾省) 如图(十三),扇形 AOB 中, OA=10, AOB =36 。
(完整)弧长与扇形面积中考题汇编(含答案),推荐文档
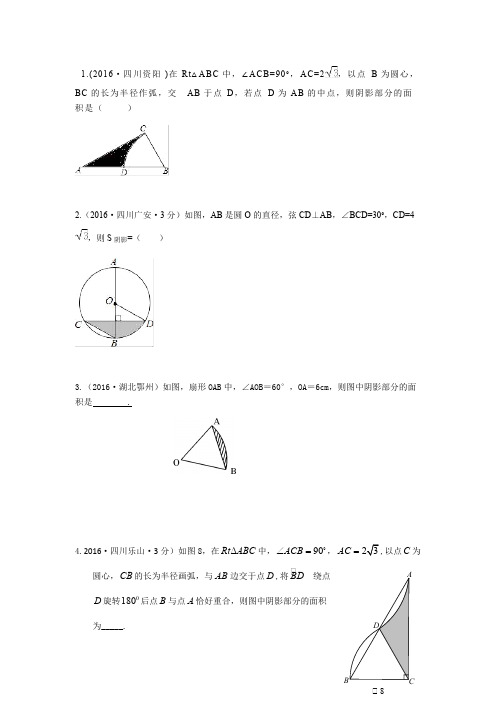
1.(2016·四川资阳)在Rt △ABC 中,∠ACB=90°,AC=2,以点B 为圆心,BC 的长为半径作弧,交AB 于点D ,若点D 为AB 的中点,则阴影部分的面积是( )2.(2016·四川广安·3分)如图,AB 是圆O 的直径,弦CD ⊥AB ,∠BCD=30°,CD=4,则S 阴影=( )3.(2016·湖北鄂州)如图,扇形OAB 中,∠AOB=60°,OA =6cm ,则图中阴影部分的面积是 .4.2016·四川乐山·3分)如图8,在中,,以点为Rt ABC ∆90ACB ∠= AC =C 圆心,的长为半径画弧,与边交于点,将 绕点CB AB D A BD旋转后点与点恰好重合,则图中阴影部分的面积D 0180B A 为_____.图85.2016年浙江省宁波市)如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°影部分的面积为 .6.(2016·江苏苏州)如图,AB是⊙O的直径,AC是⊙O的弦,过点C交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为.图8图87. (2016·新疆)如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=,以O为圆心,OC为半径作,交OB于E点.(1)求⊙O的半径OA的长;(2)计算阴影部分的面积.1.【解答】解:∵D为AB的中点,∴BC=BD=AB,∴∠A=30°,∠B=60°.∵AC=2,∴BC=AC •tan30°=2•=2,∴S阴影=S △A B C ﹣S扇形C B D =×2×2﹣=2﹣π.2.【解答】解:如图,假设线段CD 、AB 交于点E ,∵AB 是⊙O 的直径,弦CD ⊥AB ,∴CE=ED=2,又∵∠BCD=30°,∴∠DOE=2∠BCD=60°,∠ODE=30°,∴OE=DE •cot60°=2×=2,OD=2OE=4,∴S 阴影=S 扇形ODB ﹣S △DOE +S △BEC =﹣OE ×DE+BE •CE=﹣2+2=.故选B .3.【解答】解:S 阴影=S 扇=π n R 2-S △AOB =π×60×62-×6×6×=6π-9.3601360121233故答案为:(6π-9)cm 2.3【点评】本题考查了求扇形的面积.要熟知不同条件下的扇形的面积的4.解析:依题意,有AD =BD ,又,所以,有90ACB ∠= CB =CD =BD ,即三角形BCD 为等边三角形∠BCD=∠B=60°,∠A=∠ACD=30°,由BC =2,AB =4,AC ==,BCD BD BCD S S S A 弓形扇形=-60423603ππ⨯-=-阴影部分面积为:=ACD AD S S S A 弓形=-23π(23π-5.【解答】解:∵弦CD ∥AB ,∴S △ACD =S △OCD ,∴S 阴影=S 扇形COD =•π•=×π×=.故答案为:.6.【考点】切线的性质;圆周角定理;扇形面积的计算.【分析】连接OC ,可求得△OCD 和扇形OCB 的面积,进而可求出图中阴影部分的面积.【解答】解:连接OC ,∵过点C 的切线交AB 的延长线于点D ,∴OC ⊥CD ,∴∠OCD=90°,即∠D+∠COD=90°,∵AO=CO ,∴∠A=∠ACO,∴∠COD=2∠A,∵∠A=∠D,∴∠COD=2∠D,∴3∠D=90°,∴∠D=30°,∴∠COD=60°∵CD=3,∴OC=3×=,∴阴影部分的面积=×3×﹣=,故答案为:.7.【解答】解;(1)连接OD,∵OA⊥OB,∴∠AOB=90°,∵CD∥OB,∴∠OCD=90°,在RT△OCD中,∵C是AO中点,CD=,∴OD=2CO,设OC=x,∴x2+()2=(2x)2,∴x=1,∴OD=2,∴⊙O的半径为2.(2)∵sin∠CDO==,∴∠CDO=30°,∵FD∥OB,∴∠DOB=∠ODC=30°,∴S圆=S△CDO+S扇形OBD﹣S扇形OCE=×+﹣=+.【点评】本题考查扇形面积、垂径定理、勾股定理、有一个角是30度的直角三角形的性质等知识,解题的关键是学会利用分割法求面积.学会把求不规则图形面积转化为求规则图形面积,属于中考常考题型.。
初三弧长和扇形面积练习题

初三弧长和扇形面积练习题(本文按照练习题的形式进行排版,分为三个部分:选择题、填空题和解答题)练习题一:初三弧长和扇形面积选择题1. 已知圆半径为6cm,弧长为12πcm,则弧度为多少?A. π/2B. πC. 2πD. 3π2. 若扇形的半径为10cm,弧长为8cm,则扇形的圆心角为多少度?A. 36B. 45C. 90D. 1803. 扇形的圆心角为60度,半径为7cm,求扇形的面积是多少?A. 14πB. 21πC. 28πD. 42π4. 在一个半径为5cm的圆中,扇形的面积是圆心角的3倍,求扇形的弧长是多少?A. 10πB. 12πC. 15πD. 20π练习题二:初三弧长和扇形面积填空题1. 已知半径为8cm的圆,一个扇形的圆心角为120度,则扇形的弧长为\_\_\_\_\_cm。
2. 在一个圆中,扇形的面积是12πcm²,圆心角是60度,则半径为\_\_\_\_\_cm。
3. 半径为6cm的圆中,扇形的面积与圆心角的比值为1:4,扇形的弧长为\_\_\_\_\_cm。
4. 若扇形的半径为5cm,弧长为10πcm,则扇形的面积为\_\_\_\_\_cm²。
练习题三:初三弧长和扇形面积解答题1. 解:根据已知条件,半径为6cm,弧长为12πcm。
弧度 = 弧长 / 半径= (12π)cm / 6cm = 2π弧度。
因此,答案为C. 2π。
2. 解:已知扇形的半径为10cm,弧长为8cm。
圆心角 = 弧长 / 半径 = 8cm / 10cm = 0.8弧度。
360度= 2π弧度,所以圆心角≈ 0.8 * 360 ≈ 288度。
因此,答案为D. 180。
3. 解:已知扇形的圆心角为60度,半径为7cm。
扇形的面积 = 圆心角 / 360度* π * 半径² = 60度 / 360度* π *(7cm)² ≈ π * 7² ≈ 49πcm²。
24.4弧长和扇形面积典型测试题

(﹣1)cm2(+1)cm2(13.2014•河北)如图,将长为8cm的铁丝首尾相接围成半径为2cm的扇形.则S扇形=_________弧长和扇形面积单元测试题1.(2014•云南)已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为()A.B.C.D.8.(2014•泰安)如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径A.B.2πC.3πD.12π作半圆,则图中阴影部分的面积为()2.(2014•衡阳)圆心角为120°,弧长为12π的扇形半径为()A.B.C.1cm2D.cm2A.6B.9C.18D.363.(2014•自贡)一个扇形的半径为8cm,弧长为cm,则扇形的圆心角为()A.60°B.120°C.150°D.180°4.(2014•包头)如图,在正方形ABCD中,对角线BD的长为.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为,则图中阴影部分的面积是()9.(2014•清新区模拟)如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半A.﹣1B.﹣C.﹣D.π﹣2圆,则图中阴影部分面积是()5.(2014•呼伦贝尔)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是()A.B.C.D.A.B.25π﹣24C.25π﹣12D.10.(2014•盐都区二模)如图,在△Rt ABC中,∠C=90°,∠A=30°,AB=2△.将ABC绕顶点A顺时针方向旋转至△AB′C′的位置,点B,A,C′在同一条直线上,则线段BC扫过的区域面积为()A.B.C.D.11.2014•绥化)一个扇形的圆心角为120°,半径为3,则这个扇形的面积为_________(结果保留π)6.(2014•牡丹江)如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2\则S阴影=(),12.(2014•常州)已知扇形的半径为3cm,此扇形的弧长是2πcm,则此扇形的圆心角等于_________度,扇形的面积是_________.(结果保留π)A.πB.2πC.D.π(cm2.7(2014•丹东)如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为()14.如图,在矩形ABCD中,E是CD边上的点,且BE BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.(1)请判断直线BE与⊙A的位置关系,并说明理由;( B . C . 3cm D . cm点上(每个小方格的顶点叫格点). ( ((2)如果 AB = 10 , BC = 5 ,求图中阴影部分的面积.FB AM(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为 _________ 米.7.一个圆锥的侧面展开图是半径为 6 的半圆,则这个圆锥的底面半径为( ) CE DA .1.5B .2C .2.5D .3(第 14 题图)8.(2014•本溪)底面半径为 4,高为 3 的圆锥的侧面积是( ) A .12π B .15π C .20π D .36π15.如图,已知△ABC ,AC =BC =6,∠C =90°.O 是 AB 的中点,⊙O 与 AC 相切于点 D 、与 BC 9.(2014•鄂州)圆锥体的底面半径为 2,侧面积为 8π,则其侧面展开图的圆心角为( ) 相切于点 E .设⊙O 交 OB 于 F ,连 DF 并延长交 CB 的延长线于 G .A . 90°B . 120°C . 150°D . 180°(1)∠BFG 与∠BGF 是否相等?为什么? (2)求由 DG 、GE 和弧 ED 围成图形的面积(阴影部分).10.(2014•呼伦贝尔)用一个圆心角为 120°,半径为 4 的扇形作一个圆锥的侧面,则这个圆锥 C 底面圆的周长为 _________ . DE11. 2014•铜仁)已知圆锥的底面直径为 20cm ,母线长为 90cm ,则圆锥的表面积是 _________AOFBcm 2.(结果保留 π)G 12.(2014•营口)如图,圆锥的底面半径 OB 长为 5cm ,母线 AB 长为 15cm ,则这个圆锥侧面展开图的圆心角 α 为 _________ 度.1.(2014•海南)一个圆锥的侧面展开图形是半径为 8cm ,圆心角为 120°的扇形,则此圆锥的底 面半径为( )A . cmcm13.在图中的方格纸中,每个小方格都是边长为 1 个单位长的正方形,△ ABC 的 3 个顶点都在格2.(2014•安顺)已知圆锥的母线长为 6cm ,底面圆的半径为 3cm ,则此圆锥侧面展开图的圆心 角是( ) A .30° B .60° C .90° D .180°3.(2014•牡丹江)如图,如果从半径为 3cm 的圆形纸片上剪去 圆周的一个扇形,将留下的扇 形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径是 _________ cm .(1)画出△ A 1B 1C 1,使得△ A 1B 1C 1 与 ABC 关于直线 l 对称;(2)画出 ABC 绕点 O 顺时针旋转 90°后的 A 2B 2C 2,并求点 A 旋转到 A 2 所经过的路线长; (3)A 1B 1C 1 与 A 2B 2C 2 成 _________ .(填”中心对称“或”轴对称“)4. 2014•铁岭)用圆心角是 216°,半径是 5cm 的扇形围成一个圆锥体的侧面(接缝处不重叠), 则这个圆锥体的高是 _________ cm .5.2014•龙岩)若圆锥的侧面展开图的弧长为 24πcm ,则此圆锥底面的半径为_________ cm .6.(2014•泉州)如图,有一直径是 米的圆形铁皮,现从中剪出一个圆周角是 90°的最大扇形 ABC ,则:(1)AB 的长为 _________ 米;。
弧长和扇形面积练习

弧长和扇形面积 练习第1题. 一条弧所对的圆心角是90o,半径是R ,则这条弧的长是 .答案:12R π第2题. 若»AB 的长为所对的圆的直径长,则»AB 所对的圆周角的度数为.答案:180πo第3题. 如图,AB 是半圆O 的直径,以O 为圆心,OE 为半径的半圆交AB 于E ,F 两点,弦AC 是小半圆的切线,D 为切点,若4OA =,2OE =,则图中阴影部分的面积为 .答案: 43π+23第4题. 如果一条弧长等于l ,它的半径等于R ,这条弧所对的圆心角增加1o,则它的弧长增加()A.l nB.180R π C.180lRπ D.360l 答案:B第5题. 在半径为3的O e 中,弦3AB =,则»AB 的长为( )O E FBCDAA.π2B.πC.32π D.2π答案:B第6题. 扇形的周长为16,圆心角为360πo,则扇形的面积是()A.16 B.32C.64D.16π答案:A第7题. 如图,扇形OAB 的圆心角为90o,且半径为R ,分别以OA ,OB 为直径在扇形内作半圆,P 和Q 分别表示两个阴影部分的面积,那么P 和Q 的大小关系是()A.P Q = B.P Q >C.P Q <D.无法确定答案:A第8题. 如图,矩形ABCD 中,1AB =,3BC =,以BC 的中点E 为圆心的¼MPN与AD 相切,则图中的阴影部分的面积为()A.23π B.34π C.34π D.π3QOAPCBEB CNDPAM答案:D第9题. 如图所示,正方形ABCD 是以金属丝围成的,其边长1AB =,把此正方形的金属丝重新围成扇形的ADC ,使AD AD =,DC DC =不变,问正方形面积与扇形面积谁大?大多少?由计算得出结果.答案:1S =正方形,121122ADC S lR 1==⨯⨯=扇形,∴面积没有变化.第10题. 如图,O e 的半径为1,C 为O e 上一点,以C 为圆心,以1为半径作弧与O e 相交于A ,B 两点,则图中阴影部分的面积为.A BDCADCOBCA答案:232π-3第11题. 如图,△ABC 中,105A ∠=o ,45B ∠=o,22AB =,AD BC ⊥,D 为垂足,以A 为圆心,以AD 为半径画弧»EF,则图中阴影部分的面积为( )A.7236-π B.7236-π+2 C.5236-πD.5236-π+2答案:B第12题. 如图,半径为r 的1O e 与半径为3r 的2O e 外切于P 点,AB 是两圆的外公切线,切点分别为A ,B ,求AB 和»PA,»PB 所围成的阴影部分的面积.答案:连结2O B ,1O A ,过1O 作12O H O B ⊥,垂足为H ,则得矩形1ABHO ,1BH O A r ∴==,1AB O H =.在Rt △21O HO 中,2232O H O B BH r r r =-=-=,CDBE AF1O2OB HAP122134O O O P O P r r r =+=+=,22112223O H O O O H r =-=,2211221cos 42O H r HO O O O r ∠===,2160HO O ∴∠=o ,1120AO P ∠=o . 21212111()(3)234322ABO O S O A O B O H r r r r =+=+=g 梯形,26033606BO PO B r r S 222π()π(3)π===2g 2扇形,122120AO PO A S r π()π==3603扇形、,21212222324311436ABO O BO P AO P S S S S r r r r ππ-π=--=--=23阴影梯形扇形扇形.第13题. 圆周角是90o,占整个周角的90360,因此它所对的弧长是圆周长的 . 答案:14第14题. 圆心角是45o,占整个周角的 ,因此它所对的弧长是圆周长的 . 答案:45360,18第15题. 圆心角是1o,占整个周角的 ,因此它所对的弧长是圆周长的 . 答案:1360,1360第16题. 扇形的圆心角为210o,弧长是28π,求扇形的面积.答案:336π第17题. 一个扇形的半径等于一个圆的半径的2倍,且面积相等.求这个扇形的圆心角.答案:90o第18题. 一服装厂里有大量形状为等腰直角三角形的边角布料(如图),现找出其中的一种,测得90C ∠=o,4AC BC ==.今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在ABC △的边上,且扇形的弧与ABC △的其他边相切,请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径). 答案:第19题. 圆心角为90o,半径为R 的弧长为( ) A.2R πB.3R πC.4R πD.6R π答案:A第20题. 已知一条弧长为l ,它所对圆心角的度数为n o,则这条弦所在圆的半径为(ACBA C B DADB CA AB CBC OO 42r =1424r =-24r =122r =).A.180n lπ B.180ln πC.360ln πD.180lnπ答案:B第21题. 半径为6cm 的圆中,60o的圆周角所对的弧的弧长为 .答案:4cm π第22题. 半径为9cm 的圆中,长为12cm π的一条弧所对的圆心角的度数为.答案:240o第23题. 已知圆的面积为281cm π,若其圆周上一段弧长为3cm π,则这段弧所对的圆心角的度数为 .答案:60o第24题. 若扇形的圆心角为120o,弧长为6cm π,则这个扇形的面积为 .答案:227cm π第25题. 弯制管道时,先按中心线计算其“展直长度”,再下料.根据如图所示的图形可算得管道的展直长度为.(单位:mm ,精确到1mm )答案:389mm第26题. 如图,在Rt △ABC 中,90C ∠=o ,60A ∠=o,3cm AC =,将△ABC 绕点B 旋转至△A BC ''的位置,且使点A ,B ,C '三点在同一直线上,则点A 经过的最短路线长是cm .答案:533π第27题. 一块等边三角形的木板,边长为1,若将木板沿水平线翻滚(如图),则点B 从开始至结束走过的路径长度为().A.3π2B.4π3C.4D.322+π 答案:BA 'C 'BC AABCBA C B第28题. 如图,扇形AOB 的圆心角为60o,半径为6cm ,C ,D 是»AB 的三等分点,则图中阴影部分的面积和是 .答案:22cm π第29题. 如图,已知在扇形AOB 中,若45AOB ∠=o,4cm AD =,3cm CD =π,则图中阴影部分的面积是 .答案:214cm π第30题. 如图4,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积为 .答案:14.2π.AC DBOA DC BO 图4。
北师大版九年级数学下册弧长及扇形面积习题

3 )米
2
C、(3π+ 9 3 )米
二、填空题
B、( 3 π+ 9 3 )米 42
D、( 3 π- 9 3 )米 4
1、圆心角是 1° ,占整个周角的 ______,因此它所对的弧长是圆周长的 ______ . 2、 一条弧所对的圆心角为 90°,半径为 3,那么这条弧长为 __________. 3、 如图所示,在 Rt△ ABC 中,已知∠ BCA =90°,∠ BAC=30°, AB=6cm,把△ ABC 以点 B 为中心逆时针旋转, 使点 C 旋转到 AB 边的延长线上的点 C’处,那么 AC 边扫过的图 形(图中阴影部分)的面积是 __________cm2.(不取近似值)
8cm 的酱油瓶,若不计绳子接头(
A 、 24cm B、 48cm C、 96cm D 、 192cm
π取 3),
8. 如图,是某公园的一角,∠ AOB=90°, AB 的半径 OA 长是 6 米,点 C 是 OA 的中
点,点 D 在 AB 上, CD∥ OB,则图中草坪区(阴影部分)的面积是(
)
9
(4)
6、如图, AD 是以等边三角形 ABC 一边 AB 为半径的四分之一圆周, P 为 AD 上任意
一点,若 AC =5,则四边形 ACBP 周长的最大值是(
)
A 、 15 B、 20 C、 15+ 5 2
D 、 15+ 5 5
D P
A
B
C
7. 如图,用两道绳子捆扎着三瓶直径均为 则捆绳总长是( )
1 1. 扇形 OEF 的面积为 4π,阴影
部分面积为
1 2- 2π
2、活动范围由 3 部分(图中阴影部分)组成:半径为 14、圆心角为 270°的扇形一个,
弧长与扇形面积 经典练习

弧长和扇形面积经典练习1、已知扇形的圆心角为120°,半径为6,则扇形的弧长是(). A.3π B.4π C.5π D.6π2、在半径为5的O中,弦AB=5,则AB的长为()A.π2B.πC.32πD.2π3、弧长等于半径的圆弧所对的圆心角是()A.π0360B.π0180C.π090D.60°4、如果一条弧长等于,它的半径等于R,这条弧所对的圆心角增加1,则它的弧长增加()A.lnB.180RπC.180lRπD.360l5、一条弧所对的圆心角是90,半径是R,则这条弧的长是.6、在半径为1的圆中,弦AB=1,则AB的长为。
7、若AB的长为所对的圆的直径长,则AB所对的圆周角的度数为.8、如图所示,OA=30B,则A D的长是B C的长的_____倍.9、一圆弧的圆心角为300°,它所对的弧长等于半径为6cm•的圆周长,求这弧所在圆的半径.10、如图,已知∠AOB=60°,⊙O’,与⊙0,OA、OB分别切于点C、D 、E求证:AB弧长的长度等于⊙O’的长的一半。
11、如图,把直角三角形ABC的斜边AB放在直线L上,•按顺时针方向在L上转动两次,使它转到△A ″B ″C ″的位置上,设BC=1,,则顶点A 运动到A•″的位置时,点A 经过的路线有多长。
12、如图,在相距60km 的两个城镇A ,B 之间,•有一近似圆形的湖泊,其半径为15km ,圆心O 恰好位于A ,B 连线的中点处,•现要绕过湖泊从A 城到B 城,假设除湖泊外,所有的地方均可行走,如路线:线段AC →CD →线段DB ,•其中C ,D 在直线AB 上,请你找出最≈1.73,π≈3.14)13.在半径为R 的圆中,n °的圆心角所对的弧长l =_______.14.____________和______所围成的图形叫做扇形.在半径为R 的圆中,圆心角为n °的扇形面积S 扇形=__________;若l 为扇形的弧长,则S 扇形=__________. 15.如图,在半径为R 的⊙O 中,弦AB 与所围成的图形叫做弓形.当为劣弧时,S 弓形=S 扇形-______; 当为优弧时,S 弓形=______+S △OAB .3题图16.半径为8cm 的圆中,72°的圆心角所对的弧长为______;弧长为8cm 的圆心角约为______(精确到1′). 17.半径为5cm 的圆中,若扇形面积为2cm 3π25,则它的圆心角为______.若扇形面积为15πcm 2,则它的圆心角为______.18.若半径为6cm 的圆中,扇形面积为9πcm 2,则它的弧长为______.19.如图,Rt △ABC 中,∠C =90°,AC =8,BC =6,两等圆⊙A ,⊙B 外切,那么图中两个扇形(即阴影部分)的面积之和为( ).7题图A .π425 B .π825 C .π1625D .π322520.如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 夹角为120°,AB 的长为30cm ,贴纸部分BD 的长为20cm ,则贴纸部分的面积为( ).8题图A .2πcm 100B .2πcm 3400C .2πcm 800D .2πcm 380021.如图,△ABC 中,BC =4,以点A 为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于E ,交AC 于F ,点P 是⊙A 上一点,且∠EPF =40°,则圆中阴影部分的面积是( ).A .9π4-B .9π84-C .94π8-D .98π8-22.已知:如图,在边长为a 的正△ABC 中,分别以A ,B ,C 点为圆心,a 21长为半径作,,,求阴影部分的面积.23.已知:如图,Rt △ABC 中,∠C =90°,∠B =30°,,34=BC 以A 点为圆心,AC 长为半径作,求∠B 与围成的阴影部分的面积.24.已知:如图,以线段AB 为直径作半圆O 1,以线段AO 1为直径作半圆O 2,半径O 1C 交半圆O 2于D 点.试比较与的长.25.已知:如图,扇形OAB 和扇形OA ′B ′的圆心角相同,设AA ′=BB ′=d .=l 1,=l 2.求证:图中阴影部分的面积.)(2121d l l S +=26. 用一圆心角为120°,半径为6cm 的扇形做成一个圆锥的侧面,这个圆锥的底面的半径形围成一个圆锥的侧面,则这个圆锥的高为( ). B C . D . .AE 为半径的圆弧交AB 于点D ,交AC 的延长于点F ,若图中两个阴影部分的面积相等,则AF 的长为(结果保留根号).答案1、B2、B3、B4、B5、12R π; 6、3π; 7、180π; 8、3 9、7.210、略11、Rt △ABC 中,BC=1,AC=,则可得AB=2,∠CAB=30°,则点A 到点A•″所经过的路线为''''l AA l A A +=1202180π⨯=(43+2)π. 12、如图所示,最短的行走路线是:线段AE →EF →线段FB ,其中E 、F 是切点,连结OC ,OD ,OE ,OF ,(A , C ,B ,D ,O 在同一直线上),∵∠AFO=90°,OE=15,OA=30,∴∠AOE=60°,同理:∠FOB=60°,EOF=60°,∴EF =16×2×15π=5π.∴AE+EF +BF=2×+5π≈67.7km .13.;180πRn 14.由组成圆心角的两条半径,圆心角所对的弧,.21,360π2lR R n 15.S △OAB ,S 扇形. 16..9157,π516o ' 17.120°,216°. 18. 3πcm . 19.A . 20.D . 21.B . 22..)8π43(2a - 23..π3838- 24.的长等于的长.提示:连结O 2D .25.提示:设A O '=R ,∠AOB =n °,由,180π,180)(π21Rn l d R n l =+=可得R (l 1-l 2)=l 2d .而.)(21212121)(2121)(21211212121d l l d l d l d l l l R R l d R l S +=+=+-=-+=26. 解:设此圆锥的底面半径为r ,由题意,得 2πr=,解得r=2cm . 故选B .27. 解:过O 点作OC ⊥AB ,垂足为D ,交⊙O 于点C , 由折叠的性质可知,OD=OC=OA , 由此可得,在Rt △AOD 中,∠A=30°,同理可得∠B=30°,在△AOB中,由内角和定理,得∠AOB=180°﹣∠A﹣∠B=120°∴弧AB的长为=2π设围成的圆锥的底面半径为r,则2πr=2π∴r=1cm∴圆锥的高为=2故选A.28. 解:由圆锥侧面积公式可得l=,属于反比例函数.故选D.29. 解:圆锥的表面积=×10π×13+π×52=90πcm2.故选A.30. ∵图中两个阴影部分的面积相等,∴S扇形ADF=S△ABC,即:=×AC×BC,又∵AC=BC=1,∴AF2=,∴AF=.故答案为.。
弧长和扇形面积

在Rt△OCD中,∵ ,∴ . …………………………8分
∴ . …………………………9分
∴图中阴影部分的面积为 . ………………………………………10分
42.如图,已知在⊙O中,AB=4 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
(1)求图中阴影部分的面积;
A.7B.8
C.9D.10
【答案】B
16.如图,在△ABC中,AB = AC,AB = 8,BC = 12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是()
A. B.
C. D.
【答案】D
17.如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为()
①如图1,⊙ 从⊙ 的位置出发,沿AB滚动到⊙ 的位置,当AB= 时,⊙ 恰好自转1周。
②如图2,∠ABC相邻的补角是n°,⊙ 在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙ 的位置转到⊙ 的位置,⊙ 绕点B旋转的角∠ = n°,⊙ 在点B处自转 周。
图1图2
解答以下问题:
⑴在阅读材料的①中,若AB=2 ,则⊙ 自转周;若AB= ,则⊙ 自转周。在阅读材料的②中,若∠ABC=120°,则⊙ 在点B处自转周;
A. B. C. D.
18.已知O为圆锥的顶点,M为底面圆周上一点,点P在OM上,一只蚂蚁从点P出发绕圆锥侧面爬行回到P时,所经过的最短路径的痕迹如图2,若沿OM将圆锥侧面剪开并展平,所得侧面展开图是()
【答案】D
19.如图,在圆心角为90°的扇形MNK中,动点P从点M出发,沿MN KM运动,最后回到点M的位置。设点P运动的路程为x,P与M两点之间的距离为y,其图象可能是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《弧长和扇形面积》经典题
1. 如果一条弧长等于l ,它的半径等于R ,这条弧所对的圆心角增加1
,则它的弧长增加
( ) A.
l n B.
180
R
π C.
180l
R
π D.
360
l 2.在半径为3的圆中,弦3AB =,则弧AB 的长为( )
A.
π2
B.π
C.
3
2
π D.2π
3. 扇形的周长为16,圆心角为360π
,则扇形的面积是(
)
A.16
B.32
C.64
D.16π
4.一条弧所对的圆心角是90
,半径是R ,则这条弧的长是
. 5. 若AB 的长为所对的圆的直径长,则AB 所对的圆周角的度数为
.
6.如图,AB 是半圆O 的直径,以O 为圆心,OE 为半径的半圆交AB 于E ,F 两点,弦AC 是小半圆的切线,D 为切点,若4OA =,2OE =,则图中阴影部分的面积为 .
7.圆周角是90
,占整个周角的
90
360
,因此它所对的弧长是圆周长的 . 8. 圆心角是45
,占整个周角的 ,因此它所对的弧长是圆周长的 . 9. 扇形的圆心角为210
,弧长是28π,求扇形的面积.
10. 一个扇形的半径等于一个圆的半径的2倍,且面积相等.求这个扇形的圆心角. 11.圆心角为90
,半径为R 的弧长为( ) A.2
R π
B.
3
R π
C.
4
R π
D.
6
R π
12已知一条弧长为l ,它所对圆心角的度数为n
,则这条弦所在圆的半径为( ).
A.
180
n l
π B.
180l
n π
C.
360l
n π
D.
180l
n
π 13.一块等边三角形的木板,边长为1,若将木板沿水平线翻滚(如图),则点B 从开始至结束走过的路径长度为( ).
A.3π2
B.
4π3
C.4
D.322
+
π
14.半径为9cm 的圆中,长为12cm π的一条弧所对的圆心角的度数为
.
15.已知圆的面积为2
81cm π,若其圆周上一段弧长为3cm π,则这段弧所对的圆心角的度数为
.
16. 若扇形的圆心角为120
,弧长为6cm π,则这个扇形的面积为
.
17. 如图,在Rt △ABC 中,90C ∠= ,60A ∠=
,AC =,将△ABC 绕点B 旋转至
△A BC ''的位置,且使点A ,B ,C '三点在同一直线上,则点A 经过的最短路线长是
cm .
18. 如图4,在两个同心圆中,三条直径把大圆分成相等的六部分,若
大圆的半径为2,则图中阴影部分的面积为 .
图4
19.如图,半径为r 的1O 与半径为3r 的2O 外切于P 点,AB 是两圆的外公切线,切点分别为A ,B ,求AB 和P A ,PB 所围成的阴影部分的面积.
20. 已知如图所示,弧AB 所在圆的半径为R ,弧AB 的长为3
R ,⊙O ′和OA 、OB 分别相切于点C 、E ,且与⊙O 内切于点D ,求⊙O ′的周长
.。
