第五章 多电子原子：泡利原理 25节 两个电子的耦合1
合集下载
原子物理第五章 多电子原子泡利原理
L 取值个数： l1 l2, 2l2 1 l1 l2, 2l1 1
例：两电子分别处于f 态和d 态，则 l1 3 , l2 1 ，合成总
轨道角动量为 Pl ， 由于l1>l2，所以L的取值总数为2l2+1=3。那么L=4、3、2。
Pl1 12 Pl2 2 L 4 , 3 , 2
PL L(L 1) 20 , 12 , 6
3P2
总轨道
L=2 1D2
l1 1 , l2 2 L3 , 2 ,1
L=3
1F3
3D3 3F4
单态
S=1
3P1
3P0
3D2
3D1
3F3
3F2
三重态
•电子组态和原子态
例如：对于1s2p组态，由L-S耦合可以构成原子态3P2.1.0和1P1。 而对于3s3p组态，由L-S耦合可以构成原子态3P2.1.0和1P1。
5、一种电子态对应于多种原子态。 不仅氦 的能级和光谱有上述特点，人们发现，元素 周期表中第二族元素：
Be(4)、Mg(12)、Ca(20)、Sr(38)、 Ba(56)、Ra(88)、Zn(30)、Cd(48)、Hg(80) 的光谱都与氦有相同的线系结构。
谱线 能级
即
原子实+2个价电子。
由此可见，能级和光谱的形成都是二个价电子 各种相互作用引起的.
次壳层电子的数目
2（2l+1）
角动量 l
0
1
2
3
4
符号
s
p
d
f
g
状态数 2（2l+1） 2
6
10 14 18
壳层电子的数目
n1
Nn 22l 1 2n2 l 0
例：两电子分别处于f 态和d 态，则 l1 3 , l2 1 ，合成总
轨道角动量为 Pl ， 由于l1>l2，所以L的取值总数为2l2+1=3。那么L=4、3、2。
Pl1 12 Pl2 2 L 4 , 3 , 2
PL L(L 1) 20 , 12 , 6
3P2
总轨道
L=2 1D2
l1 1 , l2 2 L3 , 2 ,1
L=3
1F3
3D3 3F4
单态
S=1
3P1
3P0
3D2
3D1
3F3
3F2
三重态
•电子组态和原子态
例如：对于1s2p组态，由L-S耦合可以构成原子态3P2.1.0和1P1。 而对于3s3p组态，由L-S耦合可以构成原子态3P2.1.0和1P1。
5、一种电子态对应于多种原子态。 不仅氦 的能级和光谱有上述特点，人们发现，元素 周期表中第二族元素：
Be(4)、Mg(12)、Ca(20)、Sr(38)、 Ba(56)、Ra(88)、Zn(30)、Cd(48)、Hg(80) 的光谱都与氦有相同的线系结构。
谱线 能级
即
原子实+2个价电子。
由此可见，能级和光谱的形成都是二个价电子 各种相互作用引起的.
次壳层电子的数目
2（2l+1）
角动量 l
0
1
2
3
4
符号
s
p
d
f
g
状态数 2（2l+1） 2
6
10 14 18
壳层电子的数目
n1
Nn 22l 1 2n2 l 0
原子物理学 第五章 多电子原子：Pauli原理
,
1 2
0
大连理工大学物理系
原子物理学
pp组态
两个电子都处于l 1态
L—S耦合
s1
1 2
，s2
1 2
，l1
1，l2
1
S=0, 1, L 2，1，0
S=0 J= 2，1，0
1S0，1P1，1D2
大连理工大学物理系
原子物理学
S=1, L 2
J 3, 2, 1 3D3，2，1 S=1, L 1
构成6种相互作用：
G1 s1s2 、G2 l1l2 、G3 l1s1 G4 l2s2 、G5 l1s2 、G6 l2s1
G5 l1s2 、G6 l2s1 相互作用较弱
大连理工大学物理系
原子物理学
L—S耦合
G1 s1s2 、G2 l1l2
LS耦合一般出现大部分 原子中
大连理工大学物理系
大连理工大学物理系
原子物理学
4）选择规则
li
1
i
j—j 耦合
j 0, 1 J 0, 1
大连理工大学物理系
原子物理学
5）由电子的组态到原子态 ss组态
L—S耦合
s1
1 2
，s2
1 2
，l1
0，l2
0
S=0, 1, L 0
J 0,1
1S0，3S1
J—J耦合
s1
1 2
，s2
1 2
，l1
0，l2
原子物理学
J—J耦合
G3 l1s1 、G4 l2s2
由元素组态的能级实 际情况可判断原子态 属哪种耦合。
JJ 耦 合 一 般 出 现 在 某 些 高激发态和较重的原子 中
大连理工大学物理系
多电子原子泡利原理
§25
两个电子的耦合
（1）电子组态 (configuration)
氢原子基态： 1s 2 氦原子基态： 1s1s（或1s ） 氦原子第一激发态： 1s 2 s
l
2 n3 1 0
n2
ml 2
1
0
1
2
1
0
n1 0
图25.1
对应于不同n和l可能的状态
（2）L – S 和 j – j 耦合
第五章
多电子原子：泡利原理
§24
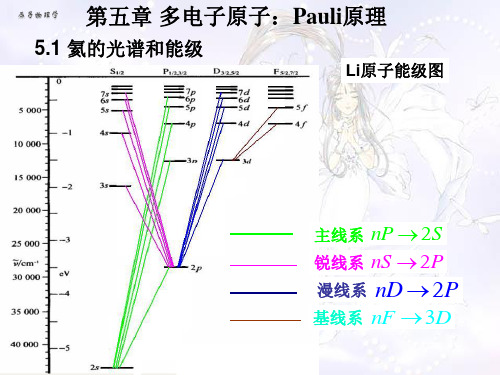
氦的光谱和能级
有两套结构，两套能级之间没有相互跃
迁； 存在几个亚稳态； 氦的基态11 S 0 与第一激发态 2 3 S1 之间能量 差别很大； 2 在三层结构的能级中没有来自 (1s ) 的能级；
氦 原 子 能 级 图
1
S
1
P
1
D
3
S
3
P
3
D
1s,3 s 1s,2 s
合成的总角动量的数值 为： J J ( J 1)
总角动量量子数的可能 取值为： J L S，L S 1， , L S 当L S时，取值数由 2 S 1决定； 当S L时，取值数由 2 L 1决定； 多数情况下满足 L S条件，故统一规定 以2 S 1表示多重数( multiplicity)。
2p3s 3p4s 4p5s 5p6s 6p7s
碳族元素原子的电子组态
碳 族 元 素 能 级 比 较
例3，求pd组态按L S耦合可能形成的原子态 。
S0
1
3 3 3
L1 L2 L3
1 1 1
P1 D2 F3
P0,1, 2 D1, 2, 3 F2, 3,4
原子物理杨家富-第五章答案
第五章
第五章 多电子原子 泡利原理
主要内容:
1．多电子原子的能级和光谱结构、多电子原子的L-S 耦 合、j-j耦合形成的原子态和对应的精细能级。
2．多电子原子的壳层结构和元素的周期性 多电子原子与氢和类氢原子不同，出现了多电子之间相 互作用。若我们先忽略这种复杂的作用，以氢的量子态 作为框架，然后再逐步考虑电子相互作用产生的影响。 这样，我们可对多电子原子系统作出定性地分析。电子 是自旋量子数为1／2的费米子，泡利指出在同一个量子 态最多只能有一个费米子占据。
J
11,1,11, S
1
S
1 0
L-S耦合得到四个原子态是 3P2，1，0；1P1。 又如3p4p电子组态的L-S耦合，
L-S耦合出十个原子态，
S=0 S=1
列表示为
S=1,0； L=2,1,0
L=0 1 2
(1S0) 3S1 1P1 (3P2,1,0) (1D2) 3D3,2,1
13
3.同科电子(等效电子)组态的原 子态 （ L-S耦合）
3
§５.1 泡利不相容原理 §５.2 双电子原子系统－ 氦原子光谱和能级 §５.3 两个电子的耦合 §５.４ 元素周期表 §５.５ 多电子原子的塞曼效应
4
§5.1 泡利不相容原理
1925年，年仅25岁的泡利提出不相容原理：原子中每个
状态只能容纳一个电子，换言之原子中不可能有两个以上
的电子占据四个量子数(n,l,ml,ms)相同的态。后来发现凡自
每个子壳层允许填充的电子数为2×(2l+1)，每个壳层 允许填充的电子数为
n1
Nn 2 (2l 1) 2n2 l 0
28
进一步考虑了电子 填充后的系统的总能 量应该最低，实际填 充壳层的顺序如图所 示。
第五章 多电子原子 泡利原理
主要内容:
1．多电子原子的能级和光谱结构、多电子原子的L-S 耦 合、j-j耦合形成的原子态和对应的精细能级。
2．多电子原子的壳层结构和元素的周期性 多电子原子与氢和类氢原子不同，出现了多电子之间相 互作用。若我们先忽略这种复杂的作用，以氢的量子态 作为框架，然后再逐步考虑电子相互作用产生的影响。 这样，我们可对多电子原子系统作出定性地分析。电子 是自旋量子数为1／2的费米子，泡利指出在同一个量子 态最多只能有一个费米子占据。
J
11,1,11, S
1
S
1 0
L-S耦合得到四个原子态是 3P2，1，0；1P1。 又如3p4p电子组态的L-S耦合，
L-S耦合出十个原子态，
S=0 S=1
列表示为
S=1,0； L=2,1,0
L=0 1 2
(1S0) 3S1 1P1 (3P2,1,0) (1D2) 3D3,2,1
13
3.同科电子(等效电子)组态的原 子态 （ L-S耦合）
3
§５.1 泡利不相容原理 §５.2 双电子原子系统－ 氦原子光谱和能级 §５.3 两个电子的耦合 §５.４ 元素周期表 §５.５ 多电子原子的塞曼效应
4
§5.1 泡利不相容原理
1925年，年仅25岁的泡利提出不相容原理：原子中每个
状态只能容纳一个电子，换言之原子中不可能有两个以上
的电子占据四个量子数(n,l,ml,ms)相同的态。后来发现凡自
每个子壳层允许填充的电子数为2×(2l+1)，每个壳层 允许填充的电子数为
n1
Nn 2 (2l 1) 2n2 l 0
28
进一步考虑了电子 填充后的系统的总能 量应该最低，实际填 充壳层的顺序如图所 示。
第五章 多电子原子：泡利原理2
偶性态（=偶数）奇性态（=奇数）∑i l ∑i l 跃迁只能发生在不同宇称状态之间，即从偶性宇称到奇性宇称或反之。
6. 辐射跃迁的普用选择定则宇称（或电子组态）跃迁选择定则j-j 耦合跃迁选择定则L-S 耦合跃迁选择定则（在两个电子同时受激发时才出现）0=∆L 10100±=±==,∆J ,∆L ∆S （J ＝0→J’＝0 除外）)0'0( 1 0,)2 ,1( 1 0,除外=→=±=∆=±=∆J J J i j i第三节：泡利原理He原子的基态电子组态是1s1s；在L-S 耦合下，可能的原子态是(1s1s) 1S0 和(1s1s) 3S1，但在能级图上，却找不到原子态3S1，事实上这个态是不存在的，这又是为什么？1925年，奥地利物理学家Pauli提出了不相容原理，回答了上述问题。
揭示了微观粒子遵从的一个重要规律。
1. 描述电子运动状态的量子数主量子数n ：n = 1, 2, 3，……角量子数l ：l = 0, 1 ,2，…，(n -1)轨道磁量子数m l ：m l = 0,±1，…，±l 自旋量子数s ：s = 1/2自旋磁量子数m s ：m s =±1/2因为s＝1/2 对所有电子都是相同的，不能作为区分状态的量子数，因此描述电子运动状态的是四个量子数（n, l, m l , m s ）；一组量子数（n, l, m l , m s ）可以完全确定电子的状态。
比如总能量，角动量，轨道的空间取向，自旋的空间取向等物理量都可以由这组量子数确定。
2．Pauli原理的描述1925年，年仅25岁的泡利提出不相容原理：原子中每个状态只能容纳一个电子，换言之原子中不可, m s)相能有两个以上的电子占据四个量子数(n, l, ml 同的态。
3．Pauli原理的应用He原子的基态在氦的基态中，两个1s 电子的n和l 都相同，ml就必须有差又都等于0，根据泡利不相容原理，ms别，m只能有两个数值+1/2 和-1/2，这就是说两s个电子的自旋必须相反。
cap5泡利原理
Be(4), Mg(12), Ca(20), Sr(38), Ba(56), Ra(88), Zn(30), Cd(48), Hg(80)
的光谱都与氦有相同的线系结构.即原子实+2个价电子. 的光谱都与氦有相同的线系结构.即原子实+2个价电子. +2个价电子 由此可见, 由此可见,能级和光谱的形成都是二个价电子各种相互作用引 起的. 起的.
ψ (r , t) 描述,如果波函数经过空间反演(即 r →r ) 后,具有 ψ (r , t) =ψ (r , t) , 则 ψ 是偶性态.
第一节: 第一节:氦的光谱和能级 3.能级和能级图的特点 能级分为两套,单层和三层能级间没有跃迁; 1)能级分为两套,单层和三层能级间没有跃迁;氦的基态 是1s1s1 S0; 1s1s下 不存在, 2)状态1s1s下3S1不存在,且基态1s1s 1S0和第一激发态 1s2s 3S1之间能差很大; 之间能差很大; 态都是单层的; 3) 所有的3S1态都是单层的; 是氦的两个亚稳态;( ;(不能跃迁到 4)1s2s 1S0和1s2s 3S1是氦的两个亚稳态;(不能跃迁到 更低能级的状态称为亚稳态,当原子处在亚稳态时, 更低能级的状态称为亚稳态,当原子处在亚稳态时,必须将 其激发到更高能,方可脱离此态回到基态) 其激发到更高能,方可脱离此态回到基态) 一种电子态对应于多种原子态. 5)一种电子态对应于多种原子态.不仅氦的能级和光谱 有上述特点,人们发现, 有上述特点,人们发现,元素周期表中第二族元素
能级
第一节: 第一节:氦的光谱和能级
氦原子的光谱由两套谱线构成, 氦原子的光谱由两套谱线构成, 一套是单层的,另一套是三层, 一套是单层的,另一套是三层,这两套 能级之间没有相互跃迁, 能级之间没有相互跃迁,它们各自内部 的跃迁便产生了两套独立的光谱, 的跃迁便产生了两套独立的光谱,早先 人们以为有两种氦, 人们以为有两种氦,把具有复杂结构的 氦称为正氦, 氦称为正氦,而产生单线光谱的称为仲 现在认识到只有一种氦, 氦,现在认识到只有一种氦,只是能级 结构分为两套. 结构分为两套.
第五篇多电子原子：泡利原理.PP
（3）电子组态的能量——壳层的次序
1s, 2s, 2 p, 3s, 3p, 4s, 3d, 4 p, 5s, 4d, 5 p, 6s, 4 f , L
等电子体系光谱的比较：
T
RZ *2 Байду номын сангаас2
T 1 (Z )
Rn
E hcT
（4）原子基态
洪特定则（1925年）：对于一个给定的电子组态形 成的一组原子态，当某原子态具有的S最大时，它处 的能级位置最低；对同一个S，又以L值大的为最低； 对同一L而不同J，正常次序（同科电子数小于或等 于满壳层的一半）和倒转次序（同科电子数大于满壳 层的一半）。
1916—1918年间，玻尔首先尝试对元素周期表给予 物理解释；
1925年，泡利提出不相容原理，结合能量最小原理， 对元素的周期性给出了成功的解释。
（2）壳层中电子的数目
决定原子中电子 状态的两条准则
泡利不相容原理 能量最小原理
决定了每一壳层 中电子的数目
决定了壳层的次序
n＝1，2，3，4……称为主壳层 K，L，M，N……
l＝0，1，2，…，（n－1）称为相应主壳层下的支壳层 s，p，d，f，g，h
电子状态由（n , l , ml , ms）表示，根据泡利不相 容原理： 每一次壳层（n，l相同）可容纳的最多电子数：
Nl 2(2l 1)
每一壳层（n相同）可容纳的最多电子数：
n1
Nn 2(2l 1) 2n2 l0
利用泡利不相容原理，可以解释原子内部的电子分布 状况和元素周期性。
（3）应用举例 1、氦原子的基态
基态电子组态1s1s
（n , l , ml , ms） （1，0，0，＋1/2）
（1，0，0，－1/2）
第五章：多电子原子 泡利原理 《原子物理学》课堂课件
能级
五
章
多
实验表明，氦原子的光谱也是由这些线系
电 构成的，与碱金属原子光谱不同的是：
子
原
子
氦原子光谱的上述四个线系都出现双份，
:
泡 即两个主线系，两个锐线系等。
利
原
理
首页
上一页
下一页
氦及周期系第二族元素的光谱和能级
➢ 第二族元素：铍、镁、钙、锶、钡、镭、锌、镉、汞。 （都具有两个价电子 光谱和化学性质） ➢ 氦及第二族元素的能级都分成两套，一套是单层的，另 一套是三层的；各自形成两套光谱。
Atomic Physics 原子物理学
第五章：多电子原子 :泡利原理
第一节 氦的光谱和能级 第二节 两个电子的耦合 第三节 泡利原理 第四节 元素周期表
H原子：
Tn
R n2
En
Rhc n2
类H离子：
Tn
Z2
R n2
En
Z 2
Rhc n2
碱金属原子：
Tnl
(n
R l)2
Enl
(n
Rhc l)2
能级
五
章
即
原子实+2个价电子。
多
电
子
原
子 由此可见，能级和光谱的形成都是二个价电子
: 泡
各种相互作用引起的.
利
原
理
首页
上一页
下一页
第二节：两个电子的耦合
电子的组态
1.定义： 两个价电子处在各种状态的组合，
称电子组态。
电子的组 态
比如，氦的两个电子都在1s态，那么氦的电
第 五
子组态是1s1s；
一个电子在1s，
若核(实)外有两个电子，由两个价电子跃迁而形 成的光谱如何？能级如何？原子态如何？