初三中考数学三角形

合集下载

中考数学考点专题复习三角形与全等三角形

剖析
先看一个事实，如图，将等腰△ABC 的底边 BC 延长线上的任一点和顶点 A 相连，所得的△DAB 和△DAC 无疑是不全等的，由此可知，有两边及其一边的对角对应相等的两个三角形(简称“边边角”)不一定全等．因此，在判定三角形全等时，一定要留心“边边角”，别上当哟．
正解证明：∵EB＝EC，∴∠3＝∠4.又∵∠1＝∠2，∴∠1＋∠3＝ ∠2＋∠4，即∠ABC＝∠ACB，∴AB＝AC.在△AEB和△AEC中， ∵EB＝EC，∠1＝∠2，AB＝AC，∴△AEB≌△AEC(SAS)， ∴∠BAE＝∠CAE
的长可能是下列哪个值( B )
A．11
B．5 C．2 D．1
(2)(2015·巴中)若 a，b，c 为三角形的三边，且 a，b 满足 a2－9＋(b－
2)2＝0，则第三边 c 的取值范围是 1＜c＜5
．
【点评】三角形三边关系性质的实质是“两点之间，线段最短”．根据三角形的三边关系，已知三角形的两边a，b，可确定三角形第三边长c的取值范围|a－b|＜c＜a＋b.
[对应训练] 1．(1)(2014·宜昌)已知三角形两边长分别为3和8，则该三角形第三边的长可能是( )B A．5 B．10 C．11 D．12
(2)(2014·淮安)若一个三角形三边长分别为2，3，x，则x的值可以为___4_．(只需填一个整数)
【例2】 (1)(2014·赤峰)如图，把一块含有30°角(∠A＝30°)的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1＝40°，那么 ∠AFE＝( ) D
A．40° B．50° C．60° D．70°
4．(2015·柳州)如图，下列条件中，不能证明△ABC≌△DCB 的是( D )

中考数学专题复习：专题五三角形

专题五三角形【专题分析】三角形在中考中的常见考点有三角形的边和角，三角形的重要线段；全等三角形的判定，全等三角形的性质及综合应用，角平分线的应用；等腰三角形的性质和判定，等边三角形的性质和判定，直角三角形的性质，勾股定理，线段的垂直平分线；比例线段与黄金分割，相似三角形的性质及判定，相似多边形的性质；锐角三角函数，解直角三角形的应用等．对三角形的考查在中考中既有客观题又有主观题，考查题型多样，关于边角的基础知识一般以选择题或填空题的形式进行考查，证明三角形全等、相似，应用三角形全等、相似解决问题一般以解答题的形式进行考查；三角形在中考中的比重约为15%～20%.【解题方法】解决三角形问题常用的数学思想是转化思想，方程思想和数形结合思想；常用的数学方法有分类讨论法和设参数法等.【知识结构】【典例精选】：如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB＝4，则AC的长是( )A．3 B．4 C．6 D．5【思路点拨】过点D作DF⊥AC，由S△ABC＝S△ABD＋S△ACD可求出AC的长．答案：A已知：如图，△ABC中，AB＝AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E.(1)求证：△ABD≌△CAE；(2)连结DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．【思路点拨】(1)由AB＝AC及AE∥BC易得∠B＝∠CAE，然后由AD是中线可得∠ADB＝∠CEA，由AAS证明两个三角形全等；(2)由(1)可得AE＝BD，结合已知条件AE∥BC可得四边形ABDE是平行四边形，根据平行四边形的性质得出DE与AB平行且相等．【自主解答】(1)证明：∵AB＝AC，∴∠B＝∠ACB.∵AE∥BC，∴∠EAC＝∠ACB.∴∠B＝∠EAC.∵AD是BC边上的中线，∴AD⊥BC，即∠ADB＝90°.∵CE⊥AE，∴∠CEA＝90°. ∴∠CEA＝∠ADB.又∵AB＝AC，∴△ABD≌△CAE(AAS)．(2)解：AB∥DE且AB＝DE.由(1)△ABD≌△CAE可得AE＝BD，又∵AE∥BD，∴四边形ABDE是平行四边形，∴AB∥DE且AB＝DE.规律方法：在求线段，角，的长度，度数或证明线段，角相等时，利用全等三角形的对应边，角相等，可将对应边，角进行转化，从而建立已知与未知之间的联系.如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，P1，P2，P3，P4，P5是△DEF边上的5个格点，请按要求完成下列各题：(1)试证明△ABC是直角三角形；(2)判断△ABC和△DEF是否相似，并说明理由；(3)画一个三角形，使它的三个顶点为P1，P2，P3，P4，P5中的3个格点，并且与△ABC相似．(要求：用尺规作图，保留痕迹，不写作法与证明) 【思路点拨】(1)分别求出△ABC三边的长度，利用勾股定理进行判断；(2)分别求出△DEF三边的长度，计算△DEF与△ABC三边长度的比值，进而作出判断；(3)观察图形，所求作的三角形满足其三边与△ABC三边的比值相等即可．【自主解答】(1)证明：根据勾股定理，得AB＝25，AC＝5，BC＝5；显然有AB2＋AC2＝BC2，根据勾股定理的逆定理，得△ABC为直角三角形．(2)解：△ABC和△DEF相似．根据勾股定理，得DE＝42，DF＝22，EF＝210.∵ABDE＝ACDF＝BCEF＝522.∴△ABC∽△DEF.(3)解：如图，△P2P4P5即为所求．规律方法：在网格中证明两个三角形相似，可分别计算两个三角形三边的长度，再计算三组对应边的比是否相等，根据三组对应边的比相等，得两三角形相似.如图，港口B位于港口O正西方向120 km处，小岛C位于港口O北偏西60°的方向．一艘游船从港口O出发，沿OA方向(北偏西30°)以v km/h的速度驶离港口O.同时一艘快艇从港口B出发，沿北偏东30°的方向以60 km/h的速度驶向小岛C，在小岛C用1 h加装补给物资后，立即按照原来的速度给游船送去．(1)快艇从港口B到小岛C需要多长时间？(2)若快艇从小岛C到与游船相遇恰好用时1 h，求v的值及相遇处与港口O的距离．【思路点拨】(1)根据题意可知∠CBO＝60°，∠COB＝30°，∴∠C＝90°，在Rt△BOC中，根据cos ∠CBO＝BCBO，求出BC，根据“路程＝速度×时间”求出时间即可；(2)根据题意游船共行驶了3个小时，所以行驶路程为 3v km，设相会点为点E，作CD⊥OA，分点E在线段OD上和在射线DA上两种情况，解非直角三角形OCE，根据DE＝90－3v或DE＝3v－90，利用CD2＋DE2＝CE2，求出速度v和路程OE即可．【自主解答】解：(1)∵∠BOC＝30°，∠CBO＝60°，∴∠BCO＝90°，∴BC＝OB·cos 60°＝120×12＝60(km)，∴快艇从港口B到小岛C需要的时间为6060＝1(h)．(2)过点C作CD⊥OA，设相遇处为点E.则OC＝OB·cos 30°＝603(km)，CD＝12OC＝303(km)，OD＝OC·cos 30°＝90(km)．分两种情况：当点E在线段OD上时，如图①，DE＝(90－3v)km，∵CE＝60 km，CD2＋DE2＝CE2，∴(303)2＋(90－3v)2＝602，∴v＝20或v＝40.∵90－3v>0，∴v＝20.当点E在射线DA上时，如图②，DE＝(3v－90)km，∵CE＝60 km，CD2＋DE2＝CE2，∴(303)2＋(3v－90)2＝602，∴v＝20或v＝40.∵3v－90>0，∴v＝40.∴当v＝20 km/h时，OE＝3×20＝60(km)；当v＝40 km/h时，OE＝3×40＝120(km)．规律方法：解决此类问题的关键在于将斜三角形转化为直角三角形，而转化的关键是作出三角形的某一条高.【能力评估检测】一、选择题1．如图，在△ABC中，∠B＝46°，∠C＝54°，AD平分∠BAC，交BC于点D，DE∥AB，交AC于点E，则∠ADE的大小是( C )A．45° B．54° C．40° D．50°2．已知三角形两边的长是3和4，第三边的长是方程x2－12x＋35＝0的根，则该三角形的周长是( B )A．14 B．12C．12或14 D．以上都不对3．如图，地面上有三个洞口A，B，C，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及三个洞口(到A，B，C三个点的距离相等)，尽快抓到老鼠，应该蹲守在( A )A．△ABC三边垂直平分线的交点B．△ABC三条角平分线的交点C．△ABC三条高所在直线的交点D．△ABC三条中线的交点4．如图，在△ABC中，∠B＝30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB，若BE＝2，则AE的长为( B )A. 3 B．1 C. 2 D．25.如图，在Rt△ABC中，∠C＝90°，∠A＝30°，E为线段AB上一点，且AE∶EB＝4∶1，EF⊥AC于点F，连结FB，则tan∠CFB的值等于( C )A.33B.233C.533D．5 36.如图，一艘海轮位于灯塔P的北偏东方向55°，距离灯塔为2海里的点A处．如果海轮沿正南方向航行到灯塔的正东位置B处，海轮航行的距离AB长是( C )A．2海里 B．2 sin 55°海里C．2cos 55°海里 D．2tan 55°海里7．如图，△ABC中，AB＝AC＝18，BC＝12.正方形DEFG的顶点E，F在△ABC 内，顶点D，G分别在AB，AC上，AD＝AG，DG＝6，则点F到BC的距离为( ) A．1B．2C．122－6D．62－6【解析】如图，过点A作AH⊥BC于点H，交DG于点I，BH＝12BC＝6，在Rt△ABH中，AH＝AB2－BH2＝182－62＝122，易知D，G分别是AB，AC的中点，则I为AH的中点，IH＝62，DG＝12BC＝6，则正方形DGFE的边长FG＝6，于是点F到BC的距离＝62－6.故选D.答案: D8．如图，在钝角三角形ABC中，AB＝6 cm，AC＝12 cm，动点D从A点出发到B点停止，动点E从C点出发到A点停止．点D运动的速度为1 cm/s，点E运动的速度为2 cm/s.如果两点同时运动，那么当以点A，D，E为顶点的三角形与△ABC相似时，运动的时间是( )A．3 s或4.8 s B．3 sC．4.5 s D．4.5 s或4.8 s【解析】根据题意，设当以点A，D，E为顶点的三角形与△ABC相似时，运动的时间是x s，①若△ADE∽△ABC，则ADAB＝AEAC，∴x6＝12－2x12，解得x＝3；②若△ADE∽△ACB，则ADAC＝AEAB，∴x12＝12－2x6，解得x＝4.8.∴当以点A，D，E为顶点的三角形与△ABC相似时，运动的时间是3 s或4.8 s．故选A.答案: A二、填空题9．如图，在等腰三角形ABC中，AB＝AC，DE垂直平分AB，已知∠ADE＝40°，则∠DBC＝15 °.10．如图，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B，D作BF⊥a于点F，DE⊥a于点E，若DE＝8，BF＝5，则EF的长为13.11．如图，已知AC＝BD，要使△ABC≌△DCB，则只需添加一个适当的条件是答案不唯一，如AB＝CD或∠ACB＝∠DBC(填一个即可)．12．如图，在△ABC中，AB＝5，AC＝3，AD，AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为 .【解析】在△ABC中，∵AE为△ABC的角平分线，CH⊥AE，∴△AFH≌△ACH.∴AF＝AC＝3.∵AB＝5，∴BF＝2.∵AF＝AC，CH⊥AE，∴FH＝HC.∵AD为△ABC的中线，∴DH为△CBF的中位线，DH＝12BF＝1.答案: 1三、解答题13．已知△ABC，AB＝AC，将△ABC沿BC方向平移得到△DEF.(1)如图①，连结BD，AF，则BD________AF(填“＞”“＜”或“＝”)．图①(2)如图②，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连结BH，GF.求证：BH＝GF.图②(1)解：＝(2)证明：如图，将△DEF沿FE方向平移，使点E与点C重合，设ED平移后与MN相交于R.∵MN∥BC，RC∥EH，∴∠GRC＝∠RHE＝∠DEF，∠RGC＝∠GCB. ∴∠GRC ＝∠RGC，∴CG＝CR.又∵MN∥BF，CR∥EH，∴CR＝EH.∴CG＝EH.由平移的性质得BC＝EF，∴BC＋CE＝CE＋EF，即BE＝CF.又∵∠HEB＝∠GCF，∴△BEH≌△FCG(SAS)，∴BH＝FG.14．如图，这是一把可调节座椅的侧面示意图，已知头枕上的点A到调节器点O处的距离为80 cm，AO与地面垂直．现调整靠背，把OA绕点O旋转35°到OA′处．求调整后点A′比调整前点A的高度降低了多少厘米？(结果取整数)(参考数据：sin 35°≈0.57，cos 35°≈0.82， tan 35°≈0.70)解：如图，过点A′作A′H⊥OA于点H，由旋转可知，OA′＝OA＝80 cm，在Rt△OA′H中，OH＝OA′cos 35°≈80×0.82＝65.6(cm)．∴AH＝OA－OH＝80－65.6＝14.4≈14(cm)．答：调整后点A′比调整前点A的高度降低了14 cm.15．如图，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E，F分别在菱形的边BC，CD上滑动，且E，F不与B，C，D重合．(1)证明：不论E，F在BC，CD上如何滑动，总有BE＝CF；(2)当点E，F在BC，CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大(或最小)值．(1)证明：如图，连结AC，在菱形ABCD中，∠BAD＝120°，∴∠BAC＝60°，∠B＝60°.∴△ABC是正三角形，∴AB＝AC.又∵△AEF为正三角形，∴∠EAF＝60°，AE＝AF，而∠BAC＝60°，∴∠BAE＝∠CAF.∴△ABE≌△ACF.∴BE＝CF.(2)解：当点E，F在BC，CD上滑动时，四边形AECF的面积不发生变化，其值为4 3.理由如下：由(1)知，S△ABE＝S△ACF.∴S四边形AECF＝S△AEC＋S△ACF＝S△AEC＋S△ABE ＝S△ABC＝12×4×4×sin 60°＝4 3.△CEF的面积发生变化，其最大值为 3.∵S△CEF＝S四边形AECF－S△AEF＝43－34×AE2，当AE⊥BC时，AE的长最小，最小值为AB·sin 60°，即AE＝4×32＝23，∴S△CEF的最大值为43－34×(23)2＝ 3.。

考点13 三角形-中考数学考点讲解

考点13 三角形一、三角形的基础知识1．三角形的三边关系（1）三角形三边关系定理：三角形的两边之和大于第三边．推论：三角形的两边之差小于第三边．（2）三角形三边关系定理及推论的作用：①判断三条已知线段能否组成三角形；②当已知两边时，可确定第三边的范围；③证明线段不等关系．2．三角形的内角和定理及推论三角形的内角和定理：三角形三个内角和等于180°．推论：①直角三角形的两个锐角互余；②三角形的一个外角等于和它不相邻的两个内角的和；③三角形的一个外角大于任何一个和它不相邻的内角．3．三角形中的重要线段（1）三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线．（2）在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线．（3）从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）．（4）连接三角形两边中点的线段叫做三角形的中位线，三角形的中位线平行于第三边，且等于第三边的一半．二、全等三角形1．三角形全等的判定定理：（1）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）；（2）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）；（3）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）；（4）对于特殊的直角三角形，判定它们全等时，还有HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）．2．全等三角形的性质：（1）全等三角形的对应边相等，对应角相等；（2）全等三角形的周长相等，面积相等；（3）全等三角形对应的中线、高线、角平分线、中位线都相等．三、等腰三角形1．等腰三角形的性质定理：等腰三角形的两个底角相等（简称：等边对等角）．推论1：等腰三角形顶角平分线平分底边并且垂直于底边，即等腰三角形的顶角平分线、底边上的中线、底边上的高重合．推论2：等边三角形的各个角都相等，并且每个角都等于60°．2．等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．推论1：三个角都相等的三角形是等边三角形．推论2：有一个角是60°的等腰三角形是等边三角形．推论3：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．四、等边三角形1．定义：三条边都相等的三角形是等边三角形．2．性质：等边三角形的各角都相等，并且每一个角都等于60°．3．判定：三个角都相等的三角形是等边三角形；有一个角等于60°的等腰三角形是等边三角形．五、直角三角形与勾股定理1．直角三角形定义：有一个角是直角的三角形叫做直角三角形．性质：（1）直角三角形两锐角互余；（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；（3）在直角三角形中，斜边上的中线等于斜边的一半．判定：（1）两个内角互余的三角形是直角三角形；（2）三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形．2．勾股定理及逆定理（1）勾股定理：直角三角形的两条直角边a、b的平方和等于斜边c的平方，即：a2+b2=c2．（2）勾股定理的逆定理：如果三角形的三条边a、b、c有关系：a2+b2=c2，那么这个三角形是直角三角形．六、锐角三角函数与解直角三角形1．锐角三角函数的定义在Rt△ABC中，∠C=90°，AB=c，BC=a，AC=b，正弦：sin A=∠的对边=斜边A ac；余弦：cos A=∠的邻边=斜边A bc；正切：tan A=∠的对边=邻边A ab．2．特殊角的三角函数值3．解直角三角形解直角三角形的常用关系：在Rt△ABC中，∠C=90°，则：（1）三边关系：a2+b2=c2；（2）两锐角关系：∠A+∠B=90°；（3）边与角关系：sin A=cos B=ac，cos A=sin B=bc，tan A=ab；（4）sin2A+cos2A=1．4．解直角三角形的应用常用知识（1）仰角和俯角仰角：在视线与水平线所成的角中，视线在水平线上方的角叫做仰角．俯角：在视线与水平线所成的角中，视线在水平线下方的角叫做俯角．（2）坡度和坡角坡度：坡面的铅直高度h和水平宽度l的比叫做坡面的坡度（或坡比），记作i=hl．坡角：坡面与水平面的夹角叫做坡角，记作α，i=tanα．坡度越大，α角越大，坡面越陡．（3）方向角（或方位角）指北或指南方向线与目标方向线所成的小于90°的水平角叫做方向角．考向一三角形的三边关系在判断三条线段能否组成一个三角形时，可以根据两条较短线段的长度之和是否大于第三条线段的长度来判断．典例1 下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是A．1 cm，2 cm，3 cm B．2 cm，2 cm，4 cm C．2 cm，3 cm，4 cm D．1 cm，2 cm，5 cm【答案】C1．若一个三角形的三条边长为别是2，2x-3，6，则x的取值范围是__________．考向二三角形的内角和外角在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角．典例2 如图，∠ABC =∠ACB ，AD 、BD 、CD 分别平分△ABC 的外角∠EAC 、内角∠ABC 、外角∠ACF ．以下结论：①AD ∥BC ；②∠ACB =2∠ADB ；③∠ADC +∠ABD =90°；④∠BDC =∠BAC ．其中正确的结论有A ．1个B ．2个C ．3个D ．4个【答案】C【解析】①∵AD 平分△ABC 的外角∠EAC ，∴∠EAD =∠DAC ，∵∠EAC =∠ACB +∠ABC ，且∠ABC =∠ACB ，∴∠EAD =∠ABC ，∴AD ∥BC ，故①正确；②由①可知AD ∥BC ，∴∠ADB =∠DBC ，∵BD 平分∠ABC ， ∴∠ABD =∠DBC ，∴∠ABC =2∠ADB ，∵∠ABC =∠ACB ，∴∠ACB =2∠ADB ，故②正确；③在△ADC 中，∠ADC +∠CAD +∠ACD =180°，∵CD 平分△ABC 的外角∠ACF ，∴∠ACD =∠DCF ，∵AD ∥BC ，∴∠ADC =∠DCF ，∠ADB =∠DBC ，∠CAD =∠ACB ，∴∠ACD =∠ADC ，∠CAD =∠ACB =∠ABC =2∠ABD ，∴∠ADC +∠CAD +∠ACD =∠ADC +2∠ABD +∠ADC =2∠ADC +2∠ABD =180°，∴∠ADC +∠ABD =90°，故③正确； ④∵∠BAC +∠ABC =∠ACF ，∴12∠BAC +12∠ABC =12∠ACF ，∵∠BDC +∠DBC =12∠ACF ，∴12∠BAC + 12∠ABC =∠BDC +∠DBC ，∵∠DBC =12∠ABC ，∴12∠BAC =∠BDC ，即∠BDC =12∠BAC ，故④错误，故选C ．【名师点睛】本题主要考查了三角形的内角和、平行线的判定和性质、三角形外角的性质等知识，解题的关键是正确找各角的关系．2．如图，CE 是△ABC 的外角ACD ∠的平分线，若3560，B ACE ∠=︒∠=︒，则A ∠=__________．3．如图，在△ABC 中，∠ACB =68°，若P 为△ABC 内一点，且∠1=∠2，则∠BPC =__________．考向三三角形中的重要线段三角形的一条中线将这个三角形分成面积相等的两个三角形．典例3 在△ABC 中，AB =3，BC =4，AC =2，D ，E ，F 分别为AB ，BC ，AC 中点，连接DF ，FE ，则四边形DBEF 的周长是A ．5B ．7C ．9D ．11【答案】B【名师点睛】三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．典例4 如图，点G 为△ABC 的重心，则S △ABG ∶S △ACG ∶S △BCG 的值是A ．1∶2∶3B ．2∶1∶2C ．1∶1∶1D ．无法确定【答案】C【解析】如图，分别延长AG 、CG 、BG ，交BC 、AB 、AC 于点D 、F 、E ，根据三角形重心的定理得到AD 、BE 、CF 是△ABC 的中线，根据三角形的中线把三角形分为面积相等的两个三角形可得，ABD ACD BDG CDG S S S S ∆∆∆==，即可得ABG ACG S S ∆∆=，同理可得ABG BCG S S ∆∆=，所以=ABG BCG ACG S S S ∆∆∆=，即S△ABG∶S△ACG∶S△BCG=1∶1∶1，故选C．4．如图，在Rt△ABC中，∠A=90°，BD平分∠ABC交AC于D点，AB=4，BD=5，点P是线段BC上的一动点，则PD的最小值是__________．考向四全等三角形1．判定两个三角形全等一般可以从三个角度考虑：（1）从三边考虑；（2）从两边和它们的夹角考虑；（3）从两角和夹边考虑．2．轴对称、平移、旋转前后的两个图形全等．典例5 如图，已知∠ADB=∠CBD，下列所给条件不能证明△ABD≌△CDB的是A．∠A=∠C B．AD=BC C．∠ABD=∠CDB D．AB=CD【答案】D【名师点睛】本题考查了全等三角形的判定方法，①三边对应相等的两个三角形全等，简记为“SSS”；②两边及其夹角对应相等的两个三角形全等，简记为“SAS ”；③两角及其夹边对应相等的两个三角形全等，简记为“ASA ”；④两角及其中一角的对边对应相等的两个三角形全等，简记为“AAS ”；⑤斜边及一直角边对应相等的两个三角形全等，根据这几种判定方法解答即可．5．如图，正方形ABCD 中，BD 是对角线，将△DCB 绕点D 顺时针旋转45︒得到△DGH ，HG 交AB 于点E ，图中全等三角形共有A ．2对B ．3对C ．4对D ．5对6．如图，在△BCE 中，AC ⊥BE ，AB =AC ，点A 、点F 分别在BE 、CE 上，BF 、AC 相交于点D ，BD =CE ．求证：AD =AE ．考向五等腰三角形1．等腰直角三角形的两个底角相等且等于45°．2．等腰三角形的底角只能为锐角，不能为钝角（或直角），但顶角可为钝角（或直角）． 3．等腰三角形的三边关系：设腰长为a ，底边长为b ，则2b<a ． 4．等腰三角形的三角关系：设顶角为顶角为∠A ，底角为∠B 、∠C ，则∠A =180°-2∠B ，∠B =∠C =2180A∠-︒．典例6 等腰三角形的一个内角为70°，它的一腰上的高与底边所夹的角的度数是A．35°B．20°C．35°或20°D．无法确定【答案】C【解析】70°是顶角，它的一腰上的高与底边所夹的角的度数是35°，70°是底角，顶角是40°，它的一腰上的高与底边所夹的角的度数是20°，故选C．典例7 如图，等腰三角形ABC中，∠BAC=90°，在底边BC上截取BD=AB，过D作DE⊥BC交AC于E，连接AD，则图中等腰三角形的个数是A．1 B．2 C．3 D．4【答案】D【名师点睛】此题考查了等腰三角形的性质和判定以及三角形的内角和定理，由已知的条件利用相关的性质，求得各个角的度数是正确解题的关键.7．等腰三角形的周长为15 cm，其中一边长为3 cm．则该等腰三角形的腰长为A．3 cm B．6 cm C．3 cm或6 cm D．3 cm或9 cm考向六直角三角形与勾股定理在直角三角形中，30°的角所对的直角边等于斜边的一半，这个性质常常用于计算三角形的边长，也是证明一边（30°角所对的直角边）等于另一边（斜边）的一半的重要依据．当题目中已知的条件或结论倾向于该性质时，我们可运用转化思想，将线段或角转化，构造直角三角形，从而将陌生的问题转化为熟悉的问题．典例8 下列几组数：①6，8，10；②7，24，25；③9，12，15；④n2-1，2n，n2+1（n）（n是大于1的整数），其中是勾股数的有A．1组B．2组C．3组D．4组【答案】D【解析】①∵62+82=100=102，∴6、8、10是勾股数；②∵72+242=252，∴7，24，25是勾股数；③∵92+122=152，∴9，12，15是勾股数；④∵（n2-1）2+（2n）2=（n2+1）2，∴n2-1，2n，n2+1（n）（n是大于1的整数）是勾股数，故选D．【名师点睛】本题考查了勾股数的判断，解题的关键是根据勾股数的定义分别对每一组数进行分析．典例9 如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若∠B=30°，BD=6，则CD的长为__________．【答案】3【解析】∵在Rt△ABC中，∠C=90°，∠B=30°，∴∠BAC=60°．又AD平分∠BAC，∴∠BAD=∠CAD=30°，∴∠BAD=∠B=30°，∴AD=BD=6，∴CD=12AD=3，故答案为：3．8．如图，一圆柱高8 cm，底面半径为6πcm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是A．12 cm B．10 cmC．8 cm D．6 cm9．已知：如图，在Rt△ABC中，∠ACB=90°，BC3tan∠ABC=2，点D是AC的中点．（1）求线段BD的长；（2）点E在边AB上，且CE=CB，求△ACE的面积．考向七锐角三角函数与解直角三角形解直角三角形的应用可解决的问题（1）测量物体的高度；（2）测量河的宽度；（3）解决航海航空问题；（4）解决坡度问题；（5）解决实际生活中其他问题.典例10 在△ABC中，∠C=90°，sin A=1213，则tan A的值为A．1213B．513C．125D．1312【答案】C【解析】∵sin A=BCAB=1213，∴设BC=12x，AB=13x，由勾股定理得：AC=22AB BC=5x，∴tan A=BCAC=125，故选C．典例11 某山的山顶B处有一个观光塔，已知该山的山坡面与水平面的夹角∠BDC为30°，山高BC为100米，点E距山脚D处150米，在点E处测得观光塔顶端A的仰角为60°，则观光塔AB的高度是A．50米B．100米C．125米D．150米【答案】A【解析】如图，作EF⊥AC于F，EG⊥DC于G，在Rt△DEG中，EG=12DE=75，∴BF=BC-CF=BC-CE=100-75=25，EF=tan tan30BF BF BEF =∠︒=253，∵∠AEF =60°，∴∠A =30°，∴AF =253tan 33EF A ==75， ∴AB =AF -BF =50（米），故观光塔AB 的高度为50米，故选A ．10．正方形网格中，△ABC 如图放置，则sin ∠BAC =A ．13B ．13C ．13D ．121311．如图，某湖心岛上有一亭子A ，在亭子A 的正东方向上的湖边有一棵树B ，在这个湖心岛的湖边C 处测得亭子A 在北偏西45︒方向上，测得树B 在北偏东36︒方向上，又测得B 、C 之间的距离等于200米，求A 、B 之间的距离（结果精确到1米）．（参考数据：2 1.414≈，sin360.588︒≈，cos360.809︒≈，tan360.727︒≈，cot36 1.376︒≈）1．三角形的三边长a，b，c满足2ab=（a+b）2-c2，则此三角形是A．钝角三角形B．锐角三角形C．直角三角形D．等边三角形2．如图，已知△ABC≌△EDF，点F，A，D在同一条直线上，AD是∠BAC的平分线，∠EDA=20°，∠F=60°，则∠DAC的度数是A．50°B．60°C．100°D．120°3．如图，△ABC中，∠A=30°，tan B=32，AC=23，则AB的长为A．3+3B．2+23C．5 D．9 24．如图，△ABC中，AB=6，AC=4，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB 于G，连接EF，则线段EF的长为__________．5．已知直角三角形的两条边分别是5和12，则斜边上的中线的长度为__________．6．如图，在等边△ABC中，点D为BC边上的点，DE⊥BC交AB于E，DF⊥AC于F，则∠EDF的度数为__________．7．如图，测量河宽AB（河的两岸平行），在C点测得∠ACB=32°，BC=60 m，则河宽AB约为__________m．（用科学计算器计算，结果精确到0.1）8．如图，AD为△ABC的中线，BE为△ABD的中线．（1）∠ABE=15°，∠BAD=40°，求∠BED的度数；（2）作图：在△BED中作出BD边上的高EF和BE边上的高DG；（3）若△ABC的面积为40，BD=5，则△BDE中BD边上的高EF为多少？若BE=6，求△BED中BE 边上的高DG为多少？9．如图，点D，E分别在AB，AC上，且AD=AE，∠BDC=∠CEB．求证：BD=CE．10．如图，在等腰三角形ABC中，AC=BC，分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE，AE与BD相交于点F，连接CF并延长交AB于点G．求证：CG垂直平分AB．11．如图，一架2.5 m长的梯子斜立在竖直的墙上，此时梯足B距底端O为0.7 m．（1）求OA的长度；（2）如果梯子顶端下滑0.4米，则梯子将滑出多少米？12．如图，小华站在河岸上的G点，看见河里有一小船沿垂直于岸边的方向划过来．此时测得小船C的俯角是∠FDC=30°．若小华的眼睛与地面的距离是3米，BG=1.5米，BG平行于AC所在的直线，迎水坡i=4∶3，坡长AB=10米，点A、B、C、D、F、G在同一平面内，则此时小船C到岸边的距离CA的长是多少？（结果保留根号）1．（2017•大庆）在△ABC中，∠A，∠B，∠C的度数之比为2∶3∶4，则∠B的度数为A．120°B．80°C．60°D．40°2．（2017•广州）如图，Rt△ABC中，159015tan8，，C BC A∠=︒==，则AB=__________．3．（2017•抚顺）如图，某城市的电视塔AB坐落在湖边，数学老师带领学生隔湖测量电视塔AB的高度，在点M处测得塔尖点A的仰角∠AMB为22.5°，沿射线MB方向前进200米到达湖边点N处，测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°，则电视塔AB的高度为__________米（结果保留根号）．4．（2017•大庆）如图，已知一条东西走向的河流，在河流对岸有一点A ，小明在岸边点B 处测得点A 在点B 的北偏东30°方向上，小明沿河岸向东走80 m 后到达点C ，测得点A 在点C 的北偏西60°方向上，则点A 到河岸BC 的距离为__________．5．（2017•广州）如图，点E ，F 在AB 上，，，AD BC A B AE BF =∠=∠=．求证：△ADF ≌△BCE ．6．（2017•张掖）美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风情线是兰州最美的景观之一．数学课外实践活动中，小林在南滨河路上的A ，B 两点处，利用测角仪分别对北岸的一观景亭D 进行了测量．如图，测得∠DAC =45°，∠DBC =65°．若AB =132米，求观景亭D 到南滨河路AC 的距离（结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）．7．（2017•重庆A卷）在△ABC中，∠ABM=45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．（1）如图①，若AB=32，BC=5，求AC的长；（2）如图②，点D是线段AM上一点，MD=MC，点E是△ABC外一点，EC=AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF=∠CEF．1．【答案】3.5<x<5.5【解析】由三角形三边关系得4<2x-3<8，解得3.5<x<5.5，故答案为：3.5<x<5.5．4．【答案】3【解析】由勾股定理知AD22543-=，BD平分∠ABC交AC于D点，所以PD=AD最小，PD=3，变式拓展故答案为：3．5．【答案】C【解析】∵四边形ABCD是正方形，∴△ABD≌△CBD．由旋转的性质得，△CBD≌GHD，DH=BD，DG=CD，∴△ABD≌△GHD，∴DH-AD=BD-DG，∴AH=BG．在△AHE和△BGE中，∵∠AEH=∠BEG，∠HAE=∠AGB=90°，AH=BG，∴△AHE≌△GBE，∴有4对三角形全等，故选C．6．【解析】∵AC⊥BE，∴∠BAD=∠CAE=90°，在Rt△ABD和Rt△ACE中，BD CE AB AC=⎧⎨=⎩，∴Rt△ABD≌Rt△ACE（HL），∴AD=AE．7．【答案】B【解析】当3 cm是底时，则腰长是（15-3）÷2=6（cm），此时能够组成三角形；当3 cm是腰时，则底是15-3×2=9（cm），此时3+3<9，不能组成三角形，应舍去，故选B．8．【答案】B【解析】如图，底面圆周长为2πr，底面半圆弧长为πr，即半圆弧长为：12×2π×6π=6（cm），展开得：∵BC=8 cm，AC=6 cm，根据勾股定理得：AB=2268+=10（cm），故选B．9．【解析】（1）Rt△ABC中，∠ACB=90°，BC=3，tan∠ABC=2，∴AC=6，∵点D是AC的中点，∴CD=12AC=162，∴Rt△BCD中，BD=2232 2BC CD+=．（2）如图，过C作CH⊥AB于H，∵BC3tan∠ABC=2，∴CH =2，BH =1，∵CE =CB ，∴EH =BH =1，∵∠ACB =90°，BC =3，AC =6，∴AB =3，∴AE =3-2=1，∴△ACE 的面积=12×AE ×CH =12×1×2=22．11．【解析】如图，过点C 作CH AB ⊥，垂足为点H ，由题意，得45ACH ∠=︒，36BCH ∠=︒，200BC =，在Rt △BHC 中，sin BH BCH BC ∠=，∴sin36200BH ︒=， ∵sin360.588︒≈，∴117.6BH ≈，又cos HC BCH BC ∠=，∴cos36200HC ︒=， ∵cos360.809︒≈，∴161.8HC ≈，在Rt △AHC 中，tan AHACH HC∠=， ∵45ACH ∠=︒，∴AH HC =，∴161.8AH ≈，又AB AH BH =+，∴279.4AB ≈，∴279AB ≈（米）．答：A 、B 之间的距离为279米．1．【答案】C【解析】∵原式可化为a 2+b 2=c 2，∴此三角形是直角三角形，故选C ． 2．【答案】A【解析】根据全等三角形的性质求出∠B =∠EDF =20°和∠C =∠F =60°，根据三角形内角和定理求出 ∠BAC =180°-∠B -∠C =100°，根据角平分线定义求出∠DAC =12∠BAC =50°，故选A ． 3．【答案】C【解析】如图，作CD ⊥AB 于D ．在直角三角形ACD 中，∠A =30°，AC =23，∴CD =3，AD =3．在直角三角形BCD 中，tan B =3，∴BD =tan CD B =2．∴AB =AD +BD =5，故选C ．4．【答案】1【解析】在△AGF 和△ACF 中，GAF CAFAF AF AFG AFC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AGF ≌△ACF ，∴AG =AC =4，GF =CF ，则BG =AB −AG =6−4=2，又∵BE =CE ，∴EF 是△BCG 的中位线，∴EF =12BG =1，故答案为：1． 5．【答案】6或6.5【解析】分两种情况：①5和12是两条直角边，根据勾股定理求得斜边为13，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6.5；②5是直角边，12为斜边，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6，故答案为：6或6.5． 6．【答案】60°考点冲关【解析】∵△ABC是等边三角形，∴∠A=∠B=60°，∵DE⊥BC交AB于E，DF⊥AC于F，∴∠BDE=∠AFD=90°．∵∠AED是△BDE的外角，∴∠AED=∠B+∠BDE=60°+90°=150°，∴∠EDF=360°−∠A−∠AED−∠AFD=360°−60°−150°−90°=60°，故答案为：60°．7．【答案】37.5【解析】由BC求AB，可利用tan32°，得到AB=BC•tan32°，代入数值即可求出AB=BC•tan32°≈60×0.625≈37.5 m，故答案为：37.5．8．【解析】（1）∵∠BED是△ABE的外角，∴∠BED=∠ABE+∠BAD=15°+40°=55°．（2）画图如下：9．【解析】∵∠ADC+∠BDC=180°，∠BEC+∠AEB=180°，又∵∠BDC=∠CEB，∴∠ADC=∠AEB．在△ADC和△AEB中，∠A=∠A（公共角），AD=AE（已知），∠ADC=∠AEB（已证），∴△ADC≌△AEB（ASA）．∴AB=AC．∴AB-AD=AC-AE．即BD=CE．10．【解析】∵CA=CB，∴∠CAB=∠CBA，∵△AEC和△BCD为等腰直角三角形，∴∠CAE=∠CBD=45°，∠FAG=∠FBG，∴∠FAB=∠FBA，∴AF=BF，在三角形ACF和△BCF中，AF BF AC BC CF CF=⎧⎪=⎨⎪=⎩，∴△ACF≌△BCF（SSS），∴∠ACF=∠BCF，∴AG=BG，CG⊥AB（三线合一），即CG垂直平分AB．12．【解析】如图，过点B作BE⊥AC于点E，延长DG交CA于点H，得Rt△ABE和矩形BEHG．∵i=43BEAE=，AB=10米，∴BE=8，AE=6．∵DG3BG=1.5，∴DH=DG+GH3+8，AH=AE+EH=6+1.5=7.5．在Rt△CDH中，∵∠C=∠FDC=30°，DH=8+3，tan30°=8333 DHCH CH+==，∴CH=83+3．又∵CH=CA+7.5，即83+3=CA+7.5，∴CA=83-4.5（米）．答：CA的长约是（83-4.5）米．1．【答案】C【解析】∵∠A∶∠B∶∠C=2∶3∶4，∴设∠A=2x，∠B=3x，∠C=4x，∵∠A+∠B+∠C=180°，∴2x+ 3x+4x=180°，解得x=20°，∴∠B的度数为60°，故选C．2．【答案】17【解析】∵Rt△ABC中，∠C=90°，∴tan A=BCAC，∵1515tan8，BC A==，∴AC=8，∴AB=22BC AC+=17，故答案为：17．3．【答案】1002【解析】如图，连接AN，由题意知，BM⊥AA'，BA=BA'，∴AN=A'N，∴∠ANB=∠A'NB=45°，∵∠AMB=22.5°，∴∠MAN=∠ANB-∠AMB=22.5°=∠AMN，∴AN=MN=200米，在Rt△ABN中，∠ANB=45°，∴AB=22AN=1002（米），故答案为：1002．4．【答案】203【解析】如图，过点A作AD⊥BC于点D．根据题意，∠ABC=90°-30°=60°，∠ACD=30°，设AD=x，直通中考在Rt△ACD中，tan∠ACD=ADCD，∴CD=3tan tan30AD xxACD==∠︒，在Rt△ABD中，tan∠ABC=ADBD，∴BD=3tan tan603AD xxABC==∠︒，∴BC=CD+BD=3x+33x=80，∴x=203，故答案为：203m．5．【解析】∵AE=BF，∴AE+EF=BF+EF，即AF=BE，在△ADF和△BCE中，AD BCA BAF BE=⎧⎪∠=∠⎨⎪=⎩，∴△ADF≌△BCE（SAS）．6．【解析】如图，过点D作DE⊥AC，垂足为E，设BE=x，在Rt△DEB中，tan∠DBE=DEBE，∵∠DBC=65°，∴DE=x·tan65°．又∵∠DAC=45°，∴AE=DE．∴132+x=x·tan65°，解得x≈115.8，∴DE≈248（米）．∴观景亭D到南滨河路AC的距离约为248米．7．【解析】（1）∵∠ABM=45°，AM⊥BM，∴AM=BM=AB·cos45°=32×2，则CM=BC-BM=5-3=2，∴AC=2222+=+=．AM CM2313（2）如图，延长EF到点G，使得FG=EF，连接BG．由DM=MC，∠BMD=∠AMC，BM=AM，∴△BMD≌△AMC（SAS），∴AC=BD，又CE=AC，因此BD=CE，由BF=FC，∠BFG=∠EFC，FG=FE，∴△BFG≌△CFE，故BG=CE，∠G=∠E，所以BD=BG=CE，因此∠BDG=∠G=∠E．。

中考数学全等三角形的五种模型

图形
结论
①△ABF≌△BCE； ②EC＝AB－FC
模型应用
7. (2016·深圳改编)如图，CB＝CA，∠ACB＝ 90°，点D在边BC上(与B，C不重合)，四边形ADEF为正方形，过点F作FG⊥CA，交CA 的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC＝FG；②S△FAB∶S四边形 CBFG＝1∶2；③∠ABC＝∠ABF. 其中正确的结论的个数是( )
∵∠1＝∠2，AD⊥FG于D，AH⊥EF于H， ∴AD＝AH， ∵AD＝AB， ∴AH＝AB，又∵AH⊥EF于H，AB⊥BC于B， ∴AE平分∠BEF，故①正确； ∵AE平分∠BEF， ∴∠AEB＝∠AEH， ∵∠AEB＋∠BAE＝90°，
∠AEH＋∠HAE＝90°， ∴∠BAE＝∠HAE，
又∵EH⊥AH于H，EB⊥AB于B， ∴BE＝HE， ∵BE＝DG， ∴HE＝DG， ∵EF＝HE＋FH，GF＝DG＋FD，EF＝GF， ∴FH＝FD，故②正确； ∵△AEF≌△AGF， ∴S△EAF＝S△GAF. ∵△ABE≌△ADG，
叠到DF，延长EF交AB于G，连接DG，现在
有如下4个结论：
①△ADG≌△FDG；②GB＝2AG；③∠GDE
＝45°；④DG＝DE.
在以上4个结论中，正确的共有
()
A. 1个
B. 2 个
C. 3 个
D. 4个
3. C 解析：由折叠可知，DF＝DC＝DA，∠DFE＝ ∠C＝90°， ∴∠DFG＝∠A＝90°， ∴△ADG≌△FDG，①正确； ∵正方形边长是12， ∴BE＝EC＝EF＝6，设AG＝FG＝x，则EG＝x＋6，BG＝12－x，由勾股定理，得EG2＝BE2＋BG2，即(x＋6)2＝62＋(12－x)2，解得x＝4， ∴AG＝GF＝4，BG＝8， ∴BG＝2AG，②正确；

初三数学13 相似三角形-2024年中考数学真题分项汇编(全国通用)(解析版)

专题13 相似三角形一．选择题1．（2022·黑龙江哈尔滨）如图，,,AB CD AC BD ∥相交于点E ，1,2,3AE EC DE ===，则BD 的长为（）A ．32B ．4C ．92D ．6【答案】C【分析】根据相似三角形对应边长成比例可求得BE 的长，即可求得BD 的长．【详解】∵//AB CD ∴ABE CDE ∽ ∴AE BE EC DE= ∵1,2,3AE EC DE ===，∴32BE =∵BD BE ED =+ ∴92BD = 故选：C ．【点睛】本题考查了相似三角形的对应边长成比例，解题的关键在于找到对应边长．2．（2022·广西贺州）如图，在ABC 中，25DE BC DE BC ==∥，，，则:ADE ABC S S 的值是（）A ．325B ．425C ．25D ．35【答案】B【分析】根据相似三角形的判定定理得到ADE ABC ，根据相似三角形的面积比等于相似比的平方计算，得到答案．【详解】解：25DE BC DE BC ==∥，，∴ADE ABC ，∴2224525ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ，故选：B ．【点睛】此题考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．3．（2022·广西梧州）如图，以点O 为位似中心，作四边形ABCD 的位似图形''''A B C D ﹐已知'13OA OA =，若四边形ABCD 的面积是2，则四边形''''A B C D 的面积是（）A ．4B ．6C ．16D ．18【答案】D 【分析】两图形位似必相似，再由相似的图形面积比等于相似比的平方即可求解．【详解】解：由题意可知，四边形ABCD 与四边形''''A B C D 相似，由两图形相似面积比等于相似比的平方可知：''''22'1139ABCD A B C D S OA S OA ⎛⎫⎛⎫= ⎪= ⎪= ⎪ ⎪⎝⎭⎝⎭，又四边形ABCD 的面积是2，∴四边形''''A B C D 的面积为18，故选：D ．【点睛】本题考察相似多边形的性质，属于基础题，熟练掌握相似图形的性质是解决本题的关键．4．（2022·四川雅安）如图，在△ABC 中，D ，E 分别是AB 和AC 上的点，DE ∥BC ，若AD BD ＝21，那么DE BC ＝（）A ．49B ．12C ．13D ．23【答案】D【分析】先求解2,3AD AB =再证明,ADE ABC ∽可得2.3DE AD BC AB ==【详解】解： AD BD ＝21，2,3AD AB ∴= DE ∥BC ，,ADE ABC ∴ ∽ 2,3DE AD BC AB ∴== 故选D 【点睛】本题考查的是相似三角形的判定与性质，证明ADE ABC △△∽是解本题的关键．5．（2022·内蒙古包头）如图，在边长为1的小正方形组成的网格中，A ，B ，C ，D 四个点均在格点上，AC 与BD 相交于点E ，连接,AB CD ，则ABE △与CDE △的周长比为（）A ．1：4B ．4：1C ．1：2D ．2：1【答案】D 【分析】运用网格图中隐藏的条件证明四边形DCBM 为平行四边形，接着证明ABE CDE ∽，最后利相似三角形周长的比等于相似比即可求出．【详解】如图：由题意可知，3DM =，3BC =， ∴DM BC =，而DM BC ∥，∴四边形DCBM 为平行四边形，∴AB DC ∥，∴BAE DCE ∠=∠，ABE CDE ∠=∠，∴ABE CDE ∽，∴21ABE CDE C AB C CD ===△△．故选：D ．【点睛】本题考查了平行四边形的判定与性质、相似三角形的判定与性质及勾股定理，熟练掌握相关知识并正确计算是解题关键．6．（2022·黑龙江绥化）如图，在矩形ABCD 中，P 是边AD 上的一个动点，连接BP ，CP ，过点B 作射线，交线段CP 的延长线于点E ，交边AD 于点M ，且使得ABE CBP =∠∠，如果2AB =，5BC =，AP x =，PM y =，其中25x < ．则下列结论中，正确的个数为（）（1）y 与x 的关系式为4y x x =-；（2）当4AP =时，ABP DPC ∽；（3）当4AP =时，3tan 5EBP ∠=．A ．0个B ．1个C ．2个D ．3个【答案】C 【分析】（1）证明ABM APB ∽，得AB AM AP AB=，将2AB =，AP x =，PM y =代入，即可得y 与x 的关系式；（2）利用两组对应边成比例且夹角相等，判定ABP DPC ∽；（3）过点M 作MF BP ⊥垂足为F ，在Rt APB △中，由勾股定理得BP 的长，证明FPM APB ∽，求出MF ，PF ，BF 的长，在Rt BMF △中，求出tan EBP ∠的值即可．【详解】解：（1）∵在矩形ABCD 中，∴AD BC ∥，90A D ∠=∠=︒，5BC AD ==，2AB DC ==，∴APB CBP ∠=∠，∵ABE CBP =∠∠，∴ABE APB ∠=∠，∴ABM APB ∽，∴AB AM AP AB=，∵2AB =，AP x =，PM y =，∴22x y x -=，解得：4y x x=-，故（1）正确；（2）当4AP =时，541DP AD AP =-=-=，∴12DC DP AP AB ==，又∵90A D ∠=∠=︒，∴ABP DPC ∽，故（2）正确；（3）过点M 作MF BP ⊥垂足为F ，∴90A MFP MFB ∠=∠=∠=︒，∵当4AP =时，此时4x =，4413y x x =-=-=，∴3PM =，在Rt APB 中，由勾股定理得：222BP AP AB =+，∴BP ===，∵FPM APB ∠=∠，∴FPM APB ∽，∴MF PF PM AB AP PB ==，∴24MF PF ==∴MF =PF =∴BF BP PF =-=∴3tan 4MF EBP BF ∠===故（3）不正确；故选：C ．【点睛】本题主要考查相似三角形的判定和性质，勾股定理的应用，矩形的性质，正确找出相似三角形是解答本题的关键．7．（2022·湖北鄂州）如图，定直线MN ∥PQ ，点B 、C 分别为MN 、PQ 上的动点，且BC =12，BC 在两直线间运动过程中始终有∠BCQ =60°．点A 是MN 上方一定点，点D 是PQ 下方一定点，且AE ∥BC ∥DF ，AE =4，DF =8，ADBC 在平移过程中，AB +CD 的最小值为（）A ．B ．C ．D ．【答案】C 【分析】如图所示，过点F 作FH CD ∥交BC 于H ，连接EH ，可证明四边形CDFH 是平行四边形，得到CH =DF =8，CD =FH ，则BH =4，从而可证四边形ABHE 是平行四边形，得到AB =HE ，即可推出当E 、F 、H 三点共线时，EH +HF 有最小值EF 即AB +CD 有最小值EF ，延长AE 交PQ 于G ，过点E 作ET ⊥PQ 于T ，过点A 作AL ⊥PQ 于L ，过点D 作DK ⊥PQ 于K ，证明四边形BEGC 是平行四边形，∠EGT =∠BCQ =60°，得到EG =BC =12，然后通过勾股定理和解直角三角形求出ET 和TF 的长即可得到答案．【详解】解：如图所示，过点F 作FH CD ∥交BC 于H ，连接EH ，∵BC DF FH CD ∥∥，，∴四边形CDFH 是平行四边形，∴CH =DF =8，CD =FH ，∴BH =4，∴BH =AE =4，又∵AE BC ∥，∴四边形ABHE 是平行四边形，∴AB =HE ，∵EH FH EF +≥，∴当E 、F 、H 三点共线时，EH +HF 有最小值EF 即AB +CD 有最小值EF ，延长AE 交PQ 于G ，过点E 作ET ⊥PQ 于T ，过点A 作AL ⊥PQ 于L ，过点D 作DK ⊥PQ 于K ，∵MN PQ BC AE ∥∥，，∴四边形BEGC 是平行四边形，∠EGT =∠BCQ =60°，∴EG =BC =12，∴=cos =6=sin GT GE EGT ET GE EGT ⋅⋅∠，∠，同理可求得8GL AL ==，，4KF DK ==，，∴2TL =，∵AL ⊥PQ ，DK ⊥PQ ，∴AL DK ∥，∴△ALO ∽△DKO ，∴2AL AO DK DO==，∴2133AO AD DO AD ====∴24OL OK ===，，∴42TF TL OL OK KF =+++=，∴EF ==故选C ．【点睛】本题主要考查了平行四边形的性质与判定，相似三角形的性质与判定，勾股定理，解直角三角形，正确作出辅助线推出当E 、F 、H 三点共线时，EH +HF 有最小值EF 即AB +CD 有最小值EF 是解题的关键．8．（2022·广西贵港）如图，在边长为1的菱形ABCD 中，60ABC ∠=︒，动点E 在AB 边上（与点A 、B 均不重合），点F 在对角线AC 上，CE 与BF 相交于点G ，连接,AG DF ，若AF BE =，则下列结论错误的是（）A ．DF CE =B ．120BGC ∠=︒C ．2AF EG EC =⋅D ．AG【答案】D【分析】先证明△BAF ≌△DAF ≌CBE ，△ABC 是等边三角形，得DF =CE ，判断A 项答案正确，由∠GCB +∠GBC =60゜，得∠BGC =120゜，判断B 项答案正确，证△BEG ∽△CEB 得BE CE GE BE= ，即可判断C 项答案正确，由120BGC ∠=︒，BC =1，得点G 在以线段BC 为弦的弧BC 上，易得当点G 在等边△ABC 的内心处时，AG 取最小值，由勾股定理求得AG D 项错误．【详解】解：∵四边形ABCD 是菱形，60ABC ∠=︒，∴AB =AD =BC =CD ，∠BAC =∠DAC =12∠BAD =12(180)ABC ⨯︒-∠=60ABC ︒=∠，∴△BAF ≌△DAF ≌CBE ，△ABC 是等边三角形，∴DF =CE ，故A 项答案正确，∠ABF =∠BCE ，∵∠ABC =∠ABF +∠CBF =60゜，∴∠GCB +∠GBC =60゜，∴∠BGC =180゜-60゜=180゜-（∠GCB +∠GBC ）=120゜，故B 项答案正确，∵∠ABF =∠BCE ，∠BEG =∠CEB ，∴△BEG ∽△CEB ，∴BE CE GE BE = ，∴2BE GE CE = ，∵AF BE =，∴2AF GE CE = ，故C 项答案正确，∵120BGC ∠=︒，BC =1，点G 在以线段BC 为弦的弧BC 上，∴当点G 在等边△ABC 的内心处时，AG 取最小值，如下图，∵△ABC 是等边三角形，BC =1，∴BF AC ⊥，AF =12AC =12，∠GAF =30゜，∴AG =2GF ，AG 2=GF 2+AF 2，∴2221122AG AG ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，解得AG D 项错误，故应选：D【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理，熟练掌握菱形的性质是解题的关键．9．（2022·贵州贵阳）如图，在ABC 中，D 是AB 边上的点，B ACD ∠=∠，:1:2AC AB =，则ADC 与ACB △的周长比是（）A ．B ．1:2C ．1:3D ．1:4【答案】B 【分析】先证明△ACD ∽△ABC ，即有12AC AD CD AB AC BC ===，则可得12AC AD CD AB AC BC ++=++，问题得解．【详解】∵∠B =∠ACD ，∠A =∠A ，∴△ACD ∽△ABC ，∴AC AD CD AB AC BC ==，∵12AC AB =，∴12AC AD CD AB AC BC ===，∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++，∴△ADC 与△ACB 的周长比1:2，故选：B ．【点睛】本题主要考查了相似三角形的判定与性质，证明△ACD ∽△ABC 是解答本题的关键．10．（2022·广西）已知△ABC 与△A 1B 1C 1是位似图形，位似比是1：3，则△ABC 与△A 1B 1C 1的面积比（）A ．1 ：3B ．1：6C ．1：9D ．3：1【答案】C【分析】根据位似图形的面积比等于位似比的平方，即可得到答案．【详解】∵△ABC 与△A 1B 1C 1是位似图形，位似比是1：3，∴△ABC 与△A 1B 1C 1的面积比为1：9，故选：C ．【点睛】本题考查位似图形的性质，熟练掌握位似图形的面积比等于位似比的平方是解题的关键．11．（2022·山东临沂）如图，在ABC 中，∥DE BC ，23AD DB =，若6AC =，则EC =（）A ．65B ．125C ．185D ．245【答案】C【分析】由∥DE BC ，23AD DB =，可得2,3AD AE DB EC ==再建立方程即可．【详解】解： ∥DE BC ，23AD DB =，2,3AD AE DB EC ∴== 6AC =，62,3CE CE -∴= 解得：18.5CE =经检验符合题意故选C 【点睛】本题考查的是平行线分线段成比例，证明“23AD AE DB EC ==”是解本题的关键．12．（2022·山东威海）由12个有公共顶点O 的直角三角形拼成如图所示的图形，∠AOB ＝∠BOC ＝∠COD ＝…＝∠LOM ＝30°．若S △AOB ＝1，则图中与△AOB 位似的三角形的面积为( )A ．（43）3B ．（43）7C ．（43）6D ．（34）6【答案】C【分析】根据题意得出A 、O 、G 在同一直线上，B 、O 、H 在同一直线上，确定与△AOB 位似的三角形为△GOH ，利用锐角三角函数找出相应规律得出OG=6x ，再由相似三角形的性质求解即可．【详解】解：∵∠AOB ＝∠BOC ＝∠COD ＝…＝∠LOM ＝30°∴∠AOG ＝180°，∠BOH ＝180°，∴A 、O 、G 在同一直线上，B 、O 、H 在同一直线上，∴与△AOB 位似的三角形为△GOH ，设OA =x ，则OB=1cos30OA x ==︒，∴OC=24cos303OB x x ==︒，∴OD=3cos30OC x ==︒，…∴OG=6x ，∴6OG OA =，∴12643GOH AOB S S ⎛⎫== ⎪⎝⎭ ，∵1AOB S = ，∴643GOH S ⎛⎫= ⎪⎝⎭ ，故选：C ．【点睛】题目主要考查利用锐角三角函数解三角形，找规律问题，相似三角形的性质等，理解题意，找出相应边的比值规律是解题关键．二．填空题13．（2022·贵州黔东南）如图，折叠边长为4cm 的正方形纸片ABCD ，折痕是DM ，点C 落在点E 处，分别延长ME 、DE 交AB 于点F 、G ，若点M 是BC 边的中点，则FG =______cm．【答案】53【分析】根据折叠的性质可得DE =DC =4，EM =CM =2，连接DF ，设FE =x ，由勾股定理得BF ，DF ，从而求出x 的值，得出FB ，再证明FEG FBM ∆∆ ，利用相似三角形对应边成比例可求出FG ．【详解】解：连接,DF 如图，∵四边形ABCD 是正方形，∴4,90.AB BC CD DA A B C CDA ︒====∠=∠=∠=∠=∵点M 为BC 的中点，∴114222BM CM BC ===⨯=由折叠得，2,4,ME CM DE DC ====∠90,DEM C ︒=∠=∴∠90DEF ︒=，90,FEG ∠=︒设,FE x =则有222DF DE EF =+∴2224DF x =+又在Rt FMB ∆中，2,2FM x BM =+=，∵222FM FB BM =+∴FB ==∴4AF AB FB =-=在Rt DAF ∆中，222,DA AF DF +=∴2224(44,x +=+解得，124,83x x ==-（舍去）∴4,3FE =∴410233FM FE ME =+=+=∴83FB ==∵∠90DEM ︒=∴∠90FEG ︒=∴∠,FEG B =∠又∠.GFE MFB =∠∴△FEG FBM∆ ∴,FG FE FM FB=即4310833FG =∴5,3FG =故答案为：53【点睛】本题主要考查了正方形的性质，折叠的性质，勾股定理，相似三角形的判定与性质，正确作出辅助线是解答本题的关键．14．（2022·上海）如图，在△ABC 中，∠A =30°，∠B =90°，D 为AB 中点，E 在线段AC 上，AD DE AB BC=，则AE AC =_____．【答案】12或14【分析】由题意可求出12DE BC =，取AC 中点E 1，连接DE 1，则DE 1是△ABC 的中位线，满足112DE BC =，进而可求此时112AE AC =，然后在AC 上取一点E 2，使得DE 1＝DE 2，则212DE BC =，证明△DE1E2是等边三角形，求出E1E2＝14AC ，即可得到214AE AC =，问题得解．【详解】解：∵D 为AB中点，∴12AD DE AB BC ==，即12DE BC =，取AC 中点E 1，连接DE 1，则DE 1是△ABC 的中位线，此时DE 1∥BC ，112DE BC =，∴112AE AD AC AB ==，在AC 上取一点E 2，使得DE 1＝DE 2，则212DE BC =，∵∠A =30°，∠B =90°，∴∠C =60°，BC ＝12AC ，∵DE 1∥BC ，∴∠DE1E2=60°，∴△DE1E2是等边三角形，∴DE 1＝DE 2＝E1E2＝12BC ，∴E1E2＝14AC ，∵112AE AC =，∴214AE AC =，即214AE AC =，综上，AE AC 的值为：12或14，故答案为：12或14．【点睛】本题考查了三角形中位线的性质，平行线分线段成比例，等边三角形的判定和性质以及含30°角的直角三角形的性质等，根据12DE BC =进行分情况求解是解题的关键．15．（2022·北京）如图，在矩形ABCD 中，若13,5,4AF AB AC FC ===，则AE 的长为_______．【答案】1【分析】根据勾股定理求出BC ，以及平行线分线段成比例进行解答即可．【详解】解：在矩形ABCD 中：AD BC ∥，90ABC ∠=︒，∴14AE AF BC FC ==，4BC =，∴144AE =，∴1AE =，故答案为：1．【点睛】此题考查了勾股定理以及平行线分线段成比例，掌握平行线分线段成比例是解题的关键．16．（2022·江苏常州）如图，在Rt ABC △中，90C ∠=︒，9AC =，12BC =．在Rt DEF 中，90F ∠=︒，3DF =，4EF =．用一条始终绷直的弹性染色线连接CF ，Rt DEF 从起始位置（点D 与点B 重合）平移至终止位置（点E 与点A 重合），且斜边DE 始终在线段AB 上，则Rt ABC △的外部被染色的区域面积是______．【答案】28【分析】过点F 作AB 的垂线交于G ，同时在图上标出,,M N F '如图，需要知道的是Rt ABC 的被染色的区域面积是MNF F S '梯形，所以需要利用勾股定理，相似三角形、平行四边形的判定及性质，求出相应边长，即可求解．【详解】解：过点F 作AB 的垂线交于G ，同时在图上标出,,M N F '如下图：90C ∠=︒ ，9AC =，12BC =，15AB ∴==，在Rt DEF 中，90F ∠=︒，3DF =，4EF =．5DE ∴==，15510AE AB DE =-=-= ，//,EF AF EF AF ''= ，∴四边形AEFF '为平行四边形，10AE FF '∴==，11622DEF S DF EF DE GF =⋅=⋅= ，解得：125GF =， //DF AC ，,DFM ACM FDM CAM ∴∠=∠∠=∠，DFM ACM ∴ ∽，13DM DF AM AC ∴==，1115344DM AM AB ∴===，//BC AF ' ，同理可证：ANF DNC ' ∽，13AF AN BC DN '∴==，345344DN AN AB ∴===，451530444MN DN DM ∴=-=-=，Rt ABC 的外部被染色的区域面积为130121028245MNF F S '⎛⎫=⨯+⨯= ⎪⎝⎭梯形，故答案为：28．【点睛】本题考查了直角三角形，相似三角形的判定及性质、勾股定理、平行四边形的判定及性质，解题的关键是把问题转化为求梯形的面积．17．（2022·广西）数学兴趣小组通过测量旗杆的影长来求旗杆的高度，他们在某一时刻测得高为2米的标杆影长为1.2米，此时旗杆影长为7.2米，则旗杆的高度为______米．【答案】12【分析】根据同时、同地物高和影长的比不变，构造相似三角形，然后根据相似三角形的性质解答．【详解】解：设旗杆为AB ，如图所示：根据题意得：ABC DEF ∆∆ ，∴DE EF AB BC= ∵2DE =米， 1.2EF =米，7.2BC =米，∴2 1.2=7.2AB 解得：AB =12米．故答案为：12．【点睛】本题考查了中心投影、相似三角形性质的应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．18．（2022·广东深圳）已知ABC 是直角三角形，90,3,5,B AB BC AE ∠=︒===连接CE 以CE 为底作直角三角形CDE 且,CD DE =F 是AE 边上的一点，连接BD 和,BF BD 且45,FBD ∠=︒则AF 长为______．【分析】将线段BD 绕点D 顺时针旋转90︒，得到线段HD ，连接BH ，HE ，利用SAS 证明EDH CDB ∆≅∆，得5EH CB ==，90HED BCD ∠=∠=︒，从而得出////HE DC AB ，则ABF EHF ∆∆∽，即可解决问题．【详解】解：将线段BD 绕点D 顺时针旋转90︒，得到线段HD ，连接BH ，HE ，BDH ∴∆是等腰直角三角形，又EDC ∆ 是等腰直角三角形，HD BD ∴=，EDH CDB ∠=∠，ED CD =，()EDH CDB SAS ∴∆≅∆，5EH CB ∴==，90HED BCD ∠=∠=︒，90EDC ∠=︒ ，90ABC ∠=︒，////HE DC AB ∴，,ABF EHF BAF HEF ∴∠=∠∠=∠，ABF EHF ∴∆∆∽，∴==-AB AF AF EH EF AE AF ，AE =∴35=AF ∴=，【点睛】本题主要考查了等腰直角三角形的性质，全等三角形的判定与性质，相似三角形的判定与性质等知识，解题的关键是作辅助线构造全等三角形．19．（2022·广西河池）如图，把边长为1：2的矩形ABCD 沿长边BC ，AD 的中点E ，F 对折，得到四边形ABEF ，点G ，H 分别在BE ，EF 上，且BG ＝EH ＝25BE ＝2，AG 与BH 交于点O ，N 为AF 的中点，连接ON ，作OM ⊥ON 交AB 于点M ，连接MN ，则tan ∠AMN ＝_____．【答案】58##0.625【分析】先判断出四边形ABEF 是正方形，进而判断出△ABG ≌△BEH ，得出∠BAG =∠EBH ，进而求出∠AOB =90°，再判断出△AOB ~△ABG ，求出OA OB ==△OBM ～△OAN ，求出BM =1，即可求出答案．【详解】解：∵点E ，F 分别是BC ，AD 的中点，∴11,22AF AD BE BC ==，∵四边形ABCD 是矩形，∴∠A =90°，AD ∥BC ，AD =BC ，∴12AF BE AD ==，∴四边形ABEF 是矩形，由题意知，AD =2AB ，∴AF =AB ，∴矩形ABEF 是正方形，∴AB =BE ，∠ABE =∠BEF =90°，∵BG =EH ，∴△ABG≌△BEH（SAS），∴∠BAG=∠EBH，∴∠BAG+∠ABO=∠EBH+∠ABO=∠ABG=90°，∴∠AOB=90°，∵BG＝EH＝25BE＝2，∴BE=5，∴AF=5，∴AG==∵∠OAB=∠BAG，∠AOB=∠ABG，∴△AOB∽△ABG，∴OA OB ABAB BG AG==，即52OA OB==∴OA OB==∵OM⊥ON，∴∠MON=90°=∠AOB，∴∠BOM=∠AON，∵∠BAG+∠FAG=90°，∠ABO+∠EBH=90°，∠BAG=∠EBH，∴∠OBM=∠OAN，∴△OBM～△OAN，∴OB BM OA AN=，∵点N是AF的中点，∴1522AN AF==，52BM=，解得：BM=1，∴AM=AB-BM=4，∴552tan48ANAMNAM∠===．故答案为：5 8【点睛】此题主要考查了矩形性质，正方形性质和判定，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，求出BM 是解本题的关键．20．（2022·内蒙古赤峰）如图，为了测量校园内旗杆AB 的高度，九年级数学应用实践小组，根据光的反射定律，利用镜子、皮尺和测角仪等工具，按以下方式进行测量：把镜子放在点O 处，然后观测者沿着水平直线BO 后退到点D ，这时恰好能在镜子里看到旗杆顶点A ，此时测得观测者观看镜子的俯角α=60°，观测者眼睛与地面距离CD =1.7m ，BD =11m ，则旗杆AB 的高度约为_________m ． 1.7≈）【答案】17【分析】如图容易知道CD ⊥BD ，AB ⊥BD ，即∠CDO =∠ABO =90°．由光的反射原理可知∠COD =∠AOB =60°，这样可以得到△COD ∽△AOB ，然后利用对应边成比例就可以求出AB ．【详解】解：由题意知∠COD =∠AOB =60°，∠CDE =∠ABE =90°，∵CD =1.7m ，∴OD =60CD tan =︒≈1(m)，∴OB =11-1=10(m)，∴△COD ∽△AOB ．∴CD OD AB OB =，即1.7110AB =，∴AB =17(m)，答：旗杆AB 的高度约为17m ．故答案为：17．【点睛】本题考查了解直角三角形的应用，相似三角形的应用，本题只要是把实际问题抽象到相似三角形中，利用相似三角形的性质就可以求出结果．21．（2022·湖北鄂州）如图，在边长为6的等边△ABC 中，D 、E 分别为边BC 、AC 上的点，AD 与BE 相交于点P ，若BD =CE =2，则△ABP 的周长为 _____．【答案】6+【分析】如图所示，过点E 作EF ⊥AB 于F ，先解直角三角形求出AF ，EF ，从而求出BF ，利用勾股定理求出BE 的长，证明△ABD ≌△BCE 得到∠BAD =∠CBE ，AD =BE ，再证明△BDP ∽△ADB ，得到62BP PD==，即可求出BP ，PD ，从而求出AP ，由此即可得到答案．【详解】解：如图所示，过点E 作EF ⊥AB 于F ，∵△ABC 是等边三角形，∴AB =BC ，∠ABD =∠BAC =∠BCE =60°，∵CE =BD =2，AB =AC =6，∴AE =4，∴cos 2sin AF AE EAF EF AE EAF =⋅∠==⋅∠=，，∴BF =4，∴BE =又∵BD =CE ，∴△ABD ≌△BCE （SAS ），∴∠BAD =∠CBE ，AD =BE ，又∵∠BDP =∠ADB ，∴△BDP ∽△ADB ，∴BD BP DP AD AB BD==，62BP PD==，∴BP PD =∴AP AD AP =-=，∴△ABP 的周长=6AB BP AP ++=故答案为：6+【点睛】本题主要考查了等边三角形的性质，解直角三角形，勾股定理，相似三角形的性质与判定，全等三角形的性质与判定，正确作出辅助线是解题的关键．22．（2022·山东潍坊）《墨子·天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，正方形ABCD 的面积为4，以它的对角线的交点为位似中心，作它的位似图形A B C D ''''，若:2:1A B AB =''，则四边形A B C D ''''的外接圆的周长为___________．【答案】【分析】根据正方形ABCD 的面积为4，求出2AB =，根据位似比求出4A B ''=，周长即可得出；【详解】解：正方形ABCD 的面积为4，∴2AB =，:2:1A B AB ''=，∴4A B ''=，∴A C ''==所求周长=；故答案为：．【点睛】本题考查位似图形，涉及知识点：正方形的面积，正方形的对角线，圆的周长，解题关键求出正方形ABCD 的边长．23．（2022·内蒙古包头）如图，在Rt ABC 中，90ACB ∠=︒，3AC BC ==，D 为AB 边上一点，且BD BC =，连接CD ，以点D 为圆心，DC 的长为半径作弧，交BC 于点E （异于点C ），连接DE ，则BE的长为___________．【答案】3##3-+【分析】过点D 作DF ⊥BC 于点F ，根据题意得出DC DE =，根据等腰三角形性质得出CF EF =，根据90ACB ∠=︒，3AC BC ==，得出AB =CF x =，则3BF x =-，证明DF AC ，得出BF BDCF AD=，列出关于x 的方程，解方程得出x 的值，即可得出3BE =．【详解】解：过点D 作DF ⊥BC 于点F ，如图所示：根据作图可知，DC DE =，∵DF ⊥BC ，∴CF EF =，∵90ACB ∠=︒，3AC BC ==，∴AB ===∵3BD BC ==，∴3AD =，设CF x =，则3BF x =-，∵90ACB ∠=︒，∴AC BC ⊥，∵DF BC ⊥，∴DF AC ，∴BF BDCF AD =，即3x x -=，解得：x =，∴226CE x ===-，∴3363BE CE =-=-+=．故答案为：3．【点睛】本题主要考查了等腰三角形的性质和判定，勾股定理，平行线分线段成比例定理，平行线的判定，作出辅助线，根据题意求出CF 的长，是解题的关键．24．（2022·江苏泰州）如图上，Δ,90,8,6,ABC C AC BC ∠=== 中O 为内心，过点O 的直线分别与AC 、AB 相交于D 、E ，若DE=CD+BE ，则线段CD 的长为__________.【答案】2或12##12或2【分析】分析判断出符合题意的DE 的情况，并求解即可；【详解】解：①如图，作//DE BC ，OF BC OG AB ⊥⊥，，连接OB ，则OD ⊥AC ，∵//DE BC ，∴OBF BOE ∠=∠∵O 为ABC ∆的内心，∴OBF OBE ∠=∠，∴BOE OBE ∠=∠∴BE OE =，同理，CD OD =，∴DE=CD+BE ，10AB ===∵O 为ABC ∆的内心，∴OF OD OG CD ===，∴BF BG AD AG==，∴6810AB BG AG BC CD AC CD CD CD =+=-+-=-+-=∴2CD =②如图，作DE AB ⊥，由①知，4BE =，6AE =，∵ACB AED CAB EAD ∠=∠∠=∠，∴ABC ADE ∆∆ ∴AB ADAC AE=∴1061582AB AE AD AC ⋅⨯===∴151822CD AC AD =-=-=∵92DE ===∴19422DE BE CD =+=+=∴12CD =故答案为：2或12．【点睛】本题主要考查三角形内心的性质、勾股定理、三角形的相似，根据题意正确分析出符合题意的情况并应用性质定理进行求解是解题的关键．25．（2022·黑龙江绥化）如图，60AOB ∠=︒，点1P 在射线OA 上，且11OP =，过点1P 作11PK OA ⊥交射线OB 于1K ，在射线OA 上截取12PP ，使1211PPPK =；过点2P 作22P K OA ⊥交射线OB 于2K ，在射线OA 上截取23P P ，使2322P P P K =.按照此规律，线段20232023P K 的长为________．20221【分析】解直角三角形分别求得11PK ，22P K ，33P K ，……，探究出规律，利用规律即可解决问题．【详解】解：11PK OA ⊥ ，11OPK ∴△是直角三角形，在11Rt OPK 中，60AOB ∠=︒，11OP =，12111tan 60PP PK OP ∴==⋅︒=11PK OA ⊥ ，22P K OA ⊥，1122PK P K ∴∥，2211OP K OPK ∴△∽△，222111P K OP PK OP ∴=，=221P K ∴，同理可得：2331P K =+，3441P K =，……，11n n n P K -∴=，2022202320231P K ∴=，20221．【点睛】本题考查了图形的规律，解直角三角形，平行线的判定，相似三角形的判定与性质，解题的关键是学会探究规律的方法．26．（2022·黑龙江）如图，在平面直角坐标系中，点1A ，2A ，3A ，4A ……在x 轴上且11OA =，212OA OA =，322OA OA =，432OA OA =……按此规律，过点1A ，2A ，3A ，4A ……作x轴的垂线分别与直线y =交于点1B ，2B ，3B ，4B ……记11OA B ，22OA B △，33 OA B ，44 OA B ……的面积分别为1S ，2S ，3S ，4S ……，则2022S =______．【答案】2【分析】先求出11A B =，可得11OA B S =112233n n A B A B A B A B ⋯⋯∥∥∥∥，从而得到11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △，再利用相似三角形的性质，可得11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231:2:2:2::2n ，即可求解．【详解】解：当x =1时，y =，∴点(1B ，∴11A B =∴11112OA B S =⨯= ，∵根据题意得：112233n n A B A B A B A B ⋯⋯∥∥∥∥，∴11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △，∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ：……∶n n OA B S = OA 12∶OA 22∶OA 32∶……∶OAn 2，∵11OA =，212OA OA =，322OA OA =，432OA OA =，……，∴22OA =，2342OA ==，3482OA ==，……，12n n OA -=，∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231246221:2:2:2::21:2:2:2::2n n --= ，∴11222n n n OA B OA B S S -= ，∴220222202222S ⨯-==故答案为：2【点睛】本题主要考查了图形与坐标的规律题，相似三角形的判定和性质，明确题意，准确得到规律，是解题的关键．27．（2022·广西）如图，在正方形ABCD 中，AB =，对角线,AC BD 相交于点O ．点E 是对角线AC 上一点，连接BE ，过点E 作EF BE ⊥，分别交,CD BD 于点F 、G ，连接BF ，交AC 于点H ，将EFH △沿EF 翻折，点H 的对应点H '恰好落在BD 上，得到EFH '△若点F 为CD 的中点，则EGH '△的周长是_________．【答案】5+【分析】过点E 作PQ //AD 交AB 于点P ，交DC 于点Q ，得到BP =CQ ，从而证得BPE ≌EQF △，得到BE =EF ，再利用BC =F 为中点，求得BF ==BE EF ===，再求出2EO ==，再利用AB //FC ，求出ABH CFH △∽△21AH CH ==，求得216833AH =⨯=，18833CH =⨯=，从而得到EH =AH -AE =1610233-=，再求得EOB GOE △∽△得到21242OG ===，求得EG OG =1，过点F 作FM ⊥AC 于点M ，作FN ⊥OD 于点N ，求得FM =2，MH =23，FN =2，证得Rt FH N '△≌Rt FMH 得到23H N MH '==，从而得到ON =2，NG =1，25133GH '=+=，从而得到答案．【详解】解：过点E 作PQ //AD 交AB 于点P ，交DC 于点Q ，∵AD //PQ ，∴AP =DQ ，BPQ CQE ∠=∠，∴BP =CQ ，∵45ACD ∠=︒，∴BP =CQ =EQ ，∵EF ⊥BE ，∴90PEB FEQ ∠+∠=︒∵90PBE PEB ∠+∠=︒∴PBE FEQ ∠=∠，在BPE 与EQF △中BPQ FQE PB EQPBE FEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BPE ≌EQF △，∴BE =EF ，又∵BC AB ==F 为中点，∴CF =∴BF ==∴BE EF ===，又∵4BO ==，∴2EO ==，∴AE =AO -EO =4-2=2，∵AB //FC ，∴ABH CFH △∽△，∴AB AH CF CH=，21AH CH ==，∵8AC ==， ∴216833AH =⨯=，18833CH =⨯=，∴EH =AH -AE =1610233-=，∵90BEO FEO ∠+∠=︒，+90BEO EBO ∠∠=︒，∴FEO EBO ∠=∠，又∵90EOB EOG ∠=∠=︒，∴EOB GOE△∽△∴EG OG OE BE OE OB==，21242OG ===，∴EG OG =1，过点F 作FM ⊥AC 于点M ，∴FM=MC 2=，∴MH =CH -MC =82233-=，作FN ⊥OD 于点N ，2,FN ==，在Rt FH N '△与Rt FMH 中FH FH FN FM'=⎧⎨=⎩∴Rt FH N '△≌Rt FHM∴23H N MH '==，∴ON =2，NG =1，∴25133GH '=+=，∴10533EGH C EH EG GH EH EG GH '''=++=++=△，故答案为：【点睛】本题考查了正方形的性质应用，重点是与三角形相似和三角形全等的结合，熟练掌握做辅助线是解题的关键．28．（2022·辽宁）如图，在正方形ABCD 中，E 为AD 的中点，连接BE 交AC 于点F ．若6AB =，则AEF 的面积为___________．【答案】3【分析】由正方形的性质可知1113222AE AD AB BC ====，//AD BC ，则有AEF CBF ∽△△，然后可得12EF AE BF BC ==，进而问题可求解．【详解】解：∵四边形ABCD 是正方形，6AB =，∴6AD BC AB ===，//AD BC ，∴AEF CBF ∽△△，∴EF AE BF BC=，∵E 为AD 的中点，∴1113222AE AD AB BC ====，∴12EF AE BF BC ==，192ABE S AE AB =⋅= ，∴13EF BE =，∴133AEF ABE S S == ；故答案为3．【点睛】本题主要考查正方形的性质及相似三角形的性质与判定，熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键．29．（2022·贵州贵阳）如图，在四边形ABCD 中，对角线AC ，BD 相交于点E ，6cm AC BC ==，90ACB ADB ∠=∠=︒．若2BE AD =，则ABE △的面积是_______2cm ，AEB ∠=_______度．【答案】 36-36- 112.5【分析】通过证明ADE BCE ，利用相似三角形的性质求出23m AE =，263m CE =-，再利用勾股定理求出其长度，即可求三角形ABE 的面积，过点E 作EF ⊥AB ，垂足为F ，证明AEF 是等腰直角三角形，再求出AE CE =，继而证明()Rt BCE Rt BFE HL ≅ ，可知122.52EBF EBC ABC ∠=∠=∠=︒，利用外角的性质即可求解．【详解】90,ACB ADB AED BEC ∠=∠=︒∠=∠ ，ADE BCE ∴ ，AD AE BC BE∴=，6,2BC AC BE AD === ，设,2AD m BE m ==，62m AE m∴=，23m AE ∴=，263m CE ∴=-，在Rt BCE 中，由勾股定理得222BC CE BE +=，22226(6)(2)2m m ∴+-=，解得236m =-或236m =+ 对角线AC ，BD 相交于点E ，236m ∴=-，12AE ∴=-，6CE ∴=，∴(2111263622ABE S AE BC =⋅⋅=⨯-⨯=- ，过点E 作EF ⊥AB ，垂足为F ，90,ACB AC BC ∠=︒= ，45BAC ABC AEF ∴∠=∠=︒=∠，6AE AF AE CE ∴====，BE BE = ，()Rt BCE Rt BFE HL ∴≅ ，122.52EBF EBC ABC ∴∠=∠=∠=︒，112.5AEB ACB EBC ∴∠=∠+∠=︒，故答案为：36-，112.5．【点睛】本题考查了相似三角形的判定和性质，勾股定理，等腰直角三角形的判定和性质，全等三角形的判定和性质及三角形外角的性质，熟练掌握知识点是解题的关键．三．解答题30．（2022·河北）如图，某水渠的横断面是以AB 为直径的半圆O ，其中水面截线MN AB ∥．嘉琪在A 处测得垂直站立于B 处的爸爸头顶C 的仰角为14°，点M 的俯角为7°．已知爸爸的身高为1.7m ．(1)求∠C 的大小及AB 的长；(2)请在图中画出线段DH ，用其长度表示最大水深（不说理由），并求最大水深约为多少米（结果保留小数点后一位）．（参考数据：tan 76︒取4 4.1）【答案】(1)=76C ∠︒， 6.8(m)AB =(2)见详解，约6.0米【分析】（1）由水面截线MN AB ∥可得BC AB ⊥，从而可求得76C ∠=︒，利用锐角三角形的正切值即可求解．（2）过点O 作O H M N ⊥，交MN 于D 点，交半圆于H 点，连接OM ，过点M 作MG ⊥OB 于G ，水面截线MN AB ∥，即可得DH 即为所求，由圆周角定理可得14BOM ∠=︒，进而可得ABC OGM ，利用相似三角形的性质可得4OG GM =，利用勾股定理即可求得GM 的值，从而可求解．(1)解：∵水面截线MN AB∥BC AB ∴⊥，90ABC ∴∠=︒，90=76C CAB ∴∠=︒-∠︒，在t R ABC 中，90ABC ∠=︒， 1.7BC =，tan 76 1.7AB AB BC ∴︒==，解得 6.8(m)AB ≈．(2)过点O 作O H M N ⊥，交MN 于D 点，交半圆于H 点，连接OM ，过点M 作MG ⊥OB 于G ，如图所示：水面截线MN AB ∥，OH AB ⊥，DH MN ∴⊥，GM OD =，DH ∴为最大水深，7BAM ∠=︒ ，214BOM BAM ∴∠=∠=︒，90ABC OGM ∠=∠=︒ ，且14BAC ∠=︒，ABC OGM ∴ ，OG MG AB CB ∴=，即6.8 1.7OG MG =，即4OG GM =，在Rt OGM △中，90OGM ∠=︒， 3.42AB OM =≈，222OG GM OM ∴+=，即2224(3.4)GM GM +=（），解得0.8GM ≈，= 6.80.86DH OH OD ∴-=-≈，∴最大水深约为6.0米．【点睛】本题考查了解直角三角形，主要考查了锐角三角函数的正切值、圆周角定理、相似三角形的判定及性质、平行线的性质和勾股定理，熟练掌握解直角三角形的相关知识是解题的关键．31．（2022·吉林）下面是王倩同学的作业及自主探究笔记，请认真阅读并补充完整．【作业】如图①，直线12l l ∥，ABC 与DBC △的面积相等吗？为什么？解：相等．理由如下：设1l 与2l 之间的距离为h ，则12ABC S BC h =⋅ ，12DBC S BC h =⋅△．∴ABC DBC S S = ．【探究】(1)如图②，当点D 在1l ，2l 之间时，设点A ，D 到直线2l 的距离分别为h ，h '，则ABC DBC S h S h ='△△．证明：∵ABC S(2)如图③，当点D 在1l ，2l 之间时，连接AD 并延长交2l 于点M ，则ABC DBC S AM S DM =△△．证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒，∴AE ∥ ．∴AEM △∽ ．∴AE AM DF DM =．由【探究】（1）可知ABC DBC S S =△△ ，∴ABC DBC S AM S DM =△△．(3)如图④，当点D 在2l 下方时，连接AD 交2l 于点E ．若点A ，E ，D 所对应的刻度值分别为5，1.5，0，ABC DBC S S △△的值为．【答案】(1)证明见解析(2)证明见解析(3)73【分析】（1）根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅ ，由此即可得证；（2）过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，先根据平行线的判定可得AE DF ，再根据相似三角形的判定可证AEM DFM ~ ，根据相似三角形的性质可得AE AM DF DM=，然后结合【探究】（1）的结论即可得证；（3）过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，先根据相似三角形的判定证出AME DNE ~ ，再根据相似三角形的性质可得73AM AE DN DE ==，然后根据三角形的面积公式可得12ABC S BC AM =⋅ ，12DBC S BC DN =⋅ ，由此即可得出答案．(1)证明：12ABC S BC h =⋅ ，12DBC BC h S '=⋅ ，ABC DBC S h S h ∴='．(2)证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒，AE DF ∴∥．AEM DFM ~∴ ．AE AM DF DM∴=．由【探究】（1）可知ABC DBC S AE S DF= ，ABC DBC S AM S DM ∴= ．(3)解：过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，则90AME DNE ∠=∠=︒，AM DN ∴ ，AME DNE ∴~ ，AM AE DN DE∴=，点,,A E D 所对应的刻度值分别为5，1.5，0，5 1.5 3.5AE ∴=-=， 1.5DE =，3.571.53AM DN ∴==，又12ABC S BC AM =⋅ ，12DBC S BC DN =⋅ ，73ABCDBC S AM S DN =∴= ，故答案为：73．【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点，熟练掌握相似三角形的判定与性质是解题关键．32．（2022·山东青岛）如图，在Rt ABC △中，90,5cm,3cm ACB AB BC ∠=︒==，将ABC 绕点A 按逆时针方向旋转90︒得到ADE ，连接CD ．点P 从点B 出发，沿BA 方向匀速运动，速度为1cm/s ；同时，点Q 从点A 出发，沿AD 方向匀速运动，速度为1cm/s ．PQ 交AC 于点F ，连接,CP EQ ．设运动时间为(s)(05)t t <<．解答下列问题：(1)当EQ AD ⊥时，求t 的值；(2)设四边形PCDQ 的面积为()2cm S ，求S 与t 之间的函数关系式；(3)是否存在某一时刻t ，使PQ CD ∥？若存在，求出t 的值；若不存在，请说明理由．【答案】(1)16s 5(2)213714210S t t =-+(3)存在，65s 29t =【分析】（1）利用AQE AED △∽△得AQ AE AE AD =，即445t =，进而求解；（2）分别过点C ，P 作,CM AD PN BC ⊥⊥，垂足分别为M ，N ，证ABC CAM △∽△得，AB BC AC CA AM CM ==，求得121655AM CM ==，再证BPN BAC △∽△得BP PN BA AC=，得出45PN t =，根据ABC ACD APQ BPC PCDQ S S S S S S ==+-- 四边形即可求出表达式；（3）当PQ CD ∥时AQP ADC ∠=∠，易证APQ MCD △∽△，得出AP AQ MC MD =，则5161355t t -=，进而求出t 值．(1)解：在Rt ABC △中，由勾股定理得，4AC ===∵ABC 绕点A 按逆时针方向旋转90︒得到ADE。

中考数学第一轮复习三角形

正整数，则这样的三角形个数为( B ) A．2 B．3 C．5 D．13
类型之二三角形的重要线段的应用命题角度： 1．三角形的中线、角平分线、高 2．三角形的中位线
[2011·成都] 如图 19－1，在△ABC 中，D、E 分别是边 AC、 BC 的中点，若 DE＝4，则 AB＝___8_____.
1．三条边对应相等的两个三角形全等(简记为________)S．SS 2．两个角和它们的夹边对应相等的两个三角形全等(简记为________)． ASA3．两个角和其中一个角的对边对应相等的两个三角形全等(简记为
________)．
4．两条边和它们的夹角对应相等的两个三角形全等(简记为________)．
命题角度： 1．等腰三角形的性质 2．等腰三角形“三线合一”的性质 3．等腰三角形两腰上的高(中线)、两底角的平分线的性质
[2011·株洲] 如图 21－1，△ABC 中，AB＝AC，∠A＝36°， AC 的垂直平分线交 AB 于 E，D 为垂足，连接 EC.
__5_0_°____.
图 19－2
全等三角形
考点1 全等图形及全等三角形
1．能够完全_____重__合_的两个图形称为全等形，全等图形的形状和 ______大__小都相同．
2．能够完全______重_合_的两个三角形叫全等三角形． [注意] 完全重合有两层含义：(1)图形的形状相同；(2)图形的大小相等
大于
[总结] 任意三角形中，最多有三个锐角，最少有两个锐角，最多有一个钝
角，最多有一个直角．
互余
类型之一三角形三边的关系
命题角度： 1．利用三角形三边的关系判断三条线段能否组成三角形 2．利用三角形三边的关系求字母的取值范围 3．三角形的稳定性

中考数学几何模型专题专题三—三角形

专题三三角形模型8 “8字”形模型展现基础模型怎么用?1.找模型两条相交的线段构成含对顶角的两个三角形,简称“有交点，想8字”2.用模型“8字”型的实质是利用三角形内角和定理进行角度转化来解题∠结论分析结论1:∠A+∠B=∠C+∠D证明:AC与BD相交于点0 , 连接AB,CD,在∠ABO中,∠.A+∠B+∠.AOB= 180°在OCD0中，∠C+∠D+∠COD= 180°因为∠AOB=∠COD(对顶角相等),所以∠A+∠B=∠C+∠D.拓展延伸角度和相等,是解决角度转化的重要思想。

“8字”型虽简单,但往往在几何综合题中推导角度时用到.∠模型拓展典例小试例1如图,线段AB , CD,EF两两相交,交点分别为G,H,I,连接AC,BE,DF，则∠A+∠B+∠C+∠D+∠E+∠F的度数是（）出现多个模型,分离模型,逐个计算A.180°B.360°C.540°D.720°考什么?对顶角相等,三角形的内角和例2如图,A,B,C,D,E是同一平面上的点,F是AB上一点,则∠A+∠B+∠C+∠D+∠E+∠DFE的度数是( )试着转化到一个四边形中,利用内角和求解A.180°B.360°C.540°D.720°考什么?对顶角相等,四边形的内角和思路点拨“8字”型能得到角度和的关系,在题目未给出具体角度的情况下,考虑将所求角度和转化到同一个多边形中,再利用多边形内角和求解.实战演练1.如图,AB∠BD,AC∠CD,∠A=30°,则∠.D的度数为____.2.一副三角板如图摆放,其中一块三角板的直角边EF落在另.一块三角板的斜边AC上,边BC与DF交于点0,则∠BOD的度数是____。

模型9 “燕尾”型模型展现基础模型怎么用?1．找模型遇到凹四边形的角度问题，考虑用“燕尾”型基础模型1 2.用模型通过“燕尾”型把“凹”的角转换成三个内角之和结论分析结论1:∠BDC=∠A+∠B+∠C证法1:如解图,延长BD交AC于点E.∠∠BEC是∠ABE的外角∠∠BEC=∠A+∠B又∠∠BDC是∠CDE的外角，∠BDC=∠BEC+∠C=∠A+∠B+∠C证法2:如解图，连接AD并延长，则∠1=∠B+∠3,∠2=∠C+∠4，∠BDC=∠1+∠2=∠B+∠3+∠C+∠4=∠A+∠B+∠C.∠∠BDC=∠A+∠B+∠C.结论2:AB+AC>BD+CD证明:如解图,延长BD交AC于点E，则AB+AE>BD+DE , DE+CE>CD，∠AC=AE+CE，∠AB+AC=AB+AE+CE>BD+DE+CE>BD+CD.巧学巧记简记:“凹角等于凸角之和”.拓展延伸也可以连接BC,使用三角形内角和定理来证明,同学们可以试试哦.:AOBAOCS S BD =:AOB COBS S AE =:BOC AOCSSBF =怎么用? 1．找模型遇到共边的两个三角形的面积相关问题,考虑用“燕尾”型基础模型2 2.用模型通过模型将面积问题转化为边的问题满分技法燕尾相邻的两个三角形共底不等高,常根据三角形的面积公式“12×底×高”可推导“共底不等高”的三角形的面积比即为应高的比. 结论分析结论3:∠::;AOBAOCSSBD CD =证明:如解图,分别过点B ,C 作 BH , CG 垂直于AD 交于点H , G ,在∠ABC 中,∠11,,22AOBAOCSAO BH S AO CG ==∠11:::,22AOB AOCSSAO BH AO CG BH CG ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭在∠BHD 和∠CGD 中，∠BHD =∠CGD =90°，∠BDH =∠CDG ， ∠∠BHD ∠∠CGD ，∠BH BDCG CD =， ∠::.AOBAOCSSBD CD =典例小试例1如图，已知点D ,E 分别在∠ABC 的边AB ,AC 上，将∠A 沿DE 折叠（点拨：折叠产生相等的角）使点A 落在点F 的位置，已知∠A =50°（点拨：∠F =50°），∠1=130°，则∠2的度数为（） A .130° B .120° C .150° D .140°考什么?三角形外角的性质,折叠的性质思路点拨折叠产生三角形全等，即ADE FDE ∆≅∆例2(2021河北)如图是可调躺椅示意图(数据如图),AE 与BD 的交点为C ,且∠A ,∠B ,∠E 保持不变.为了舒适,需调整∠D 的大小（点拨：先分析哪个角的大小随着D 点变化）,使∠EFD =110°，则图中∠D 应(填“增加”或“减少”)____度.考什么?三角形的内角和,对顶角相等实战实演1．将一副直角三角板如图放置,使两直角边重合,则∠1的度数为（） A .75° B .105° C .135° D .165°2.如图,是一块不规则的纸片,∠ABC =∠DEF = 80°,则∠A +∠C +∠D +∠F 的度数为( )A . 80°B . 160°C .240°D . 360°3.如图,∠A = 45°, ∠BDC = 135°，∠ABE =13∠ABD ，∠ACE =13∠ACD ,则∠BEC 的度数是（）A . 30°B .45°C .75°D .90°4．如图,矩形ABCD 中,点E ,F 分别是边AB ,BC 的中点,连接AF ,CE 交于点G ,若矩形ABCD 的面积为3,则四边形AGCD 的面积为________5.如图,在∠ABC 中,点 D ,E 分别在BC ,AC 边上,AD 与BE 交于点F ,若CD =3BD ,EC =4AE ,四边形CDFE 的面积是10,则∠ABC 的面积为________模型10 “风筝”型模型展现基础模型怎么用?1.找模型三角形折叠或者在角内部的角容易产生“风筝”型2.用模型三角形外角性质是解决问题的关键结论分析结论1:∠DBF+∠ECF= ∠A+∠F证明:如解图,连接AF，∠∠DBF是∠ABF的外角，∠∠DBF=∠BAF+∠BF A.∠∠FCE是∠ACF的外角，∠∠FCE=∠CAF+∠CF A，∠∠DBF+∠FCE=∠BAF+∠BF A+∠CAF+∠CF A=∠BAC+∠BFC，即∠DBF+∠ECF= ∠BAC+∠BFC.怎么用?1．找模型遇到与四边形(含对角线)相关的面积问题,考虑用“风筝”型2.用模型共边三角形面积问题可转化为线段问题例1如图,已知点D,E分别在∠ABC的边AB,AC上,将∠A沿DE 折叠(注：折叠性质产生相等的角,且有“风筝”型),使点A落在BC上,对应点为F,已知∠B=50°,∠C=60°,则么∠1+∠2的度数为（）A.100°B. 120°C. 140°D. 135°例2如图,∠ABC中,AB=BC,(等腰三角形)延长AB,AC至点D,E,点F是∠DAE内部一点,连接BF,CF.若∠ABC= 40°，∠F= 50°则∠DBF+∠ECF(寻找与求解有关的角度关系)的度数为（）A. 90°B. 100°C. 110°D. 120°实战实演1.如图,在平行四边形ABCD中,∠B= 50°,点E是BC上一点,将∠ABE沿边AE翻折得到∠AFE,延长BA至点M.若∠FEC=70°,则∠MAF的度数为（）A. 20° B．30° C. 40° D. 50°2.如图,在等边∠ABC中,点D 、E 分别是AB, BC边上一点,把∠BDE沿DE 折叠,使点B落在点B'处, DB', EB'分别交边AC于点F、G ,若∠ADF=70°,则∠AGE的度数为.3.如图,在四边形ABCD中,点E, F分别是AD, BC上的点,将四边形ABCD 沿直线EF折叠,若∠A =130°, ∠B =110°,则∠1+∠2的度数为.4.如图,在四边形ABCD中,对角线AC , BD相交于点E ,∠ADE , ∠ABE ,∠CDE 的面积分别为2,3,4,则∠BCE的面积为, AE : CE的值为.5.如图,平行四边形ABCD 的对角线交于点O,点E , F分别在BC , CD上,连接EF交OC于点G ,连接OE , OF , S∠OEF= S∠ODF =2S∠CEF, S∠BOE =6,则∠OCF的面积为；∠GCE的面为.模型11 角平分线模型模型展现基础模型结论分析结论: P A = PB , OA = OB , ∠APO = ∠BPO 证明:OP 平分∠MON , ∠∠AOP = ∠BOP ,在∠AOP 和∠BOP 中,90AOP BOPOAP OBP OPOP ∠＝∠∠＝∠＝＝∠∠AOP ∠∠BOP ,∠P A = PB , OA = OB , ∠APO = ∠BPO .怎么用? 1.找模型遇到图形中含角平分线,考虑用角平分线模型 2.用模型一般直接用角平分线的性质,或者构造等腰三角形或全等三角形解决线段和角度问题模型拓展满分技法角平分线性质:角平分线上的点到角两边的距离相等.碰到角平分线,常需要截相等线段来构造三角形全等或者作平行线产生等腰三角形来解决问题.例1(2021青海)如图,在四边形ABCD中, ∠A =90°, AD=3,BC=5,对角线BD平分∠ABC（点拨:考虑角平分线的性质）,则∠BCD 的面积为A .8B .7.5 C.15 D .无法确定考什么?角平分线的性质,三角形的面积计算公式思路点拨已知角平分线+边的垂直(直角),考虑作垂直,应用角平分线上的点到角两边的距离相等.例2(2019青岛)如图,BD是∠ ABC的角平分线, AE∠BD（点拨：角平分线的垂线产生全等），垂足为 F .若∠ABC =35°, ∠C =50°,则∠CDE 的度数为A .35°B .40°C .45°D .50°考什么?角平分线的性质,三角形的内角和,全等三角形的判定与性质,三角形的内外角关系,等腰三角形的性质思路点拨已知角平分线+角平分线的垂线,构造出等腰三角形.例3如图,已知∠ABC的平分线交AC于点E ,过点E作DE∠BC（点拨：过角平分线上的点作平行线产生等腰三角形及角相等）,交AB于点D.若∠A =70°, ∠AED =50°, BD =2,则BE长为.考什么?角平分线的性质,平行线的性质,三角形的内角和,等腰三角形的判定与性质,特殊角的三角函数值思路点拨已知角平分线+平行线,构造出等腰三角形.实战演练1.如图,已知三角形ABC 中, ∠ABC =60°, BD 是∠ABC的平分线, CE ∠AB于点E ,交BD于点F,若EF =4,则FC 的长为.2.如图,在∠ABC中, BD平分∠ABC,以点B为圆心,AB长为半径画弧,交BC于点E,连接DE,已知∠A=70° ,则∠CED的度数为______.3.如图,在∠ABC中,D,E分别是AB,AC的中点,CF平分∠ACB，交DE于点F,若AC=10,BC=12,则DF的长为________.4.如图,在矩形ABCD中,点E,F分别是BC,CD上的点,连接EF,AE,AF,若AE,AF恰好平分∠BEF,∠DFE.(1)则∠EAF的度数为__________;(2)求证:四边形ABCD是正方形;(3)若BE=EC=3,则DF的长为________.模型12 双角平分线模型模型展现基础模型111怎么用?1. 找模型三角形中,遇到两角平分线，考虑用双角平分线模型2.用模型通过三角形的内角和,内外角关系及角平分线的性质，建立两角之间的数量关系结论分析结论1:∠D=90°+12∠A证明:∠ BD平分∠ABC,CD平分∠ACB∠∠DBC=12∠ABC,∠DCB=12∠ACB∠∠D= 180°-(∠DBC+∠DCB)= 180°-(12∠ABC+12∠ACB)=180°-12(∠ABC+∠ACB)= 180°-12(180°-∠A)=90°+12∠A拓展延伸结论2的证明同学们可参考结论1和结论3,利用三角形的内外角关系进行证明.结论3：∠D =90°-12∠A证明:∠BD平分∠EBC,CD平分∠FCB，∠∠DBC=12∠EBC,∠DCB=12∠FCB，∠∠D= 180°-(∠DBC+∠DCB)= 180°-(12∠EBC +12∠FCB)= 180°-12(∠ACB+∠A+∠ABC+∠A)= 180°-12( 180°+∠A )= 90°-12∠A.模型拓展333111满分技法若将角平分线改为三等分角线,同样根据三角形的内角和及角度的倍数关系求解.典例小试例1 如图,在∠ABC中,∠ B=40°,CD∠AB于点D,∠BCD和∠BDC的平分线相交于点E（结合图形可知是双内角平分线型），则∠E的度数为（)A.105°B.110°C.140°D.145°考什么?角平分线的性质,三角形的内角和万唯中考几何模型例2如图,在四边形ABCD中，∠DAB的平分线与∠ABC的外角平分线相交于点P，且∠D+∠C=210°,则∠P=（）A. 10°B.15° C．30° D.40°考什么?角平分线的性质,三角形外角的性质,三角形的内角和思路点拨结合图形可知两角平分线分别为内角、外角平分线,根据“一内一外”角平分线结论求解即可.实战实演1.如图,在∠ABC中, ∠C= 110°，AE平分∠DAB,延长EA,交∠ABC的平分线于点F,则∠F= 。

初三中考一轮复习(15)解直角三角形题型分类含答案(全面非常好)

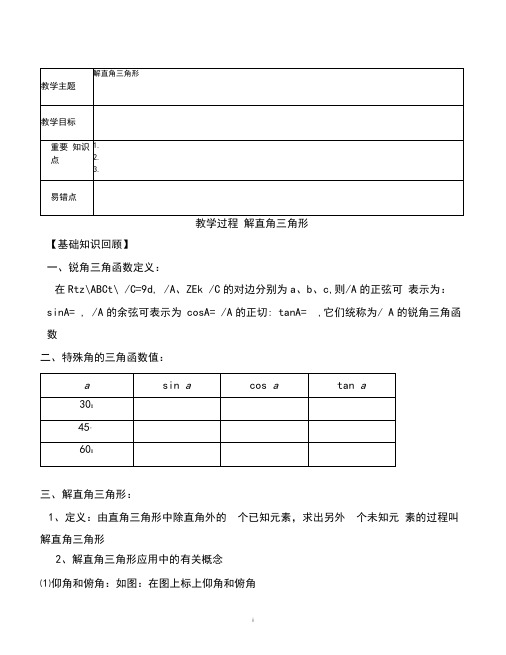
教学过程解直角三角形【基础知识回顾】一、锐角三角函数定义：在Rtz\ABCt\ /C=9d, /A、ZEk /C的对边分别为a、b、c,则/A的正弦可表示为：sinA= , /A的余弦可表示为cosA= /A的正切: tanA= ,它们统称为/ A的锐角三角函数二、特殊角的三角函数值：三、解直角三角形：1、定义：由直角三角形中除直角外的个已知元素，求出另外个未知元素的过程叫解直角三角形2、解直角三角形应用中的有关概念⑴仰角和俯角：如图：在图上标上仰角和俯角i视线水平线⑵坡度坡角：如图：斜坡AB的垂直度h和水平宽度l的比叫做坡度，用i表示, 即1= 坡面与水平面得夹角为用字母％表示，则i=tan %=上。

11 T⑶方位角：是指南北方向线与目标方向所成的小于900的水平角如图：OA^Z K OB 表木OC 表木O味示（也可称东南方向）北_ A南例2 在Rtz\ABOt\ /C=90° , AB=2BC现给出下歹U结论：①sinA= § ;②cosB=■1 ;③tanA=殍；④tanB=#,其中正确的结论是（只需填上正确结论的序号）解：如图所示：故答案为：②③④.对应训练2.计算6tan45 -2cos60 °的结果是（）A. 4 3B. 4C. 5 3D. 52. D考点三：化斜三角形为直角三角形例3 在△ABC^, AB=AC=5 sin /ABC=0.8,贝U BC=故答案为：6.对应训练3.如图，四边形ABCD勺对角线AG BD相交于点Q且B阡分AC若BD=8 AC=6/BOC=120,则四边形ABCD勺面积为 .（结果保留根号）3.12 .3考点四：解直角三角形的应用4.如图，益阳市梓山湖中有一孤立小岛，湖边有一条笔直的观光小道AR现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据：AB=80.0米,/PAB=38.5 , / PBA=26.5.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.（以A, B为参照点，结果精确到0.1米）（参考数据:sin38.5 =0.62 , cos38.5 =0.78 , tan38.5 =0.80 , sin26.5 =0.45, cos26.5 =0.89 , tan26.5 =0.50）4.解：设PD=x^,・.PDL AB,・•・/ADPN BDP=90 ,在Rt^PAD中，tan / PAD=^ ,AD・•・ AD=-—= 5x, tan38.5o0.8 4在RtWBD中，tan/PBD-DB又.78=80.0 米,55x+2x=80.0 ,4解得：x=24.6,即P[> 24.6 米,・•. DB=2x=492答：小桥PD的长度约为24.6米，位于AB之间距B点约49.2米.【聚焦中考】1.6cos30 °的值是1,但22.河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1:收，则AB的长为( )A.12B.4石米C. 5痣米D. 673米B2. A3.一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处处，望见渔船D在南偏东60方向，若海监船的速度为50海里/小时，则A, B之间的距离为（取4=1.7,结果精确到0.1海里）.5. 67.56.如图，有一艘渔船在捕鱼作业时出现故障，急需抢修，调度中心通知附近两个小岛A、B上的观测点进行观测，从A岛测得渔船在南偏东37方向C处，B岛在南偏东66°方向，从B岛测得渔船在正西方向，已知两个小岛间的距离是72海里, A岛上维修船的速度为每小时20海里，B岛上维修船的速度为每小时28.8海里，为及时赶到维修，问调度中心应该派遣哪个岛上的维修船？(参考数据：cos37 =0.8, sin37 =0.6, sin66 =0.9, cos66 =0.4)6.解：如图，作ADLBC的延长线于点D.北D C B在Rt^ADB中，AD=ABcos/BAD=72< cos66 =72X 0.4=28.8 （海里），BD=ABsin / BAD=72 sin66 =72X 0.9=64.8 （海里）.在Rt/XADC^, AC=—AD— ^88- 空=36（海里），cos DAC cos37o0.8CD=ACsin / CAD=36 sin37 =36X 0.6=21.6 （海里）.BC=BD-CD=64.8-21.6=43.2 （海里）.A岛上维修船需要时间t A=^ ^=1.8 （小时）.20 20B岛上维修船需要时间t B=坨432=1.5 （小时）.28.8 28.8- t A> t B,.•・调度中心应该派遣B岛上的维修船.10.校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CDW l垂直，测得CD的长等于21米，在l上点D的同侧取点A B,使/ CAD=30 , / CBD=60 .（1）求AB的长（精确到0.1米，参考数据：石=1.73, 72=1.41 ）;（2）已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒, 这辆校车是否超速？说明理由.S DC10.解：（1）由题意得，在Rtz\ADC^, AD= CD”马=21 阴=36.33 （米），tan30o .33在Rt^BDC^ , BD=_CD V=Z1 =75/3 = 12.11 （米），tan60 3贝U AB=AD-BD=36.33-12.11=24.22= 24.2 （米）。

中考数学三角形知识点总结

中考数学三角形知识点总结初中数学三角形知识点总结一、三角形的有关概念1.三角形：由不在同一直线上的三条线段首尾顺次相接组成的图形叫三角形。

三角形的特征：①不在同一直线上;②三条线段;③首尾顺次相接;④三角形具有稳定性。

2.三角形中的三条重要线段：角平分线、中线、高(1)角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。

(2)中线：在三角形中，连接一个顶点和它的对边中点的线段叫做三角形的中线。

(3)高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高。

说明：①三角形的角平分线、中线、高都是线段;②三角形的角平分线、中线都在三角形内部且都交于一点;三角形的高可能在三角形的内部(锐角三角形)、外部(钝角三角形)，也可能在边上(直角三角形)，它们(或延长线)相交于一点。

二、等腰三角形的性质和判定(1)性质1.等腰三角形的两个底角相等(简写成等边对等角)。

2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合(简写成等腰三角形的三线合一)。

3.等腰三角形的两底角的平分线相等(两条腰上的中线相等，两条腰上的高相等)。

4.等腰三角形底边上的垂直平分线到两条腰的距离相等。

5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。

6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。

7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。

(2)判定在同一三角形中，有两条边相等的三角形是等腰三角形(定义)。

在同一三角形中，有两个角相等的三角形是等腰三角形(简称：等角对等边)。

三、直角三角形和勾股定理有一个角是直角的三角形是直角三角形，在直角三角形中，斜边中线等于斜边的一半;30度所对的直角边等于斜边的一半;直角三角形常用面积法求斜边上的高。

勾股定理：直角三角形两直角边a，b的平方和等于斜边c的平方，即a2+b2=c2。

中考数学复习指导：任意三角形三条高的长度关系及其应用

任意三角形三条高的长度关系及其应用三角形三边之问的关系是大家是非常熟悉的性质，即“任意两边之和大于第三边，任意两边之差小于第三边”．其实任意三角形的三条高之间的长度关系也有着密切的联系．设三角形三条边分别是a 、b 、c ，对应边上的高分别为h a 、h b 、h c 不失一般性，令a ≥b ≥c ，由面积关系ah a ＝bh b ＝ch c ，知h a ≤h b ≤h c ，,c c b ah h b c a c h h ==．再由b －c<a<b ＋c ，可得,c c c b a bh h h c c c c c h h h -<<+ 化简整理，得11111b c a b ch h h h h -<<+ 同理可得11111a c b a ch h h h h -<<+， 11111a b c a bh h h h h -<<+．这就是：任意三角形两条高的倒数和大于第三条高的倒数，任意三角形两条高的倒数差小于第三条高的倒数．下面举例说明上述结论在解题中的应用．例1 试判断长度分别是1、2、3的三条线段能否作为一个三角形的三条高．解根据三角形三条高的长度关系，如果长度为l 、2、3的三条线段可以作为一个三角形的三条高，那么必须有111123-<．但11111223-=>，所以长度分别为1、2、3的三条线段不能作为一个三角形的三条高．例2已知△ABC 的两条高线的长分别为5和20，若第三条高线的长也是整数，则第三条高线长的最大值是( )(A)5 (B)6 (C)7 (D)8解令第三条高线长为m ，根据三角形三条高线的长度关系，得11111520520m -<<+ 化简得4<m<203．所以第三条高的最大值是6．例3 △ABC 的三边为a 、b 、c ，且a ＝2，S △ABC ＝1，h b 、h c (h b <h c )分别为b 、c 边上的高，试证明h c －h b <h c ·h b <h c ＋h b ．证明因为2S △ABC ＝a ·h a ，将a ＝2，S △ABC ＝1代入得h a ＝1．由11111b c a b ch h h h h -<<+，得 11c b c b b ch h h h h h -<-<•．同理可得c b c b h h h h •<+，∴h c －h b <h c ·h b <h c ＋h b ．上述结论也可理解为：有一条边上的高为单位l 的三角形中，另两边上的高的乘积大于它们的差而小于它们的和．与三角形三边关系一样，为了体现“任意”，又要快捷判断，只要用较短两条线段长相加都大于第三条线段长，那么这三条线段一定能组成三角形．同样地，只要用最短的线段长的倒数减去另外一条线段长的倒数都小于第三条线段长的倒数，那么这样的三条线段便可以作为一个三角形的三条高．。

2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题(含答案解析)

2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题（含答案解析）知识回顾1.三角形的三边关系：三角形的任意两边之和大于第三边，任意两边之差小于第三边。

三角形的三边一旦确定，这三角形就固定了，这是三角形具有稳定性。

2.三角形的内角和定理：三角形的三个内角之和等于180°。

3.三角形的外角定理：三角形的一个外角等于它不相邻的两个内角之和。

大于它不相邻的任意一个内角。

4.全等三角形的性质：若两个三角形全等，则他们的对应边相等；对应角相等；对应边上的中线相等，高线相等，角平分线也相等；且这两个三角形的周长和面积均相等。

5.全等三角形的判定：①边边边（SSS）：三条边分别对应性相等的两个三角形全等。

②边角边（SAS）：两边及其这两边的夹角对应相等的两个三角形全等。

③角边角（ASA）：两角及其这两角的夹边对应相等的两个三角形全等。

④角角边（AAS）：两角及其其中一角的对边对应相等的两个三角形全等。

⑤直角三角形判定（HL）：直角三角形中斜边与其中任意一直角边分别对应相等的两个直角三角形全等。

全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件。

在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形。

专项练习题（含答案解析）1．已知：如图，∠1＝∠2，∠3＝∠4．求证：AB＝AD．【分析】根据邻补角的定义得出∠ACB＝∠ACD，利用ASA证明△ACB≌△ACD，根据全等三角形的性质即可得解．【解答】证明：∵∠3＝∠4，∴∠ACB＝∠ACD，在△ACB和△ACD中，，∴△ACB≌△ACD（ASA），∴AB＝AD．2．如图，△ABC是等腰三角形，点D，E分别在腰AC，AB上，且BE＝CD，连接BD，CE．求证：BD＝CE．【分析】根据等腰三角形的性质得出∠EBC＝∠DCB，进而利用SAS证明△EBC与△DCB全等，再利用全等三角形的性质解答即可．【解答】证明：∵△ABC∴∠EBC＝∠DCB，在△EBC与△DCB中，，∴△EBC≌△DCB（SAS），∴BD＝CE．3．如图1是小军制作的燕子风筝，燕子风筝的骨架图如图2所示，AB＝AE，AC＝AD，∠BAD＝∠EAC，∠C＝50°，求∠D的大小．【分析】由∠BAD＝∠EAC可得∠BAC＝∠EAD，根据SAS可证△BAC≌△EAD，再根据全等三角形的性质即可求解．【解答】解：∵∠BAD＝∠EAC，∴∠BAD+∠CAD＝∠EAC+∠CAD，即∠BAC＝∠EAD，在△BAC与△EAD中，，∴△BAC≌△EAD（SAS），∴∠D＝∠C＝50°．4．如图，AC平分∠BAD，CB⊥AB，CD⊥AD，垂足分别为B，D．（1）求证：△ABC≌△ADC；（2）若AB＝4，CD＝3，求四边形的面积．【分析】（1）由AC平分∠BAD，得∠BAC＝∠DAC，根据CB⊥AB，CD⊥AD，得∠B＝90°＝∠D，用AAS 可得△ABC≌△ADC；（2）由（1）△ABC≌△ADC，得BC＝CD＝3，S△ABC＝S△ADC，求出S△ABC＝AB•BC＝6，即可得四边形ABCD的面积是12．【解答】（1）证明：∵AC平分∠BAD，∴∠BAC＝∠DAC，∵CB⊥AB，CD⊥AD，∴∠B＝90°＝∠D，在△ABC和△ADC中，，∴△ABC≌△ADC（AAS）；（2）解：由（1）知：△ABC≌△ADC，∴BC＝CD＝3，S△ABC＝S△ADC，∴S△ABC＝AB•BC＝×4×3＝6，∴S△ADC＝6，∴S四边形ABCD＝S△ABC+S△ADC＝12，答：四边形ABCD的面积是12．5．如图，在△ABC中，点D在边BC上，CD＝AB，DE∥AB，∠DCE＝∠A．求证：DE＝BC．【分析】利用平行线的性质得∠EDC＝∠B，再利用ASA证明△CDE≌△ABC，可得结论．【解答】证明：∵DE∥AB，∴∠EDC＝∠B，在△CDE和△ABC中，，∴△CDE≌△ABC（ASA），∴DE＝BC．6．如图，在等边三角形ABC中，点M为AB边上任意一点，延长BC至点N，使CN＝AM，连接MN交AC于点P，MH⊥AC于点H．（1）求证：MP＝NP；（2）若AB＝a，求线段PH的长（结果用含a的代数式表示）．【分析】（1）过点M作MQ∥BC，交AC于点Q，根据等边三角形的性质以及平行线的性质可得∠AMQ＝∠AQM＝∠A＝60°，可得△AMQ是等边三角形，易证△QMP≌△CNP（AAS），即可得证；（2）根据等边三角形的性质可知AH＝HQ，根据全等三角形的性质可知QP＝PC，即可表示出HP的长．【解答】（1）证明：过点M作MQ∥BC，交AC于点Q，如图所示：在等边△ABC中，∠A＝∠B＝∠ACB＝60°，∵MQ∥BC，∴∠AMQ＝∠B＝60°，∠AQM＝∠ACB＝60°，∠QMP＝∠N，∴△AMQ是等边三角形，∴AM＝QM，∵AM＝CN，∴QM＝CN，在△QMP和△CNP中，，∴△QMP≌△CNP（AAS），∴MP＝NP；（2）解：∵△AMQ是等边三角形，且MH⊥AC，∴AH＝HQ，∵△QMP≌△CNP，∴QP＝CP，∴PH＝HQ+QP＝AC，∵AB＝a，AB＝AC，∴PH＝a．7．如图，点A，D，C，F在同一条直线上，AB＝DE，BC＝EF．有下列三个条件：①AC＝DF，②∠ABC ＝∠DEF，③∠ACB＝∠DFE．（1）请在上述三个条件中选取一个条件，使得△ABC≌△DEF．你选取的条件为（填写序号）（只需选一个条件，多选不得分），你判定△ABC≌△DEF的依据是（填“SSS”或“SAS”或“ASA”或“AAS”）；（2）利用（1）的结论△ABC≌△DEF．求证：AB∥DE．【分析】（1）根据SSS ABC≌△DEF，即可解决问题；（2）根据全等三角形的性质可得∠A＝∠EDF，再根据平行线的判定即可解决问题．【解答】（1）解：在△ABC和△DEF中，，∴△ABC≌△DEF（SSS），∴在上述三个条件中选取一个条件，使得△ABC≌△DEF，选取的条件为①，判定△ABC≌△DEF的依据是SSS．故答案为：①，SSS；（答案不唯一）．（2）证明：∵△ABC≌△DEF．∴∠A＝∠EDF，∴AB∥DE．8．在△ABC中，∠ACB＝90°，D为△ABC内一点，连接BD，DC，延长DC到点E，使得CE＝DC．（1）如图1，延长BC到点F，使得CF＝BC，连接AF，EF．若AF⊥EF，求证：BD⊥AF；（2）连接AE，交BD的延长线于点H，连接CH，依题意补全图2．若AB2＝AE2+BD2，用等式表示线段CD与CH的数量关系，并证明．【分析】（1）证明△BCD≌△FCE（SAS），由全等三角形的性质得出∠DBC＝∠EFC，证出BD∥EF，则可得出结论；（2）由题意画出图形，延长BC到F，使CF＝BC，连接AF，EF，由（1）可知BD∥EF，BD＝EF，证出∠AEF＝90°，得出∠DHE＝90°，由直角三角形的性质可得出结论．【解答】（1）证明：在△BCD和△FCE中，，∴△BCD≌△FCE（SAS），∴∠DBC＝∠EFC，∴BD∥EF，∵AF⊥EF，∴BD⊥AF；（2）解：由题意补全图形如下：CD＝CH．证明：延长BC到F，使CF＝BC，连接AF，EF，∵AC⊥BF，BC＝CF，∴AB＝AF，由（1）可知BD∥EF，BD＝EF，∵AB2＝AE2+BD2，∴AF2＝AE2+EF2，∴∠AEF＝90°，∴AE⊥EF，∴BD⊥AE，∴∠DHE＝90°，又∵CD＝CE，∴CH＝CD＝CE．9．如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，且点D在线段BC上，连CE．（1）求证：△ABD≌△ACE；（2）若∠EAC＝60°，求∠CED的度数．【分析】（1）可利用SAS证明结论；（2）由全等三角形的性质可得∠ACE＝∠ABD，利用等腰直角三角形的性质可求得∠ACE＝∠ABD＝∠AED ＝45°，再根据三角形的内角和定理可求解∠AEC的度数，进而可求可求解【解答】（1）证明：∵∠BAC＝∠DAE＝90°，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，即∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵△ABD≌△ACE，∴∠ACE＝∠ABD，∵△ABC和△ADE都是等腰直角三角形，∴∠ACE＝∠ABD＝∠AED＝45°，∵∠EAC＝60°，∴∠AEC＝180°﹣∠ACE﹣∠EAC＝180°﹣45°﹣60°＝75°，∴∠CED＝∠AEC﹣∠AED＝75°﹣45°＝30°．10．如图，在△ABC中（AB＜BC），过点C作CD∥AB，在CD上截取CD＝CB，CB上截取CE＝AB，连接DE、DB．（1）求证：△ABC≌△ECD；（2）若∠A＝90°，AB＝3，BD＝2，求△BCD的面积．【分析】（1）由CD∥AB得∠ABC＝∠ECD，而CD＝CB，CE＝AB，即可根据全等三角形的判定定理“SAS”证明△ABC≌△ECD；（2））由∠A＝90°，根据全等三角形的对应角相等证明∠BED＝∠CED＝∠A＝90°，设BE＝x，由BD2﹣BE2＝CD2﹣EC2＝DE2，列方程（2）2﹣x2＝（3+x）2﹣32，解方程求得符合题意的x的值为2，则BC ＝5，再根据勾股定理求出DE的长，即可求出△BCD的面积．【解答】（1）证明：∵CD∥AB，CD＝CB，CE＝AB，∴∠ABC＝∠ECD，在△ABC和△ECD中，，∴△ABC≌△ECD（SAS）．（2）解：∵∠A＝90°，∴∠CED＝∠A＝90°，∴∠BED＝180°﹣∠CED＝90°，设BE＝x，∵EC＝AB＝3，BD＝2，∴CD＝BC＝3+x，∵BD2﹣BE2＝CD2﹣EC2＝DE2，∴（2）2﹣x2＝（3+x）2﹣32，整理得x2+3x﹣10＝0，解得x1＝2，x2＝﹣5（不符合题意，舍去），∴BE＝2，BC＝3+2＝5，∴DE＝＝＝4，∴S△BCD＝BC•DE＝×5×4＝10，∴△BCD的面积为10．11．如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝1，D是BC边上的一点，以AD为直角边作等腰Rt △ADE，其中∠DAE＝90°，连接CE．（1）求证：△ABD≌△ACE；（2）若∠BAD＝22.5°时，求BD的长．【分析】（1）由“SAS”可证△ACE；（2）由等腰三角形三角形的性质可得BC的长，由角度关系可求∠ADC＝67.5°＝∠CAD，可得AC＝CD ＝1，即可求解．【解答】（1）证明：∵∠BAC＝90°＝∠DAE，∴∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵∠BAC＝90°，AB＝AC＝1，∴BC＝，∠B＝∠ACB＝45°，∵∠BAD＝22.5°，∴∠ADC＝67.5°＝∠CAD，∴AC＝CD＝1，∴BD＝﹣1．12．如图，已知矩形ABCD中，AB＝8，BC＝x（0＜x＜8），将△ACB沿AC对折到△ACE的位置，AE和CD交于点F．（1）求证：△CEF≌△ADF；（2）求tan∠DAF的值（用含x的式子表示）．【分析】（1）根据矩形的性质得到∠B＝∠D＝90°，BC＝AD，根据折叠的性质得到BC＝CE，∠E＝∠B ＝90°，等量代换得到∠E＝∠D＝90°，AD＝CE，根据AAS证明三角形全等即可；（2）设DF＝a，则CF＝8﹣a，根据矩形的性质和折叠的性质证明AF＝CF＝8﹣a，在Rt△ADF中，根据勾股定理表示出DF的长，根据正切的定义即可得出答案．【解答】（1）证明：∵四边形ABCD是矩形，∴∠B＝∠D＝90°，BC＝AD，根据折叠的性质得：BC＝CE，∠E＝∠B＝90°，∴∠E＝∠D＝90°，AD＝CE，在△CEF与△ADF中，，∴△CEF≌△ADF（AAS）；（2）解：设DF＝a，则CF＝8﹣a，∵四边形ABCD是矩形，∴AB∥CD，AD＝BC＝x，∴∠DCA＝∠BAC，根据折叠的性质得：∠EAC＝∠BAC，∴∠DCA＝∠EAC，∴AF＝CF＝8﹣a，在Rt△ADF中，∵AD2+DF2＝AF2，∴x2+a2＝（8﹣a）2，∴a＝，∴tan∠DAF＝＝．13．如图，△ABC和△DEF，点E，F在直线BC上，AB＝DF，∠A＝∠D，∠B＝∠F．如图①，易证：BC+BE ＝BF．请解答下列问题：（1）如图②，如图③，请猜想BC，BE，BF之间的数量关系，并直接写出猜想结论；（2）请选择（1）中任意一种结论进行证明；（3）若AB＝6，CE＝2，∠F＝60°，S△ABC＝123，则BC＝，BF＝．【分析】（1）根据图形分别得出答案；（2）利用AAS证明△ABC≌△DFE，得BC＝EF，再根据图形可得结论；（3）首先利用含30°角的直角三角形的性质求出BH和AH的长，从而得出BC，再对点E的位置进行分类即可．【解答】解：（1）图②：BC+BE＝BF，图③：BE﹣BC＝BF；（2）图②：∵AB＝DF，∠A＝∠D，∠B＝∠F，∴△ABC≌△DFE（ASA），∴BC＝EF，∵BE＝BC+CE，∴BC+BE＝EF+BC+CE＝BF；图③：∵AB＝DF，∠A＝∠D，∠B＝∠F，∴△ABC≌△DFE（ASA），∴BC＝EF，∵BE＝BF+EF，∴BE﹣BC＝BF+EF﹣BC＝BF+BC﹣BC＝BF；（3）当点E在BC上时，如图，作AH⊥BC于H，∵∠B＝∠F＝60°，∴∠BAH＝30°，∴BH＝3，∴AH＝3，∵S△ABC＝12，∴＝12，∴BC＝8，∵CE＝2，∴BF＝BE+EF＝8﹣2+8＝14；同理，当点E在BC延长线上时，如图②，BF＝BC+BE＝8+10＝18，故答案为：8，14或18．14．△ABC和△ADE都是等边三角形．（1）将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有P A+PB ＝PC（或P A+PC＝PB）成立（不需证明）；（2）将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC 之间有怎样的数量关系？并加以证明；（3）将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC 之间有怎样的数量关系？直接写出结论，不需要证明．【分析】（2）证明△ABD≌△ACE（SAS）和△BAF≌△CAP（SAS），得AF＝AP，∠BAF＝∠CAP，再证明△AFP是等边三角形，最后由线段的和可得结论；（3）如图③，在PC上截取CM＝PB，连接AM，同理可得结论．【解答】解：（2）PB＝P A+PC，理由如下：如图②，在BP上截取BF＝PC，连接AF，∵△ABC、△ADE都是等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，∴∠BAC+∠CAD＝∠CAD+∠DAE，即∠DAB＝∠EAC，∴△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵AB＝AC，BF＝CP，∴△BAF≌△CAP（SAS），∴AF＝AP，∠BAF＝∠CAP，∴∠BAC＝∠P AF＝60°，∴△AFP是等边三角形，∴PF＝P A，∴PB＝BF+PF＝PC+P A；（3）PC＝P A+PB，理由如下：如图③，在PC上截取CM＝PB，连接AM，同理得：△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵AB＝AC，PB＝CM，∴△AMC≌△APB（SAS），∴AM＝AP，∠BAP＝∠CAM，∴∠BAC＝∠P AM＝60°，∴△AMP是等边三角形，∴PM＝P A，∴PC＝PM+CM＝P A+PB．15．【情境再现】甲、乙两个含45°角的直角三角尺如图①放置，甲的直角顶点放在乙斜边上的高的垂足O处．将甲绕点O 顺时针旋转一个锐角到图②位置．按图②作出示意图，并连接AG，BH，如图③所示，AB交HO于E，AC 交OG于F，通过证明△OBE≌△OAF，可得OE＝OF．请你证明：AG＝BH．【迁移应用】延长GA分别交HO，HB所在直线于点P，D，如图④，猜想并证明DG与BH的位置关系．【拓展延伸】小亮将图②中的甲、乙换成含30°角的直角三角尺如图⑤，按图⑤作出示意图，并连接HB，AG，如图⑥所示，其他条件不变，请你猜想并证明AG与BH的数量关系．【分析】【情境再现】由△OBE≌△OAF，得BE＝AF，OE＝OF，∠BEO＝∠AFO，可证明△BHE≌△AGF （SAS），得BH＝AG；【迁移应用】由△BHE≌△AGF，得∠BHE＝∠AGF，可得∠AGF+∠GPO＝90°，从而∠BHE+∠HPD＝90°，∠HDP＝90°，故DG⊥BH；【拓展延伸】设AB交OH于T，OG交AC于K，根据△ABC，△HOG是含30°角的直角三角形，AO⊥BC，可得OB＝AO，∠OBA＝∠OAC＝30°，∠BOT＝90°﹣∠AOT＝∠AOK，即得△BOT∽△AOK，有＝＝＝，∠BTO＝∠AKO，又OH＝GO，可得＝＝，故△BTH∽△AKG，即得＝＝，BH＝AG．【解答】【情境再现】证明：由阅读材料知△OBE≌△OAF，∴BE＝AF，OE＝OF，∠BEO＝∠AFO，∴∠BEH＝∠AFG，∵OH＝OG，∴OH﹣OE＝OG﹣OF，即EH＝GF，在△BHE和△AGF中，，∴△BHE≌△AGF（SAS），∴BH＝AG；【迁移应用】解：猜想：DG⊥BH；证明如下：由【情境再现】知：△BHE≌△AGF，∴∠BHE＝∠AGF，∵∠HOG＝90°，∴∠AGF+∠GPO＝90°，∴∠BHE+∠GPO＝90°，∵∠GPO＝∠HPD，∴∠BHE+∠HPD＝90°，∴∠HDP＝90°，∴DG⊥BH；【拓展延伸】解：猜想：BH＝AG，证明如下：设AB交OH于T，OG交AC于K，如图：由已知得：△ABC，△HOG是含30°角的直角三角形，AO⊥BC，∴∠AOB＝90°，∴OB＝AO，∠OBA＝∠OAC＝30°，∠BOT＝90°﹣∠AOT＝∠AOK，∴△BOT∽△AOK，∴＝＝＝，∠BTO＝∠AKO，∴OT＝OK，BT＝AK，∠BTH＝∠AKG，∵OH＝GO，∴HT＝OH﹣OT＝GO﹣OK＝（GO﹣OK）＝KG，∴＝＝，∴△BTH∽△AKG，∴＝＝，∴BH＝AG19。

数学中考三角形知识加例题（含答案）

a60第4题图题图NPOA三角形复习★知识点1. 三角形的定义三角形是多边形中边数最少的一种。

它的定义是：由不在同一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

顺次相接组成的图形叫做三角形。

★知识点2.三角形的分类（1）按角分类按角分类(2) 按边分类按边分类例：如果三角形的一个外角等于它相邻内角的2倍，且等于它不相邻内角的4倍，那么这个三角形一定是（么这个三角形一定是（）A 、锐角三角形、锐角三角形B 、直角三角形、直角三角形C 、钝角三角形、钝角三角形D 、正三角形、正三角形解题思路：根据角度来判断是哪一种三角形。

答案B 练习：如图，已知OA ＝a ，P 是射线ON 上一动点（即P 可在射线ON 上运动），∠AON ＝600，填空：，填空：（1）当OP ＝时，△AOP 为等边三角形；为等边三角形；（2）当OP ＝时，△AOP 为直角三角形；为直角三角形；（3）当OP 满足满足时，△AOP 为锐角三角形；为锐角三角形；（4）当OP 满足满足时，△AOP 为钝角三角形。

为钝角三角形。

答案：（1）a ；（2）a 2或2a ；（3）2a ＜OP ＜a 2；（4）0＜OP ＜2a或OP ＞a 2 ◆知识点3.三角形三条重要线段三角形中的主要线段有：三角形的角平分线、中线和高线。

这三条线段必须在理解和掌握它的定义的基础上，通过作图加以熟练掌握。

并且对这三条线段必须明确三点：握它的定义的基础上，通过作图加以熟练掌握。

并且对这三条线段必须明确三点：三角形三角形锐角三角形锐角三角形直角三角形直角三角形钝角三角形钝角三角形三角形三角形不等边三角形不等边三角形等腰三角形等腰三角形底边和腰不相等的等腰三角等边三角形等边三角形2A 1A 3题图题图DC B A（1）三角形的角平分线、中线、高线均是线段，不是直线，也不是射线。

线、中线、高线均是线段，不是直线，也不是射线。

（2）三角形的角平分线、中线、高线都有三条，角平分线、中线，都在三角形内部。

数学中考之三角形性质定理

数学中考之三角形性质定理三角形是由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

下面是作者给大家带来的数学中考之三角形性质定理，欢迎大家浏览参考，我们一起来看看吧!初中数学知识点：三角形的周长和面积构成三角形的元素：边：组成三角形的线段叫做三角形的边;顶点：相邻两边的公共端点叫做三角形的顶点;内角：相邻两边所组成的角叫做三角形的内角，简称三角形的角。

三角形有下面三个特性：(1)三角形有三条线段;(2)三条线段不在同一直线上;(3)首尾顺次相接。

三角形的表示：用符号“△，顶点是A、B、C的三角形记作“△ABC”，读作ABC”。

三角形的三边关系：在三角形中，任意两边和大于第三边，任意两边差小于第三边。

设三角形三边为a,b,c则a+b ca+c bb+c aa-ba-cb-c在直角三角形中，设a、b为直角边，c为斜边。

则两直角边的平方和等于斜边平方。

在等边三角形中，a=b=c在等腰三角形中， a,b为两腰，则a=b在三角形ABC的内角A、B、C所对边分别为a、b、c的情形下，c2=a2+b2-2abcosc三角形的三边关系定理及推论：(1)三角形三边关系定理：三角形的两边之和大于第三边。

推论：三角形的两边之差小于第三边。

(2)三角形三边关系定理及推论的作用：①判定三条已知线段能否组成三角形;②当已知两边时，可肯定第三边的范畴;③证明线段不等关系。

三角形的周长和面积：三角形的周长等于三角形三边之和。

三角形面积=(底×高)÷2。

初中数学知识点：三角形的角和定理三角形的内角和定理及推论：三角形的内角和定理：三角形三个内角和等于180°。

推论：(1)直角三角形的两个锐角互余。

(2)三角形的一个外角等于和它不相邻的来两个内角的和。

(3)三角形的一个外角大于任何一个和它不相邻的内角。

注：在同一个三角形中：等角对等边;等边对等角;大角对大边;大边对大角。

三角形的外角：三角形的一条边的延长线和另一条相邻的边组成的角，叫做三角形的外角。

中考数学专题复习三角形与多边形

第一部分夯实基础
第四章三角形
第2节三角形与多边形
上一页返回导航下一页
课标导航
·理解三角形及其内角、外角、中线、高线、角平分线等概念，会按照边长的关系和角的大小对三角形进行分类，了解三角形的稳定性．
·探索并证明三角形的内角和定理．掌握它的推论．证明三角形的任意两边之和大于第三边．
·了解三角形重心的概念． ·探索并证明三角形的中位线定理． ·了解多边形的定义，多边形的定点、边、内角、外角、对角线等概念；探索并掌握多边形内角和与外角和公式．
∴BF＝2BT＝2 3.
∵∠A F E ＝120°，∠A F B ＝∠A B F ＝30°，
∴∠B F E ＝90°.
∴S
△PE
F＝
S
△B EF
＝1·E 2
F
·BF
＝1×2×2 2
3＝2
外心三角形三边垂直平分线的交点，外心到各顶点的距离相等.
上一页返回导航下一页
3．(1)下列说法错误的是( D ) A．三角形的内心是三角形内切圆的圆心 B．三角形的外心是三角形外接圆的圆心 C．三角形的重心到每个顶点的距离等于它到对边中点距离的 2 倍 D．等腰三角形的四心重合
上一页返回导航下一页
上一页返回导航下一页
2．(1)如图，在△ABC 中，AE 是中线，AD 是∠BAC 的角平分线，AF ⊥BC 于点 F，∠B＝30°，∠C＝50°.
①BE＝ EC ； ②∠BAD＝ 50 °； ③∠DAF＝ 10 °； ④S△AEC ＝ S△ABE.(填“>”“＜”或“＝”)
上一页返回导航下一页
AD×BC×14.
上一页返回导航下一页
顶点连中点，倍长造全等点 D 是 BC 的中点，延长 AD 到 E，使 AD＝DE，则有点 D 为 BC 的中点，延长 ED △ACD≌△EBD，AC∥BE. 到点 F，使 DF＝ED，连接 CF，则有△BED≌△CFD.

中考数学三角形复习试题以及答案

三角形的概念及其性质1.三角形的概念由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三角形的分类(1)按边分类：(2)按角分类：3.三角形的内角和外角(1)三角形的内角和等于180°.(2)三角形的任一个外角等于和它不相邻的两个内角之和;三角形的一个外角大于任何一个和它不相邻的内角.4.三角形三边之间的关系三角形任意两边之和大于第三边，任意两边之差小于第三边.5.三角形内角与对边对应关系在同一个三角形内，大边对大角，大角对大边;在同一三角形中，等边对等角，等角对等边.6.三角形具有稳定性.知识点二、三角形的“四心”和中位线三角形中的四条特殊的线段是：高线、角平分线、中线、中位线.1.内心：三角形角平分线的交点，是三角形内切圆的圆心，它到各边的距离相等.2.外心：三角形三边垂直平分线的交点，是三角形外接圆的圆心，它到三个顶点的距离相等.3.重心：三角形三条中线的交点，它到每个顶点的距离等于它到对边中点距离的2倍.4.垂心：三角形三条高线的交点.5.三角形的中位线：连结三角形两边中点的线段是三角形的中位线.中位线定理：三角形的中位线平行于第三边且等于第三边的一半.要点诠释：(1)三角形的内心、重心都在三角形的内部.(2)钝角三角形的垂心、外心都在三角形的外部.(3)直角三角形的垂心为直角顶点，外心为直角三角形斜边的中点.(4)锐角三角形的垂心、外心都在三角形的内部.知识点三、全等三角形1.定义：能完全重合的两个三角形叫做全等三角形.2.性质：(1)对应边相等(2)对应角相等(3)对应角的平分线、对应边的中线和高相等(4)周长、面积相等3.判定：(1)边角边(SAS)(2)角边角(ASA)(3)角角边(AAS)(4)边边边(SSS)(5)斜边直角边(HL)(适用于直角三角形)要点诠释：判定三角形全等至少必须有一组对应边相等.知识点四、等腰三角形1.定义：有两条边相等的三角形叫做等腰三角形.2.性质：(1)具有三角形的一切性质.(2)两底角相等(等边对等角)(3)顶角的平分线，底边中线，底边上的高互相重合(三线合一)(4)等边三角形的各角都相等，且都等于60°.3.判定：(1)如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边);(2)三个角都相等的三角形是等边三角形;(3)有一个角为60°的等腰三角形是等边三角形.要点诠释：(1)腰、底、顶角、底角是等腰三角形特有的概念;(2)等边三角形是特殊的等腰三角形.知识点五、直角三角形1.定义：有一个角是直角的三角形叫做直角三角形.2.性质：(1)直角三角形中两锐角互余;(2)直角三角形中，30°锐角所对的直角边等于斜边的一半.(3)在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°.(4)勾股定理：直角三角形中，两条直角边的平方和等于斜边的平方.(5)勾股定理逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形.(6)直角三角形中，斜边上的中线等于斜边的一半;(7)SRt△ABC= ch= ab，其中a、b为两直角边，c为斜边，h为斜边上的高.3.判定：(1)两内角互余的三角形是直角三角形;(2)一条边上的中线等于该边的一半，则这条边所对的角是直角，则这个三角形是直角三角形.(3)如果三角形两边的平方和等于第三边的平方，则这个三角形是直角三角形，第三边为斜边.知识点六、线段垂直平分线和角平分线1.线段垂直平分线：经过线段的中点并且垂直这条线段的直线，叫做这条线段的垂直平分线.线段垂直平分线的定理：(1)线段垂直平分线上的点与这条线段两个端点的距离相等.(2)与一条线段两个端点距离相等的点，在这条线段的垂直平分线上.线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.2.角平分线的性质：(1)角的平分线上的点到角的两边的距离相等;(2)到角的两边的距离相等的点在角的平分线上;(3)角的平分线可以看做是到角的两边距离相等的所有点的集合.四、规律方法指导1.数形结合思想本单元中所学的三角形性质、角平分线性质、全等三角形的性质、直角三角形中的勾股定理等，都是在结合图形的基础上，求线段或角的度数，证明线段或角相等.在几何学习中，应会利用几何图形解决实际问题.2.分类讨论思想在没给图形的前提下，画三角形或三角形一边上的高、三角形的垂心、外心时要考虑分类：三种情况，锐角三角形、直角三角形、钝角三角形.3. 化归与转化思想在解决利用三角形的基础知识计算、证明问题时，通过做辅助线、利用所学知识进行准确推理等转化手段，归结为另一个相对较容易解决的或者已经有解决模式的问题，已知与未知之间的转化;数与形的转化;一般与特殊的转化.4.注意观察、分析、总结应将三角形的判定及性质作为重点，对于特殊三角形的判定及性质要记住并能灵活运用，注重积累解题思路和运用数学思想和方法解决问题的能力和培养，淡化纯粹的几何证明.学会演绎推理的方法，提高逻辑推理能力和逻辑表达能力，掌握几何证明中的分析，综合，转化等数学思想.经典例题透析考点一、三角形的概念及其性质1.(1)(2010山东济宁)若一个三角形三个内角度数的比为2︰3︰4，那么这个三角形是( )A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等边三角形思路点拨：三角形的内角和为180°，三个内角度数的份数和是9，每一份度数是20，则三个内角度数分别为40°、60°、80°，是锐角三角形.答案：B(2)三角形的三边分别为3，1-2a，8，则a的取值范围是( )A.-6-2思路点拨：涉及到三角形三边关系时，尽可能简化运算，注意运算的准确性.解析：根据三角形三边关系得：8-3<1-2a<8+3，解得-5举一反三：【变式1】已知a，b，c为△ABC的三条边，化简得_________.思路点拨：本题利用三角形三边关系，使问题代数化，从而化简得出结论.解析：∵a，b，c为△ABC的三条边∴a-b-c<0， b-a-c<0∴ =(b+c-a)+(a+c-b)=2c.【变式2】有五根细木棒，长度分别为1cm，3cm，5cm，7cm，9cm，现任取其中的三根木棒，组成一个三角形，问有几种可能( )A.1种B.2种C.3种D.4种解析：只有3、5、7或3、7、9或5、7、9三种.应选C.【变式3】等腰三角形中两条边长分别为3、4，则三角形的周长是_________.思路点拨：要分类讨论，给出的边长中，可能分别是腰或底.注意满足三角形三边关系.解析：(1)当腰为3时，周长=3+3+4=10;(2)当腰为4时，周长=3+4+4=11.所以答案为10或11.2.(1)(2010宁波市)如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是△ABC、△BCD的角平分线，则图中的等腰三角形有 ( )A.5个B.4个C.3个D.2个考点：等腰三角形答案：A(2)如图在△ABC中，∠ABC=90°，∠A=50°，BD∥AC，则∠CBD的度数是______.考点：直角三角形两锐角互余.解析：△ABC 中，∠C=∠ABC-∠A =90°-50°=40°又∵BD∥AC，∴∠CBD=∠C=40°.3.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=3∠A，则此三角形中( )A.一定有一个内角为45°B.一定有一个内角为60°C.一定是直角三角形D.一定是钝角三角形考点：三角形内角和180°.思路点拨：会灵活运和三角形内角和等于180°这一定理，即∠B+∠C=180°-∠A.解析：∵△ABC中，∠A+∠B+∠C=180°，∴∠B+∠C=180°-∠A∵∠B+∠C=3∠A，∴180°-∠A=3∠A，∴ ∠A=45°，∴选A，其它三个答案不能确定.举一反三：【变式1】下图能说明∠1>∠2的是( )考点：三角形外角性质.思路点拨：本类题目考查学生了解三角形外角大于任何一个不相邻的内角.解析：A中∠1和∠2是对顶角，∠1=∠2;B中∠1和∠2是同位角，若两直线平行则相等，不平行则不一定相等;C中∠1是三角形的一个外角，∠2是和它不相邻的内角，所以∠1>∠2.D中∠1和∠2的大小相等.故选C.总结升华：三角形内角和180°以及边角之间的关系，在习题中往往是一个隐藏的已知条件，在做题时要注意审题，并随时作为检验自己解题是否正确的标准.【变式2】如果三角形的一个内角等于其他两个内角的和，这个三角形是( )A.锐角三角形B.钝角三角形C.直角三角形D.不能确定思路点拨：理解直角三角形定义，结合三角形内角和得出结论.解析：若△ABC的三个内角∠A、∠B、∠C中，∠A+∠B=∠C又∠A+∠B+∠C=180°，所以2∠C=180°，可得∠C=90°，所以选C.【变式3】下列命题：(1)等边三角形也是等腰三角形;(2)三角形的外角等于两个内角的和;(3)三角形中最大的内角不能小于60°;(4)锐角三角形中，任意两内角之和必大于90°，其中错误的个数是( )A.0 个B.1个C.2个D.3个思路点拨：本题的解题关键是要理解定义，掌握每种三角形中角的度数的确定.解析：(2)中应强调三角形的外角等于不相邻的两个内角的和;三角形中最大的内角若小于60°，则三个角的和就小于180°，不符合三角形内角和定理，故(3)正确;(4)三角形中，任意两内角之和若不大于90°，则另一个内角就大于或等于90°，就不能是锐角三角形.所以中有(2)错，故选B.考点二、三角形的“四心”和中位线4.(1)与三角形三个顶点距离相等的点是这个三角形的( )A.二条中线的交点B. 二条高线的交点C.三条角平分线的交点D.三边中垂线的交点考点：线段垂直平分线的定理.思路点拨：三角形三边垂直平分线的交点是外心，是三角形外接圆的圆心，到三角形三个顶点距离相等.答案D若改成二边中垂线的交点也正确.(2)(2010四川眉山)如图，将第一个图(图①)所示的正三角形连结各边中点进行分割，得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割，得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割，……，则得到的第五个图中，共有________个正三角形.考点：三角形中位线找规律思路点拨：图①有1个正三角形;图②有(1+4)个正三角形;图③有(1+4+4)个正三角形;图④有(1+4+4+4)个正三角形;图⑤有(1+4+4+4+4)个正三角形;….答案：175.一个三角形的内心在它的一条高线上，则这个三角形一定是( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等边三角形考点：三角形角平分线定理.思路点拨：本题考查三角形的内心是三角形角平分线的交点，若内心在一条高线上，又符合三线合一的性质.所以该三角形是等腰三角形.故选B.举一反三：【变式1】如图，已知△ABC中，∠A=58°，如果(1)O为外心;(2)O为内心;(3)O为垂心;分别求∠BOC的度数.考点：三角形外心、内心、垂心性质.解析：∠A是锐角时，(1)O为外心时，∠BOC=2∠A =116°;(2)O为内心时，∠BOC=90°+ ∠A=119°;(3)O为垂心，∠BOC=180°-∠A=122°.【变式2】如果一个三角形的内心，外心都在三角形内，则这个三角形是( )A.锐角三角形B.只有两边相等的锐角三角形C.直角三角形D.锐角三角形或直角三角形解析：三角形的内心都在三角形内部;锐角三角形外心在三角形内部;直角三角形的外心在三角形斜边的中点上、钝角三角形的外心三角形外部.故选A.【变式3】能把一个三角形分成两个面积相等的三角形的线段，是三角形的( )A.中线B.高线C.边的中垂线D.角平分线思路点拨：三角形面积相等，可利用底、高相等或相同得到.解析：三角形的一条中线分得的两个三角形底相等，高相同.应选A.6.(1)(2010广东茂名)如图，吴伯伯家有一块等边三角形的空地ABC，已知点E、F分别是边AB、AC的中点，量得EF=5米，他想把四边形BCFE用篱笆围成一圈放养小鸡，则需用篱笆的长是( )A、15米B、20米C、25米D、30米考点：三角形中位线定理.思路点拨：BE=AE=5 ，CF=FA=5，BC=2EF=10答案：C。

中考数学三角形知识点总结

中考数学三角形知识点总结一、三角形的定义和性质1.三角形是由三条边和三个内角组成的封闭图形。

2.三角形的内角和等于180度。

3.三条边的和大于第三边，任意两边之差小于第三边。

二、三角形的分类1.根据角度分类：(1)锐角三角形：三个内角都是锐角的三角形。

(2)直角三角形：有一个内角为直角的三角形。

(3)钝角三角形：有一个内角为钝角的三角形。

2.根据边长分类：(1)等边三角形：三条边长度相等的三角形。

(2)等腰三角形：有两条边长度相等的三角形。

(3)普通三角形：三条边长度都不相等的三角形。

三、三角形的重要性质1.三角形的内角和定理：三角形的三个内角和等于180度。

2.三角形的外角和定理：三角形的一个外角等于其两个不相邻内角。

3.三角形的角平分线：三角形的内角平分线上的点到三条边的距离相等。

4.三角形的中线：三角形的中线连接相邻顶点的中点，长度相等。

5.三角形的高：三角形的高是从顶点到底边的垂直线段。

6.三角形的面积公式：S=1/2*底边长*高。

四、三角形的相似性质1.相似三角形的性质：(1)对应角相等：相似三角形的对应角相等。

(2)对应边成比例：相似三角形的对应边成比例。

(3)边角对应：相似三角形的角与边成比例。

2.判定相似三角形的定理：(1)AA相似判定定理：如果两个三角形的两个角分别相等，则它们相似。

(2)SAS相似判定定理：如果两个三角形的一个角相等，并且两个对应边的比值相等，则它们相似。

(3)SSS相似判定定理：如果两个三角形的三条边的比值相等，则它们相似。

五、三角形的勾股定理1.勾股定理的形式：直角三角形中，较长的斜边的平方等于两直角边的平方和。

(1)a²=b²+c²(2)b²=a²-c²(3)c²=a²-b²2.利用勾股定理求三角形的边长：(1)已知直角边和斜边，可以求另一个直角边的长度。

(2)已知两个直角边的长度，可以求斜边的长度。

中考数学精华复习三角形与全等三角形完美

第16讲┃ 三角形与全等三角形
11．如图16－8，给出下列四组条件： ①AB＝DE，BC＝EF，AC＝DF； ②AB＝DE，∠B＝∠E，BC＝EF； ③∠B＝∠E，BC＝EF，∠C＝∠F； ④AC＝DF，∠A＝∠D，∠B＝∠E；其中能使△ABC≌△DEF的条件共有( D )
A．1组
B．2组
图16－8 C．3组
图16－4
[解析] 如图，根据题意可知∠5＝90°， ∴∠3＋∠4＝90°，∴∠1＋∠2＝2∠5＋∠3＋∠4＝2×90°＋90° ＝270°.
第16讲┃ 三角形与全等三角形
考点3 全等三角形的定义及性质
定义性质
如果两个三角形能够完全_重__合___，那么这两个三角形全等，即对应边相__等____，对应
第16讲┃ 三角形与全等三角形
6．若一个三角形三个内角度数的比为2∶3∶4，那么这个三
角形是( B )
A．直角三角形
B．锐角三角形
C．钝角三角形
D．等边三角形
第16讲┃ 三角形与全等三角形
7．如图16－4，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1＋∠2＝___27_0____度．
考点2 三角形的边和角
三角形边的关系
三角形的内角和与外角和
三角形外角性质
三角形任意两边之和__大_于_____第三边，任意两边之差_小__于_____第三边三角形内角和等于_1_8_0_°__，外角和为
_3_6_0_°__ ①三角形的一个外角__等_于___与它不相邻的两个内角的和；②三角形的一个外角大于与__它__不__相__邻_的__任何一个内角
_三__边___对应相等的两三角形全等斜边和一条直角边对应相等的两个直角

中考数学三角形知识点总结

中考数学三角形知识点总结一、三角形的基础概念三角形呢，就是由三条线段首尾顺次相接组成的封闭图形。

这三条线段就叫做三角形的边，相邻两边组成的角就叫做三角形的内角，简称角。

三角形的角那可太重要啦，就像人的眼睛一样关键呢。

三角形有三个角，这三个角的和永远是180度哦，这可是个铁打的定律，就像太阳每天都会升起一样。

二、三角形的分类1. 按角来分的话，可以分成锐角三角形、直角三角形和钝角三角形。

锐角三角形就是三个角都是锐角的三角形，锐角就是小于90度的角啦。

直角三角形呢，有一个角是直角，也就是90度的角，这个直角就像三角形里的大明星一样，特别显眼。

钝角三角形就是有一个角是钝角，钝角是大于90度小于180度的角，这种三角形看起来就有点“歪歪扭扭”的。

2. 按边来分，有等边三角形、等腰三角形和不等边三角形。

等边三角形可厉害了，它的三条边都相等，三个角也都相等，每个角都是60度呢，就像三个好兄弟一样，完全一样，特别团结。

等腰三角形就是有两条边相等的三角形，这两条相等的边叫做腰，另一条边叫做底边。

等腰三角形的两个底角也是相等的，就像双胞胎一样。

不等边三角形就是三条边都不相等的三角形，这种三角形就比较普通啦。

三、三角形的性质1. 三角形的两边之和大于第三边，这就好比你要去两个地方，你肯定是直接走过去比绕远路要近，三角形的边也是这个道理。

比如说一个三角形的三条边分别是3、4、5，那3 + 4肯定大于5啦。

2. 三角形的稳定性。

这可是三角形的一个超酷的特性哦。

你看生活中的很多东西都利用了三角形的稳定性，像自行车的车架，就是三角形的结构，这样自行车骑起来才稳稳当当的，要是车架是四边形的，那可就东倒西歪啦。

四、三角形的高、中线和角平分线1. 高呢，就是从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段就叫做三角形的高。

每个三角形都有三条高呢，不过不同类型的三角形高的位置不太一样哦。

锐角三角形的三条高都在三角形的内部，直角三角形的两条直角边就是两条高，另一条高在三角形的内部，钝角三角形有两条高在三角形的外部，一条高在内部。

中考数学三角形问题解题方法

中考数学三角形问题解题方法
中考数学中涉及到的三角形问题是一类重要的题型，需要掌握一些解题方法。

以下是一些常用的解题方法：
1. 勾股定理：当我们知道一个直角三角形的两条直角边的长度时，可以利用勾股定理求出斜边的长度。

勾股定理公式为：直角边1的平方 + 直角边2的平方 = 斜边的平方。

2. 正弦定理：当我们知道一个三角形的某两边和其夹角时，可以利用正弦定理求出第三边的长度。

正弦定理公式为：a/sinA =
b/sinB = c/sinC，其中a、b、c分别是三角形的三条边，A、B、C
分别是它们所对的角度。

3. 余弦定理：当我们知道一个三角形的某两边和它们夹角的余弦时，可以利用余弦定理求出第三边的长度。

余弦定理公式为：c = a + b - 2abcosC，其中a、b、c分别是三角形的三条边，C是它们夹角的角度。

4. 相似三角形：当我们知道两个三角形的对应角度相等时，可以利用相似三角形的性质求出其中一些边长。

相似三角形的性质为：对应角度相等的两个三角形，它们的对应边长成比例。

5. 角平分线定理：当我们知道一个三角形的某个角的角平分线的长度时，可以利用角平分线定理求出其他相关边长。

角平分线定理公式为：在三角形ABC中，AN为角BAC的平分线，BN与AC相交于点M，则AN/BN = AC/BC。

以上是一些常用的解题方法，希望能够对同学们在中考数学中解
决三角形问题有所帮助。

初三中考数学 三角形

中考数学考点专题复习 三角形与全等三角形

中考数学专题复习：专题五 三角形

考点13 三角形-中考数学考点讲解

中考数学全等三角形的五种模型

初三数学13 相似三角形-2024年中考数学真题分项汇编(全国通用)(解析版)

中考数学第一轮复习 三角形

中考数学几何模型专题专题三—三角形

初三中考一轮复习(15)解直角三角形题型分类含答案(全面非常好)

中考数学三角形知识点总结

中考数学复习指导：任意三角形三条高的长度关系及其应用

2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题(含答案解析)

数学中考三角形知识加例题（含答案）

数学中考之三角形性质定理

中考数学专题复习 三角形与多边形

中考数学三角形复习试题以及答案

中考数学三角形知识点总结

中考数学精华复习三角形与全等三角形完美

中考数学三角形知识点总结

中考数学三角形问题解题方法

初三中考数学三角形

中考数学考点专题复习三角形与全等三角形

中考数学专题复习：专题五三角形

中考数学第一轮复习三角形

中考数学专题复习三角形与多边形