对勾函数图像及其性质
对勾函数

对勾函数图象性质对勾函数 :数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一 ) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+ (接下来写作f(x)=ax+b/x )。
当 a≠0, b≠0时, f(x)=ax+b/x 是正比例函数 f(x)=ax 与反比例函数 f(x)= b/x 叠“加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当 a , b 同号时,f(x)=ax+b/x 的图象是由直线y= ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像( ab 同号)当 a ,b 异号时, f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab 异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0 , b>0 。
之后当a<0,b<0 时,根据对称就很容易得出结论了。
1(二 ) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当 x>0 时,。
当 x<0 时,。
即对勾函数的定点坐标:(三 ) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四 ) 对勾函数的单调性y(五 ) 对勾函数的渐进线O Xy=ax由图像我们不难得到:(六 ) 对勾函数的奇偶性:对勾函数在定义域内是奇函数,二、类耐克函数性质探讨函数y ax b,在 a0或b0时为简单的单调函数,不予讨论。
对勾函数图象性质

对勾函数图象性质Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ bx的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+bx(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,f(x)=ax+bx ≥2√ab(当且尽当ax=bx时取等号),此时x=√b a。
当x<0时,f(x)=ax+bx ≤−2√ab(当且尽当ax=bx时取等号),此时x=−√ba。
即对勾函数的定点坐标:A:(√ba ,2√ab)、B:(−√ba,−2√ab)a>0 b>0 a<0 b<0对勾函数的图像(ab同对勾函数的图像(ab异号)(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
对勾函数

对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一)对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,yXOy=ax。
对勾函数的图象及性质

对勾函数一、定义对勾函数是由两个幂函数相加得到的,对勾函数是一种类似于反比例函数的一般双曲函数,其标准形式为f(x)=ax+(其中ab>0)。
由于函数图像形似两个中心对称的对勾,因此得名“对勾函数”,又被称为“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。
在许多情况下,为了简化分析,常取a=b=1,即函数形式为f(x)=x+。
研究初等函数的一般路径,背景—概念—图象—性质—应用二、图象及性质图像特征:1、对勾函数的图像是分别以y 轴和直线y=ax 为渐近线的两支曲线。
2、图像上任意一点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
3、函数图像整体呈两个“对勾”的形状,且关于原点呈中心对称。
定义域:,即除了x=0外,所有实数都是其定义域内的元素。
值域:。
单调性:函数在(−∞,−1)∪(1,+∞)上单调递增,在(1,0)∪(0,1)上单调递减。
奇偶性:对勾函数是奇函数,即满足f(−x)=−f(x)。
x 122严禁复制三、题型1、基础计算题给定对勾函数表达式,求函数在特定点的值或特定区间的最值。
2.、图像结合题根据对勾函数的图像,判断函数在哪些区间内满足特定条件(如大于某值、小于某值)。
利用图像分析函数与直线、其他曲线的交点情况。
3.、综合应用题求最值问题:利用对勾函数的性质,可以快速求解形如ax+(ab>0)的函数的最值问题。
不等式证明:在不等式证明中,对勾函数的性质也常被用来进行放缩或构造反例。
实际问题建模:在某些经济学问题中,如成本分析、收益最大化等,也可能涉及到对勾函数的应用。
4、参数变化分析:探讨参数a 和b 变化时,对勾函数图像和性质的变化规律。
5、复杂函数组合将对勾函数与其他函数(如二次函数、指数函数等)组合,分析新函数的性质和应用。
四、解题步骤1、对勾函数求最值问题的解题步骤(1)理解函数形式确认函数f(x)=ax+的形式,注意a 和b 都是正数且不相等。
换元法之对勾函数(双飘函数)模型

再次换元 (注意范围)
t
x
4
1
,
S
3 2
( x2
2x x
1)
3 2
(x
1 x
2)
Hale Waihona Puke 8y= x 1 在(3,+∞)为增函数,
x
头重脚轻分式,
S 8
对勾模型
三、高考真题
3 1
三、高考真题
43
四、课堂小结与作业布置
(一)课堂小结
1.对勾函数和飘带函数模型是高考的热门考点,一般这种题型用换元法来处理,再进一步转化用对勾函数图像性 质或基本不等式处理.
复合型
y
ax
1 ax
(
y
ax
ax
)
为偶函数)
③单调区间:当a>0,b>0时单调递增区间: ,
b a
,
b a
,
,单调递减区间:
ba,0
,
0,
b a
;
当a<0,b<0时单调递增区间: ba,0
④值域:, 2 ab 2 ab,
,当且仅当
ax
b x
,即
,0,ba
x b a
,单调递减区间: ,
微专题:
双飘函数
一、对勾函数的性质与图像
对 对勾函数是一种类似于反比例函数的一般双曲函数,又被称为“双勾函数”、“对勾函数”、“耐克函数”;
对勾函数是形如
f (x) ax b x
( ab 0 )的函数,常见
y
x
4 x
,
y 2x 3 x
;
对勾函数考点:①定义域: ,0,0, ; ②奇偶性:奇函数;(
(完整版)对勾函数详细分析

对勾函数的性质及应用一、对勾函数b y ax x =+)0,0(>>b a 的图像与性质:1. 定义域:),0()0,(+∞⋃-∞2. 值域:),2[]2,(+∞⋃--∞ab ab3. 奇偶性:奇函数,函数图像整体呈两个“对勾”的形状,且函数图像关于原点呈中心对称,即0)()(=-+x f x f 4. 图像在一、三象限, 当0x >时,by ax x=+≥ab 2(当且仅当b x a ,即)(x f 在x=a b 时,取最小值ab 2由奇函数性质知:当x<0时,)(x f 在x=ab -时,取最大值ab 2-5. 单调性:增区间为(∞+,ab ),(a b -∞-,),减区间是(0,a b ),(a b -,0)二、对勾函数的变形形式 类型一:函数by ax x=+)0,0(<<b a 的图像与性质 1.定义域:),0()0,(+∞⋃-∞ 2.值域:),2[]2,(+∞⋃--∞ab ab3.奇偶性:奇函数,函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时,)(x f 在x=ab 时,取最小值ab 2;当0x >时,)(x f 在x=ab -时,取最大值ab 2-5.单调性:增区间为(0,a b ),(a b -,0)减区间是(∞+,ab ),(a b -∞-,),类型二:斜勾函数by ax x =+)0(<ab①0,0<>b a 作图如下1.定义域:),0()0,(+∞⋃-∞2.值域:R3.奇偶性:奇函数4.图像在二、四象限,无最大值也无最小值.5.单调性:增区间为(-∞,0),(0,+∞).②0,0><b a 作图如下:1.定义域:),0()0,(+∞⋃-∞2.值域:R3.奇偶性:奇函数4.图像在二、四象限,无最大值也无最小值.5.单调性:减区间为(-∞,0),(0,+∞).类型三:函数)0()(2>++=ac xcbx ax x f 。
对勾函数
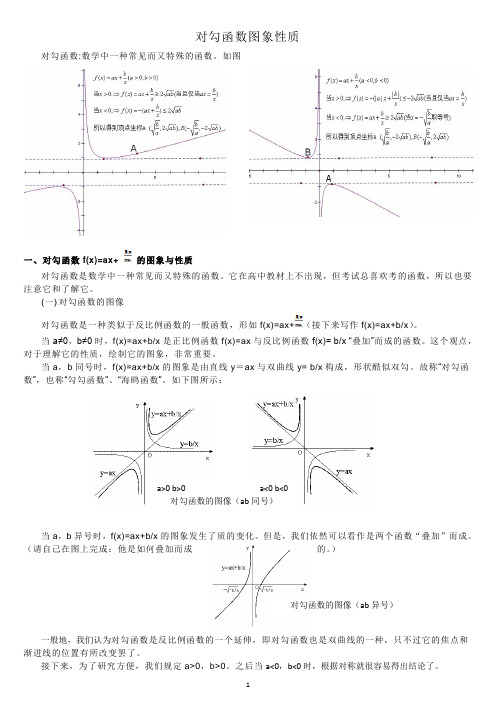
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到: 当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、类耐克函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性对勾函数的图像(ab异号)(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明: 1、求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,则22)1(2≥++=x ttt t t y 112+=+=根据对号函数t t y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
对勾函数的图像及其性质课件

在证明某些不等式时,可以利用对勾函数的单调性、奇偶性等性质进行推导。例如,在证明与根号相关的不等 式时,通过构造函数并利用对勾函数的性质,可以更加简洁地证明不等式。
数列求和与极限计算
数列求和
对勾函数在数列求和中也有广泛应用。例如,在某些含有根 号的数列求和问题中,可以通过对勾函数的变换将问题转化 为等比数列或等差数列求和,从而简化计算过程。
极限计算
在求解某些极限问题时ቤተ መጻሕፍቲ ባይዱ可以利用对勾函数的连续性、可导 性等性质进行推导。通过构造函数并利用洛必达法则等工具 ,可以更加便捷地求解极限问题。
积分变换与微分方程求解
积分变换
对勾函数在积分变换中也有重要作用。例如,在某些含有根号的积分问题中,可以通过对勾函数的变换将问题转 化为更易于求解的形式。此外,对勾函数还可以用于构建某些特殊的积分公式,为积分计算提供便利。
对勾函数拟合
利用对勾函数对需求数据 进行拟合,得到需求曲线 方程。
预测未来需求
基于拟合得到的需求曲线 方程,预测未来不同价格 水平下的需求量。
供给曲线建模与预测
供给分析
收集历史数据,分析生产 者在不同价格水平下愿意 提供的商品或服务的数量 。
对勾函数拟合
利用对勾函数对供给数据 进行拟合,得到供给曲线 方程。
单调性与增减性
单调性
对勾函数在其定义域内不是单调函数。它在某些区间内是增函数,而在另一些区 间内是减函数。
增减性
具体来说,当x从负无穷大增加到0时,对勾函数从0增加到正无穷大;当x从0增 加到正无穷大时,对勾函数从正无穷大减少到0。因此,对勾函数在x=0处达到 极大值。
凸凹性与拐点
凸凹性
对勾函数在其定义域内既不是凸函数也不是凹函数。它在某些区间内是凸函数 ,而在另一些区间内是凹函数。
对勾函数图象性质
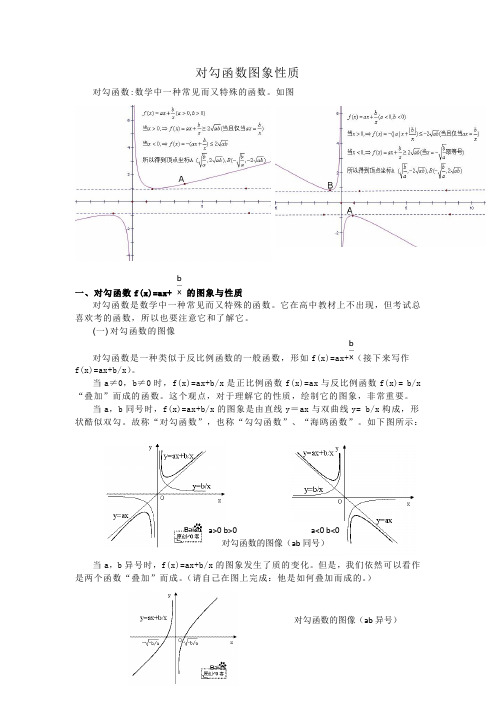
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像 对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、类对勾函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式能够得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数,二、关于求函数()01>+=x xx y 最小值的解法1. 均值不等式 0>x ,∴21≥+=xx y ,当且仅当x x 1=,即1=x 的时候不等式取到“=”。
∴当1=x 的时候,2min =y 2. ∆法 0112=+-⇒+=yx x xx y 若y 的最小值存有,则042≥-=∆y 必需存有,即2≥y 或2-≤y (舍)找到使2=y 时,存有相对应的x 即可。
对勾函数图象性质

对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一)对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、类对勾函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
在时且00≠≠b a 有如下几种情况:(1)0,0<>b a (2)0,0><b a (3)0,0>>b a (4)0,0<<b a 设ax y =1,x by =2,则xb ax y y y +=+=21,其定义域为{}0,|≠∈x R x x 且 (1)0,0<>b a 时,ax y =1,xby =2在),0(),0,(+∞-∞上分别单调递增。
数学对勾函数(详细分析“函数”共8张)

性质一
➢ 函数y=ax+b/x的性质 ➢ Ⅰ当a、b均大于零时,性质 : ➢ ⑴定义域:x≠0 ➢ ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,
+∞〕 ⑶奇偶性:奇函数 ➢ ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,
y为减函数 当x﹥根号b/a 时,y为增函 数 当x﹤0时,当- 根号b/a﹤x﹤0时,y 为减函数 当x﹤根号b/a- 时,y为增函 数
第7页,共8页。
图像三
第8页,共8页。
数学对勾函数
第1页,共8页。
简介对Biblioteka 函数:图像,性质,单调性对勾函数是数学中一种常见而又特殊的函数,见图示。 对勾函数是一种类似于反比例函数的一般函数,
又被称为“双勾函数〞、"勾函数"等。也被形象称 为“耐克函数〞
所谓的对勾函数〔双曲线函数〕,是形如 f(x)=ax+b/x的函数。由图像得名。
当x>0时,f(x)=ax+b/x有最小值〔这里为了研究方 便,规定a>0,b>0〕,也就是当x=sqrt(b/a)的时候 〔sqrt表示求二次方根〕
第6页,共8页。
图象二
Ⅰ当a、b均大于零时,性质 : 当a、b>0时,图像分布在第一、三象限两条渐近线的锐角之间局部,由于其对称性,只讨论第一象限中的情形。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 对号函数是双曲线旋转得到的,所以也有渐近线、焦点、顶点等等 对勾函数是数学中一种常见而又特殊的函数,见图示。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 Ⅰ当a、b均大于零时,性质 : ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 当a、b>0时,图像分布在第一、三象限两条渐近线的锐角之间局部,由于其对称性,只讨论第一象限中的情形。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 对号函数永远是奇函数,关于原点呈中心对称 ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,+∞〕 ⑶奇偶性:奇函数 当x>0时,f(x)=ax+b/x有最小值〔这里为了研究方便,规定a>0,b>0〕,也就是当x=sqrt(b/a)的时候〔sqrt表示求二次方根〕 ⑹对称性:图像关于原点对称 利用平均值不等式〔a>0,b>0且ab的值为定值时,a+b≥2√ab〕可知最小值是2倍根号ab,在x=根号下b/a的时候取得,所以在〔0,负根号下b/a〕 上单调递减,在〔根号下b/a,正无穷〕上单调递增
数学 对勾函数知识讲解
图象二
ቤተ መጻሕፍቲ ባይዱ
图像三
图像 四
件下 载可 自行 编辑 修改, 仅供 参考! 感谢 您的 支持, 我们 努力 做得 更好!
性质简介
1.对号函数是双曲线旋转得到的,所以也有渐近线、 焦点、顶点等等
2.对号函数永远是奇函数,关于原点呈中心对称 3.对号函数的两条渐进线永远是y轴和y=ax 4.当a、b>0时,图像分布在第一、三象限两条渐近 线的锐角之间部分,由于其对称性,只讨论第一象 限中的情形。利用平均值不等式(a>0,b>0且ab 的值为定值时,a+b≥2√ab)可知最小值是2倍根号 ab,在x=根号下b/a的时候取得,所以在(0,负根 号下b/a)上单调递减,在(根号下b/a,正无穷) 上单调递增
性质一
➢ 函数y=ax+b/x的性质 ➢ Ⅰ当a、b均大于零时,性质 : ➢ ⑴定义域:x≠0 ➢ ⑵值 域:(-∞,-2 根号ab)∪(2根号ab ,
+∞) ⑶奇偶性:奇函数 ➢ ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,
y为减函数 当x﹥根号b/a 时,y为增函 数 当x﹤0时,当- 根号b/a﹤x﹤0时,y 为减函数 当x﹤根号b/a- 时,y为增函 数
简介
对勾函数:图像,性质,单调性 对勾函数是数学中一种常见而又特殊的函数,见 图示。
对勾函数是一种类似于反比例函数的一般函 数,又被称为“双勾函数”、"勾函数"等。也被 形象称为“耐克函数”
所谓的对勾函数(双曲线函数),是形如 f(x)=ax+b/x的函数。由图像得名。
当x>0时,f(x)=ax+b/x有最小值(这里为了研 究方便,规定a>0,b>0),也就是当x=sqrt(b/a) 的时候(sqrt表示求二次方根)
对勾函数

对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性:对勾函数在定义域内是奇函数,二、类耐克函数性质探讨函数xbaxy+=,在时或00==ba为简单的单调函数,不予讨论。
对勾函数图象性质
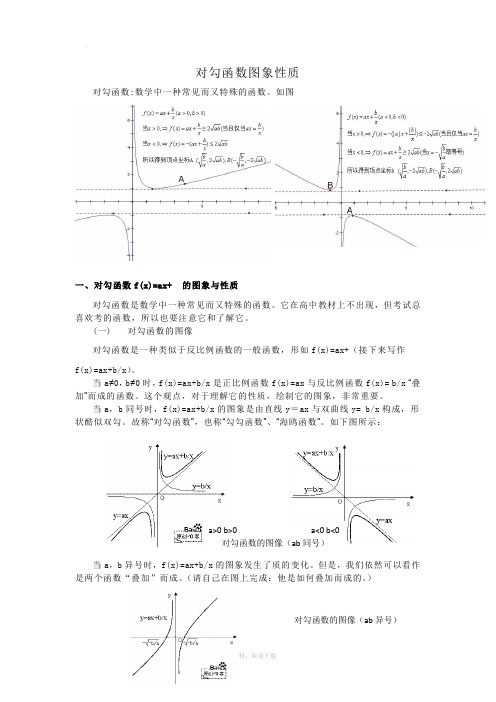
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a ≠0,b ≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,当且尽当时取等号 ,此时。
当x<0时,当且尽当时取等号 ,此时。
(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数,二、类对勾函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
专题:对勾函数
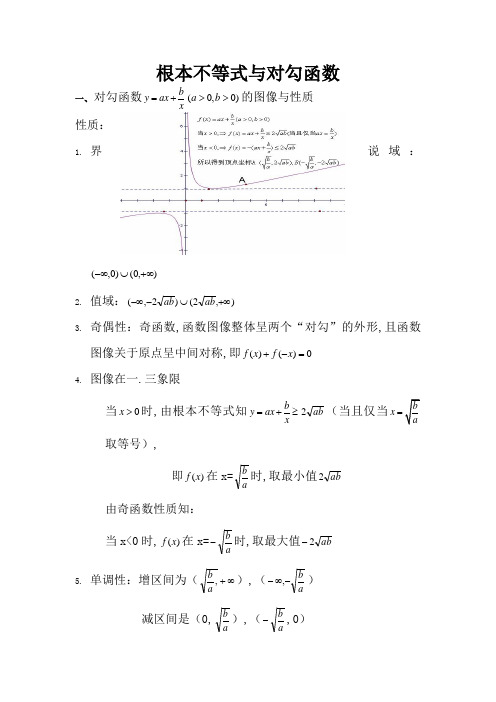
根本不等式与对勾函数一、 对勾函数by ax x=+)0,0(>>b a 的图像与性质 性质:1.界说域:),0()0,(+∞⋃-∞2. 值域:),2()2,(+∞⋃--∞ab ab3.奇偶性:奇函数,函数图像整体呈两个“对勾”的外形,且函数图像关于原点呈中间对称,即0)()(=-+x f x f4.图像在一.三象限当0x >时,由根本不等式知b y ax x =+≥ab 2(当且仅当b x a=取等号),即)(x f 在x=ab 时,取最小值ab 2由奇函数性质知: 当x<0时,)(x f 在x=ab -时,取最大值ab 2-5.单调性:增区间为(∞+,a b ),(ab -∞-,)减区间是(0,ab),(ab -,0)一、对勾函数的变形情势类型一:函数b y ax x=+)0,0(<<b a 的图像与性质此函数与对勾函数xb x a y )()(-+-=关于原点对称,故函数图像为 性质:类型二:斜勾函数b y ax x=+)0(<ab①,0<>b a 作图如下性质: ②0,0><b a 作图如下: 类型三:函数)0()(2>++=ac xc bx ax x f此类函数可变形为b x c ax x f ++=)(,则)(x f 可由对勾函数xc ax y +=高低平移得到 例1作函数xx x x f 1)(2++=的草图解:11)(1)(2++=⇒++=xx x f x x x x f 作图如下:类型四:函数)0,0()(≠>++=k a kx ax x f 此类函数可变形为kkx ak x x f -+++=)()(,则)(x f 可由对勾函数xax y +=阁下平移,高低平移得到例2作函数21)(-+=x x x f 的草图 解:2212)(21)(+-+-=⇒-+=x x x f x x x f 作图如下: 例3作函数x x x x f +++=23)(的作图:解:1212211212)(23)(-+++=+++=++++=⇒+++=x x x x x x x x f x x x x f演习:1.求函数421)(-+=x x x f 在),2(+∞上的最低点坐标2. 求函数1)(-+=x xx x f 的单调区间及对称中间类型五:函数)0,0()(2>≠+=b a bx axx f此类函数界说域为R ,且可变形为x b x axbx a x f +=+=2)( a.若0>a ,则)(x f 的单调性和对勾函数xb x y +=的单调性相反,图像如下:性质:1.界说域:),(+∞-∞ 2. 值域:)21,21(ba ba ⋅⋅-3. 奇偶性:奇函数,函数图像整体呈两个倒着的“对勾”的外形,且函数图像关于原点呈中间对称,即0)()(=-+x f x f4. 图像在一.三象限当0x >时,由根本不等式知ba xb x a x f 22)(=⋅≤(当且仅当b x =取等号),即)(x f 在b x =时,取最大值ba 2由奇函数性质知:当x<0时,)(x f 在x=b -时,取最小值ba 2-5. 单调性:减区间为(∞+,b ),(b -∞-,)增区间是],[b b -例4作函数1)(2+=x xx f 的草图 解:x x xx x f x xx f 1111)(1)(22+=+=⇒+=b.若0<a ,作出函数图像: 例5作函数42)(2+-=x xx f 的草图 类型六:函数)0()(2≠+++=a mx c bx ax x f此类函数可变形为)0()()()()(2>++++=+++++=at s mx t m x a m x t m x s m x a x f ,则)(x f 可由对勾函数xtax y +=阁下平移,高低平移得到 例6解释函数11)(2+++=x x x x f 由对勾函数xx y 1+=若何变换而来解:111111)1()1()(2-+++=+++-+=x x x x x x f故 此函数)(x f 可由对勾函数xx y 1+=向(填“左”.“右”)平移单位,向(填“上”.“下”)平移单位.草图如下: 演习:1.已知1->x ,求函数1107)(2+++=x x x x f 的最小值1<x ,求函数1109)(2--+=x x x x f 的最大值类型七:函数)0()(2≠+++=a cbx ax mx x f 例7求函数21)(2++-=x x x x f 在区间),1(+∞上的最大值解:当1=x 时,0)1(=f 当1≠x 时,3141114)1(3)1(14)1(3)1(1)(22+-+-=-+-+-=+-+--=x x x x x x x x x f问:若区间改为),4[+∞则)(x f 的最大值为 演习232)(22++++=x x x x x f 在区间),0[+∞上的最大值类型八:函数ax b x x f ++=)(此类函数可变形为尺度情势:)0()(>-+-++=+-++=a b ax a b a x ax ab a x x f例8求函数13)(-+=x x x f 的最小值解:141141)(-+-=-+-=x x x x x f演习:1.求函数15)(++=x x x f 的值域2.求函数32)(++=x x x f 的值域 类型九:函数)0()(22>++=a ax b x x f此类函数可变形为尺度情势:)()()(22222o a b ax a b a x ax ab a x x f >-+-++=+-++=例9求函数45)(22++=x x x f 的最小值解:45)(22++=x x x f 414414)(2222+++=+++=⇒x x x x x f演习:1. 求函数171)(22++=x x x f 的值域例10已知20,a >求函数的最小值.解:2=令t ≥则1t t +y=1即1a ≥时,min y1即01a <<时,2min y =。
