2012中考数学压轴题及答案40例(5)
2012年中考数学压轴题精选附答案
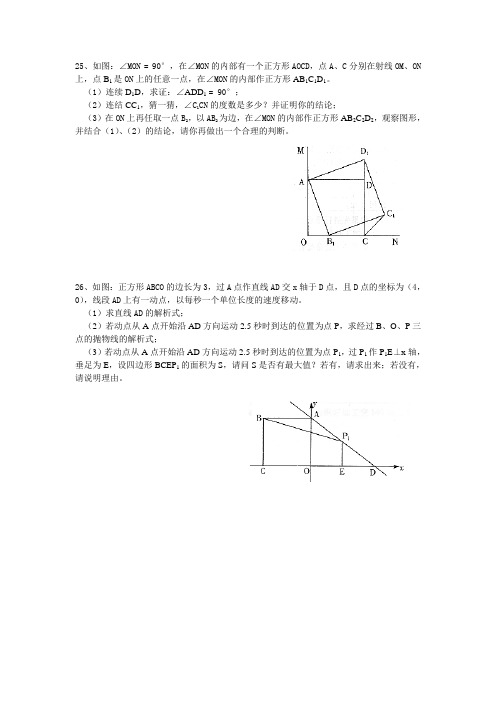
25、如图:∠MON = 90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON 上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1。
(1)连续D1D,求证:∠ADD1= 90°;(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断。
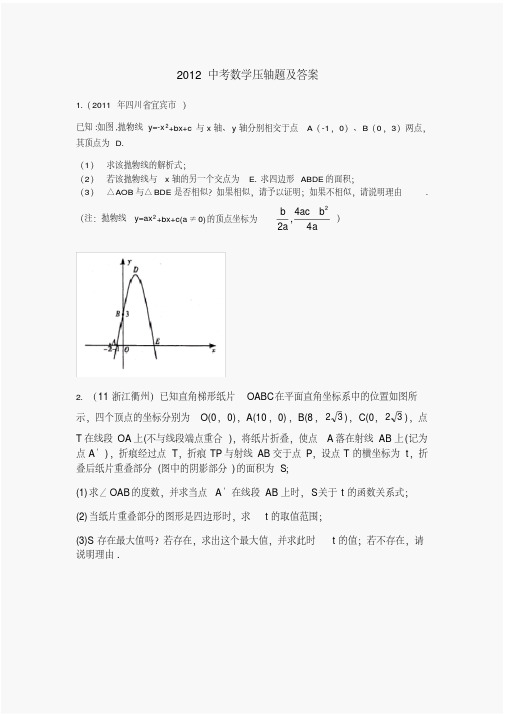
26、如图:正方形ABCO的边长为3,过A点作直线AD交x轴于D点,且D点的坐标为(4,0),线段AD上有一动点,以每秒一个单位长度的速度移动。
(1)求直线AD的解析式;(2)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P,求经过B、O、P三点的抛物线的解析式;(3)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P1,过P1作P1E⊥x轴,垂足为E,设四边形BCEP1的面积为S,请问S是否有最大值?若有,请求出来;若没有,请说明理由。
24.如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥3,AD=12.BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=5⑴求证:△ANM≌△ENM;⑵求证:FB是⊙O的切线;⑶证明四边形AMEN是菱形,并求该菱形的面积S.7),且顶点C的横坐标为4,该图象在x 轴上截25.如图,二次函数的图象经过点D(0,39得的线段AB的长为6.⑴求二次函数的解析式;⑵在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;⑶在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.七、(本大题8分)20.如图8,半圆的直径10AB =,点C 在半圆上,6BC =. (1)求弦AC 的长;(2)若P 为AB 的中点,PE AB ⊥交AC 于点E ,求PE 的长.21.如图9,已知正比例函数和反比例函数的图象都经过点(33)A ,. (1)求正比例函数和反比例函数的解析式;(2)把直线O A 向下平移后与反比例函数的图象交于点(6)B m ,,求m 的值和这个一次函数的解析式;(3)第(2)问中的一次函数的图象与x 轴、y 轴分别交于C 、D ,求过A 、B 、D 三点的二次函数的解析式;(4)在第(3)问的条件下,二次函数的图象上是否存在点E ,使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足:123S S =?若存在,求点E 的坐标;若不存在,请说明理由.P BC EA (图8)23.(本小题9分)如图,AB 是⊙O 的直径,C 是AB 延长线上一点,CD 与⊙O 相切于点E ,AD ⊥CD (1)求证:AE 平分∠DAC ; (2)若AB=3,∠ABE=60°,①求AD 的长;②求出图中阴影部分的面积。
2012中考数学压轴题及答案
( 1)求 m ,k 的值;
( 2)如果 M 为 x 轴上一点, N 为 y 轴上一点,
以点 A,B,M, N 为顶点的四边形是平行四边形,
试求直线 MN 的函数表达式.
(3) 选做题 :在平面直角坐标系中,点 P 的坐标
为( 5, 0),点 Q 的坐标为( 0, 3),把线段 PQ 向右平
移 4 个单位,然后再向上平移 2 个单位,得到线段 P1Q1,
绕着点 A按逆时针方向旋转 . 使边 AO与 AB重合 . 得到Δ ABD. ( 1)求直线 AB的解析式;
( 2)当点 P运动到点( 3 , 0 )时,求此时 DP的长及点 D的坐标;( 3 )是否存在点
P,使Δ OPD的面积等于 请说明理由 .
3
,若存在,请求出符合条件的点
4
P的坐标;若不存在,
象限 . ①说明四边形 APBQ一定是平行四边形;②设点
A.P 的横坐标分别为 m, n ,
四边形 APBQ可能是矩形吗 ?可能是正方形吗 ?若可能, 直接写出 mn应满足的条件;
若不可能,请说明理由 .
6. (2011浙江金华) 如图 1 ,在平面直角坐标系中,己知Δ
AOB是等边三角形,点
A的坐标是 (0 , 4) ,点 B在第一象限,点 P是 x轴上的一个动点,连结 AP,并把Δ AOP
11.2011 淅江宁波 )2011 年 5 月 1 日,目前世界上最长的跨海大桥——杭州湾跨海大桥 通车了. 通车后, 苏南 A 地到宁波港的路程比原来缩短了 120 千米. 已知运输车速度不 变时,行驶时间将从原来的 3 时 20 分缩短到 2 时.
(1)求 A 地经杭州湾跨海大桥到宁波港的路程.
8. (2011 浙江义乌 )如图 1 所示,直角梯形 OABC的顶点 A、C 分别在 y 轴正半轴与 x 轴 负半轴上 . 过点 B、C 作直线 l .将直线 l 平移,平移后的直线 l 与 x 轴交于点 D,与 y 轴 交于点 E.
2012年中考数学压轴题辽宁

辽宁省各市2012年中考数学试题分类解析汇编专题12:押轴题一、选择题1. (2012辽宁鞍山3分)如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=BC=4,DE⊥BC于点E,且E是BC中点;动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动;设点P的运动时间为t秒,△PBC的面积为S,则下列能反映S与t的函数关系的图象是【】A.B.C.D.【答案】B。
【考点】动点问题的函数图象。
【分析】分别求出点P在DE、AD、AB上运动时,S与t的函数关系式,结合选项即可得出答案:根据题意得:当点P在ED上运动时,S=12BC•PE=2t;当点P在DA上运动时,此时S=8;当点P在线段AB上运动时,S=12BC(AB+AD+DE-t)=5-12t。
结合选项所给的函数图象,可得B选项符合。
故选B。
2. (2012辽宁本溪3分)如图,已知点A在反比例函数4y=x图象上,点B在反比例函数ky=x(k≠0)的图象上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为C、D,若OC=13OD,则k的值为【】A 、10B 、12C 、14D 、16 【答案】B 。
【考点】反比例函数的图象和性质。
【分析】由已知,设点A (x ,4x),∵OC=13OD ,∴B (3x ,k 3x)。
∴4k =x 3x,解得k=12。
故选B 。
3. (2012辽宁朝阳3分)如图,矩形ABCD 的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数2k +4k+1y=x的图象上,若点A 的坐标为(-2,-3),则k的值为【 】A.1B. -5C. 4D. 1或-5 【答案】D 。
【考点】矩形的性质,反比例函数图象上点的坐标特征。
【分析】如图:∵四边形ABCD 、HBEO 、OECF 、GOFD 为矩形,又∵BO 为四边形HBEO 的对角线,OD 为四边形OGDF 的对角线, ∴BEO BHO OFD OGD CBD ADB S S S S S S ∆∆∆∆∆∆===,,。
2012年中考数学压轴题及解析分类汇编

中考数学压轴题:函数相似三角形问题(一)例1直线113y x =-+分别交x 轴、y 轴于A 、B 两点,△AOB 绕点O 按逆时针方向旋转90°后得到△COD ,抛物线y =ax 2+bx +c 经过A 、C 、D 三点.(1) 写出点A 、B 、C 、D 的坐标;(2) 求经过A 、C 、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;(3) 在直线BG 上是否存在点Q ,使得以点A 、B 、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.例2 Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)ky k x=≠在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m 与n 的数量关系; (2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式; (3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO 与△EFP 相似,求点P 的坐标.图12012中考数学压轴题函数相似三角形问题(二)例3 如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1 图2例4 如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22=++上.y mx mx n (1)求m、n;(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB′的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.图12012中考数学压轴题函数相似三角形问题(三) 例5 如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.,图1例6 如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域; (2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.图1 备用图 备用图例 7 如图1,在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b ).平移二次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B 、C 两点(∣OB ∣<∣OC ∣),连结A ,B .(1)是否存在这样的抛物线F ,使得OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO =23,求抛物线F 对应的二次函数的解析式.图12012中考数学压轴题函数等腰三角形问题(一)例1 如图1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P (0,m )是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .(1)求点D 的坐标(用含m 的代数式表示); (2)当△APD 是等腰三角形时,求m 的值;(3)设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H (如图2).当点P 从O 向C 运动时,点H 也随之运动.请直接写出点H 所经过的路长(不必写解答过程).图1 图2例2 如图1,已知一次函数y =-x +7与正比例函数43y x 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l//y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.图12012中考数学压轴题函数等腰三角形问题(二)例3 如图1,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N 分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN∶NP为定值;(2)若△BNP与△MNA相似,求CM的长;(3)若△BNP是等腰三角形,求CM的长.图1例4 如图1,在矩形ABCD 中,AB =m (m 是大于0的常数),BC =8,E 为线段BC 上的动点(不与B 、C 重合).连结DE ,作EF ⊥DE ,EF 与射线BA 交于点F ,设CE =x ,BF =y .(1)求y 关于x 的函数关系式;(2)若m =8,求x 为何值时,y 的值最大,最大值是多少? (3)若12y m,要使△DEF 为等腰三角形,m 的值应为多少?图12012中考数学压轴题函数相似三角形问题(三)例5 已知:如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由; (3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在成立,请说明理由.图1例6 在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM//x轴(如图1所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,联结OD.(1)求b的值和点D的坐标;(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;(3)在(2)的条件下,如果以PD为半径的圆与圆O外切,求圆O的半径.图12012中考数学压轴题函数直角三角形问题(一)例1 如图1,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B 左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段34PQ AB =时,求tan ∠CED 的值;②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.图1例2 设直线l 1:y =k 1x +b 1与l 2:y =k 2x +b 2,若l 1⊥l 2,垂足为H ,则称直线l 1与l 2是点H 的直角线.(1)已知直线①122y x =-+;②2y x =+;③22y x =+;④24y x =+和点C (0,2),则直线_______和_______是点C 的直角线(填序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC 的顶点A (3,0)、B (2,7)、C (0,7),P 为线段OC 上一点,设过B 、P 两点的直线为l 1,过A 、P 两点的直线为l 2,若l 1与l 2是点P 的直角线,求直线l 1与l 2的解析式.图12012中考数学压轴题函数直角三角形问题(三)例 5 如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).(1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1例6 已知Rt △ABC 中,︒=∠90ACB ,CB CA =,有一个圆心角为︒45,半径的长等于CA 的扇形CEF 绕点C 旋转,且直线CE ,CF 分别与直线AB 交于点M ,N .(1)当扇形CEF 绕点C 在ACB ∠的内部旋转时,如图1,求证:222BN AM MN +=;思路点拨:考虑222BN AM MN +=符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM 沿直线CE 对折,得△DCM ,连DN ,只需证BN DN =,︒=∠90MDN 就可以了.请你完成证明过程.(2)当扇形CEF 绕点C 旋转至图2的位置时,关系式222BN AM MN +=是否仍然成立?若成立,请证明;若不成立,请说明理由.图1 图2图5 图6 图72012中考数学压轴题函数平行四边形问题(一)例 1 已知平面直角坐标系xOy (如图1),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M .(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.图1例2将抛物线c 1:2y =x 轴翻折,得到抛物线c 2,如图1所示.(1)请直接写出抛物线c 2的表达式;(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(二)例3 如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1 图2例4在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1 图22012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ 的面积(用含x的代数式表示);(3)当(2)中的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB上是否存在点E,使得以点E、D、O、A为顶点的四边形是平行四边形?如果存在,直接写出BECD的值;如果不存在,请说明理由.图12012中考数学压轴题函数梯形问题(一)例1 已知平面直角坐标系xOy中,抛物线y=ax2-(a+1)x与直线y=kx的一个公共点为A(4,8).(1)求此抛物线和直线的解析式;(2)若点P在线段OA上,过点P作y轴的平行线交(1)中抛物线于点Q,求线段PQ长度的最大值;(3)记(1)中抛物线的顶点为M,点N在此抛物线上,若四边形AOMN恰好是梯形,求点N的坐标及梯形AOMN的面积.备用图图1 图2例 2 已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4,设顶点为点P ,与x 轴的另一交点为点B .(1)求二次函数的解析式及顶点P 的坐标;(2)如图1,在直线 y =2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点D 的坐标;若不存在,请说明理由;(3)如图2,点M 是线段OP 上的一个动点(O 、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN //x 轴,交PB 于点N . 将△PMN 沿直线MN 对折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.图1 图22012中考数学压轴题函数梯形问题(二)例3 如图1,在平面直角坐标系xOy 中,抛物线的解析式是y =2114x ,点C 的坐标为(–4,0),平行四边形OABC 的顶点A ,B 在抛物线上,AB 与y 轴交于点M ,已知点Q (x ,y )在抛物线上,点P (t ,0)在x 轴上.(1) 写出点M 的坐标;(2) 当四边形CMQP 是以MQ ,PC 为腰的梯形时.① 求t 关于x 的函数解析式和自变量x 的取值范围;② 当梯形CMQP 的两底的长度之比为1∶2时,求t 的值.图1例 4 已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 32-=与边BC 相交于点D . (1)求点D 的坐标;(2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式;(3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC 的边长为4,E 是边BC 上的动点,EH ⊥AC 于H ,过E 作EF ∥AC ,交线段AB 于点F ,在线段AC 上取点P ,使PE =EB .设EC =x (0<x ≤2).(1)请直接写出图中与线段EF 相等的两条线段(不再另外添加辅助线);(2)Q 是线段AC 上的动点,当四边形EFPQ 是平行四边形时,求平行四边形EFPQ 的面积(用含x 的代数式表示);(3)当(2)中 的平行四边形EFPQ 面积最大值时,以E 为圆心,r 为半径作圆,根据⊙E 与此时平行四边形EFPQ 四条边交点的总个数,求相应的r 的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB 上是否存在点E ,使得以点E 、D 、O 、A 为顶点的四边形是平行四边形?如果存在,直接写出BE CD的值;如果不存在,请说明理由.图12012中考数学压轴题函数面积问题(一)例 1 如图1,直线l 经过点A (1,0),且与双曲线m y x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和m y x=-(x <0)于M 、N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.图1例2 如图1,在平面直角坐标系xOy 中,直角梯形OABC 的顶点O 为坐标原点,顶点A 、C 分别在x 轴、y 轴的正半轴上,CB ∥OA ,OC =4,BC =3,OA =5,点D 在边OC 上,CD =3,过点D 作DB 的垂线DE ,交x 轴于点E .(1)求点E的坐标;(2)二次函数y=-x2+bx+c的图像经过点B和点E.①求二次函数的解析式和它的对称轴;②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.图12012中考数学压轴题函数面积问题(二)例3 如图1,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1).点D是线段BC上的动点(与端点B、C不重合),过点D作直线12y x b=-+交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.例 4 如图1,在△ABC中,∠C=90°,A C=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.(1)求线段AD的长;(2)若EF⊥AB,当点E在斜边AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围);②当x取何值时,y有最大值?并求出最大值.(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.图1 备用图2012中考数学压轴题函数面积问题(三)例5 如图1,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP 与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.图1 图2例6 在直角坐标系中,抛物线c=2经过点(0,10)和点(4,2).+y+xbx(1)求这条抛物线的解析式.(2)如图1,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线=2滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,y++cbxxAB落在x轴上.①求边BC的长.②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.。
人教版2012年中考数学压轴题精选

易知点F的坐标为(2,2),故BF=2,作PM⊥BF. ∵△PBF是等腰直角三角形,∴PM=BF=1. ∴点P的坐标为(3,3). ∵抛物线经过原点 ∴可设抛物线的解析式为y=ax 2+bx. 又∵抛物线经过点P(3,3)和点D(2,0) ∴ 解得 ∴过O、P、D三点的抛物线的解析式为y=x 2-2x; 7分 (3)由等腰直角三角形的对称性知D点关于∠AOC的平分线的 对称点即为C点.
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是 等腰三角形? 请直接写出相应的t值。
【004】如图,已知直线 与直线 相交于点 分别交
轴于
两点.矩形
的顶点
分别在直线
上,顶点
都在
轴上,且点
与点
重合. (1)求 的面积; (2)求矩形 的边 与 的长; (3)若矩形 从原点出发,沿 轴的反方向以每秒1个单位长度的速度平移,
F M P E ∴直线BC的解析式为y=-x+3. 当x=1时,y=-1+3=2,∴E(1,2). 当x=m时,y=-m+3,∴P(m,-m+3). 4分 将x=1代入y=-x 2+2x+3,得y=4,∴D(1,4). 将x=m代入y=-x 2+2x+3,得y=-m 2+2m+3. ∴F(m,-m 2+2m+3). 5分 ∴线段DE=4-2=2,线段PF=-m 2+2m+3-(-m+3)= -m 2+3m 6分 ∵PF∥DE,∴当PF=DE时,四边形PEDF为平行四边形. 由-m 2+3m=2,解得:m1=2,m2=1(不合题意,舍 去). ∴当m=2时,四边形PEDF为平行四边形. 7分 ②设直线PF与x轴交于点M. 由B(3,0),O(0,0),可得:OB=OM+MB=3. 则S=S△BPF +S△CPF 8分 =PF·BM+PF·OM =PF·OB =(-m 2+3m)×3 =-m 2+m(0≤m≤3) 即S与m的函数关系式为:S=-m 2+m(0≤m≤3). 9 分
2012年全国各地中考数学压轴题精选(解析版1--10)

2012年全新中考数学模拟试题四(时量:120分钟 满分:120分)一. 填空题(每小题3分,共24分) 102..-的倒数是。
2282.分解因式:。
x -=321.在函数中,自变量的取值范围是。
y x x =-41236.不等式组的解集是。
x x +≥<⎧⎨⎩5. 母线长为3cm 底面半径为1cm 的圆柱的侧面展开图的面积为_____________cm 2。
6. 如图所示,已知△ABC 中,P 为AB 上一点,连结PC ,要使△ACP ∽△ABC ,只需添加条件_____________。
(只需填入一种情况)7. 如图所示,P 是⊙O 的弦AB 上的一点,AB =10cm ,AP =4cm ,OP =5cm ,则⊙O 的半径为_____________cm 。
8. 观察下列各式:111222233334222+=⨯+=⨯+=⨯ ……请你将猜想到的规律用自然数n (n ≥1)表示出来_____________。
二. 选择题(每题3分,共24分) 98212227021211211123230..()在实数,,,,…,,--π sin tan tan .604743022o o o ·,中无理数有()-A. 2个B. 3个C. 4个D. 5个10131201222.如用换元法解方程,并设,那么原方程可x x x x y x x ---+==- 化为( ) A y y B y y ..22320320-+=+-=C y yD y y ..22230230-+=+-=11. 受季节的影响,某种商品每件按原售价降价10%,又降价a 元,现每件售价为b 元,那么该商品每件的原售价为( ) A a bB a b ..()+--+110%110%)(元元C b aD b a ..()----110%110%)(元元12. 在矩形ABCD 中,AB =3cm ,AD =2cm ,则以AB 所在直线为轴旋转一周所得的圆柱的表面积为( ) A cm B cm ..172022ππC cmD cm ..213022ππ13. 已知点P 是半径为5的⊙O 内一定点,且OP =4,则过点P 的所有弦中,弦长可能取到的整数值为( )A. 5,4,3B. 10,9,8,7,6,5,4,3C. 10,9,8,7,6D. 12,11,10,9,8,7,6 14. 下列说法错误的是( )A. 直线y =x 就是第一、三象限的角平分线 B y x.反比例函数的图象经过点(,)=212 C y x y x .函数中,随着的增大而减小=-310D y x x x .抛物线的对称轴是=-+=2211()1512102.sin tan 已知,则等于()αβαβ-+-=+A. 105°B. 75°C. 60°D. 90° 16. 若两圆的圆心距等于7,半径分别是R 、r ,且R 、r 是关于x 的方程ax ax 2560-+=的两个根,则这两圆的位置关系是()A. 相离B. 相交C. 内切D. 外切 三. 解答题(本题共6个小题,每小题6分,共36分)()172132226021.()cos 计算:-+⎛⎝ ⎫⎭⎪----o1822232.先将化简,然后自选一个合适的值,代入化简后的式x x xx xx --÷- 子求值。
2012年数学中考压轴题

已知:如图,一艘渔船正在港口A 的正东方向40海里的B 处进行捕鱼作业,突然接到通知,要该船前往C 岛运送一批物资到A 港,已知C 岛在A 港的北偏东60°方向,且在B 的北偏西45°方向.问该船从B 处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A 港(精确到1小时)(该船在C 岛停留半个小时)?)45.26,73.13,41.12(≈≈≈22.已知:如图,直线y =-x +12分别交x 轴、y 轴于A 、B 点,将△AOB 折叠,使A点恰好落在OB 的中点C 处,折痕为DE .(1)求AE 的长及sin ∠BEC 的值; (2)求△CDE 的面积.23.已知:如图,斜坡PQ 的坡度i =1∶3,在坡面上点O 处有一根1m 高且垂直于水平面的水管OA ,顶端A 处有一旋转式喷头向外喷水,水流在各个方向沿相同的抛物线落下,水流最高点M 比点A 高出1m ,且在点A 测得点M 的仰角为30°,以O 点为原点,OA 所在直线为y 轴,过O 点垂直于OA 的直线为x 轴建立直角坐标系.设水喷到斜坡上的最低点为B ,最高点为C .(1)写出A 点的坐标及直线PQ 的解析式;(2)求此抛物线AMC 的解析式; (3)求|x C -x B |;(4)求B 点与C 点间的距离.如图所示,⊙O 的内接△ABC 中,∠BAC =45°,∠ABC =15°,AD ∥OC 并交BC 的延长线于D 点,OC 交AB 于E 点.(1)求∠D 的度数;(2)求证:AC 2=AD ·CE .18.已知:如图,△ABC 中,∠BAC =90°,AB =AC =1,点D 是BC 边上的一个动点(不与B ,C 点重合),∠ADE =45°.(1)求证:△ABD ∽△DCE ;(2)设BD =x ,AE =y ,求y 关于x 的函数关系式; (3)当△ADE 是等腰三角形时,求AE 的长.19.已知:如图,△ABC 中,AB =4,D 是AB 边上的一个动点,DE ∥BC ,连结DC ,设△ABC 的面积为S ,△DCE 的面积为S ′.(1)当D 为AB 边的中点时,求S ′∶S 的值; (2)若设,,y SS x AD ='=试求y 与x 之间的函数关系式及x 的取值范围.20.已知:如图,抛物线y =x 2-x -1与y 轴交于C 点,以原点O 为圆心,OC 长为半径作⊙O ,交x 轴于A ,B 两点,交y 轴于另一点D .设点P 为抛物线y =x 2-x -1上的一点,作PM ⊥x 轴于M 点,求使△PMB ∽△ADB 时的点P 的坐标.21.在平面直角坐标系xOy 中,已知关于x 的二次函数y =x 2+(k -1)x +2k -1的图象与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C (0,-3). 求这个二次函数的解析式及A ,B 两点的坐标.22.如图所示,在平面直角坐标系xOy 内已知点A 和点B 的坐标分别为(0,6),(8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P ,Q 移动的时间为t 秒.(1)求直线AB 的解析式;(2)当t 为何值时,△APQ 与△ABO 相似? (3)当t 为何值时,△APQ 的面积为524个平方单位?23.已知:如图,□ABCD 中,AB =4,BC =3,∠BAD =120°,E 为BC 上一动点(不与B 点重合),作EF ⊥AB 于F ,FE ,DC 的延长线交于点G ,设BE =x ,△DEF 的面积为S .(1)求证:△BEF∽△CEG;(2)求用x表示S的函数表达式,并写出x的取值范围;(3)当E点运动到何处时,S有最大值,最大值为多少?。
2012年中考数学压轴题精选(含答案)

(2012年北京市)24、在△ABC 中,BA =BC ,∠BAC =α,M 是AC 的中点,P 是线段BM 上的动点,将线段PA 绕点P 顺时针旋转2α得到线段PQ 。
(1)若α=60°且点P 与点M 重合(如图1),线段CQ 的延长线交射线BM 于点D ,请补全图形,并写出∠CDB 的度数;(2)在图2中,点P 不与点B 、M 重合,线段CQ 的延长线于射线BM 交于点D ,猜想∠CDB 的大小(用含α的代数式表示),并加以证明;(3)对于适当大小的α,当点P 在线段BM 上运动到某一位置(不与点B 、M 重合)时,能使得线段CQ 的延长线与射线BM 交于点D ,且PQ =DQ ,请直接写出α的范围。
图1QM(P)C B APM图2QCBA(答案)(1)o CDB 30=∠ (2)α-=∠o CDB 90 (3)o o 6045<<α (2012年北京市)25、在平面直角坐标系xOy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”,给出如下定义:若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|; 若|x 1-x 2|<|y 1-y 2|,则点P 1与点P 2的“非常距离”为|y 1-y 2|。
例如:点P 1(1,2),点P 2(3,5),因为|1-3|<|2-5|,所以点P 1与点P 2的“非常距离”为|2-5|=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 的交点)。
(1)已知点A(-12,0),B 为y 轴上的一个动点,①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标; ②直接写出点A 与点B 的“非常距离”的最小值;(2)已知C 是直/线y =34x +3上的一个动点,①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标;②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最小值及相应的点E 和点C 的坐标。
2012中考数学压轴题及答案(5)

2012中考数学压轴题及答案(5)2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
2012中考数学压轴题及答案(5)
编辑推荐:
2012年中考生心理调节必备五大妙方
中考生早餐吃得要像“皇帝”一样
决战中考:数学必做压轴综合题(20道)
中考物理:用马铃薯确定电池正负极
近五年全国中考语文名著阅读题集锦(500篇)中考英语作文预测及范文参考
更多中考信息》》》
精心整理,仅供学习参考。
2012年全国各地中考数学压轴题汇编五

2012年全国各地中考数学压轴题汇编五【2012某某】41、如图半径分别为m,n(0<m<n)的两圆⊙O1和⊙O2相交于P,Q两点,且点P(4,1),两圆同时与两坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.(1)求两圆的圆心O1,O2所在直线的解析式;(2)求两圆的圆心O1,O2之间的距离d;(3)令四边形PO1QO2的面积为S1,四边形RMO1O2的面积为S2.试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.【2012六盘水】42、如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A 匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:(1)当t为何值时,PQ∥BC.(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.【2012某某】43、如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A.C.D均在坐标轴上,且AB=5,sinB=.(1)求过A.C.D三点的抛物线的解析式;(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值X围;(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.【2012某某】44、综合与实践:如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3与x轴交于A.B两点,与y轴交于点C,点D是该抛物线的顶点.(1)求直线AC的解析式及B.D两点的坐标;(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A.P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.(3)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.【2012某某】45、(本小题满分10分)已知抛物线1C 的函数解析式为23(0)y ax bx a b =+-<,若抛物线1C 经过点(0,3)-,方程230ax bx a +-=的两根为1x ,2x ,且124x x -=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(1)C(3,2),D(1,3); 2分 (2)设抛物线的解析式为y=ax 2+bx+c,把A(0,1),D(1, 3),C(3,2)代入 得 解得 4分 ∴抛物线的解析式为y=-x 2+x+1; 5分 (3)①当点A运动到点F(F为原B点的位置)时
∵AF==,∴t==1(秒). 当0< t ≤1时,如图1. B′F=AA′=t ∵Rt△AOF∽Rt△∠GB ′F,∴=. ∴B ′G=·B ′F=×t=t
20.已知:抛物线y=x 2-2x+a(a <0)与y轴相交于点A,顶点为M. 直线y=x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点 N. (1)填空:试用含a的代数式分别表示点M与N的坐标,则M( , ),N( , ); (2)如图,将△NAC沿轴翻折,若点N的对应点N ′恰好落在抛物线 上,AN ′与轴交于点D,连结CD,求a的值和四边形ADCN的面积; (3)在抛物线y=x 2-2x+a(a <0)上是否存在一点P,使得以 P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐 标;若不存在,试说明理由.
18.如图,已知抛物线y=a(x-1)2+(a≠0)经过点A(-2,0),抛物线 的顶点为D,过O作射线OM∥AD.过顶点D平行于轴的直线交射线OM于 点C,B在轴正半轴上,连结BC. (1)求该抛物线的解析式; (2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点 P运动的时间为t(s).问:当t为何值时,四边形DAOP分别为平行四
边形?直角梯形?等腰梯形? (3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1 个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止 运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连 接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时 PQ的长.
∴直线BC的解析式为y=x+3. 6分 联立 解得 ∴点Q的坐标为(-1,2). 7分 (3)存在. 8分 设P点的坐标为(x,-x 2-2x+3)(-3<x<0),如图 2. ∵S△PBC =S四边形PBOC -S△BOC =S四边形PBOC -×3×3=S四
边形PBOC -
2012中考数学压轴题及答案40例(5)
16.如图,已知与轴交于点和的抛物线的顶点为,抛物线与关于轴对 称,顶点为. (1)求抛物线的函数关系式; (2)已知原点,定点,上的点与上的点始终关于轴对称,则当点运动 到何处时,以点为顶点的四边形是平行四边形? (3)在上是否存在点,使是以为斜边且一个角为的直角三角形?若 存,求出点的坐标;若不存在,说明理由.
解:(1)把A(-2,0)代入y=a(x-1)2+,得0=a(-2-1)2+. ∴a=- 1分 ∴该抛物线的解析式为y=-(x-1)2+ 即y=-x 2+x+. 3分 (2)设点D的坐标为(xD,yD),由于D为抛物线的顶点 ∴xD=-=1,yD=-×1 2+×1+=. ∴点D的坐标为(1,). 如图,过点D作DN⊥x轴于N,则DN=,AN=3,∴AD== 6.
正方形落在x轴下方部分的面积为S即为△B ′FG的面积S△B
′FG
∴S=S△B′FG=B ′F·B ′G=×t×t=t 2 7分 ②当点C运动到x轴上时 ∵Rt△BCC ′∽Rt△∠AOB,∴=. ∴CC ′=·BC=×=,∴t==2(秒). 当1< t ≤2时,如图2.
∵A ′B ′=AB=,∴A ′F=t-. ∴A ′G= ∵B ′H=t ∴S=S梯形A′B′HG=(A ′G+B ′H)·A ′B ′ =(+t)· =t- 9分 ③当点D运动到x轴上时
解:(1)M(1,a-1),N(a,-a). 4分 (2)∵点N ′是△NAC沿轴翻折后点N的对应点 ∴点N ′与点N关于y轴对称,∴N ′(-a,-a). 将N ′(-a,-a)代入y=x 2-2x+a,得-a=(-a)2 -2×(-a)+a 整理得4a 2+9a=0,解得a1=0(不合题意,舍去),a2 =-. 6分 ∴N ′(3,),∴点N到轴的距离为3. ∵a=-,抛物线y=x 2-2x+a与y轴相交于点A, ∴A(0,-). ∴直线AN ′的解析式为y=x -,将y=0代入,得x =. ∴D(,0),∴点D到轴的距离为. ∴S四边形ADCN =S△ACN +S△ACN =××3+××= 8分 (3)如图,当点P在y轴的左侧时,若四边形ACPN是平行四边形, 则PN平行且等于AC. ∴将点N向上平移-2a个单位可得到点P,其坐标为(a, -a),代入抛物线的解析式,得:-a=(a)2-2×a+a, 整理得8a 2+3a=0. 解得a1=0(不合题意,舍去),a2=-. ∴P(-,) 10分 当点P在y轴的右侧时,若四边形APCN是平行OM∥AD ①当AD=OP时,四边形DAOP为平行四边形. ∴OP=6 ∴t=6(s) 5分
②当DP⊥OM时,四边形DAOP为直角梯形. 过点O作OE⊥AD轴于E. 在Rt△AOE中,∵AO=2,∠EAO=60°,∴AE=1. (注:也可通过Rt△AOE∽Rt△AND求出AE=1) ∵四边形DEOP为矩形,∴OP=DE=6-1=5. ∴t=5(s) 6分 ③当PD=OA时,四边形DAOP为等腰梯形,此时OP=AD -2AE=6-2=4. ∴t=4(s) 综上所述,当t=6s、5s、4s时,四边形DAOP分别为平行 四边形、直角梯形、等腰梯形. 7分 (3)∵∠DAO=60°,OM∥AD,∴∠COB=60°. 又∵OC=OB,∴△COB是等边三角形,∴OB=OC=AD= 6. ∵BQ=2t,∴OQ=6-2t(0<t<3) 过点P作PF⊥x轴于F,则PF=t. 8分 ∴S四边形BCPQ =S△COB -S△POQ =×6×-×(6-2t)×t =(t-)2+ 9分 ∴当t=(s)时,S四边形BCPQ的最小值为. 10分 此时OQ=6-2t=6-2×=3,OP=,OF=,∴QF=3- =,PF=. ∴PQ=== 11分 19.如图,已知直线y=-x+1交坐标轴于A、B两点,以线段AB为边向上 作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E. (1)请直接写出点C,D的坐标; (2)求抛物线的解析式; (3)若正方形以每秒个单位长度的速度沿射线AB下滑,直至顶点D 落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行 时间t的函数关系式,并写出相应自变量t的取值范围; (4)在(3)的条件下,抛物线与正方形一起平移,直至顶点D落 在x轴上时停止,求抛物线上C、E两点间的抛物线弧所扫过的面积.
当S四边形PBOC有最大值时,S△PBC就最大. ∵S四边形PBOC =SRt△PBE+S直角梯形PEOC 9分 =BE·PE+(PE+OC)·OE =(x+3)(-x 2-2x+3)+(-x 2-2x+3+3) (-x) =-(x+)2++ 当x=-时,S四边形PBOC最大值为+. ∴S△PBC最大值=+-=. 10分 当x=-时,-x 2-2x+3=-(-)2-2×(-)+3=. ∴点P的坐标为(-,). 11分
解:(1)将A(1,0),B(-3,0)代入y=-x 2+bx+c得 2分 解得 3分 ∴该抛物线的解析式为y=-x 2-2x+3. 4分 (2)存在. 5分
该抛物线的对称轴为x=-=-1 ∵抛物线交x轴于A、B两点,∴A、B两点关于抛物线的对称 轴x=-1对称. 由轴对称的性质可知,直线BC与x=-1的交点即为所求的 Q点,此时△QAC的周长最小,如图1. 将x=0代入y=-x 2-2x+3,得y=3. ∴点C的坐标为(0,3). 设直线BC的解析式为y=kx+b1, 将B(-3,0),C(0,3)代入,得 解得
解:(1)由题意知点的坐标为. 设的函数关系式为. 又点在抛物线上, ,解得. 抛物线的函数关系式为(或). (2)与始终关于轴对称, 与轴平行. 设点的横坐标为,则其纵坐标为, ,,即. 当时,解得. 当时,解得. 当点运动到或或或时, ,以点为顶点的四边形是平行四边形.
(3)满足条件的点不存在.理由如下:若存在满足条件的点在上,则 ,(或), . 过点作于点,可得. ,,. 点的坐标为. 但是,当时,. 不存在这样的点构成满足条件的直角三角形. 17.如图,抛物线y=-x 2+bx+c与x轴交于A(1,0),B(-3,0)两点. (1)求该抛物线的解析式; (2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点 Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请 说明理由; (3)在(1)中的抛物线上的第二象限内是否存在一点P,使△PBC的面积 最大?,若存在,求出点P的坐标及△PBC的面积最大值;若不存 在,请说明理由.
DD′= t==3(秒) 当2< t ≤3时,如图3.
∵A ′G= ∴GD′=-= ∴D′H=- ∴S△D′GH =()(-)=()2 ∴S=S正方形A′B′C′D′ -S△D′GH =()2-()2 =-t 2+t- 11分 (4)如图4,抛物线上C、E两点间的抛物线弧所扫过的面积为 图中阴影部分的面积. ∵t=3,BB′=AA′=DD′= ∴S阴影=S矩形BB′C′C 13分 =BB′·BC =× =15 14分
∴OA=OC,OP=ON,点P与点N关于原点对称. ∴P(-a,a),代入y=x 2-2x+a,得 a=(-a)2-2×(-a)+a,整理得8a 2+15a=0. 解得a1=0(不合题意,舍去),a2=-. ∴P(,-) 12分 ∴存在这样的点P,使得以P,A,C,N为顶点的四边形是 平行四边形,点P的坐标为 (-,)或(,-).
