激光原理第七章答案
周炳坤版激光原理习题答案第七章
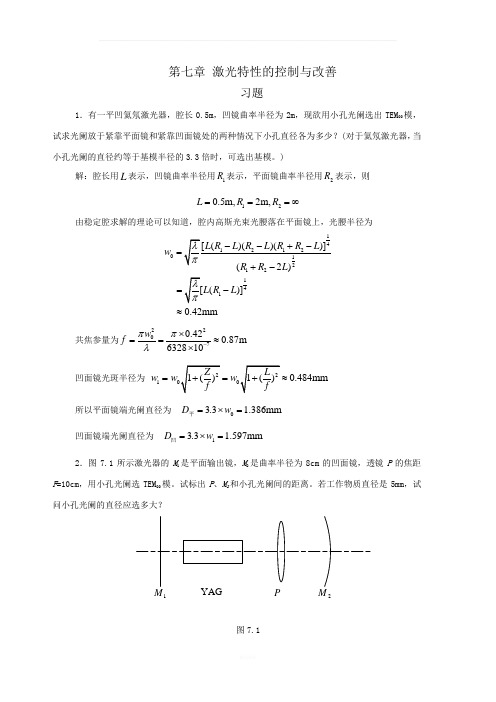
第七章 激光特性的控制与改善习题1.有一平凹氦氖激光器,腔长0.5m ,凹镜曲率半径为2m ,现欲用小孔光阑选出TEM 00模,试求光阑放于紧靠平面镜和紧靠凹面镜处的两种情况下小孔直径各为多少?(对于氦氖激光器,当小孔光阑的直径约等于基模半径的3.3倍时,可选出基模。
)解:腔长用L 表示,凹镜曲率半径用1R 表示,平面镜曲率半径用2R 表示,则120.5m,2m,L R R ===∞由稳定腔求解的理论可以知道,腔内高斯光束光腰落在平面镜上,光腰半径为012141 ()] 0.42mmw L R L ==-≈共焦参量为22070.420.87m 632810w f ππλ-⨯==≈⨯ 凹面镜光斑半径为10.484mm w w w ==≈ 所以平面镜端光阑直径为 03.3 1.386mm D w =⨯=平 凹面镜端光阑直径为 13.3 1.597mm D w =⨯=凹2.图7.1所示激光器的M 1是平面输出镜,M 2是曲率半径为8cm 的凹面镜,透镜P 的焦距F =10cm ,用小孔光阑选TEM 00模。
试标出P 、M 2和小孔光阑间的距离。
若工作物质直径是5mm ,试问小孔光阑的直径应选多大?图7.112解:如下图所示:12P小孔光阑的直径为:31.061010022mm 0.027mm 2.5f d a λππ-⨯⨯==⨯≈⨯其中的a 为工作物质的半径。
3.激光工作物质是钕玻璃,其荧光线宽F ν∆=24.0nm ,折射率η=1.50,能用短腔选单纵模吗?解:谐振腔纵模间隔222q q c LLνηλλη∆=∆=所以若能用短腔选单纵模,则最大腔长应该为215.6μm 2L ληλ=≈∆所以说,这个时候用短腔选单纵模是不可能的。
6.若调Q 激光器的腔长L 大于工作物质长l ,η及'η分别为工作物质及腔中其余部分的折射率,试求峰值输出功率P m 表示式。
解:列出三能级系统速率方程如下:2121 (1)2 (2)R dN l NcN n dt L d nN n dtστσυ=∆-'∆=-∆式中,()L l L l ηη''=+-,η及'η分别为工作物质及腔中其余部分的折射率,N 为工作物质中的平均光子数密度,/,/R c L c υητδ'==。
激光原理1-7章例题

s (1 0.2) 0.4 0.32 m
例4 发光粒子以0.3c的速度运动时,恰好可和反方 向传播的光束发生共振作用,已知该光束的频率为 51014Hz,求此粒子的固有频率. 解
0 v z ( 1)c s
0 0.3c ( 1)c 14 5 10
0 1 .3 5 1014
c c
例2 某发光粒子静止频率为5108MHz,它以 0.2c的速度向接收器方向运动,求接收器测得 该粒子所发光的频率 解 ν0 c ν 0 c 5 108 1.25 5 108 6.25 108 MHz
c vz c 0 .2 c
例3 发光粒子以0.2c的速度运动时,恰好可和同方 向传播的光束发生共振作用,已知此粒子的固有波 长为0.4m,求该光束的波长 s s s 解 v z ( 1)c 0.2c ( 0.4 1)c 0.2 0.4 1
第一章 激光基本原理 例1 求封闭腔在5000 Å处的单色模密度 解
c 3 10 14 6 10 Hz 10 5000 10
8
8 2 8 3.14 (6 1014 ) 2 5 3 m 3 3.35 10 s m 8 3 c (3 10 )
例2 求He-Ne激光器所发光子的能量、动量、 质量(光波长为6328Å) 解 E h hc 6.63 10 34 3 108 3.14 10 19 J
6328 10 10 h h 6.63 10 34 27 P k 1 . 05 10 kg m / s 10 2 6328 10 h h 6.63 10 34 36 m 2 3 . 5 10 kg 10 8 c c 6328 10 3 10
激光原理与技术_电子科技大学中国大学mooc课后章节答案期末考试题库2023年

激光原理与技术_电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.在锁模激光器中,被锁定的模式数量越多,脉冲周期越短。
参考答案:错误2.对于对称共焦腔,其傍轴光线在腔内往返传输次即可自行闭合,其自再现模式为高斯光束。
参考答案:2##%_YZPRLFH_%##二##%_YZPRLFH_%##两3.谐振腔损耗越大,品质因子越高。
参考答案:错误4.有激光输出时,激活介质不是处于热平衡条件。
参考答案:正确5.在主动锁模激光器中,调制器应该放到谐振腔的一端。
参考答案:正确6.为得到高转化效率的光学倍频,要实现匹配,使得基频波和倍频波的折射率要相等,在他们相互作用过程中,两个基频光子湮灭,产生一个倍频光子。
参考答案:相位7.尽量增加泵浦功率有利于获得单模激光输出。
参考答案:错误8.在调Q激光器中,随着Dni/Dnt的增大,峰值光子数增加,脉冲宽度。
参考答案:变窄##%_YZPRLFH_%##变小##%_YZPRLFH_%##减小9.关于基模高斯光束的特点,下面描述不正确的是。
参考答案:基模高斯光束在激光腔内往返传播时没有衍射损耗10.KDP晶体沿z轴加电场时,折射率椭球的主轴绕z轴旋转了度角。
参考答案:45##%_YZPRLFH_%##四十五11.稳定谐振腔是指。
参考答案:谐振腔对旁轴光线的几何偏折损耗为零12.形成激光振荡的充分条件是。
参考答案:光学正反馈条件和增益阈值条件13.关于谐振腔的自再现模式,下面那个说法是正确的?参考答案:自再现模式与谐振腔的稳定性有关14.三能级激光器的激光下能级是基态,需至少将原子总数的通过泵浦过程转移到激光上能级,才能实现受激辐射光放大。
参考答案:一半##%_YZPRLFH_%##1/2##%_YZPRLFH_%##50%##%_YZPRLFH_%##二分之一##%_YZPRLFH_%##百分之五十15.谱线加宽是指的光谱展宽。
参考答案:自发辐射16.关于自发辐射和受激辐射说法正确的是。
激光原理部分课后习题答案

µ
上一页 回首页 下一页 回末页 回目录
练习: 思考练习题2第 题 练习: (思考练习题 第9题).
第 二 章
§ 2 4 非 均 匀 增 宽 型 介 质 的 增 益 系 数 和 增 益 饱 和 .
连 续 激 光 器 的 原 理
µ hν 0 f (ν 0 ) πc∆ν c I s (ν 0 ) = hν 0 σ e (ν 0 ) ⇒ I s (ν 0 ) = 2 µτ σ e (ν ) = ⇒ ∆n σ e (ν 0 )τ 2 µ f (ν 0 ) = G (ν ) = ∆nB21 hνf (ν ) π∆ν c hν 0 (2) I s (ν 0 ) = σ e (ν 0 )τ ⇒ 2 c f (ν 0 ) σ e (ν 0 ) = 2 8πν 0 µ 2τ hν 0 4π 2 hcµ 2 ∆ν I s (ν 0 ) = = = 3.213 × 10 5 W / cm 2 σ e (ν 0 )τ λ3 上一页 回首页 下一页 回末页 回目录
第 二 章
§ 2 4 非 均 匀 增 宽 型 介 质 的 增 益 系 数 和 增 益 饱 和 .
练习: 思考练习题2第 题 练习: (思考练习题 第6题). 推导均匀增宽型介质,在光强I,频率为ν的光波作 用下,增益系数的表达式(2-19)。
∆ν 2 0 ) ]G (ν ) G (ν ) 2 = G (ν ) = I f (ν ) I ∆ν 2 1+ (ν − ν 0 ) 2 + (1 + )( ) I s f (ν 0 ) Is 2
.
I ( z ) = I ( 0) e
− Az
I ( z) 1 − 0.01⋅100 ⇒ =e = = 0.368 I ( 0) e
原荣版激光原理--习题解答第7章

第七章习题 1.有一平凹氦氖激光器,腔长m 5.0,凹镜曲率半径为m 2,现欲用小孔光阑选出00TEM模,试求光阑放于紧靠平面镜和紧靠凹面镜处两种情况下小孔直径各为多少?(对于氦氖激光器,当小孔光阑的直径约等于基模半径的3.3倍时,可选出基横模。
)解:由RL g -=1,可计算出75.01=g ,0.12=g ,满足1021<⋅<g g ,故该腔为一稳定腔。
对He-Ne 激光器的nm 8.632=λ,则m L os 41017.3-⨯==πλω。
由公式(2.8.7),当光阑放于紧靠凹面镜的情况下,44/121121082.4])1([1-⨯=⋅-=g g g g oss ωω,故小孔直径应为m d s 311059.13.31-⨯=⋅=ω。
当光阑放于紧靠平面镜的情况下,44/121211017.4])1([2-⨯=⋅-=g g g g os s ωω,故小孔直径应为m d s 321038.13.32-⨯=⋅=ω。
2.图7.1所示激光器的1M 是平面输出镜,2M 是曲率半径为cm 8的凹面镜,透镜P 的焦距cm F 10=,用小孔光阑选00TEM模。
试标出P 、2M 和小孔光阑间的距离。
若工作物质直径是mm 5,试问小孔光阑的直径应选多大?解:m f 5.1820==λπωmm F f 0135.0)(120=+='ωω小孔光阑直径为mm 027.020='ω 距透镜P :cm FF F l 10])(1[22022=+-='λπω 距凹面镜2M :cm F l 4222==。
3.激光工作物质是钕玻璃,其荧光线宽nm F 0.24=∆λ,折射率50.1=η,能用短腔选单纵模吗?解:1421014.2)1(-⨯=∆=∆m λλλHz c 12104.6)1(⨯=∆⋅=∆λν由短腔选模条件:ν∆>'L c 2(7.1.3)5103.22-⨯=∆<'νc Lm L μη6.15103.25max ≈⨯=-。
激光原理作业答案

J / K *300K
47.99
21
n1
h c
(3)n2
e
kT
T
h c
6252.9K
n1
k ln
n2 n1
解
2:
n2
E2 E1
e kbT
其中
h*c
h*c
n1
E E2 E1
E h *c h
(1) n e e e 1 2
h*c kb *T
6.63*1034 *3*109 1.38*10 23 *300
*
8
*
3.14 * 6.63 *1034 (6*107 )3
7.71*105 s1
s
1 A21
1.297 *106 s
(3) 60nm时 A21 7.71*108 s1
(4) 0.6nm时 A21 7.71*1014 s1
(5) v
I S
10 106
105 w / m2
W 21 B21 * 1019 *105 1014 m * s3
目录
第一章 ..............................................................................................................................................2 第二章 ..............................................................................................................................................2 第三章 ..............................................................................................................................................7 第四章 ............................................................................................................................................17 第五章 ............................................................................................................................................28 第六章 ............................................................................................................................................30 第七章 ............................................................................................................................................31 第八章 ............................................................................................................................................32 第九章 ............................................................................................................................................33
激光原理答案

激光原理答案测验1.11、梅曼(TheodoreH.Maiman)于I960年发明了世界上第一台激光器一—红宝石激光器,其波长为694.3nm。
其频率为:A:4.74某10^14(14是上标)HzB:4.32某10人14(14是上标)HzC:3.0某10人14(14是上标)Hz您的回答:B参考答案:Bnull满分:10分得分:10分2、下列说法错误的是:A:光子的某一运动状态只能定域在一个相格中,但不能确定它在相格内部的对应位置B:微观粒子的坐标和动量不能同时准确测定C:微观粒子在相空间对应着一个点您的回答:C参考答案:Cnull满分:10分得分:10分3、为了增大光源的空间相干性,下列说法错误的是:A:采用光学滤波来减小频带宽度B:靠近光源C:缩小光源线度您的回答:B参考答案:Bnull满分:10分得分:10分4、相干光强取决于:A:所有光子的数目B:同一模式内光子的数目C:以上说法都不对您的回答:B参考答案:Bnull满分:10分得分:10分5、中国第一台激光器——红宝石激光器于1961年被发明制造出来。
其波长为A:632.8nmB:694.3nmC:650nm您的回答:B参考答案:Bnull满分:10分得分:10分6、光子的某一运动状态只能定域在一个相格中,这说明了A:光子运动的连续性B:光子运动的不连续性C:以上说法都不对您的回答:参考答案:Bnull满分:10分得分:10分7、3-4在2cm的空腔内存在着带宽(A入)为1某10m、波长为0.5m的自发辐射光。
求此光的频带范围A V°A:120GHzB:3某10八18(18为上标)Hz您的回答:B参考答案:Anull满分:10分得分:0分8、接第7题,在此频带宽度范围内,腔内存在的模式数?A:2某10八18(18为上标)B:8某10八10(10为上标)您的回答:A参考答案:Bnull满分:10分得分:0分9、由两个全反射镜组成的稳定光学谐振腔腔长为L腔内振荡光的中心波长为求该光的波长带宽的近似值。
激光原理习题与答案

解: 1
1
q( z) R( z) i 2 ( z)
q0
i
2 0
,q
q0
l
q(0) 0.45i,q(0.3) 0.45i 0.3
q() 0
21.已知一二氧化碳激光谐振腔由曲个凹面 镜构成,R1=l m,R2=2m,L=0.5m。如 何选样南斯束腰斑0的大小和位置才能使它 成为该谐振腔中的自再现光束?
第二章
8.今有一球面腔,Rl=1.5m,R 2=—1m,L =80cm。试证明该腔为稳定腔;求出它的等 价共焦腔的参数;在图上画出等价共焦腔的具 体位置。
13.某二氧化碳激光器,采用平—凹腔,凹面 镜的R=2m,胶长L=1m。试给出它所产生 的高斯光束的腰斑半径0的大小和位置、该 高斯束的f及0的大小。
束腰处R1右0.37mR2左边0.13m。半径为1.28mm
第四章习题解答
第五章习题
精品课件!
精品课件!
第七章习题
z解1 : (L
L(R2 L) R1) (L
R2 )
0.37
z2
(L
L(R1 L) R1) (L
R2 )
0.13
f
sqrt(
L(
R1 L)(R2 L)(R1
(L R1) (L R2
R2
)2ຫໍສະໝຸດ L))0.48
0
f 1.28 *103 m
解: g1g2 0.5 z1 0, z2 1, f 1
0
f 1.84 *103m
0 2
3.68 *103 rad f
激光原理及应用1-6章部分课后答案

激光原理及应用部分课后答案1-4为使He-Ne 激光器的相干长度达到1KM ,它的单色性0λλ∆应是多少?2-2当每个模式内的平均光子数(光子简并数)大于1时,以受激辐射为主。
2-3如果激光器和微波激射器分别在um 10=λm 500n =λ和z 3000MH =ν输出1W 连续功率,问美秒从激光上能级向下能级跃迁的粒子数是多少?2-4当一对激光能级为E2和E1(f1=f2),相应的频率为v (波长为λ),能级上的粒子数密度分别为n2和n1,q 求:(1)当v=3000MHZ ,T=3000K 时,n2/n1=?(2)当λ=1um ,T=3000K 时,n2/n1=?(3)当λ=1um ,n2/n1=0时,温度T=?解:2-5激发态的原子从能级E2跃迁到E1时,释放出λ=5um的光子,求这个两个能级的能量差。
若能级E1和E2上的原子数分别为N1和N2,试计算室温T=300K的N2/N值。
2-7如果工作物质的某一跃迁是波长为100nm的远紫外光,自发辐射跃迁概率1621s10-=A,试问:(1)改跃迁的受激辐射爱因斯坦系数B21是多少?(2)为使受激辐射跃迁概率比自发辐射跃迁概率大三倍,腔内的单色能量密度νρ应为多少?2-9某一物质受光照射,沿物质传播1mm的距离时被吸收了1%,如果该物质的厚度是0.1m,那么入射光中有百分之几能通过该物质?并计算该物质的吸收系数α。
2-10激光在0.2m 长的增益介质中往复运动过程中,其增强了30%。
求该介质的小信号增益系数0G 。
假设激光在往复运动中没有损耗。
3-2CO2激光器的腔长L=100cm,反射镜直径D=1.5cm,两镜的光强反射系数分别为r1=0.985,r2=0.8.求由衍射损耗及输出损耗所分别引起的δ,τ。
3-4,分别按下图中的往返顺序,推导近轴光线往返一周的光学变换矩阵⎪⎪⎭⎫ ⎝⎛D C B A ,并证明这两种情况下的)(D A +21相等。
激光原理(陈玉清)答案

习题一> ※<习题一 习题一 为使氦氖激光器的相干长度达到1km,它的单色性Δλ/λ 为使氦氖激光器的相干长度达到 ,它的单色性Δ 应是多少? 应是多少? 习题二> ※<习题二 习题二 (1)一质地均匀的材料对光的吸收为 )一质地均匀的材料对光的吸收为0.01mm-1,光通过 10cm长的该材料后,出射光强为入射光强的百分之几?( ) 长的该材料后, ?(2) 长的该材料后 出射光强为入射光强的百分之几?( 一光束通过长度为1m的均匀激活的工作物质 的均匀激活的工作物质, 一光束通过长度为 的均匀激活的工作物质,如果出射光强是 入射光强的两倍,试求该物质的增益系数. 入射光强的两倍,试求该物质的增益系数. ※<习题三 习题三> 习题三 如果激光器和微波激射器分别在= 如果激光器和微波激射器分别在=10um,λ=5×10-1um和ν , = × 和 输出1W连续功率 连续功率, =3000MHz输出 连续功率,试问每秒钟从激光上能级向下 输出 能级跃迁的粒子数是多少? 能级跃迁的粒子数是多少? 习题四> ※<习题四 习题四 设一光子的波长= × 设一光子的波长=5×10-1um,单色性 =10-7,试求光子位 , 若光子的波长变为5× 射线) 置的不确定量 Δx.若光子的波长变为 ×10-4um(x射线)和 ( 射线 5×10-18um(射线),则相应的 Δx又是多少? ),则相应的 又是多少? × (射线),
习题二> ※<习题二 习题二
(1)一质地均匀的材料对光的吸收为0.01mm-1,光通 )一质地均匀的材料对光的吸收为 长的该材料后, 过10cm长的该材料后,出射光强为入射光强的百分之几? 长的该材料后 出射光强为入射光强的百分之几? 的均匀激活的工作物质, (2)一光束通过长度为 的均匀激活的工作物质,如果 )一光束通过长度为1m的均匀激活的工作物质 出射光强是入射光强的两倍, 出射光强是入射光强的两倍,试求该物质的增益系
激光原理 周炳琨版课后习题答案

当 时, 小
3. 在 波长时 ,试求在内径为 的 波导管中 模和 模的损耗 和 ,分别以 , 以及 来表示损耗的大小。当通过 长的这种波导时, 模的振幅和强度各衰减了多少(以百分数表示)?
解:由
,
, 。
当 时, ,
4.试计算用于 波长的矩形波导的 值,以 及 表示,波导由 制成, , ,计算由 制成的同样的波导的 值,计算中取 。
二、实验步骤
1.如上图所示,在高斯光束的轴线上某一点B处放入于光轴垂直的光阑(其孔半径为a),用卷尺测量出B到光腰O(此题中即为谐振腔的中心)的距离z;
2.用激光功率计测出通过小孔光阑的光功率 ;
3.移走光阑,量出高斯光束的总功率 ;
4.将所得到的数据代入(III)及(IV)式即可求出f(根据实际情况决定(IV)式根号前正负号的取舍)。
解:
一、实验原理
通过放在离光腰的距离为z的小孔(半径为a)的基模光功率为
(I)
式中, 为总的光功率, 为通过小孔的光功率。记 ,则有
(II)
注意到对基模高斯光束有
在(II)式的两端同时乘以 ,则有
令
(III)
则
解此关于f的二次方程,得
因为 、 、 、 都可以通过实验测得,所以由(III)及(IV)式就可以求得基模高斯光束的共焦参数f。
解:入射高斯光束的共焦参数
已知 ,根据
得
时, ,即将透镜放在距束腰1.39m处;
时, ,即将透镜放在距束腰23.87m处。
18.如图2.2光学系统,如射光 ,求 及 。
图2.2
解:先求经过一个透镜的作用之后的束腰半径及位置
由于 ,所以
=2cm
所以对第二个透镜,有
激光原理第六版补充参考答案(PDF)

第一章P23-1解:由cλν=,可得2cd d d λλνννν=-=- 考虑波长和频率变化的绝对值λ∆、ν∆,有λνλν∆∆=相干长度可知在时,有在 时,在P23-3解:(a )1C L km =500n m λ=3000MHz ν=(c) 如,可得,P23-4解:题中Cr +3离子浓度193210n cm -=⨯,对应激光跃迁的上下能级简并度相同,在Cr +3离子几乎全部激发到上能级时反转粒子数浓度19321210n n n cm -∆=-≈⨯,当损耗突然变小2L Q c πνδ'=变大时19321210022t n nn cm n n n -∆≈⨯>>∆=-≈-=, 假设在巨脉冲宽度10ns 时间内反转粒子数浓度从1932100cm -⨯约降到,这一过程有约2nV个上能级的Cr +3离子通过受激辐射跃迁至下能级并产生一个光子,因而可得激光输出能量216.8242n d n cE V h v l h J πλ=⋅⋅=⋅⋅≈ 得脉冲功率 9816.81.71010E P W t -==≈⨯∆注:红宝石为三能级结构,激光跃迁下能级为基态,当上能级粒子数浓度为总粒子数浓度一半时反转粒子数浓度等于0,此后仍处于上能级的粒子将在~2τ时间内通过自发辐射跃迁和无辐射跃迁的形式回到基态下能级。
另外,即使对于四能级系统的调Q 激光器,当调Q 的巨脉冲持续时间很短时,激光跃迁的下能级粒子数浓度也不能近似为0来处理,这时在巨脉冲持续阶段接近三能级情形。
巨脉冲消失后处于上能级的粒子将通过一定程度的放大的自发辐射(ASE )、自发辐射跃迁及无辐射跃迁等形式回到下能级。
P23-6解:(1)能级E 4的分子通过自发辐射跃迁到三个较低能级,有()43442414434241()()sp spsp dn dn t dn dn n t A A A dt dt dt dt ⎛⎫⎛⎫⎛⎫=---=-⋅++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 可得:()434241444040()s tA A A tn t n en eτ--++=⋅=⋅分子在E 4的自发辐射寿命8477743424111 1.110510110310s s A A A τ-==≈⨯++⨯+⨯+⨯ (2)在对能级E 4连续激发并达到稳态时,四个能级的分子数都保持动态平衡,即单位时间从E 4能级跃迁到各下能级的分子数等于单位时间各能级减少的分子数,假设各能级简并度(统计权重)相等,对E 1能级有:441111n A n τ⋅=⋅,771411431051015n A n τ-=⋅=⨯⨯⨯= 同样可得:79242241106100.06n A n τ-=⋅=⨯⨯⨯= 78343345101100.5n A n τ-=⋅=⨯⨯⨯= 进一步可得 2243340.060.120.5n n n n n n ===可知,在E 2能级和E 4能级、在E 3能级和E 4能级、在E 2能级和E 3能级之间有集居数反转。
《激光原理及应用》习题参考答案仅供大家学习参考用

《激光原理及应用》习题参考答案思考练习题11•解答:设每秒从上能级跃迁到下能级的粒子数为n 。
单个光子的能量:g = h v = he / Z 连续功率:p 二n ; 则,n = p/ ;a.对发射■ = 0.5000的光:p 1 0.5000 10-6 n — —he 6.63 10 ⑶ 3.0 108-2.514 1018(个)b.对发射、• = 3000 MHz 的光_________ 16.63 10 "4 3000 106= 5.028 1023(个)E 2 a 匹Tn 1hv些=小-1n 1hc 3T6.26 103(K)'■ ln 匹3.解答:(1) 由玻耳兹曼定律可得_E 2 -E 1e '丁 , m/g20且4g 1 =g 2, m • n 2 =10代入上式可得: n 2 :30 (个)(2 )由 (a ), (b ) ,(c)式可得:2.解答:E 2 - E<| = h..(a).(b) (1 )由 ■■■. = c/ ■ .......(a ), (b )式可得:.(c)n 2 /g 2(2) p =108 n 2(E 2 -EJ =5.028 10-(W) 4•解答:(1)由教材(1-43)式可得e kT —1因此:fT ' =2.82kh ,hc同样可求得: 一丄 =4.96九m kT故' m - m = 0.568c8h1 3 A-2000J s/m 3 -3.860 10, J s/m 3 (0.6328 10冷3 5.0 10*8- 6.63 10 ^4= 7.592 10 5•解答:(1)红宝石半径 r = 0.4cm ,长L -8cm ,铬离子浓度匸=2 1018cm‘,发射波长• =0.6943 10 “m ,巨脉冲宽度 -T = 10 ns 则输出最大能量2 ,、he18E - (:r L) 2 1034826.63 1030 108二 0.42 86(J)二 2.304(J)0.6943 10」脉冲的平均功率:P =E /.「23041010"2.304 叫) (2)自发辐射功率 _ hcN 2heP (兀r 2L)Q 自皿z-X663计 3° IO 8 *1。
激光 原理课后习题答案

激光原理复习题第一章电磁波1、麦克斯韦方程中麦克斯韦方程最重要的贡献之一是揭示了电磁场的内在矛盾和运动;不仅电荷和电流可以激发电磁场,而且变化的电场和磁场也可以相互激发。
在方程组中是如何表示这一结果?答:每个方程的意义:1)第一个方程为法拉第电磁感应定律,揭示了变化的磁场能产生电场。
2)第二个方程则为Maxwell的位移电流假设。
这组方程描述了电荷和电流激发电磁场、以及变化的电场与变化的磁场互相激发转化的普遍规律。
第二个方程是全电流安培环路定理,描述了变化的电场激发磁场的规律,表示传导电流和位移电流(即变化的电场)都可以产生磁场。
第二个方程意味着磁场只能是由一对磁偶极子激发,不能存在单独的磁荷(至少目前没有发现单极磁荷)3)第三个方程静电场的高斯定理:描述了电荷可以产生电场的性质。
在一般情况下,电场可以是库仑电场也可以是变化磁场激发的感应电场,而感应电场是涡旋场,它的电位移线是闭合的,对封闭曲面的通量无贡献。
4)第四个方程是稳恒磁场的高斯定理,也称为磁通连续原理。
2、产生电磁波的典型实验是哪个?基于的基本原理是什么?答:赫兹根据电容器经由电火花隙会产生振荡原理设计的电磁波发生器实验。
(赫兹将一感应线圈的两端接于产生器二铜棒上。
当感应线圈的电流突然中断时,其感应高电压使电火花隙之间产生火花。
瞬间后,电荷便经由电火花隙在锌板间振荡,频率高达数百万周。
有麦克斯韦理论,此火花应产生电磁波,于是赫兹设计了一简单的检波器来探测此电磁波。
他将一小段导线弯成圆形,线的两端点间留有小电火花隙。
因电磁波应在此小线圈上产生感应电压,而使电火花隙产生火花。
所以他坐在一暗室内,检波器距振荡器10米远,结果他发现检波器的电火花隙间确有小火花产生。
赫兹在暗室远端的墙壁上覆有可反射电波的锌板,入射波与反射波重叠应产生驻波,他也以检波器在距振荡器不同距离处侦测加以证实。
赫兹先求出振荡器的频率,又以检波器量得驻波的波长,二者乘积即电磁波的传播速度。
激光原理(第二版)课后习题答案

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
激光原理及应用课后答案

11.试计算连续功率均为1W 的两光源,分别发射λ=0.5000m,ν3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?q 1 0.5 ×10 6答:粒子数分别为:n1 34 8 2.5138 ×1018 hν c 6.63 ×10 ×3 ×10 6.63 ×10 34 ×λq 1 n2 34 9 5.0277 ×10 23 hν 6.63 ×10 ×3 ×10 m co2.热平衡时,原子能级E 2 的数密度为n2,下能级E1 的数密度为n1 ,设g 1 g 2 ,求:1当原子跃迁时相应频率为ν=3000MHz,T=300K 时n2/n1 为若干。
2若原子跃迁时发光波长λ=1,n2/n1 =0.1 时,则温度T 为多高?网E E )hν答:(1)nm / gm e m n kT 则有:n2 e kT exp w. 6.63 ×10 34 × 3 ×10 9 1.38 ×10 23 ×300 ≈1 案nn / gn n1 答hνn2 6.63 ×10 34 ×3 ×108 (2)e kT exp 23 6 0.1 T 6.26 ×10 3 K da n1 1.38 ×10 ×1 ×10 ×T 后课3.已知氢原子第一激发态E2 与基态E 1之间能量差为1.64×l0 -18J,设火焰T=2700K中含有1020 个氢原子。
设原子按玻尔兹曼分布,且4g1 =g2 。
求:1能级E 2 上的原子数n2 为kh多少?2设火焰中每秒发射的光子数为l0 8 n2,求光的功率为多少瓦?hνn2 g1 n 1.64 ×10 18答:(1)e kT 2 4 ×exp 23 3.11 ×10 19 n1 g 2 n1 1.38 ×10 ×2700 w. 且n1 n 2 10 20 可求出n 2 ≈31ww (2)功率=108 ×31 × 1.64 ×10 18 5.084 ×10 9 W4.1普通光源发射λ=0.6000m 波长时,如受激辐射与自发辐射光功率体密度之比q激 1 ,求此时单色能量密度ρν为若干? 2 在He —Ne 激光器中若q自2000 q激ρν 5.0 ×10 4 J s / m3 ,λ为0.6328m,设=1,求为若干?q自答:(1)1q激c3 λ3 1 0.6 ×10 6 3 =ρνρνρρν 3.857 ×10 17 J s / m3q自8πhν 3 8πh 2000 8π×6.63 ×10 34 νq激c3 λ3 0.6328 ×10 6 3 (2)=3 ρνρν34 ×5 ×10 4 7.6 ×10 9 q自8πhν8πh 8π×6.63 ×105.在红宝石Q 调制激光器中,有可能将全部Cr3+铬离子激发到激光上能级并产生巨脉冲。
激光原理答案

激光原理答案(总30页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《激光原理》习题解答第一章习题解答1 为了使氦氖激光器的相干长度达到1KM ,它的单色性0λλ∆应为多少解答:设相干时间为τ,则相干长度为光速与相干时间的乘积,即c L c ⋅=τ根据相干时间和谱线宽度的关系 cL c ==∆τν1又因为γνλλ∆=∆,0λνc=,nm 8.6320=λ由以上各关系及数据可以得到如下形式: 单色性=ννλλ∆=∆=c L 0λ=101210328.61018.632-⨯=⨯nmnm解答完毕。
2 如果激光器和微波激射器分别在10μm、500nm 和Z MH 3000=γ输出1瓦连续功率,问每秒钟从激光上能级向下能级跃迁的粒子数是多少。
解答:功率是单位时间内输出的能量,因此,我们设在dt 时间内输出的能量为dE ,则 功率=dE/dt激光或微波激射器输出的能量就是电磁波与普朗克常数的乘积,即d νnh E =,其中n 为dt 时间内输出的光子数目,这些光子数就等于腔内处在高能级的激发粒子在dt 时间辐射跃迁到低能级的数目(能级间的频率为ν)。
由以上分析可以得到如下的形式:ννh dth dE n ⨯==功率 每秒钟发射的光子数目为:N=n/dt,带入上式,得到:()()()13410626.61--⨯⋅⨯====s s J h dt n N s J νν功率每秒钟发射的光子数根据题中给出的数据可知:z H mms c13618111031010103⨯=⨯⨯==--λν z H mms c1591822105.110500103⨯=⨯⨯==--λνz H 63103000⨯=ν把三个数据带入,得到如下结果:19110031.5⨯=N ,182105.2⨯=N ,23310031.5⨯=N3 设一对激光能级为E1和E2(f1=f2),相应的频率为ν(波长为λ),能级上的粒子数密度分别为n2和n1,求(a)当ν=3000兆赫兹,T=300K 的时候,n2/n1= (b)当λ=1μm ,T=300K 的时候,n2/n1= (c)当λ=1μm ,n2/n1=时,温度T=解答:在热平衡下,能级的粒子数按波尔兹曼统计分布,即:TK E E T k h f f n n b b )(expexp 121212--=-=ν(统计权重21f f =) 其中1231038062.1--⨯=JK k b为波尔兹曼常数,T 为热力学温度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 激光特性的控制与改善习题1.有一平凹氦氖激光器,腔长0.5m ,凹镜曲率半径为2m ,现欲用小孔光阑选出TEM 00模,试求光阑放于紧靠平面镜和紧靠凹面镜处的两种情况下小孔直径各为多少?(对于氦氖激光器,当小孔光阑的直径约等于基模半径的3.3倍时,可选出基模。
)解:腔长用L 表示,凹镜曲率半径用1R 表示,平面镜曲率半径用2R 表示,则120.5m,2m,L R R ===∞由稳定腔求解的理论可以知道,腔内高斯光束光腰落在平面镜上,光腰半径为012141 ()] 0.42mmw L R L ==-≈共焦参量为22070.420.87m 632810w f ππλ-⨯==≈⨯ 凹面镜光斑半径为10.484mm w w w ==≈ 所以平面镜端光阑直径为 03.3 1.386mm D w =⨯=平 凹面镜端光阑直径为 13.3 1.597mm D w =⨯=凹2.图7.1所示激光器的M 1是平面输出镜,M 2是曲率半径为8cm 的凹面镜,透镜P 的焦距F =10cm ,用小孔光阑选TEM 00模。
试标出P 、M 2和小孔光阑间的距离。
若工作物质直径是5mm ,试问小孔光阑的直径应选多大?图7.112解:如下图所示:12P小孔光阑的直径为:31.061010022mm 0.027mm 2.5f d a λππ-⨯⨯==⨯≈⨯其中的a 为工作物质的半径。
3.激光工作物质是钕玻璃,其荧光线宽F ν∆=24.0nm ,折射率η=1.50,能用短腔选单纵模吗?解:谐振腔纵模间隔222q q c LLνηλλη∆=∆=所以若能用短腔选单纵模,则最大腔长应该为215.6μm 2L ληλ=≈∆所以说,这个时候用短腔选单纵模是不可能的。
6.若调Q 激光器的腔长L 大于工作物质长l ,η及'η分别为工作物质及腔中其余部分的折射率,试求峰值输出功率P m 表示式。
解:列出三能级系统速率方程如下:2121 (1)2 (2)R dN l NcN n dt L d nN n dtστσυ=∆-'∆=-∆式中,()L l L l ηη''=+-,η及'η分别为工作物质及腔中其余部分的折射率,N 为工作物质中的平均光子数密度,/,/R c L c υητδ'==。
由式(1)求得阈值反转粒子数密度为:21t R L n c lστ'∆=式(1)和(2)可以改写为:1 (3)2 (4)t Rt R dN n Ndt n d nn N L dt n lττη⎛⎫∆=- ⎪∆⎝⎭⎛⎫'∆∆=- ⎪∆⎝⎭(3)式除以(4)式可得:11 (5)2t n dN ld n n L η∆⎛⎫=- ⎪'∆∆⎝⎭ 将(5)式积分可得:1ln 2i i t i n l N N n n n n L η⎛⎫∆=+∆-∆+∆⋅ ⎪'∆⎝⎭当t n n ∆=∆时,m N N =,忽略初始光子数密度i N ,可由上式求出:1ln 12i i m t t t n n l N n L n n η⎛⎫∆∆=∆-- ⎪'∆∆⎝⎭设工作物质的截面积为S ,输出反射镜透射率为T ,则峰值功率为:11ln 124i i m m t t t n n c lP N h ST ch ST n L n n ννη⎛⎫∆∆==∆-- ⎪'∆∆⎝⎭7.图7.3所示Nd:Y AG 激光器的两面反射镜的透过率分别为T 2=0,T 1=0.1,021mm ω=,l =7.5cm ,L =50cm ,Nd:Y AG 发射截面1928.810cm σ-=⨯,工作物质单通损耗T i =6%,折射率η=1.836,所加泵浦功率为不加Q 开关时阈值泵浦功率的二倍,Q 开关为快速开关。
试求其峰值功率、脉冲宽度、光脉冲输出能量和能量利用率。
图7.3解:21221631916314311ln2(1)(1)(1)11 ln 0.1120.90.940.11 1.710cm 8.8107.51ln 121 1.8367.5 (2ln 21) 1.710cm 27.5 1.83642.5 6.3810cm i t i i m t t t T T T n l n n lN n L n n δδση---=---==⨯∆===⨯⨯⨯⎛⎫∆∆=∆-- ⎪'∆∆⎝⎭⨯=⨯--⨯⨯⨯+=⨯峰值功率为:102143424121(310)0.1 6.3810 6.62610()0.12 1.836 1.06102 767.7Wm m cP N h ST νηπ--=⨯=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯= 由图7.3.5可以查得,当/2i t n n ∆∆=的时候,能量利用率0.797μ=。
所以光脉冲的输出能量为:10342164()()2220.13100.10.797 6.62610()7.5 1.71020.11 1.061020.068mJ i t n T TE h S l h S l n μνμνδδπ--∆=⋅⋅=⋅⋅∆⨯=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯= 脉冲宽度为:30.068100.89ns 767.7m E P τ-⨯≈==8.Q 开关红宝石激光器中,红宝石棒截面积S =1cm 2,棒长l =15cm ,折射率为1.76,腔长L =20cm ,铬离子浓度1931.5810cm N =⨯,受激发射截面2021.2710cm σ-=⨯,光泵浦使激光上能级的初始粒子数密度1932i 10cm n -=,假设泵浦吸收带的中心波长0.45μm λ=,E 2能级的寿命23ms τ=,两平面反射镜的反射率与透射率分别为r 1=0.95,T 1=0,r 2=0.7,T 2=0.3。
试求:(1)使E 2能级保持1932i 10cm n -=所需的泵浦功率P p ;(2)Q 开关接通前自发辐射功率P ; (3)脉冲输出峰值功率P m ;(4)输出脉冲能量E ; (5)脉冲宽度τ(粗略估算)。
解:(1) 欲使19322i 10cm n n -==,所需要的泵浦功率为:1934822136210 6.626103101153100.4510 22.1KWip n P h S l ντ---⨯⨯⨯⨯⨯⨯=⋅⋅=⨯⨯⨯= (2) Q 开关接通前自发辐射功率221212120.4522.114.3KW 0.6943ip n P h S l P νντν=⋅⋅=⋅=⨯= (3)121832019322218321210211ln ln(0.70.95)0.2220.2 1.0510cm 1.271015()210(2 1.58)cm 4.210cm 1(ln 1)4115 (310) 6.6264 1.76155t i i i i i i m t t tr r n l n n n n n n n n lP ch ST n L n n δδσν----=-=-⨯=∆===⨯⨯⨯∆=--=-=⨯-=⨯∆∆=∆--'∆∆=⨯⨯⨯⨯⨯+183440.3 1.0510 4.2 4.210(ln 1)0.694310 1.05 1.05 522MW--⨯⨯⨯⨯⨯--⨯=(4) 由/4i t n n ∆∆=,可以从图7.3.5查得能量利用率0.98μ=,输出能量为:221818346()220.3310 4.210 0.98 6.626101150.40.6943102 6.63J i n T E h S l μνδ--∆=⋅⋅⨯⨯=⨯⨯⨯⨯⨯⨯⨯⨯=(5) 66.6312.752210m E ns P τ≈==⨯ 9.若有一四能级调Q 激光器,有严重的瓶颈效应(即在巨脉冲持续的时间内,激光低能级积累的粒子数不能清除)。
已知比值i t /2n n ∆∆=,试求脉冲终了时,激光高能级和低能级的粒子数n 2和n 1(假设Q 开关接通前,低能级是空的)。
解:列出速率方程如下:2211211 (1) (2) (3)t R dN nN dt n dn N n dt dn N n dtτσυσυ⎛⎫∆=- ⎪∆⎝⎭=-∆=∆ 由(2)和(3)式可以得到:2122 (4)t Rd n n NN n dt n συτ∆∆=-∆=-∆ (1)式和(4)式与三能级系统速率方程完全一样,所以,脉冲终了时有ln0f i f t tn n n n n ∆∆-∆+∆=∆根据已知条件i t /2n n ∆∆=可以求得0.407f t n n ∆=∆脉冲终了时12211210.80.420.6i f i ft ii in n n n n n n n n n n n n n n +=∆-=∆∆-∆=≈==∆-≈∆11.一锁模He-Ne 激光器振荡带宽为600MHz ,输出谱线形状近似于高斯函数,试计算其相应的脉冲宽度。
解:输出谱线的形状近似于高斯函数20()()2E a ωωω⎡⎤-=-⎢⎥⎣⎦脉冲的宽度是对时域而言的,现在知道的是频域特性。
根据傅立叶分析,时域特性可以通过傅立叶逆变换由频域特性得到,即[][]20220022001()()2() exp 21 exp ()221 exp ()22i t E t E e d i t d a at iat i t d a at i t iat d a ωωωπωωωωωωωωωωωω+∞-∞+∞-∞=⎡⎤-=-+⎢⎥⎣⎦⎧⎫=--++-⎨⎬⎩⎭⎛⎫⎧⎫=---+⎨⎬ ⎪⎩⎭⎝⎭⎰⎰利用关系式2exp()ax dx +∞-∞-⎰可以得到200()exp()exp()42at E t E i t ω=-时域里脉冲的宽度是()E t 函数的半功率点所对应的时间间隔,当0t =时222*00(0)(0)(0)48E E E E ⎛⎫=== ⎪ ⎪⎝⎭另1t t =时为半功率点,则222011()(0)216E E t E ==又有关系222*111101()()()exp()82at E t E t E t E ⎡⎤==-⎢⎥⎣⎦另上两式左端相等,可以得到2211exp()22at ⎡⎤-=⎢⎥⎣⎦求得1t =脉冲的宽度为12t τ== 下面来求a 的值,在频域中进行求解, 因为20()()2E a ωωω⎡⎤-=-⎢⎥⎣⎦当0ωω=的时候,220()E ω= 令1ωω=时为半功率点,22101()()2E E ωω=又因为222*10111()()()()exp E E E a ωωωωω⎡⎤-==-⎢⎥⎣⎦所以有222100010()1()()exp 2E E a ωωωωωω⎡⎤-=-⎢⎥⎣⎦-=半功率点的带宽为10222()ln 2a ωωνππν-∆==∆=将a 的值代入τ的表达式中去,可以得到锁模脉宽为:2ln 20.74ns τπν==≈∆ 12.一锁模氩离子激光器,腔长1m ,多普勒线宽为6 000MHz ,未锁模时的平均输出功率为3W 。
