江苏省镇江市润州区九年级数学上册2.4圆周角1学案
秋苏科版数学九上2.4《圆周角》word教案1

2015秋苏科版数学九上2.4《圆周角》w o r d教案1-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN山阳镇中心初中14---15学年度第一学期九年级数学教案课题2.4圆周角(1)课型新授教学时间:第 5周第 1 课时备课组成员李恒杨乃和赵书芳主备人:赵书芳审核:教学目标1.了解圆周角的概念;2.让学生经历圆周角与圆心角关系的探索过程;3.能用圆周角与圆心角的关系进行简单的说理。
教学重难点探索圆周角与圆心角的关系.教、学具多媒体课件学法指导学生通过讨论、总结归纳本课的知识内容。
教师活动内容、方式学生活动方式、内容旁注情境引入足球训练场上教练在球门前画了一个圆圈,进行无人防守的射门训练,如图,甲、乙两名运动员分别在C、D两地,他们争论不休,都说自己所在位置对球门AB 的张角大.如果你是教练,请评一评他们两个人,谁的位置对球门AB的张角大.1.先让学生积极思考,然后全班交流,各抒己见.2.思考:如果在⊙O上再任取一点Q,看看对球门AB的张角的大小是否变化?实践探索一:圆周角的概念激发学生的兴趣,导入新课.为下面探究圆周角的性质奠定基础.让学生加深对圆周角概念的理解.巩固给出圆周角的概念.A BO CD教师:在上面的角有什么特征如果请你命名,你叫它什么顶点在圆上,两边都和圆相交的角叫做圆周角.1.让学生自由的说,并说出命名的理由.2.口答:判断下列各图中的角是否是圆周角?并说明理由实践探索二:圆周角的性质1.操作猜想:画弧BC所对的圆心角,然后再画同弧BC所对的圆周角.你发现了什么?2.验证猜想:请同学们验证自己的猜想.合作探究,小组讨论交流.通过量一量、想一想,提出猜想:同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.例题讲解例 1 如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°,⌒BC为70°.求∠ABD、∠AED的度数.让学生自己操作、交流,提出猜想,从而进一步激发探究意识同时渗透分类的数学思想.体现了转化的数学思想.例2如图,P是△ABC的外接圆上的一点,∠APC=∠CPB=60°.求证:△ABC是等边三角形.练一练:课本练一练总结这节课你有哪些收获和困惑?开始的问题情境,你解决了吗?知识点的综合运用,进行适当的变式,进一步内化所学的知识.教后记:。
新苏科版九年级上学期数学2-4圆周角(一)学案

1新苏科版九年级数学上册2-4圆周角(一)学案教学目标1.经历探索圆周角的有关性质的过程 2.知道圆周角定义,掌握圆周角定理,会用定理进行推证和计算。
3.体会分类、转化等数学思想. 教学重点 圆周角的性质及应用. 教学难点利用圆周角的性质解决问题. 教学方法探究法,分析法,讨论法 教具 投影一、自主预习:1.通过度量教材117页操作与思考中各角的度数,使学生初步感知同弧所对的圆周角相等,进而思考这几个角的共同特征,得出圆周角的概念。
2.定义: 叫做圆周角。
3.尝试练习:(1)下列各图中,哪一个角是圆周角?( )A B C D(2)图3中有几个圆周角?( )(A )2个,(B )3个,(C )4个,(D )5个(3)写出图4中的圆周角:________________________二、合作探究:猜想:圆周角的度数与什么有关系?一条弧所对的圆周角等于它所对的圆心角的一半图3图4BA C DBC A定理:在同圆或等圆中,同弧或等弧所对的相等,都等于。
三.典型例题:例1、如图,点A、B、C在⊙O上,点D在圆外, CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由。
例2:如图,OA、OB、OC都是圆O的半径,∠AOB = 2∠BOC.求证:∠ACB = 2∠BAC.四、自主测评:1.如图,已知∠ACB = 20º,则∠AOB = _____,∠OAB =.2.如图,已知圆心角∠AOB=1000,则∠ACB = _______。
五、课后作业:FO DAB C E231.如图,△ABC 的3个顶点都在⊙O 上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。
2.如图,点A 、B 、C 、D 在同一个圆上,四边形ABCD 的对角线把4个内角分成8个角,在这8个角中,有几对相等的角?请把它们分别表示出来:___________________________________________________.3.如图,AB 是⊙O 的直径,∠BOC=120°,CD ⊥AB ,则∠ABD =___________。
(最新)苏教版九年级数学上册《圆周角》学案

∴∠BOC=∠BAC+∠OCA.
∵OA=O C,
∴∠OCA=∠BAC.
∴∠BOC=2∠BAC,即∠BAC=∠B OC.
第二 步:转化成特殊情况.
定理:圆周角的度数等于它所对弧上的圆心角度数的一半.同弧或等弧所对 的圆周角相等,
例题讲解
例1如图,⊙O 的弦AB、DC的延长线相交于点E,∠AOD=150°,为70 °.求∠ABD、∠AED的度数.
【大班交流,师生互动】
如图,P是△ABC的外接圆上的一点,∠APC=∠CPB=60°.
求证:△ABC是等边三角形.
【总结提升】
定理的证明思路:
我们根据圆周角相对于圆心的位置把圆周角分成三类,先解决 一类特殊问题,再把其他两类转化成 特殊问题。
【当堂检测】
8. P55-56练习1.2.3
【布置作业】
课本P60习题1--3
如果∠BOC=60°,画弧BC所对的圆周角。可以画多少个?你所画的圆周角为多少度?
猜想:圆周角的度数与什么有关系?
2.验证猜想:请同学们验证自己的猜想.
【小组讨论】
合作探究,小组讨论交流.
通过量一量、想一想,提出猜想:同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
第一步:特殊情况.
AB为⊙O直径,点C在⊙O上.
学习难点
通过分类讨论 ,推理、验证“圆周角与圆心角的关系”.
学习过程:
【预习检测】
1、(1)下列各图中,哪一个角是圆周角?()
(2)图3中有几个圆周角?()
(3)写出图4中的圆周角:__ _
【教学过程】
实践探索一:圆周角的概念
1.圆周角定义:叫做圆周角。
实践探索二:圆周角的性质
苏科版-数学-九年级上册-2.4 圆周角第1课时 教案

2.4 圆周角第1课时教学目标:一.知识技能1.理解圆周角概念,理解圆周用与圆心角的异同;2.掌握圆周角的性质;3.能灵活运用圆周角的性质解决问题;二.解决问题1.发现和证明圆周角定理;2.会用圆周角定理解决问题.教学重点:圆周角与圆心角的关系,圆周角的性质教学难点:发现并证明圆周角定理教学过程:一、创设情景如图是一个圆柱形的海洋馆, 在这个海洋馆里,人们可以通过其中的圆弧形玻璃窗AB观看窗内的海洋动物.大家请看海洋馆的横截面的示意图,想想看:同学甲站在圆心O的位置,同学乙站在正对着下班窗的靠墙的位置C,他们的视角(∠AOB和∠ACB)有什么关系?如果同学丙、丁分别站在其他靠墙的位置D和E,他们的视角(∠ADB和∠AEB)和同学乙的视角相同吗?下面我们就来学习相关知识.二、认识圆周角.1.观察∠ACB.∠ADB.∠AEB,这样的角有什么特点?三个角具有相同的特点:1)角的顶点在圆上;2)角的两边都与圆相交2.给出定义,顶点在圆上,并且两边都与圆相交的角叫做圆周角.(注意两点:1.角的顶点在圆上;2.角的两边都与圆相交,二者缺一不可.)3.辩一辩,图中的∠CDE是圆周角吗?引导学生识别,加深对圆周角的了解.是,符合圆周角的定义4.圆周角与圆心角的联系和区别是什么?圆周角是指顶点在圆上且角的两边是圆的弦;圆心角是指顶点是圆心,角的两边是这个圆的半径的角;它们的关系是同弧所对的圆周角等于圆心角的一半。
三、探究圆周角的性质.1.在如图中,同弧AB所对的圆周角有哪几个?【答案】∠ADB,∠ACB,∠AEB观察并测量这几个角,你有什么发现?大胆说出你的猜想.发现:∠ADB=∠ACB=∠AEB猜想:同弧所对的圆周角相等同弧AB所对的圆心角是哪个角?【答案】∠AOB观察并测量这个角,比较同弧所对的圆周角你有什么发现呢?大胆说出你的猜出想.发现:∠AOB=2∠ADB=2∠ACB=2∠AEB猜想:同弧所对的圆周角等于其所对的圆心角的一半.2.由学生总结发现规律:同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半,教师再利用几何画板从动态的角度进行演示, 验证学生的发现.四、证明圆周角定理及推论.1.问题:在圆上任取一个圆周角,观察圆心角顶点与圆周角的位置关系有几种情况?2.学生自己画出同一条弧的圆心角和圆周角, 将他们画的图归纳起来, 共有三种情况:①圆心在圆周角的一边上; ②圆心在圆周角的内部; ③圆心在圆周角的外部.3.问题:在第一种情况中,如何证明上面探究中所发现的结论呢?另外两种情况如何证明呢? 【答案】利用等腰三角形两个底角相等,三角形的外角等于与它不相邻的两个内角的和即可证明.4.怎样利用有上结论证明我们的第一个猜想:圆弧所对的圆周角相等?(利用圆弧所对的圆心角相等)5.以上结论同圆改成等圆,同弧改成等弧结论还成立吗?为什么?6.总结出圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.7.将上面定理中的“同弧或等弧”改成“同弦或等弦”,结论还成立吗?【答案】不成立,同弦或等弦所对的圆周角不一定相等,因为一条弦对着两条弧8.在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?【答案】相等总结:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等。
苏科版九年级上册数学 2.4圆周角 教案

圆周角课题名称:圆周角(九年级数学)一、教材简解:本节课是苏科版九年级上册第二章第四节内容——圆周角第一课时,是在学生学习了圆的各种概念和圆心角的概念及性质基础上,进而学习的圆的又一个重要性质,这节课是对前面所学知识的巩固和延续,又对下一节课学习圆周角定理的两个推论及应用起到铺设“桥梁”。
本节课的知识,在今后的推理、论证和计算中应用广泛,是本单元重点内容之一。
二、目标预设:知识与技能:1.了解圆周角概念,理解圆周角定理的证明。
2.让学生经历探索圆周角和圆心角的关系的过程,学会以特殊情况为基础,通过转化的方式来解决一般性问题的方法。
3.在学生经历观察、想象、验证推理等活动基础上,培养学生探究数学问题的一些能力和方法,学会“数学”地思考问题。
过程与方法:1.经历探索圆周角和圆心角的关系的过程,通过转化的方式来解决一般性问题的方法,并渗透分类思想。
2.经历观察、想象、验证推理等活动基础上,培养学生的探究数学问题的能力。
情感、态度与价值观:树立探究数学问题的意识,敢于发表自己的观点,从问题的解决中获得成功的体验,学会与他人合作,并能交流思维的过程和结果。
三、重点难点:重点:圆周角定理难点:会运用圆周角定理进行简单的计算与证明四、设计理念:九年级的学生已具备一定的知识储备和认知能力,学生两极分化开始明显,学困生增多,多数学生表现欲不强。
在教学设计时,从学生的学情出发,考虑到学生具体情况,只有通过让学生动手实践、探索、合作交流来完成本节课教学。
引导学生充分经历“圆周角定理”的探索证明过程,这种探索问题的数学活动,需要老师当好引导者、组织者和合作者,为学生提供生动有趣、富有挑战的素材和问题,为学生在学习上的“发现”创造一切条件。
五、设计思路:本节课先创设一个学生学生熟悉的问题情境,让学生带着求知欲去探索发现,然后通过学生动手,引导学生感悟:一条弧所对的圆周角有无数个,然而逐一研究它们与所对圆心角之间的数量关系是困难的,因此必须对问题进行分类,从而将无限的问题转化为有限的问题。
初中数学九年级上册苏科版2.4圆周角教学设计

2.教学过程:
(1)导入:以生活中的圆形物体为例,引导学生思考圆周角的性质,激发学生学习兴趣。
(2)探究:组织学生进行小组讨论,合作探究圆周角的定理及推论,让学生在探究中理解并掌握知识。
(3)讲解:针对重难点,进行详细的讲解和示范,帮助学生对圆周角的概念、定理、推论进行梳理,总结学习心得,尤其是解题技巧和应用方面的体会。
作业要求:
1.学生需独立完成作业,注重解题过程的规范性和逻辑性。
2.家长协助监督,关注学生的学习进度和作业质量。
3.教师在批改作业时,要及时给予反馈,指导学生改进不足,提高解题能力。
4.学生应认真对待作业,养成良好的学习习惯,不断提高自身数学素养。
(二)过程与方法
1.通过引导学生观察生活中的圆形物体,激发学生的学习兴趣,培养学生从实际中发现问题的能力。
2.通过小组讨论、合作探究,引导学生自主发现圆周角定理及推论,培养学生的合作精神和探究能力。
3.利用多媒体辅助教学,展示动态的圆周角变化,帮助学生形象地理解圆周角的概念,提高学生的空间想象力和直观感知能力。
(3)课本习题2.4第5题:运用圆周角知识解决实际问题,如测量圆形物体的周长、面积等。
2.选做题:
(1)课本习题2.4第7题:探究圆周角定理及推论在多边形中的应用。
(2)课本习题2.4第8题:研究圆周角与圆心角的关系,并运用这一关系解题。
3.创新实践题:
结合生活实际,设计一个与圆周角相关的问题,并运用所学知识解决问题。要求:问题具有一定的挑战性,解决方案需包含详细的解题过程。
(3)应用题:运用圆周角知识解决实际问题,如测量圆形物体的周长、面积等。
苏科初中数学九年级上册《2.4 圆周角》教案 (2).doc

教 学目标:1.进一步巩固圆周角的概念、圆周角定理,并能运用定理解决有关问题;
2.掌握半 圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径;
3.经历圆周角性质的过程,培养学生分析问题和解决问题的能力;
4.用联系的观点思考问题、转化问题.
教学重点:掌握直径和所对圆周角是直角之间的相互确定关系,灵活运用同弧所对的圆周角和圆心角的关系解决问题.
2.在例2中,若点E与点A在直径BC的两侧,BE交AD的延 长线于点F,其余条件不变(如下图),例2中的结论还成立吗?
解决情境引入问题
“有一个 圆形模具,现在只有一个直角三角板,请你找出它的圆心”.你现在能解决吗?
练 一练
1.如图, AB是⊙O的直径,∠A=10°,
则∠ABC=________.
2.如图,AB是⊙O的直径,D是⊙O上的任 意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断ΔABC的形状:.
今天我们学习了圆中有哪些常用辅助线?
课后作业
课本P58第1、2、3.
教后记
二次备课
3.如图,AE是⊙O的 直径,△ABC的顶点 都在⊙O上,AD是△ABC的高,△ABE和△ADC相似吗?为什么?
拓展提升
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ C=45°,求这个人工湖的直径.
教师追问:你还有哪些方法?从中你得到什么启发?
总结
这节课你有哪些收获和困惑?
例题讲解
例1如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60° ,∠ADC=50°,
求∠CEB的度数.
例2已知:BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D, = ,BE交AD于点F.
苏教版数学九年级上册教学设计《2-4圆周角(1)》

苏教版数学九年级上册教学设计《2-4圆周角(1)》一. 教材分析苏教版数学九年级上册的教学内容是《2-4圆周角(1)》,这一节主要让学生掌握圆周角的定义,性质及其在几何中的应用。
教材通过具体的例题和练习,让学生理解圆周角的概念,并能运用圆周角性质解决一些实际问题。
二. 学情分析九年级的学生已经学习了平面几何的基础知识,对图形的性质和公理有一定的理解。
但是,对于圆周角的理解可能会有一定的困难,因此,在教学过程中,需要通过具体的实例和实际操作,让学生更好地理解圆周角的概念和性质。
三. 教学目标1.知识与技能:使学生掌握圆周角的定义,性质及应用。
2.过程与方法:通过观察,操作,思考,探究等活动,培养学生的几何思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识和解决问题的能力。
四. 教学重难点1.圆周角的定义和性质。
2.如何运用圆周角性质解决实际问题。
五. 教学方法采用问题驱动法,引导学生通过观察,操作,思考,探究等活动,自主发现圆周角的性质,并在解决实际问题中运用圆周角的知识。
六. 教学准备1.准备相关的教学PPT和教学素材。
2.准备一些实际的例题和练习题。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生思考圆周角的概念。
例如:在平面内,一个圆上的两点A和B,连接圆心O和点A,B,那么∠AOB是什么角?2.呈现(10分钟)通过PPT展示圆周角的定义和性质,让学生直观地理解圆周角的概念。
同时,通过一些实际的例题,让学生了解圆周角在几何中的应用。
3.操练(10分钟)让学生通过实际的操作,发现圆周角的性质。
例如:让学生拿一个圆,用直尺和圆规画出一个圆周角,然后观察和测量这个圆周角的大小。
4.巩固(10分钟)通过一些练习题,让学生巩固圆周角的知识。
例如:已知一个圆的半径为5cm,求该圆上任意两点所对的圆周角的大小。
5.拓展(10分钟)引导学生思考如何运用圆周角的知识解决实际问题。
新苏科版九年级数学上册2.4圆周角(1)导学案

新苏科版九年级数学上册2.4圆周角(1)导学案课前参与一、预习内容: 课本P53—55;二、问题探究:1、 是圆周角。
2、如图所示,哪个是圆周角?3、试一试(1)分别量一量图(1)中弧AB 所对的两个圆周角的读数,比较一下。
再变动C 在圆周上的位置,看看圆周角的读数有没有改变?你发现了规律了吗?_______________________图(1) 图(2)(2)分别量一量上面图(2)的三个图中弧AB 所对的圆周角和圆心角的度数,你发现了其中的规律了吗?__________________ ___。
证明你所发现的结论:得到结论:在同圆或等圆中,同弧或等弧所对的圆周角________,都等于__________的圆心角的____________;1、 练一练:如图,点A 、B 、C 、D 在⊙O 上,点A 与点D 在点B 、C 所在直线的同侧,∠BAC=35°(1)∠BDC= °,理由 ;(2)∠BOC= °,理由 。
通过预习你还有什么疑惑?课中参与1.如图,ABC △内接于O ⊙,若∠AOB=124°,则C 的大小为( )A . 28°B .56°C .60°D .62°第 1题 第2题 第 3题 第 4题2、如图,在⊙O 中,弦AB 、CD 相交于点E ,∠BAC=40°,∠AED=75°,∠ABD 的度数 .3、如图,△ABC 的顶点A 、B 、C 都在⊙O 上,∠C =30 °,AB =2, 则⊙O 的半径是 。
4、如图,点A 、B 、C 在⊙O 上,(1) 若∠BAC=60°,求∠BOC=______;(2) 若∠AOB=90°,求∠ACB=______.例1、如图,∠AOB=∠BOC ,那么∠ACB 与∠BAC 相等吗?为什么?探索:若∠AOB=2∠BOC ,且其他条件不变,那么结论有怎样的变化?若∠AOB=n ∠BOC ,其他条件不变,又能得到什么变化?例2、如图,⊙O 的两条弦AB 、CD 相交于点P ,(1)试说明PA •PB=PC •PD ;(2)若PD=2PB ,PC=2cm ,求PA 的长。
苏科初中数学九年级上册《2.4 圆周角》教案 (1).doc

总结
这节课你有哪些收获和困惑?开始的问题情境,你解决了吗?
课后作业
课本P55-56第1、2、3.
教后记
情境引入
足球训练场上教练在球门前画了一个圆圈,进行无人防守的射门训练,如图,甲、乙两名运动员分别在C、D两地,他们争论不休,都说自己所在位置对球门AB的张角大.如果你是教练,请评一评他们两个人,谁的位置对球门AB的 张角大.
实践探索一:圆周角的概念
教师:在上面的角有什么特征?如果请你命名,你叫它什么?
圆周角
教学目标:1.了解圆周角的概念;
2.让学生经历圆周角与圆心角关系的探索过程,培养学生的动手操作、自主探索和合作交流的能力;
3.能用圆周角与圆心角的关系进行简单的说理,培养学生合情 推理的意识,掌握说理的基本方法,从而提高数学素养.
教学重点:探索圆周角 与圆心角的关系.
教学难点:通过分类讨论,推理、验证“圆周角与圆心角的关系”.
顶点在圆上,两边都和圆相交的角叫做圆周角.
实践探索二:圆周角的性质
1.操作猜想:
画弧BC所对的圆心角,然后再画同弧BC所对的圆周角.你发现了什么?
2.验证猜想:
请同学们验证自己的猜想.
例题讲解
例1如图,⊙O的弦A B、DC的延线相交于点E,∠AOD=150°, 为70°.求∠ABD、∠AED的度数.
例2如图,P是△ABC的外接圆上的一点,∠APC=∠CPB=60°.
求证:△ABC是等边三角形.
练一练
如图,点A、B、 C、D在⊙O上,∠BAC=35°.
(1)∠BDC=°,
理由是;
(2)∠BOC= °,
苏教科版初中数学九年级上册2.4 圆周角导学案(1)

苏教科版初中数学
重点知识精选
掌握知识点,多做练习题,基础知识很重要!苏科版初中数学和你一起共同进步学业有成!
圆周角
用
角的性质解决问题
什么是圆心角,圆心角的度数定理是什么?什么是圆周角?
: 、概念辨析:判断下列各图形中的是不是圆周角,并说
弧所对的圆周角是∠BAC,圆心角是∠
圆心在圆周角的一边上
圆周角外部)
______________
)圆周角的度数等于它所对弧度数的
相信自己,就能走向成功的第一步
教师不光要传授知识,还要告诉学生学会生活。
数学思维
可以让他们更理性地看待人生。
苏科初中数学九年级上册《2.4 圆周角》教案 (5).doc

圆周角二、知识准备复习巩固1、 叫圆心角。
2、在同圆或等圆中,圆心角的度数等于它所对的 度数。
三、学习内容活动一 操作与思考如图,点A 在⊙O 外,点B 1 、B 2 、B 3在⊙O 上,点C 在⊙O 内,度量∠A 、∠B 1 、∠B 2 、∠B 3 、∠C 的大小,你能发现什么?∠B 1 、∠B 2 、∠B 3有什么共同的特征?_________________。
归纳得出结论,顶点在_______,并且两边________________________的角叫做圆周角。
强调条件:①_______________________,②___________________________。
识别图形:判断下列各图中的角是否是圆周角?并说明理由.活动二 观察与思考如图,AB 为⊙O 的直径,∠BOC 、∠BAC分别是BC 所对的圆心角、圆周角,求出图(1)、(2)、(3)中∠BAC 的度数.通过计算发现:∠BAC =__∠BOC .试证明这个结论:(学生完成) 活动三 思考与探索1.如图,BC 所对的圆心角有多少个?BC 所对的圆周角有多少个?请在图中画出BC 所对的圆心角和圆周角,并与同学们交流。
2.思考与讨论(1)观察上图,在画出的无数个圆周角中,这些圆周角与圆心O 有几种位置关系? (2)设BC 所对的圆周角为∠BAC ,除了圆心O 在∠BAC 的一边上外,圆心O 与∠BAC 还有哪几种位置关系?对于这几种位置关系,结论∠BAC =21∠BOC 还成立吗?试证明之. 通过上述讨论发现:___________________________________。
3.尝试练习(1)如图,点A 、B 、C 、D 在⊙O 上,点A 与点D 在点B 、C 所在直线的同侧,∠BAC=350(1)∠BDC=_______°,理由是_______________________. (2)∠BOC=_______°,理由是_______________________.(2)如图,点A 、B 、C 在⊙O 上,(1) 若∠BAC=60°,求∠BOC=______°;(2) 若∠AOB=90°,求∠ACB=______°. 4、例题:如图,点A 、B 、C 在⊙O 上,点D 在圆外,CD 、BD 分别交⊙O 于点E 、F ,比较∠BAC 与∠BDC 的大小,并说明理由。
九年级数学上册2_4圆周角导学案1无答案新版苏科版

圆周角(1)学习目标: 1.了解圆周角的概念;2.让学生经历圆周角与圆心角关系的探讨进程,培育学生的动手操作、自主探讨和合作交流的能力; 3.能用圆周角与圆心角的关系进行简单的说理,培育学生合情推理的意识,把握说理的大体方式,从而提高数学素养.学习重点:.探讨圆周角与圆心角的关系.学习难点:通过度类讨论,推理、验证“圆周角与圆心角的关系””. 学习进程:【预习提纲】初步感知、激发爱好 情境引入足球训练场上教练在球门前画了一个圆圈,进行无人防守的射门训练,如图,甲、乙两名运动员别离在C 、D 两地,他们争辩不休,都说自己所在位置对球门AB 的张角大.若是你是教练,请评一评他们两个人,谁的位置对球门AB 的张角大.【新知探讨】师生互动、揭露通法问题1:在上面情境中的角有什么特点?若是请你命名,你叫它什么?极点在圆上,两边都和圆相交的角叫做圆周角.问题2:1.操作猜想:画弧BC 所对的圆心角,然后再画同弧BC 所对的圆周角.你发觉了什么?2.验证猜想:请同窗们验证自己的猜想.通过量一量、想一想,提出猜想:同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.第一步:特殊情形. 第二步:转化成特殊情形.ABOC D定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半【变式拓展】能力提升、冲破难点 =150°,⌒BC问题3:如图,⊙O 的弦AB 、DC 的延长线相交于点E ,∠AOD 为70°.求∠ABD 、∠AED 的度数.问题4:如图,P 是△ABC 的外接圆上的一点,∠APC =∠CPB =60°.求证:△ABC 是等边三角形.【回扣目标】学有所成、悟出方式 这节课你有哪些收成和困惑?开始的问题情境,你解决了吗? 【课堂反馈】分层达标、收成成功1.如图,点A 、B 、C 在⊙O 上, (1) 若∠BAC=60°,则∠BOC=______° (2) 若∠AOB=90°,则∠ACB=______°.2.如图,已知:⊙O 是△ABC 的外接圆,∠BAC=50°,∠ABC=47°,求∠AOB .3.如图;四边形ABCD的四个极点在⊙O上.求证;∠B+∠D = 180°。
苏科初中数学九年级上册《2.4 圆周角》教案 (5).doc

1圆周角二、知识准备复习巩固1、 叫圆心角。
2、在同圆或等圆中,圆心角的度数等于它所对的 度数。
三、学习内容活动一 操作与思考如图,点A 在⊙O 外,点B 1 、B 2 、B 3在⊙O 上,点C 在⊙O 内,度量∠A 、∠B 1 、∠B 2 、∠B 3 、∠C 的大小,你能发现什么?∠B 1 、∠B 2 、∠B 3有什么共同的特征?_________________。
归纳得出结论,顶点在_______,并且两边________________________的角叫做圆周角。
强调条件:①_______________________,②___________________________。
识别图形:判断下列各图中的角是否是圆周角?并说明理由.活动二 观察与思考如图,AB 为⊙O 的直径,∠BOC 、∠BAC分别是BC 所对的圆心角、圆周角,求出图(1)、(2)、(3)中∠BAC 的度数.通过计算发现:∠BAC =__∠BOC .试证明这个结论:(学生完成) 活动三 思考与探索21.如图,BC 所对的圆心角有多少个?BC 所对的圆周角有多少个?请在图中画出BC 所对的圆心角和圆周角,并与同学们交流。
2.思考与讨论(1)观察上图,在画出的无数个圆周角中,这些圆周角与圆心O 有几种位置关系? (2)设BC 所对的圆周角为∠BAC ,除了圆心O 在∠BAC 的一边上外,圆心O 与∠BAC 还有哪几种位置关系?对于这几种位置关系,结论∠BAC =21∠BOC 还成立吗?试证明之. 通过上述讨论发现:___________________________________。
3.尝试练习(1)如图,点A 、B 、C 、D 在⊙O 上,点A 与点D 在点B 、C 所在直线的同侧,∠BAC=350(1)∠BDC=_______°,理由是_______________________. (2)∠BOC=_______°,理由是_______________________.(2)如图,点A 、B 、C 在⊙O 上,(1) 若∠BAC=60°,求∠BOC=______°;(2) 若∠AOB=90°,求∠ACB=______°. 4、例题:如图,点A 、B 、C 在⊙O 上,点D 在圆外,CD 、BD 分别交⊙O 于点E 、F ,比较∠BAC 与∠BDC 的大小,并说明理由。
苏科初中数学九年级上册《2.4 圆周角》教案 (7)【精品】

O · · O FE D C B A圆周角【学习目标】1.理解圆内接四边形的概念;2.掌握圆内接四边形的性质定理、判定定理及其推论,并能解决有关问题.【自主学习】1.圆内接四边形的性质定理:定理1 圆的内接四边形的对角___ ___.定理2 圆内接四边形的外角等于它的内角的__ ____. 思考:内接于圆的平行四边形、菱形、梯形分别是矩形、正方形、等腰梯形?2.圆内接四边形的判定定理:如果一个四边形的对角互补,那么_ _____.推论 如果四边形的一个外角等于 ,那么这个四边形的四个顶点共圆. 思考:圆内接四边形的性质定理和它的判定定理及推论有何关系?【自主检测】1.如图所示,四边形ABCD 内接于⊙O ,110BOD ∠=,则BCD ∠=______度.2.如图,,AD BE 是ABC ∆的两条高,求证:CED ABC ∠=∠.【典例分析】例1.如图,⊙1O 和⊙2O 都经过A 、B 两点,经过点A 的直线CD 与⊙1O 交于点C ,与⊙2O 交于点D .经过点B 的直线EF 与⊙1O 交于点E ,与⊙2O 交于点F .求证://CE DF .例2.如图,CF 是ABC ∆的AB 边上的高,FP BC ⊥,FQ AC ⊥.求证:A 、B 、P 、Q 四点共圆.【目标检测】1.如图,四边形ABCD 是圆O 的内接四边形,延长AB 和DC 相交于点P ,若15PB PD =,则BC AD 的值为 .2.如图,D 、E 分别为ABC ∆的边AB 、AC 上的点,且不与ABC ∆的顶点重合,已知AE AC AD AB ⋅=⋅.求证:C 、B 、D 、E 四点共圆.3. 如图,已知四边形ABCD 内接于圆,延长AB 和DC 交于E ,EG 平分E ∠,且与BC 、AD 分别交于F 、G .求证:CFG DGF ∠=∠.【总结提升】证明多点共圆,当它们在一条线段同侧时,可证它们对此线段张角相等,也可以证明它们与某一定点距离相等;如两点在一条线段异侧,则证明它们与线段两端点连成的凸四边形对角互补.。
【最新苏科版精选】苏科初中数学九上《2.4 圆周角》word教案 (4).doc

(引导学生从已知条件入手,逐一进行分析,得到哪些结论? )
例2如图,P是△ABC的外接圆上的一点,∠APC=∠CPB=60°.
求证:△ABC是等边三角形.
2.先让学生独立思考,然后请学生讲评.
练 一练
如图,点A、B、C、D在⊙O上,∠BAC=35°.
第二步:转化成特殊情况.
定理:在同圆或等圆中,
同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半.
让学生自己操作、交流,提出 猜想 ,从而进一步激发 探究意识,同时渗透分类的数学思想.
体现了转化的数学思想.
例题讲解
例1如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°, 为70°.求∠A BD、∠AED的度数.
2.4圆周角(1)
教学目标
1.了解圆周角的概念 ;
2.让学生经历圆周角与圆心角关系的探索过程,培养学生的动手操作、自主探索和合作交流的能力;
3.能用圆周角与圆心角的关系进行简单的说理,培养学生合情推理的意识,掌握说理的基本方法,从而提高数学素养.
教学重点
探索圆周角与圆心角的关系.
教学难点
通 过分类讨论,推理、验证“圆周角与圆心角的关系”.
∵∠BFC是△DFC的一个外角,
∴∠BFC>∠BDC.
∵∠BAC=∠BFC(同弧所对的圆周角相等).
∴∠BAC>∠BDC.
总结
这节课你有哪些收获和困惑?开始的问题情境,你解决了吗?
各抒己见.
课后作业
课本P55-56第1、2、3.
独立完成.
(1)∠BDC=°,
理由是;
(2) ∠BOC=°,
理由是.
苏科版-数学-九年级上册-2.4 圆周角1学案
内容:2.4圆周角(1)课型:新授【学习目标】1.经历探索圆周角的有关性质的过程。
2. 理解圆周角的概念及其相关性质,并能运用相关性质解决有关问题。
【重点难点】圆周角及圆周角定理的应用【课前预习】一、课前预习:1 . 叫做圆心角.2. 叫做圆周角.3.同弧或等弧所对的相等,都等于。
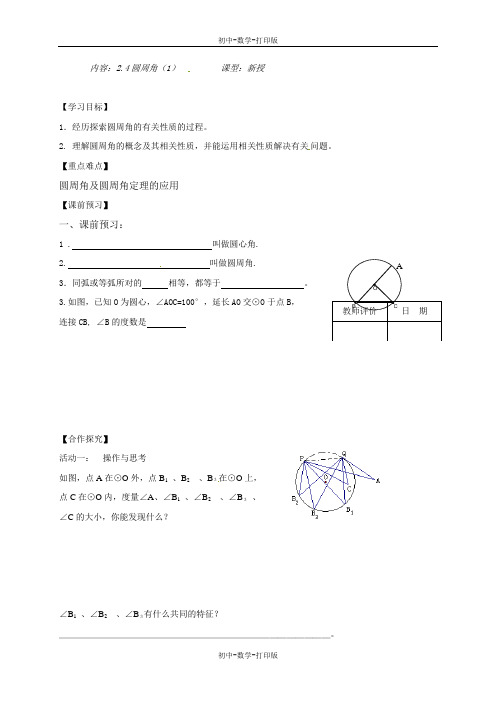
3.如图,已知O为圆心,∠AOC=100°,延长AO交⊙O于点B,连接CB, ∠B的度数是【合作探究】活动一:操作与思考如图,点A在⊙O外,点B1、B2、B3在⊙O上,点C在⊙O内,度量∠A、∠B1、∠B2、∠B3、∠C的大小,你能发现什么?∠B1、∠B2、∠B3有什么共同的特征?_______________________________。
教师评价日期OB CA归纳得出结论,顶点在_______,并且两边________________________的角叫做圆周角。
强调条件:①_______________________,②_________________________。
识别图形:判断下列各图中的角是否是圆周角?并说明理由.活动二:如图,AB为⊙O的直径,∠BOC、∠BAC分别是BC所对的圆心角、圆周角,求出图(1)、(2)、(3)中∠BAC的度数.通过计算发现:∠BAC=__∠BOC.试证明这个结论:思考与探索:1.如图,BC所对的圆心角有多少个?BC所对的圆周角有多少个?请在图中画出BC所对的圆心角和圆周角,并与同学们交流。
OCBA2.思考与讨论(1)观察上图,在画出的无数个圆周角中,这些圆周角与圆心O 有几种位置关系?(2)设BC 所对的圆周角为∠BAC ,除了圆心O 在∠BAC 的一边上外,圆心O 与∠BAC 还有哪几种位置关系?对于这几种位置关系, 结论∠BAC =21∠BOC 还成立吗?试证明之.通过上述讨论发现:_______________________。
3.尝试练习(1)如图,点A 、B 、C 、D 在⊙O 上,点A 与点D 在点B 、C 所在直线的同侧,∠BAC=350①∠BDC=_______°,理由是__________________. ②∠BOC=_______°,理由是__________________.OABCD(2)如图,点A 、B 、C 在⊙O 上,①若∠BAC=60°,求∠BOC=____°;② 若∠AOB=90°,求∠ACB=_ __°活动三: 如图,点A 、B 、C 在⊙O 上,点D 在圆外,CD 、BD 分别交⊙O 于点E 、F ,比较∠BAC 与∠BDC 的大小,并说明理由。
苏科版数学九年级上册_《圆周角》导学案1

2.4 圆周角知识梳理】1.圆周角的定义:顶点在圆上,并且两边都和圆相交的角叫做圆周角。
注:(1)圆周角要具备两个特征:①角的顶点在圆上;②角的两边与圆相交。
二者缺一不可(2)圆心角与圆周角的关系【知识梳理】1.圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
圆心与圆周角的位置关系,分三种情况:(1)圆心在角的一边上; (2)圆心在角的内部; (3)圆心在角的外部(如图).2.圆周角定理的推论:推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
【例题精讲】例1:如图所示,已知点A,B,C,D,E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C的度数为________。
例2:如图,OA、OB、OC都是O的半径,∠AOB=2∠BOC.探索∠ACB与∠BAC之间的数量关系,并说明理由。
例3:已知,如图,在△ABC中AB=AC,以AB为直径的圆交BC于点D,交AC于点E,求证:弧BD=弧DE.例4:使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,下列四种情况中合格的是( )A. B. C. D.圆的内接四边形【知识梳理】1.圆的内接四边形定义:如果四边形的各顶点在一个圆上,这个四边形叫做这个圆的内接四边形,这个圆叫做四边形的外接圆。
例如,上图中,四边形ABCD 是⊙O的内接四边形;⊙O是四边形ABCD的外接圆。
2.性质定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的相邻内角的对角。
已知:四边形ABCD中,∠B +∠D=180°求证:A,B,C,D在同一圆周上。
3.判定定理如果一个四边形的对角互补,那么它的四个顶点在同一个圆上(简称四点共圆).推论如果四边形的一个外角等于它的内角的对角,那么它的四个顶点共圆.【例题精讲】例5:如图6,⊙O1与⊙O2都经过A,B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2 交于点D,经过点B的直线EF与⊙O1交于点E,与⊙O2交与点F.求证:CE//DF.例6:如图,∠EAD是⊙O的内接四边形ABCD的一个外角,并且BD=DC.求证:AD平分∠EAC.。
2019年苏科初中数学九年级上册《2.4 圆周角》教案 (4)【精品】

(2)∠BOC=°,
理由是.
独立思考,集体反馈.
拓展提升
如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由.
变式:移动点D到圆内,其它条件不变,此时∠BAC与∠BDC的大小又如何?并说明理由.
解:连接CF,
∵∠BFC是△DFC的一个外角,
2.思考:如果在⊙O上再任取一点Q,看看对球门AB的张角的大小是否变化?
实践探索一:圆周角的概念
教师:在上面的角有什么特征?如果请你命名,你叫它什么?
顶点在圆上,两边都和圆相交的角叫做圆周角.
1.让学生自由的说,并说出命名的理由.
2.口答:判断下列各图中的角是否是圆周角?并说明理由.
实践探索二:圆周角的性质
1.操作猜想:
画弧BC所对的圆心角,然后再画同弧BC所对的圆周角.你发现了什么?
2.验证猜想:
请同学们验证自己的猜想.
合作探究,小组讨论交流.
通过量一量、想一想,提出猜想:同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
第一步:特殊情况.
AB为⊙O直径,点C在⊙O上.∵∠BOC是△AOC的外角,∴∠BOC=∠BAC+∠OCA.∵OA=OC,∴∠OCA=∠BAC.∴∠BOC=2∠BAC,即∠BAC= ∠BOC.
第二步:转化成特殊情况.
定理:在同圆或等圆中,
同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半.
让学生自己操作、交流,提出猜想,从而进一步激发探究意识,同时渗透分类的数学思想.
体现了转化的数学思想.
例题讲解
例1如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°, 为70°.求∠ABD、∠AED的度数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
活动四: 如图,点 A 、B、C 在⊙O 上,点 D 在圆外,CD、BD 分别交⊙O 于点 E、F,比较∠BAC 与∠BDC 的大小,并说明理由。
A F E O D
B
C
3
三、【课堂检测】 1.如图,在⊙O 中,弦 AB、CD 相交于点 E,∠BAC=40°, C ∠AED=75°,求∠ABD 的度数.
0
①∠BDC=_______°, 理由是__________________. ②∠BOC=_______°,理 由是____________ ______.
A O
D
B
C
(2)如图,点 A、B、C 在⊙O 上, ① 若∠BAC=60°,求∠BOC=____°; ② 若∠AOB=90°,求∠ACB=___°
O E B
D A
2. 如图,点 A、B、C、D 在⊙O 上,∠ADC=∠BDC=60°. 判断△ABC 的形状,并说明理由.
四、【课后巩固】 1.如图 1, 四边形 ABDC 内接于⊙O, ∠BOC=100°, 则∠A= °,∠D= °。
2.如图 2,A、B、C 是⊙O 上三点,D 是 AB 延长线上一点,∠CBD=65°,则 ∠AOC= °。
日期
教师评价
作业 教后感
5
3.如图 3,已知⊙O 的弦 AD、CB 交于点 E,AC 的度数为 60°,BD 的度数为 100°,则∠AEC= °。
4.如图 4, AB 是 ⊙O 的直径, C 是 ⊙O 上一点, BOC 44° ,则 A 的度 数为 . 。
C A E
5.半径为 4cm,120°的圆心角所对的弦长为
A
2
2.思考与讨论 (1)观察上图,在画出的无数个圆周角中,这些圆周角与圆心 O 有几种位置关 系? (2)设 BC 所对的圆周角为∠BAC,除了圆心 O 在∠BAC 的一边上外,圆心 O 与 ∠BAC 还有哪几种位置关系?对于这几种位置关系,
结论∠BAC=
1 ∠BOC 还成立吗?试证明之. 2
通过上述讨论发现:_______________________。 3.尝试练习 (1)如图,点 A、B、C、D 在⊙O 上,点 A 与点 D 在点 B、C 所在直线的同侧, ∠BAC=35
4.如图,已知 O 为圆心,∠AOC=100°,延长 AO 交⊙O 于点 B, 连接 CB, ∠B 的度数是 A
O B C
日期
教师评价
家长签名
二、【新知探求】 【新知导学】 活动一: 操作与思考 如图,点 A 在⊙O 外,点 B1 、B2 、B3在⊙O 上,点 C 在⊙O 内,度量∠A、 ∠B1 、∠B2 、∠B3 、∠C 的大小,你能发现什么?
1
∠B1 、∠B2 、∠B3有什么共同的特征?
归纳得出结论, 顶点在_______, 并且两边________________________的角叫做 圆周角。 强调条件:①_______________________,②_________________________。 识别图形:判断下列各图中的角是 否是圆周角?并说明理由.
活动二:如图,AB 为⊙O 的直径,∠BOC、∠BAC 分别是 BC 所对的圆心角、圆 周角,求出图(1) 、 (2) 、 (3)中∠BAC 的度数.
A
通过计算 发现:∠BAC=__∠BOC.试证明这个结论:
O C B
活动三:思考与探索 1.如图,BC 所对的圆心角有多少个?BC 所对的圆周角有多少个?请在图中画 出 BC 所对的圆心角和圆周角,并与同学们交流。
C
D
O
A
O
O
A
B 图1 D
C
C 图2 B D
图3 B
O
图4
B
6.在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°, 求这条弧所对的圆心角和圆周角的度数.
4
7.如图 5,OA、OB、OC 都是⊙O 的半径,∠ AOB=2∠BOC, 求证:∠ACB=2∠BAC。
ቤተ መጻሕፍቲ ባይዱ
五、【课后反思】
圆周角
课题 目标 圆周角 1 1.经历探索圆周角的有关性质的过程。 2. 理解圆周角的概念及其相关性质,并能运用相关性质解决有关问题。 重点 难点 教法 圆周角及圆周角定理的应用 圆周角定理的推导。 讨论,交流 教学过程 二次备课
一、【学前预习反馈】 1. 2. 3.同弧或等弧所对的 叫做圆心角. 叫做圆周角. 相等,都等于 。
